lOMoARc PSD|17327243
3. Phương pháp gom cụm (clustering)
• Tổng quan về gom cụm
• Gom cụm theo phương pháp phân hoạch
• Gom cụm theo phương pháp phân cấp
• Gom cụm dữ liệu dựa trên mật độ
• Gom cụm dữ liệu dựa trên mô hình • Các phương pháp gom 3. Phương pháp gom cụm Tổng quan về gom cụm
Ví dụ 1: Các nhà tiếp thị cần tìm ra các nhóm đặc biệt trong cơ sở khách
hàng của họ hoặc là phân khúc khách hàng để giúp họ cải thiện các
chương trình tiếp thị chính xác vào mục tiêu của họ.
Ví dụ 2: Bảo hiểm: Phân cụm rất hữu ích để nhận ra các nhóm chủ hợp
đồng bảo hiểm có chi phí yêu cầu thường xuyên cao. 103 lOMoARc PSD|17327243 3. Phương pháp gom cụm 103 Tổng quan về gom cụm
• Phân cụm là một kỹ thuật học không giám sát dùng cho tập dữ liệu không được dán nhãn.
• Kỹ thuật phân cụm chia tập dữ liệu thành các lớp/cụm sao cho các
bản ghi trong cụm có độ tương đồng cao và khác biệt cao so với các cụm khác. 104 104 lOMoARc PSD|17327243
3. Phương pháp gom cụm ≫𝑇ổ𝑛𝑔𝑞𝑢𝑎𝑛𝑣ề𝑔𝑜𝑚𝑐ụ𝑚≫
3 . Phương pháp gom cụm ≫ 105 105
Phương pháp đo khoảng cách
Dùng hàm d(x,y) để đo khoảng cách, khoảng cách là số dương.
Các phương pháp đo khoảng cách gồm: Euclidean distance
Manhattan distance (còn gọi là L1-distance) Chebyshev distance 106 lOMoARc PSD|17327243 3. Phương pháp gom cụm 106
3. Phương pháp gom cụm ≫𝑇ổ𝑛𝑔𝑞𝑢𝑎𝑛 𝑣ề 𝑔𝑜𝑚 𝑐ụ𝑚≫ Phươngpháp đo khoảngcách (𝑥
−𝑎 ) 2 +( 𝑦−𝑏 ) 2 2 1 0 1 2 (−2−2) 2 +(2+1) 2 -1 25 107 107 lOMoARc PSD|17327243
3. Phương pháp gom cụm ≫𝑇ổ𝑛𝑔𝑞𝑢𝑎𝑛𝑣ề𝑔𝑜𝑚𝑐ụ𝑚≫
Phương pháp đo khoảng cách Euclidean distance Công thức
Euclidean dist((x, y), (a, b)) = (𝑥−𝑎)2+(𝑦−𝑏)2
Ví dụ 2: Tìm điểm giống và khác nhau giữa 3 người dựa vào 3 biến đầu vào. Euclidean dist(A,B) = 18.86
Người Biến 1 Biến 2 Euclidean dist(A,C) = 53.85 A 30 70 Euclidean dist(B,C) = 40.19 B 40 54 Kết luận: C 80 50
* Trong khoảng cách Euclide,
A và B thì tương tự thuộc tính có giá trị lớn nhất A và C thì rất khác có thể chi phối khoảng cách.
Nên các thuộc tính phải ược
chia tỷ lệ chính xác trước khi áp dụng công thức. 108 108
3. Phương pháp gom cụm ≫𝑇ổ𝑛𝑔𝑞𝑢𝑎𝑛𝑣ề𝑔𝑜𝑚𝑐ụ𝑚≫ Phương pháp đo khoảng cách Manhattan distance
Công thức tính khoảng cách giữa 2 điểm (x,y) và (a,b) Manhattan
dist((x, y), (a, b)) = | x – a | + | y – b |
Ví dụ: Tìm sự giống và khác nhau giữa 3 người dựa vào 3 biến đầu vào
Manhattan dist(A,B) = |30 – 40| + |70-54| = 26 Manhattan dist(A,C) =
|30 – 80| + |70 – 50| = 70 Manhattan dist(B,C) = |40 –80| + |54 – 50| = 44 Kết luận:
Người Biến 1 Biến 2 A và B thì tương tự A 30 70 A và C thì rất khác B 40 54 109 C 80 50 lOMoARc PSD|17327243 3. Phương pháp gom cụm 109
Phương pháp đo khoảng cách Chebyshev distance
Ý nghĩa: Khoảng cách Chebyshev được xác định trên một không gian vectơ,
trong đó khoảng cách giữa hai vectơ là giá trị lớn nhất của sự khác biệt của
chúng dọc theo bất kỳ chiều tọa độ nào. Công thức
Chebyshev dist((r1, f1), (r2, f2)) = max(|r2−r1|,|f2-f1|)
Ví dụ 1: Tìm khoảng cách giữa A và B
Object A coordinate = {0,1,2,3} Object B coordinate = {6,5,4,-2} Coord 1 Coord 2 Coord 3 Coord 4 D = max(|r2−r1|,|f2−f1|) A 0 1 2 3
= max(|6-0|,|5-1|,|4-2|,|-2-3)|) B 6 5 4 -2 = max(6,4,2,5) = 6 110 110
3. Phương pháp gom cụm ≫𝑇ổ𝑛𝑔𝑞𝑢𝑎𝑛𝑣ề𝑔𝑜𝑚𝑐ụ𝑚≫ Phương pháp đo khoảng cách Chebyshev distance Công thức
Chebyshev dist((r1, f1), (r2, f2)) = max(|r2−r1|,|f2-f1|) Ví dụ 2:
Tìm sự giống và khác nhau giữa 3 người dựa vào 3 biến đầu vào
Người Biến 1 Biến 2
Chebyshev dist(A,B) = max( |30 - 40|, |70 – 54|) A 30 70 = max(|- 10 |, | 16|) = 16 B 40 54
Chebyshev dist(A,C) = max(|30 – 80| , |70 – 50|) C 80 50 = max(50,20) = 50 lOMoARc PSD|17327243
3. Phương pháp gom cụm ≫𝑇ổ𝑛𝑔𝑞𝑢𝑎𝑛𝑣ề𝑔𝑜𝑚𝑐ụ𝑚≫
Chebyshev dist(B,C) = max(|40 – 80|, |54 – 50|) Kết luận: = max(40,4) = 40 A và B thì tương tự A và C thì rất khác 111 111
Giải thuật gom cụm chính
Gom cụm theo phương pháp phân hoạch
• phân vùng ngẫu nhiên và sau đó lặp đi lặp lại tinh chỉnh chúng theo một số tiêu chí
• Gom cụm theo phương pháp phân cấp
• phân tách theo thứ bậc của tập hợp dữ liệu (hoặc đối tượng) bằng cách sử dụng một số tiêu chí.
• Gom cụm dữ liệu dựa trên mật độ • dựa trên các chức năng kết nối và mật độ
• Gom cụm dữ liệu dựa trên lưới
• dựa trên cấu trúc chi tiết nhiều cấp độ.
• Gom cụm dữ liệu dựa trên mô hình
• Một mô hình được xem xét cho từng cụm và ý tưởng là xác định cụm phù hợp nhất cho mô hình đó. 112 112 lOMoARc PSD|17327243 3. Phương pháp gom cụm
3 . Phương pháp gom cụm ≫ Gom cụm Dựa trên mật Phân hoạch Phân cấp Dựa trên lưới Dựa trên mô độ hình K-Means Agglomerative Divisive DBSCAN 113 113 lOMoARc PSD|17327243 3. Phương pháp gom cụm
Giải thuật gom cụm chính Tìm hiểu
1) k-Means (weka/SimpleKMeans) – Nhóm
2) Agglomerative (weka/ Hierarchical clustering) – Nhóm
3) Divisive (*weka/ Simple EM (expectation maximisation) – Nhóm
4) DBSCAN (weka/makeDensityBasedClusterer) – Nhóm
*** Tham khảo tài liệu số 1 114 114
3. Phương pháp gom cụm Giải thuật gom cụm chính Phân hoạch / Partitioning Clustering
• Phương pháp phân vùng nhóm các đối tượng dựa trên các thuộc tính
thành một số phân vùng.
• Ví dụ 1: cách tiếp cận định tính, các mặt hàng trong cửa hàng tạp hóa
được nhóm thành các loại khác nhau (bơ, sữa và pho mát được nhóm
lại trong các sản phẩm sữa)
• Ví dụ 2: một cách tiếp cận định lượng, đo lường các tính năng nhất
định của sản phẩm như tỷ lệ phần trăm sữa và như vậy, tức là các sản
phẩm có tỷ lệ sữa cao sẽ được nhóm lại với nhau. lOMoARc PSD|17327243 115 115 k-means clustering
• Phân cụm K-Means nhằm mục đích phân chia n quan sát thành k cụm
trong đó mỗi quan sát thuộc về cụm có giá trị trung bình gần nhất.
• Phương pháp này tạo ra chính xác k cụm khác nhau có độ phân biệt lớn nhất có thể.
• Số cụm k tốt nhất dẫn đến khoảng cách (khoảng cách) lớn nhất không
được biết trước và phải được tính toán từ dữ liệu. 116 116 • 117 lOMoARc PSD|17327243 117 k-means
Chọn một trong các phép đo khoảng cách Euclidean distance
Manhattan distance (còn gọi là L1-distance) Chebyshev distance … 118 118 119 119 lOMoARc PSD|17327243 k-means
• Ví dụ: Cho 7 quan sát có 2 thuộc tính đầu vào. Hãy phân các quan sát vào cụm 2 cụm.
Bước 1: số cụm là k = 2,
Bước 2: chọn ngẫu nhiên k tâm cụm Quan sát Biến 1 Biến 2
Tâm cụm 1 (C1) chọn quan sát 1 (1.0,1.0) 1 1.0 1.0
Tâm cụm 2 (C2) chọn quan sát 4 (5.0,7.0) 2 1.5 2.0 3 3.0 4.0 4 5.0 7.0 5 3.5 5.0 120 6 4.5 5.0 7 3.5 4.5 120 𝑥
( −𝑎 2 +( 𝑦−𝑏 ) 2
Euclidean dist((x, y), (a, b)) = ) Quan sát Tâm C1 Tâm C2 Cụm ? (1.0,1.0) (5.0,7.0) 1(1. , 0 1.0) 0 = (1−5) 2 +(1−7) 2 = 7.21 1 2(1. , 5 2.0) 1.12 6.10 1 3(3.0 , 4 .0) 3.61 3.61 1 4(5.0 , 7 .0) 7.21 0 2 5(3. , 5 5.0) 4.72 2.5 2 6(4.5 , 5 .0) 5.31 2.06 2 7(3.5 , 4 .5) 4.30 2.92 2 121 121 lOMoARc PSD|17327243 k-means
Bước 4: Tính lại tâm cụm bằng trung bình cộng các quan sát C1 = {1,2,3} C2 = {4,5,6,7} • Quan sát Biến 1 Biến 2 Tâm C1 = ( 1.0+1.5+3.0, 1 1.0 1.0 1.0+2.0+4.0) 2 1.5 2.0 3 3 3 3.0 4.0 = (1.83, 2.33) 4 5.0 7.0 • 5 3.5 5.0 Tâm C2 = ( 6 4.5 5.0
5.0+3.5+4.5+3.5, 7.0+5.0+5.0+4.5) 7 3.5 4.5 4 4 = (4.12, 5.38) 122 lOMoARc PSD|17327243 122 Quan sát Lần khởi tạo Tâm cụm 1 (1.0,1.0) (1.8 , 3 2.33) Tâm cụm 2 (5.0,7.0) (4.12 , 5 .38) Lần lặp 1 123 123 k-means
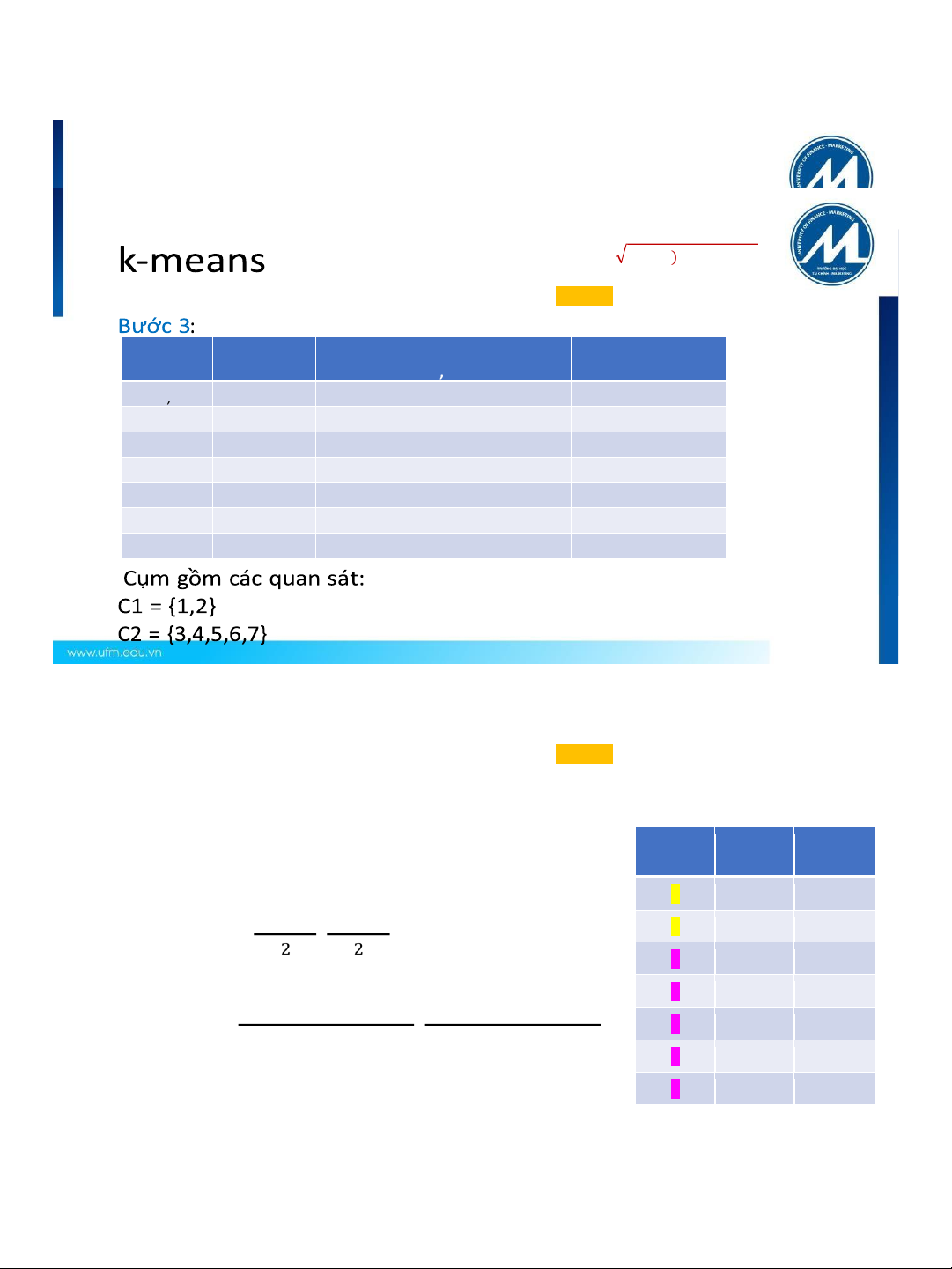
Euclidean dist((x, y), (a, b)) = (𝑥−𝑎)2+(𝑦−𝑏)2 Lần lặp 1 Bước 3: Quan sát Tâm C1 Tâm C2 Cụm ? (1.83, 2.33) (4.12, 5.38) 1(1.0, 1.0) 1.57 5.38 1 2(1.5, 2.0) 0.47 4.28 1 3(3.0, 4.0) 2.04 1.78 2 4(5.0, 7.0) 5.64 1.84 2 5(3.5, 5.0) 3.15 0.73 2 6(4.5, 5.0) 3.78 0.54 2 7(3.5, 4.5) 2.74 1.08 2 Cụm gồm các quan sát: C1 = {1,2} lOMoARc PSD|17327243 C2 = {3,4,5,6,7} 124 124 Lần lặp 1 Quan sát Biến 1 Biến 2 1 1.0 1.0 2 1.5 2.0 • 1.0+1.5 1.0+2.0 3 3.0 4.0 ) 2 2 4 5.0 7.0 5 3.5 5.0 •
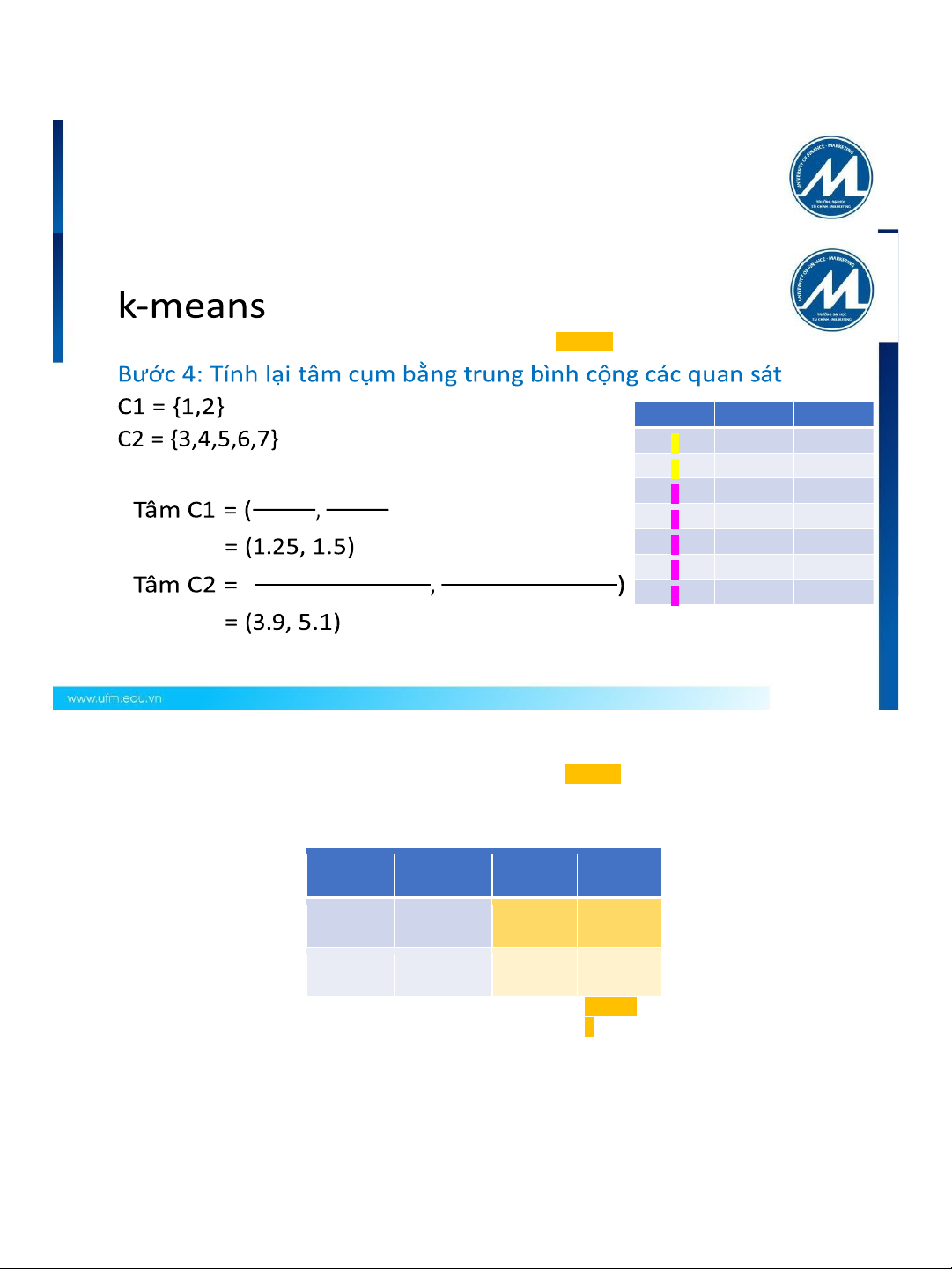
3.0+5.0+3.5+4.5+3.5 4.0+7.0+5.0+5.0+4.5 6 4.5 5.0 ( 5 5 7 3.5 4.5 125 125 Lần lặp 1 k -means Bước 5: lặp lại vì Quan sát Lần khởi Lần lặp 1 tạo Tâm cụm (1.0,1.0) (1.83, (1.25, 1 2.33) 1.5) Tâm cụm (5.0,7.0) (4.12, (3.9, 5.1) 2 5.38) Lần lặp
Quay lại Bước 2: chọn lại tâm cụm 2
Tâm cụm 1 (C1) = (1.25, 1.5)
Tâm cụm 2 (C2) = (3.9, 5.1) 126 lOMoARc PSD|17327243 126 2 2
Euclidean dist((x, y), (a, b)) = 𝑥 ( −𝑎 ) +( 𝑦−𝑏 ) Lần lặp 2 Quan sát Tâm C1 Tâm C2 Cụm ?
(1.25 , 1.5) (3. , 9 5.1) 1(1. , 0 1.0) 0.56 5.02 1 2(1.5 , 2 .0) 0.56 3.92 1 3(3.0 , 4 .0) 3.05 1.42 2 4(5.0 , 7 .0) 6.66 2.20 2 5(3.5 , 5 .0) 4.16 0.41 2 6(4.5 , 5 .0) 4.78 0.61 2 7(3.5 , 4 .5) 3.75 0.72 2 127 127 k-means Lần lặp 2
Bước 4: Tính lại tâm cụm bằng trung bình cộng các quan sát C1 = {1,2} Quan Biến 1 Biến 2 C2 = {3,4,5,6,7} sát 1 1.0 1.0 2 1.5 2.0 • Tâm C1 = (1.0+1.5, 1.0+2.0) 3 3.0 4.0 = (1.25, 1.5) 4 5.0 7.0 • Tâm C2 = ( 5 3.5 5.0
3.0+5.0+3.5+4.5+3.5, 4.0+7.0+5.0+5.0+4.5) 6 4.5 5.0 5 5 7 3.5 4.5 = (3.9, 5.1) 128 lOMoARc PSD|17327243 128 Lần lặp 2 Quan sát Lần khởi tạo Lần lặp 1 Lần lặp 2 Tâm cụm 1 (1.0,1.0) (1.8 , 3 2.33) (1.2 , 5 1.5) (1.25 , 1 .5) Tâm cụm 2 (5.0,7.0) (4.12 , 5 .38) (3.9 , 5 .1) (3.9 , 5 .1) C1 = {1,2} C2 = {3,4,5,6,7} 129 129 Tính số cụm 𝑛
• Cách 1: có n quan sát, số cụm k = 2
• Cách 2 (elbow method ): tăng dần số cụm k sao cho tổng phương sai
trong mỗi cụm giảm dần. 130 130 lOMoARc PSD|17327243 • • • • •   131 131 Phân cụm với Weka • Ignoring Attributes
• Chọn các thuộc tính bị bỏ qua khi phân cụm • Giữ phím SHIFT để chọn nhiều thuộc tính liên tục
• Giữ phím CTRL khi chọn nhiều thuộc tính không liên tục
Trực quan hóa kết quả mô hình 132 lOMoARc PSD|17327243 132 • • Quan sát Biến 1 Biến 2 1 1.0 1.0 2 1.5 2.0
1) Dữ liệu này có nhãn hay không có nhãn ? 3 3.0 4.0
2) Gọi tập dữ liệu là có giám 4 5.0 7.0 sát hay không giám sát? 5 3.5 5.0 6 4.5 5.0 7 3.5 4.5 133 133 Tiền xử lý 134 lOMoARc PSD|17327243 134 135 135 Đọc kết quả • Số lần lặp? • Bao nhiêu cụm?
• Vị trí tâm cụm lần cuối ? • Sai số như thế nào ? 136 lOMoARc PSD|17327243 Xem kết quả
• Nhấn chuột trái vào bất kỳ điểm nào để xem
thông tin của quan sát đó. 138 138