Bài tập toán 9 tuần 12 (có đáp án và lời giải chi tiết)

BÀI TẬP TOÁN 9 TUẦN 12
I. ĐẠI SỐ: ĐỒ THỊ HÀM SỐ BẬC NHẤT 1 Bài 3. Cho hàm số y  2
 x và y  x 2
a) Vẽ trên cùng hệ trục tọa độ đồ thị hai hàm số trên cùng hệ trục tọa độ. 1
b) Qua điểm 0;2  vẽ đường thẳng song song với Ox cắt hai đường thẳng y  x và 2 y  2
 x tại hai điểm A và B . Chứng minh tam giác AOB là tam giác vuông.
II. HÌNH HỌC: ÔN TẬP DÂY VÀ KHOẢNG CÁCH TỪ TÂM ĐẾN DÂY Bài 1.
Cho đường tròn tâm O; R đường kính AB , dây cung CD cắt AB tại M , biết MC  4c ,
m MD  12cm và 30o AMD  .
a) Tính khoảng cách từ O đến CD .
b) Tính bán kính đường tròn tâm O . Bài 2. Cho  ;
O R đường kính AB . Dây cung CD vuông góc với OA tại M là trung điểm của OA .
a) Tứ giác ACOD là hình gì? Vì sao?
b) Tam giác BCD là tam giác gì? Bài 3. Cho đường tròn  ;
O R đường kính AB . Gọi M , N lần lượt là trung điểm của O , A OB . Qua
M , N lần lượt vẽ các dây CD và EF song song với nhau ( C và E cùng nằm trên một nửa
đường tròn đường kính AB ).
a) Chứng minh: tứ giác CDEF là hình chữ nhật.
b) Giả sử CD và EF cùng tạo với AB một góc nhọn 30 . Tính diện tích hình chữ nhật CDEF .
………………………………HẾT……………………………… Trang 1
HƯỚNG DẪN GIẢI CHI TIẾT
I. ĐẠI SỐ: ĐỒ THỊ HÀM SỐ BẬC NHẤT 1 Bài 3. Cho hàm số y  2
 x và y  x 2
a) Vẽ trên cùng hệ trục tọa độ đồ thị hai hàm số trên cùng hệ trục tọa độ. 1
b) Qua điểm 0;2  vẽ đường thẳng song song với Ox 
cắt hai đường thẳng y x và 2 y  2
 x tại hai điểm A và B . Chứng minh tam giác AOB là tam giác vuông. Lời giải
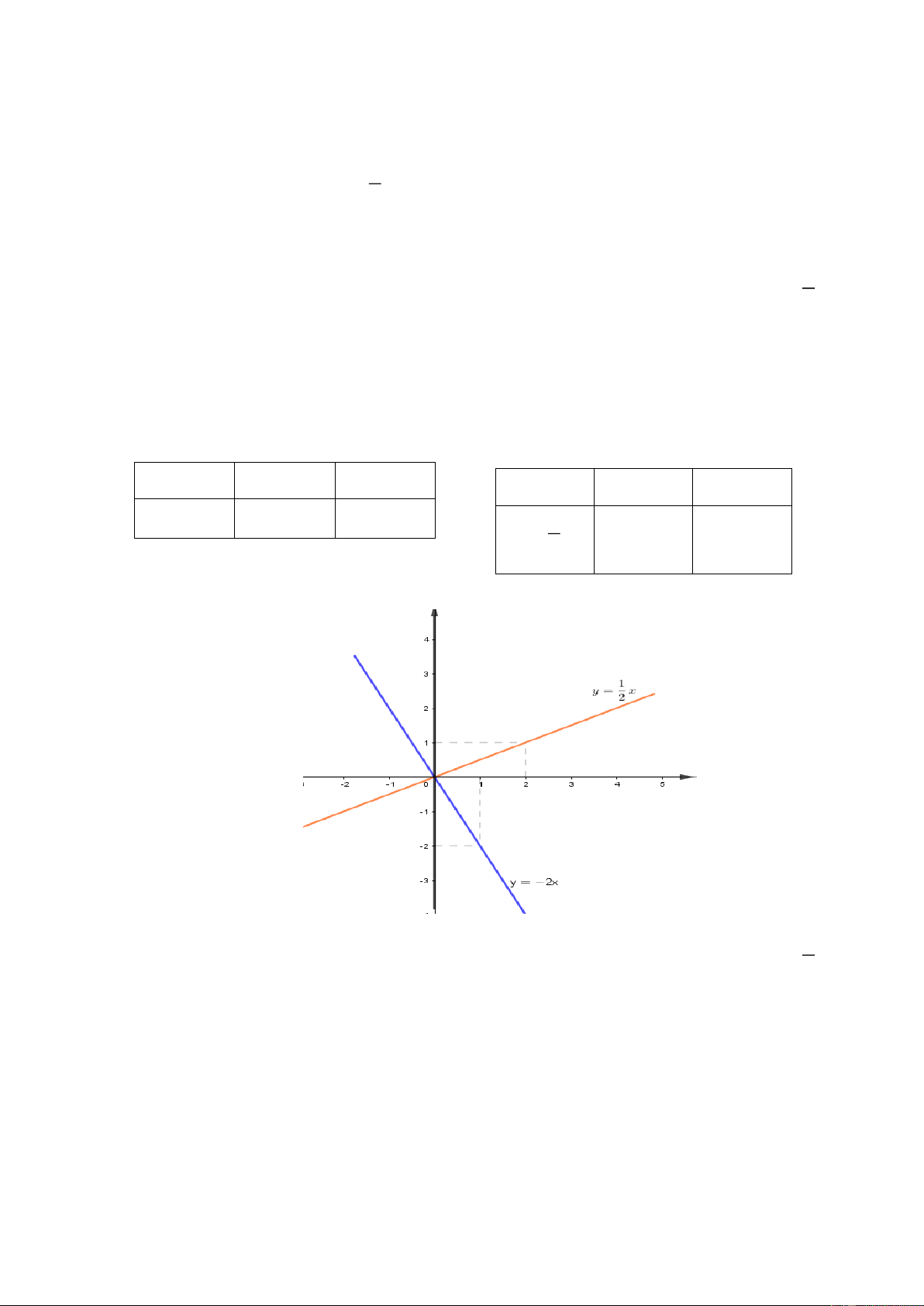
a) Vẽ đồ thị hai hàm số trên cùng một hệ trục tọa độ + Bảng giá trị x 0 1 x 0 2 y  2  x 0 2 1 0 1 y  x 2 + Hình vẽ 1
b) Qua điểm 0;2  vẽ đường thẳng song song với Ox 
cắt hai đường thẳng y x và 2 y  2
 x tại hai điểm A và B . Chứng minh tam giác AOB là tam giác vuông. Trang 2 2 2 Ta có: A 1
 ;2; B4;2, suy ra AB  4   1  2  2  5 2 1 OA  2  1  5 2 2   ; OB  2 4 20 Từ đó tính được 2 2 2
AB  OA  OB . Suy ra tam giác AOB là tam giác vuông.
II. HÌNH HỌC: ÔN TẬP DÂY VÀ KHOẢNG CÁCH TỪ TÂM ĐẾN DÂY Bài 1.
Cho đường tròn tâm O; R đường kính AB , dây cung CD cắt AB tại M , biết MC  4c ,
m MD  12cm và 30o AMD  .
a) Tính khoảng cách từ O đến CD .
b) Tính bán kính đường tròn tâm O . Lời giải
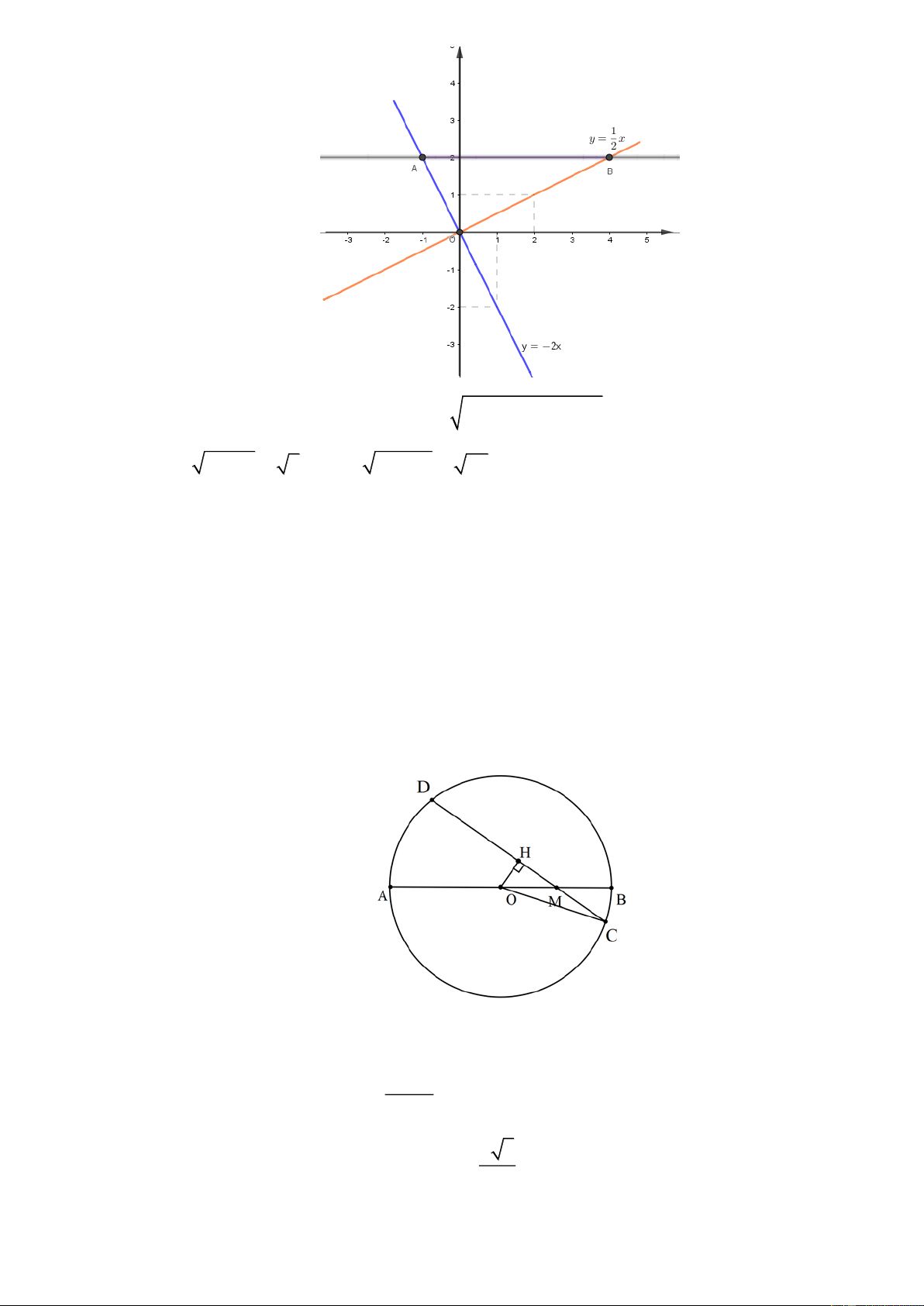
a) Tính khoảng cách từ O đến CD . 12  4
Kẻ OH  CD  HC  HD 
 8cm , MC  4 cm  MH  CH  MC  4 cm 2 o 4 3
Ta có: OH  HM .tan AMD  4.tan 30  cm 3
b) Tính bán kính đường tròn tâm O . Trang 3 Ta có: OHC  vuông tại H 2  4 3  208 2 2 2 2
CO  CH  OH  8     3 3   4 39  4 39 CO 
cm Hay R  cm. 3 3 Bài 2. Cho  ;
O R đường kính AB . Dây cung CD vuông góc với OA tại M là trung điểm của OA .
a) Tứ giác ACOD là hình gì? Vì sao?
b) Tam giác BCD là tam giác gì? Lời giải D A B M O C
a) Ta có AB  CD tại M
 M là trung điểm của CD (quan hệ vuông góc giữa đường kính và dây cung)
Tứ giác ACOD có hai đường chéo AO  DC tại M
MA  MO  gt 
MC  MD cmt 
 ACOD là hình thoi
b) Ta có AB  CD tại trung điểm M của CD nên AB là đường trung trực của đoạn thẳng CD  BC  BD  B
 CD cân tại B .
Mặt khác: tứ giác ACOD là hình thoi nên DA  DO
Lại có: OA  OD (bán kính của đường tròn O )
OA  OD  DA  ODA  là tam giác đều  DAB  60 Trang 4 1 Xét D
 AB có trung tuyến OD  AO  AB 2  D
 AB là tam giác vuông tại D  ADB  90 D
 AB là tam giác vuông tại D có DAB  60  DBA  30 B
 CD cân tại B có MB là đường cao  MB cũng là đường phân giác của DBC
 DBC  2DBA  2.30  60  B
 CD là tam giác đều (tam giác cân có góc ở đỉnh bằng 60). Bài 3. Cho đường tròn  ;
O R đường kính AB . Gọi M , N lần lượt là trung điểm của O , A OB . Qua
M , N lần lượt vẽ các dây CD và EF song song với nhau ( C và E cùng nằm trên một nửa
đường tròn đường kính AB ).
a) Chứng minh: tứ giác CDFE là hình chữ nhật.
b) Giả sử CD và EF cùng tạo với AB một góc nhọn 30 . Tính diện tích hình chữ nhật CDFE . Lời giải C E K N 30° 30° A B M O H D F
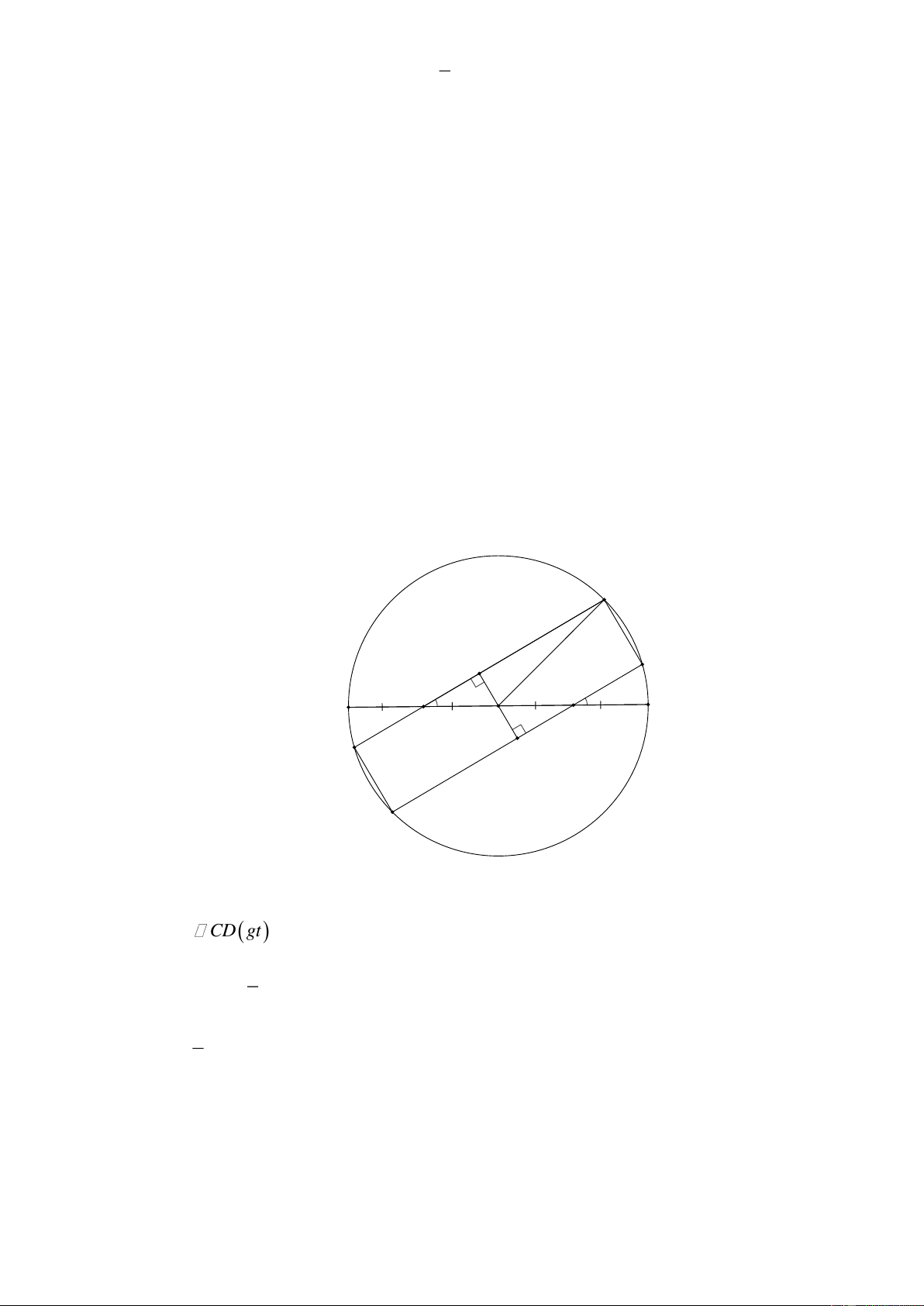
a) Qua O kẻ OH , OK lần lượt vuông góc với EF và CD . vì EF
CD  gt  nên suy ra O, H , K thẳng hàng. 1 Ta có: OM  OA 2 1 ON  OB 2
OA  OB  R OM  ON
Xét hai tam giác vuông OKM và OHN , ta có:
OKM  OHN  90 Trang 5
OM  ON cmt 
KOM  HON (2 góc đối đỉnh)  O  KM  O
 HN (cạnh huyền - góc nhọn) OK  OH
CD  EF (trong một đường tròn, hai dây cách đều tâm thì bằng nhau) Tứ giác CDFE có: CD FE  gt 
CD  FE cmt 
CDFE là hình bình hành
 CE DF hay CDFE là hình thang có đáy là CE và DF
Mặt khác OK  CD tại K
 K là trung điểm của CD
Chứng minh tương tự ta có H là trung điểm của FE
 HK là đường trung bình của hình thang CDFE  HK CE Mà HK  EF
CE  FE hay CFE  90
Hình bình hành CDFE có CFE  90  CDFE là hình chữ nhật.
b) Ta có: HK  DF  EC (vì CDFE là hình chữ nhật)
Xét tam giác vuông OKM có KMO  30 gt 1  OK  OM 2 1 R Mà OM  OA  2 2 R  OK  4 R
 HK  2OK   EC 2
Xét tam giác vuông CKO có: 2 2 2  R  R 15R 2 2 2 2 2
CK  CO  OK  R   R      4  16 16 Trang 6 R 15  CK  4 R 15
 CD  2CK  2 2 R 15 R R 15
Diện tích hình chữ nhật CDFE là S  C . D EC  .  dvdt. 2 2 4  HẾT  Trang 7