Bài tập toán 9 tuần 16 (có đáp án và lời giải chi tiết)

BÀI TẬP TOÁN 9 TUẦN 16
I. ĐẠI SỐ: PHƯƠNG TRÌNH BẬC NHẤT HAI ẨN Bài 1.
Trong mỗi trường hợp sau hãy tìm giá trị của a để:
a) Điểm A0; 
1 thuộc đường thẳng x  ay  5  ; b) Điểm B  1
 ,5;0 thuộc đường thẳng ax  4y  6 ; c) Điểm C  7  ; 
3 thuộc đường thẳng ax  6 y  3;
d) Điểm D 2,5;0 thuộc đường thẳng ax  0 y  12,5;
e) Điểm E 2;  4,5 thuộc đường thẳng 0x  ay  31,5 ; Bài 2.
Vẽ đồ thị của mỗi cặp phương trình sau trong cùng một hệ trục tọa độ rồi tìm tọa độ giao điểm
của hai đường thẳng đó:
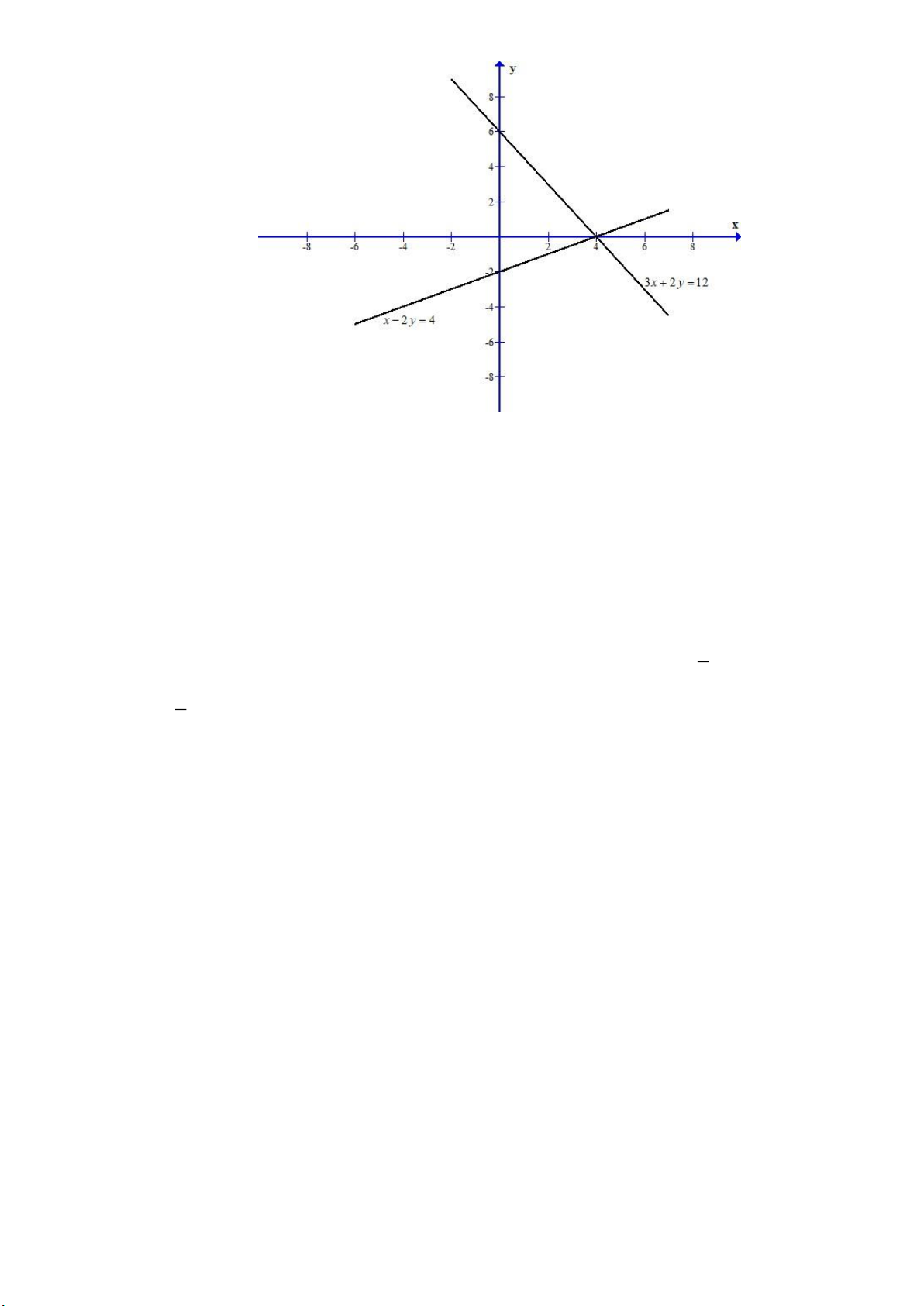
a) 2x  y  3 và 3x  y  1
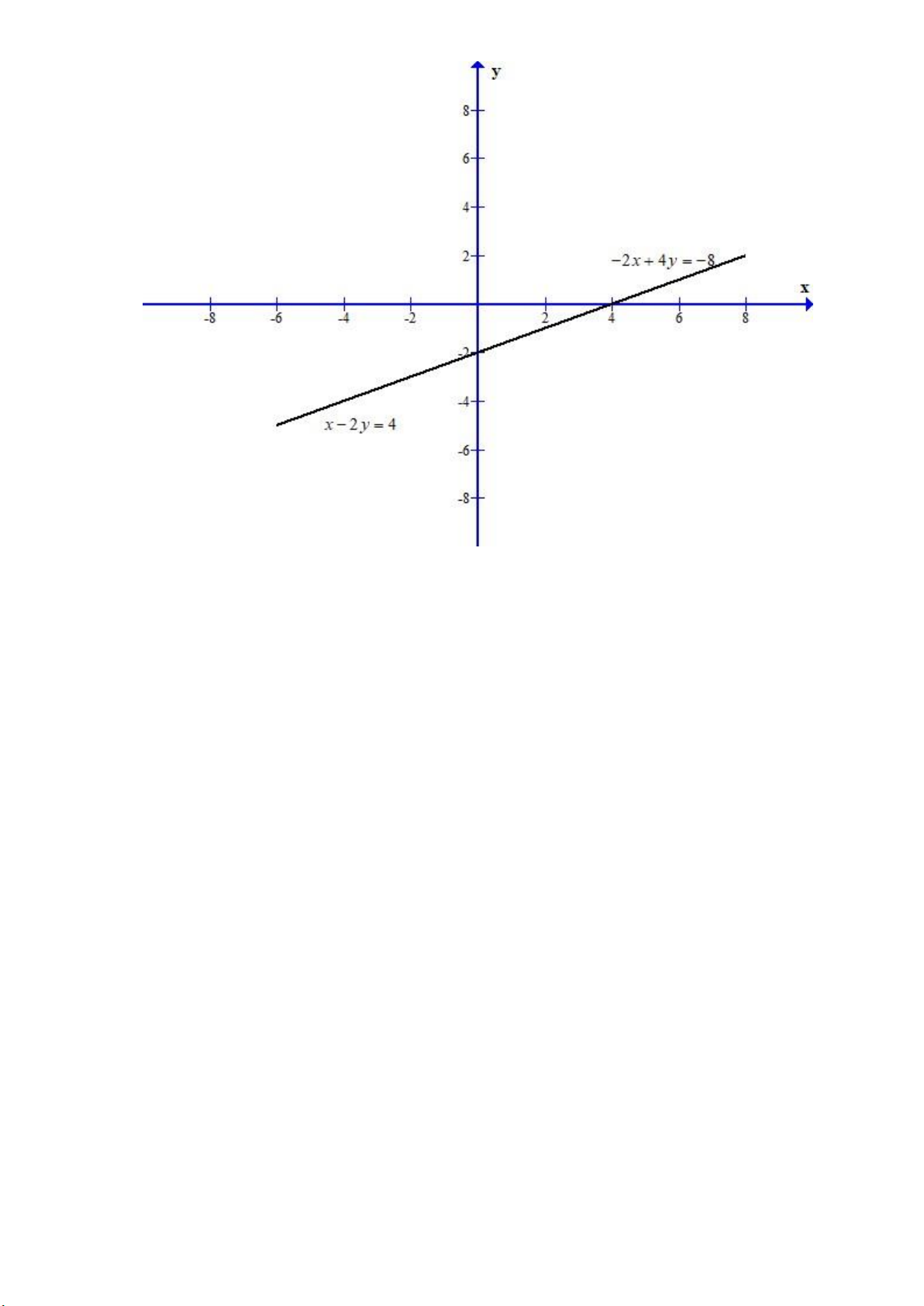
b) x  2 y  4 và 3x  2 y  12
c) x  2 y  4 và 2
 x  4y  8 
d) x  y  1 và 3
 x  3y  6  Bài 3.
a) Tìm giá trị của a để hai đường thẳng y  a  
1 x  2 và y  3  x 1 song song với nhau.
b) Xác định m và k để hai đường thẳng y  kx  m  2 và y  5  k  x  4  m trùng nhau.
c) Xác định m và k để d : y  kx  m  2 và d : y  5  k x  4  m cắt nhau tại điểm 2     1   trên trục tung.
d) Xác định k để các đường thẳng sau đồng quy?
d : y  2x 3;
d : y  x 3
d : y  kx 1 3  2  1 
II. HÌNH HỌC: VỊ TRÍ TƯƠNG ĐỐI CỦA HAI ĐƯỜNG TRÒN Bài 1.
Cho hai đường tròn (O; R) đường kính AB, đường tròn tâm (O’), đường kính OA. Dây cung
AC của đường tròn (O) cắt đường tròn (O’) ở M. Chứng minh:
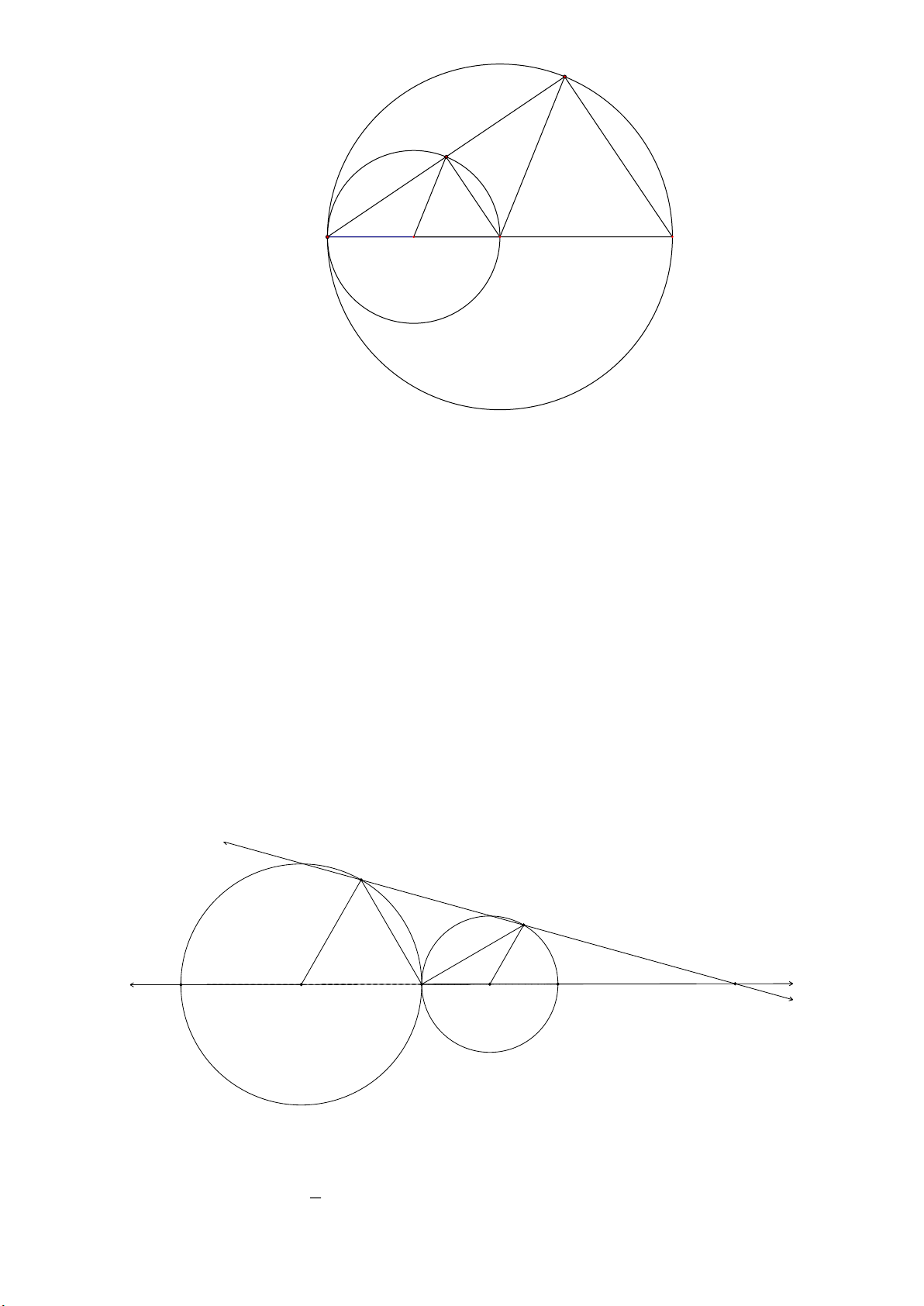
a) Đường tròn (O’) tiếp xúc (O) tại A. b) O’M // OC c) OM //BC Bài 2. Cho hai đường tròn  ;
O R và O '; R ' tiếp xúc ngoài tại A . Vẽ các bán kính OB//O' D sao
cho B , D cùng phía nửa mặt phẳng bờ OO '. Đường thẳng DB và OO ' cắt nhau tại I . a) Tính BAD .
b) Tính OI biết R  3cm và ’ R  2cm.
c) Tính OI theo R và R ' . Bài 3.
Cho hình vuông ABCD . Vẽ đường tròn  ;
D DC  và đường tròn O đường kính BC , chúng
cắt nhau tại một điểm thứ hai là E . Tia CE cắt AB tại M , tia BE cắt AD tại N . CHứng minh rằng : Trang 1
a) N là trung điểm AD .
b) M là trung điểm AB . HẾT
HƯỚNG DẪN GIẢI CHI TIẾT Bài 1.
Trong mỗi trường hợp sau hãy tìm giá trị của a để:
f) Điểm A0; 
1 thuộc đường thẳng x  ay  5  ; g) Điểm B  1
 ,5;0 thuộc đường thẳng ax  4y  6 ; h) Điểm C  7  ; 
3 thuộc đường thẳng ax  6 y  3;
i) Điểm D 2,5;0 thuộc đường thẳng ax  0 y  12,5;
j) Điểm E 2;  4,5 thuộc đường thẳng 0x  ay  31,5 ; Lời giải
a) Điểm A0; 
1 thuộc đường thẳng x  ay  5   0  . a   1  5   a  5 ; b) Điểm B  1
 ,5;0 thuộc đường thẳng ; c) Điểm C  7  ;  3 thuộc đường thẳng
ax  y    a      15 6 3 . 7 6. 3  3   a   ; 7
d) Điểm D 2,5;0 thuộc đường thẳng ax  0 y  12,5  2,5.a  0.0  12,5  a  5 ;
e) Điểm E 2;  4,5 thuộc đường thẳng
0x  ay  31,5  0.2  . a  4  ,  5  31,5  a  7  ; Bài 2.
Vẽ đồ thị của mỗi cặp phương trình sau trong cùng một hệ trục tọa độ rồi tìm tọa độ giao điểm
của hai đường thẳng đó:
a) 2x  y  3 và 3x  y  1
b) x  2 y  4 và 3x  2 y  12
c) x  2 y  4 và 2
 x  4y  8 
d) x  y  1 và 3
 x  3y  6  Lời giải
a) Các đường thẳng 2x  y  3 và 3x  y  1 là đồ thị các hàm số y  2
 x  3 và y  3x 1
trên mặt phẳng tọa độ. 3
Khi x  0  y  3 , y  0  x 
ta có đường thẳng 2x  y  3 đi qua các điểm 0;3 và 2  3  ; 0    2  1
Khi x  0  y  1
 , y  0  x  ta có đường thẳng 3x  y  1 đi qua các điểm 0;  1 và 3  1  ; 0   .  3  Trang 2
Tọa độ giao điểm của đường thẳng 2x  y  3 và đường thẳng 3x  y  1 là nghiệm của hệ
 2x  y  3 phương trình  3
 x  y  1  4  4 x  x 
 2x  y  3  5x  4    5  5        3
 x  y  1 3  x  y 1 4 7 3.   y  1 y   5  5  4 7 
Vậy tọa độ giao điểm của các đường thẳng 2x  y  3 và 3x  y  1 là ;    5 5  b) Các đườ 1
ng thẳng x  2 y  4 và 3x  2 y  12 là đồ thị các hàm số y  x  2 và 2 3 y  
x  6 trên mặt phẳng tọa độ. 2
Khi x  0  y  2
 , y  0  x  4 ta có đường thẳng x  2y  4 đi qua các điểm 0; 2 và 4;0
Khi x  0  y  6 , y  0  x  4 ta có đường thẳng 3x  2 y  12 đi qua các điểm 0;6 và 4;0 Trang 3
Tọa độ giao điểm của đường thẳng x  2 y  4 và đường thẳng 3x  2 y  12 là nghiệm của hệ
x  2y  4 phương trình 3  x  2y  12
x  2y  4 4x 16  x  4  x  4        3
 x  2y 12
x  2y  4 4  2y  4 y  0
Vậy tọa độ giao điểm của các đường thẳng x  2 y  4 và 3x  2 y  12 là 4;0 c) Các đườ 1
ng thẳng x  2 y  4 và 2
 x  4y  8
 là đồ thị các hàm số y  x  2 và 2 1 y 
x  2 trên mặt phẳng tọa độ. 2
Khi x  0  y  2
 , y  0  x  4 ta có đường thẳng x  2y  4 đi qua các điểm 0; 2 và 4;0
Khi x  0  y  2
 , y  0  x  4 ta có đường thẳng 3x  2y  12 đi qua các điểm 0; 2 và 4;0 Trang 4
Đường thẳng x  2 y  4 trùng với đường thẳng 2
 x  4y  8
 nên có vô số điểm chung, mỗi
điểm của đường thẳng x  2 y  4 đều là điểm đường thẳng 2
 x  4y  8  .
d) Các đường thẳng x  y  1 và 3
 x  3y  6
 là đồ thị các hàm số y  x 1 và y  x  2 trên mặt phẳng tọa độ.
Khi x  0  y  1
 , y  0  x  1 ta có đường thẳng x  y  1 đi qua các điểm 0;  1 và 1;0
Khi x  0  y  2
 , y  0  x  2 ta có đường thẳng 3
 x  3y  6
 đi qua các điểm 0; 2 và 2;0 Trang 5
Đường thẳng x  y  1 song song với đường thẳng 3
 x  3y  6
 , nên hai đường thẳng không có tọa độ giao điểm. Bài 3.
a) Tìm giá trị của a để hai đường thẳng y  a  
1 x  2 và y  3  x 1 song song với nhau.
b) Xác định m và k để hai đường thẳng y  kx  m  2 và y  5  k  x  4  m trùng nhau.
c) Xác định m và k để d : y  kx  m  2 và d : y  5  k x  4  m cắt nhau tại điểm 2     1   trên trục tung.
d) Xác định k để các đường thẳng sau đồng quy?
d : y  2x 3;
d : y  x 3
d : y  kx 1 3  2  1  Lời giải
a) Để hai đường thẳng y  a  
1 x  2 và y  3  x 1 song song với nhau thì: a 1  1   a  0 2  4
Vậy a  0 thì hai đường thẳng trên song song với nhau.
b) Để hai đường thẳng y  kx  m  2 và y  5  k  x  4  m trùng nhau thì:  5 k  5  k 2k  5 k       2
m  2  4  m 2m  6 m  3 5 Vậy k 
và m  3 thì hai đường thẳng trên trùng nhau. 2 Trang 6
c) Để hai đường thẳng d và d cắt nhau tại một điểm trên trục tung thì 2  1   5 k  5  k 2k  5 k       2
m  2  4  m 2m  6 m  3 5 Vậy k 
và m  3 thì hai đường thẳng d và d cắt nhau tại một điểm trên trục tung. 2  1  2
d) Gọi điểm A  d  d 1   2
Khi đó hoành độ điểm A là nghiệm của phương trình:
2x  3  x 3  3x  6   x  2  Thay x  2
 vào hàm số y  2x  3 ta được y  2. 2    3  1   A 2  ;  1
Để ba đường thẳng d , d và d đồng quy thì Ad 3  3  2  1 
 Tọa độ điểm A thỏa mãn phương trình đường thẳng d : 3  1   k. 2   1  2k  0  k  0
Vậy k  0 thì ba đường thẳng d , d và d đồng quy. 3  2  1 
II. HÌNH HỌC: ÔN TẬP TÍNH CHẤT HAI TIẾP TUYẾN CẮT NHAU. Bài 1.
Cho hai đường tròn (O; R) đường kính AB, đường tròn tâm (O’), đường kính OA. Dây cung
AC của đường tròn (O) cắt đường tròn (O’) ở M. Chứng minh:
a) Đường tròn (O’) tiếp xúc (O) tại A. b) O’M // OC c) OM //BC Lời giải Trang 7 C M A B O' O
a) Vì đường tròn tâm (O’), đường kính OA nên O’ là trung điểm của OA
OO'  OAO' A Đường tròn (O’) tiếp xúc (O) tại A.
b) Vì M O ' , đường kính AO  tam giác AMO vuông tại M  OM  AC   1
Xét (O) có OM  AC , AC là dây cung  M là trung điểm của AC Xét tam giác AOC có: M là trung điểm của AC
O’ là trung điểm của AO
 O’M là đường trung bình của tam giác AOC MO’ // OC
c) C O , đường kính AB  tam giác ABC vuông tại C  CB  AC 2 Từ (1) và (2)  OM //BC. Bài 2. Cho hai đường tròn  ;
O R và O ' ; R ' tiếp xúc ngoài tại A . Vẽ các bán kính OB//O' D sao
cho B , D cùng phía nửa mặt phẳng bờ OO '. Đường thẳng DB và OO ' cắt nhau tại I . a) Tính BAD
b) Tính OI theo R và R '
c) Tính OI biết R  3cm và ’ R  2cm Lời giải B D 1 1 1 3 O A O' I
a) Có Có OB//O' D (giả thiết)  O  O '  180 (hai góc trong cùng phía) 1 1 1 A
 OB cân tại O  A  180  O 1  1  2 Trang 8 1 A
 O'Dcân tại O'  A  180  O ' 3  1  2 1  A  A 
180  O 180  O '
 90  BAD  90 1 3  1 1  2
b) Có OB//O' D (giả thiết)  I
 O'D# I
 OB (một đường thẳng cắt hai cạnh của tam giác và
song song với cạnh thứ ba thì tạo thành tam giác mới đồng dạng với tam giác đã cho) IO ' O ' D IO O D   ' '   IO OB
IO ' OA  AO ' OB
 IO'.OB  O' .
D IO ' OA  AO '
 IO'.OB  O' .
D IO ' O ' D OA  AO '
 IO'.OB O'D  O'DOA AO'
O ' D OA  AO '
R '. R  R '  IO'   
OB  O ' D R  R'
c) Với R  3cm và ’ R  2cm, ta có
R '. R  R ' 2.3  2 IO '     . R  R ' 32 15cm Bài 3.
Cho hình vuông ABCD . Vẽ đường tròn  ;
D DC  và đường tròn O đường kính BC , chúng
cắt nhau tại một điểm thứ hai là E . Tia CE cắt AB tại M , tia BE cắt AD tại N . CHứng minh rằng :
a) N là trung điểm AD .
b) M là trung điểm AB . Lời giải 1 Xét EBC 
có EO là đường trung tuyến ứng với cạnh BC và EO  BO  CO  BC 2 Nên EBC  vuông tại E . 0
ABN  NBC  90 Ta có 
 ABN  ECB 0
ECB  EBC  90 Trang 9 Xét ABN 
vuông tại A và B
 CM vuông tại B có: AB  BC    A  BN  B
 CM cgv  gn  AN  BM   1
ABN  BCE Xét đường tròn  ;
D DC  có DC  DE Xét đường trfon  ;
O OB có OC  OE
 DO là đường trung trực của đoạn thẳng CE .
 DO  CE . 0 C
 DO  DCF  90 Ta có 
 CDO  FCB 0
FCB  DCF  90 Xét C
 DO vuông tại O và B
 CM vuông tại B có: C  D  BC    C  DO  B
 CM cgv  gn  CO  BM 2 C
 DO  BCM 1 1 1 Ta có CO  BC  AB  AD 3 2 2 2  1 AN  AD  2 Từ   1 , 2,3   1 BM  AB  2
 N là trung điểm AD và M là trung điểm AB HẾT Trang 10