







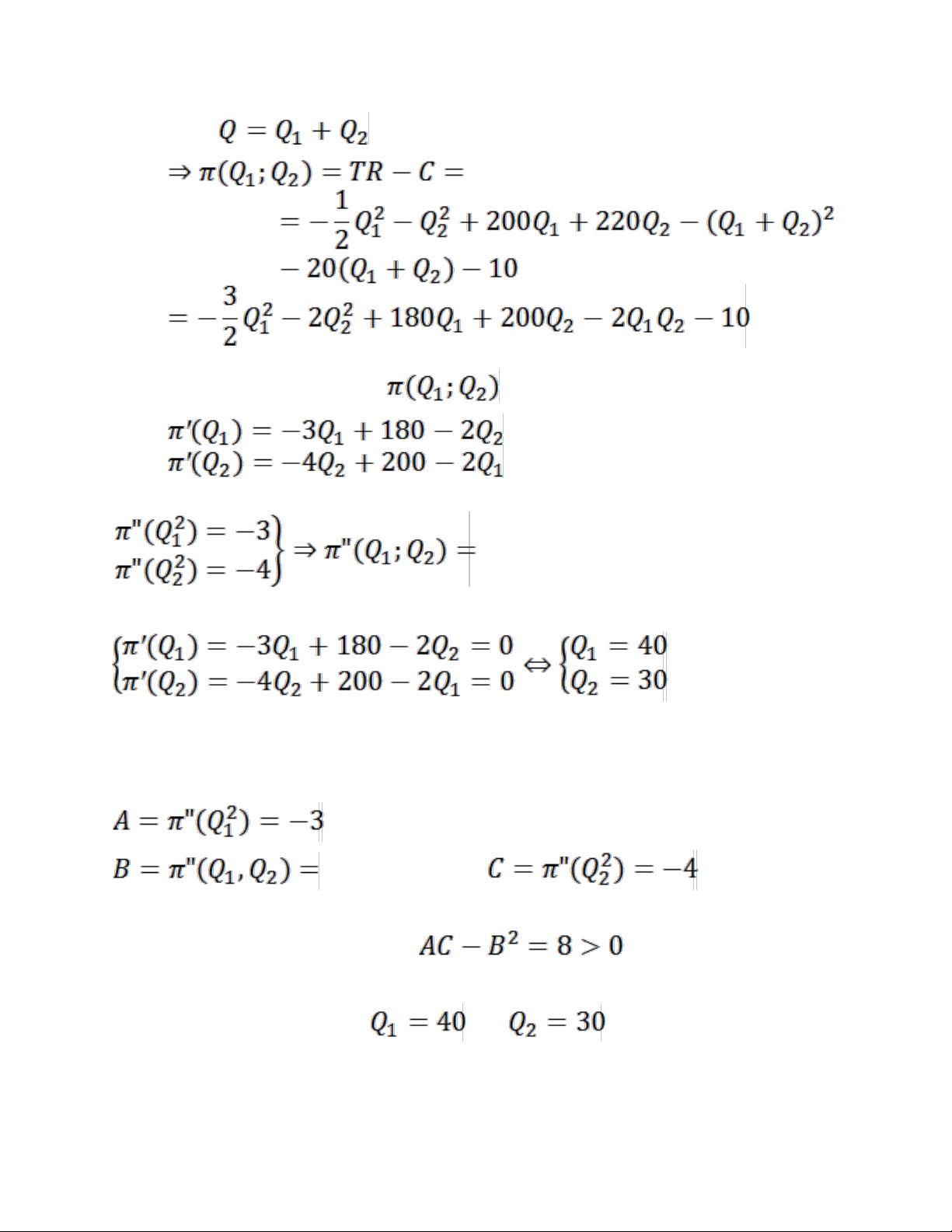



Preview text:
lOMoAR cPSD| 49519085
BÀI TẬP TOÁN CHƯƠNG 3 – TỔ 2
A. Phần Trắc Nghiệm
Câu 1 : Chọn đáp án đúng:
a)Nếu f liên tục tại x0 thì f có đạo hàm tại x0
→ f có đạo hàm tại x0 => f liên tục tại x0 ngược lại không đúng.
b)Hàm số liên tục trên [a;b] nếu f khả tích trên [a;b]
→ mọi hàm f liên tục trên [a;b] đều khả tích, điều ngược lạ không đúng.
c) f khả vi tại x0 thì f xác định tại x0
→ mọi hàm f(x) khả trên (a;b) đều liên tục trên
(a;b) ngược lại không đúng.
d) f đạt cực trị tại x0 thì f '(x0)= 0
→ f đạt cực trị tại x0 f'(x0)= 0 hoặc f'(x0) không xác định.
Chọn đáp án C
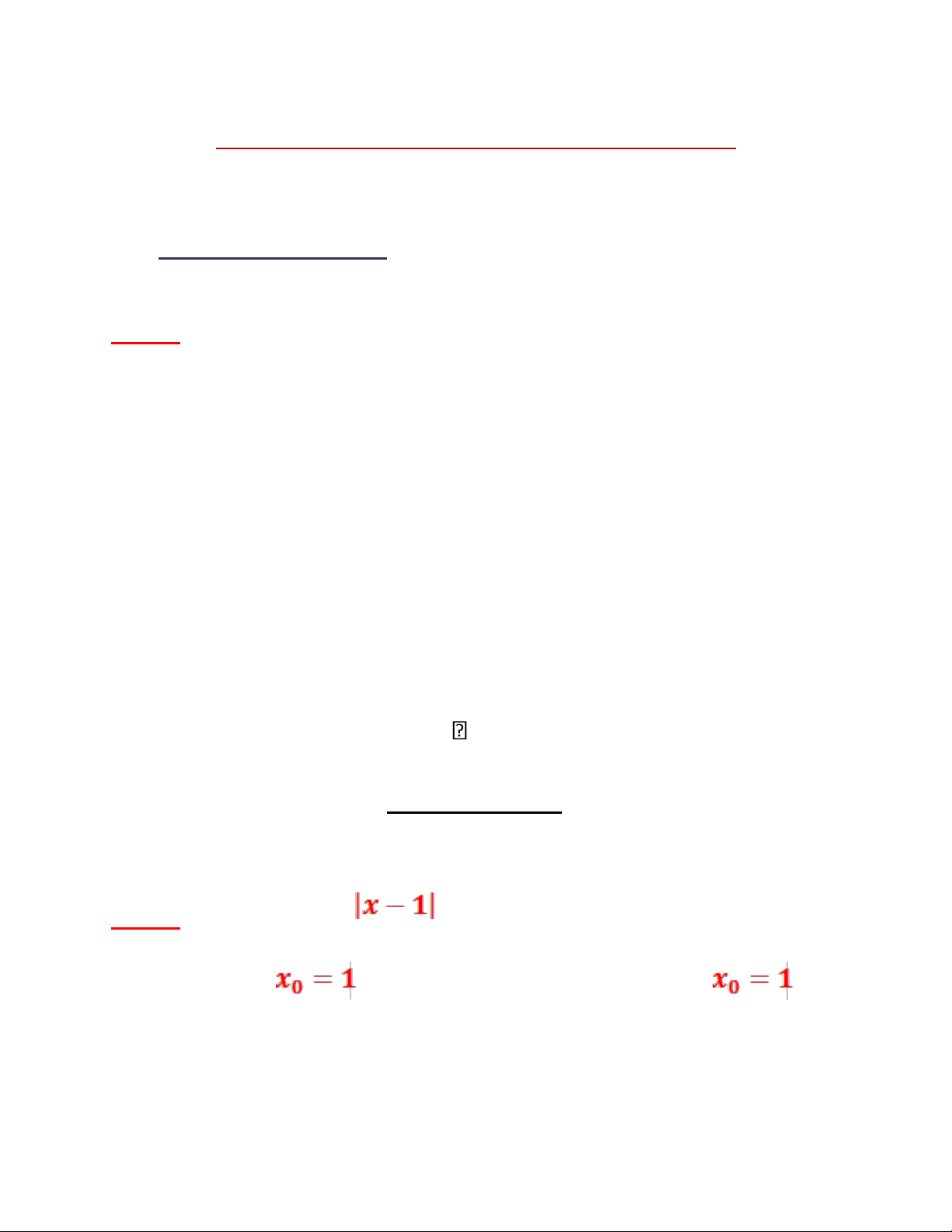
Câu 2 : Hàm f(x)= x
A.Liên tục tại
B.Có đạo hàm lOMoAR cPSD| 49519085 C.Khả vi tại
D.Cả A,B,C đều sai Bài giải
f x( ) x x 1 f x( )
x2x 2 x x(x x( 1)1) Ta có :
lim f x( ) xlim ( 1 x2 x) 0
x 1 lim f x( ) xlim ( 1 x2 x) 0 xlim 1 f x( ) xlim 1 x 1
limx 1 f x( ) lim(x 1 x2 x) 0
=>Hàm số liên tục tại x0 1
Chọn đáp án A
Câu 3: Tìm giới hạn: I = ( a>
A)I= 1/a B) I= 1
f x( ) lim f x( ) 0 lOMoAR cPSD| 49519085 x 1
C)I= 2 D) cả A, B, C đều sai Bài giải Ta có: I = = = 1 Chọn đáp án B
Câu 4 : Tính I = a) I=e b) I=1
c) I=2 d) Cả a,b,c đều sai Bài giải
Tại x=1 thương số có dạng nên ta áp dụng quy tắc L’Hospital Đặt F(x) = F’(x) =
G(x) = xln(x) => G’(x) = ln(x)+1 Ta có : I =
Chọn đáp án A lOMoAR cPSD| 49519085
Câu 5 : Nếu f(x) là hàm số liên tục trên (a,b) thì
a) f(x) có đạo hàm trên (a;b) b) f(x) bị chặn trên (a;b)
c) f(x) đạt GTLN,GTNN trên (a;b) d) Cả 3 câu đều sai Bài giải
a) Sai vì nếu f(x) có đạo hàm thì sẽ liên tục, nhưng nếu f(x)
liên tục thì không chắc có đạo hàm.
b)Sai vì f(x) thiếu điều kiện: f(x) phải xác định trên (a,b)
c) Sai vì f(x) đạt GTLN và GTNN trên [a,b]
Chọn đáp án D
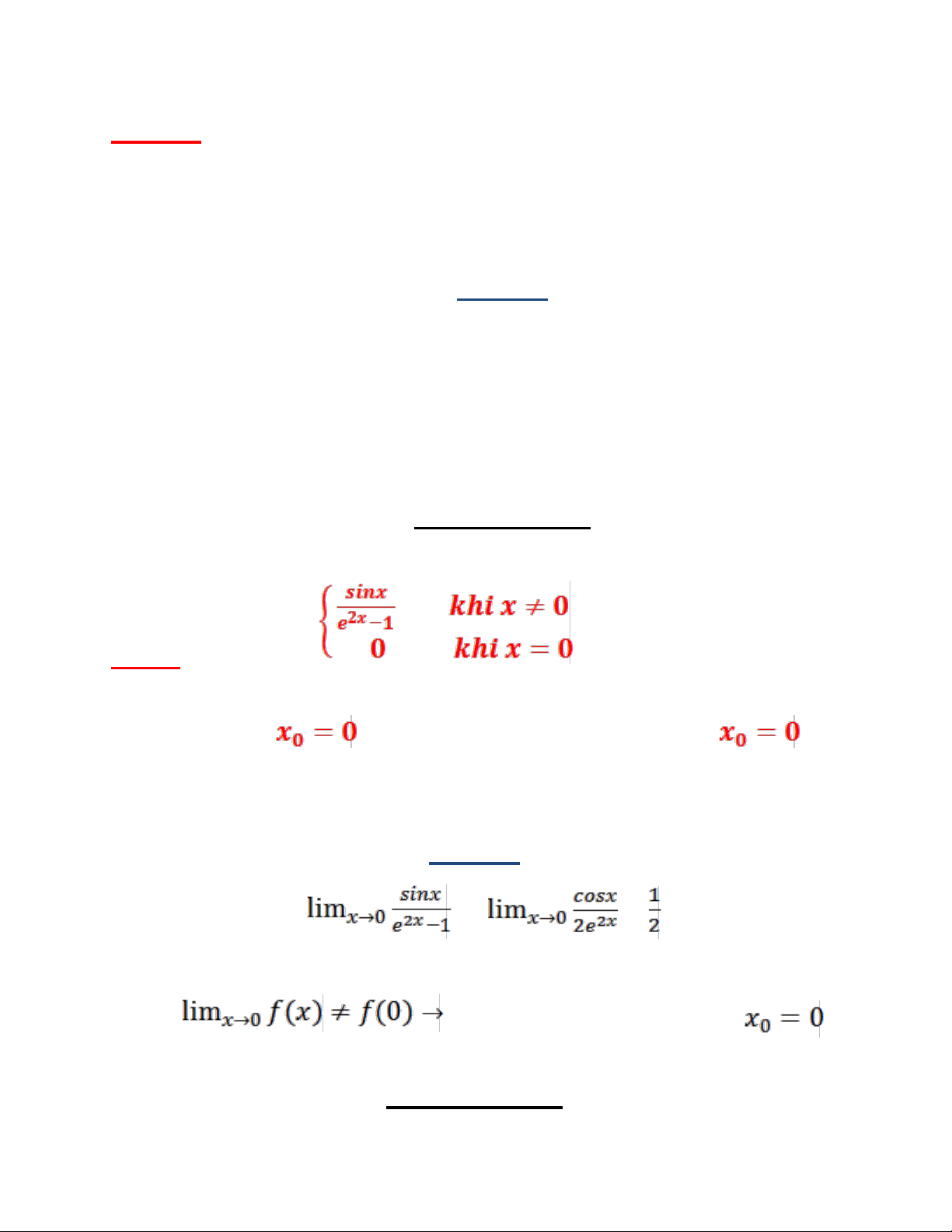
Câu 6: Hàm f(x)=
a) Liên tục tại
b) Có đạo hàm tại
c)Khả tích trên [a;b] d) Cả 3 câu trên đều sai Bài giải Ta có: = = Vì
Hàm số f(x) gián đoạn tại
Chọn đáp án D lOMoAR cPSD| 49519085
Câu 7 : Chọn đáp án đúng
a) f có giới hạn tại nếu f có f’(
) ,f’ (
b) f liên tục tại =0 thì f có đạo hàm tại =0
c) f có đạo hàm tại nếu f có f’( ,f’(
d)Cả 3 câu trên đều sai. Bài giải
a) Tìm giới hạn tại nếu f có f '(x0 ), f '(x0 ) =>SAI
Lập luận: Điều kiện cần và đủ để hàm số f(x) có giới hạn khi x
tiến về là các giới hạn bên phải và bên trái phải bằng nhau,
nghĩa là : f '(x0 ) f '(x0 )
b) f liên tục tại =0 thì f có đạo hàm tại =0 =>SAI
Lập luận: Hàm số f(x) có đạo hàm tại thì liên tục tại còn ngược lại thì sai.
Chẳng hạn như hàm số f(x)=|x| liên tục tại 0 nhưng không có đạo hàm tại 0.
c) f có đạo hàm tại nếu f có f '(x0 ), f '(x0 ) => SAI
Lập luận: Để hàm số f(x) có đạo hàm tại thì điều kiện cần và lOMoAR cPSD| 49519085
đủ là: f '(x0 ) f '(x0 ) f '(x0)
Chọn đáp án D
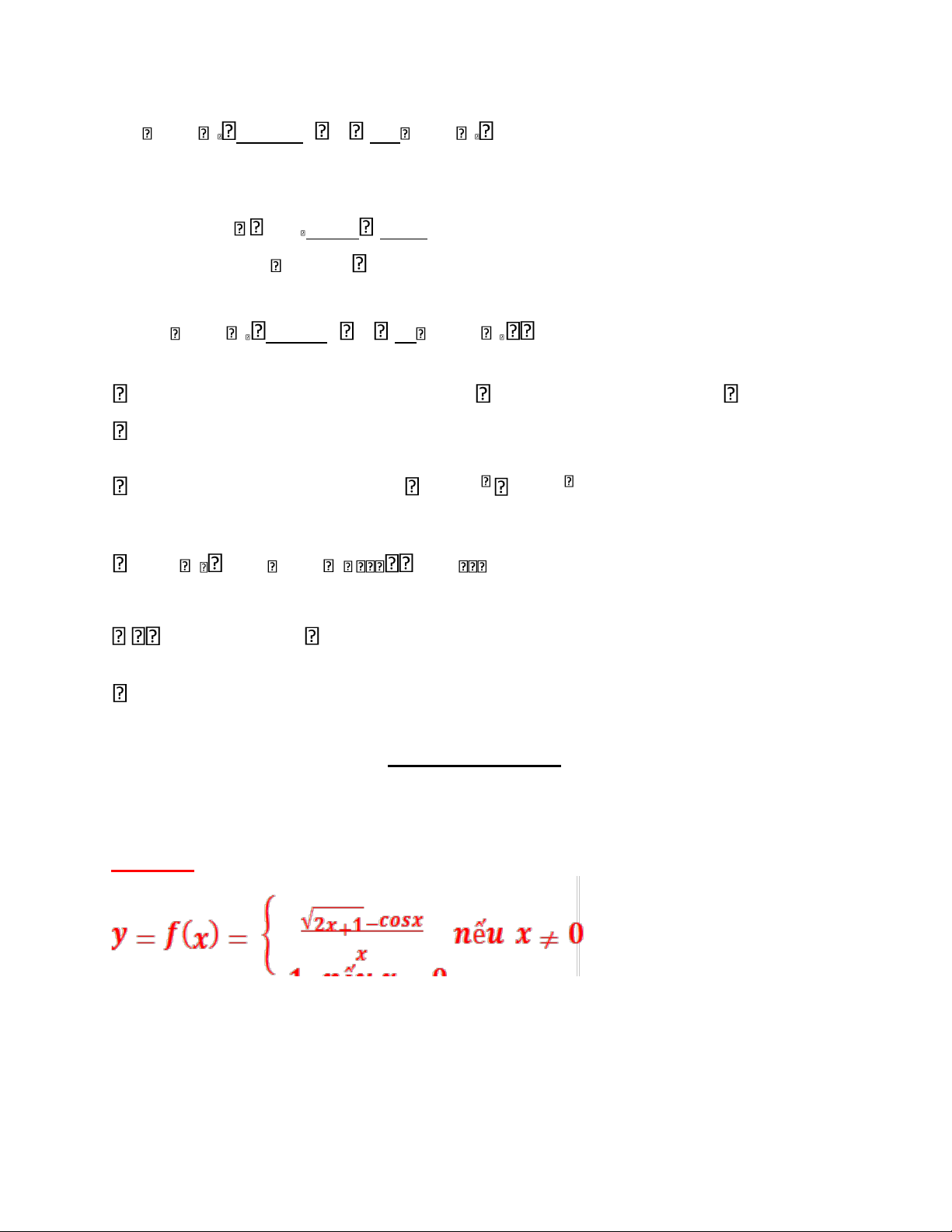
Câu 8: Cho hàm số : f(x) = Bài giải
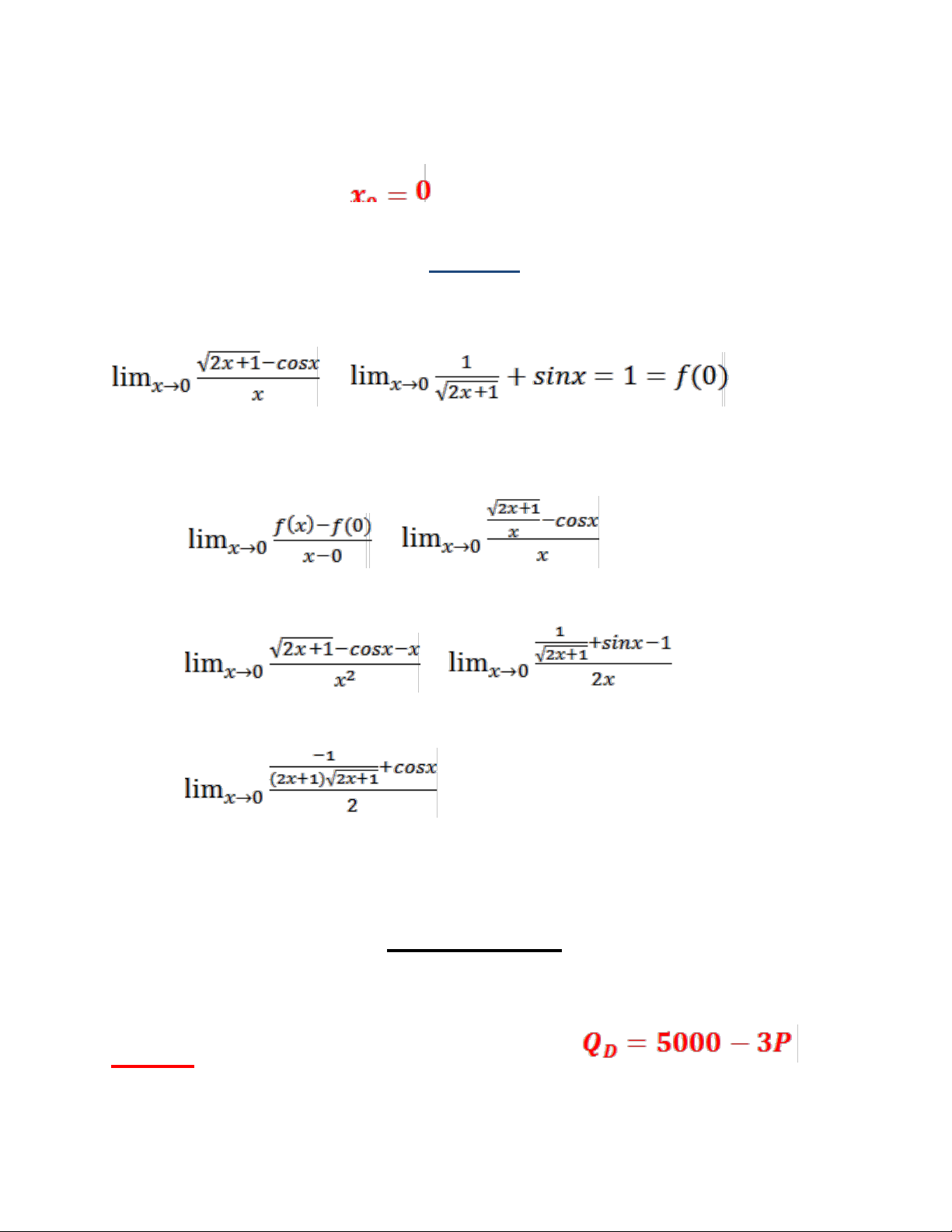
+) Miền xác định của hàm là R +) f(0)= +) = = + =m + = m – 0 = m
Đ f(x) liên t c t i ểụ ạ =0 = f(0) lOMoAR cPSD| 49519085
Chọn đáp án A
Câu 9 : Cho f(x)= x - 2 và a)
gián đoạn tại b)
không xác định được tại c)
khả vi tại d)
liên tục tại Bài giải Ta có : = = f( = f(2) = 0 = 0 = 0 Vì = f(2) = 0 Hàm liên tục tại =2 lOMoAR cPSD| 49519085
Chọn đáp án D
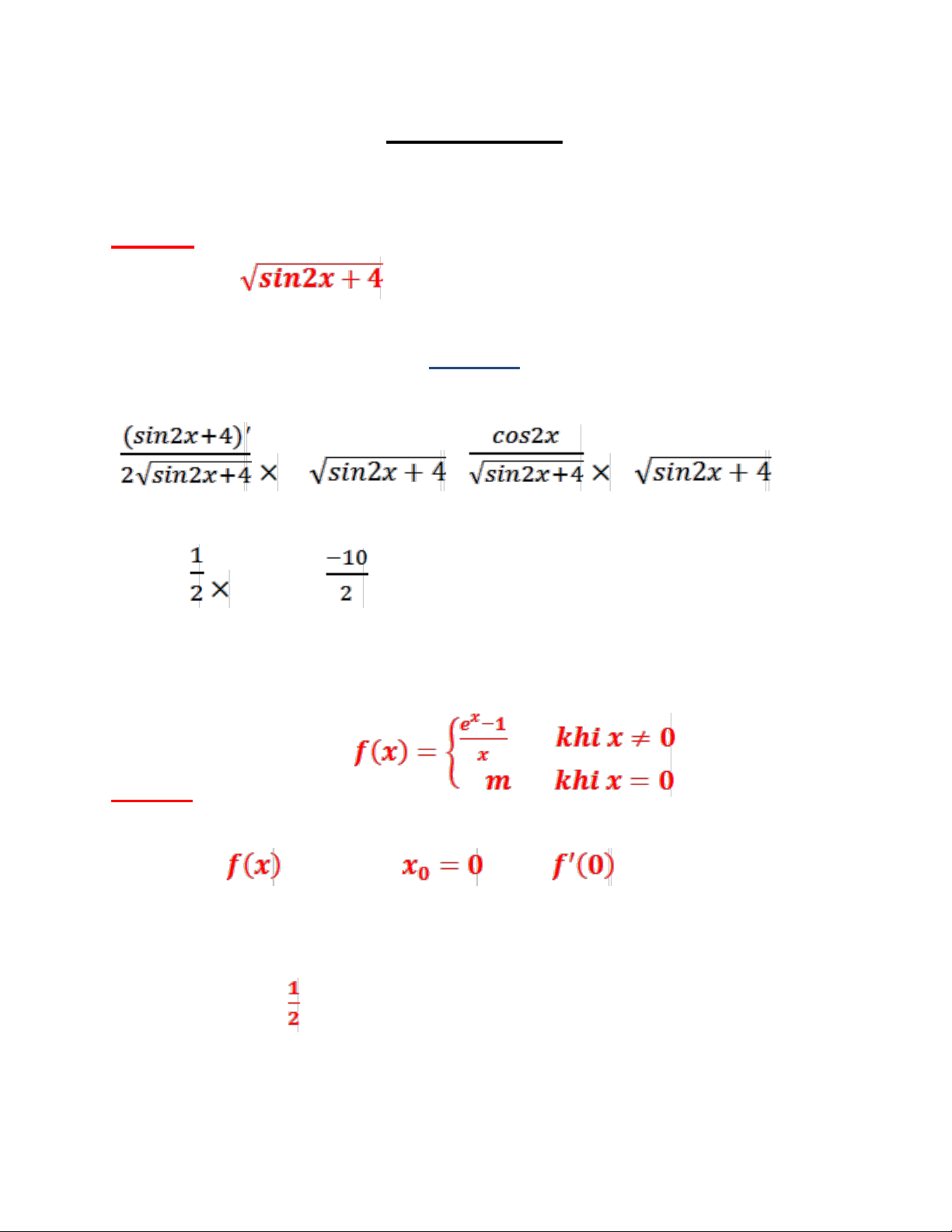
Câu 10 : Cho hàm số h(x) khả vi trên R thỏa mãn h’(2)=-10 . Đặt f(x)=h
. Tính f’(0) Bài giải f’(x)= h’ = h’ f’(0) = h’(2) = = -5
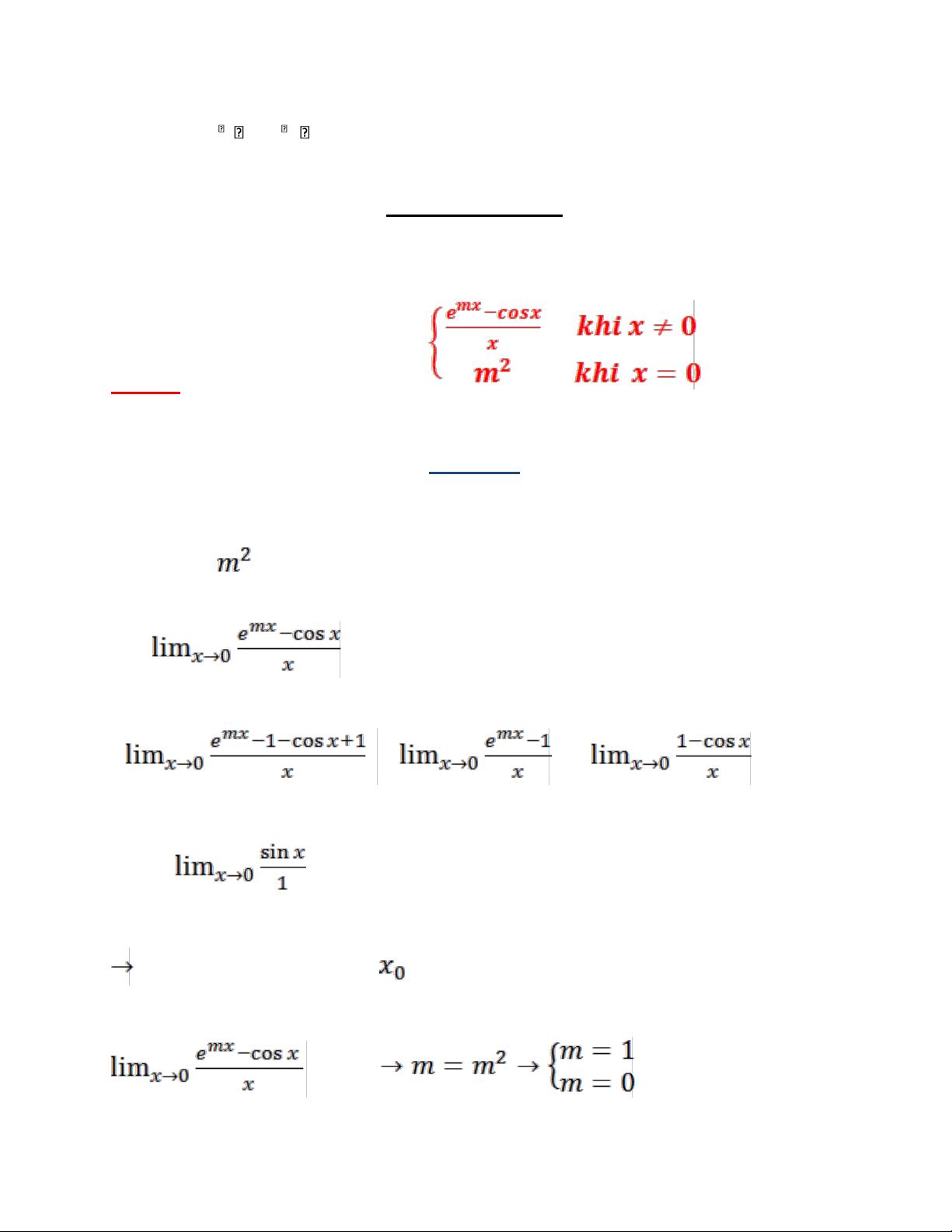
Câu 11: Cho hàm số Tìm m để khả vi tại , tính
a) m=1 , f’(0)=0 b) m=1 , f’(0)=1
c) m=1 , f’(0)= d) Cả a,b,c đều sai lOMoAR cPSD| 49519085 Bài giải Ta có: 1 Để khả vi tại thì phải liên tục tại
Chọn đáp án C
Câu 12: Đặt L= và K= a) L=0, K= b) L=1, K=
c) L=2, K=0 d) L=±∞, K= Bài giải
+) L= lim(2 )x x => dạng 00 x 0 Đặt y=(2 )x x lOMoAR cPSD| 49519085 ln y x ln(2x) x lim (ln y) lim x 0 x 0 x
Áp dụng quy tắc L’Hospital: 1 lim lim x lim x2 lim x 0 lim x 0 ln(2 )x 1 x 0 x 0 1 x 0 x x 0 x 0 x x2 lim(ln )y 0 x 0 ln(lim )y 0 ln(1) x 0 lim y 1 x 0
L 1 +) K= 1 x => dạng xlim(1 2x) 1 x 1 lim(1 )x lim 1 2x lOMoAR cPSD| 49519085 Ta có: x 2x x 1 2x
2x exlim 2xx e e K e
Chọn đáp án B
Câu 13 : Cho f(x)= với
xác định trong lân
cận của 1. Khi đó:
A. f(x) có đạo hàm trái và đạo hàm phải tại 1 nếu có
giới hạn khi x
B. f(x) có đạo hàm tại 1 nếu
là vô cùng bé khi x
C. f(x) liên tục tại 1 nếu
bị chặn trong lân cận tại 1
D.Cả ba câu trên đều đúng Bài giải f x( ) ( )x x 1 ( )(x x 1)(x 1)
( )(1x x x)( 1) Ta có : •
f '(1 ) lim f x( ) f (1) x 1 x 1 lOMoAR cPSD| 49519085
xlim 1 ( )(x xx 1 1) xlim 1 ( )x •
f '(1 ) lim f x( ) f (1) x 1 x 1
xlim 1 ( )(1xx 1 x) xlim( ( ))x 1
f(x) có đạo hàm trái / phải khi ( )x có giới hạn khi x 1 Câu A là đúng
f(x) có đạo hàm tại x=1 f '(1 ) f '(1 )
xlim 1 ( )x xlim 1 ( )x ( ) 0x khi x 1 B,D sai
Chọn đáp án A
Câu 14 : Cho hàm số lOMoAR cPSD| 49519085
a) f không liên tục tại x=0 b) f’(0) = 0
c) f không khả vi tại
d) Cả a,b,c đều sai Bài giải Ta có: =
Vậy hàm số liên tục tại x=0 f’(x)= = = = = f’(0) = 0
Chọn đáp án B
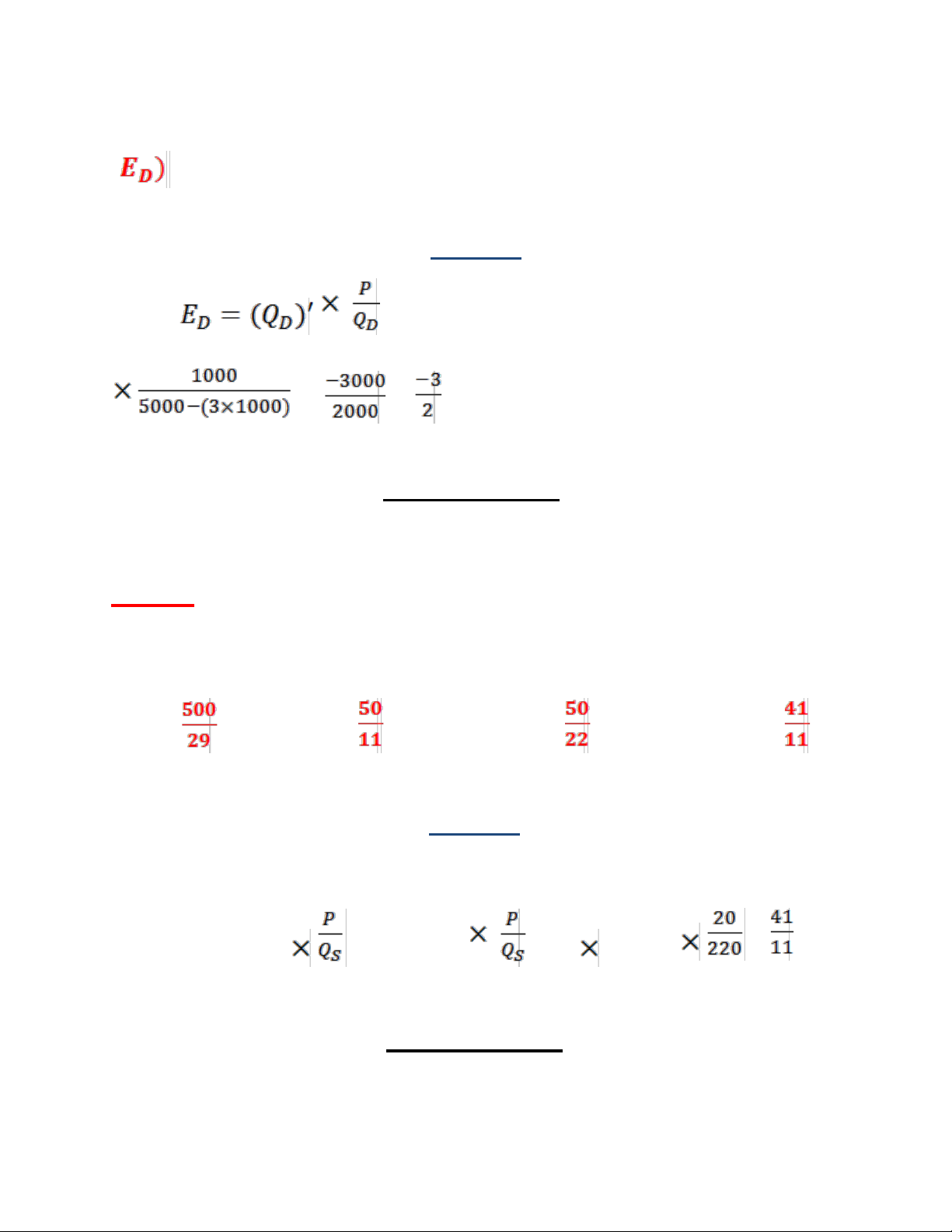
Câu 15 Cho hàm cầu của một sản phẩm với lOMoAR cPSD| 49519085
P là giá bán sản phẩm đó. Hệ số co giãn của hàm cầu theo giá ( tại P=1000. Bài giải = (-3) = =
Chọn đáp án D
Câu 16: Cho hàm cung của một sản phẩm: Qs= P2 + P- 200
với P là giá bán của sản phẩm đó. Hệ số co giãn của hàm
cung theo giá (Es) tại giá P = 20 a) Es= b) Es= c) Es= d)Es= Bài giải
Với P= 20 => Qs= 202 + 20 – 200= 220 Ta có: E = s= (Qs)' = (2P +1) = (2 20 +1)
Chọn đáp án D lOMoAR cPSD| 49519085
B. Phần tự luận
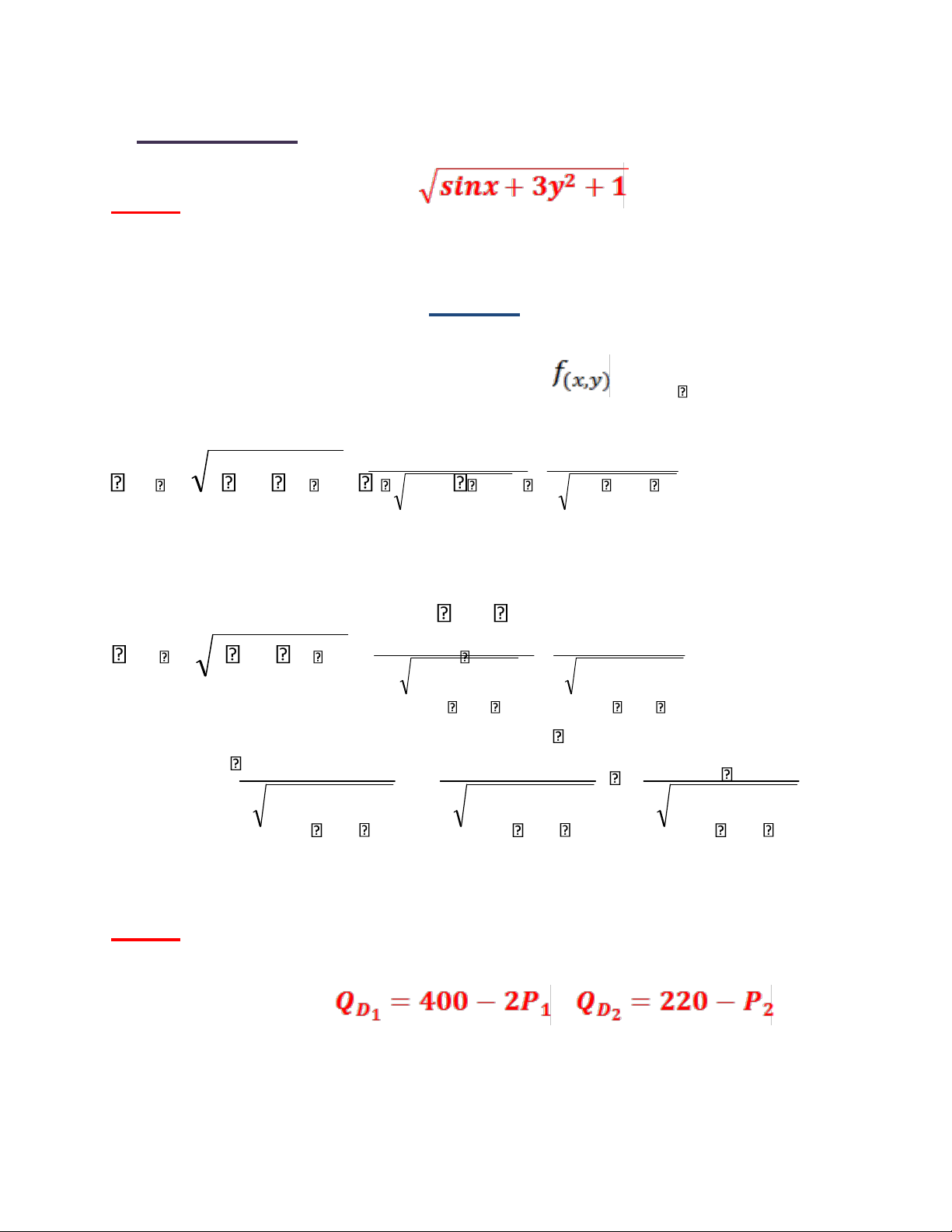
Câu 1: Cho hàm số f(x,y)=
. Tìm vi phân
toàn phần của f . Bài giải
Ta có vi phân toàn phần của f(x,y) là: d
= f 'x.dx f 'y.dy (sin x
f 'x sin x 3y2 1'x 2 sin x 33yy22 1)1 'x 2 sincosx 3xy2 1
f 'y sin x 3y2 1'y (sinx 3y22 1)'y 6y 2 2 sin x 3 y 1 2 sin x 3 y 1 cos x 6y dx cos .x dx df x y( , ) dy 6 .y dy => 2 sin x 3 y2 1 2 sin x 3 y2 1 2 sin x 3 y2 1
Câu 2: Một xí nghiệp sản xuất độc quyền một loại sản phẩm
và tiêu thụ trên hai thị trường tách biệt. Biết hàm cầu trên
từng thị trường là: ; và lOMoAR cPSD| 49519085
hàm tổng chi phí là với trong đó
là lựa hàng phân phối cho thị trường thứ i
1)Tìm doanh thu biên tế tại
2)Tìm mức sản lượng và lượng hàng phân phối cho từng
thị trường để xí nghiệp có lợi nhuận tối đa. Bài giải 1)Ta có hàm doanh thu : Doanh thu biên tế: tại 2) Hàm tổng chi phí: lOMoAR cPSD| 49519085 Với: Đạo hàm riêng của -2 Tìm điểm dừng: Tại điểm dừng ta có: -2 Xét Vậy điểm dừng và là lợi nhuận tối đa. lOMoAR cPSD| 49519085
C.Phần Sách bài tập
Câu 12d : Tính đạo hàm cấp n của các hàm số y = sin2x. Bài giải
y’ = 2cos2x = 2sin( 2x + ) y” =
2.2(-sin2x) = 22 (sin2x + ) y”’ = 23cos(2x+ ) = 23sin( 2x ) y(n) = 2nsin(2x + )
Câu 14 : Cho f(x) = xsinx. Tính f(20) (0). Bài giải f(20)= Thay x = 0 (20) f = 0 – 20cos(0) = - 20 lOMoAR cPSD| 49519085 f(20)(0) = -20
Câu 16 :Sử dụng công thức vi phân, tính gần đúng a. arctg1,05 b. ln(1,03) Bài giải a) Đặt b) Đặt Câu 28 : Cho hàm số . Tính khi Q = 9. lOMoAR cPSD| 49519085 Bài giải Khi Q = 9 PP 37 Ta có: Với Q = 9, P = 3 thì Với Q = 9, P = -7 thì




