Bài tập trắc nghiệm cực trị của hàm số

Tài liệu gồm 30 trang với nội dung gồm 2 phần: Phần 1. Các bài toán cực trị không chứa tham số; Phần 2. Các bài toán cực trị chứa tham số. Mời quý thầy cô và các bạn học sinh cùng tham khảo để phục vụ quá trình giảng dạy và học tập môn Toán lớp 12.

68 34 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Chương 2: Hàm số lũy thừa. Hàm số mũ và hàm số logarit

Môn: Toán 12

Thông tin:

30 trang 8 tháng trước

Tác giả:

Profile Nguyễn Vân
TRẦN CÔNG DIÊU
[ĐĂNG KÍ HỌC OFF TPHCM – CALL 01638.645.228]
TRUNG TÂM THẦY DIÊU – FB TRẦN CÔNG DIÊU
1
Phần 1. Các bài toán cực trị không chứa tham số
Đầu tiên chúng ta cùng nghiên cứu các bài tập tìm cực trị của hàm số không chứa tham số, các bài tập
này khá đơn giản. Thường có hai cách để tìm cực trị của hàm số như sau:
Cách 1.
Bước 1: tìm tập xác định của hàm số.
Bước 2: tính đạo hàm và giải phương trình
'0y
.
Bước 3: lập bảng biến thiên và quan sát kết luận. Nếu hàm số xác định tại
0
x
và đạo hàm đổi dấu
từ
sang
thì
0
x
là điểm cực tiểu, ngược lại đạo hàm đổi dấu từ
sang
thì
0
x
là điểm cực đại.
Cách 2.
Bước 1: tìm tập xác định của hàm số.
Bước 2: tính đạo hàm và giải phương trình
'0y
được các nghiệm
1 2 3
, , ,...,
n
x x x x
.
Bước 3: kiểm xem nếu
'' 0
i
yx
thì
i
x
điểm cực tiểu với
1,2,3,...,in
, ngược lại nếu
'' 0
i
yx
thì
i
x
điểm cực đại.
Câu 1. Cho hàm số
y f x
có bảng biến thiên như sau:
Mệnh đề nào dưới đây sai?
A. Hàm số có giá trị cực đại bằng 0. B. Hàm số có hai điểm cực tiểu.
C. Hàm số có giá tri cực đại bằng 3. D. Hàm số có ba điểm cực trị.
Trích Đề Thi THPT Quốc Gia 2017
Câu 2. Phát biểu nào sau đây là đúng?
CỰC TRỊ CỦA HÀM SỐ
TRẦN CÔNG DIÊU
[ĐĂNG KÍ HỌC OFF TPHCM – CALL 01638.645.228]
TRUNG TÂM THẦY DIÊU – FB TRẦN CÔNG DIÊU
2
A. Nếu
'( )fx
đổi dấu từ dương sang âm khi
x
qua điểm
0
x
và
()fx
liên tục tại
0
x
thì hàm số
()y f x
đạt cực đại tại điểm
0
x
.
B. Hàm số
()y f x
đạt cực trị tại
0
x
khi và chỉ khi
0
x
là nghiệm của đạo hàm.
C. Nếu
0
'( ) 0fx
và
0
''( ) 0fx
thì
0
x
không phải là cực trị của hàm số
()y f x
đã cho.
D. Nếu
0
'( ) 0fx
và
0
''( ) 0fx
thì hàm số đạt cực đại tại
0
x
.
Câu 2. Cho khoảng
( ; )ab
chứa điểm
0
x
, hàm số
()fx
có đạo hàm trong khoảng
( ; )ab
(có thể từ điểm
0
x
). Tìm mệnh đề đúng trong các mệnh đề sau:
A. Nếu
()fx
không có đạo hàm tại
0
x
thì
()fx
không đạt cực trị tại
0
x
.
B. Nếu
'( ) 0fx
thì
()fx
đạt cực trị tại điểm
0
x
.
C. Nếu
'( ) 0fx
và
''( ) 0fx
thì
()fx
không đạt cực trị tại điểm
0
x
.
D. Nếu
'( ) 0fx
và
''( ) 0fx
thì
()fx
đạt cực trị tại điểm
0
x
.
Câu 3. Phát biểu nào dưới đây là sai?
A. Nếu tồn tại số
h
sao cho
0
( ) ( )f x f x
với mọi
00
( ; )x x h x h
và
0
xx
, ta nói rằng hàm số
()fx
đạt cực đại tại điểm
0
x
.
B. Giả sử
()y f x
liên tục trên khoảng
00
( ; )K x h x h
và có đạo hàm trên
K
hoặc trên
0
\Kx
,
với
0h
. Khi đó nếu
'( ) 0fx
trên
00
;x h x
và
'( ) 0fx
trên khoảng
00
;x x h
thì
0
x
là một điểm
cực tiểu của hàm số
()fx
.
C.
xa
là hoành độ điểm cực tiểu khi và chỉ khi
'( ) 0; ''( ) 0.y a y a
D. Nếu
00
; ( )M x f x
là điểm cực trị của đồ thị hàm số thì
00
()y f x
được gọi là giá trị cực trị của
hàm số.
Câu 4. Cho hàm số
()fx
xác định và liên tục trên khoảng
( ; )ab
. Tìm mệnh đề sai?
A. Nếu
()fx
đồng biến trên khoảng
( ; )ab
thì hàm số không có cực trị trên khoảng
( ; )ab
.
B. Nếu
()fx
nghịch biến trên khoảng
( ; )ab
thì hàm số không có cực trị trên khoảng
( ; )ab
.
C. Nếu
()fx
đạt cực trị tại điểm
0
( ; )x a b
thì tiếp tuyến của đồ thị hàm số tại điểm
00
; ( )M x f x
song song hoặc trùng với trục hoành.
TRẦN CÔNG DIÊU
[ĐĂNG KÍ HỌC OFF TPHCM – CALL 01638.645.228]
TRUNG TÂM THẦY DIÊU – FB TRẦN CÔNG DIÊU
3
D. Nếu
()fx
đạt cực trị tại điểm
0
( ; )x a b
thì
()fx
đồng biến trên
0
( ; )ax
và nghịch biến trên
0
( ; ).xb
Câu 5. Cho khoảng
( ; )ab
chứa
m
. Hàm số
()y f x
xác định và liên tục trên khoảng
( ; )ab
. Có các
phát biểu sau đây:
(1)
m
là điểm cực trị của hàm số khi
'( ) 0fm
.
(2)
( ) ( ), ( ; )f x f m x a b
thì
xm
là điểm cực tiểu của hàm số.
(3)
( ) ( ), ( ; )\f x f m x a b m
thì
xm
là điểm cực đại của hàm số.
(4)
( ) , ( ; )f x M x a b
thì
M
được gọi là giá trị nhỏ nhất của hàm số trên khoảng
( ; )ab
.
Số phát biểu đúng là:
A. 0. B. 1. C. 2. D. 3.
Câu 6. Giá trị cực đại
CĐ
y
của hàm số
3
32y x x
?
A.
4.
CĐ
y
B.
1.
CĐ
y
C.
0.
CĐ
y
D.
1.
CĐ
y 
Câu 7. Hàm số
32
5 3 1y x x x
đạt cực trị khi:
A.
3
1
3
x
x


B.
0
10
3
x
x
C.
0
10
3
x
x

D.
3
1
3
x
x
Câu 8. Đồ thị của hàm số
32
3y x x
có hai điểm cực trị là:
A.
(0;0)
hoặc
(1; 2).
B.
(0;0)
hoặc
(2;4).
C.
(0;0)
hoặc
(2; 4).
D.
(0;0)
hoặc
( 2; 4).
Câu 9. Hàm số
3
31y x x
đạt cực đại là:
A.
1.x 
B.
0.x
C.
1.x
D.
2.x
Câu 10. Hàm số
32
4 3 7y x x x
đạt cực tiểu tại
CT
x
. Kết luận nào sau đây đúng?
A.
1
.
3
CT
x
B.
3.
CT
x 
C.
1
.
3
CT
x 
D.
1.
CT
x
Câu 11. Hệ thức liên hệ giữa giá trị cực đại
CĐ
y
và giá trị cực tiểu
CT
y
của hàm số
3
3y x x
là:
A.
2.
CT CĐ
yy
B.
3
.
2
CT CĐ
yy
C.
.
CCT Đ
yy
D.
.
CT CĐ
yy
TRẦN CÔNG DIÊU
[ĐĂNG KÍ HỌC OFF TPHCM – CALL 01638.645.228]
TRUNG TÂM THẦY DIÊU – FB TRẦN CÔNG DIÊU
4
Câu 12. Cho hàm số
32
3 9 4y x x x
. Nếu hàm số đạt cực đại tại
1
x
và cực tiểu tại
2
x
thì tích của
12
( ). ( )y x y x
có giá trị bằng:
A. – 302. B. – 82. C. – 207. D. 25.
Câu 13. Khoảng cách giữa 2 điểm cực đại và cực tiểu của đồ thị hàm số
2
( 1)( 2)y x x
là:
A.
2 5.
B. 2. C. 4. D.
5 2.
Câu 14. Trong các đường thẳng dưới đây, đường thẳng nào đi qua trung điểm đoạn thẳng nối các
điểm cực trị của đồ thị hàm số
32
31y x x
?
A.
2 3.yx
B.
11
.
33
yx
C.
2 3.yx
D.
2 1.yx
Câu 15. Đồ thị hàm số
42
23y x x
có
A. 1 điểm cực đại và không có điểm cực tiểu.
B. 1 điểm cực tiểu và không có điểm cực đại.
C. 1 điểm cực đại và 2 điểm cực tiểu.
D. 1 điểm cực tiểu và 2 điểm cực đại.
Câu 16. Đồ thị hàm số
42
1y x x
có bao nhiêu điểm cực trị có tung độ dương?
A. 1. B. 2. C. 3. D. 4.
Câu 17. Cho hàm số
22
( ) ( 3)f x x
. Giá trị cực đại của hàm số
'( )fx
bằng:
A. 8. B.
8.
C. 0. D.
1
.
2
Câu 18. Phát biểu nào sau đây đung?
A. Nêu
f ' x
đôi đâu tư dương sang âm khi
x
qua điêm
x
0
và
fx
liên tuc tai
x
0
thì hàm số
y f x
đat cưc đai tai điêm
x
0
.
B. Hàm số
y f x
đat cưc tri tai
x
0
khi va chi khi
x
0
là nghiệm của đạo hàm.
C. Nêu
f ' x
0
0
và
f '' x
0
0
thì
x
0
không phai la cưc tri cua ham sô
y f x
đa cho.
D. Nêu
f ' x
0
0
và
f '' x
0
0
thì hàm số đạt cưc đai tai
x
0
.
TRẦN CÔNG DIÊU
[ĐĂNG KÍ HỌC OFF TPHCM – CALL 01638.645.228]
TRUNG TÂM THẦY DIÊU – FB TRẦN CÔNG DIÊU
5
Câu 19. Cho khoang
a;b
chưa điêm
x
0
, hàm số
fx
có đạo hàm trong khoảng
a;b
(có thể trừ
điêm
x
0
). Tìm mệnh đề đúng trong các mệnh đề sau:
A. Nêu
fx
không co đao ham tai
x
0
thì
fx
không đat cưc tri tai
x
0
.
B. Nêu
f ' x 0
thì
fx
đat cưc tri tai
x
0
.
C. Nêu
f ' x 0
và
f '' x
0
0
thì
fx
không đạt cực trị tại
x
0
.
D. Nêu
f ' x 0
có nghiệm
x
0
và
f '' x
0
0
thì
fx
đat cưc tri tai
x
0
.
Câu 20. Đồ thị của hàm số
32
3x 9x 1yx
có hai điểm cực trị A và B. Điểm nào dưới đây thuộc
đường thẳng AB?
A.𝑄(−1; 10). B. 𝑀(0; −1). C.
1; 10N
D. 𝑃(1; 0).
Trích Đề Thi THPT Quốc Gia 2017
Câu 21. Phát biểu nào dưới đây là sai?
A. Nêu tôn tai sô
sao cho
f x f x
0
vơi moi
x x h; x h
00
và
xx
0
, ta noi răng ham sô
fx
đat cưc đai tai điêm
x
0
.
B. Giả sử
y f x
liên tuc trên khoang
K x h; x h
00
và có đạo hàm trên
K
hoăc
K\ x
0
, vơi
h 0
. Khi do nêu
f ' x 0
trên khoang
x h; x
00
và
f ' x 0
trên khoang
x ;h x
00
thì
x
0
là một
điêm cưc tiêu cua ham sô
y f x
.
C.
xa
là hoành độ điểm cực tiểu khi và chỉ khi
00y' a ; y'' a
.
D. Nêu
M x ; f x
00
là điểm cực trị của đồ thị hàm số thì
y f x
00
dươc goi la gia tri cưc tri cua
hàm số.
Câu 22. Cho ham sô
fx
xác định và liên tục trên khoảng
a;b
. Tìm mệnh đề sai?
A. Nêu
fx
đông biên trên khoang
a;b
thì hàm số không có cực trị trên khoang
a;b
.
B. Nêu
fx
nghịch biến trên khoảng
a;b
thì hàm số không có cực trị trên khoảng
a;b
.
TRẦN CÔNG DIÊU
[ĐĂNG KÍ HỌC OFF TPHCM – CALL 01638.645.228]
TRUNG TÂM THẦY DIÊU – FB TRẦN CÔNG DIÊU
6
C. Nêu
fx
đat cưc trị tại điểm
x a;b
0
thì tiếp tuyến của đồ thị hàm số tại điểm
M x ; f x
00
song song hoăc trung vơi truc hoanh.
D. Nêu
fx
đat cưc đai tai điêm
x a;b
0
thì
fx
đông biên trên
a; x
0
và nghịch biến trên
x ;b
0
.
Câu 23. Cho khoang
a;b
chưa
m
. Hàm số
y f x
xác định và liên tục trên khoảng
a;b
. Có các
phát biểu sau đây:
(1)
m
là điểm cực trị của hàm số khi
f ' m . 0
(2)
f x f m , x a;b
thì
xm
là điểm cực tiểu của hàm số.
(3)
f x f m , x a;b \ m
thì
xm
là điểm cực đại của hàm số.
(4)
f x M, x a;b
thì
M
là được gọi là giá trị nhỏ nhất của hàm sô trên khoang
a;b
.
Sô phat biêu đung la:
A. 0. B. 1. C. 2. D. 3.
Câu 24. Hàm số
y x x x
32
5 3 1
đat cưc tri khi:
A.
x
.
x

3
1
3
B.
x
.
x

0
10
3
C.
x
.
x


0
10
3
D.
x
.
x

3
1
3
Câu 25. Đồ thị của hàm số
y x x
32
3
có hai điểm cực trị là:
A.
;00
hoăc
;12
. B.
;00
hoăc
;24
.
C.
;00
hoăc
;24
. D.
;00
hoăc
;24
.
Câu 26. Hàm số
y x x
3
31
đat cưc đai tai:
A.
x.1
B.
x. 0
C.
x. 1
D.
x. 2
Câu 27. Hàm số
y x x x
32
4 3 7
đat cưc tiêu tai
CT
x
. Kêt luân nao sau đây đung?
A.
CT
x.
1
3
B.
CT
x.3
C.
CT
x.
1
3
D.
CT
x. 1
TRẦN CÔNG DIÊU
[ĐĂNG KÍ HỌC OFF TPHCM – CALL 01638.645.228]
TRUNG TÂM THẦY DIÊU – FB TRẦN CÔNG DIÊU
7
Câu 28. Hê thưc liên hê giưa gia tri cưc đai
CD
y
và giá trị cực tiểu
CT
y
của hàm số
y x x
3
3
là:
A.
CT CD
y y . 2
B.
CT CD
y y .
3
2
C.
CT CD
y y .
D.
CT CD
y y .
Câu 29. Cho ham sô
y x x x .
32
3 9 4
Nêu ham sô đat cưc đai tai
x
1
và cực tiểu tại
x
2
thì tích của
y x .y x
12
có giá trị bằng
A. -302. B. -82. C. -207. D. 25.
Câu 30. Khoảng cách giữa hai điểm cực đại và cực tiểu của đồ thị hàm số
y x x
2
12
là
A.
25
. B. 2. C. 4. D.
52
.
Câu 31. Trong cac đương thăng dươi đây , đương thăng nao đi qua trung điêm đoan thăng nôi cac
điêm cưc tri cua đô thi ham sô
y x x
3
31
?
A.
y x .23
B.
x
y.
1
33
C.
y x .23
D.
y x . 21
Câu 32. Đồ thị hàm số
y x x
42
23
có
A. 1 điêm cưc đai va không co điêm cưc tiêu.
B. 1 điêm cưc tiêu va không co điêm cưc đai.
C. 1 điêm cưc đai va 2 điêm cưc tiêu.
D. 1 điêm cưc tiêu va 2 cưc đai.
Câu 33. Đồ thị hàm số
y x x
42
1
có bao nhiêu điểm cực trị có tung độ dương?
A. 1. B. 2. C. 3. D. 4.
Câu 34. Cho ham sô
f x x
2
2
3
. Giá trị cực đại của hàm số
f ' x
băng:
A. 8. B. -8. C. 0. D.
.
1
2
Câu 35. Tìm cac điêm cưc tri cua ham sô
y x x
22
2
.
A.
CT
x. 1
B.
CT
x. 0
C.
CD
x.1
D.
CD
x. 2
TRẦN CÔNG DIÊU
[ĐĂNG KÍ HỌC OFF TPHCM – CALL 01638.645.228]
TRUNG TÂM THẦY DIÊU – FB TRẦN CÔNG DIÊU
8
Câu 36. Hàm số
43
y x x
có điểm cực trị
A.
3
0;
4
xx
B.
0x
C.
3
4
x
D.
1x
Câu 37. Cho hàm số
yx
. Tìm mệnh đề đúng trong các mệnh đề sau:
A. Hàm số có một điểm cực đại.
B. Hàm số đã cho không có cực trị.
C. Hàm số đã cho có đạo hàm không xác định tại
0x
nên không đạt cực trị tại
0x
.
D. Hàm số đã cho có đạo hàm không xác định tại
0x
nhưng đạt cực trị tại
0x
.
Câu 38. Hàm số nào sau đây không có cực trị ?
A.
3
3 1.y x x
B.
2
.
3
x
y
x
C.
43
4 3 1.y x x x
D.
2*
2017 ( ).
n
y x x n
Câu 39. Hàm số nào sau đây có ba điểm cực trị?
A.
42
2 10y x x
B.
42
2 3.y x x
C.
32
1
3 5 2.
3
y x x x
D.
4
24yx
.
Câu 40. Cho hàm số
42
21y x x
. Mệnh đề nào dưới đây đúng?
Câu 41. Cho hàm số
()y f x
xác định, liên tục trên
\2
và có bảng biến thiên phía dưới:
A. Hàm số có một cực đại và hai cực tiểu.
B. Hàm số có hai cực đại và một cực tiểu.
C. Hàm số có một cực đại và không có cực tiểu.
D. Hàm số có một cực đại và một cực tiểu.
TRẦN CÔNG DIÊU
[ĐĂNG KÍ HỌC OFF TPHCM – CALL 01638.645.228]
TRUNG TÂM THẦY DIÊU – FB TRẦN CÔNG DIÊU
9
Khẳng định nào sau đây là khẳng định đúng?
A. Hàm số đạt cực đại tại điểm
0x
và đạt cực tiểu tại điểm
4x
.
B. Hàm số có đúng một cực trị.
C. Hàm số có giá trị cực tiểu bằng 1.
D. Hàm số có giá trị lớn nhất bằng 1 và giá trị nhỏ nhất bằng - 15.
Câu 42. Hàm số
()y f x
liên tục trên
và có bảng biến thiên như hình vẽ bên. Mệnh đề nào sau đây
là đúng?
Câu 43. Hàm số
()y f x
có đạo hàm
2
'( ) ( 1) ( 3)f x x x
. Phát biểu nào sau đây là đúng?
A. Hàm số có một điểm cực đại.
B. Hàm số có hai điểm cực trị.
A. Hàm số đã cho có hai điểm cực trị.
B. Hàm số đã cho không có giá trị cực đại.
C. Hàm số đã cho có đúng một điểm cực trị.
D. Hàm số đã cho không có giá trị cực tiểu.
TRẦN CÔNG DIÊU
[ĐĂNG KÍ HỌC OFF TPHCM – CALL 01638.645.228]
TRUNG TÂM THẦY DIÊU – FB TRẦN CÔNG DIÊU
10
C. Hàm số có đúng 1 điểm cực trị.
D. Hàm số không có điểm cực trị.
Câu 44. Số điểm cực đại của đồ thị hàm số
4
100yx
là:
A. 0. B. 1. C. 3. D. 2.
Câu 45. Hàm số
42
2 2017y x x
có bao nhiêu điểm cực trị?
A. 1. B. 2. C. 0. D. 3.
Câu 46. Cho hàm số
32
1
4 8 5
3
y x x x
có hai điểm cực trị là
12
,xx
. Hỏi tổng
12
xx
là bao nhiêu?
A.
12
8.xx
B.
12
8.xx
C.
12
5.xx
D.
12
5.xx
Câu 47. Hàm số
()y f x
có đạo hàm
2
2
'( ) ( 1) ( 3) 2f x x x x
. Phát biểu nào sau đây là đúng?
A. Hàm số có một điểm cực đại.
B. Hàm số có hai điểm cực trị.
C. Hàm số có đúng 1 điểm cực trị.
D. Hàm số không có điểm cực trị.
Câu 48. Đồ thị hàm số
32
31y x x
có điểm cực đại là:
A.
(2; 3)I
. B.
(0;1)I
. C.
(0; 2)I
. D.
(0; 2)I
.
Câu 49. Hàm số
42
2 2017y x x
có bao nhiêu điểm cực trị?
A. 1. B. 2. C. 0. D. 3.
Câu 50. Cho hàm số
32
3 3 1y x x x
. Khẳng định nào sau đây là đúng?
A. Hàm số đạt cực tiểu tại điểm
1x
.
B. Hàm số đồng biến trên
(1; )
và nghịch biến trên
( ;1)
.
C. Hàm số đạt cực đại tại điểm
1x
.
D. Hàm số đồng biến trên
.
TRẦN CÔNG DIÊU
[ĐĂNG KÍ HỌC OFF TPHCM – CALL 01638.645.228]
TRUNG TÂM THẦY DIÊU – FB TRẦN CÔNG DIÊU
11
Câu 51. Cho hàm số
()y f x
có đồ thị như hình vẽ, các khẳng định sau khẳng định nào là đúng?
A. Hàm số đạt giá trị nhỏ nhất bằng – 1 và đạt giá trị lớn nhất bằng 3.
B. Đồ thị hàm số có điểm cực tiểu
( 1; 1)A 
và điểm cực đại
(1;3)B
.
C. Hàm số có giá trị cực đại bằng 1.
D. Hàm số đạt cực tiểu tại
( 1; 1)A 
và cực đại tại
(1;3)B
.
Câu 52. Cho hàm số
()y f x
xác định trên
\ 1;1
, liên tục trên mỗi khoảng xác định và có bảng
biến thiên sau:
Hỏi khẳng định nào dưới đây là khẳng định sai?
A. Hàm số không có đạo hàm tại
0x
nhưng vẫn đạt cực trị tại
0x
.
B. Hàm số đạt cực tiểu tại điểm
1.x
C. Đồ thị hàm số có hai tiệm cận đứng là các đường thẳng
1x 
và
1.x
TRẦN CÔNG DIÊU
[ĐĂNG KÍ HỌC OFF TPHCM – CALL 01638.645.228]
TRUNG TÂM THẦY DIÊU – FB TRẦN CÔNG DIÊU
12
D. Đồ thị hàm số có hai tiệm cận ngang là các đường thẳng
3y 
và
3.y
Câu 53. Khẳng định nào sau đây là khẳng định đúng?
A. Hàm số
1
2
1
yx
x

có hai điểm cực trị.
B. Hàm số
3
3 2016 2017y x x
có hai điểm cực trị.
C. Hàm số
21
1
x
y
x
có một điểm cực trị.
D. Hàm số
42
32y x x
có một điểm cực trị.
Câu 54. Số điểm cực trị của hàm số
3
2
43y x x
bằng:
A. 2. B. 0. C. 3. D. 4.
Câu 55. Hàm số
42
1y x x
đạt cực tiểu tại:
A.
1x 
B.
0.x
C.
2x 
D.
1.x
Câu 56. Cho hàm số
()y f x
xác định, liên tục trên
và có bảng biến thiên:
Khẳng định nào sau đây là khẳng định đúng?
A. Hàm số có đúng hai cực trị.
B. Hàm số có giá trị cực tiểu bằng – 1 hoặc 1.
C. Hàm số có giá trị lớn nhất bằng 0 và giá trị nhỏ nhất bằng – 3.
D. Hàm số đạt cực đại tại
0.x
Câu 57. Hàm số
32
31y x x
đạt cực trị đại tại các điểm nào sau đây?
TRẦN CÔNG DIÊU
[ĐĂNG KÍ HỌC OFF TPHCM – CALL 01638.645.228]
TRUNG TÂM THẦY DIÊU – FB TRẦN CÔNG DIÊU
13
A.
2x 
B.
1x 
C.
0; 2.xx
D.
0; 1.xx
Câu 58. Hệ thức liên hệ giữa giá trị cực đại
CĐ
y
và giá trị cực tiểu
CT
y
của hàm số
3
2y x x
là:
A.
0.
CCT Đ
yy
B.
2 3 .
CT CĐ
yy
C.
2.
CT CĐ
yy
D.
.
CCT Đ
yy
Câu 59. Cho hàm số
()y f x
xác định, liên tục trên
và có bảng biến thiên:
Khẳng định nào sau đây là sai?
A.
(0; 2)M
được gọi là điểm cực đại của hàm số.
B.
( 1)f
được gọi là giá trị cực tiểu của hàm số.
C. Hàm số đồng biến trên các khoảng
( 1;0)
và
(1; )
.
D.
0
1x
được gọi là điểm cực tiểu của hàm số.
Câu 60. Tính khoảng cách giữa các điểm cực tiểu của đồ thị hàm số
42
2 3 1.y x x
A.
4
2 3.
B.
3.
C.
2 3.
D.
4
3.
Câu 61. Tìm tất cả các điểm cực đại của hàm số
42
21y x x
.
A.
1x 
B.
1.x 
C.
1.x
D.
0x
.
Câu 62. Cho hàm số
()y f x
liên tục trên
và có bảng biến thiên như hình vẽ. Mệnh đề nào sau đây
là đúng?
TRẦN CÔNG DIÊU
[ĐĂNG KÍ HỌC OFF TPHCM – CALL 01638.645.228]
TRUNG TÂM THẦY DIÊU – FB TRẦN CÔNG DIÊU
14
A. Hàm số đã cho có hai điểm cực trị.
B. Hàm số đã cho không có giá trị cực đại.
C. Hàm số đã cho có đúng một điểm cực trị.
D. Hàm số đã cho không có giá trị cực tiểu.
Câu 63. Cho hàm số
4 3 2
2
3
y x x x
. Mệnh đề nào sau đây là đúng?
A. Hàm số có giá trị cực tiểu là 0.
B. Hàm số có hai giá trị cực tiểu là
2
3
và
5
.
48
C. Hàm số chỉ có một giá trị cực tiểu.
D. Hàm số có giá trị cực tiểu là
2
3
và giá trị cực đại là
5
.
48
Câu 64. Cho hàm số
2
( 1)( 2)y x x
. Trung điểm của đoạn thẳng nối hai điểm cực trị của đồ thị
hàm số nằm trên đường thẳng nào dưới đây?
A.
2 4 0.xy
B.
2 4 0.xy
C.
2 4 0.xy
D.
2 4 0.xy
Câu 65. Cho hàm số
f
có đạo hàm là
23
'( ) ( 1) ( 2)f x x x x
với mọi
x
. Số điểm cực trị của hàm
số
f
là
A. 0. B. 1. C. 2. D. 3.
Câu 66. Cho hàm số
()y f x
liên tục trên
và có bảng biến thiên như sau:
TRẦN CÔNG DIÊU
[ĐĂNG KÍ HỌC OFF TPHCM – CALL 01638.645.228]
TRUNG TÂM THẦY DIÊU – FB TRẦN CÔNG DIÊU
15
Khẳng định nào sau đây là khẳng định sai?
A. Hàm số đồng biến trên khoảng
(0; ).
B. Hàm số đạt cực tiểu tại
0.x
C. Hàm số đạt cực tiểu tại
2.x 
D. Hàm số nghịch biến trên khoảng
( 2;0)
.
Câu 67. Cho hàm số
()y f x
có đạo hàm
2
'( ) ( 1) ( 2)f x x x
xác định trên
. Mệnh đề nào sau đây
là mệnh đề đúng?
A. Hàm số
()y f x
đồng biến trên khoảng
( 2; ). 
B. Hàm số
()y f x
đạt cực đại tại
2.x 
C. Hàm số
()y f x
đạt cực tiểu tại
1.x
D. Hàm số
()y f x
nghịch biến trên khoảng
( 2;1)
.
Câu 68. Kết luận nào sau đây về cực trị của hàm số
5
x
yx
là đúng?
A. Hàm số có điểm cực đại là
1
.
ln 5
x
B. Hàm số không có cực trị.
C. Hàm số có điểm cực tiểu là
1
.
ln 5
x
D. Hàm số có điểm cực đại là
ln5x
.
Câu 69. Điêm cưc tri cua ham sô
y sin x x2
là:
TRẦN CÔNG DIÊU
[ĐĂNG KÍ HỌC OFF TPHCM – CALL 01638.645.228]
TRUNG TÂM THẦY DIÊU – FB TRẦN CÔNG DIÊU
16
A.
CD
x k k .
2
6
B.
CT
x k k .
3
C.
CD CT
x k ,x k k .


66
D.
CD
x k k .
3
Câu 70. Giá trị cực đại của hàm số
y x cos x2
trên khoang
;
0
là:
A.
.
5
3
6
B.
.
5
3
6
C.
.
3
6
D.
.
3
6
Câu 71. Cho ham sô
y sinx cosx3
. Khăng đinh nao sau đây sai:
A.
x
5
6
là một nghiệm của phương trình.
B. Trên khoang
;
0
hàm số có duy nhất một cực trị.
C. Hàm số đạt cực tiểu tại
x
5
6
.
Câu 1. Cho hàm số
32
21y x mx x
với
m
là tham số. Khẳng định nào sau đây là đúng?
A. Với mọi tham số
m
, hàm số đã cho luôn chỉ có duy nhất một cực đại.
B. Với mọi tham số
m
, hàm số đã cho luôn chỉ có duy nhất một cực tiểu.
C. Với mọi tham số
m
, hàm số đã cho luôn có một điểm cực đại và một điểm cực tiểu.
D. Với mọi tham số
m
, hàm số đã cho không có cực trị.
Câu 2. Cho hàm số
32
3 3(1 ) 1 3y x x m x m
, tìm
m
sao cho đồ thị hàm số có điểm cực đại, cực
tiểu, đồng thời tìm đường thẳng đi qua hai điểm cực trị của đồ thị hàm số đã cho.
A.
0 ; :2 2 2 0m mx y m
. B.
0 ; :2 2 2 0m mx y m
.
D.
y y'' 0,x.
Phần 2. Các bài toán cực trị chứa tham số
Như vậy chúng ta vừa tìm hiểu các bài toán cực trị không chứa tham số, sau đây chúng ta cùng đi vào các bài
toán cực trị chứa tham số, loại toán này đòi hỏi chúng ta phải vững lí thuyết và có tư duy tối hơn. Xin nhắc
rằng nếu loại không chứa tham số chưa thành thạo thì đừng nên tiếp cận ngay dạng toán này.
TRẦN CÔNG DIÊU
[ĐĂNG KÍ HỌC OFF TPHCM – CALL 01638.645.228]
TRUNG TÂM THẦY DIÊU – FB TRẦN CÔNG DIÊU
17
C.
0 ; : 202 200m y x
. D.
0 ; : 202 200m y x
.
Câu 3. Với giá trị nào của
m
thì hàm số
3 2 2
(4 3) 1y x m x m x
đạt cực đại tại
1x
?
A.
1m
và
3m 
. B.
1m
.
C.
3m 
. D.
1m 
.
Câu 4. Tìm tất cả các giá trị thực của tham số
m
sao cho hàm số
32
3 3 1y x mx m
có 2 điểm cực
trị.
A.
0.m
B.
0.m
C.
0.m
D.
0m
.
Câu 5. Cho hàm số
42
( 0)y ax bx c a
. Trong điều kiện nào sau đây thì hàm số có ba cực trị:
A.
,ab
cùng dấu và
c
bất kì. B.
,ab
trái dấu và
c
bất kì.
C.
0b
và
,ac
bất kì. D.
0c
và
,ab
bất kì.
Câu 6. Cho hàm số
42
1 ( 0)y ax bx a
. Để hàm số có một cực tiểu và hai cực đại thì
,ab
cần thỏa
mãn:
A.
0, 0.ab
B.
0, 0.ab
C.
0, 0.ab
D.
0, 0.ab
Câu 7. Tìm giá trị thực của tham số
m
để đường thẳng
2 1 3d : y ( m )x m
vuông góc với đường
thẳng đi qua hai điểm cực trị của đồ thị hàm số
32
31y x x
A.
3
2
m
. B.
3
4
m
. C.
1
2
m 
. D.
1
4
m
.
Trích Đề Thi THPT Quốc Gia 2017
Câu 8. Tìm tất cả các giá trị thực của tham số
m
sao cho hàm số
32
31y x x mx
có hai điểm cực
trị
12
,xx
thỏa mãn
22
12
3xx
.
A. – 3. B. 3. C.
3
.
2
D.
3
.
2
Câu 9. Tìm
m
để hàm số:
3 2 2
1
( 1) 1
3
y x mx m m x
đạt cực trị tại 2 điểm
12
,xx
thỏa mãn
12
4xx
.
TRẦN CÔNG DIÊU
[ĐĂNG KÍ HỌC OFF TPHCM – CALL 01638.645.228]
TRUNG TÂM THẦY DIÊU – FB TRẦN CÔNG DIÊU
18
A.
2m 
. B.
2.m 
C. Không tồn tại
m
. D.
2.m
Câu 10. Tìm tất cả các giá trị thực của tham số
m
sao cho hàm số
32
( 1) 3 1y x m x mx
đạt cực trị
tại điểm
0
1.x
A.
1.m 
B.
1.m
C.
2.m
D.
2.m 
Câu 11. Tìm tất cả các giá trị thực của tham số
m
sao cho hàm số
4 2 2
2y x mx m m
có đúng một
điểm cực trị.
A.
0m
. B.
0m
. C.
0m
. D.
0.m
Câu 12. Tìm tất cả các giá trị thực của tham số
m
để hàm số
32
4 12y x mx x
đạt cực tiểu tại điểm
2.x 
A.
9.m 
B.
2.m
C. Không tồn tại
m
. D.
9.m
Câu 13. Tìm tất cả các giá trị thực của tham số
m
sao cho hàm số
4 2 2
( 2) 2y mx m x
có hai cực
tiểu và một cực đại.
A.
2 0 2mm
. B.
20m
.
C.
2m
. D.
02m
.
Câu 14. Tìm tất cả các giá trị thực của tham số
m
sao cho đồ thị hàm số
42
22y x mx m
có ba điểm
cực trị tạo thành tam giác có diện tích bằng 1.
A.
5
1
.
4
m
B.
3.m
C.
1.m 
D.
1.m
Câu 15. Tìm tất cả các giá trị thực của tham số
m
sao cho đồ thị hàm số
4 2 4
22y x mx m m
có ba
điểm cực trị tạo thành một tam giác đều.
A.
3
3.m
B.
3
1 3.m 
C.
3
1 3.m 
D.
3
3.m 
Câu 16. Tìm
m
để đồ thị hàm số
42
2( 1) 2 5y x m x m
có ba điểm cực trị lập thành tam giác
đều?
A.
1m
. B.
3
1 3.m 
C.
3
1 3.m 
D.
13m 
.
Câu 17. Cho hàm số
4 2 2
22y x mx m
. Tìm
m
để hàm số có 3 điểm cực trị và các điểm cực trị của
đồ thị hàm số là ba đỉnh của một tam giác vuông cân?
TRẦN CÔNG DIÊU
[ĐĂNG KÍ HỌC OFF TPHCM – CALL 01638.645.228]
TRUNG TÂM THẦY DIÊU – FB TRẦN CÔNG DIÊU
19
A.
1.m
B.
1m 
C.
2.m
D.
2.m 
Câu 18. Cho hàm số
4 2 4
22y x mx m m
. Với giá trị nào của
m
thì đồ thị
m
C
có 3 điểm cực trị,
đồng thời 3 điểm cực trị đó tạo thành một tam giác có diện tích bằng 2.
A.
5
4.m
B.
16.m
C.
5
16.m
D.
3
16.m 
Câu 19. Đường thẳng đi qua điểm cực đại, cực tiểu của đồ thị hàm số
3
32y x mx
cắt đường tròn
tâm
(1;1)I
, bán kính bằng 1 tại 2 điểm phân biệt
,AB
sao cho diện tích tam giác
IAB
đạt giá trị lớn
nhất khi
m
có giá trị là:
A.
23
.
2
m
B.
13
.
2
m
C.
25
.
2
m
D.
23
.
3
m
Câu 20. Cho hàm số
3 2 2
2 (2 1) ( 1) 2y x m x m x
. Hỏi có tất cả bao nhiêu giá trị nguyên của
tham số
m
để hàm số đã cho có hai điểm cực trị.
A. 4. B. 5. C. 3. D. 6.
Câu 21. Tìm tất cả các giá trị thực của tham số
m
để hàm số
32
(2 1) 4y x x m x
có đúng hai cực
trị.
A.
4
.
3
m
B.
2
.
3
m 
C.
2
.
3
m 
D.
4
.
3
m 
Câu 22. Tìm tất cả các giá trị của tham số
m
để hàm số
32
11
( 5)
32
y x m x mx
có cực đại, cực tiểu
và
5.
CCĐ T
xx
A.
0.m
B.
6.m 
C.
6;0m
. D.
6;0m
.
Câu 23. Biết đồ thị hàm số
32
y ax bx cx d
có 2 điểm cực trị là
( 1;18)
và
(3; 16)
. Tính
.a b c d
A. 0. B. 1. C. 2. D. 3.
Câu 24. Cho hàm số
2
( ) ln( )f x x x m
. Tìm tất cả các giá trị thực của tham số
m
để hàm số đã cho
có đúng hai điểm cực trị.
A.
2.m
B.
9
.
4
m
C.
2.m 
D.
2.m
TRẦN CÔNG DIÊU
[ĐĂNG KÍ HỌC OFF TPHCM – CALL 01638.645.228]
TRUNG TÂM THẦY DIÊU – FB TRẦN CÔNG DIÊU
20
Câu 25. Cho đồ thị hàm số
32
()y f x ax bx c
có hai điểm cực trị là
(0;1)A
và
( 1;2)B
. Tính giá trị
của
.a b c
A. 0. B. 2. C. 4. D. 6.
Câu 26. Tìm tất cả các giá trị thực của tham số
m
để hàm số
32
(1 ) 3 3 5y m x x x
có cực trị?
A.
1.m
B.
1.m 
C.
01m
D.
0.m
Câu 27. Cho hàm số
32
1
(2 1) 1
3
y x mx m x
. Tìm mệnh đề sai.
A.
1m
thì hàm số có hai điểm cực trị.
B. Hàm số luôn có cực đại và cực tiểu.
C.
1m
thì hàm số có cực đại và cực tiểu.
D.
1m
thì hàm số có cực trị.
Câu 28. Tìm
m
để hàm số
4 2 2
( 9) 1y mx m x
có hai điểm cực đại và một điểm cực tiểu.
A.
3 0.m
B.
0 3.m
C.
3.m 
D.
3.m
Câu 29. Hàm số
32
36y x mx mx m
có hai điểm cực trị khi
m
thỏa mãn điều kiện:
A.
0 2.m
B.
0
8
m
m
.
C.
0
2
m
m
. D.
0 8.m
Câu 30. Hàm số
32
2017
3
m
y x x x
có cực trị khi và chỉ khi:
A.
1.m
B.
1
0
m
m
C.
1
0
m
m
D.
1.m
Câu 31. Với điều kiện nào của
a
và
b
để hàm số
3 3 3
( ) ( )y x a x b x
đạt cực đại và cực tiểu?
A.
0.ab
B.
0.ab
C.
0.ab
D.
0.ab
Câu 32. Hàm số
32
( 3) 2 3y m x mx
không có cực trị khi:
A.
3.m
B.
0m
hoặc
3.m
C.
0m
. D.
3.m
TRẦN CÔNG DIÊU
[ĐĂNG KÍ HỌC OFF TPHCM – CALL 01638.645.228]
TRUNG TÂM THẦY DIÊU – FB TRẦN CÔNG DIÊU
21
Câu 33. Tìm tất cả các giá trị của
m
để hàm số
3 2 2
11
(3 2) (2 3 1) 4
32
y x m x m m x
đạt cực đại tại
3x
hoặc
5x
, ta được
A.
0m
B.
1.m
C.
2.m
D.
3.m
Câu 34. Cho hàm số
32
y ax bx cx d
. Nếu đồ thị hàm số có hai điểm cực trị là gốc tọa độ
O
và
điểm
(2; 4)A
thì phương trình của hàm số là:
A.
32
3.y x x
B.
3
3.y x x
C.
3
3.y x x
D.
32
3.y x x
Câu 35. Tìm tất cả các giá trị của tham số
m
để hàm số
32
( ) 2 3f x x x m
có các giá trị cực trị trái
dấu:
A. – 1 và 0. B.
( ;0) ( 1; ). 
C.
( 1;0).
D.
[0;1].
Câu 36. Cho hàm số
3 2 3
2 3( 1) 6y x m x mx m
. Tìm
m
để đồ thị hàm số có hai điểm cực trị
,AB
sao cho độ dài
2.AB
A.
0m
. B.
0m
hoặc
2m
. C.
1.m
D.
2m
.
Câu 37. Hàm số
3
22
( 1) ( 3) 1
3
x
y m x m x
đạt cực trị tại
1x 
thì
m
bằng:
A.
0m
. B.
2.m 
C.
2.
0.
m
m

D.
2.
0.
m
m
Câu 38. Biết hàm số
32
33y x mx mx
có một điểm cực trị
1x 
. Khi đó, hàm số đạt cực trị tại
điểm khác có hoành độ là:
A.
1
.
4
B.
1
.
3
C.
1
.
3
D.
1
.
2
.
Câu 39. Nếu
1x 
là điểm cực tiểu của hàm số
3 2 2
1
( 4) 5
3
y x mx m x
thì tập tất cả các giá trị
của
m
có thể nhận được là:
A. 1. B. – 3. C. 1 hoặc – 3. D.
[ 3;1].
Câu 40. Hàm số
32
1y ax ax
có điểm cực tiểu
2
3
x
khi điều kiện của
a
:
A.
0.a
B.
0.a
C.
2.a
D.
0.a
TRẦN CÔNG DIÊU
[ĐĂNG KÍ HỌC OFF TPHCM – CALL 01638.645.228]
TRUNG TÂM THẦY DIÊU – FB TRẦN CÔNG DIÊU
22
Câu 41. Gọi
12
,xx
là 2 điểm cực trị của hàm số
3 2 2 3
3 3( 1)y x mx m x m m
. Giá trị của
m
để
22
1 2 1 2
7x x x x
là:
A.
0.m
B.
9
.
2
m 
C.
1
.
2
m 
D.
2.m 
Câu 42. Giá trị của
m
để hàm số
32
43y x mx x
có hai điểm cực trị
12
,xx
thỏa mãn
12
40xx
là:
A.
9
.
2
m 
B.
3
.
2
m 
C.
0.m
D.
1
.
2
m 
Câu 43. Đường thẳng đi qua hai điểm cực trị của đồ thị hàm số
32
39y x x x m
có phương trình:
A.
8.y x m
B.
8 3.y x m
C.
8 3.y x m
D.
8 3.y x m
Câu 44. Nếu
1x
là hoành độ trung điểm của đoạn thẳng nối 2 điểm cực đại, cực tiểu của đồ thị hàm
số
32
1
( 2) (2 3) 2017
3
y x m x m x
thì tập tất cả các giá trị của
m
là:
A.
1.m 
B.
1.m 
C.
3
.
2
m 
D. Không có giá trị
m
.
Câu 45. Giá trị của
m
để khoảng cách từ điểm
(0;3)M
đến đường thẳng đi qua hai điểm cực trị của
đồ thị hàm số
3
31y x mx
bằng
2
5
là:
A.
1
1
m
m

. B.
1.m 
C.
1
3
m
m

. D. Không có giá trị
m
.
Câu 46. Cho hàm số
32
2 3( 1) 6( 2) 1y x m x m x
. Xác định
m
để hàm số có điểm cực đại và điểm
cực tiểu nằm trong khoảng
( 2;3)
.
A.
( 1;3) (3;4).m
B.
(1;3)m
.
C.
(3;4)m
. D.
( 1;4)m
.
Câu 47. Để hàm số
32
6 3( 2) 6y x x m x m
có cực đại, cực tiểu tại
12
,xx
sao cho
12
1xx
thì
giá trị của
m
là:
A.
1.m
B.
1.m
C.
1.m 
D.
1.m 
Câu 48. Tìm tất cả các giá trị của tham số
m
để hàm số
32
1
( 2)
3
y x mx m x
có 2 điểm cực trị nằm
trong khoảng
(0; )
?
TRẦN CÔNG DIÊU
[ĐĂNG KÍ HỌC OFF TPHCM – CALL 01638.645.228]
TRUNG TÂM THẦY DIÊU – FB TRẦN CÔNG DIÊU
23
A.
2.m
B.
2.m
C.
2.m
D.
0 2.m
Câu 49. Với các giá trị nào của
m
thì hàm số
32
3 3 1y x x mx
có các điểm cực trị nhỏ hơn 2?
A.
0.m
B.
1.m
C.
0
1
m
m
D.
0 1.m
Câu 50. Cho hàm số
32
2 3(2 1) 6 ( 1) 2y x a x a a x
. Nếu gọi
12
,xx
lần lượt là hoành độ các điểm
cực trị của đồ thị hàm số thì giá trị
21
xx
bằng:
A.
1.a
B.
.a
C.
1.a
D.
1.
Câu 51. Cho hàm số
32
2 12 13y x mx x
. Với giá trị nào của
m
thì đồ thị có điểm cực đại, cực tiểu
cách đều trục tung?
A. 2. B. – 1. C. 1. D. 0.
Câu 52. Đồ thị hàm số
32
3 3 1y x mx m
có hai điểm cực đại, cực tiểu đối xứng với nhau qua
đường thẳng
: 8 74 0d x y
thì tập tất cả các giá trị của
m
:
A.
1.m
B.
2.m 
C.
1.m 
D.
2.m
Câu 53. Cho hàm số
32
14
( 1) (2 1)
33
y x m x m x
. Tìm tất cả các giá trị của tham số
0m
để đồ
thị hàm số cố điểm cực đại thuộc trục hoành?
A.
1
.
2
m
B.
1.m
C.
3
.
4
m
D.
4
.
3
m
Câu 54. Cho hàm số
32
32y x x mx m
với
m
là tham số, có đồ thị là
()
m
C
. Xác định
m
để
()
m
C
có các điểm cực đại và cực tiểu nằm về hai phía đối với trục hoành?
A.
2.m
B.
3.m
C.
3.m
D.
2.m
Câu 55. Cho hàm số
32
1
(2 1) 3
3
y x mx m x
với
m
là tham số, có đồ thị là
()
m
C
. Xác định
m
để
()
m
C
có các điểm cực đại và cực tiểu nằm về hai phía đối với trục tung?
A.
1
.
2
m
B.
1.m
C.
1
2
1
m
m
. D.
1
2
1
m
m
.
Câu 56. Hàm số
32
y ax bx cx d
đạt cực trị tại
12
,xx
nằm hai phía trục tung khi và chỉ khi:
TRẦN CÔNG DIÊU
[ĐĂNG KÍ HỌC OFF TPHCM – CALL 01638.645.228]
TRUNG TÂM THẦY DIÊU – FB TRẦN CÔNG DIÊU
24
A.
0, 0, 0.a b c
B.
a
và
c
trái dấu. C.
2
12 0.b ac
D.
2
12 0.b ac
Câu 57. Cho hàm số
3 2 2
3 4 2y x mx m
. Tìm
m
để đồ thị hàm số có hai điểm cực trị
,AB
sao cho
(1;0)I
là trung điểm của
AB
.
A.
0.m
B.
1.m 
C.
1.m
D.
2.m
Câu 58. Với giá trị nào của tham số
m
thì đồ thị hàm số
32
32y x mx
có hai điểm cực trị
,AB
sao
cho
,AB
và
(1; 2)M
thẳng hàng.
A.
0.m
B.
2.m
C.
2.m 
D.
2.m 
Câu 59. Với giá trị nào của tham số
m
thì đồ thị hàm số
32
31y x mx
có hai điểm cực trị
,AB
sao
cho tam giác
OAB
vuông tại
O
, với
O
là gốc tọa độ?
A.
1.m 
B.
0.m
C.
1
.
2
m
D.
0.m
Câu 60. Hàm số
y x mx mx m
32
36
có hai điêm cưc tri khi
m
thoả
A.
m.02
B.
m
.
m

0
8
C.
m
.
m

0
2
D.
m.08
Câu 61. Hàm số
m
y x x x
32
2017
3
có cực trị khi và chỉ khi
A.
m. 1
B.
m
m

1
0
. C.
m
m

1
0
. D.
m. 1
Câu 62. Vơi điêu kiên nao cua
a,b
để hàm số
y x a x b x
33
3
đat cưc đai va cưc tiêu
A.
ab . 0
B.
ab . 0
C.
ab . 0
D.
ab . 0
Câu 63. Hàm số
y m x mx
32
3 2 3
không co cưc tri khi:
A.
m. 3
B.
m 0
hoăc
m. 3
C.
m 0
. D.
m. 3
Câu 64. Tìm tất cả các giá trị của
m
để hàm sô
y x m x m m x
3 2 2
11
3 2 2 3 1 4
32
đat cưc tri tai
x 3
hoăc
x 5
ta đươc:
A.
m. 0
B.
m. 1
C.
m. 2
D.
m. 3
TRẦN CÔNG DIÊU
[ĐĂNG KÍ HỌC OFF TPHCM – CALL 01638.645.228]
TRUNG TÂM THẦY DIÊU – FB TRẦN CÔNG DIÊU
25
Câu 65. Cho ham sô
y ax bx cx d
32
. Nêu đô thị hàm số có hai điểm cực rị là gốc toạ độ
O
và
điêm
A;24
thì phương trình của hàm số là:
A.
y x x .
32
3
B.
y x x.
3
3
C.
y x x.
3
3
D.
y x x .
32
3
Câu 66. Tìm tất cả các giá trị của tham số
m
để hàm số
f x x x m
32
23
có các giá trị cực trị trái
dâu.
A. -1 và 0. B.
; ; . 01
C.
;10
. D.
;

01
.
Câu 67. Cho ham sô
y x m x mx m
3 2 3
2 3 1 6
. Tìm
m
để đồ thị hàm số có hai điểm cực trị
A,B
sao cho đô dai
AB 2
.
A.
m. 0
B.
m 0
hoăc
m 2
. C.
m. 1
D.
m 2
.
Câu 68. Hàm số
x
y m x m x
3
22
1 3 1
3
đat cưc tri tai
x 1
thì
m
băng
A.
m. 0
B.
m.2
C.
m
.
m


0
2
D.
m
.
m

0
2
Câu 69. Biêt ham sô
y x mx mx
32
33
có một điểm cực trị tại
x 1
. Khi đo ham sô đat cưc tri tai
điêm khac co hoanh đô la:
A.
.
1
4
B.
.
1
3
C.
.
1
3
D.
1
2
.
.
Câu 70. Nêu
x 1
là đivểm cực tiểu của hàm số
y x mx m x
3 2 2
1
45
3
thì tập tất cả các trị của
m
có thể nhận được là:
A. 1. B. -3. C. 1 hoăc -3. D.
;

31
.
Câu 71. Hàm số
y ax ax
32
1
có điểm cực tiểu
x
2
3
khi điêu kiên cua
a
:
A.
a. 0
B.
a. 0
C.
a. 2
D.
a. 0
Câu 72. Gọi
x ,x
12
là hai điể cực trị của hàm số
y x mx m m m
3 2 2 3
3 3 1
. Giá trị
m
để
x x x x
22
1 2 1 2
7
là:
TRẦN CÔNG DIÊU
[ĐĂNG KÍ HỌC OFF TPHCM – CALL 01638.645.228]
TRUNG TÂM THẦY DIÊU – FB TRẦN CÔNG DIÊU
26
A.
m. 0
B.
m.
9
2
C.
m.
1
2
D.
m.2
Câu 73. Giá trị
m
để hàm số
y x mx x
32
43
có hai điểm cực trị thoả
xx
12
40
là:
A.
m.
9
2
B.
m.
3
2
C.
m. 0
D.
m.
1
2
Câu 74. Đường thẳng đi qua hai điểm cực trị của đồ thị hàm số
y x x x m
32
39
có phương trình
A.
y x m. 8
B.
y x m . 83
C.
y x m . 83
D.
y x m . 83
Câu 75. Nêu
x 1
là hoành độ t rung điêm cua đoan thăng nôi hai điêm cưc đai , cưc tiêu cua đô thi
hàm số
y x m x m x
32
1
2 2 3 2017
3
thì tập tất cả các trị của
m
là:
A.
m.1
B.
m.1
C.
m.
3
2
D. Không co gia tri
m
.
Câu 78. Giá trị
m
để khoảng cách từ điểm
M;03
đến đường thẳng đi qua hai điểm cực trị của đồ
thị hàm số
y x mx
3
31
băng
2
5
là:
A.
m
.
m


1
1
B.
m 1
. C.
m
.
m
1
3
D. Không co gia tri
m
.
Câu 79. Cho ham sô
y x m x m x
32
2 3 1 6 2 1
. Xác định
m
để hà số có điểm cực đại và điểm
cưc tiêu năm trong khoang
;23
A.
m ; ; . 1 3 3 4
B.
m;13
.
C.
m; 34
. D.
m;14
.
Câu 80. Đê ham sô
y x x m x m
32
6 3 2 6
có cực đại, cưc tiêu tai
x ,x
12
sao cho
xx
12
1
thì
giá trị của
m
là:
A.
m. 1
B.
m. 1
C.
m.1
D.
m.1
Câu 81. Tìm tất cả các giá
y x mx m x
32
1
2
3
trị của tham số
m
để hàm số có hai điểm cực trị
năm trong khoang
;0
?
TRẦN CÔNG DIÊU
[ĐĂNG KÍ HỌC OFF TPHCM – CALL 01638.645.228]
TRUNG TÂM THẦY DIÊU – FB TRẦN CÔNG DIÊU
27
A.
m. 2
B.
m. 2
C.
m. 2
D.
m.02
Câu 82. Vơi cac gia tri nao cua
m
thì hàm số
y x x mx
32
3 3 1
có các điểm cực trị nhỏ hơn 2?
A.
m. 0
B.
m. 1
C.
m
.
m

0
1
D.
m.01
Câu 83. Cho ham sô
y x a x a a x
32
2 3 2 1 6 1 2
. Nêu goi
x ,x
12
lân lươt la hoanh đô cac điêm
cưc tri cua đô thi ham sô thi gia tri
xx
21
băng
A.
a.1
B.
a.
C.
a.1
D. 1.
Câu 84. Cho ham sô
y x mx x .
32
2 12 13
Vơi gia tri nao cua
m
thì đồ thị hàm số có điểm cực đại ,
cưc tiêu cac đêu truc tung?
A. 2. B. -1. C. 1. D. 0.
Câu 85. Đồ thị hàm số
y x mx m
32
3 3 1
có hai điểm cực đại, cưc tiêu đôi xưng nhau qua đương
thăng
d : x y 8 74 0
thì tập tất cả các giá trị của
m
là:
A. 1. B. -2. C. -1. D. 2.
Câu 86. Đồ thị hàm số
y x m x m x
32
14
1 2 1
33
. Tìm tập tất cả các giá trị của
m 0
để đồ
thị hàm số có điểm cực đại thuộc trục hoành?
A.
m.
1
2
B.
m. 1
C.
m.
3
4
D.
m.
4
3
Câu 87. Cho ham sô
y x x mx m
32
32
vơi
m
là tham số, có đồ thị là
m
C
. Xác định
m
để
m
C
có các điểm cực đại và cực tiểu nằm về hai phía đối với trục hoành?
A.
m. 2
B.
m. 3
C.
m. 3
D.
m. 2
Câu 88. Cho ham sô
y x mx m x
32
1
2 1 3
3
vơi
m
là tham số, có đồ thị là
m
C
. Xác định
m
để
m
C
có các điểm cực đại và cực tiểu nằm về cùng phía đối với trục tung?
A.
m.
1
2
B.
m. 1
C.
m
.
m
1
2
1
D.
m
.
m

1
1
2
TRẦN CÔNG DIÊU
[ĐĂNG KÍ HỌC OFF TPHCM – CALL 01638.645.228]
TRUNG TÂM THẦY DIÊU – FB TRẦN CÔNG DIÊU
28
Câu 89. Hàm số
y ax bx cx d
32
đat cưc tri tai
x ,x
12
năm hai phia truc tung khi va chi khi:
A.
a ,b ,c . 0 0 0
B.
a
và
c
trái dấu.
C.
b ac .
2
12 0
D.
b ac .
2
12 0
Câu 90. Cho ham sô
y x mx m
3 2 2
3 4 2
. Tìm
m
để đồ thị có hai điêm cưc tri
A,B
sao cho
I;10
là trung điểm của
AB
.
A.
m. 0
B.
m.1
C.
m. 1
D.
m. 2
Câu 91. Vơi gia tri nao cua tham sô
m
thì đồ thị hàm số
y x mx
32
32
có hai điểm cực trị
A,B
sao
cho
A,B
và
M;12
thăng hang.
A.
m. 0
B.
m. 2
C.
m. 2
D.
m. 2
Câu 92. Vơi gia tri nao cua tham sô
m
thì đồ thị hàm số
y x mx
3
31
có hai điểm cưc tri
A,B
sao
cho tam giac
OAB
vuông tai
O
, vơi
O
là gốc toạ độ?
A.
m.1
B.
m. 0
C.
m.
1
2
D.
m. 0
Câu 93. Cho ham sô
y ax bx c a
42
0
. Trong điêu kiên nao sau đây thi ham sô co ba cưc tri:
A.
a,b
cùng dấu và
c
bât ki. B.
a,b
trái dấu và
c
bât ki.
C.
b 0
và
a,c
bât ki. D.
c 0
và
a,b
bât ki.
Câu 94. Cho ham sô
y ax bx a
42
10
. Đê ham sô co môt cưc tiêu va hai cưc đai thi
a,b
cân thoa
mãn:
A.
a ,b .00
B.
a ,b .00
C.
a ,b .00
D.
a ,b .00
Câu 95. Cho ham sô
y ax bx a
42
10
. Đê ham sô co môt cưc tri va la cưc tiêu thi
a,b
cân thoa
mãn:
A.
a ,b .00
B.
a ,b .00
C.
a ,b .00
D.
a ,b .00
Câu 96. Hàm số
y x mx m m
4 2 2
2
có ba cực trị khi:
A.
m. 0
B.
m. 0
C.
m. 0
D.
m. 0
Câu 97. Đồ thị hàm số
y x x ax b
42
3
có điểm cực tiểu
A;22
. Tìm tổng
ab
TRẦN CÔNG DIÊU
[ĐĂNG KÍ HỌC OFF TPHCM – CALL 01638.645.228]
TRUNG TÂM THẦY DIÊU – FB TRẦN CÔNG DIÊU
29
A. -14. B. 14. C. -20. D. 34.
Câu 98. Đồ thị hàm số
y ax bx c
42
có điểm cực đại
A;03
và điêm cực tiểu
B;15
. Khi đo
giá trị của
a,b,c
lân lươt la:
A. -3;-1;-5. B. 2;-4;3. C. 2;4;-3. D. -2;4;-3.
Câu 99. Tìm
m
để đồ thị hàm số
y x m m x m
4 2 2
2 1 1
có một điểm cực đại , hai điêm cưc
tiêu va thoa man khoang cach giưa hai điêm cưc tiêu ngăn nhât.
A.
m.
1
2
B.
m.
1
2
C.
m.
3
2
D.
m.
3
2
Câu 100. Cho ham sô
y x mx
42
24
có đồ thị là
m
C
. Tìm các giá trị của
m
để tất cả các điểm
cưc tri cua
m
C
đều nằm trên các trục toạ độ.
A.
m. 0
B.
m. 2
C.
m. 0
D.
m 0
hoăc
m. 2
Câu 101. Giả trị của tham số
m
băng bao nhiêu đê đô thi ham sô
y x mx
42
21
có ba điểm cực trị
A ; ,B ,C01
thoả
BC 4
?
A.
m.4
B.
m. 2
C.
m. 4
D.
m. 2
Câu 102. Cho ham sô
y x m x m
4 2 2
21
,
m
là tham số thực. Tìm
m
để đồ thị hàm số có ba điểm
cưc tri tao thanh môt tam giac vuông.
A.
m.1
B.
m. 0
C.
m. 1
D.
2m.
.
Câu 103. Tìm
m
để đồ thị hàm số
y x m x m
42
1
3 1 2 1
4
có ba điểm cực trị tạo thành tam giác
có trọng tâm là gốc toạ độ.
A.
m.
2
3
B.
m.
2
3
C.
m.
1
3
D.
m.
1
3
Câu 104. Hàm số
x mx
y
x

2
1
1
có cực đại và cực tiểu thì điều kiện của
m
là:
A.
m. 0
B.
m. 0
C.
m.
D.
m. 0
Câu 105. Hàm số
x mx
y
x

2
1
1
có cực đại tại
x 2
thì giá trị thực của
m
băng:
TRẦN CÔNG DIÊU
[ĐĂNG KÍ HỌC OFF TPHCM – CALL 01638.645.228]
TRUNG TÂM THẦY DIÊU – FB TRẦN CÔNG DIÊU
30
A. -1. B. -3. C. 1. D. 3.
Câu 106. Hàm số
y sin x msinx3
đat cưc đai tai
x
3
khi
m
băng:
A. 5. B. -6. C. 6. D. -5.
Câu 107. Biêt ham sô
y asinx bcos x x x
02
đa cưc tri tai
x ; x

3
. Khi đo tông
ab
băng
A. 3. B.
.
3
1
3
C.
.31
D.
.31
| 1/30
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

TRẦN CÔNG DIÊU [ĐĂNG KÍ HỌC OFF TPHCM – CALL 01638.645.228]
CỰC TRỊ CỦA HÀM SỐ
Phần 1. Các bài toán cực trị không chứa tham số
Đầu tiên chúng ta cùng nghiên cứu các bài tập tìm cực trị của hàm số không chứa tham số, các bài tập
này khá đơn giản. Thường có hai cách để tìm cực trị của hàm số như sau: Cách 1.
 Bước 1: tìm tập xác định của hàm số.
 Bước 2: tính đạo hàm và giải phương trình y'  0 .
 Bước 3: lập bảng biến thiên và quan sát kết luận. Nếu hàm số xác định tại x và đạo hàm đổi dấu 0
từ  sang  thì x là điểm cực tiểu, ngược lại đạo hàm đổi dấu từ  sang  thì x là điểm cực đại. 0 0 Cách 2.
 Bước 1: tìm tập xác định của hàm số.
 Bước 2: tính đạo hàm và giải phương trình y'  0 được các nghiệm x , x , x ,..., x . 1 2 3 n
 Bước 3: kiểm xem nếu y' x   0 thì x điểm cực tiểu với i  1,2,3,..., n , ngược lại nếu y' x i  0 i i
thì x điểm cực đại. i
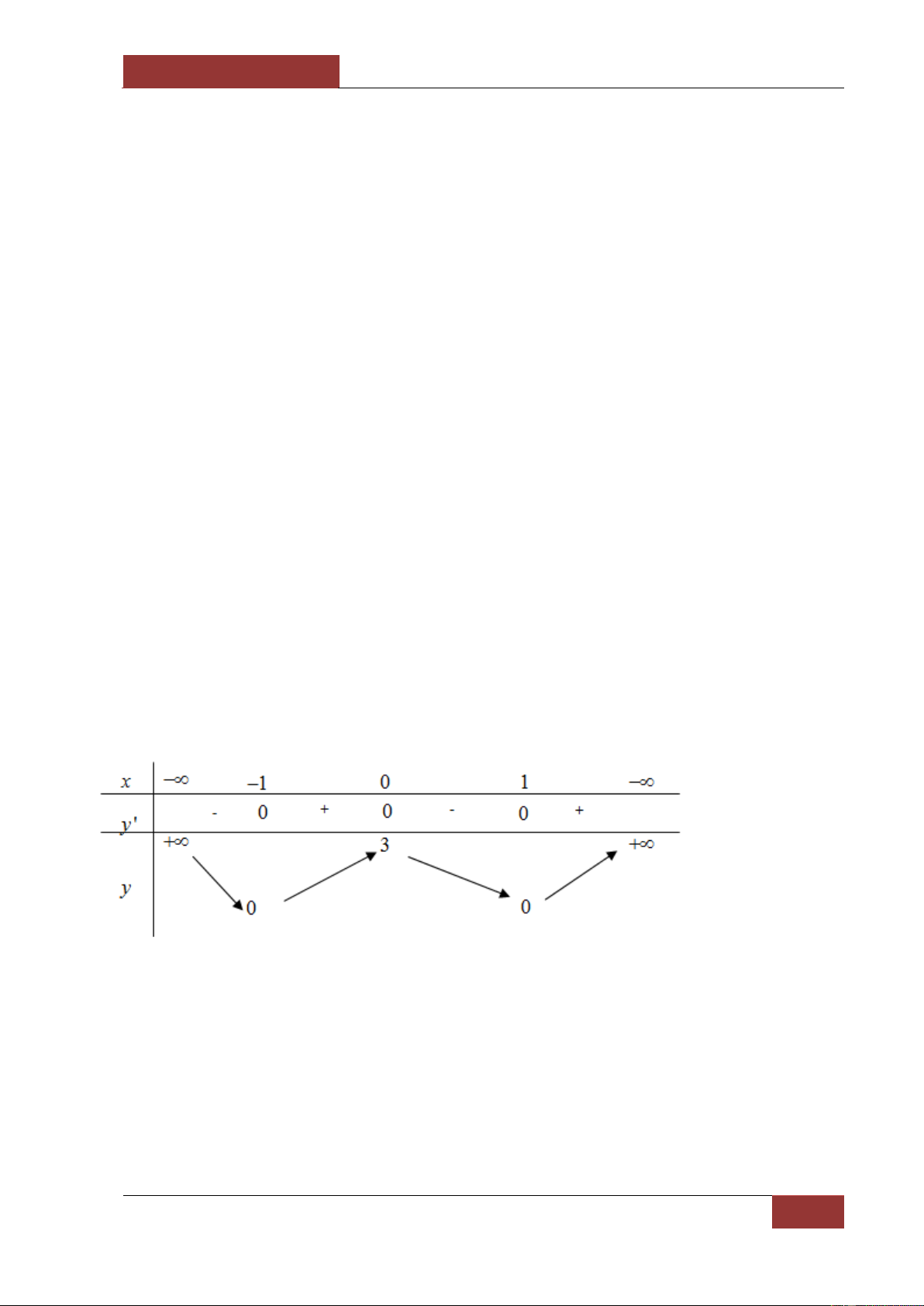
Câu 1. Cho hàm số y f x có bảng biến thiên như sau:
Mệnh đề nào dưới đây sai?
A. Hàm số có giá trị cực đại bằng 0.
B. Hàm số có hai điểm cực tiểu.
C. Hàm số có giá tri cực đại bằng 3.
D. Hàm số có ba điểm cực trị.
Trích Đề Thi THPT Quốc Gia 2017
Câu 2. Phát biểu nào sau đây là đúng?
TRUNG TÂM THẦY DIÊU – FB TRẦN CÔNG DIÊU 1
TRẦN CÔNG DIÊU [ĐĂNG KÍ HỌC OFF TPHCM – CALL 01638.645.228]
A. Nếu f '(x) đổi dấu từ dương sang âm khi x qua điểm x và f (x) liên tục tại x thì hàm số 0 0
y f (x) đạt cực đại tại điểm x . 0
B. Hàm số y f (x) đạt cực trị tại x khi và chỉ khi x là nghiệm của đạo hàm. 0 0
C. Nếu f '(x )  0 và f '(x )  0 thì x không phải là cực trị của hàm số y f (x) đã cho. 0 0 0
D. Nếu f '(x )  0 và f '(x )  0 thì hàm số đạt cực đại tại x . 0 0 0
Câu 2. Cho khoảng ( ;
a b) chứa điểm x , hàm số f (x) có đạo hàm trong khoảng ( ;
a b) (có thể từ điểm 0
x ). Tìm mệnh đề đúng trong các mệnh đề sau: 0
A. Nếu f (x) không có đạo hàm tại x thì f (x) không đạt cực trị tại x . 0 0
B. Nếu f '(x)  0 thì f (x) đạt cực trị tại điểm x . 0
C. Nếu f '(x)  0 và f '(x)  0 thì f (x) không đạt cực trị tại điểm x . 0
D. Nếu f '(x)  0 và f '(x)  0 thì f (x) đạt cực trị tại điểm x . 0
Câu 3. Phát biểu nào dưới đây là sai?
A. Nếu tồn tại số h sao cho f (x)  f (x ) với mọi x (x  ; h x  )
h và x x , ta nói rằng hàm số f (x) 0 0 0 0
đạt cực đại tại điểm x . 0
B. Giả sử y f (x) liên tục trên khoảng K  (x  ; h x  )
h và có đạo hàm trên K hoặc trên K \ x , 0 0 0
với h  0 . Khi đó nếu f '(x)  0 trên  x  ; h x
và f '(x)  0 trên khoảng  x ; x h thì x là một điểm 0 0  0 0  0
cực tiểu của hàm số f (x) .
C. x a là hoành độ điểm cực tiểu khi và chỉ khi y '(a)  0; y '(a)  0.
D. Nếu M x ; f (x ) là điểm cực trị của đồ thị hàm số thì y f (x ) được gọi là giá trị cực trị của 0 0  0 0 hàm số.
Câu 4. Cho hàm số f (x) xác định và liên tục trên khoảng ( ;
a b) . Tìm mệnh đề sai?
A. Nếu f (x) đồng biến trên khoảng ( ;
a b) thì hàm số không có cực trị trên khoảng ( ; a b) .
B. Nếu f (x) nghịch biến trên khoảng ( ;
a b) thì hàm số không có cực trị trên khoảng ( ; a b) .
C. Nếu f (x) đạt cực trị tại điểm x (  ; a )
b thì tiếp tuyến của đồ thị hàm số tại điểm M x ; f (x ) 0 0  0
song song hoặc trùng với trục hoành.
TRUNG TÂM THẦY DIÊU – FB TRẦN CÔNG DIÊU 2
TRẦN CÔNG DIÊU [ĐĂNG KÍ HỌC OFF TPHCM – CALL 01638.645.228]
D. Nếu f (x) đạt cực trị tại điểm x (  ; a )
b thì f (x) đồng biến trên ( ;
a x ) và nghịch biến trên (x ; ) b . 0 0 0
Câu 5. Cho khoảng ( ;
a b) chứa m . Hàm số y f (x) xác định và liên tục trên khoảng ( ; a b) . Có các phát biểu sau đây:
(1) m là điểm cực trị của hàm số khi f '( ) m  0 .
(2) f (x)  f ( ) m , x  (  ; a )
b thì x m là điểm cực tiểu của hàm số.
(3) f (x)  f ( ) m , x  (  ; a ) b \  
m thì x m là điểm cực đại của hàm số.
(4) f (x)  M , x  (  ; a )
b thì M được gọi là giá trị nhỏ nhất của hàm số trên khoảng ( ; a b) . Số phát biểu đúng là: A. 0. B. 1. C. 2. D. 3.
Câu 6. Giá trị cực đại y của hàm số 3
y x  3x  2 ? CĐ A. y  4. B. y 1. C. y  0. D. y  1.  CĐ CĐ CĐ CĐ Câu 7. Hàm số 3 2
y x  5x  3x 1 đạt cực trị khi: x  3 x  0 x  0 x  3 A.     1  B. 10 C. 10 D. 1 x   x  x   x   3  3  3  3
Câu 8. Đồ thị của hàm số 3 2
y x  3x có hai điểm cực trị là: A. (0;0) hoặc (1; 2  ). B. (0;0) hoặc (2;4). C. (0;0) hoặc (2; 4  ). D. (0;0) hoặc ( 2  ; 4  ). Câu 9. Hàm số 3
y x  3x 1 đạt cực đại là: A. x  1.  B. x  0. C. x  1. D. x  2. Câu 10. Hàm số 3 2
y x  4x  3x  7 đạt cực tiểu tại x . Kết luận nào sau đây đúng? CT 1 1 A. x  . B. x  3.  C. x   . D. x 1. CT 3 CT CT 3 CT
Câu 11. Hệ thức liên hệ giữa giá trị cực đại y và giá trị cực tiểu y của hàm số 3
y x  3x là: CĐ CT 3 A. y  2y . B. yy . C. yy . D. y  y . CT CĐ CT Đ 2 CĐ CT C CT CĐ
TRUNG TÂM THẦY DIÊU – FB TRẦN CÔNG DIÊU 3
TRẦN CÔNG DIÊU [ĐĂNG KÍ HỌC OFF TPHCM – CALL 01638.645.228] Câu 12. Cho hàm số 3 2
y x  3x  9x  4 . Nếu hàm số đạt cực đại tại x và cực tiểu tại x thì tích của 1 2
y(x ).y(x ) có giá trị bằng: 1 2 A. – 302. B. – 82. C. – 207. D. 25.
Câu 13. Khoảng cách giữa 2 điểm cực đại và cực tiểu của đồ thị hàm số 2
y  (x 1)(x  2) là: A. 2 5. B. 2. C. 4. D. 5 2.
Câu 14. Trong các đường thẳng dưới đây, đường thẳng nào đi qua trung điểm đoạn thẳng nối các
điểm cực trị của đồ thị hàm số 3 2
y x  3x 1? 1 1
A. y  2x  3.
B. y   x  .
C. y  2x  3. D. y  2  x 1. 3 3
Câu 15. Đồ thị hàm số 4 2
y  x  2x  3 có
A. 1 điểm cực đại và không có điểm cực tiểu.
B. 1 điểm cực tiểu và không có điểm cực đại.
C. 1 điểm cực đại và 2 điểm cực tiểu.
D. 1 điểm cực tiểu và 2 điểm cực đại.
Câu 16. Đồ thị hàm số 4 2
y x x 1 có bao nhiêu điểm cực trị có tung độ dương? A. 1. B. 2. C. 3. D. 4. Câu 17. Cho hàm số 2 2
f (x)  (x  3) . Giá trị cực đại của hàm số f '(x) bằng: 1 A. 8. B. 8.  C. 0. D. . 2
Câu 18. Phát biểu nào sau đây đúng?
A. Nếu f ' x đỗi đấu từ dương sang âm khi
x qua điễm x và f x liên tục tại x thì hàm số 0 0
y f x đạt cực đại tại điễm x . 0
B. Hàm số y f x đạt cực trị tại x khi và chĩ khi x là nghiệm của đạo hàm. 0 0
C. Nếu f 'x   0 và f ''x
0 thì x không phãi là cực trị cũa hàm số y f x đâ cho. 0   0 0
D. Nếu f 'x   0 và f ''x
0 thì hàm số đạt cực đại tại x . 0   0 0
TRUNG TÂM THẦY DIÊU – FB TRẦN CÔNG DIÊU 4
TRẦN CÔNG DIÊU [ĐĂNG KÍ HỌC OFF TPHCM – CALL 01638.645.228]
Câu 19. Cho khoãng a;b chứa điễm x , hàm số f x có đạo hàm trong khoảng a;b (có thể trừ 0
điễm x ). Tìm mệnh đề đúng trong các mệnh đề sau: 0
A. Nếu f x không có đạo hàm tại x thì f x không đạt cực trị tại x . 0 0
B. Nếu f 'x  0 thì f x đạt cực trị tại x . 0
C. Nếu f 'x  0 và f ''x   0 thì f x không đạt cực trị tại x . 0 0
D. Nếu f 'x  0 có nghiệm x và f ''x
0 thì f x đạt cực trị tại x . 0   0 0
Câu 20. Đồ thị của hàm số 3 2
y x  3x  9x 1 có hai điểm cực trị A và B. Điểm nào dưới đây thuộc đường thẳng AB? A.𝑄(−1; 10). B. 𝑀(0; −1). C. N 1; 1  0 D. 𝑃(1; 0).
Trích Đề Thi THPT Quốc Gia 2017
Câu 21. Phát biểu nào dưới đây là sai?
A. Nếu tồn tại số h sao cho f x  f x
với mọi x x h; x h và x x , ta nói rằng hàm số 0 0  0  0
f x đạt cực đại tại điễm x . 0
B. Giả sử y f x liên tục trên khoãng K  x h; x h và có đạo hàm trên K hoặc K \ x , với 0  0 0 
h  0 . Khi dó nếu f 'x  0 trên khoãng x h; x
và f 'x  0 trên khoãng x ; h x thì x là một 0 0  0 0  0
điễm cực tiễu cũa hàm số y f x .
C. x a là hoành độ điểm cực tiểu khi và chỉ khi y'a  0; y''a  0 .
D. Nếu M x ; f x
là điểm cực trị của đồ thị hàm số thì y f
dược gọi là giá trị cực trị cũa 0 x0 0 0  hàm số.
Câu 22. Cho hàm số f x xác định và liên tục trên khoảng a;b . Tìm mệnh đề sai?
A. Nếu f x đồng biến trên khoãng a;b thì hàm số không có cực trị trên khoãng a;b .
B. Nếu f x nghịch biến trên khoảng a;b thì hàm số không có cực trị trên khoảng a;b .
TRUNG TÂM THẦY DIÊU – FB TRẦN CÔNG DIÊU 5
TRẦN CÔNG DIÊU [ĐĂNG KÍ HỌC OFF TPHCM – CALL 01638.645.228]
C. Nếu f x đạt cực trị tại điểm x
thì tiếp tuyến của đồ thị hàm số tại điểm M x ; f x 0 0  0 a;b
song song hoặc trùng với trục hoành.
D. Nếu f x đạt cực đại tại điễm x
thì f x đồng biến trên a; x và nghịch biến trên 0  0 a;b x ;b . 0 
Câu 23. Cho khoãng a;b chứa m . Hàm số y f x xác định và liên tục trên khoảng a;b . Có các phát biểu sau đây:
(1) m là điểm cực trị của hàm số khi f 'm  . 0
(2) f x  f m, x
 a;b thì x m là điểm cực tiểu của hàm số.
(3) f x  f m, x  a;b  \
m thì x m là điểm cực đại của hàm số.
(4) f x  M, x
 a;b thì M là được gọi là giá trị nhỏ nhất của hàm số trên khoãng a;b .
Số phát biễu đúng là: A. 0. B. 1. C. 2. D. 3.
Câu 24. Hàm số y x3  x2 5
 3x 1 đạt cực trị khi: x  3 x  0 x  0 x  3 A.  .     1 B. . 10 C. . 10 D. . 1 x           x x x  3  3  3  3
Câu 25. Đồ thị của hàm số y x3  x2 3
có hai điểm cực trị là:
A. 0;0 hoặc 1; 2 .
B. 0;0 hoặc 2; 4 .
C. 0;0 hoặc 2; 4 .
D. 0;0 hoặc 2; 4 .
Câu 26. Hàm số y x3  3x  1 đạt cực đại tại: A. x   . 1 B. x . 0 C. x . 1 D. x . 2
Câu 27. Hàm số y x3  x2 4
 3x  7 đạt cực tiễu tại x . Kết luận nào sau đây đúng? CT A. x  1 . B. x   . 3 C. x   1 . D. x. 1 CT 3 CT CT 3 CT
TRUNG TÂM THẦY DIÊU – FB TRẦN CÔNG DIÊU 6
TRẦN CÔNG DIÊU [ĐĂNG KÍ HỌC OFF TPHCM – CALL 01638.645.228]
Câu 28. Hệ thức liên hệ giư̂a giá trị cực đại y
và giá trị cực tiểu y
của hàm số y x3  3x là: CD CT A. y  2y . B. y  3 y . C. yy . D. y  y . CT CD CT CD 2 CT CD CT CD
Câu 29. Cho hàm số y x3  x2 3  9x .
4 Nếu hàm số đạt cực đại tại x và cực tiểu tại x thì tích của 1 2
y x .yx có giá trị bằng 1 2  A. -302. B. -82. C. -207. D. 25. 2
Câu 30. Khoảng cách giữa hai điểm cực đại và cực tiểu của đồ thị hàm số y  x   1 x  2 là A. 2 5 . B. 2. C. 4. D. 5 2 .
Câu 31. Trong các đường thẵng dưới đây , đường thẵng nào đi qua trung điễm đoạn thẵng nối các
điễm cực trị cũa đồ thị hàm số y x3  3x  1 ? x
A. y  2x . 3
B. y    1 .
C. y  2x . 3
D. y  2x . 1 3 3
Câu 32. Đồ thị hàm số y  x4  x2 2  3 có
A. 1 điễm cực đại và không có điễm cực tiễu.
B. 1 điễm cực tiễu và không có điễm cực đại.
C. 1 điễm cực đại và 2 điễm cực tiễu.
D. 1 điễm cực tiễu và 2 cực đại.
Câu 33. Đồ thị hàm số y x4  x2  1 có bao nhiêu điểm cực trị có tung độ dương? A. 1. B. 2. C. 3. D. 4. 2
Câu 34. Cho hàm số f x  x2  3 . Giá trị cực đại của hàm số f 'x bằng: 1 A. 8. B. -8. C. 0. D. . 2
Câu 35. Tìm các điễm cực trị cũa hàm số y x2 x2  2 . A. x. 1 B. x. 0 C. x   . 1 D. x. 2 CT CT CD CD
TRUNG TÂM THẦY DIÊU – FB TRẦN CÔNG DIÊU 7
TRẦN CÔNG DIÊU [ĐĂNG KÍ HỌC OFF TPHCM – CALL 01638.645.228] Câu 36. Hàm số 4 3
y x x có điểm cực trị 3 3
A. x  0; x  B. x  0 C. x  D. x  1 4 4
Câu 37. Cho hàm số y x . Tìm mệnh đề đúng trong các mệnh đề sau:
A. Hàm số có một điểm cực đại.
B. Hàm số đã cho không có cực trị.
C. Hàm số đã cho có đạo hàm không xác định tại x  0 nên không đạt cực trị tại x  0 .
D. Hàm số đã cho có đạo hàm không xác định tại x  0 nhưng đạt cực trị tại x  0 .
Câu 38. Hàm số nào sau đây không có cực trị ? 2  x A. 3
y x  3x  1. B. y  . x  3 C. 4 3
y x  4x  3x  1. D. 2n *
y x  2017x (n ).
Câu 39. Hàm số nào sau đây có ba điểm cực trị? A. 4 2
y x  2x  10 B. 4 2
y  x  2x  3. 1 C. 3 2
y x  3x  5x  2. D. 4
y  2x  4 . 3 Câu 40. Cho hàm số 4 2
y  x  2x  1. Mệnh đề nào dưới đây đúng?
A. Hàm số có một cực đại và hai cực tiểu.
B. Hàm số có hai cực đại và một cực tiểu.
C. Hàm số có một cực đại và không có cực tiểu.
D. Hàm số có một cực đại và một cực tiểu.
Câu 41. Cho hàm số y f ( )
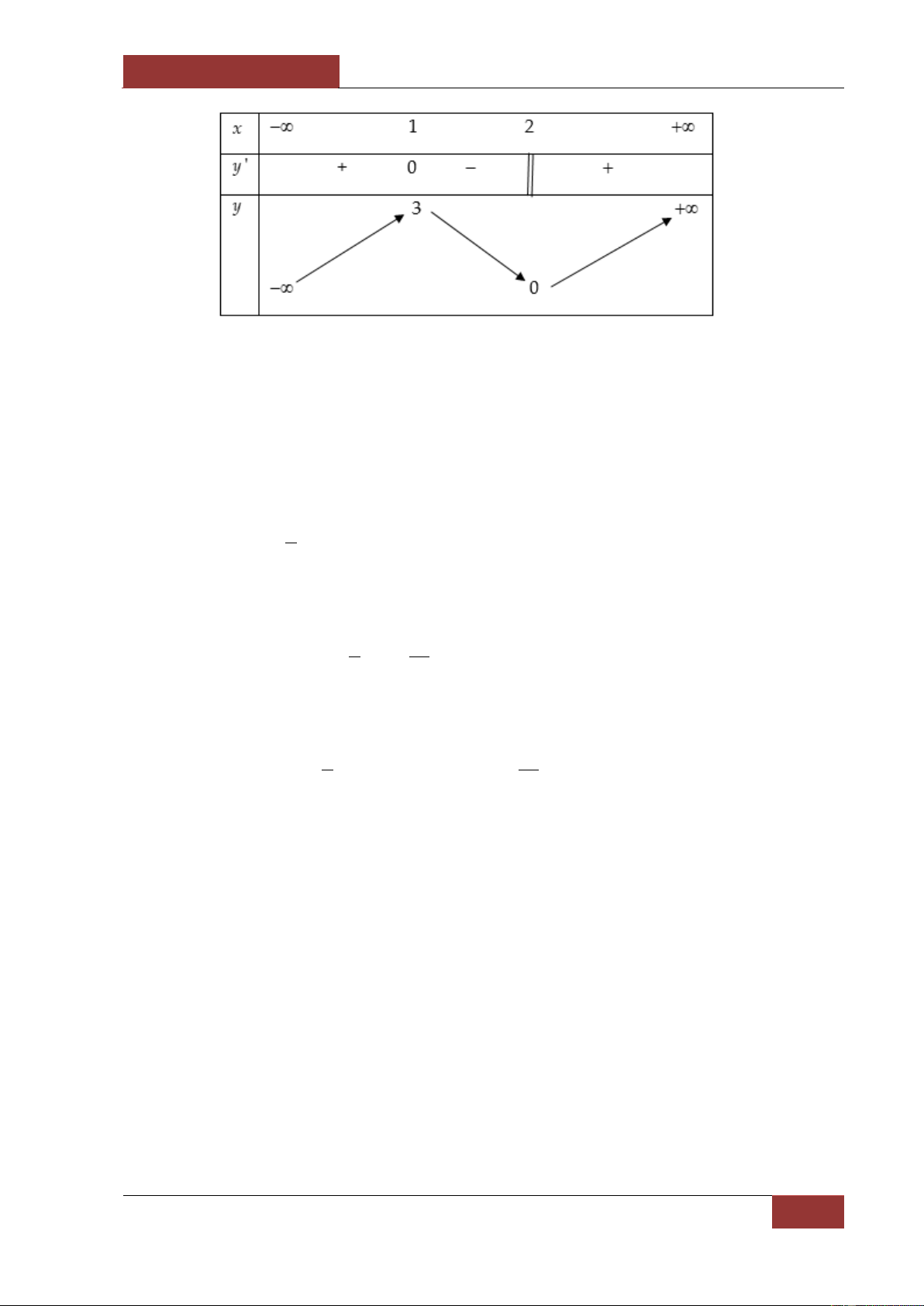
x xác định, liên tục trên   \ 
2 và có bảng biến thiên phía dưới:
TRUNG TÂM THẦY DIÊU – FB TRẦN CÔNG DIÊU 8
TRẦN CÔNG DIÊU [ĐĂNG KÍ HỌC OFF TPHCM – CALL 01638.645.228]
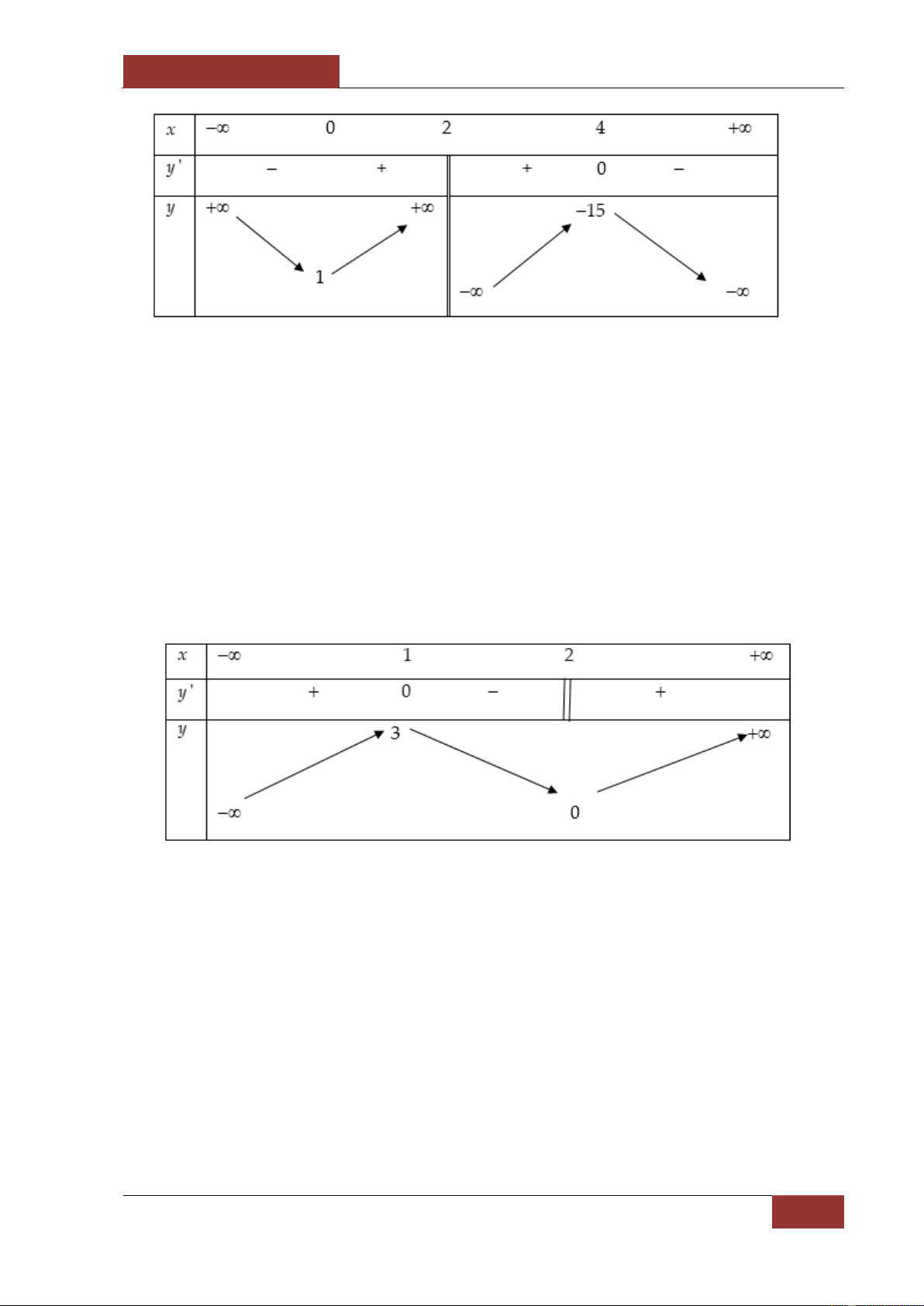
Khẳng định nào sau đây là khẳng định đúng?
A. Hàm số đạt cực đại tại điểm x  0 và đạt cực tiểu tại điểm x  4 .
B. Hàm số có đúng một cực trị.
C. Hàm số có giá trị cực tiểu bằng 1.
D. Hàm số có giá trị lớn nhất bằng 1 và giá trị nhỏ nhất bằng - 15.
Câu 42. Hàm số y f ( )
x liên tục trên  và có bảng biến thiên như hình vẽ bên. Mệnh đề nào sau đây là đúng?
A. Hàm số đã cho có hai điểm cực trị.
B. Hàm số đã cho không có giá trị cực đại.
C. Hàm số đã cho có đúng một điểm cực trị.
D. Hàm số đã cho không có giá trị cực tiểu.
Câu 43. Hàm số y f ( ) x có đạo hàm 2 f '( )
x  (x 1) (x  3) . Phát biểu nào sau đây là đúng?
A. Hàm số có một điểm cực đại.
B. Hàm số có hai điểm cực trị.
TRUNG TÂM THẦY DIÊU – FB TRẦN CÔNG DIÊU 9
TRẦN CÔNG DIÊU [ĐĂNG KÍ HỌC OFF TPHCM – CALL 01638.645.228]
C. Hàm số có đúng 1 điểm cực trị.
D. Hàm số không có điểm cực trị.
Câu 44. Số điểm cực đại của đồ thị hàm số 4
y x  100 là: A. 0. B. 1. C. 3. D. 2. Câu 45. Hàm số 4 2
y x  2x  2017 có bao nhiêu điểm cực trị? A. 1. B. 2. C. 0. D. 3. 1 Câu 46. Cho hàm số 3 2
y x  4x  8x  5 có hai điểm cực trị là x , x . Hỏi tổng x x là bao nhiêu? 3 1 2 1 2
A. x x  8.
B. x x  8.  1 2 1 2
C. x x  5.
D. x x  5.  1 2 1 2
Câu 47. Hàm số y f ( )
x có đạo hàm f x x x  x  2 2 '( ) ( 1) ( 3)
2 . Phát biểu nào sau đây là đúng?
A. Hàm số có một điểm cực đại.
B. Hàm số có hai điểm cực trị.
C. Hàm số có đúng 1 điểm cực trị.
D. Hàm số không có điểm cực trị.
Câu 48. Đồ thị hàm số 3 2
y x  3x  1 có điểm cực đại là: A. I(2; 3  ). B. I(0;1) . C. I(0; 2) . D. I(0; 2)  . Câu 49. Hàm số 4 2
y x  2x  2017 có bao nhiêu điểm cực trị? A. 1. B. 2. C. 0. D. 3. Câu 50. Cho hàm số 3 2
y x  3x  3x  1. Khẳng định nào sau đây là đúng?
A. Hàm số đạt cực tiểu tại điểm x  1.
B. Hàm số đồng biến trên (1; )
 và nghịch biến trên ( ;  1) .
C. Hàm số đạt cực đại tại điểm x  1.
D. Hàm số đồng biến trên  .
TRUNG TÂM THẦY DIÊU – FB TRẦN CÔNG DIÊU 10
TRẦN CÔNG DIÊU [ĐĂNG KÍ HỌC OFF TPHCM – CALL 01638.645.228]
Câu 51. Cho hàm số y f ( )
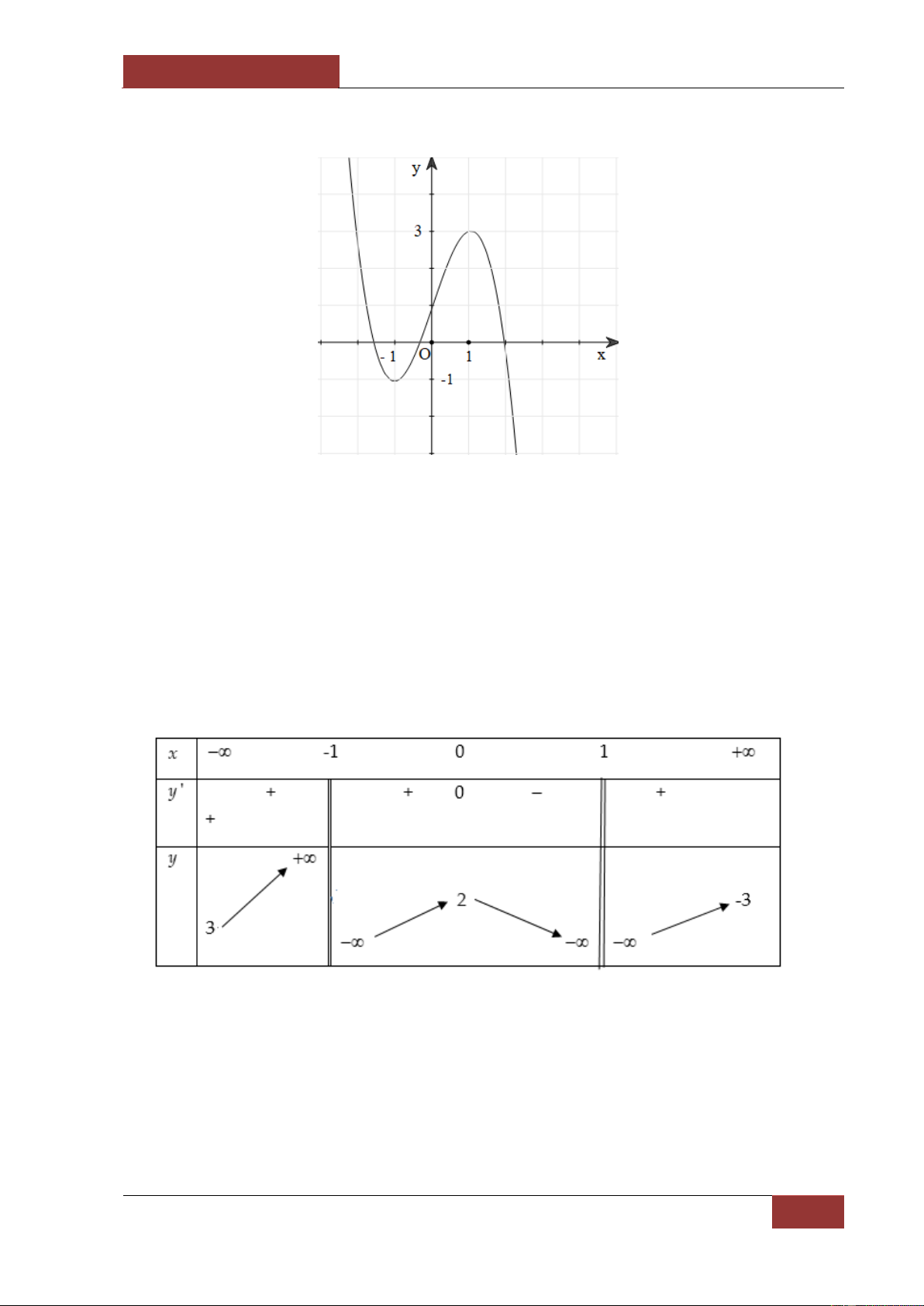
x có đồ thị như hình vẽ, các khẳng định sau khẳng định nào là đúng?
A. Hàm số đạt giá trị nhỏ nhất bằng – 1 và đạt giá trị lớn nhất bằng 3.
B. Đồ thị hàm số có điểm cực tiểu ( A 1  ; 1
 ) và điểm cực đại ( B 1; 3) .
C. Hàm số có giá trị cực đại bằng 1.
D. Hàm số đạt cực tiểu tại ( A 1  ; 1  ) và cực đại tại ( B 1; 3) .
Câu 52. Cho hàm số y f ( )
x xác định trên   \ 1  ; 
1 , liên tục trên mỗi khoảng xác định và có bảng biến thiên sau:
Hỏi khẳng định nào dưới đây là khẳng định sai?
A. Hàm số không có đạo hàm tại x  0 nhưng vẫn đạt cực trị tại x  0 .
B. Hàm số đạt cực tiểu tại điểm x  1.
C. Đồ thị hàm số có hai tiệm cận đứng là các đường thẳng x  1  và x  1.
TRUNG TÂM THẦY DIÊU – FB TRẦN CÔNG DIÊU 11
TRẦN CÔNG DIÊU [ĐĂNG KÍ HỌC OFF TPHCM – CALL 01638.645.228]
D. Đồ thị hàm số có hai tiệm cận ngang là các đường thẳng y  3  và y  3.
Câu 53. Khẳng định nào sau đây là khẳng định đúng? 1
A. Hàm số y  2x x có hai điểm cực trị. 1 B. Hàm số 3
y  3x  2016x  2017 có hai điểm cực trị. 2x  1
C. Hàm số y x có một điểm cực trị. 1 D. Hàm số 4 2
y  x  3x  2 có một điểm cực trị. 3
Câu 54. Số điểm cực trị của hàm số 2
y x  4x  3 bằng: A. 2. B. 0. C. 3. D. 4. Câu 55. Hàm số 4 2
y x x  1 đạt cực tiểu tại: A. x  1  B. x  0. C. x  2  D. x  1.
Câu 56. Cho hàm số y f ( )
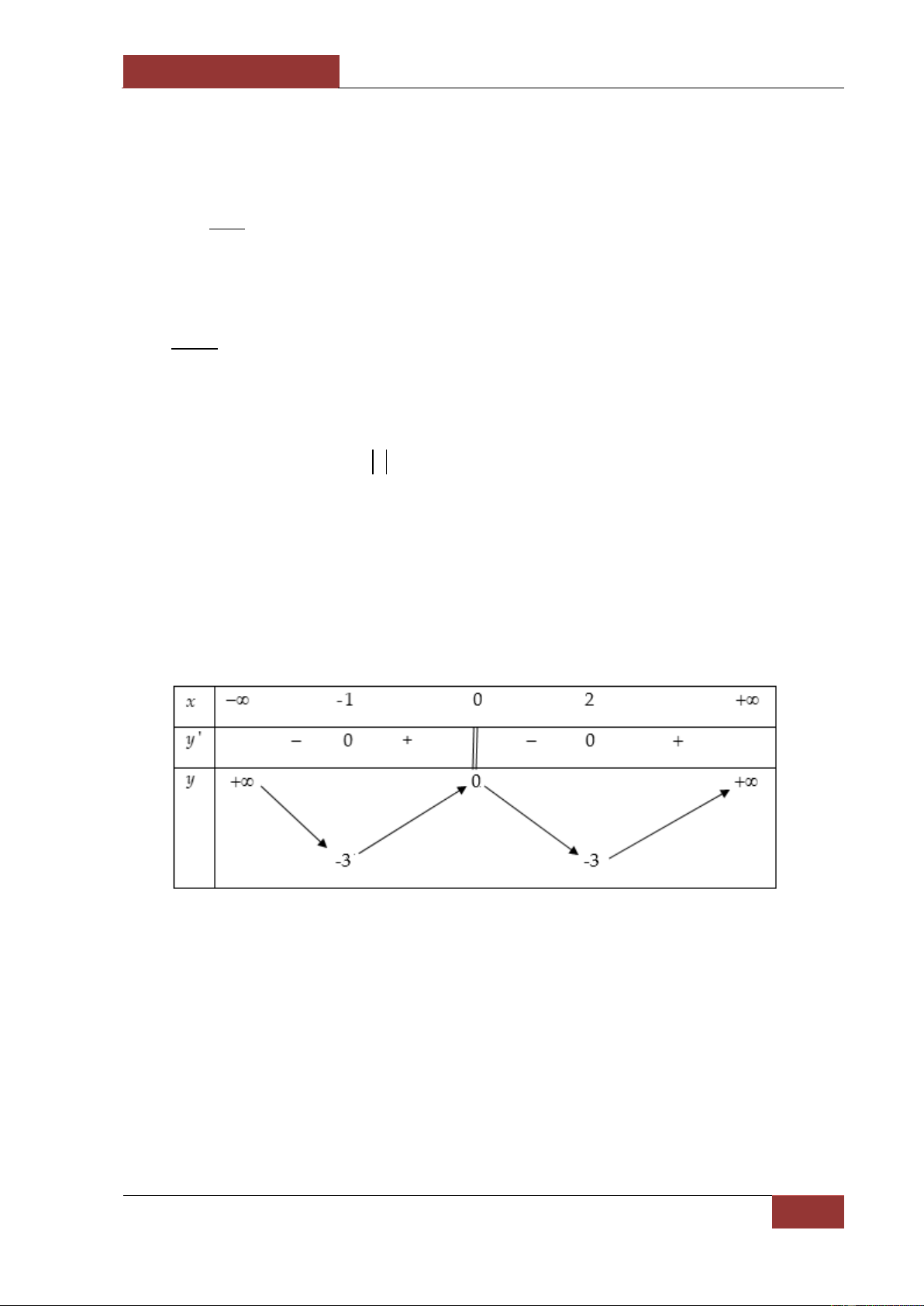
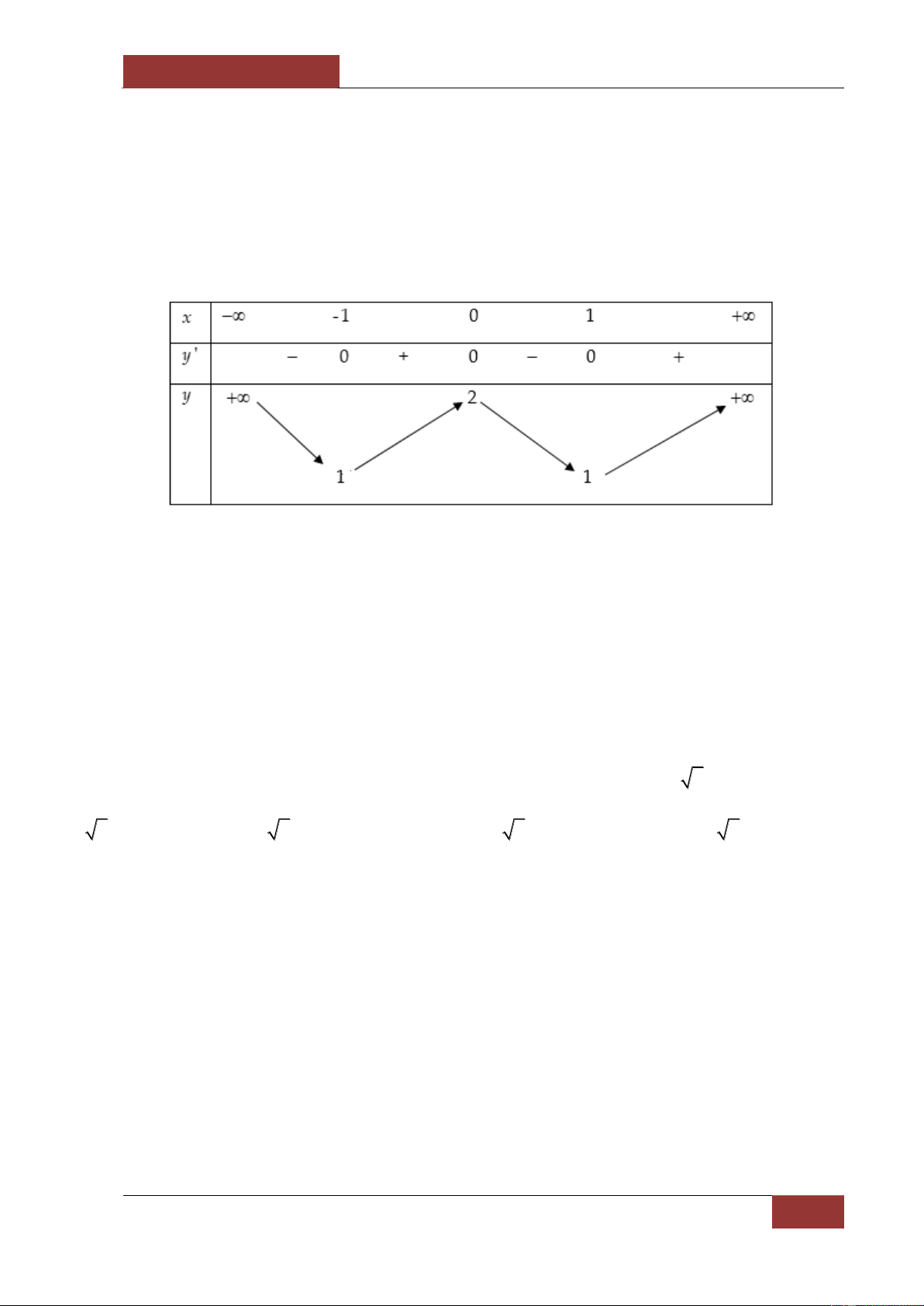
x xác định, liên tục trên  và có bảng biến thiên:
Khẳng định nào sau đây là khẳng định đúng?
A. Hàm số có đúng hai cực trị.
B. Hàm số có giá trị cực tiểu bằng – 1 hoặc 1.
C. Hàm số có giá trị lớn nhất bằng 0 và giá trị nhỏ nhất bằng – 3.
D. Hàm số đạt cực đại tại x  0. Câu 57. Hàm số 3 2
y x  3x  1 đạt cực trị đại tại các điểm nào sau đây?
TRUNG TÂM THẦY DIÊU – FB TRẦN CÔNG DIÊU 12
TRẦN CÔNG DIÊU [ĐĂNG KÍ HỌC OFF TPHCM – CALL 01638.645.228] A. x  2  B. x  1 
C. x  0; x  2.
D. x  0; x  1.
Câu 58. Hệ thức liên hệ giữa giá trị cực đại y
và giá trị cực tiểu y của hàm số 3
y x  2x là: CĐ CT A. yy  0. B. 2y  3y . C. y  2y . D. yy . CT CĐ CT CĐ CT CĐ CT CĐ
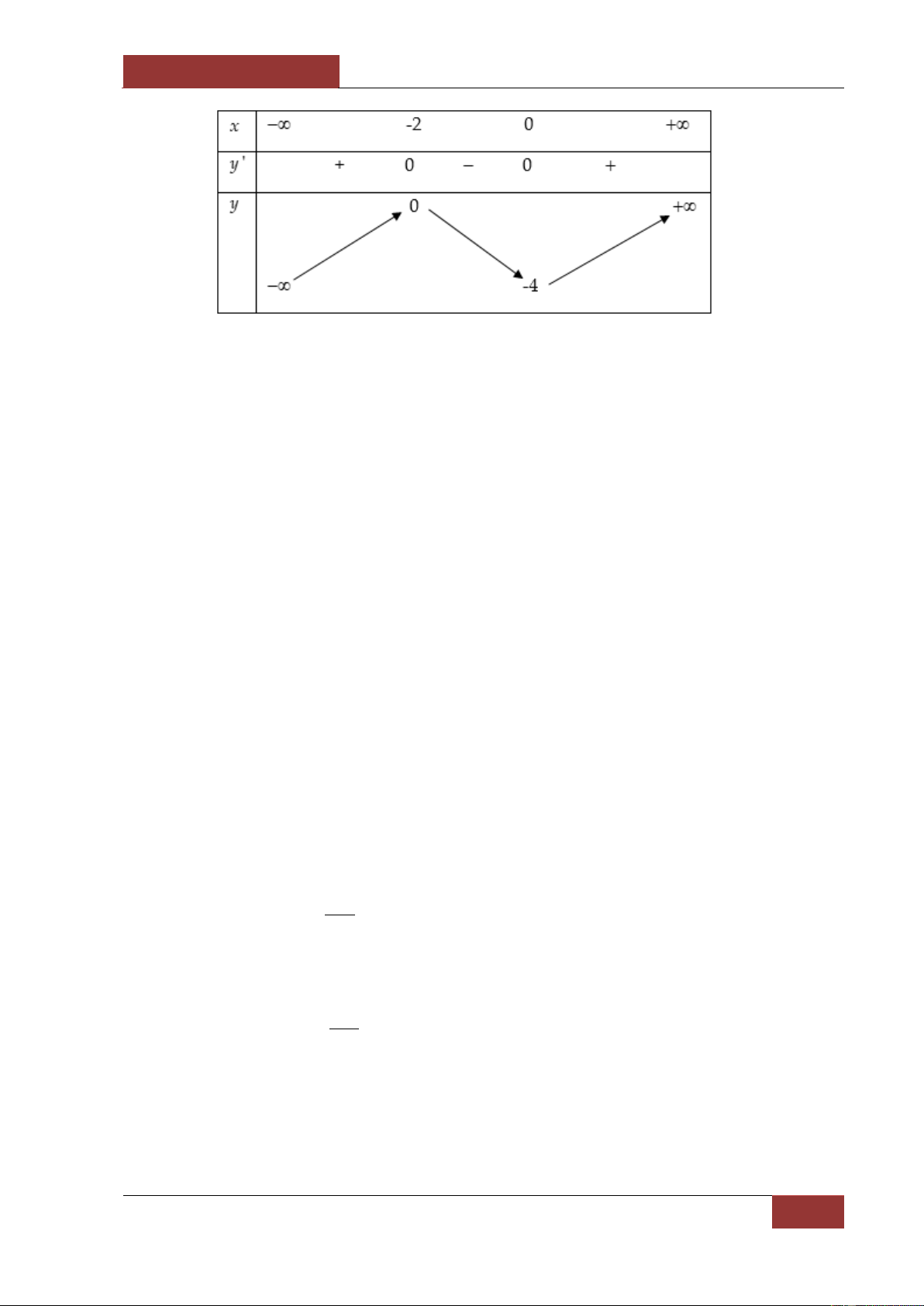
Câu 59. Cho hàm số y f ( )
x xác định, liên tục trên  và có bảng biến thiên:
Khẳng định nào sau đây là sai? A. (
M 0; 2) được gọi là điểm cực đại của hàm số. B. f ( 1
 ) được gọi là giá trị cực tiểu của hàm số.
C. Hàm số đồng biến trên các khoảng ( 1  ;0) và (1; )  .
D. x  1 được gọi là điểm cực tiểu của hàm số. 0
Câu 60. Tính khoảng cách giữa các điểm cực tiểu của đồ thị hàm số 4 2
y  2x  3x  1. A. 4 2 3. B. 3. C. 2 3. D. 4 3.
Câu 61. Tìm tất cả các điểm cực đại của hàm số 4 2
y  x  2x  1. A. x  1  B. x  1.  C. x  1. D. x  0 .
Câu 62. Cho hàm số y f ( )
x liên tục trên  và có bảng biến thiên như hình vẽ. Mệnh đề nào sau đây là đúng?
TRUNG TÂM THẦY DIÊU – FB TRẦN CÔNG DIÊU 13
TRẦN CÔNG DIÊU [ĐĂNG KÍ HỌC OFF TPHCM – CALL 01638.645.228]
A. Hàm số đã cho có hai điểm cực trị.
B. Hàm số đã cho không có giá trị cực đại.
C. Hàm số đã cho có đúng một điểm cực trị.
D. Hàm số đã cho không có giá trị cực tiểu. 2 Câu 63. Cho hàm số 4 3 2
y x x x . Mệnh đề nào sau đây là đúng? 3
A. Hàm số có giá trị cực tiểu là 0. 2 5
B. Hàm số có hai giá trị cực tiểu là  và  . 3 48
C. Hàm số chỉ có một giá trị cực tiểu. 2 5
D. Hàm số có giá trị cực tiểu là 
và giá trị cực đại là  . 3 48 Câu 64. Cho hàm số 2
y  (x 1)(x  2) . Trung điểm của đoạn thẳng nối hai điểm cực trị của đồ thị
hàm số nằm trên đường thẳng nào dưới đây?
A. 2x y  4  0.
B. 2x y  4  0.
C. 2x y  4  0.
D. 2x y  4  0.
Câu 65. Cho hàm số f có đạo hàm là 2 3 f '( ) x  (
x x 1) (x  2) với mọi x   . Số điểm cực trị của hàm số f là A. 0. B. 1. C. 2. D. 3.
Câu 66. Cho hàm số y f ( )
x liên tục trên  và có bảng biến thiên như sau:
TRUNG TÂM THẦY DIÊU – FB TRẦN CÔNG DIÊU 14
TRẦN CÔNG DIÊU [ĐĂNG KÍ HỌC OFF TPHCM – CALL 01638.645.228]
Khẳng định nào sau đây là khẳng định sai?
A. Hàm số đồng biến trên khoảng (0; )  .
B. Hàm số đạt cực tiểu tại x  0.
C. Hàm số đạt cực tiểu tại x  2. 
D. Hàm số nghịch biến trên khoảng ( 2;  0) .
Câu 67. Cho hàm số y f ( ) x có đạo hàm 2 f '( )
x  (x 1) (x  2) xác định trên  . Mệnh đề nào sau đây là mệnh đề đúng?
A. Hàm số y f ( )
x đồng biến trên khoảng ( 2;   )  .
B. Hàm số y f ( )
x đạt cực đại tại x  2. 
C. Hàm số y f ( )
x đạt cực tiểu tại x  1.
D. Hàm số y f ( )
x nghịch biến trên khoảng ( 2;  1) .
Câu 68. Kết luận nào sau đây về cực trị của hàm số 5 x y x   là đúng? 1
A. Hàm số có điểm cực đại là x  . ln 5
B. Hàm số không có cực trị. 1
C. Hàm số có điểm cực tiểu là x  . ln 5
D. Hàm số có điểm cực đại là x  ln 5 .
Câu 69. Điễm cực trị cũa hàm số y sin2 xx là:
TRUNG TÂM THẦY DIÊU – FB TRẦN CÔNG DIÊU 15
TRẦN CÔNG DIÊU [ĐĂNG KÍ HỌC OFF TPHCM – CALL 01638.645.228]   A. x   k  2 k   . B. x
   kk  . CT   CD   6 3    C. x
  k,x    kk  . D. x
  kk  . CD   CD CT   6 6 3
Câu 70. Giá trị cực đại của hàm số y x  2cos x trên khoãng 0;  là:  5  5   A.  3. B.  3. C.  3. D.  3. 6 6 6 6
Câu 71. Cho hàm số y sin x  3 cos x . Khẵng định nào sau đây sai: 
A. x  5 là một nghiệm của phương trình. 6
B. Trên khoãng 0;  hàm số có duy nhất một cực trị. 
C. Hàm số đạt cực tiểu tại x  5 . 6
D. y y''  0,x .
Phần 2. Các bài toán cực trị chứa tham số
Như vậy chúng ta vừa tìm hiểu các bài toán cực trị không chứa tham số, sau đây chúng ta cùng đi vào các bài
toán cực trị chứa tham số, loại toán này đòi hỏi chúng ta phải vững lí thuyết và có tư duy tối hơn. Xin nhắc
rằng nếu loại không chứa tham số chưa thành thạo thì đừng nên tiếp cận ngay dạng toán này. Câu 1. Cho hàm số 3 2
y x mx  2x  1 với m là tham số. Khẳng định nào sau đây là đúng?
A. Với mọi tham số m , hàm số đã cho luôn chỉ có duy nhất một cực đại.
B. Với mọi tham số m , hàm số đã cho luôn chỉ có duy nhất một cực tiểu.
C. Với mọi tham số m , hàm số đã cho luôn có một điểm cực đại và một điểm cực tiểu.
D. Với mọi tham số m , hàm số đã cho không có cực trị. Câu 2. Cho hàm số 3 2
y x  3x  3(1 )
m x  1 3m , tìm m sao cho đồ thị hàm số có điểm cực đại, cực
tiểu, đồng thời tìm đường thẳng đi qua hai điểm cực trị của đồ thị hàm số đã cho.
A. m  0 ;  :2mx y  2m  2  0 .
B. m  0 ;  :2mx y  2m  2  0 .
TRUNG TÂM THẦY DIÊU – FB TRẦN CÔNG DIÊU 16
TRẦN CÔNG DIÊU [ĐĂNG KÍ HỌC OFF TPHCM – CALL 01638.645.228]
C. m  0 ;  : y  202  200x.
D. m  0 ;  : y  202  200x .
Câu 3. Với giá trị nào của m thì hàm số 3 2 2
y x m x  (4m  3)x 1 đạt cực đại tại x  1?
A. m  1 và m  3  . B. m  1. C. m  3  . D. m  1  .
Câu 4. Tìm tất cả các giá trị thực của tham số m sao cho hàm số 3 2
y x  3mx  3m  1 có 2 điểm cực trị. A. m  0. B. m  0. C. m  0. D. m  0 . Câu 5. Cho hàm số 4 2
y ax bx c (a  0) . Trong điều kiện nào sau đây thì hàm số có ba cực trị:
A. a,b cùng dấu và c bất kì.
B. a,b trái dấu và c bất kì.
C. b  0 và a, c bất kì.
D. c  0 và a,b bất kì. Câu 6. Cho hàm số 4 2
y ax bx 1 (a  0) . Để hàm số có một cực tiểu và hai cực đại thì a,b cần thỏa mãn:
A. a  0,b  0.
B. a  0,b  0.
C. a  0,b  0.
D. a  0,b  0.
Câu 7. Tìm giá trị thực của tham số m để đường thẳng d : y (2m  1)x  3  m vuông góc với đường
thẳng đi qua hai điểm cực trị của đồ thị hàm số 3 2
y x  3x  1 3 3 1 1 A. m  . B. m  . C. m   . D. m  . 2 4 2 4
Trích Đề Thi THPT Quốc Gia 2017
Câu 8. Tìm tất cả các giá trị thực của tham số m sao cho hàm số 3 2
y x  3x mx  1 có hai điểm cực
trị x , x thỏa mãn 2 2 x x  3 . 1 2 1 2 3 3 A. – 3. B. 3. C.  . D. . 2 2 1
Câu 9. Tìm m để hàm số: 3 2 2
y x mx  (m m  1)x  1 đạt cực trị tại 2 điểm x , x thỏa mãn 3 1 2 x x  4 . 1 2
TRUNG TÂM THẦY DIÊU – FB TRẦN CÔNG DIÊU 17
TRẦN CÔNG DIÊU [ĐĂNG KÍ HỌC OFF TPHCM – CALL 01638.645.228] A. m  2  . B. m  2. 
C. Không tồn tại m . D. m  2.
Câu 10. Tìm tất cả các giá trị thực của tham số m sao cho hàm số 3 2
y x  (m 1)x  3mx  1 đạt cực trị tại điểm x  1. 0 A. m  1.  B. m  1. C. m  2. D. m  2. 
Câu 11. Tìm tất cả các giá trị thực của tham số m sao cho hàm số 4 2 2
y x  2mx m m có đúng một điểm cực trị. A. m  0 . B. m  0 . C. m  0 . D. m  0.
Câu 12. Tìm tất cả các giá trị thực của tham số m để hàm số 3 2
y  4x mx 12x đạt cực tiểu tại điểm x  2.  A. m  9.  B. m  2.
C. Không tồn tại m . D. m  9.
Câu 13. Tìm tất cả các giá trị thực của tham số m sao cho hàm số 4 2 2
y mx  (m  2)x  2 có hai cực
tiểu và một cực đại.
A. m   2  0  m  2 .
B.  2  m  0 . C. m  2 . D. 0  m  2 .
Câu 14. Tìm tất cả các giá trị thực của tham số m sao cho đồ thị hàm số 4 2
y x  2mx  2m có ba điểm
cực trị tạo thành tam giác có diện tích bằng 1. 1 A. m  . B. m  3. C. m  1.  D. m  1. 5 4
Câu 15. Tìm tất cả các giá trị thực của tham số m sao cho đồ thị hàm số 4 2 4
y x  2mx  2m m có ba
điểm cực trị tạo thành một tam giác đều. A. 3 m  3. B. 3 m  1 3. C. 3 m  1 3. D. 3 m   3.
Câu 16. Tìm m để đồ thị hàm số 4 2
y x  2(m 1)x  2m  5 có ba điểm cực trị lập thành tam giác đều? A. m  1. B. 3 m  1 3. C. 3 m  1 3. D. m  1 3 . Câu 17. Cho hàm số 4 2 2
y x  2mx m  2 . Tìm m để hàm số có 3 điểm cực trị và các điểm cực trị của
đồ thị hàm số là ba đỉnh của một tam giác vuông cân?
TRUNG TÂM THẦY DIÊU – FB TRẦN CÔNG DIÊU 18
TRẦN CÔNG DIÊU [ĐĂNG KÍ HỌC OFF TPHCM – CALL 01638.645.228] A. m  1. B. m  1  C. m  2. D. m  2.  Câu 18. Cho hàm số 4 2 4
y x  2mx  2m m . Với giá trị nào của m thì đồ thị C có 3 điểm cực trị, m
đồng thời 3 điểm cực trị đó tạo thành một tam giác có diện tích bằng 2. A. 5 m  4. B. m  16. C. 5 m  16. D. 3 m   16.
Câu 19. Đường thẳng đi qua điểm cực đại, cực tiểu của đồ thị hàm số 3
y x  3mx  2 cắt đường tròn
tâm I(1;1) , bán kính bằng 1 tại 2 điểm phân biệt A, B sao cho diện tích tam giác IAB đạt giá trị lớn
nhất khi m có giá trị là: 2  3 1  3 2  5 2  3 A. m  . B. m  . C. m  . D. m  . 2 2 2 3 Câu 20. Cho hàm số 3 2 2 y  2
x (2m1)x (m 1)x  2 . Hỏi có tất cả bao nhiêu giá trị nguyên của
tham số m để hàm số đã cho có hai điểm cực trị. A. 4. B. 5. C. 3. D. 6.
Câu 21. Tìm tất cả các giá trị thực của tham số m để hàm số 3 2
y x x (2m  1)x  4 có đúng hai cực trị. 4 2 2 4 A. m  . B. m   . C. m   . D. m   . 3 3 3 3 1 1
Câu 22. Tìm tất cả các giá trị của tham số m để hàm số 3 2
y x  (m  5)x mx có cực đại, cực tiểu 3 2 và xx  5. CĐ CT A. m  0. B. m  6.  C. m6;  0 . D. m 6;   0 .
Câu 23. Biết đồ thị hàm số 3 2
y ax bx cx d có 2 điểm cực trị là ( 1  ;18) và (3; 1  6) . Tính
a b c  . d A. 0. B. 1. C. 2. D. 3. Câu 24. Cho hàm số 2 f ( )
x x  ln(x  )
m . Tìm tất cả các giá trị thực của tham số m để hàm số đã cho
có đúng hai điểm cực trị. 9 A. m  2. B. m  . C. m   2. D. m  2. 4
TRUNG TÂM THẦY DIÊU – FB TRẦN CÔNG DIÊU 19
TRẦN CÔNG DIÊU [ĐĂNG KÍ HỌC OFF TPHCM – CALL 01638.645.228]
Câu 25. Cho đồ thị hàm số 3 2 y f ( )
x ax bx c có hai điểm cực trị là ( A 0;1) và ( B 1  ; 2). Tính giá trị
của a b  . c A. 0. B. 2. C. 4. D. 6.
Câu 26. Tìm tất cả các giá trị thực của tham số m để hàm số 3 2 y  (1 )
m x  3x  3x  5 có cực trị? A. m  1. B. m  1.  C. 0  m  1 D. m  0. 1 Câu 27. Cho hàm số 3 2
y x mx  (2m  1)x  1. Tìm mệnh đề sai. 3 A. m
  1 thì hàm số có hai điểm cực trị.
B. Hàm số luôn có cực đại và cực tiểu. C. m
  1 thì hàm số có cực đại và cực tiểu. D. m
  1 thì hàm số có cực trị.
Câu 28. Tìm m để hàm số 4 2 2
y mx  (m  9)x  1 có hai điểm cực đại và một điểm cực tiểu. A. 3   m  0. B. 0  m  3. C. m  3.  D. 3  . m Câu 29. Hàm số 3 2
y x  3mx  6mx m có hai điểm cực trị khi m thỏa mãn điều kiện: m  0 A. 0  m  2. B.  . m  8 m  0 C.  . D. 0  m  8. m  2 m Câu 30. Hàm số 3 2 y
x x x  2017 có cực trị khi và chỉ khi: 3 m  1 m  1 A. m  1. B.  C.  D. m  1. m  0 m  0
Câu 31. Với điều kiện nào của a và b để hàm số 3 3 3
y  (x a)  (x  )
b x đạt cực đại và cực tiểu? A. ab  0. B. ab  0. C. ab  0. D. ab  0. Câu 32. Hàm số 3 2
y  (m  3)x  2mx  3 không có cực trị khi: A. m  3.
B. m  0 hoặc m  3. C. m  0 . D. m  3.
TRUNG TÂM THẦY DIÊU – FB TRẦN CÔNG DIÊU 20
TRẦN CÔNG DIÊU [ĐĂNG KÍ HỌC OFF TPHCM – CALL 01638.645.228] 1 1
Câu 33. Tìm tất cả các giá trị của m để hàm số 3 2 2 y x
(3m  2)x  (2m  3m 1)x  4 đạt cực đại tại 3 2
x  3 hoặc x  5, ta được A. m  0 B. m  1. C. m  2. D. m  3. Câu 34. Cho hàm số 3 2
y ax bx cx d . Nếu đồ thị hàm số có hai điểm cực trị là gốc tọa độ O và điểm ( A 2; 4
 ) thì phương trình của hàm số là: A. 3 2 y  3
x x . B. 3 y  3  x  . x C. 3 y x  3 . x D. 3 2
y x  3x .
Câu 35. Tìm tất cả các giá trị của tham số m để hàm số 3 2
f (x)  2x  3x m có các giá trị cực trị trái dấu: A. – 1 và 0. B. ( ;  0) ( 1  ; )  . C. ( 1  ;0). D. [0;1]. Câu 36. Cho hàm số 3 2 3
y  2x  3(m 1)x  6mx m . Tìm m để đồ thị hàm số có hai điểm cực trị , A B
sao cho độ dài AB  2. A. m  0 .
B. m  0 hoặc m  2 . C. m  1. D. m  2 . 3 x Câu 37. Hàm số 2 2 y
 (m 1)x  (m  3)x 1 đạt cực trị tại x  1  thì m bằng: 3 m  2.  m  2. A. m  0 . B. m  2.  C.  D.  m  0. m  0.
Câu 38. Biết hàm số 3 2
y  3x mx mx  3 có một điểm cực trị x  1
 . Khi đó, hàm số đạt cực trị tại
điểm khác có hoành độ là: 1 1 1 1 A. . B. . C.  . D.  . . 4 3 3 2 1
Câu 39. Nếu x  1
 là điểm cực tiểu của hàm số 3 2 2 y
x mx  (m  4)x  5 thì tập tất cả các giá trị 3
của m có thể nhận được là: A. 1. B. – 3. C. 1 hoặc – 3. D. [  3;1]. 2 Câu 40. Hàm số 3 2
y ax ax 1 có điểm cực tiểu x
khi điều kiện của a : 3 A. a  0. B. a  0. C. a  2. D. a  0.
TRUNG TÂM THẦY DIÊU – FB TRẦN CÔNG DIÊU 21
TRẦN CÔNG DIÊU [ĐĂNG KÍ HỌC OFF TPHCM – CALL 01638.645.228]
Câu 41. Gọi x , x là 2 điểm cực trị của hàm số 3 2 2 3
y x  3mx  3(m 1)x m m . Giá trị của m để 1 2 2 2
x x x x  7 là: 1 2 1 2 9 1 A. m  0. B. m   . C. m   . D. m  2.  2 2
Câu 42. Giá trị của m để hàm số 3 2
y  4x mx  3x có hai điểm cực trị x , x thỏa mãn x  4x  0 là: 1 2 1 2 9 3 1 A. m   . B. m   . C. m  0. D. m   . 2 2 2
Câu 43. Đường thẳng đi qua hai điểm cực trị của đồ thị hàm số 3 2
y x  3x  9x m có phương trình: A. y  8  x  . m B. y  8
x m 3. C. y  8
x m  3. D. y  8
x m  3.
Câu 44. Nếu x  1 là hoành độ trung điểm của đoạn thẳng nối 2 điểm cực đại, cực tiểu của đồ thị hàm 1 số 3 2 y
x  (m  2)x  (2m  3)x  2017 thì tập tất cả các giá trị của m là: 3 3 A. m  1.  B. m  1.  C. m   .
D. Không có giá trị m . 2
Câu 45. Giá trị của m để khoảng cách từ điểm M (0;3) đến đường thẳng đi qua hai điểm cực trị của 2 đồ thị hàm số 3
y x  3mx 1 bằng là: 5 m 1 m  1  A.  . B. m  1.  C.  .
D. Không có giá trị m . m  1  m  3 Câu 46. Cho hàm số 3 2
y  2x  3(m 1)x  6(m  2)x 1. Xác định m để hàm số có điểm cực đại và điểm
cực tiểu nằm trong khoảng ( 2  ;3) . A. m( 1  ;3) (3;4). B. m(1;3) . C. m(3; 4) . D. m( 1  ;4) .
Câu 47. Để hàm số 3 2
y x  6x  3(m  2)x m  6 có cực đại, cực tiểu tại x , x sao cho x  1   x thì 1 2 1 2
giá trị của m là: A. m  1. B. m  1. C. m  1.  D. m  1.  1
Câu 48. Tìm tất cả các giá trị của tham số m để hàm số 3 2 y
x mx  (m  2)x có 2 điểm cực trị nằm 3 trong khoảng (0; )  ?
TRUNG TÂM THẦY DIÊU – FB TRẦN CÔNG DIÊU 22
TRẦN CÔNG DIÊU [ĐĂNG KÍ HỌC OFF TPHCM – CALL 01638.645.228] A. m  2. B. m  2. C. m  2. D. 0  m  2.
Câu 49. Với các giá trị nào của m thì hàm số 3 2
y x  3x  3mx 1 có các điểm cực trị nhỏ hơn 2? m  0 A. m  0. B. m  1. C.  D. 0  m 1. m  1 Câu 50. Cho hàm số 3 2
y  2x  3(2a 1)x  6a(a 1)x  2 . Nếu gọi x , x lần lượt là hoành độ các điểm 1 2
cực trị của đồ thị hàm số thì giá trị x x bằng: 2 1 A. a 1. B. . a C. a 1. D. 1. Câu 51. Cho hàm số 3 2
y  2x mx 12x 13. Với giá trị nào của m thì đồ thị có điểm cực đại, cực tiểu cách đều trục tung? A. 2. B. – 1. C. 1. D. 0.
Câu 52. Đồ thị hàm số 3 2
y  x  3mx  3m 1 có hai điểm cực đại, cực tiểu đối xứng với nhau qua
đường thẳng d : x  8y  74  0 thì tập tất cả các giá trị của m : A. m  1. B. m  2.  C. m  1.  D. m  2. 1 4 Câu 53. Cho hàm số 3 2 y
x  (m 1)x  (2m 1)x
. Tìm tất cả các giá trị của tham số m  0 để đồ 3 3
thị hàm số cố điểm cực đại thuộc trục hoành? 1 3 4 A. m  . B. m  1. C. m  . D. m  . 2 4 3 Câu 54. Cho hàm số 3 2
y x  3x mx m  2 với m là tham số, có đồ thị là (C ) . Xác định m để (C ) m m
có các điểm cực đại và cực tiểu nằm về hai phía đối với trục hoành? A. m  2. B. m  3. C. m  3. D. m  2. 1 Câu 55. Cho hàm số 3 2 y
x mx  (2m 1)x  3 với m là tham số, có đồ thị là (C ) . Xác định m để 3 m
(C ) có các điểm cực đại và cực tiểu nằm về hai phía đối với trục tung? m  1  1 1 m  m  A. m  . B. m  1. C.  2 . D.  2 . 2 m 1 m 1 Câu 56. Hàm số 3 2
y ax bx cx d đạt cực trị tại x , x nằm hai phía trục tung khi và chỉ khi: 1 2
TRUNG TÂM THẦY DIÊU – FB TRẦN CÔNG DIÊU 23
TRẦN CÔNG DIÊU [ĐĂNG KÍ HỌC OFF TPHCM – CALL 01638.645.228]
A. a  0,b  0,c  0.
B. a và c trái dấu. C. 2 b 12ac  0. D. 2 b 12ac  0. Câu 57. Cho hàm số 3 2 2
y x  3mx  4m  2 . Tìm m để đồ thị hàm số có hai điểm cực trị , A B sao cho
I (1; 0) là trung điểm của AB . A. m  0. B. m  1.  C. m  1. D. m  2.
Câu 58. Với giá trị nào của tham số m thì đồ thị hàm số 3 2
y x  3mx  2 có hai điểm cực trị , A B sao cho , A B và M (1; 2  ) thẳng hàng. A. m  0. B. m  2. C. m   2. D. m   2.
Câu 59. Với giá trị nào của tham số m thì đồ thị hàm số 3 2
y  x  3mx 1 có hai điểm cực trị , A B sao
cho tam giác OAB vuông tại O , với O là gốc tọa độ? 1 A. m  1.  B. m  0. C. m  . D. m  0. 2
Câu 60. Hàm số y x3  mx2 3
 6mx m có hai điễm cực trị khi m thoả m  0 m  0 A. 0  m . 2 B.  . C.  . D. 0  m . 8 m   8 m   2 m
Câu 61. Hàm số y
x3  x2  x  2017 có cực trị khi và chỉ khi 3 m  1 m  1 A. m . 1 B.  . C.  . D. m . 1 m   0 m   0 3 3
Câu 62. Với điều kiện nào cũa a,b để hàm số y  x a  x b  x3 đạt cực đại và cực tiễu A. ab . 0 B. ab . 0 C. ab . 0 D. ab . 0
Câu 63. Hàm số y  m   x3  mx2 3 2
 3 không có cực trị khi: A. m . 3
B. m  0 hoặc m . 3 C. m  0 . D. m . 3 1 1
Câu 64. Tìm tất cả các giá trị của m để hàm số y x3  3m  2 x2  2m2  3m  
1 x  4 đạt cực trị tại 3 2
x  3 hoặc x  5 ta được: A. m . 0 B. m . 1 C. m . 2 D. m . 3
TRUNG TÂM THẦY DIÊU – FB TRẦN CÔNG DIÊU 24
TRẦN CÔNG DIÊU [ĐĂNG KÍ HỌC OFF TPHCM – CALL 01638.645.228]
Câu 65. Cho hàm số y ax3  bx2  cx d . Nếu đồ thị hàm số có hai điểm cực rị là gốc toạ độ O và
điễm A2; 4 thì phương trình của hàm số là:
A. y   x3  x2 3 . B. y   x3 3  x.
C. y  x3  3 x.
D. y x3  x2 3 .
Câu 66. Tìm tất cả các giá trị của tham số m để hàm số f x  x3  x2 2 3
m có các giá trị cực trị trái dấu. A. -1 và 0.
B. ;0  ; 1 . C. 1;0 . D. 0;    1 .
Câu 67. Cho hàm số y x3  m   x2  mx m3 2 3 1 6
. Tìm m để đồ thị hàm số có hai điểm cực trị A,B
sao cho độ dài AB  2 . A. m . 0
B. m  0 hoặc m  2 . C. m . 1 D. m  2 . x3
Câu 68. Hàm số y
 m x2  m2 1
 3x 1 đạt cực trị tại x  1 thì m bằng 3 m  0 m  0 A. m . 0 B. m   . 2 C.  . D.  . m    2 m   2
Câu 69. Biết hàm số y x3  mx2 3
mx  3 có một điểm cực trị tại x  1. Khi đó hàm số đạt cực trị tại
điễm khác có hoành độ là: 1 1 1 A. . B. . C.  1 . D. . . 4 3 3 2 1
Câu 70. Nếu x  1 là đivểm cực tiểu của hàm số y
x3  mx2  m2  4 x  5 thì tập tất cả các trị của 3
m có thể nhận được là: A. 1. B. -3. C. 1 hoặc -3. D. 3;    1 .
Câu 71. Hàm số y ax3  ax2  1 có điểm cực tiểu x  2 khi điều kiện cũa a : 3 A. a . 0 B. a . 0 C. a . 2 D. a . 0
Câu 72. Gọi x , x là hai điể cực trị của hàm số
y x3  mx2  m2    m3 3 3 1
m . Giá trị m để 1 2
x2  x2  x x  7 là: 1 2 1 2
TRUNG TÂM THẦY DIÊU – FB TRẦN CÔNG DIÊU 25
TRẦN CÔNG DIÊU [ĐĂNG KÍ HỌC OFF TPHCM – CALL 01638.645.228] A. m . 0 B. m   9 . C. m   1 . D. m   . 2 2 2
Câu 73. Giá trị m để hàm số y x3  mx2 4
 3x có hai điểm cực trị thoả x  4x  0 là: 1 2 A. m   9 . B. m   3 . C. m . 0 D. m   1 . 2 2 2
Câu 74. Đường thẳng đi qua hai điểm cực trị của đồ thị hàm số y x3  x2 3
 9x m có phương trình
A. y  8x m.
B. y  8x m . 3
C. y  8x m . 3
D. y  8x m . 3
Câu 75. Nếu x  1 là hoành độ t rung điễm cũa đoạn thẵng nối hai điễm cực đại , cực tiễu cũa đồ thị 1
hàm số y x3  m  2 x2  2m  3 x  2017 thì tập tất cả các trị của m là: 3 A. m   . 1 B. m   . 1 C. m   3 .
D. Không có giá trị m . 2
Câu 78. Giá trị m để khoảng cách từ điểm M 0; 3 đến đường thẳng đi qua hai điểm cực trị của đồ 2
thị hàm số y x3  m 3 x  1 bằng là: 5 m  1 m  1 A.  . B. m  1. C.  .
D. Không có giá trị m . m    1 m   3
Câu 79. Cho hàm số y x3  m   x2 2 3 1
 6m 2x 1. Xác định m để hà số có điểm cực đại và điểm
cực tiễu nằm trong khoãng 2; 3 A. m ;
1 3 3; 4.
B. m1; 3 .
C. m3; 4 .
D. m1; 4 .
Câu 80. Đễ hàm số y x3  x2 6
 3m 2x m6 có cực đại, cực tiễu tại x ,x sao cho x  1 x thì 1 2 1 2
giá trị của m là: A. m . 1 B. m . 1 C. m   . 1 D. m   . 1 1
Câu 81. Tìm tất cả các giá y
x3  mx2  m  2 x trị của tham số m để hàm số có hai điểm cực trị 3
nằm trong khoãng 0;  ?
TRUNG TÂM THẦY DIÊU – FB TRẦN CÔNG DIÊU 26
TRẦN CÔNG DIÊU [ĐĂNG KÍ HỌC OFF TPHCM – CALL 01638.645.228] A. m . 2 B. m . 2 C. m . 2 D. 0  m . 2
Câu 82. Với các giá trị nào cũa m thì hàm số y x3  x2 3  m
3 x  1 có các điểm cực trị nhỏ hơn 2? m  0 A. m . 0 B. m . 1 C.  . D. 0  m . 1 m   1
Câu 83. Cho hàm số y x3   a   x2 2 3 2 1
 6aa  
1 x  2 . Nếu gọi x , x lần lượt là hoành độ các điễm 1 2
cực trị cũa đồ thị hàm số thì giá trị x x bằng 2 1 A. a . 1 B. a. C. a . 1 D. 1.
Câu 84. Cho hàm số y x3  mx2 2 12x 1 .
3 Với giá trị nào cũa m thì đồ thị hàm số có điểm cực đại ,
cực tiễu các đều trục tung? A. 2. B. -1. C. 1. D. 0.
Câu 85. Đồ thị hàm số y  x3  mx2 3  m
3  1 có hai điểm cực đại, cực tiễu đối xứng nhau qua đường
thẵng d : x  8y  74  0 thì tập tất cả các giá trị của m là: A. 1. B. -2. C. -1. D. 2. 1 4
Câu 86. Đồ thị hàm số y x3  m  
1 x2  2m  
1 x  . Tìm tập tất cả các giá trị của m  0 để đồ 3 3
thị hàm số có điểm cực đại thuộc trục hoành? A. m  1 . B. m . 1 C. m  3 . D. m  4 . 2 4 3
Câu 87. Cho hàm số y x3  x2 3
mx m 2 với m là tham số, có đồ thị là C . Xác định m để Cm m
có các điểm cực đại và cực tiểu nằm về hai phía đối với trục hoành? A. m . 2 B. m . 3 C. m . 3 D. m . 2 1
Câu 88. Cho hàm số y
x3  mx2  2m  
1 x  3 với m là tham số, có đồ thị là C . Xác định m để m  3
C có các điểm cực đại và cực tiểu nằm về cùng phía đối với trục tung? m      1 m 1 m   A. m  1 . B. m . 1 C.  2 . D.  . 1 2   m   1 m  2
TRUNG TÂM THẦY DIÊU – FB TRẦN CÔNG DIÊU 27
TRẦN CÔNG DIÊU [ĐĂNG KÍ HỌC OFF TPHCM – CALL 01638.645.228]
Câu 89. Hàm số y ax3  bx2  cx d đạt cực trị tại x , x nằm hai phía trục tung khi và chĩ khi: 1 2
A. a  0,b  0,c . 0
B. a và c trái dấu.
C. b2 12ac . 0
D. b2 12ac . 0
Câu 90. Cho hàm số y x3  mx2  m2 3 4
 2 . Tìm m để đồ thị có hai điễm cực trị A,B sao cho I 1;0
là trung điểm của AB . A. m . 0 B. m   . 1 C. m . 1 D. m . 2
Câu 91. Với giá trị nào cũa tham số m thì đồ thị hàm số y x3  mx2 3
 2 có hai điểm cực trị A,B sao
cho A, B và M 1; 2 thẵng hàng. A. m . 0 B. m  2. C. m   2.
D. m   2.
Câu 92. Với giá trị nào cũa tham số m thì đồ thị hàm số y  x3  m
3 x  1 có hai điểm cực trị A,B sao
cho tam giác OAB vuông tại O , với O là gốc toạ độ? A. m   . 1 B. m . 0 C. m  1 . D. m . 0 2
Câu 93. Cho hàm số y ax4  bx2  c a  0 . Trong điều kiện nào sau đây thì hàm số có ba cực trị:
A. a,b cùng dấu và c bất kì.
B. a,b trái dấu và c bất kì.
C. b  0 và a,c bất kì.
D. c  0 và a,b bất kì.
Câu 94. Cho hàm số y ax4  bx2  1a  0 . Đễ hàm số có một cực tiễu và hai cực đại thì a,b cần thoã mãn:
A. a  0,b . 0
B. a  0,b . 0
C. a  0,b . 0
D. a  0,b . 0
Câu 95. Cho hàm số y ax4  bx2  1a  0 . Đễ hàm số có một cực trị và là cực tiễu thì a,b cần thoã mãn:
A. a  0,b . 0
B. a  0,b . 0
C. a  0,b . 0
D. a  0,b . 0
Câu 96. Hàm số y x4  mx2  m2 2
m có ba cực trị khi: A. m . 0 B. m . 0 C. m . 0 D. m . 0
Câu 97. Đồ thị hàm số y x4  x2 3
ax b có điểm cực tiểu A2;2 . Tìm tổng a b
TRUNG TÂM THẦY DIÊU – FB TRẦN CÔNG DIÊU 28
TRẦN CÔNG DIÊU [ĐĂNG KÍ HỌC OFF TPHCM – CALL 01638.645.228] A. -14. B. 14. C. -20. D. 34.
Câu 98. Đồ thị hàm số y ax4  bx2  c có điểm cực đại A0; 3 và điêm cực tiểu B1; 5 . Khi đó
giá trị của a,b,c lần lượt là: A. -3;-1;-5. B. 2;-4;3. C. 2;4;-3. D. -2;4;-3.
Câu 99. Tìm m để đồ thị hàm số y x4  m2  m  x2 2 1
m 1 có một điểm cực đại , hai điễm cực
tiễu và thoã mân khoãng cách giư̂a hai điễm cực tiễu ngắn nhất. A. m   1 . B. m  1 . C. m  3 . D. m   3 . 2 2 2 2
Câu 100. Cho hàm số y  x4  mx2 2
 4 có đồ thị là C . Tìm các giá trị của m để tất cả các điểm m  cực trị cũa C
đều nằm trên các trục toạ độ. m  A. m . 0 B. m . 2 C. m . 0
D. m  0 hoặc m . 2
Câu 101. Giả trị của tham số m bằng bao nhiêu đễ đồ thị hàm số y x4  mx2 2
 1 có ba điểm cực trị A0;
1 , B,C thoả BC  4 ? A. m   . 4 B. m  2. C. m . 4
D. m   2.
Câu 102. Cho hàm số y x4  m   x2  m2 2 1
, m là tham số thực. Tìm m để đồ thị hàm số có ba điểm
cực trị tạo thành một tam giác vuông. A. m   . 1 B. m . 0 C. m . 1 D. m  2. . 1
Câu 103. Tìm m để đồ thị hàm số y
x4  3m  
1 x2  2m  
1 có ba điểm cực trị tạo thành tam giác 4
có trọng tâm là gốc toạ độ. A. m   2 . B. m  2 . C. m   1 . D. m  1 . 3 3 3 3 x2  mx  1
Câu 104. Hàm số y
có cực đại và cực tiểu thì điều kiện của m là: x  1 A. m . 0 B. m . 0 C. m.  D. m . 0 x2  mx  1
Câu 105. Hàm số y
có cực đại tại x  2 thì giá trị thực của m bằng: x  1
TRUNG TÂM THẦY DIÊU – FB TRẦN CÔNG DIÊU 29
TRẦN CÔNG DIÊU [ĐĂNG KÍ HỌC OFF TPHCM – CALL 01638.645.228] A. -1. B. -3. C. 1. D. 3. 
Câu 106. Hàm số y sin3x msin x đạt cực đại tại x  khi m bằng: 3 A. 5. B. -6. C. 6. D. -5. 
Câu 107. Biết hàm số y a sin x bcos x x0  x  
2  đạ cực trị tại x
; x   . Khi đó tỗng a b 3 bằng 3 A. 3. B.  . 1 C. 3  . 1 D. 3  . 1 3
TRUNG TÂM THẦY DIÊU – FB TRẦN CÔNG DIÊU 30