


















Preview text:
lOMoAR cPSD| 49831834 lOMoAR cPSD| 49831834 Mục lục
1 Hàm số một biến 1
1.1 Giới hạn . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 1 1.1.11.1.2
Giới hạn x → ∞ . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 12 Nhân
lượng liên hợp . . . . . . . . . . . . . . . . . . . . . . . . . . . .
1.1.3 Dạng vô định 1∞ . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 3
1.1.4 Tính giới hạn sử dụng vô cùng bé tương đương . . . . . . . . . . . . 4
1.1.5 Tính giới hạn bằng quy tắc L’ Hospital . . . . . . . . . . . . . . . . . . 7
1.2 Tìm vô cùng bé tương đương . . . . . . . . . . . . . . . . . . . . . . . . . . . 8
1.3 Dùng khai triển Maclaurin tìm vô cùng bé tương đương . . . . . . . . . . . . 9
1.4 Tọa độ cực . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 10
1.5 Tiệm cận . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 10
1.6 Hàm số liên tục . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 11 2 Đạo hàm 13
2.1 Tính đạo hàm bằng định nghĩa . . . . . . . . . . . . . . . . . . . . . . . . . . 13
2.2 Đạo hàm cấp cao . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 14
2.3 Vi phân cấp một . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 15
2.4 Vi phân cấp hai . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 16
2.5 Đạo hàm hàm ẩn . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 16 2.6 Đạo hàm của
hàm có chứa tham số . . . . . . . . . . . . . . . . . . . . . . . .
17 2.7 Tiếp tuyến . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . 19 2.8 Đơn điệu, cực trị . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
19 2.9 Giá trị lớn nhất, nhỏ nhất . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 23
2.10 Khai triển Maclaurin . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 24 3 Tích phân 27 3.1 Tích phân bất định
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 27
3.2 Đạo hàm của tích phân . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 36 3.3 Tích phân xác định
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 37
3.4 Tích phân suy rộng loại I . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 41 3.5 Tích phân suy rộng loại II
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . 44 3.6
Ứng dụng tích phân . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 46 4 Chuỗi số 50
4.1 Câu hỏi lý thuyết . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 50 4.2 Tính tổng riêng
phần . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 51 Trang ii Mục lục lOMoAR cPSD| 49831834
4.3 Chuỗi hình học . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 51
4.4 Sử dụng các tiêu chuẩn hội tụ . . . . . . . . . . . . . . . . . . . . . . . . . . . 52
4.5 Chuỗi hàm . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 60
5 Phương trình vi phân 62 5.1 Vi phân cấp 1
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 62
5.1.1 Dạng tách biến . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 62
5.1.2 Dạng đẳng cấp . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 64
5.1.3 Dạng toàn phần . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 64
5.1.4 Tuyến tính cấp 1 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 65
5.1.5 Dạng Bernoulli . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 67
5.1.6 Nhận dạng phương trình vi phân cấp 1 . . . . . . . . . . . . . . . . . 67
5.2 Phương trình vi phân cấp hai . . . . . . . . . . . . . . . . . . . . . . . . . . . 68 lOMoAR cPSD| 49831834 Chương1 Hàm số một biến Mục lục chương 1 1.1
Giới hạn . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 1
1.1.1 Giới hạn x→∞ . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 1
1.1.2 Nhân lượng liên hợp . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 2
1.1.3 Dạng vô định 1∞ . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 3
1.1.4 Tính giới hạn sử dụng vô cùng bé tương đương . . . . . . . . . . . . . . . . . . . 4
1.1.5 Tính giới hạn bằng quy tắc L’ Hospital . . . . . . . . . . . . . . . . . . . . . . . . . 7
1.2 Tìm vô cùng bé tương đương . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 8
1.3 Dùng khai triển Maclaurin tìm vô cùng bé tương đương
. . . . . . . . . . . . . . . . . 9
1.4 Tọa độ cực . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 10
1.5 Tiệm cận . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 10
1.6 Hàm số liên tục . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 11 1.1 Giới hạn 1.1.1
Giới hạn x → ∞ √ + + +
Câu 1. Tìm L = x→+∞ 2 x √ − + A. L = 1. B. L = 1/2. C. L = 0. D. L = ∞. A. L = B. L = C. L D. L lOMoAR cPSD| 49831834 Trang Câ2
u 2. Tìm L = lim
Chương 1. Hàm số một biến √ + + +
x4 + x + 1 x→+∞8x C. L = 0. D. L = +∞ . A. L = 1. B. L = 1/8. Câu 3. Tìm L 5 + x4 + x + 2 A. L = 10. x→∞ x B. L = 0. C. L = ∞. D. L = 1/2 . = Câu 4. Tìm L 10 x→∞ 10 2 . . = ∞ . Câu 5. Tìm L x ∞ x A. L = 0. → B. L = 1/3. C. L = 1/2. D. L = 1 . + 1 1.1.2
Nhân lượng liên hợp √
Câu 6. Tìm L =
+ x − √x2 − x → + x A. L = 1/2. B. L = 1/3. C. L = 1. D. L = 2 . √ − − → +
Câu 7. Tìm L = 2x x
A. L = +∞.B. L = 1.
C. L = 1.D. L = 1. − C. L = 0. D. L = 0. A. L = C. L = D. L = lOMoAR cPSD| 49831834 1.1 Giới hạn Trang 3
Câu 8. Tìm L = 2x √ − − x →− A. L = ∞.B. L = 0.
Câu 9. Tìm L = lim 2x − √x2 − 2x √ Câu 10. Tìm A. L = ∞. →∞ x B. L = 0. C. L = 0. D. L = 0.L =− p2x2 − A. L = ∞. B. L = 0. x C. L = 0. D. L = 0.
Câu 11. Tìm L = lim x A. L = ∞.
x→∞ B. L = 0. C. L = 1. D. L = 2 . Câu 12. Tìm L A. L = ∞. B. L = 0. C. L = 1. D. L = 2 . Câu 13. Tìm L A. L . B. L = √3 2. C. L = ∞. D. L = 0 .
Câu 14. Tìm L = 3 3 2
Câu 15. Tìm L = lim 3 x3 − 3x√x + 3x + 1 − 3 x4 − 3x + 4 x→+∞pB. L = 1. C. L = −1. A. L = ∞. D. L = 0 . x √ √ A. L = = + + − + − ∞. B. L = 0. C. → L = −1. = √ D. L = 1 . √ √ p − + + − − + → + √ Câu 16. Tìm L A. L = ∞. B. L = 0. C.
L = 1. D. L = 2 . = √ √ + + + − + + → Câu 17. Tìm L4 A. L = ∞. B. L = 0. C. L = 1. D. L = 2 . lOMoAR cPSD| 49831834 Trang 4
Chương 1. Hàm số một biến Câu 18. Tìm L x2 + 4 = √ √ + + − − ∞. → B. L = 0. 1. 2 .
Câu 19. Tìm L = lim √3
2x3 + 4x2 + 1 + √3 −x3 − x2 + 4 A. L = ∞.
x→∞ B. L = 0. C. L = 1. D. L = −1 . Câu 20. Tìm L A. L = ∞. B. L = 0. C. L = 1. D. L . 1.1.3
Dạng vô định 1∞ x
Câu 21. Tìm L = lim A. L = −1. B. L = 1. C. L = 2. D. L = ∞ . 1 x→∞ −
Câu 22. Tìm L = lim + x x x A. L = ∞. B. L = 1. C. L . D. L . x Câu 23. Tìm L x − A. L = ∞. B. L = 1. C. L = e2. D. L = e3 . x Câu 24. Tìm L − − A. L = ∞. B. L = 1. C. L = e2. D. L = e3 . x2+3
Câu 25. Tính L x A. L = e−2. B. L = e−1. C. L = e. D. L = e−3 .
Câu 26. Tính L A. L . B. L . C. L . D. L = e. A. L = C. L = D. L = lOMoAR cPSD| 49831834 1.1 Giới hạn Trang 5
Câu 27. Tìm L = lim(cos 3x)x2/2 x→0
D. L = e−3/2 . A. L = ∞. B. L = 1. C. L = e−9 .
Câu 28. Tìm L = lim(cos x + sin x)cot x x 0 → A. L = 1. B. L = e. C. L. D. L = +∞ .
Câu 29. Tìm L = lim(cos x)cot2x x → 0 A. L = 1. B. L = e. C. L. D. L = +∞ .
Câu 30. Tìm L = lim(cos 2x + x2)cot3x x → 0 A. L = 1. B. L = e. C. L. D. L = +∞ .
Câu 32. Tìm L = lim(cos x + sin2x)cot2x x→0 B.
L = 2/3. A. L = 0. C. L = −2/3. D. L = ∞ .
Câu 33. Tìm giới hạn L = limx1/(2x−2) x 1
Câu 31. Tìm L = lim(cos x + sin2x)cot x x→0 1. e. . = √e → A. L = 1. B. L = e. C. L = e2. D. L. 1/x
Câu 34. Tìm giới hạn L →0 2 A. L = 1. B. L . C. L . D. L = ∞ .
Câu 35. Tìm giới hạn L cot2x A. L = 1. B.x→L0 . C. L . D. L = 1/2 . A. L = 0. B. L = e. C. L = e. D. L = e.
Câu 37. Tìm giới hạn L = lim (sin x)1/ lnsin2x lOMoAR cPSD| 49831834 Trang 6
Chương 1. Hàm số một biến x 0+ Câu 36. Tìm giới
hạn L =x)(x−2) x A. L = e. B.→L = e2. C. L . D. L = 1 .
Câu 38. Tìm giới hạn L = lim (sin3x)2/ lnsin x x→0+ A. L = e. B. L = e2. C. L . D. L = 1 .
Câu 39. Tìm giới hạn L = lim (cot x)ln(1+x2) x→0+ A. L = e. B. L = e2. C. L . D. L = 1 .
1.1.4 Tính giới hạn sử dụng vô cùng bé tương đương
Câu 40. Tìm A = x A. A = B = 2.
B. A = −∞, B = 2.
C. A = −∞, B = 2.
D. A = −∞, B = 2.
Câu 41. Tìm L = lim x − +
sin5x 2 sin2x2 A. L = 1. x→04x
+B.arcsinL = −x1+. x sin22x C. L = 2. D. L = 3 . Câu 42. Tìm L sin4x
A. L = 0.B. L = 2. C. L = 1/2. D. L = 1/4 . A. L = 0. →0 x sin3x B. L = 1/3. C. L = 2/3. D. L = 4/3 . A. L = C. L = D. L = lOMoAR cPSD| 49831834 1.1 Giới hạn Trang 7
Câu 43. Tìm L =
Câu 44. Tìm L = lim − √ x 2 1 cos 2 2. x→0 sinB. Lx= 1/2. 1. 1/4 . Câu 45. Tìm L A. L = 0. → B. L = 1. C. L = 1/2. D. L = 1/4 . √
Câu 46.A. LTìm= 1/L2=. xlim→0√3 x
+B.1L−=√√3111. −− xx x + 1 − C. L = 3/2. D. L = ∞ . . x 0 x sin2x x→0 16 + x − 2 A. L = 4/5. B. L = 5/4. C. L = 3/4. D. L = 4/3 . 1 cos
Câu 48. Tìm L = lim − x + ln(1 +
tan22x) + 2arcsin3x A. L = 0. x→0
B. L =11−. cos x + sin2xC. L = 2. D. L = 3 . arcsin )
Câu 49. Tìm L = lim (x3 + tan23x +22arcsin3x A. L = 0. x→0
B. L1=− cos6. x + sin x C. L = 8. D. L = 22/3 . arcsin )
Câu 50. Tìm L = lim (x3 + tan23x +32arcsin3x D. L = 18 . lOMoAR cPSD| 49831834 Trang 8
Chương 1. Hàm số một biến A. L = 0. x→0
B. L1=− cos6. x + sin x C. L = 8.
Câu 51. Tìm L = lim x3 + sin23x + 3arcsin 3
2 x x→0 ln(1 + 2x2) + sin x A. L = 0. B. L = 6. C. L = 5/2. D. L = 3 . √ Câu 47. Tìm L Câu 52. Tìm L 0 arcsin 2 2 x + x A. L = 4. x→ B. L = 3. C. L = 2. D. L = 1 . Câu 53. Tìm L → A. L = 1/2. B. L C. L = 5/2. D. L = −3/2 . x→ A. L = −4/7. B. L = 1. C. L = −1/2. D. L = −8/7 . 0 x x Câu 54. Tìm L 0 ln(cos 4x + x ) A. L = C. L = D. L = lOMoAR cPSD| 49831834 1.1 Giới hạn Trang 9 Câu 55. Tìm L →
(2x + x + 1)(sin 2x + x ) A. L = 1. B. L = −1. C. L = 1/2. D. L = −1/2 .
Câu 56. Tìm L = lim→ 3 +( + )
3sinx +x 4 )(cossin 4x x2−−sin21 x) x 0(x D. L = 1/4 . A. L = −1/8. B. L = 1/8. C. L = −1/4.
Câu 57. Tìm L = lim
(cos 2x − ex)(x2 + 1 − cos x) x 0 2 2
x→0 x(cos 3x 3/8.. = 3/4
Câu 58. Tìm L = xlim→0
arcsinB.3Lx +=x231arcsin−. +
2x22+x x 3arcsinC. Lx= 2. D. L = 3 . A. L = 0. 2 A. L = 0.
→0 x sinB.xtanL =x1. x C. L = 1/2. D. L = 1/4 . 1 cos
Câu 60. Tìm L = lim→−4xB.+Larctanx=−1/x32x. x 0sin A. L = 0. C. L = 2. D. L = 1 . lOMoAR cPSD| 49831834 Trang 10
Chương 1. Hàm số một biến Câu 59. Tìm L 2 Câu
Câu 61. Tìm L = lim √ + x 62. − √ − x 1 3sin 1 Tìm tan L A. L = 2. x→0 B. L = 1x. C. L = 1/2. D. L = 0 . A. L √ Câu 63. Tìm L x − = 1. = x x→0 B. A. L = 1/4. →0 B.x L = 1/2. C. L = 1. D. L = 0 .L = −
Câu 64. Tìm L = lim
x x +sin5x +2sinx +2xx2 = 1.
x→0sin B. Larcsin= −1. C. L = 2. A. L
arcsin3x − sin25x + sin2x D. L = 3 .
Câu 65. Tìm L = lim 2 2 A. L = 3.
x→0 4B.x +L arcsin= −1. x + x C. L = 0. D. L = 1 . 3sin2. x
C. L = 2.D. L = 0 . x x→1 − A. L = 0. B. L = 1/2. C. L = 3/2. D. L = 2/3 . A. L = C. L = D. L = lOMoAR cPSD| 49831834 1.1 Giới hạn Trang 11 ln (
Câu 67. Tìm giới hạn L = lim 1−− x2 + 2 x) 2 x A. L = −1.
B.x→L0 =x2. arctan C. L = −2. D. L = 1 .
Câu 68. Tìm giới hạn L = lim e−x − 1 2 A. L = 0.
B.x→L0sin= −x1+. 2x C. L = 1. D. L = 1/2 . √
Câu 66. Tìm giới hạn L 1
Câu 69. Tìm giới hạn L = lim x e1/x A. L = 0. B.→L∞ .C. L = 1. D. L = 2 . x
Câu 70. Tìm giới hạn L A. L = 0. B. L =−1/2. C. L = 1. D. L = −1/2 . lOMoAR cPSD| 49831834 Trang 12
Chương 1. Hàm số một biến
Câu 71. Tìm giới hạn L
x→L0√=11+. sin2x + xx2 −√21x3+ sin 2. 1/2 . 0. B. A. L = C. L = D. L = lOMoAR cPSD| 49831834 1.1 Giới hạn Trang 13
Câu 72. Tìm giới hạn L √cos x √cos 2 A. L = 0.
B.→L0x=arcsin3/4. x + x − 2C.x L = 3/2. D. L = 2 . x
Câu 73. Tìm giới hạn L A. L = 0.
B.x→L0x=arcsin3/4. x tan x C. L = 1/2. D. L = 2 .
Câu 74. Tìm giới hạn L x→π/4 cos 2x A. L . B. L . C. L . D. L .
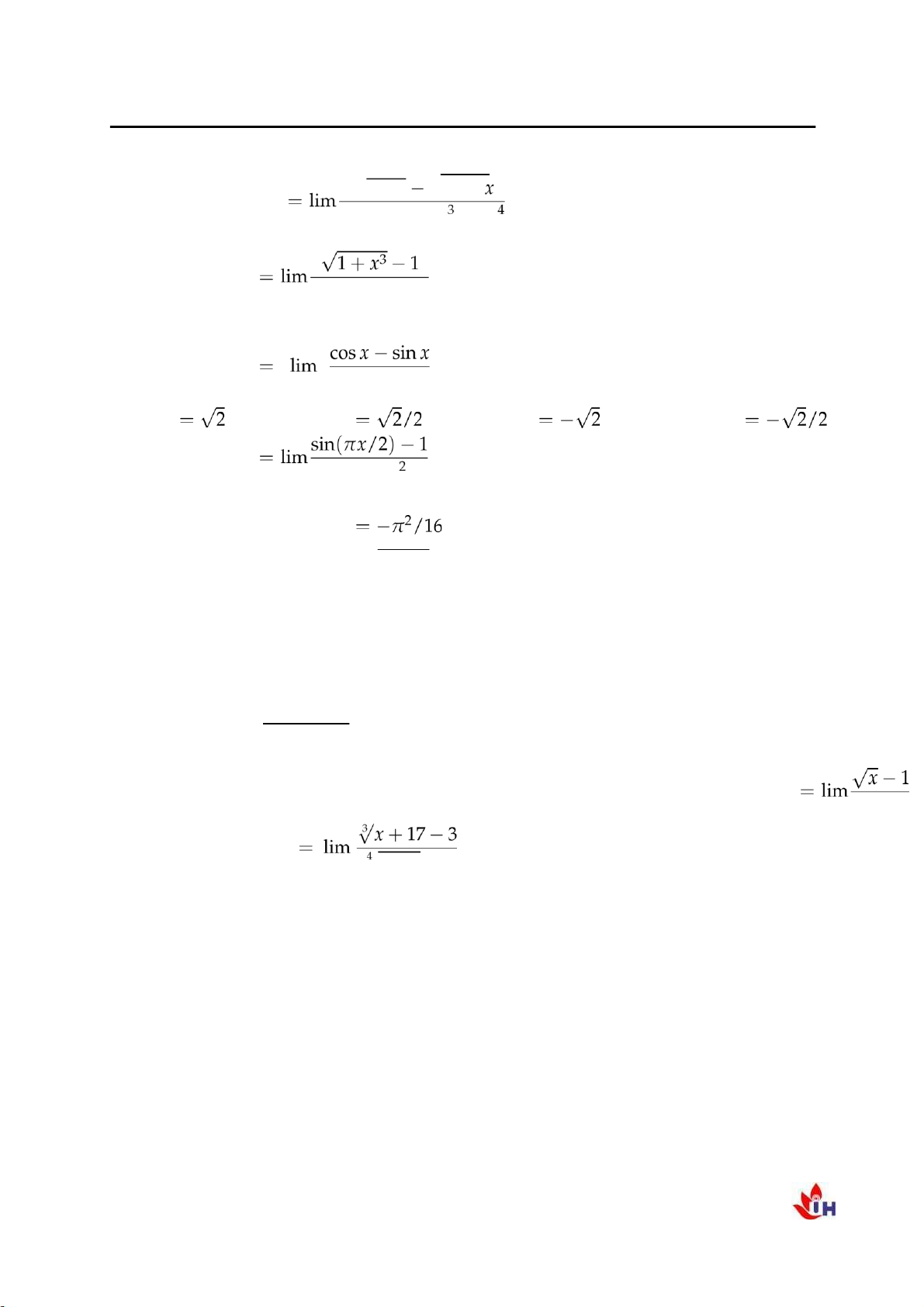
Câu 75. Tìm giới hạn L x→1 (x2 − 1) A. L = π2/16. B. L . C. L = π2/32.
D. L = −π2/32 . x→10 x + 6 − 2 = D. L −32/27 . A. L = 35/27. B. L = 32/27. C. L = 37/27. 1.1.5
Tính giới hạn bằng quy tắc L’ Hospital
Câu 77. Tìm L = lim 2 x−24−x1+ 3 A. L = 0. x→1 x B. L = −1. C. L = 2. D. L = ∞ . √
Câu 76. Tìm giới hạn L 1 x A. L = 0. A. L = = C. L D. L . lOMoAR cPSD| 49831834 Trang 14
Chương 1. Hàm số một biến Câu 78. Tìm L x→ 2 −B.1L = 1. C. L = 1/2. D. L = 1/4 . A. L = 0.
→1 x −B.1L = 1/2. x C. L = 1/3. D. L = 1/6 .
Câu 80. Tìm giới hạn L = lim x ln x A. L = ∞. B.x→L0+= 0. C. L = 1. D. L = 2 .
Câu 81. Tìm giới hạn L = lim x − arctan x 3 A. L = 0.
B.x→L0 = 1/x3. C. L = 2. D. L = −1/3 . Câu 79. Tìm L 2
Câu 82. Tìm giới hạn L =ln(x + 1)) x B. L = 1. A.C. LL == 1−.1. D. L = 1.
Câu 83. Tìm giới hạn L = lim xex B. L = 0. D. L = 0. A. L = −∞ . x→−∞ C. L = 0. ex − 1 − x L = 0 2
Câu 84. Tìm giới hạn lim
x→L 1.x = 2. = 1/2 0. B. 3
Câu 85. Tìm giới hạn L = limex − 1 − x3 6 A. L = 0.
B.x→L0 = 1sin. x C. L = 1/2. D. L = 2 .
Câu 86. Tìm giới hạn L =
ex−1 − e1−x → B. L = 1. 1 x D. L = 1. A. C. D. lOMoAR cPSD| 49831834 Trang 15 A. L = 0. C. L = 1.
Câu 87. Tìm giới hạn L = L →1 A. L = 1. B. L = 1/2. C. L = 1/4. D. L = 1/8 . x 1 − 1 ln + 2ln x
Câu 88. Tìm giới hạn L = lim | ln x| A. L = 0.
B.x→L0 = 1.ln |x| C. L = 2. D. L = ∞ . 2tan
Câu 89. Tìm giới hạn L = lim 32x
+xln−(1tan2+ xx3) + x4 x→0arcsin A. L = 2/9. B. L = −2/9. C. L = 3/4. D. L = 1 . 2sin
Câu 90. Tìm giới hạn L = lim x − sin2x A. L = 1.
B.x→L02=tan−1x. − tan2x C. L = 1/2. D. L = −1/2 .
Câu 91. Tìm giới hạn L = lim x − arcsin x A. L = 1.
B.x→L0 =x−−1tan. x C. L = 1/2. D. L = −1/2 . 2
Câu 92. Tìm giới hạn L = lim
x − arcsin 2x 3
x→0ln(1 + 2x2) + arcsin x A. L = 0. B. L = −2/9. C. L = −4/9. D. L = 8/9 .
Câu 93. Tìm giới hạn L = lim(cot x − 1/x) x→L0 = 1/2. C. L = −1/2. A. L = 0. B. D. L = 1 . A. C. D. lOMoAR cPSD| 49831834 Trang 16
Chương 1. Hàm số một biến
Câu 94. Tìm giới hạn L →0 A. L = 0. B. L = 2/3. C. L = −2/3. D. L = ∞ . 5x − 4x
Câu 95. Tìm giới hạn L = lim 2 + x x→0 x 6223 A. L = ln . B. L . C. L = . D. L = 0 . 51000 1.2
Tìm vô cùng bé tương đương
Câu 96. Cho f(x) = (cos 2x − ex)(x2 + 1 − cos x) + x(cos 3x − cos x) ln(1 + ex − cos x). Khi x → 0 thì x3 2x2 3x3 x2 f . B. f . f . f .
1.3 Dùng khai triển Maclaurin tìm vô cùng bé tương đương Câu 97. Cho
fx Khi x → 0 thì 2 2 ( ) ∼ A. f(x) ∼ x . B. (x) ∼ x . C. x . D. f x . Câu 98. Cho fKhi x → 0 thì x2 x x x2 A. f . B. f(x) ∼ . C. f(x) ∼ − . D. f . 5 5
Câu 99. Khi x → 0, VCB tương đương với 3xx3 3x2 x A. f(x) ∼ . B. f . C. f .
D. f(x) ∼ − . A. C. D.




