lOMoAR cPSD| 47206071 TỔ 2 BÀI TẬP CHƯƠNG 2 A. TRẮC NGHIỆM
Chọn câu kết luận úng Câu 1: ax by c Cho hệ phương trình bx cy a
với a,b ,c là các tham số cx ay b
Gọi A A, là ma trận hệ số và ma trận mở rộng a) Rank A=3 b) A a b c3 3 3 3abc
c) Nếu hệ có úng một nghiệm thì A 0
d) Nếu hệ có nghiệm thìa b c3 3 3 3abc Lời giải a b a b c Ta có : A b cc a , A a b c T b c a , A b c ac a b a) R A R A T 2 câu A sai
b) A 3abc a b c ( 3 3 3) câu B sai
c) Để có 1 nghiệm duy nhất R A R A A 0 câu C sai
d) Để hệ có nghiệm R A R A
2 A 0 a b c3 3 3 3abc 1 lOMoAR cPSD| 47206071 TỔ 2 Chọn D Câu 2:
x 2y 2z 3 Cho hệ phương trình :
2x (m 3)y 7z m 9
x (m 3)y mz 1
Tìm m ể hệ phương trình a) m 1 b) m 1 c) m 1, m 1 d) Cả 3 câu ều sai Lời giải 1 2 1 5 1 2 1 A 1 2 mm A , 1 2 m m 2 2m m 2 2
A 2 2m2 2 2m 2m 2 2m2 4m 2 A 0 m 1 1 5 1 1 2 d dd d3 12 1 5 1 2 A 1 0 0 4 1 2 2 1 1 1 4 0 2 1 0 0 RankA 2
R A( ) R A( ) m 1 2 lOMoAR cPSD| 47206071 TỔ 2 RankA 3
Để hệ ã cho có vô số nghiệm R A( ) R A( ) 2 3 m 1 0 m 1 CHỌN B Câu 3: x 2y z 5 Cho hệ phương trình: x 2y mz m
. Kết luận nào sau ây úng
mx 2y 2z m
a) Hệ luôn có nghiệm với mọi m
b) Tồn tại m ể hệ vô nghiệm
c) Hệ luôn có úng một nghiệm với mọi m
d) Tồn tại m ể hệ có vô số nghiệm Lời giải 1 2 1 5 1 2 1 A 1 2 m m , A 1 2 m m 2 2m m 2 2
A 2 2m2 2 2m 2m 2 2m2 4m 2
TH1: A 0: Hệ phương trình có 1 nghiệm duy nhất m 1
TH2: A 0: Hệ phương trình có vô số nghiệm hoặc vô nghiệm m 1 1 2 1 5 1 2 1 5 A 1 2 1 1 d dd d3 12 1 0 0 0 4 3 lOMoAR cPSD| 47206071 TỔ 2 1 2 2 1 0 0 1 4 RankA 2
R A R A( ) ( ) m 1 RankA 3
Vậy hệ phương trình vô nghiệm CHỌN B
Câu 4: Gọi s là số nghiệm của hệ nghiệm cơ bản của hệ phương trình
x1 x2 x3 x4 x5 0
2x1 3x2 4x3 5x4 6x5 0. Ta có:
4x1 5x2 6x3 7x4 8x5 0 A. s = 1 B. s = 2 C. s = 3 D. s = 4 Lời giải 2 1 0 1 2 1 0 1 2 1 3 1 3 0 1 0 4 0 1 2 0 dd d4 2 13 d2 dd dd d2 2 m m 00 A 134 d11 12 00 4 4 2 0 4 1 0 7 1 1 2 0 1 0 0 1 5 5 0 1 0 0 2 0 2 m 2 4 0 0 0 0
Vậy hệ vô ịnh nên số nghiệm của hệ cơ bản là 5 – 2 = 3 CHỌN C
Câu 5: Gọi s là số nghiệm của hệ nghiệm cơ bản của hệ phương trình
x1 4x2 2x3 x4 0 4 lOMoAR cPSD| 47206071 TỔ 2
2x1 7x2 3x3 4x4 0 x 1
5x2 3x3 x4 0
x1 2x2 mx3 5x4 0 Ta có s lớn nhất khi: A. m 1 B. m 0 C. m 0 D. m 1 Lời giải 1 4 2 1 0 1 4 2 1 0 1 4 2 1 0 1 1 2 0 A 127533 4 01 0 dd dd d2 2 134 d11 00 1 1 2 0 dd d4 2 13 d2 00 01 010 02 0 1 2 m 5 0 0 2 m 2 4 0 0 0 m 0 0
Để s lớn nhất m 0 s 4 2 2 CHỌN C
Câu 6: Cho hệ phương trình tuyến tính (I): x
y 2z 3t 0
2y 5z 8t 0 .Hệ vecto nào sau ây là 2x
một hệ nghiệm cơ bản của hệ (I)
B. u1 (1,0, 2,1), u2 ( 2,2,0,0),u3 (0,1, 2,
A. u1 (1,0, 2,1), u2 (1,1, 1, 0) 1)
C. u1 (1,0, 2,1), u2 (0,1, 2, 1)
D. u (1,0, 2, 1) Lời giải 5 lOMoAR cPSD| 47206071 TỔ 2 A 1 2 13 0 d2 2 1 d 1 1 2 3 0 5 2 2 8 0 0 0 1 2 0
R A( ) R A( ) 2 4
Hệ vô ịnh phụ thuộc vào 4 - 2 = 2 tham số Hệ tương ương: xz 2yt 20z 3t 0 xz
y2t2( 2 )t 3t 0, x y, tz
x 2(yx y), x y, x X y 2(x y) x y x 1, y
0 z 2,t 1 x 0, y 1 z 2,t 1 CHỌN C 0,3 0,1 0,2
Câu 7: Trong mô hình input, output mở biết ma trận A 0,2 0,4 0,1 Giả sử sản 0,3 0,2 0,3
lượng của ba ngành lần lượt là 80, 100 và 50. Phát biểu nào sau ây là úng?
A. Tổng giá trị nguyên liệu mà ngành 1 ã sử dụng là 40
B. Giá trị nguyên liệu mà ngành 2 cung cấp cho ngành 3 là 10 6 lOMoAR cPSD| 47206071 TỔ 2
C. Giá trị sản lượng mà các ngành cung cấp cho ngành mở là 40, 50, 28
D. Các phát biểu trên là úng Lời giải 0,3 0,1 0,2 80 A 0,2 0,4 0,1 , X 100 0,3 0,2 0,3 60 Xét áp án A:
Tổng giá trị của ngành 1: X1 0,3.80 0,1.100 0,2.60 46 40 (A sai) Xét áp án B:
Giá trị nguyên liệu ngành 2 cung cấp cho ngành 3: X23 0,1.60 6 10 (B sai) Xét áp án C:
Giá trị sản lượng mà các ngành cung cấp cho ngành mở: 1 0 0 0,3 0,1 0,2 80 34
D (In A X). 0 1 0 0,2 0,4 0,1 . 100 38 0 0 1 0,3 0,20,3 60 2 C sai
Vậy cả ba áp án ều sai B. TỰ LUẬN x y 2z 0
Bài 1: Giải và biện luận hệ phương trình: ax y 2z 1 x y az 2 1 1 2 0 1 1 20 7 lOMoAR cPSD| 47206071 TỔ 2 A a1 11a2 12 d add d23 11 0 1 a 2(1 a) 1 0 0 a 22 a 2
TH1: 1 Hệ phương trình có 1 nghiệm duy nhất a 1 x 1
x y 2z 0 a
Hệ phương trình tương ương : (0ax
2)(1z a y)2 2(1 a z) 1 y 2 (a 5 a 6 2)( a 1) z a 2 TH2: a 2 1 1 2 0 1 1 2 0 A 12 11 2 22 1 8 lOMoAR cPSD| 47206071 TỔ 2 d d d2 2 13 1 d 0 0 0 1 0 22 1 R A( ) R A( )
Vậy hệ phương trình vô nghiệm. TH3: a 1 9 lOMoAR cPSD| 47206071 TỔ 2 1 1 2 0 1 1 2 0 A 1 1 2 11 1 1 2 d dd d2 13 1 0 00 0 0 112 R A( ) R A( )
Vậy hệ phương trình vô nghiệm 2x 3y z m
Bài 2: Cho hệ phương trình 3x 2y mz 1 x y z 2 Lời giải 2 3 1m 1 1 22 1 1 22 A 3 2m 1 d1 d3 3 2m 1 dd3 2 12 3 1 dd 0 5 m 6 5 1 1 22 2 3 1m 0 5 5m 4 1 1 22 d d3 4 0 5 m 65 0 0 m 1m 1
R A( ) R A( ) 2 3 ycbt m 1 10 lOMoAR cPSD| 47206071 TỔ 2
Bài 3: Trong mô hình Input – Output mở, cho ma trận hệ số ầu vào
a) Tìm ma trận nghịch ảo của ma trận I-A, với I là ma trận ơn vị cấp 3.
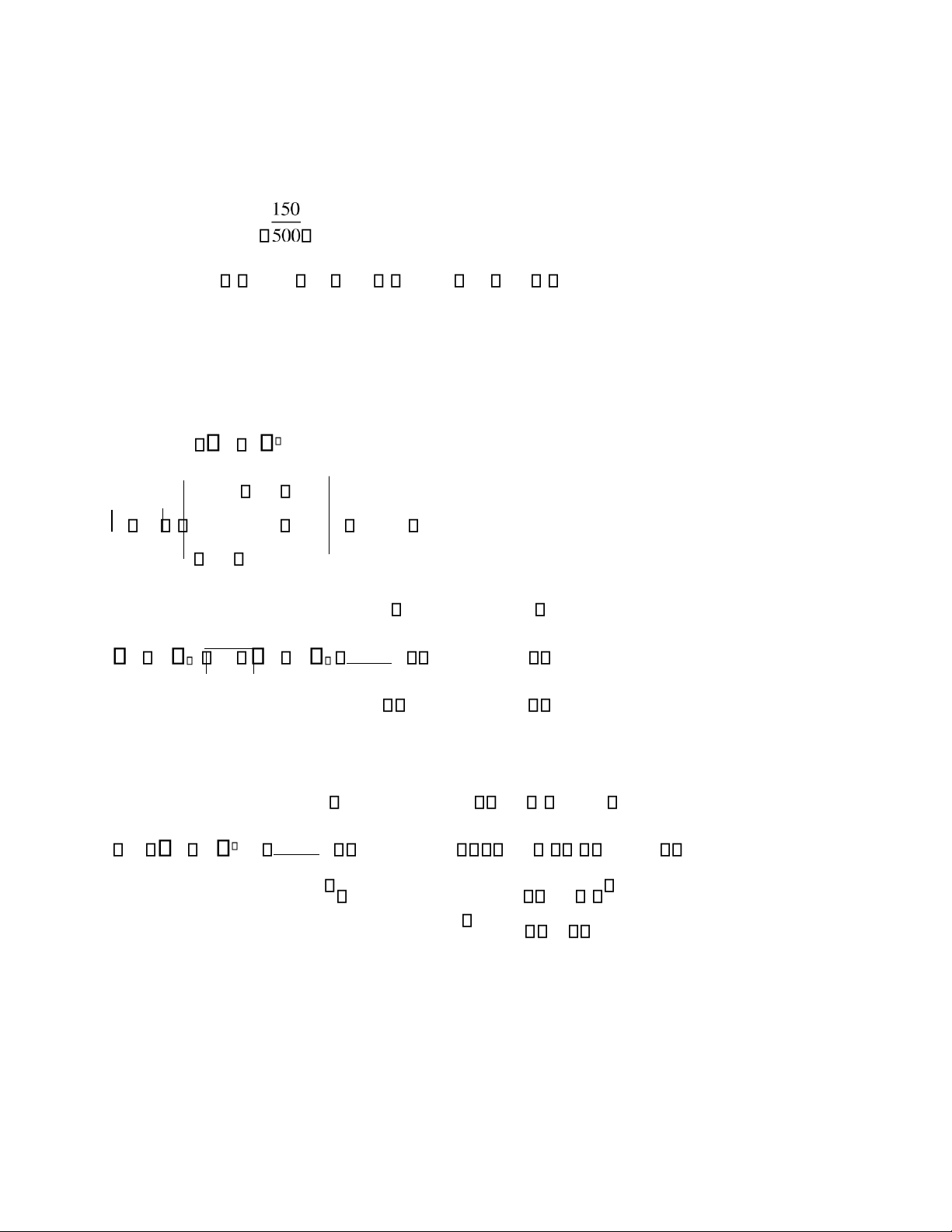
b) Tìm sản lượng của 3 ngành, biết yêu cầu của ngành mở ối với 3 ngành là D = (68, 86, 29) Lời giải a) 0,9 0,2 0,1 (I3 A) 0,2 0,8 0,1 0,3 0,1 0,8 I A 503 100 3 26 15 68 63 17 10 10 . 19 69 11 503 26 15 68 10 68 6036 120 11 . 86 29 50310 . b) 7545 5030 3 1 10 . 19 63 X (I A) .D 150100 17 503 26 69 15 68 11 lOMoAR cPSD| 47206071 TỔ 2 63 17 10 (I3 A) 1 1
.(I3 A) 1000. 1 . 19 69 11
Vậy sản lượng của 3 ngành lần lượt là 120, 150, 100.
Bài 4: Xét mô hình Input-Output mở gồm 3 ngành kinh tế với ma trận hệ số ầu vào 0,1 0,2 0,2 10 A 0,2 0,20,3 , X 10 0,4 0,1 0,2 10 0,1 0,2 0,2 10 5 Y AX 0,2 0,20,3 . 10 7 0,4 0,10,2 10 7 175 a13.100 0,2.100 20 a)
Tìm tổng nguyên liệu ầu vào của ba ngành ể sản xuất ra ược 10 ơn vị ầu ra của từng ngành. b)
Tìm sản lượng ngành 1, biết rằng ngành 3 phải cung cấp cho ngành 1 với lượng
nguyên liệu giá trị 7 ( vt). 12 lOMoAR cPSD| 47206071 TỔ 2 c)
Nếu biết sản lượng của ngành 3 là 100, thì ngành 1 phải cung cấp cho ngành 3 là bao nhiêu? Lời giải a) 0,1 0,2 0,2 10 A 0,2 0,20,3 , X 10 0,4 0,1 0,2 10 0,1 0,2 0,2 10 5 Y AX 0,2 0,20,3 . 10 7 0,4 0,10,2 10 7
Vậy tổng nguyên liệu ầu vào của ba ngành ể sản xuất ra ược 10 ơn vị ầu ra của từng ngành lần lượt là 5, 7, 7. b) Sản lượng ngành 1 175 ( vt) c)
Sản lượng ngành 1 phải cung cấp cho ngành 3 là 100.0,2=20 ( ơn vị tiền) 13 lOMoAR cPSD| 47206071 TỔ 2
BÀI TẬP SÁCH BÀI TẬP 11. 1 2 31 1 2 31 1 2 31 2 m 3 m 1 m 1 72 10 10 A dd d2 2 13 1 d 0 d d3 2 0 m 0 m 1 m 1 m m 1 2 0 m 2 3 0 m m 3 3 1 Với m = 3 1 2 3 1 A 00 021 00 0
R A( ) R A( ) 2 3
Vậy hệ pt có vô số nghiệm
Ta có hệ phương trình tương ương x 2y 30z 1 xy 12 2y 3z 1 2z z z , 2y z
Vậy nghiệm tổng quát của hệ phương trình là 1 2z X z , z 2 z 14 lOMoAR cPSD| 47206071 TỔ 2 13.
Để hệ ã cho là hệ Cramer khi và chỉ khi 1 1 2 D A a a 1 2 (a 1)(a 2) 0 a 12 1 1 a CHỌN D 14. 2 35 2 35 2 11 35 1
d3 (6 a a d 3 2) 23 11 A 2 22 2d 2 0 a dd d 211 0 0 (a 1)(a 4) a 2 3a4 0
6a 3a28 5a2 0
Để hệ ã cho có úng một nghiệm khi và chỉ khi
R A( ) R A( ) 2 (a 10(a 4) 0 a 14 a CHỌN C 15. 1 2 m3 m 1 2 m3 m 1 2 m3 m A 2 m 3 m 1 dd2 2 13 2 1 dd
0 m 4 (3 2 )m (7 m)
(m 4) 3 (d m 2) 2d 0 m 4 (3 2 )m (7 m) 2 m m2 2 0 (m 4) 0 (8 2 )m 0 0
(3 2 )(m m 4) (m 4)(m 1) 15 lOMoAR cPSD| 47206071 TỔ 2 Với m = - 4 0,9 0,2 0,3 I3 A 0,3 0,9 0,1 0,2 0,3 0,8 I3 A 0,488 0 0,69 0,25 0,29 (I 1 3
A) 1 I3 A . I3 A 0,4881 00,,2726 00,,6631 00,,1875 0,69 0,25 0,29 39 89,75
X (I3 A) 1D 1 0,26 0,660,18 . 49 92,95 0,488 0,27 0,310,75 16 77,3 x1 3,22 x x2
(I3 A) 1 D 1,11 x3 0,39
Vậy hệ phương trình có vô số nghiệm CHỌN A 18. a)
Ý nghĩa kinh tế của hệ số a21= 0,3 là 0,3 giá trị của lượng nguyên liệu mà ngành 1
nhận ược từ ngành 2 ể sản xuất ra một lượng sản phẩm có giá trị một ơn vị tiền. b)
Khi sản lượng của ngành 2 là 100, giá trị của lượng nguyên liệu mà các ngành cung cấp lần lượt là: 16 lOMoAR cPSD| 47206071 TỔ 2
Ngành 1 cung cấp: a12.100 0,2.100 20
Ngành 2 cung cấp: a22.100 0,1.100 10
Ngành 3 cung cấp: a32.100 0,3.100 30 c) 0,9 0,2 0,3 I3 A 0,3 0,9 0,1 0,2 0,3 0,8
I3 A 0,488 0 , tồn tại ma trận nghịch ảo I3 A 0,69 0,25 0,29 0,66
(I3 A) 1 I3 1 A . I3 A 0,4881 0,31 0,18 00,,2726 0,75 d)
Gọi X là vecto biểu thị giá trị sản lượng của 3 ngành ta có: 0,69 0,25 0,29 39 0,66 89,75 X (I 0,31 3 A) 1D 0,4881 00,,2726 0,18 . 49 92,95 0,75 16 77,3
Vậy sản lượng của 3 ngành lần lượt là 89,75, 92,95, 77,3. e) 17 lOMoAR cPSD| 47206071 TỔ 2
Mức sản lượng thay ổi của các ngành là: a23.200 20 a03.1000 400 0,7 0,1 0,2 I3 A 0,2 0,6 0,1 0,219 0,3 0,2 0,7 0,4 0,11 0,13 I 1 3
A 1 I3 A I3 A 0,2191 00,,1722 00,,1743 00,,114 0,4 0,11 0,13 66 242,19 X I3 A 1.D 1 0,170,430,11 124 344,93 0,219 0,22 0,170,4 100 345,21
Vậy ngành 1 tăng 3,22, ngành 2 giảm 1,11, ngành 3 tăng 0,39. 20.
a) Ý nghĩa kinh tế của hệ số a23 0,1 là cần một lượng hàng hóa ầu vào của ngành 2 có giá
trị là 0,1 ( vt) ể sản xuất ra một lượng hàng hóa của ngành 3 có giá trị 1 ( ddvt) Khi giá trị
ầu vào của ngành 3 là 200 (dddvt0 thì số tiền mà ngành 2 phải óng góp cho ngành 3 là: a23.200 20( vt) b)
a03 1 (a13 a23 a33) 0,4
Ngành mở óng góp 0,4 ( vt) cho ngành 3 ể ngành 3 sản xuất 1 lượng hàng hóa có giá trị 1 ( vt)
Khi giá trị sản lượng của ngành 3 là 1000 (dvt) thì ngành mở óng góp cho ngành 3 là: a03.1000 400(dvt) 18 lOMoAR cPSD| 47206071 TỔ 2 c)
Theo giả thiết: a02 0,3
Ta lại có : a02 1 (a12 a22 a32) 1 (0,3 m) 0,3 m 4 d)
Với m = 0,4. Gọi X là vecto biểu thị sản lượng của 3 ngành Ta có : X I3 A 1.D 0,7 0,1 0,2 I3 A 0,2 0,6 0,1 0,219 0 0,3 0,2 0,7 0,4 0,11 0,13 I3 A 1 3 1 I3 A 1 0,170,43 0,11 I A 0,219 0,22 0,17 0,4 0,4 0,11 0,13 66 242,19 X I3 A 1.D 1 0,17 0,430,11 124 344,93 0,219 0,22 0,17 0, 100 345,21 4
Vậy giá trị sản lượng của 3 ngành lần lượt là 242,19, 344,93, 345,21. 19