Bộ đề thi môn toán cao cấp | Trường Đại học Kinh tế Thành phố hồ Chí Minh

lOMoAR cPSD| 49831834
Môn thi: TOÁN CAO CẤP Đề số 01 Câu 1 (2 điểm). 3 1 4
1) Tính định thức của ma trận : A 2 4m 5 5 2 3 3 5 7 9
2) Tìm hạng của ma trận : A 5 8 11 14 7 11 15 19 9 14 19 24 Câu 2 (2 điểm). 1 3 7
1) Tìm ma trận nghịch đảo của ma trận A 2 1 2 (nếu có). 7 1 4 1 3
2) Tìm A sao cho AB BA với B 2 0 . x 4 3 x 8
Câu 3 (1 điểm). Tính giới hạn: lim. x 0 4 x 16 2
Câu 4 (1 điểm). Khảo sát tính tăng, giảm và cực trị của hàm sau: f x lnx3 x . dx
Câu 5 (1 điểm). Tính tích phân suy rộng: 2 2 12x 60. 3x lOMoAR cPSD| 49831834
Câu 6 (1 điểm). Cho hàm số: f(x,y) x5 5xy y5 2019. Tính vi phân toàn phần cấp 2 của
hàm số trên tại điểm (0, 0).
Câu 7 (1 điểm). Sử dụng phương pháp nhân tử Lagrange tìm cực trị của hàm số z x2 2y2 với điều kiện 3x 2y 22.
Câu 8 (1 điểm). Giải phương trình vi phân: y/ 5y 2 2019x. Đề số 02 Câu 1 (2 điểm). 3 1 1
1) Tính định thức của ma trận : A 2 4m 7 8 1 1 3 5 7 9
2) Tìm hạng của ma trận : A 2 3 4 5 7 11 15 19 9 14 19 24
Câu 2 (2 điểm). 1 3 7
1) Tìm ma trận nghịch đảo của ma trận A 3 4 9 (nếu có). 6 4 11 1 2 2) Cho ma trận B 3 4
. Tìm ma trận A sao cho AB BA. x2 1lnx
Câu 3 (1 điểm). Tính giới hạn: lim ex e . x 1
Câu 4 (1 điểm). Khảo sát tính tăng, giảm và cực trị của hàm sau: f x x23 (x 1)2 . dx 2 lOMoAR cPSD| 49831834
Câu 5 (1 điểm). Tính tích phân suy rộng: 2 10x 130. 4 5x
Câu 6 (1 điểm). Cho hàm số: f(x,y) x4 4xy y4 2019. Tính vi phân toàn phần cấp 2 của
hàm số trên tại điểm (0,0).
Câu 7 (1 điểm). Khảo sát cực trị của hàm số: f x,y x 4ey ex 2e2y 2019.
Câu 8 (1 điểm). Giải phương trình vi phân: y/ 2y 1 2019x. Đề số 03 Câu 1 (2 điểm). 3 1 4
1) Tính định thức của ma trận : A 2 4m 5 2 3 1 3 5 7 9
2) Tìm hạng của ma trận : A 5 8 11 14 7 11 15 19 2 3 4 5
Câu 2 (2 điểm). Cho hai ma trận: 1 3 7
1) Tìm ma trận nghịch đảo của ma trận A 2 1 2 (nếu có). 6 4 11 2 1 2) Cho ma trận B 1 2
. Tìm ma trận A sao cho AB BA. x
Câu 3 (1 điểm). Tính giới hạn: lim 1 x tan . x 1 2 ex . f x
Câu 4 (1 điểm). Khai sát tính tăng, giảm và cực trị của hàm số : lOMoAR cPSD| 49831834 x 1
Câu 5 (1 điểm). Tính tích phân suy rộng: dx 7x2 42 x 126 .
Câu 6 (1 điểm). Cho hàm số: f(x,y) x3 6xy y3 2019. Tính vi phân toàn phần cấp 2
của hàm số trên tại điểm (0, 0).
Câu 7 (1 điểm). Sử dụng phương pháp nhân tử Lagrange tìm cực trị của hàm số z 3x y
với điều kiện 3x2 4y2 208.
Câu 8 (1 điểm). Giải phương trình vi phân: y/ 3y 3 2019x. Đề số 04 Câu 1 (2 điểm). 3 5 7 9
1) Tìm hạng của ma trận : A 5 8 11 14 7 11 15 19 4 6 8 10 x1 3x2 7x3 1
2) Giải hệ phương trình : 2x1 x2 2x3 2 5x1 2x2 6x3 m
Câu 2 (2 điểm). 4 5 13
1) Tìm ma trận nghịch đảo của ma trận A 2 1 2 (nếu có). 5 2 6 2 2 trong đó f(x) x3 3x2 2x 4. f A , 2) Cho ma trận A 3 1 . Tìm 1 3 x 1 4 x 4 lOMoAR cPSD| 49831834
Câu 3 (1 điểm). Tính giới hạn: lim 2 . x 1 1 x 31 x cosx
Câu 4 (1 điểm). Cho hàm số khi f x x x 0
. Định m để hàm f liên m khi x 0
tục tại x 0. Với m tìm được tính f / 0 .
Câu 5 (1 điểm). Tính tích phân suy rộng: 1 5x2 dx20x 65 .
Câu 6 (1 điểm). Cho hàm số: f(x,y) x2 y .2 Tính vi phân toàn phần cấp 1 của hàm số trên tại điểm (3, 4).
Câu 7 (1 điểm). Tìm cực trị của hàm số: f x,y 3x2 4y2 2xy 2x 3y 2019.
Câu 8 (1 điểm). Giải phương trình vi phân: y/ 6y 2019. Đề số 05 Câu 1 (2 điểm). 2 3 4 5
1) Tìm hạng của ma trận : A 5 8 11 14 7 11 15 19 9 14 19 24 x1 3x2 7x3 3
2) Giải hệ phương trình : 2x x2 2x3 2 1 3x1 3x2 8x3 m Câu 2 (2 điểm). 1 3 7
1) Tìm ma trận nghịch đảo của ma trận : A 2 1 2 (nếu có). lOMoAR cPSD| 49831834 4 5 13 1 2 , trong đó f(x) 2x3 4x 5. 2) Cho ma trận A 4 3 . Tìm f A 1 4 x 1 5 x
Câu 3 (1 điểm). Tính giới hạn: lim 2 . x 1 (1 x) 31 2x cosx
Câu 4 (1 điểm). Cho hàm số f x khi x x 0
. Định m để hàm f liên m khi x 0
tục tại x 0. Với m tìm được tính f / 0 . 2x 1
Câu 5 (1 điểm). Tính tích phân suy rộng: 3x dx . 0 e
Câu 6 (1 điểm). Cho hàm số: f(x,y) x2 y .2 Tính vi phân toàn phần cấp 1 của hàm số trên tại điểm (4, 3).
Câu 7 (1 điểm). Khảo sát cực trị của hàm số: f x,y x 2ey ex e2y 2019.
Câu 8 (1 điểm). Giải phương trình vi phân: y/ 2y 2019. Đề số 06 Câu 1 (2 điểm). 3 5 7 9
1) Tìm hạng của ma trận : A 5 8 11 14 1 2 3 4 9 14 19 24 x1 3x2 7x3 1 6 lOMoAR cPSD| 49831834
2) Giải hệ phương trình : 3x1 3x2 8x3 3 5x1 2x2 6x3 m Câu 2 (2 điểm). 1 3 7
1) Tìm ma trận nghịch đảo của ma trận : A 2 1 2 (nếu có). 3 3 8 1 2
, trong đó f(x) x3 2x 11. 2) Cho f A ma trận A 4 3 . Tính 1 5 x 1 6 x
Câu 3 (1 điểm). Tính giới hạn: lim 2 . x 1 (1 x) 31 3x cosx
Câu 4 (1 điểm). Cho hàm số f x khi x x 0
. Định m để hàm f liên m khi x 0
tục tại x 0. Với m tìm được tính f / 0 . dx
Câu 5 (1 điểm). Tính tích phân suy rộng: 3 . e xln x
Câu 6 (1 điểm). Cho hàm số: f(x,y) x3 y .3 Tính vi phân toàn phần cấp 1 của hàm số trên tại điểm (1,1).
Câu 7 (1 điểm). Tìm cực trị của hàm số: f x,y 8x3 2xy 3x2 y2 2019.
Câu 8 (1 điểm). Giải phương trình vi phân: y/ 4y 2019. Đề số 07
Câu 1 (2 điểm). Giải hệ phương trình tuyến tính sau bằng quy tắc Cramer: x1 2x2 x3 1 lOMoAR cPSD| 49831834 x2 4x3 2 2x1 3x1 2x2 2x3 m
Câu 2 (2 điểm). Cho hai ma trận 1 2 1 1 3 1 A 2 2 1 ; B 0 1 2 3 3 2 2 4 5
1) Tìm ma trận nghịch đảo của ma trận A (nếu có). 2)
Tìm ma trận X sao cho AXAT B AB.T 1 2x 3x x
Câu 3 (1 điểm). Tính giới hạn: lim . x 2
Câu 4 (1 điểm). Khai triển Maclorint của hàm số sau tới lũy thừa bậc 4: f x 2 42x 3. x
Câu 5 (1 điểm). Tính tích phân suy rộng: I 1 dx. 1 x 1 ln x2
Câu 6 (1 điểm). Cho hàm số: y f(x) thỏa mãn đẳng thức x3 y3 3xy 2019, với f 0 1. Tính f (0)./
Câu 7 (1 điểm). Tìm cực trị của hàm f x,y 4x 18y 28, với ràng buộc 2x2 3y2 116.
Câu 8 (1 điểm). Giải phương trình vi phân: y/ y ex 2x 3 . Đề số 08 8 lOMoAR cPSD| 49831834
Câu 1 (2 điểm). Giải hệ phương trình tuyến tính sau bằng quy tắc Cramer: x1 2x2 x3 1 2x1 x2 4x3 3 3x1 2x2 2x3 m
Câu 2 (2 điểm). Cho hai ma trận 1 2 1 1 3 1 A 2 2 1 ; B 2 4 3 4 5 3 3 5 4
1) Tìm ma trận nghịch đảo của ma trận A (nếu có). 2)
Tìm ma trận X sao cho AXAT B AB.T 1 4x 5x x
Câu 3 (1 điểm). Tính giới hạn: lim . x 2
Câu 4 (1 điểm). Khai triển Maclorint của hàm số sau tới lũy thừa bậc 4: f x 2 35x 4. x
Câu 5 (1 điểm). Tính tích phân suy rộng: I 1 dx. 1 x 4 ln x2
Câu 6 (1 điểm). Cho hàm số: y f(x) thỏa mãn đẳng thức x4 y4 4xy 2019, với f 0 1. Tính f (0)./
Câu 7 (1 điểm). Tìm cực trị của hàm f x,y 2x 12y 13, với ràng buộc x2 3y2 52.
Câu 8 (1 điểm). Giải phương trình vi phân: y/ 2y e2x 2x 1 . Đề số 09
Câu 1 (2 điểm). Giải hệ phương trình tuyến tính sau bằng quy tắc Cramer: lOMoAR cPSD| 49831834 x1 2x2 x3 2 2x x2 4x3 3 1 3x1 2x2 2x3 m
Câu 2 (2 điểm). Cho hai ma trận 1 2 1 1 4 1 A 2 2 1 ; B 2 0 3 2 3 2 3 5 6
1) Tìm ma trận nghịch đảo của ma trận A (nếu có). 2)
Tìm ma trận X sao cho AXAT B AB.T 1 3x 4x x
Câu 3 (1 điểm). Tính giới hạn: lim . x 2
Câu 4 (1 điểm). Khai triển Maclorint của hàm số sau tới lũy thừa bậc 4: f x 2 64x 5. x
Câu 5 (1 điểm). Tính tích phân suy rộng: I 1 dx. 1 x 9 ln x2
Câu 6 (1 điểm). Cho hàm số: y f(x) thỏa mãn đẳng thức x5 y5 5xy 2019, với f 0 1. Tính f (0)./
Câu 7 (1 điểm). Tìm cực trị của hàm f x,y 4x 12y 15, với ràng buộc x2 3y2 36.
Câu 8 (1 điểm). Giải phương trình vi phân: y/ 3y e3x 2x 5 . Đề số 10
Câu 1 (2 điểm). Giải hệ phương trình tuyến tính sau bằng quy tắc Cramer: x1 2x2 x3 1 10 lOMoAR cPSD| 49831834 2x2 x3 3 2x1 x1 x2 x3 m
Câu 2 (2 điểm). Cho hai ma trận 1 2 1 1 3 1 A 2 2 1 ; B 3 0 3 4 5 3 1 3 1
1) Tìm ma trận nghịch đảo của ma trận A (nếu có).
2) Tìm ma trận X sao cho A XAT BAB .T 3x sin3x
Câu 3 (1 điểm). Tính giới hạn: x 0lim x3 .
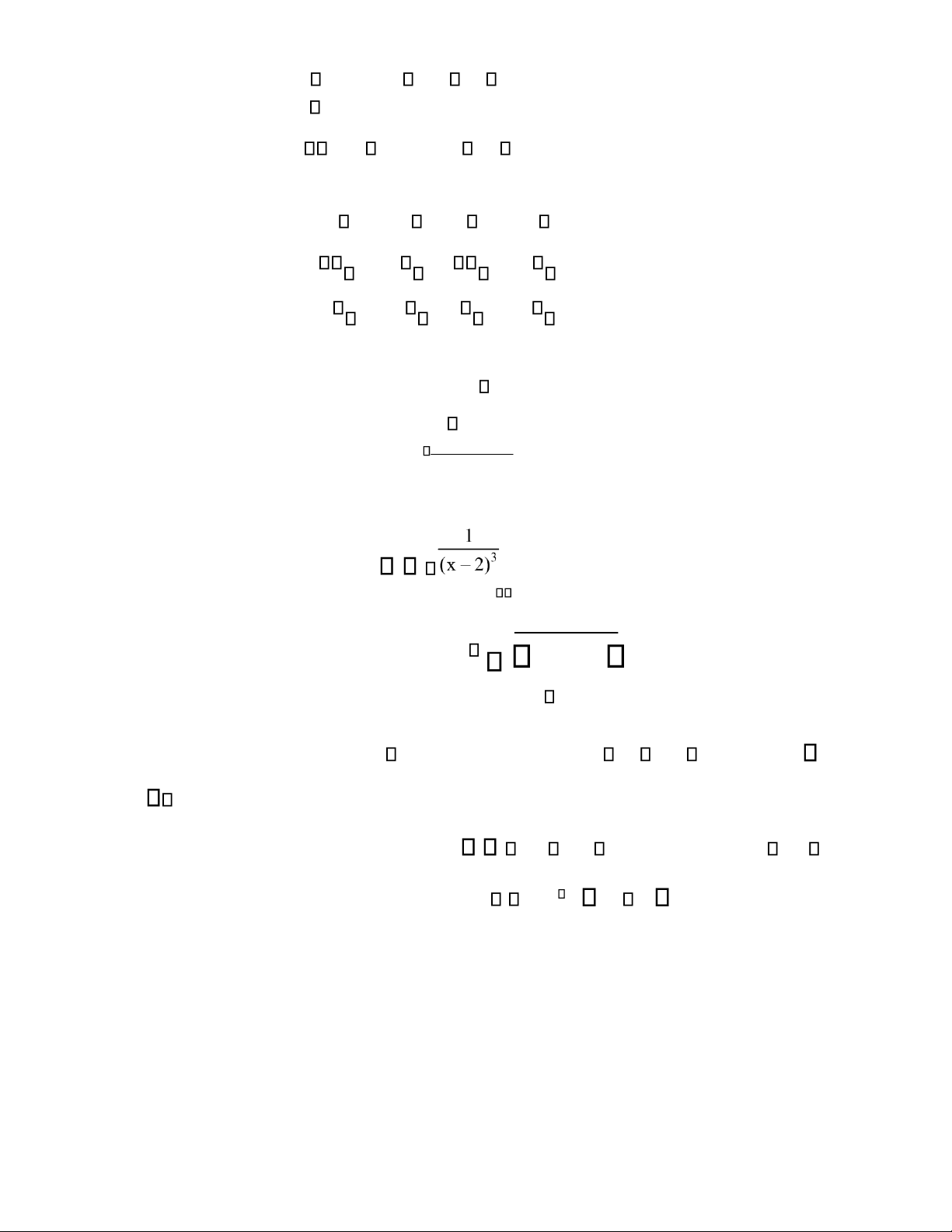
Câu 4 (1 điểm). Khai triển Maclorint của hàm số sau tới lũy thừa bậc 4: f x .
Câu 5 (1 điểm). Tính tích phân suy rộng: I 1 dx. 1 x 4 9ln x2
Câu 6 (1 điểm). Cho hàm số: y f(x) thỏa mãn đẳng thức x4 y4 8xy 2019, với f 0 2. Tính f (0)./
Câu 7 (1 điểm). Tìm cực trị của hàm f x,y 2x 18y 17 , với ràng buộc x2 3y2 112
Câu 8 (1 điểm). Giải phương trình vi phân: y/ 2y e 2x 2x 1 .