9 trang 22 lượt tải

Chia đoạn lấy tích phân thành n phần bằng nhau | Bài giảng môn Phương pháp tính và matlab CTTT | Đại học Bách khoa hà nội

44

Chia đoạn lấy tích phân thành n phần bằng nhau. Tài liệu trắc nghiệm môn Phương pháp tính và matlab CTTT giúp bạn tham khảo, ôn tập và đạt kết quả cao. Mời bạn đọc đón xem!

Môn: Phương pháp tính và matlab CTTT 42 tài liệu

Trường: Đại học Bách Khoa Hà Nội 2.8 K tài liệu

Tác giả:

Profile

Lê Na

7 tháng trước
Danh sách Quiz
/9
TÍNH GẦN ĐÚNG
TÍCH PHÂN XÁC ĐỊNH
Ý tưởng
( ) ( )
bb
n
aa
f x dx P x dx=

( ) ( )
n
f x P x
PP HÌNH THANG
• Chia đoạn lấy tích phân thành n phần
bằng nhau
0 1 1 2 1
, , , ,
nn
a b x x x x x x
−
=
PP HÌNH THANG
• Trên mỗi đoạn ta có:
( ) ( )
( )
( ) ( )
( )
11
11
11
,
.
2
ii
ii
i i i i i
xx
i i i
xx
f x P x y f x x x x
h
f x dx P x dx y y
++
+
+
= + −
= +

1
,
ii
xx
+
PP HÌNH THANG
• Công thức tính:
• Sai số:
( )
( )
0 1 1
22
2
b
nn
a
h
f x dx y y y y
−
+ + + +
( )
*2
2
12
M
I I b a h− −
PP SIMPSON (PARABOL)
• Chia đoạn lấy tích phân thành 2n phần
bằng nhau
PP SIMPSON
• Trên mỗi đoạn ta có:
2 2 2
,
ii
xx
+
( )
( )
( )
( )
( ) ( )
22
2
2
2
2 2 2 2
2
2 2 2 2 1 2 2
0
1
2!
4.
3
i
i
i
i i i i
x
i i i i i
x
y
f x P x th y y t t t
h
f x dx P x th hdt y y y
+
++
+ = + + −
+ = + +

PP SIMPSON
• Công thức tính:
( )
( )
0 1 2 2
1 1 3 2 1
2 2 4 2 2
42
3
b
n
a
n
n
h
f x dx y y
y y y
y y y

−
−
+ + +
= + + +
= + + +
PP SIMPSON
• Sai số
( )
*4
4
180
M
I I b a h− −

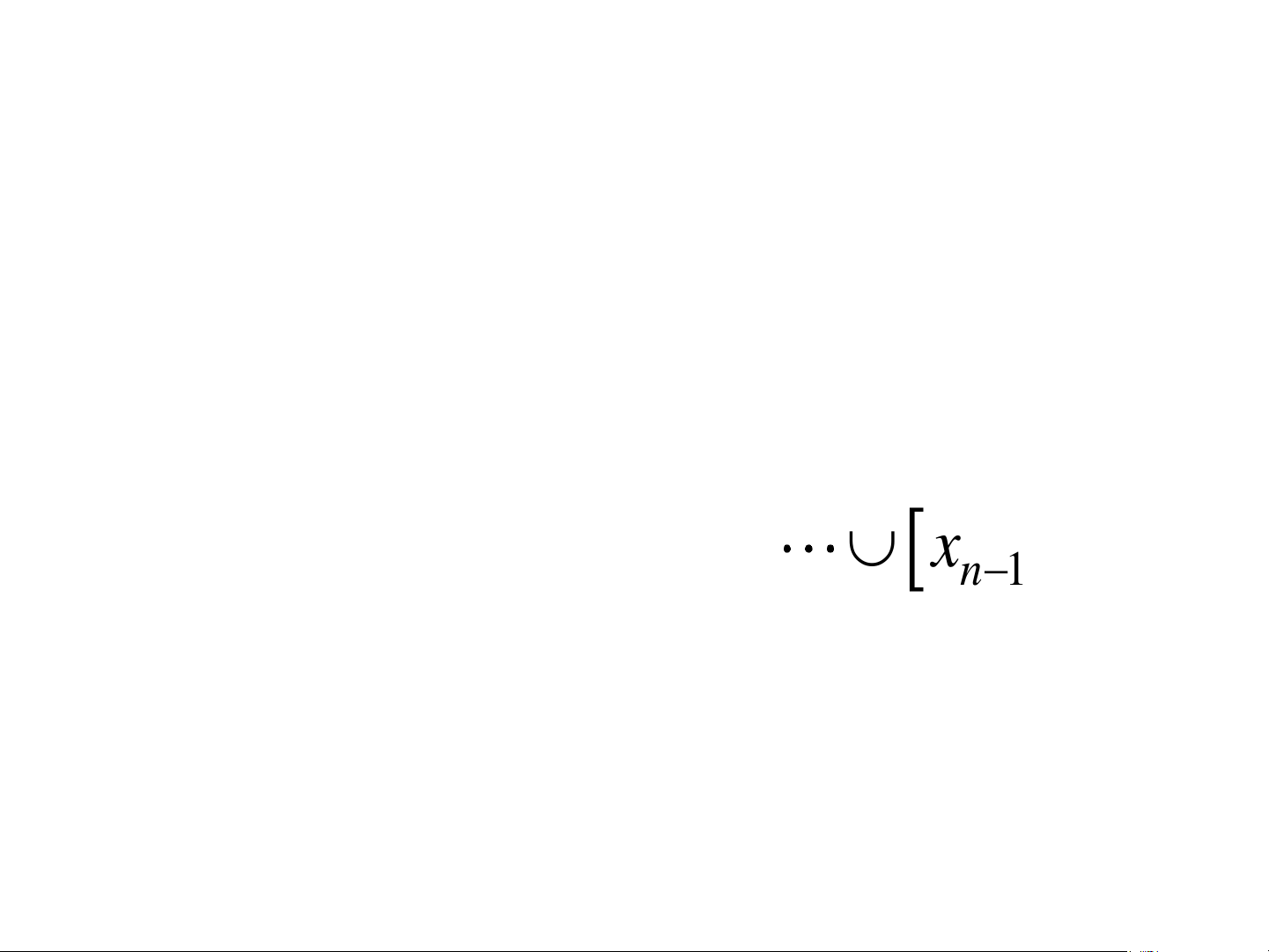
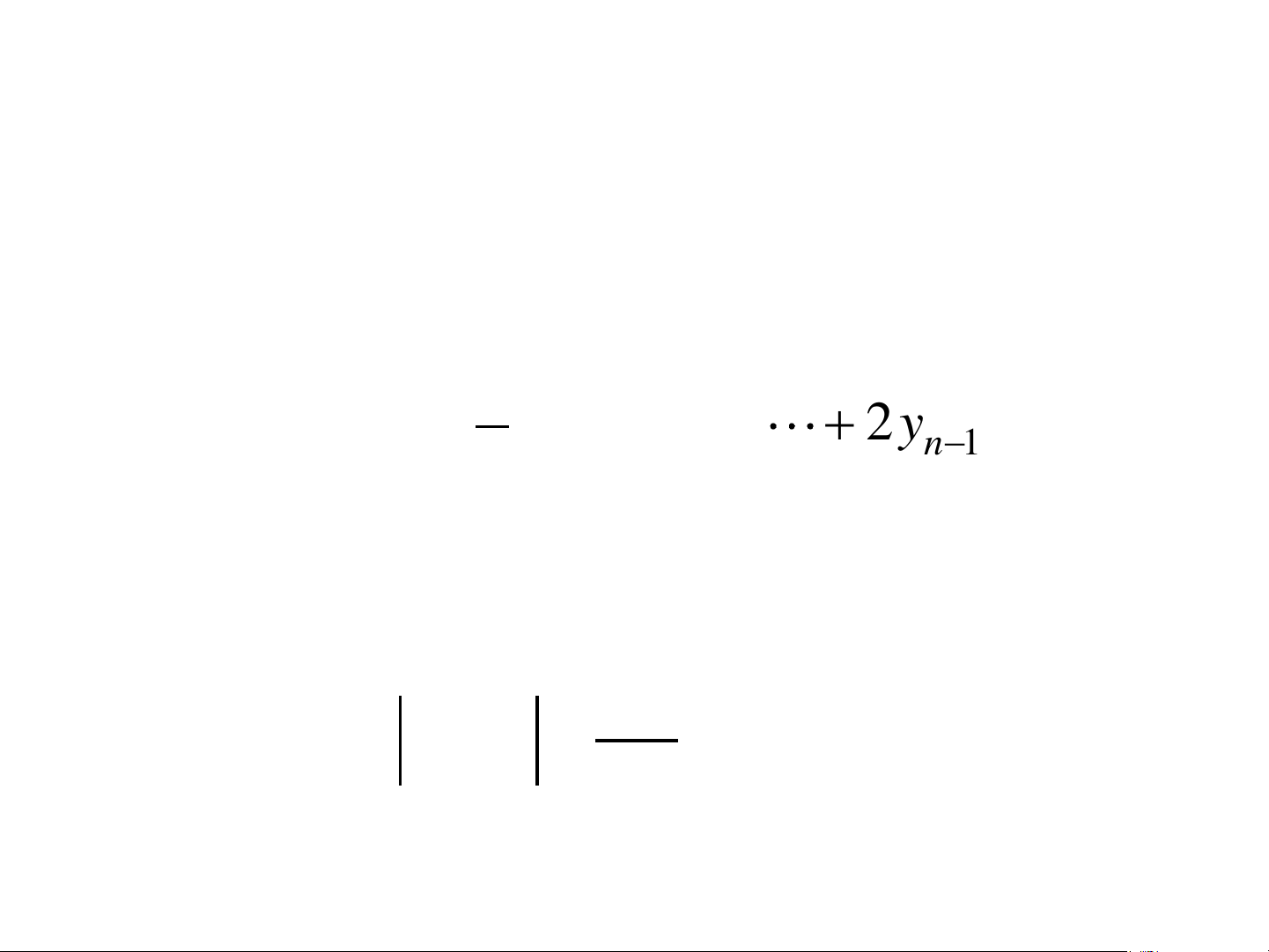
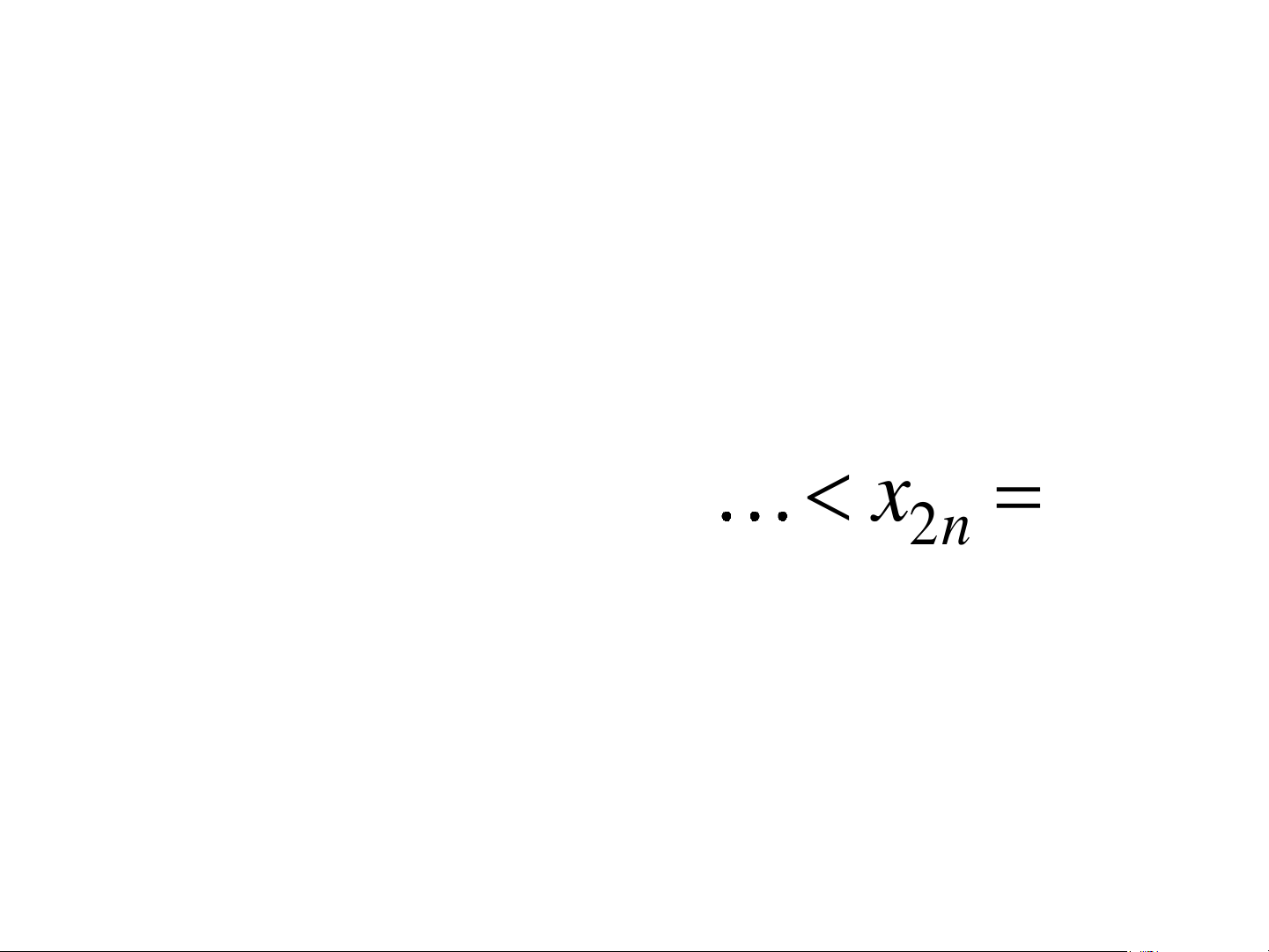
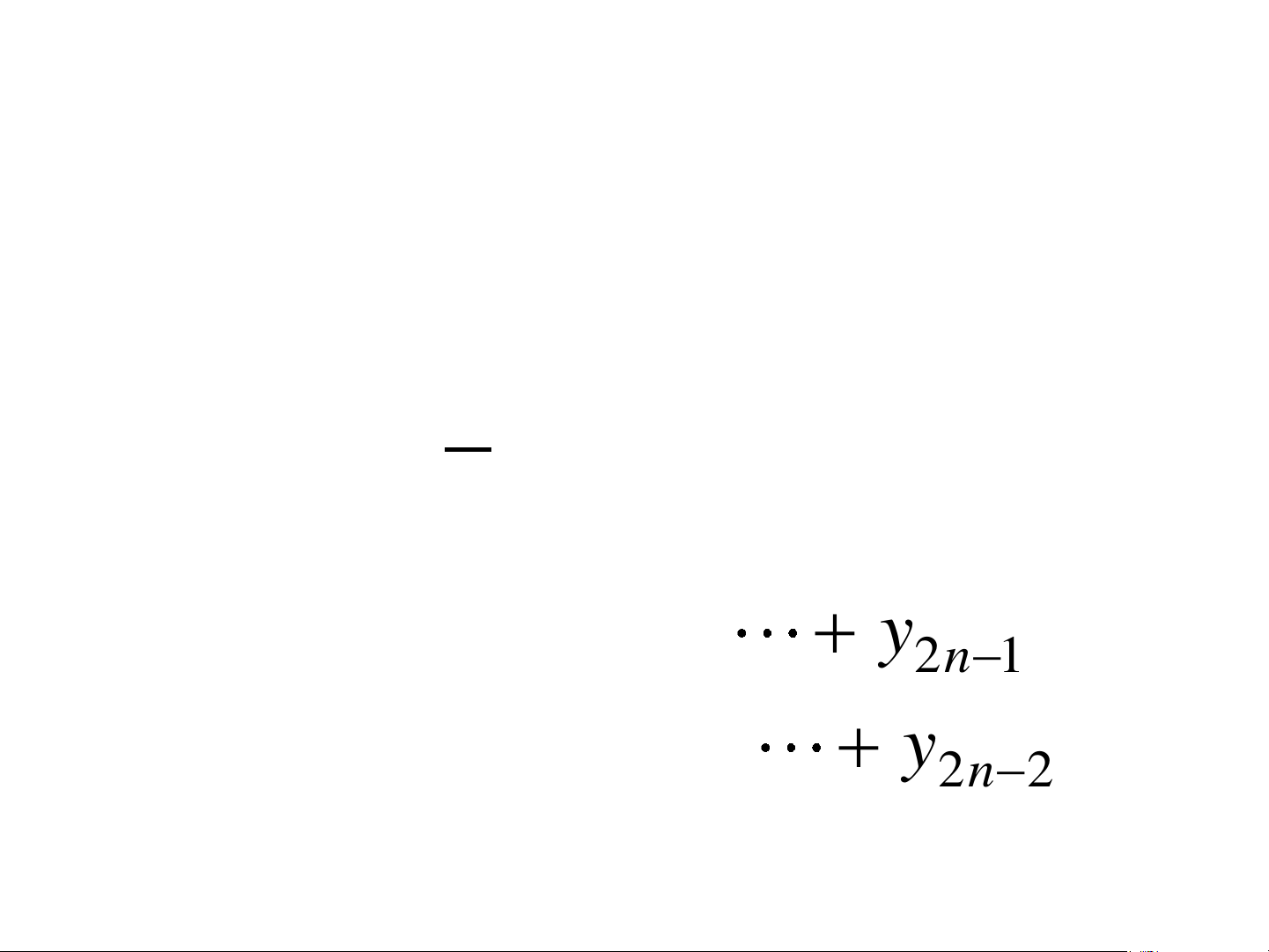
Tài liệu khác của Đại học Bách Khoa Hà Nội

Preview text:

TÍNH GẦN ĐÚNG
TÍCH PHÂN XÁC ĐỊNH Ý tưởng
f ( x)  P x n ( ) b b f
 (x)dx = P x dxn( ) a a PP HÌNH THANG
• Chia đoạn lấy tích phân thành n phần bằng nhau
a,b=x ,x x ,x   x ,x 0 1  1 2  n 1− n PP HÌNH THANG • Trên mỗi đoạn  x , x i i 1 +  ta có:
f ( x)  P x = y + f x , x x − x 1i ( ) ii i 1+( i ) i x 1 x + +  ( ) i 1 h f x dx P x dx = y + y .  1i( ) ( i i 1+) 2 i x i x PP HÌNH THANG • Công thức tính: b  ( ) h f x dx
( y + 2y + + 2y + y 0 1 n 1 − n ) 2 a • Sai số: * M 2 I − I  (b − a) 2 h 12 PP SIMPSON (PARABOL)
• Chia đoạn lấy tích phân thành 2n phần bằng nhau
a = x x x   x = b 0 1 2 2n
x = x + kh k 0 PP SIMPSON • Trên mỗi đoạn  x , x 2i 2i+2  ta có: ( )  y
f x P x + th = y + yt + t t − i ( i ) 2 2i 1 2 2 2i 2i ( ) 2! 2 x i+2 2  ( ) h
f x dx P x + th hdt = y + 4y + y .  2i( 2i ) ( 2i 2i 1 + 2i+2 ) 3 2 x 0 i PP SIMPSON • Công thức tính: b  ( ) h f x dx
( y + 4 + 2 + y 0 1 2 2n ) 3 a
 = y + y + + y 1 1 3 2n 1 −
 = y + y + + y 2 2 4 2n−2 PP SIMPSON • Sai số * M 4 I − I  (b − a) 4 h 180

Tài liệu liên quan: