Chương 1: Vật lý và đo lường | Tài liệu môn Vật lý Trường đại học sư phạm kỹ thuật TP. Hồ Chí Minh

Vật lý học cổ điển bao gồm các nguyên lý của cơ học cổ điển, nhiệt động lực học, quang học và điện tử học đã được trước năm 1900. Newton là người đã có những đóng góp quan trọng cho vật lý học cổ điển, ông cũng là một trong những người khai sinh ra phép tính vi tích phân như là một công cụ toán học. Các phát triển chủ yếu của cơ học được tiếp diễn trong thế kỷ 18, Tài liệu giúp bạn tham khảo, ôn tập và đạt kết quả cao. Mời bạn đọc đón xem!

17 9 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Môn: vật lý 1, 2

Trường: Đại học Sư phạm Kỹ thuật Thành phố Hồ Chí Minh

Thông tin:

18 trang 2 tuần trước

Tác giả:

Profile Lê Kim Dung
http://ipt.hcmute.edu.vn B môn v t lý ộ ậ
1
Chương 1: Vật lý và đo lường
ũng như các khoa h c khác, v t lý là khoa h c d a trên các quan sát th c nghi m và ọ ậ ọ ự ự ệ
các phép đo định lượ ật lý là xác địng. Mục tiêu chính của v nh số lượng có hạn các
định lu n chi phật cơ bả ối các hi ng trong tện tượ ự nhiên và sử d phát ụng chúng để
triển các lý thuy t có th d c k t qu cế ể ự đoán đượ ế ả ủa các thí nghiệm trong tương lai.
Các đị ật cơ này đượ ễn đạnh lu bản c di t bằng ngôn ngữ toán học, một công cụ để để gắn kết
lý thuy t v i th c nghi m. ế ớ ự ệ
Mỗi khi có s không nh t quán gi a a lý thuy t và k t qu th c nghi m thì ự ấ ữ tiên đoán củ ế ế ả ự ệ
cần ph t lý thuyải đưa ra mộ ết m i ho c ch nh s a lý thuy lo i b s không nh t ớ ặ ỉ ử ết đã có để ạ ỏ ự ấ
quán đó. Nế ững điề ất địu một lý thuyết chỉ được thỏa mãn trong nh u kiện nh nh thì một lý
thuyết t ng quát ổ hơn sẽ có th th a mãn ể ỏ được mà không c n các u ki n này. Ví d ầ điề ệ ụ như các
định luật chuy c Newton (1642-1727) khám phá mô tển động đượ ả chính xác chuy ng ển độ
của các v t có t i không áp d c cho các v t chuyậ ốc độ bình thường nhưng lạ ụng đượ ậ ển động
với t g v i t c l i, thuy i h p cốc độ tương đươn ớ ốc độ ánh sáng. Ngượ ạ ết tương đố ẹ ủa Einstein
(1879-1955) cho các k t qu gi ng v nh lu i v i t nhế ả ố ới các đị ật Newton đố ớ ốc độ ỏ nhưng cũng
mô t chính xác chuy ng c a các v t có t g n b ng t t ả ển độ ủ ậ ốc độ ầ ằ ốc độ ánh sáng. Do đó, thuyế
tương đố ển độ ổng quát hơn so với hẹp của Einstein là một thuyết về chuy ng t i thuyết được
xây d ng t nh lu t Newton. ự ừ các đị ậ
Vật lý h c c ọ ổ điển bao g m các nguyên lý c a ồ ủ cơ học c ổ điển, nhiệt động l c hự ọc, quang
học và điện t hừ ọc đã đượ ển trước năm 1900. Newton là người đã có những đóng c phát tri
góp quan tr ng cho v t lý h c c t trong nh i khai sinh ra phép ọ ậ ọ ổ điển, ông cũng là mộ ững ngườ
tính vi tích phân như là mộ ủa cơ học đượt công cụ toán học. Các phát triển chủ yếu c c tiếp
diễn trong th kế ỷ 18, nhưng ngành nhiệt động lực h n t thì ph n n a sau c a th ọc và điệ ừ ải đế ử ủ ế
kỷ 19 mới được phát tri n. Nguyên nhân ch y u là do các thi t b thí nghi m thể ủ ế ế ị ệ ời đó quá thô
sơ hoặc thiếu thốn.
Cuộc cách m ng l n c a v t lý, có liên quan v i v t lý hi i, b u vào g n cu i th ạ ớ ủ ậ ớ ậ ện đạ ắt đầ ầ ố ế
kỷ 19. V t lý hi c phát tri n là do v t lý cậ ện đại đượ ể ậ ổ điển không th gi c nhi u ể ải thích đượ ề
hiện tượng v t lý. Hai s phát tri n quan tr ng nh t trong k nguyên hiậ ự ể ọ ấ ỷ ện đại là thuyết tương
đối và cơ học lượng tử. Thuyết tương đối h p c a Einstein không nh ng ch mô t chính xác ẹ ủ ữ ỉ ả
chuyển động của các vật có t i t ánh sáng mà còn hi u ch nh m t ốc độ tươndg đương vớ ố ộc đ ệ ỉ ộ
cách tr n v n các khái ni m truy n th ng v không gian, th ng. Lý thuy t ọ ẹ ệ ề ố ề ời gian và năng lượ ế
này còn ch ra r ng t ánh sáng là gi i h n trên c c a m t v t và kh ng và ỉ ằ ốc độ ớ ạ ủa tốc độ ủ ộ ậ ối lượ
năng lượ ới nhau. Cơ học lượng có liên hệ v ng tử được hình thành bởi nhiều nhà khoa học
khác nhau, mô t các hi ng v t lý c nguyên t . Nhi u thi t b th c ti c ả ện tượ ậ ở ấp độ ử ề ế ị ự ễn đã đượ
chế t o d a vào các nguyên lý c c lạ ự ủa cơ họ ượng t . ử
Các nhà khoa h c làm vi c không ng c i thi n hi u bi t c a chúng ta v nh ọ ệ ừng để ả ệ ể ế ủ ề các đị
luật cơ bả ại như tàu vũ trụ không ngườn. Nhiều tiến bộ về công nghệ trong hiện t i lái, hàng
loạt ng d ng ti na nô, vi m ch và máy tính siêu t c, kứ ụ ềm năng trong công nghệ ạ ố ỹ thu t ch p ậ ụ
C
Trường Đạ ọc Sư phại h m Kỹ thu t Tp. H Chí Minh 2021 ậ ồ
2
ảnh tinh x o dùng trong nghiên c u khoa hả ứ ọc và y khoa cũng như nhiều kết qu ả đáng kể trong
kỹ thu t gien là k t qu c a nh ng n l c c a nhi u nhà khoa hậ ế ả ủ ữ ỗ ự ủ ề ọc, k thu t. nh ỹ sư, nhà kỹ ậ Ả
hưở ủ ộ ớng c a những phát tri n xã hển và khám phá này đế i của chúng ta quả thực là to l n và
chắc ch n là các khám phá và phát triắ ển trong tương lai cũng sẽ đầy h ng thú, thách th c và ứ ứ
mang l i nhi u l i ích cho nhân lo i. ạ ề ợ ạ
Các chu dài, kh i ng và thẩn độ ố lượ ời gian
Để mô tả các hi ng vện tượ ật lý, ta cần phải ng nhiđo lườ ều khía cạnh khác nhau của tự
nhiên. Mỗi phép đo tương ứng với một đại lượng v t lý, ví d ậ ụ như chiều dài của một vật. Các
đị ợ ợnh luật vật lý đư c di i quan hễn đạt như là các mố ệ toán học giữa các đại lư ng vật lý.
Trong cơ học, ba đại lượng cơ bả ối lượ ọi đạn nhất là chiều dài, kh ng và thời gian. M i
lượng khác trong cơ họ ễn thông qua ba đạc có thể được biểu di i lượng này.
Do các qu c gia khác nhau s d ng các chu n khác nhau nên c n ph i có chu n chung ố ử ụ ẩ ầ ả ẩ
cho các đạ ẩ ải lượng. Cái được chọn làm chu n ph i:
có s n; ẵ
có m t vài thu c tính có th c m t cách tin c y; ộ ộ ể đo lường đượ ộ ậ
phải cho cùng một k t qu i b t kế ả khi đo bở ấ ỳ ai và b t kấ ỳ nơi nào;
không thay đổi theo thời gian.
Vào năm 1960, một ủy ban qu c t ố ế đã đưa ra mộ ẩn cho các đại lượng cơ bảt bộ các chu n
của khoa h c. i là SI (Système International H qu c t ). B ng ọ Nó được gọ d’unités – ệ đơn vị ố ế ả
dưới đây là các đạ ợng cơ bả ất và đơn vị tương ứi lư n nh ng.
Đạ ợi lư ng
Đơn vị trong SI
độ dài
mét (m),
khối lượng
ki-lô-gam (kg)
thời gian
giây (s).
nhiệt độ
Kelvin (K)
cường độ dòng điệ n
Ampère (A)
cường độ sáng
Candela Cd –
lượng chất
mole (mol)
Các đại lượng cơ bản dùng trong cơ họ ối lượ ời gian. Các đạc là chiều dài, kh ng và th i
lượ ợng còn l c biại đượ ểu diễn qua các đại lư ng này.
1.1.1 Chiều dài
Chiều dài được xác định bằng khoảng cách giữa hai điểm trong không gian.
Năm 1799, khi mét đượ ọn làm đơn vị đo hợc ch p pháp của chiều dài tại Pháp, thì mét
được định nghĩa bằ ủa đoạ ến đi qua Paris, tính từng 1/10.000.000 chiều dài c n kinh tuy xích
đạ ịo lên cực bắc c t. C ng giá trủa Trái đấ ần lưu ý rằ này không th a mãn yêu c u là có th s ỏ ầ ể ử
dụng trong toàn vũ trụ.
http://ipt.hcmute.edu.vn B môn v t lý ộ ậ
3
Năm 1960, mét được định nghĩa là khoả –ng cách giữa hai vạch trên một thanh platinum
iridium đặ ợc lưu trữc biệt đư tạ ềi Pháp trong đi u kiện kiểm soát được.
Trong nh ng 1.650.763,73 l c sóng ững năm 1960 và 1970, mét được định nghĩa bằ ần bướ
c - cam phát ra t -86. ủa ánh sáng đỏ ừ đèn khí kripton
Năm 1983, mét được định nghĩa là quãng đường mà ánh sáng đi được trong chân
không trong kho ng th i gian 1/299.792.458 sả ờ . Trong th c tự ế, định nghĩa này thiết lập tốc
độ ánh sáng trong chân không chính xác b p lằng 299.792.458 m/s. Định nghĩa này là hợ ệ
trong toàn vũ trụ ằng ánh sáng là như nhau ở ọi nơi. và dựa trên giả thiết r khắp m Bảng
1.1Bảng li t kê các giá trệ ị ướ ợc lư ng c t s chi c. ủa mộ ố ều dài đã đo đạc đượ
Bảng 1.1: ng giá tr s a m dài (m)Ước lượ ị ố đo củ ột vài độ
Độ dài (m)
Khoảng cách t n chu n tinh xa nh n ừ Trái đất đế ẩ ất được biết đế
1,4
10
26
Khoảng cách t n thiên hà xa nh t ừ Trái đất đế ấ
9 10
25
Khoảng cách t n thiên hà l n g n nh t (Andromeda) ừ Trái đất đế ớ ầ ấ
2 10
22
Khoảng cách t M t trừ ặ ời đến ngôi sao g n nh t (Proxima Centauri) ầ ấ
4 10
16
Một năm ánh sáng
9,46 10
15
Bán kính quĩ đạ ủa Trái đấo trung bình c t quanh Mặt trời
1,50 10
11
Khoảng cách trung bình t n M ừ Trái đất đế ặt trăng
3,84 10
8
Khoảng cách t n B c ừ xích đạo đế ắc cự
1,00 10
7
Bán kính trung bình c t ủa Trái đấ
6,37 10
6
Độ ủ cao điển hình (tính từ bề mặt) c a vệ tinh bay quanh Trái đất
2 10
5
Chiều dài c a m ủ ột sân bóng đá
9,1 10
1
Chiều dài c a m t con ru i nhà ủ ộ ồ
5 10
3
Kích thước củ ỏa các hạt b i nhụ nhất
~ 10
4
Kích thước củ ốa tế bào trong hầu hết các cơ quan s ng
~ 10
5
Đường kính của nguyên tử hidro
~ 10
10
Đường kính của hạt nhân nguyên tử
~ 10
14
Đườ ộng kính của m t proton
~ 10
15
1.1.2 Khối lượng
Đơn vị ối lượ gram (kg), được định nghĩa là khối lượ của kh ng trong SI là ki-lô- ng của
một khối platinum iridium hình tr– ụ đặc bi t c t v kh ng và ệt lưu trữ ại văn phòng quố ế ề ối lượ
Trường Đạ ọc Sư phại h m Kỹ thu t Tp. H Chí Minh 2021 ậ ồ
4
đo lườ ối lượng được đưa ra vào năm 1887 và từ đó đếng tại Sèvres, Pháp. Chuẩn kh n nay
chưa thay đổ ợp kim đặi, do platinum-iridium là h c biệt bền. Một bản sao của khối trụ này
được giữ tại Viện quốc tế về tiêu chuẩn và công nghệ (NIST) tại Gaithersburd, Maryland.
Bảng 1.2 li t kê các giá trệ ị g a kh ng các v t th khác nhau. ần đúng củ ối lượ ậ ể
Bảng 1.2: ng kh ng c a các v t th khác nhauƯớc lượ ối lượ ủ ậ ể
Khối lượng (kg)
Phần vũ trụ quan sát đượ c
10
52
Dải Ngân hà
10
42
Mặt trời
1,99 10
30
Trái đất
5,98 10
24
Mặt trăng
7,36 10
22
Cá m p ậ
~ 10
3
Con người
~ 10
2
Con ch ế
~ 10
1
Con mu i ỗ
~ 10
5
Vi khuẩn
~ 10
15
Nguyên t hidro ử
1,67 10
27
Điện tử
9,11 10
31
1.1.3 Thời gian
Trước năm 1967, chuẩ ời gian được định nghĩa theo n về th ngày m t tr i trung bìnhặ ờ (là
khoảng thời gian gi a hai l n m t tr ng bóng liên tiữ ầ ặ ời đứ ếp). Đơn vị giây (second c – s) đượ
định nghĩa là
c a ngày mủ ặt tr a trên s quay ời trung bình. Định nghĩa này dự ự
của m t nên không th xem là chuột hành tinh là Trái đấ ể ẩn th i gian c . ờ ủa vũ trụ
Vào năm 1967, ịnh nghĩa lạ đo thờgiây được đ i khi xuất hiện dụng cụ i gian với độ chính
xác cao – đồng h nguyên tồ ử (hình 1.1b), đồng hồ này đo các dao động c a nguyên t Cesium ủ ử
(Cs). Theo đó, 1 giây là 9.192.631.770 chu k ng c a nguyên t Cs133ỳ dao độ ủ ử . Bảng 1.3
trình bày m t s giá tr g i gian. ộ ố ị ần đúng của thờ
http://ipt.hcmute.edu.vn B môn v t lý ộ ậ
5
Bảng 1.3: ng giá tr c a m t s kho ng th i gian Ước lượ ị ủ ộ ố ả ờ
Khoảng th i gian (s) ờ
Tuổi c ủa Vũ trụ
4 10
17
Tuổi c t ủa Trái đấ
1,3 10
17
Tuổi trung bình c i hủa sinh viên đạ ọc
6,3 10
8
Một năm
3,2 10
7
Một ngày
8,6 10
4
Một giờ h c ọ
3,0 10
3
Thời gian gi a hai nh ng ữ ịp tim bình thườ
8
10
21
Chu k c c) ỳ ủa sóng âm (mà tai nghe đượ
~ 10
–23
Chu k n hình c a sóng vô tuy n ỳ điể ủ ế
~ 10
–26
Chu k ỳ dao động c a m t nguyên t trong ch t r n ủ ộ ử ấ ắ
~ 10
–13
Chu k c a ánh sáng kh ki n ỳ ủ ả ế
~ 10
–15
Thời gian va ch m c a hai h t nhân ạ ủ ạ
~ 10
–22
Thời gian để ánh sáng đi qua mộ t proton
~10
–24
Ngoài các đơn vị n mét, kg và s nói trên, ta có thcơ bả ể mm dùng các đơn vị khác như là
(mili-mét), ns (nano giây), v i mili và nano là các ti u ng ch các b i s c a 10. ớ ếp đầ ữ ỉ ộ ố ủ
Các ti u ngếp đầ ữ: Các ti u ng (ti n tếp đầ ữ ề ố) được ghép vào trướ ột đơn vị đo đểc m biểu
diễn m t b i sộ ộ ố c a 10. M i ti u ng có m t tên và cách vi t t t riêng. Có th ghép ti p ủ ỗ ếp đầ ữ ộ ế ắ ể ế
đầ ớ ỳu ngữ v i bất k n nào. Nó chính là hđơn vị cơ bả ệ số n. nhân thêm vào đơn vị cơ bả
Ví dụ:
3
1mm 10 m
;
3
1mg 10 g
.
Đại lượng cơ bản và đại lượng phái sinh: Độ ối lượ dài, kh ng và thời gian là ví dụ cho
các đại lượng cơ bản. Hầu hết các đại lượng còn l ng phái sinh, t c là có th c ại là đại lượ ứ ể đượ
biểu di i d ng các t hễn dướ ạ ổ ợp toán h c c n. Ví dọ ủa các đại lượng cơ bả ụ thường g p là ặ diện
tích (tích c a hai chi u dài) và ủ ề tốc độ (t s giỉ ố ữa độ dài và kho ng th i gian). Ho c ả ờ ặ khối lượng
riêng, ng c a m th tích được định ngh a là ĩ khối lượ ủ ột đơn vị ể
m
V
Trường Đạ ọc Sư phại h m Kỹ thu t Tp. H Chí Minh 2021 ậ ồ
6
Tính h p lý c a các k t quợ ủ ế ả: Khi gi i bài t p, b n c n ph i ki m tra câu tr l i cả ậ ạ ầ ả ể ả ờ ủa mình
xem chúng có h p lý không. Vi c xem l i các b ng giá tr g dài, kh ng ợ ệ ạ ả ị ần đúng của độ ối lượ
và th i gian có th giúp b n ki m tra tính h p lý này. ờ ể ạ ể ợ
Bảng 1.4: Các ti u ng cho b c a 10 ếp đầ ữ ội/ước số ủ
Lũy thừa
10
Tiếp đầu
ngữ
Viết t t ắ
Lũy thừa
10
Tiếp đầu
ngữ
Viết t t ắ
10
22
yocto
y
10
3
kilo
k
10
21
zepto
z
10
6
mega
M
10
18
atto
a
10
9
giga
G
10
15
femto
f
10
12
tera
T
10
12
pico
p
10
15
peta
P
10
9
nano
n
10
18
exa
E
10
6
micro

10
21
zetta
Z
10
3
milli
m
10
24
yotta
Y
10
2
centi
c
10
1
deci
d
Câu h i 1.1:ỏ Trong một xưởng cơ khí, người ta ch t o hai bánh cam, m t b ng nhôm và m t ế ạ ộ ằ ộ
bằng s t. Hai bánh cam này có cùng kh ng. Bánh cam nào l ắ ối lượ ớn hơn?
(a) bánh b ng nhôm (b) bánh b ng s t (c) hai bánh có cùng kích cằ ằ ắ ỡ
http://ipt.hcmute.edu.vn B môn v t lý ộ ậ
7
Vật chất và xây d ng mô hình ự
Nếu nhà v t lý ậ không th c ti p v i ể tương tác trự ế ớ
một s hiố ện tượng, h ọ thường hình dung ra m t ộ mô hình
cho h vệ ật lý có liên quan đến các hiện tượng này. Ví d , ụ
ta không th c ti p v i các nguyên t vì ể tương tác trự ế ớ ử
chúng quá nh ng m ng ỏ. Do đó, ta xây dự ột mô hình tưở
tượng về nguyên tử như một hệ gồm một hạt nhân và
một ho c nhi u electron n m bên ngoài h t nhặ ề ằ ạ ân. Khi đã
xác định được các thành ph n v t lý c a mô hìnhầ ậ ủ thì ta
đưa ra các tiên đoán trên cơ sở v c a chúng ề hành vi ủ
các tương tác ặc tương giữa các thành phần của hệ ho
tác gi a h v ng bên ngoài hữ ệ ới môi trườ ệ.
Hãy xem xét hành vi c a v t chủ ậ ất để làm ví d . Hình ụ
đầu tiên của hình 1.1 cho thấy một mi c. Có ếng vàng đặ
phải mi ng vàng này toàn là vàng, không có ch tr ng ế ỗ ố
nào? N u c ng vàng này, hai mi ng vàng thu ế ắt đôi miế ế
được vẫn giữ nguyên đặ ọc như miếc tính hóa h ng vàng
nguyên. Chuy n gì s x y ra n u ta c ệ ẽ ả ế ứ chia đôi các miếng
này liên t c, vô h n l n? Các mi ng ngày càng nh d n ụ ạ ầ ế ỏ ầ
này có luôn là vàng hay không? Nh ng câu h y ữ ỏi như vậ
đã được đặt ra từ rất lâu bởi . các nhà tri t h c Hi Lế ọ ạp
Hai trong s h , Leucippus và h c trò c a ông là ố ọ ọ ủ
Democritus, không ch p nh ng r ng s chia c t ấ ận ý tưở ằ ự ắ
như vậy có th di n ra mãi mãi. Hể ễ ọ xây d ng m t mô ự ộ
hình m t mô hình v t chộ ậ ất với suy đoán rằng quá trình nói trên cuối cùng cũng phải kết thúc
khi nó t o ra ạ một h t không th b chia cạ ể ị ắt được nữa. Trong ti ng Hi lế ạp, “atomos” có nghĩa
là “không chia cắt được”. Từ ếng Anh “atom” (nguyên tử ti ) bắt nguồn từ cách gọi này trong
tiếng Hi l p. ạ
Mô hình Hi l p v c u trúc v t ch t cho r ng m i v t chạ ề ấ ậ ấ ằ ọ ậ ất bình thường đều có các nguyên
tử (xem hình gi a c a hình 1.1). Ngoài ra, không có thêm c nh ữ ủ ấu trúc nào khác được xác đị
trong mô hình này; các nguyên t ho t nhử ạt động như các hạ ỏ có tương tác với nhau, nhưng
mô hình này không đề ập đế c n cấu trúc bên trong nguyên tử.
Vào năm 1897, J. J. Thomson đã xác định electron là m t hộ ạt tích điện và là m t thành ộ
phần của nguyên tử. Điề ẫn đếu này d n mô hình nguyên tử đầu tiên có cấu trúc bên trong.
Mô hình này s c th o lu ẽ đượ ả ận trong chương 42.
Sau s phát hi n các h t mô hình nguyên t ự ệ ạt nhân vào năm 1911, người ta đã đưa ra mộ ử
trong đó nguyên tử được tạo thành từ các electron bao quanh một hạt nhân ở giữa. Tuy vậy,
mô hình này d n m t câu h i m i: H t nhân có cẫn đế ộ ỏ ớ ạ ấu trúc hay không? Nghĩa là, phải chăng
hạt nhân là một h hay là m t t p h p các h u nh i ta ạt đơn lẻ ộ ậ ợ ạt? Vào đầ ững năm 1930, ngườ
đưa ra mộ ần cơ bảt mô hình mô tả hai thành ph n trong hạt nhân: proton và neutron. Proton
mang điện tích dương và một nguyên t hóa h nh b ng s ng proton trong ố ọc được xác đị ằ ố lượ
Hình 1.1
Trường Đạ ọc Sư phại h m Kỹ thu t Tp. H Chí Minh 2021 ậ ồ
8
hạt nhân c a nó. Con sủ ố này được gọi là nguyên tử số (atomic number) của nguyên tố. Bên
cạnh nguyên t s , m t s khác, kh i s ng t ng c a s ử ố ộ ố ố ố (mass number), được định nghĩa bằ ổ ủ ố
proton và s neutron t o nên h t nhân. Nguyên t s c a m t nguyên t không bao gi thay ố ạ ạ ử ố ủ ộ ố ờ
đổ ối, còn khối s có thể thay đổi.
Tuy nhiên, có ph i s phân chia v t ch t thúc? Hiả ự ậ ất đã kế ện nay, người ta đã biết rằng các
proton, neutron và m t s o các h t ngo i lai 6 h t khác g i là ộ ố đông đả ạ ạ được t o nên tạ ừ ạ ọ
quark, các h t tên là ạt này được đặ up down strange charmed bottom top, , , , và . Các h t quark ạ
up charmed top, và n tích +2 n tích ccó điệ /3 điệ ủa proton trong khi 3 hạt còn l n tích ại có điệ
–1/3 điệ ủa proton. Proton đượ ần lượn tích c c tạo thành từ 2 hạt và 1 hup ạt (ký hidown ệu l t
là u và d trong hình 1.2). Tương tự, neutron được tạo thành từ 2 hạt và 1 hdown ạt . up
Khi h c v t lý, b n ph i phát tri n m t ti n trình xây d ng các mô hình.ọ ậ ạ ả ể ộ ế ự B n s c ạ ẽ đượ
thử thách v i vi c gi i quy t nhi u v toán h c. M t kớ ệ ả ế ề ấn đề ọ ộ ỹ thu t gi i quy t bài toán quan ậ ả ế
trọng nh t là : ấ xây d ng mô hình cho v c n gi i quyự ấn đề ầ ả ết
Xác định m t h các thành ph n v t lý cho bài toán và ộ ệ ầ ậ
Đưa ra dự đoán về ống trên cơ sở các tương tác giữ hành vi của hệ th a các thành phần
của hệ ho này v ng xung quanh. ặc tương tác của hệ ới môi trườ
Phân tích th nguyên ứ
Trong v t lý, t b n ch t v t lý c a m t ng. Ví d , ậ ừ “thứ nguyên” được dùng để ả ấ ậ ủ ộ đại lượ ụ
khoảng cách gi m có th ữa hai điể ể được đo bằng feet , mét hay fulong , t t c
1 2
ấ ả đều là các cách
khác nhau để nguyên độ biểu thị thứ dài.
Trong sách này, chúng tôi dùng các ký hi u cho th dài, kh ng và th i ệ ứ nguyên độ ối lượ ờ
gian tương ứng là L, M và T
3
. Chúng tôi cũng thường dùng c p d u ngo c [ bi u th các ặ ấ ặ ] để ể ị
thứ nguyên c ng. Ví d , chủa các đại lượ ụ v được dùng để ỉ t , th nguyên cốc độ ứ ủa t s ốc độ ẽ
đượ ị ớ
c biểu th là [ ]=L/T. Vv i diện tích (ký hiệu là ) thì ta có [ . BA A]=L
2
ảng 1.5Error!
Reference source not found. gi i thi u th nguyên c a m t s ng. ớ ệ ứ ủ ộ ố đại lượ
Bảng 1.5: Các th c t ứ nguyên và đơn vị ủa 4 đại lượng đã biế
Đạ ợi lư ng
Diện tích ( ) A
Thể tích ( ) V
Tốc độ ( ) v
Gia tốc ( ) a
Thứ nguyên
L
2
L
3
L / T
L / T
2
Đơn vị SI
m
2
m
3
m / s
m / s
2
Đơn vị trong hệ
đo lường của
Mỹ
ft
2
ft
3
ft / s
ft / s
2
Trong nhiều trườ ột phương trình cụng hợp, có thể bạn phải kiểm tra m thể để xem nó có
phù h p v i d tính c a bợ ớ ự ủ ạn hay không. Để làm điều đó, bạ n có thể sử dụng một thủ thuật
1
F u dài c a Anh, b ng 0,3048m eet: đơn vị đo chiề ủ ằ
2
Fulong: đơn vị đo chiề u dài, bằng 1/8 dặm Anh, tức khoảng 201m
3
Th nguyên c a m c vi t b ng ch vi t hoa, th ng; còn ký hi i s c ký ứ ủ ột đại lượng đượ ế ằ ữ ế ẳ ệu đạ ố cho đại lượng đượ
hiệu b ng ch in nghiêng: ằ ữ L cho độ dài và t cho th i gian. ờ
http://ipt.hcmute.edu.vn B môn v t lý ộ ậ
9
hữu ích, , vì các th nguyên có th i phân tích th nguyênứ ứ ể được xem như là các đại lượng đạ
số. C ần lưu ý:
Chỉ có th c ng hoể ộ ặc trừ các đại lượng v i nhau n u chúng có cùng th nguyên. ớ ế ứ
Vế trái và v ph i c a m ng th ng th n ph i có cùng th nguyên. ế ả ủ ột đẳ ức (bấ ẳt đ ức) cầ ả ứ
Tuân theo quy t n này, ta có th s d ng phép ki m tra ắc cơ bả ể ử ụ phân tích th nguyênứ để ể
tính đúng đắn của một biểu th c. M t quan h b t k ch có th u th nguyên cứ ộ ệ ấ ỳ ỉ ể đúng nế ứ ủa hai
vế ng nhau. phương trình là giố
Để minh họa cho thủ thuật này, gi thi t r ng b n m v ả ế ằ ạn quan tâm đế ột phương trình về ị
trí c a m t chi c xe và th i gian n u xe kh i hành t tr ng yên t i v trí =0 và x ủ ộ ế ờ t ế ở ừ ạng thái đứ ạ ị x
chuy
ển độ ốc không đổ ức đúng cho trường với gia t i . Bia ểu th ng hợp này là = ½ x at
2
(xem
chương 2). Đại lượng x ở vế trái có thứ nguyên là L. Để cho phương trình này đúng về thứ
nguyên thì v bên ph i c i có th nguyên là L. Ta có th ti n hành ế ả ủa phương trình cũng phả ứ ể ế
ki
ểm tra th nguyên b ng cách thay th th nguyên cho gia t , và thứ ằ ế ứ ốc là L/T
2
ời gian là T vào
phương trình. Ta được:
L
L=
T
2
T
2
L
Các th nguyên th c kh ứ ời gian đượ ử đi như trên nên chỉ còn lại th dài. Hai v ứ nguyên độ ế
trái và ph i kh p v i nhau. ả ớ ớ
Một th thu t t d ng phép phân tích th nguyên là l p m t bi u th c ủ ậ ổng quát hơn khi sử ụ ứ ậ ộ ể ứ
có d ng: ạ
n m
x a t
Với , là các s c n tìm và là d u tm n ố ầ ấ ỉ l . Quan h này chệ ệ ỉ đúng nếu thứ nguyên c a ủ
hai v nguyên c a v bên trái là chi u dài nên th nguyên c a ph n bên ế là như nhau. Vì thứ ủ ế ề ứ ủ ầ
phải cũng là chiều dài. Nghĩa là:
1 0
L L T
n m
a t
Do gia t
ốc a có th nguyên là L ứ /T
2
(xem chương 2) nên ta có:
2 1 0 2 1 0
(L / T ) T LT L / T L T
n m m n
Từ phương trình trên, ta dễ thấy là =1 và =2. Tn m ức là:
2
x at
Phép phân tích th nguyên ch có m t h n ch là không ki s b ng s ứ ỉ ộ ạ ế ểm tra được các hệ ố ằ ố
trong công th c. ứ
Các ký hi u dùng trong công th c không nh t thi t ph i là ký hi u dùng cho th nguyên ệ ứ ấ ế ả ệ ứ
của đại lượ ệu đượ g thường vật lý. Một số ký hi c dùn ng xuyên (ví d ). M ng ụ như t ột đại lượ
có th c bi u di n b i nhi u ký hi u (ví d , có th dùng , ho c ), tùy theo ể đượ ể ễ ở ề ệ ụ như tọa độ ể x y ặ z
trườ ợ ụng h p sử d ng.
Trường Đạ ọc Sư phại h m Kỹ thu t Tp. H Chí Minh 2021 ậ ồ
10
Câu h i 1.2ỏ : Nói r có th cho ra giá tr b ng s c a các h ng s ằng “Phép phân tích đơn vị ể ị ằ ố ủ ằ ố
của các t lỉ ệ có thể xu t hi n trong các bi u th i s ấ ệ ể ức đạ ố” là đúng hay sai?
Bài t p m u 1.1: ậ ẫ
Hãy ch ng t r ng bi u th c ứ ỏ ằ ể ứ
v at
(v i v là t , a là gia t c và t là kho ng th i ớ ốc độ ố ả ờ
gian) là đúng về thứ nguyên.
Bài t p m u 1.2: ậ ẫ
Giả s ử người ta b o r ng gia t c c t h t chuy ng v i tả ằ ố ủa mộ ạ ển độ ớ ốc độ không đổ i theo v
một đường tròn bán kính t l v i r ỉ ệ ớ r
n
và v i . Hãy tìm giá tr c a và n và vi t bi u ớ v
m
ị ủ m ế ể
thức tối gi n c a gia t c. ả ủ ố
Giải:
Ta có th vi t bi u th u c c v i là h s t l , không có th nguyên: ể ế ể ức ban đầ ủa gia tố ớ k ệ ố ỉ ệ ứ
m
n
a kr v
Thay các th nguyên c c: ứ ủa gia tốc, tốc độ và bán kính vào, ta đượ
2
L L
L
T T
m
n
Cân b ng các s m c c ằ ố ũ ủa L và T ta đượ
1; 2 n m m
Từ đó:
1 n
Biểu thức của gia t là ốc sẽ
2
1 2
v
a kr v k
r
Trong ph n 4.4 v sau, ta s th y r ng 1 v i h c ch n phù h p. N u ầ ề ẽ ấ ằ k= ớ ệ đơn vị đượ ọ ợ ế
dùng h khác thì s khác 1. Ví d n v n t c là km/h và ta mu n có ệ đơn vị k ẽ ụ ếu đơn vị ậ ố ố
gia t c tính b ng m/s .
ố ằ
2
Phép đổi đơn vị
Trong các bài toán, đôi khi ta phải đổi đơn vị đơn vị đơn vị từ một hệ này sang một hệ
khác (ví d t inch sang cm) ho trong cùng m t h (ví d t km sang m). Xem ụ ừ ặc đổi đơn vị ộ ệ ụ ừ
phụ lục A v danh sách các h sề ệ ố qui đổi.
Cũng như vớ xem đơn vị là các đại lượng đạ ước lượi thứ nguyên, có thể i số và có thể c
lẫn nhau trong m t công th c. ộ ứ
Cần lưu ý là phải luôn ghi kèm đơn vị ỗi đại lượ ần thì ghi đơn vị cho m ng, nếu c trong
suốt quá trình y thì có th phát hi c các sai sót trong tính toán. tính toán. Làm như vậ ể ện đượ
http://ipt.hcmute.edu.vn B môn v t lý ộ ậ
11
Khi đổi đơn vị thì c n ph ng g c v i m t phân s mà giá tr c a phân s này là ầ ải nhân đại lượ ố ớ ộ ố ị ủ ố
1.
Ví dụ:
15in ? cm
. Ta bi ến đổi như sau:
15,0 in 15,0 in
2,54cm
1 in
38,1 cm
.
Trong tính toán ở trên, ph n trong d u ngo c có giá tr là 1 vì ầ ấ ặ ị
1 in 2,54 cm
.
Câu h i 1.3:ỏ Khoảng cách gi a hai thành ph là 100 d m. Kho ng cách này tính theo ki-lô-ữ ố ặ ả
mét s là: ẽ
(a) Nh (b) L ng 100 ỏ hơn 100 ớn hơn 100 (c) bằ
Bài t p m u 1.3: ậ ẫ
Trên m ng cao t t chi y v i t 38,0 i lái xe có ột đườ ốc, mộ ếc xe đang chạ ớ ố ộc đ m/s. Ngườ
vượ ớt gi i hạn tốc độ 75,0 mi/h (dặm/h) hay không?
Giải:
Đổi mét sang d i giây sang giặm và đổ ờ
1mi
38,0 m / s
1609 m
3600 s
85,0 mi / h
1h
Như vậy, người lái xe đã vượ qui địt quá tốc độ nh và cần phải chạy ch m l i. ậ ạ
Ước lượng và phép tính b l n ậc độ ớ
Trong nhiều trườ chính xác cho đại lượng hợp, ta không cần phải có một con số ng vật lý
mà ch c n m t giá tr g u di i d ng s dùng trong khoa h c. Giá tr c ỉ ầ ộ ị ần đúng, biể ễn dướ ạ ố ọ ị ướ
lượng này có th thi a (more approximate) n c bi u di n theo b c ể ếu chính xác hơn nữ ếu đượ ể ễ ậ
độ ớ ộ l n (order of magnitute). Cách tính theo bậc đ l ớn như sau:
Biểu di n sễ ố dưới d ng khoa h c: là tích c a m t s (có giá trạ ọ ủ ộ ố x ị t n 10) vừ 1 đế ới m t ộ
lũy thừ ột đơn vị đo. (ví dụ
a của 10 kèm theo m 1,2310
–2
m)
Nếu nh x ỏ hơn 3,162 (
10
) thì b c c l n là s ậ ủa độ ớ ố mũ củ đã cho a 10 khi biểu diễn số
dưới dạng khoa học.
Nếu l l n b ng s a 10 c ng thêm 1. x ớn hơn 3,162 thì bậc củ ộa đ ớ ằ ố mũ củ ộ
Ta dùng d u ch c v d xem xét m t s giá tr v ấ để ỉ “cùng bậ ới”. Sử ụng qui ước này để ộ ố ị ề
độ dài, ta được kết quả như sau:
0,002 1 m = 2,1 m 10 m; (b l n b ng s a 10 ng h p này
10
–3
–3
ậc độ ớ ằ ố mũ củ , trong trườ ợ
là 3) –
0,008 6 m = 8.6 10 m; (b l n b ng s a 10 c ng thêm 1)
10
–3
m
–2
ậc độ ớ ằ ố mũ củ ộ
720 m = 7,2 m 10 m; (b l n b ng s a 10 c ng thêm 1)
10
2
3
ậc độ ớ ằ ố mũ củ ộ
Trường Đạ ọc Sư phại h m Kỹ thu t Tp. H Chí Minh 2021 ậ ồ
12
Khi s d ng theo b l n thì các k t qu ch tin c c trong ph m vi ử ụng ước lượ ậc độ ớ ế ả ỉ ậy đượ ạ
một b i s c a 10. Nộ ố ủ ếu một đ i lưạ ợng ltăng 3 bậc độ ớn thì giá trị c c nhân vủa nó đượ ới m t ộ
hệ số là
10
3
= 1, 000.
Bài t p m u 1.4: ậ ẫ
Hãy ướ ột ngườ ộc đờc lượng số lần hít vào – thở ra trung bình của m i trong suốt cu i.
Giải:
Ta b u b i th trung bình cắt đầ ằng cách ước đoán tuổ ọ ủa người là 70 năm. Nghĩ xem
trong 1 phút thì m i th bao nhiêu l n. Giá tr này ph thu c vào viột ngườ ở ầ ị ụ ộ ệc người nay
đang tập th dể ụng, đang ngủ, đang tứ ận, hay đang bình thản… Ta có thểc gi ước lượng
rằng s l n th trong m t phút là 10 l n. S này ch c ch n là g n v i giá tr th c t ố ầ ở ộ ầ ố ắ ắ ầ ớ ị ự ế
hơn là 1 lần hoặc 100 lần trong một phút.
Tìm s : ố phút trong 1 năm
5
400days 24hr 60mins
1yr 6 10 min
1 1day 1hr
yr
Tìm s : ố phút trong 70 năm
5 7
min
6 10 70yrs 4 10 mins
yr
Tìm s l n th trong c i: ố ầ ở ả đời ngườ
7 8
breaths
4 10 mins 10 4 10 breaths
min
Từ đó, có thể ột ngườ ộc đờ nói rằng số lần thở của m i trong suốt cu i vào khoảng 1 tỉ
lần. Qua ví d này y r ng thì ch n con s tính ụ , ta cũng thấ ằng để ước lượ ọ ố 400 ngày để
thì thu n ti ậ ện hơn là 365 ngày.
Các ch s ữ ố có nghĩa
Khi đo một đại lượ đó, các giá trị đo đượ ết đếng nào c chỉ được bi n trong gi i h n c a sai ớ ạ ủ
số th c nghi m. Giá tr c này ph thuự ệ ị ủa sai số ụ ộc vào nhiều y u t khác nhau. ế ố
Các sai s này có th là do d ng c i làm thí nghi m và/ho c s ố ể ụ ụ đo, kỹ năng của ngườ ệ ặ ố
lượng phép đo được thực hiện.
Ta c n có m t k thu n các sai s này. ầ ộ ỹ ật để tính đế ố
Ta s d ng các qui t c v ch s ẽ ụ ắ ề ữ ố có nghĩa để ước lượng sai s trong k t qu c a các phép ố ế ả ủ
tính.
Số ch sữ ố có nghĩa trong một phép đo có thể mô tả được ít nhi u v sai s . Nó có liên ề ề ố
quan v i s ch s t qu c ớ ố ữ ố được ghi trong kế ả ủa phép đo.
Ví d ta c a m c mét. Gi s r chính xác ụ ần đo bán kính củ ột cái đĩa CD bằng thướ ả ử ằng độ
mà ta có th c là ± 0,1 cm. N c 6,0 cm thì ta ch có th c r ng bán ể đạt đượ ếu ta đo đượ ỉ ể nói đượ ằ
http://ipt.hcmute.edu.vn B môn v t lý ộ ậ
13
kính c ng 5,9 cm n 6,1 ng h p này, giá trủa đĩa nằm đâu đó trong khoả đế cm. Trong trườ ợ ị đo
6,0 cm có 2 ch s ng ch s c tính là ữ ố có nghĩa. Lưu ý rằ ữ ố được ước lượng đầu tiên cũng đượ
chữ số y ta có th vi t giá tr bán kính c ± 0,1) cm. có nghĩa. Vì vậ ể ế ị ủa đĩa là (6,0
Chữ s số có nghĩa là chữ ố đáng tin. Số có nghĩa hoặ không (0) có thể c không có nghĩa.
Số 0 dùng để xác định vị trí của dấu thập phân thì . Ví dkhông có nghĩa ụ như các số
0 trong các s 0,03 và 0,007 ch s a hai giá tr ố 5 là không có nghĩa. Số ữ ố có nghĩa củ ị
này l t là 1 và 2. Tuy nhiên, s 10,0 l i có 3 ch s ần lượ ố ạ ữ ố có nghĩa.
Nếu s 0 n m sau các ch s khác thì có th b nh m l n. Ví d ng c a ố ằ ữ ố ể ị ầ ẫ ụ như khối lượ ủ
một v c ghi là 1 500 g thì các ch sật đượ ữ ố 0 có ph i là sả ố có nghĩa hay không. Để đỡ
nh
ầm l n thì ph i dùng d ng s khoa h ng hẫ ả ạ ố ọc. Trong trườ ợp này, n u ghi là 1,5 10 ế
3
thì có 2 ch s u ghi là 1,50 10 thì có 3 ch s u ghi
ữ ố có nghĩa. Nế
3
ữ ố có nghĩa và nế
1,500 10 thì có 4 ch s
3
ữ ố có nghĩa. Các giá trị nhỏ c xem xét v i qui hơn 1 cũng đượ ớ
t
ắc tương tự nghĩa, trong khi 2,30: 2,3 10
–4
(hoặc 0,000 23) thì có 2 chữ số có 10
–
4
(ho c 0,000 230) thì có 3 ch s ặ ữ ố có nghĩa.
Khi gi i bài tả ập, ta thường kết hợp các đại lượng v i nhau b ng các phép toán nhân, chia, ớ ằ
cộng, tr y thì cừ… Khi làm như vậ ần ph i b m r ng kả ảo đả ằ ết quả có m t s ch sộ ố ữ ố có nghĩa
thích h p. ợ
Khi nhân hoặc chia các đại lượng, số chữ số có nghĩa ở kết quả là số ch s ữ ố có nghĩa
nh tỏ nhấ trong các giá trị tham gia vào phép tính.
Tính diện tích c a m t hình ch nh t có 2 c nh là 25,57 m và 2,45 m, ta có: ủ ộ ữ ậ ạ
25,57 m 2,45 m = 62,6 m
2
do s ch s a hai th a s l t là 4 và 3 nên l y 3 là s ch số ữ ố có nghĩa củ ừ ố ần lượ ấ ố ữ ố có nghĩa cho
kết qu phép nhân. ả
Tính diện tích c a m t hình tròn bán kính 6,0 cm: ủ ộ
2 2
cm 1,1 10 cm
2
2
A= r 6,0 =
Nếu dùng máy tính thì b n có thạ ể thu được k t qu là 113,097 335 5. T t nhiên là không ế ả ấ
th
ể ghi h t các ch s ế ữ ố như vậy nên có th là b n s ghi k t qu là 113 cm . K t qu này không ể ạ ẽ ế ả
2
ế ả
đúng vì nó có đến 3 ch s ữ ố có nghĩa trong khi bán kính của hình tròn ch có 2 ch s ỉ ữ ố có nghĩa.
Vì v y, k t qu ph (ch không ph i là 110 cm )
ậ ế ả ải được ghi là 1,110
2
cm
2
ứ ả
2
Nếu c ng và tr các s thì k t qu s l y trong các s ộ ừ ố ế ả ẽ ấ s tố ch s th p phân nh nhữ ố ậ ỏ ấ ố
hạng của phép tính.
Ví dụ: T ng c a 135 cm và 3,25 cm s là: ổ ủ ẽ
135 cm + 3,25 cm = 138 cm (do s 135 cm không có s th p phân nào). ố ố ậ
Tương tự như vậ 28,4 (Lưu ý là không thể y, ta có: 23,2 + 5,174 = ghi kết quả là 28,374
vì s 23,2 ch có 1 ch s th p phân). ố ỉ ữ ố ậ
Trường Đạ ọc Sư phại h m Kỹ thu t Tp. H Chí Minh 2021 ậ ồ
14
Qui t c v c ng ho c tr có th d ng h p mà s ch s a k t qu ắ ề ộ ặ ừ ể ẫn đến trườ ợ ố ữ ố có nghĩa củ ế ả
không gi ng v i s ch s a các s h ng trong phép tính. Xét c i ố ớ ố ữ ố có nghĩa củ ố ạ ác phép tính dướ
đây:
1,000 1 + 0,000 3 = 1,000 4
1,002 0,998 = 0,004 –
Ở ố phép tính thứ nhất, số chữ số có nghĩa của kết quả là 5, trong khi s chữ số có nghĩa
của các s hố ạng l t là 5 và 1. phép tính th 2, s ch s a kần lượ Ở ứ ố ữ ố có nghĩa củ ết qu là 1, ả
trong khi s ch s a các s h ng l t là 4 và 3. ố ữ ố có nghĩa củ ố ạ ần lượ
Lưu ý: Trong sách này, các ví d v s ụ ề ố cũng như các bài toán ở cu dùng các ối chương sẽ
số với 3 ch s ữ ố có nghĩa.
Qui tắc về làm tròn s : ố
Chữ s cu c gi l i s n u ch s cu i cùng b bố ối cùng đượ ữ ạ ẽ tăng lên 1 đơn vị ế ữ ố ố ị ỏ đi lớn
hơn 5. (Ví dụ, 1,346 được làm tròn thành 1,35)
Giữ nguyên ch s cu c gi l i n u ch s cu i cùng bữ ố ối cùng đượ ữ ạ ế ữ ố ố ị bỏ đi nhỏ hơn 5.
(Ví d c làm tròn thành 1,34) ụ, 1,342 đượ
Nếu ch s cu c b s c gi l c làm tròn thành ữ ố ối cùng đượ ỏ đi là 5 thì chữ ố đượ ữ ại đượ số
ch tẵn g n nhầ ấ .
4
(Qui t tránh sai s t lo t phép ắc này được đưa ra để ố tích lũy trong mộ ạ
tính s h c liên ti p). ố ọ ế
Khi làm toán, n u có nhi tránh c ng d n sai s , ta ế ều phép tính trung gian thì để ộ ồ ố chỉ
làm tròn phép tính cu i cùngở ố .
Bài t p m u 1.5: ậ ẫ
Người ta tr i m t t m th m trong phòng hình ch nh t có các s ả ộ ấ ả ữ ậ ố đo chiều dài là 12,71 m
và chi u r ng là 3,56 m. Hãy tìm di n tích c ề ộ ệ ủa căn phòng.
Giải:
N
ếu nhân 12,71 m v i 3,46 m bớ ằng máy tính bỏ túi thì ta sẽ được kết quả là 43,9766 m . Ta
2
sẽ ch p nh n bao nhiêu ch s trong k t qu này. Áp dấ ậ ữ ố ế ả ụng qui t c v s ch s có ắ ề ố ữ ố
nghĩa thì con số có nghĩa nhấ có ít chữ số t là 3,46 m. Vì vậy ta phải biểu diễn kết quả
là 44,0 m .
2
4
Qui t c này d a trên l p lu n là trong quá trình tính toán thì 50% các s c làm tròn lên và 50% còn l i ắ ự ậ ậ ố đã đượ ạ
được làm tròn xuống. Theo qui tắc này, khi bỏ ố đi chữ s 5 cu c làm tròn thành 2,32 ối cùng thì 2,315 và 2,325 đều đượ
http://ipt.hcmute.edu.vn B môn v t lý ộ ậ
15
Tóm t t 1 ắ chương
Đị ĩnh ngh a:
Ba đại lượ ật lý cơ bả ủa cơ họ đơn vịng v n c c là và . Trong hđộ dài, khối lượng thời gian ệ
quốc t , chúng lế ần lượt có đơn vị là mét (m), kilogram (kg) và giây (s). Không th ể định nghĩa
các đại lư i lượng này bằng các đạ ợng khác cơ bản hơn chúng.
Khối lượng riêng của m t ch ng cộ ất được định nghĩa là khối lượ ủa m th tích ột đơn vị ể
m
V
Khái ni m và nguyên lý: ệ
Phương pháp ữu ích đốphân tích th nguyênứ là rất h i với việc giải bài tập vật lý. Có thể xử
lý các th ứ nguyên như là các đạ ượng đại l i s . Bố ằng cách ước lượng và tính toán theo b c c a ậ ủ
độ ớ ờ l n, ta có thể áng ch c câu trừng đượ ả l i cho bài tập n thông tin cếu không có đủ ần thiết
để ờ tìm ra một l i giải hoàn toàn chính xác.
Khi tính một kết quả từ mộ ốt s giá tr ị đo mà mỗi giá tr chính xác nh nh thì c n ị đều có độ ất đị ầ
phải ghi k t qu v i m t s chính xác các ch s . Khi ế ả ớ ộ ố ữ ố có nghĩa nhân m ng, sột vài đại lượ ố
chữ số có nghĩa trong kết quả cuối cùng bằng số chữ số có nghĩa của đại lượng có ít chữ số
có nghĩa nhất. Qui t ng cho . ắc này cũng áp dụ phép chia
Khi c các s , s ch s sau d u th p phân ph i b ng s ch s th p phân c cộng hoặ trừ ố ố ữ ố ấ ậ ả ằ ố ữ ố ậ ủa số
hạng có ít ch sữ ố sau d u th p phân nh t. ấ ậ ấ
Câu h i lý thuy ỏ ết chương 1
1. Gi ả s ba chu n c a h mét là chi u dài, kh ng riêng và thử ẩn cơ bả ủ ệ ề ối lượ ời gian (thay vì
chiều dài, khối lượng và th i gian). Chu n khờ ẩ ối lượng riêng trong h thệ ống này được định
nghĩa từ ối lượ ủa nướ ải quan tâm đế ủa nước để kh ng riêng c c. Cần ph n tính chất nào c
bảo đảm rằng chuẩn khối lượng riêng này càng chính xác càng tốt?
2. T ại sao h mét lệ đơn vị ại được dùng nhi i các h khác? ều hơn so vớ ệ đơn vị
3. Có th s dể ử ụng hi ng t nhiên nào làm chu n thay th c i gian? ện tượ ự ẩ ế ủa thờ
4. Hãy bi u di n các giá trể ễ ị ng các ti u ng cho trong dưới đây bằ ếp đầ ữ b ng 1.4.ả
(a) 3 10 m (b) 5 10 m (c) 72 10 m
4
5
2
Trường Đạ ọc Sư phại h m Kỹ thu t Tp. H Chí Minh 2021 ậ ồ
16
Bài t p ậ chương 1
1. Một sinh viên sử dụng thước mét để ốn sách và thu đượ do bề dày của một cu c kết quả là
4,3cm ± 0,1cm. sinh viên khác s d c 4 k t qu khác nhau: M tộ ử ụng thước cặp và thu đượ ế ả
(a) 4,32 cm ± 0,01 cm,
(b) 4,31 cm ± 0,01 cm,
(c) 4,24 cm ± 0,01 cm,
(d) 4,43 cm 0,01 cm, ±
Số đo nào trong bốn s nói trên phù hố ợp với s nhố đo mà sinh viên thứ ất thu được?
2. M ột ngôi nhà được qu ng cáo là có di n tích s d ng 1420 feet vuông. Di n tích này tính ả ệ ử ụ ệ
theo mét vuông là bao nhiêu?
(a) 4660 m (b) 432 m
2 2
(c) 158 m (d) 132 m (e) 40,2 m
2 2 2
3. Hai đại lượng có c n ph i cùng th nguyên hay không n u ầ ả ứ ế
(a) ta cộng chúng v i nhau? ớ
(b) ta nhân chúng với nhau?
(c) ta trừ chúng cho nhau?
(d) ta chia chúng cho nhau?
(e) ta so sánh chúng với nhau?
4. S ố nào dưới đây là ước lượ ối lượng tốt nhất cho kh ng của toàn bộ người s ng trên Trái ố
đất?
(a) 2 10 (b) 1 10 kg (c) 2 10 (d) 3 10 (e) 4 10
8
kg
9
10
kg
11
kg
12
kg
5. Định lu u r ng tích c a kh ng c a m t v t vật 2 Newton (chương 5) phát biể ằ ủ ối lượ ủ ộ ậ ới gia
tốc c a nó thì b ng t ng l c tác d c a l c (a) ủ ằ ổ ự ụng lên nó. Cái nào dưới đây là đơn vị ủ ự
kg m/s (b) kg m (c) kg/m s m
2
2
/s
2
2
(d) kg
2
/s (e) không có cái nào đúng.
6. M
ột máy tính b túi hi n th k t qu 1,365 248 0 ỏ ể ị ế ả 10 kg. Sai s c a k t qu này là 62 %.
7
ố ủ ế ả
Có bao nhiêu ch s c xem là ch s t qu này? ữ ố đượ ữ ố có nghĩa trong kế ả
(a) Không có s nào (b) mố ột (c) hai (d) ba (e) bốn
7. M ẫu kilogram chu n là mẩ ột hình tr b ng platinum-iridium có chi u cao 39,0 mm và ụ ằ ề
đường kính 39,0 mm. Tính kh ng riêng cối lượ ủa nó?
ĐS: 2,15
10 kg/m
4 3
8. C ần m t khộ ố ợi lư ng v t li u, khậ ệ ố ợi lư ng riêng là
b làm m t hình c u ằng bao nhiêu để ộ ầ
rỗng có bán kính trong là và bán kính ngoài là ? r
1
r
2
ĐS:
3 3
2 1
4
3
r r
9. Kh ối lượng của một nguyên tử đồng là
25
1,06 10 kg
và kh ng riêng c ng là ối lượ ủa đồ
3
k8 20 g / m9
. nh s nguyên t ng có trong 1 cm ng. Cho r ng m t centimet
Xác đị ố ử đồ
3
đồ ằ ộ
http://ipt.hcmute.edu.vn B môn v t lý ộ ậ
17
kh giối đồng được hình thành b ng cách x p các kh i lằ ế ố ập phương ống h t nhau, vệ ới m t ộ
nguyên t ng tâm c a m i kh nh th tích c i kh i l ử đồ ở ủ ỗ ối. Xác đị ể ủa mỗ ố ập phương này.
Tính cạnh c a m i kh i l ng cách gi a các nguyên t . ủ ỗ ố ập phương, xem như là khoả ữ ử
ĐS: a)
22 3
8,42 10 atom/ cm
b)
23 3
1,19 10 cm / atom
c)
10
2,28 10 m
10. Hình bên bi u di n m t hình nón cể ễ ộ ụt. Hãy ch n bi u th c ọ ể ứ đúng để
mô t : ả
Tổng chu vi đáy lớn và đáy nhỏ
Thể tích
Diện tích toàn ph n ầ
của hình nón c t. ụ
a)
1/2
2
2
1 2 1 2
hr r r r
b)
1 2
2 r r
c)
2 2
1 1 2 2
3
r rr r
h
11. Định lu t v n v t h p d n c u di n b ng công th c ậ ạ ậ ấ ẫ ủa Newton được biể ễ ằ ứ
2
GMm
F
r
trong đó ối lượF là lực hấp dẫn của vật này lên vật khác, và là khM m ng của hai vật, và
r
là kho ng cách gi a hai v t. Lả ữ ậ ực có đơn vị trong hệ SI là kg . V y h ng s h p d n m/s
2
ậ ằ ố ấ ẫ
G có đơn vị gì?
ĐS:
3 2
m s / kg
12. (a) Gi s ả ử phương trình
3
x At Bt
mô t chuy ng c a mả ển độ ủ ột vật, v i có th nguyên ớ x ứ
độ dài và t có thứ nguyên th nh thời gian. Xác đị ứ nguyên của và . A B
(a) Xác định th nguyên c a o hàm ứ ủ đạ
2
3
dx
At B
dt
ĐS: (a)
3
A L / T
và
B L / T
b)
L / T
13. Gi ả s t phát tri n c a tóc b n là 1/32 (inchử ốc độ ể ủ ạ /ngày). Hãy đổi ra đơn vị (nano mét
/giây). B i vì kho ng cách gi a các nguyên t trong m t phân t là kho ng 0,1 nm, câu ở ả ữ ử ộ ử ả
trả lời c a b n cho th y các l p nguyên t ủ ạ ấ ớ ử nhanh chóng được lắp ráp trong quá trình t ng ổ
hợp protein này như thế nào.
ĐS: 9,19 n/s
14. Có bao nhiêu qu v a vào m c tiêu chu n? ả bóng bàn để ừ ột căn phòng có kích thướ ẩ
ĐS:
10
6
quả
Trường Đạ ọc Sư phại h m Kỹ thu t Tp. H Chí Minh 2021 ậ ồ
18
15. M ột l c dùng cho 50 000 miles (d c bao nhiêu vòng trong ốp ô tô đượ ặm). Nó quay đượ
cuộc đời c a nó? Gi s lủ ả ử ốp xe có đường kính là 2,5 ft, chu vi kho ng 8 ft. 1 mile = 5280 ả
ft
ĐS: 1
0
7
vòng
16. Năm dương lị ột Xuân phân này đếch, khoảng thời gian từ m n một Xuân phân tiếp theo,
là cơ sở ột năm dương cho lịch chúng ta. Nó có 365,242 199 ngày. Tìm số giây trong m
lịch.
ĐS: 31556926,0 s
17. Trong bãi đỗ ủa trường đạ ộng đồ xe bình thườ ớn hơn số xe c i học c ng, số ng l xe thể thao
tiện ích (SUV) là 94,7 %. Hi u c a chúng là 18. Tìm s xe . ệ ủ ố lượng SUV trong bãi đỗ
ĐS: 19
18. Bán kính của m t qu c u r ng ch ng c a ộ ả ầ ắn đồ ất được đo là (6,50 ± 0,20) cm, và khối lượ ủ
nó được đo là (1,85 ± 0,02) kg. Xác định khối lượng riêng c a qu c u tính b ng kilôgam ủ ả ầ ằ
trên mét kh i và sai s c a nó. ố ố ủ
ĐS:
1,6 ± 0,2 kg 10
3
19. 10
Khoảng cách t M t tr n ngôi sao g n nh t là kho ng 4 ừ ặ ời đế ầ ấ ả
16
m. Có th xem d i ể ả
Ngân hà là m
ột đĩa và độhình trụ đường kính ~10 m
21
dày ~10 m. Hãy tìm s ngôi sao
19
ố
trong d i Ngân hà theo b c c l n. Xem kho ng cách gi a M t tr i và ngôi sao g n ả ậ ủa độ ớ ả ữ ặ ờ ầ
nhất là kho ng cách ả điển hình.
ĐS:
10
11
ngôi sao.
| 1/18
| | Tải xuống

Có thể bạn quan tâm:

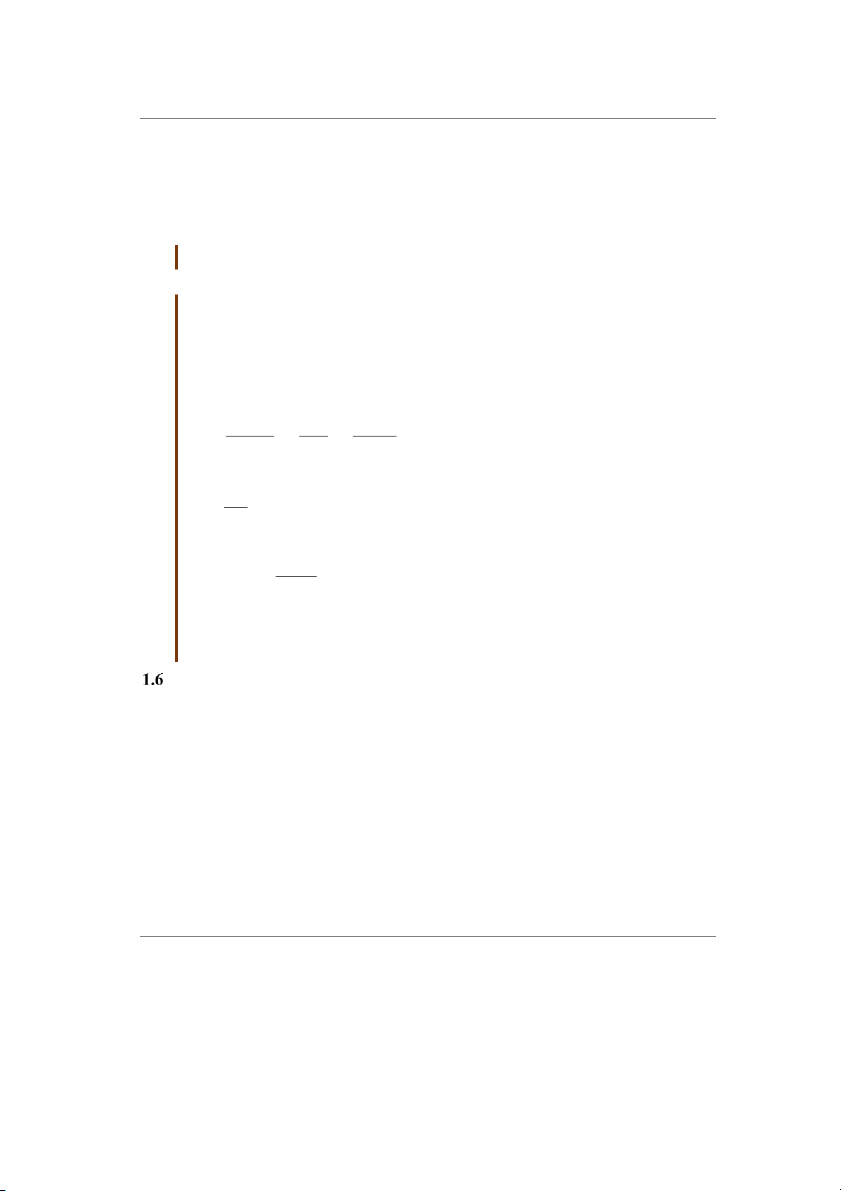
Preview text:

http://ipt.hcmute.edu.vn Bộ môn vật lý
Chương 1: Vật lý và đo lường
ũng như các khoa học khác, vật lý là khoa học dựa trên các quan sát thực nghiệm và
các phép đo định lượng. Mục tiêu chính của vật lý là xác định số lượng có hạn các
Cđịnh luật cơ bản chi phối các hiện tượng trong tự nhiên và sử dụng chúng để phát
triển các lý thuyết có thể dự đoán được kết quả của các thí nghiệm trong tương lai.
Các định luật cơ bản này được diễn đạt bằng ngôn ngữ toán học, một công cụ để để gắn kết
lý thuyết với thực nghiệm.
Mỗi khi có sự không nhất quán giữa tiên đoán của lý thuyết và kết quả thực nghiệm thì
cần phải đưa ra một lý thuyết mới hoặc chỉnh sửa lý thuyết đã có để loại bỏ sự không nhất
quán đó. Nếu một lý thuyết chỉ được thỏa mãn trong những điều kiện nhất định thì một lý
thuyết tổng quát hơn sẽ có thể thỏa mãn được mà không cần các điều kiện này. Ví dụ như các
định luật chuyển động được Newton (1642-1727) khám phá mô tả chính xác chuyển động
của các vật có tốc độ bình thường nhưng lại không áp dụng được cho các vật chuyển động
với tốc độ tương đương với tốc độ ánh sáng. Ngược lại, thuyết tương đối hẹp của Einstein
(1879-1955) cho các kết quả giống với các định luật Newton đối với tốc độ nhỏ nhưng cũng
mô tả chính xác chuyển động của các vật có tốc độ gần bằng tốc độ ánh sáng. Do đó, thuyết
tương đối hẹp của Einstein là một thuyết về chuyển động tổng quát hơn so với thuyết được
xây dựng từ các định luật Newton.
Vật lý học cổ điển bao gồm các nguyên lý của cơ học cổ điển, nhiệt động lực học, quang
học và điện từ học đã được phát triển trước năm 1900. Newton là người đã có những đóng
góp quan trọng cho vật lý học cổ điển, ông cũng là một trong những người khai sinh ra phép
tính vi tích phân như là một công cụ toán học. Các phát triển chủ yếu của cơ học được tiếp
diễn trong thế kỷ 18, nhưng ngành nhiệt động lực học và điện từ thì phải đến nửa sau của thế
kỷ 19 mới được phát triển. Nguyên nhân chủ yếu là do các thiết bị thí nghiệm thời đó quá thô sơ hoặc thiếu thốn.
Cuộc cách mạng lớn của vật lý, có liên quan với vật lý hiện đại, bắt đầu vào gần cuối thế
kỷ 19. Vật lý hiện đại được phát triển là do vật lý cổ điển không thể giải thích được nhiều
hiện tượng vật lý. Hai sự phát triển quan trọng nhất trong kỷ nguyên hiện đại là thuyết tương
đối và cơ học lượng tử. Thuyết tương đối hẹp của Einstein không những chỉ mô tả chính xác
chuyển động của các vật có tốc độ tươndg đương với tốc độ ánh sáng mà còn hiệu chỉnh một
cách trọn vẹn các khái niệm truyền thống về không gian, thời gian và năng lượng. Lý thuyết
này còn chỉ ra rằng tốc độ ánh sáng là giới hạn trên của tốc độ của một vật và khối lượng và
năng lượng có liên hệ với nhau. Cơ học lượng tử được hình thành bởi nhiều nhà khoa học
khác nhau, mô tả các hiện tượng vật lý ở cấp độ nguyên tử. Nhiều thiết bị thực tiễn đã được
chế tạo dựa vào các nguyên lý của cơ học lượng tử.
Các nhà khoa học làm việc không ngừng để cải thiện hiểu biết của chúng ta về các định
luật cơ bản. Nhiều tiến bộ về công nghệ trong hiện tại như tàu vũ trụ không người lái, hàng
loạt ứng dụng tiềm năng trong công nghệ na nô, vi mạch và máy tính siêu tốc, kỹ thuật chụp 1
Trường Đại học Sư phạm Kỹ thuật Tp. Hồ Chí Minh 2021
ảnh tinh xảo dùng trong nghiên cứu khoa học và y khoa cũng như nhiều kết quả đáng kể trong
kỹ thuật gien là kết quả của những nỗ lực của nhiều nhà khoa học, kỹ sư, nhà kỹ thuật. Ảnh
hưởng của những phát triển và khám phá này đến xã hội của chúng ta quả thực là to lớn và
chắc chắn là các khám phá và phát triển trong tương lai cũng sẽ đầy hứng thú, thách thức và
mang lại nhiều lợi ích cho nhân loại.
Các chuẩn độ dài, khối lượng và thời gian
Để mô tả các hiện tượng vật lý, ta cần phải đo lường nhiều khía cạnh khác nhau của tự
nhiên. Mỗi phép đo tương ứng với một đại lượng vật lý, ví dụ như chiều dài của một vật. Các
định luật vật lý được diễn đạt như là các mối quan hệ toán học giữa các đại lượng vật lý.
Trong cơ học, ba đại lượng cơ bản nhất là chiều dài, khối lượng và thời gian. Mọi đại
lượng khác trong cơ học có thể được biểu diễn thông qua ba đại lượng này.
Do các quốc gia khác nhau sử dụng các chuẩn khác nhau nên cần phải có chuẩn chung
cho các đại lượng. Cái được chọn làm chuẩn phải:  có sẵn;
 có một vài thuộc tính có thể đo lường được một cách tin cậy;
 phải cho cùng một kết quả khi đo bởi bất kỳ ai và bất kỳ nơi nào;
 không thay đổi theo thời gian.
Vào năm 1960, một ủy ban quốc tế đã đưa ra một bộ các chuẩn cho các đại lượng cơ bản
của khoa học. Nó được gọi là SI (Système International d’unités – Hệ đơn vị quốc tế). Bảng
dưới đây là các đại lượng cơ bản nhất và đơn vị tương ứng. Đại lượng Đơn vị trong SI độ dài mét (m), khối lượng ki-lô-gam (kg) thời gian giây (s). nhiệt độ Kelvin (K) cường độ dòng điện Ampère (A) cường độ sáng Candela – Cd lượng chất mole (mol)
Các đại lượng cơ bản dùng trong cơ học là chiều dài, khối lượng và thời gian. Các đại
lượng còn lại được biểu diễn qua các đại lượng này.
1.1.1 Chiều dài
Chiều dài được xác định bằng khoảng cách giữa hai điểm trong không gian.
Năm 1799, khi mét được chọn làm đơn vị đo hợp pháp của chiều dài tại Pháp, thì mét
được định nghĩa bằng 1/10.000.000 chiều dài của đoạn kinh tuyến đi qua Paris, tính từ xích
đạo lên cực bắc của Trái đất. Cần lưu ý rằng giá trị này không thỏa mãn yêu cầu là có thể sử dụng trong toàn vũ trụ. 2 http://ipt.hcmute.edu.vn Bộ môn vật lý
Năm 1960, mét được định nghĩa là khoảng cách giữa hai vạch trên một thanh platinum– iridium đặc biệt đ ợc
ư lưu trữ tại Pháp trong điều kiện kiểm soát được.
Trong những năm 1960 và 1970, mét được định nghĩa bằng 1.650.763,73 lần bước sóng
 của ánh sáng đỏ - cam phát ra từ đèn khí kripton-86.
Năm 1983, mét được định nghĩa là quãng đường mà ánh sáng đi được trong chân
không trong khoảng thời gian 1/299.792.458 s. Trong thực tế, định nghĩa này thiết lập tốc
độ ánh sáng trong chân không chính xác bằng 299.792.458 m/s. Định nghĩa này là hợp lệ
trong toàn vũ trụ và dựa trên giả thiết rằng ánh sáng là như nhau ở khắp mọi nơi. Bảng
1.1Bảng liệt kê các giá trị ước lượng của một số chiều dài đã đo đạc được.
Bảng 1.1: Ước lượng giá trị số đo của một vài độ dài (m) Độ dài (m)
Khoảng cách từ Trái đất đến chuẩn tinh xa nhất được biết đến 1,4 1026
Khoảng cách từ Trái đất đến thiên hà xa nhất 9  1025
Khoảng cách từ Trái đất đến thiên hà lớn gần nhất (Andromeda) 2  1022
Khoảng cách từ Mặt trời đến ngôi sao gần nhất (Proxima Centauri) 4  1016 Một năm ánh sáng 9,46  1015
Bán kính quĩ đạo trung bình của Trái đất quanh Mặt trời 1,50  1011
Khoảng cách trung bình từ Trái đất đến Mặt trăng 3,84  108
Khoảng cách từ xích đạo đến Bắc cực 1,00  107
Bán kính trung bình của Trái đất 6,37  106
Độ cao điển hình (tính từ bề mặt) của vệ tinh bay quanh Trái đất 2  105
Chiều dài của một sân bóng đá 9,1  101
Chiều dài của một con ruồi nhà 5  103
Kích thước của các hạt bụi nhỏ nhất ~ 104
Kích thước của tế bào trong hầu hết các cơ quan sống ~ 105
Đường kính của nguyên tử hidro ~ 1010
Đường kính của hạt nhân nguyên tử ~ 1014
Đường kính của một proton ~ 1015
1.1.2 Khối lượng
Đơn vị của khối lượng trong SI là ki-lô-gram (kg), được định nghĩa là khối lượng của
một khối platinum–iridium hình trụ đặc biệt lưu trữ tại văn phòng quốc tế về khối lượng và 3
Trường Đại học Sư phạm Kỹ thuật Tp. Hồ Chí Minh 2021
đo lường tại Sèvres, Pháp. Chuẩn khối lượng được đưa ra vào năm 1887 và từ đó đến nay
chưa thay đổi, do platinum-iridium là hợp kim đặc biệt bền. Một bản sao của khối trụ này
được giữ tại Viện quốc tế về tiêu chuẩn và công nghệ (NIST) tại Gaithersburd, Maryland.
Bảng 1.2 liệt kê các giá trị gần đúng của khối lượng các vật thể khác nhau.
Bảng 1.2: Ước lượng khối lượng của các vật thể khác nhau Khối lượng (kg)
Phần vũ trụ quan sát được 1052 Dải Ngân hà 1042 Mặt trời 1,99  1030 Trái đất 5,98  1024 Mặt trăng 7,36  1022 Cá mập ~ 103 Con người ~ 102 Con ếch ~ 101 Con muỗi ~ 105 Vi khuẩn ~ 1015 Nguyên tử hidro 1,67  1027 Điện tử 9,11  1031
1.1.3 Thời gian
Trước năm 1967, chuẩn về thời gian được định nghĩa theo ngày mặt trời trung bình (là
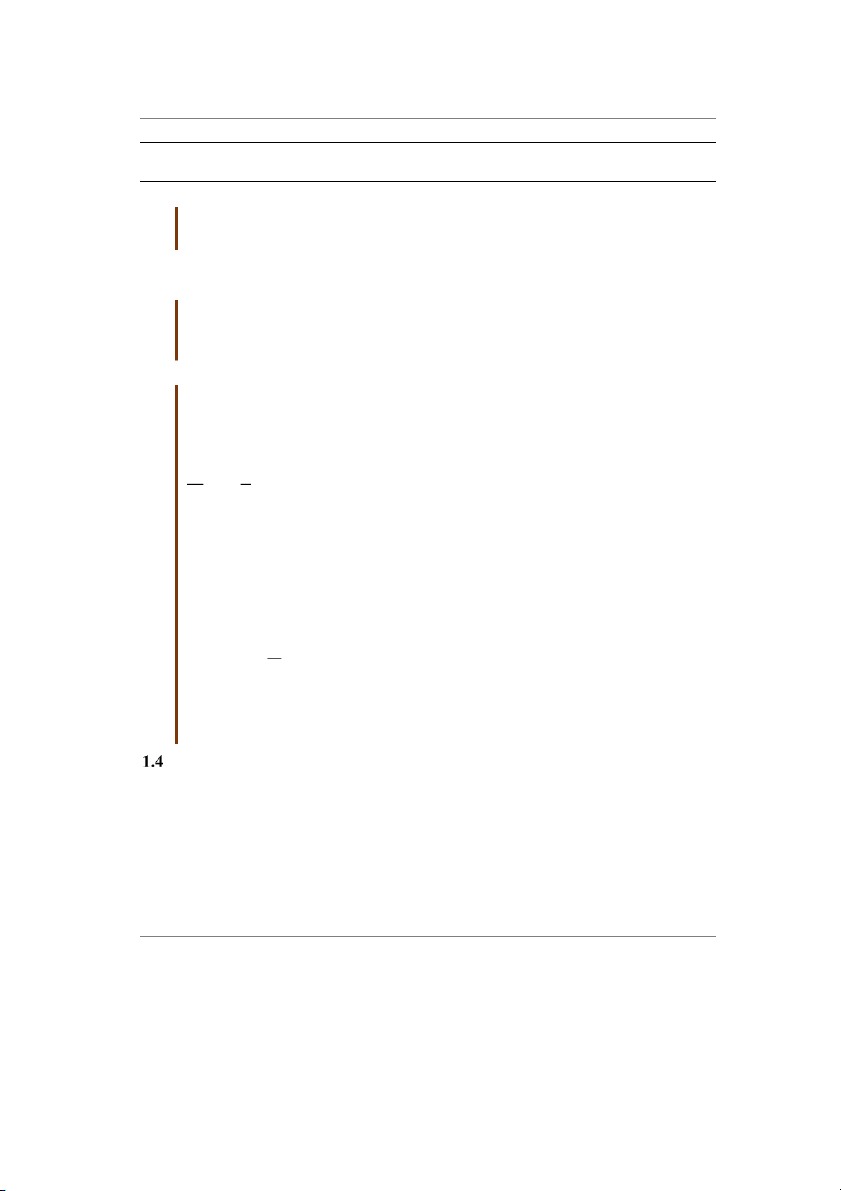
khoảng thời gian giữa hai lần mặt trời đứng bóng liên tiếp). Đơn vị giây (second – s) được  1  1  1 định nghĩa là  
của ngày mặt trời trung bình. Định nghĩa này dựa trên sự quay 60  60  24     
của một hành tinh là Trái đất nên không thể xem là chuẩn thời gian của vũ trụ.
Vào năm 1967, giây được định nghĩa lại khi xuất hiện dụng cụ đo thời gian với độ chính
xác cao – đồng hồ nguyên tử (hình 1.1b), đồng hồ này đo các dao động của nguyên tử Cesium
(Cs). Theo đó, 1 giây là 9.192.631.770 chu kỳ dao động của nguyên tử Cs133. Bảng 1.3
trình bày một số giá trị gần đúng của thời gian. 4 http://ipt.hcmute.edu.vn Bộ môn vật lý
Bảng 1.3: Ước lượng giá trị của một số khoảng thời gian Khoảng thời gian (s) Tuổi của Vũ trụ 4  1017 Tuổi của Trái đất 1,3  1017
Tuổi trung bình của sinh viên đại học 6,3  108 Một năm 3,2  107 Một ngày 8,6  104 Một giờ học 3,0  103
Thời gian giữa hai nhịp tim bình thường 81021
Chu kỳ của sóng âm (mà tai nghe được) ~ 10–23
Chu kỳ điển hình của sóng vô tuyến ~ 10–26
Chu kỳ dao động của một nguyên tử trong chất rắn ~ 10–13
Chu kỳ của ánh sáng khả kiến ~ 10–15
Thời gian va chạm của hai hạt nhân ~ 10–22
Thời gian để ánh sáng đi qua một proton ~10–24
Ngoài các đơn vị cơ bản mét, kg và s nói trên, ta có thể dùng các đơn vị khác như là mm
(mili-mét), ns (nano giây), với mili và nano là các tiếp đầu ngữ chỉ các bội số của 10.
Các tiếp đầu ngữ: Các tiếp đầu ngữ (tiền tố) được ghép vào trước một đơn vị đo để biểu
diễn một bội số của 10. Mỗi tiếp đầu ngữ có một tên và cách viết tắt riêng. Có thể ghép tiếp
đầu ngữ với bất kỳ đơn vị cơ bản nào. Nó chính là hệ số nhân thêm vào đơn vị cơ bản. Ví dụ: 3 1mm 10  m ; 3 1mg 10  g .
Đại lượng cơ bản và đại lượng phái sinh: Độ dài, khối lượng và thời gian là ví dụ cho
các đại lượng cơ bản. Hầu hết các đại lượng còn lại là đại lượng phái sinh, tức là có thể được
biểu diễn dưới dạng các tổ hợp toán học của các đại lượng cơ bản. Ví dụ thường gặp là diện
tích (tích của hai chiều dài) và tốc độ (tỉ số giữa độ dài và khoảng thời gian). Hoặc khối lượng
riêng, được định nghĩa là khối lượng của một đơn vị thể tích m   V 5
Trường Đại học Sư phạm Kỹ thuật Tp. Hồ Chí Minh 2021
Tính hợp lý của các kết quả: Khi giải bài tập, bạn cần phải kiểm tra câu trả lời của mình
xem chúng có hợp lý không. Việc xem lại các bảng giá trị gần đúng của độ dài, khối lượng
và thời gian có thể giúp bạn kiểm tra tính hợp lý này.
Bảng 1.4: Các tiếp đầu ngữ cho bội/ước số của 10 Lũy thừa Tiếp đầu Viết tắt Lũy thừa Tiếp đầu Viết tắt 10 ngữ 10 ngữ 1022 yocto y 103 kilo k 1021 zepto z 106 mega M 1018 atto a 109 giga G 1015 femto f 1012 tera T 1012 pico p 1015 peta P 109 nano n 1018 exa E 106 micro  1021 zetta Z 103 milli m 1024 yotta Y 102 centi c 101 deci d
Câu hỏi 1.1: Trong một xưởng cơ khí, người ta chế tạo hai bánh cam, một bằng nhôm và một
bằng sắt. Hai bánh cam này có cùng khối lượng. Bánh cam nào lớn hơn?
(a) bánh bằng nhôm (b) bánh bằng sắt (c) hai bánh có cùng kích cỡ 6 http://ipt.hcmute.edu.vn Bộ môn vật lý
Vật chất và xây dựng mô hình
Nếu nhà vật lý không thể tương tác trực tiếp với
một số hiện tượng, họ thường hình dung ra một mô hình
cho hệ vật lý có liên quan đến các hiện tượng này. Ví dụ,
ta không thể tương tác trực tiếp với các nguyên tử vì
chúng quá nhỏ. Do đó, ta xây dựng một mô hình tưởng
tượng về nguyên tử như một hệ gồm một hạt nhân và
một hoặc nhiều electron nằm bên ngoài hạt nhân. Khi đã
xác định được các thành phần vật lý của mô hình thì ta
đưa ra các tiên đoán về hành vi của chúng trên cơ sở
các tương tác giữa các thành phần của hệ hoặc tương
tác giữa hệ với môi trường bên ngoài hệ.
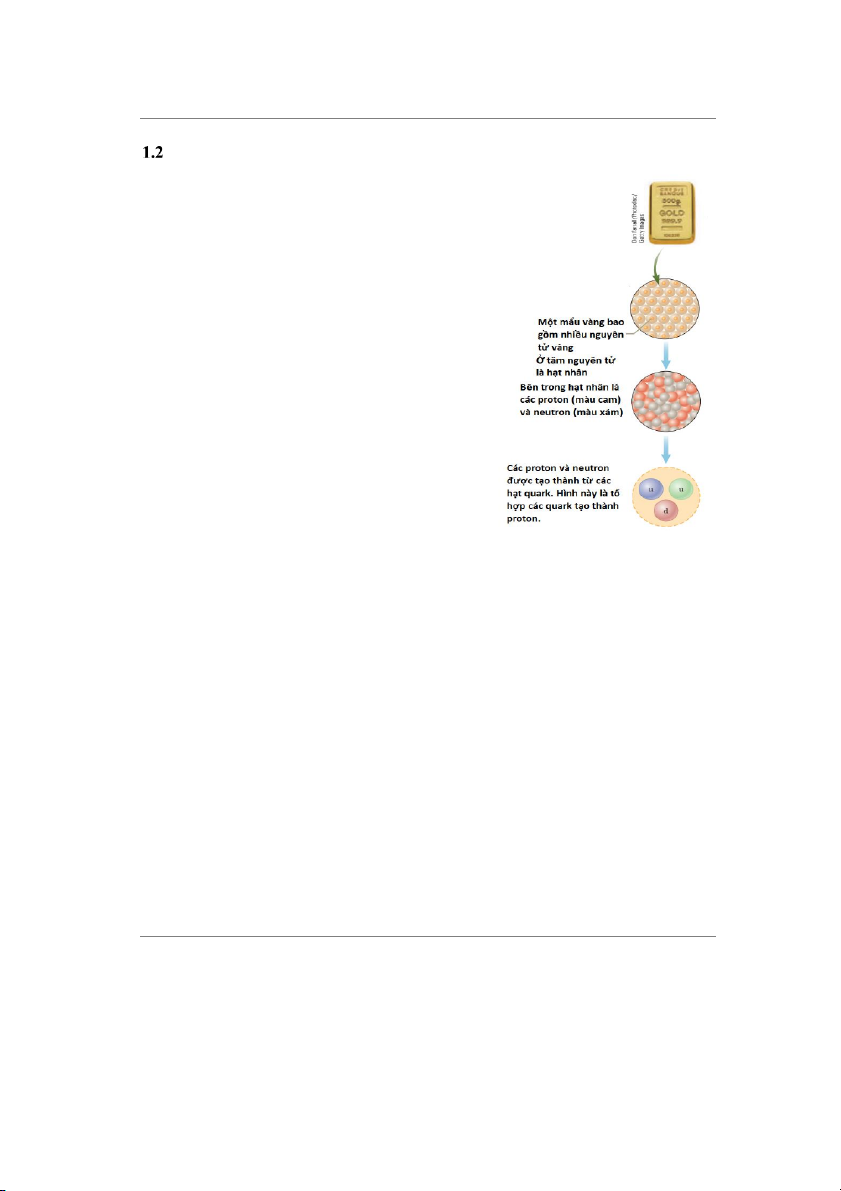
Hãy xem xét hành vi của vật chất để làm ví dụ. Hình
đầu tiên của hình 1.1 cho thấy một miếng vàng đặc. Có
phải miếng vàng này toàn là vàng, không có chỗ trống
nào? Nếu cắt đôi miếng vàng này, hai miếng vàng thu
được vẫn giữ nguyên đặc tính hóa học như miếng vàng
nguyên. Chuyện gì sẽ xảy ra nếu ta cứ chia đôi các miếng
này liên tục, vô hạn lần? Các miếng ngày càng nhỏ dần
này có luôn là vàng hay không? Những câu hỏi như vậy
đã được đặt ra từ rất lâu bởi các nhà triết học Hi Lạp.
Hai trong số họ, Leucippus và học trò của ông là Hình 1.1
Democritus, không chấp nhận ý tưởng rằng sự chia cắt
như vậy có thể diễn ra mãi mãi. Họ xây dựng một mô
hình một mô hình vật chất với suy đoán rằng quá trình nói trên cuối cùng cũng phải kết thúc
khi nó tạo ra một hạt không thể bị chia cắt được nữa. Trong tiếng Hi lạp, “atomos” có nghĩa
là “không chia cắt được”. Từ tiếng Anh “atom” (nguyên tử) bắt nguồn từ cách gọi này trong tiếng Hi lạp.
Mô hình Hi lạp về cấu trúc vật chất cho rằng mọi vật chất bình thường đều có các nguyên
tử (xem hình giữa của hình 1.1). Ngoài ra, không có thêm cấu trúc nào khác được xác định
trong mô hình này; các nguyên tử hoạt động như các hạt nhỏ có tương tác với nhau, nhưng
mô hình này không đề cập đến cấu trúc bên trong nguyên tử.
Vào năm 1897, J. J. Thomson đã xác định electron là một hạt tích điện và là một thành
phần của nguyên tử. Điều này dẫn đến mô hình nguyên tử đầu tiên có cấu trúc bên trong.
Mô hình này sẽ được thảo luận trong chương 42.
Sau sự phát hiện các hạt nhân vào năm 1911, người ta đã đưa ra một mô hình nguyên tử
trong đó nguyên tử được tạo thành từ các electron bao quanh một hạt nhân ở giữa. Tuy vậy,
mô hình này dẫn đến một câu hỏi mới: Hạt nhân có cấu trúc hay không? Nghĩa là, phải chăng
hạt nhân là một hạt đơn lẻ hay là một tập hợp các hạt? Vào đầu những năm 1930, người ta
đưa ra một mô hình mô tả hai thành phần cơ bản trong hạt nhân: proton và neutron. Proton
mang điện tích dương và một nguyên tố hóa học được xác định bằng số lượng proton trong 7
Trường Đại học Sư phạm Kỹ thuật Tp. Hồ Chí Minh 2021
hạt nhân của nó. Con số này được gọi là nguyên tử số (atomic number) của nguyên tố. Bên
cạnh nguyên tử số, một số khác, khối số (mass number), được định nghĩa bằng tổng của số
proton và số neutron tạo nên hạt nhân. Nguyên tử số của một nguyên tố không bao giờ thay
đổi, còn khối số có thể thay đổi.
Tuy nhiên, có phải sự phân chia vật chất đã kết thúc? Hiện nay, người ta đã biết rằng các
proton, neutron và một số đông đảo các hạt ngoại lai được tạo nên từ 6 hạt khác gọi là
quark, các hạt này được đặt tên là up, down, strange, charmed, bottom và top. Các hạt quark
up, charmed và top có điện tích +2/3 điện tích của proton trong khi 3 hạt còn lại có điện tích
–1/3 điện tích của proton. Proton được tạo thành từ 2 hạt up và 1 hạt down (ký hiệu lần lượt
là u và d trong hình 1.2). Tương tự, neutron được tạo thành từ 2 hạt down và 1 hạt up.
Khi học vật lý, bạn phải phát triển một tiến trình xây dựng các mô hình. Bạn sẽ được
thử thách với việc giải quyết nhiều vấn đề toán học. Một kỹ thuật giải quyết bài toán quan
trọng nhất là xây dựng mô hình cho vấn đề cần giải quyết:
 Xác định một hệ các thành phần vật lý cho bài toán và
 Đưa ra dự đoán về hành vi của hệ thống trên cơ sở các tương tác giữa các thành phần
của hệ hoặc tương tác của hệ này với môi trường xung quanh.
Phân tích thứ nguyên
Trong vật lý, từ “thứ nguyên” được dùng để bản chất vật lý của một đại lượng. Ví dụ,
khoảng cách giữa hai điểm có thể được đo bằng feet1, mét hay fulong2, tất cả đều là các cách
khác nhau để biểu thị thứ nguyên độ dài.
Trong sách này, chúng tôi dùng các ký hiệu cho thứ nguyên độ dài, khối lượng và thời
gian tương ứng là L, M và T 3. Chúng tôi cũng thường dùng cặp dấu ngoặc [ ] để biểu thị các
thứ nguyên của các đại lượng. Ví dụ, v được dùng để chỉ tốc độ, thứ nguyên của tốc độ sẽ
được biểu thị là [v]=L/T. Với diện tích (ký hiệu là A) thì ta có [A]=L2. Bảng 1.5Error!
Reference source not found. giới thiệu thứ nguyên của một số đại lượng.
Bảng 1.5: Các thứ nguyên và đơn vị của 4 đại lượng đã biết Đại lượng Diện tích ( A ) Thể tích ( V ) Tốc độ ( v ) Gia tốc ( a ) Thứ nguyên L2 L3 L / T L / T2 Đơn vị SI m2 m3 m / s m / s2 Đơn vị trong hệ ft2 ft3 ft / s ft / s2 đo lường của Mỹ
Trong nhiều trường hợp, có thể bạn phải kiểm tra một phương trình cụ thể để xem nó có
phù hợp với dự tính của bạn hay không. Để làm điều đó, bạn có thể sử dụng một thủ thuật
1 Feet: đơn vị đo chiều dài của Anh, bằng 0,3048m
2 Fulong: đơn vị đo chiều dài, bằng 1/8 dặm Anh, tức khoảng 201m
3 Thứ nguyên của một đại lượng được viết bằng chữ viết hoa, thẳng; còn ký hiệu đại số cho đại lượng được ký
hiệu bằng chữ in nghiêng: L cho độ dài và t cho thời gian. 8 http://ipt.hcmute.edu.vn Bộ môn vật lý
hữu ích, phân tích thứ nguyên, vì các thứ nguyên có thể được xem như là các đại lượng đại số. Cần lưu ý:
 Chỉ có thể cộng hoặc trừ các đại lượng với nhau nếu chúng có cùng thứ nguyên.
 Vế trái và vế phải của một đẳng thức (bất ẳ
đ ng thức) cần phải có cùng thứ nguyên.
Tuân theo quy tắc cơ bản này, ta có thể sử dụng phép phân tích thứ nguyên để kiểm tra
tính đúng đắn của một biểu thức. Một quan hệ bất kỳ chỉ có thể đúng nếu thứ nguyên của hai
vế phương trình là giống nhau.
Để minh họa cho thủ thuật này, giả thiết rằng bạn quan tâm đến một phương trình về vị
trí x của một chiếc xe và thời gian t nếu xe khởi hành từ trạng thái đứng yên tại vị trí x=0 và
chuyển động với gia tốc không đổi a. Biểu thức đúng cho trường hợp này là x= ½ at2 (xem
chương 2). Đại lượng x ở vế trái có thứ nguyên là L. Để cho phương trình này đúng về thứ
nguyên thì vế bên phải của phương trình cũng phải có thứ nguyên là L. Ta có thể tiến hành
kiểm tra thứ nguyên bằng cách thay thế thứ nguyên cho gia tốc là L/T2, và thời gian là T vào phương trình. Ta được: L L= T 2  L T 2
Các thứ nguyên thời gian được khử đi như trên nên chỉ còn lại thứ nguyên độ dài. Hai vế
trái và phải khớp với nhau.
Một thủ thuật tổng quát hơn khi sử dụng phép phân tích thứ nguyên là lập một biểu thức có dạng:  n m x a t
Với m, n là các số cần tìm và  là dấu tỉ lệ. Quan hệ này chỉ đúng nếu thứ nguyên của
hai vế là như nhau. Vì thứ nguyên của vế bên trái là chiều dài nên thứ nguyên của phần bên
phải cũng là chiều dài. Nghĩa là: n m 1 0 a t   L  LT  
Do gia tốc a có thứ nguyên là L/T2 (xem chương 2) nên ta có: 2 n m 1 0 m 2  n 1 0 (L / T ) T  LT  L / T  L T
Từ phương trình trên, ta dễ thấy là n=1 và m=2. Tức là: 2 x at
Phép phân tích thứ nguyên chỉ có một hạn chế là không kiểm tra được các hệ số bằng số trong công thức.
Các ký hiệu dùng trong công thức không nhất thiết phải là ký hiệu dùng cho thứ nguyên
của đại lượng vật lý. Một số ký hiệu được dùng thường xuyên (ví dụ như t). Một đại lượng
có thể được biểu diễn bởi nhiều ký hiệu (ví dụ như tọa độ, có thể dùng x, y hoặc z), tùy theo trường hợp sử dụng. 9
Trường Đại học Sư phạm Kỹ thuật Tp. Hồ Chí Minh 2021
Câu hỏi 1.2: Nói rằng “Phép phân tích đơn vị có thể cho ra giá trị bằng số của các hằng số
của các tỉ lệ có thể xuất hiện trong các biểu thức đại số” là đúng hay sai?
Bài tập mẫu 1.1:
Hãy chứng tỏ rằng biểu thức v at (với v là tốc độ, a là gia tốc và t là khoảng thời
gian) là đúng về thứ nguyên.
Bài tập mẫu 1.2:
Giả sử người ta bảo rằng gia tốc của một hạt chuyển động với tốc độ không đổi v theo
một đường tròn bán kính r tỉ lệ với rn và với vm. Hãy tìm giá trị của m và n và viết biểu
thức tối giản của gia tốc. Giải:
Ta có thể viết biểu thức ban đầu của gia tốc với k là hệ số tỉ lệ, không có thứ nguyên: m  n a kr v
Thay các thứ nguyên của gia tốc, tốc độ và bán kính vào, ta được: L n  L m L   2 T  T   
Cân bằng các số mũ của L và T ta được
n m  1; m  2 Từ đó: n  1 
Biểu thức của gia tốc sẽ là 2 1  2   v a kr v k r
Trong phần 4.4 về sau, ta sẽ thấy rằng k=1 với hệ đơn vị được chọn phù hợp. Nếu
dùng hệ đơn vị khác thì k sẽ khác 1. Ví dụ nếu đơn vị vận tốc là km/h và ta muốn có gia tốc tính bằng m/s2.
Phép đổi đơn vị
Trong các bài toán, đôi khi ta phải đổi đơn vị từ một hệ đơn vị này sang một hệ đơn vị
khác (ví dụ từ inch sang cm) hoặc đổi đơn vị trong cùng một hệ (ví dụ từ km sang m). Xem
phụ lục A về danh sách các hệ số qui đổi.
Cũng như với thứ nguyên, có thể xem đơn vị là các đại lượng đại số và có thể ước lược
lẫn nhau trong một công thức.
Cần lưu ý là phải luôn ghi kèm đơn vị cho mỗi đại lượng, nếu cần thì ghi đơn vị trong
suốt quá trình tính toán. Làm như vậy thì có thể phát hiện được các sai sót trong tính toán. 10 http://ipt.hcmute.edu.vn Bộ môn vật lý
Khi đổi đơn vị thì cần phải nhân đại lượng gốc với một phân số mà giá trị của phân số này là 1.
Ví dụ: 15in  ? cm . Ta biến đổi như sau:  2,54cm  15,0 in 15,0 in    38,1 cm 1 in   .
Trong tính toán ở trên, phần trong dấu ngoặc có giá trị là 1 vì 1 in  2,54 cm .
Câu hỏi 1.3: Khoảng cách giữa hai thành phố là 100 dặm. Khoảng cách này tính theo ki-lô- mét sẽ là:
(a) Nhỏ hơn 100 (b) Lớn hơn 100 (c) bằng 100
Bài tập mẫu 1.3:
Trên một đường cao tốc, một chiếc xe đang chạy với tốc độ 38,0 m/s. Người lái xe có
vượt giới hạn tốc độ 75,0 mi/h (dặm/h) hay không? Giải:
Đổi mét sang dặm và đổi giây sang giờ  1mi   3600 s  38,0 m / s        85,0 mi / h 1609 m 1h    
Như vậy, người lái xe đã vượt quá tốc độ qui định và cần phải chạy chậm lại.
Ước lượng và phép tính bậc độ lớn
Trong nhiều trường hợp, ta không cần phải có một con số chính xác cho đại lượng vật lý
mà chỉ cần một giá trị gần đúng, biểu diễn dưới dạng số dùng trong khoa học. Giá trị ước
lượng này có thể thiếu chính xác hơn nữa (more approximate) nếu được biểu diễn theo bậc
độ lớn (order of magnitute). Cách tính theo bậc độ lớn như sau:
 Biểu diễn số dưới dạng khoa học: là tích của một số x (có giá trị từ 1 đến 10) với một
lũy thừa của 10 kèm theo một đơn vị đo. (ví dụ 1,2310–2 m)
 Nếu x nhỏ hơn 3,162 ( 10 ) thì bậc của độ lớn là số mũ của 10 khi biểu diễn số đã cho dưới dạng khoa học.
 Nếu x lớn hơn 3,162 thì bậc của độ lớn bằng số mũ của 10 cộng thêm 1.
Ta dùng dấu  để chỉ “cùng bậc với”. Sử dụng qui ước này để xem xét một số giá trị về
độ dài, ta được kết quả như sau:
0,002 1 m = 2,110–3 m  10–3 m; (bậc độ lớn bằng số mũ của 10, trong trường hợp này là –3)
0,008 6 m = 8.610–3 m  10–2 m; (bậc độ lớn bằng số mũ của 10 cộng thêm 1)
720 m = 7,2102 m  103 m; (bậc độ lớn bằng số mũ của 10 cộng thêm 1) 11
Trường Đại học Sư phạm Kỹ thuật Tp. Hồ Chí Minh 2021
Khi sử dụng ước lượng theo bậc độ lớn thì các kết quả chỉ tin cậy được trong phạm vi
một bội số của 10. Nếu một đại lượng tăng 3 bậc độ lớn thì giá trị của nó được nhân với một hệ số là 103 = 1, 000.
Bài tập mẫu 1.4:
Hãy ước lượng số lần hít vào – thở ra trung bình của một người trong suốt cuộc đời. Giải:
Ta bắt đầu bằng cách ước đoán tuổi thọ trung bình của người là 70 năm. Nghĩ xem
trong 1 phút thì một người thở bao nhiêu lần. Giá trị này phụ thuộc vào việc người nay
đang tập thể dụng, đang ngủ, đang tức giận, hay đang bình thản… Ta có thể ước lượng
rằng số lần thở trong một phút là 10 lần. Số này chắc chắn là gần với giá trị thực tế
hơn là 1 lần hoặc 100 lần trong một phút. Tìm s ố phút trong 1 năm:
 400days   24hr   60mins  5 1yr     610 min  1   yr 1day   1hr        Tìm s ố phút trong 70 năm: min 5 7 6 1  0 70yrs  4 1  0 mins yr Tìm s l
ố ần thở trong cả đời người: 7 breaths 8 4 1  0 mins 1  0  4 1  0 breaths min
Từ đó, có thể nói rằng số lần thở của một người trong suốt cuộc đời vào khoảng 1 tỉ
lần. Qua ví dụ này, ta cũng thấy rằng để ước lượng thì chọn con số 400 ngày để tính
thì thuận tiện hơn là 365 ngày.
Các chữ số có nghĩa
Khi đo một đại lượng nào đó, các giá trị đo được chỉ được biết đến trong giới hạn của sai
số thực nghiệm. Giá trị của sai số này phụ thuộc vào nhiều yếu tố khác nhau.
 Các sai số này có thể là do dụng cụ đo, kỹ năng của người làm thí nghiệm và/hoặc số
lượng phép đo được thực hiện.
 Ta cần có một kỹ thuật để tính đến các sai số này.
Ta sẽ dụng các qui tắc về chữ số có nghĩa để ước lượng sai số trong kết quả của các phép tính.
Số chữ số có nghĩa trong một phép đo có thể mô tả được ít nhiều về sai số. Nó có liên
quan với số chữ số được ghi trong kết quả của phép đo.
Ví dụ ta cần đo bán kính của một cái đĩa CD bằng thước mét. Giả sử rằng độ chính xác
mà ta có thể đạt được là ± 0,1 cm. Nếu ta đo được 6,0 cm thì ta chỉ có thể nói được rằng bán 12 http://ipt.hcmute.edu.vn Bộ môn vật lý
kính của đĩa nằm đâu đó trong khoảng 5,9 cm đến 6,1 cm. Trong trường hợp này, giá trị đo
6,0 cm có 2 chữ số có nghĩa. Lưu ý rằng chữ số được ước lượng đầu tiên cũng được tính là
chữ số có nghĩa. Vì vậy ta có thể viết giá trị bán kính của đĩa là (6,0 ± 0,1) cm.
Chữ số có nghĩa là chữ số đáng tin. Số không (0) có thể có nghĩa hoặc không có nghĩa.
 Số 0 dùng để xác định vị trí của dấu thập phân thì không có nghĩa. Ví dụ như các số
0 trong các số 0,03 và 0,007 5 là không có nghĩa. Số chữ số có nghĩa của hai giá trị
này lần lượt là 1 và 2. Tuy nhiên, số 10,0 lại có 3 chữ số có nghĩa.
 Nếu số 0 nằm sau các chữ số khác thì có thể bị nhầm lẫn. Ví dụ như khối lượng của
một vật được ghi là 1 500 g thì các chữ số 0 có phải là số có nghĩa hay không. Để đỡ
nhầm lẫn thì phải dùng dạng số khoa học. Trong trường hợp này, nếu ghi là 1,5  103
thì có 2 chữ số có nghĩa. Nếu ghi là 1,50  103 thì có 3 chữ số có nghĩa và nếu ghi
1,500  103 thì có 4 chữ số có nghĩa. Các giá trị nhỏ hơn 1 cũng được xem xét với qui
tắc tương tự: 2,3  10–4 (hoặc 0,000 23) thì có 2 chữ số có nghĩa, trong khi 2,30  10–
4 (hoặc 0,000 230) thì có 3 chữ số có nghĩa.
Khi giải bài tập, ta thường kết hợp các đại lượng với nhau bằng các phép toán nhân, chia,
cộng, trừ… Khi làm như vậy thì cần phải bảo đảm rằng kết quả có một số chữ số có nghĩa thích hợp.
 Khi nhân hoặc chia các đại lượng, số chữ số có nghĩa ở kết quả là số chữ số có nghĩa
nhỏ nhất trong các giá trị tham gia vào phép tính.
Tính diện tích của một hình chữ nhật có 2 cạnh là 25,57 m và 2,45 m, ta có: 25,57 m  2,45 m = 62,6 m2
do số chữ số có nghĩa của hai thừa số lần lượt là 4 và 3 nên lấy 3 là số chữ số có nghĩa cho kết quả phép nhân.
Tính diện tích của một hình tròn bán kính 6,0 cm:
A = r   6,02 2 2 2 cm = 1,110 cm
Nếu dùng máy tính thì bạn có thể thu được kết quả là 113,097 335 5. Tất nhiên là không
thể ghi hết các chữ số như vậy nên có thể là bạn sẽ ghi kết quả là 113 cm2. Kết quả này không
đúng vì nó có đến 3 chữ số có nghĩa trong khi bán kính của hình tròn chỉ có 2 chữ số có nghĩa.
Vì vậy, kết quả phải được ghi là 1,1102 cm2 (chứ không phải là 110 cm2)
 Nếu cộng và trừ các số thì kết quả sẽ lấy số chữ số thập phân nhỏ nhất trong các số hạng của phép tính.
Ví dụ: Tổng của 135 cm và 3,25 cm sẽ là:
135 cm + 3,25 cm = 138 cm (do số 135 cm không có số thập phân nào).
Tương tự như vậy, ta có: 23,2 + 5,174 = 28,4 (Lưu ý là không thể ghi kết quả là 28,374
vì số 23,2 chỉ có 1 chữ số thập phân). 13
Trường Đại học Sư phạm Kỹ thuật Tp. Hồ Chí Minh 2021
Qui tắc về cộng hoặc trừ có thể dẫn đến trường hợp mà số chữ số có nghĩa của kết quả
không giống với số chữ số có nghĩa của các số hạng trong phép tính. Xét các phép tính dưới đây: 1,000 1 + 0,000 3 = 1,000 4 1,002 – 0,998 = 0,004
Ở phép tính thứ nhất, số chữ số có nghĩa của kết quả là 5, trong khi số chữ số có nghĩa
của các số hạng lần lượt là 5 và 1. Ở phép tính thứ 2, số chữ số có nghĩa của kết quả là 1,
trong khi số chữ số có nghĩa của các số hạng lần lượt là 4 và 3.
Lưu ý: Trong sách này, các ví dụ về số cũng như các bài toán ở cuối chương sẽ dùng các
số với 3 chữ số có nghĩa.
Qui tắc về làm tròn số:
 Chữ số cuối cùng được giữ lại sẽ tăng lên 1 đơn vị nếu chữ số cuối cùng bị bỏ đi lớn
hơn 5. (Ví dụ, 1,346 được làm tròn thành 1,35)
 Giữ nguyên chữ số cuối cùng được giữ lại nếu chữ số cuối cùng bị bỏ đi nhỏ hơn 5.
(Ví dụ, 1,342 được làm tròn thành 1,34)
 Nếu chữ số cuối cùng được bỏ đi là 5 thì chữ số được giữ lại được làm tròn thành số
chẵn gần nhất.4 (Qui tắc này được đưa ra để tránh sai số tích lũy trong một loạt phép
tính số học liên tiếp).
 Khi làm toán, nếu có nhiều phép tính trung gian thì để tránh cộng dồn sai số, ta chỉ
làm tròn ở phép tính cuối cùng.
Bài tập mẫu 1.5:
Người ta trải một tấm thảm trong phòng hình chữ nhật có các số đo chiều dài là 12,71 m
và chiều rộng là 3,56 m. Hãy tìm diện tích của căn phòng. Giải:
Nếu nhân 12,71 m với 3,46 m bằng máy tính bỏ túi thì ta sẽ được kết quả là 43,9766 m2. Ta
sẽ chấp nhận bao nhiêu chữ số trong kết quả này. Áp dụng qui tắc về số chữ số có
nghĩa thì con số có ít chữ số có nghĩa nhất là 3,46 m. Vì vậy ta phải biểu diễn kết quả là 44,0 m2.
4 Qui tắc này dựa trên lập luận là trong quá trình tính toán thì 50% các số đã được làm tròn lên và 50% còn lại
được làm tròn xuống. Theo qui tắc này, khi bỏ đi chữ số 5 cuối cùng thì 2,315 và 2,325 đều được làm tròn thành 2,32 14 http://ipt.hcmute.edu.vn Bộ môn vật lý
Tóm tắt chương 1 Định nghĩa:
Ba đại lượng vật lý cơ bản của cơ học là độ dài, khối lượng và thời gian. Trong hệ đơn vị
quốc tế, chúng lần lượt có đơn vị là mét (m), kilogram (kg) và giây (s). Không thể định nghĩa
các đại lượng này bằng các đại lượng khác cơ bản hơn chúng.
Khối lượng riêng của một chất được định nghĩa là khối lượng của một đơn vị thể tích   m V
Khái niệm và nguyên lý:
Phương pháp phân tích thứ nguyên là rất hữu ích đối với việc giải bài tập vật lý. Có thể xử
lý các thứ nguyên như là các đại lượng đại số. Bằng cách ước lượng và tính toán theo bậc của
độ lớn, ta có thể áng chừng được câu trả lời cho bài tập nếu không có đủ thông tin cần thiết
để tìm ra một lời giải hoàn toàn chính xác.
Khi tính một kết quả từ một số giá trị đo mà mỗi giá trị đều có độ chính xác nhất định thì cần
phải ghi kết quả với một số chính xác các chữ số có nghĩa. Khi nhân một vài đại lượng, số
chữ số có nghĩa trong kết quả cuối cùng bằng số chữ số có nghĩa của đại lượng có ít chữ số
có nghĩa nhất. Qui tắc này cũng áp dụng cho phép chia.
Khi cộng hoặc trừ các số, số chữ số sau dấu thập phân phải bằng số chữ số thập phân của số
hạng có ít chữ số sau dấu thập phân nhất.
Câu hỏi lý thuyết chương 1
1. Giả sử ba chuẩn cơ bản của hệ mét là chiều dài, khối lượng riêng và thời gian (thay vì
chiều dài, khối lượng và thời gian). Chuẩn khối lượng riêng trong hệ thống này được định
nghĩa từ khối lượng riêng của nước. Cần phải quan tâm đến tính chất nào của nước để
bảo đảm rằng chuẩn khối lượng riêng này càng chính xác càng tốt?
2. Tại sao hệ đơn vị mét lại được dùng nhiều hơn so với các hệ đơn vị khác?
3. Có thể sử dụng hiện tượng tự nhiên nào làm chuẩn thay thế của thời gian?
4. Hãy biểu diễn các giá trị dưới đây bằng các tiếp đầu ngữ cho trong bảng 1.4.
(a) 3 104 m (b) 5  105 m (c) 72  102 m 15
Trường Đại học Sư phạm Kỹ thuật Tp. Hồ Chí Minh 2021
Bài tập chương 1
1. Một sinh viên sử dụng thước mét để do bề dày của một cuốn sách và thu được kết quả là
4,3cm ± 0,1cm. Một sinh viên khác sử dụng thước cặp và thu được 4 kết quả khác nhau: (a) 4,32 cm ± 0,01 cm, (b) 4,31 cm ± 0,01 cm, (c) 4,24 cm ± 0,01 cm,
(d) 4,43 cm ± 0,01 cm,
Số đo nào trong bốn số nói trên phù hợp với số đo mà sinh viên thứ nhất thu được?
2. Một ngôi nhà được quảng cáo là có diện tích sử dụng 1420 feet vuông. Diện tích này tính
theo mét vuông là bao nhiêu?
(a) 4660 m2 (b) 432 m2(c) 158 m2 (d) 132 m2 (e) 40,2 m2
3. Hai đại lượng có cần phải cùng thứ nguyên hay không nếu
(a) ta cộng chúng với nhau?
(b) ta nhân chúng với nhau? (c) ta trừ chúng cho nhau? (d) ta chia chúng cho nhau?
(e) ta so sánh chúng với nhau?
4. Số nào dưới đây là ước lượng tốt nhất cho khối lượng của toàn bộ người sống trên Trái đất?
(a) 2  108 kg (b) 1  109 kg (c) 2  1010 kg (d) 3  1011 kg (e) 4  1012 kg
5. Định luật 2 Newton (chương 5) phát biểu rằng tích của khối lượng của một vật với gia
tốc của nó thì bằng tổng lực tác dụng lên nó. Cái nào dưới đây là đơn vị của lực (a)
kg  m/s2 (b) kg  m2/s2 (c) kg/m  s2 (d) kg  m2/s (e) không có cái nào đúng.
6. Một máy tính bỏ túi hiển thị kết quả 1,365 248 0  107 kg. Sai số của kết quả này là 62 %.
Có bao nhiêu chữ số được xem là chữ số có nghĩa trong kết quả này?
(a) Không có số nào (b) một (c) hai (d) ba (e) bốn
7. Mẫu kilogram chuẩn là một hình trụ bằng platinum-iridium có chiều cao 39,0 mm và
đường kính 39,0 mm. Tính khối lượng riêng của nó? ĐS: 2,15  104 kg/m3
8. Cần một khối lượng vật liệu, khối lượng riêng là  bằng bao nhiêu để làm một hình cầu
rỗng có bán kính trong là r1 và bán kính ngoài là r2? 3 3 r r ĐS: 2 1 4   3
9. Khối lượng của một nguyên tử đồng là  25
1,0610 kg và khối lượng riêng của đồng là 3 8 2
9 0kg / m . Xác định số nguyên tử đồng có trong 1 cm3 đồng. Cho rằng một centimet 16 http://ipt.hcmute.edu.vn Bộ môn vật lý
khối đồng được hình thành bằng cách xếp các khối lập phương giống hệt nhau, với một
nguyên tử đồng ở tâm của mỗi khối. Xác định thể tích của mỗi khối lập phương này.
Tính cạnh của mỗi khối lập phương, xem như là khoảng cách giữa các nguyên tử. ĐS: a) 22 3 8,42 1  0 atom / cm b) 23 3 1,1910 cm / atom c)  10 2,28 1  0 m
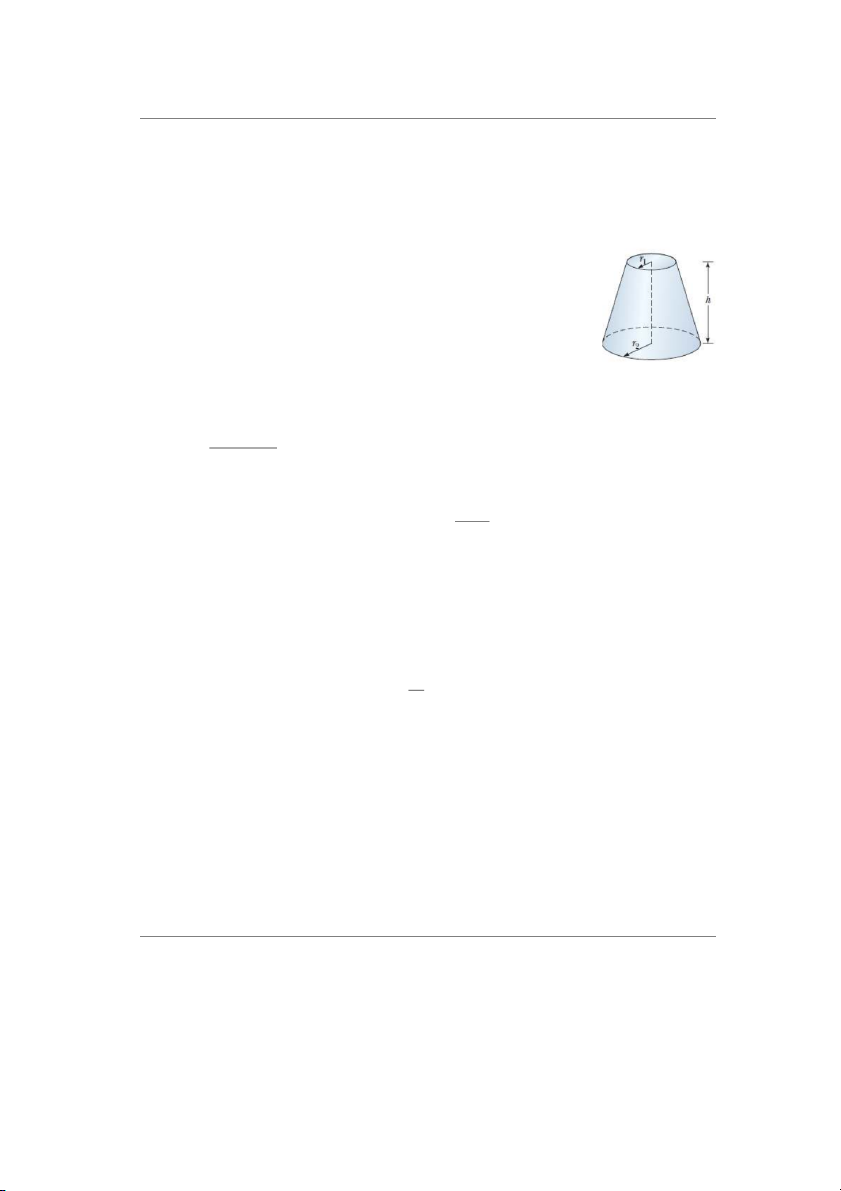
10. Hình bên biểu diễn một hình nón cụt. Hãy chọn biểu thức đúng để mô tả:
 Tổng chu vi đáy lớn và đáy nhỏ  Thể tích  Diện tích toàn phần của hình nón cụt.
a)  r r  h  r r  1/2 2 2  1 2 1 2  
b) 2 r r 1 2  2 2 c)
r rr r 1 1 2 2 h  3
11. Định luật vạn vật hấp dẫn của Newton được biểu diễn bằng công thức GMm F  2 r
trong đó F là lực hấp dẫn của vật này lên vật khác, M và m là khối lượng của hai vật, và
r là khoảng cách giữa hai vật. Lực có đơn vị trong hệ SI là kgm/s2. Vậy hằng số hấp dẫn G có đơn vị gì? ĐS: 3 2 m s / kg
12. (a) Giả sử phương trình 3
x At Bt mô tả chuyển động của một vật, với x có thứ nguyên
độ dài và t có thứ nguyên thời gian. Xác định thứ nguyên của A và B. (a) dx
Xác định thứ nguyên của đạo hàm 2  3 At Bdt
ĐS: (a)       3 A
L / T và B  L / T  b) L / T 
13. Giả sử tốc độ phát triển của tóc bạn là 1/32 (inch/ngày). Hãy đổi ra đơn vị (nano mét
/giây). Bởi vì khoảng cách giữa các nguyên tử trong một phân tử là khoảng 0,1 nm, câu
trả lời của bạn cho thấy các lớp nguyên tử nhanh chóng được lắp ráp trong quá trình tổng
hợp protein này như thế nào. ĐS: 9,19 n/s
14. Có bao nhiêu quả bóng bàn để vừa vào một căn phòng có kích thước tiêu chuẩn? ĐS: 106 quả 17
Trường Đại học Sư phạm Kỹ thuật Tp. Hồ Chí Minh 2021
15. Một lốp ô tô được dùng cho 50 000 miles (dặm). Nó quay được bao nhiêu vòng trong
cuộc đời của nó? Giả sử lốp xe có đường kính là 2,5 ft, chu vi khoảng 8 ft. 1 mile = 5280 ft ĐS: 107 vòng
16. Năm dương lịch, khoảng thời gian từ một Xuân phân này đến một Xuân phân tiếp theo,
là cơ sở cho lịch chúng ta. Nó có 365,242 199 ngày. Tìm số giây trong một năm dương lịch. ĐS: 31556926,0 s
17. Trong bãi đỗ xe của trường đại học cộng đồng, số xe bình thường lớn hơn số xe thể thao
tiện ích (SUV) là 94,7 %. Hiệu của chúng là 18. Tìm số lượng SUV trong bãi đỗ xe . ĐS: 19
18. Bán kính của một quả cầu rắn đồng chất được đo là (6,50 ± 0,20) cm, và khối lượng của
nó được đo là (1,85 ± 0,02) kg. Xác định khối lượng riêng của quả cầu tính bằng kilôgam
trên mét khối và sai số của nó. ĐS: 1,6 ± 0,2 103 kg
19. Khoảng cách từ Mặt trời đến ngôi sao gần nhất là khoảng 4 1016 m. Có thể xem dải
Ngân hà là một đĩa hình trụ đường kính ~1021 m và độ dày ~1019 m. Hãy tìm số ngôi sao
trong dải Ngân hà theo bậc của độ lớn. Xem khoảng cách giữa Mặt trời và ngôi sao gần
nhất là khoảng cách điển hình. ĐS: 1011 ngôi sao. 18