Chương 2: Hệ phương trình tuyến tính và ứng dụng trong phân tích kinh tế | Môn toán cao cấp

lOMoAR cPSD| 49519085
Bài tập Toán Cao cấp dành cho Kinh tế & Quản trị Chương II :
HỆ PHƯƠNG TRÌNH TUYẾN TÍNH
& ỨNG DỤNG TRONG PHÂN TÍCH KINH TẾ
A. TÓM TẮT LÝ THUYẾT.
I. Hệ phương trình tuyến tính tổng quát.
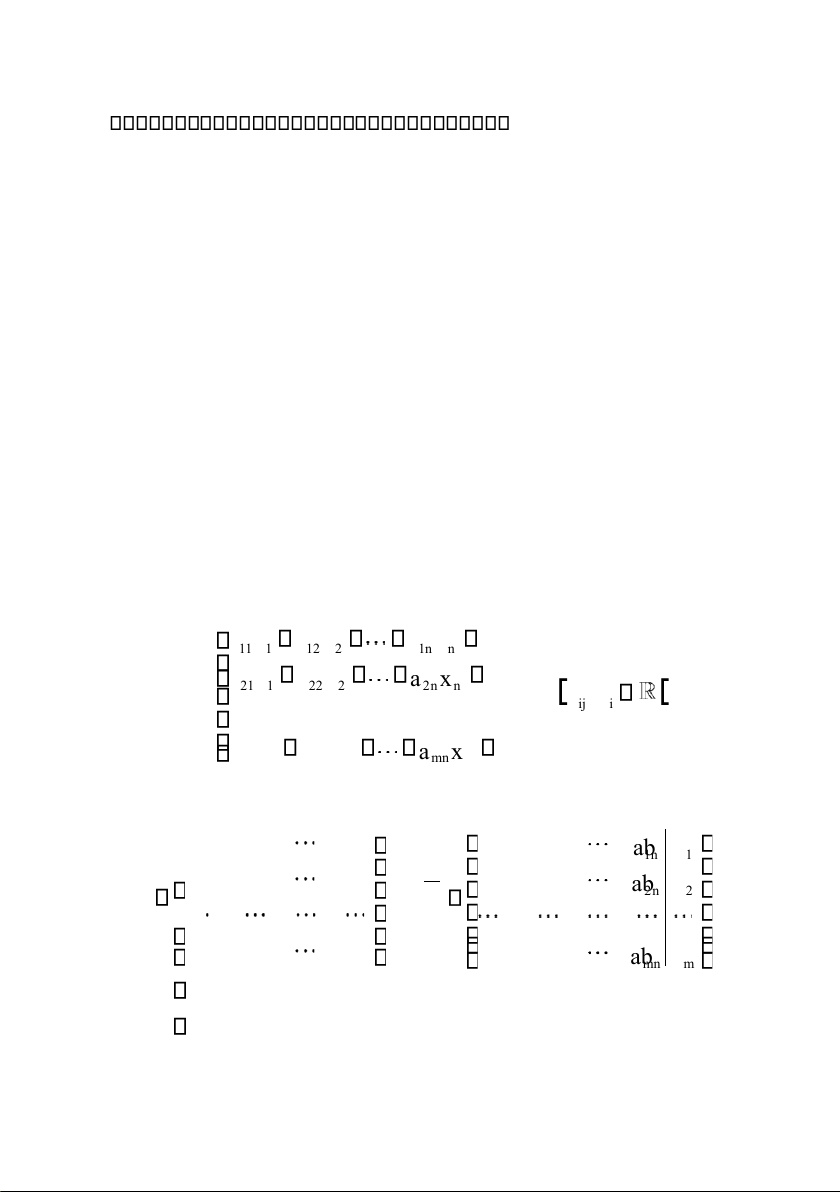
Hệ phương trình tuyến tính có n ẩn số và cómphương
trình là hệ phương trình có dạng như sau 11 ax 1 12 ax 2 n 1 ax n 1 b ax ax a x b ( 21 1 22 2 2 n n 2 I) : a ij ,b i
........................................... a m1 x1 am2 x2 amn xn bm C ác ma trận 11 a12 a1 n a11 a12 n 1 ab 1 a21 a22 a2 n a a ab A 21 22 2n 2 và A a m1 am2 amn a m1 am2 mn ab m a lOMoAR cPSD| 49519085
Bài tập Toán Cao cấp dành cho Kinh tế & Quản trị
ược gọi lần lượt là ma trận hệ số và ma trận hệ số mở rộng (hay
còn gọi là ma trận bổ sung) của hệ (I). Ma trận A còn ược ký hiệu là A B . x1 b1 Nếu ta ặt X x2 và B b2 thì hệ (I) A.X B ... ... xn bm Mỗi bộ n số X x ,x ,...,x1 2 n thỏa mãn n a xijj b ,i i1,m j 1
ược gọi là một nghiệm riêng của hệ.
• Hệ (I) có nghiệm R(A) R(A)
• Hai hệ phương trình ược gọi là tương ương nếu hai tập nghiệm của chúng trùng nhau. 54 lOMoAR cPSD| 49519085
Bài tập Toán Cao cấp dành cho Kinh tế & Quản trị
II. Phương pháp giải một hệ phương trình tuyến tính.
1. Phương pháp khử ẩn liên tiếp (phương pháp Gauss) : Ta biết
rằng mỗi hệ phương trình tuyến tính có duy nhất một ma trận hệ số
mở rộng và ngược lại khi ã có ma trận hệ số mở rộng thì ta luôn
viết ược hệ phương trình tuyến tính, vì thế khi giải phương trình
tuyến tính bằng phương pháp khử ẩn liên tiếp (phương pháp
Gauss), ta sử dụng các phép biến ổi sơ cấp theo dòng của ma trận
trên ma trận hệ số mở rộng của nó (nếu ổi cột trong n cột ầu thì
phải ổi thứ tự của ẩn số).
Trong quá trình biến ổi, nếu xuất hiện một dòng của ma trận hệ số
mở rộng có dạng 0,0,...,b với b 0 thì ta kết luận ngay hệ vô
nghiệm. Trái lại, hệ sẽ có nghiệm và khi ó bao giờ cũng ưa ược ma
trận hệ số mở rộng về dạng hình thang chuẩn (sau khi ã ổi n cột ầu) 1 0 0 0 1 c k 1 1 c n d1 0 1 0 0 c 2 k 1 c2 n d2 0 0 1 0 c 3 k 1 c3 n d3 0 0 0 1 ck k1 ckn dk
Không giảm tính tổng quát ta có thể coi cột thứ j là cột lOMoAR cPSD| 49519085
Bài tập Toán Cao cấp dành cho Kinh tế & Quản trị
biểu diễn các hệ số ẩn x j j 1,...,n
. Khi ó nghiệm tổng quát của hệ là : x1 d1 c1 k 1 k 1 ... c 1n n
........................................... xk dk ck k 1 k 1 ...ckn n xk 1 k 1 ................. xn n
với k 1 ,..., n là những số thực tùy ý.
Ta gọi x , x ,..., x1 2 k là các ẩn chính và xk 1 , xk 2 ,..., xn là các ẩn phụ.
Chú ý : Trong thực hành, ể tránh sự nhầm lẫn thì chỉ nên ổi chỗ các
dòng (mà không nên ổi chỗ các cột). 56 lOMoAR cPSD| 49519085
Bài tập Toán Cao cấp dành cho Kinh tế & Quản trị
2. Định lý Kronecker-Capelli. Xét
hệ phương trình tuyến tính a x111 a x122 a x1n n b1 a x 211 a x222 a2nxn b2 ij i (I) : a ,b
............................................... am1x1 am2x2 amnxn bn
Gọi A là ma trận hệ số , A là ma trận hệ số mở rộng. Khi ó : Nếu R(A) R(A) : hệ (I) vô nghiệm.
Nếu R(A) R(A) : hệ (I) có nghiệm.
Từ ó, Gauss ưa ra phương pháp tổng quát ể giải hệ phương trình tuyến tính (I) như sau.
Bằng các phép biến ổi sơ cấp trên ma trận, ta biến ổi ma trận hệ số
mở rộng A B về dạng bậc thang A B . Tính R A B và R(A). lOMoAR cPSD| 49519085
Bài tập Toán Cao cấp dành cho Kinh tế & Quản trị + R(A) R A B : hệ (I) vô nghiệm. + R(A) R A B n
: hệ (I) có duy nhất nghiệm. + R(A) R A B k n
: hệ (I) có vô số nghiệm
Khi (I) có nghiệm, ta có : (I) AX B III. Hệ Cramer.
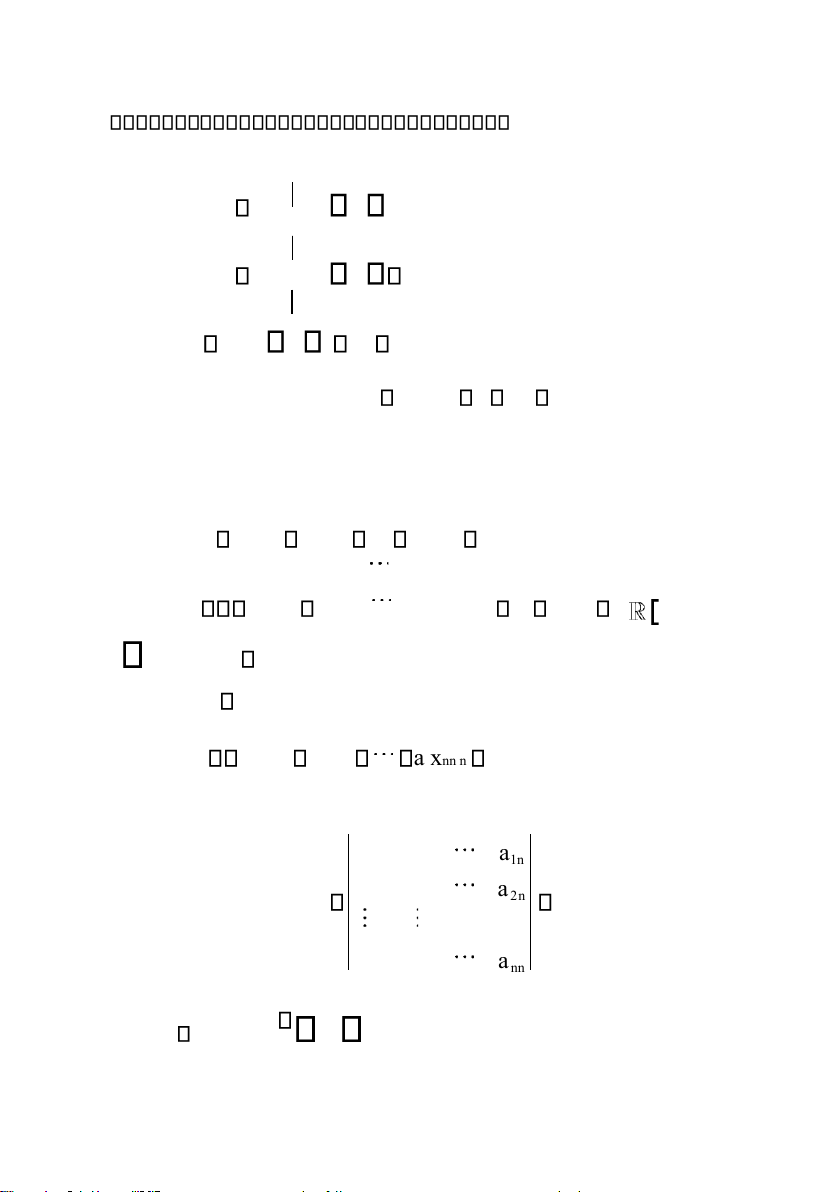
Cho hệ phương trình tuyến tính a x111 a x122 a x1n n b1 a x211 a x22 2 a2nxn b2 a ,b ij i
......................................... a xn11 an2x2 a xnn n bn
Hệ trên ược gọi là hệ Cramer nếu a11 a12 a1 n a21 a22 a2 n D 0 an1 an2 ann ♦ Do D 0 nên A
aij n n là ma trận không suy biến vì thế nên 58 lOMoAR cPSD| 49519085
Bài tập Toán Cao cấp dành cho Kinh tế & Quản trị
tồn tại A 1 . Ta viết hệ dưới dạng A.X B . Hệ có úng một nghiệm X A B 1 .
♦ Ngoài phương pháp giải trên, ta còn có thể sử dụng công thức sau
ây (còn gọi là công thức Cramer) : x1 DD1 x D2 2 D n x D n D
trong ó D j ( j 1,n ) là ịnh thức của ma trận có ược bằng cách thay
cột j của ma trận A bởi ma trận B.
IV. Hệ phương trình tuyến tính thuần nhất. lOMoAR cPSD| 49519085
Bài tập Toán Cao cấp dành cho Kinh tế & Quản trị
Hệ phương trình tuyến tính thuần nhất là hệ phương trình tuyến
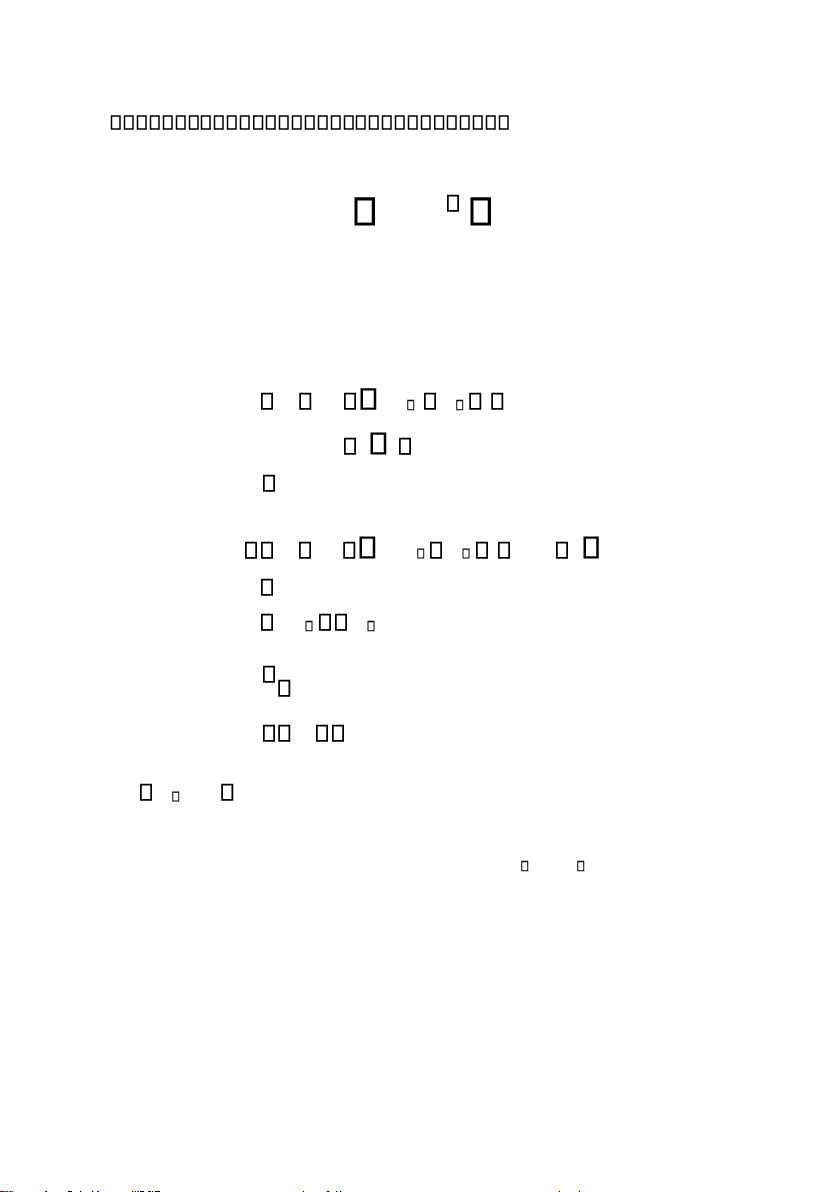
tính có dạng biểu diễn như sau : a x111 a x122 a x1n n 0 (II) : a x211 a x22 2 a2nxn 0 a ,b ij i
......................................... a a m1x1 am2x2 mn x n 0 Nghĩa là (II) A.X 0 .
Chú ý rằng hệ (II) luôn có nghiệm X 0 .
V. Một vài ứng dụng trong phân tích kinh tế.
1. Mô hình cân bằng thị trường :
Xét một thị trường có n loại hàng hóa với giá bán lần lượt là P ,P ,1 2 ,P . Giả n
sử, các hàm cung QSi QSi P,P ,1 2 ,Pn và các hàm cầu QD Q P,P , ,P
1,n là các hàm bậc i Di 1 2 n i
nhất của các giá P ,P , ,P . 12 n
Để tìm iểm cân bằng thị trường, ta giải hệ phương trình 60 lOMoAR cPSD| 49519085
Bài tập Toán Cao cấp dành cho Kinh tế & Quản trị tuyến tính QS Q i
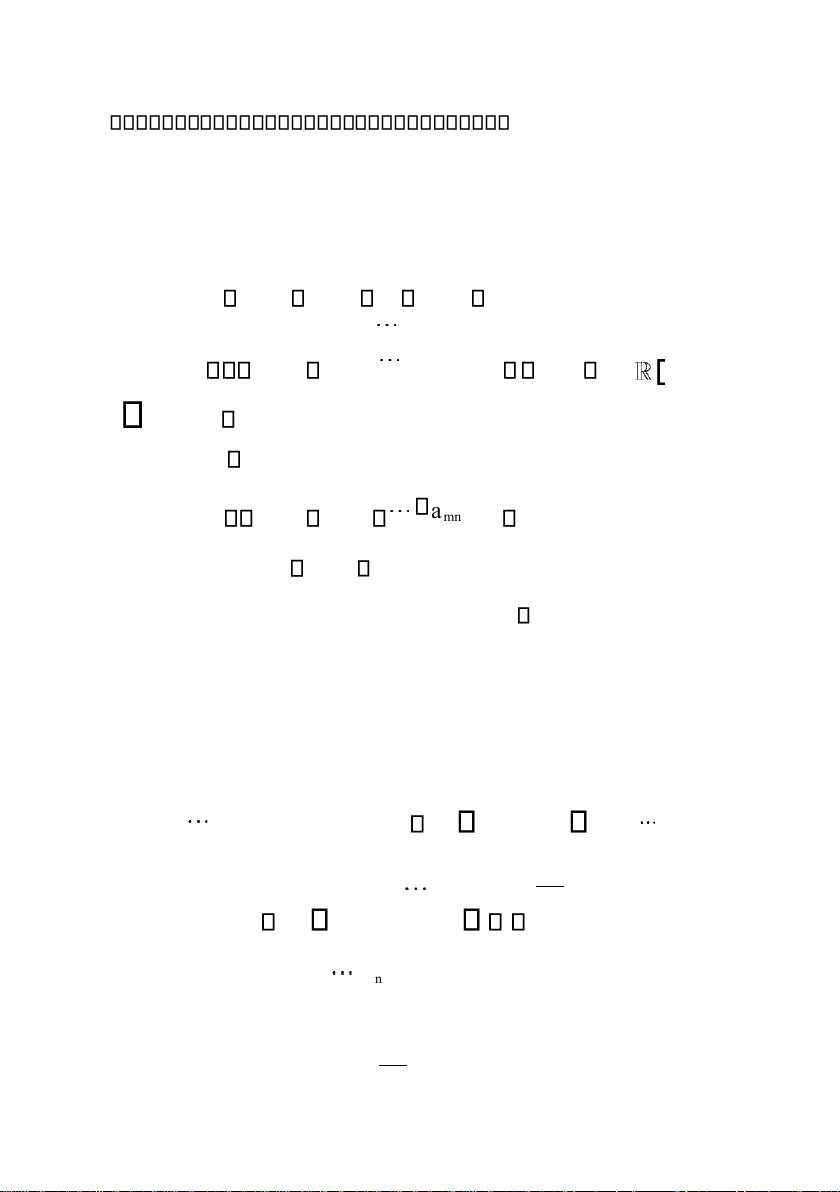
Di ( i 1,n ), nghĩa là giải hệ phương trình tuyến tính sau ây E1 P ,P ,1 2 ,P n 0 E2 P ,P ,1 ,P 2 n 0 (1) .......................... En P ,P ,1 ,P 2 n 0
Do ặc iểm của các hàm cung, hàm cầu và ý nghĩa của các hệ số
của giá Pi trong các hàm QS và Q , nên hệ phương trình tuyến tính i Di
(1) ược ưa về dạng như sau a P11 1 a P122 a P1nn b1 a P21 1 a P22 2 a2nPn b2 (2) a Pn1 1 an2P2 a Pnnn bn
trong ó aij 0, bi 0, i, j 1,n lOMoAR cPSD| 49519085
Bài tập Toán Cao cấp dành cho Kinh tế & Quản trị
Để tìm giá của các loại hàng tại iểm cân bằng thị trường,
ta phải giải hệ phương trình tuyến tính 2 .
Lời giải của (2) có ý nghĩa kinh tế khi các thành phần của nghiệm
phải dương và khi thay những giá trị ó vào các hàm cung và cầu,
giá trị các hàm ó cũng phải dương.
Ký hiệu các ma trận của hệ (2) : a 11 a12 a1 n a a a 21 22 2 n A n1 an2 ann a P1 b1 P P2 , B b2 Pn bn
Khi ó, hệ (2) ược viết dưới dạng :A.P B 2 62 lOMoAR cPSD| 49519085
Bài tập Toán Cao cấp dành cho Kinh tế & Quản trị
Và ta giải hệ 2 bằng một trong hai phương pháp ã nêu ở
phần hệ phương trình tuyến tính.
2. Mô hình Input – Output Mở Leontief :
Mô hình này nhằm xác ịnh ầu ra của mỗi ngành trong n ngành sao
cho vừa ủ ể thỏa mãn toàn bộ nhu cầu của cả nền kinh tế ó (kể cả
dự trữ và xuất khẩu).
- Các ơn vị ược sử dụng trong mô hình ược quy thành ơn vị tiền.
- Ký hiệu aij là giá trị của lượng nguyên liệu mà ngành j nhận
ược từ ngành i ể sản xuất ra một lượng sản phẩm có giá trị một ơn vị tiền. - Giả sử rằng :
✓ Mỗi ngành chỉ sản xuất một loại sản phẩm.
✓ Các ngành sử dụng một tỷ lệ cố ịnh nguyên liệu ầu vào từ các ngành khác.
✓ Nếu lượng ầu vào tăng lên k lần thì ầu ra cũng tăng thêm k lần. lOMoAR cPSD| 49519085
Bài tập Toán Cao cấp dành cho Kinh tế & Quản trị a 11 a12 a1 n 21 a22 a2 n n1 an2 ann - Ma trận A
a ược gọi là ma trận hệ a
số ầu vào hay còn gọi là ma trận hệ số kỹ thuật.
Bên cạnh n ngành, mô hình còn có một ngành ặc biệt khác ược gọi
là ngành mở, cung ứng những ầu vào thiết yếu (ví dụ như lao ộng,
dịch vụ) cho n ngành trên. Ngược lại, sản lượng của các ngành ược
xác ịnh bởi yêu cầu nguyên liệu của các ngành trong nền kinh tế và
yêu cầu cuối (yêu cầu dự trữ, xuất khẩu). Lượng yêu cầu cuối này
ược xem là yếu tố ể lập kế hoạch cho toàn bộ nền kinh tế.
- Gọi lượng ầu ra của n ngành lần lượt là x ,x , ,x ; 1 2 n yêu
cầu cuối cùng cho ầu ra của ngành thứ i (còn gọi là yêu cầu
cuối cùng của ngành mở ối với ngành thứ i) là di với i 1,n . 64 lOMoAR cPSD| 49519085
Bài tập Toán Cao cấp dành cho Kinh tế & Quản trị
- Giả sử ngành thứ i sản xuất một lượng ầu ra xi vừa ủ ể áp
ứng những iều kiện ầu vào của n ngành và áp ứng yêu cầu
cuối cùng của ngành mở. Khi ó, ta có : In A .X D (*)
trong ó In là ma trận ơn vị cấp n, A là ma trận các hệ số ầu vào, X
là véctơ cột của lượng ầu ra, D là vectơ cột biểu thị các yêu cầu
cuối cùng của ngành mở.
Từ (*), ta tìm ược nghiệm X In A 1 .D
Chú ý : ta có thể tìm X từ (*) bằng phương pháp Cramer. B. BÀI TẬP
Bài 1 : Giải hệ phương trình sau ây bằng phương pháp Cramer x1 x2 x3 6 2x1 x2 x3 3 x1 x2 2x3 5 Giải : lOMoAR cPSD| 49519085
Bài tập Toán Cao cấp dành cho Kinh tế & Quản trị 1 1 1 Tính D 1 1 5 0 nên hệ có nghiệm duy 2 1 nhất. 1 2 Ta có 6 1 1 D1 3 1 1 5 5 1 2 1 6 1 D2 2 3 1 10 1 5 2 66 lOMoAR cPSD| 49519085
Bài tập Toán Cao cấp dành cho Kinh tế & Quản trị 1 1 6 D3 2 1 3 15 1 1 5
Áp dụng công thức Cramer, ta tính ược nghiệm của hệ là x1 DD1 1 x2 D2 2 D x3 DD3 3
Cách khác : Hệ phương trình ược viết dưới dạng AX B XA B 1 1 3 2 Vì A 1 15 13 12 13 nên 1 3 2 6 1 1 X A B 1 1 2 3 2 lOMoAR cPSD| 49519085
Bài tập Toán Cao cấp dành cho Kinh tế & Quản trị 5 1 1 3 3 5 3 Vậy nghiệm của hệ là x1 1 X x2 2 x3 3
Bài 2 : Giải hệ phương trình tuyến tính sau ây x 1 3x2 4x3 11 1 x2 3x3 3 2x 2x1 x2 x3 1 Giải :
Cách 1 : Biến ổi ma trận: 2 4 11 1 3 4 11 1 7 11 25 2 1 3 3 0 dd 23 d 2dd d23 4 4 21 0 68 lOMoAR cPSD| 49519085
Bài tập Toán Cao cấp dành cho Kinh tế & Quản trị A 2 1 1 1 0
Ta có hệ phương trình tương ương : x1 3x2 4x3 11 x1 1 7x2 11x3 25 x2 2 4x3 4 x3 1 x1 1
Vậy, nghiệm duy nhất là x2 2 x3 1
Cách 2 : Dùng phương pháp Cramer 1 3 4 D 2 1 3 28 0 2 1 1
Nên hệ phương trình ã cho là hệ Cramer, do ó hệ có nghiệm duy nhất. 11 3 4 lOMoAR cPSD| 49519085
Bài tập Toán Cao cấp dành cho Kinh tế & Quản trị D1 3 1 3 28 1 1 1 1 11 4 D2 2 3 3 56 2 1 1 1 3 11 D3 2 1 328 2 1 1 x1 DD1 1 2 D2 2
Nghiệm duy nhất của hệ là : x D x3 DD3 1
Cách 3 : Dùng phương pháp tính ma trận nghịch ảo.
Hệ ã cho ược viết dưới dạng :AX B 1 70 lOMoAR cPSD| 49519085
Bài tập Toán Cao cấp dành cho Kinh tế & Quản trị 1 3 4 x1 11 trong ó A 2 13 , X x2 , B 3 2 1 1 x3 1 Ta có : A 28 0 Ta tính ược 4 7 5 A 1 1 8 7 11 28 0 7 7 4 7 5 11 1 Từ 1 cho ta : X A B 1 281 08 77 117 31 21
Bài 3 : Giải hệ phương trình tuyến tính sau ây 2x1 7x2 3x3 x4 6 lOMoAR cPSD| 49519085
Bài tập Toán Cao cấp dành cho Kinh tế & Quản trị 3x1 5x2 2x3 2x4 4 1 9x1 4x2 x3 7x4 2
Giải : Xét ma trận hệ số mở rộng 2 7 3 1 6 A 3 5 2 2 4 9 4 1 7 2
Bằng kiến thức trong các phần trước, ta tính ược r A 2 và r A 2 Vì r A r A
2 số ẩn hệ có vô số nghiệm và nghiệm
của hệ phụ thuộc vào hai tham số.
Nếu chọn x3 và x4 làm các tham số thì ta có hệ phương trình tuyến tính sau ây : 2x1 7x2 6 3x3 x4 3x1 5x 1 2 4 2x3 2x4
Ta giải hệ 1 như sau (với x1 và x2 là các ẩn số). Ta có : 2 7 72