Chương 2. Một số vấn đề mở rộng giải tích hàm một biến số | Môn toán cao cấp

lOMoAR cPSD| 49519085
Chương 2. Một số vấn ề mở rộng giải tích hàm một biến số
2.1. Các ịnh lí hàm số khả vi
Định lý Fermat: Giả sử hàm f(x) thoả mãn các iều kiện sau:
i) f(x) có ạo hàm tại iểm x0 (a, b). ii) f(x) có cực trị ịa phương tại iểm x0. Khi ó
f (x0) = 0. Định lý
Rolle: Giả sử hàm số f(x) thoả mãn các iều kiện: i) f(x)
liên tục trên [a, b] ii) f(x) khả vi trong khoảng (a, b) iii) f(a) = f(b)
Khi ó, tồn tại iểm c (a, b) sao cho f (c) = 0.
Định lý Lagrance: Giả sử hàm số f(x) thoả mãn các iều kiện:
i) f(x) liên tục trên [a, b] ii) f(x) khả vi trong khoảng (a, b) Khi
ó, tồn tại iểm c (a, b) sao cho f c f(b) - f(a) . b - a
Định lý Cauchy: Giả sử các hàm số f(x) và g(x) thoả mãn các iều kiện:
i) f(x) và g(x) liên tục trên [a, b] ii) f(x) và g(x) khả vi trong khoảng (a, b) iii) g (x) 0, x (a, b)
Khi ó, tồn tại iểm c (a, b) sao cho f (c) f(b) - f(a) . g (c) g(b) - g(a)
2.2. Quy tắc Lôpitan khử dạng vô ịnh
2.2.1. Quy tắc Lôpitan khử dạng vô ịnh
Định lý 1. Giả sử các hàm số f(x) và g(x) thoả mãn các iều kiện sau:
i) f(x) và g(x) liên tục trên một lân cận U nào ó của iểm a; ii) f(x) và
g(x) khả vi trong lân cận U (có thể trừ a).
iii) f(a) = g(a) = 0; f (x) iv) lim (hữu hạn hay vô hạn). x a g (x) Khi ó
GV: Nguyễn Dương Nguyễn, BM Toán, Khoa Cơ bản, FTU lOMoAR cPSD| 49519085 f(x) f (x) lim = lim . x a g(x) x a g (x) 2x - x2 Ví dụ 1. Tính lim . x 2 x - 2
Giải. Áp dụng Quy tắc Lôpitan, ta có: 2x - x2 2xln2 - 2x lim = lim = 4(ln2 -1). x 2 x - 2 x 2 1 3 1+2x 1
Ví dụ 2. Tính lim. x 0 x Giải. Ta có 1 2x) lim 3 1 lim (1 2x)1/3 1 lim 3.2.(1 2/3 2 . 1+2x x 0 x x 0 x x 0 1 3 ex3 1 x3 Ví dụ 3. Tính xlim 0 sin 2x6 . Giải.
Cách 1: lim ex3 1 x3 lim ex3 1 x3 lim 3x e2 x3 3x2 1 lim ex3 1 1 . x 0 sin 2x6 x 0 (2x)6 x 0 2 .66 .x5 128x 0 x3 128 Cách 2: ex3 1 x 0lim 3sin 2x6 x 0lim 12 3x esin 2xc2 x53
os2x3x2 x 0lim 4cos2x1 .215 .sin 2xx53 4.215 1281 . ex 1 x3 (2x)5
2.2.2. Quy tắc Lôpitan khử dạng vô ịnh lOMoAR cPSD| 49519085
Định lý 2. Giả sử các hàm số f(x) và g(x) thoả mãn các iều kiện i), ii), iv) trong Định lý
1 và iều kiện iii) trong Định lý 1 ược thay thế bởi iều kiện: lim f(x) = , lim g(x) = . x a x a Khi ó f(x) f (x) lim = lim . x a g(x) x a g (x) ln x2 Ví dụ. Tính lim . x 0 cot x Giải. Ta có 2x ln x2sin x2 2 x lim = lim = - 2.limx. 2 = 0. x 0 cot x x 0 x 0 x
2.2.3. Một số chú ý 0
a) Sau khi áp dụng quy tắc Lôpitan mà giới hạn ó vẫn có dạng hoặc thì ta có 0 thể áp
dụng quy tắc Lôpitan một lần nữa: Ví dụ. Tính lim e - ex -x 2x d¹ng 0 x 0 x - sinx 0
Giải. Áp dụng quy tắc Lôpitan, ta ược: e - ex -x 2x ex + e - 2-x 0 lim = lim d¹ng x 0 x - sinx x 0 1 - cosx 0 ex e x 0 = lim d¹ng x 0 sinx 0 ex e x = lim = 2. x 0 cosx
b) Quy tắc Lôpitan vẫn úng nếu các giới hạn xét trong các Định lý trên là giới hạn một phía. lnsinx Ví dụ. Tính xlim 0 lnsin5x (dạng ). Giải. Ta có
GV: Nguyễn Dương Nguyễn, BM Toán, Khoa Cơ bản, FTU lOMoAR cPSD| 49519085 cosx sin5x xlim 0
lnsin5xlnsinx = xlim 0 5cos5xsinx = xlim 0 5cos5xcosx .sin5xsinx = xlim 0 cos5xcosx . sinx5x = 1. sin5x x
c) Quy tắc Lôpitan vẫn úng cho cả trường hợp khi x . x2 Ví dụ. Tính lim (dạng ) x e2x Giải. Ta có lim x2 lim 2x lim 2 0. x e2x x 2e2x x 4e2x 0
d) Ngoài việc dùng quy tắc Lôpitan ể khử các dạng vô ịnh và , quy tắc Lôpitan 0
còn ược dùng ể khử các dạng vô ịnh khác như 0. , - , 00, 1 , 0 : Khử dạng vô
ịnh 0. : Giả sử cần tính lim f(x).g(x), trong ó x a lim f(x) 0; lim g(x ) , ta biến ổi như sau: x a x a f(x) 0 lim f(x).g(x) = lim (dạng 1 ) x a x a0 g(x) hoặc g(x)
lim f(x).g(x)= lim (dạng ). x a x a 1 f(x)
Ví dụ. Tính lim x.lnx (dạng 0. ). x 0 Giải. Ta có 1 lOMoAR cPSD| 49519085
ln x x = lim( x) = 0. x 0lim x.lnx = xlim0 = x 0lim 1 x 0 1 x x2 Khử dạng vô ịnh : Giả sử cần tính lim(f(x) g(x)), trong ó x a lim f(x) ; lim g(x) , ta biến ổi như sau: x a x a 1 1 g(x) f(x) lim(f(x) g(x)) = lim 0 (d¹ng ). x a x a 1 0 f(x).g(x) 1 1 - ) Ví dụ. Tính lim 1 lnx - x - 1 (dạng x Giải. Ta có 1 1 x - 1 - lnx 0 xlim - = lim 1 (x - 1)lnx (d¹ng 0) 1 lnx x - 1 x 1 1 - = lim x x 1 x - 1 lnx + x x - 1 0 = lim (d¹ng ) x 1xlnx + x - 1 0 1 1 = lim = . x 1lnx + 1 + 1 2
Khử dạng vô ịnh 00, 1 , 0 : Khi tính giới hạn lim f(x) g(x), ta thường gặp x a
GV: Nguyễn Dương Nguyễn, BM Toán, Khoa Cơ bản, FTU lOMoAR cPSD| 49519085
các dạng vô ịnh 00, 1 , hoặc 0, ể tính giới hạn ó trước hết ta ặt y f(x) g(x) ln y g(x)lnf(x) Sau ó, tính giới hạn
lim ln y = lim g(x).lnf(x) (có dạng vô ịnh 0. ). x a x a
Nếu tính ược lim ln y = k thì x a
lim f(x) g(x) lim y = lim elny= elimln yx a = ek. x a x a x a
Ví dụ 1. Tính lim π 2 x cosx ( dạng 00) x Giải. Đặt y π2x cosx lny cosx.ln π 2x . Ta có lim ln y
lim c osx.ln π 2 x (dạng 0. ) π x π x 2 2 lim ln π 1 x 2 (dạng ) π x 2 cosx π 2 x 2 2 lim sin π x .cosx 1.0 0. lim x π sinx x π π x sinx 2 cos x2 2 2 Vậy lim π 2 x cosx e0 1. x
Ví dụ 2. Tính lim(cosx)cot2x (dạng 1 ) x 0 lOMoAR cPSD| 49519085
Giải. Đặt y (cosx)cot2x lny = cot2x.ln(cosx) Ta có
lim(ln )y = lim cot2x.ln(cosx) (dạng 0. ) x 0 x 0 ln(cosx) 0 = lim 2 (dạng ) x 0 tan x 0 = lim tanx lim cos2x 1 . 1 x 02 tanx. x 0 2 2 cos2x 2 1
Vậy, lim(cosx)cot x e 2. x 0 1
Ví dụ 3. Tính lim xx (dạng 0). x + 1 1
Giải. Đặt y = xx lny = lnx x Ta có lnx lim (lny) = lim (dạng ) x x x 1 = lim = 0. x x Vậy 1 lim xx = e0 = 1. x +
e) Mặc dù quy tắc Lôpitan là một công cụ mạnh ể tính giới hạn nhưng nó không thể thay
thế toàn bộ các phương pháp tính giới hạn ã biết. Ví dụ. Tính lim x sin(1/ x)2 (dạng vô ịnh 0 ). x 0 sinx 0 Giải. Ta có
GV: Nguyễn Dương Nguyễn, BM Toán, Khoa Cơ bản, FTU lOMoAR cPSD| 49519085 x sin(1/ x) 2 2x.sin(1/ x) cos(1/x) . sinx cosx Ta xét giới hạn 2x.sin(1/x) cos(1/x) 2x.sin(1/x) lim cos(1/x) . lim = lim x 0 cosx x 0 cosx x 0 cosx
Do không tồn tại giới hạn cos(1/x) lim x 0 cosx
nên không tồn tại giới hạn 2x.sin(1/ x) cos(1/x) lim , x 0 cosx
tức là không tồn tại giới hạn x sin(1/ x)2 lim . x 0 sinx
Do ó, quy tắc Lôpitan không áp dụng ược. Tuy nhiên, ta vẫn tính ược giới hạn này
bằng phương pháp như sau x sin(1/ x)2 x 1 lim = lim . lim xsin = 1.0 = 0. x 0 sinx x 0 sinx x 0 x
2.3. Khai triển Taylor
Định lý. Cho hàm số f(x) xác ịnh trong một lân cận U nào ó của iểm x0 và có ạo hàm
ến cấp n + 1 trong lân cận ó . Khi ó f(x) có thể ược biểu diễn dưới dạng f x f x 0 f (x 0)(x - x0) f (x
0)(x - x0)2 ... f(n)(x0)(x - x0)n Rn x 1! 2! n!
Công thức này ược gọi là công thức khai triển Taylor của hàm số f(x) ến bậc n tại iểm x 0 với phần dư Rn x .
Rn(x) = O((x – x0)n), , x x0: phần dư dưới dạng Peano lOMoAR cPSD| 49519085
Rn(x) = f(n + 1)(x 0 (x - xθ 0))(x - x0)n + 1, 0 < < 1: phần dư dưới dạng (n + 1)! Lagrange. Chú ý:
1) Cả hai số hạng dư (dạng Peano và Lagrange) là bằng nhau. 2)
Khi x0 = 0 ta thu ược công thức Maclaurin: f(x) = f(0) + f (0 ) x + f (0 ) x2 + … + f(n)(0) xn + Rn(x) 1! 2! n! với phần dư
+) dạng Peano Rn(x) = O(x n), x 0. +) dạng Lagrange Rn(x) = f(n + 1)(θ )x x n + 1 , 0 < < 1. (n + 1)!
Sau ây là khai triển Maclaurin của một số hàm sơ cấp: x x 2 + … + xn + O(xn) = n xk + O(xn) i) e = 1 + x + 2! n! k 0 k!
ii) sinx = x - x3 + … + (-1)n-1 x2n - 1 + O(x2n) = n ( 1) k 1 x2k 1 + O(x2n) 3! (2n - 1)! k 1 (2k 1)! x 2n+1 x2 x4 n x2n n k 2k + O(x2n+1). = iii) cosx = 1 - + - … + (-1) + O(x ) ( 1) 2! 4! (2n)! k 1 (2k)! iv) (1 + x) = 1 + x + α(α - 1) x2 + … + α(α - 1) ... ( - n + 1)α xn + O(xn) = n C k xk + 2! n! k 0 k! O(xn) 1 Đặc biệt: 1 x x2 x3 ... ( 1)n nx O(x )n n ( 1) k kx O(x )n 1 x k 0
GV: Nguyễn Dương Nguyễn, BM Toán, Khoa Cơ bản, FTU lOMoAR cPSD| 49519085 x x x 2 3 ... ( 1)n 1 n O(x )n ( 1) = n
k 1 xk + O(xn) v) ln(1 + x) = x 2 3 n k 1 k
2.4. Tích phân suy rộng
2.4.1 Tích phân suy rộng có cận vô hạn 1) Định nghĩa:
+) Cho hàm số f(x) liên tục trên [a, + ). Khi ó, tích phân suy rộng của hàm số f(x)
trên khoảng [a, + ), ký hiệu là f(x)dx , ược ịnh nghĩa như sau: a B f(x)dx = lim f(x)dx (2.1) B a a
+) Cho hàm số f(x) liên tục trên (- , b]. Khi ó, tích phân suy rộng của hàm số f(x) b
trên khoảng (- , b], ký hiệu là f(x)dx , ược ịnh nghĩa như sau: b b f(x)dx = lim f(x)dx , (2.2) A A
+) Cho hàm số f(x) liên tục trên (
, ) . Khi ó, tích phân suy rộng của hàm số f(x) trên khoảng ( ,
), ký hiệu là f(x)dx , ược ịnh nghĩa như sau: c f(x)dx f(x)dx f(x)dx c (2.3) c B lim f(x)dx lim f(x)dx, A B A c lOMoAR cPSD| 49519085
ở ây ta chọn số c sao cho f(x) liên tục tại x c .
Nếu các giới hạn ở vế phải của (2.1), (2.2), (2.3) là tồn tại hữu hạn thì ta nói tích phân
suy rộng tương ứng ở vế trái là hội tụ. Ngược lại, thì ta nói tích phân suy rộng ó phân kỳ.
Ví dụ. Tính các tích phân sau a) xe xdx b) dxx2 1 1 c) dx2 d) dx (với a > 0, 0) 2 1 a xα x x Giải. a) Ta có B xe xdx lim xe xdx. B 1 1 Đặt u x du dx dv e dx x v e x. B xe xdx xe x B B e xdx Be B e 1 e B e 1. 1 1 1 Suy ra
xe xdx lim ( Be B e 1 e B e ) 1 2e 1. B 1
Vậy, tích phân xe xdx hội tụ. 1
GV: Nguyễn Dương Nguyễn, BM Toán, Khoa Cơ bản, FTU lOMoAR cPSD| 49519085 b) Ta có 1 dx dx dx . 1 x2 1 x2 1 1 x2 1 dx lim 1 dx lim π π 3π arctan1 arctanA . 1 x2 A A1 x2 A 4 2 4 π π π dx lim B dx lim 2 B 1 x2 B arctanB arctan1 2 4 4 . 1 1 x 1 Vậy, dx 3π π π, 1 x2 4 4 tức là, tích phân dxx2 hội tụ. 1 c) Đặt t x2 1 t2 x2 1 tdt
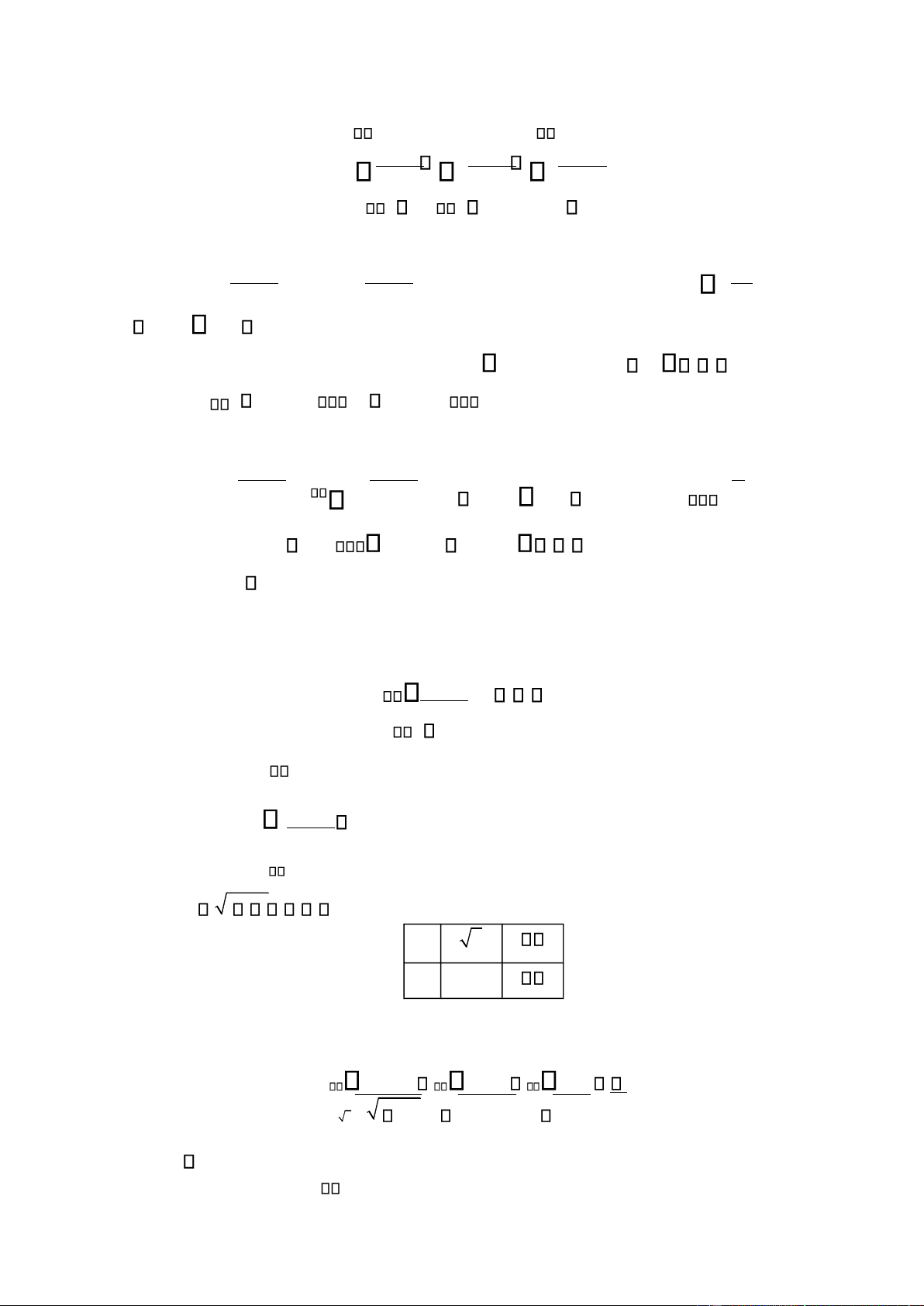
xdx. Khi ó, ta có bảng ổi cận sau x 2 t 1 Ta có dx2 tdt 2 dt 2 . 2 x x 1 1 t(1 t ) 1 1 t 4 d) * Với = 1, ta có B lOMoAR cPSD| 49519085
dx = lim dx = lim (lnB - lna) = + . a x B a x B * Với 1, ta có a dxxα B Ba dx lim x1 B = lim B 1 - 1a 1 = lim α = B 1 a B 1 x a1 , nÕu > 1 = 1 + , nÕu < 1 dx Vậy, tích phân α (a > 0, 0) hội tụ khi 1 và phân kỳ khi a x 0 1.
Ví dụ. Xét sự hội tụ hay phân kỳ của các tích phân sau dx dx dx a) b) x c) 3 x 2 x 1 11 Giải. d x a) Tích phân 2 hội tụ vì 2 1. 1 x 1 dx (0,1].
b) Tích phân phân kỳ vì x 2
GV: Nguyễn Dương Nguyễn, BM Toán, Khoa Cơ bản, FTU lOMoAR cPSD| 49519085 1 3 dx 1. c) Tích phân hội tụ vì 2 3 x 1
2) Dấu hiệu hội tụ: Xét sự hội tụ của tích phân f(x)dx a
a) Dấu hiệu so sánh:
Định lý. Giả sử các hàm số f(x) và g(x) liên tục trên [a, + ) và f(x) g(x), x [a, + ) . Khi ó
i) Õu N g(x)dx héi tô th× f(x)dx héi tô. a a
ii) NÕu f(x)dx ph©n kú th× g(x)dx ph©n kú. a a
Ví dụ. Xét sự hội tụ hay phân kỳ của các tích phân sau ln(1 x 2 x) a) e dx b) dx 1 x 1 Giải. a) Ta có 0 < e x2 e x , x [1, + ). Ta có B
e xdx = lim e xdx = lim (-e-x)B = lim (-e B + 1 ) = 1 . 1 B 1 B 1B e e lOMoAR cPSD| 49519085
Do ó, tích phân e xdx hội tụ. Theo dấu hiệu so sánh, tích phân e x2dx hội tụ. 1 1 b) Ta có ln(1 x) ln2 0, x [1, + ). x x dx ln(1 x) Mặt khác,
phân kỳ. Theo dấu hiệu so sánh, tích phân dx phân kỳ. 1 x 1 x
Hệ quả. Nếu f(x) liên tục trên [a, + ) với a 0 , f(x) 0, x [a, + ) và 1 , +
thì f(x)dx hội tụ nếu > 1 và phân kỳ nếu f(x) ~ ( > 0) x x a 0 1.
Ví dụ. Xét sự hội tụ hay phân kỳ của các tích phân sau xdx xdx a) 2 2 b) 1 x5 5 2 x Giải. a) Ta có x ~ x 1 ,x . x2 2 x2 x Vậy, tích phân xdx phân kỳ. 2 x2 2 b) Ta có x ~ x1/2 1 ,x . x5 5 x5/2 x2
GV: Nguyễn Dương Nguyễn, BM Toán, Khoa Cơ bản, FTU lOMoAR cPSD| 49519085 Vậy, tích phân xdx hội tụ. 1 x5 5
b) Dấu hiệu Dirichlê Xét tích phân suy rộng f(x)g(x)dx a
Định lý. Nếu các hàm số f(x) và g(x) thỏa mãn các iều kiện sau
i) f(x) liên tục trên [a, + ) ,
ii) f(x) có một nguyên hàm bị chặn trên [a, + ) , tức là tồn tại hàm F(x) sao cho F (x) = f(x), F(x) m, x [a, + ) ,
ở ây m là một hằng số dương nào ó.
iii) g(x) khả vi trên [a, + ) , iv) g(x) giảm trên [a, + ) và lim g(x) = 0 . x
Khi ó, tích phân f(x)g(x)dx hội tụ. a
Ví dụ. Xét sự hội tụ hay phân kỳ của tích phân cosx dx . 1 x + 100 1
Giải. Đặt f(x) = cosx, g(x) = . Ta có
x + 100 +) f(x) liên tục trên [1, + ).
+) f(x) có 1 nguyên hàm F(x) = sinx, |F(x)| = |sinx| 1, x [1, + ).
+) g(x) khả vi trên [1, + ) . +) g(x) giảm trên [1, + ), lim 1 g(x) = lim = 0. x x x + 100 cosx
Theo dấu hiệu Dirichlê, tích phân dx hội tụ. lOMoAR cPSD| 49519085 1 x + 100 b
Chú ý. Các tích phân f(x)dx; f(x)dx cũng có dấu hiệu hội tụ tương tự.
2.4.2. Tích phân suy rộng của hàm số không bị chặn 1) Định nghĩa:
+) Cho hàm số f(x) liên tục trên (a, b] và f(x) không bị chặn tại x a ( lim f(x) ). x a Khi
ó, tích phân suy rộng của hàm f(x) trên [a, b] ược ịnh nghĩa như sau: b b f(x)dx = lim f(x)dx (2.4) t a a t
+) Cho hàm số f(x) liên tục trên [a, b) và f(x) không bị chặn tại x b ( lim f(x) ). x b Khi
ó, tích phân suy rộng của hàm f(x) trên [a, b] ược ịnh nghĩa như sau: b t f(x )dx = lim f(x)dx (2.5) t b aa
+) Cho hàm số f(x) liên tục trên [a, b]\{c}, với a < c < b và f(x) không bị chặn tại x c (limf(x)
). Khi ó, tích phân suy rộng của hàm f(x) trên [a, b] ược ịnh nghĩa như x c sau: b c b f(x)dx f(x)dx f(x)dx a a c (2.6) t b lim f(x)dx lim f(x)dx t c t c a t
+) Cho hàm số f(x) liên tục trên (a, b), f(x) không bị chặn tại x a và x b ( lim f(x) , lim f(x)
). Khi ó, tích phân suy rộng của hàm f(x) trên [a, b] ược
GV: Nguyễn Dương Nguyễn, BM Toán, Khoa Cơ bản, FTU lOMoAR cPSD| 49519085 x a x b ịnh nghĩa như sau: b d b f(x)dx f(x)dx f(x)dx a a d (2.7) d t lim f(x)dx lim f(x)dx, t a t b t d
ở ây d là một số nào ó thuộc (a; b) sao cho f(x) liên tục tại x d .
Nếu các giới hạn ở vế phải của (2.4), (2.5), (2.6), (2.7) là tồn tại hữu hạn thì ta
nói tích phân suy rộng tương ứng ở vế trái hội tụ. Ngược lại, thì ta nói tích phân suy rộng ó phân kỳ. b dx
Ví dụ. Tính
α ( > 0; a, b là các số thực cho trước). a (x - a) Giải. * Với = 1, ta có: b xdx a = tlim a bt xdx a = tlim ln(x a a)bt = tlim a [ln(b-a) - ln(t-a) ] = + . a * Với 1, ta có b α = tlim a b (x a) = tlim a (x - a1 - ) 1 - bt dx dx a (x - a) t 1 1- (t a)1 ] = lim[(b-a) 1 - t a lOMoAR cPSD| 49519085 (b a)1 , nÕu < 1 = 1 - + , nÕu > 1 b dx Vậy, tích phân
α ( > 0; a, b là các số thực cho trước) hội tụ khi < 1 và a (x - a) phân kỳ khi 1. b dx
Tương tự, ta chứng minh ược
α ( > 0; a, b là các số thực cho trước) hội tụ a (b - x)
khi < 1 và phân kỳ khi 1.
2) Dấu hiệu hội tụ b
Xét sự hội tụ của tích phân suy rộng f(x)dx, trong ó f liên tục trên (a; b] và f(x) a
không bị chặn tại x a .
Định lý. Giả sử hàm số f(x) thỏa mãn các iều kiện
i) f(x) liên tục trên (a, b] và f(x) không bị chặn tại x a , ii) f(x) 0, x (a, b],
iii) 1/f(x) ~ (x - a) ( 0), khi x a+. b
Khi ó, tích phân suy rộng f(x)dx hội tụ khi < 1 và phân kỳ khi 1. a
Chú ý. Các tích phân suy rộng của hàm số không bị chặn còn lại cũng có dấu hiệu hội tụ tương tự.
Ví dụ. Khảo sát sự hội tụ của các tích phân suy rộng sau: 1 11 2 dx xdx x dx a) I = b) c) 3 2 5
GV: Nguyễn Dương Nguyễn, BM Toán, Khoa Cơ bản, FTU lOMoAR cPSD| 49519085 0 0 esinx 1 0 (1 x ) ln(1 + x) Giải. 1 a) Xét hàm số f(x) = . Ta có ln(1 + x)
+) f(x) liên tục trên (0, 1], +)
f(x) không bị chặn tại x 0 , +) f(x) > 0, x (0, 1] . Mặt khác 1 = ln(1 + x) ~ x, x 0+ f(x) 1 dx
Theo dấu hiệu trên, tích phân phân kỳ. 0 ln(1 + x) b) Xét hàm số f(x) x . Ta có esinx 1
+) f(x) liên tục trên (0, 1], +)
f(x) không bị chặn tại x 0 , +) f(x) > 0, x (0, 1] . Mặt khác 1 esinx 1 ~ sinx ~ x x1/2, x 0 1 / 2 f(x) x x x xdx hội tụ . 1/2
1 Theo dấu hiệu trên, tích phân 0 esinx 1 c) Xét hàm số f(x) x2 . 3 (1 x2 5)