Chương 25: Điện thế | Tài liệu môn vật lý 1 Trường đại học sư phạm kỹ thuật TP. Hồ Chí Minh

Điện trường đã được nghiên cuứ về phương diện tác dụng lực trong các chương trước. Trong chương này, điện trường sẽ được khảo sát ở khía cạnh năng lượng, Bằng cách tiếp cận theo hướng năng lượng, các bài toán có thể đựơc giải theo hướng không cần đến việc sử dụng lực. Khái niệm về thế năng có giá trị lớn trong các nghiên cứu về điện. Tài liệu giúp bạn tham khảo, ôn tập và đạt kết quả cao. Mời bạn đọc đón xem!

9 5 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Môn: vật lý 1, 2

Trường: Đại học Sư phạm Kỹ thuật Thành phố Hồ Chí Minh

Thông tin:

25 trang 1 tháng trước

Tác giả:

Profile Lê Kim Dung
1
Chương 25: Điện thế
iện trường c nghiên c u v n tác d ng l đã đượ ứ ề phương diệ ụ ực trong các chương trước.
Trong chương này, điệ năng lượn trường sẽ được khảo sát ở khía cạnh ng. Bằng cách
tiếp c ng, các bài toán có th c gi ng không c n ận theo hướng năng lượ ể đượ ải theo hướ ầ
đế ớn việc sử dụng lực. Khái niệm về thế năng có giá trị l n trong các nghiên cứu về
điệ ợn. Do l n là lực tĩnh điệ ực bảo toàn, hi n có thện tượng tĩnh điệ ể đư c mô tả một cách dễ
dàng dướ ạng năng lượng điệi d n thế.
Điệ ến th và hi n thệu điệ ế
25.1
Khi m n tích ột điệ
q
đặt trong điện trường
,E
nó s u tác d ng m c b ng ẽ chị ụ ột lự ằ
.F qE
Đây là lự ất, các tương tác đều tuân theo địc bảo toàn bởi vì theo bản ch nh luật
Coulomb. Hãy xem xét dưới góc độ kín các điện tích, khi điệ một hệ n tích
q
chuy ng ển độ
chỉ dưới tác d ng c n tích còn l i. V i m t chuy n d i vô cùng bé ụ ủa các điệ ạ ớ ộ ể ờ
,ds
trường lực
thế Coulomb sinh m t công b ng ộ ằ
.F ds
Trong cơ họ ằng, công do trườc ta biết r ng lực thế
sinh ra bằng đúng độ năng, cho nên: suy giảm thế
dU F ds
Khi điện tích
q
di chuy n t v n v bi n thiên thể ừ ị trí A đế ị trí B trong điện trường, độ ế ế năng
bằng:
(25.1)
Ở đây tích phân đườ ủa điệng tính dọc theo quỹ đạo di chuyển c n tích
q
t n B. Tuy ừ A đế
nhiên vì trườ ảo toàn nên dù đi theo con đườ ủa tích phân này cũng ng lực b ng nào, giá trị c
không thay đổi.
Khi đã có biể ức tính độ năng, chỉ ột điểm O nào đó làm u th biến thiên thế cần chọn m
gốc thế năng (
0U
), ta đã có thể tính thế năng c ng: ủa điện tích đặ ện trườt trong đi
(P)
(O) (P)
U q E ds q E ds
Thế năng của điện tích
q
t i v trí P b ng có tr s b ng công c a lạ ị ất kì trong điện trườ ị ố ằ ủ ực
điện trườ ển điệng làm di chuy n tích
q
g đó từ P về ốc thế năng.
Thế năng t i v trí P c a mạ ị ủ ột đơn vị điện tích trong n ng điệ trườ
E
được g i là ọ điện thế
tại điểm đó:
Đ
2
(P)
(O) (P)
U
V E ds E ds
q
(25.2)
Điện thế tạ ằ ủi vị trí P b ng có tr sất kì trong điện trườ ị ố b ng công c a l ng làm di ực điện trườ
chuyển điện tích 1 Coulomb từ P về gốc c thđiện thế (gố ế năng).
Tương tự như độ năng biến thiên thế
U
ta cũng có khái niệm hiệu điện thế gi a hai ữ
điểm B và A:
( )
( )
B
B A
A
V V V E ds
(25.3)
Từ (25.1) và (25.3), ta có mối liên h gi bi n thiên th n th : ệ ữa độ ế ế năng và hiệu điệ ế
U q V
(25.4)
Theo đị ảo toàn năng lượnh luật b ng:
0,U K
suy ra động năng mà điện tích
q
thu
đượ độ năng:c khi di chuyển từ điểm A đến điểm B nói trên bằng suy giảm của thế
( )
A B
K U q V q V V
Điệ ến th và hi n thệu điệ ế có thứ nguyên c ng trên mủa năng lượ ột đơn vị điện tích, được
gán cho m c bi SI : 1V = 1J/C. ột đơn vị đặ ệt trong hệ – Volt
Mối liên h khác c ng là ệ (25.2), (25.3) cũng cho ta một đơn vị ủa cường độ điện trườ
V/m: 1N/C = 1V/m.
Khi m n tích nguyên t ột electron mang điệ ố
e
chuyển
động dướ ủa điện trường, đi qua đoạn đười tác dụng c ng có
hiệu điệ ằng electron đã thu đượn thế bằng 1V, ta nói r c thêm
động năng bằng 1 : electron-volt
19 19
1 1,6 10 1 1,6 10eV C V J
Câu h i 25.1:ỏ Hai điể ột điện trườm A và B nằm trong m ng
như hình 25.1. ệu điệ(i) Hi n thế
B A
V V V
có giá trị như
thế nào? (a) dương (b) âm (c) bằ ột điệng không. (ii) M n tích
âm ban đầ ại A, sau đó di chuyển đếu nằm t n vị trí B. Sự biến
thiên c a thủ ế năng
U
có giá tr nào? L a ch n trong ị như thế ự ọ
các khả năng như phần trước.
Hiệu điệ trong điệ ờng đền thế n trư u 25.2
Ta ti n hành kh o sát m ng s ng ế ả ột điện trường đều, theo đó các đườ ức điện trường hướ
song song và đều đặn như miêu tả phương trình (25.3) suy ra đượ trên hình 25.2a. Từ c hiệu
điệ ờn thế gi m A và B nữa hai điể ằm trên cùng một đư ng sức điện trường:
Hình 25.1: Hai điện tích
điểm trong điện trường
3
( ) ) ( )
0
( ) ( ) ( )
cos(0 )
B B
B A
A A A
V V V E ds E ds E ds
Trong điện trường đều
E
l i nên có th u tích phân: có độ ớn không đổ ể đưa ra ngoài dấ
( )
( )
B
A
V E ds
V Ed
(25.6)
Dấu “–“ ở đây nói rằng, điệ ấp hơn điện thế tại B th n thế tại A:
.
B A
V V
Như vậy, các
đường sức điện trường luôn hướ ủa điệng theo chiều suy giảm c n thế.
Khi một điện tích
q
di chuy n t n B, a hể ừ A đế thế năng củ ạt trong điện trường thay đổi
một lượng b ng ằ
U q V qEd
(25.7)
Có nghĩa nế ạt mang điện tích dương: u h
0,q
thế năng sẽ giảm:
0.U
Nói cách khác,
khi m n xuôi theo chi u c ng s ng, thột điện tích dương di chuyể ề ủa đườ ức điện trườ ế năng của
nó s gi a miêu t , n u hẽ ảm. Như hình 25.2 ả ếu ban đầ ạt mang điện tích dương
q
thả t do t ự ừ
trạng thái đứng yên, nó sẽ chịu tác dụng một lực
F qE
hướng xu i, b u ống dướ ắt đầ đi
xuống và tăng tố ần thu động năng từ năng. Đó là minh c. Hạt d chính sự suy giảm của thế
chứng rõ ràng cho đị ảo toàn năng lượnh luật b ng.
Hình 25.2b miêu t hình , khi m t h t kh ng ả ảnh tương tự ộ ạ ối lượ
m
rơi tự do trong trường
hấp d n g n mẫ ầ ặt đất. H u tác dạt cũng chị ụng của trọng l ng xu ng ực hướ ống và tăng tốc. Độ
năng tích luỹ năng trọng trườ tự sự suy giảm của thế ng.
Phép so sánh nói trên gi a h ng v i h t chuyữ ạt mang điện tích dương trong điện trườ ớ ạ ển
động dưới trườ ện tượng tĩnh điệng trọng lực rất hữu ích cho việc hình dung về các hi n. Chỉ
Hình 25.2: (a) Hạt mang điệ ển độn tích chuy ng dọc theo
đường sức điện trường đề rơi trong u (b) Hạt khối lượng
trường trọng lực đều.
4
một điểm lưu ý rằ ối lượng thì luôn dương, nhưng điệ dương, cũng có thểng: kh n tích có thể
âm.
Với trườ ợp điệ ủa đườ ức điện trường h n tích âm, khi hạt di chuyển theo chiều c ng s ng,
thế năng của hạt sẽ tăng, thay vì giả ếu ban đầ ạt đứm. N u h ng yên, nó s c v phía ẽ tăng tố ề
ngượ ờc chiều của đư ng sức.
Ta kh ng h p t t mang ảo sát trườ ợ ổng quát hơn, khi hạ
điệ ị ịn tích di chuyển từ v trí A đến v trí B trong điện trường
đều, nhưng không nằ ột đườ ức như hình m trên cùng m ng s
25.3. Lúc này hi n th gi a A và B b ng: ệu điệ ế ữ ằ
( )
( ) ( )
B
B A
A A
V V V E ds E ds E s
Ở đây vector
E
c u có thủa điện trường đề ể đưa ra ngoài dấu
tích phân. Độ bi n thiên c ế ủa thế năng:
U q V qE s
Tích vô hướng (25.8) có thể tính qua hình học:
B A
V V V Ed
Mặt khác hi n th gi m A và C n m trên cùng ệu điệ ế ữa hai điể ằ
một đường s ức:
C A
V V Ed
Từ đây suy ra rằng
.
B C
V V
T ng quát lên có th y r ng, ổ ể thấ ằ
mọi điể ới đườ ức điện trường đềm nằm trên cùng một mặt phẳng vuông góc v ng s u có cùng
một điện thế. Ta g i m t ph ng ch a t t c n th y là mọ ặ ẳ ứ ấ ả các điểm có cùng điệ ế như vậ ột mặt
đẳng thế. Đố ới điện trường đềi v u, họ các mặt đẳng thế cấu thành từ những mặt phẳng song
song với nhau và cùng vuông góc v ng s ng. ới các đườ ức điện trườ
Hình 25.3: Hạt mang điện
tích chuyển động không
song song với đường sức
của điện trường đều
Câu h i 25.2:ỏ Các điểm được đánh dấu trên hình 25.4 nằm
trên các m ng th . Hãy s p x p công th c hi n cặt đẳ ế ắ ế ự ệ ủa điện
trường lên m tột điện tích dương theo thứ ự giảm dần, khi
điện tích này di chuyển từ A sang B, từ B sang C, từ C sang
D và từ D sang E.
Bài t p m ng gi a hai bậ ẫu 25.1: Điện trườ ữ ản
phẳng song song tích điện trái dấu
Một ắc-quy hi n th 12V m c vào hai bệu điệ ế ắ ản
phẳng đặ song như hình 25.5. Khoảt song ng cách
giữa hai b n ả
0,3d
cm, đủ ằng điệ nhỏ để xem r n
trườ điệng giữa hai bản là đều. Tính cường độ n
trường giữa hai bản phẳng.
Gi i:ả
Dùng công th c (25.6), có th n ứ ể tính cường độ điệ
trường giữa hai bản phẳng song song:
3
2
12
4 10 /
0,3 10
B A
V V
V
E V m
d m
Bài tập m u 25.2: Chuy a h u ẫ ển động củ ạt proton trong điện trường đề
Một proton đượ ạng thái đức thả ra từ tr ng yên tại
vị trí A trong m l n ột điện trường đều có độ ớ
4
8,0 10
V/m (hình 25.6). Proton di chuy n ển đế
điểm B cách đó một đoạn
0,50d
m d c theo ọ
hướng c ng ủa điện trườ
E
. Tìm t c a proton ốc độ ủ
sau đoạn đường đó.
Gi i:ả
Khái niệm. Hình dung r ng h ng ằ ạt proton rơi xuố
tựa như đang ở ột trườ trong m ng trọng lực. Trong
Hình 25.5: Hai bản ph ng ẳ
song song nối vào ngu n ồn điệ
Hình 25.6: Proton tăng tốc theo
hướng c ng ủa điện trườ
Hình 25.4: Các mặt đẳng th ế
6
bài t p này, h u tác d ng m t gia t ng. ậ ạt cũng chị ụ ộ ố ổc không đ i bởi lực điện trườ
Phân loại. Do h i bên ngoài nên ta có th quy v v ệ không tương tác vớ ể ấn đề ề chủ đề
bảo toàn năng lượng.
Phân tích. nh lu m B: Áp dụng đị ật bảo toàn năng lượng cho điểm A và điể
0K U
Thế bi u th ng: ể ức của động năng và thế năng tại A và B tương ứ
2
1
0 0
2
mv e V
Từ đó suy ra vận tốc
v
đồng th i tính ờ
V
theo công thức (25.6):
19 4
27
6
2 2 ( ) 2
2(1,6 10 )(8,0 10 V)(0,50 )
1,67 10
2,8 10 /
e V e Ed eEd
v
m m m
C m
kg
m s
Nhận định. Điện thế giảm theo chi u chuy ng c a proton,ề ển độ ủ
0,V
kéo theo s ự
suy gi m c a thả ủ ế năng:
0.U
Để ỹ cân bằng sự suy giảm này, proton lại tích lu
động năng trong chuyển độ ảo toàn năng lượng có gia tốc, tuân theo định luật b ng.
Điệ ế ến th và th o bnăng tạ ởi điện tích điểm
25.3
Từ trình bày ở chương 23, ta đã biế ột điệt rằng m n
tích điểm
0q
t o ra trong không gian xung quanh mạ ột
điện trường đố ững đười xứng xuyên tâm với nh ng sức
hướng ra ngoài. Hiệu điệ ữa hai điển thế gi m A và B bất
kì (hình 25.7) có th tính theo công th ể ức (25.3):
( )
( )
B
B A
A
V V E ds
Vector cường độ điện trườ ng
E
đối v ng cới điện trườ ủa
điện tích điểm có dạng
3
E r
r
Thế c vào thu đượ
( )
3
( )
B
e
B A
A
k q
V V r ds
r
Từ hình 25.7 có th ể thấy tích vô hướng
,r ds r dr
nên:
Hình 25.7: Tính hiệu điện
thế giữa hai điểm bất kì
trong điện trường đối xứng
xuyên tâm
7
( ) ( )
3 2
( ) ( )
1
B
A
r
B B
e
B A e e
rA A
k q dr
V V r dr k q k q
r r r
A
r
và
B
r
l t là kho ng cách t m, th ần lượ ả ừ A và từ B đến điện tích điể ế vào thu được:
1 1
B A e
B A
V V k q
r r
(25.10)
Phương trình (25.10) cho thấy, hiệu điệ ữa hai điể ủa điện trườn thế gi m bất kì c ng đối
xứng xuyên tâm chỉ phụ thuộc vào v u và v trí cu i, không phị trí đầ ị ố ụ thuộc vào đường lấy
tích phân. Kh nh này l i càng c ng c r ng l n luôn là m ng ẳng đị ạ ủ ố ằng, trườ ực tĩnh điệ ột trườ
bảo toàn, b ng l n v b n ch t là sởi trườ ực tĩnh điệ ề ả ấ ự chồng ch ng cập điện trườ ủa r t nhiấ ều
điện tích điểm.
Nếu chọn g n th ốc điệ ế
0V
tại
,r
điện th t i m t kì nế ạ ột điểm P bấ ằm cách điện
tích
q
m t kho ng ộ ả
r
c tính b ng công th c (25.2): đượ ằ ứ
3 2
(P)
1
e
e e
r
r r
q dr
V E ds r dr k q k q
r r r
Hay:
e
q
V k
r
(25.11)
Khi c n th t i m m b ng do nhi m tần tính điệ ế ạ ột điể ất kì trong điện trườ ều điện tích điể ạo
ra, ta sử d ng phép ch ng ch p: ụ ồ ậ
i
e
i
q
V k
r
(25.12)
Hình 25.8a miêu tả điện tích điểm
1
q
t o ra m n th t i mạ ột điện trường cũng như điệ ế ạ ọi
điểm xung quanh nó. Điện thế tại vị trí P bằng:
Hình 25.8: Hệ hai điện tích điểm
8
1
1
12
e
q
V k
r
Bây gi n i v trí P mờ ếu đặt tạ ị ột điện tích điểm
2
q
khác (hình 25.8b), h ệ hai điện tích điểm sẽ
có thế năng bằng:
1 2
2 1
12
e
q q
U q V k
r
(25.13)
Lưu ý rằ năng lấ ạng thái hai điệng gốc thế y ở tr n tích cách xa nhau vô cùng. Nếu
1 2
,q q
cùng d u, chúng có s c m y nhau ra xa nh t có th , ch ng t h ng ấ ứ ạnh đẩ ấ ể ứ ỏ ệ có mang năng lượ
0.U
Ngược l i n u ạ ế
1 2
,q q
trái d u, c n ph i b sung m ng nh m t l c bên ấ ầ ả ổ ột năng lượ ờ ộ ự
ngoài m c, ch ng t h ng âm. N u bi n lu n theo ới tách chúng ra xa đượ ứ ỏ ệ mang năng lượ ế ệ ậ
hướng cho r n tích ằng điệ
1
q
n ng do ằm trong điện trườ
2
q
t n k t quạo ra, ta cũng đi đế ế ả như
(25.13).
Nếu h c u thành t nhi ệ ấ ừ ều điện tích điểm, như ví dụ
hình 25.9, th a h có th tính b ng cách c ng hế năng củ ệ ể ằ ộ ợp
theo từng đôi một:
2 3 3 11 2
12 23 31
e
q q q qq q
U k
r r r
)
Câu h i 25.3:ỏ Trên hình 25.8b, cho điện tích điểm
2
q
mang
giá tr âm, ị còn điện tích điểm
1
q
có th i d u. Ban ể thay đổ ấ
đầu
1
q
mang điện tích dương, sau đó chuyển sang tích điện
âm v l n. n th n tích ới cùng độ ớ (i) Điệ ế do điệ
2
q
t o ra t i v ạ ạ ị
trí của
1
q
s m (c) gi nguyên? (ii) Thẽ: (a) tăng (b) giả ữ ế năng
của hệ n tích nói trên s m (c) gi nguyên? hai điệ ẽ: (a) tăng (b) giả ữ
Bài tập m n th t o b m ẫu 25.3: Điệ ế ạ ởi hai điện tích điể
Hai điện tích điểm
1
2,00q C
đặt t i g c toạ ố ạ độ
xOy
và
2
6,00q C
đặt t i v ạ ị
trí (0;3,00)m như hình 25.10a miêu tả.
(A) Tính tổng th o b n tích này t m P có to (4,00;0). ế năng tạ ởi hai điệ ạ ểi đi ạ độ
Hình 25.10: Tính điệ ởi hai điện tích điển thế tạo b m
Hình 25.9: Hệ c u thành t 3 ấ ừ
điện tích điểm
9
Gi i:ả
Cần hi u r n n th tể ằng, hai điệ tích điểm nói trên đã tạo ra điện trường cũng như điệ ế ại
mọi điểm trong không gian, trong đó có điểm P.
Dùng công thức (25.12) cho h ệ hai điện tích điểm:
1 2
1 2
6 6
9 2 2
3
2,00 10 6,00 10
(8,988 10 / )
4,00 5,00
6,29 10
P e
q q
V k
r r
C C
N m C
m m
V
(B) Tính s i th a h m, g n tích ự thay đổ ế năng củ ệ 3 điện tích điể ồm hai điệ
1
q
,
2
q
nói
trên và điện tích điểm
3
3,00q C
khi
3
q
di chuy n t xa vô cùng v ể ừ ề P.
Gi i:ả
Mức bi c (25.2):ến đổi thế năng có thể tính theo công thứ
3
6 3
2
(3,00 10 C)( 6,29 10 )
1,89 10
P
U q V
V
J
Giá tr ng, c n sinh m i ngo i l c thì m i có ị âm thu được có nghĩa rằ ầ ột công dương bở ạ ự ớ
thể n tích kéo điệ
3
q
ra xa vô cùng.
Mối liên h ệ giữa điện trường và điện thế 25.4
Công thức (25.3) vi t l ng vi phân ế ại dưới dạ
dV E ds
(25.15)
cho ta giá tr c a hi n th n u bi ng ị ủ ệu điệ ế ế ết trước điện trườ
E
t m trong không gian. ại các điể
Câu h t ra: n u bi n th ỏi đặ ế ết điệ ế
V
t m trong không gian, li u có th c ra ại các điể ệ ể suy ngượ
vector cường độ điện trườ ng
?E
Để ờ trả l i câu hỏi trên, ta viết lại tích ng vô hướ
E ds
giữa
x y z
E E i E j E k
và
ds dxi dy j dzk
dưới dạng:
x y z
E ds E dx E dy E dz
(25.15) viết l i thành ạ
x y z
dV E dx E dy E dz
Khi xem xét theo hướng củ ụa tr c
,x
nh ng bi n thiên ữ ế
dy
và
dz
b ng không, nên: ằ
10
x
V
E
x
Có nghĩa thành phần
x
E
c ng b o hàm c n th ủa vector cường độ điện trườ ằng đạ riêng ủa điệ ế
theo bi n ế
x
đảo dấu. Ta cũng thu đượ ận tương tực kết lu đối với thành phần theo
y
và
,z
viết thành bộ đầy đủ:
, ,
x y z
V V V
E E E
x y z
(25.16)
Hình chi u c a vector ế ủ
E
theo hướng của vector
l
b c tính theo cách ất kì cũng đượ
tương tự như thế:
l
dV
E
dl
Xét hai điể ặt đẳ ệu điệ ữa hai điểm lân cận nằm trên cùng một m ng thế, hi n thế gi m này:
0.dV
Do v y, hình chi u c a vector ậ ế ủ
E
theo phương tiế ặt đẳp tuyến với m ng thế cũng
bằng không. Nói cách khác, vector cường độ điện trườ ng
E
luôn hướng vuông góc với mặt
đẳng thế.
Hình 25.11 miêu t h các m ng th ng h ng ả ọ ặt đẳ ế trong các trườ ợp khác nhau: điện trườ
đều, điện trườ ởi điện tích điểm và điện trườ ởi lưỡ ực điệng sinh ra b ng tạo b ng c n. Trong tất
cả các trườ ặt đẳ ững đườ ức điện trường hợp, các m ng thế luôn vuông góc với nh ng s ng tại
giao điểm:
Trên m c r ng, h các m ng th u ục 25.2 ta đã phân tích đượ ằ ọ ặt đẳ ế trong điện trường đề
là những m t ph ng song song, c nhiên vuông góc v ng s ng. ặ ẳ ố ới đườ ức điện trườ
Ở m r n thục 25.3 ta cũng làm sáng tỏ ằng, điệ ế ạ t o b m ch ph thuởi điện tích điể ỉ ụ ộc
vào kho m, nên h các m ng th là nh ng m t c u, giao ảng cách đến điện tích điể ọ ặt đẳ ế ữ ặ ầ
nhau vuông góc v ng s ng xuyên tâm. ớ ời đư ức đối xứ
Hãy th suy vector ử
E
c ng t o b m t bi u th c c n th ủa điện trườ ạ ởi điện tích điể ừ ể ứ ủa điệ ế
(25.11):
e
q
V k
r
Các m ng th có d ng c u nên vector ặt đẳ ế ạ ầ
E
ph ng xuyên tâm. ải hướng vuông góc theo hướ
Nói cách khác
E
chỉ có thành ph n: ầ
r
V
E
r
(25.17)
Thế bi u th n th ể ức của điệ ế
V
vào (25.17) suy ra:
2
r e e
q q
E E k k
r r r
Kết quả c hoàn toàn quen thuthu đượ ộc!
Điệ ến th sinh ra b i s phân b n tích liên t c 25.5 ở ự ố điệ ụ
Ở ở m n thục 25.3, chúng ta tính được điệ ế sinh ra b i tập
hợp các điện tích điểm rời rạc. Mục này trình bày phương pháp
tính điện thế sinh ra bởi sự phân bố điện tích liên tục, tức vật
tích điện có kích thước đáng kể. Có hai phương pháp tiến hành:
phương pháp chia nhỏ và phương pháp dùng đị nh lý Gauss.
Phương pháp chia nhỏ
Ta chia v c l n nói trên thành ật tích điện có kích thướ ớ
những ph n r t nh , nhầ ấ ỏ ỏ đến m c có th xem m i ph ứ ể ỗ ần như thế
là m i v i m m v a c t ra ột điện tích điểm. Đố ớ ỗi điện tích điể ừ ắ
Hình 25.11: Họ các m ng th ng h n ặt đẳ ế trong các trườ ợp: (a) điện trường đều (b) điệ
trường c ng t o bủa điện tích điểm (c) điện trườ ạ ởi lưỡng cực điện
Hình 25.12: Tính điện thế
sinh ra bởi sự phân b ố
điện tích liên tục
12
ấy, ta đã có thể ức (25.11) để tính điệ áp dụng công th n thế
dV
do nó t o ra t m P cạ ại điể ần
khảo sát:
e
dq
dV k
r
(25.18)
trong đó
r
là kho ng cách t ph n nh m P. n th do v t sinh ra tả ừ ầ ỏ đang xét đến điể Điệ ế ậ ại
điểm P là sự tổng hợp của tất cả các phần nhỏ trên toàn bộ v n: ật tích điệ
e
dq
V dV dV k
r
(25.19)
Cần lưu ý ở phương pháp này rằ ấy điệ ng: gốc l n thế
( 0)V
n xa vô cùng ằm ở
( ).
Phương pháp dùng định lý Gauss
Đố ới v i những hệ tích điện mang tính đố dùng định lý Gauss đểi xứng, ta có thể tính
điện trường
E
n th : trước. Sau đó dùng công thức () để tính điệ ế
(O)
(P)
V E ds
trong đó gốc lấy điện thế
( 0)V
i m có thể quy ước tạ ột điểm O nào đó.
Bài t p m n th t o b i vành tròn ậ ẫu 25.4: Điệ ế ạ ở
tích điện đều
(A) Tìm bi u th c c n th t m P nể ứ ủa điệ ế ại điể ằm
trên tr i x ng c a m t vành tròn bán kính ục đố ứ ủ ộ
a
với điện tích
Q
phân b u, cách tâm vành tròn ố đề
một đoạn
.x
Gi i:ả
Chia vành tròn ra r t nhi u ph n nh , m i phấ ề ầ ỏ ỗ ần
có điện tích
dq
nh n m c có thỏ đế ứ ể xem như
điện tích điểm. Áp dụng công thức ), ta có (20.20
thể n th t m P: tính điệ ế ại điể
e
dq
V k
r
Để ý r m P n u tằng điể ằm cách đề ất cả các phần của vành tròn, do vậy tích phân trên
dễ dàng chuy n thành: ể
e
k
V dq
r
Tích phân trên th hi ng toàn b n tích ch a trên vành. Còn kho ng cách ể ện tổ ộ điệ ứ ả
r
có
thể bi u di n thành ể ễ
2 2
r a x
Hình 25.13: Tính điệ ến th tại
điể ụm nằm trên tr c của vành
tròn tích điện đều
13
2 2
e
k Q
V
a x
(B) Tìm bi u th ng t ể ức của cường độ điện trườ ại P.
Gi i:ả
Do tính ch i x ng, có th k t lu n r ng ất đố ứ ể ế ậ ằng vector cường độ điện trườ
E
tại điểm
P ph ng d c theo tr c x. Nói cách khác ải hướ ọ ụ
E
chỉ có thành phần theo
.x
T mừ ối
liên hệ (25.16) gi ng và th ữa cường độ điện trườ ế năng:
3/2
2 2
2 2
1
e
x e
k xdV d
E k Q Q
dx dx
a x
a x
Bài tập m n th t o b u ẫu 25.5: Điệ ế ạ ởi thanh tích điện đề
Một thanh có chi u dài ề
l
đặt d c theo trọ ục
x
như hình vẽ.
Thanh có điện tích
Q
phân b u v i m dài ố đề ớ ật độ
.
Tính
điện thế t m P nại điể ằm trên trục
y
cách đầu thanh một
đoạn bằng
.a
Gi i:ả
Điệ ến th t c tại P đượ ạo b i các ph n tích phân bở ần điệ ố
khắp chi u dài thanh. Xét m n ề ột đoạ
dx
r t nh trên thanh, ấ ỏ
mang điện tích
dq dx
đủ nh có th n ỏ để ể xem như điệ
tích điểm.
Điện thế do điện tích điểm
dq
nói trên t o ra t i P: ạ ạ
2 2
e e
dq dx
dV k k
r
a x
Điệ ấn thế do r t nhi trên toàn bều điện tích điểm như thế ộ thanh tạ ạo ra t i P là tích
phân:
2 2
0
l
e
dx
V k
a x
Theo đó cận tích phân lấy từ
0x
n cho đế
.x l
Để ý rằng
e
k
và
/Q l
là những số không đổi, có thể cho ra ngoài dấu tích phân:
Hình 25.14: Tính điện
thế t o b i thanh tícạ ở h
điện đều
2 2
2 2
0
0
2 2
ln(x )
ln
l
l
e e
e
dx Q
V k k a x
l
a x
Q l a l
k
l a
Điệ ến th tạo bởi v t d n 25.6 ậ ẫn tích điệ
Từ chương 24, ta biế ằng đốt r i với vật d n ng thái cân b n tích ch ẫn điệ ở trạ ằng, điệ ỉ
phân b trên b m t v t d ng ch t n t i bên ngoài ố ề ặ ậ ẫn. Ngoài ra ta cũng biết rằng, điện trườ ỉ ồ ạ
vật d n và vuông góc v i bẫ ớ ề m t v t d Bên trong v t d ng hoàn toàn b triặ ậ ẫn. ậ ẫn điện trườ ị ệt
tiêu.
Chương này ta tiế ục bàn đế ẫn điệ phương diện điệp t n vật d n về n thế. Áp dụng công
thức (25.3) cho hai điểm A và B bất kì n t v t dằm trong ho c trên b mặ ề ặ ậ ẫn, ta có:
( )
( )
0
B
B A
A
V V E ds
Như vậy mọi điể ẫn đều có điệm thuộc vật d n thế bằng nhau.
Hình 25.15 miêu t n th t m bên trong và bên ả điệ ế ại các điể
ngoài qu c u làm b ng v t li u d n. Theo trình bày ả ầ ằ ậ ệ ẫn điệ ở
chương 24, việ ụng đị ằng: điệc áp d nh lý Gauss cho ra kết quả r n
trường bên ngoài quả c n có dầu tích điệ ạng y h ng ệt như điện trườ
tạo bởi điện tích điểm:
2
e
q
E k
r
Do đó điệ ột điể ầu cũng sẽn thế tại m m bất kì nằm ngoài quả c có
dạng như điệ ện tích điển thế sinh ra bởi đi m đặt tại tâm quả cầu:
e
q
V k
r
Từ đó suy ra điện thế ngay trên bề mặt quả c n: ầu tích điệ
e
q
V k
R
(25.20)
với
R
là bán kính qu c ng h p qu c u làm b ng ả ầu. Trong trườ ợ ả ầ ằ
vật li u d n, bi u th n th t i mệ ẫn điệ ể ức (25.20) cũng chính là điệ ế ạ ọi
điểm thuộc quả cầu. Hình 25.15b diễn tả điều đó bằng đoạn nằm
ngang tương ứ ới các điểng v m bên trong quả cầu.
Bài tập m u 25.6: Hai qu c i nhau ẫ ả ầu tích điện nố
Hình 25.15: (a) vật d n ẫ
hình c n th (c) ầu (b) điệ ế
điện trường
Hai v t d n hình c u có bán kính l t b ng ậ ẫ ầ ần lượ ằ
1
r
và
2
r
ban đầu đặt cách xa nhau.
Sau đó chúng đượ ẫn điện như hình 25.16c nối với nhau nhờ sợi dây d . Khi hệ cân
bằng, điệ ần lượn tích trên mỗi quả cầu l t bằng
1
q
và
2
q
, phân b u trên m i b ố đề ỗ ề
mặt. Tìm t s c ng trên b m a hai qu c u này. ỉ ố ủa cường độ điện trườ ề ặt củ ả ầ
Gi i:ả
Do hai qu c xa, s ng l n nhau v ng là không ả ầu đặt cách nhau đủ ự ảnh hưở ẫ ề điện trườ
đáng kể ẫn đến điệ ặt và điện trườ, d n tích mỗi bên vẫn phân bố đều trên mỗi bề m ng
trên m c u v n gi i x ng. ỗi quả ầ ẫ ữ được nguyên tính đố ứ
Việc n i hai qu c u b ng dây d n th c hai b ng ố ả ầ ằ ẫn làm cho điệ ế ả ằ
nhau:
1 2
1 2
e e
q q
V k k
r r
hay:
1 1
2 2
(1)
q r
q r
Cường độ điện trườ ầu có độ ng trên bề mặt mỗi quả c lớn:
1 2
1 2
2 2
1 2
,
e e
q q
E k E k
r r
Lấy t s c ng: ỉ ố ủa cường độ điện trườ
2
1 1 2
2
2 2 1
E q r
E q r
Thế (1) vào thu được:
2
1 1 2 2
2
2 2 1 1
E r r r
E r r r
Từ k c có thết quả thu đượ ể thấy r ng, khi hai qu c u n i nhau b ng dây d n, ằ ả ầ ố ằ ẫn điệ
điện trườ ớn hơn điện trường trên bề mặt của quả cầu nhỏ thì l ng trên bề mặt quả cầu
lớn.
Vật dẫn rỗng ru t ộ
Vật d n r ng ru t có th miêu t . Vẫ ỗ ộ ể ả như hình 25.17 ới
loại v t d n h t s c bi t này, ta s ng minh rậ ẫ ế ức đặ ệ ẽ chứ ằng
điện trường bên trong phần rỗng của vật dẫn phải luôn
luôn b ng khôngằ , dù điện trường bên ngoài có thay đổi
Hình 25.16: Hai
quả ầ c u d n ẫn điệ
nối v i nhauớ
16
thế nào đi nữa! Th c v m A và B b t kì thuự ậy, xét hai điể ấ ộc thành bên trong sát phần r ng, ỗ
theo (25.3) ta có:
( )
( )
B
B A
A
V V E ds
Nhưng đố ất kì ta cũng đã chứi với vật dẫn b ng minh r n th t i m m trong nó ằng điệ ế ạ ọi điể
đều bằng nhau:
.
A B
V V
Nên vector cường độ điện trường
E
bu ng không. ộc phải bằ
Vật d n rẫ ỗng ru t ộ dưới d ng nh ng h p có v b ng kim lo i có nhi u ng d ng trong ạ ữ ộ ỏ ằ ạ ề ứ ụ
việc cách ly các v t bên trong kh ng cậ ỏi ảnh hưở ủa điện
trường ngoài.
Tia lửa điện
Tia l ng quan sát th g n v t d n cao th ng g n vửa điện thườ ấy ở ầ ậ ẫn điệ ế. Khi điện trườ ầ ật
dẫn đủ lớn, các electron tự do, vốn phát sinh do sự ion hoá ngẫu nhiên của phân tử khí, sẽ
đượ ị đẩ ớc gia tốc và b y xa khỏi phân tử mẹ. Chúng chuy ng nhanh và va chển độ ạm v i nhiều
phân t khí xung quanh, làm phát sinh thêm r t nhi u s ion hoá th c p, kéo theo s xuử ấ ề ự ứ ấ ự ất
hiện càng lúc càng nhi u electron t do khác. Các electron này tái k t hề ự sau đó ế ợp với nh ng ữ
ion phân t , di chuy n t ng thái t do sang tr ng thái liên k m ng th p ử ể ừ trạ ự ạ ết ở ức năng lượ ấ
hơn làm phát ra năng lượng dướ ạng ánh sáng. Đó chính là tia lửi d a điện.
Ở những phần nhọn của vật d n tích tẫn, điệ ập trung nhi ng ều hơn và sinh ra điện trườ
lớn hơn so vớ ần khác. Do đó tia lửa điện thườ ững điểi những ph ng hay xuất hiện ở nh m
nhọn này.
Tia lửa điện có th máy quay t ngo i ể được quan sát rõ hơn nhờ ử ạ
Hình 25.17: Vật dẫn r ng ru t ỗ ộ
Thí nghi m gi t dệ ọ ầu Millikan 25.7
Trong giai đoạ 1913, Robert Millikan đã tiến hành phép đo điện 1909- n tích của
electron, xác đ a điị ịnh giá tr củ ện tích nguyên tố
.e
Thiết bị thí nghi c mô t ệm đượ ả như hình
25.18. B ph n chính c a thi t b g i u vào hai c c cộ ậ ủ ế ị ồm hai đĩa kim loạ đặt song song, đấ ự ủa
ắc quy để ạo ra điện trườ ữa chúng. Millikan dùng bình phun sương phun nhữ t ng gi ng giọt
dầu li ti vào kho ng trả ống gi ng th i rữa hai đĩa, đồ ờ ọi x-quang làm ion hoá không khí, khi n ế
cho các electron đượ ầu được giải phóng và dính vào những giọt dầu. Những giọt d c chiếu
sáng, hi n gi a ng kính quan sát ng ngôi sao hi n gi ệ ữ ố như nhữ ệ ữa trời đêm.
Khi ng t ngu n ra kh i, gi t dắ ồn điệ ỏi đĩa kim loạ ọ ầu
rơi dưới tác dụng của trọng lực
mg
, nhưng nhanh chóng
đạt đế ốc độn t tới hạn do tác dụng của ma sát nhớt
1
6
D
F r v

t l thu n v i t , vỉ ệ ậ ớ ốc độ ới
r
là bán kính
giọt d u, ầ
là độ nhớt của không khí (hình 25.19 . a) Do
giọt dầu rơi đều nên hai lực này cân bằng nhau:
1
6mg rv

Khi ngu n b t, gi i xu t hi n mồ ậ ữa hai đĩa kim loạ ấ ệ ột
hiệu điệ ạo ra điện trường hướn thế và t ng từ trên xuống
dưới (hình 25.19b). Giọt dầu bị nhiễm các electron nên
tích điệ ực điện trườn âm, cho nên chịu tác dụng bởi l ng
qE
hướng lên trên. L c này l n m c gi t d u b ự ớn đế ứ ọ ầ ị
kéo đi lên, tă ốc và đạng t t tốc độ tới hạn
2
v
. Khi ấy:
2
6qE mg rv

Hình 25.19: Giọt d u khi không ầ
có điện trường (a) và khi có điện
trường (b)
Hình 25.18: Thí nghi m giệ ọt dầu Millikan
Ở đây cường độ điện trường đượ ệu điệ c tính qua hi n thế giữa hai bản kim loại và khoảng
cách giữa chúng:
V
E
d
Từ nh n tích c u: ững phương trình trên có thể suy ra điệ ủa giọt dầ
2
1
1
mg v
q
E v
Khối lượng
m
c t d u ch bi c bán kính ủa giọ ầ ỉ có thể ết được sau khi tính đượ
r
theo (25.21):
3
1
4
6
3
g r rv

Kết quả cu c:ối cùng thu đượ
2 3
1 2
1
1
9 2 1
v v
q
g E v
Như vậy để xác định được điệ h độ n tích của giọt dầu, bên cạn nhớt của không khí và
khối lượng riêng
c a d u, c ủ ầ ần đo các tốc độ
1
v
khi rơi không có điện trường,
2
v
hướng
lên khi có điện trường.
Kết qu thí nghi m c a Millikan cho th y, ả ệ ủ ấ điện tích
q
t o ra trên nh ng gi t d u khác ạ ữ ọ ầ
nhau luôn có giá tr là b i nguyên c a con s ị ộ ủ ố
19
1,6 10
C.
Millikan kh nh r ng, hi ng này x y ra do gi t d u b ẳng đị ằ ện tượ ả ọ ầ ị
bám b i m t s nguyên electron cùng lúc. Nói cách khác, ở ộ ố
19
1,6 10
C là điện tích của một electron riêng rẽ. Nhờ phát
hiện này, Robert Millika c trao gi i Nobel v t lý vào n đã đượ ả ậ năm
1923.
Một s ố ứng dụng các hiện tượng tĩnh điện 25.8
Các hi n có nhi u ng d ng dân d ng trong ện tượng tĩnh điệ ề ứ ụ ụ
việc thu lôi, kh b i, in m t. Trong khoa h c, có ử ụ ấn, sơn bề ặ ọ
những thi t bế ị ho ng dạt độ ựa trên nguyên lý tĩnh điện như máy
phát tĩnh điệ ển vi trườ ion, động cơ tên lửa ion… n, kính hi ng-
Dưới đây ta sẽ bàn đế n hai trong số đó.
Máy phát tĩnh điện Van de Graaff
Thực nghi ra r ng, ệm đã chỉ ằ khi m t v t d n tiộ ậ ẫn tích điệ ếp
xúc v t r ng bên trong c a m t v t d n r ng, toàn bới mặ ỗ ủ ộ ậ ẫ ỗ ộ điện
tích s y sang v t d n r ng và ch y h t ra phía b m t ngoàiẽ chạ ậ ẫ ỗ ạ ế ề ặ .
19
Lợi d ng hi o ra nh ng thi t b cho phép tích lu n tích và ụ ện tượng này, người ta đã tạ ữ ế ị ỹ điệ
điệ ớn áp g không giần như i hạn.
Máy phát tĩnh điện do Van de Graaff phát minh năm 1929 có sơ đồ nguyên lý thể hiện
hình 25.20. Bên trong máy phát có m n tu n hoàn trên hai trột dây đai có thể cuộ ầ ục. Dây đai
luôn được tích điệ ần điể V. Điện tích theo “băng
n tại vị trí g m A ở điện thế khoảng 10
4
chuyền” di chuyển đế ần điển g m B, lúc này hoàn toàn nằm bên trong quả cầu kim loại rỗng,
sẽ đi theo những đầu kim tiếp xúc rồi ra ngoài bề mặt của quả cầu kim loại. Quá trình có thể
lặp đi lặ o đế ầu tích điện đủ tích điện đếp lại ch n khi quả c nhiều. Trên thực tế, nó có thể n
hàng tri u volt, v m gia t c cho các proton trong các ph ng hệ ới điện trường đủ ạnh để ố ản ứ ạt
nhân.
Bộ l c b n ọ ụi tĩnh điệ
Hiện tượng phóng điệ ụi nơi n trong không khí có vai trò quan trọng trong việc khử b
công xưở phóng điệ ẩm cháy như ng. Thiết bị dựa trên sự n này có thể giúp khử các sản ph
khói t o ra t t than và nhi u ho ng công nghi p khác. ạ ừ việc đố ề ạt độ ệ
Sơ đồ ụi đượ . Theo đó, mộ nguyên lý của thiết bị lọc b c miêu tả trên hình 25.21 t hiệu
điệ ỏ ị ọn thế rất lớn, tầm 40- c t100 kV, đượ ạo ra giữa v thiết b và sợi dây treo giữa bình l c.
Sợi dây mang điệ ỏ. Điện thế âm so với v n thế âm cực lớn từ sợi
dây t o ra nh ng tia l n, làm ion hoá không khí xung quanh, ạ ữ ửa điệ
tạo ra các electron t bự do, ion dương và ion âm. Các ion âm sẽ ị
đẩ ớy về phía những vỏ bình lọc, va chạm v i những hạt bụi li ti.
Phần đa nhữ tích điện âm và cũng bịng hạt bụi này bị đẩy về phía những vỏ bình lọc, làm
không khí s ạch bớt.
Hình 25.20: Máy phát
tĩnh điện
20
Tóm t ắt chương 25
Định nghĩa
Hiệu điệ hai điểm A và B trong điện trườn thế giữa ng
E
được định nghĩa qua công thức:
( )
( )
B
A
U
V E ds
q
trong đó
U
- chênh l ch th n th độ ệ ế năng. Điệ ế
/V U q
là m ng, có ột đại lượng vô hướ
đơn vị Volt (V): 1V = 1J/C
Khái niệm và nguyên lý
Hình 25.21: Bộ l c b n ọ ụi tĩnh điệ
| 1/25
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

Chương 25: Điện thế
iện trường đã được nghiên cứu về phương diện tác dụng lực trong các chương trước.
Trong chương này, điện trường sẽ được khảo sát ở khía cạnh năng lượng. Bằng cách
tiếp cận theo hướng năng lượng, các bài toán có thể được giải theo hướng không cần
Đđến việc sử dụng lực. Khái niệm về thế năng có giá trị lớn trong các nghiên cứu về
điện. Do lực tĩnh điện là lực bảo toàn, hiện tượng tĩnh điện có thể được mô tả một cách dễ dàng dưới ạ
d ng năng lượng điện thế.
25.1 Điện thế và hiệu điện thế
Khi một điện tích q đặt trong điện trường E, nó sẽ chịu tác dụng một lực bằng
F qE. Đây là lực bảo toàn bởi vì theo bản chất, các tương tác đều tuân theo định luật
Coulomb. Hãy xem xét dưới góc độ một hệ kín các điện tích, khi điện tích q chuyển động
chỉ dưới tác dụng của các điện tích còn lại. Với một chuyển dời vô cùng bé ds, trường lực
thế Coulomb sinh một công bằng F d .
s Trong cơ học ta biết rằng, công do trường lực thế
sinh ra bằng đúng độ suy giảm thế năng, cho nên:
dU F ds
Khi điện tích q di chuyển từ vị trí A đến vị trí B trong điện trường, độ biến thiên thế năng bằng: ( ) B U
   F ds  q E ds   (25.1) ( ) A ( A)
Ở đây tích phân đường tính dọc theo quỹ đạo di chuyển của điện tích q từ A đến B. Tuy
nhiên vì trường lực bảo toàn nên dù đi theo con đường nào, giá trị của tích phân này cũng không thay đổi.
Khi đã có biểu thức tính độ biến thiên thế năng, chỉ cần chọn một điểm O nào đó làm
gốc thế năng (U  0), ta đã có thể tính thế năng của điện tích đặt trong điện trường: (P) U  q
E ds q E ds   (O) (P)
Thế năng của điện tích q tại vị trí P bất kì trong điện trường có trị số bằng công của lực
điện trường làm di chuyển điện tích q đó từ P về gốc thế năng.
Thế năng tại vị trí P của một đơn vị điện tích trong điện trường E được gọi là điện thế tại điểm đó: 1 (P) U V
  E ds E ds   (25.2) q (O) (P)
Điện thế tại vị trí P bất kì trong điện trường có trị số bằng công của lực điện trường làm di
chuyển điện tích 1 Coulomb từ P về gốc điện thế (gốc thế năng).
Tương tự như độ biến thiên thế năng U
 ta cũng có khái niệm hiệu điện thế giữa hai điểm B và A: (B ) V
  V V   E ds  (25.3) B A (A )
Từ (25.1) và (25.3), ta có mối liên hệ giữa độ biến thiên thế năng và hiệu điện thế: U   q V  (25.4)
Theo định luật bảo toàn năng lượng: U   K
  0, suy ra động năng mà điện tích q thu
được khi di chuyển từ điểm A đến điểm B nói trên bằng độ suy giảm của thế năng: K    U   q V
  q(V V ) A B
Điện thế và hiệu điện thế có thứ nguyên của năng lượng trên một đơn vị điện tích, được
gán cho một đơn vị đặc biệt trong hệ SI – Vol : t 1V = 1J/C.
Mối liên hệ (25.2), (25.3) cũng cho ta một đơn vị khác của cường độ điện trường là V/m: 1N/C = 1V/m.
Khi một electron mang điện tích nguyên tố e  chuyển
động dưới tác dụng của điện trường, đi qua đoạn đường có
hiệu điện thế bằng 1V, ta nói rằng electron đã thu được thêm
động năng bằng 1 electron-volt: 1  9 1  9
1eV  1,610 C1V  1,610 J
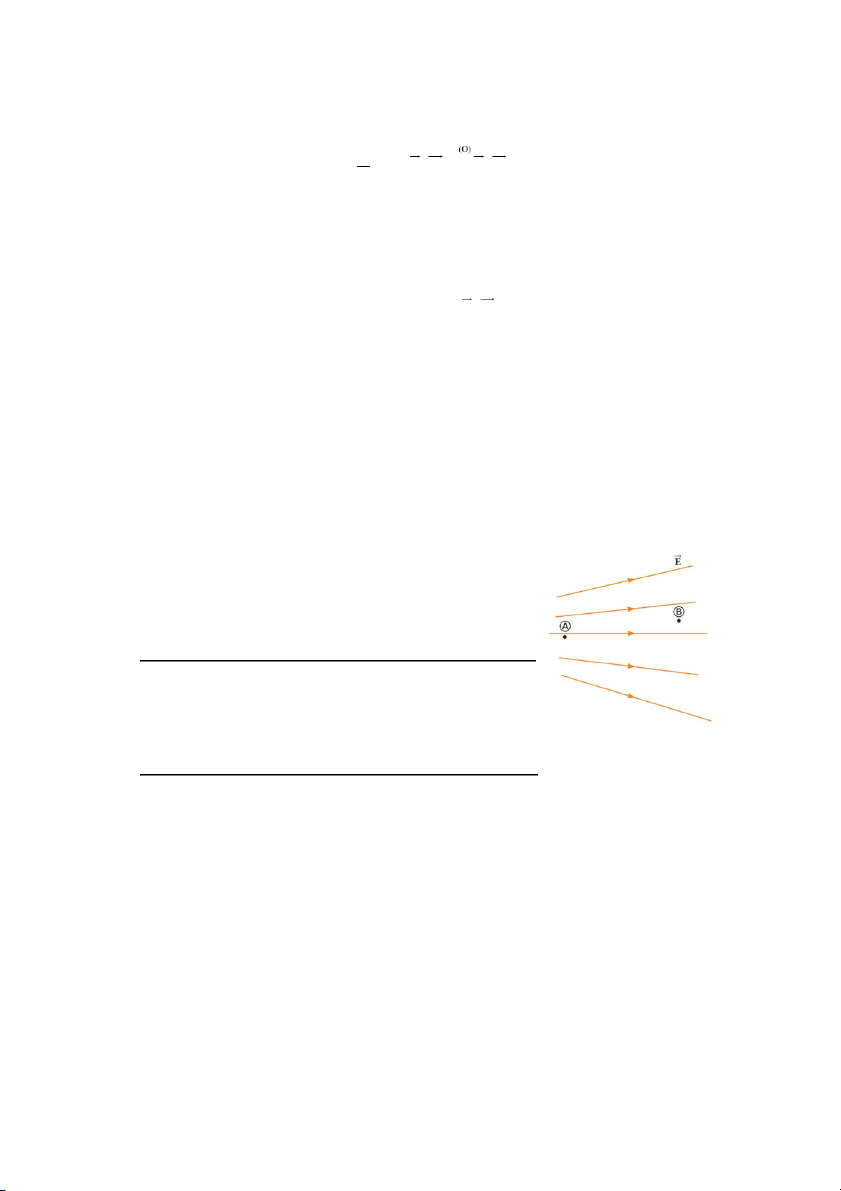
Câu hỏi 25.1: Hai điểm A và B nằm trong một điện trường
như hình 25.1. (i) Hiệu điện thế V V V có giá trị như B A
thế nào? (a) dương (b) âm (c) bằng không. (ii) Một điện tích
âm ban đầu nằm tại A, sau đó di chuyển đến vị trí B. Sự biến
thiên của thế năng U
 có giá trị như thế nào? Lựa chọn trong Hình 25.1: Hai điện tích
các khả năng như phần trước.
điểm trong điện trường 25.
2 Hiệu điện thế trong điện trường đều
Ta tiến hành khảo sát một điện trường đều, theo đó các đường sức điện trường hướng
song song và đều đặn như miêu tả trên hình 25.2a. Từ phương trình (25.3) suy ra được hiệu
điện thế giữa hai điểm A và B nằm trên cùng một đ ờ
ư ng sức điện trường: 2
Hình 25.2: (a) Hạt mang điện tích chuyển động dọc theo
đường sức điện trường đều (b) Hạt khối lượng rơi trong
trường trọng lực đều. (B ) ) (B ) 0 V
  V V   E ds   E ds  cos(0 )   E ds    B A (A ) (A ) (A )
Trong điện trường đều E có độ lớn không đổi nên có thể đưa ra ngoài dấu tích phân: (B ) V   E ds  (A ) V   Ed (25.6)
Dấu “–“ ở đây nói rằng, điện thế tại B thấp hơn điện thế tại A: V V . Như vậy, các B A
đường sức điện trường luôn hướng theo chiều suy giảm của điện thế.
Khi một điện tích q di chuyển từ A đến B, thế năng của hạt trong điện trường thay đổi một lượng bằng U   q V   qEd (25.7)
Có nghĩa nếu hạt mang điện tích dương: q  0, thế năng sẽ giảm: U   0. Nói cách khác,
khi một điện tích dương di chuyển xuôi theo chiều của đường sức điện trường, thế năng của
nó sẽ giảm. Như hình 25.2a miêu tả, nếu ban đầu hạt mang điện tích dương q thả tự do từ
trạng thái đứng yên, nó sẽ chịu tác dụng một lực F qE hướng xuống dưới, bắt đầu đi
xuống và tăng tốc. Hạt dần thu động năng từ chính sự suy giảm của thế năng. Đó là minh
chứng rõ ràng cho định luật ả b o toàn năng lượng.
Hình 25.2b miêu tả hình ảnh tương tự, khi một hạt khối lượng m rơi tự do trong trường
hấp dẫn gần mặt đất. Hạt cũng chịu tác dụng của trọng lực hướng xuống và tăng tốc. Động
năng tích luỹ tự sự suy giảm của thế năng trọng trường.
Phép so sánh nói trên giữa hạt mang điện tích dương trong điện trường với hạt chuyển
động dưới trường trọng lực rất hữu ích cho việc hình dung về các hiện tượng tĩnh điện. Chỉ 3
một điểm lưu ý rằng: khối lượng thì luôn dương, nhưng điện tích có thể dương, cũng có thể âm.
Với trường hợp điện tích âm, khi hạt di chuyển theo chiều của đường sức điện trường,
thế năng của hạt sẽ tăng, thay vì giảm. Nếu ban đầu hạt đứng yên, nó sẽ tăng tốc về phía
ngược chiều của đường sức.
Ta khảo sát trường hợp tổng quát hơn, khi hạt mang
điện tích di chuyển từ vị trí A đến vị trí B trong điện trường
đều, nhưng không nằm trên cùng một đường sức như hình
25.3. Lúc này hiệu điện thế giữa A và B bằng: (B ) V
  V V   E ds  E ds  E s   B A (A ) (A )
Ở đây vector E của điện trường đều có thể đưa ra ngoài dấu
tích phân. Độ biến thiên của thế năng: U   q V
  qE s
Tích vô hướng (25.8) có thể tính qua hình học: V
  V V  Ed B A
Mặt khác hiệu điện thế giữa hai điểm A và C nằm trên cùng Hình 25.3: Hạt mang điện một đường sức:
tích chuyển động không
song song với đường sức
V V  Ed C A
của điện trường đều
Từ đây suy ra rằng V V . Tổng quát lên có thể thấy rằng, B C
mọi điểm nằm trên cùng một mặt phẳng vuông góc với đường sức điện trường đều có cùng
một điện thế. Ta gọi mặt phẳng chứa tất cả các điểm có cùng điện thế như vậy là một mặt
đẳng thế. Đối với điện trường đều, họ các mặt đẳng thế cấu thành từ những mặt phẳng song
song với nhau và cùng vuông góc với các đường sức điện trường. 4
Hình 25.4: Các mặt đẳng thế
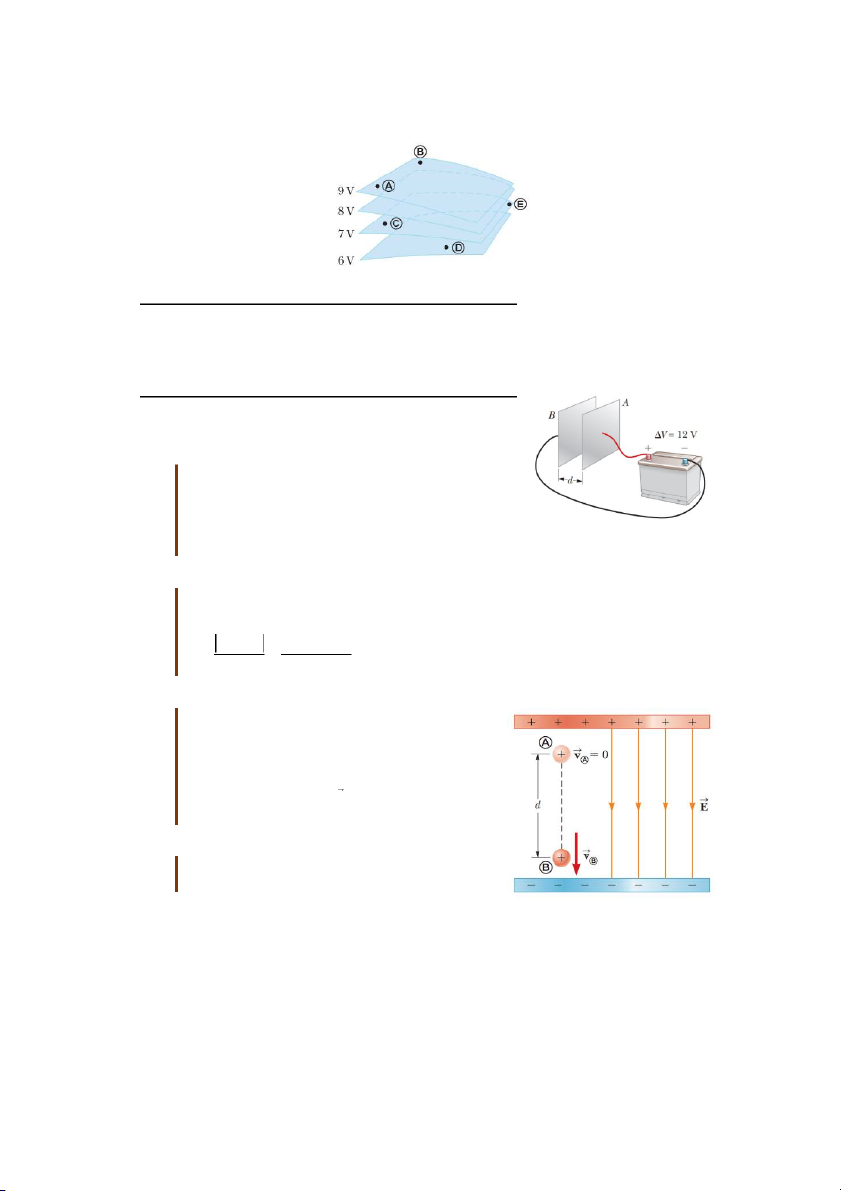
Câu hỏi 25.2: Các điểm được đánh dấu trên hình 25.4 nằm
trên các mặt đẳng thế. Hãy sắp xếp công thực hiện của điện
trường lên một điện tích dương theo thứ tự giảm dần, khi
điện tích này di chuyển từ A sang B, từ B sang C, từ C sang D và từ D sang E.
Bài tập mẫu 25.1: Điện trường giữa hai bản
phẳng song song tích điện trái dấu
Một ắc-quy hiệu điện thế 12V mắc vào hai bản
phẳng đặt song song như hình 25.5. Khoảng cách
giữa hai bản d  0,3cm, đủ nhỏ để xem rằng điện
trường giữa hai bản là đều. Tính cường độ điện
trường giữa hai bản phẳng. Giải:
Hình 25.5: Hai bản phẳng
Dùng công thức (25.6), có thể tính cường độ điện song song nối vào nguồn điện
trường giữa hai bản phẳng song song: V V B A 12 V 3 E  
 410 V / m 2 d 0,310 m
Bài tập mẫu 25.2: Chuyển động của hạt proton trong điện trường đều
Một proton được thả ra từ t ạ r ng thái đứng yên tại
vị trí A trong một điện trường đều có độ lớn 4
8,010 V/m (hình 25.6). Proton di chuyển đến
điểm B cách đó một đoạn d  0,50m dọc theo
hướng của điện trường E . Tìm tốc độ của proton sau đoạn đường đó. Giải:
Khái niệm. Hình dung rằng hạt proton rơi xuống
tựa như đang ở trong một trường trọng lực. Trong
Hình 25.6: Proton tăng tốc theo
hướng của điện trường
bài tập này, hạt cũng chịu tác dụng một gia tốc không đổi bởi lực điện trường.
Phân loại. Do hệ không tương tác với bên ngoài nên ta có thể quy vấn đề về chủ đề bảo toàn năng lượng.
Phân tích. Áp dụng định luật bảo toàn năng lượng cho điểm A và điểm B: K   U   0
Thế biểu thức của động năng và thế năng tại A và B tương ứng:  1  2
mv  0  eV  0  2   
Từ đó suy ra vận tốc v đồng thời tính V  theo công thức (25.6): 2  eV 2  ( e Ed ) 2eEd v    m m m 1  9 4 2(1,6 1  0 C)(8,0 1  0 V)(0,50 ) m  27 1,67 10 kg 6
 2,810 m / s
Nhận định. Điện thế giảm theo chiều chuyển động của proton, V   0, kéo theo sự
suy giảm của thế năng: U
  0. Để cân bằng sự suy giảm này, proton lại tích luỹ
động năng trong chuyển động có gia tốc, tuân theo định luật ả b o toàn năng lượng.
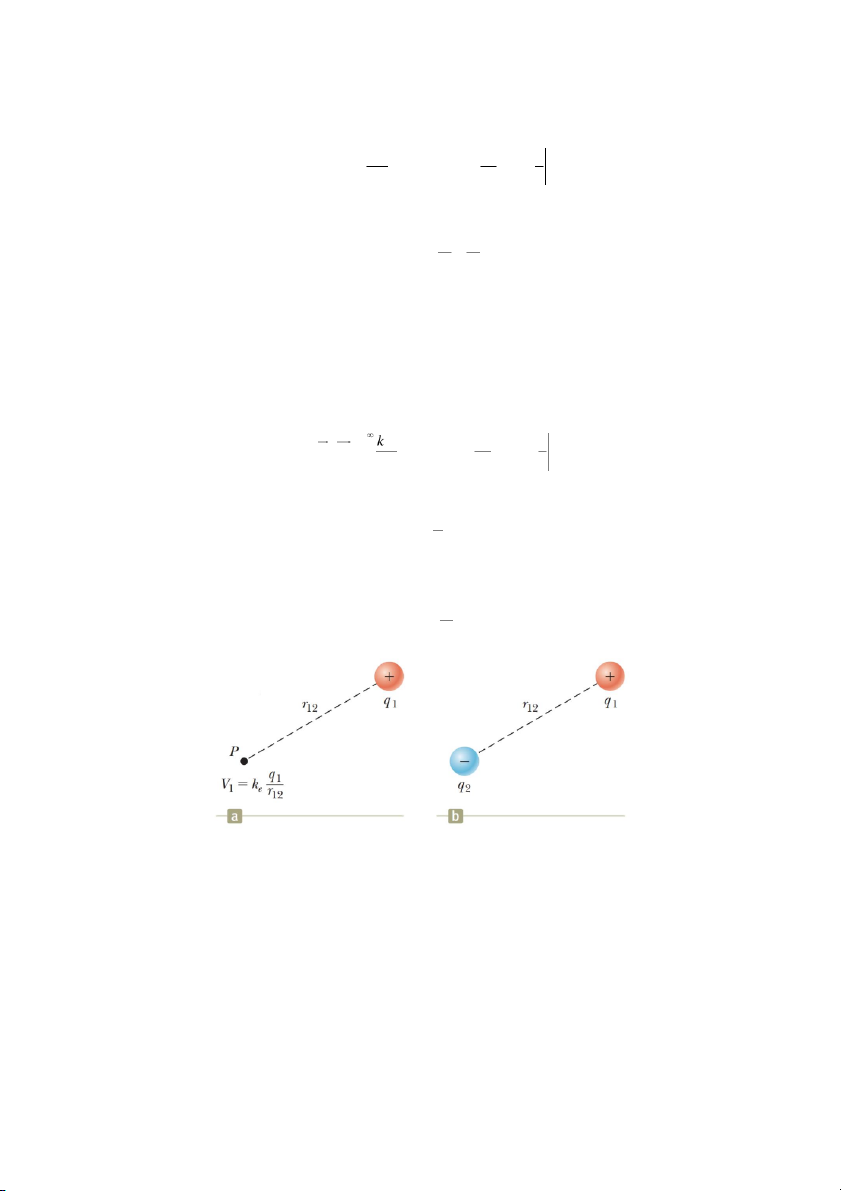
25.3 Điện thế và thế năng tạo bởi điện tích điểm
Từ trình bày ở chương 23, ta đã biết rằng một điện
tích điểm q  0 tạo ra trong không gian xung quanh một
điện trường đối xứng xuyên tâm với những đường sức
hướng ra ngoài. Hiệu điện thế giữa hai điểm A và B bất
kì (hình 25.7) có thể tính theo công thức (25.3): ( B) V V   E dsB A ( A)
Vector cường độ điện trường E đối với điện trường của
điện tích điểm có dạng E r 3 r Thế vào thu được
Hình 25.7: Tính hiệu điện ( )
thế giữa hai điểm bất kì B k q e V V   r ds
trong điện trường đối xứng B A 3 r ( ) A xuyên tâm
Từ hình 25.7 có thể thấy tích vô hướng r ds r dr, nên: 6 (B ) (B ) k q dr 1 rB e V V  
r dr  k qk q   B A 3 e 2 e ( r r r A ) (A ) rA
r và r lần lượt là khoảng cách từ A và từ B đến điện tích điểm, thế vào thu được: A B  1 1 
V V k q  (25.10) B A e   r rB A
Phương trình (25.10) cho thấy, hiệu điện thế giữa hai điểm bất kì của điện trường đối
xứng xuyên tâm chỉ phụ thuộc vào vị trí đầu và vị trí cuối, không phụ thuộc vào đường lấy
tích phân. Khẳng định này lại càng củng cố rằng, trường lực tĩnh điện luôn là một trường
bảo toàn, bởi trường lực tĩnh điện về bản chất là sự chồng chập điện trường của rất nhiều điện tích điểm.
Nếu chọn gốc điện thế V  0 tại r  ,
 điện thế tại một điểm P bất kì nằm cách điện
tích q một khoảng r được tính bằng công thức (25.2):    q dr 1 e V E ds
r dr k q  k q   3  e 2 e (P) r r r r r r Hay: q V k (25.11) e r
Khi cần tính điện thế tại một điểm bất kì trong điện trường do nhiều điện tích điểm tạo
ra, ta sử dụng phép chồng chập: q i V k  (25.12) e ri
Hình 25.8: Hệ hai điện tích điểm
Hình 25.8a miêu tả điện tích điểm ạ
ột điện trường cũng như điệ ế ạ ọi 1 q t o ra m n th t i m
điểm xung quanh nó. Điện thế tại vị trí P bằng: 7 q 1 V k 1 e 1 r 2
Bây giờ nếu đặt tại vị trí P một điện tích điểm
ệ hai điện tích điểm sẽ 2
q khác (hình 25.8b), h có thế năng bằng: q q 1 2 U   (25.13) 2 q 1 V ke 1 r 2
Lưu ý rằng gốc thế năng lấy ở t ạ
r ng thái hai điện tích cách xa nhau vô cùng. Nếu q , q 1 2
cùng dấu, chúng có sức mạnh đẩy nhau ra xa nhất có thể, chứng tỏ hệ có mang năng lượng
U  0. Ngược lại nếu q , ấ ầ ả ổ ột năng lượ ờ ộ ự 1 2
q trái d u, c n ph i b sung m ng nh m t l c bên
ngoài mới tách chúng ra xa được, chứng tỏ hệ mang năng lượng âm. Nếu biện luận theo
hướng cho rằng điện tích ằm trong điện trườ ạo ra, ta cũng đi đế ế ả như 1 q n ng do 2 q t n k t qu (25.13).
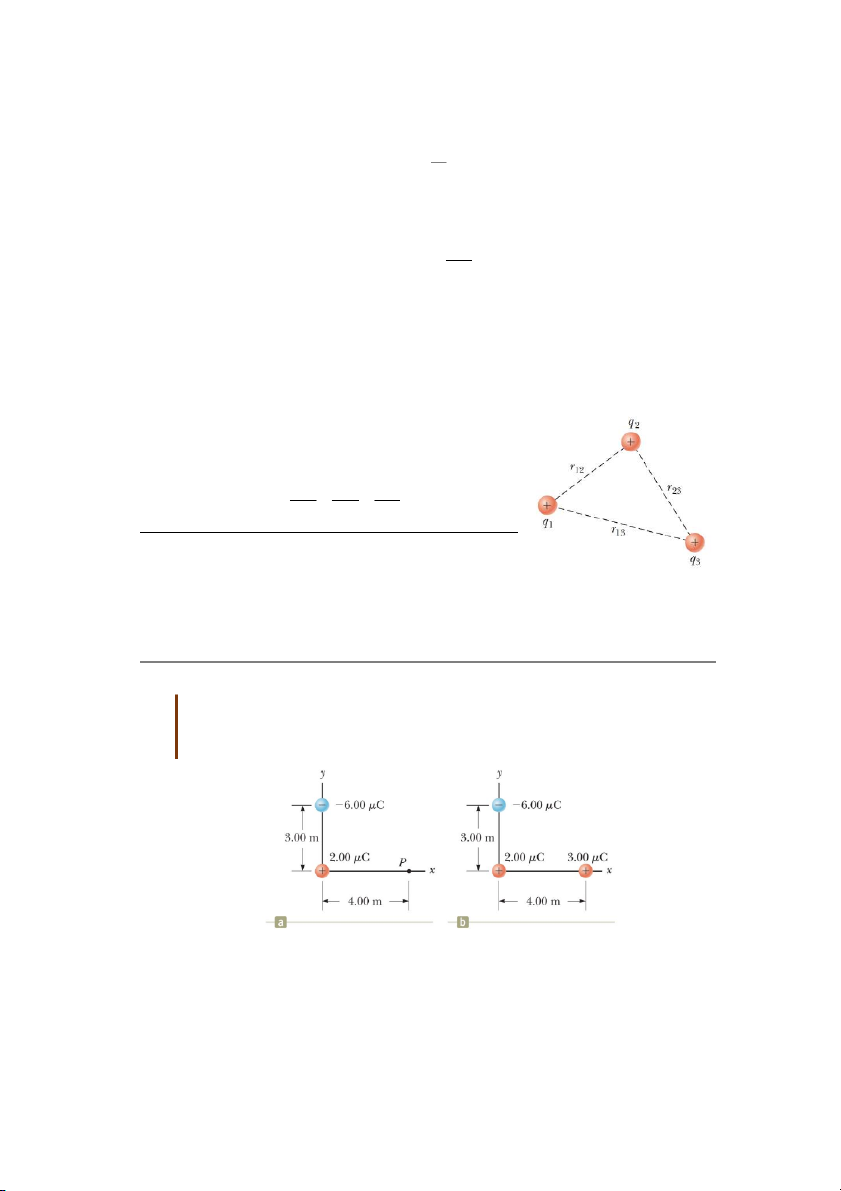
Nếu hệ cấu thành từ nhiều điện tích điểm, như ví dụ
hình 25.9, thế năng của hệ có thể tính bằng cách cộng hợp theo từng đôi một:  q q q q q q  1 2 2 3 3 1 U k   ) e   r r r  12 23 31 
Câu hỏi 25.3: Trên hình 25.8b, cho điện tích điểm 2 q mang
giá trị âm, còn điện tích điểm ể thay đổ ấ 1 q có th i d u. Ban đầu
Hình 25.9: Hệ cấu thành từ 3 1
q mang điện tích dương, sau đó chuyển sang tích điện
âm với cùng độ lớn. (i) Điện thế do điện tích ạ ạ ị điện tích điểm 2 q t o ra t i v trí của ẽ: (a) tăng (b) giả ữ ế năng 1 q s m (c) gi nguyên? (ii) Th
của hệ hai điện tích nói trên sẽ: (a) tăng (b) giảm (c) giữ nguyên?
Bài tập mẫu 25.3: Điện thế tạo bởi hai điện tích điểm
Hai điện tích điểm q  2,00 đặt tại gốc toạ độ q  6  ,00 đặt tại vị 1 C xOy và 2 C
trí (0;3,00)m như hình 25.10a miêu tả.
(A) Tính tổng thế năng tạo bởi hai điện tích này tại đ ể
i m P có toạ độ (4,00;0). 8
Hình 25.10: Tính điện thế tạo bởi hai điện tích điểm Giải:
Cần hiểu rằng, hai điện tích điểm nói trên đã tạo ra điện trường cũng như điện thế tại
mọi điểm trong không gian, trong đó có điểm P.
Dùng công thức (25.12) cho hệ hai điện tích điểm:   1 q 2 q V kP e   r r  1 2   6  6  2,0010 C 6  ,0010 C  9 2 2
 (8,98810 N m / C )     4,00 m 5,00 m  3  6,2910 V
(B) Tính sự thay đổi thế năng của hệ 3 điện tích điểm, gồm hai điện tích 1 q , 2 q nói
trên và điện tích điểm q 3,00 khi ể ừ ề P. 3 C 3
q di chuy n t xa vô cùng v Giải:
Mức biến đổi thế năng có thể tính theo công thức (25.2): U  3 q VP 6  3
 (3,00 10 C)(6,2910 V ) 2  1,8910 J
Giá trị âm thu được có nghĩa rằng, cần sinh một công dương bởi ngoại lực thì mới có thể kéo điện tích 3 q ra xa vô cùng. 25.
4 Mối liên hệ giữa điện trường và điện thế
Công thức (25.3) viết lại dưới dạng vi phân
dV  E ds (25.15)
cho ta giá trị của hiệu điện thế nếu biết trước điện trường E tại các điểm trong không gian.
Câu hỏi đặt ra: nếu biết điện thế V tại các điểm trong không gian, liệu có thể suy ngược ra
vector cường độ điện trường E ?
Để trả lời câu hỏi trên, ta viết lại tích vô hướng E ds giữa E E i E j E k và x y z
ds dxi dy j dzk dưới dạng:
E ds E dx E dy E dz x y z (25.15) viết lại thành
dV E dx E dy E dz x y z
Khi xem xét theo hướng của trục x, những biến thiên dy và dz bằng không, nên: 9 V E   x x
Có nghĩa thành phần E của vector cường độ điện trường bằng đạo hàm riên
g của điện thế x
theo biến x đảo dấu. Ta cũng thu được kết luận tương tự đối với thành phần theo y và z,
viết thành bộ đầy đủ: VVV E   , E   , E   (25.16) x y zxyz
Hình chiếu của vector E theo hướng của vector l bất kì cũng được tính theo cách tương tự như thế: dV E   l dl
Xét hai điểm lân cận nằm trên cùng một mặt đẳng thế, hiệu điện thế giữa hai điểm này:
dV  0. Do vậy, hình chiếu của vector E theo phương tiếp tuyến với mặt đẳng thế cũng
bằng không. Nói cách khác, vector cường độ điện trường E luôn hướng vuông góc với mặt đẳng thế.
Hình 25.11 miêu tả họ các mặt đẳng thế trong các trường hợp khác nhau: điện trường
đều, điện trường sinh ra bởi điện tích điểm và điện trường tạo bởi lưỡng cực điện. Trong tất
cả các trường hợp, các mặt đẳng thế luôn vuông góc với những đường sức điện trường tại giao điểm:
 Trên mục 25.2 ta đã phân tích được rằng, họ các mặt đẳng thế trong điện trường đều
là những mặt phẳng song song, cố nhiên vuông góc với đường sức điện trường.
 Ở mục 25.3 ta cũng làm sáng tỏ rằng, điện thế tạo bởi điện tích điểm chỉ phụ thuộc
vào khoảng cách đến điện tích điểm, nên họ các mặt đẳng thế là những mặt cầu, giao nhau vuông góc với đ ờ
ư ng sức đối xứng xuyên tâm. 10
Hình 25.11: Họ các mặt đẳng thế trong các trường hợp: (a) điện trường đều (b) điện
trường của điện tích điểm (c) điện trường tạo bởi lưỡng cực điện
Hãy thử suy vector E của điện trường tạo bởi điện tích điểm từ biểu thức của điện thế (25.11): q V k e r
Các mặt đẳng thế có dạng cầu nên vector E phải hướng vuông góc theo hướng xuyên tâm.
Nói cách khác E chỉ có thành phần:  V E   (25.17) r r
Thế biểu thức của điện thế V vào (25.17) suy ra:   q q E E   kk re e 2 r   r r
Kết quả thu được hoàn toàn quen thuộc! 25.
5 Điện thế sinh ra bởi sự phân bố điện tích liên tục
Ở mục 25.3, chúng ta tính được điện thế sinh ra bởi tập
hợp các điện tích điểm rời rạc. Mục này trình bày phương pháp
tính điện thế sinh ra bởi sự phân bố điện tích liên tục, tức vật
tích điện có kích thước đáng kể. Có hai phương pháp tiến hành:
phương pháp chia nhỏ và phương pháp dùng định lý Gauss. Phương pháp chia nhỏ
Ta chia vật tích điện có kích thước lớn nói trên thành
những phần rất nhỏ, nhỏ đến mức có thể xem mỗi phần như thế
là một điện tích điểm. Đối với mỗi điện tích điểm vừa cắt ra
Hình 25.12: Tính điện thế
sinh ra bởi sự phân bố
điện tích liên tục
ấy, ta đã có thể áp dụng công thức (25.11) để tính điện thế dV do nó tạo ra tại điểm P cần khảo sát: dq dV k (25.18) e r
trong đó r là khoảng cách từ phần nhỏ đang xét đến điểm P. Điện thế do vật sinh ra tại
điểm P là sự tổng hợp của tất cả các phần nhỏ trên toàn bộ vật tích điện: dq V dV   dV k   (25.19) e r
Cần lưu ý ở phương pháp này rằng: gốc lấy điện thế (V  0) nằm ở xa vô cùng ().
Phương pháp dùng định lý Gauss
Đối với những hệ tích điện mang tính đối xứng, ta có thể dùng định lý Gauss để tính
điện trường E trước. Sau đó dùng công thức () để tính điện thế: (O) V E ds  (P)
trong đó gốc lấy điện thế (V  0) có thể quy ước tại một điểm O nào đó.
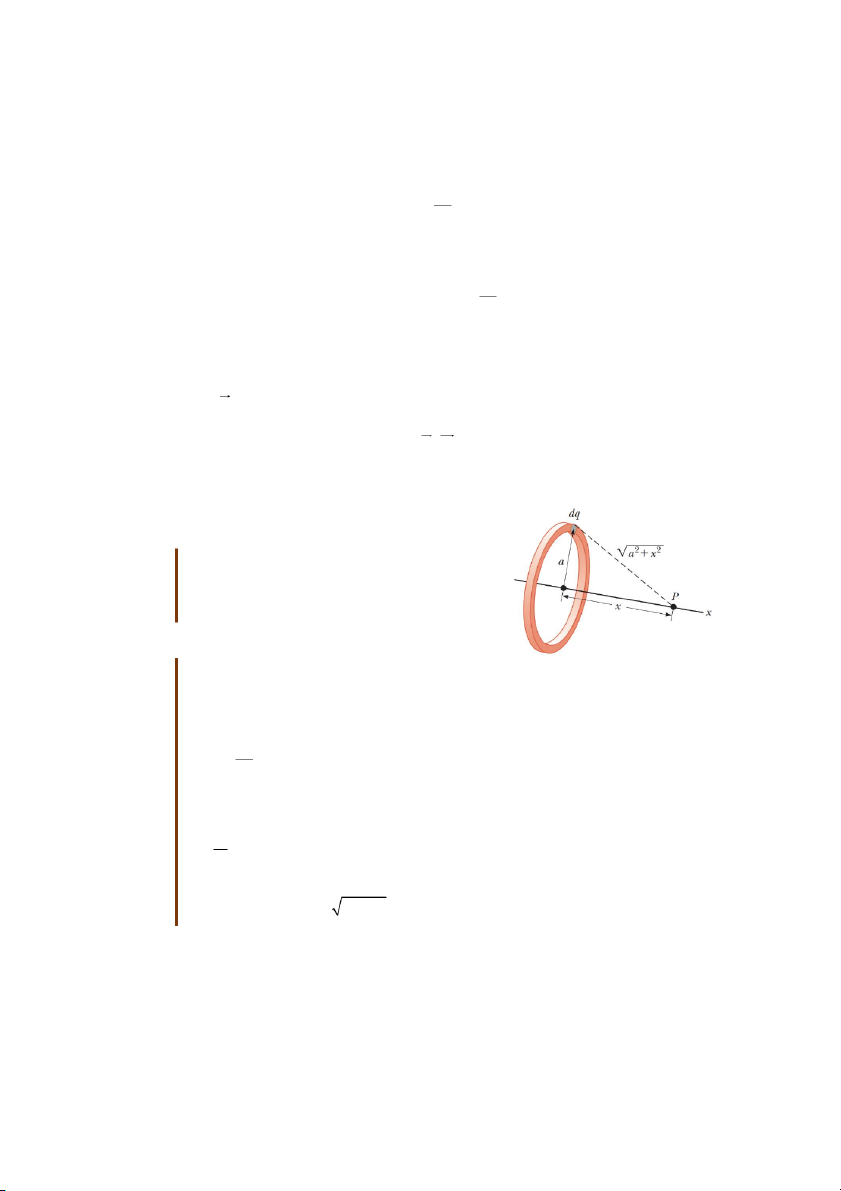
Bài tập mẫu 25.4: Điện thế tạo bởi vành tròn tích điện đều
(A) Tìm biểu thức của điện thế tại điểm P nằm
trên trục đối xứng của một vành tròn bán kính a
với điện tích Q phân bố đều, cách tâm vành tròn một đoạn . x Giải:
Chia vành tròn ra rất nhiều phần nhỏ, mỗi phần
Hình 25.13: Tính điện thế tại
có điện tích dq nhỏ đến mức có thể xem như
điểm nằm trên trục của vành
điện tích điểm. Áp dụng công thức (20.20), ta có
tròn tích điện đều
thể tính điện thế tại điểm P: dq V k e r
Để ý rằng điểm P nằm cách đều tất cả các phần của vành tròn, do vậy tích phân trên dễ dàng chuyển thành: ke V dqr
Tích phân trên thể hiện tổng toàn bộ điện tích chứa trên vành. Còn khoảng cách r có thể biểu diễn thành 2 2
r a x 12 k Q e V  2 2 a x
(B) Tìm biểu thức của cường độ điện trường tại P . Giải:
Do tính chất đối xứng, có thể kết luận rằng vector cường độ điện trường E tại điểm
P phải hướng dọc theo trục x. Nói cách khác E chỉ có thành phần theo . x Từ mối
liên hệ (25.16) giữa cường độ điện trường và thế năng: dV d  1  k x e E    k Q    Q x e dx
dx a x  a x 3/2 2 2 2 2
Bài tập mẫu 25.5: Điện thế tạo bởi thanh tích điện đều
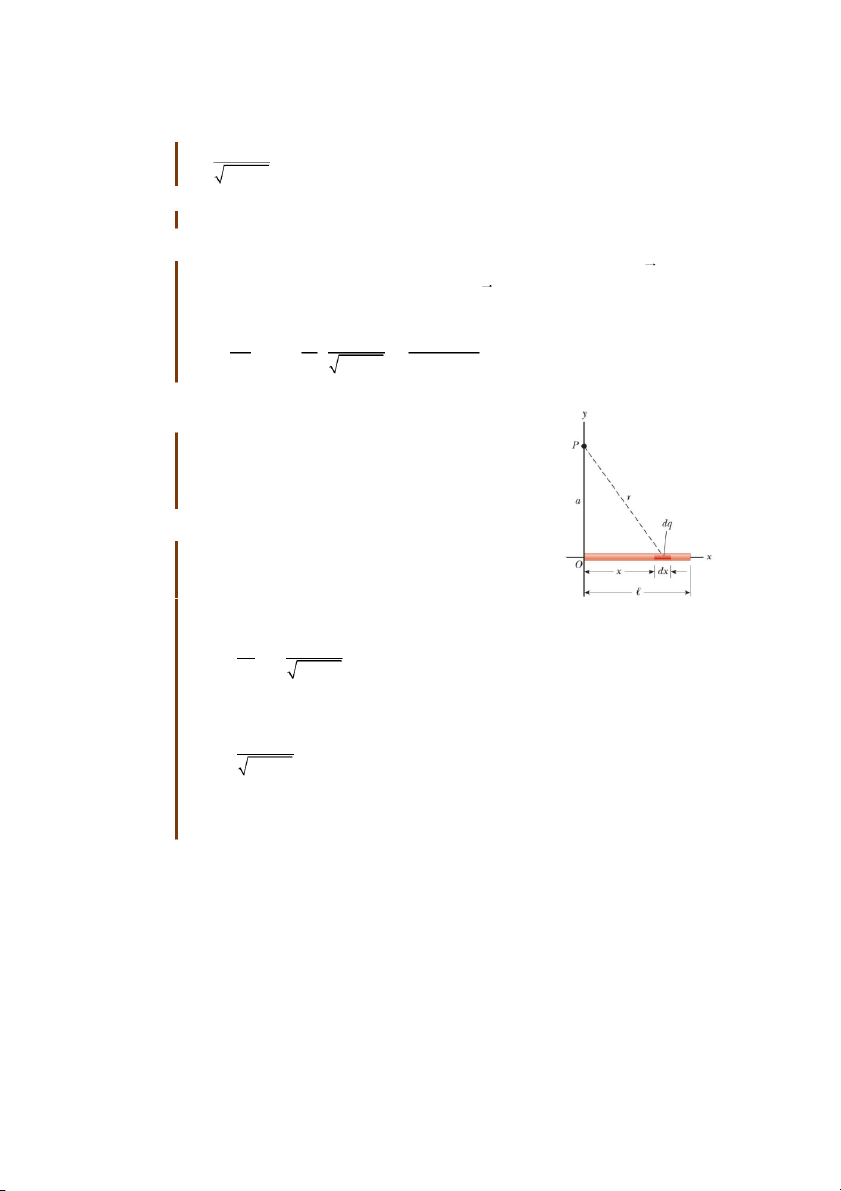
Một thanh có chiều dài l đặt dọc theo trục x như hình vẽ.
Thanh có điện tích Q phân bố đều với mật độ dài . Tính
điện thế tại điểm P nằm trên trục y cách đầu thanh một đoạn bằng . a Giải:
Điện thế tại P được tạo bởi các phần điện tích phân bố
khắp chiều dài thanh. Xét một đoạn dx rất nhỏ trên thanh,
mang điện tích dq  dx đủ nhỏ để có thể xem như điện tích điểm.
Hình 25.14: Tính điện
Điện thế do điện tích điểm dq nói trên tạo ra tại P:
thế tạo bởi thanh tích dqdx điện đều dV kk e e 2 2 r a x
Điện thế do rất nhiều điện tích điểm như thế trên toàn bộ thanh tạo ra tại P là tích phân: ldx V ke 2 2 0 a x
Theo đó cận tích phân lấy từ x  0 cho đến x l.
Để ý rằng k và   Q / l là những số không đổi, có thể cho ra ngoài dấu tích phân: e 13 l l dx Q 2 2 V k   k
ln(x  a x )  e 2 2 e a x l 0 0 2 2 Q      ln l a l k   e la    25.
6 Điện thế tạo bởi vật dẫn tích điện
Từ chương 24, ta biết rằng đối với vật dẫn điện ở trạng thái cân bằng, điện tích chỉ
phân bố trên bề mặt vật dẫn. Ngoài ra ta cũng biết rằng, điện trường chỉ tồn tại bên ngoài
vật dẫn và vuông góc với bề mặt vật dẫn. Bên trong vật dẫn điện trường hoàn toàn bị triệt tiêu.
Chương này ta tiếp tục bàn đến vật dẫn điện về phương diện điện thế. Áp dụng công
thức (25.3) cho hai điểm A và B bất kì nằm trong hoặc trên bề mặt vật dẫn, ta có: ( ) B V V   E ds  0  B A ( ) A
Như vậy mọi điểm thuộc vật ẫ
d n đều có điện thế bằng nhau.
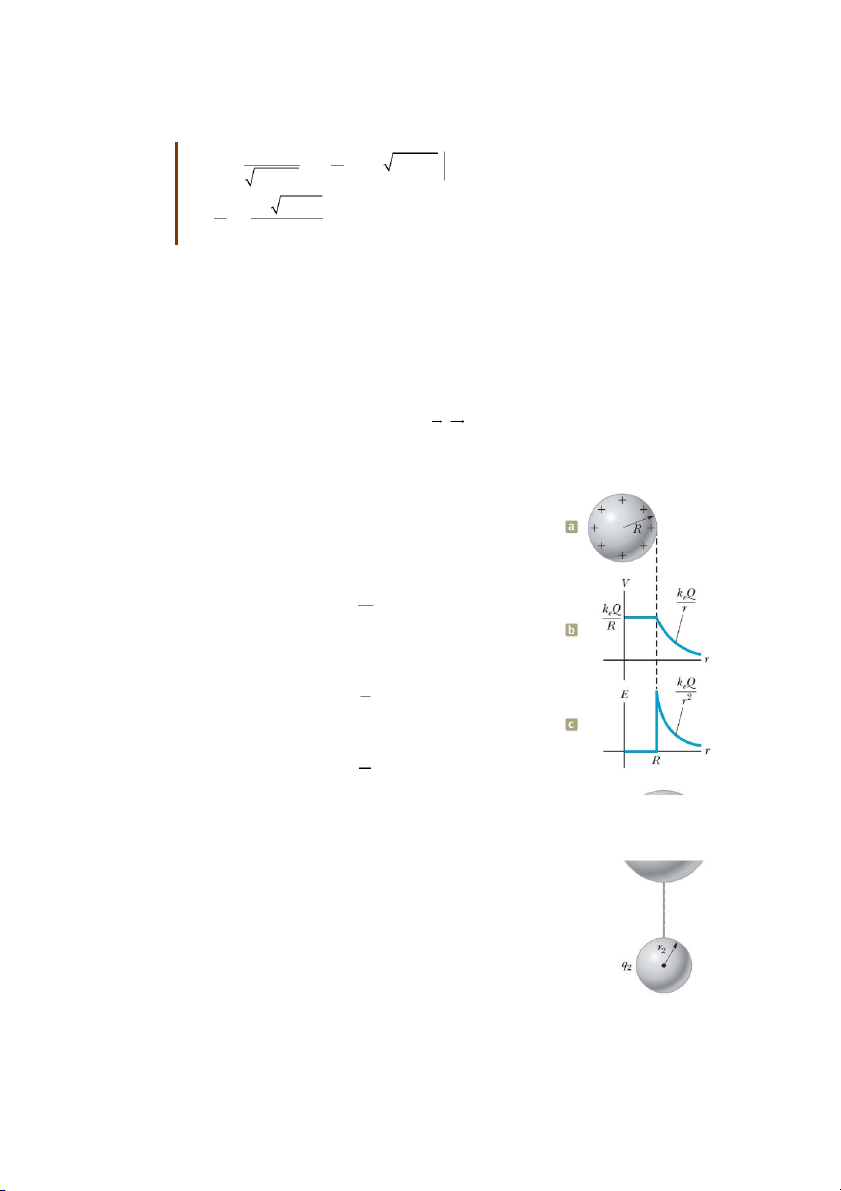
Hình 25.15 miêu tả điện thế tại các điểm bên trong và bên
ngoài quả cầu làm bằng vật liệu dẫn điện. Theo trình bày ở
chương 24, việc áp dụng định lý Gauss cho ra kết quả rằng: điện
trường bên ngoài quả cầu tích điện có dạng y hệt như điện trường
tạo bởi điện tích điểm: q E k e 2 r
Do đó điện thế tại một điểm bất kì nằm ngoài quả cầu cũng sẽ có
dạng như điện thế sinh ra bởi đ ệ
i n tích điểm đặt tại tâm quả cầu: q V k e r
Từ đó suy ra điện thế ngay trên bề mặt quả cầu tích điện: q V k (25.20) e R
với R là bán kính quả cầu. Trong trường hợp quả cầu làm bằng Hình 25.15: (a) vật dẫn
vật liệu dẫn điện, biểu thức (25.20) cũng chính là điện thế tại mọi hình cầu (b) điện thế (c)
điểm thuộc quả cầu. Hình 25.15b diễn tả điều đó bằng đoạn nằm điện trường
ngang tương ứng với các điểm bên trong quả cầu.
Bài tập mẫu 25.6: Hai quả cầu tích điện nối nhau
Hai vật dẫn hình cầu có bán kính lần lượt bằng 1r và 2r ban đầu đặt cách xa nhau.
Sau đó chúng được nối với nhau nhờ sợi dây dẫn điện như hình 25.16. Khi hệ cân
bằng, điện tích trên mỗi quả cầu lần lượt bằng ố đề ỗ ề 1
q và q , phân b u trên m i b 2
mặt. Tìm tỉ số của cường độ điện trường trên bề mặt của hai quả cầu này. Giải:
Do hai quả cầu đặt cách nhau đủ xa, sự ảnh hưởng lẫn nhau về điện trường là không
đáng kể, dẫn đến điện tích mỗi bên vẫn phân bố đều trên mỗi bề mặt và điện trường
trên mỗi quả cầu vẫn giữ được nguyên tính đối xứng.
Việc nối hai quả cầu bằng dây dẫn làm cho điện thế cả hai bằng Hình 25.16: Hai nhau:
quả cầu dẫn điện
nối với nhau q q 1 2 V kk e e r r 1 2 hay: 1 q 1 r  (1) q r 2 2
Cường độ điện trường trên bề mặt mỗi quả cầu có độ lớn: q q 1 2 E k ,  1 E k e 2 2 e 2 r r 1 2
Lấy tỉ số của cường độ điện trường: 2 E q r 1 1 2  2 2 E 2 q 1r Thế (1) vào thu được: 2 1 E 1 r 2 r 2 r   2 2 E 2 r 1r 1 r
Từ kết quả thu được có thể thấy rằng, khi hai quả cầu nối nhau bằng dây dẫn điện,
điện trường trên bề mặt của quả cầu nhỏ thì lớn hơn điện trường trên bề mặt quả cầu lớn.
Vật dẫn rỗng ruột
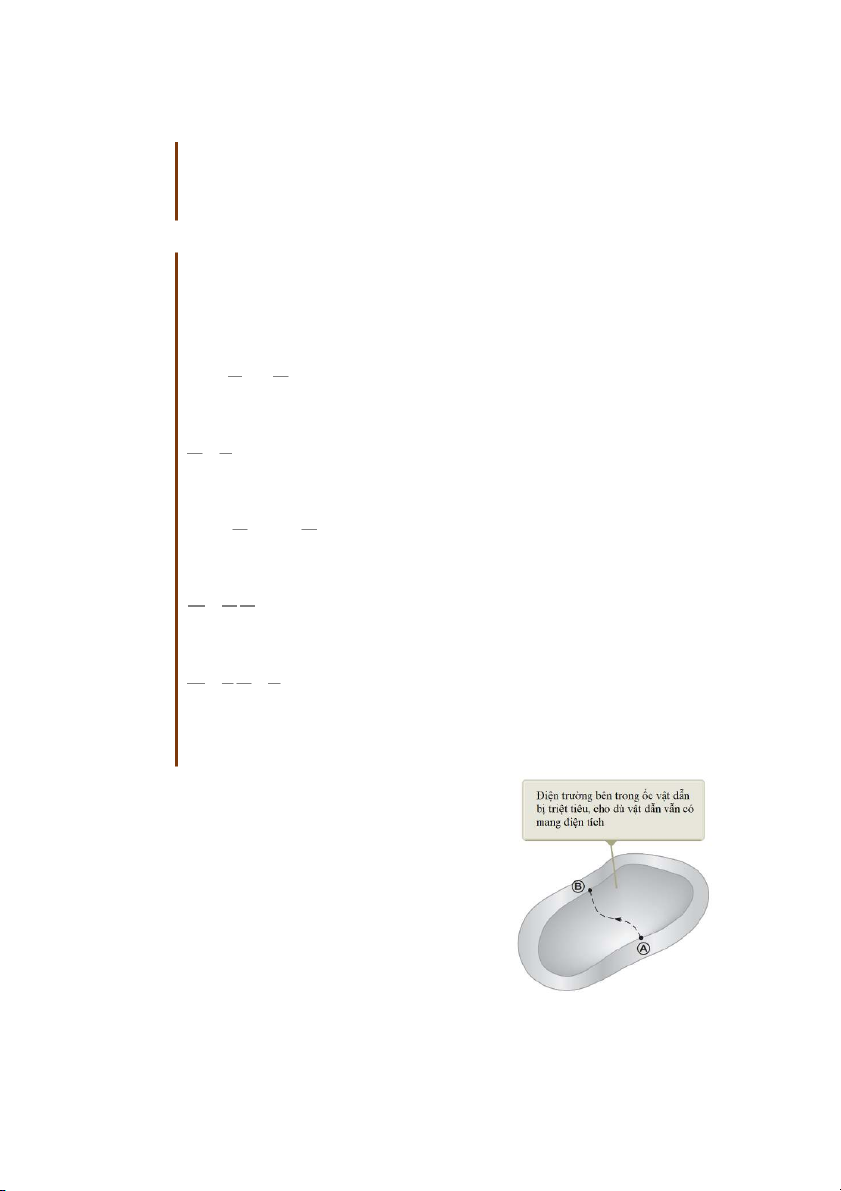
Vật dẫn rỗng ruột có thể miêu tả như hình 25.17. Với
loại vật dẫn hết sức đặc biệt này, ta sẽ chứng minh rằng
điện trường bên trong phần rỗng của vật dẫn phải luôn
luôn bằng không, dù điện trường bên ngoài có thay đổi
thế nào đi nữa! Thực vậy, xét hai điểm A và B bất kì thuộc thành bên trong sát phần rỗng, theo (25.3) ta có: ( B) V V   E dsB A ( A)
Nhưng đối với vật dẫn bất kì ta cũng đã chứng minh rằng điện thế tại mọi điểm trong nó
đều bằng nhau: V V . Nên vector cường độ điện trường E buộc phải bằng không. A B
Vật dẫn rỗng ruột dưới dạng những hộp có vỏ bằng kim loại có nhiều ứng dụng trong
việc cách ly các vật bên trong khỏi ảnh hưởng của điện Hình 25.17: Vật dẫn rỗng ruột trường ngoài. Tia lửa điện
Tia lửa điện thường quan sát thấy ở gần vật dẫn điện cao thế. Khi điện trường gần vật
dẫn đủ lớn, các electron tự do, vốn phát sinh do sự ion hoá ngẫu nhiên của phân tử khí, sẽ
được gia tốc và bị đẩy xa khỏi phân tử mẹ. Chúng chuyển động nhanh và va chạm với nhiều
phân tử khí xung quanh, làm phát sinh thêm rất nhiều sự ion hoá thứ cấp, kéo theo sự xuất
hiện càng lúc càng nhiều electron tự do khác. Các electron này sau đó tái kết hợp với những
ion phân tử, di chuyển từ trạng thái tự do sang trạng thái liên kết ở mức năng lượng thấp
hơn làm phát ra năng lượng dưới ạ
d ng ánh sáng. Đó chính là tia lửa điện.
Ở những phần nhọn của vật dẫn, điện tích tập trung nhiều hơn và sinh ra điện trường
lớn hơn so với những phần khác. Do đó tia lửa điện thường hay xuất hiện ở những điểm nhọn này.
Tia lửa điện có thể được quan sát rõ hơn nhờ máy quay tử ngoại 16 25.
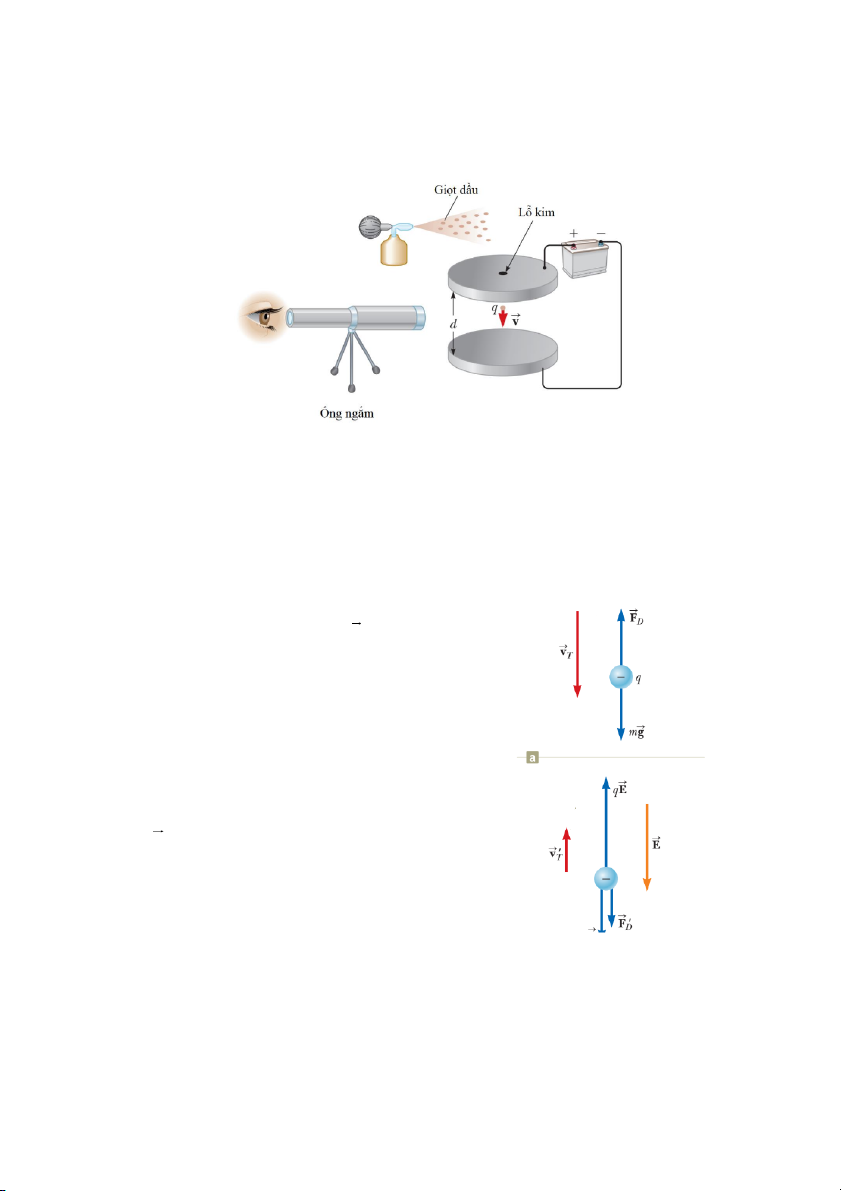
7 Thí nghiệm giọt dầu Millikan
Hình 25.18: Thí nghiệm giọt dầu Millikan
Trong giai đoạn 1909-1913, Robert Millikan đã tiến hành phép đo điện tích của
electron, xác định giá trị của điện tích nguyên tố .
e Thiết bị thí nghiệm được mô tả như hình
25.18. Bộ phận chính của thiết bị gồm hai đĩa kim loại đặt song song, đấu vào hai cực của
ắc quy để tạo ra điện trường giữa chúng. Millikan dùng bình phun sương phun những giọt
dầu li ti vào khoảng trống giữa hai đĩa, đồng thời rọi x-quang làm ion hoá không khí, khiến
cho các electron được giải phóng và dính vào những giọt dầu. Những giọt dầu được chiếu
sáng, hiện giữa ống kính quan sát như những ngôi sao hiện giữa trời đêm.
Khi ngắt nguồn điện ra khỏi đĩa kim loại, giọt dầu
rơi dưới tác dụng của trọng lực mg , nhưng nhanh chóng
đạt đến tốc độ tới hạn do tác dụng của ma sát nhớt
F  6r v tỉ lệ thuận với tốc độ, với r là bán kính D 1
giọt dầu,  là độ nhớt của không khí (hình 25.19a). Do
giọt dầu rơi đều nên hai lực này cân bằng nhau:
mg  6rv 1
Khi nguồn bật, giữa hai đĩa kim loại xuất hiện một
hiệu điện thế và tạo ra điện trường hướng từ trên xuống
dưới (hình 25.19b). Giọt dầu bị nhiễm các electron nên
tích điện âm, cho nên chịu tác dụng bởi lực điện trường
qE hướng lên trên. Lực này lớn đến mức giọt dầu bị
kéo đi lên, tăng tốc và đạt tốc độ tới hạn v . Khi ấy: 2
qE mg  6 rv 2
Hình 25.19: Giọt dầu khi không
có điện trường (a) và khi có điện trường (b)
Ở đây cường độ điện trường được tính qua hiệu điện thế giữa hai bản kim loại và khoảng cách giữa chúng: V E d
Từ những phương trình trên có thể suy ra điện tích của giọt dầu: mg v  2 q  1  E v  1 
Khối lượng m của giọt dầu chỉ có thể biết được sau khi tính được bán kính r theo (25.21): 4 3
g  r  6r 1 v 3
Kết quả cuối cùng thu được: 2 3  v 1  v  1 2 q  9 2  1   g E v  1 
Như vậy để xác định được điện tích của giọt dầu, bên cạnh độ nhớt của không khí và
khối lượng riêng  của dầu, cần đo các tốc độ 1v khi rơi không có điện trường, 2 v hướng
lên khi có điện trường.
Kết quả thí nghiệm của Millikan cho thấy, điện tích q tạo ra trên những giọt dầu khác
nhau luôn có giá trị là bội nguyên của con số 19 1,6 10   C.
Millikan khẳng định rằng, hiện tượng này xảy ra do giọt dầu bị
bám bởi một số nguyên electron cùng lúc. Nói cách khác, 19 1,6 10  
C là điện tích của một electron riêng rẽ. Nhờ phát
hiện này, Robert Millikan đã được trao giải Nobel vật lý vào năm 1923. 25.
8 Một số ứng dụng các hiện tượng tĩnh điện
Các hiện tượng tĩnh điện có nhiều ứng dụng dân dụng trong
việc thu lôi, khử bụi, in ấn, sơn bề mặt. Trong khoa học, có
những thiết bị hoạt động dựa trên nguyên lý tĩnh điện như máy
phát tĩnh điện, kính hiển vi trường-ion, động cơ tên lửa ion…
Dưới đây ta sẽ bàn đến hai trong số đó.
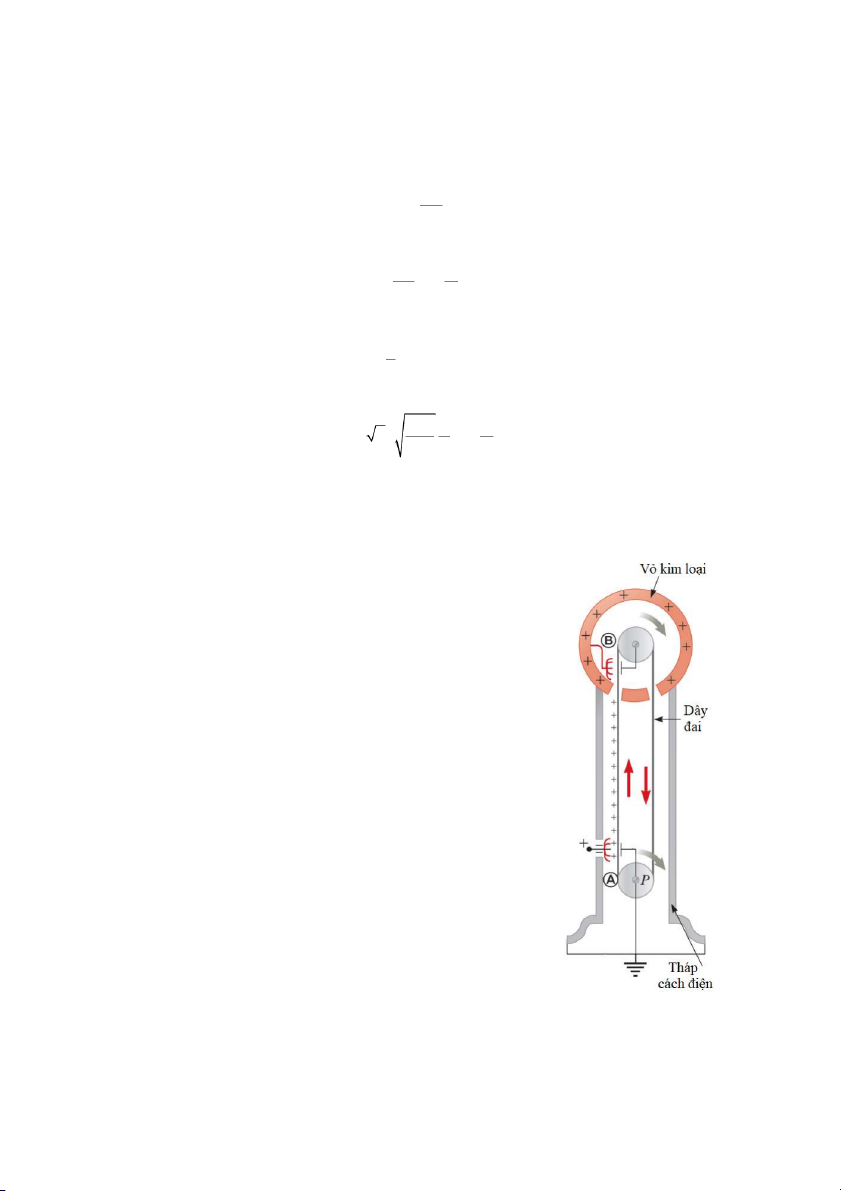
Máy phát tĩnh điện Van de Graaff
Thực nghiệm đã chỉ ra rằng, khi một vật dẫn tích điện tiếp
xúc với mặt rỗng bên trong của một vật dẫn rỗng, toàn bộ điện
tích sẽ chạy sang vật dẫn rỗng và chạy hết ra phía bề mặt ngoài.
Lợi dụng hiện tượng này, người ta đã tạo ra những thiết bị cho phép tích luỹ điện tích và
điện áp gần như không giới hạn.
Máy phát tĩnh điện do Van de Graaff phát minh năm 1929 có sơ đồ nguyên lý thể hiện
hình 25.20. Bên trong máy phát có một dây đai có thể cuộn tuần hoàn trên hai trục. Dây đai
luôn được tích điện tại vị trí gần điểm A ở điện thế khoảng 104 V. Điện tích theo “băng
chuyền” di chuyển đến gần điểm B, lúc này hoàn toàn nằm bên trong quả cầu kim loại rỗng,
sẽ đi theo những đầu kim tiếp xúc rồi ra ngoài bề mặt của quả cầu kim loại. Quá trình có thể
lặp đi lặp lại cho đến khi quả cầu tích điện đủ nhiều. Trên thực tế, nó có thể tích điện đến
hàng triệu volt, với điện trường đủ mạnh để gia tốc cho các proton trong các phản ứng hạt nhân.
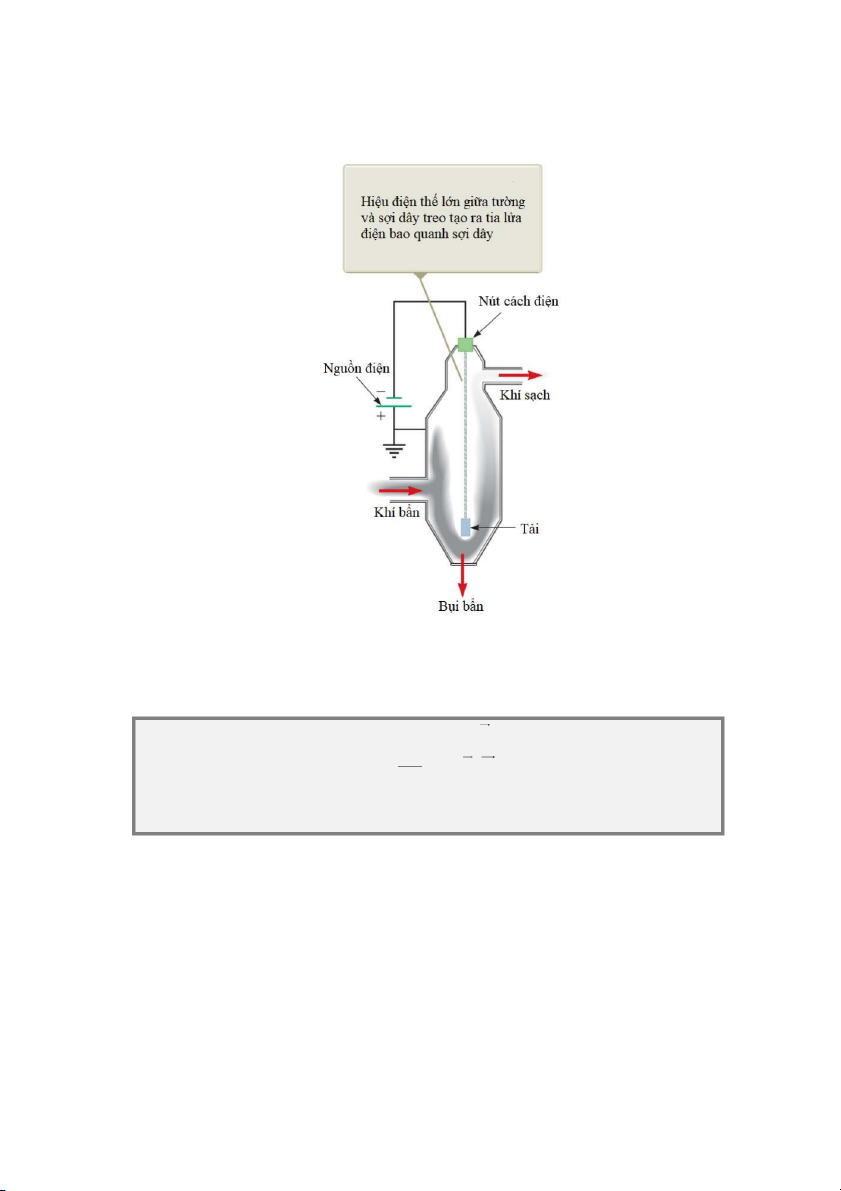
Bộ lọc bụi tĩnh điện
Hiện tượng phóng điện trong không khí có vai trò quan trọng trong việc khử bụi nơi
công xưởng. Thiết bị dựa trên sự phóng điện này có thể giúp khử các sản phẩm cháy như
khói tạo ra từ việc đốt than và nhiều hoạt động công nghiệp khác.
Sơ đồ nguyên lý của thiết bị lọc bụi được miêu tả trên hình 25.21. Theo đó, một hiệu
điện thế rất lớn, tầm 40-100 kV, được tạo ra giữa vỏ thiết bị và sợi dây treo giữa bình lọc.
Sợi dây mang điện thế âm so với vỏ. Điện thế âm cực lớn từ sợi
dây tạo ra những tia lửa điện, làm ion hoá không khí xung quanh, Hình 25.20: Máy phát
tạo ra các electron tự do, ion dương và ion âm. Các ion âm sẽ bị tĩnh điện
đẩy về phía những vỏ bình lọc, va chạm với những hạt bụi li ti.
Phần đa những hạt bụi này bị tích điện âm và cũng bị đẩy về phía những vỏ bình lọc, làm không khí sạch bớt. 19
Hình 25.21: Bộ lọc bụi tĩnh điện
Tóm tắt chương 25 Định nghĩa
Hiệu điện thế giữa hai điểm A và B trong điện trường E được định nghĩa qua công thức: ( ) B UV     E dsq ( ) A trong đó U
 - độ chênh lệch thế năng. Điện thế V U / q là một đại lượng vô hướng, có
đơn vị Volt (V): 1V = 1J/C
Khái niệm và nguyên lý 20