Chương 7: Năng lượng của một hệ | Tài liệu môn Vật lý 1 trường đại học sư phạm kĩ thuật TP. Hồ Chí Minh

Nhiều bài toán có thể giải được nhờ các định luật Newton và các nguyên lý liên quan. Tuy nhiên, về mặt  lý thuyế có nhiều bài toán có thể giải được nhờ các định luật Newton nhưng thực tế thì rất phức tạp. Các bài toán đó lại có thể giải một cách dễ dàng bằng một cách khác. Khái niệm về năng lượng là một trong những chủ đề quan trọng..Tài liệu giúp bạn tham khảo, ôn tập và đạt kết quả cao. Mời bạn đọc đón xem!

5 3 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Môn: vật lý 1, 2

Trường: Đại học Sư phạm Kỹ thuật Thành phố Hồ Chí Minh

Thông tin:

18 trang 2 tuần trước

Tác giả:

Profile Lê Kim Dung
1
Chương Năng 7 lượng của m t hộ ệ
hi nhều bài toán có thể giải được ờ các định luật Newton và các nguyên lý liên quan.
Tuy nhiên, v mề ặt lý thuyế ềt có nhi u bài toán có th ng nh luể giải được bằ các đị ật
Newton nhưng thực t ế thì r t ph c tấ ứ ạp. Các bài toán đó lại có th ể giải m t cách d dàng ộ ễ
bằng một cách khác.
Khái ni m v là m t trong nh ng ch quan tr ng nh t trong khoa h c và ệ ề năng lượng ộ ữ ủ đề ọ ấ ọ
kỹ thu t.ậ M i quá trình v t lý xỗ ậ ảy ra trong vũ trụ liên quan đế đều n vi c chuy n hóa t d ng ệ ể ừ ạ
năng lượ ạng năng lượ Trên cơ sở ệm năng lượng, người ta đã ng này sang d ng khác. khái ni
phát tri n nhể ững phương pháp mới cho phép gi i các bài toán vả ật lý một cách dễ dàng khi mà
gi giải b nh lu t Newton thì l i r . C sằng các đị ậ ạ ất khó khăn hương này ẽ ới thi u khái ni ệ ệm hệ
và các trong m t h . cách lưu trữ năng lượ ng ộ ệ
Hệ và môi trường
Một h là m t ph n nh c a cệ ộ ầ ỏ ủ ả vũ trụ. Một hệ có thể là mộ ột vật hoặc m t chất điểm, một
tập h p nhi u v t ho c nhi u ch m, hay m t vùng không gian t h s có ranh ợ ề ậ ặ ề ất điể ộ nào đó. Mộ ệ ẽ
giới v i bên ngoài. Bên ngoài biên gi i c a h là . Biên gi i c a m t h có thớ ớ ủ ệ môi trường ớ ủ ộ ệ ể là
một b m t thề ặ ực ho c m t b m ng ng, không nh t thi t trùng v i m t b m t thặ ộ ề ặt tưở tượ ấ ế ớ ộ ề ặ ực.
Biên giới chia vũ trụ h thành ệ và môi trường. Kích thước và hình d ng c a mạ ủ ột h có th ệ ể thay
đổi theo thời gian.
Ví d mụ ột hệ: Khi có m t l c tác d ng vào m t v t trong không gian tr ng r ng thì hộ ự ụ ộ ậ ố ỗ ệ là
vật đó, bề mặt của vật là ranh gi i c a h . ớ ủ ệ
Những điều cần chú ý khi gi ải toán:
Xác định hệ
Cũng xác định một ranh giới hệ
Lực ng lên h t ng xuyên qua ranh gi i c a h . ảnh hưở ệ ừ môi trường tác độ ớ ủ ệ
Công th c hi n b i m c i ự ệ ở ột lự không đổ
Công (ký hi u là ) c hi n b i mệ W thự ệ ở ột tác nhân tác dụ ộng m t ngoại l i lên h ực không đổ ệ
là m nh b ng tích cột đại lượng được xác đị ằ ủa độ ới độ ủa điể lớn lực F v dịch chuyển Δr c m
đặ ựt l c nhân với cos vθ, ới θ là góc tạo bởi vectơ lực và vectơ độ dich chuyển.
W = FΔr cosθ (7.1)
N
2
Chú ý r d ch chuy d ch chuy n ằng độ ị ển ở đây là độ ị ể
của điểm mà l c tác d ng vào. ự ụ
Lực s không th c hi n công trên mẽ ự ệ ột vật chuyển động
nếu c không chuy ng cùng vđiểm đặt lự ển độ ới phương
dịch chuy n. Công th c hi n b i m t l c làm cho v t dể ự ệ ở ộ ự ậ ịch
chuyển có độ lớn bằng 0 khi l c vuông góc vự ới phương
dịch chuy n. ể
Độ ị ứ d ch chuyển trong công th c tính công
Nếu l c tác d ng vào m t v n ự ụ ộ ật rắ được xem như một
chất điểm d ch chuy n gi d ch chuy n thì độ ị ể ống như độ ị ể
của chất điểm. Đối v i vớ ật bi n d d ch chuy n ế ạng thì độ ị ể
của vật không gi ng v d ch chuyố ới độ ị ển mà l c tác d ng vào. ự ụ
Do đó, để xác đị nh độ dịch chuyển chúng ta chỉ xét đến điểm
mà l c tác d ng vào. ự ụ
Phản l c pháp n và l c h p d n không sinh ra công trên ự tuyế ự ấ ẫ
vật vì = cos 90° = 0cos θ . Chỉ có lực
F
thực hi n công trên v ệ ật.
Dấu c a công phủ ụ thuộc vào hướ ực và hướng của l ng của
độ dịch chuyển. Công dương khi lực và độ dịch chuyển có cùng
hướng, công âm khi chúng ngược hướng.
Công là m c a công là joule ột đại lượng vô hướng. Đơn vị ủ
(J).
1 joule = 1 newton. 1 meter = kg.m²/s²
J = N. m
Công là m t d i ộ ạng năng lượng trao đổ
Nếu công th c hi n trên m t h nh n giá ự ệ ộ ệ ậ trị dương thì năng
lượng được truyền vào h ; còn n u công thệ ế ực hiện trên một h ệ
nhận giá trị âm thì năng lượng thoát ra kh i hỏ ệ. N u m t h ế ộ ệ tương
tác với môi trường ngoài thì s ự tương tác đó có thể xem như sự
trao đổi năng lượng truyền qua biên giới của hệ. Điều này dẫn
đế ựn một s thay đổ ủa năng lượi c ng d trong h . ự trữ ệ
Câu h i 7.1:ỏ L c h p d n M t tr i tác d t gi ự ấ ẫ ặ ờ ụng lên Trái đấ ữ
cho Trái đấ ển đột chuy ng trên quỹ đạo quanh Mặt trời. Giả sử
quỹ đạo là đường tròn. H i công c a l c h p d n này th c hi n ỏ ủ ự ấ ẫ ự ệ
khi Trái đất di chuy n mể ột quãng đường trong m t khoộ ảng thời
gian ng n trên qu o là: (a) b ng không? (b) (c) ắ ỹ đạ ằ dương?
âm? (d) không th ể xác định được?
Hình 7.1 t d ch chuy n Một vậ ị ể
dướ ựi tác dụng của một l c
không đổi.
Hình 7.2 n l c pháp Phả ự
tuyến và tr ng l c không ọ ự
sinh công, ch có l
ỉ ực 𝐹
sinh công.
Hình 7.3 Hình cho câu h i 7.2.ỏ
3
Câu h i 7.2:ỏ Trên hình 7.3, các l l n bực có độ ớ ằng nhau, quãng đường dịch chuyển của vật
sang ph i b ng nhau. Hãy s p x p theo th t giá tr c a công do l c th c hi n trên v t t ả ằ ắ ế ứ ự ị ủ ự ự ệ ậ ừ
dương nhất đến âm nhất.
Tích vô hướng 2 vectơ
Tích vô hướ vectơ ng của hai
A
r
và
B
r
, được kí hi u ệ là
và có giá tr bị ằng:
A B
r r
A B cos
Với là góc gi hai θ ữa vectơ
A
r
và
B
r
Tích vô hướng có tính chất giao hoán:
và tính ch t k t h p: ấ ế ợ
Áp d ng vào công th ụ ức tính công, ta được:
cos
F r
r
r
W F r
(7.2)
Công đượ ực có độ ớn thay đổc thực hiện bởi l l i
Để ử ứ ự s dụng công th c W = FΔrcos θ l c ph c này không thải không đổi, do đó công thứ ể
s m biử d ng cho vi c tính công cụ ệ ủa ột lực ến . thiên Giả sử r ng trong kho ng d ch chuy n rằ ả ị ể ất
nhỏ Δx, F là h ng s
x
ằ ố thì trong khoảng đó W = F
x
Δx. Vì v y, trên c ậ ả quãng đường d ch chuy n ị ể
từ v u xị trí đầ
i
đến vị trí cu i x ố
f
thì:
f
i
x
x
x
W F x
Hình 7.5 (a) Công sinh ra b i thành ph n F c a l t l c d ch chuy n m n ở ầ
x
ủ ực khi điểm đặ ự ị ể ột đoạ
Δx (b) Công sinh ra b i thành ph n F c a l t l c d ch chuy n t x n x ở ầ
x
ủ ực khi điểm đặ ự ị ể ừ
i
đế
f
Nếu đoạn dịch chuyển Δx tiến t i 0. Ta có:ớ
Hình 7.4 Tích vô hướng 2 vectơ.
A B B A
r r r r
A B C A B A C
r rr r r r r
4
0
lim
x
f
x
f
F x F dx
x x
x
xx
i
i
Do đó,
f
i
x
x
x
W F dx
(7.3)
Trên đồ ông đượ thị, c c tính bằng di n tích gi i h n b ng cong n m và ệ ớ ạ ởi đườ ằ giữa x
i
x
f.
Công th c hi n b i nhi u l c ự ệ ở ề ự
Nếu có nhi u l c tác d ng lên h và h có th t ch m, thì t ng công tác ề ự ụ ệ ệ ể xem như mộ ất điể ổ
dụng lên h là công tác d ng b i h p l ệ ụ ở ợ ực:
f
i
x
ext x
x
W W F dx
Kí hi u công th c hi n b i các yệ “ext” để chỉ ự ệ ở ếu t ng t bên ngoài h . ố tác độ ừ ệ
Trong trườ ổng quát, độ thay đổi, lúc đó:ng hợp t lớn và chiều của hợp lực có thể
F r
r
r
f
i
x
ext
x
W W d
(7.4)
Nếu h không thệ ể xem như một chất điểm thì t ng công b ng t i s các công thổ ằ ổng đạ ố ực
hiện b i tở ừng l c: ự
forces
ext
rdFWW
.
(7.5)
Công th c hi n b i m t lò xo ự ệ ở ộ
Đây là một mô hình vật lý cho
trường h p l i phợ ực thay đổ ụ thuộc
vào v ị trí.
Lực đàn hồi (Định luật
Hooke)
Lực tác d ng b i lò xo là ụ ở
F
s
= - kx (7.6)
Trong đó, x là vị trí của chiếc hộp
cách v trí cân b ng (x = 0), k ị ằ được
gọi là h s i và ệ ố đàn hồ được đo bởi
mức độ cứng c a lò xo. ủ
Dạng vectơ của định luật
Hooke:
ˆ ˆ
F i i
r
s x
F kx
(7.7)
Hình 7.6 L c lò xo tác d ng lên chi c hự ụ ế ộp thay đổi
theo v trí x c a chi c hị ủ ế ộp
5
Lực tác d ng b i lò xo luôn có chi ng v vụ ở ều hướ ề ị ả trí cân bằng. Nếu th hộp ra, nó s dao ẽ
động gi a 2 v ữ ị trí –x và x. Khi x dương (lò xo bị giãn), lực F nh n giá tr âm; khi b ng 0 (tậ ị x ằ ại
vị trí cân b ng), lằ ực F b ng 0; và khi âm (lò xo bằ x ị nén), lực F dương.
Xem cái h p là m t h công th c hi n khi h p chuy ng gi a 2 v trí t - ộ ộ ệ, ự ệ ộ ển độ ữ ị ừ x
i
= x
max
đến = 0 l x
f
à:
max
0
2
max
ˆ ˆ
1
2
F r i i
r
r
f
i
x
s s
x
x
W d kx dx
kx dx kx
(7.8)
Còn t ng công th c hi n khi h p d ch chuy n t n b ng 0. ổ ự ệ ộ ị ể ừ -x
max
đế x
max
ằ
Khi h p d ch chuy n m n tùy ý t ông th c hi n b i lò xo ộ ị ể ột đoạ ừ x = x
i
đến x = x thì c
f
ự ệ ở
trên h p là: ộ
f
i
x
s i f
x
W kx dx kx kx
2 2
1 1
2 2
(7.9)
Nếu điểm cuối trùng với điểm đầu thì W = 0.
Bài t p m u 7.1: Lò xo u s ng c a m t l c ậ ẫ chị ự tác dụ ủ ộ ự
Giả s r ng có m t ngo i l ử ằ ộ ạ ực F
app
kéo giãn lò xo, l c tác d ng này ự ụ
bằng v i l i c a lò xo. ớ ực đàn hồ ủ
app app s
F kx kx
ˆ ˆ ˆ
F i F i i
Đố ịi với m n dột đoạ ch chuyển bất
kì t x n x công th c hi n ừ
i
đế
f
thì ự ệ
bởi l c tác d ng là: ự ụ
f
i
x
app f i
x
W kx dx kx kx
2 2
1 1
2 2
Công th c hi n b i lự ệ ở ực F
app
khi hộp
chuyển động từ vị trí –x
max
đến x
= 0 thì b ng -
ằ ½ kx
2
max
.
Câu h i 7.3:ỏ M t cái phi tiêu c n p vào m t kh u súng lò xo. L n thộ đượ ạ ộ ẩ ầ ứ nhất lò xo b nén ị
một đoạn x, lần thứ hai lò lo b nén mị ột đoạn 2x. Hỏi công để nạp phi tiêu l n th hai lầ ứ ớn hơn
lần thứ nh t bao nhiêu l n: (a) 4 l n? (b) 2 l n? (c) b ng nhau? (d) m t n a? (e) mấ ầ ầ ầ ằ ộ ữ ột phần tư?
Hình 7.7 Lò xo ch u tác d ng c a ngoị ụ ủ ại
l
ực 𝐹
𝑎𝑝𝑝 trong quá trình v t di chuy n t v ậ ể ừ ị
trí x n x = 0.
i
= -x
max
đế
f
6
Động nh lý công - năng và đị động năng
Một k t qu c a công tác d ng vào h là làm cho h i v n t a nói h c ế ả ủ ụ ệ ệ thay đổ ậ ốc, t ệ thu đượ
động năng. Sự thay đổi của động năng là một k t qu ế ả khả dĩ của vi c th c hiệ ự ện công để truyền
năng lượng cho hệ.
Xét m t h có m
ộ ệ chỉ ột vật khối lượng m chuyển động dưới tác d ng c a t ng h p lụ ủ ổ ợ ực
∑
𝐹
như trên hình vẽ ật và điểm đặ ực đề. Nếu cả v t l u thực hiện một dịch chuyển ∆𝑟= ∆𝑥𝑖=
(𝑥
𝑓
− 𝑥
𝑖
)𝑖 thì công mà t ng h p l c hi n là: ổ ợ ực đã thự ệ
𝑊
𝑒𝑥𝑡
= ∫ ∑𝐹
𝑥
𝑓
𝑥
𝑖
𝑑𝑥= ∫ 𝑚𝑎
𝑥
𝑓
𝑥
𝑖
𝑑𝑥
f
i
v
ext
v
W mv dv
ext f i
W mv mv
2 2
1 1
2 2
(7.10)
Trong đó v ốc độ trí ban đầ
i
và v là t
f
của vật tại vị u
x
i
và v trí cuị ối x .
f
Phương trình trên cho thấy công của tổng hợp
lực thực hi n trên v t b ng hi u sệ ậ ằ ệ ố giữa hai giá trị
cuối và đầ ột đại lượng. Đại lượng này đượu của m c
gọi là động năng của vật.
K
= ½ mv
2
11) (7.
Động năng là năng lượng g n v i chuy ng c a v t, là m ng và ắ ớ ển độ ủ ậ ột đại lượng vô hướ
có đơn vị ống như đơn vị gi của công là jun (J).
Định lý công - động năng
Phương trình cuối cùng thu được trên đây là phương trình của định lý công – động năng.
W
ext
= K K K (7.12)
f
–
i
= Δ
Khi công th c hi n trên m t h và ch ự ệ ộ ệ ỉ làm thay đổi tốc độ c a h , thì t ng công th c hiủ ệ ổ ự ện
trên h bệ ằng độ thay đổi động năng củ a hệ. Tốc độ của h sệ ẽ tăng nếu công dương, tốc độ của
hệ sẽ giảm n u công âm. ế
Đị ố độ ứnh lý công - áp dđộng năng ụng cho t c ch không ph n t nh lý công - ải vậ ốc. Đị
động năng không đúng nế thay đổ thay đổ ốc độu có sự i khác trong hệ bên cạnh sự i về t hoặc
có s ng ngoài. ự tương tác khác với môi trườ
Hình 7.8. i tác d ng c a t ng Dướ ụ ủ ổ
hợp l c, v t d ch chuy n m n ự ậ ị ể ột đoạ
Δx.
7
Bài t p m u 7.2 ậ ẫ
Một v t kh ng 6,0 kậ ối lượ g đang nằm yên trên
một b m t không ma sát bề ặ ị kéo sang ph i bả ởi
một lực có phương năm ngang, độ ớn 12 N như l
hình 7.9. Hãy tính t c a v t sau khi nó di ốc độ ủ ậ
chuyển m n dài 3,0 m. ột đoạ
Giải:
Chọn h g m v t. Có 3 ngo i l c tác d ng ệ chỉ ồ ậ ạ ự ụ
lên h . Ph n l c pháp tuy n và l c h p d n ệ ả ự ế ự ấ ẫ
không th c hi n công vì chúng vuông góc vự ệ ới
phương dị ệ. Theo địch chuyển của h nh lý công
– động năng, ta có:
W
ext f
= ΔK = ½ mv
2
– 0
𝑣
𝑓
=
√
2𝑊
𝑒𝑥𝑡
𝑚
=
√
2𝐹∆𝑥
𝑚
=
√
2.12.3,0
6,0
=3,5𝑚/𝑠
Thế năng của một hệ
Bây gi chúng ta hãy xem xét mờ ột hệ gồm nhiều hơn một
vật mà các vật bên trong h ệ tương tác lực v i nhau. Ví d , mớ ụ ột
hệ g m cu t, hai v i nhau ồ ốn sách và Trái đấ ật này tương tác vớ
bằng l c h p d n. Ta s th n mự ấ ẫ ẽ ực hiệ ột công trên cuốn sách
bằng cách nâng quy n sách th t chể ậ ậm theo phương thẳng
đứng, cu t dốn sách đã có mộ ời chuyển
ˆ
r j
f i
y y
Công th c hi n ự ệ trên h ph i xu t hiệ ả ấ ện như là sự ăng năng t
lượng c a h . Không có s khi ủ ệ ự thay đổi động năng trước
quyển sách b u chuy ng và sau khi quy n sách d ng ắt đầ ển độ ể ừ
l iạ . Như vậy, năng lượng cung cấp cho hệ từ bên ngoài phải
tồn trữ ở m t dộ ạng khác động năng của hệ. Khi cuốn sách
được thả rơi hệ có động năng; như vậy, trướ c khi cuốn sách
đượ ảc th rơi hệ năng (potential) để thu đượ phải có một khả c
động năng. Ta gọi cơ chế năng lượng trướ tích trữ c khi cuốn
sách đượ rơi là c thả thế năng (potential energy).
Thế năng là dạng năng lượng được xác định b i c u hình c a m t h ở ấ ủ ộ ệ mà trong đó các
thành ph n c a h i nhau b ng các lầ ủ ệ tương tác vớ ằ ực. Các l c này là n i l , chự ộ ực của hệ ỉ liên
quan đến tương tác năng luôn gắgiữa các thành phần của hệ với nhau. Thế n liền với một hệ
của 2 hay nhiều v n nhau. ật tương tác lẫ
Hình 7.9 Bài t p 7.2. ậ
Hình 7.10 Tác nhân bên
ngoài nâng t t n sách ừ ừ cuố
ở độ cao h cao h .
i
lên độ
f
8
7.6.1 Thế năng hấp dẫn
Xét h gệ ồm Trái Đất và cuốn sách như hình vẽ. Cuốn sách có khối lượng m đang nằm tại
độ cao y
i
so v i b mớ ề ặt Trái đất. Một tác nhân bên ngoài h nâng cu n sách l cao yệ ố ến độ
f
một
cách ch m ch d ch chuy n không có gia t l n b ng l c h p ậ ạp để ị ể ốc và do đó lực nâng có độ ớ ằ ự ấ
dẫn mà Trái đất tác dụng lên cuốn sách. Công mà lực ngoài thực hiện trên hệ Cuốn sách -
Trái đất là:
app
ˆ ˆ
( )
ext
ext f i
ext f i
W
W mg y y
W mgy mgy
F r
j j
(7.13)
Phương trình trên cho thấy công của ngoại lực th c hi n trên h b ng hi u s a hai giá ự ệ ệ ằ ệ ố giữ
trị cuối và đầ ột đại lượ Công này đã truyề ột năng lượng và năng lượu của m ng. n cho hệ m ng
đó tích trữ ở m t d c g i là thộ ạng đượ ọ ế năng. Đại lượng mgy được gọi là thế năng hấp dẫn
U
g
c v t khủa hệ ậ ối lượng m và Trái đất.
U
g
= mgy (7.14)
Thế năng là một đại lượng vô hướ Đơn vịng. của thế năng là joules (J).
Công có th i th p d n c a h ể làm thay đổ ế năng hấ ẫ ủ ệ
W
ext
= ΔU
g
(7.15)
Thế năng hấp dẫn là năng lượng liên kết với một vật, phụ thuộc vào độ ật đó cao của v
trên b m t c t. p d n ch ph cao c a v t so v i b mề ặ ủa Trái Đấ Thế năng hấ ẫ ỉ ụ thuộc vào độ ủ ậ ớ ề ặt
Trái Đất. Khi giải các bài toán, chúng ta cần phải chọn một mốc quy chiếu sao cho thế năng
hấp d n t ng mẫ ại đó bằ ột giá tr tham ị chiếu ng là b ng 0. nào đó, thườ ằ Việc chọn l a mự ốc thế
năng là tùy ý. Thông thường m t v t n m trên b m t cộ ậ ằ ề ặ ủa Trái Đất được xem như có thế năng
hấp d n b ng 0. các bài toán s xu t mẫ ằ Hoặc ẽ đề ấ ột mố ục thế năng để sử d ng.
Câu h i 7.4:ỏ Hãy ch n câu tr l p d n c a m t h (aọ ả ời đúng: Thế năng hấ ẫ ủ ộ ệ ) luôn luôn dương.
(b) luôn luôn âm. (c) có th âm ho ể ặc dương.
7.6.2 Thế năng đàn hồi
Thế năng đàn hồi là m t loộ ại năng lượng mà m t h có lò xo s tích tr . ộ ệ ẽ ữ Khi đó lực tương
tác gi a các thành ph n bên trong h là l i c a lò xo. ữ ầ ệ ực đàn hồ ủ
Xét h gệ ồ ộm có m t vật và m ên hình vột lò xo như tr ẽ. Lực đàn hồi lò xo tác dụng lên cái
hộp là
F
s
= - kx
Công th c hi n b i ngo i l c F tác d ng lên h lò xo - h p là: ự ệ ở ạ ự
app
ụ ệ ộ
W
ext
= ½ kx
f
2
– ½ kx
i
2
(7.16)
9
Trong đó x
i
và x là v
f
ị trí đầu và cuối của vật tính t vừ ị trí cân b ng x = 0. Công này b ng ằ ằ
với độ ột đại lượ chênh lệch giữa giá trị đầu và giá trị cuối của m ng gắn với cấu hình của hệ.
Do đó thế năng đàn hồ được xác đị i của hệ vậ ểt - lò xo có th nh bởi hệ thức:
U
s
= ½ kx
2
(7.17)
Lúc đó ta cũng có phương trình:
W
ext
= ΔU
s
(7.18)
Thế năng đàn hồ ểu là năng lượi có thể hi ng d trong m lò xo b bi n dự trữ ột ị ế ạng. Năng
lượng d này có th ự trữ ể chuyển hóa thành động năng. Quan sát sự biến dạng c a lò xo, có th ủ ể
nhận thấy: Thế năng đàn hồi dự trữ trong lò xo b ng 0 khi lò xo không biằ ến d ng (Uạ
s
= 0 khi x
= 0); n c d trong lò xo ch khi lò xo b giãn hay nén; th i l n ăng lượng đượ ự trữ ỉ ị ế năng đàn hồ ớ
nhất khi lò xo đạt đến độ nén ho giãn l n nh t; thặc độ ớ ấ ế năng đàn hồ dương bởi luôn n luô i vì
x
2
luôn dương.
Hình 7.11 S bi ng gi a th i a h . ự ến đổi năng lượ ữ ế năng đàn hồ và động năng củ ệ
Trên hình 7.11 là m t bi u di quan tr ng vộ ể ễn đồ thị ọ ề năng lượ ệ, đượng của một h c gọi là
biểu đồ thanh năng lượ ng. Biểu đồ thanh năng lượ ọng đểng là một đồ thị quan tr biểu diễn
thông tin v ng c a h . u ng, tr c tung bi u di n giá tr ề năng lượ ủ ệ Trên biể đồ thanh năng lượ ụ ể ễ ị
năng lượng, trục hoành cho th y các loấ ại năng lượng có trong hệ.
10
Trong hình 7.11a, không có năng lượ ởi vì lò xo đang thảng nào cả, b lỏng còn hộp thì
không chuy ng. ển độ
Trong hình 7.11b và c, tác nhân bên ngoài th c hi n công trên h . Do lò xo b nén l i nên ự ệ ệ ị ạ
có th i trong h vì h p v c gi ế năng đàn hồ ệ. Không có động năng trong hệ ộ ẫn đang đượ ữ
Trong hình 7.11d, hộp được th ra cho chuy ng v phía bên ph i trong khi vả ển độ ề ả ẫn tương
tác với lò xo. Do đó, thế năng đàn hồ ảm trong khi động năng củ i của hệ gi a hệ tăng.
Trong hình 7.11e, lò xo tr v u và hở ề chiều dài ban đầ ệ chỉ còn động năng do sự chuyển
độ ộng của cái h p.
Câu h i 7.5:ỏ Một trái banh
gắn v i mớ ột lò xo nhẹ được
treo thẳng đứng như hình
7.12. Khi kéo trái banh xu ng ố
dưới kh i v trí cân b ng rỏ ị ằ ồi
thả ra thì trái banh s dao ẽ
động lên xuống.
(i) Nếu hệ gồm trái banh, lò
xo và Trái đất thì có nh ng ữ
dạng năng lượng nào trong
quá trình chuy ển động đó: (a)
động năng và thế năng đàn hồi (b) động năng và thế năng hấp
dẫn (c) i và thđộng năng, thế năng đàn hồ ế năng hấp dẫn (d)
thế năng đàn hồi và thế năng hấp dẫn.
(ii) Nếu thì có nh ng dhệ g m trái banh và lò xoồ ữ ạng năng
lượng nào trong quá trình chuyển động đó: (a) động năng và
thế năng đàn hồi (b) động năng và thế năng hấ p dẫn (c) động
năng, thế năng đàn hồ năng hấ năng đàn i và thế p dẫn (d) thế
hồi và th p d n. ế năng hấ ẫ
L c b o toàn và l không b o toàn ự ả ực ả
Trong ph n này ta s tìm hi u m t loầ ẽ ể ộ ại năng lượng có th ể
tồn trữ trong m t h . Loộ ệ ại năng lượng đó liên hệ với nhi ệt độ
của h c gệ, đượ ọi là nội năng, E
int.
Trong ví d trên hình 7.13ụ ,
giả s ta dùng tay tác d ng l c gia t c cu t sang ử ụ ự ố ốn sách trượ
phải trên một b m t c a mề ặ ủ ột chi c bàn n ng. mế ặ Ở đây, bề ặt
có ma sát nên sau khi thôi tác d ng l c thì cu n sách s ụ ự ố ẽ
chuyển động chậm lại rồi dừng hẳn. Xét hệ chỉ là bề mặt mà
cuốn sách trượt trên đó. Lực ma sát mà cu n sách tác d ng ố ụ
lên b m t th c hi n công. Khi cu n sách chuy ng sang ề ặ ự ệ ố ển độ
bên ph i, l c ma sát tác d ng lên b m ng sang ph i và ả ự ụ ề ặt hướ ả
điểm đặ ực cũng dị ải. Do đó công thựt l ch chuyển sang ph c
hiện trên bề mặt là dương nhưng bề mặt không dịch chuyển
Hình 7.12 Câu h i 7.5. ỏ
Hình 7.13 Biểu đồ năng
lượng khi có ma sát: động
năng của hệ (gồm cuốn sách
và b m t) bi i thành nề ặ ến đổ ội
năng khi cuốn sách chuyển
động chậm dần
11
sau khi cu n sách ng t. Công th c hi n trên hố ừng trượ ự ệ ệ là công dương song cả động năng và
thế năng của hệ không thay đổ ậy năng lượng đó nằi. V m ở đâu?
Từ kinh nghi m h ng ngày, có th nh n bi t r ng khi cu t trên b mệ ằ ể ậ ế ằ ốn sách trượ ề ặt thì sẽ
làm b m y, công th c hi n trên hề ặt nóng lên. Như vậ ự ệ ệ đã làm nóng hệ lên mà không tăng tố c
độ hay thay đổ ệ. Ngườ ọi năng lượ ệt đội cấu hình của h i ta g ng liên hệ với nhi của hệ là nội
năng, ký hi u là ng hệ E
int.
Trong trườ ợp này, ma sát đã thực hiện công trên b m t, truy n cho ề ặ ề
hệ một năng lượng dướ ội năng còn động năng và thế năng củi dạng n a hệ vẫn giữ nguyên
không thay đổi.
Bây gi , ta xét h g m có cu n sách và b m t. B u h n sách ờ ệ ồ ố ề ặ an đầ ệ có động năng vì cuố
đang di chuyển. Trong khi cuốn sách trượt trên b m t thì nề ặ ội năng của hệ tăng lên vì cả cuốn
sách và b mề ặt đều ấm hơn trước đó. Khi cuốn sách d ng l a hừ ại, động năng củ ệ đã chuyển
hóa hoàn toàn thành n a h c ma sát m t l c không b o toàn, tác d ng ội năng củ ệ. Ở đây, lự – ộ ự ả ụ
giữa các thành ph n c a hầ ủ ệ đã chuyển hóa động năng củ ội năng.a hệ thành n
7.7.1 Lực b o toàn (lả ực thế)
Công th c hi n b i m t l c tác d ng lên m t ch m làm ch m này chuy ng ự ệ ở ộ ự ụ ộ ất điể ất điể ển độ
giữa hai điể ển độ ất điểm đó thì lựm mà không phụ ộ thu c vào quỹ đạo chuy ng của ch c này
đượ ọc g i là lực b o toàn (lả ực thế).
Do đó, công thực hi n b i l c b o toàn tác d ng lên mệ ở ự ả ụ ột ch m chuy ng trên mất điể ển độ ột
quỹ đạo kín b ng 0. Qu o kín là qu u trùng v m cu ằ ỹ đạ ỹ đạo mà điểm đầ ới điể ối.
Lực h p d n và l i là nh ng ví d n hình c a l c b o toàn. ấ ẫ ực đàn hồ ữ ụ điể ủ ự ả
Thế năng của một hệ gắ ền li n với một l c b ng gi a các thành phự ảo toàn nào đó tác dụ ữ ần
của h t cách t ng quát, công W c th c hiệ đó. Mộ ổ
int
đượ ự ện b i m t l c b o toàn do m t thành ở ộ ự ả ộ
phần c a h tác d ng lên m t thành ph n khác c a h khi c u hình c a h i s b ng ủ ệ ụ ộ ầ ủ ệ ấ ủ ệ thay đổ ẽ ằ
hiệu th a h t i vế năng củ ệ ạ ị trí đầu và vị trí cuối.
W
int
= U U -
i
–
f
= ΔU (7.19)
Công dương thực hiện bởi một tác nhân bên ngoài W
ext
làm
tăng thế năng củ Trong khi đó, c a hệ. ông do một thành phần của
hệ thực hi n W b i l c b o toàn bên trong m t h cô l p là ệ
int
ở ự ả ộ ệ ậ
nguyên nhân làm gi m th a h . ả ế năng củ ệ
7.7.2 Lực không b o toàn (lả ực phi th ) ế
Các l c không thự ỏa mãn các điều ki n c a l c bệ ủ ự ảo toàn được
gọi là l c không b o toàn. Công th c hi n b i m t lự ả ự ệ ở ộ ực không b o ả
toàn phụ thuộc vào quãng đường dịch chuyển.
Lực không b o toàn tác d ng bên trong h s làm biả ụ ệ ẽ ến đổi cơ
năng E
mech
của hệ.
E
mech
= K + U (7.20)
với K bao gồm động năng của tất c các thành ph n chuyả ầ ển động
của h , và U bao g m tệ ồ ất cả các dạng thế năng của hệ.
Hình 7.14 Công thực
hiện b i lở ực ma sát ph ụ
thuộc vào quãng đường
dịch chuy n cể ủa vật
12
Như trên hình 7.14, nếu ta dịch chuy n cu n sách t ể ố ừ điểm A đến điểm B theo m ng ột đườ
thẳng v i m t t i t ng l i l nh ớ ộ ốc độ không đổ hì công để chố ạ ực ma sát trên quãng đường đó sẽ ỏ
hơn khi ta dị ốn sách theo đườ A đếch chuyển cu ng cong từ n B. Bởi vì công thực hiện phụ
thuộc vào quãng đường dịch chuyển nên lực ma sát là lực không bảo toàn (không phải lực
thế).
Liên h gi a l o toàn và th ệ ữ ực bả ế năng
Ta định nghĩa ột đại lượng được xác địhàm thế năng của một hệ là m nh sao cho công
thự ực hiện bởi một l c bảo toàn bên trong hệ bằng nhưng trái dấ ới độ năng u v biến thiên thế
của h . ệ
Gi
ả s l c b o toàn ử ự ả 𝐹
tác d ng gi a các h t trong m t h làm cho m t h t di chuy n dụ ữ ạ ộ ệ ộ ạ ể ọc
theo tr c th c hi n b i l
ục x thì công đượ ự ệ ở ực 𝐹
là:
(7.21)
ΔU = U
f
– U
i
âm khi F và x cùng hướng.
Do đó, lự năng theo hệc bảo toàn liên hệ với hàm thế thức:
x
dU
F
dx
(7.22)
Mối liên hệ này có nghĩa là thành phần theo phương x của lực bảo toàn tác dụng lên một
phần t c a h bử ủ ệ ằng nhưng trái dấu với đạo hàm c a hàm th ủ ế năng theo biến x. Từ đây ta thấy
thế năng U là một đại lượng quan trọng bởi vì có thể tìm được lực thế từ nó.
Xét l ng h p l c tác d ng c a lò xo, ta có: ại trườ ợ ự ụ ủ
2
1
2
s
s
dU
d
F kx kx
dx dx
(7.23)
Kết qu nh lu t Hooke. ả thu được đúng như đị ậ
Giản đồ năng lượ ng và sự cân bằng
Chuyển độ ợc quan sát qua đồ trí và năng lượng của một hệ có thể đư thị biểu diễn vị ng
của nó.
Cân b ng bằ ền
Trong ví d c a m t h lò xo h , chi c h ng gi a 2 v ụ ủ ộ ệ – ộp như trên hình vẽ ế ộp dao độ ữ ị trí x
= ±x
max
, chiếc h p luôn chuy ng có gia t c vộ ển độ ố ề phía = 0 và khi nó nx ằ ạm yên t i v trí này ị
thì ch có tác d ng m t l c t bên ngoài m i làm cho nó r i kh i v v = 0 ỉ ụ ộ ự ừ ớ ờ ỏ ị trí đó. Do đó, ị trí x
là vị ệ trí h n ng thái ằm ở trạ cân b ng bằ ền. B t c s d ch chuy n nào kh i vấ ứ ự ị ể ỏ ị trí cân b ng bằ ền
này đề trí đó. Mộu có một lực kéo vật trở về vị t cách tổng quát, những cấu hình của một hệ
nằm ở trạng thái cân b ng b ng v i m t hàm th c c tiằ ền tương ứ ớ ộ ế năng U(x) có giá trị ự ểu.

int
f
i
x
x
x
W F dx U
13
Trạng thái cân b ng b c bi u di ng hình vằ ền đượ ể ễn trên đồ thị năng lượ như ẽ. Ta thấy cân
bằng b n s ng v i v trí U(x) có giá tr nh nh t, còn và ề ẽ tương ứ ớ ị ị ỏ ấ x = x
max
x = -x
max
được gọi
là các . điểm quay đầu
Hình 7.15 a- Hàm th c v trí x b- L c h i ph c lò xo tác d ng lên v t luôn ế năng phụ thuộ ị ự ồ ụ ụ ậ
hướ ịng về v trí cân bằng bền x = 0.
Cân b ng không b n ằ ề
Bây gi , ta xét mờ ột chất điểm chuy ng d c theo ển độ ọ
trục x dưới tác dụng c a m t l c b ủ ộ ự ảo toàn F(x) có đồ thị
bi iểu diễn U(x) như hình vẽ bên dướ . Trong trường hợp
này, F
x
= 0 t = 0, cho nên ch ng thái cân ại x ất điểm ở trạ
bằng. t vTuy nhiên, đây là mộ ị trí cân b ng không bằ ền
bởi vì khi ch m r i khất điể ờ ỏi v trí x = 0 sang trái hay ị
sang ph u có l c tác d y v t xa kh i v trí ải thì đề ự ụng đẩ ậ ỏ ị
đó hướ ăng nhỏ hơn. Mộng tới một vị trí có thế n t cách
tổng quát, những c u hình c a m t hấ ủ ộ ệ n ng thái ằm ở trạ
cân b ng không b ng v i m t hàm thằ ền tương ứ ớ ộ ế năng
U(x) có giá tr c ị ực đại.
Trạng thái cân b ng không b c bi u di n trên ằ ền đượ ể ễ
đồ ị th năng lượ như tương ứng hình vẽ. Ta thấy cân bằng không bền sẽ ng với vị trí U(x) có
giá tr l n nh t. ị ớ ấ
Cân b ng phiằ ếm định là tr ng thái mà th i trong mạ ế năng U không đổ ột vùng nào đó, do
đó một sự dịch chuyển nhỏ khỏi một vị trí trong vùng này không gây ra sự xuất hiện của lực
kéo v v y ra v trí m ề ị trí cũ hoặc đẩ ị ới.
Tóm tắt chương 7
Một hệ thường g p nh t là m t ch m, m t h m ho c m t vùng không gian có ặ ấ ộ ất điể ộ ệ chất điể ặ ộ
thể thay đổi kích thướ ới môi trườc và hình dạng. Biên giới của hệ phân chia hệ v ng.
Hình 7.16 Hàm th ế năng phụ
thuộc v i v i m t chị trí x đố ớ ộ ất
điể ịm có v trí cân bằng không
bền x = 0.
14
Công (ký hi u là ) c hi n b i m t tác nhân tác d ng m t ngo i l i lên hệ W thự ệ ở ộ ụ ộ ạ ực không đổ ệ là
một đại lượng được xác định bằng tích c l n l c F v d ch chuy n của độ ớ ự ới độ ị ể Δr ủa điểm đặt
lực nhân v i cos vớ θ, ới θ là góc t o b dich chuy n. ạ ởi vectơ lực và vectơ độ ể
W = FΔr cosθ
Nếu l c tác d ng lên m t ch i thì công l c sinh ra khi ch m chuy ng ự ụ ộ ất điểm thay đổ ự ất điể ển độ
dọc theo trục x trên quãng đường d ch chuy n t vị ể ừ ị trí đầu x
i
đến vị trí cu i x ố
f
là:
f
i
x
x
x
W F dx
F
x
là thành ph n hình chi u c a lầ ế ủ ực 𝐹
󰇍
󰇍
󰇍
trên tr c x. ụ
Động năng c a m t ch m có kh ng m chuy ng v i t v là ủ ộ ất điể ối lượ ển độ ớ ốc độ
K=
1
2
mv
2
Thế năng hấp dẫn c a h t khi ch m n cao y phía trên b mủ ệ chất điểm-Trái đấ ất điể ằm ở độ ề ặt
Trái đất là
U
g
= mgy
Thế năng đàn hồi tích tr trong m c ng k là ữ ột lò xo có độ ứ
𝑈
𝑠
=
1
2
kx
2
Một lực được g i là ọ lực b o toàn (l c th ) ả ự ế nếu công c hi n b i l ên m t chthự ệ ở ực đó tr ộ ất điểm
làm ch m này chuy ng gi hai m không ph c vào qu o chuyất điể ển độ ữa điể ụ thuộ ỹ đạ ển động
của ch Ngoài ra, m t l ) nất điểm đó. ộ ực là lực b o toàn (lả ực thế ếu công thực hi n b i lệ ở ực đó
trên m t ch m làm ch m này chuy ng trên m t qu o kín b ng 0. M t lộ ất điể ất điể ển độ ộ ỹ đạ ằ ộ ực
không th a mãn nh u ki n trên c g i là ỏ ững điề ệ đượ ọ l )ực không b o toàn (lả ực phi thế
Cơ năng của mộ ổt hệ ằ b ng t ng c ủa động năng và thế năng
E
mech
= K + U
Định lý công – động năng: Công do ngo i lạ ự ự ỉc th c hiện trên một hệ và làm cho hệ ch thay
đổ
i t cốc độ ủa nó thì
W
ext
= W
f
− W
i
= ∆K=
1
2
mv
f
2
−
1
2
mv
i
2
Hàm th
ế năng U có th ể được liên kết ch vỉ ới một l c b o toàn. N u mự ả ế ột lực 𝐹
tác d ng giụ ữa
các thành ph n c a mầ ủ ột hệ và một phần t c a h ử ủ ệ đó chuyển động d c theo tr c x t v u ọ ụ ừ ị trí đầ
x
i
đến v trí cu i xị ố
f
thì độ biến thiên thế năng củ ằng nhưng trái dấ ực đó a hệ b u với công do l
thực hiện
15
∆U= U − U = −
f i
∫ F
x
dx
x
f
x
i
Câu h i lý thuyỏ ết chương 7
1. Alex và John đang đưa các tủ giống hệt nhau lên xe tải. Alex nh c t c a mình th ng t ấ ủ ủ ẳ ừ
mặt đất lên xe tải, trong khi John trượ ặt đất tủ của mình trên một tấm ván nghiêng từ m t
lên xe t i. Tuyên b nào c th c hi n trên h t - Trái ả ố sau đây là chính xác về công đượ ự ệ ệ ủ
đất?
(a) Alex và c hi n cùng m John thự ệ ột lượng công như nhau.
(b) Alex th c hi n nhi ự ệ ều công hơn John.
(c) John th c hi n nhiự ệ ều công hơn Alex.
(d) Không có phát bi vì không bi t l c ma sát. ểu nào đúng cả ế ự
(e) Không có phát bi c vì không bi t góc nghiêng. ểu nào đúng ả ế
2. L ực pháp tuy n có th c hi n công không? N u không thì cho bi t t i sao không? Nế ể thự ệ ế ế ạ ếu
có thì hãy cho ví d ? ụ
3. Thảo lu n xem li u có b t kậ ệ ấ ỳ công nào đượ ởi các đối tượng sau đây hay c thực hiện b
không và n u có thì li m: ế ệu công đó là công dương hay công â
(a) Một con gà bươi đất,
(b) Một người đang nghiên cứu,
(c) Một c n c u nâng m t thùng bê tông, ầ ẩ ộ
(d) Lực hấp dẫn tác dụng lên thùng bê tông trong ph n (c), ầ
(e) Cơ chân người trong hành độ của ng ngồi.
4. 4. Khi một con l ng qua l i, lắc dao độ ạ ực tác d ng lên v t treo g m có: (a) l c h p d n, ụ ậ ồ ự ấ ẫ
(b) l a dây treo, và c) l c c n c a không khí. ực căng củ ự ả ủ
(i) Lực nào trong s u có, không sinh công trên v t treo vào b t c lúc nào? ố đó, nế ậ ấ ứ
(ii) Lực nào trong s t treo trong su t quá trình ng cố đó sinh công âm trên vậ ố chuyển độ ủa
con l ắc?
5. Bạn đang sắ ếp sách trong thư việ sàn lên đếp x n. Bạn nhấc một quyển sách từ n giá trên
cùng. Động năng củ ốn sách trên sàn là không và động năng của cu a cuốn sách ở giá trên
cùng cũng là không, vì vậy không có thay đổi động năng nhưn ạn đã thựg b c hiện công
khi nâng quy n sách. V nh lý công - ng có b vi ph m? Hãy gi i thích. ể ậy đị độ năng ị ạ ả
6. Một v t có kh c th t ng thậ ối lượng m đượ ả rơi từ ầ ứ 4 của tòa nhà xu ng, v t có t v ố ậ ốc độ
khi ch t. H i nên thạm đấ ỏ ả rơi vật đó từ ấy để ốc độ ủa nó tăng gấp đôi khi tầng thứ m t c
chạm đấ ầng đềt? Giả sử độ cao của các t u bằng nhau.
(a) Tầng 6
(b) Tầng 8
(c) Tầng 10
(d) Tầng 12
(f) Tầng 16
16
Bài t p ậ chương 7
1.
Một hạt mưa khối lượ kg rơi thẳng đứng 3,35.10
-5
ng với tốc độ không đổi dưới tác dụng
của tr ng l c và l c c n không khí. Xem h t ch m. Hãy tính công thọ ự ự ả ạt mưa là mộ ất điể ực
hiện trên hạt mưa khi nó rơi một đoạn 100 m b i ở
(a) Lực hấp dẫn.
(b) Lực cản không khí.
2. Một cái h p có ộ khối lượng m = 2,50 kg được đẩy trượt trên
một m t bàn n m ngang, không ma sát m n d = 2,20 ặ ằ ột đoạ
m b i m l F = 12 N, h p vở ột lực không đổi có độ ớn ợ ới
phương ngang
một góc . Hãy tính = 25,0
o
như hình vẽ
công c hi n trên cái h p b thự ệ ộ ởi:
(a) Lực tác dụng.
(b) Phản l c l c pháp tuy n c a bàn. ự ự ế ủ
(c) Trọng l ực.
(d) Tổng h p l c tác d ng lên cái h p. ợ ự ụ ộ
3. L ực tác d ng lên m t chụ ộ ất điểm thay đổi như trên
hình v . Hãy tính công l c th c hi n trên chẽ ự ự ệ ất điểm
khi nó di chuy n ể
(a) Từ x = 0 đến x = 8,00 m
(b) Từ x = 8,00 m đến x = 10,0 m
(c) Từ x = 0 đến x = 10,0 m.
4. Khi m t v t có kh ng 4,00 kg u ộ ậ ối lượ được treo ở đầ
một lò xo nh thì lò xo b dãn ra m n 2,50 cm. N u v t th 4,00 c l y ra, ẹ ị ột đoạ ế ậ ể kg đượ ấ
(a) Hỏi lò xo s dài bao nhiêu n u vẽ ra ế ật có kh ng 1,50 c treo lên ối lượ kg đượ đó?
(b) Tính công ngo i lạ ực ph i th c hi n kéo dãn lò xo dài ra 4,00 cm t v trí bả ự ệ để ừ ị ình
thường c a nó? ủ
5. 5. Giữ cho m t lò xo nh ộ ẹ có độ c ng 3,85 N/m b nén mứ ị ột đoạn 8,00 cm v i m t v t n ng ớ ộ ậ ặ
0,250 kg ở u bên trái và m t v t n ng 0,500 kg u bên ph i c a lò xo, c hai vđầ ộ ậ ặ ở đầ ả ủ ả ật đều
nằm yên trên m t ph ng n ngang. Lò xo tác d ng l c lên m i vặ ẳ ằm ụ ự ỗ ật và có xu hướng đẩy
hai v t ra xa. Th cho hai v ng th i chuy ng t ng thái ngh . Tính gia tậ ả ật đồ ờ ển độ ừ trạ ỉ ốc
chuyển độ ma sát động của mỗi vật nếu hệ số ng giữa mỗi vật và bề mặt là a- 0, b- 0,100
và c- 0,462.
6. Tác động một lực F
󰇍
= (4x + 3yi j), trong đó F
󰇍
đo bằng Newton và x và y ng m, lđo bằ ên
1 v v t di chuy n theo x t g c hật để ậ ể trục ừ ố ệ trụ đếc tọa độ n vị trí x= 5,00 m. Tính công
W
=
∫
𝐹
𝑑𝑟 l c hi n trên v ực đã thự ệ ật.
7. Một v t n ng 3,00 kg có v n t c (6,00 - 2,00 ) m/s ậ ặ ậ ố 𝑖 𝑗 .
(a) Tính động năng của vật.
17
(b) Nếu v n t c c a v i t i giá tr (8,00 + 4,00 ) m/s thì công th c hi n trên vậ ố ủ ật thay đổ ớ ị 𝑖 𝑗 ự ệ ật
là bao nhiêu?
8. Một người đẩy m t thùng g n ng 35,0 kg vộ ỗ ặ ới tốc độ không đổ ột đoại m n dài 12,0 m trên
một sàn gỗ. Lực đẩy F có phương ngang, ớn không đổ ực đã thự độ l i. Công mà l c hiện là
350 J.
(a) Xác định độ lớn của lực F.
(b) Hãy mô t ng ti p theo c a cái thùng n u bây gi ng mả chuyển độ ế ủ ế ờ người đó tác dụ ột
lực l c F. ớn hơn lự
(c) Điều gì s x i v i cái thùng n u l c tác d ng nh ẽ ảy ra đố ớ ế ự ụ ỏ hơn F?
9. Một v t nậ ặng 5,75 kg băng qua gố ọa độ ời điểc của hệ trục t tại th m t = 0 v i v n t c có ớ ậ ố
thành ph n theo tr c x là 5,00 m/s và theo tr c y là -3,00 m/s. ầ ụ ụ
(a) Động năng củ ời điểm đó là bao nhiêu?a vật tại th
(b) Tại mộ ởt thời điểm sau đó t = 2,00 s, vật tại vị trí x = 8,50 m và y = 5,00 m. H i lỏ ực
không đổ ời gian đó là bao nhiêu?i tác dụng lên vật trong khoảng th
(c) Tốc độ ời điể của vật tại th m t = 2,00 s là bao nhiêu?
10. Một tảng đá 0,20 kg được giữ ở độ cao 1,30 phía nh c a m c và sau m trên đỉ ủ ột giếng nướ
đó rơi vào đthả ó. Giếng có chi u sâu 5,0 m. n g c th a gi c, ề Chọ ố ế năng tại đĩnh củ ếng nướ
tính
(a) Thế năng hấ hòn đá – Trái đất trước khi đá rơi.p dẫn của hệ
(b) Thế năng hấ hòn đá – Trái đất khi hòn đá ở đáy giếp dẫn của hệ ng.
(c) Độ ừ thay đổ năng hấi thế p dẫn của hệ t lúc đầu đế úc hòn đá ở đáy giến l ng.
11. Một v t chuy ng trong m t ph ng xy trong hình ậ ển độ ặ ẳ như
vẽ và chịu m t lộ ực ma sát v l n ới độ ớ không đổi 3,00 N,
luôn hướng ngược với vận tốc của vật. Hãy tính công mà
bạn ph c hi n ải thự ệ để trượt v t v i t khi ậ ớ ốc độ không đổi
vật chuy n ể động
(a) Dọc theo đường màu tím t n A r i quay l i theo ừ O đế ồ ạ
đường màu tím trở về O.
(b) Dọc theo đường màu tím từ O đến C rồi theo đường
dẫn màu xanh dương trở về O.
(c) Theo đường màu xanh t O t i C r v O. ừ ớ ồi theo đường màu xanh dương trở ề
(d) Mỗi câu tr l i c a b n ph khác a vi c quan sát này là gì. ả ờ ủ ạ ải không. Ý nghĩa củ ệ
12.
Hàm thế năng củ ực tác độa một hệ có dạng U = 3x y
3
– 7x. Tìm l ng tại điểm (x,y).
13. Một lực thế
2 4
x
F x
(N; m) tác d ng lên chụ ất điểm nặng 5 kg. Khi chất điểm d ịch
chuyển theo tr c x t ụ ừ
1 5x m x m
. Hãy tính:
(a) Công c a lủ ực
x
F
thực hi n lên ch ệ ất điểm.
(b) Độ biến thiên thế năng của hệ vật.
(c) Động năng củ ất điểa ch m tại
5x m
nếu tại điểm
1x m
vận t c nó là 3 m/s. ố
18
14. Một toa xe lửa n ng 6000 kg ch y d ng ray v i ma sát nh có th b qua. Toa ặ ạ ọc theo đườ ớ ỏ ể ỏ
xe được dừng l i nh c ng là k = 1600 N/m ạ ờ hai lò xo như trên hình vẽ. Hai lò xo có độ ứ
1
và k = 3400 N/m. Sau khi lò xo th nh t b nén m t kho ng 30,0 m thì lò xo th hai b
2
ứ ấ ị ộ ả ứ ắt
đầ ụ ự ổ ịu tác d ng và l c t ng hợp của hai lò xo tăng lên như đồ th bên dưới. Sau khi lò xo
thứ ị ừ nhất tiếp xúc với toa xe và b nén m n 50,0 cm thì toa xe dột đoạ ng lại. Hãy tìm tốc
độ ban đầu của toa xe.
15. Một lò xo có độ ứng k = 500 N/m đượ c c buộc chặt tại
đáy của một mặt phẳng nằm nghiêng có góc nghiêng =
20,0
o
như hình vẽ ối lượng m = 2,50 kg đặ. Một vật kh t
phía trên m t ph ng nghiêng cách lò xo m t kho ng d = ặ ẳ ộ ả
0,300 m. Đẩ ển động hướy cho vật chuy ng về phía lò xo
với t dài bốc độ v = 0,750 m/s. Độ ị nén c a lò xo ủ ở thời
điể ừm vật tạm thời d ng l i là bao nhiêu? ạ
| 1/18
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

Chương 7 Năng lượng của một hệ
hiều bài toán có thể giải được nhờ các định luật Newton và các nguyên lý liên quan.
Tuy nhiên, về mặt lý thuyết có nhiều bài toán có thể giải được bằng các định luật
Newton nhưng thực tế thì rất phức tạp. Các bài toán đó lại có thể giải một cách dễ dàng Nbằng một cách khác.
Khái niệm về năng lượng là một trong những chủ đề quan trọng nhất trong khoa học và
kỹ thuật. Mỗi quá trình vật lý xảy ra trong vũ trụ đều liên quan đến việc chuyển hóa từ dạng
năng lượng này sang dạng năng lượng khác. Trên cơ sở khái niệm năng lượng, người ta đã
phát triển những phương pháp mới cho phép giải các bài toán vật lý một cách dễ dàng m à khi
giải bằng các định luật Newton thì lại rất khó khăn. Chương này sẽ giới thiệu khái niệm hệ
và các cách lưu trữ năng lượng trong một hệ.
Hệ và môi trường
Một hệ là một phần nhỏ của cả vũ trụ. Một hệ có thể là một vật hoặc một chất điểm, một
tập hợp nhiều vật hoặc nhiều chất điểm, hay một vùng không gian nào đó. Một hệ sẽ có ranh
giới với bên ngoài. Bên ngoài biên giới của hệ là môi trường. Biên giới của một hệ có thể là
một bề mặt thực hoặc một bề mặt tưởng tượng, không nhất thiết trùng với một bề mặt thực.
Biên giới chia vũ trụ thàn
h hệ và môi trường. Kích thước và hình dạng của một hệ có thể thay đổi theo thời gian.
Ví dụ một hệ: Khi có một lực tác dụng vào một vật trong không gian trống rỗng thì hệ là
vật đó, bề mặt của vật là ranh giới của hệ.
Những điều cần chú ý khi giải toán:  Xác định hệ
 Cũng xác định một ranh giới hệ
 Lực ảnh hưởng lên hệ từ môi trường tác động xuyên qua ranh giới của hệ.
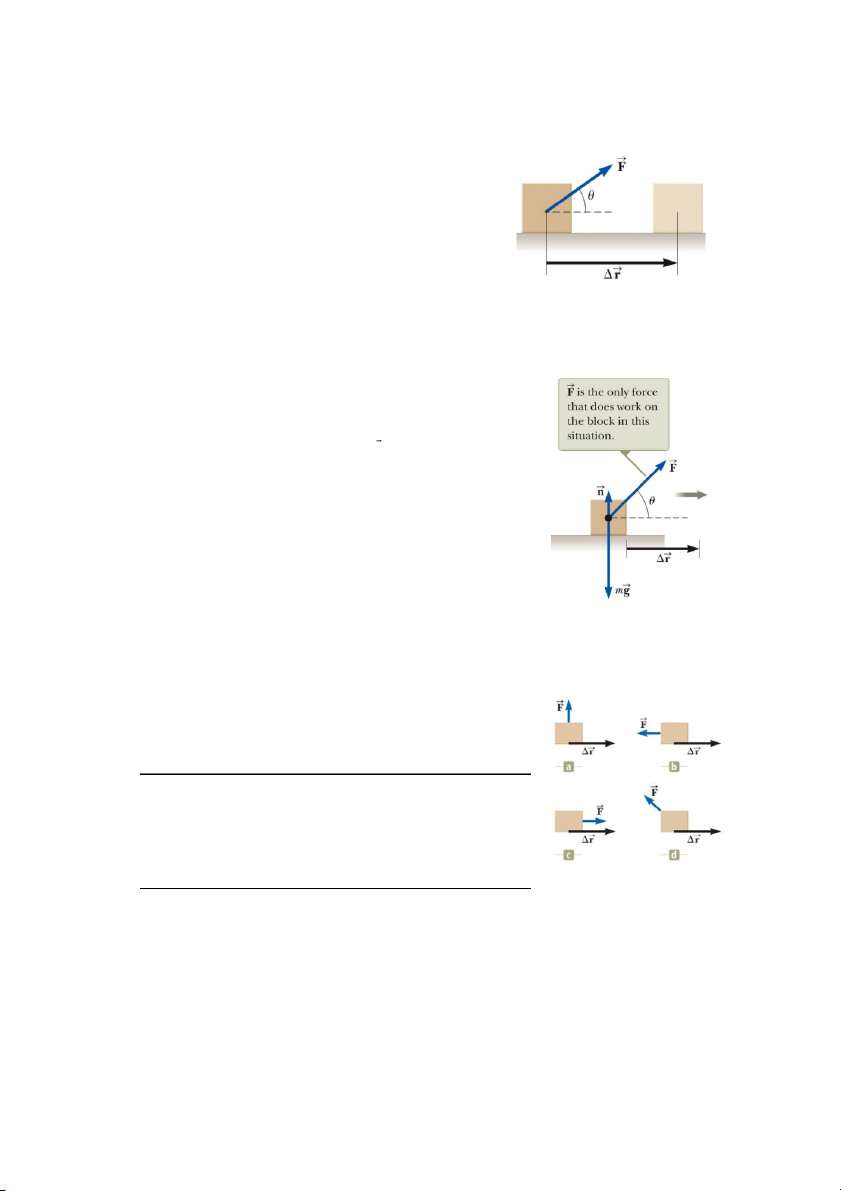
Công thực hiện bởi một lực không đổi
Công (ký hiệu là W) thực hiện bởi một tác nhân tác dụng một ngoại lực không đổi lên hệ
là một đại lượng được xác định bằng tích của độ lớn lực F với độ dịch chuyển Δr của điểm
đặt lực nhân với cosθ, với θ là góc tạo bởi vectơ lực và vectơ độ dich chuyển.
W = FΔr cosθ (7.1) 1
Chú ý rằng độ dịch chuyển ở đây là độ dịch chuyển
của điểm mà lực tác dụng vào.
Lực sẽ không thực hiện công trên một vật chuyển động
nếu điểm đặt lực không chuyển động cùng với phương
dịch chuyển. Công thực hiện bởi một lực làm cho vật dịch
chuyển có độ lớn bằng 0 khi lực vuông góc với phương dịch chuyển.
Độ dịch chuyển trong công thức tính công
Hình 7.1 Một vật dịch chuyển
Nếu lực tác dụng vào một vật rắn được xem như một
dưới tác dụng của một lực
chất điểm thì độ dịch chuyển giống như độ dịch chuyển không đổi.
của chất điểm. Đối với vật biến dạng thì độ dịch chuyển
của vật không giống với độ dịch chuyển mà lực tác dụng vào.
Do đó, để xác định độ dịch chuyển chúng ta chỉ xét đến điểm mà lực tác dụng vào.
Phản lực pháp tuyến và lực hấp dẫn không sinh ra công trên
vật vì cos θ = cos 90° = 0. Chỉ có lực F thực hiện công trên vật .
Dấu của công phụ thuộc vào hướng của lực và hướng của
độ dịch chuyển. Công dương khi lực và độ dịch chuyển có cùng
hướng, công âm khi chúng ngược hướng.
Công là một đại lượng vô hướng. Đơn vị của công là joule (J).
 1 joule = 1 newton. 1 meter = kg.m²/s²  J = N.m
Hình 7.2 Phản lực pháp
Công là một dạng năng lượng trao đổi
tuyến và trọng lực không
Nếu công thực hiện trên một hệ nhận giá trị dương thì năng
sinh công, chỉ có lực 𝐹
lượng được truyền vào hệ; còn nếu công thực hiện trên một hệ sinh công.
nhận giá trị âm thì năng lượng thoát ra khỏi hệ. Nếu một hệ tương
tác với môi trường ngoài thì sự tương tác đó có thể xem như sự
trao đổi năng lượng truyền qua biên giới của hệ. Điều này dẫn
đến một sự thay đổi của năng lượng dự trữ trong hệ.
Câu hỏi 7.1: Lực hấp dẫn Mặt trời tác dụng lên Trái đất giữ
cho Trái đất chuyển động trên quỹ đạo quanh Mặt trời. Giả sử
quỹ đạo là đường tròn. Hỏi công của lực hấp dẫn này thực hiện
khi Trái đất di chuyển một quãng đường trong một khoảng thời
gian ngắn trên quỹ đạo là: (a) bằng không? (b) dương? (c)
âm? (d) không thể xác định được?
Hình 7.3 Hình cho câu hỏi 7.2. 2
Câu hỏi 7.2: Trên hình 7.3, các lực có độ lớn bằng nhau, quãng đường dịch chuyển của vật
sang phải bằng nhau. Hãy sắp xếp theo thứ tự giá trị của công do lực thực hiện trên vật từ
dương nhất đến âm nhất.
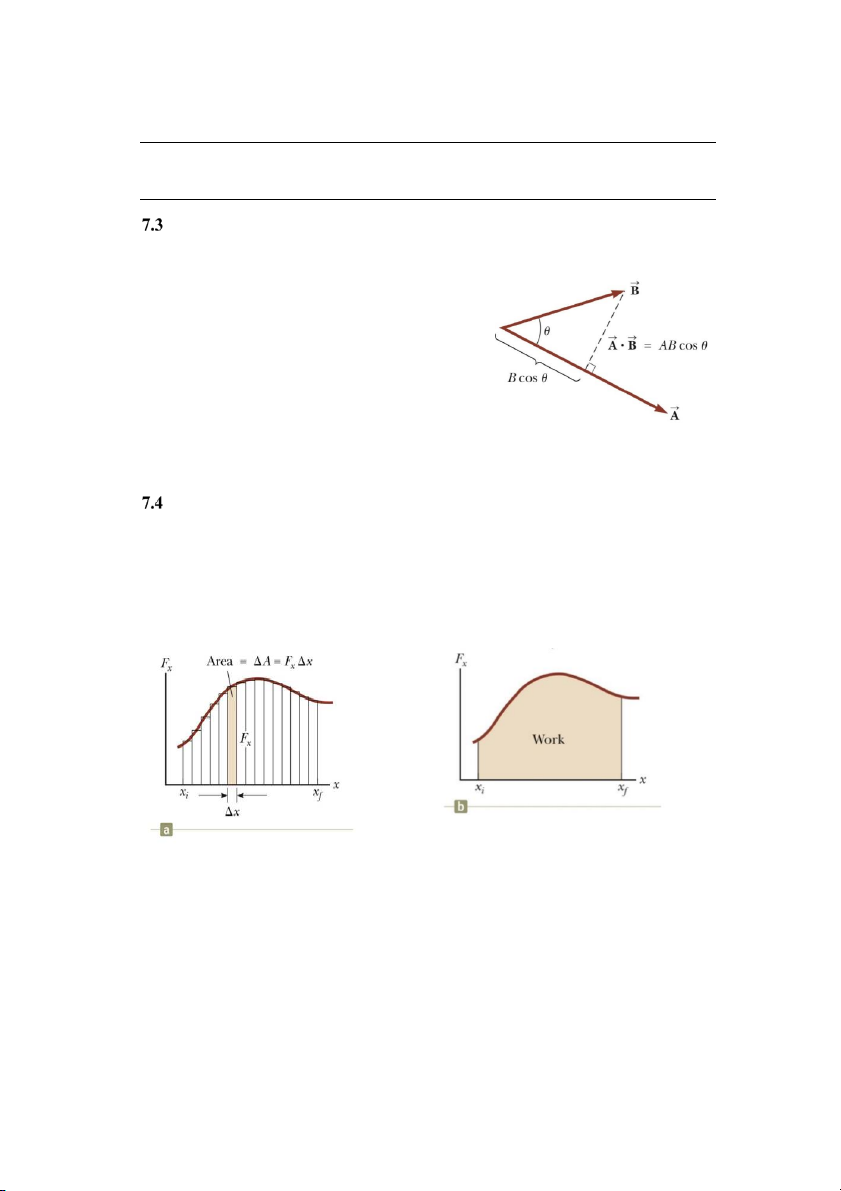
Tích vô hướng 2 vectơ r r r r
Tích vô hướng của hai vectơ A và B , được kí hiệu là AB và có giá trị bằng: r r
A B A B cos r r
Với θ là góc giữa hai vectơ A và B
Tích vô hướng có tính chất giao hoán: r r r r
AB BA và tính chất kết hợp: r r r r r r r
A BC ABAC
Áp dụng vào công thức tính công, ta được:
Hình 7.4 Tích vô hướng 2 vectơ. r r
W F r cos  F  r (7.2)
Công được thực hiện bởi lực có độ lớn thay đổi
Để sử dụng công thức W = FΔrcos θ lực phải không đổi, do đó công thức này không thể
sử dụng cho việc tính công của một lực biến thiê .
n Giả sử rằng trong khoảng dịch chuyển rất
nhỏ Δx, Fx là hằng số thì trong khoảng đó W = FxΔx. Vì vậy, trên cả quãng đường dịch chuyển
từ vị trí đầu xi đến vị trí cuối xf thì: x W F  f x x xi
Hình 7.5 (a) Công sinh ra bởi thành phần Fx của lực khi điểm đặt lực dịch chuyển một đoạn
Δx (b) Công sinh ra bởi thành phần Fx của lực khi điểm đặt lực dịch chuyển từ xi đến xf
Nếu đoạn dịch chuyển Δx tiến tới 0. Ta có: 3 x lim f x    f F x F dx x x x x 0 x i i Do đó,
W   fx F dx (7.3) x xi
Trên đồ thị, công được tính bằng diện tích giới hạn bởi đường cong nằm giữa xi và xf.
Công thực hiện bởi nhiều lực
Nếu có nhiều lực tác dụng lên hệ và hệ có thể xem như một chất điểm, thì tổng công tác
dụng lên hệ là công tác dụng bởi hợp lực:
W W   fx F dx ext  x x i
Kí hiệu “ext” để chỉ công thực hiện bởi các yếu tố tác động từ bên ngoài hệ.
Trong trường hợp tổng quát, độ lớn và chiều của hợp lực có thể thay đổi, lúc đó: x r f r W W   d (7.4) ext  Fr x i
Nếu hệ không thể xem như một chất điểm thì tổng công bằng tổng đại số các công thực hiện bởi từng lực:    W WF. r d ext  (7.5) forces
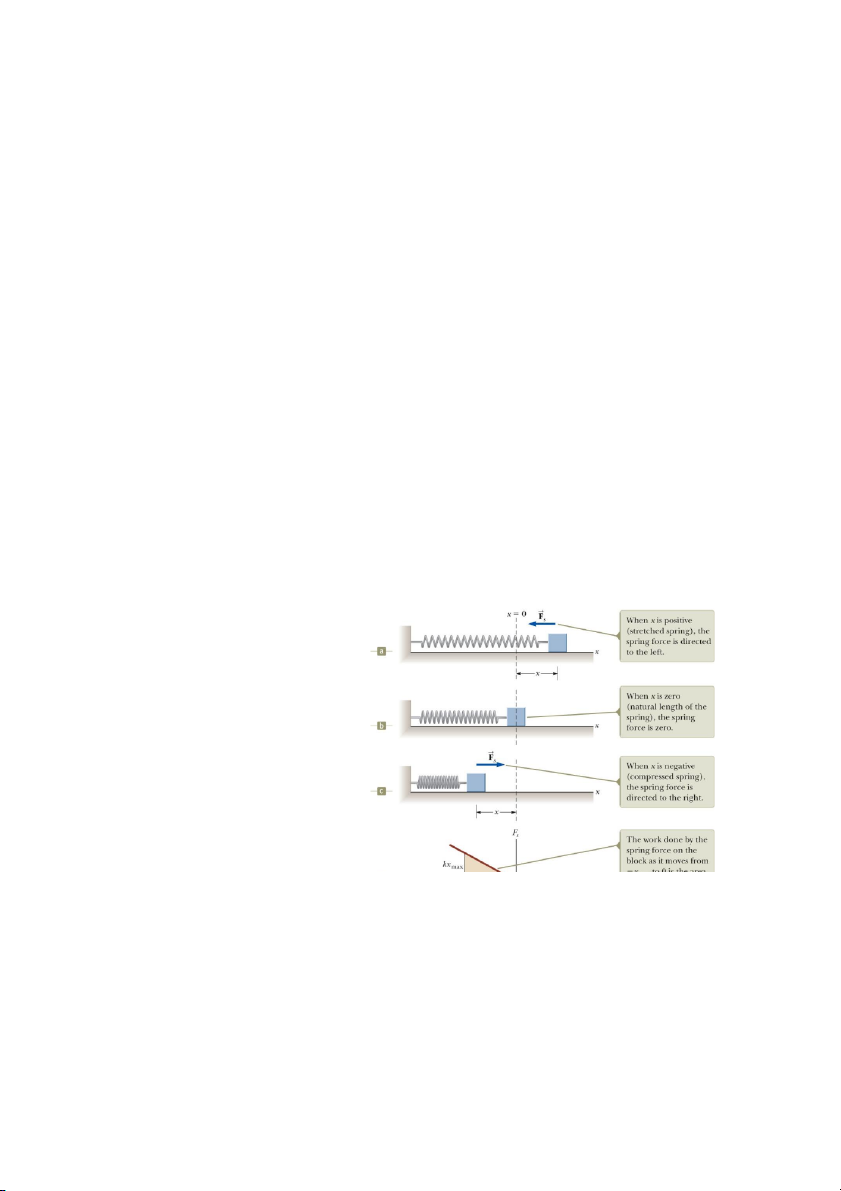
Công thực hiện bởi một lò xo
Đây là một mô hình vật lý cho
trường hợp lực thay đổi phụ thuộc vào vị trí .
Lực đàn hồi (Định luật Hooke)
Lực tác dụng bởi lò xo là
Fs = - kx (7.6)
Trong đó, x là vị trí của chiếc hộp
cách vị trí cân bằng (x = 0), k được
gọi là hệ số đàn hồi và được đo bởi
mức độ cứng của lò xo.
Dạng vectơ của định luật Hooke: r ự ụ ế ộp thay đổi
F F ˆi  kxˆi s x (7.7)
Hình 7.6 L c lò xo tác d ng lên chi c h
theo vị trí x của chiếc hộp 4
Lực tác dụng bởi lò xo luôn có chiều hướng về vị trí cân bằng. Nếu thả hộp ra, nó sẽ dao
động giữa 2 vị trí –x và x. Khi x dương (lò xo bị giãn), lực F nhận giá trị âm; khi x bằng 0 (tại
vị trí cân bằng), lực F bằng 0; và khi x âm (lò xo bị nén), lực F dương.
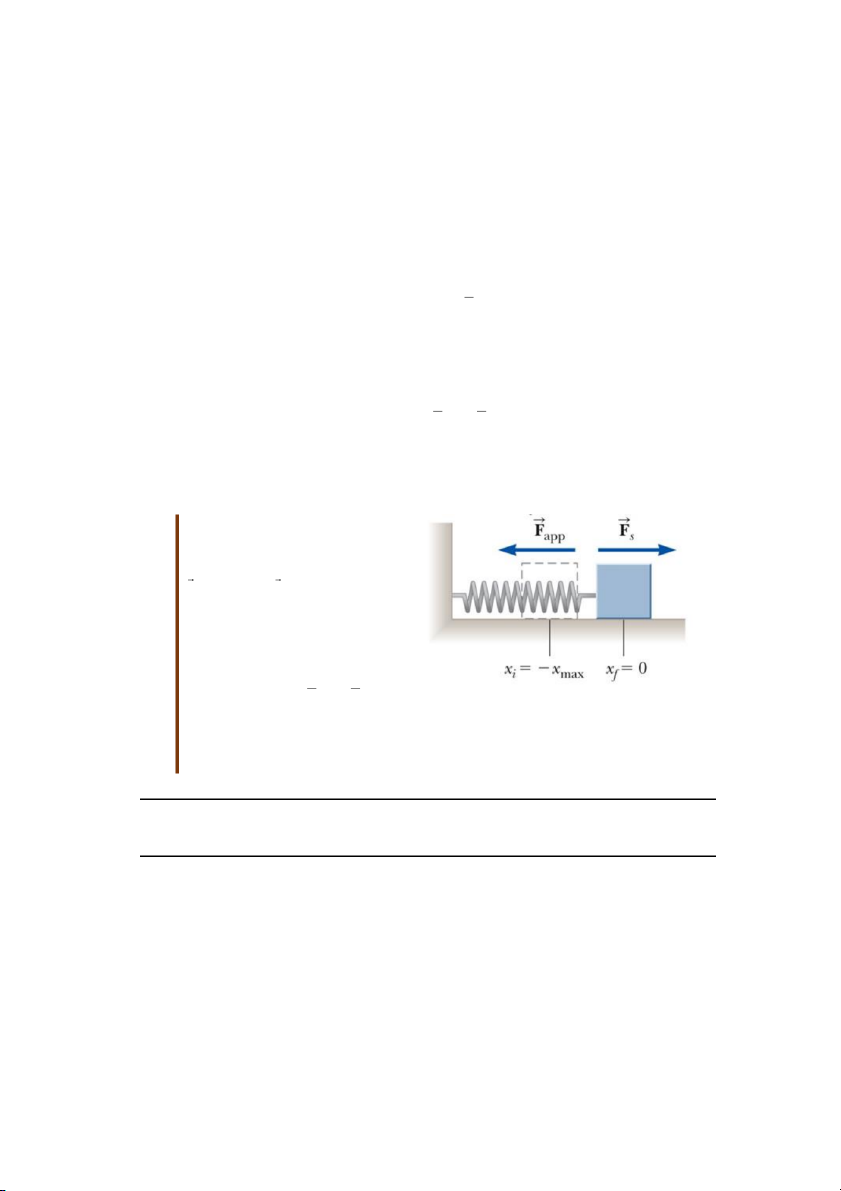
Xem cái hộp là một hệ, công thực hiện khi hộp chuyển động giữa 2 vị trí từ xi = - xmax đến xf = 0 là: r r W xf
F dr kx dx ss
   iˆ  iˆ x i 0   kx 1 2 dx kxmax xmax 2 (7.8)
Còn tổng công thực hiện khi hộp dịch chuyển từ -xmax đến xmax bằng 0.
Khi hộp dịch chuyển một đoạn tùy ý từ x = xi đến x = xf thì công thực hiện bởi lò xo trên hộp là: 1 1 W x kx dx kx 2 kx 2 s      f i f xi 2 2 (7.9)
Nếu điểm cuối trùng với điểm đầu thì W = 0.
Bài tập mẫu 7.1: Lò xo chịu sự tác dụng của một lực
Giả sử rằng có một ngoại lực Fapp
kéo giãn lò xo, lực tác dụng này
bằng với lực đàn hồi của lò xo. F
F ˆi  F   kxˆi  kxˆi app app s
Đối với một đoạn dịch chuyển bất
kì từ xi đến xf th ì công thực hiện bởi lực tác dụng là: x 1 1 Wkx dx kx2 kx2 app      f f i xi 2 2
Hình 7.7 Lò xo chịu tác dụng của ngoại
Công thực hiện bởi lực Fapp khi hộp lực 𝐹𝑎𝑝𝑝 trong quá trình vật di chuyển từ vị
chuyển động từ vị trí –xmax đến x trí xi = -xmax đến xf = 0.
= 0 thì bằng -½ kx2max.
Câu hỏi 7.3: Một cái phi tiêu được nạp vào một khẩu súng lò xo. Lần thứ nhất lò xo bị nén
một đoạn x, lần thứ hai lò lo bị nén một đoạn 2x. Hỏi công để nạp phi tiêu lần thứ hai lớn hơn
lần thứ nhất bao nhiêu lần: (a) 4 lần? (b) 2 lần? (c) bằng nhau? (d) một nữa? (e) một phần tư? 5
Động năng và định lý công - động năng
Một kết quả của công tác dụng vào hệ là làm cho hệ thay đổi vận tốc, ta nói hệ thu được
động năng. Sự thay đổi của động năng là một kết quả khả dĩ của việc thực hiện công để truyền năng lượng cho hệ.
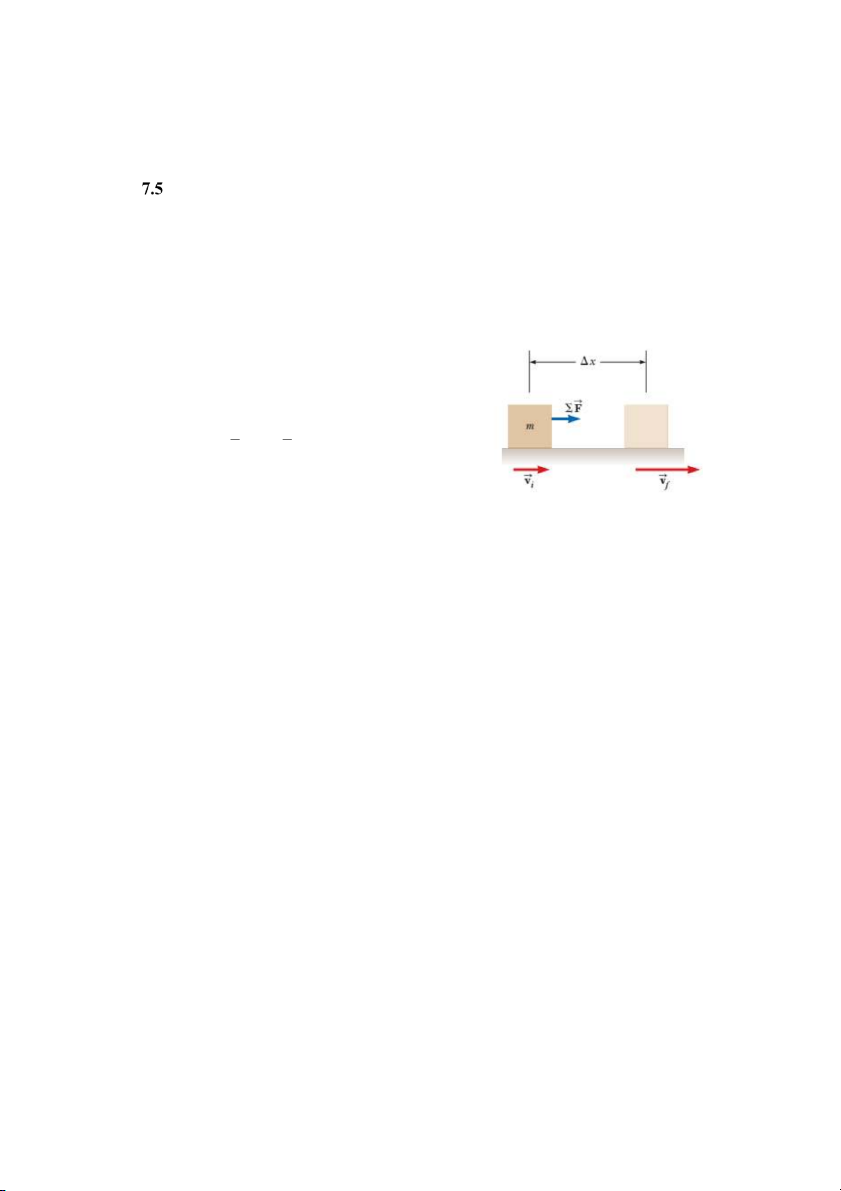
Xét một hệ chỉ có một vật khối lượng m chuyển động dưới tác dụng của tổng hợp lực ∑ 𝐹
như trên hình vẽ. Nếu cả vật và điểm đặt lực đều thực hiện một dịch chuyển ∆𝑟 = ∆𝑥𝑖 =
(𝑥𝑓 − 𝑥𝑖)𝑖 thì công mà tổng hợp lực đã thực hiện là: 𝑥𝑓 𝑥𝑓
𝑊𝑒𝑥𝑡 = ∫ ∑ 𝐹 𝑑𝑥 = ∫ 𝑚𝑎 𝑑𝑥 𝑥𝑖 𝑥𝑖 v Wmv dv extf v i 1 1 W
mv 2  mv 2 ext f i 2 2 (7.10)
Trong đó vi và vf là tốc độ của vật tại vị trí ban đầu xi và vị trí cuối xf.
Hình 7.8. Dưới tác dụng của tổng
Phương trình trên cho thấy công của tổng hợp
hợp lực, vật dịch chuyển một đoạn
lực thực hiện trên vật bằng hiệu số giữa hai giá trị Δx.
cuối và đầu của một đại lượng. Đại lượng này được
gọi là động năng của vật.
K = ½ mv2 (7.11)
Động năng là năng lượng gắn với chuyển động của vật, là một đại lượng vô hướng và có đơn vị g ố
i ng như đơn vị của công là jun (J).
Định lý công - động năng
Phương trình cuối cùng thu được trên đây là phương trình của định lý công – động năng. Wext = Kf – Ki = ΔK (7.12)
Khi công thực hiện trên một hệ và chỉ làm thay đổi tốc độ của hệ, thì tổng công thực hiện
trên hệ bằng độ thay đổi động năng của hệ. Tốc độ của hệ sẽ tăng nếu công dương, tốc độ của
hệ sẽ giảm nếu công âm.
Định lý công - động năng áp dụng cho tốc độ chứ không phải vận tốc. Định lý công -
động năng không đúng nếu có sự thay đổi khác trong hệ bên cạnh sự thay đổi về tốc độ hoặc
có sự tương tác khác với môi trường ngoài. 6
Bài tập mẫu 7.2
Một vật khối lượng 6,0 kg đang nằm yên trên
một bề mặt không ma sát bị kéo sang phải bởi
một lực có phương năm ngang, độ lớn 12 N như
hình 7.9. Hãy tính tốc độ của vật sau khi nó di
chuyển một đoạn dài 3,0 m. Giải:
Chọn hệ chỉ gồm vật. Có 3 ngoại lực tác dụng
lên hệ. Phản lực pháp tuyến và lực hấp dẫn
không thực hiện công vì chúng vuông góc với
Hình 7.9 Bài tập 7.2.
phương dịch chuyển của hệ. Theo định lý công – động năng, ta có:
Wext = ΔK = ½ mv 2 f – 0
𝑣𝑓 = √2𝑊𝑒𝑥𝑡 𝑚 = √2𝐹∆𝑥 𝑚 = √2.12.3,0 6,0 = 3,5𝑚/𝑠
Thế năng của một hệ
Bây giờ chúng ta hãy xem xét một hệ gồm nhiều hơn một
vật mà các vật bên trong hệ tương tác lực với nhau. Ví dụ, một
hệ gồm cuốn sách và Trái đất, hai vật này tương tác với nhau
bằng lực hấp dẫn. Ta sẽ thực hiện một công trên cuốn sách
bằng cách nâng quyển sách thật chậm theo phương thẳng
đứng, cuốn sách đã có một dời chuyển
r  y y ˆj f i
Công thực hiện trên hệ phải xuất hiện như là sự tăng năng
lượng của hệ. Không có sự thay đổi động năng trước khi
quyển sách bắt đầu chuyển động và sau khi quyển sách dừng
lại. Như vậy, năng lượng cung cấp cho hệ từ bên ngoài phải
tồn trữ ở một dạng khác động năng của hệ. Khi cuốn sách
Hình 7.10 Tác nhân bên
được thả rơi hệ có động năng; như vậy, trước khi cuốn sách ngoài nâng từ từ cuốn sách
được thả rơi hệ phải có một khả năng (potential) để thu được
ở độ cao hi lên độ cao hf.
động năng. Ta gọi cơ chế tích trữ năng lượng trước khi cuốn
sách được thả rơi là thế năng (potential energy).
Thế năng là dạng năng lượng được xác định bởi cấu hình của một hệ mà trong đó các
thành phần của hệ tương tác v i
ớ nhau bằng các lực. Các lực này là nội lực của hệ, chỉ liên
quan đến tương tác giữa các thành phần của hệ với nhau. Thế năng luôn gắn liền với một hệ
của 2 hay nhiều vật tương tác lẫn nhau. 7
7.6.1 Thế năng hấp dẫn
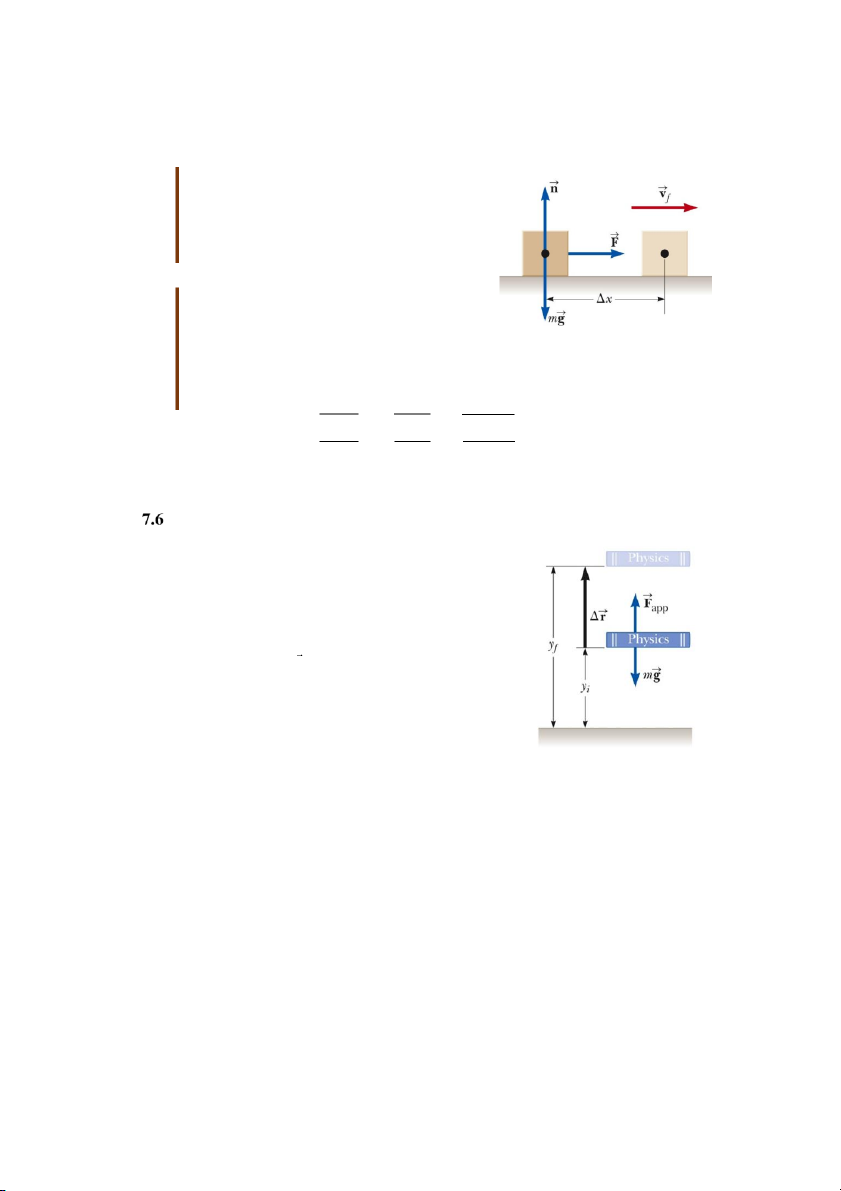
Xét hệ gồm Trái Đất và cuốn sách như hình vẽ. Cuốn sách có khối lượng m đang nằm tại
độ cao yi so với bề mặt Trái đất. Một tác nhân bên ngoài hệ nâng cuốn sách lến độ cao yf một
cách chậm chạp để dịch chuyển không có gia tốc và do đó lực nâng có độ lớn bằng lực hấp
dẫn mà Trái đất tác dụng lên cuốn sách. Công mà lực ngoài thực hiện trên hệ Cuốn sách - Trái đất là: WF r ext  app  W (m ˆ
gj)  y y j ext   f i  ˆ    Wmgy mgy ext f i (7.13)
Phương trình trên cho thấy công của ngoại lực thực hiện trên hệ bằng hiệu số giữa hai giá
trị cuối và đầu của một đại lượng. Công này đã truyền cho hệ một năng lượng và năng lượng
đó tích trữ ở một dạng được gọi là thế năng. Đại lượng mgy được gọi là thế năng hấp dẫn
Ug của hệ vật khối lượng m và Trái đất. Ug = mgy (7.14)
Thế năng là một đại lượng vô hướng. Đơn vị của thế năng là joules (J).
Công có thể làm thay đổi thế năng hấp dẫn của hệ Wext = ΔUg (7.15)
Thế năng hấp dẫn là năng lượng liên kết với một vật, phụ thuộc vào độ cao của vật đó
trên bề mặt của Trái Đất. Thế năng hấp dẫn chỉ phụ thuộc vào độ cao của vật so với bề mặt
Trái Đất. Khi giải các bài toán, chúng ta cần phải chọn một mốc quy chiếu sao cho thế năng
hấp dẫn tại đó bằng một giá trị tham chiếu nào đó, thường là bằng 0. Việc chọn lựa mốc thế
năng là tùy ý. Thông thường một vật nằm trên bề mặt của Trái Đất được xem như có thế năng
hấp dẫn bằng 0. Hoặc các bài toán sẽ đề xuất một mốc thế năng để sử dụng.
Câu hỏi 7.4: Hãy chọn câu trả lời đúng: Thế năng hấp dẫn của một hệ (a) luôn luôn dương.
(b) luôn luôn âm. (c) có thể âm hoặc dương.
7.6.2 Thế năng đàn hồi
Thế năng đàn hồi là một loại năng lượng mà một hệ có lò xo sẽ tích trữ. Khi đó lực tương
tác giữa các thành phần bên trong hệ là lực đàn hồi của lò xo.
Xét hệ gồm có một vật và một lò xo như trên hình vẽ. Lực đàn hồi lò xo tác dụng lên cái hộp là Fs = - kx
Công thực hiện bởi ngoại lực Fapp tác dụng lên hệ lò xo - hộp là: W 2 2
ext = ½ kxf – ½ kxi (7.16) 8
Trong đó xi và xf là vị trí đầu và cuối của vật tính từ vị trí cân bằng x = 0. Công này bằng
với độ chênh lệch giữa giá trị đầu và giá trị cuối của một đại lượng gắn với cấu hình của hệ.
Do đó thế năng đàn hồi của hệ vật - lò xo có thể được xác định bởi hệ thức:
Us = ½ kx2 (7.17)
Lúc đó ta cũng có phương trình: Wext = ΔUs (7.18)
Thế năng đàn hồi có thể hiểu là năng lượng dự trữ trong một lò xo bị biến dạng. Năng
lượng dự trữ này có thể chuyển hóa thành động năng. Quan sát sự biến dạng của lò xo, có thể
nhận thấy: Thế năng đàn hồi dự trữ trong lò xo bằng 0 khi lò xo không biến dạng (Us = 0 khi x
= 0); năng lượng được dự trữ trong lò xo chỉ khi lò xo bị giãn hay nén; thế năng đàn hồi lớn
nhất khi lò xo đạt đến độ nén hoặc độ giãn lớn nhất; thế năng đàn hồi luôn lu n ô dương bởi vì x2 luôn dương.
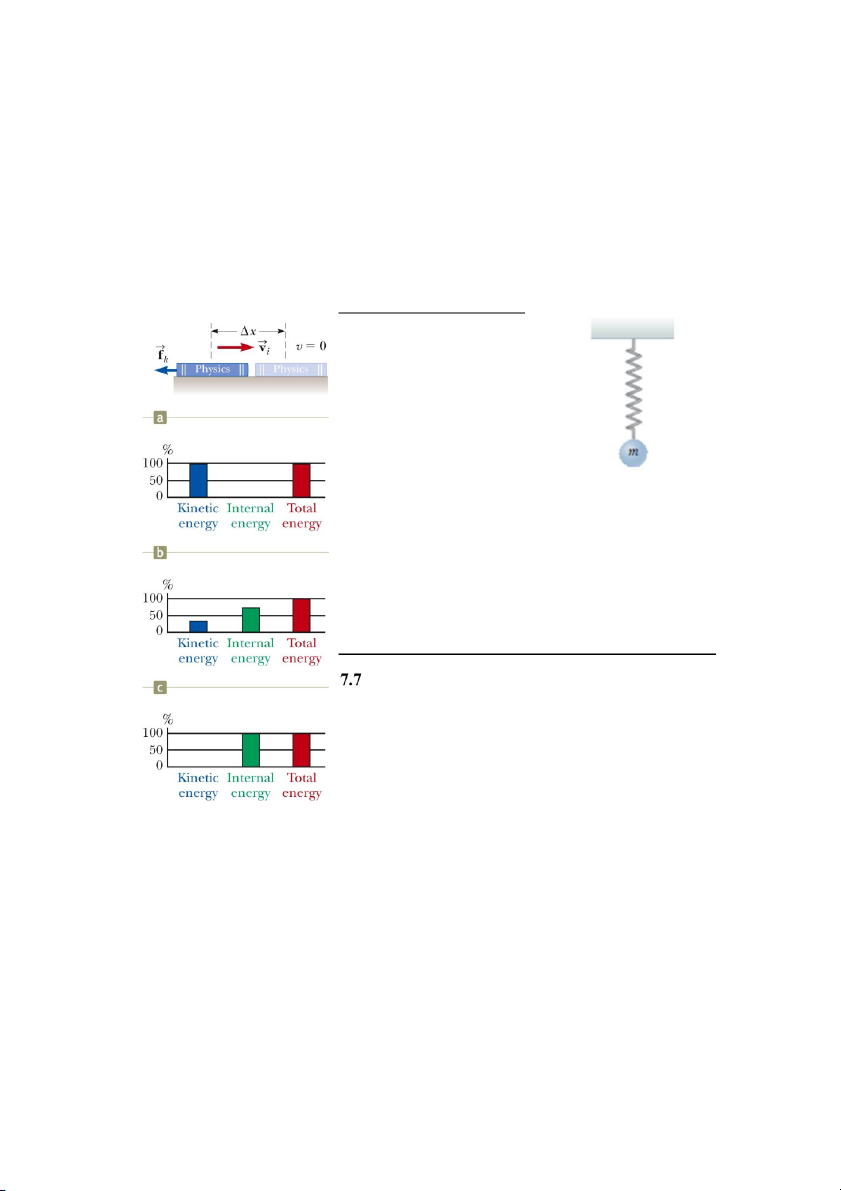
Hình 7.11 Sự biến đổi năng lượng giữa thế năng đàn hồi và động năng của hệ.
Trên hình 7.11 là một biểu diễn đồ thị quan trọng về năng lượng của một hệ, được gọi là
biểu đồ thanh năng lượng. Biểu đồ thanh năng lượng là một đồ thị quan trọng để biểu diễn
thông tin về năng lượng của hệ. Trên biểu đồ thanh năng lượng, trục tung biểu diễn giá trị
năng lượng, trục hoành cho thấy các loại năng lượng có trong hệ. 9
Trong hình 7.11a, không có năng lượng nào cả, bởi vì lò xo đang thả lỏng còn hộp thì không chuyển động.
Trong hình 7.11b và c, tác nhân bên ngoài thực hiện công trên hệ. Do lò xo bị nén lại nên
có thế năng đàn hồi trong hệ. Không có động năng trong hệ vì hộp vẫn đang được giữ
Trong hình 7.11d, hộp được thả ra cho chuyển động về phía bên phải trong khi vẫn tương
tác với lò xo. Do đó, thế năng đàn hồi của hệ g ả
i m trong khi động năng của hệ tăng.
Trong hình 7.11e, lò xo trở về chiều dài ban đầu và hệ chỉ còn động năng do sự chuyển động của cái hộp.
Câu hỏi 7.5: Một trái banh
gắn với một lò xo nhẹ được
treo thẳng đứng như hình
7.12. Khi kéo trái banh xuống
dưới khỏi vị trí cân bằng rồi
thả ra thì trái banh sẽ dao động lên xuống.
(i) Nếu hệ gồm trái banh, lò
xo và Trái đất thì có những
dạng năng lượng nào trong
Hình 7.12 Câu hỏi 7.5.
quá trình chuyển động đó: (a)
động năng và thế năng đàn hồi (b) động năng và thế năng hấp
dẫn (c) động năng, thế năng đàn hồi và thế năng hấp dẫn (d)
thế năng đàn hồi và thế năng hấp dẫn.
(ii) Nếu hệ gồm trái banh và lò xo thì có những dạng năng
lượng nào trong quá trình chuyển động đó: (a) động năng và
thế năng đàn hồi (b) động năng và thế năng hấp dẫn (c) động
năng, thế năng đàn hồi và thế năng hấp dẫn (d) thế năng đàn
hồi và thế năng hấp dẫn.
Lực bảo toàn và lực không bảo toàn
Trong phần này ta sẽ tìm hiểu một loại năng lượng có thể
tồn trữ trong một hệ. Loại năng lượng đó liên hệ với nhiệt độ
của hệ, được gọi là nội năng, Eint. Trong ví dụ trên hình 7.13,
giả sử ta dùng tay tác dụng lực gia tốc cuốn sách trượt sang
phải trên một bề mặt của một chiếc bàn nặng. Ở đây, bề mặt
có ma sát nên sau khi thôi tác dụng lực thì cuốn sách sẽ
Hình 7.13 Biểu đồ năng
chuyển động chậm lại rồi dừng hẳn. Xét hệ chỉ là bề mặt mà
lượng khi có ma sát: động
cuốn sách trượt trên đó. Lực ma sát mà cuốn sách tác dụng
năng của hệ (gồm cuốn sách lên bề mặt thực hiện công. Khi cuốn sách chuyển động sang
và bề mặt) biến đổi thành nội bên phải, lực ma sát tác dụng lên bề mặt hướng sang phải và
năng khi cuốn sách chuyển
điểm đặt lực cũng dịch chuyển sang phải. Do đó công thực
động chậm dần
hiện trên bề mặt là dương nhưng bề mặt không dịch chuyển 10
sau khi cuốn sách ngừng trượt. Công thực hiện trên hệ là công dương song cả động năng và
thế năng của hệ không thay đổi. Vậy năng lượng đó nằm ở đâu?
Từ kinh nghiệm hằng ngày, có thể nhận biết rằng khi cuốn sách trượt trên bề mặt thì sẽ
làm bề mặt nóng lên. Như vậy, công thực hiện trên hệ đã làm nóng hệ lên mà không tăng tốc
độ hay thay đổi cấu hình của hệ. Người ta gọi năng lượng liên hệ với nhiệt độ của hệ là nội
năng, ký hiệu là Eint. Trong trường hợp này, ma sát đã thực hiện công trên bề mặt, truyền cho
hệ một năng lượng dưới dạng nội năng còn động năng và thế năng của hệ vẫn giữ nguyên không thay đổi.
Bây giờ, ta xét hệ gồm có cuốn sách và bề mặt. Ban đầu hệ có động năng vì cuốn sách
đang di chuyển. Trong khi cuốn sách trượt trên bề mặt thì nội năng của hệ tăng lên vì cả cuốn
sách và bề mặt đều ấm hơn trước đó. Khi cuốn sách dừng lại, động năng của hệ đã chuyển
hóa hoàn toàn thành nội năng của hệ. Ở đây, lực ma sát – một lực không bảo toàn, tác dụng
giữa các thành phần của hệ đã chuyển hóa động năng của hệ thành nội năng.
7.7.1 Lực bảo toàn (lực thế)
Công thực hiện bởi một lực tác dụng lên một chất điểm làm chất điểm này chuyển động
giữa hai điểm mà không phụ th ộ
u c vào quỹ đạo chuyển động của chất điểm đó thì lực này
được gọi là lực bảo toàn (lực thế).
Do đó, công thực hiện bởi lực bảo toàn tác dụng lên một chất điểm chuyển động trên một
quỹ đạo kín bằng 0. Quỹ đạo kín là quỹ đạo mà điểm đầu trùng với điểm cuối .
Lực hấp dẫn và lực đàn hồi là những ví dụ điển hình của lực bảo toàn.
Thế năng của một hệ gắn liền với một lực bảo toàn nào đó tác dụng giữa các thành phần
của hệ đó. Một cách tổng quát, công Wint được thực hiện bởi một lực bảo toàn do một thành
phần của hệ tác dụng lên một thành phần khác của hệ khi cấu hình của hệ thay đổi sẽ bằng
hiệu thế năng của hệ tại vị trí đầu và vị trí cuối. Wint = Ui – Uf = - ΔU (7.19)
Công dương thực hiện bởi một tác nhân bên ngoài Wext làm
tăng thế năng của hệ. Trong khi đó, công do một thành phần của
hệ thực hiện Wint bởi lực bảo toàn bên trong một hệ cô lập là
nguyên nhân làm giảm thế năng của hệ.
7.7.2 Lực không bảo toàn (lực phi thế)
Các lực không thỏa mãn các điều kiện của lực bảo toàn được
gọi là lực không bảo toàn. Công thực hiện bởi một lực không bảo
toàn phụ thuộc vào quãng đường dịch chuyển.
Lực không bảo toàn tác dụng bên trong hệ sẽ làm biến đổi cơ năng Emech của hệ.
Hình 7.14 Công thực Emech = K + U (7.20)
hiện bởi lực ma sát phụ
với K bao gồm động năng của tất cả các thành phần chuyển động thuộc vào quãng đường
của hệ, và U bao gồm tất cả các dạng thế năng của hệ.
dịch chuyển của vật 11
Như trên hình 7.14, nếu ta dịch chuyển cuốn sách từ điểm A đến điểm B theo một đường
thẳng với một tốc độ không đổi thì công để chống lại lực ma sát trên quãng đường đó sẽ nhỏ
hơn khi ta dịch chuyển cuốn sách theo đường cong từ A đến B. Bởi vì công thực hiện phụ
thuộc vào quãng đường dịch chuyển nên lực ma sát là lực không bảo toàn (không phải lực thế).
Liên hệ giữa lực bảo toàn và thế năng
Ta định nghĩa hàm thế năng của một hệ là một đại lượng được xác định sao cho công
thực hiện bởi một lực bảo toàn bên trong hệ bằng nhưng trái dấu với độ biến thiên thế năng của hệ.
Giả sử lực bảo toàn 𝐹 tác dụng giữa các hạt trong một hệ làm cho một hạt di chuyển dọc
theo trục x thì công được thực hiện bởi lực 𝐹 là: x f (7.21) WF dx  U int  x xi
ΔU = Uf – Ui âm khi F và x cùng hướng.
Do đó, lực bảo toàn liên hệ với hàm thế năng theo hệ thức: dU F   (7.22) x dx
Mối liên hệ này có nghĩa là thành phần theo phương x của lực bảo toàn tác dụng lên một
phần tử của hệ bằng nhưng trái dấu với đạo hàm của hàm thế năng theo biến x. Từ đây ta thấy
thế năng U là một đại lượng quan trọng bởi vì có thể tìm được lực thế từ nó.
Xét lại trường hợp lực tác dụng của lò xo, ta có: dU d s  1 2  F     kx  kx s   dx dx  2  (7.23)
Kết quả thu được đúng như định luật Hooke.
Giản đồ năng lượng và sự cân bằng
Chuyển động của một hệ có thể được quan sát qua đồ thị biểu diễn vị trí và năng lượng của nó.
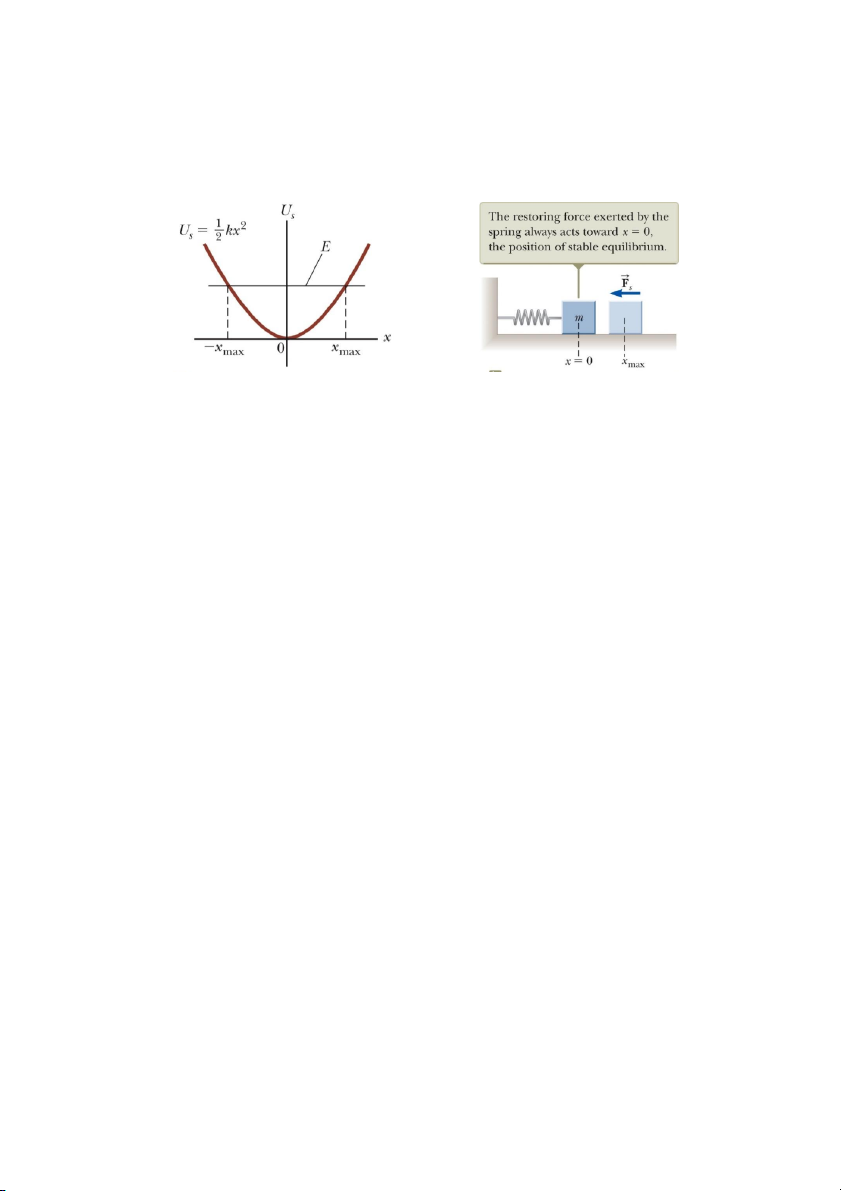
Cân bằng bền
Trong ví dụ của một hệ lò xo – hộp như trên hình vẽ, chiếc hộp dao động giữa 2 vị tr íx
= ±xmax, chiếc hộp luôn chuyển động có gia tốc về phía x = 0 và khi nó nằm yên tại vị trí này
thì chỉ có tác dụng một lực từ bên ngoài mới làm cho nó rời khỏi vị trí đó. Do đó, vị trí x = 0
là vị trí hệ nằm ở trạng thái cân bằng bền. Bất cứ sự dịch chuyển nào khỏi vị trí cân bằng bền
này đều có một lực kéo vật trở về vị trí đó. Một cách tổng quát, những cấu hình của một hệ
nằm ở trạng thái cân bằng bền tương ứng với một hàm thế năng U(x) có giá trị cực tiểu. 12
Trạng thái cân bằng bền được biểu diễn trên đồ thị năng lượng như hình vẽ. Ta thấy cân
bằng bền sẽ tương ứng với vị trí U(x) có giá trị nhỏ nhất, còn x = xmax và x = -xmax được gọi
là các điểm quay đầu.
Hình 7.15 a- Hàm thế năng phụ thuộc vị trí x b- Lực hồi phục lò xo tác dụng lên vật luôn
hướng về vị trí cân bằng bền x = 0.
Cân bằng không bền
Bây giờ, ta xét một chất điểm chuyển động dọc theo
trục x dưới tác dụng của một lực bảo toàn F(x) có đồ thị
biểu diễn U(x) như hình vẽ bên dưới. Trong trường hợp
này, Fx = 0 tại x = 0, cho nên chất điểm ở trạng thái cân
bằng. Tuy nhiên, đây là một vị trí cân bằng không bền
bởi vì khi chất điểm rời khỏi vị trí x = 0 sang trái hay
sang phải thì đều có lực tác dụng đẩy vật xa khỏi vị trí
đó hướng tới một vị trí có thế năng nhỏ hơn. Một cách
tổng quát, những cấu hình của một hệ nằm ở trạng thái
Hình 7.16 Hàm thế năng phụ
cân bằng không bền tương ứng với một hàm thế năng
thuộc vị trí x đối với một chất
U(x) có giá trị cực đại .
điểm có vị trí cân bằng không bền x = 0.
Trạng thái cân bằng không bền được biểu diễn trên đồ t ị
h năng lượng như hình vẽ. Ta thấy cân bằng không bền sẽ tương ứng với vị trí U(x) có giá trị lớn nhất.
Cân bằng phiếm định là trạng thái mà thế năng U không đổi trong một vùng nào đó, do
đó một sự dịch chuyển nhỏ khỏi một vị trí trong vùng này không gây ra sự xuất hiện của lực
kéo về vị trí cũ hoặc đẩy ra vị trí mới .
Tóm tắt chương 7
Một hệ thường gặp nhất là một chất điểm, một hệ chất điểm hoặc một vùng không gian có
thể thay đổi kích thước và hình dạng. Biên giới của hệ phân chia hệ với môi trường. 13
Công (ký hiệu là W) thực hiện bởi một tác nhân tác dụng một ngoại lực không đổi lên hệ là
một đại lượng được xác định bằng tích của độ lớn lực F với độ dịch chuyển Δr của điểm đặt
lực nhân với cosθ, với θ là góc tạo bởi vectơ lực và vectơ độ dich chuyển. W = FΔr cosθ
Nếu lực tác dụng lên một chất điểm thay đổi thì công lực sinh ra khi chất điểm chuyển động
dọc theo trục x trên quãng đường dịch chuyển từ vị trí đầu x x
i đến vị trí cuối xf là:W   f F dx x xi F 󰇍󰇍
x là thành phần hình chiếu của lực 𝐹 trên trục x.
Động năng của một chất điểm có khối lượng m chuyển động với tốc độ v là 1 K = 2mv2
Thế năng hấp dẫn của hệ chất điểm-Trái đất khi chất điểm nằm ở độ cao y phía trên bề mặt Trái đất là Ug = mgy
Thế năng đàn hồi tích trữ trong một lò xo có độ cứng k là 1 𝑈𝑠 = 2kx2
Một lực được gọi là lực bảo toàn (lực thế) nếu công thực hiện bởi lực đó trên một chất điểm
làm chất điểm này chuyển động giữa hai điểm không phụ thuộc vào quỹ đạo chuyển động
của chất điểm đó. Ngoài ra, một lực là lực bảo toàn (lực thế) nếu công thực hiện bởi lực đó
trên một chất điểm làm chất điểm này chuyển động trên một quỹ đạo kín bằng 0. Một lực
không thỏa mãn những điều kiện trên được gọi là lực không bảo toàn (lực phi thế)
Cơ năng của một hệ bằng tổng của động năng và thế năng Emech = K + U
Định lý công – động năng: Công do ngoại lực thực hiện trên một hệ và làm cho hệ chỉ thay
đổi tốc độ của nó thì 1 1 W 2 2 ext = Wf − Wi = ∆K = 2 mvf − 2 mvi
Hàm thế năng U có thể được liên kết chỉ với một lực bảo toàn. Nếu một lực 𝐹 tác dụng giữa
các thành phần của một hệ và một phần tử của hệ đó chuyển động dọc theo trục x từ vị trí đầu
xi đến vị trí cuối xf thì độ biến thiên thế năng của hệ bằng nhưng trái dấu với công do lực đó thực hiện 14 xf
∆U = Uf − Ui = − ∫ Fxdx xi
Câu hỏi lý thuyết chương 7
1. Alex và John đang đưa các tủ giống hệt nhau lên xe tải. Alex nhấc tủ của mình thẳng từ
mặt đất lên xe tải, trong khi John trượt tủ của mình trên một tấm ván nghiêng từ mặt đất
lên xe tải. Tuyên bố nào sau đây là chính xác về công được thực hiện trên hệ tủ - Trái đất?
(a) Alex và John thực hiện cùng một lượng công như nhau.
(b) Alex thực hiện nhiều công hơn John.
(c) John thực hiện nhiều công hơn Alex.
(d) Không có phát biểu nào đúng cả vì không biết lực ma sát.
(e) Không có phát biểu nào đúng cả vì không biết góc nghiêng.
2. Lực pháp tuyến có thể thực hiện công không? Nếu không thì cho biết tại sao không? Nếu có thì hãy cho ví dụ?
3. Thảo luận xem liệu có bất kỳ công nào được thực hiện bởi các đối tượng sau đây hay
không và nếu có thì liệu công đó là công dương hay công âm:
(a) Một con gà bươi đất,
(b) Một người đang nghiên cứu,
(c) Một cần cẩu nâng một thùng bê tông,
(d) Lực hấp dẫn tác dụng lên thùng bê tông trong phần (c),
(e) Cơ chân của người trong hành động ngồi.
4. 4. Khi một con lắc dao động qua lại, lực tác dụng lên vật treo gồm có: (a) lực hấp dẫn,
(b) lực căng của dây treo, và c) lực cản của không khí.
(i) Lực nào trong số đó, nếu có, không sinh công trên vật treo vào bất cứ lúc nào?
(ii) Lực nào trong số đó sinh công âm trên vật treo trong suốt quá trình chuyển động của con lắc?
5. Bạn đang sắp xếp sách trong thư viện. Bạn nhấc một quyển sách từ sàn lên đến giá trên
cùng. Động năng của cuốn sách trên sàn là không và động năng của cuốn sách ở giá trên
cùng cũng là không, vì vậy không có thay đổi động năng nhưng bạn đã thực hiện công
khi nâng quyển sách. Vậy định lý công - động năng có bị vi phạm? Hãy giải thích.
6. Một vật có khối lượng m được thả rơi từ tầng thứ 4 của tòa nhà xuống, vật có tốc độ v
khi chạm đất. Hỏi nên thả rơi vật đó từ tầng thứ mấy để tốc độ của nó tăng gấp đôi khi
chạm đất? Giả sử độ cao của các tầng đều bằng nhau. (a) Tầng 6 (b) Tầng 8 (c) Tầng 10 (d) Tầng 12 (f) Tầng 16 15
Bài tập chương 7
1. Một hạt mưa khối lượng 3,35.10-5 kg rơi thẳng đứng với tốc độ không đổi dưới tác dụng
của trọng lực và lực cản không khí. Xem hạt mưa là một chất điểm. Hãy tính công thực
hiện trên hạt mưa khi nó rơi một đoạn 100 m bởi (a) Lực hấp dẫn. (b) Lực cản không khí.
2. Một cái hộp có khối lượng m = 2,50 kg được đẩy trượt trên
một mặt bàn nằm ngang, không ma sát một đoạn d = 2,20
m bởi một lực không đổi có độ lớn F = 12 N, hợp với
phương ngang một góc  = 25,0o như hình vẽ. Hãy tính
công thực hiện trên cái hộp bởi: (a) Lực tác dụng.
(b) Phản lực lực pháp tuyến của bàn. (c) Trọng lực.
(d) Tổng hợp lực tác dụng lên cái hộp.
3. Lực tác dụng lên một chất điểm thay đổi như trên
hình vẽ. Hãy tính công lực thực hiện trên chất điểm khi nó di chuyển
(a) Từ x = 0 đến x = 8,00 m
(b) Từ x = 8,00 m đến x = 10,0 m
(c) Từ x = 0 đến x = 10,0 m.
4. Khi một vật có khối lượng 4,00 kg được treo ở đầu
một lò xo nhẹ thì lò xo bị dãn ra một đoạn 2,50 cm. Nếu vật thể 4,00 kg được lấy ra,
(a) Hỏi lò xo sẽ dài ra bao nhiêu nếu vật có khối lượng 1,50 kg được treo lên đó?
(b) Tính công ngoại lực phải thực hiện để kéo dãn lò xo dài ra 4,00 cm từ vị trí bình thường của nó?
5. 5. Giữ cho một lò xo nhẹ có độ cứng 3,85 N/m bị nén một đoạn 8,00 cm với một vật nặng
0,250 kg ở đầu bên trái và một vật nặng 0,500 kg ở đầu bên phải của lò xo, cả hai vật đều
nằm yên trên mặt phẳng nằm ngang. Lò xo tác dụng lực lên mỗi vật và có xu hướng đẩy
hai vật ra xa. Thả cho hai vật đồng thời chuyển động từ trạng thái nghỉ. Tính gia tốc
chuyển động của mỗi vật nếu hệ số ma sát động giữa mỗi vật và bề mặt là a- 0, b- 0,100 và c- 0,462.
6. Tác động một lực F󰇍 = (4xi + 3yj), trong đó F󰇍 đo bằng Newton và x và y đo bằng m, lên
1 vật để vật di chuyển theo trục x từ gốc hệ trục tọa độ đến vị trí x= 5,00 m. Tính công
W = ∫ 𝐹𝑑𝑟 lực đã thực hiện trên vật .
7. Một vật nặng 3,00 kg có vận tốc (6,00𝑖 - 2,00𝑗) m/s.
(a) Tính động năng của vật. 16
(b) Nếu vận tốc của vật thay đổi tới giá trị (8,00𝑖 + 4,00𝑗) m/s thì công thực hiện trên vật là bao nhiêu?
8. Một người đẩy một thùng gỗ nặng 35,0 kg với tốc độ không đổi một đoạn dài 12,0 m trên
một sàn gỗ. Lực đẩy F có phương ngang, độ lớn không đổi. Công mà lực đã thực hiện là 350 J.
(a) Xác định độ lớn của lực F.
(b) Hãy mô tả chuyển động tiếp theo của cái thùng nếu bây giờ người đó tác dụng một lực lớn hơn lực F.
(c) Điều gì sẽ xảy ra đối với cái thùng nếu lực tác dụng nhỏ hơn F?
9. Một vật nặng 5,75 kg băng qua gốc của hệ trục tọa độ tại thời điểm t = 0 với vận tốc có
thành phần theo trục x là 5,00 m/s và theo trục y là -3,00 m/s.
(a) Động năng của vật tại thời điểm đó là bao nhiêu?
(b) Tại một thời điểm sau đó t = 2,00 s, vật ở
tại vị trí x = 8,50 m và y = 5,00 m. Hỏi lực
không đổi tác dụng lên vật trong khoảng thời gian đó là bao nhiêu?
(c) Tốc độ của vật tại thời điểm t = 2,00 s là bao nhiêu?
10. Một tảng đá 0,20 kg được giữ ở độ cao 1,30 m phía trên đỉnh của một giếng nước và sau
đó thả rơi vào đó. Giếng có chiều sâu 5,0 m. Chọn gốc thế năng tại đĩnh của giếng nước, tính
(a) Thế năng hấp dẫn của hệ hòn đá – Trái đất trước khi đá rơi.
(b) Thế năng hấp dẫn của hệ hòn đá – Trái đất khi hòn đá ở đáy giếng.
(c) Độ thay đổi thế năng hấp dẫn của hệ từ lúc đầu đến lúc hòn đá ở đáy giếng.
11. Một vật chuyển động trong mặt phẳng xy như trong hình
vẽ và chịu một lực ma sát với độ lớn không đổi 3,00 N,
luôn hướng ngược với vận tốc của vật. Hãy tính công mà
bạn phải thực hiện để trượt vật với tốc độ không đổi khi vật chuyển động
(a) Dọc theo đường màu tím từ O đến A rồi quay lại theo
đường màu tím trở về O.
(b) Dọc theo đường màu tím từ O đến C rồi theo đường
dẫn màu xanh dương trở về O.
(c) Theo đường màu xanh từ O tới C rồi theo đường màu xanh dương trở về O.
(d) Mỗi câu trả lời của bạn phải k
hác không. Ý nghĩa của việc quan sát này là gì.
12. Hàm thế năng của một hệ có dạng U = 3x3y – 7x. Tìm lực tác động tại điểm (x,y).
13. Một lực thế F  2x  4 (N; m) tác dụng lên chất điểm nặng 5 kg. Khi chất điểm dịch x
chuyển theo trục x từ x 1m x  5m . Hãy tính:
(a) Công của lực F thực hiện lên chất điểm. x
(b) Độ biến thiên thế năng của hệ vật.
(c) Động năng của chất điểm tại x  5 m nếu tại điểm x  1m vận tốc nó là 3 m/s. 17
14. Một toa xe lửa nặng 6000 kg chạy dọc theo đường ray với ma sát nhỏ có thể bỏ qua. Toa
xe được dừng lại nhờ hai lò xo như trên hình vẽ. Hai lò xo có độ cứng là k1 = 1600 N/m
và k2 = 3400 N/m. Sau khi lò xo thứ nhất bị nén một khoảng 30,0 m thì lò xo thứ hai bắt
đầu tác dụng và lực tổng hợp của hai lò xo tăng lên như đồ t ị
h bên dưới. Sau khi lò xo
thứ nhất tiếp xúc với toa xe và bị nén một đoạn 50,0 cm thì toa xe dừng lại. Hãy tìm tốc
độ ban đầu của toa xe.
15. Một lò xo có độ cứng k = 500 N/m được buộc chặt tại
đáy của một mặt phẳng nằm nghiêng có góc nghiêng  =
20,0o như hình vẽ. Một vật khối lượng m = 2,50 kg đặt
phía trên mặt phẳng nghiêng cách lò xo một khoảng d =
0,300 m. Đẩy cho vật chuyển động hướng về phía lò xo
với tốc độ v = 0,750 m/s. Độ dài bị nén của lò xo ở thời
điểm vật tạm thời dừng lại là bao nhiêu? 18