Chương 8: Định luật bảo toàn năng lượng | Tài liệu môn Vật lý 1 trường đại học sư phạm kĩ thuật TP. Hồ Chí Minh

Hệ không cô lập về năng lượng là một hệ có trao đổi năng lượng với môi trường qua biên giới của nó. Một hệ không cô lập sẽ tương tác với môi trường. Một vật bị tác dụng lực là một ví dụ của hệ không cô lập. Hệ cô lập là một hệ trao đổi năng lượng với môi trường qua biên giới của hệ. Tài liệu giúp bạn tham khảo, ôn tập và đạt kết quả cao. Mời bạn đọc đón xem!

13 7 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Môn: vật lý 1, 2

Trường: Đại học Sư phạm Kỹ thuật Thành phố Hồ Chí Minh

Thông tin:

18 trang 2 tháng trước

Tác giả:

Profile Lê Kim Dung
1
Chương 8: Định luật bảo toàn năng lượng
Hệ không cô lập
Hệ không cô lập về năng lượng là một hệ có trao đổi năng lượ ới môi trường v ng qua
biên i c nó. M t h không cô l p sgiớ ủa ộ ệ ậ ẽ tương tác với môi trường. M t vộ ật bị tác d ng lụ ực
là m t ví d c a h không cô l p. ộ ụ ủ ệ ậ
Hệ cô lập là m t h không t ng v ng qua biên i c a h . ộ ệ rao đổi năng lượ ới môi trườ giớ ủ ệ
Đối với một hệ không cô lập, năng lượng được truyền qua biên giới của hệ trong thời
gian h ệ tương tác với môi trường bên ngoài. Sau đây là những phương thức truyền năng lượng
vào ho c ra kh i mặ ỏ ột hệ.
Công ( ) là m t hình th n ng b ng cách tác d ng l lên h và Work ộ ức truyề năng lượ ằ ụ ực ệ điểm
đặ ự ị ịt của l c b d ch chuyển (hình 8.1a).
Sóng cơ ( ) là hình th n ng thông qua s lan truyMechanical waves ức truyề năng lượ ự ền
nhiễu lo n trong ng. Âm thanh r i khạ môi trườ ờ ỏi chi c loa radio ế ở hình 8.1b hay sóng địa
chấn, sóng bi n là s ng b ng ể ự truyền năng lượ ằ sóng cơ.
Nhiệt ( ) là mHeat ột cơ chế trao đổi năng lượng giữa hệ và môi trường do có sự khác nhau
về nhiệt độ. Năng lượ ới đuôi cáing truyền t thìa trong hình 8.1c từ phần bị nhúng trong tách
cà phê nóng là dưới dạng nhiệt.
a
b
c
d
e
f
Hình 8.1 Các ng. cơ chế truyền năng lượ
2
Trao đổi chất (Matter transfer) là hình th c truy ng xuyên qua biên ứ ền năng lượ giới của
hệ dưới d ng v t chạ ậ ất mang theo năng lượ xăng cho xe như ởng. Ví dụ đổ hình 8.1d hay đối
lưu là sự ền năng lượng dướ ạng trao đổ truy i d i chất.
Truyền điện (Electrical transmission) là s truy n ng vào ho c ra kh i h b ng ự ề năng lượ ặ ỏ ệ ằ
dòng điện. Năng lượng cung c p cho máy s y tóc là nh s n (hình 8.1e). ấ ấ ờ ự truyền điệ
Sóng điện từ ( ) là Electromagnatic radiation năng lượng được trao đổ ởi sóng điệi b n từ.
Năng lượ ỏi bóng đèn (hình f) là dướ ạng sóng điệng truyền kh 8.1 i d n từ.
Định luật bảo toàn năng lượng
Năng lượng luôn được bảo toàn.
Điều này nghĩa là nếu năng lượng t ng c ng c a mổ ộ ủ ột h ệ thay đổi thì đã có một năng lượng
truyền qua biên gi i c a h b ng mớ ủ ệ ằ ột phương pháp trao đổi năng lượng nào đó. Dạng tổng
quát c nh lu t b ng có th c bi u di n b ng ủa đị ậ ảo toàn năng lượ ể đượ ể ễ ằ phương trình bảo toàn
năng lượng như sau:
ΔE
system
= ΣT (8.1)
Trong đó, E
system
là t ng c a h ng truy n qua biên giổng năng lượ ủ ệ, T (Transfer) là năng lượ ề ới
của h ệ.
Phương trình toán họ ủa đị ăng lượng đốc c nh luận bảo toàn n i với một hệ không cô lập
thể hi các loện đầy đủ ại năng lượng trao đổ ễn dưới có thể được biểu di i dạng:
Δ K + Δ U + Δ E
int
= W + Q + T
MW
+ T
MT
+ T + T
ET ER
(8.2)
Với K là động năng, U là thế năng và E ội năng củ năng lượ
int
là n a hệ; ng truy n qua biên giề ới
của h i d ng công i d ng nhiệ dướ ạ là T
work
= W, dướ ạ ệt là T
heat
= Q, T
MW
là năng lượng được
truyền bởi sóng cơ, T
MT
là năng lượng trao đổ là năng lượi chất, T
ET
ng do truyền điện và T
ER
là năng lượng trao đổ ởi sóng điệi b n từ.
Trong th c tự ế, phương trình của định lu t bậ ảo toàn năng lượng s ẽ đơn giản hơn nhiều. Ví
dụ, n u có mế ộ ụt l c tác dự ng lên h và sinh công và gi s ng ệ ả ử chỉ có cơ chế truyền năng lượ
này làm thay đổ ốc độ thì phương trình của đị ảo toàn năng lượi t của hệ nh luật b ng sẽ rút về
phương trình của đị động năng:nh lý công-
ΔK = W
Câu h i 8.1:ỏ Hãy cho bi ng nào qua m t h là: a- M t chi c tivi, b- ết cơ chế truyền năng lượ ộ ệ ộ ế
Một máy c t cắ ỏ chạy xăng, c- Một cái gọt bút chì bằng tay.
Câu h i 8.2:ỏ Xét một cái h t có ma sát trên mộp trượ ột bề mặt nằm ngang.
i) N u h là chi c h p thì h là a- cô l p, b- không cô l p, c- không th ế ệ ế ộ ệ ậ ậ ể xác định được.
ii) N u h là b m t n m ngang thì h là a- cô l p, b- không cô l p, c- không thế ệ ề ặ ằ ệ ậ ậ ể xác định
được.
iii) N u h là cái h p và b m t n m ngang thì h là a- cô l p, b- không cô l p, c- không th ế ệ ộ ề ặ ằ ệ ậ ậ ể
xác định được.
3
Hệ cô l p ậ
Đối với một hệ cô l p, không có b t kậ ấ ỳ hình thức trao đổi năng lượng nào với môi trường
bên ngoài qua biên gi i c a h , thì t t c các s h ng bên v phớ ủ ệ ấ ả ố ạ ế ải trong phương trình (8.2)
đều b nh luằng 0 do đó phương trình của đị ật b ng có dảo toàn năng lượ ạng:
ΔE
system
= 0 (8.3)
E
system
là tổng động năng, thế năng và nội năng củ a hệ.
Như vậy, năng lượng của một hệ cô lập không đổi.
Trên hình v i mô t các dẽ bên dướ ả ạng năng lượng tồn trữ bên trong m t h cô l p gộ ệ ậ ồm
có động năng, thế năng và nội năng. Các dạng năng lượ ến đổ ẫn nhau nhưng tổ ng này bi i l ng
năng lượng của hệ bảo toàn.
Hình 8.2 Các d ng n ng t n tr bên trong h . ạ ăng lượ ồ ữ ệ
Định luật bảo toàn cơ năng
Định luật b ng h p riêng ảo toàn cơ năng là một trườ ợ
của định luật bảo toàn năng lượ Đây là mô hình thường. ng
g mặp nh i vất đố ới ột hệ ả cô lập mà trong hệ chỉ ự có l c b o
toàn tác d ng. ụ
Hãy xét m t h gộ ệ ồm m t cu n sách kh ng m và ộ ố ối lượ
Trái đất. Sau khi nâng cu n sách lên mố ột độ cao nào đó thì
bên trong h s t n tr mệ ẽ ồ ữ ột năng lượng dưới dạng th ế năng
hấp d n b ng công mà tác nhân bên ngoài th c hi n trên ẫ ằ ự ệ
cuốn sách:
W = U
g
Khi cu cao y xuốn sách rơi từ độ
i
ống đến vị trí y thì
f
công mà l c h p d n s c hi n trên cu n sách là: ự ấ ẫ ẽ thự ệ ố
fifionbook
mgymgyjyyjmgrgmW
ˆ
.
ˆ
.
(8.4)
Hình 8.3 c th ra và Cuốn sách đượ ả
rơi do công thực hiện bởi lực hấp
dẫn
4
Theo đị động năng, công thự ằng độ ến đổi độnh lý công – c hiện trên cuốn sách b bi ng
năng của cuốn sách:
W
on book
= K
book
Suy ra,
K
book
= mgy mgy - ) = -
i
–
f
= -(mgy
f
mgy
i
U
g
(8.5)
Trong đó, Ug = mgy là thế năng hấ p dẫn c a h . Trong h n sách ủ ệ ệ cuố – Trái đất, chỉ có cuốn
sách chuy ng nên a cu n sách Kển độ động năng củ ố
book
cũng chính là động năng của hệ K, do
đó:
K
book
= K
Phương trình (8.4) có thể được vi t l i là: ế ạ
K = - U
g
(8.6)
K + U
g
= 0
Phương trình trên đã đượ Trái đất, trong đó U năng c dẫn xuất từ hệ cuốn sách –
g
là thế
hấp d n song th c t cho thẫ ự ế ấy nó cũng đúng đối với bất kỳ một loạ ếi th năng nào. Phương
trình tổng quát đó là phương trình của đị ảo toàn cơ năng: nh luật b
K + U = 0 (8.7)
ΔE
mech
= 0 (8.8)
Với E = K + U a h
mech
là cơ năng củ ệ, K là động năng tổng cộng của hệ, U là tổng tất cả các
loại th a h . ế năng củ ệ
Định lu t bậ ảo toàn cơ năng chỉ đúng trong trường h p h là cô l p và không có l c không ợ ệ ậ ự
bảo toàn tác dụng bên trong h nh lu t có th c phát biệ. Đị ậ ể đượ ểu như sau: Cơ năng của một
hệ cô l p mà trong h không có các l c không b o toàn tác d ng thì b o toànậ ệ ự ả ụ ả .
Sự thay đổi năng lượng có thể được vi t l i d ng sau: ế ại dướ ạ
K
f
+ U = K + U (8.9)
f i i
Đối với hệ cuốn sách – Trái đất, ta có phương trình:
iiff
mgymvmgymv
22
2
1
2
1
Trong đó, v
i
và v
f
là t c a cu n sách t i v trí y và y . ốc độ ủ ố ạ ị
i f
Câu h i 8.3:ỏ Ba quả banh được ném từ đỉnh một tòa nhà với cùng t u. Qu bóng ốc độ ban đầ ả
thứ nhất được ném theo phương ngang, quả thứ hai hướng l ch lên trên so vệ ới phương ngang,
còn qu ng l ch xuả thứ ba hướ ệ ống dưới so với phương ngang. Bỏ qua sức cản không khí, hãy
sắp x p theo thế ứ tự từ lớn đế ốc độn bé t c a ba qu bóng khi chúng ch ủ ả ạm đất.
5
Bài t p m u 8.1: ậ ẫ Quả bóng rơi tự do
Một trái banh khối lượng m đượ rơi từc thả độ cao h trên
mặt đất như hình 8.4.
(A) B qua s c c n không khí, hãy x nh tỏ ứ ả ác đị ốc độ của
trái banh tại độ cao y so với mặt đất. Hệ c ch n là trái đượ ọ
banh – Trái đất.
(B) Hãy x nh t c trái banh t so vác đị ốc độ ủa ại độ cao y ới
mặt đất nếu hệ được chọn là trái banh.
Giải:
(A) T c a trái banh t y khi h là trái banh ốc độ ủ ại độ cao ệ
– Trái đất.
Vì h bao g trái banh ệ ồm và Trái Đất nên khi bỏ qua sức
cản không khí ch có m t l c tác d ng ỉ ộ ự ụ giữa các thành
ph bần c a h ng lủ ệ là trọ ực - là lđó ực ảo toàn. Do đó, cơ
năng củ ụng đị ảo toàn cơ a hệ bảo toàn. Áp d nh luật b
năng, ta có phương trình:
K
f
+ U = K + U
gf i gi
Với K
i
= 0 u khi qu bóng b , U = mgh là thlà động năng ban đầ ả ắt đầu rơi
gi
ế năng ban
đầ
u của hệ. Khi quả bóng đến độ cao y thì động năng K
f
= mv
f
2
/2 và thế năng của hệ
U
gf
= mgy. Ta có,
Từ đó, suy ra v n t c c a trái banh cao y là ậ ố ủ ở độ
2 ( )
f
v g h y
(B) Tốc độ của trái banh t cao y khi h là trái banh. ại độ ệ
Trong trường h p này, ch có mợ ỉ ột loại năng lượng thay đổi là động năng của trái banh.
Hệ không có th ế năng. Trọng l c th c hi n công trên trái banh. Áp d nh lu t bự ự ệ ụng đị ậ ảo
toàn năng lượng cho h không cô l p, ta có: ệ ậ
K = W
mgymghhymgymgjyjmgrgmmv
f
)(
ˆ
.
ˆ
.0
2
1
2
2 ( )
f
v g h y
K t quế ả cũng giống như trong câu a bất kể ệ h c chđượ ọn là không gi ng nhau. ố
Hình 8.4 Bài t p 8.1. ậ
6
Bài t p m u 8.2: Súng lò xo ậ ẫ
Trên hình 8.5 mô t n n c a mả cơ chế ạp đạ ủ ột cây súng trò chơi.
Khi nạp đạn, lò xo được nén lại đến vị trí y
A
. Khi bóp cò, viên
đạ đượ ịn sẽ c b n vắn lên đế trí y phía trên v
C
ị trí y = 0 lúc viên
B
đạn rời khỏi lò xo. Trong một lần bắn, m = ,0 g, 35 y
A
= -0,120
m và = 20,0 m. y
C
(A) B qua m i l c c n, hãy tính h s i c a lò xo. ỏ ọ ự ả ệ ố đàn hồ ủ
(B) Tính t cốc độ ủa viên đạn khi nó đi qua vị trí cân bằng của lò
xo y .
B
Gi iả :
(A) Hệ s i c a lò xoố đàn hồ ủ
Trong bài toán c a chúng ta, v n trong ng phóng bủ iên đạ ố ắt đầu
từ trạng thái ngh vì y nó lên phía trên. ỉ, được tăng tốc lò xo đẩ
Khi r i kh i nòng súng, l c h p d n sờ ỏ ự ấ ẫ ẽ làm viên đạn chuyển động
chậm lại.
Chọn h bao g Khi b qua ệ ồm viên đạn, súng và Trái Đất. ỏ
mọi l c c n thì mô hình c a bài toán là mự ả ủ ột hệ cô l p vậ ới các
lực tác d ng chụ ỉ có các lực bảo . toàn
Viên đạ ắt đầ động năng ban đầ năng n b u từ trạng thái nghỉ nên u K = 0.
i
Chọn gốc thế
hấp d n tẫ ại điểm viên đạ úc đó, thế năng đàn hồ cũng n rời khỏi lò xo y = 0 thì l
B
i U
s
bằng 0. i vĐố ới hệ cô l nh lu t bập, đị ậ ảo toàn năng lượng vi t cho hai c u hình lúc viên ế ấ
đạ ịn tại v trí y
A
và y có d
C
ạng:
0
g S
K U U
Bởi vì viên đạn đạ khi động năng củt trí vị cao nhất y
C
a nó bằng 0 nên K = 0, ta có:
f
2
1
2
(0 0) ( ) (0 ) 0
C A
mgy mgy kx
=>
2
2 ( )
C A
mg y y
k
x
mNk /958
120,0
)120,0(0,20.80,9.0350,0.1
2
(B) Tốc độ ủa viên đạ c n trí cân bkhi đi qua vị ằng
Khi viên đạn đi qua vị ằng, năng lượ có động năng còn thế năng trí cân b ng của hệ chỉ
hấp d n và th ẫ ế năng đàn hồi đều băng 0. Phương trình bảo toàn năng lượng đối v i hai ớ
vị trí y và y :
A B
0
g S
K U U
Hình 8.5 Bài t p 8.2. ậ
7
0
2
1
000
2
1
22
kxmgymv
AB
AB
gy
m
kx
v 2
2
smv
B
/8,19120,0.80,9.2
0350,0
120
,0.958
2
Lưu ý là trong bài toán này có hai dạng th ế năng và trong việc giải bài toán theo phương
pháp năng lượ đây, chúng ta không cần quan tâm đế ốc độ ủa viên đạng ở n t c n tại
những vị trí khác trong quá trình chuy ng mà ch c n các vển độ ỉ ần quan tâm đế ị trí đầu
và v trí cu m m nh c ị ối. Đó là một điể ạ ủa phương pháp này.
Ma sát động (ma sát trượt)
Hình 8.5 mô t mả ột mô hình đơn giản để giải thích sự
xuất hiện ma sát trượt giữa b mề ặt c a hai v t ti p xúc vủ ậ ế ới
nhau. Theo mô hình này thì l c ma sát tác d ng gi a hai ự ụ ữ
v nhật là do tương tác giữa ững ph n g trên b mầ ồ ghề ề ặt
ti trếp xúc gi a hai v t. Tuy nhiên, l c ma sát ữ ậ ự ải rộng trên
toàn b di n tích ộ ệ tiếp xúc. Do đó, không thể tính được độ
dịch chuy n cể ủa điểm đặt mà l c ma sát tác d ng vào. ự ụ Vì
vậy, cũng không thể tính đượ c công th c hi n b i l c ma ự ệ ở ự
sát. Thực tế đã chứng t khi có ma sát thì v t b nóng lên ỏ ậ ị
trong quá trình chuyển động. Điều đó cho thấ ội năng y n
của v i vật đã tăng lên. Đố ới trường hợp hệ không b bi n ị ế
dạng và l lực ma sát có độ ớn không thay đổi thì có th ể
phát tri n mể ột cách thức để đánh giá sự ến đổ ội năng bi i n
của h n l c ma sáệ liên quan đế ự t như sau.
Xét m t h g m m t vộ ệ ồ ộ ật (ví d m t cuụ ộ ốn sách) trượt
trên m t chi c bàn nộ ế ằm ngang có ma sát dưới tác dụng
của các l c tác d ng t bên ngoài h . Công c a t t cự ụ ừ ệ ủ ấ ả các
lực tác d ng lên v t thụ ậ ực hi ện được xác định như sau:
otherforces otherforces
W W dr
(8.10)
Trong công th c trên, ứ
dr
là độ dịch chuyển của vật
cũng chính là độ dịch chuyển của các điểm đặt lực bởi vì
vật không bị bi n d ng. Thêm vào m i vế ạ ỗ ế của phương
trình trên m t s h ng ộ ố ạ
k
f .dr
ta được:
Hình 8.6 Mô hình để gi i thích ả
ma sát gi a v t và b m ữ ậ ề ặt.
8
otherforces k otherforces k
otherforces k
W f .dr W dr f .dr
W f .dr F .dr
Sử d ng nh lu t 2 Newton s ụ đị ậ ẽ thu được:
otherforces k
W f .dr ma.dr m .dr mv.dv
dt
Vì
2
1 1
v.dv d(v.v) dv
2 2
Nên
i
v
2 2 2
otherforces k f i
v
1 1
W f .dr m.dv mv mv K
2 2 2
Công và năng lượng khi có ma sát
Một cách t ng quát, n u l c ma sát tác d ng vào m t h ổ ế ự ụ ộ ệ thì
ΔK = ΣW
other forces
ƒ
k
d (8.11)
Đây là một dạng khác của định lý động năng và được sử dụng nếu lực ma sát tác dụng
lên vật. Nếu không có ma sát, phương trình này trở thành đị nh lu t bậ ảo toàn cơ năng. Lực ma
sát biến động năng thành nội năng của hệ.
Độ tăng nội năng bằng với độ ảm động năng củ gi a hệ:
ΔE
int
= ƒ
k
d 12) (8.
Một cách t ng quátổ , phương trình trên sẽ được viết dưới
dạng sau:
ΣW
other forces
= W = ΔK + ΔE
int
(8.13)
Phương trình này có thể được sử d ng trong các h ụ ệ
không cô l p v i các l c không ph i l o toàn. ậ ớ ự ả ực bả
Bài t p m u 8.3: Chuy ng c a chi p trên ậ ẫ ển độ ủ ếc hộ
bề m t có ma sát ặ
Một chi c h p n ng 6,0 kg c kéo b ng m t l có ế ộ ặ đượ ằ ộ ực
phương ngang không đổi 12 trên m t b mN ộ ề ặt nhám
từ trạng thái ngh . ỉ
(A) Hãy tính t c a cái h p sau khi nó di chuyốc độ ủ ộ ển
một đoạ ma sát độn dài 3,0 m. Biết hệ số ng giữa bề
mặt và cái h p là 0,15. ộ
Hình 8.7 Bài t p 8.3. ậ
9
Giải:
Bề mặt nhám s tác d ng l c ma sát vào ẽ ụ ự cái hộp. L c ma sát có chiự ều ngược chiều của
lực kéo. H h p ệ ộ – b mề ặt là h không cô l p vệ ậ ới l c không b o toàn tác d ng bên trong ự ả ụ
hệ.
Cả ph n lả ực pháp tuy n và lế ực h p dấ ẫn đều không sinh công trong trường hợp này.
Theo phương thẳng đứng thì vật ở trạng thái cân b ng. T ằ ừ đó tìm ra độ lớn c a l c ma ủ ự
sát:
k k
f mg
Công do l c tác d c hi n trên h ự ụng theo phương ngang thự ệ ệ là:
ΣW
other forces
= F. x
Suy ra
F.
x = K + E
int
= (mv
f
2
/2 – 0) + f
k
d
Tốc độ cuối cùng c a vủ ật đó là:
2
( )
f k
v f d F x
m
v
f
=
√
2
6,0
(
−8, .3,0 + .3,082 12
)
=1,8 m/s
Giá tr v n t c ph i nhị ậ ốc thu đượ ả ỏ hơn trong ví dụ Trong trườ không có lực ma sát. ng
hợp này, động năng của hệ giảm còn n a h h p b mội năng củ ệ ộ – ề ặt đã ăng lên.t
(B) Nếu l c tác d ng h p v t góc thì góc nghiêng có giá tr ự ụ ợ ới phương ngang mộ ị
bằng bao nhiêu để tốc độ c a chi c h p có giá tr l n nh t có th khi nó di chuyủ ế ộ ị ớ ấ ể ển được
một đoạn dài 3,0 m?
Giải:
Chọn h g m cái h p và b mệ ồ ộ ề ặt Đây là một hệ không cô lập và bên trong h có lệ ực
không b o toàn tác d ng. ả ụ
. Công l c bên ngoài th c hi n trên h ự ự ệ ệ là:
ΣW
other forces
= W
F
= F.x.cos = Fdcos
Theo phương thẳng đứng, hệ cân bằng nên:
n + Fsin -mg = 0
n = mg - Fsin
W
F
= K + E
int f
= (K – 0) + f
k
d
K
f
= W - f d = Fdcos - nµ d = Fdcos - µ d(mg -
F
k
k
k
Fsin)
Để t cốc độ ủa chiếc hộp cực đại thì phải thỏa mãn:
10
𝑑𝐾
𝑓
𝑑𝜃
= -Fdsin + µ = 0
k
dFcos
tan = 0
= tan = tan 0,15 = 8,5
-1
µ
k
-1 o
Bài t p m 8.4: Hậ ẫu ệ khối hộp – lò xo
Một v t khậ ối lượng m = 1,6 kg được đẩy vào một
chiếc lò xo nằm ngang có độ cứng 1000 N/m trên
bề m Lò xo b nén m n 2,0 ặt như hình vẽ. ị ột đoạ
cm c th và sau đó đượ ả ra.
(A) Hãy tính t c a v ốc độ ủ ật khi đi ngang qua vị
trí cân b ng x = 0 n u b mằ ế ề ặt không ma sát.
Giải:
Hệ được ch n là v t. không cô l p. ọ ậ Đây là hệ ậ
Công do lực đàn hồi của lò xo th c hi n trên h ự ệ ệ
từ vị trí x = x
i max
đến vị trí x = 0 là:
f
W
s
= kx
max
2
/2
Theo định lý động năng, ta có:
𝑊
𝑠
=
1
2
𝑚𝑣
𝑓
2
−
1
2
𝑚𝑣
𝑖
2
=
1
2
𝑚𝑣
𝑓
2
−0
𝑣
𝑓
= √
2𝑊
𝑠
𝑚
=
√
𝑘𝑥
𝑚𝑎𝑥
2
𝑚
=
√
1000.(2,0.10
−2
)
2
1,6
=0,50 𝑚/𝑠
(B) Hãy tính t c a vốc độ ủ ật khi đi ngang qua vị cân b ng x = 0 n u btrí ằ ế ề ặ m t tác d ng ụ
lên v t m t l i 4,0 N. ậ ộ ực ma sát không đổ
Giải:
Hệ được ch n g m v t và b m t. ọ ồ ậ ề ặ Đây là hệ không cô l p và bên trong h có m t lậ ệ ộ ực
không b o toàn ả (lực ma sát) tác d ng. ụ Phương trình của định lu t bậ ảo toàn năng lượng
áp d ng cho h ng h p này có d ng: ụ ệ trong trườ ợ ạ
𝑊
𝑠
= ∆𝐾+ ∆𝐸
𝑖𝑛𝑡
=
1
2
𝑚𝑣
𝑓
2
+ 𝑓
𝑘
𝑑
𝑣
𝑓
=
√
2 𝑊(
𝑠
−𝑓
𝑘
𝑑)
𝑚
=
√
2(
1
2
𝑘𝑥
𝑚𝑎𝑥
2
−𝑓
𝑘
𝑑)
𝑚
=
√
2(
1
2
1000.(
2,0.10
−2
)
2
−4,0.0,020
1,6
= 0, 𝑚/𝑠39
Có th y r ng t c a v ng h p này nhể thấ ằ ốc độ ủ ật trong trườ ợ ỏ hơn trong câu A.
Hình 8.8: Bài t p 8.4ậ
11
Thay đổi cơ năng khi có lực không bảo toàn
Nếu có l c ma sát tác d ng ự ụ thì cơ năng củ thay đổa hệ i.
ΔE
mech
= ΔK + ΔU = ƒ
k
d = -ΔE
int
(8.14)
ΔU là độ biến đổi của tất cả các dạng thế năng.
Trong trường hợp tổng quát, khi có lực không b o toàn tác d ng bên trong mả ụ ột hệ cô lập
thì phương trình của định luật bảo toàn có dạng:
ΔK + ΔU + ΔE
int
= 0 (8.15)
Đối với một hệ không cô l p ng bên ngoài b ng cách th c hi n công ậ và các tác độ lên hệ ằ ự ệ
ΣW
other forces
ƒ
k
d = ΔE
mech
(8.16)
Như vậy, đối với m t hộ ệ không cô l p có th ậ ế năng thay đổi và có tác d ng c a l c không ụ ủ ự
bảo toàn thì
ΣW
other forces
= W = ΔK + ΔU + ΔE
int
(8.17)
Bài tập mẫu 8.5: Ma sát trên mặt
phẳng nghiêng
Một thùng hàng n ng 3,00 kg ặ trượt
xu mống trên ột m t ph ng nghiêng có ặ ẳ
ma sát. M t nghiên có chi u dài 1,00 ặ ề
m và độ
nghiêng là = 30,0 . Thùng
o
hàng b t không v n t c ban ắt đầu trượ ậ ố
đầu t ừ đỉnh c a m t nghiêng và l c ma ủ ặ ự
sát có độ ớn 5,00 N. Sau khi trượ l t hết
mặt ph ng nghiêng, nó còn di chuyẳ ển
một đoạn ngắn trên mặt phẳng nằm
ngang.
(A) Hãy tìm t c a thùng tốc độ ủ ại đáy mặt phẳng nghiêng.
Giải:
Xác định hệ bao gồm: thùng hàng, bề mặt và Trái đấ Đây là một. t hệ kín có l c không ự
bảo toàn tác dụng.
Chọn g c tính thố ế năng hấp dẫn của hệ tại mặt phẳng ngang y = 0có tọa độ . Khi đó,
phương trình của đị ảo toàn năng lượnh luật b ng cho h có d ng: ệ ạ
ΔK + ΔU + ΔE
int
= 0
(K
f
– K ) + (U U ) +f .d = 0
i f
–
i k
(½ mv
f
2
– 0) + (0 - ) + f .d = 0 mgy
i k
𝑣
𝑓
= √
2
𝑚
(
𝑚𝑔𝑦
𝑖
− 𝑓
𝑘
𝑑
)
Hình 8.9: Bài t p 8.5 ậ
12
𝑣
𝑓
=
√
2
3,
00
(
3, × 9, × 0, × 1,00 80 500 − 5,00 00
)
= 2,54 𝑚/𝑠
(B) Thùng hàng ti p t t m n dài bao nhiêu trên mế ục trượ ột đoạ ặ ẳt ph ng ngang nếu nó
tiếp t c ch u l c ma sát tác dụ ị ự ụng có độ lớn bằng 5,00 N?
Giải:
Lúc này th a h không th ế năng củ ệ ay đổi nên ta có phương trình:
ΔK + ΔE
int
= 0
(0
- ½ mv
i
2
) + f .d = 0
k
𝑑 =
𝑚𝑣
𝑖
2
2𝑓
𝑘
=
3, ×2,00 54
2
2×5,
00
=1,94 𝑚
Bài t p mậ ẫu 8.6: Va
chạm gi a chiữ ếc hộp
và lò xo
Một chi c h p có ế ộ
khối lượng 0,8 kg
được cung cấp một
vận t u 1,2 ốc ban đầ
m/s sang bên ph i và ả
va ch m v i mạ ớ ột lò xo
khối lượng nh ỏ có độ
cứng k = 50 N/m.
Giả s b m t không ử ề ặ
ma sát. Hãy tính độ
nén cực đại của lò xo
sau va ch ạm.
Giải:
Nếu không có ma sát,
năng lượng được
chuyển hóa giữa động
năng và thế năng đàn
hồi và tổng năng
lượng không đổi
Chọn h g m có h p và lò xo. H ệ ồ ộ ệ là cô l p vậ ới các l c tác d ng ự ụ đều là l o toànực bả .Tất
cả chuyển động di n ra trên m t ph ng n m ngang. Vì v y không có s i cễ ặ ẳ ằ ậ ự thay đổ ủa
thế năng hấp dẫn. Trước va ch m, t ng c a h l a h p. Khi ạ ổng năng lượ ủ ệ à động năng củ ộ
Hình 8.10: Bài t p m u 8.6ậ ẫ
13
lò xo b ng 0 và toàn b ng là thị nén hoàn toàn, động năng bằ ộ năng lượ ế năng đàn hồi
của lò xo. C a h c b o toànơ năng củ ệ đượ ả .
Phương trình của đị ảo toàn năng lượng trong trườnh luật b ng h p này là: ợ
ΔK + ΔU = 0
(0
- ½ mv
A
2
) + (½ kx
max
2
- 0) = 0
𝑥
𝑚𝑎𝑥
=
√
𝑚
𝑘
𝑣
𝐴
= √
0,80
50
× 1,2 = 0,15 𝑚
(B) Giả s h s ng gi a chi c h p và b mử ệ ố ma sát độ ữ ế ộ ề ặt là µ = 0,50. N
k
ếu t cốc độ ủa
chiếc h p t i th m nó va ch m v nén c i c a lò xo ộ ạ ời điể ạ ới lò xo là 1,2 m/s thì độ ực đạ ủ
là bao nhiêu?
Giải:
Đây là bài toán có l c ma sát. Lự ực ma sát s biẽ ến đổi động năng của h thành nệ ội năng.
Chọn h g m chi c h p, b mệ ồ ế ộ ề ặt và lò xo. Đó là h kín v i l c không b o toàn tác d ng. ệ ớ ự ả ụ
Trong trườ ợp này, cơ năng củng h a hệ E
mech s
= K + U không bảo toàn; trong đó U
s
là
thế năng đàn ồi. Phương trình của đị ảo toàn năng lượng đố h nh luật b i với hệ là:
ΔK + ΔU + ΔE
int
= 0
Trong đó,
ΔE
int
= ƒ
k
d, f = µ .n = µ .mg
k k k
Thay vào phương trình trên, ta được:
(0
- ½ mv
A
2
) + (½ kx
max
2
- 0) + µ
k
.mgx
max
= 0
kx
max
2
+ 2µ
k
.mgx
max
- mv
A
2
= 0
50x
max
2
+ 2.0,50.0,8.9,8x 0,8.1,2 = 0
max
–
2
50x
max
2
+ 7,84x 1,15 = 0
max
–
Phương trình có hai nghiệm x = 0,092 m và x -0,25 m. Giá tr
max max
= ị có ý nghĩa vật
lý là x = 0,092 m.
max
So v i k t qu trong câu (A) có giá tr nh ớ ế ả , x
max
ị ỏ hơn. Lý do là gì?
Công su t ấ
Định nghĩa: Công su c th i là tất tứ ờ ốc độ truyền năng lượng theo i gian và c tính thờ đượ
theo công th ức:
dE
P
dt
(8.18)
14
Nếu năng lượng trao đổi dướ ạng công đượi d c thực hiện bởi một lực và trong khoảng
thời gian t công do l c sinh ra là W công su t trung bình P ự thì ấ
avg
được xác định bởi công
thức:
avg
W
P
t
(8.19)
Công su t t c th i là i h n c công su t trung bình khi n t i 0. ấ ứ ờ giớ ạ ủa ấ Δt tiế ớ
0
lim
F F v
t
W dW d
P
t dt dt
Đơn vị
Trong hệ đơn vị SI, đơn vị của công suất là watt (W).
1 watt = 1 joule/second = 1 kg.m
2 3
/s
Một đơn vị công suất hay sử dụng nữa tại Mỹ là mã lực (horsepower – hp)
1 hp = 746 W
Một cđơn vị ủa năng lượng thường b m l n vị nhầ ẫ ới đơn vị công suất là kWh. Nhớ rằng
kWh là đơn vị đo năng lượng, được xác định như sau:
1 kWh = 1kW.1h = (1000 W)(3600 s) = 3.6 x10 J
6
Tóm tắt chương 8
Hệ không cô lập về năng lượng là m t h ng vộ ệ có trao đổi năng lượ ới môi trường qua biên
giới c a nó. ủ
Hệ cô lập là m t hộ ệ không trao đổi năng lượ ới môi trường v ng qua biên gi i c a h . ớ ủ ệ
Định luật b ng: ảo toàn năng lượ Năng lượng c a m t h cô lủ ộ ệ ập là không đổi.
Một lực ma l n f tác d ng trên msát có độ ớ
k
ụ ột quãng đườ ội năng củ thay đổng d thì n a hệ i
một lượng:
E
int
= f
k
.d
Công suất là tốc độ truyền năng lượng theo thòi gian:
dE
P
dt
Phương trình củ ảo toàn năng lượng đốa định luật b i với hệ không cô lập
ΔE
system
= ΣT
Δ K + Δ U + Δ E
int
= W + Q + T
MW
+ T
MT
+ T + T
ET ER
15
Phương trình củ ảo toàn năng lượa định luật b ng i vđố ới hệ ậ cô l p
ΔE
system
= 0
ΔK + ΔU + ΔE
int
= 0
Nếu các l tác d ng bên trong h u là l o toàn ta có nh lu t b ực ụ ệ đề ực bả thì đị ậ ảo toàn cơ năng
ΔE
mech
= 0
ΔK + ΔU = 0
Câu h i lý thuyỏ ết chương 8
1. Một người thả một quả bóng t nh c a mừ trên đỉ ủ ột tòa nhà trong khi người khác thì đang
đứng ở dưới để ển độ ệu 2 người này có đồ quan sát chuy ng của nó. Li ng ý
(a) Về giá tr thị ế năng hấ Trái Đấp dẫn của hệ quả bóng - t.
(b) Về s i c p d n. ự thay đổ ủa thế năng hấ ẫ
(c) Về động năng của quả bóng t t ong quá trình ng cại mộ điểm nào đó tr chuyển độ ủa
nó.
2. L ực ma sát tĩnh có thể sinh công hay không? N u không, hãy gi i thích t i sao không. ế ả ạ
Nếu có thì hãy cho m t ví d ộ ụ.
3. Một người nặng 70,0 kg leo lên m nh núi cao 325m trong 90 phút. Công su t trung ột đỉ ,0 ấ
bình người đó sinh ra là bao nhiêu?
(a) 39,1 W (b) 54,6 W (c) 25,5 W (d) 67,0 W (e) 88,4 W
4. Một v c g n v i m t lò xo treo trên tr n nhà. Gi s s c c c b ật đượ ắ ớ ộ ầ ả ử ứ ản không khí đượ ỏ
qua, hãy mô t các bi ng x y ra trong h g - t - lò xo khi v t ả ến đổi năng lượ ả ệ ồm vật trái đấ ậ
chuyển độ theo phương ng thẳng đứng.
5. Phương trình của định lý công - ng độ năng W = K chỉ đúng trong trường hợp không có
thay đổi đối với bấ ết kỳ loại năng lượng nào khác như th năng h ội năng xảy ra đốay n i
với m t h . Hãy cho vài ví d cho th y công th c hi n trên m t hộ ệ ụ ấ ự ệ ộ ệ nhưng sự thay đổi
năng lượng của hệ không ph i là thay . ả đổi động năng
Bài t p ậ chương 8
1. Một qu bóng khả ối lượng m rơi từ độ cao h xuống sàn.
(a) Viết phương trình của đị ảo toàn năng lượnh luật b ng (dạng 8.2) cho hệ quả bóng -
Trái đấ ụng nó để ốc độ bóng ngay trướ ạm đất và sử d tính t của quả c khi nó ch t.
(b) Viết phương trình của đị ảo toàn năng lượnh luật b ng (dạng 8.2) cho hệ chỉ có quả
bóng và s dử ụng nó để ốc độ tính t của quả bóng ngay trước khi nó ch ạm đất.
2. Một quả đạn pháo nặng 20,0 kg được bắn ra t m t kh i bác v i từ ộ ẩu đạ ớ ốc độ là 1000 m/s
theo phương hợ
p với phương ngang một góc 37,0 . M
o
ột quả đạn khác b n v i góc 90,0ắ ớ
o
.
Xét m ột hệ kín để tính:
(a) Độ ỗ đạ cao c i cực đạ ủa m i quả n.
16
(b) Cơ năng củ trái đấa hệ quả đạn- t t cao c i c a m i qu . Ch n y = 0 t i vại độ ực đạ ủ ỗ ả ọ ạ ị trí
đặt kh i bác. ẩu đạ
3. Một v t kh ng m = 5,00 kg r i khậ ối lượ ờ ỏi điểm A và trượt trên một rãnh không ma sát
như trong hình vẽ Hãy xác đị . nh:
(a) Tốc độ ại các điể của vật t m B và C.
(b) Công th c hi n b i l c h p d n trên v t khi nó di chuy n tự ệ ở ự ấ ẫ ậ ể ừ điểm A đến điểm C.
4. Một kh i nố ặng 2,00 kg được gắn vào một lò xo có độ cứng
k = 500 N/m như trên hình vẽ ối đó đượ. Kh c kéo tới vị trí x
i
= 5,00 cm v phía bên ph i c a v trí cân b c th ề ả ủ ị ằng và đượ ả
ra t ng thái ngh . Tìm t c a kh trí ừ trạ ỉ ốc độ ủ ối khi đi qua vị
cân b ng n u: ằ ế
(a) Bề mặt ngang không có ma sát.
(b) Hệ s ma sát gi a kh i và b m t là = 0,350. ố ữ ố ề ặ
k
5. Một vòng tròn trơn có bán kính 0,500 m đặt trên mặ ạt sàn. Một h t nặng 0,400-kg trượt
quanh c nh bên trong c a vòng. T u c a nó là 8,00 m/s. Sau m t vòng, tạ ủ ốc độ ban đầ ủ ộ ốc
độ còn lại là 6,00 m/s do có ma sát.
(a) Tìm năng lượ ển đổ cơ năng sang nội năng củ Trái đấng chuy i từ a hệ hạt – vòng – t
(do ma sát) sau khi k t thúc 1 vòng chuy ng. ế ển độ
(b) Tổng s vòng hố ạt đi được đến khi d ng l i là bao nhiêu? Gi s lừ ạ ả ử ực ma sát không đổi
trong quá trình chuy ng. ển độ
6. Hệ s ma sát giố ữa vật kh ng m = 3,00 kg v i m t bàn là ối lượ
1
ớ ặ
µ
k
= 0,400 (xem hình v ). Cho hai v t chuy ng tẽ ậ ển độ ừ trạng
thái ngh . Tính t c a v t m ng ỉ ốc độ ủ ậ
2
= 5,00 kg khi nó đi xuố
một đoạn h = 1,50 m.
7. Đẩy cho m t v t n ng m = 5,00 kg chuy i tộ ậ ặ ển động đi lên vớ ốc
độ u là vi = 8,00 m/s trên m t m t d nghiêng ban đầ ộ ặ ốc có độ
= 30,0o. V t d ng lậ ừ ại sau khi đi đượ ột đc m oạn d = 3,00 m.
Hãy tính:
(a) Độ bi a vến thiên động năng củ ật.
(b) Độ biến thiên thế năng của hệ vật-Trái đất.
(c) Lự ục ma sát tác d ng lên vật.
(d) Hệ số ma sát trượt.
8. Một động cơ điện c a m t chi c xe l a mô hình gia tủ ộ ế ử ốc
chiếc xe t ng thái ngh n t 0,620 m/s ừ trạ ỉ đế ốc độ trong
thời gian 21,0 ms. Kh ng c a chi c xe là 875 g. ối lượ ủ ế
(a) Tính công su t t i thi u c n cung c p cho xe lấ ố ể ầ ấ ửa
trong quá trình gia t ốc.
17
(b) Giải thích tại sao đó là gia tốc tối thiểu?
9. Một chi c thang máy n ng 650 kg chuyế ặ ển động đi lên từ trạng thái ngh vỉ ới gia t c không ố
đổi. Sau th t t di chuy u b ng 1,75 m/s. ời gian 3,00 s nó đạ ốc độ ển đề ằ
(a) Công su t trung bình cấ ủa động cơ thang máy trong khoảng th ng bao ời gian đó bằ
nhiêu?
(b) Hãy so sánh giá tr ị tính được với công su t cấ ủa động cơ khi thang máy di chuyển đều.
10. Một v t nh c thậ ỏ khối lượng m = 200 g đượ ả cho
chuyển độ ọc theo đường d ng kính bên trong c a mủ ột
cái chén hình bán c u, không ma sát. Bán kính c a cái ầ ủ
chén bán c u là R = 30,0 cm. Hãy tính: ầ
(a) Thế năng hấ Trái đấp dẫn của hệ vật- t khi vật ở
điểm A. Chọn gốc tính thế năng tại điểm B.
(b) Động năng củ ại điểa vật t m B.
(c) Tốc độ của vật tại B.
(d) Động năng củ năng của vật và thế a hệ khi vật ở t m C. ại điể
11. Vật m
1
= 3,50 kg ban đầu nằm yên trên m t m t bàn nộ ặ ằm
ngang cách sàn một khoảng h = 1,20 m được nối với vật
m
2
= 1,90 kg b ng mằ ột dây nhẹ không co dãn. u Lúc đầ
vật m
2
cách mặt sàn m t kho ng d = 0,900 m. M t bàn và ộ ả ặ
cạnh bàn đều không ma sát. Các v t b u chuy ng ậ ắt đầ ển độ
từ trạng thái ngh , v t m t trên m t bàn r i bay ra ỉ ậ
1
trượ ặ ồ
ngoài còn v t mậ
2
đi xuống và d ng l i trên sàn. Xem h ừ ạ ệ
gồm có hai v ật và Trái đất.
(a) Tính t c a vốc độ ủ ật m khi r
1
ời khỏi mép bàn.
(b) Tính t c a mốc độ ủ
1
khi ch m m t sàn. ạ ặ
(c) Chiều dài ng n nh t c a s i dây không b ắ ấ ủ ợ ị căng khi m
1
đang bay là bao nhiêu?
(d) Năng lượng c a h khi nó b u chuy ng có b ng c a h c khi ủ ệ ắt đầ ển độ ằng năng lượ ủ ệ trướ
m
1
chạm đất hay không? Hãy giải thích tại sao bằng hay tại sao không?
12. Một tài xế đạp chân ga làm cho c xe kh ng 1160 kg c t ng thái nghchiế ối lượ tăng tố ừ trạ ỉ.
Trong 2 giây đầ ếc xe tăng theo thời gian và đượu tiên, gia tốc của chi c biểu diễn bởi
phương trình
𝑎 = 1, 𝑡 −0, + 0,16 210𝑡
2
240𝑡
3
(
𝑚
𝑠
2
).
Trong đó t đo bằng s và a đo bằ
ng m/s .
2
(a) Tính độ ến thiên động năng củ t = 0 s đế bi a xe từ n t = 2,5 s.
(b) Tính công su t trung bình t i thi u cấ ố ể ủa động cơ trong khoảng th i gian trên. ờ
(c) Tại sao giá tr b là giá tr nh nh ị ở câu ị ỏ ất.
18
13. Một lò xo n ngang có ằm độ cứng = 850 k
N/m được gắn vào m t b ng. Mộ ức tườ ột vật
khối lượ 1,00 kg đượng m = c gắn vào lò xo
và n m yên trên mằ ột b mề ặt ngang không ma
sát như trong hình vẽ.
(a) Vật được kéo đến m t v trí x = 6,00 cm ộ ị
i
so v i v trí cân b ng. Tìm thớ ị ằ ế năng đàn
hồi được lưu trữ trong lò xo khi nó n m t i vằ ạ ị trí 6,00 cm và khi v trí cân ật đi qua vị
bằng.
(b) Tìm t c cân b ng. ốc độ ủa vật khi nó đi qua vị trí ằ
(c) Tính tốc độ của vật khi nó ở vị trí x = 3,00 cm.
i
/2
(d) Tại sao t trong câu c không b ng m t n a câu (b) ốc độ ằ ộ ử ?
14. Một vật khối lượng 10,0 kg đượ ại điểm A như hình vẽ. Rãnh trược thả t t là không ma
sát ngo i tr ph n giạ ừ ầ ữa điểm B và C, có chi u dài 6,00 m. Về ật trượt xu ng r i va vào mố ồ ột
lò xo có độ ứng 2250 N/m đẩ c y lò xo ép l i m t kho ng 0,300 m t vạ ộ ả ừ ị trí cân bằng trước
khi t m d ng l nh h s cạ ừ ại . Hãy xác đị ệ ố ủa ma sát động gi a vữ ật và máng trượt trên đoạn
giữa điểm B và C.
15. Một v t kh ng m = 20,0 kg n i v i v t kh ng mậ ối lượ
1
ố ớ ậ ối lượ
2
=
30,0 kg b ng 1 s i dây m nh, nh v t qua m t ròng r c nhằ ợ ả ẹ ắ ộ ọ ẹ,
không ma sát. Đầu còn l i c a mạ ủ
2
n i vố ới lò xo có độ cứng k =
250 N/m như hình vẽ. Bỏ qua ma sát trên mặt nghiêng, góc
nghiêng u, h cân b ng, lò xo không b giãn. θ = 40,0o. Ban đầ ệ ằ ị
Kéo m
1
đi xuống một đoạn h = 20,0 cm r i th ra. Tìm tồ ả ốc độ mỗi
vật khi lò xo tr l i tr ng thái không bở ạ ạ ị giãn.
| 1/18
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

Chương 8: Định luật bảo toàn năng lượng
Hệ không cô lập
Hệ không cô lập về năng lượng là một hệ có trao đổi năng lượng với môi trường qua
biên giới của nó. Một hệ không cô lập sẽ tương tác với môi trường. Một vật bị tác dụng lực
là một ví dụ của hệ không cô lập.
Hệ cô lập là một hệ không trao đổi năng lượng với môi trường qua biên giới của hệ.
Đối với một hệ không cô lập, năng lượng được truyền qua biên giới của hệ trong thời
gian hệ tương tác với môi trường bên ngoài. Sau đây là những phương thức truyền năng lượng
vào hoặc ra khỏi một hệ.
Công (Work) là một hình thức truyền năng lượng bằng cách tác dụng lực lên hệ và điểm
đặt của lực bị dịch chuyển (hình 8.1a). a b c d e f
Hình 8.1 Các cơ chế truyền năng lượng.
Sóng cơ (Mechanical waves) là hình thức truyền năng lượng thông qua sự lan truyền
nhiễu loạn trong môi trường. Âm thanh rời khỏi chiếc loa radio ở hình 8.1b hay sóng địa
chấn, sóng biển là sự truyền năng lượng bằng sóng cơ.
Nhiệt (Heat) là một cơ chế trao đổi năng lượng giữa hệ và môi trường do có sự khác nhau
về nhiệt độ. Năng lượng truyền tới đuôi cái thìa trong hình 8.1c từ phần bị nhúng trong tách
cà phê nóng là dưới dạng nhiệt. 1
Trao đổi chất (Matter transfer) là hình thức truyền năng lượng xuyên qua biên giới của
hệ dưới dạng vật chất mang theo năng lượng. Ví dụ đổ xăng cho xe như ở hình 8.1d hay đối lưu là sự tru ề
y n năng lượng dưới dạng trao đổi chất.
Truyền điện (Electrical transmission) là sự truyền năng lượng vào hoặc ra khỏi hệ bằng
dòng điện. Năng lượng cung cấp cho máy sấy tóc là nhờ sự truyền điện (hình 8.1e).
Sóng điện từ (Electromagnatic radiatio )
n là năng lượng được trao đổi bởi sóng điện từ.
Năng lượng truyền khỏi bóng đèn (hình 8.1f) là dưới dạng sóng điện từ.
Định luật bảo toàn năng lượng
Năng lượng luôn được bảo toàn.
Điều này nghĩa là nếu năng lượng tổng cộng của một hệ thay đổi thì đã có một năng lượng
truyền qua biên giới của hệ bằng một phương pháp trao đổi năng lượng nào đó. Dạng tổng
quát của định luật bảo toàn năng lượng có thể được biểu diễn bằng phương trình bảo toàn
năng lượng như sau:
ΔEsystem = ΣT (8.1)
Trong đó, Esystem là tổng năng lượng của hệ, T (Transfer) là năng lượng truyền qua biên giới của hệ.
Phương trình toán học của định luận bảo toàn năng lượng đối với một hệ không cô lập
thể hiện đầy đủ các loại năng lượng trao đổi có thể được biểu diễn dưới dạng:
Δ K + Δ U + Δ Eint = W + Q + TMW + TMT + TE T + TE R (8.2)
Với K là động năng, U là thế năng và Eint là nội năng của hệ; n
ăng lượng truyền qua biên giới
của hệ dưới dạng công là Twork = W, dưới dạng nhiệt là Theat = Q, TMW l à năng lượng được
truyền bởi sóng cơ, TMT là năng lượng trao đổi chất, TET là năng lượng do truyền điện và TER
là năng lượng trao đổi bởi sóng điện từ.
Trong thực tế, phương trình của định luật bảo toàn năng lượng sẽ đơn giản hơn nhiều. Ví
dụ, nếu có một lực tác dụng lên hệ và sinh công và giả sử chỉ có cơ chế truyền năng lượng
này làm thay đổi tốc độ của hệ thì phương trình của định luật bảo toàn năng lượng sẽ rút về
phương trình của định lý công-động năng: ΔK = W
Câu hỏi 8.1: Hãy cho biết cơ chế truyền năng lượng nào qua một hệ là: a- Một chiếc tivi, b-
Một máy cắt cỏ chạy xăng, c- Một cái gọt bút chì bằng tay.
Câu hỏi 8.2: Xét một cái hộp trượt có ma sát trên một bề mặt nằm ngang.
i) Nếu hệ là chiếc hộp thì hệ là a- cô lập, b- không cô lập, c- không thể xác định được.
ii) Nếu hệ là bề mặt nằm ngang thì hệ là a- cô lập, b- không cô lập, c- không thể xác định được.
iii) Nếu hệ là cái hộp và bề mặt nằm ngang thì hệ là a- cô lập, b- không cô lập, c- không thể xác định được. 2
Hệ cô lập
Đối với một hệ cô lập, không có bất kỳ hình thức trao đổi năng lượng nào với môi trường
bên ngoài qua biên giới của hệ, thì tất cả các số hạng bên vế phải trong phương trình (8.2)
đều bằng 0 do đó phương trình của định luật bảo toàn năng lượng có dạng: ΔEsystem = 0 (8.3)
Esystem là tổng động năng, thế năng và nội năng của hệ.
Như vậy, năng lượng của một hệ cô lập không đổi.
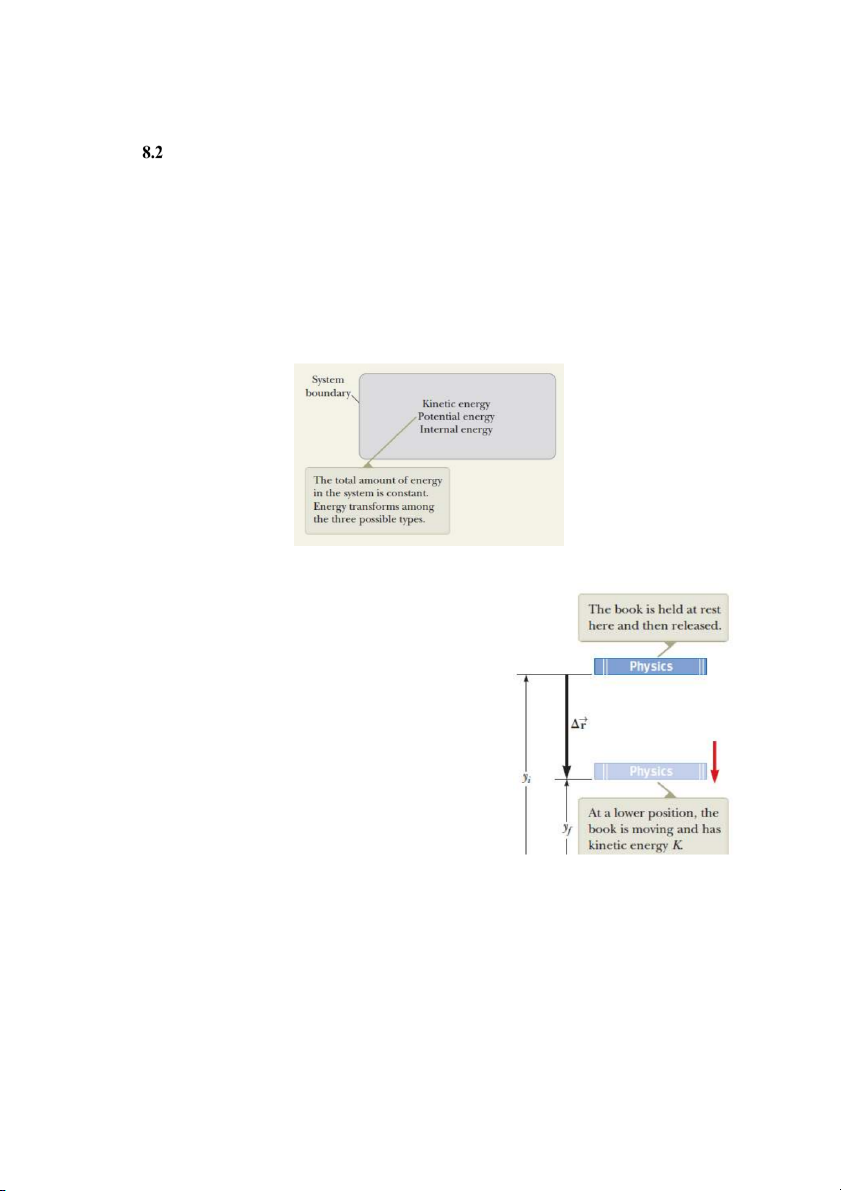
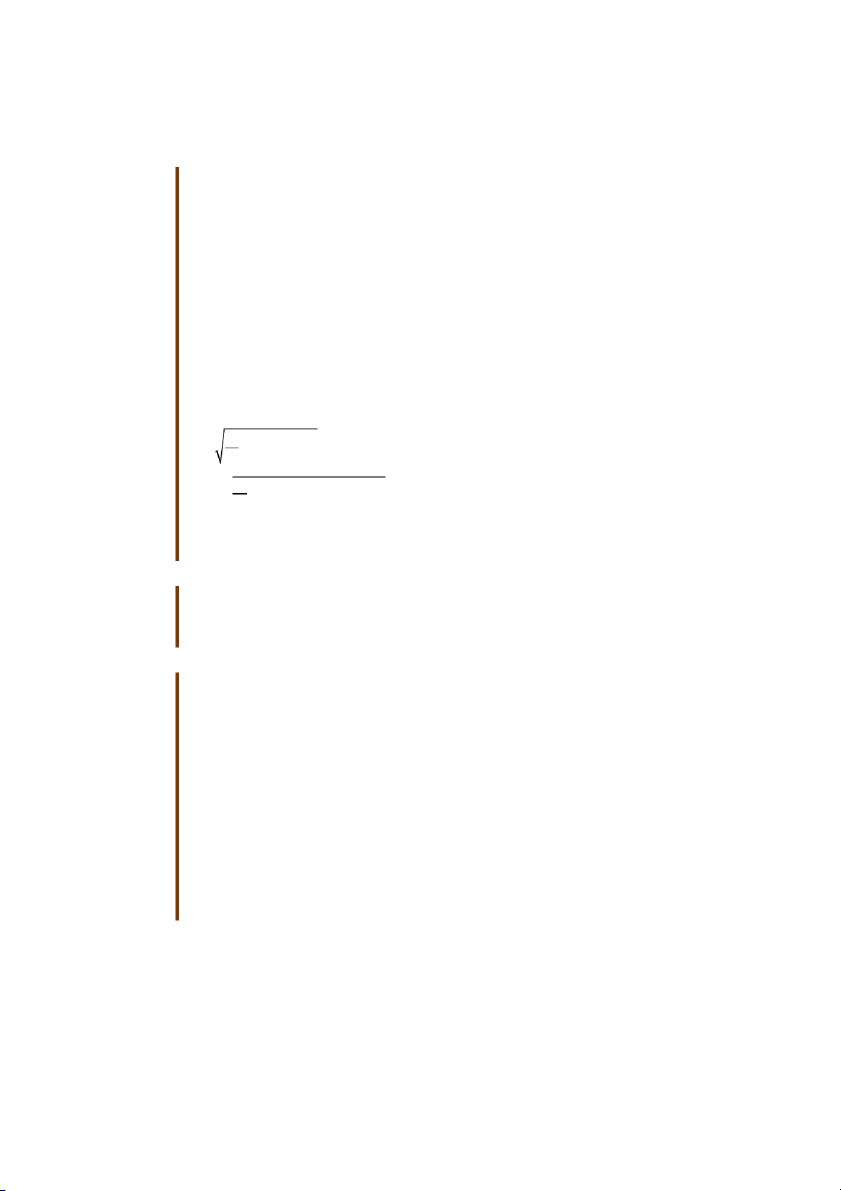
Trên hình vẽ bên dưới mô tả các dạng năng lượng tồn trữ bên trong một hệ cô lập gồm
có động năng, thế năng và nội năng. Các dạng năng lượng này biến đổi lẫn nhau nhưng tổng
năng lượng của hệ bảo toàn.
Hình 8.2 Các dạng năng lượng tồn trữ bên trong hệ.
Định luật bảo toàn cơ năng
Định luật bảo toàn cơ năng là một trường hợp riêng
của định luật bảo toàn năng lượng. Đây là mô hình thường
gặp nhất đối với một hệ cô lập mà trong hệ chỉ có lực bảo toàn tác dụng.
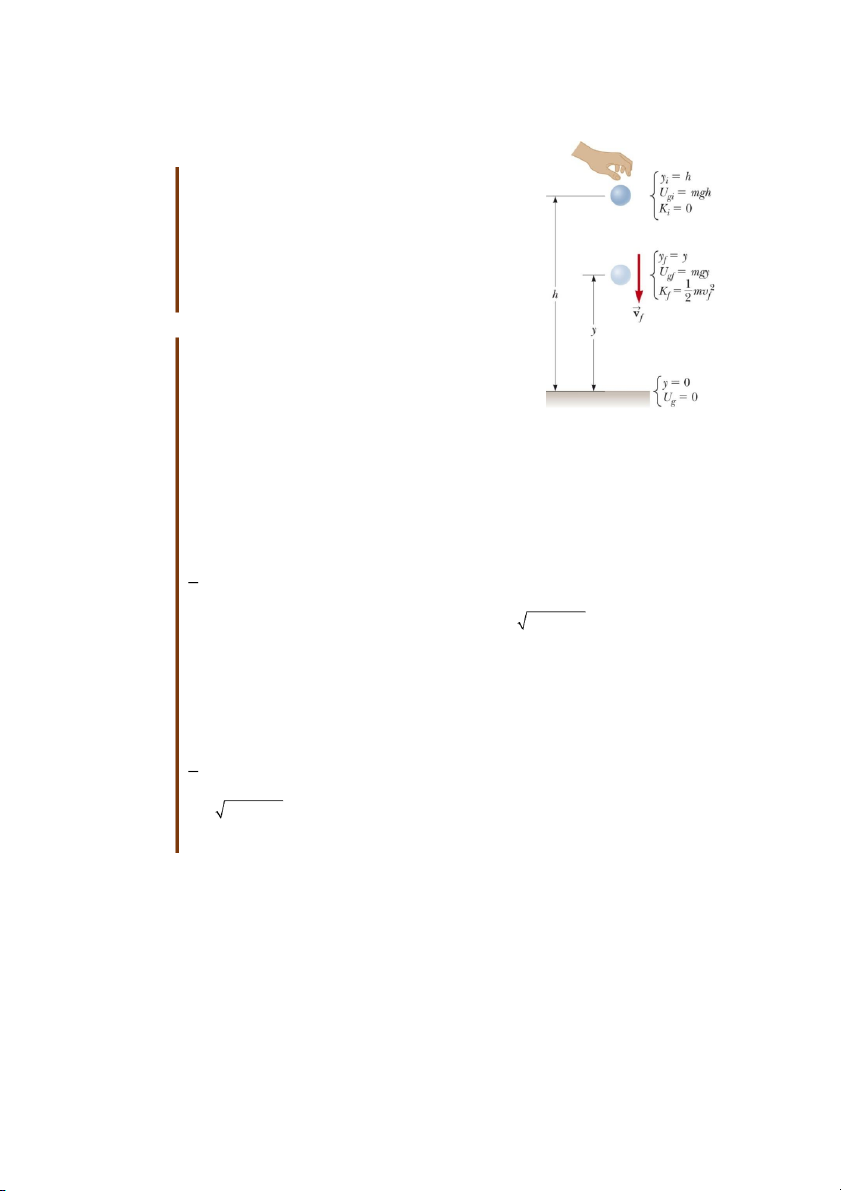
Hãy xét một hệ gồm một cuốn sách khối lượng m và
Trái đất. Sau khi nâng cuốn sách lên một độ cao nào đó thì
bên trong hệ sẽ tồn trữ một năng lượng dưới dạng thế năng
hấp dẫn bằng công mà tác nhân bên ngoài thực hiện trên cuốn sách: W = Ug
Khi cuốn sách rơi từ độ cao yi xuống đến vị trí yf thì
công mà lực hấp dẫn sẽ thực hiện trên cuốn sách là:   Wg m r
  mgj y y jˆ . ˆ .  mgy mgy Cuốn sách đượ ả onbooki f i
f (8.4) Hình 8.3 c th ra và
rơi do công thực hiện bởi lực hấp dẫn 3
Theo định lý công – động năng, công thực hiện trên cuốn sách bằng độ biến đổi động năng của cuốn sách: Won book = Kbook Suy ra,
Kbook = mgyi – mgyf = -(mgyf - mgyi) = -Ug (8.5)
Trong đó, Ug = mgy là thế năng hấp dẫn của hệ. Trong hệ cuốn sách – Trái đất, chỉ có cuốn
sách chuyển động nên động năng của cuốn sách Kbook cũng chính là động năng của hệ K, do đó: Kbook =  K
Phương trình (8.4) có thể được viết lại là: K = -Ug (8.6) K + Ug = 0
Phương trình trên đã được dẫn xuất từ hệ cuốn sách – Trái đất, trong đó Ug là thế năng
hấp dẫn song thực tế cho thấy nó cũng đúng đối với bất kỳ một loại thế năng nào. Phương
trình tổng quát đó là phương trình của định luật bảo toàn cơ năng: K + U = 0 (8.7) ΔEmech = 0 (8.8)
Với Emech = K + U là cơ năng của hệ, K là động năng tổng cộng của hệ, U là tổng tất cả các
loại thế năng của hệ.
Định luật bảo toàn cơ năng chỉ đúng trong trường hợp hệ là cô lập và không có lực không
bảo toàn tác dụng bên trong hệ. Định luật có thể được phát biểu như sau: Cơ năng của một
hệ cô lập mà trong hệ không có các lực không bảo toàn tác dụng thì bảo toàn.
Sự thay đổi năng lượng có thể được viết lại dưới dạng sau: Kf + Uf = Ki + Ui (8.9)
Đối với hệ cuốn sách – Trái đất, ta có phương trình: 1 2 1 2 mv    f mgy f mvi mgyi 2 2
Trong đó, vi và vf là tốc độ của cuốn sách tại vị trí yi và yf.
Câu hỏi 8.3: Ba quả banh được ném từ đỉnh một tòa nhà với cùng tốc độ ban đầu. Quả bóng
thứ nhất được ném theo phương ngang, quả thứ hai hướng lệch lên trên so với phương ngang,
còn quả thứ ba hướng lệch xuống dưới so với phương ngang. Bỏ qua sức cản không khí, hãy
sắp xếp theo thứ tự từ lớn đến bé tốc độ của ba quả bóng khi chúng chạm đất . 4
Bài tập mẫu 8.1: Quả bóng rơi tự do
Một trái banh khối lượng m được thả rơi từ độ cao h trên mặt đất như hình 8.4.
(A) Bỏ qua sức cản không khí, hãy xác định tốc độ của
trái banh tại độ cao y so với mặt đất. Hệ được chọn là trái banh – Trái đất .
(B) Hãy xác định tốc độ của trái banh tại độ cao y so với
mặt đất nếu hệ được chọn là trái banh. Giải:
(A) Tốc độ của trái banh tại độ cao y khi hệ là trái banh – Trái đất.
Vì hệ bao gồm trái banh và Trái Đất nên khi bỏ qua sức
cản không khí chỉ có một lực tác dụng giữa các thành phần của hệ l
à trọng lực - đó là lực bảo toàn. Do đó, cơ
Hình 8.4 Bài tập 8.1.
năng của hệ bảo toàn. Áp dụng định luật bảo toàn cơ
năng, ta có phương trình: Kf + Ugf = Ki + Ugi
Với Ki = 0 là động năng ban đầu khi quả bóng bắt đầu rơi, Ug i= mgh là thế năng ban
đầu của hệ. Khi quả bóng đến độ cao y thì động năng K 2
f = mvf /2 và thế năng của hệ Ugf = mgy. Ta có,
1 mv2 mgy  0 mgh f 2
Từ đó, suy ra vận tốc của trái banh ở độ cao y là v  2g(h y ) f
(B) Tốc độ của trái banh tại độ cao y khi hệ là trái banh.
Trong trường hợp này, chỉ có một loại năng lượng thay đổi là động năng của trái banh.
Hệ không có thế năng. Trọng lực thực hiện công trên trái banh. Áp dụng định luật bảo
toàn năng lượng cho hệ không cô lập, ta có: K = W 1  mv2   0  g m r
  mgj j yˆ . ˆ .  mg y   m
g(y h)  mgh mgy f 2
v  2g (h y ) f
Kết quả cũng giống như trong câu a bất kể hệ được chọn là không giống nhau. 5
Bài tập mẫu 8.2: Súng lò xo
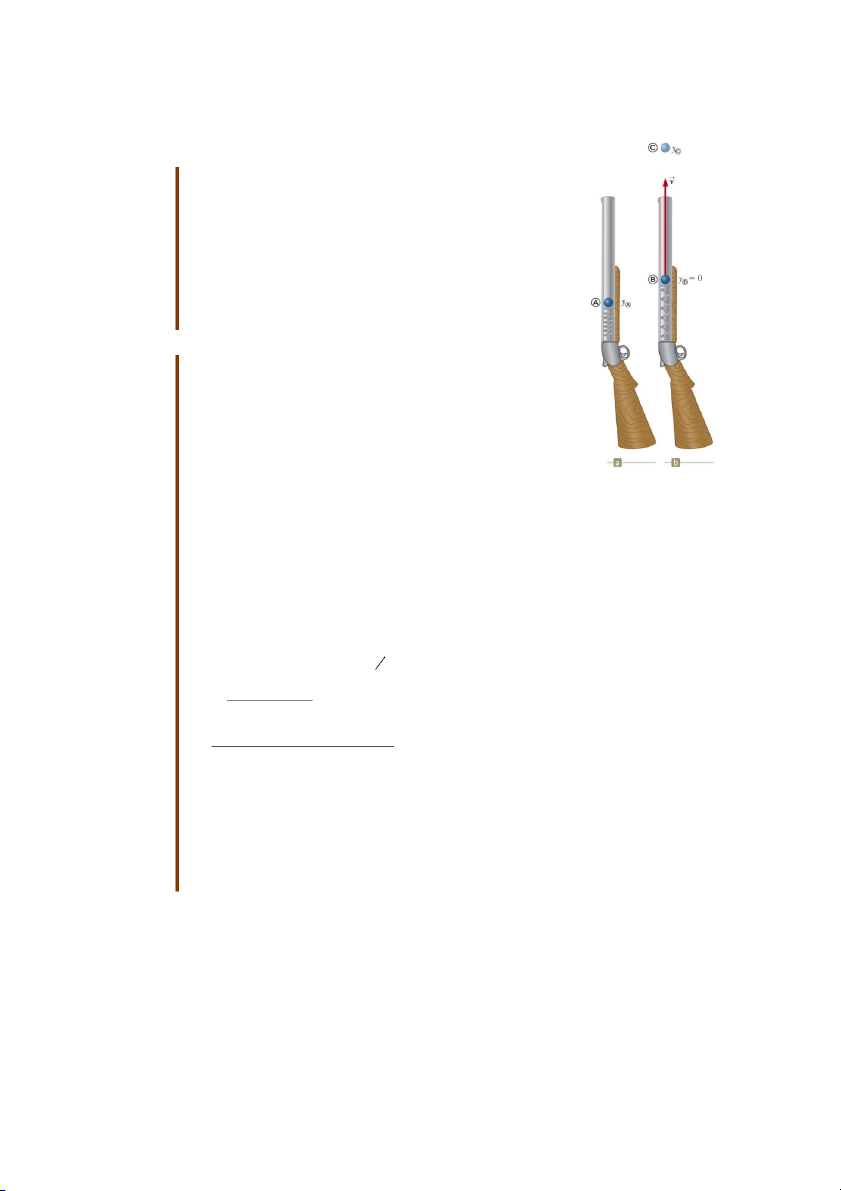
Trên hình 8.5 mô tả cơ chế nạp đạn của một cây súng trò chơi.
Khi nạp đạn, lò xo được nén lại đến vị trí yA. Khi bóp cò, viên
đạn sẽ được bắn lên đến vị trí yC phía trên vị trí yB = 0 lúc viên
đạn rời khỏi lò xo. Trong một lần bắn, m = 35,0 g, yA = -0,120 m và yC = 20,0 m.
(A) Bỏ qua mọi lực cản, hãy tính hệ số đàn hồi của lò xo.
(B) Tính tốc độ của viên đạn khi nó đi qua vị trí cân bằng của lò xo yB. Giải:
(A) Hệ số đàn hồi của lò xo
Trong bài toán của chúng ta, viên đạn trong ống phóng bắt đầu
từ trạng thái nghỉ, được tăng tốc vì lò xo đẩy nó lên phía trên.
Khi rời khỏi nòng súng, lực hấp dẫn sẽ làm viên đạn chuyển động chậm lại.
Chọn hệ bao gồm viên đạn, súng và Trái Đất. Khi bỏ qua
mọi lực cản thì mô hình của bài toán là một hệ cô lập với các Hình 8.5 Bài tập 8.2.
lực tác dụng chỉ có các lực bảo toàn.
Viên đạn bắt đầu từ trạng thái nghỉ nên động năng ban đầu Ki = 0. Chọn gốc thế năng
hấp dẫn tại điểm viên đạn rời khỏi lò xo yB = 0 thì lúc đó, thế năng đàn hồi Us cũng
bằng 0. Đối với hệ cô lập, định luật bảo toàn năng lượng viết cho hai cấu hình lúc viên
đạn tại vị trí yA và yC có dạng:
K  U  U  0 g S
Bởi vì viên đạn đạt vị trí cao nhất yC khi động năng của nó bằng 0 nên Kf = 0, ta có:
(0 0) (mgy mgy ) (0  2 1 kx ) 0 C A 2  2m ( g y  => k y ) C A 2 x , 0 . 1 0350 8 , 9 . 0 .20 0 ,  ( 1 , 0 20) k   958 N / m 1 , 0 20 2
(B) Tốc độ của viên đạn khi đi qua vị trí cân bằng
Khi viên đạn đi qua vị trí cân bằng, năng lượng của hệ chỉ có động năng còn thế năng
hấp dẫn và thế năng đàn hồi đều băng 0. Phương trình bảo toàn năng lượng đối với hai vị trí yA và yB:
K  U  U  0 g S 6  1 2     mv  0  B 0mgy A  1   0 2  kx   0  2   2  kx2 v  2 gy B A m 958 1 , 0 . 20 2 v   8 , 9 . 2 0. 1 , 0 2  0  19 8 , m / s B 0 , 0 350
Lưu ý là trong bài toán này có hai dạng thế năng và trong việc giải bài toán theo phương
pháp năng lượng ở đây, chúng ta không cần quan tâm đến tốc độ của viên đạn tại
những vị trí khác trong quá trình chuyển động mà chỉ cần quan tâm đến các vị trí đầu
và vị trí cuối. Đó là một điểm mạnh của phương pháp này.
Ma sát động (ma sát trượt)
Hình 8.5 mô tả một mô hình đơn giản để giải thích sự
xuất hiện ma sát trượt giữa bề mặt của hai vật tiếp xúc với
nhau. Theo mô hình này thì lực ma sát tác dụng giữa hai
vật là do tương tác giữa những phần gồ ghề trên bề mặt
tiếp xúc giữa hai vật. Tuy nhiên, lực ma sát trải rộng trên
toàn bộ diện tích tiếp xúc. Do đó, không thể tính được độ
dịch chuyển của điểm đặt mà lực ma sát tác dụng vào. Vì
vậy, cũng không thể tính được công thực hiện bởi lực ma
sát. Thực tế đã chứng tỏ khi có ma sát thì vật bị nóng lên
trong quá trình chuyển động. Điều đó cho thấy nội năng
của vật đã tăng lên. Đối với trường hợp hệ không bị biến
dạng và lực ma sát có độ lớn không thay đổi thì có thể
phát triển một cách thức để đánh giá sự biến đổi nội năng
của hệ liên quan đến lực ma sát như sau.
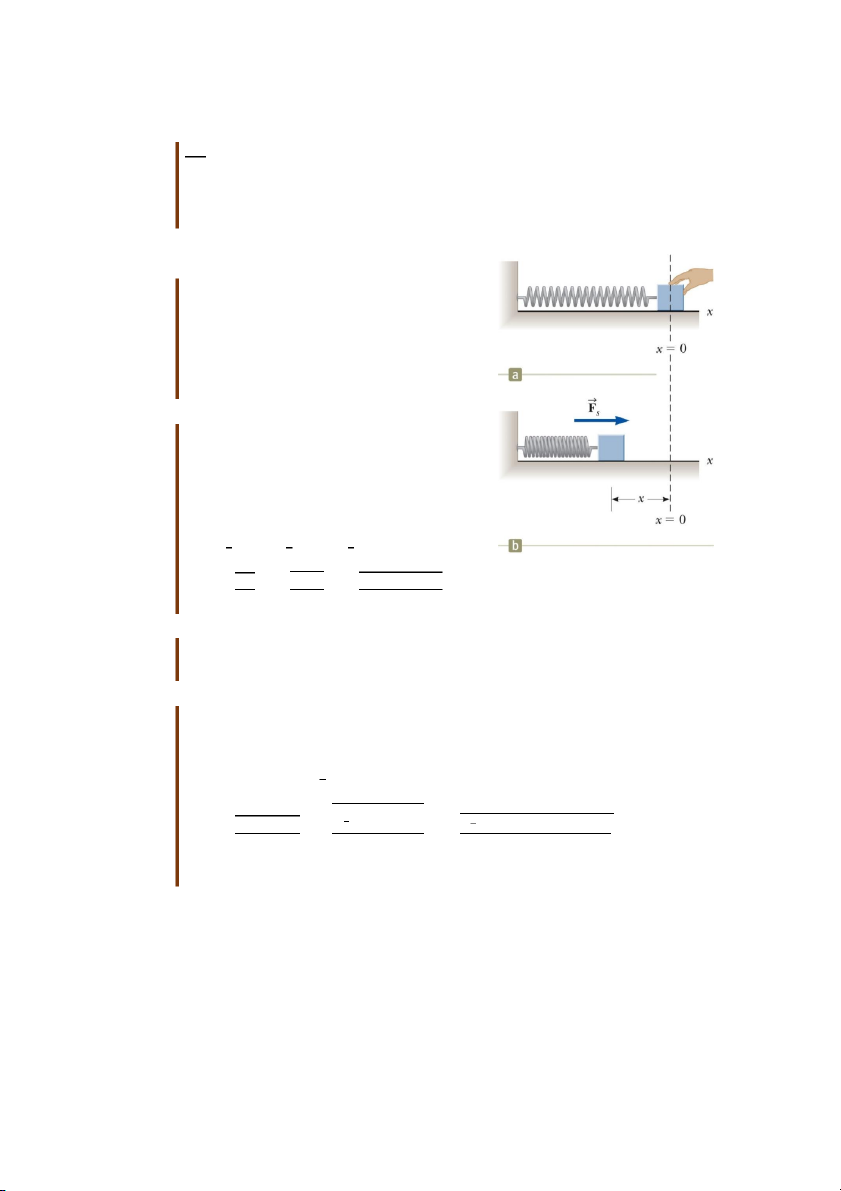
Xét một hệ gồm một vật (ví dụ một cuốn sách) trượt
trên một chiếc bàn nằm ngang có ma sát dưới tác dụng
của các lực tác dụng từ bên ngoài hệ. Công của tất cả các
lực tác dụng lên vật thực hiện được xác định như sau:   W   W dr (8.10) otherforces  otherforces   
Trong công thức trên, dr là độ dịch chuyển của vật
cũng chính là độ dịch chuyển của các điểm đặt lực bởi vì
vật không bị biến dạng. Thêm vào mỗi vế của phương
trình trên một số hạng f .dr  ta được: k
Hình 8.6 Mô hình để giải thích
ma sát giữa vật và bề mặt . 7 W  f .dr    W dr  f .dr otherforces k  otherforces   k       W  f .dr   F .dr  otherforces k       
Sử dụng định luật 2 Newton sẽ thu được: W  f .dr  ma.dr  m .dr   mv.dv otherforces  k    dt Vì 1 1 2 v.dv  d(v.v)  dv 2 2 Nên v 2 1 2 1 2 W  f .dr  m.dv  mv  mv  K   otherforces  k  f i 2 2 2 vi
Công và năng lượng khi có ma sát
Một cách tổng quát, nếu lực ma sát tác dụng vào một hệ thì
ΔK = ΣWother forcesƒkd (8.11)
Đây là một dạng khác của định lý động năng và được sử dụng nếu lực ma sát tác dụng
lên vật. Nếu không có ma sát, phương trình này trở thành định luật bảo toàn cơ năng. Lực ma
sát biến động năng thành nội năng của hệ.
Độ tăng nội năng bằng với độ g ả i m động năng của hệ: ΔEint = ƒk d (8.12)
Một cách tổng quát, phương trình trên sẽ được viết dưới dạng sau:
ΣWother forces = W = ΔK + ΔEint (8.13)
Phương trình này có thể được sử dụng trong các hệ
không cô lập với các lực không phải lực bảo toàn.
Bài tập mẫu 8.3: Chuyển động của chiếc hộp trên
bề mặt có ma sát
Một chiếc hộp nặng 6,0 kg được kéo bằng một lực có
phương ngang không đổi 12 N trên một bề mặt nhám từ trạng thái nghỉ.
(A) Hãy tính tốc độ của cái hộp sau khi nó di chuyển
một đoạn dài 3,0 m. Biết hệ số ma sát động giữa bề
mặt và cái hộp là 0,15.
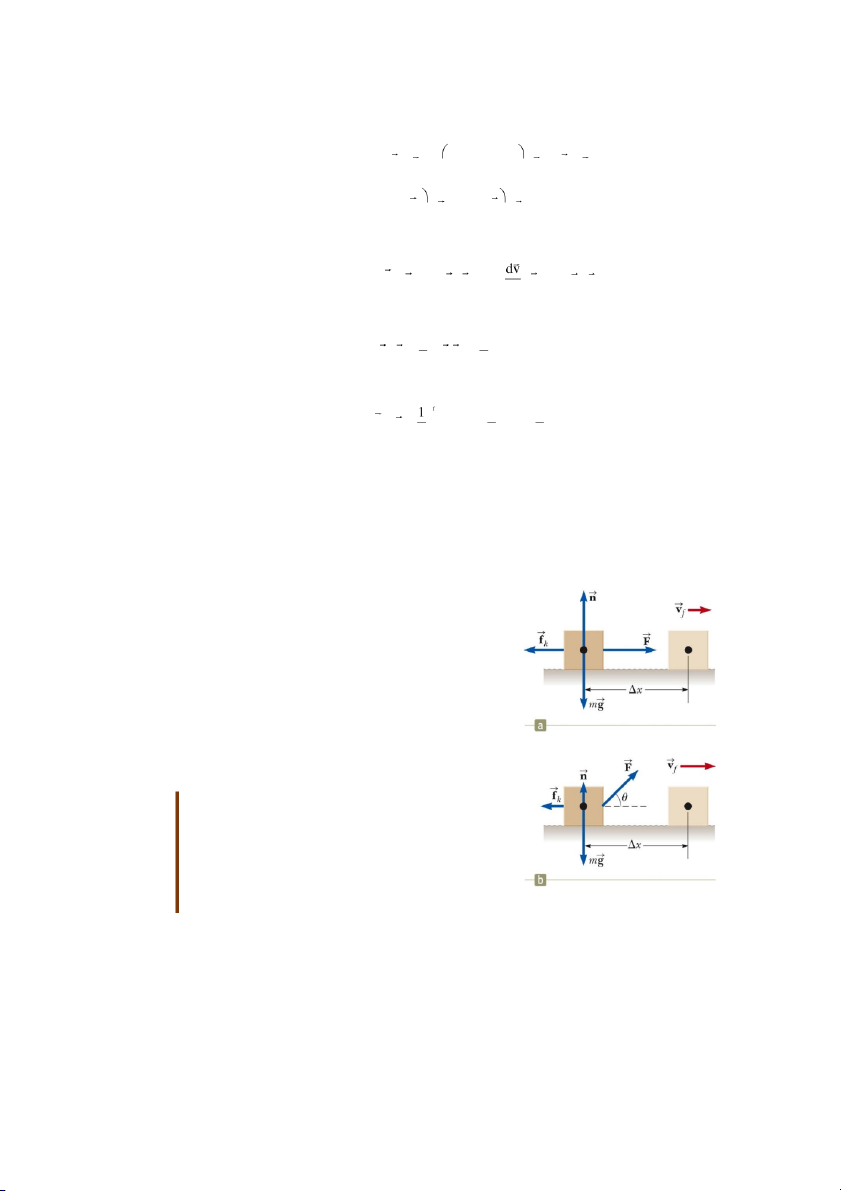
Hình 8.7 Bài tập 8.3. 8 Giải:
Bề mặt nhám sẽ tác dụng lực ma sát vào cái hộp. Lực ma sát có chiều ngược chiều của
lực kéo. Hệ hộp – bề mặt là hệ không cô lập với lực không bảo toàn tác dụng bên trong hệ.
Cả phản lực pháp tuyến và lực hấp dẫn đều không sinh công trong trường hợp này.
Theo phương thẳng đứng thì vật ở trạng thái cân bằng. Từ đó tìm ra độ lớn của lực ma
sát: f   mg k k
Công do lực tác dụng theo phương ngang thực hiện trên hệ là : ΣWother forces = F.x Suy ra F.x = K + E 2
int = (mvf /2 – 0) + fkd
Tốc độ cuối cùng của vật đó là: v
2 ( f d F ) x f k m
vf = √ 2 (−8,82.3,0 + 12.3,0) = 1,8 m/s 6,0
Giá trị vận tốc thu được phải nhỏ hơn trong ví dụ không có lực ma sát. Trong trường
hợp này, động năng của hệ giảm còn nội năng của hệ hộp – bề mặt đã tăng lên.
(B) Nếu lực tác dụng hợp với phương ngang một góc  thì góc nghiêng  có giá trị
bằng bao nhiêu để tốc độ của chiếc hộp có giá trị lớn nhất có thể khi nó di chuyển được một đoạn dài 3,0 m? Giải:
Chọn hệ gồm cái hộp và bề mặt Đây là một hệ không cô lập và bên trong hệ có lực
không bảo toàn tác dụng.
. Công lực bên ngoài thực hiện trên hệ là :
ΣWother forces = WF = F.x.cos = Fdcos
Theo phương thẳng đứng, hệ cân bằng nên: n + Fsin -mg = 0 n = mg - Fsin
WF = K + Eint = (Kf – 0) + fkd
Kf = WF - fkd = Fdcos - nµkd = Fdcos - µkd(mg - Fsin)
Để tốc độ của chiếc hộp cực đại thì phải thỏa mãn: 9
𝑑𝐾𝑓 = -Fdsin + µkdFcos = 0 𝑑𝜃 tan = 0  = tan-1µ -1 o k = tan 0,15 = 8,5
Bài tập mẫu 8.4: Hệ khối hộp – lò xo
Một vật khối lượng m = 1,6 kg được đẩy vào một
chiếc lò xo nằm ngang có độ cứng 1000 N/m trên
bề mặt như hình vẽ. Lò xo bị nén một đoạn 2,0
cm và sau đó được thả ra.
(A) Hãy tính tốc độ của vật khi đi ngang qua vị
trí cân bằng x = 0 nếu bề mặt không ma sát. Giải:
Hệ được chọn là vật. Đây là hệ không cô lập.
Công do lực đàn hồi của lò xo thực hiện trên hệ
từ vị trí xi = xmax đến vị trí xf = 0 là: W 2 s = kxmax /2
Theo định lý động năng, ta có: 𝑊 2 2 2
𝑠 = 1 𝑚𝑣 − 1 𝑚𝑣 = 1 𝑚𝑣 − 0 2 𝑓 2 𝑖 2 𝑓
Hình 8.8: Bài tập 8.4 𝑣 2
𝑓 = √2𝑊𝑠 = √𝑘𝑥𝑚𝑎𝑥 = √1000.(2,0.10−2)2 = 0,50 𝑚/𝑠 𝑚 𝑚 1,6
(B) Hãy tính tốc độ của vật khi đi ngang qua vị trí c
ân bằng x = 0 nếu bề mặt tác dụng
lên vật một lực ma sát không đổi 4,0 N. Giải:
Hệ được chọn gồm vật và bề mặt. Đây là hệ không cô lập và bên trong hệ có một lực
không bảo toàn (lực ma sát) tác dụng. Phương trình của định luật bảo toàn năng lượng
áp dụng cho hệ trong trường hợp này có dạng: 𝑊 2
𝑠 = ∆𝐾 + ∆𝐸𝑖𝑛𝑡 = 1 𝑚𝑣 + 𝑓 2 𝑓 𝑘𝑑 2 −𝑓 𝑣 ( 𝑠−𝑓𝑘𝑑) 𝑘𝑑) 𝑓 = √2 𝑊 = √2(12𝑘𝑥𝑚𝑎𝑥
= √2(121000.(2,0.10−2)2−4,0.0,020 = 0,39 𝑚/𝑠 𝑚 𝑚 1,6
Có thể thấy rằng tốc độ của vật trong trường hợp này nhỏ hơn trong câu A. 10
Thay đổi cơ năng khi có lực không bảo toàn
Nếu có lực ma sát tác dụng thì cơ năng của hệ thay đổi.
ΔEmech = ΔK + ΔU = ƒk d = -ΔEint (8.14)
ΔU là độ biến đổi của tất cả các dạng thế năng.
Trong trường hợp tổng quát, khi có lực không bảo toàn tác dụng bên trong một hệ cô lập
thì phương trình của định luật bảo toàn có dạng: ΔK + ΔU + ΔEint = 0 (8.15)
Đối với một hệ không cô lập và các tác động bên ngoài lên hệ bằng cách thực hiện công
ΣWother forces ƒkd = ΔEmech (8.16)
Như vậy, đối với một hệ không cô lập có thế năng thay đổi và có tác dụng của lực không bảo toàn thì
ΣWother forces = W = ΔK + ΔU + ΔEint (8.17)
Bài tập mẫu 8.5: Ma sát trên mặt phẳng nghiêng
Một thùng hàng nặng 3,00 kg trượt
xuống trên một mặt phẳng nghiêng có
ma sát. Mặt nghiên có chiều dài 1,00
m và độ nghiêng là  = 30,0o. Thùng
hàng bắt đầu trượt không vận tốc ban
đầu từ đỉnh của mặt nghiêng và lực ma
sát có độ lớn 5,00 N. Sau khi trượt hết
mặt phẳng nghiêng, nó còn di chuyển
một đoạn ngắn trên mặt phẳng nằm ngang.
Hình 8.9: Bài tập 8.5
(A) Hãy tìm tốc độ của thùng tại đáy mặt phẳng nghiêng. Giải:
Xác định hệ bao gồm: thùng hàng, bề mặt và Trái đất. Đây là một hệ kín có lực không bảo toàn tác dụng.
Chọn gốc tính thế năng hấp dẫn của hệ tại mặt phẳng ngang có tọa độ y = 0. Khi đó,
phương trình của định luật bảo toàn năng lượng cho hệ có dạng: ΔK + ΔU + ΔEint = 0
(Kf – Ki) + (Uf – Ui) +fk.d = 0
(½ mv 2f – 0) + (0 - mgyi) + fk.d = 0 𝑣𝑓 = √2 (𝑚𝑔𝑦 𝑚 𝑖 − 𝑓𝑘𝑑) 11
𝑣𝑓 = √ 2 (3,00 × 9,80 × 0,500 − 5,00 × 1,00) = 2,54 𝑚/𝑠 3,00
(B) Thùng hàng tiếp tục trượt một đoạn dài bao nhiêu trên mặt phẳng ngang nếu nó
tiếp tục chịu lực ma sát tác dụng có độ lớn bằng 5,00 N? Giải:
Lúc này thế năng của hệ không thay đổi nên ta có phương trình: ΔK + ΔEint = 0 (0 - ½ mv 2i) + fk.d = 0 2
𝑑 = 𝑚𝑣𝑖 = 3,00×2,542 = 1,94 𝑚 2𝑓𝑘 2×5,00
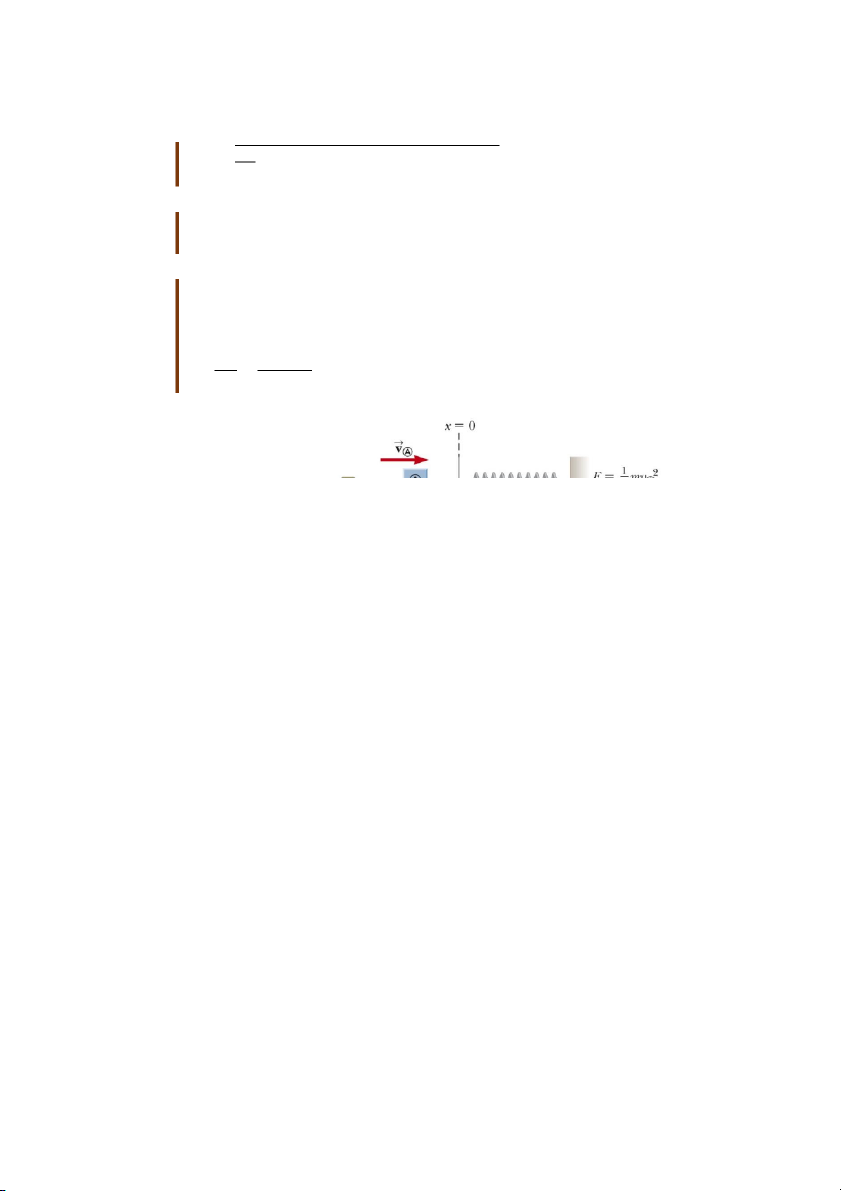
Bài tập mẫu 8.6: Va
chạm giữa chiếc hộp và lò xo Một chiếc hộp có khối lượng 0,8 kg được cung cấp một vận tốc ban đầu 1,2 m/s sang bên phải và va chạm với một lò xo
khối lượng nhỏ có độ cứng k = 50 N/m. Giả sử bề mặt không ma sát. Hãy tính độ
nén cực đại của lò xo sau va chạm. Giải: Nếu không có ma sát, năng lượng được chuyển hóa giữa động năng và thế năng đàn
Hình 8.10: Bài tập m u ẫ 8.6 hồi và tổng năng lượng không đổi
Chọn hệ gồm có hộp và lò xo. Hệ là cô lập với các lực tác dụng đều là lực bảo toàn.Tất
cả chuyển động diễn ra trên mặt phẳng nằm ngang. Vì vậy không có sự thay đổi của
thế năng hấp dẫn. Trước va chạm, tổng năng lượng của hệ là động năng của hộp. Khi 12
lò xo bị nén hoàn toàn, động năng bằng 0 và toàn bộ năng lượng là thế năng đàn hồi
của lò xo. Cơ năng của hệ được bảo toàn.
Phương trình của định luật bảo toàn năng lượng trong trường hợp này là: ΔK + ΔU = 0 (0 - ½ mv 2 2 A ) + (½ kxmax - 0) = 0
𝑥𝑚𝑎𝑥 = √𝑚 𝑣 × 1,2 = 0,15 𝑚 𝑘 𝐴 = √0,80 50
(B) Giả sử hệ số ma sát động giữa chiếc hộp và bề mặt là µk = 0,50. Nếu tốc độ của
chiếc hộp tại thời điểm nó va chạm với lò xo là 1,2 m/s thì độ nén cực đại của lò xo là bao nhiêu? Giải:
Đây là bài toán có lực ma sát. Lực ma sát sẽ biến đổi động năng của hệ thành nội năng.
Chọn hệ gồm chiếc hộp, bề mặt và lò xo. Đó là hệ kín với lực không bảo toàn tác dụng.
Trong trường hợp này, cơ năng của hệ Emech = K + Us không bảo toàn; trong đó Us là
thế năng đàn hồi. Phương trình của định luật bảo toàn năng lượng đối với hệ là: ΔK + ΔU + ΔEint = 0 Trong đó,
ΔEint = ƒk d, fk = µk.n = µk.mg
Thay vào phương trình trên, ta được: (0 - ½ mv 2 2
A ) + (½ kxmax - 0) + µk.mgxmax = 0 kx 2 2 max + 2µk.mgxmax - mvA = 0 50x 2 2
max + 2.0,50.0,8.9,8xmax – 0,8.1,2 = 0 50x 2 max + 7,84xmax – 1,15 = 0
Phương trình có hai nghiệm xmax = 0,092 m và xmax = -0,25 m. Giá trị có ý nghĩa vật lý là xmax = 0,092 m.
So với kết quả trong câu (A), xmax có giá trị nhỏ hơn. Lý do là gì? Công suất
Định nghĩa: Công suất tức thời là tốc độ truyền năng lượng theo thời gian và được tính theo công thức:  dE P (8.18) dt 13
Nếu năng lượng trao đổi dưới dạng công được thực hiện bởi một lực và trong khoảng
thời gian t công do lực sinh ra là W thì công suất trung bình Pavg được xác định bởi công thức:  W P (8.19) avgt
Công suất tức thời là giới hạn của công suất trung bình khi Δt tiến tới 0.  W dW d P lim   F  Fv   t 0 t dt dt Đơn vị
Trong hệ đơn vị SI, đơn vị của công suất là watt (W).
1 watt = 1 joule/second = 1 kg.m2 3 /s
Một đơn vị công suất hay sử dụng nữa tại Mỹ là mã lực (horsepower – hp) 1 hp = 746 W
Một đơn vị của năng lượng thường bị nhầm lẫn với đơn vị công suất là kWh. Nhớ rằng
kWh là đơn vị đo năng lượng, được xác định như sau:
1 kWh = 1kW.1h = (1000 W)(3600 s) = 3.6 x106 J
Tóm tắt chương 8
Hệ không cô lập về năng lượng là một hệ có trao đổi năng lượng với môi trường qua biên giới của nó.
Hệ cô lập là một hệ không trao đổi năng lượng với môi trường qua biên giới của hệ.
Định luật bảo toàn năng lượng: Năng lượng của một hệ cô lập là không đổi.
Một lực ma sát có độ lớn fk tác dụng trên một quãng đường d thì nội năng của hệ thay đổi một lượng: Eint = fk.d
Công suất là tốc độ truyền năng lượng theo thòi gian:  dE P dt
Phương trình của định luật bảo toàn năng lượng đối với hệ không cô lập ΔEsystem = ΣT
Δ K + Δ U + Δ Eint = W + Q + TMW + TMT + TE T + TER 14
Phương trình của định luật bảo toàn năng lượng đối với hệ cô lập ΔEsystem = 0 ΔK + ΔU + ΔEint = 0
Nếu các lực tác dụng bên trong hệ đều là lực bảo toàn thì ta có định luật bảo toàn cơ năng ΔEmech = 0 ΔK + ΔU = 0
Câu hỏi lý thuyết chương 8
1. Một người thả một quả bóng từ trên đỉnh của một tòa nhà trong khi người khác thì đang
đứng ở dưới để quan sát chuyển động của nó. L ệ
i u 2 người này có đồng ý
(a) Về giá trị thế năng hấp dẫn của hệ quả bóng - Trái Đất.
(b) Về sự thay đổi của thế năng hấp dẫn.
(c) Về động năng của quả bóng tại một điểm nào đó t o
r ng quá trình chuyển động của nó.
2. Lực ma sát tĩnh có thể sinh công hay không? Nếu không, hãy giải thích tại sao không.
Nếu có thì hãy cho một ví dụ.
3. Một người nặng 70,0 kg leo lên một đỉnh núi cao 325m trong 90,0 phút. Công suất trung
bình người đó sinh ra là bao nhiêu?
(a) 39,1 W (b) 54,6 W (c) 25,5 W (d) 67,0 W (e) 88,4 W
4. Một vật được gắn với một lò xo treo trên trần nhà. Giả sử sức cản không khí được bỏ
qua, hãy mô tả các biến đổi năng lượng xảy ra trong hệ gồm vật -
trái đất - lò xo khi vật
chuyển động theo phương thẳng đứng.
5. Phương trình của định lý công - động năng W = K chỉ đúng trong trường hợp không có
thay đổi đối với bất kỳ loại năng lượng nào khác như t ế
h năng hay nội năng xảy ra đối
với một hệ. Hãy cho vài ví dụ cho thấy công thực hiện trên một hệ nhưng sự thay đổi
năng lượng của hệ không phải là thay đổi động năng.
Bài tập chương 8
1. Một quả bóng khối lượng m rơi từ độ cao h xuống sàn.
(a) Viết phương trình của định luật bảo toàn năng lượng (dạng 8.2) cho hệ quả bóng -
Trái đất và sử dụng nó để tính tốc độ của quả bóng ngay trước khi nó chạm đất.
(b) Viết phương trình của định luật bảo toàn năng lượng (dạng 8.2) cho hệ chỉ có quả
bóng và sử dụng nó để tính tốc độ của quả bóng ngay trước khi nó chạm đất .
2. Một quả đạn pháo nặng 20,0 kg được bắn ra từ một khẩu đại bác với tốc độ là 1000 m/s
theo phương hợp với phương ngang một góc 37,0o. Một quả đạn khác bắn với góc 90,0o.
Xét một hệ kín để tính:
(a) Độ cao cực đại của mỗi quả đạn. 15
(b) Cơ năng của hệ quả đạn-trái đất tại độ cao cực đại của mỗi quả. Chọn y = 0 tại vị trí đặt khẩu đại bác.
3. Một vật khối lượng m = 5,00 kg rời khỏi điểm A và trượt trên một rãnh không ma sát
như trong hình vẽ . Hãy xác định:
(a) Tốc độ của vật tại các điểm B và C.
(b) Công thực hiện bởi lực hấp dẫn trên vật khi nó di chuyển từ điểm A đến điểm C.
4. Một khối nặng 2,00 kg được gắn vào một lò xo có độ cứng
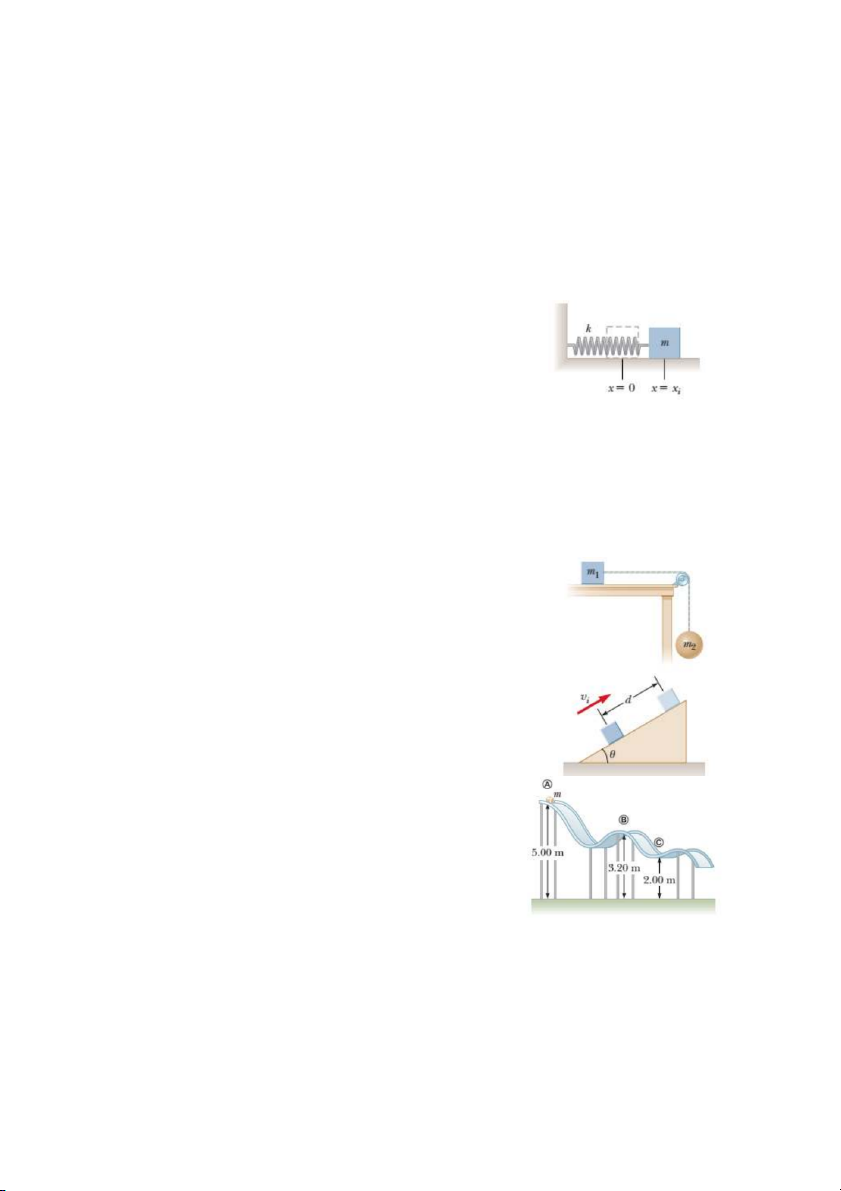
k = 500 N/m như trên hình vẽ. Khối đó được kéo tới vị trí xi
= 5,00 cm về phía bên phải của vị trí cân bằng và được thả
ra từ trạng thái nghỉ. Tìm tốc độ của khối khi đi qua vị trí cân bằng nếu:
(a) Bề mặt ngang không có ma sát.
(b) Hệ số ma sát giữa khối và bề mặt là k = 0,350.
5. Một vòng tròn trơn có bán kính 0,500 m đặt trên mặt sàn. Một hạt nặng 0,400-kg trượt
quanh cạnh bên trong của vòng. Tốc độ ban đầu của nó là 8,00 m/s. Sau một vòng, tốc
độ còn lại là 6,00 m/s do có ma sát.
(a) Tìm năng lượng chuyển đổi từ cơ năng sang nội năng của hệ hạt – vòng – Trái đất
(do ma sát) sau khi kết thúc 1 vòng chuyển động.
(b) Tổng số vòng hạt đi được đến khi dừng lại là bao nhiêu? Giả sử lực ma sát không đổi
trong quá trình chuyển động.
6. Hệ số ma sát giữa vật khối lượng m1 = 3,00 kg với mặt bàn là
µk = 0,400 (xem hình vẽ). Cho hai vật chuyển động từ trạng
thái nghỉ. Tính tốc độ của vật m2 = 5,00 kg khi nó đi xuống một đoạn h = 1,50 m.
7. Đẩy cho một vật nặng m = 5,00 kg chuyển động đi lên với tốc
độ ban đầu là vi = 8,00 m/s trên một mặt dốc có độ nghiêng 
= 30,0o. Vật dừng lại sau khi đi được một đoạn d = 3,00 m. Hãy tính:
(a) Độ biến thiên động năng của vật.
(b) Độ biến thiên thế năng của hệ vật-Trái đất.
(c) Lực ma sát tác dụng lên vật.
(d) Hệ số ma sát trượt.
8. Một động cơ điện của một chiếc xe lửa mô hình gia tốc
chiếc xe từ trạng thái nghỉ đến tốc độ 0,620 m/s trong
thời gian 21,0 ms. Khối lượng của chiếc xe là 875 g.
(a) Tính công suất tối thiểu cần cung cấp cho xe lửa trong quá trình gia tốc. 16
(b) Giải thích tại sao đó là gia tốc tối thiểu?
9. Một chiếc thang máy nặng 650 kg chuyển động đi lên từ trạng thái nghỉ với gia tốc không
đổi. Sau thời gian 3,00 s nó đạt tốc độ di chuyển đều bằng 1,75 m/s.
(a) Công suất trung bình của động cơ thang máy trong khoảng thời gian đó bằng bao nhiêu?
(b) Hãy so sánh giá trị tính được với công suất của động cơ khi thang máy di chuyển đều.
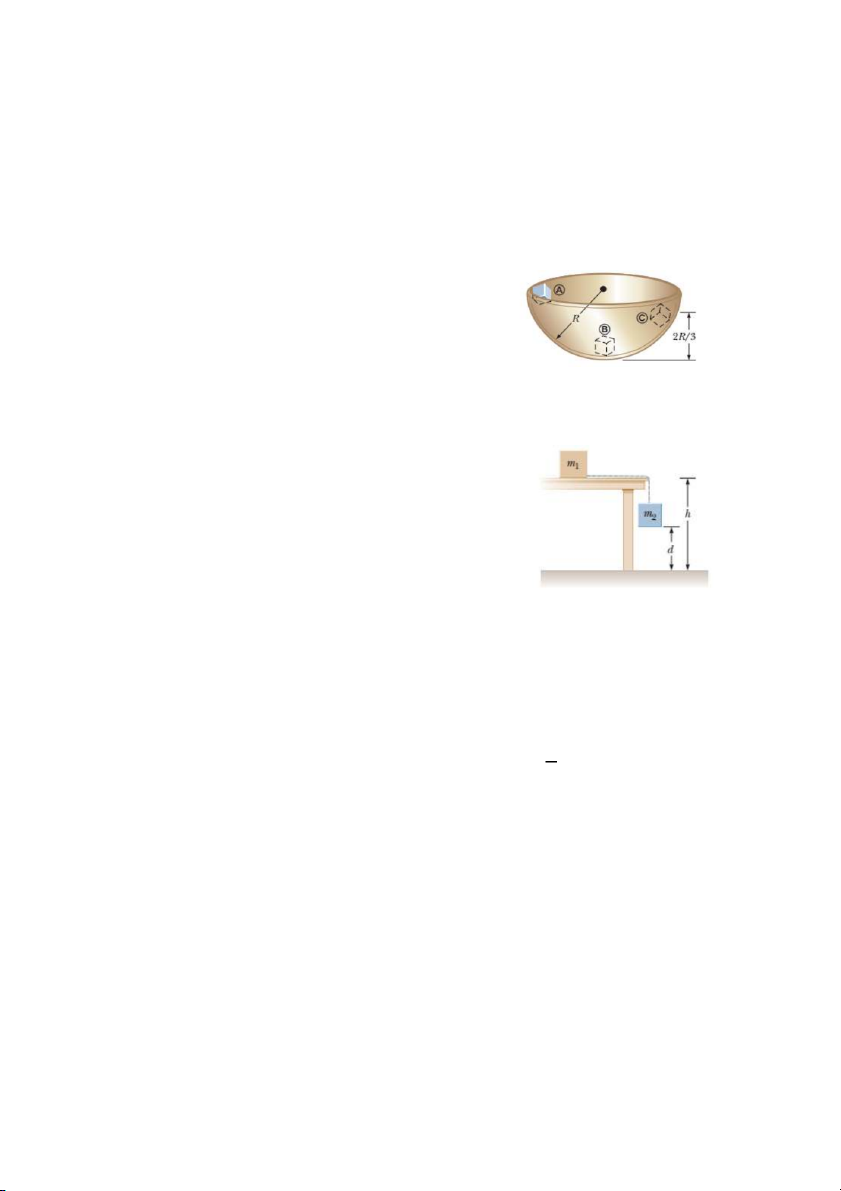
10. Một vật nhỏ khối lượng m = 200 g được thả cho
chuyển động dọc theo đường kính bên trong của một
cái chén hình bán cầu, không ma sát. Bán kính của cái
chén bán cầu là R = 30,0 cm. Hãy tính:
(a) Thế năng hấp dẫn của hệ vật-Trái đất khi vật ở
điểm A. Chọn gốc tính thế năng tại điểm B.
(b) Động năng của vật tại điểm B.
(c) Tốc độ của vật tại B.
(d) Động năng của vật và thế năng của hệ khi vật ở tại điểm C.
11. Vật m1 = 3,50 kg ban đầu nằm yên trên một mặt bàn nằm
ngang cách sàn một khoảng h = 1,20 m được nối với vật
m2 = 1,90 kg bằng một dây nhẹ không co dãn. Lúc đầu
vật m2 cách mặt sàn một khoảng d = 0,900 m. Mặt bàn và
cạnh bàn đều không ma sát. Các vật bắt đầu chuyển động
từ trạng thái nghỉ, vật m1 trượt trên mặt bàn rồi bay ra
ngoài còn vật m2 đi xuống và dừng lại trên sàn. Xem hệ
gồm có hai vật và Trái đất .
(a) Tính tốc độ của vật m1 khi rời khỏi mép bàn.
(b) Tính tốc độ của m1 khi chạm mặt sàn.
(c) Chiều dài ngắn nhất của sợi dây không bị căng khi m1 đang bay là bao nhiêu?
(d) Năng lượng của hệ khi nó bắt đầu chuyển động có bằng năng lượng của hệ trước khi
m1 chạm đất hay không? Hãy giải thích tại sao bằng hay tại sao không?
12. Một tài xế đạp chân ga làm cho chiếc xe khối lượng 1160 kg tăng tốc từ trạng thái nghỉ.
Trong 2 giây đầu tiên, gia tốc của chiếc xe tăng theo thời gian và được biểu diễn bởi phương trình
𝑎 = 1,16𝑡 − 0,210𝑡2 + 0,240𝑡3 (𝑚 ). 𝑠2
Trong đó t đo bằng s và a đo bằng m/s2.
(a) Tính độ biến thiên động năng của xe từ t = 0 s đến t = 2,5 s.
(b) Tính công suất trung bình tối thiểu của động cơ trong khoảng thời gian trên.
(c) Tại sao giá trị ở câu b là giá trị nhỏ nhất . 17
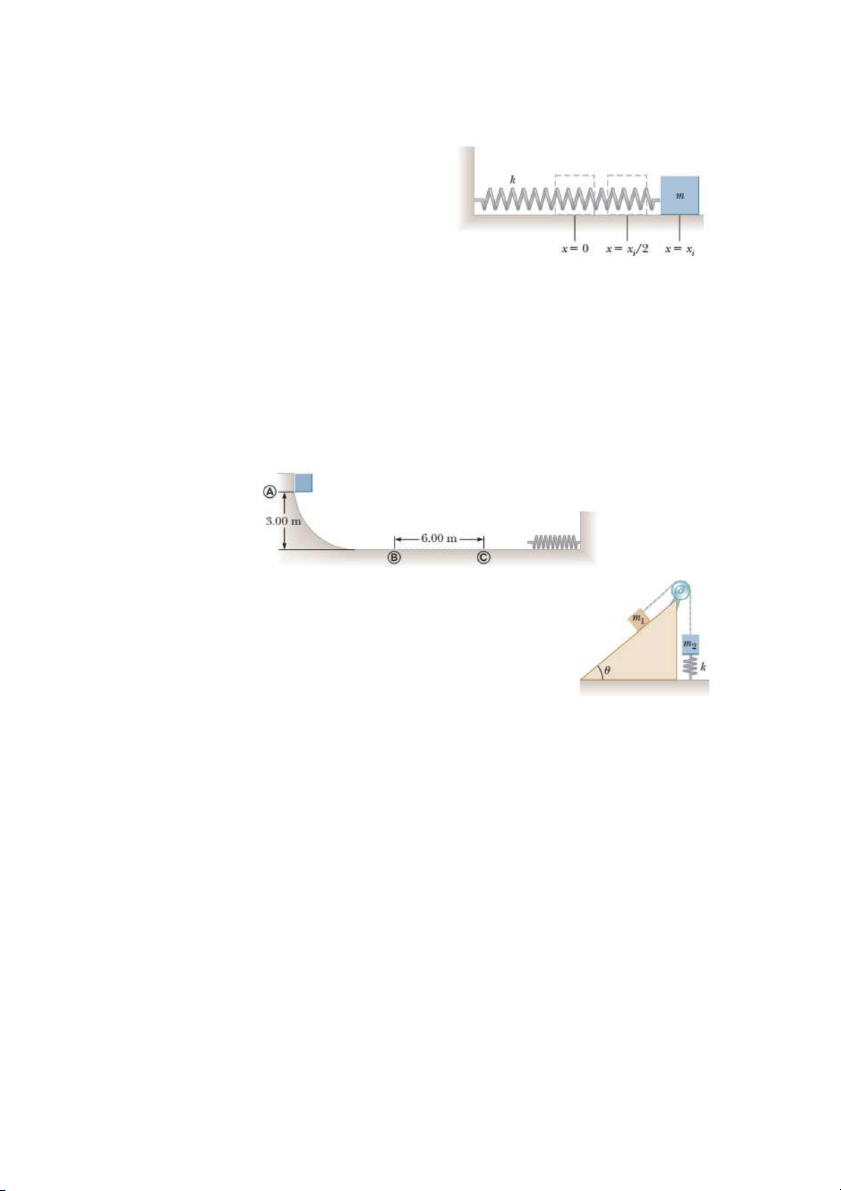
13. Một lò xo nằm ngang có độ cứng k = 850
N/m được gắn vào một bức tường. Một vật
khối lượng m = 1,00 kg được gắn vào lò xo
và nằm yên trên một bề mặt ngang không ma sát như trong hình vẽ.
(a) Vật được kéo đến một vị trí xi = 6,00 cm
so với vị trí cân bằng. Tìm thế năng đàn
hồi được lưu trữ trong lò xo khi nó nằm tại vị trí 6,00 cm và khi vật đi qua vị trí cân bằng.
(b) Tìm tốc độ của vật khi nó đi qua vị trí c ân bằng.
(c) Tính tốc độ của vật khi nó ở vị trí xi/2 = 3,00 cm.
(d) Tại sao tốc độ trong câu c không bằng một nửa câu (b)?
14. Một vật khối lượng 10,0 kg được thả tại điểm A như hình vẽ. Rãnh trượt là không ma
sát ngoại trừ phần giữa điểm B và C, có chiều dài 6,00 m. Vật trượt xuống rồi va vào một
lò xo có độ cứng 2250 N/m đẩy lò xo ép lại một khoảng 0,300 m từ vị trí cân bằng trước
khi tạm dừng lại . Hãy xác định hệ số của ma sát động giữa vật và máng trượt trên đoạn giữa điểm B và C.
15. Một vật khối lượng m1 = 20,0 kg nối với vật khối lượng m2 =
30,0 kg bằng 1 sợi dây mảnh, nhẹ vắt qua một ròng rọc nhẹ,
không ma sát. Đầu còn lại của m2 nối với lò xo có độ cứng k =
250 N/m như hình vẽ. Bỏ qua ma sát trên mặt nghiêng, góc
nghiêng θ = 40,0o. Ban đầu, hệ cân bằng, lò xo không bị giãn.
Kéo m1 đi xuống một đoạn h = 20,0 cm rồi thả ra. Tìm tốc độ mỗi
vật khi lò xo trở lại trạng thái không bị giãn. 18