Chương 9: Động lượng và va chạm | Tài liệu lý thuyết môn Vật lý 1 trường đại học sư phạm kĩ thuật TP. Hồ Chí Minh

Khi giải quyết một bài toán cơ học ta có thể sử dụng nhiều phương pháp khác nhau. Đối với một số bài toán nếu ta dùng phương pháp này thì sẽ phức tạp nhưng nếu ta dùng phương pháp khác thì lại trở nên dễ dàng hơn. Ví dụ trường hợp người đàn ông đứng trên bang bán cung tên or tình huống các viên bi-da va chạm với nhau. Tài liệu giúp bạn tham khảo, ôn tập và đạt kết quả cao. Mời bạn đọc đón xem!

4 2 lượt tải Tải xuống

Chia sẻ Báo cáo tài liệu

http://ipt.hcmute.edu.vn B môn v t lý ộ ậ

Chương 9: Động lượng và va chạm

hi gi i quy t m c ta có th s d ng nhiả ế ột bài toán cơ họ ể ử ụ ều phương pháp khác nhau.

Đố ới v i một s bài toán nố ếu ta dùng phương pháp này thì sẽ ạp nhưng nế phức t u ta

dùng phương pháp khác thì lạ dàng hơn. Ví dụ ngưßi đàn i trá nên dễ trưßng hợp

ông đứng trên băng b n cung tên ho c tình hu ng các viên bi-da va ch m v i nhau. ắ ặ ố ạ ớ

Giả s xét m t tình hu n là cho bi t v n tử ộ ống đơn giả ế ậ ốc c a c b n ra ủ mũi tên ngay sau khi đượ ắ

và yêu c u tính v n t c c i b n cung ngay khi . Ta không th gi i bài toán này v i ầ ậ ố ủa ngưß ắ đó ể ả ớ

các mô hình độ ọc (chương 2), độ ọc (chương 5), hoặc năng lượng (chương 7). ng h ng lực h

Tuy nhiên, ta có th gi i quyể ả ế ết bài toán này một cách dễ dàng dùng cách ti p cận liên quan

đến động lượng.

Chương này sẽ ệm động lượng, xung lượng, các đị trình bày các khái ni nh lý liên quan

đến động lượng, xung lượng, từ đó đưa ra phương pháp giải các bài toán cơ học liên quan đến

động lượng, đặc biệt là các bài toán va chạm.

Động lượng

Xét h cô l p g m 2 ch m có kh ng m m , chuy n ệ ậ ồ ất điể ối lượ

1, 2

ể

độ ớng v i các vận tốc ă

và ă

(hình 9.1). Vì h cô l p nên l c tác ệ ậ ự

dụng lên ch m này là do ch m kia gây ra. N u ch m 1 ất điể ấ ểt đi ế ất điể

tác d ng lên ch m 2 m t l c ụ ất điể ộ ự þ



thì ch ng ất điểm 2 cũng tác dụ

lên chất điểm 1 một lực þ



b ng v l c chi u. Các ằ ề độ ớn nhưng ngượ ề

l c-phực này t o thành m t c p lạ ộ ặ ự ản l nh lu t 3 Newton, ực theo đị ậ



= 2þ



, nên ta có: þ



+ þ



= 0.

Theo đị ất điểnh luật 2 Newton: lực tác dụng lên mỗi ch m bằng

ÿ�㕎 nên:

ÿ �㕎 + ÿ �㕎

1 1 2 2

= 0

Thay các gia t ng bi u thốc bằ ể ức định nghĩa của nó theo phương

trình 4.5, ta có:

þă

þā

+ ÿ

þă

þā

= 0

Nếu các khối lượng m , m i, ta có th o hàm:

1 2

không đổ ể đưa chúng vào trong dấu đạ

þ(ÿ ă )

1 1

þā

þ(ÿ

ă )

þā

= 0

1 1 2 2

d m v

(9.1)

Hình 9.1 Hai chất

điểm tương tác với

nhau

Trưßng Đạ ọc Sư phại h m Kỹ thu t Tp. H Chí Minh 2021 ậ ồ

Vì đạo hàm của tổng ÿ

ă + ÿ ă

1 2 2

theo th i gian b ng không, nên t ng này là không ß ằ ổ

đổi. Đại lượng

c g i đượ ọ là động lượng của một chất điểm, và đối v i h các chớ ệ ất điểm cô

lập, t o toàn. ổng các đạ ợng này đượi lư c bả

Định nghĩa độ ất điểng lượng của ch m:

Động lượng c a m t chủ ộ ất điểm có khối lượng m chuyển động với v n t c ậ ố ă được xác định

bằng tích của kh ng và vối lượ ận tốc của nó:

(9.2)

Động lượng là một đại lượng vectơ, hướng dọc theo ă, th ứ nguyên là ML/T, đơn vị trong

hệ SI là kg.m/s.

Nếu ch m chuy ng th ng b t kất điể ển độ eo hướ ấ ỳ thì động lượng Ă có 3 thành ph n, và ầ

phương trình (9.2) viết cho các thành phần là:

= ÿă

Khái ni ng giúp ta phân bi t m ng gi a các v t n ng và v t ệm động lượ ệ ột cách định lượ ữ ậ ặ ậ

nhẹ chuy ng vển độ ới cùng v n t c. Ví d ng c a mậ ố ụ động lượ ủ ột qu bóng bowling thì lả ớn hơn

nhiều so v ng c a mới động lượ ủ ột qu bóng tennis chuy ng vả ển độ ới cùng v n tậ ốc. Newton đã

gọi ÿă là ; thu t ng này có l t ng khối lượ ển động chuy ng ậ ữ ẽ sinh động hơn thuậ ữ động lượng

ta dùng hi n nay. ệ

Phân biệt động năng và động lượng:

Thứ nhất, động năng là đ¿i lượng vô hướng còn động lượng là đ¿i lượng vectơ. Ví d ụ

xét hai ch m có kh ng b ng nhau chuy ng v phía nhau theo m ng th ng ất điể ối lượ ằ ển độ ề ột đưß ẳ

với cùng tốc độ. Độ năng củng a hệ này khác không, động lượng của hệ này bằng không.

Thứ hai là động năng có thể chuyển hóa thành các d¿ng năng lượng khác ch ng hẳ ¿n như

thế năng hoặc nội năng, còn động lượng không chuyển đổi được thành năng lượng. Các khác

biệt này đủ ựa vào động lượ để tạo ra các mô hình phân tích d ng, tách biệt với các mô hình

dựa vào năng lượng, cung cấp một công cụ độc l s dập để ử ụng trong vi c gi i quy t các bài ệ ả ế

toán.

Theo định luật 2 Newton, ta có:

∑þ



= ÿ�㕎 = ÿ

þă

þā

Giả s kh ng m là khô i, ta có th ng m vào trong d o hàm, ử ối lượ ng đổ ể đưa khối lượ ấu đạ

nên:

dt dt

ý ý

(9.3)

Phương trình (9.3) là d¿ ủa đị ật 2 Newton đống khác c nh lu i v i chớ ất điểm. Phương trình

này ch ra ỉ rằng t bi n thiên theo th i gian c ng c a ch m thì b ng ốc độ ế ờ ủa động lượ ủ ất điể ằ

h mợp lực tác dụng lên chất điể . D ng này t i thi u ạ ổng quát hơn dạng đã giớ ệ á chương 5, và

có th s dể ử ụng để khảo sát các hiện tượ đó khối lượng thay đổi, ngoài các trưßng trong ng h p ợ

http://ipt.hcmute.edu.vn B môn v t lý ộ ậ

trong đó ốc thay đổ ối lượ ửa thay đổvận t i. Ví dụ trưßng hợp kh ng của tên l i do nhiên liệu bị

đố ị

t và b phóng ra khỏi tên lửa, ta không thể sử dụng phương trình

∑



= ÿ�㕎 để phân tích

mà ph i dùng cách ti p c trình bày trong m c 9.9. ả ế ận động lượng như sẽ ụ

Câu h i 9.1:ỏ Hai v l ng c a chúng so v i nhau th ật có động năng bằng nhau. Độ ớn động lượ ủ ớ ế

nào? ( ) p < p ( ) p = p ( ) p > p ( phát bi u. a

1 2

d) không đủ thông tin để ể

Câu h i 9.2:ỏ Giáo viên th d c ném m t qu bóng chày v phía b n v i m t tể ụ ộ ả ề ạ ớ ộ ốc độ nào đó

và b n b t l y nó. Ti p theo giáo viên s ném m t qu bóng t p n ng g p 10 l n qu bóng ạ ắ ấ ế ẽ ộ ả ậ ặ ấ ầ ả

chày. B n có các l a ch n sau: B n có th b c qu bóng t c ném v i ( ) cùng t c ạ ự ọ ạ ể ắt đượ ả ập đượ ớ a ố

độ ớ ớ v i quả bóng chày, (b) cùng động lượng v i quả bóng chày, hoặc ( vc) cùng động năng ới

quả bóng chày. Hãy s p x p các l n này t d b t. ắ ế ựa chọ ừ ễ đến khó để ắ

Mô hình phân tích: H cô lệ ập (động lượng)

Sử d ng, bi u th c 9.1 có th vi t là: ụng định nghĩa động lượ ể ứ ể ế

þā

(Ă

+ Ă

) = 0

Vì đạo hàm của động lượng toàn phần Ă

þĀþ

= Ă

+ Ă

b ng toàn ằng không, nên động lượ

phần c hai ch m cô l p trong hình 9.1 là i: ủa hệ ất điể ậ không đổ

tot

(9.4)

Hay:

tot

p ý

9.5)

hoặc vi t theo d ng khác là: ế ạ

Ă

1�㕖

+ Ă

2�㕖

= Ă

1Ā

+ Ă

2Ā

với Ă

1�㕖

, Ă

2�㕖

là các giá tr u và ị đầ Ă

1Ā

, Ă

2Ā

là các giá tr cu i c ng ng c a hai ch t ị ố ủa độ lượ ủ ấ

điểm.

Phương trình (9.5) chứ động lượ ần theo các hướng x, y, z đều đượng tỏ ng toàn ph c bảo

toàn m p: ột cách độc lậ

1 2 1 2 1 2 1 2 1 2 1 2ix ix fx fx iy iy fy fy iz iz fz fz

p p p p p p p p p p p p ý   ý   ý 

(9.6)

Phương trình (9.5) là dạng toán học của một mô hình phân tích mới, gọi là mô hình hệ

cô lập ( . Mô hình này có th m r ng cho h cô l p nhi u ch m b t kđộng lượng) ể á ộ ệ ậ ề ất điể ấ ỳ như

sẽ trình bày trong mục 9.7.

Từ phương trình (9.5) ta có thể ểu như sau: phát bi Khi hai hay nhi u ch m c a m t ề ất điể ủ ộ

hệ cô l ng toàn phập tương tác với nhau, động lượ ần của hệ luôn không đổi. Như vậy động

lượng toàn phần của hệ cô lập tại các th m bßi điể ất kì đều b u cằng động lượng ban đầ ủa nó.

Trưßng Đạ ọc Sư phại h m Kỹ thu t Tp. H Chí Minh 2021 ậ ồ

Mô hình phân tích h cô l p không c n ngo i l c tác d ng lên h c ệ ậ ần xét đế ạ ự ụ ệ, cũng như lự

đó là lực bảo toàn hay không b o toàn, l c bi n thiên hay không bi n thiên theo th i gian. ả ự ế ế ß

Yêu c u duy nh t là các l c ph i là n i l c c a h u này cho th y t m quan tr ng c a mô ầ ấ ự ả ộ ự ủ ệ. Điề ấ ầ ọ ủ

hình m i này. ớ

Mô hình phân tích: H cô l ng) ệ ập (động lượ

Giả s c n phân tích và biên cử ta đã xác định được hệ ầ ủa nó. N u không có ngo i l c nào ế ạ ự

tác d ng lên h thì h là cô l ng toàn ph n c o toàn: ụ ệ ệ ập. Khi đó động lượ ầ ủa hệ được bả

ø ù

0 9.5

tot

p ý

Ví dụ:

 Viên bi da cái đánh vào các viên bi da khác

trên bàn

 Tàu vũ trụ ển độ bắn tên lửa ra và chuy ng

nhanh hơn trong không gian

 Các phân t ch t khí m t nhi nh ử ấ á ộ ệt độ xác đị

chuyển động và va chạm với nhau

Bài t p m u 9.1: ậ ẫ

Một ngưß ắn cung đứ ặt băng không ma sát bắ ột mũi tên nặi b ng trên m n m ng 0.03 kg

theo phương ngang với vận t u 85 m/s. (A) H i v n t c cốc đầ ỏ ậ ố ủa ngưßi sau khi mũi tên

được b n ra. (Bắ ) Điều gì x y ra nả ếu mũi tên được bắn theo hướng h p vợ ới phương nằm

ngang m u này s i v n t c gi t lùi c i bột góc θ? Điề ẽ làm thay đổ ậ ố ậ ủa ngưß ắn cung như

thế nào?

Giải:

Phân tích bài toán: Hãy tưáng tượng mũi tên bị bắn đi trên một

đưßng th i bẳng và ngưß ắn cung thủ chuy ng giển độ ật lùi theo

hướng ngược l i. Ta không th gi i bài toán này v i các mô hình ạ ể ả ớ

dựa trên chuy ng, l c, ho ng. Tuy nhiên, ta có ển độ ự ặc năng lượ

thể gi i quy t v này m t cách d dàng vả ế ấn đề ộ ễ ới cách ti p c n ế ậ

liên quan đến động lượ ồm có ngưßng. Ta xét hệ g i bắn cung

(bao g m c không cô l p vì có l c h p ồ ả cung) và mũi tên. Hệ ậ ự ấ

dẫn và ph n l c pháp tuy n t ả ự ế ừ băng tác dụng lên hệ. Tuy nhiên,

các l ng và vuông góc v i chi u ực này theo phương thẳng đứ ớ ề

chuyển động của hệ. Không có ngoại lực tác dụng lên hệ theo

phương ngang, và ta có thể ập (độ áp dụng mô hình hệ cô l ng

lượng) đố ần động lượng theo hưới với các thành ph ng này.

(A) Áp dụng mô hình h cô l ng theo ệ ập (động lượng) theo phương ngang, động lượ

phương nga ắn đề ọn hướ ắn mũi tên là ng của hệ trước và sau khi b u bằng 0. Ta ch ng b

hướng dương củ ục x. Xem ngưß ất điểm 1 và mũi tên là chất điểa tr i bắn cung là ch m

2, theo phương trình 9.5 ta được:

1 1 2 2

f i f i f ftot

p ý 

Hình 9.2 Bài t p ậ

mẫu 9.1 – Người

bắn cung

http://ipt.hcmute.edu.vn B môn v t lý ộ ậ

Theo đề bài ta có m = 60 kg, m = 0,030 kg và

1 2

m/s.

Giải phương trình này và thay số ta đượ c:

1 2

f f

v i m s

Dấu tr ch ra r i b n cung chuyừ ỉ ằng ngưß ắ ển động về phía bên trái trên hình 9.2 sau khi

bắn mũi tên, phù hợ ới đị ủa ngưßp v nh luật 3 Newton. Gia tốc và vận tốc c i bắn cung

nhỏ hơn nhiều so với gia tốc và v n t c cậ ố ủa mũi tên vì khối lượng của ngưßi bắn cung

rất l n so v ớ ới mũi tên.

(B) Độ ốc mũi tên là lớn của vận tốc giật lùi sẽ giảm vì chỉ một thành phần của vận t

theo hướ ớng x. Sự b ng theo ảo toàn động lượ hư ng x cho ta:

1 1 2 2

cos 0

f f

m v m v



 ý

dẫn t i ớ

1 2

cos

f f

v v



ý 

Với các giá tr ị



thì

1 f

nhỏ hơn

1 f

khi



vì

cos 1



Mô hình phân tích: H không cô l ng) ệ ập (động lượ

Đố ớ ụ ểi v i các kh ng, nảo sát động lượ h pệ không cô lậ ếu có lực tác d ng lên hệ. Ta có th

hình dung động lượng đượ môi trưßng đế ểu được chuyển từ n hệ thông qua lực. Việc hi c lực

là nguyên nhân gây ra s bi ng ng r t quan tr ng khi gi i quy t m t s lo i bài ự ến thiên độ lượ ấ ọ ả ế ộ ố ạ

toán.

ả s có m t hử ộ ợp l c ự

∑



tác d ng lên ch m và h p l c này có th bi n thiên theo ụ ất điể ợ ự ể ế

thßi gian. Theo định lu t 2 Newton: ậ

∑þ



þĂ

þā

hay

þĂ = þ∑



þā (9.7)

Ta có th l y tích phân bi u thể ấ ể ức (9.7) để tìm độ ến thiên động lượ bi ng của ch m khi ất điể

có l c tác d ng lên nó trong m t kho ng th ng c a ch m ự ụ ộ ả ßi gian nào đó. Nếu động lượ ủ ất điể

thay đổi từ Ă

�㕖

t i th i m ạ ß điể ā

�㕖

t i ớ Ă

t i th m ạ ßi điể ā

, l c: ấy tích phân phương trình 9.7 ta đượ

∆Ă = Ă

2 Ă

� 㕖

= ∫ ∑þ



þā

�㕓

� 㕖

(9.8

Để tính tích phân này, ta c n bi t h p l c tác d ng lên ch m bi n thiên theo th i gian ầ ế ợ ự ụ ất điể ế ß

như thế nào. Đại lượ ủa phương trình (9.8) đượ

ng á vế phải c c gọi là xung c a h p lủ ợ ực

∑



tác d ng lên ch m trong kho ng th i gian

ụ ất điể ả ß ∆ā = ā

2 ā

�㕖

, kí hi u là ệ �㔼



Trưßng Đạ ọc Sư phại h m Kỹ thu t Tp. H Chí Minh 2021 ậ ồ

�㔼



∫

∑



þā

�㕓

� 㕖

(9.9)

Giả s l c bi n thiên theo thử ự ế ßi gian

như trên hình 9.3a và khác không trong

khoảng thßi gian ∆ā = ā

2 ā

�㕖

. Vectơ

xung l c

ự �㔼



cùng hướng với vectơ độ bi n ế

thiên động lượng ∆Ă. Xung l c có th ự ứ

nguyên c ng là ML/T. Xung ủa động lượ

lực không ph i là m t thu c tính c a ả ộ ộ ủ

chất điểm, mà là s ố đo mức độ ngo i l c ạ ự

làm thay đổ ộng lượi đ ng của chất điểm.

Do h p l c truy n xung l c cho ch t ợ ự ề ự ấ

điểm thưßng thay đổi theo th i gian, nên ß

để thuận ti p ện, ngưßi ta định nghĩa hợ

lực trung bình theo th i gian: ß

(∑þ



)

�㕎ÿā

∆ā

∫ ∑ þ



þā

�㕓

� 㕖

(9.10

trong đó ∆ā = ā

2 ā

�㕖

. (Phương trình 9.11 là một áp d ng c nh lý giá tr trung bình trong ụ ủa đị ị

giải tích.) Do đó có thể bi u di ể ễn phương trình 9.9 như là:

�㔼



= (∑þ



)

�㕎ÿā

∆ā (9.11)

Lực trung bình này, như chỉ ực không đổ ra trên hình 9.3b, có thể xem là l i tác dụng lên

chất điểm trong khoảng thßi gian , có cùng xung l∆ā ực với xung lực của lực biến thiên theo

thßi gian tác d ng lên ch m trong kho ng th ụ ất điể ả ßi gian đó.

ếu

∑



là m t hàm c a th i gian, có th c xung l c t c ộ ủ ß ể tính đượ ự ừ phương trình 9.9. Việ

tính toán tr nên r n n c tác d ng lên ch ng á ất đơn giả ếu như lự ụ ất điểm là không đổi. Trong trưß

ợp này, (

∑



)

�㕎ÿā

∑



, trong đó

∑



là h p l i tác d ng lên ch m, và ợ ực không đổ ụ ất điể

phương trình (9.11) trá thành:

�㔼



= ∑þ



∆ā (9.12)

Kết h c ợp các phương trình (9.8) và (9.9) ta đượ định lý xung lượng- ngđộng lượ :

Độ bi ng cến thiên động lượ ủa một ch m thì b ng cất điể ằng xung lượ ủa hợp lực tác dụng

lên ch ất điểm đó:

∆Ă = �㔼



(9.13)

Phát bi nh lu t 2 Newton. Khi nói m t xung l c truy n cho ểu này tương đương với đị ậ ộ ực đượ ề

chất điểm, ta mu n nói rố ằng động lượng được truy n t m t tác nhân bên ngoài t i ch m ề ừ ộ ớ ất điể

Hình 9.3 (a) L c tác d ng lên ch n thiên ự ụ ất điểm biế

theo th i gian. (b) Giá tr c a l ngờ ị ủ ực không đổi (đườ

nét đứ ằm ngang) đượt n c lấy sao cho diện tích của

hình ch nh t b ng di ng cong ữ ậ ằ ện tích dưới đườ ở

hì h ( )

http://ipt.hcmute.edu.vn B môn v t lý ộ ậ

đó. Phương trình ạng tương tự ới các phương trình bảo toàn năng lượ(9.13) có d v ng (8.1) và

(8.2).

Phương trình 9.13 là phát biểu tổng quát nhất của nguyên lý và bảo toàn động lượng

được gọi là phương trình bảo toàn động lượng. Trong cách tiếp c ng, hận động lượ ệ cô lập

xuất hiện thưßng xuyên hơn hệ không cô lập, nên phương trình (9.13) có thể xem như trưßng

hợp đặ ủa phương trình ủa phương trình là độ ến thiên độc biệt c (9.5). Vế trái c (9.13) bi ng

lượ ủng c a hệ. Vế phải là số đo động lượng đi qua biên của hệ khi có lực tác dụng lên hệ.

Phương trình (9.13) là phát biểu toán học của một mô hình phân tích mới, gọi là mô hình h ệ

không cô lập (động lượng). Phương trình này có dạng tương tự phương trình (8.1) nhưng có

một s khác bi t khi áp d (9.13) ố ệ ụng cho các bài toán. Trước tiên, phương trình là phương

trình vectơ, trong khi phương trình là phương trình vô hướng. Do đó hướ(8.1) ng là quan

trọng đố phương trình ại động lượi với (9.13). Thứ hai, chỉ có một lo ng nên chỉ có một cách

duy nhất để tích tr ữ động lượng trong hệ. Ngược lại, như thấy t ừ phương trình (8.2), có 3 cách

để ỉ tích năng lượ là động năng, thế năng ội năng. Thứng cho hệ và n ba, ch có m ột cách để

truyền động lượ ßi gian. Phương trình ng cho hệ là tác dụng lực lên hệ trong một khoảng th

(8.2) ch truy ng cho m t h m ỉ ra 6 cách mà ta đã biết để ền năng lượ ộ ệ. Do đó, không có sự á

rộng phương trình tương tự(9.13) như phương trình (8.2).

Trong nhi u tình huề ống ngưßi ta dùng <xấp xỉ xung l , b ng cách gi s m t trong các ực= ằ ả ử ộ

lực tác d ng lên ch m tác d ng trong m t kho ng th i gian ngụ ất điể ụ ộ ả ß ắn nhưng lớn hơn nhiều so

ới các l c khác cùng có m p l c ự ặt. Khi đó, hợ ự

∑



trong phương trình (9.9) được thay thế

bằng một lực đơn þ



để ỉ tính xung l c tác d ng lên ch m. S x p xự ụ ất điể ự ấ này rất hữu ích khi

xét các bài toán va ch ng th i gian va ch m r t ng n. Khi s d ng x p x ạm trong đó khoả ß ạ ấ ắ ử ụ ấ ỉ

này, l c xem là m t xung l c. Ví d khi qu bóng chày b ng cái g y, th i ực đơn đượ ộ ự ụ ả ị đánh bằ ậ ß

gian va ch m kho ng 0,01s và l c trung bình mà g y tác d ng lên qu bóng là vài ngàn ạ ả ự ậ ụ ả

Newton. Vì l c này l u so v i tr ng l c tác d ng lên qu bóng và cái g y, nên s ự ớn hơn nhiề ớ ọ ự ụ ả ậ ự

xấp x xung l c cho th y vi c bỉ ự ấ ệ ỏ qua trọng l n. Khi dùng x p x này, c n nh ực là đúng đắ ấ ỉ ầ ớ

rằng Ă

�㕖

và Ă

là các động lượng t c thứ ßi trước và sau khi va chạm. Do đó trưßng hợp phù h p ợ

để ỉ dùng xấp x xung là khi va chạm chấ ểt điểm di chuy n một đoạn rất ngắn.

Câu h i 9.3:ỏ Hai v t n m yên trên m t b m t không có ma sát. V t 1 có kh ng lậ ằ ộ ề ặ ậ ối lượ ớn hơn

vật 2. ( ) Khi mi ột l i tác dực không đổ ụng lên v t 1, nó gia tậ ốc v ng d theo ật trên quãng đưß

một đưßng thẳng. Ngừng cho lực tác dụng lên vật 1 mà cho nó tác dụng lên vật 2. Tại thßi

điểm vật 2 được gia tốc qua cùng quãng đưßng d, phát biểu nào đúng? (a) p

< p , (b) p = p ,

2 1 2

1 2 1 2 1 2 1 2

ii ộ ực không đổ ụ ậ

1, nó gia t c v t trong m t kho ng th i gian ố ậ ộ ả ß



t. Ng ng cho l c tác d ng lên v t 1 mà cho nó ừ ự ụ ậ

tác d ng lên v t 2. T danh sách các l a ch t 2 ụ ậ ừ ự ọn như trên, phát biểu nào là đúng sau khi vậ

đượ ßc gia tốc trong cùng khoảng th i gian



Câu h i 9.4:ỏ Hãy x p h ng t l n nh n nh nh t m t b u khi n ô tô, m t dây an ế ạ ừ ớ ất đế ỏ ấ ộ ảng điề ể ộ

toàn và một túi khí, mỗi cái được s d ng m t mình trong các va ch m có cùng t , v (a) ử ụ ộ ạ ốc độ ề

xung l c và (b) l c trung bình mà m i cái mang l i cho m t hành khách ng i c. ự ự ỗ ạ ộ ồ phía trướ

Trưßng Đạ ọc Sư phại h m Kỹ thu t Tp. H Chí Minh 2021 ậ ồ

Mô hình phân tích: H không cô l ng ệ ập (độ

lượng)

Giả s c h c n phân tích và ử ta đã xác định đượ ệ ầ

biên c a nó. N u có ngo i l c tác d ng lên h thì h ủ ế ạ ự ụ ệ ệ

là không cô lập. Khi đó độ biến thiên động lượng toàn

phần của h b ng xung l c tác d ng lên h nh lý ệ ằ ự ụ ệ (đị

xung l c - ng): ự động lượ

ø ù

9.13

tot

p I ý

Ví dụ:

 Cái g bóng chày ậy đánh vào quả

 Dùng sợi dây kéo m t ng ch t trên bàn ộ ố ỉ đặ

Bài t p m va t nào? ậ ẫu 9.3: Cái đỡ ốt như thế

Trong m t th nghi m va ch m, mộ ử ệ ạ ột xe hơi

có kh ng 1500 kg va ch m v i m t b c ối lượ ạ ớ ộ ứ

tưßng như trên hình 9.4. Vận t c c a ố ủ xe trước

và sau khi va ch m l t là ạ ần lượ

m/s

và

m/s. (A) Va ch m kéo dài trong ạ

0.15 s, hãy tìm xung l c c a v va ch m và ự ủ ụ ạ

lực trung bình tác dụng lên xe. (B u gì ) Điề

xảy ra n u chi c xe không b t ra khế ế ậ ỏi b c ứ

tưß ống? Giả sử t cuốc độ i cùng của xe bằng

không và kho ng th i gian c a va ch m v n ả ß ủ ạ ẫ

á mức 0.15 s. Điều đó có thể hiện là lực lớn hơn hoặc nh ỏ hơn tác dụng lên xe không?

Giải:

(A) S d ng công th tính xung l c tác d ử ụ ức 9.13 để ự ụng lên xe hơi:

ø ù

f i f i f i

I iý 

kg.m/s

Dùng công th c (9.11) ứ để tính l c trung bình tác d ng lên xe: ự ụ

ø ù

1760 i 00

avg

F ý ý



Lực tính được trên là t ng h p c a ph n l ng tác d ng lên xe và á ổ ợ ủ ả ực vuông góc do tưß ụ

lực ma sát gi a các l p xe và m u xe b bi n d ng. N u các bánh xe quay ữ ố ặt đất khi đầ ị ế ạ ế

tự do, l i nhực ma sát này là tương đố ỏ.

(B) Trong tình hu ng trên, khi mà chi c xe b t ra khố ế ậ ỏi tưßng, lực tác d ng lên xe th c ụ ự

hiện hai vi c trong kho ng th i gian 0.15s: (1) nó d ng xe, và (2) nó làm cho xe chuy n ệ ả ß ừ ể

động ra kh ng vỏi tưß ới t 2.60 m/s sau khi va chốc độ ạm. Nếu chiếc xe không bật ra,

lực chỉ th c hiự ện bước đầu tiên đó là dừng xe - đòi hỏi một l c nh ng ự ỏ hơn. Trong trưß

hợp này, xung l c là: ự

Hình 9.4 Bài t p m u 9.3 ậ ẫ

http://ipt.hcmute.edu.vn B môn v t lý ộ ậ

ø ù

f i i f i

I iý 

kg.m/s và l c trung bình tác d ng lên xe ự ụ

là:

ø ù

1500 i 00

avg

F ý ý



Va ch m mạ ột chiều

Thuật ng va ch m bi u th s ki n hai chữ ạ ể ị ự ệ ất điểm đi lại gần

nhau và tương tác với nhau b ng các l c. Các lằ ự ực tương tác được

giả s r t lử ấ ớn so v i các ngo i l c có m t, nên có th s d ng ớ ạ ự ặ ể ử ụ

xấp x xung l c. ỉ ự

Va ch m không ch x y ra khi có s ti p xúc tr c ti p gi a ạ ỉ ả ự ế ự ế ữ

hai v t th trên hình 9.5a, mà ph c hi u ậ ể vĩ mô, như mô tả ải đượ ể

tổng quát hơn. Ví dụ xét một va chạm á tỉ lệ nguyên tử giữa

proton và h t alpha (hình 9.5b). Vì c hai h n ạ ả ạt đều mang điệ

dương, chúng đẩy nhau, va chạm với nhau thông qua trưßng

điện từ.

Khi hai v t có kh ng m và m va chậ ối lượ

1 2

ạm như trên hình

9.5, các xung l c có th i r t ph c t p, ch ng hự ể thay đổ ấ ứ ạ ẳ ạn như

trên hình 9.3. Tuy nhiên, b t k s ph c t p c a xung l c, l c ấ ể ự ứ ạ ủ ự ự

luôn là n i l c c a h hai v t t o thành m t h ộ ự ủ ệ ật. Do đó, hai vậ ạ ộ ệ

cô l ng c a h c b o toàn trong va ch m b t ập và động lượ ủ ệ đượ ả ạ ấ

kỳ. Tuy nhiên, t a h có th b o toàn ho c ổng động năng củ ệ ể ả ặ

không, tùy thu c vào lo i va ch m. ộ ạ ạ

Phân lo i va chạ ạm: Va ch¿m được chia thành va ch¿m đàn hồi ho c va chặ ¿m không đàn

hồi tùy thuộc vào việc động năng của hệ có bÁo toàn hay không.

Va ch hai v t là va ch m mà t ng c a h ¿m đàn hồi g a ữ ậ ¿ ổng động năng và tổng động lượ ủ ệ

trước và sau khi va ch¿m là như nhau. Va ch m gi a các v t trong th gi ng h n ạ ữ ậ ế ới vĩ mô, chẳ ạ

giữa các qu bóng bi a, chả ỉ là x p xấ ỉ đàn hồi vì có xảy ra s bi n d ng và mự ế ạ ất động năng. Ví

dụ ta có th nghe th y ti ng các qu bi a va ch y có mể ấ ế ả ạm nhau, như vậ ột số năng lượng từ hệ

đã bị ền đi xa bá ạm đàn truy i âm thanh. Va ch hồi phải hoàn toàn yên lặng

Va ch¿m không đàn hồi là va ch m mà t a h c và sau khi va ch m ¿ ổng động năng củ ệ trướ ¿

khác nhau (m ng c a h c b o toàn).ặc dù động lượ ủ ệ đượ Á Các va ch i có hai ạm không đàn hồ

loại. Khi các v t dính vào nhau sau khi va ch c g i làậ ạm đượ ọ va ch¿m hoàn toàn không đàn

hồi, ví dụ khi một thiên thạch va chạm v t. Khi các với Trái đấ ật va chạm nhưng không dính

vào nhau, nhưng mộ ần năng lượt ph ng bị chuyển sang d ng khác hoạng năng lượ ặc b truyị ền

ra xa, như trưß ạm đượng hợp quả bóng cao su va chạm với một bề mặt cứng, thì va ch c gọi

là . Khi qu bóng cao su va ch m v i n n c ng, m t ph a qu không đàn hồi ả ạ ớ ề ứ ộ ần động năng củ ả

bóng b chuy n i (sang nhi t) khi qu bóng b bi n d ng trong khi nó ti p xúc v i b m t ị ể đổ ệ ả ị ế ạ ế ớ ề ặ

cứng. Các va ch c mô tạm không đàn hồi đượ ả b ng cách di n gi ng c a mô hình ằ ễ ải động lượ ủ

hệ cô l p. ậ

Hình 9.5 (a) Va

ch¿m giữa hai vật

như kết quÁ của sự

tiếp xúc tr c ti p, (b) ự ế

"Va ch m" gi a hai ¿ ữ

h¿t tích điện.

Trưßng Đạ ọc Sư phại h m Kỹ thu t Tp. H Chí Minh 2021 ậ ồ

Va chạm hoàn toàn không đàn hồi

Xét 2 v t kh ng m và m , chuy n ậ ối lượ

1 2

ể

độ ớng v i các vận t u ốc ban đầ ă

1�㕖

, ă

2�㕖

d c ọ

theo m ng thột đưß ẳng như trên hình 9.6.

Hai v t va ch m tr c di n v i nhau, dính ậ ạ ự ệ ớ

vào nhau và sau va ch m chúng chuyạ ển

độ ớng v i vận tốc chung ă

. Do động lượng

của m t hộ ệ cô l c b o toàn trong va ập đượ ả

chạm b t kì, ta có t c ấ ổng động lượng trướ

khi va ch m b ng v ng c a h ạ ằ ới động lượ ủ ệ

hợp l i sau khi va ch m: ạ ạ

ÿ ă

1 1�㕖

+ ÿ

ă ÿ + ÿ

2�㕖

(

1 2

)

ă

(9.14)

Gi mải phương trình này đối với ẩn số là vận tốc sau va chạ , ta được:

ă

1�㕖

+ ÿ

ă

2�㕖

ÿ + ÿ

1 2

(9.15)

Va chạm đàn hồi

Xét 2 v t kh ng m và m , chuy n ậ ối lượ

1 2

ể

động với các vận t u ốc ban đầ ă

1�㕖

, ă

2�㕖

d c ọ

theo m ng thột đưß ẳng như trên hình 9.7.

Hai chất điểm v a ch m tr c di n v i nhau, ạ ự ệ ớ

sau đó tách ra ển độ và chuy ng với các vận

tốc ă

1Ā

, ă

2Ā

Trong va chạm đàn hồi, c ả động lượng

và động năng của h ệ được bảo toàn. Do đó,

xét các v n tậ ốc theo hướ ằm ngang như ng n

trên hình 9.7 ta có:

1 1 2 2 1 1 2 2i f i i f f

p p m vý 

(9.16)

2 2 2 2

1 1 2 2 1 1 2 2

1 1 1 1

2 2 2 2

i f i i f f

K K m v m v m v m vý   ý 

(9.17)

Vì va ch m m t chi u nên ta có th bi u di n các v n t c b ng các t ạ ộ ề ể ể ễ ậ ố ằ ốc độ tương ứng, với các

dấu để chỉ hướng: t ốc độ v là dương nế ất điểu ch m chuy ng sang ph i, là âm n u chuy n ển độ ả ế ể

động sang trái.

Trong bài toán va ch i, có hai t nên c n gi i hạm đàn hồ đại lượng chưa biế ầ ả ệ các phương

trình (9.16) và (9.17) tìm chúng. Ta b các th ½ trong (9.17) và vi t l để ỏ ừa số ế ại như sau:

(ă

1�㕖

2 ă

1Ā

) = ÿ

(ă

2Ā

2 ă

2�㕖

)

Khai tri n c hai v ta có: ể ả ế

(ă

1�㕖

2 ă

1Ā

)(ă

1�㕖

+ ă

1Ā

) = ÿ

(ă

2Ā

2 ă

2�㕖

)(ă

2Ā

+ ă

2�㕖

) (9.18)

Hình 9.6 Gi m xuyên tâm Án đồ biểu diễn va ch¿

hoàn toàn không đàn hồi giữa hai chất điểm

Hình 9.7 m t va ch m tr c di i Sơ đồ ộ ¿ ự ện đàn hồ

giữa hai ch m. ất điể

http://ipt.hcmute.edu.vn B môn v t lý ộ ậ

Tiếp theo ta nhóm các s h ng ch a (9.16) ố ạ ứ m

, m

trong phương trình để có:

(ă

1�㕖

2 ă

1Ā

) = ÿ

(ă

2Ā

2 ă

2�㕖

) (9.19)

Để ợ để thu đư c kết quả cuối cùng, ta chia (9.18) cho (9.19) có:

1�㕖

+ ă

1Ā

= ă

2Ā

+ ă

2�㕖

1�㕖

2 ă

2�㕖

= 2(ă

1Ā

2 ă

2Ā

) (9.20)

Phương trình này và phương trình (9.16) được dùng để gi i các bài toán va chả ạm đàn hồi.

Cặp phương trình ụng hơn cặp các phương trình (9.16) và (9.20) dễ sử d (9.16) và (9.17) vì

không có các s h ng bố ạ ậc 2 như trong phương trình . Theo phương trình (9.17) (9.20), vận t c ố

tương đố ất điểm trướ ốc tương i của 2 ch c khi va chạm, , bă 2 ă

1�㕖 2�㕖

ằng và trái dấu với vận t

đố ủi c a chúng sau khi va chạm, 2(ă

1Ā

2 ă

2Ā

Nếu bi t kh ng và v n t c cế ối lượ ậ ố ủa các v c khi va ch m, ta giật trướ ạ ải các phương trình

(9.16) và (9.20) tìm các v n t c sau va ch m theo các v n t m: để ậ ố ạ ậ ốc trước va chạ

1Ā

= (

2 ÿ

ÿ + ÿ

1 2

)ă

1�㕖

+ (

2ÿ

ÿ + ÿ

1 2

)ă

2�㕖

(9.21)

2Ā

= (

2ÿ

ÿ + ÿ

1 2

)ă

1�㕖

+ (

2 ÿ

ÿ + ÿ

1 2

)ă

2�㕖

(9.22)

Lưu ý dùng đúng các dấ phương trình u cho các (9.21) và (9.22).

Ta hãy xét m t s ng h c bi t . ộ ố trưß ợp đặ ệ sau đây

 Nếu (9.21) và (9.22) cho th y ÿ

= ÿ

, các phương trình ấ ă

1Ā

= ă

2�㕖

, ă

2Ā

= ă

1�㕖

, t c ứ

là các ch m s i v n t c cho nhau n u kh ng c a chúng b ng nhau. Ví d ất điể ẽ đổ ậ ố ế ối lượ ủ ằ ụ

va ch m tr c di n c a 2 qu bi-a: sau khi va ch m viên bi cái d ng l y viên bi ạ ự ệ ủ ả ạ ừ ại và đẩ

kia đi xa vớ ốc ban đầi vận t u của viên bi cái.

 Nếu ch ng yên, (9.21), (9.22) tr thành: ất điểm 2 lúc đầu đứ ă

2�㕖

= 0, các phương trình á

1Ā

= (

2 ÿ

ÿ + ÿ

1 2

)ă

1�㕖

(9.23)

2Ā

= (

2ÿ

ÿ + ÿ

1 2

)ă

1�㕖

(9.24)

 Nếu ÿ

≫ ÿ

, t ừ các phương trình 9.23 và 9.24 ta thấy ă

1Ā

≈ ă

1�㕖

và ă

2Ā

≈ 2ă

1�㕖

. T c ứ

là khi m t v t r t n ng va ch m tr n v i m t v t r t nh ộ ậ ấ ặ ạ ực diệ ớ ộ ậ ấ ẹ đang đứng yên, vật nặng

sẽ ti p t c chuy ng mà không bế ụ ển độ ị thay đổi gì sau khi va chạm, còn vật nhẹ bị bật

lại với t b ng 2 l n t u c a v t n ng. ốc độ ằ ầ ố ộc đ lúc đầ ủ ậ ặ

 Nếu ÿ

≫ ÿ

và chất điểm 2 lúc đầu đứng yên, , ta th y ă

2�㕖

= 0 ấ ă

1Ā

≈ 2ă

1�㕖

và ă ≈

2Ā

0, t c là khi m t v t r t nh va ch m tr c di n v i m t v t r t n ng yên, ứ ộ ậ ấ ẹ ạ ự ệ ớ ộ ậ ấ ặng đang đứ

vận tốc của v t nh s b i chi u còn v t n ng g ng yên. ậ ẹ ẽ ị đổ ề ậ ặ ần như vẫn đứ

Trưßng Đạ ọc Sư phại h m Kỹ thu t Tp. H Chí Minh 2021 ậ ồ

Câu h i 9.5:ỏ Trong m t va ch m m t chiộ ạ ộ ều hoàn toàn không đàn hồi gi a hai vữ ật đang chuyển

động, điều kiện nào là cần thi i cùng c a h b ng không sau va ch m? ( ) ết để động năng cuố ủ ệ ằ ạ a

Động lượng ban đầ ải có cùng độ ớn nhưng ngược hướu của các vật ph l ng. ( ) Các vb ật phải

có cùng kh ng. ( ) Các v t ph i có cùng v n t u. ( ) Các v t ph i có cùng t c ối lượ c ậ ả ậ ốc ban đầ d ậ ả ố

độ ớ u, v n tban đầ ới các vectơ vậ ốc ngược hư ng.

Câu h i 9.6:ỏ M t qu c ném v phía m t qu ng yên. ộ ả bóng bàn đượ ề ộ ả bóng bowling đang đứ

Quả bóng bàn gây ra m t va chộ ạm đàn hồi m t chi u và b n y l i trên cùng mộ ề ị ả ạ ột đưßng th ng. ẳ

So v i qu bóng bowling sau va ch m, qu bóng bàn có ( l n c ng lớ ả ạ ả a) độ ớ ủa động lượ ớn hơn

và động năng lớn hơn, ( ) độ ủa động lượ hơn và động năng lớn hơn, ( ) độb lớn c ng nhỏ c lớn

của động lượ ớn hơn và động năng nhỏng l hơn, ( l n c ng nh ng d) độ ớ ủa động lượ ỏ hơn và độ

năng lớn hơn, hoặ ) cùng độ ộng lượng và cùng động năng?c (e lớn của đ

Chiến lược giải bài toán va chạm m t chiộ ều

 Tưáng tượng va ch m x y ra. V các giạ ả ẽ ản đồ đơn giản v các về ật trước và sau va ch m. ạ

Đoán hướng của các vectơ vận t c sau khi va chố ạm.

 Hệ chất điểm có ph i là cô l p không? N u có hãy phân lo i va chả ậ ế ạ ạm là đàn hồi, không

đàn hồi hoặc hoàn toàn đàn hồi.

 Viết các phương trình:

- Nếu va ch i, vi (9.15). ạm là hoàn toàn không đàn hồ ết phương trình

- Nếu va ch m là i, vi (9.16) và (9.17). ạ đàn hồ ết phương trình

- Nếu va ch i, vi (9.16). ạm là không đàn hồ ết phương trình

 Dựa vào các thông số đề bài đã cho và tính các thông số còn lại.

Bài t p m u 9.5: Th c hi n b o hi m va ch m! ậ ẫ ự ệ ả ể ạ

Một xe hơi n ng 1800 kg ng thì bặ đang dừng đèn giao thô ị m t xe ng 900 ộ hơi khác nặ

kg húc t phía sau. Hai xe ng vào nhau và chuy ng d ng th ng mà ừ vướ ển độ ọc theo đưß ẳ

chiếc xe nh ẹ ban đầ đang chuyển độu ng. Trước khi va ch m xe nh ạ ẹ hơn đang chạy v i ớ

tố ộc đ 20.0 m/s, h i t c ỏ ố độ c a hai xe sau khi va ch m b ng bao nhiêu? ủ ạ ằ

Giải:

Sau khi va chạm hai xe vướng vào nhau nên đây là va chạm hoàn toàn không đàn hồi.

Dùng mô hình h cô l i v ng cho h hai xe ta có: ệ ập đố ới động lượ ệ

ø ù

1 1 2

i f i f

m v m m vpý  ý 

Từ đây ta tính được tốc độ của hai xe sau khi va chạm là:

1 2

6,67

m v

m m

ý ý



m/s

http://ipt.hcmute.edu.vn B môn v t lý ộ ậ

Bài t p m u 9.6: Con l n ậ ẫ ắc thử đạ

Con l c th n (Hình 9.8) là thi t b ắ ử đạ ế ị được sử d ụng để đo tốc độ c a m t v t ủ ộ ậ được bắn

ra và chuy ng nhanh ch ng h n n. M n kh ng m c ển độ ẳ ạ như viên đạ ột viên đạ ối lượ

đượ

ắn vào một kh i g l n có kh i ng mố ỗ ớ ố lượ

c treo b i mđượ á ột s s i dây nh . ố ợ ẹ Viên đạn

cắm vào kh i g và hố ỗ ệ đạn - gỗ được nâng lên m cao h. Làm thột độ ế nào nh để xác đị

đượ đạc tố ộc đ của viên n bằng cách cao h? đo độ

Giải:

Va ch m gi n và kh i g là va ch i vì sau khi va ạ ữa viên đạ ố ỗ ạm hoàn toàn không đàn hồ

chạm viên đạ động lượn cắm vào khối gỗ. Hệ đạn – gỗ tạo thành một hệ cô lập về ng.

Tốc độ ạm hoàn toàn không đàn hồi được xác đị của các vật sau khi va ch nh theo

phương trình (9.15):

1 1

1 2

m v

m m



(1)

Động lượng của hệ ngay sau khi va chạm là:

ø ù

1 2

B B

K m m vý 

(2)

Thay v t c:

ừ (1) vào (2) ta đượ

ø ù

2 2

1 1

1 2

m v

m m



Động năng của hệ đạn – g ngay sau khi va ch m này nh ỗ ạ ỏ hơn động năng ban đầu của

viên đạn.

Chọn g c th i kh i g , U = 0. Th ố ế năng tạ ố ỗ

ế năng của hệ đạn g– ỗ tại độ cao h là:

ø ù

1 2C

U m m ghý 

Hình 9.8 Bài t p m u 9.6 m t con l n. ậ ẫ (a) Sơ đồ ộ ắc thử đ¿

là v n t c va ch m và là v n t a ậ ốc của đ¿n ngay trướ ¿ ậ ốc củ

hệ đ¿n g ngay sau va ch i. (b) – ỗ ¿m hoàn toàn không đàn hồ

Ành chụ ủ ộ ắp nhiều lần chớp c a m t con l c thử đ¿n dùng trong

Trưßng Đạ ọc Sư phại h m Kỹ thu t Tp. H Chí Minh 2021 ậ ồ

Áp dụng mô hình h cô l p cho h n g ta có: ệ ậ ệ đạ – ỗ

ø ù ø ù

0 0

C B C B

K U K K U U   ý     ý

ø ù

2 2

1 1

1 2

0 0 0

m v

m m gh

m m

ö ö

     ýù ù

÷ ÷

 

÷ ÷



ø ø

Giải phương trình này ta được:

1 2

m m

v gh

ö ö



÷ ÷

ø ø

Ta đã giải bài t p ậ này theo hai bước. Mỗi bước liên quan đến một hệ khác nhau và m t ộ

mô hình phân tích khác nhau: h cô l ng c th nh t và h cô l p ệ ập (độ lượng) cho bướ ứ ấ ệ ậ

(năng lượ đàn hồ cơ ng) cho bước thứ hai. Vì va chạm là hoàn toàn không i, một lượng

năng đã năng trong Do đó, sẽ không đúng được chuyển thành nội quá trình va chạm.

khi s d ng mô hình h cô lử ụ ệ ập (năng lượng) cho toàn b quá trình b ng cho ộ ằ động năng

ban đầu của viên đạn bằng với thế năng hấp dẫn của hệ đạn – gỗ á độ cao h.

Va ch m hai chi u ạ ề

Trong m c 9.2 ta bi t r ng ụ ế ằng độ

lượng của hệ hai ch m cô l c ất điể ập đượ

bảo toàn. Trong va ch m b t kì c a hai ạ ấ ủ

chất điểm thì động lượ ỗi hướng theo m ng

x, y, z được bảo toàn.

Xét va ch m x y ra trên m t ph ng, ạ ả ặ ẳ

ví d i v i các va ch m hai ụ chơi bi da. Đố ớ ạ

chiều, ta có hai phương trình thành phần

cho bảo toàn ng: động lượ

ÿ ă

1 1 2�㕖ā

+ ÿ

�㕖ā

= ÿ

1Āā

+ ÿ

2Āā

ÿ ă

1 1 2�㕖Ă

+ ÿ

�㕖Ă

= ÿ

1ĀĂ

+ ÿ

2ĀĂ

trong đó 3 chỉ số dưới các thành ph n v n tầ ậ ốc trong các phương trình này tương ứng biểu th : ị

kí hi u c a v t th (1,2), các giá tr c và sau va ch m (i,f), và thành ph n v n t c (x,y). ệ ủ ậ ể ị trướ ạ ầ ậ ố

Xét trưßng h c bi t khi v t th nh t kh ng m va ch m v i v t th 2 khợp đặ ệ ậ ứ ấ ối lượ

ạ ớ ậ ứ ối lượng

ban đầu đứ ển động yên (hình 9.11). Sau va chạm (hình 9.11b),

vật 1 chuy ng theo góc �㔃

so v t 2 chuy ng theo góc so v m này ới phương ngang và vậ ển độ �㔑 ới phương ngang. Va chạ

gọi là va ch m ạ sượt qua (glancing). Áp d nh lu t b ng d ng thành ph n ụng đị ậ ảo toàn động lượ ạ ầ

và lưu ý thành phầ ộng lượng ban đần y của đ u bằng 0, ta có:

1 1 1 1 2 2

0 cos cos

x ix fx i f f

p p p m v m v m v

 

 ý  ý  ý 

(9.25)

1 1 2 2

0 0 sin sin

y iy fy f f

p p p m v m v

 

 ý  ý  ý 

(9.26)

Hình 9.9 Va ch i không xuyên tâm gi a ¿m đàn hồ ữ

hai chất điểm.

http://ipt.hcmute.edu.vn B môn v t lý ộ ậ

trong đó dấ ạm hướu trừ á (9.26) là do thành phần y của vận tốc vật 2 sau va ch ng xuống. Kí

hiệu v trong các phương trình này là tốc độ, hướ ủa vectơ thành phần đượng c c chỉ rõ bái các

dấu c ng ho c l ng, n u có không quá 2 n s ộ ặc trừ. Ta có hai phương trình độ ập vơi 7 đại lượ ế ẩ ố

thì ta có th gi i bài toán này. ể ả

Nếu va chạm là đàn hồi, ta có th ể dùng phương trình 9.17 (bảo toàn động năng) với v =0.

2 2 2

1 1 1 1 2 2

1 1 1

2 2 2

i f i f f

K K m v m v m vý  ý 

(9.27)

Biết t u c a v t 1 và kh ng c a 2 v t, ta còn l i 4 n s (ốc độ ban đầ ủ ậ ối lượ ủ ậ ạ ẩ ố ă

1Ā 2Ā

,ă ,�㔃,�㔑).

Vì ch ng còn l i ph nh chuy n ỉ có 3 phương trình, nên 1 trong 4 đại lượ ạ ải được cho để xác đị ể

độ ỉng sau va ch i chạm đàn hồ từ các nguyên lý bảo toàn.

Nếu va ch o toàn và khạm không đàn h i, đồ ộng năng không bả ông được áp dụng phương

trình (9.27).

Chiến lược giải bài toán va chạm hai chiều

 Tưáng tượ đoán các hướ ần đúng mà các hạng va chạm xảy ra và dự ng g t sẽ chuyển

động sau khi va chạm.

 Thiết l p m t h t nh các v n t c d a vào h t thu n ti n ậ ộ ệ ọa độ và xác đị ậ ố ự ệ ọa độ đó. Để ậ ệ

nên ch n tr c x trùng v i m t trong nh ng v n t u c a các ch m. ọ ụ ớ ộ ữ ậ ốc ban đầ ủ ất điể

 Vẽ và ghi tên c a các v n t n t t c ủ ậ ốc, và tính đế ấ ả các thông tin đã cho.

 Xem xét h các ch m có ph i th c s cô l p? N u có hãy phân lo i va ch m là ệ ất điể ả ự ự ậ ế ạ ạ

đàn hồi, không đàn hồi hoặc hoàn toàn đàn hồi.

 Viết các bi u th i vể ức đố ới các thành ph n x và y cầ ủ ớa động lượng của mỗi vật trư c và

sau khi va ch m. Nh ạ ớ tính đến các dấu phù hợp cho các thành ph n c n ầ ủa các vectơ vậ

tốc và chú ý c n th n các d u trong su t quá trình tính toán. ẩ ận đế ấ ố

 Viết các bi u th i vể ức đố ới động lượng tổng c ng theo tr c x và khi va ch m ộ ụ trước sau ạ

rồi cho chúng b ng nhau. L p l i th t i v ng t ng c ng theo tr c ằ ặ ạ ủ ục này đố ới động lượ ổ ộ ụ

 Tiến hành gi t. ải các phương trình động lượng cho các đạ ợng chưa biếi lư

- Nếu va ch c b o toàn, và có l i ạm là không đàn hồi, động năng không đượ ả ẽ đòi hỏ

thông tin b sung. ổ

- Nếu va ch i, các v n t c sau va ch m c a hai v t là ạm là hoàn toàn không đàn hồ ậ ố ạ ủ ậ

bằng nhau.

- Nếu va chạm là đàn hồi, động năng được b o toàn, và b n có th cho t ng ả ạ ể ổ động năng

của hệ trước và sau khi va ch m b ng nhau, cho ta m t m i liên h b sung gi a các ạ ằ ộ ố ệ ổ ữ

độ ớ ố l n vận t c.

 Khi bạn đã xác định được kết qu , ki m tra l i xem chúng có phù h p v i các miêu t ả ể ạ ợ ớ ả

về a, và có phù h p v i th không. ý nghĩa minh họ ợ ớ ực tế

Trưßng Đạ ọc Sư phại h m Kỹ thu t Tp. H Chí Minh 2021 ậ ồ

Bài t p m u 9.8: Va ch m t i m t ngã ba ậ ẫ ạ ạ ộ

Tại m t ngã ba, chi ng 1500 kg ch y v ng ộ ếc xe hơi nặ ạ ề hướ

đông vớ ốc đội t 25.0 m/s va chạm với chiếc xe tải nặng

2500 kg ch y v phía b c v i tạ ề ắ ớ ốc độ 20.0 m/s như trên Hình

9.10. Hãy tìm hướng và độ lớn của vận tốc của các xe sau

va ch m, gi s các xe dính vào v i nhau sau va ch m. ạ ả ử ớ ạ

Giải:

Ta ch n trọ ục x, y như hình 9.10. Xem hai xe như một h cô ệ

lập v ng. Va ch m gi a hai xe là va ch m hoàn ề động lượ ạ ữ ạ

toàn không đàn hồi vì chúng dính vào nhau sau va chạm.

Trước khi va ch m, chi c ạ ế xe hơi có động lượng theo hướng

x, còn chi c xe t ng y. ế ải có động lượng theo hướ

Giả s sau khi va ch m hai xe chuy ng vử ạ ển độ ới t v ng hốc độ

theo hướ ợp với trục x

một góc



Áp dụng mô hình h cô l p v ng x: ệ ậ ề động lượng cho hướ

ø ù

1 1 1 2

0 cos

x xi xf i f

p p p m v m m v



 ý  ý  ý 

õ õ

(1)

Áp dụng mô hình h cô l p v ng y: ệ ậ ề động lượng cho hướ

ø ù

2 2 1 2

0 sin

y yi yf i f

p p p m v m m v



 ý  ý  ý 

õ õ

(2)

Chia (2) cho (1) ta có:

2 2 2 2

1 1 1 1

tan tan

i i

m v m v

 



ö ö

ý  ý

÷ ÷

ø ø

Thay s c ố ta đượ

53,1



Từ (2) ta tính được giá tr c ị ủa v

ø ù

2 2

1 2

15,6

sin

m v

m m



ý ý



m/s

Ta th y tấ ốc độ c a h hai xe sau va ch m nh ủ ệ ạ ỏ hơn tốc độ của mỗi xe trước khi va ch m. ạ

Kết qu ả này cũng phù hợp v i lý thuy t là trong va chớ ế ạm không đàn hồi thì động năng

của hệ gi m. ả

Khối tâm

Trong m c này ta mô t chuyụ ả ển độ ển độ ột điểm đặng của một hệ bằng chuy ng của m c

biệt gọi là khối tâm c a h . H có th g m m t s ch m, ch ng h n các nguyên t trong ủ ệ ệ ể ồ ộ ố ất điể ẳ ạ ử

một bình ch c là m t v t th t v ng viên nh y lên trong không khí. Ta ứa, hoặ ộ ậ ể dài, như mộ ận độ ả

sẽ th y r ng chuy ng t nh ti n c a kh i tâm gi t c kh ng c c t p ấ ằ ển độ ị ế ủ ố ống như tấ ả ối lượ ủa hệ đượ ậ

trung t c là h chuy t ng ngo i l c tác d ng vào kh i tâm. ại điểm đó, tứ ệ ển động như thể ổ ạ ự ụ ố

Chuyển động này độc l p v i các chuyậ ớ ển động khác c a h , ch ng hủ ệ ẳ ạn như chuyển động quay

Hình 9.10 Bài t p m u ậ ẫ

9.8

http://ipt.hcmute.edu.vn B môn v t lý ộ ậ

hoặc rung, ho c bi n d ng (ch ng h n khi v ng viên g i l i). Mô hình này là mô ặ ế ạ ẳ ạ ận độ ập ngưß ạ

hình ch i thi ất điểm đã giớ ệu trong chương 2.

Hình 9.11 L c tác d ng lên h g n v i nhau ự ụ ệ ồm 2 chất điểm khối lượng khác nhau được gắ ớ

bằng m t thanh c ng, nh . ộ ứ ẹ

Xét h hai v t có kh c k t n i v i nhau b ng m t thanh r n, mệ ậ ối lượng khác nhau đượ ế ố ớ ằ ộ ắ ảnh

và nh (hình 9.11). V trí kh i tâm c a h là ẹ ị ố ủ ệ vị trí trung bình c a khủ ối lượng c a h . Kh i tâm ủ ệ ố

của hệ n ng n i hai v t và g n v t có kh ng l u l c tác d ng vào ằm trên đưß ố ậ ầ ậ ối lượ ớn hơn. Nế ự ụ

một điể ều kim đồm trên thanh, á phần phía trên khối tâm thì hệ sẽ quay theo chi ng hồ (hình

9.11a). N u l c này tác d ng vào m m n i kh i tâm thì h s c ế ự ụ ột điể ằm phía dướ ố ệ ẽ quay ngư ợ

chiều kim đồ ển động hồ (hình 9.11b). Nếu lực này tác dụng vào khối tâm thì hệ sẽ chuy ng

theo chi u tác d ng c a l c mà không b quay (xem hình 9.11c). V trí kh i tâm có th c ề ụ ủ ự ị ị ố ể đượ

xác định theo cách này.

Khối tâm c a c p ch m trên hình 9.12 n m trên ủ ặ ất điể ằ

trục x, á gi m. Vữa các chất điể ị trí c a nó là: ủ

�㔶�㕀

1 2

+ ÿ ý

ÿ + ÿ

1 2

(9.28)

Ví d n u x =0, x =d và m = 2m ta có

ụ ế

1 2 2 1

�㔶�㕀

þ. T c là ứ

khối tâm n m g n v t nằ ầ ậ ặng hơn. Nếu hai v t có khậ ối lượng

bằng nhau, kh i tâm s n m t n th ng nố ẽ ằ ại trung điểm đoạ ẳ ối

hai v t. ậ

Có th m r ng khái ni m kh i tâm cho h nhi u ch t ể á ộ ệ ố ệ ề ấ

điểm trong không gian 3 chiều, ch m thất điể ứ i có khối

lượng m .

Tọ ộa đ x c a khủ ối tâm c g m n ch m là: ủa hệ ồ ất điể

�㔶�㕀

1 2 3

+ ÿ ý

+ ⋯+ ÿ

ÿ + ÿ + ÿ + ⋯+ ÿ

1 2 3 ÿ

∑

�㕖

�㕖�㕖

∑

�㕖�㕖

∑

�㕖

�㕖�㕖

� 㕀

∑ÿ

�㕖

� 㕖

(9.29)

Hình 9.12 Kh i tâm c a h 2 ố ủ ệ

chất điểm có kh ng khác ối lượ

nhau trên tr c x n m t i x_CM,ụ ằ ¿

giữa các ch m, và gất điể ần

chất điểm có kh ng l n ối lượ ớ

hơn

Trưßng Đạ ọc Sư phại h m Kỹ thu t Tp. H Chí Minh 2021 ậ ồ

Trong đó

�㕖

là t x c a ch m th i, và t ng kh ng c a h là ọa độ ủ ất điể ứ ổ ối lượ ủ ệ �㕀 =

∑

�㕖�㕖

. Các t a ọ

độ y và z của kh t : ối tâm đượ ịnh tươngc xác đ ự, theo các phương trình

�㔶�㕀

� 㕀

∑ÿ

�㕖

� 㕖

�㔶�㕀

� 㕀

∑ÿ

�㕖

� 㕖

(9.30)

Trong không gian 3 chiều, v trí c nh bị ủa khối tâm được xác đị ái bán kính vectơ ÿ

�㔶�㕀

, v i ớ

3 thành ph n ầ ý ,þ

�㔶�㕀 �㔶�㕀

, ÿ

�㔶�㕀

: xác định theo các phương trình 9.29 và 9.30. Do đó

ÿ

�㔶�㕀

= ý

�㔶�㕀

ÿ+ þ

�㔶�㕀

Ā+ ÿ �㕘

�㔶�㕀

󰇍



� 㕀

∑ÿ

�㕖

� 㕖

ÿ+

� 㕀

∑ÿ

�㕖

� 㕖

Ā+

� 㕀

∑ÿ

�㕖

� 㕖

�㕘

󰇍



ÿ

�㔶�㕀

� 㕀

∑ÿ

�㕖

� 㕖

ÿ

�㕖

(9.31)

trong đó ÿ

�㕖

ý ÿ+ þ

�㕖 � 㕖

Ā+ ÿ

�㕖

�㕘

󰇍



a ch m th i. là bán kính vectơ củ ất điể ứ

Các ý tưáng cơ bản đã thả ận trên đây cũng đượo lu c áp

dụng để xác định vị trí khối tâm của vật rắn. Xem vật rắn

như là hệ ột lượ ập phương gồm m ng lớn các phần tử hình l

như hình 9.13. Do s n t là r t nh ự ngăn cách giữa các phầ ử ấ ỏ

nên v t r n có th xem là có phân b kh ng liên t c. ậ ắ ể ố ối lượ ụ

Bằng cách chia v t r n thành các y u t có kh ng ậ ắ ế ố ối lượ ∆ÿ

�㕖

với các tọa độ ý

�㕖

, þ

�㕖

,ÿ

�㕖

, ta th y tấ ọa độ x c a kh i tâm x p x ủ ố ấ ỉ

bằng:

�㔶�㕀

� 㕀

∑ý

�㕖

∆ÿ

�㕖

Các tọa độ þ

�㔶�㕀

, ÿ

�㔶�㕀 �㔶�㕀

bi u thể ức cũng tương tự như ý .

Nếu s ph n t n ti n t c c a m i ố ầ ử ế ới vô cùng thì kích thướ ủ ỗ

phần t s ti n tử ẽ ế ới 0, và gý

�㔶�㕀

ần như chính xác. Khi đó ta

thay t ng b ng tích phân, và thay b ng y u t vi phân ổ ằ ∆ÿ

�㕖

ằ ế ố

dm:

�㔶�㕀

= lim

∆þ

�㕖→0

� 㕀

∑ý

�㕖

∆ÿ

�㕖

� 㕖

� 㕀

∫ýþÿ (9.32)

Tương tự, ta có:

�㔶�㕀

� 㕀

∫þþÿ ÿ

�㔶�㕀

� 㕀

∫ÿþÿ (9.33)

Ta có th bi u di i tâm v t r i d ng: ể ể ễn bán kính véctơ của khố ậ ắn dướ ạ

ÿ

�㔶�㕀

� 㕀

∫ ÿþÿ (9.34)

Hình 9.13 Kh nh ối tâm được đị

vị bằng bán kính vectơ

ÿ

�㔶�㕀

, có

các thành phần ý

�㔶�㕀

,þ

�㔶�

http://ipt.hcmute.edu.vn B môn v t lý ộ ậ

Biểu th i 3 bi u th c cho trong ức này tương đương vớ ể ức đượ

(9.32) và (9.33). Đối với vật r ng nh t và có d i x ng, ắn đồ ấ ạng đố ứ

khối tâm c a v t n m trên m t tr i x ng và m t m t ph ng ủ ậ ằ ộ ục đố ứ ộ ặ ẳ

đố ụ ái xứng. Ví d , khối tâm của m ng nhột thanh đồ ất nằm trên

thanh, m c a thanh. Kh i tâm c a m t hình c u ho c á trung điể ủ ố ủ ộ ầ ặ

một hình l m ập phương nằ á tâm hình h c cọ ủa nó.

Vì v t r n là m t phân b kh ng liên t c, m i y u t ậ ắ ộ ố ối lượ ụ ỗ ế ố

khối lượng chịu tác dụng c a tr ng l c. Tác d ng t ng c ng c a ủ ọ ự ụ ổ ộ ủ

các l i tác d ng c t l c duy nh t ực này tương đương vớ ụ ủa mộ ự ấ �㕀ý

lên một điểm đặc bi c g i là tr ng tâm. N u ệt đượ ọ ọ ế ý là không đổi

trên toàn b phân b khộ ố ối lượng thì tr ng tâm trùng v i kh i tâm ọ ớ ố

của vật. N u vế ật rắn được treo ngay tại tr ng tâm c a nó thì nó ọ ủ

cân b ng trong m ng b t kì. ằ ọi định hướ ấ

Trọng tâm của m t v t th có hình d n, ví ộ ậ ể ạng không đều đặ

dụ cái m l t, có th ỏ ế ể được xác định b ng cách treo vằ ật, trước tiên

treo á một điểm, sau đó treo á điểm khác. Trên hình 9.14, cái m ỏ

lết lúc đầu được treo á điểm A, khi nó ngừng quay, v ng ẽ đưß

AB th ng (có th dùng dây d i). Ti l t t i ẳng đứ ể ọ ếp đó treo mỏ ế ạ

điểm C, r i v ồ ẽ đưßng thẳng đứng CD. Tr ng tâm c a mọ ủ ỏ l t n m ế ằ

á ủ nửa bề dày c m của nó, bên trong giao điể a AB và CD. Tổng

quát, n u m lế ỏ ết được treo t do t i mự ạ ột điểm bất kì, đưßng th ng ẳ

đứng đi qua điểm này phải đi qua trọng tâm.

Câu h i 9.7:ỏ Một cây g y bóng chày có m ng ậ ật độ đồ

nhất đượ ủa nó như trên hình c cắt tại vị trí khối tâm c

9.15. Ph n nào có kh ng nh n bên ầ ối lượ ỏ hơn? (a) phầ

phải (b) ph n bên trái (c) c hai ph n có cùng kh i ầ ả ầ ố

lượng (d) không thể xác định.

Bài t p m u 9.10: Kh i tâm c a ba ch m ậ ẫ ố ủ ất điể

Một h g m ba chệ ồ ất điểm được b trí nhố ư trên Hình

9.16. Kh ng c a các ch m là m = m = ối lượ ủ ất điể

1 2

1.0 kg và m = 2.0 kg. Hãy tìm kh i tâm c .

ố ủa hệ

Giải:

Sử d ng các công th i v i các toụ ức định nghĩa đố ớ ạ

độ khối tâm (9.29) và (9.30) và thay s ta có: ố

1 1 2 2 3 3

1 2 3

0,75

m x m x m x

m m m

 

ý ý

 

1 1 2 2 3 3

1 2 3

1,0

y y ym m m

m m m

 

ý ý

 

z ý

Hình 9.14 Một phương

pháp th c nghi xác ự ệm để

định trọng tâm của cái mỏ

lết

Hình 9.15 M t cây g y bóng chày b ộ ậ ị

đôi cắt t¿i vị trí khối tâm của nó.

Hình 9.16 Bài t p m u 9.10 ậ ẫ

Trưßng Đạ ọc Sư phại h m Kỹ thu t Tp. H Chí Minh 2021 ậ ồ

Vậy véctơ vị trí của khối tâm của hệ là:

ø ù

0,75 1,0

CM CM CM

r i y j i j m ý 

Bài t p m u 9.11: Kh i tâm c a m t thanh r n ậ ẫ ố ủ ộ ắ

(A) Hãy ch ra r ng kh i tâm c a m t thanh có ỉ ằ ố ủ ộ

khối lượ trung điểng M và chiều dài L nằm á m

của nó, gi s thanh có m kh ng không ả ử ật độ ối lượ

đổi. (B) Gi s mả ử ột thanh không đồng nh t và m t ấ ậ

độ kh ng c i tuyối lượ ủa nó thay đổ ến tính với x

theo công th c ứ

 

, v i ớ



là h ng s . Tìm t a ằ ố ọ

độ dướ x của tâm kh ng ối lượ i dạng một phân số

của L.

Giải:

Chọn h toệ ạ độ có g c toố ạ độ n m ằ á m u thanh và tr ng d c theo thanh ột đầ ục x hướ ọ

như trên hình 9.17. Dễ thấy khối tâm của thanh nằm trên trục x, và y = 0, z = 0.

CM CM

(A) S d ng công th c (9.32) ta có: ử ụ ứ

x xdm x

M M M



ýý ý

 

Thay

M L



ta có:

2 2

L M

x L

M L

ý ý

Trong trưßng hợp này ta có th dùng nh n xét v i x c cùng k t ể ậ ề tính đố ứng để thu đượ ế

quả.

(B) Trong trưßng hợp này do m kh ng t l thu n v i x nên càng xa g c to ật độ ối lượ ỉ ệ ậ ớ ố ạ

độ ộ thì thanh càng nặng. M t phần tử c dài dx có kh ng dm và ủa thanh có độ ối lượ

d x = xm d x d

 

Sử d ng công th c (9.32) ta có: ụ ứ

0 0

1 1 1

dx dx

L L

x xdm x x x

M M M M



 

ýý ýý

  

Khố ợi lư ng c a thanh là: ủ

0 0

x x

L L

M dm d x d



 

ý ý ý ý

  

Thay bi u th a M vào bi u th ể ức củ ể ức c a xủ

ta được:

x Lý

Ta th y kh i tâm n m cách xa g c to ng h p (A) trên. ấ ố ằ ố ạ độ hơn trong trưß ợ á

Hình 9.17 Hình v dùng ẽ để xác

định khối tâm của một thanh rắn

Bấm Tải xuống để xem toàn bộ.

| 1/33

| | Tải xuống

Preview text:

http://ipt.hcmute.edu.vn Bộ môn vật lý
Chương 9: Động lượng và va chạm
hi giải quyết một bài toán cơ học ta có thể sử dụng nhiều phương pháp khác nhau.
Đối với một số bài toán nếu ta dùng phương pháp này thì sẽ phức tạp nhưng nếu ta
Kdùng phương pháp khác thì lại trá nên dễ dàng hơn. Ví dụ trưßng hợp ngưßi đàn
ông đứng trên băng bắn cung tên hoặc tình huống các viên bi-da va chạm với nhau.
Giả sử xét một tình huống đơn giản là cho biết vận tốc của mũi tên ngay sau khi được bắn ra
và yêu cầu tính vận tốc của ngưßi bắn cung ngay khi đó. Ta không thể giải bài toán này với
các mô hình động học (chương 2), động lực học (chương 5), hoặc năng lượng (chương 7).
Tuy nhiên, ta có thể giải quyết bài toán này một cách dễ dàng dùng cách tiếp cận liên quan đến động lượng.
Chương này sẽ trình bày các khái niệm động lượng, xung lượng, các định lý liên quan
đến động lượng, xung lượng, từ đó đưa ra phương pháp giải các bài toán cơ học liên quan đến
động lượng, đặc biệt là các bài toán va chạm.
Động lượng
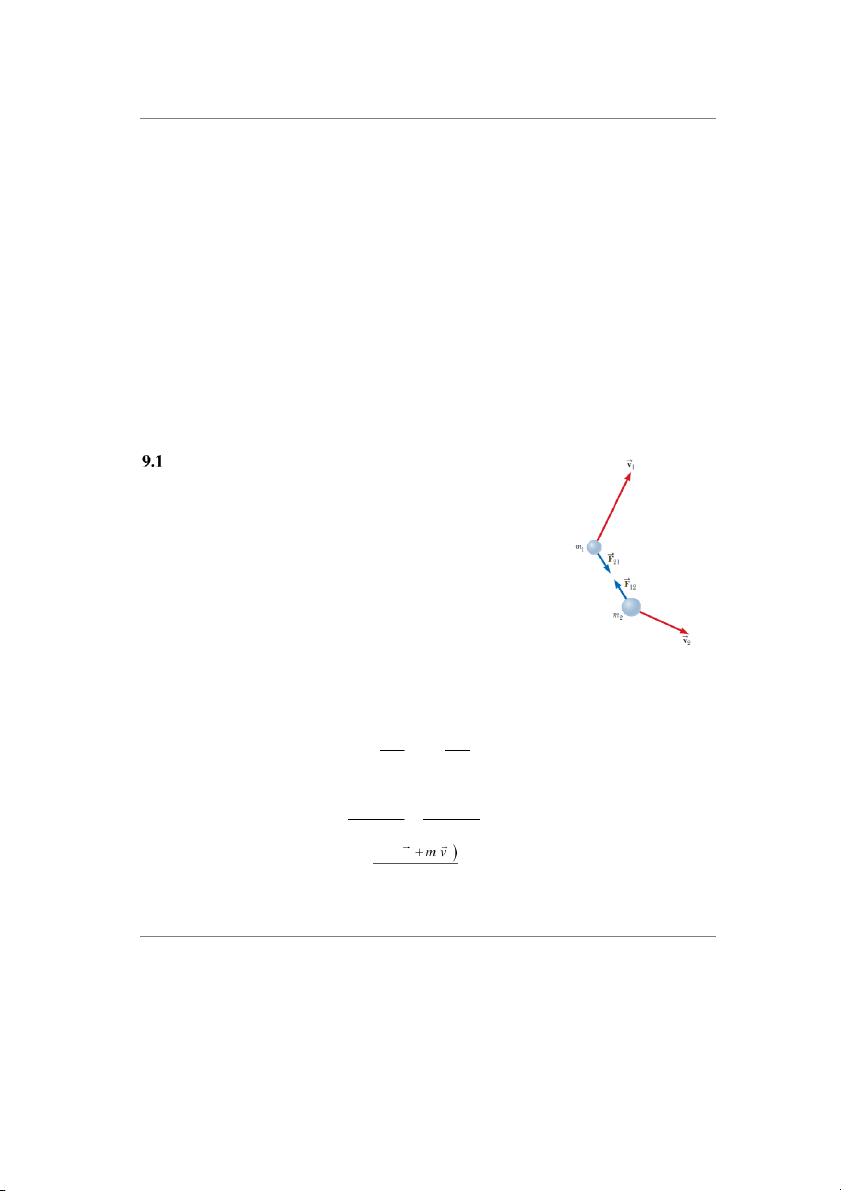
Xét hệ cô lập gồm 2 chất điểm có khối lượng m1, m2, chuyển
động với các vận tốc ă1 và ă2 (hình 9.1). Vì hệ cô lập nên lực tác
dụng lên chất điểm này là do chất đ ể
i m kia gây ra. Nếu chất điểm 1
tác dụng lên chất điểm 2 một lực þ12 thì chất điểm 2 cũng tác dụng
lên chất điểm 1 một lực þ21 bằng về độ lớn nhưng ngược chiều. Các
lực này tạo thành một cặp lực-phản lực theo định luật 3 Newton,
þ12 = 2þ21, nên ta có: þ12 + þ21 = 0.
Theo định luật 2 Newton: lực tác dụng lên mỗi chất điểm bằng ÿ�㕎 nên: ÿ �㕎
Hình 9.1 Hai chất 1 1 + ÿ �㕎 2 2 = 0
điểm tương tác với
Thay các gia tốc bằng biểu thức định nghĩa của nó theo phương nhau trình 4.5, ta có: þă þă ÿ 1 2 1 þā + ÿ2 þā = 0
Nếu các khối lượng m1, m2 không đổi, ta có thể đưa chúng vào trong dấu đạo hàm: þ(ÿ1ă1) þ(ÿ2ă2) þā + þā = 0 d ø 1 m 1 v 2 2 ý 0 (9.1) dt 1
Trưßng Đại học Sư phạm Kỹ thuật Tp. Hồ Chí Minh 2021
Vì đạo hàm của tổng ÿ1ă1 + ÿ2ă2 theo thßi gian bằng không, nên tổng này là không
đổi. Đại lượng mv được gọi là động lượng của một chất điểm, và đối với hệ các chất điểm cô
lập, tổng các đại lượng này được bảo toàn.
Định nghĩa động lượng của chất điểm:
Động lượng của một chất điểm có khối lượng m chuyển động với vận tốc ă được xác định
bằng tích của khối lượng và vận tốc của nó: (9.2)
Động lượng là một đại lượng vectơ, hướng dọc theo ă, thứ nguyên là ML/T, đơn vị trong hệ SI là kg.m/s.
Nếu chất điểm chuyển động theo hướng bất kỳ thì động lượng Ă có 3 thành phần, và
phương trình (9.2) viết cho các thành phần là:
Ăā = ÿăā ĂĂ = ÿăĂ Ăă = ÿăă
Khái niệm động lượng giúp ta phân biệt một cách định lượng giữa các vật nặng và vật
nhẹ chuyển động với cùng vận tốc. Ví dụ động lượng của một quả bóng bowling thì lớn hơn
nhiều so với động lượng của một quả bóng tennis chuyển động với cùng vận tốc. Newton đã
gọi ÿă là khối lượng chuyển động; thuật ngữ này có lẽ sinh động hơn thuật ngữ động lượng ta dùng hiện nay.
Phân biệt động năng và động lượng:
Thứ nhất, động năng là đ¿i lượng vô hướng còn động lượng là đ¿i lượng vectơ. Ví dụ
xét hai chất điểm có khối lượng bằng nhau chuyển động về phía nhau theo một đưßng thẳng
với cùng tốc độ. Động năng của hệ này khác không, động lượng của hệ này bằng không.
Thứ hai là động năng có thể chuyển hóa thành các d¿ng năng lượng khác chẳng h¿n như
thế năng hoặc nội năng, còn động lượng không chuyển đổi được thành năng lượng. Các khác
biệt này đủ để tạo ra các mô hình phân tích dựa vào động lượng, tách biệt với các mô hình
dựa vào năng lượng, cung cấp một công cụ độc lập để sử dụng trong việc giải quyết các bài toán.
Theo định luật 2 Newton, ta có: þă
∑ þ  = ÿ�㕎 = ÿþā
Giả sử khối lượng m là không đổi, ta có thể đưa khối lượng m vào trong dấu đạo hàm, nên: d F õ ý ý (9.3) dt dt
Phương trình (9.3) là d¿ng khác của định luật 2 Newton đối với chất điểm. Phương trình
này chỉ ra rằng tốc độ biến thiên theo thời gian của động lượng của chất điểm thì bằng
hợp lực tác dụng lên chất điểm. Dạng này tổng quát hơn dạng đã giới thiệu á chương 5, và
có thể sử dụng để khảo sát các hiện tượng trong đó khối lượng thay đổi, ngoài các trưßng hợp 2 http://ipt.hcmute.edu.vn Bộ môn vật lý
trong đó vận tốc thay đổi. Ví dụ trưßng hợp khối lượng của tên lửa thay đổi do nhiên liệu bị
đốt và bị phóng ra khỏi tên lửa, ta không thể sử dụng phương trình ∑ þ = ÿ�㕎 để phân tích
mà phải dùng cách tiếp cận động lượng như sẽ trình bày trong mục 9.9.
Câu hỏi 9.1: Hai vật có động năng bằng nhau. Độ lớn động lượng của chúng so với nhau thế
nào? (a) p1 < p2 (b) p1 = p2 (c) p1 > p2 (d) không đủ thông tin để phát biểu.
Câu hỏi 9.2: Giáo viên thể dục ném một quả bóng chày về phía bạn với một tốc độ nào đó
và bạn bắt lấy nó. Tiếp theo giáo viên sẽ ném một quả bóng tập nặng gấp 10 lần quả bóng
chày. Bạn có các lựa chọn sau: Bạn có thể bắt được quả bóng tập được ném với (a) cùng tốc
độ với quả bóng chày, (b) cùng động lượng với quả bóng chày, hoặc (c) cùng động năng với
quả bóng chày. Hãy sắp xếp các lựa chọn này từ dễ đến khó để bắt.
Mô hình phân tích: Hệ cô lập (động lượng)
Sử dụng định nghĩa động lượng, biểu thức 9.1 có thể viết là: þ þā (Ă1 + Ă2) = 0
Vì đạo hàm của động lượng toàn phần ĂþĀþ = Ă1 + Ă2 bằng không, nên động lượng toàn
phần của hệ hai chất điểm cô lập trong hình 9.1 là không đổi: t (9.4) tot Hay:  p ý 0 9.5) tot
hoặc viết theo dạng khác là:
Ă1�㕖 + Ă2�㕖 = Ă1Ā + Ă2Ā
với Ă1�㕖, Ă2�㕖 là các giá trị đầu và Ă1Ā, Ă2Ā là các giá trị cuối của động lượng của hai chất điểm.
Phương trình (9.5) chứng tỏ động lượng toàn phần theo các hướng x, y, z đều được bảo
toàn một cách độc lập:  ý   ý   ý  (9.6) 1 p p p p p p p p p p p p ix 2ix 1 fx 2 fx 1iy 2iy 1 fy 2 fy 1iz 2iz 1 fz 2 fz
Phương trình (9.5) là dạng toán học của một mô hình phân tích mới, gọi là mô hình hệ
cô lập (động lượng). Mô hình này có thể má rộng cho hệ cô lập nhiều chất điểm bất kỳ như
sẽ trình bày trong mục 9.7.
Từ phương trình (9.5) ta có thể phát biểu như sau: Khi hai hay nhiều chất điểm của một
hệ cô lập tương tác với nhau, động lượng toàn phần của hệ luôn không đổi. Như vậy động
lượng toàn phần của hệ cô lập tại các thßi điểm bất kì đều bằng động lượng ban đầu của nó. 3
Trưßng Đại học Sư phạm Kỹ thuật Tp. Hồ Chí Minh 2021
Mô hình phân tích hệ cô lập không cần xét đến ngoại lực tác dụng lên hệ, cũng như lực
đó là lực bảo toàn hay không bảo toàn, lực biến thiên hay không biến thiên theo thßi gian.
Yêu cầu duy nhất là các lực phải là nội lực của hệ. Điều này cho thấy tầm quan trọng của mô hình mới này.
Mô hình phân tích: Hệ cô lập (động lượng)
Giả sử ta đã xác định được hệ cần phân tích và biên của nó. Nếu không có ngoại lực nào
tác dụng lên hệ thì hệ là cô lập. Khi đó động lượng toàn phần của hệ được bảo toàn:  p ý 0 ø9.5 tot ù Ví dụ:
 Viên bi da cái đánh vào các viên bi da khác trên bàn
 Tàu vũ trụ bắn tên lửa ra và chuyển động nhanh hơn trong không gian
 Các phân tử chất khí á một nhiệt độ xác định
chuyển động và va chạm với nhau
Bài tập mẫu 9.1:
Một ngưßi bắn cung đứng trên mặt băng không ma sát bắn một mũi tên nặng 0.03 kg
theo phương ngang với vận tốc đầu 85 m/s. (A) Hỏi vận tốc của ngưßi sau khi mũi tên
được bắn ra. (B) Điều gì xảy ra nếu mũi tên được bắn theo hướng hợp với phương nằm
ngang một góc θ? Điều này sẽ làm thay đổi vận tốc giật lùi của ngưßi bắn cung như thế nào? Giải:
Phân tích bài toán: Hãy tưáng tượng mũi tên bị bắn đi trên một
đưßng thẳng và ngưßi bắn cung thủ chuyển động giật lùi theo
hướng ngược lại. Ta không thể giải bài toán này với các mô hình
dựa trên chuyển động, lực, hoặc năng lượng. Tuy nhiên, ta có
thể giải quyết vấn đề này một cách dễ dàng với cách tiếp cận
liên quan đến động lượng. Ta xét hệ gồm có ngưßi bắn cung
(bao gồm cả cung) và mũi tên. Hệ không cô lập vì có lực hấp
dẫn và phản lực pháp tuyến từ băng tác dụng lên hệ. Tuy nhiên,
các lực này theo phương thẳng đứng và vuông góc với chiều
chuyển động của hệ. Không có ngoại lực tác dụng lên hệ theo
Hình 9.2 Bài tập
phương ngang, và ta có thể áp dụng mô hình hệ cô lập (động
mẫu 9.1 – Người
lượng) đối với các thành phần động lượng theo hướng này. bắn cung
(A) Áp dụng mô hình hệ cô lập (động lượng) theo phương ngang, động lượng theo
phương ngang của hệ trước và sau khi bắn đều bằng 0. Ta chọn hướng bắn mũi tên là
hướng dương của trục x. Xem ngưßi bắn cung là chất điểm 1 và mũi tên là chất điểm
2, theo phương trình 9.5 ta được:  p ý 0  tot f i f i 1 1 f 2 2 f 4 http://ipt.hcmute.edu.vn Bộ môn vật lý Theo đề bài ta có m v
1 = 60 kg, m2 = 0,030 kg và 2 f m/s.
Giải phương trình này và thay số ta được: v i m / 1 s f 2 f 1 m
Dấu trừ chỉ ra rằng ngưßi bắn cung chuyển động về phía bên trái trên hình 9.2 sau khi
bắn mũi tên, phù hợp với định luật 3 Newton. Gia tốc và vận tốc của ngưßi bắn cung
nhỏ hơn nhiều so với gia tốc và vận tốc của mũi tên vì khối lượng của ngưßi bắn cung
rất lớn so với mũi tên.
(B) Độ lớn của vận tốc giật lùi sẽ giảm vì chỉ một thành phần của vận tốc mũi tên là
theo hướng x. Sự bảo toàn động lượng theo hướng x cho ta: m
m v  m v cos  ý 0 dẫn tới 2 v ý  v cos . 1 1 f 2 2 f 1 f 2 f m1
Với các giá trị  ù 0 thì  ý vì cos ü1. 1
v nhỏ hơn v khi 0 f 1 f
Mô hình phân tích: Hệ không cô lập (động lượng)
Đối với các khảo sát động lượng, hệ không cô lập nếu có lực tác dụng lên hệ. Ta có thể
hình dung động lượng được chuyển từ môi trưßng đến hệ thông qua lực. Việc hiểu được lực
là nguyên nhân gây ra sự biến thiên động lượng rất quan trọng khi giải quyết một số loại bài toán.
Giả sử có một hợp lực ∑ þ tác dụng lên chất điểm và hợp lực này có thể biến thiên theo
thßi gian. Theo định luật 2 Newton: þĂ ∑ þ  = þā hay
þĂ = ∑ þ  þā (9.7)
Ta có thể lấy tích phân biểu thức (9.7) để tìm độ biến thiên động lượng của chất điểm khi
có lực tác dụng lên nó trong một khoảng thßi gian nào đó. Nếu động lượng của chất điểm
thay đổi từ Ă�㕖 tại thßi điểm ā�㕖 tới ĂĀ tại thßi điểm āĀ, lấy tích phân phương trình 9.7 ta được: þ�㕓
∆Ă = ĂĀ 2 Ă� 㕖 = ∫ ∑ þ  þā (9.8 þ� 㕖
Để tính tích phân này, ta cần biết hợp lực tác dụng lên chất điểm biến thiên theo thßi gian
như thế nào. Đại lượng á vế phải của phương trình (9.8) được gọi là xung của hợp lực ∑ þ
tác dụng lên chất điểm trong khoảng thßi gian ∆ā = āĀ 2 ā�㕖, kí hiệu là �㔼: 5
Trưßng Đại học Sư phạm Kỹ thuật Tp. Hồ Chí Minh 2021 �㔼 = þ�∫㕓  ∑þþā (9.9) þ� 㕖
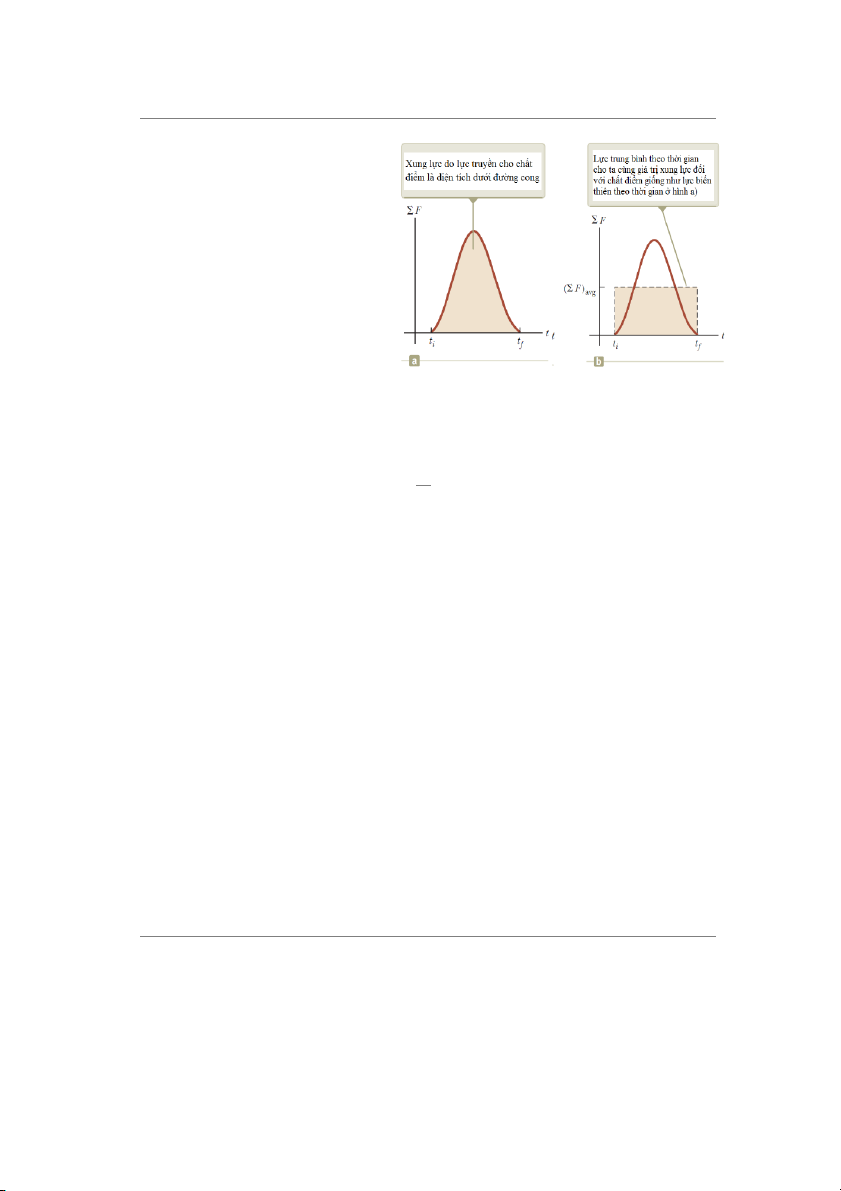
Giả sử lực biến thiên theo thßi gian
như trên hình 9.3a và khác không trong
khoảng thßi gian ∆ā = āĀ 2 ā�㕖. Vectơ
xung lực �㔼 cùng hướng với vectơ độ biến
thiên động lượng ∆Ă. Xung lực có thứ
nguyên của động lượng là ML/T. Xung
lực không phải là một thuộc tính của
chất điểm, mà là số đo mức độ ngoại lực làm thay đổi ộ
đ ng lượng của chất điểm.
Do hợp lực truyền xung lực cho chất
điểm thưßng thay đổi theo thßi gian, nên ự ụ ất điể
để thuận tiện, ngưßi ta định nghĩa hợp Hình 9.3 (a) L c tác d ng lên ch m biến thiên ờ
ị ủ ực không đổi (đườ
lực trung bình theo thßi gian:
theo th i gian. (b) Giá tr c a l ng
nét đứt nằm ngang) được lấy sao cho diện tích của
hình chữ nhật bằng diện tích dưới đường cong ở þ�㕓 hì h ( ) 1 (∑ þ ) = (9.10
�㕎ÿā ∆ā ∫ ∑ þ  þā þ� 㕖
trong đó ∆ā = āĀ 2 ā�㕖. (Phương trình 9.11 là một áp dụng của định lý giá trị trung bình trong
giải tích.) Do đó có thể biểu diễn phương trình 9.9 như là: �㔼 = (∑ þ ) ∆ā (9.11) �㕎ÿā
Lực trung bình này, như chỉ ra trên hình 9.3b, có thể xem là lực không đổi tác dụng lên
chất điểm trong khoảng thßi gian ∆ā, có cùng xung lực với xung lực của lực biến thiên theo
thßi gian tác dụng lên chất điểm trong khoảng thßi gian đó.
Nếu ∑ þ là một hàm của thßi gian, có thể tính được xung lực từ phương trình 9.9. Việc
tính toán trá nên rất đơn giản nếu như lực tác dụng lên chất điểm là không đổi. Trong trư n ß g hợp này, (∑ þ) = ∑ þ
, trong đó ∑ þ là hợp lực không đổi tác dụng lên chất điểm, và �㕎ÿā
phương trình (9.11) trá thành: �㔼 = ∑ þ ∆ā (9.12)
Kết hợp các phương trình (9.8) và (9.9) ta được định lý xung lượng-động lượng:
Độ biến thiên động lượng của một chất điểm thì bằng xung lượng của hợp lực tác dụng
lên chất điểm đó: ∆Ă = �㔼 (9.13)
Phát biểu này tương đương với định luật 2 Newton. Khi nói một xung lực được truyền cho
chất điểm, ta muốn nói rằng động lượng được truyền từ một tác nhân bên ngoài tới chất điểm 6 http://ipt.hcmute.edu.vn Bộ môn vật lý
đó. Phương trình (9.13) có dạng tương tự với các phương trình bảo toàn năng lượng (8.1) và (8.2).
Phương trình 9.13 là phát biểu tổng quát nhất của nguyên lý bảo toàn động lượng và
được gọi là phương trình bảo toàn động lượng. Trong cách tiếp cận động lượng, hệ cô lập
xuất hiện thưßng xuyên hơn hệ không cô lập, nên phương trình (9.13) có thể xem như trưßng
hợp đặc biệt của phương trình (9.5). Vế trái của phương trình (9.13) là độ biến thiên động
lượng của hệ. Vế phải là số đo động lượng đi qua biên của hệ khi có lực tác dụng lên hệ.
Phương trình (9.13) là phát biểu toán học của một mô hình phân tích mới, gọi là mô hình hệ
không cô lập (động lượng). Phương trình này có dạng tương tự phương trình (8.1) nhưng có
một số khác biệt khi áp dụng cho các bài toán. Trước tiên, phương trình (9.13) là phương
trình vectơ, trong khi phương trình (8.1) là phương trình vô hướng. Do đó hướng là quan
trọng đối với phương trình (9.13). Thứ hai, chỉ có một loại động lượng nên chỉ có một cách
duy nhất để tích trữ động lượng trong hệ. Ngược lại, như thấy từ phương trình (8.2), có 3 cách
để tích năng lượng cho hệ là động năng, thế năng và nội năng. Thứ ba, chỉ có một cách để
truyền động lượng cho hệ là tác dụng lực lên hệ trong một khoảng thßi gian. Phương trình
(8.2) chỉ ra 6 cách mà ta đã biết để truyền năng lượng cho một hệ. Do đó, không có sự má
rộng phương trình (9.13) tương tự như phương trình (8.2).
Trong nhiều tình huống ngưßi ta dùng lực tác dụng lên chất điểm tác dụng trong một khoảng thßi gian ngắn nhưng lớn hơn nhiều so
với các lực khác cùng có mặt. Khi đó, hợp lực ∑ þ trong phương trình (9.9) được thay thế
bằng một lực đơn þ để tính xung lực tác dụng lên chất điểm. Sự xấp xỉ này rất hữu ích khi
xét các bài toán va chạm trong đó khoảng thßi gian va chạm rất ngắn. Khi sử dụng xấp xỉ
này, lực đơn được xem là một xung lực. Ví dụ khi quả bóng chày bị đánh bằng cái gậy, thßi
gian va chạm khoảng 0,01s và lực trung bình mà gậy tác dụng lên quả bóng là vài ngàn
Newton. Vì lực này lớn hơn nhiều so với trọng lực tác dụng lên quả bóng và cái gậy, nên sự
xấp xỉ xung lực cho thấy việc bỏ qua trọng lực là đúng đắn. Khi dùng xấp xỉ này, cần nhớ
rằng Ă�㕖 và ĂĀ là các động lượng tức thßi trước và sau khi va chạm. Do đó trưßng hợp phù hợp
để dùng xấp xỉ xung là khi va chạm chất điểm di chuyển một đoạn rất ngắn.
Câu hỏi 9.3: Hai vật nằm yên trên một bề mặt không có ma sát. Vật 1 có khối lượng lớn hơn
vật 2. (i) Khi một lực không đổi tác dụng lên vật 1, nó gia tốc vật trên quãng đưßng d theo
một đưßng thẳng. Ngừng cho lực tác dụng lên vật 1 mà cho nó tác dụng lên vật 2. Tại thßi
điểm vật 2 được gia tốc qua cùng quãng đưßng d, phát biểu nào đúng? (a) p1 < p2, (b) p1 = p2,
(c) p1 > p2, (d) K1 < K2, (e) K1 = K2, (f) K1 > K2. (ii) Khi một lực không đổi tác dụng lên vật
1, nó gia tốc vật trong một khoảng thßi gian t. Ngừng cho lực tác dụng lên vật 1 mà cho nó
tác dụng lên vật 2. Từ danh sách các lựa chọn như trên, phát biểu nào là đúng sau khi vật 2
được gia tốc trong cùng khoảng thßi gian t?
Câu hỏi 9.4: Hãy xếp hạng từ lớn nhất đến nhỏ nhất một bảng điều khiển ô tô, một dây an
toàn và một túi khí, mỗi cái được sử dụng một mình trong các va chạm có cùng tốc độ, về (a)
xung lực và (b) lực trung bình mà mỗi cái mang lại cho một hành khách ngồi phía trước. 7
Trưßng Đại học Sư phạm Kỹ thuật Tp. Hồ Chí Minh 2021
Mô hình phân tích: Hệ không cô lập (động lượng)
Giả sử ta đã xác định được hệ cần phân tích và
biên của nó. Nếu có ngoại lực tác dụng lên hệ thì hệ
là không cô lập. Khi đó độ biến thiên động lượng toàn
phần của hệ bằng xung lực tác dụng lên hệ (định lý
xung lực - động lượng):  p ý I ø9.13 tot ù Ví dụ:
 Cái gậy đánh vào quả bóng chày
 Dùng sợi dây kéo một ống chỉ đặt trên bàn
Bài tập mẫu 9.3: Cái đỡ va tốt như thế nào?
Trong một thử nghiệm va chạm, một xe hơi
có khối lượng 1500 kg va chạm với một bức
tưßng như trên hình 9.4. Vận tốc của xe trước
và sau khi va chạm lần lượt là v m/s i và v
m/s. (A) Va chạm kéo dài trong f
0.15 s, hãy tìm xung lực c ủa vụ va chạm và
lực trung bình tác dụng lên xe. (B) Điều gì
xảy ra nếu chiếc xe không bật ra khỏi bức
tưßng? Giả sử tốc độ cuối cùng của xe bằng
Hình 9.4 Bài tập mẫu 9.3
không và khoảng thßi gian của va chạm vẫn
á mức 0.15 s. Điều đó có thể hiện là lực lớn hơn hoặc nhỏ hơn tác dụng lên xe không? Giải:
(A) Sử dụng công thức 9.13 để tính xung lực tác dụng lên xe hơi: I ý  ø ù 0i kg.m/s f i f i f i
Dùng công thức (9.11) để tính lực trung bình tác dụng lên xe: ø F õ ù ý ý176000i avg t  N
Lực tính được á trên là tổng hợp của phản lực vuông góc do tưßng tác dụng lên xe và
lực ma sát giữa các lốp xe và mặt đất khi đầu xe bị biến dạng. Nếu các bánh xe quay
tự do, lực ma sát này là tương đối nhỏ.
(B) Trong tình huống trên, khi mà chiếc xe bật ra khỏi tưßng, lực tác dụng lên xe thực
hiện hai việc trong khoảng thßi gian 0.15s: (1) nó dừng xe, và (2) nó làm cho xe chuyển
động ra khỏi tưßng với tốc độ 2.60 m/s sau khi va chạm. Nếu chiếc xe không bật ra,
lực chỉ thực hiện bước đầu tiên đó là dừng xe - đòi hỏi một lực nhỏ hơn. Trong trưßng hợp này, xung lực là: 8 http://ipt.hcmute.edu.vn Bộ môn vật lý I ý  ø ù
0i kg.m/s và lực trung bình tác dụng lên xe f i i f i là: ø F õ ù ý ý150000 i N. avg t
Va chạm một chiều
Thuật ngữ va chạm biểu thị sự kiện hai chất điểm đi lại gần
nhau và tương tác với nhau bằng các lực. Các lực tương tác được
giả sử rất lớn so với các ngoại lực có mặt, nên có thể sử dụng xấp xỉ xung lực.
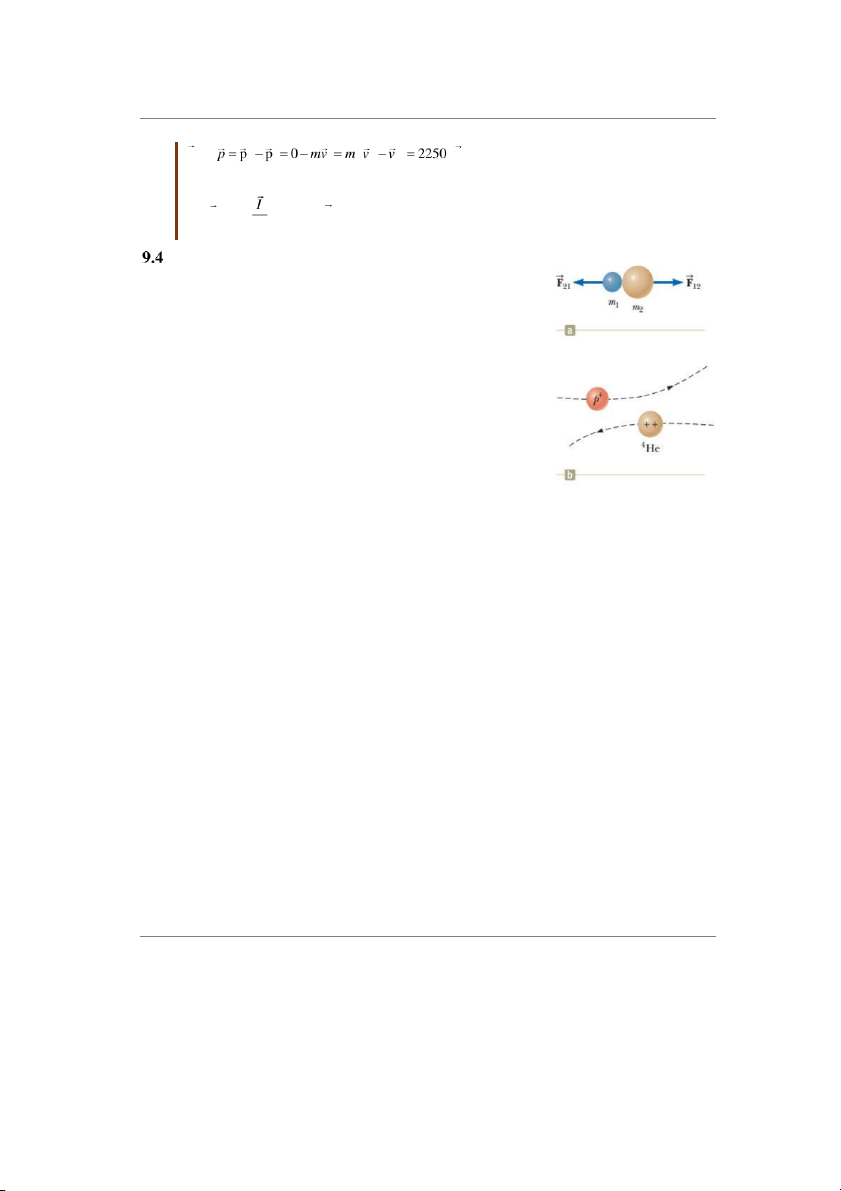
Va chạm không chỉ xảy ra khi có sự tiếp xúc trực tiếp giữa
hai vật thể vĩ mô, như mô tả trên hình 9.5a, mà phải được hiểu
tổng quát hơn. Ví dụ xét một va chạm á tỉ lệ nguyên tử giữa
proton và hạt alpha (hình 9.5b). Vì cả hai hạt đều mang điện
dương, chúng đẩy nhau, va chạm với nhau thông qua trưßng điện từ.
Khi hai vật có khối lượng m1 và m2 va chạm như trên hình
9.5, các xung lực có thể thay đổi rất phức tạp, chẳng hạn như Hình 9.5 (a) Va
trên hình 9.3. Tuy nhiên, bất kể sự phức tạp của xung lực, lực
ch¿m giữa hai vật
luôn là nội lực của hệ hai vật. Do đó, hai vật tạo thành một hệ
như kết quÁ của sự
cô lập và động lượng của hệ được bảo toàn trong va chạm bất
tiếp xúc trực tiếp, (b)
kỳ. Tuy nhiên, tổng động năng của hệ có thể bảo toàn hoặc
"Va ch¿m" giữa hai
không, tùy thuộc vào loại va chạm.
h¿t tích điện.
Phân loại va chạm: Va ch¿m được chia thành va ch¿m đàn hồi hoặc va ch¿m không đàn
hồi tùy thuộc vào việc động năng của hệ có bÁo toàn hay không.
Va ch¿m đàn hồi gữa hai vật là va ch¿m mà tổng động năng và tổng động lượng của hệ
trước và sau khi va ch¿m là như nhau. Va chạm giữa các vật trong thế giới vĩ mô, chẳng hạn
giữa các quả bóng bi a, chỉ là xấp xỉ đàn hồi vì có xảy ra sự biến dạng và mất động năng. Ví
dụ ta có thể nghe thấy tiếng các quả bi a va chạm nhau, như vậy có một số năng lượng từ hệ
đã bị truyền đi xa bái âm thanh. Va chạm đàn hồi phải hoàn toàn yên lặng
Va ch¿m không đàn hồi là va ch¿m mà tổng động năng của hệ trước và sau khi va ch¿m
khác nhau (mặc dù động lượng của hệ được bÁo toàn). Các va chạm không đàn hồi có hai
loại. Khi các vật dính vào nhau sau khi va chạm được gọi là va ch¿m hoàn toàn không đàn
hồi, ví dụ khi một thiên thạch va chạm với Trái đất. Khi các vật va chạm nhưng không dính
vào nhau, nhưng một phần năng lượng bị chuyển sang dạng năng lượng khác hoặc bị truyền
ra xa, như trưßng hợp quả bóng cao su va chạm với một bề mặt cứng, thì va chạm được gọi
là không đàn hồi. Khi quả bóng cao su va chạm với nền cứng, một phần động năng của quả
bóng bị chuyển đổi (sang nhiệt) khi quả bóng bị biến dạng trong khi nó tiếp xúc với bề mặt
cứng. Các va chạm không đàn hồi được mô tả bằng cách diễn giải động lượng của mô hình hệ cô lập. 9
Trưßng Đại học Sư phạm Kỹ thuật Tp. Hồ Chí Minh 2021
Va chạm hoàn toàn không đàn hồi
Xét 2 vật khối lượng m1 và m2, chuyển
động với các vận tốc ban đầu ă1�㕖, ă2�㕖 dọc
theo một đưßng thẳng như trên hình 9.6.
Hai vật va chạm trực diện với nhau, dính
vào nhau và sau va chạm chúng chuyển
động với vận tốc chung ăĀ. Do động lượng
của một hệ cô lập được bảo toàn trong va
chạm bất kì, ta có tổng động lượng trước Hình 9.6 GiÁn đồ biểu diễn va ch¿m xuyên tâm
khi va chạm bằng với động lượng của hệ hoàn toàn không đàn hồi giữa hai chất điểm
hợp lại sau khi va chạm:
ÿ1ă1�㕖 + ÿ2ă2�㕖 = (ÿ1 + ÿ2)ăĀ (9.14)
Giải phương trình này đối với ẩn số là vận tốc sau va chạm, ta được: ÿ ă
1ă1�㕖 + ÿ2ă2�㕖 Ā = ÿ (9.15) 1 + ÿ2
Va chạm đàn hồi
Xét 2 vật khối lượng m1 và m2, chuyển
động với các vận tốc ban đầu ă1�㕖, ă2�㕖 dọc
theo một đưßng thẳng như trên hình 9.7.
Hai chất điểm v a chạm trực diện với nhau,
sau đó tách ra và chuyển động với các vận tốc ă1Ā, ă2Ā.
Trong va chạm đàn hồi, cả động lượng Hình 9.7 Sơ đồ một va ch¿m trực diện đàn hồi
và động năng của hệ được bảo toàn. Do đó,
giữa hai chất điểm.
xét các vận tốc theo hướng nằm ngang như trên hình 9.7 ta có:
p ý p  m v (9.16) i f 1 1i 2 2i 1 1 f 2 2 f 1 2 1 2 1 2 1 2 K ý K  m v  m v ý m v  m v (9.17) i f 1 1i 2 2i 1 1f 2 2 2 2 2 2 f
Vì va chạm một chiều nên ta có thể biểu diễn các vận tốc bằng các tốc độ tương ứng, với các
dấu để chỉ hướng: tốc độ v là dương nếu chất điểm chuyển động sang phải, là âm nếu chuyển động sang trái.
Trong bài toán va chạm đàn hồi, có hai đại lượng chưa biết nên cần giải hệ các phương
trình (9.16) và (9.17) để tìm chúng. Ta bỏ các thừa số ½ trong (9.17) và viết lại như sau: ÿ 2 2 2 2 1(ă1�㕖
2 ă1Ā) = ÿ2(ă2Ā 2 ă2�㕖)
Khai triển cả hai vế ta có:
ÿ1(ă1�㕖 2 ă1Ā)(ă1�㕖 + ă1Ā) = ÿ2(ă2Ā 2 ă2�㕖)(ă2Ā + ă2�㕖) (9.18) 10 http://ipt.hcmute.edu.vn Bộ môn vật lý
Tiếp theo ta nhóm các số hạng chứa m1, m2 trong phương trình (9.16) để có:
ÿ1(ă1�㕖 2 ă1Ā) = ÿ2(ă2Ā 2 ă2�㕖) (9.19) Để thu đ ợ
ư c kết quả cuối cùng, ta chia (9.18) cho (9.19) để có:
ă1�㕖 + ă1Ā = ă2Ā + ă2�㕖
ă1�㕖 2 ă2�㕖 = 2(ă1Ā 2 ă2Ā) (9.20)
Phương trình này và phương trình (9.16) được dùng để giải các bài toán va chạm đàn hồi.
Cặp phương trình (9.16) và (9.20) dễ sử dụng hơn cặp các phương trình (9.16) và (9.17) vì
không có các số hạng bậc 2 như trong phương trình (9.17). Theo phương trình (9.20), vận tốc
tương đối của 2 chất điểm trước khi va chạm, ă1�㕖 2 ă , b ốc tương 2�㕖
ằng và trái dấu với vận t
đối của chúng sau khi va chạm, 2(ă1Ā 2 ă2Ā).
Nếu biết khối lượng và vận tốc của các vật trước khi va chạm, ta giải các phương trình
(9.16) và (9.20) để tìm các vận tốc sau va chạm theo các vận tốc trước va chạm: ÿ 2ÿ ă 1 2 ÿ2 2 1Ā = ( ) ă ÿ ) ă1�㕖 + ( 2�㕖 (9.21) 1 + ÿ2 ÿ1 + ÿ2 2ÿ ÿ ă 1 2 2 ÿ1 2Ā = ( ) ă ÿ ) ă1�㕖 + ( 2�㕖 (9.22) 1 + ÿ2 ÿ1 + ÿ2
Lưu ý dùng đúng các dấu cho các phương trình (9.21) và (9.22).
Ta hãy xét một số trưßng hợp đặc biệt sau đây.  Nếu ÿ (9.21) và (9.22) cho th y 1 = ÿ2, các phương trình
ấ ă1Ā = ă2�㕖, ă2Ā = ă1�㕖, tức
là các chất điểm sẽ đổi vận tốc cho nhau nếu khối lượng của chúng bằng nhau. Ví dụ
va chạm trực diện của 2 quả bi-a: sau khi va chạm viên bi cái dừng lại và đẩy viên bi
kia đi xa với vận tốc ban đầu của viên bi cái.
 Nếu chất điểm 2 lúc đầu đứng yên, ă (9.21), (9.22) tr thành:
2�㕖 = 0, các phương trình á ÿ ă 1 2 ÿ2 1Ā = (ÿ ) ă1�㕖 (9.23) 1 + ÿ2 2ÿ ă 1 2Ā = ( ÿ ) ă1�㕖 (9.24) 1 + ÿ2
 Nếu ÿ1 ≫ ÿ2, từ các phương trình 9.23 và 9.24 ta thấy ă1Ā ≈ ă1�㕖 và ă2Ā ≈ 2ă1�㕖. Tức
là khi một vật rất nặng va chạm trực diện với một vật rất nhẹ đang đứng yên, vật nặng
sẽ tiếp tục chuyển động mà không bị thay đổi gì sau khi va chạm, còn vật nhẹ bị bật
lại với tốc độ bằng 2 lần tốc độ lúc đầu của vật nặng.
 Nếu ÿ2 ≫ ÿ1 và chất điểm 2 lúc đầu đứng yên, ă , ta th y 2�㕖 = 0
ấ ă1Ā ≈ 2ă1�㕖 và ă2Ā ≈
0, tức là khi một vật rất nhẹ va chạm trực diện với một vật rất nặng đang đứng yên,
vận tốc của vật nhẹ sẽ bị đổi chiều còn vật nặng gần như vẫn đứng yên. 11
Trưßng Đại học Sư phạm Kỹ thuật Tp. Hồ Chí Minh 2021
Câu hỏi 9.5: Trong một va chạm một chiều hoàn toàn không đàn hồi giữa hai vật đang chuyển
động, điều kiện nào là cần thiết để động năng cuối cùng của hệ bằng không sau va chạm? (a)
Động lượng ban đầu của các vật phải có cùng độ lớn nhưng ngược hướng. (b) Các vật phải
có cùng khối lượng. (c) Các vật phải có cùng vận tốc ban đầu. (d) Các vật phải có cùng tốc
độ ban đầu, với các vectơ vận tốc ngược hướng.
Câu hỏi 9.6: Một quả bóng bàn được ném về phía một quả bóng bowling đang đứng yên.
Quả bóng bàn gây ra một va chạm đàn hồi một chiều và bị nảy lại trên cùng một đưßng thẳng.
So với quả bóng bowling sau va chạm, quả bóng bàn có (a) độ lớn của động lượng lớn hơn
và động năng lớn hơn, (b) độ lớn của động lượng nhỏ hơn và động năng lớn hơn, (c) độ lớn
của động lượng lớn hơn và động năng nhỏ hơn, (d) độ lớn của động lượng nhỏ hơn và động
năng lớn hơn, hoặc (e) cùng độ lớn của động lượng và cùng động năng?
Chiến lược giải bài toán va chạm một chiều
 Tưáng tượng va chạm xảy ra. Vẽ các giản đồ đơn giản về các vật trước và sau va chạm.
Đoán hướng của các vectơ vận tốc sau khi va chạm.
 Hệ chất điểm có phải là cô lập không? Nếu có hãy phân loại va chạm là đàn hồi, không
đàn hồi hoặc hoàn toàn đàn hồi.
 Viết các phương trình:
- Nếu va chạm là hoàn toàn không đàn hồi, viết phương trình (9.15).
- Nếu va chạm là đàn hồi, viết phương trình (9.16) và (9.17).
- Nếu va chạm là không đàn hồi, viết phương trình (9.16).
 Dựa vào các thông số đề bài đã cho và tính các thông số còn lại.
Bài tập mẫu 9.5: Thực hiện bảo hiểm va chạm!
Một xe hơi nặng 1800 kg đang dừng đèn giao thông thì bị một xe hơi khác nặng 900
kg húc từ phía sau. Hai xe vướng vào nhau và chuyển động dọc theo đưßng thẳng mà
chiếc xe nhẹ ban đầu đang chuyển động. Trước khi va chạm xe nhẹ hơn đang chạy với
tốc độ 20.0 m/s, hỏi tốc độ của hai xe sau khi va chạm bằng bao nhiêu? Giải:
Sau khi va chạm hai xe vướng vào nhau nên đây là va chạm hoàn toàn không đàn hồi.
Dùng mô hình hệ cô lập đối với động lượng cho hệ hai xe ta có: 
ý p  m v ý m  m v i f 1 i ø 1 2 ù f
Từ đây ta tính được tốc độ của hai xe sau khi va chạm là: 1 m vi v ý ý 6,67 m/s f m  m 1 2 12 http://ipt.hcmute.edu.vn Bộ môn vật lý
Bài tập mẫu 9.6: Con lắc thử đạn
Con lắc thử đạn (Hình 9.8) là thiết bị được sử dụng để đo tốc độ của một vật được bắn
ra và chuyển động nhanh chẳng hạn như viên đạn. Một viên đạn khối lượng m1 được
bắn vào một khối gỗ lớn có khối lượng m2 được treo bái một số sợi dây nhẹ. Viên đạn
cắm vào khối gỗ và hệ đạn - gỗ được nâng lên một độ cao h. Làm thế nào để xác định
được tốc độ của viên đạn bằng cách đo độ cao h?
Hình 9.8 Bài tập mẫu 9.6 (a) Sơ đồ một con lắc thử đ¿n.
là vận tốc của đ¿n ngay trước va ch¿m và
là vận tốc của
hệ đ¿n – gỗ ngay sau va ch¿m hoàn toàn không đàn hồi. (b)
Ành chụp nhiều lần chớp của một con lắc thử đ¿n dùng trong Giải:
Va chạm giữa viên đạn và khối gỗ là va chạm hoàn toàn không đàn hồi vì sau khi va
chạm viên đạn cắm vào khối gỗ. Hệ đạn – gỗ tạo thành một hệ cô lập về động lượng.
Tốc độ của các vật sau khi va chạm hoàn toàn không đàn hồi được xác định theo phương trình (9.15): 1 m 1 v A v ý (1) B m  m 1 2
Động lượng của hệ ngay sau khi va chạm là: 1 K ý m  m v (2) B ø ù 2 1 2 2 B
Thay vB từ (1) vào (2) ta được: 2 2 1 m 1 v A K ý B 2ø  1 m 2 m ù
Động năng của hệ đạn – gỗ ngay sau khi va chạm này nhỏ hơn động năng ban đầu của viên đạn.
Chọn gốc thế năng tại khối gỗ, UB = 0. Thế năng của hệ đạn – gỗ tại độ cao h là:
U ý m  m gh C ø 1 2 ù 13
Trưßng Đại học Sư phạm Kỹ thuật Tp. Hồ Chí Minh 2021
Áp dụng mô hình hệ cô lập cho hệ đạn – gỗ ta có: K   U
 ý 0  øK  K ù  øU U ù ý 0 C B C B 2 2 ö m v ö 1 1  ÷0 A  ÷ ù ÷
÷ øm  m gh  0ù ý 0 1 2 ù 2ø  m  m ø 1 2 ù ø
Giải phương trình này ta được: ö  ö 1 m 2 m v ý 2gh 1A ÷ ÷ m ø 1 ø
Ta đã giải bài tập này theo hai bước. Mỗi bước liên quan đến một hệ khác nhau và một
mô hình phân tích khác nhau: hệ cô lập (động lượng) cho bước thứ nhất và hệ cô lập
(năng lượng) cho bước thứ hai. Vì va chạm là hoàn toàn không đàn hồi, một lượng cơ
năng đã được chuyển thành nội năng trong quá trình va chạm. Do đó, sẽ không đúng
khi sử dụng mô hình hệ cô lập (năng lượng) cho toàn bộ quá trình bằng cho động năng
ban đầu của viên đạn bằng với thế năng hấp dẫn của hệ đạn – gỗ á độ cao h.
Va chạm hai chiều
Trong mục 9.2 ta biết rằng động
lượng của hệ hai chất điểm cô lập được
bảo toàn. Trong va chạm bất kì của hai
chất điểm thì động lượng theo mỗi hướng x, y, z được bảo toàn.
Xét va chạm xảy ra trên mặt phẳng,
ví dụ chơi bi da. Đối với các va chạm hai
chiều, ta có hai phương trình thành phần
cho bảo toàn động lượng:
Hình 9.9 Va ch¿m đàn hồi không xuyên tâm giữa
ÿ1ă1�㕖ā + ÿ2ă2�㕖ā = ÿ1ă1Āā + ÿ2ă2Āā
hai chất điểm.
ÿ1ă1�㕖Ă + ÿ2ă2�㕖Ă = ÿ1ă1ĀĂ + ÿ2ă2ĀĂ
trong đó 3 chỉ số dưới các thành phần vận tốc trong các phương trình này tương ứng biểu thị:
kí hiệu của vật thể (1,2), các giá trị trước và sau va chạm (i,f), và thành phần vận tốc (x,y).
Xét trưßng hợp đặc biệt khi vật thứ nhất khối lượng m1 va chạm với vật thứ 2 khối lượng
m2 ban đầu đứng yên (hình 9.11). Sau va chạm (hình 9.11b), vật 1 chuyển động theo góc �㔃
so với phương ngang và vật 2 chuyển động theo góc �㔑 so với phương ngang. Va chạm này
gọi là va chạm sượt qua (glancing). Áp dụng định luật bảo toàn động lượng dạng thành phần
và lưu ý thành phần y của động lượng ban đầu bằng 0, ta có: p
 ý 0  p ý p  m v ý m v cos  m v cos  (9.25) x ix fx 1 1i 1 1 f 2 2 f p
 ý 0 p ý p 
0ý m v sin  m v sin (9.26) y iy fy 1 1 f 2 2 f 14 http://ipt.hcmute.edu.vn Bộ môn vật lý
trong đó dấu trừ á (9.26) là do thành phần y của vận tốc vật 2 sau va chạm hướng xuống. Kí
hiệu v trong các phương trình này là tốc độ, hướng của vectơ thành phần được chỉ rõ bái các
dấu cộng hoặc trừ. Ta có hai phương trình độc lập vơi 7 đại lượng, nếu có không quá 2 ẩn số
thì ta có thể giải bài toán này.
Nếu va chạm là đàn hồi, ta có thể dùng phương trình 9.17 (bảo toàn động năng) với v2i=0. 1 1 1 2 2 2 K ý K  m v ý m v  m v (9.27) i f 1 1i 1 1f 2 2 2 2 2 f
Biết tốc độ ban đầu của vật 1 và khối lượng của 2 vật, ta còn lại 4 ẩn số (ă1Ā, ă2Ā, �㔃, �㔑).
Vì chỉ có 3 phương trình, nên 1 trong 4 đại lượng còn lại phải được cho để xác định chuyển
động sau va chạm đàn hồi chỉ từ các nguyên lý bảo toàn.
Nếu va chạm không đàn hồi, động năng không bảo toàn và không được áp dụng phương trình (9.27).
Chiến lược giải bài toán va chạm hai chiều
 Tưáng tượng va chạm xảy ra và dự đoán các hướng gần đúng mà các hạt sẽ chuyển động sau khi va chạm.
 Thiết lập một hệ tọa độ và xác định các vận tốc dựa vào hệ tọa độ đó. Để thuận tiện
nên chọn trục x trùng với một trong những vận tốc ban đầu của các chất điểm.
 Vẽ và ghi tên của các vận tốc, và tính đến tất cả các thông tin đã cho.
 Xem xét hệ các chất điểm có phải thực sự cô lập? Nếu có hãy phân loại va chạm là
đàn hồi, không đàn hồi hoặc hoàn toàn đàn hồi.
 Viết các biểu thức đối với các thành phần x và y của động lượng của mỗi vật tr ớ ư c và
sau khi va chạm. Nhớ tính đến các dấu phù hợp cho các thành phần của các vectơ vận
tốc và chú ý cẩn thận đến các dấu trong suốt quá trình tính toán.
 Viết các biểu thức đối với động lượng tổng cộng theo trục x trước và sau khi va chạm
rồi cho chúng bằng nhau. Lặp lại thủ tục này đối với động lượng tổng cộng theo trục y.
 Tiến hành giải các phương trình động lượng cho các đại lượng chưa biết.
- Nếu va chạm là không đàn hồi, động năng không được bảo toàn, và có lẽ đòi hỏi thông tin bổ sung.
- Nếu va chạm là hoàn toàn không đàn hồi, các vận tốc sau va chạm của hai vật là bằng nhau.
- Nếu va chạm là đàn hồi, động năng được bảo toàn, và bạn có thể cho tổng động năng
của hệ trước và sau khi va chạm bằng nhau, cho ta một mối liên hệ bổ sung giữa các độ lớn vận tốc.
 Khi bạn đã xác định được kết quả, kiểm tra lại xem chúng có phù hợp với các miêu tả
về ý nghĩa minh họa, và có phù hợp với thực tế không. 15
Trưßng Đại học Sư phạm Kỹ thuật Tp. Hồ Chí Minh 2021
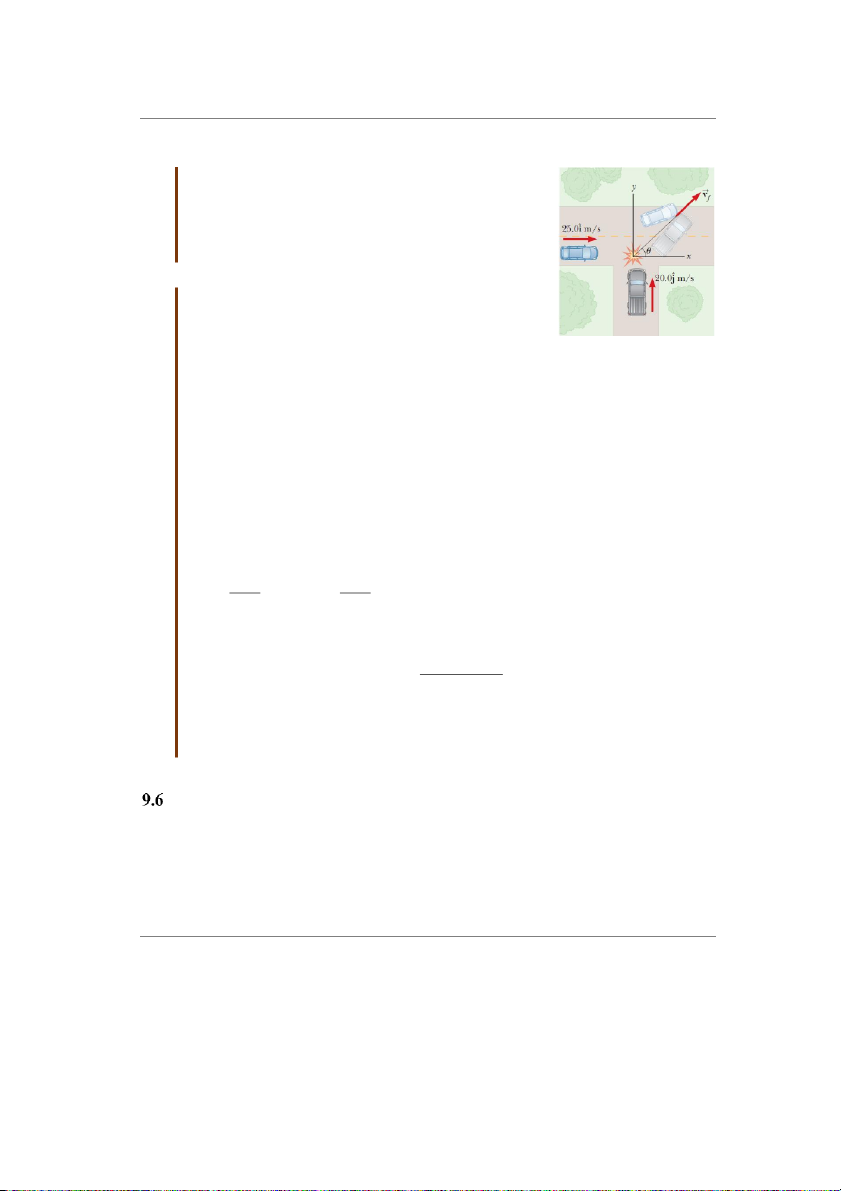
Bài tập mẫu 9.8: Va chạm tại một ngã ba
Tại một ngã ba, chiếc xe hơi nặng 1500 kg chạy về hướng
đông với tốc độ 25.0 m/s va chạm với chiếc xe tải nặng
2500 kg chạy về phía bắc với tốc độ 20.0 m/s như trên Hình
9.10. Hãy tìm hướng và độ lớn của vận tốc của các xe sau
va chạm, giả sử các xe dính vào với nhau sau va chạm. Giải:
Ta chọn trục x, y như hình 9.10. Xem hai xe như một hệ cô
lập về động lượng. Va chạm giữa hai xe là va chạm hoàn
toàn không đàn hồi vì chúng dính vào nhau sau va chạm.
Trước khi va chạm, chiếc xe hơi có động lượng theo hướng Hình 9.10 Bài tập mẫu
x, còn chiếc xe tải có động lượng theo hướng y. 9.8
Giả sử sau khi va chạm hai xe chuyển động với tốc độ vf theo hướng hợp với trục x một góc  .
Áp dụng mô hình hệ cô lập về động lượng cho hướng x: p  ý  p ý p
 m v ý m  m v  õ õ (1) x 0 xi xf i f cos 1 1 ø 1 2 ù
Áp dụng mô hình hệ cô lập về động lượng cho hướng y: p
 ý õ p ýõ p  m v ý m  m v  (2) y 0 yi yf i f sin 2 2 ø 1 2 ù Chia (2) cho (1) ta có: m v ö ö  m v 2 2i 1 2 2 tan ý   ý tan i ÷ ÷ m v m v 1 1i ø 1 1i ø Thay số ta được 53,1o  ý
Từ (2) ta tính được giá trị của v m v 2 2i f: v ý ý m/s f ø 15,6 m  m sin 1 2 ù
Ta thấy tốc độ của hệ hai xe sau va chạm nhỏ hơn tốc độ của mỗi xe trước khi va chạm.
Kết quả này cũng phù hợp với lý thuyết là trong va chạm không đàn hồi thì động năng của hệ giảm. Khối tâm
Trong mục này ta mô tả chuyển động của một hệ bằng chuyển động của một điểm đặc
biệt gọi là khối tâm của hệ. Hệ có thể gồm một số chất điểm, chẳng hạn các nguyên tử trong
một bình chứa, hoặc là một vật thể dài, như một vận động viên nhảy lên trong không khí. Ta
sẽ thấy rằng chuyển động tịnh tiến của khối tâm giống như tất cả khối lượng của hệ được tập
trung tại điểm đó, tức là hệ chuyển động như thể tổng ngoại lực tác dụng vào khối tâm.
Chuyển động này độc lập với các chuyển động khác của hệ, chẳng hạn như chuyển động quay 16 http://ipt.hcmute.edu.vn Bộ môn vật lý
hoặc rung, hoặc biến dạng (chẳng hạn khi vận động viên gập ngưßi lại). Mô hình này là mô
hình chất điểm đã giới thiệu trong chương 2.
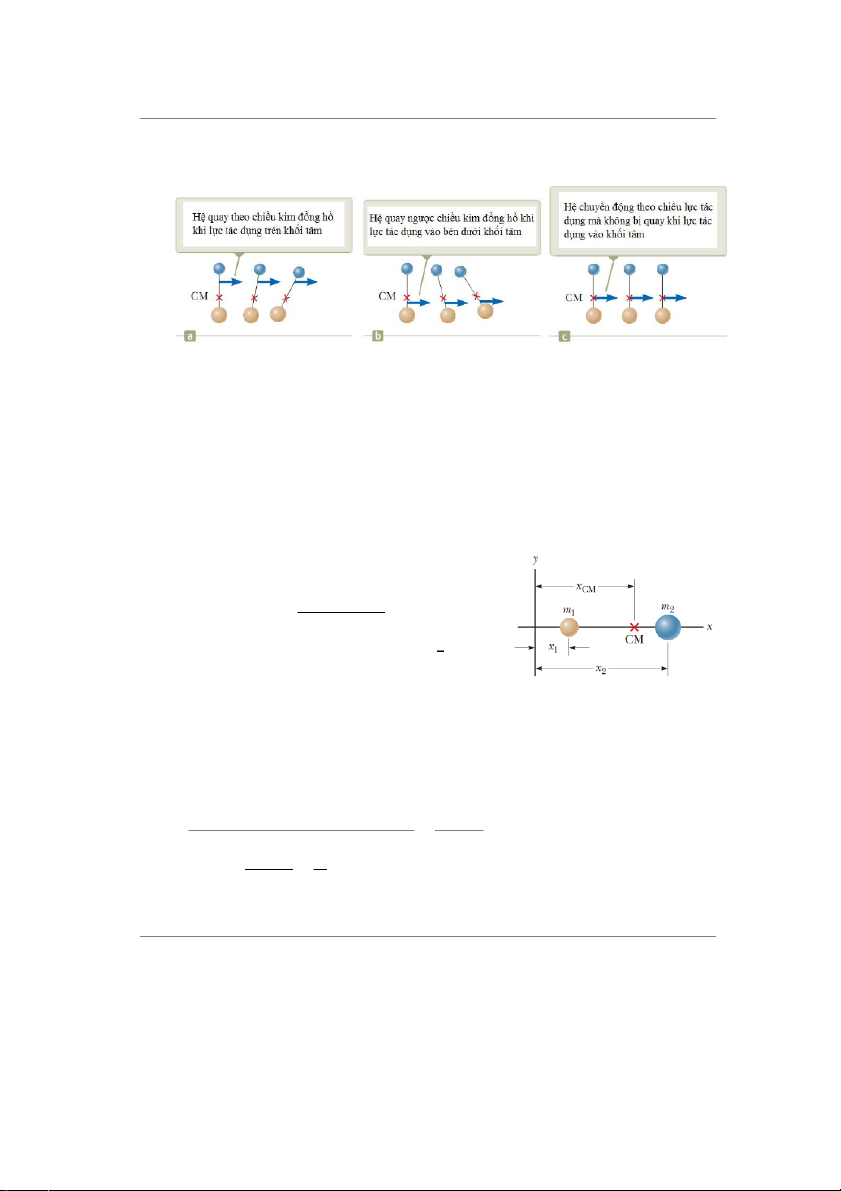
Hình 9.11 Lực tác dụng lên hệ gồm 2 chất điểm khối lượng khác nhau được gắn với nhau
bằng một thanh cứng, nhẹ.
Xét hệ hai vật có khối lượng khác nhau được kết nối với nhau bằng một thanh rắn, mảnh
và nhẹ (hình 9.11). Vị trí khối tâm của hệ là vị trí trung bình của khối lượng của hệ. Khối tâm
của hệ nằm trên đưßng nối hai vật và gần vật có khối lượng lớn hơn. Nếu lực tác dụng vào
một điểm trên thanh, á phần phía trên khối tâm thì hệ sẽ quay theo chiều kim đồng hồ (hình
9.11a). Nếu lực này tác dụng vào một điểm nằm phía dưới khối tâm thì hệ sẽ quay ngư ợc
chiều kim đồng hồ (hình 9.11b). Nếu lực này tác dụng vào khối tâm thì hệ sẽ chuyển động
theo chiều tác dụng của lực mà không bị quay (xem hình 9.11c). Vị trí khối tâm có thể được xác định theo cách này.
Khối tâm của cặp chất điểm trên hình 9.12 nằm trên
trục x, á giữa các chất điểm. Vị trí của nó là: ÿ ý ý ý 1 1 + ÿ2 2 �㔶�㕀 = ÿ (9.28) 1 + ÿ2
Ví dụ nếu x1=0, x2=d và m2= 2m1 ta có ý�㔶�㕀 = 2 þ. Tức là 3
khối tâm nằm gần vật nặng hơn. Nếu hai vật có khối lượng
bằng nhau, khối tâm sẽ nằm tại trung điểm đoạn thẳng nối hai vật.
Hình 9.12 Khối tâm của hệ 2
chất điểm có khối lượng khác
Có thể má rộng khái niệm khối tâm cho hệ nhiều chất nhau trên trục x nằm t¿i x_CM,
điểm trong không gian 3 chiều, chất điểm thứ i có khối
giữa các chất điểm, và gần lượng mi.
chất điểm có khối lượng lớn
Tọa độ x của khối tâm của hệ gồm n chất điểm là: hơn ÿ ý ý ý ∑ ý
1 1 + ÿ2 2 + ÿ3 3 + ⋯ + ÿÿýÿ ÿ�㕖ý � � 㕖㕖 �㔶�㕀 = ÿ = 1 + ÿ2 + ÿ3 + ⋯ + ÿÿ ∑ ÿ�㕖 ∑ ÿ 1 = �㕖ý � � 㕖㕖 � 㕀㕀 ∑ ÿ� = 㕖ý�㕖 (9.29) � 㕖 17
Trưßng Đại học Sư phạm Kỹ thuật Tp. Hồ Chí Minh 2021
Trong đó ý�㕖 là tọa độ x của chất điểm thứ i, và tổng khối lượng của hệ là �㕀 = ∑ ÿ�㕖 . Các tọa
độ y và z của khối tâm được xác định tương tự, theo các phương trình: 1 1 þ�㔶� ú 㕀
� 㕀 ∑ ÿ�㕖þ�㕖 ú ÿ�㔶�㕀
� 㕀 ∑ ÿ�㕖ÿ�㕖 (9.30) � 㕖 � 㕖
Trong không gian 3 chiều, vị trí của khối tâm được xác định bái bán kính vectơ ÿ�㔶�㕀, với
3 thành phần ý�㔶�㕀, þ�㔶�㕀, ÿ�㔶�㕀 xác định theo các phương trình 9.29 và 9.30. Do đó: 1 1 1 ÿ 󰇍 󰇍
�㔶�㕀 = ý�㔶�㕀ÿ + þ�㔶�
= 㕀Ā + ÿ�㔶�㕀�㕘 � 㕀 ∑ ÿ�㕖ý�㕖 ÿ + � 㕀 ∑ ÿ�㕖þ�㕖 Ā + � 㕀 ∑ ÿ�㕖ÿ �㕖 �㕘 � 㕖 � 㕖 � 㕖 1 ÿ�㔶�
ú 㕀� 㕀 ∑ÿ�㕖 ÿ�㕖 (9.31) � 㕖 trong đó ÿ�㕖
úý�㕖ÿ + þ�㕖󰇍Ā   l+à ÿ b � án 㕖 k � ín 㕘
h vectơ của chất điểm thứ i.
Các ý tưáng cơ bản đã thảo luận trên đây cũng được áp
dụng để xác định vị trí khối tâm của vật rắn. Xem vật rắn
như là hệ gồm một lượng lớn các phần tử hình lập phương
như hình 9.13. Do sự ngăn cách giữa các phần tử là rất nhỏ
nên vật rắn có thể xem là có phân bố khối lượng liên tục.
Bằng cách chia vật rắn thành các yếu tố có khối lượng ∆ÿ�㕖
với các tọa độ ý�㕖, þ�㕖, ÿ�㕖, ta thấy tọa độ x của khối tâm xấp xỉ bằng: 1 ý�㔶� û 㕀
� 㕀 ∑ ý�㕖 ∆ÿ�㕖 �㕖
Các tọa độ þ�㔶�㕀, ÿ�㔶�㕀 biểu thức cũng tương tự như ý�㔶�㕀.
Hình 9.13 Khối tâm được định
Nếu số phần tử n tiến tới vô cùng thì kích thước của mỗi vị bằng bán kính vectơ ÿ , có
phần tử sẽ tiến tới 0, và ý �㔶�㕀
�㔶�㕀 gần như chính xác. Khi đó ta
các thành phần ý
thay tổng bằng tích phân, và thay ∆ÿ �㔶�㕀, þ�㔶�
�㕖 bằng yếu tố vi phân dm: 1 1 ý�㔶�㕀 = lim =
∆þ�㕖→0� 㕀 ∑ ý�㕖∆ÿ�㕖 � 㕀 ∫ ýþÿ (9.32) � 㕖 Tương tự, ta có: 1 1 þ�㔶�㕀 =
� 㕀 ∫ þþÿ ÿ�㔶�㕀 = � 㕀 ∫ ÿþÿ (9.33)
Ta có thể biểu diễn bán kính véctơ của khối tâm vật rắn dưới dạng: 1 ÿ�㔶�㕀 = � 㕀 ∫ ÿþÿ (9.34) 18 http://ipt.hcmute.edu.vn Bộ môn vật lý
Biểu thức này tương đương với 3 biểu thức được cho trong
(9.32) và (9.33). Đối với vật rắn đồng nhất và có dạng đối xứng,
khối tâm của vật nằm trên một trục đối xứng và một mặt phẳng
đối xứng. Ví dụ, khối tâm của một thanh đồng nhất nằm á trên
thanh, á trung điểm của thanh. Khối tâm của một hình cầu hoặc
một hình lập phương nằm á tâm hình học của nó.
Vì vật rắn là một phân bố khối lượng liên tục, mỗi yếu tố
khối lượng chịu tác dụng của trọng lực. Tác dụng tổng cộng của
các lực này tương đương với tác dụng của một lực duy nhất �㕀ý
lên một điểm đặc biệt được gọi là trọng tâm. Nếu ý là không đổi
trên toàn bộ phân bố khối lượng thì trọng tâm trùng với khối tâm
của vật. Nếu vật rắn được treo ngay tại trọng tâm của nó thì nó
cân bằng trong mọi định hướng bất kì.
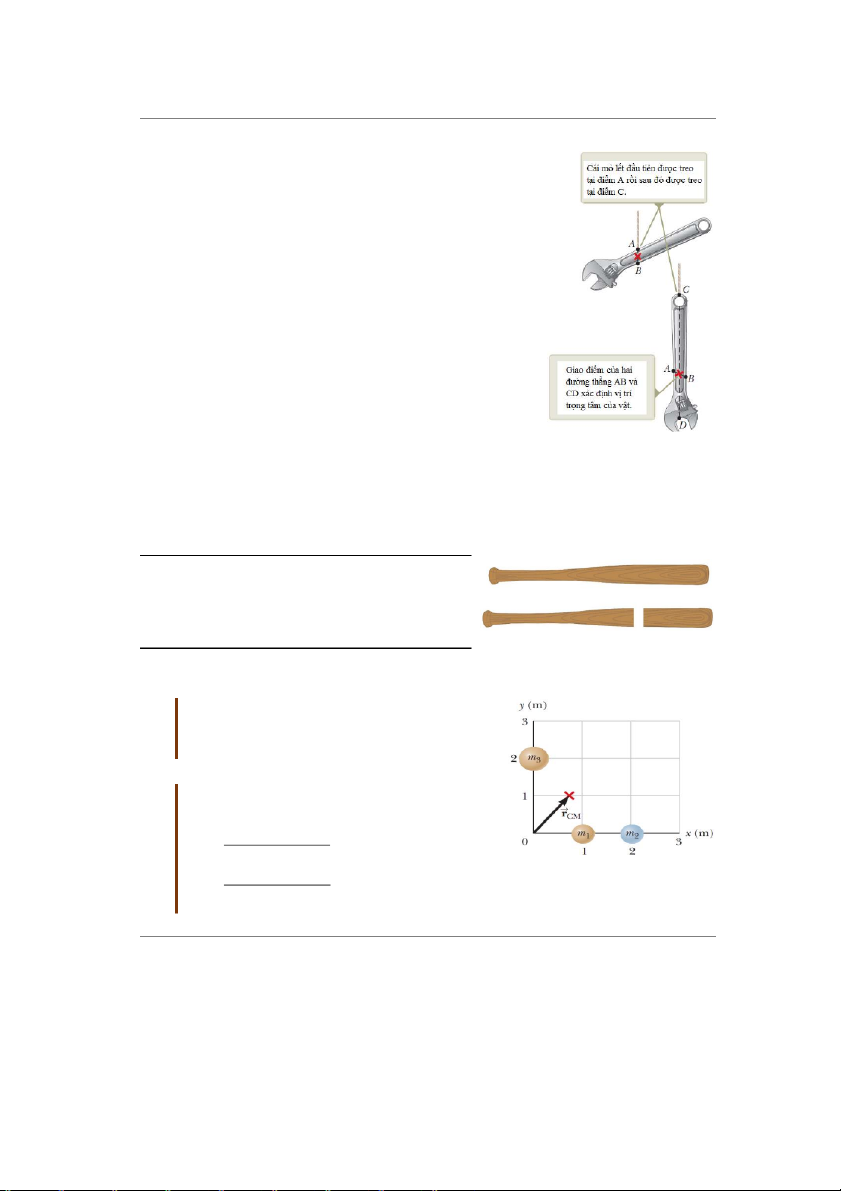
Trọng tâm của một vật thể có hình dạng không đều đặn, ví
dụ cái mỏ lết, có thể được xác định bằng cách treo vật, trước tiên
treo á một điểm, sau đó treo á điểm khác. Trên hình 9.14, cái mỏ
lết lúc đầu được treo á điểm A, khi nó ngừng quay, vẽ đưßng
Hình 9.14 Một phương ự ệm để
AB thẳng đứng (có thể dùng dây dọi). Tiếp đó treo mỏ lết tại pháp th c nghi xác đị
điểm C, rồi vẽ đưßng thẳng đứng CD. Trọng tâm của mỏ lết nằm
nh trọng tâm của cái mỏ
á nửa bề dày của nó, bên trong giao điểm của AB và CD. Tổng lết
quát, nếu mỏ lết được treo tự do tại một điểm bất kì, đưßng thẳng
đứng đi qua điểm này phải đi qua trọng tâm.
Câu hỏi 9.7: Một cây gậy bóng chày có mật độ đồng
nhất được cắt tại vị trí khối tâm của nó như trên hình
9.15. Phần nào có khối lượng nhỏ hơn? (a) phần bên
phải (b) phần bên trái (c) cả hai phần có cùng khối
lượng (d) không thể xác định.
Hình 9.15 Một cây gậy bóng chày bị
đôi cắt t¿i vị trí khối tâm của nó.
Bài tập mẫu 9.10: Khối tâm của ba chất điểm
Một hệ gồm ba chất điểm được bố trí như trên Hình
9.16. Khối lượng của các chất điểm là m1 = m2 =
1.0 kg và m3 = 2.0 kg. Hãy tìm khối tâm của hệ. Giải:
Sử dụng các công thức định nghĩa đối với các toạ
độ khối tâm (9.29) và (9.30) và thay số ta có:
m x  m x  m x 1 1 2 2 3 3 x ý ý 0,75 m, CM   1 m m2 m3  
Hình 9.16 Bài tập mẫu 9.10 1 m 1 y 2 m y2 3 m y3 y ý ý m, z ý 0 CM 1,0
m  m  m CM 1 2 3 19
Trưßng Đại học Sư phạm Kỹ thuật Tp. Hồ Chí Minh 2021
Vậy véctơ vị trí của khối tâm của hệ là: r i  y
j ý ø0,75 i 1,0 j m CM CM CM ù
Bài tập mẫu 9.11: Khối tâm của một thanh rắn
(A) Hãy chỉ ra rằng khối tâm của một thanh có
khối lượng M và chiều dài L nằm á trung điểm
của nó, giả sử thanh có mật độ khối lượng không
đổi. (B) Giả sử một thanh không đồng nhất và mật
độ khối lượng của nó thay đổi tuyến tính với x
theo công thức  ý x , với  là hằng số. Tìm tọa
độ x của tâm khối lượng dưới dạng một phân số Hình 9.17 Hình vẽ dùng để xác của L.
định khối tâm của một thanh rắn Giải:
Chọn hệ toạ độ có gốc toạ độ nằm á một đầu thanh và trục x hướng dọc theo thanh
như trên hình 9.17. Dễ thấy khối tâm của thanh nằm trên trục x, và yCM = 0, zCM = 0.
(A) Sử dụng công thức (9.32) ta có: 2 1 1  ý L ý  dx L x xdm x ý CM   0 M M 2M 2 Thay  ý L M 1 M L ta có: x ý ý L . CM 2M L 2
Trong trưßng hợp này ta có thể dùng nhận xét về tính đối xứng để thu được cùng kết quả.
(B) Trong trưßng hợp này do mật độ khối lượng tỉ lệ thuận với x nên càng xa gốc toạ
độ thì thanh càng nặng. Một phần tử của thanh có độ dài dx có khối lượng dm và dm ý  x d =  x x d
Sử dụng công thức (9.32) ta có: 3 1 1 L 1 L x ý xdm ý xdx L ý x xdx ý CM    0 0 M M M 3M
Khối lượng của thanh là: 2 L  ý ý  x L ý  x L M dm d x d ý    0 0 2 2
Thay biểu thức của M vào biểu thức của xCM ta được: x ý L . CM 3
Ta thấy khối tâm nằm cách xa gốc toạ độ hơn trong trưßng hợp (A) á trên. 20

Chương 9: Động lượng và va chạm | Tài liệu lý thuyết môn Vật lý 1 trường đại học sư phạm kĩ thuật TP. Hồ Chí Minh

Thông tin :

Tài liệu liên quan:

Chapter 2 Motion in One Dimension| Tài liệu môn vật lý 1,2 Trường đại học sư phạm kĩ thuật TP. Hồ Chí Minh

Overview of particle accumulation | Tài liệu môn Vật lý 1,2 Trường đại học sư phạm kĩ thuật TP. Hồ Chí Minh

Bài 20B: Xác định tỉ số nhiệt dung phân tử chất khí | Tài liệu môn thí nghiệm vật lý 1 Trường Đại học sư phạm kỹ thuật TP Hồ Chí Minh

Chương I: Tính chất hạt của ánh sáng | Lý thuyết môn Vật lý 1 Trường đại học sư phạm kĩ thuật TP. Hồ Chí Minh

Giáo trình môn vật lý 1 – Bộ môn vật lý | Trường Đại học sư phạm kỹ thuật TP Hồ Chí Minh