
CHUYÊN ĐỀ II – TOÁN – 11 – DÃY SỐ – CẤP SỐ CỘNG – CẤP SỐ NHÂN
Page 1
Sưu tầm và biên soạn
BÀI 5: DÃY SỐ
1. ĐỊNH NGHĨA DÃY SỐ
Mỗi hàm số
u
xác định trên tập các số nguyên dương
*
được gọi là một dãy số vô hạn.
Kí hiệu:
( )
*
:
.
u
n un
→
Người ta thường viết dãy số dưới dạng khai triển
123
, , , ..., , ...,
n
uuu u
trong đó
n
u un
hoặc viết tắt là
,
n
u
và gọi
1
u
là số hạng đầu,
n
u
là số hạng thứ
n
và là số
hạng tổng quát của dãy số.
Chú ý: Nếu
*
,
n
n uc∀∈ =
thì
n
u
là dãy số không đổi.
Mỗi hàm số
u
xác định trên tập
1,2,3,...,Mm
với
*
m
được gọi là một dãy số hữu hạn.
Dạng khai triển của nó là
123
, , , ..., ,
n
uuu u
trong đó
1
u
là số hạng đầu,
m
u
là số hạng cuối.
2. CÁC CÁCH CHO MỘT DÃY SỐ
a) Dãy số cho bằng liệt kê các số hạng
b) Dãy số cho bằng công thức của số hạng tổng quát
c) Dãy số cho bằng phương pháp mô tả
d) Dãy số cho bằng phương pháp truy hồi
Cách cho một dãy số bằng phương pháp truy hồi, tức là:
Cho số hạng đầu.
Cho hệ thức truy hồi, tức là hệ thức biểu thị số hạng thứ
n
qua số hạng đứng trước nó.
3. DÃY SỐ TĂNG, DÃY SỐ GIẢM VÀ DÃY SỐ BỊ CHẶN
Dãy số
n
u
được gọi là dãy số tăng nếu ta có
1nn
uu
với mọi
*
.n
Dãy số
n
u
được gọi là dãy số giảm nếu ta có
1nn
uu
với mọi
*
.n
CHƯƠNG
II
DÃY SỐ
CẤP SỐ CỘNG – CẤP SỐ NHÂN
CHUYÊN ĐỀ II – TOÁN – 11 – DÃY SỐ – CẤP SỐ CỘNG – CẤP SỐ NHÂN
Page 2
Sưu tầm và biên soạn
Chú ý: Không phải mọi dãy số đều tăng hoặc giảm. Chẳng hạn, dãy số
n
u
với
3
n
n
u
tức là
dãy
3, 9, 27,81,...
không tăng cũng không giảm.
Dãy số
n
u
được gọi là bị chặn trên nếu tồn tại một số
M
sao cho
*
, .
n
u Mn
Dãy số
n
u
được gọi là bị chặn dưới nếu tồn tại một số
m
sao cho
*
, .
n
u mn
Dãy số
n
u
được gọi là bị chặn nếu nó vừa bị chặn trên vừa bị chặn dưới, tức là tồn tại các số
, mM
sao cho
*
, .
n
mu M n
Lưu y: + Dãy tăng sẽ bị chặn dưới bởi
1
u
+ Dãy giảm sẽ bị chặn trên bởi
1
u
DẠNG 1: TÌM SỐ HẠNG CỦA DÃY SỐ
Bài toán 1: Cho dãy số
()
n
u
:
()
n
u fn=
. Hãy tìm số hạng
k
u
.
Tự luận: Thay trực tiếp
nk=
vào
n
u
.
MTCT: Dùng chức năng CALC:
Nhập:
()fx
Bấm r nhập
X k
=
Bấm
=
→
Kết quả
Câu 1: Cho dãy số
()
n
u
biết
115 15
22
5
nn
n
u
+−
= −
. Tìm số hạng
6
u
.
Câu 2: Cho dãy số
()
n
u
có số hạng tổng quát
21
2
n
n
u
n
+
=
+
. Số
167
84
là số hạng thứ mấy?
Bài toán 2: Cho dãy số
()
n
u
cho bởi
1
1
()
nn
ua
u fu
+
=
=
. Hãy tìm số hạng
k
u
.
HỆ THỐNG BÀI TẬP.
II
PHƯƠNG PHÁP.
1
BÀI TẬP TỰ LUẬN.
2

CHUYÊN ĐỀ II – TOÁN – 11 – DÃY SỐ – CẤP SỐ CỘNG – CẤP SỐ NHÂN
Page 3
Sưu tầm và biên soạn
Tự luận: Tính lần lượt
23
; ;...;
k
uu u
bằng cách thế
1
u
vào
2
u
, thế
2
u
vào
3
u
, …, thế
1k
u
−
vào
1k
u
+
.
MTCT: Cách lập quy trình bấm máy:
- Nhập giá trị của số hạng u
1
:
a =
- Nhập biểu thức của
( )
1nn
u fu
+
=
- Lặp dấu
=
lần thứ
1k −
cho ra giá trị của số hạng
k
u
.
Câu 3: Cho dãy số
()
n
u
biết
1
1
1
2
1
n
n
n
u
u
u
u
+
=
+
=
+
. Tìm số hạng
10
u
.
Câu 4: Cho dãy số
()
n
u
được xác định như sau:
1
1
1
2
nn
u
uu
+
=
= +
. Tìm số hạng
50
u
.
Bài toán 3: Cho dãy số
()
n
u
cho bởi
12
21
,
..
nnn
u au b
u cu du e
++
= =
= ++
. Hãy tìm số hạng
k
u
.
Tự luận: Tính lần lượt
34
; ;... ;
k
uu u
bằng cách thế
12
,uu
vào
3
u
; thế
23
,uu
vào
4
u
; …; thế
21
,
kk
uu
−−
vào
k
u
.
MTCT: Cách lập quy trình bấm máy:
- Nhập
C .B .A : A B : B Ccd e
=++ = =
- Bấm r nhập
B b
=
, ấn =, nhập
A a=
ấn
=
- Lặp dấu = cho đến khi xuất hiện lần thứ
2k −
giá trị của C thì đó chính là giá trị của số hạng
k
u
.
Câu 5: Cho dãy số
()
n
u
được xác định như sau:
12
21
1; 2
2 35
n nn
uu
u uu
++
= =
= ++
. Tìm số hạng
8
u
.
PHƯƠNG PHÁP.
1
BÀI TẬP TỰ LUẬN.
2
PHƯƠNG PHÁP.
1
BÀI TẬP TỰ LUẬN.
2

CHUYÊN ĐỀ II – TOÁN – 11 – DÃY SỐ – CẤP SỐ CỘNG – CẤP SỐ NHÂN
Page 4
Sưu tầm và biên soạn
Bài toán 4: Cho dãy số
()
n
u
cho bởi
{ }
(
)
1
1
,
nn
ua
u f nu
+
=
=
. Trong đó
{ }
( )
,
n
f nu
là kí hiệu của biểu thức
1n
u
+
tính theo
n
u
và
n
. Hãy tìm số hạng
k
u
.
Tự luận: Tính lần lượt
23
; ;...;
k
uu u
bằng cách thế
{
}
1
1, u
vào
2
u
; thế
{ }
2
2,u
vào
3
u
; …; thế
{ }
1
1,
k
ku
−
−
vào
k
u
.
MTCT: Cách lập quy trình bấm máy:
- Sử dụng 3 ô nhớ:
A
: chứa giá trị của n
B
: chứa giá trị của u
n
C
: chứa giá trị của u
n+1
- Lập công thức tính u
n+1
thực hiện gán
A
: =
A
+ 1 và
B
:=
C
để tính số hạng tiếp theo
của dãy
- Lặp phím dấu
=
cho đến khi giá trị của C xuất hiện lần thứ
1k −
thì đó là giá trị của số hạng
k
u
.
Câu 6: Cho dãy số
()
n
u
được xác định như sau:
( )
1
1
0
1
1
nn
u
n
uu
n
+
=
= +
+
. Tìm số hạng
11
u
.
Câu 7: Cho dãy số
()
n
u
được xác định bởi:
1
1
1
2
2
nn
u
u un
+
=
= +
. Tìm số hạng
50
u
.
DẠNG 2: XÉT TÍNH TĂNG, GIẢM CỦA DÃY SỐ
Cách 1: Xét hiệu
1nn
uu
+
−
Nếu
*
1
0
nn
uu n
+
− > ∀∈
thì
()
n
u
là dãy số tăng.
Nếu
*
1
0
nn
uu n
+
− < ∀∈
thì
()
n
u
là dãy số giảm.
Cách 2 : Khi
*
0
n
un> ∀∈
ta xét tỉ số
1n
n
u
u
+
PHƯƠNG PHÁP.
1
BÀI TẬP TỰ LUẬN.
2
PHƯƠNG PHÁP.
1

CHUYÊN ĐỀ II – TOÁN – 11 – DÃY SỐ – CẤP SỐ CỘNG – CẤP SỐ NHÂN
Page 5
Sưu tầm và biên soạn
Nếu
1
1
n
n
u
u
+
>
thì
()
n
u
là dãy số tăng.
Nếu
1
1
n
n
u
u
+
<
thì
()
n
u
là dãy số giảm.
Cách 3 : Nếu dãy số
()
n
u
được cho bởi một hệ thức truy hồi thì ta có thể sử dụng phương pháp quy nạp
để chứng minh
*
1
nn
u un
+
> ∀∈
* Công thức giải nhanh một số dạng toán về dãy số
Dãy số
()
n
u
có
n
u an b= +
tăng khi
0a >
và giảm khi
0a <
Dãy số
()
n
u
có
n
n
uq=
Không tăng, không giảm khi
0q <
Giảm khi
01q<<
Tăng khi
1q >
Dãy số
()
n
u
có
n
an b
u
cn d
+
=
+
với điều kiện
*
cn d 0 n+ > ∀∈
Tăng khi
0
ad bc−>
Giảm khi
0ad bc−<
Dãy số đan dấu cũng là dãy số không tăng, không giảm
Nếu dãy số
()
n
u
tăng hoặc giảm thì dãy số
(
)
.
n
n
qu
không tăng, không giảm
Dãy số
()
n
u
có
1
nn
u au b
+
= +
tăng nếu
21
0
0
a
uu
>
−>
; giảm nếu
21
0
0
a
uu
>
−<
và không tăng
không giảm nếu
0a <
Dãy số
()
n
u
có
1
*
, 0, 0
n
n
n
n
au b
u
cu d
cd u n
+
+
=
+
> > ∀∈
tăng nếu
21
0
0
ad bc
uu
−>
−>
và giảm nếu
21
0
0
ad bc
uu
−>
−<
Dãy số
()
n
u
có
1
*
, 0, 0
n
n
n
n
au b
u
cu d
cd u n
+
+
=
+
> > ∀∈
không tăng không giảm nếu
0ad bc−<
Nếu
()
()
n
n
u
v
↑
↑
thì dãy số
( )
nn
uv+↑
Nếu
()
()
n
n
u
v
↓
↓
thì dãy số
( )
nn
uv+↓

CHUYÊN ĐỀ II – TOÁN – 11 – DÃY SỐ – CẤP SỐ CỘNG – CẤP SỐ NHÂN
Page 6
Sưu tầm và biên soạn
Nếu
*
*
( ); 0
(); 0
nn
nn
uu n
vv n
↑ ≥ ∀∈
↑ ≥ ∀∈
thì dãy số
( )
.
nn
uv ↑
Nếu
*
*
( ); 0
(); 0
nn
nn
uu n
vv n
↓ ≥ ∀∈
↓ ≥ ∀∈
thì dãy số
( )
.
nn
uv ↓
Nếu
()
n
u ↑
và
*
0
n
un
≥ ∀∈
thì dãy số
( )
n
u
↑
và dãy số
(
)
*
()
m
n
um↑∀ ∈
Nếu
()
n
u
↓
và
*
0
n
un≥ ∀∈
thì dãy số
( )
n
u ↓
và dãy số
( )
*
()
m
n
um↓∀ ∈
Nếu
()
n
u
↑
và
*
0
n
un
> ∀∈
thì dãy số
1
n
u
↓
Nếu
()
n
u
↓
và
*
0
n
un> ∀∈
thì dãy số
1
n
u
↑
Câu 8: Xét tính đơn điệu của dãy số
()
n
u
biết
36
n
un= +
.
Câu 9: Xét tính đơn điệu của dãy số
()
n
u
biết
5
2
n
n
u
n
+
=
+
.
Câu 10: Xét tính đơn điệu của dãy số
()
n
u
biết
2
5
n
n
u
n
=
.
Câu 11: Cho dãy số
()
n
u
biết
1
1
2
( ):
31
2
4
n
n
n
u
u
u
un
−
=
+
= ∀≥
.
DẠNG 3: XÉT TÍNH BỊ CHẶN CỦA DÃY SỐ
Phương pháp 1: Chứng minh trực tiếp bằng các phương pháp chứng minh bất đẳng thức
Cách 1: Dãy số
()
n
u
có
()
n
u fn=
là hàm số đơn giản.
Ta chứng minh trực tiếp bất đẳng thức
*
() ,
n
u fn M n= ≤ ∀∈
hoặc
*
() ,
n
u fn m n= ≥ ∀∈
Cách 2: Dãy số
()
n
u
có
12
... ...
n kn
u vv v v=+ ++ ++
Ta làm trội
1
k kk
vaa
+
≤−
Lúc đó
( ) ( )
( )
12 23 1
...
n nn
u aa aa a a
+
≤−+−+ −
Suy ra
*
11
,
nn
u aa Mn
+
≤ − ≤ ∀∈
Cách 3: Dãy số
()
n
u
có
1 23
. ...
nn
u v vv v=
với
*
0,
n
vn> ∀∈
Ta làm trội
1k
k
k
a
v
a
+
≤
Lúc đó
31
2
12
. ...
n
n
n
aa
a
u
aa a
+
≤
BÀI TẬP TỰ LUẬN.
2
PHƯƠNG PHÁP.
1
CHUYÊN ĐỀ II – TOÁN – 11 – DÃY SỐ – CẤP SỐ CỘNG – CẤP SỐ NHÂN
Page 7
Sưu tầm và biên soạn
Suy ra
*
1
1
,
n
n
a
u Mn
a
+
≤ ≤ ∀∈
Phương pháp 2: Dự đoán và chứng minh bằng phương pháp quy nạp.
Nếu dãy số
()
n
u
được cho bởi một hệ thức truy hồi thì ta có thể sử dụng phương pháp quy nạp
để chứng minh
Chú ý: Nếu dãy số
()
n
u
giảm thì bị chặn trên, dãy số
()
n
u
tăng thì bị chặn dưới
* Công thức giải nhanh một số dạng toán về dãy số bị chặn
Dãy số
()
n
u
có
(
)
1
n
n
uq q= ≤
bị chặn
Dãy số
()
n
u
có
(
)
1
n
n
uq q= <−
không bị chặn
Dãy số
()
n
u
có
n
n
uq=
với
1q >
bị chặn dưới
Dãy số
()
n
u
có
n
u an b= +
bị chặn dưới nếu
0a
>
và bị chặn trên nếu
0a <
Dãy số
()
n
u
có
2
n
u an bn c= ++
bị chặn dưới nếu
0a
>
và bị chặn trên nếu
0a <
Dãy số
()
n
u
có
1
1 10
...
mm
nm m
u a n a n an a
−
−
= + ++ +
bị chặn dưới nếu
0
m
a >
và bị chặn trên nếu
0
m
a
<
Dãy số
()
n
u
có
( )
1
1 10
...
nm m
n mm
u q a n a n an a
−
−
= + ++ +
với
0
m
a ≠
và
1
q <−
không bị chặn
Dãy số
()
n
u
có
1
1 10
...
mm
nm m
u a n a n an a
−
−
= + ++ +
bị chặn dưới với
0
m
a
>
Dãy số
()
n
u
có
1
3
1 10
...
mm
nm m
u a n a n an a
−
−
= + ++ +
bị chặn dưới nếu
0
m
a >
và bị chặn trên
nếu
0
m
a <
Dãy số
()
n
u
có
( )
( )
n
Pn
u
Qn
=
trong đó
( )
Pn
và
( )
Qn
là các đa thức, bị chặn nếu bậc của
( )
Pn
nhỏ hơn hoặc bằng bậc của
( )
Qn
Dãy số
()
n
u
có
( )
( )
n
Pn
u
Qn
=
trong đó
( )
Pn
và
( )
Qn
là các đa thức, bị chặn dưới hoặc bị chặn
trên nếu bậc của
( )
Pn
lớn hơn bậc của
( )
Qn
Câu 12: Xét tính bị chặn của dãy số
()
n
u
biết
1
23
n
u
n
−
=
+
.
Câu 13: Xét tính bị chặn của dãy số
()
n
u
biết
45
1
n
n
u
n
+
=
+
.
BÀI TẬP TỰ LUẬN.
2

CHUYÊN ĐỀ II – TOÁN – 11 – DÃY SỐ – CẤP SỐ CỘNG – CẤP SỐ NHÂN
Page 8
Sưu tầm và biên soạn
Câu 14: Xét tính bị chặn của dãy số
()
n
u
biết
3
2
1
n
n
u
n
=
+
.
Câu 15: Xét tính bị chặn của dãy số
()
n
u
biết
22 2
11 1 1
...
22 3
n
u
n
=+ + ++
. Mệnh đề nào sau đây đúng ?
DẠNG 4: TÍNH TỔNG CỦA DÃY SỐ
Dạng 4.1: Tính tổng của dãy số cách đều
Giải sử cần tính tổng:
12
...
n
Saa a= + ++
. Trong đó:
1nn
aa d
−
= +
- Tự luận:
Ta có:
(
) ( ) ( ) ( )
1 21 1 1
2 ...
nn n n
S aa aa a a naa
−
=+++ +++= +
Từ đó suy ra:
( )
1
n.
2
n
aa
S
+
=
- Trắc nghiệm:
Công thức tính nhanh:
+ Số hạng tổng quát của dãy số cách đều là:
(
)
1
1
n
uu n d
=+−
với d là khoảng cách giữa 2 số
hạng
+ Số số hạng =: + 1
+ Tổng = •: 2
- Casio
Bước 1: Từ công thức của tổng tìm số hạng tổng quát của tổng và số số hạng.
Bước 2: Sử dụng công cụ tính:
∑
y
nhập số hạng tổng quát của dãy số
y
nhập
x
chạy từ 1
tới
n =
số số hạng
y
=.
Câu 16: Tính
1 3 5 ... 4001
S
=+++ +
?
Câu 17: Cho tổng
( ) 2 4 6 ... 2Sn n=+++ +
. Khi đó
30
S
bằng?
Câu 18: Cho dãy số
( )
n
u
xác định bởi:
1
150u =
và
1
3
nn
uu
−
= −
với mọi
2n ≥
Khi đó tổng
100
số hạng
đầu tiên là:
Dạng 4.2: Tính tổng của dãy số bằng phương pháp khử liên tiếp
PHƯƠNG PHÁP.
1
BÀI TẬP TỰ LUẬN.
2
PHƯƠNG PHÁP.
1
CHUYÊN ĐỀ II – TOÁN – 11 – DÃY SỐ – CẤP SỐ CỘNG – CẤP SỐ NHÂN
Page 9
Sưu tầm và biên soạn
Giả sử cần tính tổng: .
- Tự luận:
Bước 1: Ta tìm cách tách: ; ;.
Bước 2: Rút gọn:
- Trắc nghiệm:
+ Một số công thức tách thường sử dụng:
+ Nhận định kết quả của tổng là:
- Casio:
Làm tương tự như dạng 1
Câu 19: Tính tổng sau:
Câu 20: Cho tổng . Khi đó công thức của là:
Câu 21: Cho tổng . Tính
Dạng 4.3: Tính tổng bằng cách chuyển về phương trình có ẩn là tổng cần tính
Giả sử cần tính tổng: .
- Tự luận:
Sơ đồ giải: Từ công thức của tổng S ta chuyển về phương trình chứa ẩn
S
Giải pt
S
- Trắc nghiệm:
Tổng có dạng: với
- Casio:
Làm tương tự như dạng 1
12
...
n
Saa a= + ++
112
a bb= −
2 23
a bb= −
122 3 11 1
b ...
nn n
Sbbb bb bb
++
=− + −++ − =−
11
n(n a)
a
n na
•=−
++
2 11
n(n a)(n 2a) ( ) ( )( 2 )
a
nna nan a
•=−
++ + + +
2
2 22 2
2 11
n (n a) ( )
na a
n na
+
•=−
++
. ! ( 1)! !nn n n• =+−
11n
Sbb
+
= −
222 2
...
1.3 3.5 5.7 97.99
S = + + ++
111 1
...
1.2.3 2.3.4 3.4.5 n(n 1)(n 2)
n
S = + + ++
++
n
S
222 2
3 5 7 21
...
(1.2) (2.3) (3.4) [n( 1)]
n
n
S
n
+
=++++
+
10
S
12
...
n
Saa a= + ++
( )
1
1
2
11 1 1
1
...
1
n
n
ua
S u ua ua ua S
a
+
−
= + + ++ ⇒=
−
1a ≠
BÀI TẬP TỰ LUẬN.
2
PHƯƠNG PHÁP.
1

CHUYÊN ĐỀ II – TOÁN – 11 – DÃY SỐ – CẤP SỐ CỘNG – CẤP SỐ NHÂN
Page 10
Sưu tầm và biên soạn
Câu 22: Tính tổng: ?
Câu 23: Tính tổng ?
Câu 24: Tính tổng: . Tính
Dạng 4.4: Tính tổng bằng cách đưa về các tổng đã biết
Giải sử cần tính tổng: .
- Tự luận:
Tìm cách tách: . Trong đó: đã biết công thức tính tổng.
- Trắc nghiệm:
Ta có thể dùng phương pháp thử giá trị
n
vào các đáp án để loại trừ và chọn ra đáp án đúng.
- Casio:
Làm tương tự như dạng 1
Câu 25: Tính: . Biết rằng:
Câu 26: Cho: . Tính biết rằng:
.
Câu 27: Cho tổng: với . Biết: . Giá trị của k là:
DẠNG 5: XÁC ĐỊNH CÔNG THỨC SỐ HẠNG TỔNG QUÁT CỦA DÃY SỐ
Nếu có dạng thì biến đổi thành hiệu của hai số hạng, dựa vào đó thu
gọn .
2 50
1 3 3 ... 3S =++ + +
100
2 3 100
11 1 1
4.5 . ... 1
55 5 5
S
= + + ++ +
111 1
1 1 1 ... 1
248 2
n
S
=− +− +− ++−
10
S
12
...
nn
S aa a= + ++
123
...
n
S SS S=+++
12 3
; ;S ...SS
1.3 2.5 3.7 ... (2 1)
n
S nn=++++ +
2 22 2
11
( 1) ( 1)(2 1)
1 2 3 ... ; 1 2 3 ...
26
nn
ii
nn nn n
i ni n
= =
+ ++
=++++= =+ + ++ =
∑∑
1.2 3.4 5.6 ... (2 1).2
n
S nn=++++ −
100
S
2 22 2
11
( 1)(2 1)
2 2 4 6 ... 2 ( 1); 1 2 3 ...
6
nn
ii
nn n
i n nn i n
= =
++
=++++ = + =+ + ++ =
∑∑
1.4 2.7 3.10 ... .(3 1)
n
S nn= + + ++ +
*
n ∈
294
k
S =
( )
n
u
12
...
nn
u aa a= + ++
k
a
n
u
BÀI TẬP TỰ LUẬN.
2
PHƯƠNG PHÁP.
1
BÀI TẬP TỰ LUẬN.
2
PHƯƠNG PHÁP.
1

CHUYÊN ĐỀ II – TOÁN – 11 – DÃY SỐ – CẤP SỐ CỘNG – CẤP SỐ NHÂN
Page 11
Sưu tầm và biên soạn
Nếu dãy số được cho bởi một hệ thức truy hồi, tính vài số hạng đầu của dãy số, từ đó dự
đoán công thức tính theo n, rồi chứng minh công thức này bằng phương pháp quy nạp. Ngoài
ra cũng có thể tính hiệu dựa vào đó để tìm công thức tính theo n.
Câu 28: Cho dãy số có . Đặt . Xác định công thức tính theo n.
Câu 29: Xác định công thức tính số hạng tổng quát theo n của dãy số sau: .
Câu 30: Xác định công thức tính số hạng tổng quát theo n của dãy số sau:
( )
n
u
n
u
1nn
uu
+
−
( )
n
u
( )
n
a
( )
1
1
k
a
kk
=
+
1
n
nk
k
ua
=
=
∑
( )
n
u
n
u
1
1
3
2
nn
u
uu
+
=
= +
n
u
1
3
1
1
1.
nn
u
n
u un
+
=
∀≥
= +
BÀI TẬP TỰ LUẬN.
2

CHUYÊN ĐỀ II – TOÁN – 11 – DÃY SỐ – CẤP SỐ CỘNG – CẤP SỐ NHÂN
Page 1
Sưu tầm và biên soạn
BÀI 5: DÃY SỐ
1. ĐỊNH NGHĨA DÃY SỐ
Mỗi hàm số
u
xác định trên tập các số nguyên dương
*
được gọi là một dãy số vô hạn.
Kí hiệu:
( )
*
:
.
u
n un
→
Người ta thường viết dãy số dưới dạng khai triển
123
, , , ..., , ...,
n
uuu u
trong đó
n
u un
hoặc viết tắt là
,
n
u
và gọi
1
u
là số hạng đầu,
n
u
là số hạng thứ
n
và là số
hạng tổng quát của dãy số.
Chú ý: Nếu
*
,
n
n uc∀∈ =
thì
n
u
là dãy số không đổi.
Mỗi hàm số
u
xác định trên tập
1,2,3,...,Mm
với
*
m
được gọi là một dãy số hữu hạn.
Dạng khai triển của nó là
123
, , , ..., ,
n
uuu u
trong đó
1
u
là số hạng đầu,
m
u
là số hạng cuối.
2. CÁC CÁCH CHO MỘT DÃY SỐ
a) Dãy số cho bằng liệt kê các số hạng
b) Dãy số cho bằng công thức của số hạng tổng quát
c) Dãy số cho bằng phương pháp mô tả
d) Dãy số cho bằng phương pháp truy hồi
Cách cho một dãy số bằng phương pháp truy hồi, tức là:
Cho số hạng đầu.
Cho hệ thức truy hồi, tức là hệ thức biểu thị số hạng thứ
n
qua số hạng đứng trước nó.
3. DÃY SỐ TĂNG, DÃY SỐ GIẢM VÀ DÃY SỐ BỊ CHẶN
Dãy số
n
u
được gọi là dãy số tăng nếu ta có
1nn
uu
với mọi
*
.n
Dãy số
n
u
được gọi là dãy số giảm nếu ta có
1nn
uu
với mọi
*
.n
CHƯƠNG
II
DÃY SỐ
CẤP SỐ CỘNG – CẤP SỐ NHÂN
CHUYÊN ĐỀ II – TOÁN – 11 – DÃY SỐ – CẤP SỐ CỘNG – CẤP SỐ NHÂN
Page 2
Sưu tầm và biên soạn
Chú ý: Không phải mọi dãy số đều tăng hoặc giảm. Chẳng hạn, dãy số
n
u
với
3
n
n
u
tức là
dãy
3, 9, 27,81,...
không tăng cũng không giảm.
Dãy số
n
u
được gọi là bị chặn trên nếu tồn tại một số
M
sao cho
*
, .
n
u Mn
Dãy số
n
u
được gọi là bị chặn dưới nếu tồn tại một số
m
sao cho
*
, .
n
u mn
Dãy số
n
u
được gọi là bị chặn nếu nó vừa bị chặn trên vừa bị chặn dưới, tức là tồn tại các số
, mM
sao cho
*
, .
n
mu M n
Lưu y: + Dãy tăng sẽ bị chặn dưới bởi
1
u
+ Dãy giảm sẽ bị chặn trên bởi
1
u
DẠNG 1: TÌM SỐ HẠNG CỦA DÃY SỐ
Bài toán 1: Cho dãy số
()
n
u
:
()
n
u fn=
. Hãy tìm số hạng
k
u
.
Tự luận: Thay trực tiếp
nk=
vào
n
u
.
MTCT: Dùng chức năng CALC:
Nhập:
()fx
Bấm r nhập
X k
=
Bấm
=
→
Kết quả
Câu 1: Cho dãy số
()
n
u
biết
115 15
22
5
nn
n
u
+−
= −
. Tìm số hạng
6
u
.
Lời giải
Cách 1: Giải theo tự luận:
HỆ THỐNG BÀI TẬP.
II
PHƯƠNG PHÁP.
1
BÀI TẬP TỰ LUẬN.
2

CHUYÊN ĐỀ II – TOÁN – 11 – DÃY SỐ – CẤP SỐ CỘNG – CẤP SỐ NHÂN
Page 3
Sưu tầm và biên soạn
Thế trực tiếp:
66
6
11 5 1 5
8
22
5
u
.
Cách 2: Dùng chức năng CALC của máy tính cầm tay:
Nhập:
115 15
22
5
xx
+−
−
Bấm
CALC
nhập
X6=
Máy hiện: 8
Câu 2: Cho dãy số
()
n
u
có số hạng tổng quát
21
2
n
n
u
n
+
=
+
. Số
167
84
là số hạng thứ mấy?
Lời giải
Cách 1: Giải theo tự luận:
1Giả sử
+
= ⇔ = ⇔ += +
+
167 2 1 167
84(2 1) 167( 2)
84 2 84
n
n
u nn
n
250n⇔=
.
Vậy
167
84
là số hạng thứ 250 của dãy số
()
n
u
.
Cách 2: Sử dụng MTCT:
Nhập:
+
+
21
2
x
x
Bấm
CALC
nhập
X 250
=
Máy hiện:
167
84
Bài toán 2: Cho dãy số
()
n
u
cho bởi
1
1
()
nn
ua
u fu
+
=
=
. Hãy tìm số hạng
k
u
.
Tự luận: Tính lần lượt
23
; ;...;
k
uu u
bằng cách thế
1
u
vào
2
u
, thế
2
u
vào
3
u
, …, thế
1k
u
−
vào
1k
u
+
.
MTCT: Cách lập quy trình bấm máy:
- Nhập giá trị của số hạng u
1
:
a =
- Nhập biểu thức của
( )
1nn
u fu
+
=
- Lặp dấu
=
lần thứ
1k −
cho ra giá trị của số hạng
k
u
.
PHƯƠNG PHÁP.
1

CHUYÊN ĐỀ II – TOÁN – 11 – DÃY SỐ – CẤP SỐ CỘNG – CẤP SỐ NHÂN
Page 4
Sưu tầm và biên soạn
Câu 3: Cho dãy số
()
n
u
biết
1
1
1
2
1
n
n
n
u
u
u
u
+
=
+
=
+
. Tìm số hạng
10
u
.
Lời giải
Cách 1: Giải theo tự luận:
1
2
1
2
12 3
1 11 2
u
u
u
+
+
= = =
++
;
2
3
2
3
2
2
7
2
3
15
1
2
u
u
u
+
+
= = =
+
+
;
3
4
3
7
2
2
17
5
7
1 12
1
5
u
u
u
+
+
= = =
+
+
;
4
5
4
17
2
2
41
12
17
1 29
1
12
u
u
u
+
+
= = =
+
+
;
5
6
5
41
2
2
99
29
41
1 70
1
29
u
u
u
+
+
= = =
+
+
;
6
7
6
99
2
2
239
70
99
1 169
1
70
u
u
u
+
+
= = =
+
+
7
8
7
239
2
2
577
169
239
1 408
1
169
u
u
u
+
+
= = =
+
+
;
8
9
8
577
2
2
1393
408
577
1 985
1
408
u
u
u
+
+
= = =
+
+
;
9
10
9
1393
2
2
3363
985
1393
1 2378
1
985
u
u
u
+
+
= = =
+
+
Cách 2: Sử dụng MTCT:
Lập quy trình bấm phím tính số hạng của dãy số như sau:
Nhập: 1
=
1
()
u
Nhập
ANS 2
ANS 1
+
+
Lặp dấu
=
ta được giá trị số hạng
10
3363
2378
u =
.
Câu 4: Cho dãy số
()
n
u
được xác định như sau:
1
1
1
2
nn
u
uu
+
=
= +
. Tìm số hạng
50
u
.
Lời giải
Cách 1: Giải theo tự luận:
Từ giả thiết ta có:
1
21
32
50 49
1
2
2
...
2
u
uu
uu
uu
=
= +
= +
= +
Cộng theo vế các đẳng thức trên, ta được:
BÀI TẬP TỰ LUẬN.
2
CHUYÊN ĐỀ II – TOÁN – 11 – DÃY SỐ – CẤP SỐ CỘNG – CẤP SỐ NHÂN
Page 5
Sưu tầm và biên soạn
50
1 2.49 99u
=+=
Cách 2: Sử dụng MTCT:
Lập quy trình bấm phím tính số hạng của dãy số như sau:
Nhập: 1
=
1
()u
Nhập
ANS 2+
Lặp dấu
=
ta được giá trị số hạng
50
99u =
.
Bài toán 3: Cho dãy số
()
n
u
cho bởi
12
21
,
..
nnn
u au b
u cu du e
++
= =
= ++
. Hãy tìm số hạng
k
u
.
Tự luận: Tính lần lượt
34
; ;... ;
k
uu u
bằng cách thế
12
,uu
vào
3
u
; thế
23
,uu
vào
4
u
; …; thế
21
,
kk
uu
−−
vào
k
u
.
MTCT: Cách lập quy trình bấm máy:
- Nhập
C .B .A : A B : B Ccd e=++ = =
- Bấm r nhập
B
b=
, ấn =, nhập
A a
=
ấn
=
- Lặp dấu = cho đến khi xuất hiện lần thứ
2k −
giá trị của C thì đó chính là giá trị của số hạng
k
u
.
Câu 5: Cho dãy số
()
n
u
được xác định như sau:
12
21
1; 2
2 35
n nn
uu
u uu
++
= =
= ++
. Tìm số hạng
8
u
.
Lời giải
Cách 1: Giải theo tự luận:
3 21
2 3 5 12u uu= + +=
4 32
2 3 5 35u uu= + +=
5 43
2 3 5 111u uu= + +=
6 54
2 3 5 332u uu= + +=
7 65
2 3 5 1002u uu
= + +=
8 76
2 3 5 3005u uu= + +=
Cách 2: Dùng máy tính cầm tay:
Sử dụng 3 ô nhớ:
A
: chứa giá trị của
n
u
B
: chứa giá trị của
1n
u
+
C
: chứa giá trị của
2n
u
+
Lập quy trình bấm máy:
PHƯƠNG PHÁP.
1
BÀI TẬP TỰ LUẬN.
2

CHUYÊN ĐỀ II – TOÁN – 11 – DÃY SỐ – CẤP SỐ CỘNG – CẤP SỐ NHÂN
Page 6
Sưu tầm và biên soạn
Nhập:
C 2B 3A+5:A B:B C
=+==
Bấm
CALC
nhập
B2=
, ấn
=
, nhập
A1=
ấn
=
Lặp dấu
=
cho đến khi giá trị của C xuất hiện lần thứ 6 thì đó là giá trị của số hạng
8
u
bằng
3005.
Bài toán 4: Cho dãy số
()
n
u
cho bởi
{ }
(
)
1
1
,
nn
ua
u f nu
+
=
=
. Trong đó
{ }
(
)
,
n
f nu
là kí hiệu của biểu thức
1n
u
+
tính theo
n
u
và
n
. Hãy tìm số hạng
k
u
.
Tự luận: Tính lần lượt
23
; ;...;
k
uu u
bằng cách thế
{
}
1
1,
u
vào
2
u
; thế
{ }
2
2,u
vào
3
u
; …; thế
{ }
1
1,
k
ku
−
−
vào
k
u
.
MTCT: Cách lập quy trình bấm máy:
- Sử dụng 3 ô nhớ:
A
: chứa giá trị của n
B
: chứa giá trị của u
n
C
: chứa giá trị của u
n+1
- Lập công thức tính u
n+1
thực hiện gán
A
: =
A
+ 1 và
B
:=
C
để tính số hạng tiếp theo
của dãy
- Lặp phím dấu
=
cho đến khi giá trị của C xuất hiện lần thứ
1k
−
thì đó là giá trị của số hạng
k
u
.
Câu 6: Cho dãy số
()
n
u
được xác định như sau:
( )
1
1
0
1
1
nn
u
n
uu
n
+
=
= +
+
. Tìm số hạng
11
u
.
Lời giải
Cách 1: Giải theo tự luận:
21
11
( 1)
22
uu= +=
32
2
( 1) 1
3
uu= +=
43
33
( 1)
42
uu= +=
54
4
( 1) 2
5
uu= +=
65
55
( 1)
62
uu= +=
76
6
( 1) 3
7
uu= +=
87
77
( 1)
82
uu= +=
98
8
( 1) 4
9
uu= +=
10 9
99
( 1)
10 2
uu= +=
11 10
10
( 1) 5
11
uu= +=
PHƯƠNG PHÁP.
1
BÀI TẬP TỰ LUẬN.
2

CHUYÊN ĐỀ II – TOÁN – 11 – DÃY SỐ – CẤP SỐ CỘNG – CẤP SỐ NHÂN
Page 7
Sưu tầm và biên soạn
Cách 2: Dùng máy tính cầm tay:
Sử dụng 3 ô nhớ:
A
: chứa giá trị của
n
B
: chứa giá trị của
n
u
C
: chứa giá trị của
1n
u
+
Lập quy trình bấm máy:
Nhập:
( )
A
C B 1 :A A 1:B C
A1
= + =+=
+
Bấm
CALC
nhập
A1=
, ấn =, nhập
B0=
ấn =
Lặp dấu = cho đến khi giá trị của C xuất hiện lần thứ 10 thì đó là giá trị của số hạng
11
u
bằng 5.
Câu 7: Cho dãy số
()
n
u
được xác định bởi:
1
1
1
2
2
nn
u
u un
+
=
= +
. Tìm số hạng
50
u
.
Lời giải
Cách 1: Giải theo tự luận:
Từ giả thiết ta có:
1
21
32
50 49
1
2
2.2
2.3
...
2.50
u
uu
uu
uu
=
= +
= +
= +
Cộng theo vế các đẳng thức trên, ta được:
50
50
2
11
2.(2 3 ... 50) 2. 2548,5
22
x
ux
=
= + ++ + = + =
∑
Cách 2: Dùng máy tính cầm tay:
Nhập:
C B 2A:A A 1:B C=+ =+=
Bấm
CALC
nhập
1
B
2
=
, ấn =, nhập
A1=
ấn =
Lặp dấu = cho đến khi giá trị của C xuất hiện lần thứ 49 thì đó là giá trị của số hạng
50
u
bằng
2548,5
.
DẠNG 2: XÉT TÍNH TĂNG, GIẢM CỦA DÃY SỐ
PHƯƠNG PHÁP.
1

CHUYÊN ĐỀ II – TOÁN – 11 – DÃY SỐ – CẤP SỐ CỘNG – CẤP SỐ NHÂN
Page 8
Sưu tầm và biên soạn
Cách 1: Xét hiệu
1nn
uu
+
−
Nếu
*
1
0
nn
uu n
+
− > ∀∈
thì
()
n
u
là dãy số tăng.
Nếu
*
1
0
nn
uu n
+
− < ∀∈
thì
()
n
u
là dãy số giảm.
Cách 2 : Khi
*
0
n
un> ∀∈
ta xét tỉ số
1n
n
u
u
+
Nếu
1
1
n
n
u
u
+
>
thì
()
n
u
là dãy số tăng.
Nếu
1
1
n
n
u
u
+
<
thì
()
n
u
là dãy số giảm.
Cách 3 : Nếu dãy số
()
n
u
được cho bởi một hệ thức truy hồi thì ta có thể sử dụng phương pháp quy nạp
để chứng minh
*
1nn
u un
+
> ∀∈
* Công thức giải nhanh một số dạng toán về dãy số
Dãy số
()
n
u
có
n
u an b
= +
tăng khi
0
a >
và giảm khi
0a <
Dãy số
()
n
u
có
n
n
uq=
Không tăng, không giảm khi
0q <
Giảm khi
01
q<<
Tăng khi
1q >
Dãy số
()
n
u
có
n
an b
u
cn d
+
=
+
với điều kiện
*
cn d 0 n+ > ∀∈
Tăng khi
0ad bc−>
Giảm khi
0ad bc−<
Dãy số đan dấu cũng là dãy số không tăng, không giảm
Nếu dãy số
()
n
u
tăng hoặc giảm thì dãy số
( )
.
n
n
qu
không tăng, không giảm
Dãy số
()
n
u
có
1
nn
u au b
+
= +
tăng nếu
21
0
0
a
uu
>
−>
; giảm nếu
21
0
0
a
uu
>
−<
và không tăng
không giảm nếu
0a <
Dãy số
()
n
u
có
1
*
, 0, 0
n
n
n
n
au b
u
cu d
cd u n
+
+
=
+
> > ∀∈
tăng nếu
21
0
0
ad bc
uu
−>
−>
và giảm nếu
21
0
0
ad bc
uu
−>
−<
Dãy số
()
n
u
có
1
*
, 0, 0
n
n
n
n
au b
u
cu d
cd u n
+
+
=
+
> > ∀∈
không tăng không giảm nếu
0ad bc−<
CHUYÊN ĐỀ II – TOÁN – 11 – DÃY SỐ – CẤP SỐ CỘNG – CẤP SỐ NHÂN
Page 9
Sưu tầm và biên soạn
Nếu
()
()
n
n
u
v
↑
↑
thì dãy số
( )
nn
uv
+↑
Nếu
()
()
n
n
u
v
↓
↓
thì dãy số
(
)
nn
uv+↓
Nếu
*
*
( ); 0
(); 0
nn
nn
uu n
vv n
↑ ≥ ∀∈
↑ ≥ ∀∈
thì dãy số
( )
.
nn
uv ↑
Nếu
*
*
( ); 0
(); 0
nn
nn
uu n
vv n
↓ ≥ ∀∈
↓ ≥ ∀∈
thì dãy số
( )
.
nn
uv ↓
Nếu
()
n
u ↑
và
*
0
n
un≥ ∀∈
thì dãy số
( )
n
u ↑
và dãy số
(
)
*
()
m
n
um↑∀ ∈
Nếu
()
n
u ↓
và
*
0
n
un≥ ∀∈
thì dãy số
( )
n
u ↓
và dãy số
( )
*
()
m
n
um↓∀ ∈
Nếu
()
n
u ↑
và
*
0
n
un> ∀∈
thì dãy số
1
n
u
↓
Nếu
()
n
u ↓
và
*
0
n
un
> ∀∈
thì dãy số
1
n
u
↑
Câu 8: Xét tính đơn điệu của dãy số
()
n
u
biết
36
n
un= +
.
Lời giải
Ta có
( )
1
3 6 3 1 63 9
nn
un u n n
+
= +⇒ = + += +
Xét hiệu
( ) ( )
*
1
3 9 3 6 30
nn
uu n n n
+
− = + − + = > ∀∈
Vậy
()
n
u
là dãy số tăng
Giải nhanh: Dãy này có dạng
n
u an b= +
;
a30= >
nên dãy số tăng
Câu 9: Xét tính đơn điệu của dãy số
()
n
u
biết
5
2
n
n
u
n
+
=
+
.
Lời giải
Ta có
1
53 3
11
22 3
nn
n
uu
nn n
+
+
= =+ ⇒=+
++ +
Xét hiệu
( )( )
*
1
33 3
0
3 2 23
nn
uu n
nn nn
+
−
− = − = < ∀∈
++ ++
Vậy
()
n
u
là dãy số giảm
Giải nhanh: Dãy này có dạng
n
an b
u
cn d
+
=
+
Mẫu
*
20nn+>∀∈
và
25 30ad bc− = − =−<
nên
()
n
u
là dãy số giảm
Câu 10: Xét tính đơn điệu của dãy số
()
n
u
biết
2
5
n
n
u
n
=
.
Lời giải
BÀI TẬP TỰ LUẬN.
2

CHUYÊN ĐỀ II – TOÁN – 11 – DÃY SỐ – CẤP SỐ CỘNG – CẤP SỐ NHÂN
Page 10
Sưu tầm và biên soạn
Ta có
(
)
1
*
1
2
2
55
0,
1
nn
nn
u nu
n
n
+
+
= > ∀∈ ⇒ =
+
Xét tỉ số
( )
12 2 2 2
1
2
22
5 5 2 14 2 1
.
5 21 21
1
n
n
n
n
u
n n nn nn
u nn nn
n
+
+
+ ++ − −
= = =
++ ++
+
( )
2
*
2
2 12 1
1 1,
21
nn n
n
nn
−+ −
=+ > ∀∈
++
Vậy
()
n
u
là dãy số tăng
Câu 11: Cho dãy số
()
n
u
biết
1
1
2
( ):
31
2
4
n
n
n
u
u
u
un
−
=
+
= ∀≥
.
Lời giải
Ta dự đoán dãy số giảm sau đó ta sẽ chứng minh nó giảm
Ta có
11
11
31 1
44
nn
nn n
uu
uu u
−−
−−
+−
−= −=
Do đó, để chứng minh dãy
()
n
u
giảm ta chứng minh
1 1
n
un>∀≥
bằng phương pháp quy nạp
toán học. Thật vậy
Với
1
1 21nu=⇒=>
Giả sử
1
31
31
11
44
k
kk
u
uu
+
+
+
>⇒ = > =
Theo nguyên lí quy nạp ta có
1 1
n
un>∀≥
Suy ra
11
0 2
nn n n
uu uu n
−−
− < ⇔ < ∀≥
hay dãy
()
n
u
giảm
Giải nhanh: Dãy
()
n
u
có dạng
1
nn
u au b
+
= +
Ở đây
3
0
4
a = >
và
21
71
20
44
uu− = −=−<
Suy ra dãy số giảm
Tổng quát ta có thể chứng minh dãy số
(
)
1
1
1
( ):
, a,b>0 2
n
n
n
uc
u
au b
un
ab
−
= >
+
= ∀≥
+
giảm tương tự như
trên.
DẠNG 3: XÉT TÍNH BỊ CHẶN CỦA DÃY SỐ
Phương pháp 1: Chứng minh trực tiếp bằng các phương pháp chứng minh bất đẳng thức
Cách 1: Dãy số
()
n
u
có
()
n
u fn
=
là hàm số đơn giản.
PHƯƠNG PHÁP.
1

CHUYÊN ĐỀ II – TOÁN – 11 – DÃY SỐ – CẤP SỐ CỘNG – CẤP SỐ NHÂN
Page 11
Sưu tầm và biên soạn
Ta chứng minh trực tiếp bất đẳng thức
*
() ,
n
u fn M n= ≤ ∀∈
hoặc
*
() ,
n
u fn m n= ≥ ∀∈
Cách 2: Dãy số
()
n
u
có
12
... ...
n kn
u vv v v=+ ++ ++
Ta làm trội
1k kk
vaa
+
≤−
Lúc đó
( ) ( ) ( )
12 23 1
...
n nn
u aa aa a a
+
≤−+−+ −
Suy ra
*
11
,
nn
u aa Mn
+
≤ − ≤ ∀∈
Cách 3: Dãy số
()
n
u
có
1 23
. ...
nn
u v vv v=
với
*
0,
n
vn
> ∀∈
Ta làm trội
1k
k
k
a
v
a
+
≤
Lúc đó
31
2
12
. ...
n
n
n
aa
a
u
aa a
+
≤
Suy ra
*
1
1
,
n
n
a
u Mn
a
+
≤ ≤ ∀∈
Phương pháp 2: Dự đoán và chứng minh bằng phương pháp quy nạp.
Nếu dãy số
()
n
u
được cho bởi một hệ thức truy hồi thì ta có thể sử dụng phương pháp quy nạp
để chứng minh
Chú ý: Nếu dãy số
()
n
u
giảm thì bị chặn trên, dãy số
()
n
u
tăng thì bị chặn dưới
* Công thức giải nhanh một số dạng toán về dãy số bị chặn
Dãy số
()
n
u
có
( )
1
n
n
uq q= ≤
bị chặn
Dãy số
()
n
u
có
( )
1
n
n
uq q= <−
không bị chặn
Dãy số
()
n
u
có
n
n
uq
=
với
1q >
bị chặn dưới
Dãy số
()
n
u
có
n
u an b= +
bị chặn dưới nếu
0a >
và bị chặn trên nếu
0a <
Dãy số
()
n
u
có
2
n
u an bn c= ++
bị chặn dưới nếu
0a >
và bị chặn trên nếu
0a <
Dãy số
()
n
u
có
1
1 10
...
mm
nm m
u a n a n an a
−
−
= + ++ +
bị chặn dưới nếu
0
m
a >
và bị chặn trên nếu
0
m
a <
Dãy số
()
n
u
có
(
)
1
1 10
...
nm m
n mm
u q a n a n an a
−
−
= + ++ +
với
0
m
a ≠
và
1q <−
không bị chặn
Dãy số
()
n
u
có
1
1 10
...
mm
nm m
u a n a n an a
−
−
= + ++ +
bị chặn dưới với
0
m
a >
Dãy số
()
n
u
có
1
3
1 10
...
mm
nm m
u a n a n an a
−
−
= + ++ +
bị chặn dưới nếu
0
m
a >
và bị chặn trên
nếu
0
m
a <

CHUYÊN ĐỀ II – TOÁN – 11 – DÃY SỐ – CẤP SỐ CỘNG – CẤP SỐ NHÂN
Page 12
Sưu tầm và biên soạn
Dãy số
()
n
u
có
(
)
( )
n
Pn
u
Qn
=
trong đó
( )
Pn
và
( )
Qn
là các đa thức, bị chặn nếu bậc của
( )
Pn
nhỏ hơn hoặc bằng bậc của
(
)
Qn
Dãy số
()
n
u
có
( )
( )
n
Pn
u
Qn
=
trong đó
(
)
Pn
và
( )
Qn
là các đa thức, bị chặn dưới hoặc bị chặn
trên nếu bậc của
( )
Pn
lớn hơn bậc của
(
)
Qn
Câu 12: Xét tính bị chặn của dãy số
()
n
u
biết
1
23
n
u
n
−
=
+
.
Lời giải
Ta có
** *
11 1 1
2 3 5, 0 , 0,
235 523
nn n n
nn
−
+ ≥ ∀∈ ⇒ < ≤ ∀∈ ⇒− ≤ < ∀∈
++
1
0
5
n
u⇒− ≤ <
Suy ra dãy số
()
n
u
bị chặn
Giải nhanh: dãy số
()
n
u
có
n
u
có bậc của tử thấp hơn bậc của mẫu nên bị chặn
Câu 13: Xét tính bị chặn của dãy số
()
n
u
biết
45
1
n
n
u
n
+
=
+
.
Lời giải
Ta có
*
45
0,
1
n
n
un
n
+
= > ∀∈
+
*
4 5 4( 1) 1 1 1 9 9
44 ,
1 1 1 22 2
nn
nn
u un
nn n
+ ++
= = = + ≤ + = ⇒ ≤ ∀∈
++ +
Suy ra
*
9
0,
2
n
un< ≤ ∀∈
Vậy dãy số
()
n
u
bị chặn
Giải nhanh: dãy số
()
n
u
có
n
u
có bậc của tử bằng bậc của mẫu nên bị chặn
Câu 14: Xét tính bị chặn của dãy số
()
n
u
biết
3
2
1
n
n
u
n
=
+
.
Lời giải
Ta có
3
*
2
0, ( )
1
nn
n
u nu
n
= > ∀∈ ⇒
+
bị chặn dưới
BÀI TẬP TỰ LUẬN.
2

CHUYÊN ĐỀ II – TOÁN – 11 – DÃY SỐ – CẤP SỐ CỘNG – CẤP SỐ NHÂN
Page 13
Sưu tầm và biên soạn
Câu 15: Xét tính bị chặn của dãy số
()
n
u
biết
22 2
11 1 1
...
22 3
n
u
n
=+ + ++
. Mệnh đề nào sau đây đúng ?
Lời giải
Xét
( )
2
1 1 11
,2
11
k
k k kk k
< = − ∀≥
−−
Suy ra
1 1 11 11 11 1 1 31 3
1 ...
2 2 23 34 56 1 2 2
n
u
nn n
<+− + − + − + − ++ − =−<
−
3
0 ,*
2
n
un⇒ < < ∀∈
Vậy
()
n
u
bị chặn
DẠNG 4: TÍNH TỔNG CỦA DÃY SỐ
Dạng 4.1: Tính tổng của dãy số cách đều
Giải sử cần tính tổng:
12
...
n
Saa a= + ++
. Trong đó:
1nn
aa d
−
= +
- Tự luận:
Ta có:
( ) ( ) ( ) ( )
1 21 1 1
2 ...
nn n n
S aa a a a a naa
−
=+++ +++= +
Từ đó suy ra:
( )
1
n.
2
n
aa
S
+
=
- Trắc nghiệm:
Công thức tính nhanh:
+ Số hạng tổng quát của dãy số cách đều là:
(
)
1
1
n
uu n d
=+−
với d là khoảng cách giữa 2 số
hạng
+ Số số hạng =: + 1
+ Tổng = •: 2
- Casio
Bước 1: Từ công thức của tổng tìm số hạng tổng quát của tổng và số số hạng.
Bước 2: Sử dụng công cụ tính:
∑
y
nhập số hạng tổng quát của dãy số
y
nhập
x
chạy từ 1
tới
n =
số số hạng
y
=.
PHƯƠNG PHÁP.
1
BÀI TẬP TỰ LUẬN.
2

CHUYÊN ĐỀ II – TOÁN – 11 – DÃY SỐ – CẤP SỐ CỘNG – CẤP SỐ NHÂN
Page 14
Sưu tầm và biên soạn
Câu 16: Tính
1 3 5 ... 4001S =+++ +
?
Lời giải
Ta có:
2 (1 4001) (3 3999) (5 3997) ... (4001 1) 4002 2001S =++++++++=⋅
⇒
4002.2001
4004001
2
S = =
+) Giải theo phương pháp trắc nghiệm:
Số số hạng:
4001 1
1 2001
2
n
−
= +=
Tổng:
(1 4001).2001
4004001
2
S
+
= =
+) Giải theo Casio
Công thức số hạng tổng quát của dãy là:
1
( 1) 1 ( 1).2 2 1
n
uu n d n n=+− =+− = −
Số số hạng của dãy là 2001
Nhập máy tính cho ta kết quả: 4004001
+) Những sai lầm thường gặp:
- Tính sai số số hạng của dãy
- Tìm sai công thức số hạng tổng quát của dãy số khi làm với máy tính Casio
Lời bình: Nhận thấy việc tìm số hạng tổng quát của dãy đối với HS trung bình, yếu là tương
đối khó khăn. Vì thế ta nên sử dụng công thức giải nhanh để tìm số số hạng và tổng của dãy
một cách nhanh chóng. Ở bài tập này thì việc vận dụng công thức tính nhanh sẽ nhanh hơn
Casio nhé các em!
Câu 17: Cho tổng
( ) 2 4 6 ... 2Sn n=+++ +
. Khi đó
30
S
bằng?
Lời giải
Ta có:
50
2 4 6 60S = + + +…+
2 (2 60) (4 58) (6 56) (60 2)S
=++++++…++
(2 60).30
( ) 930
2
Sn
+
= =
+) Giải theo phương pháp trắc nghiệm:
Số hạng thứ 30:
50
2.30 60u = =
Số số hạng:
30n =
Tổng:
(2 60).30
930
2
S
+
= =
+) Giải theo Casio
Công thức số hạng tổng quát của dãy là:
2n
Số số hạng của dãy là:
30
Nhập máy tính cho ta kết quả:
930
Những sai lầm thường gặp:
- Tìm sai số hạng thứ
n
.

CHUYÊN ĐỀ II – TOÁN – 11 – DÃY SỐ – CẤP SỐ CỘNG – CẤP SỐ NHÂN
Page 15
Sưu tầm và biên soạn
Lời bình: Trong bài tập này HS cần chú ý tới số hạng tổng quát trong dãy đã cho sẵn. Từ đó sử
dụng để tìm số hạng thứ n hoặc sử dụng trong việc bấm máy tính Casio một cách nhanh chóng
tìm được kết quả.
Câu 18: Cho dãy số
( )
n
u
xác định bởi:
1
150u =
và
1
3
nn
uu
−
= −
với mọi
2n ≥
Khi đó tổng
100
số hạng
đầu tiên là:
Lời giải
+) Giải tự luận:
Ta có:
21
32
100 99
3 150 3 150 1.3 147
3 150 3 3 150 2.3 144
3 150 99.3 147
= −= −= − =
= −= −−= − =
= −= − =−
uu
uu
uu
100
150 147 144 147S = + + +…+−
100
2 (150 147) (147 144) (144 141) ( 147 150)S =−+−+−+…+−+
100
(150 147) 100
150
2
S
−⋅
= =
+) Giải theo phương pháp trắc nghiệm:
Số hạng thứ 100:
100 1
( 1) 150 99.( 3) 147u und= + − = + −=−
Số số hạng:
100n =
Tổng:
(150 147) 100
150
2
S
−⋅
= =
+) Giải theo Casio
Công thức số hạng tổng quát của dãy là:
150 3( 1) 3 153
n
u nn= − −=−+
Số số hạng của dãy là:
100n =
Nhập máy tính cho ta kết quả:
150
Những sai lầm thường gặp:
- Tìm sai số hạng thứ n của dãy
- Tìm sai công thức số hạng tổng quát của dãy số khi làm với máy tính Casio
Lời bình: HS cần ghi nhớ công thức số hạng tổng quát của dãy số cách đều để sử dụng tìm số
hạng thứ
n
và rút ra công thức số hạng tổng quát của dãy một cách nhanh chóng để xử lý bài
toán.
Dạng 4.2: Tính tổng của dãy số bằng phương pháp khử liên tiếp
Giả sử cần tính tổng: .
- Tự luận:
12
...
n
Saa a= + ++
PHƯƠNG PHÁP.
1

CHUYÊN ĐỀ II – TOÁN – 11 – DÃY SỐ – CẤP SỐ CỘNG – CẤP SỐ NHÂN
Page 16
Sưu tầm và biên soạn
Bước 1: Ta tìm cách tách: ; ;.
Bước 2: Rút gọn:
- Trắc nghiệm:
+ Một số công thức tách thường sử dụng:
+ Nhận định kết quả của tổng là:
- Casio:
Làm tương tự như dạng 1
Câu 19: Tính tổng sau:
Lời giải
Ta có:
Do đó:
+) Giải theo phương pháp trắc nghiệm:
Nhận thấy:
Nhận định:
+) Giải bằng Casio
Số hạng tổng quát của dãy là:
Số số hạng của dãy là:
Nhập máy tính cho ta kết quả:
Những sai lầm thường gặp:
- Tách sai các số hạng
112
a bb= −
2 23
a bb= −
122 3 11 1
b ...
nn n
Sbbb bb bb
++
=− + −++ − =−
11
n(n a)
a
n na
•=−
++
2 11
n(n a)(n 2a) ( ) ( )( 2 )
a
nna nan a
•=−
++ + + +
2
2 22 2
2 11
n (n a) ( )
na a
n na
+
•=−
++
. ! ( 1)! !nn n n• =+−
11n
Sbb
+
= −
222 2
...
1.3 3.5 5.7 97.99
S = + + ++
1 111 11
; ;...
1.3 1 3 3.5 3 5
=−=−
1 1 1 1 1 1 1 98
... 1
1 3 3 5 97 99 99 99
S =−+−++ − =− =
1 111 11
; ;...
1.3 1 3 3.5 3 5
=−=−
1 98
1
99 99
S =−=
2
(2 1)(2 1)
n
u
nn
=
−+
49n =
( )
2 1 97 49nn−= ⇔ =
98
99
S =
BÀI TẬP TỰ LUẬN.
2

CHUYÊN ĐỀ II – TOÁN – 11 – DÃY SỐ – CẤP SỐ CỘNG – CẤP SỐ NHÂN
Page 17
Sưu tầm và biên soạn
- Tìm sai số hạng tổng quát của dãy số
Lời bình: Học sinh cần chuyển các số hạng của dãy về đúng dạng và tách theo công thức:
. Ở bài tập này việc làm bằng máy tính Casio là khó khăn và phức tạp hơn
vì chưa có sẵn số hạng tổng quát và số số hạng.
Câu 20: Cho tổng . Khi đó công thức của là:
Lời giải
Ta có:
Suy ra:
Vậy:
+) Giải theo phương pháp trắc nghiệm:
Nhận thấy:
Nhận định:
Những sai lầm thường gặp:
- Tách sai các số hạng
Lời bình: Học sinh cần chuyển các số hạng của dãy về đúng dạng và tách theo công thức:
Câu 21: Cho tổng . Tính
Lời giải
Cách 1:
Ta có:
Suy ra:
Vậy:
11
n(n a)
a
n na
•=−
++
111 1
...
1.2.3 2.3.4 3.4.5 n(n 1)(n 2)
n
S = + + ++
++
n
S
2.1 1 1 2.1 1 1
; ;...
1.2.3 1.2 2.3 2.3.4 2.3 3.4
=−=−
1 1 1 1 1 1 1 1 ( 3)
2 ...
1.2 2.3 2.3 3.4 ( 1) ( 1)( 2) 1.2 ( 1)( 2) 2( 1)( 2)
n
nn
S
nn nn nn nn
+
=−+−++ − =− =
+ ++ ++ ++
( 3)
4( 1)( 2)
n
nn
S
nn
+
=
++
2.1 1 1 2.1 1 1
; ;...
1.2.3 1.2 2.3 2.3.4 2.3 3.4
=−=−
1 1 1 ( 3)
2 1.2 ( 1)( 2) 4( 1)( 2)
n
nn
S
nn nn
+
=−=
++ ++
2 11
n(n a)(n 2a) ( ) ( )( 2 )
a
nna nan a
•=−
++ + + +
222 2
3 5 7 21
...
(1.2) (2.3) (3.4) [n( 1)]
n
n
S
n
+
=++++
+
10
S
( ) ( )
22
3 11 1 11
; ;...
14 49
1.2 2.3
=−=−
( )
2
2 22
1 1 1 1 1 1 1 1 ( 2)
...
1 4 4 9 1 ( 1) ( 1)
1
n
nn
S
n nn
n
+
=−+−++ − =− =
++
+
10
2
10(10 2) 120
(10 1) 121
S
+
= =
+

CHUYÊN ĐỀ II – TOÁN – 11 – DÃY SỐ – CẤP SỐ CỘNG – CẤP SỐ NHÂN
Page 18
Sưu tầm và biên soạn
Cách 2:
Ta có:
Suy ra:
+) Giải theo phương pháp trắc nghiệm:
Nhận thấy:
( )
( )
22
3 11 5 11
; ;...
14 49
1.2 2.3
=−=−
Nhận định: . Suy ra:
+) Casio
Công thức số hạng tổng quát của dãy là:
Số số hạng của dãy là:
Nhập máy tính cho ta kết quả:
Những sai lầm thường gặp:
- Tách sai các số hạng
Lời bình: Học sinh cần chuyển các số hạng của dãy về đúng dạng và tách theo công thức:
.
Dạng 4.3: Tính tổng bằng cách chuyển về phương trình có ẩn là tổng cần tính
Giả sử cần tính tổng: .
- Tự luận:
Sơ đồ giải: Từ công thức của tổng S ta chuyển về phương trình chứa ẩn
S
Giải pt
S
- Trắc nghiệm:
Tổng có dạng: với
- Casio:
Làm tương tự như dạng 1
( )
10
2
222
3 5 7 21
...
(1.2) (2.3) (3.4)
10.11
S =++++
10
22 2
1 1 1 1 1 1 1 1 120
...
1 4 4 9 10 11 1 11 121
S =−+−++ − =− =
22
1 1 ( 2)
1 ( 1) ( 1)
n
nn
S
nn
+
=−=
++
10
2
10(10 2) 120
(10 1) 121
S
+
= =
+
( )
2
21
1
n
n
u
nn
+
=
+
10n =
120
121
2
2 22 2
2 11
n (n a) ( )
na a
n na
+
•=−
++
12
...
n
Saa a= + ++
( )
1
1
2
11 1 1
1
...
1
n
n
ua
S u ua ua ua S
a
+
−
= + + ++ ⇒=
−
1a ≠
PHƯƠNG PHÁP.
1

CHUYÊN ĐỀ II – TOÁN – 11 – DÃY SỐ – CẤP SỐ CỘNG – CẤP SỐ NHÂN
Page 19
Sưu tầm và biên soạn
Câu 22: Tính tổng: ?
Lời giải
Ta có:
.
+) Giải theo phương pháp trắc nghiệm:
Áp dụng công thức tính nhanh với ta có: .
+) Giải theo Casio
Công thức số hạng tổng quát của dãy là:
Số số hạng của dãy là:
Nhập máy tính cho ta kết quả: .
Ta gán: )
Lấy từng kết quả ở 4 đáp án trừ cho A khi nào bằng 0 thì chọn đáp án đó.
+) Những sai lầm thường gặp:
- Tìm sai số hạng tổng quát của dãy số
Lời bình: Khi làm với máy tính Caiso các em cần tìm chính xác số hạng tổng quát của dãy số
việc này quyết định máy có đưa ra được kết quả chính xác hay không. Ở bài tập này nếu các em
thuộc được công thức tính nhanh thì ta có thể giải quyết bài toán hết sức nhanh chóng. Chú ý
rằng bài toán này có thể hạn chế Casio bằng cách cho 2 đáp án ở “gần nhau” chẳng hạn phương
án B. thì khi làm bằng Casio sẽ có 2 đáp án không phân biệt được là
B và C
Câu 23: Tính tổng ?
Lời giải
Đặt:
Ta có:
2 50
1 3 3 ... 3S =++ + +
2 3 51
3 3 3 3 ... 3S =++ +
( ) ( )
2 3 51 2 50
3 3 3 3 ... 3 1 3 3 ... 3SS⇒ − = + + + − ++ +
51
51
31
2 31
2
SS
−
⇒ = −⇒ =
1
1; 3ua= =
51
31
2
S
−
=
1
3
n
n
u
−
=
51n =
24
1,076846982.10
24
1,076846982.10 A→
51
3
2
100
2 3 100
11 1 1
4.5 . ... 1
55 5 5
S
= + + ++ +
2 3 100
11 1 1
...
55 5 5
M =+ + ++
2 99
11 1
5 1 ...
55 5
M =++ ++
BÀI TẬP TỰ LUẬN.
2
CHUYÊN ĐỀ II – TOÁN – 11 – DÃY SỐ – CẤP SỐ CỘNG – CẤP SỐ NHÂN
Page 20
Sưu tầm và biên soạn
+) Giải theo phương pháp trắc nghiệm:
Đặt:
Áp dụng công thức tính nhanh với: ta có:
Câu 24: Tính tổng: . Tính
Lời giải
Cách 1:
Ta có:
Đặt:
Ta có:
Cách 2:
Ta có:
Đặt:
2 99 2 3 100 100
11 1 11 1 1 1
5 1 ... ... 1
55 5 55 5 5 5
MM
⇒ − = ++ ++ − + + ++ =−
100
100 100
1 51
41
5 4.5
MM
−
⇒ =− ⇒=
100
100 100
100
51
45 1 5
4.5
S
−
⇒ =⋅ ⋅ +=
2 3 100
11 1 1
...
55 5 5
M =+ + ++
1
11
;
55
ua= =
100
100
100
11
1
55
51
1
4.5
1
5
M
−
−
= =
−
100
100 100
100
51
45 1 5
4.5
S
−
⇒ =⋅ ⋅ +=
111 1
1 1 1 ... 1
248 2
n
S
=− +− +− ++−
10
S
10
2 3 10 2 3 10
1 1 1 1 11 1 1
1 1 1 ... 1 10 ...
2 2 2 2 22 2 2
S
=− +− +− ++− =− + + ++
2 3 10
11 1 1
...
22 2 2
M =+ + ++
29
11 1
2 1 ...
22 2
M =++ ++
2 9 2 3 10 10
11 1 11 1 1 1
2 1 ... ... 1
22 2 22 2 2 2
MM M
⇒ − = = ++ ++ − + + ++ =−
10 10
11
10 1 9
22
S⇒ = −+ = +
23
11 1 1
...
22 2 2
n
n
Sn
=− + + ++
23
11 1 1
...
22 2 2
n
M =+ + ++

CHUYÊN ĐỀ II – TOÁN – 11 – DÃY SỐ – CẤP SỐ CỘNG – CẤP SỐ NHÂN
Page 21
Sưu tầm và biên soạn
Ta có:
+) Giải theo phương pháp trắc nghiệm:
Ta có:
+) Giải theo Casio
Nhận xét:
Nhập máy tính tổng với số hạng tổng quát: , số số hạng:
ta được kết quả: . Nhập tiếp: 10 – Ans được kết quả:
Ta gán: )
Lấy từng kết quả ở 4 đáp án trừ cho A khi nào bằng 0 thì chọn đáp án đó.
Dạng 4.4: Tính tổng bằng cách đưa về các tổng đã biết
Giải sử cần tính tổng: .
- Tự luận:
Tìm cách tách: . Trong đó: đã biết công thức tính tổng.
- Trắc nghiệm:
21
11 1
2 1 ...
22 2
n
M
−
=++ ++
2 1 23
11 1 11 1 1 1
2 1 ... ... 1
22 2 22 2 2 2
n nn
MM M
−
⇒ − = = ++ ++ − + + ++ =−
1
1
2
n
n
Sn⇒ = −+
10
10 10
11
10 1 9
22
S⇒ = −+ = +
10
2 3 10
11 1 1
10 ...
22 2 2
S
= − + + ++
10
2 3 10 10
11
1
22
11 1 1 1
... 1
1
22 2 2 2
1
2
−
+ + ++ = =−
−
10 10
11
10 1 9
22
S⇒ = −+ = +
23
11 1 1
...
22 2 2
n
n
Sn
=− + + ++
23
11 1 1
...
22 2 2
n
+ + ++
1
2
n
n
u =
10
n
u =
1023
1024
9217
1024
9217
1024
A→
12
...
nn
S aa a= + ++
123
...
n
S SS S=+++
12 3
; ;S ...SS
PHƯƠNG PHÁP.
1
CHUYÊN ĐỀ II – TOÁN – 11 – DÃY SỐ – CẤP SỐ CỘNG – CẤP SỐ NHÂN
Page 22
Sưu tầm và biên soạn
Ta có thể dùng phương pháp thử giá trị
n
vào các đáp án để loại trừ và chọn ra đáp án đúng.
- Casio:
Làm tương tự như dạng 1
Câu 25: Tính: . Biết rằng:
Lời giải
Câu 26: Cho: . Tính biết rằng:
.
Lời giải
Ta có:
Câu 27: Cho tổng: với . Biết: . Giá trị của k là:
Lời giải
Ta có:
DẠNG 5: XÁC ĐỊNH CÔNG THỨC SỐ HẠNG TỔNG QUÁT CỦA DÃY SỐ
Nếu có dạng thì biến đổi thành hiệu của hai số hạng, dựa vào đó thu
gọn .
Nếu dãy số được cho bởi một hệ thức truy hồi, tính vài số hạng đầu của dãy số, từ đó dự
đoán công thức tính theo n, rồi chứng minh công thức này bằng phương pháp quy nạp. Ngoài
ra cũng có thể tính hiệu dựa vào đó để tìm công thức tính theo n.
1.3 2.5 3.7 ... (2 1)
n
S nn=++++ +
2 22 2
11
( 1) ( 1)(2 1)
1 2 3 ... ; 1 2 3 ...
26
nn
ii
nn nn n
i ni n
= =
+ ++
=++++= =+ + ++ =
∑∑
22
1 1 11
2 ( 1)(2 n 1) ( 1) ( 1)(4 5)
(2 1) (2i ) 2
626
n n nn
i i ii
nn nn nn n
S ii i i i
= = = =
++ + ++
= += += + = + =
∑ ∑ ∑∑
1.2 3.4 5.6 ... (2 1).2
n
S nn=++++ −
100
S
2 22 2
11
( 1)(2 1)
2 2 4 6 ... 2 ( 1); 1 2 3 ...
6
nn
ii
nn n
i n nn i n
= =
++
=++++ = + =+ + ++ =
∑∑
22
1 1 11
4 ( 1)(2 n 1) ( 1)(4 1)
2 (2 1) (4 i 2 ) 4 2 ( 1)
63
n n nn
n
i i ii
nn nn n
S i i i i i nn
= = = =
++ +−
= −= − = − = − +=
∑ ∑ ∑∑
100
100.(100 1)(4.100 1)
1343300
3
S
+−
⇒= =
1.4 2.7 3.10 ... .(3 1)
n
S nn= + + ++ +
*
n ∈
294
k
S =
22 2
1 1 11
3 ( 1)(2 n 1) ( 1)
(3 1) (3i ) 3 ( 1)
62
n n nn
n
i i ii
nn nn
S i i i i i nn
= = = =
++ +
= += += + = + = +
∑ ∑ ∑∑
2 32 2
( 1) 294 2 294 ( 6)( 8 49) 0 6
k
S kk k k k k k k k⇒ = + = ⇔ + += ⇔ − + + =⇔=
( )
n
u
12
...
nn
u aa a= + ++
k
a
n
u
( )
n
u
n
u
1nn
uu
+
−
( )
n
u
BÀI TẬP TỰ LUẬN.
2
PHƯƠNG PHÁP.
1

CHUYÊN ĐỀ II – TOÁN – 11 – DÃY SỐ – CẤP SỐ CỘNG – CẤP SỐ NHÂN
Page 23
Sưu tầm và biên soạn
Câu 28: Cho dãy số có . Đặt . Xác định công thức tính theo n.
Lời giải
Ta có , do đó:
.
Câu 29: Xác định công thức tính số hạng tổng quát theo n của dãy số sau: .
Lời giải
Ta có:
Từ các số hạng đầu trên, ta dự đoán số hạng tổng quát có dạng:
Ta dùng phương pháp chứng minh quy nạp để chứng minh công thức đúng.
Với . Vậy đúng với
Giả sử đúng với Có nghĩa ta có:
Ta cần chứng minh đúng với Có nghĩa là ta phải chứng minh:
Thật vậy từ hệ thức xác định dãy số và theo ta có:
Vậy đúng khi Kết luận đúng với mọi số nguyên dương
n
.
Câu 30: Xác định công thức tính số hạng tổng quát theo n của dãy số sau:
Lời giải
( )
n
a
( )
1
1
k
a
kk
=
+
1
n
nk
k
ua
=
=
∑
( )
n
u
( )
1 11
11
k
a
kk k k
= = −
++
1
1 11 1 1 1 1 1
1 ... 1
2 23 1 1 1
n
nk
k
ua
n n nn n
=
= =−+−++ −+− =−
− ++
∑
n
u
1
1
3
2
nn
u
uu
+
=
= +
21
2325.uu= +=+=
32
2 5 2 7.uu= +=+=
43
2 7 2 9.uu= +=+=
54
2 9 2 11.uu= +=+=
n
u
( )
2 1 1
n
un n= + ∀≥ ∗
( )
∗
1
1; 2.1 1 3nu= = +=
( )
∗
1.n =
( )
∗
.nk=
( )
2 1 2
k
uk= +
( )
∗
1.nk= +
( )
1
2 1 1 2 3.
k
uk k
+
= + += +
( )
2
1
22 122 3.
kk
uu k k
+
= += ++= +
( )
∗
1.nk= +
( )
∗
n
u
1
3
1
1
1.
nn
u
n
u un
+
=
∀≥
= +
BÀI TẬP TỰ LUẬN.
2

CHUYÊN ĐỀ II – TOÁN – 11 – DÃY SỐ – CẤP SỐ CỘNG – CẤP SỐ NHÂN
Page 24
Sưu tầm và biên soạn
Ta có:
Từ đó suy ra:
Cộng từng vế n đẳng thức trên:
Bằng phương pháp quy nạp ta chứng minh được:
Vậy
Mở rộng phương pháp:
Nếu dãy số
( )
n
u
được cho dưới dạng liệt kê thì ta có thể thử giá trị
n
vào từng đáp án.
Nếu dãy số
( )
n
u
được cho bởi một hệ thức truy hồi tính vài số hạng đầu của dãy số sau đó ta có
thể thử giá trị
n
vào từng đáp án.
33
11
.
n n nn
u un u un
++
=+⇒ −=
1
1u =
3
21
1uu−=
3
32
2uu−=
3
43
3uu−=
..............
( )
3
12
2
nn
uu n
−−
−=−
( )
3
1
1
nn
uu n
−
−=−
( ) ( )
33
333
12132 1 2 1
... 1 1 2 3 ... 2 1
n n nn
uuuuu u u uu n n
−− −
+ −+ − ++ − + − =++ + ++ − + −
( ) ( )
33
333
1 1 2 3 ... 2 1 .
n
u nn⇔=+++++− +−
( )
( )
2
2
3
333
1.
1 2 3 ... 1
4
nn
n
−
+ + ++ − =
( )
2
2
1
1
4
n
nn
u
−
= +
CHUYÊN ĐỀ II – TOÁN – 11 – DÃY SỐ - CẤP SỐ CỘNG – CẤP SỐ NHÂN
Page 12
Sưu tầm và biên soạn
BÀI 5: DÃY SỐ
DẠNG 1. BIỂU DIỄN DÃY SỐ, TÌM CÔNG THỨC TỔNG QUÁT
Câu 1: Cho dãy số có các số hạng đầu là:9; 99; 999; 9999,… Số hạng tổng quát của dãy số này là:
A.
1
n
n
u
n
=
+
B.
10 1
n
n
u = −
. C.
9
n
n
u =
D.
9
n
un=
Câu 2: Cho dãy số
1325
, , , ,...
2537
. Công thức tổng quát
n
u
nào là của dãy số đã cho?
A.
*
1
n
n
un
n
= ∀∈
+
. B.
*
2
n
n
n
un
= ∀∈
. C.
*
1
3
n
n
un
n
+
= ∀∈
+
. D.
*
2
21
n
n
un
n
= ∀∈
+
.
Câu 3: Cho dãy số có các số hạng đầu là:
5;10;15;20;25;...
Số hạng tổng quát của dãy số này là:
A.
5( 1)
n
un= −
. B.
5
n
un
=
. C.
5
n
un= +
. D.
5. 1
n
un
= +
.
Câu 4: Cho dãy số có các số hạng đầu là:
8,15,22,29,36,...
.Số hạng tổng quát của dãy số này là:
A.
77
n
un= +
. B.
7.
n
un=
.
C.
7. 1
n
un= +
. D.
n
u
: Không viết được dưới dạng công thức.
Câu 5: Cho dãy số có các số hạng đầu là:
;...
5
4
;
4
3
;
3
2
;
2
1
;0
.Số hạng tổng quát của dãy số này là:
A.
1
n
n
u
n
+
=
. B.
1
n
n
u
n
=
+
. C.
1
n
n
u
n
−
=
. D.
2
1
n
nn
u
n
−
=
+
.
Câu 6: Cho dãy số có các số hạng đầu là:
1;1; 1;1; 1; ...−−−
.Số hạng tổng quát của dãy số này có dạng
A.
1
=
n
u
. B.
1−=
n
u
. C.
n
n
u )1(−=
. D.
( )
1
1
n
n
u
+
= −
.
Câu 7: Cho dãy số
( )
n
u
xác định bởi
( )
1
1
1
1
3
nn
u
n
uu
+
=
≥
=
. Tìm công thức số hạng tổng quát của dãy số
trên.
A.
3=
n
n
u
. B.
1
3
−
=
n
n
u
. C.
1
32
+
= −
n
n
u
. D.
32
= −
n
n
u
.
Câu 8: Cho dãy số có các số hạng đầu là:
0.1;0.01;0.001;0.0001...
. Số hạng tổng quát của dãy số này có
dạng?
A.
=
0
0.00...01
n
n sè
u
. B.
−
=
10
0.00...01
n
n sè
u
. C.
1
1
10
n
n
u
−
=
. D.
1
1
10
n
n
u
+
=
.
CHƯƠNG
II
DÃY SỐ
CẤP SỐ CỘNG – CẤP SỐ NHÂN
HỆ THỐNG BÀI TẬP TRẮC NGHIỆM.
III

CHUYÊN ĐỀ II – TOÁN – 11 – DÃY SỐ - CẤP SỐ CỘNG – CẤP SỐ NHÂN
Page 13
Sưu tầm và biên soạn
Câu 9: Cho dãy số
( )
n
u
xác định bởi:
( )
1
1
1
1
2
nn
u
n
uu
+
=
≥
= +
. Xác định công thức của số hạng tổng quát.
A.
21
n
un= −
. B.
32
n
un= −
. C.
43
n
un= −
. D.
87
n
un= −
.
Câu 10: Cho dãy số có các số hạng đầu là:
2345
11 1 1 1
; ; ; ; ;...
33 3 3 3
Số hạng tổng quát của dãy số này là?
A.
1
11
.
33
n
n
u
+
=
. B.
1
1
3
n
n
u
+
=
. C.
1
3
n
n
u =
. D.
1
1
3
n
n
u
−
=
.
Câu 11: Cho dãy số
( )
n
u
với
1
1
5
nn
u
u un
+
=
= +
.Số hạng tổng quát
n
u
của dãy số là số hạng nào dưới đây?
A.
( )
1
2
n
nn
u
−
=
. B.
( )
1
5
2
n
nn
u
−
= +
. C.
( )
1
5
2
n
nn
u
+
= +
. D.
( )( )
12
5
2
n
nn
u
++
= +
.
Câu 12: Cho dãy số với . Công thức số hạng tổng quát của dãy số này là:
A. . B. . C. . D. .
Câu 13: Cho dãy số có các số hạng đầu là:
2;0; 2; 4; 6;...−
.Số hạng tổng quát của dãy số này có dạng?
A.
nu
n
2−=
. B.
( )
nu
n
+−= 2
. C.
( )
)1(2 +−= nu
n
. D.
( ) ( )
22 1
n
un=−+ −
.
Câu 14: Cho dãy số có các số hạng đầu là:
;
3
1
;
3
1
;
3
1
;
3
1
;
3
1
5432
….Số hạng tổng quát của dãy số này là?
A.
1
3
1
3
1
+
=
n
n
u
. B.
1
3
1
+
=
n
n
u
. C.
n
n
u
3
1
=
. D.
1
3
1
−
=
n
n
u
.
Câu 15: Cho dãy số
( )
n
u
với
( )
1
2
1
1
1
n
nn
u
uu
+
=
= +−
. Số hạng tổng quát
n
u
của dãy số là số hạng nào dưới
đây?
A.
1
n
un= +
. B.
1
n
un= −
. C.
( )
2
11
n
n
u =+−
. D.
n
un=
.
Câu 16: Cho dãy số
( )
n
u
với
( )
1
21
1
1
1
n
nn
u
uu
+
+
=
= +−
. Số hạng tổng quát
n
u
của dãy số là số hạng nào dưới
đây?
A.
2
n
un= −
. B.
n
u
không xác định. C.
1
n
un= −
. D.
n
un= −
với mọi
n
.
Câu 17: Cho dãy số
( )
n
u
với
1
2
1
1
nn
u
u un
+
=
= +
. Số hạng tổng quát
n
u
của dãy số là số hạng nào dưới đây?
A.
( )( )
12 1
1
6
n
nn n
u
++
= +
. B.
( )( )
12 2
1
6
n
nn n
u
−+
= +
.
C.
( )( )
12 1
1
6
n
nn n
u
−−
= +
. D.
( )( )
12 2
1
6
n
nn n
u
+−
= +
.
( )
n
u
1
1
1
2
2
+
=
= −
nn
u
uu
( )
1
21
2
=+−
n
un
( )
1
21
2
=−−
n
un
1
2
2
= −
n
un
1
2
2
= +
n
un

CHUYÊN ĐỀ II – TOÁN – 11 – DÃY SỐ - CẤP SỐ CỘNG – CẤP SỐ NHÂN
Page 14
Sưu tầm và biên soạn
Câu 18: Cho dãy số
( )
n
u
với
1
1
2
21
nn
u
uun
+
=
−=−
. Số hạng tổng quát
n
u
của dãy số là số hạng nào dưới
đây?
A.
( )
2
21
n
un=+−
. B.
2
2
n
un
= +
. C.
( )
2
21
n
un=++
. D.
( )
2
21
n
un=−−
.
Câu 19: Cho dãy số
( )
n
u
với
1
1
2
1
2
n
n
u
u
u
+
= −
=−−
. Công thức số hạng tổng quát của dãy số này là:
A.
1
n
n
u
n
−
= −
. B.
1
n
n
u
n
+
=
. C.
1
n
n
u
n
+
= −
. D.
1
n
n
u
n
= −
+
.
Câu 20: Cho dãy số
( )
n
u
với
1
1
1
2
2
nn
u
uu
+
=
= −
. Công thức số hạng tổng quát của dãy số này là:
A.
( )
1
21
2
n
un=+−
. B.
( )
1
21
2
n
un=−−
. C.
1
2
2
n
un= −
. D.
1
2
2
n
un= +
.
Câu 21: Cho dãy số
( )
n
u
với
1
1
1
2
n
n
u
u
u
+
= −
=
. Công thức số hạng tổng quát của dãy số này là:
A.
( )
1
1.
2
n
n
u
= −
. B.
( )
1
1
1.
2
n
n
u
+
= −
. C.
1
1
2
n
n
u
−
=
. D.
(
)
1
1
1.
2
n
n
u
−
= −
.
Câu 22: Cho dãy số
( )
n
u
với
1
1
2
2
nn
u
uu
+
=
=
. Công thức số hạng tổng quát của dãy số này:
A.
1n
n
un
−
=
. B.
2
n
n
u =
. C.
1
2
n
n
u
+
=
. D.
2
n
u =
.
Câu 23: Cho dãy số
(
)
n
u
với
1
1
1
2
2
nn
u
uu
+
=
=
. Công thức số hạng tổng quát của dãy số này:
A.
1
2
n
n
u
−
= −
. B.
1
1
2
n
n
u
−
−
=
. C.
1
2
n
n
u
−
=
. D.
2
2
n
n
u
−
=
.
Câu 24: Cho dãy số
( )
n
u
xác định bởi
1
*
1
2
1
2,
n
n
u
un
u
+
= −
=−− ∀∈
.
Tìm công thức số hạng tổng quát của dãy số.
A.
31−
= −
n
n
u
n
. B.
1
= −
+
n
n
u
n
. C.
1+
=
n
n
u
n
. D.
1+
= −
n
n
u
n
.
Câu 25: Cho dãy số
( )
n
u
với
( )
1
2
1
1
1
+
=
= +−
n
nn
u
uu
.Công thức tổng quát
n
u
nào dưới đây là của dãy số đã
cho?
A.
=
n
un
. B.
1= −
n
un
. C.
( )
2
11= +−
n
n
u
. D.
1= +
n
un
.
Câu 26: Gọi
( )( )
111 1
....
1.3 3.5 5.7 2 1 2 1
n
S
nn
= + + ++
−+
với mọi
*
n
. Ta có:
CHUYÊN ĐỀ II – TOÁN – 11 – DÃY SỐ - CẤP SỐ CỘNG – CẤP SỐ NHÂN
Page 15
Sưu tầm và biên soạn
A.
1
21
n
n
S
n
−
=
−
. B.
2
21
n
n
S
n
=
+
. C.
21
n
n
S
n
=
+
. D.
1
23
n
n
S
n
+
=
+
.
Câu 27: Cho dãy số
( )
n
u
xác định bởi
1
1
1
2 1, 1
nn
u
u u nn
+
=
=++ ≥
. Giá trị của
n
để
2017 2018 0
n
un−+ + =
là
A. Không có
n
. B.
1009
. C.
2018
. D.
2017
.
Câu 28: Cho hai cấp số cộng
:1;6;11;...
n
u
và
: 4;7;10;...
n
v
Mỗi cấp số có 2018 số. Hỏi có bao nhiêu
số có mặt trong cả hai dãy số trên.
A.
403
. B.
401
. C.
402
. D.
504
.
Câu 29: Cho dãy số
( )
n
u
thỏa
1
2
1
3
2 3, , 2
nn
u
u u nn n n
−
=
= + − − ∀∈ ≥
. Tính tổng
20 1 2 20
...
S uu u= + ++
A.
2022
. B.
8385080
. C.
2021
. D.
8385087
.
DẠNG 2. TÌM HẠNG TỬ TRONG DÃY SỐ
Câu 30: Cho dãy số
,
n
u
biết
2
2
21
.
3
n
n
u
n
Tìm số hạng
5
.u
A.
5
1
.
4
u =
B.
5
17
.
12
u =
C.
5
7
.
4
u =
D.
5
71
.
39
u =
Câu 31: Cho dãy số
,
n
u
biết
n
n
un1 .2 .
Mệnh đề nào sau đây sai?
A.
1
2.u
B.
2
4.u
C.
3
6.u
D.
4
8.u
Câu 32: Cho dãy số
,
n
u
biết
2
1. .
n
n
n
u
n
Tìm số hạng
3
.u
A.
3
8
.
3
u
B.
3
2.u
C.
3
2.u
D.
3
8
.
3
u
Câu 33: Cho dãy số
,
n
u
biết
2
n
n
n
u
=
. Chọn đáp án đúng.
A.
4
1
.
4
u =
B.
5
1
.
16
u =
C.
5
1
.
32
u =
D.
3
1
.
8
u =
Câu 34: Cho dãy số
,
n
u
biết
( 1) sin( )
2
n
n
n
un
π
= −
. Số hạng thứ 9 của dãy số đó là:
A. 0. B. 9. C.
−1.
D.
−9.
Câu 35: Cho dãy số
,
n
u
biết
1
1
n
u
n
=
+
. Ba số hạng đầu tiên của dãy số đó lần lượt là những số nào
dưới đây?
A.
111
;;.
234
B.
11
1; ; .
23
C.
111
;;.
246
D.
11
1; ; .
35
Câu 36: Cho dãy số
,
n
u
biết
21
2
n
n
u
n
+
=
+
. Viết năm số hạng đầu của dãy số.

CHUYÊN ĐỀ II – TOÁN – 11 – DÃY SỐ - CẤP SỐ CỘNG – CẤP SỐ NHÂN
Page 16
Sưu tầm và biên soạn
A.
12345
3 7 3 11
1,,,,
452 7
uuuuu= = = = =
. B.
12345
5 7 3 11
1,,,,
452 7
uuuuu= = = = =
.
C.
12345
5 8 3 11
1,,,,
452 7
uuuuu= = = = =
D.
12345
5 7 7 11
1,,,,
452 3
uuuuu= = = = =
.
Câu 37: Cho dãy số
,
n
u
biết
31
n
n
n
u =
−
. Ba số hạng đầu tiên của dãy số đó là
A.
111
;;.
248
B.
11 3
;; .
2426
C.
11 1
;; .
2 4 16
D.
123
;;.
234
Câu 38: Cho dãy số
,
n
u
biết
1
21
n
n
u
n
. Số
8
15
là số hạng thứ mấy của dãy số?
A. 8. B. 6. C. 5. D. 7.
Câu 39: Cho dãy số
,
n
u
biết
25
.
54
n
n
u
n
Số
7
12
là số hạng thứ mấy của dãy số?
A. 6. B. 8. C. 9. D. 10.
Câu 40: Cho dãy số
,
n
u
biết
2
1
.
1
n
n
u
n
Số
2
13
là số hạng thứ mấy của dãy số?
A. Thứ 3. B. Thứ tư. C. Thứ năm. D. Thứ 6.
Câu 41: Cho dãy số
,
n
u
biết
32
8 5 7.
n
un n n
Số
33
là số hạng thứ mấy của dãy số?
A. 5. B. 6. C. 8. D. 9.
Câu 42: Cho dãy số
n
u
với
2
37
1
n
nn
u
n
++
=
+
. Hỏi dãy số trên có bao nhiêu số hạng nhận giá trị nguyên.
A. 2. B. 4. C. 1. D. Không có.
Câu 43: Cho dãy số
n
u
với
2.
n
n
u =
Tìm số hạng
1
.
n
u
+
A.
1
2 .2.
n
n
u
B.
1
2 1.
n
n
u
C.
1
2 1.
n
un
D.
1
2 2.
n
n
u
Câu 44: Cho dãy số
n
u
với
3.
n
n
u =
Tìm số hạng
21
.
n
u
A.
2
21
3 .3 1.
n
n
u
B.
1
21
3 .3 .
nn
n
u
C.
2
21
3 1.
n
n
u
D.
21
21
3.
n
n
u
Câu 45: Cho dãy số
n
u
với
3.
n
n
u =
Số hạng
1n
u
+
bằng:
A.
31
n
+
. B.
33
n
+
. C.
3 .3
n
. D.
3( 1)n +
.
Câu 46: Cho dãy số
n
u
với
3.
n
n
u
=
Số hạng
2n
u
bằng:
A.
33
n
+
. B.
9
n
. C.
3 .3
n
. D.
2
4
n
.
Câu 47: Cho dãy số
n
u
với
1
5.
n
n
u
+
=
Tìm số hạng
1n
u
−
.
A.
1
1
5
n
n
u
−
−
=
. B.
1
5
n
n
u
−
=
. C.
1
1
5.5
n
n
u
+
−
=
. D.
1
1
5.5
n
n
u
−
−
=
.
Câu 48: Cho dãy số
n
u
với
23
1
.
1
n
n
n
u
n
+
−
=
+
Tìm số hạng
1n
u
+
.

CHUYÊN ĐỀ II – TOÁN – 11 – DÃY SỐ - CẤP SỐ CỘNG – CẤP SỐ NHÂN
Page 17
Sưu tầm và biên soạn
A.
2 13
1
1
.
1
n
n
n
u
n
B.
2 13
1
1
.
1
n
n
n
u
n
C.
23
1
.
2
n
n
n
u
n
D.
25
1
.
2
n
n
n
u
n
Câu 49: Cho dãy số
n
u
xác định bởi
1
1
2
.
1
1
3
nn
u
uu
Tìm số hạng
4
.u
A.
4
5
.
9
u
B.
4
1.u
C.
4
2
.
3
u
D.
4
14
.
27
u
Câu 50: Cho dãy số
n
u
xác định bởi
1
1
3
.
2
2
n
n
u
u
u
Mệnh đề nào sau đây sai?
A.
2
5
.
2
u
B.
3
15
.
4
u
C.
4
31
.
8
u
D.
5
63
.
16
u
Câu 51: Cho dãy số
n
u
xác định bởi
1
1
7
23
nn
u
uu
+
=
= +
khi đó
5
u
bằng:
A. 317. B. 157. C. 77. D. 112.
Câu 52: Cho dãy số
n
u
xác định bởi
1
1
1
3
nn
u
uu
+
= −
= +
. Ba số hạng đầu tiên của dãy số đó là
A.
1;2;5.−
B.
1; 4; 7.
C.
4; 7;10
D.
1; 3; 7.−
Câu 53: Cho dãy số
n
u
xác định bởi
+
=
= +
1
1
3
5
nn
u
uu
. Ba số hạng đầu tiên của dãy số đó là
A.
−3; 6; 9.
B.
−−3; 2; 7.
C.
3; 8;13
. D.
3; 5;7.
Câu 54: Cho dãy số
n
u
xác định bởi
−
= −
≥
= +
1
2
1
2
( 2)
2
nn
u
n
uun
. Số hạng thứ tư của dãy số đó bằng
A. 0. B. 93. C. 9. D. 34.
Câu 55: Cho dãy số
( )
n
u
, biết
21
n
n
n
u =
−
. Ba số hạng đầu tiên của dãy số là
A.
123
;;
234
. B.
11
1; ;
2 16
C.
11
1; ;
48
D.
23
1; ;
37
.
Câu 56: Cho dãy số
n
u
xác định bởi
1
1
1
2
1
,2
2
n
n
u
un
u
. Khi đó
3
u
có giá trị bằng
A.
3
4
. B.
4
3
. C.
2
3
. D.
3
2
.
Câu 57: Cho dãy số
( )
n
u
với
23
n
un= +
. Tìm số hạng thứ 6 của dãy số.
A.
17
. B.
5
. C.
15
. D.
7
.

CHUYÊN ĐỀ II – TOÁN – 11 – DÃY SỐ - CẤP SỐ CỘNG – CẤP SỐ NHÂN
Page 18
Sưu tầm và biên soạn
Câu 58: Cho dãy số
( )
n
u
, biết
2.3
n
n
u =
. Giá trị của
20
u
bằng
A.
19
2.3 .
. B.
20
2.3 .
. C.
20
3.
. D.
21
2.3 .
Câu 59: Cho dãy số
( )
n
u
, biết công thức số hạng tổng quát
23
n
un
= −
. Số hạng thứ 10 của dãy số bằng:
A.
17
B.
20
C.
10
D.
7
Câu 60: Cho dãy số
( )
n
u
có công thức số hạng tổng quát
83
n
un= −
. Tính
4
.
u
A.
2
. B.
7−
. C.
5−
. D.
4
−
.
Câu 61:
Cho dãy số
(
)
n
u
xác định bởi
2
1
23
n
n
u
nn
−
=
++
. Giá trị
21
u
là
A.
11
243
. B.
10
243
. C.
21
443
. D.
19
443
.
Câu 62: Cho dãy số
( )
n
u
có
2
2
1
1
n
n
u
n
−
=
+
. Tính
2
u
.
A.
2
1
5
u
=
. B.
2
2
5
u =
. C.
2
3
5
u =
. D.
2
4
5
u
=
.
Câu 63: Cho dãy số
(
)
n
u
được xác định bởi
1
1
2
3 1, 2
nn
u
uu n
−
= −
= − ∀≥
. Tìm số hạng
4
u
.
A.
4
76u
= −
. B.
4
77u = −
.
C.
4
66u
= −
. D.
4
67u
= −
.
Câu 64: Cho dãy số
( )
n
u
, biết
( )
( )
3
2
n
nn
u
−
=
. Ba số hạng đầu tiên của dãy số là
A.
13
;1;
22
. B.
1
1; ; 0
2
−−
. C.
1; 1; 0−−
. D.
13
;1;
22
.
Câu 65: Cho dãy số
( )
n
u
với
23
n
un= −
. Số hạng thứ 5 của dãy số là
A.
5
. B.
4
. C.
13
. D.
7
.
Câu 66: Cho dãy số
( )
n
u
thỏa mãn
21
n
n
u
n
+
=
. Tìm số hạng thứ
10
của dãy số đã cho.
A.
2,1
. B.
2, 2
. C.
2,0
. D.
2, 4
.
Câu 67: Cho dãy số
( )
n
u
có số hạng tổng quát
2
1
1
n
n
u
n
= −
+
. Số hạng đầu tiên của dãy là:
A.
2
. B.
3
5
. C.
0
. D.
1
2
.
Câu 68: Cho dãy số
( )
n
u
có
2
1
n
u nn=− ++
. Số
19−
là số hạng thứ mấy của dãy?
A.
5
. B.
7
. C.
6
. D.
4
.
Câu 69: Cho dãy số
( )
n
u
với
3
n
n
u
=
. Khi đó số hạng
21n
u
−
bằng
A.
1
3 .3
nn−
. B.
21
31
n−
−
. C.
2
31
n
−
. D.
2
3 .3 1
n
−
.
Câu 70: Cho dãy số
n
u
xác định bởi
1 cos
n
n
un
π
. Giá trị
99
u
bằng

CHUYÊN ĐỀ II – TOÁN – 11 – DÃY SỐ - CẤP SỐ CỘNG – CẤP SỐ NHÂN
Page 19
Sưu tầm và biên soạn
A.
99
. B.
1
. C.
1
. D.
99
.
Câu 71: Cho dãy số
(
)
n
u
với
21
n
un= +
số hạng thứ
2019
của dãy là
A.
4039
. B.
4390
. C.
4930
. D.
4093
.
Câu 72: Cho dãy số
( )
n
u
với
1 2.
n
n
u
= +
Khi đó số hạng
2018
u
bằng
A.
2018
2
. B.
2017
2017 2
+
. C.
2018
12+
. D.
2018
2018 2+
.
Câu 73: Cho dãy số
(
)
n
u
với
2
,n 1.
31
n
n
u
n
−
= ≥
+
Tìm khẳng định sai.
A.
3
1
.
10
u =
B.
10
8
.
31
u =
C.
21
19
.
64
u =
D.
50
47
.
150
u =
Câu 74: Cho dãy số
2
21
1
n
nn
u
n
+−
=
+
. Tính
11
u
.
A.
11
182
12
u
=
. B.
11
1142
12
u =
. C.
11
1422
12
u =
. D.
11
71
6
u =
.
Câu 75: Cho dãy số
( )
n
u
có số hạng tổng quát là
2
21
1
n
n
u
n
+
=
+
. Khi đó
39
362
là số hạng thứ mấy của dãy
số?
A.
20
. B.
19
. C.
22
. D.
21
.
Câu 76: Cho dãy số
( )
1
1
5
:
n
nn
u
u
u un
+
=
= +
. Số
20
là số hạng thứ mấy trong dãy?
A.
5
. B.
6
. C.
9
. D.
10
.
Câu 77: Cho dãy số
(
)
n
u
thỏa mãn
1
21
n
n
u
n
−
+
=
. Tìm số hạng thứ
10
của dãy số đã cho.
A.
51, 2
. B.
51, 3
. C.
51,1
. D.
102,3
.
Câu 78: Cho dãy số
1
1
4
nn
u
u un
+
=
= +
. Tìm số hạng thứ
5
của dãy số.
A.
16
. B.
12
. C.
15
. D.
14
.
Câu 79: Cho dãy số
( )
n
u
, biết
.
1
n
n
u
n
−
=
+
Năm số hạng đầu tiên của dãy số đó lần lượt là những số nào
dưới đây?
A.
12345
;;;;.
23456
−−−−−
B.
23456
;;;;.
34567
−−−−−
C.
12345
;;;;.
23456
D.
23456
;;;;.
34567
Câu 80: Cho dãy số
(
)
n
u
, biết
31
n
n
n
u =
−
. Ba số hạng đầu tiên của dãy số đó lần lượt là những số nào
dưới đây?
A.
111
;;.
248
B.
11 3
;; .
2426
C.
11 1
;; .
2 4 16
D.
123
;;.
234

CHUYÊN ĐỀ II – TOÁN – 11 – DÃY SỐ - CẤP SỐ CỘNG – CẤP SỐ NHÂN
Page 20
Sưu tầm và biên soạn
Câu 81: Cho dãy số
( )
n
u
, biết
1
1
1
3
nn
u
uu
+
= −
= +
với
0n ≥
. Ba số hạng đầu tiên của dãy số đó là lần lượt là
những số nào dưới đây?
A.
1; 2; 5.−
B.
1; 4; 7.
C.
4;7;10.
D.
1; 3; 7.−
Câu 82: Cho dãy số
( )
,
n
u
biết
1
21
n
n
u
n
+
=
+
. Số
8
15
là số hạng thứ mấy của dãy số?
A.
8.
B.
6.
C.
5.
D.
7.
Câu 83: Cho dãy số
(
)
,
n
u
biết
25
.
54
n
n
u
n
+
=
−
Số
7
12
là số hạng thứ mấy của dãy số?
A.
8.
B.
6.
C.
9.
D.
10.
Câu 84: Cho dãy số
( )
,
n
u
biết
2.
n
n
u =
Tìm số hạng
1
.
n
u
+
A.
1
2 .2.
n
n
u
+
=
B.
1
2 1.
n
n
u
+
= +
C.
( )
1
2 1.
n
un
+
= +
D.
1
2 2.
n
n
u
+
= +
Câu 85: Cho dãy số
( )
n
u
, biết
3.
n
n
u
=
Tìm số hạng
21
.
n
u
−
A.
2
21
3 .3 1.
n
n
u
−
= −
B.
1
21
3 .3 .
nn
n
u
−
−
=
C.
2
21
3 1.
n
n
u
−
= −
D.
( )
21
21
3.
n
n
u
−
−
=
Câu 86: Cho dãy số
( )
,
n
u
với
1
5.
n
n
u
+
=
Tìm số hạng
1
.
n
u
−
A.
1
1
5.
n
n
u
−
−
=
B.
1
5.
n
n
u
−
=
C.
1
1
5.5 .
n
n
u
+
−
=
D.
1
1
5.5 .
n
n
u
−
−
=
Câu 87: Cho dãy số
(
)
n
u
bởi công thức truy hồi sau
1
1
0
; 1
nn
u
u u nn
+
=
=+≥
;
218
u
nhận giá trị nào sau đây?
A.
23653
. B.
46872
. C.
23871
. D.
23436
.
DẠNG 3. DÃY SỐ TĂNG, DÃY SỐ GIẢM
Câu 88: Cho các dãy số sau. Dãy số nào không là dãy số tăng?
A.
1;1;1;1; ...
. B.
1;3;5;7;...
. C.
2;4;6;8;...
. D.
13
;1; ;2;...
22
Câu 89: Cho dãy số
()
n
u
biết
52
n
un= +
. Mệnh đề nào sau đây đúng?
A. Dãy số tăng B. Dãy số giảm
C. Dãy số không tăng, không giảm D. Dãy số vừa tăng vừa giảm
Câu 90: Cho dãy số
()
n
u
biết
1
32
n
u
n
=
+
. Mệnh đề nào sau đây đúng?
A. Dãy số tăng B. Dãy số giảm
C. Dãy số không tăng, không giảm D. Dãy số vừa tăng vừa giảm
Câu 91: Cho dãy số
()
n
u
biết
10
3
n
n
u =
. Mệnh đề nào sau đây đúng?
A. Dãy số tăng B. Dãy số giảm
C. Dãy số không tăng, không giảm D. Dãy số vừa tăng vừa giảm
Câu 92: Cho dãy số
()
n
u
biết
2
2 31
n
u nn
= ++
. Mệnh đề nào sau đây đúng?

CHUYÊN ĐỀ II – TOÁN – 11 – DÃY SỐ - CẤP SỐ CỘNG – CẤP SỐ NHÂN
Page 21
Sưu tầm và biên soạn
A. Dãy số tăng B. Dãy số giảm
C. Dãy số không tăng, không giảm D. Dãy số vừa tăng vừa giảm
Câu 93: Cho dãy số
()
n
u
biết
(
)
( )
2
11
n
n
un=−+
. Mệnh đề nào sau đây đúng?
A. Dãy số tăng B. Dãy số giảm
C. Dãy số không tăng, không giảm D. Dãy số là dãy hữu hạn
Câu 94: Cho dãy số
()
n
u
biết
2
400
n
un n= −
. Mệnh đề nào sau đây đúng?
A. Dãy số tăng B. Dãy số giảm
C. Dãy số không tăng, không giảm D. Mọi số hạng đều âm
Câu 95: Trong các dãy số
( )
n
u
cho bởi số hạng tổng quát
n
u
sau, dãy số nào tăng?
A.
1
.
3
n
n
u =
B.
1
.
21
n
u
n
=
+
C.
1
.
32
n
n
u
n
+
=
+
D.
42
.
3
n
n
u
n
−
=
+
Câu 96: Trong các dãy số
( )
n
u
cho bởi số hạng tổng quát
n
u
sau, dãy số nào giảm?
A.
4
.
3
n
n
u
=
B.
( )
(
)
1 5 1.
n
n
n
u
=−−
C.
3.
n
n
u = −
D.
4.
n
un= +
Câu 97: Trong các dãy số
( )
n
u
cho bởi số hạng tổng quát
n
u
sau, dãy số nào không tăng, không giảm?
A.
1
.
n
un
n
= +
B.
5 3.
n
n
un= +
C.
3.
n
n
u
= −
D.
( )
2
3. 1
n
n
un=−+
Câu 98: Cho dãy số
()
n
u
biết
54
nn
n
u = −
. Mệnh đề nào sau đây đúng?
A. Dãy số tăng B. Dãy số giảm
C. Dãy số không tăng, không giảm D. Dãy số có số hạng thứ 100 bé hơn 1
Câu 99: Cho dãy số
()
n
u
biết
2
31
n
an
u
n
+
=
+
. Tìm tất cả các giá trị của a để dãy số tăng.
A.
6a =
B.
6a >
C.
6a <
D.
6a ≥
Câu 100: Cho dãy số
()
n
u
biết
2
n
n
u an
= −
. Tìm tất cả các giá trị của a để dãy số tăng.
A.
2a =
B.
2a >
C.
2a
<
D.
2a
≥
Câu 101: Cho dãy số
()
n
u
biết
3
n
n
u
an
=
. Tìm tất cả các giá trị của a để dãy số tăng.
A.
0a∀<
B. Không tồn tại a C.
*
a∀∈
D.
0a >
Câu 102: Cho dãy số
()
n
u
biết
32 31
n
un n= +− +
. Mệnh đề nào sau đây đúng?
A. Dãy số tăng B. Dãy số giảm
C. Dãy số không tăng, không giảm D. Dãy số vừa tăng vừa giảm
Câu 103: Cho dãy số
()
n
u
biết
2
1
n
un n=−+
. Mệnh đề nào sau đây đúng?
A. Dãy số tăng B. Dãy số giảm
C. Dãy số không tăng, không giảm D. Các số hạng đều dương
Câu 104: Cho dãy số
()
n
u
biết
2
21
2
n
nn
u
n
−−
=
+
. Mệnh đề nào sau đây đúng?
A. Dãy số tăng B. Dãy số giảm

CHUYÊN ĐỀ II – TOÁN – 11 – DÃY SỐ - CẤP SỐ CỘNG – CẤP SỐ NHÂN
Page 22
Sưu tầm và biên soạn
C. Dãy số không tăng, không giảm D. Có số hạng âm
Câu 105: Trong các dãy số
( )
n
u
cho bởi số hạng tổng quát
n
u
sau, dãy số nào tăng?
A.
sin
.
n
n
u
n
=
B.
2
1
.
21
n
n
u
n
+
=
+
C.
2
3
.
n
n
u
n
=
D.
32
4 3 1.
n
u nn=−+
Câu 106: Cho dãy số
()
n
u
biết
1
1
1
15
33
nn
u
uu
−
=
= +
. Mệnh đề nào sau đây đúng?
A. Dãy số tăng B. Dãy số giảm
C. Dãy số không tăng, không giảm D. Dãy số vừa tăng vừa giảm
Câu 107: Cho dãy số
()
n
u
biết
1
2
1
1
3,
nn
u
uu n
∗
+
=
= + ∀∈
. Mệnh đề nào sau đây đúng?
A. Dãy số tăng B. Dãy số giảm
C. Dãy số không tăng, không giảm D. Dãy số vừa tăng vừa giảm
Câu 108: Cho dãy số
()
n
u
biết
1
1
3
3
3
n
n
n
u
u
u
u
+
=
=
+
. Mệnh đề nào sau đây đúng?
A. Dãy số tăng B. Dãy số giảm
C. Dãy số không tăng, không giảm D. Có
10
2u =
Câu 109: Cho dãy số
()
n
u
biết
11 1
...
12
n
u
n n nn
= + ++
++ +
. Mệnh đề nào sau đây đúng?
A. Dãy số tăng B. Dãy số giảm
C. Dãy số không tăng, không giảm D. Có hữu hạn số hạng
Câu 110: Cho dãy số
()
n
u
biết
1
*
1
1
1
nn
u
u au n
+
=
= +∀∈
. Tìm tất cả các giá trị của a để
()
n
u
tăng?
A.
0.a <
B.
0.a ≤
C.
0.a >
D.
1.a >
Câu 111: Trong các dãy số dưới đây, dãy số nào là dãy giảm?
A.
2
n
un=
. B.
1
3
n
u
n
= −
. C.
3
n
un=
. D.
3
2
n
un= −
.
Câu 112: Trong các dãy số sau, dãy số nào là dãy số giảm?
A.
2
3
n
u
n
=
. B.
3
1
n
n
u
n
−
=
+
. C.
2
n
n
u =
. D.
( )
1
3
n
n
n
u
−
=
.
Câu 113: Dãy số nào sau đây là dãy số giảm?
A.
*
53
,
23
n
n
un
n
−
= ∈
+
. B.
*
5
,
41
n
n
un
n
−
= ∈
+
.
C.
2*
2 3,
n
un n= +∈
. D.
( )
*
cos 2 1 ,
n
u nn= +∈
.
Câu 114: Trong các dãy số
( )
n
u
cho bởi số hạng tổng quát
n
u
sau, dãy số nào là dãy số giảm?

CHUYÊN ĐỀ II – TOÁN – 11 – DÃY SỐ - CẤP SỐ CỘNG – CẤP SỐ NHÂN
Page 23
Sưu tầm và biên soạn
A.
1
2
n
n
u =
. B.
31
1
n
n
u
n
−
=
+
. C.
2
n
un=
. D.
2
n
un= +
.
Câu 115: Trong các dãy số
( )
n
u
cho bởi số hạng tổng quát
n
u
sau, dãy số nào là dãy số tăng?
A.
1
2
n
n
u =
. B.
31
1
n
n
u
n
−
=
+
. C.
2
1
n
un= −
. D.
1
2
n
u
n
=
+
.
Câu 116: Trong các dãy số sau, dãy số nào là dãy số giảm
A.
3
1
n
n
u
n
−
=
+
. B.
2
n
n
u =
. C.
2
2
n
u
n
=
. D.
( )
1
3
n
n
n
u
−
=
.
Câu 117: Dãy số nào sau đây là dãy số giảm?
A.
( )
53
,*
23
n
n
un
n
−
= ∈
+
. B.
( )
5
,*
41
n
n
un
n
−
= ∈
+
.
C.
( )
3
2 3, *
n
un n=+∈
. D.
( ) ( )
cos 2 1 , *
n
u nn= +∈
.
Câu 118: Trong các dãy số
( )
n
u
cho bởi số hạng tổng quát
n
u
sau, dãy số nào là dãy số tăng?
A.
1
.
2
n
n
u =
B.
1
.
n
u
n
=
C.
5
.
31
n
n
u
n
+
=
+
D.
21
.
1
n
n
u
n
−
=
+
Câu 119: Trong các dãy số
( )
n
u
cho bởi số hạng tổng quát
n
u
sau, dãy số nào là dãy số tăng?
A.
2
.
3
n
n
u =
B.
3
.
n
u
n
=
C.
2.
n
n
u
=
D.
( )
2.
n
n
u = −
Câu 120: Trong các dãy số sau, dãy số nào là dãy số giảm?
A.
21
1
n
n
u
n
+
=
−
. B.
3
1
n
un= −
. C.
2
n
un=
. D.
2
n
un=
.
DẠNG 4. DÃY SỐ BỊ CHẶN TRÊN, BỊ CHẶN DƯỚI, BỊ CHẶN
Câu 121: Xét tính bị chặn của các dãy số sau:
( 1)
= −
n
n
u
A. Bị chặn. B. Không bị chặn. C. Bị chặn trên. D. Bị chặn dưới.
Câu 122: Xét tính bị chặn của các dãy số sau:
31= −
n
un
A. Bị chặn. B. Bị chặn trên. C. Bị chặn dưới. D. Không bị chặn dưới.
Câu 123: Trong các dãy số
n
u
cho bởi số hạng tổng quát
n
u
sau, dãy số nào bị chặn?
A.
2
.
n
un=
B.
2.
n
n
u =
C.
1
.
n
u
n
=
D.
1.
n
un= +
Câu 124: Trong các dãy số
( )
n
u
cho bởi số hạng tổng quát
n
u
sau, dãy số nào bị chặn?
A.
1
.
2
n
n
u =
B.
3.
n
n
u =
C.
1.
n
un= +
D.
2
1.
n
un= +
Câu 125: Xét tính bị chặn của các dãy số sau:
21
2
+
=
+
n
n
u
n
A. Bị chặn. B. Không bị chặn. C. Bị chặn trên. D. Bị chặn dưới.

CHUYÊN ĐỀ II – TOÁN – 11 – DÃY SỐ - CẤP SỐ CỘNG – CẤP SỐ NHÂN
Page 24
Sưu tầm và biên soạn
Câu 126: Xét tính tăng, giảm và bị chặn của dãy số
()
n
u
, biết:
2 13
32
−
=
−
n
n
u
n
A. Dãy số tăng, bị chặn.
B. Dãy số giảm, bị chặn.
C. Dãy số không tăng không giảm, không bị chặn.
D. Cả A, B, C đều sai.
Câu 127: Xét tính bị chặn của các dãy số sau:
2
1
1
+
=
+
n
n
u
n
A. Bị chặn. B. Không bị chặn. C. Bị chặn trên. D. Bị chặn dưới.
Câu 128: Xét tính bị chặn của các dãy số sau:
2
43=−−
n
u nn
A. Bị chặn. B. Không bị chặn. C. Bị chặn trên. D. Bị chặn dưới.
Câu 129: Trong các dãy số
()
n
u
sau, dãy số nào bị chặn?
A.
1
.
n
un
n
= +
B.
1
n
un= +
. C.
2
21
n
n
u
n
=
+
. D.
2
1
n
unn= ++
.
Câu 130: Trong các dãy số
()
n
u
sau, dãy số nào bị chặn?
A.
sin 3
n
un n= −
B.
2
1
n
n
u
n
+
=
. C.
( )
1
1
n
u
nn
=
+
. D.
(
)
.sin 3 1
n
un n= −
.
Câu 131: Trong các dãy số
( )
n
u
cho dưới đây dãy số nào là dãy số bị chặn ?
A.
3
2
.
1
n
n
u
n
=
+
B.
2
2017.
n
un
= +
C.
( 1) ( 2).
n
n
un
=−+
D.
2
.
1
n
n
u
n
=
+
Câu 132: Xét tính tăng giảm và bị chặn của dãy số sau:
1
( ):
2
+
=
+
nn
n
uu
n
A. Tăng, bị chặn. B. Giảm, bị chặn. C. Tăng, chặn dưới. D. Giảm, chặn trên.
Câu 133: Xét tính tăng, giảm và bị chặn của dãy số
()
n
u
, biết:
3
( ): 2 1=++
nn
uun n
A. Tăng, bị chặn. B. Giảm, bị chặn. C. Tăng, chặn dưới. D. Giảm, chặn trên.
Câu 134: Cho dãy số
31
( ):
31
nn
n
uu
n
−
=
+
. Dãy số
n
u
bị chặn trên bởi số nào dưới đây?
A.
1
3
. B. 1. C.
1
2
. D. 0.
Câu 135: Cho dãy số
n
u
, biết
cos sin .
n
u nn
Dãy số
n
u
bị chặn trên bởi số nào dưới đây?
A. 0. B. 1. C.
2
. D. Không bị chặn trên.
Câu 136: Cho dãy số
n
u
, biết
cos sin .
n
u nn
Dãy số
n
u
bị chặn dưới bởi số nào dưới đây?
A. 0. B.
1−
. C.
2−
. D. Không bị chặn dưới.
Câu 137: Xét tính bị chặn của các dãy số sau:
(
)( )
11 1
...
1.3 3.5 2 1 2 1
= + ++
−+
n
u
nn
A. Bị chặn. B. Không bị chặn. C. Bị chặn trên. D. Bị chặn dưới.
CHUYÊN ĐỀ II – TOÁN – 11 – DÃY SỐ - CẤP SỐ CỘNG – CẤP SỐ NHÂN
Page 25
Sưu tầm và biên soạn
Câu 138: Xét tính bị chặn của các dãy số sau:
11 1
...
1.3 2.4 .( 2)
= + ++
+
n
u
nn
A. Bị chặn. B. Không bị chặn. C. Bị chặn trên. D. Bị chặn dưới.
Câu 139: Xét tính tăng, giảm và bị chặn của dãy số
()
n
u
, biết:
22 2
11 1
1 ...
23
=+ + ++
n
u
n
.
A. Dãy số tăng, bị chặn. B. Dãy số tăng, bị chặn dưới.
C. Dãy số giảm, bị chặn trên. D. Cả A, B, C đều sai.
Câu 140: Xét tính bị chặn của các dãy số sau:
1
1
1
1
2
, ( 2)
1
−
−
=
+
= ≥
+
n
n
n
u
u
un
u
A. Bị chặn. B. Không bị chặn. C. Bị chặn trên. D. Bị chặn dưới.
Câu 141: Xét tính tăng giảm và bị chặn của dãy số sau:
1
1
2
( ):
1
, 2
2
+
=
+
= ∀≥
n
n
n
u
u
u
un
A. Tăng, bị chặn. B. Giảm, bị chặn.
C. Tăng, chặn dưới, không bị chặn trên. D. Giảm, chặn trên, không bị chặn dưới.
Câu 142: Cho dãy
( )
n
u
với
2018
.
2018 1
n
n
u
n
+
=
+
Chọn khẳng định đúng trong các khẳng định sau.
A. Dãy
( )
n
u
bị chặn dưới nhưng không bị chặn trên
B. Dãy
(
)
n
u
bị chặn.
C. Dãy
( )
n
u
không bị chặn trên, không bị chặn dưới.
D. Dãy
( )
n
u
bị chặn trên nhưng không bị chặn dưới
Câu 143: Trong các dãy số
( )
n
u
có số hạng tổng quát
n
u
dưới đây, dãy số nào là dãy bị chặn?
A.
2
2
n
un= +
. B.
21
n
n
u
n
=
+
. C.
31
n
n
u = −
. D.
2
n
un
n
= +
.
Câu 144: Cho dãy số
( )
n
u
với
1
25
n
n
u
−
= +
. Kết luận nào sau đây là đúng?
A. Dãy số không đơn điệu. B. Dãy số giảm và không bị chặn.
C. Dãy số tăng. D. Dãy số giảm và bị chặn.
Câu 145: Trong các dãy số sau, dãy nào là dãy số bị chặn?
A.
21
1
n
n
u
n
+
=
+
. B.
( )
2 sin
n
un n= +
. C.
2
n
un=
. D.
3
1
n
un
= −
.
Câu 146: Chọn kết luận sai:
A. Dãy số
21n
tăng và bị chặn trên. B. Dãy số
1
1n
giảm và bị chặn dưới.
C. Dãy số
1
n
tăng và bị chặn trên. D. Dãy số
1
3.2
n
giảm và bị chặn dưới.
Câu 147: Cho dãy số
()
n
u
biết
22 2
11 1 1
...
22 3
n
u
n
=+ + ++
. Mệnh đề nào sau đây đúng ?

CHUYÊN ĐỀ II – TOÁN – 11 – DÃY SỐ - CẤP SỐ CỘNG – CẤP SỐ NHÂN
Page 26
Sưu tầm và biên soạn
A. Dãy số bị chặn dưới. B. Dãy số bị chặn trên.
C. Dãy số bị chặn. D. Không bị chặn.
Câu 148: Cho dãy số
()
n
u
xác định bởi
*
1
3
1
1
,
nn
u
u un n
+
=
= +
∈∀
. Tìm số nguyên dương
n
nhỏ nhất sao
cho
20391901
n
u ≥−
.
A.
2017n =
. B.
2019
n =
. C.
2020n =
. D.
2018n =
.
Câu 149: Cho dãy số
()
n
u
thỏa mãn
2
11
log log 6 0uu+ −=
và
1
5
nn
uu
+
= +
, với mọi
1,
n nN≥∈
. Giá trị
lớn nhất của
n
để
500
n
u
<
bằng:
A.
80
. B.
100
. C.
99
. D.
82
.
Câu 150: Cho dãy số
(
)
n
u
thỏa mãn:
1
5
u
=
và
1
4
3
3
nn
uu
+
= +
với
1.
n∀≥
Giá trị nhỏ nhất của
n
để
100
12
... 5
nn
S uu u= + ++ >
bằng?
A.
142
. B.
146
. C.
141
. D.
145
.
Câu 151: Cho dãy số
( )
n
u
xác định bởi
12
11
2, 3
32
n nn
uu
u uu
+−
= =
= −
2,n nN≥∈
.Khi đó
1
....
n
uu++
bằng?
A.
21
n
−
. B.
2
n
. C.
22
n
n+
. D.
21
n
n+−
.
Câu 152: Cho dãy số
{ }
n
u
xác định bởi
3 32 3 2 3 2
44 4 4
1
2 3 31
n
u
n nn n nn n n n
=
+++++++++
,
1n ≥
.
Tính tổng
4
12
2018 1
...Suu u
−
= + ++
.
A.
2016
. B.
2017
. C.
2018
. D.
2019
.
Câu 153: Cho dãy số
( )
n
u
được xác định bởi
1
2
3
u
=
và
( )
1
22 1 1
n
n
n
u
u
nu
+
=
++
,
( )
*
n ∈
. Tính tổng
2018
số hạng đầu tiên của dãy số đó?
A.
4036
4035
. B.
4035
4034
. C.
4038
4037
. D.
4036
4037
.
Câu 154: Cho dãy số
(
)
n
u
thỏa mãn
1
6
nn
uu
−
= +
,
2n∀≥
và
25 9
2
log log 8 11uu+ +=
. Đặt
12
...
nn
S uu u
= + ++
. Tìm số tự nhiên
n
nhỏ nhất thỏa mãn
20172018
n
S ≥
.
A.
2587
. B.
2590
. C.
2593
. D.
2584
.
Câu 155: Cho dãy số
(
)
n
u
thỏa mãn
18 18
11
44
e5ee e
uu
uu
+ −=
và
1
3
nn
uu
+
= +
với mọi
1n ≥
. Giá trị lớn
nhất của
n
để
3
log ln 2018
n
u <
bằng
A.
1419
. B.
1418
. C.
1420
. D.
1417
.
Câu 156: Tổng:
2 4 6 2018A = + + +…+
có giá trị là:
A.
2018001
. B.
1209900
. C.
1010101
. D.
1019090
.
Câu 157: Tổng:
1 4 7 3031B = + + +…+
bằng:
A.
1532676
. B.
1435000
. C.
1351110
. D.
1322300
.
Câu 158: Giá trị của tổng:
13 9 5 387C = − − − +…+
bằng:

CHUYÊN ĐỀ II – TOÁN – 11 – DÃY SỐ - CẤP SỐ CỘNG – CẤP SỐ NHÂN
Page 27
Sưu tầm và biên soạn
A.
23455
. B.
18887
. C.
36778
. D.
43234
.
Câu 159: Giá trị của tổng:
1 101 201 1001
100 100 100 100
S = + + +…+
bằng:
A.
5514
100
. B.
5501
100
. C.
5511
100
. D.
5515
100
.
Câu 160: Cho tổng:
*
1 3 5 2 1, .
n
S nn= + + +…+ + ∀ ∈
Tìm
100
S
?
A.
10201
. B.
10000
. C.
10200
. D.
10202
.
Câu 161: Cho tổng:
246 2
n
Sn= + + +…+
với
*
n ∈
. Khi đó công thức của
n
S
là?
A.
( 2)nn+
. B.
( 1)
2
nn+
. C.
( 1)nn+
. D.
2
n
.
Câu 162: Tìm
x
biết:
( 3) ( 7) ( 11) ( 79) 860xxx x+++++ +…++ =
A.
2x =
. B.
1x =
. C.
4x =
. D.
3x =
.
Câu 163: Tìm
x
biết:
( ) ( ) ( ) ( )
2 3 2 7 2 11 ... 2 79 1720xxx x++++++++=
A.
35x =
. B.
45
2
x =
.
C.
10x =
. D.
15x =
.
Câu 164: Tính giá trị biểu thức:
1 2 3 2018
1 3 5 1009
A
+ + +…+
=
+ + +…+
A.
2030071
255025
. B.
2037171
200025
. C.
2037111
255000
. D.
2037171
255025
.
Câu 165: Cho tổng:
159 4 3
n
Sn= + + +…+ −
với
*
n ∈
. Khi đó:
22
10 15
SS+
bằng:
A.
225325
. B.
255325
. C.
225355
. D.
225525
.
Câu 166: Tính tổng sau: .
A. B. C. D.
Câu 167: Tổng: bằng:
A. B. C. D.
Câu 168: Giá trị của tổng: là:
A. B. C. D.
Câu 169: Tổng
100 100 100 100
...
10.15.20 15.20.25 20.25.30 110.115.120
S = + + ++
có giá trị bằng:
A. B. C. D.
Câu 170: Giá trị của tổng:
12 20 28 84
...
4.16 16.36 36.64 400.484
S = + + ++
là:
33 3 3
...
1.4 4.7 7.10 91.94
S = + + ++
93
94
94
95
94
93
1
111 1
...
2.4 4.6 6.8 100.102
S = + + ++
53
102
25
102
1
2
1
4
444 4
...
1.3.5 3.5.7 5.7.9 91.93.95
S = + + ++
2941
8835
2942
8835
2944
8835
1
3
93
1380
91
13800
9
138
91
1380

CHUYÊN ĐỀ II – TOÁN – 11 – DÃY SỐ - CẤP SỐ CỘNG – CẤP SỐ NHÂN
Page 28
Sưu tầm và biên soạn
A. B. C. D.
Câu 171: Cho tổng:
( )
111 1
...
1.2 2.3 3.4 1
S
nn
=++++
+
với . Lựa chọn đáp án đúng.
A. B. C. D.
Câu 172: Cho tổng:
( )( )
111 1
...
1.2.3 2.3.4 3.4.5 1 2
n
S
nn n
= + + ++
++
. Khi đó:
30
S
bằng:
A. B.
495
992
C. D.
Câu 173: Tìm
x
biết:
2 2 2 2 1430
...
1.3 3.5 5.7 51.53 53
xxx x
+ ++ ++ +++ =
A. B. C. D.
Câu 174: Tìm
x
biết:
2 2 2 2 9125
...
1.2.3 2.3.4 3.4.5 20.21.22 231
xx x x
− +− +− ++− =
A. B. C. D.
Câu 175: Tính:
2 3 10
11 1 1
...
55 5 5
M =+ + ++
A. B. C. D.
Câu 176: Cho
5 55 5
...
1024 512 256 2
M = + + ++
. Khi đó M bằng:
A. B. C. D.
Câu 177: Cho
55 5
5 ...
3 9 729
M =++++
. Khi đó
729M
bằng:
A. B. C. D.
Câu 178: Cho tổng:
2
1 2 2 ... 2
n
n
S =++ ++
. Chọn mệnh đề đúng:
A.
10
2047S =
B.
10
2048S =
C.
10
1024S =
D.
10
1023S =
Câu 179: Tính tổng:
1.2 3.4 5.6 ... 11.12S =++++
A. B. C. D.
Câu 180: Tổng:
2.3 4.5 6.7 ... 20.21S = + + ++
có giá trị bằng:
A. B. C. D.
Câu 181: Giá trị của tổng: là:
A. B. C. D.
Câu 182: Tính tổng:
( ) ( )
1.5 3.7 5.9 ... 2 1 . 2 3
n
S nn= + + ++ − +
khi
A. B. C. D.
31
121
30
121
32
121
33
121
*
n ∈
3
1
.
12
S =
2
1
.
6
S =
2
2
.
3
S =
3
1
.
4
S =
31
121
496
1987
31
121
1x =
2x =
3x =
4x =
1x =
2x =
3x =
4x =
10
11
1
45
−
11
11
1
45
−
10
1
1
5
−
10
11
1
55
−
1023
1024
5111
1024
1024
1023
5115
1024
5465
729
5460
5465
5460
729
322
321
320
319
1550
1655
1650
1450
1.2 2.5 3.8 ... 20.59S = + + ++
8450
8300
8850
8400
15n =
5450
5400
5395
5650

CHUYÊN ĐỀ II – TOÁN – 11 – DÃY SỐ - CẤP SỐ CỘNG – CẤP SỐ NHÂN
Page 29
Sưu tầm và biên soạn
Câu 183: Giá trị của tổng:
( )
1.4 3.8 5.12 ... 2 1 .4
n
S nn= + + ++ −
khi
10n =
là:
A. B. C. D.
Câu 184: Cho tổng
( )
1.2 3.4 5.6 ... 2 1 2=++++ −
n
S nn
. Tính giá trị của
50
S
A. B. C. D.
Câu 185: Tìm
x
biết:
( ) ( ) ( ) ( )
1.2 2.5 3.8 ... 10.29 1200xxx x+ ++ ++ +++ =
A. B. C. D.
1650
2860
2650
1950
169150
155000
165050
165000
7x =
8x =
9x =
10x =
CHUYÊN ĐỀ II – TOÁN – 11 – DÃY SỐ - CẤP SỐ CỘNG – CẤP SỐ NHÂN
Page 1
Sưu tầm và biên soạn
BÀI 5: DÃY SỐ
DẠNG 1. BIỂU DIỄN DÃY SỐ, TÌM CÔNG THỨC TỔNG QUÁT
Câu 1: Cho dãy số có các số hạng đầu là:9; 99; 999; 9999,… Số hạng tổng quát của dãy số này là:
A.
1
n
n
u
n
=
+
B.
10 1
n
n
u = −
. C.
9
n
n
u =
D.
9
n
un=
Lời giải
Nhận xét:
1
1
10 1u
= −
;
2
2
10 1
u = −
;
3
3
10 1u = −
;
4
4
10 1u = −
.
Câu 2: Cho dãy số
1325
, , , ,...
2537
. Công thức tổng quát
n
u
nào là của dãy số đã cho?
A.
*
1
n
n
un
n
= ∀∈
+
. B.
*
2
n
n
n
un
= ∀∈
. C.
*
1
3
n
n
un
n
+
= ∀∈
+
. D.
*
2
21
n
n
un
n
= ∀∈
+
.
Lời giải
Viết lại dãy số:
2345
, , , ,...
4567
1
3
n
n
un
n
∗
+
⇒ = ∀∈
+
.
Câu 3: Cho dãy số có các số hạng đầu là:
5;10;15;20;25;...
Số hạng tổng quát của dãy số này là:
A.
5( 1)
n
un= −
. B.
5
n
un=
. C.
5
n
un
= +
. D.
5. 1
n
un= +
.
Lời giải
Ta có:
5 5.1=
10 5.2=
15 5.3=
20 5.4=
25 5.5=
Suy ra số hạng tổng quát
5
n
un
=
.
CHƯƠNG
II
DÃY SỐ
CẤP SỐ CỘNG – CẤP SỐ NHÂN
HỆ THỐNG BÀI TẬP TRẮC NGHIỆM.
III

CHUYÊN ĐỀ II – TOÁN – 11 – DÃY SỐ - CẤP SỐ CỘNG – CẤP SỐ NHÂN
Page 2
Sưu tầm và biên soạn
Câu 4: Cho dãy số có các số hạng đầu là:
8,15,22,29,36,...
.Số hạng tổng quát của dãy số này là:
A.
77
n
un= +
. B.
7.
n
un=
.
C.
7. 1
n
un= +
. D.
n
u
: Không viết được dưới dạng công thức.
Lời giải
Ta có:
8 7.1 1= +
15 7.2 1= +
22 7.3 1= +
29 7.4 1= +
36 7.5 1= +
Suy ra số hạng tổng quát
71
n
un= +
.
Câu 5: Cho dãy số có các số hạng đầu là:
;...
5
4
;
4
3
;
3
2
;
2
1
;0
.Số hạng tổng quát của dãy số này là:
A.
1
n
n
u
n
+
=
. B.
1
n
n
u
n
=
+
. C.
1
n
n
u
n
−
=
. D.
2
1
n
nn
u
n
−
=
+
.
Lời giải
Ta có:
0
0
01
=
+
11
2 11
=
+
22
3 21
=
+
33
4 31
=
+
44
5 41
=
+
Suy ra
1
n
n
u
n
=
+
.
Câu 6: Cho dãy số có các số hạng đầu là:
1;1; 1;1; 1; ...
−−−
.Số hạng tổng quát của dãy số này có dạng
A.
1
=
n
u
. B.
1−=
n
u
. C.
n
n
u
)1(−=
. D.
( )
1
1
n
n
u
+
= −
.
Lời giải
Ta có:
Các số hạng đầu của dãy là
( ) ( ) ( ) ( ) ( ) ( )
12345
1;1;1;1;1;... 1
n
n
u−−−−− ⇒=−
.

CHUYÊN ĐỀ II – TOÁN – 11 – DÃY SỐ - CẤP SỐ CỘNG – CẤP SỐ NHÂN
Page 3
Sưu tầm và biên soạn
Câu 7: Cho dãy số
( )
n
u
xác định bởi
( )
1
1
1
1
3
nn
u
n
uu
+
=
≥
=
. Tìm công thức số hạng tổng quát của dãy số
trên.
A.
3=
n
n
u
. B.
1
3
−
=
n
n
u
. C.
1
32
+
= −
n
n
u
. D.
32= −
n
n
u
.
Lời giải
Ta có
0
1
1
2
2
3
13
3
3
u
u
u
= =
=
=
…
Dự đoán
1*
3,
n
n
un
−
= ∈
. Ta dễ dàng chứng minh được công thức này bằng quy nạp
+ với
=⇒=
1
11nu
suy ra khẳng định đúng
+ Giả sử
= ≥ 2
nk
ta có
−
=
1
3
k
k
u
. Ta phải chứng minh
+
=
1
3
k
k
u
Thật vậy, theo công thức truy hồi ta có
−
+
= = =
1
1
3. 3.3 3
kk
kk
uu
Vậy theo nguyên lý quy nạp ta dã chứng minh được
1*
3,
n
n
un
−
= ∈
Câu 8: Cho dãy số có các số hạng đầu là:
0.1;0.01;0.001;0.0001...
. Số hạng tổng quát của dãy số này có
dạng?
A.
=
0
0.00...01
n
n sè
u
. B.
−
=
10
0.00...01
n
n sè
u
.
C.
1
1
10
n
n
u
−
=
. D.
1
1
10
n
n
u
+
=
.
Lời giải
Ta có
1
2
2
3
3
1
0.1
10
1
0.01
10
1
0.001
10
u
u
u
= =
= =
= =
…
Dự đoán
= =
0
1
0.00...01
10
n
n
n sè
u
.
Câu 9: Cho dãy số
( )
n
u
xác định bởi:
( )
1
1
1
1
2
nn
u
n
uu
+
=
≥
= +
. Xác định công thức của số hạng tổng quát.

CHUYÊN ĐỀ II – TOÁN – 11 – DÃY SỐ - CẤP SỐ CỘNG – CẤP SỐ NHÂN
Page 4
Sưu tầm và biên soạn
A.
21
n
un= −
. B.
32
n
un= −
. C.
43
n
un= −
. D.
87
n
un= −
.
Lời giải
Ta có
=
=
=
1
2
3
1
3
5
u
u
u
…
Dự đoán
=−∈
*
2 1,
n
u nn
. Ta dễ dàng chứng minh được công thức dự đoán bằng quy nạp
Câu 10: Cho dãy số có các số hạng đầu là:
2345
11 1 1 1
; ; ; ; ;...
33 3 3 3
Số hạng tổng quát của dãy số này là?
A.
1
11
.
33
n
n
u
+
=
. B.
1
1
3
n
n
u
+
=
. C.
1
3
n
n
u =
. D.
1
1
3
n
n
u
−
=
.
Lời giải
Từ các số hạng đầu tiên của dãy số ta dự đoán
= ∈
*
1
,
3
n
n
un
Câu 11: Cho dãy số
( )
n
u
với
1
1
5
nn
u
u un
+
=
= +
.Số hạng tổng quát
n
u
của dãy số là số hạng nào dưới đây?
A.
( )
1
2
n
nn
u
−
=
. B.
( )
1
5
2
n
nn
u
−
= +
.
C.
( )
1
5
2
n
nn
u
+
= +
. D.
( )( )
12
5
2
n
nn
u
++
= +
.
Lời giải
Theo công thức truy hồi ta có
+
−=
1nn
u un
. Khi đó
−
=
−=
−=
−=−
1
21
32
1
5
1
2
...
1
nn
u
uu
uu
uu n
Cộng vế theo vế các đẳng thức trên ta được
( )
( )
−
=+ +++ − =+
1
5 1 2 3 ... 1 5
2
n
nn
un
Câu 12: Cho dãy số với . Công thức số hạng tổng quát của dãy số này là:
A. . B. . C. . D. .
Lời giải
( )
n
u
1
1
1
2
2
+
=
= −
nn
u
uu
( )
1
21
2
=+−
n
un
( )
1
21
2
=−−
n
un
1
2
2
= −
n
un
1
2
2
= +
n
un

CHUYÊN ĐỀ II – TOÁN – 11 – DÃY SỐ - CẤP SỐ CỘNG – CẤP SỐ NHÂN
Page 5
Sưu tầm và biên soạn
Ta có: . Cộng hai vế ta được .
Câu 13: Cho dãy số có các số hạng đầu là:
2;0; 2; 4; 6;...−
.Số hạng tổng quát của dãy số này có dạng?
A.
nu
n
2−=
. B.
( )
nu
n
+−= 2
. C.
( )
)1(2 +−= nu
n
. D.
( ) ( )
22 1
n
un=−+ −
.
Lời giải
Dãy số là dãy số cách đều có khoảng cách là
2
và số hạng đầu tiên là
( )
2−
nên
( ) ( )
2 2. 1
n
un=−+ −
.
Câu 14: Cho dãy số có các số hạng đầu là:
;
3
1
;
3
1
;
3
1
;
3
1
;
3
1
5432
….Số hạng tổng quát của dãy số này là?
A.
1
3
1
3
1
+
=
n
n
u
. B.
1
3
1
+
=
n
n
u
. C.
n
n
u
3
1
=
. D.
1
3
1
−
=
n
n
u
.
Lời giải
5 số hạng đầu là
2345
1
11111
; ; ; ; ;...
33333
nên
1
3
n
n
u =
.
Câu 15: Cho dãy số
( )
n
u
với
( )
1
2
1
1
1
n
nn
u
uu
+
=
= +−
. Số hạng tổng quát
n
u
của dãy số là số hạng nào dưới
đây?
A.
1
n
un= +
. B.
1
n
un= −
. C.
( )
2
11
n
n
u =+−
. D.
n
un=
.
Lời giải
Ta có:
( )
2
1 234
1 1 2; 3; 4;...
n
nn n
uu u u u u
+
= +− = +⇒ = = =
Dễ dàng dự đoán được
n
un=
.
Thật vậy, ta chứng minh được
n
un=
( )
*
bằng phương pháp quy nạp như sau:
+ Với
1
11nu=⇒=
. Vậy
( )
*
đúng với
1n =
+ Giả sử
( )
*
đúng với mọi
( )
*
n kk= ∈
, ta có:
k
uk=
. Ta đi chứng minh
( )
*
cũng đúng với
1nk= +
, tức là:
1
1
k
uk
+
= +
+ Thật vậy, từ hệ thức xác định dãy số
( )
n
u
ta có:
( )
2
1
11
k
kk
uu k
+
= +− = +
. Vậy
( )
*
đúng với
mọi
*
n ∈
.
Câu 16: Cho dãy số
( )
n
u
với
( )
1
21
1
1
1
n
nn
u
uu
+
+
=
= +−
. Số hạng tổng quát
n
u
của dãy số là số hạng nào dưới
đây?
1
21
32
1
1
2
2
2
...
2
−
=
= −
= −
= −
nn
u
uu
uu
uu
( )
11
2 2... 2 2 1
22
= −− −= − −
n
un

CHUYÊN ĐỀ II – TOÁN – 11 – DÃY SỐ - CẤP SỐ CỘNG – CẤP SỐ NHÂN
Page 6
Sưu tầm và biên soạn
A.
2
n
un
= −
. B.
n
u
không xác định. C.
1
n
un
= −
. D.
n
un= −
với mọi
n
.
Lời giải
Ta có:
23 4
0; 1; 2uu u= =−=−
,. Dễ dàng dự đoán được
2
n
un= −
.
Câu 17: Cho dãy số
(
)
n
u
với
1
2
1
1
nn
u
u un
+
=
= +
. Số hạng tổng quát
n
u
của dãy số là số hạng nào dưới đây?
A.
( )
(
)
12 1
1
6
n
nn n
u
++
= +
. B.
( )( )
12 2
1
6
n
nn n
u
−+
= +
.
C.
(
)( )
12 1
1
6
n
nn n
u
−−
= +
. D.
( )( )
12 2
1
6
n
nn n
u
+−
= +
.
Lời giải
Ta có:
( )
1
2
21
2
32
2
1
1
1
2
...
1
nn
u
uu
uu
uu n
−
=
= +
= +
= +−
.
Cộng hai vế ta được
(
)
(
)( )
2
22
12 1
1 1 2 ... 1 1
6
n
nn n
un
−−
=++ ++ − =+
Câu 18: Cho dãy số
( )
n
u
với
1
1
2
21
nn
u
uun
+
=
−=−
. Số hạng tổng quát
n
u
của dãy số là số hạng nào dưới
đây?
A.
( )
2
21
n
un=+−
. B.
2
2
n
un= +
. C.
( )
2
21
n
un=++
. D.
( )
2
21
n
un=−−
.
Lời giải
Ta có:
1
21
32
1
2
1
3
...
23
nn
u
uu
uu
uu n
−
=
= +
= +
= +−
. Cộng hai vế ta được
( ) ( )
2
2 1 3 5 ... 2 3 2 1
n
u nn= ++ ++ + − = + −
Câu 19: Cho dãy số
( )
n
u
với
1
1
2
1
2
n
n
u
u
u
+
= −
=−−
. Công thức số hạng tổng quát của dãy số này là:
A.
1
n
n
u
n
−
= −
. B.
1
n
n
u
n
+
=
. C.
1
n
n
u
n
+
= −
. D.
1
n
n
u
n
= −
+
.
Lời giải
Ta có:
123
345
; ; ;...
234
uuu=−=−=−
Dễ dàng dự đoán được
1
n
n
u
n
+
= −
.

CHUYÊN ĐỀ II – TOÁN – 11 – DÃY SỐ - CẤP SỐ CỘNG – CẤP SỐ NHÂN
Page 7
Sưu tầm và biên soạn
Câu 20: Cho dãy số
( )
n
u
với
1
1
1
2
2
nn
u
uu
+
=
= −
. Công thức số hạng tổng quát của dãy số này là:
A.
( )
1
21
2
n
un=+−
. B.
( )
1
21
2
n
un=−−
. C.
1
2
2
n
un= −
. D.
1
2
2
n
un= +
.
Lời giải
Ta có:
1
21
32
1
1
2
2
2
...
2
nn
u
uu
uu
uu
−
=
= −
= −
= −
. Cộng hai vế ta được
( )
11
2 2... 2 2 1
22
n
un= −− −= − −
.
Câu 21: Cho dãy số
( )
n
u
với
1
1
1
2
n
n
u
u
u
+
= −
=
. Công thức số hạng tổng quát của dãy số này là:
A.
( )
1
1.
2
n
n
u
= −
. B.
( )
1
1
1.
2
n
n
u
+
= −
. C.
1
1
2
n
n
u
−
=
. D.
( )
1
1
1.
2
n
n
u
−
= −
.
Lời giải
Ta có:
1
1
2
2
3
1
1
2
2
...
2
n
n
u
u
u
u
u
u
u
−
= −
=
=
=
.
Nhân hai vế ta được
( ) ( ) ( )
1
123 1
123
1
1 lan
. . ...
11
. . ... 1. 1. 1.
2.2.2...2 2 2
n
n
nn
n
n
uuu u
uuu u u
−
−
−
−
=− ⇔=− =−
Câu 22: Cho dãy số
( )
n
u
với
1
1
2
2
nn
u
uu
+
=
=
. Công thức số hạng tổng quát của dãy số này:
A.
1n
n
un
−
=
. B.
2
n
n
u =
. C.
1
2
n
n
u
+
=
. D.
2
n
u =
.
Lời giải
Ta có:
1
21
32
1
2
2
2
...
2
nn
u
uu
uu
uu
−
=
=
=
=
. Nhân hai vế ta được
1
123 12 1
. . ... 2.2 . . ... 2
nn
n nn
uuu u uu u u
−
−
= ⇔=

CHUYÊN ĐỀ II – TOÁN – 11 – DÃY SỐ - CẤP SỐ CỘNG – CẤP SỐ NHÂN
Page 8
Sưu tầm và biên soạn
Câu 23: Cho dãy số
( )
n
u
với
1
1
1
2
2
nn
u
uu
+
=
=
. Công thức số hạng tổng quát của dãy số này:
A.
1
2
n
n
u
−
= −
. B.
1
1
2
n
n
u
−
−
=
. C.
1
2
n
n
u
−
=
. D.
2
2
n
n
u
−
=
.
Lời giải
Ta có:
1
21
32
1
1
2
2
2
...
2
nn
u
uu
uu
uu
−
=
=
=
=
. Nhân hai vế ta được
12
123 12 1
1
. . ... .2 . . ... 2
2
nn
n nn
uuu u uu u u
−−
−
= ⇔=
Câu 24: Cho dãy số
( )
n
u
xác định bởi
1
*
1
2
1
2,
n
n
u
un
u
+
= −
=−− ∀∈
.
Tìm công thức số hạng tổng quát của dãy số.
A.
31−
= −
n
n
u
n
. B.
1
= −
+
n
n
u
n
. C.
1+
=
n
n
u
n
. D.
1+
= −
n
n
u
n
.
Lời giải
Từ
1
1
2
n
n
u
u
+
=−−
1
. 21
nn n
uu u
+
⇔ =−−
1 11
.1
nnnn n n
uuuu u u
+ ++
⇔ + + += −
( )( )
11
11
n n nn
u u uu
++
⇔ + += −
( )( )
1
1
1
11
nn
nn
uu
uu
+
+
−
⇔=
++
1
11
1
11
nn
uu
+
⇔− =
++
Đặt
1
1
n
n
v
u
=
+
. Khi đó
11
11
nn n n
vv v v
++
− =⇔ −=−
( )( )
1
11
n
vv n⇔ =+− −
1
1
1
1
n
v nn
u
⇔ = −+=−
+
1
1
n
n
u
⇔=−
+
1
1
n
u
n
⇔ +=−
11
1
n
n
u
nn
+
⇔ =− −=−
.
Câu 25: Cho dãy số
( )
n
u
với
( )
1
2
1
1
1
+
=
= +−
n
nn
u
uu
.Công thức tổng quát
n
u
nào dưới đây là của dãy số đã
cho?
A.
=
n
un
. B.
1= −
n
un
. C.
( )
2
11= +−
n
n
u
. D.
1= +
n
un
.
Lời giải
Ta có:
( )
2
1
11
+
= +− = +
n
nn n
uu u
⇒
2
2;=u
3
3;=u
4
4;...=u

CHUYÊN ĐỀ II – TOÁN – 11 – DÃY SỐ - CẤP SỐ CỘNG – CẤP SỐ NHÂN
Page 9
Sưu tầm và biên soạn
Dự đoán được
*
,
= ∀∈
n
u nn
.
Ta chứng minh
*
,
= ∀∈
n
u nn
( )
*
bằng phương pháp quy nạp:
+ Với
1
11=⇒=nu
.Vậy
( )
*
đúng với
1=n
.
+ Giả sử
(
)
*
đúng với
( )
*
= ∈n kk
, tức là ta có:
=
k
uk
.
+ Ta đi chứng minh
( )
*
cũng đúng với
1= +nk
,tức là cần chứng minh:
1
1
+
= +
k
uk
.
Thật vậy, từ hệ thức xác định dãy số
( )
n
u
ta có:
( )
2
1
11
+
= +− = +
k
kk
uu k
.
Vậy
(
)
*
đúng với mọi
*
∈
n
.
Câu 26: Gọi
( )
( )
111 1
....
1.3 3.5 5.7 2 1 2 1
n
S
nn
= + + ++
−+
với mọi
*
n
. Ta có:
A.
1
21
n
n
S
n
−
=
−
. B.
2
21
n
n
S
n
=
+
. C.
21
n
n
S
n
=
+
. D.
1
23
n
n
S
n
+
=
+
.
Lời giải
Ta có:
( )( )
111 1
....
1.3 3.5 5.7 2 1 2 1
n
S
nn
= + + ++
−+
.
( ) ( )
11 1 1 1 1 1 1 1
....
2133557 2 1 2 1nn
= −+−+−+ + −
−+
Câu 27: Cho dãy số
( )
n
u
xác định bởi
1
1
1
2 1, 1
nn
u
u u nn
+
=
=++ ≥
. Giá trị của
n
để
2017 2018 0
n
un
−+ + =
là
A. Không có
n
. B.
1009
. C.
2018
. D.
2017
.
Lời giải
Ta có:
( )
1
21
32
43
1
1
2.1 1
2.2 1
2.3 1
....
2 11
nn
u
uu
uu
uu
uu n
−
=
=++
=++
=++
= + −+
Cộng vế với vế các đẳng thức trên ta được:
( )
( )( )
2*
11 1
2 1 2 3 ... 1 2. ,
2
n
nn
u n n nn n
−+ −
= ++++−+= += ∀∈
.

CHUYÊN ĐỀ II – TOÁN – 11 – DÃY SỐ - CẤP SỐ CỘNG – CẤP SỐ NHÂN
Page 10
Sưu tầm và biên soạn
Do đó:
2
1
2017 2018 0 2017 2018 0
2018
n
n
un nn
n
= −
−+ +=⇔−+ +=⇔
=
Vậy
2018.
n =
Câu 28: Cho hai cấp số cộng
:1;6;11;...
n
u
và
: 4;7;10;...
n
v
Mỗi cấp số có 2018 số. Hỏi có bao nhiêu
số có mặt trong cả hai dãy số trên.
A.
403
. B.
401
. C.
402
. D.
504
.
Lời giải
Dãy
n
u
có số hạng tổng quát là
1 5 1 5 4, 1 2018
n
u nn n
.
Dãy
m
v
có số hạng tổng quát là
4 3 1 3 1, 1 2018
m
v mm m
.
Một số có mặt trong cả hai dãy số trên nếu tồn ại
,mn
thỏa mãn điều kiện:
1 , 2018
(*)
mn
mn
uu
.
Ta có
* 5 4 3 1 5 1 3 **nm n m
Từ
**
suy ra
5m
, mặt khác
1 2018
m
nên ta được tập các giá trị của
m
là
5;10;...;2015
.
Xét với
2015m
thì
3.2015
1 1210 2018
5
n
, thỏa điều kiện
1 2018n
.
Do tập
5;10;...;2015
có
403
số nên có tất cả
403
số có mặt trong cả hai dãy đã cho.
Câu 29: Cho dãy số
( )
n
u
thỏa
1
2
1
3
2 3, , 2
nn
u
u u nn n n
−
=
= + − − ∀∈ ≥
. Tính tổng
20 1 2 20
...S uu u= + ++
A.
2022
. B.
8385080
. C.
2021
. D.
8385087
.
Lời giải
Ta có:
( ) (
)
( )
( )
(
)
2
1
22
1
2
2
1
2
2
1
23
3 12 2 4 26 62
312 21612
3 12 1 3 1 1
nn
nn
nn
nn
u u nn
un n u n n n
un n u n n
un n u n n
−
−
−
−
= + −−
⇔+++= + −++−+
⇔ + + += + − + − +
⇔ + + += + − + − +
,1nn∀∈ ≥
, đặt
( )
( )
2
11
2
2
11
1 3.1 1 8
31
1 3 11
nn
nn
vu
vun n
vu n n
−−
= + + +=
= + + +⇒
= + − + −+
Ta có dãy
( )
1
1
8
:
2, , 2
n
nn
v
v
vvn n
−
=
= ∀∈ ≥
là một cấp số nhân với
1
8v =
, công bội là
2q =
12
8.2 2
nn
n
v
−+
⇒= =
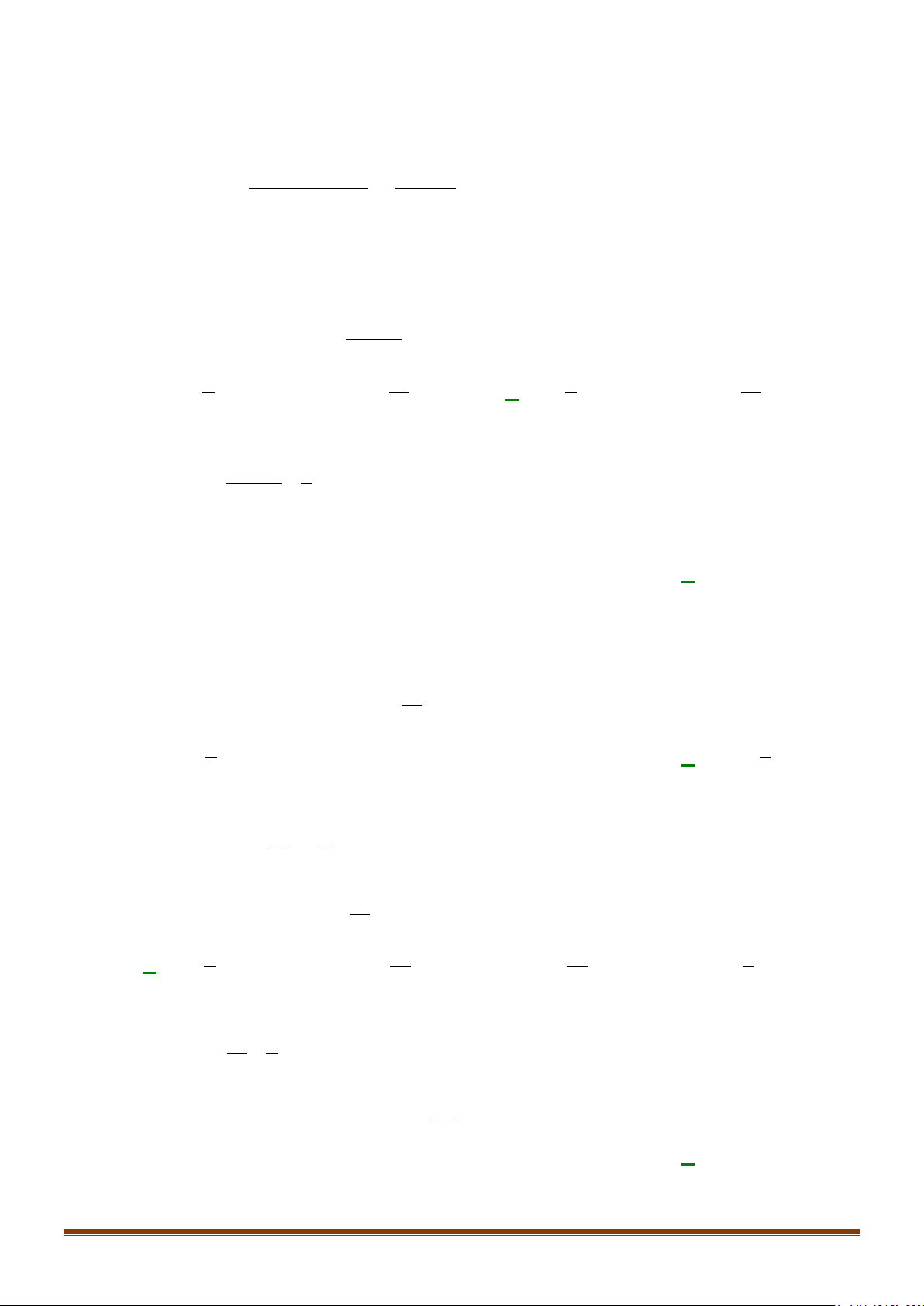
CHUYÊN ĐỀ II – TOÁN – 11 – DÃY SỐ - CẤP SỐ CỘNG – CẤP SỐ NHÂN
Page 11
Sưu tầm và biên soạn
Vậy
22
2 31
n
n
u nn
+
= −−−
Vậy
( )
( )
22 2 2
1
... 2 2 2 ... 2 1 2 ... 3 1 2 ...
n
nn
S u u n nn
= ++ = + ++ −− −− − +++ −
( )
( )( )
( )
3
12 1 1
22 1 3
62
n
nn n nn
n
++ +
= −− − −
Vậy
20
8385087S =
.
DẠNG 2. TÌM HẠNG TỬ TRONG DÃY SỐ
Câu 30: Cho dãy số
,
n
u
biết
2
2
21
.
3
n
n
u
n
Tìm số hạng
5
.u
A.
5
1
.
4
u =
B.
5
17
.
12
u =
C.
5
7
.
4
u =
D.
5
71
.
39
u =
Lời giải
Ta có
2
5
2
2.5 1 7
53 4
u
−
= =
+
Câu 31: Cho dãy số
,
n
u
biết
n
n
un1 .2 .
Mệnh đề nào sau đây sai?
A.
1
2.u
B.
2
4.u
C.
3
6.u
D.
4
8.
u
Lời giải
Vì
( )
4
4
1 .2.4 8u =−=
Câu 32: Cho dãy số
,
n
u
biết
2
1. .
n
n
n
u
n
Tìm số hạng
3
.u
A.
3
8
.
3
u
B.
3
2.u
C.
3
2.u
D.
3
8
.
3
u
Lời giải
Ta có
( )
3
3
3
28
1
33
u =−=−
Câu 33: Cho dãy số
,
n
u
biết
2
n
n
n
u =
. Chọn đáp án đúng.
A.
4
1
.
4
u =
B.
5
1
.
16
u =
C.
5
1
.
32
u =
D.
3
1
.
8
u =
Lời giải
Ta có
4
4
41
24
u = =
Câu 34: Cho dãy số
,
n
u
biết
( 1) sin( )
2
n
n
n
un
π
= −
. Số hạng thứ 9 của dãy số đó là:
A. 0. B. 9. C.
−1.
D.
−9.
Lời giải

CHUYÊN ĐỀ II – TOÁN – 11 – DÃY SỐ - CẤP SỐ CỘNG – CẤP SỐ NHÂN
Page 12
Sưu tầm và biên soạn
Ta có
(
)
9
9
9
9. 1 .sin 9
2
u
π
=−=−
Câu 35: Cho dãy số
,
n
u
biết
1
1
n
u
n
=
+
. Ba số hạng đầu tiên của dãy số đó lần lượt là những số nào
dưới đây?
A.
111
;;.
234
B.
11
1; ; .
23
C.
111
;;.
246
D.
11
1; ; .
35
Lời giải
Ta có
123
111
,,
234
uuu= = =
Câu 36: Cho dãy số
,
n
u
biết
21
2
n
n
u
n
+
=
+
. Viết năm số hạng đầu của dãy số.
A.
12345
3 7 3 11
1,,,,
452 7
uuuuu= = = = =
. B.
12345
5 7 3 11
1,,,,
452 7
uuuuu= = = = =
.
C.
12345
5 8 3 11
1,,,,
452 7
uuuuu= = = = =
D.
12345
5 7 7 11
1,,,,
452 3
uuuuu= = = = =
.
Lời giải
Câu 37: Cho dãy số
,
n
u
biết
31
n
n
n
u
=
−
. Ba số hạng đầu tiên của dãy số đó là
A.
111
;;.
248
B.
11 3
;; .
2426
C.
11 1
;; .
2 4 16
D.
123
;;.
234
Lời giải
Câu 38: Cho dãy số
,
n
u
biết
1
21
n
n
u
n
. Số
8
15
là số hạng thứ mấy của dãy số?
A. 8. B. 6. C. 5. D. 7.
Lời giải
Ta có
( )
*
8 18
15 15 16 8 7
15 2 1 15
n
n
u n n nn
n
+
= ⇔ = ∈ ⇔ + = +⇔ =
+
Câu 39: Cho dãy số
,
n
u
biết
25
.
54
n
n
u
n
Số
7
12
là số hạng thứ mấy của dãy số?
A. 6. B. 8. C. 9. D. 10.
Lời giải
Ta có
( )
*
7 257
24 60 35 28 11 88 8
12 5 4 12
n
n
u n n n nn
n
+
= ⇔ = ∈ ⇔ + = − ⇔ = ⇔=
−
Câu 40: Cho dãy số
,
n
u
biết
2
1
.
1
n
n
u
n
Số
2
13
là số hạng thứ mấy của dãy số?
A. Thứ 3. B. Thứ tư. C. Thứ năm. D. Thứ 6.
Lời giải

CHUYÊN ĐỀ II – TOÁN – 11 – DÃY SỐ - CẤP SỐ CỘNG – CẤP SỐ NHÂN
Page 13
Sưu tầm và biên soạn
Ta có
( )
( )
( )
* 22
2
5
2 12
13 13 2 2 2 13 15 0
3
13 1 13
2
n
nn
n
u n n n nn
n
nl
=
−
= ⇔ = ∈ ⇔ − = +⇔ − + =⇔
+
=
Câu 41: Cho dãy số
,
n
u
biết
32
8 5 7.
n
un n n
Số
33
là số hạng thứ mấy của dãy số?
A. 5. B. 6. C. 8. D. 9.
Lời giải
Ta có
( )
( )
(
)
32 * 32
8
33 8 5 7 33 8 5 40 0
5
n
nn
u nnn n nnn
nl
=
=−⇔− −+=− ∈ ⇔− −+=⇔
= ±
Câu 42: Cho dãy số
n
u
với
2
37
1
n
nn
u
n
++
=
+
. Hỏi dãy số trên có bao nhiêu số hạng nhận giá trị nguyên.
A. 2. B. 4. C. 1. D. Không có.
Lời giải
Ta có
( )
2
*
37 5
2
11
n
nn
u nn
nn
++
= =++ ∈
++
Để
n
u
nhận giá trị nguyên thì
( )
*
5
1
n
n
∈
+
là số nguyên hay
4n =
Vậy dãy số
( )
n
u
chỉ có một số hạng nhận giá trị nguyên.
Câu 43: Cho dãy số
n
u
với
2.
n
n
u =
Tìm số hạng
1
.
n
u
+
A.
1
2 .2.
n
n
u
B.
1
2 1.
n
n
u
C.
1
2 1.
n
un
D.
1
2 2.
n
n
u
Lời giải
Ta có
1
1
2 2.2
nn
n
u
+
+
= =
Câu 44: Cho dãy số
n
u
với
3.
n
n
u =
Tìm số hạng
21
.
n
u
A.
2
21
3 .3 1.
n
n
u
B.
1
21
3 .3 .
nn
n
u
C.
2
21
3 1.
n
n
u
D.
21
21
3.
n
n
u
Lời giải
Ta có
21 1
21
3 3 .3
n nn
n
u
−−
−
= =
Câu 45: Cho dãy số
n
u
với
3.
n
n
u =
Số hạng
1n
u
+
bằng:
A.
31
n
+
. B.
33
n
+
. C.
3 .3
n
. D.
3( 1)n +
.
Lời giải
Ta có
1
1
3 3 .3
nn
n
u
+
+
= =
Câu 46: Cho dãy số
n
u
với
3.
n
n
u =
Số hạng
2n
u
bằng:
A.
33
n
+
. B.
9
n
. C.
3 .3
n
. D.
2
4
n
.
Lời giải
Ta có
2
2
39
nn
n
u = =

CHUYÊN ĐỀ II – TOÁN – 11 – DÃY SỐ - CẤP SỐ CỘNG – CẤP SỐ NHÂN
Page 14
Sưu tầm và biên soạn
Câu 47: Cho dãy số
n
u
với
1
5.
n
n
u
+
=
Tìm số hạng
1n
u
−
.
A.
1
1
5
n
n
u
−
−
=
. B.
1
5
n
n
u
−
=
. C.
1
1
5.5
n
n
u
+
−
=
. D.
1
1
5.5
n
n
u
−
−
=
.
Lời giải
Ta có
( )
11
1
55
n
n
n
u
−+
−
= =
Câu 48: Cho dãy số
n
u
với
23
1
.
1
n
n
n
u
n
+
−
=
+
Tìm số hạng
1n
u
+
.
A.
2 13
1
1
.
1
n
n
n
u
n
B.
2 13
1
1
.
1
n
n
n
u
n
C.
23
1
.
2
n
n
n
u
n
D.
25
1
.
2
n
n
n
u
n
Lời giải
Ta có
( )
2 13 2 5
1
11
11 2
nn
n
nn
u
nn
++ +
+
+−
= =
++ +
Câu 49: Cho dãy số
n
u
xác định bởi
1
1
2
.
1
1
3
nn
u
uu
Tìm số hạng
4
.u
A.
4
5
.
9
u
B.
4
1.u
C.
4
2
.
3
u
D.
4
14
.
27
u
Lời giải
Ta có
( )
(
)
23 4
1 1 2 12 5
2 1 1, 1 1 , 1
3 3 3 33 9
uu u
= += = += = +=
Câu 50: Cho dãy số
n
u
xác định bởi
1
1
3
.
2
2
n
n
u
u
u
Mệnh đề nào sau đây sai?
A.
2
5
.
2
u
B.
3
15
.
4
u
C.
4
31
.
8
u
D.
5
63
.
16
u
Lời giải
Vì
2
37
2
22
u =+=
Câu 51: Cho dãy số
n
u
xác định bởi
1
1
7
23
nn
u
uu
+
=
= +
khi đó
5
u
bằng:
A. 317. B. 157. C. 77. D. 112.
Lời giải
Ta có
23 4 5
2.7 3 17, 2.17 3 37, 2.37 3 77, 2.77 3 157
uu u u= += = += = += = +=
Câu 52: Cho dãy số
n
u
xác định bởi
1
1
1
3
nn
u
uu
+
= −
= +
. Ba số hạng đầu tiên của dãy số đó là

CHUYÊN ĐỀ II – TOÁN – 11 – DÃY SỐ - CẤP SỐ CỘNG – CẤP SỐ NHÂN
Page 15
Sưu tầm và biên soạn
A.
1;2;5.−
B.
1; 4; 7.
C.
4; 7;10
D.
1; 3; 7.
−
Lời giải
Ta có
12 3
1, 1 3 2, 2 3 5uu u
=− =−+= =+=
Câu 53: Cho dãy số
n
u
xác định bởi
+
=
= +
1
1
3
5
nn
u
uu
. Ba số hạng đầu tiên của dãy số đó là
A.
−3; 6; 9.
B.
−−3; 2; 7.
C.
3; 8;13
. D.
3; 5;7.
Lời giải
Ta có
12 3
3, 3 5 8, 8 5 13uu u
= =+= =+=
Câu 54: Cho dãy số
n
u
xác định bởi
−
= −
≥
= +
1
2
1
2
( 2)
2
nn
u
n
uun
. Số hạng thứ tư của dãy số đó bằng
A. 0. B. 93. C. 9. D. 34.
Lời giải
Ta có
( )
23 2
2 34
2. 2 2 0, 2.0 3 9, 2.9 4 34u uu=−+= = += = +=
Câu 55: Cho dãy số
( )
n
u
, biết
21
n
n
n
u =
−
. Ba số hạng đầu tiên của dãy số là
A.
123
;;
234
. B.
11
1; ;
2 16
C.
11
1; ;
48
D.
23
1; ;
37
.
Lời giải
12 3
23
1, ,
37
uu u= = =
.
Câu 56: Cho dãy số
n
u
xác định bởi
1
1
1
2
1
,2
2
n
n
u
un
u
. Khi đó
3
u
có giá trị bằng
A.
3
4
. B.
4
3
. C.
2
3
. D.
3
2
.
Lời giải
Theo công thức truy hồi ta có
2
12
1
3
2
2
u
3
13
2
4
2
3
u
.
Câu 57: Cho dãy số
( )
n
u
với
23
n
un= +
. Tìm số hạng thứ 6 của dãy số.
A.
17
. B.
5
. C.
15
. D.
7
.
Lời giải
Ta có số hạng thứ 6 của dãy là
6
2.6 3 15u = +=
.
Câu 58: Cho dãy số
( )
n
u
, biết
2.3
n
n
u =
. Giá trị của
20
u
bằng
A.
19
2.3 .
. B.
20
2.3 .
. C.
20
3.
. D.
21
2.3 .
Lời giải

CHUYÊN ĐỀ II – TOÁN – 11 – DÃY SỐ - CẤP SỐ CỘNG – CẤP SỐ NHÂN
Page 16
Sưu tầm và biên soạn
Ta có
2.3
n
n
u
=
suy ra
20
20
2.3u =
.
Câu 59: Cho dãy số
( )
n
u
, biết công thức số hạng tổng quát
23
n
un= −
. Số hạng thứ 10 của dãy số bằng:
A.
17
B.
20
C.
10
D.
7
Lời giải
10
2 3 2.10 3 17
n
un u
= − →⇒ = − =
Câu 60: Cho dãy số
( )
n
u
có công thức số hạng tổng quát
83
n
un= −
. Tính
4
.u
A.
2
. B.
7−
. C.
5−
. D.
4−
.
Lời giải
4
8 3.4 4.u =−=−
Câu 61:
Cho dãy số
(
)
n
u
xác định bởi
2
1
23
n
n
u
nn
−
=
++
. Giá trị
21
u
là
A.
11
243
. B.
10
243
. C.
21
443
. D.
19
443
.
Lời giải
Ta có:
21
2
21 1 10
21 2.21 3 243
u
−
= =
++
.
Câu 62: Cho dãy số
( )
n
u
có
2
2
1
1
n
n
u
n
−
=
+
. Tính
2
u
.
A.
2
1
5
u =
. B.
2
2
5
u =
. C.
2
3
5
u
=
. D.
2
4
5
u
=
.
Lời giải
Ta có
2
2
2
213
2 15
u
−
= =
+
.
Câu 63: Cho dãy số
(
)
n
u
được xác định bởi
1
1
2
3 1, 2
nn
u
uu n
−
= −
= − ∀≥
. Tìm số hạng
4
u
.
A.
4
76u = −
. B.
4
77u = −
.
C.
4
66u = −
. D.
4
67u = −
.
Lời giải
Cách 1. Ta có
( )
( )
( )
21
32
43
3 1 3. 2 1 7
3 1 3. 7 1 22
3 1 3. 22 1 67
uu
uu
uu
= −= − −=−
= −= − −=−
= −= − −=−
Cách 2.

CHUYÊN ĐỀ II – TOÁN – 11 – DÃY SỐ - CẤP SỐ CỘNG – CẤP SỐ NHÂN
Page 17
Sưu tầm và biên soạn
11
1
31
3 13
22
11
3
22
nn n
nn
uu u
uu
−−
−
= −= − +
⇒ −= −
Xét dãy số
( )
n
v
có
1
5
2
1
2
nn
v
vu
−
=
= −
Khi đó ta có
1
3
nn
vv
−
=
là cấp số nhân có công bội bằng
3
.
1
5
.3
2
n
n
v
−
−
⇒=
Vậy
1
15
.3
22
n
n
u
−
= −
.
Câu 64: Cho dãy số
( )
n
u
, biết
(
)
( )
3
2
n
nn
u
−
=
. Ba số hạng đầu tiên của dãy số là
A.
13
;1;
22
. B.
1
1; ; 0
2
−−
. C.
1; 1; 0
−−
. D.
13
;1;
22
.
Lời giải
( )
1
11 3
1
2
u
−
= = −
;
( )
2
22 3
1
2
u
−
= = −
;
( )
1
33 3
0
2
u
−
= =
Vậy ba số hạng đầu tiên của dãy số là
1, 1, 0−−
.
Câu 65: Cho dãy số
( )
n
u
với
23
n
un= −
. Số hạng thứ 5 của dãy số là
A.
5
. B.
4
. C.
13
. D.
7
.
Lời giải
Ta có:
5
2.5 3 7u = −=
.
Câu 66: Cho dãy số
( )
n
u
thỏa mãn
21
n
n
u
n
+
=
. Tìm số hạng thứ
10
của dãy số đã cho.
A.
2,1
. B.
2, 2
. C.
2,0
. D.
2, 4
.
Lời giải
Ta có:
10
2.10 1
10
u
+
=
2,1=
.
Câu 67: Cho dãy số
( )
n
u
có số hạng tổng quát
2
1
1
n
n
u
n
= −
+
. Số hạng đầu tiên của dãy là:
A.
2
. B.
3
5
. C.
0
. D.
1
2
.
Lời giải
Chọn D

CHUYÊN ĐỀ II – TOÁN – 11 – DÃY SỐ - CẤP SỐ CỘNG – CẤP SỐ NHÂN
Page 18
Sưu tầm và biên soạn
Ta có
1
2
11
1
112
u
=−=
+
.
Câu 68: Cho dãy số
( )
n
u
có
2
1
n
u nn
=− ++
. Số
19−
là số hạng thứ mấy của dãy?
A.
5
. B.
7
. C.
6
. D.
4
.
Lời giải
Chọn A
Giả sử
19
n
u = −
,
(
)
*
n
∈
.
Suy ra
2
1 19
nn
− + +=−
2
20 0nn
⇔− + + =
(
)
5
4
n
nl
=
⇔
= −
.
Vậy số
19−
là số hạng thứ
5
của dãy.
Câu 69: Cho dãy số
( )
n
u
với
3
n
n
u
=
. Khi đó số hạng
21
n
u
−
bằng
A.
1
3 .3
nn−
. B.
21
31
n−
−
. C.
2
31
n
−
. D.
2
3 .3 1
n
−
.
Lời giải
Chọn A
21 1
21
3 3 3 .3
n n nn
nn
uu
−−
−
=⇒==
Câu 70: Cho dãy số
n
u
xác định bởi
1 cos
n
n
un
π
. Giá trị
99
u
bằng
A.
99
. B.
1
. C.
1
. D.
99
.
Lời giải
Chọn C
Ta có:
99
99
1 cos 99 cos 98 cos 1.u
π ππ π
Câu 71: Cho dãy số
( )
n
u
với
21
n
un= +
số hạng thứ
2019
của dãy là
A.
4039
. B.
4390
. C.
4930
. D.
4093
.
Lời giải
Ta có:
2019
2.2019 1 4039u = +=
.
Câu 72: Cho dãy số
(
)
n
u
với
1 2.
n
n
u = +
Khi đó số hạng
2018
u
bằng
A.
2018
2
. B.
2017
2017 2+
. C.
2018
12
+
. D.
2018
2018 2+
.
Lời giải
Ta có
2018
2018
12 .u = +
Câu 73: Cho dãy số
( )
n
u
với
2
,n 1.
31
n
n
u
n
−
= ≥
+
Tìm khẳng định sai.
A.
3
1
.
10
u =
B.
10
8
.
31
u =
C.
21
19
.
64
u
=
D.
50
47
.
150
u =
Lời giải
Ta có:
50
50 2 48
.
3.50 1 151
u
−
= =
+

CHUYÊN ĐỀ II – TOÁN – 11 – DÃY SỐ - CẤP SỐ CỘNG – CẤP SỐ NHÂN
Page 19
Sưu tầm và biên soạn
Câu 74: Cho dãy số
2
21
1
n
nn
u
n
+−
=
+
. Tính
11
u
.
A.
11
182
12
u
=
. B.
11
1142
12
u
=
. C.
11
1422
12
u
=
. D.
11
71
6
u
=
.
Lời giải
Ta có:
2
11
11 2.11 1 71
11 1 6
u
+−
= =
+
.
Câu 75: Cho dãy số
( )
n
u
có số hạng tổng quát là
2
21
1
n
n
u
n
+
=
+
. Khi đó
39
362
là số hạng thứ mấy của dãy
số?
A.
20
. B.
19
. C.
22
. D.
21
.
Lời giải
Ta có
2
2 1 39
1 362
n
n
+
=
+
2
39 724 323 0nn⇔ − −=
19
17
39
n
n
=
⇔
= −
, do
*
n ∈
nên
19n =
.
Câu 76: Cho dãy số
(
)
1
1
5
:
n
nn
u
u
u un
+
=
= +
. Số
20
là số hạng thứ mấy trong dãy?
A.
5
. B.
6
. C.
9
. D.
10
.
Lời giải
Cách 1:
1234 5 6
5, 6, 8, 11, 15, 20uu uu u u= = = = = =
Vậy số
20
là số hạng thứ
6
.
Cách 2:
Dựa vào công thức truy hồi ta có
(
)
1
2
3
4
5
51
512
5123
.....
1
5 1 2 ... 1 5
2
n
u
u
u
u
nn
un
=
= +
= ++
= ++ +
−
⇒ = ++ + + −= +
( )
( )
1
20 5 *
2
nn
n
−
⇒=+ ∈
=
⇔ −− =⇔
= −
2
6
30 0
5(lo¹i )
n
nn
n
Vậy
20
là số hạng thứ
6
.
Cách 3: Sử dụng máy tính CASIO fx – 570VN PLUS
1 SHIFT STO A
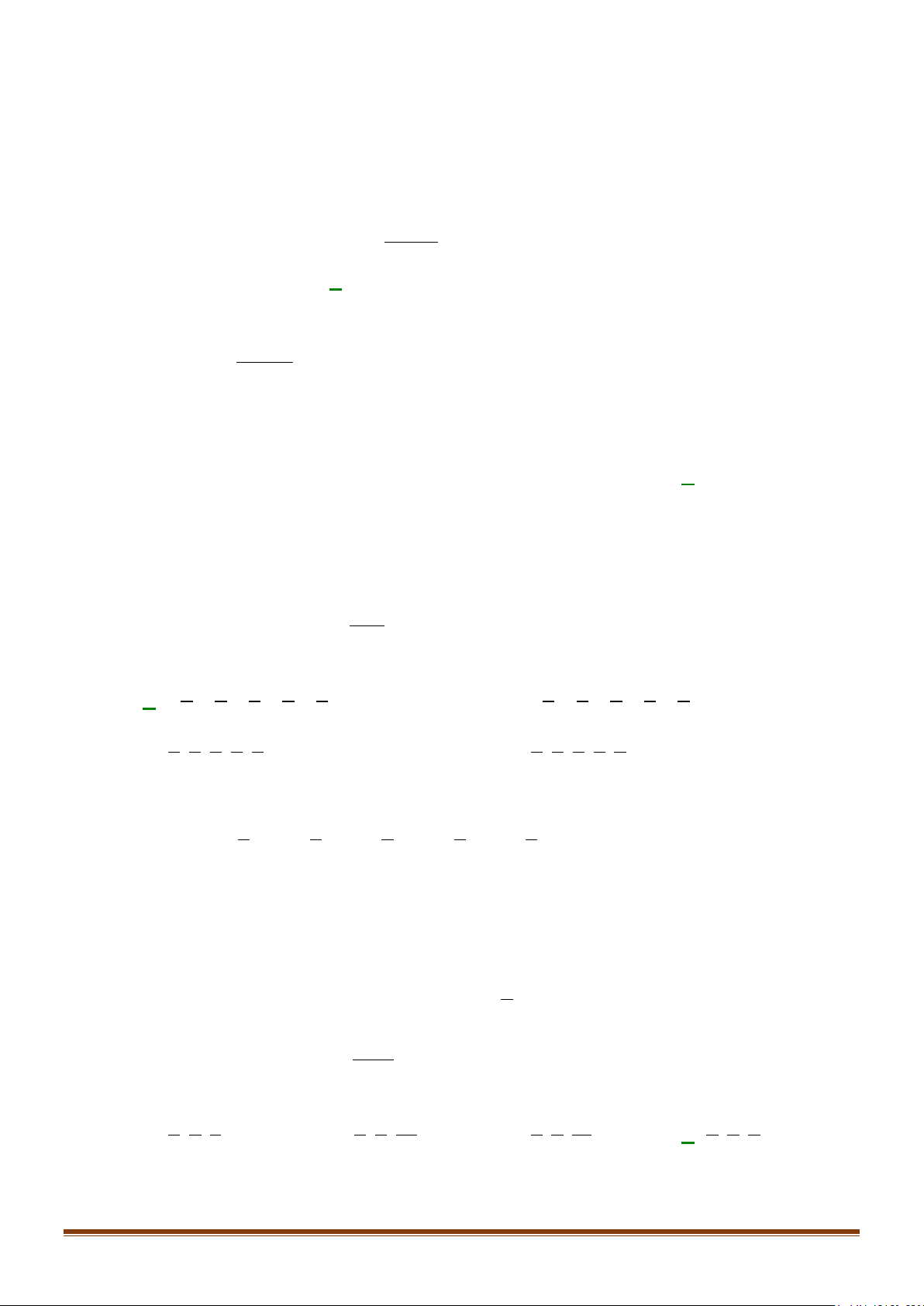
CHUYÊN ĐỀ II – TOÁN – 11 – DÃY SỐ - CẤP SỐ CỘNG – CẤP SỐ NHÂN
Page 20
Sưu tầm và biên soạn
5 SHIFT STO B
Ghi vào màn hình C = B + A: A = A + 1: B = C
Ấn CALC và lặp lại phím =
Ta tìm được số 20 là số hạng thứ 6
Câu 77: Cho dãy số
( )
n
u
thỏa mãn
1
21
n
n
u
n
−
+
=
. Tìm số hạng thứ
10
của dãy số đã cho.
A.
51, 2
. B.
51, 3
. C.
51,1
. D.
102,3
.
Lời giải
Ta có:
10 1
10
21
10
u
−
+
=
51, 3=
.
Câu 78: Cho dãy số
1
1
4
nn
u
u un
+
=
= +
. Tìm số hạng thứ
5
của dãy số.
A.
16
. B.
12
. C.
15
. D.
14
.
Lời giải
Ta có
21
15uu= +=
;
32
27uu
= +=
;
43
3 10uu= +=
. Do đó số hạng thứ
5
của dãy số là
54
4 14uu= +=
.
Câu 79: Cho dãy số
( )
n
u
, biết
.
1
n
n
u
n
−
=
+
Năm số hạng đầu tiên của dãy số đó lần lượt là những số nào
dưới đây?
A.
12345
;;;;.
23456
−−−−−
B.
23456
;;;;.
34567
−−−−−
C.
12345
;;;;.
23456
D.
23456
;;;;.
34567
Lời giải
Ta có
12345
12345
;;;;.
23456
uuuuu=−=−=−=−=−
Nhận xét: Dùng MTCT chức năng CALC để kiểm tra nhanh.
Ta thấy dãy
( )
n
u
là dãy số âm nên loại các phương án C, D. Đáp án đúng là A
hoặc B. Ta chỉ cần kiểm tra một số hạng nào đó mà cả hai đáp án khác nhau
là được. Chẳng hạng kiểm tra
1
u
thì thấy
1
1
2
u = −
Câu 80: Cho dãy số
( )
n
u
, biết
31
n
n
n
u =
−
. Ba số hạng đầu tiên của dãy số đó lần lượt là những số nào
dưới đây?
A.
111
;;.
248
B.
11 3
;; .
2426
C.
11 1
;; .
2 4 16
D.
123
;;.
234
Lời giải
Dùng MTCT chức năng CALC: ta có

CHUYÊN ĐỀ II – TOÁN – 11 – DÃY SỐ - CẤP SỐ CỘNG – CẤP SỐ NHÂN
Page 21
Sưu tầm và biên soạn
12 3
23
1 2 21 3 3
; ;.
2 3 1 8 4 3 1 26
uu u= = = = = =
−−
Câu 81: Cho dãy số
( )
n
u
, biết
1
1
1
3
nn
u
uu
+
= −
= +
với
0n ≥
. Ba số hạng đầu tiên của dãy số đó là lần lượt là
những số nào dưới đây?
A.
1; 2; 5.−
B.
1; 4; 7.
C.
4;7;10.
D.
1; 3; 7.
−
Lời giải
Ta có
1 21 32
1; 3 2; 3 5.u uu uu=− = += = +=
Nhận xét: Dùng chức năng “lặp” của MTCT để tính:
Nhập vào màn hình:
3.XX= +
Bấm CALC và cho
1
X = −
Vì
1
1u = −
nên loại các đáp án B, C. Còn lại các đáp án A,
C; để biết đáp án nào ta chỉ cần kiểm tra
2
u
:
21
32uu
= +=
Câu 82: Cho dãy số
( )
,
n
u
biết
1
21
n
n
u
n
+
=
+
. Số
8
15
là số hạng thứ mấy của dãy số?
A.
8.
B.
6.
C.
5.
D.
7.
Lời giải
Ta cần tìm
n
sao cho
18
15 15 16 8 7.
2 1 15
n
n
u n nn
n
+
= = ⇔ + = +⇔ =
+
Nhận xét: Có thể dùng chức năng CALC để kiểm tra nhanh.
Câu 83: Cho dãy số
(
)
,
n
u
biết
25
.
54
n
n
u
n
+
=
−
Số
7
12
là số hạng thứ mấy của dãy số?
A.
8.
B.
6.
C.
9.
D.
10.
Lời giải
Dùng chức năng “lặp” để kiểm tra đáp án. Hoặc giải cụ thể như sau:
257
24 60 35 28 11 88 8.
5 4 12
n
n
u n n nn
n
+
= = ⇔ + = − ⇔ = ⇔=
−
Câu 84: Cho dãy số
( )
,
n
u
biết
2.
n
n
u =
Tìm số hạng
1
.
n
u
+
A.
1
2 .2.
n
n
u
+
=
B.
1
2 1.
n
n
u
+
= +
C.
( )
1
2 1.
n
un
+
= +
D.
1
2 2.
n
n
u
+
= +
Lời giải
Thay
n
bằng
1n +
trong công thức
n
u
ta được:
1
1
2 2.2
nn
n
u
+
+
= =
.
Câu 85: Cho dãy số
( )
n
u
, biết
3.
n
n
u
=
Tìm số hạng
21
.
n
u
−
A.
2
21
3 .3 1.
n
n
u
−
= −
B.
1
21
3 .3 .
nn
n
u
−
−
=
C.
2
21
3 1.
n
n
u
−
= −
D.
( )
21
21
3.
n
n
u
−
−
=
Lời giải
Ta có
21
21 1
21
3 3 3 .3 .
nn
n n nn
nn
uu
↔−
−−
−
= → = =

CHUYÊN ĐỀ II – TOÁN – 11 – DÃY SỐ - CẤP SỐ CỘNG – CẤP SỐ NHÂN
Page 22
Sưu tầm và biên soạn
Câu 86: Cho dãy số
( )
,
n
u
với
1
5.
n
n
u
+
=
Tìm số hạng
1
.
n
u
−
A.
1
1
5.
n
n
u
−
−
=
B.
1
5.
n
n
u
−
=
C.
1
1
5.5 .
n
n
u
+
−
=
D.
1
1
5.5 .
n
n
u
−
−
=
Lời giải
( )
11
1
1
1
5 5 5.
n
nn
nn
nn
uu
−+
↔−
+
−
= → = =
Câu 87: Cho dãy số
( )
n
u
bởi công thức truy hồi sau
1
1
0
; 1
nn
u
u u nn
+
=
=+≥
;
218
u
nhận giá trị nào sau đây?
A.
23653
. B.
46872
. C.
23871
. D.
23436
.
Lời giải
Đặt
1nn n
vu un
+
= −=
, suy ra
( )
n
v
là một câp số cộng với số hạng đầu
1 21
1vuu
=−=
và công
sai
1d
=
.
Xét tổng
217 1 2 217
...
S vv v=+ ++
.
Ta có
217 1 2 217
...S vv v=+ ++
(
)
1 217
217.
2
vv
+
=
( )
217. 1 217
23653
2
+
= =
.
Mà
1nn n
vu u
+
= −
suy ra
(
) ( ) (
)
217 1 2 217 2 1 3 2 218 217
... ...S vv v u u uu u u=+ ++ = − + − ++ −
218 1
uu= −
218 217 1
23653u Su
⇒ = +=
.
DẠNG 3. DÃY SỐ TĂNG, DÃY SỐ GIẢM
Câu 88: Cho các dãy số sau. Dãy số nào không là dãy số tăng?
A.
1;1;1;1; ...
. B.
1;3;5;7;...
. C.
2;4;6;8;...
. D.
13
;1; ;2;...
22
Lời giải
Xét đáp án A ta có dãy
1;1;1;1; ...
là dãy hằng nên không tăng không giảm.
Câu 89: Cho dãy số
()
n
u
biết
52
n
un= +
. Mệnh đề nào sau đây đúng?
A. Dãy số tăng B. Dãy số giảm
C. Dãy số không tăng, không giảm D. Dãy số vừa tăng vừa giảm
Lời giải
* Trắc nghiệm: Tính vài số hạng đầu của dãy số rồi suy ra kết quả
* Tự luận:
Ta có
( )
11
5 12 52 57 520
nn n n
uu n n n n u u
++
− = ++− += +− +>⇔ >
Câu 90: Cho dãy số
()
n
u
biết
1
32
n
u
n
=
+
. Mệnh đề nào sau đây đúng?
A. Dãy số tăng B. Dãy số giảm
C. Dãy số không tăng, không giảm D. Dãy số vừa tăng vừa giảm
Lời giải
Ta có
( ) ( )( )
1
1 111 3
0
3 12323532 3532
nn
uu
n n n n nn
+
−= −=−=− <
++ + + + + +
.

CHUYÊN ĐỀ II – TOÁN – 11 – DÃY SỐ - CẤP SỐ CỘNG – CẤP SỐ NHÂN
Page 23
Sưu tầm và biên soạn
Vậy
*
11
0,
nn n n
u u u un
++
− < ⇔ < ∀∈
Câu 91: Cho dãy số
()
n
u
biết
10
3
n
n
u =
. Mệnh đề nào sau đây đúng?
A. Dãy số tăng B. Dãy số giảm
C. Dãy số không tăng, không giảm D. Dãy số vừa tăng vừa giảm
Lời giải
Ta có
1
1
10 10 10 10 20
0
3 3 3.3 3 3.3
nn
nnnnn
uu
+
+
−
−= −= −= <
Vậy
*
11
0,
nn n n
u u u un
++
− < ⇔ < ∀∈
Câu 92: Cho dãy số
()
n
u
biết
2
2 31
n
u nn= ++
. Mệnh đề nào sau đây đúng?
A. Dãy số tăng B. Dãy số giảm
C. Dãy số không tăng, không giảm D. Dãy số vừa tăng vừa giảm
Lời giải
Ta có
(
) ( )
2
2*
1
2 1 3 1 1 2 3 1 4 5 0,
nn
uu n n nn n n
+
− = + + + +− − −= + > ∀∈
Vậy
*
11
0,
nn n n
u u u un
++
− < ⇔ < ∀∈
Câu 93: Cho dãy số
()
n
u
biết
( )
( )
2
11
n
n
un=−+
. Mệnh đề nào sau đây đúng?
A. Dãy số tăng B. Dãy số giảm
C. Dãy số không tăng, không giảm D. Dãy số là dãy hữu hạn
Lời giải
Dãy không tăng, không giảm vì các số hạng đan dấu
Câu 94: Cho dãy số
()
n
u
biết
2
400
n
un n= −
. Mệnh đề nào sau đây đúng?
A. Dãy số tăng B. Dãy số giảm
C. Dãy số không tăng, không giảm D. Mọi số hạng đều âm
Lời giải
Ta có
( ) ( )
2
2
1
1 400 1 400 2 399
nn
u u n n n nn
+
− = + − +− + = −
Do
2 399 0n
−>
khi
399
2
n >
và
2 399 0n −<
khi
399
2
n <
.
Vậy dãy số đã cho không tăng, không giảm
Câu 95: Trong các dãy số
( )
n
u
cho bởi số hạng tổng quát
n
u
sau, dãy số nào tăng?
A.
1
.
3
n
n
u =
B.
1
.
21
n
u
n
=
+
C.
1
.
32
n
n
u
n
+
=
+
D.
42
.
3
n
n
u
n
−
=
+
Lời giải
Ta có:
1
1
11 11 2
0
3 3 3.3 3 3.3
nn
nnnnn
uu
+
+
−
−= −= −= <
→
loại A

CHUYÊN ĐỀ II – TOÁN – 11 – DÃY SỐ - CẤP SỐ CỘNG – CẤP SỐ NHÂN
Page 24
Sưu tầm và biên soạn
(
) ( )( )
1
1 111 2
0
2 11212321 2321
nn
uu
n nnn nn
+
−
−= −=−= <
+++++ ++
→
loại B
( )( )
1
21 1
0
3532 3532
nn
nn
uu
n n nn
+
++
−= − =− <
++ ++
→
loại C
( )( )
1
4 2 4 2 14
0
4 3 43
nn
nn
uu
n n nn
+
+−
−= − = >
+ + ++
Câu 96: Trong các dãy số
( )
n
u
cho bởi số hạng tổng quát
n
u
sau, dãy số nào giảm?
A.
4
.
3
n
n
u
=
B.
(
)
(
)
1 5 1.
n
n
n
u =−−
C.
3.
n
n
u
= −
D.
4.
n
un= +
Lời giải
Ta có:
1
1
4 4 44 4 14
. .0
3 3 33 3 33
n n nn n
nn
uu
+
+
−= − = − = >
→
loại A
Dãy
( )
n
u
với
( )
( )
1 5 1.
n
n
n
u =−−
có các số hạng đan dấu nên dãy không tăng, không giảm
→
loại B
1
1
3 3 3.3 3 2.3 0
nnnnn
nn
uu
+
+
−=− +=− +=− <
→
Chọn C
1
1
54 0
54
nn
uu n n
nn
+
− = +− += >
++ +
→
loại D
Câu 97: Trong các dãy số
( )
n
u
cho bởi số hạng tổng quát
n
u
sau, dãy số nào không tăng, không giảm?
A.
1
.
n
un
n
= +
B.
5 3.
n
n
un= +
C.
3.
n
n
u = −
D.
( )
2
3. 1
n
n
un=−+
Lời giải
Dãy không tăng, không giảm vì các số hạng đan dấu
Dãy trong đáp án A và B tăng, dãy trong đáp án C là dãy giảm
Câu 98: Cho dãy số
()
n
u
biết
54
nn
n
u = −
. Mệnh đề nào sau đây đúng?
A. Dãy số tăng B. Dãy số giảm
C. Dãy số không tăng, không giảm D. Dãy số có số hạng thứ 100 bé hơn 1
Lời giải
Ta có
( )
11 *
1
5 4 5 4 4 5 4 0,
n n nn nn
nn
uu n
++
+
− = − − + = − > ∀∈
Vậy
*
11
0,
nn n n
u u u un
++
− > ⇔ > ∀∈
Câu 99: Cho dãy số
()
n
u
biết
2
31
n
an
u
n
+
=
+
. Tìm tất cả các giá trị của a để dãy số tăng.
A.
6a =
B.
6a >
C.
6a <
D.
6a ≥
Lời giải
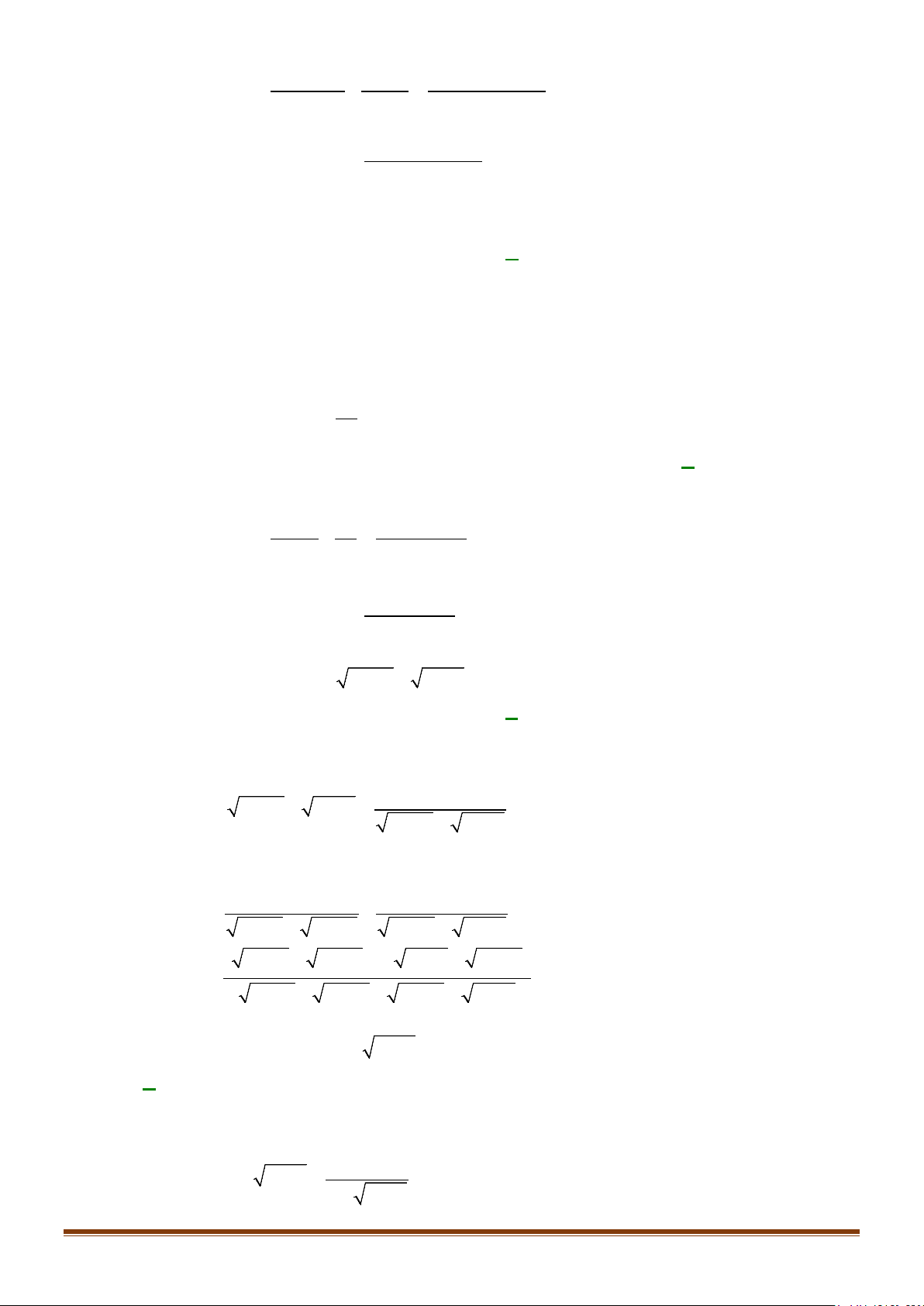
CHUYÊN ĐỀ II – TOÁN – 11 – DÃY SỐ - CẤP SỐ CỘNG – CẤP SỐ NHÂN
Page 25
Sưu tầm và biên soạn
Ta có
( )( )
*
1
22 6
,
34 31 3431
nn
an a an a
uu n
n n nn
+
++ + −
− = − = ∀∈
+ + ++
Để dãy số tăng thì
( )( )
*
1
6
0, 6
3 43 1
nn
a
uu n a
nn
+
−
− = > ∀∈ ⇔ >
++
Câu 100: Cho dãy số
()
n
u
biết
2
n
n
u an= −
. Tìm tất cả các giá trị của a để dãy số tăng.
A.
2a =
B.
2a >
C.
2a <
D.
2a ≥
Lời giải
Ta có
1*
1
2 2 2 a,
n nn
nn
u u an a an n
+
+
− = − − − + = − ∀∈
Để dãy số tăng thì
* **
1
2 a 0, 2 , 2,
nn
nn
uu nanan
+
− = − > ∀∈ ⇔ < ∀∈ ⇔ < ∀∈
Câu 101: Cho dãy số
()
n
u
biết
3
n
n
u
an
=
. Tìm tất cả các giá trị của a để dãy số tăng.
A.
0a
∀<
B. Không tồn tại a C.
*
a∀∈
D.
0a >
Lời giải
Ta có
( )
( )
1
*
1
22
.3 2 1
33
,
n
nn
nn
an
uu n
an a an
an n
+
+
−
− = − = ∀∈
+
+
Để dãy số tăng thì
( )
( )
*
1
22
.3 2 1
0, 0
n
nn
an
uu n a
an n
+
−
− = > ∀∈ ⇔ >
+
Câu 102: Cho dãy số
()
n
u
biết
32 31
n
un n= +− +
. Mệnh đề nào sau đây đúng?
A. Dãy số tăng B. Dãy số giảm
C. Dãy số không tăng, không giảm D. Dãy số vừa tăng vừa giảm
Lời giải
Ta có
1
32 31
32 31
n
un n
nn
= +− +=
++ +
Khi đó
( )
( )
( )
( )
1
*
11
35 34 32 31
32 35 31 34
0,
35 34 32 31
nn
uu
nn nn
n n nn
n
nnnn
+
−= −
+++ +++
+−++ +−+
= < ∀∈
+++ +++
Câu 103: Cho dãy số
()
n
u
biết
2
1
n
un n=−+
. Mệnh đề nào sau đây đúng?
A. Dãy số tăng B. Dãy số giảm
C. Dãy số không tăng, không giảm D. Các số hạng đều dương
Lời giải
Ta có
2
2
1
1
1
n
un n
nn
−
=− +=
++

CHUYÊN ĐỀ II – TOÁN – 11 – DÃY SỐ - CẤP SỐ CỘNG – CẤP SỐ NHÂN
Page 26
Sưu tầm và biên soạn
Khi đó
(
)
( )
( )
( )
(
)
(
)
2
2
*
1
22
2
2
1 11 1
11
0,
1
1 11
1 11 1
nn
nn
uu n
nn
nn
n n nn
+
+ + +− +
−
− = + = > ∀∈
++
++ + +
++ + + + +
Vậy dãy số đã cho là dãy tăng
Câu 104: Cho dãy số
()
n
u
biết
2
21
2
n
nn
u
n
−−
=
+
. Mệnh đề nào sau đây đúng?
A. Dãy số tăng B. Dãy số giảm
C. Dãy số không tăng, không giảm D. Có số hạng âm
Lời giải
Ta có
( )( )
22 2
*
1
2 3 2 1 2 10 3
0,
3 2 32
nn
n n nn n n
uu n
n n nn
+
+ −− + +
− = − = > ∀∈
+ + ++
Vậy dãy số đã cho là dãy tăng
Câu 105: Trong các dãy số
( )
n
u
cho bởi số hạng tổng quát
n
u
sau, dãy số nào tăng?
A.
sin
.
n
n
u
n
=
B.
2
1
.
21
n
n
u
n
+
=
+
C.
2
3
.
n
n
u
n
=
D.
32
4 3 1.
n
u nn=−+
Lời giải
* Với
(
)
sin
k 2 ; 2 , sin 0 0
n
n kk n
n
ππ π
∈ + ∈ ⇒ >⇒ >
và
( )
sin
2 ;2 2 , sin 0 0
n
n k kk n
n
ππππ
∈ + + ∈ ⇒ <⇒ <
. Suy ra dãy số trong đáp án A không
tăng, không giảm
→
loại A
* Ta có
( )
22
2
11
21
21
n
nn
u
n
n
++
= =
+
+
. Xét dãy
( )
n
v
với
( )
2
2
1
21
n
n
v
n
+
=
+
( ) ( )
2 22
1
22
22
22 1 4 27
4 12 9 4 4 1
2321
nn
nn n nn
vv
n n nn
nn
+
++ + −−
−= − =
+ + ++
++
Do
1
nn
vv
+
−
vừa nhận giá trị âm lẫn dương nên dãy số
( )
n
v
không tăng, không giảm
→
loại B
*
( )
( )
( )
2
1
22
2
2
32 2 1
3.3 3
11
n
nn
nn
nn
uu
n
n nn
+
−−
−= − =
++
. Do
1
nn
uu
+
−
nhận giá trị âm lẫn dương nên dãy đã
cho không tăng, không giảm
→
loại C
* Theo phương pháp loại trừ ta chọn D
Câu 106: Cho dãy số
()
n
u
biết
1
1
1
15
33
nn
u
uu
−
=
= +
. Mệnh đề nào sau đây đúng?
A. Dãy số tăng B. Dãy số giảm

CHUYÊN ĐỀ II – TOÁN – 11 – DÃY SỐ - CẤP SỐ CỘNG – CẤP SỐ NHÂN
Page 27
Sưu tầm và biên soạn
C. Dãy số không tăng, không giảm D. Dãy số vừa tăng vừa giảm
Lời giải
Ta có
123
uuu<<
. Dự đoán dãy số đã cho tăng, ta chứng minh bằng quy nạp
Từ giả thiết thì
*
0,
n
un> ∀∈
Giả sử
1
,2
kk
uuk
−
>≥
. Ta chứng minh
1kk
uu
+
>
Thật vậy:
(
)
1 11
1
0
3
k k kk k k
u u uu u u
+ −+
− = − >⇔ >
. Vậy dãy đã cho là dãy tăng
Câu 107: Cho dãy số
()
n
u
biết
1
2
1
1
3,
nn
u
uu n
∗
+
=
= + ∀∈
. Mệnh đề nào sau đây đúng?
A. Dãy số tăng B. Dãy số giảm
C. Dãy số không tăng, không giảm D. Dãy số vừa tăng vừa giảm
Lời giải
Ta có
123
0
uuu<<<
. Dự đoán dãy số đã cho tăng, ta chứng minh bằng quy nạp
Từ giả thiết thì
*
0,
n
un> ∀∈
Giả sử
1
,2
kk
uuk
−
>≥
. Ta chứng minh
1kk
uu
+
>
Thật vậy:
( )( )
11
22
11 1
22
1
33 0
33
kk kk
kk k k k k
kk
uu uu
uu u u uu
uu
−−
+− +
−
−+
− = +− += >⇔ >
++ +
. vậy dãy đã cho
là dãy tăng
Câu 108: Cho dãy số
()
n
u
biết
1
1
3
3
3
n
n
n
u
u
u
u
+
=
=
+
. Mệnh đề nào sau đây đúng?
A. Dãy số tăng B. Dãy số giảm
C. Dãy số không tăng, không giảm D. Có
10
2u =
Lời giải
Ta có
123
uuu>>
. Dự đoán dãy số đã cho giảm, ta chứng minh bằng quy nạp
Từ giả thiết thì
*
0,
n
un> ∀∈
Giả sử
1
,2
kk
uuk
−
<≥
. Ta chứng minh
1kk
uu
+
<
Thật vậy:
( )
( )( )
1
1
11
11
9
33
0
3 3 33
kk
kk
kk k k
k k kk
uu
uu
uu uu
u u uu
−
−
++
−−
−
− = − = <⇔ <
++ ++
. vậy dãy đã cho là dãy
giảm
Câu 109: Cho dãy số
()
n
u
biết
11 1
...
12
n
u
n n nn
= + ++
++ +
. Mệnh đề nào sau đây đúng?
A. Dãy số tăng B. Dãy số giảm
C. Dãy số không tăng, không giảm D. Có hữu hạn số hạng

CHUYÊN ĐỀ II – TOÁN – 11 – DÃY SỐ - CẤP SỐ CỘNG – CẤP SỐ NHÂN
Page 28
Sưu tầm và biên soạn
Lời giải
Xét hiệu
( )( )
2
*
1
2
1 1 1 4 31
0
2 12 2 1
22 1 1
nn
nn
uu n
n nn
nn
+
++
− = + − = > ∀∈
+ ++
++
Câu 110: Cho dãy số
()
n
u
biết
1
*
1
1
1
nn
u
u au n
+
=
= +∀∈
. Tìm tất cả các giá trị của a để
()
n
u
tăng?
A.
0.
a <
B.
0.a ≤
C.
0.a
>
D.
1.a >
Lời giải
Xét hiệu
11
11
n n nn
u au u au
+−
= +⇒ = +
( )
11n n nn
u u au u
+−
⇒ −= −
( )
(
)
2
32 21
3
43 32
1
...
0
n
nn
u u au u a
u u au u a
u ua
+
⇒−= − =
⇒−= − =
⇒ −=>
Để dãy số
()
n
u
tăng suy ra
a0>
.
Câu 111: Trong các dãy số dưới đây, dãy số nào là dãy giảm?
A.
2
n
un=
. B.
1
3
n
u
n
= −
. C.
3
n
un=
. D.
3
2
n
un= −
.
Lời giải
Xét đáp án A, ta có
( )
2
2*
1
1 2 1 0,
nn
uun n n n
+
− = + − = +> ∀∈
nên dãy này là dãy tăng.
Xét đáp án B, ta có
( )
*
1
11 1
0,
11
nn
uu n
n n nn
+
−
− = − = < ∀∈
++
nên dãy này là dãy giảm.
Xét đáp án C, ta có
( )
*
1
3 1 3 3 0,
nn
uu n n n
+
− = + − = > ∀∈
nên dãy này là dãy tăng.
Xét đáp án D, ta có
( )
3
3*
1
1 0,
nn
uun n n
+
− = + − > ∀∈
nên dãy này là dãy tăng.
Câu 112: Trong các dãy số sau, dãy số nào là dãy số giảm?
A.
2
3
n
u
n
=
. B.
3
1
n
n
u
n
−
=
+
. C.
2
n
n
u =
. D.
( )
1
3
n
n
n
u
−
=
.
Lời giải
Xét A:
Ta có
2
3
n
u
n
=
,
( )
1
2
3
1
n
u
n
+
=
+
( )
22
1
2
2
1,
1
n
n
u
nn
n
un
n
∗
+
= < = ∀∈
+
. Vậy
( )
n
u
là dãy giảm.
Xét B:

CHUYÊN ĐỀ II – TOÁN – 11 – DÃY SỐ - CẤP SỐ CỘNG – CẤP SỐ NHÂN
Page 29
Sưu tầm và biên soạn
Ta có
3
;
1
n
n
u
n
−
=
+
1
2
2
n
n
u
n
+
−
=
+
. Khi đó:
( )
(
)
1
23 4
0
2 1 12
nn
nn
uu
n n nn
+
−−
−= − = >
+ + ++
n
∀∈
Vậy
( )
n
u
là dãy số tăng.
Xét C:
Ta có
;
2
n
n
u
=
1
1
2
n
n
u
+
+
=
. Khi đó:
1
11
0
2 22
nn
nn
uu
+
+
− = −=>
n∀∈
Vậy
( )
n
u
là dãy số tăng.
Xét D:
Ta có
1
1
;
3
u
−
=
2
1
;
9
u =
3
1
27
u
−
=
. Vậy
( )
n
u
là dãy số không tăng không giảm.
Câu 113: Dãy số nào sau đây là dãy số giảm?
A.
*
53
,
23
n
n
un
n
−
= ∈
+
. B.
*
5
,
41
n
n
un
n
−
= ∈
+
.
C.
2*
2 3,
n
un n= +∈
. D.
(
)
*
cos 2 1 ,
n
u nn= +∈
.
Lời giải
* Với dãy
53
23
n
n
u
n
−
=
+
.
Ta có
(
)
(
)
( )( ) ( )( )
(
)( ) ( )(
)
1
*
53 1
53 23 53
2 13232523
2323 5325
19
0
2523 2325
nn
n
n nn
uu
n n nn
nn nn
n
nn nn
+
−+
− −−
−= − = −
++ + + +
− +−− +
−
= = < ∀∈
++ ++
Suy ra
( )
n
u
là dãy giảm.
Câu 114: Trong các dãy số
( )
n
u
cho bởi số hạng tổng quát
n
u
sau, dãy số nào là dãy số giảm?
A.
1
2
n
n
u =
. B.
31
1
n
n
u
n
−
=
+
. C.
2
n
un=
. D.
2
n
un= +
.
Lời giải
Ta có
1
2
n
n
u =
1
1
1
2
n
n
u
+
+
<=
*
n∀∈
.
Câu 115: Trong các dãy số
( )
n
u
cho bởi số hạng tổng quát
n
u
sau, dãy số nào là dãy số tăng?
A.
1
2
n
n
u =
. B.
31
1
n
n
u
n
−
=
+
. C.
2
1
n
un= −
. D.
1
2
n
u
n
=
+
.
Lời giải
Câu 116: Trong các dãy số sau, dãy số nào là dãy số giảm

CHUYÊN ĐỀ II – TOÁN – 11 – DÃY SỐ - CẤP SỐ CỘNG – CẤP SỐ NHÂN
Page 30
Sưu tầm và biên soạn
A.
3
1
n
n
u
n
−
=
+
. B.
2
n
n
u
=
. C.
2
2
n
u
n
=
. D.
( )
1
3
n
n
n
u
−
=
.
Lời giải
Xét A:
Ta có
3
;
1
n
n
u
n
−
=
+
1
2
2
n
n
u
n
+
−
=
+
. Khi đó:
( )(
)
1
23 4
0
2 1 12
nn
nn
uu
n n nn
+
−−
−= − = >
+ + ++
n∀∈
Vậy
( )
n
u
là dãy số tăng.
Xét B:
Ta có
;
2
n
n
u =
1
1
2
n
n
u
+
+
=
. Khi đó:
1
11
0
2 22
nn
nn
uu
+
+
− = −=>
n∀∈
Vậy
( )
n
u
là dãy số tăng.
Xét C:
Ta có
2
2
n
u
n
=
,
( )
1
2
2
1
n
u
n
+
=
+
(
)
22
1
2
2
1,
1
n
n
u
nn
n
un
n
∗
+
= < = ∀∈
+
. Vậy
( )
n
u
là dãy giảm.
Xét D:
Ta có
1
1
;
3
u
−
=
2
1
;
9
u =
3
1
27
u
−
=
. Vậy
( )
n
u
là dãy số không tăng không giảm.
Câu 117: Dãy số nào sau đây là dãy số giảm?
A.
( )
53
,*
23
n
n
un
n
−
= ∈
+
. B.
( )
5
,*
41
n
n
un
n
−
= ∈
+
.
C.
( )
3
2 3, *
n
un n=+∈
. D.
( )
( )
cos 2 1 , *
n
u nn= +∈
.
Lời giải
Xét
( )
53
,*
23
n
n
un
n
−
= ∈
+
, ta có
( )
( )
1
53 1
53
2 1 32 3
nn
n
n
uu
nn
+
−+
−
−= −
++ +
23 53
2523
nn
nn
−−
= −
++
( )( ) ( )( )
( )( )
2323 2553
2523
nn n n
nn
− +− + −
=
++
( )( )
22
4 6 6 9 10 6 25 15
2523
nn n nn n
nn
− +− − + − +
=
++
( )(
)
19
0, *
2523
n
nn
−
= < ∀∈
++
.
Vậy
( )
53
,*
23
n
n
un
n
−
= ∈
+
là dãy giảm.
Câu 118: Trong các dãy số
( )
n
u
cho bởi số hạng tổng quát
n
u
sau, dãy số nào là dãy số tăng?
A.
1
.
2
n
n
u =
B.
1
.
n
u
n
=
C.
5
.
31
n
n
u
n
+
=
+
D.
21
.
1
n
n
u
n
−
=
+
Lời giải
Vì
2;
n
n
là các dãy dương và tăng nên
11
;
2
n
n
là các dãy giảm, do đó loại các đáp án A và
B.

CHUYÊN ĐỀ II – TOÁN – 11 – DÃY SỐ - CẤP SỐ CỘNG – CẤP SỐ NHÂN
Page 31
Sưu tầm và biên soạn
Xét đáp án C:
1
12
2
3
5
2
7
31
6
n
u
n
u uu
n
u
=
+
= → → > →
+
=
loại C.
Xét đáp án D:
1
21 3 1 1
2 30
1 1 12
n nn
n
u uu
n n nn
+
−
= =− ⇒ −= − >
+ + ++
Câu 119: Trong các dãy số
( )
n
u
cho bởi số hạng tổng quát
n
u
sau, dãy số nào là dãy số tăng?
A.
2
.
3
n
n
u =
B.
3
.
n
u
n
=
C.
2.
n
n
u =
D.
( )
2.
n
n
u = −
Lời giải
Xét đáp án C:
1
1
2 2 220
n n nn
n nn
u uu
+
+
= → − = − = > →
Chọn C
Vì
2;
n
n
là các dãy dương và tăng nên
11
;
2
n
n
là các dãy giảm, do đó loại các đáp án A và
B.
Xét đáp án D:
( )
2
23
3
4
2
8
n
n
u
u uu
u
=
= − → → > →
= −
loại D.
Câu 120: Trong các dãy số sau, dãy số nào là dãy số giảm?
A.
21
1
n
n
u
n
+
=
−
. B.
3
1
n
un= −
. C.
2
n
un=
. D.
2
n
un=
.
Lời giải
Với mọi
n ∈
,
1
n >
. Ta có
( )
( )
1
2 11
212321
11 1 1
nn
n
nnn
uu
n n nn
+
++
+++
−= − = −
+− − −
(
)( ) ( )
(
)
( )
( ) (
)
(
) (
)
23 1 21 23 1 21
3
0
1 11
n n nn n n nn
nn nn nn
+ −− + + −− +
−
= = = <
− −−
, với mọi
n ∈
,
1n >
.
Suy ra dãy số giảm.
DẠNG 4. DÃY SỐ BỊ CHẶN TRÊN, BỊ CHẶN DƯỚI, BỊ CHẶN
Câu 121: Xét tính bị chặn của các dãy số sau:
( 1)= −
n
n
u
A. Bị chặn. B. Không bị chặn. C. Bị chặn trên. D. Bị chặn dưới.
Lời giải
Câu 122: Xét tính bị chặn của các dãy số sau:
31= −
n
un
A. Bị chặn. B. Bị chặn trên. C. Bị chặn dưới. D. Không bị chặn dưới.
Lời giải
Ta có
*
2,
n
un
≥ ∀∈ →
Dãy bị chặn dưới
Khi
n
tiến tới dương vô cực thì
n
u
cũng tiến tới dương vô cực nên dãy số không bị chặn trên
Vậy dãy đã cho bị chặn dưới

CHUYÊN ĐỀ II – TOÁN – 11 – DÃY SỐ - CẤP SỐ CỘNG – CẤP SỐ NHÂN
Page 32
Sưu tầm và biên soạn
Câu 123: Trong các dãy số
n
u
cho bởi số hạng tổng quát
n
u
sau, dãy số nào bị chặn?
A.
2
.
n
un=
B.
2.
n
n
u =
C.
1
.
n
u
n
=
D.
1.
n
un= +
Lời giải
Ta có:
1
1
0
n
u
n
với mọi
*
n
nên dãy
n
u
bị chặn.
Nhận xét: Các dãy số
2
;2; 1
n
nn
là các dãy tăng đến vô hạn khi
n
tăng lên vô hạn nên chúng
không bị chặn trên.
Câu 124: Trong các dãy số
(
)
n
u
cho bởi số hạng tổng quát
n
u
sau, dãy số nào bị chặn?
A.
1
.
2
n
n
u =
B.
3.
n
n
u
=
C.
1.
n
un= +
D.
2
1.
n
un
= +
Lời giải
Ta có:
1
0
2
1
2
n
n
u
với mọi
*
n
nên dãy
n
u
bị chặn.
Câu 125: Xét tính bị chặn của các dãy số sau:
21
2
+
=
+
n
n
u
n
A. Bị chặn. B. Không bị chặn. C. Bị chặn trên. D. Bị chặn dưới.
Lời giải
Ta có
2 1 2 4 2( 2)
0 2
22 2
n
nn n
un
nn n
++ +
<= < = =∀
++ +
nên dãy
()
n
u
bị chặn.
Câu 126: Xét tính tăng, giảm và bị chặn của dãy số
()
n
u
, biết:
2 13
32
−
=
−
n
n
u
n
A. Dãy số tăng, bị chặn.
B. Dãy số giảm, bị chặn.
C. Dãy số không tăng không giảm, không bị chặn.
D. Cả A, B, C đều sai.
Lời giải
Ta có:
1
2 11 2 13 34
0
3 1 3 2 (3 1)(3 2)
+
−−
−= − = >
+ − +−
nn
nn
uu
n n nn
với mọi
1≥
n
.
Suy ra
1
1
+
> ∀≥⇒
nn
u un
dãy
()
n
u
là dãy tăng
⇒
dãy bị chặn dưới bởi
1
9
4
u
= −
.
Mặt khác:
2 35 9 2
1
3 3(3 2) 4 3
nn
u un
n
= − ⇒− ≤ < ∀ ≥
−
Vậy dãy
()
n
u
là dãy bị chặn.
Câu 127: Xét tính bị chặn của các dãy số sau:
2
1
1
+
=
+
n
n
u
n
A. Bị chặn. B. Không bị chặn. C. Bị chặn trên. D. Bị chặn dưới.
Lời giải

CHUYÊN ĐỀ II – TOÁN – 11 – DÃY SỐ - CẤP SỐ CỘNG – CẤP SỐ NHÂN
Page 33
Sưu tầm và biên soạn
Ta có:
2
22
2
1 21 2 2
0 1 1 2 , ( )
1 12
1
nn
n nn n n
u nu
n nn
n
+ ++
< = = = + ≤ + = ∀⇒
++
+
bị chặn.
Câu 128: Xét tính bị chặn của các dãy số sau:
2
43=−−
n
u nn
A. Bị chặn. B. Không bị chặn. C. Bị chặn trên. D. Bị chặn dưới.
Lời giải
Ta có:
2
25 3 25
()
4 24
nn
un u
= −+ < ⇒
bị chặn trên; dãy
()
n
u
không bị chặn dưới.
Câu 129: Trong các dãy số
()
n
u
sau, dãy số nào bị chặn?
A.
1
.
n
un
n
= +
B.
1
n
un= +
. C.
2
21
n
n
u
n
=
+
. D.
2
1
n
unn= ++
.
Lời giải
Câu 130: Trong các dãy số
()
n
u
sau, dãy số nào bị chặn?
A.
sin 3
n
un n= −
B.
2
1
n
n
u
n
+
=
. C.
( )
1
1
n
u
nn
=
+
. D.
( )
.sin 3 1
n
un n= −
.
Lời giải
Ta có
( )
*
11
0,
12
n
un
nn
< = ≤ ∀∈ ⇒
+
Dãy
()
n
u
với
( )
1
1
n
u
nn
=
+
bị chặn
Câu 131: Trong các dãy số
( )
n
u
cho dưới đây dãy số nào là dãy số bị chặn ?
A.
3
2
.
1
n
n
u
n
=
+
B.
2
2017.
n
un= +
C.
( 1) ( 2).
n
n
un
=−+
D.
2
.
1
n
n
u
n
=
+
Lời giải
Ta có
*
2
1
0,
12
n
n
un
n
< = ≤ ∀∈ ⇒
+
Dãy
()
n
u
với
2
1
n
u
n
n
=
+
bị chặn
Câu 132: Xét tính tăng giảm và bị chặn của dãy số sau:
1
( ):
2
+
=
+
nn
n
uu
n
A. Tăng, bị chặn. B. Giảm, bị chặn. C. Tăng, chặn dưới. D. Giảm, chặn trên.
Lời giải
Ta có
2
1
2 1 ( 2) ( 3)( 1)
3 2 ( 2)( 3)
+
+ + + −+ +
−= − =
+ + ++
nn
n n n nn
uu
n n nn
1
0,
( 2)( 3)
= >∀
++
n
nn
.
Và
*
12
0 1,
22
n
nn
un
nn
++
< = < = ∀∈
++
Vậy dãy
()
n
u
là dãy tăng và bị chặn.
Câu 133: Xét tính tăng, giảm và bị chặn của dãy số
()
n
u
, biết:
3
( ): 2 1=++
nn
uun n
A. Tăng, bị chặn. B. Giảm, bị chặn. C. Tăng, chặn dưới. D. Giảm, chặn trên.
Lời giải

CHUYÊN ĐỀ II – TOÁN – 11 – DÃY SỐ - CẤP SỐ CỘNG – CẤP SỐ NHÂN
Page 34
Sưu tầm và biên soạn
Ta có:
33
1
( 1) 2( 1) 2
+
− = + + +− −
nn
uun n nn
2
3 3 3 0, = + +> ∀nn n
Mặt khác:
1, >∀
n
un
và khi
n
càng lớn thì
n
u
càng lớn.
Vậy dãy
()
n
u
là dãy tăng và bị chặn dưới.
Câu 134: Cho dãy số
31
( ):
31
nn
n
uu
n
−
=
+
. Dãy số
n
u
bị chặn trên bởi số nào dưới đây?
A.
1
3
. B. 1. C.
1
2
. D. 0.
Lời giải
Ta có
31 2
1 1.
31 31
n
n
u
nn
Mặt khác:
2
511
0
723
u
nên suy ra dãy
n
u
bị chặn
trên bởi số 1.
Câu 135: Cho dãy số
n
u
, biết
cos sin .
n
u nn
Dãy số
n
u
bị chặn trên bởi số nào dưới đây?
A. 0. B. 1. C.
2
. D. Không bị chặn trên.
Lời giải
Ta có
1
sin1 cos1 1 0
MTCT
n
uu
nên loại các đáp án A và B
Ta có
cos sin 2 sin
4
2
n
u nn n
Câu 136: Cho dãy số
n
u
, biết
cos sin .
n
u nn
Dãy số
n
u
bị chặn dưới bởi số nào dưới đây?
A. 0. B.
1−
. C.
2−
. D. Không bị chặn dưới.
Lời giải
5
sin 5 cos5 1 0
MTCT
n
uu
loại A và B
Ta có
2 sin
4
2
n
un
Câu 137: Xét tính bị chặn của các dãy số sau:
( )( )
11 1
...
1.3 3.5 2 1 2 1
= + ++
−+
n
u
nn
A. Bị chặn. B. Không bị chặn. C. Bị chặn trên. D. Bị chặn dưới.
Lời giải
Rõ ràng
n
u 0, n *> ∀∈
nên
( )
n
u
bị chặn dưới.
Lại có:
( )( )
1 11 1
2121 22121kk k k
= −
−+ − +
. Suy ra
1 1 11 1 1 1 1 1
1 ... 1
2 3 35 2121 2 21 2
n
u
nn n
= −+−++ − = − <
−+ +
với mọi số nguyên dương
n
, nên
( )
n
u
bị chặn trên.
Kết luận
( )
n
u
bị chặn.

CHUYÊN ĐỀ II – TOÁN – 11 – DÃY SỐ - CẤP SỐ CỘNG – CẤP SỐ NHÂN
Page 35
Sưu tầm và biên soạn
Câu 138: Xét tính bị chặn của các dãy số sau:
11 1
...
1.3 2.4 .( 2)
= + ++
+
n
u
nn
A. Bị chặn. B. Không bị chặn. C. Bị chặn trên. D. Bị chặn dưới.
Lời giải
Ta có:
11 1 1
0 ... 1 1
1.2 2.3 .( 1) 1
< < + ++ =− <
++
n
u
nn n
Dãy
()
n
u
bị chặn.
Câu 139: Xét tính tăng, giảm và bị chặn của dãy số
()
n
u
, biết:
22 2
11 1
1 ...
23
=+ + ++
n
u
n
.
A. Dãy số tăng, bị chặn. B. Dãy số tăng, bị chặn dưới.
C. Dãy số giảm, bị chặn trên. D. Cả A, B, C đều sai.
Lời giải
Ta có:
1
2
1
0
( 1)
+
− = >⇒
+
nn
uu
n
dãy
()
n
u
là dãy số tăng.
Do
11 1 1
1 ... 2
1.2 2.3 ( 1)
n
u
nn n
<+ + + + = −
−
1 2, 1
n
un⇒< < ∀≥⇒
dãy
()
n
u
là dãy bị chặn.
Câu 140: Xét tính bị chặn của các dãy số sau:
1
1
1
1
2
, ( 2)
1
−
−
=
+
= ≥
+
n
n
n
u
u
un
u
A. Bị chặn. B. Không bị chặn. C. Bị chặn trên. D. Bị chặn dưới.
Lời giải
Bằng quy nạp ta chứng minh được
12<<
n
u
nên dãy
()
n
u
bị chặn.
Câu 141: Xét tính tăng giảm và bị chặn của dãy số sau:
1
1
2
( ):
1
, 2
2
+
=
+
= ∀≥
n
n
n
u
u
u
un
A. Tăng, bị chặn. B. Giảm, bị chặn.
C. Tăng, chặn dưới, không bị chặn trên. D. Giảm, chặn trên, không bị chặn dưới.
Lời giải
Trước hết bằng quy nạp ta chứng minh:
1 2, <≤∀
n
un
Điều này đúng với
1=n
, giả sử
12<<
n
u
ta có:
1
1
12
2
+
+
<= <
n
n
u
u
nên ta có đpcm.
Mà
1
1
0,
2
+
−
−= <∀
n
nn
u
uu n
.
Vậy dãy
()
n
u
là dãy giảm và bị chặn.

CHUYÊN ĐỀ II – TOÁN – 11 – DÃY SỐ - CẤP SỐ CỘNG – CẤP SỐ NHÂN
Page 36
Sưu tầm và biên soạn
Câu 142: Cho dãy
( )
n
u
với
2018
.
2018 1
n
n
u
n
+
=
+
Chọn khẳng định đúng trong các khẳng định sau.
A. Dãy
( )
n
u
bị chặn dưới nhưng không bị chặn trên
B. Dãy
( )
n
u
bị chặn.
C. Dãy
( )
n
u
không bị chặn trên, không bị chặn dưới.
D. Dãy
(
)
n
u
bị chặn trên nhưng không bị chặn dưới
Lời giải
Chọn B
Ta có:
( )
2018 1 2017.2019
2018 1 2018 2018 2018 1
n
n
u
nn
+
= = +
++
.
Do đó
( )
n
u
là dãy giảm, mà
1
1u =
, dễ thấy
*
,0
n
nu∀∈ >
0 1.
n
u⇒< ≤
Suy ra: Dãy
( )
n
u
bị chặn.
Câu 143: Trong các dãy số
( )
n
u
có số hạng tổng quát
n
u
dưới đây, dãy số nào là dãy bị chặn?
A.
2
2
n
un= +
. B.
21
n
n
u
n
=
+
. C.
31
n
n
u = −
. D.
2
n
un
n
= +
.
Lời giải
Chọn B
2
lim 2n + = +∞
⇒
dãy số
2
2
n
un= +
không bị chặn.
111
212212
n
n
u
nn
==−<
++
⇒
1
2
n
u <
.
Mặt khác ta thấy ngay
0*
21
n
n
un
n
= > ∀∈
+
1
0
2
n
u⇒< <
⇒
dãy số
21
n
n
u
n
=
+
bị chặn.
Câu 144: Cho dãy số
( )
n
u
với
1
25
n
n
u
−
= +
. Kết luận nào sau đây là đúng?
A. Dãy số không đơn điệu. B. Dãy số giảm và không bị chặn.
C. Dãy số tăng. D. Dãy số giảm và bị chặn.
Lời giải
Xét
( ) ( )
1
1
25 25
nn
nn
uu
−−
+
−=+ −+
1
55
nn−−
= −
1
11
55
nn−
= −
15
55
nn
= −
*
4
0,
5
n
n=− < ∀∈
.
( )
n
u⇒
là dãy số giảm.
Ta có:
1*
2 5 2,
n
n
un
−
= + > ∀∈
;
*
5
2 3,
5
n
n
un= + ≤ ∀∈
.
( )
n
u⇒
là dãy số bị chặn.
Câu 145: Trong các dãy số sau, dãy nào là dãy số bị chặn?
A.
21
1
n
n
u
n
+
=
+
. B.
( )
2 sin
n
un n= +
. C.
2
n
un=
. D.
3
1
n
un= −
.
Lời giải

CHUYÊN ĐỀ II – TOÁN – 11 – DÃY SỐ - CẤP SỐ CỘNG – CẤP SỐ NHÂN
Page 37
Sưu tầm và biên soạn
Xét dãy số
21
1
n
n
u
n
+
=
+
ta có:
*
*
21
0;
1
n
n
un
n
+
= > ∀∈ ⇒
+
dãy
( )
n
u
bị chặn dưới bởi giá trị
0
.
*
*
21 1
2 2;
11
n
n
un
nn
+
= = − < ∀∈ ⇒
++
dãy
( )
n
u
bị chặn trên bởi giá trị
2
.
⇒
dãy
( )
n
u
là dãy bị chặn.
Câu 146: Chọn kết luận sai:
A. Dãy số
21n
tăng và bị chặn trên. B. Dãy số
1
1n
giảm và bị chặn dưới.
C. Dãy số
1
n
tăng và bị chặn trên. D. Dãy số
1
3.2
n
giảm và bị chặn dưới.
Lời giải
Đáp án B đúng vì dãy số
1
1n
giảm và bị chặn dưới bởi 0.
Đáp án C đúng vì dãy số
1
n
tăng và bị chặn trên bởi 0.
Đáp án D đúng vì dãy số
1
3.2
n
giảm và bị chặn dưới bởi 0.
Đáp án A sai vì dãy số
21n
tăng nhưng không bị chặn trên.
Câu 147: Cho dãy số
()
n
u
biết
22 2
11 1 1
...
22 3
n
u
n
=+ + ++
. Mệnh đề nào sau đây đúng ?
A. Dãy số bị chặn dưới. B. Dãy số bị chặn trên.
C. Dãy số bị chặn. D. Không bị chặn.
Lời giải
Xét
( )
2
1 1 11
,2
11
k
k k kk k
< = − ∀≥
−−
Suy ra
1 1 11 11 11 1 1 31 3
1 ...
2 2 23 34 56 1 2 2
n
u
nn n
<+− + − + − + − ++ − =−<
−
3
0 ,*
2
n
un⇒ < < ∀∈
.
Vậy
()
n
u
bị chặn.
Câu 148: Cho dãy số
()
n
u
xác định bởi
*
1
3
1
1
,
nn
u
u un n
+
=
= +
∈∀
. Tìm số nguyên dương
n
nhỏ nhất sao
cho
20391901
n
u ≥−
.

CHUYÊN ĐỀ II – TOÁN – 11 – DÃY SỐ - CẤP SỐ CỘNG – CẤP SỐ NHÂN
Page 38
Sưu tầm và biên soạn
A.
2017
n =
. B.
2019
n =
. C.
2020n =
. D.
2018n =
.
Lời giải
Theo hệ thức đã cho ta có:
3 3 3 33 3
12 1
( 1) ( 2) ( 1) ... 1 2 ... ( 1)
nn n
uu n u n n u n
−−
= +− = +− +− ==++++−
.
Lại có
22
33 3 2
( 1)
1 2 ... ( 1) (1 2 ... ( 1))
4
nn
nn
−
+ ++ − =+++ − =
.
Suy ra:
22
( 1) ( 1)
11
42
nn
n n nn
uu
−−
=+ ⇒ −=
.
Sử dụng mode
7
cho
n
chạy từ
2017
đến
2020
, ta được kết quả
2020n =
.
Câu 149: Cho dãy số
()
n
u
thỏa mãn
2
11
log log 6 0uu+ −=
và
1
5
nn
uu
+
= +
, với mọi
1,n nN≥∈
. Giá trị
lớn nhất của
n
để
500
n
u
<
bằng:
A.
80
. B.
100
. C.
99
. D.
82
.
Lời giải
+)
11
2
11
11
log 3 0,001
log log 6 0
log 2 100
uu
uu
uu
=−=
+ −=⇔ ⇔
= =
+) Từ giả thiết suy ra
()
n
u
là cấp số cộng có công sai
5d =
. Do đó, ta có
1
( 1)
n
uu n d=+−
.
+) Vậy
0,001 5( 1) 5 4,999
100 5( 1) 5 95
n
n
u nn
u nn
= + −= −
= + −= +
. Suy ra
100,9998
500
81
n
n
u
n
<
<⇔
<
.
Vậy số
n
lớn nhất để
500
n
u
<
là 100.
Câu 150: Cho dãy số
( )
n
u
thỏa mãn:
1
5u
=
và
1
4
3
3
nn
uu
+
= +
với
1.n∀≥
Giá trị nhỏ nhất của
n
để
100
12
... 5
nn
S uu u
= + ++ >
bằng?
A.
142
. B.
146
. C.
141
. D.
145
.
Lời giải
11
422
33
333
nn n n
uu u u
++
= +⇔ += +
Đặt
2
3
nn n
vu v= +⇒
là cấp số nhân với
1
17
3
v =
, công bội
3
q =
.
Khi đó
12
...
nn
S uu u
= + ++
12
22 2
...
33 3
n
vv v
=−+ −++ −
12
2
...
3
n
n
vv v=+ ++ −
1
12
.
13
n
qn
v
q
−
= −
−
17.3 17 4
6
n
n−−
=
Bằng cách thử trực tiếp ta có
n
bé nhất để
100
5
n
S >
là
146n =
.
Câu 151: Cho dãy số
( )
n
u
xác định bởi
12
11
2, 3
32
n nn
uu
u uu
+−
= =
= −
2,n nN≥∈
.Khi đó
1
....
n
uu++
bằng?

CHUYÊN ĐỀ II – TOÁN – 11 – DÃY SỐ - CẤP SỐ CỘNG – CẤP SỐ NHÂN
Page 39
Sưu tầm và biên soạn
A.
21
n
−
. B.
2
n
. C.
22
n
n+
. D.
21
n
n+−
.
Lời giải.
Ta có:
11
32
n nn
u uu
+−
= −
.
12
32
nn n
uu u
−−
= −
123
32
nnn
uuu
−−−
= −
….
432
32uuu= −
3 21
32uuu= −
13 1321
.... 3 .... 2
n nn
u u uu uu u
+−
⇒ ++= + +++−
1 21
2 221
nn n
u uu u u
+
⇔ = +− = −
1
21
n
n
u
+
⇒=+
.
Vậy
( ) ( ) ( ) ( )
012 1
1
.... 2 1 2 1 2 1 .... 2 1 2 1
nn
n
uu n
−
+ + = ++ ++ ++ + += +−
.
Câu 152: Cho dãy số
{ }
n
u
xác định bởi
3 32 3 2 3 2
44 4 4
1
2 3 31
n
u
n nn n nn n n n
=
+++++++++
,
1n ≥
.
Tính tổng
4
12
2018 1
...
Suu u
−
= + ++
.
A.
2016
. B.
2017
. C.
2018
. D.
2019
.
Lời giải
Ta có:
( )
3
3
4
44
4
1
.1 .1 1
n
u
n nn nn n
=
+ ++ ++ +
( )
( )
44 44
1
1 1. 1nnn n nn
=
++++ ++
( )
( )
44
1
11nn nn
=
++ ++
44
1
1
nn
nn
+−
=
++
( ) ( )
44
1 .1
1
nnnn
nn
+− +−
=
+−
44
1nn= +−
.
Do đó
44
44
44 4
4
2 1 3 2 ... 2018 1 1 2018 1
S = − + − + + −+− −
4
4
1 2018=−+
1 2018=−+
2017=
.
Câu 153: Cho dãy số
( )
n
u
được xác định bởi
1
2
3
u =
và
( )
1
22 1 1
n
n
n
u
u
nu
+
=
++
,
( )
*
n ∈
. Tính tổng
2018
số hạng đầu tiên của dãy số đó?
A.
4036
4035
. B.
4035
4034
. C.
4038
4037
. D.
4036
4037
.
Lời giải

CHUYÊN ĐỀ II – TOÁN – 11 – DÃY SỐ - CẤP SỐ CỘNG – CẤP SỐ NHÂN
Page 40
Sưu tầm và biên soạn
- Ta có:
( )
1
22 1 1
1
n
nn
nu
uu
+
++
=
1
42
n
n
u
=++
( )
1
1
4 12 4 2
n
nn
u
−
= + −+ + +
Tương tự ta đươc:
( ) ( ) ( )
11
11
4.1 2 4.2 2 ... 4 2
n
n
uu
+
=+ ++ +++ +
( )
3
22 1
2
n nn=++ +
2
4 83
2
nn++
=
1
2
2
4 83
n
u
nn
+
⇒=
++
( )( )
2
2 12 3nn
=
++
( )
( )
2
2 12 1
n
u
nn
⇒=
−+
11
2 12 1nn
= −
−+
1
1
1
21
n
k
k
u
n
=
⇒=−
+
∑
2
21
n
n
=
+
2018
1
4036
4037
k
k
u
=
⇒=
∑
.
Câu 154: Cho dãy số
(
)
n
u
thỏa mãn
1
6
nn
uu
−
= +
,
2n∀≥
và
25 9
2
log log 8 11
uu+ +=
. Đặt
12
...
nn
S uu u
= + ++
. Tìm số tự nhiên
n
nhỏ nhất thỏa mãn
20172018
n
S ≥
.
A.
2587
. B.
2590
. C.
2593
. D.
2584
.
Lời giải
Ta có dãy số
( )
n
u
là cấp số cộng có công sai
6d =
.
( )
25 9 25 9
2
log log 8 11 log 8 11u u uu+ += ⇔ + =
( )
*
với
5
0u >
.
Mặt khác
51 1
4 24u u du=+=+
và
91 1
8 48
u u du=+=+
.
Thay vào
( )
*
ta được
15
15
8 32
88 64
uu
uu
=⇒=
=−⇒=−
. Suy ra
1
8u
=
.
( )
2
1
20172018 2 1 20172018 3 5 20172018 0
2
n
n
S un d n n≥⇔+−≥⇔+−≥
.
Vậy số tự nhiên
n
nhỏ nhất thỏa mãn
20172018
n
S ≥
là
2593n =
.
Câu 155: Cho dãy số
( )
n
u
thỏa mãn
18 18
11
44
e5ee e
uu
uu
+ −=
và
1
3
nn
uu
+
= +
với mọi
1n ≥
. Giá trị lớn
nhất của
n
để
3
log ln 2018
n
u <
bằng
A.
1419
. B.
1418
. C.
1420
. D.
1417
.
Lời giải
Ta có
1
3
nn
uu
+
= +
với mọi
1n ≥
nên
n
u
là cấp số cộng có công sai
3d =
18 18 18 18
11 11
44 44
e5ee e 5ee ee
uu u u
uu uu
+ −=⇔ −=−
( )
1
Đặt
18
1
4
ee
u
u
t = −
( )
0t ≥

CHUYÊN ĐỀ II – TOÁN – 11 – DÃY SỐ - CẤP SỐ CỘNG – CẤP SỐ NHÂN
Page 41
Sưu tầm và biên soạn
Phương trình
( )
1
trở thành
2
0
50
25
t
tt t
tt
≤
=−⇔ ⇔ =
=
( )
5 5 0 50 0 0t t t t tt t t=−⇔ + = ⇔ + = ⇔ = ⇔ =
Với
0t =
ta có :
18
1
4
1811 11
e e 4 51 4 17
u
u
u uu uu
= ⇔ = ⇔+= ⇔=
Vậy
( ) ( )
1
1 17 1 3 3 14
n
uu n d n n=+− =+− =+
Có :
ln2018
ln2018 ln 2018
3
3 14
log ln 2018 3 3 14 3 1419,98
3
nn
u un n
−
< ⇔<⇔+<⇔< ≈
Vậy giá trị lớn nhất của
n
là
1419
.
Câu 156: Tổng:
2 4 6 2018A = + + +…+
có giá trị là:
A.
2018001
. B.
1209900
. C.
1010101
. D.
1019090
.
Lời giải
Ta có
( ) ( ) ( )
2 2 2018 4 2016 ... 2018 2A =++++++
Do đó
(
)
1009 2 2018
1019090
2
A
+
= =
Câu 157: Tổng:
1 4 7 3031B = + + +…+
bằng:
A.
1532676
. B.
1435000
. C.
1351110
. D.
1322300
.
Lời giải
Ta có
( ) ( ) ( )
2 1 3031 4 3028 ... 3031 1B =++++++
Do đó
( )
1011 1 3031
1532676
2
B
+
= =
Câu 158: Giá trị của tổng:
13 9 5 387C = − − − +…+
bằng:
A.
23455
. B.
18887
. C.
36778
. D.
43234
.
Lời giải
Ta có
( ) ( ) ( )
2 13 387 9 383 ... 387 13C =−++−+++−
Do đó
( )
101 13 387
18887
2
C
−+
= =
Câu 159: Giá trị của tổng:
1 101 201 1001
100 100 100 100
S = + + +…+
bằng:
A.
5514
100
. B.
5501
100
. C.
5511
100
. D.
5515
100
.
Lời giải
Ta có
1 1001 101 901 1001 1
2 ...
100 100 100 100 100 100
S
=+ ++++ +

CHUYÊN ĐỀ II – TOÁN – 11 – DÃY SỐ - CẤP SỐ CỘNG – CẤP SỐ NHÂN
Page 42
Sưu tầm và biên soạn
Do đó
1 1001
11
5511
100 100
2 100
S
+
= =
.
Câu 160: Cho tổng:
*
1 3 5 2 1, .
n
S nn
= + + +…+ + ∀ ∈
Tìm
100
S
?
A.
10201
. B.
10000
. C.
10200
. D.
10202
.
Lời giải
Ta có
100
1 3 5 ... 201S =+++ +
Suy ra
( ) (
)
( )
100
2 1 201 3 199 ... 201 1S
=++++++
Vậy
( )
100
101 1 201
10201
2
S
+
= =
Câu 161: Cho tổng:
246 2
n
Sn= + + +…+
với
*
n
∈
. Khi đó công thức của
n
S
là?
A.
( 2)nn+
. B.
( 1)
2
nn+
. C.
( 1)
nn+
. D.
2
n
.
Lời giải
Ta có
( ) ( ) ( )
2 2 2 4 2 2 ... 2 2
n
S nn n=+++−+++
Vậy
( )
( )
22
1
2
n
nn
S nn
+
= = +
Câu 162: Tìm
x
biết:
( 3) ( 7) ( 11) ( 79) 860xxx x+++++ +…++ =
A.
2
x =
. B.
1x =
. C.
4x =
. D.
3
x =
.
Lời giải
Ta có
( ) ( ) ( )
1720 3 79 7 75 ... 79 3xx xx x x= +++ + +++ ++ + ++
Do đó
( ) ( )
1720 20 3 79 1720 20 2 82 2xx x x= +++ ⇔ = + ⇔ =
Câu 163: Tìm
x
biết:
( ) ( ) ( ) ( )
2 3 2 7 2 11 ... 2 79 1720xxx x++++++++=
A.
35x =
. B.
45
2
x =
.
C.
10
x =
. D.
15x
=
.
Lời giải
Ta có
( )
( ) (
)
3440 2 3 2 79 2 7 2 75 ... 2 79 2 3xx xx x x
= +++ + +++ ++ +++
Do đó
( ) ( )
45
3440 20 2 3 2 79 3440 20 4 82
2
xx x x= ++ + ⇔ = + ⇔ =
Câu 164: Tính giá trị biểu thức:
1 2 3 2018
1 3 5 1009
A
+ + +…+
=
+ + +…+
A.
2030071
255025
. B.
2037171
200025
. C.
2037111
255000
. D.
2037171
255025
.
Lời giải
Đặt
1 2 3 ... 2018, 1 3 5 ... 1009PQ=+++ + =+++ +
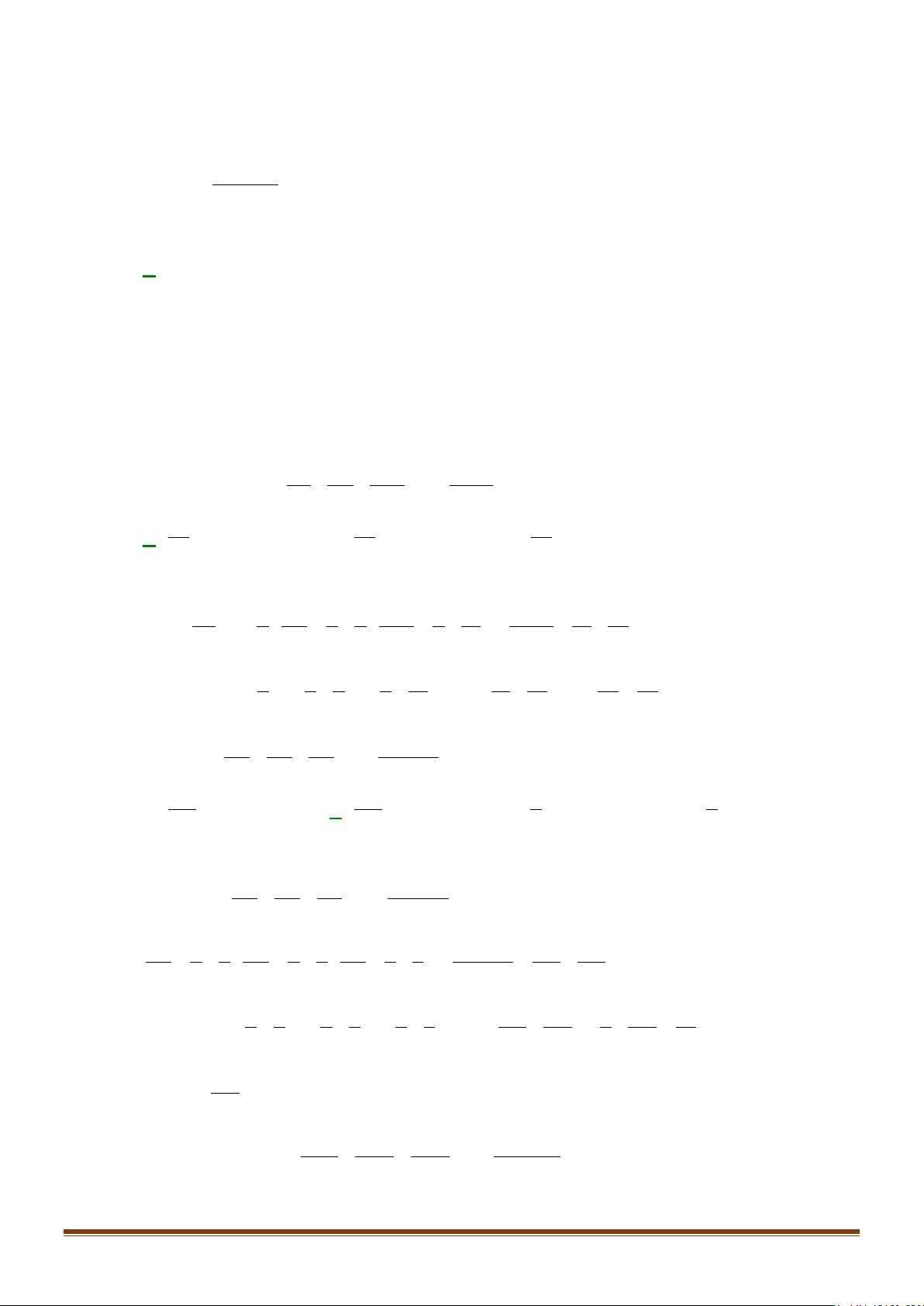
CHUYÊN ĐỀ II – TOÁN – 11 – DÃY SỐ - CẤP SỐ CỘNG – CẤP SỐ NHÂN
Page 43
Sưu tầm và biên soạn
Ta có
( ) ( ) ( )
2 1 2018 2 2017 ... 2018 1 2018.2019 2037171PP=++++++= ⇒=
( ) ( ) ( )
2 1 1009 2 1007 ... 1009 1 505.1010 255025QQ=++++++= ⇒=
Vậy
2037171
255025
A =
Câu 165: Cho tổng:
159 4 3
n
Sn= + + +…+ −
với
*
n ∈
. Khi đó:
22
10 15
SS+
bằng:
A.
225325
. B.
255325
. C.
225355
. D.
225525
.
Lời giải
Ta có
( )
2
10 10
1 5 9 ... 37 190 36100SS=+++ + = ⇒ =
( )
2
15 15
1 5 9 ... 57 435 189225SS=+++ + = ⇒ =
Vậy
22
10 15
225325SS+=
Câu 166: Tính tổng sau: .
A. B. C. D.
Lời giải
Ta có
3 1 3 11 3 1 1 3 1 1
1 ; ; ;...;
1.4 4 4.7 4 7 7.10 7 10 91.94 91
94
=−=− =− =−
Do đó
11111 11 193
1 ... 1
4 4 7 7 10 91 94 94 94
S
=−+−+− ++ − =−=
Câu 167: Tổng: bằng:
A. B. C. D.
Lời giải
Ta có
222 2
2 ...
2.4 4.6 6.8 100.102
S = + + ++
211211211 2 1 1
; ; ;...;
2.4 2 4 4.6 4 6 6.8 6 8 100.102 100 102
=−=−=− =−
Do đó
1 1 1 1 1 1 1 1 1 1 50
2 ...
2 4 4 6 6 8 100 102 2 102 51
S
=−+−+−++ − =− =
Vậy
50
102
S =
Câu 168: Giá trị của tổng: là:
33 3 3
...
1.4 4.7 7.10 91.94
S = + + ++
93
94
94
95
94
93
1
111 1
...
2.4 4.6 6.8 100.102
S = + + ++
53
102
25
102
1
2
1
4
444 4
...
1.3.5 3.5.7 5.7.9 91.93.95
S = + + ++

CHUYÊN ĐỀ II – TOÁN – 11 – DÃY SỐ - CẤP SỐ CỘNG – CẤP SỐ NHÂN
Page 44
Sưu tầm và biên soạn
A. B. C. D.
Lời giải
Ta có
4 11 4 11 4 11 4 1 1
;;;
1.3.5 1.3 3.5 3.5.7 3.5 5.7 5.7.9 5.7 7.9 91.93.95 91.93 93.95
=−=−=− =−
Khi đó
1 1 1 1 1 1 1 1 1 1 2944
...
1.3 3.5 3.5 5.7 5.7 7.9 91.93 93.95 1.3 93.95 8835
S
=−+−+−++ − =− =
Câu 169: Tổng
100 100 100 100
...
10.15.20 15.20.25 20.25.30 110.115.120
S = + + ++
có giá trị bằng:
A. B. C. D.
Lời giải
Ta có
100 1 1 100 1 1
10 ; 10 ;
10.15.20 10.15 15.20 15.20.25 15.20 20.25
100 1 1 100 1
1
10 ; 10
20.25.30 20.25 25.30 110.115.120 110.115 115.120
=−=−
=−=−
Khi đó
11 11 11 1 1
10 10 10 ... 10
10.15 15.20 15.20 20.25 20.25 25.30 110.115 115.120
1 1 91
15 115.12 1380
S
= − + − + − ++ −
=−=
Câu 170: Giá trị của tổng:
12 20 28 84
...
4.16 16.36 36.64 400.484
S = + + ++
là:
A. B. C. D.
Lời giải
Ta có
12 1 1 20 1 1 28 1 1 84 1 1
;; ;
4.16 4 16 16.36 16 36 36.64 36 64 400.484 400 484
=−=− =− =−
Khi đó
1 1 1 1 1 1 1 1 1 1 30
...
4 16 16 36 36 64 400 484 4 484 121
S
=−+−+−++ − =−=
Câu 171: Cho tổng:
( )
111 1
...
1.2 2.3 3.4 1
S
nn
=++++
+
với . Lựa chọn đáp án đúng.
A. B. C. D.
Lời giải
Ta có
2
1 12
1.2 2.3 3
S =+=
2941
8835
2942
8835
2944
8835
1
3
93
1380
91
13800
9
138
91
1380
31
121
30
121
32
121
33
121
*
n ∈
3
1
.
12
S =
2
1
.
6
S =
2
2
.
3
S =
3
1
.
4
S =

CHUYÊN ĐỀ II – TOÁN – 11 – DÃY SỐ - CẤP SỐ CỘNG – CẤP SỐ NHÂN
Page 45
Sưu tầm và biên soạn
Câu 172: Cho tổng:
( )( )
111 1
...
1.2.3 2.3.4 3.4.5 1 2
n
S
nn n
= + + ++
++
. Khi đó:
30
S
bằng:
A. B.
495
992
C. D.
Lời giải
Ta có
( )( )
222 2
2 ...
1.2.3 2.3.4 3.4.5 1 2
n
S
nn n
= + + ++
++
Trong đó
( )( )
( ) ( )( )
2 112 11 2 11
;; ;
1.2.3 1.2 2.3 2.3.4 2.3 3.4 3.4.5 3.4 4.5
2 11
12 1 12nn n nn n n
=−=− =−
= −
++ + ++
Khi đó
( )
( )( )
( )( )
( )( )
( )( )
22
111111 1 1
2 ...
1.2 2.3 2.3 3.4 3.4 4.5 1 1 2
11 3 3
1.2 12
12 212
n
n
S
nn n n
nn nn
S
nn nn nn
=−+−+−++ −
+ ++
++
= − = ⇒=
++ ++ ++
Vậy
( )( )
2
30
30 3.30 495
2. 30 1 30 2 992
S
+
= =
++
Câu 173: Tìm
x
biết:
2 2 2 2 1430
...
1.3 3.5 5.7 51.53 53
xxx x
+ ++ ++ +++ =
A. B. C. D.
Lời giải
Ta có
2 2 2 2 1430
...
1.3 3.5 5.7 51.53 53
1 1 1 1 1 1 1 1430 52 1430
26 1 ... 26 1
3 3 5 5 7 51 53 53 53 53
xxx x
x xx
+ ++ ++ +++ =
⇔ + −+−+−++ − = ⇔ + = ⇔=
Câu 174: Tìm
x
biết:
2 2 2 2 9125
...
1.2.3 2.3.4 3.4.5 20.21.22 231
xx x x
− +− +− ++− =
A. B. C. D.
Lời giải
Ta có
31
121
496
1987
31
121
1x =
2x =
3x =
4x =
1x =
2x =
3x =
4x =

CHUYÊN ĐỀ II – TOÁN – 11 – DÃY SỐ - CẤP SỐ CỘNG – CẤP SỐ NHÂN
Page 46
Sưu tầm và biên soạn
2 2 2 2 9125
...
1.2.3 2.3.4 3.4.5 20.21.22 231
1 1 1 1 1 1 1 1 9125
20 ...
1.2 2.3 2.3 3.4 3.4 4.5 20.21 21.22 231
1 1 9125 115 9125
20 20 2
1.2 21.22 231 231 231
xx x x
x
x xx
− +− +− ++− =
⇔ − −+−+−++ − =
⇔− − = ⇔−= ⇔=
Câu 175: Tính:
2 3 10
11 1 1
...
55 5 5
M =+ + ++
A. B. C. D.
Lời giải
Chọn A
Ta có
( )
( )
10 3 2
10 3 2
10 3 2
11
10 10
10 10
1 1 11 1 1 1 1
... 1 ... 1
5 555 5 5 5 5
1 1 1 1 11
1
1 1 ... 1
5 5 5 5 55
4 1 5.5
1 5 1 1 1
1 11 1
5 5 4.5 4.5 4 5
MM
M
M MM
= ++ + +⇔ +=
++ + ++
⇔ + − = − ++ + ++
−−
⇔− + = − ⇔ + = ⇔ = = −
10
Câu 176: Cho
5 55 5
...
1024 512 256 2
M = + + ++
. Khi đó M bằng:
A. B. C. D.
Lời giải
Chọn D
Ta có
( )
( )
10 9 8
10 9 8
10 9 8 11
11 11
5 5 5 5 1 11 1
... 5 ...
1024 512 256 2 2 2 2 2
111 1
5 5 ...
1
2 22 2
1 11111 1 1
5 1 5 1 ...
1 5
5 1
2 2 2 22 2 2 2
1 1
511
5 10 1 10
1 5
22
M
M
MM
MM
= + + ++= + +
++
⇔ += +
+ +++
⇔ + − = − + + + + + ⇔−
+ = −
⇔ += −
⇔ = − −=
5
1024
Câu 177: Cho
55 5
5 ...
3 9 729
M =++++
. Khi đó
729M
bằng:
A. B. C. D.
10
11
1
45
−
11
11
1
45
−
10
1
1
5
−
10
11
1
55
−
1023
1024
5111
1024
1024
1023
5115
1024
5465
729
5460
5465
5460
729

CHUYÊN ĐỀ II – TOÁN – 11 – DÃY SỐ - CẤP SỐ CỘNG – CẤP SỐ NHÂN
Page 47
Sưu tầm và biên soạn
Lời giải
Chọn C
Ta có
26
26
77
76 6
55 5 1 1 1
5 ... 5 1 ...
3 9 729 3 3 3
1 1 11 1
1 5 1 1 ...
3 3 33 3
2 1 531 5
31
5 1 729 729. . 5465
3 3
23 2 3
M
M
MM M
=
++++ = +
+ ++
⇔ − = − ++ ++
−−
⇔ = − ⇔= ⇒ = =
Câu 178: Cho tổng:
2
1 2 2 ... 2
n
n
S =++ ++
. Chọn mệnh đề đúng:
A.
10
2047S =
B.
10
2048S =
C.
10
1024S =
D.
10
1023S =
Lời giải
Chọn A
Ta có
( )
( )
2 21
1 2 2 ... 2 2 1 1 2 2 ... 2 2 1
n nn
nn
SS
+
=++ + + ⇔ = − ++ + + = −
Vậy
11
10
2 1 2047S = −=
Câu 179: Tính tổng:
1.2 3.4 5.6 ... 11.12S =++++
A. B. C. D.
Lời giải
Chọn A
Ta có
( ) ( )
( )
( )( )
( )
( )( )
*
1
2
1 11
2 1 2 , . 1.2 3.4 5.6 ... 2 1 2
2 12 4 2
4 12 1 14 1
1
63
n
k nk
k
n nn
n
k kk
n
a k kk S a n n
S kk k k
nn n nn n
S nn
=
= = =
= − ∈ = =++++ −
⇔= − = −
++ +−
⇔ = − +=
∑
∑ ∑∑
Vậy
( )( )
6 6 1 4.6 1
1.2 3.4 5.6 ... 11.12 322
3
S
+−
=++++ = =
Câu 180: Tổng:
2.3 4.5 6.7 ... 20.21S = + + ++
có giá trị bằng:
A. B. C. D.
Lời giải
Chọn C
Ta có
322
321
320
319
1550
1655
1650
1450

CHUYÊN ĐỀ II – TOÁN – 11 – DÃY SỐ - CẤP SỐ CỘNG – CẤP SỐ NHÂN
Page 48
Sưu tầm và biên soạn
( )
( )
( )
( )( )
( )
( )( )
*
1
2
1 11
2 2 1 , . 2.3 4.5 6.7 ... 2 2 1
22 1 4 2
4 12 1 14 5
1
63
n
k nk
k
n nn
n
k kk
n
a kk k S a nn
S kk k k
nn n nn n
S nn
=
= = =
= + ∈ = = + + ++ +
⇔ = += +
++ ++
⇔ = + +=
∑
∑ ∑∑
Vậy
( )( )
10 10 1 40 5
2.3 4.5 6.7 ... 20.21 1650
3
S
++
= + + ++ = =
Câu 181: Giá trị của tổng: là:
A. B. C. D.
Lời giải
Chọn D
Ta có
( )
( )
( )
( )( )
( )
( )
*
1
2
1 11
2
3 1 , . 1.2 2.5 3.8 ... 3 1
313
12 1 1
1
22
n
k nk
k
n nn
n
k kk
n
a kk k S a nn
S kk k k
nn n nn
S nn
=
= = =
= − ∈ = = + + ++ −
⇔ = −= −
++ +
⇔= − = +
∑
∑ ∑∑
Vậy
( )
2
1.2 2.5 3.8 ... 20.59 20 20 1 8400S = + + ++ = +=
Câu 182: Tính tổng:
( ) ( )
1.5 3.7 5.9 ... 2 1 . 2 3
n
S nn= + + ++ − +
khi
A. B. C. D.
Lời giải
Chọn C
Ta có
( )( ) ( )( )
( )( )
( )( )
( )
( )( )
*
1
2
1 11
2 1 2 3 , . 1.5 3.7 5.9 ... 2 1 2 3
2 12 3 4 4 3
2 12 1 2 12 4
2 13 3
33
n
k nk
k
n nn
n
k kk
n
ak kk S a n n
S k k k kn
nn n nn n
S nn n n
=
= = =
= − + ∈ = = + + ++ − +
⇔ = − += + −
++ ++
⇔ = + +− = −
∑
∑ ∑∑
Vậy
( ) ( )
15
30.16.34
1.5 3.7 5.9 ... 2 1 . 2 3 45 5395
3
n
S nn S= + + ++ − + ⇒ = − =
Câu 183: Giá trị của tổng:
( )
1.4 3.8 5.12 ... 2 1 .4
n
S nn= + + ++ −
khi
10n =
là:
A. B. C. D.
Lời giải
Chọn B
1.2 2.5 3.8 ... 20.59S = + + ++
8450
8300
8850
8400
15n =
5450
5400
5395
5650
1650
2860
2650
1950

CHUYÊN ĐỀ II – TOÁN – 11 – DÃY SỐ - CẤP SỐ CỘNG – CẤP SỐ NHÂN
Page 49
Sưu tầm và biên soạn
Ta có
( ) ( )
( )
( )( )
( )
( )( )
*
1
2
1 11
2 1 4k, . 1.4 3.8 5.12 ... 2 1 4
2 14 8 4
4 12 1 2 14 1
21
33
n
k nk
k
n nn
n
k kk
n
ak k S a nn
S kk k k
nn n nn n
S nn
=
= = =
= − ∈ = = + + ++ −
⇔= − = −
++ +−
⇔ = − +=
∑
∑ ∑∑
Vậy
( )
10
20.11.39
1.4 3.8 5.12 ... 2 1 .4 2860
3
n
S n nS= + + ++ − ⇒ = =
Câu 184: Cho tổng
( )
1.2 3.4 5.6 ... 2 1 2=++++ −
n
S nn
. Tính giá trị của
50
S
A. B. C. D.
Lời giải
Chọn A
Ta có
( )
( )
( )
( )( )
( )
( )( )
*
1
2
1 11
2 1 2 , . 1.2 3.4 5.6 ... 2 1 2
2 12 4 2
4 12 1 14 1
1
63
n
k nk
k
n nn
n
k kk
n
a k kk S a n n
S kk k k
nn n nn n
S nn
=
= = =
= − ∈ = =++++ −
⇔= − = −
++ +−
⇔ = − +=
∑
∑ ∑∑
Vậy
( )
( )( )
50
14 1
50.51.199
1.2 3.4 5.6 ... 2 1 2 169150
33
n
nn n
S nn S
+−
=++++ − = ⇒= =
Câu 185: Tìm
x
biết:
( ) ( ) ( ) ( )
1.2 2.5 3.8 ... 10.29 1200xxx x+ ++ ++ +++ =
A. B. C. D.
Lời giải
Chọn D
Ta có
( ) ( ) ( ) ( )
( )
1.2 2.5 3.8 ... 10.29 1200
10 1.2 2.5 3.8 ... 10.29 1200 10 1100 1200 10
xxx x
x xx
+ ++ ++ +++ =
⇔+++++ = ⇔+ = ⇔=
169150
155000
165050
165000
7x =
8x =
9x =
10x =
CHUYÊN ĐỀ II – TOÁN – 11 – DÃY SỐ - CẤP SỐ CỘNG – CẤP SỐ NHÂN
Page 30
Sưu tầm và biên soạn
BÀI 6: CẤP SỐ CỘNG
1. ĐỊNH NGHĨA
Cấp số cộng là một dãy số (hữu hạn hoặc vô hạn), trong đó kể từ số hạng thứ hai, mỗi
số hạng đều bằng số hạng đứng ngay trước nó cộng với một số không đổi
d
.
Số không đổi
d
được gọi là công sai của cấp số cộng.
Đặc biệt, khi
0d =
thì cấp số cộng là một dãy số không đổi (tất cả các số hạng đều
bằng nhau).
Nhận xét: Từ định nghĩa, ta có:
1) Nếu
( )
n
u
là một cấp số cộng với công sai
d
, ta có công thức truy hồi
2) Cấp số cộng
( )
n
u
là một dãy số tăng khi và chỉ khi công sai
0d >
.
3) Cấp số cộng
( )
n
u
là một dãy số giảm khi và chỉ khi công sai
0d <
.
NHẬN XÉT
Để chứng minh dãy số
( )
n
u
là một cấp số cộng, chúng ta cần chứng minh
1nn
uu
+
−
là một hằng
số với mọi số nguyên dương
n
.
Ví dụ 1. Chứng minh rằng dãy số hữu hạn sau là một cấp số cộng:
2;1;4;7;10;13;16;19−
.
Lời giải
Vì
Nên theo định nghĩa cấp số cộng, dãy số
2;1;4;7;10;13;16;19−
là một cấp số cộng với công sai
3d =
.
Ví dụ 2. Trong các dãy số dưới đây, dãy số nào là cấp số cộng? Tìm số hạng đầu và công sai của nó.
a) Dãy số , với
43
n
an= −
. b) Dãy số
( )
n
b
, với
23
4
n
n
b
−
=
.
Lời giải
*
1
,.
nn
u u dn
+
=+∈
( )
1
1 2 3; 4 1 3; 7 4 3; 10 7 3;=−+ =+ = + = +
13 10 3; 16 13 3; 19 16 3.=+=+=+
( )
n
a
CHƯƠNG
II
DÃY SỐ
CẤP SỐ CỘNG – CẤP SỐ NHÂN
LÝ THUYẾT.
I
VÍ DỤ.

CHUYÊN ĐỀ II – TOÁN – 11 – DÃY SỐ - CẤP SỐ CỘNG – CẤP SỐ NHÂN
Page 31
Sưu tầm và biên soạn
a) Ta có
(
)
1
4 1 34 1
n
an n
+
= + −= +
nên
( ) ( )
1
4 1 4 3 4, 1
nn
aa n n n
+
− = + − − = ∀≥
.
Do đó
( )
n
a
là cấp số cộng với số hạng đầu
1
1a =
và công sai
4
d =
.
b) Ta có
(
)
1
23 1
13
44
n
n
n
b
+
−+
−−
= =
nên
1
13 23 3
,1
4 44
nn
nn
bb n
+
−− −
− = − =− ∀≥
.
Suy ra
( )
n
b
là cấp số cộng với số hạng đầu
1
1
4
b = −
và công sai
3
4
d = −
.
Ví dụ 3. Cho cấp số cộng
( )
n
u
có
7
số hạng với số hạng đầu
1
2
3
u =
và công sai
4
3
d = −
. Viết dạng
khai triển của cấp số cộng đó.
Lời giải
Ta có
21
2
3
u ud
=+=−
;
32
2uud= +=−
;
43
10
3
u ud= +=−
54
14
3
uud
= +=−
;
65
6
uud= +=−
;
76
22
3
uud= +=−
.
Vậy dạng khai triển của cấp số cộng
( )
n
u
là
2 2 10 14 22
; ; 2; ; ; 6;
33 3 3 3
−−−−−−
.
2. SỐ HẠNG TỔNG QUÁT CỦA CẤP SỐ CỘNG.
Nếu cấp số cộng
( )
n
u
có số hạng đầu
1
u
và công sai
d
thì số hạng tổng quát
n
u
được
xác định bởi công thức:
( )
1
1, 2
n
u u n dn
= + − ∀≥
(2).
NHẬN XÉT
Từ kết quả của định lý 1, ta rút ra nhận xét sau:
Cho cấp số cộng
( )
n
u
biết hai số hạng
p
u
và
q
u
thì số hạng đầu và công sai được tính
theo công thức:
(1):
pq
uu
d
pq
−
=
−
.
(2):
( )
1
1
p
uu p d=−−
Cho cấp số cộng
( )
n
u
có
1
2u
=
và
5d = −
.
a) Tìm
20
u
.
b) Số
2018−
là số hạng thứ bao nhiêu của cấp số cộng?
Lời giải
a) Ta có
(
)
20 1
19 2 19. 5 93uu d=+ =+ −=−
.
b) Số hạng tổng quát của cấp số cộng là
( )
1
1 75
n
uu n d n=+− =−
.
Vì
2018
n
u = −
nên
7 5 2018 405nn− =− ⇔=
.
Do
405n =
là số nguyên dương nên số
2018−
là số hạng thứ
405
của cấp số cộng đã cho.
20 1
(20 1) 2 19.( 5) 93.= + − =+ −=−uu d
VÍ DỤ.

CHUYÊN ĐỀ II – TOÁN – 11 – DÃY SỐ - CẤP SỐ CỘNG – CẤP SỐ NHÂN
Page 32
Sưu tầm và biên soạn
Chú ý : Trong một cấp số cộng
( )
n
u
, mỗi số hạng (trừ số hạng đầu và cuối) đều là trung bình
cộng của hai số hạng đứng kề với nó, nghĩa là
11
2
kk
k
uu
u
−+
+
=
với
2k ≥
. (3)
NHẬN XÉT
Một cách tổng quát, ta có:
Nếu
( )
n
u
là cấp số cộng thì.
2
pk pk
p
uu
u
−+
+
=
,
1
kp≤<
a) Cho cấp số cộng
( )
n
u
có
99
101u
=
và
101
99u
=
. Tìm
100
u
.
b) Cho cấp số cộng
2; ;6;xy−
Tính giá trị của biểu thức
22
Px y= +
.
Lời giải
a) Theo tính chất của cấp số cộng, ta có
99 101
100
2
uu
u
+
=
nên
100
100
u =
.
b) Theo tính chất của cấp số cộng, ta có
26
2
2
x
−+
= =
và
6
2
xy+
=
.
Vì
2x =
nên
10y
=
.
Vậy .
222 2
2 10 104Px y=+=+ =
.
3. TỔNG
n
SỐ HẠNG ĐẦU TIÊN CỦA CẤP SỐ CỘNG.
Cho một cấp số cộng
( )
n
u
có số hạng đầu
1
u
và công sai
d
. Đặt
12
...
nn
S uu u= + ++
Khi đó:
( )
1
2
n
n
nu u
S
+
=
(4) hoặc
( )
1
1
2
n
nn d
S nu
−
= +
(5)
Cho cấp số cộng
( )
n
u
có
1
2u = −
và
3d
=
.
a) Tính tổng của
25
số hạng đầu tiên của cấp số cộng.
b) Biết
6095374
n
S =
, tìm
n
.
Lời giải
Ta có
( )
( )
( )
2
1
3
1 37
2
2 22
n
nn
nn n n
S nu d n
−
−−
= + =−+ =
a) Ta có .
( )
25
25 3.25 7
850
2
S
−
= =
.
b) Vì
6095374
n
S =
nên
( )
2
37
6095374 3 7 12190748 0
2
nn
nn
−
= ⇔ −− =
Giải phương trình
bậc hai trên với
n
nguyên dương, ta tìm được
2017n =
.
222 2
2 10 104
=+=+ =
Px y
25
25(3.25 7)
850
2
−
= =
S
VÍ DỤ.
VÍ DỤ.
HỆ THỐNG BÀI TẬP TỰ LUẬN.
II

CHUYÊN ĐỀ II – TOÁN – 11 – DÃY SỐ - CẤP SỐ CỘNG – CẤP SỐ NHÂN
Page 33
Sưu tầm và biên soạn
Câu 1: Cho một cấp số cộng
( )
n
u
có
1
1
3
u =
,
8
26.u =
Tìm công sai
d
Câu 2: Cho dãy số
( )
n
u
là một cấp số cộng có
1
3u =
và công sai
4d =
. Biết tổng
n
số hạng đầu của
dãy số
( )
n
u
là
253
n
S =
. Tìm
n
.
Câu 3: Cho một cấp số cộng
n
u
có
1
1
3
u
,
8
26u
. Tìm công sai
Câu 4: Một gia đình cần khoan một cái giếng để lấy nước. Họ thuê một đội khoan giếng nước. Biết giá
của mét khoan đầu tiên là
80.000
đồng, kể từ mét khoan thứ hai giá của mỗi mét khoan tăng
thêm
5.000
đồng so với giá của mét khoan trước đó. Biết cần phải khoan sâu xuống
50m
mới
có nước. Hỏi phải trả bao nhiêu tiền để khoan cái giếng đó?
Câu 5: Cho cấp số cộng
( )
n
u
có số hạng tổng quát là
32
n
un= −
. Tìm công sai
d
của cấp số cộng.
Câu 6: Cho cấp số cộng
( )
n
u
có
1
3u = −
,
6
27u =
. Tính công sai
d
.
Câu 7: Cho cấp số cộng
( )
n
u
có
1
3u = −
,
6
27u =
. Tính công sai
d
.
Câu 8: Cho một cấp số cộng
(
)
n
u
có
1
5u =
và tổng của
50
số hạng đầu bằng
5150
. Tìm công thức của
số hạng tổng quát
n
u
.
Câu 9: Cho cấp số cộng
( )
n
u
thỏa mãn
4
46
10
26
u
uu
=
+=
có công sai là
Câu 10: Cho cấp số cộng
( )
n
u
có
5
15u = −
,
20
60u =
. Tổng của
10
số hạng đầu tiên của cấp số cộng
Câu 11: Cho cấp số cộng
( )
n
u
có
4
12u = −
,
14
18
u =
. Tính tổng
16
số hạng đầu tiên của cấp số cộng
này.
Câu 12: Trong hội chợ tết Mậu Tuất
2018
, một công ty sữa muốn xếp
900
hộp sữa theo số lượng
1
,
3
,
5
,
...
từ trên xuống dưới (số hộp sữa trên mỗi hàng xếp từ trên xuống là các số lẻ liên tiếp - mô
hình như hình bên). Hàng dưới cùng có bao nhiêu hộp sữa?
Câu 13: Người ta trồng
465
cây trong một khu vườn hình tam giác như sau: Hàng thứ nhất có
1
cây,
hàng thứ hai có
2
cây, hàng thứ ba có
3
cây….Số hàng cây trong khu vườn là
Câu 14: Cho cấp số cộng
( )
n
u
có
1
3u
=
và công sai
7d
=
. Hỏi kể từ số hạng thứ mấy trở đi thì các số
hạng của
( )
n
u
đều lớn hơn
2018
?
Câu 15: Bốn số tạo thành một cấp số cộng có tổng bằng
28
và tổng các bình phương của chúng bằng
276
. Tích của bốn số đó là :
Câu 16: Chu vi một đa giác là
158cm
, số đo các cạnh của nó lập thành một cấp số cộng với công sai
3d cm=
. Biết cạnh lớn nhất là
44cm
. Số cạnh của đa giác đó là?
Câu 17: Cho cấp số cộng
( )
n
u
biết
5
18=u
và
2
4 =
nn
SS
. Tìm số hạng đầu tiên
1
u
và công sai
d
của cấp
số cộng.

CHUYÊN ĐỀ II – TOÁN – 11 – DÃY SỐ - CẤP SỐ CỘNG – CẤP SỐ NHÂN
Page 34
Sưu tầm và biên soạn
Câu 18: Biết bốn số
5
;
x
;
15
;
y
theo thứ tự lập thành cấp số cộng. Giá trị của biểu thức
32xy+
bằng.
Câu 19: Cho cấp số cộng , biết , . Số là số hạng thứ bao nhiêu?
Câu 20: Cho cấp số cộng có tổng
n
số hạng đầu là
2
34
n
Snn= +
,
*n ∈
. Giá trị của số hạng thứ
10
của cấp số cộng là
Câu 21: Cho cấp số cộng có tổng
n
số hạng đầu là
2
43
n
S nn= +
,
*
n ∈
thì số hạng thứ 10 của cấp số
cộng là
Câu 22: Cho cấp số cộng có tổng
n
số hạng đầu là
2
43
n
S nn= +
,
*
n ∈
thì số hạng thứ 10 của cấp số
cộng là
Câu 23: Người ta viết thêm
999
số thực vào giữa số
1
và số
2018
để được cấp số cộng có
1001
số hạng.
Tìm số hạng thứ
501
.
Câu 24: Cho cấp số cộng có
1
1u =
và công sai
2d = −
. Tổng
n
số hạng đầu tiên của cấp số cộng này là
9800
n
S = −
. Giá trị
n
là
( )
n
u
1
5u = −
2d =
81
CHUYÊN ĐỀ II – TOÁN – 11 – DÃY SỐ - CẤP SỐ CỘNG – CẤP SỐ NHÂN
Page 1
Sưu tầm và biên soạn
BÀI 6: CẤP SỐ CỘNG
1. ĐỊNH NGHĨA
Cấp số cộng là một dãy số (hữu hạn hoặc vô hạn), trong đó kể từ số hạng thứ hai, mỗi
số hạng đều bằng số hạng đứng ngay trước nó cộng với một số không đổi
d
.
Số không đổi
d
được gọi là công sai của cấp số cộng.
Đặc biệt, khi
0d =
thì cấp số cộng là một dãy số không đổi (tất cả các số hạng đều
bằng nhau).
Nhận xét: Từ định nghĩa, ta có:
1) Nếu
( )
n
u
là một cấp số cộng với công sai
d
, ta có công thức truy hồi
2) Cấp số cộng
( )
n
u
là một dãy số tăng khi và chỉ khi công sai
0d >
.
3) Cấp số cộng
( )
n
u
là một dãy số giảm khi và chỉ khi công sai
0d <
.
NHẬN XÉT
Để chứng minh dãy số
( )
n
u
là một cấp số cộng, chúng ta cần chứng minh
1nn
uu
+
−
là một hằng
số với mọi số nguyên dương
n
.
Ví dụ 1. Chứng minh rằng dãy số hữu hạn sau là một cấp số cộng:
2;1;4;7;10;13;16;19−
.
Lời giải
Vì
Nên theo định nghĩa cấp số cộng, dãy số
2;1;4;7;10;13;16;19−
là một cấp số cộng với công sai
3d =
.
Ví dụ 2. Trong các dãy số dưới đây, dãy số nào là cấp số cộng? Tìm số hạng đầu và công sai của nó.
a) Dãy số , với
43
n
an= −
. b) Dãy số
( )
n
b
, với
23
4
n
n
b
−
=
.
Lời giải
*
1
,.
nn
u u dn
+
=+∈
( )
1
1 2 3; 4 1 3; 7 4 3; 10 7 3;=−+ =+ = + = +
13 10 3; 16 13 3; 19 16 3.=+=+=+
( )
n
a
CHƯƠNG
II
DÃY SỐ
CẤP SỐ CỘNG – CẤP SỐ NHÂN
LÝ THUYẾT.
I
VÍ DỤ.

CHUYÊN ĐỀ II – TOÁN – 11 – DÃY SỐ - CẤP SỐ CỘNG – CẤP SỐ NHÂN
Page 2
Sưu tầm và biên soạn
a) Ta có
(
)
1
4 1 34 1
n
an n
+
= + −= +
nên
( ) ( )
1
4 1 4 3 4, 1
nn
aa n n n
+
− = + − − = ∀≥
.
Do đó
( )
n
a
là cấp số cộng với số hạng đầu
1
1a =
và công sai
4
d =
.
b) Ta có
(
)
1
23 1
13
44
n
n
n
b
+
−+
−−
= =
nên
1
13 23 3
,1
4 44
nn
nn
bb n
+
−− −
− = − =− ∀≥
.
Suy ra
( )
n
b
là cấp số cộng với số hạng đầu
1
1
4
b = −
và công sai
3
4
d = −
.
Ví dụ 3. Cho cấp số cộng
( )
n
u
có
7
số hạng với số hạng đầu
1
2
3
u =
và công sai
4
3
d = −
. Viết dạng
khai triển của cấp số cộng đó.
Lời giải
Ta có
21
2
3
u ud
=+=−
;
32
2uud= +=−
;
43
10
3
u ud= +=−
54
14
3
uud
= +=−
;
65
6
uud= +=−
;
76
22
3
uud= +=−
.
Vậy dạng khai triển của cấp số cộng
( )
n
u
là
2 2 10 14 22
; ; 2; ; ; 6;
33 3 3 3
−−−−−−
.
2. SỐ HẠNG TỔNG QUÁT CỦA CẤP SỐ CỘNG.
Nếu cấp số cộng
( )
n
u
có số hạng đầu
1
u
và công sai
d
thì số hạng tổng quát
n
u
được
xác định bởi công thức:
( )
1
1, 2
n
u u n dn
= + − ∀≥
(2).
NHẬN XÉT
Từ kết quả của định lý 1, ta rút ra nhận xét sau:
Cho cấp số cộng
( )
n
u
biết hai số hạng
p
u
và
q
u
thì số hạng đầu và công sai được tính
theo công thức:
(1):
pq
uu
d
pq
−
=
−
.
(2):
( )
1
1
p
uu p d=−−
Cho cấp số cộng
( )
n
u
có
1
2u
=
và
5d = −
.
a) Tìm
20
u
.
b) Số
2018−
là số hạng thứ bao nhiêu của cấp số cộng?
Lời giải
a) Ta có
(
)
20 1
19 2 19. 5 93uu d=+ =+ −=−
.
b) Số hạng tổng quát của cấp số cộng là
( )
1
1 75
n
uu n d n=+− =−
.
Vì
2018
n
u = −
nên
7 5 2018 405nn− =− ⇔=
.
Do
405n =
là số nguyên dương nên số
2018−
là số hạng thứ
405
của cấp số cộng đã cho.
20 1
(20 1) 2 19.( 5) 93.= + − =+ −=−uu d
VÍ DỤ.

CHUYÊN ĐỀ II – TOÁN – 11 – DÃY SỐ - CẤP SỐ CỘNG – CẤP SỐ NHÂN
Page 3
Sưu tầm và biên soạn
Chú ý : Trong một cấp số cộng
( )
n
u
, mỗi số hạng (trừ số hạng đầu và cuối) đều là trung bình
cộng của hai số hạng đứng kề với nó, nghĩa là
11
2
kk
k
uu
u
−+
+
=
với
2k ≥
. (3)
NHẬN XÉT
Một cách tổng quát, ta có:
Nếu
( )
n
u
là cấp số cộng thì.
2
pk pk
p
uu
u
−+
+
=
,
1
kp≤<
a) Cho cấp số cộng
( )
n
u
có
99
101u
=
và
101
99u
=
. Tìm
100
u
.
b) Cho cấp số cộng
2; ;6;xy−
Tính giá trị của biểu thức
22
Px y= +
.
Lời giải
a) Theo tính chất của cấp số cộng, ta có
99 101
100
2
uu
u
+
=
nên
100
100
u =
.
b) Theo tính chất của cấp số cộng, ta có
26
2
2
x
−+
= =
và
6
2
xy+
=
.
Vì
2x =
nên
10y
=
.
Vậy .
222 2
2 10 104Px y=+=+ =
.
3. TỔNG
n
SỐ HẠNG ĐẦU TIÊN CỦA CẤP SỐ CỘNG.
Cho một cấp số cộng
( )
n
u
có số hạng đầu
1
u
và công sai
d
. Đặt
12
...
nn
S uu u= + ++
Khi đó:
( )
1
2
n
n
nu u
S
+
=
(4) hoặc
( )
1
1
2
n
nn d
S nu
−
= +
(5)
Cho cấp số cộng
( )
n
u
có
1
2u = −
và
3d
=
.
a) Tính tổng của
25
số hạng đầu tiên của cấp số cộng.
b) Biết
6095374
n
S =
, tìm
n
.
Lời giải
Ta có
( )
( )
( )
2
1
3
1 37
2
2 22
n
nn
nn n n
S nu d n
−
−−
= + =−+ =
a) Ta có .
( )
25
25 3.25 7
850
2
S
−
= =
.
b) Vì
6095374
n
S =
nên
( )
2
37
6095374 3 7 12190748 0
2
nn
nn
−
= ⇔ −− =
Giải phương trình
bậc hai trên với
n
nguyên dương, ta tìm được
2017n =
.
222 2
2 10 104
=+=+ =
Px y
25
25(3.25 7)
850
2
−
= =
S
VÍ DỤ.
VÍ DỤ.
HỆ THỐNG BÀI TẬP TỰ LUẬN.
II

CHUYÊN ĐỀ II – TOÁN – 11 – DÃY SỐ - CẤP SỐ CỘNG – CẤP SỐ NHÂN
Page 4
Sưu tầm và biên soạn
Câu 1: Cho một cấp số cộng
( )
n
u
có
1
1
3
u =
,
8
26.u =
Tìm công sai
d
Lời giải
81
7uu d= +
1
26 7
3
d⇔=+
11
3
d⇔=
.
Câu 2: Cho dãy số
( )
n
u
là một cấp số cộng có
1
3u =
và công sai
4d =
. Biết tổng
n
số hạng đầu của
dãy số
( )
n
u
là
253
n
S
=
. Tìm
n
.
Lời giải
Ta có
( )
( )
( )
( )
1
2 1 2.3 1 .4
253
22
n
nu n d n n
S
+− +−
=⇔=
( )
2
11
4 2 506 0
23
2
n
nn
nL
=
⇔ +− =⇔
= −
.
Câu 3: Cho một cấp số cộng
n
u
có
1
1
3
u
,
8
26
u
. Tìm công sai
Lời giải
Ta có
81
1 11
7 26 7
33
uu d dd
.
Câu 4: Một gia đình cần khoan một cái giếng để lấy nước. Họ thuê một đội khoan giếng nước. Biết giá
của mét khoan đầu tiên là
80.000
đồng, kể từ mét khoan thứ hai giá của mỗi mét khoan tăng
thêm
5.000
đồng so với giá của mét khoan trước đó. Biết cần phải khoan sâu xuống
50m
mới
có nước. Hỏi phải trả bao nhiêu tiền để khoan cái giếng đó?
Lời giải
* Áp dụng công thức tính tổng của
n
số hạng đầu của cấp số nhân có số hạng đầu
1
80.000u =
,
công sai
5.000d =
ta được số tiền phải trả khi khoan đến mét thứ
n
là
( )
( )
1
1
21
22
n
n
nu n d
nu u
S
+−
+
= =
* Khi khoan đến mét thứ
50
, số tiền phải trả là
( )
50
50 2.80000 50 1 .5000
10.125.000
2
S
+−
= =
đồng.
Câu 5: Cho cấp số cộng
( )
n
u
có số hạng tổng quát là
32
n
un= −
. Tìm công sai
d
của cấp số cộng.
Lời giải
Ta có
( )
1
3 1 23 23
nn
uu n n
+
− = + −− +=
Suy ra
3d =
là công sai của cấp số cộng.
Câu 6: Cho cấp số cộng
( )
n
u
có
1
3u = −
,
6
27u =
. Tính công sai
d
.
Lời giải
Ta có
61
5 27 6uu d d=+ = ⇒=
.

CHUYÊN ĐỀ II – TOÁN – 11 – DÃY SỐ - CẤP SỐ CỘNG – CẤP SỐ NHÂN
Page 5
Sưu tầm và biên soạn
Câu 7: Cho cấp số cộng
( )
n
u
có
1
3
u = −
,
6
27u =
. Tính công sai
d
.
Lời giải
Ta có
61
5 27 6uu d d
=+ = ⇒=
.
Câu 8: Cho một cấp số cộng
( )
n
u
có
1
5u
=
và tổng của
50
số hạng đầu bằng
5150
. Tìm công thức của
số hạng tổng quát
n
u
.
Lời giải
Ta có:
(
)
50 1
50
2 49 5150
2
S ud= +=
4d⇒=
.
Số hạng tổng quát của cấp số cộng bằng
( )
1
1 14
n
uu n d n=+− =+
.
Câu 9: Cho cấp số cộng
( )
n
u
thỏa mãn
4
46
10
26
u
uu
=
+=
có công sai là
Lời giải
Gọi
d
là công sai.
Ta có:
4
1
1
46
1
10
3 10
1
26
2 8 26
3
u
ud
u
uu
ud
d
=
+=
=
⇔⇔
+=
+=
=
.
Vậy công sai
3d =
.
Câu 10: Cho cấp số cộng
( )
n
u
có
5
15
u = −
,
20
60
u =
. Tổng của
10
số hạng đầu tiên của cấp số cộng
Lời giải
Gọi
1
u
,
d
lần lượt là số hạng đầu và công sai của cấp số cộng.
Ta có:
5
20
15
60
u
u
= −
=
⇔
1
1
4 15
19 60
ud
ud
+=−
+=
⇔
1
35
5
u
d
= −
=
.
Vậy
( )
10 1
10
.2 9
2
S ud= +
( )
5. 2. 35 9.5
= −+
125= −
.
Câu 11: Cho cấp số cộng
( )
n
u
có
4
12u = −
,
14
18u =
. Tính tổng
16
số hạng đầu tiên của cấp số cộng
này.
Lời giải
Gọi
d
là công sai của cấp số cộng. Theo giả thiết, ta có
1
1
3 12
13 18
ud
ud
+=−
+=
1
21
3
u
d
= −
⇔
=
.
Khi đó,
(
)
1
16
2 15 .16
2
ud
S
+
=
( )
8 42 45 24
=−+ =
.
Câu 12: Trong hội chợ tết Mậu Tuất
2018
, một công ty sữa muốn xếp
900
hộp sữa theo số lượng
1
,
3
,
5
,
...
từ trên xuống dưới (số hộp sữa trên mỗi hàng xếp từ trên xuống là các số lẻ liên tiếp - mô
hình như hình bên). Hàng dưới cùng có bao nhiêu hộp sữa?

CHUYÊN ĐỀ II – TOÁN – 11 – DÃY SỐ - CẤP SỐ CỘNG – CẤP SỐ NHÂN
Page 6
Sưu tầm và biên soạn
Lời giải
Cách 1: p dụng công thức tính tổng n số hạng liên tiếp của CSC:
( )
1
21
2
n
n
S un d
= +−
( )
900 2.1 1 .2
2
n
n⇔ = +−
2
900n⇔=
30.n⇒=
Vậy
30
1 29*2 59.u =+=
Cách 2: Áp dụng công thức
( )
2
1 3 5 ..... 2 1nn+++ + − =
, suy ra
30.n =
Vậy
2 1 59.n −=
.
Câu 13: Người ta trồng
465
cây trong một khu vườn hình tam giác như sau: Hàng thứ nhất có
1
cây,
hàng thứ hai có
2
cây, hàng thứ ba có
3
cây….Số hàng cây trong khu vườn là
Lời giải
Cách trồng
465
cây trong một khu vườn hình tam giác như trên lập thành một cấp số cộng
( )
n
u
với số
n
u
là số cây ở hàng thứ
n
và
1
1u
=
và công sai
1d =
.
Tổng số cây trồng được là:
465
n
S
=
( )
1
465
2
nn+
⇔=
2
930 0nn⇔ +− =
( )
30
31
n
nl
=
⇔
= −
.
Như vậy số hàng cây trong khu vườn là
30
.
Câu 14: Cho cấp số cộng
( )
n
u
có
1
3u =
và công sai
7d =
. Hỏi kể từ số hạng thứ mấy trở đi thì các số
hạng của
( )
n
u
đều lớn hơn
2018
?
Lời giải
Ta có:
( )
1
1
n
uu n d
=+−
( )
37 1n=+−
74
n= −
;
2018
n
u >
7 4 2018n⇔ −>
2022
7
n⇔>
Vậy
289n =
.
Câu 15: Bốn số tạo thành một cấp số cộng có tổng bằng
28
và tổng các bình phương của chúng bằng
276
. Tích của bốn số đó là :
Lời giải
Gọi
4
số cần tìm là
3
ar
−
,
ar−
,
ar+
,
3ar+
.
Ta có:
( ) ( ) ( ) ( )
222 2
3 3 28
3 3 276
a rarara r
arararar
− +−++++ =
− +− ++ ++ =
2
7
4
a
r
=
⇔
=
7
2
a
r
=
⇔
= ±
.
Bốn số cần tìm là
1
,
5
,
9
,
13
có tích bằng
585
.
Câu 16: Chu vi một đa giác là
158cm
, số đo các cạnh của nó lập thành một cấp số cộng với công sai
3d cm=
. Biết cạnh lớn nhất là
44cm
. Số cạnh của đa giác đó là?
CHUYÊN ĐỀ II – TOÁN – 11 – DÃY SỐ - CẤP SỐ CỘNG – CẤP SỐ NHÂN
Page 7
Sưu tầm và biên soạn
Lời giải
Giả sử đã giác đã cho có
n
cạnh thì chu vi của đa giác là:
( )
1
2
n
n
u un
S
+
=
với
1
u
là cạnh nhỏ
nhất. Suy ra:
( )
1
44
158
2
un+
=
( )
1
316 44un⇔=+
( )
2
1
2 .79 44un⇔=+
Do đó
1
44u +
là ước nguyên dương của
2
316 2 .79=
và đa giác có ít nhất ba cạnh nên
1
316
44 44
3
u>+ >
. Suyra:
11
44 79 35uu+ = ⇔=
.
Số cạnh của đa giác đã cho là:
44 35
14
3
−
+=
( cạnh ).
Câu 17: Cho cấp số cộng
( )
n
u
biết
5
18=u
và
2
4 =
nn
SS
. Tìm số hạng đầu tiên
1
u
và công sai
d
của cấp
số cộng.
Lời giải
Ta có:
51
18 4 18= ⇔+ =u ud
( )
1
.
2
4 =
nn
SS
( ) ( )
11
1 22 1
42
22
−−
⇔+ =+
nnd n
nd
nu nu
11
42 222⇔+−=+−u nd d u nd d
1
20⇔ −=ud
( )
2
.
Từ
( )
1
và
( )
2
suy ra
1
2=u
;
4=d
.
Câu 18: Biết bốn số
5
;
x
;
15
;
y
theo thứ tự lập thành cấp số cộng. Giá trị của biểu thức
32xy+
bằng.
Lời giải
Ta có:
5 15
10
2
x
+
= =
20y⇒=
. Vậy
3 2 70xy+=
.
Câu 19: Cho cấp số cộng , biết , . Số là số hạng thứ bao nhiêu?
Lời giải
Ta có .
Vậy là số hạng thứ .
Câu 20: Cho cấp số cộng có tổng
n
số hạng đầu là
2
34
n
Snn= +
,
*n∈
. Giá trị của số hạng thứ
10
của cấp số cộng là
Lời giải
Từ giả thiết ta có
2
11
3.1 4.1 7Su== +=
.
Ta có
( )
2
86
34
2
n
nn
Snn
+
= +=
( )
76 1
2
nn++
=
61
n
un⇒=+
10
61u⇒=
.
( )
n
u
1
5u = −
2d =
81
( )
1
1
n
uu n d=+−
( )
81 5 1 2n⇔ =−+ −
44n⇔=
81
44

CHUYÊN ĐỀ II – TOÁN – 11 – DÃY SỐ - CẤP SỐ CỘNG – CẤP SỐ NHÂN
Page 8
Sưu tầm và biên soạn
Câu 21: Cho cấp số cộng có tổng
n
số hạng đầu là
2
43
n
S nn= +
,
*
n ∈
thì số hạng thứ 10 của cấp số
cộng là
Lời giải
Theo công thức ta có
(
)
1
2
43
2
n
nu u
nn
+
= +
1
86
n
uu n
⇔+= +
1
86
n
u un⇒ =−+ +
.
Mà
11
7uS
= =
do đó
10
7 8.10 6 79u =−+ + =
.
Câu 22: Cho cấp số cộng có tổng
n
số hạng đầu là
2
43
n
S nn= +
,
*
n
∈
thì số hạng thứ 10 của cấp số
cộng là
Lời giải
Theo công thức ta có
(
)
1
2
43
2
n
nu u
nn
+
= +
1
86
n
uu n⇔+= +
1
86
n
u un⇒ =−+ +
.
Mà
11
7uS= =
do đó
10
7 8.10 6 79
u =−+ + =
.
Câu 23: Người ta viết thêm
999
số thực vào giữa số
1
và số
2018
để được cấp số cộng có
1001
số hạng.
Tìm số hạng thứ
501
.
Lời giải
Áp dụng công thức cấp số cộng ta có:
( ) (
) ( )
1 1001 1
2017
1 1001 1 2018 1 1001 1
1000
n
uu n du u d d d=+−⇒ =+ −⇔ =+ −⇒=
.
Vậy số hạng thứ
501
là
( )
501 1
2019
501 1
2
uu d=+ −=
.
Câu 24: Cho cấp số cộng có
1
1u
=
và công sai
2d = −
. Tổng
n
số hạng đầu tiên của cấp số cộng này là
9800
n
S
= −
. Giá trị
n
là
Lời giải
( )
( )
( )
1
2 1 9800 2 2 1 19600 0
2
n
n
S un d n n= +− =− ⇔ − − + =
100n⇔=
.
CHUYÊN ĐỀ II – TOÁN – 11 – DÃY SỐ - CẤP SỐ CỘNG – CẤP SỐ NHÂN
Page 35
Sưu tầm và biên soạn
BÀI 6: CẤP SỐ CỘNG
DẠNG 1. NHẬN DIỆN CẤP SỐ CỘNG
Câu 1: Trong các dãy số sau, dãy số nào là một cấp số cộng?
A.
1;2;4;6;8−−−−
. B.
1;3;6;9;12.−−−−
C.
1;3;7;11;15.−−− −
D.
1;3;5;7;9−−−−
.
Câu 2: Trong các dãy số sau, dãy số nào không phải cấp số cộng?
A.
13579
;;;;
22222
. B.
1;1;1;1;1
. C.
8; 6; 4; 2;0
−−−−
. D.
3;1;1;2;4
−−−
.
Câu 3: Cho cấp số cộng
( )
n
u
với
52
n
un= −
. Tìm công sai của cấp số cộng
A.
3
d
=
. B.
2d = −
. C.
1d =
. D.
2d =
.
Câu 4: Trong các dãy số có công thức tổng quát sau, dãy số nào là cấp số cộng?
A.
2021
n
n
u
. B.
2 2021
n
un= +
. C.
2
2021
n
u
n
=
+
. D.
2
2
n
un= −
.
Câu 5: Trong các dãy số sau, dãy nào là một cấp số cộng?
A.
1;3;6;9;12−−−−
. B.
1;3;7;11;15−−− −
. C.
1;3;5;7;9−−−−
. D.
1;2;4;6;8−−−−
.
Câu 6: Trong các dãy số sau đây, dãy số nào là cấp số cộng?
A.
3
n
n
u =
. B.
( )
1
3
n
n
u
+
= −
. C.
31
n
un= +
. D.
1
2
+
=
n
n
u
.
Câu 7: Trong các dãy số
( )
n
u
sau đây, dãy số nào là cấp số cộng?
A.
1
1
3
21
nn
u
uu
+
=
= +
. B.
1
1
1
2
nn
u
uu
+
= −
−=
. C.
1
3
1
1
1
nn
u
uu
+
=
= −
. D.
1
1
1
nn
u
u un
+
=
= +
.
Câu 8: Dãy số nào sau đây là cấp số cộng?
A.
4;8;16;32
. B.
4;6;8;10
. C.
1;1; 1;1−−
. D.
3; 5; 7;10
.
Câu 9: Xác định
a
để 3 số
2
1 2 ; 2 1; 2aa a+ −−
theo thứ tự thành lập một cấp số cộng?
A. Không có giá trị nào của
a
. B.
3
4
a = ±
.
C.
3a = ±
. D.
3
2
a = ±
.
CHƯƠNG
II
DÃY SỐ
CẤP SỐ CỘNG – CẤP SỐ NHÂN
HỆ THỐNG BÀI TẬP TRẮC NGHIỆM.
III

CHUYÊN ĐỀ II – TOÁN – 11 – DÃY SỐ - CẤP SỐ CỘNG – CẤP SỐ NHÂN
Page 36
Sưu tầm và biên soạn
Câu 10: Trong các dãy số sau đây, dãy số nào là cấp số cộng?
A.
2
3 2017
= +
n
un
.
B.
3 2018= +
n
un
.
C.
3=
n
n
u
. D.
(
)
1
3
+
= −
n
n
u
.
Câu 11: Dãy số nào sau đây là cấp số cộng?
A.
( )
1
:
nn
uu
n
=
. B.
( )
1
: 2, 2
nnn
uuu n
−
= − ∀≥
.
C.
( )
: 21
n
nn
uu= −
. D.
( )
1
: 2, 2
nn n
uu u n
−
= ∀≥
.
Câu 12: Trong các dãy số sau đây, dãy số nào là một cấp số cộng?
A.
2
1, 1
n
un n
=+≥
.
B.
2, 1
n
n
un= ≥
.
C.
1, 1
n
u nn=+≥
.
D.
2 3, 1
n
un n=−≥
Câu 13: Trong các dãy số sau, dãy nào
là cấp số cộng:
A.
1
3
n
n
u
+
=
. B.
2
1
n
u
n
=
+
. C.
2
1
n
un= +
. D.
52
3
n
n
u
−
=
.
DẠNG 2. TÌM CÁC YẾU TỐ CỦA CẤP SỐ CỘNG
Câu 14: Cho cấp số cộng
( )
n
u
có
1
1u =
có
1
1u =
và
2
3u
=
. Giá trị của
3
u
bằng
A.
6.
B.
9.
C.
4.
D.
5.
Câu 15: Cho cấp số cộng
( )
n
u
với
1
2u
=
và
2
7u =
. Công sai của cấp số cộng đã cho bằng
A.
5
. B.
2
7
. C.
5−
. D.
7
2
.
Câu 16: ] Cho cấp số cộng
()
n
u
với
1
11u
=
và công sai
3
d =
. Giá trị của
2
u
bằng
A.
8
. B.
33
. C.
11
3
. D.
14
.
Câu 17: Cho cấp số cộng
( )
n
u
với
1
9
u =
và công sai
2d =
. Giá trị của
2
u
bằng
A.
11
. B.
9
2
. C.
18
. D.
7
.
Câu 18: Cho cấp số cộng
( )
n
u
với
1
8u =
và công sai
3d =
. Giá trị của
2
u
bằng
A.
8
3
. B.
24
. C.
5
. D.
11
.
Câu 19: Cho cấp số cộng
( )
n
u
với
1
2u =
và
2
6u
=
. Công sai của cấp số cộng đã cho bằng
A.
4
. B.
4−
. C.
8
. D.
3
.
Câu 20: Cho cấp số cộng
( )
n
u
với
1
1u =
và
2
4u =
. Công sai của cấp số cộng đã cho bằng
A.
4
. B.
3−
. C.
3
. D.
5
.
Câu 21: Cho cấp số cộng với
1
3u =
và
2
9u =
. Công sai của cấp số cộng đã cho bằng
A.
6−
. B.
3
. C.
12
. D.
6
.
Câu 22: Cho cấp số cộng
( )
n
u
với
1
2u =
và
2
8
u =
. Công sai của cấp số cộng đã cho bằng
A.
10
. B.
6
. C.
4
. D.
6−
.

CHUYÊN ĐỀ II – TOÁN – 11 – DÃY SỐ - CẤP SỐ CỘNG – CẤP SỐ NHÂN
Page 37
Sưu tầm và biên soạn
Câu 23: Cho cấp số cộng
(
)
n
u
với
1
2022u =
và công sai
7
d
=
. Giá trị của
6
u
bằng
A.
2043
. B.
2064
. C.
2050
. D.
2057
.
Câu 24: Tìm công sai
d
của cấp số cộng
( )
n
u
,
*
n ∈
có
14
1; 13
uu
= =
.
A.
3
d =
. B.
1
4
d =
. C.
4d =
. D.
1
3
d =
.
Câu 25: Cấp số cộng
( )
n
u
có số hạng đầu
1
3,u =
công sai
2
d = −
thì số hạng thứ
5
là
A.
5
1u =
. B.
5
8u =
. C.
5
7u = −
. D.
5
5
u = −
.
Câu 26: Cho cấp số cộng có
3
2
u =
, công sai
2d = −
. Số hạng thứ hai của cấp số cộng đó là
A.
2
4u =
B.
2
0u =
C.
2
4
u = −
D.
2
3u =
Câu 27: Cho cấp số cộng
( )
n
u
có
1
1, 2ud= =
. Tính
10
u
A.
10
20u =
.
B.
10
10.
u =
C.
10
19u =
.
D.
10
15.u =
Câu 28: Cho cấp số cộng
( )
n
u
có
1
3u
= −
,
6
27u =
. Tính công sai
d
.
A.
7d =
. B.
5d =
. C.
8d =
. D.
6d
=
.
Câu 29: Cho cấp số cộng
( )
n
u
có số hạng tổng quát là
32
n
un= −
. Tìm công sai
d
của cấp số cộng.
A.
3d =
. B.
2d =
. C.
2d = −
. D.
3d = −
.
Câu 30: Cho cấp số cộng
( )
n
u
với
17
33
u =
và
33
65u =
thì công sai bằng
A.
1
. B.
3
. C.
2−
. D.
2
.
Câu 31: Một cấp số cộng gồm
5
số hạng. Hiệu số hạng đầu và số hạng cuối bằng
20
. Tìm công sai
d
của
cấp số cộng đã cho
A.
5d = −
. B.
4d =
. C.
4d = −
. D.
5d =
.
Câu 32: Cho cấp số cộng
n
u
có các số hạng đầu lần lượt là
5;9;13;17;...
. Tìm số hạng tổng quát
n
u
của
cấp số cộng?
A.
41
n
un= +
. B.
51
n
un= −
. C.
51
n
un= +
. D.
41
n
un= −
.
Câu 33: Xác định số hàng đầu
1
u
và công sai
d
của cấp số cộng
( )
n
u
có
92
5uu=
và
13 6
25uu= +
.
A.
1
3u =
và
4d =
. B.
1
3u =
và
5d =
. C.
1
4u =
và
5d =
. D.
1
4u =
và
3d =
.
Câu 34: Cho
( )
n
u
là một cấp số cộng thỏa mãn
13
8uu+=
và
4
10u =
. Công sai của cấp số cộng đã cho
bằng
A.
3
. B.
6
. C.
2
. D.
4
.
Câu 35: Tìm công thức số hạng tổng quát của cấp số cộng
( )
n
u
thỏa mãn:
235
16
7
12
uuu
uu
−+=
+=
A.
23
n
un= +
. B.
21
n
un= −
. C.
21
n
un= +
. D.
23
n
un= −
.
Câu 36: Cấp số cộng
( )
n
u
có số hạng đầu
1
3
u =
, công sai
2d = −
thì số hạng thứ 5 là
A.
5
8u =
. B.
5
1u =
. C.
5
5
u = −
. D.
5
7u = −
.

CHUYÊN ĐỀ II – TOÁN – 11 – DÃY SỐ - CẤP SỐ CỘNG – CẤP SỐ NHÂN
Page 38
Sưu tầm và biên soạn
Câu 37: Cho cấp số cộng có
1
3u
= −
,
4
d
=
. Chọn khẳng định đúng trong các khẳng định sau?
A.
5
15u =
. B.
4
8u
=
. C.
3
5u =
. D.
2
2u =
.
Câu 38: Cho cấp số cộng
( )
n
u
có
1
11u =
và công sai
4
d
=
. Hãy tính
99
u
.
A.
401
. B.
403
. C.
402
. D.
404
.
Câu 39: Cho cấp số cộng
( )
n
u
, biết:
1
3
u =
,
2
1u = −
. Chọn đáp án đúng.
A.
3
4u =
. B.
3
7u =
. C.
3
2u =
. D.
3
5u = −
.
Câu 40: Một cấp số cộng
(
)
n
u
có
13
8u =
và
3
d = −
. Tìm số hạng thứ ba của cấp số cộng
(
)
n
u
.
A.
50
. B.
28
. C.
38
. D.
44
Câu 41: Cho cấp số cộng
( )
n
u
có số hạng đầu
1
3u =
và công sai
2d =
. Giá trị của
7
u
bằng:
A.
15
. B.
17
. C.
19
. D.
13
.
Câu 42: Cho cấp số cộng
( )
n
u
có số hạng đầu
1
2u =
và công sai
4d =
. Giá trị
2019
u
bằng
A.
8074
. B.
4074
. C.
8078
. D.
4078
.
Câu 43: Tìm số hạng thứ
11
của cấp số cộng có số hạng đầu bằng
3
và công sai
2d = −
.
A.
21−
. B.
23
. C.
19−
. D.
17−
.
Câu 44: Cho cấp số cộng
( )
n
u
có số hạng đầu
1
2u = −
và công sai
7.d = −
Giá trị
6
u
bằng
A.
37
. B.
37−
. C.
33−
. D.
33
.
Câu 45: Cho cấp số cộng
( )
n
u
có số hạng đầu
1
2u =
và công sai
5d =
. Giá trị
4
u
bằng
A. 22. B. 17. C. 12. D. 250.
Câu 46: Cho cấp số cộng
( )
n
u
với số hạng đầu tiên
1
2
u
=
và công sai
2d =
. Tìm
2018
u
?
A.
2018
2018
2
u =
. B.
2017
2018
2u =
. C.
2018
4036u
=
. D.
2018
4038u
=
.
Câu 47: Cho cấp số cộng
( )
n
u
có
1
3u =
và công sai
7
d =
. Hỏi kể từ số hạng thứ mấy trở đi thì các số
hạng của
( )
n
u
đều lớn hơn
2018
?
A.
287
. B.
289
. C.
288
. D.
286
.
Câu 48: Viết ba số xen giữa
2
và
22
để ta được một cấp số cộng có
5
số hạng?
A.
6
,
12
,
18
. B.
8
,
13
,
18
. C.
7
,
12
,
17
. D.
6
,
10
,
14
.
Câu 49: Cho cấp số cộng có
1
2u = −
và
4d =
. Chọn khẳng định đúng trong các khẳng định sau ?
A.
4
8u =
. B.
5
15u =
. C.
2
3u
=
. D.
3
6u =
.
Câu 50: Cho cấp số cộng
(
)
n
u
với
1
2u
=
;
9d =
. Khi đó số
2018
là số hạng thứ mấy trong dãy?
A.
226
. B.
225
. C.
223
. D.
224
.
Câu 51: Cho cấp số cộng
1,4,7,...
. Số hạng thứ 100 của cấp số cộng là
A.
297
. B.
301
. C.
295
. D.
298
.
Câu 52: Cho cấp số cộng
( )
n
u
biết
1
3u =
,
8
24u =
thì
11
u
bằng
A.
30
. B.
33
. C.
32
. D.
28
.

CHUYÊN ĐỀ II – TOÁN – 11 – DÃY SỐ - CẤP SỐ CỘNG – CẤP SỐ NHÂN
Page 39
Sưu tầm và biên soạn
Câu 53: Cho cấp số cộng có số hạng thứ 3 và số hạng thứ 7 lần lượt là 6 và −2. Tìm số hạng thứ 5.
A.
5
2.u =
B.
5
2.u = −
C.
5
0.u =
D.
5
4.u =
Câu 54: Cho cấp số cộng
(
)
n
u
, biết
2
3u =
và
4
7u =
. Giá trị của
15
u
bằng
A.
27
. B.
31
. C.
35
. D.
29
.
Câu 55: Cho cấp số cộng
( )
n
u
có
1
123u =
và
3 15
84uu−=
. Số 11 là số hạng thứ bao nhiêu của cấp số
cộng đã cho?
A. 17. B. 16. C. 18. D. 19.
Câu 56: Cho cấp số cộng
()
n
u
biết
1
1;
u = −
2;d =
43
n
u =
. Hỏi cấp số cộng đó có bao nhiêu số hạng?
A. 20. B. 23. C. 22. D. 21.
Câu 57: Cho cấp số cộng
(
)
n
u
có số hạng đầu là
2
1u =
,
5
19u =
. Số
103
là số hạng thứ mấy trong cấp
số cộng đã cho?
A.
19
. B.
18
. C.
20
. D.
17
.
Câu 58: Cho cấp số cộng
( )
n
u
có
1
5=u
và công sai
3= −d
. Biết rằng
289−
là một số hạng của cấp số
cộng trên. Hỏi đó là số hạng thứ bao nhiêu?
A.
98
. B.
99
. C.
101
. D.
100
.
Câu 59: Cho cấp số cộng
( )
n
u
có
2
2001u =
và
5
1995u =
. Khi đó
1001
u
bằng
A.
4005
. B.
1
. C.
3
. D.
4003
.
Câu 60: Một cấp số cộng có số hạng đầu
1
2018u
công sai
5
d
. Hỏi bắt đầu từ số hạng nào của
cấp số cộng đó thì nó nhận giá trị âm.
A.
406
u
. B.
403
u
. C.
405
u
. D.
404
u
.
Câu 61: Cho cấp số cộng
( )
n
u
có
1 56
37
2 15
46
u uu
uu
− +=−
+=
. Số hạng đầu
1
u
là
A.
1
5u = −
. B.
1
5u =
. C.
1
3u =
. D.
1
3u = −
.
Câu 62: Cho dãy số
( )
n
U
xác định bởi
1
*
1
2
5,
nn
u
u u nN
+
=
=+∈
Tính
10
u
?
A.
57
. B.
62
. C.
47
. D.
52
.
Câu 63: Cho cấp số cộng
( )
n
u
thỏa mãn
5 32
74
3 21
3 2 34
u uu
uu
+ −=−
−=−
. Tính số hạng thứ
100
của cấp số.
A.
100
243u = −
. B.
100
295u = −
. C.
100
231u = −
. D.
100
294u = −
.
Câu 64: Cho cấp số cộng
n
u
có công sai
2d =
và biểu thức
222
234
uuu++
đạt giá trị nhỏ nhất. Số 2018 là
số hạng thứ bao nhiêu của cấp số cộng
n
u
?
A.
1011
. B.
1014
. C.
1013
. D.
1012
.

CHUYÊN ĐỀ II – TOÁN – 11 – DÃY SỐ - CẤP SỐ CỘNG – CẤP SỐ NHÂN
Page 40
Sưu tầm và biên soạn
Câu 65: Cho cấp số cộng
( )
n
u
, biết
1
5u = −
,
2
d
=
. Số
81
là số hạng thứ bao nhiêu?
A.
100
. B.
50
. C.
75
. D.
44
.
Câu 66: Một cấp số cộng
(
)
n
u
có
9
47u =
, công sai
5d =
. Số
10092
là số hạng thứ mấy trong cấp số cộng
đó?
A.
2018
. B.
2017
.
C.
2016
. D.
2019
.
Câu 67: Cho hai cấp số cộng
( )
:4
n
x
,
7
,
10
,… và
( )
n
y
:
1
,
6
,
11
,…. Hỏi trong
2018
số hạng đầu tiên
của mỗi cấp số có bao nhiêu số hạng chung?
A.
404
. B.
673
. C.
403
. D.
672
.
DẠNG 3. TÍNH TỔNG VÀ MỘT SỐ BÀI TOÁN LIÊN QUAN
Câu 68: Cho cấp số cộng
( )
n
u
có
1
1u =
và công sai
2d =
. Tổng
10 1 2 3 10
.....S uu u u=++ +
bằng:
A.
10
110S =
. B.
10
100S =
. C.
10
21S
=
. D.
10
19S =
.
Câu 69: Cho dãy số
( )
n
u
là một cấp số cộng có
1
3u =
và công sai
4d =
. Biết tổng
n
số hạng đầu của
dãy số
( )
n
u
là
253
n
S =
. Tìm
n
.
A.
9
. B.
11
. C.
12
. D.
10
.
Câu 70: Cho cấp số cộng
( )
n
u
,
*
n ∈
có số hạng tổng quát
13
n
un= −
. Tổng của
10
số hạng đầu tiên
của cấp số cộng bằng.
A.
59049−
. B.
59048−
. C.
155−
. D.
310−
.
Câu 71: Cho dãy số vô hạn
{ }
n
u
là cấp số cộng có công sai
d
, số hạng đầu
1
u
. Hãy chọn khẳng định sai?
A.
19
5
2
uu
u
+
=
. B.
1nn
uu d
−
= +
,
2
n ≥
.
C.
( )
12 1
2 11
2
n
S ud= +
. D.
1
( 1).
n
uu n d=+−
,
*
n∀∈
.
Câu 72: Cho
( )
n
u
là cấp số cộng biết
3 13
80uu+=
. Tổng 15 số hạng đầu của cấp số cộng đó bằng
A.
800
. B.
600
. C.
570
. D.
630
Câu 73: Cho cấp số cộng
( )
n
u
với số hạng đầu
1
6u = −
và công sai
4.d =
Tính tổng
S
của 14 số hạng đầu
tiên của cấp số cộng đó.
A.
46S =
. B.
308S =
. C.
644S =
. D.
280S =
.
Câu 74: Cho cấp số cộng
(
)
n
u
có
25
8, 17uu= =
. Công sai
d
bằng:
A.
3d = −
. B.
5d = −
. C.
3d =
. D.
5d =
.
Câu 75: Cho dãy
( )
n
u
là một cấp số cộng với số hạng đầu
2
và số hạng thứ
36
là
72
. Công sai của
cấp số cộng
( )
n
u
là
A.
3d =
B.
2d = −
. C.
2d =
. D.
1
2
d =
.

CHUYÊN ĐỀ II – TOÁN – 11 – DÃY SỐ - CẤP SỐ CỘNG – CẤP SỐ NHÂN
Page 41
Sưu tầm và biên soạn
Câu 76: Cho cấp số cộng
( )
n
u
và gọi
n
S
là tổng
n
số hạng đầu tiên của nó. Biết
21
19
u
= −
và
22
0S =
.
Tìm số hạng tổng quát
n
u
của cấp số cộng đó.
A.
21 2
n
un= +
. B.
21 2
n
un
= −
. C.
23 2
n
un= −
. D.
23 2
n
un= +
.
Câu 77: Cho cấp số cộng
( )
n
u
có
18
5; 30uu=−=
. Công sai của cấp số cộng bằng:
A.
4
. B.
5
. C.
6
. D.
3
Câu 78: Cho cấp số cộng
( )
n
u
với
1
10u =
,
2
13
u =
. Giá trị của
4
u
là
A.
4
20u =
. B.
4
19u
=
. C.
4
16u =
. D.
4
18u =
.
Câu 79: Cho cấp số cộng
(
)
n
u
biết
24
1, 7uu=−=
. Tìm
3
.u
A.
4.
B.
10
. C.
8
. D.
3
.
Câu 80: Cho cấp số cộng
( )
n
u
, biết
1
2u
=
và
4
8u =
. Giá trị của
5
u
bằng
A.
12
. B.
10
. C.
9
. D.
11
.
Câu 81: Cho cấp số cộng
( )
n
u
có
5
15u = −
;
20
60u =
. Tổng
20
số hạng đầu tiên của cấp số cộng là
A.
20
250S =
. B.
20
200S =
. C.
20
200S = −
. D.
20
25S = −
.
Câu 82: Cho cấp số cộng
( )
n
u
biết
38
6, 16.
uu= =
Tính công sai
d
và tổng của
10
số hạng đầu tiên.
A.
10
2; 100dS= =
. B.
10
1; 80dS= =
. C.
10
2; 120dS= =
. D.
10
2; 110
dS= =
.
Câu 83: Cho cấp số cộng
( )
n
u
với
32
n
un= −
thì
60
S
bằng
A.
6960
−
. B.
117−
. C.
3840−
. D.
116−
.
Câu 84: Cho cấp số cộng
( )
n
u
có
2013 6
1000uu+=
. Tổng 2018 số hạng đầu tiên của cấp số cộng đó là:
A.
1009000
. B.
100800
. C.
1008000
. D.
100900
.
Câu 85: Cho cấp số cộng
(u )
n
thỏa mãn
14
32
8
2
uu
uu
+=
−=
. Tính tổng
10
số hạng đầu của cấp số cộng trên.
A.
100
. B.
110
. C.
10
. D.
90
.
Câu 86: Cho cấp số cộng
{
}
n
u
có
4
12u = −
;
14
18u =
. Tổng của 16 số hạng đầu tiên của cấp số cộng là:
A.
24S =
. B.
25S = −
. C.
24S = −
. D.
26S =
.
Câu 87: Cho cấp số cộng
( )
n
u
thỏa
235
46
10
26
uuu
uu
−+=
+=
. Tính
1 4 7 2011
...Su u u u= + + ++
A.
2023736S =
. B.
2023563S =
. C.
6730444S =
. D.
6734134S =
.
Câu 88: Cho một cấp số cộng
(
)
n
u
có
1
5u =
và tổng của
50
số hạng đầu bằng
5150
. Tìm công thức của
số hạng tổng quát
n
u
.
A.
14
n
un= +
. B.
5
n
un=
. C.
32
n
un= +
. D.
23
n
un= +
.

CHUYÊN ĐỀ II – TOÁN – 11 – DÃY SỐ - CẤP SỐ CỘNG – CẤP SỐ NHÂN
Page 42
Sưu tầm và biên soạn
Câu 89: Một cấp số cộng có tổng của n số hạng đầu
n
S
tính theo công thức
2*
5 3,
n
S n nn
.
Tìm số hạng đầu
1
u
và công sai d của cấp số cộng đó.
A.
1
8; 10ud
. B.
1
8; 10
ud
. C.
1
8; 10ud
. D.
1
8; 10ud
.
Câu 90: Cho cấp số cộng
( )
n
u
biết
5
18u =
và
2
4
nn
SS=
. Giá trị
1
u
và
d
là
A.
1
2u =
,
3
d
=
. B.
1
3u =
,
2d =
. C.
1
2u =
,
2d =
. D.
1
2u =
,
4
d
=
.
Câu 91: Gọi
n
S
là tổng
n
số hạng đầu tiên trong cấp số cộng
(
)
.
n
a
Biết
69
,SS
=
tỉ số
3
5
a
a
bằng:
A.
9
5
. B.
5
9
. C.
5
3
. D.
3
5
.
Câu 92: Cho cấp số cộng
( )
n
u
và gọi
n
S
là tổng
n
số hạng đầu tiên của nó. Biết
7
77
S
=
và
12
192S
=
.
Tìm số hạng tổng quát
n
u
của cấp số cộng đó
A.
54
n
un= +
. B.
32
n
un= +
. C.
23
n
un= +
. D.
45
n
un= +
.
Câu 93: Giải phương trình
1 8 15 22 7944x
+ + + +…+ =
A.
330x =
. B.
220
x =
. C.
351x =
. D.
407
x =
.
Câu 94: Cho cấp số cộng
(
)
n
u
có số hạng đầu bằng
1
và tổng
100
số hạng đầu bằng
14950
. Giá trị của
tổng
1 2 2 3 49 50
11 1
...
uu u u u u
+ ++
bằng.
A.
49
74
. B.
148
. C.
49
148
. D.
74
.
Câu 95: Cho một cấp số cộng
(
)
n
u
có
1
1u =
và tổng
100
số hạng đầu bằng
10000
. Tính tổng
1 2 2 3 99 100
11 1
...S
uu u u u u
= + ++
.
A.
100
201
=S
. B.
200
201
=S
. C.
198
199
=S
. D.
99
199
=
S
.
Câu 96: Cho tam giác đều
111
ABC
có độ dài cạnh bằng
4
. Trung điểm của các cạnh tam giác
111
ABC
tạo
thành tam giác
222
ABC
, trung điểm của các cạnh tam giác
222
ABC
tạo thành tam giác
333
ABC
…
Gọi
123
, , ,...PP P
lần lượt là chu vi của tam giác
111
ABC
,
222
ABC
,
333
ABC
,…Tính tổng chu vi
123
...PPPP=+++
A.
8P =
. B.
24P =
. C.
6P =
. D.
18P
=
.
Câu 97: Lan đang tiết kiệm để mua laptop. Trong tuần đầu tiên, cô ta để dành
200
đô la, và trong mỗi
tuần tiếp theo, cô ta đã thêm
16
đô la vào tài khoản tiết kiệm của mình. Chiếc laptop Lan cần
mua có giá
1000
đô la. Hỏi vào tuần thứ bao nhiêu thì cô ấy có đủ tiền để mua chiếc laptop đó?
A.
49
. B.
50
. C.
51
. D.
52
.
Câu 98: Một người làm việc cho một công ty. Theo hợp đồng trong năm đầu tiên, tháng lương thứ nhất
là 6 triệu đồng và lương tháng sau cao hơn tháng trước là 200 ngàn đồng. Hỏi theo hợp đồng,
tháng thứ 7 người đó nhận được lương là bao nhiêu?
A. 7,0 triệu. B. 7,3 triệu. C. 7,2 triệu. D. 7,4 triệu.

CHUYÊN ĐỀ II – TOÁN – 11 – DÃY SỐ - CẤP SỐ CỘNG – CẤP SỐ NHÂN
Page 43
Sưu tầm và biên soạn
Câu 99: Trong tháng 12, lớp 12A dự kiến quyên góp tiền để đi làm từ thiện như sau: Ngày đầu quyên góp
được mỗi bạn bỏ 2000 đồng vào lợn, từ ngày thứ hai trở đi mỗi bạn bỏ vào lợn hơn ngày liền
trước là 500 đồng. Hỏi sau 28 ngày lớp 11A quyên góp được bao nhiêu tiền? Biết lớp có 40 bạn.
A.
8800000
đồng. B.
9800000
đồng. C.
10800000
đồng. D.
7800000
đồng
Câu 100: Trong sân vận động có tất cả 30 dãy ghế, dãy đầu tiên có 15 ghế. Các dãy sau, mỗi dãy nhiều
hơn dãy ngay trước nó 4 ghế. Hỏi sân vận động có tất cả bao nhiêu ghế?
A.
1740
. B.
2250
. C.
4380
. D.
2190
.
Câu 101: Hùng đang tiết kiệm để mua một cây đàn piano có giá 142 triệu đồng. Trong tháng đầu tiên, anh
ta để dành được 20 triệu đồng. Mỗi tháng tiếp theo anh ta để dành được 3 triệu đồng và đưa số
tiền tiết kiệm của mình. Hỏi ít nhất vào tháng thứ bao nhiêu thì Hùng mới có đủ tiền để mua cây
đàn piano đó?
A.
43
. B.
41
. C.
40
. D.
42
.
Câu 102: Người ta trồng
820
cây theo một hình tam giác như sau: Hàng thứ nhất trồng 1 cây, kể từ hàng
thứ hai trở đi số cây trồng mỗi hàng nhiều hơn
1
cây so với hàng liền trước nó. Hỏi có tất cả bao
nhiêu hàng cây?
A.
42
. B.
41
. C.
40
. D.
39
.
Câu 103: Một cầu thang đường lên cổng trời của một điểm giải trí ở công viên tỉnh X được hàn bằng sắt
có hình dáng các bậc thang đều là hình chữ nhật với cùng chiều rộng là 35cm và chiều dài của
nó theo thứ tự mỗi bậc đều giảm dần đi 7cm. Biết rằng bậc đầu tiên của cầu thang là hình chữ
nhật có chiều dài 189cm và bậc cuối cùng cầu thang là hình chữ nhật có chiều dài 63cm. Hỏi giá
thành làm cầu thang đó gần với số nào dưới đây nếu giá thành làm một mét vuông cầu thang đó
là
1250000
đồng trên một mét vuông?
A.
9500000
đồng. B.
11000000
đồng. C.
10000000
đồng. D.
10500000
đồng.
Câu 104: Công ty A muốn thuê hai mảnh đất để làm 2 nhà kho, một mảnh trong vòng10 năm và 1 mảnh
trong vòng 15 năm ở hai chỗ khác nhau. Công ty bất động sản C, công ty bất động sản B đều
muốn cho thuê. Hai công ty đưa ra phương án cho thuê như sau
Công ty C: Năm đầu tiên tiền thuê đất là 60 triệu và kể từ năm thứ hai trở đi mỗi năm tăng
thêm 3 triệu đồng.
Công ty B: Trả tiền theo quí, quý đầu tiên là 8 triệu đồng và từ quý thứ hai trở đi mỗi quý tăng
thêm 500000 đồng.
Hỏi công ty A nên lựa chọn thuê đất của công ty bất động sản nào để chi phí là thấp nhất biết
rằng các mảnh đất cho thuê về diện tích, độ tiện lợi đều như nhau?
A. Chọn công ty B để thuê cả hai mảnh đất.
B. Chọn công ty C để thuê cả hai mảnh đất.
C. Chọn công ty C để thuê đất 10 năm, công ty B thuê đất 15 năm.
D. Chọn công ty B để thuê đất 10 năm, công ty C thuê đất 15 năm.
Câu 105: Hùng đang tiết kiệm để mua một cây guitar. Trong tuần đầu tiên, anh ta để dành 42 đô la, và
trong mỗi tuần tiếp theo, anh ta đã thêm 8 đô la vào tài khoản tiết kiệm của mình. Cây guitar
Hùng cần mua có giá 400 đô la. Hỏi vào tuần thứ bao nhiêu thì anh ấy có đủ tiền để mua cây
guitar đó?
A.
47
. B.
45
. C.
44
. D.
46
.

CHUYÊN ĐỀ II – TOÁN – 11 – DÃY SỐ - CẤP SỐ CỘNG – CẤP SỐ NHÂN
Page 44
Sưu tầm và biên soạn
Câu 106: Một công ti trách nhiệm hữu hạn thực hiện việc trả lương cho các kĩ sư theo phương thức sau:
Mức lương của quý làm việc đầu tiên cho công ti là
4,5
triệu đồng/quý, và kể từ quý làm việc
thứ hai, mức lương sẽ được tăng thêm
0,3
triệu đồng mỗi quý. Hãy tính tổng số tiền lương một
kĩ sư nhận được sau
3
năm làm việc cho công ti.
A.
83, 7
. B.
78,3
. C.
73,8
. D.
87,3
.
Câu 107: Người ta trồng
465
cây trong một khu vườn hình tam giác như sau: Hàng thứ nhất có
1
cây,
hàng thứ hai có
2
cây, hàng thứ ba có
3
cây….Số hàng cây trong khu vườn là
A.
31
. B.
30
. C.
29
. D.
28
.
Câu 108: Trong sân vận động có tất cả
30
dãy ghế, dãy đầu tiên có
15
ghế, các dãy liền sau nhiều hơn dãy
trước
4
ghế, hỏi sân vận động đó có tất cả bao nhiêu ghế?
A.
2250
. B.
1740
. C.
4380
. D.
2190
.
Câu 109: Cho
4
số thực
,,,abcd
là
4
số hạng liên tiếp của một cấp số cộng. Biết tổng của chúng bằng 4
và tổng các bình phương của chúng bằng
24
. Tính
333 3
Pabcd=+++
.
A.
64
P
=
. B.
80P =
. C.
16P =
. D.
79P =
.
Câu 110: Cho cấp số cộng
( )
n
u
có
1
4u =
. Tìm giá trị nhỏ nhất của
12 23 31
uu u u uu++
?
A.
20
. B.
6
. C.
8
. D.
24
.
Câu 111: Một tam giác vuông có chu vi bằng
3
và độ dài các cạnh lập thành một cấp số cộng. Độ dài các
cạnh của tam giác đó là:
A.
15
;1;
33
. B.
17
;1;
44
. C.
35
;1;
44
. D.
13
;1;
22
.
Câu 112: Trong hội chợ, một công ty sơn muốn xếp
1089
hộp sơn theo số lượng
1,3,5,...
từ trên xuống
dưới. Hàng cuối cùng có bao nhiêu hộp sơn?
A.
63
. B.
65
. C.
67
. D.
69
.
Câu 113: Người ta trồng
1275
cây theo hình tam giác như sau: Hàng thứ nhất có
1
cây, hàng thứ
2
có
2
cây, hàng thứ
3
có
3
cây,.hàng thứ
k
có
k
cây
( )
1.k ≥
Hỏi có bao nhiêu hàng ?
A.
51
. B.
52
. C.
53
. D.
50
.
Câu 114: Người ta trồng
3003
cây theo hình tam giác như sau: Hàng thứ nhất trồng
1
cây, hàng thứ hai
trồng
2
cây, hàng thứ ba trồng
3
cây,….Hỏi có bao nhiêu hàng cây.
A.
78
. B.
243
. C.
77
. D.
244
.

CHUYÊN ĐỀ II – TOÁN – 11 – DÃY SỐ - CẤP SỐ CỘNG – CẤP SỐ NHÂN
Page 45
Sưu tầm và biên soạn
Câu 115: Bà chủ quán trà sữa
X
muốn trang trí quán cho đẹp nên quyết định thuê nhân công xây một bức
tường bằng gạch với xi măng, biết hàng dưới cùng có
500
viên, mỗi hàng tiếp theo đều có ít hơn
hàng trước 1 viên và hàng trên cùng có 1 viên. Hỏi số gạch cần dùng để hoàn thành bức tường
trên là bao nhiêu viên?
A.
25250.
B.
250500.
C.
12550.
D.
125250.
Câu 116: Người ta trồng
3240
cây theo một hình tam giác như sau: hàng thứ nhất trồng 1 cây, kể từ hàng
thứ hai trở đi số cây trồng mỗi hàng nhiều hơn
1
cây so với hàng liền trước nó. Hỏi có tất cả bao
nhiêu hàng cây?
A.
81
. B.
82
. C.
80
. D.
79
.
Câu 117: Cho hai cấp số cộng hữu hạn, mỗi cấp số cộng có 100 số hạng là
4, 7, 10, 13, 16,...
và
1, 6, 11, 16, 21,...
. Hỏi có tất cả bao nhiêu số có mặt trong cả hai cấp số cộng trên?
A.
20
. B.
18
. C. 21. D. 19.
Câu 118: Sinh nhật bạn của An vào ngày
01
tháng năm. An muốn mua một món quà sinh nhật cho bạn
nên quyết định bỏ ống heo
100
đồng vào ngày
01
tháng
01
năm
2016
, sau đó cứ liên tục ngày
sau hơn ngày trước
100
đồng. Hỏi đến ngày sinh nhật của bạn, An đã tích lũy được bao nhiêu
tiền?.
A.
738.100
đồng. B.
726.000
đồng. C.
714.000
đồng. D.
750.300
đồng.
Câu 119: Gọi
S
là tập hợp tất cả các số tự nhiên
k
sao cho
14
k
C
,
1
14
k
C
+
,
2
14
k
C
+
theo thứ tự đó lập thành một
cấp số cộng. Tính tổng tất cả các phần tử của
S
.
A.
12
. B.
8
. C.
10
. D.
6
.
Câu 120: Cho
22
1
;;
2
xy
theo thứ tự lập thành một cấp số cộng. Gọi
,Mm
lần lượt là giá trị lớn nhất và giá
trị nhỏ nhất của biểu thức
2
3P xy y
= +
. Tính
SMm
= +
A.
1
. B.
2
. C.
3
. D.
31
22
−
.
Câu 121: Cho dãy số
( )
n
u
thỏa mãn
1
2018
u =
và
1
2
1
n
n
n
u
u
u
+
=
+
với mọi
1n ≥
. Giá trị nhỏ nhất của
n
để
1
2018
n
u <
bằng
A.
4072325
B.
4072324
C.
4072326
D.
4072327
Câu 122: Cho cấp số cộng
( )
n
u
có
1
3u =
và công sai
2d =
, và cấp số cộng
( )
n
v
có
1
2v =
và công sai
3d
′
=
. Gọi
,XY
là tập hợp chứa
1000
số hạng đầu tiên của mỗi cấp số cộng. Chọn ngẫu nhiên
2
phần tử bất kỳ trong tập hợp
XY∪
. Xác suất để chọn được
2
phần tử bằng nhau gần với số
nào nhất trong các số dưới đây?
A.
4
0,83.10
−
. B.
4
1,52.10
−
. C.
4
1,66.10
−
. D.
4
0,75.10
−
.

CHUYÊN ĐỀ II – TOÁN – 11 – DÃY SỐ - CẤP SỐ CỘNG – CẤP SỐ NHÂN
Page 46
Sưu tầm và biên soạn
Câu 123: Nếu
2a +
,
b
,
2c
theo thứ tự lập thành cấp số cộng thì dãy số nào sau đây lập thành cấp số cộng?
A.
4
b
−
;
24a−−
;
4
c
. B.
22
a
−−
;
2b
−
;
42c−−
.
C.
2 b+
;
2a
;
22c +
. D.
24a +
;
4b
;
4c
.
Câu 124: Cho một cấp số cộng
n
u
có
1
5u
và tổng của
40
số hạng đầu là
3320
. Tìm công sai của cấp
số cộng đó.
A.
4
−
. B.
8
. C.
8−
. D.
4
.
CHUYÊN ĐỀ II – TOÁN – 11 – DÃY SỐ - CẤP SỐ CỘNG – CẤP SỐ NHÂN
Page 1
Sưu tầm và biên soạn
BÀI 6: CẤP SỐ CỘNG
DẠNG 1. NHẬN DIỆN CẤP SỐ CỘNG
Câu 1: Trong các dãy số sau, dãy số nào là một cấp số cộng?
A.
1;2;4;6;8−−−−
. B.
1;3;6;9;12.−−−−
C.
1;3;7;11;15.−−− −
D.
1;3;5;7;9−−−−
.
Lời giải
Dãy số
( )
n
u
có tính chất
1nn
u ud
+
= +
thì được gọi là một cấp số cộng.
Ta thấy dãy số:
1;3;7;11;15−−− −
là một cấp số cộng có số hạng đầu là 1 và công sai bằng
4.−
Câu 2: Trong các dãy số sau, dãy số nào không phải cấp số cộng?
A.
13579
;;;;
22222
. B.
1;1;1;1;1
. C.
8; 6; 4; 2; 0
−−−−
. D.
3;1;1;2;4−−−
.
Lời giải
Cấp số cộng là một dãy số mà trong đó kể từ số hạng thứ hai, mỗi số hạng đều bằng tổng của số
hạng đứng ngay trước nó và một số d không đổi.
Đáp án A: Là cấp số cộng với
1
1
;1
2
ud= =
.
Đáp án B: Là cấp số cộng với
1
1; 0ud= =
.
Đáp án C: Là cấp số cộng với
1
8; 2ud=−=
.
Đáp án D: Không là cấp số cộng vì
( ) ( )
21 43
2; 1uu uu= +− = +−
.
Câu 3: Cho cấp số cộng
( )
n
u
với
52
n
un= −
. Tìm công sai của cấp số cộng
A.
3d
=
. B.
2d = −
. C.
1d =
. D.
2d =
.
Lời giải
Ta có
( )
( )
( )
1
52 1 52 52 252 2 2.
nn
uu n n n n d
+
− = − + − − = − − −+ =−⇒ =−
Câu 4: Trong các dãy số có công thức tổng quát sau, dãy số nào là cấp số cộng?
A.
2021
n
n
u
. B.
2 2021
n
un= +
. C.
2
2021
n
u
n
=
+
. D.
2
2
n
un= −
.
Lời giải
CHƯƠNG
II
DÃY SỐ
CẤP SỐ CỘNG – CẤP SỐ NHÂN
HỆ THỐNG BÀI TẬP TRẮC NGHIỆM.
III

CHUYÊN ĐỀ II – TOÁN – 11 – DÃY SỐ - CẤP SỐ CỘNG – CẤP SỐ NHÂN
Page 2
Sưu tầm và biên soạn
Với
2 2021
n
un
= +
thì
1
2( 1) 2021 2
nn
un u
+
= ++ = +
, như vậy dãy số này là một cấp số cộng.
Câu 5: Trong các dãy số sau, dãy nào là một cấp số cộng?
A.
1;3;6;9;12
−−−−
. B.
1;3;7;11;15−−− −
. C.
1;3;5;7;9
−−−−
. D.
1;2;4;6;8
−−−−
.
Lời giải
Ta có dãy số
1;3;7;11;15
−−− −
là một cấp số cộng có công sai
4d = −
.
Câu 6: Trong các dãy số sau đây, dãy số nào là cấp số cộng?
A.
3
n
n
u
=
. B.
( )
1
3
n
n
u
+
= −
. C.
31
n
un= +
. D.
1
2
+
=
n
n
u
.
Lời giải
Ta có:
Xét đáp án A:
( )
1*
1
3 3 2.3
nn n
nn
uu n
+
+
− = − = ∀ ∈Ν
nên
3
n
n
u =
không phải là cấp số cộng.
Xét đáp án B:
( ) ( ) ( )
( )
1
*
1
3 3 4. 3
nn n
nn
uu n
+
+
− = − − − =− − ∀ ∈Ν
nên
( )
1
3
n
n
u
+
= −
không phải là
cấp số cộng.
Xét đáp án C:
( ) (
)
( )
*
1
3 11 3 1 3
nn
uu n n n
+
− = + + − + = ∀ ∈Ν
không đổi, nên
31
n
un= +
là
cấp số cộng.
Xét đáp án D:
( )
21 1 *
1
222
+++
+
− = − = ∀ ∈Ν
nnn
nn
uu n
nên
1
2
+
=
n
n
u
không phải là cấp số cộng.
Câu 7: Trong các dãy số
( )
n
u
sau đây, dãy số nào là cấp số cộng?
A.
1
1
3
21
nn
u
uu
+
=
= +
. B.
1
1
1
2
nn
u
uu
+
= −
−=
. C.
1
3
1
1
1
nn
u
uu
+
=
= −
. D.
1
1
1
nn
u
u un
+
=
= +
.
Lời giải
Xét phương án A:
23
7, 15uu= =
vì
2132
uuuu−≠−
do đó
( )
n
u
không phải là cấp số cộng.
Xét phương án B: theo giả thiết ta có
1
2,
nn
uu n
∗
+
− = ∀∈
do đó
( )
n
u
là cấp số cộng.
Xét phương án C:
23 4 5
0, 1, 2; 9
uu u u= =−=−=−
do đó
( )
n
u
không phải là cấp số cộng.
Xét phương án C:
23
2, 4uu= =
vì
2132
uuuu−≠−
do đó
( )
n
u
không phải là cấp số cộng.
Câu 8: Dãy số nào sau đây là cấp số cộng?
A.
4;8;16;32
. B.
4;6;8;10
. C.
1;1; 1;1−−
. D.
3; 5; 7;10
.
Lời giải
Ta có
642
862
10 8 2
= +
= +
= +
Nên dãy số
4;6;8;10
là một cấp số cộng.

CHUYÊN ĐỀ II – TOÁN – 11 – DÃY SỐ - CẤP SỐ CỘNG – CẤP SỐ NHÂN
Page 3
Sưu tầm và biên soạn
Câu 9: Xác định
a
để 3 số
2
1 2 ; 2 1; 2aa a+ −−
theo thứ tự thành lập một cấp số cộng?
A. Không có giá trị nào của
a
. B.
3
4
a = ±
.
C.
3a = ±
. D.
3
2
a
= ±
.
Lời giải
Theo công thức cấp số cộng ta có:
22
33
2(2 1) (1 2) (2)
42
a a aa a− = + +− ⇔ = ⇔ =±
.
Câu 10: Trong các dãy số sau đây, dãy số nào là cấp số cộng?
A.
2
3 2017= +
n
un
.
B.
3 2018= +
n
un
.
C.
3=
n
n
u
. D.
( )
1
3
+
= −
n
n
u
.
Lời giải
Ta có
11
3( 1) 2018 (3 2018) 3 3
++
− = ++ − + =⇔ = +
nn n n
uu n n u u
.
Vậy dãy số trên là cấp số cộng có công sai
3=d
.
Câu 11: Dãy số nào sau đây là cấp số cộng?
A.
( )
1
:
nn
uu
n
=
. B.
( )
1
: 2, 2
nnn
uuu n
−
= − ∀≥
.
C.
( )
: 21
n
nn
uu= −
. D.
( )
1
: 2, 2
nn n
uu u n
−
= ∀≥
.
Lời giải
Xét dãy số
( )
1
: 2, 2
nnn
uuu n
−
= − ∀≥
Ta có
1
2, 2
nn
uu n
−
− =−∀≥
Vậy dãy số đã cho là cấp số cộng với công sai
2d = −
Câu 12: Trong các dãy số sau đây, dãy số nào là một cấp số cộng?
A.
2
1, 1
n
un n
=+≥
.
B.
2, 1
n
n
un= ≥
.
C.
1, 1
n
u nn
=+≥
.
D.
2 3, 1
n
un n=−≥
Lời giải
Theo định nghĩa cấp số cộng ta có:
11
, 1,
n n nn
u u d u u d n d const
++
= + ⇔ − = ∀≥ =
Thử các đáp án ta thấy với dãy số:
2 3, 1
n
un n=−≥
thì:
( )
1
1
23
2
2 1 32 1
n
nn
n
un
u u const
un n
+
+
= −
⇒ −==
= + −= −
Câu 13: Trong các dãy số sau, dãy nào
là cấp số cộng:
A.
1
3
n
n
u
+
=
. B.
2
1
n
u
n
=
+
. C.
2
1
n
un= +
. D.
52
3
n
n
u
−
=
.
Lời giải
Ta có dãy
n
u
là cấp số cộng khi
*
1
, n
nn
u ud
+
− = ∀∈
với
d
là hằng số.
Bằng cách tính
3
số hạng đầu của các dãy số ta dự đoán đáp án D.

CHUYÊN ĐỀ II – TOÁN – 11 – DÃY SỐ - CẤP SỐ CỘNG – CẤP SỐ NHÂN
Page 4
Sưu tầm và biên soạn
Xét hiệu
( )
*
1
5 12
5 25
,n
3 33
nn
n
n
uu
+
+−
−
− = − = ∀∈
.
Vậy dãy
52
3
n
n
u
−
=
là cấp số cộng.
DẠNG 2. TÌM CÁC YẾU TỐ CỦA CẤP SỐ CỘNG
Câu 14: Cho cấp số cộng
( )
n
u
có
1
1u =
có
1
1u =
và
2
3u =
. Giá trị của
3
u
bằng
A.
6.
B.
9.
C.
4.
D.
5.
Lời giải
Công sai
21
2duu
nên
32
5.uud
Câu 15: Cho cấp số cộng
(
)
n
u
với
1
2u =
và
2
7u =
. Công sai của cấp số cộng đã cho bằng
A.
5
. B.
2
7
. C.
5−
. D.
7
2
.
Lời giải
Ta có
2 1 21
725u u d du u= + ⇔ = − =−=
.
Câu 16: ] Cho cấp số cộng
()
n
u
với
1
11u =
và công sai
3d =
. Giá trị của
2
u
bằng
A.
8
. B.
33
. C.
11
3
. D.
14
.
Lời giải
Ta có
21
11 3 14u ud= + = +=
.
Câu 17: Cho cấp số cộng
( )
n
u
với
1
9u
=
và công sai
2d =
. Giá trị của
2
u
bằng
A.
11
. B.
9
2
. C.
18
. D.
7
.
Lời giải
Ta có:
21
9211
u ud= +=+=
.
Câu 18: Cho cấp số cộng
( )
n
u
với
1
8u =
và công sai
3d =
. Giá trị của
2
u
bằng
A.
8
3
. B.
24
. C.
5
. D.
11
.
Lời giải
Áp dụng công thức ta có:
21
8 3 11u ud= + =+=
.
Câu 19: Cho cấp số cộng
( )
n
u
với
1
2u =
và
2
6u =
. Công sai của cấp số cộng đã cho bằng
A.
4
. B.
4−
. C.
8
. D.
3
.
Lời giải
Ta có
2
6u = ⇔
1
6 ud= +
4d⇔=
.

CHUYÊN ĐỀ II – TOÁN – 11 – DÃY SỐ - CẤP SỐ CỘNG – CẤP SỐ NHÂN
Page 5
Sưu tầm và biên soạn
Câu 20: Cho cấp số cộng
(
)
n
u
với
1
1
u
=
và
2
4
u
=
. Công sai của cấp số cộng đã cho bằng
A.
4
. B.
3
−
. C.
3
. D.
5
.
Lời giải
Vì
( )
n
u
là cấp số cộng nên
2 1 21
413u u d du u= + ⇔ = − = −=
.
Câu 21: Cho cấp số cộng với
1
3
u =
và
2
9
u =
. Công sai của cấp số cộng đã cho bằng
A.
6−
. B.
3
. C.
12
. D.
6
.
Lời giải
Ta có:
21
6du u
=−=
.
Câu 22: Cho cấp số cộng
( )
n
u
với
1
2u =
và
2
8u =
. Công sai của cấp số cộng đã cho bằng
A.
10
. B.
6
. C.
4
. D.
6−
.
Lời giải
Vì
( )
n
u
là cấp số cộng nên ta có
2 1 21
826u u d du u= +⇔ = − =−=
.
Câu 23: Cho cấp số cộng
( )
n
u
với
1
2022u =
và công sai
7d =
. Giá trị của
6
u
bằng
A.
2043
. B.
2064
. C.
2050
. D.
2057
.
Lời giải
Ta có công thức tính số hạng thứ
n
của cấp số cộng
( )
1 61
1 5 2022 5.7 2057
n
uu n duu d=+− ⇒=+ = + =
Câu 24: Tìm công sai
d
của cấp số cộng
( )
n
u
,
*
n
∈
có
14
1; 13uu= =
.
A.
3d
=
. B.
1
4
d =
. C.
4d =
. D.
1
3
d =
.
Lời giải
Ta có
41
13 3 13 1 3 13 3 12 4.u ud d d d=⇔+=⇔+=⇔=⇔=
Câu 25: Cấp số cộng
( )
n
u
có số hạng đầu
1
3,u =
công sai
2d = −
thì số hạng thứ
5
là
A.
5
1u =
. B.
5
8u =
. C.
5
7u = −
. D.
5
5u = −
.
Lời giải
Ta có:
51
4 3 4.( 2) 5uu d=+ =+ −=−
.
Câu 26: Cho cấp số cộng có
3
2u =
, công sai
2d = −
. Số hạng thứ hai của cấp số cộng đó là
A.
2
4u
=
B.
2
0
u =
C.
2
4u = −
D.
2
3u =
Lời giải
Ta có
( )
32 2 2
2 2 4.u u du u= + = +− = ⇒ =
Câu 27: Cho cấp số cộng
( )
n
u
có
1
1, 2ud= =
. Tính
10
u
A.
10
20u =
.
B.
10
10.u =
C.
10
19u =
.
D.
10
15.u =
Lời giải

CHUYÊN ĐỀ II – TOÁN – 11 – DÃY SỐ - CẤP SỐ CỘNG – CẤP SỐ NHÂN
Page 6
Sưu tầm và biên soạn
Ta có:
10 1
9 1 2.9 19
uud=+=+ =
.
Câu 28: Cho cấp số cộng
( )
n
u
có
1
3
u
= −
,
6
27u =
. Tính công sai
d
.
A.
7d
=
. B.
5d =
. C.
8
d =
. D.
6d
=
.
Lời giải
Ta có
61
5 27 6uu d d=+ = ⇒=
.
Câu 29: Cho cấp số cộng
( )
n
u
có số hạng tổng quát là
32
n
un= −
. Tìm công sai
d
của cấp số cộng.
A.
3d
=
. B.
2d
=
. C.
2d = −
. D.
3d = −
.
Lời giải
Ta có
( )
1
3 1 23 23
nn
uu n n
+
− = + −− +=
Suy ra
3d =
là công sai của cấp số cộng.
Câu 30: Cho cấp số cộng
( )
n
u
với
17
33u =
và
33
65u =
thì công sai bằng
A.
1
. B.
3
. C.
2−
. D.
2
.
Lời giải
Gọi
1
u
,
d
lần lượt là số hạng đầu và công sai của cấp số cộng
( )
n
u
.
Khi đó, ta có:
17 1
16uu d= +
,
33 1
32uu d= +
Suy ra:
33 17
65 33 16 32 2uu d d− = − ⇔ = ⇔=
Vậy công sai bằng:
2
.
Câu 31: Một cấp số cộng gồm
5
số hạng. Hiệu số hạng đầu và số hạng cuối bằng
20
. Tìm công sai
d
của
cấp số cộng đã cho
A.
5d = −
. B.
4d =
. C.
4d = −
. D.
5d =
.
Lời giải
Gọi năm số hạng của cấp số cộng đã cho là:
1 2345
;;;;.uuuuu
Theo đề bài ta có:
15 1 1
20 ( 4 ) 20 5uu u u d d− = ⇔ − + = ⇔=−
Câu 32: Cho cấp số cộng
n
u
có các số hạng đầu lần lượt là
5;9;13;17;...
. Tìm số hạng tổng quát
n
u
của
cấp số cộng?
A.
41
n
un= +
. B.
51
n
un= −
. C.
51
n
un= +
. D.
41
n
un= −
.
Lời giải
( )
1
1
n
uu n d=+−
▪
( )
31
3 1 13 5 2 13 4uu d d d= + − = ⇔+ = ⇔ =
▪
( )
5 1 .4 4 1
n
un n=+− = +
Câu 33: Xác định số hàng đầu
1
u
và công sai
d
của cấp số cộng
( )
n
u
có
92
5uu=
và
13 6
25uu= +
.
A.
1
3u
=
và
4
d =
. B.
1
3u
=
và
5d =
. C.
1
4u =
và
5d =
. D.
1
4u =
và
3d =
.
Lời giải

CHUYÊN ĐỀ II – TOÁN – 11 – DÃY SỐ - CẤP SỐ CỘNG – CẤP SỐ NHÂN
Page 7
Sưu tầm và biên soạn
Ta có:
( )
1
1
n
uu n d=+−
. Theo đầu bài ta có hpt:
( )
(
)
11
11
85
12 2 5 5
u d ud
u d ud
+= +
+= ++
1
1
1
430
3
25
4
ud
u
ud
d
−=
=
⇔⇔
−=−
=
.
Câu 34: Cho
( )
n
u
là một cấp số cộng thỏa mãn
13
8uu+=
và
4
10u =
. Công sai của cấp số cộng đã cho
bằng
A.
3
. B.
6
. C.
2
. D.
4
.
Lời giải
Ta có
13
11 1
1
11
4
8
28 228
1
3 10 3 10
10
3
uu
uud ud
u
ud ud
u
d
+=
++= +=
=
⇔ ⇔⇔
+= +=
=
=
.
Vậy công sai của cấp số cộng là
3d =
.
Câu 35: Tìm công thức số hạng tổng quát của cấp số cộng
(
)
n
u
thỏa mãn:
235
16
7
12
uuu
uu
−+=
+=
A.
23
n
un= +
. B.
21
n
un= −
. C.
21
n
un= +
. D.
23
n
un= −
.
Lời giải
Chọn B
Giả sử dãy cấp số cộng
(
)
n
u
có công sai là
d
. Khi đó,
235
16
7
12
uuu
uu
−+=
+=
trở thành:
( ) ( ) ( )
( )
11 1
1
1
1
11
2 47
37
1
2 5 12
2
5 12
ududud
ud
u
ud
d
uu d
+− + + + =
+=
=
⇔⇔
+=
=
++ =
Số hạng tổng quát của cấp số cộng
( )
n
u
:
( ) ( )
1
1 1 1 .2 2 1
n
uu n d n n=+− =+− = −
Vậy
21
n
un= −
.
Câu 36: Cấp số cộng
( )
n
u
có số hạng đầu
1
3
u =
, công sai
2d = −
thì số hạng thứ 5 là
A.
5
8
u =
. B.
5
1u
=
. C.
5
5u = −
. D.
5
7u = −
.
Lời giải
Ta có:
( )
51
4 3 4. 2 5uu d=+ =+ −=−
.
Câu 37: Cho cấp số cộng có
1
3u = −
,
4d =
. Chọn khẳng định đúng trong các khẳng định sau?
A.
5
15u =
. B.
4
8u =
. C.
3
5
u =
. D.
2
2u
=
.
Lời giải
Ta có
31
2
uu d= +
3 2.4=−+
5=
.
Câu 38: Cho cấp số cộng
( )
n
u
có
1
11
u =
và công sai
4d =
. Hãy tính
99
u
.
A.
401
. B.
403
. C.
402
. D.
404
.
Lời giải

CHUYÊN ĐỀ II – TOÁN – 11 – DÃY SỐ - CẤP SỐ CỘNG – CẤP SỐ NHÂN
Page 8
Sưu tầm và biên soạn
Ta có :
99 1
98
uu d= +
11 98.4= +
403=
.
Câu 39: Cho cấp số cộng
( )
n
u
, biết:
1
3
u =
,
2
1
u = −
. Chọn đáp án đúng.
A.
3
4u =
. B.
3
7u
=
. C.
3
2u =
. D.
3
5u
= −
.
Lời giải
Ta có
( )
n
u
là cấp số cộng nên
2 13
2u uu= +
suy ra
3 21
25u uu= −=−
.
Câu 40: Một cấp số cộng
( )
n
u
có
13
8u =
và
3
d
= −
. Tìm số hạng thứ ba của cấp số cộng
( )
n
u
.
A.
50
. B.
28
. C.
38
. D.
44
Lời giải
Ta có:
13 1
12uu d= +
( )
1
8 12. 3u⇔= + −
1
44u⇒=
31
2 44 6 38uu d⇒ = + = −=
.
Câu 41: Cho cấp số cộng
(
)
n
u
có số hạng đầu
1
3u =
và công sai
2d =
. Giá trị của
7
u
bằng:
A.
15
. B.
17
. C.
19
. D.
13
.
Lời giải
Ta có
71
6. 3 6.2 15uu d=+=+=
.
Câu 42: Cho cấp số cộng
( )
n
u
có số hạng đầu
1
2u =
và công sai
4d =
. Giá trị
2019
u
bằng
A.
8074
. B.
4074
. C.
8078
. D.
4078
.
Lời giải
Áp dụng công thức của số hạng tổng quát
( )
1
1
n
uu n d=+−
2 2018.4 8074=+=
.
Câu 43: Tìm số hạng thứ
11
của cấp số cộng có số hạng đầu bằng
3
và công sai
2d = −
.
A.
21−
. B.
23
. C.
19−
. D.
17−
.
Lời giải
Áp dụng công thức số hạng tổng quát của cấp số cộng ta có
( )
11 1
10 3 10. 2 17uu d=+ =+ −=−
.
Câu 44: Cho cấp số cộng
( )
n
u
có số hạng đầu
1
2u = −
và công sai
7.d = −
Giá trị
6
u
bằng
A.
37
. B.
37−
. C.
33−
. D.
33
.
Lời giải
Ta có
61
5 2 35 37uu d= + =−− =−
.
Câu 45: Cho cấp số cộng
( )
n
u
có số hạng đầu
1
2u =
và công sai
5d =
. Giá trị
4
u
bằng
A. 22. B. 17. C. 12. D. 250.
Lời giải
Ta có:
41
3uu d= +
2 15 17=+=
.
Câu 46: Cho cấp số cộng
( )
n
u
với số hạng đầu tiên
1
2u =
và công sai
2d =
. Tìm
2018
u
?
A.
2018
2018
2u =
. B.
2017
2018
2u =
. C.
2018
4036u =
. D.
2018
4038u =
.
Lời giải
Ta có:
( ) ( )
1 2018
1 2 2018 1 .2 4036
n
uu n du=+− ⇒ =+ − =
.

CHUYÊN ĐỀ II – TOÁN – 11 – DÃY SỐ - CẤP SỐ CỘNG – CẤP SỐ NHÂN
Page 9
Sưu tầm và biên soạn
Câu 47: Cho cấp số cộng
(
)
n
u
có
1
3
u
=
và công sai
7
d
=
. Hỏi kể từ số hạng thứ mấy trở đi thì các số
hạng của
( )
n
u
đều lớn hơn
2018
?
A.
287
. B.
289
. C.
288
. D.
286
.
Lời giải
Ta có:
( )
1
1
n
uu n d
=+−
(
)
37 1
n
=+−
74n= −
;
2018
n
u
>
7 4 2018n⇔ −>
2022
7
n⇔>
.
Vậy
289n =
.
Câu 48: Viết ba số xen giữa
2
và
22
để ta được một cấp số cộng có
5
số hạng?
A.
6
,
12
,
18
. B.
8
,
13
,
18
. C.
7
,
12
,
17
. D.
6
,
10
,
14
.
Lời giải
Xem cấp số cộng cần tìm là
(
)
n
u
có:
1
5
2
22
u
u
=
=
. Suy ra:
1
2
5
u
d
=
=
.
Vậy cấp số cộng cần tìm là
( )
n
u
:
2
,
7
,
12
,
17
,
22
.
Câu 49: Cho cấp số cộng có
1
2u = −
và
4d =
. Chọn khẳng định đúng trong các khẳng định sau ?
A.
4
8u =
. B.
5
15u =
. C.
2
3u =
. D.
3
6u =
.
Lời giải
Ta có:
1
2u = −
và
4d
=
suy ra
21
242
uud
= + =−+ =
31
2 2 2.4 6uu d= + =−+ =
;
41
3 2 3.4 10uu d= + =−+ =
;
51
4 2 4.4 14uu d= + =−+ =
Nên đáp án D đúng.
Câu 50: Cho cấp số cộng
(
)
n
u
với
1
2u =
;
9d =
. Khi đó số
2018
là số hạng thứ mấy trong dãy?
A.
226
. B.
225
. C.
223
. D.
224
.
Lời giải
( )
1
1
n
uu n d
=+−
( )
2018 2 1 .9n⇔ =+−
225n⇔=
.
Câu 51: Cho cấp số cộng
1,4,7,...
. Số hạng thứ 100 của cấp số cộng là
A.
297
. B.
301
. C.
295
. D.
298
.
Lời giải
Cấp số cộng
1,4,7,...
. có số hạng đầu
1
1u =
và công sai
3d =
.
Số hạng thứ 100 của cấp số cộng là:
100 1
99. 1 99.3 298uu d=+=+=
.
Câu 52: Cho cấp số cộng
( )
n
u
biết
1
3u =
,
8
24u =
thì
11
u
bằng
A.
30
. B.
33
. C.
32
. D.
28
.
Lời giải
Ta có:
81
81
24 3
73
77
uu
uu d d
−
−
=+ ⇒= = =
.

CHUYÊN ĐỀ II – TOÁN – 11 – DÃY SỐ - CẤP SỐ CỘNG – CẤP SỐ NHÂN
Page 10
Sưu tầm và biên soạn
11 1
10 33uu d=+=
.
Câu 53: Cho cấp số cộng có số hạng thứ 3 và số hạng thứ 7 lần lượt là 6 và −2. Tìm số hạng thứ 5.
A.
5
2.
u =
B.
5
2.u = −
C.
5
0.u =
D.
5
4.u =
Lời giải
Theo giả thiết ta có
3
1
1
71
6
26
2
10
2 62
u
ud
d
u
u ud
Vậy
5
2u
.
Câu 54: Cho cấp số cộng
( )
n
u
, biết
2
3u =
và
4
7u =
. Giá trị của
15
u
bằng
A.
27
. B.
31
. C.
35
. D.
29
.
Lời giải
Từ giả thiết
2
3u =
và
4
7u
=
suy ra ta có hệ phương trình:
1
1
3
37
ud
ud
+=
+=
1
1
2
u
d
=
⇒
=
.
Vậy
15 1
14 29uu d=+=
.
Câu 55: Cho cấp số cộng
(
)
n
u
có
1
123
u =
và
3 15
84
uu−=
. Số 11 là số hạng thứ bao nhiêu của cấp số
cộng đã cho?
A. 17. B. 16. C. 18. D. 19.
Lời giải
Ta có:
(
)
3 15 1 1
84 2 14 84 7
uu u du d d− = ⇔+ − + = ⇔=−
.
Số hạng tổng quát:
7 130
n
un=−+
.
Ta có:
11 17
n
un= ⇔=
.
Câu 56: Cho cấp số cộng
()
n
u
biết
1
1;
u = −
2;d =
43
n
u =
. Hỏi cấp số cộng đó có bao nhiêu số hạng?
A. 20. B. 23. C. 22. D. 21.
Lời giải
1
( 1)
n
uu n d=+−
43 1 ( 1).2n⇔ =−+ −
23n⇔=
.
Câu 57: Cho cấp số cộng
( )
n
u
có số hạng đầu là
2
1u =
,
5
19
u =
. Số
103
là số hạng thứ mấy trong cấp
số cộng đã cho?
A.
19
. B.
18
. C.
20
. D.
17
.
Lời giải
Ta có
2
1
1
5
1
1
1
5
19
4 19
6
u
ud
u
u
ud
d
=
+=
= −
⇔⇔
=
+=
=
.
Lại có
( ) ( )
1
1 103 5 1 6 19
n
uu n d n n=+− ⇔ =−+−⋅⇔=
.
Vậy số
103
là số hạng thứ 19 trong cấp số cộng đã cho.

CHUYÊN ĐỀ II – TOÁN – 11 – DÃY SỐ - CẤP SỐ CỘNG – CẤP SỐ NHÂN
Page 11
Sưu tầm và biên soạn
Câu 58: Cho cấp số cộng
( )
n
u
có
1
5=u
và công sai
3
= −
d
. Biết rằng
289−
là một số hạng của cấp số
cộng trên. Hỏi đó là số hạng thứ bao nhiêu?
A.
98
. B.
99
. C.
101
. D.
100
.
Lời giải
Số hạng tổng quát của cấp số cộng có
1
5=u
và công sai
3= −d
là
(
)
53 1
=−−
n
un
,
∗
∀∈
n
.
Ta có
( )
289 5 3 1−=−−n
( )
294 3 1⇔− =− −n
98 1⇔=−n
99⇔=n
.
Vậy
289
−
là số hạng thứ
99
của cấp số cộng trên.
Câu 59: Cho cấp số cộng
( )
n
u
có
2
2001
u
=
và
5
1995u
=
. Khi đó
1001
u
bằng
A.
4005
. B.
1
. C.
3
. D.
4003
.
Lời giải
Gọi
1
u
và
d
lần lượt là số hạng đầu tiên và công sai của cấp số công.
Ta có:
2
1
1
5
1
2001
2001
2003
1995
4 1995
2
u
ud
u
u
ud
d
=
+=
=
⇔⇔
=
+=
= −
.
Vậy
1001 1
1000 3uu d=+=
.
Câu 60: Một cấp số cộng có số hạng đầu
1
2018u
công sai
5d
. Hỏi bắt đầu từ số hạng nào của
cấp số cộng đó thì nó nhận giá trị âm.
A.
406
u
. B.
403
u
. C.
405
u
. D.
404
u
.
Lời giải
Ta có
( ) ( )
1
1 2018 5 1
n
uu n d n=+− = − −
Có
( )
2023
0 2018 5 1 0 5 2023
5
n
u n nn<⇔ − −<⇔ > ⇔>
,
405nn∈⇒≥
.
Vậy từ
405
u
thì số hạng của cấp số cộng đó nhận giá trị âm.
Câu 61: Cho cấp số cộng
( )
n
u
có
1 56
37
2 15
46
u uu
uu
− +=−
+=
. Số hạng đầu
1
u
là
A.
1
5u = −
. B.
1
5u
=
. C.
1
3u =
. D.
1
3u = −
.
Lời giải
Gọi
d
là công sai của CSC. Ta có
( )
1
1
n
uu n d=+−
.
( ) (
)
( ) ( )
11 1
1 56
1
1
37
11
2 4 5 15
2 15
5
3
2 8 46
46
2 6 46
u udud
u uu
d
u
ud
uu
udud
− + ++ =−
− +=−
=
⇔ ⇔ ⇒=
+=
+=
+ ++ =
.
Câu 62: Cho dãy số
( )
n
U
xác định bởi
1
*
1
2
5,
nn
u
u u nN
+
=
=+∈
Tính
10
u
?
A.
57
. B.
62
. C.
47
. D.
52
.

CHUYÊN ĐỀ II – TOÁN – 11 – DÃY SỐ - CẤP SỐ CỘNG – CẤP SỐ NHÂN
Page 12
Sưu tầm và biên soạn
Lời giải:
Cách 1: Dùng casio 570VN
B1 : Nhập vào máy tính “2”=>SHIFT=>STO=>A
B2: Nhập
5:BA AB=+=
B3: Ấn CALC rồi bấm liên tiếp dấu “=” cho kết quả
10
47u =
.
Cách 2: Từ
1
*
1
2
5,
nn
u
u u nN
+
=
=+∈
.
Ta có
1
5
nn
uu
+
−=
nên dãy
( )
n
U
là một cấp số cộng với công sai
5d =
nên
10 1
9 2 45 47uud=+=+=
.
Câu 63: Cho cấp số cộng
( )
n
u
thỏa mãn
5 32
74
3 21
3 2 34
u uu
uu
+ −=−
−=−
. Tính số hạng thứ
100
của cấp số.
A.
100
243u = −
. B.
100
295u = −
. C.
100
231u = −
. D.
100
294u
= −
.
Lời giải
5 32
74
3 21
3 2 34
u uu
uu
+ −=−
−=−
(
)
( )
( )
1 11
11
4 3 2 21
3 6 2 3 34
ud udud
ud ud
+ + + −−=−
⇔
+− +=−
1
1
37
12 34
ud
ud
+=−
⇔
+=−
1
2
3
u
d
=
⇔
= −
.
Số hạng thứ
100
là
( )
100
2 99 3 295u =+ −=−
.
Câu 64: Cho cấp số cộng
n
u
có công sai
2d
=
và biểu thức
222
234
uuu++
đạt giá trị nhỏ nhất. Số 2018 là
số hạng thứ bao nhiêu của cấp số cộng
n
u
?
A.
1011
. B.
1014
. C.
1013
. D.
1012
.
Lời giải
Ta có:
( ) ( ) ( ) ( )
21
222 2
222 2
31234111 11 1
41
2
4 2 4 6 3 24 56 3 4 8 8
6
uu
uu uuu u u u u u u
uu
= +
=+⇒++=+++++= + += ++≥
= +
Vậy
222
234
uuu++
đạt giá trị nhỏ nhất khi
1
4u = −
.
Từ đó suy ra
( ) ( )
1
2018 1 2018 4 1 2 1012.un d n n=+− ⇔ =−+− ⇔=
Câu 65: Cho cấp số cộng
( )
n
u
, biết
1
5
u = −
,
2d =
. Số
81
là số hạng thứ bao nhiêu?
A.
100
. B.
50
. C.
75
. D.
44
.
Lời giải
Ta có
( )
1
1
n
uu n d=+−
( )
81 5 1 2n⇔ =−+ −
44n⇔=
.
Vậy
81
là số hạng thứ
44
.

CHUYÊN ĐỀ II – TOÁN – 11 – DÃY SỐ - CẤP SỐ CỘNG – CẤP SỐ NHÂN
Page 13
Sưu tầm và biên soạn
Câu 66: Một cấp số cộng
( )
n
u
có
9
47u =
, công sai
5d =
. Số
10092
là số hạng thứ mấy trong cấp số cộng
đó?
A.
2018
. B.
2017
.
C.
2016
. D.
2019
.
Lời giải
Ta có
91 1
87uu d u=+ ⇒=
.
Gọi
10092
là số hạng thứ
n
trong khai triển, ta có:
(
)
1
10092 7
10092 1 1 2018
5
un dn
−
= + − ⇒ = +=
.
Câu 67: Cho hai cấp số cộng
( )
:4
n
x
,
7
,
10
,… và
( )
n
y
:
1
,
6
,
11
,…. Hỏi trong
2018
số hạng đầu tiên
của mỗi cấp số có bao nhiêu số hạng chung?
A.
404
. B.
673
. C.
403
. D.
672
.
Lời giải
Số hạng tổng quát của cấp số cộng
(
)
n
x
là:
( )
4 1 .3
n
xn=+−
31n= +
.
Số hạng tổng quát của cấp số cộng
( )
n
y
là:
( )
1 1 .5
m
ym=+−
54m= −
.
Giả sử
k
là
1
số hạng chung của hai cấp số cộng trong
2018
số hạng đầu tiên của mỗi cấp số.
Vì
k
là
1
số hạng của cấp số cộng
( )
n
x
nên
31ki
= +
với
1 2018i≤≤
và
*
i ∈
.
Vì
k
là
1
số hạng của cấp số cộng
( )
n
y
nên
54kj= −
với
1 2018j≤≤
và
*
j ∈
.
Do đó
3 15 4ij+= −
355ij⇒= −
5i
⇒
{ }
5;10;15;...;2015i⇒∈
⇒
có
403
số hạng chung.
DẠNG 3. TÍNH TỔNG VÀ MỘT SỐ BÀI TOÁN LIÊN QUAN
Câu 68: Cho cấp số cộng
( )
n
u
có
1
1u =
và công sai
2d =
. Tổng
10 1 2 3 10
.....S uu u u=++ +
bằng:
A.
10
110S =
. B.
10
100S =
. C.
10
21S =
. D.
10
19S =
.
Lời giải
* Áp dụng công thức
( )
( )
1
1
21
22
n
n
nu n d
nu u
S
+−
+
= =
ta được:
( )
10
10 2 10 1 2
100
2
S
+−
= =
.
Câu 69: Cho dãy số
( )
n
u
là một cấp số cộng có
1
3u =
và công sai
4d =
. Biết tổng
n
số hạng đầu của
dãy số
( )
n
u
là
253
n
S =
. Tìm
n
.
A.
9
. B.
11
. C.
12
. D.
10
.
Lời giải

CHUYÊN ĐỀ II – TOÁN – 11 – DÃY SỐ - CẤP SỐ CỘNG – CẤP SỐ NHÂN
Page 14
Sưu tầm và biên soạn
Ta có
(
)
(
)
(
)
( )
1
2 1 2.3 1 .4
253
22
n
nu n d n n
S
+− +−
=⇔=
(
)
2
11
4 2 506 0
23
2
n
nn
nL
=
⇔ +− =⇔
= −
.
Câu 70: Cho cấp số cộng
( )
n
u
,
*
n
∈
có số hạng tổng quát
13
n
un= −
. Tổng của
10
số hạng đầu tiên
của cấp số cộng bằng.
A.
59049−
. B.
59048
−
. C.
155−
. D.
310−
.
Lời giải
Ta có:
1
2
u
= −
;
10
29u = −
;
(
)
1 10
10
10
155
2
uu
S
+
= = −
.
Câu 71: Cho dãy số vô hạn
{ }
n
u
là cấp số cộng có công sai
d
, số hạng đầu
1
u
. Hãy chọn khẳng định sai?
A.
19
5
2
uu
u
+
=
. B.
1nn
uu d
−
= +
,
2n ≥
.
C.
( )
12 1
2 11
2
n
S ud= +
. D.
1
( 1).
n
uu n d=+−
,
*
n∀∈
.
Lời giải
Ta có công thức tổng
n
số hạng đầu tiên của cấp số cộng là:
( )
1
1
2
n
nn d
S nu
−
= +
Suy ra
12 1
12.11.
12
2
d
Su= +
( )
1
6 2 11ud= +
( )
1
2 11
2
n
ud≠+
.
Câu 72: Cho
( )
n
u
là cấp số cộng biết
3 13
80uu+=
. Tổng 15 số hạng đầu của cấp số cộng đó bằng
A.
800
. B.
600
. C.
570
. D.
630
Lời giải
( ) ( ) ( )
( )
15 1 2 3 15 1 15 2 14 3 13 7 9 8
... ...S uuu u uu uu uu uu u= + + ++ = + + + + + ++ + +
Vì
1 15 2 14 3 13 7 9 8
... 2uu uu uu u u u+ =+ =+ ==+=
và
3 13
80uu+=
7.80 40 600S⇒= + =
.
Câu 73: Cho cấp số cộng
(
)
n
u
với số hạng đầu
1
6u = −
và công sai
4.d =
Tính tổng
S
của 14 số hạng đầu
tiên của cấp số cộng đó.
A.
46S =
. B.
308S =
. C.
644S =
. D.
280S =
.
Lời giải
Tổng
n
số hạng đầu tiên của một cấp số cộng là
( )
1
21
2
n
u n dn
S
+−
=
.
Vậy
( ) (
)
2 6 14 1 4 14
280
2
S
−+ −
= =
.
Câu 74: Cho cấp số cộng
( )
n
u
có
25
8, 17uu= =
. Công sai
d
bằng:
A.
3d = −
. B.
5d = −
. C.
3d =
. D.
5d =
.
Lời giải

CHUYÊN ĐỀ II – TOÁN – 11 – DÃY SỐ - CẤP SỐ CỘNG – CẤP SỐ NHÂN
Page 15
Sưu tầm và biên soạn
Theo giả thiết ta có:
1
25
1
1
8
3
8, 17
5
4 17
ud
d
uu
u
ud
+=
=
==⇒⇔
=
+=
.
Câu 75: Cho dãy
( )
n
u
là một cấp số cộng với số hạng đầu
2
và số hạng thứ
36
là
72
. Công sai của
cấp số cộng
( )
n
u
là
A.
3
d =
B.
2d
= −
. C.
2d =
. D.
1
2
d
=
.
Lời giải
Ta có
36 1
35uu d= +
mà
36 1
72, 2uu= =
nên ta có:
72 2 35 2dd=+ ⇔=
.
Vậy
2d =
.
Câu 76: Cho cấp số cộng
( )
n
u
và gọi
n
S
là tổng
n
số hạng đầu tiên của nó. Biết
21
19u = −
và
22
0S =
.
Tìm số hạng tổng quát
n
u
của cấp số cộng đó.
A.
21 2
n
un= +
. B.
21 2
n
un= −
. C.
23 2
n
un= −
. D.
23 2
n
un= +
.
Lời giải
Giả sử cấp số cộng có số hạng đầu là
1
u
và công sai
d
.
Ta có:
21 1
21 1
1
22 1
22 1
20
19 20 19
21
22.21
0 2 21 0
2
22
2
uu d
u ud
u
d
S ud
d
Su
= +
=− +=−
=
⇔ ⇔⇔
= +=
= −
= +
.
Khi đó:
( ) ( )
1
1 21 2 1 23 2
n
uu n d n n=+ − = − −= −
.
Câu 77: Cho cấp số cộng
( )
n
u
có
18
5; 30
uu=−=
. Công sai của cấp số cộng bằng:
A.
4
. B.
5
. C.
6
. D.
3
Lời giải
Gọi công sai của cấp số cộng là
d
khi đó ta có
81
7 30 5 7 5uu d d d=+⇔=−+⇔=
.
Câu 78: Cho cấp số cộng
( )
n
u
với
1
10u =
,
2
13u =
. Giá trị của
4
u
là
A.
4
20u =
. B.
4
19u =
. C.
4
16u =
. D.
4
18u =
.
Lời giải
Ta có:
12
41
10, 13 3
3 10 3.3 19
uu d
uu d B
= = ⇒=
=+=+=⇒
.
Câu 79: Cho cấp số cộng
( )
n
u
biết
24
1, 7uu=−=
. Tìm
3
.u
A.
4.
B.
10
. C.
8
. D.
3
.
Lời giải
Áp dụng tính chất của các số hạng trong dãy cấp số cộng, ta có:
24
3
17
3.
22
uu
u
+
−+
= = =

CHUYÊN ĐỀ II – TOÁN – 11 – DÃY SỐ - CẤP SỐ CỘNG – CẤP SỐ NHÂN
Page 16
Sưu tầm và biên soạn
Câu 80: Cho cấp số cộng
( )
n
u
, biết
1
2u =
và
4
8u =
. Giá trị của
5
u
bằng
A.
12
. B.
10
. C.
9
. D.
11
.
Lời giải
Từ giả thiết
1
2u =
và
41
38 2uu d d=+ =⇒=
Vậy
51
4 2 4.2 10uu d=+=+=
.
Câu 81: Cho cấp số cộng
( )
n
u
có
5
15u = −
;
20
60u =
. Tổng
20
số hạng đầu tiên của cấp số cộng là
A.
20
250S =
. B.
20
200S =
. C.
20
200S
= −
. D.
20
25S = −
.
Lời giải
Ta có
( )
5
1
1
1 20
20
20 1
15
4 15
35
20
250
60 19 60
5
2
u
ud
u
uu
S
u ud
d
= −
+=−
= −
+
⇔ ⇔ ⇒= =
= +=
=
.
Câu 82: Cho cấp số cộng
( )
n
u
biết
38
6, 16.
uu= =
Tính công sai
d
và tổng của
10
số hạng đầu tiên.
A.
10
2; 100
dS
= =
. B.
10
1; 80
dS
= =
. C.
10
2; 120dS= =
. D.
10
2; 110dS= =
.
Lời giải
3
1
1
81
6
26
2
16 7 16
2
u
ud
u
u ud
d
=
+=
=
⇔⇔
= +=
=
.
( ) ( )
10 1
10 10 1 10 10 1
10. . 10.2 .2 110
22
Su d
−−
=+=+=
.
Câu 83: Cho cấp số cộng
( )
n
u
với
32
n
un= −
thì
60
S
bằng
A.
6960−
. B.
117−
. C.
3840−
. D.
116
−
.
Lời giải
Ta có
1
12
n
un
+
= −
, Ta có
*
1
2,
nn
uu n
+
− =− ∀∈
, suy ra
( )
n
u
là cấp số cộng có
1
1u =
và công
sai
2d = −
. Vậy
( )
60 1
60
2 59 3840
2
S ud= +=−
.
Câu 84: Cho cấp số cộng
( )
n
u
có
2013 6
1000uu+=
. Tổng 2018 số hạng đầu tiên của cấp số cộng đó là:
A.
1009000
. B.
100800
. C.
1008000
. D.
100900
.
Lời giải
Gọi
d
là công sai của cấp số cộng. Khi đó:
2013 6
1000
uu+=
11
2012 5 1000u du d⇔+ ++ =
1
2 2017 1000ud⇔+ =
.
Ta có:
2018 1
2017.2018
2018
2
Su d= +
( )
1
1009. 2 2017ud= +
1009000=
.
Câu 85: Cho cấp số cộng
(u )
n
thỏa mãn
14
32
8
2
uu
uu
+=
−=
. Tính tổng
10
số hạng đầu của cấp số cộng trên.
A.
100
. B.
110
. C.
10
. D.
90
.
Lời giải

CHUYÊN ĐỀ II – TOÁN – 11 – DÃY SỐ - CẤP SỐ CỘNG – CẤP SỐ NHÂN
Page 17
Sưu tầm và biên soạn
Gọi cấp cố cộng có công sai là
d
ta có
21 31 41
; 2 ; 3u u du u du u d=+=+ =+
Khi đó
14
11
32
8
238 1
2
22
uu
ud u
uu
dd
+=
+= =
⇔⇔
−=
= =
Áp dụng công thức
1
( 1)
2
nn
S nu d
−
= +
Vậy tổng của
10
số hạng đầu của cấp số cộng là
10
10.9
10.1 .2 100
2
S =+=
Câu 86: Cho cấp số cộng
{ }
n
u
có
4
12u
= −
;
14
18
u =
. Tổng của 16 số hạng đầu tiên của cấp số cộng là:
A.
24S
=
. B.
25S = −
. C.
24S = −
. D.
26S =
.
Lời giải
Ta có:
41
1
14 1
12 3 12
21
18 13 18
3
u ud
u
u ud
d
=− +=−
= −
⇔⇔
= +=
=
.
Tổng của 16 số hạng đầu tiên của cấp số cộng là:
( )
16
16.15
16. 21 .3 24
2
S = −+ =
.
Câu 87: Cho cấp số cộng
( )
n
u
thỏa
235
46
10
26
uuu
uu
−+=
+=
. Tính
1 4 7 2011
...Su u u u= + + ++
A.
2023736S =
. B.
2023563S =
. C.
6730444
S =
. D.
6734134S
=
.
Lời giải
235
46
10
26
uuu
uu
−+=
+=
11 1
11
2 4 10
3 5 26
u du du d
u du d
+− − + + =
⇔
+ ++ =
1
1
3 10
2 8 26
ud
ud
+=
⇔
+=
1
1
3
u
d
=
⇔
=
.
4
10u =
,
7
19u
=
,
10
28u =
…
Ta có
1
u
,
4
u
,
7
u
,
10
u
, …,
2011
u
là cấp số cộng có
1
1
9
671
u
d
n
=
=
=
(
)
671
2.1 670.9 2023736
2
S
= +=
.
Câu 88: Cho một cấp số cộng
( )
n
u
có
1
5u =
và tổng của
50
số hạng đầu bằng
5150
. Tìm công thức của
số hạng tổng quát
n
u
.
A.
14
n
un= +
. B.
5
n
un=
. C.
32
n
un= +
. D.
23
n
un
= +
.
Lời giải
Ta có:
( )
50 1
50
2 49 5150
2
S ud= +=
4d⇒=
.
Số hạng tổng quát của cấp số cộng bằng
( )
1
1 14
n
uu n d n=+− =+
.

CHUYÊN ĐỀ II – TOÁN – 11 – DÃY SỐ - CẤP SỐ CỘNG – CẤP SỐ NHÂN
Page 18
Sưu tầm và biên soạn
Câu 89: Một cấp số cộng có tổng của n số hạng đầu
n
S
tính theo công thức
2*
5 3,
n
S n nn
.
Tìm số hạng đầu
1
u
và công sai d của cấp số cộng đó.
A.
1
8; 10ud
. B.
1
8; 10
ud
. C.
1
8; 10ud
. D.
1
8; 10ud
.
Lời giải
Ta có:
11
8= =uS
.
2 21 21
18 18 8 10= − = ⇒ = − = −=u S S du u
.
Câu 90: Cho cấp số cộng
( )
n
u
biết
5
18u =
và
2
4
nn
SS=
. Giá trị
1
u
và
d
là
A.
1
2u
=
,
3d
=
. B.
1
3u =
,
2
d
=
. C.
1
2u =
,
2
d
=
. D.
1
2u
=
,
4d =
.
Lời giải
Ta có
5
18u =
⇔
1
4 18
ud+=
.
Lại có
5 10
4SS=
⇔
11
5.4 10.9
4 5 10
22
u du d
+=+
⇔
1
20ud−=
.
Khi đó ta có hệ phương trình
1
1
4 18
20
ud
ud
+=
−=
⇔
1
2
4
u
d
=
=
.
Câu 91: Gọi
n
S
là tổng
n
số hạng đầu tiên trong cấp số cộng
( )
.
n
a
Biết
69
,SS=
tỉ số
3
5
a
a
bằng:
A.
9
5
. B.
5
9
. C.
5
3
. D.
3
5
.
Lời giải
Ta có
( ) (
)
11
69 1
62 5 92 8
7.
22
ad ad
SS a d
++
=⇔ = ⇔=−
3
1
51
2
72 5
.
4 74 3
a
ad
dd
aa d dd
+
−+
= = =
+ −+
Câu 92: Cho cấp số cộng
( )
n
u
và gọi
n
S
là tổng
n
số hạng đầu tiên của nó. Biết
7
77S
=
và
12
192S =
.
Tìm số hạng tổng quát
n
u
của cấp số cộng đó
A.
54
n
un
= +
. B.
32
n
un
= +
. C.
23
n
un= +
. D.
45
n
un= +
.
Lời giải
Giả sử cấp số cộng có số hạng đầu là
1
u
và công sai
d
.
Ta có:
1
7
1
1
1
12
1
7.6.
7 77
77
7 21 77
5
2
12.11. 12 66 192
192
2
12 192
2
d
u
S
ud
u
d ud
S
d
u
+=
=
+=
=
⇔ ⇔⇔
+=
=
=
+=
.
Khi đó:
( ) ( )
1
1 52 1 32
n
uu n d n n=+ − =+ −=+
.
Câu 93: Giải phương trình
1 8 15 22 7944x+ + + +…+ =
A.
330x =
. B.
220x =
. C.
351x =
. D.
407x =
.
Lời giải

CHUYÊN ĐỀ II – TOÁN – 11 – DÃY SỐ - CẤP SỐ CỘNG – CẤP SỐ NHÂN
Page 19
Sưu tầm và biên soạn
Ta có cấp số cộng với
1
1
u =
,
7
d
=
,
n
ux=
,
7944
n
S =
.
Áp dụng công thức
( ) ( )
1
2
2 1 2.1 1 7
7944 7 5 15888 0
22
n
u n dn n n
S nn
+− +−
= ⇔ = ⇔ −− =
( )
(
)
48 /
331
7
n tm
n loai
=
⇔
= −
.
Vậy
48
1 47.7 330xu==+=
.
Câu 94: Cho cấp số cộng
( )
n
u
có số hạng đầu bằng
1
và tổng
100
số hạng đầu bằng
14950
. Giá trị của
tổng
1 2 2 3 49 50
11 1
...
uu u u u u
+ ++
bằng.
A.
49
74
. B.
148
. C.
49
148
. D.
74
.
Lời giải
Gọi
d
là công sai của cấp số cộng. Ta có
( )
100 1
50 2 99 14950S ud= +=
với
1
13ud=⇒=
Đặt
1 2 2 3 49 50
11 1
...S
uu u u u u
= + ++
.
Ta có
1 2 2 3 49 50
. ...
dd d
Sd
uu u u u u
= + ++
3 2 50 49
21
1 2 2 3 49 50
...
uu u u
uu
uu u u u u
−−
−
= + ++
1 50
11
uu
= −
1 147
1
1 49.3 148
=−=
+
.
Với
3d =
nên
49
148
S =
.
Câu 95: Cho một cấp số cộng
(
)
n
u
có
1
1u
=
và tổng
100
số hạng đầu bằng
10000
. Tính tổng
1 2 2 3 99 100
11 1
...S
uu u u u u
= + ++
.
A.
100
201
=
S
. B.
200
201
=S
. C.
198
199
=S
. D.
99
199
=S
.
Lời giải
Gọi
d
là công sai của cấp số cộng đã cho.
Ta có:
( )
1
100 1
200 2
50 2 99 10000 2
99
u
S ud d
−
= + = ⇒= =
.
1 2 2 3 99 100
22 2
2 ...
S
uu u u u u
⇒ = + ++
3 2 99 100
21
1 2 2 3 99 100
...
uu u u
uu
uu u u u u
−−
−
= + ++
1 2 2 3 98 99 99 100
1111 1 1 1 1
...
uu u u u u u u
= − + − ++ − + −
CHUYÊN ĐỀ II – TOÁN – 11 – DÃY SỐ - CẤP SỐ CỘNG – CẤP SỐ NHÂN
Page 20
Sưu tầm và biên soạn
1 100 1 1
1 1 1 1 198
99 199uu uu d
=−=− =
+
99
199
S⇒=
.
Câu 96: Cho tam giác đều
111
ABC
có độ dài cạnh bằng
4
. Trung điểm của các cạnh tam giác
111
ABC
tạo
thành tam giác
222
ABC
, trung điểm của các cạnh tam giác
222
ABC
tạo thành tam giác
333
ABC
…
Gọi
123
, , ,...
PPP
lần lượt là chu vi của tam giác
111
ABC
,
222
ABC
,
333
ABC
,…Tính tổng chu vi
123
...PPP P
=+++
A.
8
P =
. B.
24P =
. C.
6P =
. D.
18P =
.
Lời giải
Chọn B
Ta có:
21
1
2
PP
=
;
321
11
24
PPP= =
;
4 31
11
28
PPP= =
…;
1
1
1
2
n
n
PP
−
=
…
Vậy
1
123 1111 1
111
... ... 2 24.
1
248
1
2
P
PPPP PPPP P=+ + +=+ + + += = =
−
B
3
C
3
A
3
C
2
A
2
B
2
C
1
B
1
A
1

CHUYÊN ĐỀ II – TOÁN – 11 – DÃY SỐ - CẤP SỐ CỘNG – CẤP SỐ NHÂN
Page 21
Sưu tầm và biên soạn
DẠNG 4. BÀI TOÁN THỰC TẾ VÀ MỘT SỐ BÀI TOÁN KHÁC
Câu 97: Lan đang tiết kiệm để mua laptop. Trong tuần đầu tiên, cô ta để dành
200
đô la, và trong mỗi
tuần tiếp theo, cô ta đã thêm
16
đô la vào tài khoản tiết kiệm của mình. Chiếc laptop Lan cần
mua có giá
1000
đô la. Hỏi vào tuần thứ bao nhiêu thì cô ấy có đủ tiền để mua chiếc laptop đó?
A.
49
. B.
50
. C.
51
. D.
52
.
Lời giải
Gọi
n
là số tuần cô ta đã thêm
16
đô la vào tài khoản tiết kiệm của mình
Số tiền cô ta tiết kiệm được sau
n
tuần đó là
200 16 .Tn= +
Theo đề bài, ta có
200 16 1000 50.Tnn= + = ⇔=
Vậy kể cả tuần đầu thì tuần thứ
51
cô ta có đủ tiền để mua chiếc laptop đó.
Câu 98: Một người làm việc cho một công ty. Theo hợp đồng trong năm đầu tiên, tháng lương thứ nhất
là 6 triệu đồng và lương tháng sau cao hơn tháng trước là 200 ngàn đồng. Hỏi theo hợp đồng,
tháng thứ 7 người đó nhận được lương là bao nhiêu?
A. 7,0 triệu. B. 7,3 triệu. C. 7,2 triệu. D. 7,4 triệu.
Lời giải
Gọi lương tháng thứ
n
của người đó là
n
A
.
Ta có
1
6=A
.
Lương tháng sau hơn tháng trước
0, 2
triệu nên ta có
{
}
n
A
là một cấp số cộng với số hạng đầu
1
6=A
và công sai
0, 2
=d
.
Số hạng tổng quát của dãy số là
(
) ( )
1
11
=+− >
n
A A n dn
.
Vậy tới tháng thứ 7, người đó nhận được lương là
71
6 6 6.0,2 7, 2
=+=+ =AA d
.
Câu 99: Trong tháng 12, lớp 12A dự kiến quyên góp tiền để đi làm từ thiện như sau: Ngày đầu quyên góp
được mỗi bạn bỏ 2000 đồng vào lợn, từ ngày thứ hai trở đi mỗi bạn bỏ vào lợn hơn ngày liền
trước là 500 đồng. Hỏi sau 28 ngày lớp 11A quyên góp được bao nhiêu tiền? Biết lớp có 40 bạn.
A.
8800000
đồng. B.
9800000
đồng. C.
10800000
đồng. D.
7800000
đồng
Lời giải
Số tiền mỗi bạn lớp 11A quyên góp để làm từ thiện lập thành một cấp số cộng có số hạng đầu
1
2000u =
, công sai
d 500=
Vậy sau
28
ngày số tiền mỗi bạn quyên góp được là:
27.28.500
28.2000 245000
2
+=
đồng
Vậy sau 28 ngày tổng số tiền quyên góp được của lớp 11A là:
245000.40 9800000=
đồng
Câu 100: Trong sân vận động có tất cả 30 dãy ghế, dãy đầu tiên có 15 ghế. Các dãy sau, mỗi dãy nhiều
hơn dãy ngay trước nó 4 ghế. Hỏi sân vận động có tất cả bao nhiêu ghế?
A.
1740
. B.
2250
. C.
4380
. D.
2190
.
Lời giải
Số ghế trong mỗi dãy của sân vận động lập thành một cấp số cộng có
1
15U =
và
4d =
.

CHUYÊN ĐỀ II – TOÁN – 11 – DÃY SỐ - CẤP SỐ CỘNG – CẤP SỐ NHÂN
Page 22
Sưu tầm và biên soạn
Vậy tổng tất cả các ghế của sân vận động là tổng 30 số hạng đầu của cấp số cộng trên, do đó áp
dụng công thức
(
)
1
1
2
n
nn d
S nU
−
= +
ta có
(
)
30
30 30 1 4
30.15 2190
2
S
−
=+=
Vậy sân vận động có tất cả 2190 ghế.
Câu 101: Hùng đang tiết kiệm để mua một cây đàn piano có giá 142 triệu đồng. Trong tháng đầu tiên, anh
ta để dành được 20 triệu đồng. Mỗi tháng tiếp theo anh ta để dành được 3 triệu đồng và đưa số
tiền tiết kiệm của mình. Hỏi ít nhất vào tháng thứ bao nhiêu thì Hùng mới có đủ tiền để mua cây
đàn piano đó?
A.
43
. B.
41
. C.
40
. D.
42
.
Lời giải
Tổng số tiền Hùng tiết kiệm được vào mỗi tháng lập thành một cấp số cộng
( )
n
u
có số hạng đầu
1
20u =
và công sai
3
d
=
.
Tổng số tiền Hùng tiết kiệm được vào tháng thứ
n
bằng
( ) ( )
1
1 20 1 .3 3 17
n
uu n d n n=+− =+− =+
Hùng có đủ tiền mua cây đàn
3 17 142
n
⇔+≥
125
41,67
3
n⇔≥ ≈
.
Vậy ít nhất vào tháng thứ 42 thì Hùng mới có đủ tiền để mua cây đàn piano đó.
Câu 102: Người ta trồng
820
cây theo một hình tam giác như sau: Hàng thứ nhất trồng 1 cây, kể từ hàng
thứ hai trở đi số cây trồng mỗi hàng nhiều hơn
1
cây so với hàng liền trước nó. Hỏi có tất cả bao
nhiêu hàng cây?
A.
42
. B.
41
. C.
40
. D.
39
.
Lời giải
Giả sử trồng được
n
hàng cây
( )
1,nn≥∈
.
Số cây ở mỗi hàng lập thành cấp số cộng có
1
1u =
và công sai
1d =
.
Theo giả thiết:
820
n
S =
( )
1
2 1 820
2
n
un d⇔ +− =
( )
1 1640nn⇔ +=
2
1640 0nn⇔ +− =
40
41
n
n
=
⇔
= −
So với điều kiện, suy ra:
40n =
. Vậy có tất cả
40
hàng cây.
Câu 103: Một cầu thang đường lên cổng trời của một điểm giải trí ở công viên tỉnh X được hàn bằng sắt
có hình dáng các bậc thang đều là hình chữ nhật với cùng chiều rộng là 35cm và chiều dài của
nó theo thứ tự mỗi bậc đều giảm dần đi 7cm. Biết rằng bậc đầu tiên của cầu thang là hình chữ
nhật có chiều dài 189cm và bậc cuối cùng cầu thang là hình chữ nhật có chiều dài 63cm. Hỏi giá
thành làm cầu thang đó gần với số nào dưới đây nếu giá thành làm một mét vuông cầu thang đó
là
1250000
đồng trên một mét vuông?
A.
9500000
đồng. B.
11000000
đồng. C.
10000000
đồng. D.
10500000
đồng.
Lời giải

CHUYÊN ĐỀ II – TOÁN – 11 – DÃY SỐ - CẤP SỐ CỘNG – CẤP SỐ NHÂN
Page 23
Sưu tầm và biên soạn
Ta có chiều dài của mỗi mặt cầu thang theo thứ tự lập thành một cấp số cộng với số hạng đầu
tiên là
1
189
u =
, công sai
7d = −
và số hạng cuối cùng là
63
n
u =
.
Khi đó áp dụng công thức tính số hạng tổng quát ta có:
1
( 1) 63 189 7( 1) 19
n
uu n d n n= + − ⇔ = − −⇔=
Tổng chiều dài của 19 hình chữ nhật đó là:
1 19
19
19. 2394
2
uu
S
+
= =
.
Diện tích của 19 bậc thang là:
22
35.2394 83790( ) 8,379( )S cm m= = =
Tổng số tiền để làm cầu thang đó là:
8,379.1250000 10473750
T
= =
đồng.
Vậy chọn đáp án D.
Câu 104: Công ty A muốn thuê hai mảnh đất để làm 2 nhà kho, một mảnh trong vòng10 năm và 1 mảnh
trong vòng 15 năm ở hai chỗ khác nhau. Công ty bất động sản C, công ty bất động sản B đều
muốn cho thuê. Hai công ty đưa ra phương án cho thuê như sau
Công ty C: Năm đầu tiên tiền thuê đất là 60 triệu và kể từ năm thứ hai trở đi mỗi năm tăng
thêm 3 triệu đồng.
Công ty B: Trả tiền theo quí, quý đầu tiên là 8 triệu đồng và từ quý thứ hai trở đi mỗi quý tăng
thêm 500000 đồng.
Hỏi công ty A nên lựa chọn thuê đất của công ty bất động sản nào để chi phí là thấp nhất biết
rằng các mảnh đất cho thuê về diện tích, độ tiện lợi đều như nhau?
A. Chọn công ty B để thuê cả hai mảnh đất.
B. Chọn công ty C để thuê cả hai mảnh đất.
C. Chọn công ty C để thuê đất 10 năm, công ty B thuê đất 15 năm.
D. Chọn công ty B để thuê đất 10 năm, công ty C thuê đất 15 năm.
Lời giải
Gọi
,
nn
BC
lần lượt là số tiền công ty A cần trả theo các tính của hai công ty B và C
Theo bài ra ta có :
n
B
là tổng
n
số hạng đầu tiên của một cấp số cộng với
1
8u =
triệu đồng
0,5d =
triệu đồng.
n
C
là tổng
n
số hạng đầu tiên của một cấp số cộng với
1
60u =
triệu đồng
3d =
triệu đồng.
Do đó : Nếu thuê đất của công ty B trong vòng 15 năm = 60 quý số tiền công ty A phải trả là
60
(2.8 59.0,5).30 1365B =+=
triệu đồng
Nếu thuê đất của công ty C trong vòng 15 năm số tiền công ty A phải trả là
15
(2.60 14.3).7,5 1215C =+=
triệu đồng
Vậy thuê mảnh đất trong vòng 15 năm của công ty C
Nếu thuê đất của công ty B trong vòng 10 năm = 40 quý số tiền công ty A phải trả là
40
(2.8 39.0,5).20 710B =+=
triệu đồng

CHUYÊN ĐỀ II – TOÁN – 11 – DÃY SỐ - CẤP SỐ CỘNG – CẤP SỐ NHÂN
Page 24
Sưu tầm và biên soạn
Nếu thuê đất của công ty C trong vòng 10 năm số tiền công ty A phải trả là
10
(2.60 9.3).4,5 661,5
C
=+=
triệu đồng
Vậy thuê mảnh đất trong vòng 10 năm của công ty. C.
Câu 105: Hùng đang tiết kiệm để mua một cây guitar. Trong tuần đầu tiên, anh ta để dành 42 đô la, và
trong mỗi tuần tiếp theo, anh ta đã thêm 8 đô la vào tài khoản tiết kiệm của mình. Cây guitar
Hùng cần mua có giá 400 đô la. Hỏi vào tuần thứ bao nhiêu thì anh ấy có đủ tiền để mua cây
guitar đó?
A.
47
. B.
45
. C.
44
. D.
46
.
Lời giải
Sau tuần đầu, Hùng cần thêm 358 đô la. Như vậy Hùng cần thêm
358:8 44,75=
tuần.
Vậy đến tuần thứ 46 Hùng đủ tiền.
Câu 106: Một công ti trách nhiệm hữu hạn thực hiện việc trả lương cho các kĩ sư theo phương thức sau:
Mức lương của quý làm việc đầu tiên cho công ti là
4,5
triệu đồng/quý, và kể từ quý làm việc
thứ hai, mức lương sẽ được tăng thêm
0,3
triệu đồng mỗi quý. Hãy tính tổng số tiền lương một
kĩ sư nhận được sau
3
năm làm việc cho công ti.
A.
83, 7
. B.
78,3
. C.
73,8
. D.
87,3
.
Lời giải
Ta có
3
năm bằng
12
quý.
Gọi
1
u
,
2
u
, …,
12
u
là tiền lương kĩ sư đó trong các quý.
Suy ra
( )
n
u
là cấp số cộng với công sai
4,5
.
Vậy số tiền lương kĩ sư nhận được là
( )
1
12
21
2
un d
Sn
+−
=
2 4,5 11 0,3
12 73,8
2
× +×
= =
.
Câu 107: Người ta trồng
465
cây trong một khu vườn hình tam giác như sau: Hàng thứ nhất có
1
cây,
hàng thứ hai có
2
cây, hàng thứ ba có
3
cây….Số hàng cây trong khu vườn là
A.
31
. B.
30
. C.
29
. D.
28
.
Lời giải
Cách trồng
465
cây trong một khu vườn hình tam giác như trên lập thành một cấp số cộng
( )
n
u
với số
n
u
là số cây ở hàng thứ
n
và
1
1u =
và công sai
1d =
.
Tổng số cây trồng được là:
465
n
S =
( )
1
465
2
nn+
⇔=
2
930 0nn⇔ +− =
( )
30
31
n
nl
=
⇔
= −
.
Như vậy số hàng cây trong khu vườn là
30
.
Câu 108: Trong sân vận động có tất cả
30
dãy ghế, dãy đầu tiên có
15
ghế, các dãy liền sau nhiều hơn dãy
trước
4
ghế, hỏi sân vận động đó có tất cả bao nhiêu ghế?
A.
2250
. B.
1740
. C.
4380
. D.
2190
.
Lời giải

CHUYÊN ĐỀ II – TOÁN – 11 – DÃY SỐ - CẤP SỐ CỘNG – CẤP SỐ NHÂN
Page 25
Sưu tầm và biên soạn
Gọi
1 2 30
, ,...uu u
lần lượt là số ghế của dãy ghế thứ nhất, dãy ghế thứ hai,… và dãy ghế số ba
mươi. Ta có công thức truy hồi ta có
( )
1
4 2,3,...,30
nn
uu n
−
=+=
.
Ký hiệu:
30 1 2 30
...S uu u= + ++
, theo công thức tổng các số hạng của một cấp số cộng, ta được:
( )
( )
( )
30 1
30
2 30 1 4 15 2.15 29.4 2190
2
Su= +− = + =
.
Câu 109: Cho
4
số thực
,,,abcd
là
4
số hạng liên tiếp của một cấp số cộng. Biết tổng của chúng bằng 4
và tổng các bình phương của chúng bằng
24
. Tính
333 3
Pabcd=+++
.
A.
64P =
. B.
80P =
. C.
16P =
. D.
79P =
.
Lời giải
Theo giả thiết ta có: .
.
.
Câu 110: Cho cấp số cộng
( )
n
u
có
1
4u =
. Tìm giá trị nhỏ nhất của
12 23 31
uu u u uu++
?
A.
20
. B.
6
. C.
8
. D.
24
.
Lời giải
Ta gọi
d
là công sai của cấp số cộng.
( ) ( )( ) ( )
12 23 31
44 4 4 2 44 2uu uu uu d d d d+ +=+++ +++
( )
2
2
2 24 48 2 6 24 24dd d= + + = + − ≥−
Dấu
""=
xảy ra khi
6d = −
.
Vậy giá trị nhỏ nhất của
12 23 31
uu u u uu++
là
24−
.
Câu 111: Một tam giác vuông có chu vi bằng
3
và độ dài các cạnh lập thành một cấp số cộng. Độ dài các
cạnh của tam giác đó là:
A.
15
;1;
33
. B.
17
;1;
44
. C.
35
;1;
44
. D.
13
;1;
22
.
Lời giải
Gọi
d
là công sai của cấp số cộng và các cạnh có độ dài lần lượt là
ad−
,
a
,
ad+
( )
0 da<<
.
Vì tam giác có chu vi bằng
3
nên
33a =
1a⇔=
.
Vì tam giác vuông nên theo định lý Pytago ta có
( ) ( )
22
2
1 11dd+=−+
41d⇔=
1
4
d⇔=
.
Suy ra ba cạnh của tam giác có độ dài là
35
;1;
44
.
2
4
ad bc
ad bc
abcd
+=+
⇒+ =+=
+++ =
( ) ( ) ( )
22
222 2
2a b c d a d b c ad bc+++ =+ ++ − +
( ) ( )
22
222 2
8ad bc a b c d a d b c⇒ + = +++ −+ −+ =−
333 3
Pabcd=+++
( )
( )
( )
( )
2 2 22
a d a ad d b c b bc c=+ − + ++ −+
( )
222 2
2 a b c d ad bc= +++ − −
64=

CHUYÊN ĐỀ II – TOÁN – 11 – DÃY SỐ - CẤP SỐ CỘNG – CẤP SỐ NHÂN
Page 26
Sưu tầm và biên soạn
Câu 112: Trong hội chợ, một công ty sơn muốn xếp
1089
hộp sơn theo số lượng
1,3,5,...
từ trên xuống
dưới. Hàng cuối cùng có bao nhiêu hộp sơn?
A.
63
. B.
65
. C.
67
. D.
69
.
Lời giải
Giả sử
1089
được xếp thành
n
hàng. Từ giả thiết ta có số hộp sơn trên mỗi hàng là số hạng của
một cấp số cộng
n
u
với số hạng đầu
1
1u
công sai
2d
. Do đó
1089 1 1089 33
n
S n nn n
.
Vậy số hộp sơn ở hàng cuối cùng là:
33
1 32.2 65u
.
Câu 113: Người ta trồng
1275
cây theo hình tam giác như sau: Hàng thứ nhất có
1
cây, hàng thứ
2
có
2
cây, hàng thứ
3
có
3
cây,.hàng thứ
k
có
k
cây
( )
1.k ≥
Hỏi có bao nhiêu hàng ?
A.
51
. B.
52
. C.
53
. D.
50
.
Lời giải
Đặt
k
u
là hàng thứ
k
Ta có :
( )
12
1
... 1 2 3 ...
2
k
kk
Suu u k
+
= + ++ =++++=
Theo giả thiết ta có :
(
)
50
1
1275
51 0
2
k
kk
k
=
+
= ⇔
=−<
Vậy
50k =
nên có 50 hàng.
Câu 114: Người ta trồng
3003
cây theo hình tam giác như sau: Hàng thứ nhất trồng
1
cây, hàng thứ hai
trồng
2
cây, hàng thứ ba trồng
3
cây,….Hỏi có bao nhiêu hàng cây.
A.
78
. B.
243
. C.
77
. D.
244
.
Lời giải
Giả sử có
n
hàng cây.
Theo đề bài ta có:
2
77 ( )
.( 1)
1 2 3 .... 3003 3003 6006 0
78 ( )
2
n TM
nn
n nn
nL
=
+
+++ + = ⇔ = ⇔ +− = ⇔
= −
.
Câu 115: Bà chủ quán trà sữa
X
muốn trang trí quán cho đẹp nên quyết định thuê nhân công xây một bức
tường bằng gạch với xi măng, biết hàng dưới cùng có
500
viên, mỗi hàng tiếp theo đều có ít hơn

CHUYÊN ĐỀ II – TOÁN – 11 – DÃY SỐ - CẤP SỐ CỘNG – CẤP SỐ NHÂN
Page 27
Sưu tầm và biên soạn
hàng trước 1 viên và hàng trên cùng có 1 viên. Hỏi số gạch cần dùng để hoàn thành bức tường
trên là bao nhiêu viên?
A.
25250.
B.
250500.
C.
12550.
D.
125250.
Lời giải
Ta có số gạch ở mỗi hàng là các số hạng của 1 cấp số cộng:
500
,
499
,
498
,.,
2
,
1
.
⇒ Tổng số gạch cần dùng là tổng của cấp số cộng trên, bằng
500
500(500 1)
250.501 125250
2
S
+
= = =
Câu 116: Người ta trồng
3240
cây theo một hình tam giác như sau: hàng thứ nhất trồng 1 cây, kể từ hàng
thứ hai trở đi số cây trồng mỗi hàng nhiều hơn
1
cây so với hàng liền trước nó. Hỏi có tất cả bao
nhiêu hàng cây?
A.
81
. B.
82
. C.
80
. D.
79
.
Lời giải
Giả sử trồng được
n
hàng cây
( )
1,nn
≥∈
.
Số cây ở mỗi hàng lập thành cấp số cộng có
1
1
u =
và công sai
1d =
.
Theo giả thiết:
3240
n
S =
(
)
1
2 1 3240
2
n
un d
⇔ +− =
( )
1 6480nn⇔ +=
2
6480 0nn⇔ +− =
80
81
n
n
=
⇔
= −
So với điều kiện, suy ra:
80n =
.
Vậy có tất cả
80
hàng cây.
Câu 117: Cho hai cấp số cộng hữu hạn, mỗi cấp số cộng có 100 số hạng là
4, 7, 10, 13, 16,...
và
1, 6, 11, 16, 21,...
. Hỏi có tất cả bao nhiêu số có mặt trong cả hai cấp số cộng trên?
A.
20
. B.
18
. C. 21. D. 19.
Lời giải
Cấp số cộng đầu tiên có số hạng tổng quát là
( )
( )
*
4 1 .3 3 1 .
n
u n nn=+− =+ ∈
Cấp số cộng thứ hai có số hạng tổng quát là
( )
( )
*
1 1 .5 5 4 .
m
u m mm=+− = − ∈
Ta cần có
( )
3 1 5 4 3 5 1.n m nm+= − ⇔ = −
Ta thấy để thỏa mãn yêu cầu bài toán thì
3 5 5.nn⇔
Vì cấp số cộng có 100 số hạng nên từ
đó suy ra có 20 số hạng chung.
Câu 118: Sinh nhật bạn của An vào ngày
01
tháng năm. An muốn mua một món quà sinh nhật cho bạn
nên quyết định bỏ ống heo
100
đồng vào ngày
01
tháng
01
năm
2016
, sau đó cứ liên tục ngày

CHUYÊN ĐỀ II – TOÁN – 11 – DÃY SỐ - CẤP SỐ CỘNG – CẤP SỐ NHÂN
Page 28
Sưu tầm và biên soạn
sau hơn ngày trước
100
đồng. Hỏi đến ngày sinh nhật của bạn, An đã tích lũy được bao nhiêu
tiền?.
A.
738.100
đồng. B.
726.000
đồng. C.
714.000
đồng. D.
750.300
đồng.
Lời giải
Số ngày bạn An để dành tiền là
31 29 31 30 121+++=
ngày.
Số tiền bỏ ống heo ngày đầu tiên là:
1
100u =
.
Số tiền bỏ ống heo ngày thứ hai là:
2
100 1.100u
= +
.
Số tiền bỏ ống heo ngày thứ ba là:
3
100 2.100
u = +
.
…
Số tiền bỏ ống heo ngày thứ
n
là:
( )
1
1
n
uu n d=+−
( )
100 1 100n= +−
100n=
.
Số tiền bỏ ống heo ngày thứ
121
là:
121
100.121u =
12100
=
.
Sau
121
ngày thì số tiền An tích lũy được là tổng của
121
số hạng đầu của cấp số cộng có số
hạng đầu
1
100u =
, công sai
100d =
.
Vậy số tiền An tích lũy được là
( )
121 1 121
121
2
S uu= +
( )
121
100 12100
2
= +
738100=
đồng.
Câu 119: Gọi
S
là tập hợp tất cả các số tự nhiên
k
sao cho
14
k
C
,
1
14
k
C
+
,
2
14
k
C
+
theo thứ tự đó lập thành một
cấp số cộng. Tính tổng tất cả các phần tử của
S
.
A.
12
. B.
8
. C.
10
. D.
6
.
Lời giải
Điều kiện:
, 12
kk
14
k
C
,
1
14
k
C
+
,
2
14
k
C
+
theo thứ tự đó lập thành một cấp số cộng ta có
21
14 14 14
2
kk k
CC C
++
+=
( ) ( ) ( )
( ) ( )
14! 14! 14!
2
! 14 ! 2 ! 12 ! 1 ! 13 !k kk k k k
⇔+ =
− + − +−
( )( ) ( )( )
( )( )
1 12
14 13 1 2 1 13k kk k k k
⇔ +=
− − ++ + −
( )( ) ( )( ) (
)( )
14 13 1 2 2 14 2k k k k kk⇔ − −++ += − +
2
4 (tm)
12 32 0
8 (tm)
k
kk
k
=
⇔− +=⇔
=
.
Có
4 8 12.+=
Câu 120: Cho
22
1
;;
2
xy
theo thứ tự lập thành một cấp số cộng. Gọi
,Mm
lần lượt là giá trị lớn nhất và giá
trị nhỏ nhất của biểu thức
2
3P xy y= +
. Tính
SMm= +
A.
1
. B.
2
. C.
3
. D.
31
22
−
.

CHUYÊN ĐỀ II – TOÁN – 11 – DÃY SỐ - CẤP SỐ CỘNG – CẤP SỐ NHÂN
Page 29
Sưu tầm và biên soạn
Lời giải
Ta có:
22
1
;;
2
xy
theo thứ tự lập thành một cấp số cộng
22
1xy
+=
.
Đặt
sin
x
α
=
,
cosy
α
=
.
22
3 1 cos 2
3 3 sin .cos cos sin2
22
P xy y
α
αα α α
+
= += + = +
2 1 3 sin2 cos 2P
αα
⇔ −= +
.
Giả sử
P
là giá trị của biểu thức
2 1 3 sin2 cos 2P
αα
⇒ −= +
có nghiệm.
( )
(
)
2
2
2
13
21 3 1
22
PP⇔ − ≤ + ⇔− ≤ ≤
.
Vậy
31
;1
22
Mm S= =−⇒=
.
Câu 121: Cho dãy số
( )
n
u
thỏa mãn
1
2018u =
và
1
2
1
n
n
n
u
u
u
+
=
+
với mọi
1n ≥
. Giá trị nhỏ nhất của
n
để
1
2018
n
u <
bằng
A.
4072325
B.
4072324
C.
4072326
D.
4072327
Lời giải
Từ giả thiết suy ra
0, 1
n
un> ∀≥
Ta có
1
2
1
n
n
n
u
u
u
+
=
+
,
1n∀≥
⇔
2
2
1
2
1
n
n
n
u
u
u
+
=
+
⇔
22
1
11
1
nn
uu
+
= +
Đặt
2
1
n
n
v
u
=
, khi đó
1
2
1
2018
v
=
và
1
1
nn
vv
+
= +
nên
( )
n
v
là cấp số cộng có công sai là
1
.
( )
1
2
1
11
2018
n
vv n n= + − = +−
suy ra
22
11
1
2018
n
n
u
= +−
.
Để
1
2018
n
u <
⇔
2
2
1
2018
n
u
>
⇔
2
2
1
( 1) 2018
2018
n −+ >
⇔
2
2
1
1 2018
2018
n >− +
⇔
2
1
4072325
2018
n >−
Vậy giá trị nhỏ nhất của
n
thỏa mãn điều kiện là
4072325
.
Câu 122: Cho cấp số cộng
( )
n
u
có
1
3u =
và công sai
2d =
, và cấp số cộng
( )
n
v
có
1
2v =
và công sai
3d
′
=
. Gọi
,XY
là tập hợp chứa
1000
số hạng đầu tiên của mỗi cấp số cộng. Chọn ngẫu nhiên
2
phần tử bất kỳ trong tập hợp
XY∪
. Xác suất để chọn được
2
phần tử bằng nhau gần với số
nào nhất trong các số dưới đây?
A.
4
0,83.10
−
. B.
4
1,52.10
−
. C.
4
1,66.10
−
. D.
4
0,75.10
−
.
Lời giải
Chọn ngẫu nhiên
2
phần tử bất kỳ trong tập hợp
XY∪
ta có
2
2000
C
cách chọn.
Gọi
2
phần tử bằng nhau trong
,XY
là
k
u
và
l
v
.

CHUYÊN ĐỀ II – TOÁN – 11 – DÃY SỐ - CẤP SỐ CỘNG – CẤP SỐ NHÂN
Page 30
Sưu tầm và biên soạn
Do
kl
uv=
( ) ( )
32 1 23 1kl+ −=+ −
3
1
2
l
k
= −
Do
1 1000k≤≤
1 667l≤≤
. Mặt khác
2lx=
1
333,5
2
x
≤≤
có
333
số
Vậy xác suất để chọn được
2
phần tử bằng nhau là:
4
2
2000
333
1,665832916.10
C
−
≈
.
Câu 123: Nếu
2a +
,
b
,
2c
theo thứ tự lập thành cấp số cộng thì dãy số nào sau đây lập thành cấp số cộng?
A.
4b−
;
24a−−
;
4c
. B.
22a−−
;
2b−
;
42c−−
.
C.
2 b
+
;
2a
;
22c +
. D.
24a +
;
4b
;
4c
.
Lời giải
Ta có
22 2a cb++ =
(
) (
)
2 2 2 2. 2
ac b⇒− + + =−
( ) ( ) ( )
2 2 4 2 22ac b⇔− − +− − = −
.
Vậy
22a−−
,
2
b−
,
42c−−
theo thứ tự lập thành cấp số cộng.
Câu 124: Cho một cấp số cộng
n
u
có
1
5u
và tổng của
40
số hạng đầu là
3320
. Tìm công sai của cấp
số cộng đó.
A.
4−
. B.
8
. C.
8−
. D.
4
.
Lời giải
Gọi
d
là công sai của cấp số cộng.
Ta có tổng
40
số hạng đầu của cấp số cộng là:
1
40
40 2 39
3320
2
ud
S
.
40 2.5 39
3320 4
2
d
d
.
CHUYÊN ĐỀ II – TOÁN – 11 – DÃY SỐ - CẤP SỐ CỘNG – CẤP SỐ NHÂN
Page 47
Sưu tầm và biên soạn
BÀI 6: CẤP SỐ NHÂN
1. ĐỊNH NGHĨA: Cấp số nhân là một dãy số, trong đó kể từ số hạng thứ hai, mỗi số hạng đều là tích của
số hạng đứng ngay trước nó với một số không đổi
q.
Số
q
được gọi là công bội của cấp số nhân.
Nếu
( )
n
u
là cấp số nhân với công bội
q,
ta có công thức truy hồi:
1nn
u uq
+
=
với
*
n.∈
Đặc biệt:
•
Khi
0q,=
cấp số nhân có dạng
1
00 0
u , , , ..., , ...
•
Khi
1q,=
cấp số nhân có dạng
111 1
u , u , u , ..., u , ...
•
Khi
1
0
u =
thì với mọi
q,
cấp số nhân có dạng
000 0, , , ..., , ...
2. SỐ HẠNG TỔNG QUÁT
Nếu cấp số nhân có số hạng đầu
1
u
và công bội
q
thì số hạng tổng quát
n
u
được xác định bởi
công thức
1
1
n
n
u u .q
−
=
với
2n.≥
Chú ý: Trong một cấp số nhân, bình phương của mỗi số hạng đều là tích của hai số hạng đứng
kề với nó, nghĩa là
2
11k kk
u u .u
−+
=
với
2k.≥
3. TỔNG
n
SỐ HẠNG ĐẦU TIÊN CỦA CẤP SỐ NHÂN
Cho cấp số nhân
( )
n
u
với công bội
1q.≠
Đặt
12nn
S u u ... u .= + ++
Khi đó
( )
1
1
1
n
n
uq
S.
q
−
=
−
Chú ý: Nếu
1q =
thì cấp số nhân là
111 1
u , u , u , ..., u , ...
khi đó
1n
S nu .=
CHƯƠNG
II
DÃY SỐ
CẤP SỐ CỘNG – CẤP SỐ NHÂN
LÝ THUYẾT.
I

CHUYÊN ĐỀ II – TOÁN – 11 – DÃY SỐ - CẤP SỐ CỘNG – CẤP SỐ NHÂN
Page 48
Sưu tầm và biên soạn
Dạng 1: Chứng minh một dãy là cấp số nhân.
Dạng 2. Xác định các đại lượng của cấp số nhân
Dạng 3. Tổng n số hạng đầu tiên của cấp số nhân
Dạng 4. Một số bài toán liên quan đến cấp số nhân
DẠNG 1: CHỨNG MINH MỘT DÃY LÀ CẤP SỐ NHÂN.
+ Chứng minh
1nn
u u q, n *
+
= ∀∈
trong đó q là một số không đổi.
+ Nếu
0 *
n
un≠ ∀∈
thì
n
u
là một cấp số nhân
1
: *
n
n
u
q const n
u
+
⇔ = ∀∈
+ Để chứng minh dãy không phải là cấp số nhân, ta chỉ cần chỉ ra ba số hạng liên tiếp
không tạo thành cấp số nhân, chẳng hạn
3
2
21
u
u
uu
≠
.
+ Để chứng minh
a,b,c
theo thứ tự đó lập thành CSN, ta chứng minh
2
ac b=
hoặc
b ac=
Câu 1: Chứng minh rằng dãy số
( )
( )
2
13
n
n
nn
v :v .= −
là một cấp số nhân.
Câu 2: Giá trị của
a
để
11
; ;
5 125
a
−−
theo thứ tự lập thành cấp số nhân?
DẠNG 2. XÁC ĐỊNH CÁC ĐẠI LƯỢNG CỦA CẤP SỐ NHÂN
Vận dụng các công thức ở định nghĩa, số hạng tổng quát, tính chất của cấp số nhân.
Câu 3: Cho cấp số nhân
( )
n
u
với công bội q < 0 và
24
49u ,u= =
. Tìm
1
u
.
Câu 4: Cho cấp số nhân
( )
n
u
biết
15 26
51 102u u ;u u+= +=
. Hỏi số 12288 là số hạng thứ mấy của
cấp số nhân
( )
n
u
?
Câu 5: Cho cấp số nhân
()
n
u
thỏa:
4
38
2
27
243
u
uu
=
=
.
( )
n
u
( )
n
u
( )
n
u
HỆ THỐNG BÀI TẬP.
II
PHƯƠNG PHÁP.
1
BÀI TẬP TỰ LUẬN.
2
PHƯƠNG PHÁP.
1
BÀI TẬP TỰ LUẬN.
2

CHUYÊN ĐỀ II – TOÁN – 11 – DÃY SỐ - CẤP SỐ CỘNG – CẤP SỐ NHÂN
Page 49
Sưu tầm và biên soạn
a) Viết năm số hạng đầu của cấp số nhân:
b) Số
2
6561
là số hạng thứ bao nhiêu của cấp số?
Câu 6: Cho tứ giác ABCD có 4 góc tạo thành 1 cấp số nhân có công bội bằng 2. Tìm 4 góc ấy
Câu 7: Cho 5 số lập thành một cấp số nhân. Biết công bội bằng một phần tư số hạng đầu tiên và tổng 2
số hạng đầu bằng 8.
DẠNG 3: TỔNG N SỐ HẠNG ĐẦU TIÊN CỦA CẤP SỐ NHÂN
Ghi nhớ công thức
(
)
( )
1
1
1
1
n
n
uq
S ,q .
q
−
= ≠
−
Câu 8: Tính tổng tất cả các số hạng của một cấp số nhân, biết số hạng đầu bằng 18, số hạng thứ hai bằng
54 và số hạng cuối bằng 39366.
Câu 9: Cho cấp số nhân
()
n
u
thỏa:
4
38
2
27
243
u
uu
=
=
.Tính tổng 10 số hạng đầu của cấp số;
Câu 10: Tính các tổng sau:
22 2
11 1
24 2
24 2
n
n
n
S ...
=++++++
Câu 11:
8
8 88 888 ... 88...8
n
n so
S =+ + ++
DẠNG 4: MỘT SỐ BÀI TOÁN LIÊN QUAN ĐẾN CẤP SỐ NHÂN
Câu 12: Chu kì bán rã của nguyên tố phóng xạ poloni 210 là 138 ngày. Tính khối lượng còn lại của 20
gam poloni 210 sau 7314 ngày.
Câu 13: Người ta thiết kế một cái tháp gồm 11 tầng. Diện tích bề mặt trên của mỗi tầng bằng nữa diện
tích của mặt trên của tầng ngay bên dưới và diện tích mặt trên của tầng 1 bằng nửa diện tích của
đế tháp. Tính diện tích mặt trên cùng.
Câu 14: Một du khách vào trường đua ngựa đặt cược, lần đầu đặt
20000
đồng, mỗi lần sau tiền đặt gấp
đôi lần tiền đặt cọc trước. Người đó thua
9
lần liên tiếp và thắng ở lần thứ
10.
Hỏi du khác trên
thắng hay thua bao nhiêu?
Câu 15: Tìm m để phương trình sau có 3 nghiệm lập thành CSN.
( ) ( )
32
5 65 6 0x mx mx m+− +− − =
PHƯƠNG PHÁP.
1
BÀI TẬP TỰ LUẬN.
2
PHƯƠNG PHÁP.
1
BÀI TẬP TỰ LUẬN.
2

CHUYÊN ĐỀ II – TOÁN – 11 – DÃY SỐ - CẤP SỐ CỘNG – CẤP SỐ NHÂN
Page 50
Sưu tầm và biên soạn
Câu 16: Một người bắt đầu đi làm được nhận được số tiền lương là 7000000đ một tháng. Sau 36 tháng
người đó được tăng lương 7%. Hằng tháng người đó tiết kiệm 20% lương để gửi vào ngân hàng
với lãi suất 0,3%/tháng theo hình thức lãi kép. Biết rằng người đó nhận lương vào đầu tháng và
số tiền tiết kiệm được chuyển ngay vào ngân hàng.
a) Hỏi sau 36 tháng tổng số tiền người đó tiết kiệm được là bao nhiêu?
b) Hỏi sau 60 tháng tổng số tiền người đó tiết kiệm được là bao nhiêu?
CHUYÊN ĐỀ II – TOÁN – 11 – DÃY SỐ - CẤP SỐ CỘNG – CẤP SỐ NHÂN
Page 1
Sưu tầm và biên soạn
BÀI 6: CẤP SỐ NHÂN
1. ĐỊNH NGHĨA: Cấp số nhân là một dãy số, trong đó kể từ số hạng thứ hai, mỗi số hạng đều là tích của
số hạng đứng ngay trước nó với một số không đổi
q.
Số
q
được gọi là công bội của cấp số nhân.
Nếu
( )
n
u
là cấp số nhân với công bội
q,
ta có công thức truy hồi:
1nn
u uq
+
=
với
*
n.∈
Đặc biệt:
•
Khi
0q,=
cấp số nhân có dạng
1
00 0
u , , , ..., , ...
•
Khi
1q,=
cấp số nhân có dạng
111 1
u , u , u , ..., u , ...
•
Khi
1
0
u =
thì với mọi
q,
cấp số nhân có dạng
000 0, , , ..., , ...
2. SỐ HẠNG TỔNG QUÁT
Nếu cấp số nhân có số hạng đầu
1
u
và công bội
q
thì số hạng tổng quát
n
u
được xác định bởi
công thức
1
1
n
n
u u .q
−
=
với
2n.≥
Chú ý: Trong một cấp số nhân, bình phương của mỗi số hạng đều là tích của hai số hạng đứng
kề với nó, nghĩa là
2
11k kk
u u .u
−+
=
với
2k.≥
3. TỔNG
n
SỐ HẠNG ĐẦU TIÊN CỦA CẤP SỐ NHÂN
Cho cấp số nhân
( )
n
u
với công bội
1q.≠
Đặt
12nn
S u u ... u .= + ++
Khi đó
( )
1
1
1
n
n
uq
S.
q
−
=
−
Chú ý: Nếu
1q =
thì cấp số nhân là
111 1
u , u , u , ..., u , ...
khi đó
1n
S nu .=
CHƯƠNG
II
DÃY SỐ
CẤP SỐ CỘNG – CẤP SỐ NHÂN
LÝ THUYẾT.
I

CHUYÊN ĐỀ II – TOÁN – 11 – DÃY SỐ - CẤP SỐ CỘNG – CẤP SỐ NHÂN
Page 2
Sưu tầm và biên soạn
Dạng 1: Chứng minh một dãy là cấp số nhân.
Dạng 2. Xác định các đại lượng của cấp số nhân
Dạng 3. Tổng n số hạng đầu tiên của cấp số nhân
Dạng 4. Một số bài toán liên quan đến cấp số nhân
DẠNG 1: CHỨNG MINH MỘT DÃY LÀ CẤP SỐ NHÂN.
+ Chứng minh
1nn
u u q, n *
+
= ∀∈
trong đó q là một số không đổi.
+ Nếu
0 *
n
un≠ ∀∈
thì
n
u
là một cấp số nhân
1
: *
n
n
u
q const n
u
+
⇔ = ∀∈
+ Để chứng minh dãy không phải là cấp số nhân, ta chỉ cần chỉ ra ba số hạng liên tiếp
không tạo thành cấp số nhân, chẳng hạn
3
2
21
u
u
uu
≠
.
+ Để chứng minh
a,b,c
theo thứ tự đó lập thành CSN, ta chứng minh
2
ac b=
hoặc
b ac=
Câu 1: Chứng minh rằng dãy số
( )
( )
2
13
n
n
nn
v :v .= −
là một cấp số nhân.
Lời giải
( )
( )
( )
1
21
1
2
13
9
13
n
n
*
n
n
n
n
v
,n
v
+
+
+
−
= =− ∀∈
−
. Vậy
( )
( )
2
13
n
n
nn
v :v .= −
là một cấp số nhân.
Câu 2: Giá trị của
a
để
11
; ;
5 125
a
−−
theo thứ tự lập thành cấp số nhân?
Lời giải
Ta có:
2
111 1
.
5 125 625 25
aa
=− − = ⇔=±
DẠNG 2. XÁC ĐỊNH CÁC ĐẠI LƯỢNG CỦA CẤP SỐ NHÂN
Vận dụng các công thức ở định nghĩa, số hạng tổng quát, tính chất của cấp số nhân.
( )
n
u
( )
n
u
( )
n
u
HỆ THỐNG BÀI TẬP.
II
PHƯƠNG PHÁP.
1
BÀI TẬP TỰ LUẬN.
2
PHƯƠNG PHÁP.
1
BÀI TẬP TỰ LUẬN.
2
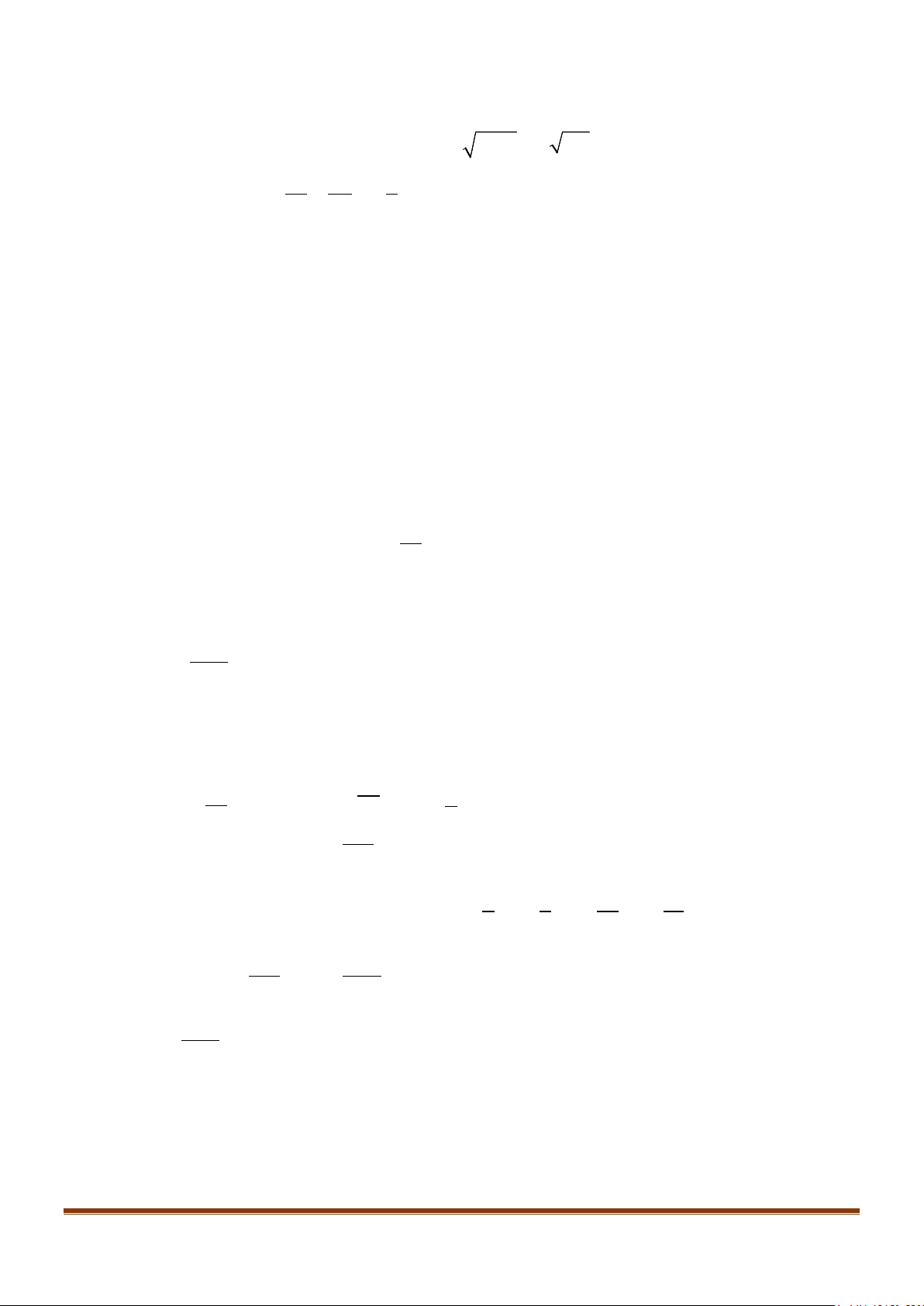
CHUYÊN ĐỀ II – TOÁN – 11 – DÃY SỐ - CẤP SỐ CỘNG – CẤP SỐ NHÂN
Page 3
Sưu tầm và biên soạn
Câu 3: Cho cấp số nhân
( )
n
u
với công bội q < 0 và
24
49
u ,u
= =
. Tìm
1
u
.
Lời giải
Vì
2
00q ,u<>
nên
3
0u
<
. Do đó
3 24
49 6
u u .u .=− =−=−
;
22
2
2
2 13 1
3
48
63
u
u u .u u
u
= ⇒= = =−
−
. Chọn đáp án A
Câu 4: Cho cấp số nhân
( )
n
u
biết
15 26
51 102u u ;u u+= +=
. Hỏi số 12288 là số hạng thứ mấy của
cấp số nhân
( )
n
u
?
Lời giải
Gọi q là công bội của cấp số nhân đã cho. Theo đề bài, ta có
( )
(
)
4
1
15
1
1
4
26
1
1 51
51
2 3 32
102
1 102
n
n
uq
uu
q u u.
uu
uq q
−
+=
+=
⇔ ⇒=⇒ =⇒ =
+=
+=
.
Mặt khác
1 1 12
12288 3 2 12288 2 2 13
nn
n
u. n
−−
= ⇔ = ⇔ = ⇔=
.
Câu 5: Cho cấp số nhân
()
n
u
thỏa:
4
38
2
27
243
u
uu
=
=
.
a) Viết năm số hạng đầu của cấp số nhân:
b) Số
2
6561
là số hạng thứ bao nhiêu của cấp số?
Lời giải
Gọi
q
là công bội của cấp số. Theo giả thiết ta có:
3
3
1
1
27
5
1
11
2
2
1
27
27
3
1
2
243.
243
uq
uq
q
u
uq uq
q
=
=
=
⇔⇔
=
=
=
a)Năm số hạng đầu của cấp số là:
12 3 4 5
22 2 2
2, , ; ,
3 9 27 81
uu u u u
= = = = =
.
b)Ta có:
18
1
22
3 6561 3 9
6561
3
n
nn
n
uu n
−
−
= ⇒ = ⇔ = = ⇒=
Vậy
2
6561
là số hạng thứ 9 của cấp số.
Câu 6: Cho tứ giác ABCD có 4 góc tạo thành 1 cấp số nhân có công bội bằng 2. Tìm 4 góc ấy
Lời giải
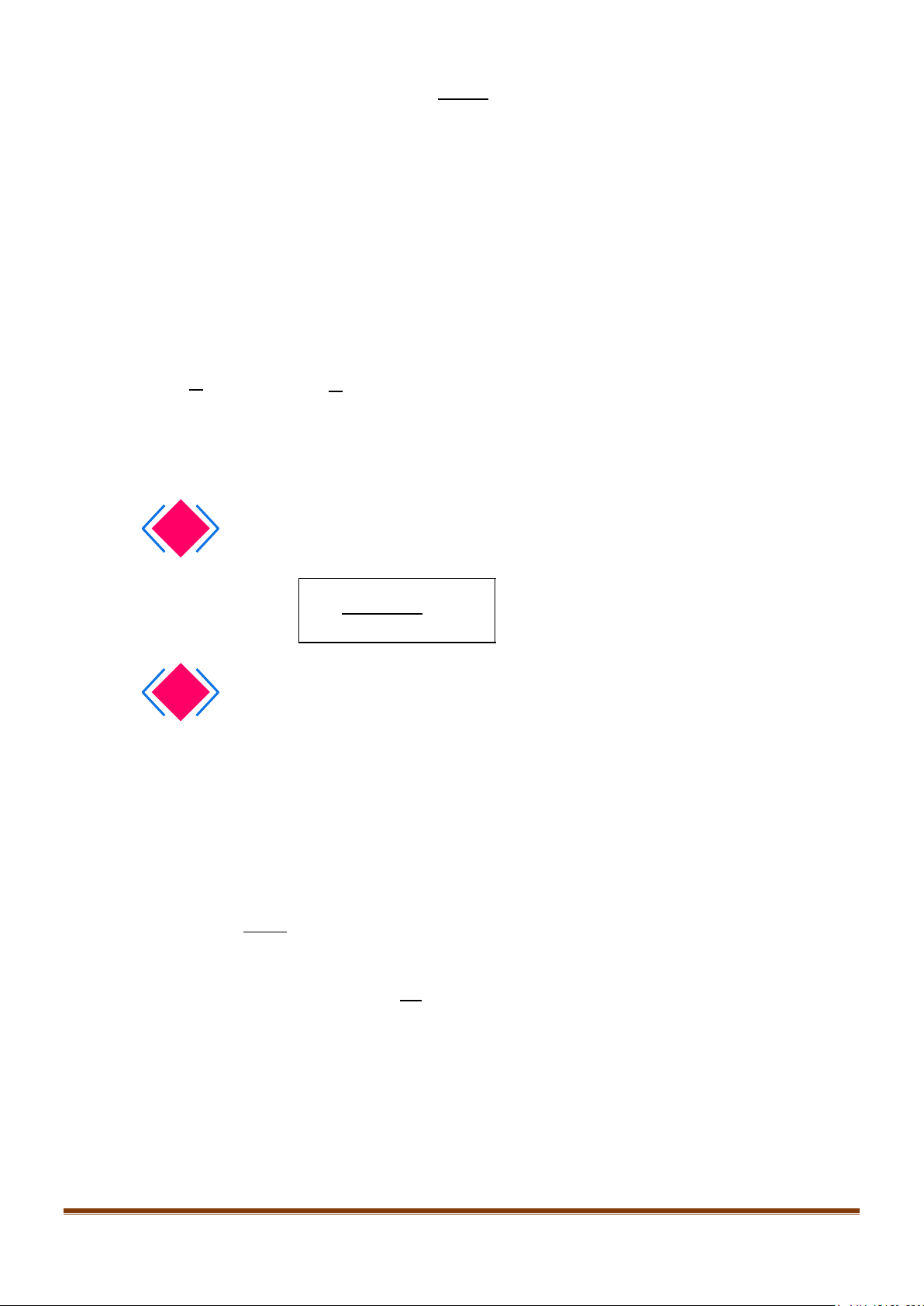
CHUYÊN ĐỀ II – TOÁN – 11 – DÃY SỐ - CẤP SỐ CỘNG – CẤP SỐ NHÂN
Page 4
Sưu tầm và biên soạn
4
0
0
0
1
1234
1
1
360
360
24
1
2
2
2
q
U
UUUU
U
q
q
q
q
−
=
+++=
=
⇔⇔
−
=
=
=
Vậy 4 góc là: 24, 48, 96, 192.
Câu 7: Cho 5 số lập thành một cấp số nhân. Biết công bội bằng một phần tư số hạng đầu tiên và tổng 2
số hạng đầu bằng 8.
Lời giải
1
2
12
11
1
1
1
8
8
4 32
4
1
1
2
4
4
1
U
UU
UU
U
qU
q
qU
q
=−
+=
+=
=
⇔⇔
=
= −
=
=
Vậy CSN là: -8, 16, -32, 64, -128; 4,4,4,4,4
DẠNG 3: TỔNG N SỐ HẠNG ĐẦU TIÊN CỦA CẤP SỐ NHÂN
Ghi nhớ công thức
( )
(
)
1
1
1
1
n
n
uq
S ,q .
q
−
= ≠
−
Câu 8: Tính tổng tất cả các số hạng của một cấp số nhân, biết số hạng đầu bằng 18, số hạng thứ hai bằng
54 và số hạng cuối bằng 39366.
Lời giải
12
18 54 3u ,u q .= = ⇒=
1 1 17
1
39366 39366 18 3 39366 3 3 8
n nn
n
u u .q . n
− −−
= ⇔ = ⇔ = ⇔ = ⇔=
.
Vậy
8
8
13
18 59040
13
S.
−
= =
−
.
Câu 9: Cho cấp số nhân
()
n
u
thỏa:
4
38
2
27
243
u
uu
=
=
.Tính tổng 10 số hạng đầu của cấp số;
Lời giải
Gọi
q
là công bội của cấp số. Theo giả thiết ta có:
PHƯƠNG PHÁP.
1
BÀI TẬP TỰ LUẬN.
2

CHUYÊN ĐỀ II – TOÁN – 11 – DÃY SỐ - CẤP SỐ CỘNG – CẤP SỐ NHÂN
Page 5
Sưu tầm và biên soạn
3
3
1
1
27
5
1
11
2
2
1
27
27
3
1
2
243.
243
uq
uq
q
u
uq uq
q
=
=
=
⇔⇔
=
=
=
Tổng 10 số hạng đầu của cấp số
10
10
10
10 1
1
1
1
3
1 59048
2. 3 1
1
1 3 19683
1
3
q
Su
q
−
−
= = =−=
−
−
.
Câu 10: Tính các tổng sau:
22 2
11 1
24 2
24 2
n
n
n
S ...
=++++++
Lời giải.
( )
24 2
24 2
24 2
24 2
11 1
22222 2
22 2
11 1
22 2 2
22 2
1
1
14 1 4 1 1
4
4 2 42
1
14 4 3 4
1
4
n
n
n
n
n
nn
n
n
S ...
... ... n
. n n.
= + ++ + ++ + + +
= + ++ + + ++ +
−
−−
= + + = −+
−
−
Câu 11:
8
8 88 888 88 8
n
n so
S ... ...=+ + ++
Lời giải.
( )
9
23
8
9 99 999 99 9
9
8
10 1 10 1 10 1 10 1
9
n
n so
n
S ...
...
= ++ +
= −+ −+ −+ + −
( )
( )
23
8
10 10 10 10
9
80 10 1
8 1 10 8
10
9 1 10 81 9
n
n
n
... n
. n n.
= + + ++ −
−
−
= −= −
−
DẠNG 4: MỘT SỐ BÀI TOÁN LIÊN QUAN ĐẾN CẤP SỐ NHÂN
PHƯƠNG PHÁP.
1
BÀI TẬP TỰ LUẬN.
2

CHUYÊN ĐỀ II – TOÁN – 11 – DÃY SỐ - CẤP SỐ CỘNG – CẤP SỐ NHÂN
Page 6
Sưu tầm và biên soạn
Câu 12: Chu kì bán rã của nguyên tố phóng xạ poloni 210 là 138 ngày. Tính khối lượng còn lại của 20
gam poloni 210 sau 7314 ngày.
Lời giải
Kí hiệu
n
u
là khối lượng còn lại của 20 gam poloni 210 sau n chu kì án rã.
Ta có 7314 ngày gồm 53 chu kì bán rã. Theo đề bài ra, ta cần tính
53
u
.
Từ giả thiết suy ra dãy (
n
u
) là một cấp số nhân với số hạng đầu là
1
20
10
2
u = =
và công bội
q=0,5. Do đó
52
15
53
1
10 2 22 10
2
u . ,.
−
= ≈
.
Câu 13: Người ta thiết kế một cái tháp gồm 11 tầng. Diện tích bề mặt trên của mỗi tầng bằng nữa diện
tích của mặt trên của tầng ngay bên dưới và diện tích mặt trên của tầng 1 bằng nửa diện tích của
đế tháp. Tính diện tích mặt trên cùng.
Lời giải
Diện tích bề mặt của mỗi tầng lập thành một cấp số nhân có công bội
1
2
q
=
và
1
12288
6 144
2
u.= =
Khi đó diện tích mặt trên cùng là
10
11 1
10
6144
6
2
u uq .= = =
Câu 14: Một du khách vào trường đua ngựa đặt cược, lần đầu đặt
20000
đồng, mỗi lần sau tiền đặt gấp
đôi lần tiền đặt cọc trước. Người đó thua
9
lần liên tiếp và thắng ở lần thứ
10.
Hỏi du khác trên
thắng hay thua bao nhiêu?
Lời giải
Số tiền du khác đặt trong mỗi lần là một cấp số nhân có
1
20 000u =
và công bội
2q.=
Du khách thua trong 9 lần đầu tiên nên tổng số tiền thua là:
( )
9
1
9 12 9
1
10220000
1
up
S u u ... u
p
−
= + ++ = =
−
Số tiền mà du khách thắng trong lần thứ
10
là
9
10 1
10240000u u .p= =
Ta có
10 9
20 000 0uS−= >
nên du khách thắng 20 000.
Câu 15: Tìm m để phương trình sau có 3 nghiệm lập thành CSN.
( ) ( )
32
5 65 6 0x mx mx m+− +− − =
Lời giải

CHUYÊN ĐỀ II – TOÁN – 11 – DÃY SỐ - CẤP SỐ CỘNG – CẤP SỐ NHÂN
Page 7
Sưu tầm và biên soạn
(
)
(
) (
)
(
)
32 2
5 65 6 0 5 6 0
2
3
x mx mx m x m x x
xm
x
x
+− +− − =⇔− + +=
=
⇔=−
= −
Để 3 nghiệm lập thành CSN xét 3 TH
TH1:
2
6
32 6 6
6
m
mm m
m
=
− < <− ⇒ = ⇔ ⇒ =−
= −
TH2:
4
32 43
3
m mm− <− < ⇒ =− ⇔ =−
TH3:
9
329 2
2
m mm<− <− ⇒ =− ⇔ =−
Vậy có 3 giá trịn của m thỏa mãn
Câu 16: Một người bắt đầu đi làm được nhận được số tiền lương là 7000000đ một tháng. Sau 36 tháng
người đó được tăng lương 7%. Hằng tháng người đó tiết kiệm 20% lương để gửi vào ngân hàng
với lãi suất 0,3%/tháng theo hình thức lãi kép. Biết rằng người đó nhận lương vào đầu tháng và
số tiền tiết kiệm được chuyển ngay vào ngân hàng.
a) Hỏi sau 36 tháng tổng số tiền người đó tiết kiệm được là bao nhiêu?
b) Hỏi sau 60 tháng tổng số tiền người đó tiết kiệm được là bao nhiêu?
Lời giải
a) Đặt
7.000.000
a =
,
20%m =
,
0,3%
n =
,
7%t =
.
Hết tháng thứ nhất, người đó có tổng số tiền tiết kiệm là
1
1
(1 )T am n= +
.
Hết tháng thứ hai, người đó có tổng số tiền tiết kiệm là
21
21
( )(1 ) (1 ) (1 )T T am n am n am n= + += + + +
.
.
Hết tháng thứ 36, người đó có tổng số tiền tiết kiệm là
36
36 35
36
(1 ) 1
(1 ) (1 ) ... (1 ) .(1 )
n
T am n am n am n am n
n
+−
=++++++= +
Thay số ta được
36
53 297 648,73T ≈
.
b) Hết tháng thứ 37, người đó có tổng số tiền tiết kiệm là
[ ]
1
37 36 36
(1 ) (1 ) .(1 ) (1 ) .(1 )T T a tm n T n a tm n= ++ += +++ +
Hết tháng thứ 38, người đó có tổng số tiền tiết kiệm là

CHUYÊN ĐỀ II – TOÁN – 11 – DÃY SỐ - CẤP SỐ CỘNG – CẤP SỐ NHÂN
Page 8
Sưu tầm và biên soạn
[ ]
22
38 37 36
(1 ) (1 ) .(1 ) (1 ) (1 ) (1 )T T a tm n T n a tm n n
= ++ += +++ +++
.
.
Hết tháng thứ 60, người đó có tổng số tiền tiết kiệm là
24 24 23
60 36
24
24
36
(1 ) (1 ) (1 ) (1 ) ... (1 )
(1 ) 1
(1 ) (1 ) .(1 ) .
T T n a tm n n n
n
T n a tm n
n
= + + + + ++ +++
+−
= + ++ +
Thay số và tính ta được tổng số tiền tiết kiệm sau 60 tháng của người đó là:
60
94 602156,59T
≈
.
CHUYÊN ĐỀ II – TOÁN – 11 – DÃY SỐ - CẤP SỐ CỘNG – CẤP SỐ NHÂN
Page 51
Sưu tầm và biên soạn
BÀI 6: CẤP SỐ NHÂN
DẠNG 1. NHẬN DIỆN CẤP SỐ NHÂN
Câu 1: Dãy số nào sau đây không phải là cấp số nhân?
A.
1; 1; 1; 1−−
. B.
1; 3; 9;10−
. C.
1; 0; 0; 0
. D.
32; 16; 8; 4
.
Câu 2: Dãy số nào sau đây không phải là cấp số nhân?
A.
1; 3;9; 27;54
−−
. B.
1;2;4;8;16
. C.
1; 1;1; 1;1
−−
. D.
1; 2;4; 8;16
−−
.
Câu 3: Trong các dãy số cho dưới đây, dãy số nào là cấp số nhân?
A.
1; 2;3;4;5
. B.
1;3;6;9;12
. C.
2; 4;6;8;10
. D.
2; 2; 2; 2; 2
.
Câu 4: Trong các dãy số sau, dãy số nào là một cấp số nhân?
A.
1;2;3;4;5;6;...
. B.
2;4;6;8;16;32;...
.
C.
2; 3; 4; 5; 6; 7;...−−−−−−
. D.
1;2;4;8;16;32;...
.
Câu 5: Trong các dãy số sau, dãy số nào là một cấp số nhân?
A.
128 64 32 16 8; ; ; ; ; ...−−
B.
22442
; ; ; ; ....
C.
5678; ; ; ; ...
D.
1
15 5 1
5
; ; ; ; ...
Câu 6: Trong các dãy số sau, dãy số nào không phải là một cấp số nhân?
A.
2 4 8 16; ; ; ;
B.
1111; ; ; ; −−
C.
2222
123; ; ; 4 ;
D.
( )
357
0a; a ; a ; a ; a .≠
Câu 7: Dãy số nào sau đây không phải là cấp số nhân?
A.
1248; ; ; ;
B.
234
33 3 3; ; ; ;
C.
11
42
24
; ; ; ;
D.
246
11 1 1
; ; ; ;
ππππ
Câu 8: Dãy số
33
n
n
u.= +
là một cấp số nhân với:
A. Công bội là 3 và số hạng đầu tiên là 1. B. Công bội là 2 và số hạng đầu tiên là 1.
C. Công bội là 4 và số hạng đầu tiên là 2. D. Công bội là 2 và số hạng đầu tiên là 2.
CHƯƠNG
II
DÃY SỐ
CẤP SỐ CỘNG – CẤP SỐ NHÂN
HỆ THỐNG BÀI TẬP TRẮC NGHIỆM.
III

CHUYÊN ĐỀ II – TOÁN – 11 – DÃY SỐ - CẤP SỐ CỘNG – CẤP SỐ NHÂN
Page 52
Sưu tầm và biên soạn
Câu 9: Cho dãy số
( )
n
u
với
3
5
2
n
n
u ..
=
Khẳng định nào sau đây đúng?
A.
( )
n
u
không phải là cấp số nhân.
B.
( )
n
u
là cấp số nhân có công bội
5q =
và số hạng đầu
1
3
2
u.
=
C.
(
)
n
u
là cấp số nhân có công bội
5q =
và số hạng đầu
1
15
2
u.
=
D.
(
)
n
u
là cấp số nhân có công bội
5
2
q =
và số hạng đầu
1
3u.=
Câu 10: Chọn cấp số nhân trong các dãy số sau:
A.
1; 0,2; 0,04; 0,0008; ...
B.
2; 22; 222;2222; ...
C.
; 2 ; 3 ; 4 ; ...xxxx
D.
24 6
1; ; ; ; ...xx x−−
Câu 11: Trong các số sau, dãy số nào là một cấp số nhân:
A.
1, 3,9, 27,81.
−−
B.
1,3,6,9,12.−−−−
C.
1,2,4,8,16.−−−−
D.
0,3,9,27,81.
Câu 12: Xác định
x
để 3 số
2; 1; 3xx x− +−
theo thứ tự lập thành một cấp số nhân:
A. Không có giá trị nào của
.x
B.
1.x = ±
C.
2.x =
D.
3.x = −
Câu 13: Xác định
x
để 3 số
2 1; ; 2 1
x xx−+
theo thứ tự lập thành một cấp số nhân:
A.
1
.
3
x = ±
B.
3.x = ±
C.
1
.
3
x = ±
D. Không có giá trị nào của
x
.
Câu 14: Trong các dãy số
( )
n
u
sau, dãy nào là cấp số nhân?
A.
2
1
n
unn= ++
. B.
( )
23
n
n
un.= +
.
C.
1
1
2
6
*
n
n
u
.
u ,n
u
+
=
= ∀∈
D.
( )
21
4
n
n
u
+
= −
.
Câu 15: Dãy số nào sau đây là cấp số nhân?
A.
1
1
1
.
1, 1
nn
u
uu n
B.
1
1
1
.
3 , 1
nn
u
u un
C.
1
1
2
.
2 3, 1
nn
u
u un
D.
1
2
.
sin , 1
1
n
u
un
n
Câu 16: Cho dãy số
n
u
với
3
.5 .
2
n
n
u
Khẳng định nào sau đây đúng?
A.
n
u
không phải là cấp số nhân.
B.
n
u
là cấp số nhân có công bội
5q
và số hạng đầu
1
3
.
2
u
C.
n
u
là cấp số nhân có công bội
5q
và số hạng đầu
1
15
.
2
u
D.
n
u
là cấp số nhân có công bội
5
2
q
và số hạng đầu
1
3.u

CHUYÊN ĐỀ II – TOÁN – 11 – DÃY SỐ - CẤP SỐ CỘNG – CẤP SỐ NHÂN
Page 53
Sưu tầm và biên soạn
Câu 17: Trong các dãy số
n
u
cho bởi số hạng tổng quát
n
u
sau, dãy số nào là một cấp số nhân?
A.
2
1
.
3
n
n
u
B.
1
1.
3
n
n
u
C.
1
.
3
n
un
D.
2
1
.
3
n
un
Câu 18: Trong các dãy số
n
u
cho bởi số hạng tổng quát
n
u
sau, dãy số nào là một cấp số nhân?
A.
7 3.
n
un
B.
7 3.
n
n
u
C.
7
.
3
n
u
n
D.
7.3 .
n
n
u
Câu 19: Cho dãy số
n
u
là một cấp số nhân với
*
0, .
n
un
Dãy số nào sau đây không phải là cấp số
nhân?
A.
135
; ; ; ...uuu
B.
12 3
3 ; 3 ; 3 ; ...uu u
C.
123
111
; ; ; ...
uuu
D.
123
2; 2; 2; ...uuu
Câu 20: Trong các dãy số
( )
n
u
sau đây, dãy số nào là cấp số nhân?
A.
n
un= 3
. B.
n
n
u = 2
. C.
n
u
n
=
1
. D.
n
n
u = +21
.
Câu 21:
n
u
được cho bởi công thức nào dưới đây là số hạng tổng quát của một cấp số nhân?
A.
1
1
2
n
n
u
+
=
. B.
2
1
2
n
un= −
. C.
1
1
2
n
n
u = −
. D.
2
1
2
n
un= +
.
Câu 22: Trong các dãy số sau, dãy nào là cấp số nhân?
A.
( )
1
n
n
un
= −
. B.
2
n
un=
. C.
2
n
n
u =
. D.
3
n
n
n
u =
.
Câu 23: Cho dãy số
n
u
có số hạng tổng quát là
1*
3.2
n
n
un
. Chọn kết luận đúng:
A. Dãy số là cấp số nhân có số hạng đầu
1
12u
.
B. Dãy số là cấp số cộng có công sai
2
d
.
C. Dãy số là cấp số cộng có số hạng đầu
1
6u
.
D. Dãy số là cấp số nhân có công bội
3
q
.
Câu 24: Dãy nào sau đây là một cấp số nhân?
A.
1, 2,3, 4,...
. B.
1,3,5,7,...
. C.
2, 4,8,16,...
. D.
2, 4,6,8,...
Câu 25: Cho dãy số:
1 11 1
1; ; ; ;
3 9 27 81
−− −
. Khẳng định nào sau đây là sai?
A. Dãy số không phải là một cấp số nhân.
B. Dãy số này là cấp số nhân có
1
1
1; q=
3
=−−u
.
C. Số hạng tổng quát.
(
)
1
1
1.
3
−
= −
n
n
n
u
D. Là dãy số không tăng, không giảm.
Câu 26: Tập hợp các giá trị x thỏa mãn
,2 , 3x xx+
theo thứ tự lập thành một cấp số nhân là
A.
{ }
0;1
. B.
∅
. C.
{ }
1
. D.
{ }
0

CHUYÊN ĐỀ II – TOÁN – 11 – DÃY SỐ - CẤP SỐ CỘNG – CẤP SỐ NHÂN
Page 54
Sưu tầm và biên soạn
Câu 27: Có bao nhiêu giá trị nguyên dương của
x
để ba số
1; ; 2xx+
theo thứ tự đó lập thành một cấp số
nhân?
A.
2
. B.
1
. C.
3
. D.
0
.
Câu 28: Tìm tất cả các giá trị của
x
để ba số
2 1, , 2 1
x xx−+
theo thứ tự đó lập thành một cấp số nhân.
A.
1
3
x = ±
B.
1
3
x
= ±
C.
3x = ±
D.
3x = ±
Câu 29: Trong các phát biểu sau, phát biểu nào là sai?
A. Dãy số có tất cả các số hạng bằng nhau là một cấp số nhân.
B. Dãy số có tất cả các số hạng bằng nhau là một cấp số cộng.
C. Một cấp số cộng có công sai dương là một dãy số tăng.
D. Một cấp số cộng có công sai dương là một dãy số dương.
Câu 30: Xác định
x
dương để
23−x
;
x
;
23+x
lập thành cấp số nhân.
A.
3x
=
. B.
3x =
.
C.
3x = ±
. D. không có giá trị nào của
x
.
Câu 31: Giả sử
sin
6
α
,
cos
α
,
tan
α
theo thứ tự đó là một cấp số nhân. Tính
cos 2
α
.
A.
3
2
. B.
3
2
−
. C.
1
2
. D.
1
2
−
.
Câu 32: Cho dãy số có các số hạng đầu là
234
11 1 1
; ; ; ;...
3
333
Số hạng tổng quát của dãy số này là
A.
1
1
3
n−
B.
2
1
3
n+
. C.
1
3
n
. D.
1
1
3
n+
.
Câu 33: Cho cấp số nhân
( )
n
u
với
1
3
u =
và công bội
2q =
. Số hạng tổng quát
n
u
( )
2n ≥
bằng
A.
3.2
n
. B.
2
3.2
n+
. C.
1
3.2
n+
. D.
1
3.2
n−
.
Câu 34: Cho dãy số
( )
n
u
biết
1
*
1
3
,
3
nn
u
nN
uu
+
=
∀∈
=
. Tìm số hạng tổng quát của dãy số
( )
n
u
.
A.
3=
n
n
u
. B.
1+
=
n
n
un
. C.
1
3
+
=
n
n
u
. D.
1
3
−
=
n
n
u
.
Câu 35: Cho dãy số
(
)
n
u
thỏa mãn
1 12 2
*
1
33 6
2,
nn
u uu u
u un
+
= −++
= ∀∈
. Tìm giá trị nhỏ nhất của
n
để
2021
2
n
u ≥
.
A.
2021
. B.
1012
. C.
2022
. D.
1011
.
DẠNG 2. TÌM CÔNG THỨC CỦA CẤP SỐ NHÂN
Câu 36: Cho cấp số nhân
()
n
u
với
1
1u =
và
2
2u =
. Công bội của cấp số nhân đã cho là
A.
1
2
q =
. B.
2q =
. C.
2q = −
. D.
1
2
q = −
.
Câu 37: Cho cấp số nhân
( )
n
u
với
1
3u =
và
2
9u =
. Công bội của cấp số nhân đã cho bằng
A.
6−
. B.
1
3
. C.
3
. D.
6
.

CHUYÊN ĐỀ II – TOÁN – 11 – DÃY SỐ - CẤP SỐ CỘNG – CẤP SỐ NHÂN
Page 55
Sưu tầm và biên soạn
Câu 38: Cho cấp số nhân
( )
n
u
với
1
3
u =
và
2
12
u =
. Công bội của cấp số nhân đã cho bằng
A.
9
. B.
9
−
. C.
1
4
. D.
4
.
Câu 39: Cho cấp số nhân
()
n
u
với
1
3
u
=
và
2
15.u =
Công bội của cấp số nhân đã cho bằng
A.
12−
. B.
1
5
. C.
5
. D.
12
.
Câu 40: Cho cấp số nhân
( )
n
u
với
1
2=
u
và
2
6=u
. Công bội của cấp số nhân đã cho bằng
A.
3
. B.
4
−
. C.
4
. D.
1
3
.
Câu 41: Cho cấp số nhân
( )
n
u
với
1
3u
=
và công bội
2q =
. Giá trị của
2
u
bằng
A.
8
. B.
9
. C.
6
. D.
3
2
.
Câu 42: Cho cấp số nhân
( )
n
u
với
1
2u =
và công bội
3q =
. Giá trị của
2
u
bằng
A.
6
. B.
9
. C.
8
. D.
2
3
.
Câu 43: Cho cấp số nhân
(
)
n
u
với
1
3u =
và công bội
4q =
. Giá trị của
2
u
bằng
A.
64
. B.
81
. C.
12
. D.
3
4
.
Câu 44: Tìm công bội
q
của một cấp số nhân
( )
n
u
có
1
1
2
u =
và
6
16u =
.
A.
1
2
q =
. B.
2q = −
. C.
2q
=
. D.
1
2
q = −
.
Câu 45: Cho cấp số nhân
( )
n
u
, biết
1
1u =
,
4
64u =
. Tính công bội
q
của cấp số nhân đã cho
A.
4q =
. B.
4
q = −
. C.
21q =
. D.
22q =
.
Câu 46: Cho cấp số nhân
n
u
có
1
2u
và
5
162u
.Công bội
q
bằng:
A.
3q
. B.
3q
. C.
3; 3qq
. D.
2q
.
Câu 47: Cho cấp số nhân
( )
n
u
có
1
2u =
và
4
54u =
. Giá trị của công bội
q
bằng
A.
3
. B.
9
. C.
27
. D.
3−
.
Câu 48: Cho cấp số nhân
( )
n
u
với
1
2u
=
và công bội
3q =
. Tìm số hạng thứ
4
của cấp số nhân?
A.
24
. B.
54
. C.
162
. D.
48
.
Câu 49: : Cấp số nhân
( )
n
u
có
45
9, 81uu= =
có công bội là
A.
3
. B.
72
. C.
18
. D.
9
.
Câu 50: Tìm công bội
q
của một cấp số nhân
( )
n
u
có
1
1
2
u =
và
6
16u =
.
A.
1
2
q =
. B.
2q = −
. C.
2q =
. D.
1
2
q = −
.
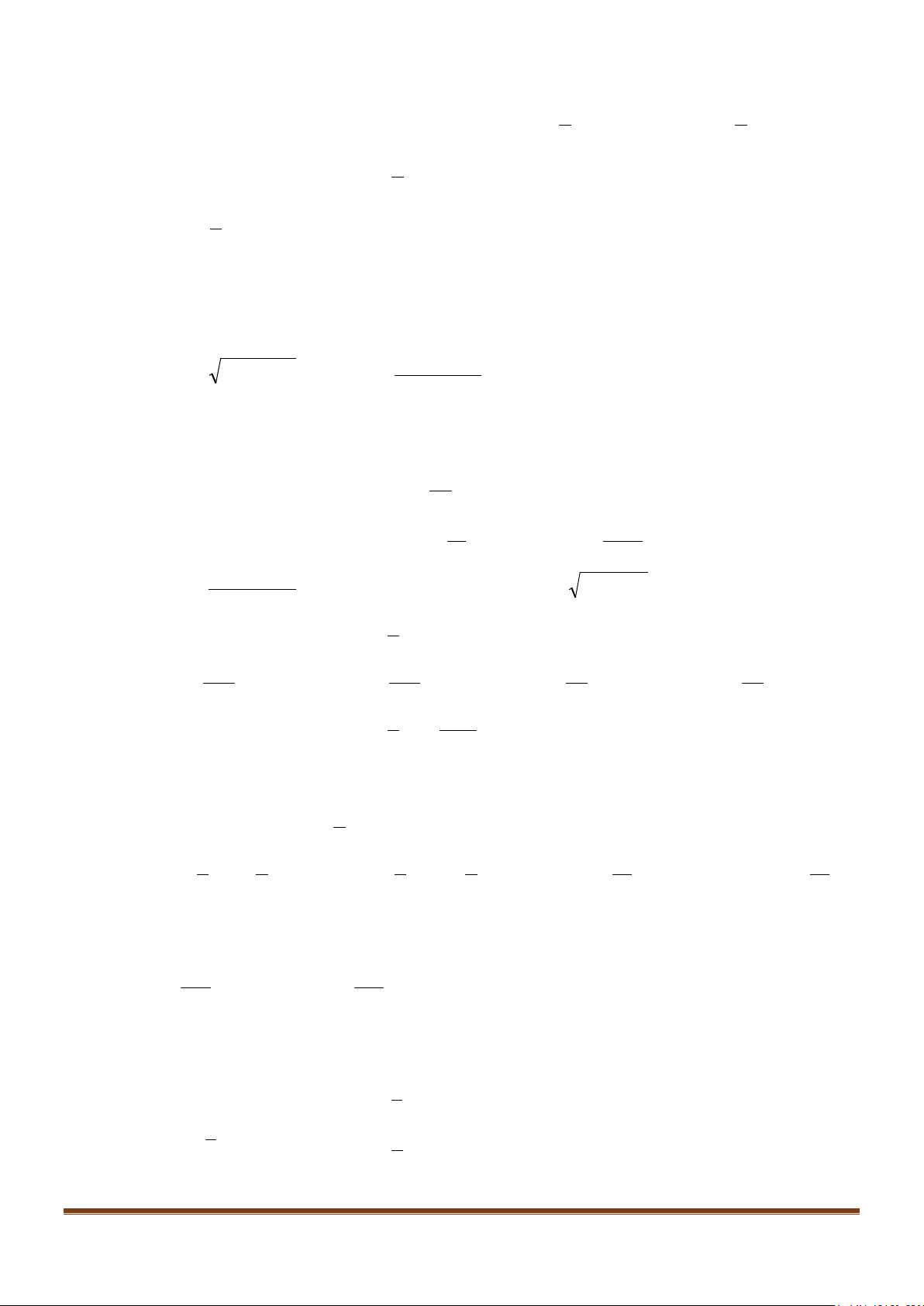
CHUYÊN ĐỀ II – TOÁN – 11 – DÃY SỐ - CẤP SỐ CỘNG – CẤP SỐ NHÂN
Page 56
Sưu tầm và biên soạn
Câu 51: Cho cấp số nhân
(
)
n
u
có số hạng đầu
1
2u =
và
6
486
u
=
. Công bội q bằng
A.
3
q =
. B.
5q =
. C.
3
2
q =
. D.
2
3
q =
.
Câu 52: Cho cấp số nhân
( )
n
u
với
17
1
; u 32
2
=−=−
u
. Tìm q ?
A.
1
2
= ±q
. B.
2
= ±q
. C.
4= ±q
. D.
1= ±q
.
Câu 53: Biết ba số
2
; 8;
xx
theo thứ tự lập thành cấp số nhân. Giá trị của
x
bằng
A.
4x
B.
5x
C.
2x
D.
1x
Câu 54: Cho cấp số nhân
( )
n
u
có công bội
q
. Chọn hệ thức đúng trong các hệ thức sau:
A.
21
.
++
=
kkk
uuu
B.
2
11 +−
+
=
kk
k
uu
u
.
C.
1
1
..
k
k
u uq
−
=
D.
( )
1
1.
k
uu k q=+−
Câu 55: Cho dãy số
( )
n
u
xác định bởi:
−
=
−=
+
n
n
u
u
u
.
10
1
2
1
1
. Chọn hệ thức đúng:
A.
( )
n
u
là cấp số nhân có công bội
1
.
10
q = −
B.
1
1
( 2) .
10
n
n
u
−
= −
C.
2
1
1 +−
+
=
nn
n
uu
u
( )
2n ≥
. D.
11
.
+−
=
nn
n
uu
u
( )
2n ≥
.
Câu 56: Cho cấp số nhân có
1
3u
= −
,
2
3
q =
. Tính
5
?u
A.
5
27
.
16
u
−
=
B.
5
16
.
27
u
−
=
C.
5
16
.
27
u
=
D.
5
27
.
16
u
=
Câu 57: Cho cấp số nhân có
1
3
u = −
,
2
3
q =
. Số
243
96−
là số hạng thứ mấy của cấp số này?
A. Thứ 5. B. Thứ 6.
C. Thứ 7. D. Không phải là số hạng của cấp số.
Câu 58: Cho cấp số nhân có
2
1
4
u =
;
5
16u =
. Tìm
q
và
1
u
.
A.
1
11
; .
22
qu= =
B.
1
11
; .
22
qu=−=−
C.
1
1
4; .
16
qu
= =
D.
1
1
4; .
16
qu=−=−
Câu 59: Với
x
là số nguyên dương, ba số
2,3 3,5 5xx x++
theo thứ tự là ba số hạng liên tiếp của một
cấp số nhân. Số hạng tiếp theo của cấp số nhân đó là
A.
250
3
−
. B.
250
3
. C.
250
. D.
250−
.
Câu 60: Cho ba số thực
,,xyz
trong đó
0x ≠
. Biết rằng
,2 ,3xyz
lập thành cấp số cộng và
,,xyz
lập
thành cấp số nhân; tìm công bội
q
của cấp số nhân đó.
A.
1
1
3
q
q
=
=
B.
1
3
2
3
q
q
=
=
C.
2q =
D.
1q =

CHUYÊN ĐỀ II – TOÁN – 11 – DÃY SỐ - CẤP SỐ CỘNG – CẤP SỐ NHÂN
Page 57
Sưu tầm và biên soạn
DẠNG 3. TÌM HẠNG TỬ TRONG CẤP SỐ NHÂN
Câu 61: Cho cấp số nhân
( )
n
u
có
1
2u = −
và công bội
3q =
. Số hạng
2
u
là:
A.
2
6u
= −
. B.
2
6u
=
. C.
2
1u
=
. D.
2
18u
= −
.
Câu 62: Cho cấp số nhân
( )
n
u
có
5
2u =
và
9
6u =
. Tính
21
u
.
A.
18
. B.
54
. C.
162
. D.
486
.
Câu 63: Cho cấp số nhân
(
)
n
u
có số hạng đầu
1
2u =
và công bội
5
q
=
. Giá trị của
68
uu
bằng
A.
6
2.5
. B.
7
2.5
. C.
8
2.5
. D.
5
2.5
.
Câu 64: Cho cấp số nhân
(
)
n
u
có
1
3u =
, công bội
2
q =
. Ta có
5
u
bằng
A.
24
. B.
11
. C.
48
. D.
9
.
Câu 65: Cho cấp số nhân
( )
n
u
có công bội dương và
2
1
4
u =
,
4
4u =
. Giá trị của
1
u
là
A.
1
1
6
u =
. B.
1
1
16
u =
. C.
1
1
16
u = −
. D.
1
1
2
u =
.
Câu 66: Cho cấp số nhân
( )
n
u
có số hạng đầu
1
2u
=
và công bội
3
q
=
. Giá trị
2019
u
bằng
A.
2018
2.3
. B.
2018
3.2
. C.
2019
2.3
. D.
2019
3.2
.
Câu 67: Cho cấp số nhân
( )
1
; 1, 2
n
uu q= =
. Hỏi số
1024
là số hạng thứ mấy?
A.
11
. B.
9
. C.
8
. D.
10
.
Câu 68: Cho cấp số nhân
( )
n
u
có số hạng đầu
1
5u =
và công bội
2q = −
. Số hạng thứ sáu của
( )
n
u
là
A.
6
320u
=
. B.
6
160u = −
. C.
6
320u = −
. D.
6
160u =
.
Câu 69: Tìm số hạng đầu
1
u
của cấp số nhân
( )
n
u
biết rằng
123
168
uuu++=
và
456
21uuu++=
A.
1
24u =
. B.
1
1334
11
u =
. C.
1
96u =
. D.
1
217
3
u =
.
Câu 70: Cho dãy số
( )
n
u
xác định bởi
1
1
1
25
nn
u
uu
+
=
= +
. Tính số hạng thứ
2018
của dãy số trên
A.
2017
2018
6.2 5
u = −
. B.
2018
2018
6.2 5
u = −
. C.
2017
2018
6.2 1u = +
. D.
2018
2018
6.2 5u = +
.
Câu 71: Cho
( )
n
u
là cấp số nhân, công bội
0.q >
Biết
13
1, 4 .uu
= =
Tìm
4
u
.
A.
11
2
. B.
2.
C.
16.
D.
8.
Câu 72: Cho cấp số nhân
( )
,1≥
n
un
với công bội
2q =
và có số hạng thứ hai
2
5.
=u
Số hạng thứ
7
của
cấp số nhân là
A.
7
320=u
. B.
7
640=u
. C.
7
160=u
. D.
7
80=u
.
Câu 73: Cho một cấp số nhân có số hạng thứ
4
gấp
4096
lần số hạng đầu tiên. Tổng hai số hạng đầu tiên
là 34. Số hạng thứ
3
của dãy số có giá trị bằng:
A.
1
. B.
512
. C.
1024
. D.
32
.
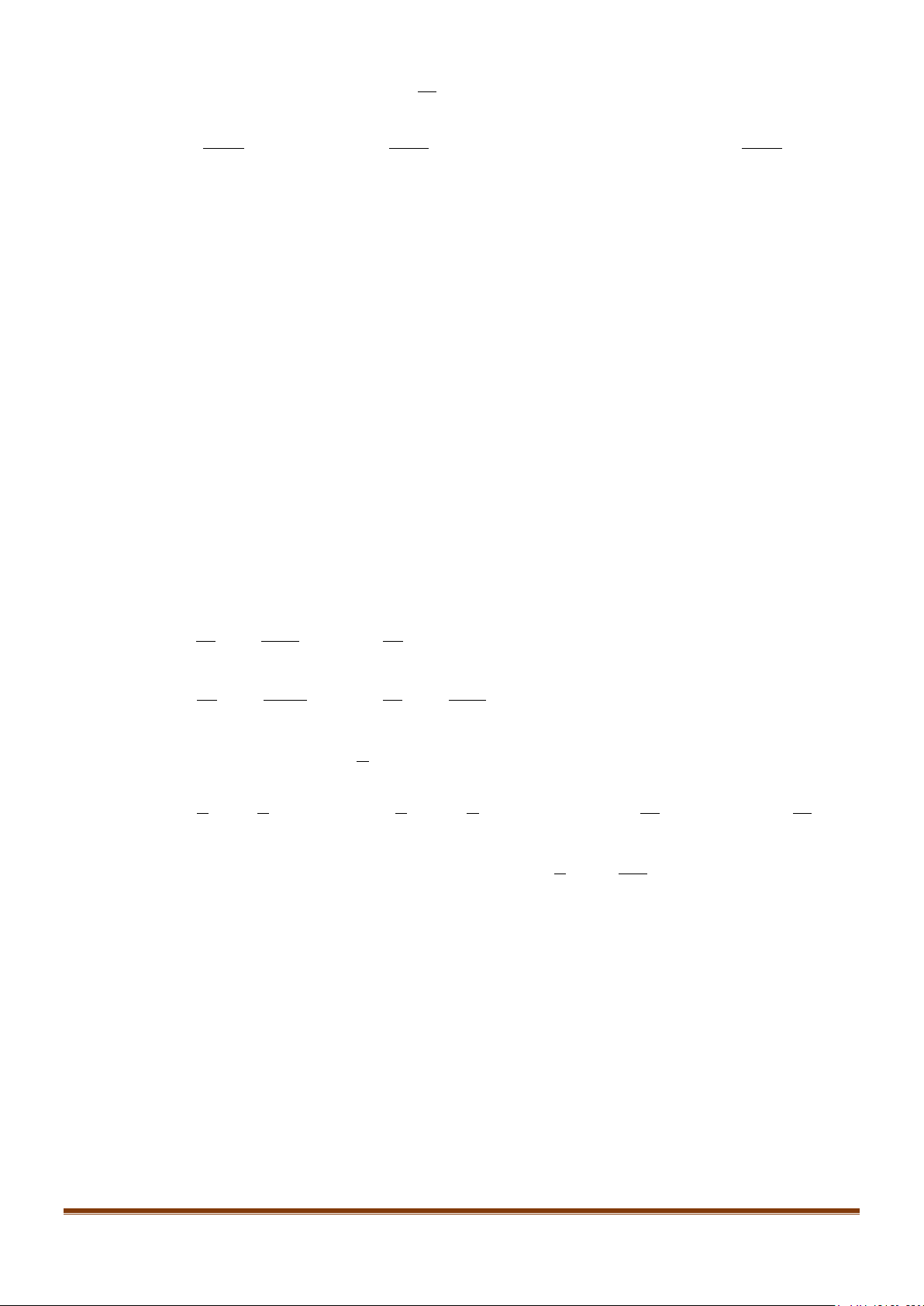
CHUYÊN ĐỀ II – TOÁN – 11 – DÃY SỐ - CẤP SỐ CỘNG – CẤP SỐ NHÂN
Page 58
Sưu tầm và biên soạn
Câu 74: Cho cấp số nhân
( )
n
u
, biết
1
12u =
,
3
8
243
u
u
=
. Tìm
9
u
.
A.
9
2
2187
u =
. B.
9
4
6563
u =
. C.
9
78732u =
. D.
9
4
2187
u =
.
Câu 75: Cho cấp số nhân
( )
n
u
có tổng
n
số hạng đầu tiên là
51
n
n
S = −
với
1,2,...
n
=
. Tìm số hạng đầu
1
u
và công bội
q
của cấp số nhân đó?
A.
1
5
u =
,
4q =
. B.
1
5u =
,
6
q =
. C.
1
4u =
,
5q =
. D.
1
6u =
,
5q =
.
Câu 76: Cho cấp số nhân
( )
n
u
biết
42
53
54
108
uu
uu
−=
−=
. Tìm số hạng đầu
1
u
và công bội
q
của cấp số nhân
trên.
A.
1
9u =
;
2q =
. B.
1
9u
=
;
2q = −
. C.
1
9u = −
;
2q = −
. D.
1
9u = −
;
2q =
.
Câu 77: Xen giữa số
3
và số
768
là
7
số để được một cấp số nhân có
1
3u =
. Khi đó
5
u
là:
A.
72
. B.
48−
. C.
48±
. D.
48
.
Câu 78: Cấp số nhân
( )
n
u
có
20 17
15
8
.
272
uu
uu
=
+=
Tìm
1
u
, biết rằng
1
100u ≤
.
A.
1
16.
u =
B.
1
2.
u =
C.
1
16.u = −
D.
1
2.u = −
Câu 79: Cho cấp số nhân
1
1u = −
,
6
0,00001
u
=
. Khi đó
q
và số hạng tổng quát là?
A.
1
10
q =
,
1
1
10
n
n
u
−
−
=
. B.
1
10
q
−
=
,
1
10
n
n
u
−
= −
.
C.
1
10
q
−
=
,
( )
1
1
10
n
n
n
u
−
−
=
. D.
1
10
q =
,
1
1
10
n
n
u
−
=
.
Câu 80: Cho cấp số nhân
n
u
có
2
1
4
u =
,
5
16u =
. Tìm công bội
q
và số hạng đầu
1
u
.
A.
1
2
q =
,
1
1
2
u =
. B.
1
2
q = −
,
1
1
2
u = −
. C.
4q = −
,
1
1
16
u
= −
. D.
4q =
,
1
1
16
u =
.
Câu 81: Cho cấp số nhân có số hạng đầu
1
2,
u = −
công bội
3
4
q =
. Số
81
128
−
là số hạng thứ mấy của cấp
số này?
A.
5
. B.
4
. C.
6
. D.
3
.
Câu 82: Cho dãy số
4,12,36,108,324,...
. Số hạng thứ 10 của dãy số đó là?
A.
73872
. B.
77832
. C.
72873
. D.
78732
.
Câu 83: Cho tứ giác
ABCD
có bốn góc tạo tành cấp số nhân có công bội
2
q =
, góc có số đo nhỏ nhất
trong bốn góc đó là:
A.
0
1
B.
0
30
C.
0
12
D.
0
24
Câu 84: Cho cấp số nhân
( )
n
u
thỏa mãn
135
17
65
325
uuu
uu
−+=
+=
. Tính
3
.u
A.
3
15u =
. B.
3
25u =
. C.
3
10u =
. D.
3
20u =
.

CHUYÊN ĐỀ II – TOÁN – 11 – DÃY SỐ - CẤP SỐ CỘNG – CẤP SỐ NHÂN
Page 59
Sưu tầm và biên soạn
Câu 85: Cho cấp số nhân
( )
n
u
có tổng
n
số hạng đầu tiên là
61
n
n
S = −
. Tìm số hạng thứ năm của cấp
số nhân đã cho.
A. 120005. B. 6840. C. 7775. D. 6480.
Câu 86: Cho dãy số
( )
n
u
xác định bởi
1
1
1
.
25
nn
u
uu
+
=
= +
Tìm số hạng thứ
2020
của dãy.
A.
2020
2020
3.2 5.u = −
B.
2019
2020
3.2 5.u = +
C.
2019
2020
3.2 5.u = −
D.
2020
2020
3.2 5.
u = +
Câu 87: Số hạng đầu và công bội
q
của CSN với
7 10
5, 135uu=−=
là:
A.
1
5
,3
729
uq= = −
. B.
1
5
,3
729
uq=−=
. C.
1
5
,3
729
uq= =
. D.
1
5
,3
729
uq=−=−
.
Câu 88: Cho dãy số
( )
n
u
được xác định bởi
1
2
u =
;
1
2 31
nn
uu n
−
= +−
. Tìm số hạng thứ
2019
của dãy
số.
A.
2019
2019
5.2 6062.u = −
B.
2019
2019
5.2 6062.u = +
C.
2020
2019
5.2 6062.u = −
D.
2020
2019
5.2 6062.u = +
Câu 89: Cho dãy số
n
u
xác định bởi
11
2
34
1; , 1
2 32
nn
n
uu u n
nn
. Giá trị của
50
u
gần nhất
với số nào dưới đây?
A.
312540600
. B.
312540500
. C.
212540500
. D.
212540600
.
DẠNG 4. TÍNH TỔNG VÀ MỘT SỐ BÀI TOÁN LIÊN QUAN
Câu 90: Cho cấp số nhân
( )
n
u
có
1
3u = −
và
2q = −
. Tính tổng
10
số hạng đầu tiên của cấp số nhân.
A.
10
511S = −
. B.
10
1023S =
. C.
10
1025S =
. D.
10
1025S = −
.
Câu 91: Cho một cấp số nhân có các số hạng đều không âm thỏa mãn
2
6u =
,
4
24u =
. Tính tổng của
12
số hạng đầu tiên của cấp số nhân đó.
A.
12
3.2 3−
. B.
12
21−
. C.
12
3.2 1−
. D.
12
3.2
.
Câu 92: Cho dãy
( )
n
u
với
1
1
2
n
n
u
= +
,
*
n∀∈
. Tính
2019 1 2 3 2019
...S uu u u= + + ++
, ta được kết quả
A.
2019
1
2020
2
−
. B.
4039
2
. C.
2019
1
2019
2
+
. D.
6057
2
.
Câu 93: Cho cấp số nhân
( )
n
u
có
3
12u =
,
5
48u =
, có công bội âm. Tổng
7
số hạng đầu của cấn số nhân
đã cho bằng
A.
129
. B.
129−
. C.
128
. D.
128−
.
Câu 94: Cho
( )
n
u
là cấp số nhân, đặt
12
...
nn
S uu u= + ++
. Biết
23
4; 13SS= =
và
2
0u <
, giá trị
5
S
bằng
A.
2
. B.
181
16
. C.
35
16
. D.
121
.

CHUYÊN ĐỀ II – TOÁN – 11 – DÃY SỐ - CẤP SỐ CỘNG – CẤP SỐ NHÂN
Page 60
Sưu tầm và biên soạn
Câu 95: Giá trị của tổng
2 2018
1 3 3 ... 3
S =++ + +
bằng
A.
2019
31
2
S
−
=
. B.
2018
31
2
S
−
=
. C.
2020
31
2
S
−
=
. D.
2018
31
2
S
−
= −
.
Câu 96: Biết rằng
2 10
21.3
1 2.3 3.3 ... 11.3 .
4
b
Sa=+ + ++ =+
Tính
.
4
b
Pa= +
A.
1.P
B.
2.P
C.
3.P
D.
4.P
Câu 97: Cho cấp số nhân
(
)
n
u
có
2
4S =
và
3
13.S
=
Tìm
5
.S
A.
5
121S =
hoặc
5
181
.
16
S =
B.
5
121
S
=
hoặc
5
35
.
16
S =
C.
5
114S =
hoặc
5
185
.
16
S =
D.
5
141S =
hoặc
5
183
.
16
S
=
Câu 98: Cho cấp số nhân
( )
n
u
có
1
8
u
=
và biểu thức
32 1
4 2 15uu u+−
đạt giá trị nhỏ nhất. Tính
10
.S
A.
( )
11
10
9
24 1
5.4
S
+
=
. B.
( )
10
10
8
24 1
5.4
S
+
=
. C.
10
10
6
21
3.2
S
−
=
. D.
11
10
7
21
3.2
S
−
=
Câu 99: Cho cấp số nhân
( )
n
u
có
1
2,u =
công bội dương và biểu thức
4
7
1024
u
u
+
đạt giá trị nhỏ nhất.
Tính
11 12 20
... .
Su u u
= + ++
A.
2046.S =
B.
2097150.S =
C.
2095104.S =
D.
1047552.S
=
Câu 100: Cho cấp số nhân
( )
n
u
có
46
35
540
180
uu
uu
+=−
+=
. Tính
21
.S
A.
( )
21
21
1
31
2
S = +
B.
21
21
3 1.S
= −
C.
21
21
1 3.S = −
D.
( )
21
21
1
3 1.
2
S =−+
Câu 101: Cho cấp số nhân có các số hạng lần lượt là
1; 4; 16; 64;
Gọi
n
S
là tổng của
n
số hạng đầu tiên
của cấp số nhân đó. Mệnh đề nào sau đây đúng?
A.
1
4.
n
n
S
B.
1
14
.
2
n
n
n
S
C.
41
.
3
n
n
S
D.
44 1
.
3
n
n
S
Câu 102: Cho cấp số nhân có các số hạng lần lượt là
11
; ; 1; ; 2048.
42
Tính tổng
S
của tất cả các số hạng
của cấp số nhân đã cho.
A.
2047,75.S
B.
2049,75.S
C.
4095,75.S
D.
4096,75.S
Câu 103: Số thập phân vô hạn tuần hoàn
(
)
3,1555... 3,1 5=
viết dưới dạng số hữu tỉ là:
A.
63
20
. B.
142
45
. C.
1
18
. D.
7
2
.
Câu 104: Tính tổng
( )
1
2
11 1
1 ... 1 ...
66 6
n
n
S
−
=−+ − + +− +
A.
7
6
S =
B.
6
7
S
= −
C.
6
7
S =
D.
7
6
S = −

CHUYÊN ĐỀ II – TOÁN – 11 – DÃY SỐ - CẤP SỐ CỘNG – CẤP SỐ NHÂN
Page 61
Sưu tầm và biên soạn
Câu 105: Số thập phân vô hạn tuần hoàn
0,121212...
được biểu diễn bởi phân số
A.
3
25
. B.
12
99
. C.
1
11
. D.
3
22
.
Câu 106: Viết thêm bốn số vào giữa hai số
160
và
5
để được một cấp số nhân. Tổng các số hạng của cấp
số nhân đó là
A.
215
. B.
315
. C.
415
. D.
515
.
Câu 107: Cho cấp số nhân
(
)
n
u
thỏa mãn
123
41
13
26
uuu
uu
++=
−=
. Tổng
8
số hạng đầu của cấp số nhân
(
)
n
u
là
A.
8
1093S =
. B.
8
3820S
=
. C.
8
9841S =
. D.
8
3280S
=
.
Câu 108: Tổng
2
11 1
33 3
n
S = + +⋅⋅⋅+ +⋅⋅⋅
có giá trị là:
A.
1
9
. B.
1
4
. C.
1
3
. D.
1
2
.
Câu 109: Cho dãy số
(
)
n
a
xác định bởi
1
2a =
,
1
2
nn
aa
+
= −
,
1n ≥
,
n ∈
. Tính tổng của
10
số hạng đầu
tiên của dãy số.
A.
2050
3
. B.
2046
. C.
682−
. D.
2046−
.
Câu 110: Tính tổng tất cả các số hạng của một cấp số nhân có số hạng đầu là
1
2
, số hạng thứ tư là
32
và
số hạng cuối là
2048
?
A.
1365
2
. B.
5416
2
. C.
5461
2
. D.
21845
2
.
Câu 111: Một cấp số nhân
( )
n
u
có
n
số hạng, số hạng đầu
1
7
u
=
, công bội
2q =
. Số hạng thứ
n
bằng
1792
. Tính tổng
n
số hạng đầu tiên của cấp số nhân
( )
n
u
?
A.
5377
. B.
5737
. C.
3577
. D.
3775
.
Câu 112: Tính tổng cấ số nhân lùi vô hạn
( )
2
1
11 1
, , ,..., ,...
24 8 2
n
−
−−
là.
A.
1−
. B.
1
2
. C.
1
4
−
. D.
1
3
−
.
Câu 113: Giá trị của tổng
7 77 777 ... 77...7
bằng
A.
2018
70
10 1 2018
9
. B.
2018
7 10 10
2018
99
.
C.
2019
7 10 10
2018
99
. D.
2018
7
10 1
9
.
Câu 114: Giá trị của tổng
4 44 444 ... 44...4+ + ++
bằng
A.
( )
2018
40
10 1 2018
9
−+
. B.
2019
4 10 10
2018
99
−
−
.
C.
2019
4 10 10
2018
99
−
+
. D.
( )
2018
4
10 1
9
−
.

CHUYÊN ĐỀ II – TOÁN – 11 – DÃY SỐ - CẤP SỐ CỘNG – CẤP SỐ NHÂN
Page 62
Sưu tầm và biên soạn
Câu 115: Cho dãy số xác định bởi
1
1u =
,
*
1
2
11
2 ;
3 32
nn
n
uu n
nn
+
−
=+∈
++
. Khi đó
2018
u
bằng:
A.
2016
2018
2017
21
3 2019
u = +
. B.
2018
2018
2017
21
3 2019
u = +
.
C.
2017
2018
2018
21
3 2019
u = +
.
D.
2017
2018
2018
21
3 2019
u
= +
.
Câu 116: Cho dãy số
(
)
n
U
xác định bởi:
1
1
3
U =
và
1
1
.
3
nn
n
UU
n
+
+
=
. Tổng
3 10
2
1
...
2 3 10
UU
U
SU= + + ++
bằng:
A.
3280
6561
. B.
29524
59049
. C.
25942
59049
. D.
1
243
.
Câu 117: Cho dãy số
()
n
u
thỏa mãn
1
1
1
2 1; 2
nn
u
uu n
−
=
= +≥
. Tổng
1 2 20
...Suu u= + ++
bằng
A.
20
2 20.
−
B.
21
2 22.
C.
20
2.
D.
21
2 20.−
DẠNG 5. KẾT HỢP CẤP SỐ NHÂN VÀ CẤP SỐ CỘNG
Câu 118: Ba số theo thứ tự lập thành một cấp số nhân có số hạng cuối lớn hơn số hạng đầu
16
đơn vị. Ba
số đó là các số hạng thứ nhất, thứ hai và thứ năm của một cấp số cộng. Tìm ba số đó.
A.
2,6,18
. B.
4,8, 20
. C.
1 7 49
,,
33 3
. D.
4,4 5,20
.
Câu 119: Ba số dương
,,xyz
theo thứ tự lập thành một cấp số cộng và có tổng bằng
30
. Biết
2; 2; 18xyz+++
theo thứ tự lập thành một cấp số nhân. Tính
22
.Tx z
= +
A.
328.T =
B.
424.T =
C.
296.T =
D.
428.T =
Câu 120: Ba số
,,xyz
theo thứ tự lập thành một cấp số cộng tăng có tổng bằng
24
. Nếu cộng thêm lần
lượt các số
1, 4, 13
vào ba số
,,xyz
ta được ba số theo thứ tự lập thành cấp số nhân. Tính giá trị
biểu thức
2 22
Px y z
=++
.
A.
200
. B.
210
. C.
220
. D.
190
.
Câu 121: Ba số theo thứ tự lập thành một cấp số nhân có số hạng cuối lớn hơn số hạng đầu
16
đơn vị. Ba
số đó là các số hạng thứ nhất, thứ hai và thứ năm của một cấp số cộng. Tìm ba số đó.
A.
2,6,18
. B.
4,8, 20
. C.
1 7 49
,,
33 3
. D.
4,4 5,20
.
Câu 122: Cho ba số
a
,
b
,
c
là ba số liên tiếp của một cấp số cộng có công sai là
2
. Nếu tăng số thứ nhất
thêm
1
, tăng số thứ hai thêm
1
và tăng số thứ ba thêm
3
thì được ba số mới là ba số liên tiếp của
một cấp số nhân. Tính
( )
abc++
.
A.
12
. B.
18
. C.
3
. D.
9
.
Câu 123: Cho ba số
x
;
5
;
2y
theo thứ tự lập thành cấp số cộng và ba số
x
;
4
;
2y
theo thứ tự lập thành cấp
số nhân thì
2xy−
bằng
A.
2 10xy
−=
. B.
29xy−=
. C.
26xy−=
. D.
28xy−=
.

CHUYÊN ĐỀ II – TOÁN – 11 – DÃY SỐ - CẤP SỐ CỘNG – CẤP SỐ NHÂN
Page 63
Sưu tầm và biên soạn
Câu 124: Tính tổng của cấp số nhân lùi vô hạn
()
n
u
biết
1
1u
=
và
134
,,uuu
theo thứ tự là ba số hạng liên
tiếp trong một cấp số cộng.
A.
51
2
+
. B.
51
2
−
. C.
1
51−
. D.
2
.
Câu 125: Ba số phân biệt có tổng là
217
có thể coi là các số hạng liên tiếp của một cấp số nhân, cũng có
thể coi là số hạng thứ
2
, thứ
9
, thứ
44
của một cấp số cộng. Hỏi phải lấy bao nhiêu số hạng
đầu của cấp số cộng này để tổng của chúng bằng
820
?
A.
20
. B.
42
. C.
21
. D.
17
.
DẠNG 6. BÀI TOÁN THỰC TẾ VÀ MỘT SỐ BÀI TOÁN KHÁC
Câu 126: Người ta thiết kế một cái tháp
11
tầng. Diện tích bề mặt trên của mỗi tầng bằng nửa diện tích
của mặt trên của tầng ngay bên dưới và diện tích mặt trên của tầng
1
bằng nửa diện tích của đế
tháp. Tính diện tích mặt trên cùng.
A.
2
8 .
m
B.
2
6 .
m
C.
2
10 .
m
D.
2
12 .m
Câu 127: Một hình vuông
ABCD
có cạnh
AB a
=
, diện tích
1
S
. Nối 4 trung điểm
1
A
,
1
B
,
1
C
,
1
D
theo
thứ tự của 4 cạnh
AB
,
BC
,
CD
,
DA
ta được hình vuông thứ hai là
111 1
ABC D
có diện tích
2
S
.
Tiếp tục như thế ta được hình vuông thứ ba
222 2
ABC D
có diện tích
3
S
và cứ tiếp tục như thế, ta
được diện tích
45
, ,...SS
Tính
1 2 3 100
...SS S S S= + + ++
.
A.
100
99 2
21
.
2
S
a
−
=
B.
( )
100
99
21
.
2
a
S
−
=
C.
( )
2 100
99
21
.
2
a
S
−
=
D.
(
)
2 99
99
21
.
2
a
S
−
=
Câu 128: Dân số tỉnh Bình Phước theo điều tra vào ngày
1/1/ 2011
là
905300
người. Nếu duy trì tốc độ
tăng trưởng dân số không đổi là
10%
một năm thì đến
1/1/ 2020
dân số của tỉnh Bình Phước là
bao nhiêu?
A.
22582927
. B.
02348115
. C.
2134650
. D.
11940591
.
Câu 129: Bạn A thả quả bóng cao su từ độ cao
10
m theo phương thẳng đứng. Mỗi khi chạm đất nó lại nảy
lên theo phương thẳng đứng có độ cao bằng
3
4
độ cao trước đó. Tính tổng quãng đường bóng đi
được đến khi bóng dừng hẳn.
A.
40
m. B.
70
m. C.
50
m. D.
80
m.
Câu 130: Một loại vi khuẩn sau mỗi phút số lượng tăng gấp đôi biết rằng sau
5
phút người ta đếm được
có
64000
con hỏi sau bao nhiêu phút thì có được
2048000
con.
A.
10
. B.
11
. C.
26
. D.
50
.
Câu 131:
Trên một bàn cờ vua kích thước 8x8 người ta đặt số hạt thóc theo cách như sau. Ô thứ nhất đặt
một hạt thóc, ô thứ hai đặt hai hạt thóc, các ô tiếp theo đặt số hạt thóc gấp đôi ô đứng liền kề
trước nó. Hỏi phải tối thiểu từ ô thứ bao nhiêu để tổng số hạt thóc từ ô đầu tiên đến ô đó lớn hơn
20172018 hạt thóc.
A.
26
B.
23
C.
24
D.
25

CHUYÊN ĐỀ II – TOÁN – 11 – DÃY SỐ - CẤP SỐ CỘNG – CẤP SỐ NHÂN
Page 64
Sưu tầm và biên soạn
Câu 132: Cho tam giác
ABC
cân tại đỉnh
A
, biết độ dài cạnh đáy
BC
, đường cao
AH
và cạnh bên
AB
theo thứ tự lập thành cấp số nhân với công bội
q
. Giá trị của
2
q
bằng
A.
22
2
+
. B.
22
2
−
. C.
21
2
+
. D.
21
2
−
Câu 133: Cho dãy số
( )
n
a
xác định bởi
11
5, . 3
nn
a a qa
+
= = +
với mọi
1n
≥
, trong đó
q
là hằng số,
0q ≠
,
1
q
≠
. Biết công thức số hạng tổng quát của dãy số viết được dưới dạng
1
1
1
.
1
n
n
n
q
aq
q
αβ
−
−
−
= +
−
. Tính
2
αβ
+
?
A.
13
. B.
9
. C.
11
. D.
16
.
Câu 134: Cho bốn số
, ab
,
, cd
theo thứ tự đó tạo thành cấp số nhân với công bội khác
1
. Biết tổng ba
số hạng đầu bằng
148
9
, đồng thời theo thứ tự đó chúng lần lượt là số hạng thứ nhất, thứ tư và thứ
tám của một cấp số cộng. Tính giá trị biểu thức
T abcd=−+−
.
A.
101
27
T =
. B.
100
27
T =
. C.
100
27
T = −
. D.
101
27
T = −
.
Câu 135: Từ độ cao
55,8m
của tháp nghiêng Pisa nước Italia người ta thả một quả bóng cao su chạm xuống
đất. Giả sử mỗi lần chạm đất quả bóng lại nảy lên độ cao bằng
1
10
độ cao mà quả bóng đạt trước
đó. Tổng độ dài hành trình của quả bóng được thả từ lúc ban đầu cho đến khi nó nằm yên trên
mặt đất thuộc khoảng nào trong các khoảng sau đây?
A.
( )
67 ;69mm
. B.
( )
60 ;63mm
. C.
( )
64 ;66mm
. D.
( )
69 ;72mm
.
Câu 136: Để trang trí cho quán trà sữa sắp mở cửa của mình, bạn Việt quyết định tô màu một mảng tường
hình vuông cạnh bằng
1m
. Phần tô màu dự kiến là các hình vuông nhỏ được đánh số lần lượt là
1,2,3...n,..
, trong đó cạnh của hình vuông kế tiếp bằng một nửa cạnh hình vuông trước đó. Giả
sử quá trình tô màu của Việt có thể diễn ra nhiều giờ. Hỏi bạn Việt tô màu đến hình vuông thứ
mấy thì diện tích của hình vuông được tô bắt đầu nhỏ hơn
( )
2
1
1000
m
?
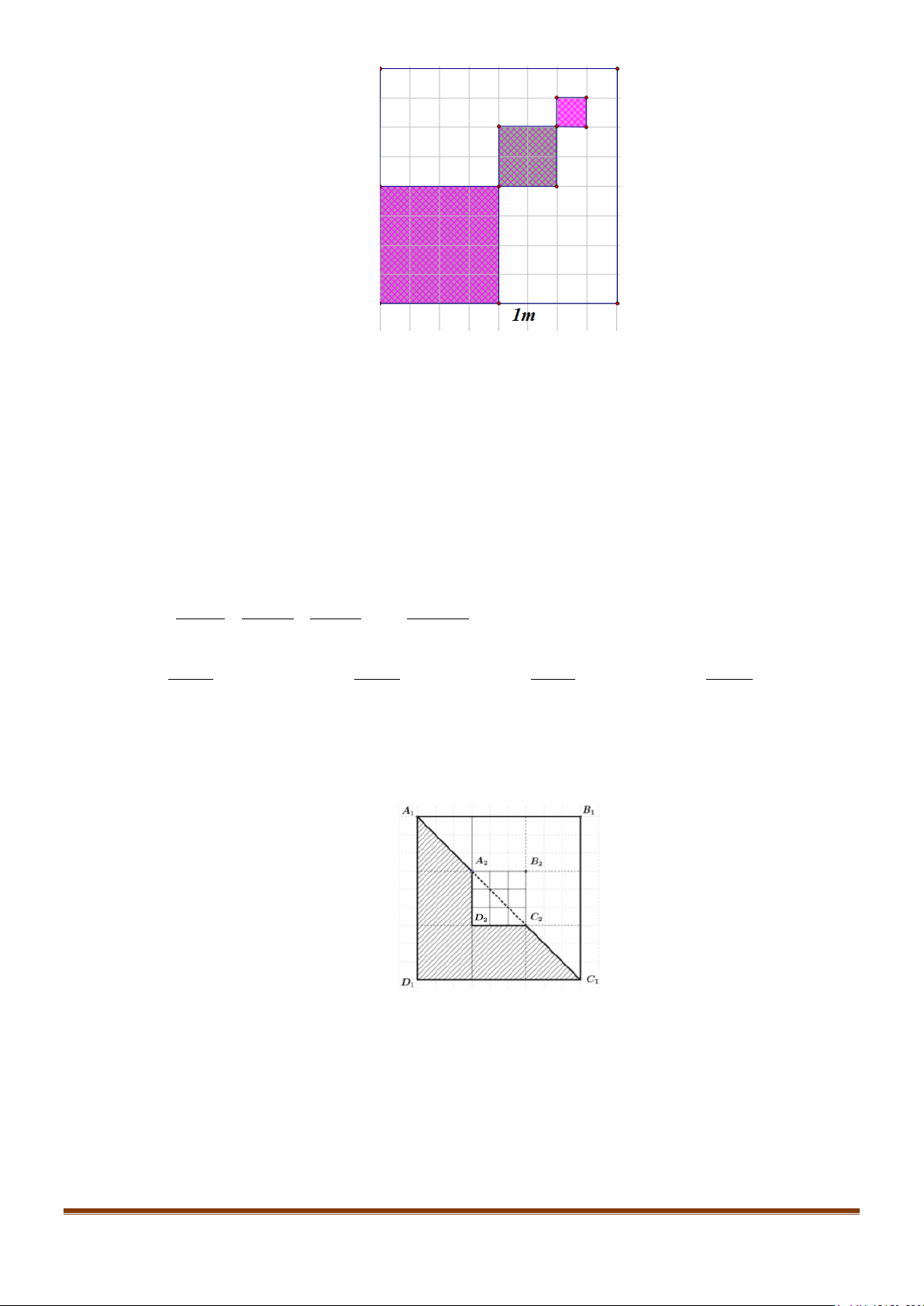
CHUYÊN ĐỀ II – TOÁN – 11 – DÃY SỐ - CẤP SỐ CỘNG – CẤP SỐ NHÂN
Page 65
Sưu tầm và biên soạn
A.
6
. B.
3
. C.
5
. D.
4
.
Câu 137: Có bao nhiêu giá trị thực của tham số
m
để phương trình
( )( )( )
13 0x x xm− − −=
có 3 nghiệm
phân biệt lập thành cấp số nhân tăng?
A.
4
. B.
3
. C.
2
. D. 1.
Câu 138: Biết rằng tồn tại đúng hai giá trị của tham số
m
để phương trình
(
)
32 2
7 2 6 80x x m mx− + + −=
có ba nghiệm phân biệt lập thành một cấp số nhân. Tính tổng lập phương của hai giá trị đó.
A.
342
−
. B.
216−
. C.
344
. D.
216
.
Câu 139: Cho dãy số
( )
n
u
là một cấp số nhân có số hạng đầu
1
1u =
, công bội
2q =
. Tính tổng
1 5 2 6 3 7 20 24
111 1
...T
uu uu uu u u
= + + ++
−−− −
.
A.
19
18
12
15.2
−
. B.
20
19
12
15.2
−
. C.
19
18
21
15.2
−
. D.
20
19
21
15.2
−
Câu 140: Với hình vuông
111 1
ABC D
như hình vẽ bên, cách tô màu như phần gạch sọc được gọi là cách tô
màu “đẹp”. Một nhà thiết kế tiến hành tô màu cho một hình vuông như hình bên, theo quy trình
sau:
Bước 1: Tô màu “đẹp” cho hình vuông
111 1
ABC D
.
Bước 2: Tô màu “đẹp” cho hình vuông
222 2
ABC D
là hình vuông ở chính giữa khi chia hình
vuông
111 1
ABC D
thành
9
phần bằng nhau như hình vẽ.
Bước 3: Tô màu “đẹp” cho hình vuông
333 3
ABC D
là hình vuông ở chính giữa khi chia hình
vuông
222 2
ABC D
thành
9
phần bằng nhau. Cứ tiếp tục như vậy. Hỏi cần ít nhất bao nhiêu bước
để tổng diện tích phần được tô màu chiếm
49,99%
.
A.
9
bước. B.
4
bước. C.
8
bước. D.
7
bước.
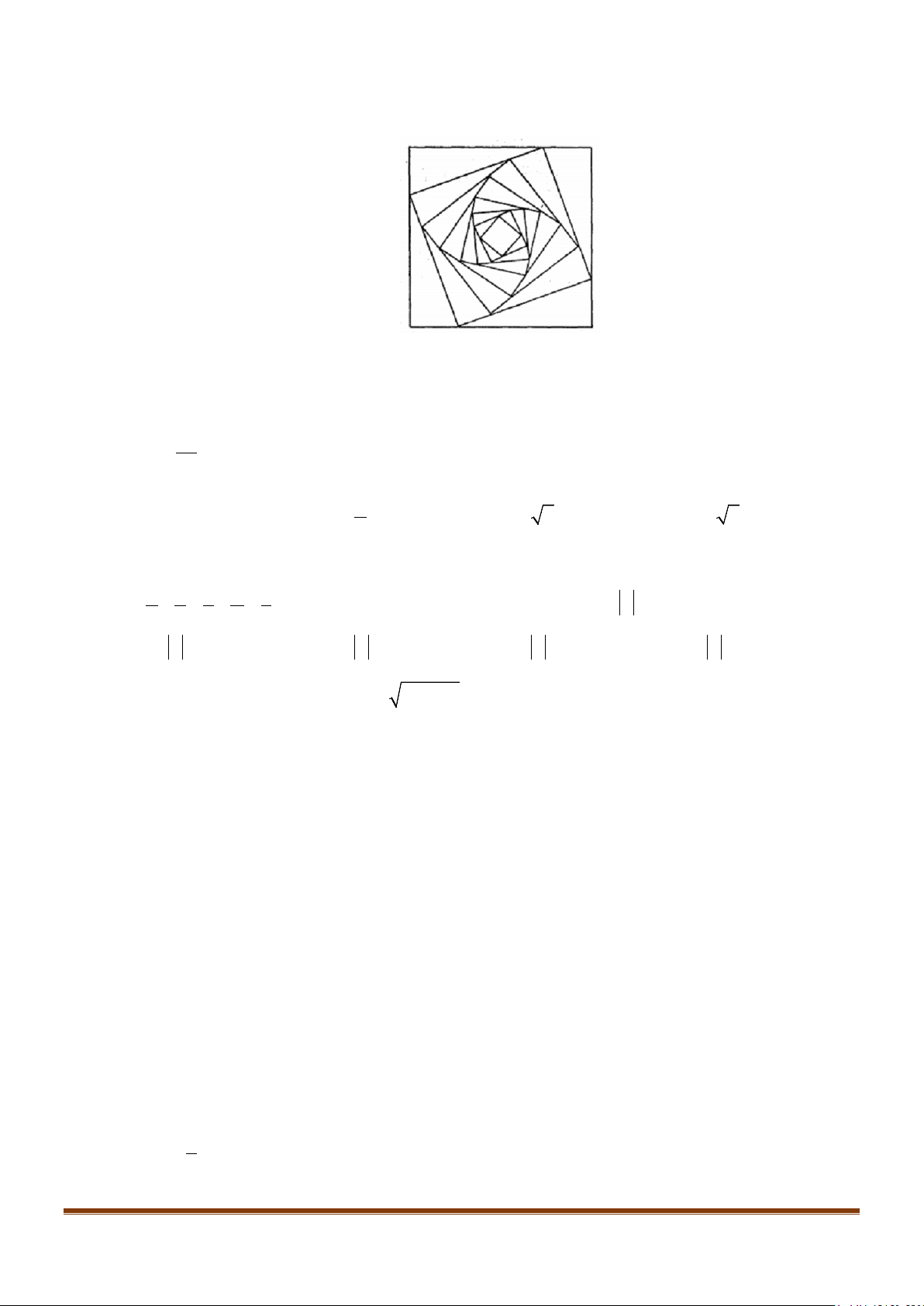
CHUYÊN ĐỀ II – TOÁN – 11 – DÃY SỐ - CẤP SỐ CỘNG – CẤP SỐ NHÂN
Page 66
Sưu tầm và biên soạn
Câu 141: Cho hình vuông
(
)
1
C
có cạnh bằng
a
. Người ta chia mỗi cạnh của hình vuông thành bốn phần
bằng nhau và nối các điểm chia một cách thích hợp để có hình vuông
( )
2
C
.
Từ hình vuông
( )
2
C
lại tiếp tục làm như trên ta nhận được dãy các hình vuông
1
C
,
2
C
,
3
C
,.,
n
C
. Gọi
i
S
là diện tích của hình vuông
{ }
( )
1,2,3,.....
i
Ci∈
. Đặt
123
... ...
n
TSS S S=+++ +
. Biết
32
3
T =
, tính
a
?
A.
2
. B.
5
2
. C.
2
. D.
22
.
Câu 142: Cho năm số
a
,
b
,
c
,
d
,
e
tạo thành một cấp số nhân theo thứ tự đó và các số đều khác
0
, biết
11111
10
abcde
+++ +=
và tổng của chúng bằng
40
. Tính giá trị
S
với
S abcde=
.
A.
42S =
. B.
62S =
. C.
32S
=
. D.
52S =
.
Câu 143: Cho dãy số
( )
n
u
thỏa mãn
1 12 2
*
1
55 6
3
nn
u uu u
u un
+
+ −=+
= ∀∈
. Giá trị nhỏ nhất của
n
để
2018
2.3
n
u ≥
bằng:
A.
2017
. B.
2018
. C.
2019
. D.
2010
Câu 144: Tìm tất cả các giá trị của tham số
m
để phương trình sau có ba nghiệm phân biệt lập thành một
cấp số nhân:
( )
32 2
7 2 6 80x x m mx .− + + −=
A.
7
m.= −
B.
1m.=
C.
1m = −
hoặc
7m.=
D.
1m =
hoặc
7m.= −
Câu 145: Bốn góc của một tứ giác tạo thành cấp số nhân và góc lớn nhất gấp 27 lần góc nhỏ nhất. Tổng
của góc lớn nhất và góc bé nhất bằng:
A.
0
56 .
B.
0
102 .
C.
0
252 .
D.
0
168 .
Câu 146: Người ta thiết kế một cái tháp gồm 11 tầng. Diện tích bề mặt trên của mỗi tầng bằng nữa diện
tích của mặt trên của tầng ngay bên dưới và diện tích mặt trên của tầng 1 bằng nửa diện tích của
đế tháp. Tính diện tích mặt trên cùng.
A.
2
6.m
B.
2
8.m
C.
2
10 .m
D.
2
12 .m
Câu 147: Một tứ giác lồi có số đo các góc lập thành một cấp số nhân. Biết rằng số đo của góc nhỏ nhất
bằng
1
9
số đo của góc nhỏ thứ ba. Hãy tính số đo của các góc trong tứ giác đó.
A.
00 0 0
5 ,15 ,45 ,225 .
B.
0 00 0
9 ,27 ,81 ,243 .
C.
000 0
7 , 21 ,63 , 269 .
D.
000 0
8 ,32 ,72 ,248 .

CHUYÊN ĐỀ II – TOÁN – 11 – DÃY SỐ - CẤP SỐ CỘNG – CẤP SỐ NHÂN
Page 67
Sưu tầm và biên soạn
Câu 148: Cho cấp số nhân
( )
n
a
có
1
7,a =
6
224a =
và
3577.
k
S =
Tính giá trị của biểu thức
( )
1.
k
Tk a= +
A.
17920.T
=
B.
8064.
T
=
C.
39424.T =
D.
86016.T =
Câu 149: Các số
6 , 5 2 , 8xyxyxy
theo thứ tự đó lập thành một cấp số cộng; đồng thời các số
1, 2 , 3x y xy
theo thứ tự đó lập thành một cấp số nhân. Tính
22
.xy
A.
22
40.xy
B.
22
25.xy
C.
22
100.xy
D.
22
10.xy
Câu 150: Ba số
; ;
xyz
theo thứ tự lập thành một cấp số nhân với công bội
q
khác
1;
đồng thời các số
; 2 ; 3
x yz
theo thứ tự lập thành một cấp số cộng với công sai khác
0.
Tìm giá trị của
q
.
A.
1
.
3
q
B.
1
.
9
q
C.
1
.
3
q
D.
3.q
Câu 151: Các số
6,
xy+
5x 2 ,y+
8x y
+
theo thứ tự đó lập thành một cấp số cộng, đồng thời, các số
5
,
3
x +
1,y −
2x 3y
−
theo thứ tự đó lập thành một cấp số nhân. Hãy tìm
x
và $y.$
A.
3, 1xy=−=−
hoặc
31
,.
88
xy
= =
B.
3, 1xy= =
hoặc
31
,.
88
xy
=−=−
C.
24, 8xy= =
hoặc
3, 1xy
=−=−
.D.
24, 8xy=−=−
hoặc
3, 1xy= =
Câu 152: Ba số
,,xyz
lập thành một cấp số cộng và có tổng bằng 21. Nếu lần lượt thêm các số
2;3;9
vào
ba số đó thì được ba số lập thành một cấp số nhân. Tính
2 22
.Fx y z=++
A.
389.F =
hoặc
395.F =
B.
395.F =
hoặc
179.
F =
C.
389.F =
hoặc
179.F =
D.
441F =
hoặc
357.F =
Câu 153: Cho bố số
,,,abcd
biết rằng
,,abc
theo thứ tự đó lập thành một cấp số nhân công bội
1
q
; còn
,,
bcd
theo thứ tự đó lập thành cấp số cộng. Tìm
q
biết rằng
14ad
và
12.bc
A.
18 73
.
24
q
B.
19 73
.
24
q
C.
20 73
.
24
q
D.
21 73
.
24
q
Câu 154: Một người đem 100 triệu đồng đi gửi tiết kiệm với kỳ han 6 tháng, mỗi tháng lãi suất là
0,7%
số tiền mà người đó có. Hỏi sau khi hết kỳ hạn, người đó được lĩnh về bao nhiêu tiền?
A.
( )
5
8
10 . 0,007
B.
( )
5
8
10 . 1,007
C.
(
)
6
8
10 . 0,007
D.
( )
6
8
10 . 1,007
Câu 155: Tỷ lệ tăng dân số của tỉnh M là
1, 2%.
Biết rằng số dân của tỉnh M hiện nay là 2 triệu người. Nếu
lấy kết quả chính xác đến hàng nghìn thì sau 9 năm nữa số dân của tỉnh M sẽ là bao nhiêu?
A.
10320
nghìn người. B.
3000
nghìn người. C.
2227
nghìn người. D.
2300
nghìn người.
Câu 156: Tế bào E. Coli trong điều kiện nuôi cấy thích hợp cứ 20 phút lại nhân đôi một lần. Nếu lúc đầu
có
12
10
tế bào thì sau 3 giờ sẽ phân chia thành bao nhiêu tế bào?
A.
12
1024.10
tế bào. B.
12
256.10
tế bào. C.
12
512.10
tế bào. D.
13
512.10
tế bào.

CHUYÊN ĐỀ II – TOÁN – 11 – DÃY SỐ - CẤP SỐ CỘNG – CẤP SỐ NHÂN
Page 1
Sưu tầm và biên soạn
BÀI 6: CẤP SỐ NHÂN
DẠNG 1. NHẬN DIỆN CẤP SỐ NHÂN
Câu 1: Dãy số nào sau đây không phải là cấp số nhân?
A.
1; 1; 1; 1−−
. B.
1; 3; 9;10−
. C.
1; 0; 0; 0
. D.
32; 16; 8; 4
.
Lời giải
Nếu
( )
n
u
là cấp số nhân với công bội
q
ta có:
1
1
.
n
nn
n
u
u uq q
u
+
+
= ⇒=
.
1; 1;1; 1−−
là cấp số nhân với
1
q = −
.
1;3;9;10−
không là cấp số nhân.
1;0;0;0
là cấp số nhân với
0q =
.
32;16;8;4
là cấp số nhân với
1
2
q =
.
Câu 2: Dãy số nào sau đây không phải là cấp số nhân?
A.
1; 3;9; 27;54−−
. B.
1;2;4;8;16
. C.
1; 1;1; 1;1−−
. D.
1; 2;4; 8;16−−
.
Lời giải
Dãy
1;2;4;8;16
là cấp số nhân với công bội
2q =
.
Dãy
1; 1;1; 1;1−−
là cấp số nhân với công bội
1q = −
.
Dãy
1; 2;4; 8;16−−
là cấp số nhân với công bội
2q = −
.
Dãy
1; 3;9; 27;54
−−
không phải là cấp số nhân vì
3 1.( 3);( 27).( 3) 81 54−= − − − = ≠
.
Câu 3: Trong các dãy số cho dưới đây, dãy số nào là cấp số nhân?
A.
1; 2;3;4;5
. B.
1;3;6;9;12
. C.
2; 4;6;8;10
. D.
2; 2; 2; 2; 2
.
Lời giải
Ta thấy ở đáp án D có
12345
2uuuuu= = = = =
nên đây là cấp số nhân với công bội
1q =
.
Câu 4: Trong các dãy số sau, dãy số nào là một cấp số nhân?
CHƯƠNG
II
DÃY SỐ
CẤP SỐ CỘNG – CẤP SỐ NHÂN
HỆ THỐNG BÀI TẬP TRẮC NGHIỆM.
III

CHUYÊN ĐỀ II – TOÁN – 11 – DÃY SỐ - CẤP SỐ CỘNG – CẤP SỐ NHÂN
Page 2
Sưu tầm và biên soạn
A.
1;2;3;4;5;6;...
. B.
2;4;6;8;16;32;...
.
C.
2; 3; 4; 5; 6; 7;...−−−−−−
. D.
1;2;4;8;16;32;...
.
Lời giải
Nhận thấy
3
2
12
u
u
uu
≠
nên các dãy số ở đáp án A, B và C không phải là cấp số nhân.
Riêng đối với dãy
1,2,4,8,16,32,...
ở đáp án D thỏa mãn:
*
1
2.
nn
u un
+
= ∀∈
.
Vậy dãy số
1,2,4,8,16,32,...
là cấp số nhân với
1
1u =
và công bội
2q =
.
Câu 5: Trong các dãy số sau, dãy số nào là một cấp số nhân?
A.
128 64 32 16 8; ; ; ; ; ...
−−
B.
22442; ; ; ; ....
C.
5678; ; ; ; ...
D.
1
15 5 1
5
; ; ; ; ...
Câu 6: Trong các dãy số sau, dãy số nào không phải là một cấp số nhân?
A.
2 4 8 16; ; ; ;
B.
1111; ; ; ;
−−
C.
2222
123; ; ; 4 ;
D.
( )
357
0a; a ; a ; a ; a .≠
Câu 7: Dãy số nào sau đây không phải là cấp số nhân?
A.
1248; ; ; ;
B.
234
33 3 3; ; ; ;
C.
11
42
24
; ; ; ;
D.
246
11 1 1
; ; ; ;
ππππ
Câu 8: Dãy số
33
n
n
u.= +
là một cấp số nhân với:
A. Công bội là 3 và số hạng đầu tiên là 1.
B. Công bội là 2 và số hạng đầu tiên là 1.
C. Công bội là 4 và số hạng đầu tiên là 2.
D. Công bội là 2 và số hạng đầu tiên là 2.
Câu 9: Cho dãy số
( )
n
u
với
3
5
2
n
n
u ..=
Khẳng định nào sau đây đúng?
A.
( )
n
u
không phải là cấp số nhân.
B.
( )
n
u
là cấp số nhân có công bội
5q =
và số hạng đầu
1
3
2
u.
=
C.
( )
n
u
là cấp số nhân có công bội
5q =
và số hạng đầu
1
15
2
u.=
D.
( )
n
u
là cấp số nhân có công bội
5
2
q
=
và số hạng đầu
1
3u.=
Câu 10: Chọn cấp số nhân trong các dãy số sau:
A.
1; 0,2; 0,04; 0,0008; ...
B.
2; 22; 222;2222; ...
C.
; 2 ; 3 ; 4 ; ...xxxx
D.
24 6
1; ; ; ; ...xx x−−
Lời giải

CHUYÊN ĐỀ II – TOÁN – 11 – DÃY SỐ - CẤP SỐ CỘNG – CẤP SỐ NHÂN
Page 3
Sưu tầm và biên soạn
Dãy số :
24 6
1; ; ; ; ...xx x
−−
là cấp số nhân có số hạng đầu
1
1; u
=
công bội
2
qx= −
.
Câu 11: Trong các số sau, dãy số nào là một cấp số nhân:
A.
1, 3,9, 27,81.−−
B.
1,3,6,9,12.−−−−
C.
1,2,4,8,16.−−−−
D.
0,3,9,27,81.
Lời giải
Câu 12: Xác định
x
để 3 số
2; 1; 3xx x− +−
theo thứ tự lập thành một cấp số nhân:
A. Không có giá trị nào của
.x
B.
1.x = ±
C.
2.x =
D.
3.x = −
Lời giải
Ba số
2; 1; 3xx x− +−
theo thứ tự lập thành một cấp số nhân
( )( ) (
)
2
23 1x xx⇔− −=+
2
2 3 70xx⇔ − +=
Câu 13: Xác định
x
để 3 số
2 1; ; 2 1x xx−+
theo thứ tự lập thành một cấp số nhân:
A.
1
.
3
x
= ±
B.
3.
x
= ±
C.
1
.
3
x = ±
D. Không có giá trị nào của
x
.
Lời giải
Ba số:
2 1; ; 2 1x xx−+
theo thứ tự lập thành cấp số nhân
( )( )
2
2 12 1xxx⇔ − +=
22
41xx⇔ −=
2
31x⇔=
1
.
3
x⇔=±
Câu 14: Trong các dãy số
( )
n
u
sau, dãy nào là cấp số nhân?
A.
2
1
n
unn= ++
. B.
( )
23
n
n
un.= +
.
C.
1
1
2
6
*
n
n
u
.
u ,n
u
+
=
= ∀∈
D.
( )
21
4
n
n
u
+
= −
.
Lời giải
A.
2
1
2
33
1
*
n
n
u
nn
,n
u nn
+
++
= ∀∈
++
, không phải là hằng số. Vậy
( )
n
u
không phải là cấp số nhân.
B.
( )
(
)
(
)
1
1
33 3 3
23 2
n
*
n
n
n
n. n
u
,n
u n. n
+
+
++
= = ∀∈
++
, không phải là hằng số. Vậy
( )
n
u
không phải là cấp
số nhân.
C. Từ công thức truy hồi của dãy số, suy ra
1234
2323u ;u ;u ;u ;...= = = =
Vì
3
2
21
u
u
uu
≠
nên
( )
n
u
không phải là cấp số nhân.
D.
( )
( )
( )
2 11
1
21
4
16
4
n
*
n
n
n
u
,n
u
++
+
+
−
= = ∀∈
−
. Vậy
( )
n
u
là một cấp số nhân.

CHUYÊN ĐỀ II – TOÁN – 11 – DÃY SỐ - CẤP SỐ CỘNG – CẤP SỐ NHÂN
Page 4
Sưu tầm và biên soạn
Câu 15: Dãy số nào sau đây là cấp số nhân?
A.
1
1
1
.
1, 1
nn
u
uu n
B.
1
1
1
.
3 , 1
nn
u
u un
C.
1
1
2
.
2 3, 1
nn
u
u un
D.
1
2
.
sin , 1
1
n
u
un
n
Lời giải
n
u
là cấp số nhân
1nn
u qu
Chọn B
Câu 16: Cho dãy số
n
u
với
3
.5 .
2
n
n
u
Khẳng định nào sau đây đúng?
A.
n
u
không phải là cấp số nhân.
B.
n
u
là cấp số nhân có công bội
5q
và số hạng đầu
1
3
.
2
u
C.
n
u
là cấp số nhân có công bội
5
q
và số hạng đầu
1
15
.
2
u
D.
n
u
là cấp số nhân có công bội
5
2
q
và số hạng đầu
1
3.u
Lời giải
3
.5
2
n
n
u
là cấp số nhân công bội
5
q
và
1
15
2
u
Chọn C
Câu 17: Trong các dãy số
n
u
cho bởi số hạng tổng quát
n
u
sau, dãy số nào là một cấp số nhân?
A.
2
1
.
3
n
n
u
B.
1
1.
3
n
n
u
C.
1
.
3
n
un
D.
2
1
.
3
n
un
Lời giải
Dãy
2
11
9.
3
3
n
n
n
u
là cấp số nhân có
1
3
1
3
u
q
Chọn A
Câu 18: Trong các dãy số
n
u
cho bởi số hạng tổng quát
n
u
sau, dãy số nào là một cấp số nhân?
A.
7 3.
n
un
B.
7 3.
n
n
u
C.
7
.
3
n
u
n
D.
7.3 .
n
n
u
Lời giải.
Dãy
7.3
n
n
u
là cấp số nhân có
1
21
3
u
q
Chọn D
Câu 19: Cho dãy số
n
u
là một cấp số nhân với
*
0, .
n
un
Dãy số nào sau đây không phải là cấp số
nhân?
A.
135
; ; ; ...uuu
B.
12 3
3 ; 3 ; 3 ; ...uu u
C.
123
111
; ; ; ...
uuu
D.
123
2; 2; 2; ...
uuu
Lời giải
Giả sử
n
u
là cấp số nhân công bội
,q
thì

CHUYÊN ĐỀ II – TOÁN – 11 – DÃY SỐ - CẤP SỐ CỘNG – CẤP SỐ NHÂN
Page 5
Sưu tầm và biên soạn
Dãy
135
; ; ; ...
uuu
là cấp số nhân công bội
2
.
q
Dãy
12 3
3 ; 3 ; 3 ; ...uu u
là cấp số nhân công bội
2.q
Dãy
123
111
; ; ; ...
uuu
là cấp số nhân công bội
1
.
q
Dãy
123
2; 2; 2; ...uuu
không phải là cấp số nhân. Chọn D
Câu 20: Trong các dãy số
( )
n
u
sau đây, dãy số nào là cấp số nhân?
A.
n
un
= 3
. B.
n
n
u
= 2
. C.
n
u
n
=
1
. D.
n
n
u = +21
.
Lời giải
Ta thấy, với
2,nn
∀≥ ∈
dãy số
(
)
2
n
n
u =
có tính chất:
1
1
2
2
2
n
n
n
n
u
u
−
−
= =
nên là cấp số nhân với
công bội
qu= =
1
2, 2
.
Câu 21:
n
u
được cho bởi công thức nào dưới đây là số hạng tổng quát của một cấp số nhân?
A.
1
1
2
n
n
u
+
=
. B.
2
1
2
n
un= −
. C.
1
1
2
n
n
u = −
. D.
2
1
2
n
un
= +
.
Lời giải
1
1
1 11
.
2 42
n
n
n
u
−
+
= =
là số hạng tổng quát của một cấp số nhân có
1
1
4
u =
và
1
2
q
=
.
2
1
2
n
un= −
có
12 3
1 7 1 17 7
; .7; .7
2 22 2 2
uu u= = = = ≠
nên không phải số hạng tổng quát của một
cấp số nhân.
1
1
2
n
n
u = −
có
12 3
1 3 13 7 33
; .; .
2 4 22 8 42
uu u=− =−=− =−≠−
nên không phải số hạng tổng quát
của một cấp số nhân.
2
1
2
n
un= +
có
12 3
3 9 3 19 9
; .3; .3
2 22 2 2
uu u= = = = ≠
nên không phải số hạng tổng quát của một
cấp số nhân.
Câu 22: Trong các dãy số sau, dãy nào là cấp số nhân?
A.
( )
1
n
n
un= −
. B.
2
n
un=
. C.
2
n
n
u =
. D.
3
n
n
n
u =
.
Lời giải
Lập tỉ số
1n
n
u
u
+
A:
( ) ( )
( )
1
1
1. 1
1
1.
n
n
n
n
n
u
n
un
n
+
+
−+
+
= = −
−
( )
n
u⇒
không phải cấp số nhân.

CHUYÊN ĐỀ II – TOÁN – 11 – DÃY SỐ - CẤP SỐ CỘNG – CẤP SỐ NHÂN
Page 6
Sưu tầm và biên soạn
B:
(
)
2
1
2
1
n
n
n
u
un
+
+
=
( )
n
u⇒
không phải là cấp số nhân.
C:
1
1
1
2
22
2
n
n
nn
n
n
u
uu
u
+
+
+
= =⇒=
( )
n
u⇒
là cấp số nhân có công bội bằng
2
.
D:
1
1
3
n
n
u
n
un
+
+
=
(
)
n
u
⇒
không phải là cấp số nhân.
Câu 23: Cho dãy số
n
u
có số hạng tổng quát là
1*
3.2
n
n
un
. Chọn kết luận đúng:
A. Dãy số là cấp số nhân có số hạng đầu
1
12u
.
B. Dãy số là cấp số cộng có công sai
2d
.
C. Dãy số là cấp số cộng có số hạng đầu
1
6u
.
D. Dãy số là cấp số nhân có công bội
3q
.
Lời giải
Dãy số
n
u
có số hạng tổng quát là
1* 2
1
3.2 3.2
nn
nn
u nu
.
Xét thương
2
1
1
3.2
2
3.2
n
n
n
n
u
const
u
với
*
n
nên dãy số
n
u
là một cấp số nhân có công
bội
2q
và có số hạng đầu là
11
1
3.2 12u
.
Câu 24: Dãy nào sau đây là một cấp số nhân?
A.
1, 2,3, 4,...
. B.
1,3,5,7,...
. C.
2, 4,8,16,...
. D.
2, 4,6,8,...
Lời giải
Ta có:
2, 4,8,16,...
là cấp số nhân có số hạng đầu
1
2u =
và công bội
2q =
.
Câu 25: Cho dãy số:
1 11 1
1; ; ; ;
3 9 27 81
−− −
. Khẳng định nào sau đây là sai?
A. Dãy số không phải là một cấp số nhân.
B. Dãy số này là cấp số nhân có
1
1
1; q=
3
=−−
u
.
C. Số hạng tổng quát.
( )
1
1
1.
3
−
= −
n
n
n
u
D. Là dãy số không tăng, không giảm.
Lời giải
Ta có:
1 1 1 111 11
1. ; . ; . ;.......
3 3 9 3 3 27 9 3
=− − −=− − =− −
Vậy dãy số trên là cấp số nhân với
1
1
1; q=-
3
= −u
.
Áp dụng công thức số hạng tổng quát cấp số nhân ta có
( )
1
1
1
1
11
1 1.
33
−
−
−
= =−− =−
n
n
n
n
n
u uq
.
Câu 26: Tập hợp các giá trị x thỏa mãn
,2 , 3x xx+
theo thứ tự lập thành một cấp số nhân là
A.
{ }
0;1
. B.
∅
. C.
{ }
1
. D.
{ }
0
Lời giải

CHUYÊN ĐỀ II – TOÁN – 11 – DÃY SỐ - CẤP SỐ CỘNG – CẤP SỐ NHÂN
Page 7
Sưu tầm và biên soạn
Gọi
q
là công bội của cấp số nhân.
Ta có
2. 2. 2
3 2 . 3 2.2 1
x xq x xq q
x xq x x x
= = =
⇔⇒
+= += =
Tập hợp các giá trị x thỏa mãn
,2 , 3x xx+
theo thứ tự lập thành một cấp số nhân là
{ }
1
.
Câu 27: Có bao nhiêu giá trị nguyên dương của
x
để ba số
1; ; 2xx+
theo thứ tự đó lập thành một cấp số
nhân?
A.
2
. B.
1
. C.
3
. D.
0
.
Lời giải
Để
1; ; 2xx+
theo thứ tự đó lập thành một cấp số nhân thì:
2
1
2
2
x
xx
x
= −
=+⇔
=
.
Vậy có đúng
1
số nguyên dương
2x
=
.
Câu 28: Tìm tất cả các giá trị của
x
để ba số
2 1, , 2 1x xx−+
theo thứ tự đó lập thành một cấp số nhân.
A.
1
3
x
= ±
B.
1
3
x = ±
C.
3
x = ±
D.
3
x = ±
Lời giải
Để ba số đó lập thành một cấp số nhân thì:
( )( )
2 22 2
11
2 12 1 4 1
3
3
x x x xx x x= − +⇔= −⇔=⇔=±
Câu 29: Trong các phát biểu sau, phát biểu nào là sai?
A. Dãy số có tất cả các số hạng bằng nhau là một cấp số nhân.
B. Dãy số có tất cả các số hạng bằng nhau là một cấp số cộng.
C. Một cấp số cộng có công sai dương là một dãy số tăng.
D. Một cấp số cộng có công sai dương là một dãy số dương.
Lời giải
A. Đúng vì dãy số đã cho là cấp số nhân với công bội
1q =
.
B. Đúng vì dãy số đã cho là cấp số cộng với công sai
0d =
.
C. Đúng vì dãy số đã cho là cấp số cộng có công sai dương nên:
1
0
nn
u ud
+
−=>
1nn
uu
+
⇒>
.
D. Sai. Ví dụ dãy
5−
;
2−
;
1
;
3
; … là dãy số có
30d = >
nhưng không phải là dãy số dương.
Câu 30: Xác định
x
dương để
23−x
;
x
;
23+x
lập thành cấp số nhân.
A.
3x =
. B.
3
x =
.
C.
3
x = ±
. D. không có giá trị nào của
x
.
Lời giải
23−x
;
x
;
23+x
lập thành cấp số nhân
( )( )
2
2 32 3xx x⇔= − +
22
49xx⇔= −
2
3x⇔=
3x⇔=±
.
Vì
x
dương nên
3x =
.
Câu 31: Giả sử
sin
6
α
,
cos
α
,
tan
α
theo thứ tự đó là một cấp số nhân. Tính
cos 2
α
.

CHUYÊN ĐỀ II – TOÁN – 11 – DÃY SỐ - CẤP SỐ CỘNG – CẤP SỐ NHÂN
Page 8
Sưu tầm và biên soạn
A.
3
2
. B.
3
2
−
. C.
1
2
. D.
1
2
−
.
Lời giải
Điều kiện:
cos 0
2
k
π
αα π
≠⇔ ≠ +
( )
k ∈
.
Theo tính chất của cấp số nhân, ta có:
2
sin
cos .tan
6
α
αα
=
2
2
sin
6cos
cos
α
α
α
⇔=
.
32
6cos sin 0
αα
⇔ −=
32
6cos cos 1 0
αα
⇔ + −=
1
cos
2
α
⇔=
.
Ta có:
2
2
11
cos2 2cos 1 2. 1
22
αα
= −= −=−
.
Câu 32: Cho dãy số có các số hạng đầu là
234
11 1 1
; ; ; ;...
3
333
Số hạng tổng quát của dãy số này là
A.
1
1
3
n
−
B.
2
1
3
n+
. C.
1
3
n
. D.
1
1
3
n
+
.
Lời giải
Ta có
1
1
2
22
3
33
11
3
3
11
33
11
33
...............
u
u
u
Vậy
1
.
3
n
n
u
.
Câu 33: Cho cấp số nhân
( )
n
u
với
1
3u =
và công bội
2q
=
. Số hạng tổng quát
n
u
( )
2n ≥
bằng
A.
3.2
n
. B.
2
3.2
n+
. C.
1
3.2
n+
. D.
1
3.2
n−
.
Lời giải
Ta có
11
1
. 3.2
nn
n
u uq
−−
= =
.
Câu 34: Cho dãy số
(
)
n
u
biết
1
*
1
3
,
3
nn
u
nN
uu
+
=
∀∈
=
. Tìm số hạng tổng quát của dãy số
( )
n
u
.
A.
3=
n
n
u
. B.
1+
=
n
n
un
. C.
1
3
+
=
n
n
u
. D.
1
3
−
=
n
n
u
.
Lời giải
Ta có
1
3=u
và
1
3
+
=
n
n
u
u
Suy ra dãy số
( )
n
u
là cấp số nhân với
1
3
3
=
=
u
q
Do đó
1
1 1
. 3.3 3
−−
== =
nnn
n
u uq

CHUYÊN ĐỀ II – TOÁN – 11 – DÃY SỐ - CẤP SỐ CỘNG – CẤP SỐ NHÂN
Page 9
Sưu tầm và biên soạn
Câu 35: Cho dãy số
( )
n
u
thỏa mãn
1 12 2
*
1
33 6
2,
nn
u uu u
u un
+
= −++
= ∀∈
. Tìm giá trị nhỏ nhất của
n
để
2021
2
n
u
≥
.
A.
2021
. B.
1012
. C.
2022
. D.
1011
.
Lời giải
Ta có:
*
1
1
2 2,
n
nn
n
u
uu n
u
+
+
= ⇒ = ∀∈
nên dãy
(
)
n
u
là cấp số nhân với công bội
2q =
.
21
2uu⇒=
.
Mà
1 12 2
33 6
u uu u
= −++
12 12
3 3 60uu uu⇔ − − − −=
( )
2
12 12
3 3 60
uu uu
⇔ − − − −=
(
)
(
)
12
12
32
33
uu N
uu L
−=
⇔
−=−
12
34uu⇔ −=
.
Từ và ta có:
21
1
12
2
4
34
uu
u
uu
=
⇒=
−=
( )
n
u⇒
là cấp số nhân với công bội
1
2, 4qu= =
. Nên số hạng tổng quát là:
( )
21
1 21 *
2.4 2.2 2 ,
n
nn
n
un
−
−−
= = = ∀∈
.
2021 2 1 2021
2 2 2 2 1 2021 1011
n
n
u nn
−
≥⇔≥⇔−≥ ⇔≥
.
Vậy giá trị nhỏ nhất thỏa mãn là
1011
.
DẠNG 2. TÌM CÔNG THỨC CỦA CẤP SỐ NHÂN
Câu 36: Cho cấp số nhân
()
n
u
với
1
1u =
và
2
2u =
. Công bội của cấp số nhân đã cho là
A.
1
2
q =
. B.
2q =
. C.
2q = −
. D.
1
2
q = −
.
Lời giải
Ta có
2
21
1
2
. 2.
1
u
u uq q
u
= ⇒= ==
Câu 37: Cho cấp số nhân
( )
n
u
với
1
3u =
và
2
9
u =
. Công bội của cấp số nhân đã cho bằng
A.
6−
. B.
1
3
. C.
3
. D.
6
.
Lời giải
Ta có
21
.u uq=
⇒
2
1
3
u
q
u
= =
.

CHUYÊN ĐỀ II – TOÁN – 11 – DÃY SỐ - CẤP SỐ CỘNG – CẤP SỐ NHÂN
Page 10
Sưu tầm và biên soạn
Câu 38: Cho cấp số nhân
( )
n
u
với
1
3u =
và
2
12
u =
. Công bội của cấp số nhân đã cho bằng
A.
9
. B.
9
−
. C.
1
4
. D.
4
.
Lời giải
Công bội của cấp số nhân đã cho là
2
1
12
4
3
u
q
u
= = =
Câu 39: Cho cấp số nhân
()
n
u
với
1
3u =
và
2
15.u =
Công bội của cấp số nhân đã cho bằng
A.
12−
. B.
1
5
. C.
5
. D.
12
.
Lời giải
Từ định nghĩa cấp số nhân ta có
2
1
5
u
q
u
= =
.
Câu 40: Cho cấp số nhân
( )
n
u
với
1
2=u
và
2
6
=u
. Công bội của cấp số nhân đã cho bằng
A.
3
. B.
4−
. C.
4
. D.
1
3
.
Lời giải
Công bội của cấp số nhân là
2
1
6
3
2
= = =
u
q
u
.
Câu 41: Cho cấp số nhân
( )
n
u
với
1
3u
=
và công bội
2q =
. Giá trị của
2
u
bằng
A.
8
. B.
9
. C.
6
. D.
3
2
.
Lời giải
Ta có:
21
. 3.2 6u uq= = =
.
Câu 42: Cho cấp số nhân
( )
n
u
với
1
2
u
=
và công bội
3
q =
. Giá trị của
2
u
bằng
A.
6
. B.
9
. C.
8
. D.
2
3
.
Lời giải
Ta có
21
. 2.3 6u uq= = =
.
Câu 43: Cho cấp số nhân
( )
n
u
với
1
3u =
và công bội
4q =
. Giá trị của
2
u
bằng
A.
64
. B.
81
. C.
12
. D.
3
4
.
Lời giải
Ta có
21
. 3.4 12u uq= = =
.
Câu 44: Tìm công bội
q
của một cấp số nhân
( )
n
u
có
1
1
2
u =
và
6
16u =
.

CHUYÊN ĐỀ II – TOÁN – 11 – DÃY SỐ - CẤP SỐ CỘNG – CẤP SỐ NHÂN
Page 11
Sưu tầm và biên soạn
A.
1
2
q =
. B.
2q = −
. C.
2q =
. D.
1
2
q
= −
.
Lời giải
Ta có
55
6
61
1
16
32
1
2
u
u uq q
u
=⋅⇒= = =
2
q
⇒=
.
Câu 45: Cho cấp số nhân
( )
n
u
, biết
1
1u =
,
4
64u =
. Tính công bội
q
của cấp số nhân đã cho
A.
4q =
. B.
4q = −
. C.
21
q
=
. D.
22q
=
.
Lời giải
Ta có
33
41
64 . 64 64 4
uuqqq= ⇔ = ⇔ = ⇔=
.
Câu 46: Cho cấp số nhân
n
u
có
1
2u
và
5
162u
.Công bội
q
bằng:
A.
3q
. B.
3q
.
C.
3; 3
qq
. D.
2
q
.
Lời giải
Ta có
44
51
1
162 162
162 . 162 81 3
2
u uq q q
u
.
Câu 47: Cho cấp số nhân
( )
n
u
có
1
2u =
và
4
54u =
. Giá trị của công bội
q
bằng
A.
3
. B.
9
. C.
27
. D.
3−
.
Lời giải
Ta có:
33
3
4
1
54
27 27 3
2
u
qq q
u
= ⇒ = = ⇒= =
Câu 48: Cho cấp số nhân
( )
n
u
với
1
2u =
và công bội
3q =
. Tìm số hạng thứ
4
của cấp số nhân?
A.
24
. B.
54
. C.
162
. D.
48
.
Lời giải
Có
33
41
. 2.3 54.
u uq
= = =
Câu 49: : Cấp số nhân
( )
n
u
có
45
9, 81
uu
= =
có công bội là
A.
3
. B.
72
. C.
18
. D.
9
.
Lời giải
Ta có công bội
5
4
81
9
9
u
q
u
= = =
.
Câu 50: Tìm công bội
q
của một cấp số nhân
( )
n
u
có
1
1
2
u =
và
6
16u =
.
A.
1
2
q =
. B.
2q = −
. C.
2q =
. D.
1
2
q = −
.
Lời giải

CHUYÊN ĐỀ II – TOÁN – 11 – DÃY SỐ - CẤP SỐ CỘNG – CẤP SỐ NHÂN
Page 12
Sưu tầm và biên soạn
Ta có
55
61
1
. 16 . 2
2
u uq q q= ⇒ = ⇔=
.
Câu 51: Cho cấp số nhân
( )
n
u
có số hạng đầu
1
2u =
và
6
486
u
=
. Công bội q bằng
A.
3q
=
. B.
5q =
. C.
3
2
q =
. D.
2
3
q =
.
Lời giải
Chọn A
Theo đề ra ta có:
1
6
2
486
u
u
=
=
1
5
1
2
486 .
u
uq
=
⇔
=
55
243 3q⇒= =
3
q⇒=
.
Câu 52: Cho cấp số nhân
(
)
n
u
với
17
1
; u 32
2
=−=−u
. Tìm q ?
A.
1
2
= ±q
. B.
2= ±q
. C.
4= ±q
. D.
1= ±q
.
Lời giải
Áp dụng công thức số hạng tổng quát cấp số nhân ta có
1 66
1 71
2
. 64
2
−
=
= ⇒= ⇒=⇒
= −
n
n
q
u uq u u q q
q
Câu 53: Biết ba số
2
; 8;xx
theo thứ tự lập thành cấp số nhân. Giá trị của
x
bằng
A.
4x
B.
5x
C.
2x
D.
1x
Lời giải
Do ba số
2
; 8;xx
theo thứ tự lập thành cấp số nhân nên theo tính chất cấp số nhân ta được
23
.8 8 2xx x x
.
Câu 54: Cho cấp số nhân
( )
n
u
có công bội
q
. Chọn hệ thức đúng trong các hệ thức sau:
A.
21
.
++
=
kkk
uuu
B.
2
1
1 +−
+
=
kk
k
uu
u
.
C.
1
1
..
k
k
u uq
−
=
D.
( )
1
1.
k
uu k q
=+−
Lời giải
Theo tính chất các số hạng của cấp số nhân.
Câu 55: Cho dãy số
( )
n
u
xác định bởi:
−
=
−=
+
nn
uu
u
.
10
1
2
1
1
. Chọn hệ thức đúng:
A.
( )
n
u
là cấp số nhân có công bội
1
.
10
q = −
B.
1
1
( 2) .
10
n
n
u
−
= −
C.
2
11 +
−
+
=
n
n
n
u
u
u
( )
2n ≥
. D.
11
.
+−
=
nnn
uu
u
( )
2n ≥
.
Lời giải

CHUYÊN ĐỀ II – TOÁN – 11 – DÃY SỐ - CẤP SỐ CỘNG – CẤP SỐ NHÂN
Page 13
Sưu tầm và biên soạn
Ta có:
1
1
10
n
n
u
u
+
= −
nên
( )
n
u
là cấp số nhân có công bội
1
.
10
q = −
Câu 56: Cho cấp số nhân có
1
3u
= −
,
2
3
q =
. Tính
5
?u
A.
5
27
.
16
u
−
=
B.
5
16
.
27
u
−
=
C.
5
16
.
27
u =
D.
5
27
.
16
u =
Lời giải
Chọn B
Ta có:
(
)
4
4
51
2 16
.3 .
3 27
u uq
==−=−
Câu 57: Cho cấp số nhân có
1
3u
= −
,
2
3
q =
. Số
243
96−
là số hạng thứ mấy của cấp số này?
A. Thứ 5. B. Thứ 6.
C. Thứ 7. D. Không phải là số hạng của cấp số.
Lời giải
Chọn B
Giả sử số
243
96−
là số hạng thứ
n
của cấp số này.
Ta có:
( )
1
1
1
96 2 96
. 3 6
243 3 243
n
n
uq n
−
−
−−
= ⇔− = ⇔ =
.
Vậy số
243
96−
là số hạng thứ 6 của cấp số.
Câu 58: Cho cấp số nhân có
2
1
4
u =
;
5
16u =
. Tìm
q
và
1
u
.
A.
1
11
; .
22
qu= =
B.
1
11
; .
22
qu=−=−
C.
1
1
4; .
16
qu= =
D.
1
1
4; .
16
qu=−=−
Lời giải
Ta có:
21 1
1
. .
4
u uq uq
= ⇔=
;
44
51 1
. 16 .u uq uq= ⇔=
Suy ra:
3
64 4qq= ⇔=
. Từ đó:
1
1
.
16
u =
Câu 59: Với
x
là số nguyên dương, ba số
2,3 3,5 5xx x++
theo thứ tự là ba số hạng liên tiếp của một
cấp số nhân. Số hạng tiếp theo của cấp số nhân đó là
A.
250
3
−
. B.
250
3
. C.
250
. D.
250−
.
Lời giải

CHUYÊN ĐỀ II – TOÁN – 11 – DÃY SỐ - CẤP SỐ CỘNG – CẤP SỐ NHÂN
Page 14
Sưu tầm và biên soạn
Ba số
2,3 3,5 5xx x
++
theo thứ tự là ba số hạng liên tiếp của một cấp số nhân nên
( )
(
)
2
2
1
255 33 890 9
9
x
xx x x x x
x
= −
+ = + ⇔ − −=⇔ ⇒=
=
.
Với
9x =
, suy ra
3.9 3 30 5
2.9 18 3
q
+
= = =
Số hạng tiếp theo của cấp số nhân đó là:
( )
5 250
5.9 5 .
33
+=
.
Câu 60: Cho ba số thực
,,xyz
trong đó
0
x
≠
. Biết rằng
,2 ,3xyz
lập thành cấp số cộng và
,,xyz
lập
thành cấp số nhân; tìm công bội
q
của cấp số nhân đó.
A.
1
1
3
q
q
=
=
B.
1
3
2
3
q
q
=
=
C.
2q =
D.
1q =
Lời giải
,,
xyz
lập thành cấp số nhân công bội
q
nên
2
;y qx z q x= =
,2 ,3xyz
lập thành cấp số cộng nên
2
33
22
22
x z x qx
y qx
++
= ⇒=
Vì
0x ≠
nên
2
2
1
3
2 4 13
1
2
3
q
x qx
qx q q
q
=
+
= ⇒=+ ⇒
=
DẠNG 3. TÌM HẠNG TỬ TRONG CẤP SỐ NHÂN
Câu 61: Cho cấp số nhân
( )
n
u
có
1
2
u = −
và công bội
3
q =
. Số hạng
2
u
là:
A.
2
6u = −
. B.
2
6u
=
. C.
2
1
u
=
. D.
2
18
u
= −
.
Lời giải
Số hạng
2
u
là:
21
.u uq=
6= −
Câu 62: Cho cấp số nhân
( )
n
u
có
5
2u =
và
9
6u
=
. Tính
21
u
.
A.
18
. B.
54
. C.
162
. D.
486
.
Lời giải
Ta có
5
9
2
6
u
u
=
=
4
1
8
1
2
6
uq
uq
=
⇔
=
1
4
2
3
3
u
q
=
⇔
=
.
Suy ra
( )
5
20 4 5
21 1 1
2
.3 162
3
u uq u q= = = =
.
Câu 63: Cho cấp số nhân
( )
n
u
có số hạng đầu
1
2u
=
và công bội
5q =
. Giá trị của
68
uu
bằng
A.
6
2.5
. B.
7
2.5
. C.
8
2.5
. D.
5
2.5
.
Lời giải
Vì
( )
n
u
là cấp số nhân nên
2
68 7
uu u=
, suy ra
66
68 7 1
. 2.5uu u u q= = =
.

CHUYÊN ĐỀ II – TOÁN – 11 – DÃY SỐ - CẤP SỐ CỘNG – CẤP SỐ NHÂN
Page 15
Sưu tầm và biên soạn
Câu 64: Cho cấp số nhân
( )
n
u
có
1
3
u =
, công bội
2q
=
. Ta có
5
u
bằng
A.
24
. B.
11
. C.
48
. D.
9
.
Lời giải
Công thức số hạng tổng quát của cấp số nhân:
1
1
.
n
n
u uq
−
=
.
Do đó
4
5
3.2 48u = =
.
Câu 65: Cho cấp số nhân
( )
n
u
có công bội dương và
2
1
4
u =
,
4
4u =
. Giá trị của
1
u
là
A.
1
1
6
u =
. B.
1
1
16
u =
. C.
1
1
16
u = −
. D.
1
1
2
u =
.
Lời giải
Theo tính chất của cấp số nhân với
2k ≥
thì
2
11
.
k kk
u uu
−+
=
ta suy ra
3
2
3 24
3
1
1
. .4 1
1
4
u
u uu
u
=
= = = ⇔
= −
Vì
( )
n
u
là cấp số nhân có công bội dương nên
3
1
u =
. Gọi
q
là công bội ta được
4
3
4
4
1
u
q
u
= = =
Từ đó ta có
2
1
1
1
4
4 16
u
u
q
= = =
.
Câu 66: Cho cấp số nhân
( )
n
u
có số hạng đầu
1
2u
=
và công bội
3q =
. Giá trị
2019
u
bằng
A.
2018
2.3
. B.
2018
3.2
. C.
2019
2.3
. D.
2019
3.2
.
Lời giải
Áp dụng công thức của số hạng tổng quát
1 2018
1
. 2.3
n
n
u uq
−
= =
.
Câu 67: Cho cấp số nhân
( )
1
; 1, 2
n
uu q= =
. Hỏi số
1024
là số hạng thứ mấy?
A.
11
. B.
9
. C.
8
. D.
10
.
Lời giải
Ta có
1 1 1 10
1
. 1.2 1024 2 2 1 10 11
nn n
n
u uq n n
−− −
= ⇔ = ⇔ = ⇔ −= ⇔ =
.
Câu 68: Cho cấp số nhân
( )
n
u
có số hạng đầu
1
5u =
và công bội
2q = −
. Số hạng thứ sáu của
( )
n
u
là
A.
6
320u =
. B.
6
160u = −
. C.
6
320u = −
. D.
6
160
u =
.
Lời giải
Ta có:
( )
5
5
61
. 5. 2 160u uq
= =−=−
.
Câu 69: Tìm số hạng đầu
1
u
của cấp số nhân
( )
n
u
biết rằng
123
168uuu++=
và
456
21uuu++=
A.
1
24u =
. B.
1
1334
11
u =
. C.
1
96u =
. D.
1
217
3
u =
.
Lời giải

CHUYÊN ĐỀ II – TOÁN – 11 – DÃY SỐ - CẤP SỐ CỘNG – CẤP SỐ NHÂN
Page 16
Sưu tầm và biên soạn
Ta có :
2
123
11 1
345
456
111
168
. . 168
21
. . . 21
uuu
u uq uq
uuu
uq uq uq
++=
++ =
⇔
++=
++=
( )
( )
2
1
32
1
1 168
1 21
u qq
uq q q
++ =
⇔
++ =
1
2
3
168
1
1
8
u
qq
q
=
++
⇔
=
1
96
1
2
u
q
=
⇔
=
.
Vậy
1
96u =
,
Câu 70: Cho dãy số
( )
n
u
xác định bởi
1
1
1
25
nn
u
uu
+
=
= +
. Tính số hạng thứ
2018
của dãy số trên
A.
2017
2018
6.2 5u = −
. B.
2018
2018
6.2 5u = −
. C.
2017
2018
6.2 1u = +
. D.
2018
2018
6.2 5u = +
.
Lời giải
Ta có
5
nn
uv= −
,
1
25
nn
uu
+
= +
( )
1
52 5 5
nn
vv
+
⇔ −= − +
1
2
nn
vv
+
⇔=
.
Do đó
n
v
là cấp số nhân với
1
6v =
,
2q =
,
1
6.
n
n
vq
−
=
,
2017
2018
6.2v
=
2017
2018
6.2 5
u⇒= −
.
Câu 71: Cho
( )
n
u
là cấp số nhân, công bội
0.q >
Biết
13
1, 4 .uu= =
Tìm
4
u
.
A.
11
2
. B.
2.
C.
16.
D.
8.
Lời giải
Ta có:
1
1
1
23
1 41
3
1
1
1
. 4 . 8.
4
2
0
u
u
u
uq u uq
u
q
q
=
=
=
⇔ =⇔ ⇒= =
=
=
>
Câu 72: Cho cấp số nhân
( )
,1≥
n
un
với công bội
2q =
và có số hạng thứ hai
2
5.=u
Số hạng thứ
7
của
cấp số nhân là
A.
7
320
=u
. B.
7
640=u
. C.
7
160=u
. D.
7
80=u
.
Lời giải
Ta có
( )
,1≥
n
un
là cấp số nhân có công bội
2q =
nên có số hạng tổng quát
1
1
.
−
=
n
n
u q u
.
Vì
6
2 11 7
55
5 .2 .2
2
1.
2
60⇒== =⇒= =u u uu

CHUYÊN ĐỀ II – TOÁN – 11 – DÃY SỐ - CẤP SỐ CỘNG – CẤP SỐ NHÂN
Page 17
Sưu tầm và biên soạn
Vậy số hạng thứ
7
của cấp số là
160.
Đáp án C.
Câu 73: Cho một cấp số nhân có số hạng thứ
4
gấp
4096
lần số hạng đầu tiên. Tổng hai số hạng đầu tiên
là 34. Số hạng thứ
3
của dãy số có giá trị bằng:
A.
1
. B.
512
. C.
1024
. D.
32
.
Lời giải
Theo bài ra ta có:
3
41
11
12
1
4096.
16 16
4096
17. 34 2
34
.(1 ) 34
uu
qq
q
uu
uu
uq
=
= =
=
⇔ ⇔⇔
= =
+=
+=
.
Vậy
22
31
. 2.16 512u uq= = =
.
Câu 74: Cho cấp số nhân
(
)
n
u
, biết
1
12u =
,
3
8
243
u
u
=
. Tìm
9
u
.
A.
9
2
2187
u =
. B.
9
4
6563
u
=
. C.
9
78732u =
. D.
9
4
2187
u =
.
Lời giải
Gọi
q
là công bội của cấp số nhân
( )
n
u
.
Ta có
2
31
u uq=
,
7
81
u uq=
3
5
8
1
243
u
uq
⇒==
1
3
q⇒=
.
Do đó
8
91
u uq=
8
1
12.
3
=
4
2187
=
.
Câu 75: Cho cấp số nhân
( )
n
u
có tổng
n
số hạng đầu tiên là
51
n
n
S = −
với
1,2,...n =
. Tìm số hạng đầu
1
u
và công bội
q
của cấp số nhân đó?
A.
1
5
u =
,
4q =
. B.
1
5u =
,
6q =
. C.
1
4
u
=
,
5q =
. D.
1
6
u =
,
5q =
.
Lời giải
Ta có:
11
1
2
21
12 2
51 4
4
24 20
5 1 24
uS
u
uu
uu S
= = −=
=
⇒
= −=
+ = = −=
1
4
u
⇒=
,
2
1
5
u
q
u
= =
.
Câu 76: Cho cấp số nhân
( )
n
u
biết
42
53
54
108
uu
uu
−=
−=
. Tìm số hạng đầu
1
u
và công bội
q
của cấp số nhân
trên.
A.
1
9u =
;
2q
=
. B.
1
9u =
;
2q = −
. C.
1
9
u = −
;
2q = −
. D.
1
9u = −
;
2q =
.
Lời giải
Ta có:
42
53
54
108
uu
uu
−=
−=
3
11
42
11
54
108
uq uq
uq uq
−=
⇔
−=
( )
( )
2
1
22
1
1 54
1 108
uq q
uq q
−=
⇔
−=
1
9
2
u
q
=
⇔
=
.
Vậy
1
9u =
;
2q =
.
Câu 77: Xen giữa số
3
và số
768
là
7
số để được một cấp số nhân có
1
3u =
. Khi đó
5
u
là:
A.
72
. B.
48−
. C.
48±
. D.
48
.
Lời giải
Ta có
1
3u =
và
9
768
u =
nên
8
768 3.
q=
8
256q⇒=
2q⇒=±
.

CHUYÊN ĐỀ II – TOÁN – 11 – DÃY SỐ - CẤP SỐ CỘNG – CẤP SỐ NHÂN
Page 18
Sưu tầm và biên soạn
Do đó
44
51
. 3.2 48u uq= = =
.
Câu 78: Cấp số nhân
( )
n
u
có
20 17
15
8
.
272
uu
uu
=
+=
Tìm
1
u
, biết rằng
1
100u ≤
.
A.
1
16.u =
B.
1
2.u =
C.
1
16.u = −
D.
1
2.u = −
Lời giải
Ta có:
(
)
(
)
(
)
( )
16 3
19 16
1
20 17
11
4
4
15
11
1
8 01
8
.8
272
. 272
1 272 2
uq q
uu
u q uq
uu
u uq
uq
−=
=
=
⇔⇔
+=
+=
+=
.
Từ
( )
2
suy ra
1
0u ≠
do đó:
(
)
0
1
2
q
q
=
⇔
=
.
Nếu
0q =
thì
( )
1
2 272u⇔=
không thõa điều kiện
1
100u ≤
.
Nếu
2q =
thì
(
)
1
2 16u⇔=
thõa điều kiện
1
100
u ≤
.
Câu 79: Cho cấp số nhân
1
1u = −
,
6
0,00001u =
. Khi đó
q
và số hạng tổng quát là?
A.
1
10
q =
,
1
1
10
n
n
u
−
−
=
. B.
1
10
q
−
=
,
1
10
n
n
u
−
= −
.
C.
1
10
q
−
=
,
( )
1
1
10
n
n
n
u
−
−
=
. D.
1
10
q =
,
1
1
10
n
n
u
−
=
.
Lời giải
Ta có:
5
61
. 0,00001u uq= =
5
5
1
10
q
−
⇔=
1
10
q
−
⇔=
.
1
1
.
n
n
u uq
−
⇒=
1
1
1.
10
n−
−
= −
( )
1
1
10
n
n−
−
=
.
Vậy đáp án đúng là: C.
Câu 80: Cho cấp số nhân
n
u
có
2
1
4
u =
,
5
16u =
. Tìm công bội
q
và số hạng đầu
1
u
.
A.
1
2
q =
,
1
1
2
u =
. B.
1
2
q = −
,
1
1
2
u = −
. C.
4q = −
,
1
1
16
u = −
. D.
4q =
,
1
1
16
u =
.
Lời giải
Ta có
2
5
1
4
16
u
u
=
=
( )
( )
1
4
1
1
.1
4
. 16 2
uq
uq
=
⇔
=
.
Chia hai vế của
( )
2
cho
( )
1
ta được
3
64q =
4q⇔=
1
1
16
u⇒=
.
Câu 81: Cho cấp số nhân có số hạng đầu
1
2,u = −
công bội
3
4
q =
. Số
81
128
−
là số hạng thứ mấy của cấp
số này?
A.
5
. B.
4
. C.
6
. D.
3
.

CHUYÊN ĐỀ II – TOÁN – 11 – DÃY SỐ - CẤP SỐ CỘNG – CẤP SỐ NHÂN
Page 19
Sưu tầm và biên soạn
Lời giải
Áp dụng công thức cấp số nhân
14 1
1
1
81 3 3 3
2. 5
128 4 4 4
nn
n
n
u uq n
−−
−
= ⇒− =− ⇔ = ⇔ =
.
Câu 82: Cho dãy số
4,12,36,108,324,...
. Số hạng thứ 10 của dãy số đó là?
A.
73872
. B.
77832
. C.
72873
. D.
78732
.
Lời giải
Xét dãy số
4,12,36,108,324,...
là cấp số nhân có
1
4u =
,
3
q =
.
Số hạng thứ
10
của dãy số là
10
u
9
1
.uq=
9
4.3=
78732=
.
Câu 83: Cho tứ giác
ABCD
có bốn góc tạo tành cấp số nhân có công bội
2q =
, góc có số đo nhỏ nhất
trong bốn góc đó là:
A.
0
1
B.
0
30
C.
0
12
D.
0
24
Lời giải
Giả sử: Bốn góc
,,,ABCD
theo thứ tự lập thành cấp số nhân và
A
nhỏ nhất.
Khi đó
2, 4, 8B AC AD A
= = =
Nên
00
2 4 8 360 24AAAA A+++= ⇒=
Câu 84: Cho cấp số nhân
(
)
n
u
thỏa mãn
135
17
65
325
uuu
uu
−+=
+=
. Tính
3
.u
A.
3
15u
=
. B.
3
25u =
. C.
3
10u =
. D.
3
20u
=
.
Lời giải
Ta có:
( )
( )
24
24
1
135
11 1
6
6
17
11
1
1 65 (1)
65
. . 65
325
. 325
1 325 (2)
u qq
uuu
u uq uq
uu
u uq
uq
−+ =
−+=
−+=
⇔⇔
+=
+=
+=
Chia từng vế của
( )
1
cho
( )
2
ta được phương trình :
( )
24
642
6
11
5 5 4 0 *
15
qq
qqq
q
−+
= ⇔ − + −=
+
Đặt
2
,0t qt= ≥
.
Phương trình
(
)
*
trở thành :
( )
( )
32 2
2
4
5 5 40 4 1 0
1 0( )
t
t t t t tt
t t vn
=
− + − = ⇔ − −+ = ⇔
−+=
Với
2
44 2tq q=⇒ =⇔=±
.
Với
2q = ±
thay vào
( )
2
ta được
1
5u =
.
Vậy
2
31
. 5.4 20.
u uq= = =
Câu 85: Cho cấp số nhân
( )
n
u
có tổng
n
số hạng đầu tiên là
61
n
n
S = −
. Tìm số hạng thứ năm của cấp
số nhân đã cho.
A. 120005. B. 6840. C. 7775. D. 6480.
Lời giải

CHUYÊN ĐỀ II – TOÁN – 11 – DÃY SỐ - CẤP SỐ CỘNG – CẤP SỐ NHÂN
Page 20
Sưu tầm và biên soạn
Cấp số nhân
( )
n
u
có số hạng đầu
1
u
và công bội
q
.
Do
61
n
n
S = −
nên
1q ≠
. Khi đó
( )
1
1
61
1
n
n
n
uq
S
q
−
= = −
−
.
Ta có:
( )
1
11
1
61 5
1
uq
Su
q
−
= = −⇔ =
−
.
(
)
2
1
2
2
1
6 1 6.
1
uq
Sq
q
−
= = −⇔ =
−
Vậy
44
51
. 5.6 6480.u uq
= = =
Câu 86: Cho dãy số
( )
n
u
xác định bởi
1
1
1
.
25
nn
u
uu
+
=
= +
Tìm số hạng thứ
2020
của dãy.
A.
2020
2020
3.2 5.u = −
B.
2019
2020
3.2 5.
u = +
C.
2019
2020
3.2 5.u = −
D.
2020
2020
3.2 5.u = +
Lời giải
Đặt
11
5 5 2.( 5) 5 2
nn n n n n
uv v v v v
++
= −⇒ −= − +⇒ =
Có
11
11
1 6 5 6.2 6.2 5
nn
nn
uv u u
−−
=⇒ =⇒ += ⇒ = −
Vậy
2019 2020
2020
6.2 5 3.2 5u = −= −
Câu 87: Số hạng đầu và công bội
q
của CSN với
7 10
5, 135uu=−=
là:
A.
1
5
,3
729
uq= = −
. B.
1
5
,3
729
uq=−=
. C.
1
5
,3
729
uq
= =
. D.
1
5
,3
729
uq
=−=−
.
Lời giải
Vì
( )
n
u
là CSN nên:
6
71
.5u uq= = −
,
9
10 1
u . 135uq= =
9
10
1
6
71
135
27 3
5
u
uq
q
u uq
⇒ = ⇔ =− ⇒=−
−
7
1
6
5
729
u
u
q
⇒= =−
.
Câu 88: Cho dãy số
( )
n
u
được xác định bởi
1
2u =
;
1
2 31
nn
uu n
−
= +−
. Tìm số hạng thứ
2019
của dãy
số.
A.
2019
2019
5.2 6062.u = −
B.
2019
2019
5.2 6062.u = +
C.
2020
2019
5.2 6062.u = −
D.
2020
2019
5.2 6062.u = +
Lời giải
Ta có
1
2 31
nn
uu n
−
= +−
( )
1
3 52 3 1 5
nn
un u n
−
⇔ + += + − +
, với
2n ≥
;
n∈
.
Đặt
35
nn
vu n=++
, ta có
1
2
nn
vv
−
=
với
2n ≥
;
n∈
.
Như vậy,
( )
n
v
là cấp số nhân với công bội
2q =
và
1
10
v
=
, do đó
1
10.2 5.2
nn
n
v
−
= =
.
Do đó
3 5 5.2
n
n
un+ +=
, hay
5.2 3 5
n
n
un= −−
với
2
n ≥
;
n∈
.
Nên
2019
2019
5.2 6062.u = −

CHUYÊN ĐỀ II – TOÁN – 11 – DÃY SỐ - CẤP SỐ CỘNG – CẤP SỐ NHÂN
Page 21
Sưu tầm và biên soạn
Câu 89: Cho dãy số
n
u
xác định bởi
11
2
34
1; , 1
2 32
nn
n
uu u n
nn
. Giá trị của
50
u
gần nhất
với số nào dưới đây?
A.
312540600
. B.
312540500
. C.
212540500
. D.
212540600
.
Lời giải
Ta có
11 1
2
3 4 332 333
1
2 32 212 221
nn nn n n
n
uu uu u u
nn n n n n
Đặt
3
,1
1
nn
vu n
n
, ta có
11
31
22
vu
và từ
1
thu được
1
3
2
nn
vv
.
Suy ra dãy số
n
v
là một cấp số nhân với công bội
3
2
q
, ta có
11
1
3 13
..
2 22
nn
n
vv
Từ đó ta được
1
50
13 3
. 212540500
22 1
n
n
uu
n
DẠNG 4. TÍNH TỔNG VÀ MỘT SỐ BÀI TOÁN LIÊN QUAN
Câu 90: Cho cấp số nhân
( )
n
u
có
1
3u = −
và
2
q = −
. Tính tổng
10
số hạng đầu tiên của cấp số nhân.
A.
10
511S = −
. B.
10
1023S =
. C.
10
1025
S =
. D.
10
1025
S = −
.
Lời giải
Ta có:
( )
( )
10
10 1
12
1
. 3. 1023
1 12
n
q
Su
q
−−
−
==−=
− −−
.
Câu 91: Cho một cấp số nhân có các số hạng đều không âm thỏa mãn
2
6u =
,
4
24u =
. Tính tổng của
12
số hạng đầu tiên của cấp số nhân đó.
A.
12
3.2 3−
. B.
12
21−
. C.
12
3.2 1−
. D.
12
3.2
.
Lời giải
Gọi công bội của CSN bằng
q
. Suy ra
2
42
.u uq=
2q⇒=±
. Do CSN có các số hạng không âm
nên
2q =
.
Ta có
12
12 1
1
.
1
q
Su
q
−
=
−
12
12
3.
12
−
=
−
( )
12
32 1= −
.
Câu 92: Cho dãy
( )
n
u
với
1
1
2
n
n
u
= +
,
*
n∀∈
. Tính
2019 1 2 3 2019
...S uu u u= + + ++
, ta được kết quả
A.
2019
1
2020
2
−
. B.
4039
2
. C.
2019
1
2019
2
+
. D.
6057
2
.
Lời giải

CHUYÊN ĐỀ II – TOÁN – 11 – DÃY SỐ - CẤP SỐ CỘNG – CẤP SỐ NHÂN
Page 22
Sưu tầm và biên soạn
2019
1 2 2019
2019
2019
1
1
11 1 1 1
2
2019 ... 2019 . 2020
1
22 2 2 2
1
2
S
−
= + + ++ = + = −
−
.
Câu 93: Cho cấp số nhân
( )
n
u
có
3
12
u
=
,
5
48u
=
, có công bội âm. Tổng
7
số hạng đầu của cấn số nhân
đã cho bằng
A.
129
. B.
129−
. C.
128
. D.
128
−
.
Lời giải
Ta có:
2
4 35
. 576u uu= =
.
Vì
35
0, 0uu
>>
và công bội âm nên:
4
24 2uq
=− ⇒=−
.
Lại có:
2
3
31 1
2
12
3
4
u
u uq u
q
= ⇒= = =
.
Áp dụng công thức ta có:
( )
( )
7
7
71
12
1
3. 129
1 12
q
Su
q
−−
−
= = =
− −−
.
Câu 94: Cho
( )
n
u
là cấp số nhân, đặt
12
...
nn
S uu u= + ++
. Biết
23
4; 13SS= =
và
2
0u <
, giá trị
5
S
bằng
A.
2
. B.
181
16
. C.
35
16
. D.
121
.
Lời giải
Gọi
1
,uq
lần lượt là số hạng đầu tiên và công bội của cấp số nhân cần tìm.
Từ giả thiết ta có
( )
( )
( )
1
1
2
2
3
1
14
14
4
3
13
1 13
3
4
uq
uq
S
q
S
u qq
q
+=
+=
=
=
⇔⇔
=
++ =
−
=
.
Vì
2
3
3 32
2
0
0
90
u
u
q
uSS
u
<
⇒= <
=−=>
nên cấp số nhân cần tìm có
1
16
3
4
u
q
=
= −
.
Do đó
5
51
1 181
1 16
q
Su
q
−
= =
−
.
Câu 95: Giá trị của tổng
2 2018
1 3 3 ... 3S =++ + +
bằng
A.
2019
31
2
S
−
=
. B.
2018
31
2
S
−
=
. C.
2020
31
2
S
−
=
. D.
2018
31
2
S
−
= −
.
Lời giải
Ta thấy
S
là tổng của 2019 số hạng đầu tiên của cấp số nhân với số hạng đầu là
1
1u =
, công
bội
3q =
.

CHUYÊN ĐỀ II – TOÁN – 11 – DÃY SỐ - CẤP SỐ CỘNG – CẤP SỐ NHÂN
Page 23
Sưu tầm và biên soạn
Áp dụng công thức tính tổng của cấp số nhân ta có
2019 2019
13 3 1
1.
13 2
S
−−
= =
−
.
Câu 96: Biết rằng
2 10
21.3
1 2.3 3.3 ... 11.3 .
4
b
Sa=+ + ++ =+
Tính
.
4
b
Pa
= +
A.
1.P
B.
2.P
C.
3.
P
D.
4.P
Lời giải
Từ giả thiết suy ra
2 3 11
3 3 2.3 3.3 ... 11.3
S
. Do đó
11 11
2 10 11 11 11
1 3 1 21.3 1 21
2 3 1 3 3 ... 3 10.3 11.3 .3 .
13 2 2 4 4
SS S S
Vì
11
1 21.3 21.3 1 1 11
, 11 3.
4 4 4 4 44
b
S a ab P
Câu 97: Cho cấp số nhân
( )
n
u
có
2
4S
=
và
3
13.S =
Tìm
5
.S
A.
5
121S =
hoặc
5
181
.
16
S =
B.
5
121S =
hoặc
5
35
.
16
S =
C.
5
114S =
hoặc
5
185
.
16
S =
D.
5
141S
=
hoặc
5
183
.
16
S
=
Lời giải
Ta có
3 32
9u SS=−=
2
11
2
9
9uq u
q
⇒ =⇒=
Vì
2
4
S =
nên
11
4.u uq
+=
Do đó
2
99
4
qq
+=
2
4 9 90
qq⇔ − −=
3q⇔=
hoặc
3
.
4
q = −
+ Với
3q =
thì
1
1,u =
5
61
243.u uq= =
Suy ra
16
5
1 243
121.
1 13
uu
S
q
−
−
= = =
−−
+ Với
3
4
q = −
thì
1
16,u =
6
243
.
64
u = −
Suy ra
16
5
181
.
1 16
uu
S
q
−
= =
−
Câu 98: Cho cấp số nhân
( )
n
u
có
1
8u =
và biểu thức
32 1
4 2 15uu u+−
đạt giá trị nhỏ nhất. Tính
10
.S
A.
( )
11
10
9
24 1
5.4
S
+
=
. B.
( )
10
10
8
24 1
5.4
S
+
=
. C.
10
10
6
21
3.2
S
−
=
. D.
11
10
7
21
3.2
S
−
=
Lời giải
Gọi
q
là công bội của cấp số nhân. Khi đó
(
)
2
32 1
4 2 15 2 4 1 122 122, .uu u q q+ − = + − ≥− ∀
Dấu bằng xảy ra khi
4 10q +=
1
.
4
q
⇔=−
Suy ra:
( )
10
10
10
10 1
8
1
1
24 1
1
4
. 8.
1
1 5.4
1
4
q
Su
q
−−
−
−
= = =
−
−−

CHUYÊN ĐỀ II – TOÁN – 11 – DÃY SỐ - CẤP SỐ CỘNG – CẤP SỐ NHÂN
Page 24
Sưu tầm và biên soạn
Câu 99: Cho cấp số nhân
( )
n
u
có
1
2,
u =
công bội dương và biểu thức
4
7
1024
u
u
+
đạt giá trị nhỏ nhất.
Tính
11 12 20
... .Su u u= + ++
A.
2046.S =
B.
2097150.S =
C.
2095104.
S =
D.
1047552.S =
Lời giải
Gọi
q
là công bội của cấp số nhân,
0.
q >
Ta có
3
4
6
7
1024 512
2.uq
uq
+=+
Áp dụng bất đẳng thức Cô-si, ta có:
3 3 3 33
3
6 66
512 512 512
2 3 . . 24.q q q qq
q qq
+ =++ ≥ =
Suy ra
4
7
1024
u
u
+
đạt giá trị nhỏ nhất bằng
24
khi
3
6
512
q
q
=
2.q⇔=
Ta có
( )
10
1
11
10
1
2 2;
1
uq
S
q
−
= = −
−
( )
20
1
21
10
1
2 2.
1
uq
S
q
−
= = −
−
Do đó
20 10
2095104.SS S=−=
Vậy phương án đúng là
.C
Câu 100: Cho cấp số nhân
( )
n
u
có
46
35
540
180
uu
uu
+=−
+=
. Tính
21
.S
A.
( )
21
21
1
31
2
S
= +
B.
21
21
3 1.S
= −
C.
21
21
1 3.S
= −
D.
( )
21
21
1
3 1.
2
S =−+
Lời giải
Ta có
46
540uu+=−
( )
35
540.u uq
⇔+ =−
Kết hợp với phương trình thứ hai trong hệ, ta tìm được
3.q = −
Lại có
35
180uu+=
( )
24
1
180.uq q⇔ +=
Vì
3q = −
nên
1
2.u =
Suy ra
( )
(
)
21
1
21
21
1
1
3 1.
12
uq
S
q
−
= = +
−
Vậy phương án đúng là
.A
Câu 101: Cho cấp số nhân có các số hạng lần lượt là
1; 4; 16; 64;
Gọi
n
S
là tổng của
n
số hạng đầu tiên
của cấp số nhân đó. Mệnh đề nào sau đây đúng?
A.
1
4.
n
n
S
B.
1
14
.
2
n
n
n
S
C.
41
.
3
n
n
S
D.
44 1
.
3
n
n
S
Lời giải
Cấp số nhân đã cho có
1
1
1
1 14 4 1
. 1. .
4
1 14 3
n nn
n
u
q
Su
q
q
Câu 102: Cho cấp số nhân có các số hạng lần lượt là
11
; ; 1; ; 2048.
42
Tính tổng
S
của tất cả các số hạng
của cấp số nhân đã cho.

CHUYÊN ĐỀ II – TOÁN – 11 – DÃY SỐ - CẤP SỐ CỘNG – CẤP SỐ NHÂN
Page 25
Sưu tầm và biên soạn
A.
2047,75.
S
B.
2049,75.S
C.
4095,75.S
D.
4096,75.S
Lời giải
Cấp số nhân đã cho có
11 1 1 2
1
1
1
1
2048 2 .2 2 13.
4
2
2
n nn
u
uq n
q
Vậy cấp số nhân đã cho có tất cả 13 số hạng. Vậy
13 13
13 1
1 11 2
. . 2047,75
1 41 2
q
Su
q
Câu 103: Số thập phân vô hạn tuần hoàn
( )
3,1555... 3,1 5
=
viết dưới dạng số hữu tỉ là:
A.
63
20
. B.
142
45
. C.
1
18
. D.
7
2
.
Lời giải
3,1555... 3,1 0,05 0,005 0,0005 ...
=++ + +
Dãy số
0,05;0,005; 0,0005; 0,00005;...
là một cấp số nhân lùi vô hạn có
1
0,05u =
;
0,1
q =
.
Vậy
0,05
3,1555... 3,1
1 0,1
= +
−
142
45
=
.
Câu 104: Tính tổng
(
)
1
2
11 1
1 ... 1 ...
66 6
n
n
S
−
=−+ − + +− +
A.
7
6
S =
B.
6
7
S = −
C.
6
7
S =
D.
7
6
S = −
Lời giải
Ta có:
( )
3
2
12
1
... 1
6
u
u
qq
uu
====−<
. Do đó:
1
16
1
17
1
6
u
S
q
−−
= = =
−
+
Câu 105: Số thập phân vô hạn tuần hoàn
0,121212...
được biểu diễn bởi phân số
A.
3
25
. B.
12
99
. C.
1
11
. D.
3
22
.
Lời giải
Ta có
246 2
12 12 12 12
0,121212... ... ...
10 10 10 10
n
= + + ++ +
24 2
11 1
12 ... ...
10 10 10
n
= + ++ +
1
100
12
1
1
100
=
−
4 12
33 99
= =
.
Câu 106: Viết thêm bốn số vào giữa hai số
160
và
5
để được một cấp số nhân. Tổng các số hạng của cấp
số nhân đó là
A.
215
. B.
315
. C.
415
. D.
515
.

CHUYÊN ĐỀ II – TOÁN – 11 – DÃY SỐ - CẤP SỐ CỘNG – CẤP SỐ NHÂN
Page 26
Sưu tầm và biên soạn
Lời giải
Từ giả thiết ta có
1
6
5
6
1
160
1
5
2
u
u
q
u
u
=
⇒= =
=
.
Suy ra tổng các số hạng của cấp số nhân đó là:
( )
6
6
1
1
160 1
12
315
1
1
2
uq
S
q
−
−
= = =
−
.
Câu 107: Cho cấp số nhân
( )
n
u
thỏa mãn
123
41
13
26
uuu
uu
++=
−=
. Tổng
8
số hạng đầu của cấp số nhân
( )
n
u
là
A.
8
1093
S
=
. B.
8
3820S =
. C.
8
9841
S
=
. D.
8
3280
S
=
.
Lời giải
Ta có
123
41
13
26
uuu
uu
++=
−=
2
11 1
3
11
. . 13
. 26
u uq uq
uq u
++ =
⇔
−=
( )
( )
( )
2
1
2
1
1 13
. 1 1 26
u qq
uq qq
++ =
⇔
− ++ =
( )
2
1
1 13
3
u qq
q
++ =
⇔
=
1
1
3
u
q
=
⇔
=
.
Vậy tổng
(
)
8
1
8
1
1
uq
S
q
−
=
−
( )
8
11 3
3280
13
−
= =
−
.
Câu 108: Tổng
2
11 1
33 3
n
S = + +⋅⋅⋅+ +⋅⋅⋅
có giá trị là:
A.
1
9
. B.
1
4
. C.
1
3
. D.
1
2
.
Lời giải
Ta có
2
11 1
33 3
n
S = + +⋅⋅⋅+ +⋅⋅⋅
là tổng của cấp số nhân lùi vô hạn
(
)
n
u
với
1
3
n
n
u =
có số hạng
đầu
1
1
3
u =
, công sai
1
3
q =
.
Do đó
1
1
1
3
1
12
1
3
u
S
q
= = =
−
−
.
Câu 109: Cho dãy số
( )
n
a
xác định bởi
1
2a =
,
1
2
nn
aa
+
= −
,
1n ≥
,
n ∈
. Tính tổng của
10
số hạng đầu
tiên của dãy số.
A.
2050
3
. B.
2046
. C.
682−
. D.
2046−
.
Lời giải
Vì
1
2
n
n
a
a
+
= −
suy ra
( )
n
a
là một cấp số nhân với
1
2
2
a
q
=
= −
.

CHUYÊN ĐỀ II – TOÁN – 11 – DÃY SỐ - CẤP SỐ CỘNG – CẤP SỐ NHÂN
Page 27
Sưu tầm và biên soạn
Suy ra
( )
10
1
10
1
682
1
aq
S
q
−
= = −
−
.
Câu 110: Tính tổng tất cả các số hạng của một cấp số nhân có số hạng đầu là
1
2
, số hạng thứ tư là
32
và
số hạng cuối là
2048
?
A.
1365
2
. B.
5416
2
. C.
5461
2
. D.
21845
2
.
Lời giải
Theo bài ra ta có
1
1
2
u =
,
4
32u
=
và
2048
n
u =
.
3
41
.u uq=
3
1
32 .
2
q
⇒=
4q⇒=
2048
n
u =
1
1
. 2048
n
uq
−
⇒=
16
44
n−
⇒=
7n⇒=
Khi đó tổng của cấp số nhân này là
( )
( )
7
7
1
7
1
14
1
5461
2
1 14 2
uq
S
q
−
−
= = =
−−
.
Câu 111: Một cấp số nhân
( )
n
u
có
n
số hạng, số hạng đầu
1
7
u
=
, công bội
2q
=
. Số hạng thứ
n
bằng
1792
. Tính tổng
n
số hạng đầu tiên của cấp số nhân
( )
n
u
?
A.
5377
. B.
5737
. C.
3577
. D.
3775
.
Lời giải
Ta có
1
1
.
n
n
u uq
−
=
1
8
7.2 1792 9 3577
n
nS
−
⇒ = ⇔=⇒ =
Câu 112: Tính tổng cấ số nhân lùi vô hạn
( )
2
1
11 1
, , ,..., ,...
24 8 2
n
−
−−
là.
A.
1−
. B.
1
2
. C.
1
4
−
. D.
1
3
−
.
Lời giải
Cấp số nhân có
1
1
2
u = −
công bội
1
2
q = −
nên tổng của cấp số nhân lùi vô hạng là.
( )
1
1
1
1
lim lim
1 13
n
n
uq
u
S
qq
−
= = = −
−−
Câu 113: Giá trị của tổng
7 77 777 ... 77...7
bằng
A.
2018
70
10 1 2018
9
. B.
2018
7 10 10
2018
99
.
C.
2019
7 10 10
2018
99
. D.
2018
7
10 1
9
.
Lời giải

CHUYÊN ĐỀ II – TOÁN – 11 – DÃY SỐ - CẤP SỐ CỘNG – CẤP SỐ NHÂN
Page 28
Sưu tầm và biên soạn
Ta có
7 77 777 ... 77...7
7
9 99 999 ... 99...9
9
2 3 2018
7
10 1 10 1 10 1 ... 10 1
9
2 3 2018
7
10 10 10 ... 10 2018
9
Mặt khác,ta có
2 3 2018
10 10 10 ... 10
là tổng của một cấp số nhân với
1
10u
và công bội
10q
2 3 2018
10 10 10 ... 10
2018 2019
10 1 10 10
10
99
.
Do đó
2 3 2018
7
10 10 10 ... 10 2018
9
2019
7 10 10
2018
99
.
Câu 114: Giá trị của tổng
4 44 444 ... 44...4
+ + ++
bằng
A.
( )
2018
40
10 1 2018
9
−+
. B.
2019
4 10 10
2018
99
−
−
.
C.
2019
4 10 10
2018
99
−
+
. D.
( )
2018
4
10 1
9
−
.
Lời giải
Đặt
4 44 444 ... 44...4S =+ + ++
. Ta có:
9
9 99 999 ... 99...9
4
S
=+ + ++
( )
(
) ( )
( )
2 3 2018
10 1 10 1 10 1 ... 10 1= −+ −+ −+ −
Suy ra:
9
4
S =
( )
2 3 2018
10 10 10 ... 10 2018+ + ++ − =
2018A −
.
Với
2 3 2018
10 10 10 ... 10A = + + ++
là tổng
2018
số hạng của một cấp số nhân có số hạng đầu
1
10u =
, công bội
10q =
nên ta có
2018
1
1
1
q
Au
q
−
=
−
2018
1 10
10
9
−
=
−
2019
10 10
9
−
=
.
Do đó
2019
9 10 10
2018
49
S
−
= −
2019
4 10 10
2018
99
S
−
⇔= −
.
Câu 115: Cho dãy số xác định bởi
1
1u =
,
*
1
2
11
2 ;
3 32
nn
n
uu n
nn
+
−
=+∈
++
. Khi đó
2018
u
bằng:
A.
2016
2018
2017
21
3 2019
u = +
. B.
2018
2018
2017
21
3 2019
u = +
.
C.
2017
2018
2018
21
3 2019
u = +
.
D.
2017
2018
2018
21
3 2019
u = +
.
Lời giải
Ta có:
1
2
11
u 2u
3 32
nn
n
nn
+
−
= +
++
1 32
2
3 21
n
u
nn
= +−
++
2 1 21
.
3 23 1
n
u
nn
=+−
++
.

CHUYÊN ĐỀ II – TOÁN – 11 – DÃY SỐ - CẤP SỐ CỘNG – CẤP SỐ NHÂN
Page 29
Sưu tầm và biên soạn
1
12 1
23 1
nn
uu
nn
+
⇔− = −
++
( )
1
Đặt
1
1
nn
vu
n
= −
+
, từ
( )
1
ta suy ra:
1
2
3
nn
vv
+
=
.
Do đó
( )
n
v
là cấp số nhân với
11
11
22
vu=−=
, công bội
2
3
q =
.
Suy ra:
1
1
1
12
..
23
n
n
n
v vq
−
−
= =
1
1 12
.
123
n
n
u
n
−
⇔− =
+
1
12 1
.
23 1
n
n
u
n
−
⇔= +
+
.
Vậy
2017
2018
12 1
.
2 3 2019
u
= +
2016
2017
21
3 2019
= +
.
Câu 116: Cho dãy số
( )
n
U
xác định bởi:
1
1
3
U =
và
1
1
.
3
nn
n
UU
n
+
+
=
. Tổng
3 10
2
1
...
2 3 10
UU
U
SU= + + ++
bằng:
A.
3280
6561
. B.
29524
59049
. C.
25942
59049
. D.
1
243
.
Lời giải
Theo đề ta có:
1
1
.
3
nn
n
UU
n
+
+
=
1
1
13
nn
UU
nn
+
⇔=
+
mà
1
1
3
U =
hay
1
1
13
U
=
Nên ta có
2
2
11 1
.
2 33 3
U
= =
;
23
3
11 1
.
3 33 3
U
= =
; … ;
10
10
1
10 3
U
=
.
Hay dãy
n
U
n
là một cấp số nhân có số hạng đầu
1
1
3
U =
, công bội
1
3
q =
.
Khi đó
3 10
2
1
...
2 3 10
UU
U
SU= + + ++
2
1
.2 . 3
3
π
=
10
10
31
2.3
−
=
10
59048
2.3
=
29524
59049
=
.
Câu 117: Cho dãy số
()
n
u
thỏa mãn
1
1
1
2 1; 2
nn
u
uu n
−
=
= +≥
. Tổng
1 2 20
...
Suu u= + ++
bằng
A.
20
2 20.−
B.
21
2 22.
C.
20
2.
D.
21
2 20.−
Lời giải
( )
11
2 1 12 1
nn n n
uu u u
−−
= +⇔ += +
Đặt
1,
nn
vu= +
ta có
1
2
nn
vv
−
=
trong đó
1
2v =
Vậy
()
n
v
là cấp số nhân có số hạng đầu
1
2
v
=
và công bội bằng
2,
nên số hạng tổng quát
2
n
n
v =
12 1
n
nn
uv⇒ = −= −
1 2 20
...Suu u⇒= + ++
(
) ( ) ( )
1 2 20
2 1 2 1 ... 2 1= −+ −++ −
( )
1 2 20
2 2 ... 2 20= + ++ −
( )
20 21
2. 2 1 20 2 22.S = −− = −

CHUYÊN ĐỀ II – TOÁN – 11 – DÃY SỐ - CẤP SỐ CỘNG – CẤP SỐ NHÂN
Page 30
Sưu tầm và biên soạn
DẠNG 5. KẾT HỢP CẤP SỐ NHÂN VÀ CẤP SỐ CỘNG
Câu 118: Ba số theo thứ tự lập thành một cấp số nhân có số hạng cuối lớn hơn số hạng đầu
16
đơn vị. Ba
số đó là các số hạng thứ nhất, thứ hai và thứ năm của một cấp số cộng. Tìm ba số đó.
A.
2,6,18
. B.
4,8, 20
. C.
1 7 49
,,
33 3
. D.
4,4 5,20
.
Lời giải
Ta gọi ba số đó lần lượt là
,,
abc
và
d
là công sai của cấp số cộng.
Theo đề bài ta có:
16
4
4
ca
d
ca d
= +
⇒=
= +
.
Ngoài ra
( ) ( )
2
2
4 16 2b ac a a a a= ⇔ + = + ⇔=
Suy ra
6, 18bc= =
.
Vậy các số cần tìm là
2,6,18
.
Câu 119: Ba số dương
,,xyz
theo thứ tự lập thành một cấp số cộng và có tổng bằng
30
. Biết
2; 2; 18xyz+++
theo thứ tự lập thành một cấp số nhân. Tính
22
.
Tx z= +
A.
328.T =
B.
424.T =
C.
296.T =
D.
428.T
=
Lời giải
Theo tính chất của cấp số cộng, ta có
2xz y+=
.
Kết hợp với giả thiết
30
xyz++=
, ta suy ra
3 30 10
yy
= ⇔=
.
Gọi
d
là công sai của cấp số cộng thì
10x yd d=−= −
và
10z yd d=+= +
.
2; 2; 18xyz
+++
là cấp số nhân hay
12 ,12,28dd−+
.
Theo tính chất của cấp số nhân, ta có :
( )
( )
22
12 28 12 16 192 0d d dd
− += ⇔+ − =
.
( ) (
)
( ) ( )
8 ; ; 2;10;18
24 ; ; 34; 10; 14 ( )
d xyz
d xyz l
=⇒=
=−⇒ = −
22 22
18 2 328.Tx z
=+= +=
Câu 120: Ba số
,,xyz
theo thứ tự lập thành một cấp số cộng tăng có tổng bằng
24
. Nếu cộng thêm lần
lượt các số
1, 4, 13
vào ba số
,,xyz
ta được ba số theo thứ tự lập thành cấp số nhân. Tính giá trị
biểu thức
2 22
Px y z
=++
.
A.
200
. B.
210
. C.
220
. D.
190
.
Lời giải
Ba số
,,xyz
theo thứ tự lập thành một cấp số cộng có tổng bằng 24 nên ta có hệ
phương trình

CHUYÊN ĐỀ II – TOÁN – 11 – DÃY SỐ - CẤP SỐ CỘNG – CẤP SỐ NHÂN
Page 31
Sưu tầm và biên soạn
24
2
xyz
xz y
++=
+=
3 24 8yy⇒ = ⇒=
.
Ta viết lại 3 số
,,xyz
lần lượt bằng
8 d−
, 8,
8 d+
.
Nếu cộng thêm lần lượt các số
1, 4, 13
vào ba số
,,xyz
ta được ba số là
9 ,12, 21dd−+
.
Vì ba số này theo thứ tự lập thành cấp số nhân nên ta có phương trình
(
)(
)
2
9 21 12
dd− +=
2
12 45 0dd⇔+ −=
3
15
d
d
=
⇔
= −
.
Vì cấp số cộng tăng nên
03dd>⇒ =⇒
ba số
,,xyz
lần lượt bằng
5, 8, 11
.
Suy ra
2 22 22 2
5 8 11 210Px y z=++=++ =
.
Câu 121: Ba số theo thứ tự lập thành một cấp số nhân có số hạng cuối lớn hơn số hạng đầu
16
đơn vị. Ba
số đó là các số hạng thứ nhất, thứ hai và thứ năm của một cấp số cộng. Tìm ba số đó.
A.
2,6,18
. B.
4,8, 20
. C.
1 7 49
,,
33 3
. D.
4,4 5,20
.
Lời giải
Ta gọi ba số đó lần lượt là
,,
abc
và
d
là công sai của cấp số cộng.
Theo đề bài ta có:
16
4
4
ca
d
ca d
= +
⇒=
= +
.
Ngoài ra
( ) ( )
2
2
4 16 2b ac a a a a= ⇔ + = + ⇔=
Suy ra
6, 18bc= =
.
Vậy các số cần tìm là
2,6,18
.
Câu 122: Cho ba số
a
,
b
,
c
là ba số liên tiếp của một cấp số cộng có công sai là
2
. Nếu tăng số thứ nhất
thêm
1
, tăng số thứ hai thêm
1
và tăng số thứ ba thêm
3
thì được ba số mới là ba số liên tiếp của
một cấp số nhân. Tính
( )
abc
++
.
A.
12
. B.
18
. C.
3
. D.
9
.
Lời giải
Chọn D
+)
a
,
b
,
c
là ba số hạng liên tiếp của cấp số cộng có công sai bằng
2d =
⇒
2
4
ba
ca
= +
= +
.
+) Ba số
1a +
,
3a +
,
7a +
là ba số hạng liên tiếp của một cấp số nhân
( ) ( ) ( )
2
3 1. 7a aa⇔+ =+ +
22
69 87aa aa⇔ + += + +
22 1aa⇔ =⇔=
.
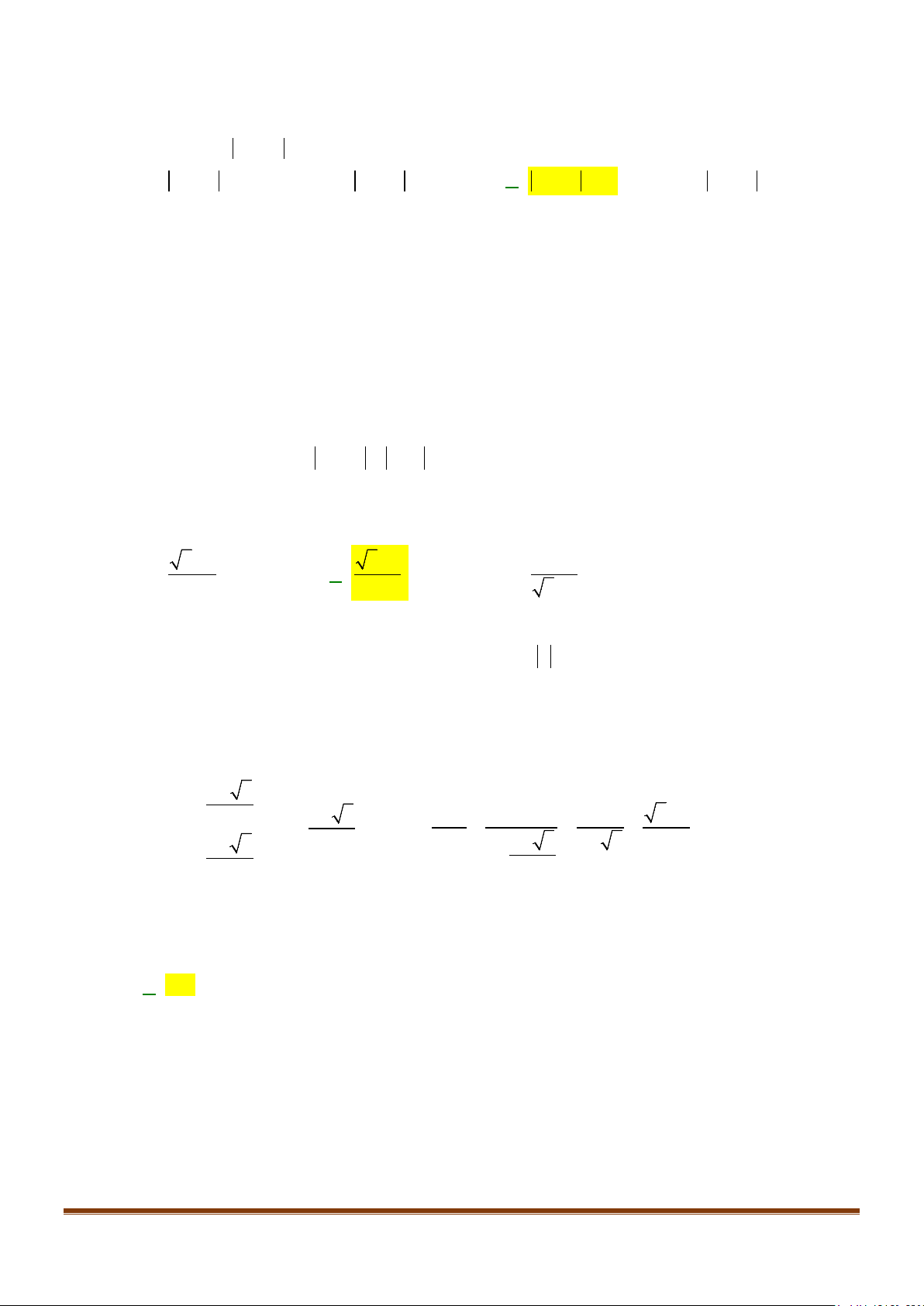
CHUYÊN ĐỀ II – TOÁN – 11 – DÃY SỐ - CẤP SỐ CỘNG – CẤP SỐ NHÂN
Page 32
Sưu tầm và biên soạn
3 69
T abc a
⇒ =++= +=
.
Câu 123: Cho ba số
x
;
5
;
2
y
theo thứ tự lập thành cấp số cộng và ba số
x
;
4
;
2
y
theo thứ tự lập thành cấp
số nhân thì
2xy−
bằng
A.
2 10xy−=
. B.
29xy−=
. C.
26
xy−=
. D.
28
xy−=
.
Lời giải
Do ba số
x
;
5
;
2y
theo thứ tự lập thành cấp số cộng, ta có:
(
)
2 10 1Sx y=+=
Ta lại có ba số
x
;
4
;
2y
theo thứ tự lập thành cấp số nhân nên:
( )
.2 16 2P xy= =
Từ
( ) ( )
1,2
suy ra hai số
x
;
2y
là nghiệm của phương trình
2
.0X SX P− +=
hay
2
10 16 0XX− +=
2
8
X
X
=
⇒
=
Theo yêu cầu bài toán
2 28 6xy− =−=
Câu 124: Tính tổng của cấp số nhân lùi vô hạn
()
n
u
biết
1
1u =
và
134
,,uuu
theo thứ tự là ba số hạng liên
tiếp trong một cấp số cộng.
A.
51
2
+
. B.
51
2
−
. C.
1
51−
. D.
2
.
Lời giải
()
n
u
là cấp số nhân lùi vô hạn có công bội
q
, suy ra
1q <
và
22 33
31 41
.,.u uq q u uq q= = = =
.
Mà và
134
,,uuu
theo thứ tự là ba số hạng liên tiếp trong một cấp số cộng nên
14 3
2.uu u+=
.
Từ đó ta có
3 23 2 2 2
1 2. q 2. 1 0 ( 1)( 1) 0 1 0q q q q qq qq+ = ⇔ − +=⇔ − −− =⇔ −−=
15
15
2
2
15
2
q
q
q
+
=
−
⇔ ⇒=
−
=
.Vậy
1
1 2 51
12
1 51 5
1
2
u
S
q
−
= = = =
−
−+
−
.
Câu 125: Ba số phân biệt có tổng là
217
có thể coi là các số hạng liên tiếp của một cấp số nhân, cũng có
thể coi là số hạng thứ
2
, thứ
9
, thứ
44
của một cấp số cộng. Hỏi phải lấy bao nhiêu số hạng
đầu của cấp số cộng này để tổng của chúng bằng
820
?
A.
20
. B.
42
. C.
21
. D.
17
.
Lời giải
Gọi ba số đó là
x
,
y
,
z
. Do ba số là các số hạng thứ
2
, thứ
9
và thứ
44
của một cấp số cộng
nên ta có:
x
;
7yx d
= +
;
42zx d= +
.
Theo giả thiết, ta có:
xyz++
7 42xx dx d
=++ ++
3 49xd= +
217=
.
Mặt khác, do
x
,
y
,
z
là các số hạng liên tiếp của một cấp số nhân nên:

CHUYÊN ĐỀ II – TOÁN – 11 – DÃY SỐ - CẤP SỐ CỘNG – CẤP SỐ NHÂN
Page 33
Sưu tầm và biên soạn
2
y xz=
(
) ( )
2
7 42x d xx d⇔+ = +
( )
47 0d xd⇔ −+ =
0
47 0
d
xd
=
⇔
−+ =
Với
0
d =
, ta có:
217
3
xyz
= = =
. Suy ra
217 2460
820 :
3 217
n = = ∉
.
Với
47 0xd−+ =
, ta có:
47 0
3 49 217
xd
xd
−+ =
+=
7
4
x
d
=
⇔
=
. Suy ra
1
743u =−=
.
Do đó,
820
n
S
=
( )
1
21
820
2
u n dn +−
⇔=
( )
[ ]
2.3 4 1
820
2
nn+−
⇔=
20
41
2
n
n
=
⇔
= −
Vậy
20n
=
.
DẠNG 6. BÀI TOÁN THỰC TẾ VÀ MỘT SỐ BÀI TOÁN KHÁC
Câu 126: Người ta thiết kế một cái tháp
11
tầng. Diện tích bề mặt trên của mỗi tầng bằng nửa diện tích
của mặt trên của tầng ngay bên dưới và diện tích mặt trên của tầng
1
bằng nửa diện tích của đế
tháp. Tính diện tích mặt trên cùng.
A.
2
8 .
m
B.
2
6 .m
C.
2
10 .
m
D.
2
12 .m
Lời giải
Gọi
0 1 2 11
, , a ,...,aaa
lần lượt là diện tích mặt trên của đế tháp, tầng 1, tầng 2,., tầng 11.
Khi đó ta có:
0 10
11
12288; a , 1,2,...,11
22
n
nn
a aa n
.
Diện tích mặt trên tầng trên cùng là:
11 11
11 0
11
12288 6
22
aa
2
m
Câu 127: Một hình vuông
ABCD
có cạnh
AB a=
, diện tích
1
S
. Nối 4 trung điểm
1
A
,
1
B
,
1
C
,
1
D
theo
thứ tự của 4 cạnh
AB
,
BC
,
CD
,
DA
ta được hình vuông thứ hai là
111 1
ABC D
có diện tích
2
S
.
Tiếp tục như thế ta được hình vuông thứ ba
222 2
ABC D
có diện tích
3
S
và cứ tiếp tục như thế, ta
được diện tích
45
, ,...SS
Tính
1 2 3 100
...SS S S S= + + ++
.
A.
100
99 2
21
.
2
S
a
−
=
B.
( )
100
99
21
.
2
a
S
−
=
C.
( )
2 100
99
21
.
2
a
S
−
=
D.
( )
2 99
99
21
.
2
a
S
−
=
Lời giải
Dễ thấy:
22 2
2
1 2 3 100
99
; ; ;...; .
24 2
aa a
S aS S S= = = =
Như vậy
1 2 3 100
, , ,...,SS S S
là cấp số nhân với công bội
1
2
q =
.
( )
2 100
2
1 2 100
2 99 99
21
11 1
... 1 ... .
22 2 2
a
SS S S a
−
= + ++ = ++ ++ =

CHUYÊN ĐỀ II – TOÁN – 11 – DÃY SỐ - CẤP SỐ CỘNG – CẤP SỐ NHÂN
Page 34
Sưu tầm và biên soạn
Câu 128: Dân số tỉnh Bình Phước theo điều tra vào ngày
1/1/ 2011
là
905300
người. Nếu duy trì tốc độ
tăng trưởng dân số không đổi là
10%
một năm thì đến
1/1/ 2020
dân số của tỉnh Bình Phước là
bao nhiêu?
A.
22582927
. B.
02348115
. C.
2134650
. D.
11940591
.
Lời giải
Sau
9
năm thì số dân của tỉnh Bình Phước là:
9
905300.1,1 2134650≈
người.
Câu 129: Bạn A thả quả bóng cao su từ độ cao
10
m theo phương thẳng đứng. Mỗi khi chạm đất nó lại nảy
lên theo phương thẳng đứng có độ cao bằng
3
4
độ cao trước đó. Tính tổng quãng đường bóng đi
được đến khi bóng dừng hẳn.
A.
40
m. B.
70
m. C.
50
m. D.
80
m.
Lời giải
Các quãng đường khi bóng đi xuống tạo thành một cấp số nhân lùi vô hạn có
1
10u =
và
3
4
q =
.
Tổng các quãng đường khi bóng đi xuống là
1
1
u
S
q
=
−
10
3
1
4
=
−
40=
.
Tổng quãng đường bóng đi được đến khi bóng dừng hẳn
2 10 70S −=
.
Câu 130: Một loại vi khuẩn sau mỗi phút số lượng tăng gấp đôi biết rằng sau
5
phút người ta đếm được
có
64000
con hỏi sau bao nhiêu phút thì có được
2048000
con.
A.
10
. B.
11
. C.
26
. D.
50
.
Lời giải
Số lượng vi khuẩn tăng lên là cấp số nhân
( )
n
u
với công bội
2q =
.
Ta có:
6
64000u =
5
1
. 64000uq⇒=
1
2000u⇒=
.
Sau
n
phút thì số lượng vi khuẩn là
1n
u
+
.
1
2048000
n
u
+
=
1
. 2048000
n
uq⇒=
2000.2 2048000
n
⇒=
10n⇒=
.
Vậy sau
10
phút thì có được
2048000
con.
Câu 131:
Trên một bàn cờ vua kích thước 8x8 người ta đặt số hạt thóc theo cách như sau. Ô thứ nhất đặt
một hạt thóc, ô thứ hai đặt hai hạt thóc, các ô tiếp theo đặt số hạt thóc gấp đôi ô đứng liền kề
trước nó. Hỏi phải tối thiểu từ ô thứ bao nhiêu để tổng số hạt thóc từ ô đầu tiên đến ô đó lớn hơn
20172018 hạt thóc.
A.
26
B.
23
C.
24
D.
25
Lời giải
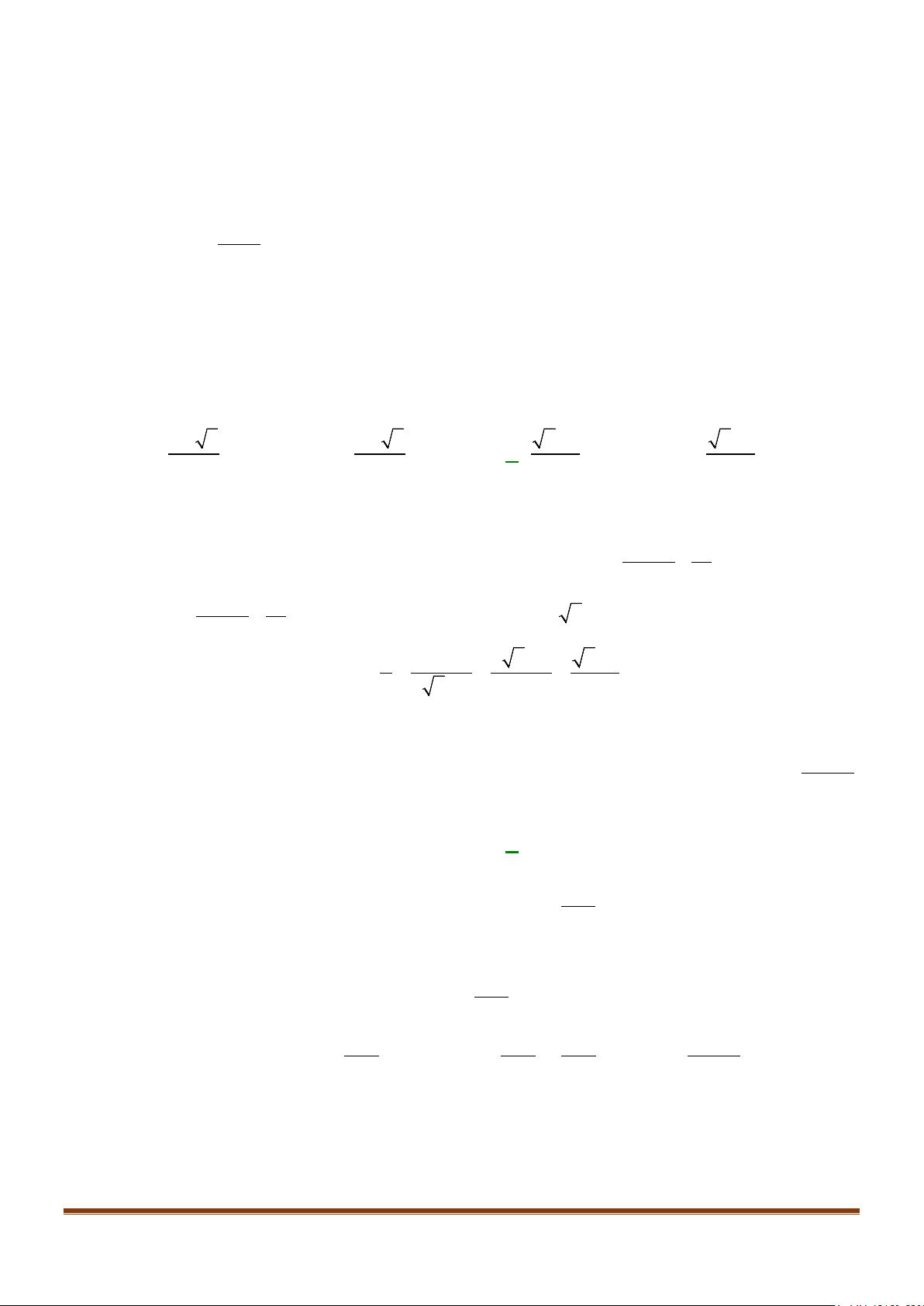
CHUYÊN ĐỀ II – TOÁN – 11 – DÃY SỐ - CẤP SỐ CỘNG – CẤP SỐ NHÂN
Page 35
Sưu tầm và biên soạn
Số thóc ở ô sau gấp đôi ở ô trước, đặt
n
u
là số thóc ở ô thứ
n
thì số thóc ở mỗi ô sẽ lập thành
một cấp số nhân:
0
1
1
12
.
22
n
nn
u
uu
+
= =
= =
Khi đó tổng số thóc từ ô đầu tới ô thứ
k
là
11
12
12 2
k
kk
S uu u
−
= + +…+ = + +…+
Vậy
21
21
21
k
k
k
S
−
= = −
−
Theo đề ta có:
2
2 1 20172018 2 20172019 log 20172019
kk
k−> ⇔ > ⇔ >
Vậy phải lấy tối thiểu từ ô thứ
25
Câu 132: Cho tam giác
ABC
cân tại đỉnh
A
, biết độ dài cạnh đáy
BC
, đường cao
AH
và cạnh bên
AB
theo thứ tự lập thành cấp số nhân với công bội
q
. Giá trị của
2
q
bằng
A.
22
2
+
. B.
22
2
−
. C.
21
2
+
. D.
21
2
−
Lời giải
Đặt
;;BC a AB AC b AH h= = = =
. Theo giả thiết ta có
,,ahb
lập cấp số nhân, suy ra
2
.h ab=
Mặt khác tam giác
ABC
cân tại đỉnh
A
nên
22 2
22
24
a
bb a
hm
+
= = −
Do đó
( )
22 2
22
4 4 0 22 2
24
bb a
ab a ab b a b
+
− = ⇔ + − =⇔= −
Lại có
2
b qa=
nên suy ra
2
1 22 2 2 1
42
22 2
b
q
a
++
= = = =
−
.
Câu 133: Cho dãy số
( )
n
a
xác định bởi
11
5, . 3
nn
a a qa
+
= = +
với mọi
1n ≥
, trong đó
q
là hằng số,
0q ≠
,
1q ≠
. Biết công thức số hạng tổng quát của dãy số viết được dưới dạng
1
1
1
.
1
n
n
n
q
aq
q
αβ
−
−
−
= +
−
. Tính
2
αβ
+
?
A.
13
. B.
9
. C.
11
. D.
16
.
Lời giải
Cách 1. Ta có:
( )
1nn
a k qa k
+
−= −
3k kq⇔− =
3
1
k
q
⇔=
−
Đặt
nn
v ak= −
2
1 11
. . ... .
n
n nn
v qv q v q v
+−
⇒== ==
Khi đó
( )
11 1
11
3
. . .5
1
nn n
n
v qv q ak q
q
−− −
= = −= −
−
Vậy
1
11 1
3 33 1
. 5 . 5 5. 3.
1 11 1
n
nn n
nn
q
a v kq kq q
q qq q
−
−− −
−
= += − += − + = +
− −− −
.
Do đó:
5; 3
αβ
= =
2 5 2.3 11
αβ
⇒+=+=
.
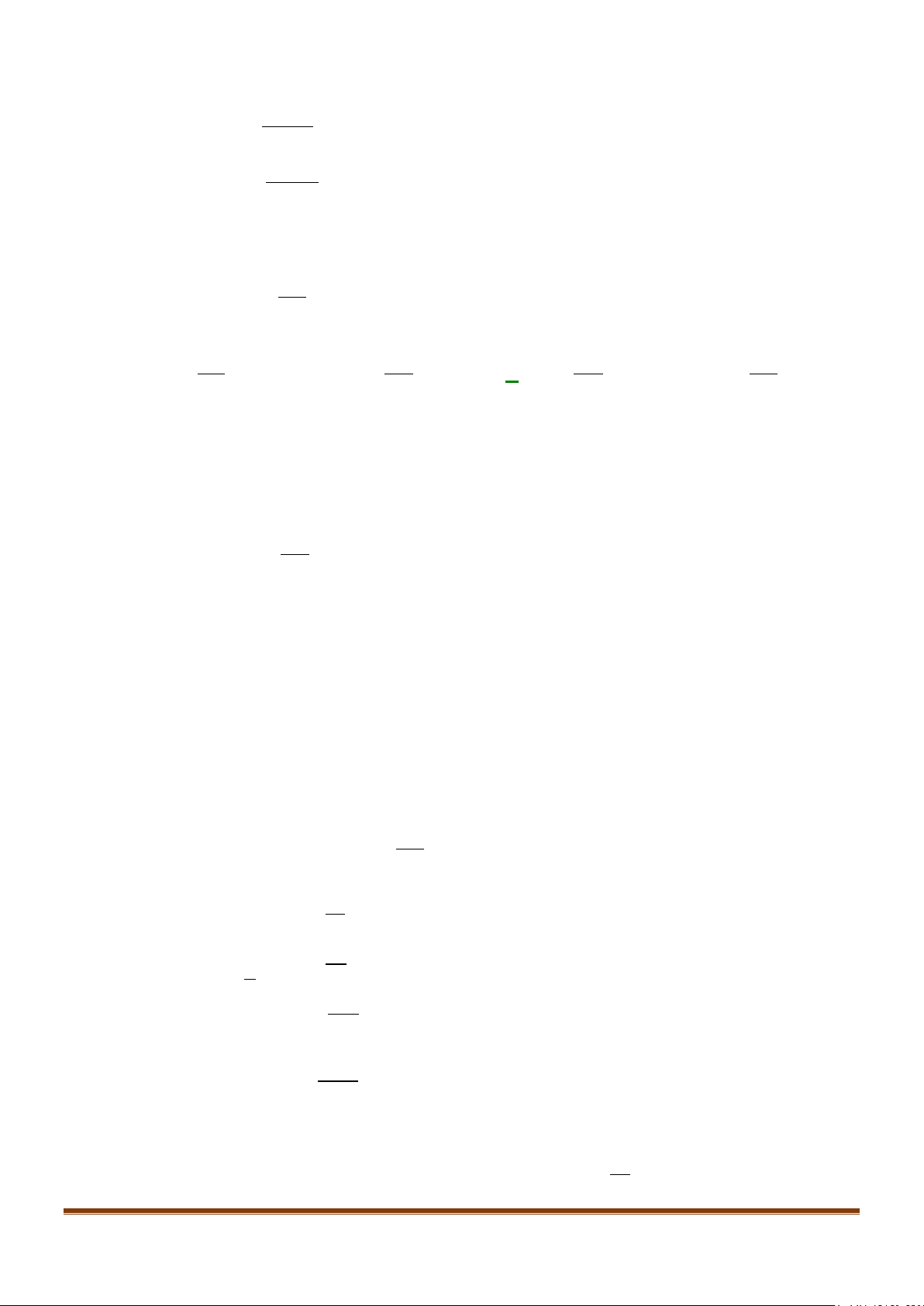
CHUYÊN ĐỀ II – TOÁN – 11 – DÃY SỐ - CẤP SỐ CỘNG – CẤP SỐ NHÂN
Page 36
Sưu tầm và biên soạn
Cách 2. Theo giả thiết ta có
12
5, 5 3a aq
= = +
. Áp dụng công thức tổng quát, ta được
11
11
1
21
21
2
1
.
1
1
.
1
q
aq
q
q
aq
q
q
αβ
αβ
α
αβ
−
−
−
−
−
=+=
−
−
=+=
−
+
, suy ra
5
53
q
q
α
αβ
=
+=
+
, hay
5
3
α
β
=
=
2 5 2.3 11
αβ
⇒+=+=
Câu 134: Cho bốn số
,
ab
,
, cd
theo thứ tự đó tạo thành cấp số nhân với công bội khác
1
. Biết tổng ba
số hạng đầu bằng
148
9
, đồng thời theo thứ tự đó chúng lần lượt là số hạng thứ nhất, thứ tư và thứ
tám của một cấp số cộng. Tính giá trị biểu thức
T abcd=−+−
.
A.
101
27
T =
. B.
100
27
T =
. C.
100
27
T = −
. D.
101
27
T = −
.
Lời giải
Ta có
(
)
(
)
( )
2
2
1
2
148
3
9
ac b
bd c
abc
=
=
++=
.
Và cấp số cộng có
1
ua=
,
4
ub=
,
8
uc=
. Gọi
x
là công sai của cấp số cộng. Vì cấp số nhân
có công bội khác
1
nên
0x ≠
.
Ta có :
3
7
ba x
ca x
= +
= +
(
)
4
.
Từ
( )
1
và
( )
4
ta được :
(
)
( )
2
73
aa x a x+=+
2
90ax x⇔− =
.
Do
0x ≠
nên
9ax=
.
Từ
( )
3
và
( )
4
, suy ra
148
3 10
9
ax+=
.
Do đó :
4
4
9
a
x
=
=
16
3
64
9
256
27
b
c
d
=
⇒=
=
.
Vậy
100
27
T abcd
−
=−+− =
.
Câu 135: Từ độ cao
55,8m
của tháp nghiêng Pisa nước Italia người ta thả một quả bóng cao su chạm xuống
đất. Giả sử mỗi lần chạm đất quả bóng lại nảy lên độ cao bằng
1
10
độ cao mà quả bóng đạt trước

CHUYÊN ĐỀ II – TOÁN – 11 – DÃY SỐ - CẤP SỐ CỘNG – CẤP SỐ NHÂN
Page 37
Sưu tầm và biên soạn
đó. Tổng độ dài hành trình của quả bóng được thả từ lúc ban đầu cho đến khi nó nằm yên trên
mặt đất thuộc khoảng nào trong các khoảng sau đây?
A.
( )
67 ;69mm
. B.
( )
60 ;63mm
. C.
( )
64 ;66mm
. D.
( )
69 ;72mm
.
Lời giải
Gọi
n
h
là độ dài đường đi của quả bóng ở lần rơi xuống thứ
(
)
*
nn
∈
.
Gọi
n
l
là độ dài đường đi của quả bóng ở lần nảy lên thứ
(
)
*
nn
∈
.
Theo bài ra ta có
1
55,8h =
,
1
1
.55,8 5,58
10
l = =
và các dãy số
( )
n
h
,
( )
n
l
là các cấp số nhân lùi
vô hạn với công bội
1
10
q =
.
Từ đó ta suy ra tổng độ dài đường đi của quả bóng là:
( )
( )
11
11
10
68, 2
11
9
11
10 10
hl
S hl m= + = +=
−−
.
Câu 136: Để trang trí cho quán trà sữa sắp mở cửa của mình, bạn Việt quyết định tô màu một mảng tường
hình vuông cạnh bằng
1m
. Phần tô màu dự kiến là các hình vuông nhỏ được đánh số lần lượt là
1,2,3...n,..
, trong đó cạnh của hình vuông kế tiếp bằng một nửa cạnh hình vuông trước đó. Giả
sử quá trình tô màu của Việt có thể diễn ra nhiều giờ. Hỏi bạn Việt tô màu đến hình vuông thứ
mấy thì diện tích của hình vuông được tô bắt đầu nhỏ hơn
( )
2
1
1000
m
?
A.
6
. B.
3
. C.
5
. D.
4
.
Lời giải

CHUYÊN ĐỀ II – TOÁN – 11 – DÃY SỐ - CẤP SỐ CỘNG – CẤP SỐ NHÂN
Page 38
Sưu tầm và biên soạn
Diện tích của hình vuông lập thành cấp số nhân với số hạng đầu tiên là
1
11
,
44
uq
= =
.
Do đó số hạng tổng quát là
( )
1
11 1
.1
44 4
n
n
n
un
−
= = ≥
. Để diện tích của hình vuông tô màu nhỏ
hơn
1 11
4 1000 5
1000 4 1000
n
n
n⇔ < ⇔ > ⇒≥
. Vậy tô màu từ hình vuông thứ
5
thỏa mãn yêu
cầu bài toán.
Câu 137: Có bao nhiêu giá trị thực của tham số
m
để phương trình
( )( )
( )
13 0x x xm− − −=
có 3 nghiệm
phân biệt lập thành cấp số nhân tăng?
A.
4
. B.
3
. C.
2
. D. 1.
Lời giải
Ta có:
( )( )( )
1
13 0 3
x
x x xm x
xm
=
− − −=⇔=
=
.
Để phương trình có 3 nghiệm phân biệt thì:
{ }
1;3m ∉
.
Trường hợp 1:
13m <<
.
Để 3 số
;1;3
m
lập thành cấp số nhân tăng thì:
2
1
.3 1
3
mm
=⇔=
Cấp số nhân tăng đó là:
1
;1;3
3
Trường hợp 2:
13m<<
.
Để 3 số
1; ;3m
lập thành cấp số nhân tăng thì:
2
3
1.3
3
m
m
m
=
= ⇔
= −
Đối chiếu điều kiện
13m<<
ta chọn
3
m =
.
Cấp số nhân tăng đó là:
1; 3;3
Trường hợp 3:
13m<<
.
Để 3 số
1;3;
m
lập thành cấp số nhân tăng thì:
2
1. 3 9mm=⇔=
Cấp số nhân tăng đó là:
1;3;9
Vậy
1
; 3;9
3
m
∈
thì phương trình
( )( )( )
13 0x x xm− − −=
có 3 nghiệm phân biệt lập thành
cấp số nhân tăng.
Câu 138: Biết rằng tồn tại đúng hai giá trị của tham số
m
để phương trình
( )
32 2
7 2 6 80x x m mx− + + −=
có ba nghiệm phân biệt lập thành một cấp số nhân. Tính tổng lập phương của hai giá trị đó.
A.
342−
. B.
216−
. C.
344
. D.
216
.
Lời giải
Giả sử phương trình đã cho có 3 nghiệm là:
123
,,xx x
.
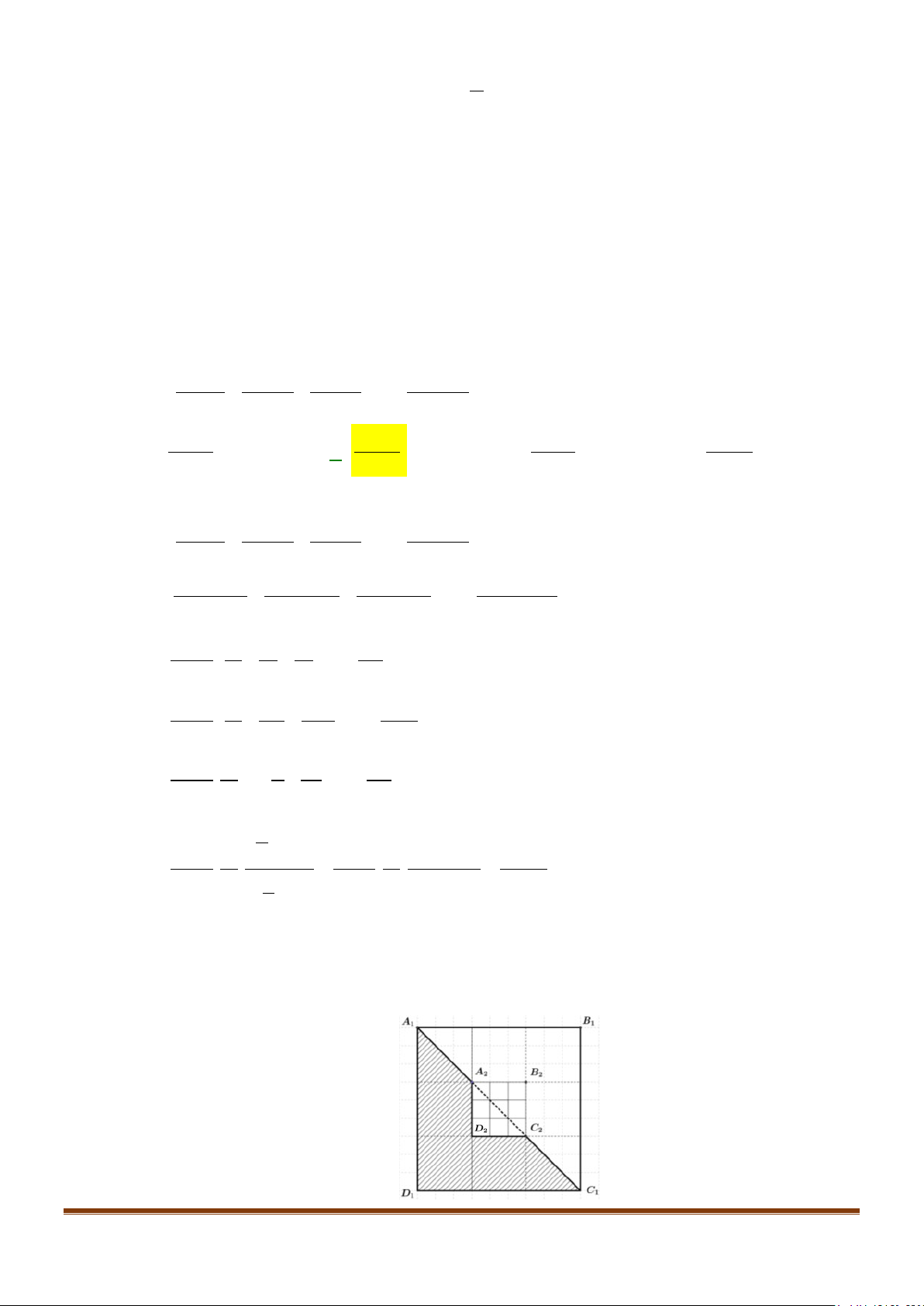
CHUYÊN ĐỀ II – TOÁN – 11 – DÃY SỐ - CẤP SỐ CỘNG – CẤP SỐ NHÂN
Page 39
Sưu tầm và biên soạn
Theo định lí Viet, tích 3 nghiệm:
123
8
d
xxx
a
=−=
.
Vì ba nghiệm này lập thành một cấp số nhân nên
2
2 13
x xx=
. Do đó ta có:
3
22
82xx=⇔=
.
Thay
2
x =
vào phương trình ta được:
(
)
2
1
4 6 28
7
m
mm
m
=
+=⇔
= −
.
Theo giả thiết hai giá trị này của
m
đều nhận.
Tổng lập phương của hai giá trị
m
là:
(
)
3
3
1 7 342+− =−
.
Câu 139: Cho dãy số
( )
n
u
là một cấp số nhân có số hạng đầu
1
1u =
, công bội
2
q
=
. Tính tổng
1 5 2 6 3 7 20 24
111 1
...T
uu uu uu u u
= + + ++
−−− −
.
A.
19
18
12
15.2
−
. B.
20
19
12
15.2
−
. C.
19
18
21
15.2
−
. D.
20
19
21
15.2
−
Lời giải
( ) ( ) ( ) (
)
1 5 2 6 3 7 20 24
444 4
1 2 3 20
4
1 2 3 20
4 2 19
11 1 1
4 2 19
1
20
4
1
111 1
...
111 1
...
111 1
1 111 1
...
1
1 11 1 1
...
1
1 1 11 1
. 1 ...
1
1
1
11
..
1
1
T
uu uu uu u u
u qu qu q u q
qu u u u
q u uq uq uq
qu qq q
q
qu
q
= + + ++
−−− −
= + + ++
−−− −
= + + ++
−
= + + ++
−
= ++ ++
−
−
=
−
−
( )
( )
20
20
4 19 19
1
1
1 1 12
..
1 1 15.2
1
q
q u qq
−
−
= =
−−
Câu 140: Với hình vuông
111 1
ABC D
như hình vẽ bên, cách tô màu như phần gạch sọc được gọi là cách tô
màu “đẹp”. Một nhà thiết kế tiến hành tô màu cho một hình vuông như hình bên, theo quy trình
sau:
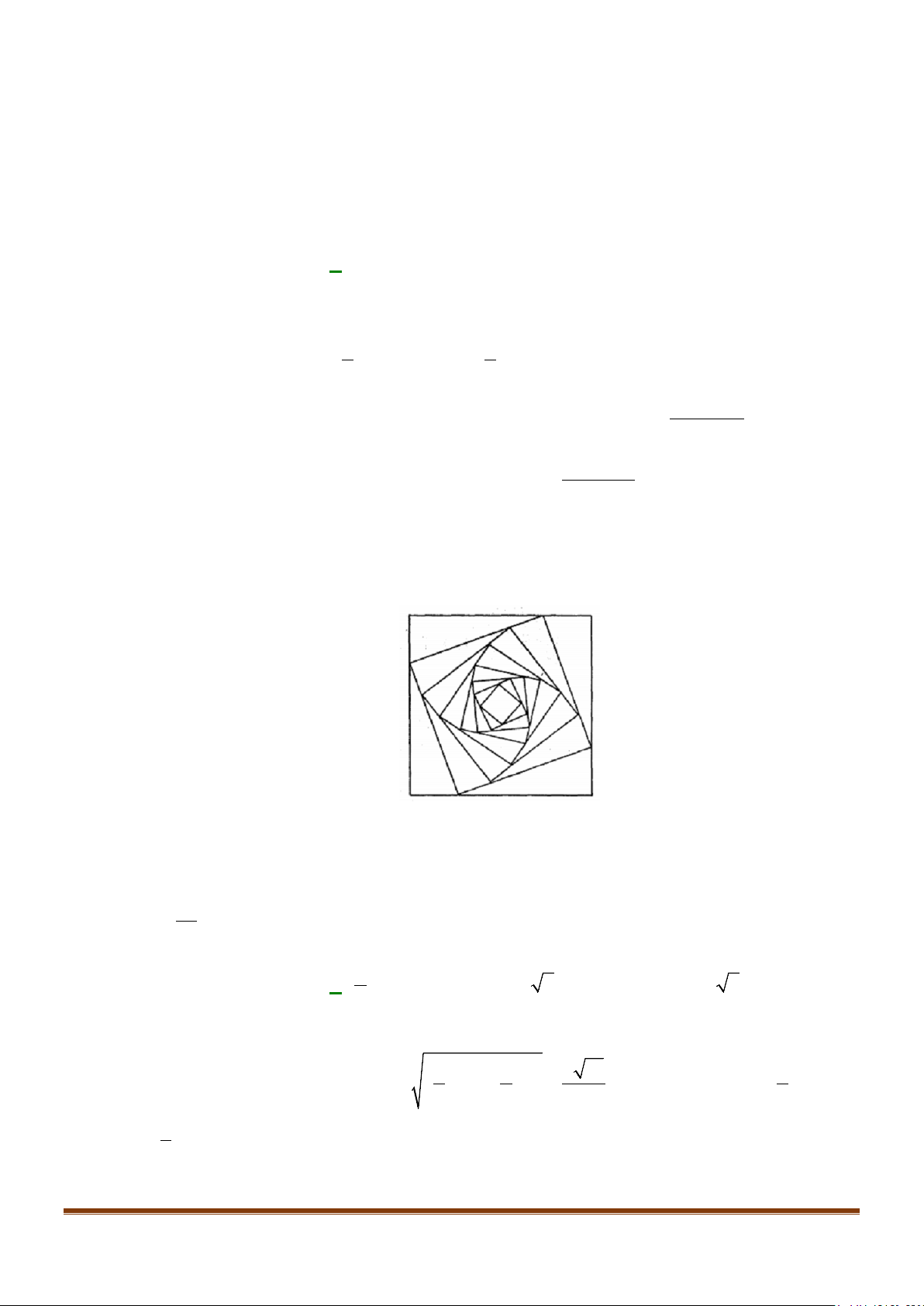
CHUYÊN ĐỀ II – TOÁN – 11 – DÃY SỐ - CẤP SỐ CỘNG – CẤP SỐ NHÂN
Page 40
Sưu tầm và biên soạn
Bước 1: Tô màu “đẹp” cho hình vuông
111 1
ABC D
.
Bước 2: Tô màu “đẹp” cho hình vuông
222 2
ABC D
là hình vuông ở chính giữa khi chia hình
vuông
111 1
ABC D
thành
9
phần bằng nhau như hình vẽ.
Bước 3: Tô màu “đẹp” cho hình vuông
333 3
ABC D
là hình vuông ở chính giữa khi chia hình
vuông
222 2
ABC D
thành
9
phần bằng nhau. Cứ tiếp tục như vậy. Hỏi cần ít nhất bao nhiêu bước
để tổng diện tích phần được tô màu chiếm
49,99%
.
A.
9
bước. B.
4
bước. C.
8
bước. D.
7
bước.
Lời giải
Gọi diện tích được tô màu ở mỗi bước là
n
u
,
*
n ∈
. Dễ thấy dãy các giá trị
n
u
là một cấp số
nhân với số hạng đầu
1
4
9
u =
và công bội
1
9
q =
.
Gọi
k
S
là tổng của
k
số hạng đầu trong cấp số nhân đang xét thì
(
)
1
1
1
k
k
uq
S
q
−
=
−
.
Để tổng diện tích phần được tô màu chiếm
49,99%
thì
( )
1
1
0,4999 3,8
1
k
uq
k
q
−
≥ ⇔≥
−
.
Vậy cần ít nhất
4
bước.
Câu 141: Cho hình vuông
( )
1
C
có cạnh bằng
a
. Người ta chia mỗi cạnh của hình vuông thành bốn phần
bằng nhau và nối các điểm chia một cách thích hợp để có hình vuông
( )
2
C
.
Từ hình vuông
( )
2
C
lại tiếp tục làm như trên ta nhận được dãy các hình vuông
1
C
,
2
C
,
3
C
,.,
n
C
. Gọi
i
S
là diện tích của hình vuông
{ }
( )
1,2,3,.....
i
Ci∈
. Đặt
123
... ...
n
TSS S S=+++ +
. Biết
32
3
T =
, tính
a
?
A.
2
. B.
5
2
. C.
2
. D.
22
.
Lời giải
Cạnh của hình vuông
( )
2
C
là:
22
2
3 1 10
44 4
a
a aa
= +=
. Do đó diện tích
2
2
5
8
Sa=
1
5
8
S=
.
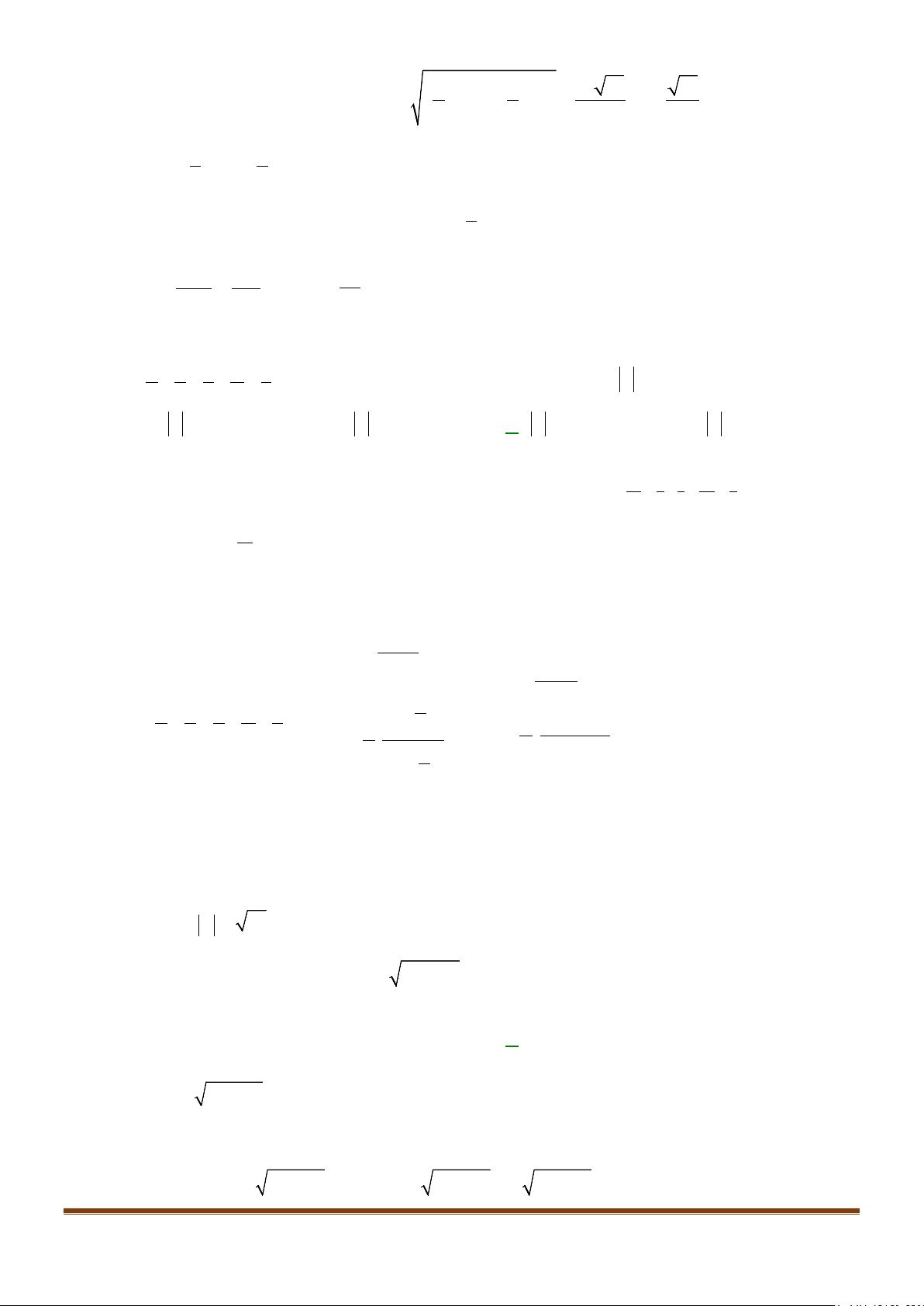
CHUYÊN ĐỀ II – TOÁN – 11 – DÃY SỐ - CẤP SỐ CỘNG – CẤP SỐ NHÂN
Page 41
Sưu tầm và biên soạn
Cạnh của hình vuông
( )
3
C
là:
2
22
2
32 2
10
3 1 10
44 4 4
a
aa a a
= +==
. Do đó diện tích
2
2
32
55
88
S aS
= =
. Lý luận tương tự ta có các
1
S
,
2
S
,
3
,... ...
n
SS
. tạo thành một dãy cấp số
nhân lùi vô hạn có
11
uS=
và công bội
5
8
q
=
.
1
1
S
T
q
=
−
2
8
3
a
=
. Với
32
3
T
=
ta có
2
42aa=⇔=
.
Câu 142: Cho năm số
a
,
b
,
c
,
d
,
e
tạo thành một cấp số nhân theo thứ tự đó và các số đều khác
0
, biết
11111
10
abcde
+++ +=
và tổng của chúng bằng
40
. Tính giá trị
S
với
S abcde=
.
A.
42S =
. B.
62S =
. C.
32S =
. D.
52
S
=
.
Lời giải
Gọi
q
( )
0q ≠
là công bội của cấp số nhân
a
,
b
,
c
,
d
,
e
. Khi đó
1
a
,
1
b
,
1
c
,
1
d
,
1
e
là cấp số nhân
có công bội
1
q
.
Theo đề bài ta có
40
11111
10
abcde
abcde
+++ +=
+++ +=
5
5
1
. 40
1
1
1
1
. 10
1
1
q
a
q
q
a
q
−
=
−
⇔
−
=
−
( )
5
5
4
1
. 40
1
11
. 10
1
q
a
q
q
aq q
−
=
−
⇔
−
=
−
24
4aq
⇔=
.
Ta có
S abcde=
234
.. . .a aq aq aq aq=
5 10
aq=
.
Nên
( )
2
2 5 10
S aq=
( )
5
24 5
4aq= =
.
Suy ra
5
4 32
S = =
.
Câu 143: Cho dãy số
( )
n
u
thỏa mãn
1 12 2
*
1
55 6
3
nn
u uu u
u un
+
+ −=+
= ∀∈
. Giá trị nhỏ nhất của
n
để
2018
2.3
n
u ≥
bằng:
A.
2017
. B.
2018
. C.
2019
. D.
2010
Lời giải
( )
( )
1 12 2
*
1
5 5 6 1
3 2
nn
u uu u
u un
+
+ −=+
= ∀∈
.
Từ
( )
1
có
( )
2
1 12 2 12 12
5 5 6 5 5 60u uu u uu uu+−=+⇔ −+−−=

CHUYÊN ĐỀ II – TOÁN – 11 – DÃY SỐ - CẤP SỐ CỘNG – CẤP SỐ NHÂN
Page 42
Sưu tầm và biên soạn
12 12
5 25 4uu uu⇔ −=⇔ −=
.
Từ
( )
2
có
1 21
33
nn
u uuu
+
= ⇒=
. Giải hệ
12
21
54
3
uu
uu
−=
=
được
1
2u
=
.
Dãy
( )
n
u
là cấp số nhân với
1
2
3
u
q
=
=
có SHTQ:
1
2.3
n
n
u
−
=
với
*
n ∈
2018 1 2018
2.3 2.3 2.3 1 2018 2019
n
n
u nn
−
≥⇔≥⇔−≥⇔≥
.
Vậy giá trị nhỏ nhất thỏa mãn là
2019
.
Câu 144: Tìm tất cả các giá trị của tham số
m
để phương trình sau có ba nghiệm phân biệt lập thành một
cấp số nhân:
( )
32 2
7 2 6 80x x m mx .− + + −=
A.
7
m.
= −
B.
1m.=
C.
1m
= −
hoặc
7m.=
D.
1
m =
hoặc
7
m.
= −
Lời giải
+ Điều kiện cần: Giả sử phương trình đã cho có ba nghiệm phân biệt
123
x ,x ,x
lập thành một
cấp số nhân.
Theo định lý Vi-ét, ta có
123
8xx x .=
Theo tính chất của cấp số nhân, ta có
2
13 2
xx x=
. Suy ra ta có
3
22
82x x.=⇔=
Với nghiệm x=2, ta có
2
1
6 70
7
m
mm
m
=
+ −=⇔
= −
+ Điều kiện đủ: Với
1m =
hoặc
7m = −
thì
2
67mm+=
nên ta có phương trình
32
7 14 8 0xx x .− + −=
Giải phương trình này, ta được các nghiệm là
124,,.
Hiển nhiên ba nghiệm này lập thành một
cấp số nhân với công bôị
2q.=
Vậy
1m =
và
7m = −
là các giá trị cần tìm. Chọn đáp án D.
Câu 145: Bốn góc của một tứ giác tạo thành cấp số nhân và góc lớn nhất gấp 27 lần góc nhỏ nhất. Tổng
của góc lớn nhất và góc bé nhất bằng:
A.
0
56 .
B.
0
102 .
C.
0
252 .
D.
0
168 .
Lời giải.
Giả sử 4 góc A, B, C, D theo thứ tự đó lập thành cấp số nhân thỏa yêu cầu với công bội
.
q
Ta
có
23
3
3
3
1 360
360
9 252.
27
27
243
q
A qq q
ABC D
A AD
DA
Aq A
D Aq

CHUYÊN ĐỀ II – TOÁN – 11 – DÃY SỐ - CẤP SỐ CỘNG – CẤP SỐ NHÂN
Page 43
Sưu tầm và biên soạn
Câu 146: Người ta thiết kế một cái tháp gồm 11 tầng. Diện tích bề mặt trên của mỗi tầng bằng nữa diện
tích của mặt trên của tầng ngay bên dưới và diện tích mặt trên của tầng 1 bằng nửa diện tích của
đế tháp. Tính diện tích mặt trên cùng.
A.
2
6.m
B.
2
8.m
C.
2
10 .
m
D.
2
12 .m
Lời giải
Diện tích bề mặt của mỗi tầng lập thành một cấp số nhân có công bội
1
2
q
và
1
12288
6 144.
2
u
Khi đó diện tích mặt trên cùng là
10
11 1
10
6144
6
2
u uq
Câu 147: Một tứ giác lồi có số đo các góc lập thành một cấp số nhân. Biết rằng số đo của góc nhỏ nhất
bằng
1
9
số đo của góc nhỏ thứ ba. Hãy tính số đo của các góc trong tứ giác đó.
A.
00 0 0
5 ,15 ,45 ,225 .
B.
0 00 0
9 ,27 ,81 ,243 .
C.
000 0
7 , 21 ,63 , 269 .
D.
000 0
8 ,32 ,72 ,248 .
Lời giải
Gọi các góc của tứ giác là
23
,, , ,
a aq aq aq
trong đó
1.q >
Theo giả thiết, ta có
2
1
9
a aq=
nên
3.q =
Suy ra các góc của tứ giác là
,3 ,9 ,27 .aaa a
Vì tổng các góc trong tứ giác bằng
0
360
nên ta có:
0
3 9 27 360aaa a
+++ =
0
9.a⇔=
Do đó, phương án đúng là
B
.
Câu 148: Cho cấp số nhân
( )
n
a
có
1
7,a =
6
224a =
và
3577.
k
S =
Tính giá trị của biểu thức
( )
1.
k
Tk a= +
A.
17920.T =
B.
8064.T =
C.
39424.T =
D.
86016.T =
Lời giải
Ta có
6
224a =
5
1
224
aq⇔=
2q⇒=
.
Do
( )
( )
1
1
72 1
1
k
k
k
aq
S
q
−
= = −
−
nên
3577
k
S =
( )
7 2 1 3577
k
⇔ −=
9
22
k
⇔=
9.k⇔=
Suy ra
8
91
10 10 17920.T a aq= = =
Vậy phương án đúng là
.A
Câu 149: Các số
6 , 5 2 , 8xyxyxy
theo thứ tự đó lập thành một cấp số cộng; đồng thời các số
1, 2 , 3x y xy
theo thứ tự đó lập thành một cấp số nhân. Tính
22
.xy
A.
22
40.xy
B.
22
25.xy
C.
22
100.xy
D.
22
10.xy
Lời giải

CHUYÊN ĐỀ II – TOÁN – 11 – DÃY SỐ - CẤP SỐ CỘNG – CẤP SỐ NHÂN
Page 44
Sưu tầm và biên soạn
Theo giả thiết ta có
2
6 8 25 2
13 2
xy xy xy
x xy y
22
33
6
.
2
3 13 3 2 0 2
xy xy
x
y
y yy y y
Suy ra
22
40.xy
Chọn A
Câu 150: Ba số
; ; xyz
theo thứ tự lập thành một cấp số nhân với công bội
q
khác
1;
đồng thời các số
; 2 ; 3x yz
theo thứ tự lập thành một cấp số cộng với công sai khác
0.
Tìm giá trị của
q
.
A.
1
.
3
q
B.
1
.
9
q
C.
1
.
3
q
D.
3.q
Lời giải
2
22
2
0
;
3 4 3 410 .
3 22
3 4 10
x
y xq z xq
x xq xq x q q
xz y
qq
Nếu
00x yz
công sai của cấp số cộng:
;2 ;3xyz
bằng 0.
Nếu
2
1
1
3 4 10 .
1
3
3
1
q
qq q q
q
Câu 151: Các số
6,xy
+
5x 2 ,y
+
8x y+
theo thứ tự đó lập thành một cấp số cộng, đồng thời, các số
5
,
3
x
+
1,
y −
2x 3y−
theo thứ tự đó lập thành một cấp số nhân. Hãy tìm
x
và $y.$
A.
3, 1xy=−=−
hoặc
31
,.
88
xy
= =
B.
3, 1xy
= =
hoặc
31
,.
88
xy=−=−
C.
24, 8xy= =
hoặc
3, 1xy=−=−
.D.
24, 8xy=−=−
hoặc
3, 1xy= =
Lời giải
+ Ba số
6,5 2,8x yx yxy+++
lập thành cấp số cộng nên
( ) (
) ( )
6 8 25 2 3x y xy x y x y+ + + = + ⇔=
.
+ Ba số
5
, 1, 2 3
3
x y xy+−−
lập thành cấp số nhân nên
( )
( )
2
5
23 1
3
x xy y
+ −=−
.
Thay
3xy=
vào ta được
2
8 7 10 1yy y+ −= ⇔ =−
hoặc
1
8
y =
.
Với
1y = −
thì
3x = −
; với
1
8
y =
thì
3
8
x
=
.
Câu 152: Ba số
,,xyz
lập thành một cấp số cộng và có tổng bằng 21. Nếu lần lượt thêm các số
2;3;9
vào
ba số đó thì được ba số lập thành một cấp số nhân. Tính
2 22
.Fx y z=++
A.
389.F =
hoặc
395.F =
B.
395.F =
hoặc
179.F =
C.
389.F =
hoặc
179.F =
D.
441F =
hoặc
357.F =
Lời giải

CHUYÊN ĐỀ II – TOÁN – 11 – DÃY SỐ - CẤP SỐ CỘNG – CẤP SỐ NHÂN
Page 45
Sưu tầm và biên soạn
Theo tính chất của cấp số cộng, ta có
2
xz y
+=
.
Kết hợp với giả thiết
21
xyz++=
, ta suy ra
3 21 7yy= ⇔=
.
Gọi
d
là công sai của cấp số cộng thì
7x yd d=−=−
và
7z yd d=+=+
.
Sau khi thêm các số
2;3;9
vào ba số
,,xyz
ta được ba số là
2, 3, 9xyz
+ ++
hay
9 ,10,16dd−+
.
Theo tính chất của cấp số nhân, ta có
( )( )
22
9 16 10 7 44 0d d dd− += ⇔+−=
.
Giải phương trình ta được
11d = −
hoặc
4
d
=
.
Với
11d = −
, cấp số cộng
18,7, 4−
. Lúc này
389F =
.
Với
4
d =
, cấp số cộng
3,7,11
. Lúc này
179F =
.
Câu 153: Cho bố số
,,,abcd
biết rằng
,,abc
theo thứ tự đó lập thành một cấp số nhân công bội
1q
; còn
,,bcd
theo thứ tự đó lập thành cấp số cộng. Tìm
q
biết rằng
14ad
và
12.
bc
A.
18 73
.
24
q
B.
19 73
.
24
q
C.
20 73
.
24
q
D.
21 73
.
24
q
Lời giải
Giả sử
,,abc
lập thành cấp số cộng công bội
.
q
Khi đó theo giả thiết ta có:
2
2
2
,
21
2
14 2
14
12 3
12
b aq c aq
aq d aq
bd c
ad
ad
aq q
bc
Nếu
00q bc d
Nếu
1; 0
q b ac a b c
.
Vậy
0, 1,qq
từ và ta có:
14da
và
2
12
a
qq
thay vào ta được:
23
32
22 2
2
12 14 14 12 24
12 7 13 6 0
19
1 12 19 6
73
0
24
q qq q
qq q
qq qq qq
q qq q
Vì
1q
nên
19 73
.
24
q
Chọn B
Câu 154: Một người đem 100 triệu đồng đi gửi tiết kiệm với kỳ han 6 tháng, mỗi tháng lãi suất là
0,7%
số tiền mà người đó có. Hỏi sau khi hết kỳ hạn, người đó được lĩnh về bao nhiêu tiền?
A.
(
)
5
8
10 . 0,007
B.
( )
5
8
10 . 1,007
C.
( )
6
8
10 . 0,007
D.
( )
6
8
10 . 1,007
Lời giải
Số tiền ban đầu là
8
0
10M =
.
Đặt
0,7% 0,007r = =
.
Số tiền sau tháng thứ nhất là
( )
100 0
1M M Mr M r=+= +
.

CHUYÊN ĐỀ II – TOÁN – 11 – DÃY SỐ - CẤP SỐ CỘNG – CẤP SỐ NHÂN
Page 46
Sưu tầm và biên soạn
Số tiền sau tháng thứ hai là
(
)
2
2 11 0
1
M M Mr M r=+= +
.
Lập luận tương tự, ta có số tiền sau tháng thứ sáu là
(
)
6
60
1
MM r= +
.
Do đó
( )
6
8
6
10 1,007M =
.
Câu 155: Tỷ lệ tăng dân số của tỉnh M là
1, 2%.
Biết rằng số dân của tỉnh M hiện nay là 2 triệu người. Nếu
lấy kết quả chính xác đến hàng nghìn thì sau 9 năm nữa số dân của tỉnh M sẽ là bao nhiêu?
A.
10320
nghìn người. B.
3000
nghìn người. C.
2227
nghìn người. D.
2300
nghìn người.
Lời giải
Đặt
6
0
2000000 2.10P = =
và
1,2% 0,012
r
= =
.
Gọi
n
P
là số dân của tỉnh
M
sau
n
năm nữa.
Ta có:
( )
1
1
n nn n
P P Pr P r
+
=+= +
.
Suy ra
( )
n
P
là một cấp số nhân với số hạng đầu
0
P
và công bội
1qr= +
.
Do đó số dân của tỉnh
M
sau
10
năm nữa là:
(
)
( )
9 10
6
90
1 2.10 1,012 2227000PM r= += ≈
.
Câu 156: Tế bào E. Coli trong điều kiện nuôi cấy thích hợp cứ 20 phút lại nhân đôi một lần. Nếu lúc đầu
có
12
10
tế bào thì sau 3 giờ sẽ phân chia thành bao nhiêu tế bào?
A.
12
1024.10
tế bào. B.
12
256.10
tế bào. C.
12
512.10
tế bào. D.
13
512.10
tế bào.
Lời giải
Lúc đầu có
22
10
tế bào và mỗi lần phân chia thì một tế bào tách thành hai tế bào nên ta có cấp số
nhân với
22
1
10u =
và công bội
2q =
.
Do cứ
20
phút phân đôi một lần nên sau
3
giờ sẽ có
9
lần phân chia tế bào. Ta có
10
u
là số tế bào
nhận được sau
3
giờ. Vậy, số tế bào nhận được sau
3
giờ là
9 12
10 1
512.10u uq
= =
.
Bấm Tải xuống để xem toàn bộ.




