Chuyên đề đồ thị hàm số y = ax + b (a khác 0)

Tài liệu gồm 46 trang, được biên soạn bởi tác giả Toán Học Sơ Đồ, tổng hợp kiến thức trọng tâm, phân dạng và hướng dẫn giải các dạng bài tập tự luận & trắc nghiệm chuyên đề đồ thị hàm số y = ax + b (a khác 0). Mời bạn đọc đón xem.

125 63 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Chương 4: Phương trình bậc hai một ẩn

Môn: Toán 9

Thông tin:

33 trang 8 tháng trước

Tác giả:

Profile Hà Việt Anh
1/
CHUYÊN ĐỀ ĐỒ THỊ HÀM SỐ
yaxb
(0)a
A.KIẾN THỨC CẦN NHỚ
1. Đồ thị hàm số bậc nhất
Hàm số bậc nhất y = ax + b với có đồ thị là một đường thẳng,
kí hiệu là d: y = ax + b
2. Cách vẽ đồ thị của hàm số bậc nhất
Xét đường thẳng d: y = ax + b với
.Nếu b = 0 ta có d: y = ax đi qua gốc tọa độ O(0;0) và điểm A(1; a).
.Nếu thì d đi qua hai điểm A(0; b) và
3. Chú ý
.Trục hoành là đường thẳng : y = 0
.Trục tung là đường thẳng : x = 0
B.CÁC DẠNG BÀI TẬP MINH HỌA
Dạng 1: Vẽ đồ thị hàm số bậc nhất
Phương pháp giải: Xét đường thẳng d: y = ax + b với
.Nếu b = 0 ta có d: y = ax đi qua gốc tọa độ O(0;0) và điểm A(1; a).
.Nếu thì d đi qua hai điểm A(0; b) và
Bài 1 : Cho hàm số

1
3
2
yfx x

.
a. Tính
b. Vẽ đồ thị của hàm số trên.
Bài 2: Biểu diễn các điểm sau trên mặt phẳng tọa độ.

3;2; 1;4; 5;0; 0;3; 1;4ABCDE
Dạng 2: Tìm tham số
m
để hàm số là hàm số bậc nhất, đồng biến, nghịch biến.
1. Tìm điều kiện xác định của hàm số là bậc nhất…
2. Xét x
1
; x
2
thuộc tập xác định của hàm số với x
1
< x
2
a. Nếu
12 21
f(x ) f(x ) f( (x) fx) 0
Hàm số

yfx
đồng biến
a0
a0
b0
b
B;0
a



a0
b0
b
B;0
a



0; 1; 1; 2; 2; 8;fff ff f
2/
b. Nếu

12 21
f(x ) f(x ) f( f(x) x) 0
Hàm số

yfx
nghịch biến
Bài 3: Tìm
m
để hàm số sau là hàm số bậc nhất?
a.

4 2009ym x
b.

23 21ymxm
c.
2
4
2
m
yx
m

d.
3.53ymx m
Bài 4: Cho hàm số

5 2010ym x
. Tìm
m
để hàm số trên là
a. Hàm số bậc nhất
b. Hàm số đồng biến, nghịch biến
Bài 5 : Cho hàm số

2
56 2ym m x

. Tìm
m
để
a. Hàm số trên là hàm số bậc nhất
b. Hàm số đồng biến, nghịch biến
c. Đồ thị hàm số đi qua điểm

1; 4A
Dạng 3 : Xét tính đồng quy của ba đường thẳng.
Phương pháp giải:
‐
Ba đường thẳng đồng quy là ba đường thẳng phân biệt và cùng đi qua một điểm
‐
Để xét tính đồng quy của ba đường thẳng ( phân biệt) cho trước, ta làm như sau:
1. Tìm tọa độ giao điểm của hai trong ba đường thẳng đã cho.
2. Kiểm tra nếu giao điểm vừa tìm được thuộc đường thẳng còn lại thì kết luận ba đường thẳng đó đồng
quy.
Bài 6 : Cho ba đường thẳng.
;
2
:31dy x ;
3
:3dyx
Chứng minh rằng
123
;;ddd đồng quy.
1
:43dy x
3/
Bài 7 : Cho ba đường thẳng.
1
:4dyx ;
2
:23dy x ;
3
:1dymxm
Tìm
m
để ba đường thẳng trên đồng quy.
Bài 8 : Cho ba đường thẳng.
1
:38dy x ;
2
:23dy x ;
3
:3 21dy mx m
Tìm
m
để ba đường thẳng trên đồng quy.
Dạng 4: Tìm điểm cố định của đường thẳng phụ thuộc tham số
Phương pháp giải: Cho đường thẳng d: y = ax + b phụ thuộc tham số m
1. Điểm I(x
0
;y
0
) được gọi là điểm cố định của d nếu I luôn thuộc d với mọi giá trị của m.
2. Để tìm điểm cố định của d, ta làm như sau:
.Gọi I(x
0
;y
0
) là điểm cố định của d => y
0
= ax
0
+ b với mọi m.
.Biến đổi y
0
= ax
0
+ b về dạng A(x
0
;y
0
)m + B(x
0
;y
0
) = 0
Hoặc A(x
0
;y
0
) m
2
+ B(x
0
;y
0
) m + C(x
0
;y
0
) = 0
.Ta có A(x
0
;y
0
)m + B(x
0
;y
0
) = 0 với mọi m
.Tương tự A(x
0
;y
0
) m
2
+ B(x
0
;y
0
) m + C(x
0
;y
0
) = 0 với mọi m
.Từ đó tìm được x
0
; y
0
và kết luận.
Bài 9 :
a.Chứng minh
00
2xy là điểm cố định mà đường thẳng

7
:12
2
ymxm
luôn đi qua với
mọi giá trị của tham số
m
b.Cho đường thẳng với
m
là tham số. Tìm điểm cố định mà luôn đi qua
với mọi
m

00
00
Ax;
y
0
Bx;
y
0


00
00
00
Ax;
y
0
Bx;
y
0
Cx;
y
0

:21 2dy m x m
d
4/
Dạng 5: Tính chu vi và diện tích tam giác
Phương pháp giải toán
1. Cho đồ thị hàm số

yfx
.
2. Một điểm

00
x;y
được gọi là thuộc đồ thị hàm số nếu khi ta thay các giá trị toạ độ của điểm đó vào
phương trình của hàm số và thoả mãn

00
yfx y
3. Một điểm

00
x;y
được gọi là không thuộc đồ thị hàm số nếu khi ta thay các giá trị toạ độ của điểm
đó vào phương trình của hàm số mà không thoả mãn

00
yfx y
.
4.Vận dụng công thức chu vi và diện tích tích theo yêu cầu bài toán
Bài 10: Xác định các điểm sau trên hệ trục toạ độ Oxy.

A0;3;Bl;3,C 2;2;D2;6;M0;4
Bài 11: Cho hàm số

yfx x
 .Trong các điểm


A 4;2 , B 2;1 , C 9;3 , D 8;2 2
, điểm nào
thuộc và điểm nào không thuộc đồ thị của hàm số.
Bài 12 : Vẽ trên mặt phẳng Oxy các điểm

Al;2; B l;0; C2;0
a.Tính diện tích tam giác ABC (theo đơn vị đo của trục toạ độ).
b. Tính chu vi tam giác ABC (theo đơn vị đo của trục toạ độ).
HƯỚNG DẪN
Dạng 1: Vẽ đồ thị hàm số bậc nhất
Bài 1 :
a.Lập bảng giá trị tương ứng của
x
và

fx
.
5/
2

1
3
2
f
xx

4
b.Hs tự vẽ ĐTHS
Bài 2 :
Dạng 2: Tìm tham số
m
để hàm số là hàm số bậc nhất, đồng biến, nghịch biến.
Bài 3:
...... 4 0 4
3
...... 2 3 0
2
20 2
2
...... 0
20 2
2
...... 3 0 3 0 3
am m
bm m
mm
m
c
mm
m
dmmm









Bài 4
:
...... 5 0 5am m
b.
+ hàm số đồng biến
50 5mm
+ hàm số nghịch biến
50 5mm
E
B
D
C
A
-5
-3
-1
2
1
-2
-4
4
3
21
O
y
x
6/
Bài 5
:
a.
Hàm số đã cho là hàm số bậc nhất

2
20
560 2 30
30
m
mm m m
m



b.
Hàm số đồng biến

2
20 2
30 3
3
560 2 30
2
20 2
30 3
mm
mm
m
mm m m
m
mm
mm

















*) Hàm số nghịch biến

2
20 2
30 3
23
560 2 30
20 2
30 3
mm
mm
m
mm m m
khong tm
mm
mm


















a.
Vì đồ thị hàm số đi qua

1; 4A
nên :


22
456.12540140
10 1
40 4
mm mm m m
mm
mm







Dạng 3 : Xét tính đồng quy của ba đường thẳng.
Bài 6
:
Gọi
12
Id d
Tìm được

2;5I
Thay tọa độ
I
vào
3
d thấy thỏa mãn
Vậy
123
;;ddd đồng quy.
Bài 7
:
Gọi
12
Id d
7/
Tìm được

7; 11I 
Thay tọa độ
I
vào
3
d tìm được
2m
Với
2m
suy ra
3
:23dy x trùng với
2
d
Vậy: Không có giá trị nào của
m
để 3 đường thẳng trên đồng quy.
Bài 8
:
Giải tương tự Bài tập 7. Tìm được
6
5
m
Dạng 4: Tìm điểm cố định của đường thẳng phụ thuộc tham số
Bài 9:
a.
Thay
1
;3
2
xy
vào
ta thấy luôn thỏa mãn vói mọi
m
.
b.
Gọi

00
;Ixy
là điểm cố định của
d
Suy ra :

00
21 2ymxm
với mọi
m

000
21 20xmxy
với mọi
m
0
00
210
20
x
xy


Từ đó ta tìm được
15
;
22




là điểm cố định của
d
Dạng 5: Tính chu vi và diện tích tam giác
Bài 10:

A0;3;Bl;3,C 2;2;D2;6;M0;4
8/
Bài 11:
Thay toạ độ từng điểm đã cho vào phương trình

yfx x
.
+ x
A
= 4 thay vào hàm số:

A
f4 4 2 y
, suy ra A thuộc đồ thị hàm số.
+ x
B
= 2 thay vào hàm số:

B
f2 2 y
, suy ra B không thuộc đồ thị hàm số.
+ x
C
= 9 thay vào hàm số:

C
f9 9 3 y
 , suy ra C thuộc đồ thị hàm số.
+ x
D
= 8 thay vào hàm số:

D
f8 8 22 y
 , suy ra D thuộc đồ thị hàm số.
Vậy, các điểm A, C, D thuộc đồ thị, điểm B không thuộc đồ thị.
Bài 12:
Biểu diễn các điểm

Al;2; B l;0; C2;0
trên hệ trục toạ độ Oxy.
a.
Ta có:
BC BO OC 1 2 3
, AH = 2
ABC
11
S BC.AH .3.2 3
22
 (đơn vị diện tích)
b.
Ta có:
BH BO OH l l 2
Tam giác AHB vuông tại H, theo định lý Phytago, ta có:
22222
AB AH BH 2 2 8
Suy ra
AB 2 2
.
9/
Tương tự, tam giác AHC vuông tại H, ta có:
22222
AC AH CH 2 1 5
.
Suy ra
AC 5
Vậy chu vi tam giác ABC bằng:
AB BC CA 2 2 3 5
(đơn vị độ dài)
Dạng 6.Nâng cao phát triển tư duy
Dạng 1: Tính đồng biến – nghịch biến - điểm thuộc đồ thị .
Bài 1:
Tìm m để mỗi hàm số sau đây đồng biến hoặc nghịch biến
a)
(1)2
ym x
b)
2
1ymx c)
(1 3 ) 2
ymxm
Bài 2:
a) Cho
(3)7ym x
. Tìm m để hàm số trên là hàm số đồng biến, nghịch biến.
b) Cho
2
(k 4) 2yx . Tìm k để hàm số trên là hàm số đồng biến, nghịch biến.
Bài 3:
Cho hàm số
(1)
ym xm
a) Tìm m để đồ thị hàm số cắt trục tung tại điểm có tung độ bằng 2
b) Tìm m để đồ thị hàm số cắt trục hoành tại điểm có hoành độ bằng -3
Bài 4:
Cho hàm số
(1)3
ym x
a) Tìm m để đồ thị hàm số đi qua điểm A(1;2)
b) Tìm m để đồ thị hàm số đi qua điểm B(1;-2)
Bài 5:
Xác định a, b để đồ thị hàm số
yaxb
đi qua các điểm
a)
(1; 2) (2;1)AvàB
b)
(1; 2) (3; 4)PvàQ
Dạng 2: TỔNG HỢP:
Vẽ đồ thị - Tính khoảng cách- Tam giác( Diện tích, chu vi).
Bài 1:
Cho hai đường thẳng (d
1
)
1
2
2
yx
2
(): 2dyx ;
3
(): 3dyx
a) Vẽ (d
1
), (d
2
); (d3) trên cùng một hệ tọa độ
b) Gọi A, B lần lượt giao điểm của(d
1
), (d
2
) trên Ox, C là giao điểm của (d
1
), (d
2
). Tính chu vi tam giác
ABC
c) Tính khoảng cách từ gốc tọa độ O đến (d
2
)
Bài 2
: Cho 3 đường thẳng
12 3
11
( ): 1;( ): 2 4;( ): 4
22
dy x d y x dy x 
10/
a) Vẽ đồ thị các đường thẳng thẳng trên cùng một hệ trục tọa độ
b) Cho (d
2
) cắt (d
1
) và (d
3
) tại A, B, (d
1
) cắt trục Ox tại C. Tính
ABC
S
Bài 3:
Cho hàm số
(2 1) 3ymx
có đồ thị là đường thẳng (d)
a) Tìm m để (d) đi qua điểm A(2 ;5)
b) Vẽ đồ thị của (d) ứng với m vừa tìm được ở câu a. Gọi giao điểm của (d) với hai trục Ox và Oy là M,
N. Tính diện tích tam giác OMN.
c) Tìm m để khoảng cách từ gốc tọa độ O đến (d) lớn nhất
d) Tìm điểm cố định mà (d) luôn đi qua với mọi m
Bài 4:
Cho hàm số
(2)2ym x
có đồ thị là đường thẳng (d)
a) Tìm m để hàm số đồng biến, nghịch biến
b) Tìm m để khoảng cách từ gốc tọa độ O đến (d) bằng 1.
c) Tìm m để khoảng cách từ gốc tọa độ O đến (d) lớn nhất
d) Tìm điểm cố định mà (d) luôn đi qua
e) Tìm m để (d) cắt hai trục Ox, Oy tại A và B sao cho 4
AOB
S
Bài 5:
Cho hàm số
(2 1) 4ymx
có đồ thị là đường thẳng (d)
a) Tìm m để hàm số trên đồng biến, nghịch biến.
b) Vẽ (d) khi m = 2.
c) Tìm m để khoảng cách từ gốc tọa độ O đến (d) bằng 2
d) Tìm m để khoảng cách từ gốc tọa độ O đến (d) lớn nhất.
Bài 6.
Cho hàm số

22ym x
có đồ thị là đường thẳng (d)
a)
Tìm m để hàm số trên là hàm số bậc nhất
b)
Tìm m để (d) cắt
Ox
tại điểm có hoành độ bằng 2
c)
Tìm m để khoảng cách từ gốc tọa độ đến (d) bằng
HƯỚNG DẪN
Dạng 1: Tính đồng biến – nghịch biến - điểm thuộc đồ thị .
Bài 1:
Tìm m để mỗi hàm số sau đây đồng biến hoặc nghịch biến
a)
(1)2ym x
b)
2
1ymx c)
(1 3 ) 2ymxm
Lời giải
Hàm số bậc nhất đồng biến khi
0a
và nghịch biến khi
0a
.
11/
a,

12ym x
đồng biến khi
1m
nghịch biến khi
1m
.
b,
2
1ymx
do
2
0mm
nên hàm số luôn nghịch biến khi
0m
.
c,
(1 3 ) 2ymxm
hàm số đồng biến khi
1
3
m
và nghịch biến khi
1
3
m
.
Bài 2:
a) Cho
()
m+3 7yx=+
. Tìm
m
để hàm số trên là đồng biến, nghịch biến.
b) Cho
()
2
k4 2yx=--
. Tìm
k
để hàm số trên là đồng biến, nghịch biến.
Lời giải
a) *Để hàm số
()
m+3 7yx=+
đồng biến khi:
m + 3 > 0
m > -3
*Để hàm số
()
m+3 7yx=+
nghịch biến khi:
m + 3 < 0
m < -3
b)
*Để hàm số
()
2
k4 2yx=--
đồng biến khi:
()()
2
4 0
22 0
-2; 2
k
kk
kk
->
- + >
< >
*Để hàm số
()
2
k4 2yx=--
nghịch biến khi:
()()
2
4 < 0
22 < 0
-2 < 2
k
kk
k
-
- +
<
Bài 3:
Cho hàm số
(1)ym xm
a) Tìm m để đồ thị hàm số cắt trục tung tại điểm có tung độ bằng 2
b) Tìm m để đồ thị hàm số cắt trục hoành tại điểm có hoành độ bằng -3
Lời giải
a, Khi hàm số cắt trục tung tại điểm có tung độ bằng 2, tức là đồ thị hàm số đã cho sẽ đi qua điểm
(0;2)
. Vậy
2( 2).0 2mmm
.
b, Khi hàm số cắt trục hoành tại điểm có hoành độ bằng -3, tức là đồ thị hàm số đi qua điểm
(3;0)
. Vậy:
0( 2).(3) 62 0 3mmmm
.
Bài 4:
Cho hàm số
(1)3ym x
a) Tìm m để đồ thị hàm số đi qua điểm A(1;2)
b) Tìm m để đồ thị hàm số đi qua điểm B(1;-2)
12/
Lời giải
a, Để hàm số đi qua điểm
(1; 2)A
thì
2( 1).13 0mm
.
b, Để hàm số đi qua điểm
(1; 2)B
thì
2( 1).13 4mm
.
Bài 5:
Xác định a, b để đồ thị hàm số
yaxb
đi qua các điểm
a)
(1; 2) (2;1)
AvàB
b)
(1; 2) (3; 4)
PvàQ
Lời giải
Cho hàm số
yaxb
. Để đồ thị hàm số đi qua:
a,
(1; 2)A
và
(2;1)B
thì
2.1 1
1.2 3
ab a
ab b





b,
(1; 2)P
và
(3;4)Q
thì
2.1 1
4.3 1
ab a
ab b





Dạng 2: TỔNG HỢP:
Vẽ đồ thị - Tính khoảng cách- Tam giác( Diện tích, chu vi).
Bài 1.
Cho hai đường thẳng

1
1
:2
2
dy x
và

2
:2dy x
;
3
(): 3dyx
a) Vẽ

1
d
và

2
d
; (d3)
trên cùng một hệ trục tọa độ.
b) Gọi
A
và
B
lần lượt là giao điểm của

1
d
và

2
d
với trục
.Ox C
là giao điểm của

1
d
và

2
d
. Tính chu vi tam giác
.ABC
c) Tính khoảng cách từ gốc tọa độ O đến

2
.d
Lời giải
13/
a) Vẽ

1
d
:
Cho
0x
thì
2y
ta được điểm

0;2 .
Cho
0y
thì
4x 
ta được điểm

4;0

1
d
là đường thẳng đi qua 2 điểm

0;2 ; 4;0
Vẽ

2
d
:
Cho
0x
thì
2y
ta được điểm

0;2 .
Cho
0y
thì
2x
ta được điểm

2;0

1
d
là đường thẳng đi qua 2 điểm

0;2 ; 2;0
b) Theo câu a ta có

4;0A
và

2;0B
;
Tọa độ giao điểm của
C
là nghiệm của hệ:

1
0
2
0;2
2
2
2
x
yx
C
y
yx




Theo công thức tính khoảng cách giữa hai điểm ta tính được:
6; 2 5; 2 2AB AC BC
Vậy chu vi tam giác ABC bằng:
62522
(đơn vị độ dài)
c) Gọi
m
là khoảng cách từ
O
đến

2
d
. Áp dụng hệ thức lượng trong tam giác vuông
OBC
ta có:
222222
11 1 111
2
22
m
mOBOC m

(đơn vị độ dài)
Bài 3:
Cho 3 đường thẳng

1
1
:1
2
dy x
;

2
:24dy x
;

3
1
:4
2
dy x
.
a)
Vẽ đồ thị các đường thẳng trên cùng một hệ trục tọa độ.
b)
Cho

2
d
cắt

1
d
và

3
d
tại
A
và
B
,

1
d
cắt trụ
Ox
tại
C
. Tính
ABC
S
.
Giải:
14/
a)
Ta có

1
d
cắt trục tung tại

0; 1
cắt trục hoành tại

2;0
.

2
d
cắt trục tung tại

0; 4
cắt trục hoành tại
2;0

3
d
cắt trục tung tại

0; 4
cắt trục hoành tại

8;0
Nên ta có đồ thị hình bên
b)
Tọa độ của
A
là nghiệm của hệ
6
1
1
5
2
8
24
5
x
yx
yx
y





Dễ thấy

0; 4B
;

2;0C
và

12
dd
Do đó
1
.
2
ABC
SABAC
Ta có
 
22
22
68 270
04
55 5
AB A B
AB x x y y







22
22
6885
20
555
AC AC
AC x x y y





Suy ra
12 7085 814
..
25 5 5
ABC
S

Vậy
814
5
ABC
S
đvdt
Bài 4:
Cho hàm số
(2 1) 3ymx
có đồ thị là đường thẳng (d)
a) Tìm m để (d) đi qua điểm A(2 ;5)
b) Vẽ đồ thị của (d) ứng với m vừa tìm được ở câu a. Gọi giao điểm của (d) với hai trục Ox và Oy là M,
N. Tính diện tích tam giác OMN.
c) Tìm m để khoảng cách từ gốc tọa độ O đến (d) lớn nhất
d) Tìm điểm cố định mà (d) luôn đi qua với mọi m
Lời giải
a) Vì

2;5Ad thay
2; 5xy
vào

d ta được:

521.23 1mm
b) Với

1: 3mdyx .
15/
Giao của đồ thị

d với

:0 3 3;0Ox y x M
Giao của đồ thị

d với

:0 3 0;3Oy x y N
Diện tích
OMN
là:
119
. . .3.3
222
SOMON (đvdt)
c) Với

1
:3
2
mdy khoảng cách từ điểm
O
đến

d là 3 (*)
Với
1
2
m . Đồ thị hàm số cắt
Ox
tại
3
;0
21
A
m



, cắt
Oy
tại

0;3B .
Kẻ
OH AB
khoảng cách từ
O
đến

d là
OH
.
Áp dụng hệ thức lượng cho tam giác vuông
OAB
ta có:
222
111
OH OA OB


2
21
111
3
999
m
OH
OH
 (**)
Từ (*) và (**) suy ra
max 3OH
. Dấu bằng xảy ra khi
1
2
m
Vậy
1
2
m thì khoảng cách lớn nhất từ
O
đến đường thẳng

d là 3.
d) Ta có:

:21323 0 1dy m x mx xy
Gọi

;Ixy là điểm cố định, suy ra phương trình

1 có nghiệm với
0
30
x
m
xy



0
0;3
3
x
I
y

. Vậy đường thẳng

d luôn đi qua điểm cố định

0;3I .
H
A
B
0
-3
3
0
1
1
16/
Bài 4:
Cho hàm số
(2)2ym x
có đồ thị là đường thẳng (d)
a) Tìm m để hàm số đồng biến, nghịch biến
b) Tìm m để khoảng cách từ gốc tọa độ O đến (d) bằng 1.
c) Tìm m để khoảng cách từ gốc tọa độ O đến (d) lớn nhất
d) Tìm điểm cố định mà (d) luôn đi qua
e) Tìm m để (d) cắt hai trục Ox, Oy tại A và B sao cho 4
AOB
S
Lời giải
a) Hàm số đồng biến khi
20 2mm
Hàm số nghịch biến khi:
20 2mm
b) Với

2:2mdy : Không thỏa mãn.
Với
2m
, đường thẳng

d cắt
Ox
tại
2
;0
2
A
m



, cắt
Oy
tại

0; 2B .
Kẻ
1.OH AB OH
Áp dụng hệ thức lượng cho tam giác vuông
OAB
ta có:

2
222
2
1111 1
23
144
m
m
OH OA OB

c) Với

2:2mdy nên khoảng cách từ O đến đường thẳng là 2.
Với
2m
. Theo ý b ta có:

2
222 2
2
111 1 11
2
444
m
OH
OH OA OB OH

Vậy
max 2OH
. Dấu bằng xảy ra khi
2m
.
Vậy
2m
thì
max 2OH
.
d) Đường thẳng

:22dy m x luôn đi qua điểm cố định

0; 2I .
e) Đường thẳng

d cắt hai trục tọa độ tại
,2AB m
. Khi đó
2
;0
2
A
m



;

0; 2B
Vì
5
112 1
2
4.4 .242
222 2
3
2
OAB
m
SOAOB m
m
m
  
(tmđk) .
Bài 5:

2 1 4 ymx d
17/
a)
Tìm m để hàm số đồng biến, nghịch biến trên tập xác định R
b)
Vẽ (d) khi m = 2 .
c)
Tìm m để khoảng cách từ gốc tọa độ O đến (d) bằng 2.
d)
Tìm m để khoảng cách từ gốc tọa độ O đến (d) lớn nhất.
GIẢI
2 1 4 ymx d
a. Tìm m để hàm số đồng biến, nghịch biến
* Để hàm số đồng biến
1
02 10
2
am m
* Để hàm số nghịch biến
1
< 0 2 1 0
2
am m
* Vậy để hàm số đồng biến
1
2
m
; nghịch biến
1
2
m
b. Vẽ (d) khi m = 2
Thay m = 2 vào hs (d) ta có:
(d) :

2 . 2 – 1 4 3 4yxyx
Cho
0 4 0 ; 4xy A
44
0 (;0)
33
yx B


Ta vẽ đồ thị
c. Tìm m để khoảng cách từ gốc tọa độ O đến (d) bằng 2.
Cho

0 4 0 ; 4xyA
4
0
21
yx
m

41
;0
21 2
Bm
m




8
6
4
2
2
4
15 10 5 5 10 15
y = 3x + 4
B
A
O
18/
+ Kẻ OH AB = {H}
+ Vì khoảng cách từ (O) đến AB = 2 OH = 2 (đvđd)
+ Xét ∆ OAB (vuông tại O) có OH là đường cao :
22 2
11 1
(HTL)
OA OB OH

2
22
111
42
4
21m




22
3
1(2 1) 1 (2 1) 3
16 16 4 16 16
(2 1) 3 2 1 3
31
2.1 3
2
(/ )
21 3 31
2
mm
mm
m
m
tm
m
m





+ Vậy để khoảng cách từ O đến đường thẳng (d) bằng 2
31
2
(/ )
31
2
m
tm
m

d) Tìm m để khoảng cách từ gốc tọa độ O đến (d) lớn nhất.
Xét ∆ OAB (vuông tại O): OH AB
8
6
4
2
2
4
15 10 5 5 10 15
d
y = 3x + 4
B
A
O
H
19/
22 2
2
2
2
2
2
2
2
11 1
()() ( )
1(2 1) 1
16 16
(2 1) 1 1
16
16
(2 1) 1
4
(2 1) 1
OA OB OH
m
OH
m
OH
OH
m
OH
m








+ Ta có: A(0; 4) là điểm mà (d) luôn đi qua
+ Xét ∆ OAB (vuông tại O) :
OH OA
(quan hệ đường, điểm)
+ Dấu “ =” xảy ra H A
2
4
4
(2 1) 1m


22
( 2 1) 1 1 ( 2 1) 1 1
1
21 0 (kot/m)
2
mm
mm


Vậy không có giá trị của m để khoảng cách từ gốc tọa độ O đến (d) lớn nhất.
Bài 6.
Cho hàm số

22ym x
có đồ thị là đường thẳng (d)
d)
Tìm m để hàm số trên là hàm số bậc nhất
e)
Tìm m để (d) cắt
Ox
tại điểm có hoành độ bằng 2
f)
Tìm m để khoảng cách từ gốc tọa độ đến (d) bằng 1
Giải :
Hàm số

22ym x
có
2, 2am b
a)
Để hàm số trên là hàm số bậc nhất thì
0a
20 2mm
b)
Ta có đồ thị hàm số
yaxb
(
0a
) luôn cắt trục hoành tại điểm có tọa độ
;0
b
a



nên theo đề bài, để (d) cắt
Ox
tại điểm có hoành độ bằng 2 thì
2
22
2
b
am

1m
( thỏa mãn điều kiện
2m
)
c)
Gọi
,AB
theo thứ tự là giao điểm của đường thẳng (d) với trục hoành và trục tung.
20/
Suy ra
2
;0
2
A
m



và

0; 2B
Khi đó
22
22
OA
mm


,
2OB
Kẻ
OH AB
(
HAB
) thì
OH
là khoảng cách từ gốc tọa độ
đến đường thẳng (d)
Xét
OAB
vuông tại O đường cao
OH
, ta có:

2
2
222
2
111 1 45
44 4
m
mm
OH OA OB


mặt khác,
2
1454OH m m

2
23 2 3mm
 
23
23
m
m


.
Vậy với
23m  hoặc 23m  thì khoảng cách từ gốc tọa độ đến (d) bằng 1
C.TRẮC NGHIỆM RÈN PHẢN XẠ
Câu 1
. Chọn khẳng định
đúng
về đồ thị hàm số
(0)yaxba=+ ¹
.
A.
Là đường thẳng đi qua gốc tọa độ.
B.
Là đường thẳng song song với trục hoành.
C.
Là đường thẳng đi qua hai điểm
(0; ), ; 0
b
AbB
a
æö
÷
ç
÷
-
ç
÷
ç
÷
ç
èø
với
0b ¹
.
D.
Là đường cong đi qua gốc tọa
độ.
Câu 2
. Chọn khẳng định
đúng
về đồ thị hàm số
(0)yaxba=+ ¹
với
0b =
A.
Là đường thẳng đi qua gốc tọa độ.
B.
Là đường thẳng song song với trục hoành.
C.
Là đường thẳng đi qua hai điểm
(1;0), ;0
b
AB
a
æö
÷
ç
÷
-
ç
÷
ç
÷
ç
èø
.
D.
Là đường cong đi qua gốc tọa độ.
Câu 3
. Trong các hình vẽ sau, hình vẽ nào là đồ thị hàm số
21yx=+
x
y
2
1
H
B
A
d
-2
m-2
2
1
A
O
21/
A.
Hình 4.
B.
Hình 2.
C.
Hình 3.
D.
Hình 1.
Câu 4.
Trong các hình vẽ sau, hình vẽ nào là đồ thị hàm số
32yx=-
.
A.
Hình 4.
B.
Hình 2.
C.
Hình 3.
D.
Hình 1.
Câu 5
. Đồ thị hàm số
2
5
5
yx=-
đi qua điểm nào sau đây?
A.
22
1;
5
A
æö
÷
ç
÷
ç
÷
ç
÷
ç
èø
.
B.
13
;
55
B
æö
÷
ç
÷
ç
÷
ç
÷
ç
èø
.
C.
23
;
25 5
C
æö
÷
ç
÷
--
ç
÷
ç
÷
ç
èø
.
D.
()
2;10D
.
Câu 6
. Cho hai đường thẳng
1
:1dy x=-
và
2
:23dy x=-
. Tung độ giao điểm của
12
;dd
có tọa độ
là:
22/
A.
4y =-
.
B.
7
4
y =
.
C.
1
4
y =
.
D.
1
4
y =-
.
Câu 7
. Cho hai đường thẳng
1
:22dy x=-
và
2
34dx=-
. Tung độ giao điểm của
21
;dd
có tọa độ là.
A.
1
3
y =-
.
B.
2
3
y =
.
C.
1y =
.
D.
1y =-
.
Câu 8
. Cho đường thẳng
:26dy x=+
. Giao điểm của
d
với trục tung là:
A.
1
0;
6
P
æö
÷
ç
÷
ç
÷
ç
÷
ç
èø
.
B.
(6; 0)N
.
C.
(0;6)M
.
D.
(0; 6)D -
.
Câu 9
. Cho đường thẳng
1
:3
2
dy x=-
. Giao điểm của
d
với trục tung là:
A.
1
;0
6
A
æö
÷
ç
÷
ç
÷
ç
÷
ç
èø
.
B.
1
0;
2
B
æö
÷
ç
÷
ç
÷
ç
÷
ç
èø
.
C.
1
0;
6
C
æö
-
÷
ç
÷
ç
÷
ç
÷
ç
èø
.
D.
1
0;
2
D
æö
÷
ç
÷
-
ç
÷
ç
÷
ç
èø
.
Câu 10
. Cho hàm số
(1 )ymxm=- +
. Xác định
m
để đồ thị hàm số cắt trục hoành tại điểm có hoành
độ
3x =-
.
A.
1
2
m =
.
B.
3
4
m =
.
C.
3
4
m =-
.
D.
4
5
m =
.
Câu 11
. Cho hàm số
2
21
3
m
yxm
+
=-+
. Xác định
m
để đồ thị hàm số cắt trục hoành tại điểm có
hoành độ
9x =
.
A.
7m =-
.
B.
7m =-
.
C.
2m =-
.
D.
3m =-
.
Câu 12
. Cho hàm số
(3 2 ) 2ymxm=- +-
, xác định
m
để đồ thị hàm số cắt trục tung tại điểm có
tung độ
4y =-
.
A.
1m =
.
B.
1m =-
.
C.
2m =-
.
D.
2m =
.
Câu 13
. Cho hàm số
5
(2 )
2
m
ymx
+
=- -
. Xác định
m
để hàm số cắt trục
tung tại điểm có tung độ
3y =
.
A.
11m =
.
B.
11m =-
.
C.
12m =-
.
D.
1m =
.
Câu 14
. Cho hàm số
2ymx=-
có đồ thị là đường thẳng
1
d
và hàm số
1
1
2
yx=+
có đồ thị là đường
thẳng
2
d
. Xác định
m
để hai đường thẳng
1
d
và
2
d
cắt nhau tại một điểm có hoành độ
4x =-
.
23/
A.
1
4
m =-
.
B.
1
4
m =
.
C.
1
2
m =
.
D.
1
2
m =-
.
Câu 15
. Cho hàm số
2ymx=-
có đồ thị là đường thẳng
1
d
và hàm số
1
1
2
yx=+
có đồ thị là đường
thẳng
2
d
. Xác định
m
để hai đường thẳng
1
d
và
2
d
cắt nhau tại một điểm có hoành độ
4x =-
.
A.
3m =
.
B.
12m =
.
C.
12m =-
.
D.
3m =-
.
Câu 16
. Cho hàm số
2( 2)ymxm=-+
có đồ thị là đường thẳng
1
d
và hàm số
2yx=- -
có đồ thị
là đường thẳng
2
d
. Xác định
m
để hai đường thẳng
1
d
và
2
d
cắt nhau tại một điểm có tung độ
3y =
.
A.
7
13
m =
.
B.
7
13
m =-
.
C.
13
7
m =-
.
D.
13
7
m =
.
Câu 17
. Cho hàm số
(1)1ym x=+-
có đồ thị là đường thẳng
1
d
và hàm số
1yx=+
có đồ thị là
đường thẳng
2
d
. Xác định
m
để hai đường thẳng
1
d
và
2
d
cắt nhau tại một điểm có tung độ
4y =
.
A.
3
2
m =
.
B.
3
2
m =-
.
C.
2
3
m =
.
D.
2
3
m =-
.
Câu 18
. Với giá trị nào của
m
thì hàm số
32yxm=-
và
1yx m=- + -
cắt nhau tại một điểm trên
trục tung?
A.
1m =
.
B.
0m =
.
C.
1m =-
.
D.
2m =
.
Câu 19
. Với giá trị nào của
m
thì hàm số
22yxm=- + +
và
552yx m=+-
cắt nhau tại một
điểm trên trục tung?
A.
1m =
.
B.
0m =
.
C.
1m =-
.
D.
2m =
.
Câu 20
. Cho ba đường thẳng
12 3
:2;:31;: 3dy xdy x dy x=- =- - = +
. Khẳng định nào dưới đây
là đúng?
A.
Giao điểm của
1
d
và
3
d
là
(2;1)A
.
B.
Ba đường thẳng trên không đồng quy.
C.
Đường thẳng
2
d
đi qua điểm
(1; 4)B
.
D.
Ba đường thẳng trên đồng quy tại điểm
(1;2)M -
.
Câu 21
. Cho ba đường thẳng
123
:5;:51;:26dy x dy x dy x=- + = - =- +
. Khẳng định nào dưới
đây là đúng?
24/
A.
Giao điểm của
1
d
và
2
d
là
(0;5)M
.
B.
Ba đường thẳng trên đồng quy tại
(1; 4)N
.
C.
Ba đường thẳng trên không đồng quy.
D.
Ba đường thẳng trên đồng quy tại điểm
(0;5)M
.
Câu 22
. Với giá trị nào của
m
thì ba đường thẳng
12 3
:;:43;: 3dy xdy xdy mx==- =-
đồng quy?
A.
1m =
.
B.
0m =
.
C.
1m =-
.
D.
4m =
.
Câu 23
. Với giá trị nào của
m
thì ba đường thẳng
12 3
:65;:(2) ;:32dy xdy m xmdy x=- = + + = +
đồng quy.
A.
5
3
m =
.
B.
3
5
m =
.
C.
5
3
m =-
.
D.
2m =-
.
Câu 24
. Cho đường thẳng
:32dy x=- +
. Gọi
,AB
lần lượt là giao điểm của
d
với trục hoành và
trục tung. Tính diện tích tam giác
OAB
.
A.
4
3
.
B.
2
3
-
.
C.
3
2
.
D.
2
3
.
Câu 25
. Cho đường thẳng
:24dy x=- -
. Gọi
,AB
lần lượt là giao điểm của
d
với trục hoành và
trục tung. Tính diện tích tam giác
OAB
.
A.
2
.
B.
4
.
C.
3
.
D.
8
.
Câu 26
. Cho đường thẳng
1
4
:
3
x
dy
-
=
và
2
:82dy x=-
. Gọi
,AB
lần lượt là giao điểm của
1
d
với
2
d
và
1
d
với trục tung. Tổng tung độ giao điểm của
A
và
B
là:
A.
4
3
.
B.
2
3
.
C.
9
.
D.
8
.
Câu 27
. Cho đường thẳng
1
:2dy x=- +
và
2
:54dy x=-
. Gọi
,AB
lần lượt là giao điểm của
1
d
với
2
d
và
1
d
với trục hoành. Tổng tung độ giao điểm của
A
và
B
là:
A.
2
.
B.
4
.
C.
3
.
D.
8
.
Câu 28
. Gọi
1
d
là đồ thị hàm số
(2 2) 4ymxm=- - +
và
2
d
là đồ thị hàm số
41yx=-
. Xác định
giá trị của
m
để
(1; 3)M
là giao điểm của
1
d
và
2
d
.
A.
1
2
m =
.
B.
1
2
m =-
.
C.
2m =
.
D.
2m =-
.
25/
Câu 29
. Gọi
1
d
là đồ thị hàm số
1ymx=+
và
2
d
là đồ thị hàm số
1
2
2
yx=-
. Xác định giá trị của
m
để
(2; 1)M -
là giao điểm của
1
d
và
2
d
.
A.
1m =
.
B.
2m =
.
C.
1m =-
.
D.
2m =-
.
Câu 30
. Với giá trị nào của m thì ba đường thẳng phân biệt
123
:(2)33;: 2;: 2dy m x m dy x dy mx=+-- =+ = +
giao nhau tại một
điểm?
A.
1
3
m =
.
B.
5
3
m =-
.
C.
5
1;
3
mm==-
.
D.
5
6
m
-
=
.
Câu 31
. Hình vẽ bên là đồ thị của hàm số nào dưới đây?
A.
22yx=-
.
B.
33yx=-
.
C.
1yx=-
.
D.
1yx=+
.
Câu 32
.
A.
21yx=-
.
B.
1yx=-
.
C.
2yx=-
.
D.
21yx=- -
.
HƯỚNG DẪN
26/
Câu 1. Đáp án C.
Đồ thị hàm số
(0)yaxba=+ ¹
là một đường thẳng
Trường hợp 1: Nếu
0b =
ta có hàm số
yax=
. Đồ thị của
yax=
là đường thẳng đi qua gốc tọa
độ
(0; 0)O
và điểm
(1; ).Aa
Trường hợp 2: Nếu
0b ¹
thì đồ thị
yaxb=+
là đường thẳng đi qua các điểm
(0; ), ; 0 .
b
AbB
a
æö
÷
ç
÷
-
ç
÷
ç
÷
ç
èø
Câu 2. Đáp án A.
Đồ thị hàm số
(0)yaxba=+ ¹
là một đường thẳng
Trường hợp 1: Nếu
0b =
ta có hàm số
yax=
. Đồ thị của
yax=
là đường thẳng đi qua gốc tọa
độ
(0; 0)O
và điểm
(1; ).Aa
Trường hợp 2: Nếu
0b ¹
thì đồ thị
yaxb=+
là đường thẳng đi qua các điểm
(0; ), ; 0 .
b
AbB
a
æö
÷
ç
÷
-
ç
÷
ç
÷
ç
èø
Câu 3. Đáp án D.
Đồ thị hàm số
21yx=+
là đường thẳng đi qua hai điểm có tọa độ
(0;1)
và
(1; 3)
nên hình 1 là đồ thị
hàm số
21yx=+
.
Câu 4. Đáp án B.
Đồ thị hàm số
32yx=-
là đường thẳng đi qua hai điểm có tọa độ
(0; 2)-
và
(1; 1)
nên hình 2 là đồ
thị hàm số
32yx=-
.
Câu 5. Đáp án B.
Thay tọa độ từng điểm vào hàm số ta được
+) Với
22
1;
5
A
æö
÷
ç
÷
ç
÷
ç
÷
ç
èø
. Thay
22
1;
5
xy==
vào
2
5
5
yx=-
ta được:
222 2322
5.1
55 5 5
-= =
(vô lý).
+) Với
13
;
55
B
æö
÷
ç
÷
ç
÷
ç
÷
ç
èø
. Thay
13
;
55
xy==
vào
2
5
5
yx=-
ta được
12 2 3
5. 1
55 5 5
-=-=
(luôn đúng).
+) Với
23
;
25 5
C
æö
÷
ç
÷
--
ç
÷
ç
÷
ç
èø
. Thay
23
;
25 5
xy=- =-
vào
2
5
5
yx=-
, ta được:
22 3 4 3
5.
25 5 5 5 5
-
-=--=-
(vô lý).
+) Với
(2;10)D
. Thay
2; 10xy==
vào
2
5
5
yx=-
ta được:
248
5.2 10 10
55
-= =
(vô lý).
27/
13
;
55
B
æö
÷
ç
÷
ç
÷
ç
÷
ç
èø
thuộc đồ thị hàm số
2
5
5
yx=-
.
Câu 6. Đáp án D.
Xét phương trình hoành độ giao điểm của
1
d
và
2
d
ta được
3
123 4 3
4
xxxx-=- = =
Thay
3
4
x =
vào phương trình đường thẳng
1
:1dy x=-
ta được
31
1
44
y =-=-
.
Câu 7. Đáp án A.
Xét phương trình hoành độ giao điểm của
1
d
và
2
d
ta được
5
2234 6 5
6
xxxx-=- = =
Thay
5
6
x =
vào phương trình đường thẳng
1
:22dy x=-
, ta được
51
2. 2
63
y =-=-
.
Câu 8. Đáp án C.
Giao điểm của đường thẳng
d
và trục tung có hoành độ
0x =
. Thay
0x =
vào phương
trình
26yx=+
ta được
2.0 6 6y =+=
Vậy tọa độ giao điểm cần tìm là
(0;6)M
.
Câu 9. Đáp án D.
Giao điểm của đường thẳng
d
và trục tung có hoành độ
0x =
. Thay
0x =
vào phương
trình
1
3
2
yx=-
ta được
11
3.0
22
y =-=-
Vậy tọa độ giao điểm cần tìm là
1
0;
2
D
æö
÷
ç
÷
-
ç
÷
ç
÷
ç
èø
.
Câu 10. Đáp án B.
Đồ thị hàm số cắt trục hoành tại điểm có hoành độ
3x =-
nên tọa độ giao điểm là
(3;0)-
Thay
3; 0xy=- =
vào
(1 )ymxm=- +
ta được
(1 ).( 3) 0mm--+=
3
430 .
4
mm-==
Vậy
3
.
4
m =
Câu 11. Đáp án
A
.
Đồ thị hàm số cắt trục hoành tại điểm có hoành độ
9x =
nên tọa độ giao điểm là
(9; 0)
Thay
9; 0xy==
vào
2
21
3
m
yxm
+
=-+
28/
Ta được
2
.9 2 1 0 3 6 2 1 0 7
3
m
mmmm
+
-+= +-+==-
Vậy
7m =-
.
Câu 12. Đáp án C.
Đồ thị hàm số cắt trục tung tại điểm có tung độ
4y =-
nên tọa độ giao điểm là
(0; 4)-
Thay
0; 4xy==-
vào
(3 2 ) 2ymxm=- +-
ta được
(3 2 ).0 2 4 2mm m-+-=-=-
Vậy
2m =-
.
Câu 13. Đáp án B.
Đồ thị hàm số cắt trục tung tại điểm có tung độ
3y =
nên tọa độ giao điểm là
(0; 3)
Thay
0; 3xy==
ta được
5
(2 ).0 3 5 6 11.
2
m
mmm
+
-- =+=-=-
Vậy
11m =-
.
Câu 14. Đáp án A.
Ta có phương trình hoành độ giao điểm của
1
d
và
2
d
:
1
21
2
mx x-= +
(*)
Để hai đường thẳng
1
d
và
2
d
cắt nhau tại một điểm có hoành độ
4x =-
thì
4x =-
thỏa mãn
phương trình (*).
Suy ra
11
.( 4) 2 .( 4) 1 4 2 2 1 4 1
24
mmmm--= - +- -=-+- = =-
.
Câu 15. Đáp án B.
Ta có phương trình hoành độ giao điểm của
1
d
và
2
d
là
13 2
2
m
xx+= -
(*)
Để hai đường thẳng
1
d
và
2
d
cắt nhau tại một điểm có hoành độ
1x =-
thì
1x =-
thỏa mãn
phương trình (*).
Suy ra
.( 1) 1 3.( 1) 2 1 5 6 12.
222
mmm
m- + = - - - + =- - =- =
Câu 16. Đáp án D.
Thay
3y =
vào phương trình đường thẳng
2
d
ta được
13 4xx-- = =-
Suy ra tọa độ giao điểm của
1
d
và
2
d
là
(4;3)-
Thay
4; 3xy=- =
vào phương trình đường thẳng
1
d
ta
được
13
2( 2).( 4) 3 7 16 3
7
mmm m--+=-+==
Vậy
13
7
m =
.
Câu 17. Đáp án C.
29/
Thay
4y =
vào phương trình đường thẳng
2
d
ta được
14 3xx+= =
Suy ra tọa độ giao điểm của
1
d
và
2
d
là
(3; 4)
Thay
3; 4xy==
vào phương trình đường thẳng
1
d
ta
được
52
(1).314 1
33
mmm+-=+==
Vậy
2
3
m =
.
Câu 18. Đáp án C.
Để hai đồ thị hàm số
32yxm=-
và
1yx m=- + -
cắt nhau tại một điểm trên trục tung thì
31
1
21
m
mm
ì
ï
¹-
ï
=-
í
ï
-=-
ï
î
Câu 19. Đáp án A.
Để hai đồ thị hàm số
22yxm=- + +
và
552yx m=+-
cắt nhau tại một điểm trên trục tung thì
25
33 1
252
mm
mm
ì
ï
-¹
ï
==
í
ï
+=-
ï
î
Câu 20. Đáp án D.
+) Thay tọa độ điểm
(2;1)A
vào phương trình đường thẳng
1
d
ta
được
12.214=- =-
( vô lý) nên
1
AdÏ
hay
(2;1)A
không là giao điểm của
1
d
và
3
d
. Suy ra
A sai.
+) Thay tọa độ điểm
(1; 4)B
vào phương trình đường thẳng
2
d
ta được
43.1144=- - =-
(vô
lý )
Nên
2
BdÏ
. Suy ra C sai.
+) Xét tính đồng quy của ba đường thẳng
* Phương trình hoành độ giao điểm của
1
d
và
2
d
231 1 2.(1) 2xx x y y-=--=-=--=
Suy ra tọa độ giao điểm của
1
d
và
2
d
là
(1;2)-
.
* Thay
1; 2xy=- =
vào phương trình đường thẳng
3
d
ta được
21322=- + =
(luôn đúng)
Vậy ba đường thẳng trên đồng quy tại điểm
(1;2)M -
.
Câu 21. Đáp án B.
+) Thay tọa độ điểm
(0;5)M
vào phương trình đường thẳng
2
d
ta được
55.01 5 1=-=-
(vô lý
)
Nên
2
BdÏ
. Suy ra A,D sai.
30/
+) Xét tính đồng quy của ba đường thẳng
* Phương trình hoành độ giao điểm của
1
d
và
2
:d
55 1 6 6 1 15 4xx xxy y-+ = - = = =-+ =
Suy ra tọa độ giao điểm của
1
d
và
2
d
là
(1; 4)
* Thay
1; 4xy==
vào phương trình đường thẳng
3
d
ta được
42.1644=- + =
(luôn đúng)
Vậy ba đường thẳng trên đồng quy tại điểm
(1; 4)N
.
Câu 22. Đáp án D.
Xét phương trình hoành độ giao điểm của
1
d
và
2
d
:
43 1 1xxxy=- ==
.
Suy ra giao điểm của
1
d
và
2
d
là
(1; 1)M
Để ba đường thẳng trên đồng quy thì
3
MdÎ
nên
1.13 4mm=-=
.
Vậy
4m =
.
Câu 23. Đáp án A.
Xét phương trình hoành độ giao điểm của
1
d
và
3
d
:
17
65 3 2 8 4
22
xx x x y-=+ ===
.
Suy ra giao điểm của
1
d
và
3
d
là
17
;
22
M
æö
÷
ç
÷
ç
÷
ç
÷
ç
èø
Để ba đường thẳng trên đồng quy thì
2
MdÎ
nên
71375
(2). 1 .
22223
m
mm m=+ + +==
Vậy
5
3
m =
Câu 24. Đáp án D.
31/
(;0)Bx
là giao điểm của
d
với trục hoành nên
22
032 ;0
33
xx B
æö
÷
ç
÷
=- + =
ç
÷
ç
÷
ç
èø
(0; )Ay
là giao điểm của
d
với trục tung nên
3.0 2 2 (0;2)yyA=- + =
Suy ra
22
22;
33
OA OB== = =
Vì tam giác
OAB
vuông tại
O
nên
2
2.
.2
3
223
OAB
OAOB
S ===
(đvdt).
Câu 25. Đáp án B.
(;0)Ax
là giao điểm của
d
với trục hoành nên
024 2(2;0)xx A=- - =- -
(0; )By
là giao
điểm của
d
với trục tung nên
2.0 4 4 (0; 4)yyB=- - =- -
Suy ra
22; 44OA OB
=- = =- =
.
Vì tam giác
OAB
vuông tại
O
nên
.2.4
4
22
OAB
OAOB
S ===
(đvdt)
Câu 26. Đáp án A.
+) Phương trình hoành độ giao điểm của
1
d
và
2
d
là
4
82 246 4 5 20 4
3
x
xxxxx
-
=- - =- = =
0y=
nên
()4; 0A
+)
(0; )
B
By
là giao điểm của đường thẳng
1
d
và trục tung. Khi đó ta có
40 4
33
BB
yy
-
==
Suy ra tổng tung độ
44
0.
33
AB
yy+=+=
Câu 27. Đáp án C.
+) Phương trình hoành độ giao điểm của
1
d
và
2
d
là
254 3 3 1xxxx-+ = - = =
nên
1
A
x =
32/
+)
(;0)
B
Bx
là giao điểm của đường thẳng
1
d
và trục hoành. Khi đó ta có
022
BB
xx=- + =
.
Suy ra tổng hoành độ
12 3
AB
xx+=+=
.
Câu 28. Đáp án A.
Nhận thấy
2
MdÎ
. Ta thay tọa độ điểm
M
vào phương trình
1
d
được phương
trình
1
3(22).14
2
mmm=- - + =
Vậy
1
.
2
m =
Câu 29. Đáp án C.
+) Nhận thấy
2
MdÎ
+) Ta thay tọa độ điểm
M
vào phương trình
1
d
được phương trình
12. 1 1mm-= + =-
Vậy
1m =-
.
Câu 30. Đáp án B.
Để 3 đường thẳng trên là ba đường thẳng phân biệt thì
21
1
1
1
2
m
m
m
m
mm
ì
ï
+¹
ï
ì
ï
ï
¹
ï
ï
¹
íí
ïï
¹-
ïï
î
¹+
ï
ï
î
Xét phương trình hoành độ giao điểm của
2
d
và
3
d
:
()
0
22 10
()1
x
xmx xm
mktm
é
=
ê
+= + - =
ê
=
ê
ë
Với
02xy==
nên giao điểm của
23
,dd
là
(0;2)M
Để ba đường thẳng trên giao nhau tại 1 điểm thì
1
MdÎ
.
Nên
5
2( 2).03 3 3 5 ()
3
mmmmtm=+ -- =-=-
Vậy
5
3
m
-
=
.
Câu 31. Đáp án B.
Từ hình vẽ suy ra đồ thị hàm số đi qua hai điểm có tọa độ
(1; 0)
(2; 3)
.
Thay tọa độ hai điểm vào mỗi hàm số ta thấy với hàm số
33yx=-
+) Thay
1; 0xy==
và vào hàm số
33yx=-
ta được
033 00=-=
(luôn đúng)
+) Thay
2; 3xy==
và vào hàm số
33yx=-
ta được
33.23 33=-=
(luôn đúng)
Vậy đồ thị hàm số
33yx=-
là đường thẳng như hình vẽ.
Câu 32. Đáp án A.
33/
Từ hình vẽ suy ra đồ thị hàm số đi qua hai điểm có tọa độ
(0; 1)-
và
(2; 3)
Thay tọa độ hai điểm vào mỗi hàm số ta thấy với hàm số
21yx=-
+) Thay
0; 1xy==-
và vào hàm số
21yx=-
ta được
12.01 1 1-= - -=-
(luôn đúng)
+) Thay
2; 3xy==
và vào hàm số
21yx=-
ta được
32.21 33=-=
(luôn đúng)
Vậy đồ thị hàm số
21yx=-
là đường thẳng như hình vẽ.
| 1/33
| | Tải xuống

Có thể bạn quan tâm:

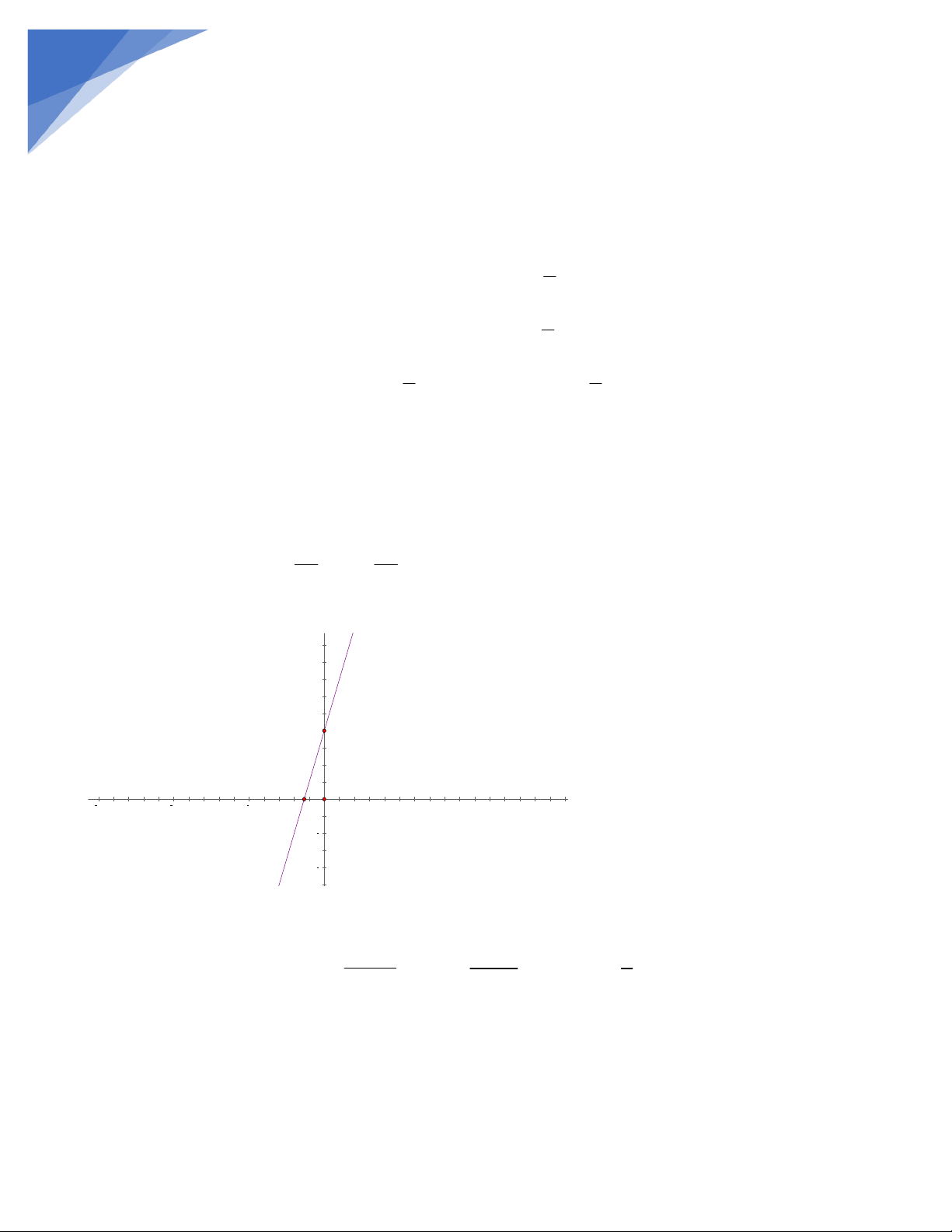
Preview text:

1/
CHUYÊN ĐỀ ĐỒ THỊ HÀM SỐ y ax b (a  0)
A.KIẾN THỨC CẦN NHỚ
1. Đồ thị hàm số bậc nhất
Hàm số bậc nhất y = ax + b với a  0 có
đồ thị là một đường thẳng, kí hiệu là d: y = ax + b
2. Cách vẽ đồ thị của hàm số bậc nhất
Xét đường thẳng d: y = ax + b với a  0
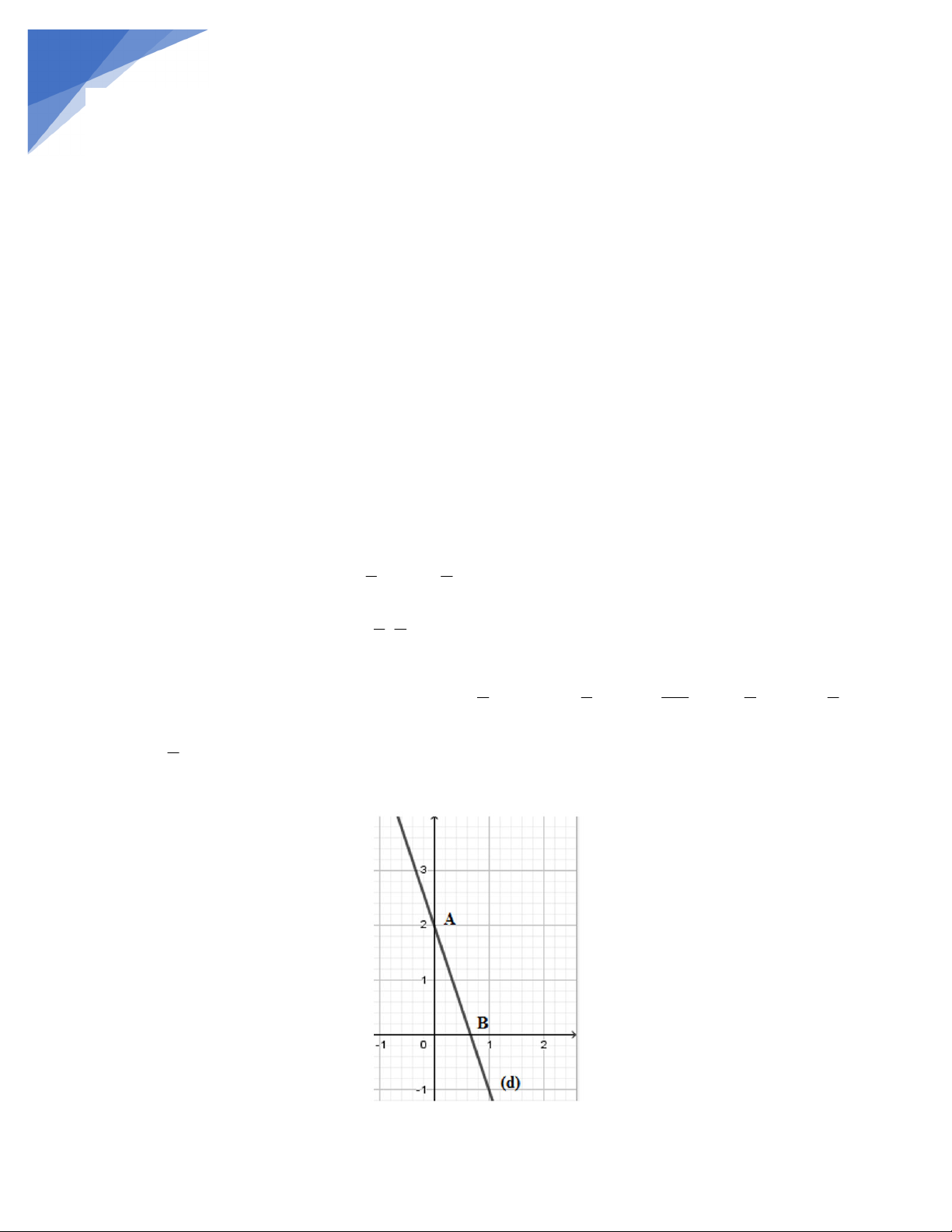
.Nếu b = 0 ta có d: y = ax đi qua gốc tọa độ O(0;0) và điểm A(1; a). .Nếu  
b  0 thì d đi qua hai điểm A(0; b) và b B  ;0    a  3. Chú ý
.Trục hoành là đường thẳng : y = 0
.Trục tung là đường thẳng : x = 0
B.CÁC DẠNG BÀI TẬP MINH HỌA
Dạng 1: Vẽ đồ thị hàm số bậc nhất
Phương pháp giải: Xét đường thẳng d: y = ax + b với a  0
.Nếu b = 0 ta có d: y = ax đi qua gốc tọa độ O(0;0) và điểm A(1; a).
.Nếu b  0 thì d đi qua hai điểm A(0; b) và  b  B  ; 0    a  
Bài 1 : Cho hàm số y f x 1 
x  3 . 2 a. Tính
f 0; f   1 ; f  
1 ; f 2; f  2  ; f 8;
b. Vẽ đồ thị của hàm số trên.
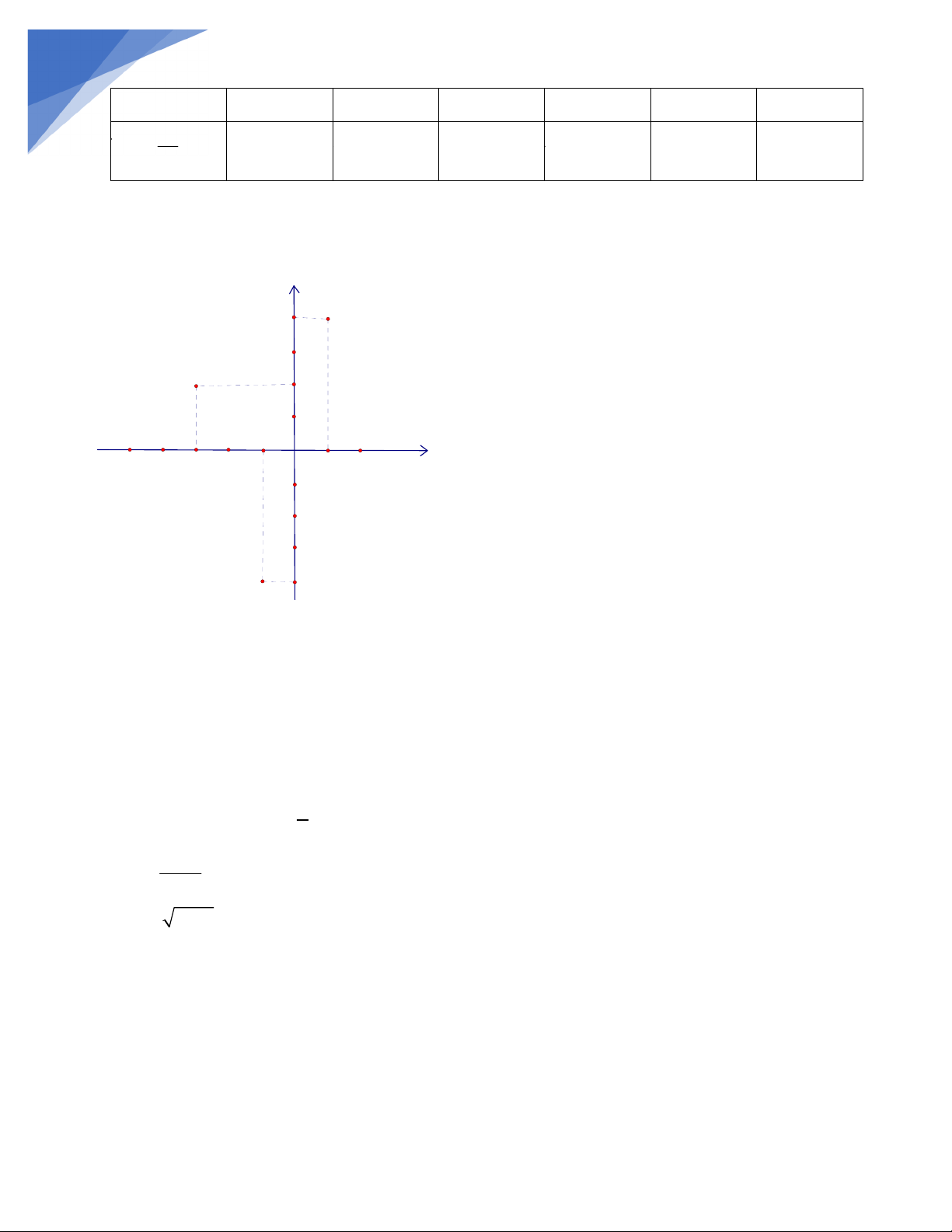
Bài 2: Biểu diễn các điểm sau trên mặt phẳng tọa độ.
A3; 2; B 1;4;C 5;0; D 0;3; E 1;4
Dạng 2: Tìm tham số m để hàm số là hàm số bậc nhất, đồng biến, nghịch biến.
1. Tìm điều kiện xác định của hàm số là bậc nhất…
2. Xét x1; x2 thuộc tập xác định của hàm số với x1 < x2
a. Nếu f(x )  f(x )  f(x ) f(x )  0  Hàm số y  f x đồng biến 1 2 2 1 2/
b. Nếu f(x )  f(x )  f(x )
f(x )  0  Hàm số y  f x nghịch biến 1 2 2 1
Bài 3: Tìm m để hàm số sau là hàm số bậc nhất?
a. y  m  4 x  2009
b. y  2m  3 x  2m 1 m  2 c. y x  4 m  2
d. y  3  m.x  5 3  m
Bài 4: Cho hàm số y  m  5 x  2010 . Tìm m để hàm số trên là
a. Hàm số bậc nhất
b. Hàm số đồng biến, nghịch biến
Bài 5 : Cho hàm số y   2
m  5m  6 x  2 . Tìm m để
a. Hàm số trên là hàm số bậc nhất
b. Hàm số đồng biến, nghịch biến
c. Đồ thị hàm số đi qua điểm A1;4
Dạng 3 : Xét tính đồng quy của ba đường thẳng. Phương pháp giải: ‐
Ba đường thẳng đồng quy là ba đường thẳng phân biệt và cùng đi qua một điểm ‐
Để xét tính đồng quy của ba đường thẳng ( phân biệt) cho trước, ta làm như sau:
1. Tìm tọa độ giao điểm của hai trong ba đường thẳng đã cho.
2. Kiểm tra nếu giao điểm vừa tìm được thuộc đường thẳng còn lại thì kết luận ba đường thẳng đó đồng quy.
Bài 6 : Cho ba đường thẳng.
d : y  4x  3 ; d : y  3x 1 ; d : y x  3 1 2 3
Chứng minh rằng d ; d ; d đồng quy. 1 2 3 3/
Bài 7 : Cho ba đường thẳng.
d : y x  4 ; d : y  2x  3 ; d : y mx m 1 1 2 3
Tìm m để ba đường thẳng trên đồng quy.
Bài 8 : Cho ba đường thẳng.
d : y  3x  8 ; d : y  2x  3 ; d : y  3mx  2m 1 1 2 3
Tìm m để ba đường thẳng trên đồng quy.
Dạng 4: Tìm điểm cố định của đường thẳng phụ thuộc tham số
Phương pháp giải: Cho đường thẳng d: y = ax + b phụ thuộc tham số m
1. Điểm I(x0;y0) được gọi là điểm cố định của d nếu I luôn thuộc d với mọi giá trị của m.
2. Để tìm điểm cố định của d, ta làm như sau:
.Gọi I(x0;y0) là điểm cố định của d => y0= ax0 + b với mọi m.
.Biến đổi y0= ax0 + b về dạng A(x0;y0)m + B(x0;y0) = 0
Hoặc A(x0;y0) m2 + B(x0;y0) m + C(x0;y0) = 0 A x ;y  0 0 0 
.Ta có A(x0;y0)m + B(x0;y0) = 0 với mọi m   B  x ;y  0 0 0 
.Tương tự A(x0;y0) m2 + B(x0;y0) m + C(x0;y0) = 0 với mọi m A x ;y  0 0 0     B x ;y  0 0 0   C  x ;y  0 0 0 
.Từ đó tìm được x0; y0 và kết luận. Bài 9 :
a.Chứng minh x y  2 là điểm cố định mà đường thẳng  y    m 7 : 1 2
x m  luôn đi qua với 0 0 2
mọi giá trị của tham số m
b.Cho đường thẳng v
d : y  2m  
1 x m  2 ới m là tham số. Tìm điểm cố định mà d luôn đi qua với mọi m 4/
Dạng 5: Tính chu vi và diện tích tam giác
Phương pháp giải toán
1. Cho đồ thị hàm số y  f x .
2. Một điểm x ;y được gọi là thuộc đồ thị hàm số nếu khi ta thay các giá trị toạ độ của điểm đó vào 0 0 
phương trình của hàm số và thoả mãn
 y  f x  y 0  0
3. Một điểm x ;y được gọi là không thuộc đồ thị hàm số nếu khi ta thay các giá trị toạ độ của điểm 0 0 
đó vào phương trình của hàm số mà không thoả mãn  y  f x  y . 0  0
4.Vận dụng công thức chu vi và diện tích tích theo yêu cầu bài toán
Bài 10: Xác định các điểm sau trên hệ trục toạ độ Oxy.
A 0;3;Bl;3,C2;2;D2;6;M0;4
Bài 11: Cho hàm số y  f x  x .Trong các điểm A4;2, B2; 
1 , C9;3, D8;2 2 , điểm nào
thuộc và điểm nào không thuộc đồ thị của hàm số.
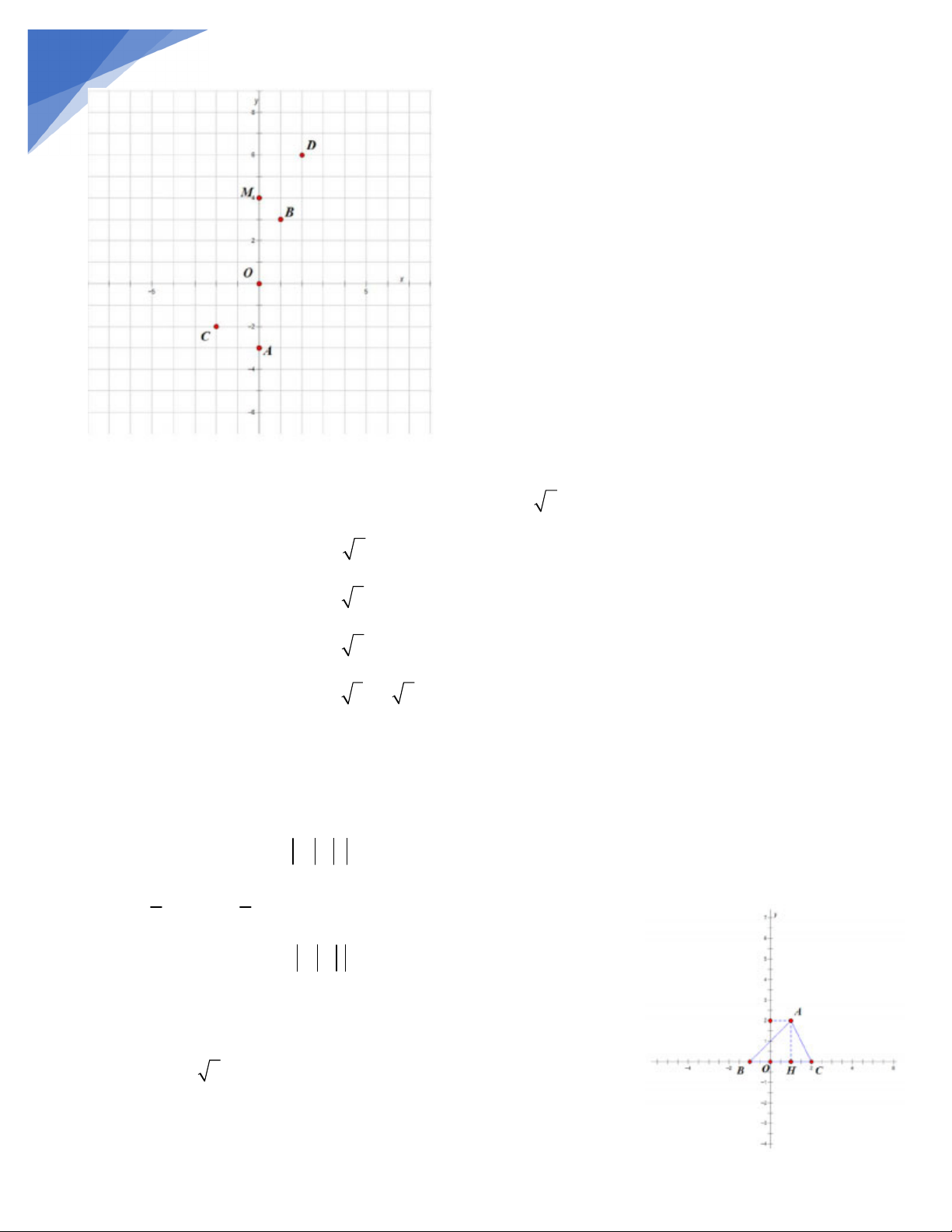
Bài 12 : Vẽ trên mặt phẳng Oxy các điểm A l;2; Bl;0; C2;0
a.Tính diện tích tam giác ABC (theo đơn vị đo của trục toạ độ).
b. Tính chu vi tam giác ABC (theo đơn vị đo của trục toạ độ). HƯỚNG DẪN
Dạng 1: Vẽ đồ thị hàm số bậc nhất Bài 1 :
a.Lập bảng giá trị tương ứng của x và f x . 5/ 2  4 f x 1  x  3 2
b.Hs tự vẽ ĐTHS Bài 2 : y B 4 D 3 A 2 1 C -1 x -5 -3 O 1 2 -2 E -4
Dạng 2: Tìm tham số m để hàm số là hàm số bậc nhất, đồng biến, nghịch biến. Bài 3:
a ......  m  4  0  m  4 3
b ......  2m  3  0  m  2 m  2 m  2  0 m  2  c ......   0     m  2 m  2  0 m  2
d ......  3  m  0  3  m  0  m  3 Bài 4:
a......  m  5  0  m  5
b. + hàm số đồng biến  m  5  0  m  5
+ hàm số nghịch biến  m  5  0  m  5 6/ Bài 5:
a.Hàm số đã cho là hàm số bậc nhất m  2  0 2
m  5m  6  0  m  2m  3  0   m  3  0
b.Hàm số đồng biến m  2  0 m  2   m  3  0 m  3 m  3 2
m  5m  6  0  m  2m  3  0      m  2  0
m  2 m  2   m  3  0 m  3 *) Hàm số nghịch biến m  2  0 m  2   m  3  0 m  3 2  m  3 2
m  5m  6  0  m  2m  3  0      m 2 0    m  2 khong tm   m 3  0 m  3
a. Vì đồ thị hàm số đi qua A1;4 nên :   2 m m   2 4 5
6 .1 2  m  5m  4  0  m   1 m  4  0 m 1  0 m  1     m  4  0 m  4
Dạng 3 : Xét tính đồng quy của ba đường thẳng. Bài 6:
Gọi I d d 1 2
Tìm được I  2;5
Thay tọa độ I vào d thấy thỏa mãn 3
Vậy d ; d ; d đồng quy. 1 2 3 Bài 7:
Gọi I d d 1 2 7/
Tìm được I  7;1  1
Thay tọa độ I vào d tìm được m  2 3
Với m  2 suy ra d : y  2x  3 trùng với d 3 2
Vậy: Không có giá trị nào của m để 3 đường thẳng trên đồng quy. 6
Bài 8: Giải tương tự Bài tập 7. Tìm được m  5
Dạng 4: Tìm điểm cố định của đường thẳng phụ thuộc tham số Bài 9: 1
a.Thay x  ; y  3 vào  ta thấy luôn thỏa mãn vói mọi m . 2
b.Gọi I   x ; y là điểm cố định của d 0 0  Suy ra :
y  2m 1 x m  2 với mọi m 0   0
 2x 1 m x y  2  0 với mọi m 0   0 0   2x 1  0 0  
x y  2  0  0 0  1 5 
Từ đó ta tìm được  ;  
 là điểm cố định của d  2 2 
Dạng 5: Tính chu vi và diện tích tam giác Bài 10:
A 0;3;Bl;3,C2;2;D2;6;M0;4 8/ Bài 11:
Thay toạ độ từng điểm đã cho vào phương trình y  f x  x .
+ xA = 4 thay vào hàm số: f 4  4  2  y , suy ra A thuộc đồ thị hàm số. A
+ xB = 2 thay vào hàm số: f 2  2  y , suy ra B không thuộc đồ thị hàm số. B
+ xC = 9 thay vào hàm số: f 9  9  3  y , suy ra C thuộc đồ thị hàm số. C
+ xD = 8 thay vào hàm số: f 8  8  2 2  y , suy ra D thuộc đồ thị hàm số. D
Vậy, các điểm A, C, D thuộc đồ thị, điểm B không thuộc đồ thị. Bài 12:
Biểu diễn các điểm A l;2; Bl;0; C2;0 trên hệ trục toạ độ Oxy.
a. Ta có: BC  BO  OC  1  2  3 , AH = 2 1 1 S
 BC.AH  .3.2  3 (đơn vị diện tích) AB  C 2 2
b. Ta có: BH  BO  OH  l  l  2
Tam giác AHB vuông tại H, theo định lý Phytago, ta có: 2 2 2 2 2
AB  AH  BH  2  2  8 Suy ra AB  2 2 . 9/
Tương tự, tam giác AHC vuông tại H, ta có: 2 2 2 2 2
AC  AH  CH  2 1  5 . Suy ra AC  5
Vậy chu vi tam giác ABC bằng: AB  BC  CA  2 2  3  5 (đơn vị độ dài)
Dạng 6.Nâng cao phát triển tư duy
Dạng 1: Tính đồng biến – nghịch biến - điểm thuộc đồ thị .
Bài 1:Tìm m để mỗi hàm số sau đây đồng biến hoặc nghịch biến
a) y  (m 1)x  2 b) 2
y  m x 1 c) y  (1 3m)x  2m Bài 2:
a) Cho y  (m  3)x  7 . Tìm m để hàm số trên là hàm số đồng biến, nghịch biến. b) Cho 2
y  (k  4)x  2 . Tìm k để hàm số trên là hàm số đồng biến, nghịch biến.
Bài 3: Cho hàm số y  (m 1)x m
a) Tìm m để đồ thị hàm số cắt trục tung tại điểm có tung độ bằng 2
b) Tìm m để đồ thị hàm số cắt trục hoành tại điểm có hoành độ bằng -3
Bài 4: Cho hàm số y  (m 1)x  3
a) Tìm m để đồ thị hàm số đi qua điểm A(1;2)
b) Tìm m để đồ thị hàm số đi qua điểm B(1;-2)
Bài 5: Xác định a, b để đồ thị hàm số y ax b đi qua các điểm a) (1
A ; 2) và B(2;1) b) P(1; 2) và Q(3; 4)
Dạng 2: TỔNG HỢP:
Vẽ đồ thị - Tính khoảng cách- Tam giác( Diện tích, chu vi). 1
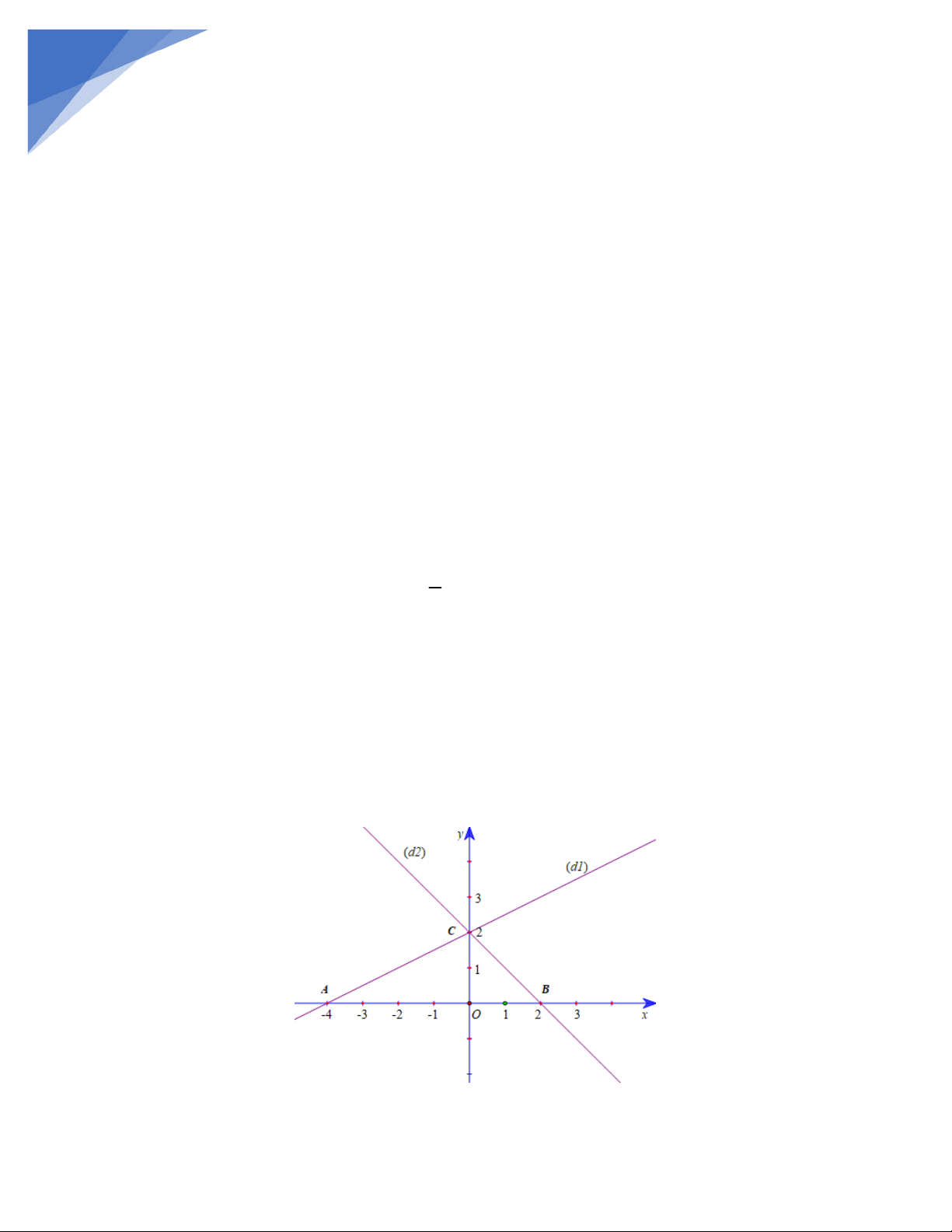
Bài 1: Cho hai đường thẳng (d1) y x  2 2
(d ) : y  x  2 ; (d ) : y  3x 2 3
a) Vẽ (d1), (d2); (d3) trên cùng một hệ tọa độ
b) Gọi A, B lần lượt giao điểm của(d1), (d2) trên Ox, C là giao điểm của (d1), (d2). Tính chu vi tam giác ABC
c) Tính khoảng cách từ gốc tọa độ O đến (d2) 1 1
Bài 2: Cho 3 đường thẳng (d ) : y x 1; (d ) : y  2x  4; (d ) : y x  4 1 2 3 2 2 10/
a) Vẽ đồ thị các đường thẳng thẳng trên cùng một hệ trục tọa độ
b) Cho (d2) cắt (d1) và (d3) tại A, B, (d1) cắt trục Ox tại C. Tính S ABC
Bài 3: Cho hàm số y  (2m 1)x  3 có đồ thị là đường thẳng (d)
a) Tìm m để (d) đi qua điểm A(2 ;5)
b) Vẽ đồ thị của (d) ứng với m vừa tìm được ở câu a. Gọi giao điểm của (d) với hai trục Ox và Oy là M,
N. Tính diện tích tam giác OMN.
c) Tìm m để khoảng cách từ gốc tọa độ O đến (d) lớn nhất
d) Tìm điểm cố định mà (d) luôn đi qua với mọi m
Bài 4: Cho hàm số y  (m  2)x  2 có đồ thị là đường thẳng (d)
a) Tìm m để hàm số đồng biến, nghịch biến
b) Tìm m để khoảng cách từ gốc tọa độ O đến (d) bằng 1.
c) Tìm m để khoảng cách từ gốc tọa độ O đến (d) lớn nhất
d) Tìm điểm cố định mà (d) luôn đi qua
e) Tìm m để (d) cắt hai trục Ox, Oy tại A và B sao cho S  4 AOB
Bài 5: Cho hàm số y  (2m 1)x  4 có đồ thị là đường thẳng (d)
a) Tìm m để hàm số trên đồng biến, nghịch biến. b) Vẽ (d) khi m = 2.
c) Tìm m để khoảng cách từ gốc tọa độ O đến (d) bằng 2
d) Tìm m để khoảng cách từ gốc tọa độ O đến (d) lớn nhất.
Bài 6. Cho hàm số y  m  2 x  2 có đồ thị là đường thẳng (d)
a) Tìm m để hàm số trên là hàm số bậc nhất
b) Tìm m để (d) cắt Ox tại điểm có hoành độ bằng 2
c) Tìm m để khoảng cách từ gốc tọa độ đến (d) bằng HƯỚNG DẪN
Dạng 1: Tính đồng biến – nghịch biến - điểm thuộc đồ thị .
Bài 1: Tìm m để mỗi hàm số sau đây đồng biến hoặc nghịch biến
a) y  (m 1)x  2 b) 2
y  m x 1 c) y  (1 3m)x  2m Lời giải
Hàm số bậc nhất đồng biến khi a  0 và nghịch biến khi a  0 . 11/
a, y  m  
1 x  2 đồng biến khi m  1 nghịch biến khi m  1. b, 2
y  m x  1 do 2 m  0 m
 nên hàm số luôn nghịch biến khi m  0 . 1 1
c, y  (1 3m)x  2m hàm số đồng biến khi  m và nghịch biến khi  m . 3 3 Bài 2: a) Cho y = ( m+3)x
+ 7 . Tìm m để hàm số trên là đồng biến, nghịch biến. b) Cho y = ( 2 k - ) 4 x
- 2. Tìm k để hàm số trên là đồng biến, nghịch biến. Lời giải
a) *Để hàm số y = ( m+3)x + 7 đồng biến khi: m + 3 > 0 m >  -3 *Để hàm số y = ( m+3)x + 7 nghịch biến khi: m + 3 < 0 m <  -3
b) *Để hàm số y = ( 2 k - ) 4 x - 2 đồng biến khi: 2 k 4 - > 0 (  k 2 - )(k 2 + ) > 0 k  < -2; k > 2
*Để hàm số y = ( 2 k - ) 4 x - 2 nghịch biến khi: 2 k 4 < - 0 (  k 2 - )(k+ 2) < 0 -2  < k < 2
Bài 3: Cho hàm số y  (m 1)x m
a) Tìm m để đồ thị hàm số cắt trục tung tại điểm có tung độ bằng 2
b) Tìm m để đồ thị hàm số cắt trục hoành tại điểm có hoành độ bằng -3 Lời giải
a, Khi hàm số cắt trục tung tại điểm có tung độ bằng 2, tức là đồ thị hàm số đã cho sẽ đi qua điểm (0;2)
. Vậy 2  (m  2).0  m m  2 .
b, Khi hàm số cắt trục hoành tại điểm có hoành độ bằng -3, tức là đồ thị hàm số đi qua điểm ( 3  ;0) . Vậy: 0  (m  2).( 3
 )  m  6  2m  0  m  3 .
Bài 4: Cho hàm số y  (m 1)x  3
a) Tìm m để đồ thị hàm số đi qua điểm A(1;2)
b) Tìm m để đồ thị hàm số đi qua điểm B(1;-2) 12/ Lời giải
a, Để hàm số đi qua điểm (1
A ;2) thì 2  (m  1).1 3  m  0 .
b, Để hàm số đi qua điểm B(1;2) thì 2
  (m  1).1 3  m  4  .
Bài 5: Xác định a, b để đồ thị hàm số y ax b đi qua các điểm a) (1
A ; 2) và B(2;1) b) P(1; 2) và Q(3; 4) Lời giải
Cho hàm số y ax b . Để đồ thị hàm số đi qua: 2  . a 1 ba  1 a, (1
A ;2) và B(2;1) thì    1   . a 2  bb  3 2  . a 1 b a   1
b, P(1;2) và Q(3;4) thì    4  . a 3  bb  1
Dạng 2: TỔNG HỢP:
Vẽ đồ thị - Tính khoảng cách- Tam giác( Diện tích, chu vi). 1 Bài 1.
Cho hai đường thẳng d : y x  2 và d : y  x  2 (d ) : y  3x 2  1  2 ; 3
a) Vẽ d và d
trên cùng một hệ trục tọa độ. 2  1  ; (d3)
b) Gọi A và B lần lượt là giao điểm của d và d với trục .
Ox C là giao điểm của d và d2  1  2  1 
. Tính chu vi tam giác ABC.
c) Tính khoảng cách từ gốc tọa độ O đến d . 2  Lời giải 13/ a) Vẽ d : 1 
Cho x  0 thì y  2 ta được điểm 0;2.
Cho y  0 thì x  4 ta được điểm  4;  0
d là đường thẳng đi qua 2 điểm0;2; 4;  0 1  Vẽ d : 2 
Cho x  0 thì y  2 ta được điểm 0;2.
Cho y  0 thì x  2 ta được điểm 2;0
d là đường thẳng đi qua 2 điểm0;2;2;0 1 
b) Theo câu a ta có A 4;
 0 và B2;0 ;
Tọa độ giao điểm của C là nghiệm của hệ:  1
y x  2 x  0  2    C 0;2  y  2
y  x  2
Theo công thức tính khoảng cách giữa hai điểm ta tính được:
AB  6; AC  2 5; BC  2 2
Vậy chu vi tam giác ABC bằng: 6  2 5  2 2 (đơn vị độ dài)
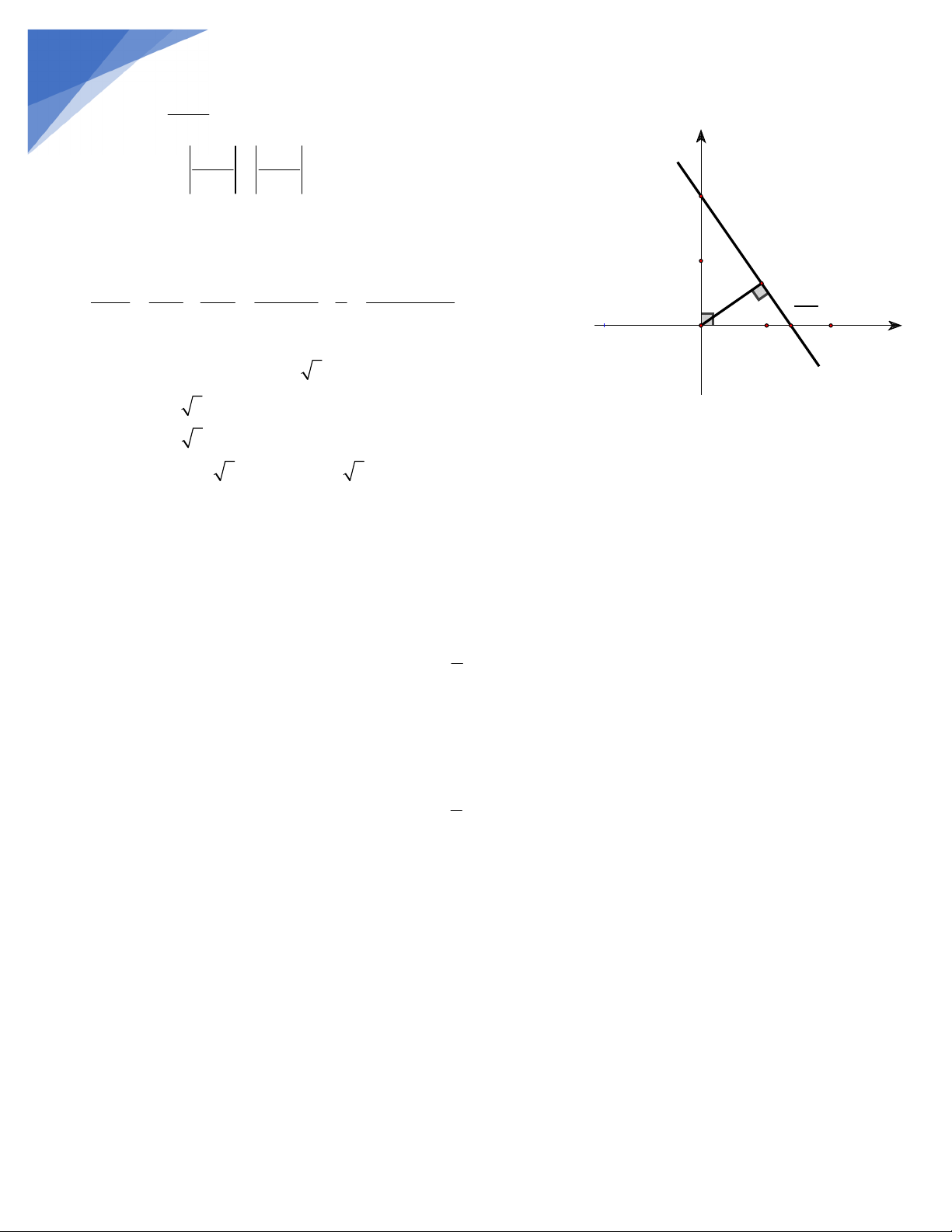
c) Gọi m là khoảng cách từ O đến d . Áp dụng hệ thức lượng trong tam giác vuông OBC ta có: 2  1 1 1 1 1 1     
m  2 (đơn vị độ dài) 2 2 2 2 2 2 m OB OC m 2 2 1 1
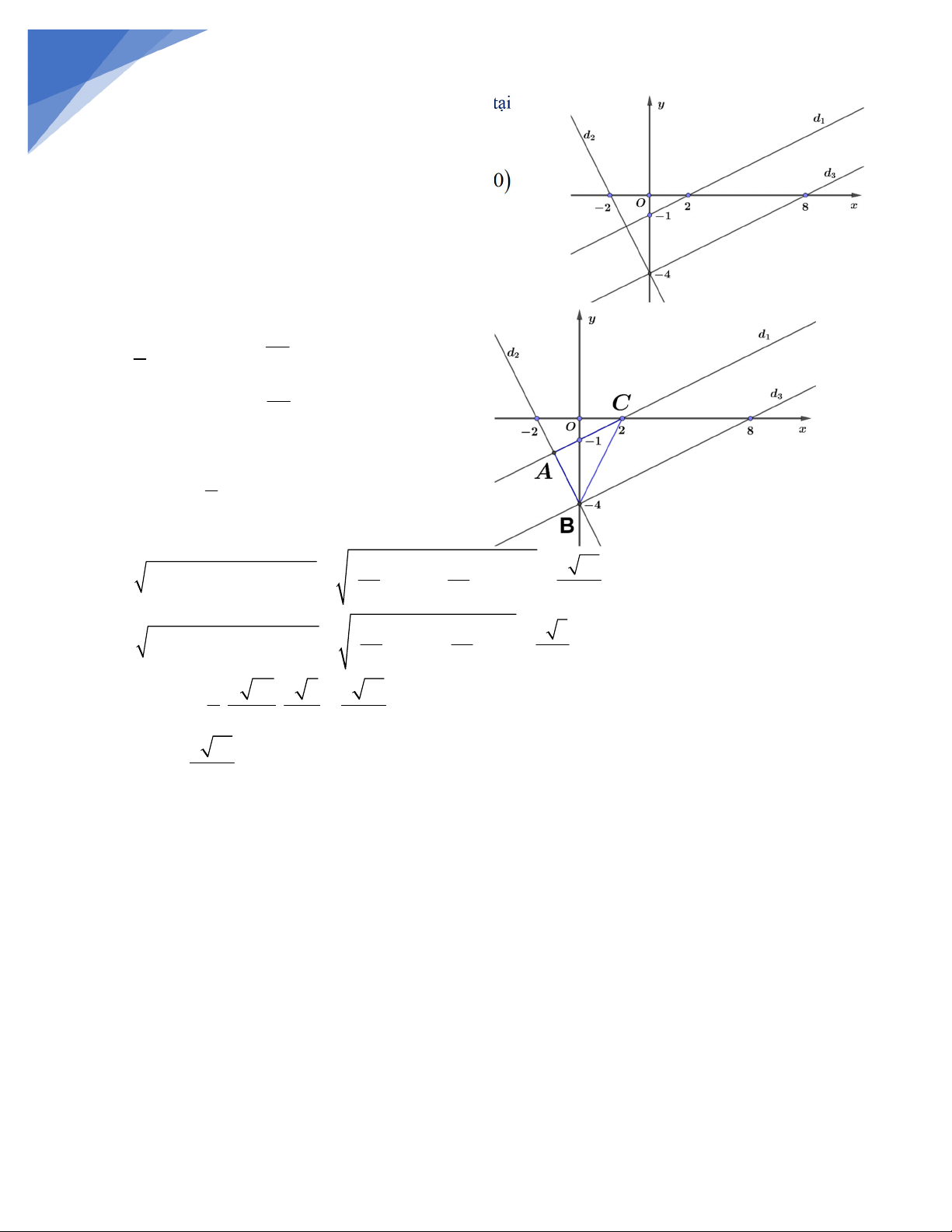
Bài 3: Cho 3 đường thẳng d : y x 1 ; d : y  2
x  4 ; d : y x  4 . 3  2  1  2 2
a) Vẽ đồ thị các đường thẳng trên cùng một hệ trục tọa độ.
b) Cho d cắt d và d tại A và B , d cắt trụ Ox tại C . Tính S 1  3  1  2   . ABC Giải: 14/
a) Ta có d cắt trục tung tại 0;  1  cắt trục hoành tại 1  2;0.
d cắt trục tung tại 0; 4
  cắt trục hoành tại  2;  0 2 
d cắt trục tung tại 0; 4
  cắt trục hoành tại 8;0 3 
Nên ta có đồ thị hình bên
b) Tọa độ của A là nghiệm của hệ  6   1 x  y x 1  5  2   8  y  2  x  4 y   5 Dễ thấy B 0; 4
  ; C 2;0 và d d 1   2 1 Do đó SA . B AC ABC  2 Ta có 2 2     
AB   x xy y       A B 2  A B 2 6 8     2 70 0 4 5  5      5 2 2      
AC   x xy y      A C 2  A C 2 6 8 8 5 2 0      5   5  5 1 2 70 8 5 8 14 Suy ra S  . .  ABC  2 5 5 5 8 14 Vậy S  đvdt ABC 5
Bài 4: Cho hàm số y  (2m 1)x  3 có đồ thị là đường thẳng (d)
a) Tìm m để (d) đi qua điểm A(2 ;5)
b) Vẽ đồ thị của (d) ứng với m vừa tìm được ở câu a. Gọi giao điểm của (d) với hai trục Ox và Oy là M,
N. Tính diện tích tam giác OMN.
c) Tìm m để khoảng cách từ gốc tọa độ O đến (d) lớn nhất
d) Tìm điểm cố định mà (d) luôn đi qua với mọi m Lời giải
a) Vì A 2;5    d   thay x  2; y  5 vào  d  ta được: 5   2m  1.2  3  m  1
b) Với m  1   d  : y x  3 . 15/
Giao của đồ thị  d  với Ox : y  0  x  3   M  3  ;0 
Giao của đồ thị  d  với Oy : x  0  y  3  N  0;3  y y 3 B H -3 0 1 x A 0 1 x 1 1 9
Diện tích OMN là: S  . OM .ON  .3.3  (đvdt) 2 2 2 1 c) Với m
  d  : y  3  khoảng cách từ điểm O đến  d  là 3 (*) 2 1  3 
Với m  . Đồ thị hàm số cắt Ox tại A ;0  
 , cắt Oy tại B 0;3 . 2  2m 1 
Kẻ OH AB  khoảng cách từ O đến  d  là OH . 1 1 1
Áp dụng hệ thức lượng cho tam giác vuông OAB ta có:   2 2 2 OH OA OB 1  2m 1 1 1  
   OH  3 (**) 2 OH 9 9 9 1
Từ (*) và (**) suy ra max OH  3 . Dấu bằng xảy ra khi m  2 1
Vậy m  thì khoảng cách lớn nhất từ O đến đường thẳng  d  là 3. 2
d) Ta có:  d  : y   2m  1 x  3  2mx  3  x y  0 1  x  0 Gọi I  ;
x y  là điểm cố định, suy ra phương trình 1 có nghiệm với m   
3  x y  0  x  0  
I  0;3 . Vậy đường thẳng  d  luôn đi qua điểm cố định I  0;3 .  y  3 16/
Bài 4: Cho hàm số y  (m  2)x  2 có đồ thị là đường thẳng (d)
a) Tìm m để hàm số đồng biến, nghịch biến
b) Tìm m để khoảng cách từ gốc tọa độ O đến (d) bằng 1.
c) Tìm m để khoảng cách từ gốc tọa độ O đến (d) lớn nhất
d) Tìm điểm cố định mà (d) luôn đi qua
e) Tìm m để (d) cắt hai trục Ox, Oy tại A và B sao cho S  4 AOB Lời giải
a) Hàm số đồng biến khi m  2  0  m  2
Hàm số nghịch biến khi: m  2  0  m  2
b) Với m  2   d  : y  2 : Không thỏa mãn.  2 
Với m  2 , đường thẳng  d  cắt Ox tại A ;0  
, cắt Oy tại B  0; 2  .  m 2   
Kẻ OH AB OH  1.
Áp dụng hệ thức lượng cho tam giác vuông OAB ta có: 1 1 1 1  m  2 2 1       m  2  3 2 2 2 OH OA OB 1 4 4
c) Với m  2   d  : y  2 nên khoảng cách từ O đến đường thẳng là 2.
Với m  2 . Theo ý b ta có: 1 1 1 1  m  2 2 1 1        OH  2 2 2 2 2 OH OA OB OH 4 4 4
Vậy max OH  2 . Dấu bằng xảy ra khi m  2 .
Vậy m  2 thì max OH  2 .
d) Đường thẳng  d  : y   m  2  x  2 luôn đi qua điểm cố định I  0;2  .  2 
e) Đường thẳng  d  cắt hai trục tọa độ tại  ,
A B m  2 . Khi đó A ;0 ; B  0;2   m 2     5  1 1 2 1 m  Vì 2 S           OA OB m (tmđk) . OAB 4 . 4 .2 4 2 2 2 m 2 2   3  m   2
Bài 5: y  2m   1 x  4  d  17/
a) Tìm m để hàm số đồng biến, nghịch biến trên tập xác định R b) Vẽ (d) khi m = 2 .
c) Tìm m để khoảng cách từ gốc tọa độ O đến (d) bằng 2.
d) Tìm m để khoảng cách từ gốc tọa độ O đến (d) lớn nhất. GIẢI
y  2m   1 x  4  d
a. Tìm m để hàm số đồng biến, nghịch biến 1
* Để hàm số đồng biến  a  0  2m  1  0  m  2 1
* Để hàm số nghịch biến  a < 0  2m  1  0  m  2 1 1
* Vậy để hàm số đồng biến
m  ; nghịch biến  m  2 2 b. Vẽ (d) khi m = 2
Thay m = 2 vào hs (d) ta có:
(d) : y  2 . 2 – 
1 x  4  y  3x  4 Cho
x  0  y  4  A 0 ; 4 4  4  y  0  x   B ( ;0) 3 3 Ta vẽ đồ thị 8 6 y = 3x + 4 4 A 2 B 15 10 5 5 10 15 O 2 4
c. Tìm m để khoảng cách từ gốc tọa độ O đến (d) bằng 2. Cho x  0  y  4  A  0 ;  4 4   4    1 
y  0  x   B ;0 m      2m 1  2m 1   2  18/ 8 d 6 y = 3x + 4 4 A 2 H B 15 10 5 5 10 15 O 2 4 + Kẻ OH  AB = {H}
+ Vì khoảng cách từ (O) đến AB = 2  OH = 2 (đvđd)
+ Xét ∆ OAB (vuông tại O) có OH là đường cao : 1 1 1   (HTL) 2 2 2 OA OB OH 1 1 1    2 2 2 4  4  2    2m 1 2 2 1 (2m 1) 1 (2m 1) 3      16 16 4 16 16 3
 (2m 1)  3  2m 1   3  3 1    2 .1  3 m m 2     (t / m) 2m 1   3   3 1 m   2  3 1 m
+ Vậy để khoảng cách từ O đến đường thẳng (d) bằng 2 2   (t / m)   3 1 m   2
d) Tìm m để khoảng cách từ gốc tọa độ O đến (d) lớn nhất.
Xét ∆ OAB (vuông tại O): OH  AB 19/ 1 1 1   2 2 2 ( ) OA (OB) (OH ) 2 1 (2m 1) 1    2 16 16 OH 2 (2m 1) 1 1   2 16 OH 16 2   OH 2 (2m 1) 1  4  OH  2 (2m 1) 1
+ Ta có: A(0; 4) là điểm mà (d) luôn đi qua
+ Xét ∆ OAB (vuông tại O) : OH OA (quan hệ đường, điểm)
+ Dấu “ =” xảy ra  H  A 4   4 2 (2m 1) 1 2 2  (2m 1  ) 1  1 (2m 1  ) 1  1 1  2m 1  0 m  (ko t/ m) 2
Vậy không có giá trị của m để khoảng cách từ gốc tọa độ O đến (d) lớn nhất.
Bài 6. Cho hàm số y  m  2 x  2 có đồ thị là đường thẳng (d)
d) Tìm m để hàm số trên là hàm số bậc nhất
e) Tìm m để (d) cắt Ox tại điểm có hoành độ bằng 2
f) Tìm m để khoảng cách từ gốc tọa độ đến (d) bằng 1 Giải : Hàm
số y  m  2 x  2 có a m  2, b  2
a) Để hàm số trên là hàm số bậc nhất thì a  0  m  2  0  m  2  b
b) Ta có đồ thị hàm số y ax b ( a  0 ) luôn cắt trục hoành tại điểm có tọa độ  ;0    a b 2 
nên theo đề bài, để (d) cắt Ox tại điểm có hoành độ bằng 2 thì   2   2 a m  2
m 1( thỏa mãn điều kiện m  2 ) c) Gọi ,
A B theo thứ tự là giao điểm của đường thẳng (d) với trục hoành và trục tung. 20/  2  Suy ra A ;0   và B 0;2  m  2  y 2  2 Khi đó OA   , OB  2 d m  2 2  m 2 B
Kẻ OH AB ( H AB ) thì OH là khoảng cách từ gốc tọa độ đến đường thẳng (d)
Xét OAB vuông tại O đường cao OH , ta có: H 1 1 1 2 m2 2 1 m  4m  5      1 -2 2 2 2 OH OA OB 4 4 4 m-2 mặt khác, 2
OH 1  m  4m  5  4 1 A 2 O x A  m  2
2  3  m  2   3 m  2  3   . m  2  3
Vậy với m  2  3 hoặc m  2  3 thì khoảng cách từ gốc tọa độ đến (d) bằng 1
C.TRẮC NGHIỆM RÈN PHẢN XẠ
Câu 1. Chọn khẳng định đúng về đồ thị hàm số y = ax + b (a ¹ 0).
A. Là đường thẳng đi qua gốc tọa độ.
B. Là đường thẳng song song với trục hoành. æ b ö
C. Là đường thẳng đi qua hai điểm (0
A ;b),B ç- ç ; 0÷÷ ç với b ¹ 0 .
D. Là đường cong đi qua gốc tọa çè a ÷÷ø độ.
Câu 2. Chọn khẳng định đúng về đồ thị hàm số y = ax + b (a ¹ 0) với b = 0
A. Là đường thẳng đi qua gốc tọa độ.
B. Là đường thẳng song song với trục hoành. æ b ö
C. Là đường thẳng đi qua hai điểm ( A 1;0),B ç- ç ; 0÷÷ ç .
D. Là đường cong đi qua gốc tọa độ. çè a ÷÷ø
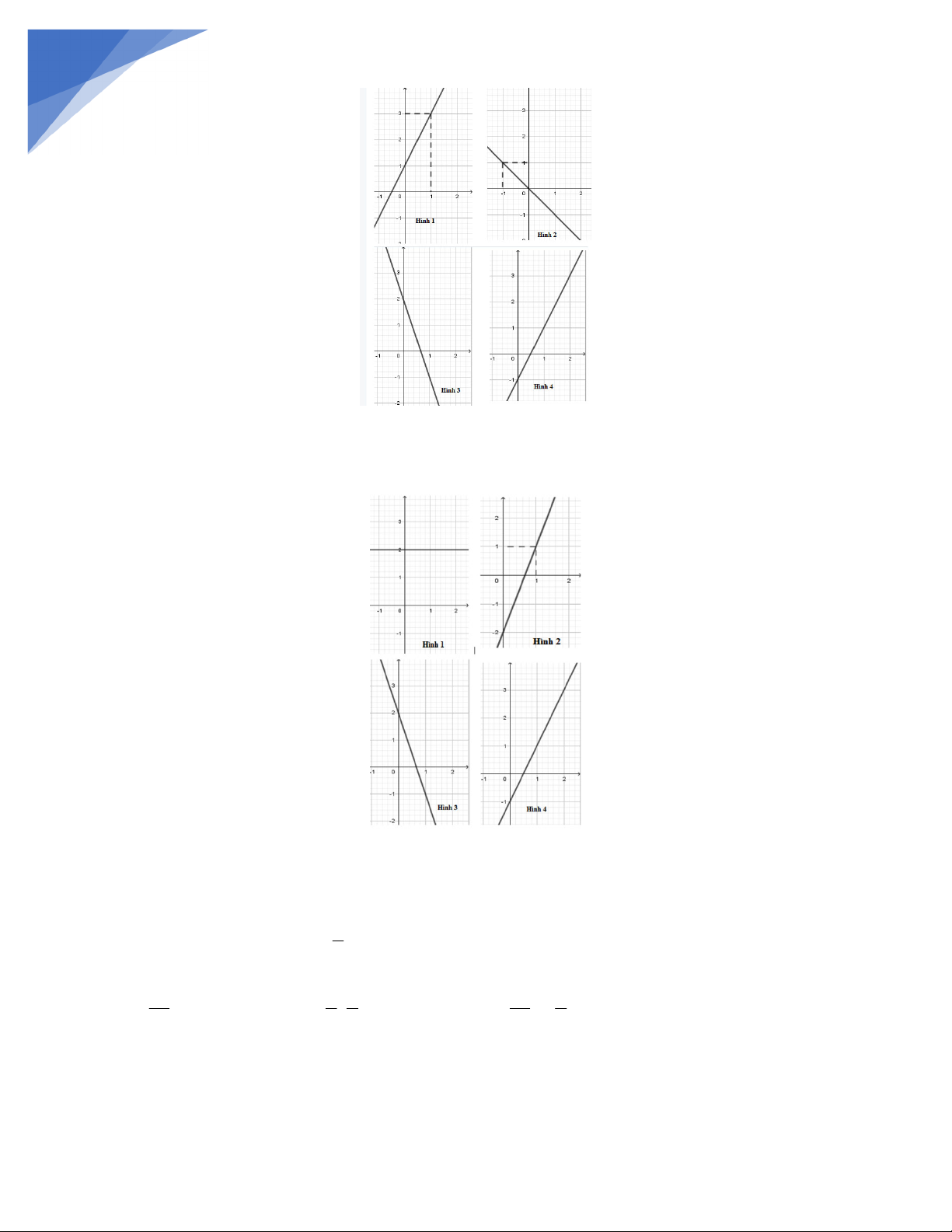
Câu 3. Trong các hình vẽ sau, hình vẽ nào là đồ thị hàm số y = 2x + 1 21/ A. Hình 4. B. Hình 2. C. Hình 3. D. Hình 1.
Câu 4. Trong các hình vẽ sau, hình vẽ nào là đồ thị hàm số y = 3x - 2 . A. Hình 4. B. Hình 2. C. Hình 3. D. Hình 1. 2
Câu 5. Đồ thị hàm số y = 5x - đi qua điểm nào sau đây? 5 æ 22ö æ1 3ö æ 2 3ö A. A 1; ç ÷ ç ÷ ç ÷ ç ÷ ç
. B. B ç ; ÷ . C. C - ç ;- ÷. D. D (2;1 ) 0 . çè 5 ÷÷ø çè5 5÷÷ø çè 25 5÷÷ø
Câu 6. Cho hai đường thẳng d :y = x - 1 và d : y = 2 - 3x . Tung độ giao điểm của d ;d có tọa độ 1 2 1 2 là: 22/ 7 1 1
A. y = -4 . B. y = . C. y = . D. y = - . 4 4 4
Câu 7. Cho hai đường thẳng d : y = 2x - 2 và d = 3 - 4x . Tung độ giao điểm của d ;d có tọa độ là. 1 2 1 2 1 2
A. y = - . B. y = .
C. y = 1. D. y = -1 . 3 3
Câu 8. Cho đường thẳng d : y = 2x + 6 . Giao điểm của d với trục tung là: æ 1ö A. P çç0; ÷÷ ç . B. N(6; 0) . C. M(0;6) . D. D(0;-6). çè 6÷÷ø 1
Câu 9. Cho đường thẳng d : y = 3x - . Giao điểm của d với trục tung là: 2 æ1 ö æ 1ö æ 1ö - æ 1ö A. Açç ;0÷÷ ç ÷ ç ÷ ç ÷ ç . B. B 0; ç ÷ . C. C ç0; ÷. D. D ç0;- ÷. çè6 ÷÷ø çè 2÷÷ø çè 6 ÷÷ø çè 2÷÷ø
Câu 10. Cho hàm sốy = (1 - m)x + m . Xác định m để đồ thị hàm số cắt trục hoành tại điểm có hoành độ x = -3 . 1 3 3 4
A. m = . B. m = . C. m = - . D. m = . 2 4 4 5 m + 2
Câu 11. Cho hàm sốy =
x - 2m + 1 . Xác định m để đồ thị hàm số cắt trục hoành tại điểm có 3 hoành độ x = 9 . A. m = 7 - . B. m = 7 - . C. m = -2 . D. m = -3 .
Câu 12. Cho hàm sốy = (3 - 2m)x + m - 2 , xác định m để đồ thị hàm số cắt trục tung tại điểm có tung độ y = -4 .
A. m = 1. B. m = -1 . C. m = -2 . D. m = 2 . 5 + m
Câu 13. Cho hàm sốy = (2 - m)x -
. Xác định m để hàm số cắt trục 2
tung tại điểm có tung độ y = 3 .
A. m = 11. B. m = -11 . C. m = -12 . D. m = 1. 1
Câu 14. Cho hàm số y = mx - 2 có đồ thị là đường thẳng d và hàm số y = x + 1 có đồ thị là đường 1 2
thẳng d . Xác định m để hai đường thẳng d và 2 1
d cắt nhau tại một điểm có hoành độ x = -4 . 2 23/ 1 1 1 1 A. m = - . B. m = . C. m = . D. m = - . 4 4 2 2 1
Câu 15. Cho hàm số y = mx - 2 có đồ thị là đường thẳng d và hàm số y = x + 1 có đồ thị là đường 1 2
thẳng d . Xác định m để hai đường thẳng d và 2 1
d cắt nhau tại một điểm có hoành độ x = -4 . 2
A. m = 3 . B. m = 12 . C. m = -12 . D. m = -3 .
Câu 16. Cho hàm số y = 2(m - 2)x + m có đồ thị là đường thẳng d và hàm số y = x - - 2 có đồ thị 1
là đường thẳng d . Xác định m để hai đường thẳng d và 2 1
d cắt nhau tại một điểm có tung độ y = 3 . 2 7 7 13 13 A. m = . B. m = - . C. m = - . D. m = . 13 13 7 7
Câu 17. Cho hàm số y = (m + 1)x - 1 có đồ thị là đường thẳng d và hàm số y = x + 1 có đồ thị là 1
đường thẳng d . Xác định m để hai đường thẳng d và d cắt nhau tại một điểm có tung độ y = 4 . 2 1 2 3 3 2 2 A. m = . B. m = - . C. m = . D. m = - . 2 2 3 3
Câu 18. Với giá trị nào của m thì hàm số y = 3x - 2m và y = x
- + 1 - m cắt nhau tại một điểm trên trục tung?
A. m = 1. B. m = 0 . C. m = -1 . D. m = 2 .
Câu 19. Với giá trị nào của m thì hàm số y = -2x + m + 2 và y = 5x + 5 - 2m cắt nhau tại một điểm trên trục tung?
A. m = 1. B. m = 0 . C. m = -1 . D. m = 2 .
Câu 20. Cho ba đường thẳng d : y = 2
- x;d : y = 3
- x - 1;d : y = x + 3 . Khẳng định nào dưới đây 1 2 3 là đúng? d
A. Giao điểm của d và 3 là (2
A ;1) . B. Ba đường thẳng trên không đồng quy. 1
C. Đường thẳng d đi qua điểm B(1; 4) . D. Ba đường thẳng trên đồng quy tại điểm M (-1;2) . 2
Câu 21. Cho ba đường thẳng d : y = x
- + 5;d : y = 5x - 1;d : y = 2
- x + 6 . Khẳng định nào dưới 1 2 3 đây là đúng? 24/ d d
A. Giao điểm của 1 và 2 là M(0;5) . B. Ba đường thẳng trên đồng quy tại N (1; 4).
C. Ba đường thẳng trên không đồng quy.
D. Ba đường thẳng trên đồng quy tại điểm M(0;5) .
Câu 22. Với giá trị nào của m thì ba đường thẳng
d : y = x;d : y = 4 - 3x;d : y = mx - 3 đồng quy? 1 2 3
A. m = 1. B. m = 0 . C. m = -1 . D. m = 4 .
Câu 23. Với giá trị nào của
m thì ba đường thẳng
d : y = 6 - 5x;d : y = (m + 2)x + m;d : y = 3x + 2 đồng quy. 1 2 3 5 3 5 A. m = . B. m = . C. m = - . D. m = -2 . 3 5 3
Câu 24. Cho đường thẳng d : y = -3x + 2 . Gọi ,
A B lần lượt là giao điểm của d với trục hoành và
trục tung. Tính diện tích tam giác OAB . 4 2 3 2 A. . B. - . C. . D. . 3 3 2 3
Câu 25. Cho đường thẳng d : y = -2x - 4 . Gọi ,
A B lần lượt là giao điểm của d với trục hoành và
trục tung. Tính diện tích tam giác OAB . A. 2 . B. 4 . C. 3 . D. 8 . 4 - x
Câu 26. Cho đường thẳng d : y =
và d : y = 8 - 2x . Gọi ,
A B lần lượt là giao điểm của d với 1 3 2 1
d và d với trục tung. Tổng tung độ giao điểm của A và B là: 2 1 4 2 A. . B. . C. 9 . D. 8 . 3 3
Câu 27. Cho đường thẳng d : y = x
- + 2 và d : y = 5 - 4x . Gọi ,
A B lần lượt là giao điểm của d 1 2 1
với d và d với trục hoành. Tổng tung độ giao điểm của 2 1 A và B là: A. 2 . B. 4 . C. 3 . D. 8 .
Câu 28. Gọi d là đồ thị hàm số y = (2
- m - 2)x + 4m và d là đồ thị hàm số y = 4x - 1 . Xác định 1 2
giá trị củam để M (1; 3) là giao điểm của d và d . 1 2 1 1
A. m = . B. m = - . C. m = 2 . D. m = -2 . 2 2 25/ 1
Câu 29. Gọi d là đồ thị hàm số y = mx + 1 và d là đồ thị hàm số y = x - 2 . Xác định giá trị của 1 2 2
m để M (2;-1) là giao điểm của d và d . 1 2
A. m = 1. B. m = 2 . C. m = -1 . D. m = -2 .
Câu 30. Với giá trị nào của m thì ba đường thẳng phân biệt
d : y = (m + 2)x - 3m - 3;d : y = x + 2;d : y = mx + 2 giao nhau tại một 1 2 3 điểm? 1 5 5 5 - A. m = . B. m = - .
C. m = 1;m = - . D. m = . 3 3 3 6
Câu 31. Hình vẽ bên là đồ thị của hàm số nào dưới đây?
A. y = 2x - 2 . B. y = 3x - 3 . C. y = x - 1 .
D. y = x + 1 . Câu 32.
A. y = 2x - 1. B. y = x - 1 .
C. y = x - 2 .
D. y = -2x - 1 . HƯỚNG DẪN 26/ Câu 1. Đáp án C.
Đồ thị hàm số y = ax + b (a ¹ 0) là một đường thẳng
Trường hợp 1: Nếu b = 0 ta có hàm số y = ax . Đồ thị của y = ax là đường thẳng đi qua gốc tọa
độ O(0; 0) và điểm (1 A ;a). æ b ö (0
A ;b), B ç- ç ; 0÷÷. çè a ÷÷
Trường hợp 2: Nếu b ¹ 0 thì đồ thị y = ax + b là đường thẳng đi qua các điểm ø Câu 2. Đáp án A.
Đồ thị hàm số y = ax + b (a ¹ 0) là một đường thẳng
Trường hợp 1: Nếu b = 0 ta có hàm số y = ax . Đồ thị của y = ax là đường thẳng đi qua gốc tọa
độ O(0; 0) và điểm (1 A ;a). æ b ö (0
A ;b), B ç- ç ; 0÷÷. çè a ÷÷
Trường hợp 2: Nếu b ¹ 0 thì đồ thị y = ax + b là đường thẳng đi qua các điểm ø Câu 3. Đáp án D.
Đồ thị hàm số y = 2x + 1 là đường thẳng đi qua hai điểm có tọa độ (0;1) và (1; 3) nên hình 1 là đồ thị
hàm số y = 2x + 1. Câu 4. Đáp án B.
Đồ thị hàm số y = 3x - 2 là đường thẳng đi qua hai điểm có tọa độ (0;-2) và (1;1) nên hình 2 là đồ
thị hàm số y = 3x - 2 . Câu 5. Đáp án B.
Thay tọa độ từng điểm vào hàm số ta được æ 22ö A 1; ç ÷ ç ÷ 22 2 2 22 23 22 çè 5 ÷÷ x = 1;y = y = 5x - 5.1 - =  = +) Với ø . Thay 5 vào 5 ta được: 5 5 5 5 (vô lý). æ1 3ö B çç ; ÷÷ 1 3 2 1 2 2 3 çè5 5÷÷ x = ;y = y = 5x - 5. - = 1 - = +) Với ø . Thay 5 5 vào 5 ta được 5 5 5 5 (luôn đúng). æ 2 3ö C ç- ç ; ÷ - ÷ 2 3 2 çè 25 5÷÷ x = - ;y = - y = 5x - +) Với ø. Thay 25 5 vào 5 , ta được: -2 2 3 4 3 5. - = -  - = - 25 5 5 5 5 (vô lý). 2 y = 5x -
+) Với D(2;10). Thay x = 2;y = 10 vào 5 ta được: 2 48 5.2 - = 10  = 10 5 5 (vô lý). 27/ æ1 3ö  B çç ; ÷÷ 2 çè5 5÷÷ø y = 5x -
thuộc đồ thị hàm số 5 . Câu 6. Đáp án D. d d
Xét phương trình hoành độ giao điểm của 1 và 2 ta được 3
x - 1 = 2 - 3x  4x = 3  x = 4 3 3 1 x =
d : y = x - 1 y = - 1 = - Thay
4 vào phương trình đường thẳng 1 ta được 4 4 . Câu 7. Đáp án A. 5 d d
2x - 2 = 3 - 4x  6x = 5  x =
Xét phương trình hoành độ giao điểm của 1 và 2 ta được 6 5 5 1 x =
d : y = 2x - 2 y = 2. - 2 = - Thay
6 vào phương trình đường thẳng 1 , ta được 6 3 . Câu 8. Đáp án C.
Giao điểm của đường thẳng d và trục tung có hoành độ x = 0 . Thay x = 0 vào phương
trình y = 2x + 6 ta được y = 2.0 + 6 = 6
Vậy tọa độ giao điểm cần tìm là M(0;6) . Câu 9. Đáp án D.
Giao điểm của đường thẳng d và trục tung có hoành độ x = 0 . Thay x = 0 vào phương 1 1 1 y = 3x - y = 3.0 - = - trình 2 ta được 2 2 æ 1ö D çç0; ÷ - ÷ çè 2÷÷
Vậy tọa độ giao điểm cần tìm là ø. Câu 10. Đáp án B.
Đồ thị hàm số cắt trục hoành tại điểm có hoành độ x = -3 nên tọa độ giao điểm là (-3; 0)
Thay x = -3;y = 0 vào y = (1 - m)x + m ta được (1 - m).(-3) + m = 0 3
 4m - 3 = 0  m = . 4 3 m = . Vậy 4
Câu 11. Đáp án A.
Đồ thị hàm số cắt trục hoành tại điểm có hoành độ x = 9 nên tọa độ giao điểm là (9; 0) m + 2 y = x - 2m + 1
Thay x = 9;y = 0 vào 3 28/
m + 2 .9 -2m +1 = 0  3m + 6 -2m +1 = 0  m = -7 Ta được 3 Vậy m = 7 - . Câu 12. Đáp án C.
Đồ thị hàm số cắt trục tung tại điểm có tung độ y = -4 nên tọa độ giao điểm là (0;-4)
Thay x = 0;y = -4 vào y = (3 - 2m)x + m - 2 ta được (3 - 2m).0 + m - 2 = -4  m = -2 Vậy m = -2 . Câu 13. Đáp án B.
Đồ thị hàm số cắt trục tung tại điểm có tung độ y = 3 nên tọa độ giao điểm là (0; 3) 5 + m (2 - m).0 -
= 3  5 + m = -6  m = -11.
Thay x = 0;y = 3 ta được 2 Vậy m = -11 . Câu 14. Đáp án A. d d 1
Ta có phương trình hoành độ giao điểm của 1 và 2 : mx - 2 = x + 1 (*) 2
Để hai đường thẳng d và d cắt nhau tại một điểm có hoành độ x = -4 thì x = -4 thỏa mãn 1 2 phương trình (*). 1 1
m.(-4) - 2 = .(-4) + 1  -4m - 2 = -2 + 1  -4m = 1  m = - Suy ra 2 4 . Câu 15. Đáp án B. m x +1 = 3x -2
Ta có phương trình hoành độ giao điểm của d và d là 2 (*) 1 2
Để hai đường thẳng d và d cắt nhau tại một điểm có hoành độ x = -1 thì x = -1 thỏa mãn 1 2 phương trình (*). m m m .(-1) + 1 = 3.(-1) - 2  - + 1 = -5  - = -6  m = 12. Suy ra 2 2 2 Câu 16. Đáp án D. d
Thay y = 3 vào phương trình đường thẳng 2 ta được x - - 1 = 3  x = 4 - d d
Suy ra tọa độ giao điểm của - 1 và 2 là ( 4; 3) d
Thay x = -4;y = 3 vào phương trình đường thẳng 1 ta 13
2(m - 2).(-4) + m = 3  -7m + 16 = 3  m = được 7 13 m = Vậy 7 . Câu 17. Đáp án C. 29/ d
Thay y = 4 vào phương trình đường thẳng 2 ta được x + 1 = 4  x = 3
Suy ra tọa độ giao điểm của d và d là (3; 4) 1 2 d
Thay x = 3;y = 4 vào phương trình đường thẳng 1 ta 5 2
(m + 1).3 - 1 = 4  m + 1 =  m = được 3 3 2 m = Vậy 3 . Câu 18. Đáp án C.
Để hai đồ thị hàm số y = 3x - 2m và y = x
- + 1 - m cắt nhau tại một điểm trên trục tung thì 3 ìï ¹ -1 ïí  m = -1 ï-2m = 1 - m ïî Câu 19. Đáp án A.
Để hai đồ thị hàm số y = -2x + m + 2 và y = 5x + 5 - 2m cắt nhau tại một điểm trên trục tung thì ìï-2 ¹ 5 ïí
 3m = 3  m = 1 m ï + 2 = 5 - 2m ïî
Câu 20. Đáp án D. d +) Thay tọa độ điểm (2
A ;1) vào phương trình đường thẳng 1 ta A Ï d d được 1 = 2 - .2  1 = 4 - ( vô lý) nên 1 hay (2
A ;1) không là giao điểm của 1 và d . Suy ra 3 A sai. d
+) Thay tọa độ điểm B(1; 4) vào phương trình đường thẳng 2 ta được 4 = 3 - .1 -1  4 = 4 - (vô lý ) B Ï d Nên 2 . Suy ra C sai.
+) Xét tính đồng quy của ba đường thẳng d
* Phương trình hoành độ giao điểm của d và 2 1
-2x = -3x - 1  x = -1  y = -2.(-1)  y = 2 d d
Suy ra tọa độ giao điểm của - 1 và 2 là ( 1;2) . d
* Thay x = -1;y = 2 vào phương trình đường thẳng 3 ta được 2 = 1
- + 3  2 = 2 (luôn đúng)
Vậy ba đường thẳng trên đồng quy tại điểm M (-1;2) . Câu 21. Đáp án B. d
+) Thay tọa độ điểm M(0;5) vào phương trình đường thẳng 2 ta được 5 = 5.0 - 1  5 = 1 - (vô lý ) B Ï d Nên 2 . Suy ra A,D sai. 30/
+) Xét tính đồng quy của ba đường thẳng d d :
* Phương trình hoành độ giao điểm của 1 và 2 x
- + 5 = 5x - 1  6x = 6  x = 1  y = -1 + 5  y = 4 d d
Suy ra tọa độ giao điểm của 1 và 2 là (1; 4) d
* Thay x = 1;y = 4 vào phương trình đường thẳng 3 ta được 4 = 2
- .1 + 6  4 = 4 (luôn đúng)
Vậy ba đường thẳng trên đồng quy tại điểm N (1; 4). Câu 22. Đáp án D. d d
Xét phương trình hoành độ giao điểm của = -  =  = 1 và 2 : x 4 3x x 1 y 1 . d d
Suy ra giao điểm của 1 và 2 là M(1;1) M Î d
Để ba đường thẳng trên đồng quy thì 3 nên 1 = .
m 1 - 3  m = 4 . Vậy m = 4 . Câu 23. Đáp án A. d d
Xét phương trình hoành độ giao điểm của 1 và 3 : 1 7
6 - 5x = 3x + 2  8x = 4  x =  y = . 2 2 æ1 7ö M çç ; ÷÷ çè2 2÷÷
Suy ra giao điểm của d và d là ø 1 3 7 1 3m 7 5 M Î d
= (m + 2). + m  + 1 =  m = .
Để ba đường thẳng trên đồng quy thì 2 nên 2 2 2 2 3 5 Vậym = 3 Câu 24. Đáp án D. 31/ 2 æ2 ö
0 = -3x + 2  x =  B çç ;0÷÷ ç ÷ B(x; 0) 3 çè3 ÷
là giao điểm của d với trục hoành nên ø (0
A ;y) là giao điểm của d với trục tung nên y = -3.0 + 2  y = 2  ( A 0;2) 2 2 OA = 2 = 2;OB = = 3 3 Suy ra 2 2. . OAOB 2 3 S = = =
Vì tam giácOAB vuông tại O nên OAB 2 2 3 (đvdt). Câu 25. Đáp án B. (
A x; 0) là giao điểm của d với trục hoành nên 0 = -2x - 4  x = -2  (
A -2; 0) B(0;y) là giao
điểm của d với trục tung nên y = -2.0 - 4  y = -4  B(0;-4)
OA = -2 = 2;OB = -4 = 4 Suy ra .
Vì tam giác OAB vuông tại O nên . OAOB 2.4 S = = = 4 OAB 2 2 (đvdt) Câu 26. Đáp án A.
+) Phương trình hoành độ giao điểm của d1 4 - x và d là
= 8 - 2x  24 - 6x = 4 - x  5x = 20  x = 4  y = 0 nên ( A 4; ) 0 2 3 4 - 0 4 B(0;y ) y =  y = +) B B
B là giao điểm của đường thẳng d và trục tung. Khi đó ta có 3 3 1 4 4
Suy ra tổng tung độ y + y = 0 + = . A B 3 3 Câu 27. Đáp án C.
+) Phương trình hoành độ giao điểm của d và d là x
- + 2 = 5 - 4x  3x = 3  x = 1 1 2 x = 1 nên A 32/ 0 = x - + 2  x = 2
+)B(x ;0) là giao điểm của đường thẳng d và trục hoành. Khi đó ta có B B . B 1
x + x = 1 + 2 = 3
Suy ra tổng hoành độ A B . Câu 28. Đáp án A. M Î d Nhận thấy
2 . Ta thay tọa độ điểm M vào phương trình d được phương 1 1 3 = (
- 2m - 2).1 + 4m m = trình 2 1 m = . Vậy 2 Câu 29. Đáp án C. M Î d +) Nhận thấy 2
+) Ta thay tọa độ điểm M vào phương trình d được phương trình 1
- = 2.m + 1  m = 1 - 1 Vậy m = -1 . Câu 30. Đáp án B. m ìï + 2 ¹ 1 ïï m ìï ¹ 1
Để 3 đường thẳng trên là ba đường thẳng phân biệt thì m ïí ¹ 1 ï  í ï m ï ¹ -1 m ïï ¹ m + 2 ïî ïî d
Xét phương trình hoành độ giao điểm của d và 3 : 2 éx = 0 x 2 mx 2 x(m ) 1 0 ê + = +  - =  m ê = ( 1 ktm) êë d ,d
Với x = 0  y = 2 nên giao điểm của 2 3 là M(0;2)
Để ba đường thẳng trên giao nhau tại 1 điểm thì M Î d . 1 5
2 = (m + 2).0 - 3m - 3  3m = -5  m = - (tm) Nên 3 5 - m = Vậy 3 . Câu 31. Đáp án B.
Từ hình vẽ suy ra đồ thị hàm số đi qua hai điểm có tọa độ (1; 0) (2; 3) .
Thay tọa độ hai điểm vào mỗi hàm số ta thấy với hàm số y = 3x - 3
+) Thay x = 1;y = 0 và vào hàm số y = 3x - 3 ta được 0 = 3 - 3  0 = 0 (luôn đúng)
+) Thay x = 2;y = 3 và vào hàm số y = 3x - 3 ta được 3 = 3.2 - 3  3 = 3 (luôn đúng)
Vậy đồ thị hàm số y = 3x - 3 là đường thẳng như hình vẽ. Câu 32. Đáp án A. 33/
Từ hình vẽ suy ra đồ thị hàm số đi qua hai điểm có tọa độ (0;-1) và (2; 3)
Thay tọa độ hai điểm vào mỗi hàm số ta thấy với hàm số y = 2x - 1
+) Thay x = 0;y = -1 và vào hàm số y = 2x - 1 ta được 1 - = 2.0 -1  1 - = 1 - (luôn đúng)
+) Thay x = 2;y = 3 và vào hàm số y = 2x - 1 ta được 3 = 2.2 - 1  3 = 3 (luôn đúng)
Vậy đồ thị hàm số y = 2x - 1 là đường thẳng như hình vẽ.