Chuyên đề hàm số

Tài liệu gồm 33 trang, được biên soạn bởi tác giả Toán Học Sơ Đồ, tổng hợp kiến thức trọng tâm, phân dạng và hướng dẫn giải các dạng bài tập tự luận & trắc nghiệm chuyên đề hàm số. Mời bạn đọc đón xem.

126 63 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Chương 4: Phương trình bậc hai một ẩn

Môn: Toán 9

Thông tin:

33 trang 8 tháng trước

Tác giả:

Profile Hà Việt Anh
1.
TOÁNHỌCSƠĐỒ‐THCS.TOANMATH.com
CHUYÊN ĐỀ HÀM SỐ
2
yax

0a
A. KIẾN THỨC TRỌNG TÂM
* Tập xác định của hàm số:
+ Hàm số

2
0yaxa
xác định với mọi
Rx
.
* Tính chất biến thiên của hàm số:
+ Nếu
0a
thì hàm số

2
0yaxa
nghịch biến khi
0x
, và đồng biến khi
0x
.
+ Nếu
0a
thì hàm số

2
0yaxa
đồng biến khi
0x
và nghịch biến khi
0x
.
* Đồ thị của hàm số:

2
0yaxa
+ Đồ thị của hàm số

2
0yaxa
là một đường cong đi qua gốc toạ độ và nhận trục Oy làm trục
đối xứng. Đường cong đó được gọi là một Parabol

P
với đỉnh O.
+ Nếu
0a
thì
0y
với mọi
0x
,
0y
khi
0x
. Do đó, đồ thị

P
nằm phía trên trục hoành

Ox
, đỉnh O là điểm thấp nhất của đồ thị.
+ Nếu
0a
thì
0y
với mọi
0x
,
0y
khi
0x
. Do đó, đồ thị

P
nằm phía trên trục hoành

Ox
, đỉnh O là điểm cao nhất của đồ thị.
+ Vì đồ thị

2
0yaxa
luôn đi qua gốc toạ độ và nhận trục Oy làm trục đối xứng nên để vẽ đồ thị
của hàm số này, ta chỉ cần tìm một điểm ở bên phải trục Oy rồi lấy các điểm đối xứng với chúng qua
Oy.
B. CÁC DẠNG BÀI TOÁN MINH HỌA
Dạng 1. Xác định hàm số bậc hai
Cho hàm số

yfx
được gọi là hàm số bậc hai một ẩn nếu phương trình của hàm số có:
Vậy, để xác định một hàm số là hàm số bậc hai một ẩn phải thoả mãn điểu kiện sau:
+ Hàm số chỉ chứa một ẩn duy nhất, với bậc cao nhất của ẩn là bậc hai.
+ Hàm số có dạng
2
0ax bx c
với

0a
.
+ Hàm số có dạng
2
yax b có hệ số
0a
.
+ Hàm số
2
yax
có hệ số
0a
.
Ví dụ minh hoạ 1:
Trong các hàm số sau, hàm số nào là hàm số bậc hai một ẩn?
a.
2
1
3y
x

b.
2
1
5
x
y  c.
2
1
yx
x

2.
TOÁNHỌCSƠĐỒ‐THCS.TOANMATH.com
d.
2
2
1
yx
y
 e.
2
1yxx
f.

2
31yx
Hướng dẫn giải:
Các hàm số là hàm số bậc hai một ẩn là:
2
1
5
x
y  và
2
1yxx

2
2
31363yx xx
.
Ví dụ minh hoạ 2:
Tìm m để hàm số sau là hàm số bậc hai một ẩn.
a.

2
2ym x
b.

22
2ym x
Hướng dẫn giải:
a. Để hàm số

2
2ym x
là hàm số bậc hai khi và chỉ khi:
20 2mm
Vậy, với
2m 
thì hàm số đã cho là hàm số bậc hai.
b. Để hàm số

22
2ym x
là hàm số bậc hai khi và chỉ khi:
22
2
20 2
2
m
mm
m


Vậy, với
2m 
thì hàm số đã cho là hàm số bậc hai.
Dạng 2. Điểm thuộc đồ thị hàm số - Vẽ đồ thị hàm số
* Cho hàm số

2
0yaxa
có đồ thị là Parabol

P
.
+ Điểm M có toạ độ

00
;xy
thuộc đồ thị parabol

P
khi và chỉ khi
2
00
yax
+ Điểm M có toạ độ

00
;xy
không thuộc đồ thị parabol

P
2
00
yax
* Vẽ đồ thị hàm số

2
0yaxa
+ Xác định đỉnh của Parabol là gốc toạ độ

0;0O
.
+ Xác định các điểm thuộc đồ thị hàm số:
–2 –1 0 1 2
4a A 0 a 4a
+ Hình dạng parabol:
0a
0a
Parabol nhận trục tung làm trục đối xứng.
3.
TOÁNHỌCSƠĐỒ‐THCS.TOANMATH.com
Ví du minh họa 1: Cho hàm số
2
1
10
yx
a. Vẽ đồ thị

P
của hàm số.
b. Các điểm sau có thuộc đồ thị hay không:
9
3;
10
A



,
5
5;
2
B



,

10;1C
Hướng dẫn giải:
Hàm số
2
1
10
yx
có đồ thị là parabol

P
.
a. Đồ thị

P
có đỉnh là

0;0O
, nằm phía trên trục hoành, nhận trục Oy làm trục đối xứng và đồ thị
đi qua các điểm sau:
–10 –5 0 5 10
10
5
2
0
5
2
10
b. Thay toạ độ điểm
9
3;
10
A



vào phương trình parabol

P
:
2
1
10
yx
Ta có:

2
91 99
3
10 10 10 10

(đúng). Vậy điểm A thuộc đồ thị hàm số.
Thay toạ độ điểm
5
5;
2
B



vào phương trình parabol

P
:
2
1
10
yx
Ta có:

2
51 525 55
5
210 210 22

(đúng).
Vậy điểm B thuộc đồ thị hàm số.
4.
TOÁNHỌCSƠĐỒ‐THCS.TOANMATH.com
Thay toạ độ điểm

10;1C
vào phương trình parabol

P
:
2
1
10
yx
Ta có:

2
1100
110 110
10 10

(vô lý).
Vậy điểm B không thuộc đồ thị hàm số.
Dạng 3. Sự đồng biến - nghịch biến của đồ thị hàm số.
Cho hàm số

2
0yaxa
xác định với mọi
Rx
.
+ Nếu
0a
: Hàm số

2
0yaxa
nghịch biến khi
0x
, và đồng biến khi
0x
.
x

0

2
0yaxa
0
+ Nếu
0a
: Hàm số

2
0yaxa
đồng biến khi
0x
và nghịch biến khi
0x
.
x

0

2
0yaxa
0
Ví dụ minh hoạ 1: Cho hàm số

22
ymmx
. Tìm giá trị của m để:
a. Hàm số đồng biến với mọi
0x
.
b. Hàm số nghịch biến với mọi
0x
.
Hướng dẫn giải:
Hàm số

22
ymmx
.
a. Hàm số đồng biến với mọi

2
00 0 10xammmm 
Khi
00
1
10 1
mm
m
mm






Hoặc
00
0
10 1
mm
m
mm






Vậy với
0m
hoặc
1m
thì hàm số đã cho đồng biến với mọi
0x
.
b. Hàm số nghịch biến với mọi

2
00 0 10xammmm 
Khi
00
01
10 1
mm
m
mm






Hoặc
00
10 1
mm
mm






Không có giá trị nào của m thoả mãn điều kiện này.
5.
TOÁNHỌCSƠĐỒ‐THCS.TOANMATH.com
Vậy với
01m
thì hàm số đã cho nghịch biến với mọi
0x
.
Dạng 4. Giá trị lớn nhất, giá trị nhỏ nhất của hàm số
* Hàm số

2
0yaxa
+ Nếu
0a
hàm số có giá trị nhỏ nhất bằng 0 khi
0x
.
+ Nếu
0a
hàm số có giá trị lớn nhất bằng 0 khi
0x
.
* Hàm số

2
0yax bxca
+ Nếu
0a
hàm số

2
0yax bxca
có giá trị nhỏ nhất khi
2
b
x
a

+ Nếu
0a
hàm số

2
0yax bxca
có giá trị lớn nhất khi
2
b
x
a

Dạng 5. Viết phương trình parabol

2
0yaxa
(tìm hệ số a)
Khi biết toạ độ của một điểm thuộc đồ thị hàm số

2
0yaxa
, ta đi tìm hệ số a của nó bằng cách
thay toạ độ điểm đó vào phương trình hàm số.
Ví dụ minh hoạ 1: Cho hàm số

22
ymmx
. Tìm giá trị của m để đồ thị của hàm số đi qua điểm

1; 2A
.
Hướng dẫn giải:
Đồ thị hàm số

22
ymmx
đi qua điểm

1; 2A


2
222
21 2 20mm mm mm 

1
120
2
m
mm
m


Vậy, với
1m 
hoặc
2m
thì đồ thị hàm số đã cho đi qua điểm

1; 2A
Ví dụ minh hoạ 2: Viết phương trình parabol
2
yax
. Biết đồ thị của nó đi qua điểm

2;8M
.
Hướng dẫn giải:
Phương trình parabol
2
yax đi qua điểm

2;8M

2
82 2aa 
Vậy, hàm số cần tìm là:
2
2yx
.
Dạng 6. Tương giao giữa Parabol với đường thẳng
Cho parabol

2
0yaxa
và đường thẳng
ykxb
.
+ Lập phương trình hoành độ giao điểm:
2
ax kx b

1
Số nghiệm của phương trình

1
chính là số giao điểm của parabol với đường thẳng.
6.
TOÁNHỌCSƠĐỒ‐THCS.TOANMATH.com
+ Toạ độ giao điểm

00
;xy
vừa là nghiệm của phương trình
2
yax
, vừa là nghiệm của phương
trình
ykxb
.
Ví dụ minh hoạ 1: Cho hàm số
2
ymx có đồ thị là parabol

P
. Tìm giá trị của m biết rằng đồ thị
của hàm số
2
ymx cắt đường thẳng

:3dyx
tại điểm có hoành độ bằng 5.
Hướng dẫn giải:
Gọi

00
;Mxy
là toạ độ giao điểm của

P
và

d
.
Theo đề,
0
5x và M thuộc

d
nên ta có:
00 0 0
3532yx y y
Vậy

5; 2M
. Điểm

5; 2M
thuộc đồ thị hàm số
2
ymx

2
2
25
25
mm
. Vậy, hàm số cần tìm là:
2
2
25
yx
.
BÀI TẬP LUYỆN TẠI LỚP
Bài 1: Cho hàm số
2
3yx
a. Lập bảng tính giá trị của hàm số tại các điểm có hoành độ

x
sau:
–2; –1;
1
2
; 0;
1
2
; 1; 2
b. Với giá trị nào của x thì hàm số

y
nhận các giá trị sau:
0; 27; –27; 5;
1
9
; –81; –3
Bài 2: Cho hàm số

2
4ym x
. Tìm giá trị của m để:
a. Hàm số đồng biến với mọi
0x
.
b. Hàm số nghịch biến với mọi
0x
.
Bài 3: Cho hàm số

22
23yk k x
a. Xét sự biến thiên của hàm số trên tập xác định của nó?
b. Tìm k biết đồ thị hàm số đi qua điểm

1; 6
?
Bài 4: Cho hàm số
2
1
2
yx
a. Vẽ đồ thị của hàm số;
b. Cho các điểm sau:

0;1A
;

2; 2B
;
5
3;
2
C



;
5
5;
2
D



điểm nào thuộc đồ thị hàm số, điểm
nào không thuộc đồ thị hàm số?
Bài 5: Cho hàm số

2
1ym x
. Xác định hệ số a trong mỗi trường hợp sau:
7.
TOÁNHỌCSƠĐỒ‐THCS.TOANMATH.com
a. Đồ thị của hàm số đi qua điểm

1; 9A
b. Đồ thị của hàm số đi qua điểm

4;32B
.
Bài 6: Cho hàm số
2
1
3
yx
.
a. Biết điểm

3;Am
thuộc đồ thị hàm số, tìm m? Hỏi điểm

3;Am
có thuộc đồ thị hàm số không?
Vì sao?
b. Biết điểm

;9Mk
thuộc đồ thị hàm số, tìm k? Hỏi điểm

;9Mk
có thuộc đồ thị hàm số không?
Vì sao?
Bài 7: Cho hàm số
2
yax .
a. Xác định hàm số biết đồ thị của nó đi qua điểm

2;2A .
Vẽ đồ thị hàm số với giá trị tìm được của a.
b. Biết

2;2B là một điểm thuộc đồ thị hàm số trong câu a, O là gốc toạ độ. Tam giác OAB là tam
giác gì? Tính diện tích tam giác OAB.
Bài 8: Cho hàm số

2
1
2
yxP
và
22yx
.
a. Vẽ hai đồ thị hàm số này trên cùng một mặt phẳng toạ độ.
b. Tìm toạ độ giao điểm của hai đồ thị trên.
Bài 9: Cho hàm số
2
3yx .
a. Tìm các điểm thuộc đồ thị hàm số có tung độ bằng –9;
b. Tìm các điểm thuộc đồ thị hàm số cách đều hai trục toạ độ
c. Tìm các điểm thuộc đồ thị hàm số có tung độ gấp 9 lần hoành độ.
Bài 10: Cho hàm số
2
ykx .
a. Xác định k biết đồ thị hàm số có đồ thị cắt đường thẳng
34yx
tại điểm có hoành độ
2x 
.
b. Với giá trị k tìm được ở câu a, hãy vẽ đồ thị hàm số
2
ykx
và
34yx
trên cùng một mặt
phẳng toạ độ.
c. Bằng đồ thị hãy xác định toạ độ giao điểm của đồ thị hàm số
2
ykx
và
34yx
.
HƯỚNG DẪN GIẢI:
Bài 1: Cho hàm số
2
3yx
a. Lập bảng tính giá trị của hàm số tại các điểm có hoành độ

x
sau:
x –2 –1
1
2
0
1
2
1 2
8.
TOÁNHỌCSƠĐỒ‐THCS.TOANMATH.com
2
3yx
–12 –3
3
4
0
3
4
–3 –12
b. Với giá trị nào của x thì hàm số

y
nhận các giá trị sau:
Với
0y
, ta có
22
30 0 0xxx
;
Với
27y
, ta có
22
327 9xx
không có giá trị của x thoả mãn;
Với
27y 
, ta có
22
327 9 3xxx
;
Với
1
9
y 
, ta có
22
11 1
3
927
33
xxx ;
Với
3y 
, ta có
22
33 1 1xxx
Bài 2: Cho hàm số

2
4ym x
.
a. Hàm số đồng biến với mọi
0x
.
40 4mm
Vậy với
4m
thì hàm số đã cho đồng biến với mọi
0x
.
b. Hàm số nghịch biến với mọi
0x
.
40 4mm
Vậy với
4m
thì hàm số đã cho nghịch biến với mọi
0x
.
Bài 3: Cho hàm số

22
23yk k x
a. Hàm số

22
23yk k x
có hệ số

2
2
23 1 20
ak k k
với mọi giá trị của k.
Do đó, hàm số đã cho nghịch biến khi
0x
; và đồng biến khi
0x
.
b. Đồ thị hàm số đi qua điểm



2
2
1; 6 6 2 3 1kk
22
236 230kk kk

1
13
3
k
kk
k


Vậy, với
1k 
hoặc
3k
thì đồ thị hàm số đi qua điểm

1; 6
Bài 4: Cho hàm số
2
1
2
yx
a. Vẽ đồ thị của hàm số:
Đồ thị hàm số
2
1
2
yx
là parabol

P
có đỉnh là

0;0O
, nhận trục Oy
làm trục đối xứng, và đi qua các điểm sau:
x –2 0 2
9.
TOÁNHỌCSƠĐỒ‐THCS.TOANMATH.com
2
1
2
yx
2 0 2
b. Ta có:
Thay hoành độ điểm

0;1A
vào hàm số:

2
01
1
0
2
A
y
Vậy điểm

0;1A
không thuộc đồ thị hàm số.
Thay hoành độ điểm

2; 2B
vào hàm số:

2
2
1
2
2
B
y
Vậy điểm

2; 2B
thuộc đồ thị hàm số.
Thay hoành độ điểm
5
3;
2
C



vào hàm số:

2
95
2
3
2
1
2
C
y
Vậy điểm
5
3;
2
C



không thuộc đồ thị hàm số.
Thay hoành độ điểm
5
5;
2
D



vào hàm số:

2
22
51
5
D
y
Vậy điểm
5
5;
2
D



thuộc đồ thị hàm số.
KL: Vậy điểm B và điểm D thuộc đồ thị hàm số.
Bài 5: Cho hàm số

2
1ym x
. Xác định hệ số a trong mỗi trường hợp sau:
a. Đồ thị của hàm số

2
1ym x
đi qua điểm

1; 9A

2
911 19 8
mmm
Vậy, với
8m
thì đồ thị hàm số đi qua điểm

1; 9A
b. Đồ thị của hàm số

2
1ym x
đi qua điểm

4;32B
.
 
2
32 1 4 16 1 32mm
12 1mm
Vậy, với
1m
thì đồ thị hàm số đi qua điểm

4;32B
.
Bài 6: Cho hàm số
2
1
3
yx
.
a. Vì điểm

3;Am
thuộc đồ thị hàm số
2
1
3
yx
, nên

2
19
33
32
mmm  
10.
TOÁNHỌCSƠĐỒ‐THCS.TOANMATH.com
Suy ra toạ độ điểm

3; 3A 
và

3; 3A
là hai điểm đối xứng nhau qua trục Oy (tính chất đối xứng
của hàm số
2
yax
với

0a
). Mà điểm

3; 3A 
thuộc đồ thị hàm số nên điểm

3; 3A
cũng
thuộc đồ thị hàm số.
b. Điểm

;9Mk
thuộc đồ thị hàm số
2
1
3
yx
, nên:

2
2
1
92733
3
kk k
Với
33k  thay vào phương trình hàm số ta được

2
33
1
3
9
M
yy 
.
Do đó điểm

;9Mk
không thuộc đồ thị hàm số.
Bài 7: Cho hàm số
2
yax .
a. Đồ thị hàm số
2
yax đi qua điểm
 
2
2;2 2 2 1Aaa .
Vậy,
1a
và hàm số cần tìm là
2
yx
Đồ thị hàm số
2
yx
là parabol có đỉnh

0;0O
, có trục đối xứng Oy.
Đồ thị hàm số
2
yx đi qua các điểm sau:
x –1 0 1
2
yx
1 0 1
b. Điểm

2;2A và

2;2B thuộc đồ thị hàm số
2
yx .
Vì
AB
AB
xx
yy

nên hai điểm A và B đối xứng nhau qua trục Oy.
Do đó, Oy là đường trung trực của đoạn thẳng AB, suy ra
OA OB
.
Vậy tam giác OAB là tam giác cân tại O.
Ta có:
2; 2 2
A
OH y AB
Diện tích tam giác OAB:
11
..2.2222
22
OAB
SOHAB
(đvdt)
11.
TOÁNHỌCSƠĐỒ‐THCS.TOANMATH.com
Bài 8: Cho hàm số

2
1
2
yxP
và
22yx
.
a. * Đồ thị hàm số
2
1
2
yx
là parabol

P
có đỉnh

0;0O
, có
trục đối xứng Oy.
Đồ thị hàm số
2
1
2
yx
đi qua các điểm sau:
x –2 0 2
2
1
2
yx
2 0 2
* Đồ thị hàm số
22yx
là đường thẳng

d
đi qua hai điểm

0; 2
và

1; 0
b. Tìm toạ độ giao điểm của hai đồ thị trên.
Phương trình hoành độ giao điểm của

P
và

d
là:

2
22
11 1
22 220 2 0 2
22 2
xx xx x x
Với
22xy
. Vậy toạ độ giao điểm là

2; 2
.
Bài 9: Cho hàm số
2
3yx

P
.
a. Gọi

;
MM
Mx y
là điểm thuộc đồ thị hàm số và có 9
M
y 
Vì M thuộc

P
nên ta có:
22
93 3 3
MM M
xx x
Vậy điểm thuộc đồ thị hàm số và có tung độ bằng –9 là:

1
3; 9M  và

2
3; 9M
b. Gọi

;
NN
Nx y
là điểm thuộc đồ thị hàm số và có khoảng cách đến các trục toạ độ bằng nhau.
N thuộc đồ thị hàm số nên:
2
3
NN
yx
N có khoảng cách đến hai trục toạ độ bằng nhau nên:


1
2
NN
NN
NN
yx
yx
yx


Giải

1
:
2
3
NN N N
yx x x

00
13 0
11
33
NN
NN
NN
xy
xx
xy


 
Ta có điểm

0;0
;
11
;
33




12.
TOÁNHỌCSƠĐỒ‐THCS.TOANMATH.com
Giải

2
:
2
3
NN N N
yx x x 

00
13 0
11
33
NN
NN
NN
xy
xx
xy



Ta có điểm

0;0
;
11
;
33



Vậy, các điểm thuộc đồ thị hàm số cách đều hai trục toạ độ là:

0;0
;
11
;
33



;
11
;
33




c. Tìm các điểm thuộc đồ thị hàm số có tung độ gấp 9 lần hoành độ.
Điểm

;
AA
Ax y
có tung độ gấp 9 lần hoành độ: 9
AA
yx .
Điểm A thuộc đồ thị hàm số nên:
22
393 
AA AA
yx xx

00
330
327
AA
AA
AA
xy
xx
xy


 
Vậy toạ độ các điểm thuộc đồ thị hàm số có tung độ gấp 9 lần hoành độ là:

0;0
;

3; 27
.
Bài 10: Cho hàm số
2
ykx .
a. Đồ thị hàm số có đồ thị cắt đường thẳng

d
:
34yx
tại điểm có hoành độ
2x 
.
Gọi

00
;Mxy
là toạ độ giao điểm của

P
và

d
. Theo
đề ta có
0
2x 
M thuộc đường thẳng

d
nên:
00 0
34 3.242yx y  
Suy ra

2; 2M 
. Thay vào phương trình

P
, ta có:

2
1
22
2
kk
Vậy, đồ thị hàm số cần tìm là:
2
1
2
yx
b. Đồ thị hàm số
2
1
2
yx

P
và đường thẳng

d
:
34yx
Đồ thị hàm số
2
1
2
yx

P
là parabol có đỉnh

0;0O
, có trục đối xứng là Oy và đi qua các điểm:
x –2 0 2
13.
TOÁNHỌCSƠĐỒ‐THCS.TOANMATH.com
2
1
2
yx
–2 0 –2
* Đồ thị hàm số
34yx
là đường thẳng

d
đi qua hai điểm

0; 4
và

1;1
c. Dựa vào đồ thị ta thấy toạ độ giao điểm của đồ thị hàm số
2
1
2
yx

P
và đường thẳng

d
:
34yx
là:

2; 2 ; 4; 8AB
.
C.TRẮC NGHIỆM RÈN LUYỆN PHẢN XẠ (Hàm số bậc hai một ẩn và đồ thị hàm số y=ax
2
)
Câu 1. Cho hàm số
2
yax=
với
0a ¹
. Kết luận nào sau đây là đúng?
A. Hàm số nghịch biến khi
0a >
và
0x >
. B. Hàm số nghịch biến khi
0a <
và
0x <
.
C. Hàm số nghịch biến khi
0a >
và
0x <
. D. Hàm số nghịch biến khi
0a >
và
0x =
.
Câu 2. Cho hàm số
2
yax=
với 0a ¹ .Kết luận nào sau đây là đúng?
A. Hàm số đồng biến khi
0a >
và
0x <
. B. Hàm số đồng biến khi
0a >
và
0x >
.
C. Hàm số đồng biến khi
0a >
và
0x <
. D. Hàm số đồng biến khi
0a <
và
0x =
.
Câu 3. Kết luận nào sau đây là sai khi nói về đồ thị của hàm số
2
yax=
với 0a ¹ .
A. Đồ thị hàm số nhận trục tung làm trục đối xứng.
B. Với
0a >
đồ thị nằm phía trên trục hoành và
O
là điểm cao nhất của đồ thị.
C. Với
0a <
đồ thị nằm phía dưới trục hoành và
O
là điểm cao nhất của đồ thị.
D. Với
0a >
đồ thị nằm phía trên trục hoành và
O
là điểm thấp nhất của đồ thị.
Câu 4. Giá trị của hàm số
2
() 7yfx x==-
tại
0
2x =-
là:
A.
28
. B.
14
. C.
21
. D.
28-
.
Câu 5. Giá trị của hàm số
2
4
()
5
yfx x== tại
0
5x =-
là
A.
20
. B.
10
. C.
4
. D.
20-
.
Câu 6. Cho hàm số
2
() ( 2 1)
yfx m x==-+
. Tìm giá trị của
m
để đồ thị đi qua điểm
(2;4)A -
.
A. 0m = . B.
1m =
. C.
2m =
. D.
2m =-
.
Câu 7. Cho hàm số
2
23
()
3
m
yfx x
-
== . Tìm giá trị của
m
để đồ thị đi qua điểm
(3;5)B -
A.
1
m
=
. B.
3
7
m = . C.
7
3
m = . D.
3
m
=
.
Câu 8. Cho hàm số
2
(5 2)
ymx=+
với
2
5
m ¹- . Tìm
m
để hàm số nghịch biến với mọi
0x >
.
A.
2
5
m <- . B.
2
5
m > . C.
2
5
m < . D.
5
2
m >- .
14.
TOÁNHỌCSƠĐỒ‐THCS.TOANMATH.com
Câu 9. Cho hàm số với
2
7
3
m
yx
-
=
-
. Tìm
m
để hàm số nghịch biến với mọi
0x <
.
A.
7m >
. B.
7m <
. C.
7m <-
. D.
7m >-
.
Câu 10. Cho hàm số
2
(4 3 )
ymx=-
với
4
3
m ¹ . Tìm
m
để hàm số đồng biến với mọi
0
x
>
.
A.
4
3
m > . B.
4
3
m <- . C.
4
3
m < . D.
4
3
m <- .
Câu 11. Cho hàm số
2
2
52
yx
m
=
-
với
5
2
m ¹ . Tìm
m
để hàm số đồng biến với mọi
0
x
<
A.
5
2
m > . B.
5
2
m < . C.
2
5
m > . D.
2
5
m < .
Câu 12. Trong các điểm
(1;2); ( 1; 1); (10; 200); ( 10; 10)AB C D-- - -
có bao nhiêu điểm thuộc đồ thị
hàm số
2
yx=-
.
A.
1
. B.
4
. C.
3
. D.
2
.
Câu 13. Cho hàm số
2
() 3
fxyx==
. Tìm
b
biết
() 6 9fb b³+
A.
13b<<
. B.
13b-£ £
. C.
1
3
b
b
é
£-
ê
ê
³
ê
ë
. D.
1
3
b
b
é
<-
ê
ê
>
ê
ë
.
Câu 14. Cho hàm số
2
() 2
fxyx=-=
. Tìm
b
biết
() 5 2fb b£- +
A.
1
2
2
b<<. B.
1
2
2
b££. C.
1
2
2
b
b
é
ê
<
ê
ê
>
ê
ë
. D.
1
2
2
b
b
é
ê
£
ê
ê
³
ê
ë
.
Câu 15. Cho hàm số
2
(2 2)
ymx=+
. Tìm
m
để đồ thị hàm số đi qua điểm
(; )Ax y
với
(; )xy
là
nghiệm của hệ phương trình
1
23
xy
xy
ì
ï
-=
ï
í
ï
-=
ï
î
A.
7
4
m = . B.
1
4
m = . C.
7
8
m = . D.
7
8
m =- .
Câu 16. Cho hàm số
2
(3 1)
ymx=- +
. Tìm
m
để đồ thị hàm số đi qua điểm
(; )Ax y
với
(; )xy
là
nghiệm của hệ phương trình
43 2
23
xy
xy
ì
ï
-=-
ï
í
ï
-=-
ï
î
A.
1
3
m = . B.
1
3
m =- . C.
3m =
. D.
3m =-
.
Câu 17. Cho hàm số
22
(45)
ymmx=- + -
. Kết luận nào sau đây là đúng
A. Đồ thị của hàm số nằm phía trên trục hoành.
15.
TOÁNHỌCSƠĐỒ‐THCS.TOANMATH.com
B. Đồ thị của hàm số nhận gốc tọa độ
O
là điểm cao nhất.
C. Hàm số nghịch biến với
0x <
.
D. Hàm số đồng biến với
0
x
>
.
Câu 18. Cho hàm số
22
(4 12 11)
ym m x=++
. Kết luận nào sau đây là sai?
A. Đồ thị của hàm số nằm phía trên trục hoành.
B. Đồ thị của hàm số nhận gốc tọa độ
O
là điểm thấp nhất.
C. Hàm số nghịch biến với
0
x
>
.
D. Hàm số đồng biến với
0x >
.
Câu 19. Hình vẽ dưới đây là của đồ thị hàm số nào?
A.
2
yx=-
. B.
2
yx=
. C.
2
2
yx=
. D.
2
2
yx=-
.
Câu 20. Hình vẽ dưới đây là của đồ thị hàm số nào?
A.
2
yx=
. B.
2
1
2
yx= . C.
2
3
yx=
. D.
2
1
3
yx= .
Câu 21. Cho hàm số
2
3yx=
có đồ thị là
()P
. Có bao nhiêu điểm trên
()P
có tung độ gấp đôi
hoành độ.
A. 5 . B.
4
. C.
3
. D.
2
.
Câu 22. Cho hàm số
2
2
5
yx=- có đồ thị là
()P
. Điểm trên
()P
(khác gốc tọa độ
(0; 0)O
) có tung độ
gấp ba lần hoành độ thì có hoành độ là:
A.
15
2
. B.
15
2
-
. C.
2
15
. D.
2
15
- .
Câu 23. Cho
2
;
11
(): ():
22
yPy xd x==- . Tìm tọa độ giao điểm của
()P
và
()d
A.
1
1;
2
æö
÷
ç
÷
ç
÷
ç
÷
ç
èø
. B.
(1; 2)
. C.
1
;1
2
æö
÷
ç
÷
ç
÷
ç
÷
ç
èø
. D.
(2;1)
.
Câu 24. Cho
2
(): 3 (): 4;1yPy xd x==--
. Tìm tọa độ giao điểm
()P
và
()d
16.
TOÁNHỌCSƠĐỒ‐THCS.TOANMATH.com
A.
11
;;(1;3)
33
æö
÷
ç
÷
-
ç
÷
ç
÷
ç
èø
. B.
11
;;(1;3)
33
æö
÷
ç
÷
ç
÷
ç
÷
ç
èø
. C.
11
;;(1;3)
33
æö
÷
ç
÷
--
ç
÷
ç
÷
ç
èø
. D.
11
;
33
æö
÷
ç
÷
-
ç
÷
ç
÷
ç
èø
.
Câu 25. Cho parabol .
2
1
4
yx= Xác định
m
để điểm
(2; )Am
nằm trên parabol.
A.
1
2
m = . B.
1
2
m =- . C.
2m =
. D.
2m =-
.
Câu 26. Cho parabol
2
5yx=-
. Xác định
m
để điểm
()
5; 2 5Am -
nằm trên parabol.
A.
5
2
m =- . B.
2
5
m = . C.
5
2
m = . D.
2
5
m =- .
Câu 27. Cho parrabol
2
(): ( 1)
Py m x=-
và đường thẳng
(): 3 2dy x=-
. Tìm
m
để đường thẳng
d
cắt
()P
tại điểm có tung độ 5y = .
A. 5m = . B.
7m =
. C.
6
m
=
. D.
6
m
=-
.
Câu 28. Cho parrabol
2
(): 5 1.Py m x=+
và đường thẳng
(): 5 4dy x=+
. Tìm
m
để đường
thẳng
d
cắt
()P
tại điểm có tung độ
9y =
.
A. 5m = . B.
15
m
=
. C.
6
m
=
. D.
16
m
=
.
Câu 29. Cho parrabol
2
12
(): .
m
Py x
m
æö
-
÷
ç
÷
=
ç
÷
ç
÷
ç
èø
và đường thẳng
(): 2 2dy x=+
. Biết đường thẳng
d
cắt tại một điểm có tung độ
4y =
. Tìm hoành độ giao điểm còn lại của
d
và parabol
()P
A.
1
2
x =- . B.
1
2
x = . C.
1
4
x =- . D.
1
4
x = .
Câu 30. Cho parrabol
2
7
34()
4
: ym xP
æö
÷
ç
÷
=+-
ç
÷
ç
÷
ç
èø
và đường thẳng
5(): 3dy x=-
. Biết đường
thẳng
d
cắt tại một điểm có tung độ
1y =
. Tìm
m
và hoành độ giao điểm còn lại của và
parabol
()P
A.
0; 2mx==
. B.
1
;10
4
mx==-. C.
2; 8mx==
. D.
0; 10mx==
.
Câu 31. Cho đồ thị hàm số
2
2
yx=
như hình vẽ. Dựa vào đồ thị, tìm
m
để phương trình
2
250xm--=
có hai nghiệm phân biệt.
()P
()P
d
17.
TOÁNHỌCSƠĐỒ‐THCS.TOANMATH.com
A.
5m <-
. B.
0m >
. C.
0m <
. D.
5m >-
.
HƯỚNG DẪN
Câu 1. Đáp án C.
Cho hàm số
2
(0)yaxa=¹
a) Nếu
0a >
thì hàm số nghịch biến khi
0x <
và đồng biến khi
0x >
b) Nếu
0a <
thì hàm số đồng biến khi
0x <
và nghịch biến khi
0x >
.
Câu 2. Đáp án B.
Cho hàm số
2
(0)yaxa=¹
a) Nếu
0a >
thì hàm số nghịch biến khi
0x <
và đồng biến khi
0x >
b) Nếu
0
a
<
thì hàm số đồng biến khi
0
x
<
và nghịch biến khi
0
x
>
.
Câu 3. Đáp án B.
Đồ thị của hàm số
2
(0)yaxa=¹
là một parabol đi qua gốc tọa độ
,O
nhận
Oy
là trục đối xứng (
O
là đỉnh của parabol).
- Nếu
0a >
thì đồ thị nằm phía trên trục hoành,
,O
là điểm thấp nhất của đồ thị.
- Nếu
0
a
<
thì đồ thị nằm phía dưới trục hoành,
,O
là điểm cao nhất của đồ thị.
Câu 4. Đáp án D.
Thay
0
2x =-
vào hàm số
2
() 7
yfx x==-
ta được
() (22 8)27. 2f -=-- =-
.
Câu 5. Đáp án A.
Thay
0
5x =-
vào hàm số
2
4
()
5
yfx x== ta được
545.() ( 2)520f -= - =
Câu 6. Đáp án A.
Thay tọa độ điểm
(2;4)A -
vào hàm số
2
() ( 2 1)
yfx m x==-+
ta được
2
(2 1).(2) 4 2 1 1 0
mmm-+-=-+==
Vậy
0m =
là giá trị cần tìm.
Câu 7. Đáp án C.
18.
TOÁNHỌCSƠĐỒ‐THCS.TOANMATH.com
Thay tọa độ điểm
(3;5)B -
vào hàm số
2
23
()
3
m
yfx x
-
== ta được
2
23 7
.( 3) 5 3(2 3) 5 6 9 5 6 14
33
m
mmmm
-
-= -= -= == Vậy
7
3
m = là giá trị
cần tìm.
Câu 8. Đáp án A.
Để hàm số nghịch biến với mọi
0x >
thì
0a <
nên
2
520
5
mm+< <-.
Vậy
2
5
m <- thỏa mãn điều kiện đề bài.
Câu 9. Đáp án B.
Để hàm số nghịch biến với mọi
0x <
thì
0a >
nên
7
0707
3
m
mm
-
> -< <
-
Vậy
7m <
thỏa mãn điều kiện đề bài
Câu 10. Đáp án C.
Để hàm số đồng biến với mọi
0
x
>
thì
0
a
>
nên
4
43 0
3
mm-><
Vậy
4
3
m < thỏa mãn điều kiện đề bài
Câu 11. Đáp án A.
Để hàm số đồng biến với mọi
0x <
thì
0a <
nên
25
052 02 5
52 2
mmm
m
<- < > >
-
. Vậy
5
2
m > thỏa mãn điều kiện đề bài
Câu 12. Đáp án D.
+) Thay tọa độ điểm
(1; 2)A
vào hàm số
2
yx=-
ta được
2
21=-
(vô lý) nên
()APÏ
.
+) Thay tọa độ điểm
(10; 200)C -
vào hàm số
2
yx=-
ta được
2
200 (10) 200 100
-=- -=-
(
vô lý) nên loại
()CPÏ
+) Thay tọa độ điểm
()
10; 10D -
vào hàm số
2
yx=-
ta được
()
2
10 10 10 10-=- -=-
(
luôn đúng) nên
()DPÎ
+) Thay tọa độ điểm
(1; 1)B --
vào hàm số
2
yx=-
ta được
2
1(1) 11
-=-- -=-
(luôn đúng)
()BPÎ
Câu 13. Đáp án C.
19.
TOÁNHỌCSƠĐỒ‐THCS.TOANMATH.com
Ta có
22
() 6 9 3 6 9 2 3 0
fb b b b b b³+ ³+--³
. Vậy
1
3
b
b
é
£-
ê
ê
³
ê
ë
là giá trị cần tìm.
Câu 14. Đáp án D.
Ta có
£- + - £- + - + ³
22
() 52 2 522 520
fb b b b b b
--+³ ---³ - -³
2
2 4 20 2( 2)( 2)0 (2 1)( 2)0
bbb bb b b b
Vậy
1
210
2
2
20 2
1
210 1
2
2
20
2
b
b
b
bb
b
b
b
b
b
é
ì
ï
ï
ê
é
³
ì
ï
ï
ï
-³
ê
ï
ê
í
é
ê
í
ï
ê
³
ï
ï
-³ ³
ê
ê
ê
ï
ï
ï
îî
ê
ê

ê
ìì
ê
ê
ïï
-£
ê
£
ïï
ê
ê
£
ê
ï
ï
í
ë
ê
í
ê
ï
-£
ï
ï
ê
ê
î
ë
ï
£
ê
ï
ï
î
ë
.
Vậy
1
2
2
b
b
é
ê
£
ê
ê
³
ê
ë
là giá trị cần tìm.
Câu 15. Đáp án D.
Ta có
11 2
2;1
23
()
23(1)1
xy x y x
A
xy y y y
ìì ì
ïï ï
-= =+ =
ïï ï

íí í
ïï ï
-= + -= =
ïï ï
îî î
Thay
2; 1xy==
vào hàm số
2
(2 2)
ymx=+
ta được
2
177
1(2 2).2 2 2 2
448
mm mm
--
=+ +===
Vậy
7
8
m =- là giá trị cần tìm.
Câu 16. Đáp án B.
Ta có:
23 23 2
1; 2
42 3 3 2 5 10
43 2
()
213()
xy xy y
A
yy
xy
xyyx
ììì
ïïï
=- =- =
ïïï

ííí
ïïï
-- =- = =
ï
ì
ï
-=-
ï
í
ï
-=-
ïïï
îîîî
Thay
1; 2xy==
vào hàm số
2
(3 1)
ymx=- +
ta được
2
1
2(3 1).1 3 12 3 1
3
mm mm
-
=- + - + = - = =
Vậy
1
3
m =-
là giá trị cần tìm.
Câu 17. Đáp án B.
Ta thấy hàm số
22
(45)
ymmx=- + -
có
22 2
45( 44)1(2)110,amm mm m m"=-+-=--+-=---£-<
20.
TOÁNHỌCSƠĐỒ‐THCS.TOANMATH.com
Nên hàm số đồng biến khi
0x <
và nghịch biến khi
0x >
. Suy ra C,D sai.
Và đồ thị hàm số nằm phía dưới trục hoành, O là điểm cao nhất của đồ thị.
Suy ra A sai.
Câu 18. Đáp án C.
Ta thấy hàm số
22
(4 12 11)
ym m x=++
có
22 2
41211(4129)2(23)220,am m m m m m"=++= +++=++³>
Nên hàm số đồng biến khi
0
x
>
và nghịch biến khi
0
x
<
.
Suy ra C sai, D đúng.
Và đồ thị hàm số nằm phía trên trục hoành, O là điểm thấp nhất của đồ thị.
Câu 19. Đáp án A.
Từ hình vẽ suy ra
0a <
nên loại B,C
Vì đồ thị đi qua điểm có tọa độ
(1; 1)-
nên loại D.
Câu 20. Đáp án D.
Từ hình vẽ ta thấy đồ thị đi qua điểm có tọa độ
(3; 3)
, ta thay
3; 3xy==
vào từng hàm số ở các
đáp án ta được:
+ Đáp án A:
22
33 39
yx===
(vô lý) nên loại A.
+ Đáp án B:
22
119
333
222
yx=== (vô lý) nên loại B.
+ Đáp án C:
22
3 3 3.3 3 27
yx== =
(vô lý) nên loại C.
+ Đáp án D:
22
11
3.333
33
yx== = (luôn đúng) nên chọn D.
Câu 21. Đáp án D.
Gọi điểm
(; )Mxy
là điểm cần tìm.
Vì
M
có tung độ gấp đôi hoành độ nên
(;2)Mx x
Thay tọa độ điểm
M
vào hàm số ta được
2
00
23
23 43
33
xy
xx
xy
é
==
ê
ê
=
ê
==
ê
ë
Hay có hai điểm thỏa mãn điều kiện là
2343
(0;0), ;
33
OM
æö
÷
ç
÷
ç
÷
ç
÷
ç
÷
ç
èø
Câu 22. Đáp án B.
Gọi điểm
(; )Mxy
là điểm cần tìm. Vì
M
có tung độ gấp ba lần hoành độ nên
(;3)Mx x
Thay tọa độ điểm
M
vào hàm số ta được
21.
TOÁNHỌCSƠĐỒ‐THCS.TOANMATH.com
22
00
22 2
33030
15 45
55 5
22
xy
xxxx xx
xy
é
==
æö
ê
÷
ç
ê
÷
=- + = + =
ç
÷
ç
ê
÷
ç
=- =-
èø
ê
ë
Hay điểm khác gốc tọa độ thỏa mãn điều kiện là
15 45
;
22
M
æö
--
÷
ç
÷
ç
÷
ç
÷
ç
èø
Câu 23. Đáp án A.
Xét phương trình hoành độ giao điểm của parabol
()P
và đường thẳng
()d
=- - += - =-==
22 2
11
210(1)0 10 1
22
xx x x x x x
Thay
1x =
vào hàm số
2
1
2
yx= ta được
2
11
.1
22
y ==
Nên tọa độ giao điểm cần tìm là
1
1;
2
æö
÷
ç
÷
ç
÷
ç
÷
ç
èø
Câu 24. Đáp án C.
Xét phương trình hoành độ giao điểm của parabol
()P
và đường thẳng
()d
22
2
3413410
3 3 103( 1) 10
xx xx
xxx xx x
=- - + + =
+++= +++=
2
2
11
310
3
31 10
33
()(
10
133
)
x
xyx
xx
x
xyx
é
é
ê
+=
=- = =
ê
ê
+ +=
ê
ê
+=
ê
=- = =
ëê
ë
Nên tọa độ giao điểm cần tìm là
11
;;(1;3)
33
æö
÷
ç
÷
--
ç
÷
ç
÷
ç
èø
Câu 25. Đáp án A.
Thay
2;xym==
vào hàm số
2
1
4
yx= ta được
()
2
11
.2 .
42
m == Vậy
1
2
m =
Câu 26. Đáp án D.
Thay
5; 2 5xm y==-
vào hàm số
2
5yx=-
ta được
()
2
2
25 5. 5 5 5 25
5
mm m-=- - = =-. Vậy
2
5
m =- .
Câu 27. Đáp án C.
Thay 5y = vào phương trình đường thẳng
d
ta được
532 1xx=- =-
22.
TOÁNHỌCSƠĐỒ‐THCS.TOANMATH.com
Nên tọa độ giao điểm của đường thẳng
d
và parabol
()P
là
(1;5)-
Thay
1; 5xy=- =
vào hàm
số
2
(1)
ym x=-
ta được
2
(1).(1)5 15 6
mmm--=-==
Vậy
6m =
là giá trị cần tìm.
Câu 28. Đáp án D.
ĐK:
1
5
m
-
>
Thay
9y =
vào phương trình đường thẳng
d
ta được
95 4 1xx=+=
Nên tọa độ giao điểm của đường thẳng và parabol
()P
là
(1; 9)
Thay
1; 9xy==
vào hàm số
2
51.ymx=+
ta được
2
51.19 51951815 80 16()mmmmmTM+= +=+=== Vậy
16m =
là giá
trị cần tìm.
Câu 29. Đáp án A.
Thay
4y =
vào phương trình đường thẳng
d
ta được
224 1xx+= =
Nên tọa độ giao điểm của đường thẳng
d
và parabol
()P
là
(1; 4)
Thay
1; 4xy==
vào hàm số
2
12
2
m
yx
æö
-
÷
ç
÷
=
ç
÷
ç
÷
ç
èø
ta được
2 2
12 7
.1 4 1 2 8 ( ) : 4
22
m
mm Pyx
-
=- = =- =
Xét phương trình hoành độ giao điểm của
d
và :
é
=
ê
ê
=+ --= + -=
ê
=-
ê
ë
22
1
4222 1021)10
1
2
(()
x
xx xx x x
x
Vậy hoành độ giao điểm còn lại là
1
2
x =- .
Câu 30. Đáp án D.
Thay
1y =
vào phương trình đường thẳng
d
ta được
351 2xx-= =
Nên tọa độ giao điểm của đường thẳng và parabol
là
(2;1)
Thay
2; 1xy==
vào hàm
số
2
7
34
4
ym x
æö
÷
ç
÷
=+-
ç
÷
ç
÷
ç
èø
ta được
()
2
2
771
34 .21 34 342
444
1
344 0 :
4
mmm
mmPyx
æö
÷
ç
÷
+- = +- = +=
ç
÷
ç
÷
ç
èø
+== =
d
()P
d
()P
23.
TOÁNHỌCSƠĐỒ‐THCS.TOANMATH.com
Xét phương trình hoành độ giao điểm của
và :
22
2
1
3 5 12 20 0 2()( 0)10
10
4
x
xx x x x x
x
é
=
ê
=-- +=- - =
ê
=
ê
ë
Vậy hoành độ giao điểm còn lại là
10x =
.
Câu 31. Đáp án D.
Ta có
2
250xm--=
(*)
2
25xm=+
Số nghiệm của phương trình (*) là số giao điểm của parabol
2
(): 2
Py x=
đường
thẳng
:5dy m=+
.
Để (*) có hai nghiệm phân biệt thì cắt
()P
tại hai điểm phân biệt. Từ đồ thị hàm số ta thấy
Với
50 5
mm
+> >-
thì cắt
()P
tại hai điểm phân biệt hay phương trình (*) có hai
nghiệm phân biệt khi
5m >-
.
D.PHIẾU BÀI TỰ LUYỆN Ở NHÀ
Bài 1:Cho hàm số

2
3
2
yfx x
. Hãy tính

2f
;

3f
;

5f
;
2
3
f




Bài 2: Cho hàm số
2
yf(x)ax
.Biết rằng khi
x2
thì
4
y
3
. Tìm hệ số a
Bài 3: Cho hàm số ym xm
2
(2)( 2) . Tìm giá trị của m để:
a) Hàm số đồng biến với
x0
.
b) Có giá trị
y 4
khi
x 1
.
Bài 4:Cho hàm số

2
y1 m1x
a) Tìm điều kiện để hàm số đồng biến khi
x0
b) Tìm điều kiện để hàm số nghịch biến khi
x0
Bài 5 :Cho hàm số
2
yf(x)ax
có đồ thị (P) đi qua
9
A3;
4



.
a) Tính a.
b) Các điểm nào sau đây thuộc (P):
B( 3 2; 4); C( 2 3; 3)
.
Bài 6 :Cho hàm số
22
y(m 2m3)x Chứng tỏ rằng hàm số nghịch biến với mọi
x0
.
Bài 7:Cho hàm số
22
y (m 6m 12)x
.
a) Chứng tỏ rằng hàm số nghịch biến trong khoảng
( 2005;0)
, đồng biến trong khoảng
(0;2005)
b) Khi
m2
.Tìm x để y = 8
d
()P
d
d
24.
TOÁNHỌCSƠĐỒ‐THCS.TOANMATH.com
Bài 8: Cho hàm số
yfx x
2
()
. Tìm a R sao cho
fa(1)4

.
Bài 9: Cho hình lập phương có cạnh bằng x cm. Gọi S là diện tích toàn phần của hình lập phương
a) Tính S theo x
b) S thay đổi như thế nào khi x tăng, khi x giảm?
c) Khi x tăng 3 lần thì S tăng hay giảm mấy lần?
Bài 10: Cho hàm số
2
yf(x)ax.Biết rằng khi
x5
thì
75
y
2
.Tìm giá trị nhỏ nhất và giá trị lớn
nhất của y khi x thõa mãn điều kiện
4x2
Bài 11: Cho hàm số
2
1
yf(x) x
3

.Biết
12
f(x ) f(x ) .Hãy so sánh
1
x và
2
x trong các trường hợp
sau :
a)
1
x ,
2
x là những số dương .
b)
1
x ,
2
x là những số âm .
Bài 12: Cho hàm số
2
yf(x) 2x..Chứng minh rằng với mọi giá trị của x thõa mãn điều kiện
3x 1
ta điều có
2
f( 3) 2x f( 1)
.Suy ra rằng x biến đổi thõa mãn điều kiện
3x 1
thì
y có giá trị bé nhất là
18
và giá trị lớn nhất là
2
Bài 13: Cho hàm số

2
yfx ax
a)Hãy xác định hàm số biết rằng đồ thị của nó đi qua điểm

2;4A
.
b)Vẽ đồ thị của hàm số đã cho .
c)Tìm các điểm trên Parabol có tung độ bằng 16.
d)Tìm
m
sao cho

3
;Bmm
thuộc Parabol.
d)Tìm các điểm trên Parabol (khác gốc tọa độ) cách đều hai trục tọa độ.
Bài 14:
a) Vẽ đồ thị hàm số
1
yx.x
3
b) Vẽ đồ thị hàm số
y2x.x
Bài 15: Trên mặt phẳng tọa độ
Oxy
cho đường thẳng

:6dy x
và parabol

2
:Pyx
.
a)Tìm tọa độ các giao điểm của

d
và

P
.
b)Gọi
,AB
là hai giao điểm của

d
và

P
. Tính diện tích tam giác
OAB
.
Bài 16:
25.
TOÁNHỌCSƠĐỒ‐THCS.TOANMATH.com
a)Xác định điểm
M
thuộc đường Parabol

2
:Pyx
sao cho độ dài đoạn
IM
là nhỏ nhất, trong đó

0;1I
.
b)Giả sử điểm
A
chạy trên Parabol

2
:Pyx
. Tìm tập hợp trung điểm
J
của đoạn
OA
.
Bài 17: Trong mặt phẳng tọa độ
Oxy
, cho hai điểm
A
và
B
chạy trên parabol

2
:Pyx
sao cho

,0;0AB O
và
OA OB
. Giả sử
I
là trung điểm của đoạn
AB
.
a) Tìm quỹ tích điểm trung điểm
I
của đoạn
AB
.
b) Đường thẳng
AB
luôn luôn đi qua một điểm cố định.
c) Xác định tọa độ điểm
A
và
B
sao cho độ dài đoạn
AB
nhỏ nhất.
Bài 18: Trong mặt phẳng tọa độ
Oxy
cho Parabol

2
:Pyx
, trên

P
lấy hai điểm

1;1 , 3; 9AB
a)Tính diện tích tam giác
OAB
.
b)Xác định điểm
C
thuộc cung nhỏ
AB
của

P
sao cho diện tích tam giác
ABC
lớn nhất.
Bài 19: Một xe tải có chiều rộng là 2,4 m chiều cao là 2,5 m muốn đi qua một cái cổng hình Parabol.
Biết khoảng cách giữa hai chân cổng là 4m và khoảng cách từ đỉnh cổng tới mỗi chân cổng là
25
m
(Bỏ qua độ dày của cổng).
a)Trong mặt phẳng tọa độ
Oxy
gọi Parabol

2
:Pyax
với
0a
là hình biểu diễn cổng mà xe tải
muốn đi qua. Chứng minh
1a 
.
b)Hỏi xe tải có đi qua cổng được không? Tại sao?
HƯỚNG DẪN
Bài 1: Ta có:
 
2
33
2.2 .46
22
f 
;

2
3327
3.3.9
222
f 
;
 
2
3315
5.5 .5
222
f 
;
2
23 2 321
..
323 293
f





Bài 2: Thay
x2
;
4
y
3
vào hàm số
2
yf(x)ax
có
2
441
a.( 2) 4a a
333

 
Bài 3:Cho hàm số ym xm
2
(2)( 2) . Tìm giá trị của m để:
a) Tìm điều kiện để hàm số đồng biến khi
x0
Để hàm số đồng biến khi x < 0
20 2mm
Vậy để hàm số đồng biến khi
x0
thì
m2
b) Thay
y4;x 1
vào hàm số ym xm
2
(2)( 2) ta có :
26.
TOÁNHỌCSƠĐỒ‐THCS.TOANMATH.com
2
4(m2)(1)
m2


Vậy khi
m2
thì hàm số giá trị
y 4
khi
x 1
.
Bài 4: Hàm số

2
y1 m1x
(ĐK:
1m
;
2m
)
a) Tìm điều kiện để hàm số đồng biến khi
x0
Để hàm số đồng biến khi x < 0
1m10 m11m11m2
Vậy để hàm số đồng biến khi x < 0
m2
b) Tìm điều kiện để hàm số nghịch biến khi
x0
Để hàm số nghịch biến khi
x0
1m10 m11m11m2
Vậy để hàm số nghịch biến khi
x0
1m2
Bài 5:
a) Đồ thị (P) đi qua
9
A3;
4




2
91
3
44
aa

.
b) Thay

32;4B vào (P) ta được:

2
19
4324
42

(vô lý)
Vậy B không thuộc (P).
Thay

23;3C vào (P) ta được:

2
1
32333
4

(đúng)
Vậy C thuộc (P).
Bài 6:
Hàm số đã cho có dạng
2
yax
,

22 2
am 2m3 m 2m1 2(m1) 20
với mọi m
Do đó : Hàm số đã cho nghịch biến với mọi
x0
Bài 7:
a) hàm số
22
y(m 6m12)x .
22
y(m 6m12)x
22
(m 3) 3 x



Vì
2
a(m3)30



với mọi x nên trong khoảng
( 2005;0)
thì
x0
, do đó hàm số nghịch biến,
trong khoảng
(0;2005)
thì
x0
, do đó hàm số nghịch biến.
b) Với
m2
, ta có
2
y4x
27.
TOÁNHỌCSƠĐỒ‐THCS.TOANMATH.com
2
y8 4x 8 x 2 
Bài 8 :
Ta có



fa
aaa
aa
22
(1)4
(1) 4 230
(1)(3)0
a1
hoặc
a3
Vậy với
a1
hoặc
a3
thì hàm số
yfx x
2
()
có
fa(1)4

.
Bài 9:
a) Mỗi hình lập phương là một hình vuôngvới cạnh có độ dài bằng
x
cm nên diện tích mỗi mặt là
22
x(cm).Vì hình lập phương có
6
mặt bằng nhau nên
22
S6x(cm)
b)
2
S6x
là một hàm số có dạng
2
yax , với
a60
. Hàm số này đồng biến khi
x0
. Vì x là độ
dài nên
x0
. Do đó khi x tăng thì S cũng tăng , x giàm thì S cũng giảm
c) Giả sử cho
1
x là độ dài của cạnh hình lập phương .Khi đó
S
có giá trị tương ứng là
2
11
S6x
.Khi
cạnh tăng lên
3
lần , đặt
22 22
212 2 1 1 1 1
x 3x S 6x 6(3x ) 6.9x 9.6x 9S
. Vậy khi
x
tăng lên 3
lần thì
S
tăng lên 9 lần .
Bài 10: Cho hàm số
2
yf(x)ax
.Biết rằng khi
x5
thì
75
y
2
.Tìm giá trị nhỏ nhất và giá trị lớn
nhất của y khi x thõa mãn điều kiện
4x2
Thay
x5
;
75
y
2
vào hàm số
2
yf(x)axta có :
2
75 3
a.5 a
22

Vì
3
a0
2

nên
y0
là giá trị nhỏ nhất của hàm số và hàm số nghịch biến khi
x0
, đồng biến khi
x0
, do đó khi
4x2
thì
2
3
f( 4) ( 4) 24 f(x) f(0) 0
2

và khi
0x2
thì
2
3
0f(0)f(x)f(2) .2 6
2

Vậy khi x biến đổi , thõa mãn
4x2
thì giá trị nhỏ nhất của
y
bằng
0
và giá trị lớn nhất của
y
bằng 24 .
Bài 11: Vì
1
a0
3

nên hàm số nghịch biến khi
x0
và đồng biến khi
x0
.Vậy
+ Khi
1
x ,
2
x cùng dương thì
1212
f(x ) f(x ) x x
+ Khi
1
x ,
2
x cùng âm thì
1212
f(x ) f(x ) x x
28.
TOÁNHỌCSƠĐỒ‐THCS.TOANMATH.com
Bài 12: Cho hàm số
2
yf(x) 2x
..Chứng minh rằng với mọi giá trị của x thõa mãn điều kiện
3x 1
ta điều có
2
f( 3) 2x f( 1)
Vì
a20
nên hàm số đồng biến khi
x0
.Do đó
f( 3) f(x) f( 1)
hay
22
2( 3) f (x) 2( 1) 
2
18 2x 2  
Vậy khi x biến đổi thõa mãn điều kiện
3x 1
thì y có giá trị bé nhất là
18
và giá trị lớn nhất là
2
Bài 13: Cho hàm số

2
yfx ax
a)Hãy xác định hàm số biết rằng đồ thị của nó đi qua điểm

2;4A
.
b)Vẽ đồ thị của hàm số đã cho .
c)Tìm các điểm trên Parabol có tung độ bằng 16.
d)Tìm
m
sao cho

3
;
Bmm
thuộc Parabol.
e)Tìm các điểm trên Parabol (khác gốc tọa độ) cách đều hai trục tọa độ.
Lời giải:
a) Ta có

2
4.2 1AP a a
b) Đồ thị Parabol có đỉnh là gốc tọa độ

0;0O
quay bề lồi xuống dưới, có trục
đối xứng là
Oy
đi qua các điểm

1;1 , 1;1 , 3; 9 , 3; 9MN E F
c) Gọi
C
là điểm thuộc

P
có tung độ bằng 16.
Ta có:
2
16 16 4
CCC
yx x
 
. Vậy

4;16C
hoặc

4;16C
.
d) Thay tọa độ điểm
B
vào

P
ta được:

32 32 2
0100mm mm mm m
hoặc
1m
.
e) Gọi
D
là điểm thuộc

P
cách đều hai trục tọa độ. Ta có:
 
2
,;,
DD D
dDOx y x dDOy x
.
Theo giả thiết ta có:
2
0
DD D
xx x
(loại) hoặc
1
D
x
. Vậy

1;1D
hoặc

1;1D
.
Bài 14:
a) Vẽ đồ thị hàm số
1
yx.x
3
b) Vẽ đồ thị hàm số
y2x.x
Lời giải:
y
=
x
2
-3
9
3
1
-1
1
y
x
O
29.
TOÁNHỌCSƠĐỒ‐THCS.TOANMATH.com
a) Với
x0
⇒
2
1
yx
3
Với
x0
⇒
2
1
yx
3

b) Với
x0
⇒
2
y2x
Với
x0
⇒
2
y2x
Bài 15: Trên mặt phẳng tọa độ
Oxy
cho đường thẳng

:6dy x
và parabol

2
:Pyx
.
a)Tìm tọa độ các giao điểm của

d
và

P
.
b)Gọi
,
AB
là hai giao điểm của

d
và

P
. Tính diện tích tam giác
OAB
.
Lời giải:
a) Phương trình hoành độ giao điểm của

P
và

d
là:
22
660
xx xx

23xx
.Ta có

24; 39yy
.
Vậy tọa độ giao điểm của

P
và

d
là

2; 4B
và

3; 9A
.
b) Gọi
', '
AB
lần lượt là hình chiếu của
,
AB
xuống trục hoành.
Ta có
'' ' '
OAB AA B B OAA OBB
SS SS


Ta có
'' ''
'' 5; ' 9; ' 4
BA BA A B
ABxx xx AAy BBy
30.
TOÁNHỌCSƠĐỒ‐THCS.TOANMATH.com
''
'' 9465
.'' .5
222
AA BB
AA BB
SAB


(đvdt),
'
127
'.'
22
OAA
SAAAO

(đvdt)
'' ' '
65 27
415
22
OAB AA B B OAA OBB
SS SS


 


(đvdt).
Bài 16 :
a) Xác định điểm
M
thuộc đường Parabol

2
:Pyx
sao cho độ dài đoạn
IM
là nhỏ nhất, trong đó

0;1I
.
b) Giả sử điểm
A
chạy trên Parabol

2
:Pyx
. Tìm tập hợp trung điểm
J
của đoạn
OA
.
Lời giải
a) Giả sử điểm
M
thuộc đường Parabol

2
:Pyx
suy ra

2
;Mmm
. Khi đó

2
22 2 42
11IM m m m m . Vậy
2
2
133
242
IM m




. Ta thấy
IM
nhỏ nhất bằng
3
2
khi
2
2
m 
hay
21
;
22
M




.
b) Giả sử điểm

2
;
Aaa
thuộc

2
:Pyx
. Gọi

11
;Ixy
là trung điểm đoạn
OA
.Suy ra
1
2
2
11
2
2
2
a
x
a
yx

Vậy tập hợp các trung điểm
I
của đoạn
OA
là đường Parabol

2
1
:2Py x
.
Bài 17 :Trong mặt phẳng tọa độ
Oxy
, cho hai điểm
A
và
B
chạy trên parabol

2
:Pyx
sao cho

,0;0AB O
và
OA OB
. Giả sử
I
là trung điểm của đoạn
AB
.
a) Tìm quỹ tích điểm trung điểm
I
của đoạn
AB
.
b) Đường thẳng
AB
luôn luôn đi qua một điểm cố định.
c) Xác định tọa độ điểm
A
và
B
sao cho độ dài đoạn
AB
nhỏ nhất.
Lời giải:
a) Giả sử

2
;
Aaa
và

2
;
Bbb
là hai điểm thuộc

P
. Để

,0;0AB O
và
OA OB
ta cần điều
kiện:
0ab
và
22 2
OA OB AB
hay
0ab
và


2
2
2424 22
aabb ab ab . Rút gọn hai
31.
TOÁNHỌCSƠĐỒ‐THCS.TOANMATH.com
vế ta được:
1ab 
. Gọi

11
;Ixy
là trung điểm đoạn
AB
. Khi đó:

1
2
22
2
11
2
2
21
22
ab
x
ab ab
ab
yx


Vậy tọa độ điểm
I
thỏa mãn phương trình
2
21yx
.
Ta cũng có thể tìm điều kiện để
OA OB
theo cách sử dụng hệ số góc: Đường thẳng
OA
có hệ số
góc là
2
1
a
ka
a
, đường thẳng
OB
có hệ số góc là
2
2
b
kb
b
. Suy ra điều kiện để
OA OB
là
.1ab
b) Phương trình đường thẳng đi qua
A
và
B
là

2
22
:
xa ya
AB
ba b a


hay

:1AB y a b x ab a b x 
. Từ đây ta dễ dàng suy ra đường thẳng

:1AB y a b x
luôn luôn đi qua điểm cố định

0;1
.
c) Vì
OA OB
nên
1ab 
. Độ dài đoạn


2
2
22
AB a b a b
hay
22 44 22
22AB ab abab ab
Áp dụng bất đẳng thức Cô si ta có
22 22
22ab ab ab
,
44 22
2aab b
. Ta có:
22 22
222 2 2AB ab ab ab. Vậy
AB
ngắn nhất bằng
2
khi
22
,1abab
. Ta có thể chỉ ra cặp điểm đó là:

1;1A
và

1;1B
.
Bài 18 : Trong mặt phẳng tọa độ
Oxy
cho Parabol

2
:Pyx
, trên

P
lấy hai điểm

1;1 , 3; 9AB
.
a)Tính diện tích tam giác
OAB
.
b)Xác định điểm
C
thuộc cung nhỏ
AB
của

P
sao cho diện tích tam giác
ABC
lớn nhất.
Lời giải:
32.
TOÁNHỌCSƠĐỒ‐THCS.TOANMATH.com
a) Gọi
yaxb
là phương trình đường thẳng
AB
.
Ta có

.1 1
2
3
.3 9
ab
a
b
ab



Suy ra phương trình đường thẳng
AB
là

:23dy x
.
Đường thẳng
AB
cắt trục
Oy
tại điểm

0;3I
.
Diện tích tam giác
OAB
là:
11
..
22
OAB OAI OBI
SSS AHOIBKOI
.
Ta có
1; 3, 3AH BK OI
.
Suy ra
6
OAB
S
(đvdt).
b) Giả sử

2
;Ccc
thuộc cung nhỏ

P
với
13c
.
Diện tích tam giác:
'' '' ''ABC ABB A ACC A BCC B
SS S S
.
Các tứ giác
'', '', ''ABB A AA C C CBB C
đều là hình thang vuông nên ta có:
 
22
2
19 1 9
.4 . 1 . 3 8 2 1 8
22 2
ABC
cc
Sccc

 .
Vậy diện tích tam giác
ABC
lớn nhất bằng
8
(đvdt) khi

1;1C
.
Bài 19: Một xe tải có chiều rộng là 2,4 m chiều cao là 2,5 m muốn đi qua một cái cổng hình Parabol.
Biết khoảng cách giữa hai chân cổng là 4m và khoảng cách từ đỉnh cổng tới mỗi chân cổng là
25 m(
Bỏ qua độ dày của cổng).
a)Trong mặt phẳng tọa độ
Oxy
gọi Parabol

2
:Pyax
với
0a
là hình biểu diễn cổng mà xe tải
muốn đi qua. Chứng minh
1a 
.
b)Hỏi xe tải có đi qua cổng được không? Tại sao?
Lời giải:
a) Giả sử trên mặt phẳng tọa độ, độ dài các đoạn thẳng được tính theo đơn vị mét. Do khoảng cách
giữa hai chân cổng là 4 m nên
2MA NA m
. Theo giả thiết ta có 25OM ON , áp dụng định lý
Pitago ta tính được:
4OA
vậy

2; 4 , 2; 4MN
. Do

2; 4M
thuộc parabol nên tọa độ điểm
M
thỏa mãn phương trình:

2
:Pyax
hay
2
4.2 1aa
và

2
:Py x
.
b) Để đáp ứng chiều cao trước hết xe tải phải đi vào chính giữa cổng.
K
H
I
A'
B'
C'
C(c;c
2
)
y
=
x
2
-3
9
3
1
-1
1
y
x
O
33.
TOÁNHỌCSƠĐỒ‐THCS.TOANMATH.com
Xét đường thẳng

3
:
2
dy
(ứng với chiều cao của xe). Đường
thẳng này cắt Parabol tại 2 điểm
có tọa độ thỏa mãn hệ:
2
3
2
yx
y


2
3
2
3
2
x
y

32 3
;
22
32 3
;
22
xy
xy

 
suy ra tọa độ hai giao điểm là
32 3 323
;; ; 322,4
22 22
THHT





.
Vậy xe tải có thể đi qua cổng.
----------Toán Học Sơ Đồ---------
A
B
H
T
N
M
-4
y
=-
x
2
2
-2
y
x
O
| 1/33
| | Tải xuống

Có thể bạn quan tâm:

Preview text:


CHUYÊN ĐỀ HÀM SỐ 2
y ax a0
A. KIẾN THỨC TRỌNG TÂM
* Tập xác định của hàm số: + Hàm số 2
y ax a  0 xác định với mọi x R .
* Tính chất biến thiên của hàm số:
+ Nếu a  0 thì hàm số 2
y ax a  0 nghịch biến khi x  0 , và đồng biến khi x  0 .
+ Nếu a  0 thì hàm số 2
y ax a  0 đồng biến khi x  0 và nghịch biến khi x  0 .
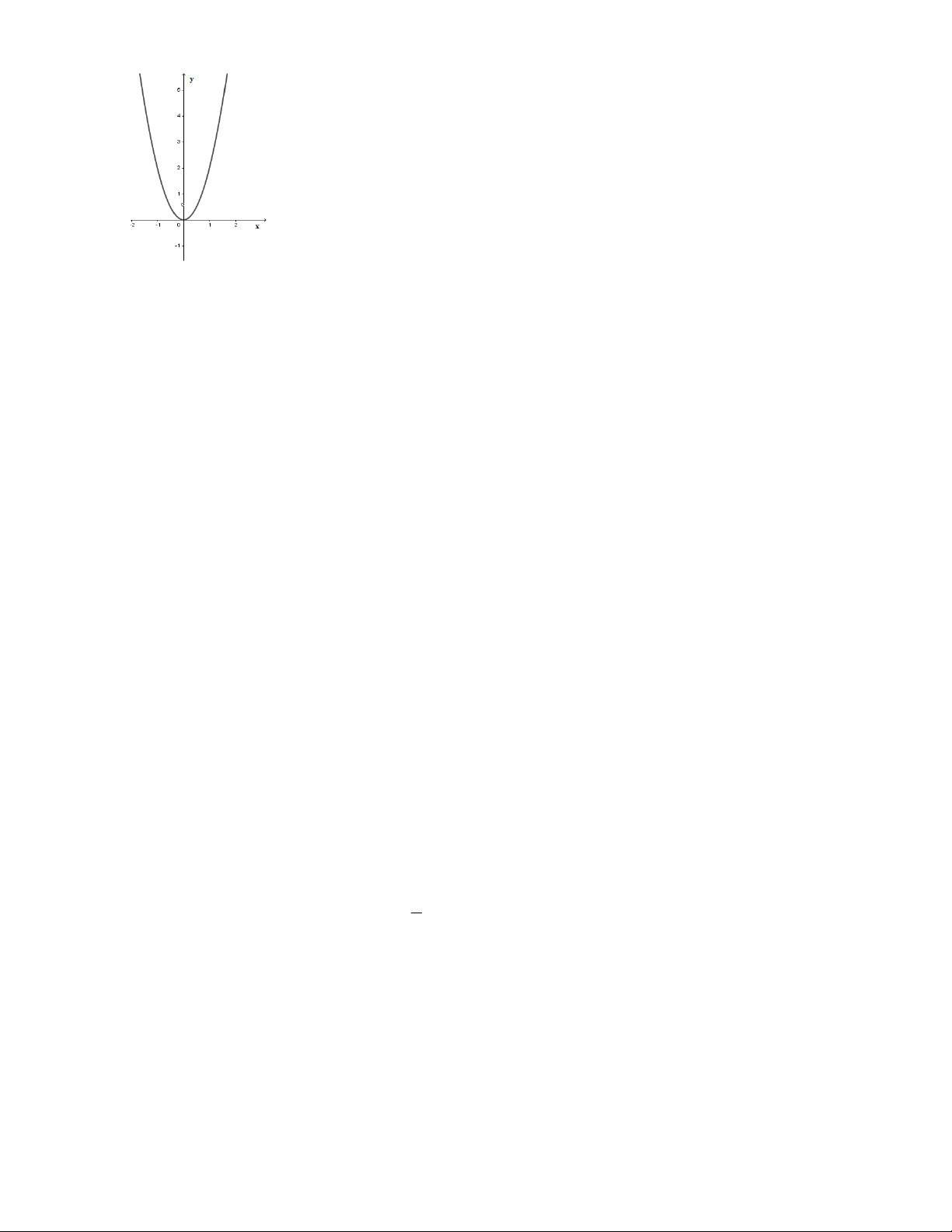
* Đồ thị của hàm số: 2
y ax a  0 + Đồ thị của hàm số 2
y ax a  0 là một đường cong đi qua gốc toạ độ và nhận trục Oy làm trục
đối xứng. Đường cong đó được gọi là một Parabol P với đỉnh O.
+ Nếu a  0 thì y  0 với mọi x  0 , y  0 khi x  0 . Do đó, đồ thị P nằm phía trên trục hoành
Ox , đỉnh O là điểm thấp nhất của đồ thị.
+ Nếu a  0 thì y  0 với mọi x  0 , y  0 khi x  0 . Do đó, đồ thị P nằm phía trên trục hoành
Ox , đỉnh O là điểm cao nhất của đồ thị. + Vì đồ thị 2
y ax a  0 luôn đi qua gốc toạ độ và nhận trục Oy làm trục đối xứng nên để vẽ đồ thị
của hàm số này, ta chỉ cần tìm một điểm ở bên phải trục Oy rồi lấy các điểm đối xứng với chúng qua Oy.
B. CÁC DẠNG BÀI TOÁN MINH HỌA
Dạng 1. Xác định hàm số bậc hai
Cho hàm số y f x được gọi là hàm số bậc hai một ẩn nếu phương trình của hàm số có:
Vậy, để xác định một hàm số là hàm số bậc hai một ẩn phải thoả mãn điểu kiện sau:
+ Hàm số chỉ chứa một ẩn duy nhất, với bậc cao nhất của ẩn là bậc hai. + Hàm số có dạng 2
ax bx c  0 với a  0 . + Hàm số có dạng 2
y ax b có hệ số a  0 . + Hàm số 2
y ax có hệ số a  0 . Ví dụ minh hoạ 1:
Trong các hàm số sau, hàm số nào là hàm số bậc hai một ẩn? 1 2 x 1 a. y   3 b. y  1 c. 2 y  x  2 x 5 x
1. TOÁN HỌC SƠ ĐỒ ‐ THCS.TOANMATH.com 1 d. 2 y   x e. 2
y  1 x x f.
y   x  2 3 1 2 y Hướng dẫn giải: 2 x
Các hàm số là hàm số bậc hai một ẩn là: y  1 và 2
y  1 x x 5
y   x  2 2 3
1  3x  6x  3. Ví dụ minh hoạ 2:
Tìm m để hàm số sau là hàm số bậc hai một ẩn.
a. y  m   2 2 x b. y   2 m   2 2 x Hướng dẫn giải:
a. Để hàm số y  m   2
2 x là hàm số bậc hai khi và chỉ khi: m  2  0  m  2  Vậy, với m  2
 thì hàm số đã cho là hàm số bậc hai. m  2
b. Để hàm số y   2 m   2
2 x là hàm số bậc hai khi và chỉ khi: 2 2
m  2  0  m  2   m   2
Vậy, với m   2 thì hàm số đã cho là hàm số bậc hai.
Dạng 2. Điểm thuộc đồ thị hàm số - Vẽ đồ thị hàm số * Cho hàm số 2
y ax a  0 có đồ thị là Parabol P.
+ Điểm M có toạ độ x ; y thuộc đồ thị parabol P khi và chỉ khi 2 y ax 0 0  0 0
+ Điểm M có toạ độ x ; y không thuộc đồ thị parabol P 2  y ax 0 0  0 0
* Vẽ đồ thị hàm số 2
y ax a  0
+ Xác định đỉnh của Parabol là gốc toạ độ O 0;0 .
+ Xác định các điểm thuộc đồ thị hàm số: –2 –1 0 1 2 4a A 0 a 4a
+ Hình dạng parabol: a  0 a  0
Parabol nhận trục tung làm trục đối xứng.
2. TOÁN HỌC SƠ ĐỒ ‐ THCS.TOANMATH.com 1
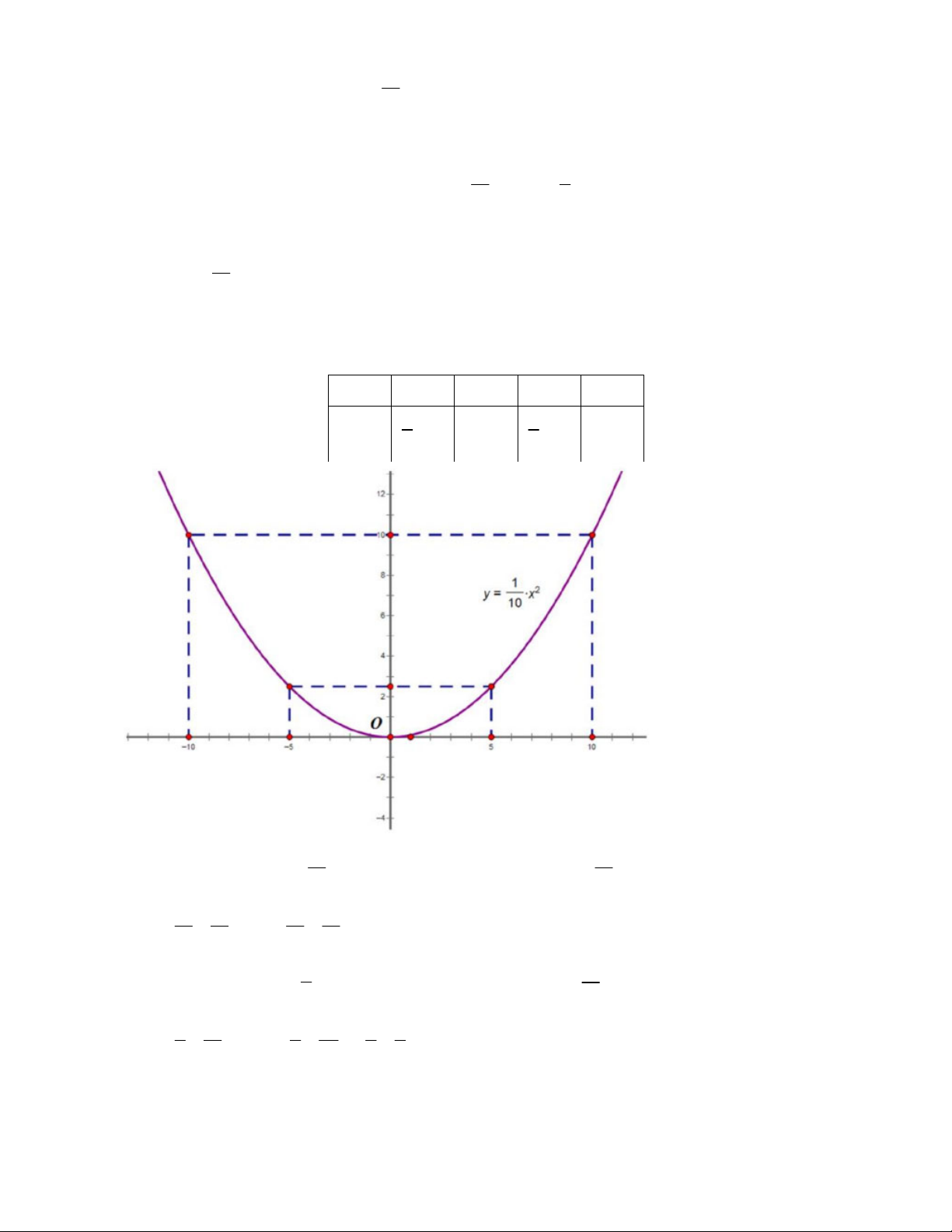
Ví du minh họa 1: Cho hàm số 2 y x 10
a. Vẽ đồ thị P của hàm số.  9   5 
b. Các điểm sau có thuộc đồ thị hay không: A 3;   , B 5;   , C  10  ;  1  10   2  Hướng dẫn giải: 1 Hàm số 2 y
x có đồ thị là parabol P . 10
a. Đồ thị P có đỉnh là O0;0 , nằm phía trên trục hoành, nhận trục Oy làm trục đối xứng và đồ thị đi qua các điểm sau: –10 –5 0 5 10 5 5 10 0 10 2 2  9  1
b. Thay toạ độ điểm A 3; 
 vào phương trình parabol P : 2 y x  10  10 9 1 9 9 Ta có: 
32   (đúng). Vậy điểm A thuộc đồ thị hàm số. 10 10 10 10  5  1
Thay toạ độ điểm B 5; 
 vào phương trình parabol P : 2 y x  2  10 5 1 5 25 5 5 Ta có:  52     (đúng). 2 10 2 10 2 2
Vậy điểm B thuộc đồ thị hàm số.
3. TOÁN HỌC SƠ ĐỒ ‐ THCS.TOANMATH.com 1
Thay toạ độ điểm C  10  
;1 vào phương trình parabol P : 2 y x 10 1 100 Ta có: 1   1  02   1  10 (vô lý). 10 10
Vậy điểm B không thuộc đồ thị hàm số.
Dạng 3. Sự đồng biến - nghịch biến của đồ thị hàm số. Cho hàm số 2
y ax a  0 xác định với mọi x R .
+ Nếu a  0 : Hàm số 2
y ax a  0 nghịch biến khi x  0 , và đồng biến khi x  0 . x  0  2
y ax a  0 0
+ Nếu a  0 : Hàm số 2
y ax a  0 đồng biến khi x  0 và nghịch biến khi x  0 . x  0  2
y ax a  0 0
Ví dụ minh hoạ 1: Cho hàm số   2   2 y m
m x . Tìm giá trị của m để:
a. Hàm số đồng biến với mọi x  0 .
b. Hàm số nghịch biến với mọi x  0 . Hướng dẫn giải: Hàm số   2   2 y m m x .
a. Hàm số đồng biến với mọi 2
x  0  a  0  m m  0  mm   1  0 m  0 m  0 Khi     m 1 m 1  0 m 1 m  0 m  0 Hoặc     m  0 m 1  0 m  1
Vậy với m  0 hoặc m 1 thì hàm số đã cho đồng biến với mọi x  0 .
b. Hàm số nghịch biến với mọi 2
x  0  a  0  m m  0  mm   1  0 m  0 m  0 Khi     0  m 1 m 1  0 m 1 m  0 m  0 Hoặc   
 Không có giá trị nào của m thoả mãn điều kiện này. m 1  0 m 1
4. TOÁN HỌC SƠ ĐỒ ‐ THCS.TOANMATH.com
Vậy với 0  m 1 thì hàm số đã cho nghịch biến với mọi x  0 .
Dạng 4. Giá trị lớn nhất, giá trị nhỏ nhất của hàm số * Hàm số 2
y ax a  0
+ Nếu a  0 hàm số có giá trị nhỏ nhất bằng 0 khi x  0 .
+ Nếu a  0 hàm số có giá trị lớn nhất bằng 0 khi x  0 . * Hàm số 2
y ax bx c a  0 b
+ Nếu a  0 hàm số 2
y ax bx c a  0 có giá trị nhỏ nhất khi x   2a b
+ Nếu a  0 hàm số 2
y ax bx c a  0 có giá trị lớn nhất khi x   2a
Dạng 5. Viết phương trình parabol 2
y ax a  0 (tìm hệ số a)
Khi biết toạ độ của một điểm thuộc đồ thị hàm số 2
y ax a  0 , ta đi tìm hệ số a của nó bằng cách
thay toạ độ điểm đó vào phương trình hàm số.
Ví dụ minh hoạ 1: Cho hàm số   2   2 y m
m x . Tìm giá trị của m để đồ thị của hàm số đi qua điểm A1;2 . Hướng dẫn giải:
Đồ thị hàm số   2   2 y m
m x đi qua điểm A1;2
  m m 2 2 2 2 2
1  m m  2  m m  2  0     
m  m   m 1 1 2  0   m  2 Vậy, với m  1
 hoặc m  2 thì đồ thị hàm số đã cho đi qua điểm A1;2
Ví dụ minh hoạ 2: Viết phương trình parabol 2
y ax . Biết đồ thị của nó đi qua điểm M  2;  8 . Hướng dẫn giải: Phương trình parabol 2
y ax đi qua điểm M  2;  8
   a  2 8 2  a  2
Vậy, hàm số cần tìm là: 2 y  2  x .
Dạng 6. Tương giao giữa Parabol với đường thẳng Cho parabol 2
y ax a  0 và đường thẳng y kx b .
+ Lập phương trình hoành độ giao điểm: 2
ax kx b  1
Số nghiệm của phương trình  
1 chính là số giao điểm của parabol với đường thẳng.
5. TOÁN HỌC SƠ ĐỒ ‐ THCS.TOANMATH.com
+ Toạ độ giao điểm x ; y vừa là nghiệm của phương trình 2
y ax , vừa là nghiệm của phương 0 0 
trình y kx b .
Ví dụ minh hoạ 1: Cho hàm số 2
y mx có đồ thị là parabol P . Tìm giá trị của m biết rằng đồ thị của hàm số 2
y mx cắt đường thẳng d  : y x  3 tại điểm có hoành độ bằng 5. Hướng dẫn giải:
Gọi M x ; y là toạ độ giao điểm của P và d  . 0 0 
Theo đề, x  5 và M thuộc d  nên ta có: y x  3  y  5  3  y  2 0 0 0 0 0
Vậy M 5;2 . Điểm M 5;2 thuộc đồ thị hàm số 2 y mx   2 m  2 2 2 5  m
. Vậy, hàm số cần tìm là: 2 y x . 25 25
BÀI TẬP LUYỆN TẠI LỚP Bài 1: Cho hàm số 2 y  3  x
a. Lập bảng tính giá trị của hàm số tại các điểm có hoành độ  x sau: 1 1 –2; –1;  ; 0; ; 1; 2 2 2
b. Với giá trị nào của x thì hàm số  y nhận các giá trị sau: 1
0; 27; –27; 5;  ; –81; –3 9
Bài 2: Cho hàm số y  m   2
4 x . Tìm giá trị của m để:
a. Hàm số đồng biến với mọi x  0 .
b. Hàm số nghịch biến với mọi x  0 .
Bài 3: Cho hàm số y   2
k k   2 2 3 x
a. Xét sự biến thiên của hàm số trên tập xác định của nó?
b. Tìm k biết đồ thị hàm số đi qua điểm 1;6 ? 1 Bài 4: Cho hàm số 2 y x 2
a. Vẽ đồ thị của hàm số;  5   5 
b. Cho các điểm sau: A0; 
1 ; B 2;2 ; C 3;   ; D  5; 
 điểm nào thuộc đồ thị hàm số, điểm  2   2 
nào không thuộc đồ thị hàm số?
Bài 5: Cho hàm số y  m   2
1 x . Xác định hệ số a trong mỗi trường hợp sau:
6. TOÁN HỌC SƠ ĐỒ ‐ THCS.TOANMATH.com
a. Đồ thị của hàm số đi qua điểm A1;9
b. Đồ thị của hàm số đi qua điểm B  4;  32 . 1 Bài 6: Cho hàm số 2 y   x . 3
a. Biết điểm A 3;
m thuộc đồ thị hàm số, tìm m? Hỏi điểm A3;m có thuộc đồ thị hàm số không? Vì sao?
b. Biết điểm M k; 9
  thuộc đồ thị hàm số, tìm k? Hỏi điểm Mk;9 có thuộc đồ thị hàm số không? Vì sao? Bài 7: Cho hàm số 2 y ax .
a. Xác định hàm số biết đồ thị của nó đi qua điểm A 2;2 .
Vẽ đồ thị hàm số với giá trị tìm được của a.
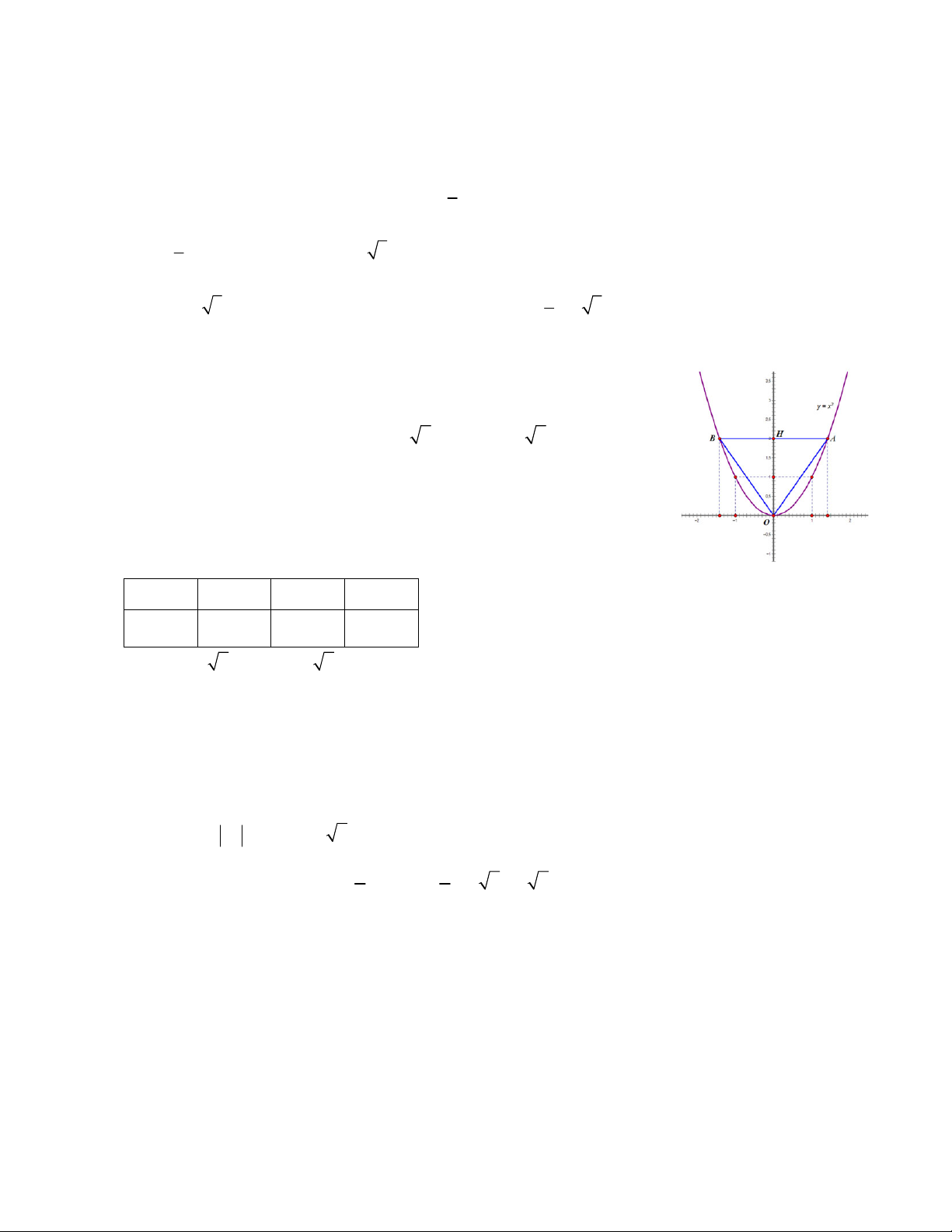
b. Biết B  2;2 là một điểm thuộc đồ thị hàm số trong câu a, O là gốc toạ độ. Tam giác OAB là tam
giác gì? Tính diện tích tam giác OAB. 1 Bài 8: Cho hàm số 2
y x P và y  2x  2 . 2
a. Vẽ hai đồ thị hàm số này trên cùng một mặt phẳng toạ độ.
b. Tìm toạ độ giao điểm của hai đồ thị trên. Bài 9: Cho hàm số 2 y  3  x .
a. Tìm các điểm thuộc đồ thị hàm số có tung độ bằng –9;
b. Tìm các điểm thuộc đồ thị hàm số cách đều hai trục toạ độ
c. Tìm các điểm thuộc đồ thị hàm số có tung độ gấp 9 lần hoành độ. Bài 10: Cho hàm số 2 y kx .
a. Xác định k biết đồ thị hàm số có đồ thị cắt đường thẳng y  3x  4 tại điểm có hoành độ x  2  .
b. Với giá trị k tìm được ở câu a, hãy vẽ đồ thị hàm số 2
y kx và y  3x  4 trên cùng một mặt phẳng toạ độ.
c. Bằng đồ thị hãy xác định toạ độ giao điểm của đồ thị hàm số 2
y kx và y  3x  4 . HƯỚNG DẪN GIẢI: Bài 1: Cho hàm số 2 y  3  x
a. Lập bảng tính giá trị của hàm số tại các điểm có hoành độ  x sau: 1 1 x –2 –1  0 1 2 2 2
7. TOÁN HỌC SƠ ĐỒ ‐ THCS.TOANMATH.com 3 3 2 y  3
x –12 –3  0  –3 –12 4 4
b. Với giá trị nào của x thì hàm số  y nhận các giá trị sau: Với y  0 , ta có 2 2
3x  0  x  0  x  0 ;
Với y  27 , ta có 2 2
3x  27  x  9 không có giá trị của x thoả mãn;
Với y  27 , ta có 2 2
3x  27  x  9  x  3 ; 1 1 1 1
Với y   , ta có 2 2 3
x    x   x   ; 9 9 27 3 3
Với y  3 , ta có 2 2
3x  3  x  1  x  1
Bài 2: Cho hàm số y  m   2 4 x .
a. Hàm số đồng biến với mọi x  0 .
m  4  0  m  4
Vậy với m  4 thì hàm số đã cho đồng biến với mọi x  0 .
b. Hàm số nghịch biến với mọi x  0 .
m  4  0  m  4
Vậy với m  4 thì hàm số đã cho nghịch biến với mọi x  0 .
Bài 3: Cho hàm số y   2
k k   2 2 3 x
a. Hàm số y   2
k k   2 2
3 x có hệ số a k k   k  2 2 2 3
1  2  0 với mọi giá trị của k.
Do đó, hàm số đã cho nghịch biến khi x  0 ; và đồng biến khi x  0 .
b. Đồ thị hàm số đi qua điểm 
   k k   2 2 1;6 6 2 3 1 2 2
k  2k  3  6  k  2k  3  0     
k  k   k 1 1 3   k  3 Vậy, với k  1
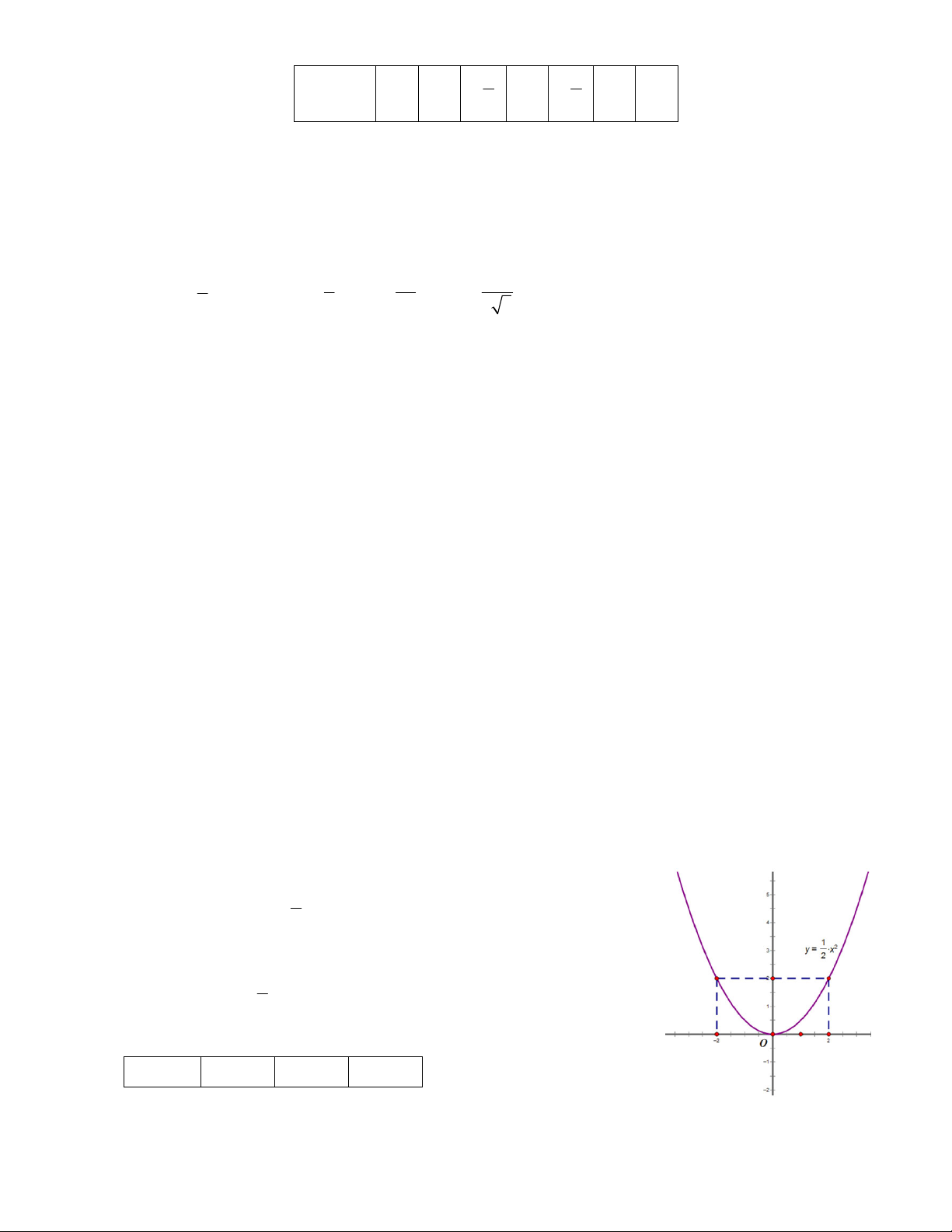
 hoặc k  3 thì đồ thị hàm số đi qua điểm 1;6 1 Bài 4: Cho hàm số 2 y x 2
a. Vẽ đồ thị của hàm số: 1 Đồ thị hàm số 2
y x là parabol P có đỉnh là O0;0 , nhận trục Oy 2
làm trục đối xứng, và đi qua các điểm sau: x –2 0 2
8. TOÁN HỌC SƠ ĐỒ ‐ THCS.TOANMATH.com 1 2 y x 2 0 2 2 b. Ta có: 1
Thay hoành độ điểm A0; 
1 vào hàm số: 02  0  y 1 2 A
Vậy điểm A0; 
1 không thuộc đồ thị hàm số. 1
Thay hoành độ điểm B 2;2 vào hàm số: 22  2  y 2 B
Vậy điểm B 2;2 thuộc đồ thị hàm số.  5  1
Thay hoành độ điểm C 3; 
 vào hàm số: 32 9 5   y   2  2 2 C 2  5  Vậy điểm C 3; 
 không thuộc đồ thị hàm số.  2   5  1 5
Thay hoành độ điểm D  5; 
 vào hàm số:  52   y  2  2 2 D  5  Vậy điểm D  5; 
 thuộc đồ thị hàm số.  2 
KL: Vậy điểm B và điểm D thuộc đồ thị hàm số.
Bài 5: Cho hàm số y  m   2
1 x . Xác định hệ số a trong mỗi trường hợp sau:
a. Đồ thị của hàm số y  m   2
1 x đi qua điểm A1;9
  m   2 9
1 1  m 1  9  m  8
Vậy, với m  8 thì đồ thị hàm số đi qua điểm A1;9
b. Đồ thị của hàm số y  m   2
1 x đi qua điểm B  4;  32 . 
 m   2 32 1 4  16m   1  32
m 1  2  m 1
Vậy, với m 1 thì đồ thị hàm số đi qua điểm B  4;  32 . 1 Bài 6: Cho hàm số 2 y   x . 3 1 a. Vì điểm A 3;
m thuộc đồ thị hàm số 2
y   x , nên 3 1 m    2 9
3  m    m  3 3 2
9. TOÁN HỌC SƠ ĐỒ ‐ THCS.TOANMATH.com
Suy ra toạ độ điểm A 3;  3   và A3; 3
  là hai điểm đối xứng nhau qua trục Oy (tính chất đối xứng của hàm số 2
y ax với a  0 ). Mà điểm A 3;  3
  thuộc đồ thị hàm số nên điểm A3; 3   cũng
thuộc đồ thị hàm số. 1
b. Điểm M k; 9
  thuộc đồ thị hàm số 2
y   x , nên: 3 1 9   k 2 2
k  27  k  3 3 3 1 Với k  3
 3 thay vào phương trình hàm số ta được y    2 3 3  9  y . 3 M
Do đó điểm M k;9 không thuộc đồ thị hàm số. Bài 7: Cho hàm số 2 y ax . a. Đồ thị hàm số 2
y ax đi qua điểm A   a 2 2; 2 2 2  a  1.
Vậy, a  1 và hàm số cần tìm là 2 y x Đồ thị hàm số 2
y x là parabol có đỉnh O 0;0 , có trục đối xứng Oy. Đồ thị hàm số 2
y x đi qua các điểm sau: x –1 0 1 2 y x 1 0 1
b. Điểm A 2;2 và B 2;2 thuộc đồ thị hàm số 2 y x . x  x Vì A B
nên hai điểm A và B đối xứng nhau qua trục Oy. y yA B
Do đó, Oy là đường trung trực của đoạn thẳng AB, suy ra OA OB .
Vậy tam giác OAB là tam giác cân tại O.
Ta có: OH y  2; AB  2 2 A 1 1
Diện tích tam giác OAB: S
OH.AB  .2.2 2  2 2 (đvdt) OAB 2 2
10. TOÁN HỌC SƠ ĐỒ ‐ THCS.TOANMATH.com 1 Bài 8: Cho hàm số 2
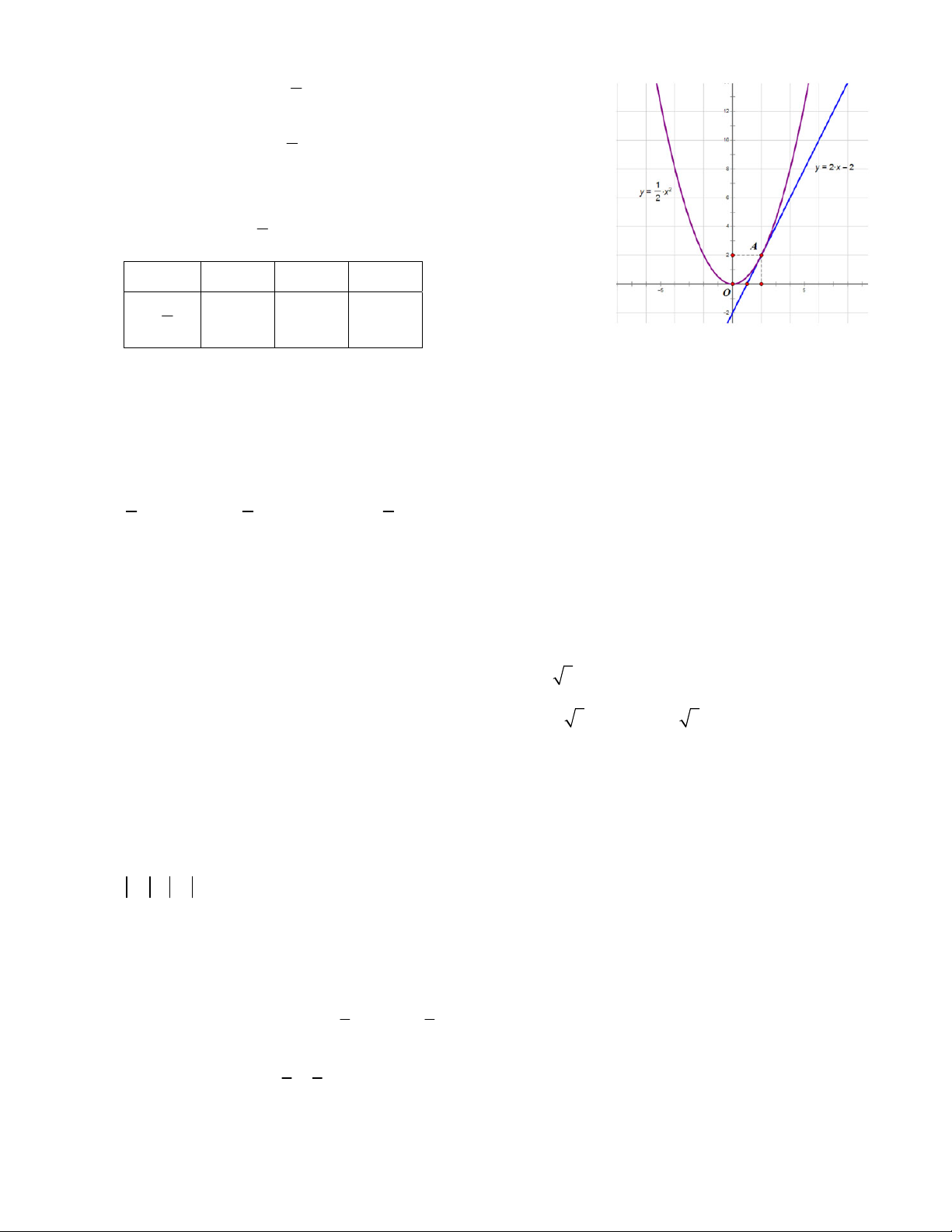
y x P và y  2x  2 . 2 1 a. * Đồ thị hàm số 2
y x là parabol P có đỉnh O0;0 , có 2 trục đối xứng Oy. 1 Đồ thị hàm số 2
y x đi qua các điểm sau: 2 x –2 0 2 1 2 y x 2 0 2 2
* Đồ thị hàm số y  2x  2 là đường thẳng d  đi qua hai điểm 0; 2   và 1;0
b. Tìm toạ độ giao điểm của hai đồ thị trên.
Phương trình hoành độ giao điểm của P và d  là: 1 1 1
x  2x  2  x  2x  2  0   x  22 2 2  0  x  2 2 2 2
Với x  2  y  2 . Vậy toạ độ giao điểm là 2;2 . Bài 9: Cho hàm số 2 y  3
x P .
a. Gọi M x ; y là điểm thuộc đồ thị hàm số và có y  9  M M M
Vì M thuộc P nên ta có: 2 2 9   3
x x  3  x   3 M M M
Vậy điểm thuộc đồ thị hàm số và có tung độ bằng –9 là: M  3; 9  và M 3; 9  2   1  
b. Gọi N x ; y là điểm thuộc đồ thị hàm số và có khoảng cách đến các trục toạ độ bằng nhau. N N
N thuộc đồ thị hàm số nên: 2 y  3x N N
N có khoảng cách đến hai trục toạ độ bằng nhau nên:  y x N N   1 y x   N Ny  xN N  2 Giải   1 : 2
y x  3xx N N N N
x  0  y  0 N N x x      N 1 3 N  0 1 1
x    y   N  3 N 3  1 1 
Ta có điểm 0;0 ;  ;    3 3 
11. TOÁN HỌC SƠ ĐỒ ‐ THCS.TOANMATH.com Giải 2 : 2
y  x  3x  x N N N N
x  0  y  0 N N x x      N 1 3 N  0 1 1
x   y   N  3 N 3  1 1  Ta có điểm 0;0 ; ;     3 3   1 1   1 1 
Vậy, các điểm thuộc đồ thị hàm số cách đều hai trục toạ độ là: 0;0 ; ;    ;  ;    3 3   3 3 
c. Tìm các điểm thuộc đồ thị hàm số có tung độ gấp 9 lần hoành độ.
Điểm Ax ; y có tung độ gấp 9 lần hoành độ: y  9x . A A A A
Điểm A thuộc đồ thị hàm số nên: 2 2
y  3x  9x  3x A A A A    
x x   x 0 y 0 3 3  0 A AA Ax  3   y  2  7  A A
Vậy toạ độ các điểm thuộc đồ thị hàm số có tung độ gấp 9 lần hoành độ là: 0;0 ;  3;  2  7 . Bài 10: Cho hàm số 2 y kx .
a. Đồ thị hàm số có đồ thị cắt đường thẳng d  : y  3x  4
tại điểm có hoành độ x  2  .
Gọi M x ; y là toạ độ giao điểm của P và d  . Theo 0 0  đề ta có x  2  0
M thuộc đường thẳng d  nên: y  3
x  4  y  3  .2  4  2  0 0 0 Suy ra M  2;  2
  . Thay vào phương trình P , ta có:   k  2 1 2 2  k   2 1
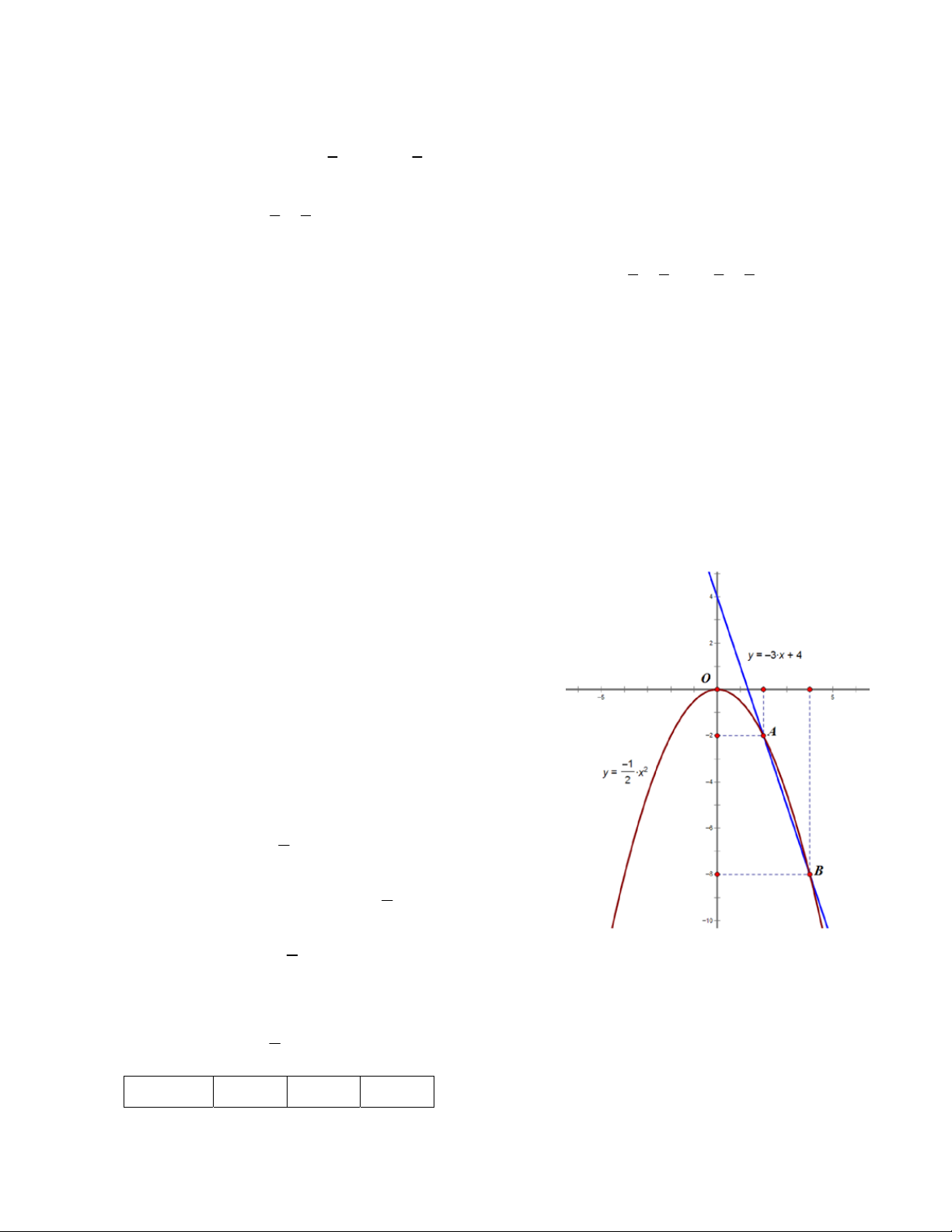
Vậy, đồ thị hàm số cần tìm là: 2 y   x 2 1 b. Đồ thị hàm số 2
y   x P và đường thẳng d  : 2
y  3x  4 1 Đồ thị hàm số 2
y   x P là parabol có đỉnh O0;0 , có trục đối xứng là Oy và đi qua các điểm: 2 x –2 0 2
12. TOÁN HỌC SƠ ĐỒ ‐ THCS.TOANMATH.com 1 2
y   x –2 0 –2 2
* Đồ thị hàm số y  3x  4 là đường thẳng d  đi qua hai điểm 0;4 và 1;  1 1
c. Dựa vào đồ thị ta thấy toạ độ giao điểm của đồ thị hàm số 2
y   x P và đường thẳng d  : 2
y  3x  4 là: A2; 2  ; B4; 8  .
C.TRẮC NGHIỆM RÈN LUYỆN PHẢN XẠ (Hàm số bậc hai một ẩn và đồ thị hàm số y=ax2 ) Câu 1. Cho hàm số 2
y = ax với a ¹ 0 . Kết luận nào sau đây là đúng?
A. Hàm số nghịch biến khi a > 0 và x > 0 .
B. Hàm số nghịch biến khi a < 0 và x < 0 .
C. Hàm số nghịch biến khi a > 0 và x < 0 .
D. Hàm số nghịch biến khi a > 0 và x = 0 . Câu 2. Cho hàm số 2
y = ax với a ¹ 0 .Kết luận nào sau đây là đúng?
A. Hàm số đồng biến khi a > 0 và x < 0 .
B. Hàm số đồng biến khi a > 0 và x > 0 .
C. Hàm số đồng biến khi a > 0 và x < 0 .
D. Hàm số đồng biến khi a < 0 và x = 0 .
Câu 3. Kết luận nào sau đây là sai khi nói về đồ thị của hàm số 2
y = ax với a ¹ 0 .
A. Đồ thị hàm số nhận trục tung làm trục đối xứng.
B. Với a > 0 đồ thị nằm phía trên trục hoành và O là điểm cao nhất của đồ thị.
C. Với a < 0 đồ thị nằm phía dưới trục hoành và O là điểm cao nhất của đồ thị.
D. Với a > 0 đồ thị nằm phía trên trục hoành và O là điểm thấp nhất của đồ thị.
Câu 4. Giá trị của hàm số 2
y = f (x) = -7x tại x = 2 - là: 0 A. 28 . B. 14 . C. 21 . D. -28 . 4
Câu 5. Giá trị của hàm số 2
y = f (x) = x tại x = 5 - là 5 0 A. 20 . B. 10 . C. 4 . D. -20 . Câu 6. Cho hàm số 2
y = f (x) = (-2m + 1)x . Tìm giá trị của m để đồ thị đi qua điểm ( A -2; 4). A. m = 0 . B. m = 1. C. m = 2 . D. m = -2 . 2m - 3 Câu 7. Cho hàm số 2
y = f (x) =
x . Tìm giá trị của m để đồ thị đi qua điểm B(-3;5) 3 3 7 A. m = 1. B. m = . C. m = . D. m = 3 . 7 3 2 Câu 8. Cho hàm số 2
y = (5m + 2)x với m ¹ - . Tìm m để hàm số nghịch biến với mọi x > 0 . 5 2 2 2 5 A. m < - . B. m > . C. m < . D. m > - . 5 5 5 2
13. TOÁN HỌC SƠ ĐỒ ‐ THCS.TOANMATH.com m - 7
Câu 9. Cho hàm số với 2 y =
x . Tìm m để hàm số nghịch biến với mọi x < 0 . 3 - A. m > 7 . B. m < 7 . C. m < 7 - . D. m > 7 - . 4 Câu 10. Cho hàm số 2
y = (4 - 3m)x với m ¹
. Tìm m để hàm số đồng biến với mọi x > 0 3 . 4 4 4 4 A. m > . B. m < - . C. m < . D. m < - . 3 3 3 3 2 5 Câu 11. Cho hàm số 2 y =
x với m ¹ . Tìm m để hàm số đồng biến với mọi x < 0 5 - 2m 2 5 5 2 2 A. m > . B. m < . C. m > . D. m < . 2 2 5 5
Câu 12. Trong các điểm (
A 1;2);B(-1;-1);C (10;-200);D( 10;-10) có bao nhiêu điểm thuộc đồ thị hàm số 2 y = x - . A. 1 . B. 4 . C. 3 . D. 2 . Câu 13. Cho hàm số 2
y = f (x) = 3x . Tìm b biết f (b) ³ 6b + 9 b é £ -1 b é < -1
A. 1 < b < 3 .
B. -1 £ b £ 3 . C. ê . D. ê . b ê ³ 3 ê ê > ë b 3 êë Câu 14. Cho hàm số 2
y = f (x) = -2x . Tìm b biết f (b) £ -5b + 2 é 1 é 1 1 1 b ê < b ê £
A. < b < 2 . B. £ b £ 2 . C. ê 2 . D. ê 2 . 2 2 ê ê b ê > 2 ê ³ ë b 2 ë Câu 15. Cho hàm số 2
y = (2m + 2)x . Tìm m để đồ thị hàm số đi qua điểm (
A x;y) với (x;y) là x ìï -y = 1
nghiệm của hệ phương trình ïí 2 ï x - y = 3 ïî 7 1 7 7 A. m = . B. m = . C. m = . D. m = - . 4 4 8 8 Câu 16. Cho hàm số 2
y = (-3m + 1)x . Tìm m để đồ thị hàm số đi qua điểm (
A x;y) với (x;y) là 4 ìï x - 3y = 2 -
nghiệm của hệ phương trình ïí x ï - 2y = 3 - ïî 1 1 A. m = . B. m = - . C. m = 3 . D. m = -3 . 3 3 Câu 17. Cho hàm số 2 2 y = ( m -
+ 4m - 5)x . Kết luận nào sau đây là đúng
A. Đồ thị của hàm số nằm phía trên trục hoành.
14. TOÁN HỌC SƠ ĐỒ ‐ THCS.TOANMATH.com
B. Đồ thị của hàm số nhận gốc tọa độ O là điểm cao nhất.
C. Hàm số nghịch biến với x < 0 .
D. Hàm số đồng biến với x > 0 . Câu 18. Cho hàm số 2 2
y = (4m + 12m + 11)x . Kết luận nào sau đây là sai?
A. Đồ thị của hàm số nằm phía trên trục hoành.
B. Đồ thị của hàm số nhận gốc tọa độ O là điểm thấp nhất.
C. Hàm số nghịch biến với x > 0 .
D. Hàm số đồng biến với x > 0 .
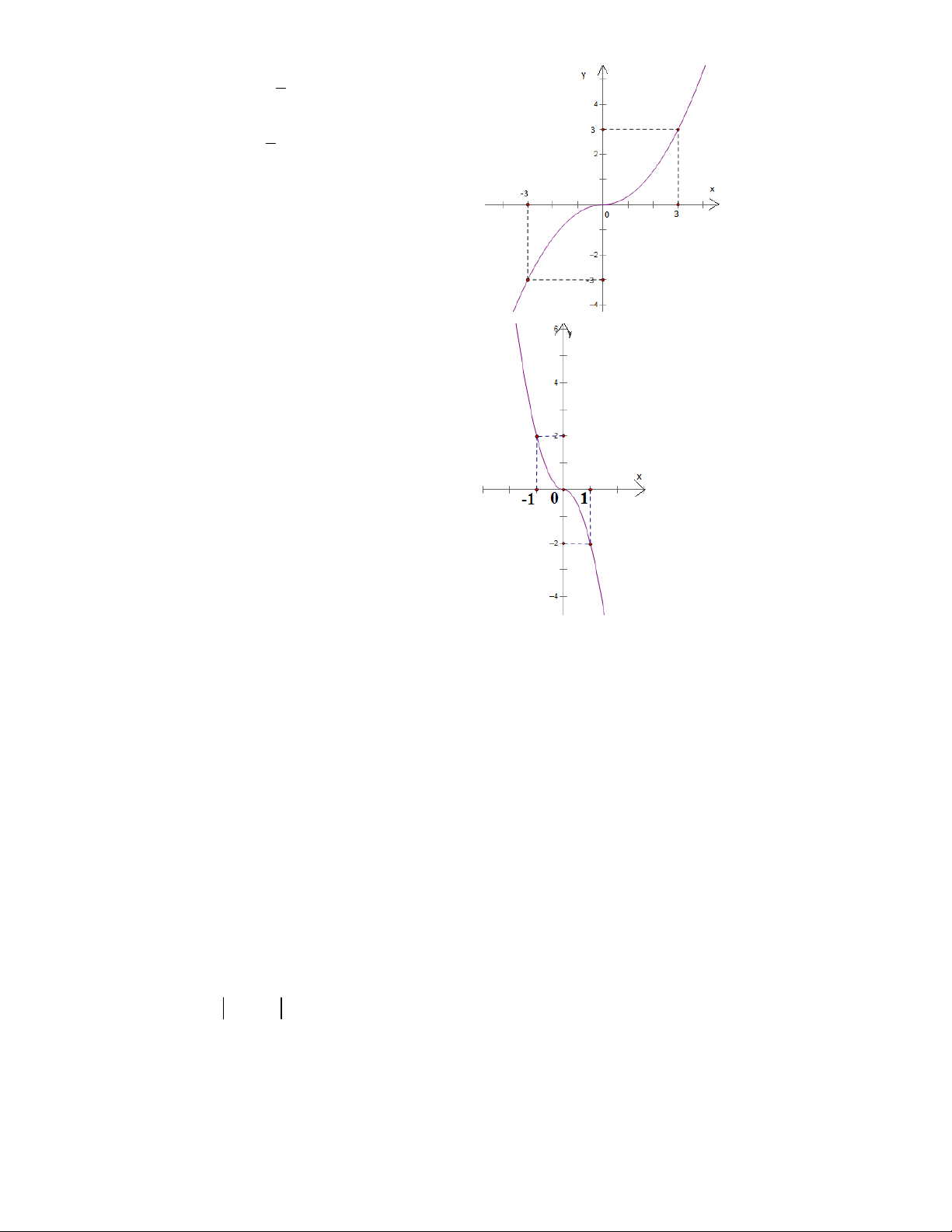
Câu 19. Hình vẽ dưới đây là của đồ thị hàm số nào? A. 2 y = x - . B. 2 y = x . C. 2 y = 2x . D. 2 y = -2x .
Câu 20. Hình vẽ dưới đây là của đồ thị hàm số nào? 1 1 A. 2 y = x . B. 2 y = x . C. 2 y = 3x . D. 2 y = x . 2 3 Câu 21. Cho hàm số 2
y = 3x có đồ thị là (P) . Có bao nhiêu điểm trên (P) có tung độ gấp đôi hoành độ. A. 5 . B. 4 . C. 3 . D. 2 . 2 Câu 22. Cho hàm số 2
y = - x có đồ thị là (P) . Điểm trên (P) (khác gốc tọa độ O(0; 0) ) có tung độ 5
gấp ba lần hoành độ thì có hoành độ là: 15 -15 2 2 A. . B. . C. . D. - . 2 2 15 15 1 1 Câu 23. Cho 2
(P) : y = x ;(d) : y = x - . Tìm tọa độ giao điểm của (P) d 2 2 và ( ) æ 1ö æ1 ö A. 1 çç ; ÷÷ ç ÷ ç
. B. (1;2). C. ç ;1÷. D. (2;1). çè 2÷÷ø çè2 ÷÷ø Câu 24. Cho 2
(P) : y = 3x ;(d) : y = 4
- x - 1. Tìm tọa độ giao điểm (P) và (d)
15. TOÁN HỌC SƠ ĐỒ ‐ THCS.TOANMATH.com æ1 1ö æ1 1ö æ 1 1ö æ 1 1ö A. çç ; ÷ - ÷;(1;3) ç ÷ ç ÷ ç ÷ ç . B. ç ; ÷;(1;3). C. - ç ; ÷;(-1; 3) . D. - ç ; ÷ . çè3 3÷÷ø çè3 3÷÷ø çè 3 3÷÷ø çè 3 3÷÷ø 1 Câu 25. Cho parabol . 2
y = x Xác định m để điểm (
A 2;m) nằm trên parabol. 4 1 1 A. m = . B. m = - . C. m = 2 . D. m = -2 . 2 2 Câu 26. Cho parabol 2
y = - 5x . Xác định m để điểm A(m 5;-2 5) nằm trên parabol. 5 2 5 2 A. m = - . B. m = . C. m = . D. m = - . 2 5 2 5 Câu 27. Cho parrabol 2
(P) : y = (m - 1)x và đường thẳng (d) : y = 3 - 2x . Tìm m để đường thẳng
d cắt (P) tại điểm có tung độ y = 5 . A. m = 5 . B. m = 7 . C. m = 6 . D. m = -6 . Câu 28. Cho parrabol 2
(P) : y = 5m + 1.x và đường thẳng (d) : y = 5x + 4 . Tìm m để đường
thẳng d cắt (P) tại điểm có tung độ y = 9 . A. m = 5 . B. m = 15 . C. m = 6 . D. m = 16 . æ1 2m ö - Câu 29. Cho parrabol ç ÷ 2 (P) : y = ç ÷.x ç
và đường thẳng (d) : y = 2x + 2 . Biết đường thẳng d çè m ÷÷ø cắt
(P) tại một điểm có tung độ y = 4 . Tìm hoành độ giao điểm còn lại của d và parabol (P) 1 1 1 1 A. x = - . B. x = . C. x = - . D. x = . 2 2 4 4 æ 7ö Câu 30. Cho parrabol ç ÷ 2
(P) : y = ç 3m + 4 - ÷x ç
và đường thẳng (d) : y = 3x - 5 . Biết đường çè 4÷÷ø thẳng d cắt
(P) tại một điểm có tung độ y = 1. Tìm m và hoành độ giao điểm còn lại của d và parabol (P) 1
A. m = 0;x = 2 .
B. m = ;x = -10 . C. m = 2;x = 8 .
D. m = 0;x = 10 . 4
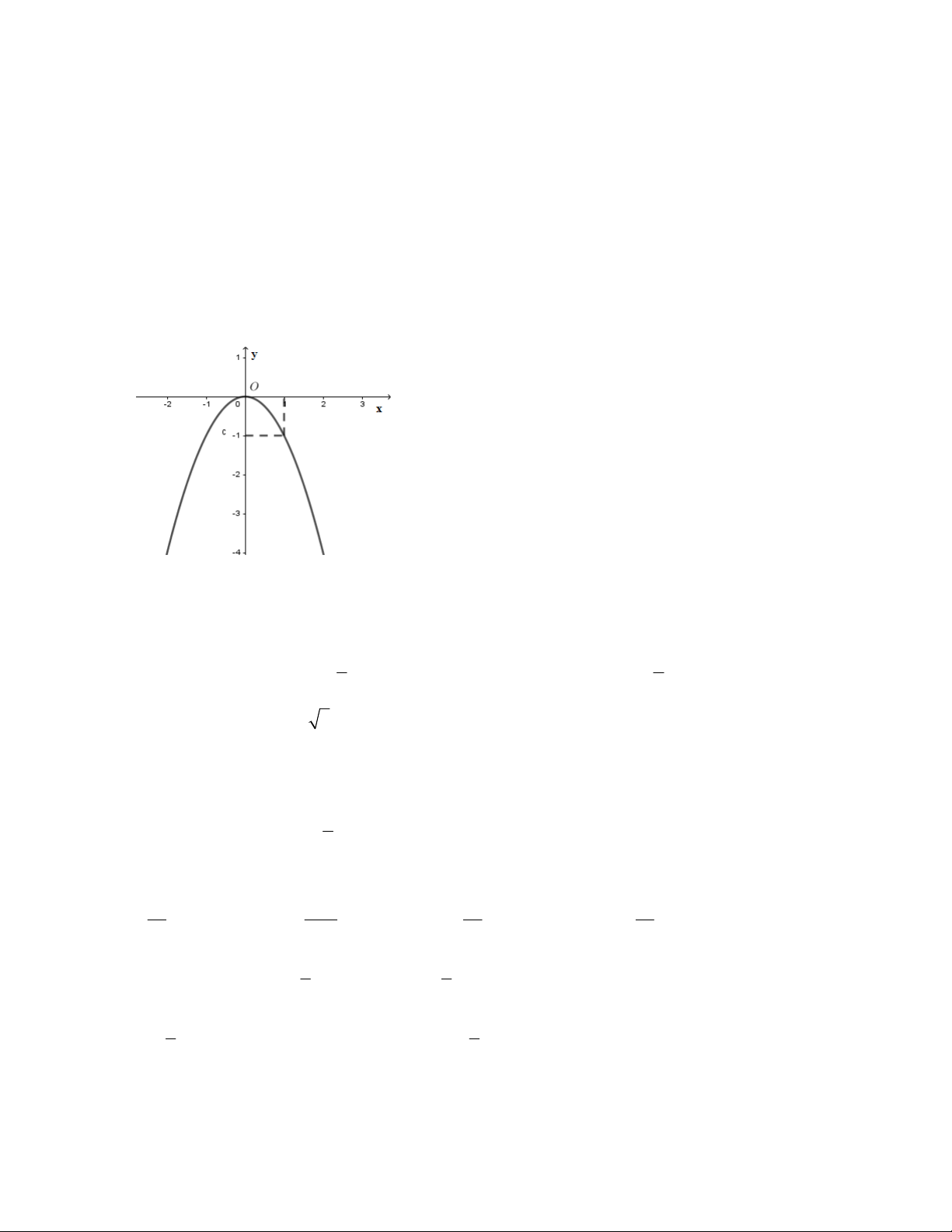
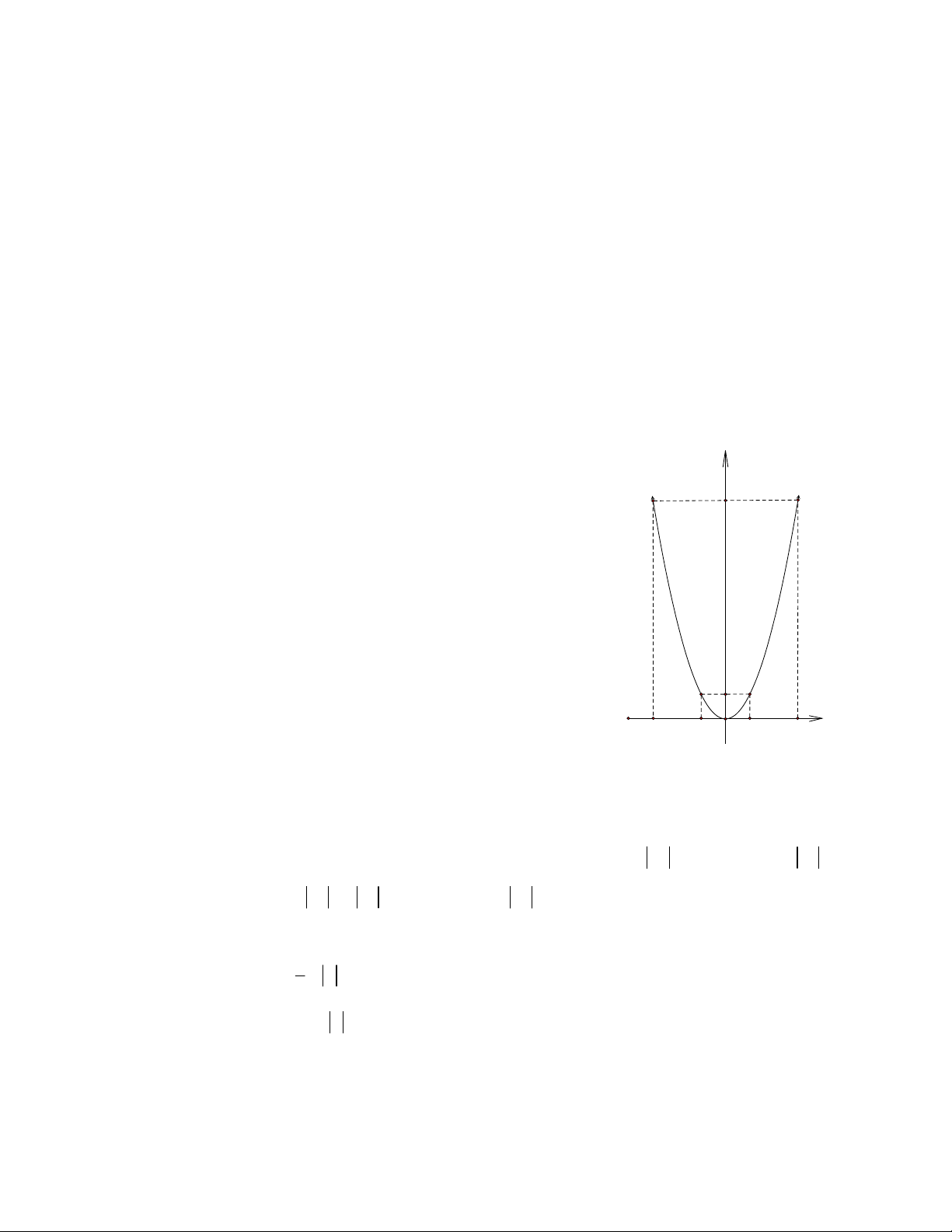
Câu 31. Cho đồ thị hàm số 2
y = 2x như hình vẽ. Dựa vào đồ thị, tìm m để phương trình 2
2x - m - 5 = 0 có hai nghiệm phân biệt.
16. TOÁN HỌC SƠ ĐỒ ‐ THCS.TOANMATH.com A. m < -5 . B. m > 0 . C. m < 0 . D. m > -5 . HƯỚNG DẪN Câu 1. Đáp án C. Cho hàm số 2
y = ax (a ¹ 0)
a) Nếu a > 0 thì hàm số nghịch biến khi x < 0 và đồng biến khi x > 0
b) Nếu a < 0 thì hàm số đồng biến khi x < 0 và nghịch biến khi x > 0 . Câu 2. Đáp án B. Cho hàm số 2
y = ax (a ¹ 0)
a) Nếu a > 0 thì hàm số nghịch biến khi x < 0 và đồng biến khi x > 0
b) Nếu a < 0 thì hàm số đồng biến khi x < 0 và nghịch biến khi x > 0 . Câu 3. Đáp án B. Đồ thị của hàm số 2
y = ax (a ¹ 0) là một parabol đi qua gốc tọa độ O, nhận Oy là trục đối xứng (
O là đỉnh của parabol).
- Nếu a > 0 thì đồ thị nằm phía trên trục hoành, O, là điểm thấp nhất của đồ thị.
- Nếu a < 0 thì đồ thị nằm phía dưới trục hoành, O,là điểm cao nhất của đồ thị. Câu 4. Đáp án D. Thay x = 2 - vào hàm số 2
y = f (x) = -7x ta được f (- ) 2 = -7.(-2 2 ) = -28 . 0 Câu 5. Đáp án A. 4 Thay x = 5 - vào hàm số 2
y = f (x) = x ta được f (-5) = 45.(- 2 ) 5 = 20 0 5 Câu 6. Đáp án A. Thay tọa độ điểm (
A -2; 4) vào hàm số 2
y = f (x) = (-2m + 1)x ta được 2
(-2m + 1).(-2) = 4  -2m + 1 = 1  m = 0
Vậy m = 0 là giá trị cần tìm. Câu 7. Đáp án C.
17. TOÁN HỌC SƠ ĐỒ ‐ THCS.TOANMATH.com 2m - 3
Thay tọa độ điểm B(-3;5) vào hàm số 2
y = f (x) = x ta được 3 2m - 3 7 7 2
.(-3) = 5  3(2m - 3) = 5  6m - 9 = 5  6m = 14  m = Vậy m = là giá trị 3 3 3 cần tìm. Câu 8. Đáp án A. 2
Để hàm số nghịch biến với mọi x > 0 thì a < 0 nên 5m + 2 < 0  m < - . 5 2
Vậy m < - thỏa mãn điều kiện đề bài. 5 Câu 9. Đáp án B. m - 7
Để hàm số nghịch biến với mọi x < 0 thì a > 0 nên
> 0  m - 7 < 0  m < 7 -3
Vậy m < 7 thỏa mãn điều kiện đề bài Câu 10. Đáp án C. 4
Để hàm số đồng biến với mọi x > 0 thì a > 0 nên 4 - 3m > 0  m < 3 4
Vậy m < thỏa mãn điều kiện đề bài 3 Câu 11. Đáp án A.
Để hàm số đồng biến với mọi x < 0 thì a < 0 nên 2 5 5
< 0  5 - 2m < 0  2m > 5  m > . Vậy m > thỏa mãn điều kiện đề bài 5 - 2m 2 2 Câu 12. Đáp án D. +) Thay tọa độ điểm (1 A ;2) vào hàm số 2 y = x - ta được 2
2 = -1 (vô lý) nên A Ï (P) .
+) Thay tọa độ điểm C (10;-200) vào hàm số 2 y = x - ta được 2 -200 = ( - 10)  -200 = -100 (
vô lý) nên loại C Ï (P)
+) Thay tọa độ điểm D ( 10;-1 ) 0 vào hàm số 2 y = x - ta được - = -( )2 10 10  10 - = 10 - (
luôn đúng) nên D Î (P)
+) Thay tọa độ điểm B(-1;-1) vào hàm số 2 y = x - ta được 2 -1 = (
- -1)  -1 = -1 (luôn đúng) B Î (P) Câu 13. Đáp án C.
18. TOÁN HỌC SƠ ĐỒ ‐ THCS.TOANMATH.com b é £ -1 Ta có 2 2
f (b) ³ 6b + 9  3b ³ 6b + 9  b - 2b - 3 ³ 0 . Vậy ê là giá trị cần tìm. b ê ³ 3 êë Câu 14. Đáp án D.
Ta có f b £ - b +  - 2 b £ - b +  2 ( ) 5 2 2 5 2 2b - 5b + 2 ³ 0  2
2b - 4b - b + 2 ³ 0  2 (
b b - 2) - (b - 2) ³ 0  (2b - 1) (b - 2) ³ 0 éìï 1 é ï ê 2 ìï -1 ³ 0 b b ï ³ ï ï ê êí 2 í ê êï b é ³ 2 b ï - 2 ³ 0 ê ê b ï ³ 2 ê ïî ï Vậy î  ê  ê  ê 1 . ê 2 ìï b -1 £ 0 ì êï 1 b ê £ ï ê ê b ï í ï £ ê ï ë 2 ê b ï - 2 £ 0 êí 2 ï êî ë b ï êï £ 2 êïîë é 1 b ê £ Vậy ê 2 là giá trị cần tìm. êbê ³ 2 ë Câu 15. Đáp án D. x ìï - y = 1 x ìï = y + 1 x ìï = 2 Ta có ï ï ï í  í  í  A 2; ( 1) 2 ï x - y = 3 2 ï (y + ) 1 - y = 3 y ï = 1 ïî ïî ïî
Thay x = 2;y = 1 vào hàm số 2
y = (2m + 2)x ta được 1 -7 -7 2
1 = (2m + 2).2  2m + 2 =  2m =  m = 4 4 8 7
Vậy m = - là giá trị cần tìm. 8 Câu 16. Đáp án B. 4 ìï x - 3y = -2 x ìï = 2y - 3 x ìï = 2y - 3 y ìï = 2 Ta có: ï ï ï ï í  í  í  í  A 1; ( 2) x ï - 2y = -3 4 ï 2
( y - 3) - 3y = -2 5 ï y = 10 x ï = 1 ïî ïî ïî ïî
Thay x = 1;y = 2 vào hàm số 2
y = (-3m + 1)x ta được -1 2
2 = (-3m + 1).1  -3m + 1 = 2  -3m = 1  m = 3 1
Vậy m = - là giá trị cần tìm. 3 Câu 17. Đáp án B. Ta thấy hàm số 2 2 y = ( m - + 4m - 5)x có 2 2 2 a = m - + 4m - 5 = (
- m - 4m + 4) - 1 = ( - m - 2) - 1 £ 1 - < 0,"m
19. TOÁN HỌC SƠ ĐỒ ‐ THCS.TOANMATH.com
Nên hàm số đồng biến khi x < 0 và nghịch biến khi x > 0 . Suy ra C,D sai.
Và đồ thị hàm số nằm phía dưới trục hoành, O là điểm cao nhất của đồ thị. Suy ra A sai. Câu 18. Đáp án C. Ta thấy hàm số 2 2
y = (4m + 12m + 11)x có 2 2 2
a = 4m + 12m + 11 = (4m + 12m + 9) + 2= (2m + 3) + 2 ³ 2 > 0,"m
Nên hàm số đồng biến khi x > 0 và nghịch biến khi x < 0 . Suy ra C sai, D đúng.
Và đồ thị hàm số nằm phía trên trục hoành, O là điểm thấp nhất của đồ thị. Câu 19. Đáp án A.
Từ hình vẽ suy ra a < 0 nên loại B,C
Vì đồ thị đi qua điểm có tọa độ (1;-1) nên loại D. Câu 20. Đáp án D.
Từ hình vẽ ta thấy đồ thị đi qua điểm có tọa độ (3; 3) , ta thay x = 3;y = 3 vào từng hàm số ở các đáp án ta được: + Đáp án A: 2 2
y = x  3 = 3  3 = 9 (vô lý) nên loại A. 1 1 9 + Đáp án B: 2 2
y = x  3 = 3  3 = (vô lý) nên loại B. 2 2 2 + Đáp án C: 2 2
y = 3x  3 = 3.3  3 = 27 (vô lý) nên loại C. 1 1 + Đáp án D: 2 2
y = x  3 = .3  3 = 3 (luôn đúng) nên chọn D. 3 3 Câu 21. Đáp án D.
Gọi điểm M(x;y) là điểm cần tìm.
Vì M có tung độ gấp đôi hoành độ nên M(x;2x) Thay tọa độ điểm M vào hàm số ta được
éx = 0  y = 0 ê 2 2x = 3x  êê 2 3 4 3 x =  y = ê ë 3 3 æç2 3 4 3ö÷
Hay có hai điểm thỏa mãn điều kiện là O(0;0),M ç ; ÷ ç ÷ ç 3 3 ÷÷ è ø Câu 22. Đáp án B.
Gọi điểm M(x;y) là điểm cần tìm. Vì M có tung độ gấp ba lần hoành độ nên M(x; 3x)
Thay tọa độ điểm M vào hàm số ta được
20. TOÁN HỌC SƠ ĐỒ ‐ THCS.TOANMATH.com x é = 0  y = 0 2 2 æ2 ö ê 2 2
3x = - x x + 3x = 0  x çç x + 3÷÷ = 0 ê ç ÷ 15 45 5 5 çè5 ÷ø x ê = -  y = - êë 2 2 æ 15 45ö - -
Hay điểm khác gốc tọa độ thỏa mãn điều kiện là M çç ; ÷÷ ç çè 2 2 ÷÷ø Câu 23. Đáp án A.
Xét phương trình hoành độ giao điểm của parabol (P) và đường thẳng (d) 1 1 2 x = x -  2
x - 2x + 1 = 0  (x - 2
1) = 0  x - 1 = 0  x = 1 2 2 1 1 1
Thay x = 1 vào hàm số 2
y = x ta được 2 y = .1 = 2 2 2 æ 1ö
Nên tọa độ giao điểm cần tìm là 1 çç ; ÷÷ ç çè 2÷÷ø Câu 24. Đáp án C.
Xét phương trình hoành độ giao điểm của parabol (P) và đường thẳng (d) 2 2
3x = -4x - 1  3x + 4x + 1 = 0 2
 3x + 3x + x + 1 = 0 3x(x + 1) + x + 1 = 0 é 1 1 é 2 3x + 1 = 0 x
ê = -  y = 3x =  3
( x + 1)(x + 1) = 0 ê   ê ê 3 3 x + 1 = 0 ê 2 êë x
ê = -1  y = 3x = 3 ë æ 1 1ö
Nên tọa độ giao điểm cần tìm là ç- ç ; ÷÷;( 1 - ;3) ç çè 3 3÷÷ø Câu 25. Đáp án A. 1 1
Thay x = 2;y = m vào hàm số 2
y = x ta được m = ( )2 1 1 . 2 = . Vậy m = 4 4 2 2 Câu 26. Đáp án D.
Thay x = m 5;y = -2 5 vào hàm số 2
y = - 5x ta được 2 - = - (m )2 2 2 5 5.
5  -5m 5 = 2 5  m = - . Vậy m = - . 5 5 Câu 27. Đáp án C.
Thay y = 5 vào phương trình đường thẳng d
ta được 5 = 3 - 2x x = 1 -
21. TOÁN HỌC SƠ ĐỒ ‐ THCS.TOANMATH.com
Nên tọa độ giao điểm của đường thẳng d và parabol (P) là (-1;5) Thay x = -1;y = 5 vào hàm 2
số y = (m - 1)x ta được 2
(m - 1).(-1) = 5  m - 1 = 5  m = 6
Vậy m = 6 là giá trị cần tìm. Câu 28. Đáp án D. -1 ĐK: m > 5
Thay y = 9 vào phương trình đường thẳng d ta được 9 = 5x + 4  x = 1
Nên tọa độ giao điểm của đường thẳng và d parabol (P) là (1;9)
Thay x = 1;y = 9 vào hàm số 2
y = 5m + 1.x ta được 2
5m + 1.1 = 9  5m + 1 = 9  5m + 1 = 81  5m = 80  m = 16(TM ) Vậy m = 16 là giá trị cần tìm. Câu 29. Đáp án A.
Thay y = 4 vào phương trình đường thẳng d ta được 2x + 2 = 4  x = 1
Nên tọa độ giao điểm của đường thẳng d và parabol (P) là (1; 4) æ1 2mö -
Thay x = 1;y = 4 vào hàm số ç ÷ 2 y = ç ÷x ç ta được çè 2 ÷÷ø 1 - 2m 7 2 2
.1 = 4  1 - 2m = 8  m = -  (P) : y = 4x 2 2
Xét phương trình hoành độ giao điểm của d và : (P) éx = ê 1 2 4x = 2x + 2  2
2x - x - 1 = 0  2
( x + 1)(x - 1) = 0  ê ê 1 x = - êë 2 1
Vậy hoành độ giao điểm còn lại là x = - . 2 Câu 30. Đáp án D.
Thay y = 1 vào phương trình đường thẳng d ta được 3x - 5 = 1  x = 2
Nên tọa độ giao điểm của đường thẳng và d parabol
(P) là (2;1) Thay x = 2;y = 1 vào hàm æ 7ö số ç ÷ 2
y = ç 3m + 4 - ÷x ç ta được çè 4÷÷ø æ 7ö ç ÷ 7 1 2
ç 3m + 4 - ÷.2 = 1  3m + 4 - =  3m + 4 = 2 çè 4÷÷ø 4 4
 3m + 4 = 4  m = 0  (P) 1 2 : y = x 4
22. TOÁN HỌC SƠ ĐỒ ‐ THCS.TOANMATH.com
Xét phương trình hoành độ giao điểm của d và : (P) 1 x é = 2 2 2 x 3x 5 x 12x 20 0 (x 2)(x ) 10 0 ê = -  - + =  - - =  4 x ê = 10 êë
Vậy hoành độ giao điểm còn lại là x = 10 . Câu 31. Đáp án D. 2 Ta có 2
2x - m - 5 = 0 (*)  2x = m + 5
Số nghiệm của phương trình (*) là số giao điểm của parabol 2
(P) : y = 2x đường
thẳng d : y = m + 5 .
Để (*) có hai nghiệm phân biệt thì d cắt (P) tại hai điểm phân biệt. Từ đồ thị hàm số ta thấy
Với m + 5 > 0  m > -5 thì d cắt (P) tại hai điểm phân biệt hay phương trình (*) có hai
nghiệm phân biệt khi m > -5 .
D.PHIẾU BÀI TỰ LUYỆN Ở NHÀ 3  2 
Bài 1:Cho hàm số y f x 2
x . Hãy tính f 2; f 3 ; f  5; f   2  3    4 Bài 2: Cho hàm số 2
y  f (x)  ax .Biết rằng khi x  2  thì y  . Tìm hệ số a 3
Bài 3: Cho hàm số y m x2 ( 2) (m  2
 ) . Tìm giá trị của m để:
a) Hàm số đồng biến với x  0 .
b) Có giá trị y  4 khi x  1  .
Bài 4:Cho hàm số      2 y 1 m 1 x
a) Tìm điều kiện để hàm số đồng biến khi x  0
b) Tìm điều kiện để hàm số nghịch biến khi x  0  9 Bài 5 :Cho hàm số 2 
y  f (x)  ax có đồ thị (P) đi qua A 3  ;   .  4  a) Tính a.
b) Các điểm nào sau đây thuộc (P): B( 3  2; 4); C( 2  3; 3) . Bài 6 :Cho hàm số 2 2
y  (m  2m  3)x Chứng tỏ rằng hàm số nghịch biến với mọi x  0 . Bài 7:Cho hàm số 2 2 y  (m  6m 12)x .
a) Chứng tỏ rằng hàm số nghịch biến trong khoảng ( 2
 005;0) , đồng biến trong khoảng (0;2005)
b) Khi m  2 .Tìm x để y = 8
23. TOÁN HỌC SƠ ĐỒ ‐ THCS.TOANMATH.com
Bài 8: Cho hàm số y f x x2 ( )
. Tìm a  R sao cho f (a 1)  4 .
Bài 9: Cho hình lập phương có cạnh bằng x cm. Gọi S là diện tích toàn phần của hình lập phương a) Tính S theo x
b) S thay đổi như thế nào khi x tăng, khi x giảm?
c) Khi x tăng 3 lần thì S tăng hay giảm mấy lần? 75 Bài 10: Cho hàm số 2
y  f (x)  ax .Biết rằng khi x  5 thì y 
.Tìm giá trị nhỏ nhất và giá trị lớn 2
nhất của y khi x thõa mãn điều kiện 4   x  2 1 Bài 11: Cho hàm số 2
y  f (x)  x .Biết f (x )  f (x ) .Hãy so sánh x và x trong các trường hợp 3 1 2 1 2 sau :
a) x , x là những số dương . 1 2
b) x , x là những số âm . 1 2 Bài 12: Cho hàm số 2 y  f (x)  2
 x ..Chứng minh rằng với mọi giá trị của x thõa mãn điều kiện
3  x  1 ta điều có 2 f ( 3  )  2  x  f ( 1
 ) .Suy ra rằng x biến đổi thõa mãn điều kiện 3  x  1 thì
y có giá trị bé nhất là 18 và giá trị lớn nhất là 2
Bài 13: Cho hàm số    2 y f x ax
a)Hãy xác định hàm số biết rằng đồ thị của nó đi qua điểm A2;4 .
b)Vẽ đồ thị của hàm số đã cho .
c)Tìm các điểm trên Parabol có tung độ bằng 16.
d)Tìm m sao cho B  3 ;
m m  thuộc Parabol.
d)Tìm các điểm trên Parabol (khác gốc tọa độ) cách đều hai trục tọa độ. Bài 14: 1
a) Vẽ đồ thị hàm số y  x. x 3
b) Vẽ đồ thị hàm số y  2  x. x
Bài 15: Trên mặt phẳng tọa độ Oxy cho đường thẳng d  : y  x  6 và parabol P 2 : y x .
a)Tìm tọa độ các giao điểm của d  và P . b)Gọi ,
A B là hai giao điểm của d  và P . Tính diện tích tam giác OAB . Bài 16:
24. TOÁN HỌC SƠ ĐỒ ‐ THCS.TOANMATH.com
a)Xác định điểm M thuộc đường Parabol P 2
: y x sao cho độ dài đoạn IM là nhỏ nhất, trong đó I 0;  1 .
b)Giả sử điểm A chạy trên Parabol P 2
: y x . Tìm tập hợp trung điểm J của đoạn OA .
Bài 17: Trong mặt phẳng tọa độ Oxy , cho hai điểm A và B chạy trên parabol P 2
: y x sao cho ,
A B O0;0 và OA OB . Giả sử I là trung điểm của đoạn AB .
a) Tìm quỹ tích điểm trung điểm I của đoạn AB .
b) Đường thẳng AB luôn luôn đi qua một điểm cố định.
c) Xác định tọa độ điểm A và B sao cho độ dài đoạn AB nhỏ nhất.
Bài 18: Trong mặt phẳng tọa độ Oxy cho Parabol P 2
: y x , trên P lấy hai điểm A 1  ;  1 , B3;9
a)Tính diện tích tam giác OAB .
b)Xác định điểm C thuộc cung nhỏ AB của P sao cho diện tích tam giác ABC lớn nhất.
Bài 19: Một xe tải có chiều rộng là 2,4 m chiều cao là 2,5 m muốn đi qua một cái cổng hình Parabol.
Biết khoảng cách giữa hai chân cổng là 4m và khoảng cách từ đỉnh cổng tới mỗi chân cổng là 2 5 m
(Bỏ qua độ dày của cổng).
a)Trong mặt phẳng tọa độ Oxy gọi Parabol P 2
: y ax với a  0 là hình biểu diễn cổng mà xe tải
muốn đi qua. Chứng minh a  1 .
b)Hỏi xe tải có đi qua cổng được không? Tại sao? HƯỚNG DẪN 3 3 3 3 27
Bài 1: Ta có: f  2    . 2
 2  .4  6 ; f 3 2  .3  .9  ; 2 2 2 2 2 2  2  3  2  3 2 1 f     2 3 3 15 5 . 5  .5  ; f     .    .  2 2 2  3  2  3  2 9 3     4  4 4 1
Bài 2: Thay x  2 ; y  vào hàm số 2 y  f (x)  ax có 2 a.(2)   4a   a  3 3 3 3
Bài 3:Cho hàm số y m x2 ( 2) (m  2
 ) . Tìm giá trị của m để:
a) Tìm điều kiện để hàm số đồng biến khi x  0
Để hàm số đồng biến khi x < 0
m  2  0  m  2 
Vậy để hàm số đồng biến khi x  0 thì m  2
b) Thay y  4; x  1 vào hàm số y m x2 ( 2) (m  2  ) ta có :
25. TOÁN HỌC SƠ ĐỒ ‐ THCS.TOANMATH.com 2 4  (m  2)(1)  m  2
Vậy khi m  2 thì hàm số giá trị y  4 khi x  1  .
Bài 4: Hàm số      2 y 1
m 1 x (ĐK: m  1; m  2 )
a) Tìm điều kiện để hàm số đồng biến khi x  0
Để hàm số đồng biến khi x < 0
 1 m 1  0  m 1 1  m 1 1  m  2
Vậy để hàm số đồng biến khi x < 0  m  2
b) Tìm điều kiện để hàm số nghịch biến khi x  0
Để hàm số nghịch biến khi x  0
 1 m 1  0  m 1 1  m 11  m  2
Vậy để hàm số nghịch biến khi x  0  1 m  2 Bài 5:  9 a) Đồ thị (P) đi qua  9 1 A 3  ;   
a32  a  .  4  4 4 b) Thay B  3
 2;4 vào (P) ta được:   2 1 9 4 3 2  4  (vô lý) 4 2 Vậy B không thuộc (P). Thay C  2
 3;3 vào (P) ta được:   2 1 3 2 3  3  3 (đúng) 4 Vậy C thuộc (P). Bài 6: Hàm số đã cho có dạng 2 y  ax , 2      2    2 a m 2m 3 m
2m 1  2  (m 1)  2  0 với mọi m
Do đó : Hàm số đã cho nghịch biến với mọi x  0 Bài 7: a) hàm số 2 2 y  (m  6m 12)x . 2 2 y  (m  6m 12)x 2 2  (m  3)  3 x   Vì 2
a  (m  3)  3  0  
với mọi x nên trong khoảng (2005;0) thì x  0 , do đó hàm số nghịch biến,
trong khoảng (0; 2005) thì x  0 , do đó hàm số nghịch biến. b) Với m  2 , ta có 2 y  4x
26. TOÁN HỌC SƠ ĐỒ ‐ THCS.TOANMATH.com 2
y  8  4x  8  x   2 Bài 8 : f (a 1)  4 Ta có  (a  2
1)  4  a2  2a  3  0
 (a 1)(a  3)  0  a  1  hoặc a  3 Vậy với a  1
 hoặc a  3 thì hàm số y f x x2 ( )
có f (a 1)  4 . Bài 9:
a) Mỗi hình lập phương là một hình vuôngvới cạnh có độ dài bằng x cm nên diện tích mỗi mặt là 2 2
x (cm ) .Vì hình lập phương có 6 mặt bằng nhau nên 2 2 S  6x (cm ) b) 2
S  6x là một hàm số có dạng 2
y  ax , với a  6  0 . Hàm số này đồng biến khi x  0 . Vì x là độ
dài nên x  0 . Do đó khi x tăng thì S cũng tăng , x giàm thì S cũng giảm
c) Giả sử cho x là độ dài của cạnh hình lập phương .Khi đó S có giá trị tương ứng là 2 S  6x .Khi 1 1 1
cạnh tăng lên 3 lần , đặt 2 2 2 2
x  3x  S  6x  6(3x )  6.9x  9.6x  9S . Vậy khi x tăng lên 3 2 1 2 2 1 1 1 1
lần thì S tăng lên 9 lần . 75 Bài 10: Cho hàm số 2
y  f (x)  ax .Biết rằng khi x  5 thì y 
.Tìm giá trị nhỏ nhất và giá trị lớn 2
nhất của y khi x thõa mãn điều kiện 4  x  2 75 75 3 Thay x  5 ; y  vào hàm số 2 y  f (x)  ax ta có : 2 a.5   a  2 2 2 3 Vì a 
 0 nên y  0 là giá trị nhỏ nhất của hàm số và hàm số nghịch biến khi x  0 , đồng biến khi 2 3
x  0 , do đó khi 4  x  2 thì 2 f (4)  ( 4
 )  24  f (x)  f (0)  0 và khi 0  x  2 thì 2 3 2
0  f (0)  f (x)  f (2)  .2  6 2
Vậy khi x biến đổi , thõa mãn 4  x  2 thì giá trị nhỏ nhất của y bằng 0 và giá trị lớn nhất của y bằng 24 . 1
Bài 11: Vì a   0 nên hàm số nghịch biến khi x  0 và đồng biến khi x  0 .Vậy 3
+ Khi x , x cùng dương thì f (x )  f (x )  x  x 1 2 1 2 1 2
+ Khi x , x cùng âm thì f (x )  f (x )  x  x 1 2 1 2 1 2
27. TOÁN HỌC SƠ ĐỒ ‐ THCS.TOANMATH.com Bài 12: Cho hàm số 2 y  f (x)  2
 x ..Chứng minh rằng với mọi giá trị của x thõa mãn điều kiện 3   x  1  ta điều có 2 f ( 3  )  2  x  f ( 1  ) Vì a  2
  0 nên hàm số đồng biến khi x  0 .Do đó
f (3)  f (x)  f (1) hay 2 2 2(  3  )  f (x)  2(  1  ) 2  18  2x  2
Vậy khi x biến đổi thõa mãn điều kiện 3   x  1
 thì y có giá trị bé nhất là 18
 và giá trị lớn nhất là 2 
Bài 13: Cho hàm số    2 y f x ax
a)Hãy xác định hàm số biết rằng đồ thị của nó đi qua điểm A2;4 .
b)Vẽ đồ thị của hàm số đã cho .
c)Tìm các điểm trên Parabol có tung độ bằng 16.
d)Tìm m sao cho B  3 ;
m m  thuộc Parabol.
e)Tìm các điểm trên Parabol (khác gốc tọa độ) cách đều hai trục tọa độ. y Lời giải: 9
a) Ta có AP 2  4  . a 2  a  1 y=x2
b) Đồ thị Parabol có đỉnh là gốc tọa độ
O0;0 quay bề lồi xuống dưới, có trục
đối xứng là Oy đi qua các điểm M 1;  1 , N  1  ; 
1 , E 3;9, F  3  ;9 1
c) Gọi C là điểm thuộc P có tung độ bằng 16. -3 -1 O 1 3 x Ta có: 2 y  16  x
 16  x  4 . Vậy C 4;16 hoặc C  4;  16 . C C C
d) Thay tọa độ điểm B vào P ta được: 3 2 3 2 2
m m m m  0  m m  
1  0  m  0 hoặc m  1.
e) Gọi D là điểm thuộc P cách đều hai trục tọa độ. Ta có: d D Ox 2 ,
y x ;d D,Oy x . D DD Theo giả thiết ta có: 2
x x x  0 (loại) hoặc x  1. Vậy D1;  1 hoặc D 1;   1 . D D D D Bài 14: 1
a) Vẽ đồ thị hàm số y  x. x 3
b) Vẽ đồ thị hàm số y  2  x. x Lời giải:
28. TOÁN HỌC SƠ ĐỒ ‐ THCS.TOANMATH.com 1 a) Với x  0 ⇒ 2 y  x 3 1 Với x  0 ⇒ 2 y   x 3 b) Với x  0 ⇒ 2 y  2  x Với x  0 ⇒ 2 y  2x
Bài 15: Trên mặt phẳng tọa độ Oxy cho đường thẳng d  : y  x  6 và parabol P 2 : y x .
a)Tìm tọa độ các giao điểm của d  và P . b)Gọi ,
A B là hai giao điểm của d  và P . Tính diện tích tam giác OAB . Lời giải:
a) Phương trình hoành độ giao điểm của P và d  là: 2 2
x  x  6  x x  6  0  x  2  x  3 
.Ta có y 2  4; y  3    9 .
Vậy tọa độ giao điểm của P và d  là B2;4 và A 3;  9 .
b) Gọi A', B ' lần lượt là hình chiếu của ,
A B xuống trục hoành. Ta có SSSSOAB AA'B 'B OAA' OBB  '
Ta có A' B '  x x x x  5; AA'  y  9; BB '  y  4 B' A' B' A' A B
29. TOÁN HỌC SƠ ĐỒ ‐ THCS.TOANMATH.com AA' BB ' 9  4 65 1 27 S  .A' B '  .5  (đvdt), SA' . A A'O  (đvdt) AA'BB ' 2 2 2 OAA' 2 2 65  27   SSSS    4  15 (đvdt). OABAA'B 'BOAA' OBB'   2  2  Bài 16 :
a) Xác định điểm M thuộc đường Parabol P 2
: y x sao cho độ dài đoạn IM là nhỏ nhất, trong đó I 0;  1 .
b) Giả sử điểm A chạy trên Parabol P 2
: y x . Tìm tập hợp trung điểm J của đoạn OA . Lời giải
a) Giả sử điểm M thuộc đường Parabol P 2
: y x suy ra M  2 ; m m  . Khi đó 2  1  3 3 3
IM m  m  2 2 2 2 4 2
1  m m 1. Vậy 2 IM m     
. Ta thấy IM nhỏ nhất bằng  2  4 2 2 2  2 1  khi m   hay M   ;  . 2  2 2   
b) Giả sử điểm A 2
a;a  thuộc P 2
: y x . Gọi I x ; y là trung điểm đoạn OA .Suy ra 1 1   a x   1  2  2 a  2 y   2x 1 1  2
Vậy tập hợp các trung điểm I của đoạn OA là đường Parabol P  2
: y  2x . 1
Bài 17 :Trong mặt phẳng tọa độ Oxy , cho hai điểm A và B chạy trên parabol P 2
: y x sao cho ,
A B O0;0 và OA OB . Giả sử I là trung điểm của đoạn AB .
a) Tìm quỹ tích điểm trung điểm I của đoạn AB .
b) Đường thẳng AB luôn luôn đi qua một điểm cố định.
c) Xác định tọa độ điểm A và B sao cho độ dài đoạn AB nhỏ nhất. Lời giải: a) Giả sử A 2
a;a  và B 2
b;b  là hai điểm thuộc P . Để ,
A B O0;0 và OA OB ta cần điều kiện: ab  0 và 2 2 2
OA OB AB hay ab  0 và       2 2 4 2 4   2 2 a a b b a b
a b 2 . Rút gọn hai
30. TOÁN HỌC SƠ ĐỒ ‐ THCS.TOANMATH.com
vế ta được: ab  1 . Gọi I x ; y là trung điểm đoạn AB . Khi đó: 1 1   a b x   1  2   a ba b2 2 2  2ab 2 y    2x 1 1 1  2 2
Vậy tọa độ điểm I thỏa mãn phương trình 2 y  2x 1.
Ta cũng có thể tìm điều kiện để OA OB theo cách sử dụng hệ số góc: Đường thẳng OA có hệ số 2 a 2 b góc là k
a , đường thẳng OB có hệ số góc là k
b . Suy ra điều kiện để OA OB là 1 a 2 b a.b  1 2 x a y a
b) Phương trình đường thẳng đi qua A và B là  AB :  hay 2 2 b a b a
AB: y  a bx ab  a bx 1. Từ đây ta dễ dàng suy ra đường thẳng AB: y  a bx 1
luôn luôn đi qua điểm cố định 0;  1 .
c) Vì OA OB nên ab  1 . Độ dài đoạn    2   2 2 AB a b
a b 2 hay 2 2 4 4 2 2
AB a b  2ab a b  2a b Áp dụng bất đẳng thức Cô si ta có 2 2 2 2
a b  2 a b  2 ab , 4 4 2 2
a b  2a b . Ta có: 2 2 2 2
AB  2 ab  2  2a b  2a b  2 . Vậy AB ngắn nhất bằng 2 khi 2 2
a b , ab  1
 . Ta có thể chỉ ra cặp điểm đó là: A 1  ;  1 và B1;  1 .
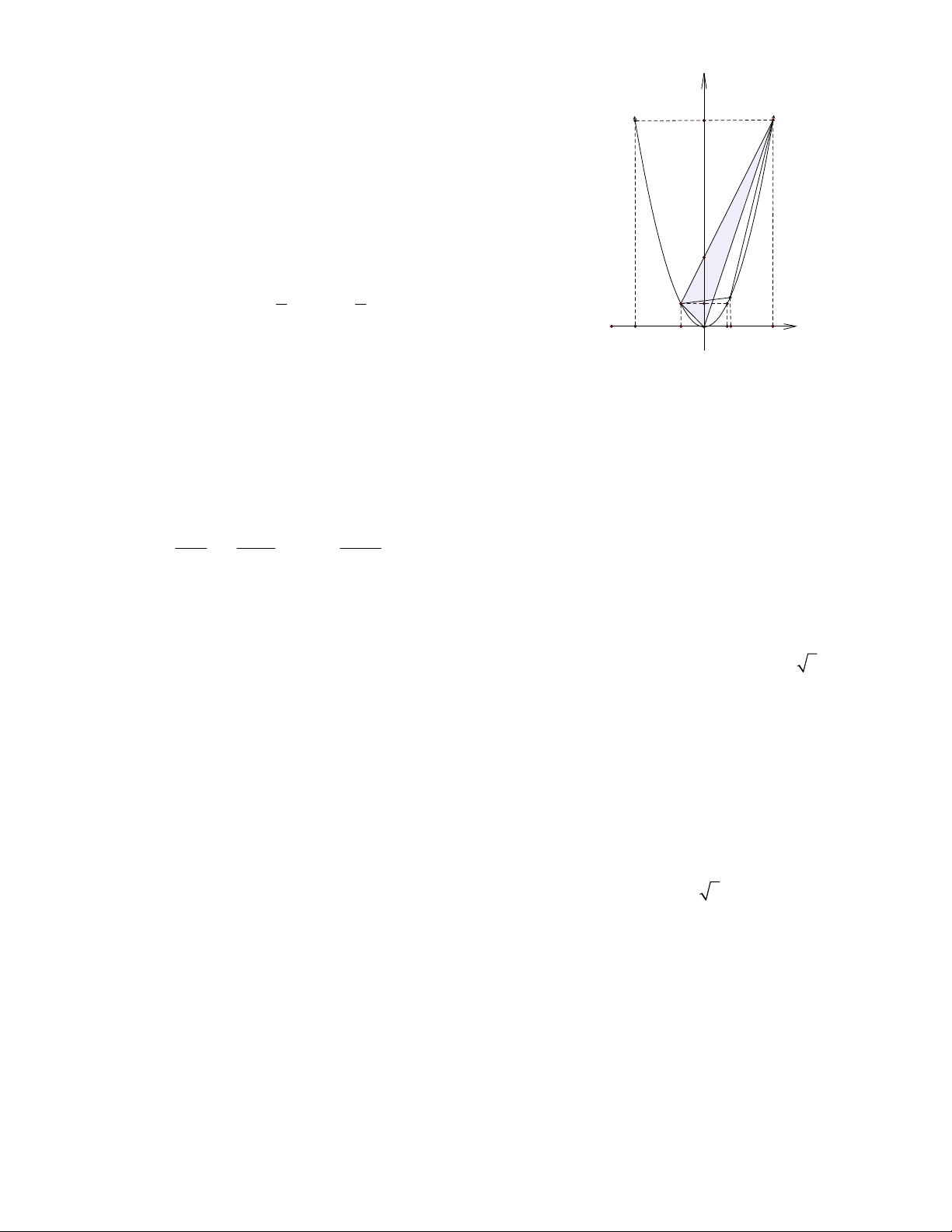
Bài 18 : Trong mặt phẳng tọa độ Oxy cho Parabol P 2
: y x , trên P lấy hai điểm A 1;   1 , B3;9 .
a)Tính diện tích tam giác OAB .
b)Xác định điểm C thuộc cung nhỏ AB của P sao cho diện tích tam giác ABC lớn nhất. Lời giải:
31. TOÁN HỌC SƠ ĐỒ ‐ THCS.TOANMATH.com
a) Gọi y ax b là phương trình đường thẳng AB . y  . a   1  b  1 a  2 9 Ta có    K B  .3 a b  9 b   3 y=x2
Suy ra phương trình đường thẳng AB là d  : y  2x  3.
Đường thẳng AB cắt trục Oy tại điểm I 0;3 .
Diện tích tam giác OAB là: I 1 1 SSS
AH.OI BK.OI . 1 C(c;c2) OAB OAI OBI A 2 2 H A' B' C' -3 -1 O 1 3 x
Ta có AH 1; BK  3,OI  3 . Suy ra S  6 (đvdt). OAB b) Giả sử C  2
c;c  thuộc cung nhỏ P với 1  c  3 .
Diện tích tam giác: SSSS . ABC ABB ' A' ACC ' A' BCC ' B '
Các tứ giác ABB' A', AA'C 'C,CBB'C ' đều là hình thang vuông nên ta có: 2 2 1 9 1 cc S   c  
c   c   . ABC   9 .4 . 1 .3  8 2 2 1 8 2 2 2
Vậy diện tích tam giác ABC lớn nhất bằng 8 (đvdt) khi C 1;  1 .
Bài 19: Một xe tải có chiều rộng là 2,4 m chiều cao là 2,5 m muốn đi qua một cái cổng hình Parabol.
Biết khoảng cách giữa hai chân cổng là 4m và khoảng cách từ đỉnh cổng tới mỗi chân cổng là 2 5 m(
Bỏ qua độ dày của cổng).
a)Trong mặt phẳng tọa độ Oxy gọi Parabol P 2
: y ax với a  0 là hình biểu diễn cổng mà xe tải
muốn đi qua. Chứng minh a  1 .
b)Hỏi xe tải có đi qua cổng được không? Tại sao? Lời giải:
a) Giả sử trên mặt phẳng tọa độ, độ dài các đoạn thẳng được tính theo đơn vị mét. Do khoảng cách
giữa hai chân cổng là 4 m nên MA NA  2m . Theo giả thiết ta có OM ON  2 5 , áp dụng định lý
Pitago ta tính được: OA  4 vậy M 2; 4  , N  2;  4   . Do M 2; 4
  thuộc parabol nên tọa độ điểm
M thỏa mãn phương trình: P 2 : y ax hay 2 4   . a 2  a  1  và P 2 : y  x .
b) Để đáp ứng chiều cao trước hết xe tải phải đi vào chính gi ữa cổng.
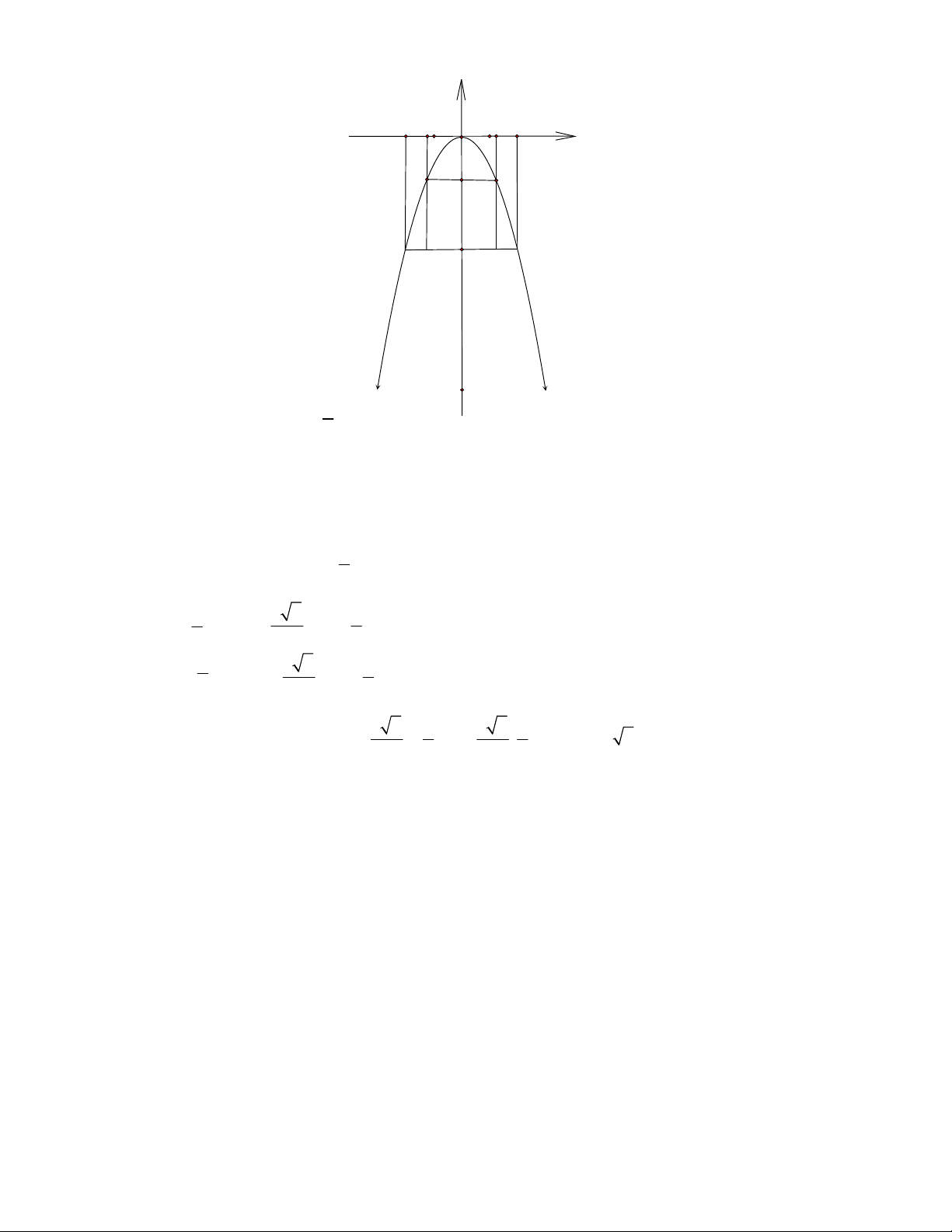
32. TOÁN HỌC SƠ ĐỒ ‐ THCS.TOANMATH.com y -2 2 O x B T H N M -4 A y=-x2
Xét đường thẳng d  3 : y   2
(ứng với chiều cao của xe). Đường
thẳng này cắt Parabol tại 2 điểm 2  y  x
có tọa độ thỏa mãn hệ:  3 y    2  3  3 2 3 2 x   x  ; y    2  2 2    3   y   3 2 3  x   ; y   2  2 2  3 2 3   3 2 3 
suy ra tọa độ hai giao điểm là T   ; ; H
;   HT  3 2  2,4  . 2 2   2 2     
Vậy xe tải có thể đi qua cổng.
----------Toán Học Sơ Đồ---------
33. TOÁN HỌC SƠ ĐỒ ‐ THCS.TOANMATH.com