














































































Preview text:
2
CHUYÊN ĐỀ PHƯƠNG TRÌNH BẬC HAI
VÀ ỨNG DỤNG HỆ THỨC VI-ÉT Lời nói đầu 1
Chủ đề 1. Phƣơng trình bậc hai một ẩn 4
1. Kiến thức cần nhớ 4
2. Bài tập vận dụng 5
Dạng 1. Giải phương trình bậc hai một ẩn 5
Dạng 2. Tìm điều kiện để phương trình bậc hai có nghiệm 6
Dạng 3. Nghiệm nguyên, nghiệm hữu tỷ của phương trình bậc hai 7
Dạng 4. Tìm giá trị của m để phương trình có hai nghiệm chung 10
Dạng 5. Chứng minh trong một hệ c{c phương trình bậc 2 có một phương trình 13 có nghiệm.
Dạng 6. Ứng dụng của phương trình bậc hai trong chứng minh bất đẳng thức và tìm GTNN và GTLN
Chủ đề 2. Khai thác các ứng dụng của định lý Vi-ét 17
A. Kiến thức cần nhớ 17
B. Các ứng dụng của định lý vi-et 17
Dạng 1: Giải phương trình bậc 2 bằng cách tính nhẩm nghiệm 17
Dạng 2: Tính giá trị biểu thức giữa các nghiệm của phương trình 18
Dạng 3. Tìm hia số khi biết tổng và tích 22
Dạng 4. Phân tích tam thức tam thức bậc hai thành nhân tử 24
Dạng 5. Tìm tham số để phương trình bậc hai có một nghiệm x = x1. Tìm nghiệm 25 thứ hai
Dạng 6. X{c định tham số để phương trình có nghiệm thỏa mãn một hệ điều 26 kiện cho trước
Dạng 7. Lập phương trình bậc hai khi biết hai nghiệm của nó hoặc hai nghiệm 30
của nó liên quan đến hai nghiệm của một phương trình đã cho
Dạng 8. Tìm hệ thức liên hệ giữa hai nghiệm của phương trình bậc hai, không 32 phụ thuộc vào tham số.
Dạng 9. Chứng minh hệ thức liên hệ giữa các nghiệm của phương trình bậc hai, 34
hoặc hai nghiệm của phương trình bậc 2.
Dạng 10. Xét dấu các nghiệm của phương trình bậc hai, so sách các nghiệm của 37
phương trình bậc hai với một số cho trước.
Dạng 11. Nghiệm chung của hai hay nhiều phương trình, hai phương trình 41 THCS.TOANMATH.com TÀI LIỆU TOÁN HỌC 3 tương đương
Dạng 12. Ứng dụng của hệ thức vi-et các bài toán số học 44
Dạng 13. Ứng dụng của hệ thức vi-et giải phương trình, hệ phương trình 46
Dạng 14. Ứng dụng hệ thức vi-ét chứng minh đẳng thức, bất đẳng thức, tìm 51 GTLN và GTNN
Dạng 15. Vận dụng định lý vi-et vào các bài toán hàm số 54
Dạng 16. Ứng dụng địng lý Vi-ét trong các bài toán hình học 57
Bài tập rèn luyện tổng hợp 60 Hƣớng dẫn giải 68
Bài tập không lời giải 98 THCS.TOANMATH.com TÀI LIỆU TOÁN HỌC 4
CHỦ ĐỀ 1. PHƢƠNG TRÌNH BẬC HAI MỘT ẨN
A/ KIẾN THỨC VÀ KỸ NĂNG CẦN NHỚ 1/ Định nghĩa:
Phương trình bậc 2 một ẩn l| phương trình có dạng: 2
ax bx c 0 trong đó x l| ẩn, a, b, c
l| c{c hệ số cho trước v| a ≠ 0.
2/ Giải phƣơng trình bậc 2.
2.1 Phương trình bậc 2 khuyết:
- Với c = 0 phương trình có dạng: x 0 2
ax bx 0 x ax c 0 c (a ≠ 0). x a
- Với b = 0 phương trình có dạng: 2 2 0 c ax c x * a
Điều kiện để phương trình có nghiệm l|: c c 0 0 (a v| c tr{i dấu) a ac 0
Với điều kiện trên ta có: * c x a
2.2 Giải phương trình bậc hai một ẩn đầy đủ bằng công thức nghiệm.
Phương trình bậc 2 một ẩn: 2
ax bx c 0 a 0 1 Xét biệt số: 2
b 4ac
+) Nếu 0 phương trình (1) vô nghiệm. b
+) Nếu 0 phương trình (1) có nghiệm kép: x x 1 2 2a b b
+) Nếu 0 phương trình (1) có hai nghiệm ph}n biệt x ; x . 1 2 2a 2a
Trường hợp: b 2b' ta có: 2
' b' ac . Khi đó:
+) Nếu ' 0 phương trình (1) vô nghiệm. b '
+) Nếu ' 0 phương trình (1) có nghiệm kép: x x 1 2 a b ' ' b ' '
+) Nếu 0 phương trình (1) có hai nghiệm ph}n biệt x ; x . 1 2 a a THCS.TOANMATH.com TÀI LIỆU TOÁN HỌC 5
2.3 Trường hợp đặc biệt có thể nhẩm nhanh nghiệm:
Phương trình bậc 2 một ẩn: 2
ax bx c 0 a 0
- Nếu a + b + c = 0 thì phương trình có nghiệm 1; c x x . 1 2 a
- Nếu a - b + c = 0 thì phương trình có nghiệm 1 ; c x x . 1 2 a
B/ BÀI TẬP VẬN DỤNG
1. Giải phƣơng trình bậc hai một ẩn
Thí dụ 1. Giải phương trình: 2
mx 2(m 3)x m 4 0 (m là tham số) (1)
a) Giải phương trình với m = 1.
b) Tìm m để phương trình có hai nghiệm phân biệt.
c) Tìm m để tập nghiệm của phương trình có một phần tử. Hƣớng dẫn giải a) Với m = 1 ta có: 2
x 4x 3 0 Ta có: 2 ' 2 1. 3 43 7 2 7 2 7 Do đó: x 2 7 ; x 2 7 1 2 1 1
Khi m = 1 thì phương trình có nghiệm l|: x 2 7 ; x 2 7 1 2
b) Điều kiện để phương trình có hai nghiệm ph}n biệt l|: a m 0 0 m 0 9 m ' 0 m3 0
2 mm 4 0 2 m 9 0 2 9
Vậy điều kiện để phương trình (1) có hai nghiệm ph}n biệt l|: 0 m 2
c) Để phương trình (1) chỉ có một phần tử thì hoặc (1) có nghiệp kép hoặc l| phương trình bậc nhất. 2
Với m = 0 phương trình có dạng: 6x 4 0 x 3
Với m ≠ 0 thì (1) l| phương trình bậc 2, có nghiệm kép khi:
m 2 mm 2 ' 0 3 4 0 2
m 9 0 m (thỏa mãn m ≠ 0) 9 2
Vậy khi m = 0 hoặc m
thì tập nghiệm của phương trình (1) có một phần tử. 9 THCS.TOANMATH.com TÀI LIỆU TOÁN HỌC 6
2. Tìm điều kiện để phƣơng trình bậc hai có nghiệm
Điều kiện có nghiệm của phương trình bậc hai l| ≥ 0 m| ta lại có: = b2 – 4ac nên
khi ac < 0 thì > 0. Do đó với nhiều trường hợp phức tạp ta chỉ cần xét ac < 0 để chứng
minh phương trình đó luôn có nghiệm.
Thí dụ 2. Chứng minh rằng phương trình sau có nghiệm với mọi a, b: a 2
1 x 2a b x b 1 0 1
(Nâng cao phát triển Vũ Hữu Bình – tập 2) Hƣớng dẫn giải
- Với a = -1 phương trình (1) trở th|nh: 2 b
1 x b 1 0 2b
1 x b 1
+) Nếu b ≠ 1 thì phương trình (1) có nghiệm: x = 0,5.
+) Nếu b = 1 thì phương trình có vô số nghiệm.
- Với a ≠ -1 thì phương trình (1) l| phương trình bậc 2 có:
' a b2 a 1 b 1 2 2
a 2ab b ab a b 1 2 2
a ab b a b 1 3
a b2 1
a b2 a b 1 4 4 2
3 a b2 1 a b 1 0 4 2
Do đó với a ≠ -1 phương trình (1) cũng luôn có nghiệm
Vậy phương trình (1) có nghiệm với mọi a, b.
Thí dụ 3. Chứng minh rằng phương trình sau có nghiệm với mọi m: 2 x 2
m m x 2 3 5 1
m 4m 5 0 1
(Nâng cao phát triển Vũ Hữu Bình – tập 2) Hƣớng dẫn giải
Ta có: ac m m m m m 2 2 2 4 5 4 4 1 2 1 0 THCS.TOANMATH.com TÀI LIỆU TOÁN HỌC 7
Do đó phương trình luôn có nghiệm. Nhận xét:
- Nếu ac ≤ 0 v| a ≠ 0 thì ≥ 0 chúng ta cũng có thể kết luận được phương trình 2
ax bx c 0 có nghiệm nghiệm.
- Nếu chỉ mỗi ac ≤ 0 chúng ta chưa thể kết luận được phương trình có nghiệm, chẳng hạn với phương trình 2
m x mx 1 0 có ac = - m2 ≤ 0 nhưng với m = 0 thì phương trình đó có dạng 0x = 1 (vô nghiệm).
2. Nghiệm nguyên, nghiệm hữu tỷ của phƣơng trình bậc hai
Thí dụ 4. Cho phương trình 2
x 2mx m 4 0 . Tìm m nguyên để phương trình có hai nghiệm nguyên.
(Trích đề thi HSG tỉnh Quảng Bình năm học 2012-2013) Hƣớng dẫn giải Ta có: 2
m m 2 '
4 m m 4
Để phương trình có nghiệm nguyên thì ' phải l| số chính phương. Do đó: 2 2
m m 4 k k Z 2 2
4m 4m 16 4k 2m 2 2 1 4k 1 5
2m 1 2k2m 1 2k 1 5
Do k2 luôn lớn hơn 0 nên không ảnh hưởng tới gi{ trị cần tìm của m ta giả sử k ≥ 0, khi đó
ta có: (2m – 1 + 2k) ≥ (2m – 1 – 2k).
Vì thế ta có c{c trường hợp sau:
2m 1 2k 1 m 4 )
2m 1 2k 15 k 4
2m 1 2k 3 m 1 )
2m 1 2k 5 k 2
2m 1 2k 5 m 0 )
2m 1 2k 3 k 2
2m 1 2k 15 m 3 )
2m 1 2k 1 k 4 THCS.TOANMATH.com TÀI LIỆU TOÁN HỌC 8
Thử lại c{c gi{ trị m = -3, m = 0, m = 1, m = 4 v|o phương trình ta thấy đều thỏa mãi điều kiện b|i to{n.
Vậy khi m = -3, m = 0, m = 1, m = 4 phương trình có nghiệm nguyên.
Cách khác: ta có thể vận dụng lý vi-ét như sau:
Gọi x , x (x x ) l| hai nghiệm nguyên của phương trình. 1 2 1 2
Ta có: x x 2 ;
m x x m 4 . 1 2 1 2
Suy ra x x 2x x 8 2(x x ) 4x x 1 15 (2x 1)(2x 1) 1 5. 1 2 1 2 1 2 1 2 1 2 2x 1 1 x 0 TH1: 1 1 m 4 2x 1 15 x 8 2 2 2x 1 5 x 2 TH2: 1 1 m 0 2x 1 3 x 2 2 2 2x 1 1 5 x 7 TH3: 1 1 m 3 2x 1 1 x 1 2 2 2x 1 3 x 1 TH4: 1 1 m 1 2x 1 5 x 3 2 2
Thử lại m = 0, m = 1, m = -3,m = 4 thỏa mãn điều kiện b|i to{n.
Thí dụ 5. Tìm c{c số nguyên n để phương trình sau có c{c nghiệm v| số nguyên: 2
x 4 n x 2n 0 1
(Nâng cao phát triển Vũ Hữu Bình – tập 2) Hƣớng dẫn giải
Ta có: n2 2 2 4
4.2n 16 8n n 8n n 16
Để phương trình có nghiệm nguyên thì phải l| số chính phương. Do đó: 2 2
n 16 k k Z 2 2
n k 16
n kn k 16
Ta thấy (n + k) – (n – k) = 2k nên (n + k) và (n – k) phải cùng chẵn hoặc cùng lẻ. Do tích l|
16 nên l| cùng chẵn. Mặt kh{c (n + k) ≥ (n – k) do đó: n + k 8 4 2 n – k -2 -4 -8 THCS.TOANMATH.com TÀI LIỆU TOÁN HỌC 9 n 3 0 -3
Thử lại c{ gi{ trị n = - 3, 0, 3 ta thấy đều thỏa mãi điều kiện phương trình có nghiệm nguyên.
Vậy n = - 3, 0, 3 l| c{c gi{ trị cần tìm.
Thí dụ 5. Cho phương trình a(a + 3)x2 - 2x - (a + 1)(a + 2) = 0 (a l| tham số, nguyên).
a) Chứng minh rằng phương trình luôn có nghiệm hữu tỷ.
b) X{c định a để phương trình có c{c nghiệm đều nguyên.
(Trích đề Chuyên Phú Yên năm 2011-2012) Hƣớng dẫn giải
a) Chứng minh phương trình luôn có nghiệm hữu tỷ:
- Với a(a+3) = 0 hay a = 0 hoặc a = -3:
Phương trình trở thành: -2x -2 = 0 có nghiệm là x = -1
- Với a(a+3) 0 hay a 0 và a -3 thì phương trình cho l| phương trình bậc hai. 2
a(a 3) x 2x (a 1)(a 2) 0 2 a 3a 2
x 2 x 1 2
a 3a 0 2
a 3a x 1 x 1 2 x 1 0 x 1 2
a 3a x 1 2 0
Nên phương trình cho có 2 nghiệm: x 1 1
(a 1)(a 2) 2 x 1 2 a(a 3) a(a 3)
Vì a nguyên nên suy ra phương trình cho luôn có nghiệm hữu tỷ. ---------------------------
Cách khác: Nếu thí sinh tính 2 2
' (a 3a 1) 0, a Vì a nguyên nên 2
' a 3a 1 là số nguyên
Vậy phương trình cho luôn có nghiệm hữu tỷ.
b) X{c định a để các nghiệm của phương trình đều là nghiệm nguyên:
- Nếu a = 0 hoặc a = -3: phương trình có 1 nghiệm nguyên x = -1.
- Nếu a 0, a -3 phương trình đã cho l| phương trình bậc 2, ta có: THCS.TOANMATH.com TÀI LIỆU TOÁN HỌC 10 2
a(a 3) x 2x (a 1)(a 2) 0 2 a 3a 2
x 2 x 1 2
a 3a 0 2
a 3a x 1 x 1 2 x 1 0 x 1 2
a 3a x 1 2 0
Nên phương trình cho có 2 nghiệm: x 1 1
(a 1)(a 2) 2 x 1 2 a(a 3) a(a 3)
Phương trình có nghiệm x1 = -1 nguyên nên để phương trình có c{c nghiệm đều nguyên
thì x2 cũng phải là nghiệm nguyên.
Nghĩa l|: 2 phải chia hết cho a(a 3) . 2
a(a 3) 2
a 3a 2 0 2 a(a 3) 1
a 3a 1 0
Khi đó ta có c{c khả năng xảy ra : 2
a(a 3) 2
a 3a 2 0 2
a(a 3) 1
a 3a 1 0
Vì a nguyên nên chỉ có phương trình 2
a 3a 2 0 có hai nghiệm nguyên a = -1 hoặc a = -2 . Vậy: a 3 ; 2 ; 1 ;
0 thì phương trình cho có c{c nghiệm đều nguyên.
3. Tìm giá trị của tham số để hai phƣơng trình có nghiệm chung
Bài toán. Hai phương trình bậc hai 2
a x b x c 0 * và 2
a x b x c 0 ** với 2 2 2 1 1 1
a , a ,b ,b , c , c 1 2 1 2 1
2 l| c{c tham số, x{c định gi{ trị của tham số để 2 phương trình có nghiệm chung. Phƣơng pháp giải.
Bƣớc 1. Giả sử x0 l| nghiệm cung của hai phương trình khi đó: 2
a x b x c 0 1 1 0 1 0 1 2
a x b x c 0 2 2 2 2
Từ hệ phương trình ta x{c định được gi{ trị của tham số.
Bƣớc 2. Thay gi{ trị của tham số v|o phương trình (*) v| (**) tính ra nghiệm chung v| kết luận.
Thí dụ 5. Tìm gi{ trị của m để hai phương trình sau có nghiệm chung THCS.TOANMATH.com TÀI LIỆU TOÁN HỌC 11 2
x m 4 x m 5 0 1 2
x m 2 x m 1 0 2 Hƣớng dẫn giải
Giả sử x0 l| nghiệm chung của hai phương trình (1) v| (2), khi đó: 2
x m 4 x m 5 0 1 0 0 2
x m 2 x m 1 0 2 0 0
Trừ theo vế (1) v| (2) ta được:
2x 4 0 x 2 0 0
Thay x0 = 2 v|o hệ ta được: m = 1.
Thay m = 1 v|o phương trình (1) v| (2) ta được phương trình: 2
x 6x 7 0 và 2
x 4x 3 0
hai phương trình trên có nghiệm chung l| 2.
Vậy m = 1 l| gi{ trị cần tìm.
Thí dụ 5. Cho hai phương trình: 2
x mx 1 0 3 2
x x m 0 4 Tìm gi{ trị của m để:
a) Hai phương trình có nghiệm chung.
b) Hai phương trình tương đương. Hƣớng dẫn giải
a) Giả sử x0 là nghiệm chung của hai phương trình (3) v| (4), khi đó: 2
x mx 1 0 3 0 0 2
x x m 0 4 0 0
Trừ theo vế (3) v| (4) ta được: x
mx 1 x m 0 x 1 m 1 0 1 0 0 0 0 m 1
Thay x0 = 1 v|o hệ ta được: m = -2. Thử lại: THCS.TOANMATH.com TÀI LIỆU TOÁN HỌC 12
- Thay m = 1 v|o phương trình (3) v| (4) ta đều được phương trình: 2
x x 1 0 vô nghiệm nên loại.
- Thay m = -2 v|o phương trình (1) v| (2) ta được phương trình: 2
x 2x 1 0 và 2
x x 2 0
hai phương trình trên có nghiệm chung l| x = 1.
Vậy m = -2 l| gi{ trị cần tìm.
b) Hai phương trình tương đương khi chúng có cùng tập nghiệm.
Trƣờng hợp 1: Hai phương trình đã cho đều vô nghiệm: 2
m 4 0 1 3 m 2. 1 4m 0 4 4
Trƣờng hợp 2: Hai phương trình có nghiệm chung, theo c}u a nếu m = -2 thì (3) v| (4) đều
có nghiệm chung l| 1 nhưng phương trình (3) chỉ có 1 nghiệm l| x = 1 còn phương trình
(4) có nghiệm là x = 1 và x = - 2, nên chúng không cùng tập nghiệm, nên chúng không tương đương. 1
Vậy phương trình (3) v| (4) tương đương khi: m 2 4
Thí dụ 5. Tìm gi{ trị của m để phương trình sau có 4 nghiệm ph}n biệt: 4 2 2
x 2mx x m m 0 5 Hƣớng dẫn giải
Phương trình (5) tương đương:
x x m
x x 1 mx x m 2 1 0 6 2 2 0 2
x x m 0 7
Để phương trình (5) có 4 nghiệm ph}n biệt thì phương trình (6) v| (7) đều phải có 2
nghiệm ph}n biệt v| c{c nghiệm của 2 phương trình n|y không được trùng nhau.
Điều kiện để phương trình (6) v| (7) có 2 nghiệm ph}n biệt l|:
4m 3 0 5 3 m . 4m 1 0 4 6
Giả sử x0 là nghiệm chung của hai phương trình (6) v| (7), khi đó: 2
x x 1 m 0 1 3 0 0
2x 1 0 x m . 0 0 2
x x m 0 2 4 0 0 3
Vậy phương trình có 4 nghiệm ph}n biệt thì x . 4 THCS.TOANMATH.com TÀI LIỆU TOÁN HỌC 13
3. Chứng minh trong một hệ các phƣơng trình bậc hai có ít nhất một phƣơng trình có nghiệm.
Phƣơng pháp: Để chứng minh có ít nhất một phương trình bậc hai trong hệ phương trình
bậc hai có nghiệm ta chứng minh tổng c{c biệt thức delta lớn hơn hoặc bằng 0.
Thí dụ 5. Cho a, b, c thỏa mãn điều kiện a + b + c = 6. Chứng minh rằng ít nhất một
phương trình sau có nghiệm: 2
x ax 1 0 1; 2
x bx 1 0 2; 2
x cx 1 0 3. Hƣớng dẫn giải
Ba phương trình lần lượt có: 2 2 2 a 4,
b 4, c 4 1 2 3
Do đó: 2 2 2
a b c 12 1 2 3
Theo bất đẳng thức AM-GM thì:
2 2 2
a b c 12 1 2 3 2 a 4 2 b 4 2 c 4 24
2 2a 2 2b 2 2c 24
4 a b c 24
4a b c 24 4.6 24 0
Do đó: 0. tổng 3 biệt số delta của 3 phương trình bằng lớn hơn 0 nên có ít 1 2 3
nhất một biệt số delta lớn hơn bằng 0.
Vậy trong 3 phương trình có một phương trình có nghiệm.
Thí dụ 5. Cho hai phương trình 2
x 6ax 2b 0 và 2
x 4bx 3a 0 với , a b l| c{c số
thực. Chứng minh nếu 3a 2b 2 thì ít nhất một trong hai phương trình đã cho có nghiệm.
(Chuyên Tây Ninh năm 2019-2020) THCS.TOANMATH.com TÀI LIỆU TOÁN HỌC 14 Hƣớng dẫn giải 2 2 Ta có: 9a 2 , b 4b 3a 1 2 3a 2 1 2b 2
1 3a 2b 2 1 2
Do 3a 2b 2 nên 0 1 2
Suy ra có ít nhất một trong hai giá trị , 1
2 không âm hay ít nhất một trong hai phương trình đã cho có nghiệm.
3. Ứng dụng của phƣơng trình bậc hai trong việc chứng minh bất đẳng thức và tìm giá
trị lớn nhất và giá trị nhỏ nhất.
Phƣơng pháp: Để một phương trình bậc 2 có nghiệm thì ta cần có biệt thức 0 , vận
dụng linh hoạt điều n|y chúng ta có thể tìm được miền gi{ trị của một biểu thức.
Thí dụ 5. Tìm gi{ trị nhỏ nhất của y = x2 + 3x – 1. Hƣớng dẫn giải
Ta có x2 + 3x – 1 – y = 0. (1) 13
Để phương trình (1) có nghiệm thì: 2 3 4 1
y 13 4y 0 y 4 3
Dấu “=” xảy ra khi = 0 hay x . 2 13 3 Vậy Min y = khi x . 4 2 2 x 1
Thí dụ 5. Tìm gi{ trị lớn nhất v| nhỏ nhất của biểu thức: P 2 x x 1 Hƣớng dẫn giải 2 1 3 Ta có 2
x x 1 x 0,
do đó P luôn x{c định với mọi x. 2 4 2 x 1 Ta có: P P 2
1 x Px P 1 0 2 x x 1 Với P = 1 thì x = 0.
Với P ≠ 1, ta có: = P2 – 4(P – 1)2 = -3P2 + 8P – 4. 2
≥ 0 ⇔ 0 P 1 hoặc P ≤ 2 (2) 3 THCS.TOANMATH.com TÀI LIỆU TOÁN HỌC 15
Dấu bằng ở (1) xảy ra khi x = -1.
Dấu bằng ở (2) xảy ra khi x = -1. 2 Vậy MinP =
khi x = - 1, MaxP = 2 khi x = 1. 3 xy
Thí dụ 5. Tìm gi{ trị lớn nhất v| gi{ trị nhỏ nhất của biểu thức P với x, y l| c{c 3y 1
số thực thỏa mãn: x2y2 + 2y + 1 = 0. Hƣớng dẫn giải 2 2 1
Ta có: 2 2 2 1 0 x y x y y y . 2 2xy 2 xy P
Px y xy P 3 3 2 0 1 2 2 x y 2 2 2 2 1 1 3x y 1
Trƣờng hợp 1: P = 0 thì xy = 0.
Trƣờng hợp 2: P ≠ 0 ta có (1) l| phương trình bậc hai với ẩn l| xy, do đó để phương trình 1 1 có nghiệm thì: 2
4 12P 0 P .
= 4 – 12P2 ≥ 0 ⇔ - ≤ P ≤ . 3 3 √ √ 1 3 2 Vậy MaxP = thì x , y . 3 2 3 1 1 2 MinP = thì x , y . 3 3 3
Thí dụ 5. Tìm số thực x, y, z thỏa mãn:
x + y + z = 1 (1) và x2 + 2y2 + 3z2 = 4 (2)
sao cho x đạt gi{ trị lớn nhất. Hƣớng dẫn giải
Từ (1) suy ra z = 1 – x – y, thay v|o biến đổi ta được
5y2 + 6(x – 1)y + 4x2 - 6x – 1 = 0. (3)
Để phương trình (3) có nghiệm thì:
= 9(x – 1)2 – 20x2 + 30x + 5 = -11x2 + 12x + 14 ≥ 0 6 190 6 190 x 11 11 THCS.TOANMATH.com TÀI LIỆU TOÁN HỌC 16
Vì x đặt gi{ trị lớn nhất nên 6 190 15 3 190 10 2 190 x y ; z . 11 55 55
CHỦ ĐỀ 2. KHAI THÁC CÁC ỨNG DỤNG CỦA ĐỊNH LÝ VI-ÉT
A/ KIẾN THỨC VÀ KỸ NĂNG CẦN NHỚ 1.Định lý thuận: Nếu phương trình 2
ax bx c 0 a 0 có hai x , x thì: 1 2 THCS.TOANMATH.com TÀI LIỆU TOÁN HỌC 17 b
S x x 1 2 a c
P x .x 1 2 a 2.Định lý đảo:
x x S
Nếu có hai số x , x thỏa mãn 1 2
thì chúng l| nghiệm của pt: 2
t St P 0 1 2
x x P 1 2
( Điều kiện để tồn tại hai số x , x là 2
S 4P 0 ) 1 2
Chú ý: Tước khi {p dụng hệ thức Vi-ét cần tìm điều kiện để pt có hai nghiệm a 0 0 ' 0
B/ CÁC ỨNG DỤNG CỦA ĐỊNH LÝ VI-ÉT:
I.GIẢI PHƢƠNG TRÌNH BẬC HAI BẰNG CÁCH TÍNH NHẨM NGHIỆM: 1) Phƣơng pháp: 2
Từ định lý Vi-ét ta có: Nếu phương thình bậc hai ax bx c 0 có: c
+) a b c 0 thì phương trình có nghiệm l| x 1, x 1 2 a c
+) a b c 0 thì phương trình có nghiệm l| x 1 , x 1 2 a 2) Ví dụ minh họa.
Thí dụ 5. Giải c{c phương trình sau: 2
a)1, 5x 1, 6x 0,1 0 b) 2 3 2
x 2 3x 2 3 0 2
c) 3x 1 3 x 1 0
d ) m 2
1 x 2m 3 x m 4 0(m 1)
( Bài 31-SGK Toán 9,tập 2) Hƣớng dẫn giải
Nhận xét: Đa số HS khi gặp yêu cầu giải phương trình thường tính ngay hoặc ' mà
không để ý đến c{c trương hợp đặc biệt a b c 0 hoặc a b c 0. Thậm chí có em khi
gặp phương trình có c{c hệ số l| số vô tỷ như pt b), c) hoặc pt có chứa tham số như pt d) THCS.TOANMATH.com TÀI LIỆU TOÁN HỌC 18
thì tỏ ra {i ngại. Rõ r|ng nếu ta để ý sẽ thấy c{c pt trong VD trên đều có dạng đặc biệt có
thể nhẩm nghiệm ngay m| không phải tính hoặc '
a) Vì pt đã cho có a b c 1,5 ( 1
,6) 0,1 0 nên pt có hai nghiệm l| : 0,1 1 x 1, x . 1 2 1,5 15
b) Vì pt đã cho có a b c
2 3 2 3 2 3 0 nên pt có hai nghiệm l|: 2 3 (2 3) 2 x 1, x 7 4 3 1 2 2 2 2 3 2 3
c) Vì pt đã cho có a b c 3 1 3 1 0 nên pt có hai nghiệm l|: ( 1 ) 1 3 x 1 , x 1 2 3 3 3
d ) Vì m 1 nên pt đã cho l| pt bậc hai, có
a b c m
1 2m 3 m 4 0 nên pt có hai nghiệm l|: m 4 x 1, x . 1 2 m 1
Trong trường hợp giải pt đơn giản ta cũng có thể nhẩm nghiệm dựa v|o định lý Vi-ét:
Thí dụ 5. Giải phương trình: 2
a)x 7x 10 0 2 )
b x 8x 15 0 Hƣớng dẫn giải
a) Vì 2 5 7; 2.5 10 nên x 2, x 5 l| nghiệm của pt đã cho. 1 2 b) Vì 3 5 8 ; 3 . 5
15 nên x 3 , x 5
l| nghiệm của pt đã cho. 1 2
Như vậy trước khi HS giải pt, gi{o viên cần tạo cho HS thói quen nhẩm nghiệm trước khi
tính theo công thức nghiệm.
II.TÍNH GIÁ TRỊ CỦA BIỂU THỨC GIỮA CÁC NGHIỆM CỦA PHƢƠNG TRÌNH BẬC HAI
1) Phƣơng pháp: Nếu phương trình 2
ax bx c 0(a 0) có hai nghiệm x , x thì ta có 1 2
thể biểu thị c{c biểu thức đối xứng giữa c{c nghiệm theo S x x và P x .x 1 2 1 2 Ví dụ: THCS.TOANMATH.com TÀI LIỆU TOÁN HỌC 19 x x
x x 2 2 2 2
2x x S 2P 1 2 1 2 1 2
(x x ) x x 2 2 2
4x x S 4P 1 2 1 2 1 2 x x
x x 3 3 3
3x x x x 3 S 3SP 1 2 1 2 1 2 1 2 x x
x x 2 2x x S 2P2 4 4 2 2 2 2 2 2 2P 1 2 1 2 1 2 1 1 x x S 1 2 x x x x P 1 2 1 2 2 2 2 x x x x S 2P 1 2 1 2 x x x x P 2 1 1 2 2 2 2 1 1 x x S 2P 1 2 2 2 2 2 2 x x x x P 1 2 1 2
x x x x x x 2 1 2 1 2 1 2 1 1 x x 2 S 2 1 2 x x
x x 2
P S 1 2 1 2
Chú ý: Khi tính gi{ trị của một biểu thức giữa c{c nghiệm thông thường ta biến đổi sao cho
trong biểu thức đó xuất hiện tổng v| tích c{c nghiệm rồi {p dụng định lý Vi-ét để giải. 2) Ví dụ minh họa:
Thí dụ 5. Cho x , x l| hai nghiệm của phương trình: 2
x x 1 0 1 2 a) Hãy tính 2 2 x x 1 2 b) Chứng minh 2 2 4 4
Q x x x x chia hết cho 5 1 2 1 2
(Trích bài trong báo Toán học & Tuổi thơ) Hƣớng dẫn giải
Phương trình đã cho có hai nghiệm ph}n biệt vì ac 1 0
Theo định lý Vi-ét ta có x x 1, x x 1 1 2 1 2
a) x x x x 2 2 2 2 2x x 1 2.( 1 ) 3 1 2 1 2 1 2
b) Q x x x x 2 2 2 2 2 2 2 2 2
2x x 3 3 2.( 1 ) 10 Q 5 1 2 1 2 1 2
Chú ý : Ta có thể chứng minh biểu thức 2008 2008 2010 2010 M x x x x cũng chia hết cho 5. 1 2 1 2
Thí dụ 5. Cho phương trình: 2
x ax a 1 0 có hia nghiệm l| x , x . Không giải 1 2
phương trình hãy tính gi{ trị biểu thức: THCS.TOANMATH.com TÀI LIỆU TOÁN HỌC 20 2 2
2x x x 2x 1 1 2 2 M 2 2 x x x x 1 2 1 2 Hƣớng dẫn giải
Trước hết ta kiểm tra xem phương trình đã cho có nghiệm hay không.
Ta có: a a a 2 2 ( ) 4 1 2
0 phương trình đã cho có hai nghiệm x , x . 1 2
{p dụng định lý Vi-et ta có: x x ; a x x a 1 1 2 1 2 2 2 2
x x x x
2 x x 2 2 5x x
2a 5a 2 1 2 1 2 1 2a 5a 5 1 2 1 2 M x x x x x x x x a a 1 a a 1 1 2 1 2 1 2 1 2
Thí dụ 5. Gọi x x l| c{c nghiệm của phương trình: 2
x 6x 1 0 . Ký hiệu n n
S x x 1, 2 n 1 2
với n l| số nguyên dương.
a) Tính S , S , S . 1 2 3
b) Tìm một hệ thức giữa S , S , S n n 1 n . 2
(Bài 281, sách Nâng cao, phát triển toán 9, tập 2) Hƣớng dẫn giải Phương trình: 2
x 6x 1 0 có 2 6
4 32 0 nên phương trình có hai nghiệm
ph}n biệt x , x . 1 2
Theo Vi-ét ta có: x x 6; x .x 1 1 2 1 2
S x x 6 1 1 2 2 a) Ta có: 2 2
S x x
x x 2
2x x 6 2.1 34 2 1 2 1 2 1 2
S x x x x 3 3 3
3x x x x 3 6 3.1.6 198 3 1 2 1 2 1 2 1 2 b) Ta có: n2 n2 n 1 n 1 n n S x x x x x x x x x x 6S S . n2 1 2 1 2 1 2 1 2 1 2 n 1 n
Chú ý: Ta còn chứng minh được trường hợp tổng qu{t: phương trình bậc hai 2
ax bx c 0(a 0) có hai nghiệm x , x với n n
S x x
thì S , S , S 1 2 n 1 2 n n 1 n liên hệ với nhau 2 bởi hệ thức: . a S . b S . c S 0 . n2 n 1 n
Vận dụng hệ thức trên cho ta lời giải thú vị của nhiều b|i to{n . THCS.TOANMATH.com TÀI LIỆU TOÁN HỌC 21
Thí dụ 5. Cho a,b l| nghiệm của phương trình 2
30x 4x 2010 . tính gi{ trị của biểu 30 2010 2010 a b 4 2009 2009 a b thức: M 2008 2008 a b Hƣớng dẫn giải
Ta thấy phương trình đã cho có 0 nên phương trình có hai nghiêm ph}n biệt x ; n n
a x b S a b . 1 2 n
{p dụng hệ thức ở chú ý trên ta có . A S . B S . C S 0 n2 n 1 n Ta có: 2008 2008 S a b n 2009 2009 S a b n 1 2010 2010 S a b n2 30S
4S 2010S 0 n2 n 1 n 30S 4S 2010S n2 n 1 n 2010Sn M 2010 Sn
Thí dụ 5. Tính gi{ trị của c{c biểu thức: 1 1 A 6 6 2 3 2 2 3 2 B
2 3 2 6 2 3 26 Hƣớng dẫn giải Đặt
x 2 3 2, x 2 3 2 thì x x 4; x x 1
4 do đó x , x l| hai nghiệm của 1 2 1 2 1 2 1 2 phương trình 2
x 4x 14 0 . Khi đó hệ thức ở chú ý trên có dạng: S
4S 14S .Ta n2 n 1 n tính được:
S 4, S 44, S 4.44 14.4 232 1 2 3
S 4.232 14.44 1544 4
S 4.1544 14.232 9424 5
A S 4.9424 14.1544 59312 6 S 59312 3707 6 B 6 14 16.47059 47059 THCS.TOANMATH.com TÀI LIỆU TOÁN HỌC 22
III.TÌM HAI SỐ KHI BIẾT TỔNG VÀ TÍCH u v S
1) Phƣơng pháp: {p dụng định lý Vi-ét đảo: Nếu hai số u, v có thì u, v là . u v P
nghiệm của phương trình: 2
x Sx P 0 .
Điều kiện để tồn tại hai số u, v là 2 S 4P . 2 2 2 2 3 3 u
v a u
v a u v a
Chú ý: C{c hệ phương trình ; ;
đều có thể đưa về hệ . u v b u v b u v b u v S . u v P 2) Ví dụ minh họa:
Thí dụ 5. Tính c{c kích thước của hình chữ nhật ABCD. Biết diện tích v| chu vi của nó theo thứ tự l| 2 2a và 6a .
(Bài 39-SGK Toán 9 Tập 2, trang 129) Hƣớng dẫn giải
Gọi c{c kích thước của hình chữ nhật l| , x y ,
x y 0 . Theo bài ra ta có:
x y 3a 2 . x y 2a Suy ra ,
x y l| hai nghiệm của phương trình: 2 2
t 3at 2a 0
Ta có a2 2 2 3
4.2a a t ; a t 2a . 1 2
Vậy c{c kích thước của hình chữ nhật l| a, 2a .
Thí dụ 5. Tìm hai số u,v trong c{c trường hợp sau:
a)u v 4; . u v 19
b)u v 10; . u v 24 2 2
c)u v 85;uv 18 Hƣớng dẫn giải
a) Ta có u, v l| hai nghiệm của phương trình: 2
x 4x 19 0 . Ta có ' 2 ( 2 ) 19 1
5 0 phương trình vô nghiệm .
Vậy không tìm được hai số u, v . THCS.TOANMATH.com TÀI LIỆU TOÁN HỌC 23 2 2 2 2
b) Ta có : u v u v 4uv u v u v 4uv 100 4.24 196
u v 14 hoặc u v 14 . u v 14 Trường hợp 1:
u,v l| hai nghiệm của phương trình: 2
t 14t 24 0 . . u v 24 Ta có ' 2 ( 7
) 24 25 0 phương trình có hai nghiệm ph}n biệt
t 12;t 2 u 12, v 2 vì u v 10 . 1 2 u v 14 Trường hợp 2:
u,v l| hai nghiệm của phương trình: 2
t 14t 24 0 . . u v 24 Ta có '
49 24 25 0 phương trình có hai nghiệm ph}n biệt t 1 2;t 2 u 2 ,v 1
2 vì u v 10 . 1 2 u 12 u 2 Vậy hoặc v 2 v 12
Chú ý : Ta có thể giảI c{ch kh{c như sau; u v 10 u ( v ) 10 Ta có
u,v l| hai nghiệm của phương trình: 2
t 10t 24 0 . u v 24 . u ( v ) 2 4 Ta có ' 2 ( 5 ) ( 2
4) 49 0 phương trình có hai nghiệm ph}n biệt t 2 ,t 12 1 2 u 2 u 12 hoặc v 12 v 2 u 12 u 2 Vậy hoặc v 2 v 12
c) Ta có u v2 2 2
u v 2uv 85 36 121 u v 11 hoặc u v 11 . u 9 u 2 u 9 u 2 Giải tiếp ta được hoặc hoặc hoặc . v 2 v 9 v 2 v 9
Thí dụ 5. Tìm c{c số p,q của phương trình 2
x px q 0 sao cho c{c nghiệm x , x của 1 2 x x 5
nó thỏa mãn điều kiện 1 2 . 3 3 x x 35 1 2 Hƣớng dẫn giải
x x p
Theo định lý Vi-ét ta có 1 2
x .x q 1 2 THCS.TOANMATH.com TÀI LIỆU TOÁN HỌC 24
x x 2 x x 2 2
4x x p 4q 25 1 2 1 2 1 2
Suy ra x x x x x x x x 5x x 2 3 3 2 2 x x 35 1 1 1 2 1 1 2 2 1 2 1 2
x x 2 2
x x p q 7 1 2 1 2 2
p 4q 25 Ta có hệ: 2
p q 7 p 1 p 1
Giải hệ trên ta được và
đều thỏa mãn điều kiện 2
p 4q 0 q 6 q 6 Vậy ; p q 1; 6 hoặc 1 ; 6 IV.
PHÂN TÍCH TAM THỨC BÂC HAI THÀNH NHÂN TỬ
1) Phƣơng pháp: Giả sử phương trình 2
ax bx c 0
* a 0 có 0 . b c
Khi đó theo Vi-ét ta có: x x ; x .x . 1 2 1 2 a a Do đó: b c 2 2 2
ax bx c a x x a x
x x x x x a
2x x x x x x x a x x x x 1 2 1 2 1 2 1 2 1 2 a a
Vậy nếu phương trình bậc hai 2
ax bx c 0 có hai nghiệm x , x thì ta có: 1 2 2
ax bx c a x x x x 1 2
Thí dụ 5. Ph}n tích th|nh nh}n tử: 2
a)2x 5x 3 2
b)3x 8x 2 Hƣớng dẫn giải 3
a) Phương trình đã cho có hai nghiệm x 1, x .Do đó ta có: 1 2 2 3 2
2x 5x 3 2 x 1 x x 1 2x 3 . 2 4 10 4 10
b)Phương trình đã cho có hai nghiệm l| x ; x . Do đó ta có: 1 2 3 3 4 10 4 10 2
3x 8x 2 3 x x 3 3
ứng dụng n|y hs r}t hay sử dung để ph}n tích c{c mẫu th|nh nh}n tử trong c{c b|i tập rút gọn THCS.TOANMATH.com TÀI LIỆU TOÁN HỌC 25
V.TÌM ĐIỀU KIỆN CỦA THAM SỐ ĐỂ PHƢƠNG TRÌNH BẬC HAI CÓ MỘT
NGHIỆM x x CHO TRƢỚC. TÌM NGHIỆM THỨ HAI. 1 1) Phƣơng pháp:
Tìm điều kiện để phương trình có nghiệm x x cho trước ta co thể l|m như sau: 1 Cách 1:
- Tìm điều kiện để phương trình có hai nghiệm ' 0 0 (*) -
Thay x x v|o phương trình đã cho tìm gi{ trị của tham số 1 -
Đối chiếu gi{ trị vừa tìm được với điều kiện (*) để kết luận
Cách 2: - Thay x x v|o phương trình đã cho tìm được gi{ trị của tham số. 1 -
Thay gi{ trị tìm được của tham số v|o phương trình v| giảI phương trình
Nếu sau khi thay gi{ trị của tham số v|o phương trình đã cho m| có 0 thì kết
luận không có gi{ trị n|o của tham số để phương trình có nghiệm x cho trước 1
Để tìm nghiệm thứ hai ta có thể l|m như sau;
Cách 1: Thay gi{ trị của tham số tìm được v|o phương trình rồi giải phương trình
Cách 2: Thay gi{ trị của tham số tìm được v|o công thức tổng 2 nghiệm để tìm nghiệm thứ hai.
Cách 3: Thay gi{ trị của tham số tìm được v|o công thức tích hai nghiệm để tìm nghiệm thứ hai.
Thí dụ 5. Với gi{ trị n|o của k thì: a) Phương trình 2
2x kx 10 0 có một nghiệm x 2 . Tìm nghiệm kia
b) Phương trình k 2
5 x k 2 x 2k 0 có một nghiệm x 2 . Tìm nghiệm kia c) Phương trình 2
kx kx 72 0 có một nghiệm x 3 . Tìm nghiệm kia ? Hƣớng dẫn giải
a) Nếu x 2 l| một nghiệm của phương trình thì:
2.4 2k 10 0 2k 2 k 1 Với k 1 ta có : 2
2x x 10 0 1 9 1 9
Cách 1: ta có 1 80 81 81 9 x 2; x 2 ,5 1 2 4 4 5 5
Cách 2: Theo hệ thức Vi-ét ta có x .x 5 x 2 ,5 1 2 2 x 2 1 THCS.TOANMATH.com TÀI LIỆU TOÁN HỌC 26 k 1 1
Cách 3: Theo hệ thức Vi-ét ta có x x x x 0 ,5 2 2 ,5 1 2 2 1 2 2 2
b) Tương tự c}u a) ta có k 3, nghiêm kia x 1,5 2
c) Tương tự c}u a) ta có k 6 , nghiệm kia x 4 2
VI.XÁC ĐỊNH THAM SỐ ĐỂ CÁC NGHIỆM CỦA PHƢƠNG TRÌNH BẬC HAI THỎA
MÃN HỆ MỘT ĐIỀU KIỆN CHO TRƢỚC.
“Điều kiện cho trước” ở đ}y có thể l| c{c nghiệm của phương trình bậc hai thỏa mãn một
đẳng thức hoặc bất đẳng thức hoặc để một biểu thức của c{c nghiệm của phương trình bậc hai đạt GTLN, GTNN v.v<
1) Phƣơng pháp: - X{c định gi{ trị của tham số để phương trình bậc hai có nghiệm x , x 1 2
x x f (m)
- {p dụng định lý Vi-ét ta có: 1 2 (*)
x .x g(m) 1 2
- Kết hợp hệ (*) với điều kiện b|i ra để suy ra điều kiện của tham số m
Chú ý: Sau khi tìm được tham số ta phải đối chiếu với điều kiện phương trình có nghiệm. 2) Ví dụ minh họa
Thí dụ 5. Cho phương trình: 2
x 6x m 0 . Tính gi{ trị của m biết phương trình có hai
nghiệm x , x thỏa mãn điều kiện: x x 4 1 2 1 2 Hƣớng dẫn giải Phương trình 2
x 6x m 0 có 9 m Phương trình có nghiệm '
0 9 m 0 m 9 (*) x x 6 (1)
Theo định lý VI-ét ta có: 1 2 x x m (2) 1 2
Theo bài ra ta có: x x 4 (3) 1 2
Từ (1) v| (3) ta có: x 5; x 1. Thay vào (2) ta có m 5 thỏa mãn điều kiện (*) 1 2
Vậy với m 5 thì phương trình đã cho có hai nghiệm thỏa mãn x x 4 1 2
Thí dụ 5. Cho phương trình: 2
x 4x m 0 . Tìm c{c gi{ trị của m để phương trình có hai
nghiệm x , x thỏa mãn: 3 3 x x 26 1 2 1 2 THCS.TOANMATH.com TÀI LIỆU TOÁN HỌC 27 Hƣớng dẫn giải
Phương trình đã cho có nghiệm khi v| chỉ khi: '
4 m 0 m 4 (*)
Theo hệ thức Vi-ét ta có: x x 4 1 2 x x m 1 2 Theo bài ra ta có: x x
26 x x 3 19 3 3
3x x x x 3 26 4 3 .
m 4 26 64 12m 26 m 1 2 1 2 1 2 1 2 6
Gi{ trị n|y của m không thỏa mãn điều kiện (*).
Vậy không có gi{ trị n|o của m để 3 3 x x 26 1 2
Thí dụ 5. Cho phương trình: 2
x m x 2 2 2
m 2m 3 0 . Tìm c{c gi{ trị của m để
phương trình có hai nghiệm ph}n biệt x , x thỏa mãn: 1 2 1 1 x x 1 2 x x 5 1 2 Hƣớng dẫn giải 2 Ta có: '
m 2 2
m 2m 3 7 6m 7
Phương trình có hai nghiệm ph}n biệt '
0 7 6m 0 m (*) 6
x x 2(m 2) (1)
Theo định lý Vi-ét ta có: 1 2 2
x x m 2m 3 (2) 1 2 1 1 x x 1 Theo bài ra ta có: 1 2
x x 5 0 (3) 1 2 x x 5 x x 1 2 1 2 m 1 Từ (3) ta suy ra 2
x x 0 m 2m 3 0 (**) 1 2 m 3
x x 0 m 2, 1 2 Mặt kh{c từ (3) suy ra 2
x x 5 m 2m 3 5 0 m 2 m 4 0 1 2
Suy ra m = 2 (loại ) hoặc m = - 4 ( thỏa mãn * v| **) 1 1 x x Vậy m = - 4 thì 1 2 x x 5 1 2 THCS.TOANMATH.com TÀI LIỆU TOÁN HỌC 28
Thí dụ 5. Cho phương trình bậc hai tham số m : 2
2x (m 3)x m 0 . Gọi x , x là hai 1 2
nghiệm của phương trình. Tìm GTNN của biểu thức P x x . 1 2
(Đề thi tuyển sinh vào lớp 10_THPT năm học 2009-2010, Sở GD-ĐT Nghệ An) Hƣớng dẫn giải
Phương trình đã cho có: m 2 2 2 3
8m m 2m 9 (m 1) 8 0 với mọi m suy ra
phương trình luôn có hai nghiệm ph}n biệt x , x x x 1 2 1 2 m 3 x x 1 2
Theo hệ thức Vi-ét ta có: 2 m x x 1 2 2
Theo bài ra ta có: P x x 2 2 2
x x x x 2x x 1 2 1 2 1 2 1 2 2 2 m 3 m x x 4x x 4. 1 2 1 2 2 2 2 2
m 6m 9 8m
m 2m 1 8 4 2 m 2 1 8 8 2 2 2
Dấu “ = ” xảy ra khi v| chỉ khi m 1
Vậy GTNN của P bằng 2 m 1
Nhận xét: Với b|i to{n trên HS có thể tính c{c nghiêm x , x theo m rồi thay v|o biểu thức 1 2 P để giải.
Thí dụ 5. Cho phương trình: 2
x m 2
2 x m 3m 4 0 .
a. Chứng minh rằng phương trình có hai nghiệm ph}n biệt với mọi m.
b. Tìm m để tỷ số giữa hai nghiệm của phương trình có gi{ trị tuyệt đối bằng 2. Hƣớng dẫn giải 3 7
a) Phương trình đã cho có .
a c 1.m 3m 4 2 2 m 0 với mọi m suy ra 2 4
phương trình luôn có hai nghiệm ph}n biệt tr{I dấu với mọi m.
b) Vì phương trình có hai nghiệm ph}n biệt tr{i dấu nên x 2
x hoặc x 2 x 1 2 2 1 THCS.TOANMATH.com TÀI LIỆU TOÁN HỌC 29
x 2x x 2x 0 x x 2x x 2 0 1 2 2 1 1 1 1 2
x x m 2
Theo hệ thức Vi-ét ta có: 1 2 2
x x m 3m 4 1 2 m
x x 2 x x 2 0 m 3m 4 2m 22 1 2 2
0 m 5m 4 0 1 2 1 2 m 4
Nhận xét: ở b|i to{n trên nếu HS chứng minh phương trình có hai nghiệm ph}n biệt bằng
c{ch chứng minh 0 thì việc đi tìm lời giải cho c}u b) sẽ rất vất vả. Vì chứng minh
được phương trình có hai nghiệm ph}n biệt tr{i dấu suy ra x 2
x và x 2 x do đó 1 2 2 1
vận dụng định lý Vi-ét một c{ch khéo léo cho ta một lời giải đẹp !
Thí dụ 5. Cho phương trình: 2 2
2x 2(m 1)x m 4m 3 0 . Tìm m để phương trình có
hai nghiệm x , x và A x x 2(x x ) đạt GTLN 1 2 1 2 1 2 Hƣớng dẫn giải
Phương trình đã cho l| phương trình bậc hai có:
m 2 m m m m m 2 ' 2 2 1 2( 4 3) 6 5 4 3
Phương trình đã cho có hai nghiệm x , x khi v| chỉ khi: 1 2
m 2 m 2 ' 0 4 3 0 3 4 2
m 3 2 5 m 1 .
Theo định lý Vi-ét ta có:
x x (m 1) 1 2 2 m 4m 3 x x 1 2 2 2 m 4m 3 1 Do đó A 2(m 1) 2
m m 3m 3 4(m 1) 2 2 1 (
m m 1) 3(m 1) 4(m 1) 2 1
m m m 1 1 3 4 1 m 1 m 7 2 2 2 1
m m 1 m 1 m 7 9 1 7 2 2 2 2
( Vì m 1 0;m 7 0 v| {p dụng bất đẳng thức Cô-si )
Dấu “=” xảy ra m
1 m 7 m 4
( thỏa mãn điều kiện ) THCS.TOANMATH.com TÀI LIỆU TOÁN HỌC 30 9 Vậy Max A m 4 2
VII. LẬP PHƢƠNG TRÌNH BẬC TRÌNH BẬC HAI MỘT ẨN KHI BIẾT HAI NGHIỆM
CỦA NÓ HOẶC HAI NGHIỆM CÓ LIÊN QUAN TỚI HAI NGHIỆM CỦA MỘT
PHƢƠNG TRÌNH ĐÃ CHO.
1) Phƣơng pháp: Để lập phương trình bậc hai khi biết hai nghiệm l| và ta cần phải
tính và . , {p dụng định lý Vi-ét đảo ta có phương trình cần lập l|: 2
x x . 0
2) Ví dụ minh họa
Thí dụ 5. Lập phương trình bậc hai có hai nghiệm l| hai số cho trong c{c trường hợp sau: 1 a) 5 và b) 3 5 và 3 5 3 Hƣớng dẫn giải 1 1 4 a) Ta có 5 và 1 5 5 . 3 3 3 3 1 14 5
Vậy phương trình bậc hai nhận 5 và l|m nghiệm l|: 2 2 x x
0 3x 14x 5 0 3 3 3
b) Ta có 3 5 3 5 6 và 3 53 5 4
Vậy phương trình bậc hai nhận 3 5 và 3 5 l|m nghiệm l|: 2
x 6x 4 0 .
Thí dụ 5. Cho phương trình: 2
x px 5 0 có hai nghiệm x , x . Hãy lập phương trình 1 2
có hai nghiệm l| hai số cho trong c{c trường hợp sau: 1 1
a) x và - x b) và . 1 2 x x 1 2 Hƣớng dẫn giải
Vì x , x l| hai nghiệm của phương trình: 2
x 6x 4 0 nên ta có: 1 2
x x p 1 2 x x 5 1 2
a) Ta có: (x ) x x x p 1 2 1 2 THCS.TOANMATH.com TÀI LIỆU TOÁN HỌC 31
x x x x 5 1 2 1 2
x ,x l| nghiệm của phương trình: 2
x px 5 0 1 2 1 1 x x p p b) Ta có: 1 2 x x x x 5 5 1 2 1 2 1 1 1 . x x 5 1 2 1 1 p 1 Suy ra và
l| nghiệm của phương trình: 2 x x 0 x x 5 5 1 2
Thí dụ 5. Gọi x , x l| hai nghiệm của phương trình: 2
x 7x 3 0 . Hãy lập phương 1 2
trình bậc hai có hai nghiệm l|: 2x x và 2x x . 1 2 2 1 Hƣớng dẫn giải Phương trình: 2
x 7x 3 0 có: 2 7
3.4 37 0 suy ra phương trình có hai nghiệm
ph}n biệt x , x . Theo hệ thức Vi-ét ta có: 1 2 x x 7 1 2 x x 3 1 2
Ta có: 2x x 2x x x x 7 1 2 2 1 1 2
2x x .2x x 9x x x x 2 2 9.3 2.7 7 1 1 2 2 1 1 2 1 2
Vậy 2x x và 2x x l| nghiệm của phương trình bậc hai: 2
x 7x 71 0 1 2 2 1
Thí dụ 5. Chứng minh rằng tồn tại một phương trình bậc hai có c{c hệ số hữu tỉ có một 2 3 nghiệm l|: . 2 3 Hƣớng dẫn giải
Cách 1: Phương trình bậc hai cần tìm có dạng 2
x ax b 0( , a b ) Q 2 2 3 2 3 Ta có:
2 6 5 2 3 2 3 2 3
Theo giả thiết 2 6 5 l| nghiệm của phương trình cần tìm nên: THCS.TOANMATH.com TÀI LIỆU TOÁN HỌC 32 2 2 6 5
a2 6 5b 0
49 20 6 2 6a 5a b 0
49 5a b 2a 20 6 0(*) 49 5a b
Nếu 2a 20 0 thì 6
Q . Vô lý vì 6 l| số vô tỷ 2a 20
Vậy 2a 20 0 a 10 . Thay a 10 v|o phương trình (*) ta được b 1.
Vậy phương trình cần tìm l|: 2
x 10x 1 0 . 2 3
Cách 2: Gọi x 2 6 5 . 1 2 3
S x x 2
6 5 2 6 5 1 0 1 2
Ta được: P x .x 2 6 5 2 6 5 1 1 2
Vậy x , x l| nghiệm của phương trình 2
x 10x 1 0 . 1 2
VIII. TÌM HỆ THỨC LIÊN HỆ GIỮA HAI NGHIỆM CỦA PHƢƠNG TRÌNH BẬC HAI
KHÔNG PHỤ THUỘC VÀO THAM SỐ:
1) Phƣơng pháp: Để tìm hệ thức liên hệ giữa c{c nghiệm không phụ thuộc v|o tham số
trong phương trình bậc hai ta l|m như sau: a 0
- Tìm điều kiện để phương trình có hai nghiệm x , x là: 1 2 0
x x S
- Theo hệ thức Vi-ét ta được: 1 2 (*)
x .x P 1 2
- Khử tham số từ hệ (*) ta được hệ thức cần tìm ( thông thường ta dùng phương ph{p
cộng hoặc phương ph{p thế ). 2) Ví dụ minh họa.
Thí dụ 5. Cho phương trình bậc hai m 2
1 x 2mx m 4 0(m 1) . Trong trường hợp
phương trình có hai nghiệm x , x ,hãy tìm một hệ thức liên hệ giữa c{c nghiệm không phụ 1 2 thuộc v|o m. Hƣớng dẫn giải
Vì phương trình đã cho l| phương trình bậc hai nên m 1 Ta có: ' 2
m m
1 m 4 5m 4 . Phương trình đã cho có hai nghiệm x , x 1 2 THCS.TOANMATH.com TÀI LIỆU TOÁN HỌC 33 4 '
0 5m 4 0 m 5 2m 2
x x S 2 1 2 m 1 m 1
Theo định lý Vi-ét ta có: m 4 3
x .x P 1 1 2 m 1 m 1 6 S 6 m 1 Do đó:
3S 2P 8 hay 3x x 2x x 8 . 1 2 6 1 2 2P 2 m 1
Chú ý: Ta có thể khử m ở ví dụ trên như sau: Cách 2: 2m S Từ S
Sm S 2m mS 2 S m m 1 S 2 S 4 m 4 3 S 8 Thế v|o P ta có: S 2 P
2P 3S 8 m 1 S 2 1 S 2
Cách 3: Xét biểu thức aP bS , trong đó a,b l| những số phải x{c định để khử tham số m
ra khỏi hệ thức đó. Ta có:
2am b m 4
2a bm4m aS bP m 1 m 1
2a bm2a b 2a 3b 2a bm 1 2a 3b m 1 m 1 2a 3b
2a b m1
Để biểu thức aS bP không phụ thuộc v|o m thì ta phải có: a 3
2a 3b 0 b 2
Thay v|o biểu thức, ta được:
3S 2P 2.3 2 8 3 x x 2x x 8 1 2 1 2
Thí dụ 5. Cho phương trình: 2
8x 4m 2 x (
m m 4) 0.Định m để phương trình có
hai nghiệm x , x . Tìm hệ thức giữa hai nghiệm độc lập với m, suy ra vị trí của c{c nghiệm 1 2 với hai số -1 và 1 Hƣớng dẫn giải
Phương trình đã cho l| phương trình bậc hai có: THCS.TOANMATH.com TÀI LIỆU TOÁN HỌC 34 m 2 '
m m 2 4 2 8 ( 4)
4 m 4m 4
Phương trình có hai nghiệm x , x khi v| chỉ khi: 1 2
m m m m m 2 ' 2 2 0 4 4 0 4 4 8 2 8
m 2 2 2 2
2 m 2 2 2
2 2 2 m 2 2 2 4(m 2) m 2 x x (1) 1 2 8 2
Khi đó theo định lý Vi-ét ta có: m(m 4) x .x (2) 1 2 8
Từ (1) ta có: m 2 x x 1 .Thay v|o (2) ta được: 1 1
8x x 2 x x 1 2 x x 1 4 1 2 1 2 1 2
8x x 2 x x 1 2 x x 1 1 2 1 2 1 2
8x x 4 x x 2 1 x x 2 2 2
2x x 1 0 x x 1 1 2 1 2 1 2 1 2 1 2
Vậy hệ thức cần tìm l|: 2 2 x x 1. 1 2
Từ hệ thức trên suy ra: 2
0 x 1 x 1 1 x 1 1 1 1 . 2 0 x 1 x 1 1 x 1 2 2 2
IX. CHỨNG MINH HỆ THỨC GIỮA CÁC NGHIỆM CỦA PHƢƠNG TRÌNH BẬC HAI
HOẶC HAI PHƢƠNG TRÌNH BẬC HAI:
Thí dụ 5. Gọi a,b l| hai nghiệm của phương trình: 2
x px 1 0. ,
b c l| hai nghiệm của phương trình: 2
x qx 2 0 . Chứng minh hệ thức: b cb a pq 6 . Hƣớng dẫn giải
Vì a,b l| hai nghiệm của phương trình 2
x px 1 0. nên theo định lý Vi-ét ta có:
a b p . a b 1
Vì p, q l| hai nghiệm của phương trình 2
x qx 2 0 nên theo định lý Vi-ét ta có: b
c q . b c 2
Ta có: b ab c 2 2
b ab bc ac b ab bc ac 2(ab bc) THCS.TOANMATH.com TÀI LIỆU TOÁN HỌC 35 ( b a )
b c(a c) 2(ab bc)
(a b)(b c) 2(ab bc)
( p)(q) 2(1 2) pq 6 Vậy ta có đpcm.
Thí dụ 5. Chứng minh rằng nếu a , a l| c{c nghiệm của phương trình 2
x px 1 0 và 1 2
b ,b l| c{c nghiệm của phương trình 2
x qx 1 0 thì: 1 2
a b a b a b a b 2 2 q p . 1 1 2 1 1 2 2 2 Hƣớng dẫn giải
Vì a , a l| c{c nghiệm của phương trình 2
x px 1 0 nên theo định lý Vi-ét ta có: 1 2
a a p 1 2 a a 1 1 2
Vì b ,b l| c{c nghiệm của phương trình 2
x qx 1 0 nên theo định lý Vi-ét ta có: 1 2 b
b q 1 2 bb 1 1 2
Ta có: a b a b a b a b
a b a b a b a b 1 1 2 1 1 2 2 2
1 1 2 2 2 1 1 2
a a a b a b b b a a a b a b b b 1 2 1 2 2 1 1 2 1 2 2 2 1 1 1 2
1 a b a b 1 1 a b a b 1 1 2 2 1 2 2 1 1
a b a b a b a b 1 2 2 1 2 2 1 1 2 2 2 2
a a b a b b a b b a a b 1 2 2 1 1 2 2 1 2 1 2 1 2 2 2 2
b a a b 2 1 2 1 2 2
b b 2 2 2 a a 2 1 2 1 2
b b 2 a a 2 1 2 1 2
q2 p2 2 2 q p
Thí dụ 5. Cho phương trình 2
ax bx c 0a 0 có hai nghiệm x , x thỏa mãn 2 x x . 1 2 1 2 Chứng minh: 3 2 2
b a c ac 3abc . Hƣớng dẫn giải Xét phương trình 2
ax bx c 0a 0 có hai nghiệm x , x thỏa mãn 2 x x . 1 2 1 2
Cách 1: Theo định lý Vi-ét ta có: THCS.TOANMATH.com TÀI LIỆU TOÁN HỌC 36 b b 2 x x x x 1 2 2 2 a a x x 3 3 b 2 2 2 3 c c a 3 x .x x 1 2 2 a a 3 b 6 3 3 2
x x 3x (x x ) 2 2 2 2 2 3 a b x
x 3x x x 3 2 3 3 3 2 2 2 2 2 2 3 a 2 3 c c c b b 2 2 3 3
ac a c 3abc b 2 3 a a a a a 3 2 2
b a c ac 3abc Cách 2: Ta có: 2 x x 2
x x 0 x 2 x x 2 x 2 x x 0 2 1 1 2 1 2 1 2 1 2 2 2 3 3
x x x x x x 1 2 1 2 1 2
x x x x 2 x x 3 3 x x x x 1 2 1 2 1 2 1 2 1 2
x x 3 x x x x 2 3 x x x x 1 2 1 2 1 2 1 2 1 2 3 2 b c c b c 3 (*) a a a a a 3 2 2
b a c ac 3abc b x x 1 2 a
Chú ý: Phần đảo ở (*) xảy ra khi
, nghĩa l| với điều kiện 3 2 2
b a c ac 3abc ta c x x 1 2 a
phải kiểm tra điều kiện có nghiệm của phương trình được thỏa mãn.
Thí dụ 5. Cho c{c phương trình: 2
ax bx c 0 (1) 2
cx dx a 0 (2)
Biết rằng phương trình (1) có c{c nghiệm m v| n, phương trình (2) có c{c nghiệm p v| q. Chứng minh rằng: 2 2 2 2
m n p q 4 . Hƣớng dẫn giải c
Vì m, n l| c{c nghiệm của phương trình (1) nên theo Vi-ét ta có: . m n a a
Vì p,q l| c{c nghiệm của phương trình (2) nên theo VI-ét ta có: . p q .Ta có: c THCS.TOANMATH.com TÀI LIỆU TOÁN HỌC 37 c 2 2 m n 2 . m n 2 a a 2 2 p q 2 . p q 2 c c a 2 2 2 2
m n p q 2 2.2 4 a c Vậy: 2 2 2 2
m n p q 4
X. XÉT DẤU CÁC NGHIÊM CỦA PHƢƠNG TRÌNH BẬC HAI, SO SÁNH NGHIỆM
CỦA PHƢƠNG TRÌNH BẬC HAI VỚI MỘT SỐ CHO TRƢỚC: 1) Phƣơng pháp
Dùng định lý Vi-ét ta có thể xét dấu c{c nghiệm của phương trình bậc hai 2
ax bx c 0a 0 dựa trên c{c kết quả sau: c
Phương trình có hai nghiệm tr{i dấu x 0 x P 0 ac 0 1 2 a 0
Phương trình có hai nghiệm cùng dấu P 0 0
Phương trình có hai nghiệm cùng dương 0 x x P 0 1 2 S 0 0
Phương trình có hai nghiệm cùng }m x x 0 P 0 1 2 S 0
Ngo|i ra {p dụng định lý Vi-ét ta có thể so s{nh được nghiệm của phương trình bậc hai
với một số cho trước. 2) Ví dụ minh họa:
Thí dụ 5. Cho phương trình: 2
x 2m 2 x 2m 1 0 .
a) Tìm m để phương trình có hai nghiệm tr{i dấu
b) Tìm m để phương trình có hai nghiệm dương Hƣớng dẫn giải
Ta có: m 2 m m m m 2 ' 2 2 2 1 2 3
1 2 0 với mọi m, suy ra phương trình
đã cho luôn có hai nghiệm ph}n biệt. THCS.TOANMATH.com TÀI LIỆU TOÁN HỌC 38
x x 2 m 2 1 2
Theo định lý Vi-ét ta có: x x 2 m 1 1 2 1
a) Phương trình có hai nghiệm tr{i dấu x x 0 2
m 1 0 m 1 2 2 m 2 x x 0 2 m 2 0 1 2 1
b) Phương trình có hai nghiệm dương 1 m x x 0 2 m 1 0 m 2 1 2 2
Thí dụ 5. Cho phương trình 2
x m 2 2
3 x m 3m 2 0 .
Tìm m để phương trình có hai nghiệm đối nhau. Hƣớng dẫn giải 2
Ta có: m 2 m m 2 2 2 3 4 3
2 4m 12m 9 4m 12m 8 1
0 với mọi m nên phương trình đã cho có hai nghiệm ph}n biệt.
x x 2m 3
Theo định lý Vi-ét ta có: 1 2 2
x x m 3m 2 1 2 3
Phương trình có hai nghiệm đối nhau x x 0 2m 3 0 m 1 2 2
Thí dụ 5. Cho phương trình: m 2
1 x 2m 3 x m 4 0 . X{c định m để phương trình có: a) Hai nghiệm tr{i dấu b) Hai nghiệm dương c) Hai nghiệm }m d) Hai nghiệm bé hơn 2 Hƣớng dẫn giải
Phương trình đã cho l| phương trình bậc hai m 1 0 m 1 2 Ta có: '
m m m 2
m m 2 3 1 4 6 9
m 5m 4 5 m
a) Phương trình có hai nghiệm tr{i dấu
x 0 x ac 0 m 1 m 4 0 1 m 4 1 2 THCS.TOANMATH.com TÀI LIỆU TOÁN HỌC 39 m 1 m 1 a 0 5 m 0 m 5 ' 0 m 4 m 1
b) Phương trình có hai nghiệm dương 0 x x 1 2 0 P 0 m 1 m 4 S 0 2m 3 m 1 0 m 1 m 3 m 1 4 m5 m 1 a 0 m 5 ' 0
c) Phương trình có hai nghiệm }m m 4
x x 0 1 2 0 P 0 m 1 S 0 2(m 3) 0 m 1 m 0 m 5
m 1 m m 4 1 m 3
d) Phương trình có hai nghiệm nhỏ hơn 2 x x 2 1 2 a 0 m 1 m 1 ' m 5 m 5 0 x 2 0
x 2 x 2 0
x x 2 x x 4 0 1 2 1 2 1 2 1 x 2 0
x 2 x 2 0
x x 4 0 2 1 2 1 2 m 1 m 1 m 1 m 5 m 5 m 5 m 4 m m 4 m 4 4 3 m 4 4 0 0 m 1 1 m 5 m 1 m 1 m 1 2m 3 2 (m 1) m 1 4 0 0 m 1 m 1 m 1
Thí dụ 5. Cho phương trình: 2
x 2(m 1)x (m 1) 0
X{c định gi{ trị của m để phương trình có một nghiệm nhỏ hơn 1, một nghiệm lớn hơn 1. Hƣớng dẫn giải THCS.TOANMATH.com TÀI LIỆU TOÁN HỌC 40
Phương trình đã cho l| phương trình bậc hai có: 2 m 2 1 7 ' 1 m 2
1 m m 2 m 0 với mọi m 2 4
phương trình đã cho có hai nghiệm ph}n biệt x , x x x . 1 2 1 2 x x 2 (m 1)
Theo định lý Vi-ét ta có: 1 2
x x (m1) 1 2
Phương trình đã cho có hai nghiệm thỏa mãn x 1 x 1 2 x 1 0 1
x 1 x 1 0 x x x x 1 0 1 2 1 2 1 2 x 1 0 2
(m 1) 2(m 1) 1 0 m 2 0 m 2
Thí dụ 5. Cho phương trình: 2
mx 2(m 3)x m 4 0 . X{c định m để phương trình có
đúng một nghiệm dương. Hƣớng dẫn giải Ta xét hai trường hợp: 2
TH1: m 0 , Phương trình đã cho có dạng: 6x 4 x ( thỏa mãn b|i ra ). 3
TH2: m 0 , phương trình đã cho l| phương trình bậc hai. Để phương trình đã cho có
đúng một nghiệm dương ta xét c{c khả năng sau:
Phương trình có nghiệm kép dương m 32 2m 9 0 ' m(m 4) 0 0 9 m 0 2(m 3) m S 0 2 0 m 3 m
Phương trình có một nghiệm bằng 0 còn nghiệm kia lớn hơn 0 tức l|: 9 2 m 9 0 ' m 0 2 m 4
x 0 x P 0 0
m 4 m 4 1 2 m S 0 m 0 2(m 3) 0 m 3 m
Phương trình có hai nghiệm tr{i dấu
x 0 x ac 0 (
m m 4) 0 0 m 4 1 2 THCS.TOANMATH.com TÀI LIỆU TOÁN HỌC 41 9
Vậy kết hợp lại c{c trường hợp ta có phương trình có đúng một nghiệm dương khi m 2 hoặc 0 m 4 .
XI. NGHIỆM CHUNG CỦA HAI HAY NHIỀU PHƢƠNG TRÌNH, HAI PHƢƠNG
TRÌNH TƢƠNG ĐƢƠNG.
Thí dụ 5. Cho phương trình: 2
ax bx c 0 có hai nghiệm dương x , x . 1 2
a) Chứng minh rằng phương trình 2
cx bx a 0 cũng có hai nghiệm dương x , x . 3 4
b) Chứng minh rằng M x x x x 4. 1 2 3 4 Hƣớng dẫn giải a) Phương trình 2
ax bx c 0 có hai nghiệm dương x , x nên: 1 2 2b 4ac 0 c 0 c 0 2 2 b b 4ac 0 b 4ac 0
x x 0 1 2 a . a b 0 . b c 0 c . a c 0 .ac 0 x x 0 1 2 a c 0 2 b 4ac 0 b
x x 0 . 3 4 c a x x 0 3 4 c phương trình 2
cx bx a 0 cũng có hai nghiệm dương x , x . 3 4
b) Nếu 0 l| nghiệm của phương trình 2
ax bx c 0 thì 2
a b c 0 , khi đó 2 1 1 1 2 . c . b
a c b a 0 , nghĩa l|
0 l| nghiệm của phương trình 2
cx bx a 0 . 1 1
Ta có: M x x x x x x 2 2 4 . 1 2 3 4 1 2 x x 1 2
Thí dụ 5. Hai phương trình 2
x ax bc 0 và 2
x bx ac 0 chỉ có một nghiệm chung
c 0. Chứng minh rằng hai nghiệm còn lại l| nghiệm của phương trình: 2
x cx ab 0 . THCS.TOANMATH.com TÀI LIỆU TOÁN HỌC 42 Hƣớng dẫn giải Giả sử phương trình 2
x ax bc 0 có nghiệm x , x v| phương trình 2
x bx ac 0 có 0 1
nghiệm x , x ( x l| nghiệm chung của hai phương trình nêu trên v| x x ) . Khi đó ta 0 2 0 1 2 có: 2
x ax bc 0 0 0
a b x c a b 0 0 2 x bx 0 0
a bx c 0 x c 0 0
( giả thiết a b để x l| nghiệm duy nhất của hai phương trình ). 0
Theo định lý Vi-ét ta có:
x x a
x x b 0 1 và 0 2 x x bc x x ac 0 1 0 2
Vì x c nên x b và x a . Mặt kh{c: 0 1 2
2x x x a b 2c a b a b a b c . 0 1 2 Ta có:
S x x a b 1 2
P x x ab 1 2
Và S P c
2 ac a b2 ac a b2 2 4 4 4
0 , do a b suy ra 2 S 4 . P Do đó theo
định lý đảo của định lý Vi-ét ta có x , x l| nghiệm của phương trình 2
x cx ab 0 . 1 2
Thí dụ 5. Tìm c{c gi{ trị m v| n để hai phương trình sau tương đương: 2
x (4m 3 ) n 9 0 ; 2
x 3m 4n x 3n 0 Hƣớng dẫn giải Phương trình 2
x (4m 3 ) n 9 0 có : . a c 9
0 nên có hai nghiệm ph}n biệt . Để hai
phương trình đã cho tương đương thì phương trình 2
x 3m 4n x 3n 0 cũng phải có
hai nghiệm ph}n biệt v| hai phương trình phải có cùng tập nghiệm.
Gọi x , x l| nghiệm của phương trình 2
x (4m 3 )
n 9 0 và x , x l| hai nghiệm của 1 2 3 4 phương trình 2
x 3m 4n x 3n 0 . Khi đó : THCS.TOANMATH.com TÀI LIỆU TOÁN HỌC 43
x x x x ( 4m 3 ) n ( 3m 4 ) n n 3 1 2 3 4
m n 3 x x x x 9 3n m n 1 2 3 4
Với m n 3
thì hai phương trình đã cho trở th|nh: 2
x 21x 9 0 và 2
x 21x 9 0
Rõ r|ng hai phương trình n|y tương đương.
Thí dụ 5. X{c định m để hai phương trình sau tương đương với nhau: 2
x 2x m 0 (1) 2
2x mx 1 0 (2) Hƣớng dẫn giải
Hai phương trình đã cho đều l| phương trình bậc hai. Gọi '
, theo thứ tự l| c{c biệt (1) (2)
số của phương trình (1), (2). Ta xét c{c khả năng sau:
*) Cả hai phương trình đều vô nghiệm: hai phương trình (1) v| (2) vô nghiệm khi v| chỉ khi: ' 0 1 m 0 m 1 (1) 2 2 m 1 (3) 2 0 m 8 0 m 2 2 (2)
**) Hai phương trình đều có cùng tập nghiệm: Hai phương trình đều có nghiệm khi v| chỉ khi: m 1 ' 0 (1) m 2 2 m 2 2. 0 (2) m 2 2
Với m 2 2 , gọi x , x l| nghiệm của phương trình (1). Để hai phương trình có cùng tập 1 2
nghiệm thì x , x cũng l| nghiệm của phương trình (2), khi đó ta phải có: 1 2 m x x 2 m 4 1 2 2 1 m (4) 1 m x x m 1 2 2 2
Kết hợp (3) v| (4) ta được 2 2 m 1
l| c{c gi{ trị cần tìm. THCS.TOANMATH.com TÀI LIỆU TOÁN HỌC 44
XII. ỨNG DỤNG CỦA ĐỊNH LÝ VI-ÉT VÀO GIẢI CÁC BÀI TOÁN SỐ HỌC
Thí dụ 5. Giải phương trình 2
x mx n 0 biết phương trình có hai nghiệm nguyên
dương ph}n biệt v| m, n l| c{c số nguyên tố. Hƣớng dẫn giải
Gọi x , x l| c{c nghiệm của phương trình đã cho. Theo định lý Vi-ét ta có: 1 2
x x m 1 2 . x x n 1 2
Do m,n l| c{c số nguyên tố suy ra x 1, x n ( giả sử x , x ). 1 2 1 2
Từ x x m 1 n m ,
m n l| hai số nguyên tố liên tiếp n 2, m 3. 1 2 Ta có phương trình: 2
x 3x 2 0 , phương trình n|y có hai nghiệm l| 1 v| 2.
Thí dụ 5. Tìm số nguyên m sao cho phương trình 2
mx 2(m 3)x m 2 0 có hai 1 1
nghiệm x , x thỏa mãn: F l| số nguyên. 1 2 x x 1 2 Hƣớng dẫn giải
Giải: Phương trình đã cho có hai nghiệm x , x 1 2 m 0 a 0 m 0 9 m 0 m 3 2 ( m m 2) 0 4m 9 0 4 2(m 3) x x 1 2 m
Theo định lý Vi-ét ta có: m 2 x x 1 2 m 1 1 x x 2(m 3) 2 Ta có 1 2 F 2 x x x x m 2 m 2 1 2 1 2 m 0 m 2 2 m 4
F l| số nguyên m 2Ư(2) m 2 1 m 1 m 1 9 Vì m
m 9;m 1
l| c{c gi{ trị cần tìm thỏa mãn b|i to{n. 4 THCS.TOANMATH.com TÀI LIỆU TOÁN HỌC 45
Thí dụ 5. Giả sử phương trình 2
x ax b 1 0 có hai nghiệm nguyên dương. Chứng minh rằng 2 2
a b l| hợp số. Hƣớng dẫn giải
Giải: Để phương trình đã cho có hai nghiệm x , x *
x , x N thì ta phải có : 1 2 1 2 2
0 a 4(b 1) 0
Theo định lý Vi-ét ta có:
x x a
a x x 1 2 1 2 x x b 1 b x x 1 1 2 1 2 2 Ta có: 2 2 2
a b
x x x x 1 1 2 1 2 2 2 2 2
x 2x x x x x 2x x 1 1 1 2 2 1 2 1 2 2 2 2 2
x x x x 1 2 x 1 2 x 1 1 2 1 2 1 2 Do *
x , x N nên suy ra: 1 2 2
x 1 N 2
x 1 N 1 và 2 2 x 1 2 2 x 1 2 1 2 Vậy 2 2 2 2 2 2
a b N, a b 4; a b 2 x 1 2 x 1 2 2
a b l| hợp số. 1 2
Thí dụ 5. Tìm c{c số nguyên dương x, y thỏa mãn phương trình: 3 3
x y 1 3xy . Hƣớng dẫn giải
Đặt u x y , v . x y .
Ta có: x y xy x y3 3 3 1 3
3xy x y 13xy 0 Hay 3
u 3uv 1 3v 0 u 2
u u v u u 2 1 1 3 ( 1) 0
1 u u 1 3v 0 . Vì ,
x y 0 u x y 0 u 1 0 1 Vậy 2
u u 1 3v 0 v
2u u 1 3
x y u
Ta phải tìm x,y nguyên dương sao cho: 1 . x y 2u u 1 3 THCS.TOANMATH.com TÀI LIỆU TOÁN HỌC 46
Suy ra x, y l| hai nghiệm của phương trình bậc hai: 1 2
X uX 2 u u 1 0 3 1 u
Ta có u 22 0 nếu u 2 . Vậy ta phải có: u x y 2 x y 1. 3 2
Thí dụ 5. Tìm c{c số nguyên a để c{c phương trình sau có nghiệm nguyên: a) 2
x a 5 x 5a 2 0 (1) b) 2
x ax 198 a (2) Hƣớng dẫn giải
a) Gọi x , x Z l| nghiệm của phương trình (1), Theo Vi-ét ta có: 1 2
x x a 5 1 2 (*) x x 5a 2 1 2 5
x 5x 5a 25 Từ (*) ta có 1 2
x x 5a2 1 2
x 5 x 5 2 1.2 2.1 ( 1 ).( 2 ) ( 2 ).( 1 ) 1 2 Suy ra a = 8 hoặc a = 2
x x a b) Ta có: 1 2
x x x x 198 1 2 1 2
x x 198 a 1 2
x 1 x 1 199 1 2
Do 199 l| số nghuyên tố nên:
x 1 x 1 1.199 199.1 ( 1 ).( 1 99) ( 1 99).( 1
) a 198 hoặc a = -2 1 2
XIII. ỨNG DỤNG CỦA ĐỊNH LÝ VI-ÉT VÀO GIẢI PHƢƠNG TRÌNH, HỆ PHƢƠNG TRÌNH. 5 x 5 x
Thí dụ 5. Giải phương trình: x x 6 . (1) x 1 x 1 Hƣớng dẫn giải
Ta có ĐKXĐ : x 1. THCS.TOANMATH.com TÀI LIỆU TOÁN HỌC 47 5 x 5 x
Đặt u x
, v x
u v 5 (2) x 1 x 1 u v 5 Từ (1) v| (2)
u,v l| nghiệm của phương trình: 2
t 5t 6 0 t 3;t 2 . u v 6 1 2 5 x x 3 x 1 u 3 5 x 2 x 2
x 2x 3 0 v 2 x 1 x 1 2
x 3x 2 0 u 2 5 x x 2 x 2 x 1 v 3 x 1 5 x x 3 x 1
Vậy phương trình đã cho có nghiệm 1; 2 .
Thí dụ 5. Giải phương trình: 1 x 4 x 3 Hƣớng dẫn giải ĐKXĐ: 4 x 1 u v 3 u v 3 u v 3 Đặt 1 x ; u
4 x v ta có u v 5 u v 2 2 2 2uv 5 . u v 2
Suy ra u,v l| hai nghiệm của phương trình: 2
X 3X 2 0 X 1; X 2 1 2 x x
u 1 hoặc u 1 1 0 2 ( thỏa mãn ĐKXĐ ). x 3 1 x 2
Vậy phương trình đã cho có tập nghiệm S 3 ; 0 .
Thí dụ 5. Cho phương trình : 3 x 6 x 3 x6 x m
a) Giải phơng trình khi m 3
b) Tìm m để phương trình có nghiệm. Hƣớng dẫn giải ĐKXĐ: 3 x 6 THCS.TOANMATH.com TÀI LIỆU TOÁN HỌC 48 u
v uv m u
v uv m (1) Đặt 3 x ; u
6 x v , ta có: u v 9 u v2 2 2 2uv 9 (2) u, v 0 u, v 0
Từ (1) suy ra: uv (u v) m thay v|o (2) ta có phương trình:
u v2 2(u v) 2m9 0 (3)
a) Với m 3 thì từ (3) ta có: u v 1
( loại ) hoặc u v 3 uv 0 u,v l| nghiệm X 0 3 x 0 x 3 của phương trình: 2
X 3X 0 ( thỏa mãn X 3 x 6 3 x 3 ĐKXĐ).
Vậy với m 3 thì phương trình đã cho có tập nghiệm S 3 ; 6 b) Xét phương trình:
u v2 2(u v) 2m9 0 (3)
Phương trình đã cho có nghiệm khi v| chỉ khi phương trình (3) có nghiệm không }m ' 0 1 0 2m 0 m 5 9
S 0 4 0 9 m 5 m 2 P 0 2m 9 0 2 1
x 2y 5 x 2y
Thí dụ 5. Giải hệ phương trình: x2y 6 x 2y Hƣớng dẫn giải 1 Đặt u
; v x 2 y x y ). x ( ĐK: 2 2 y u v 5 Ta có:
u,v l| nghiệm của phương trình: 2
t 5t 6 0 . uv 6 THCS.TOANMATH.com TÀI LIỆU TOÁN HỌC 49 7 x 4 u 2 5 y v 3 8 ( thỏa mãn ĐKXĐ ). u 3 7 x v 2 6 5 y 12
x y 5
Thí dụ 5. Giải hệ phương trình: x5 y5 8 Hƣớng dẫn giải
ĐK: x 0; y 0 Hệ đã cho x x
y y
x x 5 y y 5 13 5 5 13
x 5 x
y5 y (1) 5 5 3 3
x x 5 y y 5
Đặt u x x 5 5;v y y 5 5 . u v 13 u v 13 u v 13
Khi đó hệ (1) 1 1 3 u v 3 65 (2) uv u v 5 uv 5 3 65 39 741
Vậy u, v l| nghiệm của phương trình: 2 t 13t 0 t 1,2 3 6 u t u t
Do đó ta có nghiệm của hệ (2) l|: 1 hay 2 v t v t 2 1 39 741 Do t
0 (2) vô nghiệm . Vậy hệ (1) vô nghiệm. 2 6 2 2
x y 2xy 8 2 (1)
Thí dụ 5. Giải hệ phương trình: x y 4 (2)
( Đề thi HSG tỉnh lớp 9, năm học 2005-2006 ) Hƣớng dẫn giải THCS.TOANMATH.com TÀI LIỆU TOÁN HỌC 50
ĐKXĐ: x 0; y 0
Đặt S x y; P x. y xy
Theo bài ra ta có S 4 x y 16 2P . 2 2
Phương trình (1) x y xy xy P 2 2 2. 8 2 16 2
2P 2P 8 2 P 2 8 2
P 32P 128 8 2 2P P
P 32P 128 8 P 4 2 2
x, y l| nghiệm của phương trình: 2
t 4t 4 0 t t 2 . 1 2 x 2 x 4 Vậy ta có: ( thỏa mãn ĐKXĐ ) y 4 y 2
Vậy hệ đã cho có nghiêm , x y 4;4 . 2 2
x y 2(x y) 23
Thí dụ 5. Giải hệ phương trình: x y xy 11
(Đề thi vào lớp 10 - Khối THPT chuyên toán ĐH Vinh năm học 2009-2010, vòng 2) Hƣớng dẫn giải
x y2 2xy 2(x y) 23
Hệ đã cho x y xy 11 2 2
S 2P 2S 23
S 2P 2S 23
Đặt S x ;
y P xy hệ đã cho 2
S 4S 45 0 S P 11
2S 2P 22 S P Ta có ' 9 20 49
( C{c gi{ trị n|y đều thỏa mãn ĐK: 2 S 4P ) S 5 P 6 x 4 y 5 S 9 x 5
P 20 y 4
S 5 x 2
P 6 y 3 x 3 y 2 THCS.TOANMATH.com TÀI LIỆU TOÁN HỌC 51
Vậy hệ phương trình đã cho có nghiệm , x y 4 ; 5 , 5 ; 4
,2;3,3;2.
Nhận xét: Khi giải hệ phương trình trong đó vai trò của c{c ẩn trong c{c phương trình l|
như nhau v| khi ta thay đổi vị trí của c{c ẩn trong c{c phương trình thì hệ không thay đổi(
hệ đối xứng loại I ), ta hướng dẫn HS đặt S = x+y, P = xy để đưa hệ về hệ phương trình của
S v| P, tìm S v| P sau đó sử dụng định lý Vi-ét đảo để tìm x v| y
XIV . ỨNG DỤNG CỦA ĐỊNH LÝ VI-ÉT VÀO CÁC BÀI TOÁN CHỨNG MINH
ĐẲNG THỨC, BẤT ĐẲNG THỨC, TÌM GTLN, GTNN. Phƣơng pháp giải:
Học sinh đã được l|m quen với bất đẳng thức Cô-si, tuy nhiên ta có thể chứng minh bất
đẳng thức n|y dựa v|o định lý Vi-ét:
*) Giả sử x x S không đổi, còn P x x thay đổi. Từ điều kiện 2 S 4P 1 2 1 2 2 2 S S S P MaxP
x x . 1 2 4 4 2
Vậy nếu hai số có tổng không đổi thì tích hai số đó lớn nhất khi hai số đó bằng nhau.
*) Giả sử x 0, x 0 và x x P không đổi còn x x S thay đổi. Từ điều kiện 1 2 1 2 1 2 2
S 4P 0 S 2 P S 2 P 0 S 2 P 0 S 2 P
Vậy Min S 2 P x x P 1 2
Vậy hai số dương có tích không đổi thì tổng của hai số đó nhỏ nhất khi hai số đó bằng nhau.
Thí dụ 5. Cho a và b l| c{c số thực thỏa mãn c{c điều kiện 2 6a 20a 15 0 ; 3 2 b 6 15b 20b 6 0 ; ab 1 . Chứng minh rằng . 3 2 2015 ab 9 ab 1 Hƣớng dẫn giải
Ta ký hiệu c{c điều kiện như sau 2 6a 20a 15 0 (1). 2 15b 20b 6 0 (2). ab 1 (3).
Dễ thấy c{c phương trình (1) v| (2) đều có hai nghiệm ph}n biệt.
Do (2) nên b kh{c 0. Chia hai vế của (2) cho 2 b ta được 2 1 1 6 20 15 0 (4). b b 1
Từ (1), (3) v| (4), suy ra a và l| hai nghiệm kh{c nhau của phương trình b 2 6x 20x 15 0 (5). THCS.TOANMATH.com TÀI LIỆU TOÁN HỌC 52 1 10 a Theo định lí Vi-ét b 3 . a 5 b 2 3 2 3 3 ab 9 ab 1 a 1 5 10 2015 Từ đó 9 a 9 3 b b b 2 3 6 3 b 6 suy ra
, điều phải chứng minh. 3 2 2015 ab 9 ab 1
Nhận xét: B|i to{n sử dụng phép ẩn phụ hóa, đưa về c{c phương trình đối xứng, đồng
thời kết hợp với biểu thức đồng bậc ở giả thiết để suy ra điều phải chứng minh.
Ý tưởng: Quan s{t giả thiết b|i to{n, giữa hai phương trình bậc hai có sự đối xứng giữa c{c 1
hệ số của chúng, tuy nhiên sự kh{c biệt nằm ở 2 6a 15 và 2 15b
6 vì thế ta sẽ đặt t khi b 2 6a 20a 15 0 đó
, vì thế ta có được a,t đều l| nghiệm của phương trình 2 6t 20t 15 0 10 a t 2 3 1 10 a 5 6x 20x 15
0 . Theo định lý Viet ta có a và . Khi có được 5 b 3 b 2 at 2 3 b
điều n|y, ta sẽ khai th{c đến biểu thức
, đ}y l| một biểu thức đồng bậc ba 3 2 ab 9 ab 1
nên ta sẽ “ chia để trị “ nên chia cả tử v| mẫu cho 3 b ta được: 3 b 1 1 6 suy ra đpcm. 3 3 3 2 2015 ab 9 ab 1 a 1 5 10 9 a 9 b b 2 3 B|i to{n kết thúc.
Thí dụ 5. Trong c{c hình chữ nhật có chu vi bằng 6, tìm hình chữ nhật có diện tích lớn nhất. Hƣớng dẫn giải
Gọi độ d|i hai cạnh liên tiếp của hình chữ nhật l| x , x 0. Ta có x x 3 . Đặt x .x m 1 2 1 2 1 2
l| diện tích của hình chữ nhật. Vậy x , x l| c{c nghiệm của phương trình: 2
x 3x m 0 . 1 2 9
Phương trình n|y phải có nghiệm nên 9 4m 0 m
. Vậy diện tích lớn nhất của 4 9 3 hình chữ nhật l|
x x . Khi đó hình chữ nhật trở th|nh hình vuông. 1 2 4 2 THCS.TOANMATH.com TÀI LIỆU TOÁN HỌC 53
a b c 5
Thí dụ 5. Chứng minh rằng nếu c{c số a, , b c thỏa mãn: thì:
ab bc ca 8 7 7 7 1 a ;1 b ;1 c 3 3 3 Hƣớng dẫn giải
a b c 5 b
c 5 a b
c 5 a Ta có :
ab bc ca 8 b
c 8 a(b c) b
c 8 a(5 a) C{c số ,
b c l| nghiệm của phương trình: 2 2
x (5 a)x (a 5a 8) 0
Để phương trình có nghiệm ta phải có a2 2 0 5
4(a 5a 8) 0 2 2
a 10a 25 4a 20a 32 0 2 3
a 10a 7 0 a 1 7 3a 0 7 1 a 3 7 7
Chứng minh tương tự ta có: 1 b ;1 c . 3 3
Thí dụ 5. Biết rằng c{c số ,
x y thỏa mãn điều kiện x y 2 . Hãy tìm GTNN của 3 3
F x y . Hƣớng dẫn giải
Nhận xét : để giải b|i to{n trên có r}t nhiều c{ch giải như biến đổi biểu thức F chỉ có một
biến, đổi biến số. Tuy nhiên vận dung định lý Vi-ét cho ta một c{ch giải mới như sau: S 2
S x y x y 2 S 2 Đặt ta có: 8 F P xy 3 3
x y F 3
S 3SP F P 6 8 F Vậy ,
x y l| nghiệm của phương trình : 2 t 2t 0 ( ) 6 8 F ,
x y tồn tại (*) có nghiệm tức l| ' 0 1 0 F 2 6
Min F 2 x y 1 THCS.TOANMATH.com TÀI LIỆU TOÁN HỌC 54
x y z xyz
Thí dụ 5. Cho c{c số ,
x y, z 0 thỏa mãn điều kiện 2 x yz Chứng minh rằng 3 x 3 . Hƣớng dẫn giải 3
x y z xyz
y z xyz x x x Ta có: 2 2 x yz yz x
Vậy c{c số y, z l| c{c nghiệm của phương trình: 2 t 3 x x 2 t x 0 (*) Do tồn tại ,
x y, z thỏa mãn điều kiện đầu b|i nên phương trình (*) phải có nghiệm
Phương trình (*) có nghiệm x x x
4x 0 x 1 x 4 0 1 x 2 2 2 2 1 2 3 2 2 2 2 2 4 x 3 . 2 1 x 2
XV.VẬN DUNG ĐỊNH LÝ VI-ÉT TRONG MẶT PHẲNG TỌA ĐỘ.
Vận dung định lý Vi-ét ta có thể giải một số dạng to{n trong mặt phẳng tọa độ như khảo
s{t h|m số, viết phương trình đường thẳng, xét vị trí tương đối của đường thẳng v| Parabol< 1
Thí dụ 5. Cho Parabol ( P ) : 2 y x 4
a) Viết phương trình đi qua hai điểm A v| B thuộc Parabol có ho|nh độ lần lượt l| x 2 ; x 4. A B
b) Viết phương trình tiếp tuyến với (P) tại điểm C thuộc (P) có ho|nh độ l| 2. Hƣớng dẫn giải
Nhận xét: Hầu hết HS v| GV khi gặp b|i to{n trên đều cho lời giải như sau: A(P) 1 a) y . . Vậy ( A 2 ;1) . A 22 1 x 2 4 A B (P) 1 2
y .4 4 . Vậy B(4;4) x 4 B 4 B
Phương trình đường thẳng AB cần tìm có dạng y ax b nên ta có hệ: THCS.TOANMATH.com TÀI LIỆU TOÁN HỌC 55 1 1 2 a b a 2
4 4a b b 2 1
Vậy phương trình đường thẳng AB l|: y x 2 . 2 2 C (P) 2 b) y 1. Vậy C(2; 1). x 2 C 4 C
Phương trình đường thẳng cần tìm có dạng y ax b (d).
C (d) 1 2a b b 1 2a (d) : y ax 1 2a
Phương trình ho|nh độ giao điểm của (P) v| (d) l|: 1 2 2
x ax 1 2a x 4ax 4 8a 0 4
a a a 2 ' 2 4 4 8 4 1 (d) tiếp xúc với (P) '
0 a 1 b 1 2.1 1
Vậy phương trình tiếp tuyến cần tìm l|: y x 1
*) Nếu vận dụng định lý Vi-ét ta có lời giải đẹp như sau:
a) Phương trình đường thẳng AB cần tìm có dạng y ax b .
Phương trình ho|nh độ giao điểm của (P) v| đường thẳng AB l|: 1 2 2
x ax b x 4ax 4b 0 (*) 4 Ta có x 2
; x 4 l| nghiệm của phương trình (*), theo hệ thức Vi-ét ta có: A B 1
x x 4a a A B 2 x .x 4 b A B b 2 1
Vậy phương trình đường thẳng AB l|: y x 2 . 2
b) Phương trình tiếp tuyến (d) cần tìm có dạng: y ax b .
Phương trình ho|nh độ giao điểm của (d) v| (P) l| 1 2 2
x ax b x 4ax 4b 0 (*) 4
Vì (d) v| (P) tiếp xúc với nhau nên phương trình (*) có nghiệm kép x x 2 . 1 2
x x 4a a 1 Theo Vi-ét ta có: 1 2 x x 4 b b 1 1 2
Vậy phương trình tiếp tuyến cần tìm l|: y x 1 THCS.TOANMATH.com TÀI LIỆU TOÁN HỌC 56
**) Qua ví dụ trên ta đưa ra phương ph{p viết phương trình đường thẳng dựa v|o định lý Vi-ét:
Dạng 1: Lập phương trình đường thẳng y ax b a 0 đi qua hai điểm
A x , y ; B x , y thuộc Parabol 2
y mx (m 0) : A A B B
Vì đường thẳng v| (P) có hai giao điểm nên ho|nh độ giao điểm l| nghiệm của phương trình: 2 2
mx ax b mx ax b 0 a x x A B m Theo Vi-ét ta có : tìm được a, b. b x .x A B m
Dạng 2: Lập phương trình đường thẳng (d) tiếp xúc với (P) tại điểm M x , y M M
Do (d) v| (P) có một điểm chung duy nhất nên phương trình 2
mx ax b 0 có nghiệm kép x x 1 2 a x x 1 2 m Theo Vi-ét ta có: tìm được a,b. b x x 1 2 m
Thí dụ 5. Trong cùng mặt phẳng tọa độ Oxy, cho (P): 2 y x v| đường thẳng (D) :
y mx 1. X{c định m để (D) cắt (P) tại hai điểm ph}n biệt A x , y ; B x , y và: A A B B
a) x 2 x 2 1 1 đạt GTNN A B b) Độ d|i AB ngắn nhất. Hƣớng dẫn giải
Ta có phương trình ho|nh độ giao điểm của (D) v| (P): 2 2
x mx 1 x mx 1 0 (*) Phương trình (*) có 2
m 4 0 với mọi m nên (*) luôn có hai nghiệm ph}n biệt với mọi
m, suy ra (D) luôn cắt (P) tại hai điểm ph}n biệt A x , y ; B x , y trong đó x , x là hai A A B B A B
nghiệm của phương trình (*).
x x m
Theo hệ thức Vi-ét ta có: A B x .x 1 A B
a) x 2 x 2 2 2 1 1
x 2x 1 x 2x 1 A B A A B B
x x 2 2x x 2(x x ) 2 A B A B A B
m m m 2 2 2 2 2 1 3 3 THCS.TOANMATH.com TÀI LIỆU TOÁN HỌC 57
Dấu “=” xảy ra khi v| chỉ khi m 1 0 m 1
Vậy Min x 2 x 2 { 1 1 } 3 m 1 A B b) Do , A B ( )
D y mx 1, y mx 1 A A B B
AB x x 2 y y 2 x x 2 mx mx 2 A B A B A B A B
= x x 2 m x x 2 2 x x 2 1 4 m 1 A B A B A B 2 m 2 4 m 1 4.1 2
Dấu “=” xảy ra m 0
Vậy độ d|i đoạn thẳng AB ngắn nhất khi v| chỉ khi m = 0.
Thí dụ 5. Cho (P): 2
y x v| đường thẳng (D) có hệ số góc l| a đi qua điểm M ( 1 ; 2 )
a) Chứng minh rằng với mọi gi{ trị của a thì (D) luôn cắt (P) tại hai điểm ph}n biệt A v| B
b) X{c định a để A,B nằm về hai phía trục tung. Hƣớng dẫn giải
a) Phương trình đường thẳng (D) có hệ số góc l| a v| đi qua điểm M ( 1 ; 2 ) là:
y ax a 2
Phương trình ho|nh đọ giao điểm của (D) v| (P) l|: 2 2
x ax a 2 x ax a 2 0 (*)
Phương trình (*) có a a a 2 2 4 8 2
4 0 với mọi a, suy ra phương trình (*) luôn
có hai nghiệm ph}n biệt với mọi a. Do đó (D) luôn cắt (P) tai hai điểm ph}n biệt A v| B.
c) Để (D) cắt (P) tại hai điểm A v| B nằm về hai phía trục tung thì phương trình ho|nh
đọ giao điểm phải có hai nghiệm tr{i dấu a 2 0 a 2 .
XVI. ỨNG DỤNG CỦA ĐỊNH LÝ VI-ÉT TRONG CÁC BÀI TOÁN HÌNH HỌC:
Ta đã biết một trong những phương ph{p giải c{c b|i to{n hình học l| “phương ph{p đai
số”, phương ph{p n|y v}n dụng rất có hiệu quả trong c{c dạng b|i tập tính độ d|i đoạn
thẳng, một số b|i to{n cực trị hình học. Kết hợp với đinh lý Vi-ét sẽ cho ta những lời giải hay v| thú vị.
Thí dụ 5. Cho ABC có 0
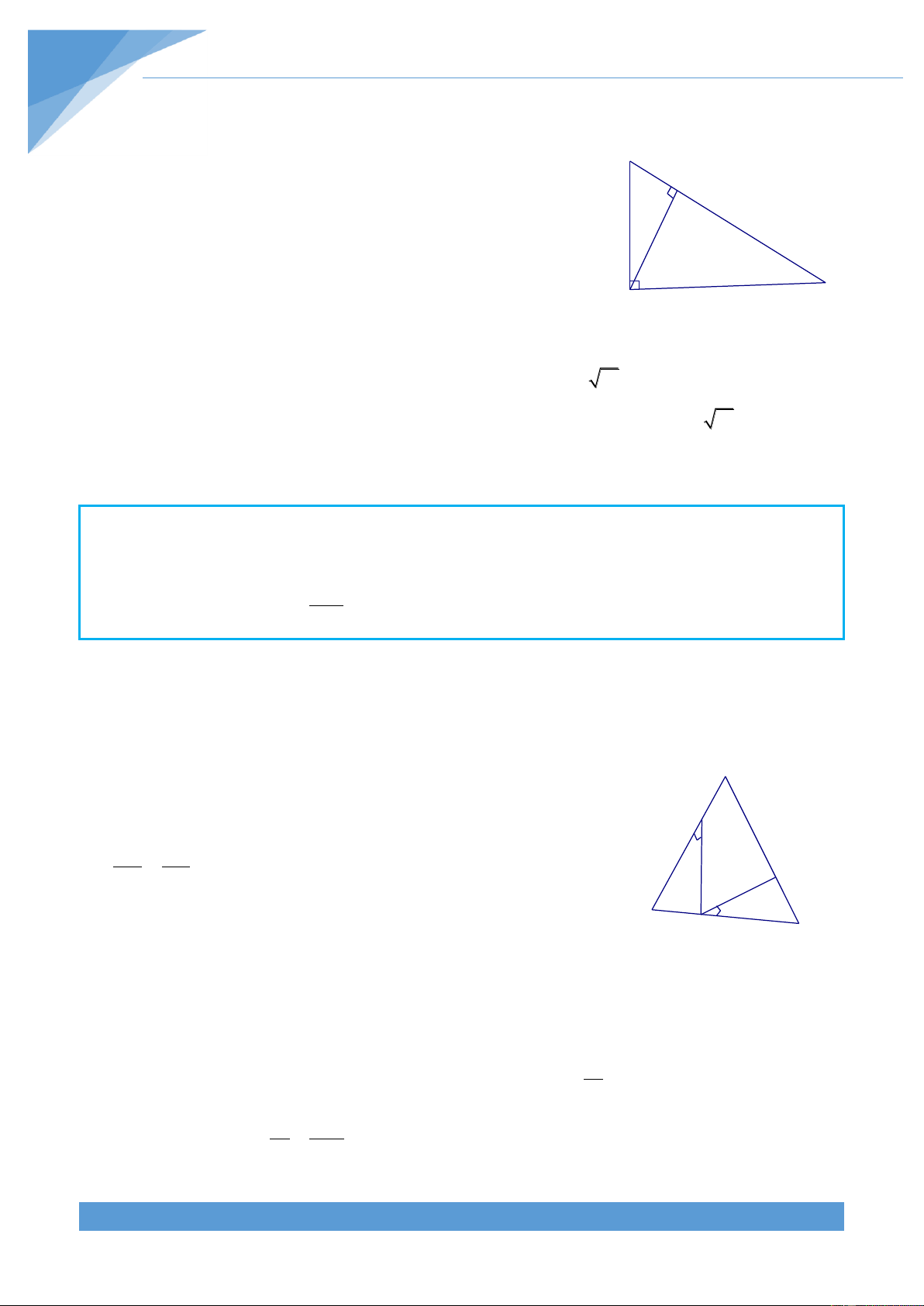
B 90 , đường cao BH 3c ,
m AC 7cm . Tính A , B BC . THCS.TOANMATH.com TÀI LIỆU TOÁN HỌC 58 Hƣớng dẫn giải C
Cách 1: Ta tìm AB, BC thông qua tìm AH, HC H
AH HC AC 7 Ta có AH, HC 2
AH.HC BH 9
l| nghiệm của phương trình: 2
x 7x 9 0 . A
Cách 2: Ta tìm trực tiếp AB,BC dựa v|o định lý Pitago v| B
Vi-ét: Ta có AB BC AC AB BC2 AB BC AB BC2 2 2 2 2 .
2AC.BH 49
AB BC2 49 42 91 AB BC 91
M| AB.BC = AC.BH = 21, Suy ra AB, BC l| nghiệm của phương trình 2
x 91x 21 0 , từ
đó ta sẽ tìm được AB,BC.
Thí dụ 5. Cho tam gi{c đều ABC , trên c{c đoạn thẳng BC,C ,
A AB lần lượt lấy c{c điểm
I , J , K sao cho K không trùng với A , B và 0 I KJ 60 . 2 AB
Chứng minh rằng AJ.BI . 4 Hƣớng dẫn giải Ta có: J KI B AC A
JK ( góc ngo|i tại đỉnh K của A JK ) Mà J KB J KI I KB ( Vì 0 B AC J KB 60 ) C A JK B KI J Vậy B
KI đồng dạng với A JK BI BK
hay AJ.BI AK.BK . I AK AJ A Đặt AK x , BK x x , x 0 ta có: 1 2 1 2 K B
AB x x a ( không đổi ) 1 2
Và AK.BK mm 0
Do đó x , x l| nghiệm của phương trình 2
x ax m 0 1 2 2 a
Phương trình n|y phải có nghiệm nên 2
a 4m 0 m 4 2 2 a AB
Vậy BI.AJ AK.BK . 4 4 THCS.TOANMATH.com TÀI LIỆU TOÁN HỌC 59 a
Dấu “=” xảy ra x x
tức K l| trung điểm của AB. 1 2 2
Thí dụ 5. Cho hình vuông ABCD có cạnh l| a v| hai điểm M, N theo thứ tự chuyển
động trên cạnh BC v| CD sao cho 0 M
AN 45 . Tìm GTNN và GTLN của diện tích tam giác AMN. Hƣớng dẫn giải Đặt MB ;
u ND v(0 ; u v a) . E B u M Ta có: S S S S S C AMN ABCD ABM ADN CMN 1 1 1 1 2
a au av a ua v 2 a uv (1) 2 2 2 2 N
Trên tia đối của tia BM lấy điểm E sao cho BE ND v v AE AN Ta có A BE A
DN(g g) E BA D AN A D 0 E AM E AB B AM B AM D
AN 45 M AN A ME A MN( . c g. )
c MN ME u v 2 2 2 C MN có 2 2 2
2 MN CM CN u v a u a v a u
v a uv at Đặt 2
t a uv , từ (1) ta có S AMN 2
Do đó tìm GTLN v| GTNN của S l| tìm GTLN, GTNN của t AMN u v t Ta có: 2 .
u v a at
u,v l| nghiệm của phương trình 2 2
X tX a at 0 (*)
Phương trình (*) có nghiệm 2 2 2
t 4at a 0 t 2a 2 1 ( vì t 0 )
Khi t 2a 2
1 thì phương trình (*) có nghiệm kép t t a
2 1 u v a 2 1 1 2
Do đó Min t 2a 2
1 u v a 2 1 . Mặt kh{c ta có: 2 2
at a uv a ( vì u, v 0 ) t a u ; a v 0
Khi t a , phương trình (*) có hai nghiệm ph}n biệt 1 1 t ; a t 0 1 2
u 0;v a 2 2 2 a
Vậy Max t = a max S khi M ,
B N C hoặc M C, N D . AMN 2 THCS.TOANMATH.com TÀI LIỆU TOÁN HỌC 60
C. BÀI TẬP VẬN DỤNG TỔNG HỢP
Câu 1. Cho ba số thực dương ph}n biệt a, ,
b c thỏa a b c 3 . Xét ba phương trình bậc hai 2 2 2
4x 4ax b 0, 4x 4bx c 0, 4x 4cx a 0 . Chứng minh rằng trong ba phương trình
trên có ít nhất một phương trình có nghiệm và có ít nhất một phương trình vô nghiệm.
(Chuyên Đà Nẵng năm 2019-2020)
Câu 2. Trong mặt phẳng tọa độ Oxy , cho đường thẳng d : y 2mx m 2 ( m l| tham số) và parabol P 2
: y 2x . Chứng minh với mọi gi{ trị của m thì d luôn cắt P tại hai
điểm ph}n biệt có ho|nh độ x , x . Tìm m sao cho 2 2 x 6x x x 0 . 1 2 1 2 1 2
(Chuyên Điện Biên 2019-2020) 2
Câu 3. Cho phương trình x 2mx m 4 (1) (m là tham số).
a) Chứng minh rằng phương trình (1) luôn có hai nghiệm phân biệt với mọi giá trị của m.
b) Với giá trị nào của m thì phương trình (1) có hai nghiệm x ; x thỏa mãn: 1 2 2 2 x x 1 2 x x 1 2 x x 2 1
(Chuyên Tuyên Quang 2019-2020)
Câu 4. Cho phương trình x2 + 4x – m = 0 (1) (m là tham số). Tìm các giá trị của m để phương 1 1
trình (1) có hai nghiệm phân biệt x 2 2 x x 4(m 2) 1 2 1, x2 thoả mãn x x 1 2
(Chuyên Hải Phòng 2019-2020) 1 1 1
Câu 5. Cho hai số thức ,
m n khác 0 thỏa mãn m n 2
Chứng minh rằng phương trình 2 2 x mx
n x nx m 0 luôn có nghiệm
(Chuyên Bình Định năm 2019-2020)
Câu 6. Cho phương trình 2
x m 2x 3m 3 0 1 với m là tham số.
Tìm các giá trị của m để phương trình 1 có hai nghiệm dương ph}n biệt x ,x sao cho 1 2
x ,x l| độ dài hai cạnh góc vuông của một tam giác vuông với cạnh huyền có độ dài bằng 1 2 5
(Chuyên Bình Phước năm 2019-2020)
Câu 7. Cho hai h|m số 2 y x và y m
1 x 1 (với m l| tham số) có đồ thị lần lượt l|
P và d . Tìm m để P cắt d tại hai điểm ph}n biệt Ax ; y Bx ; y 2 2 1 1 , sao cho 3 3 y y 18 3 3 x x 1 2 1 2 . THCS.TOANMATH.com TÀI LIỆU TOÁN HỌC 61
(Chuyên Bắc Ninh năm 2019-2020)
Câu 8. Cho parabol P 2
: y 2ax a 0 v| đường thẳng 2
d : y 4x 2a . Tìm a để d cắt 8 1
P tại hai điểm phân biệt M , N có ho|nh độ x , x sao cho K đạt giá trị M N x x 2x x M N M N nhỏ nhất.
(Chuyên Bình Dương năm 2019-2020)
Câu 9. Cho phương trình 2
x mx m 1 0
a) Tìm m để phương trình có hai nghiệm dương ph}n biệt 4x x 6
b) Tìm m để phương trình có hai nghiệm x 1 2
1, x2 thỏa mãn biểu thức A 2 2
x x 2(1 x x ) 1 2 1 2 đạt gi{ trị nhỏ nhất
(Chuyên Sơn La năm 2019-2020)
Câu 10. Cho phương trình 2
2018x m 2019 x 2020 0 ( m là tham số). Tìm m để
phương trình có hai nghiệm x , x thỏa mãn: 2 2
x 2019 x x 2019 x 1 2 1 1 1 2
(Chuyên Bạc Lưu năm 2019-2020)
Câu 11. Cho các số thực a,b thỏa mãn a b 2 . Chứng minh phương trình 2 ax
bx 2a 2 0 luôn có nghiệm.
(Chuyên Vũng Tàu năm 2019-2020)(đề 32)
Câu 12. Cho phương trình 2 2
x 2(m 2)x m 5 0 (với m l| tham số).
a) Giải phương trình với m 0 .
b) Tìm tất cả c{c gi{ trị của tham số m để phương trình có hai nghiệm ph}n biệt x , x x x
x x 1 5 1 2 (giả sử 1 2 ) thỏa mãn 1 2 .
(Chuyên Nam Định năm 2019-2020)
Câu 13. Cho phương trình (ẩn x , tham số m ): 2
x 2m
1 x 12 0 . 1
a) Với các giá trị nào của số thực m thì phương trình
1 có hai nghiệm phân biệt x , x 1 2 sao cho
x x 2x x 25 1 2 1 2 ?
b) Tìm tất cả các giá trị của số thực m để phương trình
1 có hai nghiệm phân biệt x , x 1 2 thỏa mãn 2 2
x x 7 2m 1 0 1 2 .
(Chuyên PTNK Hồ Chí Minh năm 2019-2020)
Câu 14. Cho phương trình 4 3 2 x 3x mx 9x 9 0
(Chuyên Phan Bội Châu Năm 2016-2017) THCS.TOANMATH.com TÀI LIỆU TOÁN HỌC 62 a) Với m
2. Khi đó phương trình đã cho trở th|nh 4 3 2 x 3x 2x 9x 9 0
b) Tìm tất cả c{c gi{ trị của m để phương trình đã cho có ít nhất một nghiêm dương.
Câu 15. Trong mặt phẳng Oxy cho parabol 2 (P) : y mx (m 0) v| đường thẳng 2 (d) : y 2x m .
a) Tìm m để (d) cắt (P) tại hai điểm ph}n biệt A v| B. Khi đó chứng minh rằng A v| B cùng
nằm về một phía của trục tung
b) Với m tìm được ở c}u a. Gọi x ;x theo thứ tự l| ho|nh độ c{c điểm A v| B. Tìm c{c gi{ A B 2 1
trị m để biểu thức K
đạt gi{ trị nhỏ nhất. x x 4x x 1 A B A B
(Chuyên Quốc Học Huế năm 2016-2017)
Câu 16. Cho đa thức 2 f x x bx
c . Biết b và c l| c{c hệ số dương v| f x có nghiệm. Chứng minh rằng 3 f 2 9 c .
(Chuyên Bà Rịa Vũng Tàu năm 2016-2017) Câu 17. Cho hàm số 2 y 2x .
a) Vẽ đồ thị P của hàm số (Học sinh tự vẽ hình).
b) Tìm m để đường thẳng d : y 2mx
2 cắt P tại hai điểm phân biệt có ho|nh độ x ;x 1 2 4 2 sao cho biểu thức 2 2 3 3 M x x 17 x x x x 6 x x x x 90 đạt giá trị nhỏ 1 2 1 2 1 2 1 2 1 2 nhất.
(Chuyên tỉnh Bắc Ninh năm 2016-2017)
Câu 18. Cho bốn số thực a, b, c, d kh{c 0 thỏa mãn c{c điều kiện a, b l| hai nghiệm của phương trình 2 x 10cx 11d 0 v|
c, d l| hai nghiệm của phương trình 2 x 10ax 11b
0 . Tính gi{ trị của biểu thức S a b c d .
(Chuyên Bắc Ninh vòng 2 năm 2016-2017)
Câu 19. Cho phương trình 2 x 2 m 1 x 2m 6
0 (m l| số thực). Tìm tất cả c{c gi{
trị của m để phương trình đã cho có hai nghiệm ph}n biệt x ;x thỏa mãn điều kiện 1 2 2 2 x 2x 2m 5 x 2x 2m 5 15 1 1 2 2
(Chuyên Hà Nam năm 2016-2017) THCS.TOANMATH.com TÀI LIỆU TOÁN HỌC 63 2 x 1 x mx 2m 14
Câu 20. Cho phương trình 0. x
a) Giải phương trình trên khi m 8 .
b) Tìm m để phương trình có hai nghiệm x ;x thỏa mãn 1 2 2 x m 1 x 2m 14 3 x 2 2 1
(Chuyên PTNK Hồ Chí Minh năm 2016-2017) Câu 21. Tìm a 1 để phương trình 2 ax 1 2a x 1 a 0 có hai nghiệm ph}n biệt
x ;x thỏa mãn điều kiện 2 2 x ax a a 1. 1 2 2 1
(Chuyên PTNK TP. Hồ Chí Minh năm 2016-2017 Vòng 2)
Câu 22. Giả sử phương trình bậc hai 2 x mx n 1
0 có hai nghiệm nguyên dương. Chứng minh rằng 2 2 m n là hợp số.
(Chuyên Bình Dương 2016-2017)
Câu 23. Cho phương trình 2 2 x 2mx m 4m 3
0 (m l| tham số). Tìm c{c gi{ trị của
m để phương trình có hai nghiệm x ;x sao cho biểu thức 2 2 T x x x x đạt gi{ trị 1 2 1 2 1 2 nhỏ nhất.
(Chuyên Bình Phước 2016-2017) Câu 24. Cho phương trình 2 2 x 2 2m 1 x m 8
0 (m là tham số). Tìm m để phương
trình có hai nghiệm phân biệt x ;x thỏa mãn 1 2 2 2 2 2 x 4m 1 x m x 4m 1 x m 25 . 1 1 2 2
(Chuyên Quảng Bình năm 2016-2017)
Câu 25. Cho phương trình 2 x 2 m 1 x 2m 5
0 (với m l| tham số). Tìm m để
phương trình có hai nghiệm x ,x sao cho x x 2x x 26 . 1 2 1 2 1 2
(Chuyên Long An năm 2016-2017)
Câu 26. Cho phương trình 2 x ax b
0 có hai nghiệm nguyên dương biết a, b là hai số thỏa mãn 5a b 22 . Tìm hai nghiệm đó.
(Chuyên Quảng Ngãi 2016-2017)
Câu 27. Cho phương trình 2 x x b
0 có c{c nghiệm x ;x v| phương trình 1 2 2 x 97x a 0 có c{c nghiệm l| 4 4
x ;x . Tìm gi{ trị của a. 1 2
(Chuyên Hải Phòng 2016-2017) THCS.TOANMATH.com TÀI LIỆU TOÁN HỌC 64
Câu 28. Trong mặt phẳng tọa độ Oxy, cho Parabol (P): 2 y
x v| đường thẳng (d): y 2x 2m 8 (với m l| tham số).
(Chuyên Thái Bình năm 2017-2018)
Câu 29. Cho a, b l| hai số thực bất kỳ, chứng minh có ít nhất một trong hai phương trình ẩn x sau vô nghiệm: 2 2 2 x 2ax 2a b 1 0 2 2 x 2bx 3b ab 0
(Chuyên Thái Bình năm 2017-2018 Vòng 2)
Câu 30. Cho phương trình 2 x 2 m 3 x 2m 5
0 (x là ẩn số). X{c định tất cả các
giá trị của tham số m để phương trình có hai nghiệm dương ph}n biệt x ;x thỏa mãn 1 2 1 1 4 . x x 3 1 2
(Chuyên Quốc Học Huế năm 2017-2018)
Câu 31. Cho phương trình 2 2 x 2 m 1 x 2m 3m 1
0, trong đó m l| tham số, x l| ẩn số.
a) Tìm tất cả các giá trị của m để phương trình có nghiệm.
b) Giả sử phương trình đã cho có hai nghiệm l| x , x . Chứng minh rằng 1 2 9 x x x x . 1 2 1 2 8
(Chuyên Vĩnh Phúc năm 2017-2018)
Câu 32. Cho đa thức 2 f x x – 2 m 2 x 6m
1(m l| tham số). Bằng c{ch đặt x t
2 . Hãy tính f x theo t v| tìm điều kiện của m để phương trình f x 0 có hai nghiệm lớn hơn 2.
(Chuyên Bình Định 2017-2018)
Câu 33. Cho parabol P : 2 y
x v| đường thẳng d : y 2ax
4a (với a l| tham số
(Chuyên ĐHSP Hà Nội 2017-2018) 1
a) Tìm tọa độ giao điểm của d và P khi a 2
b) Tìm tất cả c{c gi{ trị của a để đường thẳng d cắt P tại hai điểm ph}n biệt có ho|nh
độ x ;x thỏa mãn x x 3 1 2 1 2 THCS.TOANMATH.com TÀI LIỆU TOÁN HỌC 65
Bài 34. Gọi x ;x l| hai nghiệm của phương trình 2 x x 5
0 . Lập phương trình bậc hai 1 2
nhận hai nghiệm l| 2x x và x 2x . 1 2 1 2
(Chuyên Đồng Nai năm 2017-2018) 4 3 x x
Câu 35. Tìm m để phương trình sau có 4 nghiệm ph}n biệt: 2 2 x 3mx 2m . 2
(Chuyên Phú Thọ năm 2017-2018)
Câu 36. Cho phương trình 2 2 x 2 m 1 x m 3
0(x l| ẩn v| m l| tham số). Tìm c{c
gi{ trị của m để phương trình có hai nghiệm x ;x thỏa mãn 2 x 4x 2x 2mx 1 . 1 2 1 1 2 1
(Chuyên Bình Phước năm 2017-2018)
Câu 37 . (Chuyên PTNK Hồ Chí Minh năm 2017-2018) 2 Cho phương trình x m 5 x m 6 0 1 .
a) Chứng minh rằng phương trình 1 có hai nghiệm ph}n biệt x ;x với mọi số thực m. 1 2 b) Biết x
x , tìm m sao cho x 1 và 2 x 2x 2 m 1 . 1 2 2 1 2
Câu 38. (Chuyên PTNK Hồ Chí Minh năm 2017-2018 vòng 2) Cho phương trình 2 2 x 2 m 1 x 2m 4m 1 0 1 , với m l| tham số.
a) Tìm m để phương trình 1 có hai nghiệm ph}n biệt x ;x . Chứng minh rằng 1 2 x x 1 2 1 . 2 1 1
b) Giả sử hai nghiệm x ;x kh{c 0, chứng minh rằng: 2 x x . 1 2 1 2 x x 1 2
Câu 39. Cho phương trình 2
x 2mx 1 2m 0 . Chứng minh rằng phương trình luôn có 2x x 1
hai nghiệm x ; x với mọi m. Tìm m để 1 2 P 1 2 2
x 2mx 1
đạt giá trị nhỏ nhất 2m 1 2
(Chuyên Hà Tĩnh 2018-2019)
Câu 40. Cho phương trình: 2
(m 1)x 2(2m 3)x 5m 25 0 (m là tham số). Tìm các giá trị
m là số nguyên sao cho phương trình có nghiệm là số hữu tỉ.
(Chuyên Bình Định 2018-2019).
Câu 41. Cho phương trình 2
x m 2 2
1 x m 1 0 (1) (x là ẩn số)
a) Tìm m để phương trình có 2 nghiệm phân biệt THCS.TOANMATH.com TÀI LIỆU TOÁN HỌC 66
b) Gọi x ; x là 2 nghiệm phân biệt của (1). Tìm m để x ; x thỏa mãn x x x 1 2 2 1 2 1 2 1
(Chuyên Cà Mau 2018-2019)
Câu 42. Tìm các giá trị của m để đồ thị hàm số 2
y x và y x m cắt nhau tại hai điểm phân biệt 8 8
A x ; y , B x ; y sao cho x x y y 162 1 2 1 2 1 1 2 2
(Chuyên Hưng Yên 2018-2019)
Câu 43. Cho đa thức 3 2
f (x) x 2x (1 )
m x m .
1) Khi m 2 , hãy ph}n tích đa thức f (x) th|nh nh}n tử.
2) Tìm tất cả c{c gi{ trị của tham số m để phương trình f (x) 0 có ba nghiệm ph}n biệt
x , x , x thỏa mãn 2 2 2
x x x 4 . 1 2 3 1 2 3
(Chuyên Đắk –Lăk 2018-2019)
Câu 44. Cho phương trình 2
x 2m 3 x 3m 1 0 ( m là tham số)
a) Tìm tất cả các số thực m để phương trình đã cho có hai nghiệm x ; x thỏa mãn điều 1 2 kiện 2 2
x x x x 7 1 2 1 2
b) Tìm tất cả các số nguyên m để phương trình đã cho có nghiệm nguyên
(Chuyên Đại học Vinh năm 2018-2019) Câu 45.
Gọi x ; x là nghiệm của phương trình 2
x 2m
1 x 2m 6 0 . Tìm tất cả các giá trị của m 1 2 2 2 x x nguyên dương để 1 2 A có giá trị nguyên. x x 2 1
(Chuyên Bình Dương 2018-2019)
Câu 46. Cho phương trình 2
x mx 2m 3 0 ( x là ẩn số, m là tham số). Tìm m để phương
trình có hai nghiệm trái dấu mà nghiệm âm có giá trị tuyệt đối lớn hơn nghiệm dương.
(Chuyên Lâm Đồng 2018-2019)
Câu 47. Cho phương trình 2
x x 3m 11 0(1)
a) Với giá trị nào của m thì phương trình (1) có nghiệm kép ? Tìm nghiệm đó
b) Tìm m để phương trình (1) có hai nghiệm phân biệt x ; x sao cho 1 2
2017x 2018x 2019 1 2
(Chuyên PTNK Hồ Chí Minh 2018-2019)
Câu 48. Tìm tham số m để phương trình 2 2
x 2(m 1)x m 0
a) Có hai nghiệm phân biệt dương
b) Có hai nghiệm x x thỏa mãn : x m x 3m 1 2 1 2 2
(Chuyên Tuyên Quang 2018-2019) THCS.TOANMATH.com TÀI LIỆU TOÁN HỌC 67
Câu 49. Cho phương trình: 2
x ax b 0 với x là ẩn, a, b là tham số. Tìm a, b sao cho x x 5
phương trình có nghiệm thỏa mãn 1 2 3 3 x x 35 1 2
(Chuyên Bắc Ninh năm 2018-2019)
Câu 50. (Chuyên Vĩnh Long 2018-2019) Cho phương trình 2
x m 2 2
3 x m 1 0 (1) ( x l| ẩn số, m l| tham số)
a) Chứng tỏ rằng phương trình (1) có hai nghiệm ph}n biệt với mọi gi{ trị của m .
b) Giả sử x , x l| hai nghiệm của phương trình (1). Tìm m để phương trình có hai nghiệm 1 2
ph}n biệt x x thỏa mãn x x 3. 1 2 1 2
Câu 51. Cho phương trình: 2 2
x m x m 1 0 (1), m l| tham số. Tìm tất cả c{c số tự nhiên
m để phương trình (1) có nghiệm nguyên.
(Chuyên Điện Biên 2018-2019)
Câu 52. Chứng minh rằng phương trình 2
ax bx c 2
bx cx a 2 2 2
cx 2ax b 0
luôn có nghiệm với mọi số thực a, , b c
(Chuyên Đà Nẵng 2018-2019)
Câu 53. Cho a là số nguyên dương. Biết 3 nghiệm x x x của phương trình: 1 2 3 3 2
x 3x 2 a x a 0
a) CMR: Biểu thức A có giá trị không đổi: A 4 x x 2 2 2
x x x 1 2 1 2 3 b) Đặt n n n
S x x x . CMR: S là số nguyên lẻ với mọi số n tự nhiên n 1 2 3
(Chuyên Phú Thọ 2018-2019)
Câu 54. Tìm tất cả các giá trị nguyên m để phương trình: 2
x 3x m 4 0 có nghiệm thỏa x x 1 2 là số nguyên. x x 2019 1 2
(Chuyên Lào Cai 2018-2019)
Câu 55. Với a, ,
b c l| độ d|i ba cạnh của tam gi{c. Chứng minh rằng phương trình sau luôn có nghiệm: 2 2 2 2 2 2 2
(b c a )x 4bcx (b c a ) 0 .
(Chuyên Trà Vinh 2018-2019)
Câu 56. Cho các số ; a ;
b c thỏa mãn điều kiện a 2b 5c 0. Chứng minh phương trình 2
ax bx c 0 có nghiệm
(Chuyên Thái Bình năm 2018-2019) THCS.TOANMATH.com TÀI LIỆU TOÁN HỌC 68 HƢỚNG DẪN GIẢI
Câu 1Không mất tỉnh tổng quát ta có thể giả sử a > b > c > 0.
Từ a + b + c = 3 thì a 1 c 0 .
Ba phương trình đã cho lần lượt có các biệt số ' là: 2
4a 4b 2
4b 4c 2
4c 4a 1 ; 2 ; 3 Suy ra 0 2 c 1 a 2
4x 4cx a 0 3 ( vì ) phương trình vô nghiệm Và 2
4a 4a 0 2
4x 4ax b 0 1 ( vì a > b và a > 1) phương trình có nghiệm. Câu 2.
Phương trình ho|nh độ giao điểm của d và P là 2 2 2x 2mx m 2 2x 2mx m 2 0 * 2 2 Ta có m 2 m 2 m 1 3 0, m
d luôn cắt P tại hai điểm ph}n biệt
Gọi x , x l| hai nghiệm của (*). Theo định lý Viet ta có 1 2 x x m 1 2 m 2 x x 1 2 2 Theo giả thiết x 3x 2 2
x 6x x x 0 x 3x x 2x 0 1 2 1 2 1 2 1 2 1 2 x 2 x 1 2 m x2 TH1: 4 x 3x do đó ta có 1 2 3m x1 4 m 3m m 2 2 . 3m 8m 16 0 (vô nghiệm). 4 4 2 x m TH2: 2 x 2x do đó ta có 1 2 x 2m 1 m 2 1 33 2 2 2m 4m m 2 0 m 2 8 THCS.TOANMATH.com TÀI LIỆU TOÁN HỌC 69 1 33 Vậy m l| gi{ trị cần tìm. 8 Câu 3. 2
a) Phương trình: x 2mx m 4 (1)
Phương trình (1) l| phương trình bậc hai của x có:
2 2 ' m 1. m 4 m m 4 2 1 15 ' m 0 với mọi m 2 4
Vậy phương trình (1) luôn có hai nghiệm phân biệt với mọi m
b) Với mọi m phương trình (1) luôn có hai nghiệm phân biệt x ; x . 1 2 x x 2m 1 2
Theo định lí Vi-ét, ta có: x x m 4 1 2 Ta lại có: x x x x x x 2 2 2 2 3 3 x x x x 1 2 1 1 2 2 1 2 1 2 x x x x x x 1 2 1 2 1 2 x x x x x x 2 1 1 2 1 2 x x x x x x x x 1 1 2 2 1 0 x x . 0 1 2 1 2 2 2 2 1 2 x x x x 1 2 1 2 x x 1 2 2 x x 0 hoặc 1 2 x x 1 2
TH1: x x 0 2m 0 m 0 1 2 x x x x ' 0 1 2 2 1 2 TH2:
(vô nghiệm vì ' 0, m ) x x x x 0 x x 0 1 2 1 2 1 2
Vậy với m 0 thì thì phương trình (1) có hai nghiệm x ; x thỏa mãn: 1 2 2 2 x x 1 2 x x 1 2 x x 2 1 Câu 4.
Phương trình đã cho có hai nghiệm phân biệt
' 4 m 0 m 4 . THCS.TOANMATH.com TÀI LIỆU TOÁN HỌC 70
Áp dụng hệ thức Vi-ét: x x 4 1 2 . x x m x 2 416 2m gt
4m 2m 0 m 2
m 16 m 4 .
Kết hợp với điều kiện m 4
;m 0 ta được m 4 thỏa mãn. Câu 5. 1 1 1 2m n mn Ta có 2m n mn m n 2 2mn 2mn 2 x mx n 0 (1) Ta có 2 2 x mx n
x nx m 0 2 x nx m 0 (2)
Phương trình (1) l| PT bậc hai có 2 m 4n 1
Phương trình (2) l| PT bậc hai có 2 n 4m 2
Do đó m 4n n 4m m n 4m n m n 2mn m n2 2 2 2 2 2 2 0 1 2
Suy ra trong và có ít nhất một số lớn hơn hoặc bằng 0. 1 2
Vậy phương trình đã cho luôn có nghiệm Câu 6.
Điều kiện để phương trình 1 có hai nghiệm x ,x thỏa mãn điều kiện bài toán là: 1 2 2 0 m 2 4 3m 3 0 S 0 m 2 0 P 0 3m 3 0 2 2 2 x x 25 1 1 x x 2x x 25 1 2 1 2 2 m 8m 16 0 m 4 m 2 m 2 m 1 m 3 m 1 2 m 2 2 3m 3 25 m 5 hoaêc m 3 Vậy m
3 thỏa mãn yêu cầu bài toán.
Câu 7. Phương trình ho|nh độ giao điểm của d và P là 2 x m 1 x 1 0 1 . THCS.TOANMATH.com TÀI LIỆU TOÁN HỌC 71
P cắt d tại hai điểm ph}n biệt A x ;y , B x ;y khi v| chỉ khi phương trình 1 có hai 1 1 2 2 nghiệm ph}n biệt x x 1 , 2 2 m 3 m 1 4 0 m 1 2 (*). m 1
Áp dụng ĐL Vi-ét ta có x x m 1 ; x x 1 . 1 2 1 2 Từ giả thiết ta có 2 y x , 2 y x . 1 1 2 2 Khi đó 3 3 3 3 6 6 3 3 3 3 3 3 y y 18 x x x x 18 x x x x x x 18 0 2 . 1 2 1 2 1 2 1 2 1 2 1 2 3 Do x x nên 3 3 2 x x 18 0 x x 3x x x x 18 0. 1 2 1 2 1 2 1 2 1 2 Do đó, 3 2 m 1 3 m 1 18 0 m 1 3 m 1 3 m 1 6 0 m 4 (t/m (*)). Câu 8.
Phương trình ho|nh độ của P và d là: 2 2 2 2
2ax 4x 2a 2ax 4x 2a 0 *
Để d cắt P tại hai điểm phân biệt M , N thì * phải có hai nghiệm phân biệt , nghĩa l| 2 2 0 4 4.2 . a 2a 0 3 16 16a 0 3
1 a 0 a 2 1
1 a a 0 2 a 1 3 1 a
0 0 a 1 4 4 Ngoài ra, ta có: 3 3 4 16 16a 1 1 a 3 3 4 16 16a 1 1 a x x M 2.2a a N 2.2a a 3 3 1 1 a 1 1 a 2 x x M N a a a 3 3 1 1 a 1 1 a 2x .x 2. . 2a M N a a 8 1 8 1 1 BĐT Côsi 1 Mà K 4a 2 4 . a 2 2 x x 2x x 2 2a 2a 2a M N M N a
Do đó K đạt giá trị nhỏ nhất, ngĩa l| 1 2 2 4a
2 2 8a 4 2a 1 0 a 2a 4 THCS.TOANMATH.com TÀI LIỆU TOÁN HỌC 72 2 Vậy a
thì thỏa mãn yêu cầu đề bài. 4 Câu 9. a) Phương trình 2
x mx m 1 0 có hai nghiệm dương ph}n biệt khi v| chỉ khi 2 0
m 4m 4 0
m 22 0 m 0 S 0 m 0 m 1 m 1 P 0 m 1 0 m 0 Vậy với
thì phương trình đã cho có hai nghiệm dương ph}n biệt m 1 b) Vì 2
(m 2) 0 với mọi m nên phương trình đã cho luôn có hai nghiệm phân biệt x1, x2
x x m
Theo hệ thức vi – ét ta có: 1 2 x x m1 1 2 Khi đó: 4x x 6 4x x 6 4x x 6 1 2 1 2 1 2 A 2 2 2 2
x x 2(1 x x )
(x x ) 2x x 2 2x x (x x ) 2 1 2 1 2 1 2 1 2 1 2 1 2 4(m 1) 6 4m 2 A 2 2 m 2 m 2 2 (
A m 2) 4m 2 2
Am 4m 2A 2 0 (1) (1) có nghiệm khi ' 0 4 (
A 2 A 2) 0 2
2A 2A 4 0
(A 1)(A 2) 0 1 A 2 Vậy Min A = -1; khi đó 2
1 m 4m 4 0 2 (m 2) 0 m 2
Vậy với m = -2 thì phương trình có hai nghiệm thỏa mãn đề b|i Câu 10.
Do a,c < 0 nên phương trình luôn có hai nghiệm phân biệt với mọi giá trị của m. Ta có: 2 2
x 2019 x
x 2019 x . 1 i 2 2 2 2
x 2019 x 2019 x x 1 2 2 1 THCS.TOANMATH.com TÀI LIỆU TOÁN HỌC 73 2 2 x x 1 2 x x 2 1 2 2 x 2019 x 2019 1 2 x x 0 1 2 2 2
x 2019 x 2019 x x 1 2 1 2
* Trường hợp 1: x x 0 1 2 m – 2019 = 0 m = 2019
* Trường hợp 2: Không xảy ra do: 2
x 2019 x ; 2 x 2019 x 1 1 2 2 Vậy m = 2019. Câu 11. 2
Nếu a = 0 thì b 2 v| do đó phương trình có nghiệm x b Nếu a 0 thì 2 b 8a(a 1) a 0 + Nếu a(a 1) 0
0 nên phương trình có nghiệm a 1 + Nếu 0 < a < 1 thì 2 2 2 2 a b 2 b 2 a 0 b 2 a (2 a) 8a(a 1) (3a 2) 0
Nên phương trình có nghiệm
Vậy phương trình đã cho luôn có nghiệm với mọi số thực a,b thỏa mãn a b 2 Câu 12.
a) Với m = 0, ta có phương trình: 2
x 4x 5 0
Giải phương trình được x 1 ; x 5 1 2 b) Phương trình 2 2
x 2(m 2)x m 5 0 Ta có 2 ac m 5 0 m
Phương trình có hai nghiệm tr{i dấu
Mà x x x 0 x 1 2 1 2
x x ; x 1 x 1 1 1 2 2 Do đó:
x x 1 5 x x 1 5 x x 6 1 2 1 2 1 2
Lại có: x x 2 (m 2) 1 2 (theo hệ thức Vi-ét) THCS.TOANMATH.com TÀI LIỆU TOÁN HỌC 74 2 (m 2) 6 m 5
Vậy m 5 l| gi{ trị cần tìm. Câu 13. Phương trình
1 l| phương trình bậc hai ẩn x có các hệ số tương ứng a 1 , b 2m 1 và c 12
. Do a và c trái dấu nên phương trình
1 luôn có hai nghiệm phân biệt x , x trái dấu 1 2
x x 2m 1 nhau. Theo Viet, ta có: 1 2 . x x 12 1 2 a)
Do x x 2x x 25 nên ta có 2m 1 24 25 , tức m 0. 1 2 1 2
Vậy có duy nhất một giá trị m thỏa mãn yêu cầu này là m 0. b) Ta có 2 2
x x x x x x
2m 1 x x 1 2 1 2 1 2
1 2 . Dó đó, để thỏa mãn yêu cầu đều bài thì ta 1
phải có 2m
1 x x 7 0 m x x 7 1 2 , tức hoặc 1 2 . 2
Ở trường hợp thứ hai, do x x 2m 1 nên ta có x m 4 và x m 3 . 1 2 1 2
Từ đ}y, do x x 12
nên m 4m 3 1
2 , tức mm
1 0 . Suy ra m 0 hoặc m 1 . 1 2 1
Vậy có ba giá trị m thỏa mãn yêu cầu này là m 0 , m 1 và m . 2 Câu 14. a) Với m
2. Khi đó phương trình đã cho trở th|nh 4 3 2 x 3x 2x 9x 9 0 2 x 4x 3 0 x 1 Hay ta được 2 2 x 4x 3 x x 3 0 2 x x 3 0 x 3
b) Tìm tất cả c{c gi{ trị của m để phương trình đã cho có ít nhất một nghiêm dương.
Phân tích. Nhìn vào phương trình ta thấy phương trình có bậc quá cao đó là bậc 4 và đề yêu cầu
cả các giá trị của m để phương trình đã cho có ít nhất một nghiêm dương nên ta cần đưa phương
trình về phương trình bậc hai để áp dụng hệ thức Vi – ét. Ta chia phương trình đã cho cho 2 x chú ý 9 9 9 3 điều kiện x
0 , khi đó ta được 2 2 x 3x m 0 x 3 x m 0 * 2 2 x x x x 3 9 Đặt x t 2 2 x t
6. Khi đó phương trình * trở thành 2 t 3t m 6 0 x 2 x
Đến đây chi cần áp dụng định lý Vi – et là được. Ta có lời giải như sau. Lời giải. Xét x
0 , ta thấy không thỏa mãn nên x
0 không phải l| nghiệm của phương trình. Xét x
0 . Khi đó phương trình đã cho tương đương với THCS.TOANMATH.com TÀI LIỆU TOÁN HỌC 75 9 9 9 3 2 x 3x m 0 2 x 3 x m 0 * 2 x x 2 x x 3 9 Đặt x t 2 2 x t
6. Khi đó phương trình * trở th|nh: 2 t 3t m 6 0 . x 2 x
Xem phương trình trên l| phương trình ẩn t với m l| tham số. Để phương trình đã cho có
ít nhất một nghiêm dương thì phương trình ẩn t cũng có ít nhất một nghiệm dương. Khi 33
đó để phương trình ẩn t có nghiệm thì 2 3 4 m 6 4m 33 0 m . Áp 4
dụng hệ thức Vi – et ta có t t 3
0 . Do đó phương trình có ít nhất một nghiệm 1 2 dương. 33 Vậy với m
thì phương trình có ít nhất một nghiệm dương. 4 Câu 15.
a) Tìm m để (d) cắt (P) tại hai điểm ph}n biệt A v| B. Khi đó chứng minh rằng A v| B cùng
nằm về một phía của trục tung
Phân tích. Để d cắt P tại hai điểm phân biệt A và B thì phương trình 2 2 mx 2x m phải
có hai nghiệm phân biệt. Chuyển phương trình trên về phương trình bậc hai ẩn x và đi tìm điều
kiện có nghiệm cho phương trình. Ta có 2 2 2 2 mx 2x m mx 2x m 0 Khi đó 2 3 3 4 4.m .m 4 4m 0 m 1 m 1 3 3 2 4 m 2 4 m
Khi đó ta có hai nghiệm của phương trình là x ;x 2m 2m
Để chứng minh A và B cùng nằm về một phía của trục tung thì ta cần chứng minh hai hoành độ
hai giao điểm cùng dấu hay chứng minh hai nghiệm trên phải cùng dấu. Khi đó ta nghĩ đến việc xét tích hai nghiệm 3 3 3 2 4 m 2 4 m 4 4 m m . 2 2m 2m 4m 4 3 3 2 4 m 2 4 m Do m 0 nên suy ra .
0 . Đến đây ta được điều phải chứng minh. 2m 2m
Lời giải. Để đường thẳng d cắt parabol P tại hai điểm ph}n biệt A v| B thì phương trình ho|ng độ 2 2 mx 2x
m phải có hai nghiệm ph}n biệt hay 2 2 mx 2x m 0 có hai nghiệm ph}n biệt. Khi đó 2 3 3 4 4.m .m 4 4m 0 m 1 m 1. 3 3 2 4 m 2 4 m
Khi đó ta có hai nghiệm của phương trình l| x ;x 2m 2m THCS.TOANMATH.com TÀI LIỆU TOÁN HỌC 76 3 3 3 2 4 m 2 4 m 4 4 m m
Xét tích hai nghiệm trên ta có . 2 2m 2m 4m 4 3 3 2 4 m 2 4 m Vì m 0 nên .
0 , do đó hai nghiệm trên cùng dấu. 2m 2m
Vậy A v| B cùng dấu hay cùng nằm về một phía của trục tung.
b) Với m tìm được ở c}u a. Gọi x ;x theo thứ tự l| ho|nh độ c{c điểm A v| B. Tìm c{c gi{ A B 2 1
trị m để biểu thức K
đạt gi{ trị nhỏ nhất. x x 4x x 1 A B A B
Phân tích và lời giải. Với 0 m
1, khi đó phương trình ho|ng độ có hai nghiệm ph}n 2
biệt cùng dấu. Theo định lý Vi – et ta có x x ;x .x
m . Khi đó thay v|o biểu A B A B m thức K ta được 2 1 1 K m x x 4x x 1 4m 1 A B A B 1
Đến đ}y cần tìm gi{ trị nhỏ nhất của K m . 4m 1
Giả sử K l| gi{ trị nhỏ nhất của biểu thức K, khi đó phương trình sau có nghiệm 0 2 4m m 1 2 2 K 4m m 1 4K m K 4m m 1 4K 1 K 0 0 0 0 0 0 4m 1
Phương trình trên l| phương trình bậc 2 ẩn m nên để phương trình có nghiệm thì 3 K 2 0 2 4 0 1 4K 4.4 1 K 0 16K 8K 15 0 0 0 0 0 5 K0 4 3 Mặt kh{c vì m 0 nên K 0 , do đó suy ra K . 0 0 4 3 1 3 1
Suy ra gi{ trị nhỏ nhất của K l| , xẩy ra tại m m . 4 4m 1 4 4 1 2 1 Vậy với m thì biểu thức K
đạt gi{ trị nhỏ nhất. 4 x x 4x x 1 A B A B Câu 16.
+ Cách 1. Ta có f x có nghiệm nên 2 b 4c 0 b 2 c . THCS.TOANMATH.com TÀI LIỆU TOÁN HỌC 77 2 Ta lại có f 2 4 2b c 4 4 c c c 2 và 3 c 2 c 1 1 3 c 2 Do đó 3 3 f 2 3 c 9 c .
+ Cách 2. Theo hệ thức Vi – et ta có x x c và f x x x x x 1 2 1 2
Do b và c dương nên f x chỉ có nghiệm }m, suy ra x 0;x 0 1 2 Đặt x , p x q thì p 0, q 0 và pq c . Ta có f x x p x q từ đó dẫn 1 2 đến f 2 2 p 2 q 1 1 p 1 1 q 3 3 3 3 3 p.3 q 9 pq 9 c Câu 17.
Phương trình ho|nh độ giao điểm của d và P là 2 x mx 1 0 1 .
Đường thẳng d cắt P tại hai điểm ph}n biệt khi v| chỉ khi m 2 2 0 m 4 0 m 2
Áp dụng định lí Vi – et ta có x x ; m x x 1 . 1 2 1 2 2 2 4 2 4 2 2 2 M m 17m 6m 90 m 18m 81 m 6m 9 m 9 m 3 0
Vậy gi{ trị nhỏ nhất của M l| 0. Dấu bằng xảy ra khi v| chỉ khi m 3. Câu 18. a b 10c
Vì a, b l| hai nghiệm của 2 x 10cx 11d
0 nên theo hệ thức Vi – et ta có ab 11d c d 10a
Vì c, d l| hai nghiệm của 2 x 10ax 11b
0 nên theo hệ thức Vi – et ta có cd 11b
Từ c{c hệ thức trên ta có 9 a c b d S 10 a c Cũng từ ab 11d và cd
11b nên ta có ac 121.
M| a l| nghiệm của phương trình 2 x 10cx 11d 0 nên 2 a 10ac 11d 0 và c là
nghiệm của phương trình 2 x 10ax 11b 0 nên 2 c 10ac 11b 0 . Từ đó duy ra 2 2 2 a c 20ac 11 b d 0 a c 22ac 99 a c 0 2 a c 22 a c 99 a c 2662 0 a c 121 THCS.TOANMATH.com TÀI LIỆU TOÁN HỌC 78 + Với a c 22 S 220. + Với a c 121 S 1210.
Câu 19. Xét phươg trình 2 x 2 m 1 x 2m 6 0 với m l| tham số. 2 Ta có ' 2 m 4m 7 m 2 3
0 với mọi m. Do đó phương trình có nghiệm với mọi m. x x 2 m 1
Theo hệ thức Vi – et ta có 1 2 . x x 2m 6 1 2 Ta có 2 2 x 2 m 1 x 2m 6 0 x 2x 2m 5 2mx 1 .
Do x ;x l| hai nghiệm của phương trình nên ta có ta có 1 2 2 2 x 2x 2m 5 x 2x 2m 5 15 1 1 2 2 2 2mx 1 2mx 1 15 4m x x 2m x x 1 15 1 2 1 2 1 2
Kết hợp với hệ thức Vi – et ta được 2 3 2 4m 2m 6 4m m 1 16 0 2m 5m m 4 0 3 41 3 41 2 m 1 2m 3m 4 0 m 1; ; 4 4 3 41 3 41
Vậy c{c gi{ trị thỏa mãn yêu cầu b|i to{n l| m 1; ; . 4 4 Câu 20.
a) Giải phương trình trên khi m 8 .
Điều kiện x{c định của phương trình l| x 0. Khi m
8 phương trình đã cho được viết lại th|nh 2 x 1 x 8x 2 2 0 x 8x 2 0 x 4 3 2 x (Do x 0 nên x 1 0 ) Vậy với m
8 thì phương trình có tập nghiệm l| S 4 3 2;4 3 2
b) Tìm m để phương trình có hai nghiệm x ;x thỏa mãn 1 2 2 x m 1 x 2m 14 3 x . 2 2 1
Phương trình đã cho có nghiệm khi v| chỉ khi phương trình 2 x mx 2m 14 0 có nghiệm dương. THCS.TOANMATH.com TÀI LIỆU TOÁN HỌC 79
Để phương trình đã cho có hai nghiệm dương ph}n biệt x ;x thì 2 x mx 2m 14 0 1 2
phải có hai nghiệm dương ph}n biệt x ;x . Điều n|y xẩy ra khi v| chỉ khi 1 2 2 m 4 2m 14 0 S x x m 0 1 2 P x .x 2m 14 0 1 2
Do x l| nghiệm của phương trình củap hương trình 2 x mx 2m 14 0 nên ta được 2 2 2 x mx 2m 14 0 x m 1 x 2m 14 x 2 2 2 2 2 Từ đó ta được 2 x m 1 x 2m 14 3 x x 3 x x x 3 2 2 1 2 1 1 2
Bình phương hai vế v| kết hợp với hệ thức Vi – et ta được 2 x x 3 x x 2 x x 9 m 2m 14 9 1 2 1 2 1 2 m 9 m 9 2 2m 14 m 9 2 m 5 2 4 2m 14 m 9 m 10m 25 0 Thử m
5 v|o phương trình ta thấy thỏa mãn. Vậy m 5 l| gi{ trị cần tìm. Câu 21.
Điều kiện để phương trình có hai nghiệm ph}n biệt l| 2 2 1 2a 4a 1 a 8m 8a 1 0 . 2a 1
Theo định lí Vi – et ta có x x suy ra ax ax 2a 1 hay ax 2a 1 ax . 1 2 a 1 2 1 2 Kết hợp với 2 2 x ax a a 1 ta được 2 2 x ax 2a 1 a a 1. 2 1 2 2 Từ đó suy ra 2 2 3 2 ax a x a a 2a 0 . 2 2
Do x l| một nghiệm của phương trình nên ta có 2 ax 1 2a x 1 a 0 . Từ đó ta có 2 2 2 2 2 3 2 2 ax a x a a 2a ax 1 2a x 1 a 0 2 2 2 2 2 3 2 a 2a 1 x a a a 2 2 Do a 1 nên 2 a 2a 1
0 nên từ phương trình trên ta được x a 1. 2 Thế v|o phương trình 2 2 3 2 ax a x a a 2a 0 ta được 2 2 2 2 a 1 a a 1 a a 2 0 a 1;3
Thử lại v|o phương trình đã cho ta được a 1 và a
3 thỏa mãn yêu cầu b|i to{n. Câu 22. THCS.TOANMATH.com TÀI LIỆU TOÁN HỌC 80
Lời giải. Giả sử x ;x l| hai nghiệm nguyên dương của phương trình 1 2 2 x mx n 1 0 .
Khi đó theo hệ thức Vi – et ta có x x ; m x x n 1 . Do đó ta được 1 2 1 2 2 2 2 2 2 2 2 2 m n x x x x 1 x x 2x x x x 2x x 1 1 2 1 1 1 2 1 2 1 2 1 2 2 2 2 2 x x x x 1 x 1 x 1 1 2 1 2 1 2
Do x ;x l| hai nghiệm nguyên dương nên x 1 2;x 1 2 . 1 2 1 2 Từ đó suy ra 2 2 m n l| hợp số. Câu 23.
Phương trình đã cho có nghiệm x ;x khi v| chỉ khi 1 2 3 ' 2 2 m m 4m 3 4m 3 0 m 4
Theo hệ thức Vi – et ta có 2 x x 2 ; m x x m 4m 3. 1 2 1 2 2 Ta có 2 2 2 2 2 T x x x x x x 3x x 4m 3 m 4m 3 m 12m 9 1 2 1 2 1 2 1 2 2 Hay ta được T m 6 27 3 3 21 2 441 Do m nên m 6 6 nên suy ra m 6 nên 4 4 4 16 2 9 T m 6 27 . 16 9 3
Vậy gi{ trị nhỏ nhất của T l|
, đạt được tại m 16 4 Câu 24. Ta có ' 2 3m 4m 7 m 1 3m 7 m 1
Phương trình đã cho có hai nghiệm ph}n biệt khi ' m 1 3m 7 0 7 m 3 x x 4m 2
Vì x ;x l| hai nghiệm của phương trình nên theo hệ thức Vi – et ta có 1 2 1 2 2 x .x m 8 1 2 2 2 x 4m 1 x m x 8 và 1 1 1 . Khi đó: 2 2 x 4m 1 x m x 8 2 2 2 2 2 2 2 x 4m 1 x m . x 4m 1 x m 25 x 8 x 8 0 1 1 2 2 1 2 2 x x 8 x x 31 0 m 32m 31 0 m 1;31 1 2 1 2 THCS.TOANMATH.com TÀI LIỆU TOÁN HỌC 81
Kết hợp với điều kiện có nghiệm của phương trình ta được m 31 thỏa mãn yêu cầu b|i toán. Câu 25. Ta có 2 2 a b
Phương trình đã cho có nghiệm khi v| chỉ khi 2 ' 0 m 4 0 x x 2m 2
Khi đó theo định lý Vi – et ta có 1 2 x x 2m 5 1 2 Do đó ta được x x 2x x 26 2m 2 4m 10 26 m 9 1 2 1 2
Kết hợp với điều kiện có nghiệm thì m 9 thỏa yêu cần đề b|i. Câu 26. Gọi x ,x x x
l| hai nghiệm nguyên dương của phương trình 2 x ax b 0 . Ta có 1 2 1 2 x x ; a x .x b . Khi đó 1 2 1 2 5 x x x x 22 x x 5x 5x 25 47 1 2 1 2 1 2 1 2 x 5 1 1 x 5 47 x 6 2 1 x 5 x 5 47 1 2 x 5 47 x 52 1 2 x 5 1 2 Khi đó a 58 và b 312 thoả mãn 5a b 22 .
V| phương trình có nghiệm l| x 6; x 52 1 2 Câu 27. 2 x x b 0
Do x ;x l| c{c nghiệm của phương trình 2 x x b 0 nên ta có 1 1 1 2 2 x x b 0 2 2
Theo hệ thức Vi – et ta có x x 1;x x b 1 2 1 2 8 4 x 97x a 0 Do 4 4
x ;x l| c{c nghiệm của phương trình 2 x 97x a 0 nên ta có 1 1 1 2 8 4 x 97x a 0 2 2
Theo hệ thức Vi – et ta có 4 4 4 4 x x 97;x .x a 1 2 1 2 2 1 Ta có 2 2 x x x x 2x x
1 2b , từ đó suy ra 1 2b 0 b 1 2 1 2 1 2 2 2 2 Lại có 4 4 2 2 2 2 2 2 x x x x 2x .x 1 2b 2b 2b 4b 1. 1 2 1 2 1 2 Mà theo trên ta có 4 4 x x 97 nên ta được 1 2 2 2 2b 4b 1 97 b 2b 48 0 b 6;8 . THCS.TOANMATH.com TÀI LIỆU TOÁN HỌC 82 1 Do b
nên ta chọn được b 6, hay ta có x x 6 . 2 1 2 4 4 Ta có 4 4 4 4 a x .x x x b 6 6 1296 1 2 1 2 Câu 28. a) Khi m
4 , tìm tọa độ giao điểm của đường thẳng (d) v| Parabol (P) .
Xét phương trình ho|nh độ giao điểm của P và d là 2 2 x 2mx 2m 8 x 2mx 2m 8 0 x 0
Khi m = – 4, phương trình trên trở th|nh 2 x 8x 0 x 8 Với x 0 thì y 0 v| với x 8 thì y 64
Vậy khi m = – 4 thì tọa độ giao điểm của P và d là 0; 0 và 8;64 .
b) Chứng minh đường thẳng d và Parabol P luôn cắt nhau tại hai điểm ph}n biệt có
ho|nh độ x ;x . Tìm c{c gi{ trị của m để x 2x 2 . 1 2 1 2
Xét phương trình ho|n độ giao điểm 2 x 2mx 2m 8 0 . 2 Ta có ' 2 m 2m 8 m 1 7
0 với mọi m, do đó phương trình ho|nh độ luôn
có 2 nghiệm ph}n biệt. Suy ra d và P tại hai điểm ph}n biệt. x x 2m Theo hệ thức Vi – et 1 2 x x 2m 8 1 2 Theo đề b|i ta có x
0. . Kết hợp với hệ thức Vi – et trên ta có hệ x x 2m x 2 2m 1 2 1 x 2x 2 x 4m 2 1 2 2
Thay v|o hệ thức x x 2m 8 ta được 1 2 2 2 2m 4m 2 2m 8 4m 7m 2 0 1
Giải phương trình được x 0 . Vậy m 2; l| c{c gi{ trị cần tìm. 4 Câu 29.
Đặt c{c phương trình đã cho l| 2 2 2 x 2ax 2a b 1 0(1) 2 2 x 2bx 3b ab 0(2) THCS.TOANMATH.com TÀI LIỆU TOÁN HỌC 83
Để chứng minh có ít nhất một trong hai phương trình ẩn x sau vô nghiệm thì thì ta
chứng minh một trong hai biệt thức delta của phương trình nhận gi{ trị }m. Muốn vậy ta
đi tính tổng hai biệt thức delta của hai hai phương trình nhận gi{ trị }m. Ta có ' 2 2 2 2 2 a 2a b 1 a b 1 1 ' 2 2 2 b 3b ab 2b ab 2 Khi đó ta được ' ' 2 2 2 2 2 a b 1 2b ab a b 1 ab 1 2 2 Mặt kh{c dễ thấy rằng 2 2 2 2 2a 2b 2 2ab a b 2 a b 0 Do đó ta được ' '
0 . Vậy trong hai phương trình tồn tại ít nhất một phương trình 1 2 vô nghiệm. Câu 30. Phương trình 2 x 2 m 3 x 2m 5 0 có a b c 1 2 m 3 2m 5 0 nên có 2 nghiệm x 1;x 2m 5 . 1 2 m 2 2m 5 1
Phương trình có hai nghiệm dương ph}n biệt khi 5 2m 5 0 m 2 1 1 4 1 1 2m 5 3 2m 5 9 m 2 x x 3 2m 5 3 1 2 Vậy m
2 thỏa mãn yêu cầu b|i to{n. Câu 31.
a)Phương trình đã cho có nghiệm khi v| chỉ khi 2 2 2 ' m 1 2m 3m 1 0 m m 0 m m 1 0 m 0 m 1 0 0 m 1 m 0 m 0 0 m 1 m 1 0 m 1 m 0 m 1 Vậy với 0 m
1 thì phương trình đã cho luôn có nghiệm.
b) Giả sử phương trình đã cho có hai nghiệm l| x , x . Chứng minh rằng 1 2 9 x x x x . 1 2 1 2 8
Lời giải. Phương trình đã cho luôn có hai nghiệm khi 0 m 1. THCS.TOANMATH.com TÀI LIỆU TOÁN HỌC 84 x x 2 m 1
Theo hệ thức Vi – et ta có 1 2 2 x .x 2m 3m 1 1 2 2 1 9 Ta có 2 P x x x .x 2m m 1 2 m 1 2 1 2 4 16 2 1 1 3 1 9 Ta có 0 m 1 m m 4 4 4 4 16 2 9 1 9 1 Suy ra P 2 m
, dấu bằng xảy ra khi m . 16 4 8 4 Câu 32. Ta có 2 h t f t 2 t 2 2 m 2 t 2 6m 1 2 2 t 4t 4 2 mt 4m 4t 8 6m 1 t 2 mt 2m 3 Phương trình f x
0 có hai nghiệm lớn hơn 2 khi v| chỉ khi phương trình h t 0 có hai nghiệm dương 2 0 m 1 2 0 3 P 0 2m 3 0 m 2 S 0 2m 0 3 Vậy với m
thì phương trình f x
0 có hai nghiệm lớn hơn 2. 2 Câu 33. 1
a) Tìm tọa độ giao điểm của d và P khi a 2 1 Khi a
thì đường thẳng d có phương trình y x 2. 2
Ho|nh độ giao điểm của d và P l| nghiệm của phương trình 2 2 x x 2 x x 2 0 x 1;2
Từ đó ta tìm được tọa độ giao điểm của d và P là A 1;1 và B 2;4 .
b) Tìm tất cả c{c gi{ trị của a để đường thẳng d cắt P tại hai điểm ph}n biệt có ho|nh
độ x ;x thỏa mãn x x 3 1 2 1 2
Xét phương trình ho|nh độ của d và P là 2 x 2ax 4a 0 THCS.TOANMATH.com TÀI LIỆU TOÁN HỌC 85
Để d và P cắt nhau tại hai điểm ph}n biệt thì phương trình ho|nh độ phải có hai nghiệm ph}n biệt . a 0 Từ đó ta có ' 2 a 4a a a 4 0 a 4 x x 2a
Khi đó theo hệ thức Vi – et ta có 1 2 x x 4a 1 2 2 2 Ta có x x 3 x x 9 x x 2x x 2 x x 9 1 2 1 2 1 2 1 2 1 2
Kết hợp với hệ thức Vi – et ta được 2 4a 8a 8a 9 . 1 + Với a 0 ta được 2 2 4a 8a 8a 9 4a 16a 9 0 a , thỏa mãn 2 3 + Với a 4 ta được 2 2 4a 8a 8a 9 4a 9 a , không thỏa mãn. 2 1 Vậy a
thỏa mãn yêu cầu b|i to{n. 2 Bài 34. Dễ thấy phương trình 2 x x 5 0 có ac 5
0 nên phương trình luôn có hai nghiệm x ;x . 1 2
Theo hệ thức Vi – et ta có x x 1;x .x 5 1 2 1 2 Đặt S 2x x x 2x 3 x x 3 và 1 2 1 2 1 2 2 2 2 P 2x x x 2x 2 x x 5x x 2 x x x x 3 1 2 1 2 1 2 1 2 1 2 1 1 Khi đó 2x x và x
2x l| hai nghiệm của phương trình 2 x Sx P 0. 1 2 1 2
Từ đó ta có phương trình 2 x 3x 3 0 nhận 2x x và x 2x l|m nghiệm. 1 2 1 2 Câu 35.
Biến đổi phương trình đã cho ta được 4 3 x x 2 2 2 2 4 3 x 3mx 2m 4m 6mx 2x x x 0 2
Giả sử tồn tại m để phương trình đã có bốn nghiệm ph}n biệt.
Khi đó ta xem phương trình 2 2 4 3 4m 6m 2x x x
0 l| phương trình bậc hai ẩn m. 2 Ta có ' 2 2 4 3 4 3 2 2 9x 4 2x x x 4x 4x x 2x x 0 . THCS.TOANMATH.com TÀI LIỆU TOÁN HỌC 86 2 2 3x 2x x x x 2 m x x 2m 0
Khi đó phương trình có hai nghiệm 4 2 2 2 2 3x 2x x x 2x x 2x 2m 0 m 4 2
Để phương trình đã cho có bốn nghiệm ph}n biệt thì mỗi phương trình trên phải có hai
nghiệm ph}n biệt v| c{c nghiệm của hai phương trình phải kh{c nhau. 1 + Phương trình 2 x x 2m
0 có hai nghiệm ph}n biệt khi 1 8m 0 m . 8 1 + Phương trình 2 x 2x 2m
0 có hai nghiệm ph}n biệt khi 4 8m 0 m . 2
Kết hợp hai kết quả trên ta được hai phương trình trên cùng có hai nghiệm ph}n biệt khi 1 m . 8
+ Gọi x l| nghiệm chung của hai phương trình 2 x x 2m 0 và 2 x 2x 2m 0 . 0 2 4 x x 2m 0 3 4 0 m x m x 0 Khi đó ta có 0 0 0 0 3 2 2 x 2x 2m 0 x x 2m 0 2 0 0 0 0 x x 2m 0 0 0 2 4m 4m 3 Suy ra 2 2m 0 16m 6m 0 m 0; . 3 3 8 3
Do đó để hai phương trình không có nghiệm chung thì m 0; . 8 1 Vậy với m
thì phương trình đã cho có bốn nghiệm ph}n biệt. 8 Câu 36. 2
Phương trình đã cho có nghiệm khi v| chỉ khi ' 2 m 1 m 3 0 m 2 . x x 2 m 1
Theo định lí Vi – et ta có 1 2 . 2 x .x m 3 1 2
Do x l| nghiệm của phương trình đã cho nên ta được 2 2 x 2 m 1 x m 3 0 hay 1 1 1 ta được 2 2 x 2mx 2x m 3 1 1 1 Theo đề ra thì ta có 2 x 4x 2x 2mx 1 suy ra 2 x 2mx 4x 2x 1 . 1 1 2 1 1 1 1 2 Kết hợp với 2 2 x 2mx 2x m 3 ta được 1 1 1 2 2 2x m 3 4x 2x 1 2 x x m 2 0 1 1 2 1 2 THCS.TOANMATH.com TÀI LIỆU TOÁN HỌC 87
Kết hợp với hệ thức Vi – et ta được 2 2 4 m 1 m 2 0 m 4m 2 0 m 2 2 .
Kết hợp với điều kiện có nghiệm của phương trình ta được m 2 2 l| gi{ trị cần tìm. Câu 37 .
a) Chứng minh rằng phương trình 1 có hai nghiệm ph}n biệt x ;x với mọi số thực m. 1 2 2 2
Tính gi{c trị của biểu thức S x m x m 5 x x 2m . 1 2 1 2 Đặt y x
m , khi đó phương trình 1 trở th|nh 2 y 5y 6 0 y 2;3 . x m 2 x 2 m Do đó ta được . x m 3 x 3 m Dễ thấy 2 m
3 m với mọi m nên phương trình 1 luôn có hai nghiệm ph}n biệt.
Phương trình 1 có hai nghiệm x ;x tương ứng với phương trình 2 y 5y 6 0 có hai 1 2 nghiệm l| y 2 và y 3 . Khi đó ta có 1 2 2 2 2 2 2 2 S x m x m 5 x x 2m y y 5 y y 2 3 5 2 3 38 1 2 1 2 1 2 1 2 b) Biết x
x , tìm m sao cho x 1 và 2 x 2x 2 m 1 . 1 2 2 1 2 Do x x nên x 2 ; m x 3 m . Ta có x 1 3 m 1 m 2 . 1 2 1 2 2 2 2 x 2x 2 m 1 2 m 2 3 m 2 m 1 1 2 2 2 m 4m 4 6 2m 2m 2 m 8m 12 0 m 2;6
Kết hợp với điều kiện m 2 ta được m 6 l| gi{ trị cần tìm. Câu 38.
a) Tìm m để phương trình 1 có hai nghiệm ph}n biệt x ;x . Chứng minh rằng 1 2 x x 1 2 1 . 2 2 Ta có ' 2 2 2 2 m 1 2m 4m 1 m 2m 1 2m 4m 1 m 2m .
Phương trình 1 có hai nghiệm ph}n biệt x ;x khi v| chỉ khi 1 2 2 ' 2 0 m 2m 0 m 1 1 1 m 1 1 2 m 0
Khi đó theo hệ thức Vi – et ta có 2 x x 2 m 1 ;x x 2m 4m 1. 1 2 1 2 THCS.TOANMATH.com TÀI LIỆU TOÁN HỌC 88 x x Ta có 1 m 1 1 m 1 1 nên 1 2 m 1 1 2 1 1
b) Giả sử hai nghiệm x ;x kh{c 0, chứng minh rằng: 2 x x . 1 2 1 2 x x 1 2 Vì 1 m 1 1 m 1 1 nên ta được 2 2 1 2 m 1 1 1 1 2m 4m 1 1 x x 1 1 2 1 1 1 Do đó 2 2 . Mặt kh{c ta có x x x x 1 2 1 2 2 2 2 2 2 x x x x 2 x x 2 m 1 2 2m 4m 1 2 x x 1 2 1 2 1 2 1 2 2 2 x x 4 1 2 1 1 Suy ra x x 2 . Vậy ta có 2 x x . 1 2 1 2 x x 1 2 Câu 39.
m m m 2 2 ' 2 1 1 0 Ta có
nên phương trình luôn có hai nghiệm với mọi m x x 2 m 1 2
Theo định lý Vi et ta có: x x 2 m 1 1 2 2x x 1 1 2 P 2
x x x x 1 2m 1 1 2 2 2x x 1 1 2
P x x 2 x x 2m 1 2 1 2 4 m 1 4 m 1 P 11 2 2 4m 2 4m 2 2m 2 1 P 1 1 2 4m 2
Vậy giá trị nhỏ nhất của P là -1 đạt tại m = 0,5. Câu 40. Phương trình: 2
(m 1)x 2(2m 3)x 5m 25 0 (3) Có 2 2 2 ' (2m 3) (m 1)( 5
)(m 5) 9m 42m 34 (3m 7) 15
(3) có nghiệm hữu tỉ với m khi và chỉ khi ' chính phương, suy ra: 2 2
(3m 7) 15 n (n )
(3m – 7 – n)(3m – 7 + n) = 15 (m,n ) (4) THCS.TOANMATH.com TÀI LIỆU TOÁN HỌC 89
Phương trình (4) tương đương với 8 hệ phương trình: 3 m 7 n 1 5 3 m 7 n 1 3 m 7 n 5 (4.1), (4.2), (4.3), 3 m 7 n 1 3 m 7 n 1 5 3 m 7 n 3 3 m 7 n 3 (4.4) 3 m 7 n 5 3 m 7 n 15 3 m 7 n 1 3 m 7 n 3 (4.5), (4.6) (4.7), 3 m 7 n 1 3 m 7 n 15 3 m 7 n 5 3 m 7 n 5 (4.8) 3 m 7 n 3
Giải 8 hệ trên, suy ra hệ phương trình (3) có nghiệm hữu tỉ khi: m = 1 hoặc m = 5
Câu 41. a) Để phương trình đã cho có 2 nghiệm phân biệt thì
m 2 2 m 2 2 0 2 1 4
1 0 4m 4m 1 4m 4 0 3
4m 3 0 m 4 3 m Vậy
4 thì phương trình có hai nghiệm phân biệt 3 m x ; x b) Với
4 thì phương trình có hai nghiệm phân biệt 1 2
x x 2m 1 1 2
Theo hệ thức Vi-et ta có: 2 x x m 1 1 2
x x 2 x x 2x x x x 2 2 2 4x x 1 2 1 2 1 2 1 2 1 2 2m 2 1 4 2 m
1 4m 3 x1
x 2m 1 x 2m 1 4m 3 4 2m 2 1 2 )x x m 1 1 2
4m 34 2m 2 m 1 2 2
16m 8m 12 6m m 1 2
9m 22m 13 0 m 1 9m 13 0 m 1(tm) m 1 0 13 9m 13 0 m (tm) 9 13 m 1; m Vậy
9 thỏa mãn điều kiện bài toán THCS.TOANMATH.com TÀI LIỆU TOÁN HỌC 90 Câu 42.
Phương trình ho|nh độ giao điểm của hai đồ thị là: 2 2
x x m x x m 0(*)
Hai đồ thị hàm số cắt nhau tại hai điểm phân biệt
* có hai nghiệm phân biệt 1
0 1 4m 0 m 4
Gọi x , x là hai nghiệm của phương trình (*). Khi đó ta có: y x , m
y x m 1 2 1 1 2 2 x x 1
Áp dụng hệ thức Vi ét ta có: 1 2 x x m 1 2 Theo đề bài ta có:
x x 8 y y 8 162 1 2 1 2
x x 8 x m x m8 162 1 2 1 2
x x 8 x x 8 162 1 2 1 2
x x 81 38 8 1 2 x x 3 x x 3 1 2 1 2
x x 3 x x 3 1 2 1 2 1 3 1 3
+) Với x x 3 2x 3 1 x x 1 2 2 2 1 2 2 1 3 1 3 1
x x m . ( ) tm 1 2 2 2 2 1 3 1 3
+)Với x x 3 2x 3 1 x x 1 2 2 2 1 2 2 1 3 1 3 1
x x m . ( ) tm 1 2 2 2 2 1 Vậy m
thỏa mãn điều kiện bài toán. 2 Câu 43. Cho đa thức 3 2
f (x) x 2x (1 ) m x m .
1) Khi m 2 , hãy ph}n tích đa thức f (x) th|nh nh}n tử. f x 3 2
x 2x x 2
f (x) (x 1)(x 1)(x 2) .
2) Tìm tất cả c{c gi{ trị của tham số m để phương trình f (x) 0 có ba nghiệm ph}n biệt
x , x , x thỏa mãn 2 2 2
x x x 4 . 1 2 3 1 2 3 THCS.TOANMATH.com TÀI LIỆU TOÁN HỌC 91 x 1 Ph}n tích phương trình 2
(x 1)(x x m) 0 2
x x m 0 (*)
Phương trình f (x) 0 có 3 nghiệm ph}n biệt
Phương trình (*) có hai nghiệm ph}n biệt kh{c 1. m 0 m 0 1 1 4m 0 m 4
Lúc đó: x 1, x x 1; x x m 1 2 3 2 3
Điều kiện: x x x 4 x x 2 2 2 2
2x x 3 m 1. 1 2 3 2 3 2 3 1
Vậy m 1, m 0 . 4 Câu 44.
a) Tìm tất cả các số thực m…. 2
Ta có: m m 2 2 3 4 3
1 4m 5 0 m
. Do đó phương trình luôn có hai nghiệm phân biệt.
x x 2m 3
Theo định lý Vi-et, ta có: 1 2
x x 3m1 1 2 Theo đề bài ta có:
x x x x 7 x x 2 2 2 3x x 7 1 2 1 2 1 2 1 2
2m 32 33m 1 7 m 1 2 4m 3m 1 0 1 m 4 1
Vậy giá trị cần tìm là: m 1 ;m . 4
b) Tìm tất cả các số nguyên…….
Để phương trình có nghiệm nguyên thì 2
4m 5 phải là số chính phương. Khi đó: 2 2 2 2
4m 5 k k 4m 5 k 2mk 2m 5 k 2 ;
m k 2m U (5) 1;5; 1 ; 5 Ta có bảng sau: k 2m 1 5 1 5 k 2m 5 1 5 1 m 1 1 1 1 THCS.TOANMATH.com TÀI LIỆU TOÁN HỌC 92
Vậy các giá trị cần tìm là: m 1;m 1 Câu 45. 2 2
Ta có: m 2 ' 0
1 2m 6 0 m 4m 7 0 m 2 3 0 x
Suy ra phương trình đã cho luôn có hai nghiệm phân biệt với mọi m
x x 2 m 1 1 2
Áp dụng định lý Vi-et ta có: x x 2m6 1 2 Theo đề bài ta có: x x 2 2 2 2 2 2 2 4 4 2x x x x x x 1 2 1 2 1 2 1 2 A x x x x 2 x x 2 2 1 1 2 1 2
x x 2
2 2x x 2x x 2 1 2 1 2 1 2 x x 2 1 2 4m 1 22m 6 2 2
22m 62 m 2m 6 2 ( 3) 2
4m 8m44m122 2 2m 6 2 2 2 2 2 2
4m 12m 16
2m 6m 8 2 2 2m 6 m 3 2 2
2m 6m 8 A 2 m 3 2 2m 6m 8 2
2m 6m 8 m 3 m 3 Ta có: 2
2m 6m 8 2 ( m m 3) 8
Ta thấy: 2mm
3 m 3 m 3 2
2m 6m 8 m 3 m 3 2
2m 6m 8 m 3 8 m 3 hay m
3 U (8) m 3 1 ; 2 ; 4 ; 8 Ta có bảng giá trị x 3 -8 -4 -2 -1 1 2 4 8 x -5 -1 1 2 4 5 7 11
Kết hợp với điều kiện m 3ta có các giá trị thỏa mãn bài toán: m 5 ; 1 ;1;2;4;5;7;1 1 THCS.TOANMATH.com TÀI LIỆU TOÁN HỌC 93 3
Câu 46. Phương trình có hai nghiệm trái dấu ac 0 2m 3 0 m 2
x x m
Áp dụng định lý Vi ét ta có: 1 2
x x 2m3 1 2
Phương trình có hai nghiệm trái dấu trong đó nghiệm âm có giá trị tuyệt đối lớn hơn
x x 0 m 0 1 2
Vậy m 0 thỏa mãn yêu cầu bài toán 3
Vậy phương trình có hai nghiệm trái dấu m 2
Câu 47. Phương trình (1) có nghiệm kép 15
1 4(3m 11) 0 112m 44 0 m 4 1 b 1
Khi đó phương trình (1) trở thành 2 x x
0 có nghiệm kép x x 4 1 2 2a 2 15 1 Vậy với m
thì phương trình (1) có nghiệm kép, và nghiệm kép là x 4 2 15
a) Phương trình có hai nghiệm phân biệt 0 m 4
Gọi hai nghiệm phân biệt của phương trình l| x ; x , theo định lý Vi-et ta có: 1 2 x x 1 (2) 1 2
x x 3m11(3) 1 2
Theo giả thiết ta lại có 2017x 2018x 2019, kết hợp: 1 2 x x x x x x x 2 1 1 1 1 1 2 1 2 1 2 1
2017x 2018x 2019
2017 1 x 2018x 2019 x 2 x 2 1 2 2 2 2 2 Thay vào (3) ta có: 2
3m 11 m 3 (t ) m
Thử lại : với m=3 thì ta có phương trình (1) luôn có hai nghiệm phân biệt
Vậy m 3thỏa mãn yêu cầu bài toán. Câu 48.
a) Có 2 nghiệm dƣơng phân biệt Ta có:
Để phương trình đã cho có hai nghiệm dương thì: 2 2 0
4(m 1) 4m 0 8 m 4 0 1 m
S 0 2(m 1) 0
2m 1 0 2 2 2 P 0 m 0 m 0 m 0 THCS.TOANMATH.com TÀI LIỆU TOÁN HỌC 94
b) Có hai nghiệm phân biệt……
x x 2 m 1 (1) 1 2
Áp dụng định lý Vi-et ta có: 2 x x m (2) 1 2 Mặt khác :
x m2 x 3m 1 2 2 2
x 2mx m x 3m 1 1 2 2 2
x 2(m 1)x 2x m x 3m 1 1 1 2 2
x x x 2
x 2x m x 3m 1 1 2 1 1 2
x x 2x x x x 3m 1 2 1 2 1 2
2x x 3m (3) 1 2
x x 2(m 1) x m 2 Từ (1) và (3) ta có: 1 2 1
2x x 3m x m 4 1 2 2
Thay vào (2) ta có: m m 2 2
4 m 2m 8 0 m 4 (t ) m Vậy m 4 Câu 49.
Để phương trình đã cho có hai nghiệm x ; x thì 2
0 a 4b 0 1 2
x x a (1)
Áp dụng định lý Vi-et ta có: 1 2 x x b (2) 1 2 Theo đề bài ta có: x x 5 x x 5 1 2 1 2 x x 35
x x x x x x 35 1 2 2 3 3 1 2 1 2 1 2 x x 5 1 2 x x 5 (3) 1 2 5
x x 2 x x 35 x x 2 1 2 1 2 x x 7 (4) 1 2 1 2
Thế (1) (2) v|o (4) ta được: a2 2 2
b 7 a b 7 b a 7 (*)
Bình phương hai vế của (3) ta được:
x x 2 5 x x 2 2 2
4x x 25 a 4b 25 1 2 1 2 1 2
a 1 b 6 2 2 2
a 4a 28 25 a 1 a 1b 6 Vạy ; a b 1; 6 ; 1 ;6 THCS.TOANMATH.com TÀI LIỆU TOÁN HỌC 95 Câu 50.
a) Chứng tỏ rằng phương trình (1) có hai nghiệm ph}n biệt với mọi gi{ trị của m . Ta có ac 2 1. m
1 0 nên phương trình (1) có hai nghiệm ph}n biệt tr{i dấu với mọi gi{ trị m .
b) Giả sử x , x l| hai nghiệm của phương trình (1). Tìm m để phương trình có hai nghiệm 1 2
ph}n biệt x x thỏa mãn x x 3. 1 2 1 2
Do phương trình (1) có hai nghiệm ph}n biệt tr{i dấu v| x x 1 2
Suy ra x 0 , x 0 1 2
x x , x x 1 1 2 2
x x 3 x x 3 2m 3 3 m 3 1 2 1 2 Câu 51.
Phương trình có nghiệm nguyên khi 4
m 4m 4 l| số chính phương.
+ Với m 0 , hoặc m 1 thì 0 (loại). + Với m 2 thì 2 4 2 (thỏa mãn). + Với m 3 thì 2 2 (
m m 2) 5 2m 4m 5 0 2
(2m 4m 5) 4m 4 4 2 4
m 2m 1 m
m 2 m 2 2 2 1
không chính phương.
Vậy m 2 l| gi{ trị cần tìm. Câu 52. 2
ax 2bx c 0 (1) Ta có: 2
ax 2bx c 2
bx 2cx a 2
cx 2ax b 0* 2 b
x 2cx a 0 (2) 2
cx 2ax b 0 (3) 2
4b 4ac 4 2 b ac 1 2
4c 4ba 4 2 c ab 2 2
4a 4bc 4 2a bc 3
4a b c ab ac bc 2a b2 2a c2 2b c2 2 2 2 1 2 3 0 1 2 3
Luôn tôn tại 1 biểu thức 0
* luôn có nghiệm với mọi a, , b c THCS.TOANMATH.com TÀI LIỆU TOÁN HỌC 96
Câu 53. Ta có : Phương trình ban đầu tương đương với x 1 x 1 2
x 2x a 0 x 1 a 1
x 1 a 1
Ta có: 1 a 1 1 1 a 1
x 1 a 1 1 x x 2 1 3 x 1 2
x x 1 a 1 a 1 3
x 1 a 1 3 (Theo định lý Viet)
Thay vào biểu thức A ta được:
P a a 2 a 2 4 1 1 1 1 1 1 1 1
P 8 4 a 1 1 2 a 1 a 111 2 a 1 a 1 P 9
Từ đó ta có điều phải chứng minh a) Đặt n n
Q x x n 1 3
n 0 Q 2 o
n 1 Q x x 2 1 1 3 n2 n2 Q x x x x
x x x x x x Q aQ n n 1 n 1 n n 2 2 1 3 1 3 1 3 1 3 1 3 n 1 n
Theo nguyên lý Quy nạp thì Q là số chẵn với mọi số tự nhiên n
Suy ra : S 1 Q là số lẻ. n n
Ta có điều phải chứng minh. Câu 54. 9 25
Để phương trình có nghiệm thì ' 0
m 4 0 m 4 4 x x 3
Áp dụng định lý Vi-et ta có: 1 2 x x m4 1 2 x x 3
Khi đó theo đề bài ta có: 1 2 x x m4 1 2 x x
Khi đó theo đề bài ta có: 1 2 là số nguyên x x 2019 1 2
* Kết luận: Vậy phương trình (1) luôn có nghiệm. THCS.TOANMATH.com TÀI LIỆU TOÁN HỌC 97 x x 3 1 2
x x 2019 m 42019 1 2
3 m 42019 m 4U (3) m m 5
m 4 1 m 3 m 4 1
Vậy giá trị m thỏa mãn là m 5, m 3 Câu 55. Ta có: 2 2 2 2 2 2 2
(b c a )x 4bcx (b c a ) 0 (1) Vì a, ,
b c l| độ d|i ba cạnh của tam gi{c nên: , a ,
b c 0; b c a 0; a b c 0; a c b 0 (2) Xét 2 trường hợp: + TH1: 2 2 2
b c a 0
Phương trình (1) trở th|nh: 4
bcx 0 x 0 (do , b c 0)
Phương trình (1) có nghiệm + TH2: 2 2 2
b c a 0 Phương trình (1) l| phương trình bậc hai Xét 2 2 2 2 2
' (2bc) (b c a ) 2 2 2 2 2 2
(2bc b c a )(2bc b c a )
b c2 a
a b c2 2 2
a b cb c aa b ca c b
Kết hợp với (2) ' 0 Phương trình (1) có nghiệm Câu 56. a 5c
a 2b 5c 0 b 2 2 2 2 2
a 10ac 25c
a 6ac 25c a 3c 16c 2 2 2
b 4ac 4ac 0 ; a ; b c 4 4 4 Phương trình 2
ax bx c 0 luôn có nghiệm. THCS.TOANMATH.com TÀI LIỆU TOÁN HỌC 98
D. BÀI TẬP TỰ LUYỆN KHÔNG LỜI GIẢI 1. Cho phương trình 2
x 2m
1 x 3m 0 .
a) Chứng minh rằng phương trình luôn có hai nghiệm ph}n biệt x , x với mọi m 1 2 b) Tính 3 3
A x x và x x theo m. 1 2 1 2 x x
c) Tìm m để phương trình có hai nghiệm x , x thỏa mãn 1 2 5 1 2 x x 2 1
d) Tìm hệ thức liên hệ giữa x , x không phụ thuộc v|o m 1 2
e) Tìm GTNN của biểu thức: 2 2
x x 6x x . 1 2 1 2 1 1
f) Lập phương trình bậc hai nhận x , x l|m nghiệm 1 2 x x 2 1
g) Tìm m để phương trình có hai nghiệm đều dương, hai nghiệm tr{i dấu
h) Tìm m để phương trình có một nghiệm bằng ba lần nghiệm kia
i) Tìm m để phương trình có hai nghiệm thỏa mãn 2x 3x 1 . 1 2 1 1 3 2) Giải phương trình : 2 x 2 5 x HD: Đặt 2 y 5 x
xy yz zx 1 3) Giả sử ,
x y, z thỏa mãn điều kiện 2 2 2
x y z 2 4 4
Chứng minh rằng: x, y, z 3 3
4) Giả sử x , x l| nghiệm của phương trình 2
x 4x 1 0 . Chứng minh rằng 5 5
x x l| một 1 2 1 2 số nguyên
5) Trong mặt phẳng tọa độ Oxy cho đường thẳng (d): 2
2x y a 0 và Parabol (P) : 2
y ax ( a l| tham số dương ).
a) Tìm a để (d) cắt (P) tại hai điểm ph}n biệt A v| B . Chứng minh rằng khi đó A v| B nằm bên phải trục tung
b) Gọi x , x l| ho|nh độ của A v| B. tìm GTNN của biểu thức: A B 4 1 T x x x .x A B A B x y 2
6) Tìm m để hệ phương trình có nghiệm 3 3
x y m HD: Đặt x = -y THCS.TOANMATH.com TÀI LIỆU TOÁN HỌC 99
7) Gọi x , x l| nghiệm của phương trình 2
x 2009x 1 0 và x , x l| nghiệm của phương 1 2 3 4 trình 2
x 2010x 1 0 . Tính gi{ trị của biểu thức:
A x x x x x x x x 1 3 2 3 1 4 2 4
8) Cho hình thang vuông ABCD ( 0
A D 90 ) có đường chéo BD vuông góc với cạnh bên
BC. Biết AB = 12, CD = 25. Tính AB, BC, BD
9) Cho phương trình bậc hai: 2 2
x 2(m 1)x m m 1 0
a) Tìm tất cả c{c gi{ trị của tham số m để phương trình có hai nghiệm ph}n biệt đều }m.
b) Tìm tất cả c{c gi{ trị của tham số m để phương trình có hai nghiệm x , x thỏa mãn 1 2 x x 3. 1 2 10) Cho phương trình: 2
x m 2 2
3 x m 3m 0 . Định m để phương trình có hai nghiệm
x , x thỏa mãn: 1 x x 6 . 1 2 1 2
x y xy a
11) Cho hệ phương trình: 2 2
x y xy 3a 8 7
a) Giải hệ phương trình với a . 2
b) Định a để phương trình có nghiệm.
12) Cho phương trình: m 2
2 x 2m 4 x m 4m 2 0m 2
a) Với gi{ trị n|o của m thì phương trình có nghiệm kép
b) Giả sử phương trình có hai nghiệm x , x . Hãy tìm một hệ thức giữa x , x độc lập với m. 1 2 1 2 1 1
c) Tính theo m biểu thức A x 1 x 1 1 2 d) Tìm m để A = 2 13) Cho phương trình: 2
x mx 4 0 ( m l| tham số )
a) Chứng minh rằng phương trình luôn có hai nghiêm ph}n biệt với mọi m.
2 x x 7 1 2
b) Tìm GTLN của biểu thức A 2 2 x x 1 2
c) Tìm c{c gi{ trị của m sao cho hai nghiệm của phương trình đều l| số nguyên 14) Cho phương trình: 2 2 2
x 2m x 2m 2 0 m 1
a) Chứng minh rằng phương trình luôn có hai nghiệm ph}n biệt
b) Giả sử x , x l| nghiệm của phương trình đã cho v| x x hãy chứng minh 1 2 1 2 1 x 1 x 1 2 2 2 x x 1 x x . 1 1 1 2 2
15) ( Đề thi HSG huyện lớp 9 năm học 2008-2009): Tìm số nguyên x, y thỏa mãn: THCS.TOANMATH.com TÀI LIỆU TOÁN HỌC 100 2 2
2x 2y 2xy x y 0 16) Cho h|m số 2
y 2x có đồ thị l| Parabol (P) v| h|m số y 2m
1 x 1 m có đò thị l|
đường thẳng (d ) ( m l| tham số ) m
a) Chứng minh rằng khi m = 3 hoặc m = 1 thì hai đò thị (P) v| (d ) chỉ có một điểm chung m
b) Với gi{ trị n|o của m thì (d ) cắt (P) tại hai điểm ph}n biệt có ho|nh độ x , x thỏa mãn m 1 2 2 2
x x 2x x 3 0 1 2 1 2
xy x y 1005
17) GiảI hệ phương trình: x y y x 2006 THCS.TOANMATH.com TÀI LIỆU TOÁN HỌC




