Chuyên đề hàm số bậc nhất

Tài liệu gồm 16 trang, được biên soạn bởi tác giả Toán Học Sơ Đồ, tổng hợp kiến thức trọng tâm, phân dạng và hướng dẫn giải các dạng bài tập tự luận & trắc nghiệm chuyên đề hàm số bậc nhất. Mời bạn đọc đón xem.

57 29 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Chương 2: Hàm số bậc nhất

Môn: Toán 9

Thông tin:

16 trang 8 tháng trước

Tác giả:

Profile Hà Việt Anh
1.
TOÁNHỌCSƠĐỒ‐THCS.TOANMATH.com
CHUYÊN ĐỀ HÀM SỐ BẬC NHẤT
A. TÓM TẮT LÝ THUYẾT
1. Hàm số bậc nhất
Là hàm số được cho bởi công thức y= ax+b trong đó a,b là hai số đã cho và
2. Các tính chất của hàm số bậc nhất
- Hàm số bậc nhất xác định với mọi giá trị của x thuộc R
- Hàm số bậc nhất: + Đồng biến trên R khi a > 0
+ Nghịch biến trên R khi a < 0
B.CÁC DẠNG BÀI MINH HỌA
Dạng 1: Tính giá trị của hàm số tại một điểm
Phương pháp giải toán
1.
Việc tính toán theo kiểu này sẽ giúp ta xác định được toạ độ của nhiều điểm thuộc đồ thị hàm số một
cách nhanh chóng. Ngoài ra, phương pháp sử dụng kết hợp máy tính cầm tay (sử dụng Slove) sẽ giúp cải
thiện thời gian một cách hiệu quả.
2. Tính giá trị của hàm số

yfx
khi cho giá trị của ẩn
0
x là ta thay giá trị của
0
x vào biểu thức

yfx
để tìm được

00
yfx
Câu 1: Cho hai hàm số
2
()fx x
và
() 3gx x
a, Tính
1
(3), ( ), (0)
2
fff
,
(1), (2), (3)ggg
b, Xác định giá trị của
a
để
2() ()fa ga
.
Câu 2: Cho hai hàm số
2
() 2gx x
và
() 3 5hx x
a, Tính
3
( 0,4), ( ), (2), ( 1,4), ( 1)
4
ggghh

b, Xác định các giá trị của
m
để
1
() ()
2
gm hm
Dạng 2: Vẽ đồ thị hàm bậc nhất
Phương pháp giải:Theo các bước vẽ đã học
Câu 3: Vẽ đồ thị các hàm số bậc nhất sau:
a,
2yx
b,
43yx
a0
2.
TOÁNHỌCSƠĐỒ‐THCS.TOANMATH.com
c,
1
2
yx
c,
1
1
3
yx

Dạng 3: Nhận dạng hàm số bậc nhất
Phương pháp giải: Dựa vào định nghĩa hàm số bậc nhất
Câu 4: Hãy xét xem trong các hàm số sau đây , đâu là hàm số bậc nhất? Hãy chỉ rõ các hệ số a và b trong
trường đó là ham số bậc nhât .
a,
1
2
yx
b,

33 1yxx
c,
23
4
x
y
d,

2
13yx x x
Câu 5: Tìm m để hàm số sau là hàm số bậc nhất :
a,
2
y(2 6) 5mxm
b,
2
y(2 ) 8 7mx x
c,
2
(3)(1)1yxm m
d,
2
15
2
xm
y
mm


Câu 6: Chứng minh các hàm số sau là hàm số bậc nhất với mọi giá trị của tham số m:
a)
2
(1)9ymm x
b,
2
(47) 3ymmxm
Dạng 4: Xét tính đông biến và nghịch biến của hàm số bậc nhất
Phương pháp giải: xét hàm số bậc nhất y = ax + b với a, b là hằng số,
- Khi a > 0, Hàm số đồng biến trên R
- Khi a < 0, Hàm số nghịch biến trên R
Câu 7: Các hàm số sau đồng biến hay nghịch biến ? Vì sao?
a,
79yx
b,
41
72
yx
c,
3(2 1) 4 1yx x
d,
2
(2 1) 4 ( 1)yx xx
Câu 8: Tìm m để hàm số sau :
a,
(2 5) 13ymx
đồng biến trên
.
b,
2
(4 9) 2ym x
nghịch biến trên
.
c,
32
5
2
m
yx

nghịch biến trên
.
Câu 9: Cho hàm số
2
() ( 2) 9 3yfx mm x m
với
m
là tham số.
a, Chứng minh hàm số đã cho luôn là hàm số bậc nhất và nghịch biến trên
.
b, Hãy so sánh
( 10)f
và
( 3 11)f
.
a0
3.
TOÁNHỌCSƠĐỒ‐THCS.TOANMATH.com
Câu 10: Cho hàm số
2
() ( 2 3) 5yfx k k xk
a, Chứng minh hàm số đã cho luôn là hàm số bậc nhất và đồng biến trên
.
b, Hãy so sánh
(2 1)f
và
(2 3)f
.
Dạng 5. Toán thực tế
Câu 11: Mối quan hệ giữa thang nhiệt độ F(Fahrenheit) và thang nhiệt độ C (Celsius) được cho bởi công
thức 1, 8 32
FC
TT, trong đó
C
T là nhiệt độ tính theo độ C và
F
T là nhiệt độ tính theo độ F. Ví dụ
0
C
T
Ctương ứng với
32
F
T
F.
a) Hỏi
25 C
tương ứng với bao nhiêu độ
F
?
b) Các nhà khoa học đã tìm ra mối liên hệ giữa
A
là số tiếng kêu củamột con dế trong một phút và
F
T là
nhiệt độ cơ thể của nó bởi công thức 5, 6 275
F
AT, trong đó nhiệt độ
F
T tính theo độ
F
. Hỏi nếu con
dế kêu
106
tiếng trong một phút thì nhiệt độ của nó khoảng bao nhiêu độ C? (làm tròn đến hàng đơn vị).
Câu 12: Siêu thị
A
thực hiện chương trình giảm giá cho khách hàng mua loại túi bột giặt
4
kg như sau:
+ Nếu mua 1 túi thì được giảm
10 000
đồng so với giá niêm yết.
+ Nếu mua 2 túi thì túi thứ nhất được giảm
10 000
đồng và túi thứ hai được giảm
20 000
đồng so với giá
niêm yết.
+ Nếu mua từ 3 túi trở lên thì ngoài 2 túi đầu được hưởng chương trình giảm giá như trên, từ túi thứ ba trở
đi mỗi túi sẽ được giảm
20%
so với giá niêm yết.
a) Bà Tư mua
5
túi bột giặt loại 4kg ở siêu thị A thì phải trả số tiền là bao nhiêu, biết rằng loại túi bột giặt
mà bà tư mua có giá niêm yết là
150 000
đồng/túi.
b) Siêu thị B lại có hình thức giảm giá khác cho loại túi bột giặt nêu trên là: Nếu mua từ 3 túi trở lên thì sẽ
giảm giá
15%
cho mỗi túi. Nếu bà Tư mua 5 túi bột giặt thì bà Tư nên mua ở siêu thị nào để số tiền phải
trả là ít hơn?Biết rằng giá niêm yết của hai siêu thị là như nhau.
4.
TOÁNHỌCSƠĐỒ‐THCS.TOANMATH.com
HƯỚNG DẪN
Câu 1:
a,
2
(3) (3) 9f 
;
2
111
()()
224
f


;
(0) 0f
;
(1) 3 (1) 4g 
;
(2) 3 (2) 5g 
;
(3) 3 3 0g 
b, Ta có:
2
2() 2fa a
;
() 3ga a
22
2() () 2 3 2 3 0fa ga a a a a  
1
3
2
a
a
Câu 2: Tương tự câu 1:
a,
2
(0,4) 2(0,4) 0,32g 
;
39
()
48
g

;
(2) 8g 
(1,4) 0,8h 
;
(1) 2h 
;
b, Ta có
22
11
() (2)
22
gm m m
;
() 3 5hm m
22
1
() () 3 5 3 5 0
2
gm hm m m m m
( vô nghiệm)
Suy ra không có giá trị nào của m thỏa mãn.
Câu 3:
a,
2yx
b,
43yx
5.
TOÁNHỌCSƠĐỒ‐THCS.TOANMATH.com
c,
1
2
yx
d,
1
1
3
yx

Câu 4:
a, Là hàm bậc nhất với
1
2
a
và
0b
.
b, Thu gọn được
3y 
, không là hàm số bậc nhất.
c, Biến đổi được
13
24
yx
là hàm số bậc nhất với
1
2
a
và
3
4
b
.
d,

2
213 3xxyx x
là hàm số bậc nhất với
2a 
và
3b 
Câu 5:
a, y là hàm số bậc nhất
2
260 3am m
.
b, y là hàm số bậc nhất khi hệ số của
2
x
bị triệt tiêu.
20m2m 
.
c,
2
(3)(1)1yxm m
là hàm số bậc nhất


2
310 1mm m
d,
22 2
15 1 5
22 2
xm m
yx
mm mm mm


  
Để y là hàm số bậc nhất
2
1
10
21 1
20
1
m
m
mm
mm
m





Câu 6:
a,
2
(1)9ymm x
. Biến đổi được
2
13
() 0
24
am
với mọi m.
b,
2
(47) 3ymmxm
. Biến đổi được
2
(2)30am
với mọi m.
6.
TOÁNHỌCSƠĐỒ‐THCS.TOANMATH.com
Câu 7:
a, Có
90a 
Hàm số nghịch biến trên
.
b, Có
4
0
7
a 
Hàm số đồng biến trên
.
c, Thu gọn được
22 2yx a
Hàm số đồng biến trên
.
d, Thu gọn ta được
81 8yx a 
Hàm số nghịch biến trên
.
Câu 8:
a, Hàm số đồng biến
5
250
2
mm
.
b, Hàm số nghịch biến
2
33
490
22
mm

.
c, Hàm số nghịch biến
32 2
0
23
m
m


.
Câu 9:
a, Ta có
2
17
0
24
am




với mọi m.
Vì vậy hàm số đã cho luôn là hàm số bậc nhất và nghịch biến trên
.
b, Ta có
10 100 99 3 11
.Mà hàm số đã cho là hàm số nghịch biến nên


10 3 11ff
.
7.
TOÁNHỌCSƠĐỒ‐THCS.TOANMATH.com
C.TRẮC NGHIỆM RÈN LUYỆN PHẢN XẠ
Câu 1. Chọn đáp án đúng nhất. Hàm số
yaxb=+
là hàm bậc nhất khi
A.
0a =
. B.
0a <
. C.
0a >
. D.
0a ¹
.
Câu 2. Chọn đáp án đúng nhất.Với
0a ¹
hàm số
yaxb=+
A. Bậc nhất. B. Hàm hằng. C. Đồng biến. D. Nghịch biến.
Câu 3. Chọn đáp án đúng nhất. Hàm số
yaxb=+
là hàm số đồng biến khi
A. 0a = . B.
0a <
. C.
0a >
. D. 0a ¹ .
Câu 4. Hàm số nào dưới đây là hàm số bậc nhất?
A.
21yx=+
. B.
03yx=+
. C.
2
21yxx=++
. D.
24yx=++
.
Câu 5. Trong các hàm số
3
1
5; 1; 2 1; 2; 3
2
x
yy yxxy yx
x
==+=++=+= có bao nhiêu hàm số là
hàm số bậc nhất?
A.
3
. B.
2
. C.
4
. D.
1
.
Câu 6. Tìm
m
để hàm số
2.1ymx=- +
là hàm số bậc nhất?
A.
2m <
. B.
2m >
. C.
2m =
. D.
2m ¹
.
Câu 7. Tìm
m
để hàm số
1
23
2
m
yxm
m
+
=+-
-
là hàm số bậc nhất?
A.
1m ¹-
. B.
1m >-
. C.
{}
1; 2m ¹-
. D.
2m ¹
.
Câu 8. Hàm số
3
5
12
m
yx
m
=-
-
là hàm số bậc nhất khi:
A.
1
0;
2
m
ìü
ïï
ïï
¹
íý
ïï
ïï
îþ
. B.
0m >
. C.
0m ¹
. D.
1
2
m ¹ .
Câu 9. Hàm số nào sau đây là hàm số nghịch biến?
A.
21yx=-
. B.
(1 3 )yx=- -
. C.
(2 1)yx=- -
. D.
yx=
.
Câu 10. Hàm số nào sau đây là hàm số bậc nhất và đồng biến?
A.
()
24 5yx=-+
. B.
()
32 2yx=-+. C.
3
yx x=-
. D.
(9 )yx=- -
.
Câu 11. Cho hàm số
(8 4 ) 5ymx=- +
. Tìm
m
để hàm số là hàm số nghịch
biến
A.
2m >
. B.
2m <
. C.
2m =
. D.
2m ¹
.
8.
TOÁNHỌCSƠĐỒ‐THCS.TOANMATH.com
Câu 12. Với giá trị nào của
m
thì hàm số
2
1
5
22
m
yx
mm
-
=-
++
là hàm số
nghịch biến?
A.
1m <
. B.
1m >
. C.
1m =
. D. Mọi
m
.
Câu 13. Cho hàm số
52ymxxm=-+
. Tìm
m
để hàm số là hàm số đồng biến
A.
2
5
m < . B.
5
2
m > . C.
2
5
m > . D.
5
2
m < .
Câu 14. Cho hàm số
2
(2 4 5) 7 5ymmxm=- + - - +
là hàm số đồng biến khi
A.
3m <
. B.
5
2
m > . C. Không có
m
thỏa mãn. D. Mọi
m
.
Câu 15. Cho hàm số
2
3. 1ym x=++
. Kết luận nào sau đây là đúng?
A. Hàm số đã cho là hàm nghịch biến với mọi
m
. B. Hàm số đã cho là hàm nghịch biến với
3m >
.
C. Hàm số đã cho là hàm hằng. D. Hàm số đã cho là hàm số đồng biến với mọi
m
.
Câu 16. Cho hàm số
2323
5
2323
yx
æö
÷
+-
ç
÷
ç
=+ -
÷
ç
÷
ç
÷
ç
-+
èø
. Kết luận nào sau đây là đúng?
A. Hàm số đã cho là hàm nghịch biến. B. Hàm số đã cho là hàm đồng biến.
C. Hàm số đã cho là hàm hằng. D. Hàm số đã cho là hàm số đồng biến với
0x >
.
Câu 17. Cho hàm số
()
32.ym xm=---
. Giá trị nguyên nhỏ nhất của
m
để hàm số đồng biến là?
A.
8m =
. B.
9m =
. C.
3m =
. D.
7m =
.
Câu 18. Cho hàm số
()
55 . 2ymxm=- - ++
. Với giá trị nguyên lớn nhất của
m
để hàm số nghịch
biến là?
A. 5m = . B.
20m =-
. C.
19m =-
. D.
21m =-
.
Câu 19. Với giá trị nào của
m
thì hàm số
(3 1) 6ymmxm=- +
là hàm số bậc nhất
A. 0m ¹ . B.
1
3
m ¹ . C.
1
0;
3
m
ìü
ïï
ïï
¹
íý
ïï
ïï
îþ
. D. Mọi
m
.
Câu 20. Với giá trị nào của
m
thì hàm số
2
(98)10ym m x=-++
là hàm số
bậc nhất
A.
{}
1; 8m ¹
. B.
1m ¹
. C.
8m ¹
. D. Mọi
m
.
Câu 21. Cho hàm số
22
(4)(3)(2)2ya x babax=- +- + -
là hàm số bậc nhất khi
9.
TOÁNHỌCSƠĐỒ‐THCS.TOANMATH.com
A.
{}
2; 6; 4ab=¹-
. B.
{}
2; 6; 4ab=- ¹ -
. C.
2; 2aa==-
. D. Cả A, B đều đúng.
HƯỚNG DẪN
Câu 1. Đáp án D.
Hàm số bậc nhất là hàm số có dạng
(0)
yaxba=+ ¹
Câu 2. Đáp án A.
Hàm số có dạng
(0)
yaxba=+ ¹
là hàm số bậc nhất.
Câu 3. Đáp án C.
Hàm số bậc nhất
(0)
yaxba=+ ¹
xác định với mọi giá trị của
x
thuộc
và có tính chất sau
- Đồng biến trên
nếu
0a >
- Nghịch biến trên
nếu
0a <
.
Câu 4. Đáp án A.
Theo định nghĩa thì hàm số
21yx=+
là hàm số bậc nhất.
Câu 5. Đáp án B.
Theo định nghĩa thì hàm số 1; 3
2
x
yyx=+ = là hàm số bậc nhất.
Câu 6. Đáp án A.
Hàm số
2.1ymx=- +
là hàm số bậc nhất khi
20
2
2
2
20
m
m
m
m
m
ì
ì
ï
-³
ï
£
ï
ï
ï
<
íí
ïï
¹
-¹
ïï
î
ï
î
Câu 7. Đáp án C.
Hàm số
1
23
2
m
yxm
m
+
=+-
-
là hàm số bậc nhất khi
1
10 1
0
2
22
20
m
mm
m
mm
m
ì
ï
+
ìì
ï
ïï
+¹ ¹-
¹
ï
ïï
ï

ííí
-
ïïï
¹¹
ïïï
-¹
îî
ï
ï
î
.
Câu 8. Đáp án A.
Hàm số
3
5
12
m
yx
m
=-
-
là hàm số bậc nhất khi
30
30
0
12
1
21
12 0
2
mm
m
m
m
m
m
ì
ï
¹
ì
ì
ï
ï
ï
ï
ï
ï
¹
¹
ï
ï
ï

íí
-
ïï
¹
¹
ï
í
ï
ï
ï
ï
î
ï
-¹
î
ï
ï
î
.
Câu 9. Đáp án C.
Hàm số
21yx=-
có
20a =>
nên là hàm số đồng biến
Hàm số
(1 3 ) 3 1yxyx=- - = -
có
30a =>
nên là hàm số đồng biến
Hàm số
(2 1) 2 1yx yx=- - =- +
có
20a =- <
nên là hàm số nghịch biến
Hàm số
yx=
có
10a =>
nên là hàm số đồng biến
Câu 10. Đáp án D.
10.
TOÁNHỌCSƠĐỒ‐THCS.TOANMATH.com
+) Hàm số
2(4 ) 5 8 2 5 2 13yxyxyx=-+=-+=-+
có
20a =- <
nên là hàm số nghịch
biến
+) Hàm số
3(2 2) 32 2 2 32yxyxyx= - + = - -=- + -
có
20a =- <
nên là hàm
số nghịch biến
+) Hàm số
(9 )yx=- -
9yx=-
có
10a =>
nên là hàm số đồng biến.
+) Hàm số
3
yx x=-
không là hàm số bậc nhất.
Câu 11. Đáp án A.
Hàm sô
84(5)ymx=- +
là hàm số nghịch biến khi
84 0 2mm-<>
Câu 12. Đáp án A.
Hàm số
2
1
5
22
m
yx
mm
-
=-
++
là hàm số nghịch biến
2
1
0
22
m
mm
-
<
++
Nhận thấy
22
22(1)110mm m++=++³>
với mọi
m
nên
2
1
0
22
m
mm
-
<
++
10 1mm-<<
Câu 13. Đáp án C.
Hàm số
52ymxxm=-+
(5 2)ymxm= - +
là hàm số đồng biến khi
2
520
5
mm-> >
.
Câu 14. Đáp án C.
Hàm số
2
(2 4 5) 7 5ymmxm=- +--+
là hàm số đồng biến
2
2450mm-+->
Nhận thấy
"-+-=- -+=- -+-=---<
22 2 2
245(245)2(21)32(1)30,
mm mm mm m m
Nên hàm số nghịch biến với mọi
m
, nghĩa là không có giá trị nào của
m
để hàm đã cho đồng biến.
Câu 15. Đáp án D.
Hàm số
2
3. 1ym x=++
có
2
330m +³>
với mọi
m
nên là hàm số đồng biến với mọi
m
.
Câu 16. Đáp án B.
Hàm số
2323
5
2323
yx
æö
÷+-
ç
÷
ç
=+ -
÷
ç
÷
ç
÷
ç
-+
èø
có
()()
()()
+--
+-
=+=
-+
-+
22
23 23
2323
2323
2323
a
++-+-
==>
-
44334433
83 0
43
, nên là hàm số đồng biến trên
.
Câu 17. Đáp án A.
Hàm số
()
32.ym xm=---
là hàm số đồng biến khi
320m -->
.
11.
TOÁNHỌCSƠĐỒ‐THCS.TOANMATH.com
Khi đó
320 3 2mm--> ->
30 3
34 7
mm
mm
ìì
ïï
-³ ³
ïï

íí
ïï
-> >
ïï
îî
7m>
Giá trị nguyên nhỏ nhất cần tìm là
8m =
.
Câu 18. Đáp án C.
Hàm số
()
55 . 2ymxm=- - ++
là hàm số nghịch biến khi
55 0m--<
ĐK:
50 5mm-³£
Khi đó
5 5 0 5 5 5 25 20mmmm--< ->-><-
Kết hợp điều kiện ta được
20m <-
nên giá trị nguyên lớn nhất của mm thỏa mãn là
19.m =-
Câu 19. Đáp án C.
Hàm số
(3 1) 6ymmxm=- +
là hàm số bậc nhất khi
1
310
31. 0
3
0
0
()
m
m
mm
m
m
ì
ï
ì
ï
ï
-¹
¹
ï
ï
ï
-¹
íí
ïï
¹
ïï
¹
î
ï
ï
î
.
Câu 20. Đáp án A.
Hàm số
2
(98)10ym m x=-++
là hàm số bậc nhất khi
2
10 1
980 1()(80
8
)
08
mm
mm m m
mm
ìì
ïï
-¹ ¹
ïï
- +¹ - - ¹
íí
ïï
-¹ ¹
ïï
îî
.
Câu 21. Đáp án D.
Hàm số
22
(4)(3)(2)2ya x babax=- +- + -
là hàm số bậc nhất khi
2
()()
2
2
40
3
320
2
a
a
a
ba
baba
ba
ì
é
ï
=
ï
ê
ï
ï
ê
=-
ï
ê
ï
ì
ë
ï
-=
ï
ï
ïï
¹
íí
ïï
-+¹
ïï
ï
î
¹-
ï
ï
ï
ï
ï
ï
î
Với
6
2
4
b
a
b
ì
ï
¹
ï
=
í
ï
¹-
ï
î
Với
6
2
4
b
a
b
ì
ï
¹-
ï
=-
í
ï
¹
ï
î
.
12.
TOÁNHỌCSƠĐỒ‐THCS.TOANMATH.com
D.PHIẾU BÀI TỰ LUYỆN
Dạng 1. Nhận biết về khái niệm hàm số
Bài 1: Cho
y
là hàm số của
x
Trong các cách cho sau đây , cách nào là hàm số cho bởi bảng, cách nào là
hàm số cho bởi công thức ?
Cách 1:
x
-1 0 3 4 7
y
78 56 3 -5 8
Cách 2:
2
8
2 ; 2 3 ; ; y = 2 ;
1
yxyx yx x y
x

Bài 2: Trong các bảng sau ghi các giá trị tương ứng của
x
và
y
. Bảng nào xác định
y
là hàm số của
x
? Vì sao ?
Bảng 1
x
-2 -1 1 2 3
y
6 6 6 6 6
Bảng 2
x
-2 -1 1 2 3
y
8 6 5 -5 7
Bảng 3
x
-2 -1 1 2 2
y
8 6 5 -5 7
Dạng 2. Tính giá trị của hàm số, giá trị của biến số
Bài 3: Cho hàm số

23yfx x
. Tính giá trị của hàm số khi
13
2 ; ; .
22
x 
Bài 4: Cho hàm số

2
2yfx x
. Tính


3 ; 3 ; 5ff f
Bài 5: Cho hàm số

2yfx x. Tìm x để hàm số đã cho có giá trị bằng 5.
Bài 6: Cho hàm số

(m 1) 4.yfx x
. ( Với m là tham số). Tìm m biết

71.ff
Dạng 3. Tìm điều kiện xác định của hàm số
Bài 7: Tìm điều kiện của x để các hàm số sau xác định:
1) 2 6yx
2) 5 10yx
210
3)
5
x
y
2
4) 2 1yx x
Bài 8: Tìm điều kiện của x để các hàm số sau xác định:
5
1)
24
y
x
5
2)
25
y
x
5
3)
2
y
x
Bài 9: Tìm điều kiện của x để các hàm số sau xác định:
3
1)
1
x
y
x
2) (2 3)(1 )yx x
2
3) 4 3yx x
Dạng 4. Đồ thị hàm số
Bài 10: Tìm giá trị của
m
để đồ thị hàm số
3yxm
đi qua điểm
(1; 2)A
. [TS10 Nghệ An, 2018-2019]
13.
TOÁNHỌCSƠĐỒ‐THCS.TOANMATH.com
Bài 11: Tìm giá trị của tham số
m
để đồ thị hàm số
yxm
đi qua điểm
(0;3)A
.[TS10 Ninh Bình, 2018-
2019]
Bài 12: Vẽ đồ thị hàm số
44.yx x
HƯỚNG DẪN
Dạng 1. Nhận biết về khái niệm hàm số
Bài 1: Cho
y
là hàm số của
x
Trong các cách cho sau đây , cách nào là hàm số cho bởi bảng, cách nào là
hàm số cho bởi công thức ?
Cách 1:
x
-1 0 3 4 7
y
78 56 3 -5 8
Cách 2:
2
8
2 ; 2 3 ; ; y = 2 ;
1
yxyx yx x y
x

Lời giải
Cách 1: là hàm số cho bởi bảng.
Cách 2: là hàm số cho bởi công thức.
Bài 2: Trong các bảng sau ghi các giá trị tương ứng của
x
và
y
. Bảng nào xác định
y
là hàm số của
x
? Vì sao ?
Bảng 1
x
-2 -1 1 2 3
y
6 6 6 6 6
Bảng 2
x
-2 -1 1 2 3
y
8 6 5 -5 7
Bảng 3
x
-2 -1 1 2 2
y
8 6 5 -5 7
Lời giải
+ Bảng 1 và Bảng 2 xác định
y
là hàm số của
x
. Vì mỗi giá trị của x cho duy nhất một giá trị của
y
.
(Bảng 1 gọi là hàm hằng)
+ Bảng 3 không xác định
y
là hàm số của
x
. Vì tại
2x
cho hai giá trị của
y
là
5 ; 7yy
.
Dạng 2. Tính giá trị của hàm số, giá trị của biến số.
Bài 3: Cho hàm số

23yfx x
. Tính giá trị của hàm số khi
13
2 ; ; .
22
x 
( nên viết là
13
2; ; .
22
  xx x
)
Lời giải
Xét hàm số

23yfx x
.
+ Tại
2x 
ta có:

22.(2)3 1f 
14.
TOÁNHỌCSƠĐỒ‐THCS.TOANMATH.com
+ Tại
1
2
x 
ta có:
11
2. 3 1 3 2
22
f
 

 
 
+ Tại
3
2
x
ta có:
33
2. 3 3 3
22
f





Vậy giá trị của hàm số khi
13
2 ; ; .
22
x 
lần lượt là
1 ; 2 ; 3 3
Bài 4: Cho hàm số

2
2yfx x
. Tính


3 ; 3 ; 5ff f
Lời giải
Xét hàm số

2
2yfx x
.
+ Ta có:


22 2
3 2.3 18 ; 3 2.( 3) 18 ; 5 2.( 5) 10.ff f     
Vậy


318 ; 318 ; 510.ff f  
Bài 5: Cho hàm số

2yfx x. Tìm x để hàm số đã cho có giá trị bằng 5.
Lời giải
Xét hàm số

2yfx x. ĐKXĐ
2.x
Để hàm số đã cho có giá trị bằng 5 thì
25 225 27xx x
(Thỏa mãn
2.x
)
Vậy
27x
thì hàm số đã cho có giá trị bằng 5.
Bài 6: Cho hàm số

(m 1) 4.yfx x
( Với m là tham số). Tìm m biết

71.ff
Lời giải
Xét hàm số

(m 1) 4.yfx x
Theo bài ra ta có

71.ff
Suy ra
7(m1) 4 (1)(m1) 4 8(m1) 0 m 1. 
Vậy
m1
là giá trị cần tìm.
Dạng 3. Tìm điều kiện xác định của hàm số
Bài 7: Tìm điều kiện của
x
để các hàm số sau xác định:
1) 2 6yx
2) 5 10yx
210
3)
5
x
y
2
4) 2 1yx x
Lời giải:
1) Hàm số
26yx
xác định khi
260x  26 3.xx
Vậy
3x
thì hàm số
26yx
xác định.
2) Hàm số
510yx
xác định khi
1
510 0 10 5
2
xxx
Vậy
1
2
x
thì hàm số
510yx
xác định.
3) Hàm số
210
5
x
y
xác định khi
210
0
5
x
2100x
5.x
Vậy
5x
thì hàm số
210
5
x
y
xác định.
15.
TOÁNHỌCSƠĐỒ‐THCS.TOANMATH.com
4) Hàm số
2
21yx x
xác định khi
2
210xx
2
(1)0 x
(luôn đúng)
Vậy hàm số
2
21yx x
xác định với mọi
.xR
.
Bài 8: Tìm điều kiện của x để các hàm số sau xác định:
5
1)
24
y
x
5
2)
25
y
x
5
3)
2
y
x
Lời giải
1) Hàm số
5
24
y
x
xác định khi
240
2402 4 2
240
x
xxx
x



Vậy
2.x 
thì hàm số
5
24
y
x
xác định.
2) Hàm số
5
25
y
x
xác định khi
5
0
5
250
25
2
250
xx
x
x


Vậy
5
.
2
x
thì hàm số
5
25
y
x
xác định.
3) Hàm số
5
2
y
x
xác định khi
00
0
4
20 2
xx
x
x
xx








Vậy
0x
và
4x
thì hàm số
5
2
y
x
xác định.
Bài 9: Tìm điều kiện của x để các hàm số sau xác định:
3
1)
1
x
y
x
2) (2 3)(1 )yx x
2
3) 4 3yx x
Lời giải
1) Hàm số
3
1
x
y
x
xác định khi
30 3
3
10 1
1
0
1
3
30 3
10
10 1
xx
x
xx
x
x
x
xx
x
xx



















Vậy
3x
hoặc
1x 
thì hàm số
3
1
x
y
x
xác định.
2) Hàm số
(2 3)(1 )yx x
xác định khi
(2 3)(1 ) 0xx







3
230
2
10 1
3
1
2
230 3
2
10
1
x
x
xx
x
x
x
x
x
Vậy

3
1
2
x
thì hàm số
(2 3)(1 )yx x
xác định.
3) Hàm số
2
43yx x
xác định khi
2
430(3)(1)0xx x x
16.
TOÁNHỌCSƠĐỒ‐THCS.TOANMATH.com
30 3
10 1
1
3
30 3
10 1
xx
xx
x
x
xx
xx



















Vậy
1x 
hoặc
3x 
thì hàm số
2
43yx x xác định.
Dạng 4. Đồ thị hàm số
Bài 10: Tìm giá trị của
m
để đồ thị hàm số
3yxm
đi qua điểm
(1; 2)A
. [TS10 Nghệ An, 2018-2019]
Lời giải
Để đồ thị hàm số
3yxm
đi qua điểm
(1; 2)A
thì
231 23 1.mm
Vậy
1m 
.
Bài 11: Tìm giá trị của tham số
m
để đồ thị hàm số
yxm
đi qua điểm
(0;3)A
.[TS10 Ninh Bình, 2018-
2019]
Lời giải
Đồ thị hàm số
yxm
đi qua điểm
(0;3)A
nên ta có
30m
.
Vậy
3m
là giá trị cần tìm.
Bài 12: Vẽ đồ thị hàm số
44.yx x
Lời giải
Hàm số
44yx x
xác định khi
40 4
4
40 4
xx
x
xx






Với
40xy
Suy ra đồ thị hàm số là điểm
(4;0).A
‐‐‐‐‐‐‐‐‐‐ToánHọcSơĐồ‐‐‐‐‐‐‐‐‐
12
10
8
6
4
2
2
4
6
8
15 10 5 5 10 15
A
(4;0)
| 1/16
| | Tải xuống

Có thể bạn quan tâm:

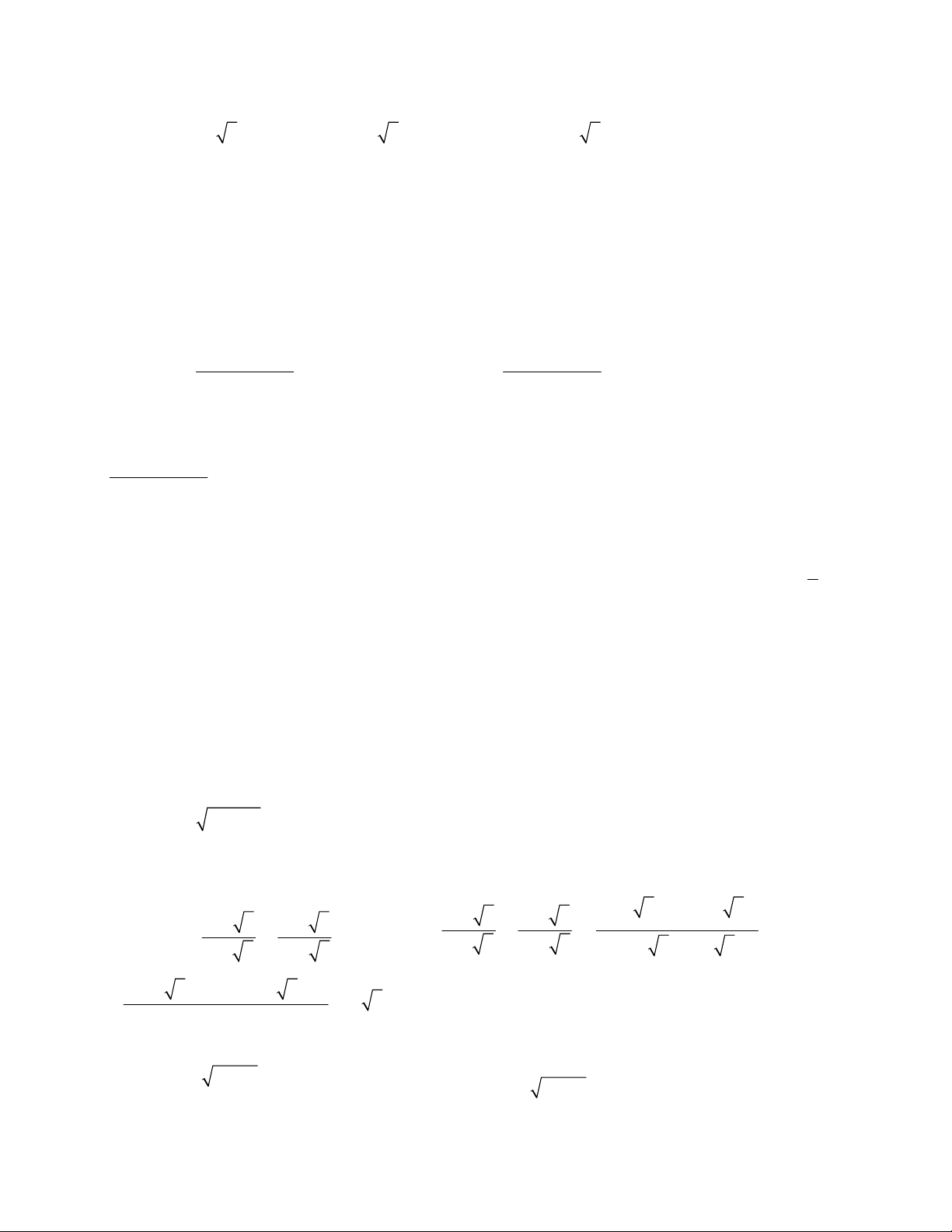
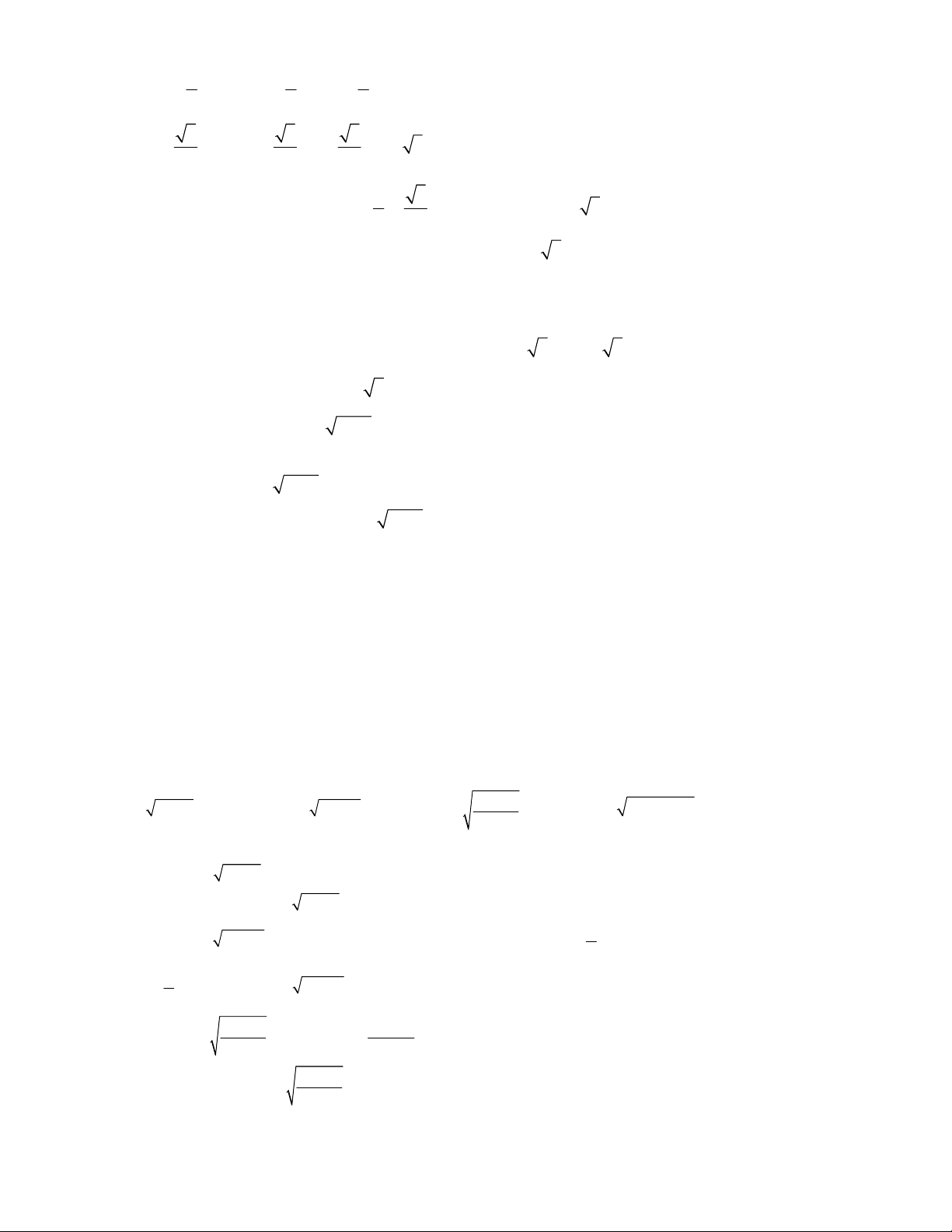
Preview text:


CHUYÊN ĐỀ HÀM SỐ BẬC NHẤT
A. TÓM TẮT LÝ THUYẾT
1. Hàm số bậc nhất
Là hàm số được cho bởi công thức y= ax+b trong đó a,b là hai số đã cho và a  0
2. Các tính chất của hàm số bậc nhất
- Hàm số bậc nhất xác định với mọi giá trị của x thuộc R
- Hàm số bậc nhất: + Đồng biến trên R khi a > 0
+ Nghịch biến trên R khi a < 0
B.CÁC DẠNG BÀI MINH HỌA
Dạng 1: Tính giá trị của hàm số tại một điểm
Phương pháp giải toán
1. Việc tính toán theo kiểu này sẽ giúp ta xác định được toạ độ của nhiều điểm thuộc đồ thị hàm số một
cách nhanh chóng. Ngoài ra, phương pháp sử dụng kết hợp máy tính cầm tay (sử dụng Slove) sẽ giúp cải
thiện thời gian một cách hiệu quả.
2. Tính giá trị của hàm số y  f x khi cho giá trị của ẩn x là ta thay giá trị của x vào biểu thức 0 0
y  f xđể tìm được y  f x 0  0
Câu 1: Cho hai hàm số 2
f (x)  x và g(x)  3  x 1
a, Tính f (3), f (
), f (0) , g(1), g(2), g(3) 2
b, Xác định giá trị của a để 2 f (a)  g(a) .
Câu 2: Cho hai hàm số 2
g(x)  2x và h(x)  3x  5 3 a, Tính g(0,4), g(
), g(2), h(1, 4), h( 1  ) 4 1 b, Xác
định các giá trị của m để g(m)  h(m) 2
Dạng 2: Vẽ đồ thị hàm bậc nhất
Phương pháp giải:Theo các bước vẽ đã học
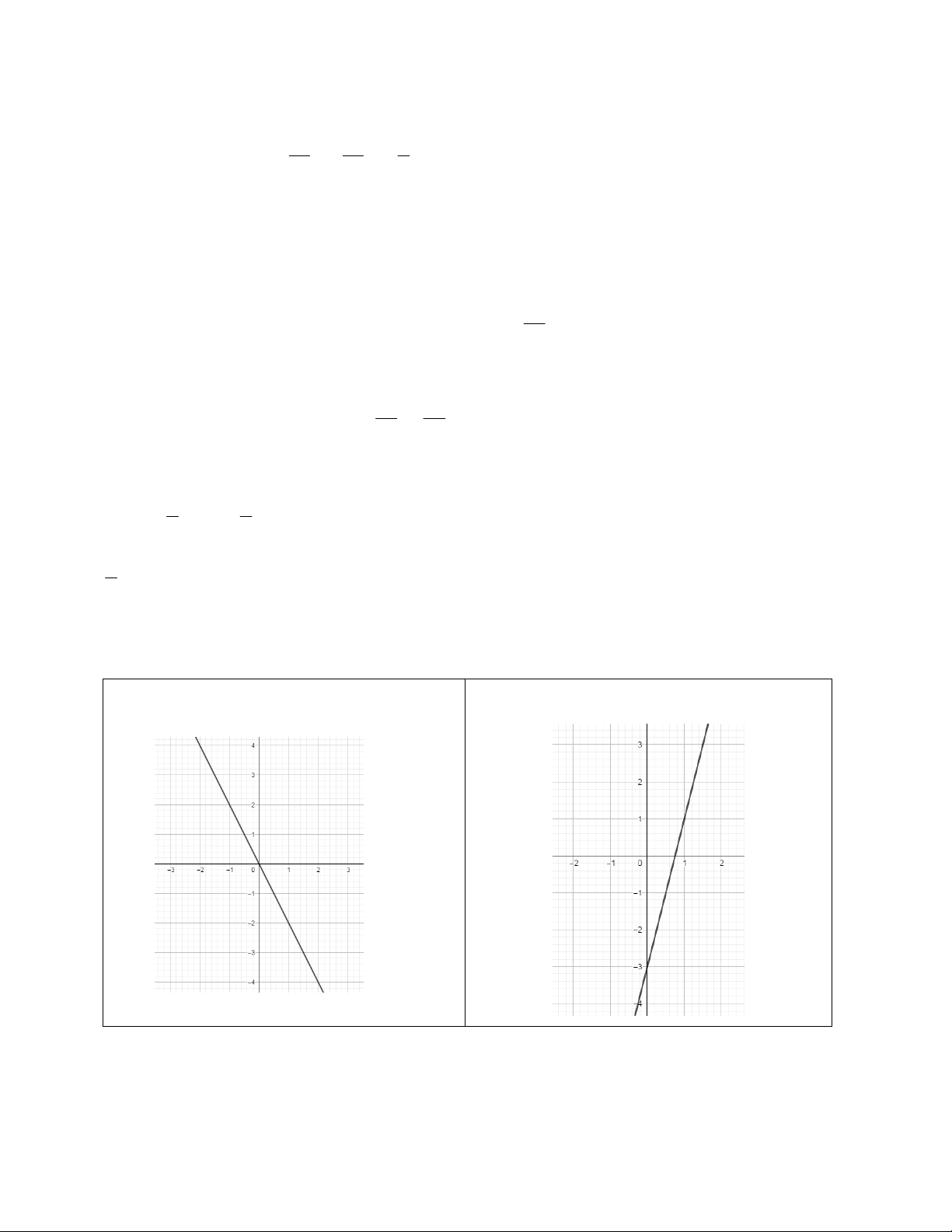
Câu 3: Vẽ đồ thị các hàm số bậc nhất sau: a, y  2x
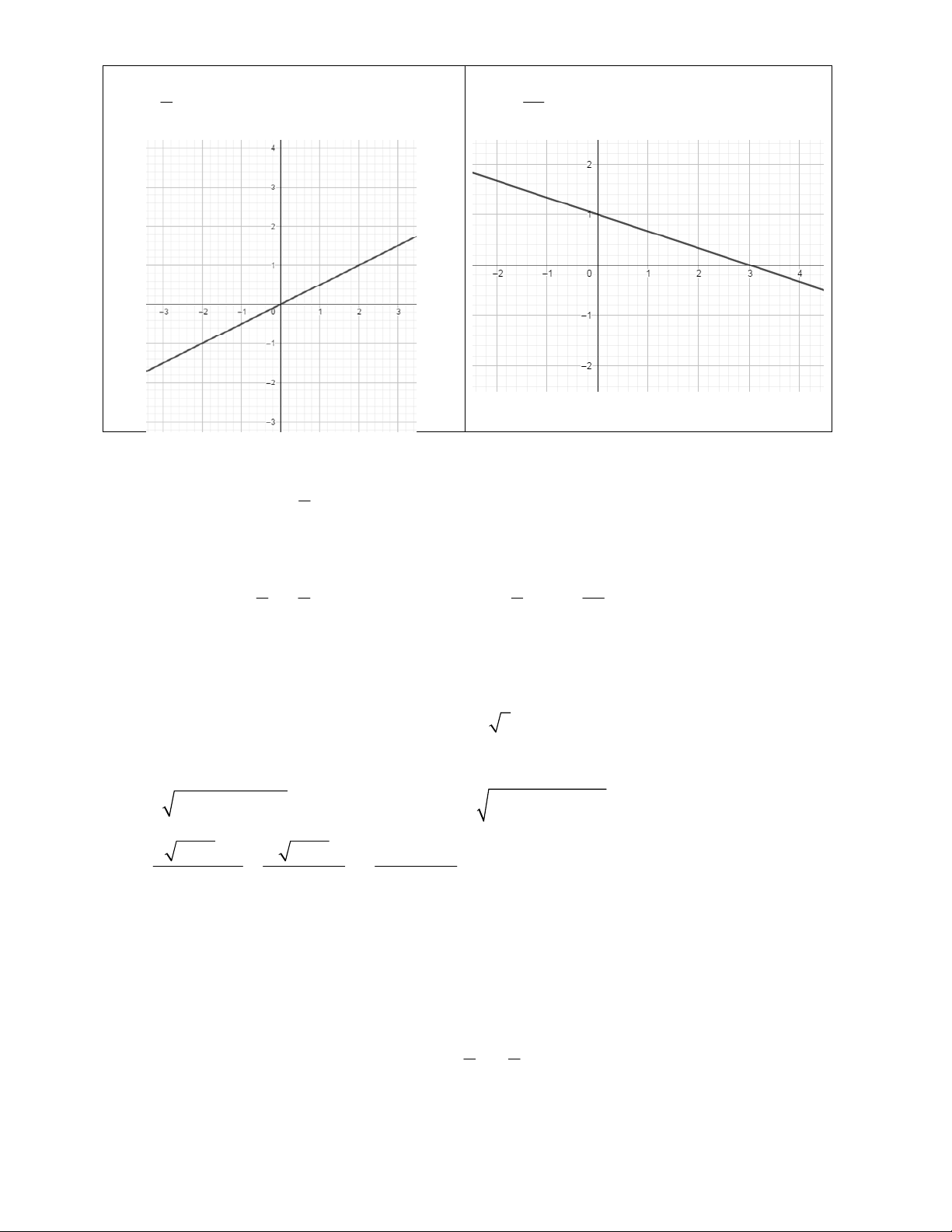
b, y  4x  3
1. TOÁN HỌC SƠ ĐỒ ‐ THCS.TOANMATH.com 1 1 c, y x c, y x 1 2 3
Dạng 3: Nhận dạng hàm số bậc nhất
Phương pháp giải: Dựa vào định nghĩa hàm số bậc nhất
Câu 4: Hãy xét xem trong các hàm số sau đây , đâu là hàm số bậc nhất? Hãy chỉ rõ các hệ số a và b trong
trường đó là ham số bậc nhât . 1 a, y x
b, y  3x  3 x   1 2 2x  3 c, y
d, y   x   x   2 1 3  x 4
Câu 5: Tìm m để hàm số sau là hàm số bậc nhất : a, 2
y  (2m  6)x m  5 b, 2
y  (2  m)x  8x  7 x m 1  5 c, 2
y x (m  3)(m 1) 1 d, y  2 m m  2
Câu 6: Chứng minh các hàm số sau là hàm số bậc nhất với mọi giá trị của tham số m: a) 2
y  (m m 1)x  9 b, 2
y  (m  4m  7)x m  3
Dạng 4: Xét tính đông biến và nghịch biến của hàm số bậc nhất
Phương pháp giải: xét hàm số bậc nhất y = ax + b với a, b là hằng số, a  0
- Khi a > 0, Hàm số đồng biến trên R
- Khi a < 0, Hàm số nghịch biến trên R
Câu 7: Các hàm số sau đồng biến hay nghịch biến ? Vì sao? 4 1
a, y  7  9x b, y x  7 2
c, y  3(2x 1)  4x  1 d, 2
y  (2x 1)  4x(x 1)
Câu 8: Tìm m để hàm số sau : a,
y  (2m  5)x 13 đồng biến trên  . b, 2
y  (4m  9)x  2 nghịch biến trên  . 3m  2 c, y
x  5 nghịch biến trên  . 2 Câu 9: Cho hàm số 2
y f (x)  (m m  2)x  9  3m với m là tham số.
a, Chứng minh hàm số đã cho luôn là hàm số bậc nhất và nghịch biến trên  .
b, Hãy so sánh f (10) và f (3 11) .
2. TOÁN HỌC SƠ ĐỒ ‐ THCS.TOANMATH.com Câu 10: Cho hàm số 2
y f (x)  (k  2k  3)x k  5 a,
Chứng minh hàm số đã cho luôn là hàm số bậc nhất và đồng biến trên  .
b, Hãy so sánh f ( 2 1) và f ( 2  3) .
Dạng 5. Toán thực tế
Câu 11: Mối quan hệ giữa thang nhiệt độ F(Fahrenheit) và thang nhiệt độ C (Celsius) được cho bởi công
thức T  1,8T  32 , trong đó T là nhiệt độ tính theo độ C và T là nhiệt độ tính theo độ F. Ví dụ T 0  F C C F C Ctương ứng với T 32  F. F
a) Hỏi 25C tương ứng với bao nhiêu độ F ?
b) Các nhà khoa học đã tìm ra mối liên hệ giữa A là số tiếng kêu củamột con dế trong một phút và T là F
nhiệt độ cơ thể của nó bởi công thức A  5, 6T  275 , trong đó nhiệt độ T tính theo độ F . Hỏi nếu con F F
dế kêu 106 tiếng trong một phút thì nhiệt độ của nó khoảng bao nhiêu độ C? (làm tròn đến hàng đơn vị).
Câu 12: Siêu thị A thực hiện chương trình giảm giá cho khách hàng mua loại túi bột giặt 4 kg như sau:
+ Nếu mua 1 túi thì được giảm 10 000 đồng so với giá niêm yết.
+ Nếu mua 2 túi thì túi thứ nhất được giảm 10 000 đồng và túi thứ hai được giảm 20 000 đồng so với giá niêm yết.
+ Nếu mua từ 3 túi trở lên thì ngoài 2 túi đầu được hưởng chương trình giảm giá như trên, từ túi thứ ba trở
đi mỗi túi sẽ được giảm 20% so với giá niêm yết.
a) Bà Tư mua 5 túi bột giặt loại 4kg ở siêu thị A thì phải trả số tiền là bao nhiêu, biết rằng loại túi bột giặt
mà bà tư mua có giá niêm yết là 150 000 đồng/túi.
b) Siêu thị B lại có hình thức giảm giá khác cho loại túi bột giặt nêu trên là: Nếu mua từ 3 túi trở lên thì sẽ
giảm giá 15% cho mỗi túi. Nếu bà Tư mua 5 túi bột giặt thì bà Tư nên mua ở siêu thị nào để số tiền phải
trả là ít hơn?Biết rằng giá niêm yết của hai siêu thị là như nhau.
3. TOÁN HỌC SƠ ĐỒ ‐ THCS.TOANMATH.com HƯỚNG DẪN Câu 1: 1 1 1 a, 2
f (3)  (3)  9 ; 2 f ( )  ( )  ; f (0)  0 ; 2 2 4
g(1)  3  (1)  4 ; g(2)  3  (2)  5 ; g(3)  3  3  0 b, Ta có: 2
2 f (a)  2a ; g(a)  3  a a 1 2 2
2 f (a)  g(a)  2a  3  a  2a a  3  0   3   a   2
Câu 2: Tương tự câu 1: 3 9 a, 2
g(0, 4)  2(0, 4)  0,32 ; g( )  ; g(2)  8 4 8
h(1, 4)  0,8 ; h(1)  2 ; 1 1 b, Ta có 2 2
g(m)  (2)m  m ; h(m)  3m  5 2 2 1 2 2
g(m)  h(m)  m  3m  5  m  3m  5  0 ( vô nghiệm) 2
Suy ra không có giá trị nào của m thỏa mãn. Câu 3: a, y  2x
b, y  4x  3
4. TOÁN HỌC SƠ ĐỒ ‐ THCS.TOANMATH.com 1 1 c, y x y x 1 2 d, 3 Câu 4: 1
a, Là hàm bậc nhất với a  và b  0. 2
b, Thu gọn được y  3 , không là hàm số bậc nhất. 1 3 1 3
c, Biến đổi được y
x  là hàm số bậc nhất với a  và b  . 2 4 2 4
d, y   x   1  x  3 2  x  2
x  3là hàm số bậc nhất với a  2 và b  3  Câu 5:
a, y là hàm số bậc nhất 2
a  2m  6  0  m   3 .
b, y là hàm số bậc nhất khi hệ số của 2
x bị triệt tiêu.  2  m  0  m  2 . c, 2
y x (m  3)(m 1) 1là hàm số bậc nhất   2
m  3m   1  0  m  1 x m 1  5 m 1 5 d, y   x  2 2 2 m m  2 m m  2 m m  2 m  1 m 1  0 
Để y là hàm số bậc nhất    m  2   1   m  1 2
m m  2  0 m  1   Câu 6: 1 3 a, 2
y  (m m 1)x  9 . Biến đổi được 2
a  (m  )   0 với mọi m. 2 4 b, 2
y  (m  4m  7)x m  3. Biến đổi được 2
a  (m  2)  3  0 với mọi m.
5. TOÁN HỌC SƠ ĐỒ ‐ THCS.TOANMATH.com Câu 7:
a, Có a  9  0  Hàm số nghịch biến trên  . 4 b, Có a
 0  Hàm số đồng biến trên  . 7
c, Thu gọn được y  2x  2  a  2  Hàm số đồng biến trên  .
d, Thu gọn ta được y  8x 1  a  8  Hàm số nghịch biến trên  . Câu 8: 5
a, Hàm số đồng biến  2m  5  0  m  . 2  b, Hàm số nghịch biến 2 3 3  4m  9  0   m  . 2 2 3m  2 2
c, Hàm số nghịch biến   0  m  . 2 3 Câu 9: 2  1  7
a, Ta có a   m    0   với mọi m.  2  4
Vì vậy hàm số đã cho luôn là hàm số bậc nhất và nghịch biến trên  .
b, Ta có 10   100   99  3 11 .Mà hàm số đã cho là hàm số nghịch biến nên
f 10  f 3 11 .
6. TOÁN HỌC SƠ ĐỒ ‐ THCS.TOANMATH.com
C.TRẮC NGHIỆM RÈN LUYỆN PHẢN XẠ
Câu 1. Chọn đáp án đúng nhất. Hàm số y = ax + b là hàm bậc nhất khi A. a = 0 .
B. a < 0 . C. a > 0 . D. a ¹ 0 .
Câu 2. Chọn đáp án đúng nhất.Với a ¹ 0 hàm số y = ax + b A. Bậc nhất. B. Hàm hằng. C. Đồng biến. D. Nghịch biến.
Câu 3. Chọn đáp án đúng nhất. Hàm số y = ax + b là hàm số đồng biến khi A. a = 0 .
B. a < 0 . C. a > 0 . D. a ¹ 0 .
Câu 4. Hàm số nào dưới đây là hàm số bậc nhất?
A. y = 2x + 1.
B. y = 0x + 3 . C. 2
y = 2x + x + 1 . D. y = x + 2 + 4 . x 1
Câu 5. Trong các hàm số 3 y = 5;y =
+ 1;y = x + 2x + 1;y =
+ 2;y = 3x có bao nhiêu hàm số là 2 x hàm số bậc nhất? A. 3 . B. 2 . C. 4 . D. 1 .
Câu 6. Tìm m để hàm số y = 2 - m.x + 1 là hàm số bậc nhất? A. m < 2 . B. m > 2 . C. m = 2 . D. m ¹ 2 . m + 1 y = x + 2m - 3
Câu 7. Tìm m để hàm số m - 2 là hàm số bậc nhất? A. m ¹ -1 . B. m > 1 - . C. m ¹ {-1; } 2 . D. m ¹ 2 . 3m
Câu 8. Hàm số y =
x - 5 là hàm số bậc nhất khi: 1 - 2m ìï 1üï 1 A. m 0; ï ï ¹ í ý . B. m > 0 . C. m ¹ 0 . D. m ¹ . ï 2ï ïî ïþ 2
Câu 9. Hàm số nào sau đây là hàm số nghịch biến?
A. y = 2x - 1. B. y = (1 - - 3x) . C. y = (2 - x - 1).
D. y = x .
Câu 10. Hàm số nào sau đây là hàm số bậc nhất và đồng biến?
A. y = 2(4 - x) + 5 . B. y = 3 - (2x + ) 2 . C. 3
y = x - x . D. y = (9 - - x) .
Câu 11. Cho hàm số y = (8 - 4m)x + 5 . Tìm m để hàm số là hàm số nghịch biến A. m > 2 . B. m < 2 . C. m = 2 . D. m ¹ 2 .
7. TOÁN HỌC SƠ ĐỒ ‐ THCS.TOANMATH.com m - 1
Câu 12. Với giá trị nào của m thì hàm số y = x - 5 là hàm số 2 m + 2m + 2 nghịch biến? A. m < 1 . B. m > 1 . C. m = 1. D. Mọi m .
Câu 13. Cho hàm số y = 5mx - 2x + m . Tìm m để hàm số là hàm số đồng biến 2 5 2 5 A. m < . B. m > . C. m > . D. m < . 5 2 5 2 Câu 14. Cho hàm số 2
y = (-2m + 4m - 5)x - 7m + 5 là hàm số đồng biến khi 5 A. m < 3 . B. m > .
C. Không có m thỏa mãn. D. Mọi m . 2 2
Câu 15. Cho hàm số y = m + 3.x + 1. Kết luận nào sau đây là đúng?
A. Hàm số đã cho là hàm nghịch biến với mọi m . B. Hàm số đã cho là hàm nghịch biến với m > 3 .
C. Hàm số đã cho là hàm hằng. D. Hàm số đã cho là hàm số đồng biến với mọi m . æç2 + 3 2 - 3 ö÷
Câu 16. Cho hàm số y = ç ÷ + ç
÷x - 5 . Kết luận nào sau đây là đúng? ç ÷ çè2 - 3 2 + 3 ÷ø
A. Hàm số đã cho là hàm nghịch biến. B. Hàm số đã cho là hàm đồng biến.
C. Hàm số đã cho là hàm hằng. D. Hàm số đã cho là hàm số đồng biến với x > 0 .
Câu 17. Cho hàm sốy = ( m - 3 - )
2 .x - m . Giá trị nguyên nhỏ nhất của m để hàm số đồng biến là? A. m = 8 . B. m = 9 . C. m = 3 . D. m = 7 .
Câu 18. Cho hàm sốy = (5 - 5 -m ).x + m + 2 . Với giá trị nguyên lớn nhất của m để hàm số nghịch biến là? A. m = 5 . B. m = -20 . C. m = -19 . D. m = -21 .
Câu 19. Với giá trị nào của m thì hàm số y = (3m - 1)mx + 6m là hàm số bậc nhất 1 ìï 1üï A. m ¹ 0 . B. m ¹ . C. m 0; ï ï ¹ í ý. D. Mọi m . 3 ï 3ï ïî ïþ
Câu 20. Với giá trị nào của m thì hàm số 2
y = (m - 9m + 8)x + 10 là hàm số bậc nhất A. m ¹ {1; } 8 . B. m ¹ 1. C. m ¹ 8 . D. Mọi m . Câu 21. Cho hàm số 2 2
y = (a - 4)x + (b - 3a)(b + 2a)x - 2 là hàm số bậc nhất khi
8. TOÁN HỌC SƠ ĐỒ ‐ THCS.TOANMATH.com
A. a = 2;b ¹ {6;- } 4 . B. a = 2; - b ¹ { 6; - } 4 .
C. a = 2;a = -2 .
D. Cả A, B đều đúng. HƯỚNG DẪN Câu 1. Đáp án D.
Hàm số bậc nhất là hàm số có dạng y = ax + b (a ¹ 0) Câu 2. Đáp án A.
Hàm số có dạng y = ax + b (a ¹ 0) là hàm số bậc nhất. Câu 3. Đáp án C.
Hàm số bậc nhất y = ax + b (a ¹ 0) xác định với mọi giá trị của x thuộc và có tính chất sau
- Đồng biến trên nếu a > 0
- Nghịch biến trên nếu a < 0 . Câu 4. Đáp án A.
Theo định nghĩa thì hàm số y = 2x + 1 là hàm số bậc nhất. Câu 5. Đáp án B. x
Theo định nghĩa thì hàm số y =
+ 1;y = 3x là hàm số bậc nhất. 2 Câu 6. Đáp án A. 2 ìï -m ³ 0 m ìï £ 2 ï
Hàm số y = 2 - m.x + 1 là hàm số bậc nhất khi ï í  í  m < 2 ï 2 - m ¹ 0 m ï ¹ 2 ï ï ïî î Câu 7. Đáp án C. m + 1 y = x + 2m - 3 ìïm + 1 ïï ¹ 0 m ìï + 1 ¹ 0 m ìï ¹ -1 Hàm số m - 2
là hàm số bậc nhất khi ï ï ï ím - 2  í  í . ï m ï ¹ 2 m ï ¹ 2 m ï - 2 ¹ 0 ï ï î ïî ïî Câu 8. Đáp án A. ìï 3m ï ì m ìï ¹ 0 3m ï ¹ 0 3 ï m ¹ 0 Hàm số y =
x - 5 là hàm số bậc nhất khi ï ï ï ï í1 - 2m  í  í . 1 - 2m 1 ï 2 ï m ¹ 1 1 ï - 2 ¹ 0 ï m m ï î ï ¹ ïî ïî 2 Câu 9. Đáp án C.
Hàm số y = 2x - 1 có a = 2 > 0 nên là hàm số đồng biến Hàm số y = (1
- - 3x)  y = 3x - 1 có a = 3 > 0 nên là hàm số đồng biến Hàm số y = (2
- x - 1)  y = -2x + 1 có a = 2
- < 0 nên là hàm số nghịch biến
Hàm số y = x có a = 1 > 0 nên là hàm số đồng biến Câu 10. Đáp án D.
9. TOÁN HỌC SƠ ĐỒ ‐ THCS.TOANMATH.com
+) Hàm số y = 2(4 - x) + 5y = 8 - 2x + 5  y = -2x + 13 có a = 2
- < 0 nên là hàm số nghịch biến
+) Hàm số y = 3 - (2x + 2)  y = 3 - 2x - 2  y = -2x + 3 - 2 có a = 2 - < 0 nên là hàm số nghịch biến +) Hàm số y = (9
- - x)  y = x - 9 có a = 1 > 0 nên là hàm số đồng biến. 3
+) Hàm số y = x - x không là hàm số bậc nhất. Câu 11. Đáp án A. Hàm sô y = 8
( - 4m)x + 5 là hàm số nghịch biến khi 8 - 4m < 0  m > 2 Câu 12. Đáp án A. m - 1 m - 1 Hàm số y =
x - 5 là hàm số nghịch biến < 0 2 m + 2m + 2 2 m + 2m + 2 Nhận thấy 2 2
m + 2m + 2 = (m + 1) + 1 ³ 1 > 0 với mọi m nên m - 1 < 0 2 m + 2m + 2
m - 1 < 0  m < 1 Câu 13. Đáp án C. 2
5m - 2 > 0  m >
Hàm số y = 5mx - 2x + m y = (5m - 2)x + m là hàm số đồng biến khi 5 . Câu 14. Đáp án C. 2 2
Hàm số y = (-2m + 4m - 5)x - 7m + 5 là hàm số đồng biến 2
- m + 4m - 5 > 0 Nhận thấy - 2 m + m - = - 2 m - m + = - 2
m - m + - = - m - 2 2 4 5 (2 4 5) 2( 2 1) 3 2( 1) - 3 < 0,"m
Nên hàm số nghịch biến với mọi m , nghĩa là không có giá trị nào của m để hàm đã cho đồng biến. Câu 15. Đáp án D. 2 2
Hàm số y = m + 3.x + 1 có m + 3 ³ 3 > 0 với mọi m nên là hàm số đồng biến với mọi m . Câu 16. Đáp án B. 2 2 æ (2+ 3) -(2- + - 3 2 3 2 3 ) ç2 + 3 2 - 3 ö÷ y = ç ÷ + a = + = ç ÷x - 5 ç ÷ çè2 - 3 2 + 3 ÷ 2 - 3 2 + 3 (2- 3)(2 + 3) Hàm số ø có 4 + 4 3 + 3 - 4 + 4 3 - 3 =
= 8 3 > 0 , nên là hàm số đồng biến trên . 4 - 3 Câu 17. Đáp án A. y = ( m - 3 - ) 2 .x - m Hàm số
là hàm số đồng biến khi m - 3 - 2 > 0 .
10. TOÁN HỌC SƠ ĐỒ ‐ THCS.TOANMATH.com m ìï - 3 ³ 0 m ìï ³ 3 ï ï  í  í m ï - 3 > 4 m ï > 7
Khi đó m - 3 - 2 > 0  m - 3 > 2 ïî ïî  m > 7
Giá trị nguyên nhỏ nhất cần tìm là m = 8 . Câu 18. Đáp án C.
y = (5 - 5 - m ).x + m + 2 Hàm số
là hàm số nghịch biến khi 5 - 5 - m < 0
ĐK: 5 - m ³ 0  m £ 5
Khi đó 5 - 5 - m < 0  5 - m > 5  5 - m > 25  m < -20
Kết hợp điều kiện ta được m < 20
- nên giá trị nguyên lớn nhất của mm thỏa mãn là m = -19. Câu 19. Đáp án C.
Hàm số y = (3m - 1)mx + 6m là hàm số bậc nhất khi ìï ì 1 3 ï m - 1 ¹ 0 ï m ïï ¹ 3 ( m 1 . ) m 0 ï - ¹  í  í 3 . m ï ¹ 0 ïî m ïï ¹ 0 ïî Câu 20. Đáp án A. 2
Hàm số y = (m - 9m + 8)x + 10 là hàm số bậc nhất khi m ìï -1 ¹ 0 m ìï ¹ 1 2 m 9m 8 0 (m 1)(m 8) 0 ï ï - + ¹  - - ¹  í  í . m ï - 8 ¹ 0 m ï ¹ 8 ïî ïî Câu 21. Đáp án D. 2 2
Hàm số y = (a - 4)x + (b - 3a)(b + 2a)x - 2 là hàm số bậc nhất khi ìï aé = 2 ïê ïïïaê = -2 ì 2 a ï - 4 = 0 ïêë ï ï ïí b ï  í ¹ 3a (
ï b - 3a)(b + 2a) ¹ 0 ï ïî b ïï ¹ -2a ïïïïïî b ìï ¹ 6 Với a 2 ï =  í b ï ¹ -4 ïî b ìï ¹ 6 - a 2 ï = -  íbï ¹ 4 Với ïî .
11. TOÁN HỌC SƠ ĐỒ ‐ THCS.TOANMATH.com
D.PHIẾU BÀI TỰ LUYỆN
Dạng 1. Nhận biết về khái niệm hàm số
Bài 1: Cho y là hàm số của x Trong các cách cho sau đây , cách nào là hàm số cho bởi bảng, cách nào là
hàm số cho bởi công thức ? Cách 1: x -1 0 3 4 7 y 78 56 3 -5 8 8 Cách 2: 2
y  2x ; y  2x  3 ; y x ; y = x  2 ; y x 1
Bài 2: Trong các bảng sau ghi các giá trị tương ứng của x và y . Bảng nào xác định y là hàm số của x ? Vì sao ? Bảng 1 x -2 -1 1 2 3 y 6 6 6 6 6 Bảng 2 x -2 -1 1 2 3 y 8 6 5 -5 7 Bảng 3 x -2 -1 1 2 2 y 8 6 5 -5 7
Dạng 2. Tính giá trị của hàm số, giá trị của biến số 1 3
Bài 3: Cho hàm số y f x  2x  3. Tính giá trị của hàm số khi x  2 ;   ; . 2 2
Bài 4: Cho hàm số y f x 2  2
x . Tính f 3 ; f  3   ; f  5
Bài 5: Cho hàm số y f x  x  2 . Tìm x để hàm số đã cho có giá trị bằng 5.
Bài 6: Cho hàm số y f x  (m1)x  4.. ( Với m là tham số). Tìm m biết f 7  f   1 .
Dạng 3. Tìm điều kiện xác định của hàm số
Bài 7: Tìm điều kiện của x để các hàm số sau xác định:
1) y  2x  6
2) y  510x 2x y  10 3) 2
4) y x  2x 1 5
Bài 8: Tìm điều kiện của x để các hàm số sau xác định: 5  1) y  5 2) y  5 3) y  2x  4 2x  5 x  2
Bài 9: Tìm điều kiện của x để các hàm số sau xác định: x  3 1) y
2) y  (2x  3)(1 x) 2
3) y x  4x  3 x 1
Dạng 4. Đồ thị hàm số
Bài 10: Tìm giá trị của m để đồ thị hàm số y  3x m đi qua điểm (1
A ;2) . [TS10 Nghệ An, 2018-2019]
12. TOÁN HỌC SƠ ĐỒ ‐ THCS.TOANMATH.com
Bài 11: Tìm giá trị của tham số m để đồ thị hàm số y x m đi qua điểm (0
A ;3) .[TS10 Ninh Bình, 2018- 2019]
Bài 12: Vẽ đồ thị hàm số
y x  4  4  x. HƯỚNG DẪN
Dạng 1. Nhận biết về khái niệm hàm số
Bài 1: Cho y là hàm số của x Trong các cách cho sau đây , cách nào là hàm số cho bởi bảng, cách nào là
hàm số cho bởi công thức ? Cách 1: x -1 0 3 4 7 y 78 56 3 -5 8 8 Cách 2: 2
y  2x ; y  2x  3 ; y x ; y = x  2 ; y x 1 Lời giải
Cách 1: là hàm số cho bởi bảng.
Cách 2: là hàm số cho bởi công thức.
Bài 2: Trong các bảng sau ghi các giá trị tương ứng của x và y . Bảng nào xác định y là hàm số của x ? Vì sao ? Bảng 1 x -2 -1 1 2 3 y 6 6 6 6 6 Bảng 2 x -2 -1 1 2 3 y 8 6 5 -5 7 Bảng 3 x -2 -1 1 2 2 y 8 6 5 -5 7 Lời giải
+ Bảng 1 và Bảng 2 xác định y là hàm số của x . Vì mỗi giá trị của x cho duy nhất một giá trị của y .
(Bảng 1 gọi là hàm hằng)
+ Bảng 3 không xác định y là hàm số của x . Vì tại x  2 cho hai giá trị của y là y  5 ;  y  7 .
Dạng 2. Tính giá trị của hàm số, giá trị của biến số. 1 3
Bài 3: Cho hàm số y f x  2x  3. Tính giá trị của hàm số khi x  2 ;   ; . 2 2 1 3
( nên viết là x  2;  ; x   x  . ) 2 2 Lời giải
Xét hàm số y f x  2x  3. + Tại x  2  ta có: f  2    2.( 2  )  3  1 
13. TOÁN HỌC SƠ ĐỒ ‐ THCS.TOANMATH.com 1  1   1 
+ Tại x   ta có: f   2.   3  1   3  2     2  2   2  3  3  3 + Tại x  ta có: f    2.  3  3  3   2 2 2   1 3
Vậy giá trị của hàm số khi x  2 ;   ;
. lần lượt là 1 ; 2 ; 3  3 2 2
Bài 4: Cho hàm số y f x 2  2
x . Tính f 3 ; f  3   ; f  5 Lời giải
Xét hàm số y f x 2  2  x . + Ta có: f   2     f   2      f   2 3 2.3 18 ; 3 2.( 3) 18 ; 5  2  .( 5)  1  0. Vậy f 3   18 ; f  3     18 ; f  5  1  0.
Bài 5: Cho hàm số y f x  x  2 . Tìm x để hàm số đã cho có giá trị bằng 5. Lời giải
Xét hàm số y f x  x  2 . ĐKXĐ x  2.
Để hàm số đã cho có giá trị bằng 5 thì x  2  5  x  2  25  x  27 (Thỏa mãn x  2.)
Vậy x  27 thì hàm số đã cho có giá trị bằng 5.
Bài 6: Cho hàm số y f x  (m1)x  4. ( Với m là tham số). Tìm m biết f 7  f   1 . Lời giải
Xét hàm số y f x  (m1)x  4.
Theo bài ra ta có f 7  f   1 .
Suy ra 7(m1)  4  ( 1
 )(m1)  4  8(m1)  0  m 1.
Vậy m 1 là giá trị cần tìm.
Dạng 3. Tìm điều kiện xác định của hàm số
Bài 7: Tìm điều kiện của x để các hàm số sau xác định:
1) y  2x  6
2) y  510x 2x y  10 3) 2
4) y x  2x 1 5 Lời giải: 1) Hàm số
y  2x  6 xác định khi 2x  6  0  2x  6   x  3  . Vậy x  3  thì hàm số
y  2x  6 xác định. 2) Hàm số
y  510x xác định khi 1
5 10x  0  10x  5  x  2 Vậy 1 x  thì hàm số
y  510x xác định. 2 3) Hàm số 2x  2x 10  2x 10  0 y  10 xác định khi   0  x  5.  5 5
Vậy x  5 thì hàm số 2x y  10 xác định. 5
14. TOÁN HỌC SƠ ĐỒ ‐ THCS.TOANMATH.com 4) Hàm số 2
y x  2x 1 xác định khi 2
x  2 x  1  0 2
 (x 1)  0 (luôn đúng) Vậy hàm số 2
y x  2x 1 xác định với mọi x  . R .
Bài 8: Tìm điều kiện của x để các hàm số sau xác định: 5  1) y  5 2) y  5 3) y  2x  4 2x  5 x  2 Lời giải    1) Hàm số 5 x y  xác định khi 2 4 0 
 2x  4  0  2x  4   x  2  2x  4 2x  4  0
Vậy x  2. thì hàm số 5 y  xác định. 2x  4  5 2) Hàm số 5    0 5 y
xác định khi 2x 5
 2x  5  0  x  2x  5 2 2x 5  0 Vậy 5  x  . thì hàm số 5 y  xác định. 2 2x  5 x  0  x  0  x  0 3) Hàm số 5 y  xác định khi      x  2  x  2  0  x  2 x  4
Vậy x  0 và x  4 thì hàm số 5 y  xác định. x  2
Bài 9: Tìm điều kiện của x để các hàm số sau xác định: x  3 1) y
2) y  (2x  3)(1 x) 2
3) y x  4x  3 x 1 Lời giải x  3  0 x  3  x  3   x  3   0 x 1  0 x  1 x  1 1) Hàm số y
xác định khi  x 1    x 1    x  3  0 x  3 x  3 x 1  0   x 1  0 x  1 x  3
Vậy x  3 hoặc x  1 thì hàm số y  xác định. x 1  3  x  2x  3  0    2 
2) Hàm số y  (2x  3)(1 x) xác định khi 1 x  0 x  1
(2 x  3)(1  x)  0    1  x  3   2x  3  0    3 2  x  1 x  0  2  x  1 Vậy  x  3 1
thì hàm số y  (2x  3)(1 x) xác định. 2 3) Hàm số 2
y x  4x  3 xác định khi 2
x  4x  3  0  (x  3)(x 1)  0
15. TOÁN HỌC SƠ ĐỒ ‐ THCS.TOANMATH.com x  3  0 x  3   x 1  0 x  1 x  1      x  3  0
x  3 x  3   x 1 0 x  1
Vậy x  1hoặc x  3 thì hàm số 2
y x  4x  3 xác định.
Dạng 4. Đồ thị hàm số
Bài 10: Tìm giá trị của m để đồ thị hàm số y  3x m đi qua điểm (1
A ;2) . [TS10 Nghệ An, 2018-2019] Lời giải
Để đồ thị hàm số y  3x m đi qua điểm (1
A ;2) thì 2  31 m m  2  3  1. Vậy m  1.
Bài 11: Tìm giá trị của tham số m để đồ thị hàm số y x m đi qua điểm (0
A ;3) .[TS10 Ninh Bình, 2018- 2019] Lời giải
Đồ thị hàm số y x m đi qua điểm (0
A ;3) nên ta có 3  0  m .
Vậy m  3 là giá trị cần tìm.
Bài 12: Vẽ đồ thị hàm số
y x  4  4  x. Lời giải      Hàm số x x
y x  4  4  x xác định khi 4 0 4     x  4 4  x  0 x  4
Với x  4  y  0 Suy ra đồ thị hàm số là điểm (4 A ;0). 12 10 8 6 4 A(4;0) 2 15 10 5 5 10 15 2 4 6 8
‐‐‐‐‐‐‐‐‐‐ Toán Học Sơ Đồ ‐‐‐‐‐‐‐‐‐
16. TOÁN HỌC SƠ ĐỒ ‐ THCS.TOANMATH.com