Chuyên đề hệ hai phương trình bậc nhất hai ẩn

Tài liệu gồm 38 trang, được biên soạn bởi tác giả Toán Học Sơ Đồ, tổng hợp kiến thức trọng tâm, phân dạng và hướng dẫn giải các dạng bài tập tự luận & trắc nghiệm chuyên đề hệ hai phương trình bậc nhất hai ẩn. Mời bạn đọc đón xem.

102 51 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Chương 3: Hệ hai phương trình bậc nhất hai ẩn

Môn: Toán 9

Thông tin:

38 trang 8 tháng trước

Tác giả:

Profile Hà Việt Anh
1.
TOÁNHỌCSƠĐỒ‐THCS.TOANMATH.com
CHUYÊN ĐỀ HỆ HAI PHƯƠNG TRÌNH BẬC NHẤT HAI ẨN
A.KIẾN THỨC TRỌNG TÂM
1. Cho hệ hai phương trình bậc nhất hai ẩn:



11 1
22 2
1
2
ax by c
I
ax by c


Nếu hai phương trình trên có nghiệm chung

00
;xy
thì

00
;xy
được gọi là một nghiệm của
hệ

I
.
Giải hệ phương trình là tìm tập nghiệm của nó.
2. Minh họa hình học tập nghiệm của hệ hai phương trình bậc nhất hai ẩn
Phương trình

11 1
1 ax by c
có thể được viết lại như sau:
11
11
ac
yx
bb




có đồ thị là
đường thẳng

1
d
với hệ số góc là
1
1
a
b



.
Phương trình

22 2
2ax by c
có thể được viết lại như sau:
22
22
ac
yx
bb




có đồ thị là
đường thẳng

2
d
với hệ số góc là
2
2
a
b



.
Do đó, tập nghiệm của hệ phương trình

I
được biểu diễn bởi tập hợp các điểm chung của hai
đường thẳng

11 1 1
:daxbyc
và

22 2 2
:daxbyc
Nếu

1
d
cắt

2
d
thì hệ

I
có một nghiệm duy nhất.
Nếu

12
//dd
thì hệ

I
vô nghiệm.
Nếu

12
dd
thì hệ

I
có vô số nghiệm.
* Tính nhanh số nghiệm của hệ phương trình bậc nhất hai ẩn:
Hệ vô nghiệm
111
222
abc
abc

Hệ có một nghiệm duy nhất
11
22
ab
ab

Hệ có vô số nghiệm
111
222
abc
abc

3. Hệ phương trình tương đương
Hai hệ phương trình được gọi là tương đương nếu chúng có cùng tập nghiệm.
2.
TOÁNHỌCSƠĐỒ‐THCS.TOANMATH.com
SƠ ĐỒ
HỆ PHƯƠNG
TRÌNH BẬC
NHẤT HAI ẨN
Phương trình (1) có đồ thị là đường thẳng
với
Phương trình (1) có đồ thị là đường thẳng
với
Nghiệm của hệ là nghiệm chung
của hai phương trình (1) và (2)
Số nghiệm của hệ
là số giao điểm
của hai đường
thẳng và
Nếu là nghiệm
của hệ
Nhìn nhanh số nghiệm của hệ:
* Vô nghiệm
* Một nghiệm duy nhất
* Vô số nghiệm
3.
TOÁNHỌCSƠĐỒ‐THCS.TOANMATH.com
B.CÁC DẠNG BÀI MINH HỌA
Dạng 1: Đoán nhận số nghiệm của hệ phương trình
Bài 1. Nối mỗi hệ phương trình với một cặp số tương ứng mà nó nhận làm nghiệm
1)
17
x2
22
19
2x
2
y
y


a)

3;1
2)
x3
-2x- 2 6
y
y

b)
1
5;
2



3)
2x 3
3x 2 4,5
y
y


c)

2; 3
4)
x2 35
x3 2 0
y
y


d)

1, 5; 0
Bài 2. Cặp số

3;1
có là nghiệm của phương trình nào sau đây ?
a)
3x 8
7x 2 19
y
y


b)
x2 5
x2 1
y
y


c)
30
x5 2
yx
y


d)


21x3 32
x214
y
y


e)
3x 2 6
2x 7
y
y


Bài 3. Không cần vẽ hình, hãy cho biết số nghiệm của mỗi hệ phương trình sau đây và giải thích vì sao.
32
);
31
yx
a
yx
ì
ï=-
ï
í
ï
=-
ï
î
1
3
2
);
1
1
2
yx
b
yx
ì
ï
ï
=+
ï
ï
ï
í
ï
ï
=- +
ï
ï
ï
î
23
);
32
yx
c
yx
ì
ï=-
ï
í
ï
=
ï
î
33
).
1
1
3
xy
d
xy
ì
ï-=
ï
ï
í
ï
-=
ï
ï
î
Bài 4. Đoán nhận số nghiệm của mỗi hệ phương trình sau, giải thích vì sao.
2
);
33 2
xy
a
xy
ì
ï+ =
ï
í
ï
+=
ï
î
32 1
);
64 0
xy
b
xy
ì
ï- =
ï
í
ï
-+ =
ï
î
44 2
);
22 1
xy
c
xy
ì
ï- =
ï
í
ï
-+ =-
ï
î
12
).
33
32
xy
d
xy
ì
ï
ï
-=
ï
í
ï
ï
-=
ï
î
4.
TOÁNHỌCSƠĐỒ‐THCS.TOANMATH.com
Bài 5. Hãy kiểm tra xem mỗi cặp số sau có phải là một nghiệm của hệ phương trình tương ứng hay
không?
a)
()
4; 5-
,
75 53
29 53
;
xy
xy
-=-
ì
ï
ï
í
+=
ï
ï
î
-
b)
()
3; 11-
,
0, 2 1, 7 18,1
3,2 20,6
;
xy
xy
+
ì
ï
ï
=
í
-
=
ï
ï
î
-
c)
()
()1,5; 2, 3;7
,
10 3 9
51,5 4,5
;
xy
xy
-=
ì
ï
ï
-
í
-=
ï
ï
î
+
d)
()
1; 8
,
52 9
14 5
.
xy
xy
ì
ï
ï
=
í
=
-
ï
ï
î
+
Bài 6. Hãy biểu diễn
y
qua
x
ở mỗi phương trình (nếu có thể) rồi đoán nhận số nghiệm của mỗi hệ
phương trình sau đây và giải thích vì sao (không vẽ đồ thị).
49 3
53
);
1
xy
a
xy
-=
--
ì
ï
ï
í
ï
ï
î
=
2, 3 0, 8 5
26
);
xy
b
y
ì
ï
ï
í
+
=
ï
ï
î
=
);
35
54
x
c
xy
ì
ï
ï
=-
+=-
í
ï
ï
î
31
62
).
5
xy
d
xy
-=
-=
ì
ï
ï
í
ï
ï
î
Bài 7. Đoán nhận số nghiệm của mỗi hệ phương trình sau, giải thích vì sao:
a)
23
31
xy
xy
ì
ï+=
ï
í
ï
-=
ï
î
; b)
32 0
23 0
xy
xy
ì
ï+ =
ï
í
ï
-=
ï
î
; c)
30 6
21
xy
xy
ì
ï+ =
ï
í
ï
+=
ï
î
;
d)
4
02
xy
xy
ì
ï- =
ï
í
ï
-=
ï
î
; e)
23
241
xy
xy
ì
ï+ =
ï
í
ï
+=
ï
î
;
f)
1
1
222
xy
y
x
ì
ï+ =
ï
ï
í
ï
+=
ï
ï
î
.
Bài 8. Chứng tỏ rằng hệ phương trình:
31
23
xy
ax y
ì
ï-=
ï
í
ï
+=
ï
î
a) Có nghiệm duy nhất với
2a =-
;
b) Vô nghiệm với
6a =-
Bài 9. Chứng tỏ rằng hệ phương trình:
32
15 10 5
xya
xy
ì
ï- =
ï
í
ï
+=
ï
î
a) Có vô số nghiệm với
1a =
;
b) Vô nghiệm với
1a =
.
Bài 10. Cho các hệ phương trình sau:
a
)
2
23
x
xy
ì
ï=
ï
í
ï
-=
ï
î
;
b)
32
24
xy
y
ì
ï+ =
ï
í
ï
=
ï
î
.
Trước hết, hãy đoán nhận số nghiệm của mỗi hệ phương trình trên (giải thích rõ lí do). Sau đó, tìm tập
nghiệm của các hệ đã cho bằng cách vẽ hình.
Bài 11. Dựa vào vị trí tương đối của hai đường thẳng dưới đây, hãy tìm mối lien hệ giữa các hằng số
,,abc
và các hằng số
ʹ;bʹ;cʹa
để hệ phương trình
ʹʹ ʹ
ax by c
ax by c
ì
ï+ =
ï
í
ï
+=
ï
î
a) Có nghiệm duy nhất;
5.
TOÁNHỌCSƠĐỒ‐THCS.TOANMATH.com
b) Vô nghiệm;
c) Có vô số nghiệm.
Áp dụng:
a) Hãy lập một hệ hai phương trình bậc nhất hai ẩn có nghiệm duy nhất.
b) Hãy lập một hệ hai phương trình bậc nhất hai ẩn vô nghiệm.
c) Hãy lập một hệ hai phương trình bậc nhất hai ẩn có vô số nghiệm.
Dạng 2: Giải hệ phương trình bằng phương pháp hình học
Bài 12. Cho hai phương trình:
3x 1y
và
5x 2 3y
a) Tìm nghiệm tổng quát của mỗi phương trình trên.
b) Vẽ đồ thị của hai phương trình trên cùng một hệ tọa độ rồi xác định nghiệm chung của hai phương
trình.
Bài 13. Bằng cách vẽ đồ thị, hãy giải các hệ phương trình:
a)
x1
x3 9
y
y


b)
x2 4
2x 4 10
y
y


c)
1,5y 0,5
2x 3 1
x
y


Bài 14. Cho hệ phương trình
2x 2
x2 6
y
y


a) Giải hệ phương trình đã cho bằng phương pháp đồ thị
b) Nghiệm của hệ phương trình đã cho có phải là nghiệm của phương trình
3x 2 8y
hay không?
c) Nghiệm của hệ phương trình đã cho có phải là nghiệm của phương trình
4,5x 7,5 25y
hay
không?
Bài 15. Cho hai đường thẳng:

1
:2x 3 8dy
và

2
:7x 5 5dy
a) Vẽ đồ thị của hai phương trình trên cùng một hệ tọa độ rồi xác định nghiệm chung của hai phương
trình.
b) Tìm các giá trị của a để đường thẳng
axy
đi qua giao điểm của

1
d
và

2
d
Dạng 2: Hai hệ phương trình tương đương
Bài 16. Trong các câu sau, câu nào đúng, câu nào sai?
a) Hai hệ phương trình bậc nhất hai ẩn vô nghiệm là hai hệ phương trình tương đương với nhau.
b) Hai hệ phương trình bậc nhất hai ẩn cùng vô số nghiệm là hai hệ phương trình tương đương.
c) Hai hệ phương trình bậc nhất hai ẩn cùng có một nghiệm là hai hệ phương trình tương đương.
Bài 17. Trong các trường hợp sau, hai hệ phương trình nào t
ương đương với nhau? Không tương đương
với nhau?
a)
x2 2
3x 6 7
y
y


và
x2 3
-4x 8 4
y
y


b)
x4
3x 3 12
y
y


và
x4
3x 4 2y

c)
2x 3 1
-x 1,5 0,5
y
y


và
3x 8
2
y
y

6.
TOÁNHỌCSƠĐỒ‐THCS.TOANMATH.com
Bài 18. Xác định a để hai hệ phương trình sau tương đương.
vaø
122
22 1
xy ax y
xy xay
ìì
ï- = ï - =
ïï
íí
ïï
+= + =
ïï
îî
Bài 19. Xác định a để hai hệ phương trình sau tương đương.
vaø
23 5 23 5
43123
xy xy
xy x ya
ìì
ï- = ï- =
ïï
íí
ïï
+= + =
ïï
îî
Bài 20. Xác định a để hai hệ phương trình sau tương đương.
vaø
2221
31 2
xy ax y
xy xay
ìì
ï- = ï - =
ïï
íí
ïï
+= + =
ïï
îî
7.
TOÁNHỌCSƠĐỒ‐THCS.TOANMATH.com
HƯỚNG DẪN
Dạng 1: Đoán nhận số nghiệm của hệ phương trình
Bài 1. Nối mỗi hệ phương trình với một cặp số tương ứng mà nó nhận làm nghiệm:
1– ;2– ;3– ;4– ;badc
Bài 2. Cặp số

3;1
có là nghiệm của hệ phương trình:
a)
3x 8
7x 2 19
y
y


và d)


21x3 32
x2142
y
y


Bài 3. Không cần vẽ hình, hãy cho biết số nghiệm của mỗi hệ phương trình sau đây và giải thích vì sao.
a) Xét
()
:32dy x=-
có 2; 3ab=- = ;
()
’: 3 –1 ’ 3; ’ 1dy xcóa b===-
;
Có
() ( )
caét ’ ʹaa d d¹
;
Hệ
32
;
31
yx
yx
ì
ï=-
ï
í
ï
=-
ï
î
có nghiệm duy nhất.
b) Xét
()
coù
11
:3;3
22
dy x a b=- + =- =
;
()
11
’: 1 ’ ; ’ 1
22
dy x cóa b=- + = =
;
Có
() ( )
//’; ’ ’aabb d d=¹
;
Hệ
1
3
2
1
1
2
yx
yx
ì
ï
ï
=+
ï
ï
ï
í
ï
ï
=- +
ï
ï
ï
î
vô nghiệm.
c) Ta có
3
23
2
2
32
3
yx
yx
yx
yx
ì
ï
ï
=-
ï
ì
ï=-
ï
ïï
íí
ïï
=
ïï
î
=
ï
ï
ï
î
Xét
()
coù
33
:;0;
22
dy x a b=- =- =
8.
TOÁNHỌCSƠĐỒ‐THCS.TOANMATH.com
()
’
22
33
:’;’0dcóayx b===
;
Có
() ( )
caét ’ ʹaa d d¹
;
Hệ
23
32
yx
yx
ì
ï=-
ï
í
ï
=
ï
î
có nghiệm duy nhất.
d) Ta có
33
33
1
33
1
3
xy
yx
yx
xy
ì
ï-=
ì
ï
ï= -
ï
ï
íí
ïï
=-
-=
ïï
î
ï
î
Nhận thấy hai đường thẳng trên trùng nhau
Hệ
33
1
1
3
xy
xy
ì
ï-=
ï
ï
í
ï
-=
ï
ï
î
có vô số nghiệm.
Bài 4. Đoán nhận số nghiệm của mỗi hệ phương trình sau, giải thích vì sao.
a) Ta có:
2
22
2
33 2 3 32
3
yx
xy y x
xy y x
yx
ì
ï=-+
ìì
ï
ï+ = ï=-+
ï
ïï

íí í
ïï ï
+= =-+
=- +
ïï ï
îî
ï
î
;
Xét
()
coù :21;2dy x a b=- + =- =
;
()
22
’: ’ 1; ’
33
dy x cóa b=- + =- =
;
Có
() ( )
//’; ’ ’aabb d d=¹
;
Hệ
2
33 2
xy
xy
ì
ï+ =
ï
í
ï
+=
ï
î
vô nghiệm.
b) Ta có:
31
32 1 2 31
22
64 0 4 6 3
2
yx
xy y x
xy yx
yx
ì
ï
ï
=-
ï
ìì
ï- = ï= -
ï
ïïï

ííí
ïïï
-+ = =
ïïï
îî
=
ï
ï
ï
î
;
Xét
()
coù
31 3 1
:;
22 2 2
dy x a b=- = =-
;
()
coù ’
33
;0
2
:
2
yxadb===
;
9.
TOÁNHỌCSƠĐỒ‐THCS.TOANMATH.com
Có
() ( )
//’; ’ ’aabb d d=¹
;
Hệ
32 1
64 0
xy
xy
ì
ï- =
ï
í
ï
-+ =
ï
î
vô nghiệm.
c) Ta có:
1
44 2 4 42
2
22 1 2 21 1
2
yx
xy y x
xy yx
yx
ì
ï
ï
=-
ï
ìì
ï- = ï= -
ï
ïïï

ííí
ïïï
-+ =- = -
ïïï
îî
=-
ï
ï
ï
î
;
Nhận thấy hai đường thẳng trên trùng nhau;
Hệ
44 2
22 1
xy
xy
ì
ï- =
ï
í
ï
-+ =-
ï
î
có vô số nghiệm.
d) Ta có:
12
12 12
33
33 33
12
32 3 2
33
yx
xy y x
xy yx
yx
ì
ï
ìì
ï
ïï
=-
ï
ïï
-= = -
ï
ïï
ï

ííí
ïïï
ïïï
-= =-
=-
ïïï
îî
ï
ï
î
;
Nhận thấy hai đường thẳng trên trùng nhau;
Hệ
12
33
32
xy
xy
ì
ï
ï
-=
ï
í
ï
ï
-=
ï
î
có vô số nghiệm.
Bài 5. Hãy kiểm tra xem mỗi cặp số sau có phải là một nghiệm của hệ phương trình tương ứng hay
không.
a) Thay
4; 5xy=- =
vào từng phương trình của hệ
75 53
29 53
xy
xy
-=-
-+ =
ì
ï
ï
í
ï
ï
î
ta được:
()
()
28 25 53
8
7. 4 5.5 53
2. 4 9.5 53
45 53
ì
ï
ì
ï- - =
ï
ï
-- =-
-
ï
íí
ï
-+
ï
+=
ïï
î
ï
=
î
Vậy cặp
()
4; 5-
là nghiệm của hệ phương trình
75 53
29 53
xy
xy
-=-
-+ =
ì
ï
ï
í
ï
ï
î
.
b) Thay
3; 11xy==-
vào từng phương trình của hệ
0,2 1, 7 18 ,1
3,2 20,6
xy
xy
+
ì
ï
ï
í
=-
-=
ï
ï
î
ta được:
()
0, 2.3 1,7 11 18,1
0,6 – 18,7 18,1
9, 6 11 20, 6
3,2.3 11 20,6
ì
ì
ï
ï
ï
ï
íí
ïï
ïï
+-=-
=-
+=
=
î
î
+
10.
TOÁNHỌCSƠĐỒ‐THCS.TOANMATH.com
Vậy cặp
()
3; 11-
là nghiệm của hệ phương trình
0, 2 1, 7 18, 1
3,2 20,6
xy
xy
+
ì
ï
ï
í
=-
-=
ï
ï
î
.
c) Thay
1,5 ; 2xy==
vào từng phương trình của hệ
10 3 9
51,5 4,5
xy
xy
-=
-
ì
ï
+=
í
-
ï
ï
ï
î
ta được:
10.1,5 – 3.2 9 15 – 6 9
5.1,5 1,5.2 4,5 7,5 3 4,5
ìì
ïï
ïï
í
==
-+ =-
í
ïï
ï
=-
î
+
î
-
ï
.
Vậy cặp
1, 5(;2)
là nghiệm của hệ phương trình
10 3 9
51,5 4,5
xy
xy
-=
-
ì
ï
+=
í
-
ï
ï
ï
î
.
Thay
3; 7xy==
vào từng phương trình của hệ
10 3 9
51,5 4,5
xy
xy
-=
-
ì
ï
+=
í
-
ï
ï
ï
î
ta được:
10.3 – 3.7 9 30 21 9
5.3 1,5.7 4,5 15 10,5 4,5
ì
ì
ï
ï
ï
ï
íí
ïï
ïï
î
=-=
-+ =- -+ =-
î
Vậy cặp
()
3;7
là nghiệm của hệ phương trình
10 3 9
51,5 4,5
xy
xy
-=
-
ì
ï
+=
í
-
ï
ï
ï
î
.
d) Thay
1; 8xy==
vào từng phương trình của hệ
52 9
14 5
,
xy
xy
ì
ï
ï
=
í
=
-
ï
ï
î
+
ta được:
()
voâ
lyù
516 21
5.
114.8 5
114
12.
.8 5
821
+
ì
ì
ï
ï
ï
ï
íí
ïï
-=
-=
+=
ï
î
î
=
ï
Vậy cặp
()
1; 8
không phải là nghiệm của hệ phương trình
52 9
14 5
.
xy
xy
ì
ï
ï
=
í
=
-
ï
ï
î
+
Bài 6.
a) Ta có:
41
93
5
49 3 9 43
53 1 3 5 11
33
xy y x
xy y
yx
yx
x
ì
ï
ï
=-
ï
ìì
ïï
ï
ïïï

ííí
ïïï
ïïï
îî
=- -
-= =-
-- = =
î
--
ï
ï
ï
Vì
45
93
¹-
nên hai đường thẳng cắt nhau.
Vậy hệ phương trình có nghiệm duy nhất.
b) Ta có:
23 25
0, 8 2,3 52, 3 0, 8
32
84
3
5
6
xy y x
y
y
y
yx
ì
ï
ìì
ï
ïï+= =-+
=- +
ï
ïï

íí í
ïï ï
=
ïï
î
=
ï
î
=
ï
î
;
Đường thẳng
23 25
84
yx=- +
cắt hai trục tọa độ mà đường thẳng
3y =
song song với trục hoành nên 2
đường thẳng trên cắt nhau.
Vậy hệ phương trình có nghiệm duy nhất.
11.
TOÁNHỌCSƠĐỒ‐THCS.TOANMATH.com
c) Ta có:
5
5
3
3
14
54
5
35
54
5
x
x
x
x
yx
yx
y
ì
ï
ì
ï
ï
=-
ï
ì
ï
ï
=-
ï
ï
ïï

ííí
ïïï
ïïï
î
=- -
=- -
ïï
î
ï
ï
î
=-
+=-
;
Đường thẳng
5
3
x =-
song song với trục tung mà đường thẳng
14
55
yx=- -
cắt hai trục tọa độ nên 2
đường thẳng đó cắt nhau;
Vậy hệ phương trình có nghiệm duy nhất.
d) Ta có:
31
31
5
265
1
2
3
3
65
2
yx
yx
y
x
x
xx
y
y
y
ì
ï= -
ìì
ï
ïï=-
ï
ïï

ííí
ïïï
=-
-=
-=
=-
ïïï
îî
ï
î
Hai đường thẳng có hệ số góc bằng nhau vì cùng bằng 3, có tung độ gốc khác nhau:
5
1
2
-¹-
nên chúng
song song với nhau. Nên hệ vô nghiệm;
Vậy hệ phương trình đã cho vô nghiệm.
Bài 7. Đoán nhận số nghiệm của mỗi hệ phương trình sau, giải thích vì sao:
a) Ta có:
23 23
31 31
xy y x
xy y x
ìì
ï+= ï=-+
ïï
íí
ïï
-= = -
ïï
îî
;
Vì
23-¹
nên hai đường thẳng cắt nhau.
Vậy hệ phương trình
23
31
xy
xy
ì
ï+=
ï
í
ï
-=
ï
î
có nghiệm duy nhất.
b) Ta có:
3
32 0 2 3
2
2
23 0 3 2
3
yx
xy y x
xy y x
yx
ì
ï
ï
=-
ï
ìì
ï+ = ï=-
ï
ïïï

ííí
ïïï
-= =
ïïï
îî
=
ï
ï
ï
î
;
Vì
32
23
-¹
nên hai đường thẳng cắt nhau.
Vậy hệ phương trình
32 0
23 0
xy
xy
ì
ï+ =
ï
í
ï
-=
ï
î
có nghiệm duy nhất.
c) Ta có:
30 6 36 2
2 1 21 21
xy x x
xy yx yx
ìì ì
ï+ = ï= ï=
ïï ï

íí í
ïï ï
+= =- + =- +
ïï ï
îî î
;
Đường thẳng
2x =
song song với trục tung mà đường thẳng
21yx=- +
cắt hai trục tọa độ nên 2
đường thẳng đó cắt nhau;
Vậy hệ phương trình
30 6
21
xy
xy
ì
ï+ =
ï
í
ï
+=
ï
î
có nghiệm duy nhất.
d) Ta có:
44
02 2
xy y x
xy y
ìì
ï- = ï= -
ïï
íí
ïï
-= =-
ïï
îî
;
Đường thẳng
4yx=-
cắt hai trục tọa độ mà đường thẳng
2y =-
song song với trục hoành nên 2
đường thẳng trên cắt nhau.
12.
TOÁNHỌCSƠĐỒ‐THCS.TOANMATH.com
Vậy hệ phương trình
4
02
xy
xy
ì
ï- =
ï
í
ï
-=
ï
î
có nghiệm duy nhất.
e) Ta có:
13
23 2 3
22
241 4 21 1 1
24
yx
xy y x
xy y x
yx
ì
ï
ï
=- +
ï
ìì
ï+ = ï =-+
ï
ïï ï

íí í
ïï ï
+= =-+
ïï ï
îî
=- +
ï
ï
ï
î
;
Hai đường thẳng có hệ số góc bằng nhau vì cùng bằng
1
2
-
, có tung độ gốc khác nhau:
13
42
¹
nên chúng
song song với nhau. Nên hệ vô nghiệm;
Vậy hệ phương trình
23
241
xy
xy
ì
ï+ =
ï
í
ï
+=
ï
î
vô nghiệm.
f) Ta có:
1
11
1
11
222
xy
yx yx
y
x
xy y x
ì
ï+ =
ìì
ï
ï=-+ ï=-+
ï
ïï

ííí
ïïï
+= =-+
+=
ïïï
îî
ï
î
;
Nhận thấy hai đường thẳng trên trùng nhau;
Vậy hệ
1
1
222
xy
y
x
ì
ï+ =
ï
ï
í
ï
+=
ï
ï
î
có vô số nghiệm.
Bài 8.
a) Thay
2a =-
vào hệ phương trình
31
23
xy
ax y
ì
ï-=
ï
í
ï
+=
ï
î
, ta được:
31
22 3
xy
xy
ì
ï-=
ï
í
ï
-+ =
ï
î
Do
3131xy y x-== -
nên tập nghiệm của phương trình thứ nhất được biểu diễn bởi đường thẳng
()
1
:31
dy x
=-
;
Do
3
22 32 23
2
xy yx yx-+ = = +=+
nên tập nghiệm của phương trình thứ nhất được biểu diễn
bởi đường thẳng
()
2
3
:
2
dyx=+
;
Hai đường thẳng
()
1
d
và
()
2
d
có hệ số góc khác nhau (
13¹
) nên chúng cắt nhau. Do đó hệ
31
22 3
xy
xy
ì
ï-=
ï
í
ï
-+ =
ï
î
có nghiệm duy nhất;
Vậy với
2a =-
thì hệ phương trình
31
23
xy
ax y
ì
ï-=
ï
í
ï
+=
ï
î
có nghiệm duy nhất.
b) Thay
6a =-
vào hệ phương trình
31
23
xy
ax y
ì
ï-=
ï
í
ï
+=
ï
î
, ta được:
31
62 3
xy
xy
ì
ï-=
ï
í
ï
-+ =
ï
î
Do
3131xy y x-== -
nên tập nghiệm của phương trình thứ nhất được biểu diễn bởi đường thẳng
()
1
:31dy x=-
;
13.
TOÁNHỌCSƠĐỒ‐THCS.TOANMATH.com
Do
3
62 3263 3
2
xy yx yx-+ = = += +
nên tập nghiệm của phương trình thứ nhất được biểu
diễn bởi đường thẳng
()
3
3
:3
2
dyx=+
;
Hai đường thẳng
()
1
d
và
()
3
d
có tung độ góc khác nhau (
3
1
2
-¹
) và có cùng hệ số góc là 3 nên song
song với nhau. Do đó, hệ
31
62 3
xy
xy
ì
ï-=
ï
í
ï
-+ =
ï
î
vô nghiệm;
Vậy với
6a =-
thì hệ phương trình
31
23
xy
ax y
ì
ï-=
ï
í
ï
+=
ï
î
vô nghiệm.
Bài 9. Chứng tỏ rằng hệ phương trình:
32
15 10 5
xya
xy
ì
ï- =
ï
í
ï
+=
ï
î
;
a) Có vô số nghiệm với
1a =
;
b) Vô nghiệm với
1a =
a) Thay
1a =
vào hệ phương trình
32
15 10 5
xya
xy
ì
ï- =
ï
í
ï
+=
ï
î
, ta được:
32 1
15 10 5
xy
xy
ì
ï- =
ï
í
ï
+=
ï
î
;
Do
31
32 12 31
22
xy y x y x-= =-= -
nên tập nghiệm của phương trình thứ nhất được biểu diễn
bởi đường thẳng
()
1
31
:
22
dy x=-
;
Do
31
15 1 0 5 10 15 5
22
xy y x yx-= =-=-
nên tập nghiệm của phương trình thứ nhất được biểu
diễn bởi đường thẳng
()
2
31
:
22
dy x=-
;
Hai đường thẳng
()
1
d
và
()
2
d
có tung độ góc bằng nhau (
11
22
--
¹
) và có cùng hệ số góc là
3
2
nên hai
đường thẳng
()
1
d
và
()
2
d
trùng nhau. Do đó, hệ
32 1
15 10 5
xy
xy
ì
ï- =
ï
í
ï
+=
ï
î
có vô số nghiệm;
Vậy với
1a =
thì hệ phương trình
32 1
15 10 5
xy
xy
ì
ï- =
ï
í
ï
+=
ï
î
có vô số nghiệm.
b) Xét hệ phương trình
32
15 10 5
xya
xy
ì
ï- =
ï
í
ï
+=
ï
î
;
Do
3
32 2 3
22
a
xya y xay x-= =-= -
nên tập nghiệm của phương trình thứ nhất được biểu diễn
bởi đường thẳng
()
3
:
22
a
dy x=-
;
Do
31
15 1 0 5 10 15 5
22
xy y x yx-= =-=-
nên tập nghiệm của phương trình thứ nhất được biểu
diễn bởi đường thẳng
()
2
31
:
22
dy x=-
;
14.
TOÁNHỌCSƠĐỒ‐THCS.TOANMATH.com
Hai đường thẳng
()
d
và
()
3
d
có tung độ góc khác nhau (
vì (baøi cho)
1
1
22
a
a
-
¹¹
) và có cùng hệ số góc
là
3
2
nên song song với nhau. Do đó, hệ
32
15 10 5
xya
xy
ì
ï- =
ï
í
ï
+=
ï
î
vô nghiệm với mọi
1a ¹
;
Vậy với
6a =-
thì hệ phương trình
31
23
xy
ax y
ì
ï-=
ï
í
ï
+=
ï
î
vô nghiệm.
Vậy với
1a ¹
thì hệ phương trình
31
23
xy
ax y
ì
ï-=
ï
í
ï
+=
ï
î
vô nghiệm.
Bài 10. Cho các hệ phương trình sau:
a) Ta có:
22
23 23
xx
xy y x
ìì
ï= ï=
ïï
íí
ïï
-= = -
ïï
îî
;
Đường thẳng
2x =
song song với trục tung mà đường thẳng
23yx=-
cắt hai trục tọa độ nên 2 đường
thẳng đó cắt nhau;
Vậy hệ phương trình
2
23
x
xy
ì
ï=
ï
í
ï
-=
ï
î
có nghiệm duy nhất.
b) Ta có
12
32 3 2
33
24 2
2
xy y x
yx
yy
y
ì
ï
ìì
ï
ï+ = ï =-+
=- +
ï
ïï

íí í
ïï ï
==
ïï ï
îî
=
ï
î
;
Đường thẳng
12
33
yx=- +
cắt hai trục tọa độ mà đường thẳng
2y =
song song với trục hoành nên 2
đường thẳng trên cắt nhau.
Vậy hệ phương trình
32
24
xy
y
ì
ï+ =
ï
í
ï
=
ï
î
có nghiệm duy nhất.
15.
TOÁNHỌCSƠĐỒ‐THCS.TOANMATH.com
Bài 11. Dựa vào vị trí tương đối của hai đường thẳng dưới đây, hãy tìm mối lien hệ giữa các hằng số
,,abc
và các hằng số
ʹ;bʹ;cʹa
để hệ phương trình
ʹʹ ʹ
ax by c
ax by c
ì
ï+ =
ï
í
ï
+=
ï
î
*Trường hợp 1: ;;ʹ; ʹ 0aba b¹
Ta có:
ʹʹ ʹ ʹ ʹʹ ʹ ʹ
ʹʹ
ac
yx
ax by c by ax c
bb
ax by c by ax c a c
yx
bb
ì
ï
ï
=- +
ï
ìì
ï+ = ï=-+
ï
ïï ï

íí í
ïï ï
+= =-+
ïï ï
îî
=- +
ï
ï
ï
î
a) Hệ phương trình có một nghiệm duy nhất khi hai đường thẳng cắt nhau. Nghĩa là hai đường thẳng có
hệ số góc khác nhau:
ʹ
ʹʹʹ
aa a b
bb a b
¹¹
b) Hệ phương trình vô nghiệm khi hai đường thẳng song song nhau. Nghĩa là hai đường thẳng có hệ số
góc bằng nhau và tung độ gốc khác nhau:
() ()
neáu hoaëc neáu
ʹ
ʹʹbʹʹ
ʹ
ʹ 00
ʹ
ʹʹ
ʹ
aa
aa c a c
bb
cc
cc
bb c a b c
bb
ì
ï
ï
=
ï
ï
ï
= ¹ ¹ = ¹ ¹
í
ï
ï
¹
ï
ï
ï
î
c) Hệ phương trình có vô số nghiệm khi hai đường thẳng trùng nhau. Nghĩa là hai đường thẳng có hệ số
góc và tung độ gốc bằng nhau:
() ()
neáu hoaëc neáu
ʹ
ʹʹbʹʹ
ʹ
ʹ 00
ʹ
ʹʹ
ʹ
aa
aa c a c
bb
cc
cc
bb c a b c
bb
ì
ï
ï
=
ï
ï
ï
= = ¹ = = ¹
í
ï
ï
=
ï
ï
ï
î
* Trường hợp 2: 0; ʹ 0aa=¹
Ta có:
()
vôùi b' 0
ʹʹ ʹ ʹ ʹ
ʹʹ
c
y
ax by c
b
ax by c a c
yx
bb
ì
ï
ï
=
ï
ì
ï+ =
ï
ïï
¹
íí
ïï
+=
ïï
î
=- +
ï
ï
ï
î
16.
TOÁNHỌCSƠĐỒ‐THCS.TOANMATH.com
hoặc
()
vôùi ʹ 0
ʹʹ ʹ ʹ
ʹ
c
y
ax by c
b
b
ax by c c
x
a
ì
ï
ï
=
ï
ì
ï+ =
ï
ïï
=
íí
ïï
+=
ïï
î
=
ï
ï
ï
î
Vì hai đường thẳng
vaø
ʹʹ ʹ
ʹʹ ʹ
ac c
yx x
bb a
=- + =
luôn luôn cắt trục hoành còn đường thẳng
c
y
b
=
song song
hoặc trùng với trục hoành nên chúng luôn luôn cắt nhau.
Vậy hệ phương trình chỉ có một nghiệm duy nhất.
* Trường hợp 3:
ʹ 0aa==
Ta có:
ʹʹ ʹ ʹ
ʹ
c
y
ax by c
b
ax by c c
y
b
ì
ï
ï
=
ï
ì
ï+ =
ï
ïï
íí
ïï
+=
ïï
î
=
ï
ï
ï
î
Hệ có vô số nghiệm khi hai đường thẳng trùng nhau, nghĩa là:
ʹ
ʹʹʹ
cc b c
bb b c
==
Hệ vô nghiệm khi hai đường thẳng song song nhau, nghĩa là:
ʹ
ʹʹʹ
cc b c
bb b c
¹¹
* Trường hợp 4: b0; ʹ 0b =¹
Ta có:
ʹʹ ʹ ʹ ʹ
ʹʹ
c
x
ax by c
a
ax by c a c
yx
bb
ì
ï
ï
=
ï
ì
ï+ =
ï
ïï
íí
ïï
+=
ïï
î
=- +
ï
ï
ï
î
(với
ʹ 0a ¹
)
hoặc
ʹʹ ʹ ʹ
ʹ
c
x
ax by c
a
ax by c c
y
b
ì
ï
ï
=
ï
ì
ï+ =
ï
ïï
íí
ïï
+=
ïï
î
=
ï
ï
ï
î
(với
0a ¹
)
Vì hai đường thẳng
vaø
ʹʹ ʹ
ʹʹ ʹ
ac c
yx y
bb b
=- + =
luôn luôn cắt trục tung còn đường thẳng
c
x
a
=
song song
hoặc trùng với trục tung nên chúng luôn luôn cắt nhau.
Vậy hệ phương trình chỉ có một nghiệm duy nhất.
* Trường hợp 5:
bʹ 0b ==
Ta có:
ʹʹ ʹ ʹ
ʹ
c
x
ax by c
a
ax by c c
x
a
ì
ï
ï
=
ï
ì
ï+ =
ï
ïï
íí
ïï
+=
ïï
î
=
ï
ï
ï
î
(với
ʹ 0a ¹
)
Hệ có vô số nghiệm khi hai đường thẳng trùng nhau, nghĩa là:
ʹ
ʹʹcʹ
cc a c
aa a
==
Hệ vô nghiệm khi hai đường thẳng song song, nghĩa là:
ʹ
ʹʹcʹ
cc a c
aa a
¹¹
Áp dụng:
a) Hệ hai phương trình bậc nhất hai ẩn có nghiệm duy nhất:
238
4
xy
xy
ì
ï+ =
ï
í
ï
+=
ï
î
b) Hệ hai phương trình bậc nhất hai ẩn vô nghiệm:
17.
TOÁNHỌCSƠĐỒ‐THCS.TOANMATH.com
238
46 4
xy
xy
ì
ï+ =
ï
í
ï
+=
ï
î
c) Hệ hai phương trình bậc nhất hai ẩn có vô số nghiệm:
25
4210
xy
xy
ì
ï+=
ï
í
ï
+=
ï
î
18.
TOÁNHỌCSƠĐỒ‐THCS.TOANMATH.com
Dạng 2: Giải hệ phương trình bằng phương pháp hình học
Bài 12. Cho hai phương trình:
3x 1y
và
-5x 2 3y
a) Nghiệm tổng quát của mỗi phương trình
3x 1y
là :

;3x1x 
Nghiệm tổng quát của mỗi phương trình
-5x 2 3y
là :
53
;x
22
x



b) Vẽ đồ thị của hai phương trình trên cùng một hệ tọa độ rồi xác định nghiệm chung của hai phương
trình.
3x 1 3x 1yy
và
53
5x 2 3 x
22
yy
Vậy nghiệm của hệ phương trình là:

1; 4
Bài 13. Bằng cách vẽ đồ thị, hãy giải các hệ phương trình:
a)
1
x1
1
x3 9
3
3
yx
y
y
yx





6
4
2
2
4
6
8
10
12
10 5 5
y
= -3x+1
y
= -5/2x+3/2
A
19.
TOÁNHỌCSƠĐỒ‐THCS.TOANMATH.com
Vậy nghiệm của hệ phương trình là:

3; 2
b)
1
2
x2 4
2
2x 4 10 1 5
22
yx
y
y
yx





Vậy hệ phương trình vô nghiệm.
c)
21
1,5y 0,5
33
2x 3 1 2 1
33
yx
x
y
yx





8
6
4
2
2
10 5 5 10
y
= 1/3x+3
y
=
x
-1
10 5 5 10
10
8
6
4
2
2
y
= -1/2x-5
y
= -1/2x+2
20.
TOÁNHỌCSƠĐỒ‐THCS.TOANMATH.com
Vậy hệ phương trình có vô số nghiệm.
Bài 14. Cho hệ phương trình
22
2x 2
1
x2 6
3
2
yx
y
y
yx





a) Giải hệ phương trình đã cho bằng phương pháp đồ thị
Vậy nghiệm của hệ phương trình là:

2; 2
b) Nghiệm của hệ phương trình đã cho không là nghiệm của phương trình
3x 2 8y
c) Nghiệm của hệ phương trình đã cho không là nghiệm của phương trình
4,5x 7,5 25y
.
Bài 15. Cho hai đường thẳng:

1
:2x 3 8dy
và

2
:7x 5 5dy
10 5 5
10
8
6
4
2
2
y
= -2/3x-1/3
y
= -2/3x-1/3
10 5 5 10
10
8
6
4
2
2
4
6
y
= 2x-2
y
= -1/2x+3
A
21.
TOÁNHỌCSƠĐỒ‐THCS.TOANMATH.com
Vậy nghiệm của hệ phương trình là:

5; 6M 
b) Để đường thẳng
axy
đi qua giao điểm của

1
d
và

2
d
thì tọa độ điểm
M
phải thỏa mãn phương
trình, ta có:
6
6a(-5) a
5

Dạng 2: Hai hệ phương trình tương đương
Bài 16. Trong các câu sau, câu nào đúng, câu nào sai?
Câu
a
là khẳng định đúng
Câu
;bc
là khẳng định sai
Bài 17. Trong các trường hợp sau, hai hệ phương trình nào tương đương với nhau? Không tương đương
với nhau?
a)
x2 2
3x 6 7
y
y


và
x2 3
-4x 8 8
y
y


Hai hệ phương trình được viết lại như sau:
x2 2
3x 6 7
y
y


và
x2 3
x2 1
y
y


Hai hệ phương trình tương đương với nhau, vì cùng có tập nghiệm là
S 
b)
x4
3x 3 12
y
y


và
x4
3x 4 2y

Hai hệ phương trình được viết lại như sau:
8
6
4
2
2
4
6
8
10 5 5 10
= 2/3x-8/3
= 7/5x+1
22.
TOÁNHỌCSƠĐỒ‐THCS.TOANMATH.com
x4
x4
y
y


và
x4
31
42
yx

Ta thấy hệ phương trình thứ nhất có vô số nghiệm, còn hệ thứ hai có nghiệm duy nhất, nên hai hệ
phương trình không tương đương với nhau.
c)
2x 3 1
-x 1,5 0, 5
y
y


và
3x 8
2
y
y

Tương tự như câu
b
, Ta có hai hệ phương trình đã cho không tương đương nhau.
Bài 18.
Ta thấy hệ phương trình
1
22
xy
xy
ì
ï- =
ï
í
ï
+=
ï
î
có nghiệm
()
1; 0
Để hai hệ đã cho tương đương nhau thì nghiệm
()
1; 0
phải là nghiệm của hệ
22
1
ax y
xay
ì
ï- =
ï
í
ï
+=
ï
î
Khi đó ta có
.1 2.0 2
2
1.01
a
a
a
ì
ï- =
ï
=
í
ï
+=
ï
î
Ngược lại với
2a =
thì hệ thứ hai trở thành:
22 2
21
xy
xy
ì
ï- =
ï
í
ï
+=
ï
î
có nghiệm
()
1; 0
Vậy với
2a =
thì hai hệ phương trình đã cho tương đương.
Bài 19.
Ta thấy hệ phương trình
23 5
43
xy
xy
ì
ï- =
ï
í
ï
+=
ï
î
có nghiệm
()
-
1; 1
Để hai hệ đã cho tương đương nhau thì nghiệm
()
-1; 1
phải là nghiệm của hệ
23 5
12 3
xy
xya
ì
ï- =
ï
í
ï
+=
ï
î
Khi đó ta có
()
()
2.1 3. 1 5
9
12.1 3. 1
a
a
ì
ï
--=
ï
ï
=
í
ï
+-=
ï
ï
î
Ngược lại với
9a =
thì hệ thứ hai trở thành:
23 5
12 3 9
xy
xy
ì
ï- =
ï
í
ï
+=
ï
î
có nghiệm
()
-
1; 1
Vậy với
9a =
thì hai hệ phương trình đã cho tương đương.
Bài 20.
Ta thấy hệ phương trình
2
310
xy
xy
ì
ï- =
ï
í
ï
+=
ï
î
có nghiệm
()
3; 1
Để hai hệ đã cho tương đương nhau thì nghiệm
()
3; 1
phải là nghiệm của hệ
221
2
ax y
xay
ì
ï-=
ï
í
ï
+=
ï
î
Khi đó ta có
()
voâ nghieäm
2.3 2.1 1 6 3 2
3.12 1 1
aaa
aaa
ììì
ï-= ï= ï=
ïïï

ííí
ïïï
+ = =- =-
ïïï
îîî
Vậy không có giá trị nào của
a
để hai hệ phương trình
vaø
2221
310 2
xy ax y
xy xay
ìì
ï- = ï - =
ïï
íí
ïï
+= + =
ïï
îî
tương đương.
23.
TOÁNHỌCSƠĐỒ‐THCS.TOANMATH.com
C.TRẮC NGHIỆM RÈN LUYỆN PHẢN XẠ
Câu 1. Hệ phương trình
ax by c
ax by c
ì
ï
+=
ï
í
ï
¢+¢=¢
ï
î
có nghiệm duy nhất khi
A.
ab
ab
¢
¹
¢
. B.
ab
ab
¢
=
¢
. C.
abc
abc
¢¢
¹
¢
= . D.
bc
bc
¢
¹
¢
.
Câu 2. Hệ phương trình
ax by c
ax by c
ì
ï
+=
ï
í
ï
¢+¢=¢
ï
î
(các hệ số
;; abc¢¢¢
khác 0 ) vô số nghiệm khi
A.
ab
ab
¢
¹
¢
. B.
abc
abc
¢¢
=
¢
= . C.
abc
abc
¢¢
¹
¢
= . D.
bc
bc
¢
¹
¢
.
Câu 3. Hệ phương trình bậc nhất hai ẩn
ax by c
ax by c
ì
ï
+=
ï
í
ï
¢+¢=¢
ï
î
(có hệ số khác 0 ) vô nghiệm khi
A.
ab
ab
¢
=
¢
. B.
abc
abc
¢¢
¹
¢
= . C.
abc
abc
¢¢
¹
¢
¹ . D.
bc
bc
¢
=
¢
.
Câu 4. Hệ phương trình
ax by c
ax by c
ì
ï
+=
ï
í
ï
¢+¢=¢
ï
î
có các hệ số khác 0 và
abc
abc
¢¢
¹
¢
= . Chọn câu đúng.
A. Hệ phương trình có nghiệm duy nhất. B. Hệ phương trình vô nghiệm.
C. Hệ phương trình vô số nghiệm. D. Chưa kết luận được về nghiệm của hệ.
Câu 5. Hệ phương trình
233
459
xy
xy
ì
ï
+=
ï
í
ï
-- =
ï
î
nhận cặp số nào sau đây là nghiệm.
A.
(21;15)-
. B.
(21; 15)-
. C.
(1; 1)
. D.
(1; 1)-
.
Câu 6. Hệ phương trình
57
321
xy
xy
ì
ï
+=
ï
í
ï
-- =
ï
î
nhận cặp số nào sau đây là nghiệm.
A.
(1; 2)
. B.
(8; 3)-
. C.
(3; 8)-
. D.
(3; 8)
.
Câu 7. Cặp số
(2;3)--
là nghiệm của hệ phương trình nào sau đây?
A.
3
24
xy
xy
ì
ï
-=
ï
í
ï
+=
ï
î
. B.
21
38
xy
xy
ì
ï
-=-
ï
í
ï
-=
ï
î
. C.
21
37
xy
xy
ì
ï
-=-
ï
í
ï
-=
ï
î
. D.
42 0
35
xy
xy
ì
ï
-=
ï
í
ï
-=
ï
î
.
Câu 8. Cặp số
(3; 5)-
là nghiệm của hệ phương trình nào sau đây?
24.
TOÁNHỌCSƠĐỒ‐THCS.TOANMATH.com
A.
31
2
xy
xy
ì
ï
-=
ï
í
ï
+=
ï
î
. B.
34
211
xy
xy
ì
ï
+=
ï
í
ï
-=
ï
î
. C.
1
35
y
xy
ì
ï
=-
ï
í
ï
-=
ï
î
. D.
40
30
xy
xy
ì
ï
-=
ï
í
ï
-=
ï
î
.
Câu 9. không giải hệ phương trình, dự đoán số nghiệm của hệ
23
32 7
xy
xy
ì
ï
-+=-
ï
í
ï
-=
ï
î
.
A. Vô s
ố nghiệm. B. Vô nghiệm. C. Có nghiệm duy nhất. D. Có hai nghiệm phân biệt.
Câu 10. Không giải hệ phương trình, dự đoán số nghiệm của hệ
51
52
xy
xy
-+ =-
+=
ì
ï
ï
í
ï
ï
î
.
A. Vô số nghiệm. B. Vô nghiệm. C. Có nghiệm duy nhất. D. Có hai nghiệm phân biệt.
Câu 11. Xác định giá trị của tham số
m
để hệ phương trình
1
2
xy
mx y m
ì
ï
+=-
ï
í
ï
+=
ï
î
vô nghiệm.
A.
1m =
. B.
1m =-
. C.
0m =
. D.
1
2
m = .
Câu 12. Xác định giá trị của tham số
m
để hệ phương trình
()
24
12
xy
mxym
ì
ï
-=
ï
í
ï
-+=
ï
î
vô nghiệm.
A.
1m =
. B.
1m =-
. C.
3m =
. D.
3m =-
.
Câu 13. Không giải hệ phương trình, dự đoán số nghiệm của hệ
22 3
32 6 5
xy
xy
ì
ï
-=
ï
ï
í
ï
-=
ï
ï
î
A. Vô số nghiệm. B. Vô nghiệm. C. Có nghiệm duy nhất. D. Có hai nghiệm phân biệt.
Câu 14. Cho hệ
1
():
1
xy
I
yx
ì
ï
=-
ï
í
ï
=+
ï
î
và hệ
235
352
()
xy
II
yx
ì
ï
ï
í
-=
+=
ï
ï
î
. Chọn kết luận đúng.
A. Hai hệ đã cho đều vô nghiệm. B. Hai hệ đã cho đề
u có nghiệm duy nhất.
C. Hệ (I) vô nghiệm, hệ (II) có nghiệm duy nhất. D. Hệ (I) và hệ (II) đều có vô số nghiệm.
Câu 15. Xác định giá trị của tham số
m
để hệ phương trình
2
21
22
mx y
xmy m
ì
ï
-=
ï
ï
í
ï
-=
ï
ï
î
có nghiệm duy nhất.
A.
2m ¹
. B.
2m ¹-
. C.
2m =
. D.
2m ¹
.
Câu 16.Xác định giá trị của tham số
m
để hệ phương trình
()22
12)5(
xm y
mxym
ì
ï
-- =
ï
í
ï
--=-
ï
î
có nghiệm duy nhất
A. 0m ¹ . B.
2m ¹
. C.
{}
0; 3m
¹
. D.
0; 3mm==
.
25.
TOÁNHỌCSƠĐỒ‐THCS.TOANMATH.com
Câu 17. Cho hệ phương trình
2
2
9
mx y m
xmy
ì
ï
-+=-
ï
ï
í
ï
+=
ï
ï
î
. Tìm các giá trị của tham số
m
để hệ phương trình
nhận cặp
(1; 2)
làm nghiệm
A. 0m = . B.
1m =-
. C.
2m =-
. D.
3m =
.
Câu 18. Cho hệ phương trình
2
228
2
()
3
mxym
mx y
ì
ï
ï
ï
í
++=-
+=-
ï
ï
ï
î
. Tìm các giá trị của tham số để hệ phương trình
nhận cặp số
(1;3)-
làm nghiệm.
A. 0m = . B.
2m =-
. C.
3m =-
. D.
3m =
.
Câu 19. Cho hệ phương trình:
32
313
mx y m
xmy m
ì
ï
+=-
ï
í
ï
-- =-+
ï
î
. Xác định các giá trị của tham số
m
để hệ
phương trình vô số nghiệm.
A. 0m = . B.
1m =
. C.
2m =
. D.
3m =
.
Câu 20. Cho hệ phương trình:
15
55
2
421
mx y
xmy m
ì
ï
ï
+=-
ï
ï
í
ï
ï
-- = +
ï
ï
î
. Xác định các giá trị của tham số
m
để hệ phương
trình vô số nghiệm.
A.
0m =
. B.
2m =
. C.
2m =-
. D.
3m =-
.
Câu 21. Bằng cách tìm giao điểm của hai đường thẳng
:2 3dxy-+=
và
:5dx y
¢
+=
ta tìm được nghiệm của hệ phương trình
23
5
xy
xy
ì
ï
-+=
ï
í
ï
+=
ï
î
là
00
(; )xy
. tính
00
yx-
.
A.
11
3
. B.
13
3
. C. 5 . D.
17
3
.
Câu 22. Bằng cách tìm giao điểm của hai đường thẳng
:4 2 5dx y+=-
và
:2 1dxy-=-
¢
ta tìm được nghiệm của hệ phương trình
42 5
21
xy
xy
ì
ï
+=-
ï
í
ï
-=-
ï
î
là
00
(; )xy
. tính
00
.xy
.
A.
21
32
. B.
21
32
- . C.
21
8
. D.
10
12
- .
Câu 23. Cho hệ phương trình
23
244
mx y m
xmy m
ì
ï
-=
ï
í
ï
-=--
ï
î
. Tìm các giá trị của tham số
26.
TOÁNHỌCSƠĐỒ‐THCS.TOANMATH.com
m
để hệ phương trình nhận cặp
(1;2)-
làm nghiệm.
A.
1m =-
. B.
1m =
. C.
3m =-
. D.
3m =
.
HƯỚNG DẪN
Câu 1. Đáp án C.
Xét hệ phương trình bậc nhất hai ẩn
ax by c
ax by c
ì
ï
+=
ï
í
ï
¢+¢=¢
ï
î
- Hệ phương trình có nghiệm duy nhất
ab
ab
¢
¹
¢
- Hệ phương trình vô nghiệm
abc
abc
¢¢
¹
¢
=
- Hệ phương trình có vô số nghiệm
abc
abc
¢¢
=
¢
=
Câu 2. Đáp án B.
Hệ phương trình
ax by c
ax by c
ì
ï
+=
ï
í
ï
¢+¢=¢
ï
î
có vô số nghiệm khi hai đường thẳng
:dax by c+=
và
:dax by c+
¢¢
=
¢¢
trùng nhau, suy ra hệ phương trình có vô số nghiệm
abc
abc
¢¢
=
¢
=
Câu 3. Đáp án B.
Xét hệ phương trình bậc nhất hai ẩn
ax by c
ax by c
ì
ï
+=
ï
í
ï
¢+¢=¢
ï
î
(có hệ số khác0 )
- Hệ phương trình có nghiệm duy nhất
ab
ab
¢
¹
¢
- Hệ phương trình vô nghiệm
abc
abc
¢¢
¹
¢
=
- Hệ phương trình có vô số nghiệm
abc
abc
¢¢
=
¢
=
Câu 4. Đáp án B.
Xét hệ phương trình bậc nhất hai ẩn
ax by c
ax by c
ì
ï
+=
ï
í
ï
¢+¢=¢
ï
î
(các hệ số
;;abc
¢¢¢
khác 0)
Hệ phương trình vô nghiệm
abc
abc
¢¢
¹
¢
=
Câu 5. Đáp án A.
Thay lần lượt các cặp số
(21; 15);(1;1);(1; 1)--
và
(21;15)-
vào hệ phương trình ta được
+) Với cặp số
(21; 15)-
thì ta có
2.21 3.15 3 87 3
4.21 5.15 9 9 9
ìì
ïï
+= =
ïï
íí
ïï
-+ = -=
ïï
îî
(vô lý) nên loại B.
27.
TOÁNHỌCSƠĐỒ‐THCS.TOANMATH.com
+) Với cặp số
(1; 1)
thì ta có
2.1 3.1 3 5 3
4.1 5.1 9 9 9
ìì
ïï
+= =
ïï
íí
ïï
-- = -=
ïï
îî
(vô lý) nên loại C.
+) Với cặp số
(1; 1)-
thì ta có
2.1 3. 1 3 1 3
4.1 5. 1 9
()
() 19
ìì
ïï
+-= -=
ïï
íí
ïï
---= =
ïï
îî
(vô lý) nên loại D.
+) Với cặp số
(21;15)-
thì ta có
2. 21 3.15 3 3 3
4. 21 5.15 9() 99
()
ìì
ïï
-+ = =
ïï
íí
ïï
-- - = =
ïï
îî
(luôn đúng) nên chọn A.
Câu 6. Đáp án C.
Thay lần lượt các cặp số
(1;2);(8; 3);(3; 8)--
và
(3; 8)
vào hệ phương trình ta được
+) Với cặp số
(1; 2)
thì ta có
5.1 2 7 7 7
13.2 21 7 21
ìì
ïï
+= =
ïï
íí
ïï
-- = - =
ïï
îî
(vô lý) nên loại B.
+) Với cặp số
(8; 3)-
thì ta có
5.8 3 7 37 7
833 21 1(2
(
)1
)
ìì
ïï
+- = =
ïï
íí
ïï
-- - = =
ïï
îî
(vô lý) nên loại C.
+) Với cặp số
(3;8)
thì ta có
5.3 8 7 23 7
3 3.8 21 27 21
ìì
ïï
+= =
ïï
íí
ïï
-- = - =
ïï
îî
(vô lý) nên loại D.
+) Với cặp số
(3; 8)-
thì ta có
5.3 8 7 7 7
3 3. 8 21 21
)
(2
(
)1
ìì
ïï
+- = =
ïï
íí
ïï
-- - = =
ïï
îî
(luôn đúng) nên chọn A.
Câu 7. Đáp án C.
+) Thay
2; 3xy=- =-
vào hệ
3
24
xy
xy
ì
ï
-=
ï
í
ï
+=
ï
î
ta được
2313
2. 2
()
()3 7 4
ì
ï
--- = ¹
ï
í
ï
--=-¹
ï
î
(vô lý) nên loại A.
+) Thay
2; 3xy=- =-
vào hệ
21
38
xy
xy
ì
ï
-=-
ï
í
ï
-=
ï
î
ta được
2. 2 3 1
23.
() )
78()3
(
ì
ï
---=-
ï
í
ï
-- - = ¹
ï
î
(vô lý) nên loại B.
+) Thay
2; 3xy=- =-
vào hệ
42 0
35
xy
xy
ì
ï
-=
ï
í
ï
-=
ï
î
ta được
4. 2 2. 3 2 0
2
() ()
()3. 3 7 5
ì
ï
-- -=-¹
ï
í
ï
-- - = ¹
ï
î
(vô lý) nên loại D.
+) Thay
2; 3xy=- =-
vào hệ
21
37
xy
xy
ì
ï
-=-
ï
í
ï
-=
ï
î
ta được
2. 2 3 1 1 1
23.3 7
() )
)77
(
(
ìì
ïï
---=- -=-
ïï
íí
ïï
-- - = =
ïï
îî
(luôn
đúng) nên chọn C.
Câu 8. Đáp án B.
+) Thay
3; 5xy==-
vào hệ
31
2
xy
xy
ì
ï
-=
ï
í
ï
+=
ï
î
ta được
335 1 18 1
352 2
()
() 2
ìì
ïï
--= =
ïï
íí
ïï
+- = - =
ïï
îî
(vô lý) nên loại A.
+) Thay
3; 5xy==-
vào hệ
1
35
y
xy
ì
ï
=-
ï
í
ï
-=
ï
î
ta được
()
51 51
33.5 5 18 5
ìì
ïï
-=- -=-
ïï
íí
ïï
--= =
ïï
îî
(vô lý) nên loại C.
+) Thay
3; 5xy==-
vào hệ
40
30
xy
xy
ì
ï
-=
ï
í
ï
-=
ï
î
ta được
4.3 5 0 17 0
33.5 0 18(0
()
)
ìì
ïï
-- = =
ïï
íí
ïï
--= =
ïï
îî
(vô lý) nên loại D.
28.
TOÁNHỌCSƠĐỒ‐THCS.TOANMATH.com
+) Thay
3; 5xy==-
vào hệ
34
211
xy
xy
ì
ï
+=
ï
í
ï
-=
ï
î
ta được
3.3 5 4 4 4
2.3 5 11 1(11)1
()
ìì
ïï
+- = =
ïï
íí
ïï
-- = =
ïï
îî
(luôn đúng) nên
chọn B.
Câu 9. Đáp án C.
Xét hệ phương trình
23
32 7
xy
xy
ì
ï
-+=-
ï
í
ï
-=
ï
î
có
21
32
-
¹
-
nên hệ phương trình có nghiệm duy nhất.
Câu 10. Đáp án C.
Xét hệ phương trình
23
32 7
xy
xy
ì
ï
-+=-
ï
í
ï
-=
ï
î
có
15
51
-
¹
nên hệ phương trình có nghiệm duy nhất.
Câu 11. Đáp án A.
Để hệ phương trình
1
2
xy
mx y m
ì
ï
+=-
ï
í
ï
+=
ï
î
vô nghiệm thì
12
11 1
mm
=¹
1
1
1
2
m
m
m
ì
ï
=
ï
ï
ï
=
í
ï
¹
ï
ï
ï
î
Câu 12. Đáp án D.
Ta có
() ()
24
24 24
1
12 21
22
yx
xy y x
mm
mxym y mxm
y
x
ì
ï
=-
ìì
ï
ïï
-= = -
ï
ïï
ï

ííí
-
ïïï
-+= =- +
=+
ïïï
îî
ï
ï
î
Để hệ phương trình
()
24
12
xy
mxym
ì
ï
-=
ï
í
ï
-+=
ï
î
vô nghiệm thì đường thẳng
:24dy x=-
song song với
đường thẳng
1
:
22
mm
dy x
-
+
¢
=
suy ra
1
2
14 3
2
3
88
4
2
m
mm
m
mmm
ì
ï
-
ï
=
ìì
ï
ïï
-= =-
ï
ïï
ï
=-
ííí
ïïï
¹- ¹-
ïïï
îî
¹-
ï
ï
ï
î
Câu 13. Đáp án B.
Xét hệ phương
22 3
32 6 5
xy
xy
ì
ï
-=
ï
ï
í
ï
-=
ï
ï
î
trình có
223113
65 335
32
-
=¹=¹
-
nên hệ phương trình vô
nghiệm.
Câu 14. Đáp án D.
Xét hệ
1
()
1
:
11
xy yx
I
yx yx
ìì
ïï
=- =+
ïï
íí
ïï
=+ =+
ïï
îî
Nhận thấy rằng hai đường thẳng
1
(): 1dyx=+
và
2
(): 1dyx=+
trùng nhau nên hệ
()I
có vô số
nghiệm.
29.
TOÁNHỌCSƠĐỒ‐THCS.TOANMATH.com
Xét hệ
25
23 5 325
33
352 325 2 5
33
()
yx
xy y x
II
yxyx
yx
ì
ï
ï
=-
ì
ï
ï
-= =-
ï
ï
ï

íí
ïï
+= = -
ì
ï
ï
í
ïï
î
=-
ï
ï
ï
î
ï
ï
î
Nhận thấy rằng hai đường thẳng
3
25
():
33
dy x=- và
4
25
():
33
dy x=-
trùng nhau nên hệ
()II
có vô
số nghiệm.
Vậy cả hai hệ đã cho đều có vô số nghiệm.
Câu 15. Đáp án D.
Để hệ phương trình
2
21
22
mx y
xmy m
ì
ï
-=
ï
ï
í
ï
-=
ï
ï
î
có nghiệm duy nhất thì
2
2
42
2
m
mm
m
-
¹¹¹
-
.
Câu 16. Đáp án C.
Xét hệ
()
() ()
() ()
22
22 2 2
15
12 52 1 5
222
myx
xm y m yx
mm
mxym ymxm
y
x
ì
ï
-=-
ìì
ï
ïï
-- = - =-
ï
ïï
ï

ííí
-
ïïï
--=- =--+
=-+
ïïï
îî
ï
ï
î
TH1: Với
20 2mm-= =
ta có hệ
0. 2 2
13 13
22 22
yx x
yx yx
ìì
ïï
=- =
ïï
ïï
ïï
íí
ïï
=+ =+
ïï
ïï
ïï
îî
Nhận thấy hệ này có nghiệm duy nhất vì hai đường thẳng
2x =
và
13
22
yx=+ cắt nhau.
TH2: Với
20 2mm-¹ ¹
ta có hệ
12
22
22
15
15
22
2
)
2
(
2
2
myx
yx
mm
m
m
ym x
ym x
ì
ï
ï
-=-
=
ì
ï
ï
ï
ï
í
-
ï
ï
ï
--
í
ï
=- -+
ï
=- -+
ï
ï
ï
î
ï
ï
ï
ï
î
Để hệ phương trình đã cho có nghiệm duy nhất thì hai đường thẳng
12
:
22
dy x
mm
=-
--
và
15
:
222
mm
dy x
-
=-+
¢
cắt nhau
-
¹--¹-+¹-¹
-
22
11
(1)(2)2 322 3 0
22
m
m m mm mm
m
()
0
30
3
m
mm
m
ì
ï
¹
ï
-¹
í
ï
¹
ï
î
. Suy ra
{}
0; 2; 3m ¹
Kết hợp cả TH1 và TH2 ta có
{}
0; 3m
¹
Vậy hệ phương trình đã cho có nghiệm duy nhất
khi
{
}
0; 3m ¹
.
Câu 17. Đáp án C.
Để hệ phương trình
2
2
9
mx y m
xmy
ì
ï
-+=-
ï
ï
í
ï
+=
ï
ï
î
nhận cặp
(1; 2)
làm nghiệm thì
30.
TOÁNHỌCSƠĐỒ‐THCS.TOANMATH.com
2
.1 2 2
2
2
2
1.29
mm
m
m
m
m
ì
ï
-+=-
=-
ï
ï
=-
í
ï
ì
ï
ï
í
ï
=
+=
ï
ï
î
ï
î
. Vậy
2m =-
.
Câu 18. Đáp án D.
Để hệ phương trình
2
228
2
()
3
mxym
mx y
ì
ï
ï
ï
í
++=-
+=-
ï
ï
ï
î
nhận cặp số
(1;3)-
làm nghiệm thì
ì
ï
=
ï
ì
ì
ï
ï
ï
+ -+= - =
--+= -
ï
ï
ï
ï
é
=
=
ííí
ê
ïïï
-+=-
-+ =- =
ïïï
ê
î
ï
î
=-
ï
ê
ï
ë
î
ì
ï
ï
ï
í
ï
ï
ï
î
2 2
3
2. 1 3 2 8 3 9
232 8
3
3
(
26 3
12.3 9
)( )
(3
3
)
m
mm m
mm
m
m
m
mm
m
.
Vậy
3m =
.
Câu 19. Đáp án B.
Để hệ phương trình
32
313
mx y m
xmy m
ì
ï
+=-
ï
í
ï
-- =-+
ï
î
có vô số nghiệm thì
31 2
313
mm
mm
-
==
-- -+
2
2
2
1
33
2310
231
m
m
mm
mm
ì
ì
ï
ï
=
=
ï
ï
ïï

íí
ïï
-+=
=-
ïï
ï
î
ï
î
1
1
1
1
21()( 0
1
2
)1
m
m
m
m
mm
m
ì
ï
=
ï
ï
ì
ï
ï
=
é
=
ï
ï
ê
=
íí
ê
ïï
--=
ïï
î
ê
ï
=
ï
ê
ï
ë
î
Câu 20. Đáp án C.
+ TH1: Với 0m = ta có hệ
3
515
1
41
4
y
y
x
x
ì
ï
=-
ì
ï
ï
=-
ï
ï
ï
íí
ïï
-=
=-
ïï
î
ï
ï
î
hay hệ phương trình có nghiệm duy nhất nên
loại 0m = .
+ TH2: Với
0m ¹
.
Để hệ phương trình
15
55
2
421
mx y
xmy m
ì
ï
ï
+=-
ï
ï
í
ï
ï
-- = +
ï
ï
î
có vô số nghiệm
thì
2
520
55 15
10 2 1 15
422
()
()1
m
m
mm
mm
-=-
-
==
+=
-
ì
ï
ï
í
-+
ï
ï
ï
ï
î
2
2
4
2
2
20 10 15
2
m
m
m
m
mm
m
ì
é
ï
ï
ê
ì
ï
ï
ï
ï
ê
ï
íí
ê
ë
ïï
ïï
ï
î
ï
ï
î
=
=
=-
=-
+=
=-
(tm)
Câu 21. Đáp án A.
Ta có
:2 3dxy-+=
23yx= +
và
:55dx y y x+==-
¢
Xét phương trình hoành độ giao điểm của
d
và
d
¢
:
2213
235 5 5
333
xxxyx+=- = =-=- = .
Vậy tọa độ giao điểm của
d
và
d
¢
là
213
;
33
æö
÷
ç
÷
ç
÷
ç
÷
ç
èø
31.
TOÁNHỌCSƠĐỒ‐THCS.TOANMATH.com
Suy ra nghiệm của hệ phương trình
23
5
xy
xy
ì
ï
-+=
ï
í
ï
+=
ï
î
là
213
;
33
æö
÷
ç
÷
ç
÷
ç
÷
ç
èø
Từ đó
00
13 2 11
33 3
yx-= -=
.
Câu 22. Đáp án A.
Ta có
:4 2 5dx y+=-
45
2
x
y
--
=
và
:2 1 2 1dxy y x-=- = +
¢
Xét phương trình hoành
độ giao điểm của
d
và
d
¢
:
--
=+--=+=-=-
45 7
21 45428 7
28
x
xxxxx
æö
÷
ç
÷
= += - +=-
ç
÷
ç
÷
ç
èø
73
212. 1
84
yx
.
Vậy tọa độ giao điểm của
d
và
d
¢
là
73
;
84
æö
÷
ç
÷
--
ç
÷
ç
÷
ç
èø
Suy ra nghiệm của hệ phương trình
42 5
21
xy
xy
ì
ï
+=-
ï
í
ï
-=-
ï
î
là
00
73
(; ) ;
84
xy
æö
÷
ç
÷
=- -
ç
÷
ç
÷
ç
èø
Từ đó
00
7321
..
8432
xy
æöæö
÷÷
çç
÷÷
=- - =
çç
÷÷
çç
÷÷
çç
èøèø
Câu 23. Đáp án A.
Để hệ phương trình
23
244
mx y m
xmy m
ì
ï
-=
ï
í
ï
-=--
ï
î
nhận cặp
(1;2)-
làm nghiệm thì
. 1 2.2 3 . 1 2.2 3 4 4
1
2. 1 .2 4 4 2. 1
() ()
() () .2 44 2 2
mmmmm
m
mmmmm
ìì ì
ïï ï
-- = -- = =-
ïï ï
=-
íí í
ïï ï
- - =- - - - =- - =-
ïï ï
îî î
Vậy
1m =-
.
32.
TOÁNHỌCSƠĐỒ‐THCS.TOANMATH.com
D.BÀI TẬP TỰ LUYỆN
Bài 1. Không giải hệ phương trình, em hãy đoán nhận số nghiệm của hệ và giải thích vì sao?
a.
42
33
yx
yx


b.
1
3
5
1
1
5
yx
yx


c.
33
1
1
3
xy
xy


d.
3
42
yx
yx

Bài 2. Xác định các nghiệm của mỗi hệ phương trình sau bằng phương pháp hình học:
a.
31
1
xy
xy


b.
35
1
xy
xy


Bài 3. Đoán nhận số nghiệm của mỗi hệ phương trình sau, và giải thích tại sao?
a.
3
55 3
xy
xy


b.
43 1
12 9 3
xy
xy


Bài 4. Cho hệ phương trình:
03
32 9
xy
xy


a. Giải hệ phương trình đã cho bằng đồ thị;
b. Nghiệm của phương trình đã cho có phải là nghiệm của phương trình
45 19xy
không?
Bài 5. Cho hệ phương trình:
23
21
xy
xy


a. Giải hệ phương trình đã cho bằng phương pháp đồ thị
b. Nghiệm của hệ phương trình đã cho có phải là nghiệm của phương trình
25 7xy
không?
Bài 6. Bằng đồ thị chứng tỏ các hệ phương trình sau luôn có nghiệm duy nhất với bất kì giá trị nào của a:
a.
1
xa
xy

b.
3xy
ya

Bài 7. Bằng đồ thị chứng tỏ hệ phương trình:
31
23
xy
ax y


a. Có nghiệm duy nhất với
2a 
;
b. Vô nghiệm với
6a 
.
Bài 8. Cho hệ phương trình:
32
15 10 5
xya
xy


a. Có vô số nghiệm với
1a
;
b. Vô nghiệm với
1a
.
Bài 9. Trong các câu sau, câu nào đúng, câu nào sai:
a. Hai hệ phương trình bậc nhất hai ẩn vô nghiệm, là hai hệ phương trình tương đương với nhau?
b. Hai hệ phương trình bậc nhất hai ẩn cùng vô số nghiệm là hai phương trình tương đương với nhau.
33.
TOÁNHỌCSƠĐỒ‐THCS.TOANMATH.com
Bài 10. Trong các trường hợp sau, hai hệ phương trình nào tương đương với nhau? Hai hệ phương trình
nào không tương đương với nhau?
a.
2
33 6
xy
xy


và
21
42 2
xy
xy


b.
3
2260
xy
xy


và
3
231
x
xy

c.
23 2
21
xy
xy


và
3
2
xy
y

HƯỚNG DẪN
Bài 1.
a. Hai đường th
ẳng
42yx
và
33yx
có hệ số góc
12
4; 3aa khác nhau nên chúng cắt nhau tại
một điểm.
Vậy hệ phương trình đã cho có nghiệm duy nhất.
b. Hai đường thẳng
1
3
5
yx
và
1
1
5
yx
có hệ số góc
12
1
5
aa
bằng nhau mà hệ số
12
31bb khác nhau nên chúng song song với nhau và không có điểm chung.
Vậy hệ phương trình đã cho vô nghiệm.
c. Biến đổi hệ phương trình về dạng:
33 33
33
11
33
11
33
xy y x
yx
yx
xy yx










Hai đường thẳng có hệ số góc
12
3aa và có tung độ gốc
12
3bb nên chúng trùng nhau.
Vậy hệ phương trình đã cho có vô số nghiệm.
d. Biến đổi hệ phương trình về dạng:
1
3
3
42
1
2
yx
yx
yx
yx



Hai đường thẳng
1
3
yx
và
1
2
yx
có hệ số góc
12
11
;
32
aa
khác nhau nên chúng cắt nhau tại
một điểm.
Vậy hệ phương trình đã cho có nghiệm duy nhất.
Bài 2.
Xác định các nghiệm của mỗi hệ phương trình sau bằng phương pháp hình học:
a. Hệ phương trình:
31
1
xy
xy


Đường thẳng

1
31xy d
có đồ thị là đường thẳng đi qua điểm

0; 1
và điểm

1; 2
.
Đường thẳng

2
1xy d
có đồ thị là đường thẳng đi qua điểm

1; 2
và điểm

1; 0
.
Hai đường thẳng

1
31xy d
và

2
1xy d
có đồ thị như hình vẽ:
34.
TOÁNHỌCSƠĐỒ‐THCS.TOANMATH.com
Dựa vào đồ thị hàm số, ta thấy hai đường thẳng cắt nhau tại

1; 2A
, suy ra nghiệm của hệ phương trình
là:
1
2
x
y

b. Hệ phương trình:
35
1
xy
xy


Đường thẳng

1
35xy d
có đồ thị đường thẳng đi qua điểm

0;5
và điểm

1; 2
.
Đường thẳng

2
1xy d
có đồ thị đường thẳng đi qua điểm

0; 1
và điểm

1; 0
.
Hai đường thẳng

1
35xy d
và

2
1xy d
có đồ thị như hình vẽ:
Dựa vào đồ thị hàm số, ta thấy hai đường thẳng cắt nhau tại

1; 2B
, suy ra nghiệm của phương trình là:
1
2
x
y

Bài 3. Đoán nhận số nghiệm của mỗi hệ phương trình sau, và giải thích tại sao?
35.
TOÁNHỌCSƠĐỒ‐THCS.TOANMATH.com
a. Biến đổi hệ phương trình đã cho:
3
3
3
55 3
5
yx
xy
xy
yx





Hệ phương trình vô nghiệm, vì hai đường thẳng
3yx
và
3
5
yx
có hệ số góc
12
1aa và tung
độ gốc
12
bb vì
3
3
5




nên chúng song song với nhau.
b. Biến đổi phương trình đã cho:
41
43 1
33
12 9 3 4 1
33
yx
xy
xy
yx





Hệ phương trình có vô số nghiệm, vì hai đường thẳng trùng nhau do có hệ số góc
12
4
3
aa
và tung
độ gốc
12
1
3
bb
.
Bài 4. Hệ phương trình:
3
03
39
32 9
22
y
xy
xy
yx




a. Dựa vào đồ thị hàm số ta thấy, hai đường thẳng
3y
và đường thẳng
39
22
yx
cắt nhau tại điểm
A có tọa độ

1; 3
.
Vậy nghiệm của hệ phương trình là
1
3
x
y

b. Với
1
3
x
y

thay vào phương trình
45 19xy
ta có:

4. 1 5.3 19 4 15 19
(VT = VP đúng).
Vậy điểm

1; 3
là nghiệm của phương trình
45 19xy
Bài 5. Biến đổi hệ phương trình:
13
23
22
21
21
xy
yx
xy
yx





a. Đồ thị hai hàm số
13
22
yx
và
21yx
được vẽ như hình:
36.
TOÁNHỌCSƠĐỒ‐THCS.TOANMATH.com
Dựa vào đồ thị hàm số ta thấy, hai đường thẳng cắt nhau tại A có tọa độ

1; 1
. Suy ra nghiệm của hệ
phương trình là
1
1
x
y
b. Với
1x
và
1y
thay vào phương trình
25 7xy
ta có:
2.1 5.1 2 5 3 7
nên
1x
và
1y
không phải là nghiệm của phương trình
25 7xy

.
Bài 6. Bằng đồ thị chứng tỏ các hệ phương trình sau luôn có nghiệm duy nhất với bất kì giá trị nào của a:
a.
11
xa xa
xy y x





Ta có: đường thẳng
xa
song song

0a
hoặc
trùng

0a
với trục Oy, mà đường thẳng
1yx

là đường thẳng xiên

0a
, cắt Oy tại
điểm

0;1
nên nó sẽ cắt đường thẳng
xa
với
mọi a.
Do đó, hệ phương trình luôn có nghiệm với mọi a.
b. Biến đổi hệ phương trình:
33xy yx
ya ya





Ta có: đường thẳng
ya
song song

0a
hoặc
trùng

0a
với trục Ox, mà đường thẳng
3yx

là đường thẳng xiên

0a
, cắt Ox tại
điểm

3; 0
nên có sẽ cắt đường thẳng
ya
với
mọi a.
Do đó hệ phương trình luôn có nghiệm với mọi a.
Bài 7. Biến đổi hệ phương trình:
31
31
3
23
22
yx
xy
a
ax y
yx





a. Khi
2a 
; thay vào hệ phương trình ta có:
31
3
2
yx
yx


Đường thẳng
31yx
và đường thẳng
3
2
yx
có hệ số góc khác nhau

31
nên cắt nhau.
Vì vậy, khi
2a 
thì hệ phương trình có nghiệm.
37.
TOÁNHỌCSƠĐỒ‐THCS.TOANMATH.com
b. Khi
6a 
, thay vào hệ phương trình ta có:
31
3
3
2
yx
yx


Đường thẳng
31yx
và
3
3
2
yx
là hai đường thẳng có hệ số góc bằng nhau

3aa

và tung độ
gốc khác nhau
3
1
2




nên chúng song song với nhau.
Vì vậy, khi
6a 
thì hệ phương trình vô nghiệm.
Bài 8. Biến đổi hệ phương trình:
3
32
22
15 10 5 3 1
22
a
yx
xya
xy
yx





a. Khi
1a
, thay vào hệ phương trình, ta có:
31
22
31
22
yx
yx


Đường thẳng
31
22
yx
và đường thẳng
31
22
yx
có hệ số góc, và tung độ gốc bằng nhau nên hai
đường thẳng trùng nhau.
Do đó, hệ phương trình đã cho có vô số nghiệm khi
1a
.
b. Khi
1a
, thay vào hệ phương trình, ta có:
3
22
31
22
a
yx
yx


Hai đường thẳng
3
22
a
yx
và đường thẳng
31
22
yx
có hệ số góc bằng nhau, nhưng tung độ gốc
khác nhau nên hai đường thẳng này song song với nhau.
Vậy, hệ phương trình đã cho vô nghiệm khi
1a
.
Bài 9. Trong các câu sau, câu nào đúng, câu nào sai:
a. Đúng. Vì hai hệ phương trình cùng vô số nghiệm thì có cùng tập nghiệm rỗng.
b. Sai.
Ví dụ chứng minh: Cho hai hệ phương trình sau:
Hệ

3
22 6
xy
I
xy


và Hệ

5
2210
xy
II
xy


Cả hệ

I
và hệ

II
đều là hệ phương trình có vô số nghiệm. Nhưng tập nghiệm của hệ phương trình

I
được biểu diễn bởi phương trình đường thẳng

1
3dy x
; còn tập nghiệm của hệ phương trình

II
được biểu diễn bởi phương trình đường thẳng

2
5dyx
. Hai đường thẳng này khác nhau nên
hai hệ phương trình đang xét không tương đương với nhau.
Bài 10. Giải các hệ phương trình nếu tập nghiệm của chúng bằng nhau ta kết luận hai hệ phương trình
tương đương, còn nếu tập nghiệm của chúng không bằng nhau ta kết luận hai hệ phương trình không
tương đương:
38.
TOÁNHỌCSƠĐỒ‐THCS.TOANMATH.com
a. Hệ phương trình
2
33 6
xy
xy


vô nghiệm.
và hệ phương trình
21
42 2
xy
xy


vô nghiệm.
Vậy hai hệ phương trình đã cho tương đương với nhau.
b. Hệ phương trình
3
2260
xy
xy


có vô số nghiệm.
và hệ phương trình
3
231
x
xy

có nghiệm
5
3;
3



.
Vì tập nghiệm của chúng khác nhau nên hai hệ phương trình đã cho không tương đương với nhau.
c. Hệ phương trình
23 2
27
xy
xy


có nghiệm là

17;12
và hệ phương trình
3
2
xy
y

có nghiệm là

1; 2
Vì tập nghiệm của chúng khác nhau nên hai hệ phương trình đã cho không tương đương với nhau.
----------Toán Học Sơ Đồ---------
| 1/38
| | Tải xuống

Có thể bạn quan tâm:

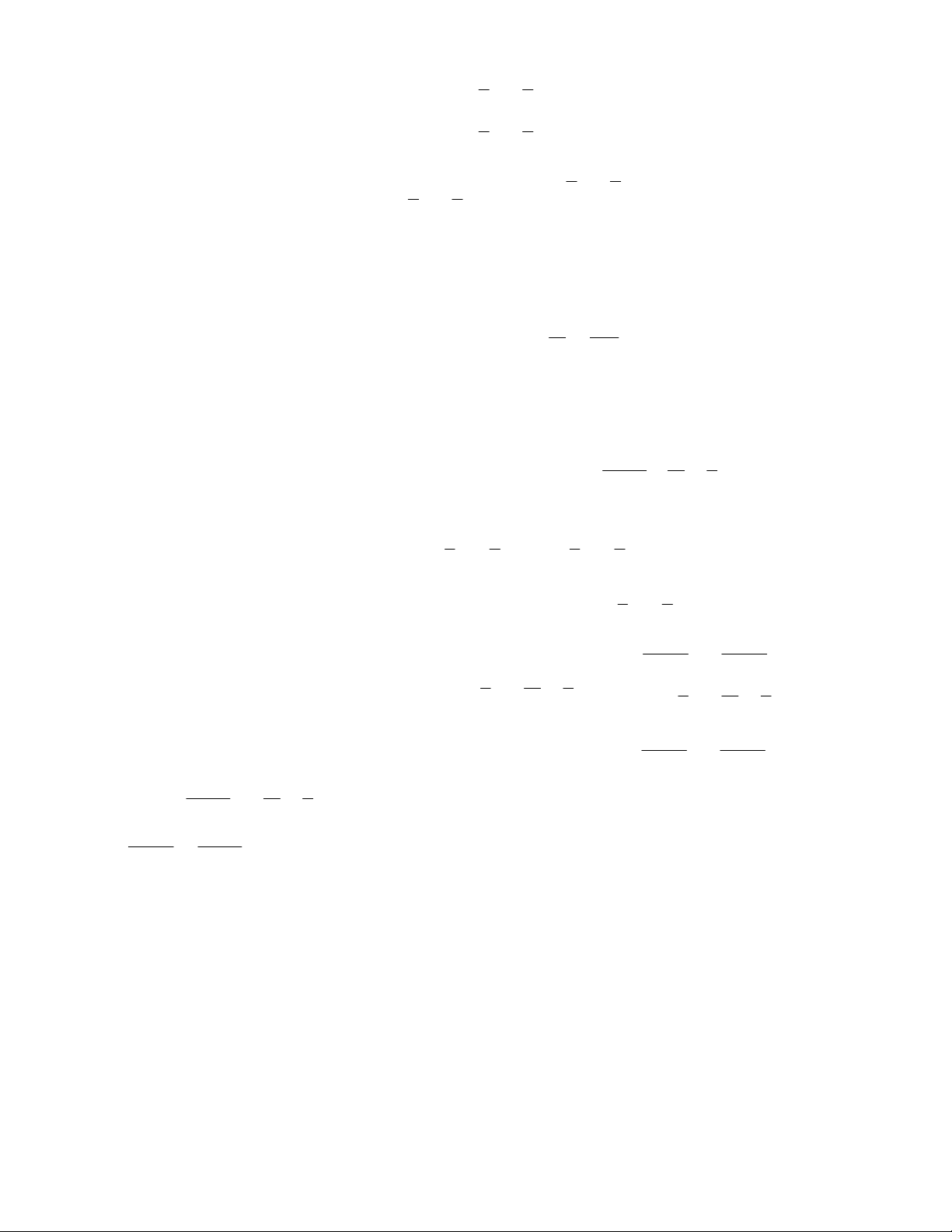
Preview text:

CHUYÊN ĐỀ HỆ HAI PHƯƠNG TRÌNH BẬC NHẤT HAI ẨN
A.KIẾN THỨC TRỌNG TÂM
a x b y c 1  1 1 1  
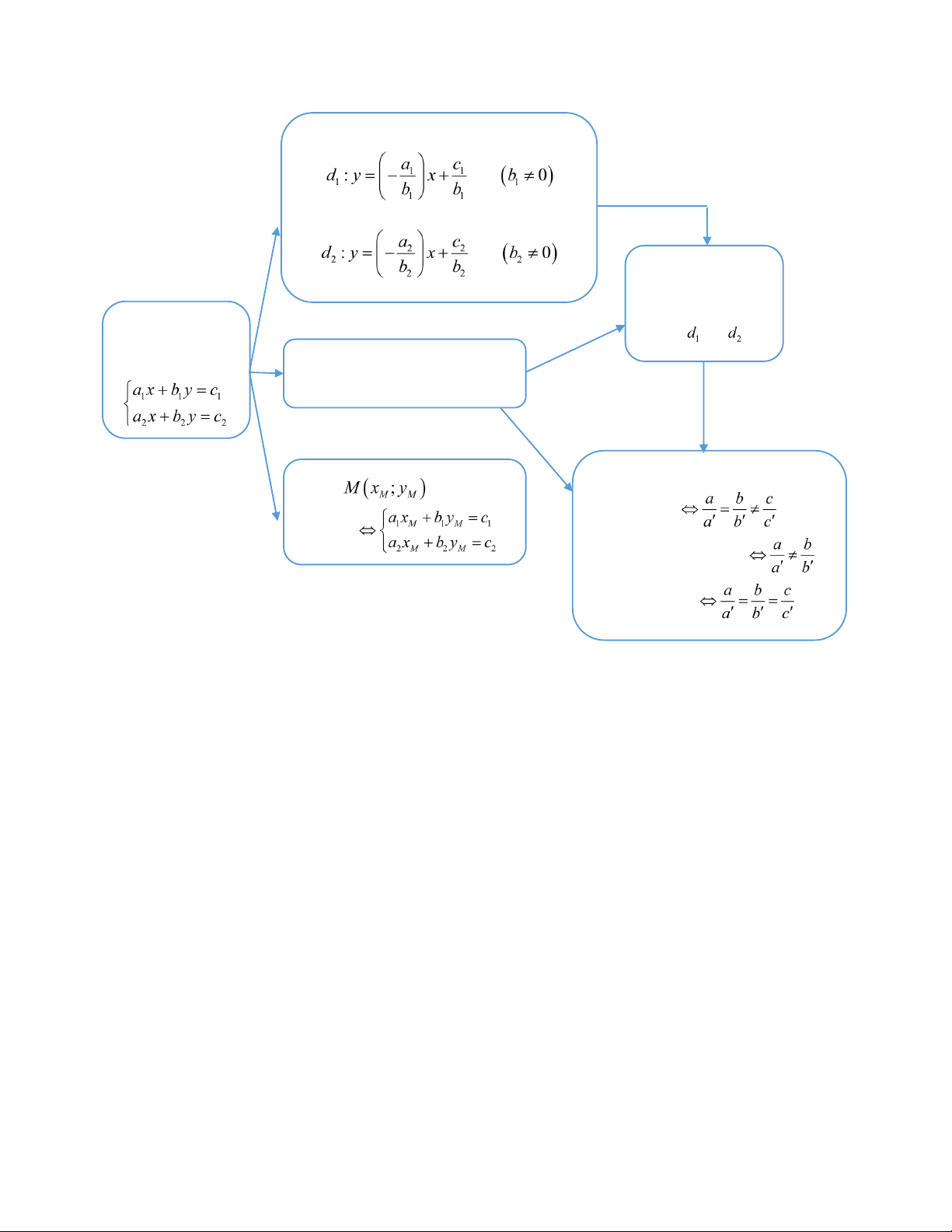
1. Cho hệ hai phương trình bậc nhất hai ẩn:
I
a x b y c 2  2 2 2  
Nếu hai phương trình trên có nghiệm chung x ; y thì x ; y được gọi là một nghiệm của 0 0  0 0 
hệ I .
Giải hệ phương trình là tìm tập nghiệm của nó.
2. Minh họa hình học tập nghiệm của hệ hai phương trình bậc nhất hai ẩn    a c
Phương trình a x b y c 1 có thể được viết lại như sau: 1 1
y     x có đồ thị là 1 1 1   b b  1  1  a
đường thẳng d với hệ số góc là 1   . 1   b  1     a c
Phương trình a x b y c 2 có thể được viết lại như sau: 2 2
y     x có đồ thị là 2 2 2   b b  2  2  a
đường thẳng d với hệ số góc là 2   . 2   b  2 
Do đó, tập nghiệm của hệ phương trình I được biểu diễn bởi tập hợp các điểm chung của hai
đường thẳng d : a x b y c và d : a x b y c 2  1  1 1 1 2 2 2
Nếu d cắt d thì hệ I có một nghiệm duy nhất. 2  1 
Nếu d // d thì hệ I vô nghiệm. 1   2
Nếu d d thì hệ I có vô số nghiệm. 1   2
* Tính nhanh số nghiệm của hệ phương trình bậc nhất hai ẩn: a b c Hệ vô nghiệm 1 1 1    a b c 2 2 2  a b
Hệ có một nghiệm duy nhất 1 1   a b 2 2  a b c
Hệ có vô số nghiệm 1 1 1    a b c 2 2 2
3. Hệ phương trình tương đương
Hai hệ phương trình được gọi là tương đương nếu chúng có cùng tập nghiệm.
1. TOÁN HỌC SƠ ĐỒ ‐ THCS.TOANMATH.com SƠ ĐỒ
Phương trình (1) có đồ thị là đường thẳng với
Phương trình (1) có đồ thị là đường thẳng với
Số nghiệm của hệ là số giao điểm của hai đường HỆ PHƯƠNG thẳng và TRÌNH BẬC NHẤT HAI ẨN
Nghiệm của hệ là nghiệm chung
của hai phương trình (1) và (2)
Nhìn nhanh số nghiệm của hệ: Nếu là nghiệm * Vô nghiệm của hệ
* Một nghiệm duy nhất * Vô số nghiệm
2. TOÁN HỌC SƠ ĐỒ ‐ THCS.TOANMATH.com
B.CÁC DẠNG BÀI MINH HỌA
Dạng 1: Đoán nhận số nghiệm của hệ phương trình
Bài 1. Nối mỗi hệ phương trình với một cặp số tương ứng mà nó nhận làm nghiệm 1 7 3; 1 x  2 y   1)  2 2  a) 19 2x  y   2 2) x  y  3  b)  1   5;   -2x- 2 y  6  2  3) 2x  y  3 c)  2; 3  3x   2y  4,5
4) x 2  y 3  5 d) 1,5;0  x 3  y 2 0
Bài 2. Cặp số 3; 
1 có là nghiệm của phương trình nào sau đây ? 3x   y  8 x  2y 5
3y x  0 a)  b)  c)  7x  2y 19 x  2y 1 x 5y   2  2   1x3y3 2 3x   2y  6 d)  e)  x  2x   y 7   2  1y 4
Bài 3. Không cần vẽ hình, hãy cho biết số nghiệm của mỗi hệ phương trình sau đây và giải thích vì sao. ìï = - ìï y 3 2x ï 1 a) í ; ïïy = x+3 ïy = 3x-1 ïî ï b 2 ) í ; ï 1 ïïy =- x+1 ïïî 2 ìï = - ìï - = 2y 3x ï 3x y 3 c) í ; ïï 3 ï y = 2x ï d) î í . 1 ïx- y = ï 1 ïî 3
Bài 4. Đoán nhận số nghiệm của mỗi hệ phương trình sau, giải thích vì sao. ìï + = ï ìï x- y = ï a x y 2 ) í ; b 3 2 1 ) í ; 3 ï x+ 3y = 2 ïî ï 6 - x + 4y = 0 ïî ìï - = ï ìï1 2 c 4x 4y 2 ) í ; ïï x-y = ï 2 - x + 2y = 1 - ïî d)í3 3 . ïïïx-3y = 2 î
3. TOÁN HỌC SƠ ĐỒ ‐ THCS.TOANMATH.com
Bài 5. Hãy kiểm tra xem mỗi cặp số sau có phải là một nghiệm của hệ phương trình tương ứng hay không? 7 ìï x-5y = 5 - 3 0, ìï 2x+1,7y 1 - 8,1 a) (- ï ï = 4 ; 5) , í ; b) (3 ; -1 ), ï 1 í ; 2x + 9y = 53 ïî- ï3,2x y = 20,6 ïî - 10 ìï x-3y = 9 5 ìï x+2y = 9 c) ï ï (1, 5 ; 2), (3 ; 7), í ; d) ( 1; 8), ï í . 5 - x 1,5y = 4 - ,5 ïî + ïx-14y = 5 ïî
Bài 6. Hãy biểu diễn y qua x ở mỗi phương trình (nếu có thể) rồi đoán nhận số nghiệm của mỗi hệ
phương trình sau đây và giải thích vì sao (không vẽ đồ thị). ìï x- y = ï ìï x + y ï = a) 4 9 3 í ; b) 2, 3 0,8 5 ï í ; 5 - x-3y 1 ïî = ï2y = 6 ïî ìï3x 5 ï = - ìï x- y = ï c) í ; d) 3 1 ï í . x + 5y = -4 ïî 6 ï x-2y = 5 ïî
Bài 7. Đoán nhận số nghiệm của mỗi hệ phương trình sau, giải thích vì sao: 2 ìï x+ y = 3 ìï3x+2y = 0 3 ìï x+0y = 6 a) ïí ; b) ïí ; c) ïí ; 3 ï x- y = 1 ïî ï2x-3y = 0 ïî 2 ï x + y = 1 ïî ìïx-y = 4 ìïx+ 2y = 3 ìïx + y = 1 d) ïí ; e) ïí ; ïï 0 ï x- y = 2 ïî ï2x + 4y = 1 ïî f) íx y 1 . ï + = ïïî2 2 2 ìï3x-y = 1
Bài 8. Chứng tỏ rằng hệ phương trình: ïí ïax + 2y = 3 ïî
a) Có nghiệm duy nhất với a = -2 ;
b) Vô nghiệm với a = -6
ìï3x-2y = a
Bài 9. Chứng tỏ rằng hệ phương trình: ïí 15 ï x +10y = 5 ïî
a) Có vô số nghiệm với a = 1 ;
b) Vô nghiệm với a = 1 .
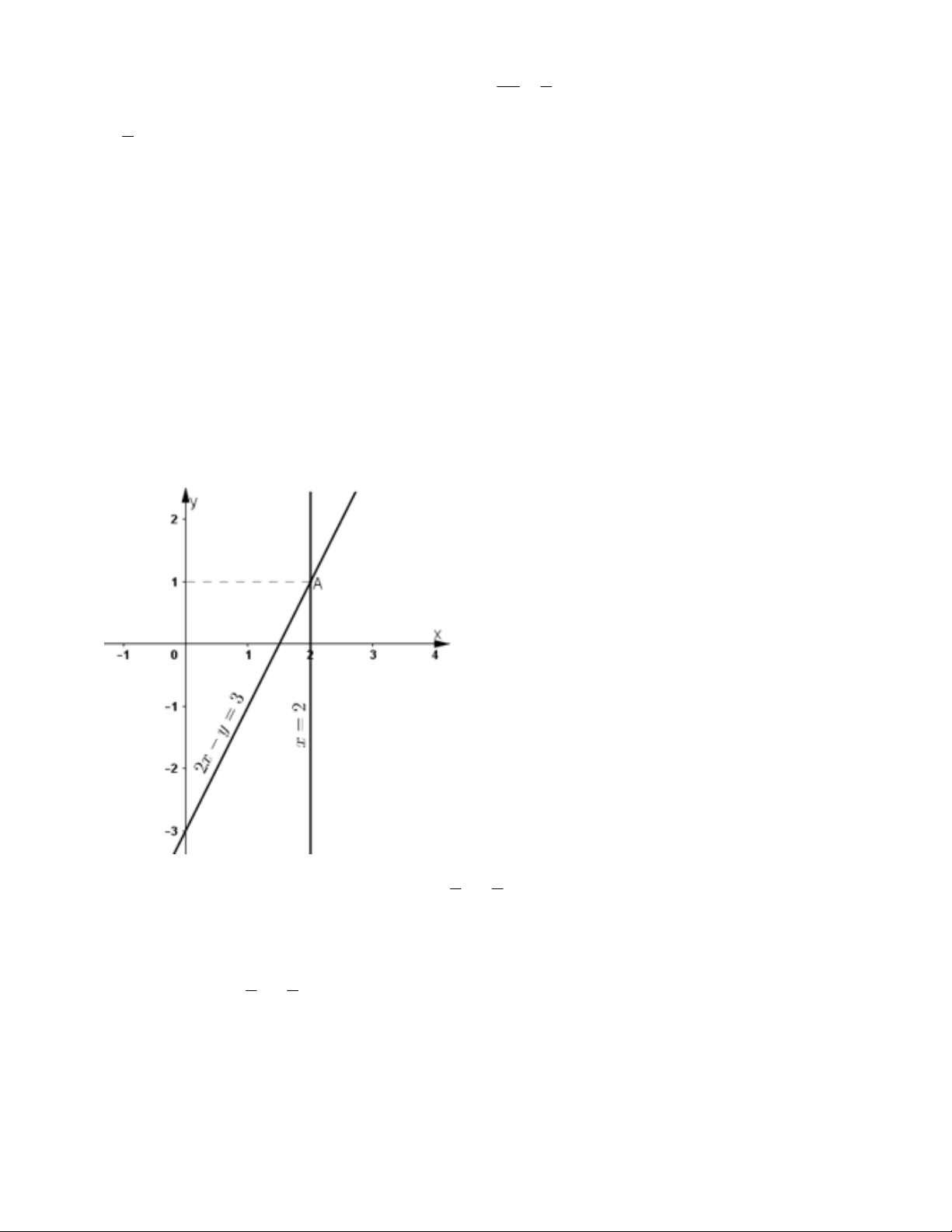
Bài 10. Cho các hệ phương trình sau: ìïx = 2 ï ìïx+3y = 2 í ï ï í - = ï = a) 2x y 3 ïî ; b) 2y 4 ïî .
Trước hết, hãy đoán nhận số nghiệm của mỗi hệ phương trình trên (giải thích rõ lí do). Sau đó, tìm tập
nghiệm của các hệ đã cho bằng cách vẽ hình.
Bài 11. Dựa vào vị trí tương đối của hai đường thẳng dưới đây, hãy tìm mối lien hệ giữa các hằng số
ìïax+by = c ï
a, b, c và các hằng số aʹ; bʹ; cʹ để hệ phương trình í
ïaʹx +bʹ y = cʹ ïî a) Có nghiệm duy nhất;
4. TOÁN HỌC SƠ ĐỒ ‐ THCS.TOANMATH.com b) Vô nghiệm; c) Có vô số nghiệm. Áp dụng:
a) Hãy lập một hệ hai phương trình bậc nhất hai ẩn có nghiệm duy nhất.
b) Hãy lập một hệ hai phương trình bậc nhất hai ẩn vô nghiệm.
c) Hãy lập một hệ hai phương trình bậc nhất hai ẩn có vô số nghiệm.
Dạng 2: Giải hệ phương trình bằng phương pháp hình học
Bài 12. Cho hai phương trình: 3x  y 1 và 5x  2y 3
a) Tìm nghiệm tổng quát của mỗi phương trình trên.
b) Vẽ đồ thị của hai phương trình trên cùng một hệ tọa độ rồi xác định nghiệm chung của hai phương trình.
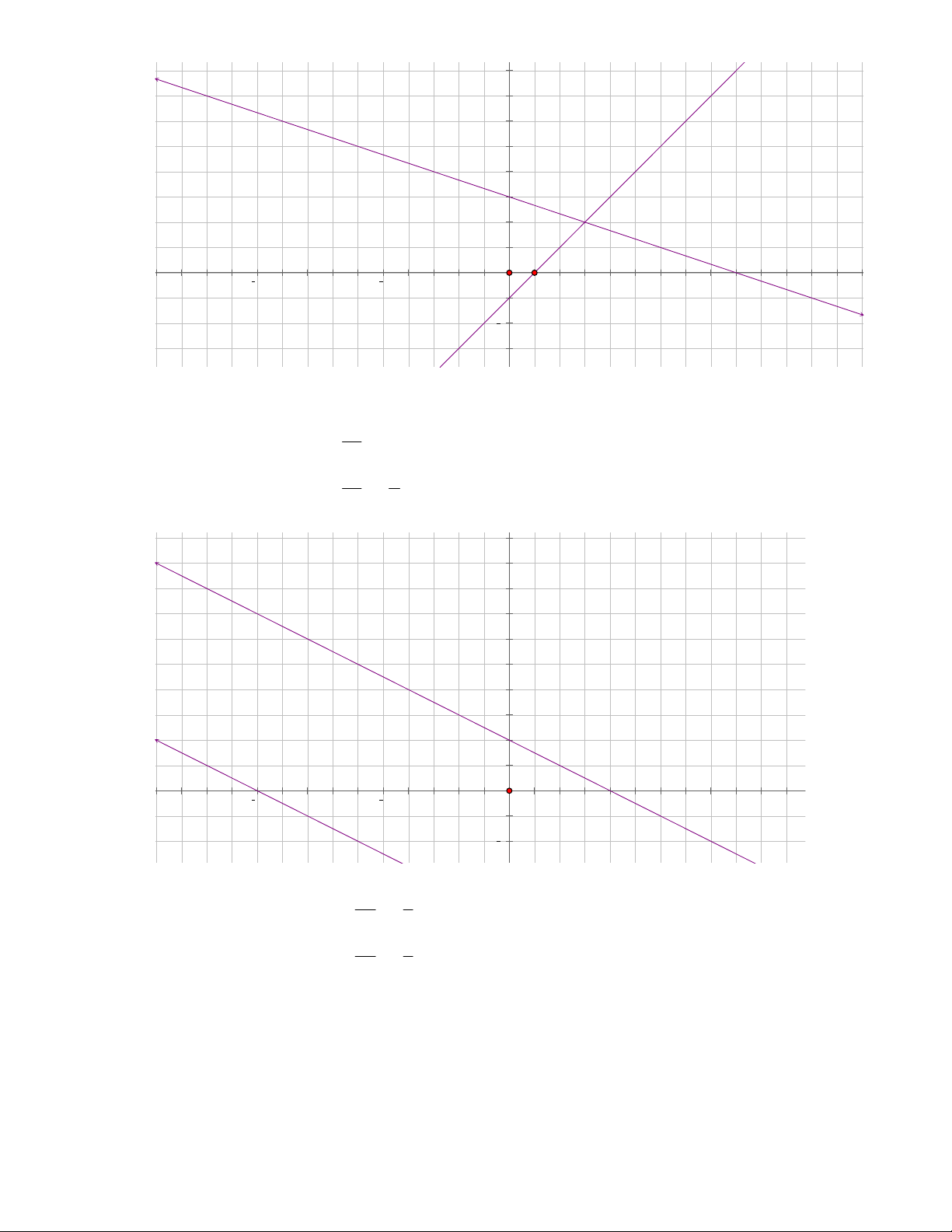
Bài 13. Bằng cách vẽ đồ thị, hãy giải các hệ phương trình: x  y 1 x  2y  4 1,5  y  x  0,5 a)  b)  c)  x 3y 9  2x   4y 10 2x 3y  1 2x  y  2
Bài 14. Cho hệ phương trình  x   2y 6
a) Giải hệ phương trình đã cho bằng phương pháp đồ thị
b) Nghiệm của hệ phương trình đã cho có phải là nghiệm của phương trình 3x  2y  8  hay không?
c) Nghiệm của hệ phương trình đã cho có phải là nghiệm của phương trình 4,5x  7,5 y  25 hay không?
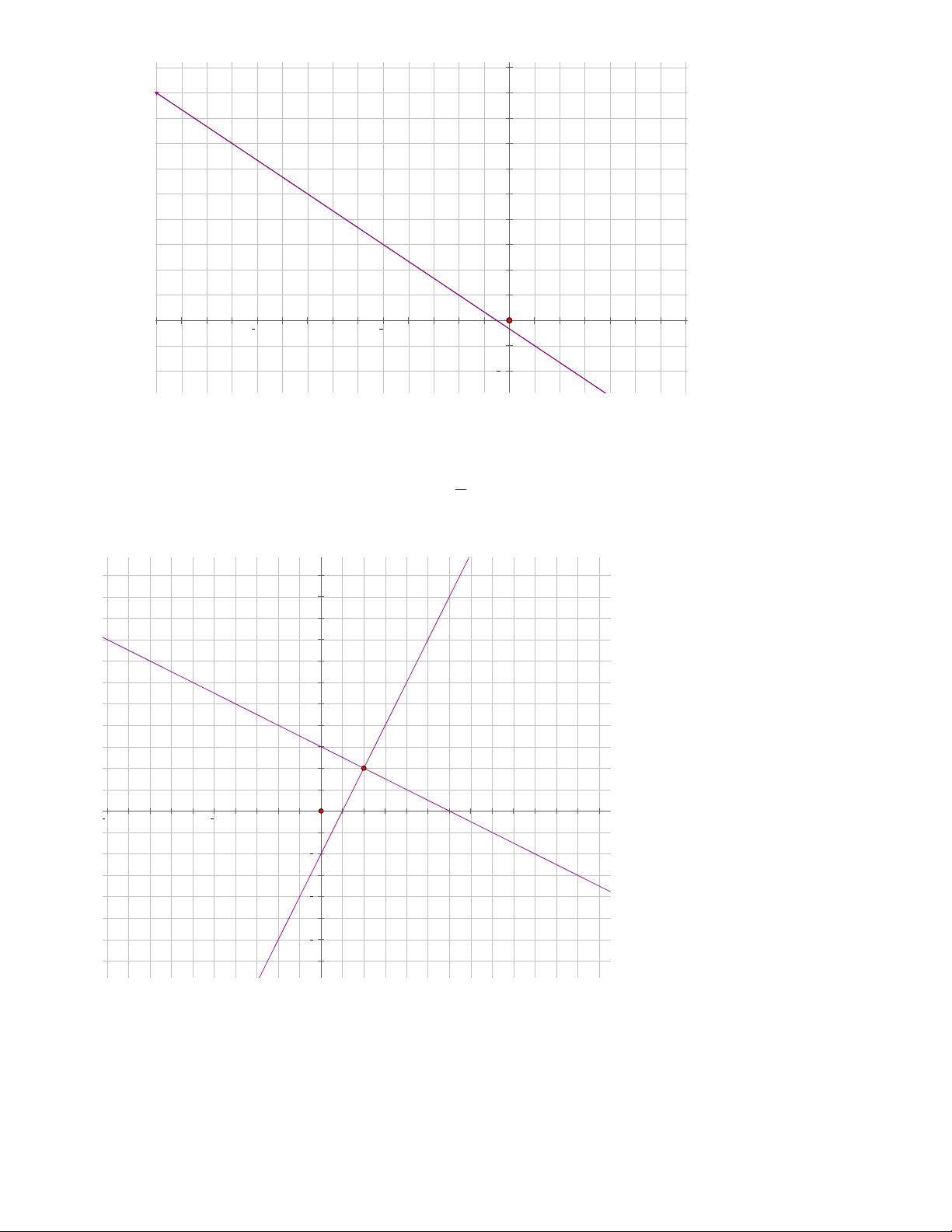
Bài 15. Cho hai đường thẳng: d : 2x 3y 8 và d : 7x  5y   5 2  1 
a) Vẽ đồ thị của hai phương trình trên cùng một hệ tọa độ rồi xác định nghiệm chung của hai phương trình.
b) Tìm các giá trị của a để đường thẳng y  ax đi qua giao điểm của d và d 2  1 
Dạng 2: Hai hệ phương trình tương đương
Bài 16. Trong các câu sau, câu nào đúng, câu nào sai?
a) Hai hệ phương trình bậc nhất hai ẩn vô nghiệm là hai hệ phương trình tương đương với nhau.
b) Hai hệ phương trình bậc nhất hai ẩn cùng vô số nghiệm là hai hệ phương trình tương đương.
c) Hai hệ phương trình bậc nhất hai ẩn cùng có một nghiệm là hai hệ phương trình tương đương.
Bài 17. Trong các trường hợp sau, hai hệ phương trình nào tương đương với nhau? Không tương đương với nhau? x  2y  2 x  2y  3 x  y  4 x  4 a)  và  b)  và  3x  6y  7 -4x 8y  4 3x 3y  12 3x  4y  2 2x 3y 1 3x   y  8  c)  và  -x  1,5y   0,5 y   2
5. TOÁN HỌC SƠ ĐỒ ‐ THCS.TOANMATH.com
Bài 18. Xác định a để hai hệ phương trình sau tương đương. ìïx- y = 1 ìï - = ï vaø ax 2y 2 ï í í ï2x + y = 2 ïx + ay = 1 ïî ïî
Bài 19. Xác định a để hai hệ phương trình sau tương đương. ìï2x-3y = 5 ìï - = ï vaø 2x 3y 5 ï í í ï4x + y = 3 1
ï 2x + 3y = a ïî ïî
Bài 20. Xác định a để hai hệ phương trình sau tương đương. ìïx-y = 2 ìï - = ï vaø 2ax 2y 1 ï í í ï3x + y = 1 ïx + ay = 2 ïî ïî
6. TOÁN HỌC SƠ ĐỒ ‐ THCS.TOANMATH.com HƯỚNG DẪN
Dạng 1: Đoán nhận số nghiệm của hệ phương trình
Bài 1. Nối mỗi hệ phương trình với một cặp số tương ứng mà nó nhận làm nghiệm: 1 – ;
b 2 – a;3 – d; 4 – c;
Bài 2. Cặp số 3; 
1 có là nghiệm của hệ phương trình:  2    3x   y  8 1 x  3y 3 2 a)  và d)  7x  2y 19 x  
 2  1y 4 2
Bài 3. Không cần vẽ hình, hãy cho biết số nghiệm của mỗi hệ phương trình sau đây và giải thích vì sao.
a) Xét (d) : y = 3-2x có a = 2; - b = 3 ;
(d )’: y = 3x – 1có a’= 3; b’=-1;
Có a ¹ a’  (d) caét (d )ʹ; ìïy = 3-2x  Hệ ïí ; có nghiệm duy nhất. ïy = 3x-1 ïî b) Xét (d) 1 y = - x + coù 1 : 3 a = - ; b = 3 ; 2 2 (d ) 1
y = - x + có 1 ’ : 1 a’ = ; b’ = 1 ; 2 2
Có a = a’; b ¹ b’  (d) // (d )’; ìï 1 ïïy = x+3  ï Hệ 2 í vô nghiệm. ï 1 ïïy =- x+1 ïïî 2 ìï 3 ï ì ï = - ï2 = -3 y x y x ï ï c) Ta có 2 í  í ï3y = 2x ï 2 ïî ïïy = x ïïî 3 Xét (d) 3 y = - x coù 3 : a = - ; b = 0; 2 2
7. TOÁN HỌC SƠ ĐỒ ‐ THCS.TOANMATH.com (d ) 2 2 ’ : y =
x có a’ = ; b’ = 0 ; 3 3
Có a ¹ a’  (d) caét (d )ʹ; ìï2y = 3 - x  Hệ ïí có nghiệm duy nhất. ï3y = 2x ïî ìï3x- y = 3 ï ìïy = 3x- ï 3 d) Ta có ï í 1  í ïx- y = ï 1 ïy = 3x-3 ïî ïî 3
Nhận thấy hai đường thẳng trên trùng nhau ìï3x- y = 3 ï  Hệ ïí 1 có vô số nghiệm. ïx- y = ï 1 ïî 3
Bài 4. Đoán nhận số nghiệm của mỗi hệ phương trình sau, giải thích vì sao. ìïy = x - + 2 ìïx + y = 2 ìïy = x - + 2 ï a) Ta có: ï ï ï í  í  í 2 ; ï3x + 3y = 2 ï3y = -3x + 2 ïy = x - + ïî ïî ïïî 3 Xét (d) : y = x - + 2 coù a = -1; b = 2 ; (d ) 2
y = -x + có a = - 2 ’ : ’ 1; b’ = ; 3 3
Có a = a’; b ¹ b’  (d) // (d )’; ìïx+ y = 2  Hệ ïí vô nghiệm. ï3x +3y = 2 ïî ìï 3 1 ï ìï - = ì ï = - 3 2 1 ï2 = 3 -1 y x x y y x ï ï ï b) Ta có: 2 2 í  í  í ; ï-6x + 4y = 0 ï4y = 6x ï 3 ïî ïî ïïy = x ïïî 2 Xét (d) 3 1 y = x - coù 3 a = 1 : ; b = - ; 2 2 2 2 (d ) 3 3 ’ : y = x coù a = ; b = 0 ; 2 2
8. TOÁN HỌC SƠ ĐỒ ‐ THCS.TOANMATH.com
Có a = a’; b ¹ b’  (d) // (d )’; ìï3x-2y = 1  Hệ ïí vô nghiệm. ï 6 - x + 4y = 0 ïî ìï 1 ï ìï - = ì ï = - 4 4 2 ï4 = 4 -2 y x x y y x ï ï ï c) Ta có: 2 í  í  í ;
ï-2x + 2y = -1 ï2y = 2x-1 ï 1 ïî ïî ïïy = x- ïïî 2
Nhận thấy hai đường thẳng trên trùng nhau; ìï4x-4y = 2  Hệ ïí có vô số nghiệm. ï 2 - x + 2y = 1 - ïî ìï 1 2 ìï1 2 ìï 1 2 ï ïï - = ï ïy = x- ï = - ï d) Ta có: x y y x 3 3 í3 3  í 3 3  í ; ï ï ï 1 2 ïïx 3y 2 ï î ï3y x 2 ï - = = - î ïy = x- ïïî 3 3
Nhận thấy hai đường thẳng trên trùng nhau; ìï1 2 ïï - =  Hệ x y í3 3 có vô số nghiệm. ïïïx-3y = 2 î
Bài 5. Hãy kiểm tra xem mỗi cặp số sau có phải là một nghiệm của hệ phương trình tương ứng hay không. 7 ìï x-5y = 5 - 3 a) Thay ï x = 4
- ; y = 5 vào từng phương trình của hệ í ta được: ï 2 - x + 9y = 53 ïî 7. ìïï ( 4) 5.5 53 ìï-28-25 = 53 ï - - = - ï í  í - ïï 2.(-4)+9.5 53 8 ï + 45 = 53 ï ï = î î 7 ìï x-5y = 5 - 3 Vậy cặp (- ï 4 ; )
5 là nghiệm của hệ phương trình í . ï 2 - x +9y = 53 ïî 0, ìï 2x+1,7y = 1 - 8,1 b) Thay ï x = 3 ; y = 1
- 1 vào từng phương trình của hệí ta được: ï3,2x- y = 20,6 ïî 0 ìï ,2.3+1,7 (- ) 11 = -18, 1 0 ìï ï ,6 – 18,7 = -18,1 ï í  í ïï3,2.3 11= 20,6 9, ï 6 +11= 20,6 î + ïî
9. TOÁN HỌC SƠ ĐỒ ‐ THCS.TOANMATH.com 0, ìï 2x+1,7y = 1 - 8,1 Vậy cặp ( ï 3 ; -1 )
1 là nghiệm của hệ phương trình í . 3, ï 2x- y = 20,6 ïî 10 ìï x-3y = 9 c) Thay ï
x = 1,5 ; y = 2 vào từng phương trình của hệ í ta được: ï 5 - x +1,5y = 4 - ,5 ïî 10.1 ìï , 5 – 3.2 = 9 15 ìï – 6 = 9 ï ï í  í . ï 5 - .1,5+1,5.2 = 4 - ,5 ï 7,5 3 4, 5 ï = - î + î- ï 10 ìï x-3y = 9 Vậy cặp 1,
( 5 ; 2) là nghiệm của hệ phương trình íï . ï 5 - x +1,5y = 4 - ,5 ïî 10 ìï x-3y = 9 Thay ï
x = 3 ; y = 7 vào từng phương trình của hệ í ta được: ï 5 - x +1,5y = 4 - ,5 ïî 10.3 ìï – 3.7 = 9 ìï30 - 21 = 9 ï ï í  í ï-5.3 +1,5.7 = -4,5 ï-15 + 10,5 = -4,5 ïî ïî 10 ìï x-3y = 9 Vậy cặp ( ï
3 ; 7) là nghiệm của hệ phương trìnhí . ï 5 - x +1,5y = 4 - ,5 ïî ìï5x+ 2y = 9 d) Thay ï x =
1 ; y = 8 vào từng phương trình của hệ í , ta được: ïx-14y = 5 ïî ìï5. 1 + 2.8 = 21 ìï5 + 16 = 21 ï ï í  í 1 ï -14.8 = 5 1 ï -14.8 = 5 ï ï ( voâ ) lyù î î ìï5x+2y = 9 Vậy cặp ( ï
1 ; 8) không phải là nghiệm của hệ phương trình í . ïx-14y = 5 ïî Bài 6. ìï 4 1 ï ìï - = ì ï = - 4x 9y 3 9 ï y = 4x-3 y x ï ï ï a) Ta có: 9 3 í  í  í
ï-5x-3y = 1 ï3y = -5x-1 ï 5 1 ïî ïî ïïy =- x- îïï 3 3 4 5 ¹ - Vì 9
3 nên hai đường thẳng cắt nhau.
Vậy hệ phương trình có nghiệm duy nhất. ìï 23 25
ìï2,3x+0,8y = 5 0, ìï 8y = 2 - ,3x + 5 ï ï ï ïy = - x + b) Ta có: í  í  í 8 4 ; ï2y 6 ïy = 3 ï ïî = ïî ïïy = 3 î 23 25 y = - x + Đường thẳng 8
4 cắt hai trục tọa độ mà đường thẳng y = 3 song song với trục hoành nên 2
đường thẳng trên cắt nhau.
Vậy hệ phương trình có nghiệm duy nhất.
10. TOÁN HỌC SƠ ĐỒ ‐ THCS.TOANMATH.com ìï 5 ìï 5 ï ìï = - ï ï = - 3x 5 x ï ï = - ï c) Ta có: x 3 í  í 3  í ; ïx + 5y = -4 ï ï 1 4 ïî ïï5y = x - - 4 ï î ïy = - x- ïïî 5 5 5 1 4 x = - y = - x - Đường thẳng
3 song song với trục tung mà đường thẳng 5
5 cắt hai trục tọa độ nên 2
đường thẳng đó cắt nhau;
Vậy hệ phương trình có nghiệm duy nhất. ìïy = 3x-1 ìï3x- y = 1 ìïy = 3x-1 ï d) Ta có: ï ï ï í  í  í 5 6 ï x-2y = 5 ï2y = 6x-5 ï î î y = 3x - ï ï ïïî 2 5 -1 ¹ -
Hai đường thẳng có hệ số góc bằng nhau vì cùng bằng 3, có tung độ gốc khác nhau: 2 nên chúng
song song với nhau. Nên hệ vô nghiệm;
Vậy hệ phương trình đã cho vô nghiệm.
Bài 7. Đoán nhận số nghiệm của mỗi hệ phương trình sau, giải thích vì sao:
ìï2x+ y = 3 ìïy = 2 - x + 3 a) Ta có: ï ï í  í ; ï3x- y = 1 ïy = 3x-1 ïî ïî
Vì -2 ¹ 3 nên hai đường thẳng cắt nhau. ìï2x+ y = 3
Vậy hệ phương trình ïí có nghiệm duy nhất. ï3x- y = 1 ïî ìï 3 ï ìï + = ì ï = - 3 2 0 ï2 = 3 y x x y y - x ï ï ï b) Ta có: 2 í  í  í ; ï2x-3y = 0 ï3y = 2x ï 2 ïî ïî ïïy = x ïïî 3 3 2 - ¹ Vì 2
3 nên hai đường thẳng cắt nhau. ìï3x+2y = 0
Vậy hệ phương trình ïí có nghiệm duy nhất. ï2x-3y = 0 ïî
ìï3x+0y = 6 ìï3x = 6 ìïx = 2 c) Ta có: ï ï ï í  í  í ; ï2x+ y = 1 ïy = 2 - x +1 ïy = 2 - x +1 ïî ïî ïî = - +
Đường thẳng x = 2 song song với trục tung mà đường thẳng y
2x 1 cắt hai trục tọa độ nên 2
đường thẳng đó cắt nhau; ìï3x+0y = 6
Vậy hệ phương trình ïí có nghiệm duy nhất. ï2x+ y = 1 ïî ìïx-y = 4 ìïy = x-4 d) Ta có: ï ï í  í ; 0 ï x- y = 2 ïy = 2 - ïî ïî = - Đường thẳng y
x 4 cắt hai trục tọa độ mà đường thẳng y = 2
- song song với trục hoành nên 2
đường thẳng trên cắt nhau.
11. TOÁN HỌC SƠ ĐỒ ‐ THCS.TOANMATH.com ìïx-y = 4
Vậy hệ phương trình ïí có nghiệm duy nhất. 0 ï x- y = 2 ïî ìï 1 3 ï ìï + = ì ï = - + 2 3 ï2 = - + 3 y x x y y x ï ï ï e) Ta có: 2 2 í  í  í ;
ï2x + 4y = 1 ï4y = -2x +1 ï 1 1 ïî ïî ïïy =- x+ ïïî 2 4 1 3 ¹
Hai đường thẳng có hệ số góc bằng nhau vì cùng bằng 1
- , có tung độ gốc khác nhau: 4 2 nên chúng 2
song song với nhau. Nên hệ vô nghiệm; ìïx+2y = 3
Vậy hệ phương trình ïí vô nghiệm. ï2x+ 4y = 1 ïî ìïx + y = 1 ï ìïy = x - +1 ìïy = x - + ï 1 f) Ta có: ï ï íx y 1  í  í ; ï + = ïx + y = 1 ïy = x - +1 ï ïî ïî ïî2 2 2
Nhận thấy hai đường thẳng trên trùng nhau; ìïx + y = 1 ï
Vậy hệ ïíx y 1 có vô số nghiệm. ï + = ïïî2 2 2 Bài 8. ìï3x-y = 1 3 ìï x-y = 1 a) Thay ï ï
a = -2 vào hệ phương trình í , ta được: ï í ax + 2y = 3 ïî ï 2 - x + 2y = 3 ïî
Do 3x- y = 1  y = 3x-1 nên tập nghiệm của phương trình thứ nhất được biểu diễn bởi đường thẳng
(d ): y = 3x-1; 1 Do 3
-2x + 2y = 3  2y = 2x + 3  y = x + nên tập nghiệm của phương trình thứ nhất được biểu diễn 2
bởi đường thẳng (d ) 3 : y = x + ; 2 2
Hai đường thẳng (d và (d có hệ số góc khác nhau (1 ¹ 3 ) nên chúng cắt nhau. Do đó hệ 2 ) 1 ) ìï3x-y = 1 ïí có nghiệm duy nhất; ï 2 - x + 2y = 3 ïî ìï3x-y = 1 Vậy với ï
a = -2 thì hệ phương trình í có nghiệm duy nhất. ïax+ 2y = 3 ïîìï3x-y=1 ìï3x-y = 1 b) Thay ï ï
a = -6 vào hệ phương trình í , ta được: ï í ax + 2y = 3 ïî ï 6 - x + 2y = 3 ïî
Do 3x- y = 1  y = 3x-1 nên tập nghiệm của phương trình thứ nhất được biểu diễn bởi đường thẳng
(d ): y = 3x-1; 1
12. TOÁN HỌC SƠ ĐỒ ‐ THCS.TOANMATH.com Do 3
-6x + 2y = 3  2y = 6x + 3  y = 3x + nên tập nghiệm của phương trình thứ nhất được biểu 2
diễn bởi đường thẳng (d ) 3 : y = 3x + ; 3 2
Hai đường thẳng (d và (d có tung độ góc khác nhau ( 3
-1 ¹ ) và có cùng hệ số góc là 3 nên song 3 ) 1 ) 2 ìï3x-y = 1
song với nhau. Do đó, hệ ïí vô nghiệm; ï 6 - x + 2y = 3 ïî ìï3x-y = 1 Vậy với ï
a = -6 thì hệ phương trình í vô nghiệm. ïax+ 2y = 3
ïî ìï3x-2y=a
Bài 9. Chứng tỏ rằng hệ phương trình: ïí ; 15 ï x +10y = 5 ïî
a) Có vô số nghiệm với a = 1 ;
b) Vô nghiệm với a = 1
ìï3x-2y = a ìï3x-2y = 1 a) Thay ï ï
a = 1 vào hệ phương trình í , ta được: í ; 15 ï x +10y = 5 ïî 15 ï x+10y = 5 ïî Do 3 1
3x - 2y = 1  2y = 3x -1  y =
x - nên tập nghiệm của phương trình thứ nhất được biểu diễn 2 2
bởi đường thẳng (d ) 3 1 : y = x - ; 1 2 2 Do 3 1
15x -10y = 5  10y = 15x - 5  y =
x - nên tập nghiệm của phương trình thứ nhất được biểu 2 2
diễn bởi đường thẳng (d ) 3 1 : y = x - ; 2 2 2 - -
Hai đường thẳng (d và (d có tung độ góc bằng nhau ( 1 1 ¹
) và có cùng hệ số góc là 3 nên hai 2 ) 1 ) 2 2 2 ìï3x-2y = 1 đường thẳng ( ï
d và (d trùng nhau. Do đó, hệ í có vô số nghiệm; 2 ) 1 ) 15 ï x+10y = 5 ïî ìï3x-2y = 1 Vậy với ï
a = 1 thì hệ phương trình í có vô số nghiệm. 15 ï x +10y = 5 ïî
ìï3x-2y = a
b) Xét hệ phương trình ïí ; 15 ï x +10y = 5 ïî Do 3 a
3x - 2y = a  2y = 3x - a y = x -
nên tập nghiệm của phương trình thứ nhất được biểu diễn 2 2 bởi đường thẳng ( ) 3 a d : y = x - ; 2 2 Do 3 1
15x -10y = 5  10y = 15x - 5  y =
x - nên tập nghiệm của phương trình thứ nhất được biểu 2 2
diễn bởi đường thẳng (d ) 3 1 : y = x - ; 2 2 2
13. TOÁN HỌC SƠ ĐỒ ‐ THCS.TOANMATH.com - Hai đường thẳng ( 1 a
d) và (d có tung độ góc khác nhau ( ¹ vì a ¹
1 (baøi cho) ) và có cùng hệ số góc 3 ) 2 2
ìï3x-2y = a
là 3 nên song song với nhau. Do đó, hệ ïí
vô nghiệm với mọi a ¹ 1 ; 2 15 ï x+10y = 5 ïî ìï3x-y = 1 Vậy với ï
a = -6 thì hệ phương trình í vô nghiệm. ïax+ 2y = 3 ïî ìï3x-y = 1 Vậy với ï
a ¹ 1 thì hệ phương trình í vô nghiệm. ïax + 2y = 3 ïî
Bài 10. Cho các hệ phương trình sau: ìïx = 2 ìïx = 2 ï ï í  í ï - = ï = - a) Ta có: 2x y 3 y 2x 3 ïî ïî ;
Đường thẳng x = 2 song song với trục tung mà đường thẳng y = 2x-3 cắt hai trục tọa độ nên 2 đường
thẳng đó cắt nhau; ìïx=2 ïíï - =
Vậy hệ phương trình 2x y 3 ïî có nghiệm duy nhất. ìï 1 2
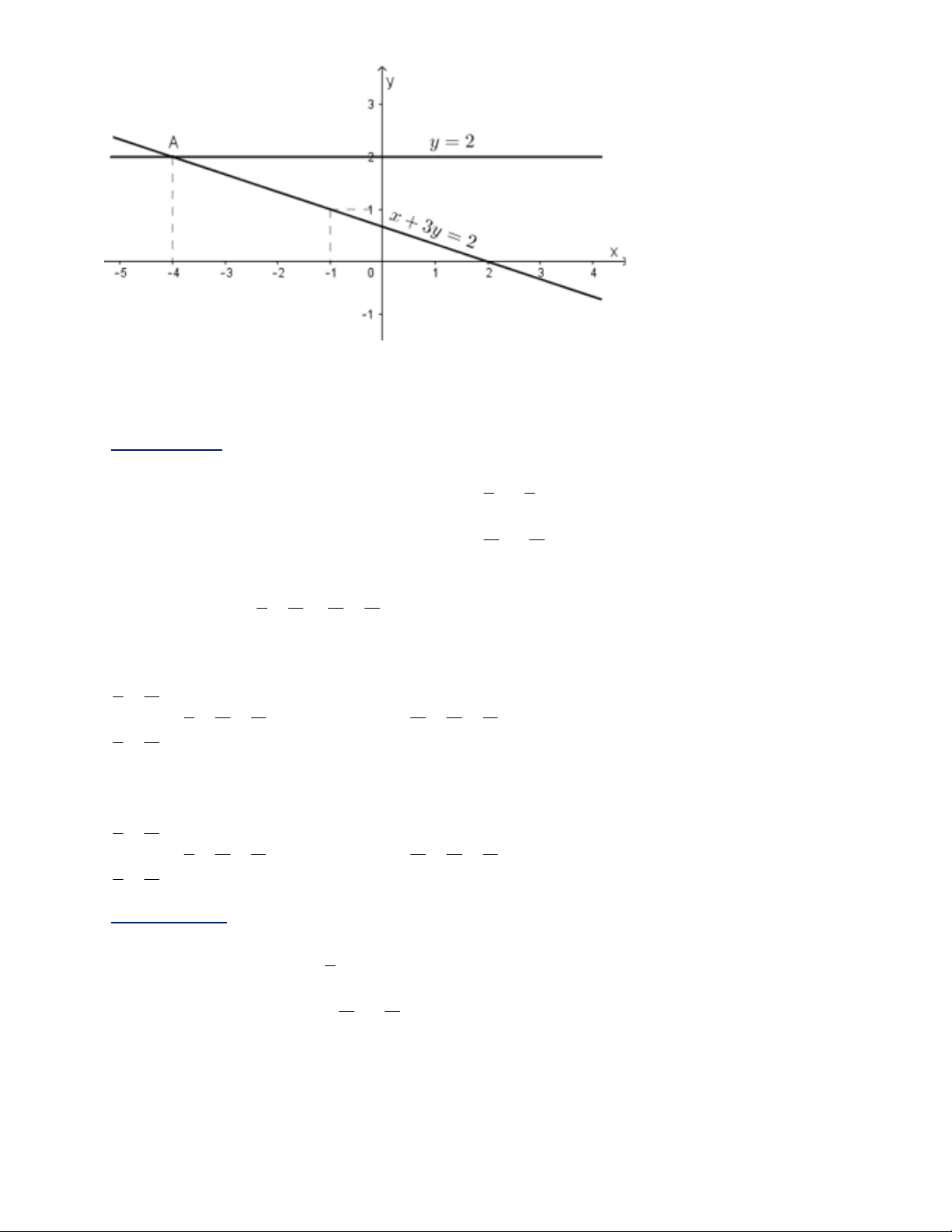
ìïx + 3y = 2 ìï3y = x - + 2 ï ï ï ïy = - x + í  í  í 3 3 ï2y = 4 ïy = 2 ï ïî ïî ïï = b) Ta có y 2 î ; 1 2 y = - x + Đường thẳng 3
3 cắt hai trục tọa độ mà đường thẳng y = 2 song song với trục hoành nên 2
đường thẳng trên cắt nhau. ìïx+3y = 2 ïíï =
Vậy hệ phương trình 2y 4 ïî có nghiệm duy nhất.
14. TOÁN HỌC SƠ ĐỒ ‐ THCS.TOANMATH.com
Bài 11. Dựa vào vị trí tương đối của hai đường thẳng dưới đây, hãy tìm mối lien hệ giữa các hằng số
ìïax+by = c ï
a, b, c và các hằng số aʹ; bʹ; cʹ để hệ phương trình í
ïaʹx +bʹ y = cʹ ïî
*Trường hợp 1: a; b; aʹ; bʹ ¹ 0 ìï a c ï ìï + = ì ïy = - x + ax by c b ï y = a - x + c ï ï ï Ta có: b b í  í  í
ïaʹ x +bʹ y = cʹ b ï ʹ y = a - ʹ x + cʹ ï aʹ c ʹ ïî ïî ïïy =- x+ ïïî bʹ bʹ
a) Hệ phương trình có một nghiệm duy nhất khi hai đường thẳng cắt nhau. Nghĩa là hai đường thẳng có
hệ số góc khác nhau: a aʹ a b ¹  ¹ b bʹ aʹ bʹ
b) Hệ phương trình vô nghiệm khi hai đường thẳng song song nhau. Nghĩa là hai đường thẳng có hệ số
góc bằng nhau và tung độ gốc khác nhau: ìïa aʹ ïï = ïb bʹ a aʹ c í  = ¹ ( neáu a c c ʹ ¹ 0) hoaëc ʹ bʹ ʹ = ¹ ( neáu c¹ 0) ïc c ʹ ï b bʹ c ʹ a b c ï ¹ ïïîb bʹ
c) Hệ phương trình có vô số nghiệm khi hai đường thẳng trùng nhau. Nghĩa là hai đường thẳng có hệ số
góc và tung độ gốc bằng nhau: ìïa aʹ ïï = ïb bʹ a aʹ c í  = = ( neáu a c c ʹ ¹ 0) hoaëc ʹ bʹ ʹ = = ( neáu c¹ 0) ïc c ʹ ï b bʹ c ʹ a b c ï = ïïîb bʹ
* Trường hợp 2: a = 0; aʹ ¹ 0 ìï c ï ì ïy =
ïax + by = c ï ï Ta có: b í  í ( vôùi b'¹ ) 0
ïaʹx +bʹ y = cʹ ï aʹ c ʹ ïî ïïy =- x+ ïïî bʹ bʹ
15. TOÁN HỌC SƠ ĐỒ ‐ THCS.TOANMATH.com ìï c ï ì ïy =
ïax + by = c ï ï hoặc b í  í ( vôùi bʹ = 0)
ïaʹx +bʹ y = cʹ ï c ʹ ïî ïïx = ïïî aʹ Vì hai đường thẳng aʹ c ʹ y = - x + vaø c ʹ x =
luôn luôn cắt trục hoành còn đường thẳng c y = song song bʹ bʹ aʹ b
hoặc trùng với trục hoành nên chúng luôn luôn cắt nhau.
Vậy hệ phương trình chỉ có một nghiệm duy nhất.
* Trường hợp 3: a = aʹ = 0 ìï c ï ì ïy =
ïax + by = c ï ï Ta có: b í  í
ïaʹx +bʹ y = cʹ ï c ʹ ïî ïïy = ïïî bʹ
Hệ có vô số nghiệm khi hai đường thẳng trùng nhau, nghĩa là: c c ʹ b c =  = b bʹ bʹ c ʹ
Hệ vô nghiệm khi hai đường thẳng song song nhau, nghĩa là: c c ʹ b c ¹  ¹ b bʹ bʹ c ʹ
* Trường hợp 4: b = 0; bʹ ¹ 0 ìï c ï ì ïx =
ïax + by = c ï ï Ta có: a í  í (với ¹ ) ï a ʹ 0
aʹ x + bʹ y = c ʹ ï aʹ c ʹ ïî ïïy =- x+ ïïî bʹ bʹ ìï c ï ì ïx =
ïax + by = c ï ï hoặc a í  í (với ) ï a ¹ 0
aʹ x + bʹ y = c ʹ ï c ʹ ïî ïïy = ïïî bʹ Vì hai đường thẳng aʹ c ʹ y = - x + vaø c ʹ y =
luôn luôn cắt trục tung còn đường thẳng c x = song song bʹ bʹ bʹ a
hoặc trùng với trục tung nên chúng luôn luôn cắt nhau.
Vậy hệ phương trình chỉ có một nghiệm duy nhất.
* Trường hợp 5: b = bʹ = 0 ìï c ï ì ïx =
ïax + by = c ï ï Ta có: a í  í (với ¹ ) ï aʹ 0
aʹ x + bʹ y = c ʹ ï c ʹ ïî ïïx = ïïî aʹ
Hệ có vô số nghiệm khi hai đường thẳng trùng nhau, nghĩa là: c c ʹ a c =  = a aʹ aʹ cʹ
Hệ vô nghiệm khi hai đường thẳng song song, nghĩa là: c c ʹ a c ¹  ¹ a aʹ aʹ cʹ Áp dụng:
a) Hệ hai phương trình bậc nhất hai ẩn có nghiệm duy nhất: ìï2x+3y = 8 ïí ïx + y = 4 ïî
b) Hệ hai phương trình bậc nhất hai ẩn vô nghiệm:
16. TOÁN HỌC SƠ ĐỒ ‐ THCS.TOANMATH.com ìï2x+3y = 8 ïí ï4x +6y = 4 ïî
c) Hệ hai phương trình bậc nhất hai ẩn có vô số nghiệm: ìï2x+ y = 5 ïí ï4x + 2y = 10 ïî
17. TOÁN HỌC SƠ ĐỒ ‐ THCS.TOANMATH.com
Dạng 2: Giải hệ phương trình bằng phương pháp hình học
Bài 12. Cho hai phương trình: 3x  y 1 và -5x  2y 3
a) Nghiệm tổng quát của mỗi phương trình 3x  y 1 là :  x; 3x   1  5 3 
Nghiệm tổng quát của mỗi phương trình -5x  2y 3 là : ; x x     2 2 
b) Vẽ đồ thị của hai phương trình trên cùng một hệ tọa độ rồi xác định nghiệm chung của hai phương trình. 5 3
3x  y 1 y  3
 x 1 và 5x  2y 3 y   x  2 2 6 4 A 2 10 5 5 2
y = -5/2x+3/2 4 y = -3x+1 6 8 10 12
Vậy nghiệm của hệ phương trình là: 1;4
Bài 13. Bằng cách vẽ đồ thị, hãy giải các hệ phương trình: y x 1 x  y 1  a)    1  x 3y 9 y x  3  3
18. TOÁN HỌC SƠ ĐỒ ‐ THCS.TOANMATH.com 8
y = 1/3x+3 6 4 2 10 5 5 10 2
y = x-1
Vậy nghiệm của hệ phương trình là: 3;2  1 y x  2 x  2y  4  b) 2    2x  4y 10 1  5  y x   2 2 10 8 6
y = -1/2x+2 4 2
y = -1/2x-5 10 5 5 10 2
Vậy hệ phương trình vô nghiệm.  2  1 y x  1,  5y  x  0  ,5  c) 3 3    2x  3y  1 2  1  y x   3 3
19. TOÁN HỌC SƠ ĐỒ ‐ THCS.TOANMATH.com 10 8
y = -2/3x-1/3 6
y = -2/3x-1/3 4 2 10 5 5 2
Vậy hệ phương trình có vô số nghiệm.
y  2x  2 2x  y  2 
Bài 14. Cho hệ phương trình    1 x  2y 6 y x  3  2
a) Giải hệ phương trình đã cho bằng phương pháp đồ thị 10 8
y = -1/2x+3 6 y = 2x-2 4 2 A 10 5 5 10 2 4 6
Vậy nghiệm của hệ phương trình là: 2;2
b) Nghiệm của hệ phương trình đã cho không là nghiệm của phương trình 3x  2y  8 
c) Nghiệm của hệ phương trình đã cho không là nghiệm của phương trình 4,5x  7,5 y  25.
Bài 15. Cho hai đường thẳng: d : 2x 3y 8 và d : 7x  5y   5 2  1 
20. TOÁN HỌC SƠ ĐỒ ‐ THCS.TOANMATH.com 8 6
y = 7/5x+1 4 2 10 5 5 10 2
y = 2/3x-8/3 4 6 8
Vậy nghiệm của hệ phương trình là: M 5;6
b) Để đường thẳng y  ax đi qua giao điểm của d và d thì tọa độ điểm M phải thỏa mãn phương 2  1  6
trình, ta có: 6  a(-5)  a  5
Dạng 2: Hai hệ phương trình tương đương
Bài 16. Trong các câu sau, câu nào đúng, câu nào sai?
Câu a là khẳng định đúng
Câu b; c là khẳng định sai
Bài 17. Trong các trường hợp sau, hai hệ phương trình nào tương đương với nhau? Không tương đương với nhau? x  2y  2 x  2y  3 a)  và  3x  6y  7 -4x 8y 8
Hai hệ phương trình được viết lại như sau: x  2y  2 x  2y  3  và  3x  6y  7 x  2y  1
Hai hệ phương trình tương đương với nhau, vì cùng có tập nghiệm là S   x  y  4 x  4 b)  và  3x 3y  12 3x  4y  2
Hai hệ phương trình được viết lại như sau:
21. TOÁN HỌC SƠ ĐỒ ‐ THCS.TOANMATH.com x  4 x  y  4   và  3 1 x  y   4 y x   4 2
Ta thấy hệ phương trình thứ nhất có vô số nghiệm, còn hệ thứ hai có nghiệm duy nhất, nên hai hệ
phương trình không tương đương với nhau. 2x 3y 1 3x   y  8  c)  và 
-x 1,5y   0,5 y  2
Tương tự như câu b , Ta có hai hệ phương trình đã cho không tương đương nhau. Bài 18. ìïx-y = 1
Ta thấy hệ phương trình ïí có nghiệm (1; 0) 2 ï x + y = 2 ïî ìïax-2y = 2
Để hai hệ đã cho tương đương nhau thì nghiệm ( ï
1; 0)phải là nghiệm của hệ í ïx + ay = 1 ïî ìï .1 a - 2.0 = 2 Khi đó ta có ïí  a = 2 1 ï + .a0 = 1 ïî ìï2x-2y = 2 Ngược lại với ï
a = 2 thì hệ thứ hai trở thành: í có nghiệm (1; 0) ïx +2y = 1 ïî
Vậy với a = 2 thì hai hệ phương trình đã cho tương đương. Bài 19. ìï2x-3y = 5
Ta thấy hệ phương trình ïí có nghiệm (1; - ) ï 1 4x + y = 3 ïî ìï2x-3y = 5
Để hai hệ đã cho tương đương nhau thì nghiệm ( ï 1; - )
1 phải là nghiệm của hệ í 12
ï x + 3y = a ïî ìï2.1-3. ï (- ) 1 = 5 Khi đó ta có ïí  = ï + (- ) a 9 12.1 3. 1 = ï a ïî ìï2x-3y = 5 Ngược lại với ï
a = 9 thì hệ thứ hai trở thành: í có nghiệm (1; - ) 1 12 ï x + 3y = 9 ïî
Vậy với a = 9 thì hai hệ phương trình đã cho tương đương. Bài 20. ìïx- y = 2
Ta thấy hệ phương trình ïí có nghiệm (3; ) ï 1 3x + y = 10 ïî ìï2ax-2y = 1
Để hai hệ đã cho tương đương nhau thì nghiệm ( ï 3; )
1 phải là nghiệm của hệ í ïx+ ay = 2 ïî ìï2 .a3-2.1= 1 6 ìï a = 3 ìïa = 2 Khi đó ta có ï ï ï í  í  í ( voâ nghieäm) ï3+ . a 1 = 2 ïa = 1 - ïa = 1 - ïî ïî ïî ìïx- y = 2 ìï2ax-2y = 1
Vậy không có giá trị nào của ï ï
a để hai hệ phương trình í vaø í tương đương. ï3x + y = 10 ïx + ay = 2 ïî ïî
22. TOÁN HỌC SƠ ĐỒ ‐ THCS.TOANMATH.com
C.TRẮC NGHIỆM RÈN LUYỆN PHẢN XẠ ax ìï +by = c
Câu 1. Hệ phương trình ïí có nghiệm duy nhất khi a ï x ¢ + b y ¢ = c¢ ïî a b a b a b c b c A. ¹ . B. = . C. = ¹ . D. ¹ . a¢ b¢ a¢ b¢ a¢ b¢ c¢ b¢ c¢ ax ìï +by = c
Câu 2. Hệ phương trình ïí a ï x ¢ + b y ¢ = c¢ ïî
(các hệ số a ;¢b ;¢c¢ khác 0 ) vô số nghiệm khi a b a b c a b c b c A. ¹ . B. = = . C. = ¹ . D. ¹ . a¢ b¢ a¢ b¢ c¢ a¢ b¢ c¢ b¢ c¢ ax ìï +by = c
Câu 3. Hệ phương trình bậc nhất hai ẩn ïí
(có hệ số khác 0 ) vô nghiệm khi a ï x ¢ + b y ¢ = c¢ ïî a b a b c a b c b c A. = . B. = ¹ . C. ¹ ¹ . D. = . a¢ b¢ a¢ b¢ c¢ a¢ b¢ c¢ b¢ c¢ ax ìï +by = c a b c
Câu 4. Hệ phương trình ïí
có các hệ số khác 0 và  = ¹ . Chọn câu đúng. a ï x ¢ + b y ¢ = c¢ ï ¢ ¢ ¢ î a b c
A. Hệ phương trình có nghiệm duy nhất.
B. Hệ phương trình vô nghiệm.
C. Hệ phương trình vô số nghiệm.
D. Chưa kết luận được về nghiệm của hệ. 2 ìï x + 3y = 3
Câu 5. Hệ phương trình ïí
nhận cặp số nào sau đây là nghiệm. ï-4x - 5y = 9 ïî A. (-21;15). B. (21;-15) .
C. (1;1). D. (1;-1) . 5 ìï x + y = 7
Câu 6. Hệ phương trình ïí
nhận cặp số nào sau đây là nghiệm. ï x - - 3y = 21 ïî
A. (1;2). B. (8;-3) . C. (3;-8) . D. (3; 8).
Câu 7. Cặp số (-2;-3) là nghiệm của hệ phương trình nào sau đây? x ìï - y = 3 2 ìï x - y = -1 2 ìï x - y = -1 4 ìï x - 2y = 0 A. ïí . B. ïí . C. ïí . D. ïí . 2 ï x + y = 4 ï ï - = ï - = ï - = î x 3y 8 ïî x 3y 7 ïî x 3y 5 ïî
Câu 8. Cặp số (3;-5) là nghiệm của hệ phương trình nào sau đây?
23. TOÁN HỌC SƠ ĐỒ ‐ THCS.TOANMATH.com x ìï - 3y = 1 3 ìï x + y = 4 y ìï = -1 4 ìï x - y = 0 A. ïí . B. ïí . C. ïí . D. ïí . x ï + y = 2 ï ï - = ï - = ï - = î 2x y 11 ïî x 3y 5 ïî x 3y 0 ïî ìï 2 - x + y = 3 -
Câu 9. không giải hệ phương trình, dự đoán số nghiệm của hệ ïí . 3 ï x - 2y = 7 ïî
A. Vô số nghiệm. B. Vô nghiệm.
C. Có nghiệm duy nhất. D. Có hai nghiệm phân biệt. ìï x - + 5y = -1
Câu 10. Không giải hệ phương trình, dự đoán số nghiệm của hệïí . 5 ï x + y = 2 ïî
A. Vô số nghiệm. B. Vô nghiệm.
C. Có nghiệm duy nhất. D. Có hai nghiệm phân biệt. x ìï + y = -1
Câu 11. Xác định giá trị của tham số m để hệ phương trình ïí vô nghiệm. mx ï + y = 2m ïî 1 A. m = 1. B. m = -1 . C. m = 0 . D. m = . 2 2 ìï x - y = 4
Câu 12. Xác định giá trị của tham số m để hệ phương trình ïí vô nghiệm. ( ï m - )
1 x + 2y = m ïî A. m = 1. B. m = -1 . C. m = 3 . D. m = -3 .
ìïï 2x -2y = 3
Câu 13. Không giải hệ phương trình, dự đoán số nghiệm của hệ ïí 3 ïï 2x - 6y = 5 ïî A. Vô số nghiệm.
B. Vô nghiệm. C. Có nghiệm duy nhất. D. Có hai nghiệm phân biệt. x ìï = y -1 2 ìï x - 3y = 5
Câu 14. Cho hệ (I ) : ïí và hệ (II )ïí . Chọn kết luận đúng. y ï = x + 1 ï ï + = î 3y 5 2x ïî
A. Hai hệ đã cho đều vô nghiệm.
B. Hai hệ đã cho đều có nghiệm duy nhất.
C. Hệ (I) vô nghiệm, hệ (II) có nghiệm duy nhất. D. Hệ (I) và hệ (II) đều có vô số nghiệm. mx ìï - 2y = 1
Câu 15. Xác định giá trị của tham số m để hệ phương trình ïí có nghiệm duy nhất. 2 2
ï x - my = 2m ïî A. m ¹ 2 . B. m ¹ -2 . C. m = 2 . D. m ¹ 2 .
Câu 16.Xác định giá trị của tham số m để hệ phương trình x ìï -(m - ) 2 y = 2 ïí có nghiệm duy nhất (
ï m - 1)x - 2y = m - 5 ïî A. m ¹ 0 . B. m ¹ 2 . C. m ¹ {0; } 3 .
D. m = 0;m = 3 .
24. TOÁN HỌC SƠ ĐỒ ‐ THCS.TOANMATH.com ìï mx - + y = -2m
Câu 17. Cho hệ phương trình ïí
. Tìm các giá trị của tham số m để hệ phương trình 2 x ï + m y = 9 ïî
nhận cặp (1;2) làm nghiệm A. m = 0 . B. m = -1 . C. m = -2 . D. m = 3 . (
ìï m + 2)x + y = 2m - 8
Câu 18. Cho hệ phương trình ïí
. Tìm các giá trị của tham số để hệ phương trình 2 m ï x + 2y = -3 ïî
nhận cặp số (-1; 3) làm nghiệm. A. m = 0 . B. m = -2 . C. m = -3 . D. m = 3 . 3
ìï mx + y = -2m
Câu 19. Cho hệ phương trình: ïí
. Xác định các giá trị của tham số m để hệ
ï-3x - my = -1 + 3m ïî
phương trình vô số nghiệm. A. m = 0 . B. m = 1. C. m = 2 . D. m = 3 . ìï 15 5 ïï mx + 5y = -
Câu 20. Cho hệ phương trình: ïí 2
. Xác định các giá trị của tham số m để hệ phương
ïï-4x -my = 2m +1 ïî trình vô số nghiệm. A. m = 0 . B. m = 2 . C. m = -2 . D. m = -3 .
Câu 21. Bằng cách tìm giao điểm của hai đường thẳng d : -2x + y = 3 và ìï 2 - x + y = 3
d¢ : x + y = 5 ta tìm được nghiệm của hệ phương trình ïí là x ï + y = 5 ïî
(x ;y ). tính y - x . 0 0 0 0 11 13 17 A. . B. . C. 5 . D. . 3 3 3
Câu 22. Bằng cách tìm giao điểm của hai đường thẳng d : 4x + 2y = -5 và 4 ìï x + 2y = -5
d¢ : 2x - y = 1
- ta tìm được nghiệm của hệ phương trình ïí là 2 ï x - y = 1 - ïî
(x ;y ). tính x .y . 0 0 0 0 21 21 21 10 A. . B. - . C. . D. - . 32 32 8 12 mx ìï - 2y = 3m
Câu 23. Cho hệ phương trình ïí
. Tìm các giá trị của tham số 2
ï x - my = -4 - 4m ïî
25. TOÁN HỌC SƠ ĐỒ ‐ THCS.TOANMATH.com
m để hệ phương trình nhận cặp (-1;2) làm nghiệm. A. m = -1 . B. m = 1. C. m = -3 . D. m = 3 . HƯỚNG DẪN Câu 1. Đáp án C. ax ìï +by = c
Xét hệ phương trình bậc nhất hai ẩn ïí a ï x ¢ + b y ¢ = c¢ ïî a b
- Hệ phương trình có nghiệm duy nhất  ¹ a¢ b¢ a b c
- Hệ phương trình vô nghiệm  = ¹ a¢ b¢ c¢ a b c  = =
- Hệ phương trình có vô số nghiệm a¢ b¢ c¢ Câu 2. Đáp án B. ax ìï +by = c Hệ phương trình ïí
có vô số nghiệm khi hai đường thẳng d : ax + by = c a ï x ¢ + b y ¢ = c¢ ïî a b c và d¢ : a x ¢ +b y
¢ = c¢ trùng nhau, suy ra hệ phương trình có vô số nghiệm = = a¢ b¢ c¢ Câu 3. Đáp án B. ax ìï +by = c
Xét hệ phương trình bậc nhất hai ẩn ïí (có hệ số khác 0 ) a ï x ¢ + b y ¢ = c¢ ïî a b
- Hệ phương trình có nghiệm duy nhất  ¹ a¢ b¢ a b c
- Hệ phương trình vô nghiệm  = ¹ a¢ b¢ c¢ a b c  = =
- Hệ phương trình có vô số nghiệm a¢ b¢ c¢ Câu 4. Đáp án B. ax ìï +by = c
Xét hệ phương trình bậc nhất hai ẩn ïí
(các hệ số a ;¢b ;¢c¢ khác 0) a ï x ¢ + b y ¢ = c¢ ïî a b c
Hệ phương trình vô nghiệm  = ¹ a¢ b¢ c¢ Câu 5. Đáp án A.
Thay lần lượt các cặp số (21;-15);(1;1);(1;-1) và (-21;15) vào hệ phương trình ta được 2.21 ìï + 3.15 = 3 8 ìï 7 = 3 ï ï í  í ï-4.21 + 5.15 = 9 ï 9 - = 9
+) Với cặp số (21;-15) thì ta có ïî ïî (vô lý) nên loại B.
26. TOÁN HỌC SƠ ĐỒ ‐ THCS.TOANMATH.com 2.1 ìï + 3.1 = 3 5 ìï = 3
+) Với cặp số (1;1)thì ta có ï ï í  í (vô lý) nên loại C. ï-4.1 - 5.1 = 9 ï-9 = 9 ïî ïî 2.1 ìï + 3.(-1) = 3 ìï-1 = 3
+) Với cặp số (1;-1) thì ta có ï ï í  í (vô lý) nên loại D. ï-4.1 - 5.(-1) = 9 1 ï = 9 ïî ïî 2. ìï (-21) + 3.15 = 3 3 ìï = 3 ï ï í  í ï-4.(-21) - 5.15 = 9 9 ï = 9
+) Với cặp số (-21;15) thì ta có ïî ïî
(luôn đúng) nên chọn A. Câu 6. Đáp án C.
Thay lần lượt các cặp số (1;2);(8;-3);(3;-8) và (3; 8) vào hệ phương trình ta được 5.1 ìï + 2 = 7 7 ìï = 7 ï ï í  í ï-1 - 3.2 = 21 ï-7 = 21
+) Với cặp số (1;2) thì ta có ïî ïî (vô lý) nên loại B. 5.8 ìï + (-3) = 7 3 ìï 7 = 7
+) Với cặp số (8;-3) thì ta có ï ï í  í (vô lý) nên loại C. ï-8 - 3(-3) = 21 1 ï = 21 ïî ïî 5.3 ìï + 8 = 7 2 ìï 3 = 7
+) Với cặp số (3; 8) thì ta có ï ï í  í (vô lý) nên loại D. ï-3 - 3.8 = 21 ï-27 = 21 ïî ïî 5.3 ìï + ( 8 - ) = 7 7 ìï = 7 ï ï í  í ï-3 - 3.( 8 - ) = 21 21 ï = 21
+) Với cặp số (3;-8) thì ta có ïî ïî
(luôn đúng) nên chọn A. Câu 7. Đáp án C. x ìï - y = 3 ìï-2 -(-3) = 1 ¹ 3
+) Thay x = -2;y = -3 vào hệ ïí ta được ïí (vô lý) nên loại A. 2 ï x + y = 4 ï ï - - = - ¹ î 2.( 2) 3 7 4 ïî 2 ìï x - y = -1 2. ìï (-2) -(-3) = -1
+) Thay x = -2;y = -3 vào hệ ïí ta được ïí (vô lý) nên loại B. x ï - 3y = 8 ï ï- - - = ¹ î 2 3.( ) 3 7 8 ïî 4 ìï x - 2y = 0 4. ìï (-2) - 2.(-3) = -2 ¹ 0
+) Thay x = -2;y = -3 vào hệ ïí ta được ïí (vô lý) nên loại D. x ï - 3y = 5 ï ï- - - = ¹ î 2 3.( ) 3 7 5 ïî 2 ìï x - y = -1 2. ìï (-2) -(-3) = -1 ìï-1 = -1
+) Thay x = -2;y = -3 vào hệ ïí ta được ï ï í  í (luôn x ï - 3y = 7 ï ï- - - = ï = î 2 3.( 3) 7 7 7 ïî ïî đúng) nên chọn C. Câu 8. Đáp án B. x ìï - 3y = 1 3 ìï - 3( 5 - ) = 1 1 ìï 8 = 1
+) Thay x = 3;y = -5 vào hệ ïí ta được ï ï í  í (vô lý) nên loại A. x ï + y = 2 ï ï + - = ï- = î 3 ( 5) 2 2 2 ïî ïî y ìï = -1 ìï-5 = -1 ìï-5 = -1
+) Thay x = 3;y = -5 vào hệ ïí ta được ï ï í  í (vô lý) nên loại C. x ï - 3y = 5 ï ï - - = ï = î 3 3.( ) 5 5 18 5 ïî ïî 4 ìï x - y = 0 4. ìï 3 -(-5) = 0 1 ìï 7 = 0
+) Thay x = 3;y = -5 vào hệ ïí ta được ï ï í  í (vô lý) nên loại D. x ï - 3y = 0 ï ï - - = ï = î 3 3.( 5) 0 18 0 ïî ïî
27. TOÁN HỌC SƠ ĐỒ ‐ THCS.TOANMATH.com 3 ìï x + y = 4 3.3 ìï + (-5) = 4 4 ìï = 4
+) Thay x = 3;y = -5 vào hệ ïí ta được ï ï í  í (luôn đúng) nên 2 ï x - y = 11 ï ï - - = ï = î 2.3 ( 5) 11 11 11 ïî ïî chọn B. Câu 9. Đáp án C. - ì 2 1 ï-2x + y = 3 - ¹ Xét hệ phương trình ïí có 3
-2 nên hệ phương trình có nghiệm duy nhất. 3 ï x - 2y = 7 ïî Câu 10. Đáp án C. - ì 1 5 ï-2x + y = 3 - ¹ Xét hệ phương trình ïí có 5
1 nên hệ phương trình có nghiệm duy nhất. 3 ï x - 2y = 7 ïî Câu 11. Đáp án A. ìï x ìï + y = -1 m = 1 m 1 2m ï Để hệ phương trình ï ï í vô nghiệm thì = ¹  í  m = 1 mx ï + y = 2m 1 ï ï î 1 1 1 m ï ¹ ïî 2 Câu 12. Đáp án D. ìï ì y ìï = 2x - 4 2x - y = 4 y ï = 2x - 4 ï ï ï ï í  í  í ( ï - ) + = ï = ( - ) 1 1 2 2 1 - m m m x y m y m x + m ïî ï y ï î ï = + Ta có ïî 2x 2 2 ìï x - y = 4
Để hệ phương trình ïí
vô nghiệm thì đường thẳng d : y = 2x - 4 song song với ( ï m - )
1 x + 2y = m ïî ìï1 - m ïï = 2 1 ìï - m = 4 m ìï = -3 ï 2 ï ï í  í  í  m = -3 1 - m m ïm m ï ¹ -8 m ï ¹ -8 d ¢ : y = x + ïï ¹ -4 ïî ïî đường thẳng 2 2 suy ra ïïî 2 Câu 13. Đáp án B. 2 -2 3 1 1 3 ìï = ¹  = ¹ ï 2x - 2y = 3 - Xét hệ phương ï 3 2 6 5 3 3 5 í trình có
nên hệ phương trình vô 3 ïï 2x - 6y = 5 ïî nghiệm. Câu 14. Đáp án D. x ìï = y -1 y ìï = x + 1 Xét hệ (I ) : ï ï í  í y ï = x + 1 y ï = x + 1 ïî ïî
(d ) : y = x + 1
(d ) : y = x + 1
Nhận thấy rằng hai đường thẳng 1 và 2
trùng nhau nên hệ (I ) có vô số nghiệm.
28. TOÁN HỌC SƠ ĐỒ ‐ THCS.TOANMATH.com ìï 2 5 ï 2 ìï - 3 = 5 3 ìï = 2 - 5 y ï = x x y y x - Xét hệ ï ï ï 3 3 (II )í  í  í 3 ï y + 5 = 2x 3 ï y = 2x - 5 ï 2 5 ïî ïî y ïï = x - ïïî 3 3 2 5 2 5
(d ) : y = x -
Nhận thấy rằng hai đường thẳng (d ) : y = x - và 4 3
3 trùng nhau nên hệ (II ) có vô 3 3 3 số nghiệm.
Vậy cả hai hệ đã cho đều có vô số nghiệm. Câu 15. Đáp án D. mx ìï - 2y = 1 m -2
Để hệ phương trình ïí có nghiệm duy nhất thì 2 ¹
m ¹ 4  m ¹ 2 . 2 2
ï x - my = 2m ïî 2 m - Câu 16. Đáp án C. ìï ì ( ìï m - )
x - (m - )y = ( ï m - ) 2 y = x - 2 2 2 2 y = x - 2 ï Xét hệ ï ï ï í  í  í (
ï m - )x - y = m - ï y = (m - ) m - 1 m 5 1 2 5 2 1 x - m + 5 ïî ï y ï î ï = - + ïî 2x 2 2 0. ìï y = x - 2 x ìï = 2 ï ï ï ï í 1 3  í 1 3 y ïï = x + y ïï = x +
TH1: Với m - 2 = 0  m = 2 ta có hệ ïî 2 2 ïî 2 2 1 3
Nhận thấy hệ này có nghiệm duy nhất vì hai đường thẳng x = 2 và y = x + cắt nhau. 2 2 ìï ì 1 2 (
ï m - 2)y = x - 2 ï y ïï = x - ï ï m - 2 m - 2 í 1 m 5  í y ïï = m - x - + ï 1 m 5 ï ïî 2 2 2 y ï = m - x - +
TH2: Với m - 2 ¹ 0  m ¹ 2 ta có hệ ïî 2 2 2 1 2
Để hệ phương trình đã cho có nghiệm duy nhất thì hai đường thẳng d : y = x - m - 2 m - 2 m - 1 m 5 và d ¢ : y = x - + cắt nhau 2 2 2 1 m - 1  ¹
 (m - 1)(m - 2) ¹ 2  2
m - 3m + 2 ¹ 2  2 m - 3m ¹ 0 m - 2 2 m ìï ¹ 0 m(m ) 3 0 ï  - ¹  ím ï ¹ 3 ïî . Suy ra m ¹ {0;2; } 3
Kết hợp cả TH1 và TH2 ta có m ¹ {0; }
3 Vậy hệ phương trình đã cho có nghiệm duy nhất khi m ¹ {0; } 3 . Câu 17. Đáp án C. ìï mx - + y = -2m
Để hệ phương trình ïí
nhận cặp (1;2) làm nghiệm thì 2 x ï + m y = 9 ïî
29. TOÁN HỌC SƠ ĐỒ ‐ THCS.TOANMATH.com ìï m - .1 + 2 = -2m m ìï = -2 ï í  ïí  m = -2 2 1 ï + m .2 = 9 m ï = 2 ïî ïî . Vậy m = -2 . Câu 18. Đáp án D. (
ìï m + 2)x + y = 2m - 8
Để hệ phương trình ïí
nhận cặp số (-1; 3) làm nghiệm thì 2 m ï x + 2y = -3 ïî ìïm = ì 3 ï(m + 2 . ) - ( 1) + 3 = 2m - ì 8 ï ì ï
-m - 2 + 3 = 2m - 8 ï3m = 9 ï ï ï ï ïé í  m 3 m 3 . 2 í  í  2 í =  = ê ïm - ( 1) + 2.3 = -3 ï-m2 + 6 = -3 ïm = 9 ï ï ï î î ï ï î ê ï m = - ïê 3 îë Vậy m = 3 . Câu 19. Đáp án B. 3
ìï mx + y = -2m 3m 1 -2m
Để hệ phương trình ïí có vô số nghiệm thì = = ï-3x - my = 1 - + 3m ïî -3 m - -1 + 3m m ìï = 1  ï ì 2 3 ï m = 3 m ìï = 1  ï ï ì ï ï m ï = 1 ïé  ï ï m = 1 í  í  í  íê  m = 1 2 2 2 ï m = 3m - 1 2
ï m - 3m + 1 = 0 ï ï ï 2 ( m - 1)(m - ) 1 = 0 ïê ïî ïî ïî ï 1 ï m ê = ïê ïîë 2 Câu 20. Đáp án C. ì y ìï = -3 5 ï y = -15 ï ï ï í  í 1 ï-4x = 1 ï x ï î ï = -
+ TH1: Với m = 0 ta có hệ ïî
4 hay hệ phương trình có nghiệm duy nhất nên loại m = 0 . + TH2: Với m ¹ 0 . ìï 15 5 ïï mx + 5y = -
Để hệ phương trình ïí 2 có vô số nghiệm
ïï-4x -my = 2m +1 ïî ì 2 5m 5 -15 - ï 5m = -20 = =  ïí ìï m é = 2 ì ï -4 m - 2 2 ( m + ) 1 10 ï 2 ( m + 1) = 15m 2 m ï = 4 ê ï thì ïî ï ï  í  í m ê = -2  m = -2 20 ï m + 10 = 15m ê ïë ïî m ïï = -2 ïî (tm) Câu 21. Đáp án A. ¢
Ta có d : -2x + y = 3  y = 2x + 3 và d : x + y = 5  y = 5 - x
Xét phương trình hoành độ giao điểm của d và d¢ : 2 2 13
2x + 3 = 5 - x x =
y = 5 - x = 5 - = . 3 3 3 æ2 13ö
Vậy tọa độ giao điểm của d và d¢ là çç ; ÷÷ ç çè3 3 ÷÷ø
30. TOÁN HỌC SƠ ĐỒ ‐ THCS.TOANMATH.com ìï 2 - x + y = 3 æ2 13ö
Suy ra nghiệm của hệ phương trình ïí là çç ; ÷÷ x ï + y = 5 ç ÷ ï ç ÷ î è3 3 ø 13 2 11 y - x = - = Từ đó 0 0 3 3 3 . Câu 22. Đáp án A. -4x - 5  y = ¢
Ta có d : 4x + 2y = -5 2
và d : 2x - y = 1
-  y = 2x + 1 Xét phương trình hoành -4x - 5 7
= 2x + 1  -4x - 5 = 4x + 2  8x = -7  x = -
độ giao điểm của d và d¢ : 2 8 æ ö ç 7÷ 3
y = 2x + 1 = 2. - ç ÷ + 1 = - ç ÷ . ç 8÷ è ø 4 æ 7 3ö
Vậy tọa độ giao điểm của d và d¢ là ç- ç ; ÷ - ÷ ç çè 8 4÷÷ø æ 7 3ö ç ÷ = - ç - ÷ 4 ìï x + 2y = -5 (x ;y ) ; 0 0 çè 8 4÷÷
Suy ra nghiệm của hệ phương trình ï ø í là 2 ï x - y = 1 - ïî æ 7ö æ 3ö ç ÷ ç ÷ 21
Từ đó x .y = - ç ÷. - ç ÷ = 0 0 çè 8÷÷ ç ø è 4÷÷ø 32 Câu 23. Đáp án A. mx ìï - 2y = 3m
Để hệ phương trình ïí
nhận cặp (-1;2) làm nghiệm thì 2 ï x - my = 4 - - 4m ïî m ìï .(-1) - 2.2 = 3m m ìï .(-1) - 2.2 = 3m 4 ìï m = -4 ï ï ï í í  í  m = -1 2.
ï (-1) - m.2 = -4 - 4m 2 ï .( 1
- ) - m.2 = -4 - 4m 2 ï m = -2 ïî ïî ïî Vậy m = -1 .
31. TOÁN HỌC SƠ ĐỒ ‐ THCS.TOANMATH.com D.BÀI TẬP TỰ LUYỆN
Bài 1. Không giải hệ phương trình, em hãy đoán nhận số nghiệm của hệ và giải thích vì sao?  1     y x 3 y  4x  2  a. 5  b. 
y  3x  3 1
y   x 1  5 3
x y  3  3  y  x c.  1 d.  x y  1  4y  2x  3
Bài 2. Xác định các nghiệm của mỗi hệ phương trình sau bằng phương pháp hình học: 3
x y  1  3
x y  5 a.  b.  x y 1
x y  1
Bài 3. Đoán nhận số nghiệm của mỗi hệ phương trình sau, và giải thích tại sao? x y  3
4x  3y  1  a.  b. 
5x  5y  3 12
x  9y  3 
0x y  3
Bài 4. Cho hệ phương trình:  3
x  2y  9 
a. Giải hệ phương trình đã cho bằng đồ thị;
b. Nghiệm của phương trình đã cho có phải là nghiệm của phương trình 4x  5y  19 không?
x  2y  3
Bài 5. Cho hệ phương trình:  2x y 1
a. Giải hệ phương trình đã cho bằng phương pháp đồ thị
b. Nghiệm của hệ phương trình đã cho có phải là nghiệm của phương trình 2x  5y  7 không?
Bài 6. Bằng đồ thị chứng tỏ các hệ phương trình sau luôn có nghiệm duy nhất với bất kì giá trị nào của a: x ax y  3 a.  b.  x y  1 y a
3x y  1
Bài 7. Bằng đồ thị chứng tỏ hệ phương trình: 
ax  2y  3
a. Có nghiệm duy nhất với a  2  ;
b. Vô nghiệm với a  6  . 3
x  2y a
Bài 8. Cho hệ phương trình:  15
x 10y  5
a. Có vô số nghiệm với a  1;
b. Vô nghiệm với a  1.
Bài 9. Trong các câu sau, câu nào đúng, câu nào sai:
a. Hai hệ phương trình bậc nhất hai ẩn vô nghiệm, là hai hệ phương trình tương đương với nhau?
b. Hai hệ phương trình bậc nhất hai ẩn cùng vô số nghiệm là hai phương trình tương đương với nhau.
32. TOÁN HỌC SƠ ĐỒ ‐ THCS.TOANMATH.com
Bài 10. Trong các trường hợp sau, hai hệ phương trình nào tương đương với nhau? Hai hệ phương trình
nào không tương đương với nhau? x y  2
2x y  1 a.  và  3
x  3y  6 
4x  2y  2 x y  3 x  3 b.  và 
2x  2y  6  0
2x  3y 1
2x  3y  2 x y  3 c.  và  x  2y 1 y  2 HƯỚNG DẪN Bài 1.
a. Hai đường thẳng y  4x  2 và y  3x  3 có hệ số góc a  4;a  3 khác nhau nên chúng cắt nhau tại 1 2 một điểm.
Vậy hệ phương trình đã cho có nghiệm duy nhất. 1 1 1
b. Hai đường thẳng y   x  3 và y   x 1 có hệ số góc a a   bằng nhau mà hệ số 5 5 1 2 5
b  3  b  1
 khác nhau nên chúng song song với nhau và không có điểm chung. 1 2
Vậy hệ phương trình đã cho vô nghiệm. 3
x y  3
y  3x  3  
y  3x  3
c. Biến đổi hệ phương trình về dạng:  1  1   x y  1 y  x 1  
y  3x  3  3 3
Hai đường thẳng có hệ số góc a a  3
 và có tung độ gốc b b  3 nên chúng trùng nhau. 1 2 1 2
Vậy hệ phương trình đã cho có vô số nghiệm.  1 y   x 3  y  x 
d. Biến đổi hệ phương trình về dạng: 3    4y  2x 1 y x  2 1 1 1 1
Hai đường thẳng y   x và y x có hệ số góc a   ; a  khác nhau nên chúng cắt nhau tại 3 2 1 2 3 2 một điểm.
Vậy hệ phương trình đã cho có nghiệm duy nhất. Bài 2.
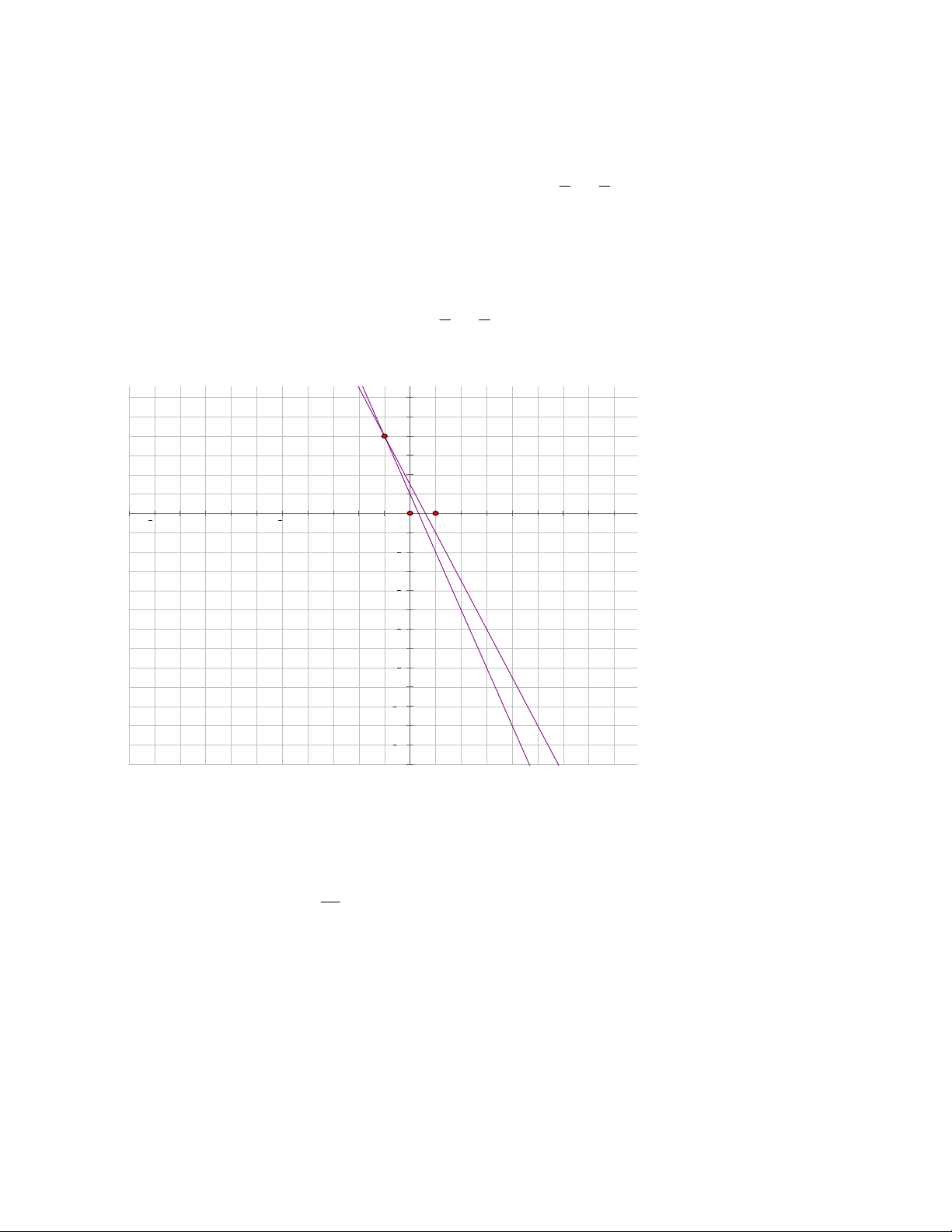
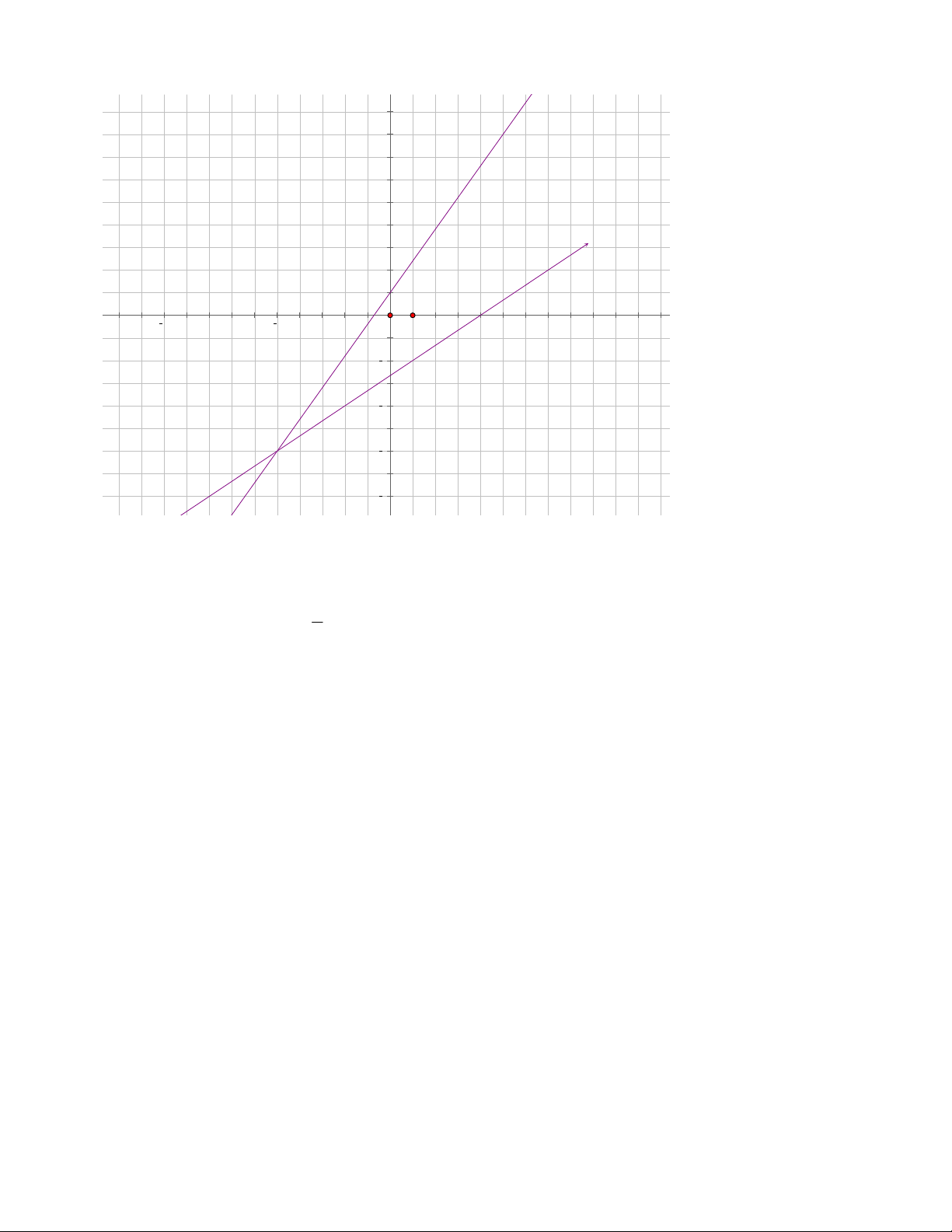
Xác định các nghiệm của mỗi hệ phương trình sau bằng phương pháp hình học: 3
x y  1  a. Hệ phương trình:  x y 1
Đường thẳng 3x y  1
 d có đồ thị là đường thẳng đi qua điểm 0;  1  và điểm  1  ;2 . 1 
Đường thẳng x y  1d có đồ thị là đường thẳng đi qua điểm  1
 ;2 và điểm 1;0 . 2 
Hai đường thẳng 3x y  1
 d và x y 1d có đồ thị như hình vẽ: 2  1 
33. TOÁN HỌC SƠ ĐỒ ‐ THCS.TOANMATH.com
Dựa vào đồ thị hàm số, ta thấy hai đường thẳng cắt nhau tại A 1
 ;2, suy ra nghiệm của hệ phương trình x  1  là:  y  2 3
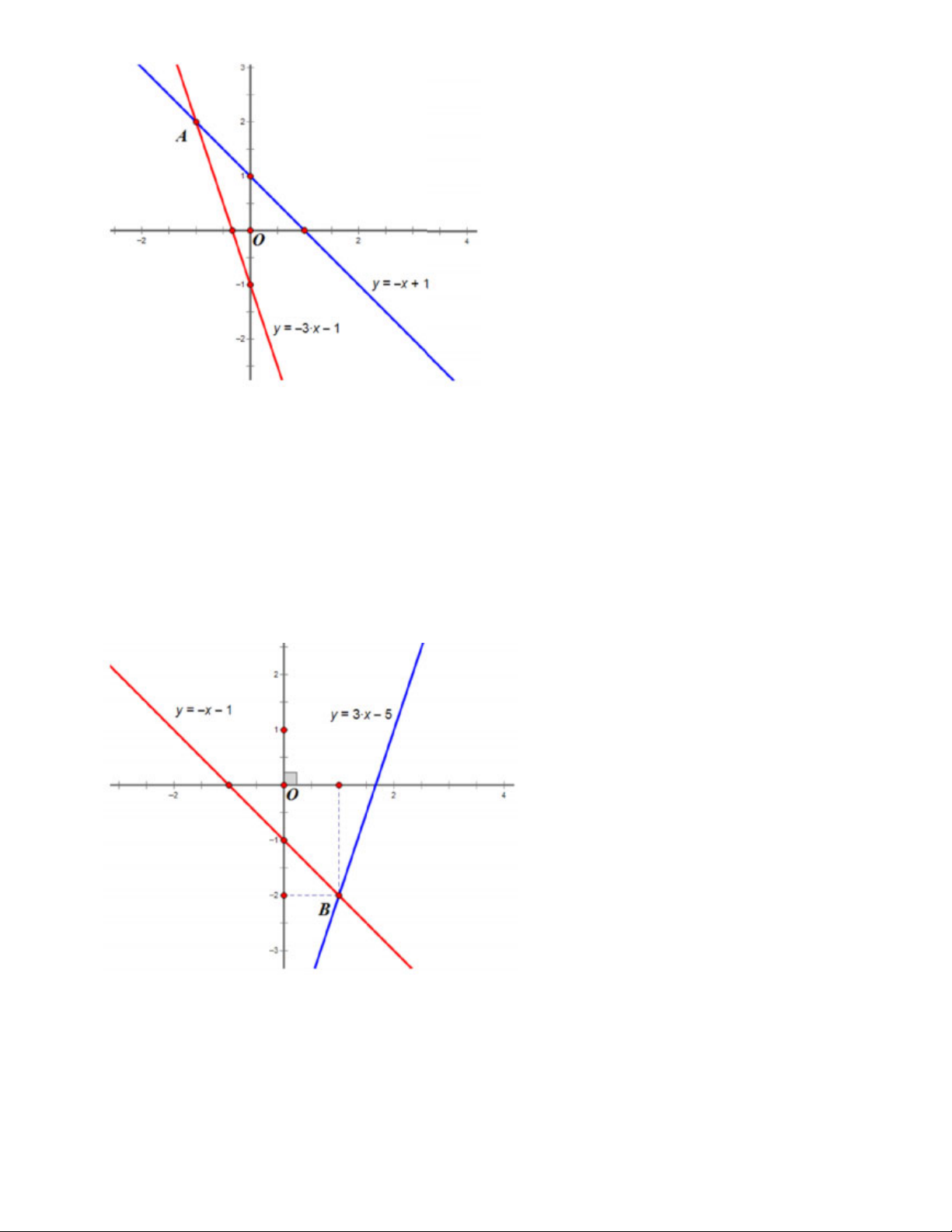
x y  5 b. Hệ phương trình: 
x y  1
Đường thẳng 3x y  5d có đồ thị đường thẳng đi qua điểm 0;5 và điểm 1; 2   . 1 
Đường thẳng x y  1d có đồ thị đường thẳng đi qua điểm 0;  1  và điểm  1  ;0 . 2 
Hai đường thẳng 3x y  5d và x y 1d có đồ thị như hình vẽ: 2  1 
Dựa vào đồ thị hàm số, ta thấy hai đường thẳng cắt nhau tại B1; 2
  , suy ra nghiệm của phương trình là: x  1   y  2
Bài 3. Đoán nhận số nghiệm của mỗi hệ phương trình sau, và giải thích tại sao?
34. TOÁN HỌC SƠ ĐỒ ‐ THCS.TOANMATH.com y x  3 x y  3 
a. Biến đổi hệ phương trình đã cho:    3 5
x  5y  3 y x   5 3
Hệ phương trình vô nghiệm, vì hai đường thẳng y x  3 và y x  có hệ số góc a a  1 và tung 5 1 2  3 
độ gốc b b vì 3  
nên chúng song song với nhau. 1 2    5   4 1 y   x
4x  3y  1  
b. Biến đổi phương trình đã cho: 3 3    12
x  9y  3  4 1
y   x   3 3 4
Hệ phương trình có vô số nghiệm, vì hai đường thẳng trùng nhau do có hệ số góc a a   và tung 1 2 3 1
độ gốc b b   . 1 2 3
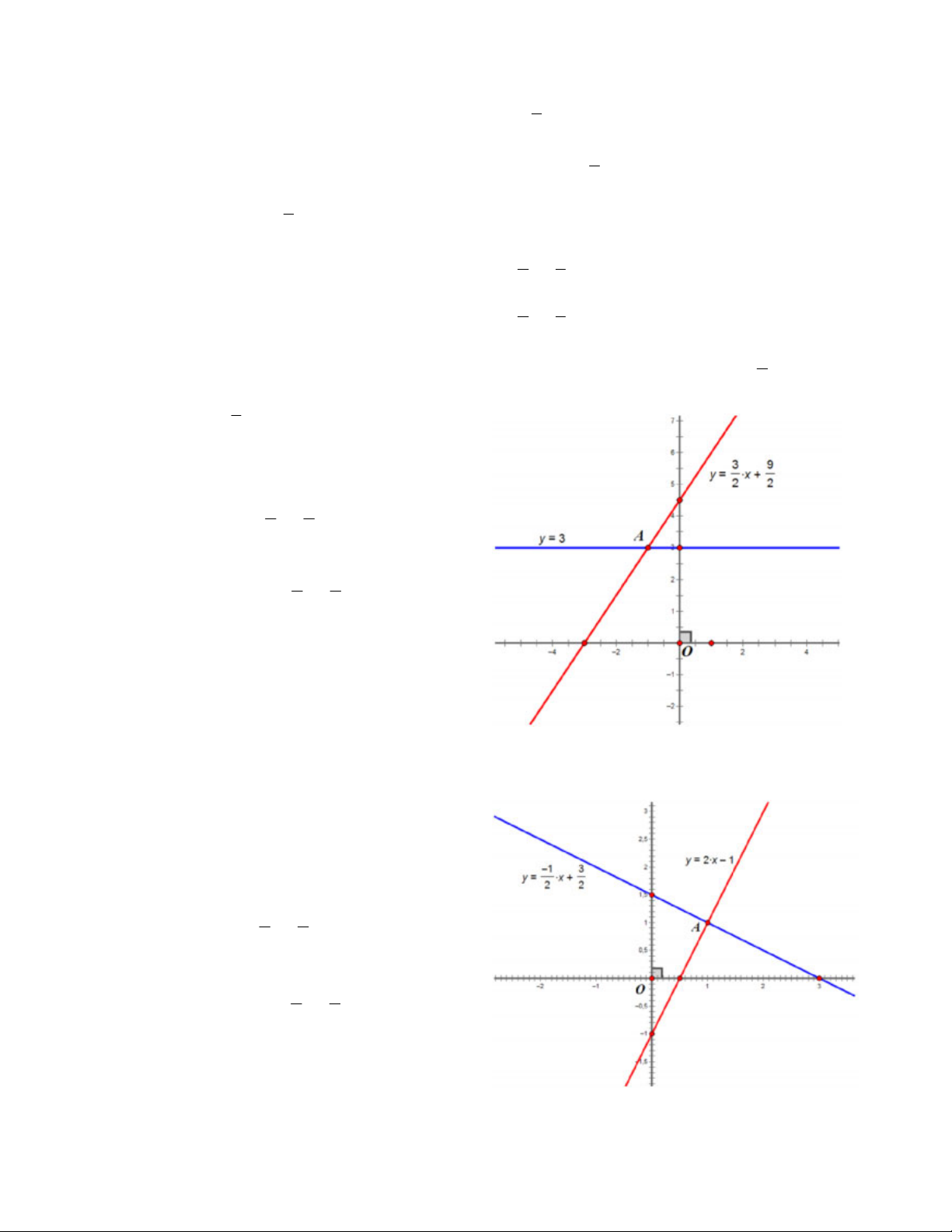
Bài 4. Hệ phương trình: y  3
0x y  3     3 9 3
x  2y  9  y x   2 2
a. Dựa vào đồ thị hàm số ta thấy, hai đường thẳng 3 9
y  3 và đường thẳng y x  cắt nhau tại điểm 2 2 A có tọa độ  1  ;3 . x  1 
Vậy nghiệm của hệ phương trình là  y  3 x  1  b. Với 
thay vào phương trình 4x  5y  19 y  3 ta có: 4.  1  5.3  19   4  15  1  9 (VT = VP đúng). Vậy điểm  1
 ;3 là nghiệm của phương trình
4x  5y  19
Bài 5. Biến đổi hệ phương trình:  1 3
x  2y  3
y   x     2 2
2x y  1
y  2x 1 1 3
a. Đồ thị hai hàm số y   x  và y  2x 1 2 2 được vẽ như hình:
35. TOÁN HỌC SƠ ĐỒ ‐ THCS.TOANMATH.com
Dựa vào đồ thị hàm số ta thấy, hai đường thẳng cắt nhau tại A có tọa độ 1; 
1 . Suy ra nghiệm của hệ x  1 phương trình là   y 1
b. Với x  1 và y  1 thay vào phương trình 2x  5y  7 ta có: 2.1 5.1  2  5  3
  7 nên x 1 và y  1 không phải là nghiệm của phương trình 2x  5y  7 .
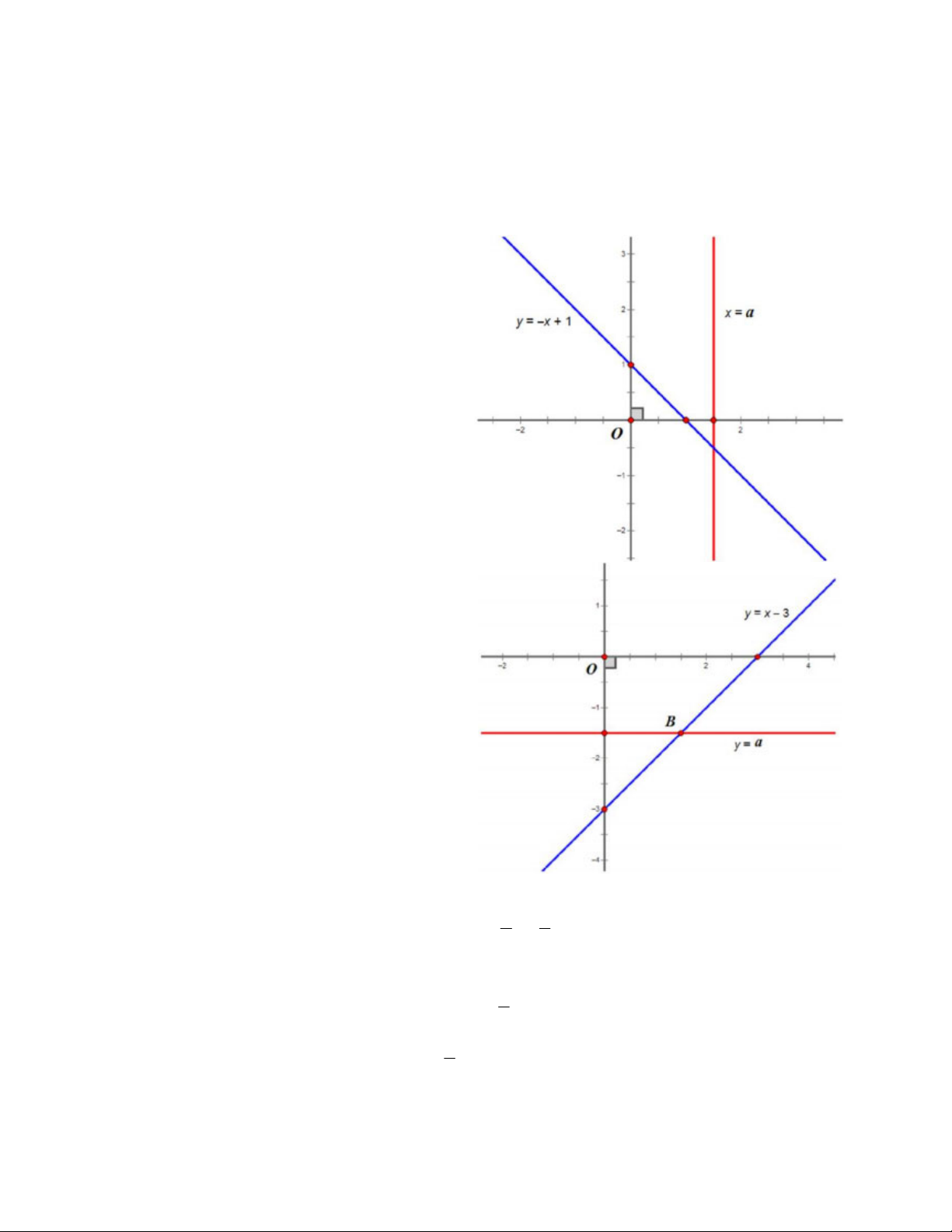
Bài 6. Bằng đồ thị chứng tỏ các hệ phương trình sau luôn có nghiệm duy nhất với bất kì giá trị nào của a: x ax a a.    x y 1
y  x 1
Ta có: đường thẳng x a song song a  0 hoặc
trùng a  0 với trục Oy, mà đường thẳng
y  x 1 là đường thẳng xiên a  0 , cắt Oy tại điểm 0; 
1 nên nó sẽ cắt đường thẳng x a với mọi a.
Do đó, hệ phương trình luôn có nghiệm với mọi a.
b. Biến đổi hệ phương trình: x y  3
y x  3     y ay a
Ta có: đường thẳng y a song song a  0 hoặc
trùng a  0 với trục Ox, mà đường thẳng
y x  3 là đường thẳng xiên a  0 , cắt Ox tại
điểm 3;0 nên có sẽ cắt đường thẳng y a với mọi a.
Do đó hệ phương trình luôn có nghiệm với mọi a. y  3x 1 3  x y 1 
Bài 7. Biến đổi hệ phương trình:    a 3
ax  2y  3 y   x   2 2 y  3x 1  a. Khi a  2
 ; thay vào hệ phương trình ta có:  3 y x   2 3
Đường thẳng y  3x 1 và đường thẳng y x  có hệ số góc khác nhau 3   1 nên cắt nhau. 2 Vì vậy, khi a  2
 thì hệ phương trình có nghiệm.
36. TOÁN HỌC SƠ ĐỒ ‐ THCS.TOANMATH.com y  3x 1  b. Khi a  6
 , thay vào hệ phương trình ta có:  3 y  3x   2 3
Đường thẳng y  3x 1 và y  3x  là hai đường thẳng có hệ số góc bằng nhau a a  3 và tung độ 2  3  gốc khác nhau 1  
 nên chúng song song với nhau.  2  Vì vậy, khi a  6
 thì hệ phương trình vô nghiệm.  3 a   3   2 y x x y a 
Bài 8. Biến đổi hệ phương trình: 2 2    15
x 10y  5 3 1 y x   2 2  3 1 y x  
a. Khi a  1, thay vào hệ phương trình, ta có: 2 2  3 1  y x   2 2 3 1 3 1
Đường thẳng y x  và đường thẳng y x  có hệ số góc, và tung độ gốc bằng nhau nên hai 2 2 2 2
đường thẳng trùng nhau.
Do đó, hệ phương trình đã cho có vô số nghiệm khi a  1.  3 a y x  
b. Khi a  1, thay vào hệ phương trình, ta có: 2 2  3 1 y x   2 2 3 a 3 1
Hai đường thẳng y x  và đường thẳng y x  có hệ số góc bằng nhau, nhưng tung độ gốc 2 2 2 2
khác nhau nên hai đường thẳng này song song với nhau.
Vậy, hệ phương trình đã cho vô nghiệm khi a  1.
Bài 9. Trong các câu sau, câu nào đúng, câu nào sai:
a. Đúng. Vì hai hệ phương trình cùng vô số nghiệm thì có cùng tập nghiệm rỗng. b. Sai.
Ví dụ chứng minh: Cho hai hệ phương trình sau: x y
x y   Hệ I  3  và Hệ II  5 
2x  2y  6  2
x  2y  10
Cả hệ I  và hệ II  đều là hệ phương trình có vô số nghiệm. Nhưng tập nghiệm của hệ phương trình
I được biểu diễn bởi phương trình đường thẳng d y  x 3; còn tập nghiệm của hệ phương trình 1 
II  được biểu diễn bởi phương trình đường thẳng d y x 5. Hai đường thẳng này khác nhau nên 2 
hai hệ phương trình đang xét không tương đương với nhau.
Bài 10. Giải các hệ phương trình nếu tập nghiệm của chúng bằng nhau ta kết luận hai hệ phương trình
tương đương, còn nếu tập nghiệm của chúng không bằng nhau ta kết luận hai hệ phương trình không tương đương:
37. TOÁN HỌC SƠ ĐỒ ‐ THCS.TOANMATH.com x y  2 a. Hệ phương trình  vô nghiệm. 3
x  3y  6 
2x y  1 và hệ phương trình  vô nghiệm.  4
x  2y  2
Vậy hai hệ phương trình đã cho tương đương với nhau. x y  3 b. Hệ phương trình  có vô số nghiệm.
2x  2y  6  0 x  3  5  và hệ phương trình  có nghiệm 3;    .
2x  3y 1  3 
Vì tập nghiệm của chúng khác nhau nên hai hệ phương trình đã cho không tương đương với nhau.
2x  3y  2 c. Hệ phương trình  có nghiệm là  17  ;12
x  2y  7 x y  3 và hệ phương trình  có nghiệm là 1;2  y  2
Vì tập nghiệm của chúng khác nhau nên hai hệ phương trình đã cho không tương đương với nhau.
----------Toán Học Sơ Đồ---------
38. TOÁN HỌC SƠ ĐỒ ‐ THCS.TOANMATH.com