Chuyên đề phương trình bậc nhất hai ẩn

Tài liệu gồm 19 trang, được biên soạn bởi tác giả Toán Học Sơ Đồ, tổng hợp kiến thức trọng tâm, phân dạng và hướng dẫn giải các dạng bài tập tự luận & trắc nghiệm chuyên đề phương trình bậc nhất hai ẩn. Mời bạn đọc đón xem.

87 44 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Chương 3: Hệ hai phương trình bậc nhất hai ẩn

Môn: Toán 9

Thông tin:

19 trang 8 tháng trước

Tác giả:

Profile Hà Việt Anh
CHUYÊN ĐỀ PHƯƠNG TRÌNH BẬC NHẤT HAI ẨN
A.KIẾN THỨC TRỌNG TÂM
B.CÁC DẠNG BÀI TẬP MINH HỌA
Dạng 1. Xác định nghiệm của phương trình bậc nhất hai ẩn.
Bài1. Trong các cặp số
0;4,–1;3,1;1,2;3,4;6cặp số nào là nghiệm của phương trình:
a)
x
y532
b)
x
y27
c)
x
y22
Bài2. Tìm nghiệm tổng quát và vẽ đường thẳng biểu diễn tập nghiệm của nó:
a)
x
y31
b)
x
y25
c)
x
y235
d)
y
x32
Dạng 2. Biện luận và vẽ đồ thị của hàm số bậc nhất:
Bài3. Cho đường thẳng
d
có phương trình:
mxm y m(1)(34) 25
. Tìm m để:
a)
d
song song với trục hoành. b)
d
song song với trục tung.
c)
d
đi qua gốc toạ độ. d)
d
đi qua điểm
)(2; –1
.
Bài 4. Trong mỗi trường hợp sau, hãy tìm giá trị của a để:
1. Phương trình bậc nhất hai ẩn là phương trình có dạng:

1 ax by c
trong đó a, b, c là các số
đã biết (
0a
hoặc
0b
), x và y lần lượt là các ẩn.
Cặp

00
;
x
y thỏa mãn
00
ax by c
được gọi là một nghiệm của phương trình

1 ax by c
.
Trong mặt phẳng tọa độ Oxy, mỗi nghiệm
00
;
x
y
của (1) được biểu diễn bởi một điểm
00
;
x
y
2. Tập nghiệm của phương trình bậc nhất hai ẩn
Phương trình bậc nhất hai ẩn

1 ax by c
(
0a
hoặc
0b
), luôn có vô số nghiệm. Tập
nghiệm của nó được biểu diễn bởi đường thẳng
ax by c d
.
Nếu
0a
và
0b
thì đường thẳng

d
là đồ thị của hàm số
ac
yx
bb

Nếu
0a
,
0b
và
0c
thì đường thẳng

d
song song với trục tung Oy và phương trình
trở thành
c
ax c x
a

.
Nếu
0a , 0b và 0c thì đường thẳng

d trùng với trục tung Oy và phương trình trở thành
00ax x.
Nếu
0a
;
0b
và
0c
thì đường thẳng

d
song song với trục hoành Ox và phương trình
trở thành
c
by c y
b

.
Nếu
0a
;
0b
và
0c
thì đường thẳng

d
trùng với trục hoành Ox và phương trình trở
thành
00by y
.
a) Điểm

0; 1A
thuộc đường thẳng
xay 5
b) Điểm

3; 0B
thuộc đường thẳng
ax y–4 6
c) Điểm

5; 2C 
thuộc đường thẳng
63ax y
d) Điểm
5
;0
2
D



thuộc đường thẳng
25
0
2
ax y
e) Điểm
9
2;
2
E


thuộc đường thẳng
010xay
.
Bài 5. Vẽ đồ thị của mỗi cặp phương trình sau trong cùng một hệ trục tọa độ, rồi tìm giao điểm của hai
đường thẳng đó.
f)
xy2– 3
và
xy3–2 5
g)
xy–2 4
và
xy3210
h)
xy–1
và
xy33 6
i)
xy–2 4
và
xy24 8
Dạng 3. Tìm nghiệm nguyên của phương trình bậc nhất hai ẩn
Bài 6. Tìm tất cả các nghiệm nguyên của phương trình:
a)
xy20
b)
xy325
c)
xy2515
d)
xy5114
e)
xy75143
f)
xy23 53 109
HƯỚNG DẪN
Dạng 1. Xác định nghiệm của phương trình bậc nhất hai ẩn
Bài 1. Thay lần lượt mỗi cặp số đã cho vào từng phương trình, rồi so sánh giá trị tìm được ở hai vế để rút
ra kết luận
a) Cặp số
(1;1),(4; 6)
là nghiệm của phương trình
53y2x
b) Cặp số
(2;3)
là nghiệm của phương trình
y72x+
c) Cặp số
(4;6)
là nghiệm của phương trình
2x y2
Bài 2. Tìm nghiệm tổng quát và vẽ đường thẳng biểu diễn tập nghiệm
a) Nghiệm tổng quát của phương trình
3x y1
là
x
yx31


hoặc
y
xy
11
33


có đồ thị hàm số là
b) Nghiệm tổng quát của phương trình
3x y1
là
x
yx31


hoặc
y
xy
11
33


có đồ thị hàm số là
c) Nghiệm tổng quát của phương trình
3x y1
là
x
yx31


hoặc
y
xy
11
33


có đồ thị hàm số là
d) Nghiệm tổng quát của phương trình
3x y1
là
x
yx31


hoặc
y
xy
11
33


có đồ thị hàm số là
Dạng 2. Biện luận và vẽ đồ thị của hàm số bậc nhất
Bài 3. Cho đường thẳng (d) có phương trình:
mxm y m(1)(34) 25
.
Phương trình đường thẳng (d) có các hệ số am b m c m1; 3 4; 2 5
a)

d
song song với trục hoành
m
am m
bm mmm
cm m
m
1
010 1
4
0340 34 1
3
025025
5
2










Vậy với
m 1 thì phương trình đường thẳng (d) song song với trục hoành
b)
d
song song với trục tung
m
am m
bm mmm
cm m
m
1
010 1
44
0340 34
33
025025
5
2


 







Vậy với
m
4
3
thì phương trình đường thẳng (d) song song với trục tung
c)
d
đi qua gốc tọa độ
m
am m
bm mmm
cm m
m
1
010 1
45
0340 34
32
025025
5
2










Vậy với
m
5
2

thì phương trình đường thẳng (d) đi qua gốc tọa độ
d)
d
đi qua điểm
A
(2; 1)
, suy ra tọa độ điểm A thỏa mãn phương trình đường thẳng




mxm y m
mm m
mm m
m
(1)(34) 25
( 1).2 (3 4).( 1) 2 5
223425
7
Vậy với
m 7
thì phương trình đường thẳng (d) đi qua điểm A.
Bài 4.
a) Điểm

0; 1A
thuộc đường thẳng
xay 5
, ta có
0.1 5 5aa
Vậy với
5a
thì điểm
0; 1A
thuộc đồ thị hàm số đã cho
b) Điểm

3; 0B thuộc đường thẳng
ax y–4 6
, ta có
.3 4.06 36 2aaa
Vậy với
2a  thì điểm
3;0B
thuộc đồ thị hàm số đã cho
c) Điểm

5; 2C 
thuộc đường thẳng
63ax y
, ta có
 
9
.5 6.2 3 5 9
5
aaa
. Vậy với
9
5
a 
thì điểm

5; 2C 
thuộc đồ thị hàm
số đã cho
d) Điểm
5
;0
2
D



thuộc đường thẳng
25
0
2
ax y
, ta có
525
.0 5
22
aa
Vậy với
5a
thì điểm
5
;0
2
D



thuộc đồ thị hàm số đã cho
Điểm
9
2;
2
E


thuộc đường thẳng
010xay
, ta
920
0.2 . 10
29
aa



. Vậy với
20
9
a
thì điểm
9
2;
2
E


thuộc đồ thị hàm số đã cho
Bài 5.
a) Đồ thị hàm số
1
2– 3 3()2xy y x d
và đồ thị hàm số
2
3
3–2 5
2
5
()
2
xy x dy 
.
Phương trình hoành độ giao điểm của hai đường thẳng là:
35
3
22
35
23
22
1
11.
22
2xx
xx
x
xy



(1; 1)A
là giao điểm của hai đường thẳng đã cho.
b) Đồ thị hàm số
1
–2 4 2( )
2
xy y
x
d
và đồ thị hàm số
2
3
321 5)0(
2
xy y x d
.
Phương trình hoành độ giao điểm của hai đường thẳng là:
3
25
22
3
7
22
71
2x 7 .
24
x
x
x
x
xy



71
(; )
24
B
là giao điểm của hai đường thẳng đã cho.
c) Đồ thị hàm số
1
)–(11xy yx d
và đồ thị hàm số
2
33 6 2()xy yx d
.
Phương trình hoành độ giao điểm của hai đường thẳng là:
12
0x 1
xx

(phương trình vô nghiệm). Vậy hai đường thẳng đã cho song song với nhau
d) Đồ thị hàm số
1
–2 4 2( )
2
x
xy y d
và
2
24 8 2()
2
x
xy y d
Vậy hai đồ thị hàm số đã cho có vô số điểm chung.
Dạng 3. Tìm nghiệm nguyên của phương trình bậc nhất hai ẩn
Bài 6.
a) Từ phương trình
xy y x20 2
Đặt
xtt y t,2
Vậy các cặp số nguyên cần tìm là
xt
ytt2,


b) Từ phương trình
xxx x
xy y x
352 5 5
32 5
22 2


. Vì
x
xy
5
,.
2


Đặt
x
tt x t y t t t
5
( ) 25 25 35
2

.
Vậy các cặp số nguyên cần tìm có dạng
xt
yt t
25
35,


c) Từ phương trình
 

yyyy y
xy x
515 515 4 15 15
2515 2
22 2 2
.
Vì
y
xy
15
,.
2


Đặt
y
tt y t x t t t
15
( ) 2 15 2(2 15) 5 30
2

Vậy các cặp số nguyên cần tìm có dạng
xt
yt t
530
215,


.
C.TRẮC NGHIỆM RÈN LUYỆN PHẢN XẠ
Câu 1. Cho phương trình
ax by c+=
với
0, 0ab¹¹
. Nghiệm của phương
trình được biểu diễn bởi.
A.
x
ac
yx
bb
ì
ï
Î
ï
ï
ï
í
ï
=- +
ï
ï
ï
î
. B.
x
ac
yx
bb
ì
ï
Î
ï
ï
ï
í
ï
=- -
ï
ï
ï
î
. C.
x
c
y
b
ì
ï
Î
ï
ï
ï
í
ï
=
ï
ï
ï
î
. D.
x
c
y
b
ì
ï
Î
ï
ï
ï
í
ï
=-
ï
ï
ï
î
.
Câu 2. Phương trình nào sau đây là phương trình bậc nhất hai ẩn?
A.
2
220x +=
. B.
315(2)yy-= -
. C. 210
2
y
x +-=
. D.
2
30xy+=.
Câu 3. Phương trình nào dưới đây nhận cặp số
(2;4)-
làm nghiệm
A.
20xy-=
. B.
20xy+=
. C.
2xy-=
. D.
210xy++=
.
Câu 4. Phương trình
570xy-+=
nhận cặp số nào sau đây làm nghiệm?
A.
(0;1)
. B.
(1;2)-
. C.
(3;2)
. D.
(2; 4)
.
Câu 5. Phương trình
548xy+=
nhận cặp số nào sau đậy là nghiệm?
A.
(2;1)-
. B.
(1;0)-
. C.
(1,5;3)
. D.
(4; 3)-
.
Câu 6. Tìm số dương
m
để phương trình
2
2( 2) 5xm y-- =
nhận cặp số
(10; 1)--
làm nghiệm.
A.
5m = . B.
7m =
. C. 3m =- . D.
7; 3mm==-
.
Câu 7. Tìm
m
để phương trình 13 1mx y-- =- nhận cặp số
(1; 1)
làm
nghiệm.
A.
5m = . B. 2m = . C. 5m =- . D. 2m =- .
Câu 8. Công thức nghiệm tổng quát của phương trình
04 16xy+=-
.
A.
4
x
y
ì
ï
Î
ï
í
ï
=-
ï
î
. B.
4
x
y
ì
ï
Î
ï
í
ï
=
ï
î
. C.
4
x
x
ì
ï
Î
ï
í
ï
=-
ï
î
. D.
4
x
x
ì
ï
Î
ï
í
ï
=
ï
î
.
Câu 9. Công thức nghiệm tổng quát của phương trình
3012xy+=
.
A.
4
xR
y
ì
ï
Î
ï
í
ï
=-
ï
î
. B.
4
xR
y
ì
ï
Î
ï
í
ï
=
ï
î
. C.
4
xR
x
ì
ï
Î
ï
í
ï
=-
ï
î
. D.
4
xR
x
ì
ï
Î
ï
í
ï
=
ï
î
.
Câu 10. Trong các cặp số
( 2;1);(0;2);( 1;0);(1,5;3);(4; 3)-- -
có bao nhiêu cặp số không là nghiệm của
phương trình
35 3xy+=-
.
A.
1 . B. 3 . C. 2 . D. 4 .
Câu 11. Cho đường thẳng
d có phương trình
(2)(31)62mxmym-+ -=-
Tìm các giá trị của tham số
m để d song song với trục hoành.
A.
1m = . B. 2m = . C. 3m = . D. 4m = .
Câu 12. Cho đường thẳng
d
có phương trình
(5 15) 2 2mxmym-+=-
Tìm các giá trị của tham số
m
để
d
song song với trục hoành.
A.
1m = . B. 2m = . C. 3m = . D. 4m = .
Câu 13. Cho đường thẳng
d có phương trình
(2)(31)62mxmym-+ -=-
Tìm các giá trị của tham số
m để d song song với trục tung.
A.
1
3
m =
. B.
2
3
m =
. C. 2m ¹ . D.
1
3
m ¹
.
Câu 14. Cho đường thẳng
d
có phương trinh
1
(1 2 ) 2
2
m
xmy
-
+- =
Tìm các giá trị của tham số
m
để
d
song song với trục tung.
A.
1m = . B.
1
2
m ¹
. C. 2m = . D.
1
2
m =
.
Câu 15. Cho đường thẳng
d có phương trình
(2 4) ( 1) 5mxmym-+-=-
Tìm các giá trị của
m
tham số
d
để đi qua gốc tọa độ.
A.
2m = . B. 1m = . C. 5m = . D. 5m ¹ .
Câu 16. Cho đường thẳng
d có phương trình
(2).(31).62mxmym-+-=-
Tìm các giá trị của tham số
m
để
d
đi qua gốc tọa độ.
A.
1
3
m =
. B.
2
3
m =
. C. 2m ¹ . D.
1
3
m ¹
.
Câu 17. Chọn khẳng định đúng.
Đường thẳng
d biểu diễn tập nghiệm của phương trình
33xy-=
là.
A. Đường thẳng song song với trục hoành. B. Đường thẳng song song với trục tung.
C. Đường thẳng đi qua gốc tọa độ. D. Đường thẳng đi qua điểm A(1;0).
Câu 18. Cho đường thẳng nào đưới đây có biểu diễn hình học là đường thẳng song song với trục hoành.
A.
57y =
. B. 39x = . C.
9xy+=
. D.
67yx+=
.
Câu 19. Tìm tất cả nghiệm nguyên của phương trình
53 8xy-=
.
A.
38
516
()
xt
tZ
yt
ì
ï
=-
ï
Î
í
ï
=-
ï
î
. B.
38
56
()
xt
tZ
yt
ì
ï
=-
ï
Î
í
ï
=- -
ï
î
.
C.
83
15 16
()
xt
tZ
yt
ì
ï
=-
ï
Î
í
ï
=-
ï
î
. D.
38
)
56
(
xt
tZ
yt
ì
ï
=+
ï
Î
í
ï
=+
ï
î
.
Câu 20. Tìm nghiệm tất cả các nghiệm nguyên của phương trình
32 5xy-=
.
A.
()
52
53
xt
tZ
yt
ì
ï
=-
ï
Î
í
ï
=- -
ï
î
. B.
5
)
5
(
2
3
xt
tZ
yt
ì
ï
=+
ï
Î
í
ï
=-
ï
î
.
C.
5
)
5
(
2
3
xt
tZ
yt
ì
ï
=-
ï
Î
í
ï
=+
ï
î
. D.
5
)
5
(
2
3
xt
tZ
yt
ì
ï
=+
ï
Î
í
ï
=+
ï
î
.
Câu 21. Tìm nghiệm nguyên âm lớn nhất của phương trình
527xy-+ =
.
A.
(7; 14)--
. B.
(1; 2)--
. C.
(3; 4)--
. D.
(5; 9)--
.
Câu 22. Nghiệm nguyên âm của phương trình
34 10xy+=-
là
();xy
. Tính
.xy
.
A.
2 . B. 2- . C. 6 . D. 4 .
Câu 23. Gọi
();xy
là nghiệm nguyên dương nhỏ nhất của phương trình
438xy-+ =
. Tính xy+
A.
5 . B. 6 . C.
7
. D. 4 .
Câu 24. Gọi
();xy
là nghiệm nguyên dương nhỏ nhất của phương trình
67 5xy-=
. Tính
xy-
.
A.
2 . B. 3 . C. 1 . D. 1- .
HƯỚNG DẪN
Câu 1. Đáp án A.
Ta có với
0, 0ab¹¹
thì
ac
by ax c y x
bb
=-+=- +
Nghiệm của phương trình được biểu diễn bởi
x
ac
yx
bb
ì
ï
Î
ï
ï
ï
í
ï
=- +
ï
ï
ï
î
Câu 2. Đáp án C.
Phương trình 210
2
y
x +-=
là phương trình bậc nhất hai ẩn.
Câu 3. Đáp án B.
Thay
2; 4xy=- =
vào từng phương trình ta được
+)
222.4100xy-=-- =-¹
nên loại A.
+)
24 6 0xy-=--=-¹
nên loại C.
+)
21 22.4170xy++=-+ +=¹
nên loại D.
+)
22.240xy+=- +=
nên chọn B.
Câu 4. Đáp án C.
+) Thay
0; 1xy==
vào phương trình
570xy-+=
ta được
05.17 0 2 0-+==
(vô lý) nên
loại A.
+) Thay
1; 2xy=- =
vào phương trình
570xy-+=
ta được
15.27 0 4 0-- + = - =
(vô
lý) nên loại B.
+) Thay
2; 4xy==
vào phương trình
570xy-+=
ta được 25.47 0 110-+=-= (vô lý)
nên loại D.
+) Thay
3; 2xy==
vào phương trình
570xy-+=
ta được
35.27 0 0 0-+==
(luôn đúng)
nên chọn C.
Câu 5. Đáp án D.
Xét phương trình
548xy+=
Cặp số
(2;1)-
không phải nghiệm của phương trình vì
5( 2) 4.1 6-+ =-
. Do đó loại A.
Cặp số
(1;0)-
không phải nghiệm của phương trình vì
5.( 1) 4.0 5-+ =-
. Do đó loại B.
Cặp số
(1,5;3)
không phải nghiệm của phương trình vì
5.1,5 4.3 19,5+=
. Do đó loại C
Cặp số
(4; 3)-
là nghiệm của phương trình vì
5.4 4.( 3) 8+-=
. Do đó chọn D.
Câu 6. Đáp án B.
Thay
10; 1xy=- =-
vào phương trình
2
2( 2) 5xm y-- =
ta được
22
25 7
2. 10 2 . 1 5
()
()( 2 25)( ) ( )
(2)53
mmN
mm
mmL
éé
-= =
êê
--- -= - =
êê
-=- =-
êê
ëë
Vậy 7m =
Câu 7. Đáp án A.
Thay
1; 1xy==
vào phương trình ta được
1.1 3.1 1m -- =-
ĐK 1m ³- 12 14mm-=-=
5m=
(thỏa mãn).
Vậy
5m =
Câu 8. Đáp án A.
Ta có
04 16 4xy y+=-=-
Nghiệm tổng quát của phương trình
4
xR
y
ì
ï
Î
ï
í
ï
=-
ï
î
.
Câu 9. Đáp án D.
Ta có
3012 4xy x+==
Nghiệm tổng quát của phương trình
4
xR
x
ì
ï
Î
ï
í
ï
=
ï
î
.
Câu 10. Đáp án B.
Xét phương trình
35 3xy+=-
Cặp số
(2;1)-
không phải nghiệm của phương trình vì
32 5.)1(1-+ =-
.
Cặp số
(0;2)
không phải nghiệm của phương trình vì
3.0 5.2 10+=
.
Cặp số
(1;0)-
là nghiệm của phương trình vì
3.( 1) 5.0 3-+ =-
.
Cặp số
(1,5;3)
không phải nghiệm của phương trình vì
3.1,5 5.3 19,5+=
.
Cặp số
(4; 3)-
là nghiệm của phương trình vì
3.4 5.( 3) 3+-=-
.
Vậy có 3 cặp số không phải nghiệm của phương trình đã cho.
Câu 11. Đáp án B.
Để d song song với trục hoành thì
20
2
310 2
1
620
3
m
m
mm
m
m
ì
ï
ì
-=
ï
=
ï
ï
ï
ï
ï
ï
-¹ =
íí
ïï
¹
ïï
-¹
ïï
ï
î
ï
î
Câu 12. Đáp án C.
Để
d
song song với trục hoành thì
5150 3
20 0 3
20 2
mm
mmm
mm
ìì
ïï
-= =
ïï
ïï
ïï
¹¹=
íí
ïï
ïï
-¹ ¹
ïï
ïï
îî
.
Câu 13. Đáp án A.
Để
d
song song với trục tung thì
2
20
11
310
33
620
1
3
m
m
mmm
m
m
ì
ï
ï
¹
ï
ì
ï
ï
-¹
ï
ï
ï
ï
ï
ï
-= = =
íí
ïï
ïï
-¹
ïï
ïï
î
ï
¹-
ï
ï
î
. Vậy
1
3
m =
.
Câu 14. Đáp án D.
Để
d
song song với trục tung thì
1
0
1
2
1
12 0
1
2
20
2
m
m
mm
m
ì
ï
-
ï
¹
ï
ì
ï
¹
ï
ï
ï
ï
ïï
-= =
íí
ïï
=
ïï
¹
ïï
ï
î
ï
ï
ï
î
. Vậy
1
2
m =
.
Câu 15. Đáp án C.
Gốc tọa độ
(0; 0)O
Để d đi qua gốc tọa độ thì tọa độ điểm O thỏa mãn phương
trình
(2 4) ( 1) 5mxmym-+-=-
hay
(2 4).0 ( 1).0 5 5 0 5mmmm m-+-=--==
Vậy 5m = .
Câu 16. Đáp án A.
Để
d đi qua gốc tọa độ thì
1
( 2).0 (3 1).0 6 2
3
mmmm-+-=-=
.
Vậy
1
3
m =
.
Câu 17. Đáp án D.
Ta có
3333xy y x-= = -
Nghiệm tổng quát của phương trình
33
xR
yx
ì
ï
Î
ï
í
ï
=-
ï
î
Biểu diễn hình học của tập nghiệm là đường thẳng
33yx=-
đi qua điểm
()1; 0A
và
(0; 3)B -
.
Câu 18. Đáp án A.
Ta thấy phương trình
57y =
có
0; 5ab==
và
70c =¹
nên biểu diễn nghiệm của phương trình là
đường thẳng
7
5
y =
song song với trục hoành.
Câu 19. Đáp án A.
Ta có
58 8
53 8 2 .
33
xx
xy y x
-+
-== =-
Đặt
()
88
38 2 238
3
)
3
(
xx
tt Z x t y x t
++
=Î=-=- = -
38
516
516
()
xt
tt tZ
yt
ì
ï
=-
ï
-= - Î
í
ï
=-
ï
î
.
Câu 20. Đáp án D.
Ta có
32 5xy-=
35 5
22
xx
yx
--
= =+
Đặt
5
() 25
2
x
tt Z x t
-
=Î=+
52
25 35
53
()
xt
yt tyt tZ
yt
ì
ï
=+
ï
= ++= + Î
í
ï
=+
ï
î
.
Câu 21. Đáp án C.
Ta có
527275xy y x-+ = =+
57 7
2
22
xx
yyx
++
= = +
Đặt
7
27
2
x
tx t
+
= = -
2.(2 7) 5 14( )yt tytt= - += - Î
Nên nghiệm nguyên của phương trình là
27
514
()
xt
tZ
yt
ì
ï
=-
ï
Î
í
ï
=-
ï
î
Vì
,xy
nguyên âm nên
7
0270
14
2
05140 14
5
5
t
xt
t
yt
t
ì
ï
ï
<
ì
ï
ï
<-<
ï
ï
ï
<
íí
ïï
<-<
ïï
î
<
ï
ì
ï
ï
ï
î
ï
î
í
ï
ï
mà
2tZ tÎ£
.
Nghiệm nguyên âm lớn nhất nhất của phương trình đạt được khi
2.2 7 3
2
5.2 14 4
xx
t
yy
ìì
ïï
=- =-
ïï
=
íí
ïï
=- =-
ïï
îî
Vậy nghiệm cần tìm là
(3; 4)--
.
Câu 22. Đáp án A.
Ta có
410 10
34 103 410
33
yy
xy x y x x y
-- +
+ =- =- - = =- -
Đặt
10
( ) 310 (310) 410
3
y
tt y t x t t t
+
= Î = - =- - - =- +
Hay nghiệm nguyên của phương trình
34 10xy+=-
là
410
31
)
0
(
xt
tZ
yt
ì
ï
=- +
ï
Î
í
ï
=-
ï
î
Vì
;xy
nguyên âm hay 0; 0xy<< nên
2, 25
4100
10
3100
3
t
t
t
t
ì
ï
>
ì
ï
ï
-+ <
ï
ï
ï
íí
ïï
-<
<
ïï
î
ï
ï
î
mà
3ttÎ=
Suy ra
4.3 10 2; 3.3 10 1xy=- + =- = - =-
nên nghiệm nguyên âm cần tìm
là
(; ) ( 2; 1) . 2xy xy=- - =
.
Câu 23. Đáp án A.
Ta có
48 8
438
33
xx
xy y yx
++
-+ == =+
Đặt
8
38 38 48( )
3
x
tx t y t ty t t
+
== -= -+= - Î
Nên nghiệm nguyên của phương trình là
38
)
48
(
xt
tZ
yt
ì
ï
ï
í
ï
ï
î
=-
Î
=-
Vì
,xy
nguyên dương nên
8
0380
8
3
0480
3
2
xt
t
t
yt
t
ì
ï
ìì
ï
ïï
>->
>
ï
ïï
ï
>
íí í
ïï ï
>->
ïï ï
>
îî
ï
ï
î
mà
3ttÎ³
.
Nghiệm nguyên dương nhỏ nhất của phương trình là
3.3 8 1
4.3 8 4
xx
yy
ìì
ïï
=- =
ïï
íí
ïï
=- =
ïï
îî
5xy+=
.
Câu 24. Đáp án C.
Ta có
75 5
67 5
66
yy
xy x xy
++
- == =+
Đặt
55
( ) 65 65 75
66
yy
tt y t x y t t t
++
=Î=-=+ =-+=-
Nên nghiệm nguyên của phương trình là
75
)
65
(
xt
tZ
yt
ì
ï
=-
ï
Î
í
ï
=-
ï
î
Vì
,xy
nguyên dương nên
5
0750
5
7
0650
5
7
6
t
xt
t
yt
t
ì
ï
ï
>
ìì
ï
ïï
>->
ï
ïï
ï
>
íí í
ïï ï
>->
ïï ï
îî
>
ï
ï
ï
î
mà
1ttÎ³
Do đó, nghiệm nguyên dương nhỏ nhất của phương trình có được khi
1t =
7.1 5 2
1
6.1 5 1
xx
xy
yy
ìì
ïï
=- =
ïï
-=
íí
ïï
=- =
ïï
îî
.
D.BÀI TẬP TỰ LUYỆN
Bài 1. Trong các cặp số
 
24
1; 2 , 2; 2 , 0; , ; 0 , 3; 3
33




, cặp số nào là nghiệm của phương trình:
a.
4313xy
b.
54xy
Bài 2. Tìm nghiệm tổng quát và vẽ đường thẳng biểu diễn tập nghiệm của nó:
a.
31
x
y
b.
25xy
c.
23 5xy
d.
32yx
Bài 3. Trong mỗi trường hợp sau, hãy tìm giá trị của
a để:
a. Điểm
0; 1A
thuộc đường thẳng
5xay
;
b. Điểm
3; 0B
thuộc đường thẳng
46ax y
;
c. Điểm
5; 2C  thuộc đường thẳng
63ax y
;
d. Điểm
5
;0
2
D



thuộc đường thẳng
25
0
2
ax y
;
e. Điểm
9
2;
2
E



thuộc đường thẳng
010xay
;
Bài 4. Cho đường thẳng

d có phương trình:
134 25mxm y m . Tìm m để:
a.

d
song song với trục hoành. b.

d
song song với trục tung.
c.

d đi qua gốc tọa độ. d.

d đi qua điểm
2; 1A .
Bài 5. Vẽ đồ thị của mỗi cặp phương trình sau trong cùng một hệ trục tọa độ, rồi tìm giao điểm của hai
đường thẳng đó.
a.
23xy
và
32 5xy
b.
24xy
và
3210xy
c.
1
x
y
và
33 6xy
d.
24xy
và
24 8xy
HƯỚNG DẪN
Bài 1. Thay lần lượt mỗi cặp số đã cho vào từng phương trình, rồi so sánh giá trị tìm được ở hai vế để rút
ra kết luận.
a. Các cặp số

2
1; 2 , 0;
3



, là nghiệm của phương trình
43 2xy
.
b. Các cặp số

4
2; 2 , ; 0
3



, là nghiệm của phương trình
35 4xy
.
Bài 2. Tìm nghiệm tổng quát và vẽ đường thẳng biểu diễn tập nghiệm của nó:
a. Nghiệm tổng quát của phương trình
31
x
y
:
31
x
yx

hoặc
11
33
y
xy

Có đồ thị hàm số là:
b. Nghiệm tổng quát của phương trình
25xy
:
15
22
x
yx

hoặc
25
y
x
y

Có đồ thị hàm số là:
c. Nghiệm tổng quát của phương trình
23 5xy
:
25
33
x
yx

hoặc
35
22
y
xy

Có đồ thị hàm số là:
d. Nghiệm tổng quát của phương trình
32yx
:
12
33
x
yx

hoặc
32
y
xy

Có đồ thị hàm số là:
Bài 3.
Trong mỗi trường hợp sau, hãy tìm giá trị của a để:
a. Điểm
0; 1A
thuộc đường thẳng
5xay
, ta có:

015 5aa.
Vậy với
5a
thì điểm A thuộc đồ thị hàm số đã cho.
b. Điểm
3; 0B
thuộc đường thẳng
46ax y
, ta có:
34.06 3 6 2aaa 
.
Vậy với
2a 
thì điểm B thuộc đồ thị hàm số đã cho.
c. Điểm
5; 2C  thuộc đường thẳng
63ax y
, ta có:
 
9
56.2 3 5 9
5
aaa 
.
Vậy với
9
5
a 
thì điểm C thuộc đồ thị hàm số đã cho.
d. Điểm
5
;1
2
D



thuộc đường thẳng
25
0
2
ax y
, ta có:
525
.0 5
22
aa
.
Vậy với
5a
thì điểm D thuộc đồ thị hàm số đã cho.
e. Điểm
9
2;
2
E



thuộc đường thẳng
010xay
, ta có:
920
0.2 10
29
aa




.
Vậy với
20
9
a
thì điểm E thuộc đồ thị hàm số đã cho.
Bài 4. Cho đường thẳng

d
có phương trình:
134 25mxm y m
.
Phương trình đường thẳng

d có các hệ số:
1; 3 4; 2 5am b m c m
a.

d
song song với trục hoành.
1
010 1
4
0340 34 1
3
025025
5
2
m
am m
bm m mm
cm m
m









Vậy với
1m thì phương trình đường thẳng

d song song với trục hoành.
b.

d
song song với trục tung
1
010 1
44
0340 34
33
025025
5
2
m
am m
bm mmm
cm m
m









Vậy với
4
3
m
thì phương trình đường thẳng

d
song song với trục hoành.
c.

d
đi qua gốc tọa độ
1
010 1
45
0340 34
32
025025
5
2
m
am m
bm mmm
cm m
m



 





Vậy với
5
2
m 
thì phương trình đường thẳng

d đi qua gốc tọa độ.
d.

d đi qua điểm
2; 1A , suy ra tọa độ điểm A thỏa mãn phương trình đường thẳng
134 25mxm y m

1.2 3 4. 1 2 5mm m
223425mm m
7m
Vậy với
7m  thì phương trình đường thẳng

d đi qua điểm A.
Bài 5. Vẽ đồ thị của mỗi cặp phương trình sau trong
cùng một hệ trục tọa độ, rồi tìm giao điểm của hai
đường thẳng đó.
a.
1
:2 3dxy và
2
:3 2 5dxy
Đồ thị hàm số
1
:2 3dxy
là đường thẳng có
phương trình là:
23yx
Đồ thị hàm số
2
:3 2 5dxy
là đường thẳng có
phương trình là:
35
22
yx
Giao điểm của hai đồ thị hàm số

1
d
và
2
d
có tọa
độ là:
1; 1
.
b.

3
:24dxy
và
4
:3 12dxy
Giao điểm của hai đồ thị hàm số
3
d
và
4
d
có tọa độ là:

4; 0
.
c.

5
:1dxy
và

6
:3 3 6dxy
Ta có:
111
33 6


. Hai đồ thị hàm số
5
d
và
6
d
song song với nhau.
d.

7
:24dxy
và
8
:2 4 8dxy
Ta có:
124
24 8


. Hai đồ thị hàm số
7
d
và
8
d
trùng nhau.
----------Toán Học Sơ Đồ---------
| 1/19
| | Tải xuống

Có thể bạn quan tâm:

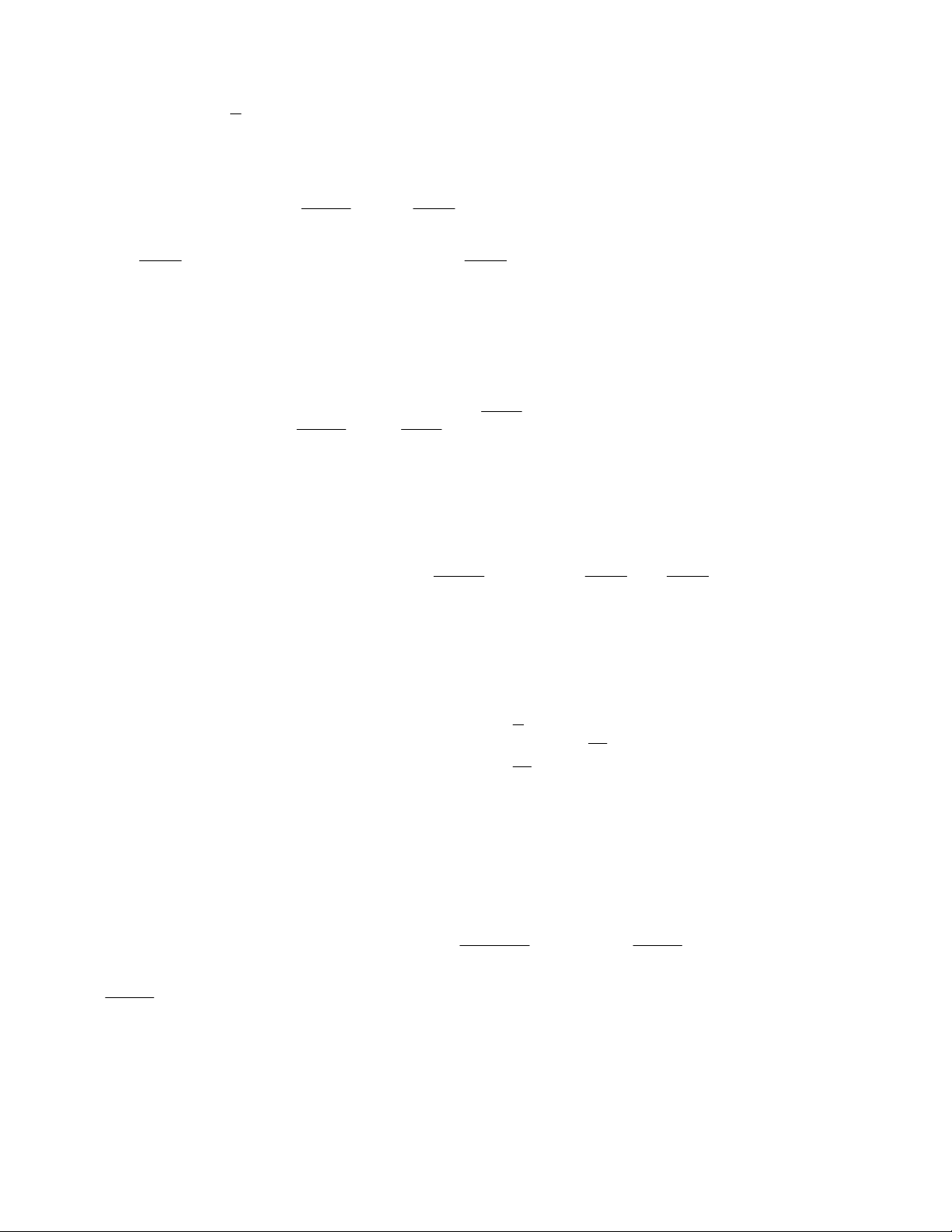
Preview text:

CHUYÊN ĐỀ PHƯƠNG TRÌNH BẬC NHẤT HAI ẨN
A.KIẾN THỨC TRỌNG TÂM
1. Phương trình bậc nhất hai ẩn là phương trình có dạng: ax by c  
1 trong đó a, b, c là các số
đã biết ( a  0 hoặc b  0 ), x và y lần lượt là các ẩn.
Cặp x ; y thỏa mãn ax by c được gọi là một nghiệm của phương trình ax by c   1 0 0  0 0 .
Trong mặt phẳng tọa độ Oxy, mỗi nghiệm x ; y của (1) được biểu diễn bởi một điểm x ; y 0 0  0 0 
2. Tập nghiệm của phương trình bậc nhất hai ẩn
Phương trình bậc nhất hai ẩn ax by c  
1 ( a  0 hoặc b  0 ), luôn có vô số nghiệm. Tập
nghiệm của nó được biểu diễn bởi đường thẳng ax by cd . a c
Nếu a  0 và b  0 thì đường thẳng d là đồ thị của hàm số y   x b b
Nếu a  0 , b  0 và c  0 thì đường thẳng d song song với trục tung Oy và phương trình c
trở thành ax c x . a
Nếu a  0 , b  0 và c  0 thì đường thẳng d trùng với trục tung Oy và phương trình trở thành
ax  0  x  0 .
Nếu a  0 ; b  0 và c  0 thì đường thẳng d song song với trục hoành Ox và phương trình c
trở thành by c y . b
Nếu a  0 ; b  0 và c  0 thì đường thẳng d trùng với trục hoành Ox và phương trình trở
thành by  0  y  0 .
B.CÁC DẠNG BÀI TẬP MINH HỌA
Dạng 1. Xác định nghiệm của phương trình bậc nhất hai ẩn.
Bài 1. Trong các cặp số 0; 4 ,–1; 3 ,1;1 ,2; 3 ,4; 6 cặp số nào là nghiệm của phương trình: a) 5x  3y  2 b) 2x y  7
c) 2x y  2
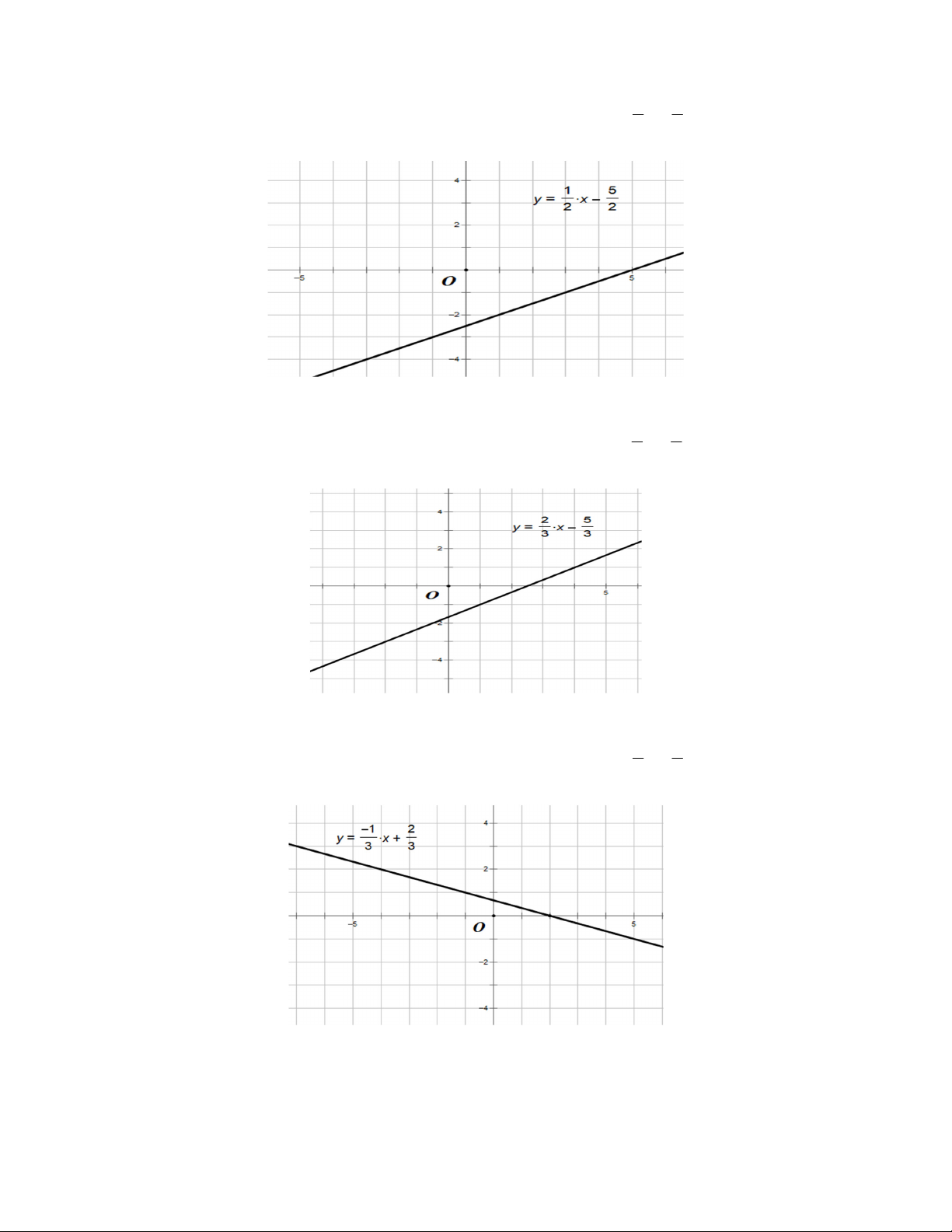
Bài 2. Tìm nghiệm tổng quát và vẽ đường thẳng biểu diễn tập nghiệm của nó: a)
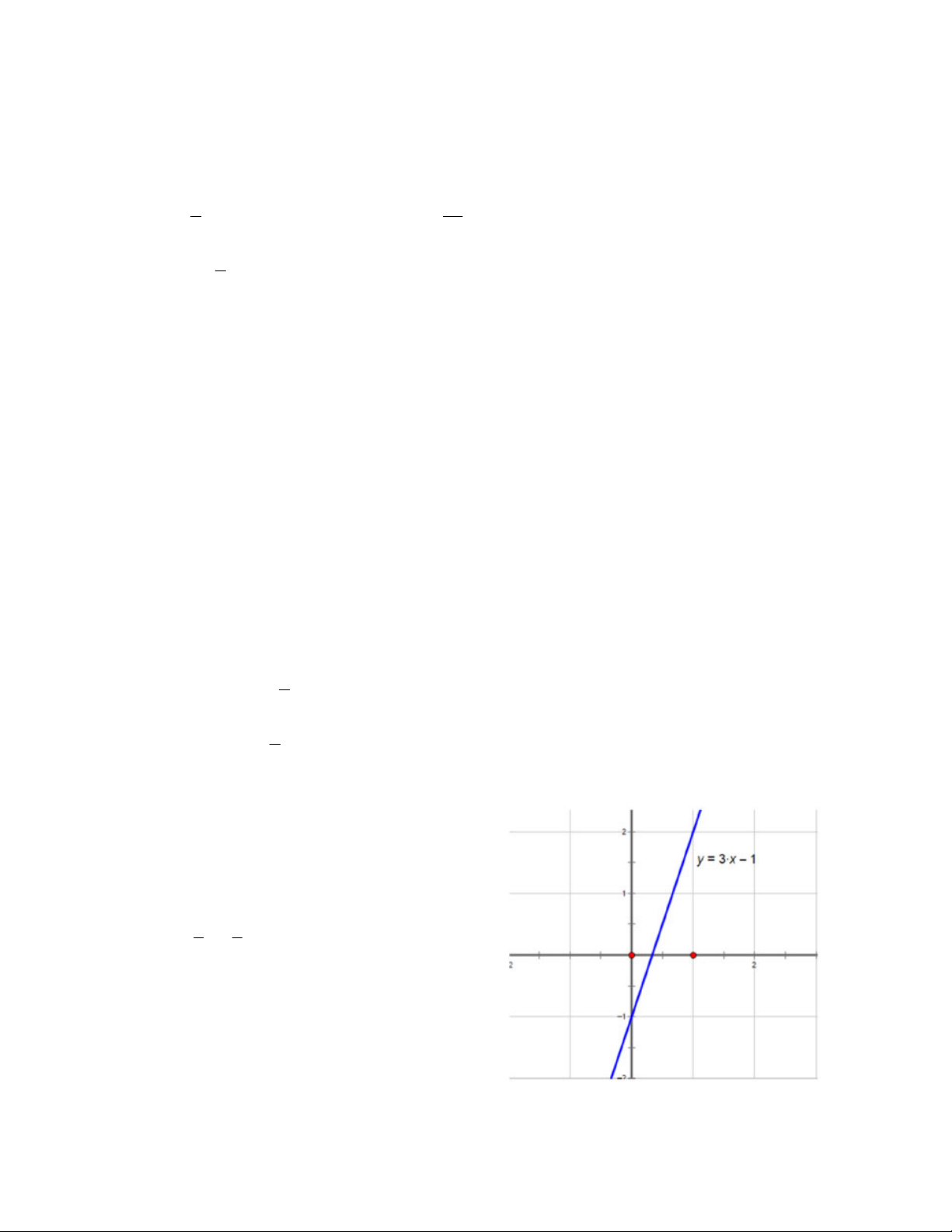
3x y 1 b) x  2y  5
c) 2x  3y  5 d) y 3  x  2
Dạng 2. Biện luận và vẽ đồ thị của hàm số bậc nhất:
Bài 3. Cho đường thẳng d có phương trình: (m 1)x  ( m
3  4)y   m 2  5. Tìm m để:
a) d song song với trục hoành.
b) d song song với trục tung.
c) d đi qua gốc toạ độ.
d) d đi qua điểm A(2; – ) 1 .
Bài 4. Trong mỗi trường hợp sau, hãy tìm giá trị của a để:
a) Điểm A0; 1thuộc đường thẳng x ay  5 
b) Điểm B3;0 thuộc đường thẳng ax – 4y  6 c) Điểm C  5;  2
  thuộc đường thẳng ax  6y  3    d) Điểm 5
D  ; 0 thuộc đường thẳng 25 ax  0y   2  2   e) Điểm 9
E 2;   thuộc đường thẳng 0x ay  1  0 .  2 
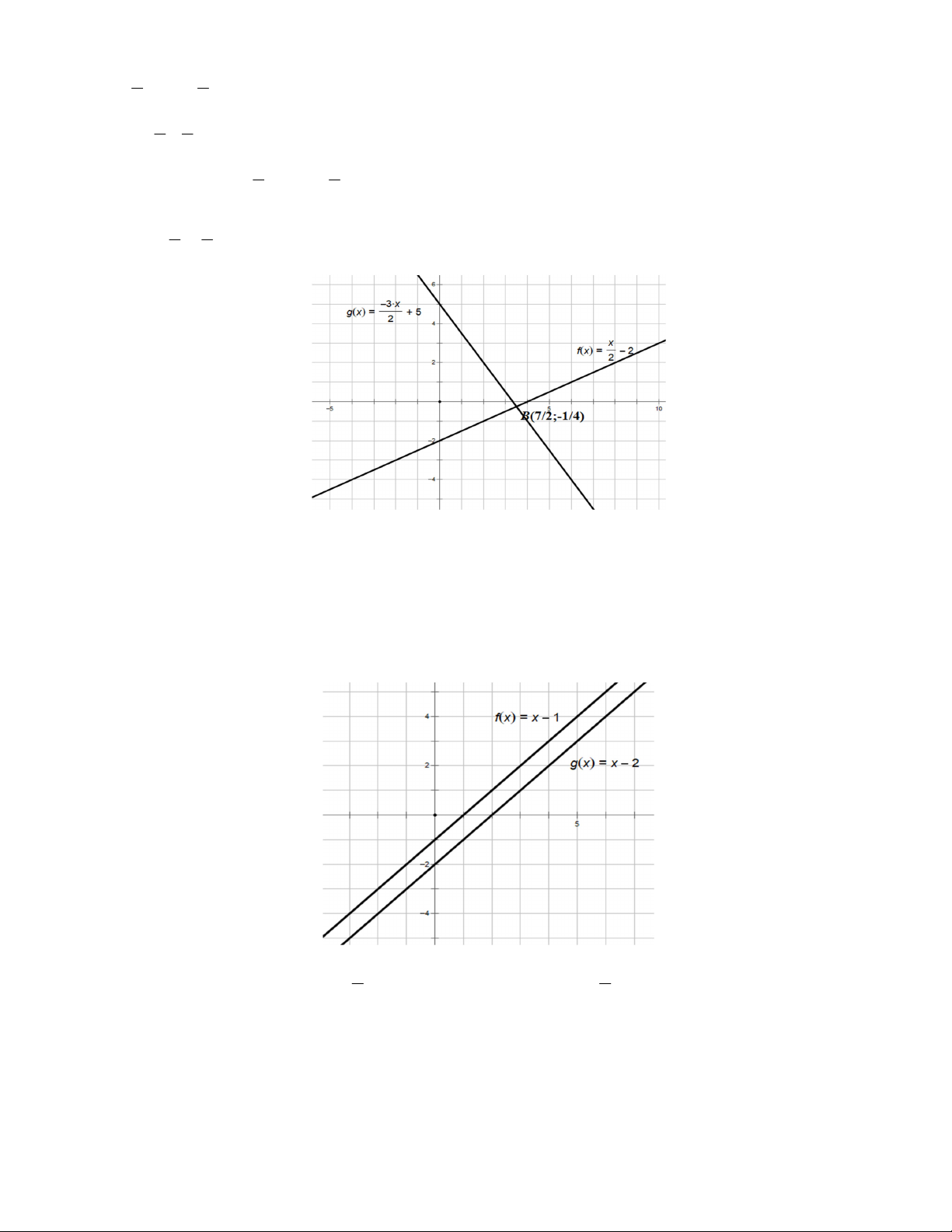
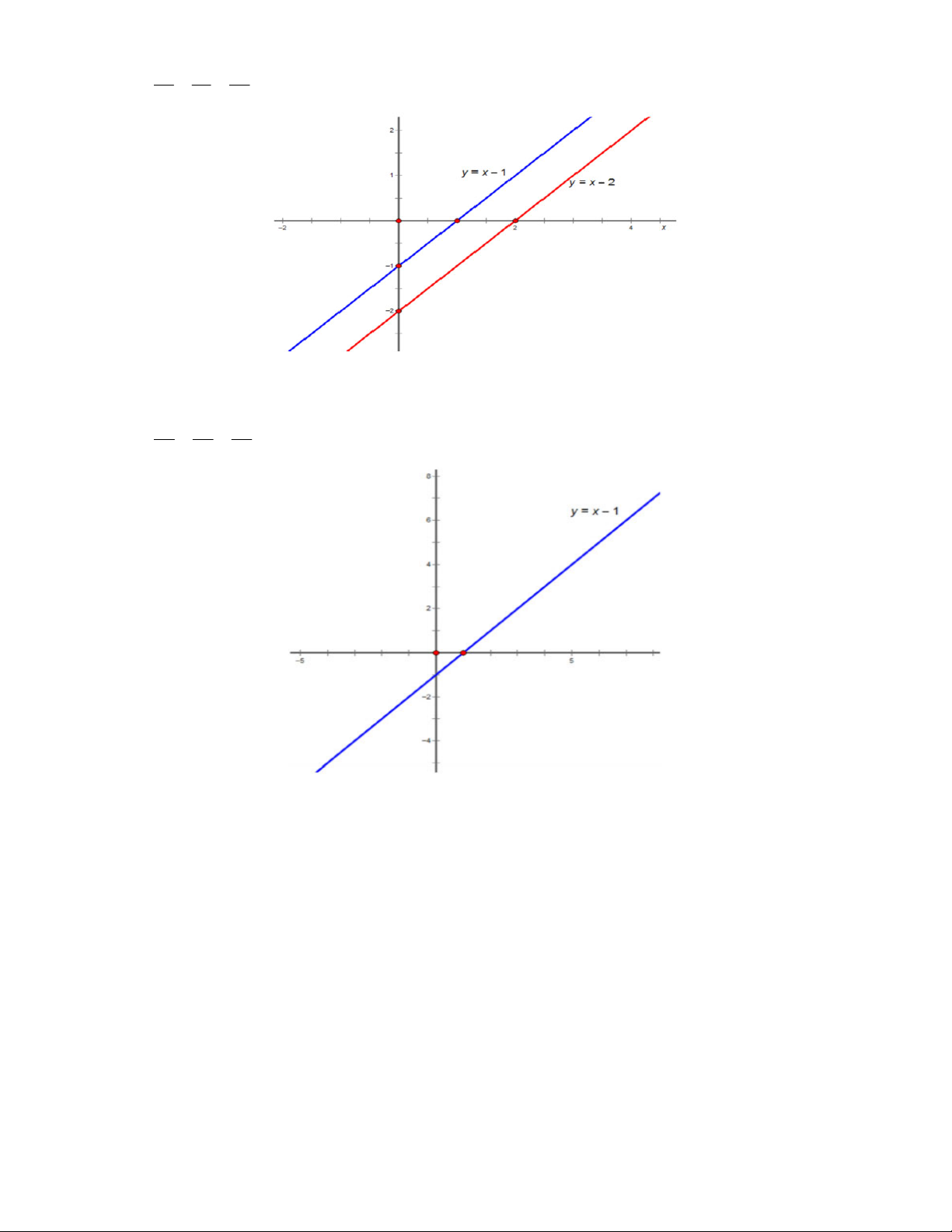
Bài 5. Vẽ đồ thị của mỗi cặp phương trình sau trong cùng một hệ trục tọa độ, rồi tìm giao điểm của hai
đường thẳng đó.
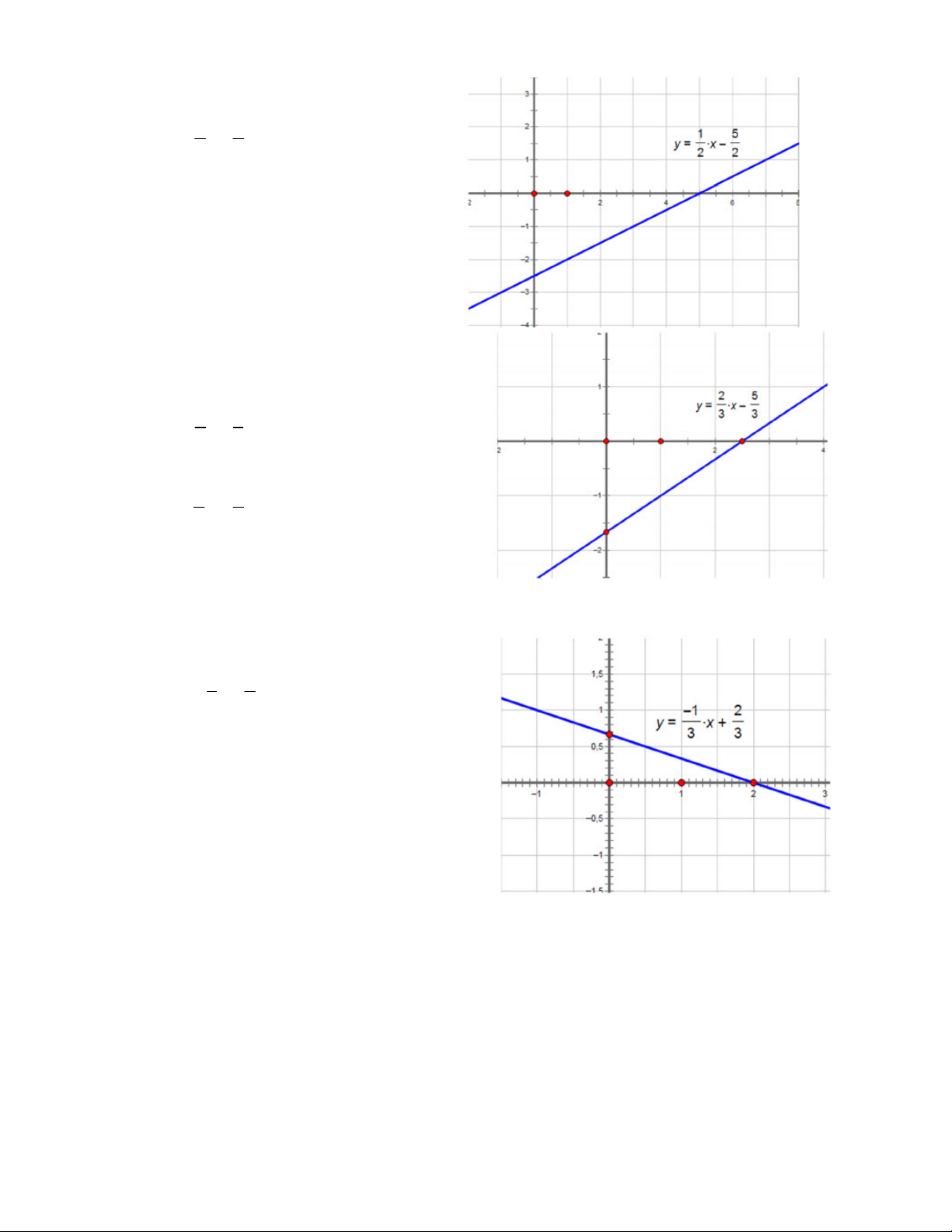
f) 2x – y  3 và 3x – y 2  5
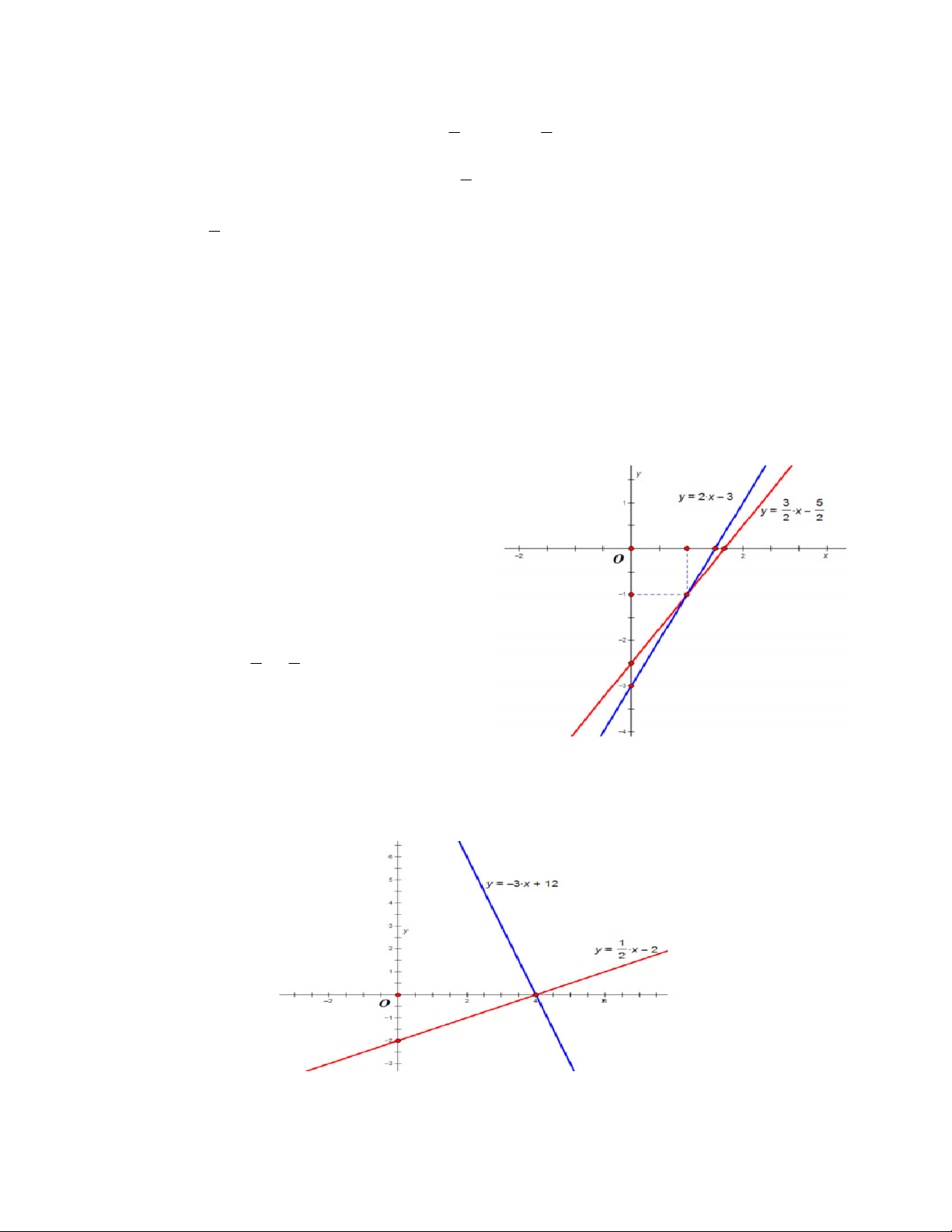
g) x – 2y  4 và 3x  2y  10
h) x – y  1 và 3
x  3y  6 
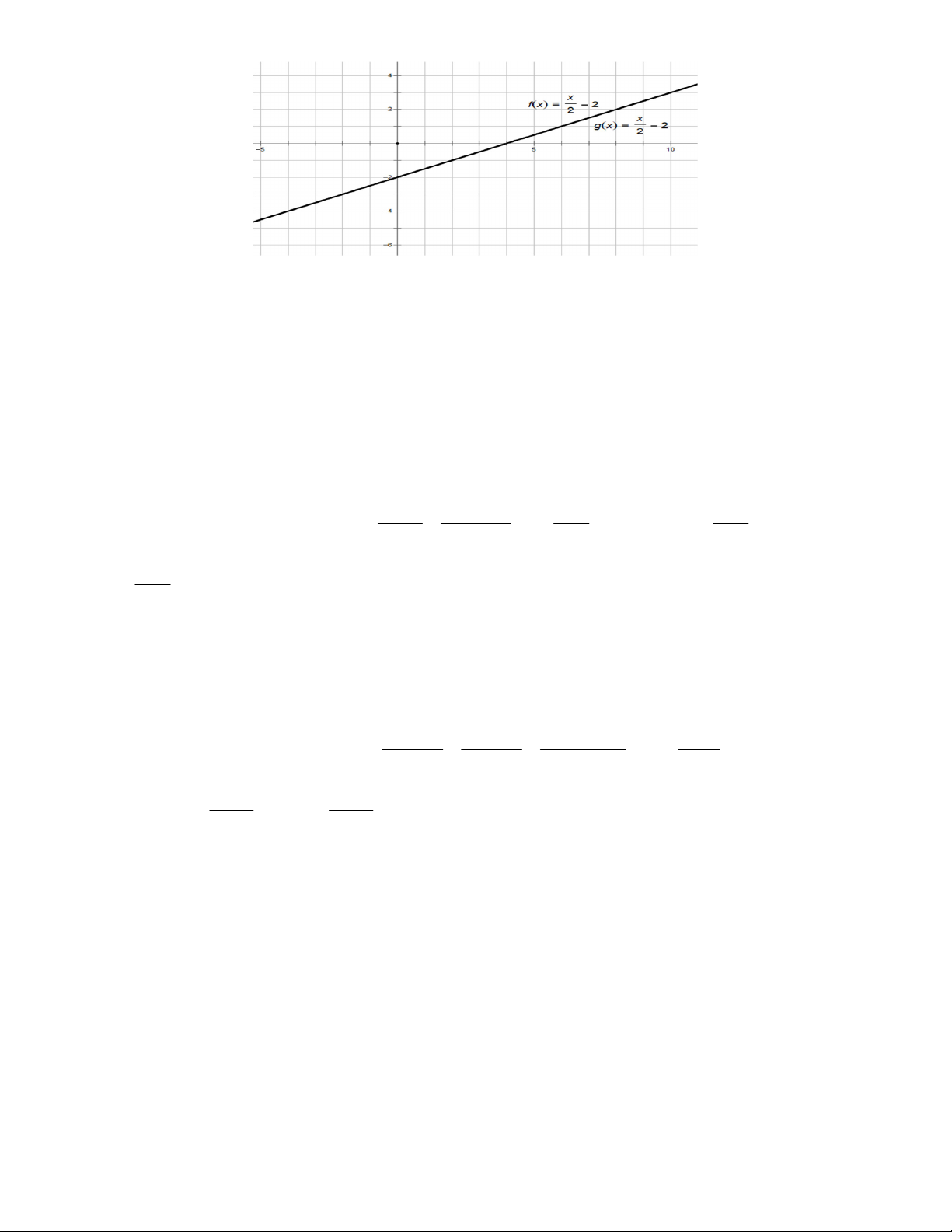
i) x – 2y  4 và 2
x  4y  8 
Dạng 3. Tìm nghiệm nguyên của phương trình bậc nhất hai ẩn
Bài 6. Tìm tất cả các nghiệm nguyên của phương trình: a)
2x y  0 b) 3x  2y  5
c) 2x  5y  15 d) 5x 1 y 1  4
e) 7x  5y  143 f)
23x  53y 109 HƯỚNG DẪN
Dạng 1. Xác định nghiệm của phương trình bậc nhất hai ẩn
Bài 1. Thay lần lượt mỗi cặp số đã cho vào từng phương trình, rồi so sánh giá trị tìm được ở hai vế để rút ra kết luận
a) Cặp số (1;1),(4; 6) là nghiệm của phương trình 5x  3y  2
b) Cặp số (2; 3) là nghiệm của phương trình 2x + y  7
c) Cặp số (4; 6) là nghiệm của phương trình 2x  y  2
Bài 2. Tìm nghiệm tổng quát và vẽ đường thẳng biểu diễn tập nghiệm   y  x   
a) Nghiệm tổng quát của phương trình 3x  y  1 là  hoặc  1 1 y  3x   1 x y   3 3 có đồ thị hàm số là   y  x   
b) Nghiệm tổng quát của phương trình 3x  y  1 là  hoặc  1 1 y  3x   1 x y   3 3 có đồ thị hàm số là   y  x   
c) Nghiệm tổng quát của phương trình 3x  y  1 là  hoặc  1 1 y  3x   1 x y   3 3 có đồ thị hàm số là   y  x   
d) Nghiệm tổng quát của phương trình 3x  y  1 là  hoặc  1 1 y  3x   1 x y   3 3 có đồ thị hàm số là
Dạng 2. Biện luận và vẽ đồ thị của hàm số bậc nhất
Bài 3. Cho đường thẳng (d) có phương trình: (m 1)x  ( m 3  4)y  2  m  5.
Phương trình đường thẳng (d) có các hệ số a m  1; b  3m  4; c  2  m  5
a) d song song với trục hoành     m  1 a  0  m 1  0 m   1      4
 b  0   3m  4  0   3m  4   m   m  1 3     c  0 2  m  5  0 2m  5      5 m       2
Vậy với m  1 thì phương trình đường thẳng (d) song song với trục hoành
b) d song song với trục tung     m  1 a  0  m 1  0 m   1      4 4
 b  0   3m  4  0   3m  4   m   m  3 3     c  0 2  m  5  0 2m  5      5 m       2 Vậy với 4 m
thì phương trình đường thẳng (d) song song với trục tung 3
c) d đi qua gốc tọa độ     m  1 a  0  m 1  0 m   1      4 5
 b  0   3m  4  0   3m  4   m   m   3 2     c  0 2  m  5  0 2m  5      5 m       2 Vậy với 5
m   thì phương trình đường thẳng (d) đi qua gốc tọa độ 2
d) d đi qua điểm A(2; 1) , suy ra tọa độ điểm A thỏa mãn phương trình đường thẳng
(m 1)x  ( m
3  4)y  2m  5
 (m 1).2  ( m
3  4).(1)  2m  5
 2m  2  m 3  4  2m  5  m  7
Vậy với m  7 thì phương trình đường thẳng (d) đi qua điểm A. Bài 4. a) Điểm A0; 1
 thuộc đường thẳng x ay  5  , ta có 0  .
a 1  5  a  5
Vậy với a  5 thì điểm A0; 1
  thuộc đồ thị hàm số đã cho
b) Điểm B3;0 thuộc đường thẳng ax – 4y  6 , ta có .
a 3  4.0  6  3a  6  a  2 Vậy với a  2
 thì điểm B3;0 thuộc đồ thị hàm số đã cho
c) Điểm C 5; 2thuộc đường thẳng ax  6y  3  , ta có
a      9 . 5 6. 2  3   5
a  9  a   . Vậy với 9
a   thì điểm C  5;  2
  thuộc đồ thị hàm 5 5 số đã cho   d) Điểm 5
D  ; 0 thuộc đường thẳng 25 ax  0y  , ta có 5 25 . a  0   a  5  2  2 2 2  
Vậy với a  5 thì điểm 5
D  ; 0 thuộc đồ thị hàm số đã cho  2      Điểm 9
E 2;   thuộc đường thẳng 0x ay  1  0 , ta 9 20 0.2  . a    1  0  a   . Vậy với 20 a   2   2  9 9   thì điểm 9
E 2;   thuộc đồ thị hàm số đã cho  2  Bài 5.
a) Đồ thị hàm số 3 5
2x – y  3  y  2x  3(d ) và đồ thị hàm số 3x – 2y  5  y x  (d ) . 1 2 2 2
Phương trình hoành độ giao điểm của hai đường thẳng là: 3 5 2x  3  x  2 2 3 5
 2x x  3  2 2 x 1
   x  1  y  1  . 2 2  (1
A ; 1) là giao điểm của hai đường thẳng đã cho.
b) Đồ thị hàm số x 3
x – 2y  4  y
 2(d ) và đồ thị hàm số 3x  2y  10  y   x  5(d ) . 1 2 2 2
Phương trình hoành độ giao điểm của hai đường thẳng là: x 3  2   x  5 2 2 x 3   x  7 2 2 7 1
 2x  7  x   y   . 2 4 7 1  ( B
;  ) là giao điểm của hai đường thẳng đã cho. 2 4
c) Đồ thị hàm số x – y  1  y x  (
1 d ) và đồ thị hàm số 3x  3y  6  y x  2(d ) . 1 2
Phương trình hoành độ giao điểm của hai đường thẳng là:
x  1  x  2  0x  1
 (phương trình vô nghiệm). Vậy hai đường thẳng đã cho song song với nhau d) Đồ thị hàm số x x
x – 2y  4  y   2(d ) và 2
x  4y  8
  y   2(d ) 1 2 2 2
Vậy hai đồ thị hàm số đã cho có vô số điểm chung.
Dạng 3. Tìm nghiệm nguyên của phương trình bậc nhất hai ẩn Bài 6.
a) Từ phương trình 2x y  0  y  2  x
Đặt x t,t   y   t 2
Vậy các cặp số nguyên cần tìm là  x ty   t 2 ,t         b) Từ phương trình 3x 5 2x x 5 x 5 5
3x  2y  5  y    x  . Vì x x, y     . 2 2 2 2 
Đặt x 5  t(t  )  x t
2  5  y t
2  5  t t 3  5 . 2
Vậy các cặp số nguyên cần tìm có dạng  x t 2  5  y t 3  5,t     y   y   y y y
c) Từ phương trình x y   x 5 15 5 15 4 15 15 2 5 15     2  . 2 2 2 2   Vì y 15 15 x, y     . Đặt y
t(t  )  y t 2  15  x  2  ( t
2  15)  t   t 5  30 2 2
Vậy các cặp số nguyên cần tìm có dạng  x   t 5  30  .
y  2t  15,t   
C.TRẮC NGHIỆM RÈN LUYỆN PHẢN XẠ
Câu 1. Cho phương trình ax + by = c với a ¹ 0,b ¹ 0 . Nghiệm của phương
trình được biểu diễn bởi. x ìï Î ì ì ì ï  x ï Î ï  x ï Î ï  x ï Î ï  A. ï ï ï ï í ï ï a c . B. í a c . C. í c . D. í c . y ïï = - x + y ïï = - x - y ïï = y ïï = - ïî b b ïî b b ïî b ïî b
Câu 2. Phương trình nào sau đây là phương trình bậc nhất hai ẩn? y A. 2 2x + 2 = 0 .
B. 3y - 1 = 5(y - 2). C. 2x + - 1 = 0 . D. 2 3 x + y = 0 . 2
Câu 3. Phương trình nào dưới đây nhận cặp số (-2; 4) làm nghiệm
A. x - 2y = 0 .
B. 2x + y = 0 .
C. x - y = 2 .
D. x + 2y + 1 = 0 .
Câu 4. Phương trình x - 5y + 7 = 0 nhận cặp số nào sau đây làm nghiệm?
A. (0;1) . B. (-1;2) .
C. (3;2) . D. (2; 4) .
Câu 5. Phương trình 5x + 4y = 8 nhận cặp số nào sau đậy là nghiệm? A. (-2;1). B. (-1; 0). C. (1, 5; 3). D. (4;-3) .
Câu 6. Tìm số dương m để phương trình 2
2x - (m - 2) y = 5 nhận cặp số (-10;-1) làm nghiệm. A. m = 5 . B. m = 7 . C. m = -3 .
D. m = 7;m = -3 .
Câu 7. Tìm m để phương trình m - 1x - 3y = 1
- nhận cặp số (1;1) làm nghiệm. A. m = 5 . B. m = 2 . C. m = -5 . D. m = -2 .
Câu 8. Công thức nghiệm tổng quát của phương trình 0x + 4y = -16 . x ìï Î  x ìï Î  x ìï Î  x ìï Î  A. ïí . B. ïí . C. ïí . D. ïí . y ï = 4 - ï ï = ï = - ï = î y 4 ïî x 4 ïî x 4 ïî
Câu 9. Công thức nghiệm tổng quát của phương trình 3x + 0y = 12 . x ìï Î R x ìï Î R x ìï Î R x ìï Î R A. ïí . B. ïí . C. ïí . D. ïí . y ï = 4 - ï ï = ï = - ï = î y 4 ïî x 4 ïî x 4 ïî
Câu 10. Trong các cặp số (-2;1);(0;2);(-1; 0);(1, 5; 3);(4;-3) có bao nhiêu cặp số không là nghiệm của
phương trình 3x + 5y = -3 . A. 1 . B. 3 . C. 2 . D. 4 .
Câu 11. Cho đường thẳng d có phương trình (m - 2)x + (3m - 1)y = 6m - 2
Tìm các giá trị của tham số m để d song song với trục hoành. A. m = 1. B. m = 2 . C. m = 3 . D. m = 4 .
Câu 12. Cho đường thẳng d có phương trình (5m - 15)x + 2my = m - 2
Tìm các giá trị của tham số m để d song song với trục hoành. A. m = 1. B. m = 2 . C. m = 3 . D. m = 4 .
Câu 13. Cho đường thẳng d có phương trình (m - 2)x + (3m - 1)y = 6m - 2
Tìm các giá trị của tham số m để d song song với trục tung. 1 2 1 A. m = . B. m = . C. m ¹ 2 . D. m ¹ . 3 3 3 m - 1
Câu 14. Cho đường thẳng d có phương trinh
x + (1 - 2m)y = 2 2
Tìm các giá trị của tham số m để d song song với trục tung. 1 1 A. m = 1. B. m ¹ . C. m = 2 . D. m = . 2 2
Câu 15. Cho đường thẳng d có phương trình (2m - 4)x + (m - 1)y = m - 5
Tìm các giá trị của m tham số d để đi qua gốc tọa độ. A. m = 2 . B. m = 1. C. m = 5 . D. m ¹ 5 .
Câu 16. Cho đường thẳng d có phương trình (m - 2).x + (3m - 1).y = 6m - 2
Tìm các giá trị của tham số m để d đi qua gốc tọa độ. 1 2 1 A. m = . B. m = . C. m ¹ 2 . D. m ¹ . 3 3 3
Câu 17. Chọn khẳng định đúng.
Đường thẳng d biểu diễn tập nghiệm của phương trình 3x - y = 3 là.
A. Đường thẳng song song với trục hoành. B. Đường thẳng song song với trục tung.
C. Đường thẳng đi qua gốc tọa độ.
D. Đường thẳng đi qua điểm A(1;0).
Câu 18. Cho đường thẳng nào đưới đây có biểu diễn hình học là đường thẳng song song với trục hoành. A. 5y = 7 . B. 3x = 9 .
C. x + y = 9 .
D. 6y + x = 7 .
Câu 19. Tìm tất cả nghiệm nguyên của phương trình 5x - 3y = 8 . x ìï = 3t - 8 x ìï = 3t - 8 A. ïí (t Î Z). B. ïí (t Î Z) . y ï = 5t - 16 ï ï = - - î y 5t 6 ïî x ìï = 8t - 3 x ìï = 3t + 8 C. ïí (t Î Z) . D. ïí (t Î Z). y ï = 15t - 16 ï ï = + î y 5t 6 ïî
Câu 20. Tìm nghiệm tất cả các nghiệm nguyên của phương trình 3x - 2y = 5 . x ìï = 5 - 2t x ìï = 5 + 2t A. ïí (t Î Z) . B. ïí (t Î Z) . y ï = -5 - 3t ï ï = - î y 5 3t ïî x ìï = 5 - 2t x ìï = 5 + 2t C. ïí (t Î Z) . D. ïí (t Î Z) . y ï = 5 + 3t ï ï = + î y 5 3t ïî
Câu 21. Tìm nghiệm nguyên âm lớn nhất của phương trình -5x + 2y = 7 . A. (-7;-14). B. (-1;-2) . C. (-3;-4) . D. (-5;-9) .
Câu 22. Nghiệm nguyên âm của phương trình 3x + 4y = -10 là (x;y) . Tính x.y . A. 2 . B. -2 . C. 6 . D. 4 .
Câu 23. Gọi (x;y) là nghiệm nguyên dương nhỏ nhất của phương trình
-4x + 3y = 8 . Tính x + y A. 5 . B. 6 . C. 7 . D. 4 .
Câu 24. Gọi (x;y) là nghiệm nguyên dương nhỏ nhất của phương trình
6x - 7y = 5 . Tính x - y . A. 2 . B. 3 . C. 1 . D. -1 . HƯỚNG DẪN Câu 1. Đáp án A. a c
Ta có với a ¹ 0,b ¹ 0 thì  by = a
- x + c y = - x + b b x ìï Î ï 
Nghiệm của phương trình được biểu diễn bởi ïí a c y ïï = - x + ïî b b Câu 2. Đáp án C. y
Phương trình 2x + - 1 = 0 là phương trình bậc nhất hai ẩn. 2 Câu 3. Đáp án B.
Thay x = -2;y = 4 vào từng phương trình ta được
+) x - 2y = -2 - 2.4 = -10 ¹ 0 nên loại A.
+) x - y = -2 - 4 = -6 ¹ 0 nên loại C.
+) x + 2y + 1 = -2 + 2.4 + 1 = 7 ¹ 0 nên loại D.
+) 2x + y = -2.2 + 4 = 0 nên chọn B. Câu 4. Đáp án C.
+) Thay x = 0;y = 1 vào phương trình x - 5y + 7 = 0 ta được 0 - 5.1 + 7 = 0  2 = 0 (vô lý) nên loại A.
+) Thay x = -1;y = 2 vào phương trình x - 5y + 7 = 0 ta được 1 - - 5.2 + 7 = 0  4 - = 0 (vô lý) nên loại B.
+) Thay x = 2;y = 4 vào phương trình x - 5y + 7 = 0 ta được 2 - 5.4 + 7 = 0  1 - 1 = 0 (vô lý) nên loại D.
+) Thay x = 3;y = 2 vào phương trình x - 5y + 7 = 0 ta được 3 - 5.2 + 7 = 0  0 = 0 (luôn đúng) nên chọn C. Câu 5. Đáp án D.
Xét phương trình 5x + 4y = 8
Cặp số (-2;1) không phải nghiệm của phương trình vì 5(-2) + 4.1 = -6 . Do đó loại A.
Cặp số (-1; 0) không phải nghiệm của phương trình vì 5.(-1) + 4.0 = -5 . Do đó loại B.
Cặp số (1, 5; 3) không phải nghiệm của phương trình vì 5.1, 5 + 4.3 = 19, 5 . Do đó loại C
Cặp số (4;-3) là nghiệm của phương trình vì 5.4 + 4.(-3) = 8 . Do đó chọn D. Câu 6. Đáp án B.
Thay x = -10;y = -1 vào phương trình 2
2x - (m - 2) y = 5 ta được m é 2 5 m é - = = 7(N ) 2 2 2.( 10) (m 2) .( 1) 5 (m 2) 25 ê ê - - - - =  - =   m ê 2 5 m ê - = - = - ( 3 L) êë êë Vậy m = 7 Câu 7. Đáp án A.
Thay x = 1;y = 1vào phương trình ta được
m - 1.1 - 3.1 = -1 ĐK m ³ 1
-  m - 1 = 2  m - 1 = 4  m = 5 (thỏa mãn). Vậy m = 5 Câu 8. Đáp án A.
Ta có 0x + 4y = -16  y = -4 x ìï Î R
Nghiệm tổng quát của phương trình ïí . y ï = 4 - ïî Câu 9. Đáp án D.
Ta có 3x + 0y = 12  x = 4 x ìï Î R
Nghiệm tổng quát của phương trình ïí . x ï = 4 ïî Câu 10. Đáp án B.
Xét phương trình 3x + 5y = -3
Cặp số (-2;1) không phải nghiệm của phương trình vì 3(-2) + 5.1 = -1.
Cặp số (0;2) không phải nghiệm của phương trình vì 3.0 + 5.2 = 10 .
Cặp số (-1; 0) là nghiệm của phương trình vì 3.(-1) + 5.0 = -3 .
Cặp số (1, 5; 3) không phải nghiệm của phương trình vì 3.1, 5 + 5.3 = 19, 5 .
Cặp số (4;-3) là nghiệm của phương trình vì 3.4 + 5.(-3) = -3 .
Vậy có 3 cặp số không phải nghiệm của phương trình đã cho. Câu 11. Đáp án B. m ìï - 2 = 0 ï m ìï = 2 ï ï
Để d song song với trục hoành thì 3 ïí m 1 0 ï - ¹  í  m = 2 1 ïï m ïï ¹ 6 ï m - 2 ¹ 0 ï ï î 3 î Câu 12. Đáp án C. 5 ìï m -15 = 0 m ìï = 3 ï ï ï ï
Để d song song với trục hoành thì 2 ïí m 0 m ï ¹
 í ¹ 0  m = 3 . ï ï m ïï 2 0 m ï - ¹ ï ¹ 2 ïî ïî Câu 13. Đáp án A. ìïm ï ì ï ¹ 2 m ï - 2 ¹ 0 ï ï ï ï ï 1 1 1
Để d song song với trục tung thì 3 ïí m 1 0 m ï - =  í =
m = . Vậy m = . ï ï 3 3 3 6 ïï m 2 0 ï - ¹ ï ïî ï 1 m ï ¹ - ïïî 3 Câu 14. Đáp án D. ìïm -1 ïï ¹ 0 ï m ìï ¹ 1 ï 2 ï ï ï 1 1 í 2m 0 ï - =  í 1  m = ïï m ïï = 2 2 ï ¹ 0 ï ï î 2 ï 1
Để d song song với trục tung thì ïî . Vậy m = . 2 Câu 15. Đáp án C.
Gốc tọa độ O(0; 0) Để d đi qua gốc tọa độ thì tọa độ điểm O thỏa mãn phương
trình (2m - 4)x + (m - 1)y = m - 5 hay (2m - 4).0 + (m - 1).0 = m - 5  m - 5 = 0  m = 5 Vậy m = 5 . Câu 16. Đáp án A. 1
(m - 2).0 + (3m - 1).0 = 6m - 2  m =
Để d đi qua gốc tọa độ thì 3 . 1 m = Vậy 3 . Câu 17. Đáp án D.
Ta có 3x - y = 3  y = 3x - 3 x ìï Î R ïíyï = 3x -3
Nghiệm tổng quát của phương trình ïî
Biểu diễn hình học của tập nghiệm là đường thẳng y = 3x - 3 đi qua điểm ( A 1; ) 0 và B(0;-3) . Câu 18. Đáp án A.
Ta thấy phương trình 5y = 7 có a = 0;b = 5 và c = 7 ¹ 0 nên biểu diễn nghiệm của phương trình là 7 đường thẳng y =
song song với trục hoành. 5 Câu 19. Đáp án A. 5x - 8 x + 8
5x - 3y = 8  y = = 2x - . Ta có 3 3 x + 8 x + 8
= t(t Î Z)  x = 3t - 8  y = 2x - = 2 3 ( t - 8) Đặt 3 3 x ìï = 3t - 8 t 5t 16 ï - = -  í (t Î Z) y ï = 5t - 16 ïî . Câu 20. Đáp án D. x - 5 3x - 5 x - 5
= t(t Î Z) x = 2t + 5
Ta có 3x - 2y = 5  y = = x + Đặt 2 2 2 x ìï = 5 + 2t y 2t 5 t y 3t 5 ï  = + +  = +  í (t Î Z) y ï = 5 + 3t ïî . Câu 21. Đáp án C. 5x + 7 x + 7 x + 7  y =  y = 2x +
= t x = 2t - 7
Ta có -5x + 2y = 7  2y = 7 + 5x 2 2 Đặt 2
y = 2.(2t - 7) + t y = 5t - 14(t Î )  x ìï = 2t - 7 ïí (t Î Z) y ï = 5t - 14
Nên nghiệm nguyên của phương trình là ïî ìï 7 ï ìï < 0 2 ìï - 7 < 0 t x t ï < ï ï ï 14 ï 2 í  í  í  t < y ï < 0 5 ï t - 14 < 0 ï 14 5 îï ïî t ïï <
Vì x,y nguyên âm nên ïî 5
mà t Î Z t £ 2 . x ìï = 2.2 - 7 x ìï = -3 t 2 ï ï =  í  í y ï = 5.2 - 14 y ï = -4
Nghiệm nguyên âm lớn nhất nhất của phương trình đạt được khi ïî ïî
Vậy nghiệm cần tìm là (-3;-4) . Câu 22. Đáp án A. -4y - 10 y + 10
3x + 4y = -10  3x = -4y - 10  x =  x = y - - Ta có 3 3 Đặt
y + 10 = t(t Î )
  y = 3t - 10  x = (
- 3t - 10) - t = -4t + 10 3 x ìï = -4t + 10 ïí (t Î Z) y ï = 3t - 10
Hay nghiệm nguyên của phương trình 3x + 4y = -10 là ïî ì t ìï > 2,25 ï-4t + 10 < 0 ï ï ï í  í 10 3 ï t - 10 < 0 ï t ï î ï <
Vì x;y nguyên âm hay x < 0;y < 0 nên ïî 3
mà t Î   t = 3
Suy ra x = -4.3 + 10 = -2;y = 3.3 - 10 = -1 nên nghiệm nguyên âm cần tìm
là (x;y) = (-2;-1)  x.y = 2 . Câu 23. Đáp án A. 4x + 8 x + 8
-4x + 3y = 8  y =  y = x + Ta có 3 3
x + 8 = t x = 3t - 8  y = 3t - 8 +t y = 4t - 8(t Î )  Đặt 3 x ìï = 3t - 8 ïí (t Î Z) y ï = 4t - 8
Nên nghiệm nguyên của phương trình là ïî ìï ìï ì 8 x > 0 3 ï t - 8 > 0 ï ï t ïï > 8 ï í  í  í 3  t > y ï > 0 4 ï t - 8 > 0 ï 3 ïî ïî t ï > 2
Vì x,y nguyên dương nên ïî
mà t Î   t ³ 3 . x ìï = 3.3 - 8 x ìï = 1 ï ï í  í y ï = 4.3 - 8 y ï = 4
Nghiệm nguyên dương nhỏ nhất của phương trình là ïî ïî
x + y = 5 . Câu 24. Đáp án C. 7y + 5 y + 5
Ta có 6x - 7y = 5  x =  x = y + 6 6 y + 5 y + 5 = t(t Î )
  y = 6t - 5  x = y +
= 6t - 5 + t = 7t - 5 Đặt 6 6 x ìï = 7t - 5 ïí (t Î Z) y ï = 6t - 5
Nên nghiệm nguyên của phương trình là ïî ìï 5 ï ìï > 0 7 ìï - 5 > 0 t x t ï > ï ï ï 5 ï 7 í  í  í  t > y ï > 0 6 ï t - 5 > 0 ï 5 7 ïî ïî t ïï >
Vì x,y nguyên dương nên ïïî 6
mà t Î   t ³ 1
Do đó, nghiệm nguyên dương nhỏ nhất của phương trình có được khi t = 1 x ìï = 7.1- 5 x ìï = 2 ï ï í  í  x - y = 1 y ï = 6.1 - 5 y ï = 1 ïî ïî .
D.BÀI TẬP TỰ LUYỆN  2   4 
Bài 1. Trong các cặp số  1
 ;2,2;2, 0; ,  ;0 ,3; 3     
 , cặp số nào là nghiệm của phương trình:  3   3 
a. 4x  3y  13 b.
x  5y  4
Bài 2. Tìm nghiệm tổng quát và vẽ đường thẳng biểu diễn tập nghiệm của nó:
a. 3x y  1 b. x  2 y  5
c. 2x  3y  5 d. 3y x  2
Bài 3. Trong mỗi trường hợp sau, hãy tìm giá trị của a để:
a. Điểm A0; 
1 thuộc đường thẳng x ay  5 ; b. Điểm B  3;
 0 thuộc đường thẳng ax  4y  6 ; c. Điểm C  5;  2
  thuộc đường thẳng ax  6y  3;  5  25 d. Điểm D ;0 
 thuộc đường thẳng ax  0y  ;  2  2  9  e. Điểm E 2;  
 thuộc đường thẳng 0x ay  10 ;  2 
Bài 4. Cho đường thẳng d  có phương trình: m  
1 x  3m  4 y  2
m  5. Tìm m để:
a. d  song song với trục hoành.
b. d  song song với trục tung.
c. d  đi qua gốc tọa độ. d.
d  đi qua điểm A2; 1.
Bài 5. Vẽ đồ thị của mỗi cặp phương trình sau trong cùng một hệ trục tọa độ, rồi tìm giao điểm của hai đường thẳng đó.
a. 2x y  3 và 3x  2 y  5
b. x  2 y  4 và 3x  2 y  10
c. x y  1 và 3x  3y  6
d. x  2 y  4 và 2x  4 y  8 HƯỚNG DẪN
Bài 1. Thay lần lượt mỗi cặp số đã cho vào từng phương trình, rồi so sánh giá trị tìm được ở hai vế để rút ra kết luận.   a. Các cặp số   2 1; 2 , 0; 
 , là nghiệm của phương trình 4x  3y  2 .  3    b. Các cặp số   4 2; 2 ,  ;0 
 , là nghiệm của phương trình 3x  5y  4 .  3 
Bài 2. Tìm nghiệm tổng quát và vẽ đường thẳng biểu diễn tập nghiệm của nó:
a. Nghiệm tổng quát của phương trình 3x y  1 : x    hoặc y  3x 1  y     1 1 x y   3 3
Có đồ thị hàm số là:
b. Nghiệm tổng quát của phương trình x  2 y  5 : x     1 5 hoặc y x   2 2 y   
x  2y  5
Có đồ thị hàm số là:
c. Nghiệm tổng quát của phương trình
2x  3y  5 : x     2 5 hoặc y x   3 3 y     3 5 x y   2 2
Có đồ thị hàm số là:
d. Nghiệm tổng quát của phương trình 3y x  2 : x     1 2 hoặc y   x   3 3 y    x  3  y  2
Có đồ thị hàm số là:
Bài 3. Trong mỗi trường hợp sau, hãy tìm giá trị của a để:
a. Điểm A0; 
1 thuộc đường thẳng x ay  5 , ta có: 0  a   1  5   a  5.
Vậy với a  5 thì điểm A thuộc đồ thị hàm số đã cho. b. Điểm B  3;
 0 thuộc đường thẳng ax  4y  6 , ta có: a  3    4.0  6  3
a  6  a  2  . Vậy với a  2
 thì điểm B thuộc đồ thị hàm số đã cho. c. Điểm C  5;  2
  thuộc đường thẳng ax  6y  3, ta có:
a      9 5
6. 2  3  5a  9  a   . 5 9
Vậy với a   thì điểm C thuộc đồ thị hàm số đã cho. 5  5  25 d. Điểm D ;1 
 thuộc đường thẳng ax  0y  , ta có:  2  2 5 25 . a  0   a  5 . 2 2
Vậy với a  5 thì điểm D thuộc đồ thị hàm số đã cho.  9  e. Điểm E 2;  
 thuộc đường thẳng 0x ay  10 , ta có:  2   9  20 0.2  a   10  a    .  2  9 20 Vậy với a
thì điểm E thuộc đồ thị hàm số đã cho. 9
Bài 4. Cho đường thẳng d  có phương trình: m  
1 x  3m  4 y  2  m  5.
Phương trình đường thẳng d  có các hệ số: a m 1;b  3m  4;c  2m  5
a. d  song song với trục hoành.  m 1 a  0 m 1  0 m 1      4  b   0  3  m  4  0  3
m  4  m   m 1 3
c 0  2m 5 0 2m 5            5 m    2
Vậy với m 1 thì phương trình đường thẳng d  song song với trục hoành.
b. d  song song với trục tung  m  1 a  0 m 1  0 m  1      4 4  b   0  3  m  4  0  3
m  4  m   m  3 3 c 0
 2m 5 0 2m 5            5 m    2 4
Vậy với m  thì phương trình đường thẳng d  song song với trục hoành. 3
c. d  đi qua gốc tọa độ  m  1 a  0 m 1  0 m  1      4 5  b   0  3  m  4  0  3
m  4  m   m   3 2 c 0
 2m 5 0 2m 5            5 m    2 5
Vậy với m   thì phương trình đường thẳng d  đi qua gốc tọa độ. 2
d. d  đi qua điểm A2; 
1 , suy ra tọa độ điểm A thỏa mãn phương trình đường thẳng
m 1 x 3m  4 y  2  m  5  m  
1 .2  3m  4.  1  2  m  5
 2m  2  3m  4  2  m 5  m  7  Vậy với m  7
 thì phương trình đường thẳng d  đi qua điểm A.
Bài 5. Vẽ đồ thị của mỗi cặp phương trình sau trong
cùng một hệ trục tọa độ, rồi tìm giao điểm của hai đường thẳng đó.
a. d : 2x y  3 và d :3x  2y  5 2  1 
Đồ thị hàm số d : 2x y  3 là đường thẳng có 1 
phương trình là: y  2x  3
Đồ thị hàm số d :3x  2y  5 là đường thẳng có 2  3 5
phương trình là: y x  2 2
Giao điểm của hai đồ thị hàm số d và d có tọa 2  1  độ là: 1;  1  .
b. d : x  2y  4 và d :3x y 12 4  3 
Giao điểm của hai đồ thị hàm số d và d có tọa độ là: 4;0 . 4  3 
c. d : x y 1 và d : 3
x  3y  6  6  5  1 1  1 Ta có:  
. Hai đồ thị hàm số d và d song song với nhau. 6  5  3  3 6
d. d : x  2y  4 và d : 2
x  4y  8  8  7  1 2 4 Ta có:  
. Hai đồ thị hàm số d và d trùng nhau. 8  7  2 4 8
----------Toán Học Sơ Đồ---------