Chuyên đề phương trình quy về phương trình bậc hai

Tài liệu gồm 39 trang, được biên soạn bởi tác giả Toán Học Sơ Đồ, tổng hợp kiến thức trọng tâm, phân dạng và hướng dẫn giải các dạng bài tập tự luận & trắc nghiệm chuyên đề phương trình quy về phương trình bậc hai. Mời bạn đọc đón xem.

104 52 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Chương 4: Phương trình bậc hai một ẩn

Môn: Toán 9

Thông tin:

39 trang 8 tháng trước

Tác giả:

Profile Hà Việt Anh
1.
TOÁNHỌCSƠĐỒ‐THCS.TOANMATH.com
CHUYÊN ĐỀ PHƯƠNG TRÌNH QUY VỀ PHƯƠNG TRÌNH BẬC HAI
A.TRỌNG TÂM CẦN ĐẠT
I. TÓM TẮT LÝ THUYẾT
1. Phương trình trùng phương
- Phương trình trùng phương là phương trình có dạng:ax
4
+ bx
2
+ c - 0 (a ≠ 0).
- Cách giải: Đặt ẩn phụ t = x
2
(t > 0) để đưa phương trình vẽ phương trình bậc hai: at
2
+ bt + c = 0 (a ≠
0).
2. Phương trình chứa ẩn ở mẫu thức
Để giải phương trình chứa ẩn ở mẫu thức, ta có các bước giải như sau:
Bước 1. Tìm điều kiện xác định của ẩn của phương trình.
Bước 2. Quy đồng mẫu thức hai vế rồi khử mẫu.
Bước 3. Giải phương trình vừa nhận được ở Bước 2.
Bước 4. So sánh các nghiệm tìm được ở B
ước 3 với điều kiện xác định và kết luận.
3. Phương trình đưa về dạng tích
Để giải phương trình đưa vể dạng tích, ta có các bước giải như sau:
Bước 1. Phân tích vế trái thành nhân tử, vế phải bằng 0.
Bước 2. Xét từng nhân tử bằng 0 để tìm nghiệm.
4. Một số dạng khác của phương trình thường gặp
- Phương trình bậc bốn dạng

xaxbxcxd m
với
abcd
- Phương trình đối xứng bậc bốn có dạng:

432
00ax bx cx bx a a
- Phương trình hồi quy có dạng

432
00ax bx cx dx e a
trong đó
2
ed
ab



- Phương trình bậc bốn dạng

44
xa xb c
- Phương trình phân thức hữu tỉ. Trong phần này chúng ta xét một số dạng sau:
2.
TOÁNHỌCSƠĐỒ‐THCS.TOANMATH.com
•
22
mx nx
p
ax bx d ax cx d


•
22
22
ax mx c ax px c
d
ax nx c ax qx c


 
•
2
22
ax mx c px
d
ax nx c ax qx c


 
II. BÀI TẬP VÀ CÁC DẠNG TOÁN
Dạng 1. Giải phương trình trùng phương
Phương pháp giải: Xét phương trình trùng phương:
ax
A
+ bx
2
+ c = 0 (a ≠ 0).
Bước 1. Đặt t = x
2
(t ≥ 0) ta được phương trình bậc hai:
at
2
+ bt + c = 0 (a ≠ 0)
Bước 2. Giải phương trình bậc hai ẩn t từ đó ta tìm được các nghiệm của phương trình trùng phương đã
cho.
1.1. Giải các phương trình sau:
a) x
4
+ 5x
2
- 6 = 0; b) ( x + 1)
4
- 5(x + 1)
2
-84 = 0.
1.2.Giải các phương trình sau:
a) 2x
4
+ 7x
2
+ 5 = 0; b) 4x
4
+ 8x
2
- 12 = 0;
Dạng 2. Phương trình chứa ẩn ở mẫu thức
Phương pháp giải: Để giải phương trình chứa ẩn ở mẫu thức, ta có các bước giải như sau:
Bước 1. Tìm điều kiện xác định của ẩn.
Bước 2. Quy đồng mẫu thức hai vế rồi khử mẫu.
Bước 3. Giải phương trình bậc hai nhận được ở Bước 2.
Bướ
c 4. So sánh các nghiệm tìm được ở Bước 3 với điều kiện xác định và kết luận.
2.1. Giải các phương trình sau:
a)
2x 5 3x
;
12xx

3.
TOÁNHỌCSƠĐỒ‐THCS.TOANMATH.com
b)
5353
;
35 35
xx
xx



c)
11 1 3
:1 .
11 1 14
xx x
xx x x






2.2. Giải các phương trình sau:
a)
2x 1 3x 1 7
3;
151
x
xxx



b)
2
2
3x 5 1
;
63
x
xx x


c)
2
2x 5 5
;
23 5x6xxx


Dạng 3. Phương trình đưa về dạng tích
Phương pháp giải: Để giải phương trình đưa về dạng tích, ta có các bước giải như sau:
Bước 1. Chuyên vế và phân tích vế trái thành nhân tử, vế phải bằng 0.
Bước 2. Xét từng nhân tử bằng 0 để tìm nghiệm.
3.1. Giải các phương trình sau:
a) x
3
- 3x
2
- 3x - 4 = 0;
b) (x - 1)
3
+ x
3
+ (x + 1)
3
- (x + 2)
3
= 0;
3.2. Giải các phương trình sau:
a) 2x
3
-7x
2
+ 4x + 1 = 0;
b) (x
2
+ 2x - 5)
2
= (x
2
- x + 5)
2
.
Dạng 4. Giải bằng phương pháp đặt ẩn phụ
Phương pháp giải:
Bước 1. Đặt điều kiện xác định (nếu có);
Bước 2. Đặt ẩn phụ, đặt điểu kiện của ẩn phụ (nếu có) và giả phương trình theo ẩn mới;
Bước 3. Tìm nghiệm ban đầu và so sánh với điều kiện xác địnl và kết luận.
4.1. Giải các phương trình sau:
4.
TOÁNHỌCSƠĐỒ‐THCS.TOANMATH.com
a) x(x + l)(x + 2)(x + 3) = 8;
b) (x
2
+ 16x + 60)(x
2
+17x + 60) = 6x
2
;
c)
22
2x 7
1.
3x 2 3x 5x 2x


4.2. Giải các phương trình sau:
a) (x
2
- 3x)
2
- 6(x
2
- 3x) -7 = 0;
b) x
6
+61x
3
- 8000 = 0;
c)
1
10 3.
1
xx
xx

Dạng 5. Phương trình chứa biếu thức trong dấu căn
Phương pháp giải: Làm mất dấu căn bằng cách đặt ẩn phụ hoặc lũy thừa hai vế.
Chú ý:
2
0
.
B
AB
AB

5.1. Giải các phương trình sau:
a)
693;xx x
b)
2
13 .xx x
5.2. Giải các phương trình sau:
a) x
2
- 3x + 2 = (1 - x) 3x 2
b
17x114x6.x 
Dạng 6. Một số dạng khác
Phương pháp giải: Ngoài các phương pháp trên, ta còn dùng các phương pháp hằng đẳng thức, thêm bớt
hạng tử, hoặc đánh giá hai vế... để giải phương trình.
6. Giải các phương trình sau bằng phương pháp thêm bớt hạng tử hoặc dùng hằng đẳng thức:
a) x
4
= 24x + 32; b) x
3
= -3x
2
+ 3x -1;
c) x
4
- x
2
+ 2x - 1 = 0;
7. Giải các phương trình sau bằng phương pháp đánh giá:
a)
44
11;xx
5.
TOÁNHỌCSƠĐỒ‐THCS.TOANMATH.com
b)
22
4x 4x 5 12x 12 9 6.
8. Giải các phương trình sau:
a) 4x
2
– 4x – 6|2x – 1| + 6 = 0;
b)
2
2
2
25x
11.
(5)
x
x

III. BÀI TẬP VỂ NHÀ
10. Giải các phương trình sau:
a) x
4
- 6x
2
- 16 = 0; b) (x + 1)
4
+(x + l)
2
- 20 = 0.
11. Giải các phương trình sau:
a)
2
24x11x2
;
1(1)( 2)
x
xxx


b)
2x 8( 1)
.
42 (2 )( 4)
xx
xxxx


12. Giải các phương trình sau:
a) (x + 1)(x-3)(x
2
- 2x) = -2;
b) (6x + 5)
2
(3x + 2)(x +1) = 35.
c) (x
2
+ 5x + 8)(x
2
+ 6x + 8) = 2x
2
;
d)
4x 1
2.
4x 1
x
x

13. Giải các phương trình sau:
a) x
3
- x
2
- 8x - 6 = 0; b)x
3
- x
2
- x =
1
3
.
HƯỚNG DẪN VÀ ĐÁP SỐ
1.1.
a) Đặt
2
0xt
, ta có:
2
560tt
Giải ra ta được t = 1 (TM) hoặc
6t 
(loại)
Từ đó tìm được
1x 
b) Đặt
2
(1) 0xt
6.
TOÁNHỌCSƠĐỒ‐THCS.TOANMATH.com
Sau khi tìm được t ta tìm được
123x  .
1.2. a)
x 
b)
1x 
2.1.
a) ĐK:
1x
và
2x
Quy đồng mẫu thức, giải được:
19 3x 
b) Tìm đượck
17x 
hoặc 131x 
c) Tìm được x = 5
2.1. a)
5
4
x 
hoặc
5x
b)
1x
c)
1
2
x
hoặc
5x
3.1.
a) Đưa PT về dạng:


2230xxx
Từ đó tìm được

2; 3x 
b) Tìm được
4x
3.2. a)
1x
hoặc
533
4
x
b)
1
;0
2
xx
hoặc
10
3
x
4.1.
a) Đặt
2
31yx x. Giải ra ta được
3y 
Từ đó tìm được
317
2
x

b) Xét hai trường hợp
Trường hợp 1: Với x = 0, thay vào thấy không là nghiệm
Trường hợp 2. Với
0x
, chia cả hai vế của PT cho x
2
sau đó đặt
60
16xy
x

. Giải ra ta được y = 2
hoặc y = -3.
Từ đó tìm được x = 15 hoặc x = -4.
c) Trường hợp 1. Xét x = 0, thay vào thấy không là nghiệm.
7.
TOÁNHỌCSƠĐỒ‐THCS.TOANMATH.com
Trường hợp 2. Xét
0x
, chia cả tử và mẫu cho x sau đó đặt
2
3yx
x

. Giải ra ta được y = -11 hoặc y =
2.
Từ đó tìm được
11 97
6
x

4.2.
a)
337
2
x
hoặc
35
2
x
b) x = 4 hoặc x = -5
c)
5
4
x
hoặc
2
3
x 
5.1.
a) ĐK:
0x
; Biến đổi phương trình ta được
33 30 0 9xxx x
b) PT
22
3
30
8
8
7
196
7
x
x
x
x
xx xx




5.2. a)
1x
b)
1x
hoặc
5x
6. a) Thêm
2
4x
ở cả hai vế của PT, ta được


2
2
2
226xx
Giải ra ta được
15x 
b) Tìm được
3
1
12
x
c) Tìm được
15
2
x

7. a) ĐK:
4
0111xxx và
4
xx
11VT x x VP
Dấu "=" xảy ra
10 1
11 0
xx
xx






Kết luận
b) Tìm được
1
2
x
.
8.
TOÁNHỌCSƠĐỒ‐THCS.TOANMATH.com
8. Đặt

2
21 0 650xtt tt 
. Tìm được t từ đó tìm được

2; 0;1;3x 
b) PT
2
55
211
55
xx
xx
xx





Đặt
2
5
x
t
x
, tìm được
11t 
hoặc
1t
Từ đó tìm được
121
2
x
10. a)
22x 
b)
1x
hoặc
3x 
11. a)
2
5
x
b) Vô nghiệm
12. a) 13x  hoặc
12x 
d) 23x 
c)
717
2
x

d) 23x 
13. a)
1x 
hoặc
17x 
b)
3
1
41
x
B.NÂNG CAO PHÁT TRIỂN TƯ DUY
Bài 1. Giải phương trình sau bằng cách đặt ẩn phụ
2
2
48 4
10
33
xx
xx




Bài 2. Giải phương trình

2
28 7 4 3 1 7xxx
Bài 3. Giải phương trình

2
2
2
3
1
x
x
x

Bài 4. Tìm m để phương trình sau vô nghiệm:
 
43 2
31 32 31 10xmxmxmx 
(m là tham
số)
Bài 5. Giải phương trình
2
2222
416 3 5 7
6135
x
xxxx


Bài 6. Giải phương trình

22 2
2222xx x x x
Bài 7 .Giải phương trình
22222
3( 2 1) 2( 3 1) 5 0xx xx x
9.
TOÁNHỌCSƠĐỒ‐THCS.TOANMATH.com
Bài 8. Giải các phương trình:
4442
)2432 )41)2128ax x bx x cx x x
Bài 9. Giải phương trình
22
3
20
252
xx
xx x x


Bài 10.

222
16 2 5
21235431024
xx x x
xx xx xx xx



.
HƯỚNG DẪN
Bài 1. Giải phương trình sau bằng cách đặt ẩn phụ
2
2
48 4
10
33
xx
xx




Hướng dẫn giải
Đặt
2
2
2
4816
393
xx
tt
xx

22
22
22
48 48
3838
33
xx
tt
xx

Khi đó phương trình trở thành
22
3810 31080tttt 
Giải ra ta được
12
4
2;
3
tt
• Với
2t
ta được
2
4
26120
3
x
xx
x

Giải ra ta được
12
321; 321xx 
• Với
4
3
t
ta được
2
44
4120
33
x
xx
x

Giải ra ta được
34
2; 6xx
Vậy tập nghiệm của phương trình là:

3 21; 3 21; 2; 6S 
Bài 2. Giải phương trình

2
28 7 4 3 1 7xxx
Hướng dẫn giải
10.
TOÁNHỌCSƠĐỒ‐THCS.TOANMATH.com
Ta có:


2
22
2 8 7 4 3 1 7 2 64 112 49 4 7 3 7xxx xxxx
Đặt
2
473yx x thì
2
64 112 49 16 1xx y
Phương trình đã cho có dạng

2
216 1 7 32 2 7 0yy y y
Giải ra ta được
12
71
;
16 2
yy

• Với
7
16
y
ta được
22
7
4 7 3 64 112 41 0
16
xx x x
Giải ra ta được
12
722 722
;
88
xx
 

• Với
1
2
y 
ta được
22
1
473 81470
2
xx x x
vô nghiệm
Vậy phương trình đã cho có tập nghiệm
722 722
;
88
S

 




Bài 3. Giải phương trình

2
2
2
3
1
x
x
x

Hướng dẫn giải
Phương trình tương đương với

22 2
2
2
2
2
2
22
223
11
1
2. 3
11
230
11
xx x
x
xx
x
xx
x
xx
xx
xx












Đặt
2
1
x
y
x
phương trình có dạng
2
230yy
Giải ra ta được
12
1; 3yy
• Với
1y
ta được
2
2
110
1
x
xx
x

. Giải ra ta được
12
15 15
;
22
xx


11.
TOÁNHỌCSƠĐỒ‐THCS.TOANMATH.com
• Với
3y 
ta được
2
2
3330
1
x
xx
x

vô nghiệm
Vậy tập nghiệm của phương trình là :
1515
;
22
S






Bài 4. Tìm m để phương trình sau vô nghiệm:
 
43 2
31 32 31 10xmxmxmx 
(m là tham
số)
Hướng dẫn giải
Nhận xét
0x
không phải là nghiệm của phương trình, nên ta chia hai vế của phương trình cho
2
x
ta
được
 
 
2
2
2
2
11
31 3 2 31 0
11
31 3201
xmxm m
xx
xmxm
xx





Đặt
1
xy
x

điều kiện
2y
hoặc
2y
tức là
2y
Khi đó phương trình có dạng
 
22
23 1 3 2 0 3 1 3 02ymym ymym
Giải ra ta được
12
1; 3yy m
Phương trình (1) có nghiệm phương trình (2) có nghiệm thỏa mãn
2
232
3
ymm 
hoặc
2
3
m
Vậy với
2
3
m
thì phương trình đã cho vô nghiệm
Bài 5. Giải phương trình
2
2222
416 3 5 7
6135
x
xxxx


Hướng dẫn giải
12.
TOÁNHỌCSƠĐỒ‐THCS.TOANMATH.com

2
2222
2
2222
2222
2222
2
2222
416 3 5 7
6135
416 3 5 7
31 1 1 0
6135
2222
0
6135
1111
20
6135
x
xxxx
x
xxxx
xxxx
xxxx
x
xxxx




 













Vì
2222
1111
0
6135
xxxx


nên
2
20 2xx
Vậy tập nghiệm của phương trình là:

2; 2S 
Bài 6. Giải phương trình

22 2
2222xx x x x
Hướng dẫn giải
Nhận xét.
0x
không phải là nghiệm của phương trình nên ta chia hai vế cho x
2
ta được:
22
122xx
xx

 


Đặt
2
1
xy
x

phương trình có dạng
.( 1) 2yy
2
20yy
giải ra ta được
1; 2yy
Trường hợp 1. Với
1y
ta có
2
2
11 2 0
xx
x

, phương trình vô nghiệm
Trường hợp 1. Với
2y 
ta có
2
2
12 3x20
xx
x

. Giải ra ta được
1; 2xx 
Vậy tập nghiệm của phương trình là:

1; 2S 
Bài 7 .Giải phương trình
22222
3( 2 1) 2( 3 1) 5 0xx xx x
Hướng dẫn giải
Nhận xét.
0x
không phải là nghiệm của phương trình nên ta chia hai vế của hai phương trình cho
2
x
ta
được:
22
11
32 23 50xx
xx

 


13.
TOÁNHỌCSƠĐỒ‐THCS.TOANMATH.com
Đặt
1
2
xy
x

phương trình có dạng

2
22
32150 430yy yy
Giải ra ta được
1; 3yy
Trường hợp 1. Với
1y
ta có
2
1
21 10
xxx
x

Giải ra ta được
12
15 15
;
22
xx
 

Trường hợp 2. Với
3y
ta có
2
1
23 10
xxx
x
 
Giải ra ta được
34
15 15
;
22
xx


Vậy tập nghiệm của phương trình là:
15151515
;;;
2222
S

 




Bài 8. Giải các phương trình:
4442
)2432 )41)2128ax x bx x cx x x
Hướng dẫn giải


42 2
2
2
2
2
2
)4442436
22 6
226
226
ax x x x
xx
xx
xx




• Giải phương trình
22
22 6 2 40xxxx
Giải ra ta được
12
15; 15xx 
Giải phương trình
22
226 280xxxx 
vô nghiệm
Vậy phương trình có nghiệm là:

15;15S 


2
2
2
42 2 2
2
12. 2
)21242 1 2. 2
122
xx
bx x x x x x
xx



• Giải phương trình
22
12. 2 2120xxxx
14.
TOÁNHỌCSƠĐỒ‐THCS.TOANMATH.com
Giải ra ta được
12
2422 2422
;
22
xx
 

• Giải phương trình
22
122 2210xxxx 
vô nghiệm
Vậy tập nghiệm của phương trình là:
2 422 2 422
;
22
S








2
2
2
42 2 2
2
12 3
)214129 123
123
xx
cxx x x x x
xx



• Giải phương trình
22
12 3 2 40xxxx
. Vô nghiệm
• Giải phương trình
22
123 220xxxx
Giải ra ta được
12
13; 13xx 
Vậy tập nghiệm của phương trình là:

13;13S 
Bài 9. Giải phương trình
22
3
20
252
xx
xx x x


Hướng dẫn giải
ĐKXĐ:
2
2
1
20
2
520
533
2
x
xx
x
xx
x






Nhận thấy
0x
không là nghiệm của phương trình
Khi
0x
thì phương trình đã cho
13
20
22
15xx
xx


Đặt
2
tx
x

ta được phương trình biểu thị theo t là
13
2
15tt


2
560 2; 3tt tt
Với
2
2
2222013tx xx x
x
 
(thỏa mãn)
15.
TOÁNHỌCSƠĐỒ‐THCS.TOANMATH.com
Với
2
2317
33320
2
tx xx x
x

(thỏa mãn)
Vậy phương trình đã cho có tập nghiệm là
317
13;
2
S






Bài 10.

222
16 2 5
21235431024
xx x x
xx xx xx xx



.
Hướng dẫn giải
Điều kiện

7; 6; 5; 4; 3; 2; 1; 0x 
. Biến đổi phương trình thành

16 2 5
2571346
xx x x
xx x x x x x x



11 1 6 1 1
22257
xx
xx x x






21 1 51 1
213 46
xx
xx xx x






11 1 1 1 1 1 1
2571346xx x x x x x x


11 1 1 1 1 1 1
72516 34xx x x x x x x x






22 2 2
11 1 1
27 0
771076712
x
xxxxxxx



 

22 2 2
7
2
11 1 1
0(*)
771076712
x
xxxx xx xx



.
Đặt
2
7ux x
thì phương trình (*) có dạng
1111 11 1 1
00
10 6 12 6 10 12uu u u uu u u





2
18 90 0uu 
.
Mặt khác

2
2
18 90 9 9 0uu u
với mọi
u
. Do đó phương trình (*) vô nghiệm. Vậy phương trình
đã cho có nghiệm duy nhất
7
2
x 
.
C.TRẮC NGHIỆM RÈN LUYỆN PHẢN XẠ
Câu 1. Phương trình
42
670xx
có bao nhiêu nghiệm?
A.
0
. B.
1
. C.
2
. D.
4
.
16.
TOÁNHỌCSƠĐỒ‐THCS.TOANMATH.com
Câu 2. Phương trình
42
2970
xx
có bao nhiêu nghiệm?
A.
0
. B.
1
. C.
2
. D.
4
.
Câu 3. Phương trình
42
(1)5(1)840xx 
có tổng các nghiệm là?
A.
12
. B.
2
. C.
1
. D.
212
.
Câu 4. Phương trình
42
(2 1) 8(2 1) 9 0xx 
có tổng các nghiệm là:
A.
1
. B.
2
. C.
1
. D.
22
.
Câu 5. Phương trình
2
25 9
23 56
x
xxxx


có số nghiệm là:
A.
2
. B.
1
. C.
0
. D.
3
.
Câu 6. Phương trình
111
0
114xxx


có số nghiệm là:
A.
1
. B.
2
. C.
0
. D.
3
.
Câu 7. Phương trình
11 1 3
:1
11 1 14
xx x
xx x x






có nghiệm là:
A.
2x
. B.
2x
. C.
3x
. D.
5x
.
Câu 8. Phương trình
22 2 2
:1
22 2 3
xx x
xx x x






có nghiệm là:
A.
2
1;
3
xx
. B.
2
1;
3
xx
. C.
3x
. D.
2
1;
3
xx 
.
Câu 9. Tích các nghiệm của phương trình
2222
(25)( 5)xx xx
là:
A.
10
3
. B.
0
. C.
1
2
. D.
5
3
.
Câu 10. Tổng các nghiệm của phương trình
22 2
(2x 3) 4( 1)x là:
A.
10
3
. B.
0
. C.
1
2
. D.
5
3
.
Câu 11. Số nghiệm của phương trình
32
33550
xxx

là:
A.
2
. B.
0
. C.
1
. D.
3
.
17.
TOÁNHỌCSƠĐỒ‐THCS.TOANMATH.com
Câu 12. Tổng các nghiệm của phương trình
(1)(2)(3)8
xx x x

là:
A.
3
. B.
3
. C.
1
. D.
4
.
Câu 13. Tổng các nghiệm của phương trình
2
( 1)( 4)( 5 6) 48xx xx là:
A.
5
4
. B.
5
. C.
5
2
. D.
5
.
Câu 14. Hai nghiệm của phương trình
1
10 3
1
xx
xx

là
12
xx . Tính
12
34xx .
A.
3
. B.
3
. C.
7
. D.
7
.
Câu 15. Số nghiệm của phương trình
241
2
2
41
xx
x
x

là?
A.
2
. B.
3
. C.
1
. D.
0
.
Câu 16. Phương trình
2
32(1)32xx xx
có bao nhiêu nghiệm?
A.
1
. B.
3
. C.
0
. D.
2
.
Câu 17. Phương trình
2
5( 2) 1 7 10xxxx
có nghiệm là?
A.
5; 10
xx

. B.
5; 10; 2
xx x

.
C.
5x
. D.
10x
.
Câu 18. Phương trình
2
13xx x
có nghiệm là:
A.
1x 
. B.
7
8
x
. C.
1x
. D.
8
7
x
.
Câu 19. Phương trình
2
261 2xx x
có nghiệm là:
A.
1; 3
xx

. B.
1; 3
xx

. C.
1x 
. D.
3x
.
Câu 20. Phương trình
22
4451212196xx x x
có nghiệm là
(, 0)
a
ab
b
. Tính
ab
.
A.
1
. B.
4
. C.
2
. D.
2
.
Câu 21. Giải phương trình
42
11xx x
?
18.
TOÁNHỌCSƠĐỒ‐THCS.TOANMATH.com
A.
0x
. B.
5
4
x
. C.
12
5
0;
4
xx
. D. Đáp án khác.
Câu 22. Giải phương trình
22
11
1
125125xxxxxx

 
.
A.
2x 
. B.
0x
. C.
1x
. D.
1x 
.
HƯỚNG DẪN
Câu 1. Đáp án C.
Đặt
2
(0)xtt ta được phương trình
2
670
tt

(*)
Nhận thấy
167 0abc
nên phương trình (*) có hai nghiệm
12
1( ); 7( )tLtN
Thay lại cách đặt ta có
2
77xx
.
Vậy phương trình đã cho có hai nghiệm.
Câu 2. Đáp án D.
Đặt
2
(0)xtt ta được phương trình
2
2970
tt

(*)
Nhận thấy
2(9)7 0
abc

nên phương trình (*) có hai nghiệm
12
7
1); ()
2
(tNt N
Thay lại cách đặt ta có
Với
2
11 1
tx x

Với
2
77 14
22 2
tx x
Vậy phương trình đã cho có bốn nghiệm phân biệt.
Câu 3. Đáp án B.
Đặt
2
(1) (0)xtt
ta được phương trình
2
5840
tt

(*)
Ta có
Δ 361
nên phương trình (*) có hai nghiệm
12
5 361 5 361
12( ); 7( )
22
tNt L


19.
TOÁNHỌCSƠĐỒ‐THCS.TOANMATH.com
Thay lại cách đặt ta có
2
(1)12 112xx
Suy ra tổng các nghiệm là
112112 2
Câu 4. Đáp án C.
Đặt
2
(2 1) ( 0)xtt
ta được phương trình
2
890
tt

(*)
Ta
1(8)(9) 0
abc

nên phương trình (*) có hai nghiệm
12
1( ); 9( )ttmt ktm
Thay lại cách đặt ta có
2
211 0
21 1
21 1
(
1
)
xx
x
xx






Suy ra tổng các nghiệm là
0(1) 1
.
Câu 5. Đáp án C.
Điều kiện:
2; 3
xx

2
2
25 9 2(3)5(2) 9
211190
2 3 5 6 ( 2)( 3) ( 2)( 3)
xxxx
xx
x x xx xx xx


 
Nhận thấy
2
Δ 11 4.19.2 31 0
nên phương trình
2
211190
xx

vô nghiệm. Suy ra phương
trình đã cho vô nghiệm.
Câu 6. Đáp án B.
111
0
114xxx


Điều kiện:
10 1
10 1
40 4
xx
xx
xx








PT
( 1)( 4) ( 1)( 4) ( 1)( 1)
0
(1)(1)( 4)(1)(1)( 4)(1)(1)( 4)
xx xx xx
xxx xxx xxx
  

  
222
2
2
( 1)( 4) ( 1)( 4) ( 1)( 1) 0
34 54 10
3810
Δ 43.(1)190
xx xx xx
xx xx x
xx




Phương trình có 2 nghiệm phân biệt:
1
2
419
3
419
3
()
()
xtm
xtm
20.
TOÁNHỌCSƠĐỒ‐THCS.TOANMATH.com
Câu 7. Đáp án D.
Điều kiện:
1; 1; 1 4
xx x

Ta có
11 1 3
:1
11 1 14
xx x
xx x x






22
(1 ) (1 ) 1 1 3
:
(1 )(1 ) 1 14
xxxx
xx x x



41 3 23
.
(1 )(1 ) 2 14 1 14
28 2 3 3 5 25 5( )
xx
xxx xx x
xx x x TM



Vậy phương trình có nghiệm
5x
Câu 8. Đáp án B.
Điều kiện:
2; 2; 0
xx x

Ta có
22 2 2
:1
22 2 3
xx x
xx x x








22
22
22 2
:
22 2 3
xx
xx
xx x x





22
82222
.
22 432 3
62403 20
xx x
xx x xx
xx xx



Phương trình này có
3(1)(2) 0
abc

nên có hai nghiệm phân biệt
2
1; ( )
3
xx TM

Vậy phương trình có hai nghiệm
2
1;
3
xx
Câu 9. Đáp án B.
Ta có

22
22
25 5xx xx
22
2
22
10
3
310
25 5
0
20
25 5
1
2
x
x
xx xx
x
xx
xx xx
x




Nên tích các nghiệm là
10 1
.0. 0
32
Câu 10. Đáp án B.
21.
TOÁNHỌCSƠĐỒ‐THCS.TOANMATH.com
Ta có
22 2
(2x 3) 4( 1)x
22
22
()
()
2321 2210
2321 2250
xx xx
xxxx






Phương trình
2
2210
xx

có
Δ 30

nên có hai nghiệm
13 13
;
22
xx


Phương trình
2
2250
xx

có
1
Δ 11 0

nên có hai nghiệm
111 111
;
22
xx
 

Nên tổng các nghiệm của phương trình đã cho là
1313 111 111
0
22 2 2


Câu 11. Đáp án C.
Ta có
32
33550
xxx

2
22
350
3151035()() ( )()10
10
x
xx x x x
x



2
()35
1
1
xL
x
x



Vậy phương trình có nghiệm duy nhất
1x 
.
Câu 12. Đáp án A.
Ta có
(1)(2)(3)8
xx x x

22
( 3)( 1)( 2) 8 ( 3 )( 3 2) 8xx xx xxxx
Đặt
2
31
xx t

, thu được phương trình
22
3
118()() 18 9
3
t
tt t t
t


+) Với
2
3313
txx

2
320
xx

có
12
317 317
Δ 17 ;
22
xx
 

+) Với
2
3313
txx
 
2
340
xx

có
Δ 70
nên phương trình vô nghiệm.
Vậy phương trình đã cho có hai nghiệm
12
317 317
;
22
xx
 

22.
TOÁNHỌCSƠĐỒ‐THCS.TOANMATH.com
Suy ra tổng các nghiệm là
317 317
3
22
 

.
Câu 13. Đáp án B.
Ta có
222
( 1)( 4)( 5 6) 48 ( 5 4)( 5 6) 48xx xx xx xx   
Đặt
2
55
xx t

, thu được phương trình
7
1182148249()()
7
t
tt t t
t


+) Với
22
7557520
txx xx

có
12
533 533
Δ 33 ;
22
xx
 

+)Với
22
7557 5120
txx xx
 
có
Δ 23 0
nên phương trình vô nghiệm.
Vậy phương trình đã cho có hai nghiệm
12
533 533
;
22
xx
 

.
Suy ra tổng các nghiệm là
533 533
5
22
 

.
Câu 14. Đáp án D.
Điều kiện:
0; 1
xx

Đặt
(0)
1
x
tt
x

, khi đó phương trình đã cho trở thành
2
1
10. 3 3 10 0ttt
t

Ta có
1
349
Δ 49 5;
2
t

2
349
2( )
2
tTM

+) Với
5t
suy ra
5
1
x
x
5
55
4
xxx
(nhận)
+) Với
2t 
suy ra
2
1
x
x

2
22
3
xxx 
(nhận)
Vậy phương trình đã cho có hai nghiệm
12
25
34
xx 
Nên
12
25
3 4 3. 4. 7
34
xx

 

 
 
23.
TOÁNHỌCSƠĐỒ‐THCS.TOANMATH.com
Câu 15. Đáp án C.
Điều kiện:
1
4
x
Đặt
2
(0)
41
x
tt
x

, khi đó phương trình đã cho trở thành
2
1
220ttt
t

(*)
Ta có
11(2) 0
abc

nên phương trình (*) có hai nghiệm
12
1( ); 2( )ttmt ktm
+) Với
1t
suy ra
22
2
12 414 414 410
41
x
xx xx xx
x
  
2
1
(2 1) 0 ( )
2
xxtm
.
Vậy phương trình đã cho có nghiệm
1
2
x
.
Câu 16. Đáp án A.
Điều kiện:
2
320
3
xx
.
Ta có
2
32(1)32xx xx
(1)( 2)(1)320 (1)(2 32)0xx x x xx x 
10 1
2320 322
()
()
xxTM
xx x x




 

Xét phương trình (*):
2
20
322
322()
x
xx
xx



2
2
2
1( )
1
760
6
x
x
xTM
x
xx
x



.
Vậy phương trình có nghiệm duy nhất
1x
.
Câu 17. Đáp án B.
Điều kiện:
10 1xx
Ta có
2
5( 2) 1 7 10xxxx
24.
TOÁNHỌCSƠĐỒ‐THCS.TOANMATH.com
5( 2) 1 ( 2)( 5) ( 2)( 5) 5( 2) 1 0xx xx xx xx
20 2
55 1 0 5 5 1
()
()
xxktm
xx x x




 

Xét phương trình (*): 51 5xx
Với
1x
ta có
22
25( 1) ( 5) 15 50 0xx xx
2
5 10 50 0 ( 5) 10( 5) 0xxx xx x
10
( 10)( 5) 0
5
()
()
xtm
xx
xtm

Vậy phương trình có nghiệm
5; 10
xx

.
Câu 18. Đáp án D.
Ta có
2
13xx x
22
3
30
3
8
8
78
7
1( )3
7
x
x
x
x
x
x
xx x




Vậy phương trình có nghiệm duy nhất
8
7
x
.
Câu 19. Đáp án A.
Ta có
2
261 2xx x
222
20 2
261(2 230)
xx
xx x xx




 

2
()(
2
2
330
330
)
x
x
xx x
xxx






2
21
1
1()(30 3
3
)
x
xx
x
xx x
x

 






Vậy phương trình có nghiệm
1; 3
xx

.
Câu 20. Đáp án A.
Ta có
22
4451212196xx x x 
2
2
1
(2 1) 4 12 16 6
2
xx




25.
TOÁNHỌCSƠĐỒ‐THCS.TOANMATH.com
Nhận thấy
2
2
1
(2 1) 4 2; 12 16 4
2
xx




Dấu “=” xảy ra khi
2
2
21 42
210
1
1
1
2
0
12 16
2
2
(
4
)x
x
x
x
x











Vậy phương trình đã cho có nghiệm duy nhất
1
2
x
Từ đó suy ra
1; 2 1
ab ab

Câu 21. Đáp án B.
42
11xx x
Điều kiện:
10 1xx
42 2 42 2
2
42 2
42 2 34
2
32 2
111 21
20
2
44
02
0
02 02
0
5
45 0 450
450
4
()
()
xx x xx x x
xx
xx xx
xx x xx
x
x
xx
x
x
xx xx
x
 




 






PT Kết hợp với điều kiện ban đầu
1x
ta thấy phương trình có nghiệm duy nhất
5
4
x
.
Câu 22. Đáp án D.
22
22
11
1
125125
11
1
1(1)4 1(1)4
xxxxxx
xx xx

 

 
Đặt
–1xt
22
22
22
11 44
11
44
44
tt tt
PT
tt tt
tt tt


 
 
26.
TOÁNHỌCSƠĐỒ‐THCS.TOANMATH.com
22
22
112121
44
tt
tx x
tt


.
Thử lại thấy
1x 
thỏa mãn phương trình.
Vậy phương trình có nghiệm duy nhất
1x 
.
D.PHIẾU BÀI TỰ LUYỆN CƠ BẢN VÀ NÂNG CAO
PHIẾU SỐ 1
Dạng 1: Phương trình trùng phương
Bài 1. Giải các phương trình sau:
a)
42
540
xx

b)
42
340
xx

c)
22
45
2
45xx


Bài 2. Tìm các giá trị của m để phương trình ẩn x sau:
42
610
xxm

có 4 nghiệm.
Dạng 2. Phương trình chứa ẩn ở mẫu
Bài 3. Giải các pt sau:
a)
858
1
43 2
x
xxx


b)
2
12 12
22 4
x
xxx


Dạng 3. Phương trình đưa về phương trình tích
Bài 4. Giải các phương trình:
a)
22
(2 5 2)( 3 1) 0xx xx  b)
22 2
(2 ) (2 1) 0xx x
Bài 5. Giải phương trình
42
430
xx x

Dạng 4. Phương pháp đặt ẩn phụ
Bài 6. Giải các phương trình sau
a)
222
(5)2(5)24xx xx
b)
22 2
(6)2(3)81xx x
c)
2
2
53
40
5
xx x
xxx



Dạng 5. Phương trình bậc 4 dạng
()()()()
xaxbxcxd m

với
abcd
Bài 7. Giải phương trình
( 5)( 6)( 8)( 9) 40
xxxx

27.
TOÁNHỌCSƠĐỒ‐THCS.TOANMATH.com
Bài 8. Giải phương trình
22
( 3 2)( 7 12) 24xx xx
Dạng 6. Phương trình đối xứng bậc bốn, phương trình hồi quy
Bài 9. Giải phương trình
43 2
2316320
xx xx

Bài 10. Giải phương trình
43 2
2 2174105500
xxx x

Dạng 7. Phương trình vô tỉ
Bài 11. Giải phương trình
a)
218xx b) 15 3 6xx
Bài 12. Giải phương trình
a)
22
24 18xx xx 
b)
2
2242xxx 
HƯƠNG DẪN – ĐÁP SỐ
Dạng 1: Phương trình trùng phương
Bài 1. Giải các phương trình sau:
a)
42
540
xx

b)
42
340
xx

c)
22
45
2
45xx


Hướng dẫn-Đáp số
a) Đặt
2
0
xt

đưa phương trình về:
2
540
tt

12
1; 4tt (thỏa mãn)
+ Với
12
11;1txx
+ Với
34
42;x2tx
Vậy phương trình đã cho có nghiệm

1; 2S 
b) Phương trình có nghiệm

2S 
c) Phương trình có nghiệm
0x
Bài 2. Tìm các giá trị của m để phương trình ẩn x sau:
42
610
xxm

có 4 nghiệm.
Hướng dẫn-Đáp số
Đặt
2
0
xt

, ta được
2
610
ttm

(1)
28.
TOÁNHỌCSƠĐỒ‐THCS.TOANMATH.com
Để pt đã cho có 4 nghiệm thì pt (1) phải có 2 nghiệm dương pb
12
12
'0 9( 1)0
010110
60
.0
m
xx m m
xx





Vậy với
110m
thì pt đã cho có 4 nghiệm.
Dạng 2. Phương trình chứa ẩn ở mẫu
Bài 3. Giải các pt sau:
a)
858
1
43 2
x
xxx


b)
2
12 12
22 4
x
xxx


Hướng dẫn-Đáp số
a) Điều kiện:
2; 3; 4
xxx

Quy đồng mẫu thức rồi khử mẫu:
2
(3 )( 2)(x 4) 8(3 )( 2) 5( 4)( 2) (8 )( 4)(3 )
7 72 128 0
xx xx x x xx x
xx


Giải ra ta được:
12
2
8; 2
7
xx
(thỏa mãn)
Vậy pt có 2 nghiệm
12
2
8; 2
7
xx
b) Pt có nghiệm
3x
Dạng 3. Phương trình đưa về phương trình tích
Bài 4. Giải các phương trình:
a)
22
(2 5 2)( 3 1) 0xx xx 
b)
22 2
(2 ) (2 1) 0xx x
Hướng dẫn-Đáp số
a)
22
(2 5 2)( 3 1) 0xx xx 
2
2
2520
310
xx
xx


(1)
(2)
Giải (1) ta được
12
1
;2
2
xx
29.
TOÁNHỌCSƠĐỒ‐THCS.TOANMATH.com
Giải (2) ta được
34
35 35
;
22
xx
 

Vậy pt có tập nghiệm
13535
;2; ;
22 2
S

 




b) Pt có tập nghiệm
317
4
S






Bài 5. Giải phương trình
42
430
xx x

Hướng dẫn-Đáp số
42 4 2 2
22 2
22
430 2 1 440
(1)(2)0
(1)(3)0
xx x x x x x
xx
xx xx
 


Giải ra ta được tập nghiệm
15
2
S






Dạng 4. Phương pháp đặt ẩn phụ
Bài 6. Giải các phương trình sau
a)
222
(5)2(5)24xx xx b)
22 2
( 6)2(3)81xx x c)
2
2
53
40
5
xx x
xxx



Hướng dẫn-Đáp số
a) Đặt
2
5xxy ta được pt
2
4
224
6
y
yy
y


Với
4
y

2
1
54
4
x
xx
x



Với
2
1
656
6
x
yxx
x
 

Vậy pt có tập nghiệm

1; 4; 6S 
b) Pt có tập nghiệm

3; 3 20S 
30.
TOÁNHỌCSƠĐỒ‐THCS.TOANMATH.com
c) Pt có tập nghiệm

1; 5; 1 6S 
Dạng 5. Phương trình bậc 4 dạng
()()()()
xaxbxcxd m

với
abcd
Bài 7. Giải phương trình
( 5)( 6)( 8)( 9) 40
xxxx

Hướng dẫn-Đáp số
Ta có
( 5)( 6)( 8)( 9) 40
xxxx

22
(1445)(1448)40xx xx
Đặt
2
545xx y
phương trình thành
5
(3)40
8
y
yy
y


Với
4
5
10
x
y
x



Với
8
y

suy ra x vô nghiệm.
Vậy phương trình có nghiệm
4; 10
xx
 
Bài 8. Giải phương trình
22
( 3 2)( 7 12) 24xx xx
Hướng dẫn-Đáp số
Ta viết dưới dạng
( 1)( 2)( 3)( 4) 24
xx x x

22
( 5 4)( 5 6) 24xx xx
Giải tương tự ta được tập nghiệm

0; 5S 
Dạng 6. Phương trình đối xứng bậc bốn, phương trình hồi quy
Bài 9. Giải phương trình
43 2
2316320
xx xx

Hướng dẫn-Đáp số
+)
0x
không là nghiệm của phương trình.
+)
0x
, chia hai vế của phương trình cho
2
x
ta được:
2
2
11
23160xx
xx




31.
TOÁNHỌCSƠĐỒ‐THCS.TOANMATH.com
Đặt
22
2
11
2xyx y
xx

. Ta được phương trình
2
4
2( 2) 3 20 0
5
2
y
yy
y


Theo cách đặt, giải pt tìm được tập nghiệm
1
23;;2
2
S




Bài 10. Giải phương trình
43 2
2 2174105500
xxx x

Hướng dẫn-Đáp số
+)
0x
không là nghiệm của phương trình.
+)
0x
, chia hai vế của phương trình cho
2
x
ta được:
2
2
25 5
221740xx
xx




Giải tương tự tìm được tập nghiệm
5
1; 5; ; 2
2
S



Dạng 7. Phương trình vô tỉ
Bài 11. Giải phương trình
a)
218xx b) 15 3 6xx
Hướng dẫn-Đáp số
a) Điều kiện
1
8
2
x
Bình phương hai vế, ta được:
2
216416
xxx

5x
(thỏa mãn);
13x
(loại)
Vậy pt có nghiệm
5x
b) Pt có nghiệm
1x 
Bài 12. Giải phương trình
a)
22
24 18xx xx 
b)
2
2242xxx 
Hướng dẫn-Đáp số
a)

3; 4S 
b)

2; 2S 
PHIẾU SỐ 2
32.
TOÁNHỌCSƠĐỒ‐THCS.TOANMATH.com
Bài 1: Giải các phương trình sau:
a)

2
x2 3x5 1x1x
b)

3
32
x 1 2x x x 2x 1
c)


23
2
xx 6 x 2 x 1
d)

22
x5 x2 x7x7 12x23
Bài 2: Giải các phương trình sau:
a)
42
x5x60
b)

42
x1 5x1 84 0 
Bài 3: Tìm các giá trị của m để phương trình ẩn số x:
42
x6xm10
có 4 nghiệm.
Bài 4: Giải các phương trình sau:
a)
858x
1
x4 3x x2


b)
2
x1 2 12
x2 x2
x4


Bài 5: Giải các phương trình:
a)

22
2x 5x 2 x 3x 1 0 
b)


2
2
2
2x x 2x 1 0
Bài 6: Giải phương trình sau:
42
xx4x30
Bài 7: Chứng minh rằng khi a và c trái dấu thì phương trình trùng phương
42
ax bx c 0
chỉ có hai
nghiệm và chúng là hai số đối nhau.
Bài 8: Giải các phương trình sau:
a)

2
22
x5x 2x5x24
b)


2
2
2
x6x 2x3 81
c)
2
2
xx5 3x
40
x
xx5



Bài 9: Giải phương trình:

x5x6x8x9 40
33.
TOÁNHỌCSƠĐỒ‐THCS.TOANMATH.com
Bài 10: Giải phương trình:

22
x3x2x7x1224
Bài 11: Giải các phương trình sau:
a)
43 2
2x 3x 16x 3x 2 0
b)
43 2
2x 21x 74x 105x 50 0
Bài 12: Giải các phương trình sau:
a)

44
x4 x2 82
b)

66
x2 x4 64
Bài 13: Giải phương trình sau:
22
4x 5x 3
2
xx3x5x3


HƯỚNG DẪN GIẢI
Bài 1:
a) Ta có:

2
x2 3x5 1x1x

22
2
2
x4x43x51x
2x x 2 0
14.2.2116170 17
 


12
117 171 117 117
x;x
2.2 4 2.2 4
  

b) Ta có:

3
32
x 1 2x x x 2x 1

32 32
32 32
2
2
x 3x 3x 1 2x x x 2x 1
x 3x 3x 1 2x x x 2x 1
2x 7x 2 0
7 4.2.2 49 16 33 0 33
 
 


12
7 337 33 7 337 33
x;x
2.2 4 2.2. 4
 

c) Ta có:


23
2
xx 6 x 2 x 1
32 32
2
2
x 6x x 4x 4 x 3x 3x 1
4x 5x 5 0
5 4.4.5 25 80 55 0


 
Vậy phương trình vô nghiệm.
d) Ta có:

22
x5 x2 x7x7 12x23
34.
TOÁNHỌCSƠĐỒ‐THCS.TOANMATH.com

222
22
2
x10x25x4x4x4912x23
3x 6x 3 0 x 2x 1 0
11.10



Vậy phương trình đã cho có nghiệm kép:
12
xx1
Bài 2:
a) Đặt
2
xt0
, đưa về phương trình
2
t5t60
Giải phương trình ta được

t1tm
hoặc

t6l
Với
t1
, ta có
2
12
x1x1;x 1
Vậy phương trình có hai nghiệm:
12
x1;x 1
b) Đặt

2
x1 t 0
, đưa về phương trình
2
t5t840
Giải phương trình ta được

t12tm
hoặc

t7l
Với
t12
, ta có

2
12
x1 12 x 123;x 123
Vậy phương trình có hai nghiệm:
12
x123;x 123 
Bài 3:
Đặt
2
xt0
ta được

2
t6tm101
Để phương trình đã cho có 4 nghiệm, thì phương trình

1
phải có 2 nghiệm dương phân biệt

0
9m10
c
0m101m10
a
60
b
a







Vậy với
1m10
thì phương trình đã cho có 4 nghiệm.
Bài 4:
a) Điều kiện:
x2;x3;x4
Quy đồng mẫu thức rồi khử mẫu:

2
3xx4x2 83xx2 5x4x2 8xx43x
7x 72x 128 0
 

Giải ra ta được:
12
2
x8;x 2
7

thỏa mãn.
Vậy phương trình có hai nghiệm:
12
2
x8;x 2
7

35.
TOÁNHỌCSƠĐỒ‐THCS.TOANMATH.com
b) Điều kiện:
x2;x2
Quy đồng mẫu thức rồi khử mẫu:



2
x2l
x1x 2 2x 2 12 x x6 0
x3tm


Vậy phương trình có một nghiệm:
x3
Bài 5:
a)



2
22
2
2x 5x 2 0 1
2x 5x 2 x 3x 1 0
x3x102

 

Giải

1
ta được:
2
2x 5x 2 0
ta được:
12
1
x;x2
2

Giải

2
ta được:
2
x3x10
ta được:
34
35 35
x;x
22
 

Vậy tập nghiệm của phương trình:
13535
S;2; ;
22 2

 




b)



2
2
222
2x x 2x1 0 2x x 2x12x x 2x1 0



2
22
2
2x x 1 0 1
2x x 1 2x 3x 1 0
2x 3x 1 0 2



Giải

1
:
1 4.2.1 7 0 
Phương trình vô nghiệm.
Giải

2
:
2
2x 3x 1 0
ta được
12
317 317
x;x
44
 

Vậy phương trình có tập nghiệm là:
317317
S;
44

 




Bài 6:





42 4 2 2
2
2
2
222
2
xx4x30 x2x1x4x40
xx301
x1 x2 0 x x3xx10
xx102
 

 

Giải

1
:
2
xx30
có
11 0
vô nghiệm.
Giải

2
:
2
12
15 15
xx10x ;x
22
 

36.
TOÁNHỌCSƠĐỒ‐THCS.TOANMATH.com
Vậy tập nghiệm của phương trình:
1515
S;
22

 




Bài 7:
Đặt
2
xm0
Ta có:
42 2
ax bx c 0 am bm c 0
Vì a và c trái dấu nên
a
0
c
. Phương trình có hai nghiệm phân biệt là
1
m
và
2
m
Theo hệ thức Vi – ét ta có:
12
c
m.m
a
Vì a và c trái dấu nên
12
c
0m.m0
a

hay
1
m
và
2
m
trái dấu nhau.
Vì
1
m
và
2
m
trái dấu nhau nên có 1 nghiệm bị loại, giả sử loại
1
m
.
Khi đó
2
22
xm x m
Vậy phương trình trùng phương
42
ax bx c 0
chỉ có hai nghiệm và chúng là hai số đối nhau khi a và
c trái dấu.
Bài 8:
a) Đặt
2
x5xy
. Ta được:
22
y4
y2y24 y2y240
y6


.Với
22
x1
y 4x5x 4x5x40
x4

 

.Với
22
x1
y6 x 5x6 x 5x60
x6
 

Vậy tập nghiệm của phương trình:

S 1;4;1;6
b)



22
2
222
x6x 2x3 81 x6x 2x6x9810
Đặt
2
x6xy
. Ta được:

22
y11
y 2 y 9 81 0 y 2y 99 0
y9


.Với
22
x3 20
y11 x 6x11 x 6x110
x3 20

 

37.
TOÁNHỌCSƠĐỒ‐THCS.TOANMATH.com
.Với
22
y 9x6x 9 x6x90 x3 
Vậy tập nghiệm

S 3 20;3 20;3
c) Điều kiện:
2
x0;x x50
Đặt
2
xx5
y
x

Ta được:
2
y1
3
y40y4y30
y3
y

 

.Với
2
2
1,2
xx5
y1 1x2x50x 16
x

  
.Với
2
2
34
xx5
y3 3x4x50x1;x 5
x

 
Vậy tập nghiệm của phương trình là:

S16;1;5
Bài 9: Ta có:

x5x6x8x9 40

22
x 14x 45 x 14x 48 40 
Đặt:
2
x14x45y
, ta có:

2
y5
yy 3 40 y 3y 40 0
y8


.Với
22
x4
y5 x 14x455 x 14x400
x10



.Với
22
y 8 x 14x 45 8 x 14x 53 0 
: vô nghiệm.
Vậy tập nghiệm của phương trình:

S4;10
Bài 10:
Ta viết dưới dạng:

x1x2x3x4 24

22
x5x4x5x624
Đặt
2
x5x4y
, ta có:
2
y4
y2y240
y6


.Với
y4
, ta có:
22
x0
x5x44 x5x0
x5


.Với
y6
, ta có:
22
x5x4 6 x 5x100
: vô nghiệm.
Vậy tập nghiệm của phương trình:

S0;5
Bài 11:
38.
TOÁNHỌCSƠĐỒ‐THCS.TOANMATH.com
a)
x0
không phải là nghiệm của phương trình.
x0
chia hai vế của phương trình cho
2
x
, ta được:
2
2
11
2x 3x 16 0
x
x




Đặt
22
2
11
xyx y2
x
x

. Ta có phương trình:

22
y4
2y 2 3y 16 0 2y 3y 20 0
5
y
2


.Với
2
x23
1
y4x 4x4x10
x
x23

 

.Với
2
1
x
515
yx 2x5x20
2
2x2
x2

Vậy tập nghiệm của phương trình:
1
S23;23;;2
2




b)
x0
không phải là nghiệm của phương trình.
x0
chia hai vế của phương trình cho
2
x
, ta được:
2
2
25 5
2x 21x 74 0
x
x




Đặt
22
2
525
xyx y10
x
x

. Ta có phương trình:

22
y6
2 y 10 21y 74 0 2y 21y 54 0
9
y
2

.Với
2
x1
5
y6 x 6 x 6x50
x5
x
 
.Với
2
5
x
959
yx 2x9x100
2
2x2
x2

Vậy tập nghiệm của phương trình là:
5
S1;5;;2
2



Bài 12:
a) Đặt
x3y
, ta được:

44
42
y2
y1 y1 82 y 6y 40 0
y2


Với
y2 x 1
39.
TOÁNHỌCSƠĐỒ‐THCS.TOANMATH.com
Với
y2x5 
Vậy tập nghiệm của phương trình là:

S1;5
b) Đặt
x3y
. Phương trình có dạng:

66
y1 y1 64
Khai triển và rút gọn ta được:
642
y15y15y310

242
y1
y1y16y310
y1


Với
y1 x 4
Với
y1x2
Vậy tập nghiệm của phương trình:

S4;2
Bài 13.
x0
không phải là nghiệm của phương trình.
x0
chia tử và mẫu của mỗi phân thức cho x:
453
33
2
x1 x5
xx


Đặt
3
x2y
x

phương trình có dạng:
453
0
y3 y3 2


. ĐK:
y3
Quy đồng, khử mẫu rồi rút gọn ta được:
2
y1
y6y70
y7


Với
2
3
y1 x 21 x 3x30
x

: vô nghiệm.
Với
2
513
x
3
2
y7x 27x5x30
x
513
x
2

 

Vậy tập nghiệm của phương trình là:
513513
S;
22

 




---------------------Toán Học Sơ Đồ--------------------
| 1/39
| | Tải xuống

Có thể bạn quan tâm:

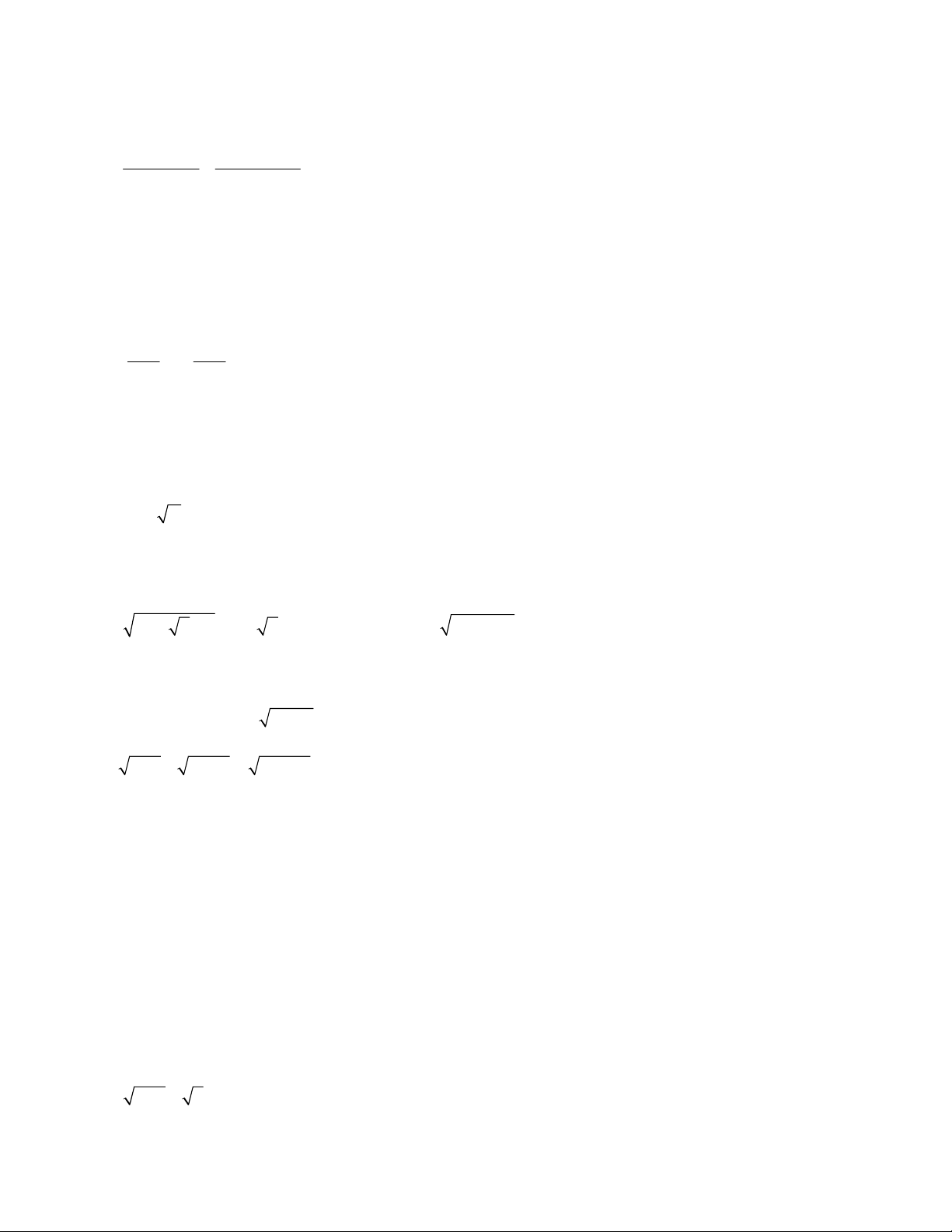
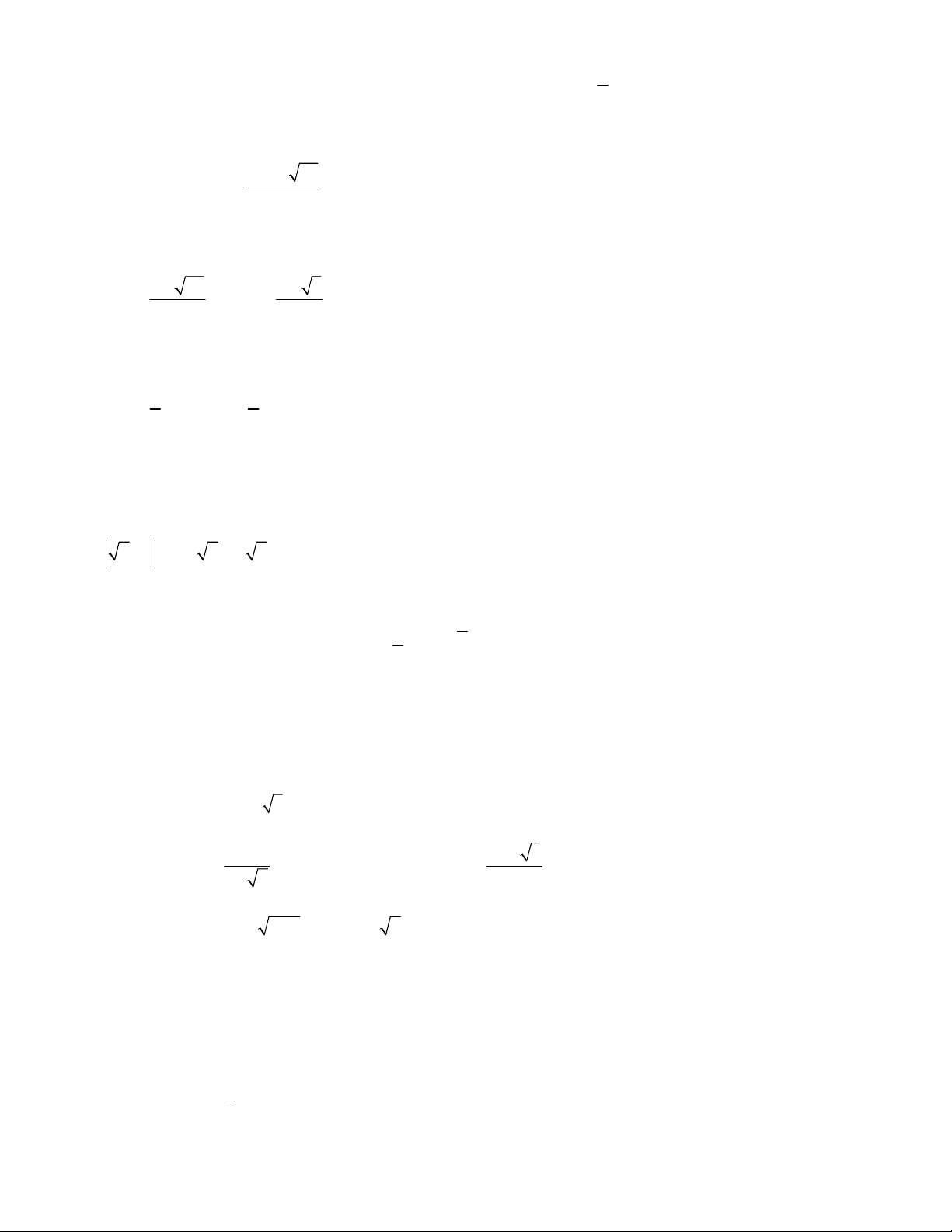
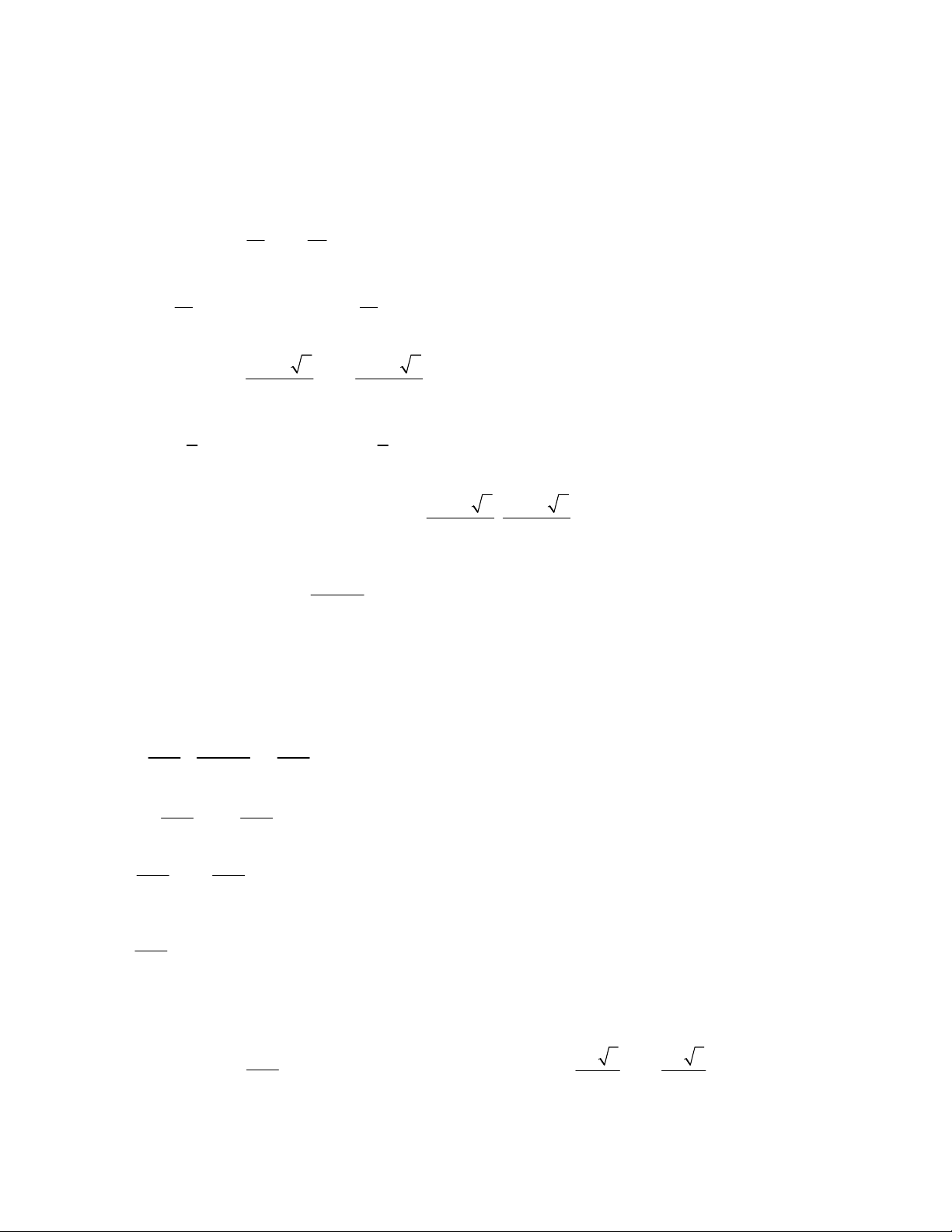
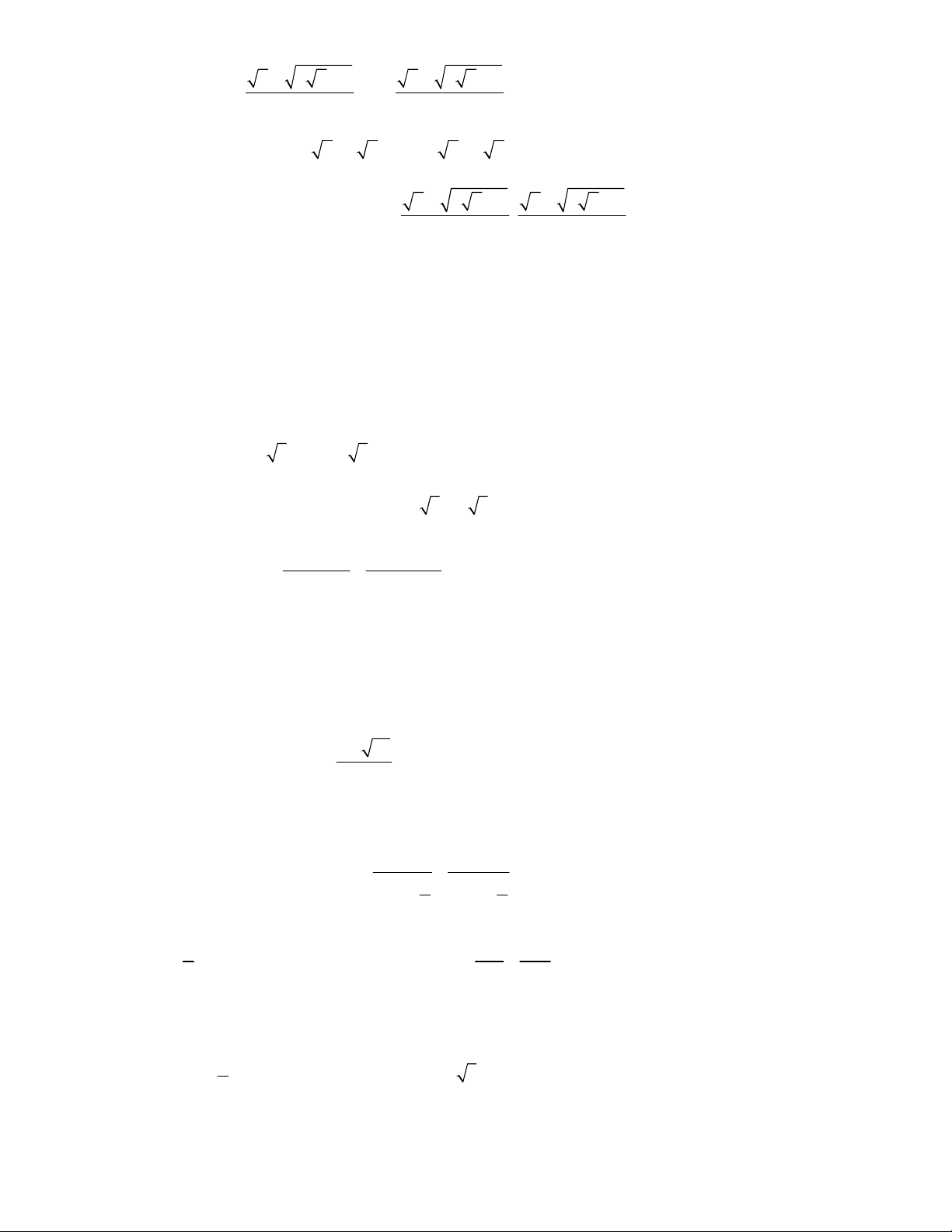
Preview text:

CHUYÊN ĐỀ PHƯƠNG TRÌNH QUY VỀ PHƯƠNG TRÌNH BẬC HAI
A.TRỌNG TÂM CẦN ĐẠT
I. TÓM TẮT LÝ THUYẾT
1. Phương trình trùng phương
- Phương trình trùng phương là phương trình có dạng:ax4 + bx2 + c - 0 (a ≠ 0).
- Cách giải: Đặt ẩn phụ t = x2 (t > 0) để đưa phương trình vẽ phương trình bậc hai: at2 + bt + c = 0 (a ≠ 0).
2. Phương trình chứa ẩn ở mẫu thức
Để giải phương trình chứa ẩn ở mẫu thức, ta có các bước giải như sau:
Bước 1. Tìm điều kiện xác định của ẩn của phương trình.
Bước 2. Quy đồng mẫu thức hai vế rồi khử mẫu.
Bước 3. Giải phương trình vừa nhận được ở Bước 2.
Bước 4. So sánh các nghiệm tìm được ở Bước 3 với điều kiện xác định và kết luận.
3. Phương trình đưa về dạng tích
Để giải phương trình đưa vể dạng tích, ta có các bước giải như sau:
Bước 1. Phân tích vế trái thành nhân tử, vế phải bằng 0.
Bước 2. Xét từng nhân tử bằng 0 để tìm nghiệm.
4. Một số dạng khác của phương trình thường gặp
- Phương trình bậc bốn dạng x a x b x c x d   m với a b c d
- Phương trình đối xứng bậc bốn có dạng: 4 3 2
ax bx cx bx a  0a  0 2 e d
- Phương trình hồi quy có dạng 4 3 2
ax bx cx dx e  0a  0 trong đó    a b
- Phương trình bậc bốn dạng   4    4 x a x b c
- Phương trình phân thức hữu tỉ. Trong phần này chúng ta xét một số dạng sau:
1. TOÁN HỌC SƠ ĐỒ ‐ THCS.TOANMATH.com mx nx •   p 2 2
ax bx d
ax cx d 2 2
ax mx c ax px c •   d 2 2
ax nx c
ax qx c 2
ax mx c px •   d 2 2
ax nx c
ax qx c
II. BÀI TẬP VÀ CÁC DẠNG TOÁN
Dạng 1. Giải phương trình trùng phương
Phương pháp giải: Xét phương trình trùng phương:
axA + bx2 + c = 0 (a ≠ 0).
Bước 1. Đặt t = x2 (t ≥ 0) ta được phương trình bậc hai:
at2 + bt + c = 0 (a ≠ 0)
Bước 2. Giải phương trình bậc hai ẩn t từ đó ta tìm được các nghiệm của phương trình trùng phương đã cho.
1.1. Giải các phương trình sau: a) x 4 + 5x2 - 6 = 0;
b) ( x + 1)4 - 5(x + 1)2 -84 = 0.
1.2.Giải các phương trình sau: a) 2x4 + 7x2 + 5 = 0; b) 4x4 + 8x2 - 12 = 0;
Dạng 2. Phương trình chứa ẩn ở mẫu thức
Phương pháp giải: Để giải phương trình chứa ẩn ở mẫu thức, ta có các bước giải như sau:
Bước 1. Tìm điều kiện xác định của ẩn.
Bước 2. Quy đồng mẫu thức hai vế rồi khử mẫu.
Bước 3. Giải phương trình bậc hai nhận được ở Bước 2.
Bước 4. So sánh các nghiệm tìm được ở Bước 3 với điều kiện xác định và kết luận.
2.1. Giải các phương trình sau: 2x  5 3x a)  ; x 1 x  2
2. TOÁN HỌC SƠ ĐỒ ‐ THCS.TOANMATH.com x  5 x  3 5 3 b)    ; 3 5 x  3 x  5
1 x 1 x  1 x  3 c)  : 1  .    
1 x 1 x  1 x  14  x
2.2. Giải các phương trình sau: 2x 1 3x 1 x  7 a)    3; x 1 x  5 x 1 2 x  3x  5 1 b)  ; 2 x x  6 x  3 2x 5 5 c)   ; 2 x  2 x  3 x  5x  6
Dạng 3. Phương trình đưa về dạng tích
Phương pháp giải: Để giải phương trình đưa về dạng tích, ta có các bước giải như sau:
Bước 1. Chuyên vế và phân tích vế trái thành nhân tử, vế phải bằng 0.
Bước 2. Xét từng nhân tử bằng 0 để tìm nghiệm.
3.1. Giải các phương trình sau:
a) x3- 3x2 - 3x - 4 = 0;
b) (x - 1)3 + x3 + (x + 1)3 - (x + 2)3 = 0;
3.2. Giải các phương trình sau: a) 2x3 -7x2 + 4x + 1 = 0;
b) (x2 + 2x - 5)2 = (x2 - x + 5)2.
Dạng 4. Giải bằng phương pháp đặt ẩn phụ Phương pháp giải:
Bước 1. Đặt điều kiện xác định (nếu có);
Bước 2. Đặt ẩn phụ, đặt điểu kiện của ẩn phụ (nếu có) và giả phương trình theo ẩn mới;
Bước 3. Tìm nghiệm ban đầu và so sánh với điều kiện xác địnl và kết luận.
4.1. Giải các phương trình sau:
3. TOÁN HỌC SƠ ĐỒ ‐ THCS.TOANMATH.com
a) x(x + l)(x + 2)(x + 3) = 8;
b) (x2 + 16x + 60)(x2 +17x + 60) = 6x2; 2x 7 c)   1. 2 2
3x  x  2 3x  5x  2
4.2. Giải các phương trình sau:
a) (x2 - 3x)2 - 6(x2 - 3x) -7 = 0; b) x6 +61x3 - 8000 = 0; x x 1 c) 10  3. x 1 x
Dạng 5. Phương trình chứa biếu thức trong dấu căn
Phương pháp giải: Làm mất dấu căn bằng cách đặt ẩn phụ hoặc lũy thừa hai vế. B  0
Chú ý: A B   . 2 A B
5.1. Giải các phương trình sau:
a) x  6 x  9  3  x; b) 2
x x 1  3  . x
5.2. Giải các phương trình sau:
a) x2 - 3x + 2 = (1 - x) 3x  2
b x 1  7x 1  14x  6.
Dạng 6. Một số dạng khác
Phương pháp giải: Ngoài các phương pháp trên, ta còn dùng các phương pháp hằng đẳng thức, thêm bớt
hạng tử, hoặc đánh giá hai vế... để giải phương trình.
6. Giải các phương trình sau bằng phương pháp thêm bớt hạng tử hoặc dùng hằng đẳng thức: a) x4 = 24x + 32; b) x3 = -3x2 + 3x -1;
c ) x 4 - x 2 + 2x - 1 = 0;
7. Giải các phương trình sau bằng phương pháp đánh giá: a) 4 4
1 x x  1;
4. TOÁN HỌC SƠ ĐỒ ‐ THCS.TOANMATH.com b) 2 2
4x  4x  5  12x 12  9  6.
8. Giải các phương trình sau:
a) 4x2 – 4x – 6|2x – 1| + 6 = 0; 2 25x b) 2 x  11. 2 (x  5)
III. BÀI TẬP VỂ NHÀ
10. Giải các phương trình sau: a) x 4 - 6x2 - 16 = 0;
b) (x + 1)4 +(x + l)2 - 20 = 0.
11. Giải các phương trình sau: 2 x  2 4x 11x  2 x 2x 8(x 1) a)  ; b)   . x 1
(1 x)(x  2) x  4 2  x
(2  x)(x  4)
12. Giải các phương trình sau:
a) (x + 1)(x-3)(x2 - 2x) = -2;
b) (6x + 5)2 (3x + 2)(x +1) = 35.
c) (x2 + 5x + 8)(x2 + 6x + 8) = 2x2; x 4x 1 d)   2. 4x 1 x
13. Giải các phương trình sau: 1 a) x3 - x2 - 8x - 6 = 0; b)x3 - x2 - x = . 3
HƯỚNG DẪN VÀ ĐÁP SỐ 1.1. a) Đặt 2
x t  0 , ta có: 2
t  5t  6  0
Giải ra ta được t = 1 (TM) hoặc t  6  (loại)
Từ đó tìm được x  1  b) Đặt 2
(x 1)  t  0
5. TOÁN HỌC SƠ ĐỒ ‐ THCS.TOANMATH.com
Sau khi tìm được t ta tìm được x  1   2 3 .
1.2. a) x  b) x  1  2.1.
a) ĐK: x  1 và x  2
Quy đồng mẫu thức, giải được: x   19  3
b) Tìm đượck x  17  hoặc x  1   31 c) Tìm được x = 5 5 1
2.1. a) x   hoặc x  5 b) x  1
c) x  hoặc x  5 4 2 3.1.
a) Đưa PT về dạng: x  2x  2x  3  0
Từ đó tìm được x  2;  3
b) Tìm được x  4 5  33 1 10
3.2. a) x  1 hoặc x
b) x  ; x  0 hoặc x  4 2 3 4.1. a) Đặt 2
y x  3x 1. Giải ra ta được y  3 3   17
Từ đó tìm được x  2 b) Xét hai trường hợp
Trường hợp 1: Với x = 0, thay vào thấy không là nghiệm 60
Trường hợp 2. Với x  0 , chia cả hai vế của PT cho x2 sau đó đặt x 16 
y . Giải ra ta được y = 2 x hoặc y = -3.
Từ đó tìm được x = 15 hoặc x = -4.
c) Trường hợp 1. Xét x = 0, thay vào thấy không là nghiệm.
6. TOÁN HỌC SƠ ĐỒ ‐ THCS.TOANMATH.com 2
Trường hợp 2. Xét x  0 , chia cả tử và mẫu cho x sau đó đặt y  3x  . Giải ra ta được y = -11 hoặc y = x 2. 11   97
Từ đó tìm được x  6 4.2. 3  37 3  5 a) x  hoặc x  2 2 b) x = 4 hoặc x = -5 5 2
c) x  hoặc x   4 3 5.1.
a) ĐK: x  0 ; Biến đổi phương trình ta được
x  3  3  x x  3  0  0  x  9 x  3 3   x  0  8 b) PT     8  x  2 2
x x 1  9  6x x x  7  7 5.2. a) x  1
b) x  1hoặc x  5 2 6. a) Thêm 2
4x ở cả hai vế của PT, ta được x     x  2 2 2 2 6
Giải ra ta được x  1 5 1 1 5 b) Tìm được x  c) Tìm được x  3 1 2 2 7. a) ĐK: 4
0  x  1  1 x  1 x và 4 x x VT 1 x x 1  VP 1   x  0 x 1 Dấu "=" xảy ra   1   x 1    x  0 Kết luận 1
b) Tìm được x  . 2
7. TOÁN HỌC SƠ ĐỒ ‐ THCS.TOANMATH.com
8. Đặt x   t t   2 2 1
0  t  6t  5  0 . Tìm được t từ đó tìm được x  2;  0;1;  3 2  5x  5x b) PT  x   2x  11    x  5  x  5 2 x Đặt
t , tìm được t  11  hoặc t 1 x  5 1 21
Từ đó tìm được x  2 10. a) x  2  2
b) x  1 hoặc x  3  2 11. a) x  b) Vô nghiệm 5 12.
a) x  1 3 hoặc x  1 2 d) x  2  3 7   17 c) x  d) x  2  3 2 1 13. a) x  1  hoặc x 1 7 b) x  3 4 1
B.NÂNG CAO PHÁT TRIỂN TƯ DUY 2 x 48  x 4 
Bài 1. Giải phương trình sau bằng cách đặt ẩn phụ  10  2   3 x  3 x
Bài 2. Giải phương trình  x  2 2 8
7 4x  3 x   1  7 2 x
Bài 3. Giải phương trình 2 x   3 x  2 1
Bài 4. Tìm m để phương trình sau vô nghiệm: 4
x   m   3
x   m   2 3 1 3
2 x  3m  
1 x 1  0 (m là tham số) 2 4x 16 3 5 7
Bài 5. Giải phương trình    2 2 2 2 x  6 x 1 x  3 x  5
Bài 6. Giải phương trình  2
x x   2 x x   2 2 2 2  2x
Bài 7 .Giải phương trình 2 2 2 2 2
3(x  2x 1)  2(x  3x 1)  5x  0
8. TOÁN HỌC SƠ ĐỒ ‐ THCS.TOANMATH.com
Bài 8. Giải các phương trình: 4 4 4 2
a)x  24x  32
b)x  4x 1 c)x  2x 12x  8 x 3x
Bài 9. Giải phương trình   2  0 2 2
x x  2 x  5x  2 x 1 x  6 x  2 x  5 Bài 10.    . x x  2 2 2 2 x 12x  35
x  4x  3 x 10x  24 HƯỚNG DẪN 2 x 48  x 4 
Bài 1. Giải phương trình sau bằng cách đặt ẩn phụ   10  2   3 x  3 x Hướng dẫn giải 2 x 4 x 8 16 Đặt 2
t    t    2 3 x 9 3 x 2 2 x 48 x 48 2 2 3t    8    3t  8 2 2 3 x 3 x
Khi đó phương trình trở thành 2 2
3t  8  10t  3t 10t  8  0 4
Giải ra ta được t  2;t  1 2 3 x 4
• Với t  2 ta được 2
  2  x  6x 12  0 3 x
Giải ra ta được x  3  21; x  3  21 1 2 4 x 4 4
• Với t  ta được 2
   x  4x 12  0 3 3 x 3
Giải ra ta được x  2; x  6 3 4
Vậy tập nghiệm của phương trình là: S  3 21;3 21; 2;  6
Bài 2. Giải phương trình  x  2 2 8
7 4x  3 x   1  7 Hướng dẫn giải
9. TOÁN HỌC SƠ ĐỒ ‐ THCS.TOANMATH.com
Ta có:  x  2  x   x      2 x x   2 2 8 7 4 3 1 7 2 64 112
49 4x  7x  3  7 Đặt 2
y  4x  7x  3 thì 2
64x 112x  49  16 y 1
Phương trình đã cho có dạng  y   2 2 16
1 y  7  32y  2y  7  0 7 1
Giải ra ta được y  ; y  1 2 16 2 7 7 • Với y  ta được 2 2
4x  7x  3 
 64x 112x  41  0 16 16 7  2 2 7  2 2
Giải ra ta được x  ; x  1 2 8 8 1 1
• Với y   ta được 2 2
4x  7x  3    8x 14x  7  0 vô nghiệm 2 2
7  2 2 7  2 2 
Vậy phương trình đã cho có tập nghiệm S   ;   8 8   2 x
Bài 3. Giải phương trình 2 x   3 x  2 1 Hướng dẫn giải
Phương trình tương đương với 2 2 2 x x x 2 x  2   2  3
x 1 x  2 1 x 1 2 2  x xx   2.  3    x 1 x 1 2 2 2  x x     2  3  0  x 1 x 1 2 x Đặt
y phương trình có dạng 2
y  2y  3  0 x 1
Giải ra ta được y  1; y  3  1 2 2 x 1 5 1 5
• Với y  1 ta được 2
1  x x 1  0 . Giải ra ta được x  ; x x 1 1 2 2 2
10. TOÁN HỌC SƠ ĐỒ ‐ THCS.TOANMATH.com 2 x
• Với y  3 ta được 2  3
  x  3x  3  0 vô nghiệm x 1 1   5 1 5 
Vậy tập nghiệm của phương trình là : S   ;   2 2  
Bài 4. Tìm m để phương trình sau vô nghiệm: 4
x   m   3
x   m   2 3 1 3
2 x  3m  
1 x 1  0 (m là tham số) Hướng dẫn giải
Nhận xét x  0 không phải là nghiệm của phương trình, nên ta chia hai vế của phương trình cho 2 x ta được 1 1 2
x  3m  
1 x  3m  2  3m   1   0 2 x x  1   1 2   x
 3m 1 x   3m  2  0 1  2          x   x  1
Đặt x   y điều kiện y  2 hoặc y  2 tức là y  2 x
Khi đó phương trình có dạng 2
y    m   y   m   2 2 3 1 3
2  0  y  3m  
1 y  3m  02
Giải ra ta được y  1; y  3  m 1 2
Phương trình (1) có nghiệm  phương trình (2) có nghiệm thỏa mãn 2 2 
y  2  3m  2  m  hoặc m  3 3 2
Vậy với m  thì phương trình đã cho vô nghiệm 3 2 4x 16 3 5 7
Bài 5. Giải phương trình    2 2 2 2 x  6 x 1 x  3 x  5 Hướng dẫn giải
11. TOÁN HỌC SƠ ĐỒ ‐ THCS.TOANMATH.com 2 4x 16 3 5 7    2 2 2 2 x  6 x 1 x  3 x  5 2  4x 16   3   5   7     3  1  1  1  0 2  2   2   2   x  6   x 1  x  3   x  5  2 2 2 2
x  2 x  2 x  2 x  2      0 2 2 2 2 x  6 x 1 x  3 x  5   1 1 1 1 2   x  2     0  2 2 2 2 
x  6 x 1 x  3 x  5  1 1 1 1 Vì     0 nên 2
x  2  0  x   2 2 2 2 2
x  6 x 1 x  3 x  5
Vậy tập nghiệm của phương trình là: S   2; 2
Bài 6. Giải phương trình  2
x x   2 x x   2 2 2 2  2x Hướng dẫn giải
Nhận xét. x  0 không phải là nghiệm của phương trình nên ta chia hai vế cho x2 ta được:  2  2 
x  1 x   2  2  x  x  2
Đặt x  1  y phương trình có dạng y.( y 1)  2 x 2
y y  2  0 giải ra ta được y  1; y  2 2
Trường hợp 1. Với y  1 ta có 2
x  1  1  x  2  0 , phương trình vô nghiệm x 2
Trường hợp 1. Với y  2 ta có 2 x  1  2
  x  3x  2  0 . Giải ra ta được x  1; x  2 x
Vậy tập nghiệm của phương trình là: S   1;    2
Bài 7 .Giải phương trình 2 2 2 2 2
3(x  2x 1)  2(x  3x 1)  5x  0 Hướng dẫn giải
Nhận xét. x  0 không phải là nghiệm của phương trình nên ta chia hai vế của hai phương trình cho 2 x ta 2 2  1   1  được: 3 x
  2    2 x   3    5  0  x   x
12. TOÁN HỌC SƠ ĐỒ ‐ THCS.TOANMATH.com 1
Đặt x  2   y phương trình có dạng y   y  2 2 2 3 2
1  5  0  y  4 y  3  0 x
Giải ra ta được y  1; y  3 1
Trường hợp 1. Với y  1 ta có 2
x  2   1  x x 1  0 x 1 5 1 5
Giải ra ta được x  ; x  1 2 2 2 1
Trường hợp 2. Với y  3 ta có 2
x  2   3  x x 1  0 x 1 5 1 5
Giải ra ta được x  ; x  3 4 2 2
1 5 1 5 1 5 1 5 
Vậy tập nghiệm của phương trình là: S   ; ; ;   2 2 2 2  
Bài 8. Giải các phương trình: 4 4 4 2
a)x  24x  32
b)x  4x 1 c)x  2x 12x  8 Hướng dẫn giải 4 2 2
a)x  4x  4  4x  24x  36 
x   x   x  2 2 2  2x  62 2 2 6 2   2
x  2  2x  6 • Giải phương trình 2 2
x  2  2x  6  x  2x  4  0
Giải ra ta được x  1 5; x  1 5 1 2 Giải phương trình 2 2
x  2  2x  6  x  2x  8  0 vô nghiệm
Vậy phương trình có nghiệm là: S  1 5;1 5 x   x
b)x  2x 1  2x  4x  2  x  2 1 2. 2 4 2 2 2 1   2.x  2 2 2   2
x 1   2x  2 • Giải phương trình 2 2
x 1  2.x  2  x  2x 1 2  0
13. TOÁN HỌC SƠ ĐỒ ‐ THCS.TOANMATH.com 2  4 2  2 2  4 2  2
Giải ra ta được x  ; x  1 2 2 2 • Giải phương trình 2 2
x 1   2x  2  x  2x  2 1  0 vô nghiệm  2 4 2 2 2 4 2 2      
Vậy tập nghiệm của phương trình là: S   ;  2 2  
x   x
c)  x  2x 1  4x 12x  9  x   2 2 1  2x  32 1 2 3 4 2 2 2   2 x 1  2  x  3 • Giải phương trình 2 2
x 1  2x  3  x  2x  4  0 . Vô nghiệm • Giải phương trình 2 2
x 1  2x  3  x  2x  2  0
Giải ra ta được x  1 3; x  1 3 1 2
Vậy tập nghiệm của phương trình là: S  1 3;1 3 x 3x
Bài 9. Giải phương trình   2  0 2 2
x x  2 x  5x  2 Hướng dẫn giải  x  1 2
x x  2  0  ĐKXĐ:   x  2 2
x  5x  2  0  5  33 x   2
Nhận thấy x  0 không là nghiệm của phương trình 1 3
Khi x  0 thì phương trình đã cho    2  0 2 2 x 1 x  5  x x 2 1 3
Đặt t x  ta được phương trình biểu thị theo t là   2 x t 1 t  5 2
t  5t  6  0  t  2;t  3 2 Với 2
t  2  x   2  x  2x  2  0  x  1 3 (thỏa mãn) x
14. TOÁN HỌC SƠ ĐỒ ‐ THCS.TOANMATH.com 2 3  17 Với 2
t  3  x   3  x  3x  2  0  x  (thỏa mãn) x 2  3  17 
Vậy phương trình đã cho có tập nghiệm là S  1   3;   2   x 1 x  6 x  2 x  5 Bài 10.    . x x  2 2 2 2 x 12x  35
x  4x  3 x 10x  24 Hướng dẫn giải
Điều kiện x  7  ; 6;  5  ; 4;  3  ; 2;  1  ; 
0 . Biến đổi phương trình thành x 1 x  6 x  2 x  5    x 1 1 1  x  6  1 1     
x x  2  x  5 x  7  x  
1  x  3  x  4 x  6     2  x x  2 
2  x  5 x  7  x  2  1 1  x  5  1 1         
2  x 1 x  3 
x x  4 x  6  1 1 1 1 1 1 1 1         x
x  2 x  5 x  7
x 1 x  3 x  4 x  6  1 1   1 1   1 1   1 1                 
x x  7   x  2 x  5   x 1 x  6x   x  3 x  4      x   1 1 1 1 2 7     0  2 2 2 2 
x  7 x  7x 10 x  7x  6 x  7x 12   7 x    2   . 1 1 1 1      0(*) 2 2 2 2
 x  7x x  7x 10 x  7x  6 x  7x 12 Đặt 2
u x  7x thì phương trình (*) có dạng 1 1 1 1  1 1   1 1      0      0     2
u 18u  90  0 .
u u 10 u  6 u 12
u u  6   u 10 u 12 
Mặt khác u u   u  2 2 18 90
9  9  0 với mọi u . Do đó phương trình (*) vô nghiệm. Vậy phương trình 7
đã cho có nghiệm duy nhất x   . 2
C.TRẮC NGHIỆM RÈN LUYỆN PHẢN XẠ
Câu 1. Phương trình 4 2
x  6x  7  0 có bao nhiêu nghiệm? A. 0 . B. 1. C. 2 . D. 4 .
15. TOÁN HỌC SƠ ĐỒ ‐ THCS.TOANMATH.com
Câu 2. Phương trình 4 2
2x  9x  7  0 có bao nhiêu nghiệm? A. 0 . B. 1. C. 2 . D. 4 .
Câu 3. Phương trình 4 2
(x 1)  5(x 1)  84  0 có tổng các nghiệm là? A.  12 . B. 2  . C. 1. D. 2 12 .
Câu 4. Phương trình 4 2
(2x 1)  8(2x 1)  9  0 có tổng các nghiệm là: A. 1. B. 2  . C. 1 . D. 2 2 . 2x 5 9
Câu 5. Phương trình   có số nghiệm là: 2 x  2 x  3 x  5x  6 A. 2 . B. 1. C. 0 . D. 3 . 1 1 1
Câu 6. Phương trình    0 có số nghiệm là:
x 1 x 1 x  4 A. 1. B. 2 . C. 0 . D. 3 .
1 x 1 x  1 x  3
Câu 7. Phương trình  : 1      có nghiệm là:
 1 x 1 x   1 x  14  x A. x  2 .
B. x  2 . C. x  3. D. x  5.
 2  x 2  x   2  x  2
Câu 8. Phương trình  : 1      có nghiệm là:
 2  x 2  x   2  x  3x 2 2 2 A. x  1;  x  .
B. x  1; x   .
C. x  3. D. x  1; x   . 3 3 3
Câu 9. Tích các nghiệm của phương trình 2 2 2 2
(x  2x  5)  (x x  5) là: 10 1 5 A. . B. 0 . C. . D. . 3 2 3
Câu 10. Tổng các nghiệm của phương trình 2 2 2
(2x  3)  4(x 1) là: 10 1 5 A. . B. 0 . C. . D. . 3 2 3
Câu 11. Số nghiệm của phương trình 3 2
3x  3x  5x  5  0 là: A. 2 . B. 0 . C. 1. D. 3 .
16. TOÁN HỌC SƠ ĐỒ ‐ THCS.TOANMATH.com
Câu 12. Tổng các nghiệm của phương trình x(x 1)(x  2)(x  3)  8 là: A. 3  . B. 3 . C. 1. D. 4  .
Câu 13. Tổng các nghiệm của phương trình 2
(x 1)(x  4)(x  5x  6)  48 là: 5 5 A.  . B. 5  . C.  . D. 5 . 4 2 x x 1
Câu 14. Hai nghiệm của phương trình 10
 3 là x x . Tính3x  4x . x 1 x 1 2 1 2 A. 3  . B. 3 . C. 7 . D. 7  . 2x 4x 1
Câu 15. Số nghiệm của phương trình   2 là? 4x 1 2x A. 2 . B. 3 . C. 1. D. 0 .
Câu 16. Phương trình 2
x  3x  2  (1 x) 3x  2 có bao nhiêu nghiệm? A. 1. B. 3 . C. 0 . D. 2 .
Câu 17. Phương trình 2
5(x  2) x 1  x  7x 10 có nghiệm là?
A. x  5; x  10 . B. x  5; x  10; x  2 . C. x  5 . D. x  10 .
Câu 18. Phương trình 2
x x 1  3  x có nghiệm là: 7 8 A. x  1  .
B. x  . C. x  1. D. x  . 8 7
Câu 19. Phương trình 2
2x  6x 1  x  2 có nghiệm là:
A. x  1; x  3.
B. x  1; x  3. C. x  1  . D. x  3. a
Câu 20. Phương trình 2 2
4x  4x  5  12x 12x 19  6 có nghiệm là (a,b  0) . Tính a b . b A. 1. B. 4 . C. 2  . D. 2 .
Câu 21. Giải phương trình 4 2
1 x x x 1?
17. TOÁN HỌC SƠ ĐỒ ‐ THCS.TOANMATH.com 5 5
A. x  0 . B. x  . C. x  0; x  . D. Đáp án khác. 4 1 2 4 1 1
Câu 22. Giải phương trình   1. 2 2
x 1 x  2x  5
x 1 x  2x  5 A. x  2  .
B. x  0 . C. x  1. D. x  1  . HƯỚNG DẪN Câu 1. Đáp án C. Đặt 2
x t(t  0) ta được phương trình 2
t  6t  7  0 (*)
Nhận thấy a b c 1 6  7  0 nên phương trình (*) có hai nghiệm t  1(
L);t  7(N) 1 2
Thay lại cách đặt ta có 2
x  7  x   7 .
Vậy phương trình đã cho có hai nghiệm. Câu 2. Đáp án D. Đặt 2
x t(t  0) ta được phương trình 2
2t  9t  7  0 (*) 7
Nhận thấy a b c  2  (9)  7  0 nên phương trình (*) có hai nghiệm t  1(N );t  (N ) 1 2 2
Thay lại cách đặt ta có Với 2
t  1  x  1  x  1 7 7 14 Với 2 t   x   x   2 2 2
Vậy phương trình đã cho có bốn nghiệm phân biệt. Câu 3. Đáp án B. Đặt 2
(x 1)  t(t  0) ta được phương trình 2
t  5t  84  0 (*) 5  361 5  361
Ta có Δ  361 nên phương trình (*) có hai nghiệm t   12(N);t   7(L) 1 2 2 2
18. TOÁN HỌC SƠ ĐỒ ‐ THCS.TOANMATH.com
Thay lại cách đặt ta có 2
(x 1)  12  x  1
  12 Suy ra tổng các nghiệm là 1   12 1 12  2  Câu 4. Đáp án C. Đặt 2
(2x 1)  t(t  0) ta được phương trình 2
t  8t  9  0 (*)
Ta a b c  1 (8)  (9)  0 nên phương trình (*) có hai nghiệm t  1(tm);t  9  (ktm) 1 2 2x 1  1 x  0
Thay lại cách đặt ta có 2 (2x 1)  1    2x 1 1     x  1 
Suy ra tổng các nghiệm là 0  (1)  1 . Câu 5. Đáp án C.
Điều kiện: x  2; x  3 2x 5 9 
2x(x  3)  5(x  2) 9  2    
 2x 11x 19  0 2 x  2 x  3 x  5x  6
(x  2)(x  3)
(x  2)(x  3) Nhận thấy 2
Δ  11  4.19.2  31  0 nên phương trình 2
2x 11x 19  0 vô nghiệm. Suy ra phương trình đã cho vô nghiệm. Câu 6. Đáp án B. 1 1 1    0
x 1 x 1 x  4 x 1  0 x  1  
Điều kiện: x 1  0  x  1  x 4 0    x  4  
(x 1)(x  4)
(x 1)(x  4) (x 1)(x 1) PT     0
(x 1)(x 1)(x  4) (x 1)(x 1)(x  4) (x 1)(x 1)(x  4)
 (x 1)(x  4)  (x 1)(x  4)  (x 1)(x 1)  0 2 2 2
x  3x  4  x  5x  4  x 1  0 2
 3x  8x 1  0 2
Δ  4  3.(1)  19  0  4  19 x  (tm) 1
Phương trình có 2 nghiệm phân biệt: 3   4  19 x  (tm) 2  3
19. TOÁN HỌC SƠ ĐỒ ‐ THCS.TOANMATH.com Câu 7. Đáp án D.
Điều kiện: x  1; x  1; x  14
1 x 1 x  1 x  3 2 2
(1 x)  (1 x) 1 x 1 x 3 Ta có  : 1       : 
1 x 1 x  1 x  14  x (1 x)(1 x) 1 x 14  x 4x 1 x 3 2 3  .   
(1 x)(1 x) 2x 14  x
x 1 14  x
 28  2x  3x  3  5x  25  x  5(TM )
Vậy phương trình có nghiệm x  5 Câu 8. Đáp án B.
Điều kiện: x  2; x  2; x  0  2 2
2  x 2  x   2  x  2
2  x 2 x 2  x  2  x 2 Ta có  : 1       : 
 2  x 2  x   2  x  3x
2  x2  x 2  x 3x 8x 2  x 2 2x 2     
x  x . 2 2 4 3x 2  x 3x 2 2
 6x  2x  4  0  3x x  2  0
Phương trình này có a b c  3  (1)  (2)  0 2 x  1; x  (TM )
nên có hai nghiệm phân biệt 3 2
Vậy phương trình có hai nghiệm x  1; x   3 Câu 9. Đáp án B.  10 x   2 2 3 2 2
x  2x  5  x x  5 3x  10  Ta có  2
x x     2 2 5
x x  5      x  0  2 2 2
x  2x 5  x x 5
2x x  0  1 x   2 10 1 Nên tích các nghiệm là .0.  0 3 2 Câu 10. Đáp án B.
20. TOÁN HỌC SƠ ĐỒ ‐ THCS.TOANMATH.com Ta có 2 2 2
(2x  3)  4(x 1) 2 2
2x  3  2(x  ) 1
2x  2x 1  0    2 2
2x  3  2(x  ) 1
2x  2x  5  0 1 3 1 3 Phương trình 2
2x  2x 1  0 có Δ  3  0 nên có hai nghiệm x  ; x  2 2 1 11 1 11 x  ; x  Phương trình 2
2x  2x  5  0 có Δ   11  0 nên có hai nghiệm 2 2 1 1 3 1 3 1 11 1 11
Nên tổng các nghiệm của phương trình đã cho là     0 2 2 2 2 Câu 11. Đáp án C. 2 3x  5  0 Ta có 3 2
3x  3x  5x  5  0 2 2
 3x (x 1)  5(x 1)  0  3
( x  5)(x  )
1  0  x10 2 3x   ( 5 L)    x  1  x   1 
Vậy phương trình có nghiệm duy nhất x  1  . Câu 12. Đáp án A.
Ta có x(x 1)(x  2)(x  3)  8 2 2
x(x  3)(x 1)(x  2)  8  (x  3x)(x  3x  2)  8 Đặt 2
x  3x 1  t , thu được phương trình t  3 2 2
(t 1)(t 1)  8  t 1  8  t  9   t  3  +) Với 2
t  3  x  3x 1  3 3  17 3  17 2
x  3x  2  0 có Δ  17  x  ; x  1 2 2 2 +) Với 2
t  3  x  3x 1  3 2
x  3x  4  0 có Δ  7
  0 nên phương trình vô nghiệm. 3  17 3  17
Vậy phương trình đã cho có hai nghiệm x  ; x  1 2 2 2
21. TOÁN HỌC SƠ ĐỒ ‐ THCS.TOANMATH.com 3  17 3  17
Suy ra tổng các nghiệm là   3 . 2 2 Câu 13. Đáp án B. Ta có 2 2 2
(x 1)(x  4)(x  5x  6)  48  (x  5x  4)(x  5x  6)  48 t  7 Đặt 2
x  5x  5  t , thu được phương trình (t 1)(t 1)  8  t2 1  48  t2  49   t  7  5  33 5  33 +) Với 2 2
t  7  x  5x  5  7  x  5x  2  0 có Δ  33  x  ; x  1 2 2 2 +)Với 2 2
t  7  x  5x  5  7  x  5x 12  0 có Δ  23
  0 nên phương trình vô nghiệm. 5  33 5  33
Vậy phương trình đã cho có hai nghiệm x  ; x  . 1 2 2 2 5   33 5   33
Suy ra tổng các nghiệm là   5  . 2 2 Câu 14. Đáp án D.
Điều kiện: x  0; x  1 x 1 Đặt
t(t  0) , khi đó phương trình đã cho trở thành 2
t 10.  3  t  3t 10  0 x 1 t 3  49
Ta có Δ  49  t   5; 1 2 3  49 t   2(TM ) 2 2 x 5
+) Với t  5 suy ra
 5  5x  5  x x   (nhận) x 1 4 x 2 +) Với t  2  suy ra  2  2
x  2  x x   (nhận) x 1 3 2 5
Vậy phương trình đã cho có hai nghiệm x    x   1 2 3 4  2   5 
Nên 3x  4x  3.  4.  7 1 2      3   4 
22. TOÁN HỌC SƠ ĐỒ ‐ THCS.TOANMATH.com Câu 15. Đáp án C. 1 Điều kiện: x  4 2x 1 Đặt
t(t  0) , khi đó phương trình đã cho trở thành 2
t   2  t t  2  0 (*) 4x 1 t
Ta có a b c  11 (2)  0 nên phương trình (*) có hai nghiệm t  1(tm);t  2  (ktm) 1 2 2x
+) Với t  1 suy ra 2 2
1 2x  4x 1  4x  4x 1  4x  4x 1  0 4x 1 2 1
 (2x 1)  0  x  (tm) . 2 1
Vậy phương trình đã cho có nghiệm x  . 2 Câu 16. Đáp án A. 2
Điều kiện: 3x  2  0  x  . 3 Ta có 2
x  3x  2  (1 x) 3x  2
 (x 1)(x  2)  (x 1) 3x  2  0  (x 1)(x  2  3x  2)  0 x 1  0 x  1(TM )    
x  2  3x  2  0
 3x  2  2  x( )  2  x  0
Xét phương trình (*): 3x  2  2  x   2 3x   2  (2  x) x  2 x  2   
 x 1  x 1(TM ) . 2
x  7x  6  0  x  6
Vậy phương trình có nghiệm duy nhất x  1. Câu 17. Đáp án B.
Điều kiện: x 1  0  x 1 Ta có 2
5(x  2) x 1  x  7x 10
23. TOÁN HỌC SƠ ĐỒ ‐ THCS.TOANMATH.com
 5(x  2) x 1  (x  2)(x  5)  (x  2)(x  5)  5(x  2) x 1  0 x  2  0 x  2  (ktm)    
x  5  5 x 1  0
x  5  5 x 1( ) 
Xét phương trình (*): 5 x 1  x  5 Với x 1 ta có 2 2
25(x 1)  (x  5)  x 15x  50  0 2
x  5x 10x  50  0  x(x  5) 10(x  5)  0 x  10(tm)
 (x 10)(x  5)  0   x   5(tm)
Vậy phương trình có nghiệm x  5; x  10 . Câu 18. Đáp án D. x  3 3   x  0 x  3  8 Ta có 2
x x 1  3  x       8  x  2 2
x x 1  (3  x) 7x  8 x  7  7 8
Vậy phương trình có nghiệm duy nhất x  . 7 Câu 19. Đáp án A. x  2  0 x  2  Ta có 2
2x  6x 1  x  2     2 2 2
2x  6x 1  (x  2)
x  2x  3  0 x  2  x  2      2 x
  3x x  3  0 x(x  ) 3  (x  3)  0 x  2  x  2   x  1     x  1   (x 1)(x 3) 0      x  3 x  3
Vậy phương trình có nghiệm x  1; x  3. Câu 20. Đáp án A. 2   Ta có 2 2
4x  4x  5  12x 12x 19  6 2 1
 (2x 1)  4  12 x  16  6    2 
24. TOÁN HỌC SƠ ĐỒ ‐ THCS.TOANMATH.com 2   Nhận thấy 2 1
(2x 1)  4  2; 12 x  16  4    2  2
 (2x 1)  4  2 2x 1  0   1 Dấu “=” xảy ra khi 2    1  1  x   x   0 2  12 x  16  4     2   2  1
Vậy phương trình đã cho có nghiệm duy nhất x  2
Từ đó suy ra a  1;b  2  a b  1 Câu 21. Đáp án B. 4 2
1 x x x 1
Điều kiện: x 1  0  x 1 4 2 2 4 2 2
 1 x x  (x 1)  1 x x x  2x 1 2
2x x  0 4 2 2
x x  2x x   4 2 2 3 4
x x  4x  4x x 0  x  2 x  0 0  x  2 0  x  2  2   x  0      5 3 2 2
4x  5x  0
x (4x  5)  0   x  4x   5  0  4 5 x
PT Kết hợp với điều kiện ban đầu x 1 ta thấy phương trình có nghiệm duy nhất 4 . Câu 22. Đáp án D. 1 1  1 2 2
x 1 x  2x  5
x 1 x  2x  5 1 1   1 2 2
x 1 (x 1)  4
x 1 (x 1)  4
Đặt x –1  t 2 2 1 1
t t  4  t t  4 PT    1   1 2 2
t t  4 t t  4  2
t t  4  2
t t  4 
25. TOÁN HỌC SƠ ĐỒ ‐ THCS.TOANMATH.com 2t 2t   1 
 1  t  2  x 1  2  x  1. 2 2 t t  4 4
Thử lại thấy x  1
 thỏa mãn phương trình.
Vậy phương trình có nghiệm duy nhất x  1  .
D.PHIẾU BÀI TỰ LUYỆN CƠ BẢN VÀ NÂNG CAO PHIẾU SỐ 1
Dạng 1: Phương trình trùng phương
Bài 1. Giải các phương trình sau: 4 5 a) 4 2
x  5x  4  0 b) 4 2
x  3x  4  0 c)   2 2 2 x  4 x  5
Bài 2. Tìm các giá trị của m để phương trình ẩn x sau: 4 2
x  6x m 1  0 có 4 nghiệm.
Dạng 2. Phương trình chứa ẩn ở mẫu
Bài 3. Giải các pt sau: 8 5 8  x x 1 2 12 a) 1   b)   x  4 3  x x  2 2 x  2 x  2 x  4
Dạng 3. Phương trình đưa về phương trình tích
Bài 4. Giải các phương trình: a) 2 2
(2x  5x  2)(x  3x 1)  0 b) 2 2 2
(2x x)  (2x 1)  0
Bài 5. Giải phương trình 4 2
x x  4x  3  0
Dạng 4. Phương pháp đặt ẩn phụ
Bài 6. Giải các phương trình sau a) 2 2 2
(x  5x)  2(x  5x)  24 b) 2 2 2
(x  6x)  2(x  3)  81 2 x x  5 3x c)   4  0 2 x x x  5
Dạng 5. Phương trình bậc 4 dạng (x a)(x b)(x c)(x d )  m với a b c d
Bài 7. Giải phương trình (x  5)(x  6)(x  8)(x  9)  40
26. TOÁN HỌC SƠ ĐỒ ‐ THCS.TOANMATH.com
Bài 8. Giải phương trình 2 2
(x  3x  2)(x  7x 12)  24
Dạng 6. Phương trình đối xứng bậc bốn, phương trình hồi quy
Bài 9. Giải phương trình 4 3 2
2x  3x 16x  3x  2  0
Bài 10. Giải phương trình 4 3 2
2x  21x  74x 105x  50  0
Dạng 7. Phương trình vô tỉ
Bài 11. Giải phương trình
a) 2x 1  8  x
b) 15  x  3  x  6
Bài 12. Giải phương trình a) 2 2
x x x x  24  18 b) 2
2  x  2  x  4  x  2
HƯƠNG DẪN – ĐÁP SỐ
Dạng 1: Phương trình trùng phương
Bài 1. Giải các phương trình sau: 4 5 a) 4 2
x  5x  4  0 b) 4 2
x  3x  4  0 c)   2 2 2 x  4 x  5
Hướng dẫn-Đáp số a) Đặt 2
x t  0 đưa phương trình về: 2
t  5t  4  0  t  1;t  4 (thỏa mãn) 1 2
+ Với t  1  x  1; x  1  1 2
+ Với t  4  x  2; x  2 3 4
Vậy phương trình đã cho có nghiệm S   1;    2
b) Phương trình có nghiệm S    2
c) Phương trình có nghiệm x  0
Bài 2. Tìm các giá trị của m để phương trình ẩn x sau: 4 2
x  6x m 1  0 có 4 nghiệm.
Hướng dẫn-Đáp số Đặt 2
x t  0 , ta được 2
t  6t m 1  0 (1)
27. TOÁN HỌC SƠ ĐỒ ‐ THCS.TOANMATH.com
Để pt đã cho có 4 nghiệm thì pt (1) phải có 2 nghiệm dương pb  '  0 9   (m 1)  0  
x x  0  m 1  0  1  m 10 1 2 x .x  0 6  0  1 2 
Vậy với 1  m  10 thì pt đã cho có 4 nghiệm.
Dạng 2. Phương trình chứa ẩn ở mẫu
Bài 3. Giải các pt sau: 8 5 8  x x 1 2 12 a) 1   b)   x  4 3  x x  2 2 x  2 x  2 x  4
Hướng dẫn-Đáp số
a) Điều kiện: x  2; x  3; x  4
Quy đồng mẫu thức rồi khử mẫu:
(3  x)(x  2)(x 4)  8(3  x)(x  2)  5(x  4)(x  2)  (8  x)(x  4)(3  x) 2
 7x  72x 128  0 2
Giải ra ta được: x  8; x  2 (thỏa mãn) 1 2 7 2
Vậy pt có 2 nghiệm x  8; x  2 1 2 7
b) Pt có nghiệm x  3
Dạng 3. Phương trình đưa về phương trình tích
Bài 4. Giải các phương trình: a) 2 2
(2x  5x  2)(x  3x 1)  0 b) 2 2 2
(2x x)  (2x 1)  0
Hướng dẫn-Đáp số a) 2 2
(2x  5x  2)(x  3x 1)  0 2
2x  5x  2  0 (1)   2
x  3x 1  0 (2) 1
Giải (1) ta được x  ; x  2 1 2 2
28. TOÁN HỌC SƠ ĐỒ ‐ THCS.TOANMATH.com 3  5 3  5
Giải (2) ta được x  ; x  3 4 2 2 1 3  5 3  5 
Vậy pt có tập nghiệm S   ;2; ;  2 2 2   3 17 
b) Pt có tập nghiệm S     4  
Bài 5. Giải phương trình 4 2
x x  4x  3  0
Hướng dẫn-Đáp số 4 2 4 2 2
x x  4x  3  0  x  2x 1 x  4x  4  0 2 2 2
 (x 1)  (x  2)  0 2 2
 (x x 1)(x x  3)  0 1 5 
Giải ra ta được tập nghiệm S     2  
Dạng 4. Phương pháp đặt ẩn phụ
Bài 6. Giải các phương trình sau 2 x x  5 3x a) 2 2 2
(x  5x)  2(x  5x)  24 b) 2 2 2
(x  6x)  2(x  3)  81 c)   4  0 2 x x x  5
Hướng dẫn-Đáp số y  4  a) Đặt 2
x  5x y ta được pt 2
y  2y  24    y  6 x  1  Với y  4 2
x  5x  4    x  4  x 1 Với 2
y  6  x  5x  6   x  6 
Vậy pt có tập nghiệm S   1  ; 4  ;  6
b) Pt có tập nghiệm S  3;3 20
29. TOÁN HỌC SƠ ĐỒ ‐ THCS.TOANMATH.com
c) Pt có tập nghiệm S  1; 5  ; 1   6
Dạng 5. Phương trình bậc 4 dạng (x a)(x b)(x c)(x d )  m với a b c d
Bài 7. Giải phương trình (x  5)(x  6)(x  8)(x  9)  40
Hướng dẫn-Đáp số
Ta có (x  5)(x  6)(x  8)(x  9)  40 2 2
 (x 14x  45)(x 14x  48)  40  y  5 Đặt 2
x  5x  45  y phương trình thành y( y  3)  40    y  8  x  4  Với y  5   x  10 
Với y  8 suy ra x vô nghiệm.
Vậy phương trình có nghiệm x  4; x  10
Bài 8. Giải phương trình 2 2
(x  3x  2)(x  7x 12)  24
Hướng dẫn-Đáp số
Ta viết dưới dạng (x 1)(x  2)(x  3)(x  4)  24 2 2
 (x  5x  4)(x  5x  6)  24
Giải tương tự ta được tập nghiệm S  0;  5
Dạng 6. Phương trình đối xứng bậc bốn, phương trình hồi quy
Bài 9. Giải phương trình 4 3 2
2x  3x 16x  3x  2  0
Hướng dẫn-Đáp số
+) x  0 không là nghiệm của phương trình.
+) x  0 , chia hai vế của phương trình cho 2 x ta được:  1   1 2  2 x   3 x  16  0  2     x   x
30. TOÁN HỌC SƠ ĐỒ ‐ THCS.TOANMATH.com y  4  1 1 Đặt 2 2
x   y x
y  2 . Ta được phương trình 2 2( y 2) 3y 20 0       2 5 x xy   2  1 
Theo cách đặt, giải pt tìm được tập nghiệm S  2  3; ;2  2 
Bài 10. Giải phương trình 4 3 2
2x  21x  74x 105x  50  0
Hướng dẫn-Đáp số
+) x  0 không là nghiệm của phương trình.
+) x  0 , chia hai vế của phương trình cho 2 x ta được:  25   5 2  2 x   21 x   74  0  2     x   x   5 
Giải tương tự tìm được tập nghiệm S  1;  5; ;2  2 
Dạng 7. Phương trình vô tỉ
Bài 11. Giải phương trình
a) 2x 1  8  x
b) 15  x  3  x  6
Hướng dẫn-Đáp số 1
a) Điều kiện  x  8 2
Bình phương hai vế, ta được: 2
2x 1  64 16x x x  5 (thỏa mãn); x  13 (loại)
Vậy pt có nghiệm x  5
b) Pt có nghiệm x  1 
Bài 12. Giải phương trình a) 2 2
x x x x  24  18 b) 2
2  x  2  x  4  x  2
Hướng dẫn-Đáp số a) S   3;   4 b) S   2;   2 PHIẾU SỐ 2
31. TOÁN HỌC SƠ ĐỒ ‐ THCS.TOANMATH.com
Bài 1: Giải các phương trình sau: a)   2
x 2  3x  5  1 x1 x b)   3 3 2
x 1  2x  x  x  2x 1 c)  2
x x  6 x  22  x  3 1
d)   2    2 x 5
x 2  x  7x  7 12x  23
Bài 2: Giải các phương trình sau: a) 4 2 x  5x  6  0
b)   4    2 x 1 5 x 1  84  0
Bài 3: Tìm các giá trị của m để phương trình ẩn số x: 4 2
x  6x  m 1  0 có 4 nghiệm.
Bài 4: Giải các phương trình sau: 8 5 8  x a) 1   x  4 3  x x  2 x 1 2 12 b)   2 x  2 x  2 x  4
Bài 5: Giải các phương trình: a)  2    2 2x 5x 2 x  3x   1  0 2 b)  2 2x  x 2x  2 1  0
Bài 6: Giải phương trình sau: 4 2 x  x  4x  3  0
Bài 7: Chứng minh rằng khi a và c trái dấu thì phương trình trùng phương 4 2
ax  bx  c  0 chỉ có hai
nghiệm và chúng là hai số đối nhau.
Bài 8: Giải các phương trình sau: 2 a)  2     2 x 5x 2 x  5x  24 2 b)  2
x  6x  2x 32  81 2 x  x  5 3x c)   4  0 2 x x  x  5
Bài 9: Giải phương trình: x  5x  6x  8x  9  40
32. TOÁN HỌC SƠ ĐỒ ‐ THCS.TOANMATH.com
Bài 10: Giải phương trình:  2    2 x 3x 2 x  7x 12  24
Bài 11: Giải các phương trình sau: a) 4 3 2
2x  3x 16x  3x  2  0 b) 4 3 2
2x  21x  74x 105x  50  0
Bài 12: Giải các phương trình sau:
a)   4    4 x 4 x 2  82
b)   6    6 x 2 x 4  64 4x 5x 3
Bài 13: Giải phương trình sau:    2 2 x  x  3 x  5x  3 2 HƯỚNG DẪN GIẢI Bài 1: a) Ta có:   2
x 2  3x  5  1 x1 x 2 2
 x  4x  4  3x  5 1 x 2  2x  x  2  0 2  1  4.2. 2
  116 17  0    17 1 17 17 1 1 17 1 17  x   ; x   1 2 2.2 4 2.2 4 b) Ta có:   3 3 2
x 1  2x  x  x  2x 1 3 2 3 2
 x  3x  3x 1 2x  x  x  2x 1 3 2 3 2
 x  3x  3x 1 2x  x  x  2x 1 2  2x  7x  2  0    7
 2  4.2.2  49 16  33  0    33 7  33 7  33 7  33 7  33  x   ; x   1 2 2.2 4 2.2. 4 c) Ta có:  2
x x  6 x  22  x  3 1 3 2 3 2
 x  6x  x  4x  4  x  3x  3x 1 2  4x  5x  5  0 2
  5  4.4.5  25  80  55  0
Vậy phương trình vô nghiệm.
d) Ta có:   2    2 x 5
x 2  x  7x  7 12x  23
33. TOÁN HỌC SƠ ĐỒ ‐ THCS.TOANMATH.com 2 2 2
 x 10x  25  x  4x  4  x  49  12x  23 2 2
 3x  6x  3  0  x  2x 1  0    2 1 1.1  0
Vậy phương trình đã cho có nghiệm kép: x  x 1 1 2 Bài 2: a) Đặt 2
x  t  0 , đưa về phương trình 2 t  5t  6  0
Giải phương trình ta được t 1tm hoặc t  6  l Với t  1, ta có 2 x  1    1 x 1; x2 1
Vậy phương trình có hai nghiệm: x 1; x  1  1 2 b) Đặt   2
x 1  t  0 , đưa về phương trình 2 t  5t  84  0
Giải phương trình ta được t  12tm hoặc t  7  l
Với t 12 , ta có x  2 1  12  x  1   2 3;x  1   2 3 1 2
Vậy phương trình có hai nghiệm: x  1   2 3;x  1   2 3 1 2 Bài 3: Đặt 2 x  t  0 ta được 2
t  6t  m 1  0   1
Để phương trình đã cho có 4 nghiệm, thì phương trình  
1 phải có 2 nghiệm dương phân biệt    0 9   m   1  0  c    0   m 1  0  1  m  10 a   6  0  b    a
Vậy với 1  m  10 thì phương trình đã cho có 4 nghiệm. Bài 4:
a) Điều kiện: x  2; x  3; x  4
Quy đồng mẫu thức rồi khử mẫu:
3 xx  4x  283 xx  2  5x  4x  2 8 xx  43 x 2  7x  72x 128  0 2
Giải ra ta được: x  8; x  2 thỏa mãn. 1 2 7 2
Vậy phương trình có hai nghiệm: x  8; x  2 1 2 7
34. TOÁN HỌC SƠ ĐỒ ‐ THCS.TOANMATH.com
b) Điều kiện: x  2; x  2
Quy đồng mẫu thức rồi khử mẫu:     x  
1 x  2  2x  2 x 2 l 2  
 12  x  x  6  0   x  3  tm
Vậy phương trình có một nghiệm: x  3 Bài 5: 2 2x  5x  2  0 1 a)  2 2x  5x  2 2 x  3x     1  0   2  x  3x 1  0  2 1 Giải   1 ta được: 2
2x  5x  2  0 ta được: x  ; x  2 1 2 2 3  5 3  5 Giải 2 ta được: 2
x  3x 1  0 ta được: x  ; x  3 4 2 2 1 3  5 3  5 
Vậy tập nghiệm của phương trình: S   ;2; ;  2 2 2   2
b)  2      2    2     2 2x x 2x 1 0 2x x 2x 1 2x  x  2x   1  0       2x  x   1 2x  3x   2 2x x 1 0 1 2 2   1  0   2 2x  3x 1  0  2 Giải   1 :   1 4.2.1  7
  0  Phương trình vô nghiệm. 3  17 3  17 Giải 2 : 2
2x  3x 1  0 ta được x  ; x  1 2 4 4  3   17 3   17 
Vậy phương trình có tập nghiệm là: S   ;   4 4   Bài 6: 4 2 4 2 2
x  x  4x  3  0  x  2x 1 x  4x  4  0   x  x  3  0 1 2 x   2 2
1  x  22  0   2 x  x  3 2 x  x     1  0   2 x  x 1  0  2 Giải   1 : 2
x  x  3  0 có   11   0  vô nghiệm. 1 5 1 5 Giải 2 : 2 x  x 1  0  x  ; x  1 2 2 2
35. TOÁN HỌC SƠ ĐỒ ‐ THCS.TOANMATH.com
1 5 1 5 
Vậy tập nghiệm của phương trình: S   ;   2 2   Bài 7: Đặt 2 x  m  0 Ta có: 4 2 2
ax  bx  c  0  am  bm  c  0 a
Vì a và c trái dấu nên  0 . Phương trình có hai nghiệm phân biệt là m và m c 1 2 c
Theo hệ thức Vi – ét ta có: m .m  1 2 a c
Vì a và c trái dấu nên  0  m .m  0 hay m và m trái dấu nhau. 1 2 a 1 2 Vì m m m 1 và
2 trái dấu nhau nên có 1 nghiệm bị loại, giả sử loại 1 . Khi đó 2 x  m  x   m 2 2
Vậy phương trình trùng phương 4 2
ax  bx  c  0 chỉ có hai nghiệm và chúng là hai số đối nhau khi a và c trái dấu. Bài 8: y  4  a) Đặt 2
x  5x  y . Ta được: 2 2
y  2y  24  y  2y  24  0    y  6 x  1  .Với 2 2 y  4   x  5x  4
  x  5x  4  0   x  4   x 1 .Với 2 2
y  6  x  5x  6  x  5x  6  0   x  6 
Vậy tập nghiệm của phương trình: S   1  ; 4  ;1;  6 2 2
b)  2      2    2     2 x 6x 2 x 3 81 x 6x
2 x  6x  9 81  0  y 11 Đặt 2
x  6x  y . Ta được: 2 y  2y  9 2
81  0  y  2y  99  0   y  9  x  3 20 .Với 2 2
y  11  x  6x  11  x  6x 11  0   x  3 20
36. TOÁN HỌC SƠ ĐỒ ‐ THCS.TOANMATH.com .Với 2 2
y  9  x  6x  9  x  6x  9  0  x  3
Vậy tập nghiệm S  3 20;3 20  ;3 c) Điều kiện: 2 x  0; x  x  5  0 2 x  x  5 Đặt  y x 3 y  1  Ta được: 2
y   4  0  y  4y  3  0  y  y  3  2 x  x  5 .Với 2 y  1 
 1  x  2x  5  0     1, x 2 1 6 x 2 x  x  5 .Với 2 y  3 
 3  x  4x  5  0  x  1; x  5 3 4 x
Vậy tập nghiệm của phương trình là: S   1   6;1;  5
Bài 9: Ta có: x  5x  6x  8x  9  40   2    2 x
14x 45 x 14x  48  40  y  5 Đặt: 2
x 14x  45  y , ta có: y y  3 2
 40  y  3y  40  0   y  8   x  4  .Với 2 2
y  5  x 14x  45  5  x 14x  40  0   x  1  0 .Với 2 2
y  8  x 14x  45  8  x 14x  53  0 : vô nghiệm.
Vậy tập nghiệm của phương trình: S   4  ; 1   0 Bài 10:
Ta viết dưới dạng: x  
1 x  2x  3x  4  24   2    2 x 5x 4 x  5x  6  24  y  4 Đặt 2
x  5x  4  y , ta có: 2 y  2y  24  0   y  6   x  0 .Với y  4 , ta có: 2 2
x  5x  4  4  x  5x  0   x  5  .Với y  6 , ta có: 2 2 x 5  x  4  6
  x  5x 10  0: vô nghiệm.
Vậy tập nghiệm của phương trình: S  0;  5 Bài 11:
37. TOÁN HỌC SƠ ĐỒ ‐ THCS.TOANMATH.com
a) x  0 không phải là nghiệm của phương trình.
x  0 chia hai vế của phương trình cho 2 x , ta được:  2 1   1  2 x   3 x  16  0  2     x   x  1 1 Đặt 2 2 x   y  x 
 y  2 . Ta có phương trình: 2 x x y  4  2 2 y 2 2 3y 16 0 2y 3y 20 0           5  y   2 1 x  2   3 .Với 2 y  4   x   4
  x  4x 1  0   x x  2   3  1 5 1 5 x  .Với 2 y x 2x 5x 2 0           2 2 x 2   x  2  1 
Vậy tập nghiệm của phương trình: S  2  3;2  3; ;2  2 
b) x  0 không phải là nghiệm của phương trình.
x  0 chia hai vế của phương trình cho 2 x , ta được:  2 25   5  2 x   21 x   74  0  2     x   x  5 25 Đặt 2 2 x   y  x 
 y 10 . Ta có phương trình: 2 x x  y  6 2 2 y 10 2 21y 74 0 2y 21y 54 0           9 y   2 5  x 1 .Với 2 y  6  x 
 6  x  6x  5  0  x  x  5  5 9 5 9 x  .Với 2 y x 2x 9x 10 0           2 2 x 2   x  2  5 
Vậy tập nghiệm của phương trình là: S  1  ;5; ;2  2  Bài 12:  y  2
a) Đặt x  3  y , ta được: y  4 1  y  4 4 2
1  82  y  6y  40  0   y  2  Với y  2  x  1
38. TOÁN HỌC SƠ ĐỒ ‐ THCS.TOANMATH.com
Với y  2  x  5
Vậy tập nghiệm của phương trình là: S   1  ;  5
b) Đặt x  3  y . Phương trình có dạng:   6    6 y 1 y 1  64
Khai triển và rút gọn ta được: 6 4 2 y 15y 15y  31  0    y  1 2 y   1  4 2 y 16y  3  1  0   y  1  Với y  1  x  4 Với y  1  x  2
Vậy tập nghiệm của phương trình: S  4;  2 Bài 13.
x  0 không phải là nghiệm của phương trình.
x  0 chia tử và mẫu của mỗi phân thức cho x: 4 5 3    3 3 2 x 1 x  5  x x 3 4 5 3
Đặt x   2  y phương trình có dạng:    0 . ĐK: y  3 x y  3 y  3 2  y 1
Quy đồng, khử mẫu rồi rút gọn ta được: 2 y  6y  7  0   y  7  3 Với 2
y  1  x   2  1  x  3x  3  0 : vô nghiệm. x  5  13 x  3 Với 2 2
y  7  x   2  7  x  5x  3  0   x  5  13 x   2
5  13 5  13 
Vậy tập nghiệm của phương trình là: S   ;   2 2  
---------------------Toán Học Sơ Đồ--------------------
39. TOÁN HỌC SƠ ĐỒ ‐ THCS.TOANMATH.com