Cực trị của hàm số - Ebook

Tài liệu ôn tập môn Toán về Cực trị của hàm số dành cho các bạn ôn thi tốt nghiệp và đại học.. Mời các bạn cùng tham khảo chi tiết tại đây nhé.

69 35 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Chương 2: Hàm số lũy thừa. Hàm số mũ và hàm số logarit

Môn: Toán 12

Thông tin:

28 trang 8 tháng trước

Tác giả:

Profile Nguyễn Vân
Nguyễn Phú Khánh – ðà Lạt 063.28.78.79 hoặc 0989.80.78.79 http://www.maths.vn
-41-
CỰC TRỊ CỦA HÀM SỐ
TÓM TẮT LÝ THUYẾT
1. Khái niệm cực trị hàm số :
Giả sử hàm số
f
xác ñịnh trên tập hợp
(
)
D D
⊂
ℝ
và
0
x D
∈
0
a x
ñược gọi là một ñiểm cực ñại của hàm số
f
nếu tồn tại một khoảng
(
)
;
a b
chứa ñiểm
0
x
sao cho
(
)
;
a b D
⊂
và
(
)
(
)
0
f x f x
< với mọi
(
)
{
}
0
; \
x a b x
∈ . Khi ñó
(
)
0
f x
ñược gọi là giá trị cực ñại của
hàm số
f
.
0
b x
ñược gọi là một ñiểm cực tiểu của hàm số
f
nếu tồn tại một khoảng
(
)
;
a b
chứa ñiểm
0
x
sao cho
(
)
;
a b D
⊂
và
(
)
(
)
0
f x f x
> với mọi
(
)
{
}
0
; \
x a b x
∈ . Khi ñó
(
)
0
f x
ñược gọi là giá trị cực tiểu của
hàm số
f
.
Giá trị cực ñại và giá trị cực tiểu ñược gọi chung là cực trị
Nếu
0
x
là một ñiểm cực trị của hàm số
f
thì người ta nói rằng hàm số
f
ñạt cực trị tại ñiểm
0
x
.
Như vậy : ñiểm cực trị phải là một ñiểm trong của tập hợp
(
)
D D
⊂
ℝ
2. ðiều kiện cần ñể hàm số ñạt cực trị:
ðịnh lý 1: Giả sử hàm số
f
ñạt cực trị tại ñiểm
0
x
. Khi ñó , nếu
f
có ñạo hàm tại ñiểm
0
x
thì
(
)
0
' 0
f x
=
Chú ý :
•
ðạo hàm
'
f
có thể bằng
0
tại ñiểm
0
x
nhưng hàm số
f
không ñạt cực trị tại ñiểm
0
x
.
•
Hàm số có thể ñạt cực trị tại một ñiểm mà tại ñó hàm số không có ñạo hàm .
•
Hàm số chỉ có thể ñạt cực trị tại một ñiểm mà tại ñó ñạo hàm của hàm số bằng
0
, hoặc tại ñó hàm
số không có ñạo hàm .
3. ðiều kiện ñủ ñể hàm số ñạt cực trị:
ðịnh lý 2: Giả sử hàm số
f
liên tục trên khoảng
(
)
;
a b
chứa ñiểm
0
x
và có ñạo hàm trên các khoảng
(
)
0
;
a x
và
(
)
0
;
x b
. Khi ñó :
)
a
Nếu
(
)
(
)
( ) ( )
0 0
0 0
' 0, ;
' 0, ;
f x x a x
f x x x b
< ∈
> ∈
thì hàm số ñạt cực tiểu tại ñiểm
0
x
. Nói một cách khác , nếu
(
)
'
f x
ñổi
dấu từ âm sang dương khi
x
qua ñiểm
0
x
thì hàm số ñạt cực tiểu tại ñiểm
0
x
.
x
a
0
x
b
(
)
'
f x
−
+
(
)
f x
(
)
f a
(
)
f b
(
)
0
f x
)
b
Nếu
(
)
(
)
( ) ( )
0 0
0 0
' 0, ;
' 0, ;
f x x a x
f x x x b
> ∈
< ∈
thì hàm số ñạt cực ñại tại ñiểm
0
x
. Nói một cách khác , nếu
(
)
'
f x
ñổi
dấu từ dương sang âm khi
x
qua ñiểm
0
x
thì hàm số ñạt cực ñại tại ñiểm
0
x
.
Nguyễn Phú Khánh – ðà Lạt 063.28.78.79 hoặc 0989.80.78.79 http://www.maths.vn
-42-
x
a
0
x
b
(
)
'
f x
+
−
(
)
f x
(
)
0
f x
(
)
f a
(
)
f b
ðịnh lý 3: Giả sử hàm số
f
có ñạo hàm cấp một trên khoảng
(
)
;
a b
chứa ñiểm
0
x
,
(
)
0
' 0
f x
=
và
f
có ñạo
hàm cấp hai khác
0
tại ñiểm
0
x
.
)
a
Nếu
(
)
0
'' 0
f x
<
thì hàm số
f
ñạt cực ñại tại ñiểm
0
x
.
)
b
Nếu
(
)
0
'' 0
f x
>
thì hàm số
f
ñạt cực tiểu tại ñiểm
0
x
.
4. Quy tắc tìm cực trị:
Quy tắc 1: Áp dụng ñịnh lý 2
•
Tìm
(
)
'
f x
•
Tìm các ñiểm
(
)
1,2,3...
i
x i
=
tại ñó ñạo hàm bằng
0
hoặc hàm số liên tục nhưng không có ñạo hàm.
•
Xét dấu của
(
)
'
f x
. Nếu
(
)
'
f x
ñổi dấu khi
x
qua ñiểm
0
x
thì hàm số có cực trị tại ñiểm
0
x
.
Quy tắc 2: Áp dụng ñịnh lý 3
•
Tìm
(
)
'
f x
•
Tìm các nghiệm
(
)
1,2,3...
i
x i
=
của phương trình
(
)
' 0
f x
=
.
•
Với mỗi
i
x
tính
(
)
'' .
i
f x
−
Nếu
(
)
'' 0
i
f x
<
thì hàm số ñạt cực ñại tại ñiểm
i
x
.
−
Nếu
(
)
'' 0
i
f x
>
thì hàm số ñạt cực tiểu tại ñiểm
i
x
.
Ví dụ 1 : Tìm cực trị của các hàm số :
( )
3 2
1 5
) 3
3 3
a f x x x x
= − − +
(
)
(
)
) 2
b f x x x
= +
(
)
(
)
) 3
c f x x x
= −
(
)
)
d f x x
=
Giải :
( )
3 2
1 5
) 3
3 3
a f x x x x
= − − +
Hàm số ñã cho xác ñịnh trên
ℝ
.
Ta có
(
)
(
)
2
' 2 3 ' 0 1, 3
f x x x f x x x
= − − = ⇔ = − =
Cách 1. Bảng biến thiên
x
−∞
1
−
3
+∞
(
)
'
f x
+
0
−
0
+
(
)
f x
10
3
+∞
−∞
22
3
−
Nguyễn Phú Khánh – ðà Lạt 063.28.78.79 hoặc 0989.80.78.79 http://www.maths.vn
-43-
Vậy hàm số ñạt cực ñại tại ñiểm
( )
10
1, 1
3
x f= − − =
, hàm số ñạt cực tiểu tại ñiểm
( )
22
3, 3
3
x f= = −
Cách 2 :
(
)
'' 2 2
f x x
= −
Vì
(
)
'' 1 4 0
f
− = − <
nên hàm số ñạt cực ñại tại ñiểm
( )
10
1, 1
3
x f= − − =
.
Vì
(
)
'' 3 4 0
f
= >
hàm số ñạt cực tiểu tại ñiểm
( )
22
3, 3
3
x f= = −
.
( ) ( )
(
)
( )
2 0
) 2
2 0
x x khi x
b f x x x
x x khi x
+ ≥
= + =
− + <
Hàm số ñã cho xác ñịnh và liên tục trên
ℝ
.
Ta có
( ) ( )
2 2 0 0
' ' 0 1
2 2 0
x khi x
f x f x x
x khi x
+ > >
= = ⇔ = −
− − <
Hàm số liên tục tại
0
x
=
, không có ñạo hàm tại
0
x
=
.
Bảng biến thiên
x
−∞
1
−
0
+∞
(
)
'
f x
+
0
−
+
(
)
f x
1
+∞
−∞
0
Vậy hàm số ñạt cực ñại tại ñiểm
(
)
1, 1 1
x f
= − − =
, hàm số ñạt cực tiểu tại ñiểm
(
)
0, 0 0
x f
= =
(
)
(
)
) 3
c f x x x
= −
Hàm số ñã cho xác ñịnh và liên tục trên
ℝ
.
( )
(
)
( )
3 0
3 0
x x khi x
f x
x x khi x
− ≥
=
− − <
.
Ta có
( )
(
)
( )
3 1
0
2
' ' 0 1
3
0 0
2
x
khi x
x
f x f x x
x
x khi x
x
−
>
= = ⇔ =
−
− > <
−
+
x
−∞
0
1
+∞
(
)
'
f x
+
−
0
+
(
)
f x
0
+∞
−∞
2
−
Hàm số ñạt ñiểm cực ñại tại ñiểm
(
)
0, 0 0
x f
= =
, hàm số ñạt ñiểm cực tiểu tại ñiểm
(
)
1, 1 2
x f
= = −
(
)
)
d f x x
=
Nguyễn Phú Khánh – ðà Lạt 063.28.78.79 hoặc 0989.80.78.79 http://www.maths.vn
-44-
Hàm số ñã cho xác ñịnh và liên tục trên
ℝ
.
( )
0
0
x khi x
f x
x khi x
≥
=
− <
.
Ta có
( )
1 0
'
1 0
khi x
f x
khi x
>
=
− <
Bảng biến thiên
x
−∞
0
+∞
(
)
'
f x
−
+
(
)
f x
+∞
+∞
0
Hàm số ñạt ñiểm cực ñại tại ñiểm
(
)
0, 0 0
x f
= =
Ví dụ 2 : Tìm cực trị của các hàm số sau :
(
)
2
) 4
a f x x x
= −
(
)
) 3 2 cos cos2
b f x x x
= − −
(
)
) 2sin 2 3
c f x x
= −
(
)
) sin 2 2
d f x x x
= − +
Giải :
(
)
2
) 4
a f x x x
= −
Hàm số ñã cho xác ñịnh trên ñoạn
2;2
−
Ta có
( ) ( ) ( )
2
2
4 2
) ' , 2;2 ' 0 2, 2
4
x
a f x x f x x x
x
−
= ∈ − = ⇔ = − =
−
(
)
'
f x
ñổi dấu từ âm sang dương khi
x
qua ñiểm
2
−
thì hàm số ñạt cực tiểu tại ñiểm
2,
x
= −
(
)
2 2
f
− = −
(
)
'
f x
ñổi dấu từ dương sang âm khi
x
qua ñiểm
2
thì hàm số ñạt cực ñại tại ñiểm
2,
x
=
(
)
2 2
f
=
Hoặc dùng bảng biến thiên hàm số ñể kết luận:
x
2
−
2
−
2
2
(
)
'
f x
−
0
+
0
−
(
)
f x
0
2
2
−
0
(
)
) 3 2 cos cos2
b f x x x
= − −
Hàm số ñã cho xác ñịnh và liên tục trên
ℝ
.
Nguyễn Phú Khánh – ðà Lạt 063.28.78.79 hoặc 0989.80.78.79 http://www.maths.vn
-45-
Ta có
(
)
(
)
' 2 sin 2 s in2 2 sin 1 2 cos
f x x x x x
= + = +
( )
sin 0
' 0 ,
1 2 2
cos cos 2
2 3 3
x x k
f x k
x x k
π
π π
π
= =
= ⇔ ⇔ ∈
= − = = ± +
ℤ
.
(
)
'' 2 cos 4 cos2
f x x x
= +
2 2
'' 2 6 cos 3 0
3 3
f k
π π
π
± + = = − <
. Hàm số ñạt cực ñại tại
2
2
3
x k
π
π
= ± + ,
2 1
2 4
3 2
f k
π
π
± + =
(
)
'' 2 cos 4 0,f k k k
π π
= + > ∀ ∈
ℤ
. Hàm số ñạt cực tiểu tại
(
)
(
)
, 2 1 cos
x k f k k
π π π
= = −
(
)
) 2sin 2 3
c f x x
= −
Hàm số ñã cho xác ñịnh và liên tục trên
ℝ
.
Ta có
( ) ( )
' 4 cos 2 , ' 0 cos 2 0 ,
4 2
f x x f x x x k k
π π
= = ⇔ = ⇔ = + ∈
ℤ
( )
8 2
'' 8 sin 2 , '' 8 sin
8 2 1
4 2 2
khi k n
f x x f k k
khi k n
π π π
π
− =
= − + = − + =
= +
Vậy hàm số ñạt cực ñại tại các ñiểm
; 1
4 4
x n f n
π π
π π
= + + = −
và ñạt cực ñại tại
( ) ( )
2 1 ; 2 1 5
4 2 4 2
x n f n
π π π π
= + + + + = −
(
)
) sin 2 2
d f x x x
= − +
Tương tự trên hàm số ñạt cực ñại tại các ñiểm
,
6
x k k
π
π
= − + ∈
ℤ
và ñạt cực tiểu tại các ñiểm
,
6
x k k
π
π
= + ∈
ℤ
.
Ví dụ 3 :
1.
Chứng minh rằng với mọi giá trị của
m
, hàm số
( )
(
)
3 3
1 1
,
x m m x m
y f x m
x m
− + + +
= =
−
luôn
có cực ñại và cực tiểu .
2 .
Với giá trị nào của
m
,hàm số
(
)
(
)
3 2
, 2 3
y f x m m x x mx m
= = + + + +
có cực ñại , cực tiểu .
3 .
Với giá trị nào của
m
,hàm số
( )
2
,
mx x m
y f x m
x m
+ +
= =
+
không có cực ñại , cực tiểu .
4 .
Xác ñịnh các giá trị của tham số
k
ñể ñồ thị của hàm số
(
)
(
)
4 2
, 1 1 2
y f x k kx k x k
= = + − + −
chỉ
có một ñiểm cực trị.
5 .
Xác ñịnh
m
ñể ñồ thị của hàm số
( )
4 2
1 3
,
2 2
y f x m y x mx
= = = − +
có cực tiểu mà không có cực
ñại.
Giải :
Nguyễn Phú Khánh – ðà Lạt 063.28.78.79 hoặc 0989.80.78.79 http://www.maths.vn
-46-
Hàm số ñã cho xác ñịnh trên
{
}
\
D m
=
ℝ .
Ta có
( )
(
)
( )
( )
2 2
2 2
2 2
2 1
' , , 2 1
g x
x mx m
y x m g x x mx m
x m x m
− + −
= = ≠ = − + −
− −
Dấu của
(
)
g x
cũng là dấu của
'
y
và
(
)
2 2
' 1 1 0 ,
g
m m m
∆ = − − = > ∀
. Do ñó
m
∀
thì
(
)
0
g x
=
luôn có
2
nghiệm phân biệt
1 2
1, 1
x m x m
= − = +
thuộc tập xác ñịnh .
x
−∞
1
m
−
m
1
m
+
+∞
(
)
'
f x
+
0
−
−
0
+
(
)
f x
+∞
+∞
−∞
−∞
'
y
ñổi dấu từ dương sang âm khi
x
qua ñiểm
1
1
x m
= −
thì hàm số ñạt cực ñại tại ñiểm
1
1
x m
= −
'
y
ñổi dấu từ âm sang dương khi
x
qua ñiểm
2
1
x m
= +
thì hàm số ñạt cực tiểu tại ñiểm
2
1
x m
= +
2 .
Hàm số ñã cho xác ñịnh trên
ℝ
.
Ta có
(
)
2
' 3 2 6
y m x x m
= + + +
Hàm số có cực ñại và cực tiểu khi phương trình
' 0
y
=
có hai nghiệm phân biệt hay
( )
( )
2
2
2 0
2
3 1
' 9 3 2 0
3 2 3 0
m
m
m
m
m m
m m
≠ −
+ ≠
≠ −
⇔ ⇔ ⇔
− < <
∆ = − + >
− − + >
Vậy giá trị
m
cần tìm là
3 1, 2
m m
− < < ≠ −
.
3 .
Hàm số ñã cho xác ñịnh trên
{
}
\
D m
= −
ℝ và có ñạo hàm
( )
2 2
2
2
'
mx m x
y
x m
+
=
+
Hàm số không có cực ñại , cực tiểu khi
' 0
y
=
không ñổi dấu qua nghiệm , khi ñó phương trình
(
)
(
)
2 2
2 0,
g x mx m x x m
= + = ≠ −
vô nghiệm hoặc có nghiệm kép
•
Xét
0 ' 0, 0
m y x m m
= ⇒ = ∀ ≠ − ⇒ =
thoả .
•
Xét
0
m
≠
. Khi ñó
4
'
m
∆ =
Vì
(
)
4
' 0, 0 0
m m g x
∆ = > ∀ ≠ ⇒ =
có hai nghiệm phân biệt nên không có giá trị tham số
m
ñể
(
)
(
)
2 2
2 0,
g x mx m x x m
= + = ≠ −
vô nghiệm hoặc có nghiệm kép
Vậy
0
m
=
thoả mãn yêu cầu bài toán .
4 .
Hàm số ñã cho xác ñịnh trên
ℝ
.
Ta có
(
)
3
' 4 2 1
y kx k x
= − −
( )
2
0
' 0
2 1 0 *
x
y
kx k
=
= ⇔
+ − =
Nguyễn Phú Khánh – ðà Lạt 063.28.78.79 hoặc 0989.80.78.79 http://www.maths.vn
-47-
Hàm số chỉ có một cực trị khi phương trình
' 0
y
=
có một nghiệm duy nhất và
'
y
ñổi dấu khi
x
ñi qua
nghiệm ñó .Khi ñó phương trình
(
)
2
2 1 0 *
kx k
+ − =
vô nghiệm hay có nghiệm kép
0
x
=
( )
0
0 0
0
0 1 1
' 2 1 0
k
k k
k
k k k
k k
=
= ≤
≠
⇔ ⇔ ⇔
< ∨ ≥ ≥
∆ = − − ≤
Vậy
0 1
k k
≤ ∨ ≥
là giá trị cần tìm .
5 .
Hàm số ñã cho xác ñịnh trên
ℝ
.
Ta có
( )
3
2
0
' 2 2 ' 0
*
x
y x mx y
x m
=
= − = ⇔
=
Hàm số có cực tiểu mà không có cực ñại khi phương trình
' 0
y
=
có một nghiệm duy nhất và
'
y
ñổi
dấu khi
x
ñi qua nghiệm ñó Khi ñó phương trình
(
)
2
*
x m= vô nghiệm hay có nghiệm kép
0
x
=
0
m
⇔ ≤
Vậy
0
m
≤
là giá trị cần tìm.
Ví dụ 4 :
1.
Xác ñịnh giá trị tham số
m
ñể hàm số
( )
2
1
x mx
y f x
x m
+ +
= =
+
ñạt cực ñại tại
2.
x
=
2.
Xác ñịnh giá trị tham số
m
ñể hàm số
(
)
(
)
3 2
3 1
y f x x m x m
= = + + + −
ñạt cực ñại tại
1.
x
= −
3.
Xác ñịnh giá trị tham số
m
ñể hàm số
(
)
(
)
3 2
6 3 2 6
y f x x x m x m
= = − + + − −
ñạt cực ñại và
cực tiểu ñồng thời hai giá trị cực trị cùng dấu.
4.
Xác ñịnh giá trị tham số
m
ñể hàm số
( )
2
2
1
x mx
y f x
x
+ +
= =
−
có ñiểm cực tiểu nằm trên Parabol
(
)
2
: 4
P y x x
= + −
Giải :
1.
Hàm số ñã cho xác ñịnh trên
{
}
\
D m
= −
ℝ và có ñạo hàm
( )
( )
2 2
2
2 1
' ,
x mx m
f x x m
x m
+ + −
= ≠ −
+
Nếu hàm số ñạt cực ñại tại
2
x
=
thì
( )
2
3
' 2 0 4 3 0
1
m
f m m
m
= −
= ⇔ + + = ⇔
= −
3
m
= −
, ta có
( )
( )
( )
2
2
2
6 8
' , 3 ' 0
4
3
x
x x
f x x f x
x
x
=
− +
= ≠ = ⇔
=
−
Bảng biến thiên :
x
−∞
2
3
4
+∞
(
)
'
f x
+
0
−
−
0
+
(
)
f x
1
+∞
+∞
Nguyễn Phú Khánh – ðà Lạt 063.28.78.79 hoặc 0989.80.78.79 http://www.maths.vn
-48-
−∞
−∞
5
Dựa vào bảng biến thiên ta thấy hàm số ñạt cực ñại tại
2
x
=
, do ñó
3
m
= −
thoả mãn .
Tương tự với
1
m
= −
Cách 2 :
Hàm số ñã cho xác ñịnh trên
{
}
\
D m
= −
ℝ và có ñạo hàm
( )
( )
2 2
2
2 1
' ,
x mx m
f x x m
x m
+ + −
= ≠ −
+
( )
3
2
'' ,
y x m
x m
= ≠ −
+
Hàm số ñạt cực ñại tại
2
x
=
khi
( )
( )
( )
( )
2
2
3
1
1 0
4 3 0
' 2 0 1 3
2
2 3
2 2
'' 2 0
0
2
2
m m
y m m
m
m m
m
y
m
m
− =
+ + =
= = − ∨ = −
+
⇔ ⇔ ≠ − ⇔ ⇔ = −
< −
<
<
< −
+
Vậy
3
m
= −
là giá trị cần tìm.
2.
Hàm số cho xác ñịnh trên
ℝ
.
Ta có
( ) ( ) ( ) ( )
2
0
' 3 2 3 3 2 6 ' 0
2 6
3
x
f x x m x x x m f x
m
x
=
= + + = + + ⇒ = ⇔
+
= −
x
−∞
2 6
3
m
+
−
0
+∞
(
)
'
f x
+
0
−
0
+
(
)
f x
Hàm số ñạt cực ñại tại
2 6 3
1 1 .
3 2
m
x m
+
= − ⇔ − = − ⇔ = −
3.
Hàm số cho xác ñịnh trên
ℝ
.
Ta có :
(
)
2
' 3 12 3 2
y x x m
= − + +
.
Hàm số có cực ñại , cực tiểu khi
' 0
y
=
có hai nghiệm phân biệt
(
)
' 36 9 2 0
m
⇔ ∆ = − + >
2 0 2
m m
⇔ − > ⇔ <
( ) ( ) ( ) ( ) ( )
2
1 1
2 . 3 12 3 2 2 2 2 2 . ' 2 2 2
3 3
y x x x m m x m x y m x m
= − − + + + − + − = − + − + −
Gọi
(
)
(
)
1 1 2 2
; , ;
A x y B x y
là các ñiểm cực trị của ñồ thị hàm số thì
1 2
,
x x
là nghiệm của phương trình
(
)
(
)
2
3 12 3 2 0
g x x x m
= − + + =
.
Trong ñó :
Nguyễn Phú Khánh – ðà Lạt 063.28.78.79 hoặc 0989.80.78.79 http://www.maths.vn
-49-
( ) ( ) ( )
( )
( )
1 1 1 1
1 1
1
1
2 . ' 2 2 2
2 2 2
3
' 0
y x y x m x m
y m x m
y x
= − + − + −
⇒ = − + −
=
( ) ( ) ( )
( )
( )
2 1 2 2
2 2
2
1
2 . ' 2 2 2
2 2 2
3
' 0
y x y x m x m
y m x m
y x
= − + − + −
⇒ = − + −
=
Theo ñịnh lý Vi-ét , ta có :
1 2 1 2
4, 2
x x x x m
+ = = +
Theo bài toán :
( ) ( ) ( ) ( )( )
2
1 2 1 2 1 2
. 0 2 2 2 2 2 2 0 2 2 1 2 1 0
y y m x m m x m m x x
> ⇔ − + − − + − > ⇔ − + + >
( ) ( ) ( ) ( ) ( ) ( )
2 2 2
1 2 1 2 1 2 1 2
2 4 2 1 0 2 4 2 1 0 2 4 17 0
m x x x x m x x x x m m
⇔ − + + + > ⇔ − + + + > ⇔ − + >
17
4
2
m
m
> −
⇔
≠
So với ñiều kiện bài toán , vậy
17
2
4
m
− < <
là giá trị cần tìm .
4.
Hàm số ñã cho xác ñịnh trên
{
}
\ 1
D =
ℝ
Ta có
( )
( )
2
2
2
2 2
' , 1 2 2
1
x x m
y x g x x x m
x
− − −
= ≠ = − − −
−
Hàm số có cực ñại , cực tiểu khi phương trình
(
)
0, 1
g x x= ≠
có hai nghiệm phân biệt khác
1
(
)
( )
' 1 2 0 3 0
3
3
1 3 0
m m
m
m
g m
∆ = − − − > + >
⇔ ⇔ > −
≠ −
= − − ≠
Khi ñó
1 1
2 2
3
1 3 1 3 1 2 2 3
3
' 0
3
1 3 1 3 1 2 2 3
3
m
x m y m m m m
m
y
m
x m y m m m m
m
+
= − + ⇒ = − + + + + = + − +
− +
= ⇔
+
= + + ⇒ = + + + + + = + + +
+
Bảng biến thiên :
x
−∞
1
x
1
2
x
+∞
(
)
'
f x
+
0
−
−
0
+
(
)
f x
1
y
+∞
+∞
−∞
−∞
2
y
Dựa vào bàng biến thiên suy ra
(
)
1 3; 2 2 3
A m m m
+ + + + +
là ñiểm cực tiểu của hàm số .
( )
(
)
2
2 2 3 1 3 1 3 4 3 1
A P m m m m m
∈ ⇔ + + + = + + + + + − ⇔ + =
Nguyễn Phú Khánh – ðà Lạt 063.28.78.79 hoặc 0989.80.78.79 http://www.maths.vn
-50-
( )
(
)
2
2 2 3 1 3 1 3 4 3 1 2
A P m m m m m m
∈ ⇔ + + + = + + + + + − ⇔ + = ⇔ = −
So với ñiều kiện bài toán ,vậy
2
m
= −
là giá trị cần tìm.
Ví dụ 5 :
1.
Tìm các hệ số
, , ,
a b c d
sao cho hàm số
(
)
3 2
f x ax bx cx d
= + + +
ñạt cực tiểu tại ñiểm
0,
x
=
(
)
0 0
f
=
và ñạt cực ñại tại ñiểm
(
)
1, 1 1
x f
= =
2.
Tìm các hệ số
, ,
a b c
sao cho hàm số
(
)
3 2
f x x ax bx c
= + + +
ñạt cực trị bằng
0
tại ñiểm
2
x
= −
và ñồ thị của hàm số ñi qua ñiểm
(
)
1; 0
A
.
3.
Tìm các hệ số
,
a b
sao cho hàm số
( )
2
ax bx ab
f x
ax b
+ +
=
+
ñạt cực trị tại ñiểm
0
x
=
và
4
x
=
.
Giải :
1.
Tìm các hệ số
, , ,
a b c d
sao cho hàm số
(
)
3 2
f x ax bx cx d
= + + +
ñạt cực tiểu tại ñiểm
(
)
0, 0 0
x f
= =
và ñạt cực ñại tại ñiểm
(
)
1, 1 1
x f
= =
Hàm số ñã cho xác ñịnh trên
ℝ
.
Ta có
(
)
(
)
2
' 3 2 , '' 6 2
f x ax bx c f x ax b
= + + = +
Hàm số
(
)
f x
ñạt cực tiểu tại
0
x
=
khi và chỉ khi
(
)
( )
( )
' 0 0 0 0
1
2 0 0
'' 0 0
f c c
b b
f
= = =
⇔ ⇔
> >
>
Hàm số
(
)
f x
ñạt cực ñại tại
1
x
=
khi và chỉ khi
(
)
( )
( )
' 1 0 3 2 0
2
6 2 0
'' 1 0
f a b c
a b
f
= + + =
⇔
+ <
<
(
)
(
)
(
)
0 0 0 , 1 1 1 1 0 3
f d f a b c d hay a b c do d= ⇒ = = ⇒ + + + = + + = =
Từ
(
)
(
)
(
)
1 , 2 , 3
suy ra
2, 3, 0, 0
a b c d
= − = = =
Ta kiểm tra lại
(
)
3 2
2 3
f x x x
= − +
Ta có
(
)
(
)
2
' 6 6 , '' 12 6
f x x x f x x
= − + = − +
(
)
'' 0 6 0
f
= >
. Hàm số ñạt cực tiểu tại
0
x
=
(
)
'' 1 6 0
f
= − <
. Hàm số ñạt cực ñại tại
1
x
=
Vậy :
2, 3, 0, 0
a b c d
= − = = =
2.
Tìm các hệ số
, ,
a b c
sao cho hàm số
(
)
3 2
f x x ax bx c
= + + +
ñạt cực trị bằng
0
tại ñiểm
2
x
= −
và ñồ thị của hàm số ñi qua ñiểm
(
)
1; 0
A
.
Hàm số ñã cho xác ñịnh trên
ℝ
.
Ta có
(
)
2
' 3 2
f x x ax b
= + +
Nguyễn Phú Khánh – ðà Lạt 063.28.78.79 hoặc 0989.80.78.79 http://www.maths.vn
-51-
Hàm số ñạt cực trị bằng
0
tại ñiểm
2
x
= −
khi và chỉ khi
(
)
( )
( )
' 2 0 4 12
1
4 2 8
2 0
f a b
a b c
f
− = − =
⇔
− + =
− =
ðồ thị của hàm số ñi qua ñiểm
(
)
1; 0
A
khi và chỉ khi
(
)
(
)
1 0 1 0 2
f a b c= ⇔ + + + =
Từ
(
)
(
)
1 , 2
suy ra
3, 0, 4
a b c
= = = −
.
3.
Hàm số ñã cho xác ñịnh khi
0
ax b
+ ≠
và có ñạo hàm
( )
2 2 2 2
2
2
'
a x abx b a b
y
ax b
+ + −
=
+
•
ðiều kiện cần :
Hàm số ñạt cực trị tại ñiểm
0
x
=
và
4
x
=
khi và chỉ khi
( )
( )
( )
( )
2 2
2 2
2
2
2
2 2 2
2 2 2
2
2
0
0
0
' 0 0 0 2
8 2 0
16 8
4
16 8 0
' 4 0
0
4 0
4
4 0
b a b
b a b
b a
y b a
b
a a
a ab b a b
b
a ab b a b
y
a a
a b
a b
− =
−
= >
=
= ≠ = −
⇔ ⇔ ⇔ + = ⇔
+ + −
=
+ + − =
=
=
+ ≠
+
+ ≠
•
ðiều kiện ñủ :
( )
2
2
2 0
4
' ' 0
4 4
2
a x
x x
y y
b x
x
= − =
−
⇒ = = ⇔
= =
− +
Bảng biến thiên
x
−∞
0
2
4
+∞
(
)
'
f x
+
0
−
−
0
+
(
)
f x
Cð
+∞
+∞
−∞
−∞
CT
Từ bảng biến thiên :hàm số ñạt cực trị tại ñiểm
0
x
=
và
4
x
=
. Vậy
2, 4
a b
= − =
là giá trị cần tìm.
Ví dụ 6:
1.
Cho hàm số
(
)
(
)
3 2
3 2
y f x x x C
= = − +
. Hãy xác ñịnh tất cả các giá trị của
a
ñể ñiểm cực ñại
và ñiểm cực tiểu của ñồ thị
(
)
C
ở về hai phía khác nhau của ñường tròn (phía trong và phía ngoài):
(
)
2 2 2
: 2 4 5 1 0
a
C x y ax ay a
+ − − + − =
2.
Cho hàm số
( )
2 2 2
2 5 3
x m x m m
y f x
x
+ + − +
= =
. Tìm
0
m
>
ñể hàm số ñạt cực tiểu tại
(
)
0;2
x m
∈
3.
3 2 2
( ) 3 .
y f x x x m x m
= = − + +
có cực ñại , cực tiểu và hai ñiểm ñó ñối xứng nhau qua
Nguyễn Phú Khánh – ðà Lạt 063.28.78.79 hoặc 0989.80.78.79 http://www.maths.vn
-52-
ñường thẳng
1 5
2 2
y x
= −
4.
Tìm tất cả các giá trị của tham số
m
thì hàm số
(
)
2 2
1 4 2
( ) .
1
x m x m m
y f x
x
− + − + −
=
−
có cực
trị ñồng thời tích các giá trị cực ñại và cực tiểu ñạt giá trị nhỏ nhất.
5.
Tìm tất cả các giá trị của tham số
m
thì hàm số
(
)
2
2 3 2
( )
1
x m x m
y f x
x
+ + + +
= =
+
có giá trị
cực trị , ñồng thời
2 2
1
2
CT
y y
+ >
CÑ
.
Giải :
1.
Hàm số ñã cho xác ñịnh trên
ℝ
và có ñạo hàm
2
0 2
' 3 6 ' 0
2 2
x y
y x x y
x y
= ⇒ =
= − = ⇔
= ⇒ = −
ðồ thị hàm số có hai ñiểm cực trị
(
)
(
)
0;2 , 2; 2
A B
−
. Hai ñiểm
(
)
(
)
0;2 , 2; 2
A B
−
ở về hai phía của hai
ñường tròn
(
)
a
C
khi
( ) ( )
( )( )
2 2 2
/ /
3
. 0 5 8 3 5 4 7 0 5 8 3 0 1
5
a a
A C B C
P P a a a a a a a
⇔ < ⇔ − + + + < ⇔ − + < ⇔ < <
Cách 2 :
( ) ( ) ( ) ( )
2 2
2 2 2
: 2 4 5 1 0 : 2 1
a a
C x y ax ay a C x a y a
+ − − + − = ⇔ − + − =
(
)
a
C
có tâm
(
)
;2
I a a
và bán kính
1
R
=
Ta có :
( ) ( )
2
2 2
2
2 36 6
2 2 2 5 4 8 5 1
5 5
5
IB a a a a a R
= − + + = + + = + + ≥ > = ⇒
ñiểm
B
nằm ngoài
(
)
a
C
, do ñó ñiểm
A
nằm trong ñường tròn
( ) ( )
2
2 2
3
1 2 2 1 5 8 3 0 1
5
a
C IA a a a a a
⇔ < ⇔ + − < ⇔ − + < ⇔ < <
2.
Hàm số ñã cho xác ñịnh trên
{
}
\ 0
D
=
ℝ và có ñạo hàm
(
)
2 2
2 2
2 5 3
' , 0
g x
x m m
y x
x x
− + −
= = ≠
Với
(
)
2 2
2 5 3
g x x m m
= − + −
Hàm số ñạt cực tiểu tại
(
)
(
)
0;2 0
x m g x
∈ ⇔ =
có hai nghiệm phân biệt
(
)
1 2 1 2
,
x x x x
<
thoả
( )
( )
2
1 2
2
0
1
0
0
1
1
2
0 2 1. 0 0 2 5 3 0
3
3
2 5 3 0
1. 2 0
2
2
3
1
2
m
m
m
m
m
x x m g m m
m
m
m m
g m
m
m
>
>
>
<
< <
< < < ⇔ < ⇔ − + − < ⇔ ⇔
>
>
+ − >
>
< −
>
Nguyễn Phú Khánh – ðà Lạt 063.28.78.79 hoặc 0989.80.78.79 http://www.maths.vn
-53-
Vậy giá trị
m
cần tìm là
1 3
1
2 2
m m
< < ∨ >
.
3.
Hàm số ñã cho xác ñịnh trên
ℝ
và có ñạo hàm
2 2
' 3 6
y x x m
= − +
.
Hàm số
có cực ñại , cực tiểu khi phương trình
' 0
y
=
có hai nghiệm phân biệt
1 2
,
x x
2
' 9 3 0
m
⇔ ∆ = − >
3 3
m
⇔ − < <
.Vi-ét, ta có
2
1 2 1 2
2 , .
3
m
x x x x
+ = =
.
Gọi
(
)
(
)
1 1 2 2
; , ;
A x y B x y
là các ñiểm cực trị của ñồ thị hàm số và
I
là trung ñiểm của ñoạn
AB
.
ðường thẳng
AB
có hệ số góc
(
)
(
)
( ) ( )
3 3 2 2 2
2
2 1 2 1 2 1
2
2 1
1 2 1 2 1 2
2 1 2 1
3
3
AB
x x x x m x x
y y
k x x x x x x m
x x x x
− − − + −
−
= = = + − − + +
− −
2 2
2
2 6
4 6
3 3
AB
m m
k m
−
= − − + =
ðường thẳng
( )
1 5
2 2
y x
= − ∆
có hệ số góc
1
2
k
=
Hai ñiểm
(
)
(
)
1 1 2 2
; , ;
A x y B x y
ñối xứng nhau qua ñường thẳng
(
)
∆
khi và chỉ khi
AB
I
⊥ ∆
∈ ∆
2
1 2 6
. 1 . 1 0
2 3
AB
m
AB k k m
−
• ⊥ ∆ ⇔ = − ⇔ = − ⇔ =
(
)
( )
( )
1 1
2
2 2
0 0 0; 0
0 ' 3 6 ' 0 1; 2
2 4 2; 4
x y A
m y x x y I
x y B
= ⇒ = ⇒
• = ⇒ = − = ⇔ ⇒ −
= ⇒ = − ⇒ −
Dễ thấy
(
)
1; 2I
− ∈ ∆
Vậy
0
m
=
thoả mãn yêu cầu bài toán .
4.
Hàm số ñã cho xác ñịnh trên
{
}
\ 1
D =
ℝ .
Ta có
( )
(
)
( )
( )
2 2
2 2
2 2
2 3 3
' , 1 2 3 3
1 1
g x
x x m m
y x g x x x m m
x x
− + − +
= = ≠ = − + − +
− −
Hàm số
có cực ñại , cực tiểu khi phương trình
(
)
0, 1
g x x
= ≠
có hai nghiệm phân biệt
1 2
,
x x
khác
1
.
( )
2
2
' 0
3 2 0
1 2
1 0
3 2 0
m m
m
g
m m
∆ >
− + − >
⇔ ⇔ ⇔ < <
≠
− + ≠
Gọi
(
)
(
)
1 1 2 2
; , ;
A x y B x y
là các ñiểm cực trị của ñồ thị hàm số thì
1 2
,
x x
là nghiệm của phương trình
(
)
0, 1
g x x
= ≠
.
Khi ñó
2 2
1 1
2 2
2 2
1 3 2 1 2 3 2
' 0
1 3 2 1 2 3 2
x m m y m m m
y
x m m y m m m
= − − + − ⇒ = − + − + −
= ⇔
= + − + − ⇒ = − − − + −
(
)
(
)
( )
(
)
2
2 2 2
1 2
. 1 2 3 2 1 2 3 2 1 4 3 2
y y m m m m m m m m m
= − + − + − − − − + − = − − − + −
Nguyễn Phú Khánh – ðà Lạt 063.28.78.79 hoặc 0989.80.78.79 http://www.maths.vn
-54-
2
2
1 2 1 2
7 4 4 4 7
. 5 14 9 5 min .
5 5 5 5 5
y y m m m y y khi m
= − + = − − ≥ − ⇒ = − =
So với ñiều kiện , vậy
7
5
m
=
là giá trị cần tìm .
5.
Hàm số ñã cho xác ñịnh trên
{
}
\ 1
D
= −
ℝ .
Ta có :
( )
(
)
( )
( )
2
2
2 2
2 2
' , 1 2 2
1 1
g x
x x m
y x g x x x m
x x
+ −
= = ≠ − = + −
+ +
Hàm số
có cực ñại , cực tiểu khi phương trình
(
)
0, 1
g x x
= ≠ −
có hai nghiệm phân biệt
1 2
,
x x
khác
( )
' 0
2 1 0
1
1
2 1 0
1 0
2
m
m
m
g
∆ >
+ >
− ⇔ ⇔ ⇔ > −
− − ≠
− ≠
Gọi
(
)
(
)
1 1 1 2 2 2
; 2 2 , ; 2 2
A x y x m B x y x m
= + + = + +
là các ñiểm cực trị của ñồ thị hàm số thì
1 2
,
x x
là
nghiệm của phương trình
(
)
0, 1
g x x
= ≠ −
Theo ñịnh lý Vi- ét
1 2 1 2
2, . 2
x x x x m
+ = − = −
Theo bài toán :
( ) ( )
(
)
( )( ) ( )
2 2 2
2 2 2 2 2 2
1 2 1 2 1 2 1 2
2 2 2 2 4 4 2 2 2
CT
y y y y x m x m x x m x x m+ = + = + + + + + = + + + + + +
CÑ
( ) ( )( ) ( ) ( ) ( ) ( )
2 2 2
2 2
1 2 1 2 1 2 1 2
4 2 4 2 2 2 4 4 4 8 2 2 2
y y x x x x m x x m m m m
+ = + − + + + + + = + − + + +
2 2 2
1 2
2 16 8
y y m m
+ = + +
Xét
( ) ( )
2
1 1
2 16 8, ' 4 16 0,
2 2
f m m m m f m m m
= + + > − = + > ∀ > −
Do ñó hàm số
(
)
f m
ñồng biến trên khoảng
1
;
2
m
∈ − +∞
và
( )
1 1 1
, ;
2 2 2
f m f m
> − = ∈ − +∞
Vậy
2 2
1 1
, ;
2 2
CT
y y m
+ > ∈ − +∞
CÑ
Ví dụ 7:
1.
Với giá trị nào của
m
thì ñồ thị của hàm số
( ) ( )
3 2
1 1
1 3 2
3 3
y mx m x m x
= − − + − +
có cực ñại ,
cực tiểu ñồng thời hoành ñộ cực ñại cực tiểu
1 2
,
x x
thỏa
1 2
2 1
x x
+ =
2.
Với giá trị nào của
m
thì ñồ thị của hàm số
(
)
2 2 3
1 4
mx m x m m
y
x m
+ + + +
=
+
tương ứng có một
ñiểm cực trị thuộc góc phần tư thứ
(
)
II
và một ñiểm cực trị thuộc góc phần tư thứ
(
)
IV
của mặt
phẳng tọa ñộ .
Giải :
1.
Hàm số cho xác ñịnh trên
ℝ
.
Nguyễn Phú Khánh – ðà Lạt 063.28.78.79 hoặc 0989.80.78.79 http://www.maths.vn
-55-
Ta có
(
)
(
)
2
' 2 1 3 2
y mx m x m
= − − + −
Hàm số có cực ñại , cực tiểu khi
'
y
ñổi dấu hai lần qua nghiệm
x
, tức là phương trình
(
)
(
)
2
2 1 3 2 0
mx m x m
− − + − =
có hai nghiệm phân biệt
1 2
,
x x
( ) ( )
2
2
0
0
0
2 6 2 6
2 4 1 0
' 1 3 2 0
2 2
m
m
m
m m
m m m
m
≠
≠
≠
⇔ ⇔
− +
− + + >
∆ = − − − >
< <
Theo ñịnh lý Vi – ét và yêu cầu bài toán, ta có:
( )
( )
( ) ( )
( )
1 2
1
2
1 2 2
1 2
3 4
2 1
2
2 1
2
3 8 4 0 0
3
2
3 2 3 2
3 4 2
.
m
x x gt
x
m
m
m m
x x x m m m
m m
m
m m
m m
x x
m m m m
−
+ =
=
−
−
=
+ = ⇔ = ⇔ − + = ≠ ⇔
=
− −
− −
= =
So với ñiều kiện bài toán , vậy
2
2
3
m m
= ∨ =
là giá trị cần tìm .
2.
Hàm số ñã cho xác ñịnh trên
{
}
\
D m
= −
ℝ và
( )
3
4
1 0
m
y mx m
x m
= + + ≠
+
Ta có :
( )
2 2 3
2
2 3
' ,
mx m x m
y x m
x m
+ −
= ≠ −
+
Gọi
(
)
(
)
1 1 2 2
; , ;
A x y B x y
là các ñiểm cực trị của ñồ thị hàm số thì
(
)
1 2 1 2
,
x x x x
< là nghiệm của phương
trình
(
)
2 2 3
2 3 0,
g x mx m x m x m
= + − = ≠ −
ðồ thị của hàm số có một ñiểm cực trị thuộc góc phần tư thứ
(
)
II
và một ñiểm cực trị thuộc góc phần tư
thứ
(
)
IV
của mặt phẳng tọa ñộ khi
(
)
( )
( )
1 2
2 1
0 1
0 2
x x
A
y y
B
• < <
⇔ ⇔ • < <
•
thuoäc goùc phaàn tö thö ù (II)
thuoäc goùc phaàn tö thö ù (IV)
He äsoá goùc cuûa tieäm caän xieân nhoû hôn 0 3
(
)
(
)
(
)
4
1 . 0 0 3 0 0
m g m m a
⇔ < ⇔ − < ⇔ ≠
(
)
2
⇔
ðồ thị của hàm số không cắt trục
(
)
(
)
2 2 3
1 4 0
Ox mx m x m m x m
⇔ + + + + = ≠ −
vô
nghiệm
( ) ( )
( )
2
4 2
2
2 3
1
0
0
0
5
1
1
15 2 1 0
1 4 4 0
5
5
m
m
m
m
b
m m
m
m m m m
m
< −
≠
≠
≠
⇔ ⇔ ⇔ ⇔
− − + <
>
∆ = + − + <
>
(
)
(
)
3 0
m c
⇔ <
Nguyễn Phú Khánh – ðà Lạt 063.28.78.79 hoặc 0989.80.78.79 http://www.maths.vn
-56-
Từ
(
)
(
)
(
)
a b c
suy ra
1
5
m < −
là giá trị cần tìm.
Ví dụ 8:
Cho hàm số
(
)
(
)
(
)
3 2
1 2 1
f x x m x m x
= + − − + −
, có ñồ thị là
(
)
,
m
C m
là tham số.
1.
Chứng minh rằng hàm số luôn có một cực ñại , một cực tiểu .
2.
Khi
1
m
=
, ñồ thị hàm số là
(
)
C
).
a
Viết phương trình ñường thẳng
(
)
d
vuông góc với ñường thẳng
3
x
y
=
và tiếp xúc với ñồ thị
(
)
C
.
).
b
Viết phương trình ñường thẳng ñi qua hai ñiểm cực trị của
(
)
C
.
Giải :
Hàm số cho xác ñịnh trên
ℝ
.
1.
Ta có
(
)
(
)
(
)
2
' 3 2 1 2 .
f x x m x m= + − − +
Vì
2
' 7 0,
m m m
∆ = + + > ∀ ∈
ℝ
nên phương trình
(
)
' 0
f x
=
luôn có hai nghiệm phân biệt . Do ñó ñồ
thị của hàm số luôn có một cực ñại , một cực tiểu với mọi giá trị của tham số
m
.
2.
(
)
(
)
3
1 : 3 1
m C f x x x
= ⇒ = − −
).
a
Gọi
(
)
0 0
;
M x y
là toạ ñộ tiếp ñiểm của ñường thẳng
(
)
d
và ñồ thị
(
)
C
3 2
0 0 0 0 0
3 1, ' 3 3
y x x y x
⇒ = − − = −
. ðường thẳng
(
)
d
vuông góc với ñường thẳng
3
x
y
=
khi
2 2
0 0 0 0 0
1
' 1 3 3 3 0 0, 1
3
y x x x y
= − ⇔ − = − ⇔ = ⇔ = = −
Vậy ñường thẳng
(
)
: 3 1
d y x
= − −
và tiếp xúc với ñồ thị
(
)
C
tại ñiểm
(
)
0; 1
−
.
).
b
ðồ thị
(
)
C
có ñiểm cực ñại là
(
)
1;1
A −
, ñiểm cực tiểu là
(
)
1; 3
B
−
. Do ñó ñường thẳng qua
AB
là :
2 1
y x
= − −
.
Ví dụ 9:
1.
Xác ñịnh giá trị tham số
m
ñể hàm số
(
)
(
)
(
)
3 2 2
2 1 3 2 4
f x x m x m m x
= − + + − + +
có hai
ñiểm cực ñại và cực tiểu nằm về hai phía trục tung .
2.
Xác ñịnh giá trị tham số
m
ñể hàm số
( )
(
)
2
1 3 2
1
x m x m
f x
x
− + + +
=
−
có hai ñiểm cực ñại và
cực tiểu cùng dấu .
3.
Cho hàm số
(
)
(
)
(
)
3 2 2 2
3 1 3 7 1 1
y f x x m x m m x m
= = − + + − + − + −
.ðịnh
m
ñể hàm số ñạt
cực tiểu tại một ñiểm có hoành ñộ nhỏ hơn
1.
4.
Tìm giá trị của
m
ñể ñồ thị hàm số
( )
2
2 2
1
x mx
f x
x
+ +
=
+
có ñiểm cực ñại, ñiểm cực tiểu và
khoảng cách từ hai ñiểm ñó ñến ñường thẳng
: 2 0
x y
∆ + + =
bằng nhau.
Giải :
1.
Hàm số cho xác ñịnh trên
ℝ
và có ñạo hàm
(
)
(
)
2 2
' 3 2 2 1 3 2
f x x m x m m
= − + + − +
Nguyễn Phú Khánh – ðà Lạt 063.28.78.79 hoặc 0989.80.78.79 http://www.maths.vn
-57-
Hàm số có hai ñiểm cực ñại và cực tiểu nằm về hai phía trục tung khi và chỉ khi phương trình
(
)
' 0
f x
=
có hai nghiệm phân biệt
1 2
,
x x
thoả mãn
(
)
1 2
0 3. ' 0 0
x x f
< < ⇔ <
2
3 2 0 1 2
m m m
⇔ − + < ⇔ < <
Vậy giá trị cần tìm là
1 2
m
< <
.
2.
Hàm số ñã cho xác ñịnh trên
{
}
\ 1
D =
ℝ
và có ñạo hàm
( )
( )
2
2
2 2 1
' , 1
1
x x m
f x x
x
− − −
= ≠
−
Hàm số có cực ñại và cực tiểu khi
(
)
' 0
f x
=
có hai nghiệm phân biệt
1
x
≠
hay phương trình
(
)
2
2 2 1 0
g x x x m
= − − − =
có hai nghiệm phân biệt
1
x
≠
, khi ñó
( )
( )
' 0
2 2 0
1 1
2 2 0
1 0
m
m
m
g
∆ >
+ >
⇔ ⇔ > −
− − ≠
≠
Gọi
(
)
(
)
1 1 2 2
; , ;
A x y B x y
là các ñiểm cực trị của ñồ thị hàm số thì
1 2
,
x x
là nghiệm của
(
)
0
g x
=
Khi ñó:
1 1
2 2
2 2
1 2 2 1 2 2 1 2 2 2
2 2
' 0
2 2
1 2 2 1 2 2 1 2 2 2
2 2
m
x m y m m m m
m
y
m
x m y m m m m
m
+
= − + ⇒ = − + − + = − − +
− +
= ⇔
+
= + + ⇒ = + + − + = − + +
+
Hai giá trị cực trị cùng dấu khi
(
)
(
)
( ) ( )
2
1 2
. 0 1 2 2 2 1 2 2 2 0 1 4 2 2 0
y y m m m m m m
> ⇔ − − + − + + > ⇔ − − + >
(
)
2
10 7 0 5 4 2 5 4 2 2
m m m m⇔ − − > ⇔ < − ∨ > +
Từ
(
)
1
và
(
)
2
suy ra
1 5 4 2 5 4 2
m m
− < < − ∨ > +
Cách khác : Hàm số ñã cho xác ñịnh trên
{
}
\ 1
D =
ℝ
và có ñạo hàm
( )
( )
2
2
2 2 1
' , 1
1
x x m
f x x
x
− − −
= ≠
−
Hàm số có cực ñại và cực tiểu khi
(
)
' 0
f x
=
có hai nghiệm phân biệt
1
x
≠
hay phương trình
(
)
2
2 2 1 0
g x x x m
= − − − =
có hai nghiệm phân biệt
( )
' 0
2 2 0
1
2 2 0
1 0
m
m
m
g
∆ >
+ >
⇔ ⇔ ⇔ > −
− − ≠
≠
Hai giá trị cực trị cùng dấu khi ñồ thị của hàm số
0
y
=
cắt trục hoành tại hai ñiểm phân biệt
1
x
≠
hay
phương trình
(
)
(
)
2
1 3 2 0 1
x m x m x
− + + + = ≠
có hai nghiệm phân biệt
1
x
≠
. Tức là
( ) ( )
( )
2
2
5 4 2
10 7 0
1 4 3 2 0
5 4 2
2 2 0
1 1 3 2 0
1
m
m m
m m
m
m
m m
m
< −
− − >
∆ = + − + >
⇔ ⇔ ⇔
> +
+ ≠
− + + + ≠
≠ −
So với ñiều kiện , giá trị
1 5 4 2 5 4 2
m m
− < < − ∨ > +
là giá trị cần tìm .
Nguyễn Phú Khánh – ðà Lạt 063.28.78.79 hoặc 0989.80.78.79 http://www.maths.vn
-58-
3.
Hàm số cho xác ñịnh trên
ℝ
và có ñạo hàm
(
)
(
)
(
)
2 2
' 3 6 1 3 7 1
f x x m x m m
= − + + − + −
.Hàm số
ñạt cực tiểu tại một ñiểm có hoành ñộ nhỏ hơn
1
(
)
(
)
(
)
2 2
' 3 6 1 3 7 1 0
f x x m x m m
⇔ = − + + − + − =
có hai nghiệm
1 2
,
x x
thoả mãn ñiều kiện :
( )
( )
(
)
(
)
( ) ( )
( )
( )
( )
( )
2
2
2
1 2
2
1 2
1 3. ' 1 0
3 3 4 0
9 1 3 3 7 1 0
1 1
' 0
1 2
2 3. ' 1 0
3 3 4 0
1 1
1
2
f
m m
m m m
x x
x x
f
m m
S
m
⇔ − <
+ − <
+ − + − >
< <
∆ >
⇔ ⇔
< ≤
⇔ − ≥
+ − ≥
+ <
<
2
4
4
1
1
3
4
3
1
4
3 12 0
3
1
4
4
3 4 0 1
3
3
0
0
m
m
m
m
m
m
m m m m
m
m
m
− < <
− < <
− < <
<
− + >
⇔ ⇔ ⇔ ⇔ <
+ − ≥ ≤ − ∨ ≥
≤ −
<
<
4.
Hàm số ñã cho xác ñịnh trên
{
}
\ 1
D
= −
ℝ
và có ñạo hàm
( )
( )
2
2
2 2 2
' , 1
1
x x m
f x x
x
+ + −
= ≠ −
+
Hàm số có cực ñại , cực tiểu khi
(
)
'
f x
ñổi dấu hai lần qua nghiệm
x
hay phương trình
(
)
2
2 2 2 0
g x x x m
= + + − =
có hai nghiệm phân biệt khác
1
−
( )
' 0
3 2 0
3
2 3 0
1 0
2
m
m
m
g
∆ >
− >
⇔ ⇔ ⇔ <
− ≠
− ≠
Gọi
(
)
(
)
1 1 1 2 2 2
; 2 2 , ; 2 2
A x y x m B x y x m
= + = +
là các ñiểm cực trị của ñồ thị hàm số thì
1 2
,
x x
là
nghiệm của phương trình
(
)
0, 1
g x x
= ≠
. Theo ñịnh lý Vi ét
1 2 1 2
2, . 2
x x x x m
+ = − = −
Theo yêu cầu bài toán
( ) ( )
1 1 2 2
1 2
2 2
, , 3 2 2 3 2 2
2 2
x y x y
d A d B x m x m
+ + + +
∆ = ∆ ⇔ = ⇔ + + = + +
( ) ( ) ( ) ( )
2 2 2 2
1 2 1 2
3 2 2 3 2 2 3 2 2 3 2 2 0
x m x m x m x m
⇔ + + = + + ⇔ + + − + + =
( ) ( ) ( ) ( ) ( )
1 2 1 2 1 2 1 2
1
3 4 4 0 3 4 4 0 3 2 4 4 0
2
x x x x m x x m x x m m
⇔ − + + + = ⇔ + + + = ≠ ⇔ − + + = ⇔ =
So với ñiều kiện, vậy
1
2
m
=
là giá trị cần tìm .
Ví dụ 10:
1.
Chứng tỏ rằng chỉ có một ñiểm
A
duy nhất trên mặt phẳng toạ ñộ sao cho nó là ñiểm cực ñại của
ñồ thị
( )
(
)
2 3
1 1
x m m x m
f x
x m
− + + +
=
−
ứng với một giá trị thích hợp của
m
và cũng là ñiểm cực
tiểu của ñồ thị ứng với một giá trị thích hợp khác. Tìm toạ ñộ của
A
.
Nguyễn Phú Khánh – ðà Lạt 063.28.78.79 hoặc 0989.80.78.79 http://www.maths.vn
-59-
2.
Tìm
m
ñể ñồ thị của hàm số
4 2 4
2 2
y x mx m m
= − + +
có cực ñại , cực tiểu ñồng thời các ñiểm
cực trị lập thành tam giác ñều.
Giải :
Hàm số ñã cho xác ñịnh trên
{
}
\
D m
=
ℝ
.
Ta có
( )
( )
( )
2 2
2 2
2
2 1
' , 2 1 1 0,
g
x mx m
f x x m g x x mx m m
x m
− + −
= ≠ = − + − ∆ = > ∀
−
Do ñó
( )
(
)
(
)
( )
( )
2 2
1 1
2 2
2 2
1 2 1; 2
' 0
1 2 1; 2
x m f x m m M m m m
f x
x m f x m m N m m m
= − ⇒ = − + − ⇒ − − + −
= ⇔
= + ⇒ = − + + ⇒ + − + +
ðặt
(
)
0 0
;
A x y
.Giả sử ứng với giá trị
1
m m
=
thì
A
là ñiểm cực ñại và ứng với giá trị
2
m m
=
thì
A
là ñiểm cực tiểu của ñồ thị hàm số
Ta có:
0 1 0 2
2 2
0 1 1 0 2 2
1 1
;
2 2
x m x m
y m m y m m
= − = +
= − + − = − + +
Theo bài toán , ta có :
( )( )
1 2
1 2
2 2
1 1 2 2
1 2 1 2
2
1 1
2 2
1 4
m m
m m
m m m m
m m m m
− =
− = +
⇔
− + − = − + +
− + − = −
1 0
1 2
1 2
2 0
1 1
2
1 7
2 2
;
1 3 7
2 4
2 4
m x
m m
A
m m
m y
= = −
− =
⇔ ⇔ ⇒ ⇒ − −
+ = −
= − = −
Vậy
1 7
;
2 4
A
− −
là ñiểm duy nhất cần tìm thoả yêu cầu bài toán .
2.
Hàm số cho xác ñịnh trên
ℝ
Ta có
( )
( )
3 2
2
0
' 4 4 4 ' 0
*
x
y x mx x x m y
x m
=
= − = − = ⇔
=
ðồ thị hàm số có cực ñại , cực tiểu khi
' 0
y
=
có
3
nghiệm phân biệt và
'
y
ñổi dấu khi
x
qua các
nghiệm ñó , khi ñó phương trình
(
)
*
có hai nghiệm phân biệt khác
0 0
m
⇔ >
Khi ñó :
(
)
(
)
(
)
4 4
4 2 4 2 4 2
0 2 0; 2
' 0
2 ; 2 , ; 2
x y m m A m m
y
x m y m m m B m m m m C m m m m
= ⇒ = + ⇒ +
= ⇔
= ± ⇒ = − + ⇒ − − + − +
Hàm số có
3
cực trị
, ,
A B C
lập thành tam giác ñều
( )
( )
3
2 2 4 3
4 3 0 3 0
AB AC
AB BC m m m m m m m
AB BC
=
⇔ ⇔ = ⇔ + = ⇔ − = ⇔ = >
=
Vậy
3
3
m
=
là giá trị cần tìm .
Ví dụ 11:
1.
Xác ñịnh tham số
a
ñể hàm số sau có cực ñại:
2
2 2 4 5
y x a x x
= − + + − +
Giải :
Nguyễn Phú Khánh – ðà Lạt 063.28.78.79 hoặc 0989.80.78.79 http://www.maths.vn
-60-
1.
Hàm số cho xác ñịnh trên
ℝ
và có ñạo hàm
(
)
( )
2 3
2
2
' 2 ''
4 5
4 5
a x
a
y y
x x
x x
−
= − + =
− +
− +
Hàm số ñạt cực ñại tại
( )
( )
(
)
( )
2
0
0 0
0
2
0
0
0 0
0
2
4 5
2' 0
1
2 2
4 5
'' 0
0
0
a x
x x
a
y x
x x
x
x x
y x
a
a
−
− +
==
=
= ⇔ ⇔ ⇔
−
− +
<
<
<
Với
0
a
<
thì
(
)
0
1 2
x
⇒ <
.
Xét hàm số :
( )
2
0 0
0 0
0
4 5
, 2
2
x x
f x x
x
− +
= <
−
( ) ( )
2 2
0 0 0 0
0 0
2 2
0 0
4 5 4 5
lim lim 1 , lim lim
2 2
x x
x x
x x x x
f x f x
x x
− −
→−∞ →−∞
→ →
− + − +
= = − = = −∞
− −
Ta có
( )
( )
( )
0 0
2
2
0 0 0
2
' 0, ;2
2 4 5
f x x
x x x
−
= < ∀ ∈ −∞
− − +
Bảng biến thiên :
x
−∞
2
(
)
'
f x
−
(
)
f x
1
−
−∞
Phương trình
(
)
1
có nghiệm
0
2 1 2
2
a
x a
< ⇔ < − ⇔ < −
BÀI TẬP TỰ LUYỆN
1. Tìm cực trị của các hàm số sau :
( )
( )
( )
3 2
3 2
1
) 2 3 1
3
1
) 2 10
3
1
)
a f x x x x
b f x x x x
c f x x
x
= + + −
= − + −
= +
( )
( )
5 3
2
1 1
) 2
5 3
3 3
)
1
d f x x x
x x
e f x
x
= − +
− +
=
−
(
)
( )
( )
( )
( )
( )
2
2
3
2
2
3 2
) 8
)
1
)
1
) 5
) 1
1 4
) 3
3 3
f f x x
x
g f x
x
x
h f x
x
i f x x
j f x x x
k f x x x x
= −
=
+
=
+
= −
= + −
= − − +
2. Tìm cực trị của các hàm số sau :
Nguyễn Phú Khánh – ðà Lạt 063.28.78.79 hoặc 0989.80.78.79 http://www.maths.vn
-61-
(
)
( )
( )
( )
3 2
4 3 2
3 2
) 2 9 12 3
) 3 4 24 48 3
) 5 3 4 5
9
) 3
2
a f x x x x
b f x x x x
c f x x x x
d f x x
x
= − + +
= − − + −
= − + − +
= − +
−
( )
( )
( )
( )
2
2
2
2
8 24
)
4
)
4
) 3
) 2 | | 2
x x
e f x
x
x
f f x
x
g f x x x
h f x x x
+ −
=
−
=
+
= −
= − +
Hướng dẫn :
(
)
2
) 2 | | 2
h f x x x
= − +
( ) ( )
2
2
2 2 0 2 2 0
'
2 2 0
2 2 0
x x khi x x khi x
f x f x
x khi x
x x khi x
+ + < + <
= ⇒ =
− >
− + ≥
(
)
' 0 1, 1
f x x x
= ⇔ = − =
Hàm số ñạt cực ñại tại ñiểm
(
)
0;2
A
và ñạt cực tiểu tại các ñiểm
(
)
(
)
1;1 , 1;1
B C−
3. Chứng minh rằng với mọi
m
ñồ thị của hàm số
3 2
4 3
y x mx x m
= − − +
luôn có cực ñại , cực tiểu
và
. 0
C CT
x x
<
Ñ
4. Cho hàm số
( ) ( )
*
1
q
f x x p
x
= + +
+
)
a
Tìm các số thực
,
p q
sao cho hàm số ñạt cực ñại tại ñiểm
2
x
= −
và
(
)
2 2
f
− = −
.
1
)
a
Trường hợp
1
p q
= =
, gọi
,
M N
là ñiểm cực ñại , cực tiểu của hàm số . Tính ñộ dài
MN
2
)
a
Trường hợp
1
p q
= =
,một ñường thẳng
(
)
t
luôn tiếp xúc với ñồ thị hàm số
(
)
*
tại
K
thuộc ñồ thị
hàm số
(
)
*
ñồng thời cắt hai trục tọa ñộ tại hai ñiểm phân biệt
,
E F
. Tìm tọa ñộ ñiểm
K
ñể
K
là trung
ñiểm
EF
)
b
Giả sử
1 2
;
x x
lần lượt là hoành ñộ cực ñại , cực tiểu của hàm số . Tìm các số thực
,
p q
sao cho
1
)
b
1 2
2
x x
= và
( ) ( )
2
1
1
2
f x f x
=
2
)
b
Khoảng cách từ
(
)
(
)
1 1
;
A x f x
ñến ñường thẳng
y x p
= +
và
1 0
x
+ =
bằng nhau .
Hướng dẫn :
)
a
Tìm các số thực
,
p q
sao cho hàm số ñạt cực ñại tại ñiểm
2
x
= −
và
(
)
2 2
f
− = −
.
( )
( )
2
' 1 , 1
1
q
f x x
x
= − ≠ −
+
0
q
• ≤
thì
(
)
' 0, 1
f x x
> ∀ ≠ −
. Do ñó hàm số
( )
1
q
f x x p
x
= + +
+
ñồng biến trên mỗi khoảng
(
)
; 1
−∞ −
và
(
)
1;
− +∞
. Hàm số không có cực ñại , cực tiểu .
Nguyễn Phú Khánh – ðà Lạt 063.28.78.79 hoặc 0989.80.78.79 http://www.maths.vn
-62-
0
q
• >
thì
( )
( )
( )
( )
2
1 2
2
1
' , 1 ' 0 1 , 1
1
x q
f x x f x x p x p
x
+ −
= ≠ − ⇒ = ⇔ = − − = − +
+
. Hàm số ñạt cực
ñại tại ñiểm
2
x
= −
và
(
)
2 2
f
− = −
khi
( )
1
2
1
1
2 2
x
q
p
f
= −
=
⇔
=
− = −
5. Cho hàm số
( ) ( ) ( )
3 2
1 2
1 2 3
3 3
f x x m x m x
= + − + − −
)
a
Chứng minh rằng
2
m
≠
thì ñồ thị của hàm số luôn có cực ñại và cực tiểu . Viết phương trình qua
hai ñiểm cực ñại và cực tiểu ñó .
)
b
Giả sử hoành ñộ cực ñại, cực tiểu là
1 2
,
x x
. Tìm
m
ñể :
1 1 2
) 3 5
b x x
+ =
2 1 2
) 5 2
b x x
− =
4
2 2
3 1 2
) 5
b x x
+ =
2
4 1 2
) 3
b x x
+ ≤
)
c
Tìm
m
ñể :
1
)
c
1 2
0 1
x x
< < <
2
)
c
1 2
1
x x
< <
3
)
c
1 2
2 0
x x
− < < <
4
)
c
1 2
0 1 2
x x
< < < <
Lưu ý : ðể làm ñược câu
)
c
học sinh xem lại so sánh nghiệm phương trình bậc hai ñã ñề cập sách ñại số
9 và có nhắc lại ñại số 10.
6. Cho hàm số
(
)
3
f x x px q
= + +
)
a
Với ñiều kiện nào ñể hàm số
f
có một cực ñại và một cực tiểu ?.
)
b
Chứng minh rằng nếu giá trị cực ñại và giá trị cực tiểu trái dấu thì phương trình
3
0
x px q
+ + =
có
3 nghiệm phân biệt?.
)
c
Chứng minh rằng ñiều kiện cần và ñủ ñể phương trình
3
0
x px q
+ + =
có ba nghiệm phân biệt là
3 2
4 27 0
p q
+ <
Hướng dẫn :
)
a
0
p
<
)
c
. 0
3 3
p p
f f
− − − <
7.
)
a
Tìm
,
a b
ñể các cực trị hàm số
( )
2 3 2
5
2 9
3
f x a x ax x b
= + − +
ñều là những số dương và
0
5
9
x
= −
là ñiểm cực ñại .
)
b
Tìm
, ,
a b c
ñể các cực trị hàm số
3 2
y x ax bx c
= + + +
có giá trị bằng
1
khi
0
x
=
và ñạt cực trị tại
2
x
=
, giá trị cực trị là
3
−
.
)
c
Tìm
,
a b
ñể các cực trị hàm số
2
2
x ax b
y
x
+ +
=
−
ñạt cực trị tại
3
x
=
và ñường tiệm cận xiên
1
y x
= −
.
)
d
Tìm
, ,
a b c
ñể các cực trị hàm số
2
2
ax bx c
y
x
+ +
=
−
có giá trị bằng
1
khi
1
x
=
và ñường tiệm cận
xiên của ñồ thị vuông góc với ñường thẳng
1
2
x
y
−
=
.
Nguyễn Phú Khánh – ðà Lạt 063.28.78.79 hoặc 0989.80.78.79 http://www.maths.vn
-63-
)
e
Tìm các hệ số
, ,
a b c
sao cho hàm số
(
)
3 2
f x x ax bx c
= + + +
ñạt cực tiểu tại
(
)
1; 3
A
−
và ñồ thị
của hàm số cắt trục tung tại ñiểm có tung ñộ bằng
2
.
Hướng dẫn :
)
a
0
a
=
: Hàm số không có cực trị
( ) ( )
2 2
9
5
0 ' 5 4 9 ' 0
1
x
a
a f x a x ax f x
x
a
= −
≠ = + − ⇒ = ⇔
=
Nếu
0
a
<
,
0
5
9
x
= −
là ñiểm cực ñại khi
0
5 1 9
9 5
x a
a
= − = ⇔ = −
, giá trị cực tiểu là số dương nên
( ) ( )
9 36
1 0
5 5
CT
f x f f b
a
= − = > ⇔ >
Nếu
0
a
>
,
0
5
9
x
= −
là ñiểm cực ñại khi
0
5 9 81
9 5 25
x a
a
= − = − ⇔ =
, giá trị cực tiểu là số dương nên
( )
1 400
0
243
CT
f x f b
a
= > ⇔ >
Vậy
9 81
5 25
36 400
5 243
a a
b b
= − =
> >
;
)
b
3, 0, 1
a b c
= − = =
)
c
3, 3
a b
= − =
)
d
2, 3, 0
a b c
= = − =
8. Cho hàm số
(
)
(
)
3 2
3 3 2 1 1,
f x x mx m x m
= − + − +
là tham số
)
a
Xác ñịnh
m
ñể hàm số ñồng biến trên tập xác ñịnh .
)
b
Xác ñịnh
m
ñể
(
)
'' 6
f x x
>
.
9.
)
a
ðịnh
a
ñể ñồ thị của hàm số
(
)
(
)
3 2
2 3 2 1 6 1 1
y x a x a a x
= − + + + +
có giá trị
1
y
>
CÑ
ðáp số:
)
a
3
0
2
a
− < ≠
10. Xác ñịnh khoảng ñơn ñiệu và cực trị ( nếu có ) của hàm số :
(
)
) sin 2
a f x x
=
(
)
) sin cos
b f x x x
= +
(
)
( )
2
) sin 3 cos , 0;
) 2 sin cos2 , 0;
c f x x x x
d f x x x x
π
π
= − ∈
= + ∈
Hướng dẫn :
(
)
) sin 2
a f x x
=
Hàm số ñã cho xác ñịnh và liên tục trên
ℝ
Nguyễn Phú Khánh – ðà Lạt 063.28.78.79 hoặc 0989.80.78.79 http://www.maths.vn
-64-
Ta có
( ) ( )
' 2 cos2 , ' 0 cos2 0 ,
4 2
f x x f x x x l l
π π
= = ⇔ = ⇔ = + ∈
ℤ
( )
4 2
'' 4 sin 2 , '' 4 sin
4 2 1
4 2 4 2
khi l k
f x x f l l k
khi l k
π π π π
− =
= − + = − + = ∈
= +
,
ℤ
Vậy
( )
4
x k k
π
π
= + ∈
ℤ
là ñiểm cực ñại của hàm số .
( )
3
4
x k k
π
π
= + ∈
ℤ
là ñiểm cực tiểu của hàm số .
Một bài toán tương tự :
(
)
sin 2
f x x x
= −
, ñể ý xét
(
)
(
)
' 0, , ?
f x x x
π π
= ∈ − ⇒ =
(
)
) sin cos
b f x x x
= +
Hàm số ñã cho xác ñịnh và liên tục trên
ℝ
( ) ( ) ( ) ( )
sin cos 2 sin ' 2 cos , ' 0
4 4 4
f x x x x f x x f x x k k
π π π
π
= + = + ⇒ = + = ⇔ = + ∈
ℤ
( )
2 2
'' 2 sin '' 2 sin
4 4 2
2 2 1
khi k n
f x x f k k
khi k n
π π π
π π
− =
= − + ⇒ + = − + =
= +
Vậy
( )
2
4
x n n
π
π
= + ∈
ℤ
là ñiểm cực ñại của hàm số .
( ) ( )
2 1
4
x n n
π
π
= + + ∈
ℤ
là ñiểm cực tiểu của hàm số .
(
)
2
) sin 3 cos , 0;
c f x x x x
π
= − ∈
(
)
(
)
(
)
(
)
2
sin 3 cos ' sin 2 cos 3 , 0;
f x x x f x x x x
π
= − ⇒ = + ∈
Vì
(
)
0; sin 0
x x
π
∈ ⇒ >
nên trong khoảng
( ) ( )
3 5
0; : ' 0 cos
2 6
f x x x
π
π
= ⇔ = − ⇔ =
( )
5
' 0, 0;
6
f x x
π
• > ∈ ⇒
hàm số ñồng biến trên ñoạn
5
0;
6
π
( )
5
' 0, ;
6
f x x
π
π
• < ∈ ⇒
hàm số ñồng biến trên ñoạn
5
;
6
π
π
•
Vì
( )
( )
5
' 0, 0;
6
5
' 0, ;
6
f x x
f x x
π
π
π
> ∈
< ∈
nên hàm số ñạt cực ñại tại ñiểm
5 5 7 3
, 1
6 6 4 4
x f
π π
= = =
Hoặc có thể kiểm tra
5 1
'' ... 0
6 2
f
π
= = − <
(
)
) 2 sin cos2 , 0;
d f x x x x
π
= + ∈
(
)
(
)
(
)
(
)
2 sin cos 2 ' 2 cos 1 2 sin , 0;
f x x x f x x x x
π
= + ⇒ = − ∈
Nguyễn Phú Khánh – ðà Lạt 063.28.78.79 hoặc 0989.80.78.79 http://www.maths.vn
-65-
Trong khoảng
( ) ( )
2
cos 0
0; : ' 0
1
6
sin
2
5
6
x
x
f x x
x
x
π
π
π
π
=
=
= ⇔ ⇔ =
=
=
Tương tự câu
)
a
học sinh tự xác ñịnh khoảng ñơn ñiệu hàm số ; hàm số ñạt cực tiểu tại
, 1
2 2
x f
π π
= =
, hàm số ñạt cực ñại tại các ñiểm
3
,
6 6 2
x f
π π
= =
và
5 5 3
,
6 6 2
x f
π π
= =
.
MỘT SỐ DẠNG TOÁN TRONG KỲ THI TÚ TÀI &TUYỂN SINH ðẠI HỌC
1. Tìm cực trị của hàm số :
)
a
(
)
.
x
f x x e
−
=
)
b
( )
3
2
3
2
f x x x
= +
)
c
(
)
2
2 3 1
f x x x
= − + +
)
d
(
)
2
3 10
f x x x
= + −
)
e
(
)
3 sin cos
f x x x
= +
2. Tìm
m
ñể ñồ thị của hàm số có cực trị :
)
a
( )
2
x mx m
y f x
x m
+ −
= =
+
)
b
( )
2
( 1)
1
x m x m
y f x
x
+ − −
= =
+
3. Tìm
m
ñể ñồ thị của hàm số:
)
a
(
)
3 2
7 3
y f x x mx x
= = + + +
có cực trị .
)
b
( )
4 3 2
1 3
2 ( 2) ( 6) 1
4 2
y f x x x m x m x
= = − + + − + +
có ba cực trị .
)
c
(
)
2
2 1
y f x x m x
= = − + +
có cực tiểu.
)
d
( )
2
2 2
1
x x m
y f x
x m
− + +
= =
+ −
có cực ñại , cực tiểu .
4. Xác ñịnh
m
ñể
ñồ thị của hàm số luôn có cực ñại , cực tiểu?.
)
a
3 2
3 5
y x mx mx
= + + +
)
b
2
2
x mx m
y
x m
+ −
=
+
)
c
(
)
2
1 1
2
mx m x
y
mx
+ + +
=
+
ðáp số :
)
a
0 9
m m
< ∨ >
)
b
1 0
m
− < <
)
c
2, 0
m m
< ≠
5. Chứng minh rằng với mọi
m
thì ñồ thị của hàm số luôn có cực ñại , cực tiểu ?.
Nguyễn Phú Khánh – ðà Lạt 063.28.78.79 hoặc 0989.80.78.79 http://www.maths.vn
-66-
)
a
( )
4 3 2
4
2
3
y f x x mx x
= = − −
)
b
( )
2
2 3
2
x mx m
y f x
x
+ + −
= =
+
)
c
( )
2
1
x mx m
y f x
x
− +
= =
−
6.
)
a
Với giá trị nào của
m
,hàm số
( )
2 2 2
2
,
1
x m x m
y f x m
x
+ +
= =
+
có cực ñại , cực tiểu
)
b
Với giá trị nào của
m
,hàm số
(
)
(
)
3 2
, 3 2 3
y f x m m x mx
= = − − +
không có cực ñại , cực tiểu
ðáp số :
)
a
1 1
m
− < <
)
b
0
m
=
7. Tìm
m
ñể ñồ thị của hàm số:
)
a
(
)
3 2 2
2
y f x x mx m
= = + +
ñạt cực ñại tại
1
x
=
)
b
( )
2
3 5
1
x mx
y f x
mx
+ +
= =
+
ñạt cực ñại tại
1 3
x
= − −
)
c
(
)
(
)
3 2
3 5
y f x x m x mx m
= = − + + + +
ñạt cực tiểu tại
2
x
=
)
d
(
)
(
)
2 3 2
5 6 6 6
y f x m m x mx x
= = − + + + −
ñạt cực ñại tại
1
x
=
)
e
( )
(
)
2
1 1
1
x m x
y f x
x m
+ − +
= =
+ −
ñạt cực ñại tại
2
x
=
8. Tìm
m
ñể ñồ thị của hàm số:
)
a
( )
2
2 3
2
x mx m
y f x
x
+ + −
= =
+
có cực ñại , cực tiểu ñối xứng nhau qua ñường thẳng
2 8 0
x y
+ + =
.
)
b
(
)
3 2
6 3( 2) 6.
y f x x x m x m
= = − + + − −
có hai cực trị trái dấu .
)
c
( )
2
2 3
1
x x m
y f x
x
− +
= =
−
có cực ñại , cực tiểu thoả mãn
8
CD CT
y y
− >
.
)
d
( )
2
3 2
4
x x m
y f x
x
− + +
= =
−
có cực ñại , cực tiểu thoả mãn
4
CD CT
y y
− =
.
9. Tìm
m
ñể ñồ thị của hàm số:
)
a
( )
2 2
2 (2 3) 4
x m x m m
y f x
x m
+ + + +
= =
+
có cực ñại , cực tiểu thoả mãn
. 0
CD CT
y y
<
.
)
b
( )
3 2 2
1
( 3) 4( 3)
3
y f x x m x m x m m
= = + + + + + −
có hoành ñộ cực ñại
1
x
, cực tiểu
2
x
thoả
mãn
1 2
1
x x
< − <
.
Nguyễn Phú Khánh – ðà Lạt 063.28.78.79 hoặc 0989.80.78.79 http://www.maths.vn
-67-
)
c
( )
3 2
1 1
( 1) 3( 2)
3 3
y f x mx m x m x
= = − − + − +
có hoành ñộ cực ñại
1
x
, cực tiểu
2
x
thoả mãn
1 2
2 1
x x
+ =
.
)
d
(
)
3 2
2 12 13
y f x x mx x
= = + − −
có ñiểm cực ñại, ñiểm cực tiểu cách ñều trục tung.
)
e
3 2
3 3 1
y x x mx m
= − + + −
có cực trị mà hoành ñộ cực trị nhỏ hơn
2
ðáp số
)
e
0 1
m
< <
10. Tìm
m
ñể ñồ thị của hàm số:
)
a
( )
2
3
4
x x m
y f x
x
− + +
= =
−
có giá trị cực ñại , cực tiểu ñồng thời
4
CT
y y
− =
CÑ
)
b
(
)
(
)
(
)
3 2 2 2
2 1 4 1 2 1
y x m x m m x m
= + − + − + − +
có cực ñại , cực tiểu
1 2
,
x x
thỏa mãn ñiều
kiện
( )
1 2
1 2
1 1 1
2
x x
x x
+ = +
)
c
( ) ( )
3 2
1 5 1
3
m
y x m x m x
= − + + − −
có cực ñại , cực tiểu
1 2
,
x x
ñồng thời hoành ñộ cực ñại,
cực tiểu thỏa mãn ñiều kiện
(
)
1 2 1 2
2 2
1 2
3 4 0
24
x x x x
x x
+ + − <
+ >
)
d
3 2
6 3 2
y x x mx m
= − + + −
có ñiểm cực ñại
(
)
1 1 1
;
M x y
và ñiểm cực tiểu
(
)
2 2 2
;
M x y
thỏa mãn
ñiều kiện
( )( )
1 2
1 2 1 2
0
2
y y
x x x x
−
<
− +
ðáp số :
)
a
3
m
=
)
b
1 5
m m
= ∨ =
)
c
1
0
7
m
− < <
)
d
2 4
m
− < <
11. Tìm
m
ñể ñồ thị của hàm số:
)
a
(
)
3 2
2 12 13
y f x x mx x
= == + − −
có cực ñại , cực tiểu và các ñiểm cực ñại , cực tiểu cách
ñều trục
Oy
)
b
( )
3 2
3
2
m
y f x x x m
= = − +
có cực ñại , cực tiểu nằm về hai phía của ñường phân giác thứ
nhất mặt phẳng toạ ñộ của hệ
Oxy
.
)
c
( )
2
8
1
x mx m
y f x
x
+ − +
= =
−
có cực ñại , cực tiểu nằm về hai phía ñường thẳng
9 7 1 0
x y
− − =
.
)
d
(
)
3 2
2 3( 1) 6( 2) 1.
y f x x m x m x
= = + − + − −
có ñường thẳng ñi qua cực ñại , cực tiểu song
song với ñường thẳng
2009
y x
= − +
Nguyễn Phú Khánh – ðà Lạt 063.28.78.79 hoặc 0989.80.78.79 http://www.maths.vn
-68-
)
e
3 2
( ) 2 3( 1) 6 (1 2 )
y f x x m x m m x
= = + − + −
có cực ñại , cực tiểu thuộc ñường thẳng
4
y x
= −
.
)
f
( )
3 2
1 1
3 2
y f x x x mx
= = + +
ñạt cực ñại và cực tiểu tại các ñiểm có hoành ñộ
x m
>
)
g
2
3 2 1
1
mx mx m
y
x
+ + +
=
−
có cực ñại , cực tiểu ñồng thời hai ñiểm cực trị nằm về hai phía ñối với
trục
Ox
.
Hướng dẫn :
)
f
2
' 0
y x x m
= + + =
có 2 nghiệm phân biệt
1 2
,
x x
thoả mãn
1 2
m x x
< <
( )
2
1
1 4 0
4
1. ' 2 0 2 0 2
1 1
2 2 2
m
m
y m m m m m m
S
m m
<
∆ = − >
⇔ = + > ⇔ < − ∨ > ⇔ < −
= − > < −
) 0 4
g m
< <
| 1/28
| | Tải xuống

Có thể bạn quan tâm:

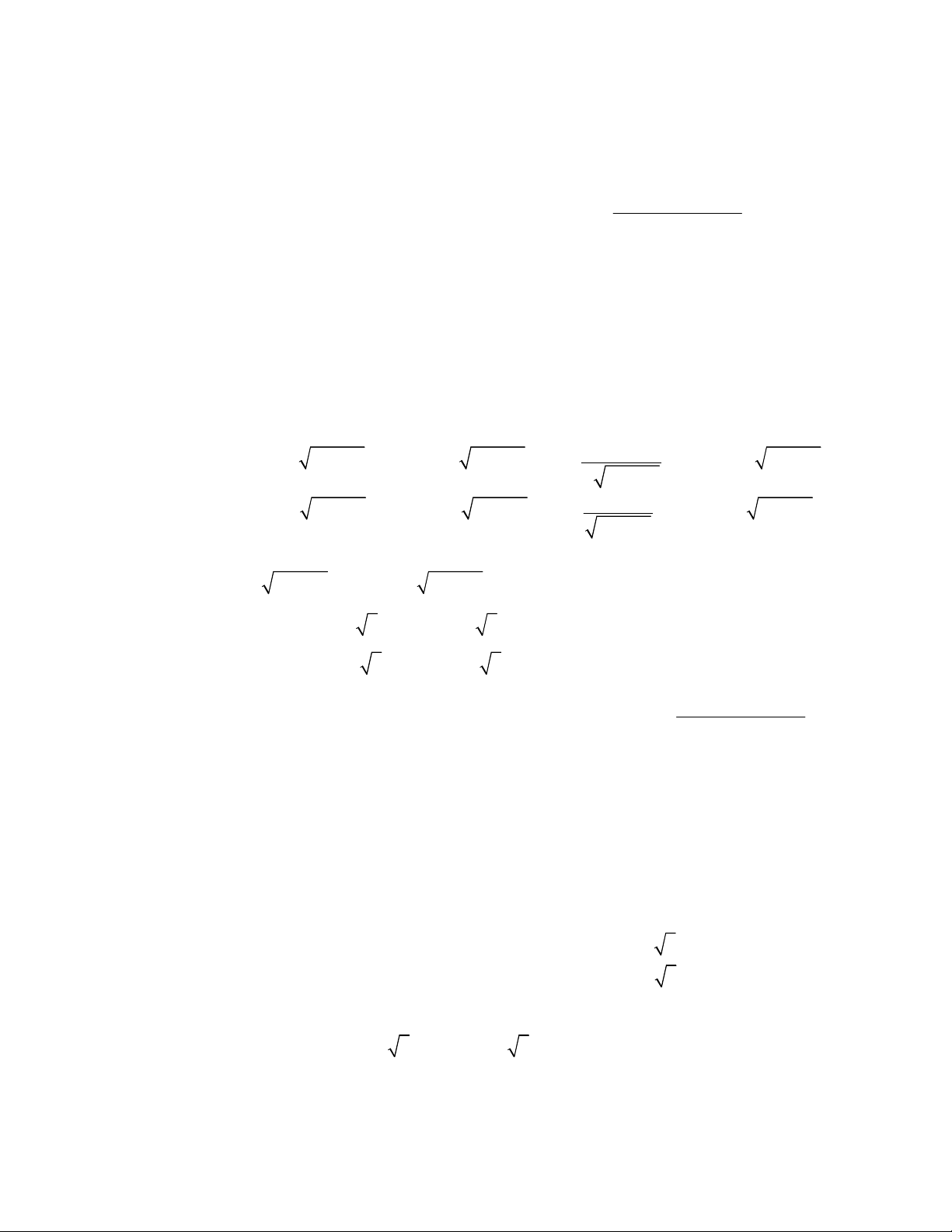
Preview text:

Nguyễn Phú Khánh – ðà Lạt 063.28.78.79 hoặc 0989.80.78.79 http://www.maths.vn CỰC TRỊ CỦA HÀM SỐ TÓM TẮT LÝ THUYẾT
1. Khái niệm cực trị hàm số :
Giả sử hàm số f xác ñịnh trên tập hợp D (D ⊂ ℝ) và x ∈ D 0 a) x
ñược gọi là một ñiểm cực ñại của hàm số f nếu tồn tại một khoảng (a;b) chứa ñiểm x sao cho 0 0
(a;b) ⊂ D và f (x) < f (x với mọi x ∈ (a;b) \{x . Khi ñó f (x ñược gọi là giá trị cực ñại của 0 ) 0} 0 ) hàm số f . b) x
ñược gọi là một ñiểm cực tiểu của hàm số f nếu tồn tại một khoảng (a;b) chứa ñiểm x sao cho 0 0
(a;b) ⊂ D và f (x) > f (x với mọi x ∈ (a;b) \{x . Khi ñó f (x ñược gọi là giá trị cực tiểu của 0 ) 0} 0 ) hàm số f .
Giá trị cực ñại và giá trị cực tiểu ñược gọi chung là cực trị
Nếu x là một ñiểm cực trị của hàm số f thì người ta nói rằng hàm số f ñạt cực trị tại ñiểm x . 0 0
Như vậy : ñiểm cực trị phải là một ñiểm trong của tập hợp D (D ⊂ ℝ)
2. ðiều kiện cần ñể hàm số ñạt cực trị:
ðịnh lý 1: Giả sử hàm số f ñạt cực trị tại ñiểm x . Khi ñó , nếu f có ñạo hàm tại ñiểm x thì f ' (x = 0 0 ) 0 0 Chú ý :
• ðạo hàm f ' có thể bằng 0 tại ñiểm x nhưng hàm số f không ñạt cực trị tại ñiểm x . 0 0
• Hàm số có thể ñạt cực trị tại một ñiểm mà tại ñó hàm số không có ñạo hàm .
• Hàm số chỉ có thể ñạt cực trị tại một ñiểm mà tại ñó ñạo hàm của hàm số bằng 0 , hoặc tại ñó hàm số không có ñạo hàm .
3. ðiều kiện ñủ ñể hàm số ñạt cực trị:
ðịnh lý 2: Giả sử hàm số f liên tục trên khoảng (a;b) chứa ñiểm x và có ñạo hàm trên các khoảng 0 (a;x và (x ;b . Khi ñó : 0 ) 0 ) f  ' (x < 0,x ∈ a;x 0 ) ( 0) a) Nếu 
thì hàm số ñạt cực tiểu tại ñiểm x . Nói một cách khác , nếu f ' (x ) ñổi f ' 0  (x > 0,x ∈ x ;b 0 ) ( 0 )
dấu từ âm sang dương khi x qua ñiểm x thì hàm số ñạt cực tiểu tại ñiểm x . 0 0 x a x b 0 f ' (x ) − + f (x ) f (a ) f (b) f (x 0 ) f  ' (x > 0,x ∈ a;x 0 ) ( 0) b) Nếu 
thì hàm số ñạt cực ñại tại ñiểm x . Nói một cách khác , nếu f ' (x ) ñổi f ' 0  (x < 0,x ∈ x ;b 0 ) ( 0 )
dấu từ dương sang âm khi x qua ñiểm x thì hàm số ñạt cực ñại tại ñiểm x . 0 0 -41-
Nguyễn Phú Khánh – ðà Lạt 063.28.78.79 hoặc 0989.80.78.79 http://www.maths.vn x a x b 0 f ' (x ) + − f (x ) f (x 0 ) f (a ) f (b)
ðịnh lý 3: Giả sử hàm số f có ñạo hàm cấp một trên khoảng (a;b) chứa ñiểm x , f ' (x = 0 và f có ñạo 0 ) 0
hàm cấp hai khác 0 tại ñiểm x . 0
a) Nếu f ' (x < 0 thì hàm số f ñạt cực ñại tại ñiểm x . 0 ) 0
b) Nếu f ' (x > 0 thì hàm số f ñạt cực tiểu tại ñiểm x . 0 ) 0
4. Quy tắc tìm cực trị:
Quy tắc 1: Áp dụng ñịnh lý 2 • Tìm f ' (x )
• Tìm các ñiểm x (i = 1,2,3... tại ñó ñạo hàm bằng 0 hoặc hàm số liên tục nhưng không có ñạo hàm. i )
• Xét dấu của f ' (x ). Nếu f '(x )ñổi dấu khi x qua ñiểm x thì hàm số có cực trị tại ñiểm x . 0 0
Quy tắc 2: Áp dụng ñịnh lý 3 • Tìm f ' (x )
• Tìm các nghiệm x (i = 1,2,3... của phương trình f '(x ) = 0. i )
• Với mỗi x tính f ' (x i ) . i
− Nếu f ' (x ) < 0 thì hàm số ñạt cực ñại tại ñiểm x . i i
− Nếu f ' (x ) > 0 thì hàm số ñạt cực tiểu tại ñiểm x . i i
Ví dụ 1 : Tìm cực trị của các hàm số : c) f (x ) = x (x − 3) a f (x ) 1 3 2 5 ) = x − x − 3x + 3 3 d) f (x ) = x b) f (x ) = x (x + 2) Giải : a f (x ) 1 3 2 5 ) = x − x − 3x + 3 3
Hàm số ñã cho xác ñịnh trên ℝ . Ta có f (x ) 2 '
= x − 2x − 3 f ' (x ) = 0 ⇔ x = −1,x = 3 Cách 1. Bảng biến thiên x −∞ −1 3 +∞ f ' (x ) + 0 − 0 + 10 f (x ) +∞ 3 22 −∞ − 3 -42-
Nguyễn Phú Khánh – ðà Lạt 063.28.78.79 hoặc 0989.80.78.79 http://www.maths.vn
Vậy hàm số ñạt cực ñại tại ñiểm x = − f (− ) 10 1, 1 =
, hàm số ñạt cực tiểu tại ñiểm x = f ( ) 22 3, 3 = − 3 3 Cách 2 : f ' (x ) = 2x − 2 Vì f '' ( 1
− ) = −4 < 0 nên hàm số ñạt cực ñại tại ñiểm x = − f (− ) 10 1, 1 = . 3
Vì f '' (3) = 4 > 0 hàm số ñạt cực tiểu tại ñiểm x = f ( ) 22 3, 3 = − . 3  + ≥ b f (x ) = x (x + ) x (x 2) khi x 0 ) 2 =  x −  (x + 2) k hi x < 0
Hàm số ñã cho xác ñịnh và liên tục trên ℝ . 2  x  + 2 > 0 k hi x > 0 Ta có f ' (x ) =  f ' (x ) = 0 ⇔ x = −1 −2x − 2 k hi x < 0 
Hàm số liên tục tại x = 0 , không có ñạo hàm tại x = 0 . Bảng biến thiên x −∞ −1 0 +∞ f ' (x ) + 0 − + f (x ) 1 +∞ −∞ 0
Vậy hàm số ñạt cực ñại tại ñiểm x = −1, f (−1) = 1 , hàm số ñạt cực tiểu tại ñiểm x = 0, f (0) = 0 c) f (x ) = x (x − 3)  x x  − 3 k hi x ≥ 0
Hàm số ñã cho xác ñịnh và liên tục trên ℝ . f (x ) ( ) =  .  x − (x − 3) k hi x < 0  3(x − 1)  k hi x > 0  Ta có ' ( ) = 2 x f x  f ' (x ) = 0 ⇔ x = 1  3 − x + x − > 0 k hi x < 0 2 x − x −∞ 0 1 +∞ f ' (x ) + − 0 + f (x ) 0 +∞ −∞ −2
Hàm số ñạt ñiểm cực ñại tại ñiểm x = 0, f (0) = 0 , hàm số ñạt ñiểm cực tiểu tại ñiểm x = 1, f (1) = 2 − d) f (x ) = x -43-
Nguyễn Phú Khánh – ðà Lạt 063.28.78.79 hoặc 0989.80.78.79 http://www.maths.vn x  k hi x  ≥
Hàm số ñã cho xác ñịnh và liên tục trên ℝ . f (x ) 0 =  . x − k hi x < 0   k hi x  > Ta có f (x ) 1 0 ' =  −1 k hi x < 0  Bảng biến thiên x −∞ 0 +∞ f ' (x ) − + f (x ) +∞ +∞ 0
Hàm số ñạt ñiểm cực ñại tại ñiểm x = 0, f (0) = 0
Ví dụ 2 : Tìm cực trị của các hàm số sau : a f (x ) 2 ) = x 4 − x c) f (x ) = 2 sin 2x − 3
b) f (x ) = 3 − 2 cosx − cos2x d) f (x ) = x − sin 2x + 2 Giải : a f (x ) 2 ) = x 4 − x
Hàm số ñã cho xác ñịnh trên ñoạn −2;2   2 4 − 2x Ta có a) f ' (x ) = , x ∈ ( 2
− ;2) f '(x ) = 0 ⇔ x = − 2,x = 2 2 4 − x
f ' (x ) ñổi dấu từ âm sang dương khi x qua ñiểm − 2 thì hàm số ñạt cực tiểu tại ñiểm x = − 2, f (− 2) = −2
f ' (x ) ñổi dấu từ dương sang âm khi x qua ñiểm 2 thì hàm số ñạt cực ñại tại ñiểm x = 2, f ( 2) = 2
Hoặc dùng bảng biến thiên hàm số ñể kết luận: x −2 − 2 2 2 f ' (x ) − 0 + 0 − f (x ) 0 2 −2 0
b) f (x ) = 3 − 2 cosx − cos2x
Hàm số ñã cho xác ñịnh và liên tục trên ℝ . -44-
Nguyễn Phú Khánh – ðà Lạt 063.28.78.79 hoặc 0989.80.78.79 http://www.maths.vn
Ta có f ' (x ) = 2 sin x + 2 s in2x = 2 sin x (1 + 2 cosx ) sin x = 0 x  = kπ   f ' (x ) = 0 ⇔ π ⇔ π , 1 2 2 k ∈  ℤ . cos x cos x  = − = = ± + k2π  2 3  3 f ' (x ) = 2 cosx + 4 cos2x  2π  2π 2π  2π  1 f '  ± + k2π  = 6 cos
= −3 < 0 . Hàm số ñạt cực ñại tại x = ± + k2π , f  ± + k2π  = 4  3  3 3  3  2
f ' (kπ ) = 2 coskπ + 4 > 0, k
∀ ∈ ℤ . Hàm số ñạt cực tiểu tại x = kπ , f (kπ ) = 2 (1 − coskπ ) c) f (x ) = 2 sin 2x − 3
Hàm số ñã cho xác ñịnh và liên tục trên ℝ . π π Ta có f ' (x ) = 4 cos 2x ,
f ' (x ) = 0 ⇔ cos 2x = 0 ⇔ x = + k ,k ∈ ℤ 4 2 (  π π   π  − = x ) 8 khi k 2n f ' = 8 − sin 2x , f '  + k  = −8 sin  + kπ  =   4 2   2 8 k hi k = 2n + 1   π  π 
Vậy hàm số ñạt cực ñại tại các ñiểm x =
+ nπ; f  + nπ  = −1 và ñạt cực ñại tại 4  4  π π  π π  x =
+ (2n + 1) ; f  + (2n + 1)  = −5 4 2  4 2  d) f (x ) = x − sin 2x + 2 π
Tương tự trên hàm số ñạt cực ñại tại các ñiểm x = −
+ kπ,k ∈ ℤ và ñạt cực tiểu tại các ñiểm 6 π x = + kπ,k ∈ ℤ . 6 Ví dụ 3 : 3 3 x − m m + 1 x + m + 1
1. Chứng minh rằng với mọi giá trị của m , hàm số y = f (x,m) ( ) = luôn x − m
có cực ñại và cực tiểu . 2 .
Với giá trị nào của m ,hàm số y = f (x m ) = (m + ) 3 2 ,
2 x + 3x + mx + m có cực ñại , cực tiểu . mx + x + m 3 .
Với giá trị nào của m ,hàm số y = f (x m ) 2 , =
không có cực ñại , cực tiểu . x + m 4 .
Xác ñịnh các giá trị của tham số k ñể ñồ thị của hàm số y = f (x k ) 4 = kx + (k − ) 2 , 1 x + 1 − 2k chỉ
có một ñiểm cực trị. 1 3 5 .
Xác ñịnh m ñể ñồ thị của hàm số y = f (x,m ) 4 2
= y = x − mx + có cực tiểu mà không có cực 2 2 ñại. Giải : -45-
Nguyễn Phú Khánh – ðà Lạt 063.28.78.79 hoặc 0989.80.78.79 http://www.maths.vn
Hàm số ñã cho xác ñịnh trên D = ℝ \ {m}. 2 2 − 2 + − 1 g (x x mx m ) Ta có y ' = = , x ≠ m , g x = x − 2mx + m − 1 2 2 ( ) 2 2 (x − m) (x − m)
Dấu của g (x ) cũng là dấu của y ' và 2 ∆ = m − ( 2 ' m − 1) = 1 > 0 , m ∀ . Do ñó m ∀ thì g (x ) = 0 g
luôn có 2 nghiệm phân biệt x = m − 1,x = m + 1 thuộc tập xác ñịnh . 1 2 x −∞ m − 1 m m + 1 +∞ f ' (x ) + 0 − − 0 + f (x ) +∞ +∞ −∞ −∞
y ' ñổi dấu từ dương sang âm khi x qua ñiểm x = m − 1 thì hàm số ñạt cực ñại tại ñiểm x = m − 1 1 1
y ' ñổi dấu từ âm sang dương khi x qua ñiểm x = m + 1 thì hàm số ñạt cực tiểu tại ñiểm x = m + 1 2 2 2 .
Hàm số ñã cho xác ñịnh trên ℝ . Ta có y = (m + ) 2 ' 3 2 x + 6x + m
Hàm số có cực ñại và cực tiểu khi phương trình y ' = 0 có hai nghiệm phân biệt hay m  + 2 ≠ 0 m  ≠ 2 − m     ≠ −2 ⇔  ⇔  ⇔  ∆ ' = 9 − 3m  (m + 2) > 0 3   ( 2 m − − 2m + 3) > 0 3 − < m < 1 
Vậy giá trị m cần tìm là −3 < m < 1,m ≠ 2 − . 2 2 mx + 2m x 3 .
Hàm số ñã cho xác ñịnh trên D = ℝ \ { m
− } và có ñạo hàm y ' = (x + m)2
Hàm số không có cực ñại , cực tiểu khi y ' = 0 không ñổi dấu qua nghiệm , khi ñó phương trình g (x ) 2 2 = mx + 2m x = 0,(x ≠ m
− ) vô nghiệm hoặc có nghiệm kép • Xét m = 0 ⇒ y ' = 0, x ∀ ≠ m − ⇒ m = 0 thoả . • Xét m ≠ 0 . Khi ñó 4 ∆ ' = m Vì 4 ∆ ' = m > 0, m ∀
≠ 0 ⇒ g (x ) = 0có hai nghiệm phân biệt nên không có giá trị tham số m ñể g (x ) 2 2 = mx + 2m x = 0,(x ≠ m
− ) vô nghiệm hoặc có nghiệm kép
Vậy m = 0 thoả mãn yêu cầu bài toán . 4 .
Hàm số ñã cho xác ñịnh trên ℝ . Ta có 3 y ' = 4kx − 2 (k − 1)x x  = 0 y ' = 0 ⇔  2 2kx + k − 1 =  0 (*)  -46-
Nguyễn Phú Khánh – ðà Lạt 063.28.78.79 hoặc 0989.80.78.79 http://www.maths.vn
Hàm số chỉ có một cực trị khi phương trình y ' = 0 có một nghiệm duy nhất và y ' ñổi dấu khi x ñi qua
nghiệm ñó .Khi ñó phương trình 2 2kx + k − 1 = 0
(*) vô nghiệm hay có nghiệm kép x = 0 k  = 0  k  = 0 k  ≤ 0 ⇔ k  ≠  0  ⇔  ⇔   < ∨ ≥ ≥   k  (k ) k 0 k 1 k 1 ' 2 1 0  ∆ = − − ≤ 
Vậy k ≤ 0 ∨ k ≥ 1 là giá trị cần tìm . 5 .
Hàm số ñã cho xác ñịnh trên ℝ . x  = 0 Ta có 3 y ' = 2x − 2mx y ' = 0 ⇔  2 x = m  (*) 
Hàm số có cực tiểu mà không có cực ñại khi phương trình y ' = 0 có một nghiệm duy nhất và y ' ñổi
dấu khi x ñi qua nghiệm ñó Khi ñó phương trình 2 x = m
(*) vô nghiệm hay có nghiệm kép x = 0 ⇔ m ≤ 0
Vậy m ≤ 0 là giá trị cần tìm. Ví dụ 4 : x + mx +
1. Xác ñịnh giá trị tham số m ñể hàm số y = f (x ) 2 1 =
ñạt cực ñại tại x = 2. x + m
2. Xác ñịnh giá trị tham số m ñể hàm số y = f (x ) 3 = x + (m + ) 2
3 x + 1 − m ñạt cực ñại tại x = 1 − .
3. Xác ñịnh giá trị tham số m ñể hàm số y = f (x ) 3 2
= x − 6x + 3 (m + 2)x − m − 6 ñạt cực ñại và
cực tiểu ñồng thời hai giá trị cực trị cùng dấu. x + mx +
4. Xác ñịnh giá trị tham số m ñể hàm số y = f (x ) 2 2 =
có ñiểm cực tiểu nằm trên Parabol x − 1 (P) 2 : y = x + x − 4 Giải : 2 2 x + 2mx + m − 1
1. Hàm số ñã cho xác ñịnh trên D = ℝ \ { m
− } và có ñạo hàm f '(x ) = , x ≠ m − (x + m)2 m  = −3
Nếu hàm số ñạt cực ñại tại x = 2 thì f ' (2) 2 = 0 ⇔ m + 4m + 3 = 0 ⇔  m = −1  2 x − 6x + 8 x  = 2 m = 3 − , ta có f ' (x ) = , x ≠ 3 f ' x = 0 ⇔  2 ( ) ( = x − ) x 4 3  Bảng biến thiên : x −∞ 2 3 4 +∞ f ' (x ) + 0 − − 0 + f (x ) 1 +∞ +∞ -47-
Nguyễn Phú Khánh – ðà Lạt 063.28.78.79 hoặc 0989.80.78.79 http://www.maths.vn −∞ −∞ 5
Dựa vào bảng biến thiên ta thấy hàm số ñạt cực ñại tại x = 2 , do ñó m = 3 − thoả mãn . Tương tự với m = 1 − Cách 2 : 2 2 x + 2mx + m − 1
Hàm số ñã cho xác ñịnh trên D = ℝ \ { m
− } và có ñạo hàm f '(x ) = , x ≠ m − (x + m)2 2 y ' = , x ≠ m − (x + m)3
Hàm số ñạt cực ñại tại x = 2 khi  1 1 − =  0  ( ) =  ( m  + m + = y 2 + m ) 2 2 4 3 0 ' 2 0  m  = 1 − ∨ m = 3 −  ⇔  ⇔ m  ≠ − ⇔  ⇔ m = − y '  (2) 2 3 < 0 2 m < −2   < 0    ( m < −  2 + m ) 2 3 Vậy m = 3
− là giá trị cần tìm.
2. Hàm số cho xác ñịnh trên ℝ . x  = 0  Ta có f ' (x ) 2
= 3x + 2 (m + 3)x = x (3x + 2m + 6) ⇒ f ' (x ) = 0 ⇔ 2m + 6 x  = −  3 2m + 6 x −∞ − 0 +∞ 3 f ' (x ) + 0 − 0 + f (x ) 2m + 6 3
Hàm số ñạt cực ñại tại x = −1 ⇔ − = −1 ⇔ m = − . 3 2
3. Hàm số cho xác ñịnh trên ℝ . Ta có : 2
y ' = 3x − 12x + 3 (m + 2) .
Hàm số có cực ñại , cực tiểu khi y ' = 0 có hai nghiệm phân biệt ⇔ ∆ ' = 36 − 9 (m + 2) > 0
⇔ 2 − m > 0 ⇔ m < 2 1 y = (x − ) 2
 x − x + (m + ) + (m − ) 1 2 . 3 12 3 2 2 2 x + m − 2 =
(x − 2).y '+ 2(m − 2)x + m − 2 3   3
Gọi A (x ;y ,B x ;y là các ñiểm cực trị của ñồ thị hàm số thì x ,x là nghiệm của phương trình 1 1 ) ( 2 2) 1 2 g (x ) 2
= 3x − 12x + 3 (m + 2) = 0 . Trong ñó : -48-
Nguyễn Phú Khánh – ðà Lạt 063.28.78.79 hoặc 0989.80.78.79 http://www.maths.vn  1 y  = x − 2 .y ' x + 2 m − 2 x + m − 2 1 ( 1 ) ( 1) ( ) 1  3 ⇒ y = 2 m − 2 x + m − 2 1 ( ) y  ' (x ) 1 = 0 1   1 y  = x − 2 .y ' x + 2 m − 2 x + m − 2 2 ( 1 ) ( 2) ( ) 2  3 ⇒ y = 2 m − 2 x + m − 2 2 ( ) y  ' (x ) 2 = 0 2 
Theo ñịnh lý Vi-ét , ta có : x + x = 4, x x = m + 2 1 2 1 2 Theo bài toán : y .y > 0 ⇔ 2   (m − 2)x + m − 2 2 
  (m − 2)x + m − 2 > 0 ⇔ 
(m − 2)2 2x + 1 2x + 1 > 0 1 2 1 2 ( 1 )( 2 ) ⇔ (m − 2)2 4x x + 2  (x + x ) + 1 > 0 ⇔  (m − 2)2 4x x + 2  (x + x ) + 1 > 0 ⇔  (m − 2)2 4m + 17 > 0 1 2 1 2 1 2 1 2 ( )  17 m  > − ⇔  4 m  ≠ 2  17
So với ñiều kiện bài toán , vậy −
< m < 2 là giá trị cần tìm . 4
4. Hàm số ñã cho xác ñịnh trên D = ℝ \ { } 1 2 x − 2x − m − 2 Ta có y ' = ,x ≠ 1 g x = x − 2x − m − 2 2 ( ) 2 (x −1)
Hàm số có cực ñại , cực tiểu khi phương trình g
(x ) = 0,x ≠ 1 có hai nghiệm phân biệt khác 1 ∆ ' = 1 − ( m − − 2) > 0 m  + 3 > 0  ⇔  ⇔ > − g  ( m 1) 3 = m − − 3 ≠ 0 m ≠ 3 −   m + 3
x = 1 − m + 3 ⇒ y = 1 − m + 3 + m + 1 + = m + 2 − 2 m +  3 1 1 = ⇔  − + Khi ñó m 3 y ' 0  m + 3
x = 1 + m + 3 ⇒ y = 1 + m + 3 + m + 1 + = m + 2 + 2 m + 3  2 2  m + 3 Bảng biến thiên : x −∞ x 1 x +∞ 1 2 f ' (x ) + 0 − − 0 + f (x ) y +∞ +∞ 1 −∞ −∞ y 2
Dựa vào bàng biến thiên suy ra A (1 + m + 3;m + 2 + 2 m + 3) là ñiểm cực tiểu của hàm số . A ∈ (P ) ⇔ m + + m + = ( + m + )2 2 2 3 1 3
+ 1 + m + 3 − 4 ⇔ m + 3 = 1 -49-
Nguyễn Phú Khánh – ðà Lạt 063.28.78.79 hoặc 0989.80.78.79 http://www.maths.vn A ∈ (P ) ⇔ m + + m + = ( + m + )2 2 2 3 1 3
+ 1 + m + 3 − 4 ⇔ m + 3 = 1 ⇔ m = −2
So với ñiều kiện bài toán ,vậy m = 2
− là giá trị cần tìm. Ví dụ 5 : 1. Tìm các hệ số a, , b , c d sao cho hàm số ( ) 3 2
f x = ax + bx + cx + d ñạt cực tiểu tại ñiểm x = 0,
f (0) = 0 và ñạt cực ñại tại ñiểm x = 1, f (1) = 1 2. Tìm các hệ số a, , b c sao cho hàm số ( ) 3 2
f x = x + ax + bx + c ñạt cực trị bằng 0 tại ñiểm x = 2
− và ñồ thị của hàm số ñi qua ñiểm A(1;0). + +
3. Tìm các hệ số a,b sao cho hàm số ( ) 2 ax bx ab f x =
ñạt cực trị tại ñiểm x = 0 và x = 4 . ax + b Giải : 1. Tìm các hệ số a, , b , c d sao cho hàm số ( ) 3 2
f x = ax + bx + cx + d ñạt cực tiểu tại ñiểm
x = 0, f (0) = 0 và ñạt cực ñại tại ñiểm x = 1, f (1) = 1
Hàm số ñã cho xác ñịnh trên ℝ . Ta có f (x ) 2 ' = 3ax + 2bx + c , f ' (x ) = 6ax + 2b f  ' (0) = 0 c  = 0 c  = 0
Hàm số f (x ) ñạt cực tiểu tại x = 0 khi và chỉ khi  ⇔  ⇔  f '  (0) (1) > 0 2b > 0 b > 0   f  ' (1) = 0 3a + 2b + c = 0
Hàm số f (x ) ñạt cực ñại tại x = 1 khi và chỉ khi  ⇔  f '  (1) (2) < 0 6a + 2b < 0  f (0) = 0 ⇒ d = 0 ,
f (1) = 1 ⇒ a + b + c + d = 1 h ay a + b + c = 1 d o d = 0 ( 3)
Từ (1),(2), (3) suy ra a = −2,b = 3,c = 0,d = 0 Ta kiểm tra lại f (x ) 3 2 = −2x + 3x Ta có f (x ) 2 ' = −6x + 6x , f ' (x ) = −12x + 6
f ' (0) = 6 > 0 . Hàm số ñạt cực tiểu tại x = 0
f ' (1) = −6 < 0 . Hàm số ñạt cực ñại tại x = 1
Vậy : a = −2,b = 3,c = 0,d = 0 2. Tìm các hệ số a, , b c sao cho hàm số ( ) 3 2
f x = x + ax + bx + c ñạt cực trị bằng 0 tại ñiểm x = 2 −
và ñồ thị của hàm số ñi qua ñiểm A (1;0) .
Hàm số ñã cho xác ñịnh trên ℝ . Ta có f (x ) 2 ' = 3x + 2ax + b -50-
Nguyễn Phú Khánh – ðà Lạt 063.28.78.79 hoặc 0989.80.78.79 http://www.maths.vn f  ' (−2) = 0 4a − b = 12
Hàm số ñạt cực trị bằng 0 tại ñiểm x = 2 − khi và chỉ khi  ⇔  f  (−2) (1) = 0 4a − 2b + c = 8 
ðồ thị của hàm số ñi qua ñiểm A (1;0) khi và chỉ khi f (1) = 0 ⇔ a + b + c + 1 = 0 ( 2)
Từ (1),(2) suy ra a = 3,b = 0,c = −4 . 2 2 2 2 a x + 2abx + b − a b
3. Hàm số ñã cho xác ñịnh khi ax + b ≠ 0 và có ñạo hàm y ' = (ax +b)2 • ðiều kiện cần :
Hàm số ñạt cực trị tại ñiểm x = 0 và x = 4 khi và chỉ khi 2 2 2 2 b  − a b b  − a b = 0 2  =  b  = a > y  '(0) 0 0 2 = 0  b b  ≠ 0  a  = −2 2  ⇔  ⇔ + + −  ⇔  a a + = ⇔  y '  (4) 2 2 2 8 2 0 16a 8ab b a b 2 2 2 ( ) = 0  = 16a + 8ab + b − a b = 0 b = 4 0     (  + ≠ a + b ) 2 2 4a a 0 4 4a + b ≠ 0   • ðiều kiện ñủ : 2 a  = −2 x − 4x x  = 0  ⇒ y ' = y ' = 0 ⇔  b = 4  ( = x − + )2 x 4 2  Bảng biến thiên x −∞ 0 2 4 +∞ f ' (x ) + 0 − − 0 + f (x ) Cð +∞ +∞ −∞ −∞ CT
Từ bảng biến thiên :hàm số ñạt cực trị tại ñiểm x = 0 và x = 4 . Vậy a = −2,b = 4 là giá trị cần tìm. Ví dụ 6: 1. Cho hàm số y = f (x ) 3 2
= x − 3x + 2 (C ) . Hãy xác ñịnh tất cả các giá trị của a ñể ñiểm cực ñại
và ñiểm cực tiểu của ñồ thị (C ) ở về hai phía khác nhau của ñường tròn (phía trong và phía ngoài): (C ) 2 2 2
: x + y − 2ax − 4ay + 5a − 1 = 0 a x + m x + m − m + 2. Cho hàm số y = f (x ) 2 2 2 2 5 3 =
. Tìm m > 0 ñể hàm số ñạt cực tiểu tại x x ∈ (0;2m ) 3. 3 2 2
y = f (x) = x − 3x + m x + m. có cực ñại , cực tiểu và hai ñiểm ñó ñối xứng nhau qua -51-
Nguyễn Phú Khánh – ðà Lạt 063.28.78.79 hoặc 0989.80.78.79 http://www.maths.vn 1 5 ñường thẳng y = x − 2 2 2 x − (m + ) 2 1 x − m + 4m − 2
4. Tìm tất cả các giá trị của tham số m thì hàm số y = f (x) .có cực x − 1
trị ñồng thời tích các giá trị cực ñại và cực tiểu ñạt giá trị nhỏ nhất. 2 x + (m + 2)x + 3m + 2
5. Tìm tất cả các giá trị của tham số m thì hàm số y = f (x) = có giá trị x + 1 cực trị , ñồng thời 2 2 1 y + y > . CÑ CT 2 Giải : x  = 0 ⇒ y = 2
1. Hàm số ñã cho xác ñịnh trên ℝ và có ñạo hàm 2 y ' = 3x − 6x y ' = 0 ⇔  x = 2 ⇒ y = −2 
ðồ thị hàm số có hai ñiểm cực trị A (0;2),B (2; 2
− ) . Hai ñiểm A(0;2),B (2; 2
− ) ở về hai phía của hai ñường tròn (C khi a ) 3 ⇔ P .P
< 0 ⇔ 5a − 8a + 3 5a + 4a + 7 < 0 ⇔ 5a − 8a + 3 < 0 ⇔ < a < 1 A C B/ C ( 2 )( 2 ) 2 /( a ) ( a ) 5 2 2 Cách 2 : (C ) 2 2 2
: x + y − 2ax − 4ay + 5a − 1 = 0 ⇔ (C ) : (x − a ) + (y − 2a ) = 1 a a
(C có tâm I (a;2a) và bán kính R = 1 a ) 2 2 2  2  36 6 Ta có : IB = (a − 2) + (2a + 2) 2 = 5a + 4a + 8 = 5 a  +  + ≥ > 1 = R ⇒ ñiểm B  5  5 5
nằm ngoài (C , do ñó ñiểm A nằm trong ñường tròn a )
(C ⇔ IA < ⇔ a + − a < ⇔ a − a + < ⇔ < a < a ) ( )2 2 2 3 1 2 2 1 5 8 3 0 1 5
2. Hàm số ñã cho xác ñịnh trên D = ℝ \ { } 0 và có ñạo hàm 2 2 − 2 + 5 − 3 g (x x m m ) y ' = = , x ≠ 0 Với g (x ) 2 2
= x − 2m + 5m − 3 Hàm số ñạt cực tiểu tại 2 2 x x
x ∈ (0;2m ) ⇔ g (x ) = 0 có hai nghiệm phân biệt x ,x x < x thoả 1 2 ( 1 2 )   m >  0 m  > 0 m  > 0  1 m  < 1 < <      x < < x < m ⇔  g ( ) m 1 2 2 0 2 1. 0 < 0
⇔ −2m + 5m − 3 < 0 ⇔  ⇔  1 2 3 m  >     1.g  (2m) 3 2 > 0 2 + 5 − 3 > 0  2 m m m >    2 m  < −  3   1  m  >   2 -52-
Nguyễn Phú Khánh – ðà Lạt 063.28.78.79 hoặc 0989.80.78.79 http://www.maths.vn 1 3
Vậy giá trị m cần tìm là < m < 1 ∨ m > . 2 2
3. Hàm số ñã cho xác ñịnh trên ℝ và có ñạo hàm 2 2 y ' = 3x − 6x + m .
Hàm số có cực ñại , cực tiểu khi phương trình y ' = 0 có hai nghiệm phân biệt x , x 1 2 2 2 ⇔ ∆ m
' = 9 − 3m > 0 ⇔ − 3 < m < 3 .Vi-ét, ta có x + x = 2 , x .x = . 1 2 1 2 3
Gọi A (x ;y ,B x ;y là các ñiểm cực trị của ñồ thị hàm số và I là trung ñiểm của ñoạn AB . 1 1 ) ( 2 2)
ðường thẳng AB có hệ số góc 3 3 x − − x − 3 ( 2 2 x − x ) 2 + m (x − x y y ) 2 1 k = = = (x + x − x x − 3 x + x + m AB 1 2 )2 2 1 2 1 2 1 1 2 ( 1 2) 2 x − x x − x 2 1 2 1 2 2 m m − 2 2 6 k = 4 − − 6 + m = AB 3 3 1 5 1 ðường thẳng y = x − (∆) có hệ số góc k = 2 2 2 A  B  ⊥ ∆
Hai ñiểm A (x ;y ,B x ;y ñối xứng nhau qua ñường thẳng (∆) khi và chỉ khi  1 1 ) ( 2 2) I ∈ ∆  2 1  2m − 6  • A B ⊥ ∆ ⇔ k .k = −1 ⇔ .  = 1 − ⇔ m = 0 AB 2 3   x  = 0 ⇒ y = 0 ⇒ A 0;0 2 1 1 ( ) • m = 0 ⇒ y ' = 3x − 6x y ' = 0 ⇔  ⇒ I 1; −2 x  = 2 ⇒ y = −4 ⇒ B 2; 4 − 2 2  ( ) ( ) Dễ thấy I (1; 2 − ) ∈ ∆
Vậy m = 0 thoả mãn yêu cầu bài toán .
4. Hàm số ñã cho xác ñịnh trên D = ℝ \ { } 1 . 2 2 − 2 + − 3 + 3 g (x x x m m ) Ta có y ' = = , x ≠ 1 g x = x − 2x + m − 3m + 3 2 2 ( ) 2 2 (x − 1) (x −1)
Hàm số có cực ñại , cực tiểu khi phương trình g (x ) = 0,x ≠ 1 có hai nghiệm phân biệt x ,x khác 1. 1 2 2 ∆ ' > 0  m  − + 3m − 2 > 0 ⇔   ( ⇔  ⇔ < m < g 1) 1 2 2 ≠ 0 m − 3m + 2 ≠ 0  
Gọi A (x ;y ,B x ;y là các ñiểm cực trị của ñồ thị hàm số thì x ,x là nghiệm của phương trình 1 1 ) ( 2 2) 1 2 g (x ) = 0,x ≠ 1 .  2 2 x = 1 − m − + 3m − 2 ⇒ y = 1 − m + 2 m − + 3m − 2 Khi ñó 1 1 y ' = 0 ⇔  2 2 x  = 1 + m −
+ 3m − 2 ⇒ y = 1 − m − 2 m − + 3m − 2 2 2  y .y = (1 − m + 2 m − + 3m − 2 )(1 − m − 2 m − + 3m − 2 ) = (1 − m)2 2 2 − 4 ( 2 m − + 3m − 2 1 2 ) -53-
Nguyễn Phú Khánh – ðà Lạt 063.28.78.79 hoặc 0989.80.78.79 http://www.maths.vn 2  7  4 4 4 7 2
y .y = 5m − 14m + 9 = 5 m −  − ≥ − ⇒ miny .y = − k hi m = 1 2 1 2  5  5 5 5 5 7
So với ñiều kiện , vậy m = là giá trị cần tìm . 5
5. Hàm số ñã cho xác ñịnh trên D = ℝ \ {− } 1 . 2 + 2 − 2 g (x x x m ) Ta có : y ' = = , x ≠ −1 g x = x + 2x − 2m 2 2 ( ) 2 (x + 1) (x + 1)
Hàm số có cực ñại , cực tiểu khi phương trình g (x ) = 0,x ≠ −1có hai nghiệm phân biệt x ,x khác 1 2 ∆ ' > 0  2  m  + 1 > 0 1 −1 ⇔  ⇔  ⇔ > − g  ( m −1) ≠ 0 2 − m − 1 ≠ 0 2  
Gọi A (x ;y = 2x + m + 2 ,B x ;y = 2x + m + 2 là các ñiểm cực trị của ñồ thị hàm số thì x ,x là 1 1 1 ) ( 2 2 2 ) 1 2
nghiệm của phương trình g (x ) = 0,x ≠ −1
Theo ñịnh lý Vi- ét x + x = −2, x .x = −2m 1 2 1 2 Theo bài toán : y + y = y + y = CÑ
(2x + m + 2)2 + (2x + m + 2)2 = 4(x + x ) + 4(m + 2)(x + x ) + 2(m + 2 CT )2 2 2 2 2 2 2 1 2 1 2 1 2 1 2  
y + y = 4 (x + x )2 − 2x x + 4 
(m + 2)(x + x ) + 2(m + 2)2 = 4(4 + 4m) − 8(m + 2) + 2(m + 2)2 2 2 1 2 1 2 1 2 1 2   2 2 2 y + y = 2m + 16m + 8 1 2 1 Xét f (m ) 2 1
= 2m + 16m + 8,m > − f ' (m) = 4m + 16 > 0, m ∀ > − 2 2  1     
Do ñó hàm số f (m ) ñồng biến trên khoảng m ∈  − ; +∞ và f (m ) 1 1 1
> f  −  = ,m ∈  − ;+∞  2   2  2  2  1  1  Vậy 2 2 y + y > ,m ∈ CÑ  − ; +∞  CT 2  2  Ví dụ 7: 1 1
1. Với giá trị nào của m thì ñồ thị của hàm số 3 y = mx − (m − 1) 2
x + 3 (m − 2)x + có cực ñại , 3 3
cực tiểu ñồng thời hoành ñộ cực ñại cực tiểu x , x thỏa x + 2x = 1 1 2 1 2 2 mx + ( 2 m + ) 3 1 x + 4m + m
2. Với giá trị nào của m thì ñồ thị của hàm số y = tương ứng có một x + m
ñiểm cực trị thuộc góc phần tư thứ (II ) và một ñiểm cực trị thuộc góc phần tư thứ (IV ) của mặt phẳng tọa ñộ . Giải :
1. Hàm số cho xác ñịnh trên ℝ . -54-
Nguyễn Phú Khánh – ðà Lạt 063.28.78.79 hoặc 0989.80.78.79 http://www.maths.vn Ta có 2
y ' = mx − 2 (m − 1)x + 3(m − 2)
Hàm số có cực ñại , cực tiểu khi y ' ñổi dấu hai lần qua nghiệm x , tức là phương trình 2
mx − 2 (m − 1)x + 3(m − 2) = 0 có hai nghiệm phân biệt x ,x 1 2 m  ≠ 0 m  ≠ 0 m  ≠   0   ⇔  ⇔  − + ∆  ' =  (m − 1)2 − 3m (m − 2) 2 2 6 2 6 > 0 −2m + 4m + 1 > 0   < m <  2 2
Theo ñịnh lý Vi – ét và yêu cầu bài toán, ta có:   3m − 4 x +  2x = 1 gt x  = 1 2 ( )   (   m − ) 1 m 2 2 1  2 − m m = 2  x  + x = ⇔ x  =
⇔ 3m − 8m + 4 = 0 m ≠ 0 ⇔ 1 2 2 ( ) 3    ( m  =  m − ) m   −   −  (m −  m m ) m 2 3 2 3 2 3 4 2 x .x =       = 1 2  m m m m      2
So với ñiều kiện bài toán , vậy m = ∨ m
= 2 là giá trị cần tìm . 3 3 4m
2. Hàm số ñã cho xác ñịnh trên D = ℝ \ { m − } và y = mx + 1 + (m ≠ 0) x + m 2 2 3 mx + 2m x − 3m Ta có : y ' = , x ≠ m − (x + m)2
Gọi A (x ;y ,B x ;y là các ñiểm cực trị của ñồ thị hàm số thì x ,x x < x là nghiệm của phương 1 2 ( 1 2 ) 1 1 ) ( 2 2) trình g (x ) 2 2 3 = mx + 2m x − 3m = 0,x ≠ m −
ðồ thị của hàm số có một ñiểm cực trị thuộc góc phần tư thứ (II ) và một ñiểm cực trị thuộc góc phần tư
thứ (IV ) của mặt phẳng tọa ñộ khi • x < 0 < x 1 1 2 ( ) A
 thuoäc goùc phaàn tö thö ù (II)    ⇔  ⇔ •  y < 0 < y 2 2 1 ( ) B
 thuoäc goùc phaàn tö thö ù (IV)  •
 He äsoá goùc cuûa tieäm caän xieân nhoû hôn 0 (3)  ( ) ⇔ m g ( ) 4 1 .
0 < 0 ⇔ −3m < 0 ⇔ m ≠ 0 ( a )
(2) ⇔ ðồ thị của hàm số không cắt trục 2 Ox ⇔ mx + ( 2 m + ) 3 1 x + 4m + m = 0 (x ≠ m − ) vô nghiệm  1  m m  ≠ ≠ 0 0 m < − m  ≠   0   ⇔  ⇔  ⇔  ⇔  5 ∆ =  ( 1 b 2 m + 1)2 − 4m ( 3 4m + m ) 4 2 2 ( ) < 0 −15m − 2m + 1 < 0 m  >  1   5 m >   5 (3) ⇔ m < 0 ( c) -55-
Nguyễn Phú Khánh – ðà Lạt 063.28.78.79 hoặc 0989.80.78.79 http://www.maths.vn 1 Từ (a ) ( b ) ( c ) suy ra m < − là giá trị cần tìm. 5 Ví dụ 8: Cho hàm số f (x ) 3 = x + (m − ) 2
1 x − (m + 2)x − 1, có ñồ thị là (C ),m là tham số. m
1. Chứng minh rằng hàm số luôn có một cực ñại , một cực tiểu .
2. Khi m = 1, ñồ thị hàm số là (C ) x
a). Viết phương trình ñường thẳng (d ) vuông góc với ñường thẳng y = và tiếp xúc với ñồ thị (C ) . 3
b). Viết phương trình ñường thẳng ñi qua hai ñiểm cực trị của (C ) . Giải :
Hàm số cho xác ñịnh trên ℝ . 1. Ta có f (x ) 2 '
= 3x + 2 (m − 1)x − (m + 2). Vì 2 ∆ ' = m + m + 7 > 0, m
∀ ∈ ℝ nên phương trình f ' (x ) = 0 luôn có hai nghiệm phân biệt . Do ñó ñồ
thị của hàm số luôn có một cực ñại , một cực tiểu với mọi giá trị của tham số m . 2. m = ⇒ (C ) f (x ) 3 1 : = x − 3x − 1
a). Gọi M (x ;y là toạ ñộ tiếp ñiểm của ñường thẳng (d ) và ñồ thị (C ) 0 0 ) x 3 2
⇒ y = x − 3x − 1,y ' = 3x − 3 . ðường thẳng (d ) vuông góc với ñường thẳng y = khi 0 0 0 0 0 3  1  2 2
y '   = −1 ⇔ 3x − 3 = 3 − ⇔ x = 0 ⇔ x = 0,y = 1 − 0 0 0 0 0  3 
Vậy ñường thẳng (d ) : y = −3x − 1 và tiếp xúc với ñồ thị (C ) tại ñiểm (0; −1) .
b). ðồ thị (C ) có ñiểm cực ñại là A( 1
− ;1), ñiểm cực tiểu là B (1;−3) . Do ñó ñường thẳng qua AB là : y = −2x − 1. Ví dụ 9:
1. Xác ñịnh giá trị tham số m ñể hàm số f (x ) 3 = x − ( m + ) 2 x + ( 2 2 1 m − 3m + 2)x + 4 có hai
ñiểm cực ñại và cực tiểu nằm về hai phía trục tung . 2 x − m + 1 x + 3m + 2
2. Xác ñịnh giá trị tham số m ñể hàm số f (x ) ( ) =
có hai ñiểm cực ñại và x − 1 cực tiểu cùng dấu . 3. Cho hàm số y = f (x ) 3 = x − + (m + ) 2 x − ( 2 m + m − ) 2 3 1 3 7
1 x + m − 1 .ðịnh m ñể hàm số ñạt
cực tiểu tại một ñiểm có hoành ñộ nhỏ hơn 1. x + mx +
4. Tìm giá trị của m ñể ñồ thị hàm số f (x ) 2 2 2 =
có ñiểm cực ñại, ñiểm cực tiểu và x + 1
khoảng cách từ hai ñiểm ñó ñến ñường thẳng ∆ : x + y + 2 = 0 bằng nhau. Giải :
1. Hàm số cho xác ñịnh trên ℝ và có ñạo hàm f (x ) 2 = x − ( m + ) 2 ' 3 2 2 1 x + m − 3m + 2 -56-
Nguyễn Phú Khánh – ðà Lạt 063.28.78.79 hoặc 0989.80.78.79 http://www.maths.vn
Hàm số có hai ñiểm cực ñại và cực tiểu nằm về hai phía trục tung khi và chỉ khi phương trình
f ' (x ) = 0 có hai nghiệm phân biệt x ,x thoả mãn x < 0 < x ⇔ 3.f ' 0 < 0 1 2 ( ) 1 2 2
⇔ m − 3m + 2 < 0 ⇔ 1 < m < 2
Vậy giá trị cần tìm là 1 < m < 2 . 2 x − 2x − 2m − 1
2. Hàm số ñã cho xác ñịnh trên D = ℝ \ { }
1 và có ñạo hàm f ' (x ) = ,x ≠ 1 (x −1)2
Hàm số có cực ñại và cực tiểu khi f ' (x ) = 0 có hai nghiệm phân biệt x ≠ 1 hay phương trình g (x ) 2
= x − 2x − 2m − 1 = 0 có hai nghiệm phân biệt x ≠ 1 , khi ñó ∆ ' > 0  2  m  + 2 > 0  ⇔  ⇔ > − g  ( m 1) 1 (1) ≠ 0 −2m − 2 ≠ 0  
Gọi A (x ;y ,B x ;y là các ñiểm cực trị của ñồ thị hàm số thì x ,x là nghiệm của g (x ) = 0 1 1 ) ( 2 2) 1 2  2m + 2
x = 1 − 2m + 2 ⇒ y = 1 − 2m + 2 − m + = 1 − m − 2 2m +  2 1 1 = ⇔  − + Khi ñó: 2m 2 y ' 0  2m + 2
x = 1 + 2m + 2 ⇒ y = 1 + 2m + 2 − m + = 1 − m + 2 2m + 2  2 2  2m + 2
Hai giá trị cực trị cùng dấu khi
y .y > 0 ⇔ (1 − m − 2 2m + 2)(1 − m + 2 2m + 2) > 0 ⇔ (1 − m)2 − 4 2m + 2 > 0 1 2 ( ) 2
⇔ m − 10m − 7 > 0 ⇔ m < 5 − 4 2 ∨ m > 5 + 4 2 ( 2)
Từ (1) và (2) suy ra −1 < m < 5 − 4 2 ∨ m > 5 + 4 2 2 x − 2x − 2m − 1
Cách khác : Hàm số ñã cho xác ñịnh trên D = ℝ \ { }
1 và có ñạo hàm f ' (x ) = ,x ≠ 1 (x −1)2
Hàm số có cực ñại và cực tiểu khi f ' (x ) = 0 có hai nghiệm phân biệt x ≠ 1 hay phương trình ∆ ' > 0  2  m  + 2 > 0 g (x ) 2
= x − 2x − 2m − 1 = 0 có hai nghiệm phân biệt ⇔  ⇔  ⇔ > − g  ( m 1) 1 ≠ 0 2 − m − 2 ≠ 0  
Hai giá trị cực trị cùng dấu khi ñồ thị của hàm số y = 0 cắt trục hoành tại hai ñiểm phân biệt x ≠ 1 hay phương trình 2
x − (m + 1)x + 3m + 2 = 0 (x ≠ 1) có hai nghiệm phân biệt x ≠ 1. Tức là  ∆ = ( m < −  m + 1)2 − 4 (3m + 2) 5 4 2 2 > 0 m  − 10m − 7 > 0   ⇔   − ( + ) ⇔  ⇔  m  > 5 + 4 2 + + ≠ 2m m m + 2 ≠ 0 1 1 3 2 0     m ≠ −1 
So với ñiều kiện , giá trị −1 < m < 5 − 4 2 ∨ m > 5 + 4 2 là giá trị cần tìm . -57-
Nguyễn Phú Khánh – ðà Lạt 063.28.78.79 hoặc 0989.80.78.79 http://www.maths.vn
3. Hàm số cho xác ñịnh trên ℝ và có ñạo hàm f (x ) 2 = − x + (m + )x − ( 2 ' 3 6 1 3m + 7m − 1).Hàm số
ñạt cực tiểu tại một ñiểm có hoành ñộ nhỏ hơn 1 ⇔ f (x ) 2 = − x + (m + )x − ( 2 ' 3 6 1 3m + 7m − 1) = 0
có hai nghiệm x , x thoả mãn ñiều kiện : 1 2 (1) ⇔ 3 − .f ' (1) < 0 3  ( 2 3m + m − 4) < 0      x < 1 < x (1)   ∆ ' > 0 9  ⇔  ⇔  (m + 1)2 − 3 ( 2 3m + 7m − 1 > 0 1 2 )   x  < x ≤ 1 (2) (2) ⇔  3 − .f ' (1) ≥ 0 3   ( 2 3m + m − 4 ≥ 0 1 2 )   S   m + 1 < 1  < 1      2  4  4 − < m <  1 − < m <  1 3   4 3  m  < 4 − < m <    1 3 − m + 12 > 0 ⇔  ⇔  3 ⇔    ⇔ m < 1   2 4 4 3m + m − 4 ≥ 0  m  ≤ − ∨ m ≥ 1 m  ≤ −  3     3  m < 0 m <   0   2 x + 2x + 2m − 2
4. Hàm số ñã cho xác ñịnh trên D = ℝ \ {− }
1 và có ñạo hàm f ' (x ) = , x ≠ −1 (x + 1)2
Hàm số có cực ñại , cực tiểu khi f ' (x ) ñổi dấu hai lần qua nghiệm x hay phương trình g (x ) 2
= x + 2x + 2m − 2 = 0 có hai nghiệm phân biệt khác −1 ∆ ' > 0   3 − 2m > 0 3 ⇔  ⇔  ⇔ < g  ( m −1) ≠ 0 2m − 3 ≠ 0 2  
Gọi A (x ;y = 2x + 2m ,B x ;y = 2x + 2m là các ñiểm cực trị của ñồ thị hàm số thì x ,x là 1 1 1 ) ( 2 2 2 ) 1 2
nghiệm của phương trình g (x ) = 0,x ≠ 1 . Theo ñịnh lý Vi ét x + x = −2, x .x = −2m 1 2 1 2 Theo yêu cầu bài toán ( x + y + x + y + d , A ∆) = d (B, ∆) 2 2 1 1 2 2 ⇔ = ⇔ 3x + 2m + 2 = 3x + 2m + 2 1 2 2 2
⇔ (3x + 2m + 2)2 = (3x + 2m + 2)2 ⇔ (3x + 2m + 2)2 − (3x + 2m + 2)2 = 0 1 2 1 2 ⇔ ( 1 x − x
3 x + x + 4m + 4 = 0 ⇔ 3 x + x + 4m + 4 = 0 x ≠ x ⇔ 3 2 − + 4m + 4 = 0 ⇔ m = 1 2 )  ( 1 2 )  ( 1 2) ( 1 2) ( ) 2 1
So với ñiều kiện, vậy m = là giá trị cần tìm . 2 Ví dụ 10:
1. Chứng tỏ rằng chỉ có một ñiểm A duy nhất trên mặt phẳng toạ ñộ sao cho nó là ñiểm cực ñại của 2 3 x − m m + 1 x + m + 1 ñồ thị f (x ) ( ) =
ứng với một giá trị thích hợp của m và cũng là ñiểm cực x − m
tiểu của ñồ thị ứng với một giá trị thích hợp khác. Tìm toạ ñộ của A . -58-
Nguyễn Phú Khánh – ðà Lạt 063.28.78.79 hoặc 0989.80.78.79 http://www.maths.vn
2. Tìm m ñể ñồ thị của hàm số 4 2 4
y = x − 2mx + 2m + m có cực ñại , cực tiểu ñồng thời các ñiểm
cực trị lập thành tam giác ñều. Giải :
Hàm số ñã cho xác ñịnh trên D = ℝ \ {m} . 2 2 x − 2mx + m − 1 Ta có f ' (x ) = , x ≠ m g x = x − 2mx + m − 1 ∆ = 1 > 0, m ∀ 2 ( ) 2 2 (x − m) g 2 2 x  = m − 1 ⇒ f x = m − + m − 2 ⇒ M m − 1; m − + m − 2 Do ñó f ' (x ) 1 ( 1) ( ) = 0 ⇔  x  = m + 1 ⇒ f (x ) 2 = m − + m + 2 ⇒ N  ( 2 m + 1; m − + m + 2 2 2 )
ðặt A (x ;y .Giả sử ứng với giá trị m = m thì A là ñiểm cực ñại và ứng với giá trị m = m thì A 0 0 ) 1 2
là ñiểm cực tiểu của ñồ thị hàm số x  = m − 1 x  = m +   1 Ta có: 0 1 0 2  ;  2 2 y = m − + m − 2 y = m − + m + 2  0 1 1   0 2 2  m  − 1 = m +  1 m  − m = 2  Theo bài toán , ta có : 1 2 1 2  ⇔  2 2 m − + m − 2 = m − + m + 2 m − m m + m − 1 = 4 −  1 1 2 2  ( 1 2)( 1 2 )   1  1  − = 2 m = x m m = −    1  0   1 2 1 7 2 2 ⇔  ⇔  ⇒  ⇒ A − ;−  m + m = 1 − 3 7   = −   2 4 1 2 m y  = − 2 0  2  4  1 7 
Vậy A  − ; −  là ñiểm duy nhất cần tìm thoả yêu cầu bài toán .  2 4 
2. Hàm số cho xác ñịnh trên ℝ x  = 0 Ta có 3 y ' = 4x − 4mx = 4x ( 2 x − m ) y ' = 0 ⇔  2 x = m  (*) 
ðồ thị hàm số có cực ñại , cực tiểu khi y ' = 0 có 3 nghiệm phân biệt và y ' ñổi dấu khi x qua các
nghiệm ñó , khi ñó phương trình (*) có hai nghiệm phân biệt khác 0 ⇔ m > 0 Khi ñó : 4 x = 0 ⇒ y = m + 2m ⇒ A( 4 0;m + 2m ) y ' 0  = ⇔ 4 2
x = ± m ⇒ y = m − m + 2m ⇒ B  ( 4 2 − m;m − m + 2m ),C ( 4 2 m ;m − m + 2m ) Hàm số có 3 cực trị ,
A B,C lập thành tam giác ñều A  B  = AC 2 2 4 ⇔ 
⇔ AB = BC ⇔ m + m = m ⇔ m ( 3 4 m − 3) 3 = 0 ⇔ m = 3 (m > 0) AB = BC  Vậy 3 m = 3 là giá trị cần tìm . Ví dụ 11:
1. Xác ñịnh tham số a ñể hàm số sau có cực ñại: 2
y = −2x + 2 + a x − 4x + 5 Giải : -59-
Nguyễn Phú Khánh – ðà Lạt 063.28.78.79 hoặc 0989.80.78.79 http://www.maths.vn a (x − 2) a
1. Hàm số cho xác ñịnh trên ℝ và có ñạo hàm y ' = −2 + y ' = 2 x − 4x + 5 (x − 4x + 5)3 2  a x −  x − x + y  '(x ) ( 2) 2 0 4 5 a =  0 0 0  = 2  = 0 1 2 ( )
Hàm số ñạt cực ñại tại x = x ⇔  ⇔  ⇔ − +  − 0 x x x y '  ( 4 5 2 2 x < 0 0 ) 0 0 0    a < 0 a < 0  
Với a < 0 thì (1) ⇒ x < 2 . 0 2 x − 4x + 5 Xét hàm số : f (x ) 0 0 = , x < 2 0 0 x − 2 0 2 2 x − x + x − x + lim f (x ) 4 5 4 5 0 0 = lim = −1 , lim f = = −∞ − (x ) 0 0 lim 0 0 x x x − 2 x 2 x 2− →−∞ →−∞ → → x − 2 0 0 −2 Ta có f ' (x = < 0, x ∀ ∈ − ; ∞ 2 0 ) 2 0 ( ) (x − 2) 2x − 4x + 5 0 0 0 Bảng biến thiên : x −∞ 2 f ' (x ) − f (x ) −1 −∞ a
Phương trình (1) có nghiệm x < 2 ⇔ < −1 ⇔ a < 2 − 0 2 BÀI TẬP TỰ LUYỆN
1. Tìm cực trị của các hàm số sau : f ) f (x ) 2 = − a) x f (x ) 1 3 2 = x + 2x + 3x − 1 8 3 x g) f (x ) = b) f (x ) 1 3 2 = x − x + 2x − 10 2 x + 1 3 x h) f (x ) 3 = c f (x ) 1 ) = x + x + 1 x i) f (x ) 2 = 5 − x d) f (x ) 1 5 1 3 = x − x + 2 2 5 3 j) f (x ) = x + x − 1 − + e 1 4 f (x ) 2 x 3x 3 ) = k) f (x ) 3 2 = x − x − 3x + x − 1 3 3
2. Tìm cực trị của các hàm số sau : -60-
Nguyễn Phú Khánh – ðà Lạt 063.28.78.79 hoặc 0989.80.78.79 http://www.maths.vn a ) f (x ) 3 2 = 2x − 9x + 12x + 3 2 x + 8x − 24 e ) f (x ) = b 2 ) f (x ) 4 3 2 = 3x − 4x − 24x + 48 − 3 x − 4 x c ) f (x ) 3 2 = 5 − x + 3x − 4x + 5 f ) f (x ) = 2 x + 4 9 d ) f (x ) = x − 3 + g ) f (x ) = x 3 − x x − 2 h ) f (x ) 2 = x − 2 | x | 2 + Hướng dẫn : h f (x ) 2 ) = x − 2 | x | 2 + 2  + + <  + < f (x ) x 2x 2 khi x 0 2x 2 khi x 0 =  ⇒ f ' x =  2 ( ) x − 2x + 2 k hi x ≥ 0 2x − 2 k hi x > 0  
f ' (x ) = 0 ⇔ x = −1,x = 1
Hàm số ñạt cực ñại tại ñiểm A (0;2) và ñạt cực tiểu tại các ñiểm B (−1;1),C (1;1)
3. Chứng minh rằng với mọi m ñồ thị của hàm số 3 2
y = 4x − mx − 3x + m luôn có cực ñại , cực tiểu và x .x < 0 C Ñ CT q
4. Cho hàm số f (x ) = x + p + ( *) x + 1 a) Tìm các số thực ,
p q sao cho hàm số ñạt cực ñại tại ñiểm x = 2 − và f (−2) = −2.
a ) Trường hợp p = q = 1 , gọi M, N là ñiểm cực ñại , cực tiểu của hàm số . Tính ñộ dài MN 1
a ) Trường hợp p = q = 1 ,một ñường thẳng (t ) luôn tiếp xúc với ñồ thị hàm số (*) tại K thuộc ñồ thị 2
hàm số (*) ñồng thời cắt hai trục tọa ñộ tại hai ñiểm phân biệt E,F . Tìm tọa ñộ ñiểm K ñể K là trung ñiểm EF
b)Giả sử x ;x lần lượt là hoành ñộ cực ñại , cực tiểu của hàm số . Tìm các số thực , p q sao cho 1 2 1 b ) x = 2x và f (x ) = f (x 2 ) 1 1 2 1 2
b ) Khoảng cách từ A (x ; f x
ñến ñường thẳng y = x + p và x + 1 = 0 bằng nhau . 1 ( 1)) 2 Hướng dẫn : a) Tìm các số thực ,
p q sao cho hàm số ñạt cực ñại tại ñiểm x = 2 − và f (−2) = −2. q f ' (x ) = 1 − , x ≠ 1 − (x + 1)2 q
• q ≤ 0 thì f ' (x ) > 0, x
∀ ≠ −1 . Do ñó hàm số f (x ) = x + p +
ñồng biến trên mỗi khoảng x + 1 (− ;
∞ −1)và (−1;+∞). Hàm số không có cực ñại , cực tiểu . -61-
Nguyễn Phú Khánh – ðà Lạt 063.28.78.79 hoặc 0989.80.78.79 http://www.maths.vn 2 x + 1 − q • q > 0 thì f ' (x ) ( ) =
,x ≠ −1 ⇒ f ' x = 0 ⇔ x = −1 − p,x = −1 + p . Hàm số ñạt cực 2 ( ) (x + 1) 1 2 x  = −2 q    = 1 ñại tại ñiểm x = 2 − và f (−2) = −2 khi 1  ⇔  f  (−2) = 2 − p = 1   1 2 5. Cho hàm số f (x ) 3 = x + (m − 1) 2 x + (2m − 3)x − 3 3
a) Chứng minh rằng m ≠ 2 thì ñồ thị của hàm số luôn có cực ñại và cực tiểu . Viết phương trình qua
hai ñiểm cực ñại và cực tiểu ñó .
b) Giả sử hoành ñộ cực ñại, cực tiểu là x , x . Tìm m ñể : 1 2 b ) x + 3x = 5 b ) x 4 − 5x = 2 2 2 b ) x + x = 5 2 b ) x + x ≤ 3 1 1 2 2 1 2 3 1 2 4 1 2 c) Tìm m ñể : c ) x < 0 < x < 1 c ) x < x < 1 c ) −2 < x < x < 0
c ) x < 0 < 1 < x < 2 1 1 2 2 1 2 3 1 2 4 1 2
Lưu ý : ðể làm ñược câuc) học sinh xem lại so sánh nghiệm phương trình bậc hai ñã ñề cập sách ñại số
9 và có nhắc lại ñại số 10. 6. Cho hàm số ( ) 3 f x = x + px + q
a) Với ñiều kiện nào ñể hàm số f có một cực ñại và một cực tiểu ?.
b) Chứng minh rằng nếu giá trị cực ñại và giá trị cực tiểu trái dấu thì phương trình 3 x + px + q = 0 có 3 nghiệm phân biệt?.
c) Chứng minh rằng ñiều kiện cần và ñủ ñể phương trình 3
x + px + q = 0 có ba nghiệm phân biệt là 3 2 4p + 27q < 0 Hướng dẫn : a) p < 0  p   p  c) f  − − .f  −  < 0  3   3      7. 5 5
a) Tìm a,b ñể các cực trị hàm số f (x ) 2 3 2
= a x + 2ax − 9x + b ñều là những số dương và x = − 3 0 9 là ñiểm cực ñại . b) Tìm a, ,
b c ñể các cực trị hàm số 3 2
y = x + ax + bx + c có giá trị bằng 1 khi x = 0 và ñạt cực trị tại
x = 2 , giá trị cực trị là −3 . 2 x + ax + b
c) Tìm a,b ñể các cực trị hàm số y =
ñạt cực trị tại x = 3 và ñường tiệm cận xiên x − 2 y = x − 1 . 2 ax + bx + c d) Tìm a, ,
b c ñể các cực trị hàm số y =
có giá trị bằng 1 khi x = 1 và ñường tiệm cận x − 2 1 − x
xiên của ñồ thị vuông góc với ñường thẳng y = . 2 -62-
Nguyễn Phú Khánh – ðà Lạt 063.28.78.79 hoặc 0989.80.78.79 http://www.maths.vn e) Tìm các hệ số a, , b c sao cho hàm số ( ) 3 2
f x = x + ax + bx + c ñạt cực tiểu tại A (1; −3) và ñồ thị
của hàm số cắt trục tung tại ñiểm có tung ñộ bằng 2 . Hướng dẫn :
a) a = 0 : Hàm số không có cực trị  9 = − ≠ ( ) x  2 2 = + − ⇒ ( ) 5 0 ' 5 4 9 ' = 0 a a f x a x ax f x ⇔  1 x  =  a 5 5 1 9 Nếu a < 0 , x = −
là ñiểm cực ñại khi x = − =
⇔ a = − , giá trị cực tiểu là số dương nên 0 9 0 9 a 5   f (x = f  −  = f > ⇔ b > CT ) 9 ( ) 36 1 0  5a  5 5 5 9 81 Nếu a > 0 , x = −
là ñiểm cực ñại khi x = − = − ⇔ a =
, giá trị cực tiểu là số dương nên 0 9 0 9 5a 25   f (x = f   > ⇔ b > CT ) 1 400 0 a   243  9  81 a = − a =     Vậy 5 25  ;  36 400 b  > b  >  5  243 b) a = 3 − ,b = 0,c = 1 d) a = 2,b = 3 − ,c = 0 c) a = −3,b = 3 8. Cho hàm số f (x ) 3 2
= x − 3mx + 3 (2m − 1)x + 1,m là tham số
a) Xác ñịnh m ñể hàm số ñồng biến trên tập xác ñịnh .
b) Xác ñịnh m ñể f ' (x ) > 6x . 9.
a) ðịnh a ñể ñồ thị của hàm số 3 y = x − ( a + ) 2 2 3 2
1 x + 6a (a + 1)x + 1 có giá trị y > 1 CÑ ðáp số: 3 a) − < a ≠ 0 2
10. Xác ñịnh khoảng ñơn ñiệu và cực trị ( nếu có ) của hàm số : a) f (x ) = sin 2x c f (x ) 2 )
= sin x − 3 cosx,x ∈ 0;π    d) f (x ) = + ∈   b) π f (x ) = sin x + cos x 2 sin x cos 2x,x 0;   Hướng dẫn : a) f (x ) = sin 2x
Hàm số ñã cho xác ñịnh và liên tục trên ℝ -63-
Nguyễn Phú Khánh – ðà Lạt 063.28.78.79 hoặc 0989.80.78.79 http://www.maths.vn π π Ta có f ' (x ) = 2 cos 2x ,
f ' (x ) = 0 ⇔ cos 2x = 0 ⇔ x = + l ,l ∈ ℤ 4 2 (  π π   π π  − = x ) 4 khi l 2k f '
= −4 sin 2x, f '  + l  = −4 sin  + l  =  , k ∈ ℤ  4 2   4 2 4 k hi l = 2k + 1   π Vậy x = + kπ (
k ∈ ℤ) là ñiểm cực ñại của hàm số . 4 3π x = + kπ (
k ∈ ℤ) là ñiểm cực tiểu của hàm số . 4
Một bài toán tương tự : f (x ) = sin 2x − x , ñể ý xét f ' (x ) = 0,x ∈ ( π − ,π ) ⇒ x = ? b) f (x ) = sin x + cos x
Hàm số ñã cho xác ñịnh và liên tục trên ℝ  π   π  π
f (x ) = sin x + cos x = 2 sin x +  ⇒ f ' (x ) = 2 cos x +  , f ' (x ) = 0 ⇔ x = + kπ ( k ∈ ℤ)  4   4  4  (  π   π   π  − = x ) 2 khi k 2n f '
= − 2 sin x +  ⇒ f '  + kπ  = − 2 sin  + kπ  =   4   4   2   2 k hi k = 2n + 1  π Vậy x = + n2π (
n ∈ ℤ) là ñiểm cực ñại của hàm số . 4 π x = + (2n + 1)π (
n ∈ ℤ) là ñiểm cực tiểu của hàm số . 4 c f (x ) 2 )
= sin x − 3 cosx,x ∈ 0;π    f (x ) 2
= sin x − 3 cosx ⇒ f ' (x ) = sinx (2cosx + 3),x ∈ (0;π ) 3 5π
Vì x ∈ (0;π ) ⇒ sin x > 0 nên trong khoảng (0;π ) : f ' (x ) = 0 ⇔ cos x = − ⇔ x = 2 6  5π   5π 
• f ' (x ) > 0,x ∈ 0;
 ⇒ hàm số ñồng biến trên ñoạn 0;   6   6   5π  5π  • f ' (x ) < 0,x ∈ 
;π  ⇒ hàm số ñồng biến trên ñoạn  ;π   6   6    π  f (x ) 5 ' > 0,x ∈ 0;    6   5π  5π  7 3 • Vì  π  =   = = 
nên hàm số ñạt cực ñại tại ñiểm x , f 1 f (x ) 5 ' < 0,x ∈  ;π  6  6  4 4   6   5π  1
Hoặc có thể kiểm tra f '   = ... = − < 0  6  2
d) f (x ) = 2 sin x + cos2x,x ∈ 0;π   
f (x ) = 2 sin x + cos2x ⇒ f ' (x ) = 2 cosx (1 − 2 sin x ),x ∈ (0;π ) -64-
Nguyễn Phú Khánh – ðà Lạt 063.28.78.79 hoặc 0989.80.78.79 http://www.maths.vn  π x =  2 cos x = 0  π  Trong khoảng (0;π ) : f ' (x ) 0  = ⇔ 1 ⇔ x =  sin x =  6  2  5π x =   6
Tương tự câu a) học sinh tự xác ñịnh khoảng ñơn ñiệu hàm số ; hàm số ñạt cực tiểu tại π  π  π  π  3 5π  5π  3 x =
, f   = 1, hàm số ñạt cực ñại tại các ñiểm x = , f   = và x = , f   = . 2  2  6  6  2 6  6  2
MỘT SỐ DẠNG TOÁN TRONG KỲ THI TÚ TÀI &TUYỂN SINH ðẠI HỌC
1. Tìm cực trị của hàm số : a) ( ) . x f x x e− = d) f (x ) 2 = 3x + 10 − x 3 b) f (x ) 3 2 = x + x e) f (x ) = 3 sin x + cosx 2 c) f (x ) 2 = 2 − x + 3 x + 1
2. Tìm m ñể ñồ thị của hàm số có cực trị : + − x + m − x − m a) = ( ) 2 x mx m y f x = b) y = f (x ) 2 ( 1) = x + m x + 1
3. Tìm m ñể ñồ thị của hàm số: a) y = f (x ) 3 2
= x + mx + 7x + 3 có cực trị . 1 3 b) y = f (x ) 4 3 2
= x − 2x + (m + 2)x − (m + 6)x + 1 có ba cực trị . 4 2 c) y = f (x ) 2
= −2x + m x + 1 có cực tiểu. x − x + m + d) y = f (x ) 2 2 2 =
có cực ñại , cực tiểu . x + m − 1
4. Xác ñịnh m ñể ñồ thị của hàm số luôn có cực ñại , cực tiểu?. a) 3 2 y = x + mx + 3mx + 5 2 mx + (m + 1)x + 1 c) y = 2 x + 2mx − m mx + 2 b) y = x + m ðáp số : a) m < 0 ∨ m > 9 c) m < 2,m ≠ 0 b) −1 < m < 0
5. Chứng minh rằng với mọi m thì ñồ thị của hàm số luôn có cực ñại , cực tiểu ?. -65-
Nguyễn Phú Khánh – ðà Lạt 063.28.78.79 hoặc 0989.80.78.79 http://www.maths.vn 4 x − mx + m a) y = f (x ) 4 3 2 = x − mx − 2x c) y = f (x ) 2 = 3 x − 1 x + mx + m − b) y = f (x ) 2 2 3 = x + 2 6. x + m x + m
a) Với giá trị nào của m ,hàm số y = f (x m ) 2 2 2 2 , =
có cực ñại , cực tiểu x + 1
b) Với giá trị nào của m ,hàm số y = f (x m ) = (m − ) 3 2 ,
3 x − 2mx + 3 không có cực ñại , cực tiểu ðáp số : a) −1 < m < 1 b) m = 0
7. Tìm m ñể ñồ thị của hàm số: a) y = f (x ) 3 2 2
= x + 2mx + m ñạt cực ñại tại x = 1 x + mx + b) y = f (x ) 2 3 5 =
ñạt cực ñại tại x = −1 − 3 mx + 1 c) y = f (x ) 3 = x − (m + ) 2
3 x + mx + m + 5 ñạt cực tiểu tại x = 2 d) y = f (x ) = − ( 2 m + m ) 3 2 5
x + 6mx + 6x − 6 ñạt cực ñại tại x = 1 2 x + m − 1 x + 1 e) y = f (x ) ( ) =
ñạt cực ñại tại x = 2 x + m − 1
8. Tìm m ñể ñồ thị của hàm số: x + mx + m − a) y = f (x ) 2 2 3 =
có cực ñại , cực tiểu ñối xứng nhau qua ñường thẳng x + 2 x + 2y + 8 = 0 . b) y = f (x ) 3 2
= x − 6x + 3(m + 2)x − m − 6.có hai cực trị trái dấu . x − x + m c) y = f (x ) 2 2 3 =
có cực ñại , cực tiểu thoả mãn y − y > 8 . x − 1 CD CT x − + x + m d) y = f (x ) 2 3 2 =
có cực ñại , cực tiểu thoả mãn y − y = 4 . x − 4 CD CT
9. Tìm m ñể ñồ thị của hàm số: x + m + x + m + m a) y = f (x ) 2 2 2 (2 3) 4 =
có cực ñại , cực tiểu thoả mãn y .y < 0 . x + m CD CT 1 b) y = f (x ) 3 2 2
= x + (m + 3)x + 4(m + 3)x + m − m có hoành ñộ cực ñại x , cực tiểu x thoả 3 1 2 mãn x < −1 < x . 1 2 -66-
Nguyễn Phú Khánh – ðà Lạt 063.28.78.79 hoặc 0989.80.78.79 http://www.maths.vn 1 1 c) y = f (x ) 3 2
= mx − (m − 1)x + 3(m − 2)x + có hoành ñộ cực ñại x , cực tiểu x thoả mãn 3 3 1 2 x + 2x = 1 . 1 2 d) y = f (x ) 3 2
= 2x + mx − 12x − 13 có ñiểm cực ñại, ñiểm cực tiểu cách ñều trục tung. e) 3 2
y = x − 3x + 3mx + 1 − m có cực trị mà hoành ñộ cực trị nhỏ hơn 2 ðáp số e) 0 < m < 1
10. Tìm m ñể ñồ thị của hàm số: x − + x + m a) y = f (x ) 2 3 =
có giá trị cực ñại , cực tiểu ñồng thời y − y = 4 x − 4 CT CÑ b) 3 y = x + (m − ) 2 x + ( 2 m − m + )x − ( 2 2 1 4 1
2 m + 1) có cực ñại , cực tiểu x ,x thỏa mãn ñiều 1 2 1 1 1 kiện + = (x + x 1 2 ) x x 2 1 2 m c) 3 y = x − (m + ) 2
1 x + (m − 5)x − 1 có cực ñại , cực tiểu x ,x ñồng thời hoành ñộ cực ñại, 3 1 2 x
 x + 3 x + x − 4 < 0 1 2 ( 1 2)
cực tiểu thỏa mãn ñiều kiện  2 2 x + x > 24  1 2  d) 3 2
y = x − 6x + 3mx + 2 − m có ñiểm cực ñại M x ;y và ñiểm cực tiểu M x ;y thỏa mãn 2 ( 2 2 ) 1 ( 1 1 ) y − y ñiều kiện 1 2 ( < 0 x − x x x + 2 1 2 ) ( 1 2 ) ðáp số : a) m = 3 1 c) − < m < 0 b) m = 1 ∨ m = 5 7 d) −2 < m < 4
11. Tìm m ñể ñồ thị của hàm số: a) y = f (x ) 3 2
== 2x + mx − 12x − 13 có cực ñại , cực tiểu và các ñiểm cực ñại , cực tiểu cách ñều trục Oy 3m b) y = f (x ) 3 2 = x −
x + m có cực ñại , cực tiểu nằm về hai phía của ñường phân giác thứ 2
nhất mặt phẳng toạ ñộ của hệ Oxy . x + mx − m + c) y = f (x ) 2 8 =
có cực ñại , cực tiểu nằm về hai phía ñường thẳng x − 1 9x − 7y − 1 = 0 . d) y = f (x ) 3 2
= 2x + 3(m − 1)x + 6(m − 2)x − 1. có ñường thẳng ñi qua cực ñại , cực tiểu song
song với ñường thẳng y = x − + 2009 -67-
Nguyễn Phú Khánh – ðà Lạt 063.28.78.79 hoặc 0989.80.78.79 http://www.maths.vn e) 3 2
y = f (x) = 2x + 3(m − 1)x + 6m(1 − 2m)x có cực ñại , cực tiểu thuộc ñường thẳng y = 4 − x . 1 1 f ) y = f (x ) 3 2
= x + x + mx ñạt cực ñại và cực tiểu tại các ñiểm có hoành ñộ x > m 3 2 2 mx + 3mx + 2m + 1 g) y =
có cực ñại , cực tiểu ñồng thời hai ñiểm cực trị nằm về hai phía ñối với x − 1 trục Ox . Hướng dẫn : f ) 2
y ' = x + x + m = 0 có 2 nghiệm phân biệt x , x thoả mãn m < x < x 1 2 1 2   1 ∆ = 1 − 4m > 0 m  <   ⇔ 1  .y ' (m) 4 2 = m + 2m > 0 ⇔ m  < 2
− ∨ m > 0 ⇔ m < −2   S 1 1  = − > m m  < −  2 2  2 g) 0 < m < 4 -68-