Đáp án kiểm tra lần 2 Môn Xác suất Thống kê - Ứng dụng | Trường đại học sư phạm kỹ thuật TP. Hồ Chí Minh
Nghi ngờ lượng nước ngọt được đóng vào chai 2 lít của nhà máy M bị thiếu, người ta kiểm tra 660 chai nước ngọt loại này của nhà máy M và tính được lượng nước ngọt trung bình là 1,985 lít và độ lệch chuẩn mẫu là 0,055 lít. Hãy kết luận về nghi ngờ nói trên với mức ý nghĩa 3%. Bài làm: Gọi a là lượng nước ngọt trung bình được đóng vào chai. Ta cần kiểm định giả thiết H: a = 2 với đối thiết K2 Tài liệu giúp bạn tham khảo, ôn tập và đạt kết quả cao. Mời bạn đọc đón xem!
Môn: Xác suất thống kê (Toán 2) 34 tài liệu
Trường: Đại học Sư phạm Kỹ thuật Thành phố Hồ Chí Minh 3.9 K tài liệu
Tác giả:
Preview text:
Kiểm tra môn: Xác suất Thống kê UD
1. Để nghiên cứu tuổi thọ X của một loại sản phẩm người ta điều tra ngẫu nhiên một số sản phẩm loại
này và thu được bảng số liệu
Tuổi thọ (tháng) 104-105 105-106 106-107 107-108 108-109 109-110 110-111 Số sản phẩm 18 21 35 43 32 23 15
a) Hãy ước lượng tuổi thọ trung bình của loại sản phẩm này với độ tin cậy 97%.
b) Tỷ lệ sản phẩm có tuổi thọ dưới 106 tháng, với độ tin cậy 95%, tối đa là bao nhiêu? Bài làm: a)
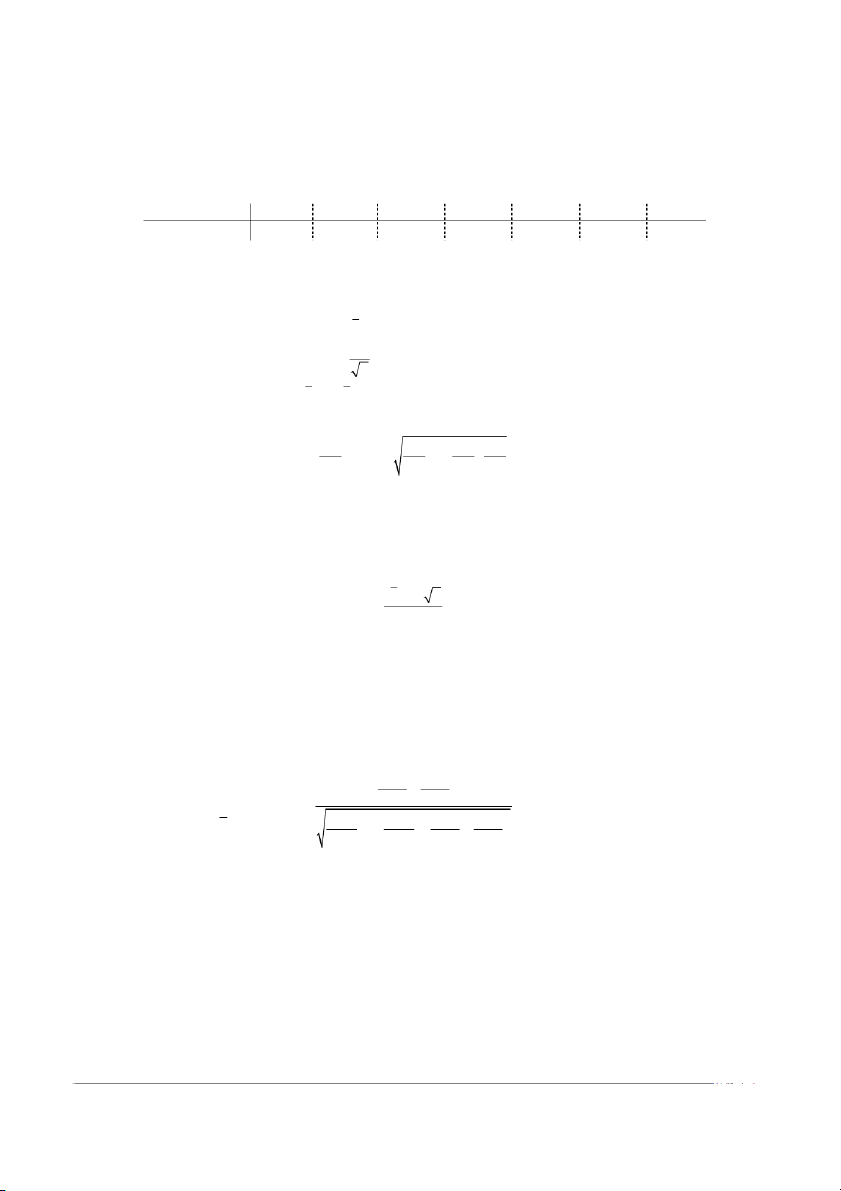
n = 187, x = 107, 4572193, s = 1, 703345467 s e = 2,17 = 0, 270297276 n
(x -e; x +e ) = (107,186922; 107,727516 )5
b) Tỷ lệ sản phẩm có tuổi thọ dưới 106 tháng, với độ tin cậy 95%, tối đa là 39 39 æ 39 ö 1 + 1,6449 1- = 0, 257425914 ç ÷ 187 187 è 187 ø187
2. Nghi ngờ lượng nước ngọt được đóng vào chai 2 lít của nhà máy M bị thiếu, người ta kiểm tra 660
chai nước ngọt loại này của nhà máy M và tính được lượng nước ngọt trung bình là 1,985 lít và độ
lệch chuẩn mẫu là 0,055 lít. Hãy kết luận về nghi ngờ nói trên với mức ý nghĩa 3%.
Bài làm: Gọi a là lượng nước ngọt trung bình được đóng vào chai.
Ta cần kiểm định giả thiết H: a = 2 với đối thiết K2: a < 2 ( x - 2) n
Ta có: a = 0, 03; ta - » za = 1,8808; t = = 7 - ,0065 < -t , n 1 a , n 1 - s Bác bỏ H, chấp nhận K ể ế ậ ờ ớ ứ ĩa là đúng
2 và có th k t lu n nghi ng nói trên v i m c ý ngh 3%
3. Điều tra ngẫu nhiên 1100 sản phẩm sản xuất theo phương pháp công nghệ thứ nhất thấy có 53 phế
phẩm. Điều tra ngẫu nhiên 1000 sản phẩm sản xuất theo phương pháp công nghệ thứ hai thấy có 70
phế phẩm. Hãy so sánh tỷ lệ phế phẩm của hai phương pháp công nghệ này với mức ý nghĩa 2%.
Bài làm: Gọi p , p lần lượt là tỷ lệ phế phẩm sản xuất theo phương pháp công nghệ thứ nhất, thứ hai. 1 2
Ta cần kiểm định giả thiết H : p = p với đối thiết K1: p ¹ p 1 2 1 2 53 70 - Ta có: 1100 1000
a = 0,02; z = 2,3265; z = = 2 - ,1265 | Þ z |< 2,3265 Þ a 2 123 æ 123 ö æ 1 1 ö 1 - + ç ÷ç ÷ 2100 è 2100 ø 1 è 100 1000 ø
Chấp nhận H hay tỷ lệ phế phẩm của hai phương pháp công nghệ này như nhau với mức ý nghĩa 2%
4. Tỷ lệ sản phẩm phải bảo hành của nhà máy M trước cải tiến kỹ thuật là 5%. Sau cải tiến kỹ thuật, điều tra
ngẫu nhiên 590 sản phẩm của nhà máy này thấy có 15 sản phẩm phải bảo hành. Cải tiến kỹ thuật có hiệu quả
hay không với mức ý nghĩa 1%?
Bài làm: Gọi p là tỷ lệ sản phẩm phải bảo hành của nhà máy M sau cải tiến kỹ thuật.
Ta cần kiểm định giả thiết H: p = 0,05 với đối thiết K2: p < 0,05 æ 15 ö - 0,05 590 ç ÷ è 590 ø
Ta có: a = 0, 01; za = 2,3265; z = = 2,
- 739 < -za Þ Bác bỏ H, chấp nhận K2 0,05(1- 0, 05)
Vậy cải tiến kỹ thuật có hiệu quả với mức ý nghĩa 1%
Kiểm tra môn: Xác suất Thống kê UD
1. Để nghiên cứu tuổi thọ X của một loại sản phẩm người ta điều tra ngẫu nhiên một số sản phẩm loại
này và thu được bảng số liệu
Tuổi thọ (tháng) 114-115 115-116 116-117 117-118 118-119 119-120 120-121 Số sản phẩm 15 25 32 45 35 22 18
a) Hãy ước lượng tuổi thọ trung bình của loại sản phẩm này với độ tin cậy 99%.
b) Tỷ lệ sản phẩm có tuổi thọ dưới 118 tháng, với độ tin cậy 98%, tối thiểu là bao nhiêu? Bài làm: a)
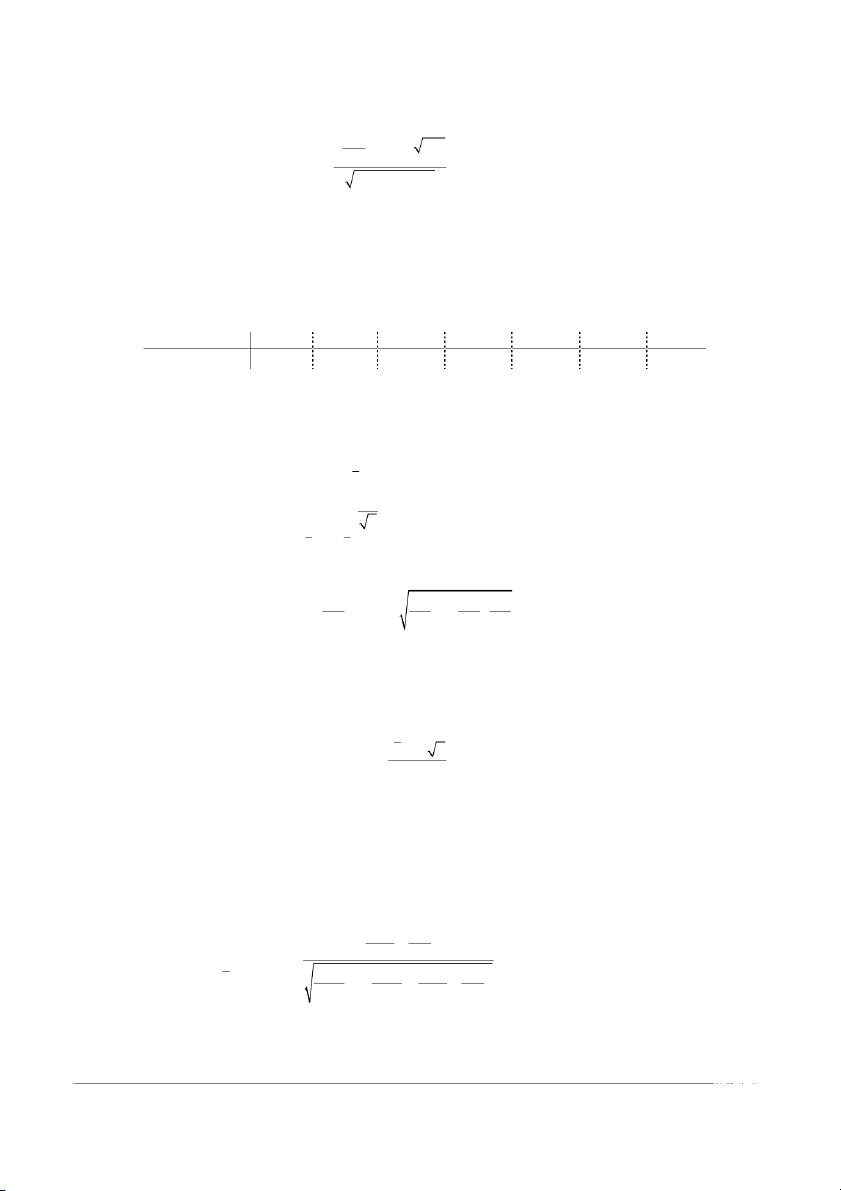
n = 192, x = 117,53125, s = 1, 699726649 s e = 2,576 = 0,315990719 n
(x -e; x +e ) = (117,2152593; 117,8472407)
b) Tỷ lệ sản phẩm có tuổi thọ dưới 118 tháng, với độ tin cậy 98%, tối thiểu là 117 117 æ 117 ö 1 - 2,0537 1 - = 0,537063274 ç ÷ 192 192 è 192 ø192
2. Nghi ngờ lượng nước ngọt được đóng vào chai 2 lít của nhà máy M bị thiếu, người ta kiểm tra 780
chai nước ngọt loại này của nhà máy M và tính được lượng nước ngọt trung bình là 1,987 lít và độ
lệch chuẩn mẫu là 0,056 lít. Hãy kết luận về nghi ngờ nói trên với mức ý nghĩa 2%.
Bài làm: Gọi a là lượng nước ngọt trung bình được đóng vào chai.
Ta cần kiểm định giả thiết H: a = 2 với đối thiết K2: a < 2 ( x - 2) n Ta có: a = 0, 02; t » z = 2,0537; t = = 6 - , 483397163 < -t a , n 1 - a a , n 1 - s Bác bỏ H, chấp nhận K ể ế ậ ờ ớ ứ ĩa là đúng
2 và có th k t lu n nghi ng nói trên v i m c ý ngh 2%
3. Điều tra ngẫu nhiên 1120 sản phẩm sản xuất theo phương pháp công nghệ thứ nhất thấy có 53 phế
phẩm. Điều tra ngẫu nhiên 990 sản phẩm sản xuất theo phương pháp công nghệ thứ hai thấy có 73
phế phẩm. Hãy so sánh tỷ lệ phế phẩm của hai phương pháp công nghệ này với mức ý nghĩa 3%.
Bài làm: Gọi p , p lần lượt là tỷ lệ phế phẩm sản xuất theo phương pháp công nghệ thứ nhất, thứ hai. 1 2
Ta cần kiểm định giả thiết H : p = p với đối thiết K ¹ 1: p p 1 2 1 2 53 73 - Ta có: 1120 990 a = 0,03; z = a 2,17; z =
= -2,555511762 Þ| z |> 2,17 Þ Bác bỏ H, 126 æ 126 ö æ 1 1 ö 2 1 - + ç ÷ç ÷ 2110 è 2110 ø è 1120 990 ø chấp nhận K1. 53 73 Vì f = < f =
nên p < p với mức ý nghĩa 3% 1 2 1 2 1120 990
4. Tỷ lệ sản phẩm phải bảo hành của nhà máy M trước cải tiến kỹ thuật là 5%. Sau cải tiến kỹ thuật, điều tra
ngẫu nhiên 540 sản phẩm của nhà máy này thấy có 15 sản phẩm phải bảo hành. Cải tiến kỹ thuật có hiệu quả
hay không với mức ý nghĩa 1%?
Bài làm: Gọi p là tỷ lệ sản phẩm phải bảo hành của nhà máy M sau cải tiến kỹ thuật.
Ta cần kiểm định giả thiết H: p = 0,05 với đối thiết K2: p < 0,05 æ 15 ö - 0,05 540 ç ÷ è 540 ø
Ta có: a = 0,01; z = 2,3265; z = = 2, - 369395511 < -z Þ a a
Bác bỏ H, chấp nhận K2 0,05(1- 0, 05)
Vậy cải tiến kỹ thuật có hiệu quả với mức ý nghĩa 1%