Đề cương giữa kỳ 1 Toán 9 năm 2023 – 2024 trường PT Thực hành Sư phạm – Đồng Nai
Giới thiệu đến quý thầy, cô giáo và các em học sinh lớp 9 đề cương ôn tập kiểm tra giữa học kỳ 1 môn Toán 9 năm học 2023 – 2024 trường Phổ thông Thực hành Sư phạm, tỉnh Đồng Nai. Mời bạn đọc đón xem.
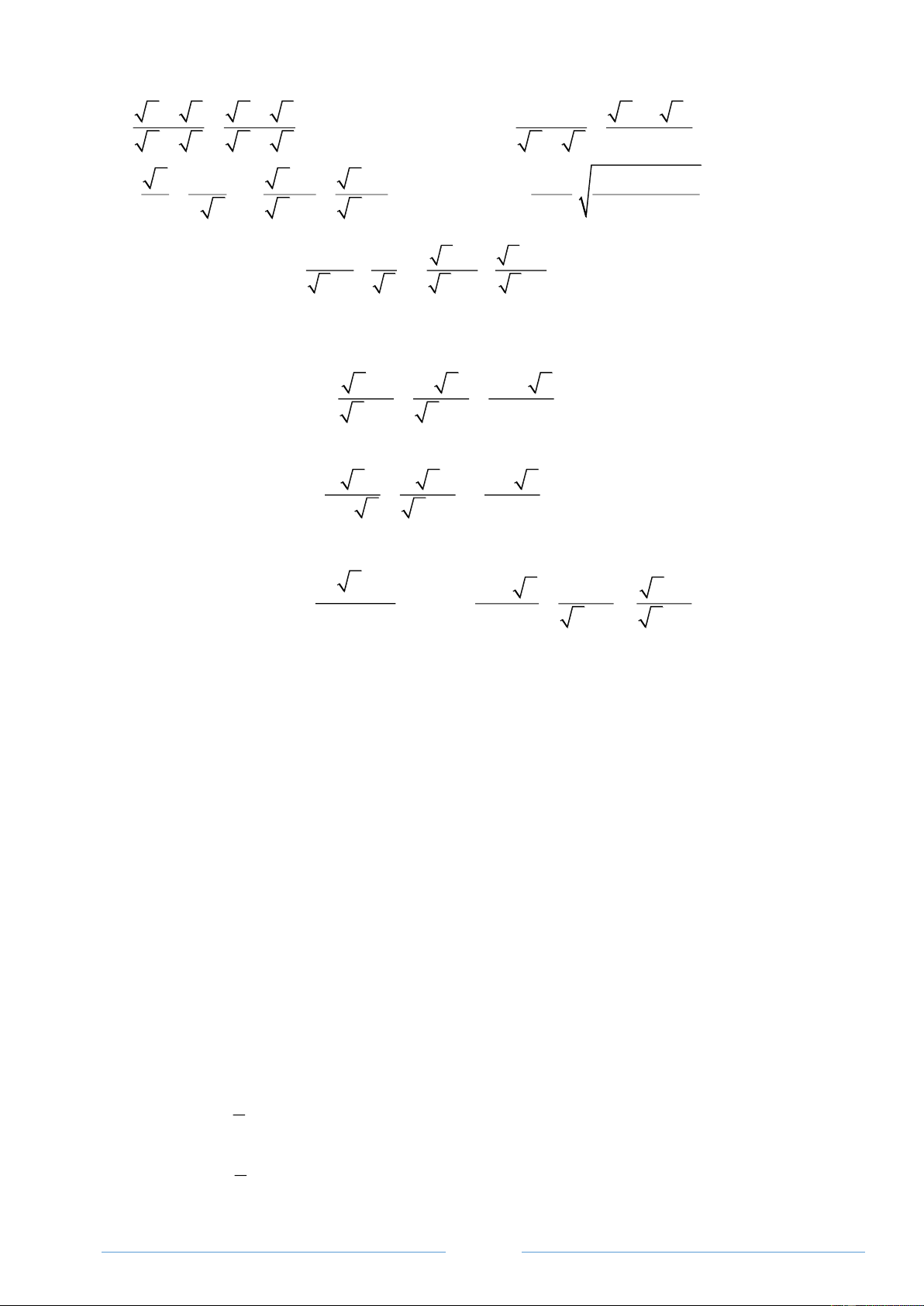
Preview text:
TRƯỜNG PT THỰC HÀNH SƯ PHẠM NĂM HỌC 2023 - 2024
ĐỀ CƯƠNG ÔN TẬP GIỮA KÌ I -TOÁN 9 NĂM HỌC 2023 - 2024 LÝ THUYẾT
Xem lại toàn bộ lý thuyết và BT trong SGK, SBT của chương I Đại số: Căn bậc hai. Căn
bậc ba và chương I Hình học: Hệ thức lượng trong tam giác vuông. BÀI TẬP THAM KHẢO PHẦN 1. ĐẠI SỐ
Bài 1. Với giá trị nào của x thì mỗi biểu thức sau có nghĩa: x x 1 a) − 3x + x − + − b) 4 − 2x c) 2 d) x 2 e) x − 2 x2 − 4 3 − 2x 2 − 4 f) g) x2 4 + 3 i) k) 3x + 4 l) 2 1 + x x + 1 x + 3
Bài 2. Thực hiện các phép tính sau: a) 12 + 2 27 + 3 75 − 9 48
b) (15 200 −3 450 + 2 50): 10 − − + c) 3 3 3 64 125 216 2 2 7 + 5 7 − 5 d) (5− 2 6) − (5+ 2 6) e) + f) 24 + 8 5 + 9 − 4 5 7 − 5 7 + 5 10 + 2 10 8 3 3 2 15 − 2 10 + 6 − 3 g) + h) ( 2 + ) 1 − ( 2 − ) 1 i) 5 + 2 1− 5 2 5 − 2 10 − 3 + 6
Bài 3. Giải các phương trình sau: 2x − 3 a) ( 9 x − ) 1 = 21 b) = 2 x −1 4 15 x −1 c) x 4 + 20 − 3 5+ x + x 9 + 45 = 6 d) x 25 − 25 − = 6+ x −1 3 2 9
e) x + x − 6 = 0 f) 2
x − 6x + 9 = 3 4x + 3 g) 3 x + 1 = 2 h) = 3 x +1 i) 2
x − 8x +16 = x + 2 k) 3x − 2 = 2 − 3
Bài 4. Chứng minh các đẳng thức sau: 2 a a +b b a + b a) ( − )+( + )2 2 2 3 2 1 2 2 − 2 6 = 9 b) − ab
=1(a,b 0;a b) a + b a − b 2 1− a a 1− a 4 4 c) + a = (
1 a 0; a ) 1 d) − = 8 − a 1 1 − a (2− 5)2 (2+ 5)2
Bài 5. Rút gọn các biểu thức sau: TRANG 1
TRƯỜNG PT THỰC HÀNH SƯ PHẠM NĂM HỌC 2023 - 2024 3 3 a + b a − b a − b a − b a) +
(a 0;b 0;a b) b) −
(a 0;b 0;a b) a − b a + b a − b a − b 2 2 4 a 1 a −1 a +1 a + b a b c) − . −
(a 0;a 1) d) .
(a + b 0;b 0) 2 2 2 2 2 a a + 1 a −1 b
a + 2ab + b 2 1 1 a +1 a + 2
Bài 6. Cho biểu thức : − : − =1 a −1 a a − 2 a −1
a) Tìm ĐKXĐ và rút gọn biểu thức A;
b) Tính giá trị của biểu thức A tại a = 16. c) Tìm a để A > 0. x + x + x
Bài 7: Cho biểu thức : 1 2 2 5 A = + + x − 2 x + 2 4 − x
a) Tìm ĐK để A có nghĩa và rút gọn P b) Tìm x để A = 2 x x + x
Bài 8 Cho biểu thức 6 P = + − 2 − x x + 2 4 − x
a) Tìm ĐKXĐ và rút gọn P. b) Tìm GTNN của P. 4( x + ) 1 15 − x 2 x +1
Bài 9 Cho biểu thức A = B = + :
(x 0; x 25) 25 − và x x − 25 x + 5 x − 5
a) Tính giá trị của biểu thức A khi x = 9 b) Rút gọn B.
c) Đặt P = A.B Tìm số thực x để P nhận giá trị nguyên PHẦN HÌNH HỌC
Bài 10. Giải tam giác vuông ABC tại A trong các trường hợp sau: a)
AB = 12 và AC = 16 . b) ˆ
B = 70 và AB = 20 .
c) C = 55 và BC = 10 .
(Độ dài làm tròn đến chữ số thập phân thứ hai, góc làm tròn đến phút)
Bài 11. Cho tam giác ABC vuông tại A, có AB = 10cm và AC = 15cm. a) Tính góc B.
b) Phân giác trong góc B cắt AC tại I. Tính AI.
c) Vẽ AH ⊥ BI tại H. Tính AH.
Bài 12 Tính giá trị của biểu thức a) 2 2 2 2 0 2 P sin 37 sin 42 sin 53 − sin 8 4 s n i 60 = − − + ; b) 2 2 2 2 2 Q cos 25 cos 35 cos 45 cos 55 cos 65 = − + − + .
Bài 13 Cho là góc nhọn. 2 a) Biết sin =
. Tính cos; tan; cot . 3 2
b) Biết cos = . Tính sin; tan; cot . 5 TRANG 2
TRƯỜNG PT THỰC HÀNH SƯ PHẠM NĂM HỌC 2023 - 2024
c) Biết tan = 9 . Tính cos; sin; cot . AB 3
Bài 14 Cho tam giác ABC vuông tại A, đường cao AH. Biết rằng = ; BC =125cm . AC 4 Tính HB, HC, AB, AC?
Bài 15 Cho tam giác ABC vuông ở A ; góc C bằng 30 độ, BC = 10cm. a) Tính AB, AC?
b) Từ A kẻ AM, AN lần lượt vuông góc với đường phân giác trong và ngoài của góc B.
Chứng minh MN//BC và MN = AB.
c) Chứng minh hai tam giác MAB và ABC đồng dạng. Tìm tỉ số đồng dạng?
Bài 16 Cho tam giác ABC vuông ở A, AB = 6cm, AC = 8cm. a) Tính BC, góc B, góc C?
b) Phân giác của góc A cắt BC tại D. Tính BD, CD?
c) Từ D kẻ DE và DF lần lượt vuông góc với AB, AC. Tứ giác AEDF là hình gì? Tính
chu vi và diện tích của tứ giác AEDF?
Bài 17. Cho tam giác ABC vuông tại A, đường cao AH. Gọi D, E lần lượt là hình chiếu của
H trên AB và AC. Biết BH = 4cm, HC = 9cm. a) Tính DE?
b) Chứng minh AD.AB = AE. AC
c) Các đường thẳng vuông góc với DE tại D và E lần lượt cắt BC tại M và N. Chứng
minh rằng: M là trung điểm BH và N là trung điểm CH. d) Tính diện tích DENM?
Bài 18. Cho tam giác ABC nhọn có góc A bằng 60 độ và K là trung điểm của AH. Các
đường cao AD, BE, CF cắt nhau tại H. Chứng minh rằng:
a) AE.AC = AF.AB và tam giác AEF đồng dạng với tam giác ABC. 1 b) 0
EKF = 120 và EF = BC 2
c) Trên BE và CF lần lượt lấy các điểm M và N sao cho 0
AMC = ANB = 90 . Chứng minh tam giác AMN cân. S d) DEF = − ( 2 2 2 1
cos A + cos B + cos C ) SABC Bài 19. Cho tam giác
ABC có góc A bằng 60 độ. Chứng minh rằng 2 2 2
BC = AB + AC − . AB AC
Bài 20. Một chiếc máy bay đang bay ở độ cao 10km. Khi bay hạ cánh xuống mặt đất đường
đi của máy bay tạo một góc nghiêng so với mặt đất.
a) Nếu phi công muốn tạo góc nghiêng 3 độ thì cách sân bay bao nhiêu km phải bắt đầu cho máy bay hạ cánh? TRANG 3
TRƯỜNG PT THỰC HÀNH SƯ PHẠM NĂM HỌC 2023 - 2024
b) Nếu cách sân bay 300km máy bay bắt đầu hạ cánh thì góc nghiêng là bao nhiêu?
Bài 21. Tàu ngầm đang ở trên mặt biển bỗng đột ngột lặn xuống theo phương tạo với mặt
nước biển một góc 21 độ.
a) Nếu tàu chuyển động theo phương lặn xuống dc 300m thì nó ở độ sâu bao nhiêu? Khi
đó khoảng cách theo phương nằm ngang so với nơi xuất phát là bao nhiêu?
b) Tàu phải chạy bao nhiên mét để đạt đến độ sâu 1000m? Bài 22. Tìm GTNN 2 2 2
x + y − 2xy + 2x − 2 y + 7 + 2 y − 8y + 2020
Bài 23. Giải phương trình: 2 2 2
3x + 6x + 7 + 5x +10x + 21 = 5 − 2x − x
Bài 24. Cho a,b,c >0 và abc = 1. Chứng minh rằng (a + ) 1 (b + ) 1 (c + ) 1 8
CHÚC CÁC EM THI THẬT TỐT. ☺☺☺ TRANG 4