

Preview text:
TRƯỜNG THCS THÀNH CÔNG NĂM HỌC 2022 - 2023
ĐỀ CƯƠNG ÔN TẬP GIỮA HỌC KÌ 1 MÔN: TOÁN 9 I. Nội dung ôn tập:
1. Đại số: Toàn bộ nội dung chương I : Căn bậc hai. Căn bậc ba
2. Hình học: Toàn bộ nội dung chương I: Hệ thức lượng trong tam giác vuông II. Bài tập tham khảo:
Bài 1: Tính giá trị của biểu thức sau (không dùng máy tính): a) 15. 33. 55 b) 2 5 80 125 180 4 3
c) ( 108 48 3 27 75) : 3 d) 2 27 6 75 3 5 8 50 e) 24 f) 5 2 6 5 2 6 3 3 1 4 g) 2
7 4 3 21 8 5 (2 5) h) 5 2 5 1 6 3 2 3 3 4 15 5 3 3 i) k) 13 4 3 2 1 2 1 3 1 2 5 1 3 2 3
Bài 2. Giải các phương trình sau: a) 3x 2 7 b) 2 4 1 x 8 0 3 2
c) 3 2x 5 8x 28 7 18x d) 16x 16 9x 9 4x 4 5 4 3 7 1 1 e) x 1 36x 36 9x 9 16 f) 2 4x 4x 1 3x 2 2 3 2 g) 2 x 6x 9 2x 4 h) x 2 x 1 3 i) x 4 x 4 2 k) 2 2
x 2x 1 x 4x 4 3
Bài 3. Rút gọn các biểu thức sau: x 1 1 x a) A với x > 0 x x x x 3 x 2 x 2 b) C
với x 0; x 4; x 9 x 2 3 x x 5 x 6 x 2 x 1 c) A với x 0; x 1 x x 1 x x 1 1 x 2 x 15 x 1 d) D : với x 0; x 25 x 5 25 x x 5 x 1 Bài 4. Cho biểu thức A = với x ≥ 0 x 2 1
a) Tính giá trị của biểu thức A khi x 4 2 3
b) Tìm giá trị của x để A = 2 1 1
c) Tìm giá trị của x để A >
d) Tìm giá trị của x để A < 3 x 2 e) So sánh A với – 1
f) So sánh A với A khi x > 1
g) CMR với 0 x 1 thì A A
h) Tìm các giá trị nguyên của x để A nhận giá trị nguyên
i) Tìm giá trị của x để A nhận giá trị là số tự nhiên x
k) Tìm giá trị lớn nhất của B A. x 1 2 x 5 x 4 x 2 Bài 5. Cho A = và B = với x 0; x 4 x 2 x 2 4 x x 2
a) Tính giá trị biểu thức A khi x = 9 b)Rút gọn biểu thức B 1
c) Đặt P = A.B . Tìm x để P = d) CMR: P < 3 2
e) Tìm số tự nhiên nhỏ nhất để P > -1
f) Tìm các số nguyên tố x để P < 0 a 1 1
Bài 6. Cho biểu thức: P với a 0;a 1 1 a 2 a 2 2 a 2 a) Rút gọn P
b) Tính P khi a 3 2 2 1 c) Tìm a để P
d) Tìm số nguyên a để P nhận giá trị nguyên 2 x 2 x 1 x 1 Bài 7. Cho A và B với x 0; x 1 x x 1 x x 1 x 1 x 1
a) Tính giá trị biểu thức B khi x = 9
b) Rút gọn biểu thức P = B:A
c) Tìm các giá trị nhỏ nhất của P
Bài 8. Cho tam giác ABC vuông tại A, đường cao AH. Biết HB = 9cm, HC = 16cm
a) Tính độ dài đoạn thẳng AH, AC b) Tính số đo góc ACB, CAH
c) Trên tia đối của tia AB, lấy điểm K sao cho 0
ACK 30 . Hãy tính các cạnh của ΔAKC
d) Vẽ AD là tia phân giác của góc
HAC (D thuộc BC). Gọi M là hình chiếu của C trên AD. 1 1 1 Chứng minh 2 2 2 CM CA CD
Bài 9. Cho tam giác ABC vuông tại A, đường cao AH, biết AB = 6cm, AC = 8cm a) Tính BH, AH
b) Vẽ HE AB tại E, HF AC tại F.
Chứng minh AE. AB = AF. AC, từ đó suy ra ΔAFE đồng dạng với ΔABC
c) Đường thẳng vuông góc với BC tại B cắt AC tại D. Trên BC lấy điểm K sao cho H là trung điểm của 2 BD AI
BK. Qua K vẽ đường thẳng song song với AH cắt AC tại I. Chứng minh BC AC
Bài 10. Cho tam giác ABC vuông tại A có AC = 8cm, 0 B 53
a) Giải tam giác vuông ABC (Kết quả làm tròn đến chữ số thập phân thứ hai)
b) Kẻ AH BC tại H. Đường thẳng vuông góc với AB tại B và vuông góc với AC tại C cắt nhau tại E.
Đường thẳng AH cắt BE tại D và cắt CE tại I. Tứ giác ABEC là hình gì?
c) Chứng minh ΔHBD đồng dạng với ΔHIC, từ đó suy ra AH2 = HD. HI
d) Gọi K là trung điểm của BC. Chứng minh 4HK2 = 2IB2 + 2IC2- BC2
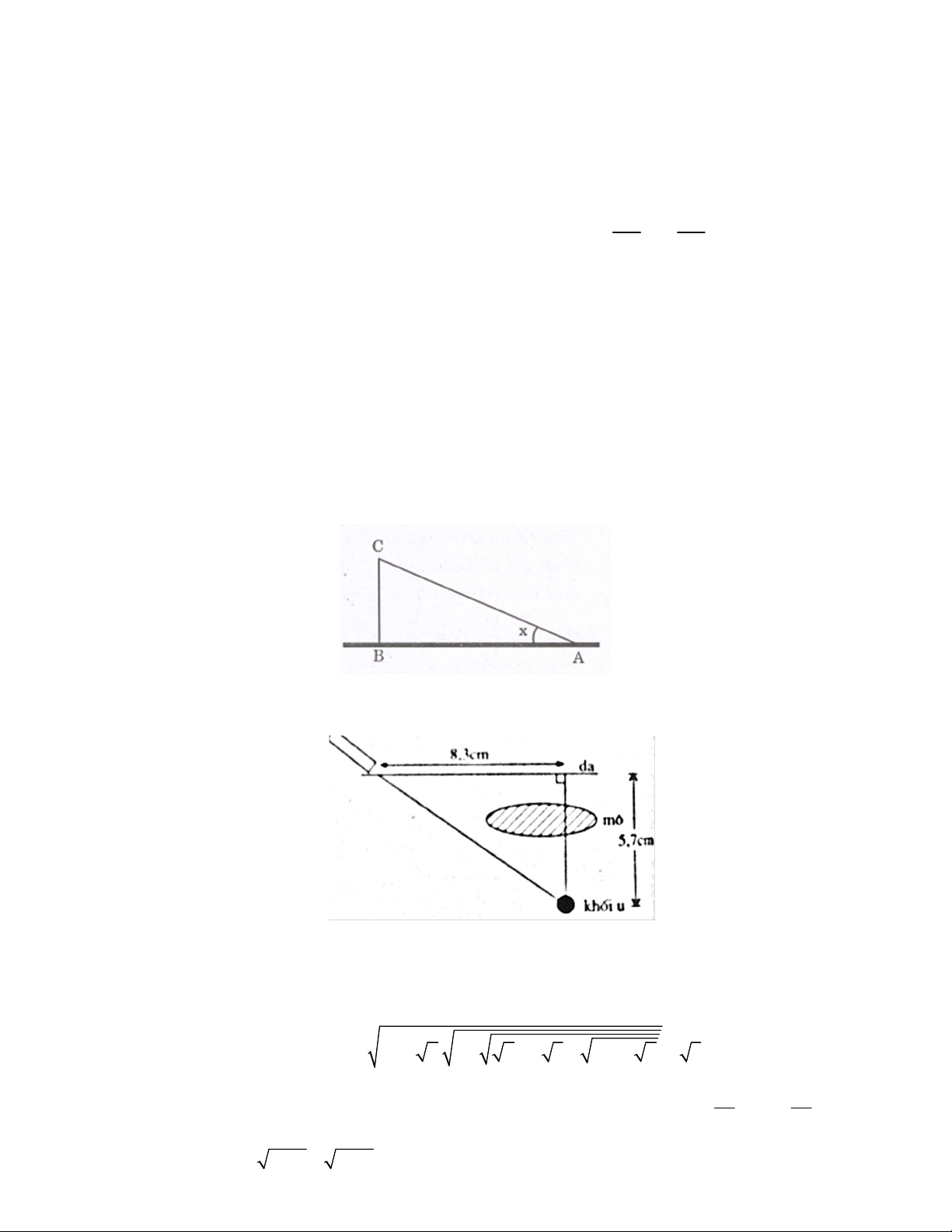
Bài 11. Một máy bay phản lực cất cánh từ vị trí A, bay lên với một góc x = 30° so với phương nằm ngang, sau
một khoảng thời gian 15 giây máy bay đạt được cao độ là BC = 3000 mét. Tính vận tốc trung bình của máy bay
(làm tròn đến hàng đơn vị).
Bài 12. Bác sĩ cần chiếu một chùm tia gamma để tiêu diệt khối u nằm dưới da 5,7cm. Để tránh làm tổn thương
mô, bác sĩ đặt nguồn tia cách khối u (trên mặt da) cách vị trí khối u 8,3cm (như hình vẽ)
a) Hỏi góc tạo bởi chùm tia với mặt da?
b) Chùm tia phải đi một đoạn dài bao nhiêu để đến được khối u?
Bài 13. Tính giá trị của biểu thức P 2013 2011 P 3x 5x
2006 với x 6 2 2. 3
2 2 3 18 8 2 3 1 1
Bài 14. Cho hai số dương x, y thỏa mãn x + y = 1. Tìm GTNN của biểu thức: 2 2 M x y 2 2 y x
Bài 15. Giải phương trình 2
4 x x 2 x 6x 11




