Đề giữa học kỳ 2 Toán 9 năm 2022 – 2023 trường THCS Phan Chu Trinh – Hà Nội

PHÒNG GD-ĐT QUẬN BA ĐÌNH
ĐỀ KIỂM TRA GIỮA HỌC KỲ II TRƯỜNG THCS PHAN CHU TRINH Năm học 2022- 2023 Môn: TOÁN 9 ĐỀ CHÍNH THỨC
Ngày kiểm tra: 30/03/2023
(Đề gồm 01 trang)
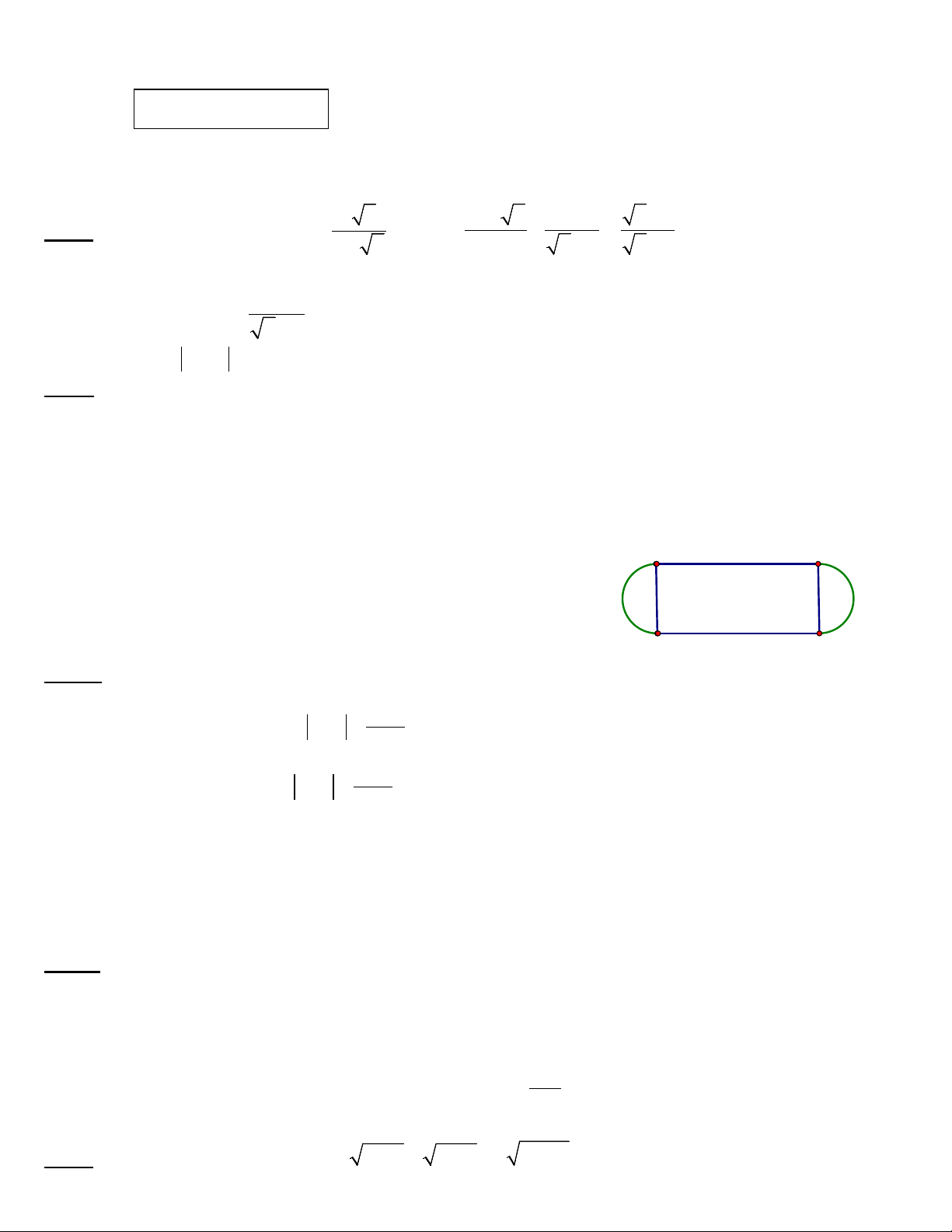
Thời gian làm bài: 120 phút 15− x 2  x + 3 Bài I: 2 ( x
2 điểm) Cho biểu thức: A = và B =  +  : (ĐKXĐ: x ≥ 0; x ≠ 25) 3+ x  x 25 x 5  − + x −   5
a) Tính giá trị của biểu thức A khi x = 9; 1 b) Chứng minh: B = ; x + 3
c) Tìm x để A− B > A− B .
Bài II: (2 điểm)
1) Giải bài toán bằng cách lập phương trình hoặc hệ phương trình
Theo kế hoạch, hai Tổ sản xuất phải làm được 330 sản phẩm. Nhưng khi thực hiện, do Tổ 1 làm vượt
mức kế hoạch 10%, Tổ 2 làm giảm 15% so với mức kế hoạch nên cả hai Tổ làm được 318 sản phẩm.
Tính số sản phẩm mà mỗi Tổ phải làm theo kế hoạch.
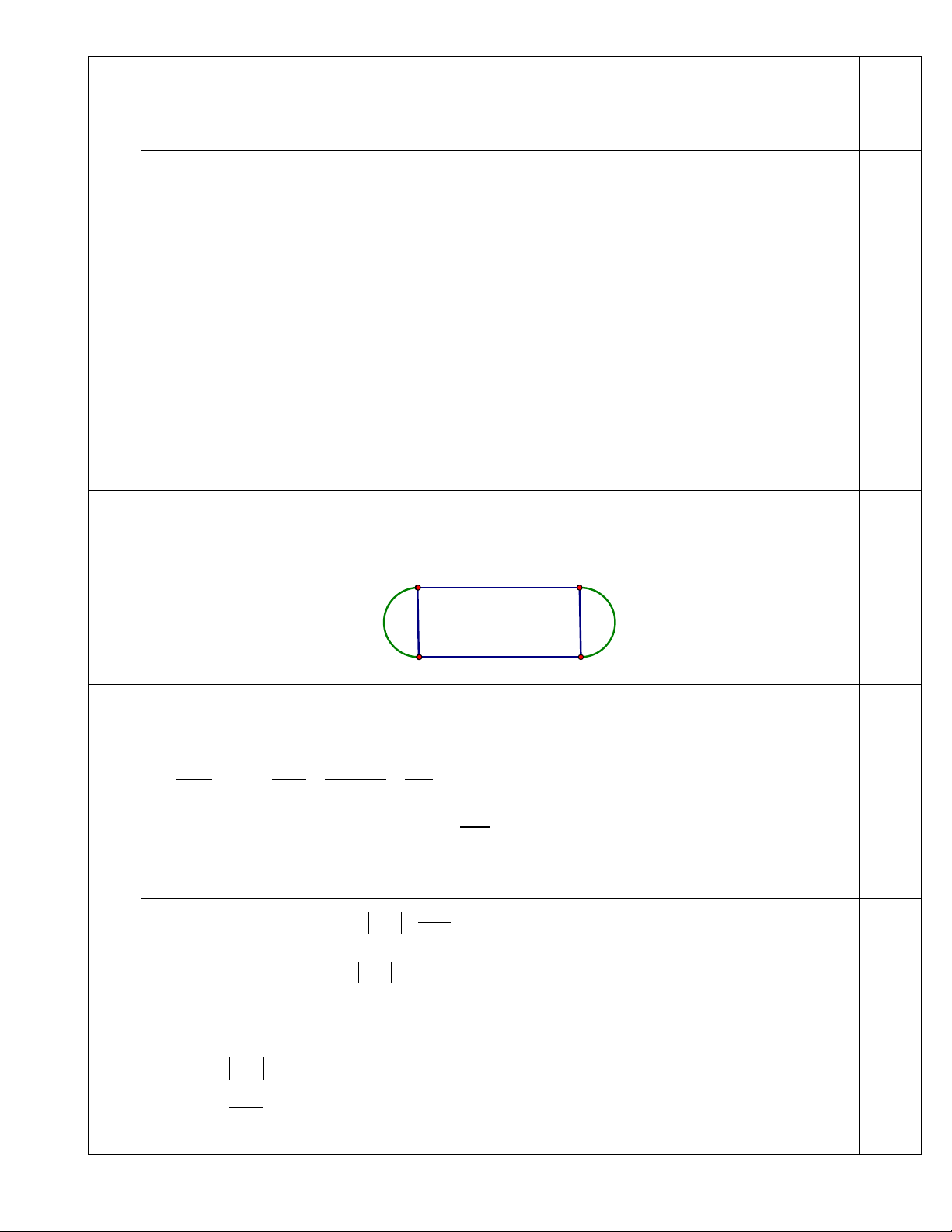
2) Một sân vận động có đường chạy đua dài 400m (hình A 100m B
bên). Đường chạy gồm các đoạn AB, CD và hai cung tròn
có đường kính là BC và AD. Biết ABCD là hình chữ nhật
và AB = 100m. Tính độ dài đường kính BC (lấy π ≈ 3,14;
kết quả làm tròn đến chữ số thập phân thứ 2) D C
Bài III: (2,5 điểm)  5 2 x −1 − = 3 −  y −1
1) Giải hệ phương trình:  2  x −1 + = 3  y −1
2) Trên mặt phẳng tọa độ Oxy cho đường thẳng (d): y = −x + 6 và parabol (P): 2 y = x .
a) Xác định tọa độ giao điểm A, B của (d) và (P) biết x < A B x ;
b) Vẽ (d) và (P). Gọi I là giao điểm của đường thẳng (d) với trục tung. Chứng minh rằng: S − = ∆ S AOI B ∆ OI 3 (đvdt).
Bài IV (3 điểm) Cho nửa đường tròn tâm (O) đường kính AB = 2R . Kẻ hai tiếp tuyến Ax, By với nửa đường
tròn. Gọi M là trung điểm của OA và lấy điểm N thuộc nửa đường tròn sao cho NA < NB. Đường thẳng đi
qua N và vuông góc với MN cắt Ax, By lần lượt tại C và D.
a) Chứng minh tứ giác MNDB nội tiếp; 2 b) Chứng minh:  ANM = 
BND và AC.BD = AM.BM = 3R ; 4
c) Xác định vị trí của N trên nửa (O) sao cho diện tích ∆ CMD đạt giá trị nhỏ nhất.
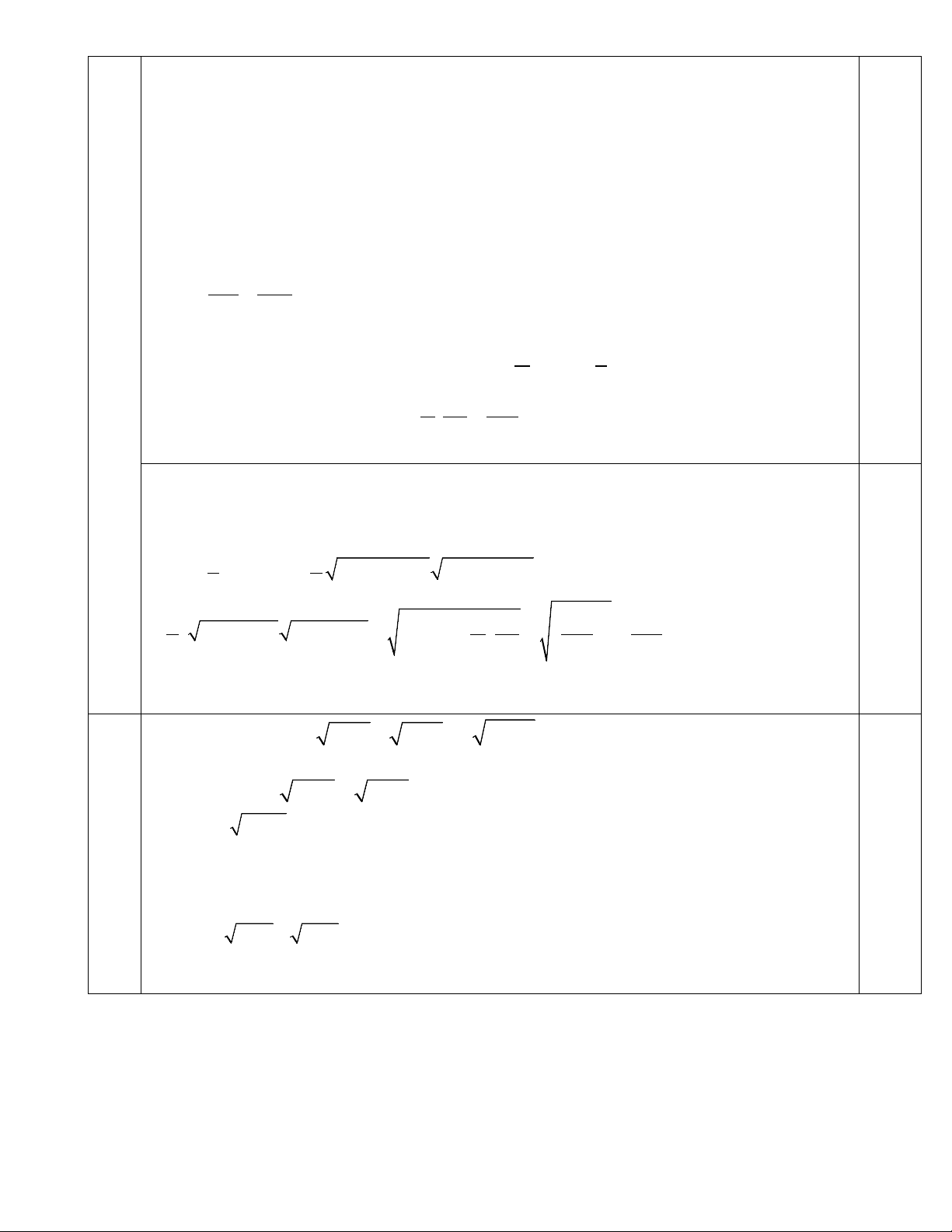
Bài V: (0,5 điểm) Giải phương trình: 2
x + 2 + x − 2 + 2 x − 4 = 2(3− x)
--------------------------Hết ------------------------
HƯỚNG DẪN CHẤM ĐỀ KIỂM TRA GIỮA KỲ 2 MÔN TOÁN 9 – PCT (2022-2023) Bài Nội dung Điểm I 2 x  −  A + = và 15 x 2 x 3 B =  +  :
(ĐKXĐ: x ≥ 0; x ≠ 25) 3+ x  x 25 x 5  − + x − 2,0   5
a) Tính giá trị của biểu thức A khi x = 9 0,5
Thay x = 9 (TMĐK) vào biểu thức A ta có : 2 9 6 0,25 A = = = 1 3+ 9 6 Vậy khi x = 9 thì A = 1 0,25 1 1 b) Chứng minh : B = x + 3 15− x 2  x + 3 B =  +  :   x − 25 x + 5 x −   5  15 x 2  − x + 3 B  0,25  (  = +  x − 5)( x +5) : x + 5  x − 5 
15 − x + 2 x −10 x + 3 B = ( 0,25
x − 5)( x +5) : x −5 x + 5 x − 5
B = ( x −5)( x +5). x +3 0,25 1 B = x + 3 (đpcm) 0,25
c) Tìm x để A− B > A− B 0,5 2 x 1 2 x −1 A − B = − = 3+ x x + 3
x + 3 (x ≥ 0; x ≠ 25) − A x
− B > A − B <=> 2 1
A − B < 0 ⇔ < 0 x + 3
=> Tử mẫu trái dấu (1) 0,25
Xét mẫu : Với mọi x thỏa mãn ĐK có :
x ≥ 0 ⇒ x ≥ 0 ⇔ x + 3 ≥ 3 > 0 => Mẫu dương (2) 1 1
2 x −1< 0 ⇔ x < ⇔ x <
Từ (1) và (2) => Tử âm => 2 4
A − B > A − B 1 0 ≤ x < 0,25
Kết hợp điều kiện: x ≥ 0; x ≠ 25 ta có:  4
Giải bài toán sau bằng cách lập hệ phương trình hoặc lập phương trình
II.1 Theo kế hoạch, hai Tổ sản xuất phải làm được 330 sản phẩm. Nhưng khi thực hiện, do
Tổ 1 làm vượt mức kế hoạch 10%, Tổ 2 làm giảm 15% so với mức kế hoạch nên cả hai
Tổ làm được 318 sản phẩm. Tính số sản phẩm mà mỗi Tổ phải làm theo kế hoạch. 1,5
Gọi số sản phẩm Tổ 1 phải làm theo kế hoạch là x (sp) (x ∈ N*, x <330) 0,25
Gọi số sản phẩm Tổ 2 phải làm theo kế hoạch là y (sp) (x ∈ N*, y <330)
Vì tổng số sản phẩm của hai Tổ là 330 nên ta có phương trình : x + y = 330 (1) 0,25
Số sản phẩm thực tế của Tổ 1 là : x + 10%x = 110%x (sản phẩm)
Số sản phẩm thực tế của Tổ 2 là: y – 15%y = 85%y (sản phẩm) 0,25
Vì thực tế cả hai Tổ làm được 318 sản phẩm nên ta có phương trình : 110% x + 85%y = 318 0,25
Từ (1) và (2) ta có hệ phương trình :  x + y = 330  x + y = 0 33  ⇔ 110% x + 85%y =  1 3 8 1, 
 1x + 0,85y = 318 0,25 x = 150(tm)
Giải hệ phương trình được  0,25  y = 180(tm)
Vậy theo kế hoạch Tổ 1 phải làm 150 sản phẩm, Tổ 2 phải làm 180 sản phẩm
II.2 Một sân vận động có đường chạy đua dài 400m (hình bên). Đường chạy gồm các 0,5
đoạn AB, CD và hai cung tròn bằng nhau có đường kính là BC và AD. Biết ABCD là
hình chữ nhật và AB = 100m. Tính độ dài đường kính BC. A 100m B D C
Vì AB = CD là hình chữ nhật => AB = DC = 100 (m)
Độ dài mỗi cung tròn AD, BC là: (400 – 100 – 100) : 2 = 100 (m) 0,25
Bán kính của mỗi cung tròn là: π Rn 180l 180.100 100 l = => R = = = (m) 180 π n π.180 π
Độ dài đường kính BC là: BC = 2R = 200 ≈ 63,69(m) π 0,25
Vậy đường kính BC là khoảng 63,69(m) III 2,5  5 2 x −1 − = 3 − 
1)Giải hệ phương trình:  y −1 1  2  x −1 + = 3  y −1 ĐKXĐ: y ≠ 1 a = x −1  0,25 
1 (a ≥ 0,b ≠ 0) Đặt b = 
thì hệ phương trình đã cho tương đương  y −1
2a −5b = 3 −
2a −5b = 3 −  9b = 9  b =1 a = 1(tm)  ⇔  ⇔  ⇔  ⇔ a 2b 3   2a 4b 6  a 2b 3  a 2.1 3  + = + = + = + = b = 1(tm) 0,25 Trả lại biến cũ:
a =1<=> x −1 =1 => x −1 = 1 ± => x ∈{2;0} 1 b =1<=>
= 1 => y −1 =1 => y = 2 0,25 y −1
Vậy hệ phương trình nghiệm ( ;x y)∈{(2;2);(0;2 } ) 0,25
1) Trên mặt phẳng tọa độ Oxy cho đường thẳng (d): y = -x + 6 và parabol (P): y = x2. 1,5
a) Xác định tọa độ giao điểm A, B của (d) và (P) biết xA < xB 0,5
Xét phương trình hoành độ giao điểm của (P) và (d): x2 = -x + 6  x2 + x – 6 = 0  (x – 2)(x+3) = 0
 x = 2 hoặc x = -3 (Hs có thể tính delta để tìm nghiệm) 0,25
Vì xA < xB nên xA = -3; xB = 2
Thay x vào (P) ta tìm được y A = 9 và yB = 4 0,25
Vậy (d) cắt (P) tại 2 điểm A(–3; 9) và B(2; 4)
b) Lập bảng và vẽ đúng đồ thị 2 hàm số: 0,5 Chứng minh rằng: S − = (đvdt) 0.5 ∆ S AOI B ∆ OI 3
Hạ AE ⊥ Oy tại E, BF ⊥ Oy tại F.
Tính được OI = 6 (đvđd); AE = 3(đvđd); BF = 2 (đvđd) 0,25
Tính được S∆AOI = 9 (đvdt); S∆BOI = 6 (đvdt)
Vậy S∆AOI - S∆BOI = 3(đvdt) 0,25
IV Cho nửa đường tròn tâm (O) đường kính AB = 2R. Kẻ hai tiếp tuyến Ax, By với nửa
đường tròn. Gọi M là trung điểm của OA và lấy điểm N thuộc nửa đường tròn sao cho
NA < NB. Đường thẳng đi qua N và vuông góc với MN cắt Ax, By lần lượt tại C và D. 3,0
Vẽ hình đúng đến câu a: 0,25 x y C N D A M O B
a) Chứng minh tứ giác MNDB nội tiếp 0,75 Chứng minh góc MBD = 900 0,25 Chứng minh góc MND = 900 0,25
Chứng minh tứ giác MNDB nội tiếp 0,25 2 b) 1,25
Chứng minh:  = 
ANM BND và AC.BD = AM.BM = 3R 4
• Xét (O) có góc ANB là góc nội tiếp chắn nửa đường tròn =>  0 ANB = 90   +  0 ANM MNB = 90 (1)
Có CD ⊥ MN tại N =>  0
MND = 90 =>  +  0 MNB BND = 90 (2)
Từ (1) và (2) =>  =  ANM BND 0.25
• Xét đường tròn ngoại tiếp tứ giác BMND có:  = 
BMD BND (2 góc nội tiếp cùng chắn cung BD) Mà  =  ANM BND (cmt) 0.25   =  BMD ANM
• Xét tứ giác ACNM có:  +  0 0 0 CAM CNM = 90 + 90 =180
Mà hai góc ở vị trí đối nhau
 Tứ giác ACNM nội tiếp   = 
ACM ANM (2 góc nội tiếp cùng chắn cung AM) Lại có:  =  BMD ANM 0.25   =  ACM BMD Xét ∆ CAM và ∆ MBD có:  =  0 CAM MBD = 90  =  ACM BMD (cmt)  ∆ CAM ~ ∆ MBD (g-g)  CA AM = (các cạnh tương ứng) MB BD 0.25  CA.BD = MB.AM
• Vì M là trung điểm của AO => R 3
AM = ; BM = R 2 2 2 0.25
• Vậy CA.BD = MB.AM = R 3R 3 . R = 2 2 4
c) Xác định vị trí của N trên nửa (O) sao cho diện tích ∆ CMD đạt giá trị nhỏ nhất 0.75
Chứng minh được: ∆ CMD vuông tại M 0.25 1 1 2 2 2 2 S = CM ⋅ MD = AC + AM BM + BD CMD 2 2 2 2 2 1 R 3R  3R  3 0.25 ≥ ⋅ 2 ⋅ 2 R AC AM
BM ⋅ BD = AC ⋅ BD ⋅ ⋅ =   = 2 2 2  4  4
Dấu “=” xảy ra khi AC = AM và BD = BM => ∆ ACM và ∆ BDM vuông cân 0.25
Vậy N là giao điểm của nửa (O) với đường thẳng vuông góc với AB tại M V Giải phương trình: 2
x + 2 + x − 2 + 2 x − 4 = 2(3− x) (1) 0.5 ĐKXĐ: x ≥ 2
Đặt ẩn phụ: t = x + 2 + x − 2(t ≥ 0) 2 2
t = 2x + 2 x − 4  = 0,25 PT (1) t 2(TM )  2
t + t = 6  2t + t − 6 = 0 <=>  t = 3( − KTM ) Trả lại biến cũ:
t = 2 <=> x + 2 + x − 2 = 2  x =2 (TMĐK) 0.25
Vậy phương trình có nghiệm: S = {2}
HS làm cách khác đúng vẫn cho điểm tối đa.
Document Outline

• Đề giữa học kì 2 Toán 9 năm 2022 – 2023 trường THCS Phan Chu Trinh – Hà Nội
• HDC giữa học kì 2 Toán 9 năm 2022 – 2023 trường THCS Phan Chu Trinh – Hà Nội