Đề giữa kì 2 Toán 9 năm 2022 – 2023 trường THCS Trưng Vương – Hà Nội
Giới thiệu đến quý thầy, cô giáo và các em học sinh lớp 9 đề tham khảo kiểm tra giữa học kỳ 2 môn Toán 9 năm học 2022 – 2023. Mời bạn đọc đón xem.
Preview text:
PHÒNG GIÁO DỤC VÀ ĐÀO TẠO KIỂM TRA GIỮA KÌ II QUẬN HOÀN KIẾM NĂM HỌC 2022 – 2023 TRƯỜNG THCS TRƯNG VƯƠNG Môn: TOÁN ĐỀ CHÍNH THỨC Ngày thi: 11/03/2023
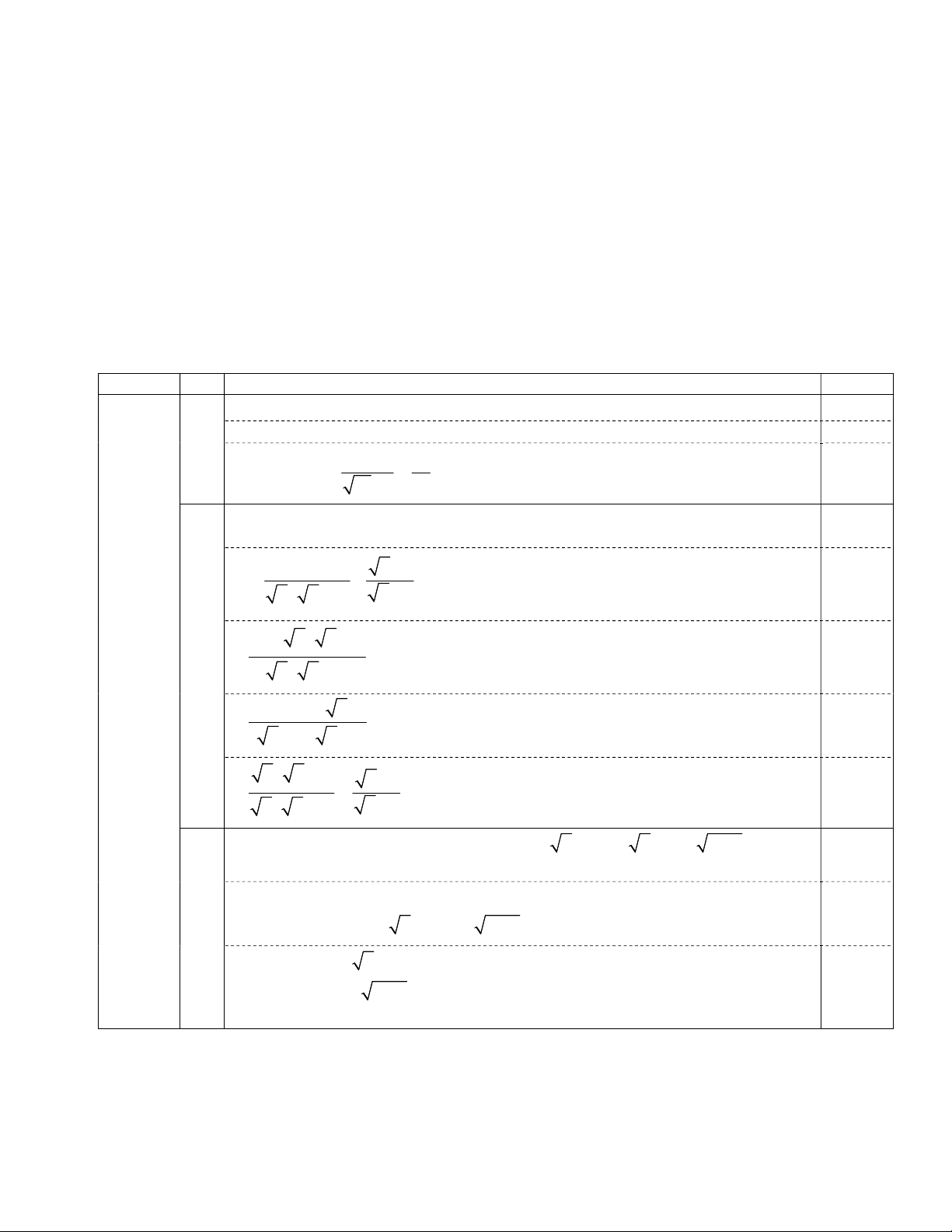
Thời gian làm bài: 90 phút Bài I (2,0 điểm) x 5 2x x 1 Cho hai biểu thức A và B
với x 0, x 1, x 9. x 1 x 3 x 3 x
1) Tính giá trị của biểu thức A khi x 16. 2) Rút gọn biểu thức . B
3) Tìm tất cả các giá trị của x sao cho A .
B x 34 x 1 2 x 4.
Bài II (2,0 điểm) Giải toán bằng cách lập hệ phương trình:
Hai lớp 9A và 9B có tổng cộng 95 học sinh. Trong đợt quyên góp vở ủng hộ các bạn học sinh nghèo, bình quân
mỗi bạn lớp 9A ủng hộ 3 quyển, mỗi bạn lớp 9B ủng hộ 4 quyển, vì vậy cả hai lớp ủng hộ 330 quyển. Tính số học sinh mỗi lớp. Bài III (2,5 điểm)
3x 1 y 1 5
1) Giải hệ phương trình: . 2 3x 1 y 1 4
2) Trong mặt phẳng tọa độ Oxy cho Parabol P 2
: y x và đường thẳng d : y 2x 3.
a) Vẽ parabol P và đường thẳng d trên cùng một mặt phẳng tọa độ.
b) Tìm tọa độ giao điểm ,
A B của d và P ( biết x x ) và tính diện tích tam giác OA . B A B Bài IV (3,0 điểm)
Cho tam giác ABC có ba góc nhọn nội tiếp đường tròn O; R. Trên cung nhỏ BC lấy điểm M sao cho
MB MC. Kẻ MI vuông góc với AB I AB và MH vuông góc với BC H BC .
1) Chứng minh tứ giác BIHM nội tiếp.
2) Gọi K là giao điểm của IH và AC. Chứng minh: MIK
MAK và MK vuông góc với AC.
3) Tìm vị trí của điểm M trên cung nhỏ BC để IK lớn nhất. Bài V (0,5 điểm)
Cho x, y, z là các số không âm thỏa mãn x y z 1. Tìm giá trị nhỏ nhất và giá trị lớn nhất của biểu thức
P 7x 9 7 y 9 7z 9.
…………..……. Hết ………………… Chúc con làm bài tốt.
PHÒNG GIÁO DỤC VÀ ĐÀO TẠO BÀI KIỂM TRA GIỮA KÌ II QUẬN HOÀN KIẾM TRƯỜNG THCS TRƯNG VƯƠNG NĂM HỌC: 2022-2023 Môn: Toán Ngày thi: 11/03/2023 HƯỚNG DẪN CHẤM HƯỚNG DẪN CHUNG
+) Điểm toàn bài để lẻ đến 0,25.
+) Các cách làm khác nếu đúng vẫn cho điểm tương ứng với biểu điểm của hướng dẫn chấm.
+) Các tình huống phát sinh trong quá trình chấm do Hội đồng chấm thi quy định, thống nhất bằng biên bản. Bài Ý Đáp án Điểm
Tính giá trị của biểu thức A khi x 16. 0,5
Thay x 16 (TMĐK) vào biểu thức . A 0,25 1) 16 5 21 Tính được A 7 0,25 16 1 3 Rút gọn biểu thức B 1,0 2x x 1 B 0,25 x x 3 x 3 2x x x 1 2) 0,25 x x 3 Bài I 2x x x 2,0 điểm 0,25 x 1 x 1 x x 1 x 1 0,25 x x 3 . x 3
Tìm tất cả các giá trị của x thỏa mãn . A .
B x 3 4 x 1 2 x 4 0,5
Điều kiện : x 4, x 9. 3) 0,25
Biến đổi được thành x 2 2 2 x 4 0. x 2 0 Lập luận để có x 4 (TMÐK) 2 x 4 0 0,25
Kết luận: x 4 là giá trị cần tìm. 1
Tính số học sinh mỗi lớp 9 , A 9B 2,0
Gọi số học sinh hai lớp 9 ,
A 9B lần lượt là x, y (học sinh). Điều kiện: x * , x, y 95. 0,25
Vì số học sinh hai lớp là 95 học sinh, ta có phương trình: x y 95. (1) 0,25
Số vở lớp 9A ủng hộ là 3x (quyển). Bài II
Số vở lớp 9B ủng hộ là 4y (quyển). 0,5 1) 2,0 điểm
Vì số vở hai lớp ủng hộ là 330 quyển. Ta có phương trình 3x 4y 330. (2) 0,25 x y 95
Từ (1) và (2) ta có hệ phương trình: 3x 4y 330 0,5
Giải hệ phương trình tìm được x 50 và y 45.
Đối chiếu điều kiện và kết luận. 0,25
Vậy số học sinh của lớp 9A là 50 học sinh, số học sinh của lớp 9B là 45 học sinh.
3x 1 y 1 5
Giải hệ phương trình: 2 3x 1 y 1 4 1,0 1 ĐKXĐ: x ; y 1 0,25 3 1) 3x 1 3 Giải ra được 0,25 y 1 2 10 x 3 . 0,25 y 3
Đối chiếu điều kiện và kết luận: Bài III
Vậy hệ phương trình có nghiệm là x y 10 ; ;3 . 0,25 2,5 điểm 3
Vẽ parabol (P) và đường thẳng (d) trên cùng một mặt phẳng tọa độ. 0,5 2a) Lập bảng giá trị 0,25 Vẽ P và d 0,25
Tìm tọa độ giao điểm A,B của (P) và (d). Tính diện tích tam giác OAB 1
Phương trình hoành độ giao điểm của (d) và (P) : 2 x 2x 3 0 (*) 0,25
Giải ra được x 1; x 3. 1 2
2b) Vì x x nên x y A A 2 1, 1 1. A B Suy ra: 2 x 3, y 3 9. 0,25 B B
Hai giao điểm của d và P là A 1 ; 1 , B 3;9.
Gọi giao điểm của d và Oy là C 0;3. 0,25
Kẻ AH, BK cùng vuông góc với O . y 2
AH x 1 1 (đvđd) , BK x 3 (đvđd). A B 1 1 S S S
AH.OC BK.OC 6 (đvdt). 0,25 OAB OAC OBC 2 2
Chứng minh tứ giác BIMH nội tiếp. 1,0 A
Vẽ đúng hình đến ý 1). 0,25 Chỉ ra BIM 90. 0,25 1) Chỉ ra BHM 90. 0,25 O I H C Xét tứ giác BIHM có: BIM BHM 90. B K
Mà I và H là hai đỉnh kề nên tứ giác BIHM nội 0,25 tiếp. M Chứng minh MIK MAK và MK AC. 1,5 Chứng minh được MIH MBH. 0,25 Chứng minh được MBH MAC. 0,25 2) Dẫn đến MIK MAK. 0,25 Vì MIK
MAK dẫn đến tứ giác AIMK nội tiếp. 0,25 Bài IV Suy ra: AIM AKM 180 . 0,25 3,0 điểm Do đó: MK AC. 0,25
Tìm vị trí của điểm M trên cung nhỏ BC để IK lớn nhất 0,5 A
Chứng minh: BMC đồng dạng với IMK (g-g). O I IK MI 0,25 H C BC MB B 3) K M
Mà MI MB (Quan hệ đường vuông góc và đường xiên) IK MI 1 IK BC. BC MB maxIK BC 0,25 MI MB IK max
M là điểm chính giữa cung BC. MK MC
Tìm giá trị nhỏ nhất và giá trị lớn nhất của biểu thức Bài V 0,5
P 7x 9 7 y 9 7z 9 0,5 điểm
Áp dụng BĐT Bunhiacopxki ta có: 0,25 3
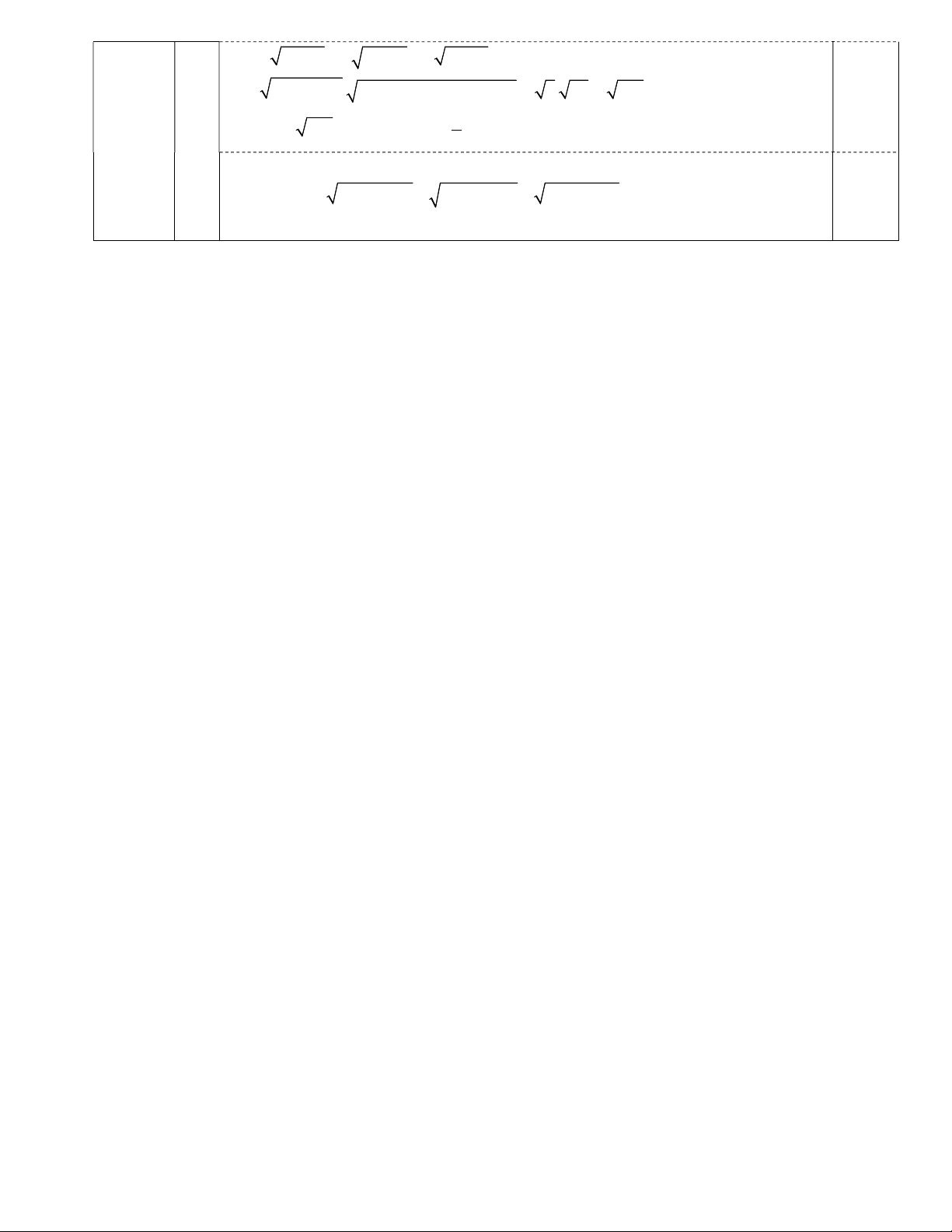
P 1. 7x 9 1. 7 y 9 1. 7z 9 2 2 2
1 1 1 . 7x 9 7 y 9 7z 9 3. 34 102 1
Max P 102 khi x y z . 3 Ta có 2 2 2
x, y, z 0, x y z 1 0 x, y, z 1 x x , y y , z z . Từ đó có 2 2 2
P x 6x 9 y 6y 9 z 6z 9 x 3 y 3 z 3 10. 0,25
min P 10 khi x, y, z là các hoán vị của 0;0; 1
…………..…… Hết …..…………… 4
Document Outline
- Đề thi giữa HK2 môn Toán 9 năm học 2022-2023 trường THCS Trưng Vương
- HDC đề thi giữa HK2 môn Toán 9 năm học 2022-2023 trường THCS Trưng Vương