Đề kiểm tra giữa học kỳ 2 Toán 9 năm 2021 – 2022 trường THCS Giảng Võ – Hà Nội

PHÒNG GD & ĐT BA ĐÌNH
ĐỀ KIỂM TRA GIỮA HỌC KỲ 2
TRƯỜNG THCS GIẢNG VÕ NĂM HỌC 2021-2022 Môn: TOÁN 9 ĐỀ CHÍNH THỨC Ngày kiểm tra: 11/3/2022
(Đề thi gồm 01 trang)
Thời gian làm bài: 90 phút
Bài I (2,0 điểm). Cho hai biểu thức: x − 2 x + 3 2 7 x − 6 A = và B = − −
với x  0; x  4. 2 x + 3 x + 2 2 − x x − 4
1) Tính giá trị của biểu thức A khi x = 16. B 2 x + 3
2) Cho biểu thức P = . Chứng minh: P = . A x + 2
3) Tìm tất cả giá trị của x để biểu thức P đạt giá trị nhỏ nhất.
Bài II (2,0 điểm). Giải bài toán bằng cách lập hệ phương trình
Một khu vườn hình chữ nhật có chu vi là 240m. Người ta dự định mở rộng khu vườn
bằng cách tăng chiều dài thêm 9 ,
m tăng chiều rộng thêm 7 ,
m sao cho khu vườn vẫn là hình
chữ nhật, do vậy diện tích khu vườn sẽ tăng thêm 2
963m . Tính chiều dài và chiều rộng của khu vườn ban đầu.
Bài III (2,5 điểm)  2 2 + = 6
x +1 y − 2
1) Giải hệ phương trình :  . 5 1  − = 3
x + 1 y − 2 2) Cho phương trình: 2 x − (m − ) 2 2
1 x + m − 3m = 0 (1) (x là ẩn số).
a) Giải phương trình (1) khi m = 5.
b) Tìm tất cả giá trị của m để phương trình (1) có hai nghiệm.
Bài IV (3,0 điểm). Cho đường tròn (O ) và điểm K nằm bên ngoài đường tròn (O). Kẻ hai tiếp tuyến K ,
A KB với đường tròn (O), A và B là các tiếp điểm. Từ điểm K vẽ đường
thẳng d cắt đường tròn (O ) tại hai điểm C,D (KC  K ,
D d không đi qua tâm O).
1) Chứng minh tứ giác KAOB là tứ giác nội tiếp.
2) Gọi giao điểm của đoạn thẳng AB với đoạn thẳng OK là M . Chứng minh 2
KA = KC.KD = KM.K . O
3) Chứng minh đường thẳng AB chứa tia phân giác của CMD.
Bài V (0,5 điểm) Cho ,
a b là các số dương thỏa mãn a + b = 3. Chứng minh rằng:  2  2 1 1 169
a +  + b +   .  b   a  18
…….……………Hết…………………. 2 HƯỚNG DẪN CHẤM Bài Ý Đáp án Điểm
Tính giá trị của biểu thức A khi x = 16. 0,5
Thay x = 16 (tmđk) vào biểu thức A 0,25 1) 16 − 2 2 Tính được A = = 0,25 2 16 + 3 11 B 2 x + 3 Cho biểu thức P = . Chứng minh: P = . 1,0 A x + 2 x + 3 2 7 x − 6 B = − − x + 2 2 − x x − 4 x + 3 2 7 x − 6 = + − x + 2 x − 2 ( x +2)( x −2) 0,25 ( x +3)( x −2) 2 ( x + 2) 7 x − 6 = + − 2)
( x +2)( x −2) ( x +2)( x −2) ( x +2)( x −2)
x − 2 x + 3 x − 6 + 2 x + 4 − 7 x + 6 x − 4 x + 4 = ( = x + 2)( x − 2) ( x +2)( x −2) 0,25 Bài I 2,0 điểm ( x − )22 x − 2 = ( = 0,25 x + 2)( x − 2) x + 2 B x − 2 2 x + 3 +  2 x 3 P = = .  P = 0,25 A x + 2 x − 2 x + 2
Tìm tất cả giá trị của x để biểu thức P đạt giá trị nhỏ nhất. 0,5 2 x + 3 2 x + 4 − 1 1 P = = = 2 − x + 2 x + 2 x + 2 1 1 x 
x  0  x + 2  2   0,25 3) Với 0 thì x + 2 2 1 3 3  2 −   P  . x + 2 2 2 3
Dấu “=” xảy ra khi x = 0 (TMĐK)  min P = khi x = 0 . 2 0,25
Vậy khi x = 0 thì P đạt giá trị nhỏ nhất.
Một khu vườn hình chữ nhật có chu vi là 240m. Người ta dự định mở Bài II
rộng khu vườn bằng cách tăng chiều dài thêm 9 ,
m tăng chiều rộng thêm 2,0 điểm 2,0 7 ,
m do vậy diện tích khu vườn sẽ tăng thêm 2
963m . Tính chiều dài và
chiều rộng của khu vườn ban đầu. 3
+) Gọi chiều dài của mảnh vườn là x (m) (x  0); chiều rộng của 0,25
mảnh vườn là y (m) (y  0,x  y).
+) Vì chu vi mảnh vườn là 240m nên ta có phương trình
2(x + y) = 240 = x + y = 120. 0,25
+) Chiều dài sau khi mở rộng là x + 9 (m); chiều rộng sau khi mở rộng 0,25 là y + 7 (m).
+) Diện tích mảnh vườn ban đầu là xy ( 2
m );diện tích mảnh vườn sau 0,25
khi mở rộng là (x + ) (y + ) ( 2 9 7 m ).
+) Vì diện tích khu vườn sẽ tăng thêm 2
963m , nên ta có phương trình: ( 0,25
x + 9)(y + 7) − xy = 963 = 7x + 9y = 900.
+) Ta có hệ phương trình: x  + y = 120 7
 x + 7y = 840 x  + y = 120  =  =  0,25 7x + 9y = 900 7x + 9y = 900 2y = 60    x  + y = 120 x  = 90 =  =  (TMĐK) y = 30 y = 30 0,25  
Vậy chiều dài, chiều rộng của khu vườn ban đầu lần lượt là 90 ; m 30 . m 0,25  2 2 + = 6
x +1 y − 2
Giải hệ phương trình :  (I ) 5 1 1,0  − = 3
x + 1 y − 2 Điều kiện x  1 − ;y  2. 0,25  1 1  + = 3 1 + 1 = 3 (   I ) x + 1 y − 2   x + 1 y −   2 5 1 0,25 6 1)  − = 3  = 6
x + 1 y − 2 x + 1 Bài III  1  1 2,5 điểm  1 + =  1  3 =  2 y − y − 2 =    2 y −   2   2 0,25  1 =  1 = x + 1 = 1  1 1   x + 1 x + 1  5 y  =   2 (TMĐK). x  = 0  0,25  
Vậy hệ phương trình có nghiệm (x y ) 5 ; = 0; . 2   2 2 2)
Cho phương trình: x − 2 (m − )
1 x + m − 3m = 0 (1) (x là ẩn số). 1,5 4
a) Giải phương trình (1) khi m = 5.
b) Tìm tất cả giá trị của m để phương trình (1) có hai nghiệm.
a) Thay m = 5 vào phương trình (1) ta nhận được: 0,25 2 x − ( − ) 2 2
2 5 1 x + 5 − 3.5 = 0 = x − 8x + 10 = 0.
+) Tính được  ' = 6 =  '  0. 0,25
Phương trình (1) có hai nghiệm phân biệt x = 4 + 6 ; x = 4 − 6. 0,25 1 2
Vậy phương trình có tập nghiệm là S = 4 + 6;4 − 6. 0,25 b)  = (m − )2 2 '
1 − m + 3m = m + 1. 0,25
Phương trình (1) có hai nghiệm  '  0  m + 1  0  m  1 − . 0,25
Kết luận phương trình có hai nghiệm khi m  1. −
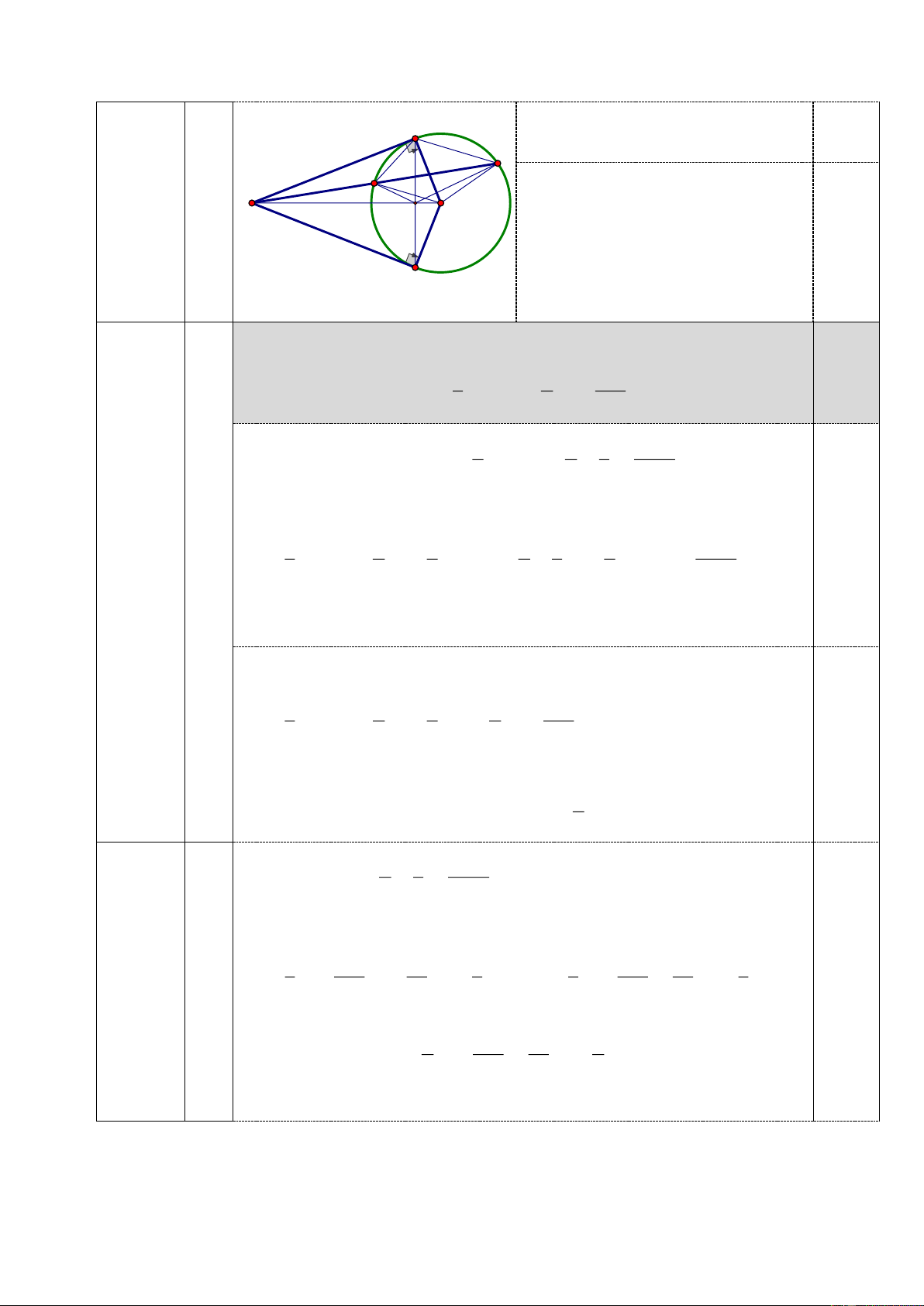
Chứng minh tứ giác KAOB là tứ giác nội tiếp. 1,25 0,25 A
+) Vẽ hình đúng đến câu 1. 0,25 D +) Lập luận được 0,25 1) C KAO = KBO = 90 .  K O
+) Tứ giác KAOB có:
KAO + KBO = 180 ,  mà hai 0,25 0,25 B
góc ở vị trí đối nhau => tứ giác
KAOB là tứ giác nội tiếp. Chứng minh 2
KA = KC.KD = KM.K . O 1,25
+) Lập luận được AB ⊥ OK tại M . 0,25 +) Lập luận được Bài IV 0,25 2
KA = KM.KO. A 3,0 điểm
+) Xét (O ) có: KAC = ADK D 2)
(góc tạo bởi tiếp tuyến và dây 0,25 C K
cung và góc nội tiếp cùng chắn M O AC . +) Chỉ ra được K  AC đồng B dạng với . KDA  0,25 2
= KA = KC.K . D 2
= KA = KC.KD = KM.K . O 0,25
Chứng minh đường thẳng AB chứa tia phân giác của CMD. 0,5 3)
+) Từ KC .KD = KM .KO lập 0,25
luận được tứ giác CMOD là tứ 5 giác nội tiếp A = DMO = OC ; D CMK = ODC. D
+) OCD cân tại O C K O M
= OCD = ODC, nên suy được
DMO = CMK = CMA = DMA 0,25 B
=> đường thẳng AB chứa tia phân giác của CMD. Cho ,
a b là các số dương thỏa mãn a + b = 3. Chứng minh rằng:  2  2 1 1 169 0,5
a +  + b +   .  b   a  18 2 1 1 1 4 +) Chứng minh: ( 2 a + 2
b )  (a + b) ; +  2 a b a + b +) Ta có:  2  2  2  2 1 1 1 1 1 1 4 0,25
a +  + b +   .a + b + +   .a + b +   (1) Bài V b a 2 a b 2 a +        b  0,5 điểm Thay a + b = 3.  2  2  2 1 1 1 4 169
a +  + b +   . 3 +  =  b   a  2  3  18 0,25
+) Dấu " = " xảy ra khi và chỉ khi a = b = 3 . 2 C2 1 1 4 +) Chứng minh: +  a b a + b +) Ta có:  2    2 1 169 13 1 1 169 13  1  a +  +  2.
a +   a +  +  a + (1)   b  36 6  b   b  36 3  b  0,25  2 1 169 13  1 
+) Tương tự, có: b +  +  b + (2)  a  36 3  a  6
+) Cộng vế với vế của (1) và (2), ta có : 2 2  1   1  169 13   
a +  + b +  +  (a + b) 1 1 +  +  b a 18 3 a b        2 2  1   1  169 13  
= a +  + b +  +  (a + b) 4 169 + =  b a 18 3 a + b 9       0,25 2 2  1   1  169
 a +  + b +   . b a 18    
+) Dấu " = " xảy ra khi và chỉ khi a = b = 3 . 2 7