Đề kiểm tra giữa học kỳ 2 Toán 9 năm 2023 – 2024 sở GD&ĐT Bắc Ninh

SỞ GIÁO DỤC VÀ ĐÀO TẠO
ĐỀ KIỂM TRA GIỮA HỌC KỲ II BẮC NINH NĂM HỌC 2023 – 2024 Môn: Toán – Lớp 9 (Đề có 01 trang)
Thời gian làm bài: 90 phút (không kể thời gian giao đề)
I. TRẮC NGHIỆM (3,0 điểm)
Câu 1. Cặp x;y nào sau đây là nghiệm của phương trình 2x y  5? A. 2;  1 . B. 2;  1 . C.  1  ;  2 . D. 3;  1 . Câu 2. Đồ thị hàm số 2 y  x  đi qua điểm nào? A. A1;  1 . B. B  1  ; 1. C. C 1;  1 . D. D 1;2. m  x  9y  4
Câu 3. Tất cả các giá trị của tham số m để hệ phương trình x my  5 có nghiệm duy nhất là  A. m  3. B. m  3. C. m  9 . D. m  3. Câu 4. Cho hàm số 2 y  2
 x . Khẳng định nào sau đây đúng?
A. Hàm số trên đồng biến khi x  0 .
B. Hàm số trên luôn nghịch biến.
C. Đồ thị hàm số trên đi qua điểm  1
 ;2. D. Hàm số trên nghịch biến khi x  0.
Câu 5. Cho đường tròn tâm O ngoại tiếp tam giác đều BCD . Lấy điểm E thuộc cung nhỏ CD . Số đo góc BEC là A. 90. B. 120. C. 30 . D. 60.
Câu 6. Tứ giác ABCD nội tiếp một đường tròn, biết  o
C  80 . Khẳng định nào sau đây SAI? A.  A  100. B.  B  100. C.  
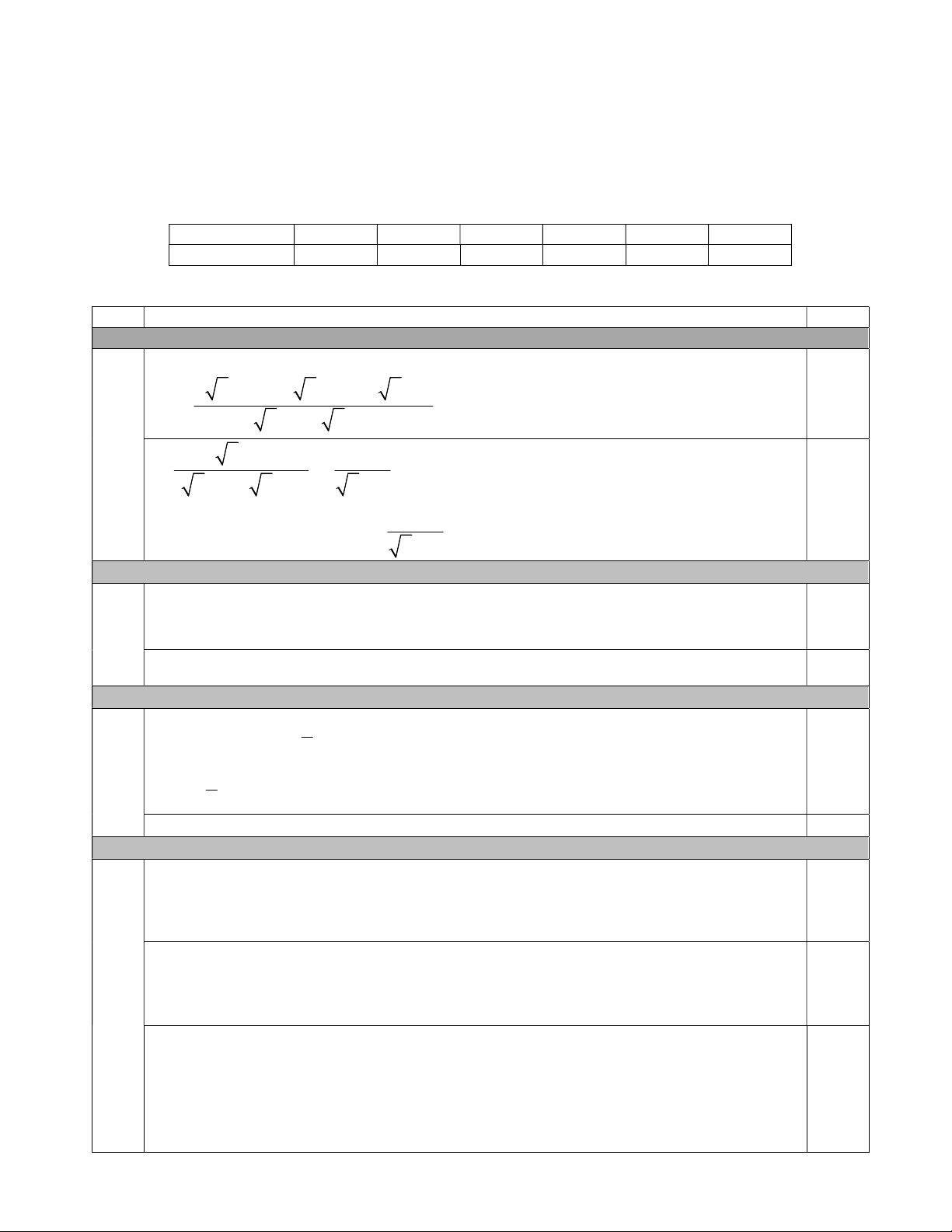
D  B  180 . D.   AC  20. II. TỰ LUẬN (7,0 điểm) Câu 7. (2,5 điểm) 4 3 6 a  2
a) Rút gọn biểu thức P    (với a  0;a  1). a 1 a 1 a 1 x  2y  4
b) Giải hệ phương trình 2x 3y  1.  1
c) Tìm giá trị của a , biết đồ thị hàm số 2
y  ax (a  0) đi qua điểm M 1; 1. 3
Câu 8. (1,0 điểm) Một mảnh đất hình chữ nhật có chu vi 80m . Nếu tăng chiều dài thêm 3m , chiều
rộng thêm 5m thì diện tích của mảnh đất tăng thêm 2
195m . Tính diện tích ban đầu của mảnh đất.
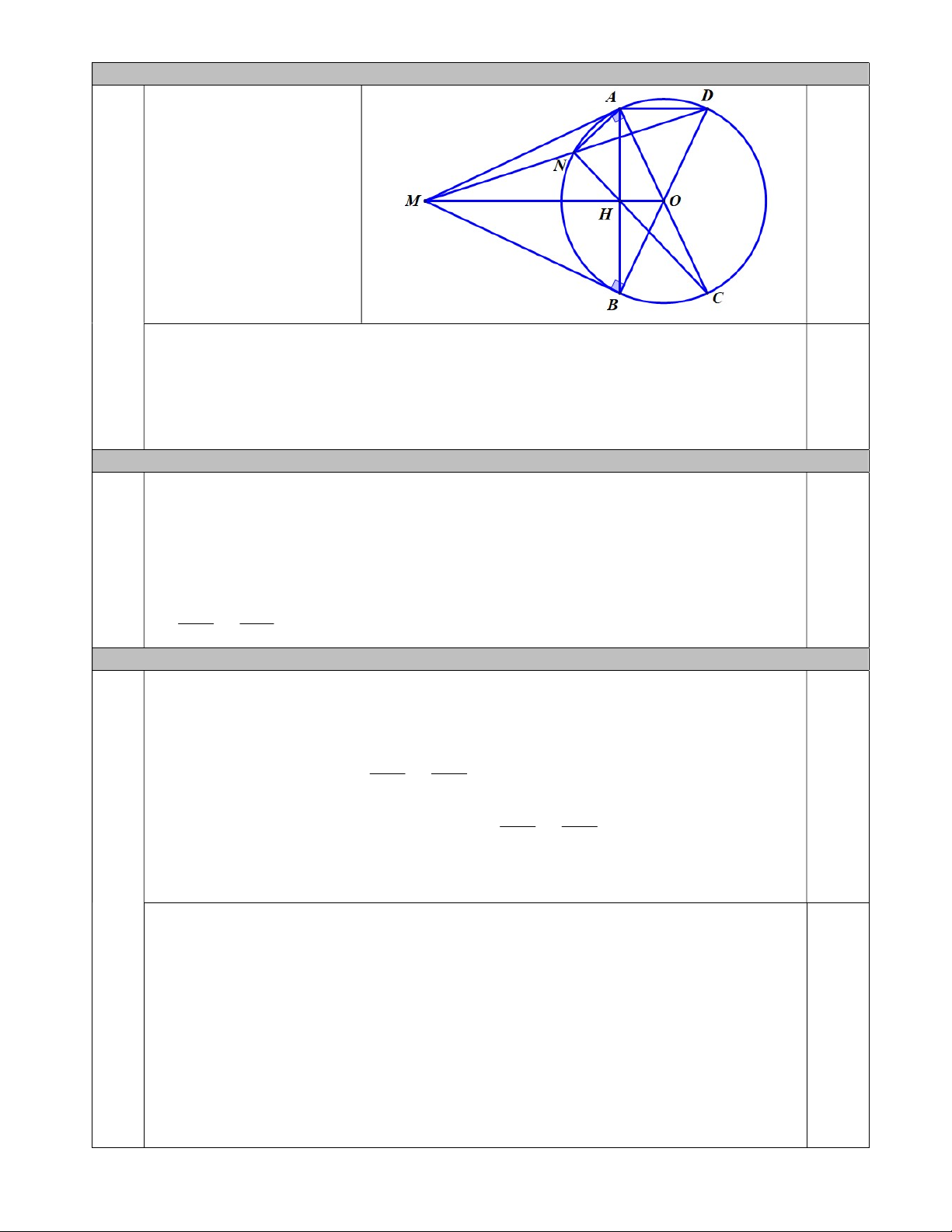
Câu 9. (3,0 điểm) Từ một điểm M nằm ngoài đường tròn O, kẻ hai tiếp tuyến M , A MB ( , A B là
tiếp điểm). Kẻ đường kính AC , gọi H là giao điểm của OM và AB , CH cắt đường tròn tại N (N
khác C ), MN cắt đường tròn O tại điểm thứ hai là D . Chứng minh rằng:
a) Tứ giác MAOB nội tiếp một đường tròn. b) 2 MA  MN.MD . c)  
MDO  MHN và D,O,B thẳng hàng.
Câu 10. (0,5 điểm) Cho a, ,
b c là các số thực dương thỏa mãn a b c  1. Tìm giá trị lớn nhất của ab bc ca biểu thứcA    . c ab a bc b ca -------- Hết--------
SỞ GIÁO DỤC VÀ ĐÀO TẠO HƯỚNG DẪN CHẤM BẮC NINH
KIỂM TRA GIỮA HỌC KỲ II ¯¯¯¯¯¯¯¯¯¯ NĂM HỌC 2023 – 2024 Môn: Toán– Lớp 9
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
I. PHẦN TRẮC NGHIỆM (3,0 điểm)
Mỗi câu trả lời đúng 0,5 điểm. Câu 1 2 3 4 5 6 Đáp án A B D C D B
II. PHẦN TỰ LUẬN (7,0 điểm) Câu Lời giải sơ lược Điểm Câu 7.a (1,0 điểm) ĐKXĐ: a  0;a  1
4 a  4  3 a  3  6 a 2 P  0,5 ( a 1)( a 1) a 1 1   ( a 1)( a 1) a 1 0,5 1
Vậy với a  0;a  1 thì P  . a 1 Câu 7.b (0,75 điểm) x  2y  4 2  x  4y  8 7  y  7 y   1     2
 x 3y  1  2x 3y  1  2x 3y  1  x      2 0,5    
Vậy hệ phương trình có nghiệm duy nhất là x;y  2;  1 . 0,25 Câu 7.c (0,75 điểm) 1 Đồ thị hàm số 2
y  ax , (a  0 ) đi qua điểm M 1; 1 khi 3 0,5 1 2 – 1  a.1  a  3 3
Vậy giá trị cần tìm là a  3 0,25 Câu 8. (1,0 điểm)
Gọi chiều dài, chiều rộng của mảnh đất hình chữ nhật ban đầu lần lượt là
x m;ym. 0  x,y  40 0,25
Do chu vi mảnh đất hình chữ nhật là 80m nên ta có phương trình x  y  40 (1)
Nếu tăng chiều dài thêm 3m , chiều rộng thêm 5m thì diện tích của mảnh đất tăng thêm 2
195m nên ta có phương trình 0,25
x 3y 5xy 195  5x 3y 180 (2) x  y  40
Từ (1) và (2) ta có hệ phương trình 5x  3y  180  0,5
Giải hệ phương trình ta được x  30;y  10 (thỏa mãn)
Vậy diện tích ban đầu của mảnh đất là 2 30.10  300m . Câu 9.a (1,0 điểm)
Vẽ hình, ghi giả thiết kết 0,5 luận Ta có M ,
A MB là hai tiếp tuyến của đường tròn O nên   MAO  MBO  90 Xét tứ giác MAOB có   0,5 MAO  MBO  180 Mà  
MAO;MBO ở vị trí đối nhau nên tứ giác MAOB nội tiếp một đường tròn. Câu 9.b (1,0 điểm)
Xét đường tròn O có góc  MDA nội tiếp và 
MAN là góc tạo bởi tia tiếp tuyến và
dây cung cùng chắn cung AN nên   MDA  MAN . Xét M  AD và M  NA có:  AMD chung;   MDA  MAN 1,0  MAD ∽ M  NA (g – g) MA MD   2  MA  MN.MD (đpcm) MN MA Câu 9.c (1,0 điểm)
Chỉ ra MO là đường trung trực của AB nên OM  AB tại H . Xét A
 MO vuông tại A, đường cao AH có 2 MA  MH.MO Lại có 2 MA  MN.MD  MD.MN  MH.MO MD MO   MH MN 0,5 MD MO Xét M  OD và M  NH có:  DMO chung ;  MH MN Suy ra M  OD ∽ M  NH (c – g – c).  
 MDO  MHN (hai góc tương ứng) (1)
Xét đường tròn O có  NDB , 
BAN là hai góc nội tiếp cùng chắn cung BN nên   NDB  BAN . Lại có  o
ANC  90 (góc nội tiếp chắn nửa đường tròn đường kính AC ) nên   o AHN  BAN  90 . 0,5 Mà   o AHN  MHN  90 Do đó suy ra được   NDB  MHN (2) Từ (1) và (2) suy ra  
NDB  MDO . Do đó hai tia DO và tia DB trùng nhau hay
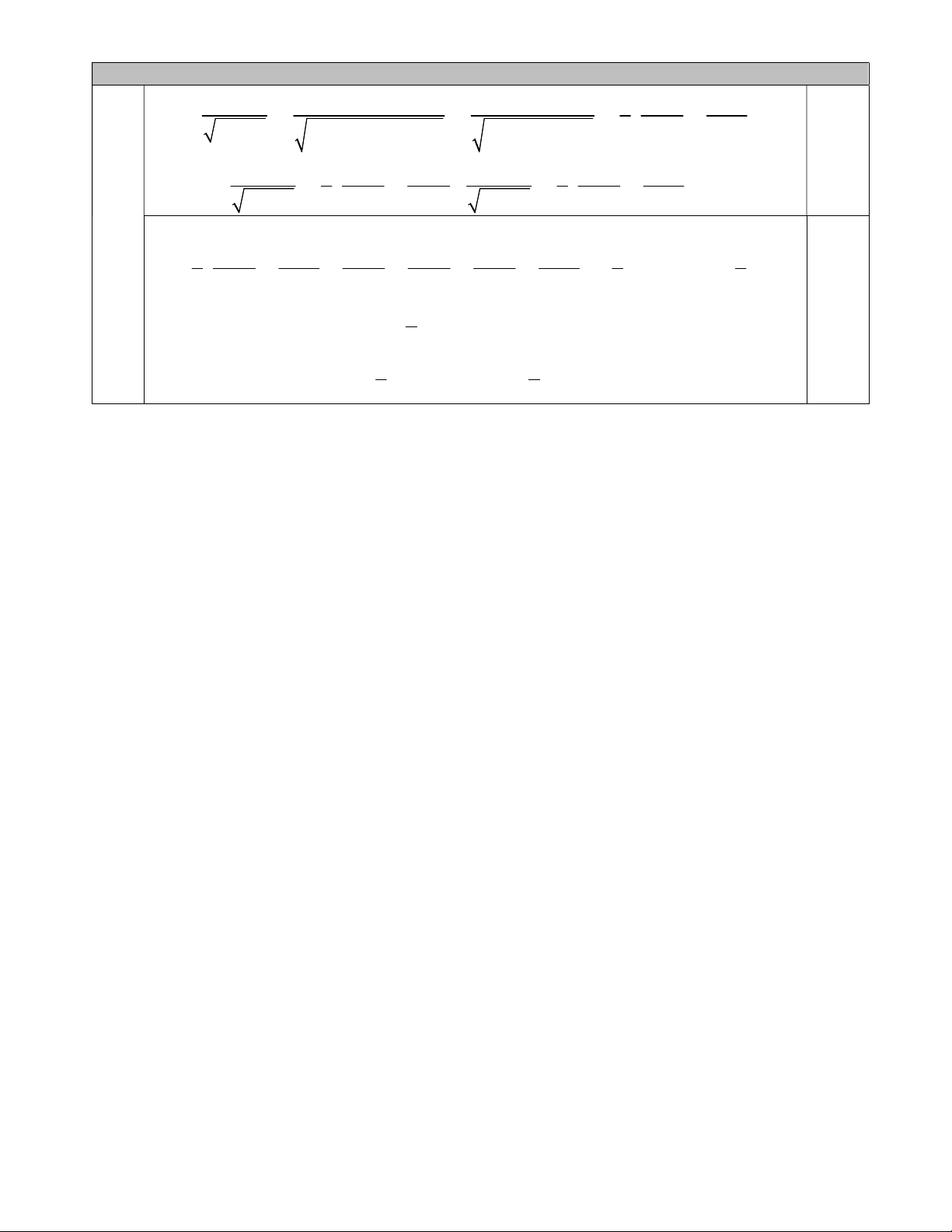
ba điểm B , O , D thẳng hàng. Câu 10. (0,5 điểm) ab ab ab 1  ab ab  Ta có         c ab   c a b cab
c ac b 2c a c b 0,25 bc 1  bc bc    ca 1  ca ca  Tương tự    ;         a bc
2 a b a c b ca 2 b  a b c Khi đó 1  ab ab bc bc ca ca    1 A            a b c 1 
2 c a c b a b a c b a b c 2 2 1 0,25
Dấu “=” xảy ra khi a  b  c  3 1 1
Vậy giá trị lớn nhất của A là khi a  b  c  . 2 3
Lưu ý: Học sinh làm cách khác đúng cho điểm tối đa. ---------- Hết ----------
Document Outline

• Toan 9.KTGK2.23.24.de
• Toan 9.KTGK2.23.24.da