Đề kiểm tra trắc nghiệm môn toán cao cấp | trường Đại học Kinh tế Thành phố Hồ Chí Minh
Cho AE M3x4 (R). Sử dụng phép biến đổi sơ cấp: cộng vào hàng thứ 3 hàng thứ nhất đã được nhân với số 2. Phép biến đổi trên tương đương với nhân bên trái ma trận A với ma trận nào sau đây? Cho các vectơ 11, #2, #3 độc lập tuyến tỉnh trong R¹ và ở là vectơ không của R³. Trong4 mệnh đề sau, mệnh đề nào là đúng? Tài liệu giúp bạn tham khảo, ôn tập và đạt kết quả cao. Mời bạn đọc đón xem !
Môn: Toán Cao Cấp (KTHCM)
Trường: Đại học Kinh tế Thành phố Hồ Chí Minh
Thông tin:
Tác giả:
Tài liệu liên quan:
Preview text:
lOMoAR cPSD| 47305584
ÑIH≈CTÀICHÍNHMARKETING TOÁNCAOCáP Khoa Kinh t∏-Lu™t N´m hÂc 2021-2022
Mã ∑ thi: BK-2021-20 Môn: Toán Cao Cßp ∑ gÁm có 3 trang 1 2x 1 1 Câu 01.
Tìm sË nghiªm phân biªt r cıa ph˜Ïng trình: 1 x2 1 1 = 0 0 0 x 1 0 0 0 2 A r = 3 B r = 4 C r = 1 D r = 2 1 1 1 1 1 0 1 3 2 0 Câu 02. Tính ‡nh th˘c ∆ = 0 2 4 0 0 0 3 0 0 0 1 0 0 0 0 A ∆ = 24 B ∆ = 24 C ∆ = 4 D ∆ = 4 1 x 1 1
Câu 03. Tìm sË nghiªm phân biªt r cıa ph˜Ïng trình: 1 x 1 1 = 0 A r = 1 B r = 2 C r D r = 0 Câu 04. Cho A
. Tính det(3AB). A 18 B 162 C 12 D 9 Câu 05.
VÓi giá tr‡ nào cıa m thì A kh£ ngh‡ch? A vÓi mÂi m B m 6= 3 C m 6= 2 D m = 1 Câu 06. Cho A
. VÓi giá tr‡ nào cıa k thì h§ng cıa ma tr™n b¨ng 3? A k = 1 B k =6= 1
C không tÁn tai k
D vÓi mÂi k 2R
Câu 07. VÓi giá tr‡ nào cıa m thì Akh£ ngh‡ch?
A vÓi mÂi m 2R B không tÁn tai m C m = 3 D m 6= 4 Câu 08. Cho ma tr
. Tìm h§ng cıa ma tr™n phˆ hÒp PA 1 lOMoAR cPSD| 47305584 A 2 B 1 C 3 D 0 ]
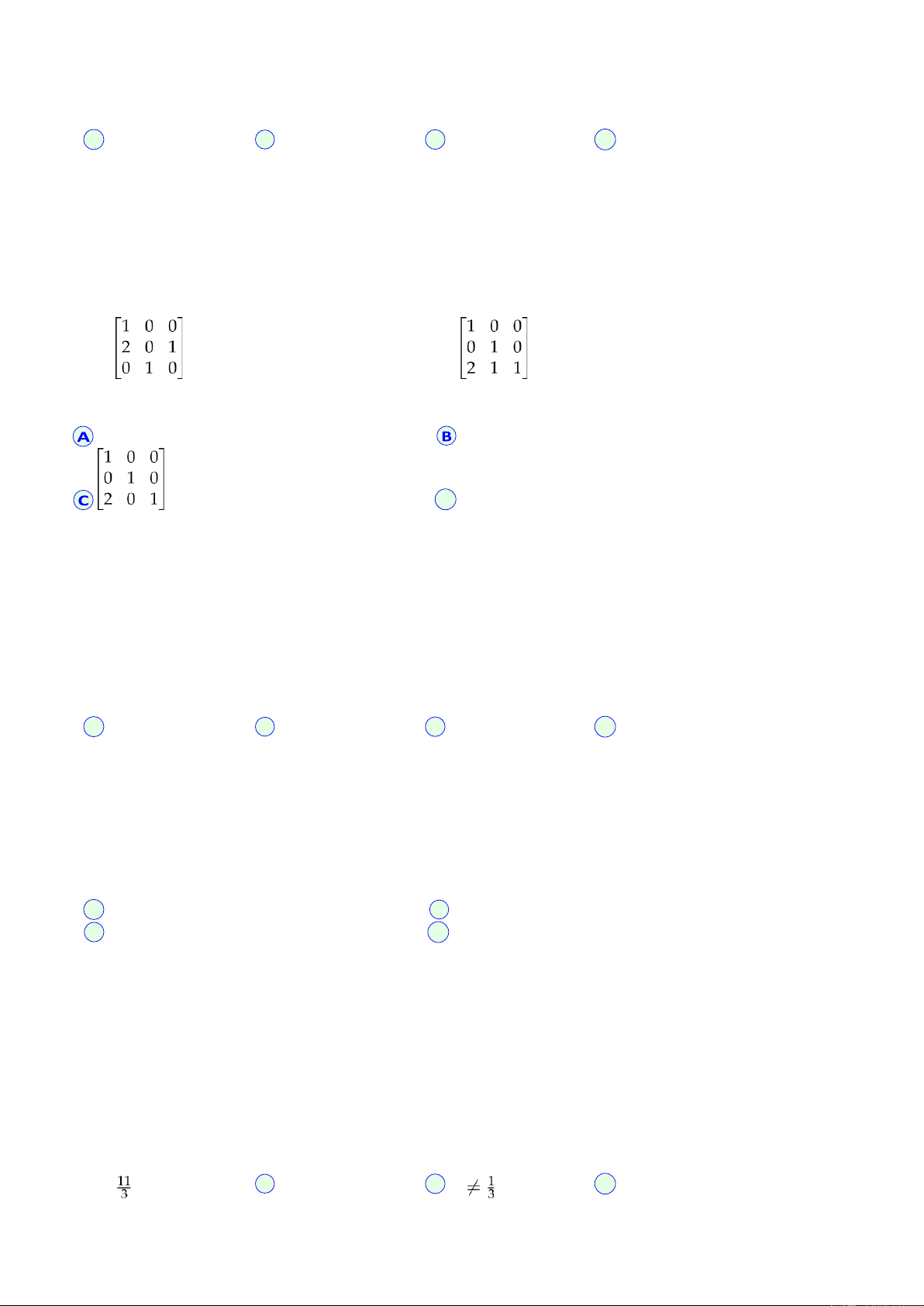
Câu 09.ã Cho A 2 M3⇥4[R . S∏˚nd͈ng phép bii trên t˜Ïng∏n˜ÏÍi sng vÏ cßÓp: ci nhân bên trái ma trÎng vào
hàng th˘™3nhàng thA vÓi ma tr˘ nh™ßnt
˜Òc nhân vÓi sË 2. Phép bi nào sau ây?
D 3 câu còn l§i ∑u sai Câu 10.
Tìm tßt c£ giá tr‡ th¸c cıa m ∫ hª ph˜Ïng trình sau có vô sË nghiªm
8>< x + 2y + 3z = 1 2x + 4y + 8z = m + 4
>:3x + 6y + z(m2 + 5) = m + 5 A m 6= 2 B m = 2 C m = ±2 D m 6= ±2 x + y + 2z = 2 Câu 11.
Tìm tßt c£ m ∫ hª ph˜Ïng trình sau vô nghiªm ><82x + y + 3z = 5
>:3x + my + 7z = m + 2 A m 6= 4
B Không tÁn t§i m C m 6= 3
D 3 câu còn l§i ∑u sai Câu 12.
VÏi giá tr‡ nào cıa m thì hª ph˜Ïng trình sau có nghiªm duy nhßt b¨ng 0:
8>< x + 2y + z = 0
2x + y + 3z = 0
>:3x + 4y + mz = 0 A m = B m 6= ±2 C m D m = 2 Câu 13. Hª vectÏ nào sau
ây không ph£i là không gian con cıa R3: lOMoAR cPSD| 47305584
A V = {(x y + z, z y, x) : x, y, z 2 R} B V = {(x y,
y,0) : x, y 2 R}
C V gÁm tßt c£ các vectÏ ˜Òc sinh ra b i hª {(1,2,1), ( 2,0,1), (1,2, 3), (3, 2,1)} D V = {(x, y, xy) :
x, y 2 R}
Câu 14. Cho các vectÏ u1, u2, u3 Îc l™p tuy∏n tính trong R4 và θ là vectÏ không cıa R4. Trong 4 mªnh ∑ sau, mªnh ∑ nào là úng?
A u1, u2, θ Îc l™p tuy∏n tính. B u1, u3, θ Îc l™p tuy∏n tính. C u1, u2, u3, θ phˆ thuÎc
tuy∏n tính. D u2, u3, θ Îc l™p tuy∏n tính. Câu 15.
Xác ‡nh m ∫ vectÏ (1, m,1) không ph£i là mÎt tÍ hÒp tuy∏n tính cıa u = (1,2,4), v = (2,1,5), w = (3,6,12) 2 A m tùy ˛. B m 6= 1. C m 6= 0, ±1. D m 6= 0. Câu 16.
Tìm m ∫ các vectÏ sau t§o thành mÎt cÏ s cıa R4: u1 = (3,1,2, m 1), u2 =
(0,0, m,0)u3 = (2,1,4,0), u4(3,2,7,0)
A Không có giá tr‡ m nào. B m tùy ˛. C m 6= 2. D m 6= 0,1.
Câu 17. Cho M = {x, y, z} là cÏ s cıa không gian vectÏ V. KhØng ‡nh nào sau ây là úng?
A Các câu còn l§i sai. B {x,2y,3z} không ph£i là cÏ s cıa V. C x, x + y, x + y + z là cÏ s cıa V. D {x,
y, x + y, x + z} không sinh ra V.
Câu 18. Tìm m ∫ các vectÏ sau t§o thành mÎt cÏ s cıa R3: u = (1,2,3), v = (m,2m + 3,3m + 3), w = (1,4,6) A m 6= 0. B m tùy ˛. C m 6= 1.
D Không có giá tr‡ m nào.
Câu 19. Tìm m ∫ h§ng cıa hª vectÏ sau b¨ng 2: u = (1,3,1), v = (1, m + 3,3), w = (1, m + 6, m + 3) A m = ±p6. B m = p6. C m = 1. D m tùy ˛.
Câu 20. Xác ‡nh m ∫ h§ng cıa hª vectÏ sau b¨ng 3: u = (m,1,0,2), v = (m, m + 2,0,2), w = (2m, m + 3,0,5)
A Không có giá tr‡ m nào. B m 6= 1. C m 6= 0, 1. D m = 0.