Đề ôn tập cuối kì tự luận | Môn toán cao cấp

lOMoAR cPSD| 47879361 1
Ôn tập cuối kỳ: Toán 1 Thời gian: 2 tiết Câu 1. Mã đề: 01 Giải phương trình
Câu 2. Giải và biện luận theo m hệ phương trình: Câu 3.
Tìm ma trận nghịch đảo của .
Câu 4. Trong không gian R4 cho họ véc tơ S = {u1;u2;u3} với u1 = (2;0;3);u2 = (1;4;−1); u3 = (3;12;−3). Hỏi:
a. S có là một cơ sở của R3 không? Vì sao?
b. Tìm số chiều và một cơ sở của Span(S).
Câu 5. Cho T : R3 →R3 xác định bởi
T(a,b,c) = (2a − b − c,−a + 2b − c,−a − b + 2c)
a. CMR T là một ánh xạ tuyến tính.
b. Tìm ma trận của T đối với cơ sở chính tắc của R3.
c. Tìm trị riêng, vecto riêng của f. lOMoAR cPSD| 47879361 2
Ôn tập cuối kỳ: Toán 1 Thời gian: 2 tiết Câu 1.
d. Tìm số chiều và cơ sở của Im(T),Ker(T).
Câu 6. Đưa dạng toàn phương sau về dạng chính tắc: . Mã đề: 02
Cho phương trình 2z2 + (3 − 5i)z − 2 − 4i = 0
a. Giải phương trình trên C;
b. Tìm các căn bậc 5 của một trong hai nghiệm tìm được ở trên.
x1 + mx2 + x3 = m + 1
Câu 2. Giải và biện luận theo m hệ phương trình:
x1 + x2 + mx3 = 2
mx1 + x2 + x3 = 2m
Câu 3. Giải phương trình ma trận AX = B với 3 2 2 2 −4 2 1 A = 1 3 1 ;B = −7 5 1 6 5 3 4 3 −6 7 −2
Câu 4. Trong R3 cho B = {u1 = (1,2,−1);u2 = (2,3,1);u3 = (3,5,−6)} và ′ ′ .
a. B,B′ có phải là các cơ sở của R3 không?
b. Tìm ma trận chuyển cơ sở từ B sang B′. lOMoAR cPSD| 47879361 3
Ôn tập cuối kỳ: Toán 1 Thời gian: 2 tiết Câu 1.
Câu 5. Cho T : R3 →R3 xác định bởi
T(a,b,c) = (a − 3b + 4c,4a − 7b + 8c,6a − 7b + 7c)
a. CMR T là một ánh xạ tuyến tính.
b. Tìm ma trận của T đối với cơ sở chính tắc của R3.
c. Tìm trị riêng, vecto riêng của f.
d. Tìm số chiều và một cơ sở của Im(T),Ker(T).
Câu 6. Đưa dạng toàn phương sau về dạng chính tắc: . Mã đề: 03 Giải phương trình sau:
z3(−1 + i) = (1 −√3i)3(−1 + i)5
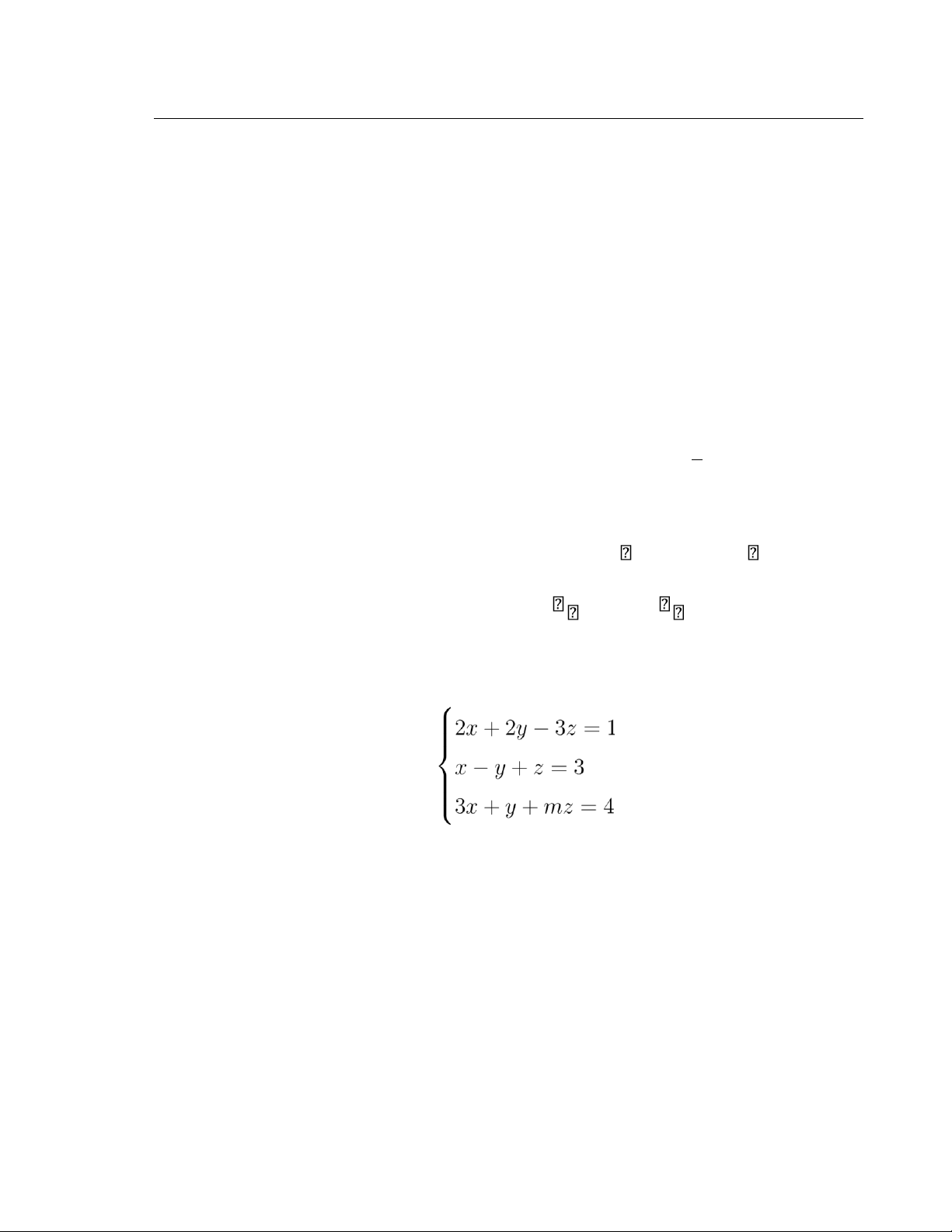
Câu 2. Giải và biện luận theo m số nghiệm của hệ phương trình:
Câu 3. Tìm ma trận nghịch đảo của 1 1 1 A = 2 −1 −3 lOMoAR cPSD| 47879361 4
Ôn tập cuối kỳ: Toán 1 Thời gian: 2 tiết Câu 1. 3 1 1
Câu 4. Trong không gian R3 cho họ véc tơ S = {u1;u2;u3} với u1 = (2;−4;2);u2 = (−2;0;−1); u3 = (4;−4;3). Hỏi:
a. S có là một cơ sở của R3 không? Vì sao?
b. Tìm số chiều và một cơ sở của Span(S).
Câu 5. Cho T : R3 →R3 xác định bởi
T(a,b,c) = (4a − 5b + 2c,5a − 7b + 3c,6a − 9b + 4c)
a. CMR T là một ánh xạ tuyến tính.
b. Tìm ma trận của T đối với cơ sở chính tắc của R3.
c. Tìm trị riêng, vec tơ riêng của f.
d. Tìm số chiều và một cơ sở của Im(T),Ker(T).
Câu 6. Đưa dạng toàn phương sau về dạng chính tắc: . lOMoAR cPSD| 47879361 5
Ôn tập cuối kỳ: Toán 1 Thời gian: 2 tiết Mã đề: 04
Câu 1. Đưa số phức sau về dạng lượng giác: .
Câu 2. Cho hệ phương trình
x1 + mx2 + x3 = m +
1 x1 + x2 + mx3 = 2
mx1 + x2 + x3 = 2m
a. Giải hệ bằng phương pháp Cramer với m = 5;
b. Biện luận theo m số nghiệm của hệ phương trình trên. Câu 3. Tìm
ma trận nghịch đảo của 5 −1 7 A = 2 −1 1 . 1 3 0
Câu 4. Trong R3 cho B = {u1 = (1,−2,−1);u2 = (−1,9,1);u3 = (3,2,−6)} và .
a. B,B′ có phải là các cơ sở của R3 không?
b. Tìm ma trận chuyển cơ sở từ B sang B′.
Câu 5. Cho T : R3 →R3 xác định bởi
T(a,b,c) = (6a − 2b − 2c,−2a + 3b,2a + 3c) lOMoAR cPSD| 47879361 6
Ôn tập cuối kỳ: Toán 1 Thời gian: 2 tiết
a. CMR T là một ánh xạ tuyến tính.
b. Tìm ma trận của T đối với cơ sở chính tắc của R3.
c. Tìm trị riêng, vecto riêng của f.
d. Tìm số chiều và một cơ sở của Im(T),Ker(T).
Câu 6. Đưa dạng toàn phương sau về dạng chính tắc:
Q = 3x1x2 − 2x2x3 + 4x1x3. Mã đề: 05
Câu 7. Tìm modun, argument của số phức: z = (−2 + 2i√3)5(1 − i)15 2 1 3
Câu 8. Tìm ma trận nghịch đảo của ma trận A = −4 −3 5 1 0 2
Câu 9. Cho hệ phương trình
a. Giải hệ với m = 2.
b. Tìm m để hệ vô nghiệm
Câu 10. Tìm cơ sở, số chiều của không gian con sinh bởi họ vecto
S = {(2,4,1,8),(1,2,3,4),(−1,3,0,1),(1,7,7,9)}
Câu 11. Cho ánh xạ tuyến tính f : R3 →R3 và
f(x,y,z) = (x − 2y + z,−2x + 3y − z,x + 3y). lOMoAR cPSD| 47879361 7
Ôn tập cuối kỳ: Toán 1 Thời gian: 2 tiết
a. CMR f là một ánh xạ tuyến tính.
b. Tìm ma trận của f đối với cơ sở chính tắc của R3.
c. Tìm ma trận của f đối với cặp cơ sở
B = {e1 = (1,−1,0), e2 = (2,1,1), e3 = (3,0,2)}
B′ = {e′1 = (1,0,0), e′2 = (0,1,0), e3′ = (0,0,1)}
d. Tìm số chiều và một cơ sở của Im(f),Ker(f).
Câu 12. Dạng toàn phương sau là xác định dương hay xác định âm? . Mã đề: 06
Câu 13. Tìm dạng lượng giác của số phức: Câu 14. Cho hệ vecto
S = {(3,−1,4),(1,5,3),(5,9,10)}.
Tìm cơ sở và số chiều của không gian vec tơ sinh bởi hệ vecto trên. −1 1 3
Câu 15. Tìm GTR và VTR của ma trận A = 0 4 0 −2 1 6
Câu 16. Tìm tọa độ của vecto x = (−3,4,2) đối với cơ sở
B = {u1 = (1,2,−1);u2 = (2,3,1);u3 = (3,5,−6)}
Câu 17. Cho ánh xạ f : R3 →R3 và lOMoAR cPSD| 47879361 8
Ôn tập cuối kỳ: Toán 1 Thời gian: 2 tiết
f(x,y,z) = (−x + 3y + 2z,2x + y − z,x + 3y).
a. CMR f là một ánh xạ tuyến tính.
b. Tìm ma trận của f đối với cơ sở chính tắc của R3.
c. Tìm số chiều và một cơ sở của ảnh, hạt nhân của ánh xạ f.
Câu 18. Tìm dạng chính tắc của dạng toàn phương sau: Mã đề: 07
Câu 19. Tìm các căn bậc 4 của số phức: z = (2 − 2i√3) 5 3 −1
Câu 20. Tìm ma trận nghịch đảo của ma trận A = 4 0 2 0 1 −1
2x + my Câu 21. Cho hệ phương trình
x − y − 8−z =z = 1−4
a) Giải hệ với m = 1. b) Tìm
x +my + 2để hệ có nghiệm duy nhất.z = 2
Câu 22. Hệ vecto sau là độc lập tuyến tính hay phụ thuộc tuyến tính
S = {(3,0,−1,4),(−1,2,5,3),(2,−9,0,1),(1,4,−2,3)} −1 1 3 lOMoAR cPSD| 47879361 9
Ôn tập cuối kỳ: Toán 1 Thời gian: 2 tiết
Câu 23. Tìm GTR và VTR của ma trận A = 0 4 0 −2 1 6
Câu 24. Dạng toàn phương sau là xác định dương hay xác định âm? Mã đề: 08
Câu 25. Giải phương trình z5 + 1 − i√3 = 0
Câu 26. Cho hệ phương trình
Biện luận theo m số nghiệm của hệ phương trình.
Câu 27. Cho ánh xạ tuyến tính f : R3 →R3 và
f(x,y,z) = (−2x + 2y + 3z,4y − 3z,−2x + 3y).
a. CMR f là một ánh xạ tuyến tính.
b. Tìm ma trận của f đối với cặp cơ sở
B = {e1 = (1,2,1), e2 = (−2,0,1), e3 = (−1,2,3)}
B′ = {e′1 = (1,0,0), e′2 = (0,1,0), e3′ = (0,0,1)}
c. Tìm số chiều và một cơ sở của ảnh, hạt nhân của ánh xạ f. 1 2 −2
Câu 28. Tìm GTR và VTR của ma trận B = 1 0 3 1 3 0 lOMoAR cPSD| 47879361 10
Ôn tập cuối kỳ: Toán 1 Thời gian: 2 tiết
Câu 29. Tìm dạng chính tắc của dạng toàn phương sau: