-
Thông tin
-
Quiz
Đề tham khảo giữa kì 2 Toán 9 năm 2024 – 2025 phòng GD&ĐT Bình Thạnh – TP HCM có đáp án
Đề tham khảo giữa kì 2 Toán 9 năm 2024 – 2025 phòng GD&ĐT Bình Thạnh – TP HCM có đáp án. Tài liệu được sưu tầm và biên soạn dưới dạng PDF gồm 89 trang giúp em củng cố kiến thức, ôn tập và đạt kết quả cao trong kì thi sắp tới. Mời bạn đọc đón xem.
Đề giữa HK2 Toán 9 178 tài liệu
Toán 9 2.5 K tài liệu
Đề tham khảo giữa kì 2 Toán 9 năm 2024 – 2025 phòng GD&ĐT Bình Thạnh – TP HCM có đáp án
Đề tham khảo giữa kì 2 Toán 9 năm 2024 – 2025 phòng GD&ĐT Bình Thạnh – TP HCM có đáp án. Tài liệu được sưu tầm và biên soạn dưới dạng PDF gồm 89 trang giúp em củng cố kiến thức, ôn tập và đạt kết quả cao trong kì thi sắp tới. Mời bạn đọc đón xem.
Chủ đề: Đề giữa HK2 Toán 9 178 tài liệu
Môn: Toán 9 2.5 K tài liệu
Thông tin:
Tác giả:
Preview text:
ĐỀ THAM KHẢO GIỮA HỌC KÌ 2 LỚP 9
Phần 1. Trắc nghiệm khách quan. (3,0 điểm) Mỗi câu sau đây đều có 4 lựa
chọn. Hãy khoanh tròn vào phương án đúng
Câu 1: Trong các điểm sau, điểm nào thuộc đồ thị hàm số P 2 :y x ?
A. (1;1). B. (1;1). C. (2;3). D. (1;2).
Câu 2: Cho parabol P: 2
y 5x và đường thẳng d: y 4x 4 . Số giao
điểm của đường thẳng d và P là A. 1. B. 0. C. 3. D. 2.
Câu 3: Phương trình nào sau đây là phương trình bậc hai một ẩn ? A. 2
3x 4x 1 0 . B. 3
x 3x 7 0 . C. 2
2x xy 3 0 . D. 2
0x 7x 5 0 .
Câu 4 :Phương trình 2
x 6x 1 0 có biệt thức ' bằng A. 13 . B. 8 . C. 10 . D. 40 .
Câu 5: Gọi S là tổng và P là tích 2 nghiệm của phương trình 2 2
− x + 5x + 3 = 0 , khi đó: A. S 3 , 5 P B. 3 5 S ;P 3 2 2 C.
S 3;P 5 . D. 5 3 S ;P 2 2
Câu 6: Khẳng định nào sau đây đúng? A. Phương trình 2
2x 5x 35 0 có hai nghiệm trái dấu. B. Phương trình 2
2x 3x 5 0 có hai nghiệm phân biệt. C. Phương trình 2
3x 4x 1 0 có hai nghiệm âm. D. Phương trình 2
2x 6x 4 0 có một nghiệm duy nhất.
Câu 7: Đường tròn ngoại tiếp tam giác là đường tròn:
A. Tiếp xúc với tất cả các cạnh của tam giác đó.
B. Đi qua tất cả các đỉnh của tam giác đó.
C. Cắt tất cả các cạnh của tam giác đó.
D. Đi qua trung điểm các cạnh của tam giác.
Câu 8: Cho tam giác ABC vuông tại A, có AB 3 cm, AC 4 cm. Độ dài của
bán kính đường tròn ngoại tiếp tam giác ABC là A. 5 cm .
B. 2 cm .
C. 3,5 cm . D. 2,5 cm .
Câu 9: Tâm đường tròn nội tiếp tam giác là giao điểm của các đường
A. Trung tuyến. B. Phân giác . C. Trung trực. D. Đáp án khác.
Câu 10: Cho tứ giác MNPQ nội tiếp đường tròn (O;R) và có 0 M 50 . Khi đó ta có A. 0 P 50 . B. 0 P 130 . C. 0 P 180 . D. 0 P 310 .
Câu 11: Trong các phát biểu sau, phát biểu nào là đúng:
A. Mọi tứ giác đều nội tiếp được đường tròn.
B. Trong một tứ giác nội tiếp, tổng số đo hai góc đối bằng 0 90 .
C. Tứ giác có tổng hai góc bằng 1800 thì tứ giác đó nội tiếp.
D. Tứ giác có 4 đỉnh cùng thuộc một đường tròn là tứ giác nội tiếp.
Câu 12: Đa giác đều là
A. một đa giác có các góc bằng nhau.
B. một đa giác lồi có các cạnh bằng nhau.
C. một đa giác có các cạnh bằng nhau và các góc bằng nhau.
D. một đa giác lồi có các cạnh bằng nhau và các góc bằng nhau.
Phần 2: Tự luận (7,0 điểm)
Bài 1: (1,5 điểm) Cho hàm số y = 𝑥𝑥2
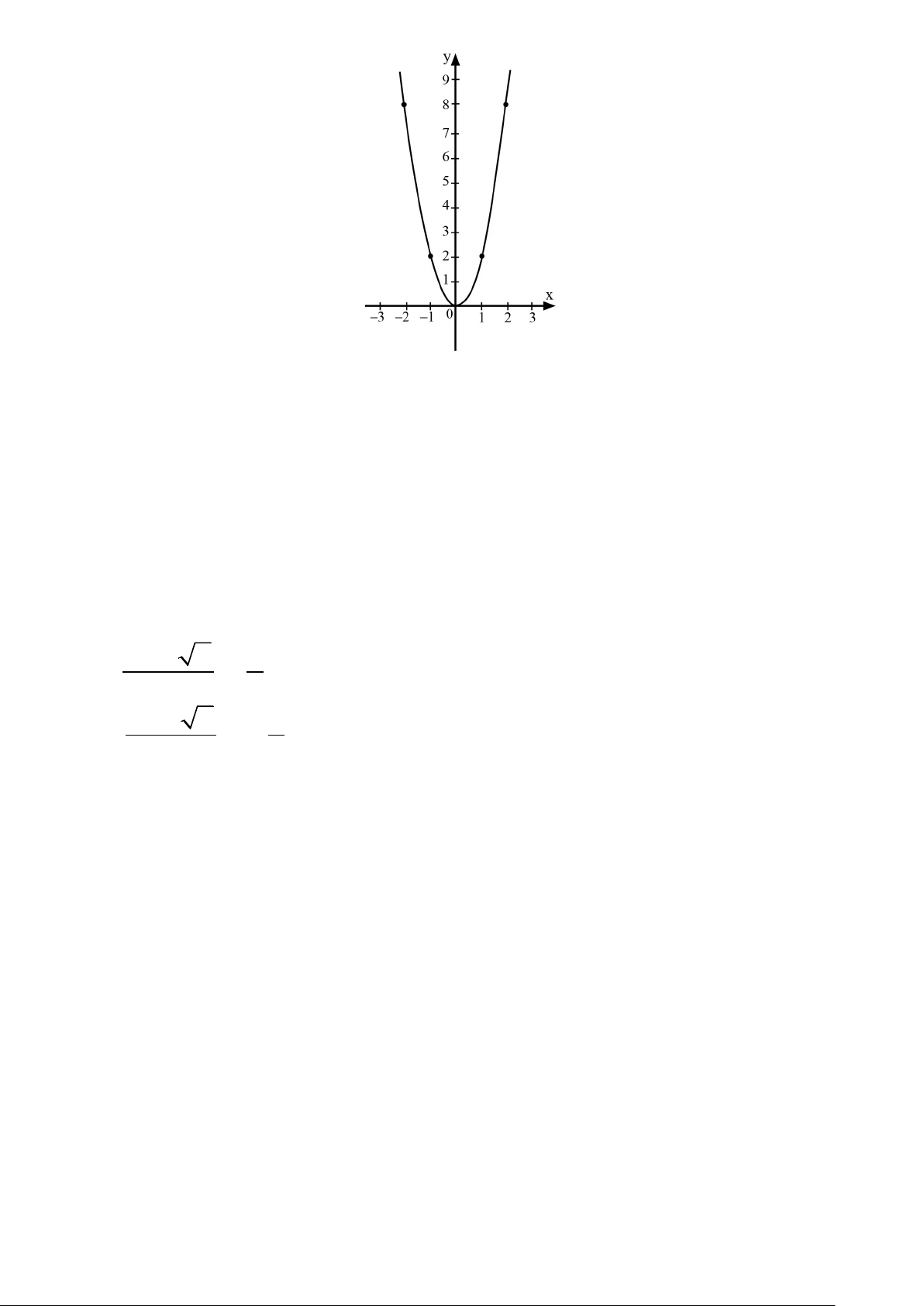
a) Vẽ đồ thị (P) của hàm số trên hệ trục tọa độ Oxy.
b) Tìm những điểm thuộc đồ thị hàm số trên có hoành độ bằng tung độ.
Bài 2 : (0,5 điểm) Giải phương trình 2
2x − 5x + 2 = 0
Bài 3: (1 điểm) Để hưởng ứng các hoạt động bảo vệ môi trường, lớp 9A nhận
trồng bổ sung 420 cây xanh ở một khu đồi gần trường và dự định chia đều số
cây cho mỗi bạn trong lớp. Đến khi thực hiện, có 7 bạn được nhà trường phân
công đi làm việc khác nên mỗi bạn còn lại trồng tăng thêm 3 cây so với dự
định. Hỏi lớp 9A có bao nhiêu học sinh?
Bài 4: (1,5 điểm) Cho phương trình x2 + 3x – 10 = 0.
a) Chứng minh phương trình có 2 nghiệm phân biệt.
b) Không giải phương trình. Gọi x1, x2 là hai nghiệm của phương trình. Hãy tính 1 1 M x x 1 2 x x 1 2
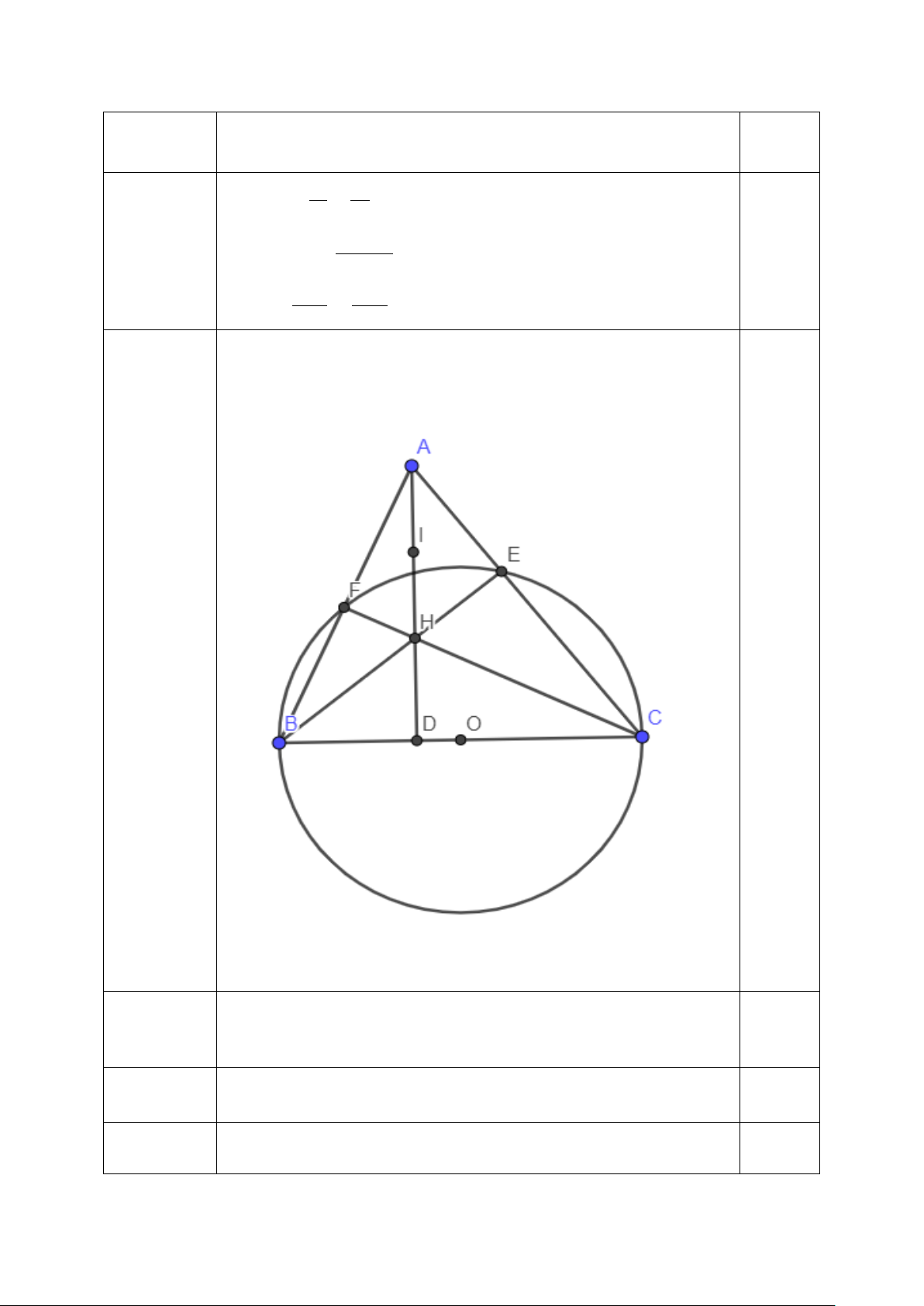
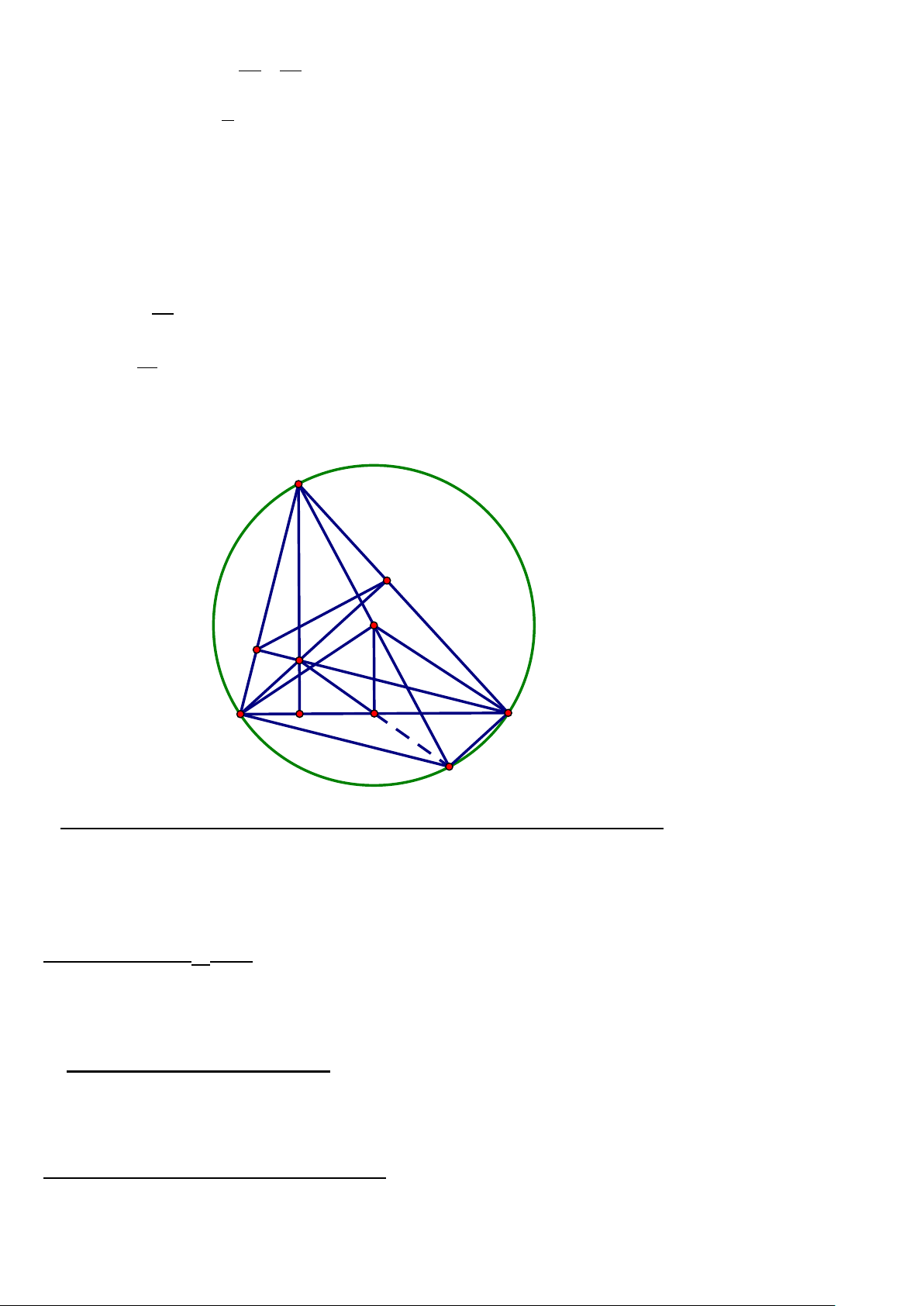
Bài 5: (2,5 điểm) Cho tam giác ABC có ba góc nhọn. Đường tròn (O; R) có
đường kính BC cắt AB, AC lần lượt tại F và E. BE cắt CF tại H.
a) Chứng minh tứ giác AFHE nội tiếp. Xác định tâm I của đường tròn ngoại tiếp tứ giác AFHE.
b) Tia AH cắt BC tại D. Chứng minh: HE.HB = 2 HD.HI
c) Tìm tâm đường tròn nội tiếp tam giác ABC và chứng minh 4 điểm D, E , I, F
cùng nằm trên một đường tròn. ĐÁP ÁN
Phần 1. Trắc nghiệm khách quan. (3,0 điểm) Câu 1 2 3 4 5 6 7 8 9 10 11 12 Đáp án B B A C D B B D B B D D
Phần 2: Tự luận (7,0 điểm) Bài Đáp án Điểm Bài 1: Cho hàm số y = 𝑥𝑥2 (1,5 điểm)
a) Vẽ đồ thị (P) của hàm số trên hệ trục tọa độ Oxy. 1,0 Lập bảng giá trị 0,25
Đồ thị (P) là 1 đường parabol đỉnh O đi qua các điểm… 0,25 Vẽ (P) 0,5
b) Tìm những điểm thuộc đồ thị hàm số trên có hoành độ 0,5 bằng tung độ.
Gọi (x;y) là điểm cần tìm
M có tung độ bằng hoành độ nên y =x 0,25 M thuộc (P) nên : 2 x = x x= 0 hoặc x= 1
Vậy điểm cần tìm là (0;0) và (1;1) 0,25 Bài 2 : Giải phương trình 2
2x − 5x + 2 = 0 (0,5 điểm) 2 ∆ = ( 5 − ) − 4.2.2 = 9 > 0
Vậy phương trình có 2 nghiệm phân biệt 0,25 −( 5) − + 9 x = = 2 1 2.2 −( 5) − − 9 1 x = = 1 2.2 2 0,25 Bài 3:
Để hưởng ứng các hoạt động bảo vệ môi trường, lớp 9A 1,0 (1 điểm)
nhận trồng bổ sung 420 cây xanh ở một khu đồi gần
trường và dự định chia đều số cây cho mỗi bạn trong lớp.
Đến khi thực hiện, có 7 bạn được nhà trường phân công
đi làm việc khác nên mỗi bạn còn lại trồng tăng thêm 3
cây so với dự định. Hỏi lớp 9A có bao nhiêu học sinh?
Gọi số học sinh lớp 9A là x (học sinh) ( * x ∈ N ) 0,25
Dự định mỗi bạn phải trồng 420 (cây) x
Vì có 7 bạn được nhà trường phân công đi làm việc khác 0,25
nên thực tế mỗi bạn phải trồng 420 (cây) x − 7
Vì mỗi bạn còn lại phải trồng tăng thêm 3 cây nên ta có 420 420 − = 3 x − 7 x 0,25
42x − 420(x − 7) = 3x(x − 7) 2
3x − 21x − 2940 = 0
PT có 2 nghiệm x = 35 ( tmđk) và x = 28 − (loại) 1 2
Vậy lớp 9A có 35 học sinh 0,25 Bài 4:
Bài 4: (1,5 điểm) Cho phương trình x2 + 3x – 10 = 0. (1,5điểm)
a) Chứng minh phương trình có 2 nghiệm phân biệt. 0,5 2 ∆ = 3 − 4.1.( 10) − = 49 > 0 0,25
Vậy phương trình có 2 nghiệm phân biệt 0,25
b) Không giải phương trình. Gọi x1, x2 là hai nghiệm của phương trình. Hãy tính 1 1 M x x 1 2 x x 1 2
Theo định lí Viete : S = x + x = 3 − 1 2
P = x .x = 10 − 1 2 1 1 M x x 1 2 x x 1 2 x x 1 2
(x x ) 1 2 x x 1 2 3 27 3 10 10 Bài 5:
Cho tam giác ABC có ba góc nhọn. Đường tròn (O; R) có
(2,5điểm) đường kính BC cắt AB, AC lần lượt tại F và E. BE cắt CF tại H.
a) Chứng minh tứ giác AFHE nội tiếp. Xác định tâm I của 1,0
đường tròn ngoại tiếp tứ giác AFHE.
b) Tia AH cắt BC tại D. Chứng minh: HE.HB = 2 HD.HI 0,5
c) Tìm tâm đường tròn nội tiếp tam giác ABC và chứng 1,0
minh 4 điểm D, E , I, F cùng nằm trên một đường tròn.
Tìm tâm đường tròn nội tiếp tam giác ABC 0,5
Chứng minh 4 điểm D, E , I, F cùng nằm t rên một đường 0,5 tròn.
UBND QUẬN BÌNH THẠNH
ĐỀ KIỂM TRA GIỮA KỲ HỌC KỲ 2
TRƯỜNG TRUNG HỌC CƠ SỞ NĂM HỌC 2024 - 2025 CÙ CHÍNH LAN MÔN TOÁN LỚP 9 ĐỀ ĐỀ NGHỊ
Thời gian: 90 phút (không kể thời gian phát đề)
A. TRẮC NGHIỆM: (3 điểm) Hãy chọn đáp án đúng nhất
Câu 1: Trong những điểm sau đây, điểm nào không thuộc đồ thị hàm số y = 4x2 ? A. (2; –16). B. (2; 16). C. (1; 4) D. (–1; 4)
Câu 2: Đồ thị hàm số 2
y = ax ,(a ≠ 0) đi qua điểm A(2; -16). Giá trị của a bằng: A. –8. B. –4. C. 4. D. 8. Câu 3: Cho hàm số 2 y = 3
− x có đồ thị là (P). Tọa độ điểm thuộc (P) có hoành độ bằng 2 là: 3 A. 2 4 ; − − B. 2 4 ; C. 2 2 ; D. 2 2 ; 3 3 3 3 3 3 3 3
Câu 4: Phương trình nào dưới đây không là phương trình bậc hai một ẩn?
A. x2 – 2 x = 0 B. 0x2 + 5x – 2 = 0. C. 4x2 – 5 = 0. D. 7x2 + 5x - 2 = 0.
Câu 5: Hãy chọn câu đúng: A. Phương trình 2
x 7x8 0 có nghiệm kép B. Phương trình 2
5x 12x 4 0 vô nghiệm C. Phương trình 2
x x 9 0 có hai nghiệm phân biệt D. Phương trình 2
3x 2x 0 có hai nghiệm phân biệt
Câu 6: Nghiệm của phương trình 3x2 – 8x + 5 = 0 là: A. 5 x = 1; − x = B. 5 x = 1; − x = − C. 5
x =1; x = − D. 5 x =1; x = 1 2 3 1 2 3 1 2 3 1 2 3
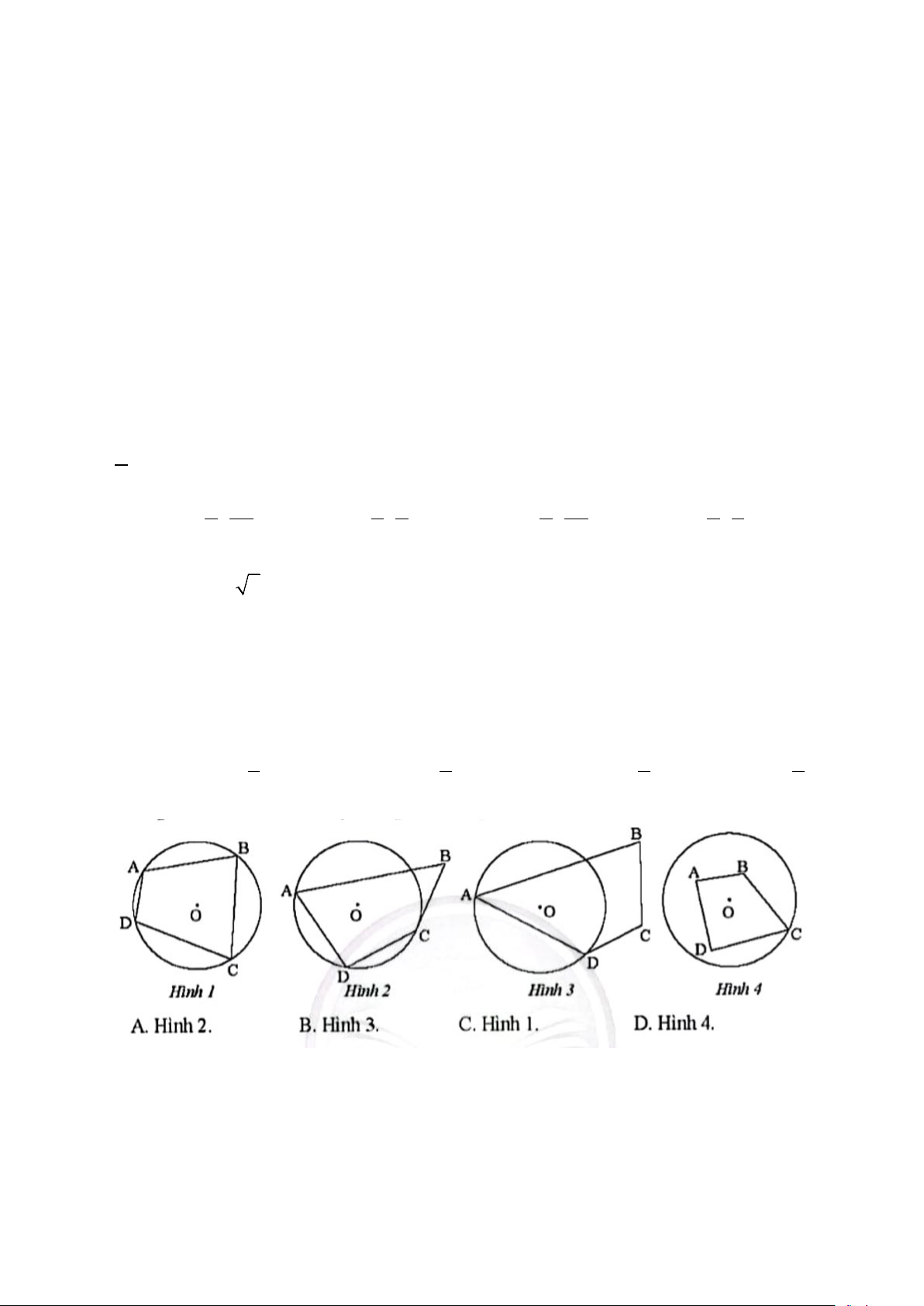
Câu 7: Tứ giác ở hình nào dưới đây là tứ giác nội tiếp đường tròn (O)
Câu 8: Trong các phát biểu sau phát biểu nào sai ?
A. Hình vuông nội tiếp đường tròn.
B. Mọi tứ giác đều nội tiếp đường tròn.
C. Hình chữ nhật là tứ giác nội tiếp.
D. Tổng số đo hai góc đối trong tứ giác nội tiếp bằng 1800.
Câu 9: Cho tứ giác MNPQ là tứ giác nội tiếp và 0
ˆM = 63 . Số đo của ˆP là: A. 0 63 B. 0 126 C. 0 36 D. 0 117
Câu 10: Cho ∆ABC đều cạnh a nội tiếp trong đường tròn tâm O có bán kính R thì: 2 A. a 3 R = B. a 3 R = C. a 3 R = D. a 3 R = 2 3 6 4
Câu 11: Cho tam giác đều cạnh 3cm. Bán kính của đường tròn nội tiếp tam giác đều đó là: A. 3 3 c ; m B. 2 c ; m C. 3 c ; m D. 2 3 c ; m 2 2 2 3
Câu 12: Cho ∆ABC vuông tại A có AB = 3 cm, AC = 4 cm. Bán kính đường tròn ngoại tiếp ∆ABC là: A. 3 cm B. 4 cm C. 2,5 cm D. 5cm
B. TỰ LUẬN (7 điểm)
Bài 1 (1,5 điểm). Cho hàm số 1 2
y = − x có đồ thị là (P). 4
a) Vẽ đồ thị của hàm số trên.
b) Tìm các điểm thuộc (P) có tung độ bằng –16.
Bài 2 (0,5 điểm) Giải các phương trình sau: 4x2 + 7x – 11 = 0
Bài 3 (1 điểm) Giải bài toán sau bằng cách lập phương trình bậc 2 một ẩn.
Hai xe ô tô khởi hành cùng một lúc từ thành phố A đến thành phố B cách nhau 210
km. Tốc độ của xe thứ nhất nhanh hơn tốc độ xe thứ hai là 9 km/h nên xe thứ nhất đã đến
sớm hơn xe thứ hai 18 phút. Tính tốc độ của mỗi xe.
Bài 4 (1,5 điểm). Cho phương trình: 2 x − x −12 = 0.
a) Chứng minh phương trình có hai nghiệm phân biệt.
b) Không giải phương trình. Gọi x , x là các nghiệm của phương trình hãy tính: 1 2
N = (x − x )2 − 3x − 3x . 1 2 1 2
Bài 5 (2,5 điểm). Cho ∆ABC nhọn (AB < AC) nội tiếp đường tròn (O), hai đường cao BM và CN cắt nhau tại H.
a) Chứng minh tứ giác BCMN là các tứ giác nội tiếp
b) Hai tia MN và CB cắt nhau tại D, AD cắt (O) tại G.
Chứng minh DB . DC = DN . DM. c) Chứng minh ˆ DGN = ˆ DMA . HẾT ĐÁP ÁN
A. PHẦN TRẮC NGHIỆM (3,0 điểm) Câu 1 2 3 4 5 6 7 8 9 10 11 12 Đáp án A B A B C D C B D B C C
B. PHẦN TỰ LUẬN (7,0 ĐIỂM) Câu 1 Cho hàm số 1 2
y = − x có đồ thị là (P). 4
a) Vẽ đồ thị của hàm số trên. 1,5đ
b) Tìm các điểm thuộc (P) có tung độ bằng –16. 1a Bảng giá trị (P): 0,5đ Vẽ đồ thị của (P) 0,5đ 1b Ta có: 1 2 y = − x 4 Mà y = –16 1 2 16 − = − x 0,25đ 4 x = 8; x = 8 − 1 2 KL 0,25đ Câu 2
Giải các phương trình sau: 4x2 + 7x – 11 = 0 0,5đ 2 2
∆ = b − 4ac = 7 − 4.4.(− ) 11 = 225 > 0 0,25đ
Vậy phương trình có hai nghiệm phân biệt: 7 225 x − + = =1 1 2.4 0,25đ 7 225 11 x − − − = = 2 2.4 4 Câu 3
Hai xe ô tô khởi hành cùng một lúc từ thành phố A đến thành 1đ
phố B cách nhau 210 km. Tốc độ của xe thứ nhất nhanh hơn
tốc độ xe thứ hai là 9 km/h nên xe thứ nhất đã đến sớm hơn
xe thứ hai 18 phút. Tính tốc độ của mỗi xe.
Gọi x (km/h) là tốc độ của xe thứ nhất (x>0) 0,25đ
Do thành phố A đến thành phố B cách nhau 210 km và tốc
độ của xe thứ nhất nhanh hơn tốc độ xe thứ hai là 9 km/h
nên xe thứ nhất đã đến sớm hơn xe thứ hai 18 phút, nên ta có phương trình: 210 3 210 + = x 10 x − 9 0,25đ
Giải phương trình ta có: x = 84(nhận) và x = 75 − (loại) 0,25đ 1 1
Vậy tốc độ của xe thứ nhất là 84 km/h, tốc độ của xe thứ 0,25đ hai là 75 km/h Câu 4 Cho phương trình: 2 x − x −12 = 0. 1,5đ
a) Chứng minh phương trình có hai nghiệm phân biệt.
b) Không giải phương trình. Gọi x , x là các nghiệm 1 2
của phương trình hãy tính: N = (x − x )2 −3x −3x . 1 2 1 2 4a
∆ = b − ac = (− )2 2 4 1 − 4.1.( 12 − ) = 49 > 0 0,25đ
Vậy phương trình có hai nghiệm phân biệt: 0,25đ 4b x + x =1 0,25đ 1 2 x .x = 12 − 0,25đ 1 2
Ta có: N = (x − x )2 −3x −3x =46 0,5đ 1 2 1 2 Câu 5
Cho ∆ABC nhọn (AB < AC) nội tiếp đường tròn (O), hai 2,,5đ
đường cao BM và CN cắt nhau tại H.
a) Chứng minh tứ giác BCMN là các tứ giác nội tiếp
b) Hai tia MN và CB cắt nhau tại D, AD cắt (O) tại G.
Chứng minh DB . DC = DN . DM. c) Chứng minh ˆ DGN = ˆ DMA . A G M N H O D C B 5a
CM: BCMN là các tứ giác nội tiếp 1d 5b CM: ∆DBN ~ ∆DMC 0,25đ CM: DB. DC = DN. DM 0,25đ 5c CM: DB. DC = DG. DA 0,5đ CM: ∆DGN ~ ∆DMA 0,25đ CM: ˆ DGN = ˆ DMA 0,25đ UBND QUẬN BÌNH THẠNH
ĐỀ KIỂM TRA GIỮA HỌC KÌ II
TRƯỜNG TRUNG HỌC CƠ SỞ
NĂM HỌC: 2024 – 2025 CỬU LONG MÔN: TOÁN 9 ĐỀ ĐỀ NGHỊ Thời gian: 90 phút (Đề gồm 2 trang)
(không tính thời gian phát đề)
PHẦN 1. TRẮC NGHIỆM KHÁCH QUAN (3,0 điểm). Câu 1: Hàm số 2 y = 3x − đồng biến khi A. x ≥ 0 . B. x < 0 . C. x ≤ 0 . D. x > 0 .
Câu 2: Khẳng định nào sau đây là đúng. Đồ thị của hàm số 2 y = ax (a ≠ 0)
A. Với a > 0 , đồ thị nằm trên trục hoành và O là điểm cao nhất đồ thị.
B. Với a < 0 , đồ thị nằm dưới trục hoành và O là điểm cao nhất đồ thị.
C. Với a > 0 , đồ thị nằm dưới trục hoành và O là điểm thấp nhất đồ thị.
D. Với a < 0 , đồ thị nằm dưới trục hoành và O là điểm thấp nhất đồ thị.
Câu 3: Phương trình nào là phương trình bậc hai một ẩn? A. 0x2 + 5x + 2 = 0 B. 6x2 + y + 5 = 0 C. x2 - 1 = 0 D. 2x + y = 3
Câu 4: Điểm thuộc (P): y = 1 x2 là 2 A. (2; 1) B. (2; 8 ) C. (2; 4) D. (2; 2)
Câu 5: Phương trình: 2
ax bx c 0 có hai nghiệm phân biệt khi nào? A. ∆ > 0 B. ∆ < 0 C. ∆ ≤ 0 D. ∆ = 0
Câu 6: Cho phương trình 2
x 14x 33 0 . Không giải phương trình, hãy tính tổng và tích các nghiệm, hãy chọn câu đúng:
A. x x 33; x x 14
x x 14; x x 33 1 2 1 2 B. 1 2 1 2 ;
C. x x 11; x x 3
x x 14; x x 33 1 2 1 2 D. 1 2 1 2 ;
Câu 7: Tứ giác ABCD nội tiếp đường tròn có A = 500. Khi đó C bằng: A. 400 B . 500 C . 1000 D . 1300
Câu 8: Đường tròn ngoại tiếp đa giác là đường tròn
A. chứa đa giác đó.
B. nằm ngoài đa giác đó.
C. tiếp xúc với tất cả các cạnh của đa giác đó.
D. đi qua tất cả các đỉnh của đa giác đó.
Câu 9: Tâm đường tròn nội tiếp của một tam giác là giao của các đường:
A. Trung trực B. Phân giác trong
C. Phân giác ngoài D. Đáp án khác
Câu 10: Một tứ giác nội tiếp đường tròn là
A. Tứ giác nằm bên trong đường tròn.
B. Tứ giác có 4 đỉnh nằm ngoài một đường tròn.
C. Tứ giác có 4 đỉnh nằm trên một đường tròn.
D. Tứ giác có 4 đỉnh nằm trong một đường tròn.
Câu 11. Tam giác đều là một đa giác
A. Có 3 cạnh và 3 góc bằng nhau.
B. Có 7 cạnh và 7 góc bằng nhau.
C. Có các cạnh và các góc bằng nhau.
D. Có 8 cạnh và 8 góc bằng nhau
Câu 12. Các phép quay có thể có với một đa giác đều tâm O là
A. Phép quay thuận chiều và phép quay đảo chiều.
B. Phép quay thuận chiều và phép quay ngược chiều.
C. Phép quay xuôi chiều và phép quay đảo chiều.
D. Phép quay xuôi chiều và phép quay ngược chiều.
PHẦN 2: TỰ LUẬN (7 điểm)
Bài 1. (1,5 điểm) Cho parabol (P): 2 y = 2x .
a. Vẽ đồ thị (P) trên hệ trục tọa độ.
b. Tìm tọa độ những điểm M thuộc (P) có tung độ bằng 2.
Bài 2 (0,5 điểm) Giải phương trình sau : 6x2 – 7x – 3 = 0.
Bài 3. (1 điểm) Giải bài toán bằng cách lập phương trình bậc hai
Một sân bóng hình chữ nhật có chiều dài là x (đơn vị: mét, x > 0) và chiều dài hơn chiều rộng là 3 m.
a) Viết biểu thức tính diện tích S của sân bóng theo x.
b) Nếu tăng chiều dài thêm 1 m và tăng chiều rộng thêm 3 m thì diện tích sân bóng tăng gấp đôi.
Tính chiều dài của sân bóng đó.
Bài 4. (1,5 điểm) Cho phương trình:
2x2 + 3x – 14 = 0 có 2 nghiệm là x , x 1 2
a. Chứng minh phương trình có hai nghiêm.
b. Tính giá trị của biểu thức sau: 2
P = (x − x ) + x x 1 2 1 2
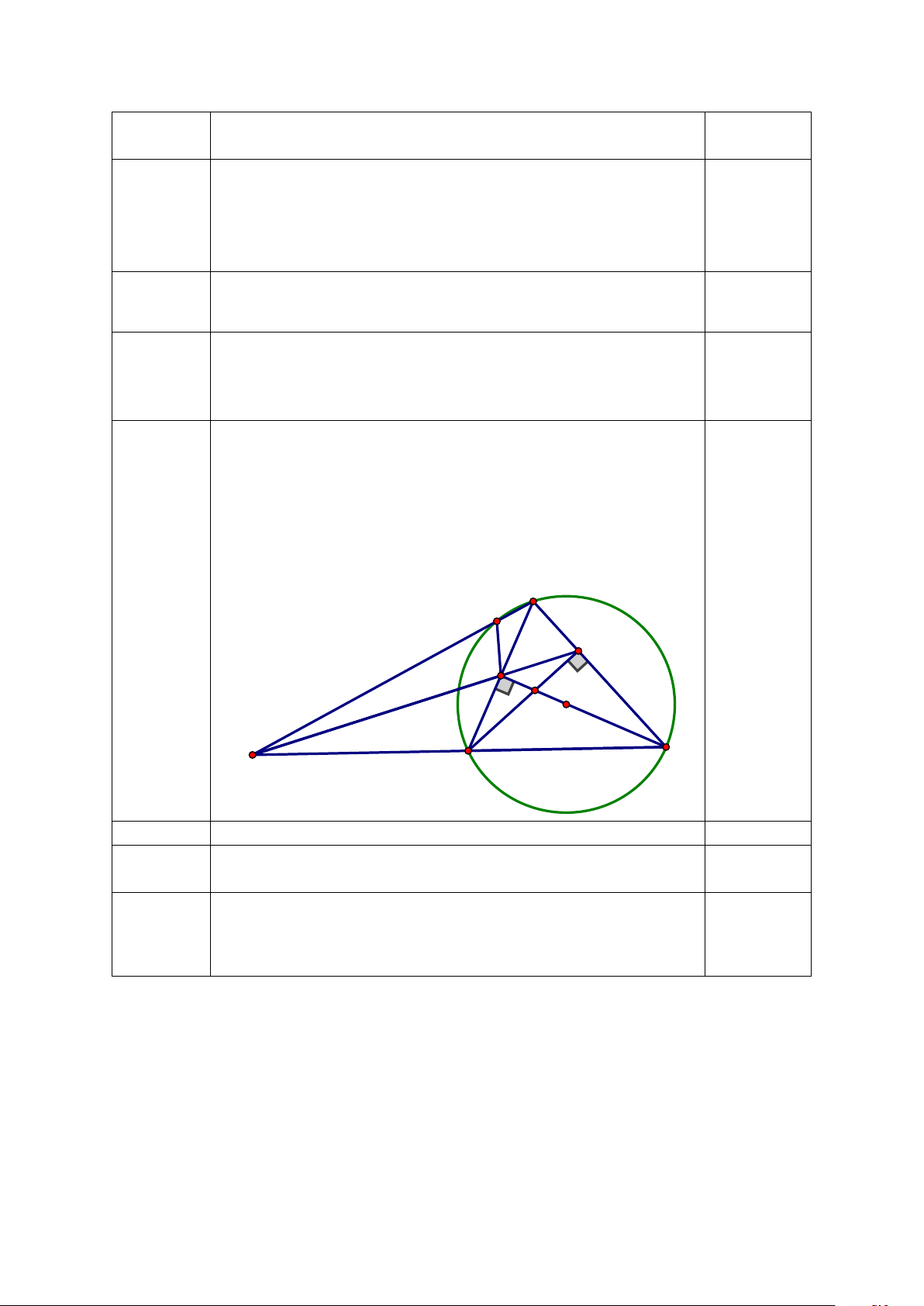
Bài 5. (2,5 điểm) Cho tam giác ABC nhọn (với AB < AC) nội tiếp (O;R). Các đường cao AD,BE,CF
của tam giác ABC cắt nhau tại H. Gọi I là trung điểm của BC.
a)Chứng minh:tứ giác BFEC nội tiếp đường tròn đường kính BC và OI vuông góc BC.
b)Kẻ đường kính AM của (O). Chứng minh: AC.AB =AD.AM và ba điểm H,I,M thẳng hàng.
c)Biết AH = R = 10cm. Tính độ dài đoạn thẳng BC và EF. Đáp án:
PHẦN I. TRẮC NGHIỆM (3,0 điểm). Mỗi câu đúng được 0,25 điểm. 1 2 3 4 5 6 7 8 9 10 11 12 B B C D B B D D B C A B
PHẦN II. TỰ LUẬN (7,0 điểm).
Bài 1. (1,5 điểm)
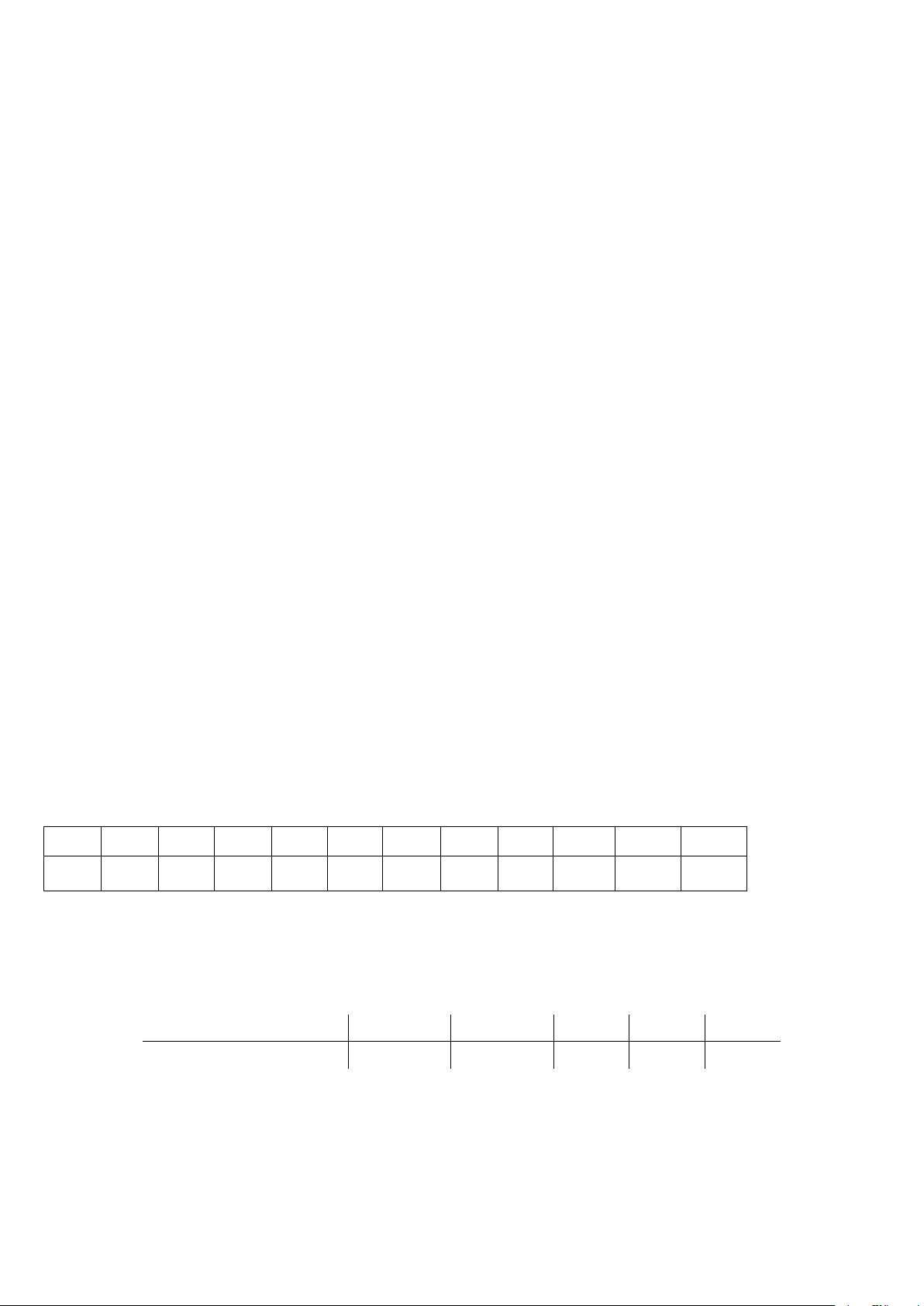
Lập bảng giá trị của (P) .................................................................................................................. 0,25đ Bảng giá trị: x –2 –1 0 1 2 y = 2x2 8 2 0 2 8
Vẽ (P) ............................................................................................................................................. 0,25đ
Đồ thị của hàm số được vẽ như hình sau
b) Điểm M thuộc (P) có tung độ bằng 2 nên tọa độ của M thỏa mãn: 2 2x 2 khi 2
x 1 ....................................................................................................................... 0,25đ
Khi đó x 1hoặc x 1
Với x 1thì y 2 ........................................................................................................................ 0,25đ
Với x 1thì y 2 .................................................................................................................... 0,25đ
Vậy tọa độ những điểm M thuộc (P) có tung độ bằng 2 là (1;2) và 1;2 .................................. 0,25đ Bài 2. 6x2 - 7x - 3 = 0 ∆ = 121 > 0
Phương trình có 2 nghiệm phân biệt: b − + 3 * x = = 1 2a 2 b − − 1 * x = = − 2 2a 3 Bài 3.
a) Viết biểu thức tính diện tích 𝑺𝑺 của sân bóng theo 𝒙𝒙.
Chiều rộng của sân bóng là: 𝑥𝑥 − 3 (𝑚𝑚)
Diện tích của sân bóng là: 𝑆𝑆 = 𝑥𝑥(𝑥𝑥 − 3) = 𝑥𝑥2 − 3𝑥𝑥 (𝑚𝑚2)
b) Sau đó người ta tăng chiều dài thêm 𝟏𝟏 m và tăng chiều rộng thêm 𝟑𝟑 𝐦𝐦 thì diện tích sân bóng
tăng gấp đôi. Tính chiều dài của sân bóng đó?
Diện tích của hình chữ nhật sau khi tăng chiều dài thêm 1 m và tăng chiều rộng thêm 3 m là:
(𝑥𝑥 + 1)(𝑥𝑥 − 3 + 3) = (𝑥𝑥 + 1) ⋅ 𝑥𝑥 = 𝑥𝑥2 + 𝑥𝑥.
Theo bài ta có phương trình: 𝑥𝑥2 + 𝑥𝑥 = 2(𝑥𝑥2 − 3𝑥𝑥) 𝑥𝑥2 − 7𝑥𝑥 = 0 𝑥𝑥(𝑥𝑥 − 7) = 0 �𝑥𝑥 = 0
𝑥𝑥 = 7 ⇒ 𝑥𝑥 = 7 (vì 𝑥𝑥 > 0)
Vậy chiều dài của hình chữ nhật là 7 𝑚𝑚 . Bài 4.
a) Chứng tỏ phương trình có 2 nghiệm phân biệt ( 0,5đ) b − 3 −
S = x + x = = 1 2 Theo viết a 2 ( 0,5đ) c P = x x = = 7 − 1 2 a
b, Ta có: P = (x − x )2 + x x 1 2 1 2 2 2
P = x + x − x x ( 0,5đ) 1 2 1 2
P = (x + x )2 −3x x ( 0,25đ) 1 2 1 2 2 3 P − = − 3( 7 − ) 2 93 P = ( 0,25đ) 4 Bài 5. A E O F H B D I C M
a)Chứng minh tứ giác BFEC nội tiếp đường tròn tâm I đường kính BC .
*C/m ba điểm B ,F ,C cùng thuộc đường tròn tâm I đường kính BC .
*C/m ba điểm B , E ,C cùng thuộc đường tròn tâm I đường kính BC .
Ta có bốn điểm B,F,E,C cùng thuộc đường tròn tâm I đường kính BC
Vậy tứ giác BFEC nội tiếp đường tròn tâm I đường kính BC .
Chứng minh OI ⊥ BC .
C/m tam giác OBC cân tại O và có OI là trung tuyến
Nên OI cũng là đường cao tam giác OBC Suy ra OI ⊥ BC.
b) Chứng minh AB.AC = AD.AM
C/m 2 tam giác ADB và ACM đồng dạng ( g-g) Suy ra AD/ AC = AB / AM Suy ra AB.AC = AD.AM.
Chứng minh ba điểm H,I,M thẳng hàng *C/m : MC // BH *C/m : MB // CH
Suy ra Tứ giác BHCM là hình bình hành
Lại có I là trung điểm của BC
Nên I cũng là trung điểm của HM
Suy ra ba điểm H , I , M thẳng hàng .
c)Tính độ dài đoạn thẳng BC Tính OI
*OI = ½ AH = ½ .10 = 5 (cm )
*Xét tam giác OIC vuông tại I
Ta có OI2 +IC2 = OC2 (đl pytago) IC = 2 2 10 − 5 = 5 3 (cm). *BC = 2 IC = 10 3 (cm).
Tính độ dài đoạn thẳng EF
*cos IOC = OI / OC = 5/10 = ½ Góc IOC = 600
Suy ra góc BOC = 2 góc IOC = 1200
*Ta có góc BAC = ½ góc BOC = 600 ( góc nội tiếp và góc ở tâm cùng chắn cung BC)
* Chứng minh Tam giác AEF và ABC đồng dạng
Suy ra EF /BC = AE/AF = cos BAC = cos 600 =1/2 Suy ra EF = ½ BC Suy ra EF = 5 3 (cm) UBND QUẬN BÌNH THẠNH
ĐỀ THAM KHẢO KIỂM TRA GIỮA HỌC KÌ 2
TRƯỜNG TRUNG HỌC CƠ SỞ MÔN TOÁN – LỚP 9 ĐIỆN BIÊN
NĂM HỌC: 2024 – 2025
Thời gian: 90 phút (không kể thời gian phát đề)
I. PHẦN TRẮC NGHIỆM (3,0 điểm) Câu 1. Cho hàm số 2 y = 3x . Khi y = 3 thì:
A. x = 1. B. x = 2 hoặc x = -2. C. x = 1 hoặc x = -1. D. x = 2 .
Câu 2. Trong các bảng giá trị sau, bảng giá trị nào là bảng giá trị của hàm số 2 y = -x ? A. B. x -2 -1 0 1 2 x -2 -1 0 1 2 2 y = -x 4 1 0 -1 4 2 y = -x -4 -1 0 -1 -4 C. D. x -2 -1 0 1 2 x -2 -1 0 1 2 2 y = -x 2 1 0 1 2 2 y = -x 4 1 0 1 4
Câu 3. Cho phương trình 2
ax + bx + c = 0 (a ≠ 0)có 2
Δ = b - 4ac = 0 . Khi đó, phương trình có hai nghiệm là: b b b b A. x = x = x = x = - x = x = x = x = - 1 2 B. C. D. 2a 1 2 2a 1 2 a 1 2 a
Câu 4. Nghiệm của phương trình 2 x − 4x + 3 = 0 là: A. x = 1; − x = 3 x = -1;x = -3 x =1;x = 3 − x =1;x = 3 1 2 . B. 1 2 . C. 1 2 . D. 1 2 .
Câu 5. Gọi S và P lần lượt là tổng và tích của hai nghiệm của phương trình 2
x − 7x+10 = 0 . Khi đó giá trị của S và P là:
A. S = 7;P =10. B. S = -7;P = 10 . C. S = -7;P = -10 . D. S = 7;P = -10.
Câu 6. Cho phương trình 2 x -5x+3 = 0. Gọi x , x 1
2 là hai nghiệm của phương trình. Khi đó giá trị của biểu thức 2 2 x + x là: 1 2
A. 19 . B. -19 . C. 25 . D. -25 .
Câu 7. Cho tam giác đều ABC có cạnh là 5 cm. Bán kính r của đường tròn nội tiếp tam giác có độ dài là:
A. 5 3 cm . B. 5 3 cm . C. 5 3 cm . D. 5 3 cm . 2 3 6
Câu 8. Cho tam giác đều có cạnh là 3 cm. Bán kính R của đường tròn ngoại tiếp tam giác có độ dài là: 3 A. 3 cm . B. 3 cm . C. cm . D. 4,5 cm . 3
Câu 9. Trong các phát biểu sau, phát biểu nào đúng?
A. Mọi tứ giác luôn nội tiếp được đường tròn.
B. Trong một tứ giác nộí tiếp, tổng số đo hai góc đối nhau bằng 90° .
C. Tổng số đo hai góc đối của một tứ giác nội tiếp luôn bằng 180°.
D. Tất cả các hình thang đều là tứ giác nội tiếp.
Câu 10. Cho tứ giác MNPQ nội tiếp đường tròn (O;R) và M 80° = . Số đo của P là:
A. 80° . B. 100°. C. 10°. D. 180°.
Câu 11. Cho lục giác đều ABCDEF nội tiếp đường tròn bán kính 5 . Độ dài cạnh AB bằng:
A. 5. B. 5 3 . C. 5 3 . D. 5 3 . 2 6
Câu 12. Phép quay nào với O là tâm biến tam giác đều thành chính nó?
A. 90° . B. 100°. C. 110°. D. 120°.
II. PHẦN TỰ LUẬN (7,0 ĐIỂM) 1
Bài 1 (1,5 điểm). Cho hàm số 2 y = - x . 2
a) Vẽ đồ thị (P) của hàm số trên.
b) Tìm những điểm thuộc (P) có hoành độ x = -2.
Bài 2. (0,5 điểm) Giải phương trình: 7x2 – 12x +5 = 0
Bài 3. (1,0 điểm) Hai xe ô tô khởi hành cùng một lúc từ thành phố A đến thành phố B cách nhau 120 km . Tốc
độ của xe thứ nhất nhanh hơn tốc độ xe thứ hai là 10 km/h nên đã đến sớm hơn xe thứ hai 24 phút. Tính tốc độ của mỗi xe.
Bài 4. (1,5 điểm) Cho phương trình 2
3x − 6x − 7 = 0.
a) Chứng minh phương trình trên có hai nghiệm phân biệt x , x . 1 2
b) Không giải phương trình, hãy tính giá trị của biểu thức A = (x − 2 x − 2 . 1 )( 2 )
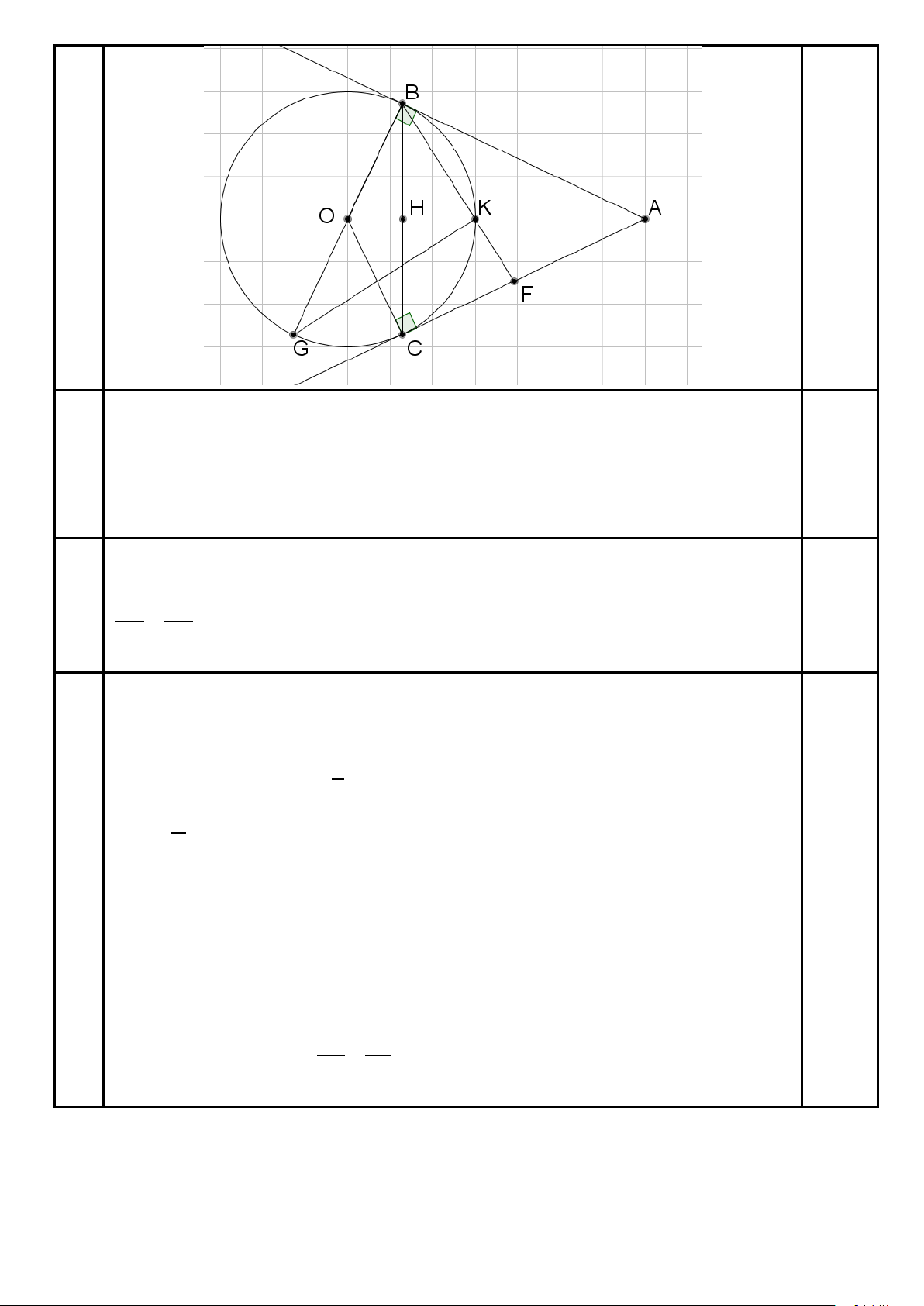
Bài 5. (2,5 điểm) Từ điểm A nằm bên ngoài đường tròn (O) vẽ hai tiếp tuyến AB, AC đến (O) (với B, C là
các tiếp điểm) AO cắt BC tại H.
a) Chứng minh tứ giác ABOC nội tiếp. Xác định tâm của đường tròn ngoại tiếp tứ giác này. b) Chứng minh AB2 = AH.AO.
c) OA cắt (O) tại K, BK cắt AC tại F. Chứng minh AB.FC = BC.FA. Hết UBND QUẬN BÌNH THẠNH
ĐÁP ÁN THAM KHẢO KIỂM TRA GIỮA HỌC KÌ 2
TRƯỜNG TRUNG HỌC CƠ SỞ MÔN TOÁN – LỚP 9 ĐIỆN BIÊN
NĂM HỌC: 2024 – 2025
I. TRẮC NGHIỆM (3,0 ĐIỂM) 1 2 3 4 5 6 7 8 9 10 11 12 C B B D A A D B C B A D
II. TỰ LUẬN (7,0 ĐIỂM) Bài Đáp án Điểm 1 1,5 Bảng giá trị x - 4 - 2 0 2 4 a 1 0,25 2
y = − x - 8 - 2 0 - 2 - 8 2 Vẽ hình đúng 0,5 Thay 1 x = 2 − vào 2
y = − x , ta được: 0,25 2 b 1
y = − .(−2)2 = −2 0,25 2
Vậy điểm thuộc (P) có hoành độ x = 2 − là (−2;−2) . 0,25
2 Giải phương trình: 7x2 – 12x +5 = 0 0,5 2 ∆ = b − 4ac 0,25 = ( 12 − )2 − 4.7.5 = 4 > 0
Phương trình có 2 nghiệm phân biệt: x =1; 5 x = 1 0,25 2 7
Hai xe ô tô khởi hành cùng một lúc từ thành phố A đến thành phố B cách nhau 120 km . Tốc
3 độ của xe thứ nhất nhanh hơn tốc độ xe thứ hai là 10 km/h nên đã đến sớm hơn xe thứ hai 1,0
24 phút. Tính tốc độ của mỗi xe?
Gọi x (km/h) là tốc độ xe thứ nhất ( x >0) 0,25
Tốc độ xe thứ hai là : x – 10 (km/h)
Thời gian xe thứ nhất đi từ A đến B: 120 x
Thời gian xe thứ hai đi từ A đến B: 120 0,25 x -10 2 Đổi 24 phút = giờ 5 0,25
Tốc độ của xe thứ nhất nhanh hơn tốc độ xe thứ hai là 10 km/h nên đã đến sớm hơn xe thứ
hai 24 phút nên ta có phương trình: 120 120 2 - = x -10 x 5 5x.120
5(x −10).120 2x(x −10) − = 5x(x −10) 5x(x −10) 5x(x −10) 2
600x − 600x + 6000 = 2x − 20x 2 2x − 20x − 6000 = 0 x =60;x = 50 − (loại) 1 2 0,25
Vậy tốc độ xe thứ nhất là 60 (km/h), tốc độ xe thứ hai là 50 (km/h).
4 Cho phương trình: 3x2 – 6x – 7 = 0 1,5
Chứng minh phương trình luôn có hai nghiệm phân biệt x , x 1 2 . 0,5 a ∆ = (− )2 6 − 4.3.( 7 − ) =120 > 0 0,25
Vậy phương trình luôn có hai nghiệm phân biệt x , x 1 2 0,25
Không giải phương trình, hãy tính giá trị của biểu thức A = (x − 2 x − 2 . 1 )( 2 ) 1,0
Theo định lí Viète ta có x + x = 2 1 2 0,5 7 x x = − 1 2 3
b A = (x −2 x −2 1 )( 2 ) 0,25
A = x x − 2 x + x + 4 1 2 ( 1 2) 7 A = − − 2.2 + 4 3 7 A = − 0,25 3
Từ điểm A nằm bên ngoài đườngtròn (O) vẽ hai tiếp tuyến AB, AC đến (O) (với B, C là
các tiếp điểm) AO cắt BC tại H.
a) Chứng minh tứ giác ABOC nội tiếp. Xác định tâm của đường tròn ngoại tiếp tứ 5 2,5 giác này. điểm b) Chứng minh AB2 = AH.AO.
c) OA cắt (O) tại K, BK cắt AC tại F. Chứng minh AB.FC = BC.FA.
△ABO vuông tại B nên nội tiếp đường tròn đường kính OA. 0,25
△ACO vuông tại C nên nội tiếp đường tròn đường kính OA. 0,25
a Suy ra 4 điểm A, B, O, C thuộc đường tròn đường kính OA. 0,25
Suy ra tứ giác ABOC nội tiếp đường tròn đường kính OA, tâm của đường tròn ngoại tiếp tứ
giác ABOC là trung điểm của OA. 0,25
Chứng minh ΔABH vuông tại H ΔABO ∽ ΔAHB (g – g) 0,25 b AB = AO AH AB 0,25 AH.AO = AB2
Vẽ đường kính BG, ta có: ABK + = 0
OBK 90 (AB là tiếp tuyến) (1) + 0 BGK OBK = 90 ( 0
BKG = 90 , góc nội tiếp chắn nửa đường tròn) (2) 0,25 Từ (1) và (2) = 1 = ABK BGK sđBK 2 0,25 CBK = 1 sđ CK (góc nội tiếp) 2 c Mà BOK =
COK (tính chất hai tiếp tuyến cắt nhau tại A) Nên sđ BK = sđ CK 0,25 ABK = CBK
BK là tia phân giác của ABC
Mà BK cắt AC tại F nên AB FA = BC FC AB.FC = BC.FA 0,25