Đề Thi Chọn HSG Toán 9 Cấp Huyện Năm 2025-2026 Có Đáp Án

UBND QUẬN ĐỀ KIỂM TRA
PHÒNG GIÁO DỤC VÀ ĐÀO TẠO CHỌN ĐỘI TUYỂN HỌC SINH GIỎI LỚP 9 CẤP QUẬN VÒNG 1 MÔN: TOÁN ĐỀ C HÍN
H THỨC Thời gian: 150 phút (không kể thời gian phát đề) 2 x − x 2x + x 2(x − ) 1
Câu 1. ( 5 điểm) Cho biểu thức A = − +
với x  0; x  1 . x + x +1 x x −1
a) Rút gọn biểu thức A . x ( + )3 5 2 17 5 − 38
b) Tính giá trị của biểu thức A khi = . 12 5 + 14 − 6 5 2 c) Đặt = x B
, chứng tỏ rằng 0  B  2 . A
Câu 2. ( 5 điểm) Giải các phương trình sau: 3 2 x 3x a) 3 x + + − = . (x − ) 28 0 3 1 x −1 1 5 b) + = 4. 3 + x 4 + x Câu 3. ( 3 điểm)
a) Tìm tất cả các số nguyên tố p thỏa mãn 2
p + 23 có đúng 6 ước số dương. 2 2 x + y 2 xy
b) Cho x, y  0 . Tìm giá trị nhỏ nhất của biểu thức M = + . xy x + y
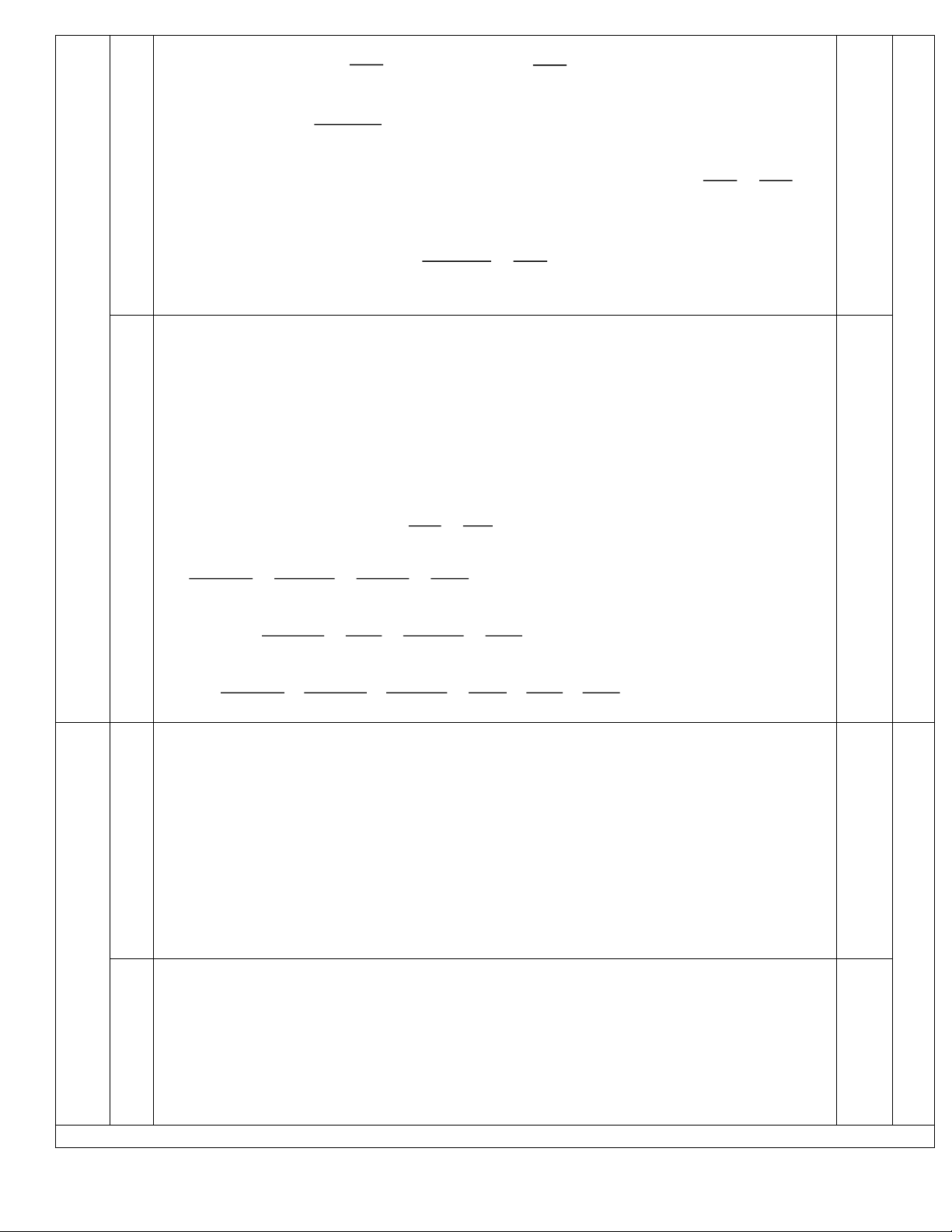
Câu 4. ( 6 điểm) Cho tam giác ABC có ba góc nhọn với các đường cao AD, BE, CF cắt
nhau tại H. Chứng minh rằng: 1 a) S = B .
A BC.sin B và AE.BF.CD = . AB BC.C . A cos . A cos . B cosC. ABC 2 b) AD tan . B tanC = . HD
c) H là giao điểm ba đường phân giác trong của tam giác DEF . d) H . B HC HC.HA H . + + A HB =1. A . B AC BC.BA C . A CB
Câu 5. ( 1 điểm) Cho 1000 điểm phân biệt trên mặt phẳng M , M , M ,..., M . Vẽ một đường 1 2 3 1000
tròn (C) tùy ý có bán kính R = 1.Chứng minh rằng tồn tại điểm A trên đường tròn (C) thỏa mãn
AM + AM + AM + ...+ AM  1000 . 1 2 3 1000
...............HẾT..............
Giám thị coi thi không giải thích gì thêm!
Họ tên thí sinh:............................................................... Số báo danh:........................ Trang 1
PHÒNG GIÁO DỤC VÀ ĐÀO TẠO HD CHẤM ĐỀ KIỂM TRA HỌC SINH GIỎI CẤP QUẬN - VÒNG 1
Môn thi: TOÁN 9
Thời gian: 150 phút (Không kể thời gian giao đề) Câu Ý
Nội dung cần đạt Điểm
Với x  0; x  1 2 x − x 2x + x 2( x − ) 1 A = − + x + x +1 x x −1 x (x x − ) 1 x (2 x + ) 1 2( x − ) 1 ( x + ) 1 = − − 0,5 a x + x +1 x x −1 = x ( x − ) 1 − (2 x + ) 1 + 2( x + ) 1 1,0 = x − x +1 0.5
Vậy A = x − x +1 . x ( + )3 5 2 17 5 − 38 ( 5 +2)( 5 −2) = = 12 5 + 14 − 6 5 5 + 3 − 5 0,5 x 1  = 1 5,0 b 12 3 0.5  x = 4 (tmđk)
Thay x = 4 vào biểu thức A ta được A = 4 − 4 +1 = 3 0.5
Vậy A = 3 khi x = 4. 2 x 2 x B = = A x − x +1 2  1  3
Vì x  0; x  1 2 x  0 và x − x +1 = x − +  0  B  0   c  2  4 ( 0.5 x − )2 2 1 Xét hiệu 2 − B =  0  B  2 x − x +1 Vậy 0  B  2 1.0 Trang 2 3 2 x 3x a) Giải phương trình 3 x + + − = x  ( . Điều kiện 1 x − ) 28 0 3 1 x −1 3 2 2  x  x  x   + − x x 3 x + + 3 − 27 = 0     0.5  x −1 x −1 x −1 x −1 3 2 2 2 2  x   x   x   − 3 + 3 −1 = 27       0.5  x −1  x −1  x −1 a 3 2  x  0.5 3  −1 = 3    x − 1  2 x 0.5  −1= 3 x −1 2
 x − 4x + 4 = 0 0.5  x = 2 (tmđk) Vậy x = 2 . 1 5
b) Giải các phương trình sau + = 4 . 3 + x 4 + x 2 1 1 1+ y 0.5 2
Điều kiện x  −3 . Đặt
= y  0  x + 3 =  x + 4 = 5,0 2 2 x + 3 y y 5y
Ta có phương trình y + = 4 2 1+ y 0.5 2 5y − 2 1+  − + y y = 2 0 2 + 1 y 2 2 5y − 4 − 4 y  y − 2 + = 0 2 2
1+ y ( 5y + 2 1+ y ) 0.5   ( y ) y + 2 2 1   − + = 0 b  2  1+ y y y 0.5  ( 2 5 + 2 1+  )  y = 2 1 11  = 2  x = − (tmđk) 3 + x 4 0.5 11 Vậy x = − . 4 Xét p = 2 2
 p + 23 = 27 có 4 ước dương (loại) 3 a Xét 2
p = 3  p + 23 = 32 có 6 ước dương (tm) 0.5 Trang 3
Xét p  3 . Ta thấy p lẻ nên 2 2
p + 23 = p −1+ 24 = ( p − ) 1 ( p + ) 1 + 24 0.5
Chia hết cho 8 nên có các ước só là 1,2,4,8 . 3.0
Mặt khác p không chia hết cho 3 nên ( p − ) 1 ( p + ) 1 chia hết cho 3. Do đó 0,5 2
p + 23 có các ước số là 3,6,12,24 (loại). Vậy p = 3.
(x + y)2 − xy xy (x + y)2 2 2 2 xy Ta có: M = + = + 4 + − 6 0.5 xy x + y xy x + y ( x + y)2 2 xy
4( x + y) 2 xy M  2 .4 + − 6 = + − 6 xy x + y xy x + y 0.5 7( x + y) x + y 2 xy 7.2 xy
x + y 2 xy = + + − 6  + 2 . − 6 = 3 . 2 xy 2 xy x + y 2 xy 2 xy x + y b 0.5   x = y  (x + y)2 Dấu bằng xảy ra   = 4  x = y . xy   x + y 2 xy  . 2 xy x + y 
Vậy gía trị nhỏ nhất của M bằng 3 khi và chỉ khi x = . y A E F H C 4 B D 1 a) Ta có: SABC = .BC.AD. 2 1 0.5
ABD vuông tại D có AD =AB.sinB, do đó SABC = BC.BA.sinB. 6.0 a 2
ABE vuông ở E có AE = AB.cosA
BFC vuông ở F có BF = BC.cosB 0,5
ACD vuông ở D có CD = AC.cosC 0,5
Do đó AE.BF.CD = AB.BC.CA.cosA.cosB.cosC 0.5 Trang 4 AD AD b) Xét ABD có tanB = ; ACD có tanC = BD CD 2 AD 0,5 suy ra tanB.tanC = (1) b BD.CD DH BD 0.5
Do HBD = CAD (cùng phụ với ACB ) nên BDH  ADC (g.g)  =  DC AD BD.DC = DH.DA 2 AD AD
Kết hợp với (1) được tanB.tanC = = . 0,5 DH.AD DH
c) Chứng minh được AEF  ABC (g.g)  AEF = ABC . 0.5
Tương tự được CED = CBA nên AEF = CED mà BE ⊥ AC
 AEB = CEB = 900. Từ đó suy ra FEB = DEB  EH là phân trong của DEF. 0.5
Tương tự DH, FH cũng là phân giác trong của DEF nên H là giao ba đường phân giác 0.5 trong của DEF. c
d) Ta có : SBHC + SCHA + SAHB = SABC. CH CE
Dễ thấy CHE  CAF(g.g)  = CA CF 0.25 d H . B HC H . B CE 2.  = = S S BHC = BHC A . B AC A . B CF 2.S S 0.25 ABC ABC HC.HA S H . A HB S Tương tự có = CHA ; = HAB . 0.25 BC.BA S C . A CB S CBA CAB H . B HC HC.HA H . A HB S S S Do đó: + +
= BHC + CHA + AHB =1 0.25 A . B AC BC.BA C . A CB S S S BAC CBA ACB
Trên đường tròn (C) ta kẻ đường kính A A tùy ý  A A = 2 1 2 1 2
Ta có A M + A M  A A = 2 1 1 2 1 1 2
A M + A M  A A = 2 1 2 2 2 1 2 …………. A M + A M  A A = 2 0.5 1 1000 2 1000 1 2  (
A M + A M + A M + ... + A M
+ A M + A M + A M + ...+ A M  2000 ( ) 1 1 1 1 2 1 3 1 1000 ) ( 2 1 2 2 2 3 2 1000 ) 5 1.0
Theo nguyên lý Dirichlet thì từ( ) 1 suy ra trong hai tổng
A M + A M + A M + ... + A M
và A M + A M + A M + ...+ A M có ít nhất một 1 1 1 2 1 3 1 1000 2 1 2 2 2 3 2 1000
trong hai tổng lớn hơn hoặc bằng 1000. Giả sử
A M + A M + A M + ... + A M 1000 . 0.5 2 1 2 2 2 3 2 1000
Chọn A  A  AM + AM + AM + ...+ AM  1000 . 2 1 2 3 1000
Học sinh làm các cách khác đúng với yêu cầu đề ra vẫn chấm điểm tối đa Trang 5