Đề thi giữa học kì 2 Toán 9 năm 2023 – 2024 phòng GD&ĐT Hiệp Hòa – Bắc Giang

PHÒNG GIÁO DỤC VÀ ĐÀO TẠO
ĐỀ KIỂM TRA GIỮA HỌC KÌ II HIỆP HÒA NĂM HỌC 2023 - 2024 MÔN: TOÁN LỚP 9
( Đề thi giồm 02 trang )
Thời gian làm bài: 90 phút, không kể thời gian giao đề
PHẦN I: TRẮC NGHIỆM
Câu 1: Hàm số y = ( − ) 2 1
2021 x đồng biến khi A. x < 0. B. x > 0. C. x∈ . R D. x ≠ 0.
Câu 2: Với giá trị nào của tham số m thì phương trình 2
x − 2x + 3m −1 = 0 có hai nghiệm x ; x 1 2 thoả mãn 2 2 x + x =10 1 2 ? A. 2 m = . B. 4 m = − . C. 2 m = − . D. 4 m = . 3 3 3 3
Câu 3: Với giá trị nào của m thì phương trình 2
x − (3m +1)x + m − 5 = 0 có nghiệm x = 1? − 3 5 5 − A. m = . B. m = . C. m = . D. m =1. 4 2 2
Câu 4: Phương trình nào sau đây có hai nghiệm phân biệt? A. 2 x + x +1 = 0 . B. 2
4x − 4x +1 = 0. C. 2
371x + 5x −1 = 0. D. 2 4x = 0 .
Câu 5: Cho đường tròn (O) có ,
MA MB là hai tiếp tuyến ( ,
A B là các tiếp điểm). Biết  0 AMB = 35 thì
số đo của cung lớn AB là A. 0 255 . B. 0 145 . C. 0 315 . D. 0 215 .
Câu 6: Trên đường tròn (O;3cm) lấy hai điểm A và B sao cho số đo cung AB lớn bằng 0 300 . Khi đó
diện tích hình quạt tạo bởi hai bán kính ,
OA OB và cung nhỏ AB là A. 15π ( 2 π π π cm ). B. 3 ( 2 cm ). C. 5 ( 2 cm ). D. ( 2 cm ). 2 2 2 2 x + 3y = 5
Câu 7: Cặp số (a;b) là nghiệm của hệ phương trình 
. Khi đó giá trị của biểu thức 2 − 3 3a b bằng x + y = 1 A. 11. − B. 1. − C. 13. D. 5. −
Câu 8: Tích hai nghiệm của phương trình 2 2
− x − 5x +16 = 0 bằng A. 8. − B. 16. − C. 8. D. 16. x + 2y =1
Câu 9: Hệ phương trình 
vô nghiệm khi a bằng 2x − ay = 3 A. 6. B. 6. − C. 4. − D. 4.
Câu 10: Cho phương trình: 2
ax + bx + c = 0, với a,b,c∈ và a ≠ 0 . Nếu 2
b − 4ac = 0 thì phương trình có nghiệm là − − − A. b x = x = . a x = x = . b x = x = . b x = x = . 1 2 B. C. D. a 1 2 2b 1 2 2a 1 2 2a
Câu 11: Phương trình nào dưới đây là phương trình bậc hai một ẩn? A. ( − ) 2
27 3 3 x − 2x + 4 = 0. B. 2 (3− 2)x = 0. C. 3
5 + y − y = 0.
D. ( 12 − 2 3)t +1 = 0.
Câu 12: Cho tam giác ABC nội tiếp đường tròn (O) . Biết  0
ACB =110 thì số đo  BOA là A. 0 140 . B. 0 70 . C. 0 220 . D. 0 305 .
Câu 13: Tam giác ABC đều ngoại tiếp đường tròn có bán kính 1cm. Diện tích tam giác ABC là A. ( 2 3 3 cm ). B. 3 3 ( 2 cm ). C. ( 2 6 3 cm ). D. 3 3 ( 2 cm ). 4 2
Câu 14: Tìm tất cả các giá trị của tham số m để phương trình 2
2x − x + m +1 = 0 có hai nghiệm phân biệt? A. 7 m − < . B. 7 m − ≥ . C. 7 m − > . D. 7 m − ≤ . 8 8 8 8
Câu 15: Phương trình 2 2x − (m − )
1 x − m −1 = 0 (với m là tham số) có một nghiệm là A. m −1. B. m +1. C. −m +1. D. −m −1. 2 2 2 2
PHẦN II. TỰ LUẬN (7,0 điểm).
Câu 16 (2,5 điểm): 3  x − y = 7
a. Giải hệ phương trình  . x + y = 5  4 x
8x   x −1 2 
b. Rút gọn biểu thức P =  +  :  −
 với x > 0; x ≠ 4; x ≠ 9 . x + 2 4 − x x −    2 x x 
c. Tìm các giá trị của tham số m để đường thẳng d: y m2x 3 m  2 song song với đường
thẳng d ': y  2024x  2025 .
Câu 17 (1,0 điểm): Cho phương trình 2
x − mx + m −1 = 0 ( ) 1 , m là tham số.
a) Giải phương trình ( ) 1 với m = 2 − .
b) Tìm m để phương trình ( ) 1 có hai nghiệm x x 2 1x 2 x + 3 =
1 , 2 và biểu thức A đạt giá trị 2 2 1 x + 2 x + 2( 1x 2 x + ) 1 lớn nhất.
Câu 18 (1,0 điểm): Trong kỳ thi Tuyển sinh vào lớp 10 THPT năm học 2022-2023, tổng chỉ tiêu tuyển
sinh của Trường THPT A và Trường THPT B là 900 học sinh. So với chỉ tiêu tuyển sinh thì số lượng thí
sinh đăng ký dự tuyển vào Trường THPT A và Trường THPT B nhiều hơn lần lượt là 15% và 10%. Biết
tổng số thí sinh đăng ký dự tuyển của cả hai trường là 1010. Hỏi chỉ tiêu tuyển sinh của mỗi trường là bao nhiêu học sinh?
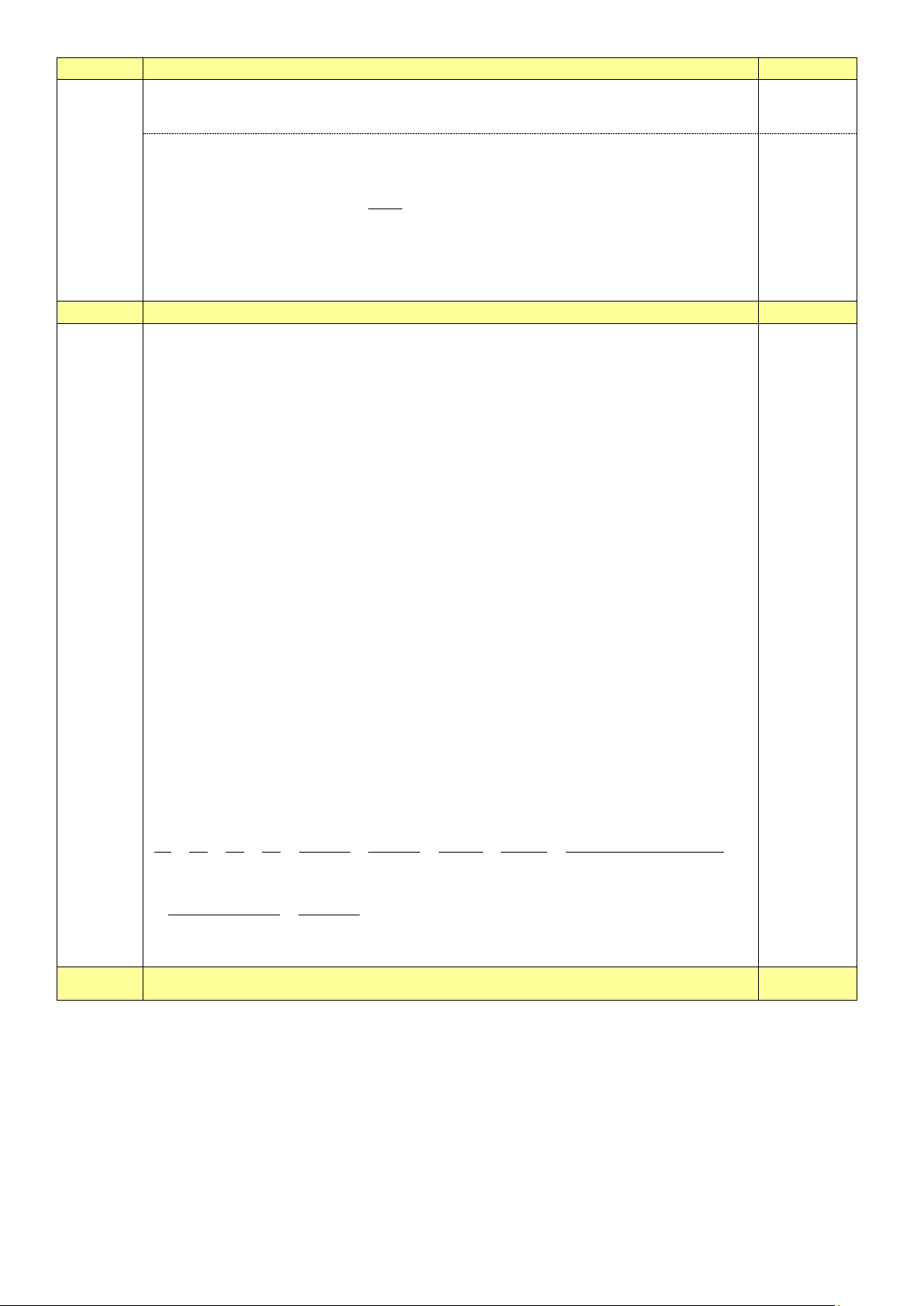
Câu 19 (2,0 điểm): Cho đường tròn ( ;
O R) và đường thẳng d không có điểm chung với đường tròn
(O) . Gọi H là hình chiếu của O trên đường thẳng d . Từ một điểm M bất kì trên đường thẳng
d (M ≠ H ), kẻ hai tiếp tuyến MA, MB với đường tròn (O) ( A và B là các tiếp điểm). Dây AB cắt
OH tại C và cắt OM tại D . Chứng minh rằng:
a) Tứ giác MAOB nội tiếp.
b) OC.OH =OD.OM .
c) Khi điểm M di chuyển trên đường thẳng d thì dây AB luôn đi qua một điểm cố định.
Câu 20 (0,5 điểm): Tìm tất cả các giá trị của tham số m để phương trình 2
(x −1)(x + 3)(x + 5) = m có 1 1 1 1
4 nghiệm phân biệt x , x , x , x + + + = 1. − 1 2 3 4 thỏa mãn: x x x x 1 2 3 4
-------------------------------Hết--------------------------------
Họ và tên học sinh: ............................................. Số báo danh:........................................................... ĐÁP ÁN
Phần 1: Trắc nghiệm Câu 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 Đáp án A C A C D B D A C D B A A A B Phần 2: Tự luận Câu
Hướng dẫn, tóm tắt lời giải Điểm Câu 16 (2,5 điểm) 3  x − y = 7 y = 5 − x y = 5 − x Ta có :  ⇔  ⇔  0,5 a x + y = 5 3
 x − (5 − x) = 7 4x = 12 (1,0 x = 3 x = 3 điểm) ⇔  ⇔ 0,25 y 5  = − x y = 2
Vậy hệ phương trình có nghiệm ( ; x y) = (3;2) . 0,25
Với x  0; x  4; x  9 ta có:  4 x 8x     x 1 2  P     :    
 x  2 4 x 
  x2 x x 
4 x . x   2 8x
x 12 x   2  0,25
 x   x   : 2 2 x  x   2 4x8 x  x 3
  x  x : 2 2 x  x   b 2 (1 điểm)
4 x  x   2 x  x   2   0,25 x   2  x  . 2  x 3 4x   x 3 4x 0,25  x3 Vậy x x
 0; x  4; x  9 thì 4 P  . 0,25 x 3
Vì 3  2025 nên đường thẳng d: y m2x 3m  2 song song với c 0,25 ( 0,5
đường thẳng d ': y  2022x 5 <=> m-2 =2024 điểm) <=> m= 2026 (t/m ĐK)
Vậy m =2026 là giá trị cần tìm 0,25 Câu 17 (1,0điểm) Với m = 2
− , phương trình (1) trở thành 2
x + 2x − 3 = 0. a) 0,25 (0,5
Giải ra được x =1, x = 3 − . điểm) 0,25 Vậy với m = 2
− phương trình (1) có tập nghiệm là 1;  3 . Ta có: 2
∆ = m − 4m + 4 = (m − 2)2 ≥ 0, m ∀ b)
Do đó phương trình  
1 luôn có hai nghiệm x ; x với mọi m . 1 2 (0,5 0,25 điểm)
x + x = m
Áp dụng hệ thức Vi-ét, ta có: 1 2  x x = m −  1 1 2 Câu
Hướng dẫn, tóm tắt lời giải Điểm 2x x + 3 2x x + 3 2(m − ) 1 + 3 Biến đổi 1 2 1 2 2m +1 A = = = = 2 2
x + x + 2(x x + ) 1 (x + x )2 2 2 1 2 1 2 1 2 + 2 m + 2 m + 2 2 2 2 + − − − 0,25 m 2 (m ) 1 (m )1 A = =1− 2 2 m + 2 m + 2
Lập luận chỉ ra A ≤1, dấu “=” xảy ra khi m = 1. Kết luận Câu 18 (1,0 điểm)
Gọi x, y (thí sinh) lần lượt là chỉ tiêu tuyển sinh của trường THPT A và THPT B . Điều kiện: *
x, y ∈ và x, y < 900.
Vì tổng chỉ tiêu tuyển sinh của Trường THPT A và trường THPT B là 900 học 0,25
sinh nên ta có phương trình: x + y = 900 ( ) 1
Số thí sinh đăng ký dự tuyển vào Trường THPT A là x + .15% x = 1,15x (thí sinh)
Số thí sinh đăng ký dự tuyển vào Trường THPT B là y + .10% y = 1,1y (thí sinh) (1,0
Vì tổng số thí sinh đăng ký dự tuyển của cả hai trường là 1010 học sinh nên ta 0,25 điểm) có phương trình:
1,15x +1,1y =1010 (2)
Từ (1) và (2) ta có hệ phương trình x + y = 900 x = 400  ⇔  (t / m). 0,25 1
 ,15x +1,1y = 1010 y = 500
Chỉ tiêu tuyển sinh của Trường THPT A là 400 học sinh.
Chỉ tiêu tuyển sinh của Trường THPT B là 500 học sinh. 0,25 Câu 19 (2,0 điểm) d H A C M D O B
Do MA, MB là hai tiếp tuyến của đường tròn (O) nên MA ⊥ O ; A MB ⊥ OB 0,5 a) ⇒  =  0 MAO MBO = 90 .
(1 điểm) Tứ giác MAOB có  +  0 0 0 MAO MBO = 90 + 90 =180 0,25
Mà đây là hai góc ở vị trí đối diện nhau nên tứ giác MAOB nội tiếp được trong 0,25 một đường tròn. b)
Chứng minh được OM ⊥ BC tại D 0,25 (0,5 điểm) Chứng minh ∆  ∆ ( − ) OD OC ODC OHM g g ⇒ = ⇒ OC.OH = OD.OM 0,25 OH OM Câu
Hướng dẫn, tóm tắt lời giải Điểm MA ∆
O vuông tại A, đường cao OD có 2 2 OA = . OD OM ⇒ . OD OM = R 0,25 Suy ra 2
OC.OH = R
Vì điểm O và đường thẳng d cố định nên H cố định do đó OH cố định và có c)
độ dài không đổi ⇒ C ∈OH cố định (1) (0,5 2 điểm) Từ 2 . R
OC OH = R ⇒ OC = không đổi (2) OH 0,25
Từ (1) và (2) suy ra điểm C cố định suy ra dây AB luôn đi qua điểm C cố định
Vậy khi điểm M di chuyển trên đường thẳng d thì dây AB luôn đi qua một điểm cố định Câu 20 (0,5 điểm) Ta có: 2
(x −1)(x + 3)(x + 5) = m (1)
⇔ (x +1)(x + 3)(x −1)(x + 5) = m 2 2
⇔ (x + 4x + 3)(x + 4x − 5) = m (2) Đặt 2 2
y = x + 4x + 4 = (x + 2) ≥ 0 ( x
∀ ∈ R) . Khi đó (2) có dạng :
(y −1)(y − 9) = m hay 2
y −10y + 9 − m = 0 (3) 0,25
Phương trình (1) có bốn nghiệm phân biệt tương đương với phương trình (3) có
hai nghiệm dương phân biệt y > y > 0 1 2 . '  ∆ =16 + m > 0 
⇔  S = y + y =10 > 0 ⇔ 16 − < m < 9 (4) 1 2 (0,5  điểm)
P = y .y = 9 − m > 0  1 2 Khi y , y 1
2 là hai nghiệm dương phân biệt của phương trình (3) thì phương
trình (2) tương đương với: 2
x + 4x + 4 − y = 0 2
x + 4x + 4 − y = 0 1 hoặc 2
Gọi x , x là hai nghiệm phân biệt của phương trình: 2
x + 4x + 4 − y = 0 1 (5) 1 2
Gọi x , x là hai nghiệm phân biệt của phương trình: 2
x + 4x + 4 − y = 0 2 (6) 3 4
Áp dụng định lý Vi-et cho các phương trình (3), (5), (6) ta có : 0,25
1 1 1 1 x + x x + x 4 − 4 − 4(y + y ) − 32 1 2 3 4 1 2 + + + = + = + = x x x x x x x x
4 − y 4 − y 16 − 4(y + y ) + y y 1 2 3 4 1 2 3 4 1 2 1 2 1 2 40 − 32 8 = = = 1 − 16 − 40 + 9 − m 15 − − m ⇔ m = 7 − ( thỏa mãn) Tổng 7,0 điểm
Lưu ý khi chấm bài tự luận:
- Trên đây chỉ là sơ lược các bước giải, lời giải của học sinh cần lập luận chặt chẽ, hợp logic. Nếu
học sinh trình bày cách làm đúng khác thì cho điểm các phần theo thang điểm tương ứng.
- Với câu 16, nếu học sinh dùng MTCT bấm và cho được kết quả đúng thì cho 0,5 điểm
- Với Câu 19, nếu học sinh không vẽ hình thì không chấm.
----------------*^*^*----------------