Đề thi giữa học kỳ 2 Toán 9 năm 2018 – 2019 phòng GD&ĐT Tây Hồ – Hà Nội

Giới thiệu đến quý thầy, cô giáo và các em học sinh lớp 9 đề tham khảo kiểm tra giữa học kỳ 2 môn Toán 9 năm học 2018 – 2019 giúp bạn ôn tập, chuẩn bị tốt kì thi sắp tới. Mời bạn đọc đón xem.

62 31 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Đề giữa HK2 Toán 9

Môn: Toán 9

Thông tin:

6 trang 8 tháng trước

Tác giả:

Profile Hà Việt Anh
PHÒNG GIÁO DỤC & ĐÀO TẠO ĐỀ KIỂM TRA GIỮA HỌC KỲ II
QUẬN TÂY HỒ NĂM HỌC 2018 - 2019
MÔN TOÁN LỚP 9
Thời gian làm bài: 90 phút (không kể thời gian giao đề)
Câu 1.
(2,0 điểm)
1) Tính giá trị biểu thức A =
1
1
x
x
−
+
khi x = 9
2) Rút gọn biểu thức B =
51 8
1
11
x
x
xx
+
−+
−
+−
với
0, 1xx≥≠
3) Tìm x để P = A.B có giá trị nguyên
Câu 2. (2,0 điểm) Giải các hệ phương trình sau:
a)
32 5
24
xy
xy
−=
+=
b)
2 13 2 5
4 1 2 17
xy
xy
+− − =
++ − =
Câu 3.
(2,0 điểm) Giải bài toán bằng cách lập hệ phương trình:
Hai vòi nước cùng chảy vào bể không có nước thì sau 12 giờ đầy bể. Nếu
người ta mở cả hai vòi chảy trong 4 giờ rồi khóa vòi hai lại và để vòi một chảy tiếp
14 giờ nữa thì mới đầy bể. Tính thời gian mỗi vòi chảy một mình đầy bể.
Câu 4 (3,5 điểm). Cho đường tròn (O; R) và đường thẳng d không có điểm chung với
đường tròn. Từ điểm M thuộc đường thẳng d kẻ hai tiếp tuyến MA, MB tới đường
tròn. Hạ OH vuông góc với đường thẳng d tại H. Nối AB cắt OH tại K, cắt OM tại I.
Tia OM cắt đường tròn (O; R) tại E.
a) Chứng minh AOBM là tứ giác nội tiếp
b) Chứng minh OI.OM = OK.OH
c) Chứng minh E là tâm đường tròn nội tiếp tam giác MAB
d) Tìm vị trí của M trên đường thẳng d để diện tích tam giác OIK có giá trị lớn
nhất.
Câu 5 (0,5 điểm). Cho hai số dương x, y thỏa mãn x + y = 1
Tìm giá trị nhỏ nhất của biểu thức A =
2
2
11
xy
xy


+ ++




_______________ HẾT _______________
HƯỚNG DẪN
Câu 1. (2,0 điểm)
1) Tính giá trị biểu thức A =
1
1
x
x
−
+
khi x = 9
2
)
Rút gọn biểu thức B
=
51 8
1
11
x
x
xx
+
−+
−
+−
với
0, 1xx≥≠
3)
T
ìm x để P = A.B có giá trị nguyên
Hướng dẫn
1)
T
ính giá trị biểu thức A =
1
1
x
x
−
+
khi x = 9
Điều kiện:
0x ≥
.Ta có:
9x =
(thỏa mãn)
Thay
9x =
vào
91 1
:A .
2
91
A
−
= =
+
Vậ
y
9x =
thì giá trị của A bằng
2) R
út gọn biểu thức B =
51 8
1
11
x
x
xx
+
−+
−
+−
với
0, 1xx≥≠
( )
( )
( )
( )
( )
( )
( )
( )
( )
( )
( )
( )
( )
( )
51 8
11
11
5 1 18
4 5 18
11 11
14
54 4
1
11 11
x
B
xx
xx
xx x
xx x
xx xx
xx
xx x
x
xx xx
+
= ++
++
−+
+ − + ++
+ −+ ++
= =
−+ −+
++
++ +
= = =
−
−+ −+
3
)
T
ìm x để P = A.B có giá trị nguyên
Điều kiện:
0; 1xx≥≠
14 4 3
.. 1
11 1 1
xx x
P AB
xx x x
−+ +
= = =
= +
+− + +
T
a có:
33
0, 1 1 1 0 0
1 1 1
11
xx x P
xx
≥ ≠⇒ +≥>⇒ >⇒+ >⇒ >
++
33
110 3 1 4 4
11
xP
xx
+≥> ⇒ ≤ ⇒+ ≤ ⇒ ≤
++
Vậy:
14P<≤
. Do
{ }
2;3; 4PZ P∈⇒∈
TH1:
( )
33
2 1 2 1 13 2 4 /
11
P x
x x tm
xx
= ⇒+ = ⇔ =⇔ += ⇔ = ⇔ =
++
TH2:
( )
3 3 3 11
31 3 2 1 /
2 24
11
P x x x tm
xx
= ⇒+ = ⇔ = ⇔ += ⇔ = ⇔ =
++
TH3:
( )
33
4 1 4 3 11 0 0 /
11
P x x x tm
xx
= ⇒+ = ⇔ = ⇔ +=⇔ = ⇔ =
++
Vậ
y:
1
0;4;
4
x

∈


Câ
u 2. (2,0 điểm) Giải các hệ phương trình sau:
a)
32 5
24
xy
xy
−=
+=
b
)
2 13 2 5
4 1 2 17
xy
xy
+− − =
++ − =
Hướng
dẫn
a)
3 2 5 6 2 10 7 14 2 2
24 24 24 224 1
xy xy x x x
xy xy xy y y
−= −= = = =

⇔ ⇔⇔⇔

+= += += += =

Vậy hệ phương trình có nghiệm duy nhất:
( ) ( )
; 2;1xy =
b)
2 13 2 5
4 1 2 17
xy
xy
+− − =
++ − =
Điều kiện:
1; 2xy≥− ≥
2 13 2 5
2 13 2 5
2 13 2 5
12 1 3 2 51
4 1 2 17 14
1 56
xy
xy
xy
xy
xy x
+− − =
+− − =
+− − =

⇔⇔

++ − =
++ − = +
=
2 1 3 2 5 2.4 3 2 5
14 14
xy y
xx

+− −= − −=

⇔⇔

+= +=


( )
( )
3/
21 21
15 /
1 16
14
y tm
yy
x tm
x
x
=
−= −=

⇔ ⇔⇔

=
+=
+=
Vậy hệ phương trình có nghiệm duy nhất:
( ) ( )
, 15;3 .xy =
Câu 3. (2,0 điểm) Giải bài toán bằng cách lập hệ phương trình:
Hai vòi nước cùng chảy vào bể không có nước thì sau 12 giờ đầy bể. Nếu
người ta mở cả hai vòi chảy trong 4 giờ rồi khóa vòi hai lại và để vòi một chảy tiếp
14 giờ nữa thì mới đầy bể. Tính thời gian mỗi vòi chảy một mình đầy bể.
Hướng dẫn
Gọi thời gian vòi một và vòi hai chảy một mình đầy bể lần lượt là x, y (giờ) (x
> 0
, y > 0)
Mỗi giờ vòi một và vòi hai chảy được
11
,
xy
(bể)
Do cả hai vòi cùng chảy thì sau 12 giờ sẽ đầy bể nên ta có phương trình:
( )
11 1
1
12xy
+=
Vì
mở cả hai vòi trong 4 giờ sau đó khóa vòi hai để vòi một chảy một mình
tiếp 14 giờ đầy bể nên ta có phương trình:
( )
11
14 1 2
3 x
+=
Từ (
1) và (2) ta có hệ phương trình:
( )
( )
11 1
21 /
12
28 /
11
14. 1
3
x tm
xy
y tm
x
+=
=

⇔⇔

=
+=
Vậy thời gian vòi một chảy một mình đầy bể là 21 giờ, vòi hai chảy một mình
đầy bể là 28 giờ.
Câu 4 (3,5 điểm). Cho đường tròn (O; R) và đường thẳng d không có điểm chung với
đường tròn. Từ điểm M thuộc đường thẳng d kẻ hai tiếp tuyến MA, MB tới đường
tròn. Hạ OH vuông góc với đường thẳng d tại H. Nối AB cắt OH tại K, cắt OM tại I.
Tia OM cắt đường tròn (O; R) tại E.
a) Chứng minh AOBM là tứ giác nội tiếp
b
) Chứng
minh OI.OM = OK.OH
c) Chứn
g minh E là tâm đường tròn nội tiếp tam giác MAB
d)
T
ìm vị trí của M trên đường thẳng d để diện tích tam giác OIK có giá trị lớ
n
nhất.
Hướng dẫn
a) Chứn
g minh AOBM là tứ giác nội tiếp
Xét tứ giác AOBM có:
180
o
MAO MBO∠ +∠ =
M
à hai hóc này ở vị tró đối nhay. Suy ra AOBM là tứ giác nội tiếp.
b) Chứng minh OI.OM = OK.OH
Ta có:
( )
OIK OHM g g∆∆ −
..
OI OK
OI OM OH OK
OH OM
=⇒=
(đpcm)
c) Chứng minh E là tâm đường tròn nội tiếp tam giác MAB
- Xét (O) có
AOE BOE∠=∠
(t/c 2 tiếp tuyến cắt nhau)
Sđ cung AE = sđ cung BE
BAE MAE⇒∠ =∠
- Xé
t
ABM∆
có:
+) MO là phân giác thứ nhất (t/c 2 tiếp tuyến cắt nhau)
+) AE là phân giác thứ hai (cmt)
+) MO cắt AE tại E
E⇒
là tâm đường tròn nội tiếp
AMB∆
(đpcm)
d)
T
ìm vị trí của M trên đường thẳng d để diện tích tam giác OIK có giá trị lớ
n
nhấ
t.
Có:
2
22 2
.. .
R
OH OK OI OM OB R OH OK R OK
OH
= = =⇒ =⇒=
M
à OH không đổi, nên OK không đổi.
Ta có:
( )
22 2
11 1
.
24 4
OIK
S OI IK OI IK OK const= ≤ += =
Để diện tích tam giác OIK đạt giá trị lớn nhất thì OI = IK. Khi đó:
1
OI OH
IK HM
= =
S
uy ra OH = HM.
Vậy điểm M nằm trên đường thẳng (d) sao cho OH = HM thì diện tích tam
giác OIK đạt giá trị lớn nhất.
Câu 5 (0,5 điểm). Cho hai số dương x, y thỏa mãn x + y = 1
Tìm giá trị nhỏ nhất của biểu thức A =
2
2
11
xy
xy


+ ++




Hướng
dẫn
Ta có:
1
20
4
x y xy xy+≥ ⇒< ≤
2
2
22
22
1 1 1 1 1 1 15
42 2 42 4
16 16
A x y x y x
y xy
x y x
y xy xy
xy


= + + + = + + + +≥ + += + + +




1 15 1 15 25
22 . 4 22. 4
1
16 16 4 2
16.
4
A xy
xy xy



⇒ ≥ + += + +=







Vậ
y
25
2
min
A =
khi
1
2
xy= =
_______________ HẾT _______________
| 1/6
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

PHÒNG GIÁO DỤC & ĐÀO TẠO
ĐỀ KIỂM TRA GIỮA HỌC KỲ II QUẬN TÂY HỒ NĂM HỌC 2018 - 2019 MÔN TOÁN LỚP 9
Thời gian làm bài: 90 phút (không kể thời gian giao đề)
Câu 1. (2,0 điểm) x −1
1) Tính giá trị biểu thức A = khi x = 9 x +1 x + 5 1 8
2) Rút gọn biểu thức B = − +
với x ≥ 0, x ≠ 1 x +1 1− x x −1
3) Tìm x để P = A.B có giá trị nguyên
Câu 2. (2,0 điểm) Giải các hệ phương trình sau: 3  x − 2y = 5
a) x+2y = 4
2 x +1−3 y − 2 = 5
b) 4 x+1+ y−2 =17 
Câu 3. (2,0 điểm) Giải bài toán bằng cách lập hệ phương trình:
Hai vòi nước cùng chảy vào bể không có nước thì sau 12 giờ đầy bể. Nếu
người ta mở cả hai vòi chảy trong 4 giờ rồi khóa vòi hai lại và để vòi một chảy tiếp
14 giờ nữa thì mới đầy bể. Tính thời gian mỗi vòi chảy một mình đầy bể.
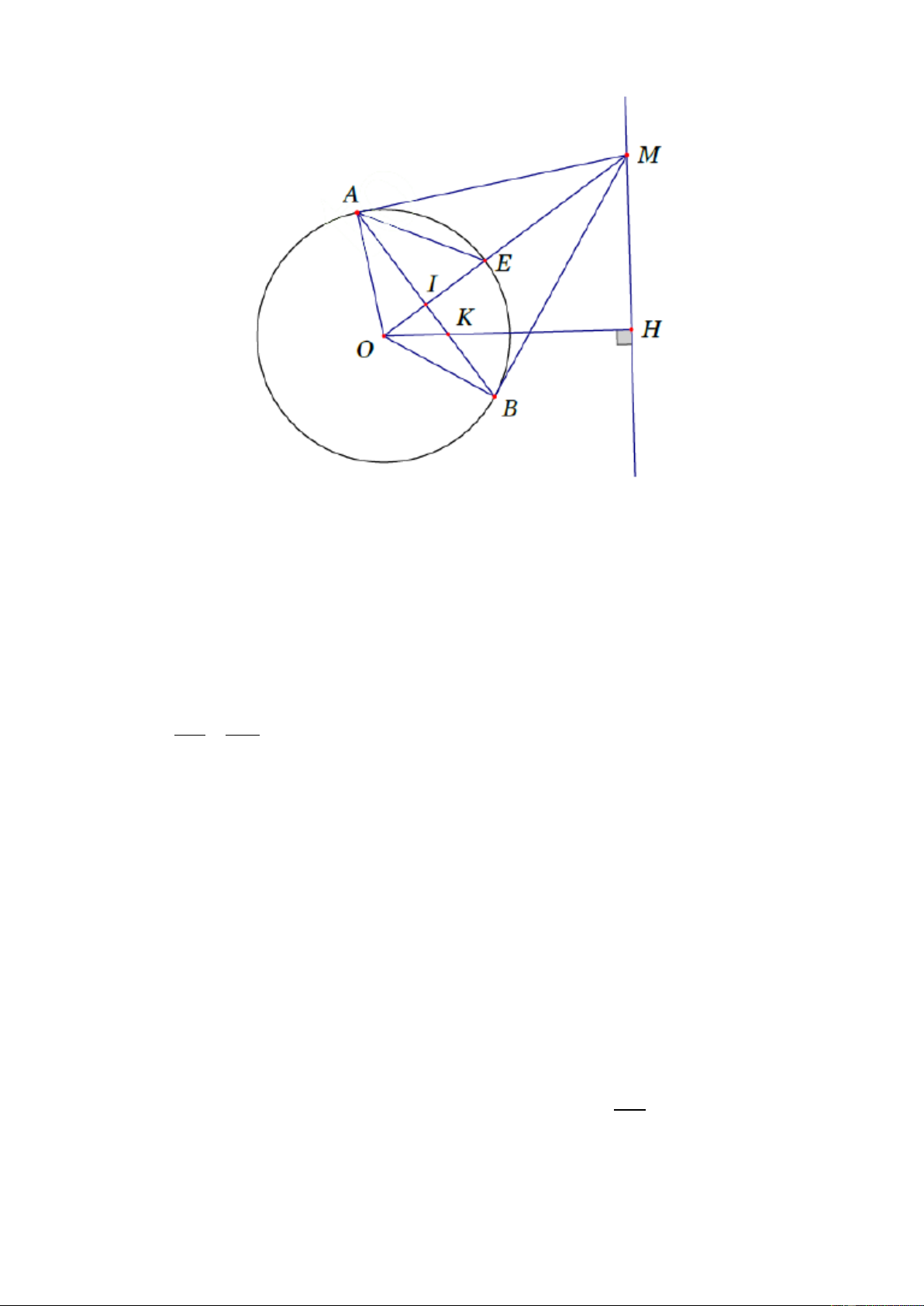
Câu 4 (3,5 điểm). Cho đường tròn (O; R) và đường thẳng d không có điểm chung với
đường tròn. Từ điểm M thuộc đường thẳng d kẻ hai tiếp tuyến MA, MB tới đường
tròn. Hạ OH vuông góc với đường thẳng d tại H. Nối AB cắt OH tại K, cắt OM tại I.
Tia OM cắt đường tròn (O; R) tại E.
a) Chứng minh AOBM là tứ giác nội tiếp b) Chứng minh OI.OM = OK.OH
c) Chứng minh E là tâm đường tròn nội tiếp tam giác MAB
d) Tìm vị trí của M trên đường thẳng d để diện tích tam giác OIK có giá trị lớn nhất.
Câu 5 (0,5 điểm). Cho hai số dương x, y thỏa mãn x + y = 1 2 2  1   1 
Tìm giá trị nhỏ nhất của biểu thức A = x + + y +      x   y
_______________ HẾT _______________ HƯỚNG DẪN
Câu 1. (2,0 điểm) x −1
1) Tính giá trị biểu thức A = khi x = 9 x +1 x + 5 1 8
2) Rút gọn biểu thức B = − +
với x ≥ 0, x ≠ 1 x +1 1− x x −1
3) Tìm x để P = A.B có giá trị nguyên Hướng dẫn x −1
1) Tính giá trị biểu thức A = khi x = 9 x +1
Điều kiện: x ≥ 0.Ta có: x = 9 (thỏa mãn) 9 − 1 1
Thay x = 9 vào A : A = = . 9 + 1 2 1
Vậy x = 9 thì giá trị của A bằng . 2 x + 5 1 8
2) Rút gọn biểu thức B = − +
với x ≥ 0, x ≠ 1 x +1 1− x x −1 x + 5 1 8 B = + + x + 1 x + 1
( x − )1( x + )1
( x +5)( x − )1+ x +1+8 x+4 x −5+ x +1+8 = ( = x − ) 1 ( x + ) 1
( x − )1( x + )1 + + x + x + ( x )1( x 4 5 4 ) x +4 = ( = = x − ) 1 ( x + ) 1
( x − )1( x + )1 x −1
3) Tìm x để P = A.B có giá trị nguyên
Điều kiện: x ≥ 0; x ≠ 1 x − 1 x + 4 x + 4 3 P = . A B = . = = 1+ x + 1 x − 1 x + 1 x + 1 3 3
Ta có: x ≥ 0, x ≠ 1 ⇒ x + 1 ≥ 1 > 0 ⇒ > 0 ⇒ 1+ > 1 ⇒ P > 1 x + 1 x + 1 3 3 x + 1 ≥ 1 > 0 ⇒ ≤ 3 ⇒ 1+ ≤ 4 ⇒ P ≤ 4 x + 1 x + 1
Vậy: 1 < P ≤ 4 . Do P ∈ Z ⇒ P ∈{2;3; } 4 3 3 TH1: P = 2 ⇒ 1 + = 2 ⇔
= 1 ⇔ x +1 = 3 ⇔ x = 2 ⇔ x = 4 (t / m) x + 1 x + 1 3 3 3 1 1 TH2: P = 3 ⇒ 1 + = 3 ⇔
= 2 ⇔ x +1 = ⇔ x = ⇔ x = (t / m) x + 1 x + 1 2 2 4 3 3 TH3: P = 4 ⇒ 1 + = 4 ⇔
= 3 ⇔ x +1 = 1 ⇔ x = 0 ⇔ x = 0 (t / m) x + 1 x + 1  1 
Vậy: x ∈ 0;4;   4 
Câu 2. (2,0 điểm) Giải các hệ phương trình sau: 3  x − 2y = 5
a) x+2y = 4
2 x +1−3 y − 2 = 5
b) 4 x+1+ y−2 =17  Hướng dẫn 3  x − 2y = 5
6x − 2y = 10  7x = 14  x = 2 x = 2 a)  ⇔  ⇔  ⇔  ⇔  x + 2y = 4 x + 2 y = 4  x + 2y = 4 2 + 2y = 4  y = 1
Vậy hệ phương trình có nghiệm duy nhất: ( ; x y ) = (2; ) 1
2 x +1−3 y − 2 = 5
b) 4 x+1+ y−2 =17 
Điều kiện: x ≥ 1 − ; y ≥ 2
2 x +1 − 3 y − 2 = 5  2 x +1 − 3 y − 2 = 5
2 x +1 − 3 y − 2 = 5  ⇔  ⇔ 
4 x +1 + y − 2 = 17 12  
x + 1 + 3 y − 2 = 51   14 x + 1 = 56
2 x +1 − 3 y − 2 = 5
2.4 − 3 y − 2 = 5 ⇔  ⇔   x + 1 = 4  x + 1 = 4
 y − 2 = 1  y − 2 = 1 y = 3 (t / m) ⇔  ⇔  ⇔   + = x + 1 = 16   x = 15 x 1 4  (t / m)
Vậy hệ phương trình có nghiệm duy nhất: ( x, y) = (15;3).
Câu 3. (2,0 điểm) Giải bài toán bằng cách lập hệ phương trình:
Hai vòi nước cùng chảy vào bể không có nước thì sau 12 giờ đầy bể. Nếu
người ta mở cả hai vòi chảy trong 4 giờ rồi khóa vòi hai lại và để vòi một chảy tiếp
14 giờ nữa thì mới đầy bể. Tính thời gian mỗi vòi chảy một mình đầy bể. Hướng dẫn
Gọi thời gian vòi một và vòi hai chảy một mình đầy bể lần lượt là x, y (giờ) (x > 0, y > 0) 1 1
Mỗi giờ vòi một và vòi hai chảy được , (bể) x y
Do cả hai vòi cùng chảy thì sau 12 giờ sẽ đầy bể nên ta có phương trình: 1 1 1 + = ( )1 x y 12
Vì mở cả hai vòi trong 4 giờ sau đó khóa vòi hai để vòi một chảy một mình 1 1
tiếp 14 giờ đầy bể nên ta có phương trình: +14 = 1 (2) 3 x  1 1 1 + =  x y 12 x = 21 (t / m)
Từ (1) và (2) ta có hệ phương trình: ⇔  ⇔  1 1   y = 28  (t / m) +14. = 1 3 x
Vậy thời gian vòi một chảy một mình đầy bể là 21 giờ, vòi hai chảy một mình đầy bể là 28 giờ.
Câu 4 (3,5 điểm). Cho đường tròn (O; R) và đường thẳng d không có điểm chung với
đường tròn. Từ điểm M thuộc đường thẳng d kẻ hai tiếp tuyến MA, MB tới đường
tròn. Hạ OH vuông góc với đường thẳng d tại H. Nối AB cắt OH tại K, cắt OM tại I.
Tia OM cắt đường tròn (O; R) tại E.
a) Chứng minh AOBM là tứ giác nội tiếp b) Chứng minh OI.OM = OK.OH
c) Chứng minh E là tâm đường tròn nội tiếp tam giác MAB
d) Tìm vị trí của M trên đường thẳng d để diện tích tam giác OIK có giá trị lớn nhất. Hướng dẫn
a) Chứng minh AOBM là tứ giác nội tiếp Xét tứ giác AOBM có: ∠ + ∠ = 180o MAO MBO
Mà hai hóc này ở vị tró đối nhay. Suy ra AOBM là tứ giác nội tiếp.
b) Chứng minh OI.OM = OK.OH Ta có: OI ∆ K OHM ∆ (g − g) OI OK =
⇒ OI.OM = OH.OK (đpcm) OH OM
c) Chứng minh E là tâm đường tròn nội tiếp tam giác MAB - Xét (O) có A ∠ OE = B
∠ OE (t/c 2 tiếp tuyến cắt nhau)
Sđ cung AE = sđ cung BE ⇒ B ∠ AE = M ∠ AE - Xét A ∆ BM có:
+) MO là phân giác thứ nhất (t/c 2 tiếp tuyến cắt nhau)
+) AE là phân giác thứ hai (cmt)
+) MO cắt AE tại E ⇒ E là tâm đường tròn nội tiếp A ∆ MB (đpcm)
d) Tìm vị trí của M trên đường thẳng d để diện tích tam giác OIK có giá trị lớn nhất. 2 R Có: 2 2 2
OH.OK = OI.OM = OB = R ⇒ OH.OK = R ⇒ OK = OH
Mà OH không đổi, nên OK không đổi. 1 1 1 Ta có: S = OI.IK ≤ OI + IK = OK = const OIK ( 2 2 ) 2 2 4 4 Để OI OH
diện tích tam giác OIK đạt giá trị lớn nhất thì OI = IK. Khi đó: 1 = = IK HM Suy ra OH = HM.
Vậy điểm M nằm trên đường thẳng (d) sao cho OH = HM thì diện tích tam
giác OIK đạt giá trị lớn nhất.
Câu 5 (0,5 điểm). Cho hai số dương x, y thỏa mãn x + y = 1 2 2  1   1 
Tìm giá trị nhỏ nhất của biểu thức A = x + + y +      x   y Hướng dẫn 1
Ta có: x + y ≥ 2 xy ⇒ 0 < xy ≤ 4 2 2  1   1  1 1 1  1 15  2 2 A = x + + y + = x + y + + + 4 ≥ 2xy + 2 + 4 = 2 xy + + + 4       2 2  x   y x y xy  16xy 16xy     1 15   1 15  25
⇒ A ≥ 2 2 x . y +  + 4 = 2 2. +  + 4 =   16xy 16xy 4 1 2    16.   4  25 1 Vậy A = khi x = y = min 2 2
_______________ HẾT _______________