Đề TS 10 Môn Toán Sở GD Bình Định 2025-2026 Có Lời Giải Chi Tiết

SỞ GIÁO DỤC ĐÀO TẠO KỲ THI TUYỂN SINH VÀO LỚP 10 THPT
BÌNH ĐỊNH Môn thi: Toán
Thời gian làm bài: 120 phút ĐỀ CHÍNH THỨC
Bài 1: (2 điểm) 2x+ 3y= 1
1.Không dùng máy tính, giải hệ phương trình:  x - 4y= 6   x 2 x 2  + − x + 1 2.Cho Q =  − . ; x  0, x  1  x + 2 x + 1 x − 1  x   a) Rút gọn biểu thức Q
b) Tìm số nguyên x để Q có giá trị nguyên lớn nhất. Bài 2: (2 điểm) 1.Cho phương trình 2
2x − (m +1)x + m −1 = 0 .Tìm các giá trị của m để phương trình có hai
nghiệm và hiệu hai nghiệm bằng tích của chúng.
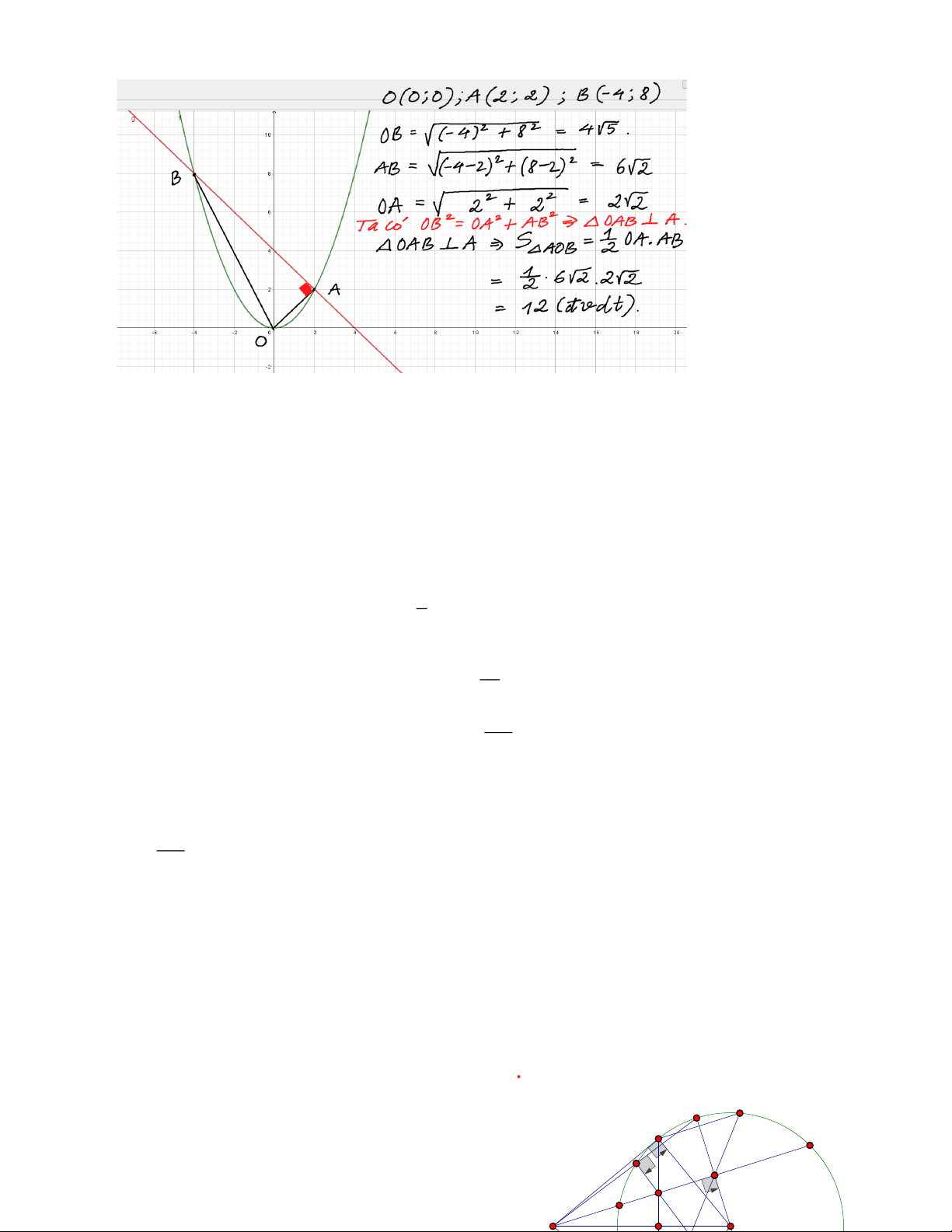
2.Trong hệ tọa độ Oxy cho đường thẳng (d) : y = −x + 4 và điểm A( 2; 2)
a) Chứng tỏ điểm A thuộc đường thẳng (d)
b)Tìm a để parabol (P) y = ax2 đi qua điểm A. Với giá trị a tìm được , hãy xác định tọa độ
điểm B là giao điểm thứ hai của (d) và (P).
c)Tìm diện tích tam giác OAB.
Bài 3: Cho tam giác vuông có cạnh huyền bằng 13cm, diện tích là 30cm2. Tính độ dài các cạnh góc vuông.
Bài 4. (3,5 điểm) Từ một điểm S ở ngoài đường tròn kẽ tiếp tuyến SB, SC (B, C là các tiếp
điểm) và một cát tuyến cắt (O) tại D và E ( D nằm giữa S và E) . Qua B kẽ đường thẳng song
song với DE cắt (O) tại điểm thứ hai là A. BC và AC cắt DE lần lượt tại F và I a) Chứng minh: SIC = SBC
b) Chứng minh: 5 điểm S, B, O, I, C cùng thuộc một đường tròn.
c) Chứng minh: FI.FS = FD.FE Trang 1
d) Đường thẳng OI cắt (O) tại M và N ( M thuộc cung nhỏ AB). Đường thẳng NF cắt đường
tròn (O) tai điểm thứ hai là K. Chứng minh ba điểm S, K, M thẳng hàng.
Bài 5: ( 1 điểm) Cho a, b, c là độ dài ba cạnh của một tam giác. Chứng minh: a b c + +  3 b + c − a a + c − b a + b − c
LỜI GIẢI CHI TIẾT Bài 1.
1.Không dùng máy tính, giải hệ phương trình: 2x+ 3y= 1 2x + 3y = 1 11  y = 11 − y = 1 −        x - 4y= 6 2x − 8y = 12 2x + 3y = 1 x = 2    
Vậy hệ phương trình có nghiệm duy nhất ( x ; y ) = ( 2; -1)  x 2 x 2  + − x + 1 2.a) Q =  − .  x + 2 x + 1 x − 1  x      x + 2 x − 2  x + 1 = ( +  ) −  . 2 ( x − )1( x +1 x 1 ) x 
( x + 2)( x − 1) − ( x − 2)( x + 1) x + 1 = . 2 ( x + 1) ( x − 1) x
x − x + 2 x − 2 − x − x + 2 x + 2 x + 1 = . 2 ( x + 1) ( x − 1) x 2 x x + 1 2 2 = . = = 2 ( x + 1) ( x − 1) x ( x − 1)( x + 1) x − 1
b) Q nguyên  2 x − 1  x − 1  U(2) =  1  ;   2 x-1 1 -1 2 -2 x 2 0 3 -1 Q 2 -2 1 Loại Thỏa
Vậy x = 2 thì Q đạt giá trị nguyên lớn nhất. Bài 2. 1/ 2
2x − (m +1)x + m −1 = 0 Trang 2  = (m + )2 1 − 4.2.(m − ) 1 2
= m + 2m +1−8m + 8
= m − 6m + 9 = (m −3)2 2  0, . m
Phương trình đã cho luôn có nghiệm x , x . Theo định lý Viet ta có: 1 2 m +1 m −1
S = x + x = , P = x x = . 1 2 1 2 2 2 Theo bài ra giả sử:
x − x = x x 1 2 1 2
 ( x − x )2 = (x x )2 1 2 1 2
 ( x + x )2 − 4x x − (x x )2 = 0 1 2 1 2 1 2 2 2  m +1
m −1  m −1  − 4. − = 0      2  2  2   −4m + 8 = 0  m = 2
Vậy m = 2 là giá trị cần tìm.
2/ a/ Thay x = 2, y = 2 vào (d ) : 2 = 2 − + 4 ( đúng)
Vậy điểm A thuộc đường thẳng (d) 1
b/ Thay x = 2, y = 2 vào (P) 1
: 4a = 2  a = . (P) 2 : y = x . 2 2
Phương trình hoành độ giao điểm (P) và (d): 1 x = 2  y = 2 2 2
x = −x + 4  x + 2x − 8 = 0   2  x 4  = −  y = 8
Vậy giao điểm còn lại là ( -4; 8). c) Trang 3 Bài 3:
Gọi độ dài hai cạnh của tam giác vuông lần lượt là ; x y(0  ; x y  13 )
Tam giác vuông có cạnh huyền bằng 13: 2 2 x + y = 169 1
Diện tích tam giác vuông là 2
30cm : xy = 30 . (cm2) 2  60 y = xy = 60  Ta có hệ phương trình: x    2 2 2 x + y =169 60  2 x + =169 2  x Ta có: 2 2 60 x + = 169 x  0 2 ( ) x 4 2 2
 x − 169x + 60 = 0 2 x = 144 x = 12  y = 5     2   x = 25 x = 5  y = 12
Vậy độ dài các cạnh của tam giác vuông là 12cm và 5cm. Bài 4. M A B E Trang 4 K I D F S O N C Giải:
a Chứng minh: SIC = SBC
Ta có: SBC = BAC ( cùng chắn BC ) Mà BAC = SIC ( đồng vị) => SBC = SIC
b)Chứng minh: 5 điểm S, B, O, I, C cùng thuộc một đường tròn. Ta có: 0 0 0 SOB + SOC = 90 + 90 = 180
 tg : SBOC nội tiếp đường tròn  SBC = SOC = SIC
Do đó B, I, O cùng nhìn SC dưới 1 góc bằng nhau
Nên 5 điểm S, B, I, O, C cùng thuộc một đường tròn.
c) Chứng minh: FI.FS = FD.FE Ta có: F  BS ∽ F  IC (g − g) FB FS  =  FI.FS = FB.FC (1) FI FC Mà F  BD ∽ F  EC (g − g) FB FD  =  FB.FC = FE.FD(2) FE FC
Từ (1) và (2) => FI.FS = FD.FE ( đpcm). Trang 5
d) Đường thẳng OI cắt (O) tại M và N ( M thuộc cung nhỏ AB). Đường thẳng NF cắt
đường tròn (O) tai điểm thứ hai là K. Chứng minh ba điểm S, K, M thẳng hàng. S  FB ∽ C  FI (g − g) FS FB  =  FB.FC = FS.FI (*) FC FI Lại có: F  BK ∽ F N C (g - g) FB FK  =  FB.FC = FN.FK (* *) FN FC
Từ (*) và (**) => FS.FI =FN.FK FS FK  =
và KFS = IFN ( đối đỉnh) FN FI Nên K  FS ∽ I  FN (c − g − c) 0  FKS = FIN = 90 Mà 0 NKM = 90 0 0 0  FKS + NKM = 90 + 90 = 180  S, K, M thẳng hàng. Bài 5:
Giải: Cách 1: Áp dụng bất đẳng thức Cauchy – Schwarz: 2 2 2 2 a b c (a + b + c) a b c + +  . Dấu “=” xảy ra khi = = x y z x + y + z x y z Ta có: a b c + + b + c − a a + c − b a + b − c 2 2 2 2 a b c (a + b + c) = + +  2 2 2 2 2 2 ab + bc − a ab + bc − b ac + bc − c
2(ab + bc + ca) − (a + b + c ) Trang 6 Mà 2 2 2
a + b + c  ab + bc + ca và 2
(a + b + c)  3(ab + bc + ca) a b c + + b + c − a a + c − b a + b − c 2 2 (a + b + c) (a + b + c)   2 2 2
2(ab + bc + ca) − (a + b + c )
2(ab + bc + ca) − (ab + bc + ca) 3(ab + bc + ca)  = 3 ab + bc + ca a b c Vậy + +
 3 . Dấu “=” xảy ra khi a = b = c. b + c − a a + c − b a + b − c Cách hai:  y + z a =  x = b + c − a 2    x + z
Đặt y = a + c − b  b = 2 z a b c  = + −  x + y c =  2  Khi đó: a b c y + z x + z x + y + + = + + b + c − a a + c − b a + b − c 2x 2y 2z 1  x y x z z y  1 = + + + + +    (2 + 2 + 2) = 3 2 y x z x y x 2   a b c Vậy + +
 3 . Dấu “=” xảy ra khi x = y =z  a = b = c b + c − a a + c − b a + b − c Trang 7