








Preview text:
TRƯỜNG ĐẠI HỌC BÁCH KHOA HÀ NỘI
ĐỒ ÁN CHUYÊN NGÀNH
Thiết kế và điều khiển mô hình con lắc ngược Furuta NGUYỄN ANH ĐỨC
Ngành Điều khiển và tự động hóa
Chuyên ngành Tự động hóa công nghiệp
Giảng viên hướng dẫn: TS. Nguyễn Danh Huy Chữ ký của GVHD Bộ môn:
Tự động hóa công nghiệp Viện: Điện HÀ NỘI, 7/2020 1 MỤC LỤC
MỤC LỤC............................................................................................................2
DANH MỤC HÌNH VẼ......................................................................................4
DANH MỤC BẢNG BIỂU.................................................................................5
LỜI NÓI ĐẦU.....................................................................................................6
CHƯƠNG 1. TỔNG QUAN...............................................................................7 1.1
Hệ con lắc ngược và bài toán điều khiển...................................................7 1.2
Đối tượng thực tế.......................................................................................7 1.3
Mục đích và phương án điều khiển...........................................................8
CHƯƠNG 2. MÔ HÌNH HÓA ĐỐI TƯỢNG THỰC TẾ..............................10 2.1
Xây dựng mô hình toán học....................................................................10 2.2
Xác định các tham số mô hình.................................................................13 2.2.1
Các tham số xác định trực tiếp..................................................13 2.2.2
Các tham số xác định gián tiếp.................................................13
2.2.2.1. Ma sát trục động cơ....................................................................13
2.2.2.2. Ma sát trụ quay con lắc...............................................................14 2.3
Kết luận mô hình và Mô phỏng trên Matlab – Simulink.........................15
CHƯƠNG 3. THIẾT KỆ BỘ ĐIỀU KHIỂN CHO CON LẮC NGƯỢC......16 3.1
Giới thiệu về điều khiển trượt..................................................................16 3.2
Thiết kế bộ điều khiển trượt....................................................................16 3.2.1
Khâu Plant................................................................................16 3.2.2
Khâu Controller........................................................................19 3.2.3
Kết quả mô phỏng....................................................................24 3.3
Thiết kế bộ điều khiển Swing - up...........................................................25 3.3.1
Cơ sở lý thuyết.........................................................................25 3.3.2
Mở rộng: Bộ điều khiển Swing – up tỉ lệ góc...........................27 3.3.3
Thiết kế trên Matlab – Simulink...............................................27 3.3.4
Chuyển đổi tín hiệu xung encoder sang rad..............................28
CHƯƠNG 4. XÂY DỰNG CHƯƠNG TRÌNH ĐIỀU KHIỂN CON LẮC
NGƯỢC TRÊN MIỀN THỜI GIAN THỰC..................................................29 4.1
Mô hình vật lý hệ thống điều khiển con lắc ngược..................................29 4.2
Giới thiệu chung về CARD ghép nối PCI – 1710....................................29 2 4.2.1
Những đặc điểm đặc trưng.......................................................30 4.2.2
Phần mềm hỗ trợ cho Card PCI – 1710....................................31
CHƯƠNG 5. KẾT LUẬN.................................................................................36
TÀI LIỆU THAM KHẢO................................................................................37
PHỤ LỤC...........................................................................................................38 DANH MỤC HÌNH VẼ
Hình 1 Mô hình con lắc ngược Er
ror! Bookmark not defined.
Hình 2 Mô hình thực tế con lắc ngược 6
Hình 3 Cấu trúc hệ thống điều khiển con lắc ngược 7
Hình 4 Mô hình đơn giản hệ con lắc ngược Furuta 8
Hình 5 Dao động tắt dần của con lắc 13
Hình 6 Sơ đồ hệ thống điều khiển trên Simulink 14
Hình 7 Mô hình Simulink đối tượng con lắc ngược 17
Hình 8 Sơ đồ cấu trúc điều khiển trượt tầng........................................................19 18
Hình 9 Mô hình Simulink của bộ điều khiển 22
Hình 10 Vị trí quay của động cơ 23
Hình 11 Vận tốc quay của động cơ 24
Hình 12 Góc lắc của con lắc ngược 24
Hình 13 Vận tốc góc của con lắc ngược 24
Hình 14 Sơ đồ bộ điều khiển Swing – up 27
Hình 15 Khối chuyển xung Encoder sang rad 27
Hình 16 Sơ đồ kết nối phần cứng hệ thống 28
Hình 17 Lựa chọn các chương trình 31
Hình 18 Sơ đồ khối CAD PCI - 1710 33
Hình 19 Mô hình Rotary Pendelum 36 Hình 20 Bộ DAQ 36
DANH MỤC BẢNG BIỂU
Bảng 1: Thông số các thiết bị trong hệ con lắc ngược...........................................7 3 LỜI NÓI ĐẦU
Trong thực tế ta bắt gặp ngày càng nhiều các hệ thống đặt ra yêu cầu phải giải
quyết bài toán giữ thăng bằng hay chống rung lắc cho hệ. Một số ví dụ quen thuộc có
thể kể đến hệ xe hai bánh tự cân bằng, hệ gimbal chống rung cho camera, robot di
chuyển bằng hai chân... Các hệ này mặc dù có kết cấu khác nhau xong mục đích điều
khiển nhìn chung đều có nguyên tắc như bài toán điều khiển hệ con lắc ngược. Hệ
con lắc ngược thực ra đã được đưa vào nghiên cứu trong lĩnh vực điều khiển tự động
từ rất sớm, khoảng từ những năm 50 của thế kỷ trước, nó vốn là đối tượng không ổn
định, thường được sử dụng để kiểm tra khả năng thực thi và tính hiệu quả của các
thuật toán điều khiển. Dù đã có từ lâu nhưng bài toán điều khiển con lắc ngược vẫn
luôn dành được nhiều sự quan tâm, các giải thuật điều khiển mới cho nó vẫn liên tục
được ra đời và kiểm nghiệm.
Xuất phát từ những bài toán thực tiễn cuộc sống cũng như tính phù hợp với
chuyên ngành, em quyết tâm lựa chọn đề tài “ Thiết kế và điều khiển mô hình con lắc
ngược Furuta ” cho đồ án chuyên ngành của mình. Mục đích khi lựa chọn đề tài này
là để em có thể vận dụng tối đa những kiến thức, kỹ năng đã có trong suốt quãng thời gian học tập của mình.
Mục tiêu thực hiện đồ án này là xây dựng một hệ thống điều khiển hoàn chỉnh
cho hệ con lắc ngược Furuta. Chúng em sẽ đi từ khâu mô hình hóa đối tượng thực,
sau đó thiết kế và chay kiểm nghiệm các giải thuật điều khiển khác nhau. Từng nội
dung sẽ được thực hiện và thể hiện trong từng chương của đồ án này.
Chương 1: Khái quát về con lắc ngược, đưa ra bài toán và phương án điều khiển.
Chương 2: Thực hiện mô hình hóa đội tượng và xác định các tham số mô hình.
Chương 3: Thiết kế bộ điều khiển cho con lắc ngược, mô phỏng Matlab – Simulink.
Chương 4: Giải thích về thiết kế và cách hoạt động của thiết bị điều khiển. Chương 5: Kết luận. 4
CHƯƠNG 1. TỔNG QUAN 1.1
Hệ con lắc ngược và bài toán điều khiển
Có hai hệ con lắc ngược thường được sử dụng để nghiên cứu là hệ xe con
lắc ngược và hệ con lắc ngược quay ( con lắc ngược Furuta ).
Hình 1 Mô hình con lắc ngược
Hai hệ này cơ bản khác nhau ở cơ cấu chấp hành để tạo ra chuyển động cho con
lắc: hệ xe con lắc ngược thì là chuyển động chạy ngang của xe, còn ở hệ con lắc ngược
quay thì là chuyển động quay của động cơ đặt thẳng đứng. Phần chung của cả hai hệ
là một thanh cứng (con lắc) được gắn một đầu vào trục quay linh hoạt.
Bài toán đặt ra là điều khiển cơ cấu chấp hành để tạo chuyển động cho con lắc
ngược, sao cho đưa được con lắc từ vị trí ban đầu thẳng đứng hướng xuống dưới đến
được vị trí cân bằng trên là vị trí thẳng đứng hướng lên, đồng thời phải giữ được nó
ổn định tại đó dù có ngoại lực hay nhiễu tác động. 1.2
Đối tượng thực tế
Đối tượng được nghiên cứu trong đồ án này là hệ con lắc ngược quay ( con lắc
ngược Furuta ). Với cơ cấu cơ khí như hình 1.2, thiết bị chấp hành tạo chuyển động
quay là một động cơ DC, thiết bị do bao gồm 2 encoder để xác định góc quay động cơ và góc quay con lắc. 5
Hình 2 Mô hình thực tế con lắc ngược
Bảng 1: Thông số các thiết bị trong hệ con lắc ngược STT Tên thiết bị Thông số Uđm=24V 1 Động cơ DC
Pđm=90W ωmax=3400rpm(u=24V ,noload) Ikđmax=21.6 A Nguồn : 5V Encoder 2 1000 xung/vòng động cơ
Đầu ra dạng NPN open collector Nguồn : 5V Encoder con 3 1000 xung/vòng lắc Đầu ra dạng Totem pole 1.3
Mục đích và phương án điều khiển
Từ mô tả bài toán ở mục 1.1, ta có thể thấy mục đích điều khiển là giải quyết hai bài toán sau :
- Bài toán điều khiển swing-up: đưa được con lắc từ vị trí ban đầu ( thẳng đứng
hướng xuống ) lên đến lân cận vị trí cân bằng trên.
- Bài toán điều khiển cân bằng: duy trì được hệ ổn định quanh vị trí cân bằng
dù chịu tác động của ngoại lực. 6
Với mỗi bài toán trên ta sẽ xây dựng một bộ điều khiển riêng và mỗi bộ điều
khiển sẽ hoạt động trong một giai đoạn khác nhau. Cụ thể quá trình hoạt động của hệ
thống như sau: Ban đầu con lắc ở vị trí thẳng đứng hướng xuống, khi bắt đầu chạy,
bộ điều khiển swing-up sẽ hoạt động trước khiến con lắc dao động, cho đến khi vị trí
con lắc đến vùng lân cận vị trí cân bằng trên thì bộ điều khiển swing-up ngừng hoạt
động, đồng thời bộ điều khiển cân bằng bắt đầu hoạt động để đưa con lắc tới vị trí cân
bằng và duy trì nó ổn định tại vị trí đó.
Ngoài hai bộ điều khiển trên, với cơ cấu chấp hành để tạo chuyển động cho con
lắc ở đây là một động cơ DC, do đó ta cần xây dựng thêm một vòng điều khiển phía
trong để điều khiển momen (điều khiển dòng) cho động cơ, giúp động cơ đáp ứng tốt
với nhiễu tải, đảm bảo giá trị momen của động cơ luôn đáp ứng đúng với tín hiệu đầu
ra của bộ điều khiển con lắc.
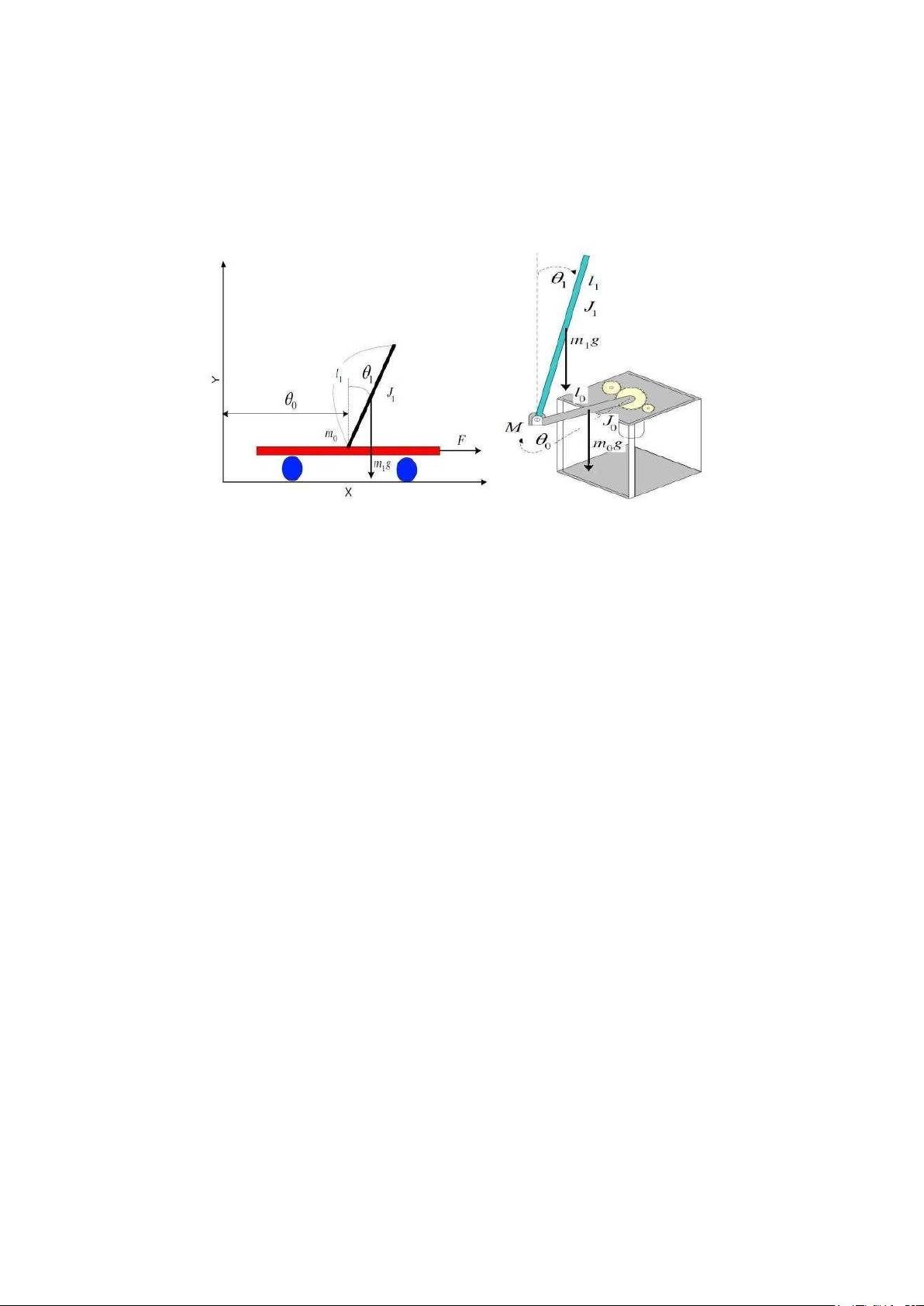
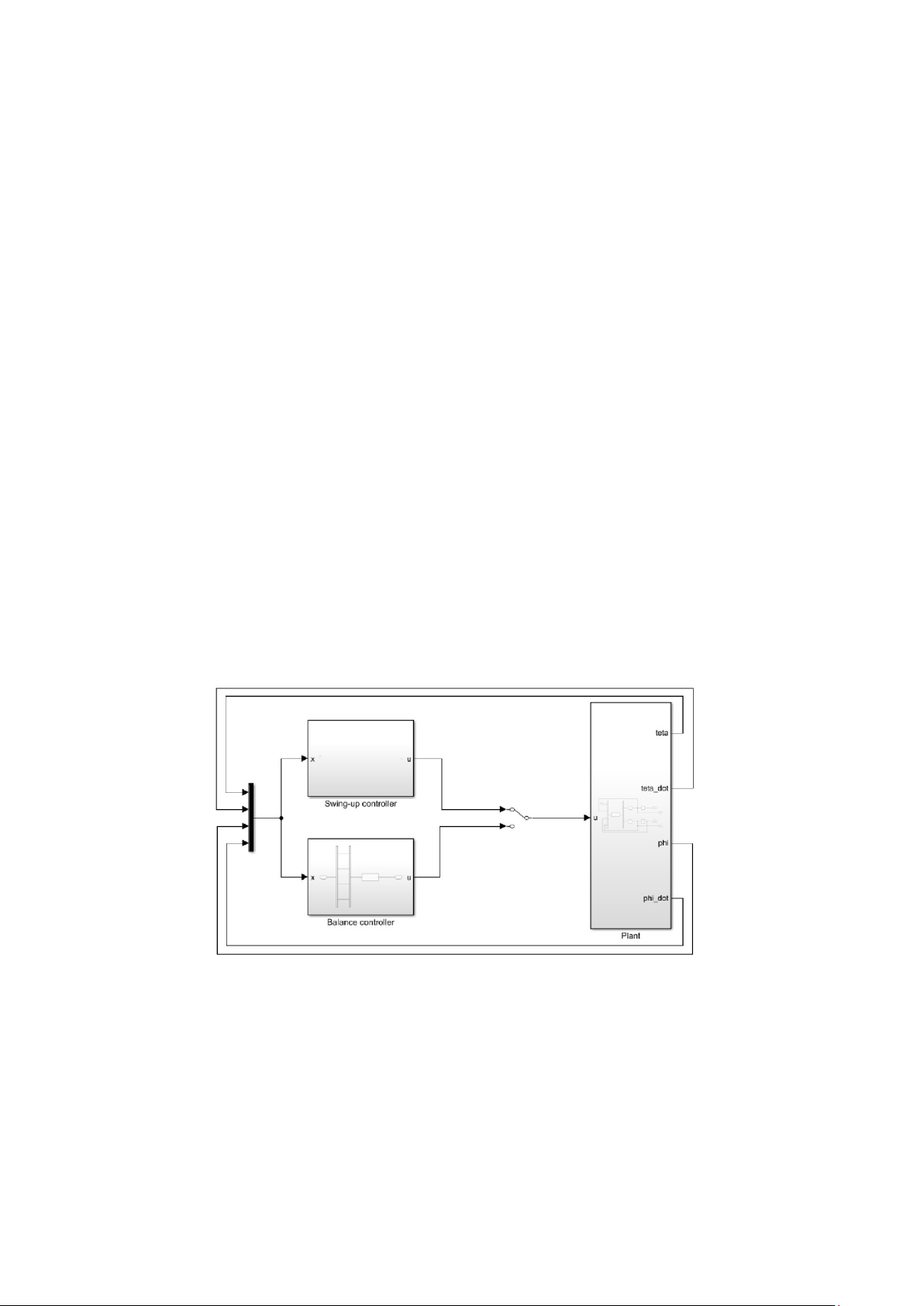
Cấu trúc hệ thống điều khiển cho con lắc ngược có thể được mô tả như hình 1.3,
gồm hai vòng điều khiển, với vòng ngoài là bộ điều khiển con lắc (bộ điều khiển
swing-up và bộ điều khiển cân bằng thay nhau hoạt động), vòng trong là bộ điều khiển
momen cho động cơ. Chi tiết cách xây dựng từng bộ điều khiển sẽ được trình bày ở các chương sau.
Hình 3 Cấu trúc hệ thống điều khiển con lắc ngược
CHƯƠNG 2. MÔ HÌNH HÓA ĐỐI TƯỢNG THỰC TẾ 2.1
Xây dựng mô hình toán học 7
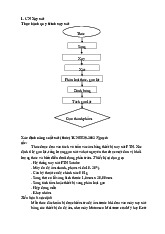
Hình 4 Mô hình đơn giản hệ con lắc ngược Furuta
Hệ con lắc ngược Furuta (chỉ gồm phần cơ khí) được mô tả một cách đơn giản
như trong hình 2.1. Hệ bao gồm: một tay quay (OA) nằm ngang, chiều dài l0 được
gắn vuông góc với trục động cơ, khi động cơ quay sẽ khiến thanh này quay trong mặt
phẳng nằm ngang; con lắc có khối lượng m, chiều dài 2l1, gắn tại A và có thể quay
linh hoạt trong mặt phẳng vuông góc với.
Một số đại lượng khác cần quan tâm:
- J0 : momen quán tính của tay quay với trục quay qua tâm O.
- J1 : momen quán tính của con lắc với khối tâm B.
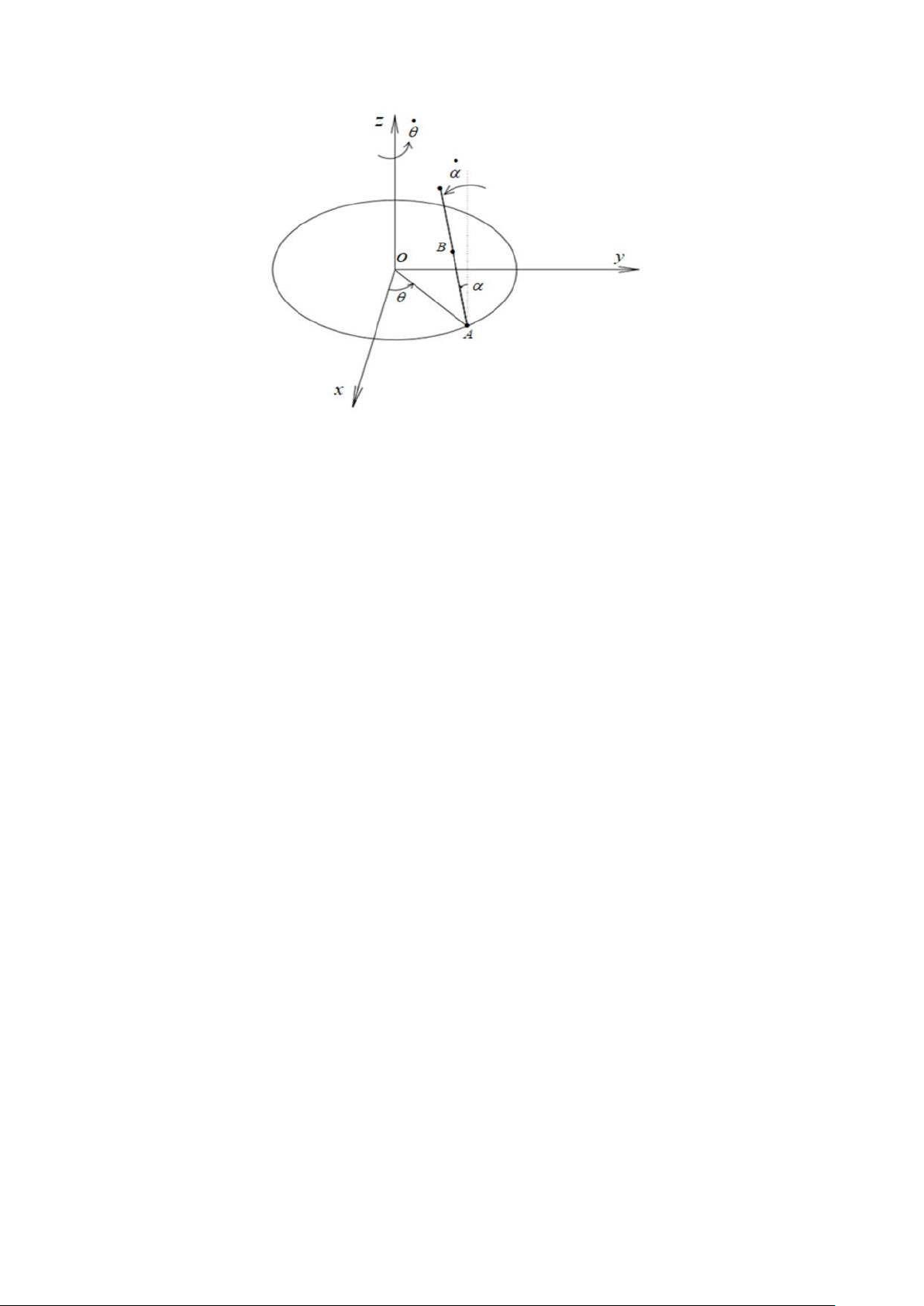
Xét trong hệ tọa độ Oxyz cố định như hình 2.1, θ và α được sử dụng là các hệ
tọa độ suy rộng. Tại một thời điểm, khi cánh tay quay được một góc θ so với trục Ox,
thì con lắc rời đi một góc α so với phương thẳng đứng.
Giả sử trọng lực của con lắc đặt tại điểm giữa B. Tọa độ khối tâm B của con lắc:
xB=l0cos(θ)+l1sin(α)sin (θ)
yB=l0sin (θ )−l1sin (α)cos (θ) (2.1) {
zB=l1cos(α )
Đạo hàm hai vế của (2.1) ta được :
x˙B=−l0sin (θ) θ˙+l1cos(α )sin (θ )α˙ +l1sin (α ) cos (θ) θ˙
y˙B=l0cos (θ )θ˙−l1cos (α )cos(θ ) α˙ +l1sin ( α) sin (θ) θ˙ (2.2) {
z˙B=−l1sin (α )α˙ 8
Suy ra được vận tốc của khối tâm B của con lắc : v 2 (2.3)
1 =x˙2B+y˙2B+z˙2B=l20θ˙2+l21sin2(α )θ˙2+l21α˙2−2l0l1cos (α)α˙ θ˙ 2 Động năng của hệ : 0 1 1 ˙ (2.4) 1 K=
(J θ˙2+J α2+mv2)
Thay (2.3) vào (2.4) ta được :
K=21 (J0+ml20+ml21sin2 (α ))θ˙2+21 (J1+ml21)α˙2−ml0l1cos(α)α˙ θ˙ (2.5)
Chọn mốc thế năng T = 0 tại vị trí cao nhất của con lắc ngược. Ta có thế năng
của hệ được tính toán như sau : T=mgl (2.6) 1(cos (α)−1)
Từ (2.5) và (2.6) ta có được công thức hàm Lagrange : L=K−T 1 2 2 2 ¿ (J (2.7)
0+ml0+ml1sin ( α))θ˙2+12 (J1+ml21) α˙2 –ml0l1cos (α)α˙ θ˙ 2
−mgl1(cos (α)−1) Gọi u là momen tác dụng của động cơ. Áp dụng công thức : Fi
Ta có hệ phương trình động lực học sau :
τ−b0θ˙=(J0+ml20+ml21sin2 (α))θ¨−ml0l1cos (α) α¨ +ml21sin (2α ) α˙ θ˙+ml0l1sin(α)α˙2
{ ⇔−b1α˙ =−ml0l1cos (α) θ¨+(J1+ml21)α¨ − ml12sin(2α )θ˙2−mgl1sin (α ) (2. 8) 9
Hệ phương trình (2.8) có thể được viết lại dưới dạng :
H (α )[θ¨ ]+V (θ,˙ α ,θ,α˙ )+G (α)=T (2. 9) α¨ Trong đó : H (α
)=J0+ml20+ml21sin2(α) −ml0l1cos2(α))
−ml0l1cos(α) J1+ml1
b0θ˙+ml21sin (2α) α˙ θ˙+ml0l1sin(α)α˙2 ( )
V (θ,˙ α,θ,α˙
)=b1α˙ −21 ml21sin (2α ) θ˙2 0 G (α )=( )
−mgl1sin(α) T=(u) 0
Từ (2.9) ta có mô hình phi tuyến của hệ con lắc ngược Furuta như sau : 10
q¨=θ¨ ]=H−1 [T−V −G]=f (θ ,˙ α,θ ,α,u˙ )=[f1(θ,˙ α ,θ,α ,u˙ )] (2.10) α¨ f2(θ
,˙ α ,θ,α ,u˙ ) Trong đó :
f1(θ,˙ α ,θ,α ,u˙)=ml0l1cos(α )(0.5ml21sin (∆2α) θ˙2+mgl1sin (α )−b1α˙ ) (2.11)
f2(θ,˙ α ,θ,α ,u˙ )= (2.12 )
Với ∆=J0J1+m2l41sin2 (α )+m2l20l21+J0ml21+J1ml20
+J1ml21sin2( α)−m2l20l21cos2(α) 2.2
Xác định các tham số mô hình 2.2.1
Các tham số xác định trực tiếp
- Khối lượng của con lắc : m=0,1kg.
- Chiều dài của con lắc : l1=1m.
- Chiều dài của tay quay : l0=1,18m.
- Momen quán tính của cả hệ tay quay với trục động cơ :
J0=4,4.10−3kgm2 11
- Momen quán tính của con lắc với khối tâm con lắc :
J1=5.5026.10−4kgm2 Chọn hằng số điện – momen
của động cơ kT=0,07 Nm/A Ta có quan hệ sau :
τ=km Ψ iA=kT iA (2.13)
Gia tốc trọng trường g = 9.8 m/s2 đã biết. 2.2.2
Các tham số xác định gián tiếp
2.2.2.1. Ma sát trục động cơ
Ta có phương trình cân bằng momen của động cơ một chiều :
¨=J1m (τ−mc) (2.14) θ Trong đó:
J : là momen quán tính so với trục quay m
mc : là momen cản do ma sát
sinh ra , được tính : mc=bcθ˙
Thay công thức tính m và công thức tính c
τ ở (2.13) vào (2.14) ta được : θ
¨=J1m (kT iA−b0θ˙) (2.15)
Khi động cơ quay với tốc độ ổn định thì θ¨=0 , ta đo được iA và tốc độ θ˙ , từ
kT iA đó theo phương trình (2.15) ta tính
được : b0= θ˙ .
Ta chọn giá trị b0=5,8.10−4.
2.2.2.2. Ma sát trụ quay con lắc
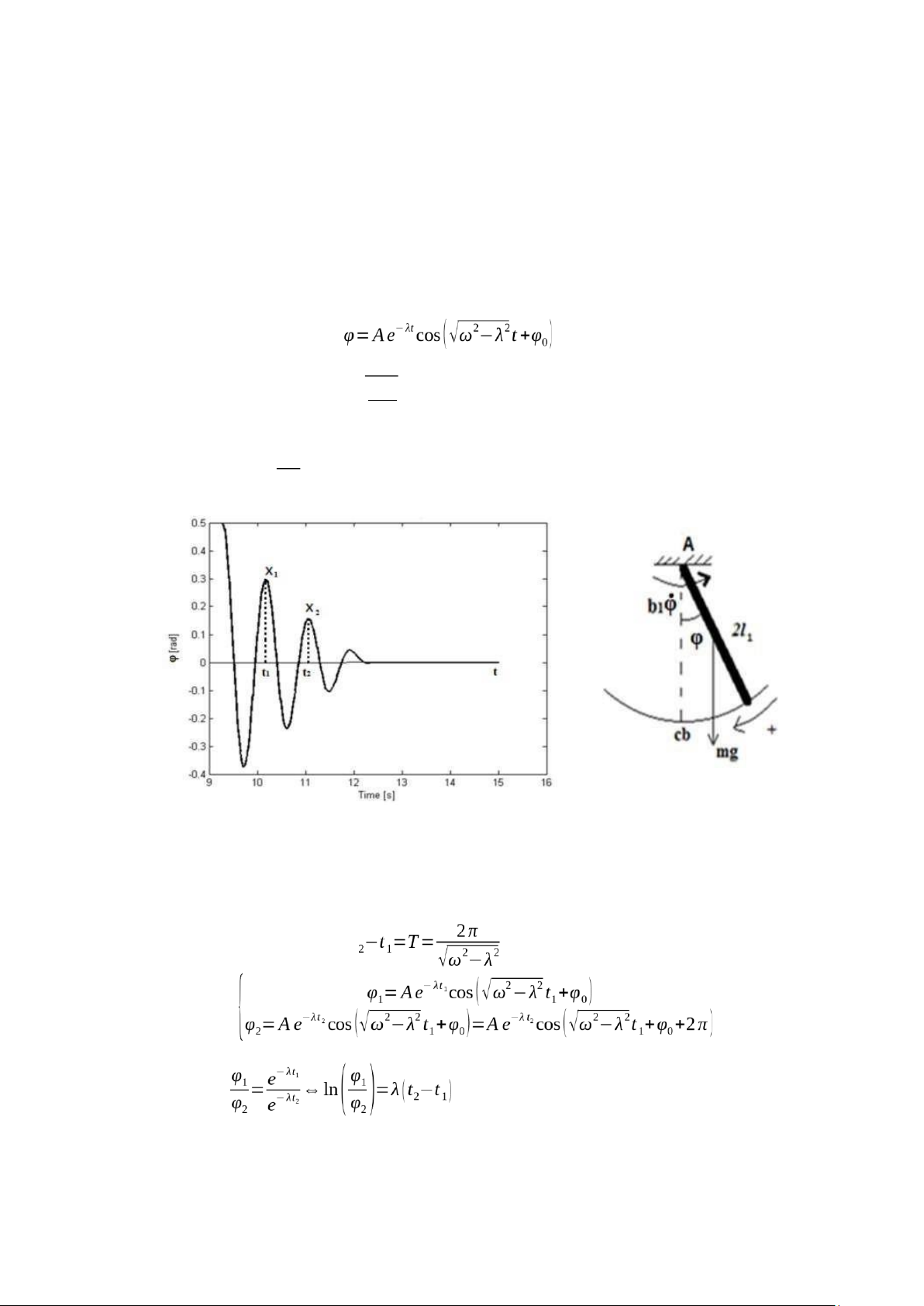
Ý tưởng: Cho con lắc dao động quanh vị trí cân bằng dưới với biên độ nhỏ, do
ảnh hưởng của ma sát nên biên độ dao động giảm gần theo thời gian. Từ việc thiết lập 12
phương trình dao động tắt dần và xác định độ giảm biên độ sau mỗi chu kỳ, ta có thể
tính được hệ số ma sát trục quay con lắc.
Ta có phương trình vi phân mô tả chuyển động của con lắc :
J φ¨ +b1φ˙+mgl1φ=0 (2.16)
với J là momen quán tính của con lắc so với tâm quay A.
Giải phương trình (2.160 ta được nghiệm là : (2.17) b1 mgl Trong đó : λ √ = , ω= 2J J
Hình 5 Dao động tắt dần của con lắc
Xét 2 thời điểm liên tiếp t1 và t2 mà góc lệch của con lắc đạt giá trị cực đại,
khoảng thời gian giữa 2 thời điểm này đúng bằng chu kì dao động T của hệ. Ta có: t (2.18) ⇒ (2.19) 13
Từ (2.18) và (2,19) ta được : ¿ (2.20 ) mgl 2 λmgl
Mặt khác ta có : J= 1 2 , b1= 1 2 suy ra : ω ω (2.21 ¿ )
Từ công thức (2.21) ta chọn b1=1,4142.10−3 2.3
Kết luận mô hình và Mô phỏng trên Matlab – Simulink
Trong nội dung đồ án này, phương pháp được lựa chọn để thiết kế bộ điều khiển
cân bằng là phương pháp điều khiển trượt. Bộ điều khiển trượt ta sẽ xây dựng từ mô
hình phi tuyến của hệ. Chương 3 sẽ đề cập đến nội dung này.
Từ mô hình phi tuyến (2.10) tìm được và phương án điều khiển đã đề ra, ta xây
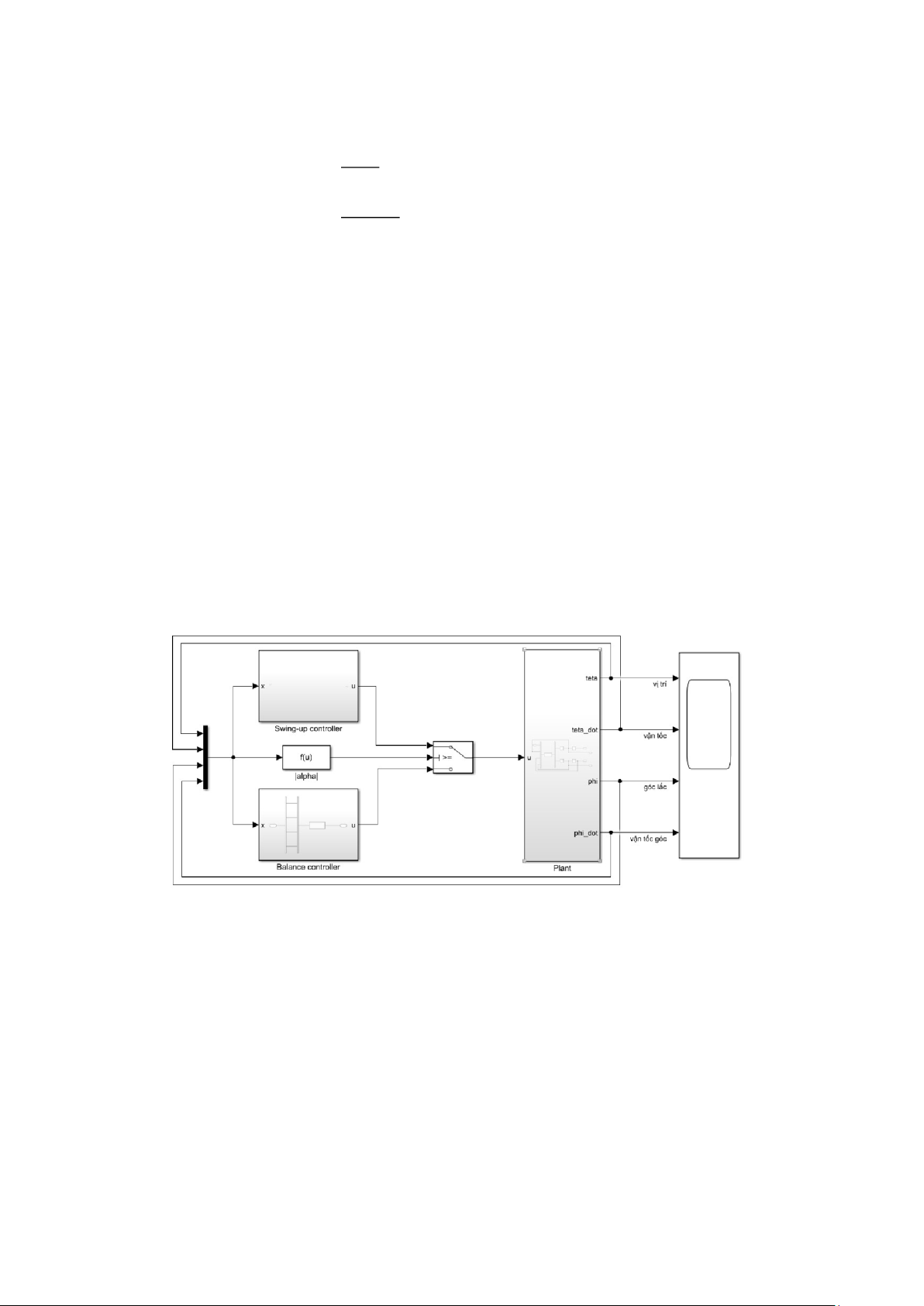
dựng được mô hình đối tượng và cấu trúc hệ thống điều khiển trên Simulink như dưới đây.
Hình 6 Sơ đồ hệ thống điều khiển trên Simulink
Điều kiện chuyển hoạt động của bộ điều khiển từ swing-up sang điều khiển cân
bằng trong khối Switch là |α|<20o.
CHƯƠNG 3. THIẾT KỆ BỘ ĐIỀU KHIỂN CHO CON LẮC NGƯỢC 3.1
Giới thiệu về điều khiển trượt 14
Con lắc ngược Furuta được coi là một hệ thiếu cơ cấu chấp hành. Hệ thiếu cơ
cấu chấp hành là hệ gồm một tín hiệu đầu vào cà nhiều tín hiệu đầu ra. Con lắc ngược
là mô hình phi tuyến mất cân bằng điển hình và chúng thường được coi là các đối
tượng chuẩn để kiểm chứng hiệu quả của các phương pháp điều khiển. Điều khiển
con lắc ngược sao cho đảm bảo hệ kín ổn định, bám vị trí đặt, góc lệch tối thiểu là bài
toán được nhiều nhà khoa học quan tâm. Vì vậy đã có các công trình công bố vè các
thuật toán điều khiển cho hệ con lắc ngược.
Phương pháp điều khiển trượt tầng ( hay còn gọi là HSMC ) là một phương pháp
điều khiển mới và phù hợp với các hệ thống chuyển động thiếu chấp hành. 3.2
Thiết kế bộ điều khiển trượt 3.2.1 Khâu Plant
Ta đặt các biến trung gian là : x1=θ;x2=θ;x˙ 3=α;x4=α˙
Từ (2.11) và (2.12) ta có các phương tình của hệ trạng thái : (
x˙1=x2 x˙2=ml0l1cos( α) (0.5ml21sin ∆2α) θ˙2+mgl1sin (α )−b1α˙ ) (3.1) x˙ 3=x4 x˙4=
Phương trình (3.1) biểu điễn dưới dạng mô hình trạng thái : 15 x˙1=x2
x˙2=f1( X )+g1( X )u x˙3=x4 (3.2)
x˙4=f2 ( X )+g2( X )u Với :
ml0l1cos(α )(0.5ml21sin (2α) θ˙2+mgl1sin (α )−b1α˙ ) f1( X )= ∆ ml21+J1 g1 ( X )= ∆ f2( X )=
ml0l1cos (α ) g2 ( X )= ∆ Trong đó :
X=¿¿ là vec-tơ biến trạng thái và u là đầu vào.
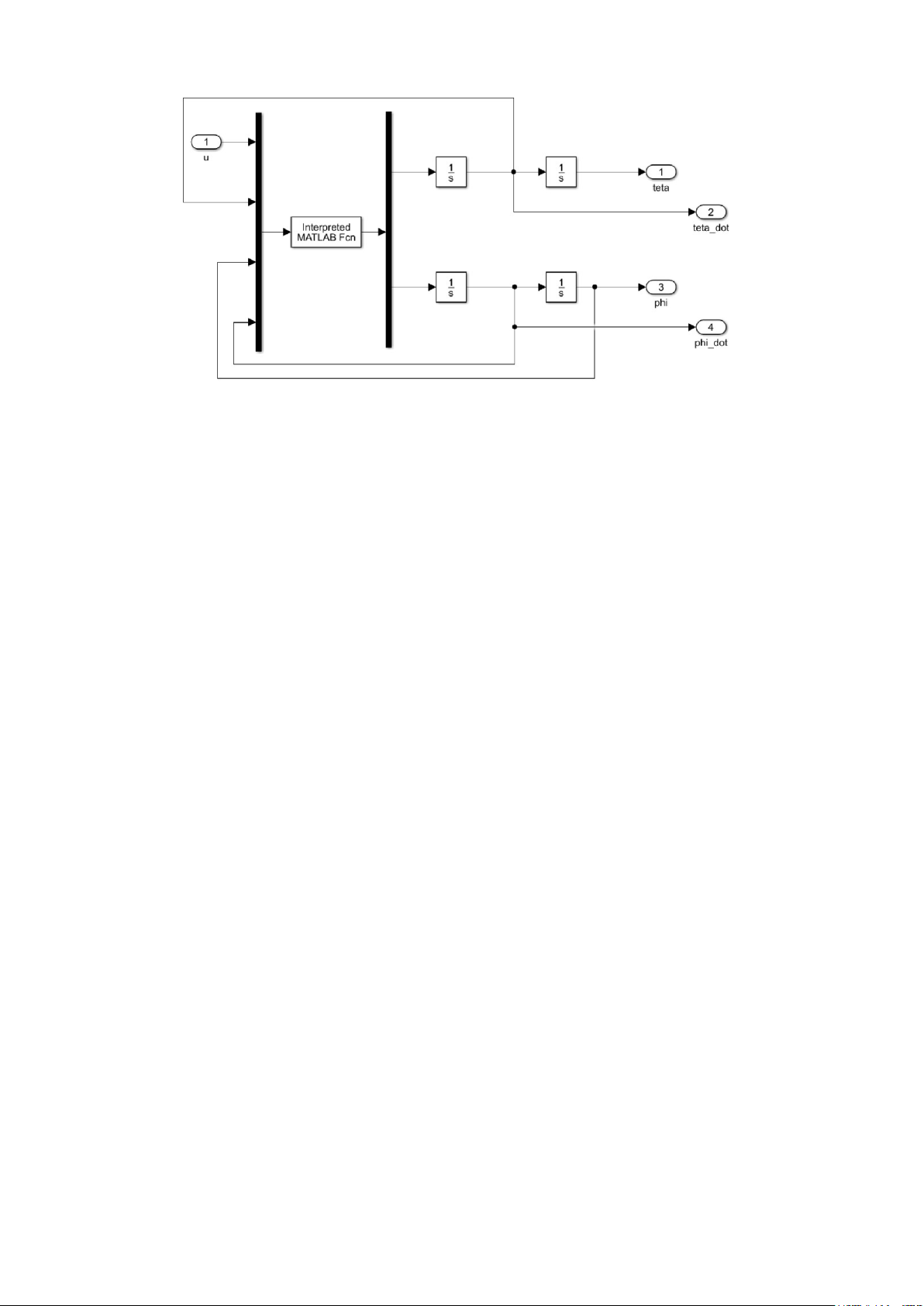
Các f i là các hàm phi tuyến bị chặn và các gi lớn hơn không và có điểm cân bằng tại gốc tọa độ. 16
Hình 7 Mô hình Simulink đối tượng con lắc ngược File “plant.m”:
function y = plant(tin_hieu) global lo lc g m J0 J1 b0 b1
%%Input u = tin_hieu(1); x_dot = tin_hieu(2); phi =
tin_hieu(3); phi_dot = tin_hieu(4); %%Plant
Denta = J0*J1 + m^2*lc^4*sin(phi)^2 + m^2*lo^2*lc^2 +
J0*m*lc^2 + J1*m*lo^2 + J1*m*lc^2*sin(phi)^2 - m^2*lo^2*lc^2*cos(phi)^2;
f1 = (m*lo*lc*cos(phi)*(0.5*m*lc^2*sin(2*phi)*x_dot^2
+ m*g*lc*sin(phi) - b1*phi_dot) - (m^lc^2 +
J1)*(m*lc^2*sin(2*phi)*phi_dot*x_dot +
m*lo*lc*sin(phi)*phi_dot^2 + b0*x_dot)) / Denta;
g1 = (m^lc^2 + J1) / Denta; f2 = ((m*lo^2 + m*lc^2*sin(phi)^2 +
J0)*(0.5*m*lc^2*sin(2*phi)*x_dot^2 + m*g*lc*sin(phi) b1*phi_dot) -
(m*lo*lc*cos(phi))*(m*lc^2*sin(2*phi)*phi_dot*x_dot +
m*lo*lc*sin(phi)*phi_dot^2 + b0*x_dot)) / Denta; g2 = (m*lo*lc*cos(phi)) / Denta;
%%Output y(1) = f1 + g1*u; y(2) = f2 + g2*u; end 17 3.2.2 Khâu Controller
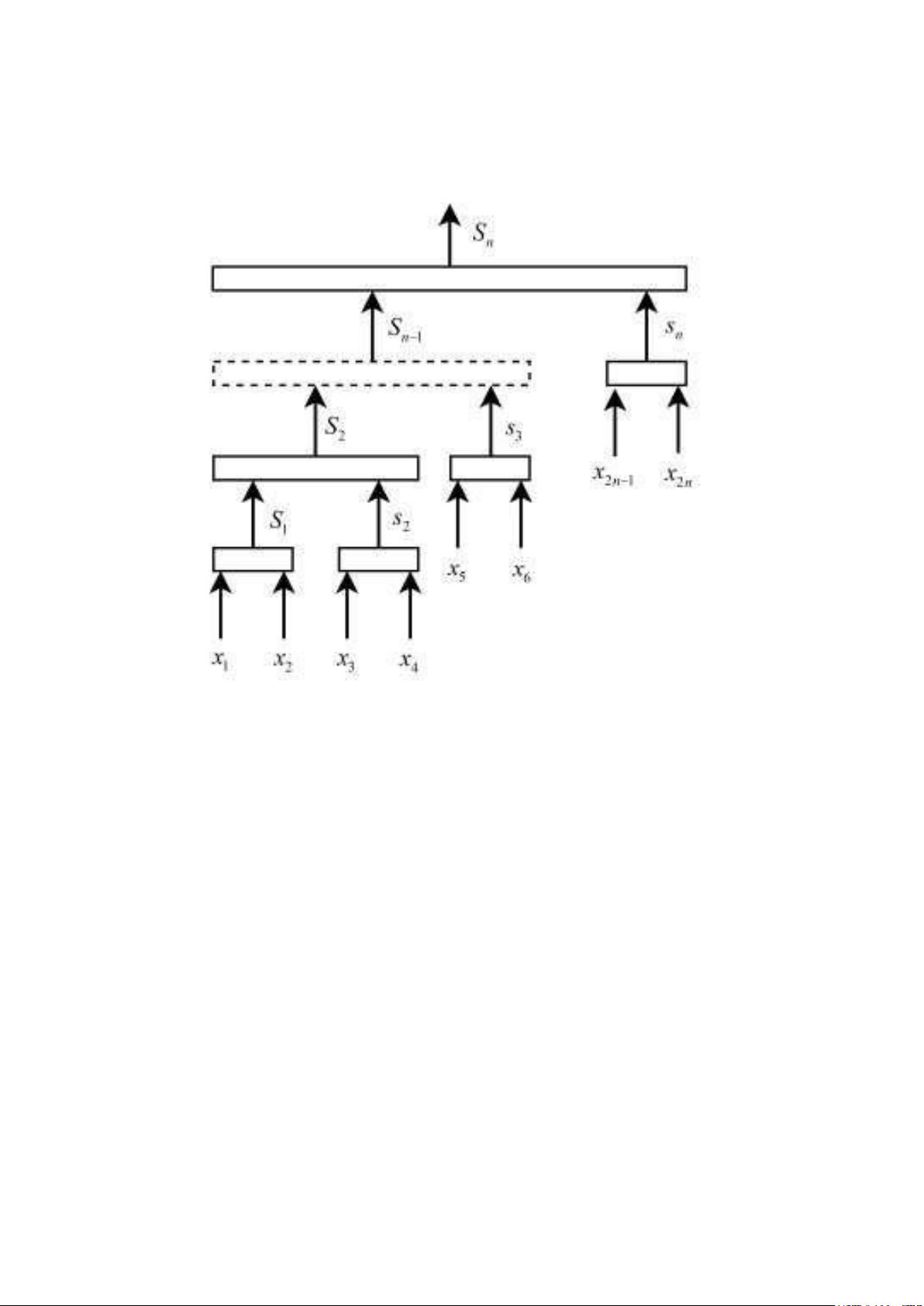
Hệ (3.2) bao gồm 4 hệ con và một tín hiệu điều khiển u. Bài toán thiết kế ở đây
là xác định tín hiệu điều u để đưa các biến trạng thái về điểm cân bằng ôn định.
Hình 8 Sơ đồ cấu trúc điều khiển trượt tầng
Ở mỗi bước ta xác định được tín hiệu điều khiển ảo ui đảm bảo cho hệ con thứ i
các hệ con trước đó ổn định theo Lyapunov, tín hiệu điều khiển u cần tìm được xác định như sau :
Bước 1: Từ (3.2), ta có mô hình của hệ con thứ nhất : x˙1=x2 (3.3)
{x˙2=f1 ( X )+g1 ( X ) u1
Ta xác định tín hiệu điều khiển ảo u để quay về gốc tọa độ khi có nhiễu đánh 1 x1
bật khỏi điểm cân bằng.
Để làm được điều này, ta định nghĩa mặt trượt s : 1 18 s1=c1 x1+x2 (3.
4) với c là hằng số dương. 1
Đạo hàm mặt trượt s theo thời gian ta được : 1
s˙1=c1 x˙1+x˙2
¿c1x2+f1+g1u1
¿c1x2+f1+g1(ueq1+usw 1) (3.5)
¿c1x2+f1+g1ueq 1−k1s1−η1sgn(s1)+k1s1+η1sgn(s1)+g1usw1
¿−k1s1−η1sgn(s1) với u1=ueq1+usw1
Từ (3.5) ta xác định được : ueq 1=−
c1gx12+f1 (3.6) và: u
−k1s1+η1sgn(s1) sw1= g1 (3.7)
Bước 2: Mặt trượt S được thiết kế cho hệ con thứ nhất và hệ con thứ hai dựa trên mặt 2
trượt đã thiết kế cho hệ con thứ nhất. S được định nghĩa như sau : 2
S2=λ1S1+β1s2=λ1s1+β1(c2 x3+x4) (3.8) Với: S
(vì là mặt trượt của bước thiết kế đầu tiên), , , là hằng số 1≡s1 s1
λ1 β1 c2
dương. Ta phải xác định tín hiệu điều khiển u để đưa mặt trượt S2→0 . Do vậy ta định
hàm Lyapunov cho Bước 2 như sau: 19 1
V (S¿¿2)= S22¿ 2 (3.9)
Đạo hàm theo thời gian của (3.9) ta có :
V˙ (S¿¿2)=S2S˙2=S2(λ1S˙1+β1s˙2)¿ (3.10) Từ (3.2) và (3.5) ta có:
S˙2=λ1S˙1+β1s˙2
¿ λ1 (c1x2+f1+g1u)+β1 (c2x4+f2+g2u) ¿ λ1(c1 x2+f1+g1(ueq1+usw 1+ueq2+usw2))+¿
β1(c2x4+f2+g2(ueq1+usw1+ueq2+usw2)) 20