Giải bài tập chương 5, 6 - Kinh tế vi mô | Đại học Kinh tế Kỹ thuật Công nghiệp

Chương 5
Bài tập 1: (chỉ làm câu d,e, câu a,b,c đã sửa trên lớp)
Một nhà sản xuất cần 2 yếu tố đầu vào K và L để sản xuất sản phẩm X. Người này chỉ
sử dụng khoản tiền C = 15.000 để mua đầu vào với giá tương ứng r = 600 và w =
300. Hàm sản xuất được cho bởi Q = 2K(L - 2)
a. Xác định hàm MP của K và L, MRTS giữa K và L.
b. Tìm phương án sản xuất tối ưu và sản lượng tối đa.
c. Xí nghiệp muốn sản xuất 900 đơn vị, tìm phương án sản xuất với chi
phí tối thiểu.
d. Từ kết quả câu c, hãy tính chi phí bình quân ATC
Q = 900, Cmin = wL + rK = 18.600 = TC
ATC = TC/Q = 18.600/900 = 20,67
e. Từ kết quả câu c, nếu giá bán sản phẩm X là P = 25, thì lợi nhuận là bao nhiêu?
P = 25, Q = 900 . Doanh thu TR = P.Q = 25 x 900 =
22.500 Lợi nhuận: π = TR – TC =22.500 – 18.600 = 3.900 Bài tập 2
Một hãng có chi phí biến đổi bình quân là
AVC = Q + 4. Chi phí cố định của hãng là 50
Viết phương trình biểu thị các đường VC, TC, MC, ATC, AFC?
Xác định chi phí bình quân tối thiểu Giải
Theo đề bài: AVC = Q + 4, FC = 50 a. VC = AVC.Q = Q2 + 4Q, TC=VC+FC=Q2+4Q+50, MC=TC’Q=VC’Q=2Q+4
ATC = TC/Q = Q + 4 + 50/Q, AFC = FC/Q = 50/Q
b. ATC min  ATC = MC  Q + 4 + 50/Q = 2Q + 4 Q=50/QQ2=50Q=7,1
=> ATCmin = 7,1 + 4 + 50/7,1 = 18,2 Bài tập 2
Một hãng biết được hàm cầu về sản phẩm của mình là P = 100 – 0,01Q. Hàm tổng chi
phí của hãng là TC = 50Q + 30000.
a. Viết phương trình biểu diễn tổng doanh thu, doanh thu cận biên và chi phí cận biên.
b. Xác định sản lượng tối đa hóa lợi nhuận.
c. Khi nào thì doanh thu của hãng là tối đa?
d. Nếu CP đánh thuế t=10đvtiền/đvsp thì sản lượng và giá là bao nhiêu để DN
tối đa hóa Lợi nhuận? Tính Lợi nhuận tối đa đó? Giải lOMoAR cPSD| 46884348 a.
Tổng doanh thu TR = P.Q = (100 - 0,01Q)Q = 100Q -
0,01Q2 doanh thu cận biên MR = TR’Q = 100 - 0,02Q
chi phí cận biên MC = TC’Q = 50 b. max khi MR = MC
=> 100 - 0,02Q = 50 => Q = 50/0,02 =
2500 =>P=100-0,01Q= 100-25=75
=> max = TR – TC = P.Q – TC = 32500
c. TRmax  MR = TR'Q = 0  100 - 0,02Q = 0  Q = 5000
=> P = 100 – 0,01Q = 50 => TRmax = P.Q = 250000
d. TCt = TC + 10Q = 60Q + 30000 => MCt = TC't = 60,
max khi MR = MCt => 100 - 0,02Q = 60 => Q =2000, P =80
max = TR – TCt = 10000
e. Nhà nước đánh thuế cố định là 5000 đợn vị tiền, thì sản lượng, giá bán
và lợi nhuận tối đa là bao nhiêu? TCT = TC + 5000 = 50Q + 35000  MCT = TC’T = 50
Lợi nhuận tối đa khi: MR = MC
=> 100 - 0,02Q = 50 => Q = 50/0,02 =
2500 =>P=100-0,01Q= 100-25=75
=> max = TR – TCT = P.Q = 27500
f. Hai cách đánh thuế này khác nhau thế nào?
Đánh thuế theo sản lượng làm cho sản lượng giảm, giá tăng và lợi
nhuận giảm Đánh thuế cố định không làm thay đổi sản lượng và giá
bán, nhưng lợi nhuận sẽ giảm. Bài 4:
Anh Nam đang làm quản lý cho công ty ABC với mức lương là 400 triệu đ ng/năm.
Anh Nam có ý định thôi việc ở công ty ABC và lấy l愃⌀i mạ t bằng nhà mình hiện
đang cho thuê với số tiền 300 triệu đ ng/năm, để mở công ty riêng và trư뀣c tiếp
điều hành. Để ra quyết định đúng đắn, anh Nam đã khảo sát thị trường và th ẩm
định dư뀣 án kinh doanh và những số liệu điều tra, tính toán được tóm tắt dưới đây
là đáng tin cậy.
Chi phí tiền lương nhân viên: 600 triệu đ ×ng/năm
Chi phí nguyên vật liệu: 1400 triệu đ ×ng/năm0
Chi phí điện, nước: 200 triệu đ ng/năm
Chi phí bao bì: 100 triệu đ ng/năm
Chi phí thuê máy móc thiết bị: 600 triệu đ ×ng/năm
Doanh thu: 3400 triệu đ ×ng/năm
a. Lợi nhuận kế toán và lợi nhuận kinh tế dư뀣 kiến của công ty anh Nam là bao nhiêu?
b. Theo anh/chị, anh Nam nên tiếp tục làm t愃⌀i công ty ABC hay mở công ty riêng?
a. Chi phí kế toán (CP hiện):
600 + 1400 + 200 + 100 + 600 = 2900 (triệu đ ×ng/năm)
Chi phí ẩn: 400 + 300 = 700 (triệu đ ×ng/năm)
Chi phí kinh tế: 2900 + 700 = 3600 (triệu đ ng/năm)
Lợi nhuận kế toán: 3400 – 2900 = 500 (triệu đ ×ng/năm)
Lợi nhuận kinh tế: 3400 – 3600 = -200 (triệu đ ng/năm)
b. anh Nam nên tiếp tục làm t愃⌀i công ty ABC (không nên mở công ty
riêng) vì công ty riêng có lợi nhuận kinh tế âm. c. Bài tập 5
Một hãng sản xuất với chi phí bình quân ATC = 300 + 97500/Q và có
đường cầu P = 1100 – Q, P tính bằng $, Q là số sản phẩm.
a. Quyết định của hãng để tối đa hóa lợi nhuận? Tính lợi nhuận đó?
b. Hãng đạ t mức giá nào để tối đa hóa doanh thu
c. Hãng đạ t mức giá nào để bán được nhiều sản phẩm nhất mà không bị lỗ Giải:
a. b. Tương tư뀣 bài tập 2b
c. Ta có ATC = 300 + 97500/Q và đường cầu P =
110 – Q, Chi phí TC = ATC.Q = 300Q + 97500
Doanh thu TR = P.Q = 110Q – Q2
Lợi nhuận = TR – TC = 1100Q – Q2 - 300Q – 97500
Để hãng không lỗ thì g 0
=> -Q2 + 800Q - 97500 g 0
Giải bất phương trình ∆=640000 – 390000 =250000
Q1 = (-800 + 500)/-2 = 150 Q2 = (-800 - 500)/-2 = 650
Vậy 150fQf650 (vì a=-1<0) thì hãng khônglỗ
Bán được nhiều sản phẩm nhất mà không lỗ thì Q = 650 (sp)
Giá P = 1100 – 650 = 450 Chương 6 Bài tập 1
Hàm tổng chi phí của một hãng CTHH là
TC = q2 + q + 100, q (sản phẩm) chi phí ($)
a. Nếu giá thị trường là 27$ thì hãng tối đa hóa lợi nhuận t愃⌀i mức sản
lượng nào? Tính lợi nhuận tối đa đó?
b. Xác định giá và sản lượng hòa vốn. Khi giá thị trường là 9$ thì hãng nên đóng cửa
hay tiếp tục sản xuất? Vì sao?
c. Xác định đường cung của hãng (phương trình và đ × thị) Giải:
a. MC = TC’q = 2q + 1, P= 27
Nguyên tắc tối đa hoá Lợi nhuận của hãng CTHH: P = MC => 27 = 2q + 1 => q= 13 ,
max = TR - TC = 27x13 - (132 + 13 + 100) = 69$
b. Điểm Hòa vốn là P = ATCmin ATCmin khi MC = ATC => 2q + 1 = q + 1 + 100/q => q2 =100 => q =10, => P = ATCmin = 21$
Điểm đóng cửa sản xuất P = AVCmin TC = (q2 + q) + 100 = VC + FC => VC = q2 + q
=> AVC = VC/q = q+1 g1 (vì q g 0)
=> AVCmin =1 (khi đó q = 0)
Hãng nên tiếp tục sx vì P=9$ > AVCmin = 1$
c. Đường cung là đường MC nằm trên điểm AVCmin =>P=MC
=> hàm cung Ps = 2q+1 (q>0) Bài 2
Một hãng c愃⌀nh tranh hoàn hảo có hàm chi phí biến đổi bình quân là: AVC = 2q + 6 ($)
a. Viết phương trình biểu diễn hàm MC và tìm mức giá mà hãng đóng cửa
sản xuất, viết pt đường cung.
b. Khi giá bán một sản phẩm là 20$ thì hãng bị lỗ 100$. Tìm mức giá và sản lượng
hoà vốn của hãng
c. Hãng sản xuất bao nhiêu sản phẩm nếu giá bán trên thị trường là 80$?
Tính lợi nhuận cư뀣c đ愃⌀i đó
d. Minh họa các kết quả trên đ × thị. Giải:
a. Ta có VC = AVCxq = 2q2 + 6q => MC = AVC'(q)= 4q + 6
Điểm đóng cửa sản xuất P = AVCmin lOMoAR cPSD| 46884348 VC = 2q2 + 6q
=> AVC = VC/q = 2q+6 g 6(vì q g 0)
=> AVCmin = 6 ($) (khi đó q = 0)
Đường cung của DN CTHH là đường MC nằm trên điểm AVCmin =>P=MC => hàm cung Ps = 4q + 6
b. Nguyên tắc sản xuất đối với DN CTHH là P = MC => 20 = 4q + 6 => q = 3,5
t愃⌀i P = 20, Lợi nhuận π = -100
π = TR - TC = Pxq - (VC + FC)
=> -100 = 3,5x20 - (2x3,52 + 6x3,5 + FC) => FC = 137,5 => TC = 2q2 + 6q + 137,5
=> ATC = TC/q = 2q + 6 + 137,5/q
Điểm hoà vốn là P = ATCmin ATCmin khi MC = ATC
=> 4q + 6 = 2q + 6 + 137,5/q => q = ????
Thay q = ??? vào ATC ta có được ATCmin
c. Câu này hoàn toàn giống câu a (bài tập 1) Bài tập 3
Một thị trường cạnh tranh hoàn hảo có 50 người bán và 60 người mua.
Mỗi người mua đều có hàm cầu giống nhau: P = 140 – 10q
Mỗi người sản xuất cũng có hàm tổng chi phí giống nhau: TC =
4q(q + 6) Xác định hàm cung và hàm cầu của thị trường
Viết phương trình hàm cầu của 1 hãng Giải
a. Hàm cầu của mỗi người mua: P = 140
– 10q => q = (140 - P)/10
Cầu thị trường là tổng cầu của 60 người mua: QD = 60q = 60x(140 - P)/10 =>QD=840-6P TC = 4q(q + 6) = 4q2 + 24q MC = TC'q = 8q + 24
Hàm cung của mỗi người bán chính là hàm MC => P = 8q + 24 => q = (P - 24)/8
Hàm cung thị trường chính là tổng cung của 50
người bán => Qs = 50x(P - 24)/8 = (25/4)P- 150 lOMoAR cPSD| 46884348
b. Cân bằng thị trường: QD =
QS => 840 - 6P = (25/4)P- 150 => P = 80,8
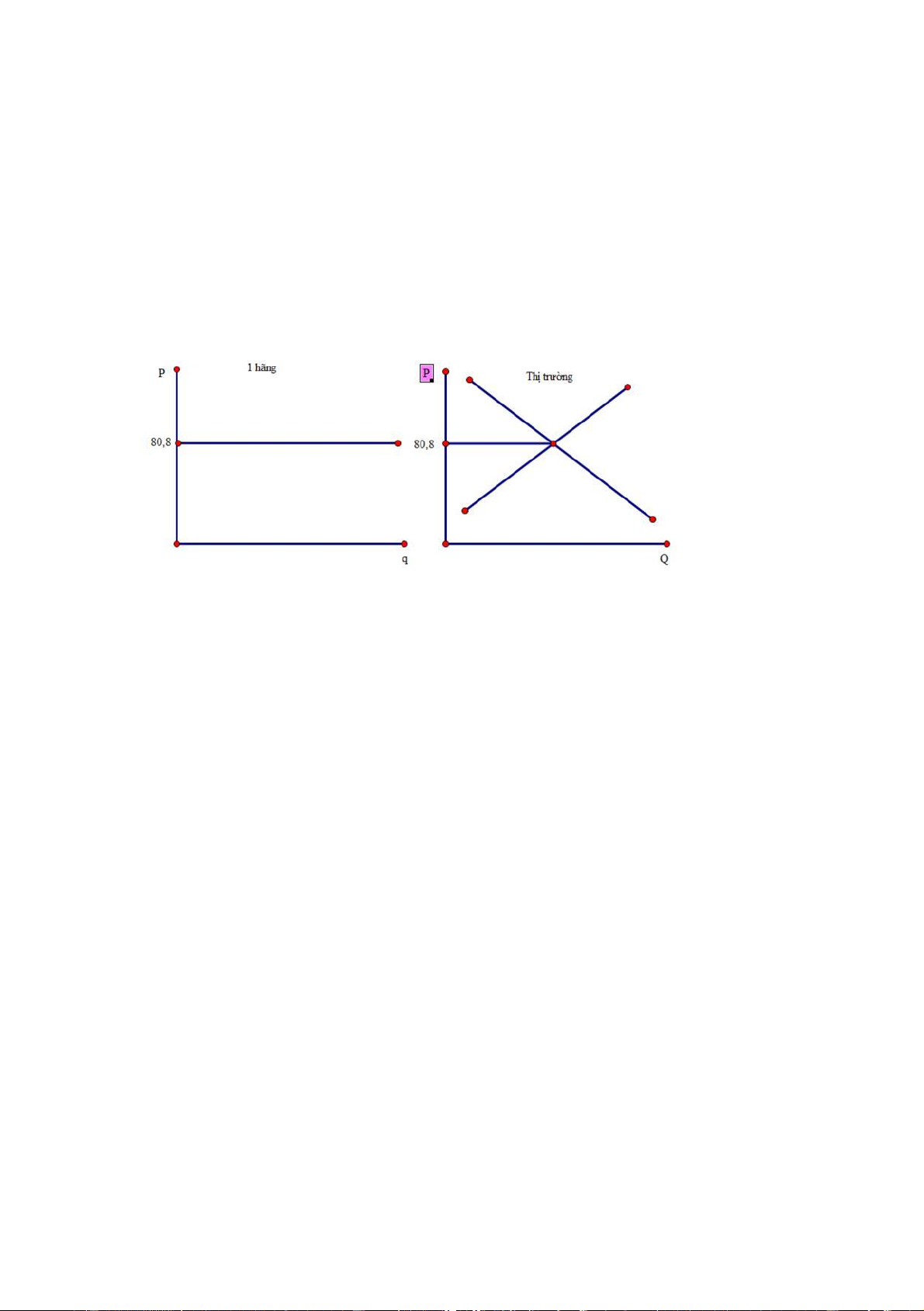
Hàm cầu của mỗi hãng chính là đường thẳng nằm ngang t愃⌀i mức
giá cần bằng => hàm cầu P = 80,8
c. Lợi nhuận tối đa khi P = MC => 80,8 = 8q + 24 => q = 7,1
Lợi nhuận tối đa = TR – TC = 7,1x80,8 – 6x7,1(7,1 + 6) = 201,64 d. Đ × thị
Bài tập 4 (khác số so với bài slide):
Một nhà độc quyền có đường cầu P = 15 - Q và hàm tổng chi phí TC = 7Q.
a. Tính sản lượng và giá bán để có lợi nhuận tối đa. Sử dụng chỉ số Lerner
để xác định sức m愃⌀nh nhà độc quyền?
b. Mức giá và sản lượng tối ưu cho xã hội là bao nhiêu? Tính khoản mất
không do nhà độc quyền này gây ra (DWL)? Giải:
a. TR = P.Q = 15Q -Q2 => MR=15-2Q , MC=TC’q = 7
Nguyên Tắc tối đa hoá lợi nhuận của nhà
độc quyền MR=MC
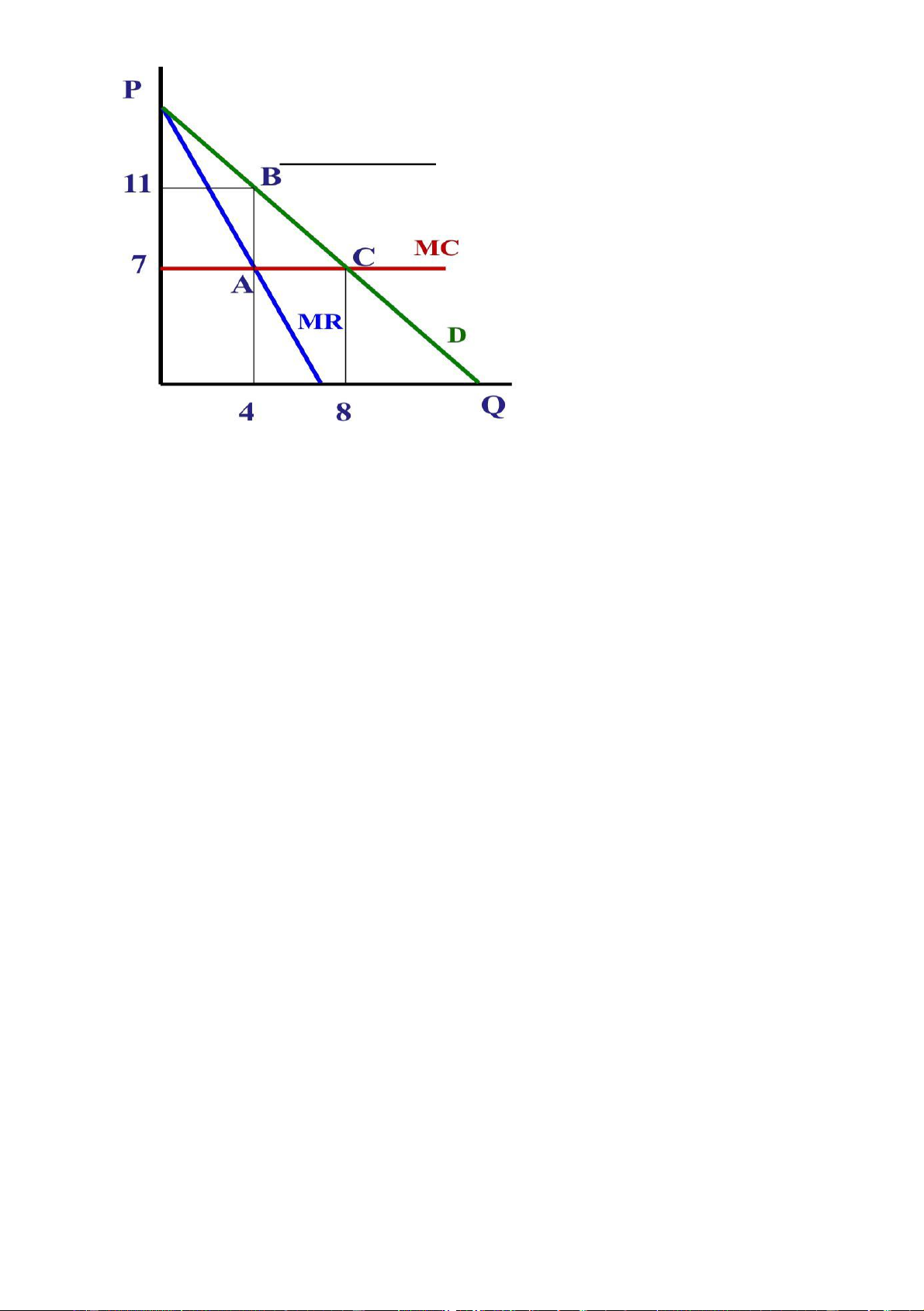
=>15–2Q=7=>Q=4,P=11
và max = TR – TC = 16
Chỉ số Lerner: L = (P-MC)/P = (11 - 7)/11 = 0,36
=> sức m愃⌀nh thị trường tương đối nhỏ (vì gần giá trị 0)
b. Mức giá và sản lượng tối ưu cho xã hội chính là mức giá và sản lượng
trong thị trường c愃⌀nh tranh hoàn hảo
Nguyên tắc tối đa há lợi nhuận trong TT CTHH là MC = P 15–Q=7, =>Q=8,P=7
Khoản mất không do nhà độc quyền này gây ra (DWL) là chênh lệch về giá
trị thạ ng dư xã hội trong 2 Thị trường (CTHH và độc quyền) DWL = TS
CTHH - TSđộc quyền (11 − = diện tích(ABC) =
= diện tích(P7C) - diện tích(PBA7) 7)(8 − 4) = 8 2 Bài tập
Giả sử một ngành cạnh tranh có thể sản xuất với tổng chi phí TC = 100 - 5Q +
Q2. Giả sử hàm cầu thị trường là: P = 55 - 2Q (P tính bằng $, Q tính bằng sp)
a. Tính lợi nhuận tối đa của ngành c愃⌀nh tranh.
b. Nếu thị trường trên là độc quyền thì lợi nhuận tối đa của hãng độc quyền là bao nhiêu?
c. Tính khoản tổn thất do độc quyền gây ra cho xã hội. Sức m愃⌀nh của nhà
độc quyền như thế nào?
d. Quyết định sản xuất của nhà độc quyền như thế nào khi CP đánh thuế t = 2$/đvsp.
e. Quyết định sản xuất của nhà độc quyền như thế nào khi CP đánh thuế 20% tổng
doanh thu? Tính lợi nhuận lúc này.
Vẽ đ thị minh họa cho từng trường hợp Giải:
a. Nguyên tắc lợi nhuận tối đa của ngành c愃⌀nh
tranh: P= MC => 55- 2Q = -5 + 2Q, => Q = 15 (sp) =>P=25($)
Lợi nhuận = TR - TC = Q.25 – 100 + 5.Q – 15.Q = 15.15 – 100 = 125 ($) b. TR = PxQ = 55Q- 2Q2
Nguyên tắc lợi nhuận tối đa của nhà độc quyền: MR = MC => 55-4Q = -5 + 2Q => Q = 10 (sp) =>P=35($)
Lợi nhuận = TR - TC = 35Q – 100 + 5.Q – 10 .Q = 30 Q – 100 = 200 ($) lOMoAR cPSD| 46884348
c. Hoàn toàn như bài tập 4
d. CP đánh thuế t = 2$/đvsp, ta có hàm chi phí mới:
TCt = TC + t.Q = 100 - 5Q + Q2 + 2Q = 100 - 3Q + Q2 => MCt = TC't = -3 + 2Q
Nguyên tắc tối đa hoá lợi nhuận: MR = MCt => 55- 2Q = -3 + 2Q, => Q = 14,5 (sp) =>P=26($)
Lợi nhuận tối đa = TR - TCt = 14,5.26 – (100 - 3.14,5 + 14,52 ) = ??? ($)
e. Khi chính phủ đánh thuế 20% tổng doanh thu
hay số thuế là T = 20%TR = 0,2(55 - 2Q)xQ= 11Q – 0,4Q2
TCt = TC + T = 100 - 5Q + Q2 + 11Q – 0,4Q2 = 0,6Q2 + 6Q
+ 100 Nguyên tắc tối đa hoá lợi nhuận: MC = MR => 1,2Q + 6 = 55-4Q =>Q=9,4
=>P=55–2.9,4=55–18,8=36,6
Lợi nhuận tối đa = TR - TCt = 9,4. 36,6 – (0,6. 9,42 + 6. 9,4 + 100) = ??? ($)