Giải SBT Toán 12 bài 5: Phương trình mũ và phương trình logarit

Giải SBT Toán 12 bài 5: Phương trình mũ và phương trình logarit
Bài 2.30 trang 125 Sách bài tập (SBT) Giải tích 12
Giải các phương trình mũ sau: a) (0,75)2x−3=(1.1/3)5−x b) 5 −5x−6=1 c) (1/7) −2x−3=7x+1
d) 32x+5/x−7=0,25.125x+17/x−3 Hướng dẫn làm bài: a) (3/4)2x−3=(4/3)5−x ⇔(3/4)2x−3=(3/4)x−5 ⇔2x−3=x−5⇔x=−2 b) 5 −5x−6=50⇔x2−5x−6=0 ⇔[x=−1;x=6 c) (1/7)
−2x−3=(1/7)−x−1⇔x2−2x−3=−x−1⇔x2−x−2=0 ⇔[x=−1;x=2
d) 25.x+5/x−7=2−2.53.x+17/x−3<=>25x+25/x−7+2=53x+51/x−3<=>27x+11/x−7=53x+51/x−3
Lấy logarit cơ số 2 cả hai vế, ta được:
7x+11/x−7=3x+51/x−3log25<=>{7x2−10x−33=(3x2+30x−357)log25;x≠7,x≠3
<=>(7−3log25)x2−2(5+15log25)−(33−357log25)=0
Ta có: Δ′=(5+15log25)2+(7−3log25)(33−357log25) =1296log2 5 25−2448log2 +256>0
Phương trình đã cho có hai nghiệm: x=5+15log25±√Δ′/7−3log25 đều thỏa mãn điều kiện
Bài 2.31 trang 125 Sách bài tập (SBT) Giải tích 12
Giải các phương trình mũ sau: a) 2x+4+2x+2=5x+1+3.5x b) 52x−7x−52x.17+7x.17=0 c) 4.9x+12x−3.16x=0 d) −8x+2.4x+2x−2=0 Hướng dẫn làm bài: a) 16.2x+4.2x=5.5x+3.5x
⇔20.2x=8.5x⇔(2/5)x=(2/5)1⇔x=1 b) 16.7x−16.52x=0
⇔7x=52x⇔(7/25)x=(7/25)0⇔x=0
c) Chia hai vế cho 12x(12x>0), ta được: 4(3/4)x+1−3(4/3)x=0
Đặt t=(3/4)x (t > 0), ta có phương trình:
4t+1−3/t=0⇔4t2+t−3=0⇔[t=−1(l);t=3/4
Do đó, (3/4)x=(3/4)1. Vậy x = 1.
d) Đặt t=2x(t>0), ta có phương trình: −t3+2t2+t−2=0
⇔(t−1)(t+1)(2−t)=0<=>⇔t=1;t=−1(l);t=2 Do đó, [2x=1;2x=2
Bài 2.32 trang 125 Sách bài tập (SBT) Giải tích 12
Giải các phương trình sau bằng phương pháp đồ thị: a) 2−x=3x+10 b) (1/3)−x=−2x+5 c) (1/3)x=x+1 d) 3x=11−x Hướng dẫn làm bài:
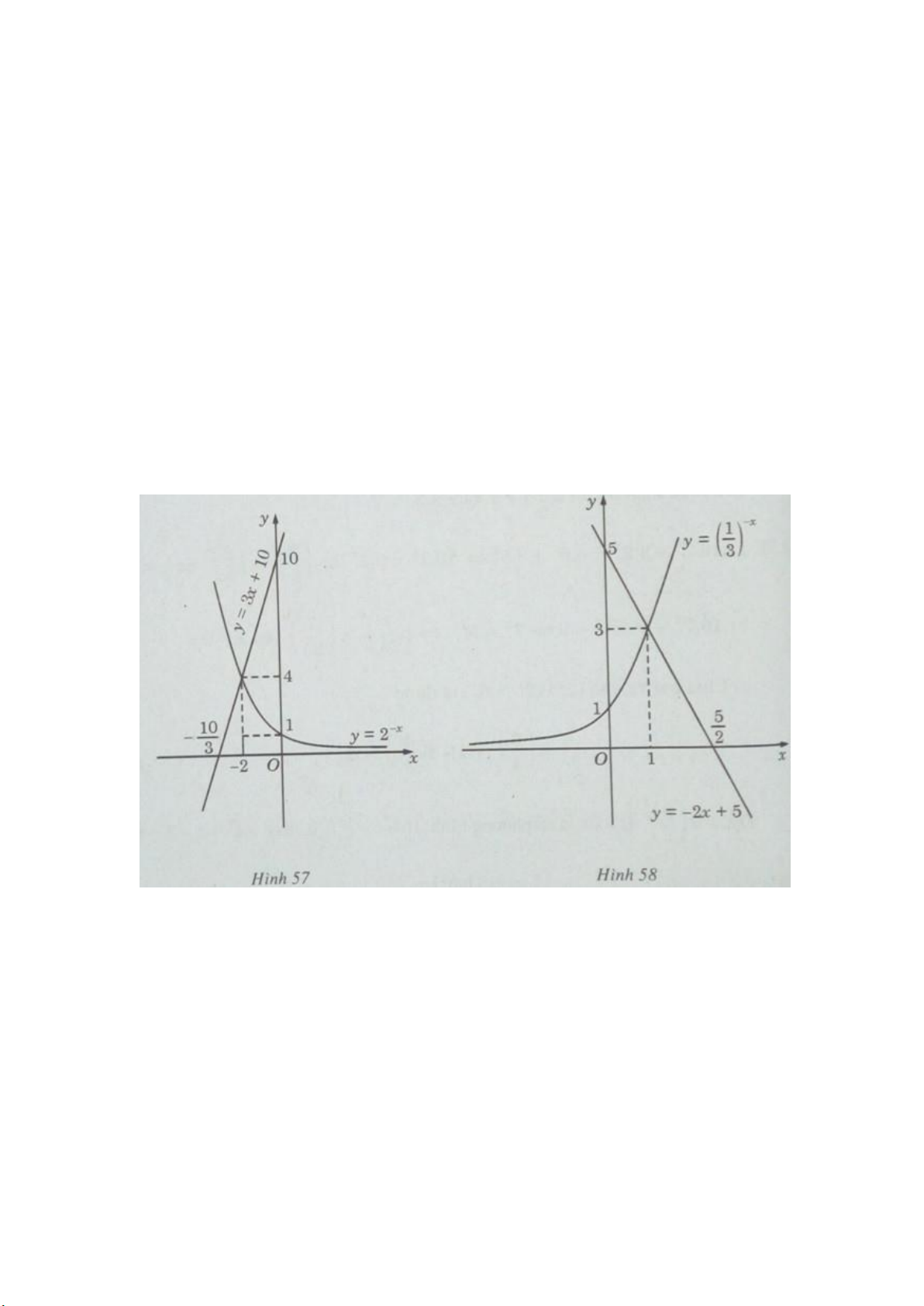
a) Vẽ đồ thị của hàm số: y=2−x và đường thẳng y = 3x +10 trên cùng một hệ trục
tọa độ (H. 57) ta thấy chúng cắt nhau tại điểm có hoành độ x = -2. Thử lại, ta
thấy x = -2 thỏa mãn phương trình đã cho.
Mặt khác, hàm số y=2−x=(1/2)x luôn nghịch biến, hàm số y = 3x + 10 luôn đồng biến.
Vậy x = -2 là nghiệm duy nhất.
b) Vẽ đồ thị của hàm số y=(1/3)−x và đường thẳng y = -2x + 5 trên cùng một hệ
trục tọa độ (H.58), ta thấy chúng cắt nhau tại điểm có hoành độ x = 1. Thử lại, ta
thấy x = 1 thỏa mãn phương trình đã cho.
Mặt khác, hàm số y=(1/3)−x=3x luôn đồng biến, hàm số y = -2x + 5 luôn nghịch biến.
Vậy x = 1 là nghiệm duy nhất.
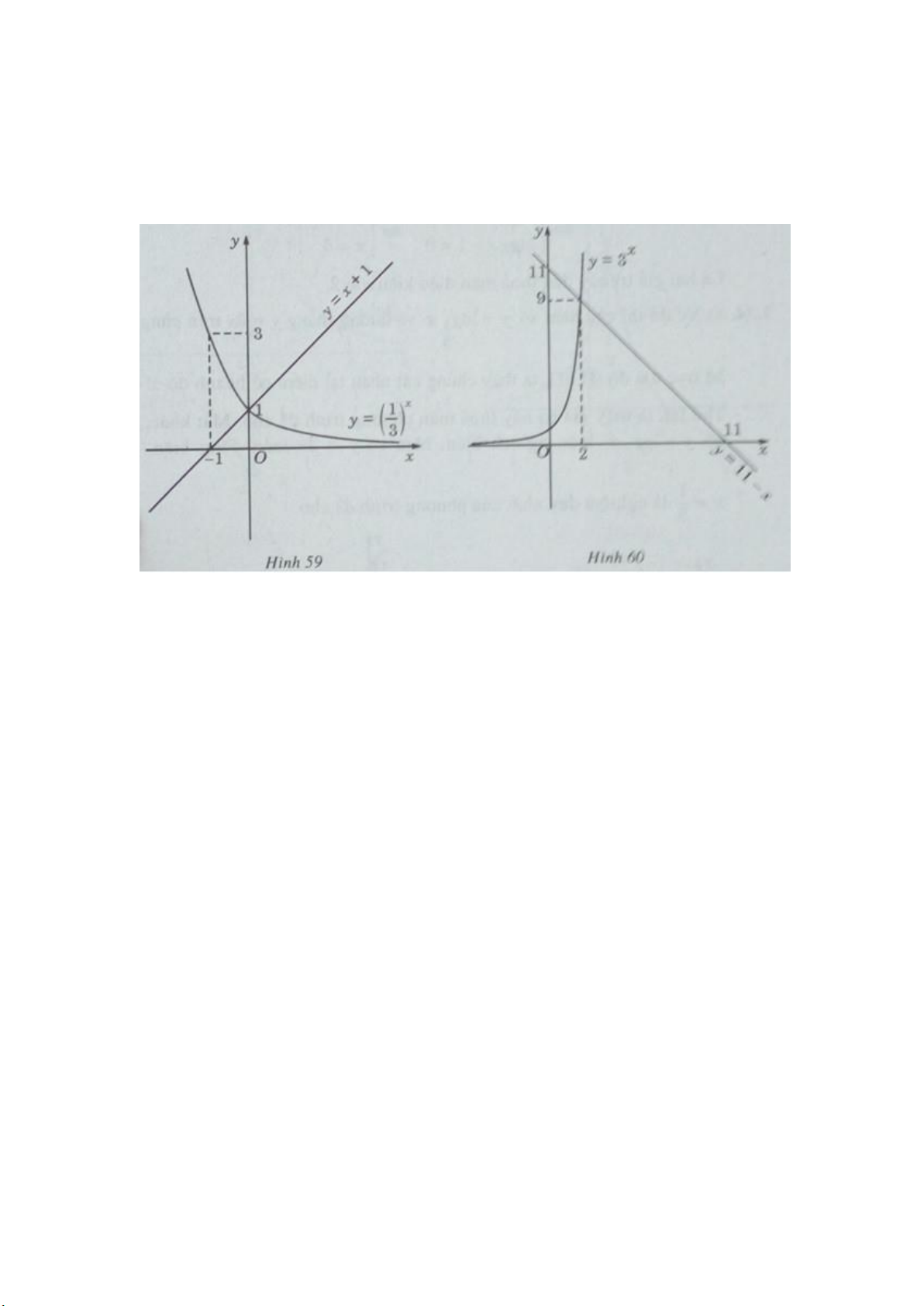
c) Vẽ đồ thị của hàm số y=(1/3)x và đường thẳng y = x + 1 trên cùng một hệ trục
tọa độ (H.59), ta thấy chúng cắt nhau tại điểm có hoành độ x = 0. Thử lại, ta
thấy x = 0 thỏa mãn phương trình đã cho. Mặt khác, y=(1/3)x là hàm số luôn
nghịch biến, hàm số y = x +1 luôn đồng biến.
Vậy x = 0 là nghiệm duy nhất.
d) Vẽ đồ thị của hàm số và đường thẳng y = 11 – x trên cùng một hệ trục tọa độ
(H.60), ta thấy chúng cắt nhau tại điểm có hoành độ x = 2. Thử lại, ta thấy x = 2
thỏa mãn phương trình đã cho. Mặt khác, y=3x luôn đồng biến, y = 11 – x luôn
nghịch biến. Vậy x = 2 là nghiệm duy nhất.
Bài 2.33 trang 125 Sách bài tập (SBT) Giải tích 12
Giải các phương trình logarit sau: a) logx+logx2=log9x b) logx4+log4x=2+logx3$
c) log4[(x+2)(x+3)]+log4x−2/x+3=2
d) log√3(x−2)log5x=2log3(x−2) Hướng dẫn làm bài:
a) Với điều kiện x > 0, ta có logx+2logx=log9+logx ⇔logx=log3⇔x=3
b) Với điều kiện x > 0, ta có 4logx+log4+logx=2log10+3logx ⇔logx=log5⇔x=5
c) Ta có điều kiện của phương trình đã cho là:
Khi đó, phương trình đã cho tương đương với: log4[(x+2)(x+3)x−2/x+3]
=log416⇔x2−4=16⇔[x=2√5;x=−2√5
Cả hai nghiệm trên đều thỏa mãn điều kiện (1).
d) Với điều kiện x > 2, ta có phương trình 2log3(x−2)(log5x−1)=0
⇔[log3(x−2)=0;log5x−1=0⇔[x=3;x=5
Cả hai giá trị này đều thỏa mãn điều kiện x > 2.
Bài 2.34 trang 125 Sách bài tập (SBT) Giải tích 12
Giải các phương trình sau bằng phương pháp đồ thị: a) log1/3x=3x b) log3x=−x+11 c) log4x=4/x d) 16x=log1/2x Hướng dẫn làm bài:
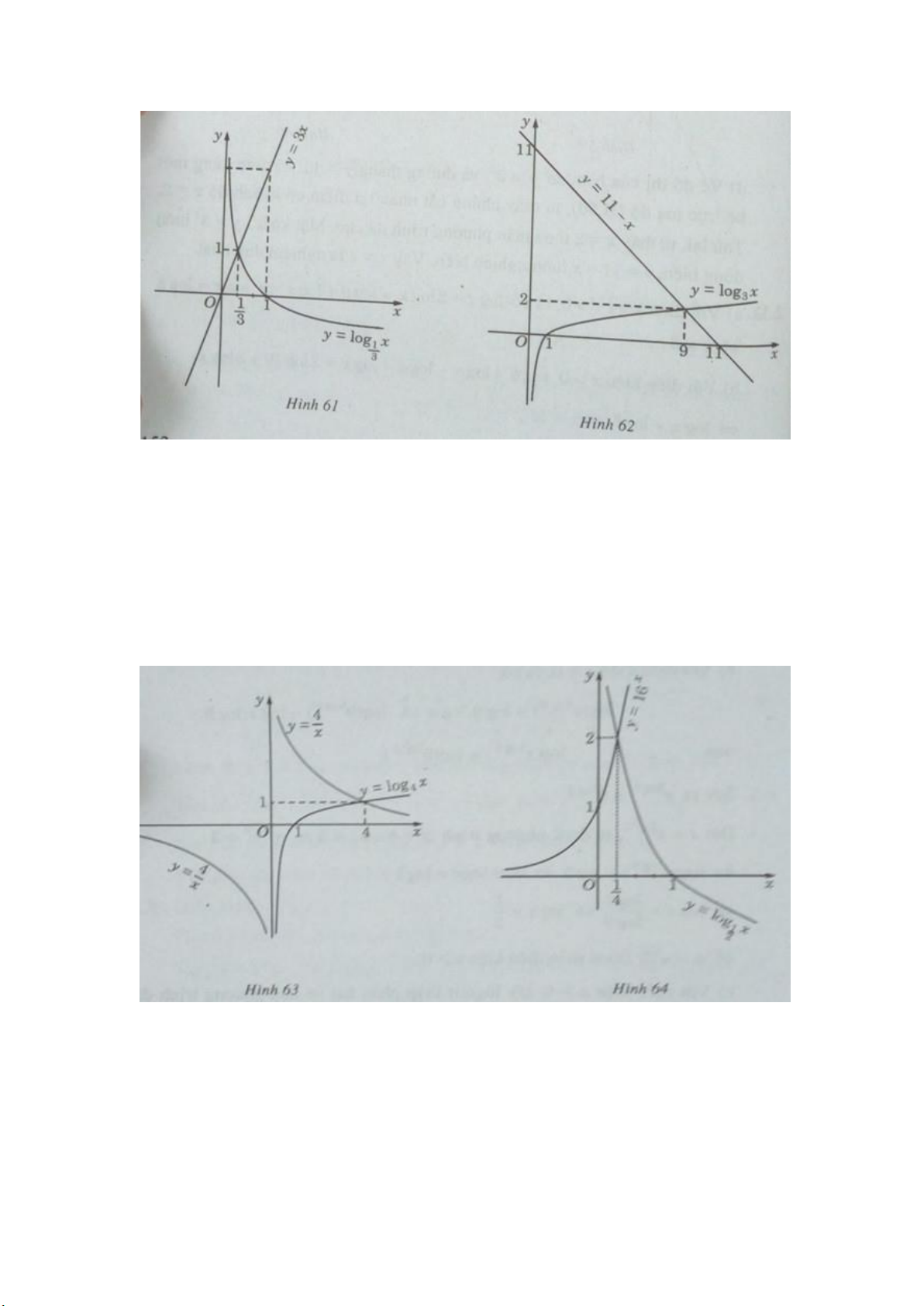
a) Vẽ đồ thị của hàm số log1/3x=3xvà đường thẳng y = 3x trên cùng một hệ trục
tọa độ (H.61), ta thấy chúng cắt nhau tại điểm có hoành độ x=1/3
Thử lại, ta thấy giá trị này thỏa mãn phương trình đã cho. Mặt khác, hàm số
y=log1/3x luôn nghịch biến, hàm số y = 3x luôn đồng biến. Vậy x=1/3 là nghiệm
duy nhất của phương trình đã cho.
b) Vẽ đồ thị của hàm số y=log3x và đường thẳng y = - x + 11 trên cùng một hệ
trục tọa độ (H.62) , ta thấy chúng cắt nhau tại điểm có hoành độ x = 9. Lập luận
tương tự câu a), ta cũng có đây là nghiệm duy nhất của phương trình đã cho.
c) Vẽ đồ thị của các hàm số y=log4x và y=4/x trên cùng một hệ trục tọa độ
(H.63), ta thấy chúng cắt nhau tại điểm có hoành độ x = 4. Ta cũng có hàm số
y=log3x luôn đồng biến, hàm số y=4/x luôn nghịch biến trên (0;+∞)(0;+∞) . Do
đó, x = 4 là nghiệm duy nhất.
d) Vẽ đồ thị của các hàm số y=16x và y=log1/2x trên cùng một hệ trục tọa độ
(H.64), ta thấy chúng cắt nhau tại điểm có hoành độ x=1/4. Thử lại, ta thấy
x=1/4 thỏa mãn phương trình đã cho. Mặt khác, hàm số luôn đồng biến, hàm số luôn nghịch biến.
Vậy x=1/4 là nghiệm duy nhất của phương trình.
Bài 2.35 trang 125 Sách bài tập (SBT) Giải tích 12
Giải các phương trình logarit: a) log2(2x+1).log2(2x+1+2)=2 b) xlog9+9logx=6 c) x3log3x−2/3logx=100 d) 1+2logx+25=log5(x+2) Hướng dẫn làm bài: a) log2(2x+1).log2[2(2x+1)]=2
⇔log2(2x+1).[1+log2(2x+1)]=2
Đặt t=log2(2x+1), ta có phương trình t(1+t)=2⇔t2+t–2=0
b) Với điều kiện x > 0, ta có: log(xlog9)=log(9logx)
log(xlog9)=log9.logx và log(9logx)=logx.log9 Nên log(xlog9)=log(9logx) Suy ra: t4+14t2−32t+17=0
⇔(t−1)2(t2+2t+17)=0⇔t=1⇔(t−1)2(t2+2t+17)=0⇔t=1 xlog9=9logx
Đặt t=xlog9, ta được phương trình 2t=6⇔t=3⇔xlog9=3 ⇔log(xlog9)=log3 ⇔log9.logx=log3 ⇔logx=log3/log9 ⇔logx=1/2
⇔x=√10⇔x=10 (thỏa mãn điều kiện x > 0)
c) Với điều kiện x > 0, lấy logarit thập phân hai vế của phương trình đã cho, ta được: (3log3x−2/3logx).logx=7/3
Đặt t=logx, ta được phương trình 3t4−2/3t2−7/3=0
⇔9t4−2t2−7=0⇔[t2=1/t2=−79(loại)[t=1;t=−1
⇔[logx=1;logx=−1⇔[x=10;x=110
d) Đặt t=log5(x+2) với điều kiện x+2>0,x+2≠1 ta có: 1+2/t=t⇔t2−t−2=0, t≠0
Bài 2.36 trang 126 Sách bài tập (SBT) Giải tích 12
Giải phương trình 25x−6.5x+5=0 (Đề thi tốt nghiệp THPT năm 2009) Hướng dẫn làm bài: Đáp số: x = 0; x = 1.
Bài 2.37 trang 126 Sách bài tập (SBT) Giải tích 12
Giải phương trình: 42x+√x+2+2 =42+√x+2+2
+4x−4 (Đề thi đại học năm 2010, khối D) Hướng dẫn làm bài: Điều kiện: x≥−2
Phương trình tương đương với: (24x−24)(22√x+2−2 −4)=0. Suy ra: ⇔[24x−24=0;22√x+2−2 −4=0⇔[x=1;2√x+2=x3−4 Nhận thấy x≥
và phương trình có một nghiệm x = 2. Trên [ ;+∞) , hàm số
f(x)=2√x+2−x3+4f(x)=2x+2−x3+4 có đạo hàm f(x)=2√x+2−x3+4 nên f(x) luôn
nghịch biến. Suy ra x = 2 là nghiệm duy nhất.
Vậy phương trình có nghiệm x = 1; x = 2.
Bài 2.38 trang 126 Sách bài tập (SBT) Giải tích 12 Giải phương trình:
f(x)=2√x+2−x3+4log2(8−x2)+log1/2(√1+x+√1−x)−2=0
(Đề thi Đại học năm 2011, khối D) Hướng dẫn làm bài: Điều kiện: −1≤x≤1
Phương trình đã cho tương đương với:
log2(8−x2)=log2[4(√1+x+√1−x)] ⇔(8−x2)2=16(2+2√1−x2) Đặt t=√1−x2 t4+14t2−32t+17=0 ⇔(t−1)2(t2+2t+17)=0 ⇔t=1
Suy ra x = 0. Vậy phương trình có nghiệm x = 0