

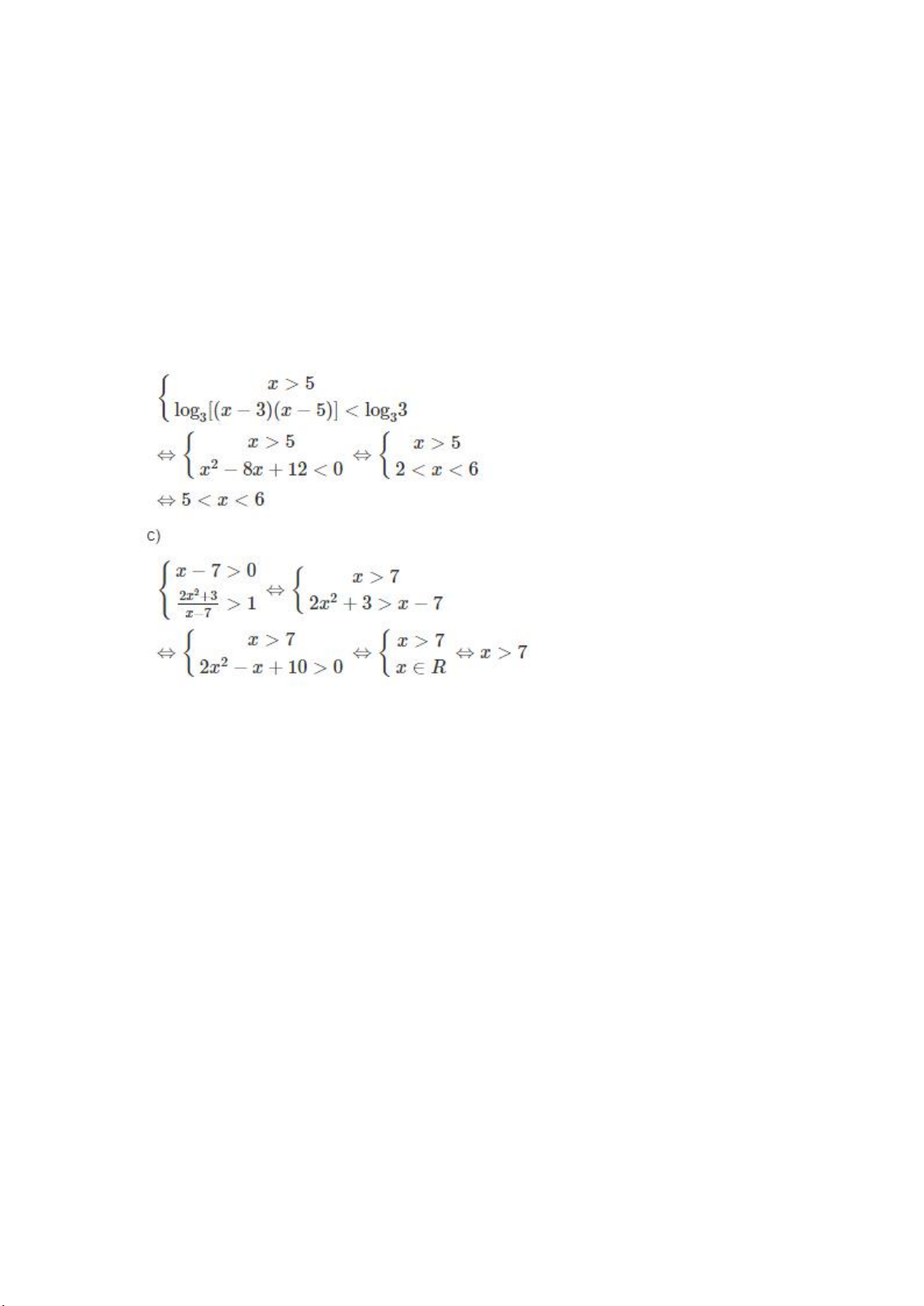
Preview text:
Giải SBT Toán 12 bài 6: Bất phương trình mũ và bất phương trình logarit
Bài 2.39 trang 131, 132 Sách bài tập (SBT) Giải tích 12
Giải các bất phương trình mũ sau: a) 3|x−2|<9 b) 4|x+1|>16 c) 2− +3x<4 d) (7/9)2 −3x≥9/7 e) 11√x+6≥11x
g) 22x−1+22x−2+22x−3≥448 h)16x−4x−6≤0 i) 3x/3x−2<3 Hướng dẫn làm bài: a) 3|x−2|<32 ⇔|x−2|<2 ⇔−2⇔0b) 4|x+1|>42
⇔|x+1|>2⇔[x+1>2;x+1<−2⇔[x>1;x<−3 c) 2− +3x<22 ⇔−x2+3x<2
⇔x2−3x+2>0⇔[x<1;x>2 d) (7/9)2 −3x≥(7/9)−1 ⇔2 −3x≤−1 ⇔2 −3x+1≤0⇔1/2≤x≤1 e) g) 1/2.22x+1/4.22x+1/8.22x≥448
⇔22x≥512⇔22x≥29⇔x≥9/2
h) Đặt t = 4x (t > 0), ta có hệ bất phương trình:
{t2−t−6≤0;t>0⇔{−2≤t≤3;t>0 ⇔0i)
3x/3x−2−3<0⇔−2.3x+6/3x−2<0⇔3x−3/3x−2>0
⇔[3x>3;3x<2⇔[x>1;xBài 2.40 trang 132 Sách bài tập (SBT) Giải tích 12
Giải các bất phương trình logarit sau: a) log1/3(x−1)≥−2
b) log3(x−3)+log3(x−5)<1 c) log1/22x2+3/x−7<0 d) log1/3log2x2>0 e) 1/5−logx+2/1+logx<1 g) 4log4x−33logx4≤1 Hướng dẫn làm bài: a) 0b) d) log1/3log2x2>log1/31 ⇔log2x2<1
⇔log2x2⇔0⇔0<|x|<√2⇔[−√2e) Đặt t=logx với điều kiện t≠5, t≠−1 ta có:
1/5−t+2/1+t<1⇔t+1+10−2t/5+4t−t2−1<0
⇔t2−5t+6/t2−4t−5>0 ⇔(t−2)(t−3)/(t+1)(t−5)>0 ⇔ t<−1;25
Suy ra log x < -1 hoặc 2 < log x < 3 hoặc log x > 5.
Vậy x<1/10 hoặc 100 < x < 1000 hoặc x > 100 000.
g) Với điều kiện x>0, x≠1 đặt t=log4x, ta có: 4t−33/t≤1
⇔4t2−t−33/t≤0⇔(4t+11)(t−3)/t≤0
Bài 2.41 trang 132 Sách bài tập (SBT) Giải tích 12
Giải các bất phương trình sau bằng đồ thị: a) (1/2)xb) (1/3)x≥x+1 c) log1/3x>3x d) log2x≤6−x Hướng dẫn làm bài:
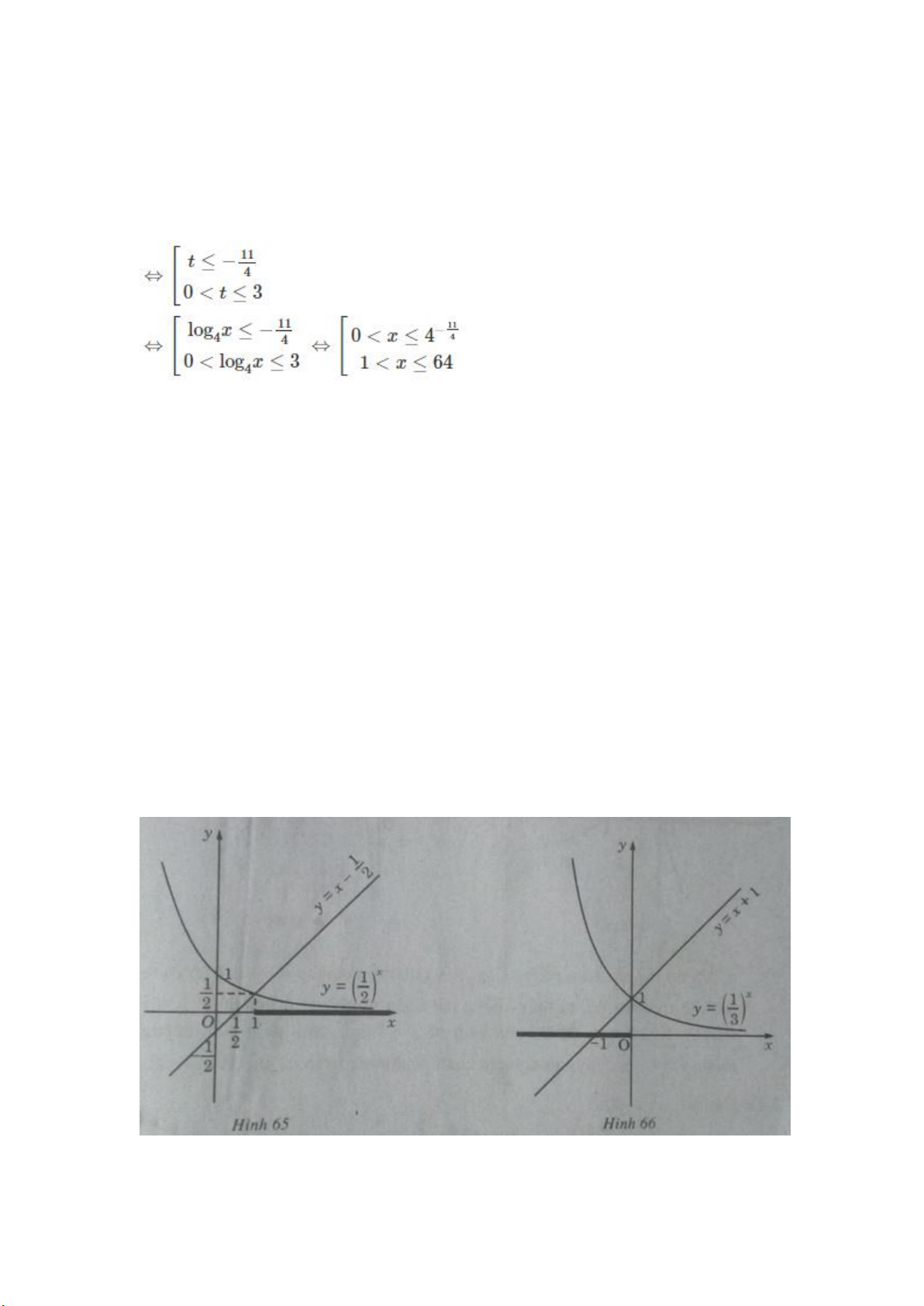
a) Vẽ đồ thị của hàm số y=(1/2)x và đường thẳng y=x−1/2 trên cùng một hệ trục tọa độ
(H.65), ta thấy chúng cắt nhau tại điểm có hoành độ x = 1. Với x > 1 đồ thị của hàm số
y=(1/2)x nằm phía dưới đường thẳng y=x−1/2. Vậy tập nghiệm của bất phương trình đã cho là (1;+∞)
b) Vẽ đồ thị của hàm số y=(1/3)x và đường thẳng y = x + 1 trên cùng một hệ trục tọa
độ (H.66), ta thấy chúng cắt nhau tại điểm có hoành độ x = 0.
Khi x < 0 đồ thị của hàm số y=(1/3)x nằm phía trên đường thẳng y = x + 1. Vậy tập
nghiệm của bất phương trình đã cho là (−∞;0]
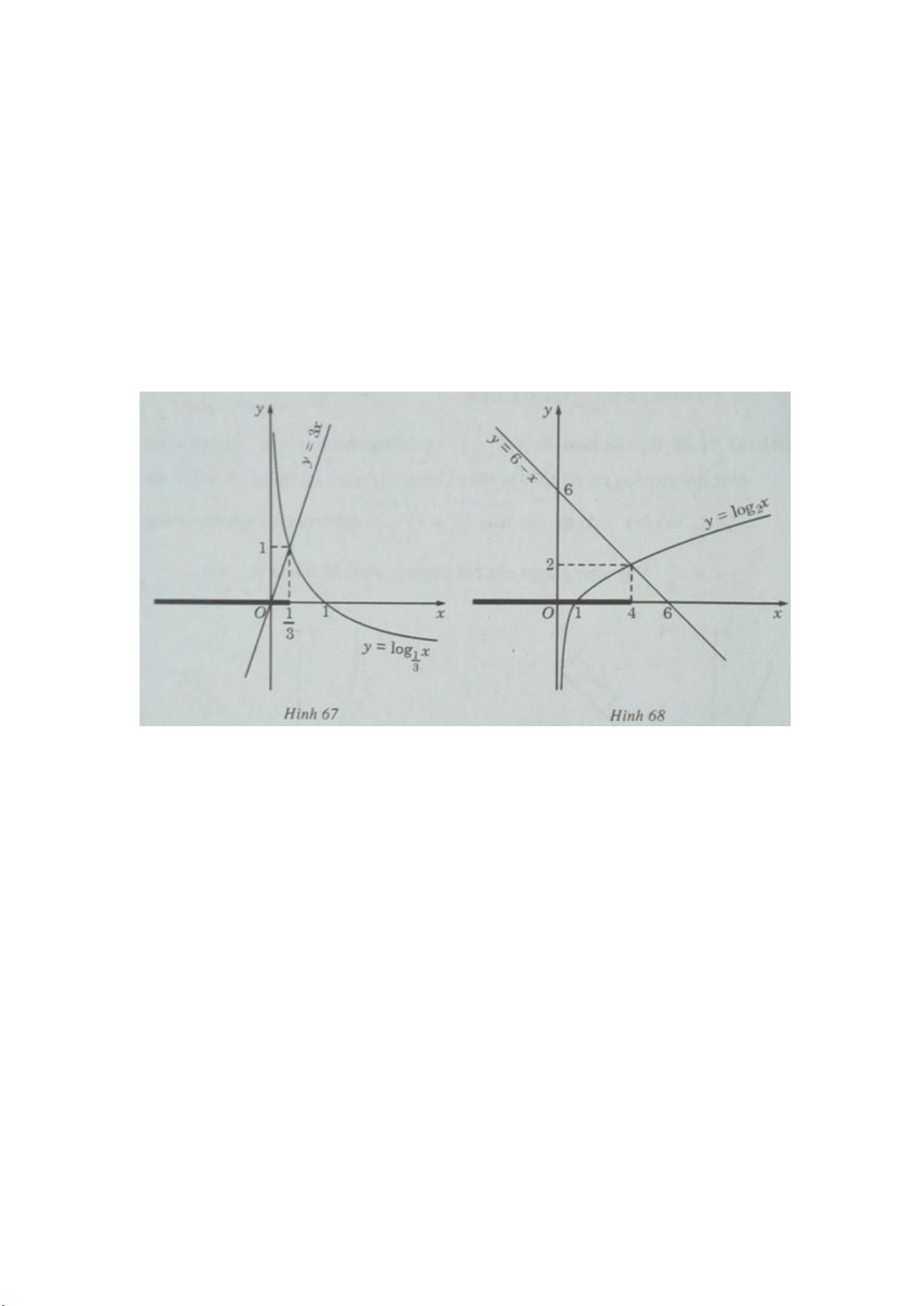
c) Vẽ đồ thị của hàm số y=log1/3x và đường thẳng y = 3x trên cùng một hệ trục tọa độ
ta thấy chúng cắt nhau tại điểm có hoành độ x=1/3 (H.67)
Khi x<1/3 đồ thị của hàm số y=log1/3x nằm phía trên đường thẳng y = 3x.
Vậy tập nghiệm của bất phương trình đã cho là (−∞;1/3).
d) Vẽ đồ thị của hàm số y=log2x và đường thẳng y = 6 – x trên cùng một hệ trục tọa độ,
ta thấy chúng cắt nhau tại điểm có hoành độ x = 4 (H.68).
Khi x < 4, đồ thị của hàm số y=log2x nằm phía dưới y = 6 – x.
Vậy tập nghiệm của bất phương trình đã cho là (−∞;4]
Bài 2.42 trang 132 Sách bài tập (SBT) Giải tích 12
Giải bất phương trình: log1/3(log22x+3/x+1)≥0 Trả lời: Đáp số: x < - 2.




