Giải SBT Toán 12 ôn tập chương 2: Hàm số lũy thừa. Hàm số mũ và hàm số logarit
Xin giới thiệu tới thầy cô và các bạn học sinh tài liệu Giải SBT Toán 12 ôn tập chương 2: Hàm số lũy thừa. Hàm số mũ và hàm số logarit, hy vọng qua bộ tài liệu các bạn học sinh sẽ có kết quả cao hơn trong học tập. Mời thầy cô và các bạn học sinh cùng tham khảo.
Chủ đề: Chương 2: Hàm số lũy thừa. Hàm số mũ và hàm số logarit
Môn: Toán 12
Thông tin:
Tác giả:
Thông tin :
Chủ đề:
Chương 2: Hàm số lũy thừa. Hàm số mũ và hàm số logarit
Môn:
Tác giả:
Tài liệu liên quan:
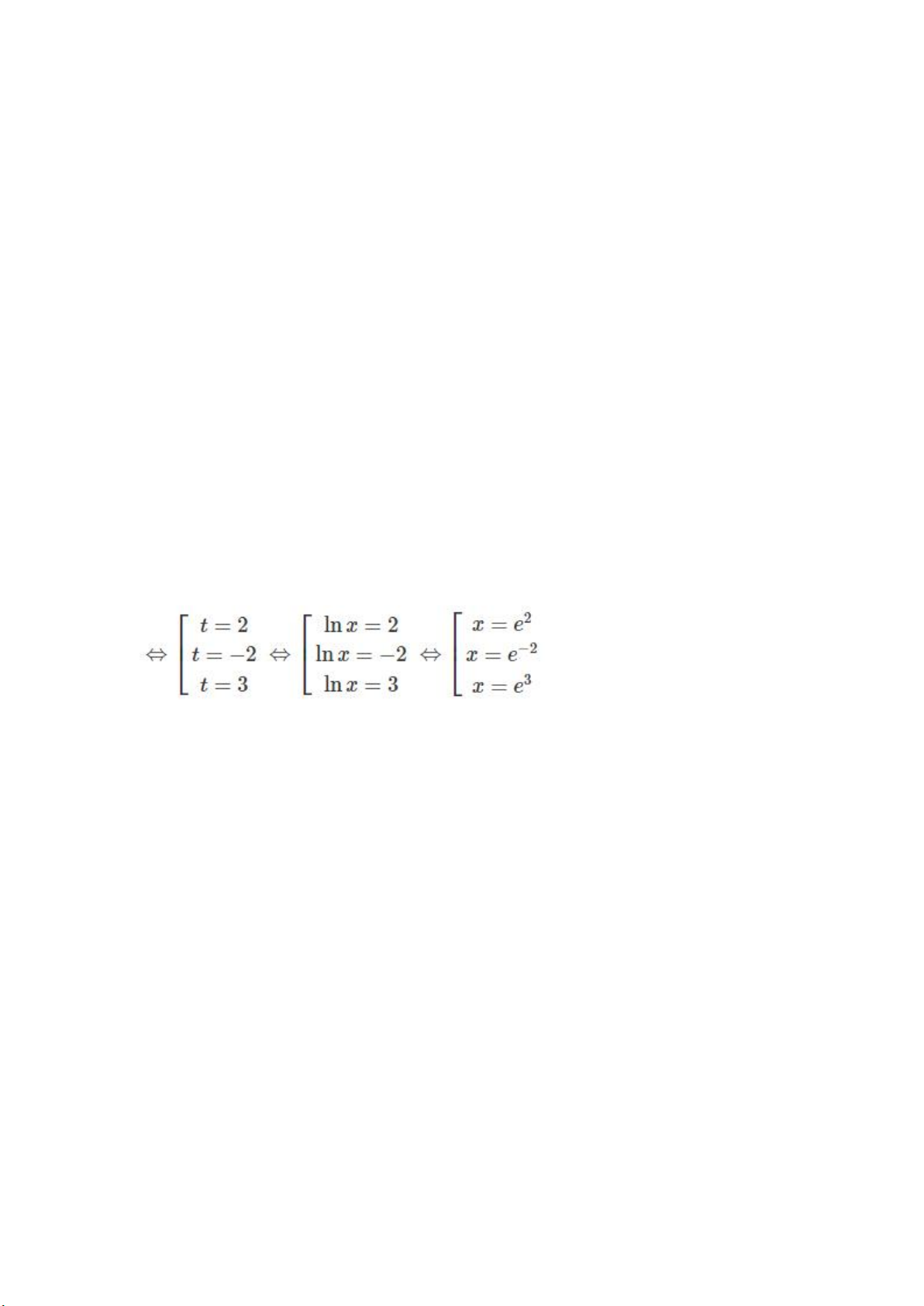
Preview text:
Giải SBT Toán 12 ôn tập chương 2: Hàm số lũy thừa. Hàm số mũ và hàm số logarit
Bài 2.43 trang 132 Sách bài tập (SBT) Giải tích 12
Khảo sát sự biến thiên và vẽ đồ thị của các hàm số sau: a) y=x√3 b) y=x1/π c) y=x−e Hướng dẫn làm bài:
a) Khảo sát sự biến thiên và vẽ đồ thị của hàm số y=x√3
Tập xác định: D=(0;+∞) y′=√3x√3−1
y′>0,∀ x∈ D nên hàm số luôn đồng biến.
limx→0+y=0, limx→+∞y=+∞
Đồ thị không có tiệm cận Bảng biến thiên: Đồ thị:
b) Khảo sát sự biến thiên và vẽ đồ thị của hàm số y=x1/π
Tập xác định: D=(0;+∞) y′=1/πx1/π−1
y′>0,∀ x∈ D nên hàm số luôn đồng biến.
limx→0+y=0,limx→+∞y=+∞
Đồ thị không có tiệm cận. Bảng biến thiên: Đồ thị
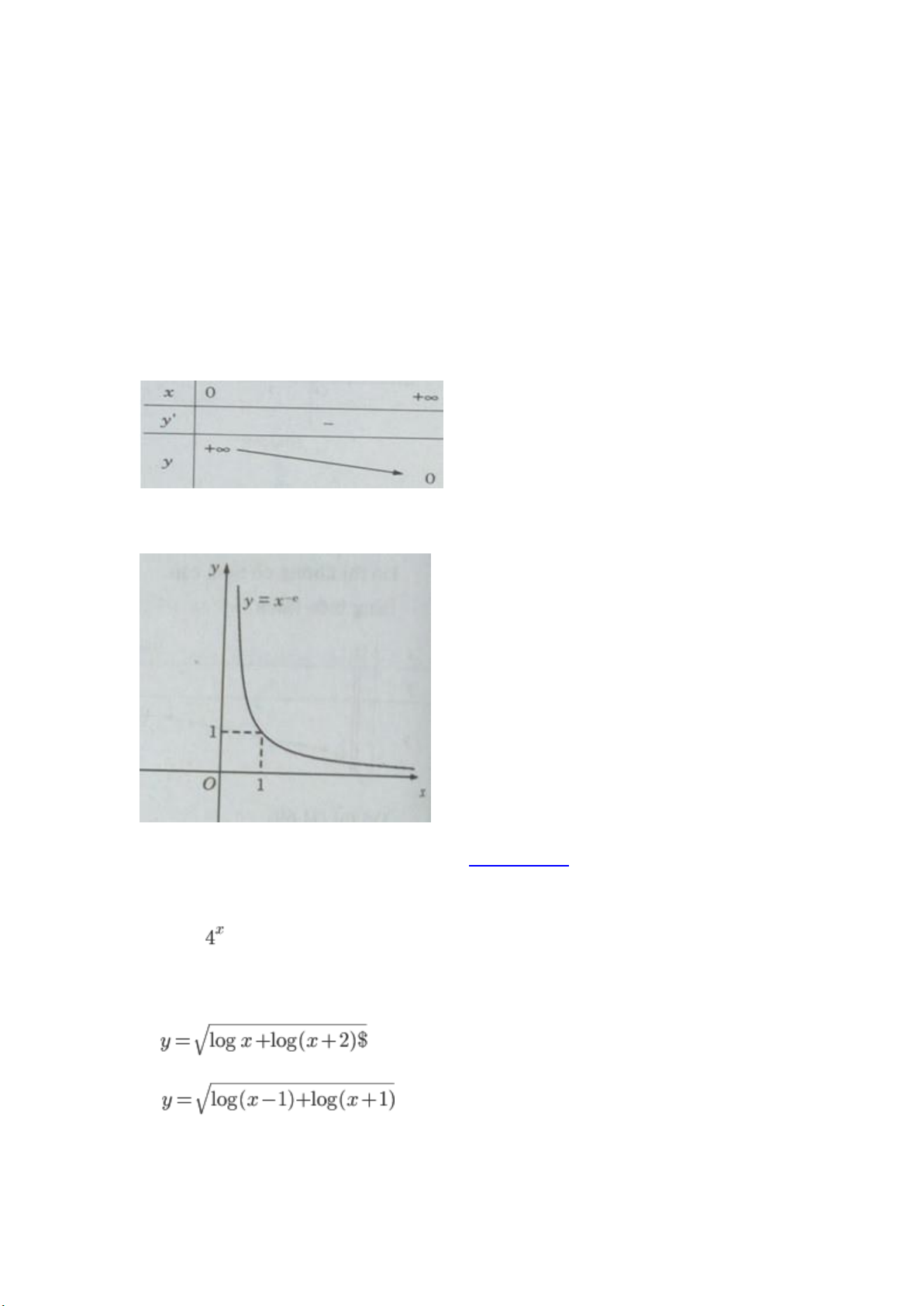
c) Khảo sát sự biến thiên và vẽ đồ thị của hàm số y=x−e
Tập xác định: D=(0;+∞) y′=−ex−e−1
y′<0,∀ x∈ D nên hàm số luôn nghịch biến
limx→0+y=+∞, limx→+∞y=0
Đồ thị có tiệm cận ngang là trục hoành, tiệm cận đứng là trục tung. Bảng biến thiên: Đồ thị:
Bài 2.44 trang 132 Sách bài tập (SBT) Giải tích 12
Tìm tập xác định của các hàm số sau: a) y=2/√ −2 b) y=log63x+2/1−x c) d) Hướng dẫn làm bài:
a) Hàm số xác định khi:
4x−2>0⇔22x>2⇔x>1/2
Vậy tập xác định là D=(12;+∞) b) D=(−2/3;1) c) logx+log(x+2)≥0
Vậy tập xác định là D=[−1+√2;+∞)
d) Tương tự câu c, D=[√2;+∞)
Bài 2.45 trang 133 Sách bài tập (SBT) Giải tích 12 Cho hai hàm số:
f(x)=ax+a−x/2, g(x)=ax−a−x/2
a) Chứng minh rằng f(x) là hàm số chẵn, g(x) là hàm số lẻ.
b) Tìm giá trị bé nhất của f(x) trên tập xác định. Hướng dẫn làm bài:
a) Ta có tập xác định của cả hai hàm số f(x), g(x) đều là R. Mặt khác:
f(−x)=a−x+ax/2=f(x),g(−x)=a−x−ax/2=−g(x)
Vậy f(x) là hàm số chẵn, g(x) là hàm số lẻ.
b) Ta có: f(x)=ax+a−x/2≥√axa−x=1,∀ x∈ R và f(0)=a0+a0/2=1 Vậy min f(x) = f(0) = 1.
Bài 2.46 trang 133 Sách bài tập (SBT) Giải tích 12
Cho a + b = c với a > 0, b > 0.
a) Chứng minh rằng am+bm 1.
b) Chứng minh rằng am+bmHướng dẫn làm bài:
a) Ta có: am+bmTheo đề bài a + b = c, a > 0, b > 0 nên 0Suy ra với m > 1 thì (a/c)m<(a/c)1;(b/c)m<(b/c)1
Từ đó ta có: (a/c)m+(b/c)mVậy (1) đúng và ta có điều phải chứng minh. b) Chứng minh tương tự.
Bài 2.47 trang 133 Sách bài tập (SBT) Giải tích 12
Vẽ đồ thị các hàm số sau: a) y=(1/2)x+3 b) y=2x+1 c) y=3x−2 Hướng dẫn làm bài:
a) Đồ thị của hàm số y=(1/2)x+3 nhận được từ đồ thị của hàm số y=(1/2)x bằng
phép tịnh tiến song song với trục tung lên trên 3 đơn vị.
b) Đồ thị của hàm số y=2x+1 nhận được từ đồ thị của hàm số y=2x bằng phép
tịnh tiến song song với trục hoành sang trái 1 đơn vị.
c) Đồ thị của hàm số y=3x−2 nhận được từ đồ thị của hàm số y=3x bằng phép tịnh
tiến song song với trục hoành sang bên phải 2 đơn vị.
Bài 2.48 trang 133 Sách bài tập (SBT) Giải tích 12
Vẽ đồ thị của các hàm số sau: a) y=log3(x−1) b) y=log1/3(x+1) c) y=1+log3x Hướng dẫn làm bài:
a) Đồ thị của hàm số y=log3(x−1)$ nhận được từ đồ thị của hàm số y=log3x
bằng cách tịnh tiến song song với trục hoành sang bên phải 1 đơn vị.
b) Đồ thị của hàm số y=log1/3(x+1) nhận được từ đồ thị của hàm số y=log1/3x
bằng cách tịnh tiến song song với trục hoành sang bên trái 1 đơn vị.
c) Đồ thị của hàm số y=1+log3x nhận được từ đồ thị của hàm số y=log3x bằng
cách tịnh tiến song song với trục tung lên trên 1 đơn vị.
Bài 2.49 trang 133 Sách bài tập (SBT) Giải tích 12
Tính đạo hàm của các hàm số sau: a) y=1/(2+3x)2 b) c) d) y=3x−3−log3x e) y=(3x2−2)log2x g) y=ln(cosx) h) y=exsinx i) y=ex−e−x/x Hướng dẫn làm bài: a) y′=−6(2+3x)−3 b)
y′=2(3x−2)−1/3,∀ x>2/3
−2(2−3x)−1/3,∀ x<2/3 c) d) y′=−9x−4−1/xln3 e) y′=6xlog2x+3x2−2/xln2 g) y′=−tanx h) y′=ex(sinx+cosx)
i) y′=x(ex+e−x)−ex+e−x/x2
Bài 2.50 trang 133 Sách bài tập (SBT) Giải tích 12
Giải các phương trình sau: a) 9x−3x−6=0 b) e2x−3ex−4+12e−x=0
c) 3.4x+1/3.9x+2=6.4x+1−1/2.9x+1 d) 2 −1−3 =3 −1−2 +2 Hướng dẫn làm bài: a) x = 1
b) Đặt t=ex(t>0), ta có phương trình t2−3t−4+12/t=0 hay t3−3t2−4t+12=0 ⇔(t−2)(t+2)(t−3)=0 ⇔t=2;t=−2(loại);t=3 Do đó [ex=2;aex=3⇔[x=ln2;x=ln3 c) 3.4x+27.9x=24.4x−9/2.9x ⇔63.9x=42.4x⇔(9/4)x=2/3
⇔(3/2)2x=(3/2)−1⇔2x=−1⇔x=−1/2 d) 1/2.2 −3 =1/3.3 −4.2
⇔9/2.2 =4/3.3 ⇔(2/3) =(2/3)3 ⇔x2=3⇔[x=√3;x=−√3
Bài 2.51 trang 133 Sách bài tập (SBT) Giải tích 12
a) Giải phương trình: 72x+1−8.7x+1=0
(Đề thi tốt nghiệp THPT năm 2011)
b) Giải phương trình: 32x+1−9.3x+6=0
(Đề thi tốt nghiệp THPT năm 2008) Hướng dẫn làm bài: a) Đáp số: x = 0; x = -1 b) Đáp số x=0;x=log32
Bài 2.52 trang 133 Sách bài tập (SBT) Giải tích 12
Giải các phương trình sau: a) ln(4x+2)−ln(x−1)=lnx
b) log2(3x+1)log3x=2log2(3x+1) c) 2log x 3 .5log3 =400 d) ln3x−3ln2x−4lnx+12=0 Hướng dẫn làm bài:
a) Với điều kiện x > 1 ta có phương trình: ln(4x+2)=ln[x(x−1)]
⇔4x+2=x2–x⇔x2–5x–2=0
⇔x=5+√33/2;x=5−√33/2(l) ⇔x=5+√33/2
b) Với điều kiện x > 0, ta có phương trình log2(3x+1)[log3x−2]=0⇔ [log2(3x+1)=0;log3x=2 ⇔[x=0(loại);x=9 ⇔x=9
c) Với điều kiện x > 0, ta có phương trình: 4log3x.5log3x=400 ⇔20log x
3 =202⇔log3x=2⇔x=9 (thỏa mãn điều kiện)
d) Đặt t=lnx(x>0), ta có phương trình:
t3–3t2–4t+12=0⇔(t–2)(t+2)(t–3)=0