-
Thông tin
-
Hỏi đáp
Giải Toán 8 Bài 10: Tứ giác | Kết nối tri thức
Giải Toán 8 Bài 10: Tứ giác | Kết nối tri thức. Tài liệu được biên soạn dưới dạng file PDF bao gồm 3 trang tổng hợp các kiến thức chọn lọc giúp các bạn tham khảo, ôn tập và đạt kết quả cao trong kỳ thi sắp tới. Mời các bạn đón xem!
Chương 3: Tứ giác (KNTT) 42 tài liệu
Toán 8 1.7 K tài liệu
Giải Toán 8 Bài 10: Tứ giác | Kết nối tri thức
Giải Toán 8 Bài 10: Tứ giác | Kết nối tri thức. Tài liệu được biên soạn dưới dạng file PDF bao gồm 3 trang tổng hợp các kiến thức chọn lọc giúp các bạn tham khảo, ôn tập và đạt kết quả cao trong kỳ thi sắp tới. Mời các bạn đón xem!
Chủ đề: Chương 3: Tứ giác (KNTT) 42 tài liệu
Môn: Toán 8 1.7 K tài liệu
Sách: Kết nối tri thức
Thông tin:
Tác giả:
Preview text:
Toán 8 Bài 10: Tứ giác Kết nối tri thức
Giải Toán 8 Kết nối tri thức Tập 1 trang 51 Bài 3.1
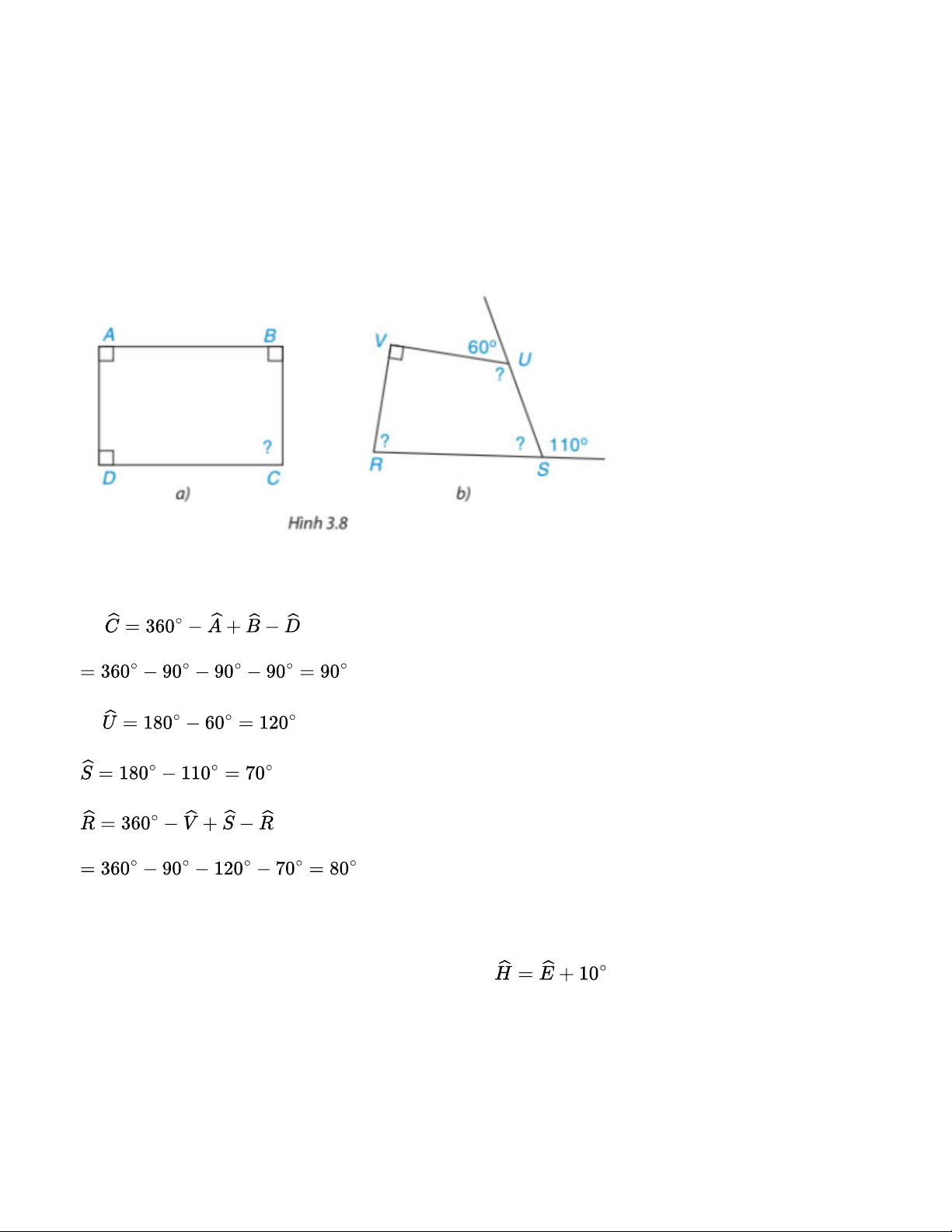
Tính góc chưa biết của các tứ giác trong Hình 3.8 Bài giải: a) b) Bài 3.2
Tính góc chưa biết củ tứ giác trong Hình 3.9. Biết Bài giải: Ta có: (1) Lại có: (2) Từ (1) và (2) suy ra Bài 3.3
Tứ giác ABCD trong Hình 3.10 có AB = AD, CB = CD, được gọi là hình "cái diều".
a) Chứng minh rằng AC là đường trung trực của đoạn BD
b) Tính các góc B, D biết rằng Bài giải:
a) Ta có: AB = AD (gt) => A thuộc đường trung trực của BD
CB = CD (gt) => C thuộc đường trung trực của BD.
Vậy AC là đường trung trực của BD.
b) Xét ABC và ADC có AB = AD (gt) BC = DC (gt) AC cạnh chung nên (c.c.c) Suy ra: Ta có Do đó