Giải Toán 8 Bài 11: Hình thang cân | Kết nối tri thức
Giải Toán 8 Bài 11: Hình thang cân | Kết nối tri thức. Tài liệu được biên soạn dưới dạng file PDF bao gồm 6 trang tổng hợp các kiến thức chọn lọc giúp các bạn tham khảo, ôn tập và đạt kết quả cao trong kỳ thi sắp tới. Mời các bạn đón xem!
Chủ đề: Chương 3: Tứ giác (KNTT)
Môn: Toán 8
Sách: Kết nối tri thức
Thông tin:
Tác giả:
Preview text:
Toán 8 Bài 11: Hình thang cân Kết nối tri thức
Giải Toán 8 Kết nối tri thức Tập 1 Bài 11 - Luyện tập Luyện tập 1
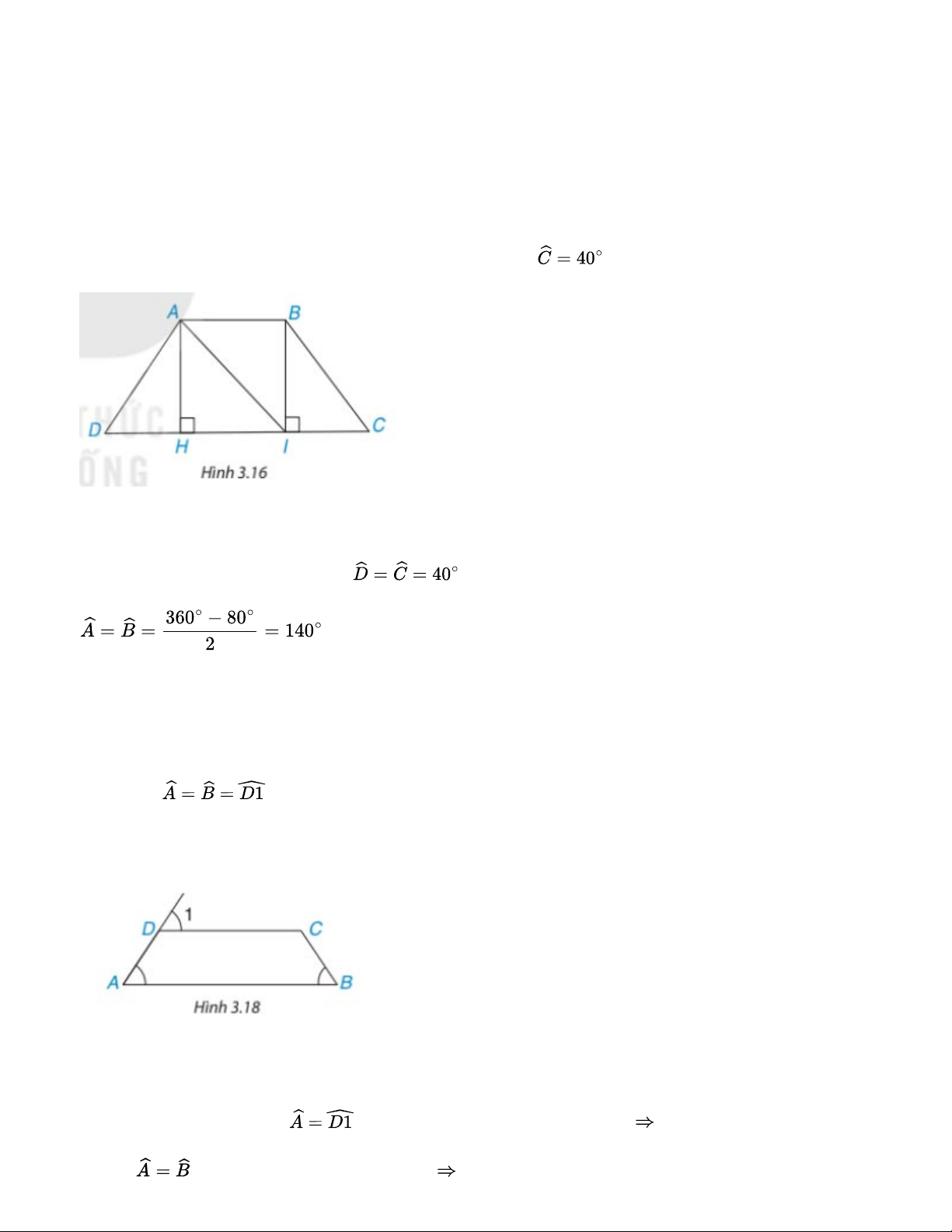
Tính các góc của hình thang cân ABCD (AB // CD, biết (H.3.15) Bài giải:
Xét hình thang cân ABCD ta có: Luyện tập 2
Cho tứ giác ABCD như Hình 3.18. Biết rằng Chứng minh rằng AD = BC Bài giải: Xét tứ giác ABCD, ta có:
(hai góc đồng vị) suy ra AB // DC ABCD là hình thang Lại có
suy ra hình thang ABCD cân AD = BC Luyện tập 3
Cho tam giác ABC cân tại A. Kẻ một đường thẳng d song song với BC, d cắt cạnh AB tại D và
cắt cạnh AC tại E (H.3.20).
a) Tứ giác DECB là hình gì? b) Chứng minh BE = CD. Bài giải:
a) Xét tứ giác DECB có: DE // BC,
suy ra DECB là hình thang cân
b) DECB là hình thang cân, BE và CD là hai đường chéo của hình thang suy ra BE = CD
Giải Toán 8 Kết nối tri thức Tập 1 trang 55 Bài 3.4
Hình thang trong Hình 3.23 có là hình thang cân không? Vì sao? Bài giải:
suy ra ABCD không là hình thang cân Bài 3.5
Cho hình thang ABCD (AB // CD). Kẻ đường thẳng vuông góc với AC tại C và đường vuông góc
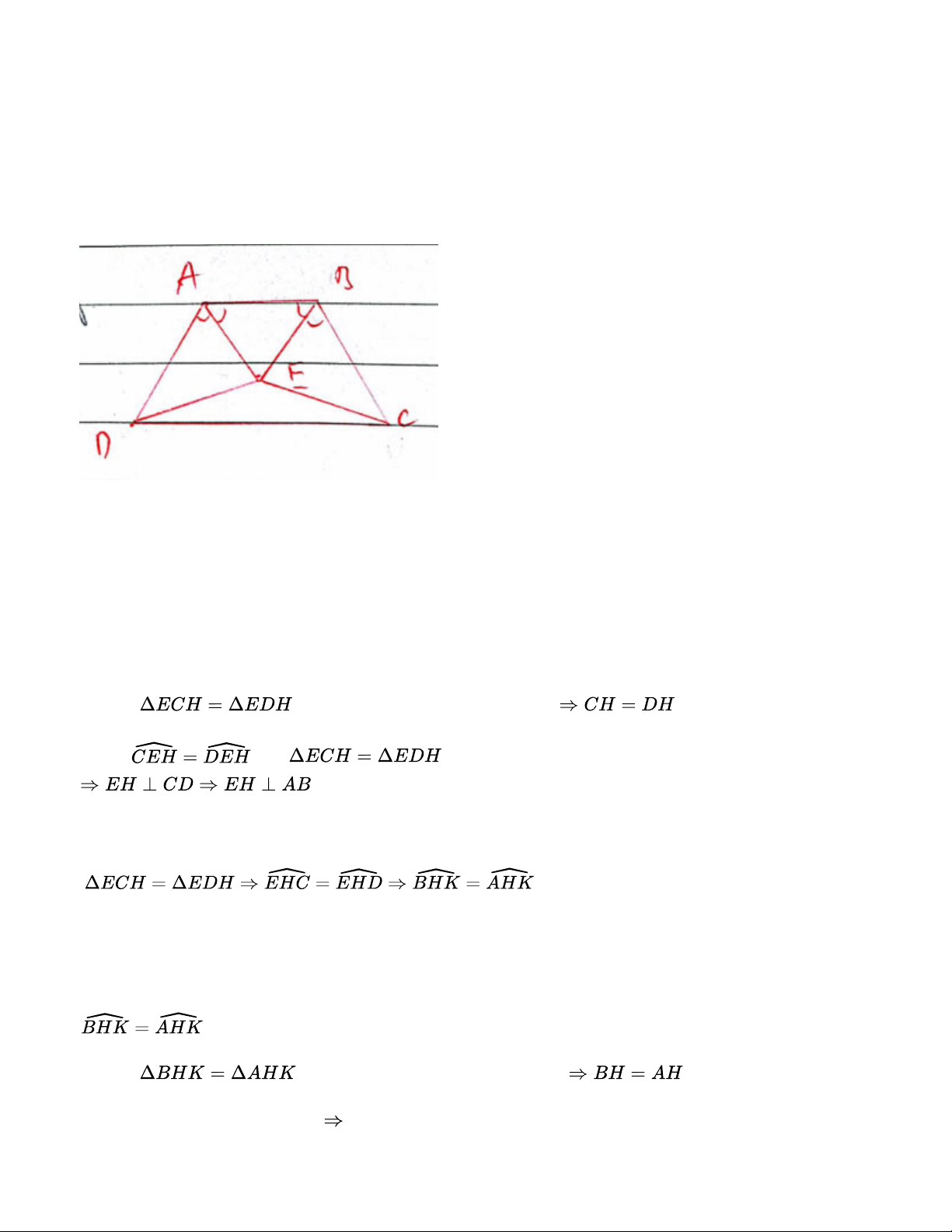
với BD tại D, hai đường thẳng này cắt nhau tại E. Chứng minh rằng nếu EC = ED thì hình thang ABCD là hình thang cân. Bài giải:
Gọi giao điểm của AC và BD là H
Xét tam giác vuông ECH và EDH, ta có: EH chung EC = ED (gt) Suy ra
(cạnh huyền - cạnh góc vuông) (1) Ta có (do
) suy ra EH là tia phân giác của tam giác cân ECD (do AB//CD)
Gọi giao điểm của EH và AB là K
Xét tam giác vuông BHK và AHK ta có: HK chung Suy ra
(cạnh góc vuông - góc nhọn kề) (2)
Từ (1) và (2) suy ra AC = BD hình thang ABCD là hình thang cân Bài 3.6
Vẽ hình thang cân ABCD (AB // CD) biết đáy lớn CD dài 4 cm, cạnh bên dài 2 cm và đường chéo dài 3 cm Bài giải: Vẽ đáy lớn CD = 4 cm
Vẽ cung tròn tâm C bán kính 2 cm, cung tròn tâm D bán kính 3 cm, giao điểm của 2 cung tròn là B
Tương tự, vẽ cung tròn tâm D bán kính 2cm, cung tròn tâm C bán kính 3 cm, giao điểm của 2 cung tròn là A
(Tất cả cung tròn đều nằm trên cùng 1 nửa mặt phẳng bờ CD) Bài 3.7
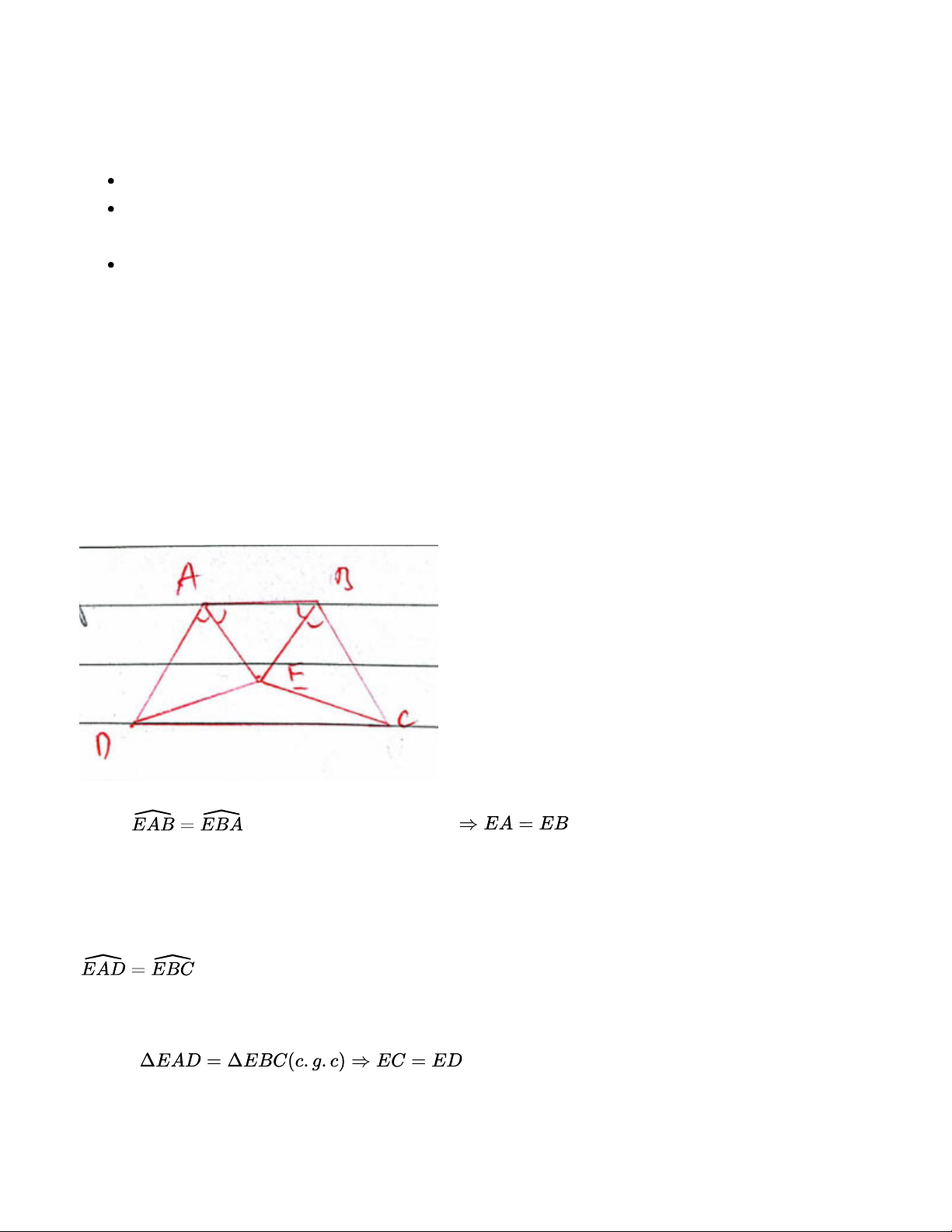
Hai tia phân giác của hai góc A, B của hình thang cân ABCD (AB// CD) cắt nhau tại điểm E trên
cạnh đáy CD. Chứng minh rằng EC = ED Bài giải: Ta có suy ra tam giác EAB cân
Xét tam giác EAD và EBC ta có: EA = EB AD = BC Suy ra Bài 3.8
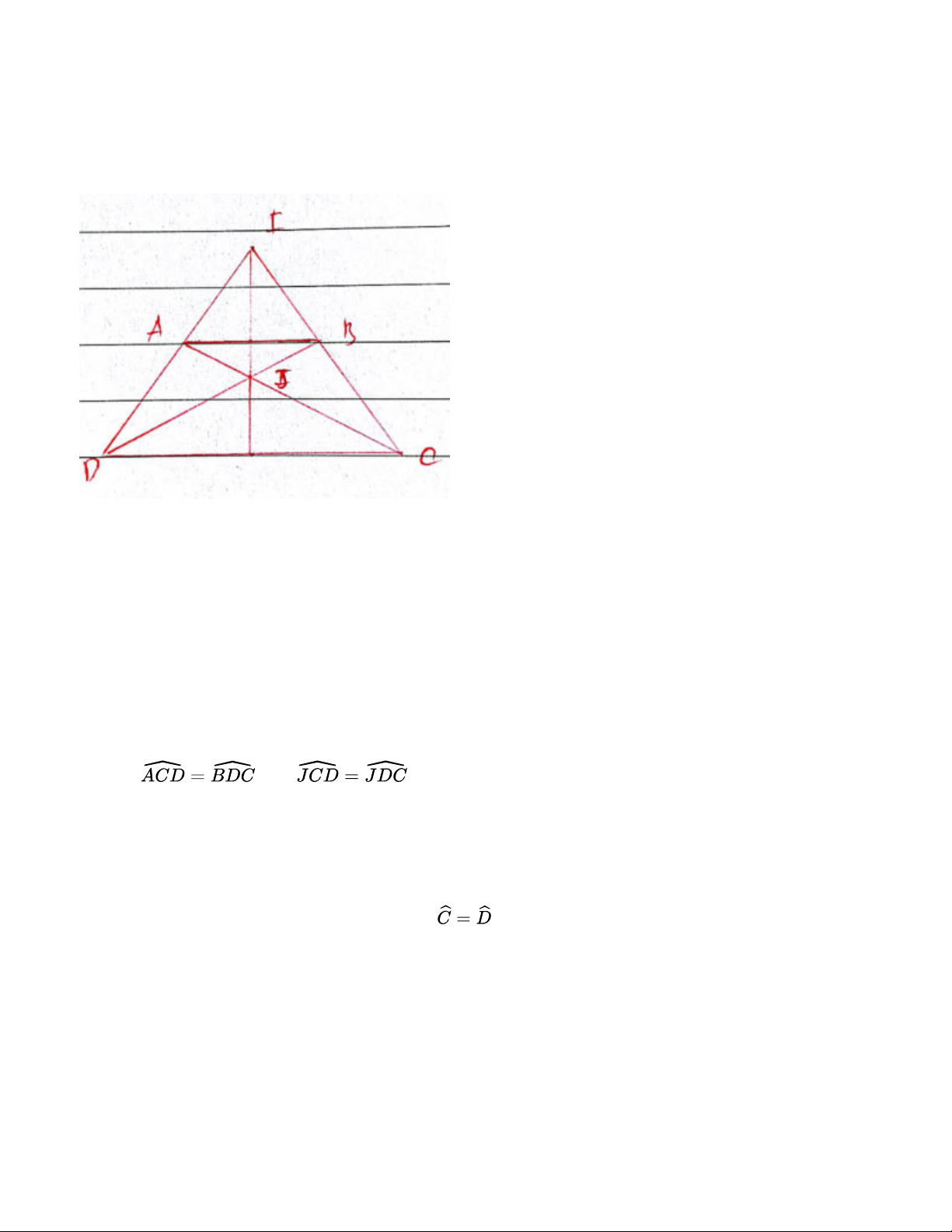
Hình thang cân ABCD (AB // CD) có các đường thẳng AD, BC cắt nhau tại I, các đường thẳng
AC, BD cắt nhau tại J. Chứng minh rằng đường thẳng IJ là đường trung trực của đoạn thẳng AB Bài giải:
Xét tam giác ACD và tam giác BDC có:
AD = BC (tính chất hình thang) CD chung
AC = BD (do ABCD là hình thang cân)
Do đó, ∆ACD = ∆BDC (c.c.c) Suy ra hay
⇒ Tam giác JCD cân tại I. Do đó JD = JC (1)
Tam giác ICD có hai góc ở đáy bằng nhau
nên tam giác ICD cân tại I ⇒ ID = IC (2)
Từ (1) và (2) suy ra IJ là đường trung trực của CD.
Chứng minh tương tự có JA = JB, IA = IB
Suy ra J và I cùng thuộc đường trung trực của đoạn thẳng AB.
Do đó, IJ là đường trung trực của AB.