














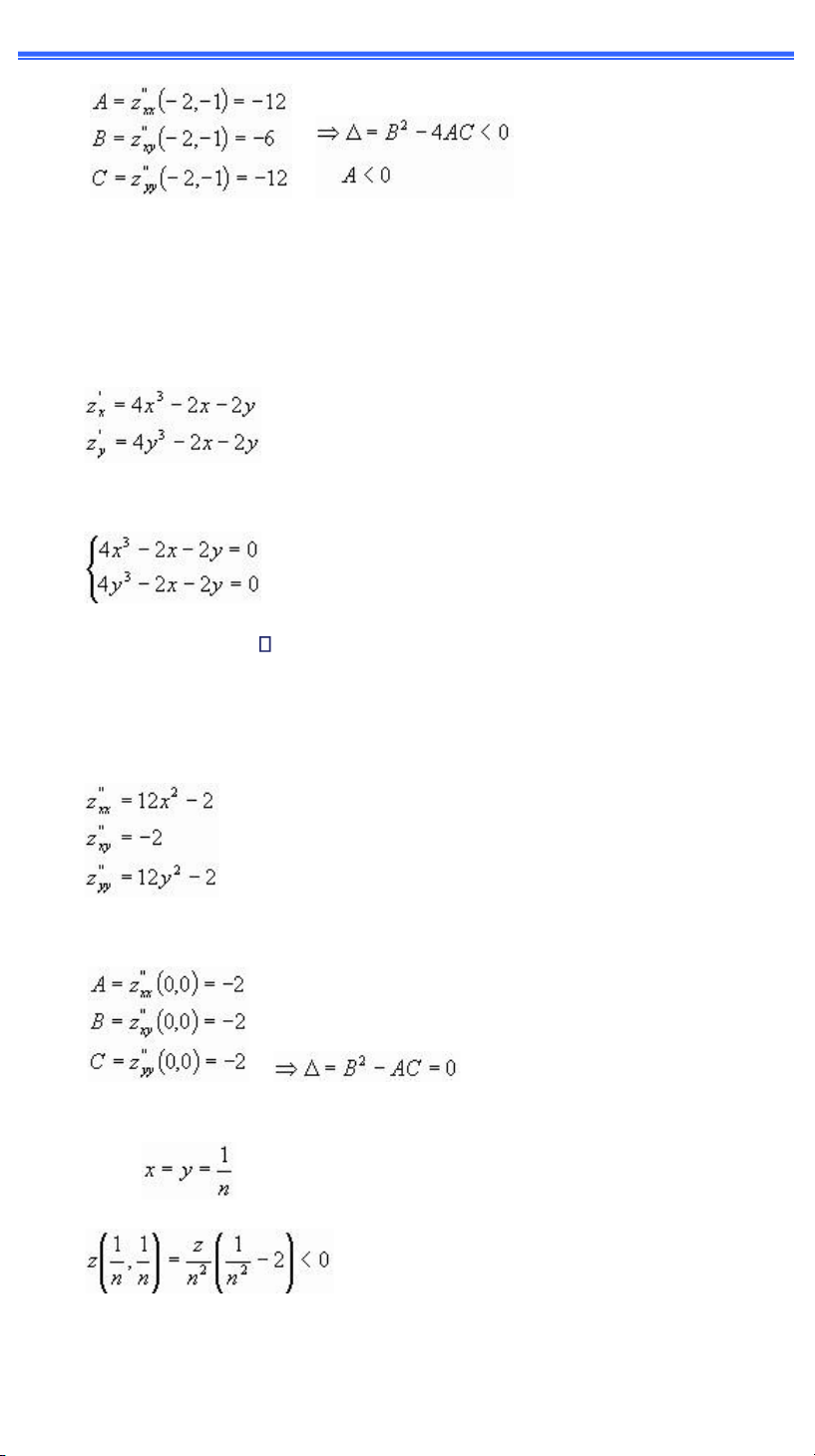
Preview text:
lOMoAR cPSD| 49519085
GI`O TR NH TO`N CAO CẤP A2 1
CH NG I: PH P T˝NH VI PH´N H M NHIỀU BIẾN
I. TẬP HỢP RN V H M NHIỀU BIẾN 1. Rn v cÆc tập con
Với n l một số nguyŒn dıngờ k hiệu Ởn ợc døng ể chỉ tập hợp tất cả cÆc bộ n số thực
ậx1, x2, ờxn) v ta th ờng gọi Ởn l kh ng gian ậthựcấ n chiềuề ẩhi bộ số thực (x1, x2, ờxn)
ợc ặt tŒn l ỳ th ta viết l ầ P(x1, x2, ờ xn)
V gọi n l một iểm trong kh ng gian Ởn. Cho 2 iểm ỳậx1, x2, ờ xn) v ẵậy1, y2,
ờ yn) trong Rn, khoảng cÆch giữa hai
iểm P v ẵờ k hiệu l dậỳờ ẵấ ợc ịnh nghĩa bởi: d(P, Q) =
Khoảng cÆch n y thỏa bất ẳng thức tam giÆc sau yầ
d(P, Q) ≤ dậỳờ R) + d(R, Q)
với ĩ iểm ỳờ ẵờ Ở tøy ề —iểm ỳậx1, x2, ờxn) cn
ợc viết gọn d ới dạng xụậx1, x2, ờxn)
với xụậx1, x2, ờ xn) v yụậy1, y2,
ờ yn), khoảng cÆch giữa x v y c n ợc viết bởiầ | x y |= Cho
v r l số thực dıngờ tập hợp B(P, r) = { | d(P, Q) < r} ợc gọi
l h nh cầu mở t m ỳ bÆn k nh rờ hay l l n cận bÆn k nh r của ỳề Tập hợp ừ trong Ởn
ợc gọi l bị chặn nếu c r ễ ế sao cho , với ẫ l iểm ẫậếờ ếờ ờ ếấề lOMoAR cPSD| 49519085
GI`O TR NH TO`N CAO CẤP A2 2 2. Hm nhiếu biến
Cho n l một số nguyŒn với n ≥ ịề ∞ột phØp tıng ứng fầ Ởn→ R ợc gọi l một h
m n biếnề Tập hợp cÆc iểm
m fậỳấ xÆc ịnh ợc gọi l miền xÆc ịnh của fề
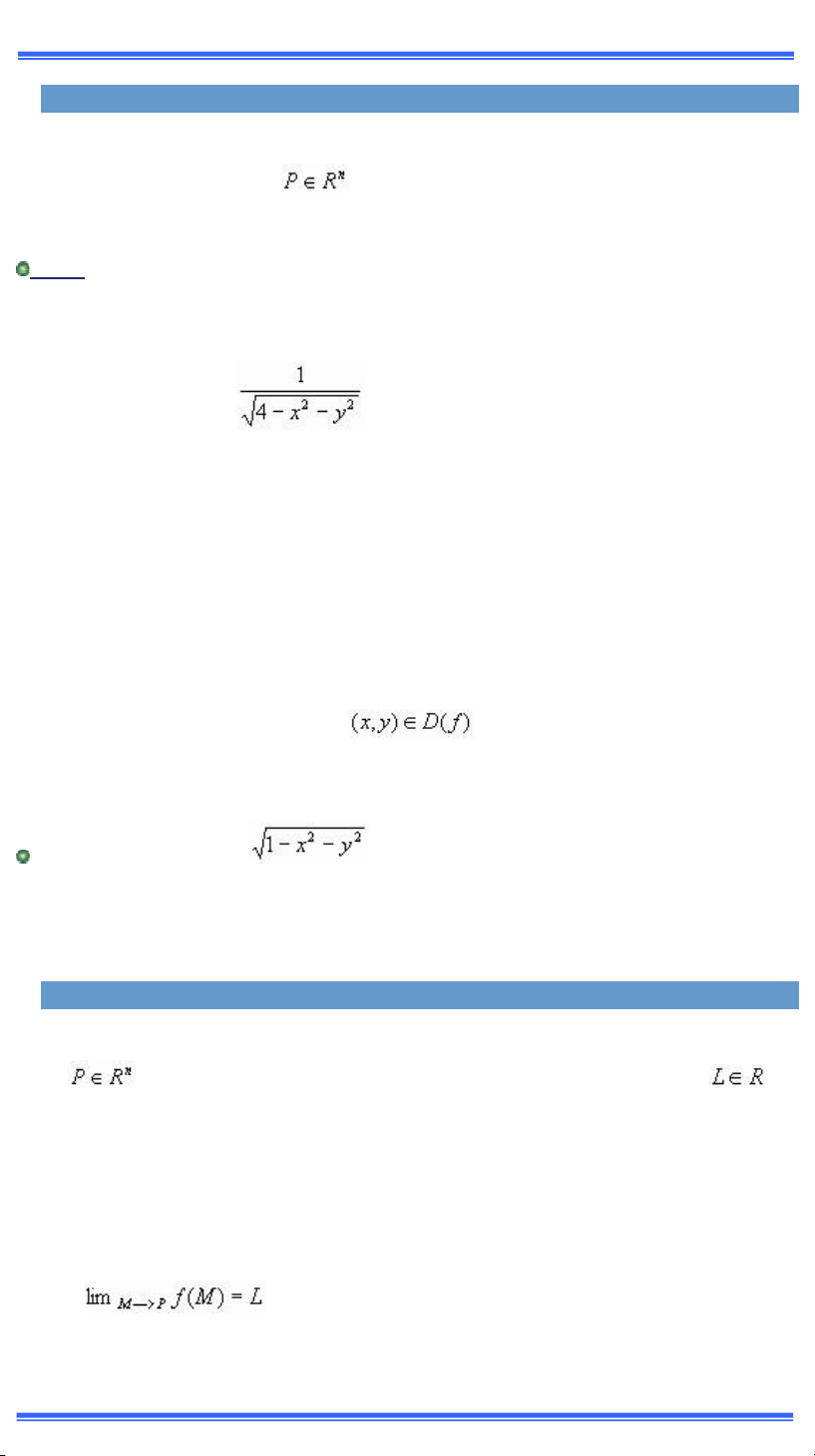
Ta k hiệu miền xÆc ịnh của f l ắậfấề V dụầ 1) Hm f ầ Ở2→ R (x, y) → f(x, y)=
L một h m ị biến c miền xÆc ịnh l tập hợp tất cả cÆc iểm ỳậxờ yấ sao cho 4-
x2-y2>0. Vậy ắậfấụửậếờ ịấờ h nh cầu mở t m ẫ bÆn k nh ị trong Ở2. 2)
g : R3→ R với gậxờ yờ zấụx2+(y+z)/2 l một h m 3 biến c miền xÆc ịnh l D(g)=R3.
Ta chỉ c thể biểu diễn h nh họcờ bằng vẽ ồ thịờ cho h m ị biến z ụ fậxờ yấề
—ồ thị của h m ị biến n y l tập hợp cÆc iểm trong kh ng gian Ở3 sau yầ G(f)={(x, y, f(x, y)) | }
—y l một mặt cong trong kh ng gian ĩ chiều với hệ tọa ộ ắescartes ẫxyzề
V dụầ ồ thị của h m z ụ
l nửa trŒn của mặt cầu t m ẫ bÆn k nh ữ
trong khng gian ĩ chiều ẫxyzề
II. GIỚI HẠN V T˝NH LI˚N TỤC
1. —ịnh nghĩa giới hạn
Cho hm n biến z ụ f ậx1, x2, ờ xn) xÆc ịnh trŒn một l n cận bÆn k nh r của một diểm
v c thể kh ng xÆc ịnh tại ỳề Ta n i z ụ f ậx1, x2, ờ xn) tiến về
(hay c giới hạn l ỡấề ẩhi ∞ ậx1, x2,
ờ xn) dần ến ỳ nếu với mọi ễ ế cho tr ớcờ tồn tại ễ ế sao choầ
0 < d (P, M) < ụễ | fậ∞ấ L | < ề Khi ta viếtầ
Trong tr ờng hợp h m ị biến z ụ f ậxờ yấ th giới hạn c thể ợc viết l ầ lOMoAR cPSD| 49519085
GI`O TR NH TO`N CAO CẤP A2 3 Hay c thể viếtầ
Tıng tự nh ối với h m một biếnờ ta cũng c cÆc ịnh nghĩa giới hạn v cøng v giới hạn ở v tận nh sauầ V dụầ 1). 2). 3). 4). 2. Sự liŒn tục
—ịnh nghĩaầ h m số z ụ f ậx1, x2, ờ xn) ợc gọi l liŒn tục tại iểm khi:
V dụầ h m fậxờ yấ ụ
liŒn tục tại mọi iểm ậxo, yo) khÆc ậếờ ếấề
Tıng tự nh h m một biến liŒn tục trŒn một oạn
, ta cũng c t nh chất ạt giÆ
trị lớn nhất v nhỏ nhất trŒn ữ miền ng v bị chặnề lOMoAR cPSD| 49519085
GI`O TR NH TO`N CAO CẤP A2 4
III. —ẠO H M V VI PH´N 1. —ạo h m riŒng
—ể ın giản cho việc tr nh b yờ ở y ta sẽ xØt cÆc ạo h m riŒng của h m ị biếnề —ối
với h m n biến th ho n to n tıng tựề
—ịnh nghĩaầ cho h m ị biến z ụ f ậxờ yấề —ạo h m riŒng theo biến x tại iểm ậxo,
yo) l giới hạn ậnếu c ấ sau yầ
v ạo h m riŒng theo biến x ợc k hiệu l hay vắn tắt l fx (xo, yo). Ta cn c thể k hiệu ạo h
m riŒng n y bởi z x (x , y ) hay (xo, yo). o o
—ạo h m riŒng theo biến y của h m x ụ f ậxờ yấ tại ậxo, yo) ợc ịnh nghĩa tıng tự bởiầ =
Nhận xØtầ dể thấy rằng f x (xo, yo) =
Từ ta c thể t nh dạo h m riŒng theo biến x tại ậxo, yo) bằng cÆch coi y ụ yo l hằng
số v t nh ạo h m của h m một biến fậxờ yo) tại x ụ xo. Tıng tựờ ể t nh ạo h m riŒng
theo biến y tại ậxo, yo) ta tnh ạo h m của h m một biến fậxờ yo) tại y ụ yo (xem x = xo l hằng sốấề V dụầ
1). Cho z = x2y. Tnh z x v z y
Xem y nh hằng số v t nh ạo h m theo biến x ta c z x = 2xy.
Tıng tựờ xem x nh hằng số v t nh ạo h m theo biến y ta v ầ x y = x2. lOMoAR cPSD| 49519085
GI`O TR NH TO`N CAO CẤP A2 5 2)
. Tnh z x, z y v z x(4, ). Xem y nh hằng sốờ ta c ầ
Xem x nh hằng sốờ ta cầ
2. —ạo h m riŒng cấp cao
CÆc ạo h m riŒng z x v z y của h m z = f(x,y) ợc gọi l cÆc ạo h m riŒng cấp ữề —
ạo h m riŒng cấp ị của một h m l ạo h m riŒng ậcấp 1) của ạo h m riŒng cấp ữ của
h m ề ổ m ị biến z = f(x, y) c bốn ạo h m riŒng cấp ị sau yầ 1)
—ạo h m riŒng cấp ị n y c n ợc k hiệu bằng cÆc cÆch khÆc nhau nh sauầ 2)
—ạo h m riŒng cấp ị n y c n ợc k hiệu bởiầ 3)
—ạo h m riŒng cấp ị n y c n ợc k hiệu bởiầ lOMoAR cPSD| 49519085
GI`O TR NH TO`N CAO CẤP A2 6 4) cn ợc k hiệu l .
Hon to n tıng tự ta cũng c ịnh nghĩa v k hiệu cho cÆc ạo h m riŒng V dụầ
1) z = x4 + y4 2x3y3. Ta cầ
z x = 4x3 4xy3 z y =
4y3 6x2y2 z"xx =
12x2 4y3 z"yy =
12y2 12x2y z"xy =
-12y2 z"yx = -12 y2 2) XØt h m số
Ta cờ với ậx, y) ≠ ậếờ ếấ th lOMoAR cPSD| 49519085
GI`O TR NH TO`N CAO CẤP A2 7
YjWҥi (0, 0) th f(0, 0) = 0. Do
tại ậx, y) ≠ ậếờ ếấ v suy ra
Hon to n tıng tựờ ta t nh ợcầ
tại ậxờ yấ ≠ ậếờ ếấ v
Qua v dụ trŒn ta thấy cÆc ạo h m riŒng theo cøng cÆc biến nh ng khÆc
thứ tự khng phải bao giờ cũng bằng nhau. Tuy nhiŒn ịnh Oêsau y cho ta iӅu
kiӋn ÿӇFic ҥo Kjm riŒng z"xyYjz"yx bҵng nhau.
—ӏnh Oê: NӃu f(x, y) c cÆc ạo h m f"xy v f"xy trong một l n cận của iểm ậx0, y0) th
chœ rằng ịnh l trŒn cũng mở rộng ѭӧc ra cho cÆc ạo h m cấp cao hın v nhiều biến hınề 3. Vi phn to n phần —ịnh nghĩa:
Hm số z = f(x, y) ợc gọi l khả vi tại ậx0, y0) nếu số gia to n phần lOMoAR cPSD| 49519085
GI`O TR NH TO`N CAO CẤP A2 8
theo cÆc số gia x, y của cÆc biến x, y tại ậx0, y0) c thể ợc viết d ới dạng
trong A, B l cÆc hằng số ậkh ng phụ thuộc x, y) v 0, 0 khi x 0, y 0. Biểu thức
ợc gọi l vi ph n của h m số f tại ậx0, y0), k hiệu l df(x0, y0). —ịnh l : (i)
Nếu f(x, y) khả vi tại ậx0, y0) th f c ạo h m riŒng cấp ữ tại v (ii)
Nếu f(x, y) c cÆc ạo h m riŒng trŒn ữ l n cận của ậx0, y0) v f x, f y
liŒn tục tại ậx0, y0) th f khả vi tại ậx0, y0).
Chœ rằng khi xØt cÆc tr ờng hợp ặc biệt f(x, y) = x v g(x, y) = y ta c vi ph nầ dx =
x v dy = y. Do c ng thức vi ph n cấp ữ của f(x, y) cn ợc viết d ới dạng
df = f x.dx + f y.dy v c n
ợc gọi l vi ph n to n phần của h m f(x, y). V dụầ Với , ta cầ vậy
Tnh chất: Tıng tự nh ối với h m một biến ta c cÆc t nh chất sau y của vi phnầ lOMoAR cPSD| 49519085
GI`O TR NH TO`N CAO CẤP A2 9
d(f + g) = df + dg d(f.g)
= g.df + f.dg (với g 0).
Ứng dụng vi ph n ể t nh gần œngầ
Giả sử z = f(x, y) khả vi tại ậx0, y0). Khi ờ theo ịnh nghĩa của vi ph n ta c thể t
nh gần œng f(x, y) bởiầ
với ậx, y) gần ậx0, y0). V dụ: Tnh gần œng
XØt h m số f(x, y) = , ta tnh gần œng
A = f(1,02; 1,97) nh sauầ
f(1,02; 1,97) f(1, 2) + f x(1, 2).(1,02 - 1) + f y(1, 2).(1,97 - 2) với f(1, 2) = = 3 Suy ra 4. Vi phn cấp cao
Cho hm ị biến z ụ fậxờ yấề Bản th n
cũng l một h m theo ị biến xờ y nŒn ta c lOMoAR cPSD| 49519085
GI`O TR NH TO`N CAO CẤP A2 10
thể xØt vi ph n của n ề ỷếu dfậxờ yấ c vi ph n th vi ph n ợc gọi l vi ph n cấp 2
của fậxờ yấờ k hiệu l d2f (x, y) hay vắn tắt l d2f. Vậyầ d2f = d(df)
Tổng quÆtờ vi ph n cấp n ậnếu c ấ của f ợc ịnh nghĩa bởiầ
Cng thức vi ph n cấp ị của zụfậxờ yấầ
Giả thiết thŒm rằngờ cÆc ạo h m hỗn hợp liŒn tục th ta c ầ v do ầ hay ta cầ
Ng ời ta døng k hiệu luỹ thừa một cÆch h nh thức ể viết lại c ng thức vi ph n cấp ị d ới dạngầ
Tıng tựờ c ng thức vi ph n cấp n của z ụ fậxờ yấ c thể ợc viết d ới dạngầ
v c ng thức n y cũng œng cho tr ờng hợp nhiều biến hınề
IV. —ẠO H M CỦA H M HỢP
1. Tr ờng hợp một biến ộc lập lOMoAR cPSD| 49519085
GI`O TR NH TO`N CAO CẤP A2 11
Giả sử z ụ fậxờ yấ v xờ y lại l cÆc h m theo tầ x ụ xậtấờ y ụ yậtấề Vậy zậtấ ụ
fậxậtấờ yậtấấ l h m ữ biến theo tề —ạo h m của zậtấ theo biến t ợc t nh theo c ng thức sau yầ V dụầ Tnh n ế u trong yụcosx
2. Tr ờng hợp nhiều biến ộc lập
Giả sử z ụ fậxờyấ v xờ y lại l cÆc h m theo cÆc biến sờ tề ẩhi ể t nh cÆc ạo h m
riŒng theo s v t của h m hợp f ậ xậsờtấờ yậsờtấấ ta cũng c cÆc c ng thức tıng tự nh
ối với h m một biến sau yầ V dụầ Tm v
nếu z ụ fậxờyấ trong x ụ uềv v y ụ Ta c , , v . Do lOMoAR cPSD| 49519085
GI`O TR NH TO`N CAO CẤP A2 12
Cho z = f(x,y,t), trong x ụ xậtấờ y ụ yậtấề
Tnh ạo h m của h m hợpầ z(t) = f (x(t), y(t), t). Ta cầ = =
V. —ẠO H M CỦA H M ẨN
1. Hm ẩn một biến
Giả sử c một hệ thức giữa hai biến xờ y dạng F(x,y) = 0
trong ≠ậxờyấ l h m ị biến xÆc ịnh trong một l n cận mở ắ của ậx0, y0) v ≠ậx0,
y0) = 0. Giả thiết rằng s l số dıng v
y duy nhất sao cho ậxờ y)
D v ≠ậxờ yấ ụ ếề
Nh vậy ta c h m số y ụ yậxấ xÆc ịnh trŒn khoảng ậx0 s, x0 + s) v thỏa ≠ậxờ yậxấấ = 0
. Hm số y ụ yậxấ n y ợc gọi l h m ẩn theo biến x xÆc ịnh
bởi phıng tr nh ≠ậxờyấ ụ ếề
Trong toÆn học ng ời ta gọi cÆc ịnh l h m ẩn l cÆc ịnh l khẳng ịnh sự tồn tại của h
m ẩn v ạo h m của n ề ắ ới y l ịnh l cı bản cho h m ẩn một biếnề
—ịnh l : Giả sử h m ≠ậxờyấ thỏa ị iều kiện sauầ (i)
F liŒn tục trong hnh tr n mở ửậỳờ ấ t m ỳậx0, y0) bÆn k nh ờ với ≠ậx0, y0) = 0; lOMoAR cPSD| 49519085
GI`O TR NH TO`N CAO CẤP A2 13 (ii)
Tồn tại cÆc ạo h m riŒng liŒn tục trong B(P, ấ v (x0, y0) ≠ ếề
Khi c ễế sao cho phıng tr nh ≠ậxờyấ ụ ế xÆc ịnh một h m ẩn yậxấ khả
vi liŒn tục trong ậx0 s, x0 + s) v .
Nhận xØt: Nếu thừa nhận sự tồn tại của h m ẩn v ạo h m của n th c ng thức ạo h
m của h m ẩn trong ịnnh l trŒn c thể suy ra dễ d ng từ c ng thức ạo h m của h m hợpầ 0 = F(x, y(x)) = F x + F y . y => y ụ -
V dụầ Tnh ạo h m của h m ẩn tại iểm ậữờ ấ nếu xềy ex.sin y = ề
Coi y l h m theo xờ lấy ạo h m phıng tr nh trŒn ta ợc
y + x.y exsiny ex cosy. y ụ ế
Tại ậxờyấ ụ ậữờ ấ ta c ầ ự y ự eềy ụ ế Suy ra y ậữấ ụ
Ghi chœ: —ể t nh ạo h m cấp ị y của h m ẩnờ từ hệ thức
0 = F x ự ≠ y ề y ta c thể tiếp tục lấy ạo h m th ợcầ
0 = F"xx + F"xy.y ự ậ≠ộyx + F"yy. y ấềy ự ≠ y.y". Từ y sẽ rœt ra y ề lOMoAR cPSD| 49519085
GI`O TR NH TO`N CAO CẤP A2 14 2. Hm ẩn 2 biến
Tıng tự nh tr ờng hợp h m ẩn ữ biếnờ với một số giả thiết th phıng tr nh F(x,y) = 0
sẽ xÆc ịnh một h m ẩn z ụ zậxờyấ theo ị biến xờ yề
—ịnh l : Giả sử h m ≠ậxờyờzấ thỏa cÆc iều kiện
(i). F liŒn tục trong h nh cầu mở ửậỳ0, ấ t m ỳ0(x0, y0,z0) bÆn k nh v F(x0,y0,z0) = 0;
(ii) Tồn tại cÆc ạo h m riŒng liŒn tục ≠ x, F y, F z trong B(P0, ấ v ≠ z(x0,y0,z0) ≠ ếề
Khi tồn tại ễế sao cho phıng tr nh ≠ậxờyờzấ ụ ế xÆc ịnh một h m ẩn trong ln
cận ửậậx0,y0), s) của iểm ậx0, y0). Hın nữa h m ẩn z ụ zậxờyấ c cÆc
ạo h m riŒng trong l n cận n y l ầ ; 9;
Ghi chœ: —ịnh l n y c thể
ợc mở rộng cho tr ờng hợp h m ẩn nhiều biến hın z
= z(x1,x2, ờxn) xÆc ịnh bởi phıng tr nhầ F(x1,x2, ờxn, z) = 0 V dụ:
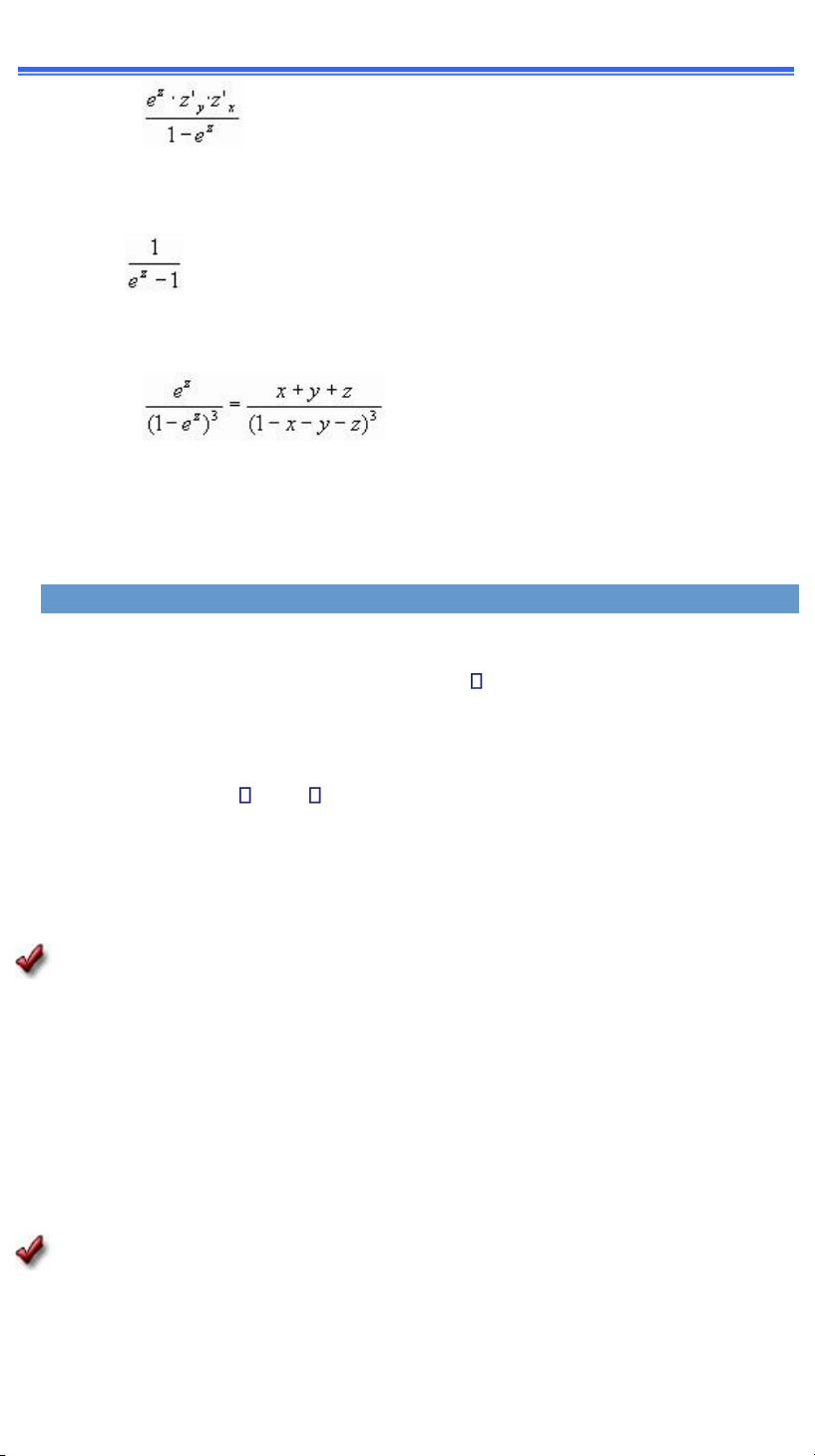
Cho hm ẩn z ụ zậxờyấ xÆc ịnh bởi phıng tr nh ez = x + y + z Tnh zx ờ zx" v zxy".
—ạo h m phıng tr nh theo biến x ta ợcầ
1 + zx ụ ez . zx ụễ zx ụ
Tiếp tục lấy ạo h m theo x v theo y th ợcầ lOMoAR cPSD| 49519085
GI`O TR NH TO`N CAO CẤP A2 15
zxx" = ez . (zx ấ2 + ez . zxx" ; zxy"
= ez . zy ề zx ự ez . zxy" Suy ra: zxx" = lOMoAR cPSD| 49519085
GI`O TR NH TO`N CAO CẤP A2 16 z xy " =
Tnh zy tıng tự nh việc t nh zx ờ ta c ầ zy ụ Do zxy" = VI. CỰC TRỊ
1.—ịnh nghĩa v iều kiện cần
XØt h m z ụ fậxờyấề —iểm ỳ0(x,y) ợc gọi l iểm cực ại ậ ịa phıngấ của h m f(x,y)
khi c ễế sao cho fậxờyấ ≤ fậx0,y0) với mọi ậxờyấ B(P0, ấề Tr ờng hợp ta c
F(x,y) < f(x0,y0) (x,y) B(P0, ấ \ {P0}th ta n i ỳ0 l iểm cực ại ậ ịa phıngấ
chặt của h m fậxờyấề
KhÆi niệm cực tiểu ậ ịa phıngấ ợc ịnh nghĩa ho n to n tıng tựề ũực ại ịa phıng v
cực tiểu ịa phıng ợc gọi chung l cực trị ịa phıngề —ịnh l : (Fermat)
Nếu h m fậxờyấ ạt cực trị ịa phıng tại ậx0,y0) v c cÆc ạo h m riŒng tại th fx ậx0,y0) = fy ậx0,y0) = 0.
—iểm m tại cÆc ạo h m riŒng của f ều bằng ế
ợc gọi l iểm dừng của h mề
Chœ rằng ịnh l trŒn chỉ cho ta iều kiện cần ể c cực trịờ nŒn iểm dừng ch a chắc l
iểm cực trịề —ịnh l sau y cho ta iều kiện ủ ể c cực trịề
—ịnh l ( iều kiện ủ):
Giả sử z ụ fậxờyấ nhận ậx0, y0) l một iểm dừngờ v fậxờyấ c cÆc ạo h m riŒng cấp ị
liŒn tục trong một l n cận của ậx0, y0). —ặt lOMoAR cPSD| 49519085
GI`O TR NH TO`N CAO CẤP A2 17
A = fxx"(x0,y0), B = fxy"(x0,y0), C = fyy"(x0,y0), v = B2 A.C Khi ta c ầ
(i). Nếu > 0 th h m số kh ng ạt cực trị tại ậx0,y0).
(ii). Nếu < 0 th h m số ạt cực trị chặt tại ậx0,y0). Hın nữa ta c ầ
(x0,y0) l iểm cực ại khi ồ ≥ 0;
(x0,y0) l iểm cực tiểu khi ồ ễ ếề
(iii). Nếu = 0 th ch a kết luận ợc l h m số fậxờyấ c ạt cực trị tại ậx0,y0) hay khngề
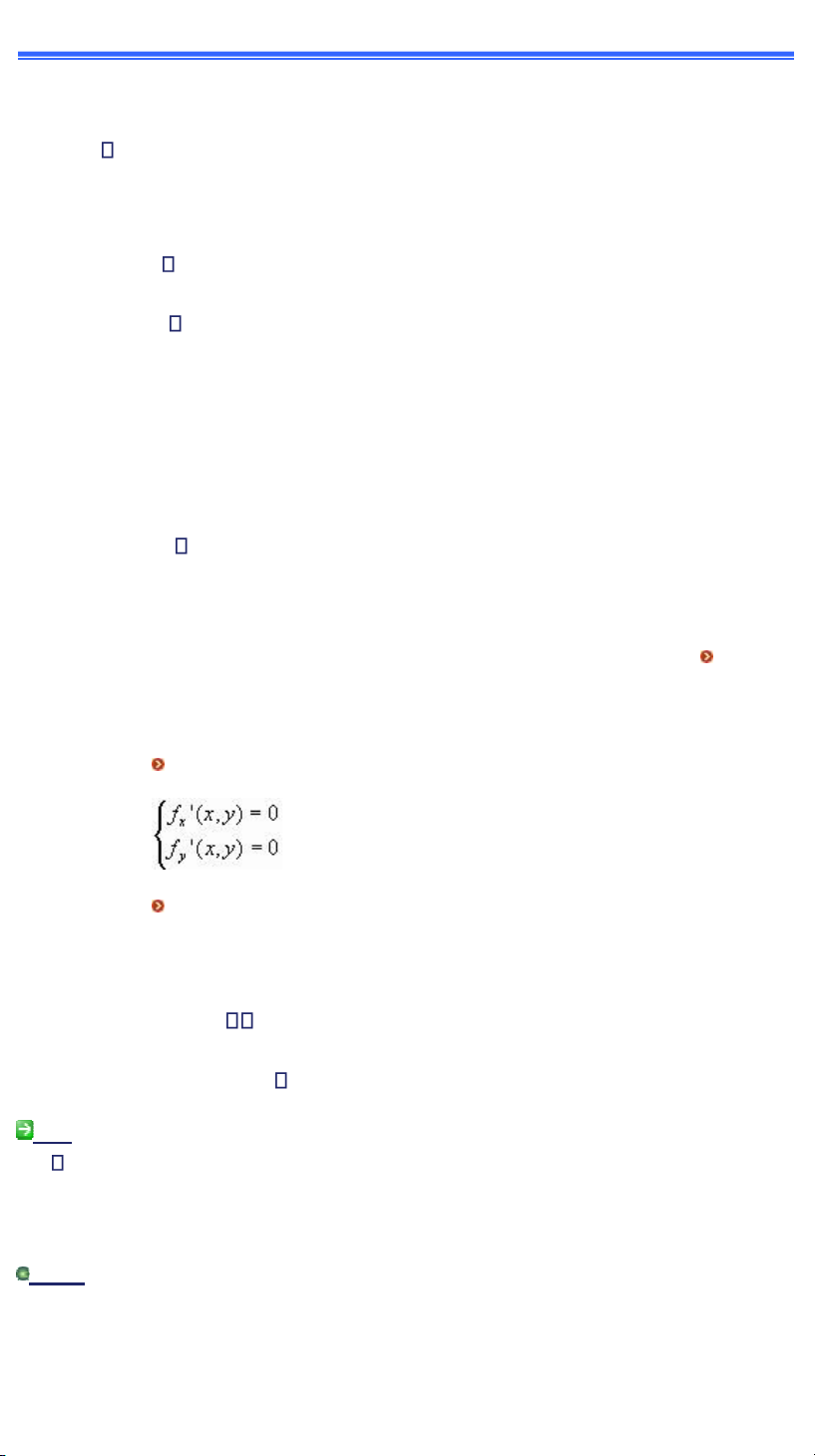
Từ ịnh l trŒn ta c thể t m cực trị của h m z ụ fậxờyấ theo cÆc b ớc sau yầ B
ớc ữầ T nh cÆc ạo h m riŒng
B ớc ịầ T m cÆc iểm dừng bằng cÆch giải hệ phıng tr nh sauầ
B ớc ĩầ Ứng với mỗi iểm dừng ậx0,y0), ặt
A = fxx"(x0,y0), B = fxy"(x0,y0), C = fyy"(x0,y0), = B2 - AC
XØt dấu của v của ồ ể kết luậnề
L u : —ể c kết luận ầy ủ về cực trị ta c n phải xØt riŒng tr ờng hợp iểm dừng m
tại = 0 v xØt cÆc iểm m tại khng tồn tại ạo h m riŒng cấp ữ hay cấp 2. V dụ:
1) Tm cực trị của h m số z ụ x3 + 3xy2 15x -12y lOMoAR cPSD| 49519085
GI`O TR NH TO`N CAO CẤP A2 18
Ta c zx ụ ĩx2 + 3y2 15, zy ụ ẳxy 12
zxx" = 6x, zxx" = 6y, zyy "= 6x
—ể t m iểm dừngờ ta giải hệ phıng tr nh sauầ
Hệ phıng tr nh c ở nghiệmờ cho ta ở iểm dừngầ
M1(1, 2); M2(2, 1); M3(-1, -2); M4(-2, -1). Tại ∞1(1, 2): A = zxx"(1, 2) = 6
B = zxy"(1, 2) = 12 => = B2 AC >0 C = zyy"(1, 2) = 6
Hm số kh ng ạt cực trị tại ∞1(1, 2). Tại ∞2(2,1): A = zxx"(2, 1) = 12
B = zxy"(2, 1) = 6 => = B2 AC <0 C = zyy"(2, 1) = 12 A > 0
Hm số ạt cực tiểu tại ∞2(2, 1), với zmin = z(2, 1) = -28 Tại ∞3(-1, -2): A = zxx"(-1, -2) = -6
B = zxy"(-1, -2) = -12 => = B2 AC >0 C = zyy"(-1, -2) = -6
Hm số kh ng ạt cực trị tại ∞3(-1, -2). Tại ∞4(-2, -1): lOMoAR cPSD| 49519085
GI`O TR NH TO`N CAO CẤP A2 19 9 ;
Hm số ạt cực ại tại ∞4(-2, -1) với zmax = z(-2,-1) = 28
2) Khảo sÆt cực trị của h m z ụ x4 + y4 x2 2xy y2 Ta cầ
Giải hệ phıng tr nh sau ể t m iểm dừngầ
Hệ phıng tr nh c ĩ nghiệm 3 iểm dừngầ P1(0, 0); P2(-1, -1); P3(1,1) Tnh cÆc ạo hm cấp ịầ
Tại ỳữậếờ ếấầ 9 ;
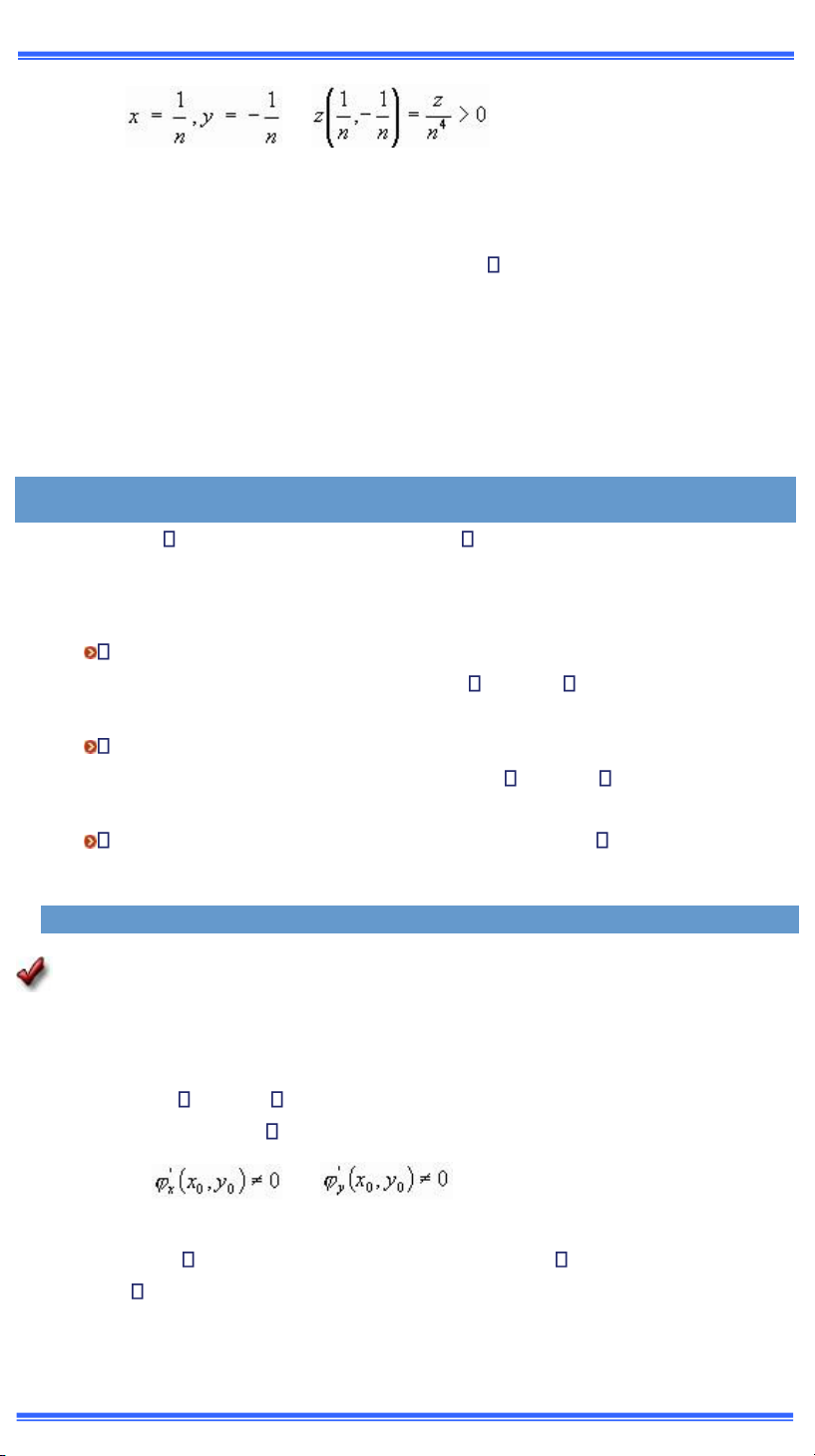
Ta ch a c kết luận về cực trị tại ỳ1 m phải khảo sÆt trực tiếpề Ta c zậếờ ếấ ụ 0, với th (n nguyŒn dıngấ lOMoAR cPSD| 49519085
GI`O TR NH TO`N CAO CẤP A2 20 Với th
. —iều n y cho thấy rằng trong
mọi l n cận của ỳ1 hm số ều c giÆ trị dıng v c giÆ trị mề Vậy ỳ1(0, 0) khng phải l iểm cực trị
Tại ỳ2(-1, -1) v ỳ3(1, 1) ta c ồ ụ ữếờ ử ụ -2, C = 10, =B2 AC = -96. Suy ra tại ỳị v ỳĩ
h m số ạt cực tiểu chặt vớiầ zmin = z(P2) = z(P3) = -2
VII. CỰC TRỊ C —IỀU KIỆN 1. —ịnh nghĩa
XØt h m số z ụ (x, y), với iều kiện r ng buộcầ (x, y) = 0 (*) Ta niầ
(x, y) ạt cực ại chặt tại ậx0, y0) với iều kiện ậảấ nếu ậx0, y0) thỏa ậảấ v với
mọi ậxờ yấ thỏa ậảấ khÆ gần ậx0,y0) ta c (x, y) < (x0, y0)
(x, y) ạt cực tiểu chặt tại ậx0, y0) với iều kiện (*) nếu ậx0, y0) thỏa ậảấ v
với mọi ậxờ yấ thỏa ậảấ khÆ gần ậx0,y0) ta c (x, y) > (x0, y0)
(x, y) ạt cực trị chặt tại ậx0, y0) với iều kiện ậảấ nếu (x,
y) ạt cực ại hoặc cực tiểu tại ậx0,y0) với iều kiện ậảấ
2. Phıng phÆp nh n tử Lagrange
—ịnh l : ( iều kiện cần của cực trị c iều kiệnấ Giả sửầ
CÆc h m (x, y) v (x, y) c ạo h m riŒng cấp ữ liŒn tục trong một l n cận
của iểm ậx0,y0) với (x0, y0) = 0 hay .
Khi ờ nếu (x, y) ạt cực trị tại ậx0,y0) với iều kiện (x0,y0)=0 th tồn tại số thực sao cho:




