
















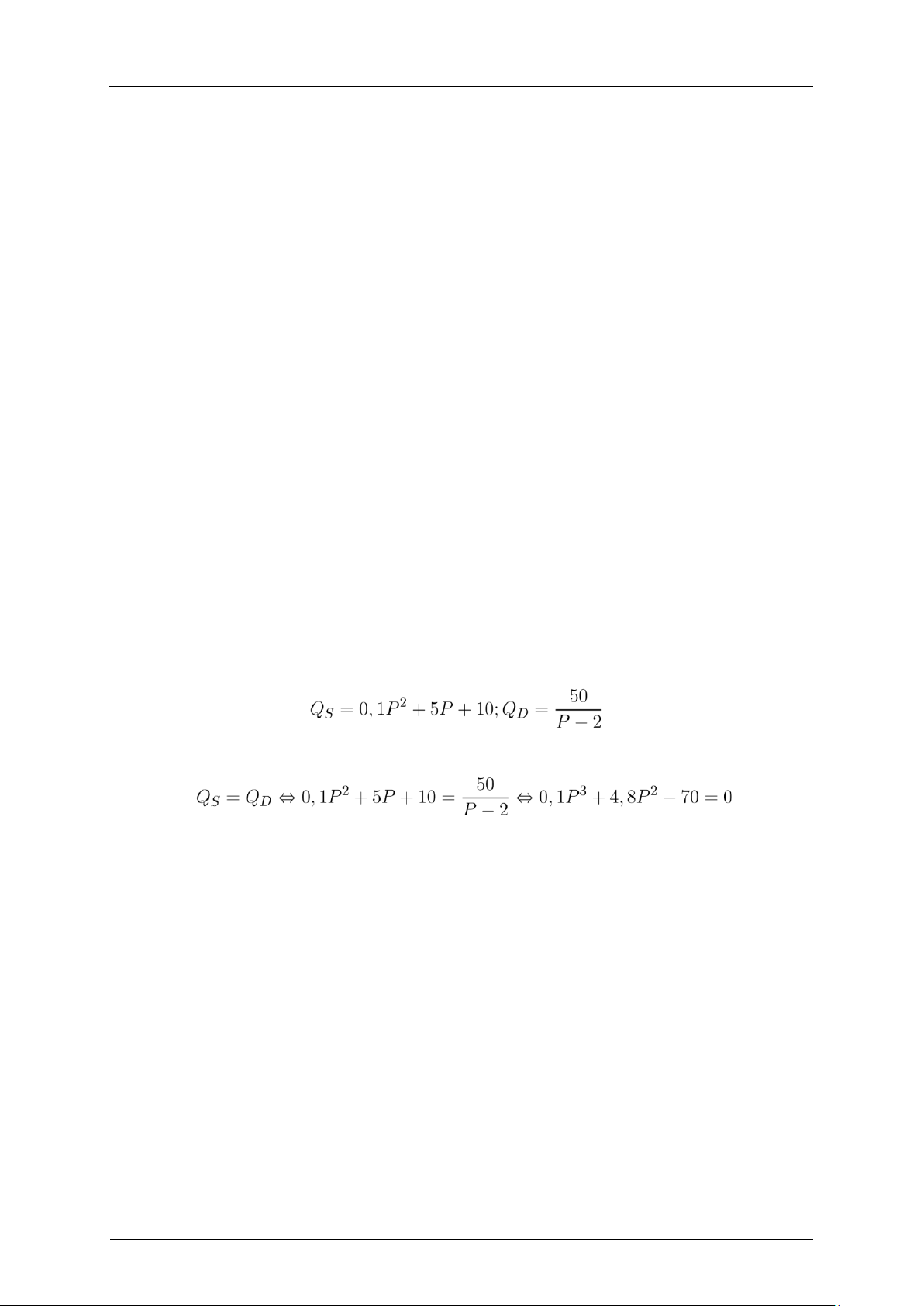

Preview text:
lOMoAR cPSD| 47207194 lOMoAR cPSD| 47207194
TRƯỜNG ĐẠI HỌC NGOẠI THƯƠNG TS. ĐẶNG LÊ QUANG Bài Giảng TOÁNCAOCẤP2
Thành phố Hồ Chí Minh - 2022 Mục lục
1. ỨNG DỤNG CỦA HÀM MỘT BIẾN TRONG KINH TẾ..... 5
1.1. Bổ trợ về phép tính vi phân hàm một biến số........................ 5 lOMoAR cPSD| 47207194
1.1.1. Các khái niệm cơ bản về hàm một biến số ............................... 5
1.1.2. Giới hạn của hàm số..................................................... 9
1.1.3. Đạo hàm ............................................................... 11
1.2. Giới thiệu hàm kinh tế một biến số................................. 12
1.3. Ứng dụng của dãy số ............................................... 14
1.3.1. Cấp số nhân............................................................ 14
1.3.2. Ứng dụng trong phân tích tài chính..................................... 14
1.4. Ứng dụng tính liên tục trong toán học và trong kinh tế ............. 17
1.5. Ứng dụng của đạo hàm trong phân tích kinh tế..................... 18
1.5.1. Đạo hàm và giá trị cận biên ............................................ 18
1.5.2. Hệ số co giãn ........................................................... 19
1.5.3. Quy luật lợi ích cận biên giảm dần...................................... 19
1.5.4. Hàm bình quân, mối quan hệ giữa hàm bình quân và hàm cận biên ..... 20
1.5.5. Cực trị hàm kinh tế một biến số ........................................ 21
1.6. Ứng dụng của tích phân trong phân tích kinh tế.................... 23
1.6.1. Một số biểu thức tích phân ............................................. 23
1.6.2. Công thức tích phân cơ bản............................................. 23
1.6.3. Tìm hàm tổng khi biết hàm cận biên ................................... 24
1.6.4. Bài toán tính thặng dư ................................................. 26
2. MỘT SỐ VẤN ĐỀ MỞ RỘNG GIẢI TÍCH HÀM MỘT BIẾN SỐ 28
2.1. Định lý hàm khả vi................................................. 28 2
2.2. Khử dạng vô định bằng quy tắc l’Hospital .......................... 30
2.2.1. Dạng tích vô định ...................................................... 31
2.2.2. Dạng hiệu vô định. ..................................................... 31
2.2.3. Dạng lũy thừa vô định.................................................. 32
2.3. Khai triển Taylor .................................................. 34
2.4. Tích phân suy rộng................................................. 35
2.4.1. Các tính chất về hội tụ và phân kỳ ..................................... 35
3. PHÉP TÍNH VI PHÂN CỦA HÀM NHIỀU BIẾN SỐ....... 38
3.1. Khái niệm cơ bản .................................................. 38 lOMoAR cPSD| 47207194
3.2. Giới hạn của hàm n biến số......................................... 39
3.3. Tính liên tục của hàm n biến số .................................... 39
3.4. Đạo hàm và vi phân của hàm n biến................................ 40
3.4.1. Đạo hàm và vi phân cấp 1.............................................. 40
3.4.2. Đạo hàm và vi phân cấp n.............................................. 43
3.4.3. Đạo hàm và vi phân của hàm hợp, hàm ẩn.............................. 44
3.5. Một số ứng dụng của phép tính vi phân của hàm n biến số ......... 46
3.5.1. Cực trị không có điều kiện ràng buộc ................................... 46
3.5.2. Cực trị có điều kiện ràng buộc.......................................... 49
3.5.3. Giá trị lớn nhất, nhỏ nhất của hàm số trên tập đóng và bị chặn......... 53
4. ỨNG DỤNG CỦA HÀM NHIỀU BIẾN SỐ TRONG KINH TẾ .. 54
4.1. Đạo hàm riêng và giá trị cận biên .................................. 54
4.2. Hệ số co giãn riêng ................................................. 57
4.3. Quy luật lợi ích cận biên giảm dần ................................. 58
4.4. Hàm thuần nhất và vấn đề hiệu quả theo quy mô sản xuất.......... 59
4.5. Phương trình đường đồng quan và đường động lượng ............... 61
4.6. Ứng dụng đạo hàm của hàm ẩn..................................... 63
4.7. Hệ số tăng trưởng .................................................. 65
4.8. Cực trị không điều kiện và có điều kiện của hàm kinh tế nhiều biến số .. 67 3 lOMoAR cPSD| 47207194 TOÁN CAO CẤP 2
TS. Đặng Lê Quang. Sđt: 0764060787
5. CHUỖI, PHƯƠNG TRÌNH VI PHÂN VÀ PHƯƠNG TRÌNH SAI
PHÂN .......................................................... 70
5.1. Chuỗi số ........................................................... 70
5.1.1. Định nghĩa và tính chất................................................. 70
5.1.2. Chuỗi đan dấu.......................................................... 73
5.2. Chuỗi lũy thừa ..................................................... 74 5.3. Phương trình vi
phân và ứng dụng trong kinh tế.................... 76
5.3.1. Phương trình vi phân................................................... 76
5.3.2. Các phương trình vi phân cấp 1 thường gặp ............................ 77 5.4. Phương
trình sai phân và ứng dụng trong kinh tế................... 82
5.4.1. Sai phân và phương trình sai phân...................................... 82
5.4.2. Giải phương trình sai phân cấp 1 ....................................... 83 5.4.3. Ứng dụng
trong kinh tế................................................. 84
TÀI LIỆU THAM KHẢO ....................................... 86 lOMoAR cPSD| 47207194 Chương1
ỨNG DỤNG CỦA HÀM MỘT BIẾN TRONG KINH TẾ
1.1. Bổ trợ về phép tính vi phân hàm một biến số
1.1.1. Các khái niệm cơ bản về hàm một biến số
Định nghĩa 1.1. Cho các tập hợp X,Y ⊂ R. Ánh xạ f : X → Y gọi là hàm một biến số. Tập X
được gọi là tập xác định thường được kí hiệu là Df, tập ảnh f(X) của ánh xạ được gọi là
tập giá trị của hàm số f. Hàm số được kí hiệu là:
f :X → Y
x 7→ f(x) = y
Hoặc y = f(x). Kí hiệu trên cho phép ta xác định được giá trị của hàm số tại điểm x, x
được gọi là biến số độc lập và y = f(x) là giá trị của hàm số tại x. Nếu f được cho bởi một
biểu thức và không nói gì thêm thì ta hiểu tập xác định ở đây là tập hợp tất cả các giá
trị của x để biểu thức có nghĩa. Ví dụ 1.1. Tìm các tập xác định của các hàm số sau:
a. Cho hàm số y = √9 − x2. Tập xác định là D = [−3,3].
b. Hàm số y = cos(x) có tập xác định là D = R. c. Cho hàm
số. Biểu thức có điều kiện xác định là 10−x > 0
và x − 2 > 0. Do đó tập xác định là D = (2,10). 5 ⋆ Hàm hợp:
Cho các tập hợp X,Y,Z ⊂ R và các hàm số f : X → Y ; g : Y → Z. Hợp của hai hàm f, g kí
hiệu g ◦ f là hàm số xác định bởi: lOMoAR cPSD| 47207194 TOÁN CAO CẤP 2
TS. Đặng Lê Quang. Sđt: 0764060787 hay
. Chẳng hạn y = cos(x3) là hàm hợp của hai hàm số y = cos(u) và u = x3. ⋆ Hàm ngược:
Cho các tập hợp X,Y ⊂ R và hàm số f : X → Y là một song ánh. Khi đó, hàm số f(x) có
hàm ngược g : Y → X sao cho .
Ta kí hiệu hàm ngược của hàm số f(x) là f−1(x). Ví dụ 1.2.
Tìm hàm ngược của các hàm số sau:
a. Hàm số y = ex có hàm ngược là y = ln(x).
b. Hàm số y = 4x − 5 có hàm ngược là . ⋆ Hàm số đơn điệu:
Cho các tập hợp X,Y ⊂ R và hàm số f : X → Y . Ta nói hàm số f(x) đơn điệu tăng ngặt
(hoặc đơn điệu giảm ngặt) trên X nếu mọi x1,x2 ∈ X thì:
x1 < x2 (hoặc x1 > x2) ⇒ f(x1) < f(x2) hoặc
Ta nói hàm số f(x) đơn điệu tăng (hoặc đơn điệu giảm) trên X nếu mọi x1,x2 ∈ X thì:
x1 ≤ x2 (hoặc x1 ≥ x2) ⇒ f(x1) ≤ f(x2) hoặc
Hàm số đơn điệu tăng hoặc giảm gọi chung là đơn điệu. Tính đơn điệu cho ta hình dung
hình dáng của đồ thị hàm số trên X: đồ thị của hàm số đơn điệu tăng (giảm) đi lên (đi
xuống) từ trái sang phải.
Ví dụ 1.3. Các hàm số sau tăng (hay giảm) trên đoạn nào:
a. Hàm số f(x) = x tăng ngặt trên R.
b. Hàm số f(x) = cos(x) tăng ngặt trên các khoảng (−π + k2π,k2π) và giảm ngặt trên các
khoảng (k2π,π + k2π).
CHƯƠNG 1. ỨNG DỤNG CỦA HÀM MỘT BIẾN TRONG KINH TẾ Trang 6 lOMoAR cPSD| 47207194 TOÁN CAO CẤP 2
TS. Đặng Lê Quang. Sđt: 0764060787 ⋆ Hàm số bị chặn:
Cho các tập hợp X,Y ⊂ R và hàm số f : X → Y . Hàm số f(x) bị chặn trên (hoặc chặn
dưới) trong tập X ⊂ R nếu tồn tại một số M sao cho:
f(x) ≤ M hoặc
với mọi x ∈ X
Nếu hàm số f(x) vừa bị chặn trên, vừa bị chặn dưới trên X thì ta nói rằng f(x) bị chặn
trên X. Nói cách khác, hàm số f(x) bị chặn trong tập X nếu tồn tại một số dương M sao
chovới mọi x ∈ X.
Ví dụ 1.4. Xét các hàm số sau:
a. Hàm số y = sin(x) bị chặn trên R vì −1 ≤ sin(x) ≤ 1.
b. Hàm số y = x2 bị chặn dưới vì x2 luôn lớn hơn hoặc bằng 0 với mọi x ∈ R.
⋆ Hàm số chẵn và hàm số lẻ:
Ta nói một tập hợp X ⊂ R đối xứng nếu với mọi x ∈ X thì −x ∈ X.
• Hàm số f(x) xác định trên tập đối xứng X được gọi là hàm chẵn nếu với mọi x ∈ X
ta có f(−x) = f(x). Chẳng hạn các hàm số y = x4, y = cos(x), y = |x| là những hàm số
chẵn. Đồ thị của hàm số chẵn nhận trục tung làm trục đối xứng.
• Hàm số f(x) xác định trên tập đối xứng X được gọi là hàm lẻ nếu với mọi x ∈ X ta có
f(−x) = −f(x). Chẳng hạn các hàm số y = x3, y = sin(x) là những hàm số lẻ. Hàm số lẻ
có đồ thị đối xứng qua gốc tọa độ.
⋆ Các hàm số thường gặp
1. Hàm số lũy thừa: y = xα (α ∈ R,α = 0)̸ . Miền xác định của hàm số này phụ thuộc vào α.
• Nếu α nguyên dương thì D = R.
• Nếu α nguyên âm thì D = R \ {0}.
• Nếu α là số dương không nguyên thì D = [0,+∞).
CHƯƠNG 1. ỨNG DỤNG CỦA HÀM MỘT BIẾN TRONG KINH TẾ Trang 7 lOMoAR cPSD| 47207194 TOÁN CAO CẤP 2
TS. Đặng Lê Quang. Sđt: 0764060787
• Nếu α là số âm không nguyên thì D = (0,+∞).
Hàm số tăng ngặt nếu α > 0 và giảm ngặt nếu α < 0. Đồ thị hàm số lũy thừa luôn đi qua điểm (1,1).
2. Hàm số mũ: y = ax (a > 0,a ̸= 1). Miền xác định là D = R. Miền giá trị là (0,+∞). Hàm số
tăng nếu a > 1 và giảm nếu 0 < a < 1. Đồ thị hàm số luôn đi qua điểm (0,1), nằm phía
trên và tiệm cận với trục hoành.
3. Hàm số logarit: y = loga(x) (a > 0,a ̸= 1). Miền xác định là D = (0,+∞). Là hàm số ngược
của hàm số y = ax. Đồ thị hàm số đối xứng với đồ thị hàm số mũ y = ax qua đường
phân giác thứ nhất. Hàm số tăng nếu a > 1 và giảm nếu 0 < a < 1.
4. Các hàm số lượng giác:
• Hàm số y = sin(x); y = cos(x). Tập xác định D = R, tập giá trị là [−1,1], tuần hoàn với chu kì 2π.
• Hàm số y = tan(x). Tập xác định
. Tập giá trị là R, tăng ngặt trong các khoảng
, tuần hoàn với chu kì π.
• Hàm số y = cot(x). Tập xác định D = R\{kπ : k ∈ Z}, tập giá trị là R, tăng ngặt trong các khoảng
, tuần hoàn với chu kì π.
⋆ Các hàm số lượng giác ngược:
1. Hàm số y = arcsin(x).
• Hàm số y = sin(x) tăng ngặt trên đoạn
nên có hàm số ngược kí hiệu là x
= arcsin(y). Nếu dùng chữ x để chỉ biến số độc lập và biến y để chỉ biến số phụ
thuộc, thì hàm số được kí hiệu là y = arcsin(x).
• Hàm số y = arcsin(x) có tập xác định là D = [−1,1], tập giá trị .
Hơn nữa, hàm số y = arcsin(x) là hàm số lẻ và tăng.
2. Hàm số y = arccos(x).
• Hàm số ngược của hàm số y = cos(x) trên đoạn [0,π] được kí hiệu là y =
CHƯƠNG 1. ỨNG DỤNG CỦA HÀM MỘT BIẾN TRONG KINH TẾ Trang 8 lOMoAR cPSD| 47207194 TOÁN CAO CẤP 2
TS. Đặng Lê Quang. Sđt: 0764060787 arccos(x).
• Hàm số y = arccos(x) có tập xác định là D = [−1,1], tập giá trị [0,π]. Hơn nữa, hàm
số y = arccos(x) là hàm giảm.
3. Hàm số y = arctan(x).
• Hàm số y = arctan(x) là hàm số ngược của hàm số y = tan(x) trong .
• Hàm số y = arctan(x) có tập xác định là D = R, tập giá trị . Hơn nữa, hàm
số y = arctan(x) là hàm số lẻ và tăng.
4. Hàm số y = arccot(x).
• Hàm số y = arccot(x) là hàm số ngược của hàm số y = cot(x) trong (0,π).
• Hàm số y = arccot(x) có tập xác định là D = R, tập giá trị (0,π). Hơn nữa, hàm số
y = arccot(x) là hàm giảm.
5. Các hàm số luỹ thừa, mũ, logarit, các hàm lượng giác và hàm số lượng giácngược
được gọi chung là các hàm sơ cấp cơ bản. Từ những hàm sơ cấp cơ bản, bằng một
số hữu hạn các phép toán cộng, trừ nhân, chia và phép hợp hàm ta xây dựng được
những hàm phức tạp hơn và gọi là các hàm sơ cấp.
1.1.2. Giới hạn của hàm số
Định nghĩa 1.2. Một hàm số f được gọi là liên tục tại a nếu:
lim f(x) = f(a) x→a
Chú ý rằng định nghĩa (1.2) yêu cầu ba điều kiện để f liên tục tại a:
1. f(a) phải xác định
(tức là a phải nằm trong miền xác định của f).
2. lim f(x) tồn tại. x→a
3. lim f(x) = f(a). x→a
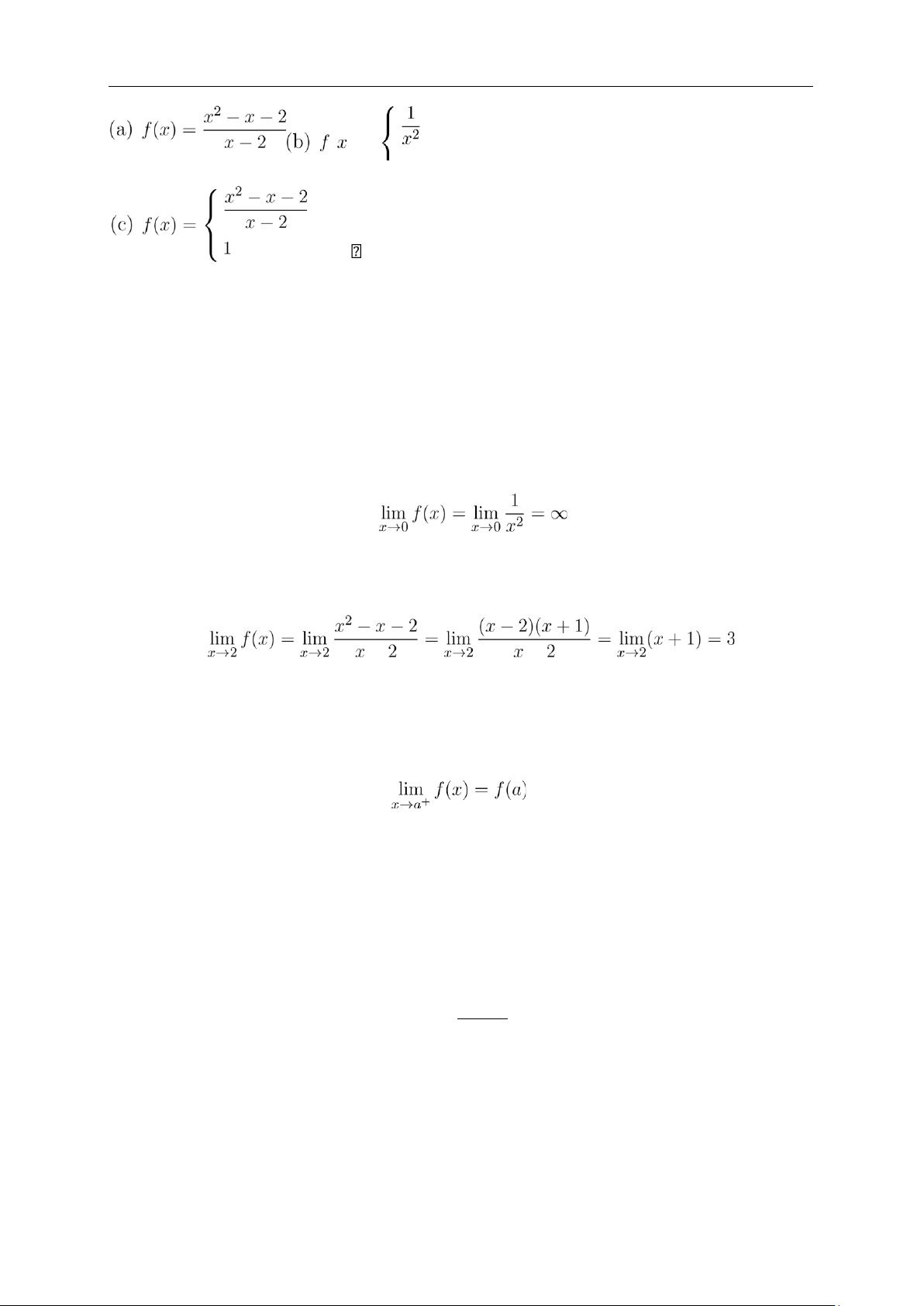
Ví dụ 1.5. Các hàm số sau đây không liên tục tại những điểm nào?
CHƯƠNG 1. ỨNG DỤNG CỦA HÀM MỘT BIẾN TRONG KINH TẾ Trang 9 lOMoAR cPSD| 47207194 TOÁN CAO CẤP 2
TS. Đặng Lê Quang. Sđt: 0764060787 nếu x ̸= 0 ( ) = 1 nếu x = 0
nếu x ̸= 2 nếu x = 2 Giải
(a) Vì f(2) không tồn tại nên f không liên tục tại 2.
(b) Ở đây f(0) = 1 xác định nhưng:
Vì vậy f không liên tục tại 0. (c) Ta xét: − −
Ta thấy vì lim→ = 3 ̸= f(2) = 1 nên f không liên tục tại 2. x 2
Định nghĩa 1.3. Một hàm số f được gọi là liên tục phải tại a nếu:
và liên tục trái tại a nếu:
lim f(x) = f(a) x→a−
Định nghĩa 1.4. Hàm số f gọi là liên tục trên một khoảng nếu nó liên tục tại mọi điểm trên khoảng đó.
Ví dụ 1.6. Chứng minh hàm số f(x) = 1 − √1
− x2 liên tục trên đoạn [−1,1]. Giải
Với −1 < a < 1, ta có:
CHƯƠNG 1. ỨNG DỤNG CỦA HÀM MỘT BIẾN TRONG KINH TẾ Trang 10 lOMoAR cPSD| 47207194 TOÁN CAO CẤP 2
TS. Đặng Lê Quang. Sđt: 0764060787
Xét trên hai đầu mút, ta có:
Vậy f liên tục phải tại −1 và liên tục trái tại 1. Vì vậy, f liên tục trên đoạn [−1,1].
Định lý 1.1. Nếu f và g liên tục tại a và c là một hằng số, thì các hàm số sau đây cũng liên tục tại a: 1. 2. 3. 4. 5. 1.1.3. Đạo hàm
Định nghĩa 1.5. Đạo hàm của hàm số f tại giá trị a, kí hiệu bởi f′(a), là:
nếu giới hạn này tồn tại. Nếu ta viết x = a+h, khi đó ta có h = x−a và h tiến đến 0 nếu và
chỉ nếu x tiến đến a. Vì vậy, một phát biểu tương đương định nghĩa của đạo hàm như
sau: nếu giới hạn trên tồn tại.
Ví dụ 1.7. Tìm đạo hàm của hàm số f(x) = x2 − 8x + 9 tại giá trị a.
CHƯƠNG 1. ỨNG DỤNG CỦA HÀM MỘT BIẾN TRONG KINH TẾ Trang 11 lOMoAR cPSD| 47207194 TOÁN CAO CẤP 2
TS. Đặng Lê Quang. Sđt: 0764060787 Giải Theo định nghĩa (1.5), ta có:
Định nghĩa 1.6. Hàm f khả vi tại a nếu f′(a) tồn tại. Hàm số khả vi trên khoảng mở (a,b)
[hoặc (a,∞) hoặc (−∞,a) hoặc (−∞,∞)] nếu nó khả vi tại mọi số trong khoảng đó.
Các công thức đạo hàm. cot( cot( arccot(
1.2. Giới thiệu hàm kinh tế một biến số ⋆ Hàm cung và hàm cầu
Các nhà kinh tế sử dụng khái niệm hàm cung và hàm cầu để biểu diễn sự phụ thuộc
của lượng cung và lượng cầu của một loại hàng hóa vào giá của hàng hóa đó. Hàm cung và hàm cầu có dạng:
• Hàm cung: QS = S(p)
• Hàm cầu: QD = D(p) Trong đó:
• p là giá hàng hóa.
CHƯƠNG 1. ỨNG DỤNG CỦA HÀM MỘT BIẾN TRONG KINH TẾ Trang 12 lOMoAR cPSD| 47207194 TOÁN CAO CẤP 2
TS. Đặng Lê Quang. Sđt: 0764060787
• QS là lượng cung: tức là lượng hàng hóa người bán bằng lòng bán ở mỗi mức giá.
• QD là lượng cầu: tức là lượng hàng hóa người mua bằng lòng mua ở mỗi mức giá.
Khi xem xét mô hình hàm cung, hàm cầu nói trên ta giả thiết rằng các yếu tố khác không đổi.
Quy luật thị trường trong kinh tế học nói rằng, đối với hàng hóa thông thường, hàm
cung là hàm đơn điệu tăng, còn hàm cầu là hàm đơn điệu giảm. Đồ thị của hàm cung
(hàm cầu) được gọi là đường cung (đường cầu). Giao điểm của đường cung và đường
cầu được gọi là điểm cân bằng của thị trường.
• Chú ý: Trong kinh tế học nhiều khi người ta vẫn gọi hàm ngược của hàm QS = S(p)
là hàm cung và hàm ngược của hàm QD = D(p) là hàm cầu:
QS = S(p) ⇔ p = S−1(QS)
QD = D(p) ⇔ p = D−1(QD)
⋆ Hàm chi phí: là hàm số biểu diễn sự phụ thuộc của tổng chi phí sản xuất (TC) vào sản
lượng (Q): TC = TC(Q).
⋆ Hàm doanh thu: là hàm số biểu diễn sự phụ thuộc của tổng doanh thu (TR) vào sản
lượng (Q): TR = TR(Q).
⋆ Hàm lợi nhuận: là hàm số biểu diễn sự phụ thuộc của tổng lợi nhuận π vào sản lượng
(Q): π = π(Q).
Hàm lợi nhuận có thể xác định bởi π(Q) = TR(Q) − TC(Q).
⋆ Hàm lợi ích (hàm tiêu dùng): Các nhà kinh tế sử dụng hàm tiêu dùng để biểu diễn sự
phụ thuộc của biến tiêu dùng (C) vào thu nhập (Y): C = C(Y ). ⋆ Hàm tiết kiệm: Là hàm
số biểu diễn sự phụ thuộc của biến tiết kiệm (S) vào thu nhập (Y ): S = S(Y ).
⋆ Hàm sản xuất ngắn hạn
Các nhà kinh tế học sử dụng khái niệm hàm sản xuất để mô tả sự phụ thuộc của sản
lượng hàng hóa (tổng số lượng sản phẩm hiện vật) của một nhà sản xuất vào các yếu
tố đầu vào, gọi là các yếu tố sản xuất, như vốn và lao động, ... Trong kinh tế học, khái
niệm ngắn hạn và dài hạn được hiểu theo nghĩa sau:
• Ngắn hạn là khoảng thời gian ít nhất một trong các yếu tố sản xuất không thể thay đổi.
• Dài hạn là khoảng thời gian mà tất cả các yếu tố sản xuất có thể thay đổi.
CHƯƠNG 1. ỨNG DỤNG CỦA HÀM MỘT BIẾN TRONG KINH TẾ Trang 13 lOMoAR cPSD| 47207194 TOÁN CAO CẤP 2
TS. Đặng Lê Quang. Sđt: 0764060787
Khi phân tích sản xuất, người ta thường quan tâm đến hai yếu tố sản xuất quan trọng
là vốn (Capital) và lao động (Labour), được kí hiệu tương ứng là K và L. Ví dụ hàm sản
xuất dạng Cobb-Douglas phụ thuộc vào một trong hai yếu tố vốn và lao động: Q = aKα;
Q = bKβ với a,b,α,β là các số dương.
⋆ Hàm đầu tư phụ thuộc vào lãi suất: I = I(r), trong đó r là lãi suất.
⋆ Hàm quỹ vốn theo thời gian: K = K(t), trong đó t là thời gian.
⋆ Hàm đầu tư theo thời gian: I = I(t), trong đó t là thời gian.
1.3. Ứng dụng của dãy số 1.3.1. Cấp số nhân
Định nghĩa 1.7. Cấp số nhân là một dãy số (un) thỏa điều kiện: un+1 = un · q, ∀n = 1,2,3,...
với q là một hằng số không đổi. Ta gọi q là công bội của cấp số nhân. Hơn nữa khi |q| <
1 thì cấp số nhân được gọi là cấp số nhân lùi vô hạn. Ta có các công thức sau:
Nếu cấp số nhân là lùi vô hạn, tức |q| < 1, thì:
1.3.2. Ứng dụng trong phân tích tài chính
a) Tính giá trị hiện tại và giá trị tương lai của tiền tệ
Giả sử một người có một khoản tiền A đồng gửi vào ngân hàng nào đó với một mức
lãi suất cố định thì sau một khoảng thời gian người đó sẽ nhận một khoản tiền lớn hơn
là B = A+ tiền lãi.
Khoản B đồng đó được gọi là giá trị tương lai của khoản A đồng hôm nay. A gọi là giá
trị hiện tại của khoản B đồng mà người đó sẽ có được trong tương lai.
Trong thị trường tiền tệ, lãi suất được xem như giá của các khoản tiền cho vay. Lãi
suất được quy định rất khác nhau. Trong kinh tế học, khi phân tích hoạt động tài chính,
người ta giả thiết rằng có một mức lãi suất chung. Ta gọi mức lãi suất chung là r.
Giả sử một người có một khoản tiền A đồng thì sau một năm, với lãi suất r một năm,
người đó sẽ có một khoản tiền gộp cả lãi lẫn gốc là:
Bt = A + rA = (1 + r)A
CHƯƠNG 1. ỨNG DỤNG CỦA HÀM MỘT BIẾN TRONG KINH TẾ Trang 14 lOMoAR cPSD| 47207194 TOÁN CAO CẤP 2
TS. Đặng Lê Quang. Sđt: 0764060787
Gọi Bt là số tiền người đó có sau t năm , ta có một dãy cấp số nhân với công bội q = 1 + r. Ta có:
Bt = B0qt = A(1 + r)t
Giá trị tương lai của A đồng người đó có hôm nay sau t năm là:
B = A(1 + r)t
Giá trị hiện tại của một khoản B đồng mà người đó nhận được sau t năm là:
Ví dụ 1.8. Một dự án đầu tư đòi hỏi chi phí hiện tại 200 triệu đồng và sẽ đem lại 300
triệu đồng sau 4 năm. Với lãi suất 6%, hãy đánh giá xem có nên thực hiện dự án này không? Giải
Ta có giá trị tương lai của 200 triệu đồng 4 năm sau là:
A = 200 · (1 + 0.06)4 ≈ 252,5 (triệu đồng)
Con số này nhỏ hơn 300 triệu sẽ thu về, nên ta sẽ thực hiện dự án.
b) Kỳ khoản và giá trị của các luồng vốn
Kỳ khoản là các khoản tiền tích góp đều đặn theo định kỳ (hàng tháng, hàng quý,
hàng năm ...). Kỳ khoản định kỳ hàng năm được gọi là niên khoản hay niên kim (annuity).
Tiền nộp đoàn phí hàng tháng, các khoản tiền thanh toán cho một hàng hóa mua
theo phương thức trả góp là các kỳ khoản.
Sử dụng phương pháp tính giá trị hiện tại và giá trị tương lai đã nêu ở trên và công
thức tính tổng các số hạng của một cấp số nhân ta có thể tính được giá trị hiện tại và
giá trị tương lai của một luồng kỳ khoản.
Ví dụ 1.9. Một dự án đầu tư sau một năm sẽ đem lại cho bạn $3000 mỗi năm, liên tiếp
trong 7 năm sau đó. Hỏi rằng luồng vốn phải đầu tư ban đầu là bao nhiêu thì bạn có
thể chấp nhận dự án đó trong điều kiện lãi suất 10% một năm? Giải Giá
trị hiện tại của luồng thu nhập (PV):
CHƯƠNG 1. ỨNG DỤNG CỦA HÀM MỘT BIẾN TRONG KINH TẾ Trang 15 lOMoAR cPSD| 47207194 TOÁN CAO CẤP 2
TS. Đặng Lê Quang. Sđt: 0764060787
Vậy dự án chỉ có thể được chấp nhận nếu số vốn phải đầu tư ban đầu nhỏ hơn $14605,26.
Ví dụ 1.10. Giả sử bạn định mua một chiếc xe ôtô theo phương thức trả góp. Theo
phương thức này, sau một tháng kể từ khi nhận hàng bạn phải trả đều đặn mỗi tháng
một lượng tiền nhất định, liên tiếp trong 60 tháng. Giả sử giá xe máy vào thời điểm bạn
mua xe là $15000 và giả sử lãi suất ngân hàng là 1%/tháng. Với mức phải trả hàng tháng
là bao nhiêu thì việc mua trả góp là chấp nhận được? Giải
Gọi a là khoản phải trả hàng tháng. Giá trị hiện tại của toàn bộ luồng tiền trả góp tại
thời điểm nhận hàng là:
Việc mua trả góp sẽ tương đương với việc mua trả ngay nếu:
PV = 49,96a = 15000 ⇔ a ≈ 300,24
CHƯƠNG 1. ỨNG DỤNG CỦA HÀM MỘT BIẾN TRONG KINH TẾ Trang 16 lOMoAR cPSD| 47207194 TOÁN CAO CẤP 2
TS. Đặng Lê Quang. Sđt: 0764060787
1.4. Ứng dụng tính liên tục trong toán học và trong kinh tế ⋆ Định lý Weierstrass
Định lý 1.2. Nếu hàm số f(x) liên tục trên đoạn [a,b] thì nó đạt giá trị lớn nhất, nhỏ nhất
trên đoạn [a,b], tức là tồn tại x1,x2 ∈ [a,b] sao cho:
f (x1) = max f(x) và f (x2) = min f(x) x∈[a,b] x∈[a,b]
⋆ Định lý giá trị trung gian
Định lý 1.3. Giả sử f(x) liên tục trên đoạn [a,b] và f(a) ̸= f(b). Khi đó nếu lấy một giá trị c
bất kì giữa f(a) và f(b) tức là f(a) < c < f(b) hay f(b) < c < f(a) thì tồn tại x0 ∈ (a,b) sao cho
f(x0) = c.
Hệ quả 1.1. Nếu hàm số f(x) liên tục trên đoạn [a,b] và f(a) · f(b) < 0 thì tồn tại x0 ∈ (a,b)
sao cho f(x0) = 0. Tức phương trình f(x) = 0 có ít nhất một nghiệm thuộc (a,b).
Ví dụ 1.11. Cho mô hình cân bằng thị trường QS = QD. Trong đó:
Chứng minh rằng mô hình trên có giá cân bằng thuộc khoảng (3,5). Ta có: (1.1)
Xét hàm số f(P) = 0,1P3 + 4,8P2 − 70 liên tục trên [3,5]. Ta có f(3) · f(5) < 0 nên phương
trình (1.1) có nghiệm trong khoảng (3,5). Suy ra mô hình trên có giá trị cân bằng thuộc khoảng (3,5).
1.5. Ứng dụng của đạo hàm trong phân tích kinh tế
1.5.1. Đạo hàm và giá trị cận biên
Cho hàm số y = f(x) với x,y là các biến số kinh tế, gọi x0 là một điểm thuộc TXĐ của hàm số. Hàm số:
My = f′(x)
được gọi là hàm cận biên. Giá trị My(x0) được gọi là giá trị cận biên của hàm số f(x) tại
điểm x0 (hay giá trị cận biên tại x0).
CHƯƠNG 1. ỨNG DỤNG CỦA HÀM MỘT BIẾN TRONG KINH TẾ Trang 17 lOMoAR cPSD| 47207194 TOÁN CAO CẤP 2
TS. Đặng Lê Quang. Sđt: 0764060787
Ý nghĩa: Tại x0, khi đối số x thay đổi một đơn vị thì giá trị hàm số f(x) thay đổi một
lượng xấp xỉ bằng My(x0) = f′(x0).
Ví dụ 1.12. Cho hàm sản xuất ngắn hạn Q = 40√K; K > 0.
a. Tìm hàm sản lượng cận biên của lao động MPK = Q′(K).
b. Tại K0 = 100, nếu tăng K thêm một đơn vị, hỏi sản lượng sẽ thay đổi bao nhiêu đơn vị? Giải a. Ta có: b. Ta có:
. Vậy K0 = 100, nếu tăng K lên một đơn vị thì sản lượng
sẽ tăng xấp xỉ 2 đơn vị.
Ví dụ 1.13. Một công ty độc quyền sản xuất một loại sản phẩm và tiêu thụ sản phẩm đó
trên thị trường với hàm cầu: Q = 1500 − 5p
Hãy tính doanh thu cận biên tại mức sản lượng Q = 650 và giải thích ý nghĩa. Giải Ta có . Do đó hàm doanh thu là:
Doanh thu cận biên của công ty là:
Tại mức sản lượng Q = 500, ta có:
Điều đó có nghĩa, tại mức sản lượng 500, nếu sản xuất thêm 1 sản phẩm thì tổng doanh
thu của công ty sẽ tăng thêm $40.
CHƯƠNG 1. ỨNG DỤNG CỦA HÀM MỘT BIẾN TRONG KINH TẾ Trang 18




