












Preview text:
lOMoAR cPSD| 47305584 MỤC LỤC Nội dung Trang
CHƢƠNG 1 TẬP HỢP VÀ ÁNH XẠ ..........................................................................
3 1.1. Tập hợp .......................................................... Error! Bookmark not defined.
1.1.1. Các khái niệm cơ bản ............................ Error! Bookmark not defined. 1.1.2.
Các phép toán trên tập hợp ................... Error! Bookmark not defined.
1.2. Ánh xạ ............................................................ Error! Bookmark not defined.
1.2.1. Khái niệm về ánh xạ .............................. Error! Bookmark not defined. 1.2.2.
Phép hợp các ánh xạ ............................. Error! Bookmark not defined.
1.3. Cấu trúc ại số ............................................... Error! Bookmark not defined. 1.3.1.
Cấu trúc nhóm ....................................... Error! Bookmark not defined. 1.3.2.
Cấu trúc vành ........................................ Error! Bookmark not defined. 1.3.3.
Cấu trúc trường ..................................... Error! Bookmark not defined.
1.4. Trƣờng số thực ............................................... Error! Bookmark not defined.
1.5. Trƣờng số phức .............................................. Error! Bookmark not defined.
1.5.1. Khái niệm .............................................. Error! Bookmark not defined. 1.5.2.
Các phép toán trên trường số phức ...... Error! Bookmark not defined. 1.5.3.
Giải phương trình .................................. Error! Bookmark not defined.
Bài tập chƣơng 1 ..................................................... Error! Bookmark not defined.
CHƢƠNG 2 MA TRẬN - ĐỊNH THỨC ..................................................................... 4
2.1. Một số khái niệm cơ bản về ma trận .................................................................. 4
2.2. Các phép toán cơ bản của ma trận ..................................................................... 7
2.2.1. Phép cộng hai ma trận cùng cấp ................................................................ 7
2.2.2. Phép nhân vô hướng một phần tử của K với một ma trận ......................... 8
2.2.3. Tích của hai ma trận ................................................................................... 8
2.3. Định thức .......................................................................................................... 10
2.3.1. Hoán vị ......................................................................................................11
2.3.2. Định thức của ma trận vuông ................................................................... 13
2.3.3. Các tính chất cơ bản của ịnh thức ........................................................... 16
2.3.4. Một số phương pháp tính ịnh thức ........................................................... 22
2.3.5. Định thức của ma trận tích ....................................................................... 29
2.4. Hạng của ma trận .............................................................................................. 31
2.4.1. Khái niệm .................................................................................................. 31
2.4.2. Một số phương pháp tính hạng của ma trận ............................................ 32
2.5. Ma trận nghịch ảo ............................................................................................. 36
2.5.1. Khái niệm .................................................................................................. 36
2.5.2. Sự duy nhất của ma trận nghịch ảo .......................................................... 36
2.5.3. Sự tồn tại của ma trận nghịch ảo .............................................................. 36
2.5.4. Một số phương pháp tìm ma trận nghịch ảo ............................................. 38
Bài tập chƣơng 2 ..................................................................................................... 42 1 lOMoAR cPSD| 47305584
CHƢƠNG 3 KHÔNG GIAN VECTƠ ....................................................................... 48
3.1. Khái niệm về không gian vectơ........................................................................ 48
3.1.1. Không gian vectơ tổng quát ..................................................................... 48
3.1.2. Không gian vectơ Rn ................................................................................. 50
3.2. Tính chất của không gian vectơ ....................................................................... 52
3.3. Mối quan hệ tuyến tính giữa các vectơ trong không gian vectơ V .................. 53
3.3.1. Các ịnh nghĩa ............................................................................................ 53
3.3.2. Các tính chất ............................................................................................. 56
3.4. Hạng của hệ vectơ – số chiều của không gian vectơ ....................................... 57
3.4.1. Hạng của hệ vectơ – số chiều của không gian vectơ V ............................. 57
3.4.2. Hạng của hệ vectơ – số chiều của không gian vectơ Rn ........................... 67
3.5. Không gian vectơ con ...................................................................................... 72
3.6. Tích vô hƣớng trong không gian Rn ................................................................ 76
Bài tập chƣơng 3 ..................................................................................................... 81
CHƢƠNG 4 HỆ PHƢƠNG TRÌNH TUYẾN TÍNH ................................................. 85
4.1. Khái niệm về hệ phƣơng trình tuyến tính ........................................................ 85
4.1.1. Các ịnh nghĩa ............................................................................................ 85
4.1.2. Các phép biến ổi tương ương hệ phương trình: ....................................... 88
4.2. Cách giải hệ phƣơng trình ............................................................................... 90
4.2.1. Hệ phương trình dạng tam giác và dạng bậc thang ................................ 90
4.2.2. Hệ Cramer ................................................................................................. 92
4.2.3. Hệ phương trình tuyến tính tổng quát ....................................................... 97
4.2.4. Hệ phương trình tuyến tính thuần nhất ................................................... 103
4.3. Một số mô hình tuyến tính trong phân tích kinh tế ........................................ 109
4.3.1. Mô hình cân bằng thị trường n hàng hóa có liên quan ......................... 109
4.3.2. Mô hình cân ối liên ngành (mô hình Input-Output của Leontief ) ........... 111
4.3.3. Mô hình cân bằng thu nhập quốc dân ..................................................... 115
Bài tập chƣơng 4 ................................................................................................... 117
CHƢƠNG 5 ÁNH XẠ TUYẾN TÍNH VÀ DẠNG TOÀN PHƢƠNG .................. 123
5.1. Ánh xạ tuyến tính ........................................................................................... 123
5.1.1. Các khái niệm .......................................................................................... 123
5.1.2. Ma trận của ánh xạ tuyến tính ................................................................ 125
5.2. Giá trị riêng và véc tơ riêng ........................................................................... 130
5.2.1. Các khái niệm .......................................................................................... 130
5.2.2. Chéo hoá một ma trận vuông .................................................................. 132
5.3. Dạng toàn phƣơng ......................................................................................... 139
5.3.1. Các khái niệm .......................................................................................... 139
5.3.2. Đưa dạng toàn phương về dạng chính tắc .............................................. 141
Bài tập chƣơng 5 ................................................................................................... 149
PHỤ LỤC: GIỚI THIỆU PHẦN MỀM MAPLE ..................................................... 152 CHƢƠNG 1 2 lOMoAR cPSD| 47305584
TẬP HỢP VÀ ÁNH XẠ (Tự ọc) 3 lOMoAR cPSD| 47305584
CHƢƠNG 2 MA TRẬN - ĐỊNH THỨC
Ma trận và ịnh thức là một công cụ hữu hiệu giúp chúng ta giải quyết các bài toán về
không gian vectơ Rn và các bài toán về hệ phƣơng trình tuyến tính dễ dàng hơn. Đặc trƣng
của ại số ma trận là xác ịnh các cấu trúc ại số trên tập hợp các ma trận cùng cấp bằng cách
ịnh nghĩa luật hợp thành trong và luật hợp thành ngoài trên tập ó. Mục ích trong chƣơng này
là chúng ta sẽ tập trung nghiên cứu tính chất của lý thuyết ma trận và lý thuyết ịnh thức ể làm
cơ sở liên hệ giải quyết các bài toán về không gian vectơ, phƣơng trình tuyến tính và dạng toàn phƣơng.
2.1. Một số khái niệm cơ bản về ma trận
Cho m, n là các số nguyên dƣơng; K là trƣờng R hoặc C.
Định nghĩa 2.1. Một bảng chữ nhật gồm m n phần tử trong trƣờng K ƣợc xếp thành m dòng và n cột: a a a 11 12 1 n a a 21 22 2 n a A = a a m1 m2 mn a
gọi là ma trận cấp m n; aij là phần tử của ma trận A nằm ở giao iểm của dòng i và cột j (aij K).
Trong chƣơng này, chúng ta chủ yếu xét các ma trận thực, tức là ma trận có các phẩn tử aij là các số thực.
Để ký hiệu ma trận, ngƣời ta thƣờng dùng hai ngoặc vuông nhƣ trên hay hai dấu ngoặc
tròn và có thể viết gọn nhƣ sau:
A = [aij]m×n hoặc A = (aij)m n hoặc Am n 2 3 7
Ví dụ 2.1. Cho A = 0 6 1
. Đây là một ma trận cấp 2 3 có: a11 = 2, a12 = -3, a13 = 7
a21 = 0, a22 = 6, a23 = -1 Ma trận cột là ma trận chỉ có một cột Am 1 (n = 1).
Ma trận dòng là ma trận chỉ có một dòng A1 n (m = 1).
Ma trận không là ma trận mà tất cả các phần tử của nó ều bằng 0. Ký hiệu ma trận không
cấp m n là m n hoặc 0 m n 4 lOMoAR cPSD| 47305584 = 00 00 00 là ma trận không cấp 2 3
Ma trận ối của ma trận A = (aij)m n là ma trận (-aij)m n, ký hiệu -A. 1 2 3 4 1 2 3 4 A2x3 = 5 6 7 8
có ma trận ối là: -A2x3 = 5 6 7 8
Ma trận vuông là ma trận có số dòng bằng số cột
Ma trận A = (aij)m n có số dòng m bằng số cột n, ta gọi A là ma trận vuông cấp n; khi ó,
ƣờng chéo chính của A i từ góc trên bên trái xuống góc dƣới bên phải chứa các phần tử a11,
a22, ..., ann, ƣờng chéo phụ của A i từ góc dƣới bên trái lên góc trên bên phải chứa an1, an-1 2, ..., a1n.
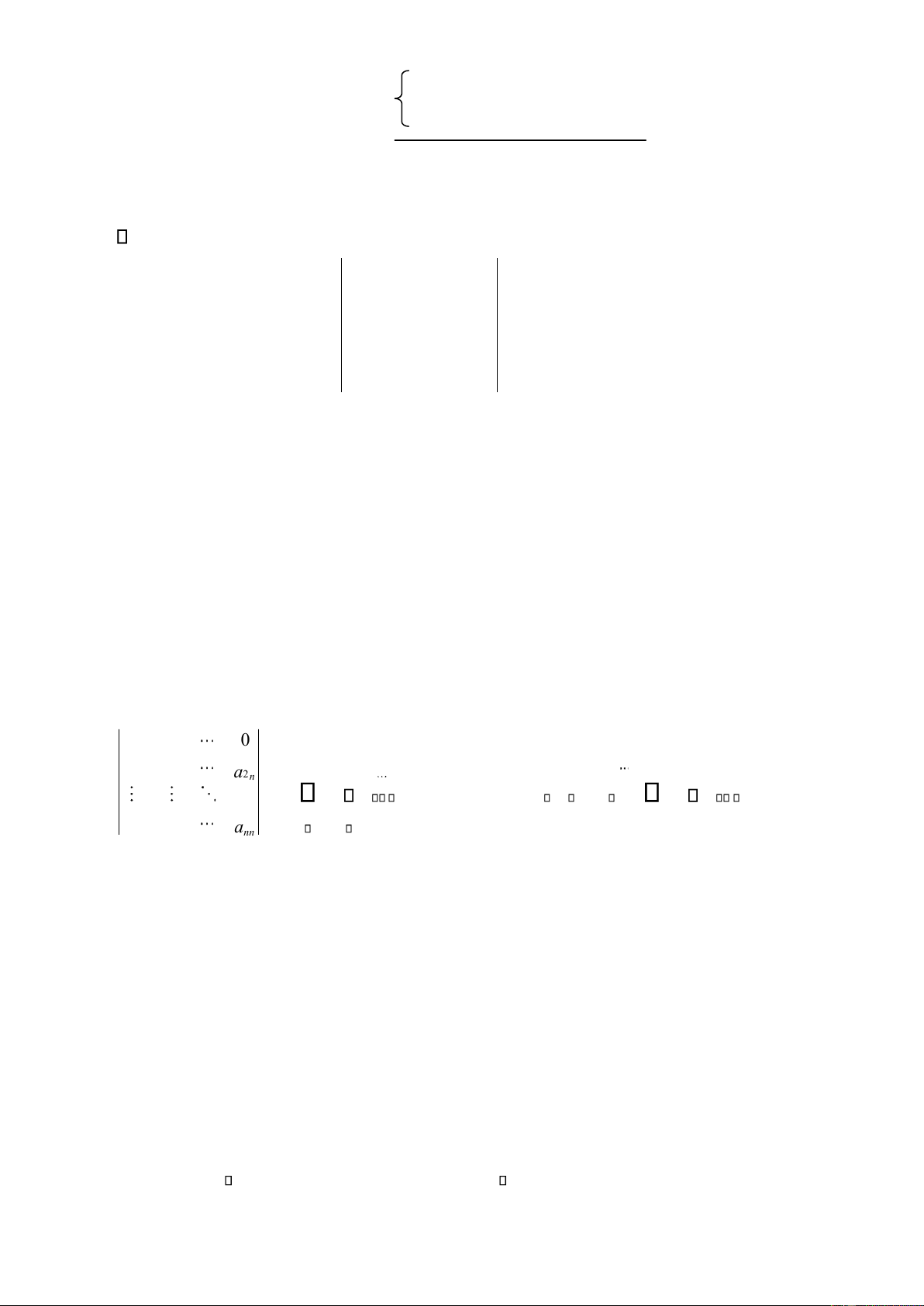
Ma trận tam giác trên là ma trận vuông có mọi phần tử nằm bên dƣới ƣờng chéo chính ều bằng 0: a a a 11 12 1 n 0 a a 22 2 n 0 ann A = (aij = 0 khi i > j) 0
Ma trận tam giác dưới là ma trận vuông có mọi phần tử nằm bên trên ƣờng chéo chính ều bằng 0: 0 11 0 a a 0 21 22 a (aij = 0 khi i < j) a a n1 n2 nn A = a
Ma trận ường chéo là ma trận vuông có mọi phần tử ở ngoài ƣờng chéo chính ều bằng 0: a (aij = 0, i j) 5 lOMoAR cPSD| 47305584 0 11 0 0 a 0 22 0 ann 0
Ma trận ơn vị là ma trận ƣờng chéo có các phần tử thuộc ƣờng chéo chính ều bằng 1, ma
trân ơn vị cấp n ký hiệu là En. 1 0 0 1 0 0 En = 0 0 1
Ma trận chuyển vị của ma trận A là ma trận ký hiệu AT, nhận ƣợc từ ma trận A bằng cách
viết các dòng của A thành các cột với thứ tự tƣơng ứng. Nhƣ vậy: a a a a 11 12 1 n a a 11 21 m1 a a a 21 22 2 n a 12 22 m2 aT A = = a a a a a m1 m2 mn 1 n 2 n mn A a a 4 1 Ví dụ 2.2. A = 3270 thì AT = 14 03 72
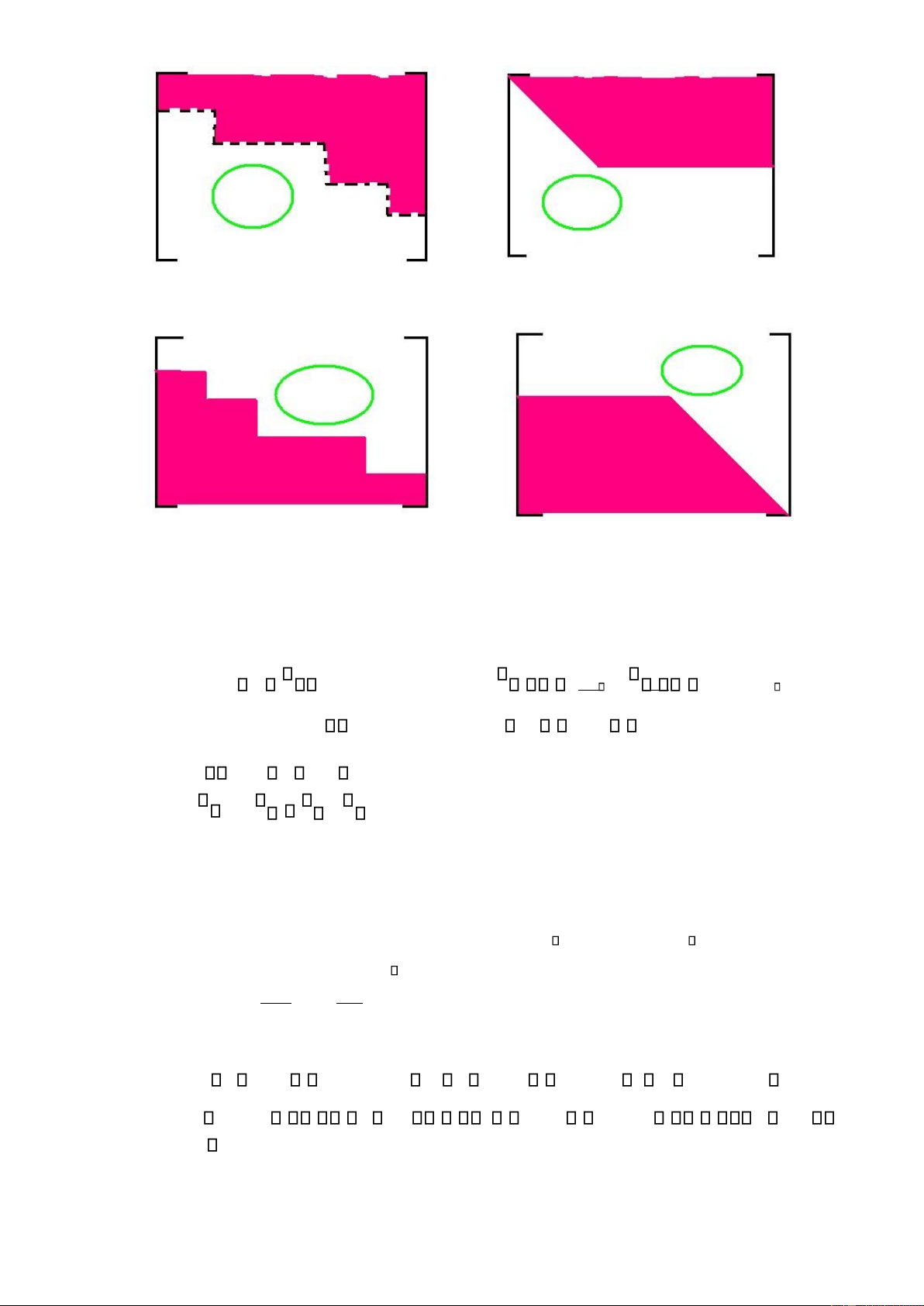
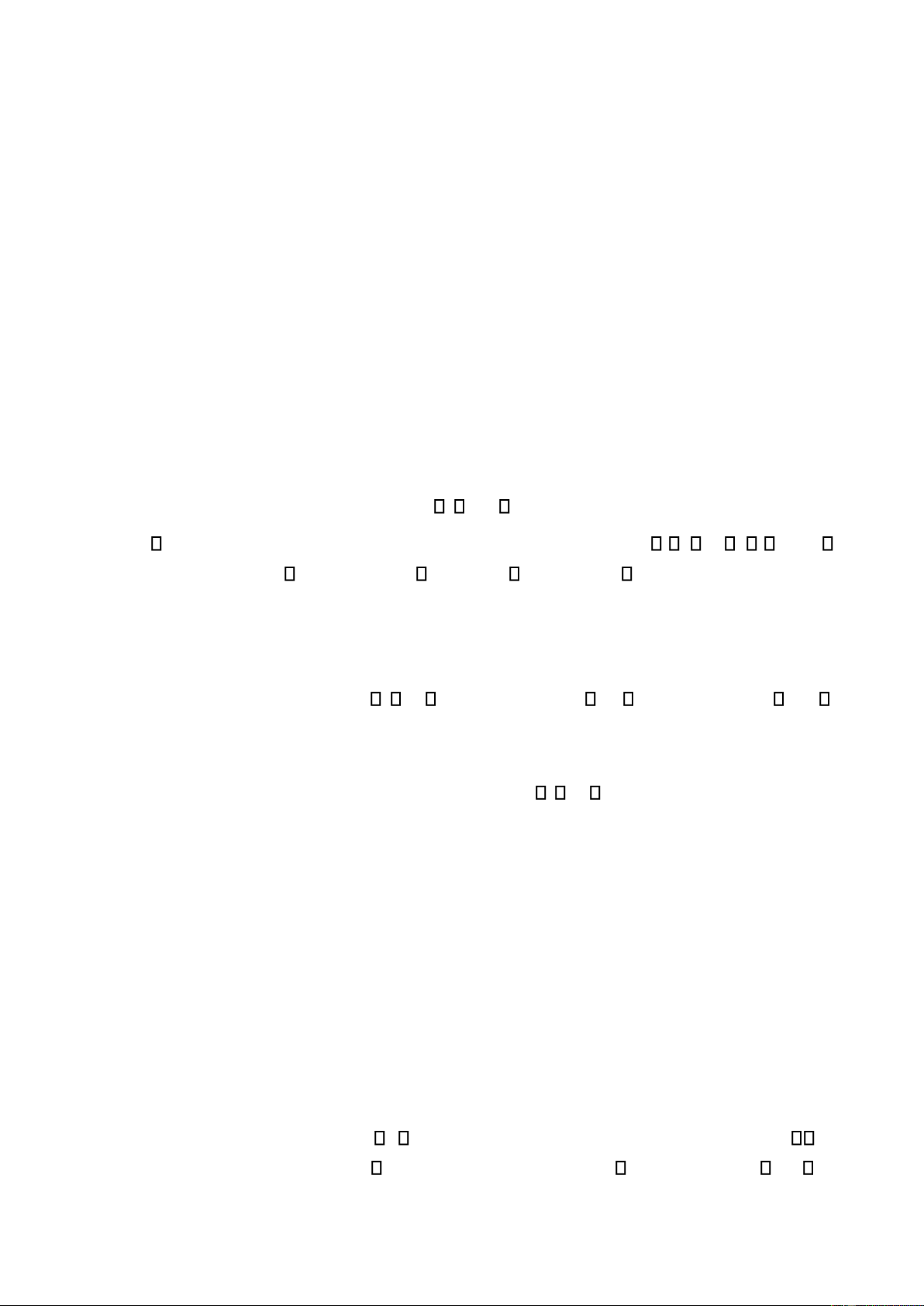
Ma trận bậc thang dòng là ma trận có phần tử khác không ầu tiên của dòng dƣới (tính từ
trái sang) luôn ứng bên phải phần tử khác không ầu tiên của dòng trên. Ma trận bậc thang cột
là ma trận có phần tử khác không ầu tiên của cột bên phải (tính từ trên xuống) luôn nằm ở
dƣới dòng chứa phần tử khác không ầu tiên của cột bên trái. 6 lOMoAR cPSD| 47305584 Ma trận bậc thang dòng Ma trận bậc thang cột
Hai ma trận A, B ược gọi là bằng nhau nếu chúng có cùng cấp và các phần tử ở các vị trí
tƣơng ứng bằng nhau, ký hiệu A = B. A A B 1) A và B cùng c p: Ê aijm n ,B bij m n 2)
aij bij , i 1,m, i 1,n 4 7 a b Ví dụ 2.3.
319 cd có nghĩa là a = -4, b = 7, c = 3, d = 19.
2.2. Các phép toán cơ bản của ma trận
2.2.1. Phép cộng hai ma trận cùng cấp
Định nghĩa 2.2. Cho hai ma trận cùng cấp A = [a ij ]m n và B = [b ij ]m n. Tổng của A và
B là một ma trận cùng cấp C = [c ij ]m n, ký hiệu C = A + B, trong ó:
c ij = a ij + b ij (i = 1, m , j = 1, n )
Nhƣ vậy, muốn cộng hai ma trận cùng cấp, ta cộng các phần tử cùng vị trí với nhau. 3 4 7 2 15 6 3 2 4 15 7 6 5 11 13 Ví dụ 2.4. 0 13 1 1 149 0 ( 1)13 ( 14)1 9 1 1 10 Tính chất 2.1 7 lOMoAR cPSD| 47305584
Từ tính chất của phép cộng hai số, ta có các tính chất sau cho các ma trận cùng cấp
t1. Tính chất giao hoán: A + B = B + A t2. Tính kết hợp: (A + B) + C = A + (B
+ C) t3. A = [aij]m×n, m n: A + m n = A
t4. A = [aij]m×n, ma trận ối của A là –A = [-aij]m×n thỏa mãn A + (-A) = m n Chú ý
2.1. Gọi Matm n (K) là tập các ma trận cấp m n trên trƣờng K. Khi ó: Matm n (K), là một nhóm giao hoán.
2.2.2. Phép nhân vô hướng một phần tử của K với một ma trận
Định nghĩa 2.3. Cho A = [a ij ]m n, k K.
Tích kA là một ma trận C = kA cấp m n xác ịnh bởi:
c ij = k.a ij ( i = 1, m , j = 1, n )
Một phần tử của trường K ta gọi là một số
Nhƣ vậy, muốn nhân một số với một ma trận, ta nhân số ó với tất cả các phần tử của ma trận. Ví dụ 2.5. 5 2 7 1 3 5 3 2 3 ( 7) 3 1 15 6 21 3 0 9 0 27 3 2 3 0 3 9 4 1 3 ( 1) 12 3 6 2 6 3 ( 2) 3 4 3 2 8 24 6 3 6 3 8 18 Tính chất 2.2.
Với mọi A B, Matm n (K), k h, K , ta có tính chất: t1. k(hA) = (k. h)A = h(kA). t2. k(A + B) = kA + kB. t3 . (k + h)A = kA + hA. t4. 1A = A.
Chú ý 2.2. Trong trƣờng hợp các ma trận cùng cấp, phép trừ hai ma trận ƣợc xác ịnh
thông qua phép cộng với ma trận ối. Hiệu của ma trận A và ma trận B ƣợc ịnh nghĩa nhƣ sau: A – B = A + (-B)
2.2.3. Tích của hai ma trận
Định nghĩa 2.4. Ta gọi tích của ma trận A = [aij]m n với ma trận B = [bij]n p là một ma
trận C = [cij]m p, ký hiệu C = AB mà các phần tử cij ƣợc xác ịnh nhƣ sau: = c n ij
a bik kj , i = 1, m , j = 1, p 8 lOMoAR cPSD| 47305584 k 1
Quy tắc này có thể minh họa bằng hình sau: 1 b j Dòng i 2 b j a 1 i i a 2 in a ij c nj b np mn mp Cột j
Chú ý 2.3. Tích AB của hai ma trận A và B chỉ ƣợc xác ịnh khi số cột của A phải bằng số
dòng của B. Khi ó, AB có số dòng bằng số dòng của ma trận A và số cột bằng số cột của ma
trận B. Muốn nhân BA (B bên trái, A bên phải) phải có iều kiện: số cột của B bằng số dòng
của A, do ó khi tồn tại tích AB nhƣng chƣa chắc tồn tại tích BA. Trƣờng hợp ặc biệt khi A
và B là hai ma trận vuông cùng cấp thì phép nhân AB và BA ều ƣợc. Ví dụ 2.6. 2 1 3 Cho A = 7 3 1 0 5 4 11 4 0 6 13 2 . Khi ó tích C = AB gồm các phần
c11 = 7.2 + (-3).(-11)+ 4.0 = 47 tử: , B =
c12 = 7.1 + (-3). 4 + 4.6 = 19
c13 = 7.3 + (-3).2 + 4.13 = 67 c21 = 1.2 + 0.(-11) + 5.0 = 2 c22 = 1.1 + 0. 4 + 5.6 = 31 c23 = 1.3 + 0. 2 + 5.13 = 68 47 19 67 Vậy: C = AB = 2 31 68 Ví dụ 2.7. 2 0 6 5 A = 13 , B = 40 , ta có: 2 ( 6) 0 4 2 5 0 0 12 10 A.B = ( 1) ( 6) = 5 (-1) 5 3 0 3 4 18 9 lOMoAR cPSD| 47305584 ( 6) 2 5 ( 6) 0 5 3 17 15 B.A = ( 1) 4 2 0 ( 4 0 0 3 = 0 1) 8
Nhƣ vậy, phép nhân hai ma trận, nói chung không có tính chất giao hoán. Điều này không
có gì bất ngờ vì trong ịnh nghĩa của ma trận tích, các ma trận A và B tham dự một cách không bình ằng. Tính chất 2.3.
Cho 3 ma trận A, B, C và k K. Giả sử A, B, C thoả mãn các iều kiện ể tồn tại tích các
ma trận. Khi ó, ta có các tính chất sau t1. Tính kết hợp: (AB)C = A(BC) t2. Tính
phân phối ối với phép cộng: (A + B)C = AC + BC A(B + C) = AB + AC t3. k(BC) = (kB)C = B(kC) a b
2 – (a + d)A + (ad – bc)E2 Ví dụ
2.8. Cho ma trận A = c d . Tính A a b 2 a2 bc b(a d) a b a(a d) b(a d) c d c(a d)d2 bc ; (a+d) cd = c(a d)d(a d) (ad – bc)E2 = (ad – bc) 10 10 = ad - bc0 ad - bc0 A2 – (a + d)A + (ad – bc)E2 = 0 0 00 2 2
Chú ý 2.4. i) Phép nhân hai ma trận là một luật hợp thành trong, xác ịnh trên tập hợp các ma trận vuông cấp n.
ii) Theo các tính chất của phép cộng và phép nhân ma trận với ma trận, ta có
thể nói rằng tập hợp các ma trận vuông cấp n trên trƣờng K lập thành một vành (không giao
hoán) gọi là vành các ma trận vuông cấp n trên trƣờng K. 2.3. Định thức
Để chuẩn bị cho việc nghiên cứu lý thuyết ịnh thức, ta giới thiệu trƣớc các khái niệm hoán
vị và nghịch thế. 10 lOMoAR cPSD| 47305584
2.3.1. Hoán vị
Ta xét tập hợp n số tự nhiên ầu tiên: 1, 2, 3, ..., n. Ngoài cách sắp xếp theo thứ tự tự nhiên,
từ nhỏ tới lớn, ta còn có thể sắp xếp chúng theo nhiều cách khác. Chẳng hạn, ta có thể sắp
xếp các số 1, 2, 3 theo 6 cách sau: 123; 132; 213; 231; 312; 321
Định nghĩa 2.5. Mỗi cách sắp xếp các số 1,2, ..., n theo một thứ tự nào ó, gọi là một hoán vị của n số ó.
Dễ dàng chứng minh ƣợc, tập n số tự nhiên ầu tiên có n! (n giai thừa) hoán vị khác nhau (n! = n.(n-1)...2.1).
Ví dụ 2.9. Với ba số 1, 2, 3 có thể lập ƣơc 3! = 3.2.1 = 6 hoán vị khác nhau: 123, 132, 213, 231, 312, 321. Nghịch thế
Mỗi hoán vị của n số tự nhiên ầu tiên ƣợc biểu diễn dƣới dạng: 1 2 ... n
trong ó i (i=1,2,...,n) là số tự nhiên ứng ở vị trí thứ i trong hoán vị (1 i n; i j khi i
j). Khi i < j thì ta nói số i ứng trƣớc số j, hoặc số j ứng sau số i trong hoán vị.
Trong hoán vị 123 của 3 số tự nhiên ầu tiên, các số ƣợc sắp xếp theo thứ tự tăng dần, còn
trong các hoán vị khác thì thứ tự ấy không còn nữa. Ví dụ hoán vị 132 có số 3 ứng trƣớc số
2. Cặp số 3 và 2 gọi là một nghịch thế của hoán vị 132.
Định nghĩa 2.6. Trong hoán vị 1 2... n, nếu i < j nhƣng i > j thì ta nói hai số i và j
tạo thành một nghịch thế. Một hoán vị ƣợc gọi là hoán vị chẵn nếu tổng số nghịch thế của nó
là số chẵn và ƣợc gọi là hoán vị lẻ nếu tổng số nghịch thế của nó là số lẻ.
Ta có thể ếm ƣợc số nghịch thế trong một hoán vị 1 2... n bằng phƣơng pháp ơn giản
sau ây: trƣớc hết. ta ếm xem có bao nhiêu số ứng trƣớc số 1, giả sử có k1 số; rồi ta xóa số 1 i
và ếm xem có bao nhiêu số ứng trƣớc số 2 (không kể số 1 ã bị xóa), giả sử có k2 số; sau ó
xóa số 2 i và ếm xem có bao nhiêu số ứng trƣớc số 3 (không kể các số 1 và 2 ã bị xóa), ...
Khi ó, tổng số các nghịch thế có trong hoán vị ã cho bằng k1+k2+...+kn.
Ví dụ 2.10. Số nghịch thế trong hoán vị 3421 ƣợc tính:
3421 (k1=3), 342 (k2=2), 34 (k3 = 0), 4 (k4=0) Nhƣ
vậy, trong hoán vị 3421 có 3 + 2 + 0 + 0 = 5 nghịch thế.
Định lý 2.1. Nếu trong một hoán vị, ta ổi chỗ hai số bất kỳ và giữ nguyên vị trí các số còn
lại thì hoán vị thay ổi tính chẵn lẻ, tức là hoán vị chẵn biến thành hoán vị lẻ hoặc ngƣợc lại. Chứng minh:
Xét trƣờng hợp 1, các số bị ổi , ứng kề nhau. Tức là hoán vị ã cho có dạng A B,
trong ó A chỉ tập các số ứng trƣớc và B chỉ tập các số ứng sau . Sau khi ổi chỗ và ta 11 lOMoAR cPSD| 47305584 ƣợc hoán vị A
B, các phần tử trong nhóm A và B giữ nguyên thứ tự. Dễ thấy rằng, trƣớc
và sau phép ổi chỗ và , số các nghịch thế tạo bởi với các nhóm A và B không thay ổi.
Tƣơng tự nhƣ thế với . Ta chỉ cần xem xét sự thay ổi số nghịch thế giữa và .
Nếu < thì ổi chỗ và làm tăng thêm một nghịch thế. Ngƣợc lại, nếu > thì ổi
chỗ và làm giảm i một nghịch thế. Do ó, cả hai trƣờng hợp tính chẵn lẻ của tổng số nghịch
thế bị thay ổi nên tính chẵn lẻ của hoán vị ban ầu bị thay ổi.
Xét trƣờng hợp 2, giữa và có m số, tức là hoán vị có dạng: A 1 2 ... m B
Ta có thể thực hiện phép ổi chỗ và bằng cách thƣc hiện lần lƣợt 2m+1 phép ổi chỗ
hai số kề nhau cho nhau, cụ thể:
Đổi chỗ lần lượt với 1, 2, ..., m. Sau m lần ổi chỗ hai số ứng kề nhau như vậy, ta ược hoán vị: A 1 2 ... m B
Đổi chỗ lần lượt với , m, ..., 2, 1. Sau m+1 lần ổi chỗ hai số ứng kề nhau như vậy, ta ược hoán vị: A 1 2 ... m B
Sau mỗi lần biến ổi, hoán vị thay ổi tính chẵn lẻ, do ó sau 2m+1 lần biến ổi thì hoán vị
chẵn trở thành hoán vị lẻ và hoán vị lẻ trở thành hoán vị chẵn.
Hệ quả 2.1. Nếu n 2 thì trong số n! hoán vị của n số tự nhiên ầu tiên, số các hoán vị
có số nghịch thế chẵn bằng số các hoán vị có số nghịch thế lẻ và bằng n!. 2 Chứng minh:
Gọi p là số hoán vị chẵn và q là số hoán vị lẻ. Đối với mỗi hoán vị chẵn, ta ổi chỗ số ứng
ầu và số ứng ở vị trí cuối cùng. Bằng cách ó, từ p hoán vị chẵn khác nhau, ta nhận ƣợc p hoán
vị lẻ khác nhau, do ó p q. Biến ổi tƣơng tự nhƣ vậy thì từ q hoán vị lẻ khác
nhau, ta nhận ƣợc q hoán vị chẵn khác nhau, do ó q p. Nhƣ vậy, p = q = n!. 2 1 2 n
Hệ quả 2.2. Nếu ổi chỗ các cột của ma trận 1 2 n , ƣa ma trận về dạng 11 22 nn
thì hai hoán vị 1 2... n và hoán vị 1 2... n có cùng tính chẵn lẻ. 12 lOMoAR cPSD| 47305584
Chứng minh: Thật vậy, mỗi phép ổi chỗ các cột của ma trận tƣơng ứng với một phép ổi
chỗ hai số của cả hai hoán vị ở dòng trên và dòng dƣới. Sau cùng một số phép ổi chỗ, hoán
vị 12...n trở thành hoán vị 1 2... n, còn hoán vị 1 2... n ƣợc biến thành hoán vị 12...n. Do
ó, hai hoán vị 1 2... n và 1 2... n có cùng tính chẵn lẻ.
2.3.2. Định thức của ma trận vuông
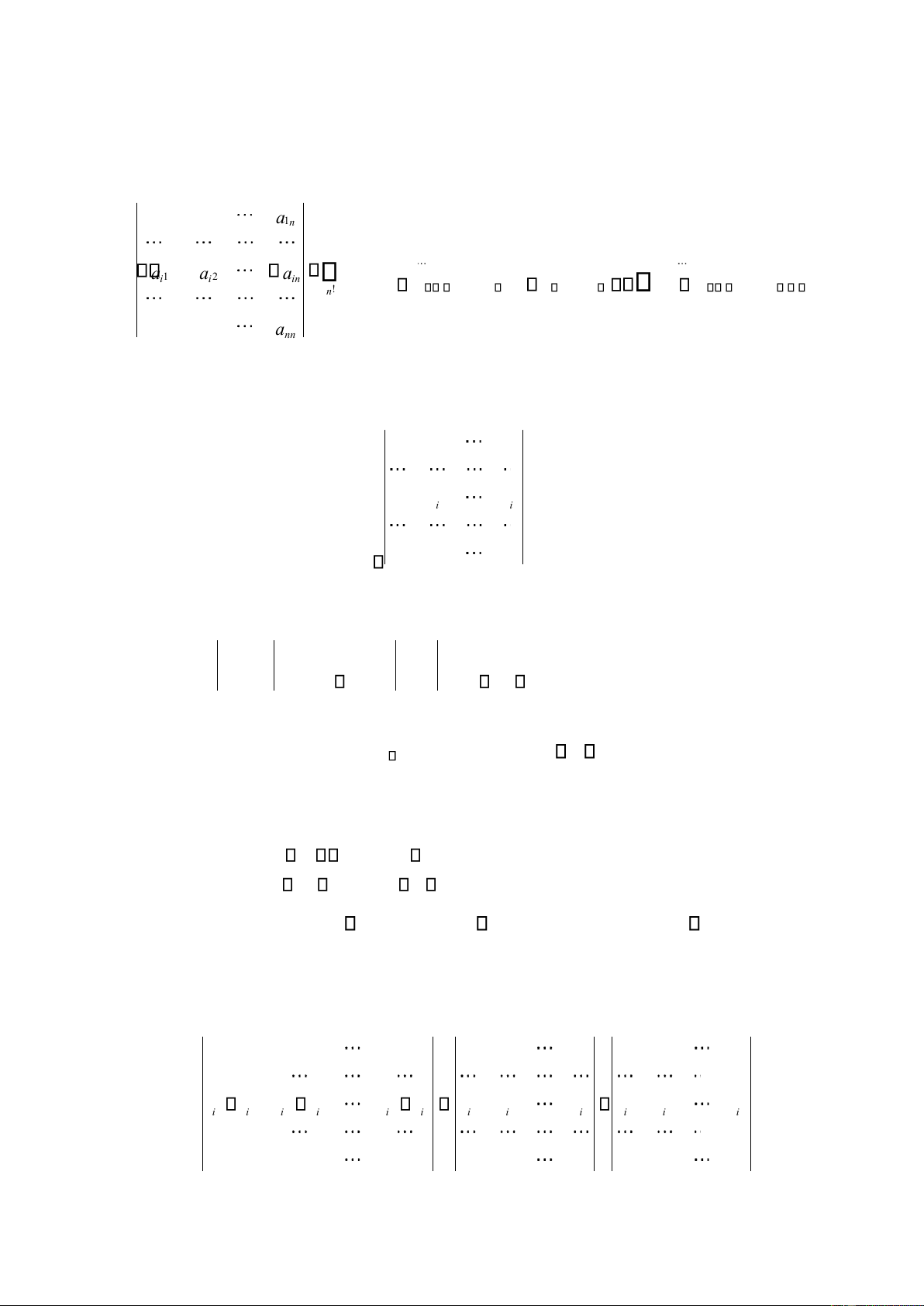
Định nghĩa 2.7. Cho ma trận vuông cấp n: 11 12 a 1 a n a 21 22 a 2 a n 1 n an 2 nn a A = a. a
Định thức cấp n liên kết với ma trận A là một số, ký hiệu là det(A) hoặc |A| hoặc 11 a 12 a 1 a n 21 a 22 a 2 a n , ƣợc tính: det(A) = ( 1) N( 1 2 n ) a1 1a2 2 ...an n n! a 1 n n a 2 nn a Trong
ó: chỉ tổng lấy theo n! số hạng, mỗi số hạng là tích của biểu n!
thứca1 a ...a (biểu thức này tƣơng ứng với n! hoán vị 1 2 2 n n 1 2
n của 1, 2, …, n) với biểu 1 thức dấu N(
1 2... n ) (trong ó N( 1 2... n ) là tổng số nghịch thế của hoán vị 1 2 n);
mỗi số hạng ƣợc gọi là một thành phần của ịnh thức.
Nhƣ vậy, ịnh thức của ma trận vuông A cấp n là tổng ại số của n! thành phần, mỗi thành
phần là tích của n phần tử của A lấy trên n dòng và n cột khác nhau, với dấu ƣợc gán theo các
hoán vị lập thành từ các chỉ số cột (dấu + nếu là hoán vị chẵn, dấu - nếu là hoán vị lẻ), còn
chỉ số dòng ƣợc sắp xếp theo thứ tự tăng dần.
Tính ịnh thức cấp n N (1 n 3)
Định thức cấp 1: det([a11]) = a11
Ví dụ 2.11. Giá trị ịnh thức cấp 1: det([-5]) = -5
Định thức cấp 2 13 lOMoAR cPSD| 47305584 a11
a12 có hai thành phần tƣơng ứng với hai hoán vị của
Định thức của ma trận A = a 21 a 22 tập hợp {1,2}.
Hoán vị 1 2 N( 1 2) ( 1) N( 1 2) a1 1a2 2 12 0 + a11a22 21 1 - a12 a22 Theo ịnh nghĩa, ta có: a11 a12– a12a21 det(A) = = a11a22 a 21 a 22
Nhƣ vậy, ịnh thức cấp 2 bằng tích hai phần tử nằm trên ƣờng chéo chính trừ i tích hai
phần tử nằm trên ƣờng chéo phụ. 1 2
Ví dụ 2.12. = 1. 4 - 2 . 3 = -2 3 4
Định thức cấp 3:
Định thức của ma trận vuông cấp 3 a11 a12 a13 A = a 21 a 22 a 23 a31 a32 a33
có 6 thành phần tƣơng ứng với 6 hoán vị của tập hợp {1, 2, 3}.
Hoán vị 1 2 3 N( 1 2 3) ( 1) N( 1 2 3) a1 1a2 2a3 3 123 0 + a11a22a33 231 2 + a12 a23a31 312 2 + a13a21a32 321 3 - a13a22a31 213 1 - a12a21a33 14 lOMoAR cPSD| 47305584 132 1 - a11a23a32
det(A) = a11a22a33 + a12a23a31 + a13a21a32 - a13a22a31 - a12a21a33 - a11a23a32 Để
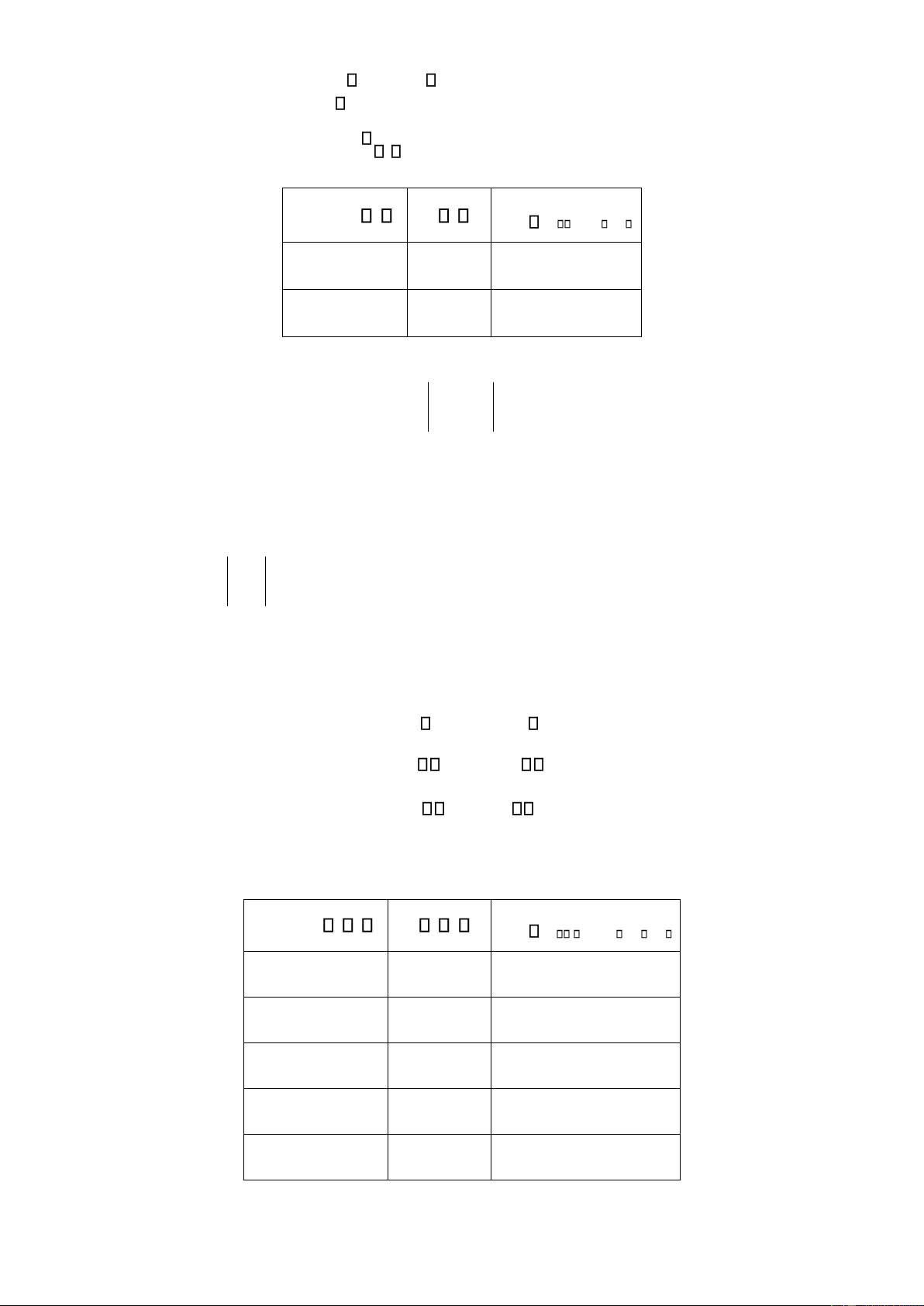
nhớ quy tắc tính ịnh thức cấp 3, ngƣời ta thƣờng dùng “quy tắc Sarrus” sau: • • • Dấu + Dấu -
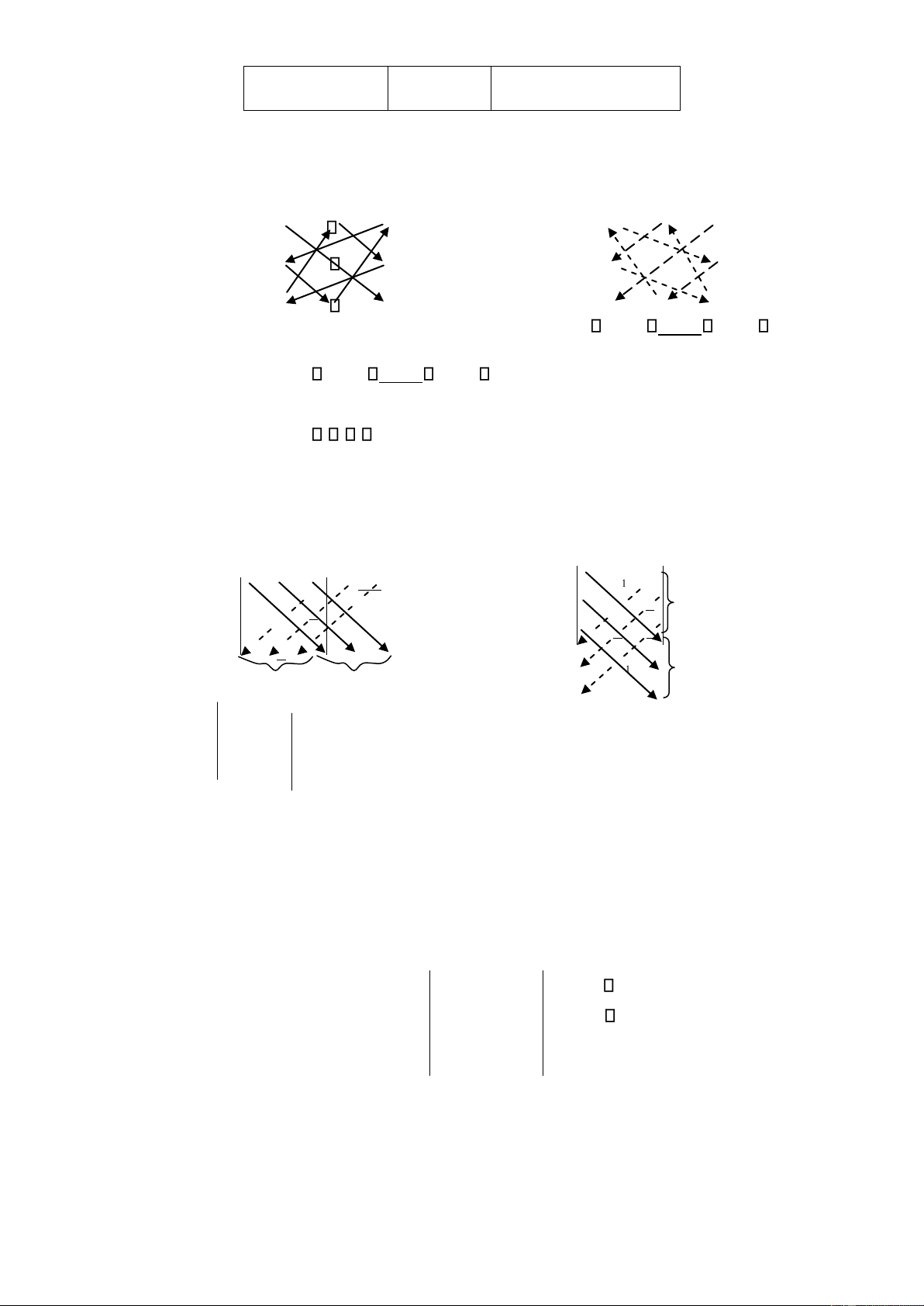
Từ quy tắc Sarrus trên, chúng ta còn một quy tắc khác ể tính nhanh ịnh thức cấp 3: ghép
thêm cột thứ nhất và cột thứ hai vào bên phải ịnh thức hoặc ghép thêm dòng thứ nhất và dòng
thứ hai xuống bên dƣới ịnh thức rồi nhân các phần tử trên các ƣờng chéo nhƣ quy tắc thể hiện trên hình: a1 a b c b1 c1 a1 b1 1 1 1 a b c a 2 2 2 2 b2 c2 a2 b2 Dấu - 3 a 3 b 3 c a3 b3 c3 a3 b3 1 a 1 b 1 c a b c
Dấu - Dấu + Dấu + 2 2 2 3 4 -5 Ví dụ
2.13. 8 7 -2 = 3.7.8 + 4.(-2).2 + (-5).8.(-1) – (-5).7.2 – 4.8.8 – 3.(-2).(-1) = 0 2 -1 8
Dùng ịnh nghĩa ể tính ịnh thức cấp lớn hơn 3 thƣờng chỉ áp dụng với các bài toán có ịnh thức dạng ặc biệt.
Ví dụ 2.14. Tính hệ số của x4 trong biểu thức 2x x x 2 1 x 1 1 f(x) = x 2 x 1 1 1 1 x Giải: 15 lOMoAR cPSD| 47305584
Các thành phần chứa x4 là: + (-1)N(1234)a11a22a33a44 = 2 x4
(-1)N(3214)a13a22a31a44 = - x4
= (-1)N(1234)a11a22a33a44 + (-1)N(3214)a13a22a31a44 = x4
Hệ số của x4 trong f(x) bằng 1.
a1 a2 a3 a4 a5 b1 b2 b3 b4 b5
Ví dụ 2.15. Tính ịnh thức c1 c 0 2 0 0 d1 d 2 0 0 0 e1 e 0 2 0 0 Giải:
Định thức ã cho là tổng ại số của 5! thành phần, mỗi thành phần (không kể dấu) là tích
của 5 phần tử lấy trên 5 dòng và 5 cột khác nhau. Dễ dàng thấy rằng, mỗi thành phần của ịnh
thức ã cho ều chứa thừa số 0 nên các thành phần ều bằng 0. Vậy ịnh thức ã cho bằng 0.
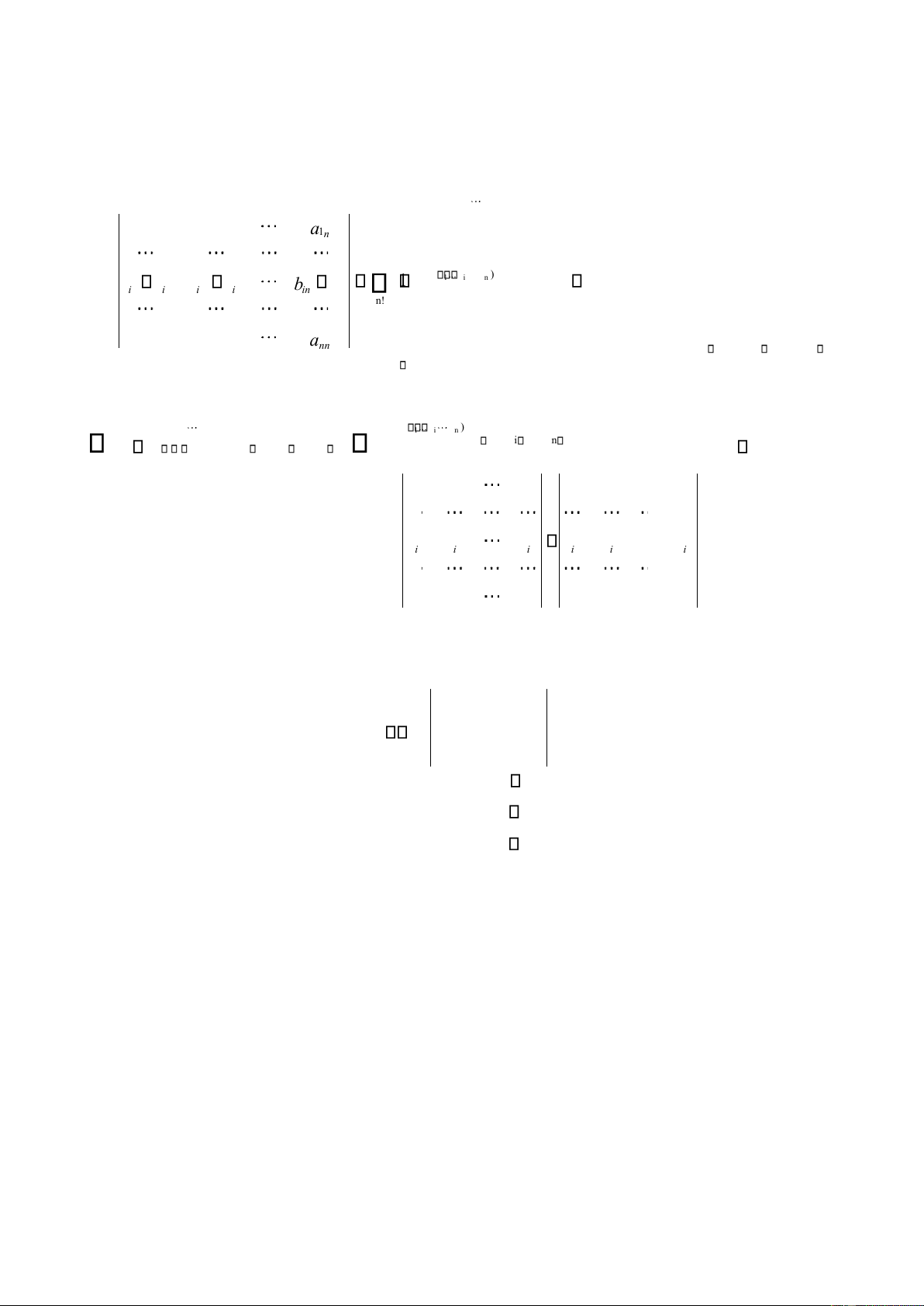
Ví dụ 2.16. Tính ịnh thức của ma trận vuông cấp n trong ó tất cả các phần tử của dòng 1 ều bằng không. Giải: 0 0 0 21 a 22 a 2 a n = ( 1) N( 1 2n ) a1 1a2 2 ...an n = ( 1) N( 1 2 n ) a 1 n n a 2 nn a 0.a2 2 ...an n = 0 n! n!
Khi tính ịnh thức cấp cao thì việc dùng ịnh nghĩa trở nên cồng kềnh, khó khăn. Do ó,
chúng ta cần thêm các phƣơng pháp khác ể tính ịnh thức. Trƣớc khi ề cập ến các phƣơng
pháp tính ịnh thức, chúng ta hãy xem xét các tính chất cơ bản của ịnh thức ể sử dụng khi tính toán.
2.3.3. Các tính chất cơ bản của ịnh thức
Tính chất 2.4. (tính chất chuyển vị)
Định thức của ma trận vuông bằng ịnh thức của ma trận chuyển vị của nó: Chứng minh:
Cho A = [aij]n n có ma trận chuyển vị AT = [bij]n n. Khi ó, bij = aji (i, j = 1, 2, …, n). 16 lOMoAR cPSD| 47305584 Ta có: det(A) = ( 1) N( 1 2 n ) a1 1a2 2 ...an n n! det(AT) = ( 1) N( 1 2 n ) b1 1b2 2 ...bn n n!
Một thành phần bất kỳ trong ịnh thức của ATlà:
( 1) N( 1 2 n ) b1 1b2 2...bn n
Sắp xếp các phần tử bij trong mỗi thành phần của det(AT) theo thứ tự chỉ số cột tăng dần, ta ƣợc:
( 1) N( 1 2 n ) b1 1b2 2...bn n = ( 1) N( 1 2 n ) b 11b 22...b nn ( 1)N( 1 2 n ) a1 1a2 2...an n
Theo hệ quả 2.2 trong mục 2.3.1, hai hoán vị 1 2… n và 1 2… n có cùng tính chẵn lẻ nên
(-1)N( 1 2… n) = (-1)N( 1 2… n) ( 1) N( 1 2 ( 1) n ) b1 1b2 2...bn n N( 1 2 n ) a1 1a2 2...an n
Nhƣ vậy, mỗi thành phần của det(AT) ồng thời cũng là một thành phần của ịnh thức det(A),
do ó n! thành phần của det(AT) ồng thời cũng là n! thành phần của det(A). Từ ó suy ra det(A) = det(AT).
Chú ý 2.5. Từ tính chất chuyển vị, mọi tính chất của ịnh thức úng cho dòng thì cũng úng
cho cột và ngƣợc lại. Do ó, trong các tính chất dƣới ây ta chỉ phát biểu cho các dòng, các tính
chất ó vẫn giữ nguyên giá trị khi thay chữ ”dòng” bằng chữ ”cột”.
Tính chất 2.5. (tính chất thay phiên)
Nếu trong ịnh thức ta ổi chỗ hai dòng cho nhau và giữ nguyên vị trí các dòng còn lại thì ịnh thức ổi dấu. Chứng minh:
Cho A = [aij]n n có det(A) = ( 1) N( 1... i... k n ) a1 1 ...ai i ...ak k ...an n n!
Nếu trong A ta ổi chỗ dòng thứ i và dòng thứ k (ilại, ta ƣợc ma trận A’ có
det(A’) = ( 1) N( 1... k ... in ) a1 1 ...ak k ...ai i ...an n n! 17 lOMoAR cPSD| 47305584 Vì ( 1) N( 1... k ... i n ) ( 1)N( 1... i ... k n ) nên det(A’) = - det(A). a b c Ví dụ 2.17. Cho a' b' c'
= 10. Tính các ịnh thức sau: a'' b'' c'' a'' c'' b''b c a a) a' b' c' b) b' c ' a' a c bb'' c'' a'' Giải: a'' a b'' c'' b c c' = - a' a) a' b'b'
c' = -10 ( ổi chỗ dòng 1 và dòng 3) a a'' b c b'' c'' b b c a a c a' = - b' b) b' c'a'
c' ( ổi chỗ cột 2 và cột 3) b'' b'' c'' a'' a'' c'' a c b c ' = - a c' '' b'
= 10 ( ổi chỗ cột 1 và cột 2) a'' b''
Hệ quả 2.3. Một ịnh thức có hai dòng nhƣ nhau thì bằng không. Chứng minh:
Gọi ịnh thức có hai dòng nhƣ nhau là . Đổi chỗ hai dòng ó ta ƣợc = - Vậy có 2 = 0, do ó = 0.
Tính chất 2.6. (tính chất thuần nhất)
Nếu nhân các phần tử một dòng nào ó với cùng một số thì ƣợc ịnh thức mới bằng ịnh thức cũ nhân với . 11 a 12 a 1 a n 11 a 12 a 1 a n a 1 i i a 2 in a a 1 i i a 2 in a a 1 n n a 2 nn a a 1 n n a 2 nn a 18 lOMoAR cPSD| 47305584
Hệ quả 2.4. i) Thừa số chung của các phần tử của một dòng của ịnh thức có thể ƣa ra
ngoài dấu ịnh thức làm thừa số nhân.
ii) Một ịnh thức có hai dòng tỉ lệ với nhau thì bằng không. Chứng minh: 11 a 12 a 1 a n i) a 1 i i a 2 in a n!
( 1) N( 1... in ) a1 1...( ai i )...an n
( 1) N( 1... i n ) a1 1...ai i ...an n a 1 n an 2 a n! nn 11 a 12 a 1 a n 1 i i a 2 in a = a 1n n a 2 nn a a
ii) Thật vậy, nếu ƣa hệ số tỷ lệ ra ngoài dấu ịnh thức thì ƣợc một ịnh thức có hai dòng
nhƣ nhau nên nó bằng không. ka a b kb Ví dụ 2.18. k
c d ad( bc) k c d
Ví dụ 2.19. Cho ma trận A = [aij]n n có aij + aji = 0 với i, j (n là số nguyên dƣơng lẻ). Tính ịnh thức của A. Giải: aij
aji, nÕu i j
Theo giả thiết, ta có: aij 0 , nÕu i j
nên AT = -A do ó |AT| = |-A| |A| = (-1)n |A| |A| = -|A| (vì n là số lẻ) |A| = 0
Tính chất 2.7. (tính chất cộng tính)
Khi tất cả các phần tử của một dòng nào ó có dạng tổng của hai số hạng thì ịnh thức
có thể phân tích thành tổng của hai ịnh thức, cụ thể: 11 a 12 a 1 a n 11 a 12 a 1 a n 11 a 12 a 1 a n b1 i c 1 i i b 2 ic2 in b in c b1 i i b 2 in b c 1 i i c 2 in c a 1 n n a 2 nn a a 1 n n a 2 nn a a 1 n a 2 n nn a 19 lOMoAR cPSD| 47305584
(Các phần tử dòng i có dạng tổng của hai số hạng) Chứng minh: 11 a 12 a 1 a n b N( 1 ... i n ) (1) a b c 1 ...( ) ...a i c 1 i i b 2 ic2 in b c = n! a 1 n n a 2 nn a in 1 1 i i i i n n = N( 1 ... i n ) a ...a ( 1) 1 ...c i n N( 1 i n 1... i n ) a1 1 ...bi i ...an n + ( 1) n! n! 11 a 12 a 1 a 11 n a 12 a 1 a n b1 i i b 2 in b i c 1 i c 2 in c = a 1 n n a 2 nn a a 1 n n a 2 nn a
Ví dụ 2.20. Tính ịnh thức a b c d g e 2a 3b 2a 3d Giải: 2e 3g 20




