












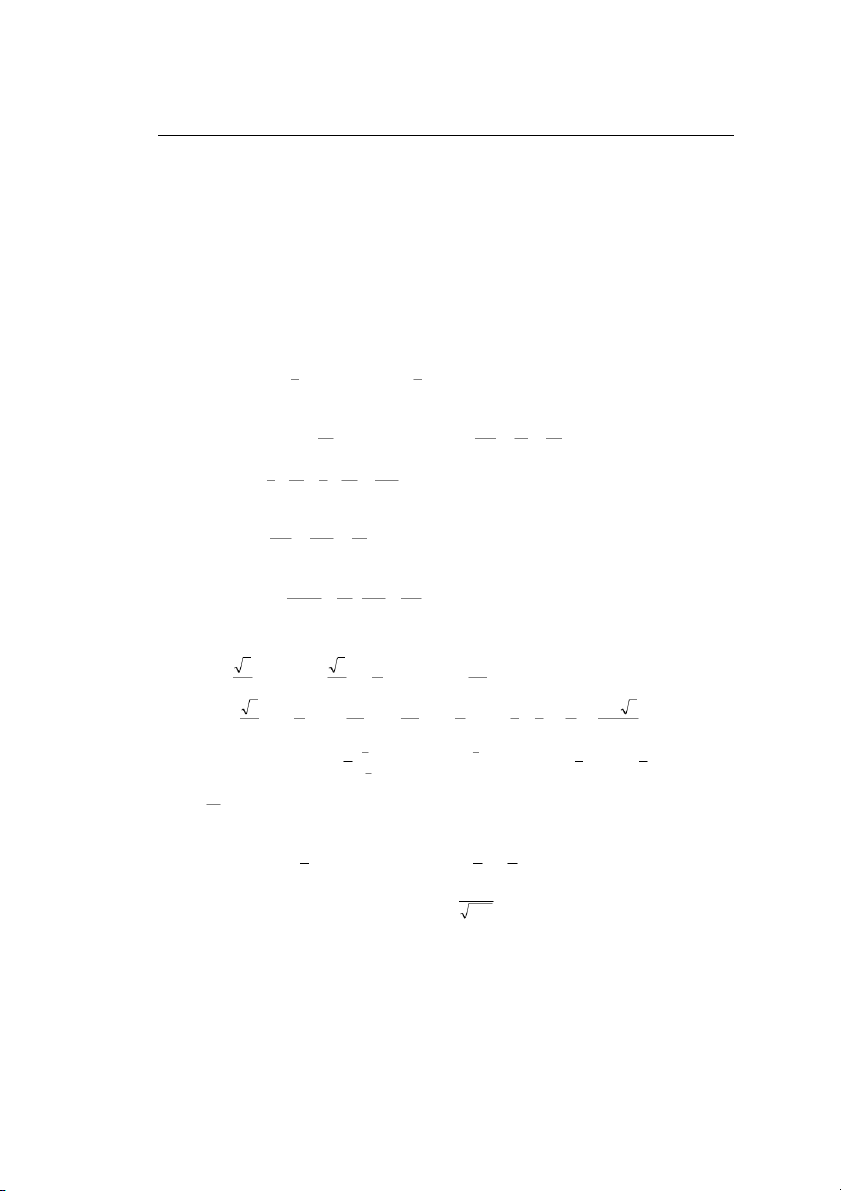
Preview text:
8. HàI QUI TUY¾N TÍNH
8.1. Tổng quan vÁ hái qui
Giả sử quan sát hai dấu hiệu X,Y trong một bối cảnh nào đó (th°ßng liên quan
trong 1 phần tử, chẳng hạn nh° chiều cao và trọng l°ợng của cùng một ng°ßi) ta có kết quả : X X1 X2 ... Xn Y Y1 Y2 ... Yn
÷ Để có một khái niệm s¡ bộ về mối quan hệ giữa hai đại l°ợng ngẫu nhiên X và Y,
ng°ßi ta th°ßng biểu diễn mỗi quan sát (xi; yi) bái một điểm trên mặt phẳng tọa
độ. Các điểm này hợp lại thành đám mây điểm trên mặt phẳng. Nhìn vào đám mây
điểm này, ta phải đọc đ°ợc mối quan hệ giữa X và Y, nh°ng quan trọng không
kém là phải dự đoán đ°ợc Y khi biết X (hoặc ng°ợc lại). Để làm đ°ợc điều này,
ng°ßi ta th°ßng vẽ một đ°ßng cong để mô tả mối quan hệ giữa hai đại l°ợng và dùng nó để dự đoán.
÷ Ph°¡ng pháp chọn một đ°ßng cong (tức là chọn một ph°¡ng trình) cho bộ dữ
liệu gọi là ph°¡ng pháp hồi qui, còn ph°¡ng trình gọi là ph°¡ng trình hồi qui (hay hàm hồi qui)
÷ Các ph°¡ng trình hồi qui đ°ợc xây dựng dựa trên ít nhất hai mục đích : Dự đoán
các quan sát mới và đánh giá mức độ t°¡ng quan giữa các biến tác động và biến đáp ứng.
÷ Ph°¡ng pháp hồi qui đ°ợc ứng dụng rộng rãi trong nhiều lĩnh vực : xã hội, khoa
học kỹ thuật, th°¡ng mại, ...
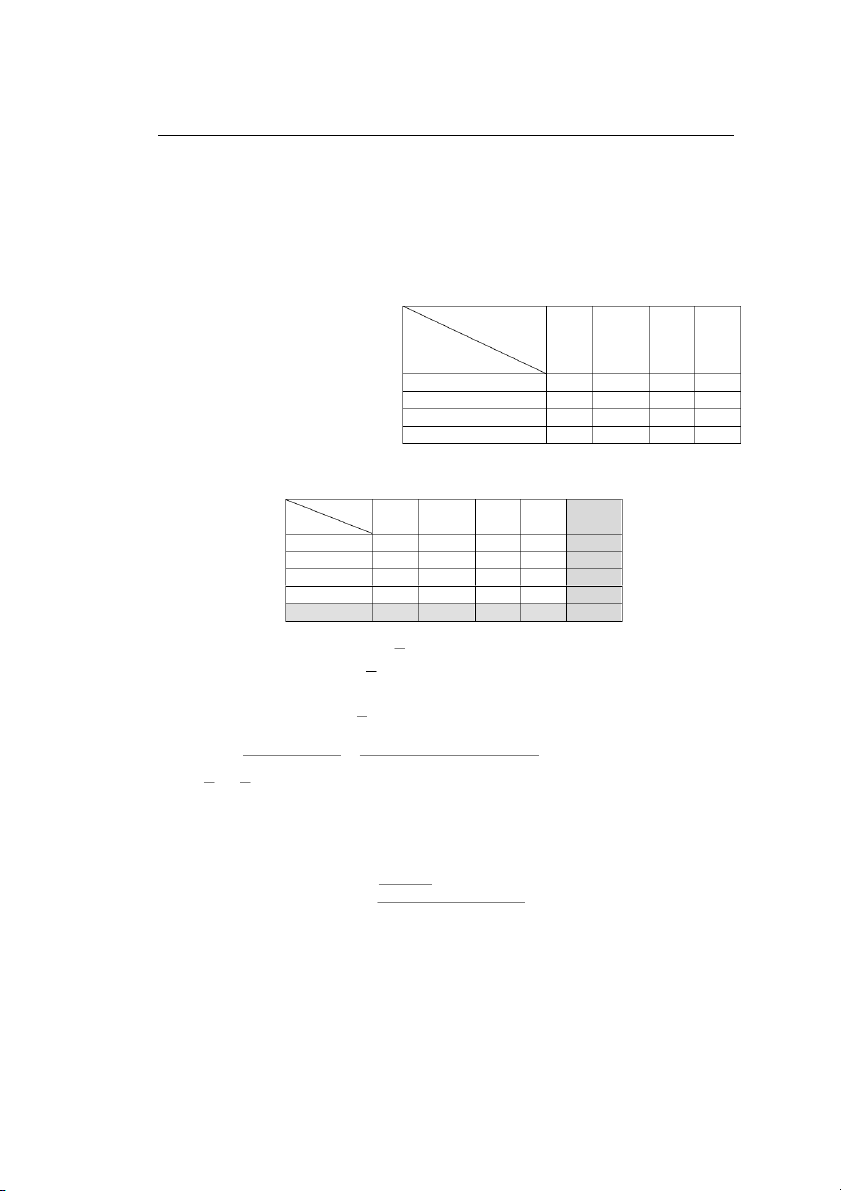
Cách chọn ph°¡ng trình : Nếu đám mây điểm có xu h°ớng tụ tập xung quanh một
đ°ßng thẳng nào đó thì ta chọn hàm hồi qui là Y = aX + b - tr°ßng hợp này ta gọi là
hồi qui tuyến tính của Y theo X; Nếu đám mây điểm có xu h°ớng tụ tập xung quanh
một parabol thì ta chọn hàm hồi qui là Y = aX2+ bX + c;... Nói chung, tùy theo
Hồi qui tuyến tính (Linear Regression) Hồi qui bậc hai (Quaratic Reg)
dáng= của đám mây điểm mà ta chọn cho nó ph°¡ng trình thích hợp. Các tr°ßng hợp
kể trên thuộc họ hồi qui có tham số.
8.2. Hái qui tuy¿n tính
Hồi qui tuyến tính (Linear Regression) là tr°ßng hợp ph°¡ng trình hồi qui có dạng : -79-
Hoài qui tuyeán tính y= ax +b
Ph°¡ng pháp bình phương bé nhất (Least squares method) : Ta phải xác định
các hệ số a, b sao cho s = õ 2 cực tiểu, với i = Yi – (aXi + b), i
Bằng cách coi S nh° là một hàm theo hai biến a,b ta sẽ tìm điểm cực tiểu của hàm
s để đ°ợc các °ớc l°ợng của a và b bằng cách giải hệ ph°¡ng trình : ü üö ö ö ö ö s 2 ý ÷ x ÷ õ a x b x y i ÷ ÷ 0 ÿ õ i ý ÷ ÷ ÷ ÷ õ i i ÿ ÿöa ÿø ø ø ø ý ý ÿös ÿö ö ÿ ý 0 ÷ x ÷ þö õ a nb n y i ý õ b ÿ÷ ÷ i i þø ø
Vậy các °ớc l°ợng của a và b là : n XY X Y õ õ õ A = ; B = Y AX nõ X øõ ù2 2 X
Để xác định các hệ số của ph°¡ng trình hồi qui tuyến tính, có thể tìm qua một trong hai công thức trên.
Ví dụ 8. 1 : Cho bộ số liệu : X 0 1 2 3 4 5 6 7 Y 0 1 1 3 4 6 9 10
Lập ph°¡ng trình hồi qui của y theo x. Giải : Tính đ°ợc : n=8; õx ý ; 28 i õy ý ; 34 i õx2 ý 140; i õx y ý 182 i i ü140a 28b ý 182 üa ý 05 , 1
Tìm hệ số a,b bằng cách giải hệ : ý ý þ28a b 8 ý 34 þb ý 1
Vậy ph°¡ng trình hồi qui cần tìm là : y=1,05x-1 -- 80
Hoài qui tuyeán tính
8.3. Hß sß tương quan
Để đánh giá mức độ phụ thuộc tuyến tính của hai biến ngẫu nhiên X & Y, ng°ßi ta dựa
vào hệ số t°¡ng quan, ký hiệu là , đ°ợc xác định nh° sau : ò ò ( E X )(Y ) = X Y ó ó x y Tính chất cơ b¿n : (i) ò þ [-1;1]
(ii) Nếu ò = 0 thì hai biến số trên không có t°¡ng quan tuyến tính.
(iii) Nếu ò càng gần 1 thì sự phụ thuộc tuyến tính giữa hai biến càng mạnh.
Ng°ßi ta sử dụng hệ số t°¡ng quan mẫu rxy (còn gọi là hệ số t°¡ng quan Pearson) để °ớc l°ợng ò : n xy x y õ õ õ rxy = nõ x øõ xù2 2 nõy øõ yù2 2 nõ xy õ xõ y = 2 n .Xó Y . ó n n õ xy X Y . = n Xó Y . ó n n
trong đó Xón , Yón lần l°ợt là độ lệch chuẩn mẫu của X và Y.
Trong thực hành, ng°ßi ta phân loại r
đối với mối liện hệ tuyến tính nh° sau: xy * 0.8 1 :
Sự liên hệ cao, rất đáng tin cậy. *
0.6 0.79 : Sự liên hệ từ vừa phải đến rõ rệt. *
0.4 0.59 : Sự liên hệ á mức trung bình. *
0.2 0.39 : Sự liên hệ á mức thấp. *
0 0.19 : Sự liên hệ không đang kể, có thể do ngẫu nhiên.
Ví dụ 8. 2 : Cho X là điểm toán thi vào đại học và Y là điểm thi cuối năm thứ I của 10
sinh viên ban toán (thang điểm 20), ta có kết quả điều tra : X 2 8 5 10 14 12 18 6 8 10 Y 4 8 6 10 12 10 15 5 9 12
a). Lập ph°¡ng trình hồi qui của Y theo X
b). Dự đoán điểm thi cuối năm của sinh viên có điểm thi toán vào đại học là 15. Giải :
a/. Ta dễ dàng tính đ°ợc n = 10
õxy = 982; õx = 93; õx2 = 1057; õy =91;
Thay vào công thức tính đ°ợc A = 0,706 và B = 2,534
Vậy ph°¡ng trình hồi qui là : Y = 0,706X +2,534 -- 81
Hoài qui tuyeán tính
b/. Sinh viên có điểm thi vào ĐH là 15 nên X = 15, thay vào ph°¡ng trình trên suy ra Y = 0,706 . 15 + 2,534 13
Vậy dự đoán điểm thi cuối năm thứ nhất của sinh viên trên là 13.
Ví dụ 8. 3 : Để nghiên cứu sự ảnh h°áng của phân bón (X) đến năng suất lúa (Y),
ng°ßi ta tiến hành thí nghiệm trên 100 mảnh ruộng và thu đ°ợc kết quả nh° sau :
a). ¯ớc l°ợng năng suất lúa Lượng phân bón
trung bình với độ tin cậy 95%. X (kg) 10 12 14 16
b). Tìm ph°¡ng trình t°¡ng Năng
quan tuyến tính giữa năng suất lúa Y(kg)
suất lúa với l°ợng phân bón. 100 22
Đánh giá mức độ chặt chẽ 150 8 10 3
của mối phụ thuộc t°¡ng 200 14 15 12 quan tuyến tính này. 250 16 Giải : X (kg) 10 12 14 16 ny Y(kg) 100 22 22 150 8 10 3 21 200 14 15 12 41 250 16 16 nx 44 25 15 16 n=100
Từ bảng trên ta tính đ°ợc :
n=100; x=1206 ; x2=15036; X =12,06; xón=2,217 ;
y=17550; y2=3332500; Y =175,5; yón=50,247. xy=219900.
a). Năng suất lúa trung bình : Y =175,5 (kg) nõ xy õ x õ y 100 2 . 19900 1206 .17550 b). Ta có A= ý 16,77 2 2 n õ x (õ x) 2 100.15036 1206
B= Y AX =175,5-16,77. 12,06 -26,75
Vậy ph°¡ng trình hồi qui tuyến tính của Y theo X là : y=16,77 x –26,75.
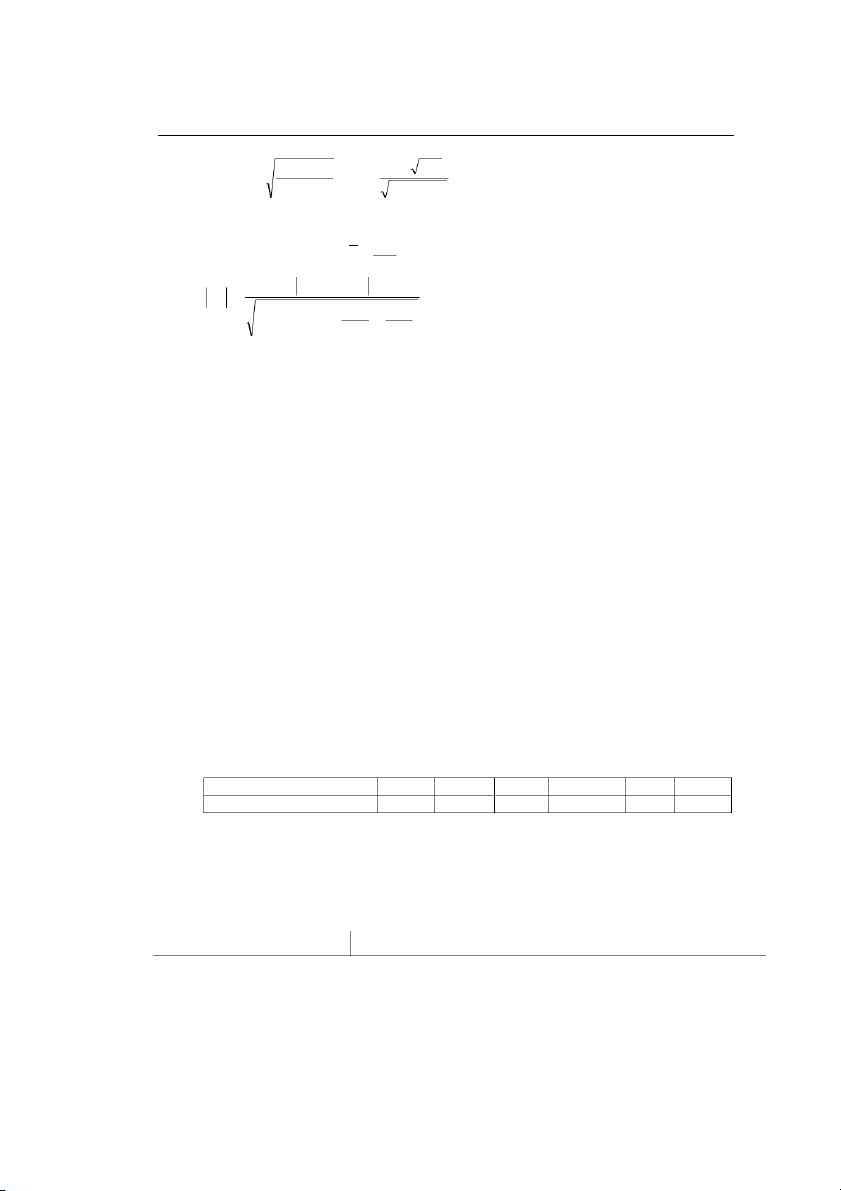
Tính hệ số t°¡ng quan Pearson, ta có 219900 12 0,6.175 5, 100 r ý 7 , 0 4 xy 2 , 2 17 5 . 0 2 , 47
Vậy mối phụ tuộc t°¡ng quan tuyến tính này khá chặt chẽ.
--------------------------------------- -- 82
Hoài qui tuyeán tính BÀI TẬP
1. Quan sát 40 lần cặp biến (X,Y) ta có bộ số liệu : xi 0-0,2 0,2-0,4 0,4-0,6 0,6-0,8 0,8-1 1-1,2 yi 10-15 4 2 15-20 2 6 20-25 2 25-30 4 30-35 4 6 35-40 6 4
a. Xác định đ°ßng hồi qui tuyến tính của y theo x (đs: y=27,81x-7,56)
b. Tính hệ số t°¡ng quan tuyến tính giữa x và y (đs:0,86)
2. Số liệu thống kê nhằm nghiên cứu quan hệ giữa tổng sản phẩm nông nhiệp y với
tổng giá trị tài sản cố định x của 10 nông trại (tính trên 100 ha) nh° sau : xi 11,3 12,9 13,6 16,8 18,8 22,0 22,2 23,7 26,6 27,5 yi 13,2 15,6 17,2 18,8 20,2 23,9 22,4 23,0 24,4 24,6
a. Hãy xác định ph°¡ng trình hồi qui tuyến tính của y theo x.
b. Dự đoán tổng sản phẩm nông nghiệp khi tổng tài sản cố định là 25.
(đs : y=0,673x+7,184; b).2400,9 ) -- 83
Hoài qui tuyeán tính BÀI TẬP ÔN
1. Cho E ý 1,2,3,4, ý
5 . Có thể lập đ°ợc từ E mấy số tự nhiên a) có 3 chữ số. (Đs:125)
b) có 3 chữ số khác nhau. (Đs:60)
c) có 3 chữ số giống nhau. (Đs:5)
d) có 3 chữ số, tận cùng bằng chừ số 4. (Đs:25)
e) có 3 chữ số khác nhau, tận cùng băng chữ số 4. (Đs:12)
f) có 3 chữ số không tận cùng bằng chữ số 4. (Đs:100)
g) có 3 chữ số khác nhau, không tận cùng bằng chữ số 4. (Đs:48) 2. Tung 3 xúc xắc.
a) Có mấy tr°ßng hợp có thể xảy ra. (Đs:216)
b) Có mấy tr°ßng hợp xuất hiện 3 mặt có số chấm đôi một khác nhau.(Đs:120)
c) Có mấy tr°ßng hợp xuất hiện 3 mặt có số chấm nh° nhau. (Đs:6)
d) Có mấy tr°ßng hợp xuất hiện mặt 5 á xúc xắc thứ nhất. (Đs:36)
e) Có mấy tr°ßng hợp xuất hiện 3 mặt 4, 5, 6. (Đs:6)
f) Có mấy tr°ßng hợp xuất hiện đúng một mặt 5. (Đs:75)
g) Có mấy tr°ßng hợp không xuất hiện mặt 5. (Đs:125)
h) Có mấy tr°ßng hợp tổng số chấm xuất hiện trên mặt 3 xúc xắc đó bằng 10. (Đs:27)
i) Tổng số chấm bằng 8 biết rằng có ít nhất 1 con ra 1 chấm. (Đs:15)
j) Tổng số chấm bằng 8. (Đs:21) H°ớng dẫn:
h) Xét các tr°ßng hợp (1;3;6) ; (1;4;5) ; (2;2;6) ; (2;3;5) ; (2;4;4) ; (3;4;3).
i) (1;1;6) ; (1;2;5) ; (1;3;4)
3. Xếp ngẫu nhiên 5 ng°ßi (trong đó có A, B) lên 7 toa tàu có đánh số.
a) Có mấy tr°ßng hợp (mấy cách xếp) có thể xảy ra. (Đs:75)
b) Có mấy tr°ßng hợp cả 5 ng°ßi lên toa thứ 3. (Đs:1)
c) Có mấy tr°ßng hợp cả 5 ng°ßi lên cùng 1 toa. (Đs:7)
d) Có mấy tr°ßng hợp 5 ng°ßi lên 5 toa đầu (mỗi ng°ßi 1 toa khác nhau).(Đs:120)
e) Có mấy tr°ßng hợp 5 ng°ßi lên 5 toa khác nhau. (Đs:2520)
f) Có mấy tr°ßng hợp A, B cùng lên toa đầu. (Đs:343)
g) Có mấy tr°ßng hợp cùng lên 1 toa. (Đs:2401)
h) Có mấy tr°ßng hợp toa đầu chỉ có A, B lên. (Đs:216)
i) Có mấy tr°ßng hợp có đúng 5 toa không có ng°ßi lên. (Đs:630)
j) Có mấy tr°ßng hợp có đúng 3 toa không có ng°ßi lên. (Đs:8400)
k) Có mấy tr°ßng hợp chỉ có 3 toa đầu đều có ng°ßi lên. (Đs:150)
l) Có mấy tr°ßng hợp chỉ có 3 toa có ng°ßi lên. (Đs:5250)
4. Xếp ngẫu nhiên 7 cuốn sách (trong đó có 3 sách toán) vào 5 ngăn tủ có đánh số
(mỗi ngăn tủ đều có thể chứa nhiều sách). a) Có mấy cách xếp. (Đs:78125)
b) Có mấy cách xếp mà 3 sách toán á cùng ngăn thứ 3. (Đs:625)
c) Có mấy cách xếp mà 3 sa1ch toán luôn cùng 1 ngăn. (Đs:3125) -- 84
Hoài qui tuyeán tính
d) Có mấy cách xếp mà 3 sách toán chỉ đ°ợc xếp á 3 ngăn đầu tiên. (Đs:3354=16875)
e) Có mấy cách xếp 3 ngăn đầu đều có sách toán. (Đs:3750)
f) Có mấy cách xếp mà3 sách toán á 3 ngăn khác nhau. (Đs:37500)
g) Có mấy cách xếp mà 3 ngăn đầu mỗi ngăn chỉ có 1 sách toán (ngoài ra không có sách nào khác). (Đs:96)
h) Có mấy cách xếp mà ngăn nào cũng có sách xếp vào. (Đs:16800)
5. Xếp 5 ng°ßi (trong đó có A, B, C) vào một ghế dài 5 chỗ có đánh số. a) Có mấy cách xếp. (Đs:120)
b) Có mấy cách xếp mà A và B luôn cạnh nhau. (Đs:48)
c) Có mấy cách xếp mà A ngồi bên phải cạnh B. (Đs:24)
d) Có mấy cách xếp mà A ngồi bên phải B. (Đs:60)
e) Có mấy cách xếp mà A và B không ngồi cạnh nhau (Đs:72)
f) Có mấy cách xếp A ngồi đầu ghế, B ngồi cuối ghế. (Đs:6)
g) Có mấy cách xếp mà A và B ngồi 2 đầu ghế. 1 (Đs: 2)
h) Có mấy cách xếp A luôn ngồi giữa B và C (cạnh nhau). (Đs:12)
i) Có mấy cách xếp mà A, B luôn cách nhau 1 ng°ßi. (Đs:36)
6. Lô chứa 6 sản phẩm loại A, 4 sản phẩm loại B. lấy ngẫu nhiêncùng lúc ra 5 sản phẩm để kiểm tra. a) Có mấy cách lấy? (Đs:252)
b) Có mấy cách lấy trong đó có đúng 2 sản phẩm loại A. (Đs:60)
c) Có mấy cách lấy có đúng 2 sản phẩm loại B. (Đs:120)
7. Hộp chứa 3 quả cầu trắng, 2 quả cầu đen, 3 quả cầu xanh. Lấy cùng lúc ra 6 quả cầu. a) Có mấy cách lấy? (Đs:210)
b) Có mấy cách lấy mỗi loại đều có 2 quả. (Đs:30)
c) Có mấy cách lấy có 2 quả cầu trắng, 4 quả cầu xanh. (Đs:15)
d) Có mấy cách lấy có đúng 2 quả cầu trắng. (Đs:105)
8. Tung 6 xúc xắc, có mấy tr°ßng hợp xuất hiện ít nhất 1 mắt lục? Tung 12 xúc xắc, có
mấy tr°ßng hợp xuất hiện ít nhất 2 mặt lục? Tung 18 xúc sắc, có mấy tr°ßng hợp
xuất hiện 3 mặt lục? (Mặt lục là mặt có 6 chấm).
ĐS: 31031 ; 1346704211 ; 6,06640199.1013
9. Hộp chứa 100 tấm thẻ đánh số từ 1 đến 100. Rút ngẫu nhiên 1 tấm thẻ. Tính xác
suất đ°ợc tấm thẻ có số đánh trên nó không chứa chữ số 5. Rút tiếp 1 tấm thẻ. Tính
xác suất để tấm thẻ rút lần 2 cũng không chứa chữ số 5. (Cả hai lần rút đều không hoàn). ĐS: 0,81 ; 0,81.
10. Hộp chứa 7 quả cầu trắng, 3 quả cầu đen. Rút ngẫu nhiên cùng lúc ra 6 quả cầu.
Tính xác suất để 6 quả cầu rút ra
a) Có đúng 4 quả cầu trắng.
b) Có từ 5 đén 6 qả cầu trắng. -- 85
Hoài qui tuyeán tính
c) Tính xác suất để 4 quả cầu còn lại có cả trắng lẫn đen. ĐS: (a) 0,5 1 5 (b) (c) 3 6
11. Hộp chứa 8 sản phẩm (5 sản phẩm tốt, 2 sản phẩm h°). Lấy ngẫu nhiên cùng lúc ra 5 sản phẩm.
a) Tính xác suất để trong 5 sản phẩm lấy ra có đúnh 4 sản phẩm tốt.
b) Lấy tiếp 1 sản phẩm (từ 3 sản phẩm còn lại). Tính xác suất để đ°ợc sản phẩm tốt. ĐS: (a) 15 (b) 0,625 56
12. Từ 5 chữ số 1, 2, 3, 4, 5 lập ngẫu nhiên 1 số tự nhiên có 3 chữ số. Tính xác suất để đ°ợc 1 số
a) Có 3 chữ số khác nhau.
b) Có 3 chữ số giống nhau.
c) Có 3 chữ số, tận cùng bằng số 4. d) Bội của 4 ĐS: (a) 0,48 (b) 0,04 (c) 0,20 (d) 0,20
13. Tung 3 xúc xắc. Tính xác suất
a) Xuất hiện 3 mặt có số chấm đôimột khác nhau.
b) Xuất hiện mặt 5 á xúc xắc thứ 2.
c) Xuất hiện đúng 1 mặt 5.
d) Xuất hiện 3 mặt chẵn.
e) Tổng số chấm 3 mặt bằng 8.
f) Có xuất hiện mặt 1 chấm, tổng số chấm 3 mặt bằng 8. 5 1 25 7 5 ĐS: (a) (b) (c) (d) 0,125 (e) (f) 9 6 72 72 72
14. Xếp ngẫu nhiên 5 ng°ßi lên 1 tàu 7 toa có đánh số. Tính xác suất :
a) 5 ng°ßi lên 5 toa khác nhau. b) Hai ng°ßi P,
Q trong họ lên cùng một toa.
c) Toa đầu chỉ có 2 trong số họ lên.
d) 5 toa không có ng°ßi lên
e) 4 toa không có ng°ßi lên ĐS: (a) 1 0,15 (b) (c) 0,1285 (d) 0,0375 (e) 0,3124 7
15. Xếp ngẫu niên 5 ng°ßi (trong đó P, Q, R) lên 1 bàn tròn 5 chỗ có đánh số. Tính xác suất: a) P, Q ngồi cạnh nhau.
b) P ngồi giữa Q và R (cạnh nhau) ĐS: (a) 0,5 1 (b) 6 -- 86
Hoài qui tuyeán tính
16. Khi gọi điện thoại, một khách hàng quên mất 2 chữ số cuối cùng của số điện thoại
cần gọi, chỉ nhớ rằng hai số đó khác nhau và lấy ngẫu nhiên 2 chữ số thay vào. Tính
xác suất để anh ta gọi đúng số cần tìm qua lần gọi đầu tiên. 1 ĐS: 90
17. Hộp chứa 3 quả cầu trắng, 2 quả cầu đen và 5 quả cầu đỏ. Lấy ngẫu nhiên cùng lúc
ra 6 quả cầu. Tính xác suất để 6 quả cầu lấy ra : a) Có 2 quả
cầu trắng, 2 quả cầu đen, 2 quả cầu đỏ. b) Có 2 quả
cầu trắng, 4 quả cầu đỏ.
c) Có đúng 2 quả cầu trắng.
d) Không có quả cầu trắng nào đ°ợc rút ra. ĐS: (a) 1 1 1 (b) (c) 0,5 (d) 7 14 30
18. Hộp chứa 5 quả cầu trắng, 2 quả cầu xanh và 3 quả cầu đen. Từ hộp rút ngẫu nhiên
(không hoàn) mỗi lần 1 quả cầu, ra 3 quả cầu. Tính xác suất để đ°ợc:
a) Lần l°ợt cầu trắng, xanh, đen b) Ba quả cầu khác màu
c) Ba quả cầu khác màu trong đó quả cầu thứ 3 màu đen. ĐS: (a) 1 1 (b) 0,25 (c) 24 12
19. Hộp chứa 7 quả cầu trắng, 3 quả cầu đen. Chia ngẫu nhiên 10 quả cầu ra 3 nhóm:
5 quả, 2 quả và 3 quả. Tính xác suất để trong mỗi nhóm đều có 1 cầu đen. ĐS: 0,25
20. D°ới tác dụng của phóng xạ, các nhiễm sắc thể của 1 tế bào có thể gãy thành 2
mảnh trong đó chỉ có 1 mảnh chứa tâm động. Sau đó các mảnh đôi một gắn lại với
nhau một cách ngẫu nhiên, và tế bào sống sót nếu các cặp gắn lại chỉ chứa 1 tâm
động. Tính xác suất để tế bào sống sót, biết rằng khi bị chiếu tia phóng xạ tế bào có
n nhiếmẵ thể bị gãy đôi. 2n(n!)2 ĐS: (2n)!
21. Hộp chứa 5 quả cầu trắng, 2 quả cầu xanh, 3 quả cầu đen. Từ hộp rút ngẫu nhiên
không hoàn lại mỗi lần 1 cầu cho tới khi đ°ợc cầu trắng thì dừng. Tính xác suất:
a) Quả cầu trắng đ°ợc rút ra á lần rút thứ 3.
b) Có 2 cầu xanh và 1 cầu đen đ°ợc rút ra.
c) Không quả cầu đen nào đ°ợc rút ra. 5 1 ĐS: (a) 5 (b) (c) ý 625 , 0 36 56 8 -- 87
Hoài qui tuyeán tính
22. Hộp chứa 40 sản phẩm tốt, 3 sản phẩm h°. Rút lần l°ợt mỗi lần 1 sản phẩm (không
hoàn) cho tới khi đ°ợc 3 sản phẩm h° thì dừng. Gọi X là số sản phẩm tốt đ°ợc rút ra. Tìm P(X=17). ĐS: 0,01386
23. Hộp chứa 7 quả cầu trắng, 3 quả cầu đen. Rút (không hoàn)mỗi lần 1 quả cầu, ra 3
quả cầu. Tính xác suất để có
a) Quả cầu thứ nhất có màu trắng.
b) Quả cầu thứ hai có màu trắng.
c) 2 quả cầu trắng, 1 quả cầu đen. ĐS: (a) 0,7 (b) 0,7 (c) 0,525
24. Ba ng°ßi bắn (độc lập) mỗi ng°ßi 1 viên đạn vào 1 con mồi. Xác suất trúng con mồi
của các viên đạn do ng°ßi thứ 1, 2, 3 bắn t°¡ng ứng bằng 0,6 ; 0,7 ; 0,8. Tính xác suất:
a) Con mồi trúng 3 viên đạn.
b) Con mồi không trúng đạn.
c) Con mồi chỉ trúng 1 viên đạn. d) Con mồi trúng đạn. ĐS: (a) 0,366 (b) 0,024 (c) 0,188 (d) 0,976
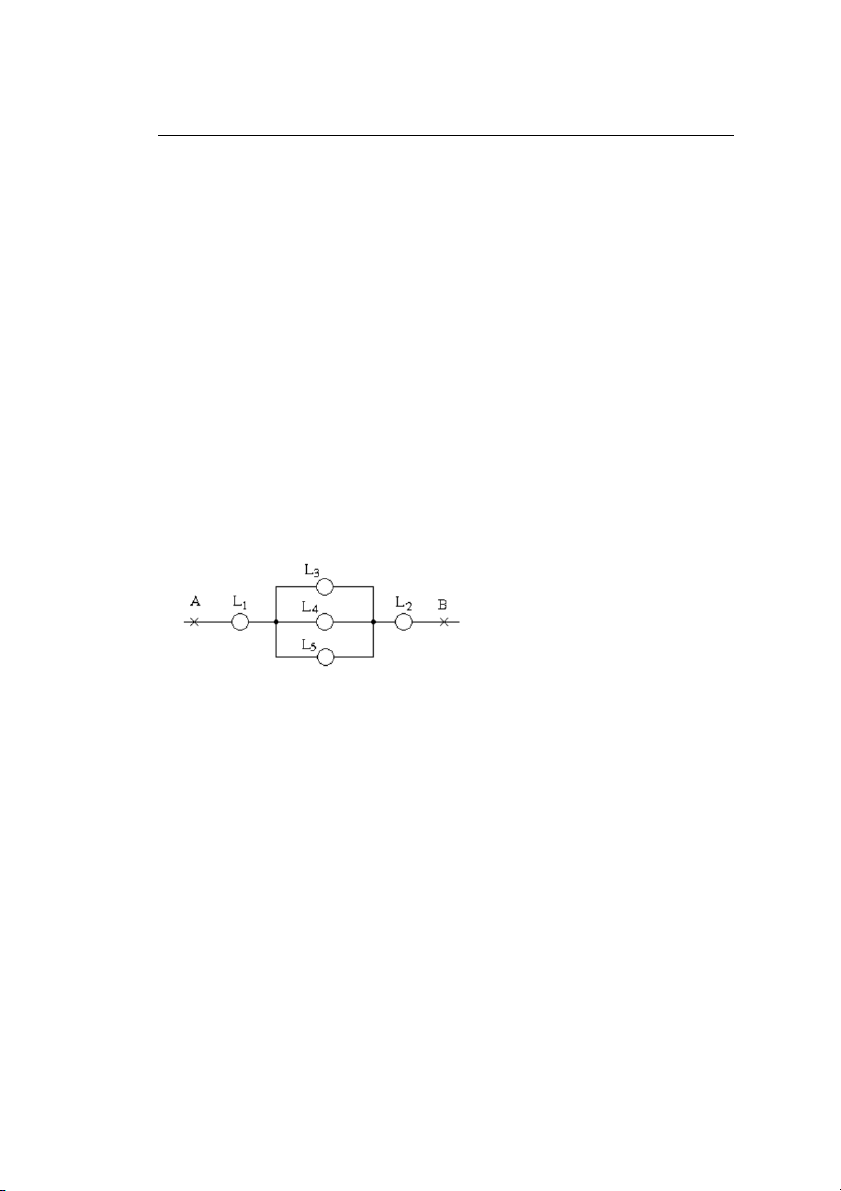
25. Một mạch điện tử từ A đến B gồm 5 linh kiện hoạt động độc lập với nhau và xác
suất h° của các linh kiện L1, L2, L3, L4, L5 trong thßi gian t°¡ng ứng bằng 0,1 ; 0,2 ;
0,4 ; 0,7 ; 0,5. Tính xác suất để mạch ng°ng hoạt động trong thßi gian T. ĐS: 0,3808
26. Lô sản phẩm gồm hai loại, kiểu dáng nh° nhau, trong đó số sản phẩm loại 1 gấp đôi
số sản phẩm loại 2. Tỉ lệ h° của loại 1 là 3%, của loại 2 là 2%. Lấy từ lô ra 1 sản
phẩm. Tính xác suất để đ°ợc sản phẩm tốt. ĐS: 0,9733
27. Cửa hàng bán 1 loại sản phẩm, trong đó có 40%sản phẩm do phân x°áng I sản
xuất, 60% do phân x°áng II sản xuất. Tỉ lệ sản phẩm loại A (loại tốt) do các phân
x°áng I, II sản xuất t°¡ng ứng bằng 80%; 90%. Mua 1 sản phẩm từ cửa hàng.
a) Tính xác suất sản phẩm mua đ°ợc là sản phẩm tốt.
b) Sản phẩm mua đ°ợc sau kiểm tra là sản phẩm xấu. Hỏi sản phẩm này có khả
năng nhiều nhất do phân x°áng nào sản xuất ra. ĐS: (a) 0,86
(b) có nhiều khả năng nhất do phân x°áng I sản xuất ra.
28. Trongsố 18 xạ thủ có 5 ng°ßi bắn trúng bia với xác suất 0,8 ; 7 ng°ßi bắn trúng bia
với xác suất 0,7 ; 4 ng°ßi bắn trúng bia với xác suất 0,6 ; 2 ng°ßi bắn trúng bia với -- 88
Hoài qui tuyeán tính
xác suất 0,5. Chọn ngẫu nhiên một xạ thủ, cho anh ta bắn 1 phát, kết quả không trúng bia.
a) Hỏi xạ thủ này có nhiều khả năng nhất thuộc về nhóm nào?
b) Cho xạ thủ này bắn thêm một phát nữa. Tính xác suất để anh ta bắn trúng. 373
ĐS: (a) có khả năng nhất thuộc về nhóm 7 ng°ßi. (b) 0,6544 570
29. Có 2 hộp. Hộp 1 chứa 8 quả cầu trắng và 2 quả cầu đen. Hộp 2 chứa 9 quả cầu
trắng và 1 quả cầu đen. Từ hộp 2 lấy ngẫu nhiên 2 quả cầu và bỏ vào hộp 1. Sau đó
từ hộp 1 lấy ngẫu nhiên cùng lúc ra 3 quả cầu.
a) Tính xác suất lấy đ°ợc 2 quả cầu trắng và 1 quả cầu đen.
b) 3 quả cầu lấy ra đều có màu trắng. Tính xác suất để 3 quả cầu này đều của hộp 1. ĐS: (a) 117 70 (b) 275 141
30. Có 3 hộp. Hộp 1 chứa 2 quả cầu trắng và 1 quả cầu đen. Hộp 2 chứa 3 quả cầu
trắng và 1 quả cầu đen. Hộp 3 chứa 2 quả cầu trắng cà 2 quả cầu đen.
a) Lấy ngẫu nhiên 1 hộp rồi từ đó lấy ra 1 quả cầu. Tính xác suất để đ°ợc quả cầu trắng.
b) Lấy ngẫu nhiên 1 hộp, từ đó lấy ra 2 quả cầu. Tính xác suất lấy đ°ợc i) 2 quả cầu trắng
ii) có ít nhất 1 quả cầu trắng
c) Lấy ngẫu nhiên mỗi hộp 1 quả cầu. Trong 3 quả cầu lấy ra này, lấy ngẫu nhiên
một quả thì đ°ợc cầu trắng. Tính xác suất để quả cầu này thuộc hộp 1. ĐS: (a) 23 1 17 (b) i/ ii/ (c) 36 3 18
31. Hộp đựng 10 sản phẩm : 6 sản phẩm do máy 1 sản xuất, 4 sản phẩm do máy 2 sản
xuất, bị mất một sản phẩm. Từ hộp lấy ngẫu nhiên cùng lúc ra 2 sản phẩm. Gọi X = i
(i = 0 ; 1 ; 2) là số sản phẩm do máy 2 sản xuất trong 2 sản phẩm lấy ra. Tính P(X =
i). Tính xác suất để trong 2 sản phẩm lấy ra có ít nhất một sản phẩm do máy 1 sản xuất. 1 8 2 13 ĐS: P(X ý 0) ý ; P (X ý 1) ý ; P (X ý 2) ý ; 3 15 15 15
32. Trong 1 kho r°ợu, số l°ợng r°ợu loại A và loại B bằng nhau. Lấy ngẫu nhiên ra 1
chai và đ°a cho 5 ng°ßi sành r°ợu thử. Giả sử mỗi ng°ßi đều có xác suất đoán
đúng là 75%. Có 4 ng°ßi kết luận chai r°ợu loại A, 1 ng°ßi kết luận chai r°ợu loại
B. Hỏi khi đó xác suất để chai r°ợu loại A bằng mấy? 27 ĐS: 28 -- 89
Hoài qui tuyeán tính
33. Một nhà máy sản xuất bóng đèn có tỉ lệ bóng đạt đại tiêu chuẩn 80%. Qua KCS, một
bóng tốt đ°ợc coi là tốt với xác suất 90%, một bóng xấu bị loại bỏ với xác suất 95%.
Tính tỉ lệ bóng đạt tiêu chuẩn sau KCS. 72 ĐS: 73
34. Tại một phòng thí khám chuyên khoa, tỉ lệ ng°ßi đến khám có bệnh là 0,8. Ng°ßi ta
áp dụng ph°¡ng pháp mới để chẩn bệnh thì thấy: nếu khẳng định có bệnh thì đúng
9 trên 10 tr°ßng hợp, còn nếu khẳng định không bệnh thì đúng 5 trên 10 tr°ßng hợp. Tính xác suất a) Chẩn đoán có bệnh. b) Chẩn đoán đúng. ĐS: (a) 0,75 (b) 0,8
35. Thống kê á một thành phố, có bảng kết quả sau:
Số con trong một gia đình 0 2 3 4 5
Tỉ lệ % số gia đình có n con 15 20 30 10 5
Xác suất sinh ra trẻ là trai hay là gái đều bằng 0,5 và không phụ thuộc vào các trẻ khác.
a) Chọn ngẫu nhiên một gia đình. Tìm xác suất để gia đình đó có đúng 2 con gái
(ngoài ra có thể có con trai).
b) Chọn ngẫu nhiên một đứa con. Tính xác suất để đứa con này thuộc gia đình có 2 con gái nh° trong câu a. ĐS: (a) 13 65 (b) 64 272
36. Thống kê á một thành phố, có bảng kết quả sau:
Số con trong một gia đình 0 1 2 3 4
Tỉ lệ % số gia đình có n con 10 20 40 20 10
Xác suất sinh ra trẻ là trai hay là gái đều bằng 0,5 và không phụ thuộc vào các trẻ khác.
a) Chọn ngẫu nhiên một gia đình. Tình xác suất để gia đình đó có có ít nhất 1 con trai.
b) Chọn ngẫu nhiên một gia đình thì đ°ợc gia đình có ít nhất 1 con trai. Tính xác
suất để gia đình đó có ít nhất 1 con gái. 107 70 ĐS: (a) (b) 160 107
37. (Bài toán của Samuel Pépys) Biến cố nào trong các biến cố sau đây có xác suất lớn h¡n:
a) Tung 6 xúc sắc, có ít nhất 1 mặt 6 xuất hiện (A).
b) Tung 12 xúc sắc, có ít nhất 2 mặt 6 xuất hiện (B). -- 90
Hoài qui tuyeán tính
c) Tung 18 xúc sắc, có ít nhất 3 mặt 6 xuất hiện (C). ĐS: P(A) 0,665 > P(B) 0,62 > P(C) 0,5973.
H°ớng dẫn: Xem bài 9 - Phần đếm.
38. Hộp đựng 3 đồng xu, trong đó có 2 đồng xu công bằng và một đòng xu có 2 mặt
hình. Chọn 1 đồng để tung, nếu đ°ợc mặt hình (H) thì tung tiếp lần 2, nếu đ°ợc mặt
số (S) thì chọn đồng xu khác để tung tiếp.
a) Tính xác suất để hai lần tung đều ra mặt hình (H).
b) Giả s° đồng xu đ°ợc tung 2 lần. Tính xác suất để đó là đồng xu có hai mặt hình (H). ĐS: (a) 0,5 (b) 0,5
39. Cặp sinh đôi đ°ợc gọi là thật nếu do cùng một trứng sinh ra và trong tr°ßng hợp đó
bao giß cũng cùng giới tính. Nếu cặp sinh đôi do các trứng khác sinh ra thì xác suất
để cùng giới tính bằng 0,5. Có một cặp sinh đôi cùng giới tính. Hỏi xác suất chúng là
cặp sinh đôi thật bằng bao nhiêu, biết rằng xác suất để cặp sinh đôi cùng trứng bằng p. 2p ĐS: p 1
40. Trên một toa tàu điện có n khách. Đến ga tiếp theo mỗi ng°ßi có thể xuống với xác
suất p. Có 1 khách mới lên với xác suất (1-po) và không có ai lên thêm với xác suất
po. Tìm xác suất để sau lần dừng đó tàu vẫn có n khách.
ĐS: (1 - p)n – 1 [ po(1 - p) + np (1 - po)]
41. Một lớp học có a học sinh giỏi, b học sinh khá, c học sinh yếu. Khi làm bài kiểm tra
học sinh giỏi bao giß cũng đ°ợc điểm giỏi; học sinh khá có thể làm bài đạt loại giỏi
hoặc khá với xác suất nh° nhau; một học sinh yếu có thể đạt khá, trung bình hoặc
yếu với xác suất nh° nhau. Sau kiểm tra, chọn ngẫu nhiên một học sinh thì đ°ợc
khá hoặc giỏi. tính xác suất để đó là học sinh yếu.
42. (Bài toán De Meré) Xác suất nào trong 2 xác suất P(A), P(B) lớn h¡n.
a) Tung 4 xúc xắc, chỉ có 1 xúc xắc xuất hiện mặt 1 chấm.
b) Tung 2 xúc xắc 24 lần chỉ xuất hiện mặt 2 chấm trên cả 2 xúc xắc.
43. (Bài toán Banach) Một ng°ßi có 2 bao diêm, mỗi bao đều có n que. Khi cần, ng°ßi
đó lấy ra 1 bao và rút 1 que để dùng. Tính xác suất khi ng°ßi đó phát hiện một bao
rỗng thì bao kia còn lại đúng k que. ĐS: n k 2n 2 C nk 2 .
44. (Bài toán truyền máu) Biết rằng một ng°ßi có máu AB có thể nhận máu của bất kì
nhóm máu nào. Nếu ng°ßi đó có nhóm máu còn lại (A, hoặc B, hoăc O) thì chỉ có
thể nhận máu của ng°ßi có cùng nhóm máu của mình hoặc ng°ßi có nhóm máu O.
a) Chọn ngẫu nhiên 1 ng°ßi cần tiếp máu và 1 ng°ßi cho máu. Tính xác suất để sự
truyền máu thực hiện đ°ợc. -- 91
Hoài qui tuyeán tính
b) Chọn ngẫu nhiên 1 ng°ßi cần tiếp máu và hai ng°ßi cho máu. Tính xác suất để
sự truyền máu thực hiện đ°ợc.
Cho biết tỉ lệ ng°ßi có nhóm máu O, A, B, AB t°¡ng ứng là 0,337 ; 0,375 ; 0,209 ; 0,079. ĐS: (a) 0,5737 (b) 0,7777
45. Một máy tự động sản xuất ra 1 loại trục máy, có thể cho cả phế phẩm. Kiểm tra
ngẫu nhiên 200 trục do máy này sản xuất ra, thấy có 25 phế phẩm . Với l°ợng tỉ lệ
phế phẩm do máy này sản xuất ra với độ tin cậy = 95%.
46. Điều tra ngẫu nhiên 250 sinh viên , thấy có 150 sinh viên có đang ký học (vi tính
hoặc anh văn) ngoài giß. ¯ớc l°ợng tỉ lệ sinh viên đăng ký học thêm với độ tin cậy = 98%
47. Điều tra ngẫu nhiên 4000 gia đình , thấy có 3200 gia đình có xe gắn máy. Với l°ợng
tỉ lệ các gia đình có xe gắn máy với đọ tin cậy = 95%.
48. Ng°ßi ta đo chiều sâu của biển bằng 1 dụng cụ có sai số phép đo tuân theo phân
phối chuẩn N( 0 ; 402). Hỏi phải đo bao nhiêu lần để kết quả đạt đ°ợc có sai
sốkhông v°ợt quá 15(m) với độ tin cậy = 90%.
49. Đo đ°ßng kính của một loại chi tiết máy do 1 máy tiện sản xuất ra (độ dài tính bằng
mm) có bảng thống kê sau : Độ dài (mm) 247 249 251 253 257 Số chi tiết 25 55 70 80 20
¯ớc l°ợng độ dài đ°ßng kính của loại trục máy này với độ tin cậy = 95%.
Muốn °ớc l°ợng đ°ßng kính trục máy với sai số không v°ợt quá 0 = 4mm, có cần
lấy thêm mẫu nữa không ? Nếu có, bằng bao nhiêu (với độ tin cậy 95%).
50. Thßi gian sản xuất 1 loại chi tiết máy là 1 biến ngẫu nhiên tuân theo phân phối
chuẩn N(a ; ó2). Ng°ßi ta quan sát 100 lần, thấy thßi gian trung bình sản xuất ra 1
chi tiết máy x100 = 5,5 giây với độ lệch quân ph°¡ng (hiệu chỉnh) sản xuất = 1,7
giây. Tìm khoảng °ớc l°ợng kì vọng a và ó2 với độ tin cậy 90%.
51. Để xác định giá trị trung bình của 1 loại hàng bán trên thị tr°ßng, ng°ßi ta điều tra
ngẫu nhiên tại 100 cửa hàng với bảng số liệu sau :
Giá xác xuấtI (nghìn đồng) 83 85 87 89 91 93 95 98 99 101 Số cửa hàng nI 6 7 12 15 30 10 8 6 4 2
a) Với độ tin cậy = 95% , tìmkhoảng tin cậy cho giá trung bình của loại hàng hóa tại
thßi điểm đang xét. Biết giá loại hàng tuân theo luật chuẩn.
b) Giả sử bán kinh khoảng tin cậy = 0,5 thì mẫu cần thiết là bao nhiêu ?
52. Kiểm tra chất l°ợng của cùng loại của 2 xí nghiệp có kết quả Xí nghiệp Số s/fẩm k/tra Số phế phẩm I 1800 60 II 1200 42 -- 92
Hoài qui tuyeán tính
Với mức ý nghĩa = 0,05, có thể coi tỉ lệ phế phẩm á 2 nhà máy này nh° nhau đ°ợc không ?
53. X(kg) là 1 chỉ tiêu của 1 loại sản phẩm thuộc xí nghiệp A. Điều tra 1 số sản phẩm
của xí nghiệp này có kết quả sau : xI
50-55 55-60 60-65 65-70 70-75 75-80 nI 5 10 25 30 18 12
a) ¯ớc l°ợng trung bình chỉ tiêu X với độ tin cậy 92%.
b) Muốn °ớc l°ợng trung bình chỉ tiêu X với độ tin cậy với độ tin cậy 95% và độ
chính xác không quá 1 kg có cần bổ sung mẫu không ? nếu có, bằng bao nhiêu ?
c) Có tài liệu nói trung bình chỉ tiêu X bằng 70(kg) . Cho nhận xét có mấy ý nghĩa = 0,05.
d) Các sản phẩm có chỉ tiêu X 70 (kg) gọi là loại 2 á xí nghiệp B, điều tra 244 sản
phẩm , thấy có 50 sản phẩm loại 2. Cho rằng tỉ lệ sản phẩm loại 2 á xí nghiệp này
nh° nhau đ°ợc không ? kiểm tra mức = 0,05.
54. Trong một nhà máy may trang phục, ng°ßi ta đo thßi gian hoàn thành một công
việc của 2 nhóm công nhân thực hiện các thao tác theo các trật tự khác nhau, đ°ợc
kết quả (tính bằng giây). Nhóm A : 220 235 214 197 206 214 Nhóm B : 247 223 215 219 207 236
Coi số liệu tuân theo phân phối chuẩn (cùng 1 đồng hồ đo). Với mức ý nghĩa =
0,05, kiểm định xem thßi gian trung bình để hoàn thành công việc của 2 nhóm có khác nhau nhiều không?
55. Theo dõi sự phát triển của 1 loại cây trồng có bảng sau : Chiều cao xI(cm) 275 325 375 425 475 525 575 Số cây nI 5 20 25 30 30 23 14
a) Cho rằng chiều cao trung bình của cây là 450 cm đ°ợc không ? kiếm định mức = 0,05
b) Tìm khoảng °ớc l°ợng chiều cao trung bình của cây với độ tin cậy = 95%.
56. Một mẫu gồm 32 cá thể đem cân, có dẫy thống kê sau (đ¡n vị tính : gr). xi 45 52 60 64 65 70 73 74 76 82 87 nI 2 2 3 4 1 2 5 4 4 3 2
a) Tìm khoảng tin cậy cho kỳ vọng a với độ tin cậy = 0,99.
b) Muốn có a = X 0,5 thì cỡ mẫu bằng bao nhiêu.
57. Kiểm tra những sản phẩm cùng loại đ°ợc chọn ngẫu nhiên từ 2 nhà máy, có bảng sau : Nhà máy Số sf đ°ợc kiểm tra Số phế phẩm A 1200 40 B 1500 100
Với mức ý nghĩa = 0,01 hãy kiểm định giả thuyết tỉ lệ phế phẩm á 2 nhà máy nh° nhau.
58. Trong 1 thí nghiệm xét sự liên quan giữa giới tính và màu sắc, sau 1 thßi gian tìm hiểu, ta có bảng sau : Phái Phụ nữ Nam giới Mầu -- 93
Hoài qui tuyeán tính Hồng 10 20 Trắng 20 10 Xanh 30 10
Hãy kiểm định giả thuyết Ho giới tính và màu sắc không liên quan với nhau với mức ý nghĩa = 0,01 -- 94
Hoài qui tuyeán tính ĐÀ THAM KH¾O
Thßi gian làm bài :90 phút, không sử dụng tài liệu.
Ghi chú : Thí sinh đ°ợc mang máy tính cầm tay, ngoài ra không đ°ợc mang theo bất
kỳ tài liệu nào khác. Bảng tra cần thiết cho phía sau đề thi. ĐÀ 1:
Câu 1 : Một dây chuyền sản xuất gồm 3 bộ phận hoạt động độc lập nhau. Biết rằng
trong một ca làm việc thì xác suất để các bộ phận bị hỏng là 0,05; 0,07; 0,1 và dây
chuyền ng°ng hoạt động nếu ít nhất một trong 3 bộ phận bị hỏng. Tính xác suất để
trong một ca làm việc, dây chuyền ng°ng hoạt động.
Câu 2 : Một lô hàng gồm 5 sản phẩm loại A và 15 sản phẩm loại B. Lấy ngẫu nhiên
cùng một lúc 4 sản phẩm để kiểm tra.
a) Tính xác suất để trong 4 sản phẩm lấy ra có đúng 3 sản phẩm loại A.
b) Gọi X là số sản phẩm loại B có trong 4 sản phẩm lấy ra, hãy lập luật phân phối xác suất của X.
c) Tính E(X), D(X) và Mod(X).
Câu 3 : Điều tra điểm môn Hóa A1 của một tr°ßng đại học ta có số liệu thống kê nh° sau : Điểm(xi) 1 2 3 4 5 6 7 8 9 10 Số sinh viên (ni) 12 18 39 25 70 65 100 72 7 10
a) Hãy °ớc l°ợng điểm trung bình môn Hóa A1 của sinh viên tr°ßng Đại học trên á độ tin cậy 98%.
b) Biết sinh viên tr°ßng đó có điểm trung bình môn Toán A1 là 5,55. Hãy so sánh điểm
trung bình môn Hóa A1 với điểm trung bình môn Toán A1 với mức ý nghĩa = 0,05.
c) Có một kết luận cho rằng tỉ lệ sinh viên thi qua môn Hóa A1 của tr°ßng này là 60%.
Theo bạn, điều đó đúng không (kết luận á = 0,01)? Gi¿i : (vắn tắt)
Câu 1 : Gọi Ai là sự kiện bộ phận thứ i bị hỏng (i=1,2,3)
A1, A2,A3 là các sự kiện độc lập và P(A1)=0.05; P(A2) =0.07; P(A3) =0.1.
Gọi A là sự kiện dây chuyền ngừng hoạt động. Khi đó dl A ý A A A ( P A ) ý ( P A ) ( P A ) (
P A ) ý 0.95x0.93x0.9= 0.79515 1 2 3 1 2 3
P(A) = 1– 0.79515=0.20485
Câu 2 : Gọi C là biến cố trong 4 sản phẩm lấy ra có 3 sản phẩm loại A.
Ap dụng công thức xác suất cổ điển, ta có 3 1 ø P ù C C . C ý 5 15 ý ... C420
b). Vì X là số sản phẩm loại B có trong 4 sản phẩm lấy ra nên X có thể nhận các giá trị :
0,1,2,3,4. Có thể thấy ngay rằng X có phân phối siêu bội H(20;15;4), nh° vậy X có
luật phân phối xác suất nh° sau : X 0 1 2 3 4 Px 1/969 10/323 70/323 455/969 91/323 -- 95
Hoài qui tuyeán tính
Thỏa tổng xác suất bằng 1.
c). E(X) = … = 3; D(X) = … =9.631579-(3)2 0.632. Mod(X) =3.
Câu 3 : Ta tính đ°ợc : n=418; X=2444; X2=16000; X =5.84689;ón-1=2.025142
a). Ap dụng công thức °ớc l°ợng khoảng cho giá trị trung bình, ta tính đ°ợc khoảng
°ớc l°ợng là (5.617087; 6.076693) á độ tin cậy 98%. b). Đặt giả thiết H
0 : =5.55 với đối thiết H1 : 5.55
Nếu giả thiết H0 đ°ợc chấp nhận thì kết luận là hai điểm trung bình này bằng nhau,
ng°ợc lại thì kết luận chúng khác nhau (và tiếp tục xét xem điểm trung bình nào lớn h¡n) tqs= … = 2.997 >1.96
nh° vậy, ta bác giả thiết H0 á mức ý nghĩa 0.05; h¡n nữa, X >5.55 nên ta kết luận
điểm trung bình Hóa A1 lớn h¡n điểm trung bình môn Toán A1. c). ….. ĐÀ 2
Câu 1: Hộp 1 chứa 8 quả cầu trắng và 2 quả cầu đen. Hộp 2 chứa 9 quả cầu trắng và 1
quả cầu đen. Từ hộp thứ 2 lấy 2 quả cầu cho vào hộp 1. sau đó từ hộp 1 lấy cùng lúc
ra 3 quả cầu thì đ°ợc 3 quả cầu trắng. Tính xác suất cả 3 quả cầu này đều là của hộp 1.
Câu 2: Cho biến ngẫu nhiên liên tục, có hàm phân phối xác suất ü ÿ 0 k hi x ü - ÿ 2 ÿ
F (x) ý ýA Bsin x k hi - x ; A , h - B s aèng c oá x aù aàn ñ c ònh ÿ 2 2 ÿ ÿ 1 k hi x þ þ 2 a. Tìm A, B. 3
b. Gọi Y = sin X. Tìm P(Y þ
) với A, B đã tính á câu a. 2
c. Tìm ph°¡ng sai D(Y) của biến ngẫu nhiên Y.
Câu 3: à một x°áng bê tông, đo ngẫu nhiên độ bền chịu nén (tính bằng kg/cm2 ), có bảng thống kê sau: Độ bền chịu 190 - 200 - 210 - 220 - 230 - 240 - nén xi(kg/cm2) 200 210 220 230 240 250 Số mẫu bê tông 10 26 56 64 30 14 ni
Giả thiết độ bền chịu nén các mẫu bê tông tuân theo phân phối chuẩn.
a. Hãy °ớc l°ợng độ bền chịu nén trung bình của các mẫu bê tông với độ tin cậy 95%. -- 96
Hoài qui tuyeán tính
b. Các mẫu bê tông có độ bền chịu nén 200 kg/cm2 gọi là loại 1. Sử dụng số liệu
thống kê trên để °ớc l°ợng tỉ lệ các mẫu bê tông loại 1 với độ chính xác o = 4%
thì độ tin cậy bằng bao nhiêu?
c. Ng°ßi ta cải tiến cách sản xuất, sau đó cho sản xuất thử, điều tra ngẫu nhiên
300 mẫu thấy có 264 mẫu loại 1 và cho rằng cải tiến có hiệu quả làm tăng tỉ lệ
các mău bê tông loại 1. cho kết luận về nhận định này, kiểm định với mức ý nghĩa = 0,05. Giải : Câu 1:
Số cầu trắng của hộp 1 sau lần rút cầu lần thứ nhất 1 4 P(Y ý 9) ý ; P(Y ý 1 ) 0 ý 5 5
B – biến cố rút lần 2 đ°ợc 2 cầu trắng 21 3 C 6 30
P(B /(Y ý ) 9 ) ý
; P (B /(Y ý 1 ) 0 ) 10 ý ý ý 55 3 C 11 55 12 1 21 4 30 141 P( ) B ý x x ý 5 55 5 55 275
H _ rút lần 2 đ°ợc 3 quả cầu trắng của hộp 1 3 C 56 14 ( P H) 8 ý ý ý 3 C 220 55 12 H B = H P (H ) 14 141 70
P(H / B) ý ý : ý P(B) 55 275 141 Câu 2: a. A = B = 0,5 3 3 2 b. Y þ sin X þ 2 k ü X ü 2 k 2 2 3 3 3 2 2 ù 1 1 ù 2 3 P(Y þ ) ý ( P ü X ü ) ý F ( ) F ( ) ý 1 sin ý . 0 067 ú ú 2 3 3 3 3 û 2 2 3 û 4 1 2 2 2 1 1 c. EY=0 ; ( E Y ) 2 ý sin x cos 2 xdx ý sin x cos xdx ý DY ý 2 0 3 3 2 Câu 3: a. x = 221kg/cm2 , s2
(12,36cm2)2 , n = 200. Độ bền chịu nén X þ N(a; n ó2). = 0,95 ( x ) ý 9 ,
1 6 xác định từ (x( )) ý (bảng hàm Laplace) 2 2 2 12 3 , 6
Độ chính xác của °ớc l°ợng ý 9 , 1 6x 7 , 1 200
P(219,3 kg/cm2 < a < 222,7 kg/cm2 = 95% -- 97
Hoài qui tuyeán tính n , 0 04 200 b. ý 2 ( ) ý 2 ( ) 2 , 1 ( ) 47 ý 2x 42922 , 0 ý % 84 , 85 f 1 ( f ) n n 82 , 0 x 18 , 0
c. p1 , p2 tỉ lệ loại 1 của hai đám đông t°¡ng ứng Ho : p 1
1 = p2 ; H : p1 p2 . Kiểm định mức ý nghĩa =0,05. 459
f1 = 0,95 ; f2 = 0,88 ; f ý ý 9 , 0 18 500 9 , 0 5 8 , 0 8 t ý ý 7 , 2 9 þ 9 , 1 6 qs 1 1 9 , 0 18x 0 , 0 82( ) 200 300 Bác bỏ Ho .
Kết luận : Sau cải tiến, tỉ lệ bê tông loại 1 sau cải tiến khác tr°ớc cải tiến.
Do f1 >f2 nên tỉ lệ bê tông loại 1 giảm. ĐÀ 3
Câu 1 : Một lô hàng gồm 10 sản phẩm, trong đó có 3 sản phẩm loại A, 7 sản phẩm loại
B. Lấy ngẫu nhiên 4 sản phẩm bày làm mẫu (không bán), còn lại đem ra cửa hàng để bán.
a). Hãy tính xác suất để trong các sản phẩm bày làm mẫu có đúng 2 sản phẩm loại A.
b). Hãy lập luật phân phối xác suất cho số sản phẩm loại B có trong các sản phẩm bày bán.
c). Giả sử một ng°ßi đến mua một sản phẩm thuộc lô hàng trên. Tính xác suất
để ng°ßi đó mua đ°ợc sản phẩm loại A.
Câu 2 : Cho biến ngẫu nhiên X có hàm mật độ dạng : A ü xsinx neáu xþ ÿ 0, f(x) = ý 0 neáu xÿ þÿ 0,
Hãy xác định hằng số A và viết hàm phân phối của X.
Câu 3 : Để có kết luận về các thông số trung bình và ph°¡ng sai của trọng l°ợng các
bao bột do một máy tự động đóng ra, ng°ßi ta cân ngẫu nhiên một số bao do
máy đóng ra và thu đ°ợc kết quả : Trọng l°ợng (xi)(kg) 18 19 20 20,5 21 22 Số bao (ni) 2 12 15 13 9 5
Giả sử trọng l°ợng do máy đóng ra có phân phối chuẩn.
a). Hãy °ớc l°ợng trọng l°ợng trung bình các bao bột do máy đóng ra với độ tin cậy 90%.
b). Muốn sai số của °ớc l°ợng trên đạt độ chính xác 0,01 kg thì phải quan sát
thêm ít nhất bao nhiêu bao?
Câu 4 : Hãy xác định hệ số t°¡ng quan r và ph°¡ng trình hồi qui tuyến tính của Y theo
X khi có các quan sát sau : Chi phí X (Tỉ đồng) 6 7 9 9 7 8 6 12 -- 98




